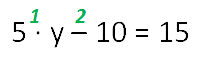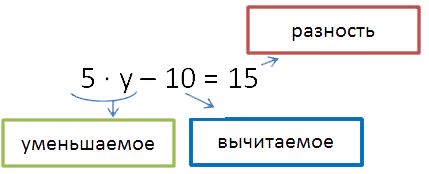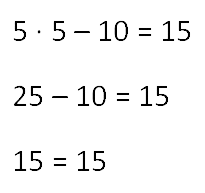Наш любимый «Д» класс.: ЗНАЙ ПРАВИЛА РЕШЕНИЯ УРАВНЕНИЙ!
1. Нахождение неизвестного слагаемого.
слагаемое слагаемое сумма
20 + 30 = 50
10 + X = 15 Нам неизвестно слагаемое.
X = 15 - 10 Чтобы найти слагаемое, нужно от суммы отнять другое слагаемое.
Х = 5
10 + 5 = 15 Делаем проверку: вместо Х подставим число и посчитаем.
15 = 15 В левой и правой части получился одинаковый ответ.
Решили правильно.2. Нахождение неизвестного уменьшаемого.уменьшаемое вычитаемое разность 70 - 30 = 40 X - 10 = 15 Нам неизвестно уменьшаемое. X = 15 + 10 Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое. Х = 25 25 - 10 = 15 Делаем проверку: вместо Х подставим число и посчитаем. 15 = 15 В левой и правой части получился одинаковый ответ. Решили правильно.уменьшаемое вычитаемое разность 70 - 30 = 40 25 - X = 15 Нам неизвестно вычитаемое. X = 25 - 15 Чтобы найти вычитаемое, нужно от уменьшаемого отнять разность. Х = 10 25 - 10 = 15 Делаем проверку: вместо Х подставим число и посчитаем. 15 = 15 В левой и правой части получился одинаковый ответ. Решили правильно.4-5. Нахождение неизвестного множителя.множитель множитель произведение 9 * 5 = 45 5 * X = 15 Нам неизвестен множитель. X = 15 : 5 Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Х = 3 5 * 3 = 15 Делаем проверку: вместо Х подставим число и посчитаем. 15 = 15 В левой и правой части получился одинаковый ответ. Решили правильно. Х * 4 = 12 Нам неизвестен множитель. X = 12 : 4 Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Х = 3 3 * 4 = 12 Делаем проверку: вместо Х подставим число и посчитаем. 12 = 12 В левой и правой части получился одинаковый ответ. Решили правильно.6. Нахождение неизвестного делимого.делимое делитель частное 20 : 4 = 5 Х : 3 = 6 Нам неизвестно делимое. X = 6 * 3 Чтобы найти делимое, нужно частное умножить на делитель. Х = 18 18 : 3 = 6 Делаем проверку: вместо Х подставим число и посчитаем. 6 = 6 В левой и правой части получился одинаковый ответ. Решили правильно. Х : 2 = 7 Нам неизвестно делимое. X = 7 * 2 Чтобы найти делимое, нужно делитель умножить на частное. Х = 14 14 : 2 = 7 Делаем проверку: вместо Х подставим число и посчитаем. 7 = 7 В левой и правой части получился одинаковый ответ. Решили правильно.делимое делитель частное 24 : 4 = 6 35 : Х = 7 Нам неизвестен делитель. X = 35 : 7 Чтобы найти делитель, нужно делимое разделить на частное. Х = 5 35 : 5 = 7 Делаем проверку: вместо Х подставим число и посчитаем. 7 = 7 В левой и правой части получился одинаковый ответ. Решили правильно.
school26d.blogspot.com
Что такое уравнение? Как решать уравнения?
Уравнение – одно из краеугольных понятий всей математики. Как школьной, так и высшей. Имеет смысл разобраться, правда? Тем более, что это очень простое понятие. Ниже сами убедитесь. 🙂 Так что же такое уравнение?
То, что это слово однокоренное со словами «равный», «равенство», возражений, думаю, ни у кого не вызывает.
Уравнение – это два математических выражения, соединённых между собой знаком «=» (равно).
Но… не каких попало. А таких, в которых (хотя бы в одном) содержится неизвестная величина. Или, по-другому, переменная величина. Или, сокращённо, просто «переменная». Которая обычно обозначается буквой «х».
Переменных может быть одна, может быть несколько. В школьной математике чаще всего рассматриваются уравнения с одной переменной. И мы тоже пока что будем рассматривать уравнения с одной переменной. С двумя переменными или более – в специальных уроках.
Что значит решить уравнение?
Идём дальше.
Переменная, входящая в уравнение, может принимать любые допустимые математикой значения. На то она и переменная. 🙂 При каких-то значениях переменной получается верное числовое равенство, а при каких-то – нет.
Так вот:
Решить уравнение означает найти ВСЕ такие значения переменной, при подстановке которых в исходное уравнение получается верное равенство. Или, более научно, верное тождество. Или доказать, что таких значений переменной не существует.
Что такое верное равенство? Это равенство, не вызывающее сомнений даже у человека, абсолютно не отягощённого глубокими математическими познаниями. Например, 5=5, 0=0, -10=-10. И так далее. 🙂
Значения переменной, при подстановке которых достигается это самое верное равенство, называются очень красиво и научно — корни уравнения.
Корень может быть один, может быть несколько. А может быть и бесконечно много корней – целый интервал или даже вообще вся числовая прямая от –∞ до +∞. Да, такое тоже бывает! Всё от конкретного уравнения зависит.)
А бывает и такое, что нельзя найти такие иксы, которые давали бы нам верное равенство. Принципиально нельзя. По определённым причинам. Нету таких иксов…
В таких случаях обычно говорят, что уравнение не имеет корней.
Для чего нужны уравнения?
Вопрос смешной. Для жизни! В школе, как правило, уравнения нужны для решения текстовых задач. Это, напоминаю, задачи на движение, на работу, на проценты и многие другие.
А во взрослой жизни без уравнений невозможны было бы ответить даже на самые обычные, но жизненно важные вопросы повседневности: какая будет погода завтра, выдержит ли заданную нагрузку здание. Или лифт. Или самолёт. Куда попадёт ракета… И не было бы сейчас среди нас ни синоптиков, ни инженеров, ни бухгалтеров, ни экономистов, ни программистов… За ненадобностью. Внушает?)
Почему это так? А потому, что уравнениями описываются почти все известные человеку природные явления и процессы. Изменение давления и температуры воздуха с высотой, закон всемирного тяготения, размножение бактерий, радиоактивный распад, химические реакции, электричество, спрос и предложение – в основе всего этого лежат математические уравнения! Простые, сложные – всякие. Какое явление или ситуация, такое и уравнение.)
Итак, запоминаем:
Уравнения – очень мощный и универсальный инструмент для решения самых разных прикладных задач.
А какие бывают уравнения?
Уравнений в математике несметное количество. Самых разных видов. Но всё многообразие уравнений можно условно разделить всего на 4 категории:
1. Линейные,
2. Квадратные,
3. Дробные (или дробно-рациональные),
4. Прочие.
Разные категории уравнений требуют и разного подхода к их решению: линейные уравнения решаются одним способом, квадратные – другим, дробные – третьим, тригонометрические, логарифмические, показательные и прочие – тоже решаются своими методами.
Прочих уравнений, разумеется, больше всего, да…) Это и иррациональные, и тригонометрические, и показательные, и логарифмические, и многие другие уравнения. И даже дифференциальные уравнения (для студентов), где роль неизвестного играет не число, а функция. Или даже семейство функций. 🙂
В соответствующих уроках мы подробно разберём все эти типы уравнений. А здесь у нас – базовые приёмы и правила.
Называются эти правила – тождественные (или – равносильные) преобразования уравнений
Как решать уравнения? Тождественные (равносильные) преобразования уравнений.
Решение любого уравнения заключается в поэтапном преобразовании входящих в него выражений. Но преобразований не абы каких, а таких, чтобы от шага к шагу суть всего уравнения не менялась. Несмотря на то, что после каждого преобразования уравнение будет видоизменяться и, в конечном счёте, станет совсем не похоже на исходное.
Такие преобразования в математике называются равносильными или тождественными. Их довольно много, но среди всего многообразия тождественных преобразований уравнений выделяется два базовых. О них и пойдёт речь в этом уроке. Да-да, всего два! Но – крайне важных! И каждое из них заслуживает отдельного внимания.
Применение этих двух тождественных преобразований в том или ином порядке гарантирует успех в решении 99% уравнений математики. Заманчиво, правда?
Итак, вперёд!
Первое тождественное преобразование:
К обеим частям уравнения можно прибавить (или отнять) любое (но одинаковое!) число или выражение (в том числе и с переменной). Суть уравнения от этого не изменится.
Это преобразование вы применяете всюду, наивно думая, что переносите какие-то члены из одной части уравнения в другую, меняя знаки. 🙂
Например, такое крутое уравнение:
Тут и думать нечего, перебрасываем тройку вправо, меняя минус на плюс:
А что же происходит в действительности? А на самом деле вы… прибавляете к обеим частям уравнения тройку!
Вот что у вас происходит:
И результат получается тем же самым:
Вот и всё. Слева остаётся чистый икс (чего мы, собственно, и добиваемся), а справа – что уж получится. Но самое главное то, что от прибавления тройки к обеим частям суть всего уравнения не изменилась!
Дело в том, что привычный нам перенос слагаемых из одной части в другую со сменой знака – это просто сокращённый вариант первого тождественного преобразования.
И зачем нам так глубоко копать? В уравнениях – незачем. Переносите себе спокойно и не парьтесь. Только знаки менять не забывайте.) А вот в неравенствах привычка к переносу может и слегка обескуражить, да…
Это было первое тождественное преобразование. Переходим ко второму.
Второе тождественное преобразование:
Обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение.
Это тождественное преобразование мы вы постоянно применяете, когда решаете что-нибудь совсем уж жуткое типа:
Тут каждому ясно, что х=3. А вот как вы получили этот ответ? Подобрали? Угадали?
Чтобы не подбирать и не гадать (мы с вами математики, а не гадалки), нужно понять, что вы просто поделили обе части уравнения на четвёрку. Которая нам и мешает.
Вот так:
Эта палка с делением означает, что на четвёрку делятся обе части нашего уравнения. Через дроби эта процедура выглядит так:
Слева четвёрки благополучно сокращаются, остаётся икс в гордом одиночестве. А справа при делении 12 на 4 получается, понятное дело, тройка. 🙂
И все дела.)
Звучит невероятно, но эти два (всего два!) простых преобразования лежат в основе решения всех уравнений математики! Да-да, именно всех, я нисколько не преувеличиваю! От линейных и квадратных в школе до дифференциальных в ВУЗе.)
Ну что, посмотрим на тождественные преобразования уравнений в действии?
Применение тождественных преобразований к решению уравнений.
Начнём с первого тождественного преобразования. Переноса вправо-влево.
Пример для новичков:
1 – х = 3 – 2х
Дело нехитрое. Это линейное уравнение. Работаем прямо по заклинанию: «С иксами влево, без иксов – вправо».
Эта мантра – универсальная инструкция по применению первого тождественного преобразования. Вот и смотрим на уравнение. Какое слагаемое с иксом у нас справа? Что? 2х? Не-а!) Справа у нас -2х (минус два икс)! Поэтому при переносе в левую часть минус поменяется на плюс:
1 – х +2х = 3
Полдела сделано, иксы собрали слева. Осталось все числа собрать справа. Слева в уравнении стоит единичка. Опять вопрос – с каким знаком? Ответ «с никаким» не катит.) Слева перед единицей и вправду ничего не написано. А это значит, что перед ней стоит знак «плюс». Так уж в математике повелось: ничего не написано – значит, плюс.)
И поэтому вправо единичка перенесётся уже с минусом:
-х + 2х = 3 — 1
Вот почти и всё. Слева приводим подобные, а справа – считаем. И получаем:
х = 2
Это было совсем примитивное уравнение.
Теперь пример покруче, для старшеклассников:
Решить уравнение:
Уравнение логарифмическое. Ну и что? Какая разница? Всё равно первым шагом делаем базовое тождественное преобразование («С иксами влево ….»). Для этого слагаемое с иксом (то есть, —log3x) переносим влево. Со сменой знака:
А числовое выражение (log34) переносим вправо. Также со сменой знака, разумеется:
Вот и всё. Справа получилась чистая формула. Кто дружит с логарифмами, тот в уме дорешает уравнение и получит:
х=3
Что? Хотите синусы? Пожалуйста, вот вам синусы:
И снова всё то же самое! Выполняем первое тождественное преобразование – переносим sin x влево (с минусом), а -0,25 переносим вправо (с плюсом):
Получили простейшее тригонометрическое уравнение с синусом, решить которое (для знающих) также не составляет никакого труда.
Видите, насколько универсально первое равносильное преобразование! Встречается везде и всюду и не обойти его никак… Именно поэтому так важно уметь его делать на автомате и без ошибок.
Собственно, ошибиться здесь можно лишь в одном – забыть сменить знак при переносе. Что и происходит сплошь и рядом. Внимательность никто не отменял, да…)
Ну что, продолжаем наши игры? Развлекаемся теперь со вторым преобразованием!)
Решить уравнение:
7х=28
Крутяк, прямо скажем.) Ладно, это эмоции…
Смотрим и соображаем: что нам мешает в этом уравнении? Что-что… Да семёрка мешает! Хорошо бы от неё избавиться. Да так, чтобы исходное уравнение не испортить.)
Но как? Перенести вправо? Ээээ… Стоп! Нельзя.) Семёрка с иксом умножением связана. Коэффициент, видите ли.) Нельзя её оторвать от икса и вправо перенести. Вот всё выражение 7х целиком – пожалуйста (вопрос – зачем?). А семёрку отдельно – никак нет.
Самое время про умножение/деление вспомнить! Нам ведь в ответе чистый икс нужен, не так ли? А семёрка – мешает. Вот и делим левую часть на семь. «Очищаем» икс от коэффициента. Так нам надо. Но тогда и правую часть тоже надо поделить на семь: этого уже математика требует. Что уж там получится, то и получится. Но пример хороший. Я старался.) 28 на 7 замечательно делится. Получится 4.
Ответ: х=4
Или такое уравнение:
Что здесь нам мешает? Дробь 1/6, не так ли? Вот давайте и избавимся от неё. Безопасно для уравнения.) Как? Ну, можно поступить аналогично – поделить обе части на эту самую 1/6. Но в уме это не очень удобно. Кое-кто и запутается…
Но мы же не только делить, мы ещё и умножать умеем!) Вспоминаем из младших классов, после какого действия у нас пропадает дробь? Правильно! Дробь у нас пропадает при умножении на число, равное (или кратное) её знаменателю. Вот и умножим обе части нашего уравнения на 6. Слева всё равно чистый икс получится, а умножение правой части на 6 – не самая трудная работа.)
Вот и всё.) Умножение обеих частей уравнения на нужное число позволяет сразу избавляться от дробей, минуя промежуточные выкладки, в которых, между прочим, запросто можно и ошибок наляпать. Короче дорога – меньше ошибок!
Теперь снова на машину времени и — в старшие классы:
Решить уравнение:
Чтобы добраться до икса и тем самым решить это крутое тригонометрическое уравнение, нам надо сначала получить слева чистый косинус, безо всяких коэффициентов. А двойка мешает. 🙂 Вот и делим на 2 всю левую часть:
Но тогда и правую часть тоже придётся разделить на двойку: это уже МАТЕМАТИКЕ надо. Делим:
Получили справа табличное значение косинуса. И теперь уравнение решается за милую душу.)
Вот и вся премудрость. Как видите, тождественные преобразования уравнений – штука полезная. И при этом не самая сложная. Перенос да умножение/деление. Однако далеко не у всех они получаются с первого раза и без ошибок, ох не у всех… Основные проблемы здесь две.
Проблема первая (для малоопытных):
Иногда ученик думает, что упрощение уравнений делается по одному, раз и навсегда установленному правилу. И никак не может уловить и понять это правило: в каких-то примерах начинают с домножения (или деления), в каких-то – с переноса. Где-то три раза переносят и ни разу не домножают…
Например, такое линейное уравнение:
10х + 5 = 5х – 20
С чего начинать? Можно начать с переноса:
10х – 5х = -20 — 5
А можно сначала поделить обе части на пятёрку, а затем уж переносить. Тогда сразу числа попроще станут:
Как видим, и так и сяк решать можно. И это – в примитивном примере! Вот и возникает у неопытных учеников вопрос: «Как правильно?»
По-всякому правильно! Кому как удобнее. 🙂 Универсального рецепта здесь нет и быть не может. Математика предлагает вам на выбор два вида преобразований уравнений. А порядок этих самых преобразований зависит исключительно от исходного уравнения, а также от личных предпочтений и привычек решающего.
Проблема вторая (для всех…ну… почти):
Ошибки в вычислениях. В преобразованиях постоянно приходится перемножать скобки. Заключать выражения в скобки и раскрывать скобки. Умножать и делить дроби. Работать со степенями… Короче, в наличии весь набор элементарных действий математики. Со всеми вытекающими…
Обе эти проблемы устраняются только одним способом – практикой. Исчезают сомнения и ошибки. Примеры становятся проще, задания — легче. И в итоге не математика командует вами, а вы – математикой. 🙂
abudnikov.ru
Как решать сложные составные уравнения?
Под сложными (составными) уравнениями мы понимаем уравнения, которые содержат два или более арифметических действия.
Решение таких уравнений выполняется по тем же правилам, которые мы рассмотрели на странице «Решение простых уравнений 5 класс» в этой же теме.
Но решение составных уравнений производится в определённой последовательности.
Рассмотрим уравнение:
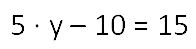
Расставляем порядок действий в уравнении.

Определяем неизвестное по последнему действию. Последнее действие в данном уравнении — это вычитание. Обращаем ваше внимание, что на этом этапе наше неизвестное — это «5y», и именно его мы рассматриваем как уменьшаемое.

Решаем как простое уравнение и находим «5y». Вспомним правило для нахождения неизвестного уменьшаемого.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

Теперь перед нами простое уравнение. Необходимо найти неизвестный множитель. Решаем уравнение по следующему правилу.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
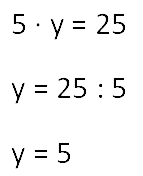
Не забудем выполнить проверку.

Всё верно. Значит уравнение решено правильно.
Другой способ решения сложных уравнений
Некоторые сложные (составные уравнения) можно решать другим способом. Зная и умея применять свойства сложения и вычитания, а также свойства умножения и деления, уравнения решаются следующем образом.
Рассмотрим уравнение.
(x + 54) − 28 = 38
Упрощаем выражение, стоящее в левой части уравнения, используя одно из свойств вычитания.
Чтобы из суммы отнять число, нужно это число вычесть из одного слагаемого и прибавить результат вычитания к другому слагаемому.

Далее решаем простое уравнение, пользуясь правилом нахождения неизвестного слагаемого.
x = 38 − 26
x = 12
Выполняем проверку.
(12 + 54) − 28 = 38
66 − 28 = 38
38 = 38
Упрощение выражений в уравнениях
Запомните!
Если в уравнении встречается выражения, которые можно упростить, то вначале упрощаем выражения, и только после этого решаем уравнение.
Решить уравнение.
5x + 2x = 49
Левую часть уравнения можно упростить. Сделаем это.
7x = 49
Теперь решим простое уравнение по правилу нахождения неизвестного множителя.
x = 49 : 7
x = 7
Завершив пример, выполним проверку.
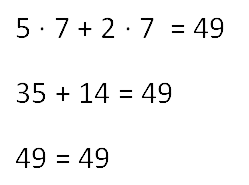
infourok.ru
1. Равносильность уравнений. Теоремы о равносильности уравнений
Определение 1.
Два уравнения с одной переменной f(x)=g(x) и p(x)=h(x) называют равносильными, если множества их корней совпадают.
Иными словами,
два уравнения называют равносильными, если они имеют одинаковые корни, или если оба уравнения не имеют корней.
Определение 2.Если каждый корень уравнения f(x)=g(x) \((1)\)
является в то же время корнем уравнения p(x)=h(x), \((2)\)
то уравнение \((2)\) называют следствием уравнения \((1)\).
Пример:
уравнение x−22=9 является следствием уравнения x−2=3.
В самом деле, решив каждое уравнение, получим:
x−22=9x−2=3;x−2=−3;x1=5;x2=−1; и x−2=3;x=5.
Корень второго уравнения является одним из корней первого уравнения, поэтому первое уравнение — следствие второго уравнения.
Очевидно следующее утверждение:
два уравнения равносильны тогда и только тогда, когда каждое из них является следствием другого.
Решение уравнения, как правило, осуществляется в три этапа:
Первый этап — технический.
На этом этапе осуществляют преобразования по схеме (1)→(2)→(3)→(4)→… и находят корни последнего (самого простого) уравнения указанной цепочки.
Второй этап — анализ решения.
На этом этапе анализируем, все ли проведённые преобразования были равносильными.
Третий этап — проверка.
Если, анализируя преобразования на втором этапе, делаем вывод, что получили уравнение-следствие, то обязательна проверка всех найденных корней их подстановкой в исходное уравнение.
Обрати внимание!
Решение уравнений, встречающихся в школьном курсе, основано на шести теоремах о равносильности.
Теорема 1.Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.
Теорема 2.Если обе части уравнения возвести в одну и ту же нечётную степень, то получится уравнение, равносильное данному.
Теорема 3.Показательное уравнение af(x)=ag(x), где \(a>0\), a≠1, равносильно
уравнению f(x)=g(x).
Определение 3.
Областью определения уравнения f(x)=g(x) или областью допустимых значений переменной (ОДЗ) называют множество тех значений переменной \(x\), при которых одновременно имеют смысл выражения \(f(x)\) и \(g(x)\).
Теорема 4.Если обе части уравнения f(x)=g(x) умножить на одно и то же выражение \(h(x)\), которое:
a) имеет смысл всюду в области определения (в области допустимых значений) уравнения f(x)=g(x);
б) нигде в этой области не обращается в \(0\)
— то получится уравнение f(x)⋅h(x)=g(x)⋅h(x), равносильное данному.
Следствие теоремы 4.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Теорема 5.Если обе части уравнения f(x)=g(x) неотрицательны в области определения уравнения, то после возведения обеих его частей в одну и ту же чётную степень \(n\) получится уравнение, равносильное данному: f(x)n=g(x)n.
Теорема 6.Если f(x)>0 и g(x)>0, то логарифмическое уравнение logaf(x)=logag(x), где \(a>0\), a≠1, равносильно уравнению f(x)=g(x).
www.yaklass.ru