Система двух линейных уравнений с двумя переменными. Математические модели реальных ситуаций
Решим такую задачу. (См. Рис. 1.)

Рис. 1. Условие задачи
В задаче речь идет о трех объектах: о кролике, птице и кабане, и неизвестными величинами являются массы этих зверей.
Сумма трех кроликов – это три кролика. Можно продолжать с картинками, но это неудобно.
Заменим массу животных на переменные (см. Рис. 2):

Рис. 2. Условные обозначения
Перепишем все, что показано на картинке, с помощью переменных:

Решим полученную систему:
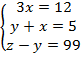
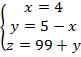
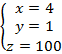
Тогда получаем, что масса трех животных:
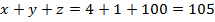
Нам нигде не пришлось думать, решать задачу. Главное, что нужно было сделать – аккуратно переписать условие задачи с помощью введенных обозначений. Таким образом, мы построили математическую модель – записали условие задачи на математическом языке и решили ее абсолютно автоматически.
Все задачи, которые будут встречаться в дальнейшем, решаются по одному алгоритму. Итак, рассмотрим этот алгоритм. В нем выделим 4 пункта.
1. Что происходит?
Читаем внимательно задачу и представляем, что происходит. Перечисляем всех участников и их характеристики (величины), которые можно измерить.
2. Моделирование
Вводим обозначения для всех этих величин. Переписываем все, что сказано в условии задачи, с помощью этих обозначений. Получаем набор алгебраических условий, уравнений, который мы называем моделью.
3. Решение
Решаем полученные уравнения. Получаем ответ в рамках модели.
4. Ответ
Возвращаемся от модели к задаче. Даем ответ на вопрос задачи.
Пример 1.
Два туриста вышли одновременно из двух городов, расстояние между которыми – 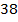 км, и встретились через
км, и встретились через 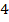
 км больше, чем второй?
км больше, чем второй?Решение
1 этап. Что происходит?
Два туриста идут навстречу друг другу и встречаются. Каждый прошел какое-то расстояние, у каждого есть скорость движения, каждый потратил какое-то время. Еще есть общее расстояние между городами. (См. Рис. 3.)

Рис. 3. Иллюстрация к задаче
2 этап. Модель
Итак, для каждого участника есть три величины и еще общее расстояние:

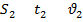
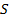
Итак, 7 величин, 7 обозначений. (См. Рис. 4.) Пока нас не интересовало, какие из них уже известны, а какие нет.

Рис. 4. Условные обозначения
А как же быть с 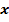 и
и 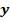 ? Будем ли мы вводить эти обозначения? Для задач на движение есть уже свои всем понятные обозначения:
? Будем ли мы вводить эти обозначения? Для задач на движение есть уже свои всем понятные обозначения: 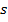
 – скорость,
– скорость, 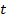 – время. И заменять их на
– время. И заменять их на  и
и  нет никакого смысла. А вообще это совершенно неважно. Делайте такие обозначения, чтобы вам было удобно и понятно.
нет никакого смысла. А вообще это совершенно неважно. Делайте такие обозначения, чтобы вам было удобно и понятно.Теперь нам нужно переписать условие задачи, используя введенные обозначения.
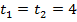
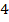 ч.
ч.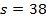 – расстояние между городами
– расстояние между городами 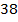 км.
км.
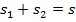 – вышли из двух городов и встретились.
– вышли из двух городов и встретились.
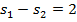 – первый прошел на
– первый прошел на  км больше, чем второй.
км больше, чем второй.
Найти нужно скорости каждого туриста.
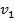 ,
, 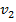 – ?
– ?
Кроме того, что сказано в задаче, мы владеем еще кое-какой важной информацией. А именно, как связаны все эти величины друг с другом. Запишем эти соотношения для каждого туриста:
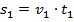
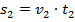
Итак, мы получили математическую модель – ввели обозначения и с помощью них переписали условие задачи. То есть мы уже выполнили 
3 этап. Решение
Наша модель содержит уже всю информацию. Никакой новой информации не будет, и никакая не пропадет. Мы просто займемся переписыванием ее в эквивалентном, но более удобном виде.
Итак, надо найти 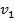 ,
, 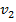 .
.
Для начала уменьшим количество записей в модели. Для этого подставим все известные величины.
Нам известны 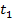 ,
,  и
и 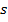
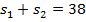
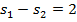
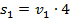
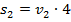
Нижние два уравнения содержат величины, которые мы ищем. Но здесь 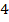 неизвестных, и если эти два уравнения взять в качестве системы, то у неё будет бесконечно много решений.
неизвестных, и если эти два уравнения взять в качестве системы, то у неё будет бесконечно много решений.
Верхние два уравнения содержат только две неизвестные. Правда, там нет нам нужных, но если решить систему этих двух уравнений, мы найдем 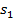
 , а затем уже и
, а затем уже и 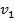 ,
, 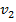 из нижних двух.
из нижних двух.То есть в качестве системы берем два верхних уравнения.

Решим систему методом сложения. Сложим почленно оба уравнения – получим первое уравнение новой системы, вычтем из первого второе – получим второе уравнение новой системы:
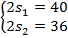
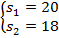
Нашли  . Теперь подставим их в два оставшихся уравнения.
. Теперь подставим их в два оставшихся уравнения.
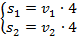
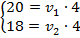
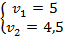
Итак, смоделированную задачу мы решили, остался последний этап.
4 этап. Ответ
Возвращаемся к исходной задаче. Заменяем наши обозначения на названия величин.
Ответ: скорость первого пешехода – 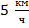 , скорость второго пешехода –
, скорость второго пешехода – 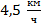 .
.
Пример 2.
На двух полках 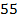 книг. Если переставить со второй полки половину книг на первую, то на первой станет в
книг. Если переставить со второй полки половину книг на первую, то на первой станет в 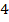 раза больше, чем останется на второй. Сколько книг на каждой полке?
раза больше, чем останется на второй. Сколько книг на каждой полке?
Решение
1 этап. Что происходит?
На двух полках стоят книги. (См. Рис. 5.)

Рис. 5. Размещение книг до перестановки
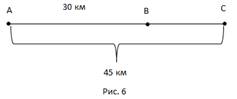
С одной полки переносят часть книг на другую. (См. Рис. 6.)

Рис. 6. Размещение книг после перестановки
2 этап. Модель
Первый момент, до перестановки. Обозначим через  и
и  количество книг на первой и второй полках. (См. Рис. 7.)
количество книг на первой и второй полках. (См. Рис. 7.)

Рис. 7. Количества книг на полках до перестановки
Второй момент, после перестановки. Теперь на полках другое количество книг. Обозначим новые количества через 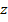 и
и 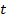 . (См. Рис. 8.)
. (См. Рис. 8.)

Рис. 8. Количества книг на полках после перестановки
Запишем все условия в этих обозначениях.
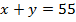 – на двух полках
– на двух полках 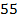 книг.
книг.
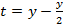 – со второй полки переставили половину книг на первую.
– со второй полки переставили половину книг на первую.
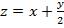 – со второй полки переставили половину книг на первую.
– со второй полки переставили половину книг на первую.
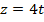 – на первой полке в
– на первой полке в 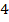 раза больше книг, чем на второй.
раза больше книг, чем на второй.
Можно еще написать, что после перестановки общее количество книг не изменилось:
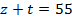
Необходимо найти:  ,
,  – ?
– ?
Мы построили модель. Пока мы будем решать эту уже математическую задачу, не станем вспоминать про книги и полки.
3 этап. Решение
Итак, мы хотим получить систему из двух уравнений с двумя неизвестными. Лучше, чтобы это были  и
и  , так как именно их нам нужно найти.
, так как именно их нам нужно найти.
Первое уравнение нам для этого подходит. А все остальные содержат еще или 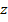 или
или 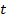 . Но можно заметить, что если в уравнение
. Но можно заметить, что если в уравнение 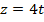 подставить выражения для
подставить выражения для 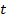 и
и 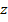 , то мы получим второе уравнение для
, то мы получим второе уравнение для  и
и  .
.
Составим и решим систему:

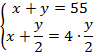
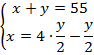
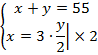
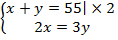

Из верхнего уравнения вычтем нижнее:

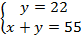
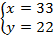
Мы получили ответ для модели, теперь возвращаемся к задаче.
4 этап. Ответ
На первой полке было  книги, на второй –
книги, на второй – 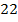 .
.
В самом деле, если половину книг со второй полки переставить на первую, то на второй останется 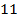 , а на первой станет
, а на первой станет 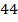 , то есть в
, то есть в 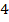 раза больше.
раза больше.
На самом деле, совершенно не обязательно при составлении модели должно получаться два уравнения с двумя неизвестными. Их может быть и 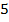 , и
, и 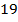 .
.
Системы уравнений с большим количеством переменных.
На самом деле, переменных столько, сколько мы ввели обозначений. Если обозначений 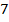 , то и уравнений должно быть
, то и уравнений должно быть 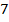 . Такой подход отличается от предыдущих только своей большей формальностью.
. Такой подход отличается от предыдущих только своей большей формальностью.
Посмотрим на первую задачу с этой точки зрения.
Два туриста вышли одновременно из двух городов, расстояние между которыми – 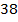 км, и встретились через
км, и встретились через 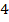 ч. С какой скоростью шел каждый турист, если первый прошел на
ч. С какой скоростью шел каждый турист, если первый прошел на  км больше, чем второй?
км больше, чем второй?
1 этап. Что происходит?
Мы это уже все обсудили. Ничего нового.
Два туриста идут навстречу друг другу и встречаются. Каждый прошел какое-то расстояние, у каждого есть скорость движения, каждый потратил какое-то время. Еще есть общее расстояние между городами. (См. Рис. 9.)

Рис. 9. О чем задача
2 этап. Модель
Мы ввели 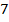 обозначений:
обозначений: 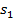 ,
, 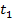 ,
, 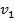 ,
,  ,
,  ,
, 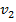 ,
, 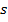 . Можно сказать, что это
. Можно сказать, что это 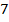 переменных. Нам необходимо для решения
переменных. Нам необходимо для решения 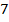 уравнений.
уравнений.
Вспомним, какие у нас были выписаны условия.

Посчитаем, сколько у нас уравнений. Вроде бы 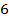 , последняя запись – вообще не уравнение.
, последняя запись – вообще не уравнение.
На самом деле, верхняя строчка – это два уравнения, их можно расписать по отдельности, и получим систему из
interneturok.ru
Презентация к уроку по алгебре (7 класс) по теме: Презентация «Системы линейных уравнений с двумя переменными» 7 класс
Слайд 1
Системы линейных уравнений с двумя переменными Автор: Малышева Л .С. Учитель математики МКОУ «СОШ №3» г. НиколаевскаСлайд 2
Устная работа Является ли линейным уравнение с двумя переменными : 5ху+3=0; у-х=13; 3у-х 2 =1; х 2 -х(х+5)+4у=3. Выразите переменную у через х из уравнения х+у =1; 3х-у=2
Слайд 3
Вычислите (- 0,3) 2 + (-0,2) 2 ; (-0,6 – 0,4) 2 ; -(0,5 – 0,3) 2 ; 0,5 2 (2 4 – 2 3 ) Решите уравнение 5. x (х + 2) = 0 ; 6. (х — 5)(2х + 7) = 0 ; 7. x 2 – 9 = 0; 8. x 2 + 4 = 0
Слайд 4
Решение системы уравнений с двумя переменными Графический способ Способ сложения Способ подстановки
Слайд 5
Система уравнений и её решение Определение: Системой двух линейных уравнений с двумя неизвестными называются два уравнения, объединенные фигурной скобкой. Фигурная скобка означает, что эти уравнения должны быть решены одновременно. а 1 х + b 1 y = c 1, а 2 х + b 2 y = c 2 ; В общем виде систему двух линейных уравнений с двумя неизвестными записывают так : где а 1 , b 1 , c 1 , а 2 , b 2 , c 2 — Заданные числа, а х и у — неизвестные
Слайд 6
Например, в системе а1 = 1, b 1 = -1, с1 = 2; а2 = 3, b 2 = -2, с2 = 9. Задание 3. (Устно.) Проверьте, являются ли числа х = 4 , у = 3 решениями системы Решение: х – у = 2, 3х – 2у = 9. 2,5 ·4 – 3 · 3 =1, 5·4 – 6 · 3 = 2. 2,5х – 3у = 1, 5х – 6у = 2. Ответ: числа х = 4 , у = 3 являются решениями системы
Слайд 8
Система линейных уравнений с двумя неизвестными Сумма двух чисел равна 12, а разность равна 2. Найдите эти числа Пусть x – первое число, а y – второе число, тогда: Сумма чисел равна: x + y = 12 Разность чисел равна: x – y = 2
Слайд 9
Система линейных уравнений с двумя неизвестными Пара значений x = 7 и y = 5 являются решением данной системы. Решением системы уравнений с двумя переменными называется пара значений переменных, при которых оба уравнения системы обращается в верное равенство
Слайд 10
Решить систему уравнений — значит найти все её решения, либо доказать, что их нет
Слайд 11
Решение системы уравнений графическим способом Ответ: (0;2). Построим в координатной плоскости графики уравнений системы. Графики пересекаются в точке А(0;2)
Слайд 12
Графический способ обычно позволяет находить решения лишь приближенно .
nsportal.ru
«Решение систем линейных уравнений с двумя переменными» ( алгебра- 7 класс)
Просмотр содержимого документа
«»Решение систем линейных уравнений с двумя переменными» ( алгебра- 7 класс)»

Решение
систем линейных уравнений
с двумя переменными
Алгебра – 7 класс

Системами уравнений называют записи, представляющие собой расположенные друг под другом уравнения, объединенные слева фигурной скобкой, которые обозначают множество всех решений уравнений, одновременно являющихся решениями каждого уравнения системы.
Решением системы уравнений с двумя переменными называется пара значений этих переменных, обращающая каждое уравнение системы в верное числовое равенство, другими словами, являющаяся решением каждого уравнения системы

Формируемые результаты
Предметные : обобщить и систематизировать знания о системах двух линейных уравнений с двумя переменными.
Личностные : формировать умение соотносить полученный результат с поставленной целью.
Метапредметные : формировать умение сравнивать, анализировать, обобщать по разным показателям, моделировать выбор способов деятельности, группировать.

Графическое решение систем
линейных уравнений с двумя переменными
- Если угловые коэффициенты прямых различны, то они пересекаются в одной точке, следовательно , система имеет единственное решение .
- Если угловые коэффициенты прямых одинаковы, а точки пересечения с осью Оу различны, то прямые параллельны, следовательно, система не имеет решения.
- Если уравнения прямых одинаковы, то их графики совпадают, следовательно, система имеет бесконечно много решений .

Решение систем линейных уравнений способом подстановки
4х + у = 2,
х– у = 3.
1-й шаг. Выразить из какого – нибудь уравнения системы одну переменную через другую.
2-й шаг. Подставить в другое уравнение системы вместо этой переменной полученное выражение.
х = 3 + у
4(3 + у) + у = 2,
3-й шаг .
х = 3 + у
4-й шаг.
4(3 + у) + у = 2,
Решить полученное уравнение с одной переменной.
12 + 4у + у = 2,
Найти соответствующее значение второй переменной.
х = 3 + у,
5-й шаг. Записать ответ
х = 3 + ( -2) ,
5у = — 12 + 2,
Ответ : ( 1 ; — 2)
5у = — 10,
х = 1.
у = — 2.

Решение систем линейных уравнений способом подстановки
3х + 2у = — 1,
5х + 4 у = — 3.
1-й шаг Умножить почленно уравнения системы на
такие множители, чтобы коэффициенты при
— 6х – 4у = 2,
2-й шаг . Сложить почленно левые и правые части
5 х + 4у = -3.
уравнений системы.
— х = — 1,
одной из переменных стали противоположными.
3-й шаг .
4-й шаг.
— х = — 1,
Решить получившееся уравнение с одной
Найти соответствующее значение второй
если х = 1 , то 3х + 2у = — 1,
х = — 1 : (-1),
5-й шаг. Записать ответ
переменной.
3 · 1 + 2у = — 1,
х = 1
переменной.
Ответ : ( 1 ; — 2)
2у = — 4,
у = — 2.

Самостоятельная
работа

Задание № 1
Умножьте одно из уравнений системы на такое число, чтобы с помощью сложения можно было исключить одну из переменных.
а) б)
в)
х – у = 7,
5х + 3у = 2 ;
х + 3у = 1,
— 4х + 2у = 5 ;
2х + 3у = — 2,
5х – 6у = 4.

Задание № 1
Умножьте одно из уравнений системы на такое число, чтобы с помощью сложения можно было исключить одну из переменных.
а) б)
в)
х – у = 7,
5х + 3у = 2 ;
х + 3у = 1,
— 4х + 2у = 5 ;
2х + 3у = — 2,
5х – 6у = 4.

Задание № 2
Решите систему уравнений способом подстановки и сделайте проверку :
а)
б)
х + 2у = -1,
х — у = — 2 ;
5 х – 3у = 14,
2х + у = 10 .

Задание № 3
Решите способом сложения систему уравнений :
а)
б)
х + у = 4,
3х — у = 20 ;
4 х – 5у = 1,
2х — 3у = 2 ;
multiurok.ru
Конспект урока по алгебре на тему «Системы линейных уравнений с двумя переменными» (7 класс)
Учитель: Табакова Татьяна Евгеньевна
Место работы: МОУ Лопаревская СОШ
Должность: учитель математики
Тема урока «Системы линейных уравнений с двумя переменными».
Тип урока: урок изучения нового материала
Цель урока: познакомить с определением системы уравнений с двумя переменными, решением системы уравнений с двумя переменными
образовательная:
— ввести понятие системы уравнений, решения системы;
— сформировать умение находить количество решений, не решая систему;
развивающая:
— развитие культуры устной и письменной речи учащихся;
— развитие мышления учащихся через умение анализировать и выделять
главное;
воспитательная:
— воспитание аккуратности.
Формы работы: фронтальная, индивидуальная
Ход урока
1. Организационный момент
13 лет – время, когда всерьёз можно задуматься над вопросом бедующей профессии. А хорошее решение может быть принято только на основе знаний. Усердное изучение математики, систематические знания учат правильно рассуждать, принимать обоснованные решения, защищать и отстаивать своё мнение, развивать память и воображение. Значит занятие математикой – это первый шаг к будущей профессии. Давайте продолжим делать этот шаг.
2. Устная работа
Работа по карточкам (задания из сборников для подготовки к ОГЭ)
2. Актуализация опорных знаний
Фронтальный опрос:
1. Какое уравнение называется линейным уравнением с двумя переменными?
2. Что является графиком уравнения?
3. Что является решением уравнения?
4. Как найти решения уравнения?
5. Как узнать будет ли пара (1;1) решением уравнения 2x + y = 5?
6. Найти три решения уравнения?
3. Объяснение нового материала
Ставит проблему: х + y = 3 и y = х — 5
Как найти решение, которое будет являться решением и одного и другого уравнения?
Чтобы найти общее решение этих уравнений надо найти такие значения переменных, которые обращают в верное равенство каждое из уравнений. В таких случаях говорят, что требуется решить систему уравнений.
Открываем тетради, записываем число, тему урока: ««Системы линейных уравнений с двумя переменными».
Систему уравнений принято записывать с помощью фигурной скобки:
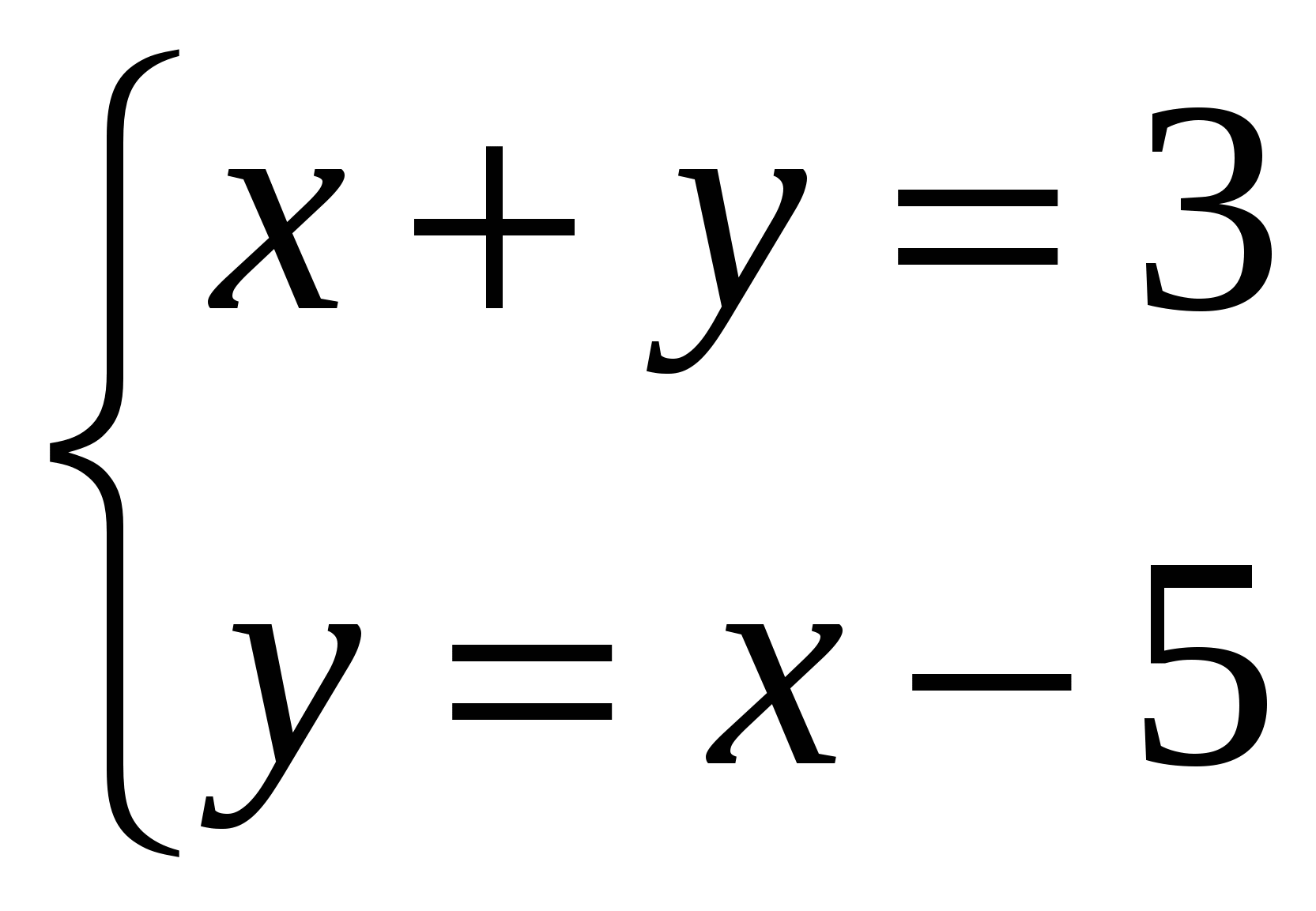
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.
Проверить является ли пара (1;2), (4;-1) решением системы (образец выполнения показывает на доске).
Как решать системы линейных уравнений вы узнаете на последующих уроках. А сейчас вы узнаете как, не решая систему уравнений, определить, сколько решений она имеет.
Рассмотрим систему:
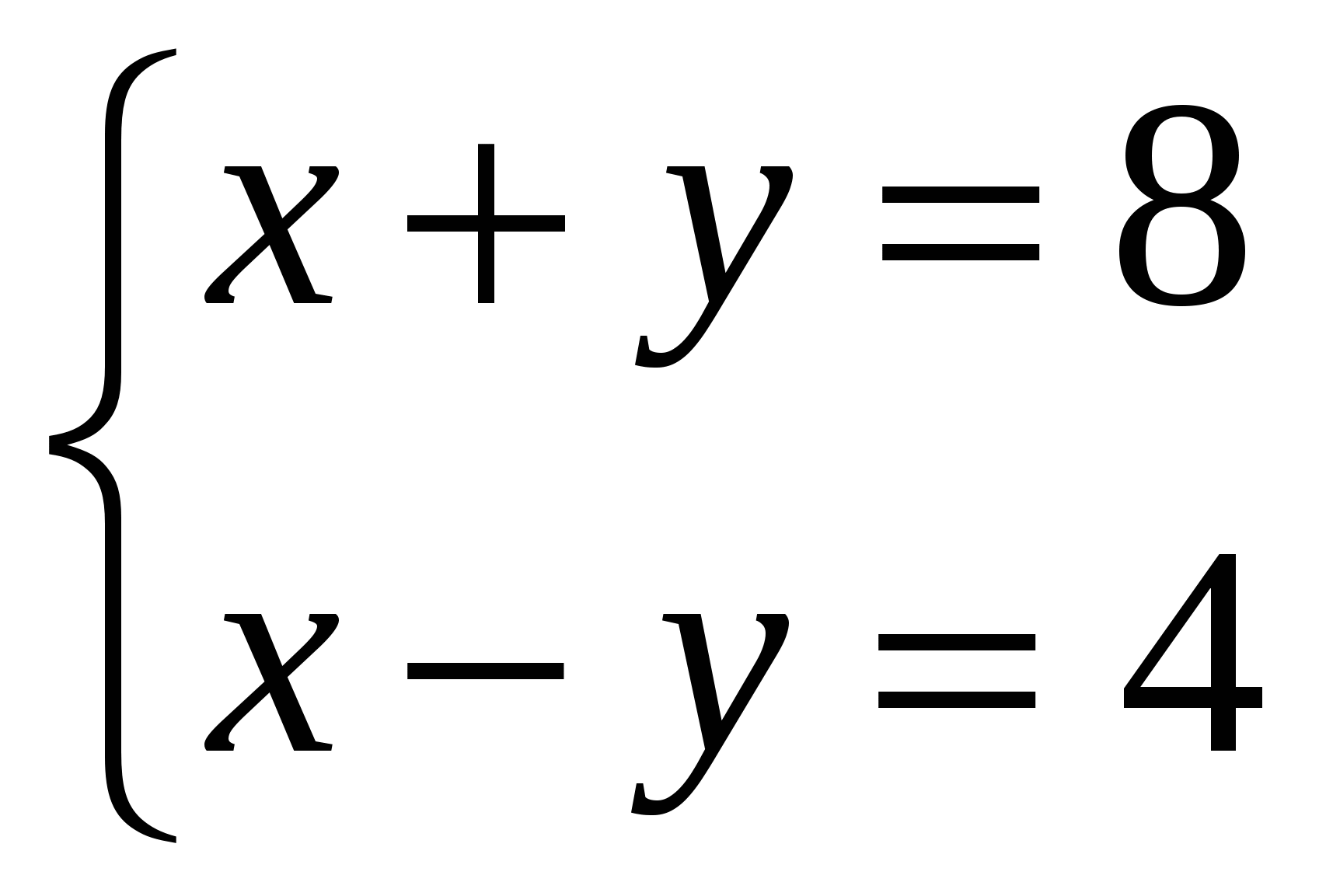
Выразим из каждого уравнения у через х:

Уравнения задаются линейными функциями. Видим, что угловые коэффициенты прямых, являющихся графиками этих функций, различны. Значит прямые пересекаются и система имеет единственное решение.
Правило:
1) если угловые коэффициенты прямых, являющихся графиками функций, различны, то система имеет единственное решение.
2) если угловые коэффициенты прямых, являющихся графиками функций, одинаковы, а b различны, то система не имеет решений.
3) если уравнения имеют одинаковый вид, то система имеет бесконечно много решений.
4. Закрепление
Работа по учебнику: №1056, №1063
5. Первичное закрепление нового материала
1. Выяснить, сколько решений имеет система.
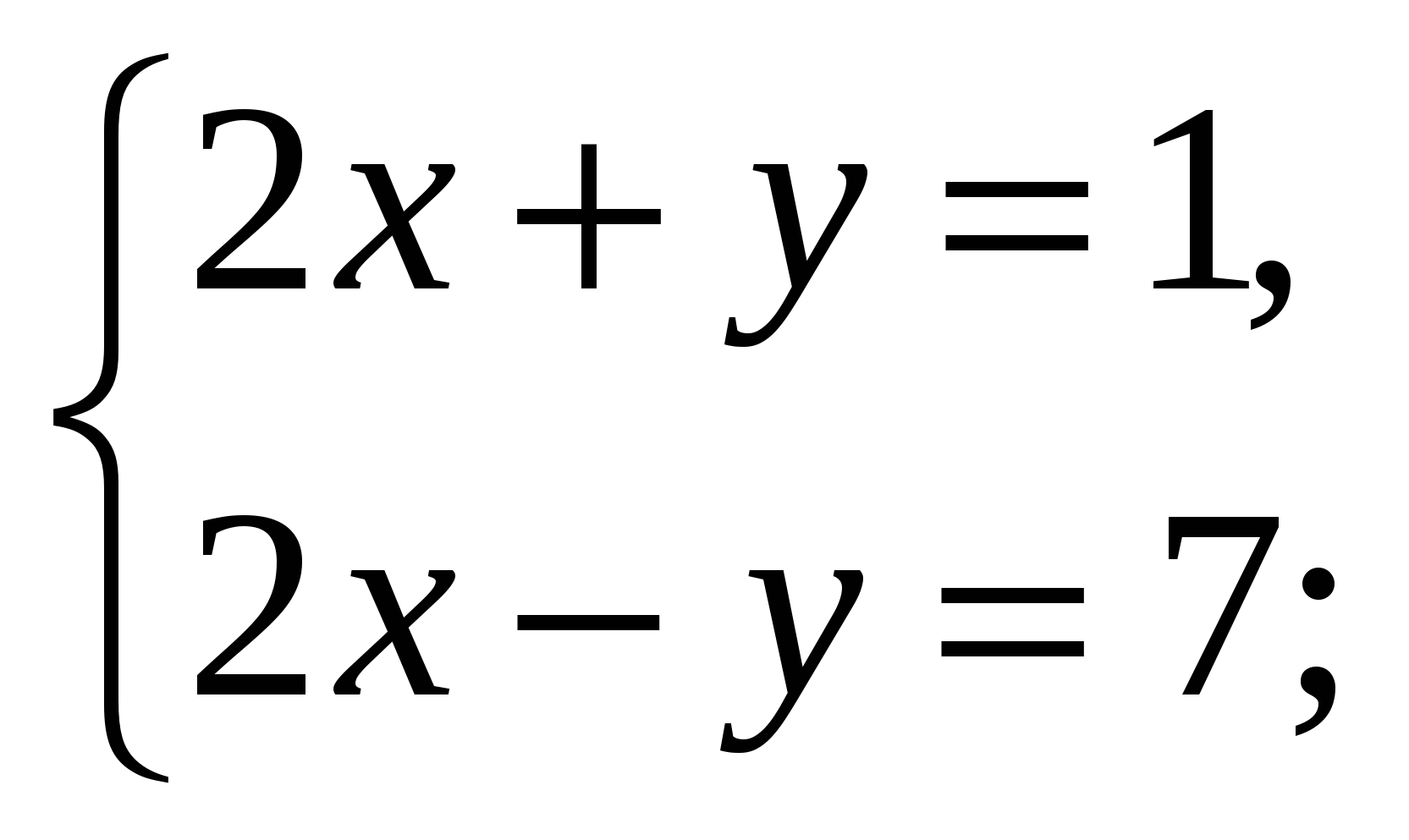
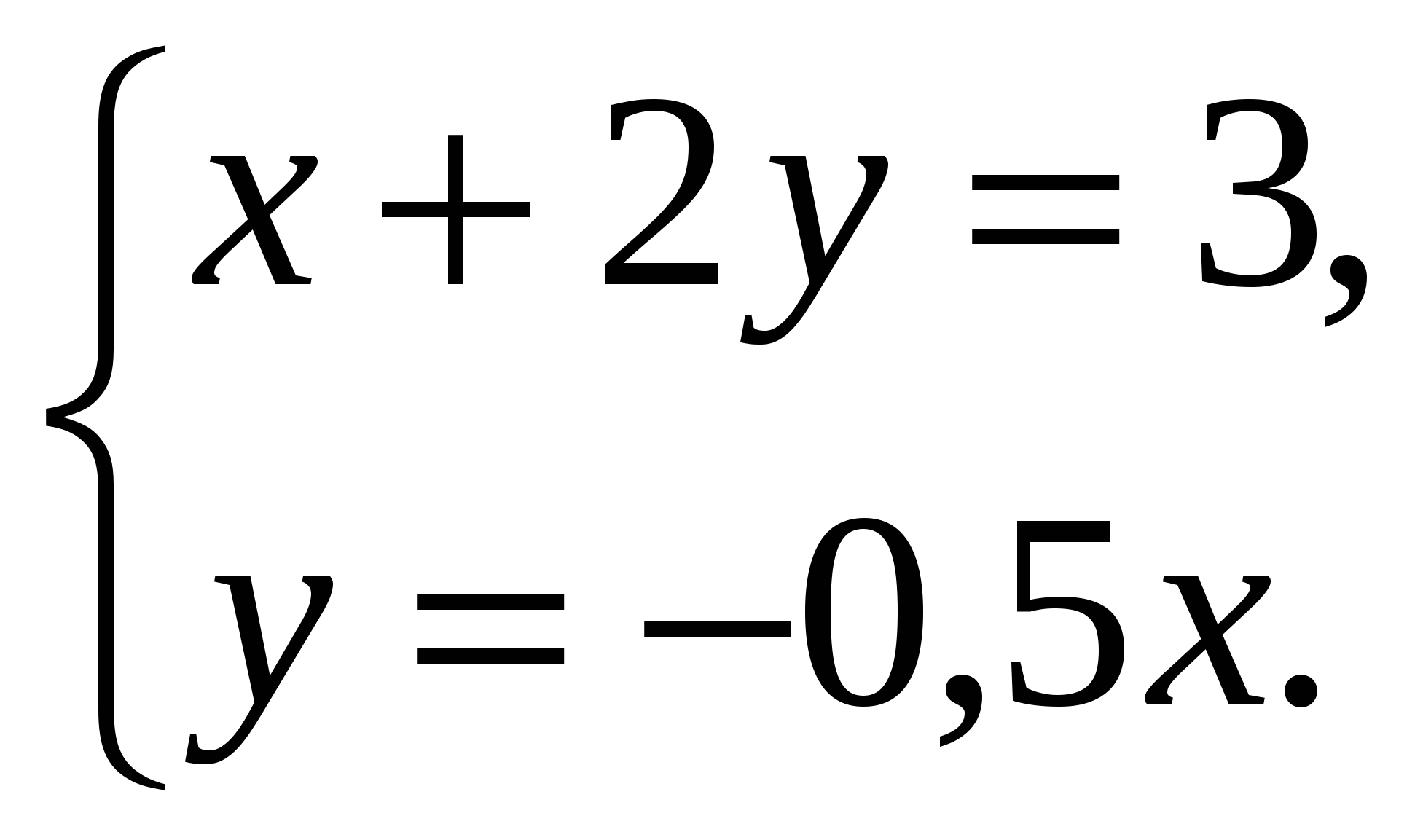
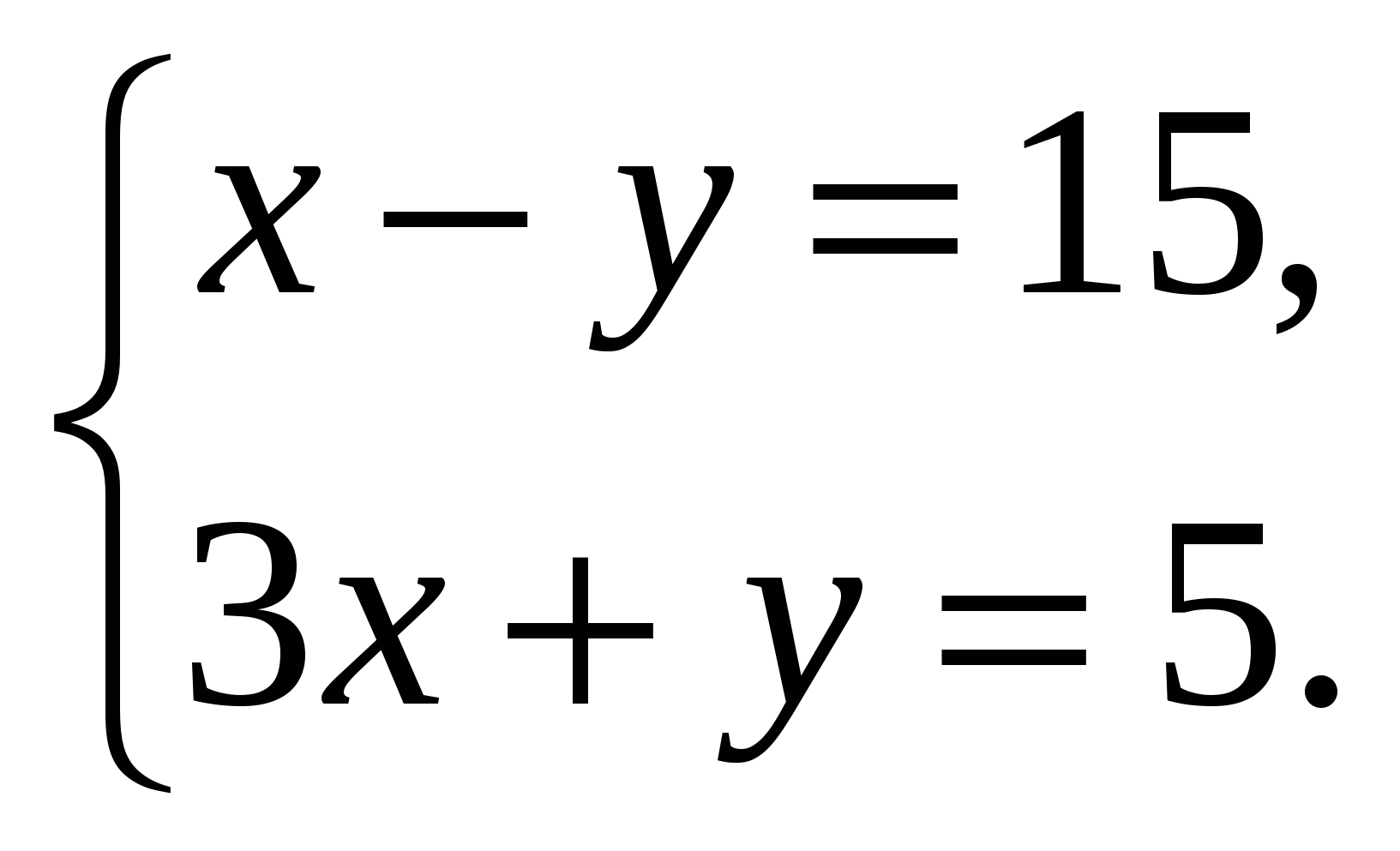
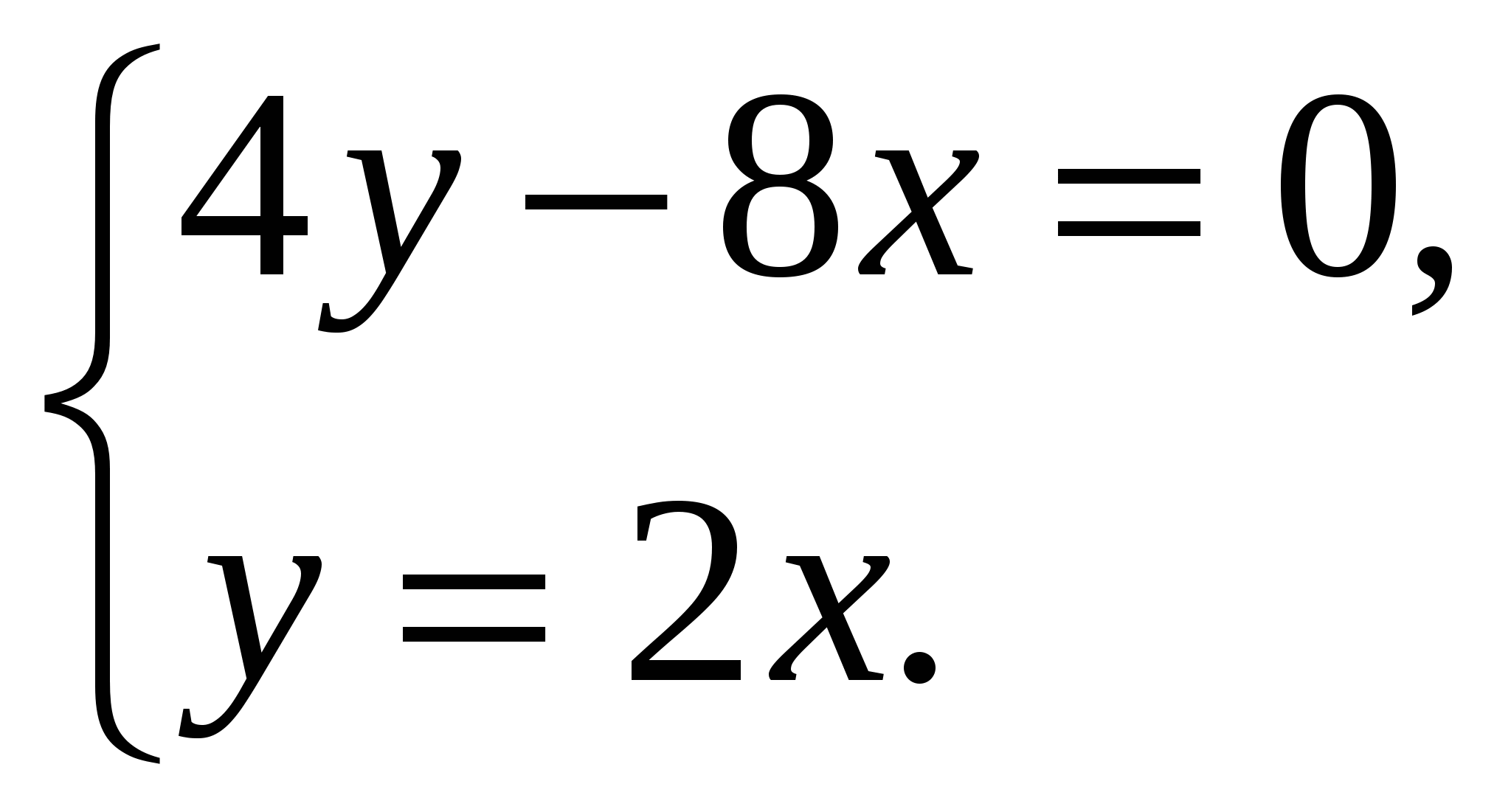
2. Является ли решением системы уравнений
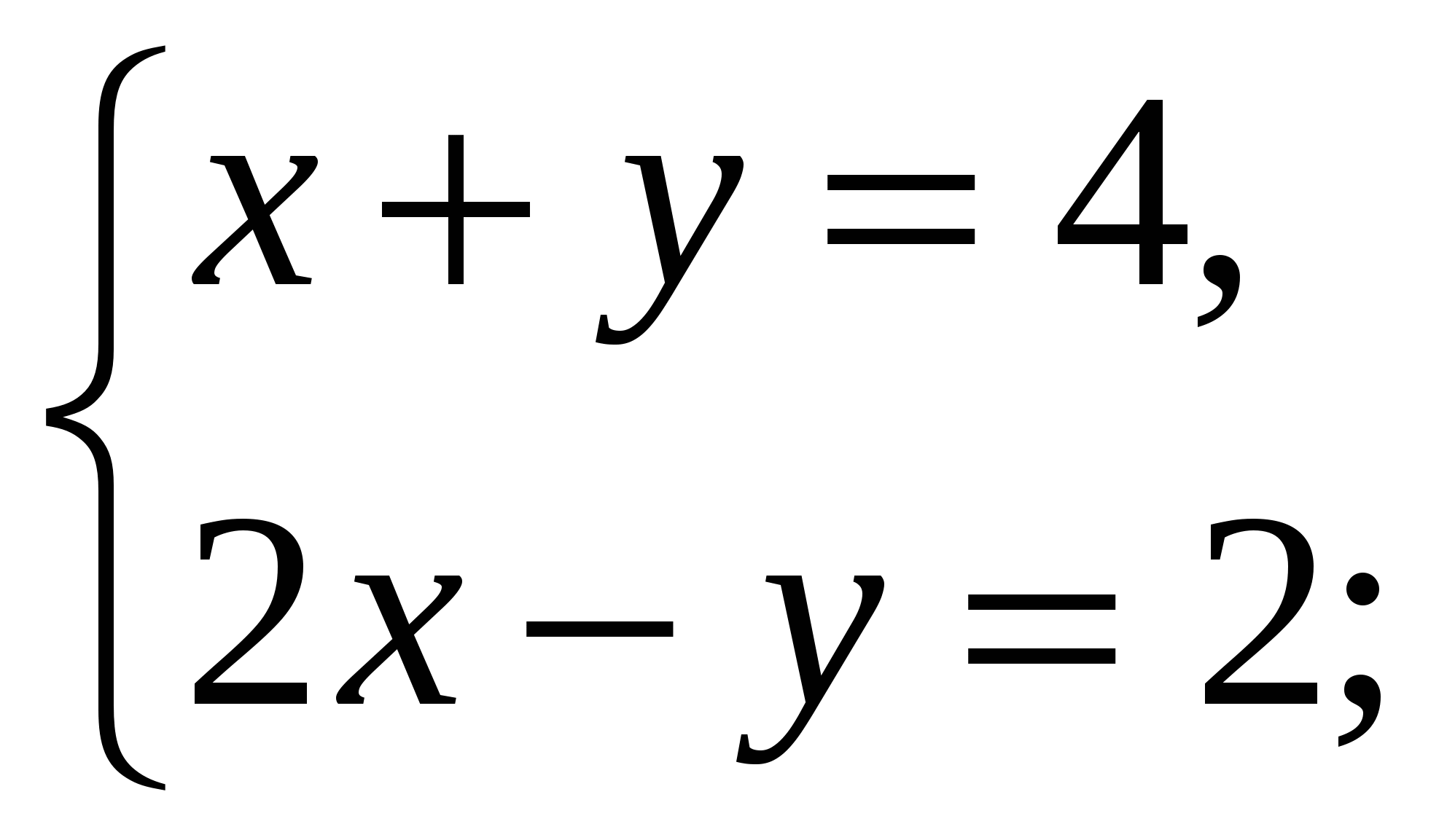
пара (3;1)
пара (2;2)
6. Постановка домашнего задания и его комментарий
п.42 (определение и примеры), №1057, №1064
7. Подведение итогов урока
Какие новые понятия узнали на уроке?
Что нового узнали на уроке.
infourok.ru
Презентация к уроку (алгебра, 7 класс) по теме: Презентация к уроку по теме: Решение систем линейных уравнений с двумя переменными. 7 класс.
Слайд 1
Решение систем линейных уравнений с двумя переменными. Алгебра 7 класс. Подготовила учитель математики Бобер Е.В. 2012год. . МБОУ лицей №82 п.Каменоломни Ростовской областиСлайд 2
Повторить определения уравнения, системы уравнений, их решений; Повторить алгоритмы решения систем уравнений; Восстановить и отработать навыки решения систем линейных уравнений с двумя переменными Цели урока:
Слайд 3
Решите линейные уравнения , ответы расположите в порядке возрастания. 3У+ 7 = 13 х – 1= -4 13 – 3У = 1 7х = 7 ( у + 5)∙ 2 = 0 2х – 1 = 9 2х –11 = 11 Задание № 1 — 5 6 15 -8 11 7 4 2 -3 1 Д И О Ф А 5 Н Е Г р Т у
Слайд 4
Диофант Александрийский, древнегреческий математик, ок . 3 века н.э. «Арифметика» из 13 книг, 6 сохранились до наших дней. В 5 книгах содержатся методы решения неопределенных уравнений. Задача. В клетке сидят кролики и фазаны вместе у них 18 ног. Узнайте сколько в клетке тех и других. Решение. Пусть: Х- число кроликов У- число фазанов Тогда 4х + 2у = 18. 2х + у = 9 у = 9 — 2х Методом перебора: (1;7), (2;5), (3;3), (4;1). Уравнение 4х+2у=18 называют неопределенным или диофантовым уравнением (уравнение в целых или натуральных числах)
Слайд 5
Определение Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой (система уравнений –это конъюнкция нескольких уравнений) Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство (решение системы уравнений – это пересечение решений всех уравнений, входящих в систему) Решить систему уравнений — это значит найти все её решения или установить, что их нет Система уравнений и её решение
Слайд 6
Решение системы графическим способом 1 0 1 2 10 x 4 6 10 -2 y y=10 — x y=x+2 у — х=2, у+х=10; Выразим у через х у=х+2, у=10-х; Построим график первого уравнения х у 0 2 -2 0 у=х+2 Построим график второго уравнения у=10 — х х у 0 10 10 0 Ответ: (4; 6)
Слайд 7
Решение системы способом сложения 7х+2у=1, 17х+6у=-9; Уравняем модули коэффициентов перед уравнением | |·(-3) -21х-6у=-3, 17х+6у=-9; + ____________ — 4х = — 12, 7х+2у=1; Сложим уравне — ния почленно Решим уравнение х=3, 7х+2у=1; Подставим х=3, 7·3+2у=1; Решим уравнение х=3, 21+2у=1; х=3, 2у=-20; х=3, у=-10. Ответ: (3; — 10)
Слайд 8
Решение системы способом подстановки -х+у=1 , 2х+у=4; У = х + 1, 2х+у=4; ____________ 2 х + х + 1= 4, 3х =4 – 1, 3х = 3 Х = 1; Подставим полученное выражение в другое уравнение Решим уравнение х=1, — 1+у=1 ; х=1, у=2; Ответ: (1; 2) Выразим у через х Подставим х и найдем у
Слайд 9
Проверочная работа 1 вариант Решите задачу: Сумма двух чисел равна 33, а их разность равна7. Найдите эти числа. 2 вариант Решите задачу: Разность чисел равна 8, а их сумма равна 22. Найдите эти числа.
Слайд 10
Проверка: 1вариант х+у=33 + х – у = 7. 2х = 40 х=20. 20+у=33 у=13. Ответ: ( 20;13) 2 вариант х — у=8 + х + у =22. 2х = 30 х=15. 15- у=8 у=7. Ответ: ( 15;7)
Слайд 11
Успехов в домашней работе Составить три системы уравнений и решить их разными способами Домашняя работа
nsportal.ru
«Системы двух уравнений с двумя переменными как математические модели реальных ситуаций»
Конспект урока алгебры для 7 класса
На тему урока: «Системы двух уравнений с двумя переменными как математические модели реальных ситуаций»
Цели урока:
— цель обучения формирование у обучающихся умения применять умение решении систем линейных уравнений для решения текстовых задач, умения различать задачи на движение и в зависимости от этого применять разные способы их решения, умения решать задачи по всем этапам, контроль и самоконтроль изученных понятий и способов.
— цель воспитания сформировать чувства коллективизма, терпимости и уважения к друг другу, взаимопомощи.
— цель развития предполагает развитие мышления, памяти, внимания, познавательные умения, самостоятельности.
УУД:
— Личностные: способность к самооценке, умение проявлять инициативу в учебно-познавательной деятельности
— Регулятивные: проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.
— Коммуникативные УУД: умение оформлять свои мысли в устной форме; слушать и понимать речь других.
— Познавательные УУД: умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя информацию, полученную на уроке и свой жизненный опыт.
План урока:
Организационный момент
Проверка домашнего задания
Актуализация знаний
Новая тема
Постановка домашнего задания
Рефлексия
Оборудование: доска, разноцветный мел, проектор.
Этапы урока
Деятельность учителя
Деятельность ученика
Организационный этап.
Добрый день, дети! Рада видеть вас.
Проверка домашнего задания.
Выяснить возникли ли проблемы, если да, то разобрать номер.
Попросить в конце урока сдать тетради домашние.
Актуализация знаний.
Давайте вспомним, чем мы с вами занимались на прошлых уроках.
Какие методы решения систем уравнений вы знаете?
А для чего нам нужны системы?
Верно, ко всему прочему системы нужны нам, чтобы решать “жизненные” задачи, поскольку системы являются моделями реальных ситуаций.
Запишем число, Классная работа. Тема урока: ” Системы двух уравнений с двумя переменными как математические модели реальных ситуаций”.
У вас на столах лежат распечатки, возьмите первую часть. Начнем ее заполнять:
Давайте вспомним с вами, алгоритм решения задачи с помощью уравнения, что мы с вами делаем?
А что такое математическая модель реальных событий и зачем она нужна?
Как мы можем описать реальные ситуации?
Чтобы решить задачу, в ходе решения наше рассуждение делится на три этапа. Прочтите их.
Давайте на примере нашей задачи распишем ее решение по всем этапам.
Методы решения систем уравнений:
– подстановки;
– алгебраического сложения;
– графический.
1.Обозначить неизвестные элементы переменными;
2.Составить по условию задачи систему уравнений;
3.Определить метод решения системы уравнений;
4.Выбрать ответ, удовлетворяющий
условию задачи.
Математическая модель-от реальной ситуации к ее матем модели(примеры)
Словесная модель (словами), алгебраическая модель(алгебраически),графическая модель(графически).
В двух классах 35 учеников. В одном на 9 учеников больше, чем в другом. Сколько в каждом классе было учеников?
I этап. Обозначим х – число овец у первого мужика, у – у второго.
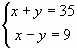
II этап. (Решаем методом алгебраического сложения.)
III этап. Ответ: 13 и 22.
Введение новых знаний.
Сегодня на уроке мы будем решать задачи на движение.
Давайте вспомним какие типы задач на движение вы уже знаете?
Сделаем чертежи пояснительные к этим задачам.
И напишем формулы.
(обсуждаем и заполняем табличку часть 2)
Решим и распишем задачу: Задача: Расстояние между двумя пунктами по реке равно 80 км. Это расстояние лодка проплывает по течению реки за 4 часа, а против течения за 5 часов. Найдите собственную скорость лодки и течения реки.
1.Встречное движение.
При решении задач на встречное движение существенной
характеристикой является скорость сближения движущихся объектов.
Расстояние, на которое сближаются движущиеся объекты за единицу
времени, называют скоростью сближения.
При встречном движении скорость сближения равна сумме скоростей
движущихся объектов, т.е.
Vсбл =V1+ V2
Расстояние между пунктами определяется по формуле
S=Vt .
2)Противоположное движение.
При решении задач такого типа суммарная скорость имеет другое
название.Расстояние, на которое удаляются движущиеся предметы за
единицу времени, называют скоростью удаления.
При движении в противоположных направлениях скорость удаления
равна сумме скоростей движущихся объектов, т.е.
Vyд= V1+V2
3.Движение в одном направлении (вдогонку).
При движении в одном направлении (вдогонку) скорость сближения
объектов равна разности их скоростей:
Vсбл=V1- V2
(V1 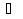 V2).
V2).
4.Движение в одном направлении(с отставанием).
При движении в одном направлении (с отставанием) скорость
удаления объектов равна разности их скоростей.
Vyд=V1- V2
(V1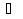 V2).
V2).
5. Движение по реке помогают знания из
жизненного опыта:
Озеро (море) – стоячая вода, поэтому при движении она не помогает,
но и не препятствует движению катера (или другого объекта).
Очевидно, что катер движется с той скоростью, которая называется
собственной скоростью катера (скоростью, обусловленной
мощностью его двигателя).
Vкатера =Vсобств
.
При движении по течению реки (часто говорят – «вниз» по реке)
скорость катера увеличивается, т.к. движущаяся вода как бы
«подталкивает», т.е. убыстряет его движение. В этом случае к
собственной скорости катера необходимо прибавить скорость течения
реки.
Vкатера= Vсобств+ Vтеч. реки
При движении против течения реки («вверх» по реке) скорость катера
уменьшается, т.к. река замедляет его движение, «сносит» катер. В
этом случае от собственной скорости катера следует вычесть скорость
течения реки.
Vкатера+Vсобств-Vтеч. реки.
Выведем две формулы, которые полезно знать:
1) формулу для нахождения собственной скорости, если
известны скорость по течению и скорость против течения.
Vпо.теч. = Vсобств +Vтеч.
(1).
Vпр.теч. = Vсобств -Vтеч.
(2).
Сложим (1) и (2), получим:
Vпо.теч. + Vпр.теч. =2Vсобств, откуда имеем:
2) формулу для нахождения скорости течения реки по тем же
известным величинам. Вычтем (2) из (1), получим:
Vпо.теч. + Vпр.теч.= 2Vсобств.
Закрепление материала.
Задача 1.
Расстояние между двумя пунктами по реке составляет 14 км. Лодка проходит этот путь по течению за 2 часа, против течения – за 2 часа 48 минут. Найдите скорость лодки в стоячей воде и скорость течения реки.
Задача 2.
Из двух городов, расстояние между которыми 700 км, одновременно навстречу друг другу отправляются два поезда, и встречаются через 5 часов. Если второй поезд отправится на 7 часов раньше первого, то они встретятся через два часа после отправления первого поезда. Найти скорость каждого поезда.
Задача 3.
Пристани В и С находятся ниже пристани А по течению реки соответственно на 30 км и 45 км. Моторная лодка отходит от пристани А, доходит до С, сразу поворачивает назад и приходит в В, затратив на весь путь 4 часа 40 минут. В другой раз эта же лодка отошла от пристани, дошла до А, сразу повернула назад и пришла в В, затратив на весь путь 7 часов. Чему равна собственная скорость лодки и скорость течения реки?
Решаем задачи:40.1, 40.2, 40.4, 40.5.
На втором уроке на третьем листе расспечатки.
Решение:
Вспомним уравнение прямолинейного равномерного движения: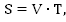
S – расстояние,
V – скорость,
T – время.
Переведем 2 часа 48 минут в часы, это составит 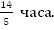
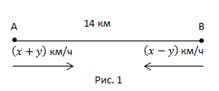
Пусть x км/ч – скорость лодки в стоячей воде, y км/ч – скорость течения реки. Составим математическую модель.
Если лодка движется по течению, то она имеет скорость 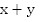 км/ч и пройдет 14 км за время
км/ч и пройдет 14 км за время 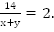 Если лодка движется против течения, она идет со скоростью
Если лодка движется против течения, она идет со скоростью 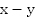 км/ч и пройдет 14 км за время
км/ч и пройдет 14 км за время 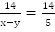 .
.
Мы получили математическую модель. То же самое можно получить с помощью таблицы.
S
V
T
По течению
14
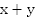
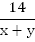
Против течения
14
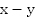

Решим полученную систему.
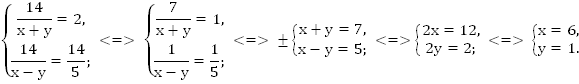
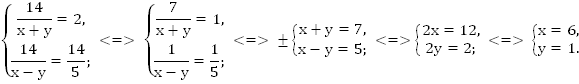
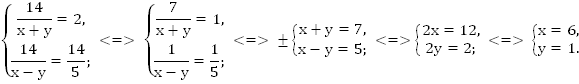
Ответ: 6 км/ч; 1 км/ч.
Решение:
Пусть x км/ч, y км/ч – скорости первого и второго поездов.
S – расстояние между городами.
Рассмотрим вначале первый случай. Легко увидеть, что это задача на сближение, т.е. мы сможем пользоваться данными, полученными в первой опорной задаче.
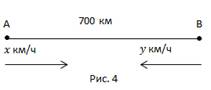
700 км оба поезда пройдут за 5 часов со скоростью сближения 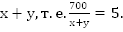
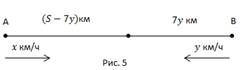
Второй случай: те же условия, но первый поезд начал движение через 7 часов после второго. За 7 часов второй поезд прошел 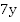 км, осталось
км, осталось 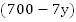 км, и только тогда начинает движение первый поезд. Начинается сближение. Поездам нужно пройти
км, и только тогда начинает движение первый поезд. Начинается сближение. Поездам нужно пройти 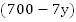 км с общей скоростью
км с общей скоростью 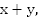 и они встретятся через 2 часа, т.е.
и они встретятся через 2 часа, т.е. 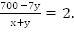
Мы получили математическую модель.
Упростим полученные уравнения.
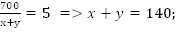
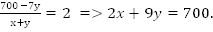
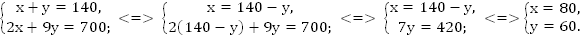
Ответ: 80 км/ч, 60 км/ч.
Решение:
Пусть x км/ч – собственная скорость лодки, y км/ч – скорость течения реки.
Время движения переведем в часы, 4 часа 40 минут = 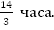
Опишем первый рейс: 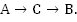
Из А в С лодка шла 45 км по течению со скоростью 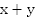 км/ч, время в пути составило
км/ч, время в пути составило 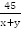 ч.
ч.
Из С в В лодка шла 15 км против течения, т.е. 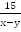 ч. Суммарное время в пути составило
ч. Суммарное время в пути составило  ч, т.е.
ч, т.е. 
Опишем второй рейс: 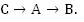
Из С в А лодка шла 45 км против течения, т.е. была в пути 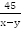 ч. Из А в В шла 30 км по течению, т.е. была в пути
ч. Из А в В шла 30 км по течению, т.е. была в пути  ч. Общее время в пути составило 7 ч, т.е.
ч. Общее время в пути составило 7 ч, т.е. 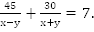
Решаем полученную систему:
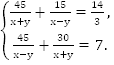
Произведем замену переменных:

Переходим к старым переменным:
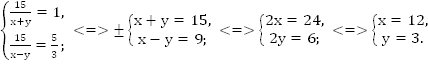
Ответ: 12 км/ч, 3 км/ч.
Домашнее задание.
40.3, 40.6 + задание.
Подведение итогов.
Что нового узнали? Чем занимались?
infourok.ru