Равносильные уравнения, преобразование уравнений
Некоторые преобразования позволяют нам перейти от решаемого уравнения к равносильным, а также к уравнениям-следствиям, благодаря чему упрощается решение первоначального уравнения. В данном материале мы расскажем, что из себя представляют эти уравнения, сформулируем основные определения, проиллюстрируем их наглядными примерами и поясним, как именно осуществляется вычисление корней исходного уравнения по корням уравнения-следствия или равносильного уравнения.
Понятие равносильных уравнений
Определение 1Равносильными называются такие уравнения, имеющие одни и те же корни, или же те, в которых корней нет.
Определения такого типа часто встречаются в различных учебниках. Приведем несколько примеров.
Определение 2Уравнение f(x)=g(x) считается равносильным уравнению r(x)=s(x), если у них одинаковые корни или у них обоих нет корней.
Определение 3Уравнения с одинаковыми корнями считаются равносильными. Также ими считаются два уравнения, одинаково не имеющие корней.
Если уравнение f(x)=g(x) имеет то же множество корней, что и уравнение p(x)=h(x), то они считаются равносильными по отношению друг к другу.
Когда мы говорим о совпадающем множестве корней, то имеем в виду, что если определенное число будет корнем одного уравнения, то оно подойдет в качестве решения и другому уравнению. Ни одно из уравнений, являющихся равносильными, не может иметь такого корня, который не подходит для другого.
Приведем несколько примеров таких уравнений.
Пример 1Например, равносильными будут 4·x=8, 2·x=4 и x=2, поскольку каждое из них имеет только один корень – двойку. Также равносильными будут x·0=0 и 2+x=x+2, поскольку их корнями могут быть любые числа, то есть множества их решений совпадают. Также равносильными будут уравнения x=x+5 и x4=−1, каждое из которых не имеет ни одного решения.
Для наглядности рассмотрим несколько примеров неравносильных уравнений.
Пример 2К примеру, таковыми будут x=2 и x2=4, поскольку их корни отличаются. То же относится и к уравнениям xx=1 и x2+5×2+5, потому что во втором решением может быть любое число, а во втором корнем не может быть 0.
Определения, данные выше, подойдут и для уравнений с несколькими переменными
Уравнение (неравенство) с параметрами — Википедия
Материал из Википедии — свободной энциклопедии
Уравнение (неравенство) с параметрами — математическое уравнение (неравенство), внешний вид и решение которого зависит от значений одного или нескольких параметров.
Решить уравнение с параметром означает:
- Найти все системы значений параметров, при которых данное уравнение имеет решение.
- Найти все решения для каждой найденной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.
Уравнения с параметром могут быть как линейными, так и нелинейными.
Пример линейного уравнения с параметром:
- ax+1=4,{\displaystyle a\,x+1=4,}
Пример нелинейного уравнения с параметром:
- logx2a+37−x=5,{\displaystyle {\mbox{log}}_{x^{2}}{\frac {a+3}{7-x}}=5,}
где x{\displaystyle x} — независимая переменная a{\displaystyle a} — параметр.
Аналогично подразделяются и неравенства. Ниже будут представлены примеры решений уравнений и неравенств с параметрами.
- Пример 1.При каком a{\displaystyle a} квадратное уравнение x2+3x−a=0{\displaystyle {x^{2}}+3\,x-a=0} имеет ровно один корень?
Решение. Любое квадратное уравнение имеет одно решение, когда его дискриминант равен нулю. Итак, дискриминант нашего уравнения: D=9+4a{\displaystyle D=9+4\,a}. Далее имеем: 9+4a=0{\displaystyle 9+4\,a=0}, откуда a=−94{\displaystyle a=-{\tfrac {9}{4}}}.
- Ответ:a=−94{\displaystyle a=-{\frac {9}{4}}}.
- Пример 2. При каком a{\displaystyle a} система уравнений :
{x2+y2−2ax−2y−8+a2=0,x2+y2−4x−2y+1=0{\displaystyle {\begin{cases}x^{2}+y^{2}-2ax-2y-8+a^{2}=0,\\x^{2}+y^{2}-4x-2y+1=0\end{cases}}}.
имеет ровно два решения?
Решение. Сначала надо преобразовать два уравнения системы, выделив в них полные квадраты: {x2+y2−2ax−2y−8+a2=0,x2+y2−4x−2y+1=0{\displaystyle {\begin{cases}x^{2}+y^{2}-2ax-2y-8+a^{2}=0,\\x^{2}+y^{2}-4x-2y+1=0\end{cases}}} ⇔{\displaystyle \Leftrightarrow } {(x2−2ax+a2)+(y2−2y+1)=9,(x2−4x+4)+(y2−2y+1)=4{\displaystyle {\begin{cases}(x^{2}-2ax+a^{2})+(y^{2}-2y+1)=9,\\(x^{2}-4x+4)+(y^{2}-2y+1)=4\end{cases}}} ⇔{\displaystyle \Leftrightarrow } {(x−a)2+(y−1)2=9,(x−2)2+(y−1)2=4{\displaystyle {\begin{cases}(x-a)^{2}+(y-1)^{2}=9,\\(x-2)^{2}+(y-1)^{2}=4\end{cases}}}
Нетрудно догадаться, что эти два равенства системы есть не что иное, как уравнения окружностей. Первая окружность имеет центр в точке (a;1){\displaystyle (a;1)}, радиус 3{\displaystyle 3}, а вторая центр в точке (2;1){\displaystyle (2;1)} и радиус 2{\displaystyle 2}. Если построить схематично эти окружности в одной системе координат, то можно заметить, что их общих точек пересечения будет две в том случае, если a∈(−3;1)∪(3;7){\displaystyle a\in (-3;1)\cup (3;7)}. И задачу можно считать решённой.
- Ответ:a∈(−3;1)∪(3;7){\displaystyle a\in (-3;1)\cup (3;7)}.
- Пример 3. При всех a{\displaystyle a} решить неравенство ax2+(a+1)x+1⩾0{\displaystyle ax^{2}+(a+1)x+1\geqslant 0}.
Решение. Рассмотрим три случая:
- Если a=0{\displaystyle a=0}, то неравенство приобретает вид x+1⩾0⇔x∈[−1;+∞){\displaystyle x+1\geqslant 0\Leftrightarrow x\in [-1;+\infty )};
- Если a⩾0{\displaystyle a\geqslant 0}, то все коэффициенты квадратного трехчлена будут положительны, значит, решение неравенства можно представить в виде x∈(−∞;x1]∪[x2;+∞){\displaystyle x\in (-\infty ;x_{1}]\cup [x_{2};+\infty )}, где x1{\displaystyle x_{1}},x2{\displaystyle x_{2}} — корни многочлена и x1⩽x2{\displaystyle x_{1}\leqslant x_{2}}. Далее находим: x1=−a−1−a2+2a+1−4a2a⇔x1=−a−1−|a−1|2a={−1,a⩾1,−1a,0⩽a⩽1{\displaystyle x_{1}={\cfrac {-a-1-{\sqrt {a^{2}+2a+1-4a}}}{2a}}\Leftrightarrow x_{1}={\cfrac {-a-1-|a-1|}{2a}}={\begin{cases}-1,a\geqslant 1,\\-{\tfrac {1}{a}},0\leqslant a\leqslant 1\end{cases}}}
x2={−1a,a⩾1,−1,0⩽a⩽1{\displaystyle x_{2}={\begin{cases}-{\tfrac {1}{a}},a\geqslant 1,\\-1,0\leqslant a\leqslant 1\end{cases}}}
Следовательно, x∈(−∞;−1]∪[−1a;+∞){\displaystyle x\in (-\infty ;-1]\cup [-{\tfrac {1}{a}};+\infty )}, если a⩾1{\displaystyle a\geqslant 1} и x∈(−∞;−1a]∪[−1;+∞){\displaystyle x\in (-\infty ;-{\tfrac {1}{a}}]\cup [-1;+\infty )}, если 0⩽a⩽1{\displaystyle 0\leqslant a\leqslant 1}.
- 3. Если a⩽0{\displaystyle a\leqslant 0}, то ветви параболы направлены вниз, естественно решение в общем виде будет выглядеть вот так: x∈[x1;x2]⇔x∈[−1;−1a]{\displaystyle x\in [x_{1};x_{2}]\Leftrightarrow x\in [-1;-{\tfrac {1}{a}}]}.
Нам остается лишь записать ответ.
- Ответ: если a=0{\displaystyle a=0}, то x∈[−1;+∞){\displaystyle x\in [-1;+\infty )}; если a⩾1{\displaystyle a\geqslant 1}, то x∈(−∞;−1]∪[−1a;+∞){\displaystyle x\in (-\infty ;-1]\cup [-{\tfrac {1}{a}};+\infty )}; если 0⩽a⩽1{\displaystyle 0\leqslant a\leqslant 1}, то x∈(−∞;−1a]∪[−1;+∞){\displaystyle x\in (-\infty ;-{\tfrac {1}{a}}]\cup [-1;+\infty )}; если a⩽0{\displaystyle a\leqslant 0}, то x∈[−1;−1a]{\displaystyle x\in [-1;-{\tfrac {1}{a}}]}.
Линейное уравнение — Википедия
Материал из Википедии — свободной энциклопедии
Линейное уравнение — это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна 1. Линейное уравнение можно представить:
- в общей форме: a1x1+a2x2+⋯+anxn+b=0{\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}+b=0};
- в канонической форме: a1x1+a2x2+⋯+anxn=−b{\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}=-b}.
Линейное уравнение одной переменной[править | править код]
Линейное уравнение от одной переменной можно привести к виду:
- ax+b=0{\displaystyle ax+b=0}.
Количество решений зависит от параметров a и b.
Если a=b=0{\displaystyle a=b=0}, то уравнение имеет бесконечное множество решений, поскольку ∀x∈R:x⋅0=0{\displaystyle \forall x\in \mathbb {R} :x\cdot 0=0}.
Если a=0,b≠0{\displaystyle a=0,b\neq 0}, то уравнение не имеет корней, поскольку ∄x∈R:0⋅x=−b≠0{\displaystyle \not \exists x\in \mathbb {R} :0\cdot x=-b\neq 0}.
Если a≠0{\displaystyle a\neq 0}, то уравнение имеет единственное решение x=−ba{\displaystyle x=-{\frac {b}{a}}}.
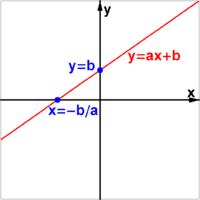 Геометрическое место точек линейного уравнения от двух переменных вида:
Геометрическое место точек линейного уравнения от двух переменных вида:y = ax + b
Линейное уравнение двух переменных можно представить:
- в общей форме: ax+by+c=0{\displaystyle ax+by+c=0};
- в канонической форме: ax+by=−c{\displaystyle ax+by=-c};
- в форме линейной функции: y=kx+m{\displaystyle y=kx+m}, где k=−ab; m=−cb{\displaystyle k=-{\frac {a}{b}};\ m=-{\frac {c}{b}}}.
Решением, или корнями, такого уравнения называют такую пару значений переменных (x;y){\displaystyle (x;y)}, которая обращает его в тождество. Таких решений (корней) линейное уравнение с двумя переменными имеет бесконечное множество. Геометрической моделью (графиком) такого уравнения является прямая y=kx+m{\displaystyle y=kx+m}.
Алгебраическое уравнение — Википедия
Материал из Википедии — свободной энциклопедии
Алгебраическое уравнение (полиномиальное уравнение, многочленное уравнение) — уравнение вида
- P(x1,x2,…,xn)=0,{\displaystyle P(x_{1},x_{2},\ldots ,x_{n})=0,}
где P{\displaystyle P} — многочлен от переменных x1,…,xn{\displaystyle x_{1},\ldots ,x_{n}}, которые называются неизвестными.
Коэффициенты многочлена P{\displaystyle P} обычно берутся из некоторого поля F{\displaystyle {F}}, и тогда уравнение P(x1,x2,…,xn)=0{\displaystyle P(x_{1},x_{2},\ldots ,x_{n})=0} называется алгебраическим уравнением над полем F{\displaystyle {F}}.
Степенью алгебраического уравнения называют степень многочлена P{\displaystyle P}.
Например, уравнение
- y4+xy2+y2z5+x3−xy2+3×2−sin1=0{\displaystyle y^{4}+{\frac {xy}{2}}+y^{2}z^{5}+x^{3}-xy^{2}+{\sqrt {3}}x^{2}-\sin {1}=0}
является алгебраическим уравнением 7-й степени от 3 переменных (с 3 неизвестными) над полем вещественных чисел.
Значения переменных x1,…,xn{\displaystyle x_{1},\ldots ,x_{n}}, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.
- Алгебраическое уравнение с одним неизвестным — уравнение вида a0xn+a1xn−1+…+an=0,{\displaystyle a_{0}x^{n}+a_{1}x^{n-1}+\ldots +a_{n}=0,} где n{\displaystyle n} — натуральное число.
- Линейное уравнение
- от одной переменной: ax+b=0,a≠0.{\displaystyle ax+b=0,\quad a\neq 0.}
- от нескольких переменных: a1x1+a2x2+⋯+anxn+b=0.{\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}+b=0.}
- Квадратное уравнение
- от одной переменной: ax2+bx+c=0,a≠0.{\displaystyle ax^{2}+bx+c=0,\quad a\neq 0.}
- Кубическое уравнение
- от одной переменной: ax3+bx2+cx+d=0,a≠0.{\displaystyle ax^{3}+bx^{2}+cx+d=0,\quad a\neq 0.}
- Уравнение четвёртой степени
- от одной переменной: ax4+bx3+cx2+dx+e=0,a≠0.{\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0.}
- Уравнение пятой степени
- от одной переменной: ax5+bx4+cx3+dx2+ex+f=0,a≠0.{\displaystyle ax^{5}+bx^{4}+cx^{3}+dx^{2}+ex+f=0,\quad a\neq 0.}
- Уравнение шестой степени
- от одной переменной: ax6+bx5+cx4+dx3+ex2+fx+g=0,a≠0.{\displaystyle ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g=0,\quad a\neq 0.}
- Возвратное уравнение — алгебраические уравнения вида: anxn+an−1xn−1+…+a1x+a0=0,{\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+\ldots +a_{1}x+a_{0}=0,} коэффициенты которых, стоящие на симметричных относительно середины позициях, равны, то есть если an−k=ak,{\displaystyle a_{n-k}=a_{k},}, при k=0,1,…,n{\displaystyle k=0,1,\ldots ,n}.
Линейное дифференциальное уравнение с постоянными коэффициентами — Википедия
Линейное дифференциальное уравнение с постоянными коэффициентами — обыкновенное дифференциальное уравнение вида:
- ∑k=0naky(k)(t)=any(n)+an−1y(n−1)+⋯+a1y′+a0y=f(t){\displaystyle \sum _{k=0}^{n}{a_{k}y^{(k)}(t)}=a_{n}y^{(n)}+a_{n-1}y^{(n-1)}+\dots +a_{1}y’+a_{0}y=f(t)}
где
- y=y(t){\displaystyle y=y(t)} — искомая функция,
- y(k)=y(k)(t){\displaystyle y^{(k)}=y^{(k)}(t)} — её k{\displaystyle k}-я производная,
- a0,a1,a2,…an{\displaystyle a_{0},a_{1},a_{2},\dots a_{n}} — фиксированные числа,
- f(t){\displaystyle f(t)} — заданная функция (когда f(t)≡0{\displaystyle f(t)\equiv 0}, имеем линейное однородное уравнение, иначе — линейное неоднородное уравнение).
Определение[править | править код]
Корень кратности k{\displaystyle k} многочлена a0xn+a1xn−1+…+an{\displaystyle a_{0}x^{n}+a_{1}x^{n-1}+\ldots +a_{n}} это число c{\displaystyle c}, такое что этот многочлен делится без остатка на (x−c)k{\displaystyle (x-c)^{k}}, но не на (x−c)k+1{\displaystyle (x-c)^{k+1}}.
Уравнение порядка n[править | править код]
Однородное уравнение:
- any(n)+an−1y(n−1)+⋯+a1y′+a0y=0{\displaystyle a_{n}y^{(n)}+a_{n-1}y^{(n-1)}+\dots +a_{1}y’+a_{0}y=0}
интегрируется следующим образом:
Пусть λ1,…,λk{\displaystyle \lambda _{1},\dots ,\lambda _{k}} — все различные корни характеристического многочлена, являющегося левой частью характеристического уравнения
- anλn+an−1λn−1+⋯+a1λ+a0=0{\displaystyle a_{n}\lambda ^{n}+a_{n-1}\lambda ^{n-1}+\dots +a_{1}\lambda +a_{0}=0}
кратностей m1,m2,…,mk{\displaystyle m_{1},m_{2},\dots ,m_{k}}, соответственно, m1+m2+⋯+mk=n{\displaystyle m_{1}+m_{2}+\dots +m_{k}=n}.
Тогда функции
- tνeλjt, 1≤j≤k, 0≤ν≤mj−1{\displaystyle t^{\nu }e^{\lambda _{j}t},\ \ 1\leq j\leq k,\ \ 0\leq \nu \leq m_{j}-1}
являются линейно независимыми (вообще говоря, комплексными) решениями однородного уравнения, они образуют фундаментальную систему решений.
Общее решение уравнения является линейной комбинацией с произвольными постоянными (вообще говоря, комплексными) коэффициентами фундаментальной системы решений.
Воспользовавшись формулой Эйлера для пар комплексно сопряженных корней λj=αj±iβj, 1≤j≤k{\displaystyle \lambda _{j}=\alpha _{j}\pm i\beta _{j},\ \ 1\leq j\leq k} можно заменить соответствующие пары комплексных функций в фундаментальной системе решений парами вещественных функций вида
- tνeαjtcos(βjt), tνeαjtsin(βjt), j∈1…k¯, 0≤ν≤mj−1{\displaystyle t^{\nu }e^{\alpha _{j}t}\cos(\beta _{j}t),\ \ t^{\nu }e^{\alpha _{j}t}\sin(\beta _{j}t),\ \ j\in {\overline {1\dots k}},\ \ 0\leq \nu \leq m_{j}-1}
и построить общее решение уравнения в виде линейной комбинации с произвольными вещественными постоянными коэффициентами.
Уравнение второго порядка[править | править код]
Однородное уравнение второго порядка:
- a2y″+a1y′+a0y=0{\displaystyle a_{2}y»+a_{1}y’+a_{0}y=0}
интегрируется следующим образом:
Пусть λ1,λ2{\displaystyle \lambda _{1},\lambda _{2}} — корни характеристического уравнения
- a2λ2+a1λ+a0=0{\displaystyle a_{2}\lambda ^{2}+a_{1}\lambda +a_{0}=0},
являющегося квадратным уравнением.
Вид общего решения однородного уравнения зависит от значения дискриминанта Δ=a12−4a2a0{\displaystyle \Delta =a_{1}^{2}-4a_{2}a_{0}}:
- при Δ>0{\displaystyle \Delta >0} уравнение имеет два различных вещественных корня
- λ1,2=α1,2=−a1±Δ2a2.{\displaystyle \lambda _{1,2}=\alpha _{1,2}={\frac {-a_{1}\pm {\sqrt {\Delta }}}{2a_{2}}}.}
Общее решение имеет вид:
- y(t)=c1eα1t+c2eα2t{\displaystyle y(t)=c_{1}e^{\alpha _{1}t}+c_{2}e^{\alpha _{2}t}}
- при Δ=0{\displaystyle \Delta =0} — два совпадающих вещественных корня
- λ1=λ2=α=−a12a2.{\displaystyle \lambda _{1}=\lambda _{2}=\alpha ={\frac {-a_{1}}{2a_{2}}}.}
Общее решение имеет вид:
- y(t)=c1eαt+c2teαt{\displaystyle y(t)=c_{1}e^{\alpha t}+c_{2}te^{\alpha t}}
- λ1,2=α±iβ=−a12a2±i|Δ|2a2.{\displaystyle \lambda _{1,2}=\alpha \pm i\beta ={\frac {-a_{1}}{2a_{2}}}\pm i{\frac {\sqrt {|\Delta |}}{2a_{2}}}.}
Общее решение имеет вид:
- y(t)=c1eαtcos(βt)+c2eαtsin(βt){\displaystyle y(t)=c_{1}e^{\alpha t}\cos(\beta t)+c_{2}e^{\alpha t}\sin(\beta t)}
Неоднородное уравнение интегрируется методом вариации произвольных постоянных (Метод Лагранжа).
Вид общего решения неоднородного уравнения[править | править код]
Если дано частное решение неоднородного уравнения y0(t){\displaystyle y_{0}(t)}, и y1(t),…,yn(t){\displaystyle y_{1}(t),\ldots ,y_{n}(t)} — фундаментальная система решений соответствующего однородного уравнения, то общее решение уравнения задается формулой
- y(t)=c1y1(t)+…+cnyn(t)+y0(t),{\displaystyle y(t)=c_{1}y_{1}(t)+\ldots +c_{n}y_{n}(t)+y_{0}(t),}
где c1,…,cn{\displaystyle c_{1},\dots ,c_{n}} — произвольные постоянные.
Принцип суперпозиции[править | править код]
Как в общем случае линейных уравнений, имеет место принцип суперпозиции, используемый в разных формулировках принципа суперпозиции в физике.
В случае, когда функция в правой части состоит из суммы двух функций
- f(t)=f1(t)+f2(t){\displaystyle f(t)=f_{1}(t)+f_{2}(t)},
частное решение неоднородного уравнения тоже состоит из суммы двух функций
- y0(t)=y01(t)+y02(t){\displaystyle y_{0}(t)=y_{01}(t)+y_{02}(t)},
где y0j(t), j∈1,2¯{\displaystyle y_{0j}(t),\ \ j\in {\overline {1,2}}} являются решениями неоднородного уравнения с правыми частями fj(t), j∈1,2¯{\displaystyle f_{j}(t),\ \ j\in {\overline {1,2}}}, соответственно.
Частный случай: квазимногочлен[править | править код]
В случае, когда f(t){\displaystyle f(t)} — квазимногочлен, то есть
- f(t)=p(t)eαtcos(βt)+q(t)eαtsin(βt){\displaystyle f(t)=p(t)e^{\alpha t}\cos(\beta t)+q(t)e^{\alpha t}\sin(\beta t)}
где p(t), q(t){\displaystyle p(t),\ q(t)} — многочлены, частное решение уравнения ищется в виде
- y0(t)=(P(t)eαtcos(βt)+Q(t)eαtsin(βt))ts{\displaystyle y_{0}(t)=(P(t)e^{\alpha t}\cos(\beta t)+Q(t)e^{\alpha t}\sin(\beta t))t^{s}}
где
В частности, когда
- f(t)=p(t)eαt{\displaystyle f(t)=p(t)e^{\alpha t}}
где p(t){\displaystyle p(t)} — многочлен, частное решение уравнения ищется в виде
- y0(t)=P(t)eαtts{\displaystyle y_{0}(t)=P(t)e^{\alpha t}t^{s}}
Здесь P(t){\displaystyle P(t)} — многочлен, deg(P)=deg(p){\displaystyle deg(P)=deg(p)}, с неопределенными коэффициентами, которые находятся подстановкой y0(t){\displaystyle y_{0}(t)} в уравнение. s{\displaystyle s} является кратностью α{\displaystyle \alpha }, как корня характеристического уравнения однородного уравнения.
Когда же
- f(t)=p(t){\displaystyle f(t)=p(t)}
где p(t){\displaystyle p(t)} — многочлен, частное решение уравнения ищется в виде
- y0(t)=P(t)ts{\displaystyle y_{0}(t)=P(t)t^{s}}
Здесь P(t){\displaystyle P(t)} — многочлен, deg(P)=deg(p){\displaystyle deg(P)=deg(p)}, а s{\displaystyle s} является кратностью нуля, как корня характеристического уравнения однородного уравнения.
Уравнение Коши — Эйлера является частным случаем линейного дифференциального уравнения вида:
- ∑k=1nak(αx+β)ky(k)(x)=an(αx+β)ny(n)(x)+…+a2(αx+β)2y″(x)+a1(αx+β)y′(x)+a0y(x)=f(x){\displaystyle \sum _{k=1}^{n}{a_{k}(\alpha x+\beta )^{k}y^{(k)}(x)}=a_{n}(\alpha x+\beta )^{n}y^{(n)}(x)+…+a_{2}(\alpha x+\beta )^{2}y»(x)+a_{1}(\alpha x+\beta )y'(x)+a_{0}y(x)=f(x)},
приводимым к линейному дифференциальному уравнению с постоянными коэффициентами подстановкой вида (αx+β)=et{\displaystyle (\alpha x+\beta )=e^{t}}.
Дифференциальные уравнения являются наиболее часто используемой и классической формой математического описания процессов. Разные формы математических описаний являются инструментальным средством аналитического анализа и синтеза динамических систем и систем автоматического управления. Дифференциальные уравнения, параметры которых, зависят от переменных называются нелинейными и не имеют общих решений. В настоящие время в теории автоматического управления широко используется математический аппарат интегральных преобразований Лапласа и Фурье. Из математики известно, что в частотную область компактно преобразуется д.у. с постоянными коэффициентами и при нулевых начальных условиях. И в теории управления такое уравнение является линейным. [1]
Если динамическая система представлена нелинейными дифференциальными уравнениями математической физики, то для применения классических методов анализа этих систем требуется их линеаризация.
- ↑ А.В. Андрюшин, В.Р.Сабанин, Н.И.Смирнов. Управление и инноватика в теплоэнергетике. — М: МЭИ, 2011. — С. 41. — 392 с. — ISBN 978-5-38300539-2.
Уравнение — это… Что такое Уравнение?
Уравне́ние — это равенство вида
или, в приведённой форме
где и — функции (в общем случае — векторные) одного или нескольких аргументов.
Решение уравнения
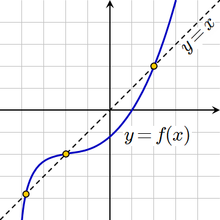 Иллюстрация графического метода нахождения корней уравнения
Иллюстрация графического метода нахождения корней уравненияРешение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.).
Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными».
Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения.
Про корни говорят, что они удовлетворяют данному уравнению.
Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет.
Равносильные уравнения
Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней.
Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому.
Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения.
Третье важное свойство задается теоремой: уравнение
эквивалентно совокупности уравнений:
Это означает, что все корни первого уравнения являются корнями одного из двух других уравнений и позволяет находить корни частями.
Основные свойства
С алгебраическими выражениями, входящими в уравнения, можно выполнять операции, которые не меняют его корней, в частности:
- В любой части уравнения можно раскрыть скобки.
- В любой части уравнения можно привести подобные слагаемые.
- Любой член уравнения можно перенести из одной части в другую, заменив его знак на противоположный.
- К обеим частям уравнения можно прибавить одно и то же выражение.
- Из обеих частей уравнения можно вычесть одно и то же выражение.
- Обе части уравнения можно умножать или делить на одно и то же число, отличное от нуля.
Уравнения, которые являются результатом этих операций, являются эквивалентными начальному уравнению. Однако для свойств 4 и 5 существует ограничение: в случае прибавления к обеим частям уравнения одного и того же выражения (или в случае вычитания из обеих частей уравнения одного и того же выражения), содержащего неизвестное и теряющего смысл при неизвестном, принимающим значения корней данного уравнения, получится уравнение, неэквивалентное исходному (начальному). Но если к обеим частям уравнения прибавить одно и то же выражение (или из обеих частей уравнения вычесть одно и то же выражение), содержащее неизвестное и теряющее смысл лишь при значениях неизвестного, не являющихся корнями данного уравнения, то получится уравнение, эквивалентное начальному.
Умножение или деление обеих частей уравнения на выражение, содержащее неизвестное, может привести, соответственно, к появлению посторонних корней или к потере корней.
Возведение обеих частей уравнения в квадрат может привести к появлению посторонних корней.
Следствие уравнения и посторонние корни
Уравнение
называется следствием уравнения
- ,
если все корни второго уравнения являются корнями первого. Первое уравнение может иметь дополнительные корни, которые для второго уравнения называются посторонними. Посторонние корни могут появиться при преобразованиях, необходимых для нахождения корней уравнений. Для того чтобы их обнаружить, необходимо проверить корень подстановкой в исходное уравнение. Если при подстановке уравнение становится тождеством, то корень настоящий, если нет — посторонний.
Пример
Уравнение
при возведении обеих частей в квадрат дает уравнение
- или
Оба уравнения являются следствием исходного. Последнее из них легко решить. Оно имеет два корня
- и .
При подстановке первого корня в исходное уравнение образуется тождество
При подстановке другого корня получается неправильное утверждение:
- .
Таким образом, второй корень нужно отбросить, как посторонний.
Виды уравнений
Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.
Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней.
К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней.
Уравнение, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны.
В общем случае, когда аналитического решения найти не удается, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определенного заранее заданного значения.
Примеры уравнений
См. также
Литература
- Бекаревич, А. Б. Уравнения в школьном курсе математики / А. Б. Бекаревич. — М., 1968.
- Маркушевич, Л. А. Уравнения и неравенства в заключительном повторении курса алгебры средней школы / Л. А. Маркушевич, Р. С. Черкасов. / Математика в школе. — 2004. — № 1.
- Каплан Я. В. Рівняння. — Киев: Радянська школа, 1968.
- Уравнение — статья из Большой советской энциклопедии
- Уравнения // Энциклопедия Кольера. — Открытое общество. 2000.
- Уравнение // Энциклопедия Кругосвет
- Уравнение // Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
Ссылки
Возвратное уравнение — Википедия
Материал из Википедии — свободной энциклопедии
Возвратное уравнение — алгебраическое уравнение вида: anxn+an−1xn−1+…+a1x+a0=0{\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+\ldots +a_{1}x+a_{0}=0} c равными друг другу коэффициентами, стоящими на симметричных относительно середины позициях, то есть если an−k=ak{\displaystyle a_{n-k}=a_{k}}, при k=0,1,…,n{\displaystyle k=0,1,…,n}. Иногда такие уравнения называют симметричными или симметрическими. Многочлены в левой части возвратного уравнения называют возвратными многочленами.
Рассмотрим возвратное уравнение четвёртой степени вида ax4+bx3+cx2+bx+a=0{\displaystyle ax^{4}+bx^{3}+cx^{2}+bx+a=0}, где a, b и c — некоторые числа, причём a≠0{\displaystyle a\neq 0}.
Алгоритм решения подобных уравнений:
Модифицированное и обобщённое уравнения четвёртой степени[править | править код]
Модифицированное возвратное уравнение четвёртой степени ax4+bx3+cx2−bx+a=0{\displaystyle ax^{4}+bx^{3}+cx^{2}-bx+a=0} может быть сведено к квадратному уравнению относительно переменной t{\displaystyle t}, если ввести t=x−1x{\displaystyle t=x-{\frac {1}{x}}}.
Обобщённое возвратное уравнение четвёртой степени сводится к квадратному уравнению подстановкой t=bx+dx{\displaystyle t=bx+{\frac {d}{x}}}. Среди всех уравнений четвёртой степени ax4+bx3+cx2+dx+e=0{\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e=0} эти уравнения выделяются тем, что для их коэффициентов справедливо соотношение:
- ea=(db)2.{\displaystyle {\frac {e}{a}}=\left({\frac {d}{b}}\right)^{2}.}
Для возвратных уравнений произвольных степеней верны следующие утверждения[1]:
- Всякий возвратный многочлен нечётной степени P2n+1(x){\displaystyle P_{2n+1}(x)} делится без остатка на x+1{\displaystyle x+1} и частное является возвратным многочленом чётной степени P2n(x){\displaystyle P_{2n}(x)}.
- ↑ Дородницын В. А, Еленин Г. Г. Симметрия нелинейных явлений // Компьютеры и нелинейные явления. — М.: Наука, 1988. — С. 131. — ISBN 5-02-006624-9 — Тираж 43 000 экз.