Решение тригонометрических уравнений

В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в заданиях C1 школьникам предлагаются для решения тригонометрические уравнения, поэтому в данной статье разобраны только они. Примеры структурированы по методам решения уравнений, от самых элементарных, до достаточно сложных.
Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.

Основные тригонометрические формулы

Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений
Пример 1. Найдите корни уравнения ![Rendered by QuickLaTeX.com \[ \cos\left(4x+\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}, \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-7cea1f5663bb6ad8fdbc9fea4f463c6b_l3.png)
принадлежащие промежутку 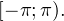
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем 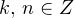
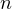 и
и 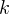 принадлежат множеству целых чисел):
принадлежат множеству целых чисел): ![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4}=\pm\operatorname{arccos \left(-\frac{\sqrt{2}}{2}\right)}+2\pi k. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-600bd6daa90af5fa4124c683eb7663ac_l3.png)
Другими словами, нам нужно подобрать такое число из промежутка ![Rendered by QuickLaTeX.com [0;2\pi],](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-6516ce3e8a2a72f3c1e75c74df6dcab5_l3.png)
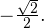 Это число
Это число  Используя это, получаем:
Используя это, получаем: ![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4} = \pm\frac{3\pi}{4}+2\pi k\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{8}+\frac{\pi k}{2}, \\ x = -\frac{\pi}{4}+\frac{\pi n}{2}.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4e1b7dcb8f1bb9b0ff44ee1900d0e206_l3.png)
Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:
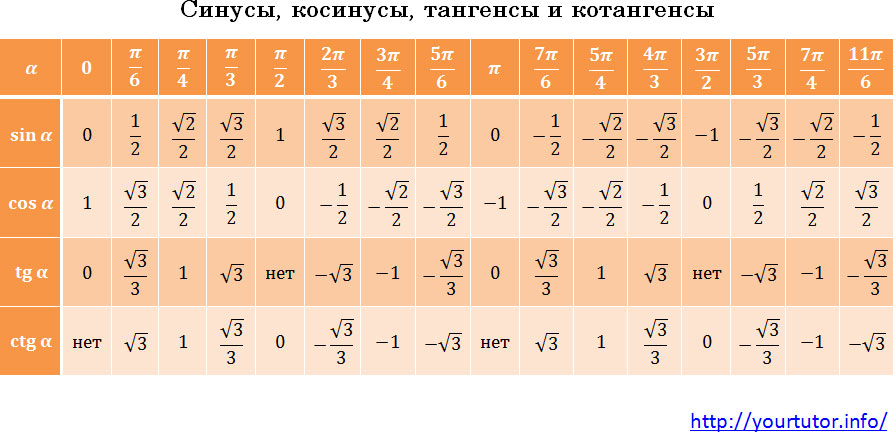
Таблица значений тригонометрических функций
Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.
Итак, вернемся к нашему заданию. Из полученных серий выбираем только те ответы, которые принадлежат промежутку 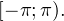 Воспользуемся для этого методом двойных неравенств. Вы помните, что
Воспользуемся для этого методом двойных неравенств. Вы помните, что 
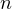 — целые числа:
— целые числа:1) 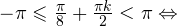
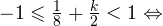
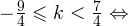
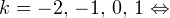

2) 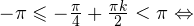
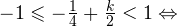

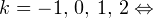
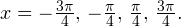
Задача для самостоятельного решения №1. Найдите корни уравнения  принадлежащие промежутку
принадлежащие промежутку 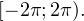
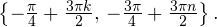
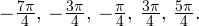
Решение линейных тригонометрических уравнений
Пример 2. Найдите корни уравнения ![Rendered by QuickLaTeX.com \[ \sin x+\sqrt{3}\cos x=1, \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c8549fd428fc2b8f8612668c1bcafa38_l3.png)
принадлежащие промежутку ![Rendered by QuickLaTeX.com [-2\pi;4\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e5ab0d4ddd997ad7264282447126bc7c_l3.png)
Решение. Подобные уравнения решаются один весьма интересным, на мой взгляд, способом. Разделим обе части на 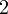 , уравнение тогда примет вид:
, уравнение тогда примет вид:
![Rendered by QuickLaTeX.com \[ \frac{1}{2}\sin x+\frac{\sqrt{3}}{2}\cos x = 1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-65ffb48c7a579b1bbdee9fbba7af59f4_l3.png)
Подберем такое число, синус которого равен 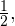 а косинус равен
а косинус равен 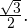 Например, пусть это будет число
Например, пусть это будет число 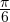
![Rendered by QuickLaTeX.com \[ \sin\frac{\pi}{6}\sin x+\cos\frac{\pi}{6}\cos x=\frac{1}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4c7a1d290000c0bba4b160c010d5f32f_l3.png)
Присмотревшись, слева от знака равенства усматриваем разложение косинуса разности 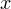 и
и  Это и есть ключ к решению. Имеем:
Это и есть ключ к решению. Имеем:
![Rendered by QuickLaTeX.com \[ \cos\left(x-\frac{\pi}{6}\right)=\frac{1}{2}\Leftrightarrow x-\frac{\pi}{6}=\pm\frac{\pi}{3}+2\pi k\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-99933eb31e68aa68196b01149d3cf7e7_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}x-\frac{\pi}{6}=\frac{\pi}{3}+2\pi k, \\ x-\frac{\pi}{6}=-\frac{\pi}{3}+2\pi n\end{array}\right.\Leftrightarrow\left[\begin{array}{l}x=\frac{\pi}{2}+2\pi k, \\ x=-\frac{\pi}{6}+2\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-a7f7798906bca8730370d50380d0b2c5_l3.png)
Осуществляем отбор решений, входящих в промежуток 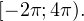 :
:
1) 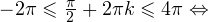

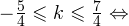

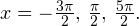
2) 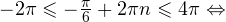
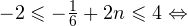
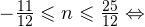
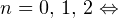
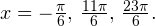
Задача для самостоятельного решения №2. Найдите корни уравнения 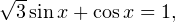 принадлежащие промежутку
принадлежащие промежутку ![Rendered by QuickLaTeX.com [-3\pi;3\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-979d4671d337b296584d0c825376e1e8_l3.png)
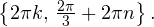
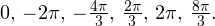
Решение тригонометрических уравнений методом замены переменной
Пример 3. Дано уравнение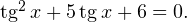
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезке ![Rendered by QuickLaTeX.com \left[-2\pi;-\frac{\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2e56a5618e53c514d925c4318432710e_l3.png)
Решение. Сразу оговорим ограничения, накладываемые на переменную 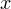 в этом уравнении:
в этом уравнении:  Откуда взялось это ограничение? Правильно, функция
Откуда взялось это ограничение? Правильно, функция 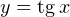 не существует при этих значениях
не существует при этих значениях 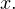 Используем замену переменной:
Используем замену переменной: 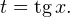 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ t^2+5t+6=0\Leftrightarrow\left[\begin{array}{l}t=-3, \\t=-2.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c8cb0eceec5f7707e25585504f135ed9_l3.png)
Переходим к обратной замене:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\operatorname{tg}x = -3,\\ \operatorname{tg}x = -2\end{array}\right.\Leftrightarrow \left[\begin{array}{l}x = -\operatorname{arctg} 3+\pi k, \\ x=-\operatorname{arctg} 2+\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-184ca285f5fe0c4b521f49f2c1fef113_l3.png)
Осуществляем отбор решений. Проведем его на этот раз с использованием единичной окружности.
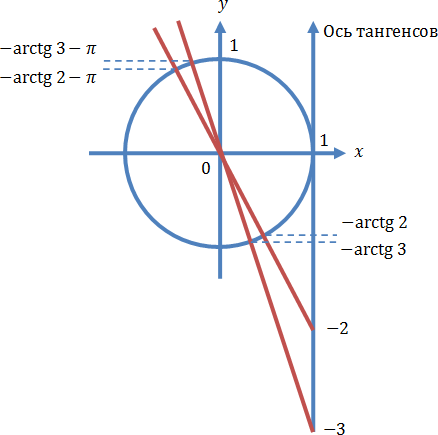
Отбор корней с помощью единичной окружности
Из рисунка видно, что в интересующий нас промежуток входят только два значения из этих серий: 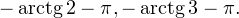 Обратите внимание на один существенный момент. На рисунке точки
Обратите внимание на один существенный момент. На рисунке точки 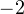 и
и 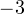 принадлежат оси тангенсов, а точки
принадлежат оси тангенсов, а точки 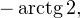
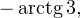
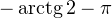 и
и 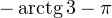 — единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
— единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
Ответ: 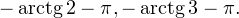
Задача для самостоятельного решения №3. Дано уравнение 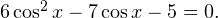
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com [-\pi;2\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-7619bf74ede16b0f138212b37cf78df2_l3.png)
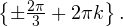
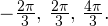
Решение тригонометрических уравнений методом разложения на множители
Пример 4. Дано уравнение ![Rendered by QuickLaTeX.com \[ \sin 2x=2\sin x-\cos x+1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-314ae6ec8084938924dcb1b7a0324414_l3.png)
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com \left[-2\pi; -\frac{\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-092d4dc81779071955ee1bdf99bce52e_l3.png)
Решение. Равносильными преобразования приводим уравнение к виду:
![Rendered by QuickLaTeX.com \[ \sin 2x=2\sin x-\cos x+1\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-26079fe9cc286a9b505cebcad4b20a54_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x\cos x-2\sin x+\cos x-1=0\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-16b853ad0976a5741efaebe9dbf734a3_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x(\cos x-1)+\cos x-1 =0\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-cb5e2726eaee2ea2b3d7aef7d4811e45_l3.png)
![Rendered by QuickLaTeX.com \[ (\cos x-1)(2\sin x+1) = 0\Lefrightarrow \left[\begin{array}{l}\cos x-1=0, \\ 2\sin x+1=0\end{array}\right.\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-1e2e696cbfce62ef0d378fc226247d45_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\cos x=1, \\ \sin x=-\frac{1}{2} \end{array}\right.\Leftrightarrow\left[\begin{array}{l}x=2\pi k, \\ x=-\frac{\pi}{6}+2\pi n, \\ x=-\frac{5\pi}{6}+2\pi z.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c0ac3379edc46ce1bf97df0f46a830ac_l3.png)
Осуществляем отбор решений с помощью единичной окружности.
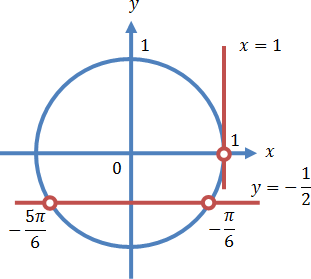
Отбор решений с помощью единичной окружности
Из рисунка видно, что в интересующий нас промежуток входят только два значения из всех этих серий: 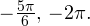
Задача для самостоятельного решения №4. Дано уравнение
![Rendered by QuickLaTeX.com \[ 3\sin 2x-4\cos x+3\sin x-2=0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-28a0aa4a8809041869a0dd165374f983_l3.png)
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com \left[\frac{\pi}{2};\frac{3\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0afd161af4c492ee4549edea05061c7b_l3.png)
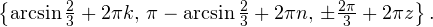
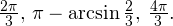
Комбинированные уравнения
При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. Именно поэтому составители вариантов ЕГЭ не просят учеников осуществлять отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение данной математической операции.
Пример 5. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \sqrt{1-2\sin 3x\sin 7x}=\sqrt{\cos 10x}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0676b2ec24b14219e132ecfeffe1beff_l3.png)
Решение. Данное уравнение эквивалентно следующей системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}1-2\sin 3x\sin 7x=\cos 10x, \\ \cos 10x\geqslant 0.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-5e7804c5a3444eda3706d8c6a9cc8bc0_l3.png)
Обратите внимание! Писать, что 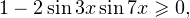 нет никакой необходимости, поскольку по условию это выражение равно выражению
нет никакой необходимости, поскольку по условию это выражение равно выражению 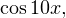 которое, в свою очередь, больше или равно нулю.
которое, в свою очередь, больше или равно нулю.
Решаем первое уравнение системы:
![Rendered by QuickLaTeX.com \[ 1-2\sin 3x\sin 7x=\cos (7x+10x)\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-85f99b88ebecfe2323a0bc59bac8e027_l3.png)
![Rendered by QuickLaTeX.com \[ 1-2\sin 3x\sin 7x=\cos 3x\cos 7x-\sin 3x\sin 7x\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-30cfd48e7e1658096abdeb1390486c83_l3.png)
![Rendered by QuickLaTeX.com \[ 1=\cos 3x\cos 7x+\sin 3x\sin 7x\Leftrightarrow \cos 4x=1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e7341e12fbea6fe289a80d2965e67b8b_l3.png)
![Rendered by QuickLaTeX.com \[ \cos 10x = 1\Leftrightarrow 4x=2\pi k\Leftrightarrow x = \frac{\pi k}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-69acc2d98a3a49c3c563dbcb9e3f3976_l3.png)
Нужно, чтобы 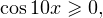 поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только
поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только 
Ответ: 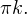
Задача для самостоятельного решения №5. Решите уравнение: 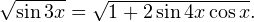
 Пример 6. Решите уравнение:
Пример 6. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \frac{2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1}{\sqrt{\sin x}}=0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-b29f83ad79819cdf0623a3f50f53cbf1_l3.png)
Решение. Данное уравение равносильно системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1=0, \\ \sin x>0\end{cases}\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-9796d3e88520ad252eea21fb51f21987_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}2\cos^2 x-\cos x-1=0,\\ \sin x>0\end{cases}\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-dbab64445b6b27423f4c9a5b3a45e710_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}\left[\begin{array}{l}\cos x = 1, \\ \cos x =-\frac{1}{2},\end{array} \\ \sin x >0\right.\end{cases}\Leftrightarrow \begin{cases}\left[\begin{array}{l}x=2\pi k, \\ x=\pm\frac{2\pi}{3}+2\pi n,\end{array} \\ \sin x >0\right.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-20bc473770ab6419cd1a45ba72b7178f_l3.png)
Тригонометрическая функция синус положительна в первой и второй координатной четвертях, поэтому из полученных серий выбираем только эту: 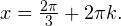
Раз уж мы с этим столкнулись, не лишним будет повторить, какие знаки принимают тригонометрические функций в различных координатных четвертях:
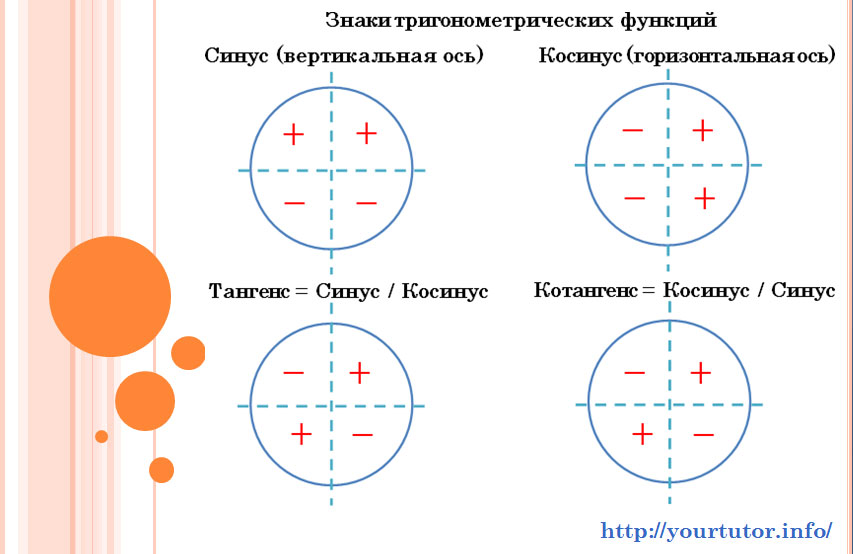
Знаки функций, входящих в тригонометрические уравнения, по координатным четвертям
Ответ: 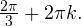
Задача для самостоятельного решения №6. Решите уравнение: 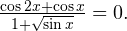
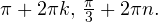 Пример 7. Решите уравнение:
Пример 7. Решите уравнение: 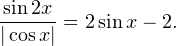
Решение. Область допустимых значения уравнения определяется условием: 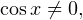 то есть
то есть  Разобьем решение на два случая:
Разобьем решение на два случая:
1) Пусть 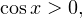 тогда уравнение принимает вид:
тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ \frac{2\sin x\cos x}{\cos x} = 2\sin x-2\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-fe301b6a371887b4ca249562d051d06c_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x=2\sin x-2\Leftrightarrow 0=-2. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-89fc402230aca1d5d103f2eba93d497e_l3.png)
Последнее равенство неверно, поэтому в данном случае решений у уравнения не будет.
2) Пусть 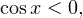 тогда уравнение принимает вид:
тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ -\frac{2\sin x\cos x}{\cos x} = 2\sin x-2\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-8bd35cba0d719a8226b8f9034ef98024_l3.png)
![Rendered by QuickLaTeX.com \[ \sin x = \frac{1}{2}\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{6}+2\pi k, \\ x=\frac{5\pi}{6}+2\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-217ffb2b7eeca2a312b56ee28296fa3a_l3.png)
Условию 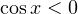 удовлетворяет только последняя серия.
удовлетворяет только последняя серия.
Ответ: 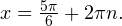
Задача для самостоятельного решения №7. Решите уравнение: 
ЕГЭ по математике 2012 позади, все в ожидании результатов, которые обещали объявить во вторник 19 июня. Сейчас уже поздно желать высоких баллов на экзаменах нынешним выпускникам. Но вот пожелать успехов сегодняшним десятиклассникам я возможности не упущу. Удачи вам в подготовке и помните, что чем раньше она начнется, тем лучше будут результаты на экзамене.

Репетитор математики
Сергей Валерьевич
P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.
yourtutor.info
Решение задач на косинус и синус разности аргументов. Видеоурок. Алгебра 10 Класс
Выпишем 2 формулы:
— косинус разности аргументов:
 ,
,
то есть косинус разности аргументов – это сумма произведений косинусов и синусов этих аргументов.
— синус разности аргументов:
 ,
,
т. е. синус разности аргументов – это разность произведений синуса α на косинус β и косинуса α на синус β.
В задачах важно понимать, что принимать за α и β.
Задача 1. Упростить .
.
Решение:

Принимаем 5x за α, т. е. 5x α, а 3x
α, а 3x β, и используем формулу синус разности аргументов.
β, и используем формулу синус разности аргументов.

Задача 2. Упростить .
.
Решение:
Подходит формула косинуса разности аргументов, но у нас разность произведений, поэтому преобразуем данное выражение, воспользовавшись свойством чётности функции косинус и свойством нечётности функции синус:


 =
=
= =
=
Мы не только упростили выражение, но и вычислили его.
Задача 3.Упростить выражение  .
.
Решение:

 =
=
Воспользовавшись свойством чётности функции косинус и свойством нечётности функции синус, получаем:
 =
= =
=
=
Т.к. 
 , то
, то
 =
= =
=
= =
= =
=
=
Вычислительные задачи по теме урока
Вычислить:

Решение:
Воспользуемся формулой косинус разности аргументов.
 =
= =
= =0
=0
Вычислить:

Решение:
Воспользуемся формулой синус разности аргументов.
 =
= =
=
Рассмотрим более сложную задачу.
Задача 4.
Дано
Найти: a)  и
и 
Решение:
а) Рассмотрим тригонометрическую окружность (рис.1):
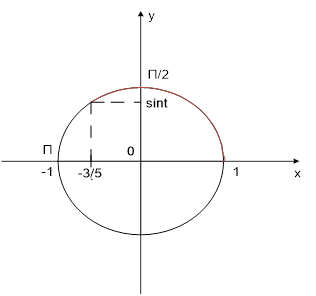
Рис. 1. Тригонометрическая окружность
Числом t является длина выделенной дуги.
а) 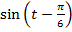 =
=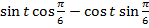
Все величины, кроме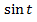 нам известны.
нам известны.
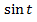 =
= =
=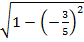 =
=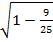 =
=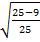 =
=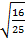 =
=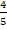
Недостающее число найдено.
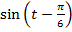 =
=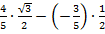 =
=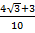 ,
,
Т. е. 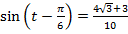
б) Сравнить поможет 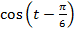 , если он отрицательный, число находится во второй четверти, если положительный – в первой (справа от
, если он отрицательный, число находится во второй четверти, если положительный – в первой (справа от  (рис. 2).
(рис. 2).
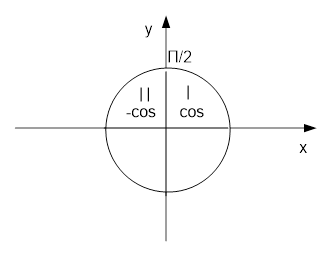
Рис. 2. Иллюстрация к задаче
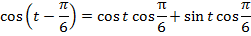
Все величины нам известны:
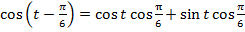 =
=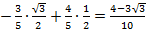 =
=
=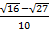
Это величина отрицательная, следовательно, и косинус отрицательный (расположен во второй четверти):
t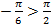 .
.
Иногда приходится применять две формулы сразу в одной задаче.
Задача 5.
Решить уравнение: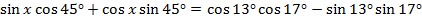 .
.
Решение:
Применяем свойство чётности функции косинуса и свойство нечётности функции синуса:
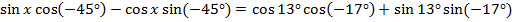
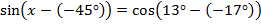
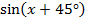 =
=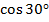 =
=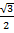
Получили простейшее тригонометрическое уравнение.
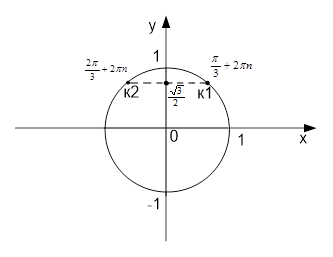
Рис. 3. Иллюстрация к задаче
Для угла t =x+45 первое множество решений даёт точка к1 (
первое множество решений даёт точка к1 (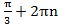 ), второе множество
), второе множество
решений — к2 ( ) (рис. 3).
) (рис. 3).
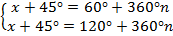 n
n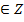
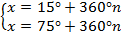 n
n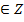
Мы решили уравнение и нашли все его решения, их бесчисленное множество.
На данном уроке были рассмотрены формулы косинуса и синуса разности аргументов и решены типовые задачи с применением данных формул.
Список литературы
- Алгебра и начала математического анализа. 10–11 классы. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович. – 10-е изд., стер. – М.: Мнемозина, 2009. – 399 с.: ил.
- Алимов А.Ш, Колягин Ю.М. и др. Алгебра и начала математического анализа. 10–11 классы. Учебник (базовый уровень).
- Карп А.П. Сборник задач по алгебре и началам анализа. 10–11 класс. – М.: Просвещение, 1995. – 176 с.
- Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10–11 классов общеобразов. учреждений). – М.: Просвещение, 2003.
Домашнее задание
- Вычислить
 .
. - Вычислить
 .
. - Упростить выражение:

- Вычислить cos(
 + α) cos(
+ α) cos( – α) – sin(
– α) – sin( + α) sin(
+ α) sin( – α).
– α).
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Sokolova-aa.ru (Источник).
- Интернет-портал Urokimatematiki.ru (Источник).
- Интернет-портал Exponenta.ru (Источник).
interneturok.ru
Решение тригонометрических уравнений

В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в заданиях C1 школьникам предлагаются для решения тригонометрические уравнения, поэтому в данной статье разобраны только они. Примеры структурированы по методам решения уравнений, от самых элементарных, до достаточно сложных.
Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.

Основные тригонометрические формулы

Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений
Пример 1. Найдите корни уравнения ![Rendered by QuickLaTeX.com \[ \cos\left(4x+\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}, \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-7cea1f5663bb6ad8fdbc9fea4f463c6b_l3.png)
принадлежащие промежутку 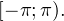
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем 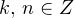 (на всякий случай, эта запись означает, что числа
(на всякий случай, эта запись означает, что числа 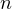 и
и 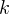 принадлежат множеству целых чисел):
принадлежат множеству целых чисел):
![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4}=\pm\operatorname{arccos \left(-\frac{\sqrt{2}}{2}\right)}+2\pi k. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-600bd6daa90af5fa4124c683eb7663ac_l3.png)
Другими словами, нам нужно подобрать такое число из промежутка ![Rendered by QuickLaTeX.com [0;2\pi],](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-6516ce3e8a2a72f3c1e75c74df6dcab5_l3.png) косинус которого был бы равен
косинус которого был бы равен 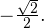 Это число
Это число  Используя это, получаем:
Используя это, получаем:
![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4} = \pm\frac{3\pi}{4}+2\pi k\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{8}+\frac{\pi k}{2}, \\ x = -\frac{\pi}{4}+\frac{\pi n}{2}.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4e1b7dcb8f1bb9b0ff44ee1900d0e206_l3.png)
Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:

Таблица значений тригонометрических функций
Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.
Итак, вернемся к нашему заданию. Из полученных серий выбираем только те ответы, которые принадлежат промежутку 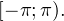 Воспользуемся для этого методом двойных неравенств. Вы помните, что
Воспользуемся для этого методом двойных неравенств. Вы помните, что 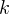 и
и 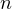 — целые числа:
— целые числа:
1) 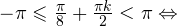
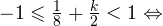
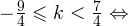
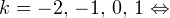

2) 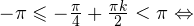
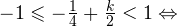

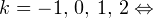
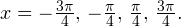
Задача для самостоятельного решения №1. Найдите корни уравнения  принадлежащие промежутку
принадлежащие промежутку 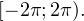
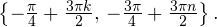
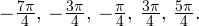
Решение линейных тригонометрических уравнений
Пример 2. Найдите корни уравнения ![Rendered by QuickLaTeX.com \[ \sin x+\sqrt{3}\cos x=1, \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c8549fd428fc2b8f8612668c1bcafa38_l3.png)
принадлежащие промежутку ![Rendered by QuickLaTeX.com [-2\pi;4\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e5ab0d4ddd997ad7264282447126bc7c_l3.png)
Решение. Подобные уравнения решаются один весьма интересным, на мой взгляд, способом. Разделим обе части на 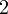 , уравнение тогда примет вид:
, уравнение тогда примет вид:
![Rendered by QuickLaTeX.com \[ \frac{1}{2}\sin x+\frac{\sqrt{3}}{2}\cos x = 1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-65ffb48c7a579b1bbdee9fbba7af59f4_l3.png)
Подберем такое число, синус которого равен 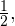 а косинус равен
а косинус равен 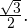 Например, пусть это будет число
Например, пусть это будет число 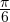 . С учетом этого перепишем уравнение в виде:
. С учетом этого перепишем уравнение в виде:
![Rendered by QuickLaTeX.com \[ \sin\frac{\pi}{6}\sin x+\cos\frac{\pi}{6}\cos x=\frac{1}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4c7a1d290000c0bba4b160c010d5f32f_l3.png)
Присмотревшись, слева от знака равенства усматриваем разложение косинуса разности 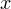 и
и  Это и есть ключ к решению. Имеем:
Это и есть ключ к решению. Имеем:
![Rendered by QuickLaTeX.com \[ \cos\left(x-\frac{\pi}{6}\right)=\frac{1}{2}\Leftrightarrow x-\frac{\pi}{6}=\pm\frac{\pi}{3}+2\pi k\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-99933eb31e68aa68196b01149d3cf7e7_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}x-\frac{\pi}{6}=\frac{\pi}{3}+2\pi k, \\ x-\frac{\pi}{6}=-\frac{\pi}{3}+2\pi n\end{array}\right.\Leftrightarrow\left[\begin{array}{l}x=\frac{\pi}{2}+2\pi k, \\ x=-\frac{\pi}{6}+2\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-a7f7798906bca8730370d50380d0b2c5_l3.png)
Осуществляем отбор решений, входящих в промежуток 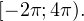 :
:
1) 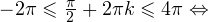

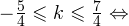

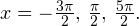
2) 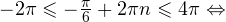
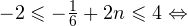
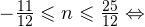
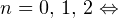
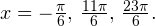
Задача для самостоятельного решения №2. Найдите корни уравнения 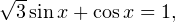 принадлежащие промежутку
принадлежащие промежутку ![Rendered by QuickLaTeX.com [-3\pi;3\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-979d4671d337b296584d0c825376e1e8_l3.png)
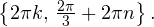
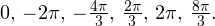
Решение тригонометрических уравнений методом замены переменной
Пример 3. Дано уравнение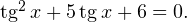
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезке ![Rendered by QuickLaTeX.com \left[-2\pi;-\frac{\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2e56a5618e53c514d925c4318432710e_l3.png)
Решение. Сразу оговорим ограничения, накладываемые на переменную 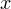 в этом уравнении:
в этом уравнении:  Откуда взялось это ограничение? Правильно, функция
Откуда взялось это ограничение? Правильно, функция 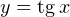 не существует при этих значениях
не существует при этих значениях 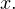 Используем замену переменной:
Используем замену переменной: 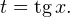 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ t^2+5t+6=0\Leftrightarrow\left[\begin{array}{l}t=-3, \\t=-2.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c8cb0eceec5f7707e25585504f135ed9_l3.png)
Переходим к обратной замене:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\operatorname{tg}x = -3,\\ \operatorname{tg}x = -2\end{array}\right.\Leftrightarrow \left[\begin{array}{l}x = -\operatorname{arctg} 3+\pi k, \\ x=-\operatorname{arctg} 2+\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-184ca285f5fe0c4b521f49f2c1fef113_l3.png)
Осуществляем отбор решений. Проведем его на этот раз с использованием единичной окружности.

Отбор корней с помощью единичной окружности
Из рисунка видно, что в интересующий нас промежуток входят только два значения из этих серий: 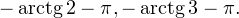 Обратите внимание на один существенный момент. На рисунке точки
Обратите внимание на один существенный момент. На рисунке точки 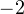 и
и 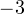 принадлежат оси тангенсов, а точки
принадлежат оси тангенсов, а точки 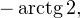
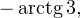
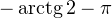 и
и 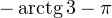 — единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
— единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
Ответ: 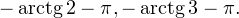
Задача для самостоятельного решения №3. Дано уравнение 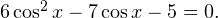
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com [-\pi;2\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-7619bf74ede16b0f138212b37cf78df2_l3.png)
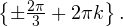
Решение тригонометрических уравнений методом разложения на множители
Пример 4. Дано уравнение ![Rendered by QuickLaTeX.com \[ \sin 2x=2\sin x-\cos x+1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-314ae6ec8084938924dcb1b7a0324414_l3.png)
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com \left[-2\pi; -\frac{\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-092d4dc81779071955ee1bdf99bce52e_l3.png)
Решение. Равносильными преобразования приводим уравнение к виду:
![Rendered by QuickLaTeX.com \[ \sin 2x=2\sin x-\cos x+1\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-26079fe9cc286a9b505cebcad4b20a54_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x\cos x-2\sin x+\cos x-1=0\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-16b853ad0976a5741efaebe9dbf734a3_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x(\cos x-1)+\cos x-1 =0\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-cb5e2726eaee2ea2b3d7aef7d4811e45_l3.png)
![Rendered by QuickLaTeX.com \[ (\cos x-1)(2\sin x+1) = 0\Lefrightarrow \left[\begin{array}{l}\cos x-1=0, \\ 2\sin x+1=0\end{array}\right.\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-1e2e696cbfce62ef0d378fc226247d45_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\cos x=1, \\ \sin x=-\frac{1}{2} \end{array}\right.\Leftrightarrow\left[\begin{array}{l}x=2\pi k, \\ x=-\frac{\pi}{6}+2\pi n, \\ x=-\frac{5\pi}{6}+2\pi z.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c0ac3379edc46ce1bf97df0f46a830ac_l3.png)
Осуществляем отбор решений с помощью единичной окружности.

Отбор решений с помощью единичной окружности
Из рисунка видно, что в интересующий нас промежуток входят только два значения из всех этих серий: 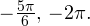
Задача для самостоятельного решения №4. Дано уравнение
![Rendered by QuickLaTeX.com \[ 3\sin 2x-4\cos x+3\sin x-2=0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-28a0aa4a8809041869a0dd165374f983_l3.png)
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com \left[\frac{\pi}{2};\frac{3\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0afd161af4c492ee4549edea05061c7b_l3.png)
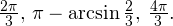
Комбинированные уравнения
При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. Именно поэтому составители вариантов ЕГЭ не просят учеников осуществлять отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение данной математической операции.
Пример 5. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \sqrt{1-2\sin 3x\sin 7x}=\sqrt{\cos 10x}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0676b2ec24b14219e132ecfeffe1beff_l3.png)
Решение. Данное уравнение эквивалентно следующей системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}1-2\sin 3x\sin 7x=\cos 10x, \\ \cos 10x\geqslant 0.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-5e7804c5a3444eda3706d8c6a9cc8bc0_l3.png)
Обратите внимание! Писать, что 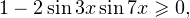 нет никакой необходимости, поскольку по условию это выражение равно выражению
нет никакой необходимости, поскольку по условию это выражение равно выражению 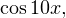 которое, в свою очередь, больше или равно нулю.
которое, в свою очередь, больше или равно нулю.
Решаем первое уравнение системы:
![Rendered by QuickLaTeX.com \[ 1-2\sin 3x\sin 7x=\cos (7x+10x)\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-85f99b88ebecfe2323a0bc59bac8e027_l3.png)
![Rendered by QuickLaTeX.com \[ 1-2\sin 3x\sin 7x=\cos 3x\cos 7x-\sin 3x\sin 7x\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-30cfd48e7e1658096abdeb1390486c83_l3.png)
![Rendered by QuickLaTeX.com \[ 1=\cos 3x\cos 7x+\sin 3x\sin 7x\Leftrightarrow \cos 4x=1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e7341e12fbea6fe289a80d2965e67b8b_l3.png)
![Rendered by QuickLaTeX.com \[ \cos 10x = 1\Leftrightarrow 4x=2\pi k\Leftrightarrow x = \frac{\pi k}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-69acc2d98a3a49c3c563dbcb9e3f3976_l3.png)
Нужно, чтобы 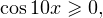 поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только
поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только 
Ответ: 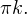
Задача для самостоятельного решения №5. Решите уравнение: 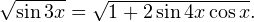
 Пример 6. Решите уравнение:
Пример 6. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \frac{2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1}{\sqrt{\sin x}}=0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-b29f83ad79819cdf0623a3f50f53cbf1_l3.png)
Решение. Данное уравение равносильно системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1=0, \\ \sin x>0\end{cases}\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-9796d3e88520ad252eea21fb51f21987_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}2\cos^2 x-\cos x-1=0,\\ \sin x>0\end{cases}\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-dbab64445b6b27423f4c9a5b3a45e710_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}\left[\begin{array}{l}\cos x = 1, \\ \cos x =-\frac{1}{2},\end{array} \\ \sin x >0\right.\end{cases}\Leftrightarrow \begin{cases}\left[\begin{array}{l}x=2\pi k, \\ x=\pm\frac{2\pi}{3}+2\pi n,\end{array} \\ \sin x >0\right.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-20bc473770ab6419cd1a45ba72b7178f_l3.png)
Тригонометрическая функция синус положительна в первой и второй координатной четвертях, поэтому из полученных серий выбираем только эту: 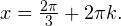
Раз уж мы с этим столкнулись, не лишним будет повторить, какие знаки принимают тригонометрические функций в различных координатных четвертях:

Знаки функций, входящих в тригонометрические уравнения, по координатным четвертям
Ответ: 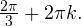
Задача для самостоятельного решения №6. Решите уравнение: 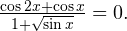
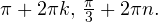 Пример 7. Решите уравнение:
Пример 7. Решите уравнение: 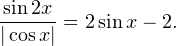
Решение. Область допустимых значения уравнения определяется условием: 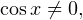 то есть
то есть  Разобьем решение на два случая:
Разобьем решение на два случая:
1) Пусть 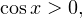 тогда уравнение принимает вид:
тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ \frac{2\sin x\cos x}{\cos x} = 2\sin x-2\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-fe301b6a371887b4ca249562d051d06c_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x=2\sin x-2\Leftrightarrow 0=-2. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-89fc402230aca1d5d103f2eba93d497e_l3.png)
Последнее равенство неверно, поэтому в данном случае решений у уравнения не будет.
2) Пусть 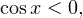 тогда уравнение принимает вид:
тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ -\frac{2\sin x\cos x}{\cos x} = 2\sin x-2\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-8bd35cba0d719a8226b8f9034ef98024_l3.png)
![Rendered by QuickLaTeX.com \[ \sin x = \frac{1}{2}\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{6}+2\pi k, \\ x=\frac{5\pi}{6}+2\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-217ffb2b7eeca2a312b56ee28296fa3a_l3.png)
Условию 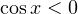 удовлетворяет только последняя серия.
удовлетворяет только последняя серия.
Ответ: 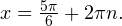
Задача для самостоятельного решения №7. Решите уравнение: 
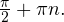
ЕГЭ по математике 2012 позади, все в ожидании результатов, которые обещали объявить во вторник 19 июня. Сейчас уже поздно желать высоких баллов на экзаменах нынешним выпускникам. Но вот пожелать успехов сегодняшним десятиклассникам я возможности не упущу. Удачи вам в подготовке и помните, что чем раньше она начнется, тем лучше будут результаты на экзамене.

Репетитор математики
Сергей Валерьевич
P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.
yourtutor.info
Формулы для решения простейших тригонометрических уравнений. Уравнение с синусом
Мы уже говорили о том, что все тригонометрические уравнения сводятся к решению четырех основных типов простейших уравнений.
В части 1 статьи мы научились решать уравнения вида  .
.
Сейчас займемся решением уравнений вида  .
.
В 3-й части статьи смотрите решение уравнений вида  .
.
Уравнение вида 
Решим уравнение  .
.
Находим на оси синусов на тригонометрическом круге  :
:
Проводя горизонталь через точку  оси синусов, выходим на точки круга
оси синусов, выходим на точки круга  и
и  :
:

Как мы знаем, за каждой из полученных точек скрывается бесконечно много других точек. Например, точка  на тригонометрическом круге располагается там же, где и
на тригонометрическом круге располагается там же, где и  , значит значение синуса в этой точке также равно
, значит значение синуса в этой точке также равно  .
.
На оси подходящие нам точки располагаются так:

Графическое решение уравнения  :
:

Мы уже знаем, что все подходящие точки взять в ответ нам позволяет счетчик. То есть мы вводим целое число 
( ).
).
И записываем ответ так:
 или
или 
Эти две серии решений можно записать и в одну строку:

Поперебирайте различные значения  , и вы убедитесь, что все нужные нам точки укладываются в эту формулу.
, и вы убедитесь, что все нужные нам точки укладываются в эту формулу.
И все же,
…

 , то есть
, то есть 



 , то есть
, то есть 

 , то есть
, то есть 
и т.д.
Убедились?
Если бы мы решали, например, уравнение  ,
,

то решением бы было

или, что тоже самое,

то есть 
Я думаю, вы уже увидели общий принцип формирования ответа.
Давайте дадим формулу, которой можно руководствоваться, решая уравнения
 , где
, где  – из
– из ![Rendered by QuickLaTeX.com [-1;\:1]](http://xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
(в противном случае, когда  – не из
– не из ![Rendered by QuickLaTeX.com [-1;\;1]](http://xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) – решений нет)
– решений нет)
Но вам формула будет понятна, если вы уже знакомы с понятием «арксинус».

или, что тоже самое

Если нам встречается уравнение с нетабличным значением синуса, вроде этого  , то ответ будет выглядеть так:
, то ответ будет выглядеть так:

то есть 
(согласно свойству функции арксинус).
Частные случаи решения уравнения 
1) 

Ответ прекрасно ложится в одну строку без всяких там  за счет полукругового счетчика
за счет полукругового счетчика  .
.
Имеем: 
2) 

У нас всего одна серия точек: 
3) 

Аналогично примеру 2 имеем: 
egemaximum.ru
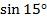 .
.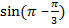 .
.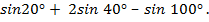
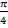 + α) cos(
+ α) cos(