Методы решения уравнений: замены, подстановки, примеры, тесты

Тестирование онлайн

Потерянные и посторонние корни

К потере корней может привести сокращение обеих частей уравнения на общий множитель.

Посторонние корни могут появится при умножении обеих частей уравнения на множитель, содержащий неизвестное.

При возведении обеих частей уравнения в квадрат (или любую четную степень) могут появляться посторонние корни.

Посторонние корни могут появляться при решении иррационального уравнения, поэтому лучше выполнять проверку.

Метод замены переменной

В ряде случаев решение уравнения можно упростить введением новой переменной (нового неизвестного).

Например, уравнение вида

где a, b, c — числа, называется биквадратным. Решается введением замены x²=t

Метод замены используют не только при решении биквадратных уравнений.

Сложные замены переменной

Основная трудность решения задач методом подстановки заключается в том, что иногда трудно угадать вид самой подстановки и вид уравнений, где подстановку можно использовать.

Очень сложные замены переменной

Графический способ решения уравнений

Графический способ решения уравнений f(x)=g(x) заключается в следующем: строят в одной системе координат графики двух функций y=f(x) и y=g(x) и находят абсциссы точек пересечения графиков. Абсциссы точек пересечения графиков и являются корнями уравнения.

Преобразуем выражение a⁴+b⁴=(a+b)⁴:

При решении уравнения f(x)=g(x) можно исследовать функции y=f(x) и y=g(x) на монотонность. Если одна из этих функций на промежутке монотонно убывает, а другая функция монотонно возрастает, то уравнение или имеет один корень, или вообще не имеет корней. Корень уравнения можно найти методом подбора или графическим методом.

Если функция y=f(x) возрастает, а y=g(x) убывает на промежутке , и при этом f(a)>g(a), то корней нет.

Примеры уравнений вида f(f(x))=x, где f(x) — некоторая функция:

1. Любой корень уравнения f(x)=x является корнем уравнения f(f(x))=x;
2. Если функция f(x) возрастает на некотором множестве и значения x и значения функции f(x) принадлежат этому множеству, то уравнения f(x)=x и f(f(x))=x равносильны на этом множестве.

Для убывающей функции f(x) правило 2 применить нельзя.

Суть метода состоит в замене переменной х тригонометрической функцией, например . Решение исходного уравнения сводится к решению тригонометрического уравнения. Но тригонометрическое уравнение обычно имеет бесконечное множество решений, а исходное — конечное.

Неравенство Коши.

Неравенство Бернулли.

Равенство достигается при x=0 или n=1.

Неравенство Коши-Буняковского.

Равенство достигается в том и только в том случае, когда существует положительная константа a такая, что x₁=ay₁, x₂=ay

2,…,x_n=ay_n.

Урок по теме «Решение уравнений методом замены переменных» (9 класс)

Решение уравнений методом замены переменных

Большинство жизненных задач

решаются как алгебраические уравнения:

приведением их к самому простому виду.

Л.Н.Толстой.

Цель урока: организовать учебную деятельность учащихся по освоению ими способов решения целых уравнений высших степеней методом замены переменной; познакомить учащихся с понятиями, приёмами решения возвратных и симметрических уравнений.

Задачи: образовательная: продолжать развивать умение применять метод замены

переменной при решении уравнений; формирование умения видеть один и тот же метод решения уравнений в различных ситуациях; сформировать представление о методах и способах решения нестандартных задач и алгебраических уравнений на уровне, превышающем уровень государственных образовательных стандартов;

развивающая: развитие мышления учащихся; развитие памяти; развитие

логического мышления, способности четко формулировать свои мысли; развитие воображения учащихся; развитие устной речи.

воспитательная: воспитание наблюдательности; воспитание аккуратности

при выполнении записей на доске и в тетради; воспитание самостоятельности при выполнении практических работ.

Ход урока

1. Организационный момент.

2. Актуализация и систематизация знаний.

Задание №1. Разгадайте кроссворд. Ответы записывайте только в именительном падеже.

3

4

5

6

7

8

9

10

11

По горизонтали:

4.Чем является выражение для квадратного уравнения? (дискриминант)

6.Значение переменной, при которой уравнение обращается в верное равенство. (корень)

8.Уравнение вида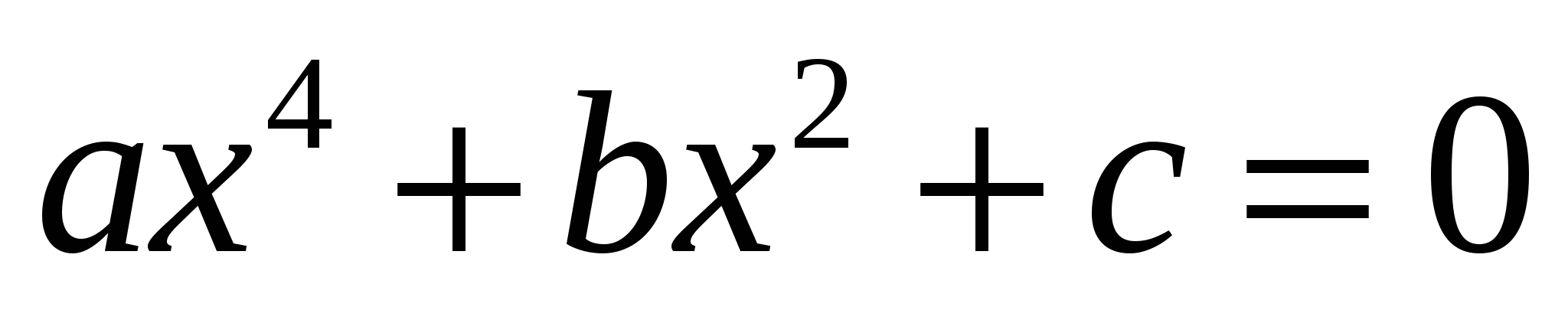

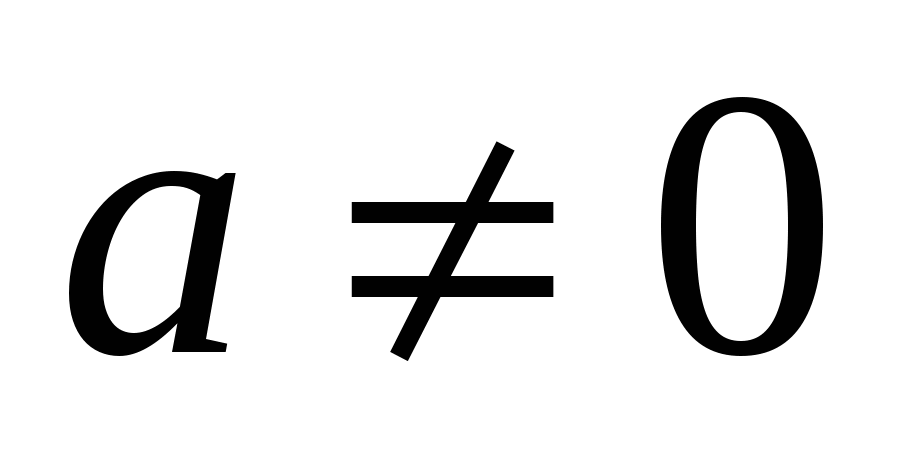, где . (биквадратное)

9.Французский математик, имеющий отношение к квадратным уравнениям. (Виет)

10.Уравнение, в котором левая и правая части являются целыми выражениями. (целое)

11. Уравнения с одной переменной, имеющие одинаковое множество корней. (равносильные)

По вертикали:

1.Множество корней уравнения. (решение)

2.Решение уравнения 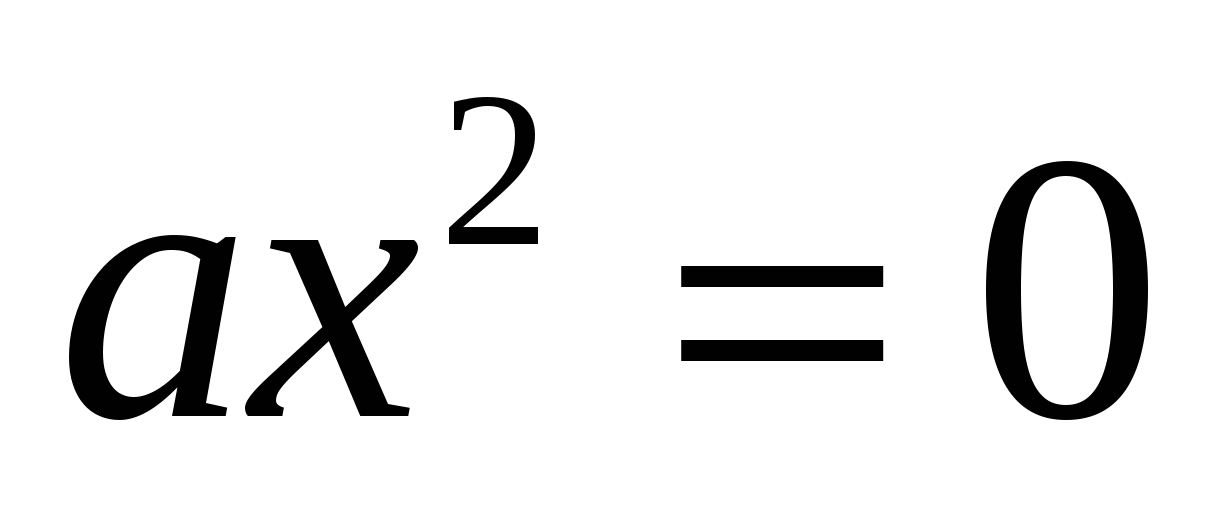. (ноль)

3.Равенство, содержащее переменную. (уравнение)

5.Квадратное уравнение, в котором один из коэффициентов b или с равен 0. (неполное)

7. Квадратное уравнение, в котором первый коэффициент равен единице.

(приведенное)

Чему мы сегодня посвятим наше занятие? (Решению уравнений)

Задание №2. Каким способом вы решали бы уравнения каждой из групп?

ОТВЕТЫ: Примеры группы 1) лучше решать разложением на множители с помощью вынесения общего множителя за скобки или с помощью формул сокращенного умножения.

Примеры группы 2) лучше решать способом группировки и разложения на множители.

Примеры группы 3) лучше решать введением новой переменной и переходом к квадратному уравнению.

1 Какой множитель вы вынесли бы за скобки в примерах группы 1 ?

ОТВЕТЫ: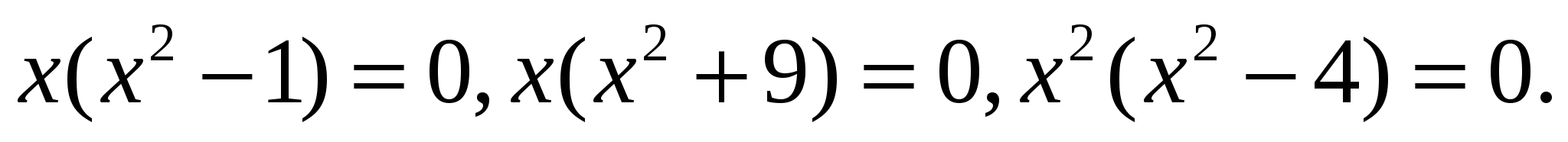

Как вы сгруппировали бы слагаемые в примерах группы 2 ?

ОТВЕТЫ: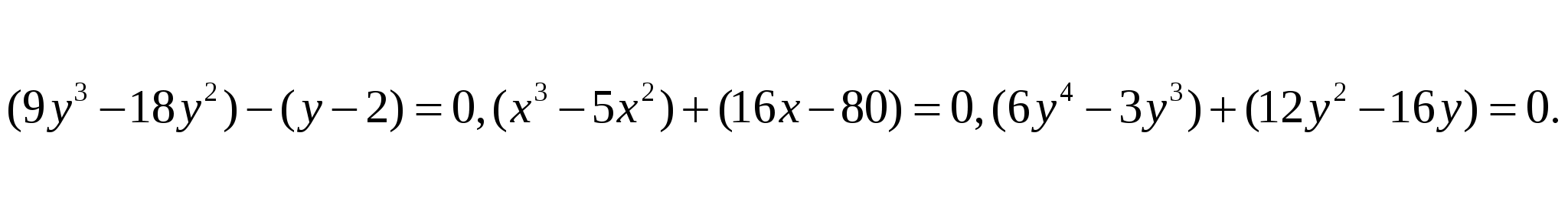

Что бы вы обозначили через новую переменную в примерах группы 3?

ОТВЕТЫ: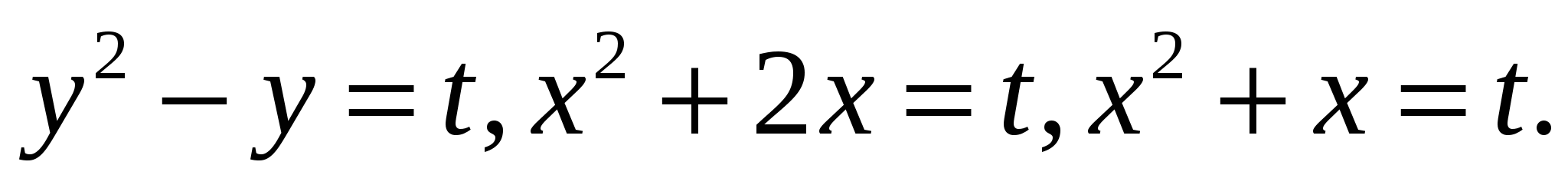

Как можно разложить на множители многочлен ?

ОТВЕТЫ: .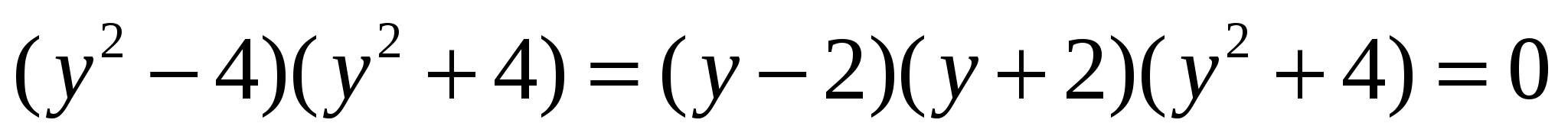

Сегодня на уроке вы покажете свои знания по теме «Решение уравнений методом замены переменной»

Запишите в тетрадях тему урока.

Сегодня на занятии мы рассмотрим один из способов решения уравнений высших степеней — метод замены переменной; познакомимся с понятиями, приёмами решения возвратных и симметрических уравнений.

Искусство производить замену переменных заключается в том, чтобы увидеть, какая замена будет более рациональна и быстрее приведет к успеху.

Задание №3.

Решите уравнение. (задание у доски одновременно решают 2 ученика.)

а) 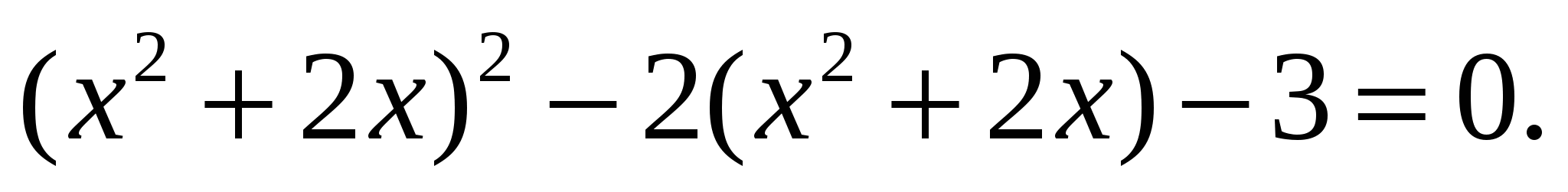(Первый ученик решает у доски с объяснением.)

б) 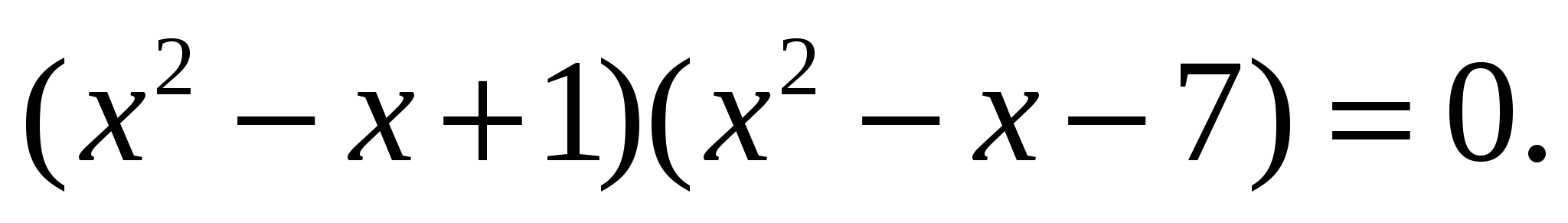(Второй учащийся решает уравнение молча, затем объясняет решение, класс слушает и задает вопросы, если что-то непонятно.)

1 ученик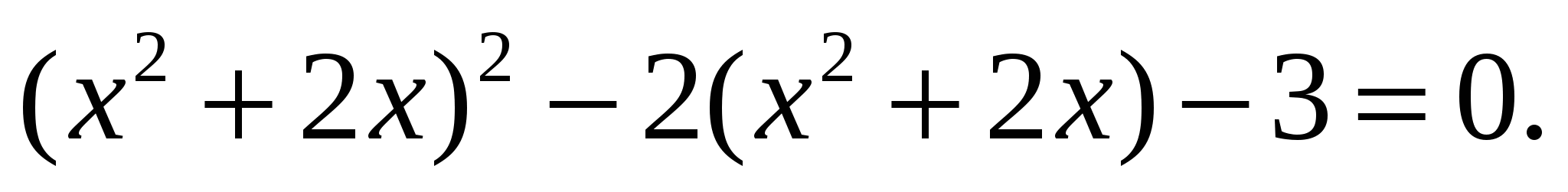

Замена: .

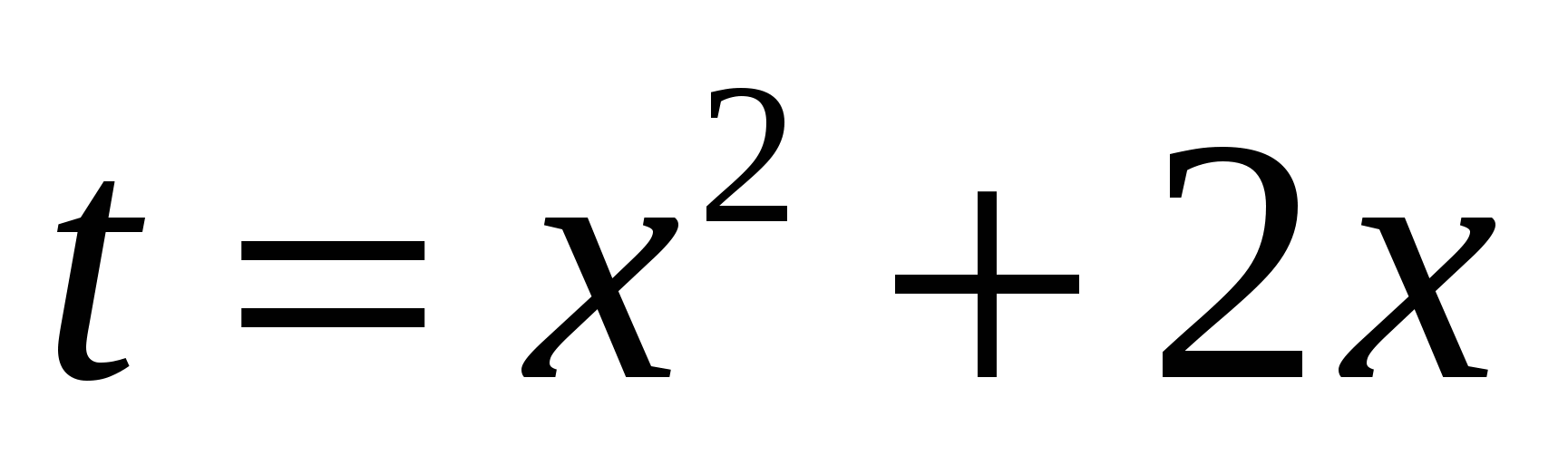2 ученик 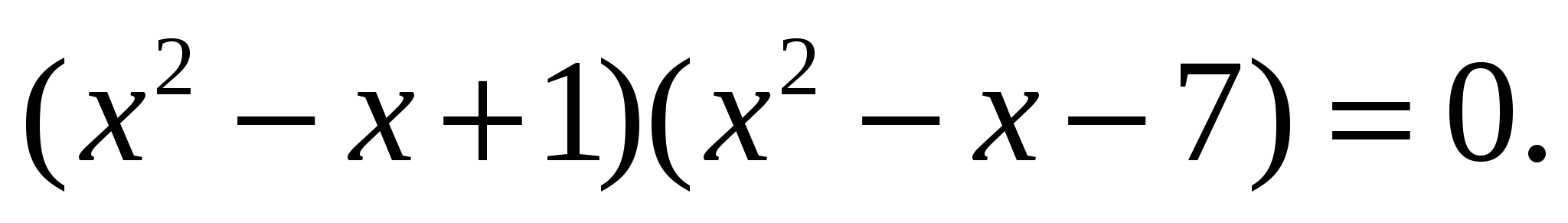Замена: .

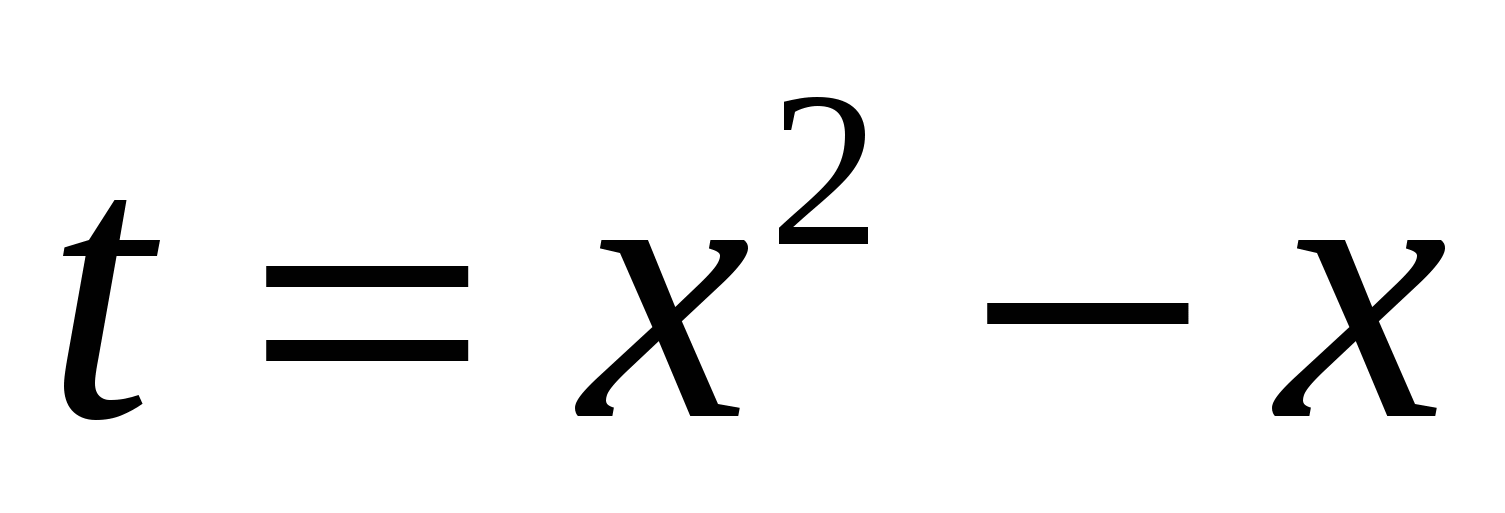(Дополнительно для тех, кто раньше справился с предыдущими уравнениями).

. .

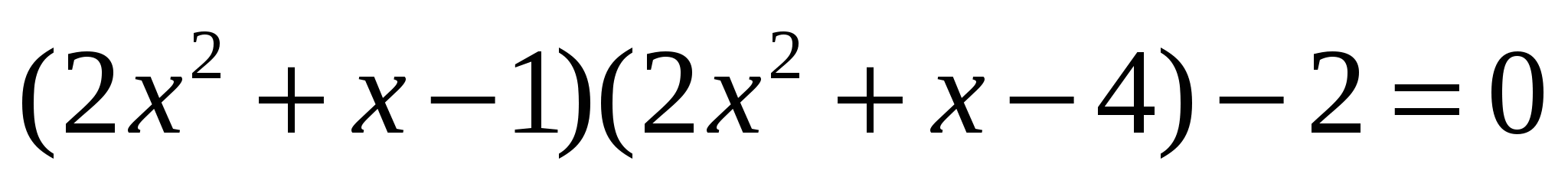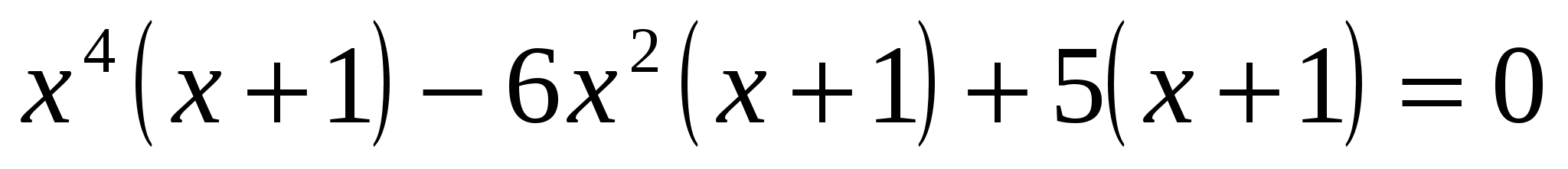
3 ученик

(Ход решения учащимися комментируется с места.)

РЕШЕНИЕ: Вынесем общий множитель: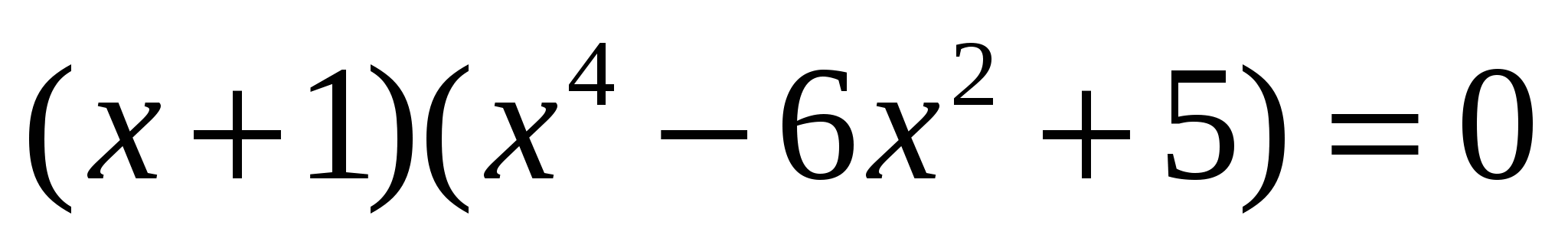

,

откуда 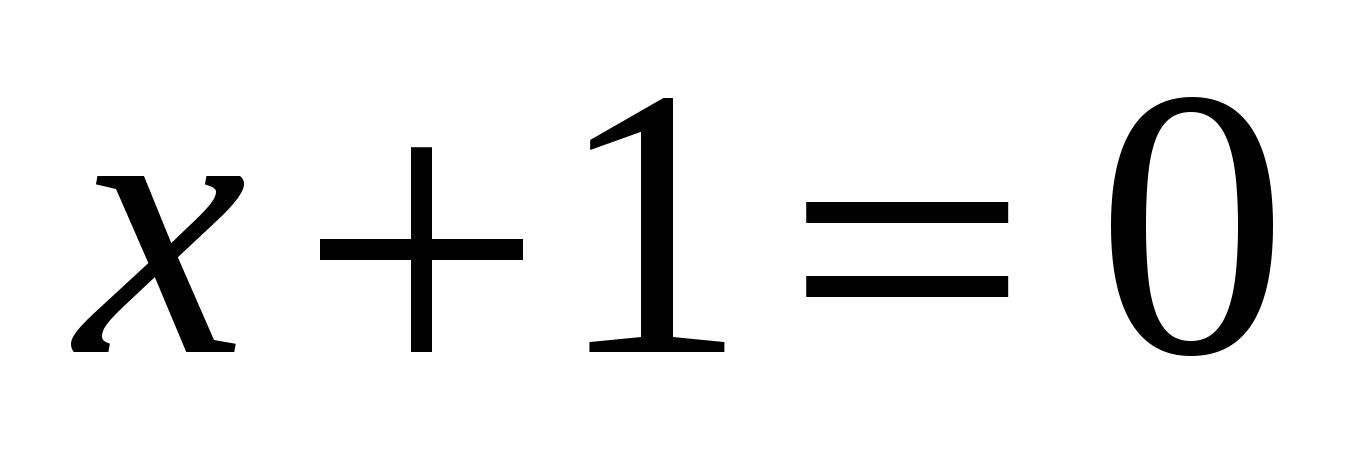или 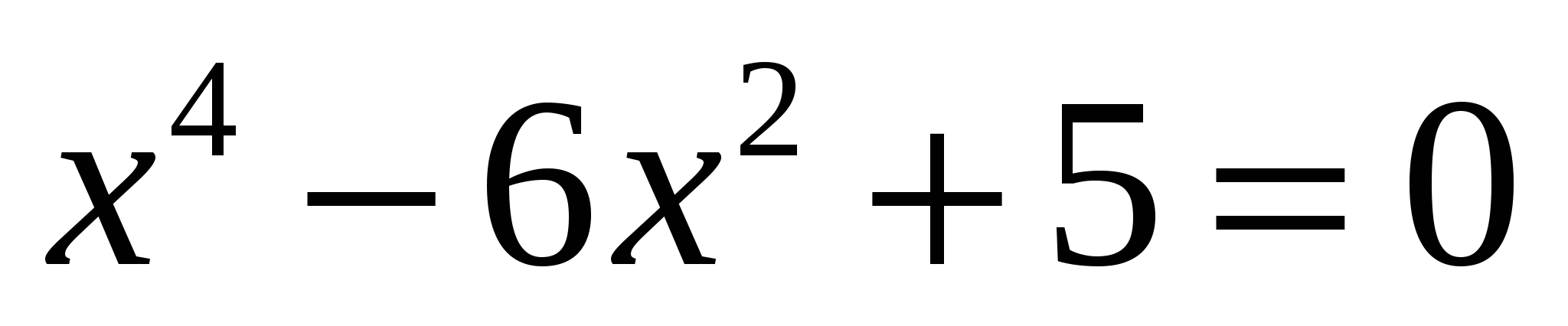, т.е.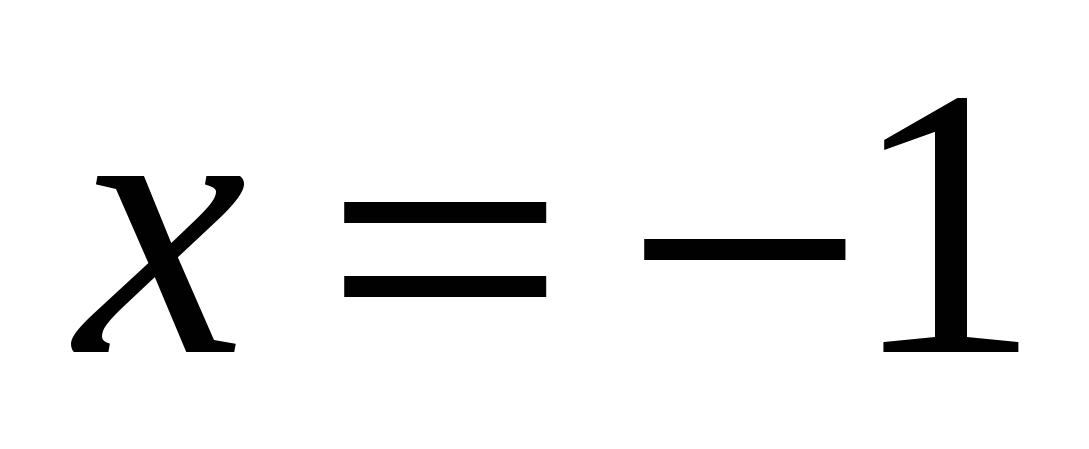

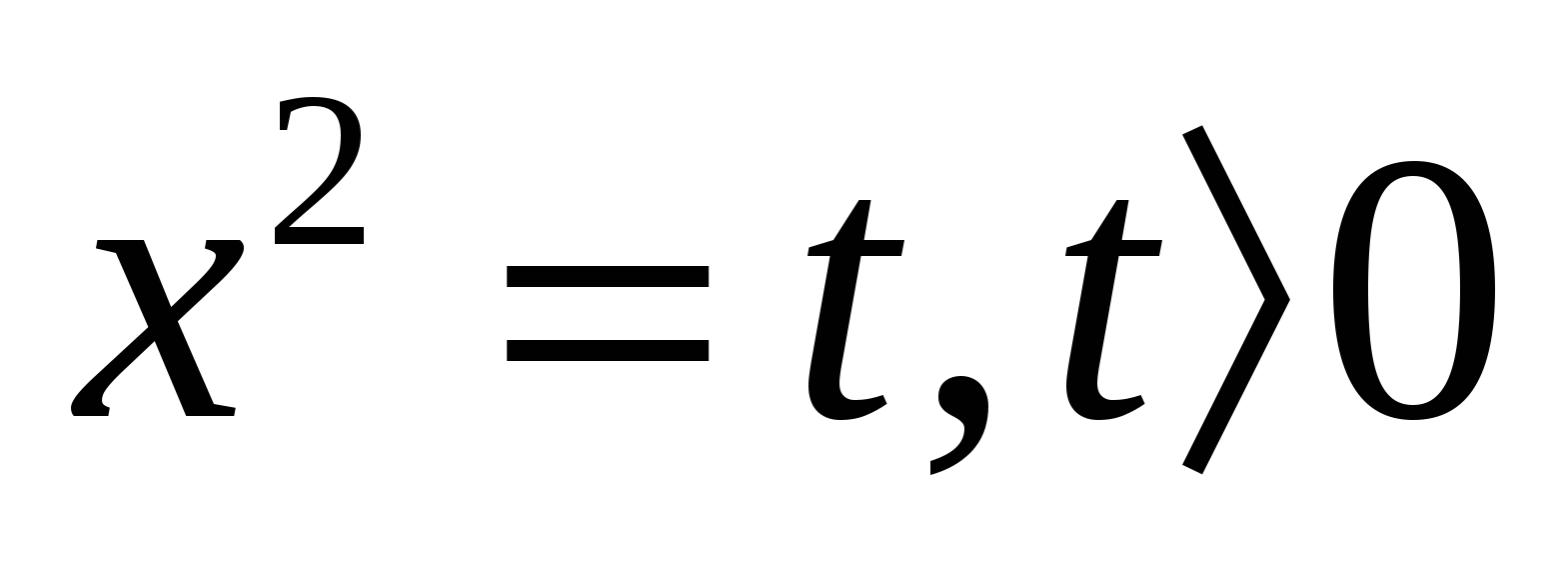
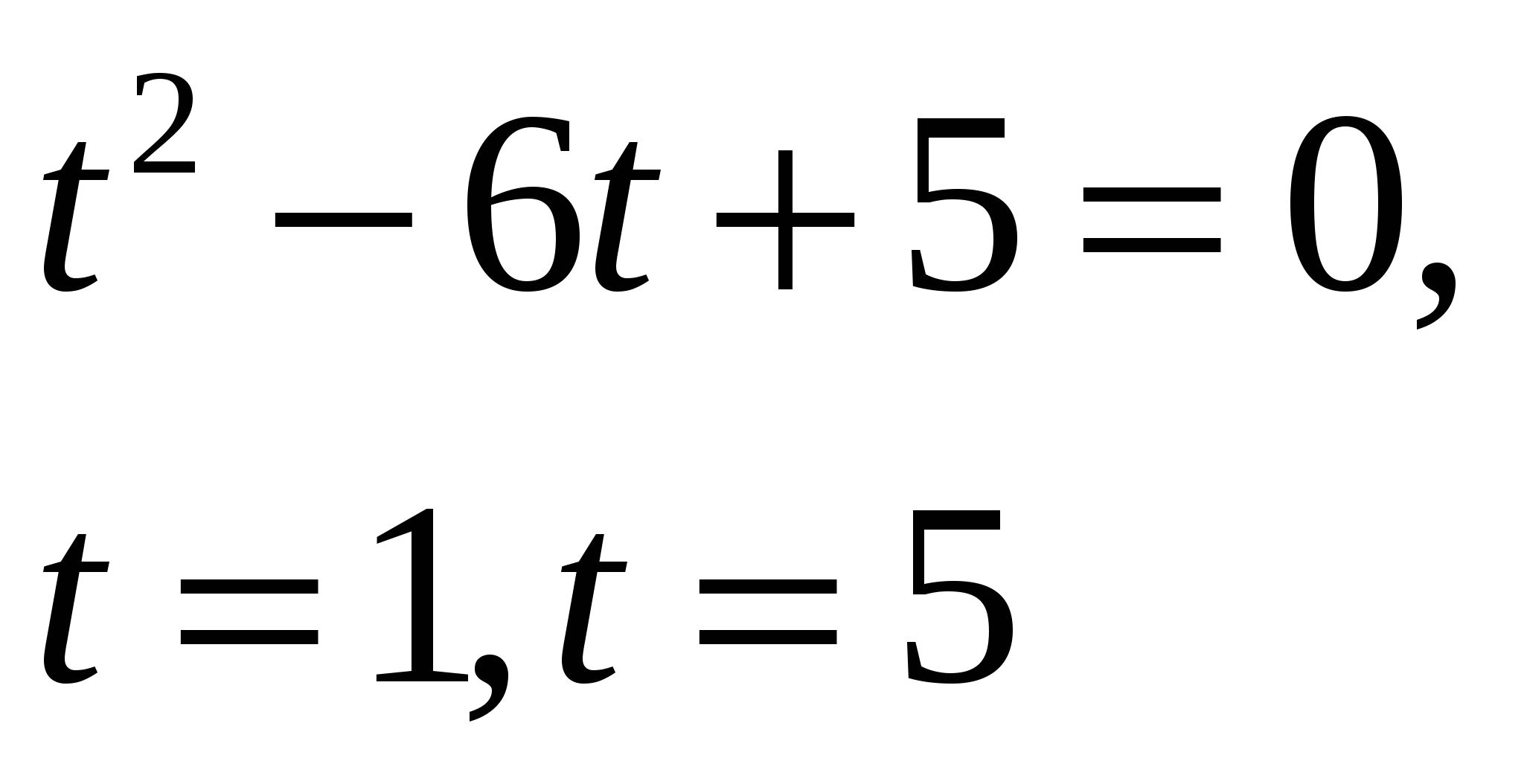
Ответ :

3. Углубление и расширение знаний

Продолжаем работу. Вы видите на слайде уравнение: х⁴-5х³+6х²-5х+1=0.

Каким способом вы предложите его решить? Как нам быть?

Возможно ли решить его в рамках школьных программ по математике? Можно ответить нет. Ведь стандартные методы решения уравнений в школе предусматривают решение уравнений не выше второй степени. Но можно вспомнить, что отдельные уравнения более высоких степеней в школе все-таки решались. Правда, способы их решения суть творческое применение известных способов, сведения их к решению одного или нескольких уравнений степени не выше второй.

Посмотрите очень внимательно на это уравнение? Что вы заметили?( в этом уравнении коэффициенты равноудалённые от концов равны)

Ребята, уравнение такого вида, когда коэффициенты, равноудалённые от концов совпадают, называются возвратными. Это уравнение сводится к квадратному с помощью подстановки.

Предлагаю вам следующий алгоритм их решения :

Алгоритм решения возвратных уравнений.

1.Разделить обе части уравнения на х² .

2.Сгруппировать слагаемые (первый с последним, второй с четвёртым).

Привести уравнение к виду а + с = 0

3. Ввести новую переменную t = 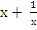,тогда выполнено t² = 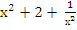, т.е.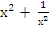= t² – 2.

4. Выполнить подстановку и решить квадратное уравнение.

5.Вернуться к замене и решить получившиеся уравнения.

6.Записать ответ.

Ребята изучают алгоритм.

Ученик у доски по алгоритму и с помощью учителя решает уравнение, остальные пишут в тетрадях.

6х⁴ – 5х³ – 38x² – 5х + 6 = 0.

Решение.

6х² – 5х – 38 – 5/х + 6/х² = 0.

6(х² + 1/х²) – 5(х + 1/х) – 38 = 0.

Вводим t: подстановка (x + 1/x) = t. Замена: (x² + 1/x²) = t² – 2, имеем:

6t² – 5t – 50 = 0.

t = -5/2 или t = 10/3.

Вернемся к переменной х. После обратной замены решим два полученных уравнения:

1) x + 1/x = -5/2;

х² + 5/2 х +1 = 0;

х = -2 или х = -1/2.

2) x + 1/x = 10/3;

х² – 10/3 х + 1 = 0;

х = 3 или х = 1/3.

Ответ: -2; -1/2; 1/3; 3.

В проблему уравнений 3-й и 4-й степеней большой вклад внесли итальянские математики 16 века Н.Тарталья, А.Фиоре, Д.Кардано и др. В 1535 г. между А.Фиоре и Н.Тартальей состоялся научный поединок, на котором последний одержал победу. Он за 2 часа решил 30 задач, предложенных Фиоре, а сам Фиоре не смог решить ни одной, заданной ему Тартальей.

Ребята, и ещё одно уравнение я хочу вам сегодня предложить, я его взяла из сборника задач для подготовки к ОГЭ.

.

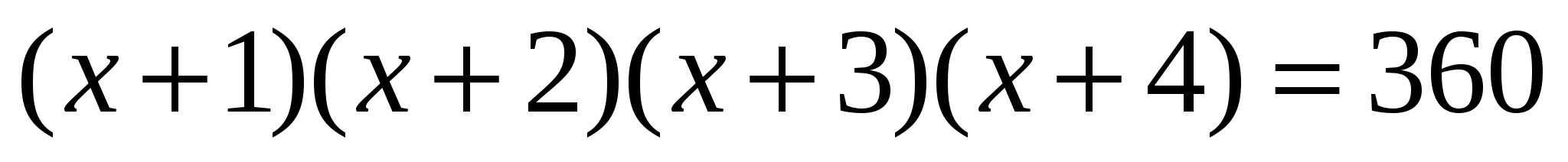Если бы вы встретили такое уравнение, то как бы вы начали его решать?

Уравнения вида (х + а)(х + b)(x + c)(x + d) = А, где а + d = c + b называются симметрическими.

Методика решения подобных уравнений заключается в частичном раскрытии скобок, а затем введении новой переменной.

РЕШЕНИЕ: Сначала сгруппируем множители:

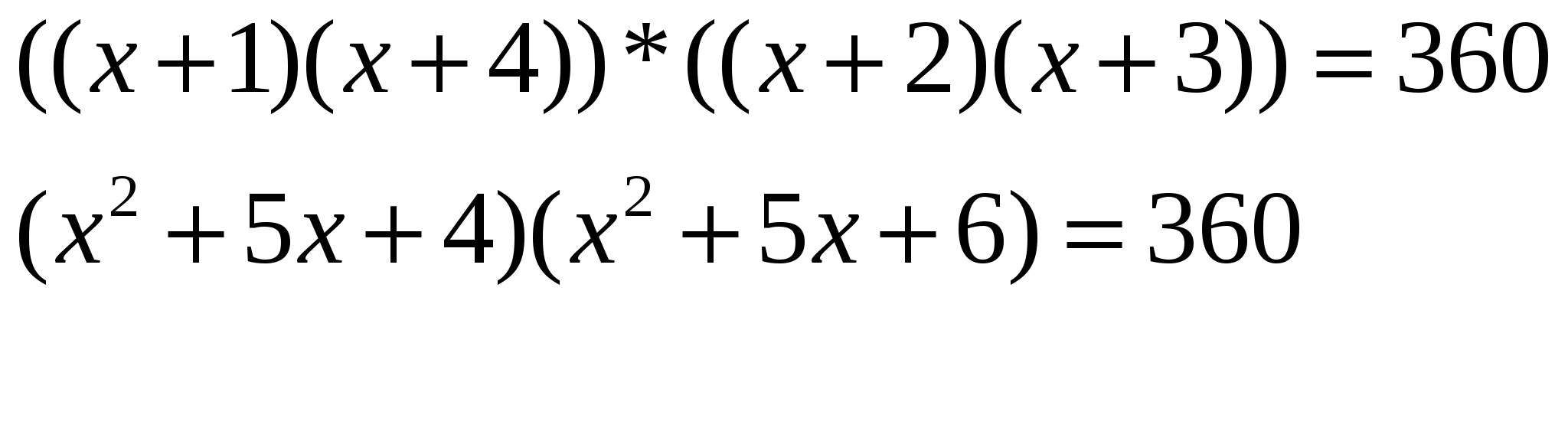Замена: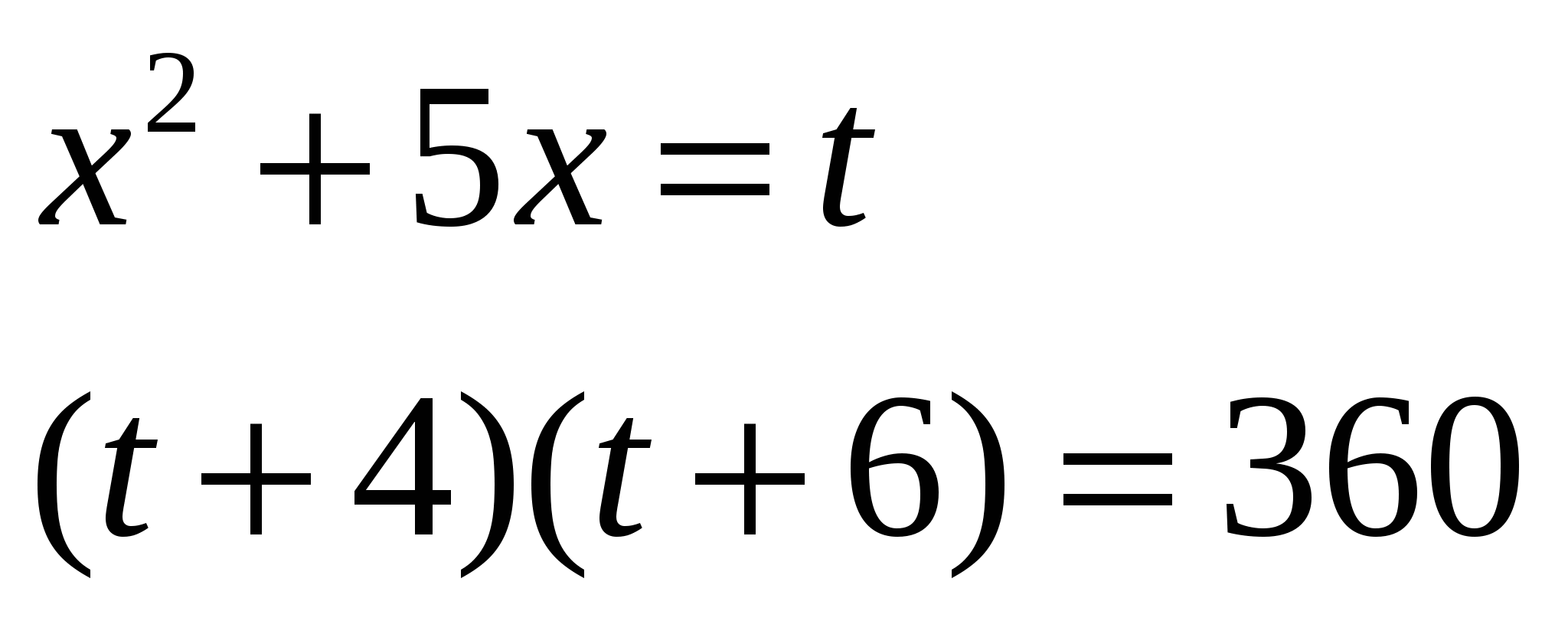

(Далее уравнение решается самостоятельно с дальнейшей устной проверкой.)

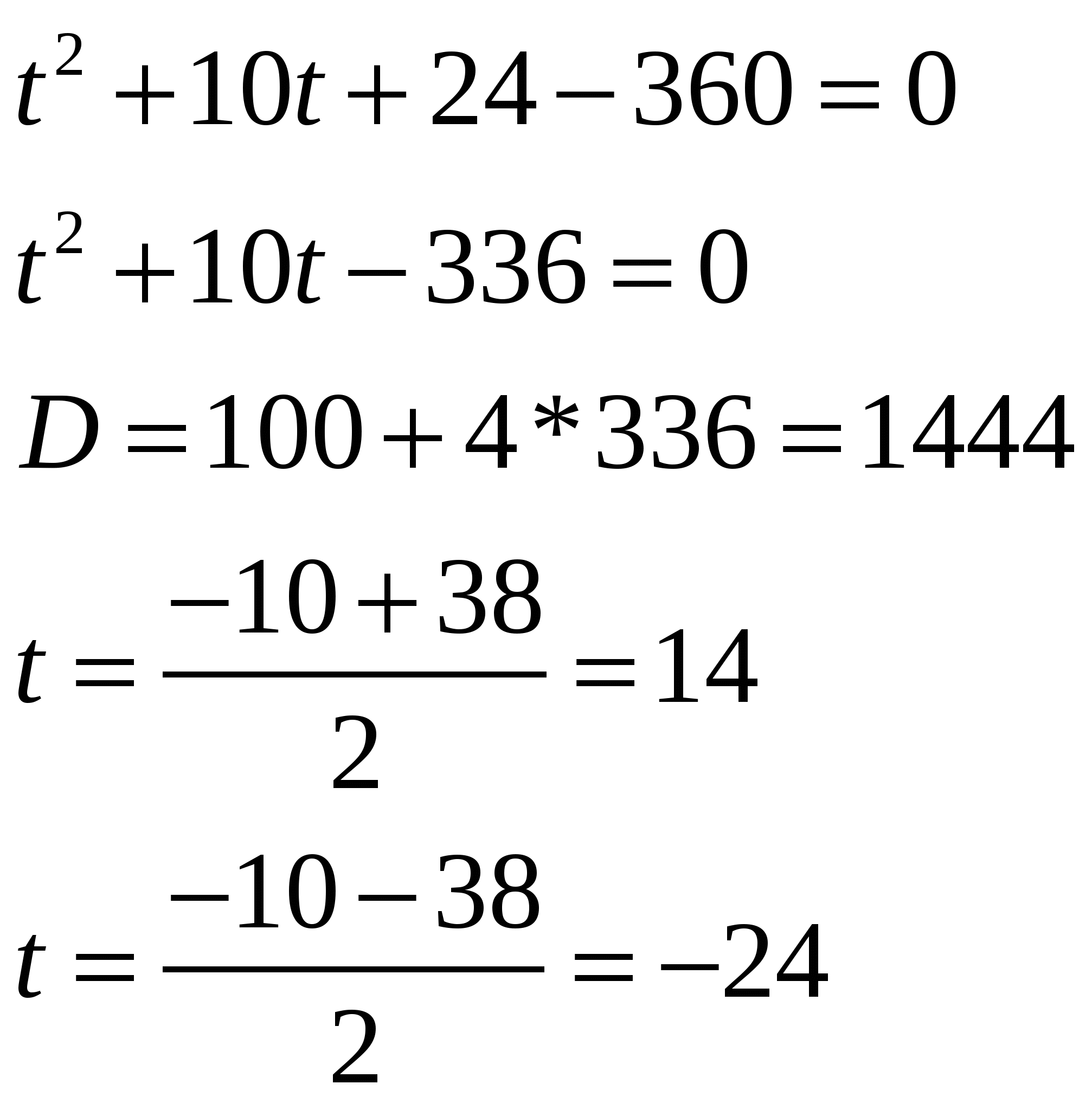
Значит, 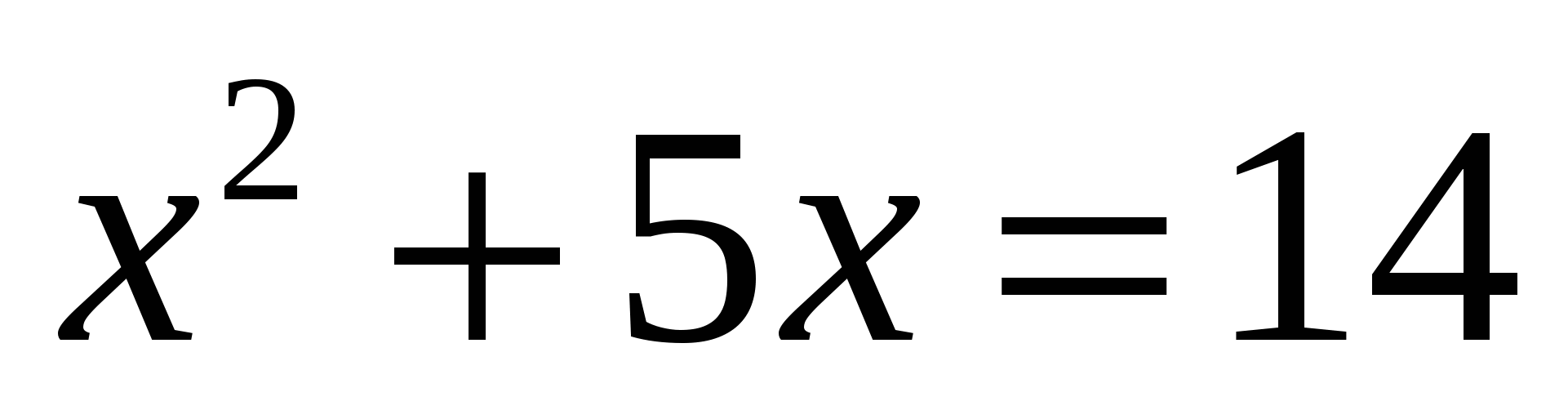или 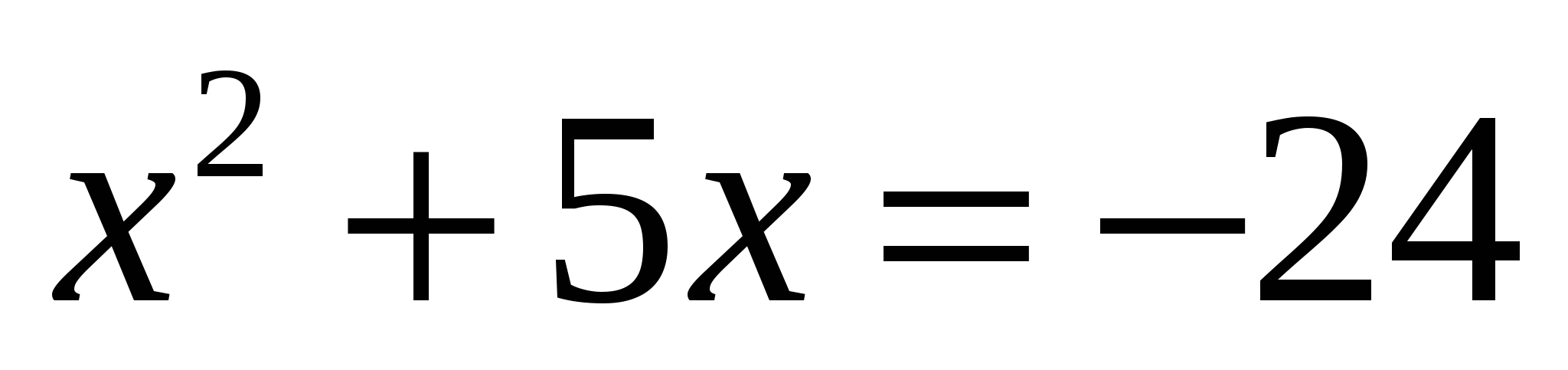(Второе уравнение корней не имеет, т.к. дискриминант меньше нуля)

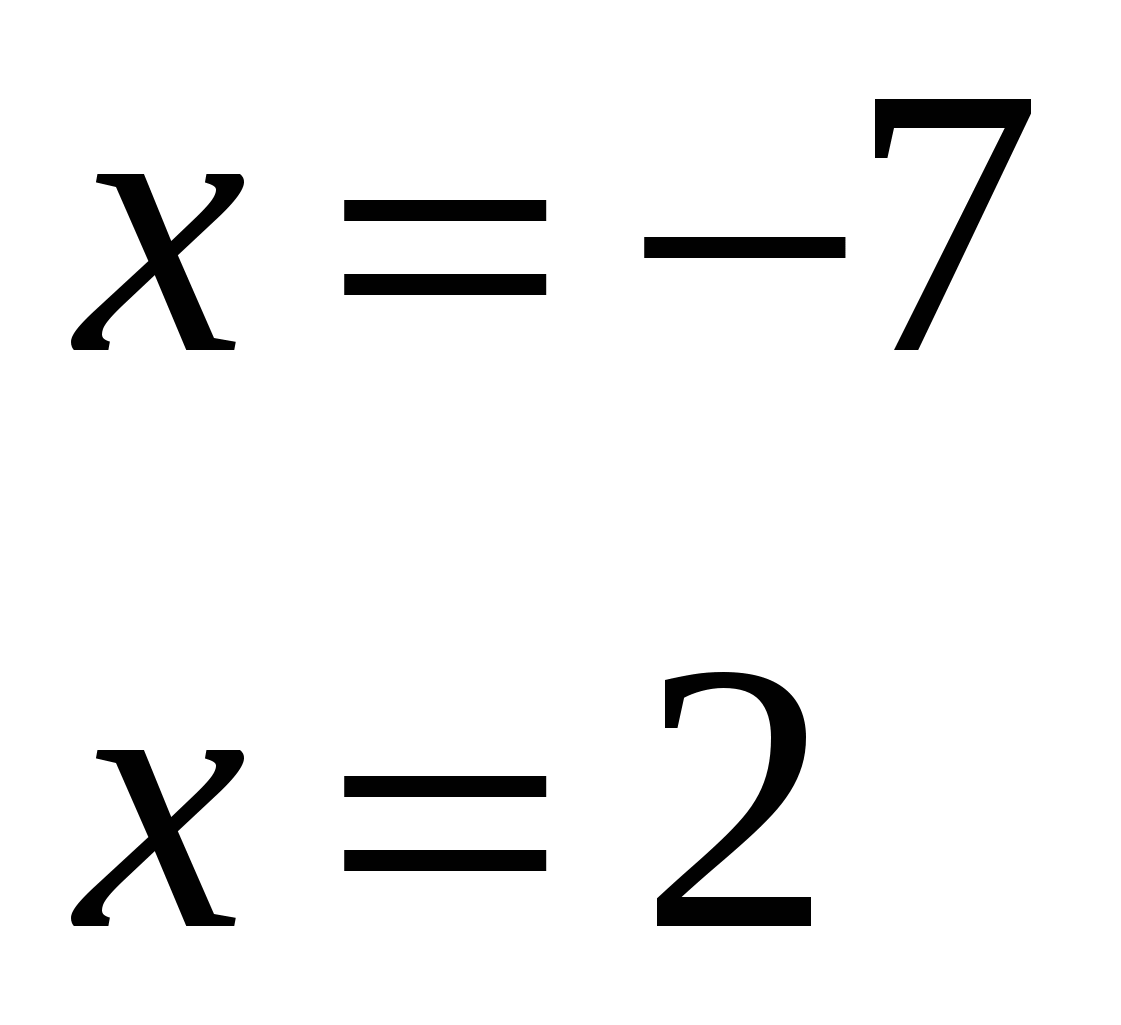
ОТВЕТ: -7; 2.

Решите самостоятельно следующее уравнение.

(х + 1)(х + 2)(x + 3)(x + 4) = 24.

Решение.

Вычисляем: 1 + 4 = 2 + 3. Группируем скобки по парам:

((х + 1)(x + 4))((х + 2)(x + 3)) = 24,

(х² + 5х + 4)(х² + 5х + 6) = 24.

Сделав замену х² + 5х + 4 = t, имеем уравнение

t(t + 2) = 24, оно является квадратным:

t² + 2t – 24 = 0.

t = -6 или t = 4.

После выполнения обратной замены, легко находим корни исходного уравнения.

Ответ: -5; 0.

4. Творческий перенос знаний и навыков в новые условия.

В начале урока говорили о том, что если в уравнении есть повторяющиеся элементы, то можно применять метод замены переменной. Мы еще не умеем решать тригонометрические и иррациональные уравнения. Давайте посмотрим, сможем ли мы применять к ним этот метод, если будем знать, как решать простейшие тригонометрические и иррациональные уравнения.

Задание 1: Назвать замену переменной в следующих уравнениях.

1. 

2. 2сos²x – 4cos x + 5 = 0

3. 

4. .

Задание 2: Составить несколько уравнений, в основе решения которых лежит метод замены переменной.

6. Подведение итогов.

Итак, ребята, наш урок подошёл к концу. Давайте подведём итоги нашего урока.

Какие цели мы ставили в начале урока?

Наши цели достигнуты?

Что нового мы узнали на уроке?

7. Домашнее задание.

4х⁴ – 8х³ + 3х² – 8х + 4 = 0

(х+1)(х+2)(х+4)(х+5) = 40

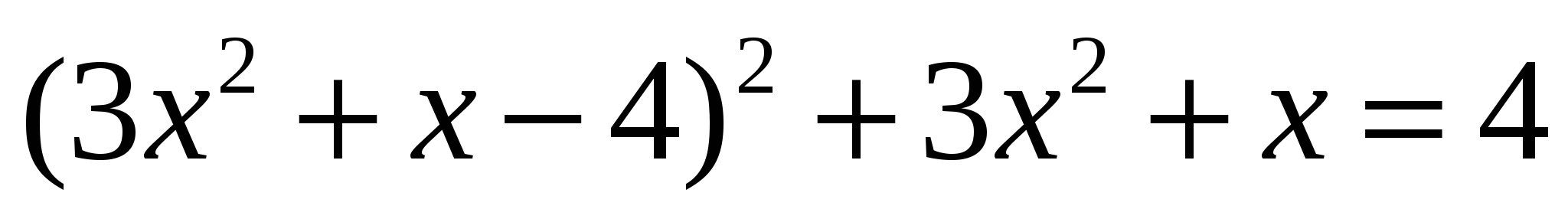. (уравнение итальянских математиков)

А закончить урок мне хочется словами великого учёного Эйнштейна А. :

« Мне приходиться делить своё время между политикой и уравнениями. Однако уравнение, по – моему, гораздо важнее, потому что политика существует только для данного момента, а уравнение будет существовать вечно».

Спасибо за урок! До свидания!

решение уравнения с заменой переменной

Для просмотра онлайн кликните на видео ⤵

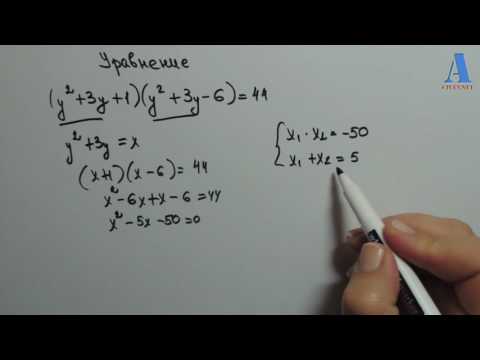
Алгебра 9 класс. Решение систем уравнений методом замены переменных Подробнее

Решение уравнения методом замены переменной Подробнее

Замена переменной. Рациональные уравнения Часть 2 из 4 Подробнее

Пример 47. Решить систему методом замены переменной Подробнее

Алгебра Система уравнений Метод замены переменной № 6.22 9 класс Подробнее

ОГЭ Задание 21 Решение уравнения методом замены Подробнее

Математический анализ, 20 урок, Метод замены переменной Подробнее

Алгебра 9 класс. 10 сентября. замена переменных при решении уравнений Подробнее

Тригонометрические уравнения с заменой переменных и сложным аргументом Алгебра 10 класс Подробнее

§101 Метод введения новой переменной Подробнее

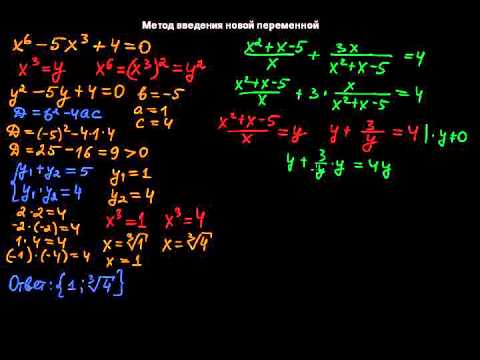
Иррациональные уравнения Урок 2 Замена переменной Подробнее

Решение систем уравнений методом подстановки Подробнее

Математика | Дробно-рациональные уравнения Подробнее

Алгебра 9к. Подготовка к экзамену. Часть 1. Урок 1. Подробнее

Решение систем уравнений методом подстановки (с решением квадратных уравнений). Алгебра 9 класс. Подробнее

Алгебра 9 класс. Область определения функции Подробнее

Понятие неопределённого интеграла и методы его вычисления Подробнее

МАТЕМАТИКА | ТОП-5 ОШИБОК Подробнее

Парадокс бесконечного отеля Подробнее

Разработка урока алгебры в 8-м классе по теме «Решение уравнений методом замены переменной»

Класс: 8.

Программа: для общеобразовательных учреждений, п/р А.Г. Мордковича.

Учебник: Алгебра 8, автор А.Г. Мордкович.

Тип урока: ознакомление с новым материалом.

Цели урока: сформировать умение решать уравнения, приводимые к квадратным, путем введения новой переменной, повторить способы решения неполных квадратных уравнений, формулы сокращенного умножения

Оборудование: компьютер, мультимедийный проектор, экран, презентация к уроку, индивидуальные доски, маркеры по доске.

Раздаточный материал: карточки с заданием для самостоятельной работы.

Ход урока

1. Оргмомент.

2. Сообщение темы урока и целей урока.

— Мы должны сегодня изучить новый метод решения уравнений. Он широко применяется при решении многих типов уравнений, которые мы будем изучать в старших классах. А сегодня мы рассмотрим, как применить его при решении уравнений, которые можно свести к квадратным. Что это за способ, вы узнаете немного позже, а сейчас проверим домашнее задание.

3. Проверка домашнего задания: (Приложение 1)

Слайд 3

4. Подготовка к изучению нового материала (работа устно).

У каждого учащегося есть индивидуальная маркерная доска, на которой он пишет ответ на задание, появляющееся на экране.

— А сейчас вспомним то, что вы изучали раньше. (Приложение 1)

Слайд 4 Решить уравнение:

х 2 = 16 х 2 — 5х = 0 2х 2 = 50

х 2 + 9 = 0 (х — 8 ) 2 = 0 х 3 — 4х = 0

Слайд 5 Разложить на множители:

1. а ² — 36 =
2. 3в ² — 12 =
3. х ² — 10х + 25 =
4. х ³ — 49х =

Раскрыть скобки:

1. (х ² + 3х ) ² =
2. (7 — х ² ) ² =
3. — (3х — 5у ) ² =

5. Изучение нового материала.

— Сейчас попробуйте решить это уравнение:

Слайд 6 (х ² — 3 ) ² + 5 (х ² — 3 ) + 6 = 0 (Проблема)

— Как? Если, как мы обычно делали, раскрывать скобки, то получится уравнение четвертой степени (вспомните устные упражнения ), а их мы решать не умеем. Значит, надо искать другие методы. Посмотрите внимательнее на это уравнение. Ничего необычного не замечаете?

Чаще всего, дети догадываются, что в уравнении встречается повторяющееся выражение.

— Мы всегда старались все упростить. И теперь давайте попробуем это сделать: заменим выражение х ² — 3 какой-нибудь буквой, например, t , Посмотрите, что получили?

t ² + 5t + 6 = 0

D = b ² — 4ac = 25 — 24 = 1

vD = 1

— Но мы нашли только t , нам нужно найти х. Что делать дальше ?

Слайд 7

— Вы узнали новый метод решения уравнений, который называется » замена переменной». Это и есть тема нашего урока. Запишите. Слайд 8

Слайд 9

— Итак, давайте попробуем сформулировать алгоритм решения уравнений методом введения новой переменной.

Слайд 10

— Посмотрите решение еще одного примера.

Слайд 11

Слайд 12

— А сейчас в тетради решим подобные уравнения и поучимся оформлять их решение.

Пример 1 (3х — 4 ) ² — 5(3х — 4 ) + 6 = 0

Сделаем замену переменной. Пусть 3х — 4 = t, получим

t ² — 5t + 6 = 0

D = b ² — 4ac = 25 — 24 = 1

vD = 1

Вернемся к замене.

1) 3х — 4 = 3 3х = 7

2) 3х — 4 = 2 3х = 6 х= 2

Ответ: ; 2.

Пример 2 2(х ² + 3 ) ² — 7 (х ² + 3) ² = — 3

Сделаем замену переменной. Пусть х ² + 3 = t, получим

2t² — 7t = — 3

2t ² — 7t + 3 = 0

D = b ² — 4ac = 49 — 24 = 25

vD = 5

Вернемся к замене:

1) х 2 + 3 = 3 х 2 = 0 х = 0

2) х 2 + 3 = х 2 = нет корней

Ответ: 0

6. Закрепление изученного материала.

— Сейчас решите из учебника № 26.22 б ; 26.23 а.в ; дополнительно 26.25.

7. Подведение итогов и задание на дом.

— Что нового вы узнали на уроке?

— Каков алгоритм решения уравнений методом замены переменной?

— Ваше домашнее задание на экране.

Слайд 13

— На следующем уроке вы узнаете, что такое биквадратные уравнения и научитесь их решать. А сейчас проверим. как вы научились решать уравнения методом замены переменной. У каждого есть карточка с заданием. Если у вас останется время, дополнительное задание на экране. Желаю успеха!

8. Самостоятельная работа. (Приложение 2)

Вариант 1	Вариант 2
Решить уравнения: 1) (х — 5 ) 2 — 2 (х — 5 ) = 8 2) (х 2 — 8 ) 2 + 3 (х 2 — 8 ) 2 - 4 = 0	Решить уравнения: 1) (2х + 3 ) 2 — 4 (2х + 3 ) = 5 2) (х 2 + х ) 2 — 11 (х 2 + х ) = 12
Вариант 3	Вариант 4
Решить уравнения: 1) (х2 - 2х ) 2 + (х 2 — 2х ) = 12 2) (х 2 + 2 ) 2 — 5 (х 2 + 2 ) — 6 = 0	Решить уравнения: 1) (х 2 - х ) 2 — 8 (х 2 — х ) + 12 = 0 2) (х 2 — 1 ) 2 + 2 (х 2 — 1 ) = 15

Слайд 14

Дополнительно.

1. (х² + 4х )( х² + 4х — 17 ) + 60 = 0
2. (х² — 5х )( х² — 5х + 10 ) = — 24

Слайд 15 — Урок закончен.

Метод замены переменной при решении рациональных неравенств

Метод замены переменной при решении рациональных неравенств
Многие неравенства удобно решать, применяя метод замены переменной (метод подстановки).
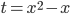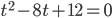Пример 1. Решить неравенство . Решение. Сделав замену переменной , получаем . Корни уравнения есть . Отсюда Поскольку 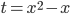, то получаем

Решаем неравенство (a):
Решаем неравенство (b):

Отсюда

Изобразим полученные множества с помощью двух координатных прямых (рис.1). Из рис.1 видим, что решением исходного неравенства является объединение множеств (-2;-1),(2;3).

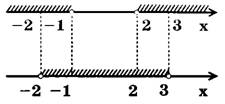
Рис.1

Ответ:
Пример 2. Решить неравенство Решение.
Обозначив , получаем из исходного неравенства Отсюда исходное неравенство равносильно следующему неравенству:

( для любого , поскольку дискриминант квадратного трехчлена
Ответ:

ЗАМЕНА ПЕРЕМЕННЫХ В ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ ПЕРВОГО ПОРЯДКА

Стр 1 из 6Следующая ⇒

Сведения из теории

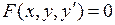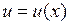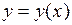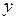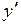Сделаем в уравнении замену переменных: введем новую неизвестную функцию , связанную с искомой функцией соотношением , где – дифференцируемая функция. Подставляя выражения и через 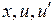в (3.1), получим для нахождения 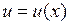уравнение вида 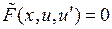, которое при удачном выборе замены может оказаться «проще» первоначального. Например, уравнение

 

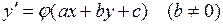
заменой переменной 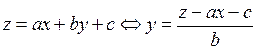сводится к уравнению с разделяющимися переменными

.

 

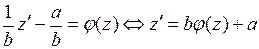Примеры решения задач

3.2.1.Решить уравнение .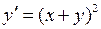

◄ Введем новую неизвестную функцию 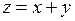. Выразим 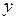и 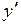через z: 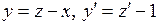. Подставим эти выражения в исходное уравнение и решим полученное уравнение с разделяющимися переменными.

.

.

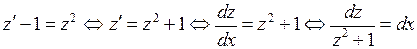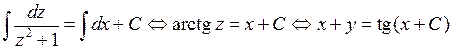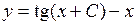– общее решение уравнения.►

3.2.2.Найти решение дифференциального уравнения , удовлетворяющее начальному условию .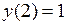

◄ Так как 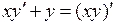, то естественно сделать замену 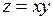. Для функции 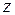получим дифференциальное уравнение 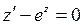с разделяющимися переменными и начальное условие 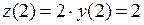. Разделяем переменные: , , 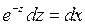интегрируем: 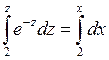, выражаем z, а затем и y через x

, , ,

, ,

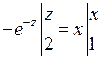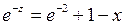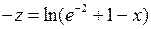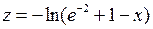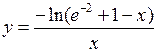– искомое решение.►

 

3.3. Задачи для самостоятельного решения

Решить уравнения.

 

Однородные уравнения

Сведения из теории

Дифференциальное уравнение, которое можно записать в виде

 

 

называется однородным. Оно сводится заменой переменной

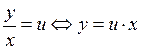
к уравнению с разделяющимися переменными для функции .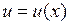

.

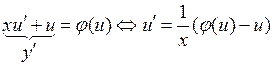Важным примером однородного уравнения является уравнение, правая часть которого – отношение однородных многочленов относительно и 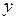одного порядка

.

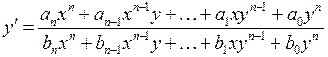Оно приводится к виду , если числитель и знаменатель разделить на .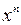

 

Примеры решения задач

4.2.1.Решить уравнение .

◄ Правая часть уравнения – отношение однородных многочленов 2-го порядка. Разделив числитель и знаменатель на 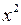, получим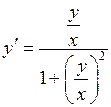

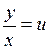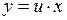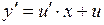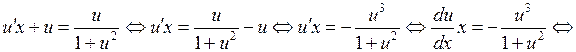
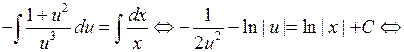
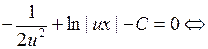
– однородное уравнение. Делаем замену . Тогда , . Для функции получаем уравнение с разделяющимися переменными: 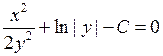— общий интеграл. ►

 

4.2.2.Найти решение дифференциального уравнения 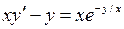, удовлетворяющее условию .

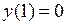◄ Приведем уравнение к нормальному виду 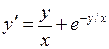. Так как х и у входят в правую часть только в виде отношения , то это – однородное уравнение. Делаем замену 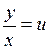, . Для функции 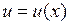получаем уравнение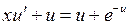 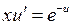и начальное условие . Разделяем переменные: 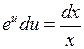, ; ; 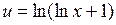, и потому 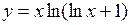– искомое решение.►

 

4.3. Задачи для самостоятельного решения

Решить уравнения.

Линейные уравнения ПЕРВОГО порядка

Сведения из теории

Дифференциальное уравнение первого порядка, разрешенное относительно производной, называется линейным, если его правая часть – линейная функция от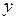

.

 

При 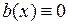получаем линейное однородное уравнение

 

.

 

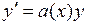Оно является уравнением с разделяющимися переменными, и его общее решение

,

 

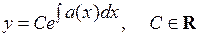где 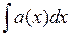– одна из первообразных функции 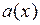. Общее решение линейного неоднородного уравнения 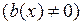можно найти одним из следующих методов.

 

1) Метод вариации произвольной постоянной (метод Лагранжа).

Сначала находится общее решение соответствующего линейного однородного уравнения . Решение неоднородного уравнения ищем в виде

,

 

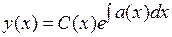получающемся из заменой постоянной 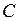на функцию 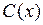. Подставляя в уравнение , получаем для новой неизвестной функции 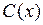уравнение 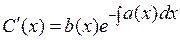. Интегрируя, находим

 

 

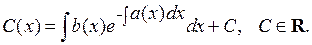
Подставляя в , получаем общее решение уравнения .

 

Метод Бернулли.

Ищем решение уравнения в виде 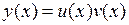. Тогда 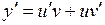. Подставляя в уравнение , получим 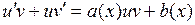. Перепишем это уравнение в виде

 

.

 

Подберем 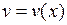так, чтобы скобка в уравнении обратилась в нуль. Для этого нужно найти какое-нибудь частное решение уравнения с разделяющимися переменными 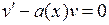. Подставляя в , получим уравнение с разделяющимися переменными для функции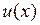

.

 

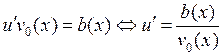Интегрируя, находим его общее решение 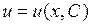. Перемножая найденные значения 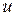и 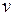, получим общее решение неоднородного уравнения .

 

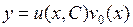Примеры решения задач

5.2.1.Решить уравнение

.

 

◄ Уравнение записано в нормальной форме. Его правая часть является линейной функцией аргумента у. Следовательно, уравнение – линейное. Решаем его методом вариации произвольной постоянной. Сначала находим общее решение однородного уравнения . . .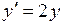

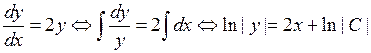Решение неоднородного уравнения ищем в ви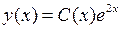де , где 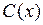– новая неизвестная функция. Подставляя в уравнение , получим

.

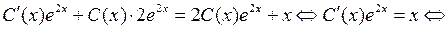
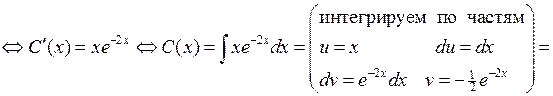
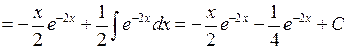Итак, общее решение 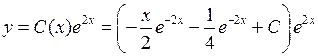, где справа буквой С обозначена, как и везде, произвольная постоянная. После преобразований запишем его в виде

. ►

 

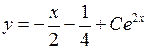5.2.2.Решить задачу Коши .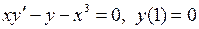

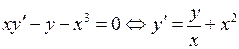◄ – линейное уравнение. Решаем методом Бернулли: 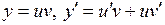. Подставляя 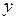и 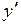в исходное уравнение, получаем 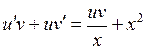. Сгруппируем члены, содержащие 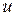в качестве множителя

.

 

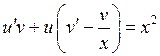Приравняем скобку к нулю и решаем полученное уравнение.

 

.

 

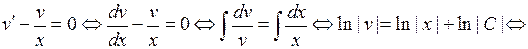
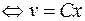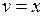Поскольку нам нужно только частное решение уравнения , то примем , тогда . Подставляя 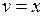в уравнение , получим

.

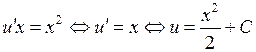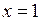Перемножая u и v, находим общее решение . Подставляя в общее решение начальные значения и 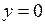, получим 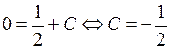. Искомое решение .►

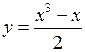5.3. Задачи для самостоятельного решения

Решить уравнения.

 

5.3.9.Известно, что сила тока 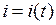в цепи, имеющей сопротивление 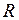, самоиндукцию 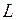удовлетворяет уравнению 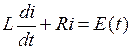, где – электродвижущая сила. Найти силу тока 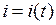, если , в случаях

а) 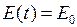, б) .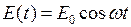

УравнениЯ Бернулли

Сведения из теории

Уравнение Бернулли – это уравнение первого порядка, имеющее в нормальной форме вид

, .

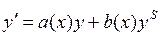Методы решения те же, что и для линейного неоднородного уравнения, являющегося частным случаем уравнения Бернулли при .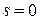

 

Примеры решения задач

6.2.1.Решить уравнение Бернулли .

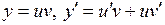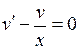◄ Решаем методом Бернулли , . Подберем v, так чтобы . Тогда 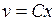. Возьмем . Подставляя 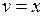в уравнение, получаем для функции u уравнение с разделяющимися переменными

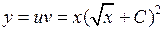– общее решение.►

6.3. Задачи для самостоятельного решения

 

Решить уравнения.



Замена переменных

Решение.

\(\triangle\) Имеем:
$$
r^2=x^2+y^2,\Longrightarrow rdr=xdx+ydy,\quad \frac{\partial r}{\partial x}=\frac{x}{r},\quad \frac{\partial r}{\partial y}=\frac{y}{r},\nonumber
$$
$$
d\varphi=\frac{xdy-ydx}{x^2+y^2},\Longrightarrow \frac{\partial \varphi}{\partial x}=-\frac{y}{r^2}=-\frac{\sin\varphi}{r},\quad \frac{\partial \varphi}{\partial y}=\frac{x}{r^2}=\frac{\cos\varphi}{r},\nonumber
$$

Тогда,
$$
\frac{\partial u}{\partial x}=\frac{\partial u}{\partial r}\frac{\partial r}{\partial x}+\frac{\partial u}{\partial \varphi}\frac{\partial\varphi}{\partial x}=\frac{x}{r}\frac{\partial u}{\partial r}-\frac{y}{r^2}\frac{\partial u}{\partial \varphi}=\cos\varphi\frac{\partial u}{\partial r}-\frac{\sin\varphi}{r}\frac{\partial u}{\partial \varphi},\nonumber
$$
$$
\frac{\partial u}{\partial y}=\frac{\partial u}{\partial r}\frac{\partial r}{\partial y}+\frac{\partial u}{\partial \varphi}\frac{\partial\varphi}{\partial y}=\sin\varphi\frac{\partial u}{\partial r}+\frac{\cos\varphi}{r}\frac{\partial u}{\partial r}.\nonumber
$$

Таким образом,
$$
\frac{\partial}{\partial x}=\cos\varphi\frac{\partial}{\partial r}-\frac{\sin\varphi}{r}\frac{\partial}{\partial\varphi},\qquad \frac{\partial}{\partial y}=\sin\varphi\frac{\partial}{\partial r}+\frac{\cos\varphi}{r}\frac{\partial}{\partial\varphi},\nonumber
$$

Для начала найдем \(\displaystyle \frac{\partial^2 u}{\partial x^2}\).
$$
\frac{\partial^2u}{\partial x^2}=\frac{\partial}{\partial x}\left(\frac{\partial u}{\partial x}\right)=\underbrace{\frac{\partial}{\partial r}\left(\frac{\partial u}{\partial r}\frac{\partial r}{\partial x}+\frac{\partial u}{\partial\varphi}\frac{\partial\varphi}{\partial x}\right)\frac{\partial r}{\partial x}}_{\boxed{1}}+\underbrace{\frac{\partial}{\partial\varphi}\left(\frac{\partial u}{\partial r}\frac{\partial r}{\partial x}+\frac{\partial u}{\partial\varphi}\frac{\partial\varphi}{\partial x}\right)\frac{\partial\varphi}{\partial x}}_{\boxed{2}}\nonumber
$$

Рассмотрим \(\boxed{1}\)
$$
\boxed{1}=\frac\partial{\partial r}\left(\frac{\partial u}{\partial r}\frac{\partial r}{\partial x}+\frac{\partial u}{\partial\varphi}\frac{\partial\varphi}{\partial x}\right)\frac{\partial r}{\partial x}=\frac\partial{\partial r}\left(\cos\varphi\frac{\partial u}{\partial r}-\frac{\sin\varphi}r\frac{\partial u}{\partial\varphi}\right)\cos\varphi=\\=\left(\cos\varphi\frac{\partial^2u}{\partial r^2}-\frac{\sin\varphi}r\frac{\partial^2u}{\partial r\partial\varphi}+\frac{\sin\varphi}{r^2}\frac{\partial u}{\partial\varphi}\right)\cos\varphi=\\=\cos^2\varphi\frac{\partial^2u}{\partial r^2}-\frac{\sin\varphi\cos\varphi}r\frac{\partial^2u}{\partial r\partial\varphi}+\frac{\sin\varphi\cos\varphi}{r^2}\frac{\partial u}{\partial\varphi}\nonumber
$$

Теперь рассмотрим \(\boxed{2}\):
$$
\boxed{2}=\frac\partial{\partial\varphi}\left(\frac{\partial u}{\partial r}\frac{\partial r}{\partial x}+\frac{\partial u}{\partial\varphi}\frac{\partial\varphi}{\partial x}\right)\frac{\partial\varphi}{\partial x}=\frac\partial{\partial\varphi}\left(\cos\varphi\frac{\partial u}{\partial r}-\frac{\sin\varphi}r\frac{\partial u}{\partial\varphi}\right)\left(-\frac{\sin\varphi}r\right)=\\=\left(-\sin\varphi\frac{\partial u}{\partial r}+\cos\varphi\frac{\partial^2u}{\partial\varphi\partial r}-\frac{\cos\varphi}r\frac{\partial u}{\partial\varphi}-\frac{\sin\varphi}r\frac{\partial^2u}{\partial\varphi^2}\right)\left(-\frac{\sin\varphi}r\right)=\\=\frac{\sin^2\varphi}r\frac{\partial u}{\partial r}-\frac{\cos\varphi\sin\varphi}r\frac{\partial^2u}{\partial\varphi\partial r}+\frac{\cos\varphi\sin\varphi}{r^2}\frac{\partial u}{\partial\varphi}+\frac{\sin^2\varphi}{r^2}\frac{\partial^2u}{\partial\varphi^2}\nonumber
$$

Сложим эти выражения вместе (\(\boxed{1}+\boxed{2}\)):
$$
\boxed{1}+\boxed{2}=\frac{\partial^2 u}{\partial x^2}=\cos^2\varphi\frac{\partial^2u}{\partial r^2}-\frac{2\sin\varphi\cos\varphi}r\frac{\partial^2u}{\partial r\partial\varphi}+\frac{\sin^2\varphi}{r^2}\frac{\partial^2u}{\partial\varphi^2}+\frac{\sin^2\varphi}r\frac{\partial u}{\partial r}+\frac{2\cos\varphi\sin\varphi}{r^2}\frac{\partial u}{\partial\varphi}\nonumber
$$

Рассуждая аналогично, найдем \(\displaystyle \frac{\partial^2 u}{\partial y^2}\)
$$
\frac{\partial^2u}{\partial y^2}=\frac{\partial}{\partial y}\left(\frac{\partial u}{\partial y}\right)=\frac{\partial}{\partial r}\left(\frac{\partial u}{\partial r}\frac{\partial r}{\partial y}+\frac{\partial u}{\partial\varphi}\frac{\partial\varphi}{\partial y}\right)\frac{\partial r}{\partial y}+\frac{\partial}{\partial\varphi}\left(\frac{\partial u}{\partial r}\frac{\partial r}{\partial y}+\frac{\partial u}{\partial\varphi}\frac{\partial\varphi}{\partial y}\right)\frac{\partial\varphi}{\partial y}=\\=\cos^2\varphi\frac{\partial^2u}{\partial r^2}+\frac{2\sin\varphi\cos\varphi}r\frac{\partial^2u}{\partial r\partial\varphi}+\frac{\cos^2\varphi}{r^2}\frac{\partial^2u}{\partial\varphi^2}+\frac{\cos^2\varphi}r\frac{\partial u}{\partial r}-\frac{2\cos\varphi\sin\varphi}{r^2}\frac{\partial u}{\partial\varphi}\nonumber
$$

Таким образом, складывая \(\displaystyle \frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\), получаем:
$$
\omega=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=\frac{\partial^2u}{\partial r}+\frac1r\frac{\partial u}{\partial r}+\frac1{r^2}\frac{\partial^2u}{\partial\varphi^2}\nonumber
$$

Пусть \(u=v(r)\) есть решение уравнения Лапласа, зависящее только от \(r\). Тогда функция \(v(r)\) должна быть решением дифференциального уравнения
$$
\frac{\partial^2v}{\partial r}+\frac1r\frac{\partial v}{\partial r}=0\quad\Longleftrightarrow\quad\frac{d}{dr}\left(r\frac{dv}{dr}\right)=0\nonumber
$$
$$
r\frac{dv}{dr}=C,\quad\Longrightarrow\quad v=C_1\ln r+C_2,\label{ref3}
$$
где \(C_1\) и \(C_2\) — произвольные постоянные. \(\blacktriangle\)
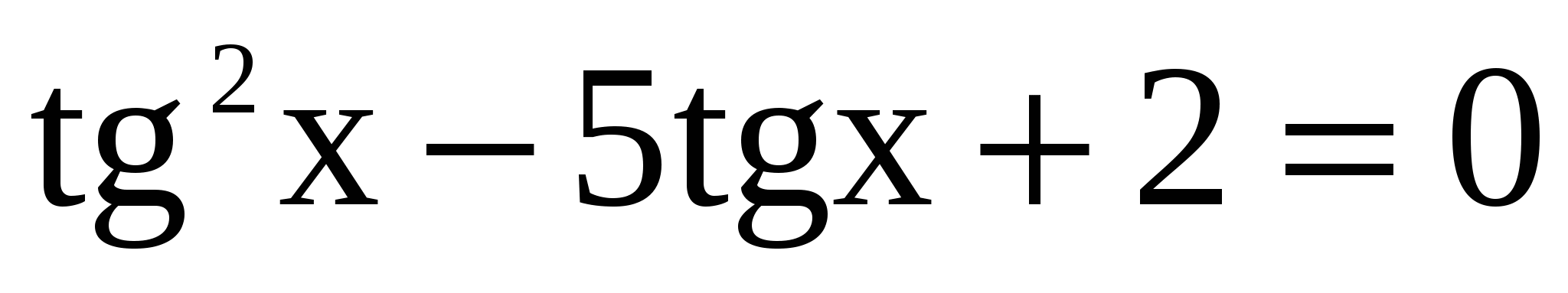
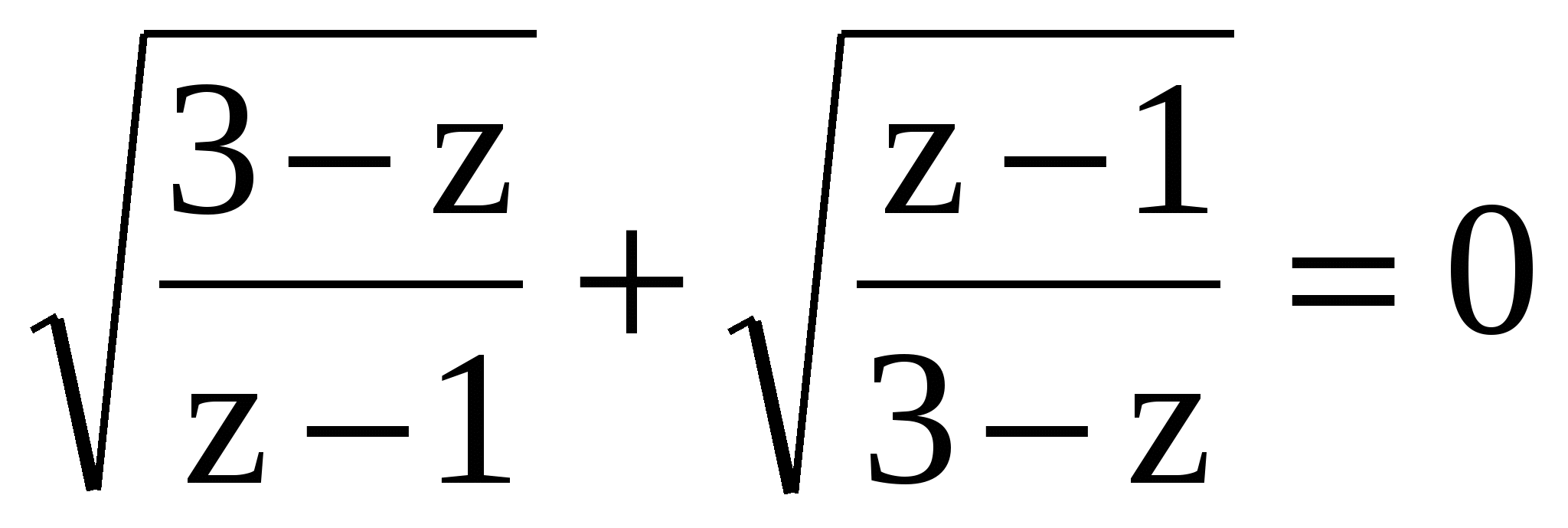