Относительность движения. Видеоурок. Физика 10 Класс
Можно ли быть неподвижным и при этом двигаться быстрее автомобиля Формулы 1? Оказывается, можно. Любое движение зависит от выбора системы отсчета, то есть любое движение относительно. Тема сегодняшнего урока: «Относительность движения. Закон сложения перемещений и скоростей». Мы узнаем, как выбрать систему отсчета в том или ином случае, как при этом найти перемещение и скорость тела.
Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени. В этом определении ключевой является фраза «относительно других тел». Каждый из нас относительно какой-либо поверхности неподвижен, но относительно Солнца мы совершаем вместе со всей Землей орбитальное движение со скоростью 30 км/с, то есть движение зависит от системы отсчета.
Система отсчета – совокупность системы координат и часов, связанных с телом, относительно которого изучается движение. Например, описывая движения пассажиров в салоне автомобиля, систему отсчета можно связать с придорожным кафе, а можно с салоном автомобиля или с движущимся встречным автомобилем, если мы оцениваем время обгона (рис. 1).

Рис. 1. Выбор системы отсчета
Какие же физические величины и понятия зависят от выбора системы отсчета?
1. Положение или координаты тела
Рассмотрим произвольную точку  . В различных системах она имеет разные координаты (рис. 2).
. В различных системах она имеет разные координаты (рис. 2).

Рис. 2. Координаты точки  в разных системах координат
в разных системах координат
2. Траектория
Рассмотрим траекторию точки, находящейся на пропеллере самолета, в двух системах отсчета: системе отсчета, связанной с пилотом, и системе отсчета, связанной с наблюдателем на Земле. Для пилота данная точка будет совершать круговое вращение (рис. 3).
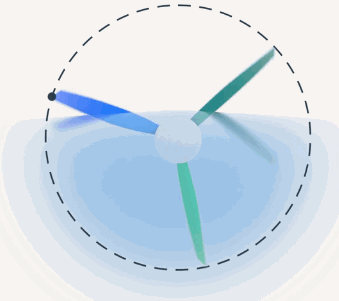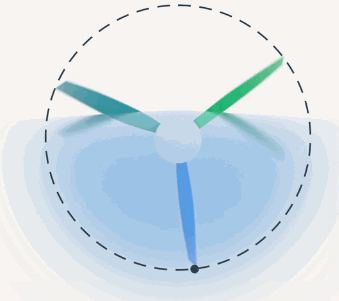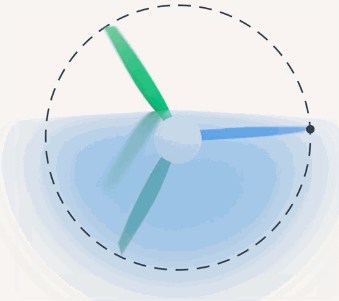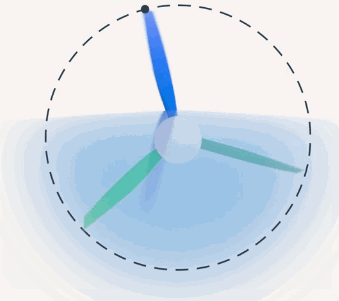
Рис. 3. Круговое вращение
В то время как для наблюдателя на Земле траекторией данной точки будет винтовая линия (рис. 4). Очевидно, что траектория зависит от выбора системы отсчета.

Рис. 4. Винтовая траектория
Относительность траектории. Траектории движения тела в различных системах отсчета
Рассмотрим, как меняется траектория движения в зависимости от выбора системы отсчета на примере задачи.
Задача
Какой будет траектория точки на конце пропеллера в разных СО?
1. В СО, связанной с летчиком самолета.
2. В СО, связанной с наблюдателем на Земле.
Решение:
1. Относительно самолета ни летчик, ни пропеллер не перемещаются. Для летчика траектория точки 

Рис. 5. Траектория точки  относительно летчика
относительно летчика
2. Для наблюдателя на Земле точка  движется двумя способами: вращаясь и двигаясь вперед. Траектория будет винтовой (рис. 6).
движется двумя способами: вращаясь и двигаясь вперед. Траектория будет винтовой (рис. 6).

Рис. 6. Траектория точки  относительно наблюдателя на Земле
относительно наблюдателя на Земле
Ответ: 1) окружность; 2) винтовая линия.
На примере данной задачи мы убедились, что траектория – это относительное понятие.
В качестве самостоятельной проверки предлагаем вам решить следующую задачу:
Какой будет траектория точки на конце колеса относительно центра колеса, если это колесо совершает поступательное движение вперед, и относительно точек, находящихся на земле (неподвижный наблюдатель)?
3. Перемещение и путь
Рассмотрим ситуацию, когда плывет плот и в какой-то момент с него спрыгивает пловец и стремится переправиться на противоположный берег. Перемещение пловца относительно рыбака, сидящего на берегу, и относительно плота будет разным (рис. 7).
Перемещение относительно земли называют абсолютным, а относительно движущегося тела – относительным. Перемещение движущегося тела (плота) относительно неподвижного тела (рыбака) называют переносным.
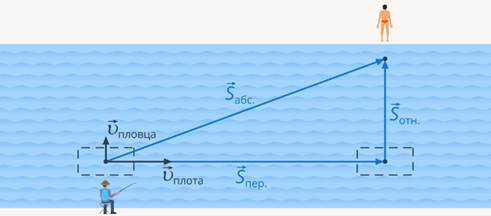
Рис. 7. Перемещение пловца
Из примера следует, что перемещение и путь являются относительными величинами.
4. Скорость
С помощью предыдущего примера можно легко показать, что скорость тоже относительная величина. Ведь скорость – это отношение перемещения ко времени. Время у нас одно и то же, а перемещение разное. Следовательно, скорость будет разной.
Зависимость характеристик движения от выбора системы отсчета называется относительностью движения.
В истории человечества были и драматичные случаи, связанные как раз с выбором системы отсчета. Казнь Джордано Бруно, отречение Галилео Галилея – все это следствия борьбы между сторонниками геоцентрической системы отсчета и гелиоцентрической системы отсчета. Уж очень сложно было человечеству привыкнуть к мысли о том, что Земля – это вовсе не центр мироздания, а вполне обычная планета. А движение можно рассматривать не только относительно Земли, это движение будет абсолютным и относительно Солнца, звезд или любых других тел. Описывать движение небесных тел в системе отсчета, связанной с Солнцем, намного удобнее и проще, это убедительно показали сначала Кеплер, а потом и Ньютон, который на основании рассмотрения движения Луны вокруг Земли вывел свой знаменитый закон всемирного тяготения.
Если мы говорим, что траектория, путь, перемещение и скорость являются относительными, то есть зависят от выбора системы отсчета, то про время мы этого не говорим. В рамках классической, или Ньютоновой, механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
Рассмотрим, как находить перемещение и скорость в одной системе отсчета, если они нам известны в другой системе отсчета.
Рассмотрим предыдущую ситуацию, когда плывет плот и в какой-то момент с него спрыгивает пловец и стремится переправиться на противоположный берег.
Как же связано перемещение пловца относительно неподвижной СО (связанной с рыбаком) с перемещением относительно подвижной СО (связанной с плотом) (рис. 8)?

Рис. 8. Иллюстрация к задаче
Перемещение в неподвижной системе отсчета мы назвали 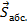 . Из треугольника векторов следует, что
. Из треугольника векторов следует, что  . Теперь перейдем к поиску соотношения между скоростями. Вспомним, что в рамках Ньютоновой механики время является абсолютной величиной (время во всех системах отсчета течет одинаково). Значит, каждое слагаемое из предыдущего равенства можно разделить на время. Получаем:
. Теперь перейдем к поиску соотношения между скоростями. Вспомним, что в рамках Ньютоновой механики время является абсолютной величиной (время во всех системах отсчета течет одинаково). Значит, каждое слагаемое из предыдущего равенства можно разделить на время. Получаем:


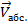 – это скорость, с которой движется пловец для рыбака;
– это скорость, с которой движется пловец для рыбака;
 – это собственная скорость пловца;
– это собственная скорость пловца;
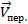 – это скорость плота (скорость течения реки).
– это скорость плота (скорость течения реки).
Задача на закон сложения скоростей
Рассмотрим закон сложения скоростей на примере задачи.
Задача
Два автомобиля движутся навстречу друг другу: первый автомобиль со скоростью 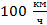
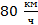 . С какой скоростью сближаются автомобили (рис. 9)?
. С какой скоростью сближаются автомобили (рис. 9)?
Рис. 9. Иллюстрация к задаче
Решение
Применим закон сложения скоростей. Для этого перейдем от привычной СО, связанной с Землей, к СО, связанной с первым автомобилем. Таким образом, первый автомобиль становится неподвижным, а второй движется к нему со скоростью 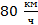 (относительная скорость). С какой скоростью, если первый автомобиль неподвижен, вращается вокруг первого автомобиля Земля? Она вращается со скоростью
(относительная скорость). С какой скоростью, если первый автомобиль неподвижен, вращается вокруг первого автомобиля Земля? Она вращается со скоростью 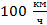
 .
.Ответ: 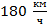 .
.
Границы применимости закона сложения скоростей. Закон сложения скоростей в теории относительности
Долгое время считалось, что классический закон сложения скоростей справедлив всегда и применим ко всем системам отсчета. Однако порядка 
Представьте себе, что вы находитесь на космической ракете, которая движется со скоростью 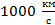 . И капитан космической ракеты включает фонарик в направлении движения ракеты (рис. 10). Скорость распространения света в вакууме составляет
. И капитан космической ракеты включает фонарик в направлении движения ракеты (рис. 10). Скорость распространения света в вакууме составляет  . Какой же будет скорость света для неподвижного наблюдателя на Земле? Будет ли она равна сумме скоростей света и ракеты?
. Какой же будет скорость света для неподвижного наблюдателя на Земле? Будет ли она равна сумме скоростей света и ракеты?

Рис. 10. Иллюстрация к задаче
Дело в том, что тут физика сталкивается с двумя противоречащими концепциями. С одной стороны, согласно электродинамике Максвелла, максимальная скорость – это скорость света, и она равна  . С другой стороны, согласно механике Ньютона, время является абсолютной величиной. Задача решилась, когда Эйнштейн предложил специальную теорию относительности, а точнее ее постулаты. Он первым предположил, что время не является абсолютным. То есть где-то оно течет быстрее, а где-то медленнее. Конечно, в нашем мире небольших скоростей мы не замечаем данный эффект. Для того чтобы почувствовать эту разницу, нам необходимо двигаться со скоростями, близкими к скорости света. На основании заключений Эйнштейна был получен закон сложения скоростей в специальной теории относительности. Он выглядит следующим образом:
. С другой стороны, согласно механике Ньютона, время является абсолютной величиной. Задача решилась, когда Эйнштейн предложил специальную теорию относительности, а точнее ее постулаты. Он первым предположил, что время не является абсолютным. То есть где-то оно течет быстрее, а где-то медленнее. Конечно, в нашем мире небольших скоростей мы не замечаем данный эффект. Для того чтобы почувствовать эту разницу, нам необходимо двигаться со скоростями, близкими к скорости света. На основании заключений Эйнштейна был получен закон сложения скоростей в специальной теории относительности. Он выглядит следующим образом:

 – это скорость относительно неподвижной СО;
– это скорость относительно неподвижной СО;
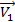 – это скорость относительно подвижной СО;
– это скорость относительно подвижной СО;
 – это скорость подвижной СО относительно неподвижной СО.
– это скорость подвижной СО относительно неподвижной СО.
Если подставить значения из нашей задачи, то получим, что скорость света для неподвижного наблюдателя на Земле будет составлять  .
.
Противоречие было решено. Также можно убедиться, что если скорости очень малы по сравнению со скоростью света, то формула для теории относительности переходит в классическую формулу для сложения скоростей.
В большинстве случаев мы будем пользоваться классическим законом.
Сегодня мы выяснили, что движение зависит от системы отсчета, что скорость, путь, перемещение и траектория – это понятия относительные. А время в рамках классической механики – понятие абсолютное. Научились применять полученные знания, разобрав некоторые типовые примеры.
Список литературы
- Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) – М.: Мнемозина, 2012.
- Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Мнемозина, 2014.
- Кикоин И.К., Кикоин А.К. Физика – 9, Москва, Просвещение, 1990.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Class-fizika.narod.ru (Источник).
- Интернет-портал Nado5.ru (Источник).
- Интернет-портал Fizika.ayp.ru (Источник).
Домашнее задание
- Дать определение относительности движения.
- Какие физические величины зависят от выбора системы отсчета?
interneturok.ru
Мгновенная скорость. Сложение скоростей
Самым простым видом механического движения является прямолинейное движение с постоянной по модулю и направлению скоростью:

Однако не будем забывать о том, что равномерно движение — это модель реального движения. В действительности же реальные тела чаще всего движутся не равномерно. Например, все вы знаете, что автомобиль в начале своего движения из состояния покоя постепенно увеличивает свою скорость. Где-то в середине пути он, возможно, будет недолго двигаться с постоянной скоростью. А при торможении его скорость будет постепенно уменьшаться. То есть движение автомобиля является неравномерным. Поэтому описать его с помощью уравнения движения мы не можем, так как скорость тела постоянно меняется.
Но нам на помощь приходить понятие мгновенной скорости, то есть скорости точки в данный момент времени (или в данной точке траектории).

Чтобы понять, как определяется мгновенная скорость, рассмотрим неравномерное движение материальной точки по криволинейной траектории. Пусть в некоторый момент времени t она занимает положение М. А спустя некоторый промежуток времени Δt1 — положение М1.
Укажем на рисунке перемещение, которое совершила точка за этот промежуток времени.

Если теперь мы с вами разделим это перемещение на промежуток времени, в течение которого оно произошло, то тем самым найдём такую скорость равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы попасть из начального положения в конечное за определённый промежуток времени. Эта скорость называется средней скоростью перемещения. Она показывает, какое перемещение в среднем совершала точка за единицу времени.

Направление этой скорости совпадает с направлением вектора перемещения точки.
Но как же нам определить скорость точки в положении М? Давайте попробуем уменьшить рассматриваемый промежуток времени. Из рисунка видим, что в этом случае точка совершит меньшее перемещение. Средняя же скорость точки на этом участке хотя и не равна скорости в точке М, но уже ближе к ней.

Если мы продолжим уменьшать промежутки времени и,
соответственно, перемещения, то очень скоро мы придём к тому, что средние
скорости будут незначительно отличаться друг от друга и от скорости точки в
положении М. В конце концов промежуток времени станет так мал, что можно
будет пренебречь изменением скорости за это время. Следовательно, при
стремлении промежутка времени к нулю отношение  будет
стремиться к своему некоторому предельному значению.
будет
стремиться к своему некоторому предельному значению.
Физическая векторная величина, равная пределу отношения перемещения к промежутку времени, в течение которого это перемещение произошло, при стремлении промежутка времени к нулю, называется мгновенной скоростью:

Направление вектора мгновенной скорости зависит от вида движения точки. Так, если точка движется прямолинейно, то направление мгновенной скорости совпадает с направлением движения. А вот в случае криволинейного движения вектор мгновенной скорости направлен по касательной к траектории.

В этом легко убедиться, если понаблюдать за раскалёнными частицами, отрывающимися от точильного камня. Или за частицами грязи, вылетающими из-под колеса буксующего автомобиля.

Для описания неравномерного движения точки, помимо понятия средней скорости перемещения, в физике чаще используют понятие средней путевой скорости. Она определяется отношением пути к промежутку времени, за который этот путь пройдён:

Проще говоря, средняя путевая скорость показывает, какой путь в среднем проходило тело за единицу времени.
Однако не стоит забывать о том, что средняя путевая скорость характеризует движение за весь промежуток времени в целом. Например, когда мы слышим, что расстояние между двумя городами автомобиль преодолел за 5 ч со скоростью 100 км/ч, мы понимаем, что в среднем он за каждый час проезжал сто километров. Но во время движения он мог заехать на заправку, где-то двигаться с бо́льшей или меньшей скоростью. Иными словами, средняя путевая скорость не даёт информации о скорости движения точки в каждый момент времени.

Для примера давайте с вами определим среднюю путевую скорость движения точки, если первую половину пути она преодолела со скоростью 15 м/с, а вторую — со скоростью 25 м/с.

Мы уже с вами не раз говорили о том, что характер движения точки зависит от того, относительно каких тел мы рассматриваем это движение (то есть от выбора системы отсчёта). Но так как тело отсчёта мы можем выбирать совершенно произвольно, то положение одного и того же тела можно одновременно рассматривать в разных системах координат.
Рассмотрим такой опыт. Пусть у нас есть стеклянная трубка, заполненная вязкой жидкостью. Опустим в неё тяжёлый шарик и будем перемещать трубку относительно школьной доски в горизонтальном направлении, не меняя ориентации трубки. Одновременно будем наблюдать за движением шарика и отмечать его положения через равные интервалы времени.

Теперь выберем две системы координат: одну свяжем с доской и назовём неподвижной, а вторую — с трубкой и назовём движущейся.
Из рисунка видно, что перемещение точки относительно неподвижной системы отсчёта равно векторной сумме её перемещения относительно движущейся системы и перемещения движущейся системы отсчёта относительно неподвижной:

В этом состоит принцип независимости движений.
Теперь разделим записанное нами уравнение на промежуток времени, в течение которого произошли эти перемещения:

И учтём, что отношения перемещений к промежутку времени равны скоростям:

Таким образом получаем, что скорость тела относительно неподвижной системы отсчёта равна векторной сумме его скорости относительно подвижной системы отсчёта и скорости подвижной системы отсчёта относительно неподвижной.
Данное утверждение называется законом сложения скоросте́й Галилея. Он справедлив как для равномерного, так и для неравномерного движения. Только в этом случае складываются мгновенные скорости.
Однако этот закон нельзя применять для точек, движение которых происходит со скоростями, близкими к скорости света в вакууме.
Для примера решим такую задачу. На какой угол следует отклонится от перпендикуляра к течению реки и сколько времени нужно плыть на лодке, чтобы пересечь реку перпендикулярно её течению, если скорость лодки относительно воды 3 м/с, скорость течения реки — 1,5 м/с, а ширина русла — 400 м?

videouroki.net
Физика. 10 класс — Конспекты
Физика. 10 класс — Конспекты
«Физика — 10 класс»
По учебнику «Физика. 10 класс» — базовый и профил. уровни, авторы Мякишев, Буховцев, Сотский.
Введение
Физика и познание мира ………. смотреть
Механика ………. смотреть
КИНЕМАТИКА
Кинематика точки и твёрдого тела
§ 1. Механическое движение. Система отсчёта ………. смотреть
§ 2. Способы описания движения ………. смотреть
§ 3. Траектория. Путь. Перемещение ………. смотреть
§ 4. Равномерное прямолинейное движение. Скорость. Уравнение движения ………. смотреть
§ 5. Примеры решения задач по теме «Равномерное прямолинейное движение» ………. смотреть
§ 6. Сложение скоростей ………. смотреть
§ 7. Примеры решения задач по теме «Сложение скоростей» ………. смотреть
§ 8. Мгновенная и средняя скорости ………. смотреть
§ 9. Ускорение ………. смотреть
§ 10. Движение с постоянным ускорением ………. смотреть
§ 11. Определение кинематических характеристик движения с помощью графиков ………. смотреть
§ 12. Примеры решения задач по теме «Движение с постоянным ускорением» ………. смотреть
§ 13. Движение с постоянным ускорением свободного падения ………. смотреть
§ 14. Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» ………. смотреть
§ 15. Равномерное движение точки по окружности ………. смотреть
§ 16. Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение ………. смотреть
§ 16. Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями ………. смотреть
§ 17. Примеры решения задач по теме «Кинематика твёрдого тела» ………. смотреть
ДИНАМИКА
Законы механики Ньютона
§ 18. Основное утверждение механики ………. смотреть
§ 19. Сила ………. смотреть
§ 19. Инертность тела. Масса. Единица массы ………. смотреть
§ 20. Первый закон Ньютона ………. смотреть
§ 21. Второй закон Ньютона ………. смотреть
§ 22. Принцип суперпозиции сил ………. смотреть
§ 23. Примеры решения задач по теме «Второй закон Ньютона» ………. смотреть
§ 24. Третий закон Ньютона ………. смотреть
§ 25. Геоцентрическая система отсчёта ………. смотреть
§ 26. Принцип относительности Галилея. Инвариантные и относительные величины ………. смотреть
Силы в механике
§ 27. Силы в природе ………. смотреть
§ 28. Сила тяжести и сила всемирного тяготения ………. смотреть
§ 29. Сила тяжести на других планетах ………. смотреть
§ 30. Примеры решения задач по теме «Закон всемирного тяготения» ………. смотреть
§ 31. Первая космическая скорость ………. смотреть
§ 32. Примеры решения задач по теме «Первая космическая скорость» ………. смотреть
§ 33. Вес. Невесомость ………. смотреть
§ 34. Деформация и силы упругости. Закон Гука ………. смотреть
§ 35. Примеры решения задач по теме «Силы упругости. Закон Гука» ………. смотреть
§ 36. Силы трения ………. смотреть
§ 37. Примеры решения задач по теме «Силы трения» ………. смотреть
§ 37. Примеры решения задач по теме «Силы трения» (продолжение) ………. смотреть
ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
Закон сохранения импульса
§ 38. Импульс материальной точки ………. смотреть
§ 38. Закон сохранения импульса ………. смотреть
§ 38. Реактивное движение. Успехи в освоении космоса ………. смотреть
§ 39. Примеры решения задач по теме «Закон сохранения импульса» ………. смотреть
Закон сохранения энергии
§ 40. Механическая работа и мощность силы ………. смотреть
§ 41. Энергия. Кинетическая энергия ………. смотреть
§ 42. Примеры решения задач по теме «Кинетическая энергия и её изменение» ………. смотреть
§ 43. Работа силы тяжести. Консервативные силы ………. смотреть
§ 43. Работа силы упругости. Консервативные силы ………. смотреть
§ 44. Потенциальная энергия ………. смотреть
§ 45. Закон сохранения энергии в механике ………. смотреть
§ 46. Работа силы тяготения. Потенциальная энергия в поле тяготения ………. смотреть
§ 47. Примеры решения задач по теме «Закон сохранения механической энергии» ………. смотреть
Динамика вращательного движения абсолютно твёрдого тела
-
§ 48. Основное уравнение динамики вращательного движения ………. смотреть
§ 49. Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси ………. смотреть
§ 50. Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела» ………. смотреть
СТАТИКА
Равновесие абсолютно твёрдых тел
§ 51. Равновесие тел ………. смотреть
§ 52. Примеры решения задач по теме «Равновесие твёрдых тел» ………. смотреть
МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕПЛОВЫЕ ЯВЛЕНИЯ
Почему тепловые явления изучаются в молекулярной физике ………. смотреть
Основы молекулярно-кинетической теории
§ 53. Основные положения молекулярно-кинетической теории. Размеры молекул ………. смотреть
§ 54. Примеры решения задач по теме «Основные положения МКТ» ………. смотреть
§ 55. Броуновское движение ………. смотреть
§ 56. Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел ………. смотреть
Молекулярно-кинетическая теория идеального газа
§ 57. Идеальный газ в МКТ. Среднее значение квадрата скорости молекул ………. смотреть
§ 57. Основное уравнение молекулярно-кинетической теории газов ………. смотреть
§ 58. Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» ………. смотреть
§ 59. Температура и тепловое равновесие ………. смотреть
§ 60. Определение температуры. Энергия теплового движения молекул ………. смотреть
§ 60. Абсолютная температура. Температура — мера средней кинетической энергии молекул ………. смотреть
§ 61. Измерение скоростей молекул газа ………. смотреть
§ 62. Примеры решения задач по теме «Энергия теплового движения молекул» ………. смотреть
Уравнение состояния идеального газа. Газовые законы
§ 63. Уравнение состояния идеального газа ………. смотреть
§ 64. Примеры решения задач по теме «Уравнение состояния идеального газа» ………. смотреть
§ 65. Газовые законы ………. смотреть
§ 66. Примеры решения задач по теме «Газовые законы» ………. смотреть
§ 67. Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов» ………. смотреть
Взаимные превращения жидкостей и газов
§ 68. Насыщенный пар ………. смотреть
§ 69. Давление насыщенного пара ………. смотреть
§ 70. Влажность воздуха ………. смотреть
§ 71. Примеры решения задач по теме «Насыщенный пар. Влажность воздуха» ………. смотреть
Твёрдые тела
§ 72. Кристаллические тела ………. смотреть
§ 72. Аморфные тела ………. смотреть
Основы термодинамики
§ 73. Внутренняя энергия ………. смотреть
§ 74. Работа в термодинамике ………. смотреть
§ 75. Примеры решения задач по теме «Внутренняя энергия. Работа» ………. смотреть
§ 76. Количество теплоты. Уравнение теплового баланса ………. смотреть
§ 77. Примеры решения задач по теме: «Количество теплоты. Уравнение теплового баланса» ………. смотреть
§ 78. Первый закон термодинамики ………. смотреть
§ 79. Применение первого закона термодинамики к различным процессам ………. смотреть
§ 80. Примеры решения задач по теме: «Первый закон термодинамики» ………. смотреть
§ 81. Второй закон термодинамики ………. смотреть
§ 81. Статистический характер второго закона термодинамики ………. смотреть
§ 82. Принцип действия тепловых двигателей. Коэффициент полезного действия (КПД) тепловых двигателей ………. смотреть
§ 83. Примеры решения задач по теме: «КПД тепловых двигателей» ………. смотреть
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
Что такое электродинамика ………. смотреть
Электростатика
§ 84. Электрический заряд и элементарные частицы. Закон сохранения заряда ………. смотреть
§ 85. Закон Кулона. Единица электрического заряда ………. смотреть
§ 86. Примеры решения задач по теме «Закон Кулона» ………. смотреть
§ 87. Близкодействие и действие на расстоянии ………. смотреть
§ 88. Электрическое поле ………. смотреть
§ 89. Напряжённость электрического поля. Силовые линии ………. смотреть
§ 90. Поле точечного заряда и заряженного шара. Принцип суперпозиции полей ………. смотреть
§ 91. Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» ………. смотреть
§ 92. Проводники в электростатическом поле ………. смотреть
§ 92. Диэлектрики в электростатическом поле ………. смотреть
§ 93. Потенциальная энергия заряженного тела в однородном электростатическом поле ………. смотреть
§ 94. Потенциал электростатического поля и разность потенциалов ………. смотреть
§ 95. Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности ………. смотреть
§ 96. Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» ………. смотреть
§ 97. Электроёмкость. Единицы электроёмкости. Конденсатор ………. смотреть
§ 98. Энергия заряженного конденсатора. Применение конденсаторов ………. смотреть
§ 99. Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора» ………. смотреть
Законы постоянного тока
§ 100. Электрический ток. Сила тока ………. смотреть
§ 101. Закон Ома для участка цепи. Сопротивление ………. смотреть
§ 102. Электрические цепи. Последовательное и параллельное соединения проводников ………. смотреть
§ 103. Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» ………. смотреть
§ 104. Работа и мощность постоянного тока ………. смотреть
§ 105. Электродвижущая сила ………. смотреть
§ 106. Закон Ома для полной цепи ………. смотреть
§ 107. Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи» ………. смотреть
Электрический ток в различных средах
§ 108. Электрическая проводимость различных веществ. Электронная проводимость металлов ………. смотреть
§ 109. Зависимость сопротивления проводника от температуры. Сверхпроводимость ………. смотреть
§ 110. Электрический ток в полупроводниках. Собственная и примесная проводимости ………. смотреть
§ 111. Электрический ток через контакт полупроводников с разным типом проводимости. Транзисторы ………. смотреть
§ 112. Электрический ток в вакууме. Электронно-лучевая трубка ………. смотреть
§ 113. Электрический ток в жидкостях. Закон электролиза ………. смотреть
§ 114. Электрический ток в газах. Несамостоятельный и самостоятельный разряды ………. смотреть
§ 115. Плазма ………. смотреть
§ 116. Примеры решения задач по теме «Электрический ток в различных средах» ………. смотреть
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
class-fizika.ru
Новые видеоуроки по физике — 10 класс
Новые видеоуроки по физике — 10 класс
Кинематика
1. Что такое механика ………. смотреть
2. Движение точки тела. Способы описания движения ………. смотреть
3. Уравнение равномерного прямолинейного движения ………. смотреть
4. Мгновенная скорость. Сложение скоростей ………. смотреть
5. Ускорение. Движение с постоянным ускорением. Единица ускорения ………. смотреть
6. Уравнение движения с постоянным ускорением ………. смотреть
7. Равномерное движение точки по окружности ………. смотреть
Динамика
8. Исаак Ньютон ………. смотреть
9. Первый закон Ньютона. Инерциальные системы отсчета ………. смотреть
10. Взаимодействие тел. Второй закон Ньютона ………. смотреть
11. Третий закон Ньютона. Понятие о системе единиц ………. смотреть
12. Силы в природе. Закон всемирного тяготения ………. смотреть
13. Первая космическая скорость. Сила тяжести и вес. Невесомость ………. смотреть
14. Деформация и силы упругости. Закон Гука ………. смотреть
15. Силы трения между соприкасающимися поверхностями твердых тел ………. смотреть
Законы сохранения в механике
16. Другая формулировка второго закона Ньютона ………. смотреть
17. Закон сохранения импульса. Реактивное движение ………. смотреть
18. Работа силы. Мощность ………. смотреть
19. Энергия. Кинетическая энергия и её изменение ………. смотреть
20. Работа силы тяжести. Работа силы упругости. Потенциальная энергия ………. смотреть
21. Закон сохранения энергии в механике ………. смотреть
Статика
22. Равновесие тел. Первое условие равновесия твердого тела ………. смотреть
23. Момент силы. Второе условие равновесия твёрдого тела ………. смотреть
Молекулярная физика. Тепловые явления
24. Основные положения молекулярно-кинетической теории ………. смотреть
25. Масса молекул. Количество вещества ………. смотреть
26. Броуновское движение. Силы взаимодействия молекул ………. смотреть
27. Строение газообразных, жидких и твердых тел ………. смотреть
28. Идеальный газ в молекулярно-кинетической теории ………. смотреть
29. Решение задач на основное уравнение МКТ идеального газа ………. смотреть
30. Температура и тепловое равновесие. Определение температуры ………. смотреть
31. Абсолютная температура ………. смотреть
32. Измерение скоростей молекул газа ………. смотреть
33. Уравнение состояния идеального газа ………. смотреть
34. Газовые законы. Изопроцессы ………. смотреть
35. Насыщенный пар. Зависимость давления пара от температуры ………. смотреть
36. Влажность воздуха и её измерение ………. смотреть
37. Строение и свойства кристаллических и аморфных тел ………. смотреть
38. Внутренняя энергия ………. смотреть
39. Работа в термодинамике ………. смотреть
40. Количество теплоты ………. смотреть
41. Первый закон термодинамики ………. смотреть
42. Необратимость процессов в природе ………. смотреть
43. Принципы действия тепловых двигателей. КПД. КПД тепловых двигателей ………. смотреть
Основы электродинамики
44. Электрический заряд и элементарные частицы ………. смотреть
45. Электрическое поле. Принцип суперпозиции полей ………. смотреть
46. Силовые линии электрического поля ………. смотреть
47. Проводники в электростатическом поле ………. смотреть
48. Диэлектрики в электростатическом поле. Поляризация диэлектриков ………. смотреть
49. Потенциальная энергия заряженного тела в электростатическом поле ………. смотреть
50. Потенциал электростатического поля, разность потенциалов ………. смотреть
51. Связь между напряженностью электростатического поля и напряжением ………. смотреть
52. Электроёмкость. Единицы электроёмкости. Конденсаторы ………. смотреть
53. Электрический ток. Закон Ома для участка цепи ………. смотреть
54. Электрические цепи. Последовательное и параллельное соединение ………. смотреть
55. Работа и мощность постоянного тока ………. смотреть
56. Электродвижущая сила. Закон Ома для полной цепи ………. смотреть
57. Электрическая проводимость различных веществ ………. смотреть
58. Электрический ток через контакт полупроводников р и n типов ………. смотреть
59. Полупроводниковый диод. Транзистор ………. смотреть
60. Электрический ток в жидкостях. Закон электролиза ………. смотреть
61. Электрический ток в газах ………. смотреть
class-fizik.ru
Презентация к уроку по физике (9, 10 класс) на тему: Презентация «Классический закон сложения скоростей и перемещений»
Слайд 1
Относительность движения. Классический закон сложения скоростей и перемещений.Слайд 2
Классический закон сложения перемещений.
Слайд 3
Скорость тела параллельна скорости ПСО
Слайд 4
Y0X — неподвижная система координат Y I 0 I X I — подвижная система координат Перемещение тела относительно неподвижной системы отсчета Перемещение тела относительно подвижной системы отсчета Перемещение подвижной системы относительно неподвижной системы отсчета
Слайд 5
X 0 Y Y 0 X X l Y l
Слайд 6
Перемещение тела относительно неподвижной системы отсчета (абсолютное) равно векторной сумме перемещения тела относительно подвижной системы отсчета (относительное) и перемещения подвижной системы отсчета относительно неподвижной (переносное). Классический закон сложения перемещений
Слайд 7
X 0 y y 0 X X l Y l
Слайд 8
Если тело и подвижная система отсчета движутся в одном направлении , перемещение относительно неподвижной системы отсчета равно сумме перемещений подвижной системы отсчета и перемещения тела в подвижной системе отсчета. Частный случай:
Слайд 9
X 0 Y Y 0 X X l Y l
Слайд 10
x 0 y y 0 x X l Y l
Слайд 11
Если тело и подвижная система отсчета движутся в противоположных направлениях , перемещение относительно неподвижной системы отсчета равно разности перемещений подвижной системы отсчета и перемещения тела в подвижной системе отсчета. Частный случай:
Слайд 12
Классический закон сложения скоростей.
Слайд 13
Скорость тела относительно неподвижной системы отсчета Скорость тела относительно подвижной системы отсчета Скорость подвижной системы относительно неподвижной системы отсчета
Слайд 14
Скорость тела относительно неподвижной системы отсчета (абсолютная) равна векторной сумме скорости тела относительно подвижной системы отсчета (относительная) и скорости подвижной системы отсчета относительно неподвижной (переносная). Классический закон сложения скоростей
Слайд 15
X 0 Y Y 0 X X l Y l
Слайд 16
Если тело и подвижная система отсчета движутся в одном направлении , скорость относительно неподвижной системы отсчета равна сумме скоростей подвижной системы отсчета и тела в подвижной системе отсчета. Частный случай:
Слайд 17
X 0 Y Y 0 X X l Y l
Слайд 18
Если тело и подвижная система отсчета движутся в противоположных направлениях , скорость относительно неподвижной системы отсчета равна разности скоростей подвижной системы отсчета и тела в подвижной системе отсчета. Частный случай:
Слайд 19
Задача
Слайд 20
Сколько времени потребуется, чтобы на катере пройти расстояние 1,5км туда и обратно по реке, скорость течения которой V 1 =2км/ч, и по озеру(в стоячей воде), если скорость катера относительно воды в обоих случаях V 2 =8км/ч? Дано: S =1,5км V 1 =2км/ч V 2 =8км/ч t 1 — ? t 2 — ? Решение:
Слайд 21
Y 1 O 1 X 1 Y O X По течению
Слайд 23
Y 1 O 1 X 1 Y O X Против течения
Слайд 25
Дано: S =1,5км V 1 =2км/ч V 2 =8км/ч t 1 — ? t 2 — ? Решение:
Слайд 26
Дано: S =1,5км V 1 =2км/ч V 2 =8км/ч t 1 — ? t 2 — ? Решение:
Слайд 27
Y 1 O 1 X 1 Y O X По озеру туда
Слайд 28
Y 1 O 1 X 1 Y O X По озеру обратно
Слайд 29
Дано: S =1,5км V 1 =2км/ч V 2 =8км/ч t 1 — ? t 2 — ? Решение: Ответ: время движения по реке составляет 0,4 часа, по озеру 0,375 часа
Слайд 30
Скорость тела направлена под углом к скорости ПСО
Слайд 31
Y l 0 X l Y 0 X
nsportal.ru
Примеры решения задач по теме «Сложение скоростей»
Примеры решения задач по теме «Сложение скоростей»
«Физика — 10 класс»
При решении задач на эту тему прежде всего надо грамотно выбрать тело отсчёта, с которым связать неподвижную систему координат. Затем выбрать тело отсчёта, движущееся относительно первого, и связать с ним подвижную систему координат. В этих двух системах рассмотреть движение тела и записать закон сложения скоростей.
Задача 1.
Два поезда движутся равномерно друг за другом. Скорость первого равна 80 км/ч, а скорость второго — 60 км/ч. Определите скорость второго поезда относительно первого.
Р е ш е н и е.
Обозначим скорость первого поезда относительно земли через 1, а скорость второго поезда — через 2. Тогда согласно закону сложения скоростей (1.9)
2 = ‘2 + 1,
где ‘2 — искомая скорость второго поезда относительно первого. Отсюда
‘2 = 2 — 1.
Это сложение скоростей поясняется на рисунке 1.21. Из рисунка видно, что скорость второго поезда относительно первого направлена в сторону, противоположную направлению движения поездов, и второй поезд удаляется от первого. Проекция скорости ‘2 на ось ОХ равна
υ’2 = υ2 — υ1 = -20 км/ч.
Задача 2.
Скорость течения реки υ = 1,5 м/с. Определите модуль скорости υ1 катера относительно воды, если катер движется перпендикулярно к берегу со скоростью υ2 = 2 м/с относительно его.
Р е ш е н и е.
Согласно закону сложения скоростей (1.9)
2 = 2 — .
Отсюда скорость катера относительно воды
1 = 1 + .
Векторное сложение скоростей и 2 показано на рисунке 1.22.
Так как полученный треугольник скоростей прямоугольный, то 1 = 2,5 м/с.
Задача 3.
Самолёт, скорость которого относительно воздуха равна 300 км/ч, летит на север. Внезапно подул северо-западный ветер со скоростью 100 км/ч относительно земли. Определите, под каким углом к направлению на запад лётчик должен направлять самолёт, чтобы продолжать лететь на север, и чему при этом будет равна скорость самолёта относительно земли.
Р е ш е н и е.
Свяжем неподвижную систему отсчёта с землёй, а подвижную — с воздухом. Тогда согласно закону сложения скоростей скорость 2 самолёта относительно земли равна сумме скоростей ‘2 самолёта относительно воздуха и ветра относительно земли:
2 = ‘2 + (1)
На рисунке 1.23 показаны скорость ветра, скорость 2 самолёта и скорость ‘2 самолёта относительно земли. Мы направляем скорости так, чтобы проекции скорости самолёта относительно ветра и скорости ветра на оси ОХ были равны по модулю и направлены в противоположные стороны: ‘2x = —x. Соответственно
‘2cosα = cos45°. (2)
В проекции на ось OY уравнение (1) запишем в виде 2y = ‘2y + y.
Тогда 2y = ‘2sinα — sin45°, это искомая скорость самолёта.
Из уравнения (2) найдем угол α:
Подставим числовые значения: α = 76°.
Из уравнения (3) выразим sinα:
Скорость самолёта
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика — Физика, учебник для 10 класса — Класс!ная физика
Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»
class-fizika.ru
Цикл поурочных планов по физике за первую четверть (10 класс, ЕМН)
Задача № 4. Определите, под каким углом к горизонту необходимо выпустить снаряд с заданной скоростью, чтобы он попал в цель?См. Приложение 4, слайд 15,16
Проверим полученные результаты с помощью действующей модели.
(Данные задачи можно предложить в классах обладающих достаточной математической подготовке).
Для подведения окончательного итога изучения темы предлагаю пройти тестирование (компьютерноеПриложение 3 или с помощью раздаточного материала Приложение 5).
На последних слайдах презентации № 18,19, 20, 21 представлены кинофрагменты (см. Приложение 6):
Основная задача механики и движение тел брошенных под углом к горизонту,
Падение снарядов, брошенных с самолета,
Полет баллистических ракет,
Полет космических ракет.
Кинофрагменты можно использовать перед началом изучения темы для создания элемента заинтересованности, в середине – для обоснования рассмотрения данных видов движений или в конце – при подведении итогов.
Урок 5 Дата_____________
Решение задач
В задачах по элементарному курсу электромагнетизма можно выделить основные группы:
а) задачи о силовом действии ЭМ-поля на проводники с током и
б) задачи о силовом действии ЭМ-поля на движущиеся в нем заряженные частицы.
Плоское движенце заряженной частицы в однородном магнитном поле.
При движении заряженной частицы в магнитном поле на нее действует сила Лоренца, которая, как известно, направлена перпендикулярно вектору скорости частицы, поэтому эта сила работы не совершает. Следовательно, при движении частицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются — изменяется только направление вектора скорости частицы.
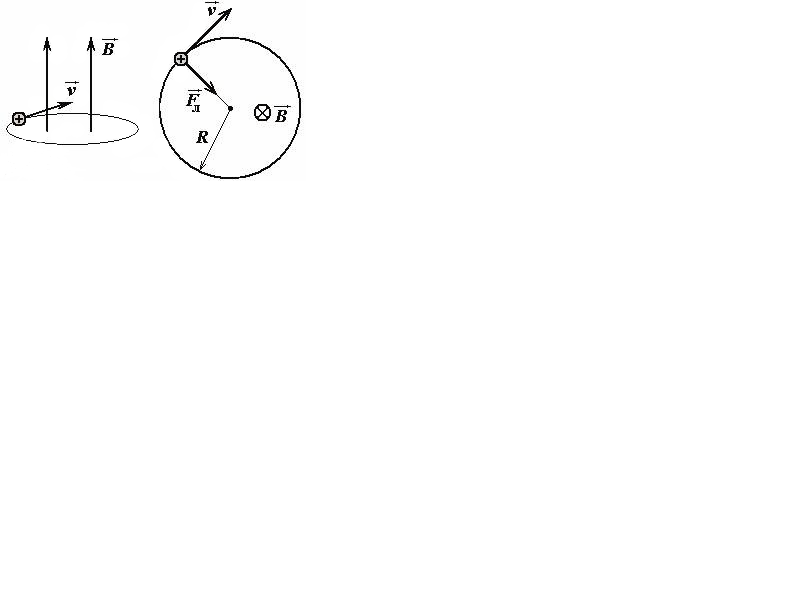
Рассмотрим движение заряженной частицы в однородном магнитном поле, когда вектор скорости частицы направлен перпендикулярно вектору индукции магнитного поля. Так как модуль скорости частицы сохраняется, сила Лоренца перпендикулярна вектору индукции поля, то вектор скорости все время будет перпендикулярен вектору индукции поля. Итак, модули векторов скорости и индукции постоянны, векторы перпендикулярны, следовательно, модуль силы Лоренца также будет оставаться постоянным и равным Fл = qυB. Сила Лоренца является центростремительной, она приводит к искривлению траектории, а, так ее модуль постоянен, то кривизна траектории частицы будет постоянна, то есть траекторией частицы будет окружность. Радиус этой окружности R можно найти на основании уравнения второго закона Ньютона.
из которого находим:
Найдем период обращения частицы в магнитном поле: .
Задача 1.
Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы при увеличении скорости движения?
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Решение:Радиус окружности по которой движется частицы зависит от скорости: . При увеличении скорости частицы радиус увеличится.
Период обращения частицы в магнитном поле не зависит от скорости частицы: , значит период останется прежним.
Кинетическая энергия зависит от скорости: , при увеличении скорости кинетическая энергия возрастает.
Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы при увеличении заряда частицы, если ее скорость не изменилась?
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Решение:Радиус окружности по которой движется частицы зависит от заряда частицы: . При увеличении заряда частицы радиус уменьшится.
Период обращения частицы в магнитном поле зависит от заряда частицы: , чем больше заряд частицы, тем период обращения меньше.
Кинетическая энергия зависит от скорости: от заряда не зависит.
Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы, если в этом поле с такой же скоростью движется частица массой 2m и зарядом q?
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Решение:Радиус окружности по которой движется частицы зависит от массы частицы: . При увеличении массы частицы в 2 раза радиус увеличится в 2 раза.
Период обращения частицы в магнитном поле зависит от массы частицы: , чем больше масса частицы, тем период обращения больше.
Кинетическая энергия зависит от скорости и массы частицы: , для частицы большей массы кинетическая энергия больше.
Домашние задание:
Урок 7 Дата_____________
Движение по окружности
Цели урока:
Изучить равномерное движение тела по окружности и познакомить учащихся с основными характеристиками данного движения.
Задачи урока:
Образовательная
(Обучающие: продолжить формирование представлений о движении тела; сформировать у учащихся представления о характеристиках равномерного движения по окружности. Развивающие: продолжить работу по формированию ключевых компетенций учащихся: умения сравнивать, анализировать, делать выводы из наблюдений, обобщать опытные данные на основе имеющихся знаний о движении тела;
развивать способность обобщать и представлять разнообразную информацию в рамках общей поставленной задачи;
формировать умения использовать основные понятия, формулы и физические законы движения тела при движении по окружности;
развивать физическое мышление учащихся через практическую деятельность; развивать умения сравнивать и анализировать.
Воспитывающие: воспитывать самостоятельность; научить детей сотрудничеству;
воспитывать уважение к мнению других (работа в группе)
Ход урока
1.Организационный момент
Актуализация знаний
В начале занятия давайте проведем физическую разминку. Повторим основные понятия кинематики.
Вопросы разминки:
Какое движение называют равномерным?
Что называют скоростью равномерного движения?
Какое движение называют равнопеременным?
Что такое ускорение тела?
Что такое путь и перемещение?
Какие типы траектории Вам известны?
При каком движении путь и перемещение совпадают? Не совпадают?
2. Объяснение нового материала
Действительно, при криволинейном движении путь и перемещение не совпадают. Давайте рассмотрим данное движение более подробно. Посмотрите внимательно на рисунок (слайд 1).
Мы видим, что движение по окружности — частный случай криволинейного движения.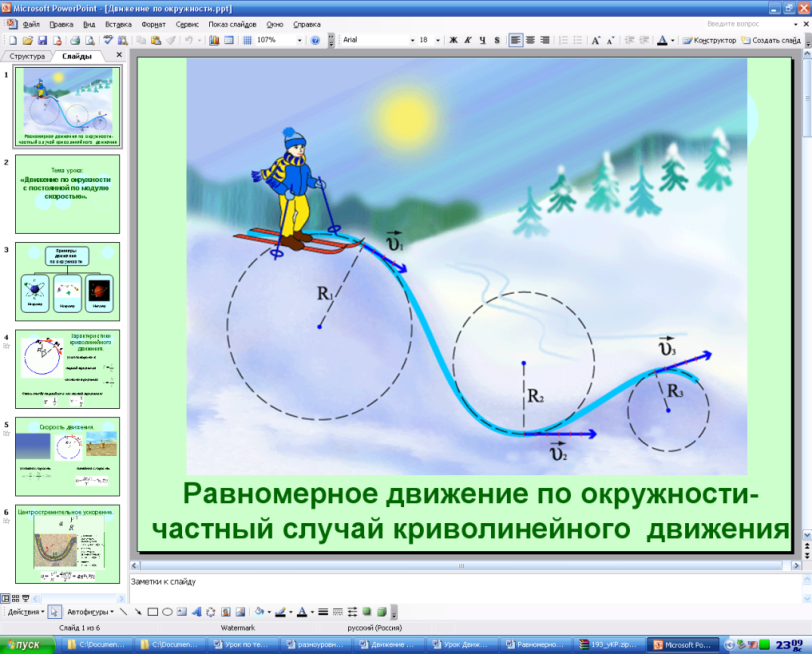
Итак, тема нашего урока: «Движение тела по окружности с постоянной по модулю скоростью» (слайд 2).
Какими же величинами можно охарактеризовать данное движение?
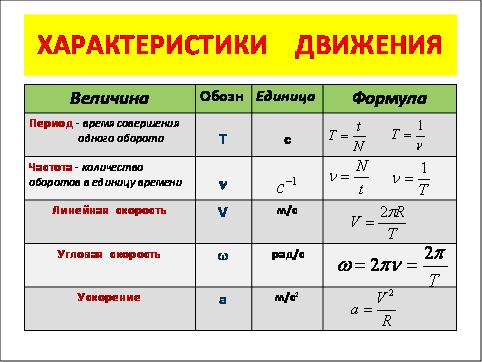
Скорость тела, направленную по касательной к окружности, называют линейной.
Если за любые равные промежутки времени радиус-вектор тела поворачивается на одинаковые углы, а линейная скорость тела по модулю не изменяется (т. е. если |v0|=|v|), движение тела по окружности называют равномерным (не следует забывать, что равномерное движение по окружности происходит с ускорением, так как скорость тела непрерывно меняется по направлению).
Угловой скоростью называют величину, равную отношению угла поворота радиуса-вектора точки, движущейся по окружности к промежутку времени t, в течение которого произошел этот поворот.
Мгновенная скорость тела в каждой точке криволинейной траектории направлена по касательной к траектории. Следовательно, в криволинейном движении направление скорости тела непрерывно изменяется. т.е. движение по окружности со скоростью, постоянной по модулю является ускоренным. 
Исходя из данной информации: Какой вопрос у Вас возникает?
/Как направлено ускорение?
Как оно называется? Центростремительное ускорение всегда направлено к центру окружности.
4. физ. пауза.
5. Закрепление нового материала (22-25 минут)
1. Тело движется равномерно по окружности в направлении часовой стрелке. Как направлен вектор ускорения при таком движении?
2. Автомобиль движется на повороте по круговой траектории радиусом 50 м с постоянной по модулю скоростью 10 м/с. Каково ускорение автомобиля?
3. Тело движется по окружности радиусом 10 м. Период его вращения равен 20с. Чему равна скорость тела?
4.Тело движется по окружности радиусом 5м со скоростью 20 м/с. Чему равна частота вращения?
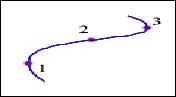
5. Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории центростремительное ускорение минимально?
Подведение итогов урока.
Домашнее задание -§
Урок 9 Дата_____________
Тема: Законы Ньютона. Динамика поступательного движения. Решение задач
Цели: изучить физическое содержание Второго закона Ньютона — основного закона динамики.
Демонстрации: взаимодействие магнитной стрелки компаса с постоянным магнитом; взаимодействие бруска и сжатой пружины.
Ход урока
I. Повторение. Проверка домашнего задания
При повторении изученного материала особое внимание необходимо уделить глубокому пониманию содержания первого закона Ньютона. Для этого, конечно, недостаточно формально пересказать содержание материала учебника.
Будет лучше, если повторение домашнего задания будет разбито на два этапа. На первом этапе два ученика могут ответить на вопросы к § 7. При этом нужно акцентировать внимание на правильном понимании реальных моделированных систем и их идеальных моделях. Точно такой же подход должен быть и в понимании инерциальных систем отсчета.
На втором этапе можно предложить ученикам ответить на ряд вопросов по теме, например:
— Может ли автомобиль двигаться по горизонтальному шоссе равномерно с выключенным двигателем?
— Парашютист равномерно спускается на землю. Действие каких сил скомпенсировано?
— Воздушный шарик, заполненный водородом, поднимается вверх. Какие силы действуют на шарик? Скомпенсированы ли они?
II. Изучение нового материала
План изложения нового материала:
1. Взаимодействие тел. Демонстрация опытов.
2. Сила как мера взаимодействия тел.
3. Второй закон Ньютона.
4. Расчет ускорения.
1. Переходя к изложению нового материала, следует обратить внимание, что в реальном мире, который нас окружает, практически не встречается изолированных тел. Следовательно, обычно тела взаимодействуют с другими, и не всегда при этом действие сил скомпенсировано.
Ранее было отмечено, что в качестве инерциальной системы отсчета можно выбирать систему, связанную с Землей. В этом случае первый закон Ньютона выполняется, если действие сил скомпенсировано.
Если рассмотреть на опыте поведение магнитной стрелки, то она выставляется определенным образом по магнитному полю Земли. Стоит только к компасу поднести постоянный магнит, как стрелка начинает менять свое положение. Значит, при этом появляется нескомпенсированная сила, выводящая стрелку из состояния покоя.
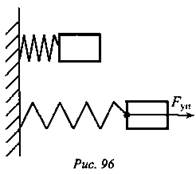
Если прикрепить брусок к сжатой пружине, а затем отпустить (см. рис. 96), тo брусок начнет двигаться по направлению силы упругости пружины.
2. Таким образом, говоря об изменении скорости тела, мы всегда подразумеваем обязательное взаимодействие тел, причем силы в этом случае нескомпенсированы.
Мерой взаимодействия тел между собой является векторная величина, I которая называется силой (F).
Основной единицей силы в системе СИ является ньютон (Н).
F = [H].
Если к телу сила не приложена, то тело не изменяет своего положения. Если тело до момента, когда F = 0, двигалось прямолинейно и равномерно, то в любой инерциальной системе отсчета такой тип движения сохранится.
В случае, когда F ≠ 0, тело начинает двигаться ускоренно. Так как масса тела m — мера инертности, то, наверное, значение ускорения должно зависеть и от массы m, и от величины силы F.
3. Ньютон установил связь между массой, силой и ускорением.
Это соотношение является Вторым законом Ньютона, его еще называют основным законом динамики:
Произведение массы тела на его ускорение равно силе, с которой на него действуют окружающие тела.
F = m · а .
Это — основное уравнение динамики поступательного движения.
Обычно к телу приложено несколько сил, и поэтому под силой F понимают равнодействующую всех сил, приложенных к телу.
Если Fp = 0, то тело покоится или движется прямолинейно и равномерно.
Если Fp ≠ 0, то тело всегда движется с ускорением.
4. Ускорение а всегда совпадает с направлением равнодействующей силы. Из второго закона Ньютона легко вывести:
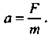
Отсюда:
а) ускорение тела прямо пропорционально силе, приложенной к телу;
б) ускорение тела обратно пропорционально массе тела. Вспомним, что сила в СИ измеряется в Ньютонах. Один Ньютон — это сила, под действием которой телу массой 1 кг, сообщается ускорение в 1 м/с2.
III. Закрепление изученного
С целью закрепления материала учитель может провести краткий опрос по изученной теме:
— От чего зависит ускорение тела?
— Как движется тело, когда векторная сумма действующих на него сил равна нулю?
— Под действием какой силы тело массой 1 кг приобретает ускорение 1 м/с2?
— Какая сила сообщает телу массой 5 кг ускорение 4 м/с2?
Для коллективного обсуждения учитель может предложить и пару более сложных задач:
1. Может ли равнодействующая трех равных по модулю сил, приложенная к одной точке, быть равной нулю?
2. При каком условии тело движется с постоянным ускорением?
Домашнее задание
Урок 10 Дата_____________
Вращательное движение твердого тела
Цель: сравнить два вида движения; линейная и угловая скорость.
Ход урока
I. Вопросы для повторения
1. Точка движется равномерно по окружности. Имеет ли она ускорение?
2. Куда направлено ускорение конца стрелки часов?
3. Может ли криволинейное движение происходить без ускорения?
II. Решение экспериментальных задач Оборудование: часы, магнитофон, линейка.
1. Определите частоту вращения секундной стрелки часов, линейную скорость и центростремительное ускорение ее конца и средней точки.
2. Определите скорость движения магнитофонной ленты при ее обратной перемотке.
3. Используя линейку и часы с секундной стрелкой, определите скорость движения магнитофонной ленты при записи или воспроизведении звука на магнитофоне. Найдите время записи. Результат проверьте прямыми измерениями (задания могут быть даны на дом).
III. Изучение нового материала
Чтобы изучить движение тела, т.е. изменение положения в пространстве, нужно, прежде всего, уметь определять само это положение. Каждое тело имеет определенные размеры, и, следовательно, разные точки тела находятся в разных местах пространства. Это не нужно тогда, когда все точки тела движутся одинаково. Например, движение чемодана, который мы поднимаем с пола.
Движение тела, при котором все его точки движутся одинаково, называется поступательным.
Тело движется поступательно, если оно одновременно не вращается и даже не поворачивается.
Вращением твердого тела вокруг неподвижной оси, называется такое движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, перпендикулярной плоскостям этих окружностей. Сама эта прямая есть ось вращения. В технике такой вид встречается часто: вращение валов двигателей, генераторов, колес.
Линейная и угловая скорость
Рассмотрим движение материальной точки М по окружности радиусом R. Положение точки на окружности в произвольный момент времени t однозначно определяется, если задан угол Д радиуса ОМ, проведенного к точке относительно некоторого неподвижного радиуса ОА, положение которого условно примем за нулевое (рис. 55).
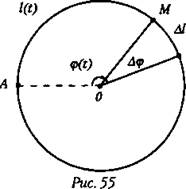
Положение точки может быть определено, если задана длина AM. Оба эти способа задания положения точки эквивалентны.
Пусть за малый промежуток времени Δt т. М проходит дугу длиной Δl, а радиус поворачивается на угол Δφ.
Линейная скорость: 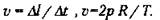
Угловая скорость: 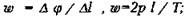
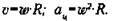
IV. Закрепление изученного
1. Что называют механическим движением?
2. Какое движение называют поступательным?
3. Какое движение называют вращательным?
4. Что называют линейной скоростью тела при движении его по окружности?
5. Что называют угловой скоростью?
6. Выведите формулу, выражающую зависимость между линейной и угловой скоростью.
Решение задач
1. Какова линейная скорость тела, движущегося равномерно по окружности радиусом 3 м, если центростремительное ускорение равно 12 см/с2.
2. Шкив вращается с угловой скоростью 50 рад/с. Определить центростремительное ускорение точек, находящихся на расстоянии 20 мм и 80 мм от оси вращения.
3. Проследите за проигрыванием граммофонной пластинки. Какова траектория кончика иглы: а) относительно корпуса проигрывателя; б) относительно пластинки; в) относительно головки звукоснимателя.
4. Измерьте частоту вращения и угловую скорость граммофонного диска. Что обозначают числа на шкале регулятора скорости? Одинакова ли линейная скорость граммофонной иглы относительно пластинки в начале и в конце проигрывания?
Домашнее задание
Урок 10 Дата_____________
Второй закон Ньютона для вращательного движения. Гироскоп
Цель: сформулировать три закона Ньютона. Побуждать учащихся к преодолению трудностей в процессе умственной деятельности, воспитать интерес к физике.
Ход урока
I. Организационный момент
II. Проверка домашнего задания. Повторение
1. Что изучает кинематика?
2. Какое движение называется центростремительным?
3. что такое линейная и угловая скорость?
4. Почему равномерное прямолинейное движение и состояние покоя физически эквивалентны и взаимозаменяемы лишь в инерциальных системах отсчета?
III. Изучение нового материала
Действия тел друг на друга, создающие ускорение, называются силами. Все силы можно разделить на два основных типа: силы, действующие при непосредственном соприкосновении, и силы, которые действуют независимо от того, соприкасаются тела или нет, т. е. на расстоянии.
Эксперимент 1
Возьмем в руки кусок мела, разожмем пальцы, и мел упадет. (Земля притягивает, действует на расстоянии.)
Эксперимент 2
Наэлектризованную палочку поднесем к висячей гильзе. Гильза притянется. (Взаимодействие на расстоянии.)
Эксперимент 3
Катнем мяч. (Непосредственное взаимодействие.)
Эксперимент 4 _
Демонстрация сегнетова колеса. (Взаимодействие.)
Наблюдая ускорение, полученное каким-либо телом под действием различных сил, видели, что ускорения могут оказаться различными как по модулю, так и по направлению. Сила векторная величина. Силу измеряют динамометром. Силы, действующие при непосредственном соприкосновении, действуют по всей соприкасающейся поверхности тел. Молоток, ударяющий по шляпке гвоздя, действует на всю шляпку. Но если площадь мала, то считают, тело действует на одну точку. Эта точка называется точкой приложения.
Если же на тело действует несколько сил, то их действие на тело можно заменить одной заменяющую силу называют суммой или равнодействующей.
I закон Ньютона
Материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны упругих тел не заставит ее (его) изменить это состояние.
Тело движется прямолинейно и равномерно, так как все действующие на него силы скомпенсированы. (Равнодействующая равна нулю.)
Во Вселенной практически невозможно найти тело, не испытывающее внешнего воздействия.
I закон — закон инерции. Непосредственно подтвердить экспериментально | его невозможно, он аксиоматичен. Однако можно объяснить ряд опытов, что является косвенным подтверждением справедливости этого закона.
Эксперимент 5
Монета, лежащая на плексигласе, закрывающем бутылку, при резком щелчке по плексигласу в горизонтальной плоскости монета упадет в бутылку. (Монета сохраняет состояние покоя по инерции.)
Следствие I закона Ньютона состоит в том, что тело может двигаться как при наличии, так и при отсутствии внешнего воздействия.
Эксперимент 6
Подвижная тележка прикреплена при помощи пружинного динамометра к перекинутой через нити с грузом на конце. Груз растягивает пружину, сообщающую своей силой упругости ускорение тележке. Чем больше подвешиваем груз, тем сильнее растянута пружина и тем больше ускорение тележки.
Опыт показывает, что направление ускорения совпадает с направлением силы, вызвавшей ускорение:
F = ma.
II закон Ньютона
Сила, действующая на тело, равна произведению массы тела на создаваемое этой силой ускорение, причем направления силы и ускорения совпадают: а =F/m
Закон можно выразить в другой форме. Ускорение, сообщаемое телу, прямо пропорционально действующей на тело силе,- обратно пропорционально массе тела и направлено так же, как и сила.
Особенности II закона Ньютона:
1. Верен для любых сил.
2. Сила — причина, определяет ускорение.
3. Вектор а сонаправлен с вектором F.
4. Если действуют на тело несколько сил, то берется равнодействующая.
5. Если равнодействующая равна нулю, то ускорение равно нулю. (Первый закон Ньютона)
6. Можно применять только по отношению к телам, скорость которых мала по сравнению со скоростью света.
III закон Ньютона
Эксперимент 7
Возьмем два динамометра, и зацепим друг за друга их крючки, и, взявшись за кольца, будем растягивать их, следя за показаниями обоих динамометров.
Что увидим? Показания будут совпадать. Сила, с которой первый действует на второй, равна силе, с которой второй действует на первый.
Эксперимент 8
Укрепим на одной тележке магнит, на другой — кусок железа и прикрепим к тележкам динамометры. Тележки могут оставаться на разном расстоянии друг от Друга, сила взаимодействия между магнитом и куском железа будет больше или меньше в зависимости от расстояния. Но во всех случаях окажется, что динамометры дадут одинаковые показания.
Силы, с которыми два тела действуют друг на друга, равны по модулю, противоположны по направлению и действуют вдоль прямой, соединяющей эти тела.
Fn = —Fn (III закон Ньютона.)
Особенности III закона Ньютона:
1. Силы возникают только парами.
2. Всегда при взаимодействии.
3. Только силы одной природы.
4. Не уравновешивают.
5. Верен для всех сил в природе.
IV. Закрепление изученного
1. Сформулируйте I закон Ньютона.
2. В чем состоит явление инерции?
3. Как движется тело, к которому приложена сила, постоянная по модулю и по направлению?
4. Как направлено ускорение тела, вызванное действующей на него силой.
5. Верно ли утверждение — силы есть, а ускорения нет.
6. Если на тело действует несколько сил, как определяется равнодействующая сил?
7. Запишите III закон Ньютона.
8. Как направлены ускорения взаимодействия между собой тел?
9. Выполняется ли III закон Ньютона при взаимодействии на расстоянии или только путем непосредственного контакта.
10. Запишите II закон Ньютона.
Домашняя работа
Урок 12 Дата_____________
Тема: «Закон всемирного тяготения. Движение в гравитационном поле»
Тип урока: комбинированный.
Цель урока – изучить закон всемирного тяготения, показать его практическую значимость. Шире раскрыть понятие взаимодействия тел на примере этого закона и ознакомить учащихся с областью действия гравитационных сил.
Задачи урока:
Оборудование к уроку:
компьютерный класс
полный интерактивный курс «Открытая астрономия»
1С: Репетитор
видеопроектор, экран
презентация учащихся (Приложение)
Домашнее задание: §15, упр15.
План урока:
1. Организация начала урока, объявление темы и цели урока – 3 мин.
2. Повторение пройденного материала по теме «Три закона Ньютона» – 7 мин.
3. Новый материал – 20 мин.
4. Работа с презентацией – 15 мин.
5. Работа с моделями в компьютерном классе – 42 мин.
6. Подведение итогов урока – 3 мин.
ХОД УРОКА
1-й урок ведет учитель физики.
1. Цель урока
– Сегодня на уроке мы с вами изучим закон всемирного тяготения, покажем его практическую значимость. Шире раскроем понятие взаимодействия тел на примере этого закона и ознакомимся с областью действия гравитационных сил.
2. Постановка проблемы
– Сможем ли мы сегодня на уроке определить массу Земли?
3. Повторение. Проверка домашнего задания
– Начнем с того, что мы уже знаем. Вспомним и отв
infourok.ru