Сложение скоростей
Ещё в младших классах вы сталкивались с тем, что иногда необходимо складывать скорости. Например, если две машины едут навстречу друг другу, то скорость их сближения — это сумма скоростей первой и второй машины.
Если же они двигаются в одном направлении, то скорость их сближения (или удаления) будет определяться разностью скоростей. Как мы уже говорили, решающее значение имеет выбор системы отсчёта.
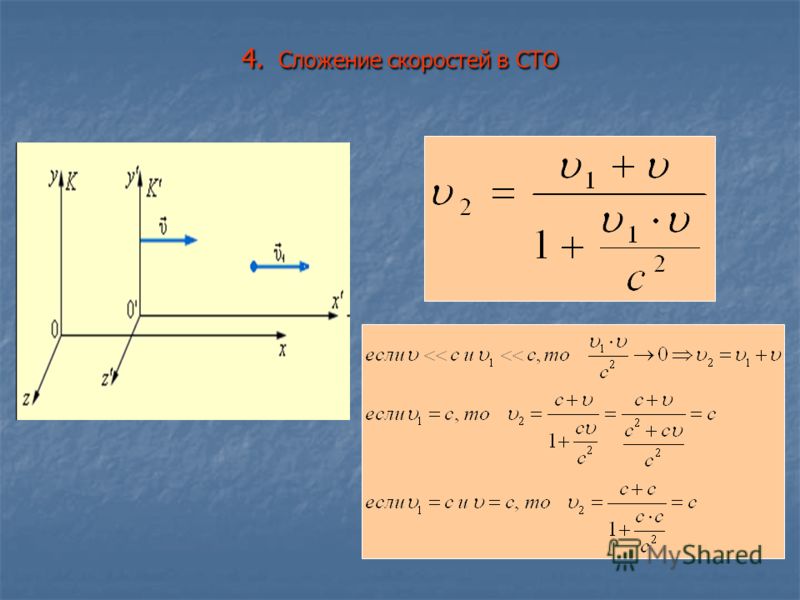
Закон сложения скоростей: если тело двигается со скоростью в системе отсчёта а система отсчёта двигается со скоростью в системе отсчёта , то скорость движения тела, относительно системы равна:
Напомним, что скорость — это векторная величина, поэтому, скорости складываются геометрически.
Пример решения задач.
Лодка двигается по реке с
собственной скоростью 8 м/с, так, как показано на рисунке.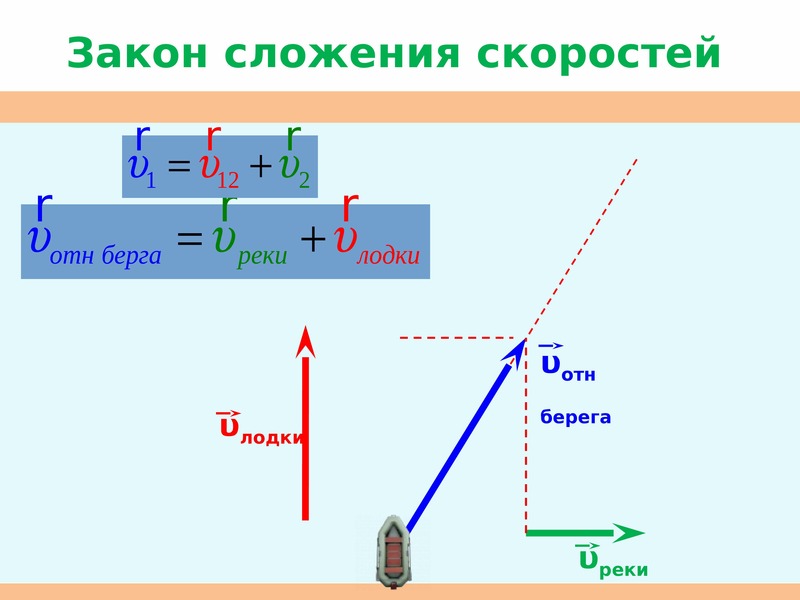
Расположим оси координат так, чтобы направление оси х совпадало с направлением течения реки. Тогда проекция скорости на ось х будет равна , т.к. на рисунке нам указан угол между направлением течения и скоростью лодки. Обратите внимание, что эта проекция будет отрицательной. В этом можно убедиться при построении проекции, да и чисто логически ясно, что лодка плывет против течения, а значит, одну из скоростей нужно обозначить за отрицательную. Проекция скорости течения на ось х, конечно же, будет равна 1 м/с, поскольку направление течение совпадает с направлением оси х. Тогда скорость движения лодки по оси х относительно берега равна:
Проекция вектора скорости лодки на ось у равнаРазумеется, проекция
скорости течения на ось у будет равна нулю, потому что вектор скорости
течения перпендикулярен этой оси. С помощью геометрической суммы проекций мы
можем найти модуль скорости лодки, относительно берега:
С помощью геометрической суммы проекций мы
можем найти модуль скорости лодки, относительно берега:
Давайте рассмотрим теперь пример, который научит вас складывать какие угодно скорости.
Найдём скорость машины, относительно самолёта в заданной системе координат. Сначала найдем проекции скорости машины на оси х и у. Точно так же, как и в предыдущем примере, проекция на ось х равна: , а проекция на ось у равна . Точно так же находим проекции скорости самолёта на координатные оси:
Напомним, что проекции являются скалярными величинами, поэтому их мы складываем алгебраически:
Теперь, когда мы нашли проекции скорости машины относительно самолёта на оси х и у, мы можем найти модуль скорости с помощью геометрической суммы:
Таким образом, мы
получили расчётную формулу для вычисления модуля скорости одного движущегося
тела, относительно другого движущегося тела. Эта формула справедлива для тех
случаев, когда оба тела двигаются в одной плоскости.
Эта формула справедлива для тех
случаев, когда оба тела двигаются в одной плоскости.
Заметим, что закон сложения скоростей справедлив и для неравномерного движения. В этом случае нужно складывать мгновенные скорости.
Пример решения задачи.
Задача. Мяч катится с постоянной скоростью 10 м/с. Ему наперерез бежит футболист со скоростью 7 м/с, так, как показано на рисунке. Через какое время футболист поймает мяч, если изначально между футболистом и мячом было 40 метров?
Начнём с того, что когда футболист поймает мяч, они будут находиться в одной точке. Расположим систему координат так, чтобы направление движения футболиста совпадало с направлением оси х. Тогда, скорость мяча будет направлена под углом 45о градусов к оси х. Сделаем проекции скорости мяча на оси х и у.
Конспект урока » Относительность движения,сложение скоростей.
 Мгновенная и средняя скорость.»10 класс
Мгновенная и средняя скорость.»10 классКласс | 10А | 10Б | 10В |
Дата |
Тема: Относительность движения,сложение скоростей.Мгновенная и средняя скорость.
Обучающая : объяснить понятие об относительности движения. Научить определять относительную скорость
Развивающая : развивать научность мышления , уметь применять знания .
Воспитывающая: формировать добросовестное отношение к учебному труду.
Ход урока.
Ι.Организационный момент.
ΙΙ. Повторение изученного материала.
Сам. работа (20 мин)
ΙΙI. Изучение новой темы.
1.Относительность движения.
Всякое движение относительно. Это означает, что одно и то же тело одновременно и движется, и покоится. Движется относительно одних тел и одновременно покоится относительно других. Мы все, земляне, можем покоиться относительно своего письменного стола и одновременно всегда движемся относительно Солнца.
В задачах на относительность движения часто приходится пользоваться правилом сложения скоростей. Правило сложения скоростей:скорость тела относительно неподвижной системы отсчета равна сумме скорости тела относительно подвижной системы отсчета и скорости самой подвижной системы относительно неподвижной, где
скорость тела относительно НСОскорость тела относительно ПСО
скорость ПСО относительно НС
Это правило применимо только к классическим скоростям, т. е. скоростям, значительно меньшим скорости света в вакууме (т.е. к скоростям порядка 106 м/с и меньше).
е. скоростям, значительно меньшим скорости света в вакууме (т.е. к скоростям порядка 106 м/с и меньше).
1) Если система отсчета и тело в ней движутся в одном направлении, то
Например, если поезд движется со скоростью 16 м/с относительно вокзала, а пассажир по ходу поезда бежит со скоростью 2 м/с относительно полок вагона, то скорость пассажира относительно вокзала равна 18 м/с.
2) Если система отсчета и тело в ней движутся в противоположных направлениях, то
Например, если в предыдущем примере пассажир будет бежать навстречу ходу поезда, то скорость, с которой он будет удаляться от вокзала, будет равна 14 м/с
3) Если в подвижной системе отсчета, движущейся со скоростью относительно неподвижной системы, тело станет двигаться со скоростью относительно подвижной системы под углом к направлению ее движения, то для определения модуля скорости тела относительно неподвижной системы придется применить теорему Пифагора или теорему косинусов — в зависимости от величины угла (рис. 10 а и б).
10 а и б).
Например, если скорость течения v0 =1 м/с, а лодка переплывает реку со скоростью v1 = 2 м/с относительно воды перпендикулярно берегу (рис. 10), то скорость лодки относительно берега будет, согласно теореме Пифагора, равна
!!! Если в условии сказано, что лодка переплывает реку по кратчайшему пути, значит, ее скорость относительно берега направлена перпендикулярно берегу, а скорость лодки относительно водынаправлена под тупым углом к вектору скорости течения (рис. 11). В таком случае скорость лодки относительно берега можно определить по теореме Пифагора:
а время t, за которое лодка переплывет реку шириной Н, двигаясь с этой скоростью, можно найти как отношение этой ширины к скорости лодки относительно берега:
Если говорится о минимальном времени, за которое лодка переплывет реку, то теперь перпендикулярно берегу надо направить вектор скорости лодки относительно воды под прямым углом к течению, как на рис. 12. В этом случае минимальное время t будет равно отношению ширины реки к скорости лодки относительно течения:Таким образом, если вам нужно переплыть реку как можно быстрее, значит, надо грести перпендикулярно течению.
12. В этом случае минимальное время t будет равно отношению ширины реки к скорости лодки относительно течения:Таким образом, если вам нужно переплыть реку как можно быстрее, значит, надо грести перпендикулярно течению.
4) Если два тела сближаются или удаляются друг от друга, т.е. движутся в противоположных направлениях со скоростями v1 и v2 относительно неподвижных объектов, то их скорость v относительно друг друга будет по модулю равна сумме их скоростей относительно неподвижных объектов:
5) Если два тела обгоняют друг друга, т.е. движутся в одном направлении со скоростями v1 и v2 относительно неподвижных объектов, то их скорость v относительно друг друга по модулю будет равна разности их скоростей относительно неподвижных объектов:
Например, если два поезда едут по параллельным рельсам навстречу друг другу со скоростями 36 км/ч и 74 км/ч относительно вокзала, то скорость их взаимного сближения, т.
А если они движутся по параллельным рельсам в одном направлении, т.е., например, если второй поезд, скорость которого равна 72 км/ч, обгоняет первый, скорость которого 36 км/ч, то скорость первого поезда относительно второго равна скорости второго минус скорость первого:
72 км/ч – 36 км/ч = 36 км/ч,
а скорость второго поезда относительно первого равна скорости
первого поезда минус скорость второго:36 км/ч – 72 км/ч = –36 км/ч.
6) Если два тела движутся со скоростями v 13, а), а чтобы найти скорость первого тела относительно второго, надо найти векторную разность (рис. 13, б).
13, а), а чтобы найти скорость первого тела относительно второго, надо найти векторную разность (рис. 13, б).
Для нахождения модуля относительной скорости можно применить теорему косинусов:
Если = 900, то удобно применить теорему Пифагора:
Если сказано, что два поезда длиной L1 и L2 каждый движутся навстречу друг другу со скоростями v1 и v2 относительно неподвижных объектов (деревьев, домов), то время t, в течение которого они будут проезжать мимо друг друга, можно найти, разделив сумму их длин на их скорость относительно друг друга, которая при встречном движении поездов равна сумме их скоростей:
А если эти поезда обгоняют друг друга, двигаясь в одном направлении, то время обгона равно:
2.Средняя и мгновенная скорости.
1. Какой простейший вид движения вам известен? (равномерное движение)
2. Как найти скорость при равномерном движении? (перемещение разделить на время v= s / t)? Равномерное движение встречается нечасто.
Как найти скорость при равномерном движении? (перемещение разделить на время v= s / t)? Равномерное движение встречается нечасто.
Обычно механическое движение — это движение с изменяющейся скоростью. Движение, при котором скорость тела с течением времени изменяется, называют неравномерным.
Например, неравномерно движется транспорт. Автобус, начиная движение, увеличивает свою скорость; при торможении его скорость уменьшается. Падающие на поверхность Земли тела также движутся неравномерно: их скорость с течением времени возрастает.
3. Как найти скорость при неравномерном движении? Как она называется? (Средняя скорость, vср = s/ t)
На практике при определении средней скорости пользуются величиной, равной отношению пути s ко времени t, за которое этот путь пройден: vср = s/t. Ее часто называют средней путевой скоростью.
4. Какие особенности есть у средней скорости? ( Средняя скорость является векторной величиной. Для определения модуля средней скорости в практических целях этой формулой можно воспользоваться лишь в том случае, когда тело движется вдоль прямой в одну сторону. Во всех остальных случаях эта формула непригодна ).
Во всех остальных случаях эта формула непригодна ).
5. Что такое мгновенная скорость? Как направлен вектор мгновенной скорости? ( Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории. Вектор мгновенной скорости в каждой точке совпадает с направлением движения в данной точке.)
6. Чем отличается мгновенная скорость при равномерном прямолинейном движении от мгновенной скорости при неравномерном движении? (В случае равномерного прямолинейного движения мгновенная скорость в любой точке и в любой момент времени одинакова; в случае неравномерного прямолинейного движения мгновенная скорость различна).
7. Можно ли определить положение тела в любой момент времени зная среднюю скорость его движения на каком-либо участке траектории? (нельзя определить его положение в любой момент времени).
Самое главное, что нужно помнить, при нахождении средней скорости — это то, что она средняя, а не средняя арифметическая скорость. Конечно, услышав задачу, сразу хочется сложить скорости и разделить на 2.Это самая распространенная ошибка.
Конечно, услышав задачу, сразу хочется сложить скорости и разделить на 2.Это самая распространенная ошибка.
Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело с этими скоростями проходит весь путь за одинаковые промежутки времени.
ΙV . Закрепление пройденного материала.
Вода в реке движется со скоростью 3 м/с. по реке плывет плот. Чему равна скорость плота относительно берега? 1. 0 2. 3 м/с 3. 6 м/с 4. 1,5 м/с 2) Человек спускается вниз по эскалатору со скоростью 1 м/с. скорость эскалатора 4 м/с. чему равна скорость человека относительно неподвижного наблюдателя, стоящего внизу? 1. 5 м/с 2. 3 м/с 3. 0 4. Недостаточно данных 3) Какова траектория движения любой точки винта , поднимающего вверх вертолет, для наблюдателя, стоящего внизу? 1. Прямая линия 2. Винтовая линия 3. Окружность 4. Парабола
V . Домашнее задание. §
План-конспект урока «Мгновенная и средняя скорость.
 Сложение скоростей.»
Сложение скоростей.»План-конспект (технологическая карта) урока физики.
Предмет: физика.
МБОУ Лесногородская СОШ
Преподаватель: Немцова А.Ю.
10 класс 9.09.2019
«Мгновенная и средняя скорость. Сложение скоростей»Номер урока (год/тема)
3/3
Тип урока:
урок совершенствования умений и навыков.
Цель:
научить различать понятия мгновенной и средней скорости; определять скорость, перемещение и пройденный путь за любой промежуток времени при равномерном прямолинейном движении.
Задачи:
Образовательные: 1) Продолжить работу по закреплению понятия скорости, зависимости проекции перемещения от времени, зависимости проекции скорости от времени для прямолинейного равномерного движения, нахождения места и времени встречи;
2) сформировать четкие представления о механическом движении и его характеристиках;
3) ввести закон сложения скоростей.
Развивающие: 1) создать условия для совершенствования интеллектуальных способностей и мыслительной деятельности обучающихся;
2) развитие умений применять знания в новой ситуации;
3) продолжить формирование у обучающихся умений сопоставлять, сравнивать, обобщать, делать выводы.
Воспитательные: создать условия для:
1) формирования коммуникативных качеств, культуры общения, воспитания наблюдательности;
2) формирование навыков коллективной работы в сочетании с самостоятельностью учащихся, навыков самоконтроля;
3) способствовать формированию научного мировоззрения, ответственного отношения к учению, содействовать воспитанию усидчивости, аккуратности при выполнении заданий.
Планируемый результат. Метапредметные результаты. 1. Сформированность познавательных интересов, направленных на развитие представлений о скорости;
2. Умение работать с источниками информации;
3. Умение преобразовывать информацию из одной формы в другую.
Умение преобразовывать информацию из одной формы в другую.
Предметные результаты:
1. Отличают понятия средней и мгновенной скорости, изучают закон сложения скоростей;
2) используют полученные теоретические знания для объяснения процессов и явлений, происходящих в жизни.
УУД
Личностные: Осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению; готовность и способность вести диалог с другими людьми и достигать в нём взаимопонимания.
Познавательные: Выделяют и формулируют познавательную цель. Строят логические цепи рассуждений. Производят анализ и преобразование информации.
Регулятивные: Умение определять потенциальные затруднения при решении учебной задачи; планировать и корректировать полученный результат.
Коммуникативные: Формируются речевые умения: учатся высказывать суждения с использованием физических терминов и понятий, формулировать вопросы и ответы в ходе выполнения задания, обмениваться знаниями.
Содержание и основные понятия темы.
Механическое движение; равномерное и неравномерное движение; относительность движения; скорость, средняя скорость, мгновенная скорость, закон сложения скоростей.
Организация пространства
1. Слушание объяснения учителя.2. Самостоятельная работа по решению задач.
3. Отвечают на вопросы и решают задачи.
1. Технология проблемного обучения.
2. Закрепление изученного материала на основе задач практического применения.
1.словесные;
2.наглядные;
3.практические.
Индивидуальная, общеклассная, парная, групповая.
Ресурсы:
Мультимедийный проектор, презентация, учебник.
Структура и ход урока.
Изучение нового материала.Решают задачи и отвечают на вопросы.
Личностные, познавательные, регулятивные
30 мин.
Рефлексивно-оценочный этап
4.
Рефлексия (подведение итогов).
Формируется адекватная самооценка личности, своих возможностей и способностей, достоинств и ограничений.
Предлагает ответить на вопросы.
Отвечают.
Личностные, познавательные, регулятивные
3 мин.
5.
Подача домашнего задания.
Закрепление изученного материала.
Запись на доске.
Записывают в тетрадь.
Личностные
1 мин.
Приложение.
Содержание урока.
Здравствуйте дети! Я рада встрече с Вами!
Давайте повторим пройденное на прошлом уроке, а для этого ответим на вопросы.
Какое движение называется равномерным прямолинейным? (Равномерным прямолинейным движением называют такое происходящее по прямолинейной траектории движение, при котором тело (материальная точка) за любые равные промежутки времени совершает одинаковые перемещения.
 )
)Приведите примеры равномерного прямолинейного движения.
В каком случае путь и перемещение совпадают? (В случае прямолинейного равномерного движения).
Как можно определить проекцию перемещения, зная конечную и начальную координаты тела? (Вычесть из конечной координаты начальную.)
Запишите уравнение равномерного прямолинейного движения. Зависимость каких величин отражает это уравнение? (x=x0+vt).
Как вы думаете, только ли формулой можно представить эту зависимость? (Нет. Эту зависимость можно также отобразить графически).
Как определить скорость при равномерном прямолинейном движении? ()
Изменение положения в пространстве движущегося тела характеризуют путь и перемещение. Однако эти величины не говорят, как быстро произошло изменение. Ребята, кто догадался какая сегодня тема урока? (Скорость движения). Правильно. Записываем тему сегодняшнего урока: «Мгновенная и средняя скорость. Сложение скоростей»
Ребята, кто догадался какая сегодня тема урока? (Скорость движения). Правильно. Записываем тему сегодняшнего урока: «Мгновенная и средняя скорость. Сложение скоростей»
Скорость является пространственно-временной характеристикой движения тела. Но всегда ли мы можем воспользоваться формулами, сказанными Вами в начале урока? (Нет.)
Предположим, что материальная точка прошла путь в 500 м за 20 с. Можно ли предположить, что тело за каждую секунду перемещалось на 25 м? (Нет, это верно только в случае равномерного прямолинейного движения.)
(Слайд 1 презентации) Действительно, тело могло первые 5 с двигаться медленно, следующие 10 с – стоять, и последние 5 с двигаться очень быстро. Поэтому, если не оговорен характер движения, путь, пройденный телом, будет характеризоваться средней скоростью: . Итак, средняя скорость – это весь путь, деленный на все время движения.
Средняя скорость, как любая средняя величина, является достаточно приблизительной характеристикой движения. Проехав путь от дома до дачи со средней скоростью 60 км/ч, всегда ли мы видим с Вами на спидометре именно это значение? (Нет.)
Проехав путь от дома до дачи со средней скоростью 60 км/ч, всегда ли мы видим с Вами на спидометре именно это значение? (Нет.)
А какую же скорость нам с Вами показывает спидометр? (Мгновенную).
(Слайд 2 презентации) Правильно. Мгновенная скорость – средняя скорость за бесконечно малый интервал времени:
Мгновенная скорость – векторная величина. Она направлена по касательной к траектории в сторону движения.
А теперь представьте, что Вы переплываете реку с течением. Как найти Вашу скорость в любой момент времени? (Сложить скорость, с которой мы плывем, и скорость течения.)
А если Вы плывете против течения? (Вычесть.)
Итак, Вы сейчас на этом примере сформулировали закон сложения скоростей. Запишем его в тетрадь.
(Слайд 3 презентации) Закон сложения скоростей:
(Слайд 4 презентации) Графические варианты интерпретации закона сложения скоростей.
Давайте решим задачи для более подробного разбора этих вопросов.
Автомобиль первую половину пути двигался со скоростью 36 км/ч, другую половину пути – со скоростью 15 м/с. Определите среднюю скорость движения автомобиля. (Ответ: 12 м/с.)
Лодочник перевозит пассажиров с одного берега на другой за 10 мин по траектории АВ. Скорость течения реки 0,3 м/с, ширина реки 240м. С какой скоростью относительно воды и под каким углом α к берегу должна двигаться лодка, чтобы достичь другого берега за указанное время? (Ответ: v’=0,5м/с, α≈53°.)
(Возможный вариант решения: скорость лодки относительно берега v=l/t, ; )
Сколько времени пассажир, сидящий у окна поезда, идущего со скоростью 54 км/ч, будет видеть проходящий мимо него встречный поезд, скорость которого 36 км/ч, длина поезда 150м? (Ответ: 6с.)
(Возможный вариант решения: Так как поезда движутся навстречу друг другу, то скорости складываются : V=V1+V2=54+36=90(км/ч)=25(м/с) теперь, зная скорость V и расстояние S ,найдём время по формуле: t=S/V=250/25=10 (с)
Лодка движется поперек реки, перпендикулярно ее берегам со скоростью 2 м/с.
 Под каким углом к выбранному направлению оси ОУ и с какой скоростью относительно поверхности воды гребец держит курс, если скорость течения реки 5 км/ч? (Ответ: 0,22 м/с.)
Под каким углом к выбранному направлению оси ОУ и с какой скоростью относительно поверхности воды гребец держит курс, если скорость течения реки 5 км/ч? (Ответ: 0,22 м/с.)
(Возможный вариант решения: vp=5 км/ч=1,38 м/с
)
Рефлексия.
Что нового узнали на уроке?
Какая форма работы вам понравилась?
Домашнее задание: §6-8, вопросы после §6-8 устно, задание ЕГЭ к §6 и 8 решить подробно).
Относительность механического движения — урок. Физика, 9 класс.
Чтобы разобраться в относительности механического движения, зададимся вопросом:
«Мы сейчас, в настоящий момент времени, движемся или находимся в состоянии покоя?»
Ты, конечно же, ответишь, что всё зависит от того, что мы делаем.
Просто сидим на месте или двигаемся куда-нибудь.
Однако это не совсем верно.
Дело в том, что даже когда ты сидишь, стоишь или лежишь на одном и том же месте —
ты всё равно движешься!
Как это понять? Да всё очень просто. Я предполагаю, что ты сейчас находишься на планете Земля, так вот знай: она движется вокруг Солнца, таким образом, и ты движешься вместе с Землёй вокруг Солнца.
Я предполагаю, что ты сейчас находишься на планете Земля, так вот знай: она движется вокруг Солнца, таким образом, и ты движешься вместе с Землёй вокруг Солнца.Магазины и деревья на улице не стоят на месте? Стоя возле них, мы же видим, что они никуда не движутся. Так движутся или нет?
Со всем разобраться поможет слово «относительно».
Пример:
Если ты находишься в движущемся вагоне маршрутного такси, то относительно окон того же самого маршрутного такси ты не движешься, а относительно мотоцикла, припаркованного возле магазина, ты движешься.
Рис. \(1\). Транспорт
Давайте примем дом за неподвижное тело. Правильно оно называется тело отсчёта. Относительно него стоящие рядом деревья находятся на месте, то есть не движутся. А пролетающие рядом птицы и едущие по дороге автомобили находятся в движении.
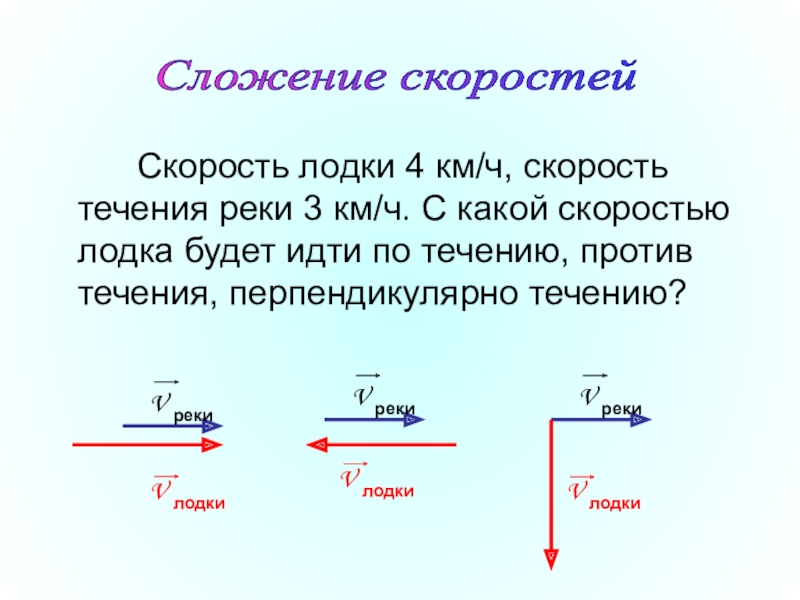
Чтобы найти скорость движения одного тела относительно другого, необходимо сложить векторы этих скоростей.
Классический закон сложения скоростей гласит:
скорость тела относительно неподвижной системы отсчёта равна геометрической сумме двух скоростей — скорости тела относительно подвижной системы отсчёта и скорости подвижной системы отсчёта относительно неподвижной.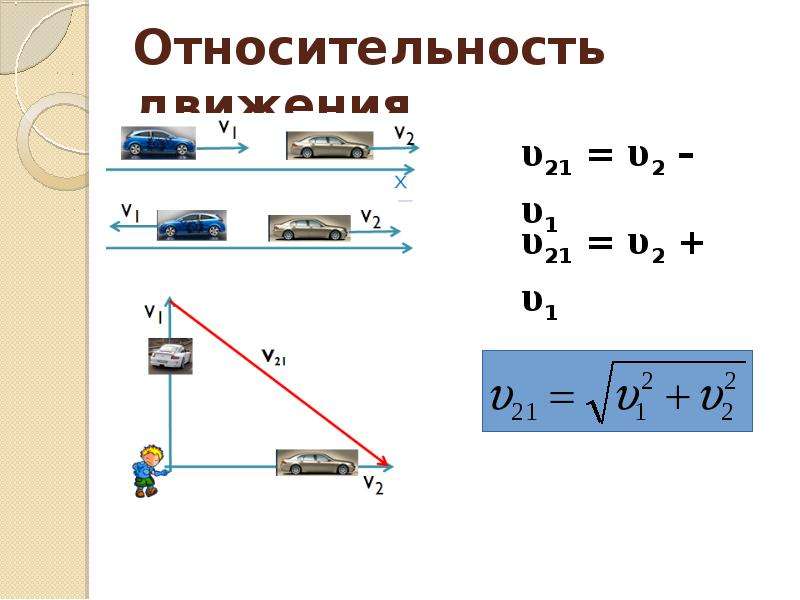
Вот они направлены в одну сторону, например, так:
Рис. \(2\). Векторы скорости, расположенные на параллельных прямых
Для того чтобы их сложить, нужно выстроить их друг за другом.
Это называется сложением векторов по правилу треугольника.
Должно получиться так:
Рис. \(3\). Векторы скорости друг за другом
В результате сложения таких векторов должен получиться один результирующий.
Покажем его красным цветом. Это вектор V→.
Он получился, когда мы соединили начало первого вектора с концом последнего.
Рис. \(4\). Вектор, получившийся в результате сложения
Два вектора V→1 и V→2 сложились, и получился один вектор V→. Всё просто.
Бывает, что векторы могут быть направлены в разные стороны. Скажем, вот так:
Рис. \(5\). Векторы направлены в разные стороны, расположены на параллельных прямых
\(5\). Векторы направлены в разные стороны, расположены на параллельных прямых
Будем пробовать их складывать по известному правилу — правилу треугольника.
Выстроим векторы друг за другом. Должно получиться примерно так:
Рис. \(6\). Выстроенные вместе векторы
Снова соединим начало первого вектора с концом последнего.
Чтобы было лучше видно, изобразим результирующий вектор красным цветом.
Рис. \(7\). Результирующий вектор
Два вектора V→1 и V→2 сложились, и получился один вектор V→.
Может случиться, что векторы лежат не так ровно, а, скажем, под углом \(90°\) друг к другу.
Например:
Рис. \(8\). Векторы, перпендикулярные друг другу
Перед нами два вектора — V→1 и V→2. Как же их сложить?
Снова выстраиваем их друг за другом, чтобы получились стороны треугольника.
Или соединяем начала этих векторов — тогда получится правило параллелограмма.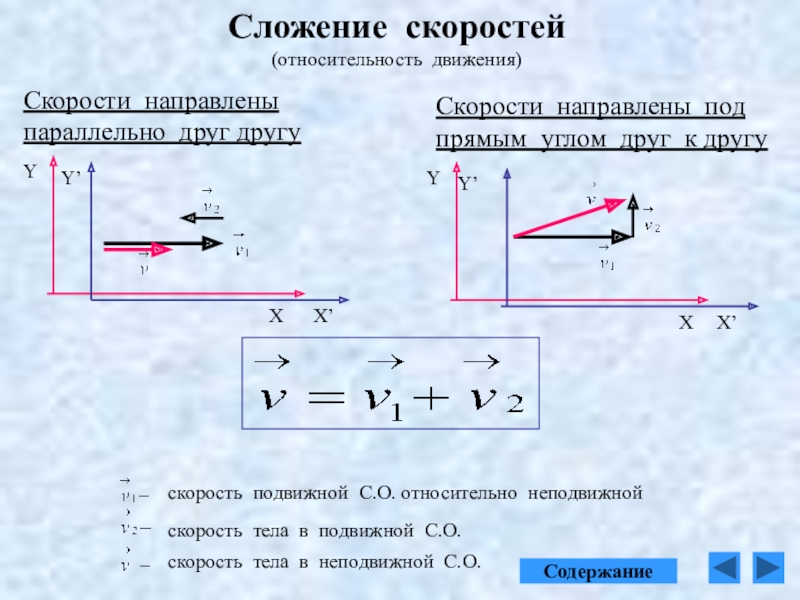
Рис. \(9\). Соединённые векторы
Правило треугольника нам уже знакомо. Просто соединяем начало первого вектора с концом последнего.
Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.
Результат сложения не зависит от выбранного правила сложения — правила треугольника или правила параллелограмма.
Должен получиться один и тот же вектор V→. Изобразим его красным.
Рис. \(10\). Результирующий вектор по правилу параллелограмма
Теперь можно приступать к решению задач на относительное движение.
Источники:
Рис. \(2\). Векторы скорости, расположенные на параллельных прямых. © ЯКласс.
Рис. \(3\). Векторы скорости друг за другом. © ЯКласс.
Рис. \(4\). Вектор, получившийся в результате сложения. © ЯКласс.
Рис. \(5\). Векторы направлены в разные стороны, расположены на параллельных прямых. © ЯКласс.
Рис. \(6\). Выстроенные вместе векторы. © ЯКласс.
© ЯКласс.
Рис. \(7\). Результирующий вектор. © ЯКласс.
Рис. \(8\). Векторы, перпендикулярные друг другу. © ЯКласс.
Рис. \(9\). Соединённые векторы. © ЯКласс.
Рис. \(10\). Результирующий вектор по правилу параллелограмма. © ЯКласс.
Относительность механического движения — Кинематика — МЕХАНИКА — ВСЕ УРОКИ ФИЗИКИ 10 класс — конспекты уроков — План урока — Конспект урока — Планы уроков — разработки уроков по физике
1-й семестр
МЕХАНИКА
1. Кинематика
Урок 3/5
Тема. Относительность механического движения
Цель урока: расширить и углубить знания об относительности движения; сформировать навыки сложения скоростей и перемещений, перехода от одной системы отсчета к другой
Тип урока: изучение нового материала
План урока
Контроль знаний |
5 мин. |
1. Прямолинейное равномерное движение. 2. Перемещение в случае прямолинейного равномерного движения. 3. Уравнение для координаты в случае прямолинейного равномерного движения |
Демонстрации |
5 мин. |
1. Относительность состояния покоя и движения. 2. Сложение перемещений. 3. Видео-фрагмент «Сложение перемещений и скоростей» |
Изучение нового материала |
25 мин. |
1. Относительность движения. 2. Сложение перемещений и скоростей. 3. Учимся решать задачи |
Закрепление изученного материала |
10 мин. |
1. Решение задач. 2. Контрольные вопросы |
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
1. Относительность движения
Напомним учащимся, что система отсчета в механике выбирается произвольно. Тогда положение того самого тела в определенный момент времени относительно разных тел отсчета будет разным. Поэтому и траектория тела, движущегося в одной системе отсчета будет иметь одну форму, а в другой — другую, то есть форма траектории зависит от выбора системы отсчета. Это означает, что движение того же самого тела для одного наблюдателя может быть прямолинейным, а для другого — криволинейным. Например, точка на обеде колеса велосипеда относительно велосипедиста описывает круг, а для прохожего — циклоїду. Следовательно, говорить о форме траектории можно только в заданной системе отсчета. В этом аспекте говорят, что траектория относительная.
Можно задать учащимся вопрос: какие еще кинематические характеристики движения являются относительными? На конкретных примерах (пловец переплывает реку с одного берега на другой, двигаясь перпендикулярно к берегам; пассажир идет по вагону, что движется, выясняем относительность перемещения и скорости.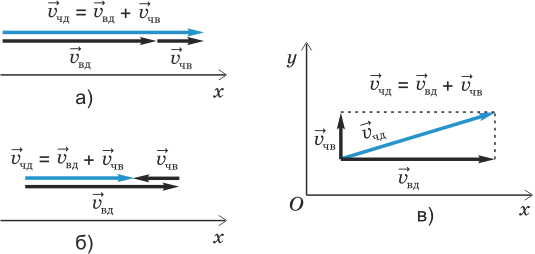
2. Сложение перемещений и скоростей
Назовем условно одну систему отсчета «неподвижной», а другую — «подвижной». Тогда правило сложения перемещений можно сформулировать так:
Ø перемещение тела в «неподвижной» системе отсчета равна векторной сумме перемещение тела 1 в «движущейся» системе отсчета и перемещения 2 «движущейся» системы отсчета относительно «неподвижной» :
Разделив соотношение на время движения t, получим закон сложения скоростей: Это означает, что
Ø скорость тела в «неподвижной» системе отсчета равна векторной сумме скорости тела 1 в «движущейся» системе отсчета и скорости 2 «движущейся» системы отсчета относительно «неподвижной».
Важно отметить, что движение тела происходит в обеих системах отсчета одновременно. Относительно каждой системы тело выполняет в любой момент времени только одно движение.
3. Учимся решать задачи
Осознать и усвоить изучаемый материал ученикам поможет решению задач.
В повседневной жизни как тело отсчета мы часто воспринимаем Землю или какое-нибудь другое тело, связанное с ней. Однако в некоторых случаях систему отсчета удобно связать с телом, что движется, тогда решение многих задач на вычисление скорости тела относительно Земли упрощается. Для подтверждения этого можно рассмотреть два варианта решения следующей задачи.
Задача. Проплывая под мостом против течения реки, гребец потерял шляпу. Обнаружив пропажу через 10 мин., гребец повернул обратно и подобрал шляпу на расстоянии d = 1 км ниже моста. Вычислите скорость течения реки.
Решения
1. Решим задачу в системе отсчета «Земля».
Очевидно, что вверх против течения лодочник до обнаружения пропажи проплыл путь
Повернув назад, он проплыл расстояние
Время, за которое он проплывет расстояние l2, вычислим как:
Общее время движения гребца будет вычисляться по формуле:
Шляпу за тот же промежуток времени прошел путь откуда
Тогда
Тогда
2. Решим эту же задачу в системе отсчета «Вода».
Решим эту же задачу в системе отсчета «Вода».
В этой системе отсчета шляпу неподвижный. Скорость лодочника относительно воды в обе стороны одинакова; следовательно, и время t1 его движения от шляпы на некоторое расстояние, и время обратного движения до шляпы t2 одинаковые. Поэтому t = t1 + t2 мин. За это время мостик «отойдет» от шляпы на расстояние d = 1 км.
Следовательно,
Вопрос к ученикам во время изложения нового материала
1. Велосипедист едет по ровной прямой дороге. Какие детали велосипеда движутся относительно земли прямолинейными траекториями, а какие — криволинейными?
2. Ветер несет воздушный шар на юг. В какую сторону отклоняется флажок, которым украшена шарик?
3. По реке плывет весельный лодка и рядом с ним — плот. Что для гребца будет проще: перегнать плот на 1 м или на столько же отстать от него?
4. Какие характеристики механического движения изменяются вследствие перехода от одной системы отсчета к другой?
ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА
1). Тренируемся решать задачи
Тренируемся решать задачи
1. Скорость моторной лодки относительно воды 6 км/ч., а скорость течения реки — 2 км/ч. Во сколько раз быстрее лодка движется по течению, чем против течения?
2. Скорость лодки относительно воды — 4 км/ч., а скорость течения — 2 км/ч. За какое время лодка пройдет 12 км по течению реки? против течения?
3. Велосипедист движется со скоростью 25 км/ч., а автомобиль — 55 км/ч. С какой скоростью движется автомобиль относительно велосипедиста, если:
а) он движется навстречу велосипедисту;
б) догоняет его;
в) удаляется от него после обгона?
4. Пловец переплывает реку шириной 150м, двигаясь со скоростью 2 м/с относительно воды. Скорость течения равна 1 м/с.
а) Каковы скорость и перемещение пловца относительно берега, если он движется перпендикулярно течению реки? Сколько времени необходимо пловцу, чтобы переплыть реку? На какое расстояние при этом его снесет течением?
б) время понадобится пловцу, чтобы переплыть реку, проплывая наименьшее расстояние относительно берега? Каким в этом случае будет его перемещения относительно воды?
2). Контрольные вопросы
Контрольные вопросы
1. Может ли человек, который находится в вагоне поезда, движущегося быть неподвижной относительно Земли?
2. Пассажир поезда, движущегося, смотрел в окно встречный поезд, проезжал мимо него. Когда встречный поезд промчался, пассажиру показалось, что его поезд замедлил ход. Почему?
3. Приведите примеры, которые подтверждают, что движение и состояние покоя являются относительными.
4. Всегда как неподвижную систему отсчета необходимо принимать ту, что связана с Землей?
5. Почему дождевые капли в безветренную погоду оставляют наклонные полосы на стеклах автомобиля, движущегося равномерно?
Что мы узнали на уроке
• Перемещение тела в «неподвижной» системе отсчета равна векторной сумме перемещение тела 1 в «движущейся» системе отсчета и перемещения 2 «движущейся» системы отсчета относительно «неподвижной»:
• Скорость тела в «неподвижной» системе отсчета равна векторной сумме скорости тела 1 в «движущейся» системе отсчета и скорости 2 «движущейся» системы отсчета относительно «неподвижной»:
Домашнее задание
1. П.:§8.
П.:§8.
2. 36.:
P1) — 3.11; 3.14; 3.15; 3.17;
р2) — 3.34; 3.36; 3.38, 3.39;
р3) — 3.63, 3.64; 3.66; 3.67.
Закон сложения скоростей определение. Правило сложения скоростей
Раздел 1 МЕХАНИКА
Механическим движением тела
механика. кинематикой .
Телом отсчёта
систему отсчёта ,
материальной точкой .
Траектория
Путь – это длина траектории ℓ(м) (рис.1.2)
перемещением этой частицыза данное время.
Модуль вектора перемещения
Скорость
Средняя скорость
Мгновенная скорость,
или 1
Сложение скоростей
Это закон сложения перемещений
Получим:
Это закон сложения скоростей: сОтносительная скорость –
υ отн =υ 1 -(- υ 2)
υ отн = υ 1 + υ 2
υ отн =υ 1 — υ 2
υ отн = υ 1 — υ 2
План решения задач по кинематике
2. Выписать числовые значения заданных величин.
Выписать числовые значения заданных величин.
3. Сделать схематический чертеж, отображающий описанное в задаче движение. Изобразить на нем траекторию движения, векторы скорости, ускорения, перемещения.
4. Выбрать систему координат, при этом координатные оси направить так, чтобы проекции векторов на них выражались возможно более простым образом.
5. Составить для данного движения уравнения, отражающие математическую связь между проекциями векторов на оси координат. Число уравнений должно быть равно числу неизвестных величин.
6. Решить составленную систему относительно искомых величин, т. е. получить расчетные формулы.
7. Подставить в расчетные формулы вместо обозначений физических величин обозначения их единиц СИ, произвести преобразования и убедиться, получаются ли в результате единицы искомых величин.
8. Подставить в расчетные формулы числовые значения физических величин и произвести вычисления. Оценить реальность полученного результата.
Раздел 1 МЕХАНИКА
Глава 1: О с н о в ы к и н е м а т и к и
Механическое движение. Траектория. Путь и перемещение. Сложение скоростей
Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени.
Механическое движение тел изучаетмеханика. Раздел механики, описывающий геометрические свойства движения без учёта масс тел и действующих сил, называется кинематикой .
Механическое движение относительно. Чтобы определить положение тела в пространстве, нужно знать его координаты. Для определения координат материальной точки следует, прежде всего, выбрать тело отсчёта и связать с ним систему координат.
Телом отсчёта называется тело, относительно которого определяется положение других тел. Тело отсчёта выбирают произвольно. Это может быть что угодно: Земля, здание, автомобиль, теплоход и т.д.
Система координат, тело отсчёта с которым она связана, и указание отсчёта времени образуют систему отсчёта , относительно которой рассматривается движение тела (рис. 1.1).
1.1).
Тело, размерами, формой и структурой которого можно пренебречь при изучении данного механического движения, называется материальной точкой . Материальной точкой можно считать тело, размеры которого намного меньше расстояний, характерных для рассматриваемого в задаче движения.
Траектория это линия, по которой движется тело.
В зависимости от вида траектории движения разделяются на прямолинейные и криволинейные
Путь – это длина траектории ℓ(м) (рис.1.2)
Вектор , проведенный из начального положения частицы в её конечное положение, называется перемещением этой частицыза данное время.
В отличие от пути, перемещение является не скалярной, а векторной величиной, так как оно показывает не только на какое расстояние, но и в каком направлении сместилось тело за данное время.
Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль перемещения не может быть больше пройденного пути. Например, если из точки А в точку Б автомобиль перемещается по криволинейной траектории, то модуль вектора перемещения меньше пройденного пути ℓ. Путь и модуль перемещения оказываются равными лишь в одном единственном случае, когда тело движется по прямой.
Но никогда модуль перемещения не может быть больше пройденного пути. Например, если из точки А в точку Б автомобиль перемещается по криволинейной траектории, то модуль вектора перемещения меньше пройденного пути ℓ. Путь и модуль перемещения оказываются равными лишь в одном единственном случае, когда тело движется по прямой.
Скорость – это векторная количественная характеристика движения тела
Средняя скорость – это физическая величина, равная отношению вектора перемещения точки к промежутку времени
Направление вектора средней скорости совпадает с направлением вектора перемещения.
Мгновенная скорость, то есть скорость в данный момент времени – это векторная физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt.
Вектор мгновенной скорости направлен по касательной к траектории движения (рис. 1.3).
В системе СИ скорость измеряется в метрах в секунду (м/с), то есть единицей скорости принято считать скорость такого равномерного прямолинейного движения, при котором за одну секунду тело проходит путь в один метр.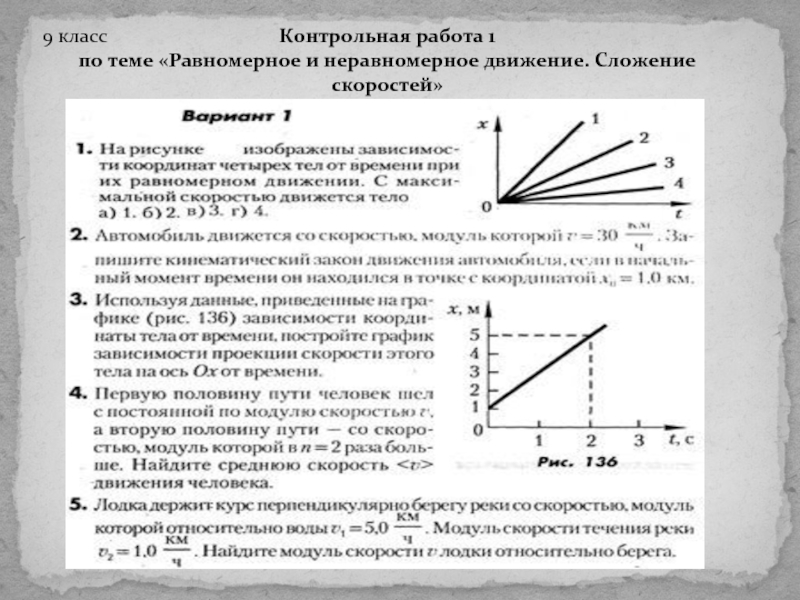 Часто скорость измеряют в километрах в час.
Часто скорость измеряют в километрах в час.
или 1
Сложение скоростей
Любые механические явления рассматриваются в какой-либо системе отсчета: движение имеет смысл только относительно других тел. При анализе движения одного и того же тела в разных системах отсчета все кинематические характеристики движения (путь, траектория, перемещение, скорость, ускорение) оказываются различными.
Например, пассажирский поезд движется по железной дороге со скоростью 60км/ч. По вагону этого поезда идёт человек со скоростью 5км/ч. Если считать железную дорогу неподвижной и принять её за систему отсчёта, то скорость человека относительно железной дороги, будет равна сложению скоростей поезда и человека, то есть
60км/ч + 5 км/ч = 65 км/ч, если человек идёт в том же направлении что и поезд и
60км/ч — 5 км/ч = 55 км/ч, если человек идёт против направления движения поезда.
Однако это справедливо только в этом случае, если человек и поезд движутся по одной линии. Если же человек будет двигаться под углом, то необходимо учитывать этот угол, и тот факт, что скорость – это векторная величина.
Если же человек будет двигаться под углом, то необходимо учитывать этот угол, и тот факт, что скорость – это векторная величина.
Рассмотрим описанный выше пример более подробно – с деталями и картинками.
Итак, в нашем случае железная дорога это неподвижная система отсчёта. Поезд, который движется по этой дороге – это подвижная система отсчёта. Вагон, по которому идёт человек, является частью поезда. Скорость человека относительно вагона (относительно подвижной системы отсчёта) равна 5км/ч. Обозначим её буквой . Скорость поезда, (а значит и вагона) относительно неподвижной системы отсчёта (то есть относительно железной дороги) равна 60 км/ч. Обозначим её буквой . Другими словами, скорость поезда – это скорость подвижной системы отсчёта относительно неподвижной системы отсчёта.
Это закон сложения перемещений . В нашем примере перемещение человека относительно железной дороги равно сумме перемещений человека относительно вагона и вагона относительно железной дороги.
Разделив обе части равенства на малый промежуток времени Dt, за которое произошло перемещение:
Получим:
Это закон сложения скоростей: с корость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и скорости самой подвижной системы отсчёта относительно неподвижной.Относительная скорость – это физическая величина, равная векторной разности скоростей, заданных относительно неподвижной системы
Понятием относительной скорости пользуются в том случае, когда рассматривают движение одного тела по отношению к другому телу. Например, движутся два автомобиля навстречу друг другу, их относительная скорость будет равна сумме скоростей (см. рис. 1.5).
υ отн =υ 1 -(- υ 2)
υ отн = υ 1 + υ 2
Если бы эти автомобили двигались в одном направлении, то относительная скорость была бы равна скорости второго минус скорость первого (см. Рис. 1).
Рис. 1).
υ отн =υ 1 — υ 2
υ отн = υ 1 — υ 2
Рис. 1.5 Относительная скорость
Сложение перемещений и скоростей проводится по правилу сложения векторов. Векторы складываются по правилу треугольника или по правилу параллелограмма (см. Рис. 1.6).
Рис. 1.6. Правила сложения векторов
Кинематика — это просто!
Формулировка закона:
Как в учебнике Буховцева для 10 класса:
Если тело движется относительно системы отсчета К 1 со скоростью V 1 ,
а сама система отсчета К 1 движется относительно другой системы отсчета К 2 со скоростью V ,
то скорость тела (V 2 ) относительно второй системы отсчета К 2
равна геометрической сумме векторов V 1 и V .
Упрощаем форммулировку, не меняя смысла:
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета.
Вторая формулировка запоминается проще, какой ползоваться решайте сами!
где всегда
К 2 — неподвижная система отсчета
V 2 — скорость тела относительно неподвижной системы отсчета (К 2 )
К 1 — подвижная система отсчета
V 1 — скорость тела относительно подвижной системы отсчета (К 1 )
V — скорость подвижной системы отсчета (К 1 ) относительно неподвижной системы отсчета (К 2 )
Алгоритм решения задачи на закон сложения скоростей
1. Определить тело — обычно это тело, о скорости которого спрашивается в задаче.
2. Выбрать неподвижную систему отсчета (дорога, берег) и подвижную систему отсчета (обычно это второе движущееся тело).
P.S. В условиях задачи скорости тел заданы обычно относительно неподвижной системы отсчета (например, дороги или берега)
3. Ввести обозначения скоростей (V 1 , V 2 , V ).
4. Сделать чертеж, на котором показать координатную ось ОХ и векторы скорости.
Лучше, если ОХ будет совпадать по направлению с вектором скорости выбранного тела .
5. Записать формулу закона сложения скоростей в векторном виде.
6. Выразить из формулы искомую скорость в векторном виде.
7. Выразить искомую скорость в проекциях.
8. Определить по чертежу знаки проекций.
9. Расчет в проекциях.
10. В ответе не забыть перейти от проекции к модулю.
Пример решения простейшей задачи на закон сложения скоростей
Задача
Два автомобиля движутся равномерно по шоссе навстречу друг другу. Модули их скоростей равны 10 м/с и 20 м/с.
Определить скорость первого автомобиля относительно второго.
Решение:
Еще раз! Если вы внимательно прочитали пояснения к формуле, то решение любой задачи, пойдет «на автомате»!
1. В задаче спрашивается о скорости первого автомобиля — значит тело — первый автомобиль.
2. По условию задачи выбираем:
K 1 — подвижная система отсчета сязана со вторым автомобилем
К 2 — неподвижная система отсчета связана с дорогой
3. Вводим обозначения скоростей:
Вводим обозначения скоростей:
V 1 — скорость тела (первого авто) относительно подвижной системы отсчета (второго авто) — найти!
V 2 — скорость тела (первого авто) относительно неподвижной систеы отсчета (дороги) — дано 10м/с
V — скоростьь подвижной системы отсчета (второго авто) относительно неподвижной системы отсчета (дороги) — дано 20двух уравнений:м/с
Теперь понятно, что в задаче надо определить V 1 .
4. Делаем чертеж, выписываем формулу:
Всё, все отдыхают! )))
P.S. Если движение происходит не по пряммой, а на плоскости, то при переводе формулы векторного вида в проекции добавляется еще одно уравнение в прекциях относительно оси OY, далее решаем систему двух уравнений:
V 2x = V 1x + V x
V 2y = V 1y + V y
Скорость – это количественная характеристика движения тела.
Средняя скорость – это физическая величина, равная отношению
вектора перемещения точки к промежутку времени
Δt, за который произошло это перемещение. Направление вектора средней скорости
совпадает с направлением вектора перемещения .
Средняя скорость определяется по формуле:
Направление вектора средней скорости
совпадает с направлением вектора перемещения .
Средняя скорость определяется по формуле:
Мгновенная скорость , то есть скорость в данный момент времени – это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Иными словами, мгновенная скорость в данный момент времени – это отношение очень малого перемещения к очень малому промежутку времени, за который это перемещение произошло.
Вектор мгновенной скорости направлен по касательной к траектории движения тела (рис. 1.6).
Рис. 1.6. Вектор мгновенной скорости.
В системе СИ скорость измеряется в метрах в секунду, то есть единицей скорости
принято считать скорость такого равномерного прямолинейного движения, при котором
за одну секунду тело проходит путь в один метр. Единица измерения скорости обозначается м/с . Часто скорость измеряют в других единицах. Например, при измерении скорости
автомобиля, поезда и т. п. обычно используется единица измерения километр в час:
п. обычно используется единица измерения километр в час:
1 км/ч = 1000 м / 3600 с = 1 м / 3,6 с или 1 м/с = 3600 км / 1000 ч = 3,6 км/ч
Сложение скоростей
Скорости движения тела в различных системах отсчёта связывает между собой классический закон сложения скоростей .
Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и самой подвижной системы отсчёта относительно неподвижной.
Например, пассажирский поезд движется по железной дороге со скоростью 60 км/ч. По вагону этого поезда идет человек со скоростью 5 км/ч. Если считать железную дорогу неподвижной и принять её за систему отсчёта, то скорость человека относительно системы отсчёта (то есть относительно железной дороги), будет равна сложению скоростей поезда и человека, то есть
60 + 5 = 65, если человек идёт в том же направлении, что и поезд и 60 – 5 = 55, если человек и поезд движутся в разных направлениях
Однако это справедливо только в том случае, если человек и поезд движутся по одной линии. Если же человек будет двигаться под углом, то придётся учитывать этот угол, вспомнив о том,
что скорость – это векторная величина .
Если же человек будет двигаться под углом, то придётся учитывать этот угол, вспомнив о том,
что скорость – это векторная величина .
А теперь рассмотрим описанный выше пример более подробно – с деталями и картинками.
Итак, в нашем случае железная дорога – это неподвижная система отсчёта . Поезд, который движется по этой дороге – это подвижная система отсчёта . Вагон, по которому идёт человек, является частью поезда.
Скорость человека относительно вагона (относительно подвижной системы отсчёта) равна 5 км/ч. Обозначим её буквой Ч.
Скорость поезда (а значит и вагона) относительно неподвижной системы отсчёта (то есть относительно железной дороги) равна 60 км/ч. Обозначим её буквой В. Иначе говоря, скорость поезда – это скорость подвижной системы отсчёта относительно неподвижной системы отсчёта.
Скорость человека относительно железной дороги (относительно неподвижной системы отсчёта) нам пока неизвестна. Обозначим её буквой .
Свяжем с неподвижной системой отсчёта (рис. 1.7) систему координат ХОY,
а с подвижной системой отсчёта – систему координат X П О П Y П
(см. также раздел ).
А теперь попробуем найти скорость человека относительно неподвижной системы отсчёта,
то есть относительно железной дороги.
1.7) систему координат ХОY,
а с подвижной системой отсчёта – систему координат X П О П Y П
(см. также раздел ).
А теперь попробуем найти скорость человека относительно неподвижной системы отсчёта,
то есть относительно железной дороги.
За малый промежуток времени Δt происходят следующие события:
Тогда за этот промежуток времени перемещение человека относительно железной дороги:Это закон сложения перемещений . В нашем примере перемещение человека относительно железной дороги равно сумме перемещений человека относительно вагона и вагона относительно железной дороги.
Рис. 1.7. Закон сложения перемещений.
Закон сложения перемещений можно записать так:
= Δ Ч Δt + Δ B ΔtСкорость человека относительно железной дороги равна.
А эта система отсчёта в свою очередь движется относительно другой системы) возникает вопрос о связи скоростей в двух системах отсчёта.
Энциклопедичный YouTube
1 / 3
Сложение скоростей (кинематика) ➽ Физика 10 класс ➽ Видеоурок
Урок 19. Относительность движения. Формула сложения скоростей.
Физика. Урок № 1. Кинематика. Закон сложения скоростей
Субтитры
Классическая механика
V → a = v → r + v → e . {\displaystyle {\vec {v}}_{a}={\vec {v}}_{r}+{\vec {v}}_{e}.}
Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей .
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.
Примеры
- Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, которую имеет точка пластинки под мухой относительно земли (то есть с которой её переносит пластинка за счёт своего вращения).

- Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.
- Если волны движутся относительно берега со скоростью 30 километров в час, и корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть относительно корабля они становятся неподвижными.
Релятивистская механика
В XIX веке классическая механика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы.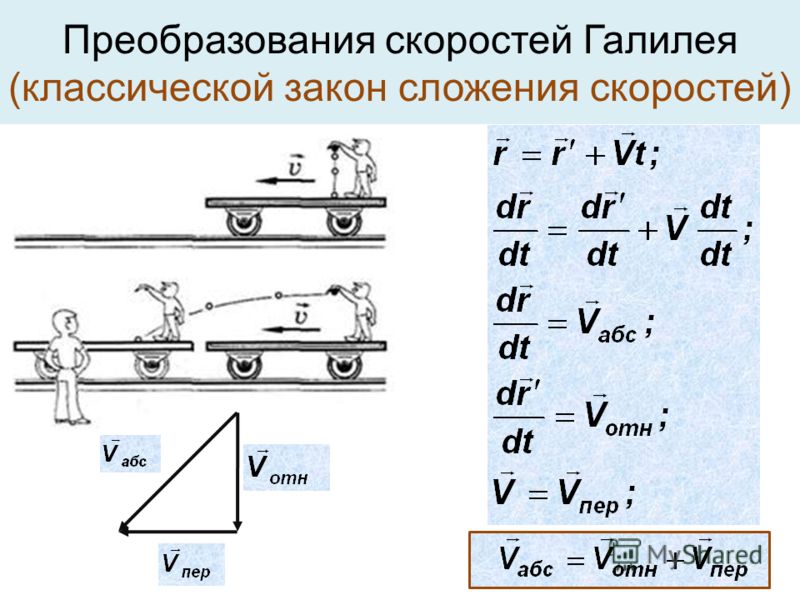 По существу произошёл конфликт между двумя идеями классической механики, перенесёнными в новую область электромагнитных процессов.
По существу произошёл конфликт между двумя идеями классической механики, перенесёнными в новую область электромагнитных процессов.
Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).
Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе , то преобразования называются галилеевыми . Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе отсчёта — всегда равно их расстоянию в другой инерциальной системе.
Вторая идея — принцип относительности . Находясь на корабле, движущимся равномерно и прямолинейно , нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое электродинамическими эффектами? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразованиям. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы.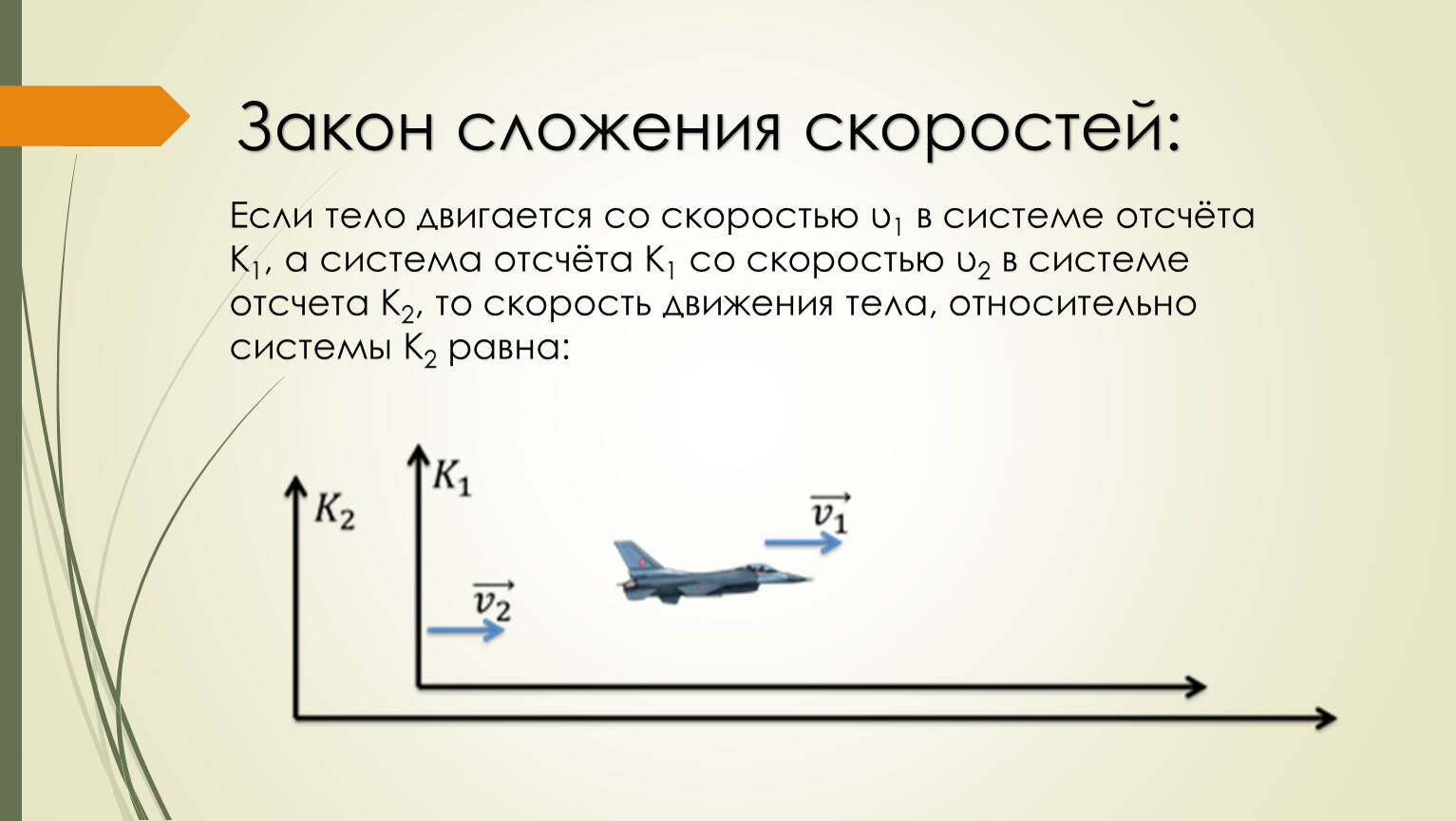 {2}}}}}.}
{2}}}}}.}
Можно заметить, что в случае, когда v / c → 0 {\displaystyle v/c\rightarrow 0} , преобразования Лоренца переходят в преобразования Галилея . Это говорит о том, что специальная теория относительности сводится к механике Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом соотносятся эти две теории — первая является обобщением второй.
Классическая механика использует понятие абсолютной скорости точки. Она определяется как сумма векторов относительной и переносной скоростей этой точки. Подобное равенство содержит утверждение теоремы о сложении скоростей. Принято представлять, что скорость движения определенного тела в неподвижной системе отсчета является равной векторной сумме скорости такого же физического тела относительно подвижной системе отсчета. В этих координатах находится непосредственно тело.
Рисунок 1. Классический закон сложения скоростей . Автор24 — интернет-биржа студенческих работ
Примеры закона сложения скоростей в классической механике
Рисунок 2. Пример сложения скоростей. Автор24 — интернет-биржа студенческих работ
Пример сложения скоростей. Автор24 — интернет-биржа студенческих работ
Существует несколько основных примеров сложения скоростей, согласно установленным правилам, взятым за основу в механической физике. В качестве простейших объектов при рассмотрении физических законов может быть взят человек и любое движущееся тело в пространстве, с которым происходит прямое или косвенное взаимодействие.
Пример 1
Например, человек, который движется по коридору пассажирского поезда со скоростью пять километров в час, при этом состав двигается со скоростью 100 километров в час, то он относительно окружающего пространства двигается со скоростью 105 километров в час. При этом направление движения человека и транспортного средства должны совпадать. Такой же принцип действует и при движении в обратном направлении. В этом случае человек будет перемещаться относительно земной поверхности со скоростью 95 километров в час.
Если значения скорости двух объектов относительно друг друга будут совпадать, то они станут неподвижными с точки зрения движущихся объектов. При вращении скорость изучаемого объекта равна сумме скоростей движения объекта относительно движущейся поверхности другого объекта.
При вращении скорость изучаемого объекта равна сумме скоростей движения объекта относительно движущейся поверхности другого объекта.
Принцип относительности Галилея
Ученые смогли сформулировать основные формулы для ускорений объектов. Из нее следует, что движущаяся система отсчета удаляется относительно другой без видимого ускорения. Это закономерно в тех случаях, когда ускорение тел происходит одинаково в разных системах отсчета.
Подобные рассуждения берут начало еще во времена Галилея, когда сформировался принцип относительности. Известно, что по второму закону Ньютона ускорение тел имеет принципиальное значение. От этого процесса зависит относительное положение двух тел в пространстве, скорость физических тел. Тогда все уравнения можно записать одинаковым образом в любой инерциальной системе отсчета. Это говорит о том, что классические законы механики не будут иметь зависимость от положения в инерциальной системе отсчета, как принято действовать при осуществлении исследования.
Наблюдаемое явление также не имеет зависимость от конкретного выбора системы отсчета. Подобные рамки в настоящее время рассматриваются как принцип относительности Галилея. Он вступает в некоторые противоречия с иными догмами физиков-теоретиков. В частности, теория относительности Альберта Эйнштейна предполагает иные условия действия.
Принцип относительности Галилея базируется на нескольких основных понятиях:
- в двух замкнутых пространствах, которые движутся прямолинейно и равномерно относительно друг друга, результат внешнего воздействия всегда будет иметь одинаковое значение;
- подобный результат будет действителен только для любого механического действия.
В историческом контексте изучения основ классической механики , подобная трактовка физических явлений сформировалась во многом, как результат интуитивного мышления Галилея, что подтвердилось в научных трудах Ньютона, когда тот представил свою концепцию классической механики . Однако подобные требования по Галилею могут накладывать на структуру механики некоторые ограничения. Это влияет на ее возможные формулировки, оформление и развитие.
Это влияет на ее возможные формулировки, оформление и развитие.
Закон движения центра масс и закон сохранения импульса
Рисунок 3. Закон сохранения импульса. Автор24 — интернет-биржа студенческих работ
Одной из общих теорем в динамике стала теорема центра инерции. Ее также называют теоремой о движении центра масс системы. Подобный закон можно вывести из общих законов Ньютона. Согласно ему, ускорение центра масс в динамической системе не является прямым следствием внутренних сил, которые действуют на тела всей системы. Оно способно связать процесс ускорения с внешними силами, которые действуют на такую систему.
Рисунок 4. Закон движения центра масс. Автор24 — интернет-биржа студенческих работ
В качестве объектов, о которых идет речь в теореме, выступают:
- импульс материальной точки;
- система тел.
Эти объекты можно описать как физическую векторную величину. Она является необходимой мерой воздействия силы, при этом полностью зависит от времени действия силы.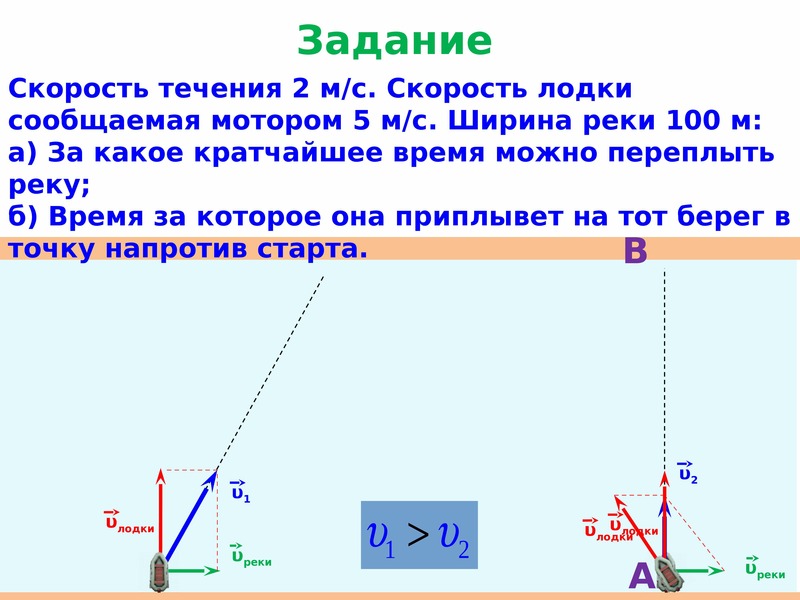
При рассмотрении закона сохранения количества движения утверждается, что векторная сумма импульсов всех тел система полностью представляется как постоянная величина. При этом векторная сумма внешних сил, которые действуют на всю систему, должна быть равна нулю.
При определении скорости в классической механике также используют динамику вращательного движения твердого тела и момент импульса. Момент импульса имеет все характерные признаки количества вращательного движения. Исследователи используют это понятие как величину, которая зависит от количества вращающейся массы, а также как она распределена по поверхности относительно оси вращения. При этом имеет значение скорости вращения.
Вращение также можно понимать не только с точки зрения классического представления вращения тела вокруг оси. При прямолинейном движении тела мимо некой неизвестной воображаемой точки, которая не лежит на линии движения, тело также может обладать моментом импульса. При описании вращательного движения момента импульса играет самую существенную роль. Это очень важно при постановке и решении разнообразных задач, связанных с механикой в классическом понимании.
Это очень важно при постановке и решении разнообразных задач, связанных с механикой в классическом понимании.
В классической механике закон сохранения импульса является следствием ньютоновской механики. Он наглядно показывает, что при движении в пустом пространстве импульс сохраняется во времени. Если существует взаимодействие, то скорость его изменения определяется суммой приложенных сил.
Вопрос: Как вычислить среднюю скорость? — Образование и коммуникации
Содержание статьи:
Урок 17. Средняя скорость. Средняя путевая скорость.
Видео взято с канала: Павел ВИКТОР
Средняя скорость. Задание 22 ОГЭ по математике
Видео взято с канала: Valery Volkov
Урок 17 (осн). Задачи на вычисление средней скорости
Видео взято с канала: Павел ВИКТОР
Мгновенная скорость. Сложение скоростей | Физика 10 класс #4 | Инфоурок
Показать описаниеВидеоуроки являются идеальными помощниками при изучении новых тем, закреплении материала, для обычных и факультативных занятий, для групповой и индивидуальной работы. Они содержат оптимальное количество графической и анимационной информации для сосредоточения внимания и удержания интереса ребят без отвлечения от сути занятия. Каждый видеоурок озвучен профессиональным мужским голосом, четким и приятным для восприятия..
Они содержат оптимальное количество графической и анимационной информации для сосредоточения внимания и удержания интереса ребят без отвлечения от сути занятия. Каждый видеоурок озвучен профессиональным мужским голосом, четким и приятным для восприятия..
Ученики ценят оригинальность подачи материала, родители радуются повышению отметок детей, а учителя в восторге от эффекта и экономии времени и денег при подготовке к урокам..
_
★Инфоурок★.
Крупнейший в России образовательный онлайн-проект.
МЫ ПРЕДЛАГАЕМ:
✓ Курсы дополнительного образования детей и взрослых: https://infourok.ru/.
✓ Тесты для учителей и воспитателей: https://infourok.ru/tests.
✓ Самые массовые международные дистанционные олимпиады: https://infourok.ru/konkurs.
✓ Видеоуроки по 14 предметам: https://infourok.ru/videouroki.
✓ Каталог репетиторов: https://infourok.ru/tutor/ru.
✓ Библиотека методических материалов для учителей: https://infourok.ru/biblioteka.
Адрес редакции и издательства: 214011, РФ,.
г. Смоленск, ул. Верхне-Сенная, 4..
[email protected]
© 2012–2017 Издатель: Проект «Инфоурок»
Видео взято с канала: ИНФОУРОК
Урок 18. Решение задач на среднюю скорость
Видео взято с канала: Павел ВИКТОР
Математика Коварная задача Найти среднюю скорость 98% дают неверный ответ
Видео взято с канала: Математика и фокусы
Физика 10 класс: Средняя скорость
Видео взято с канала: OnliSkill видеоуроки с 5 по 11 класс
Зависимость скорости от скорости
Так же, как расстояние и смещение имеют совершенно разные значения (несмотря на их сходство), то же самое делают и скорость и скорость. Скорость — это скалярная величина, которая указывает, «насколько быстро движется объект». Скорость можно представить как скорость, с которой объект преодолевает расстояние. Быстро движущийся объект имеет высокую скорость и преодолевает относительно большое расстояние за короткое время. Сравните это с медленно движущимся объектом с низкой скоростью; он преодолевает относительно небольшое расстояние за то же время.Объект, который вообще не движется, имеет нулевую скорость.
Сравните это с медленно движущимся объектом с низкой скоростью; он преодолевает относительно небольшое расстояние за то же время.Объект, который вообще не движется, имеет нулевую скорость.
Скорость — это векторная величина, которая относится к «скорости, с которой объект меняет свое положение». Представьте себе человека, который быстро движется — шаг вперед и шаг назад — всегда возвращается в исходное положение. Хотя это может привести к безумной активности, это приведет к нулевой скорости. Поскольку человек всегда возвращается в исходное положение, движение никогда не приведет к изменению положения.Поскольку скорость определяется как скорость изменения положения, это движение приводит к нулевой скорости. Если движущийся человек желает максимизировать свою скорость, он должен приложить все усилия, чтобы максимизировать величину, на которую он смещается от своего исходного положения. Каждый шаг должен продвигать этого человека дальше от того места, где он начал. Наверняка человек никогда не должен менять направление и начинать возвращаться в исходное положение.
Наверняка человек никогда не должен менять направление и начинать возвращаться в исходное положение.
Скорость — это векторная величина.Таким образом, скорость учитывает направление . Оценивая скорость объекта, нужно следить за его направлением. Недостаточно сказать, что объект имеет скорость 55 миль / час. Необходимо включить информацию о направлении, чтобы полностью описать скорость объекта. Например, вы должны описать скорость объекта как 55 миль / ч, к востоку, . Это одно из существенных различий между скоростью и скоростью. Скорость — это скалярная величина, и не отслеживает направление ; скорость является векторной величиной и учитывает направление .
Определение направления вектора скорости
Задача описания направления вектора скорости проста. Направление вектора скорости совпадает с направлением движения объекта. Неважно, ускоряется объект или замедляется. Если объект движется вправо, его скорость описывается как правая. Если объект движется вниз, его скорость описывается как нисходящая.Таким образом, самолет, движущийся на запад со скоростью 300 миль / час, имеет скорость 300 миль / час на западе. Обратите внимание, что скорость не имеет направления (это скаляр), а скорость в любой момент — это просто значение скорости с направлением.
Если объект движется вниз, его скорость описывается как нисходящая.Таким образом, самолет, движущийся на запад со скоростью 300 миль / час, имеет скорость 300 миль / час на западе. Обратите внимание, что скорость не имеет направления (это скаляр), а скорость в любой момент — это просто значение скорости с направлением.
Расчет средней скорости и средней скорости
Когда объект движется, его скорость часто меняется. Например, во время обычной поездки в школу происходит много изменений скорости.Вместо того, чтобы показания спидометра оставались стабильными, стрелка постоянно перемещается вверх и вниз, отражая остановку и запуск, а также ускорение и замедление. В один момент автомобиль может двигаться со скоростью 50 миль / час, а в другой момент он может быть остановлен (т. Е. 0 миль / час). Тем не менее, во время поездки в школу человек может в среднем 32 мили / час. Среднюю скорость во время всего движения можно рассматривать как среднее значение всех показаний спидометра. Если бы показания спидометра можно было собирать с интервалом в 1 секунду (или 0.1-секундные интервалы или …), а затем усредненные вместе, можно было определить среднюю скорость. Теперь это будет много работы. И, к счастью, есть ярлык. Читать дальше. Средняя скорость движения часто вычисляется по следующей формуле:
Если бы показания спидометра можно было собирать с интервалом в 1 секунду (или 0.1-секундные интервалы или …), а затем усредненные вместе, можно было определить среднюю скорость. Теперь это будет много работы. И, к счастью, есть ярлык. Читать дальше. Средняя скорость движения часто вычисляется по следующей формуле:Напротив, средняя скорость часто вычисляется по этой формуле
Начнем реализацию нашего понимания этих формул со следующей задачи:
Вопрос: Во время отпуска Лиза Карр преодолела расстояние в 440 миль.Поездка заняла 8 часов. Какая у нее была средняя скорость?
Чтобы вычислить ее среднюю скорость, мы просто разделим пройденное расстояние на время поездки.
Это было легко! Лиза Карр развила в среднем 55 миль в час. Возможно, она не двигалась с постоянной скоростью 55 миль / час. Она, несомненно, была остановлена в какой-то момент времени (возможно, на перерыв в ванной или на обед), и, вероятно, в другие моменты времени она, вероятно, ехала со скоростью 65 миль в час. Тем не менее, она развивала в среднем 55 миль в час. Приведенная выше формула представляет собой сокращенный метод определения средней скорости объекта.
Тем не менее, она развивала в среднем 55 миль в час. Приведенная выше формула представляет собой сокращенный метод определения средней скорости объекта.
Средняя скорость в сравнении с мгновенной скоростью
Поскольку движущийся объект часто меняет свою скорость во время движения, принято различать среднюю скорость и мгновенную скорость. Различие заключается в следующем.
- Мгновенная скорость — скорость в любой момент времени.
- Средняя скорость — среднее значение всех мгновенных скоростей; можно найти просто по соотношению расстояние / время.
Вы можете думать о мгновенной скорости как о скорости, которую показывает спидометр в любой момент времени, а о средней скорости как о среднем значении всех показаний спидометра в течение поездки. Поскольку задача усреднения показаний спидометра была бы довольно сложной (и, возможно, даже опасной), средняя скорость обычно рассчитывается как отношение расстояния / времени.
Движущиеся объекты не всегда перемещаются с неустойчивой и изменяющейся скоростью. Иногда объект будет двигаться с постоянной скоростью с постоянной скоростью. То есть объект будет преодолевать одно и то же расстояние каждый равный промежуток времени. Например, бегун может бежать с постоянной скоростью 6 м / с по прямой в течение нескольких минут. Если ее скорость постоянна, то расстояние, которое проходит каждую секунду, будет таким же. Бегун преодолевал расстояние в 6 метров каждую секунду.Если бы мы могли измерять ее положение (расстояние от произвольной начальной точки) каждую секунду, то мы бы заметили, что положение менялось бы на 6 метров каждую секунду. Это будет разительно контрастировать с объектом, который меняет свою скорость. Объект с изменяющейся скоростью будет перемещаться на разные расстояния каждую секунду. В приведенных ниже таблицах данных показаны объекты с постоянной и изменяющейся скоростью.
А теперь давайте снова рассмотрим движение того учителя физики. Учитель физики идет 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север.Все движение длилось 24 секунды. Определите среднюю скорость и среднюю скорость.
Учитель физики идет 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север.Все движение длилось 24 секунды. Определите среднюю скорость и среднюю скорость.
Учитель физики прошел дистанцию 12 метров за 24 секунды; таким образом, ее средняя скорость составляла 0,50 м / с. Однако, поскольку ее смещение составляет 0 метров, ее средняя скорость составляет 0 м / с. Помните, что смещение относится к изменению положения, а скорость основывается на этом изменении положения. В этом случае движения учителя изменяется положение на 0 метров и, следовательно, средняя скорость составляет 0 м / с.
Вот еще один пример, аналогичный тому, что мы видели ранее при обсуждении расстояния и смещения. На схеме ниже показано положение лыжника в разное время. В каждый из указанных моментов лыжник разворачивается и меняет направление движения. Другими словами, лыжник перемещается из пункта A в пункт B, затем из пункта C в пункт D.
Используйте диаграмму, чтобы определить среднюю скорость и среднюю скорость лыжника в течение этих трех минут.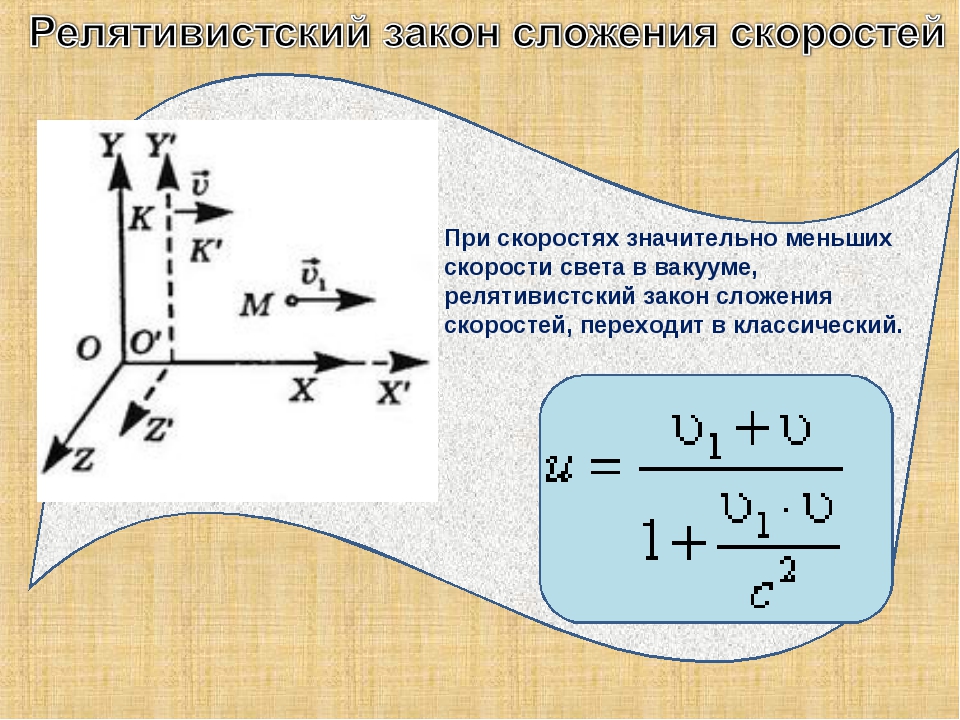 По завершении нажмите кнопку, чтобы просмотреть ответ.
По завершении нажмите кнопку, чтобы просмотреть ответ.
В качестве последнего примера рассмотрим футбольного тренера, который ходит взад и вперед по боковой линии. На диаграмме ниже показаны несколько позиций тренера в разное время. В каждой отмеченной позиции тренер делает «разворот» и движется в противоположном направлении. Другими словами, тренер переходит из позиции A в позицию B, затем из позиции C в позицию D.
Какова средняя и средняя скорость тренера? По завершении нажмите кнопку, чтобы просмотреть ответ.
В заключение, скорость и скорость — это кинематические величины, которые имеют совершенно разные определения. Скорость, будучи скалярной величиной, представляет собой скорость, с которой объект преодолевает расстояние. Средняя скорость — это отношение расстояния (скалярной величины) к временному интервалу. Скорость без учета направления . С другой стороны, скорость — это векторная величина; это с учетом направления . Скорость — это скорость изменения положения. Средняя скорость — это отношение смещения или изменения положения (векторная величина) за время.
Скорость — это скорость изменения положения. Средняя скорость — это отношение смещения или изменения положения (векторная величина) за время.
Посетите Назовите это движение.
Сложение векторов
С векторами и над векторами можно выполнять различные математические операции. Одна из таких операций — сложение векторов. Два вектора можно сложить вместе, чтобы определить результат (или полученный результат). Этот процесс добавления двух или более векторов уже обсуждался в предыдущем разделе. Вспомните в нашем обсуждении законов движения Ньютона, что чистая сила , испытываемая объектом, была определена путем вычисления векторной суммы всех индивидуальных сил, действующих на этот объект.То есть чистая сила была результатом (или результатом) сложения всех векторов силы. Во время этого блока правила суммирования векторов (например, векторов силы) оставались относительно простыми. Обратите внимание на следующие суммы двух векторов силы:
Вспомните в нашем обсуждении законов движения Ньютона, что чистая сила , испытываемая объектом, была определена путем вычисления векторной суммы всех индивидуальных сил, действующих на этот объект.То есть чистая сила была результатом (или результатом) сложения всех векторов силы. Во время этого блока правила суммирования векторов (например, векторов силы) оставались относительно простыми. Обратите внимание на следующие суммы двух векторов силы:
Эти правила суммирования векторов были применены к диаграммам свободного тела, чтобы определить результирующую силу (т. Е. Векторную сумму всех отдельных сил). Примеры приложений показаны на схеме ниже.
В этом модуле задача суммирования векторов будет расширена на более сложные случаи, когда векторы направлены в направлениях, отличных от чисто вертикального и горизонтального направлений. Например, вектор, направленный вверх и вправо, будет добавлен к вектору, направленному вверх и влево. Векторная сумма будет определена для более сложных случаев, показанных на диаграммах ниже.
Векторная сумма будет определена для более сложных случаев, показанных на диаграммах ниже.
Существует множество методов для определения величины и направления результата сложения двух или более векторов.В этом уроке будут обсуждаться два метода, которые будут использоваться на протяжении всего модуля:
Теорема Пифагора
Теорема Пифагора — полезный метод для определения результата сложения двух (и только двух) векторов , образующих прямой угол друг к другу. Этот метод не применим для добавления более двух векторов или для сложения векторов , а не под углом 90 градусов друг к другу.Теорема Пифагора — это математическое уравнение, которое связывает длину сторон прямоугольного треугольника с длиной гипотенузы прямоугольного треугольника.
Чтобы увидеть, как работает метод, рассмотрим следующую задачу:
Эрик покидает базовый лагерь и отправляется в поход на 11 км на север, а затем на 11 км на восток.Определите результирующее смещение Эрика.
В этой задаче требуется определить результат сложения двух векторов смещения, расположенных под прямым углом друг к другу.Результат (или результат) ходьбы на 11 км на север и 11 км на восток — это вектор, направленный на северо-восток, как показано на диаграмме справа. Поскольку смещение на север и смещение на восток расположены под прямым углом друг к другу, теорема Пифагора может использоваться для определения результирующей (то есть гипотенузы прямоугольного треугольника).
Результат сложения 11 км, север плюс 11 км, восток — вектор с величиной 15,6 км. Позже будет обсуждаться метод определения направления вектора.
Давайте проверим ваше понимание с помощью следующих двух практических задач. В каждом случае используйте теорему Пифагора, чтобы определить величину векторной суммы . По завершении нажмите кнопку, чтобы просмотреть ответ.
Использование тригонометрии для определения направления вектора
Направление результирующего вектора часто можно определить с помощью тригонометрических функций. Большинство студентов вспоминают значение полезной мнемоники SOH CAH TOA из своего курса тригонометрии. SOH CAH TOA — мнемоника, которая помогает запомнить значение трех общих тригонометрических функций — синуса, косинуса и тангенса. Эти три функции связывают острый угол в прямоугольном треугольнике с отношением длин двух сторон прямоугольного треугольника. Синусоидальная функция связывает меру острого угла с отношением длины стороны, противоположной углу, к длине гипотенузы.Функция косинуса связывает меру острого угла с отношением длины стороны, прилегающей к углу, к длине гипотенузы. Функция касательной связывает меру угла с отношением длины стороны, противоположной углу, к длине стороны, прилегающей к углу. Три уравнения ниже суммируют эти три функции в форме уравнения.
Большинство студентов вспоминают значение полезной мнемоники SOH CAH TOA из своего курса тригонометрии. SOH CAH TOA — мнемоника, которая помогает запомнить значение трех общих тригонометрических функций — синуса, косинуса и тангенса. Эти три функции связывают острый угол в прямоугольном треугольнике с отношением длин двух сторон прямоугольного треугольника. Синусоидальная функция связывает меру острого угла с отношением длины стороны, противоположной углу, к длине гипотенузы.Функция косинуса связывает меру острого угла с отношением длины стороны, прилегающей к углу, к длине гипотенузы. Функция касательной связывает меру угла с отношением длины стороны, противоположной углу, к длине стороны, прилегающей к углу. Три уравнения ниже суммируют эти три функции в форме уравнения.
Эти три тригонометрические функции могут быть применены к задаче туриста, чтобы определить направление общего перемещения туриста.Процесс начинается с выбора одного из двух углов (кроме прямого) треугольника. После выбора угла любую из трех функций можно использовать для определения меры угла. Напишите функцию и выполните соответствующие алгебраические шаги, чтобы найти меру угла. Работа представлена ниже.
После выбора угла любую из трех функций можно использовать для определения меры угла. Напишите функцию и выполните соответствующие алгебраические шаги, чтобы найти меру угла. Работа представлена ниже.
После определения меры угла можно определить направление вектора. В этом случае вектор составляет угол 45 градусов относительно востока.Таким образом, направление этого вектора записывается как 45 градусов. (Вспомните ранее в этом уроке, что направление вектора — это угол поворота против часовой стрелки, который вектор делает относительно востока.)
Расчетный угол не всегда соответствует направлению
Мера угла, определяемая с помощью SOH CAH TOA, составляет , а не всегда в направлении вектора. Следующая векторная диаграмма сложения является примером такой ситуации.Обратите внимание, что угол внутри треугольника определен как 26,6 градуса с использованием SOH CAH TOA. Этот угол представляет собой угол поворота на юг, который вектор R делает по отношению к Западу. Тем не менее, направление вектора, выраженное условным обозначением CCW (против часовой стрелки с востока), составляет 206,6 градуса.
Тем не менее, направление вектора, выраженное условным обозначением CCW (против часовой стрелки с востока), составляет 206,6 градуса.
Проверьте свое понимание использования SOH CAH TOA для определения направления вектора, попробовав следующие две практические задачи.В каждом случае используйте SOH CAH TOA для определения направления результирующего. По завершении нажмите кнопку, чтобы просмотреть ответ.
В приведенных выше задачах величина и направление суммы двух векторов определяется с помощью теоремы Пифагора и тригонометрических методов (SOH CAH TOA). Процедура ограничивается сложением двух векторов, образующих прямые углы друг к другу.Когда два вектора, которые должны быть добавлены, не находятся под прямым углом друг к другу, или когда необходимо сложить более двух векторов, мы будем использовать метод, известный как метод сложения векторов голова к хвосту. Этот метод описан ниже.
Этот метод описан ниже.
Величину и направление суммы двух или более векторов можно также определить с помощью точно нарисованной масштабированной векторной диаграммы.Используя масштабированную диаграмму, метод «голова к хвосту» используется для определения векторной суммы или результата. Обычная физическая лаборатория включает векторных прогулок . Либо используя смещения сантиметрового размера на карте, либо смещения метрового размера на большой открытой местности, ученик выполняет несколько последовательных смещений, начиная с назначенной начальной позиции. Предположим, вам дали карту вашего района и 18 направлений, по которым вам нужно следовать. Начиная с домашней базы , эти 18 векторов смещения можно было бы сложить вместе последовательно, чтобы определить результат сложения набора из 18 направлений. Возможно, первый вектор измеряется 5 см, восток. Когда это измерение закончится, начнется следующее измерение. Процесс будет повторяться для всех 18 направлений. Каждый раз, когда заканчивается одно измерение, начинается следующее измерение. По сути, вы использовали бы метод сложения векторов «голова к хвосту».
Возможно, первый вектор измеряется 5 см, восток. Когда это измерение закончится, начнется следующее измерение. Процесс будет повторяться для всех 18 направлений. Каждый раз, когда заканчивается одно измерение, начинается следующее измерение. По сути, вы использовали бы метод сложения векторов «голова к хвосту».
Метод «голова к хвосту» включает рисование вектора для масштабирования на листе бумаги, начиная с заданной начальной позиции.Там, где заканчивается голова этого первого вектора, начинается хвост второго вектора (таким образом, метод «голова к хвосту» ). Процесс повторяется для всех добавляемых векторов. После того, как все векторы были добавлены по направлению «голова к хвосту», результирующий результат протягивается от хвоста первого вектора к началу последнего вектора; т.е. от начала до конца. Как только результат нарисован, его длину можно измерить и преобразовать в реальных единиц, используя заданный масштаб. Направление полученного результата можно определить, используя транспортир и измерив его угол поворота против часовой стрелки с востока.
Направление полученного результата можно определить, используя транспортир и измерив его угол поворота против часовой стрелки с востока.
Пошаговый метод применения метода «голова к хвосту» для определения суммы двух или более векторов приведен ниже.
- Выберите масштаб и укажите его на листе бумаги. Наилучший выбор масштаба — такой, при котором диаграмма будет как можно больше, но при этом умещается на листе бумаги.
- Выберите начальную точку и нарисуйте первый вектор в масштабе в указанном направлении. Обозначьте величину и направление шкалы на диаграмме (например,г., МАСШТАБ: 1 см = 20 м).
- Начиная с того места, где заканчивается голова первого вектора, нарисуйте второй вектор в масштабе в указанном направлении. Обозначьте величину и направление этого вектора на диаграмме.
- Повторите шаги 2 и 3 для всех добавляемых векторов
- Нарисуйте результат от хвоста первого вектора к началу последнего вектора.
 Обозначьте этот вектор как Resultant или просто R .
Обозначьте этот вектор как Resultant или просто R . - Используя линейку, измерьте длину полученного результата и определите его величину путем преобразования в действительные единицы с помощью шкалы (4.4 см х 20 м / 1 см = 88 м).
- Измерьте направление результирующей, используя условные обозначения против часовой стрелки, о которых говорилось ранее в этом уроке.
Пример использования метода «голова к хвосту» проиллюстрирован ниже. Задача заключается в сложении трех векторов:
20 м, 45 град. + 25 м, 300 град. + 15 м, 210 град. МАСШТАБ: 1 см = 5 мМетод «голова к хвосту» используется, как описано выше, и определяется результат (выделен красным).Его величина и направление обозначены на схеме.
МАСШТАБ: 1 см = 5 м Интересно, что порядок, в котором добавляются три вектора, не влияет ни на величину, ни на направление результирующего. Результирующий по-прежнему будет иметь ту же величину и направление. Например, рассмотрим сложение тех же трех векторов в другом порядке.
Результирующий по-прежнему будет иметь ту же величину и направление. Например, рассмотрим сложение тех же трех векторов в другом порядке.
При сложении в этом другом порядке эти же три вектора по-прежнему дают результат с той же величиной и направлением, что и раньше (20. м, 312 градусов). Порядок, в котором векторы добавляются с использованием метода «голова к хвосту», не имеет значения.
МАСШТАБ: 1 см = 5 мДополнительные примеры сложения векторов методом «голова к хвосту» приведены на отдельной веб-странице.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Назови этот вектор», интерактивного элемента «Сложение векторов» или «Интерактивной игры по угадыванию векторов». Все три интерактивных элемента можно найти в разделе «Интерактивная физика» на нашем веб-сайте, и они обеспечивают интерактивный опыт с навыком добавления векторов.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Назови этот вектор», интерактивного элемента «Сложение векторов» или «Интерактивной игры по угадыванию векторов». Все три интерактивных элемента можно найти в разделе «Интерактивная физика» на нашем веб-сайте, и они обеспечивают интерактивный опыт с навыком добавления векторов.
Сложение и вычитание векторов — Практика — Гипертекст по физике
Практика
практическая задача 1
Два человека толкают инвалидную машину. Один прикладывает силу 200 N на восток, другой — 150 N на восток. Какая чистая сила действует на машину? (Предположим, трение незначительно.)
раствор
Силы направлены в одном направлении, поэтому они складываются.
| ∑ F = F 1 + F 2 ∑ F = 200 N + 150 N ∑ F = 350 N |
Две исходные силы — восток, поэтому результирующая — восток.
∑ F = 350 с.ш. восток
Никаких уловок. Некоторые проблемы решаются просто.
практическая задача 2
Два футболиста одновременно бьют по мячу с противоположных сторон. Красный № 3 бьет с силой 50 Н, а синий № 5 бьет с силой 63 Н. Какая чистая сила действует на мяч?
раствор
Силы направлены в противоположные стороны, поэтому они вычитаются. Подумайте об этом по-другому: одна из сил положительна, а другая — отрицательна. Знаки — это способ указать основные направления. Я думаю, что сделаю первый положительным, а второй отрицательным, потому что, почему бы и нет?
| ∑ F = F красный — F синий ∑ F = 50 Н — 63 Н ∑ F = −13 Н |
Как описать это направление? Никаких сторон света, таких как север, юг, восток или запад, не было.Ничего не было сказано ни о левом, ни о правом (или даже о верхнем или нижнем). Мы произвольно присвоили отрицательное значение направлению, в котором пинал Синий № 5. Ответ был отрицательным, поэтому чистая сила указывает в том направлении, в котором пинал Синий № 5. Назовем это подальше от Blue # 5.
Мы произвольно присвоили отрицательное значение направлению, в котором пинал Синий № 5. Ответ был отрицательным, поэтому чистая сила указывает в том направлении, в котором пинал Синий № 5. Назовем это подальше от Blue # 5.
∑ F = 13 N от синего # 5
Можно также написать…
∑ F = 13 с.ш. в сторону красного # 3
Это тоже был бы хороший ответ. Ни один из них не является более правильным, чем другой.
практическая задача 3
Самолет движется строго на север со скоростью 100 м / с из-за поперечного ветра 30 м / с, дующего с востока на запад. Определите результирующую скорость самолета (относительно севера).
раствор
Север (направление, в котором работают двигатели) перпендикулярно западу (направление, в котором толкает ветер). Результирующая этих двух векторов — гипотенеза прямоугольного треугольника. Воспользуемся теоремой Пифагора, чтобы найти его величину…
| против 2 = | v 2 плоскость + v 2 ветер | |
| против 2 = | (100 м / с) 2 + (30 м / с) 2 | |
| против = | 104 м / с | |
и касательная, чтобы найти его направление…
| тангенс угла θ = |
| ||||||
| тангенс угла θ = | |||||||
| θ = | 17 ° | ||||||
Эти 17 ° находятся на западной стороне севера, поэтому окончательный ответ . ..
..
v = 104 м / с, 17 ° к западу от севера
практическая задача 4
Альпинистская экспедиция устанавливает базовый лагерь и два промежуточных лагеря, A и B.Лагерь A находится в 11 200 м к востоку от базового лагеря и на 3200 м над ним. Лагерь B находится на 8400 м восточнее и на 1700 м выше лагеря A. Определите смещение между базовым лагерем и лагерем B.
раствор
Складываем векторы в одном направлении «обычным» сложением.
| x = 11 200 м + 8 400 м x = 19 600 м |
| y = 3200 м + 1700 м y = 4900 м |
Сложите векторы под прямым углом с помощью комбинации теоремы Пифагора для величины…
| r = √ ( x 2 + y 2 ) r = √ [(19 600 м) 2 + (4900 м) 2 ] r = 20 200 м |
и касательная для направления.
| тангенс угла θ = | y | = | 4900 м | |
| x | 19 600 м | |||
| θ = | 14,0 ° | |||
Не забудьте ответить на вопрос.
Лагерь B находится на расстоянии 20 200 м от базового лагеря под углом возвышения 14,0 ° .
Да, и не забудьте нарисовать рисунок.Я, наверное, должен был сказать тебе об этом раньше.
Решение задач с векторами
Мы можем использовать векторы для решения многих задач, связанных с физическими величинами, такими как скорость, скорость, вес, работа и так далее.
Скорость:
Скорость движущегося объекта моделируется вектором, направление которого является направлением движения, а величина — скоростью.
Пример :
Мяч брошен с начальной скоростью
70
футов в секунду. , под углом
35 год
°
с горизонтальным. Найдите вертикальную и горизонтальную составляющие скорости.
, под углом
35 год
°
с горизонтальным. Найдите вертикальную и горизонтальную составляющие скорости.
Позволять v представлять скорость и использовать данную информацию для записи v в форме единичного вектора:
v знак равно 70 ( потому что ( 35 год ° ) ) я + 70 ( грех ( 35 год ° ) ) j
Упростим скаляры, получим:
v ≈ 57.34 я + 40,15 j
Поскольку скаляры являются горизонтальной и вертикальной составляющими v ,
Следовательно, горизонтальная составляющая равна
57,34
футов в секунду, а вертикальная составляющая
40,15
футов в секунду.
Сила:
Сила также представлена вектором. Если на объект действуют несколько сил, результирующая сила, испытываемая объектом, является векторной суммой этих сил.
Пример :
Две силы F 1 и F 2 с величинами 20 и 30 фунт соответственно воздействуют на объект в точке п как показано. Найдите равнодействующие силы, действующие в п .
Сначала мы пишем F 1 и F 2 в компонентном виде:
v ≈ 57.34 я + 40,15 j
Упростим скаляры, получим:
F 1 знак равно ( 20 потому что ( 45 ° ) ) я + ( 20 грех ( 45 ° ) ) j знак равно 20 ( 2 2 ) я + 20 ( 2 2 ) j знак равно 10 2 я + 10 2 j F 2 знак равно ( 30 потому что ( 150 ° ) ) я + ( 30 грех ( 150 ° ) ) j знак равно 30 ( — 3 2 ) я + 30 ( 1 2 ) j знак равно — 15 3 я + 15 j
Итак, равнодействующая сила F является
F знак равно F 1 + F 2 знак равно ( 10 2 я + 10 2 j ) + ( — 15 3 я + 15 j ) знак равно ( 10 2 — 15 3 ) я + ( 10 2 + 15 ) j ≈ — 12 я + 29 j
Работа:
Работа
W
сделано силой
F
в движении по вектору
D
является
W
знак равно
F
⋅
D
.
Пример :
Сила задается вектором F знак равно 〈 2 , 3 〉 и перемещает объект из точки ( 1 , 3 ) к точке ( 5 , 9 ) . Найдите проделанную работу.
Сначала мы находим Displacement.
Вектор смещения
D знак равно 〈 5 — 1 , 9 — 3 〉 знак равно 〈 4 , 6 〉 .
Используя формулу, проделанная работа
W знак равно F ⋅ D знак равно 〈 2 , 3 〉 ⋅ 〈 4 , 6 〉 знак равно 26
Если единицей силы являются фунты, а расстояние измеряется в футах, то выполненная работа 26 фут-фунт
Лакмир Сингх Физика, класс 9 Решения, движение
Справочник формул для 9 класса по математике и естественным наукам
Лахмир Сингх Решения класса 9 по физике Движение Решения класса 9 по физике Лахмира Сингха Стр. №: 19
№: 19
Вопрос 1:
Является ли смещение скалярной величиной?
Решение:
Нет, смещение — это векторная величина.
Вопрос 2:
Укажите, является ли расстояние скалярной или векторной величиной.
Решение:
Расстояние — это скалярная величина.
Вопрос 3:
Измените скорость 6 м / с на км / ч.
Решение:
6 м / с
= 6 x (3600/1000) км / час = 21,6 км / час
Вопрос 4:
Как называется скорость в указанном направлении?
Решение:
Скорость тела в заданном направлении называется скоростью.
Вопрос 5:
Приведите два примера тел, движущихся неравномерно.
Решение:
(a) Движение автобуса по дороге
(b) Движение скаковой лошади
Вопрос 6:
Назовите физическую величину, полученную путем деления «пройденного расстояния» на «время, затраченное на прохождение этого расстояния».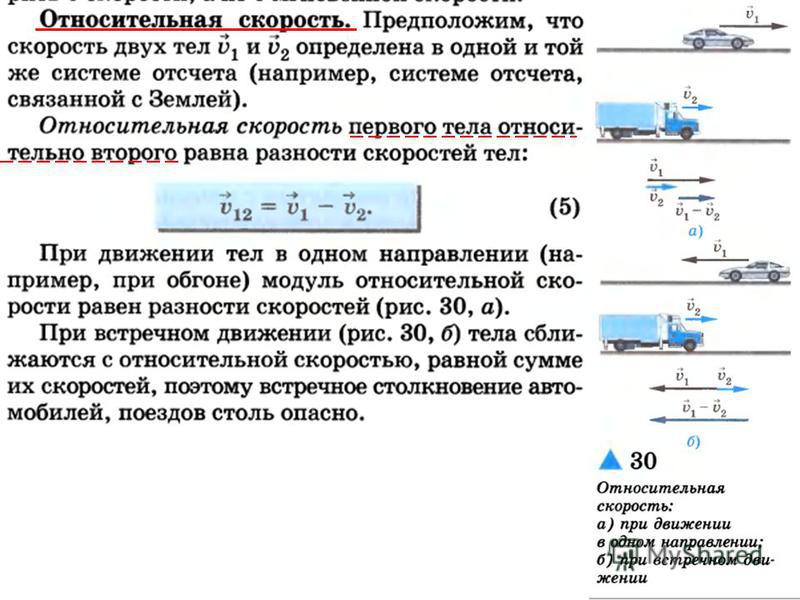
Решение:
Скорость определяется как расстояние, пройденное за единицу времени.
Вопрос 7:
Каковы следующие меры в автомобиле?
(a) Спидометр (b) Одометр
Решение:
(a) Спидометр автомобиля измеряет мгновенную скорость автомобиля.
(b) Одометр — это устройство, используемое для записи расстояния, пройденного автомобилем.
Решения класса 9 по физике Лахмира Сингха Стр. №: 20
Вопрос 8:
Назовите физическую величину, которая дает нам представление о том, насколько медленно или быстро движется тело.
Решение:
Скорость дает представление о том, насколько медленно или быстро движется тело.
Вопрос 9:
При каких условиях тело может пройти определенное расстояние, но его результирующее смещение будет равно нулю?
Решение:
Когда тело возвращается в исходную точку, оно имеет нулевое результирующее смещение, но преодолевает определенное ненулевое расстояние.
Вопрос 10:
Что еще мы должны знать, помимо скорости, для прогнозирования положения движущегося тела?
Решение:
Мы должны знать не только скорость, но и направление, в котором движется тело.
Вопрос 11:
Когда считается, что тело имеет равномерную скорость?
Решение:
Когда тело преодолевает равные расстояния за равные промежутки времени в определенном направлении, каким бы малым или большим ни был временной интервал, считается, что объект имеет равномерную скорость.
Вопрос 12:
При каком условии величина средней скорости равна средней скорости?
Решение:
Когда объект движется по одной прямой, величина средней скорости равна средней скорости.
Вопрос 13:
Что из двух может быть: нулем при определенных условиях: средняя скорость движущегося тела или средняя скорость движущегося тела?
Решение:
Средняя скорость движущегося тела может быть равна нулю.
Вопрос 14:
Приведите один пример ситуации, в которой тело имеет определенную среднюю скорость, но его средняя скорость равна нулю.
Решение:
Движение мальчика из дома в магазин (в одном направлении) и обратно домой (в обратном направлении) является примером ситуации, в которой тело имеет определенную среднюю скорость, но его средняя скорость равна нуль.
Вопрос 15:
Каково ускорение тела, движущегося с постоянной скоростью?
Решение:
Когда тело движется с постоянной скоростью, его ускорение равно нулю.
Вопрос 16:
Как еще называют отрицательное ускорение?
Решение:
Отрицательное ускорение также называется замедлением.
Вопрос 17:
Назовите физическую величину, единица измерения которой составляет:
(a) м / с (b) м / с 2
Решение:
(a) Скорость (или скорость)
(b) Разгон
Вопрос 18:
Какой тип движения совершает свободно падающее тело?
Решение:
Равномерно ускоренное движение
Вопрос 19:
Что такое единица измерения задержки в системе СИ?
Решение:
S. I. единица замедления м / с 2 .
I. единица замедления м / с 2 .
Вопрос 20:
Заполните следующие пропуски подходящими словами:
(a) Смещение — это …………………… количество, а расстояние — ………………………….
(b) Физическая величина, которая определяет скорость и направление движения тела, называется его ……………………… ..
(c) У мотоцикла есть устойчивая ……………. 3 м / с 2 . Это означает, что каждые ………………. его …………… .. увеличивается на ………….
(d) Скорость — это скорость изменения ………………………. Измеряется в дюймах.
(e) Ускорение — это скорость изменения ………………. Измеряется в
Решение:
(а) вектор, скаляр
(б) скорость
(в) ускорение, секунда, скорость, 3 м / с
(г) смещение, м / с
(д) скорость, м / с 2
Вопрос 21:
Какой тип движения, равномерный или неравномерный, демонстрирует свободно падающее тело? Обоснуйте свой ответ.
Решение:
Свободно падающее тело движется неравномерно, поскольку оно преодолевает меньшие расстояния в начальных интервалах «1 секунда» и большие расстояния в более поздних интервалах «1 секунда», т.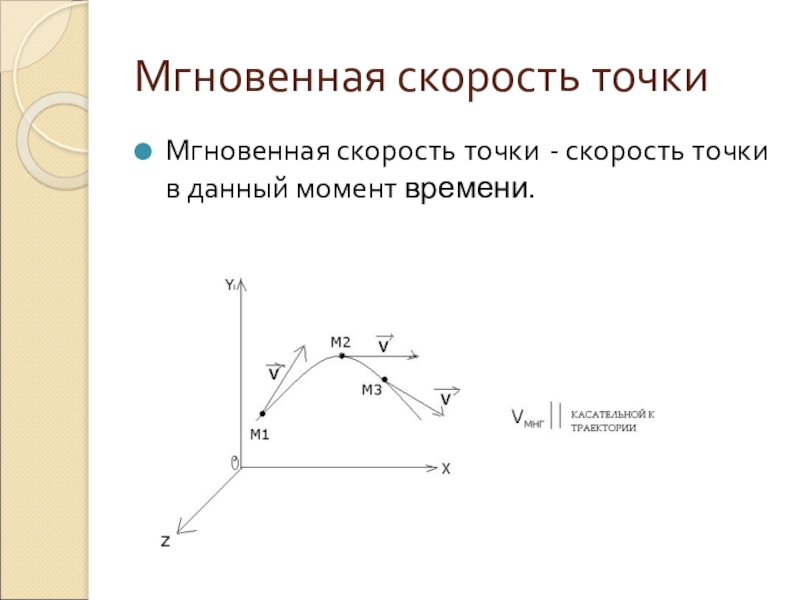 е.е., преодолевает неравные расстояния за равные промежутки времени.
е.е., преодолевает неравные расстояния за равные промежутки времени.
Вопрос 22:
Укажите, является ли скорость скалярной или векторной величиной. Обоснуйте свой выбор.
Решение:
Скорость — это скалярная величина, поскольку она имеет только величину и не имеет определенного направления.
Вопрос 23:
Автобус X преодолевает расстояние 360 км за 5 часов, тогда как автобус Y преодолевает расстояние 476 км за 7 часов. Какой автобус
едет быстрее?
Решение:
Для автобуса X,
Скорость = Расстояние / Время
Скорость = 360/5 = 72 км / ч
Для автобуса Y,
Скорость = Расстояние / Время
Скорость = 476/7 = 68 км / ч
Скорость автобуса X больше, чем автобуса Y.Следовательно, автобус X едет быстрее.
Вопрос 24:
Установите следующие скорости в порядке возрастания (сначала сохраняя наименьшую скорость):
- Спортсмен бежит со скоростью 10 м / с.

- Велосипед, движущийся со скоростью 200 м / мин.
- Самокат, движущийся со скоростью 30 км / ч.
Решение:
Скорость ателета = 10 м / с
Скорость велосипеда = 200 м / мин = 200/60 м / с = 3,33 м / с
Скорость самоката = 30 км / ч = 30000/3600 м / с = 8.33 м / с
3,33 м / с <8,33 м / с <10 м / с
т.е. 200 м / мин <30 км / ч <10 м / с
Вопрос 25:
(a) Напишите формулу ускорения. Дайте значение каждому символу, который в нем встречается.
(b) Поезд, отправляющийся с железнодорожного вокзала, развивает скорость 21 м / с за одну минуту. Найдите его ускорение.
Решение:
Вопрос 26:
(а) Какой термин используется для обозначения изменения скорости во времени?
(b) Назовите одно слово, означающее то же, что «движение с отрицательным ускорением».
(c) Смещение движущегося объекта в заданный интервал времени равно нулю. Будет ли расстояние, пройденное объектом, также равно нулю? Обоснуйте свой ответ.
Будет ли расстояние, пройденное объектом, также равно нулю? Обоснуйте свой ответ.
Решение:
(a) Ускорение
(b) Замедление
(c) Нет, потому что, если тело совершает круговой обход, так что его конечное положение совпадает с исходным положением, тогда смещение тела равно нулю, но пройденное расстояние не равно нулю.
Вопрос 27:
Улитка преодолевает расстояние 100 метров за 50 часов.Рассчитайте среднюю скорость улитки в км / ч.
Решение:
Средняя скорость = Общее пройденное расстояние / Общее время
Общее пройденное расстояние = 100 м = 0,1 км; Общее затраченное время = 50 часов
Средняя скорость = 0,1 / 50 = 0,002 км / ч
Решения класса 9 по физике Лахмира Сингха Стр. №: 21
Вопрос 28:
Черепаха преодолевает расстояние 100 метров за 15 минут. Какая средняя скорость черепахи в км / ч?
Решение:
Общее расстояние = 100 м = 0. 1 км
1 км
Общее затраченное время = 15 минут = 15/60 = 0,25 часа
Средняя скорость = Общее пройденное расстояние / Общее затраченное время
= 0,1 / 0,25 = 0,4 км / ч
Вопрос 29:
Если спринтер пробегает 100 метров за 9,83 секунды, рассчитайте его среднюю скорость в км / ч.
Решение:
Общее пройденное расстояние = 100 м
Общее затраченное время = 9,83 с
Средняя скорость = Общее пройденное расстояние / Общее затраченное время
= 100 / 9,83 = 10,172 м / с
Средняя скорость в км / ч:
10.172 x (3600/1000) = 36,62 км / ч
Вопрос 30:
Мотоциклист едет из места A в B с постоянной скоростью 30 км / ч -1 и возвращается из места B в A с постоянной скоростью 20 км / ч -1 . Найдите его среднюю скорость.
Решение:
Вопрос 31:
Мотоциклист трогается с места и достигает скорости 6 м / с после путешествия с равномерным ускорением в течение 3 с. Какое у него ускорение?
Какое у него ускорение?
Решение:
Начальная скорость = 0 м / с
Конечная скорость = 6 м / с
Время = 3 секунды
Вопрос 32:
Самолет, движущийся со скоростью 600 км / ч, постоянно ускоряется со скоростью 10 км / ч в секунду.Если принять скорость звука равной 1100 км / ч на высоте самолета, сколько времени потребуется, чтобы достичь «звукового барьера»?
Решение:
Начальная скорость, u = 600 км / ч
Конечная скорость, v = 1100 км / ч
Ускорение = 10 км / ч / с = 600 км / ч 2
Из соотношения a = (vu ) / t
t = (vu) / a
t = (1100-600) / 600 = 500/600 = 5/6 час = 50 сек
Вопрос 33:
Если автобус, движущийся со скоростью 20 м / с, подвергается постоянному замедлению 5 м / с 2 , сколько времени потребуется, чтобы остановиться?
Решение:
Торможение, a = -5 м / с 2
Начальная скорость, u = 20 м / с
Конечная скорость, v = 0 м / с
t =?
Вопрос 34:
(а) В чем разница между «пройденным телом» и «смещением»? Объясните с помощью схемы
.
(b) Муравей проходит расстояние 8 см от точки P до Q, а затем перемещается на расстояние 6 см под прямым углом к точке PQ. Найдите его результирующее смещение.
Решение:
(a) Пройденное расстояние — это фактическая длина непрямого пути, пройденного телом, тогда как смещение относится к прямолинейному пути между начальным и конечным положениями. Например, На приведенном ниже рисунке тело движется из точки A в точку B, а затем из точки B в точку C. Здесь расстояние, пройденное телом, равно AB + BC, а смещение равно AC.
Вопрос 35:
Определите движение. Что вы понимаете под терминами «равномерное движение» и «неравномерное движение»? Объясните на примерах.
(a) Определите скорость. Что такое единица измерения скорости в системе СИ?
(b) Что подразумевается под (i) средней скоростью и (ii) постоянной скоростью?
Решение:
Говорят, что тело находится в движении, если его положение непрерывно изменяется по отношению к неподвижному объекту, взятому за точку отсчета.
Тело движется равномерно, если оно проходит равные расстояния за равные промежутки времени, независимо от того, насколько малы эти промежутки времени.Например: автомобиль, движущийся с постоянной скоростью 10 м / с, будет преодолевать равное расстояние 10 м каждую секунду, поэтому его движение будет равномерным.
Неравномерное движение: тело движется неравномерно, если оно преодолевает неравные расстояния за равные промежутки времени. Например: сбросить мяч с крыши высокого здания.
Вопрос 36:
(a) Определите скорость. Что такое единица измерения скорости в системе СИ?
(b) В чем разница между скоростью и скоростью?
(c) Преобразуйте скорость 54 км / ч в м / с.
Решение:
(a) Скорость тела — это расстояние, которое оно проходит за единицу времени. Единица скорости в системе СИ — м / с.
(b) (i) Средняя скорость тела — это общее пройденное расстояние, деленное на общее время, затраченное на преодоление этого расстояния.
(ii) Под равномерной скоростью понимается постоянная скорость движущегося тела. Тело имеет равномерную скорость, если оно проходит равное расстояние за равные промежутки времени, независимо от того, насколько малы эти промежутки времени.
Вопрос 37:
(а) Что подразумевается под термином «ускорение»? Укажите единицу ускорения в системе СИ.
(b) Дайте определение термину «равномерное ускорение». Приведите один пример равноускоренного движения.
Решение:
(a) Скорость тела — это расстояние, которое оно проходит за единицу времени в заданном направлении. Единица измерения скорости в системе СИ — м / с.
(b) (i) Скорость — это скалярная величина, тогда как скорость — это векторная величина.
(ii) Скорость тела — это расстояние, пройденное им за единицу времени, тогда как скорость тела — это расстояние, пройденное им за единицу времени в заданном направлении.
(iii) Скорость всегда положительна, тогда как скорость может быть как положительной, так и отрицательной.
(c) Скорость = 54 км / ч = 54 x (1000/3600) = 15 м / с
Вопрос 38:
Расстояние между Дели и Агрой составляет 200 км. Первые 100 км поезд едет со скоростью 50 км / ч. Насколько быстро поезд должен проехать следующие 100 км, чтобы в среднем за весь путь он составлял 70 км / ч?
Решение:
(a) Ускорение тела определяется как скорость изменения его скорости во времени.Единица ускорения в системе СИ: м / с 2 .
(b) Тело имеет равномерное ускорение, если оно движется по прямой, и его скорость увеличивается на равную величину за равные промежутки времени. Например: Движение свободно падающего тела.
Вопрос 39:
Первые 15 км поезд движется с постоянной скоростью 30 км / ч; следующие 75 км с равномерной скоростью 50 км / ч; и последние 10 км с постоянной скоростью 20 км / ч. Рассчитайте среднюю скорость на всем пути следования поезда.
Решение:
Вопрос 40:
Первые 15 км поезд движется с постоянной скоростью 30 км / ч; следующие 75 км с равномерной скоростью 50 км / ч; и последние 10 км с постоянной скоростью 20 км / ч. Рассчитайте среднюю скорость на всем пути следования поезда.
Рассчитайте среднюю скорость на всем пути следования поезда.
Решение:
Вопрос 41:
Автомобиль движется по прямой дороге с постоянной скоростью. Он преодолевает 150 м за 5 секунд:
(a) Какова его средняя скорость?
(b) Как далеко он проходит за 1 секунду?
(c) Как далеко он проходит за 6 секунд?
(d) Сколько времени нужно, чтобы преодолеть 240 м?
Решение:
Решения класса 9 по физике Лахмира Сингха Стр. №: 22
Вопрос 55:
Тело движется по круговой траектории радиуса R.Какое будет пройденное расстояние и смещение тела, когда оно совершит половину оборота?
Решение:
Расстояние, пройденное за половину оборота круговой траектории, равно длине окружности полукруга, то есть
Вопрос 56:
Если в оба конца вы проехали 6 км, а затем вернулись домой:
(a) Какое расстояние вы прошли?
(б) Каково ваше окончательное перемещение?
Решение:
(i) Пройденное расстояние = 6 км
(ii) Смещение = ноль (поскольку конечное положение совпадает с исходным положением)
Вопрос 57:
Тело перемещается на 3 км на восток, затем на 4 км на север и, наконец, на 9 км на восток.
(i) Каково общее пройденное расстояние?
(ii) Каково результирующее смещение?
Решение:
(i) Общее пройденное расстояние = 3 + 4 + 9 = 16 км
(ii) Тело проходит общее расстояние 12 км в восточном направлении, то есть в направлении оси x.
И он проходит расстояние 4 км в северном направлении, то есть в направлении оси y. Следовательно, результирующее смещение составляет
Вопрос 58:
Мальчик идет из своего класса в книжный магазин по прямому коридору в сторону Севера.Он преодолевает расстояние 20 м за 25 секунд, чтобы добраться до книжного магазина. Купив книгу, он проходит такое же расстояние за то же время, чтобы вернуться в класс. Найдите (а) среднюю скорость и (б) среднюю скорость мальчика.
Решение:
(a) Общее расстояние, пройденное до книжного магазина и возвращения в класс = 20 + 20 = 40 м
Общее затраченное время = 25 + 25 = 50 секунд
Вопрос 59:
Автомобиль проезжает 100 км со скоростью 60 км / ч и возвращается со скоростью 40 км / ч. Рассчитайте среднюю скорость за весь путь.
Рассчитайте среднюю скорость за весь путь.
Решение:
В первом случае автомобиль движется со скоростью 60 км / ч на расстояние 100 км
Во втором случае автомобиль движется со скоростью 40 км / ч на расстояние 100 км
Общее пройденное расстояние = 200 км
Вопрос 60:
Мяч ударяется о стену по горизонтали на скорости 6,0 м с -1 . Он отскакивает по горизонтали на скорости 4,4 м с -1 . Мяч соприкасается со стенкой на 0.040 с. Какое ускорение у мяча?
Решение:
Начальная скорость, u = 6 м / с
Конечная скорость, v = -4,4 м / с (мяч отскакивает в противоположном направлении)
Время, t = 0,040 с
Решения класса 9 по физике Лахмира Сингха Страница №: 39
Вопрос 1:
(а) Что остается постоянным при равномерном круговом движении?
(б) Что постоянно меняется при равномерном круговом движении? ‘
Решение:
(a) Скорость
(b) Направление движения
Вопрос 2:
Укажите, верно ли следующее утверждение:
Земля движется вокруг Солнца с постоянной скоростью.
Решение:
Нет, Земля движется вокруг Солнца с постоянной скоростью, но ее скорость постоянно изменяется.
Вопрос 3:
Тело движется вокруг Солнца с постоянной скоростью по круговой орбите. Движение равномерное или ускоренное?
Решение:
Движение ускорено.
Вопрос 4:
Какой вывод вы можете сделать о скорости тела из графика смещения-времени, показанного ниже:
Решение:
Оно представляет равномерную скорость.
Вопрос 5:
Назовите величину, которая измеряется площадью, занимаемой под графиком скорость-время.
Решение:
Расстояние, пройденное движущимся телом.
Вопрос 6:
На что указывает наклон графика скорость-время?
Решение:
Наклон графика зависимости скорости от времени указывает на ускорение.
Вопрос 7:
На что указывает наклон графика «расстояние-время»?
Решение:
Наклон графика расстояние-время указывает скорость.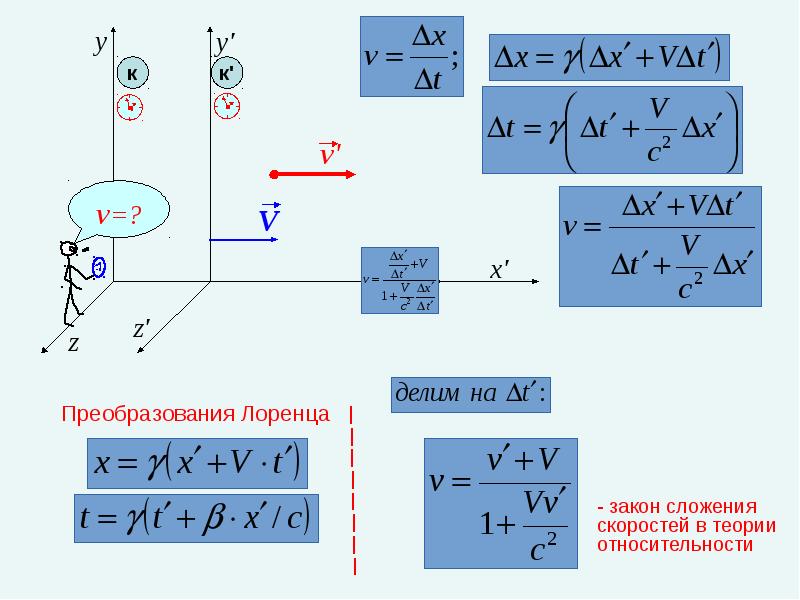
Вопрос 8:
Приведите один пример движения, при котором объект не меняет своей скорости, но его направление движения изменяется непрерывно.
Решение:
Движение Луны вокруг Земли.
Вопрос 9:
Назовите тип движения, при котором тело имеет постоянную, но не постоянную скорость.
Решение:
Равномерное круговое движение.
Вопрос 10:
Что вы можете сказать о движении тела, если его график скорость-время представляет собой прямую линию, параллельную оси времени?
Решение:
Скорость тела постоянная или равномерная.
Решения класса 9 по физике Лахмира Сингха Стр. №: 40
Вопрос 11:
Какой вывод вы можете сделать о скорости тела из следующего графика расстояние-время?
Решение:
Тело имеет равномерную скорость.
Вопрос 12:
Что вы можете сказать о движении тела, график расстояния-времени которого представляет собой прямую линию, параллельную оси времени?
Решение:
Тело не двигается.Он стационарный.
Вопрос 13:
Какой вывод вы можете сделать об ускорении тела из графика скорость-время, показанного ниже?
Решение:
Представляет неравномерное ускорение.
Вопрос 14:
Спутник движется вокруг Земли по круговой орбите с постоянной скоростью. Движение равномерное или ускоренное?
Решение:
Это ускоренное движение, поскольку скорость непрерывно изменяется.
Вопрос 15:
Какой тип движения представляет кончик «секундной» стрелки часов? Он равномерный или ускоренный?
Решение:
Кончик «секундной» стрелки часов представляет собой равномерное круговое движение. Это ускоренное движение.
Это ускоренное движение.
Вопрос 16:
Заполните следующие пропуски подходящими словами:
(a) Если тело движется с постоянной скоростью, его ускорение составляет ………………………… ..
(b) Наклон график расстояние-время показывает ………………….. движущегося тела.
(c) Наклон графика скорость-время движущегося тела дает его ……………………… ..
(d) На графике скорость-время — площадь, ограниченная кривой скорость-время и ось времени показывает …………… .. по телу.
(e) Что-то может ускоряться, но не изменять свою скорость, если оно движется ……………………… ..
Решение:
(a) нулевая
(b) скорость
(c ) ускорение
(d) пройденное расстояние
(e) круговой путь
Решения класса 9 по физике Лахмира Сингха Стр. №: 41
Вопрос 17:
Ускоряется ли равномерное круговое движение? Обоснуйте свой ответ
Решение:
Да, равномерное круговое движение ускоряется, потому что скорость изменяется из-за непрерывного изменения направления движения.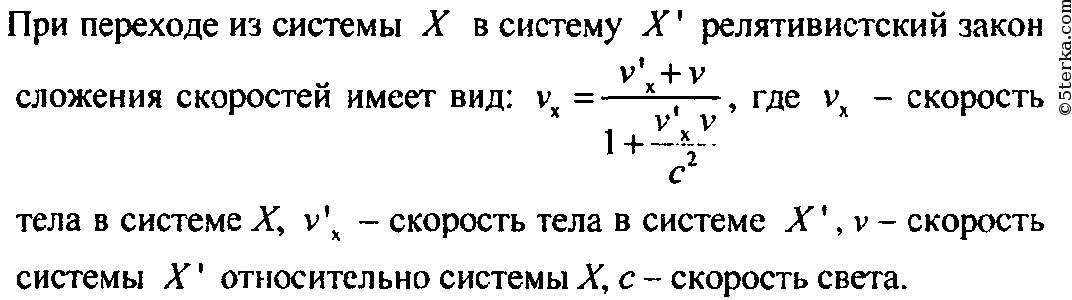
Вопрос 18:
Напишите формулу для расчета скорости тела, движущегося по круговой траектории. Дайте значение каждому символу, который в нем встречается.
Решение:
Скорость тела, движущегося по круговой траектории, определяется формулой:
где v = скорость
= 3,14 (постоянная величина)
r = радиус круговой траектории
t = время, затраченное на один виток круговой траектории
Вопрос 19:
Объясните, почему движение тела, которое движется с постоянной скоростью по круговой траектории, называется ускоренным.
Решение:
Движение тела, которое движется с постоянной скоростью по круговой траектории, называется ускоренным, потому что его скорость непрерывно изменяется из-за непрерывного изменения направления движения.
Вопрос 20:
В чем разница между равномерным линейным движением и равномерным круговым движением? Объясните на примерах.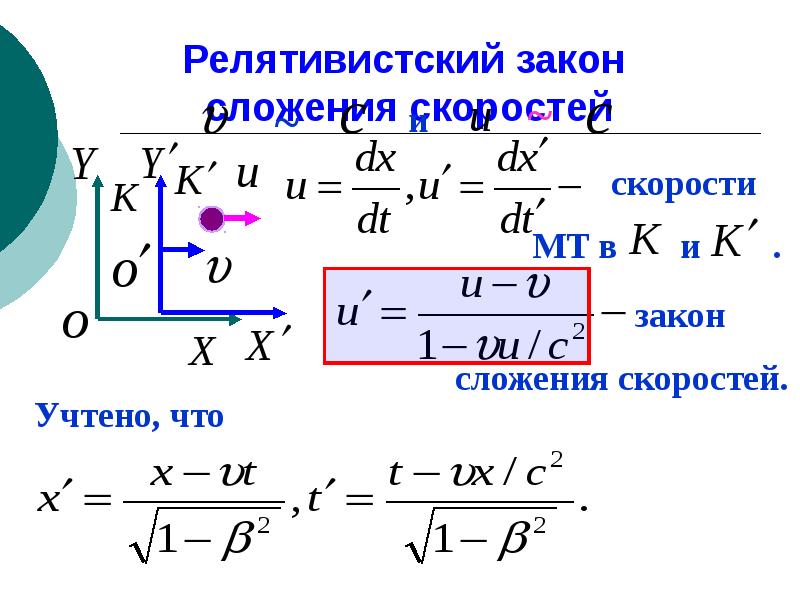
Решение:
Равномерное линейное движение — это равномерное движение по линейному пути или прямой линии.Направление движения фиксировано. Итак, это не ускоряется. Например: автомобиль движется с постоянной скоростью 10 км / ч по прямой дороге.
Равномерное круговое движение — это равномерное движение по круговой траектории. Направление движения постоянно меняется. Итак, он ускорен. Например: движение Земли вокруг Солнца.
Вопрос 21:
Укажите важную характеристику равномерного кругового движения. Назовите силу, вызывающую равномерное круговое движение.
Решение:
Важной характеристикой равномерного кругового движения является то, что направление движения в нем непрерывно изменяется со временем, поэтому оно ускоряется.
Центростремительная сила вызывает равномерное круговое движение.
Вопрос 22:
Найдите начальную скорость автомобиля, который останавливается за 10 секунд путем торможения. Тормозное замедление составляет 2,5 м / с 2 .
Тормозное замедление составляет 2,5 м / с 2 .
Решение:
Начальная скорость, u =?
Конечная скорость, v = 0 м / с (автомобиль остановлен)
Замедление, a = -2,5 м / с 2
Время, t = 10 с
v = u + при
0 = u + (- 2,5) x 10
u = 25 м / с
Вопрос 23:
Опишите движение тела, которое ускоряется с постоянной скоростью 10 мс — 2 .Если тело трогается с места, какое расстояние оно преодолеет за 2 с?
Решение:
Скорость этого тела увеличивается со скоростью ’10 метров в секунду’ каждую секунду.
Начальная скорость, u = 0 м / с
Время, t = 2 с
Ускорение, a = 10 м / с 2
Вопрос 24:
Мотоцикл, движущийся со скоростью 5 м / с, испытывает ускорение 0,2 м / с 2 . Рассчитайте скорость мотоцикла через 10 секунд и расстояние, пройденное за это время.
Решение:
Начальная скорость, u = 5 м / с
Конечная скорость, v =?
Ускорение, a = 0,2 м / с 2
Время, t = 10 с
Использование, v = u + при
v = 5 + 0,2 x 10
v = 5 + 2 = 7 м / с
Теперь пройденное расстояние по времени рассчитывается;
Вопрос 25:
Автобус, движущийся со скоростью 18 км / ч, останавливается за 2,5 секунды путем торможения. Рассчитайте произведенное замедление.
Рассчитайте произведенное замедление.
Решение:
Начальная скорость, u = 18 км / ч
Конечная скорость, v = 0 м / с
Время, t = 2.5 сек
Разгон, a =?
Использование, v = u + при
Итак, замедление составляет 2 м / с 2 .
Вопрос 26:
Поезд, трогаясь с места покоя, движется с равномерным ускорением 0,2 м / с 2 в течение 5 минут. Рассчитайте полученную скорость и пройденное за это время расстояние.
Решение:
Начальная скорость, u = 0 м / с
Конечная скорость, v =?
Ускорение, a = 0,2 м / с 2
Время, t = 5мин = 5 x60 = 300 с
Использование, v = u + при
v = 0 + 0.2 x 300 = 60 м / с
И пройденное расстояние составляет
Вопрос 27:
Назовите две величины, наклон графика которых дает:
(a) скорость и
(b) ускорение
Решение:
(a) Расстояние и время
(b) Скорость (или скорость) и Время
Вопрос 28:
Гепард стартует, отдыхает и ускоряется со скоростью 2 м / с 2 в течение 10 секунд. Вычислить:
Вычислить:
(a) конечная скорость
(b) пройденное расстояние.
Решение:
Начальная скорость,
u = 0 м / с
Конечная скорость, v =?
Ускорение, a = 2 м / с 2
Время, t = 10 с
(a) Используя,
v = u + при
v = 0 + 2 x 10 = 20 м / с
(b) Пройденное расстояние составляет:
Вопрос 29:
Поезд, движущийся со скоростью 20 м с -1 , ускоряется на 0,5 м с -2 за 30 с. Как далеко он продвинется за это время?
Решение:
Начальная скорость, u = 20 м / с
Время, t = 30 с
Ускорение,
a = 0.5 м / с 2
Пройденное расстояние:
Вопрос 30:
Велосипедист едет на скорости 15 м с -1 . Она тормозит, чтобы не столкнуться со стеной на расстоянии 18 м. Какое замедление она должна иметь?
Решение:
Начальная скорость, u = 15 м / с
Конечная скорость, v = 0 м / с
Расстояние, s = 18 м
Ускорение, a =?
Итак, замедление составляет 6,25 м / с 2 .
Вопрос 31:
Нарисуйте график скорости-времени, чтобы показать следующее движение:
Автомобиль равномерно ускоряется из состояния покоя в течение 5 с; затем он движется с постоянной скоростью в течение 5 с.
Решение:
Вопрос 32:
График скорость-время для части пути поезда представляет собой горизонтальную прямую линию. Что это говорит вам о
(а) скорости поезда и (б) о его ускорении?
Решение:
(a) Поезд движется с постоянной скоростью.
(b) Нет ускорения.
Вопрос 33:
(a) Объясните значение следующего уравнения движения: v = u + at, где символы имеют свои обычные значения.
(b) Тело, выходящее из состояния покоя, движется с равномерным ускорением. Если он преодолевает 100 м за 5 с, каково значение ускорения?
Решение:
(a) v = u + at — первое уравнение движения. Он дает скорость, приобретаемую телом за время t, когда тело имеет начальную скорость u и равномерное ускорение a. {2} \), где символы имеют обычное значение.
{2} \), где символы имеют обычное значение.
(b) Поезд, трогаясь с места и двигаясь с равномерным ускорением, развивает скорость 36 км в час за 10 минут. Найдите его ускорение.
Решение:
(a) Предположим, что тело имеет начальную скорость «u» и равномерное ускорение «a» в течение времени «t», так что его конечная скорость становится «v». Пусть расстояние, пройденное телом за это время, будет «s». Расстояние, пройденное движущимся телом за время «t», можно определить, рассматривая его среднюю скорость. Поскольку начальная скорость тела равна «u», а его конечная скорость равна «v», средняя скорость определяется как:
(b) Начальная скорость, u = 0 м / с
Конечная скорость, v = 36 км / ч = 10 м. / с
Время, t = 10мин = 10 x 60 = 600 с
Вопрос 36:
(a) Напишите три уравнения равноускоренного движения.Дайте значение каждому символу, который в них встречается.
(b) Автомобиль развивает скорость 72 км в час за 10 секунд, начиная с состояния покоя. Найдите
Найдите
(i) ускорение,
(ii) среднюю скорость и
(iii) расстояние, пройденное за это время.
Решение:
Вопрос 37:
(а) Что подразумевается под равномерным круговым движением? Приведите два примера равномерного кругового движения.
(b) Кончику секундной стрелки док-станции требуется 60 секунд, чтобы один раз повернуться по круговому циферблату часов.Если радиус циферблата часов составляет 10,5 см, рассчитайте скорость кончика секундной стрелки часов. (Учитывая \ (\ pi = \ frac {22} {7} \)).
Решение:
(a) Когда тело движется по круговой траектории с постоянной скоростью (постоянной скоростью), его движение называется равномерным круговым движением. Например,
(i) Искусственные спутники движутся равномерно по кругу вокруг Земли.
(ii) Движение велосипедиста по круговой трассе.
(b) Скорость тела, движущегося по круговой траектории, определяется формулой:
Дано, t = 60 сек.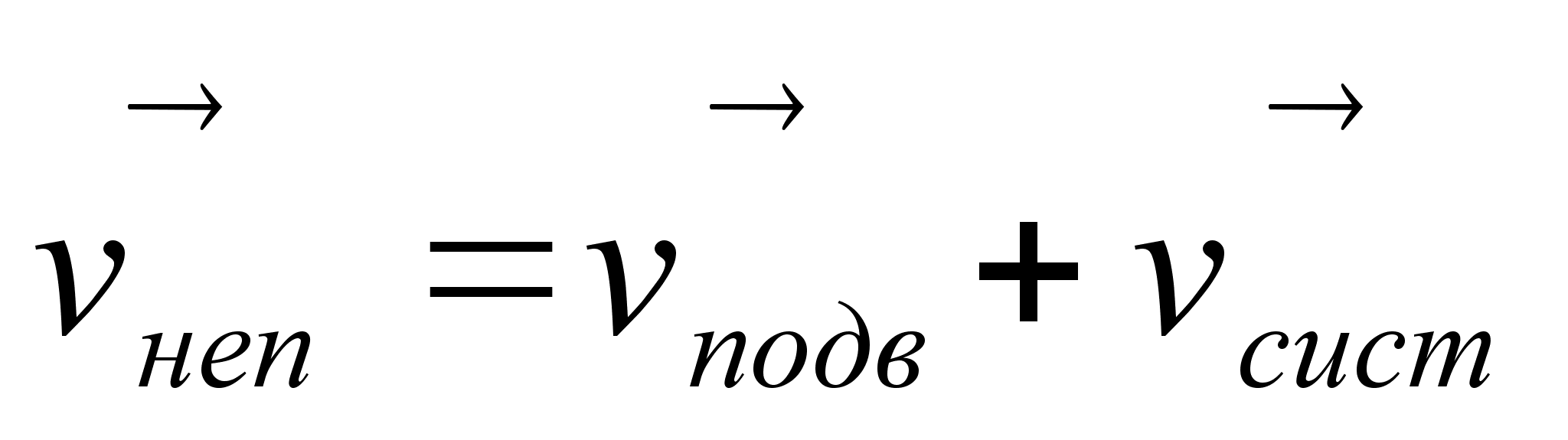
Радиус, r = 10.5 см = 0,105 м
Решения класса 9 по физике Лахмира Сингха Стр. №: 42
Вопрос 38:
С помощью графического метода покажите, что: v = u + at, где символы имеют свои обычные значения.
Решение:
Рассмотрим график скорость-время тела, показанный на рисунке.
Тело имеет начальную скорость u в точке A, а затем его скорость изменяется с постоянной скоростью от A до B за время t. Другими словами, имеется равномерное ускорение a от A до B, и по прошествии времени t его конечная скорость становится v, которая равна BC на графике.Время t обозначено OC. Чтобы завершить фигуру, мы проводим перпендикуляр CB из точки C, а AD проводим параллельно OC. BE — перпендикуляр от точки B к OE.
Итак, Начальная скорость тела, u = OA —– (1)
И, Конечная скорость тела, v = BC —— (2)
Но из графика BC = BD + DC
Следовательно, v = BD + DC —— (3)
Снова DC = OA
Итак, v = BD + OA
Теперь, из уравнения (1), OA = u
Итак, v = BD + u —— (4)
Мы должны выяснить стоимость BD сейчас. Мы знаем, что наклон графика скорости-времени равен ускорению a.{2} \), где символы имеют свое обычное значение.
Мы знаем, что наклон графика скорости-времени равен ускорению a.{2} \), где символы имеют свое обычное значение.
Решение:
Рассмотрим график скорость-время тела, показанный на рисунке. Тело имеет начальную скорость u в точке A, а затем его скорость изменяется с постоянной скоростью от A до B за время t. Другими словами, имеется равномерное ускорение a от A до B, и по прошествии времени t его конечная скорость становится v, которая равна BC на графике. Время t обозначено OC.
Предположим, что тело проходит расстояние s за время t. На рисунке расстояние, пройденное телом, определяется площадью пространства между графиком AB скорости-времени и осью времени OC, которая равна площади фигуры OABC.Таким образом:
Пройденное расстояние = Площадь фигуры OABC
= Площадь прямоугольника OADC + площадь треугольника ABD
Теперь мы найдем площадь прямоугольника OADC и площадь треугольника ABD.
(i) Площадь прямоугольника OADC = OA x OC
= uxt
= ut
(ii) Площадь треугольника ABD = (1/2) x Площадь прямоугольника AEBD
= (1/2) x AD x BD
= (1/2) xtx при
= (1/2) при 2
Пройденное расстояние, s = Площадь прямоугольника OADC + площадь треугольника ABD
Вопрос 40:
Выведите следующее уравнение движения графическим методом: v 2 = u 2 + 2as, где символы имеют свои обычные значения.
Решение:
Рассмотрим график скорость-время тела, показанный на рисунке. Тело имеет начальную скорость u в точке A, а затем его скорость изменяется с постоянной скоростью от A до B за время t. Другими словами, имеется равномерное ускорение a от A до B, и по прошествии времени t его конечная скорость становится v, которая равна BC на графике. Время t обозначено OC. Чтобы завершить фигуру, мы проводим перпендикуляр CB из точки C, а AD проводим параллельно OC. BE — перпендикуляр от точки B к OE.
Расстояние s, пройденное телом за время t, определяется площадью фигуры OABC, которая представляет собой трапецию.
Пройденное расстояние, s = Площадь трапеции OABC
Теперь, OA + CB = u + v и OC = t Подставляя эти значения в указанное выше соотношение, мы получаем:
Исключите t из приведенного выше уравнения. Это можно сделать, получив значение t из первого уравнения движения.
Решения класса 9 по физике Лахмира Сингха Стр. №: 43
№: 43
Вопрос 53:
На приведенном рядом графике показано положение тела в разное время.Рассчитайте скорость тела по мере его движения от:
(i) A до B,
(ii) от B до C и
(iii) от C до D.
Решение:
(i) Расстояние, пройденное от От A до B составляет (3-0) = 3 см
Время, необходимое для преодоления расстояния от A до B = (5-2) = 3 с
(ii) Скорость тела при движении от B к C равна нулю.
(iii) Расстояние, пройденное от C до D, составляет (7-3) = 4 см
Время, затраченное на преодоление расстояния от C до D = (9-7) = 2 с
Вопрос 54:
Что вы можете сказать о движении тела, если:
(а) его график смещения-время представляет собой прямую линию?
(b) его график скорости-времени представляет собой прямую линию?
Решение:
(a) Тело имеет равномерную скорость, если его график смещения-времени представляет собой прямую линию.
(b) Тело имеет равномерное ускорение, если его график скорости-времени представляет собой прямую линию.
Вопрос 55:
Тело с начальной скоростью x движется с равномерным ускорением y. Постройте его график скорости-времени.
Решение:
Вопрос 56:
Рядом представлен график скорость-время для движущегося тела:
Находка:
(i) Скорость тела в точке C.
(ii) Ускорение, действующее на тело между A и
(iii ) Ускорение, действующее на тело между B и C.
Решение:
(i) BC представляет собой равномерную скорость. Из графика видно, что скорость тела в точке C = 40 км / ч
(ii) Ускорение между A и B = наклон линии AB
(iii) BC представляет собой равномерную скорость, поэтому ускорение, действующее на тело между B и C равен нулю.
Вопрос 57:
Тело движется равномерно по прямой линии со скоростью 5 м / с. Найдите графически расстояние, пройденное им за 5 секунд.
Найдите графически расстояние, пройденное им за 5 секунд.
Решение:
Пройденное расстояние = Площадь прямоугольника OABC
= OA x OC
= 5 x 5 = 25 м
Вопрос 58:
Рядом приведен график скорости подъема пассажирского лифта.
Какое ускорение лифта:
(i) в течение первых двух секунд?
(ii) между второй и десятой секундами?
(iii) в течение последних двух секунд?
Решение:
Вопрос 59:
Автомобиль движется по прямой дороге с равномерным ускорением. Скорость автомобиля изменяется со временем следующим образом:
Время (с): 0 2 4 6 8 10
Скорость (м / с): 4 8 12 16 20 24
Нарисуйте график скорости-времени, выбрав удобный масштаб.Из этого графика:
(i) Рассчитайте ускорение автомобиля.
(ii) Рассчитайте расстояние, пройденное автомобилем за 10 секунд.
Решение:
Вопрос 60:
На приведенном рядом графике показано, как скорость автомобиля изменяется со временем:
(i) Какова начальная скорость автомобиля?
(ii) Какая максимальная скорость достигает автомобиля?
(iii) Какая часть графика показывает нулевое ускорение?
(iv) Какая часть графика показывает различное замедление?
(v) Найдите расстояние, пройденное за первые 8 часов.
Решение:
(i) Начальная скорость автомобиля = 10 км / ч
(ii) Максимальная скорость, достигаемая автомобилем = 35 км / ч.
(iii) BC представляет собой нулевое ускорение.
(iv) CD представляет собой различное замедление.
(в)
Вопрос 61:
Три графика скорости-времени представлены ниже:
Какой график представляет случай:
(i) мяч для крикета, брошенный вертикально вверх и возвращающийся в руки бросающего?
(ii) троллейбус замедляется до постоянной скорости, а затем ускоряется равномерно?
Решение:
(i) График (c): Скорость мяча равномерно уменьшается по мере его движения вверх, достигает нуля в наивысшей точке, а затем равномерно увеличивается по мере движения вниз.
(ii) График (a): Скорость тележки равномерно уменьшается, затем она движется с постоянной скоростью, а затем скорость равномерно увеличивается.
Решения класса 9 по физике Лахмира Сингха Стр. №: 44
№: 44
Вопрос 62:
Изучите приведенный рядом график скорости-времени автомобиля и ответьте на следующие вопросы:
(i) Какой тип движения представлен OA?
(ii) Какой тип движения представлен AB?
(iii) Какой тип движения представлен BC?
(iv) Каково ускорение автомобиля от точки 0 до точки А?
(v) Каково ускорение автомобиля от точки A до точки B?
(vi) Какое замедление автомобиля от B до C?
Решение:
(i) OA представляет собой равномерное ускорение
(ii) AB представляет постоянную скорость.
(iii) BC представляет собой равномерное замедление.
(iv) Ускорение автомобиля от O до A = наклон линии OA
(v) Ускорение от A до B равно нулю, поскольку в это время он имеет равномерную скорость.
(vi) Замедление автомобиля от B до C = наклон линии BC
Вопрос 63:
Какой тип движения представлен на каждом из следующих графиков?
Решение:
(i) График (a) представляет равномерное ускорение.
(ii) График (b) представляет постоянную скорость.
(iii) График (c) представляет равномерное замедление.
(iv) График (d) представляет неравномерное замедление.
Вопрос 64:
Автомобиль едет по дороге за 8 мс -1 . Ускоряется за 1 мс -2 на расстояние 18 м. Как быстро он тогда путешествует?
Решение:
Начальная скорость, u = 8 м / с
Ускорение, a = 1 м / с 2
Расстояние, s = 18 м
Вопрос 65:
Автомобиль движется по дороге со скоростью 20 м / с.В 50 м впереди на дорогу выбегает ребенок, водитель автомобиля нажимает на педаль тормоза. Каким должно быть замедление машины, если она должна остановиться прямо перед тем, как подъехать к ребенку?
Решение:
Начальная скорость, u = 20 м / с
Конечная скорость, v = 0 м / с
Расстояние, s = 50 м
Торможение кабины должно составлять 4 м / с 2 .
Скалярное сложение: определение, использование и пример
Scalar Addition How-To
Скалярное сложение очень просто, как и базовое сложение: все, что вам нужно сделать, это сложить значения вместе.Вам не о чем больше беспокоиться.
Например, вам даны эти две скалярные величины: 20 и 54. Вы можете сложить эти две величины так же, как и обычные числа.
И готово.
Использует
В физике две скалярные величины, с которыми вы часто будете работать, это масса и заряд . Масса объекта показывает, из какого количества вещества он сделан. Когда вы встаете на весы с балансировочной ручкой, вы получаете свою массу.Заряд объекта — это то, сколько напряжения он излучает.
Поскольку обе эти величины являются скалярными, их можно сложить с помощью скалярного сложения.
Примеры
Давайте рассмотрим некоторые примеры, использующие массу и заряд.
Вам нужно использовать лифт, чтобы поднять тяжелые ящики на третий этаж здания. Лифт имеет грузоподъемность 600 фунтов, что означает, что лифт может поднять только 600 фунтов. Вам нужно выяснить массу ваших ящиков, чтобы увидеть, сможет ли лифт справиться с этим.Общая масса всех объектов не должна превышать 600 фунтов. Что вы делаете? Вот список ваших ящиков и их масс.
Лифт имеет грузоподъемность 600 фунтов, что означает, что лифт может поднять только 600 фунтов. Вам нужно выяснить массу ваших ящиков, чтобы увидеть, сможет ли лифт справиться с этим.Общая масса всех объектов не должна превышать 600 фунтов. Что вы делаете? Вот список ваших ящиков и их масс.
| Ящик 1 | 45 фунтов |
| Ящик 2 | 20 фунтов |
| Ящик 3 | 95 фунтов |
| Ящик 4 | 70 фунтов |
| Ящик 5 | 80 фунтов |
Вы понимаете, что масса является скалярной величиной, поэтому для решения этой проблемы вы можете пойти дальше и использовать скалярное сложение, чтобы найти ответ.Вы можете сложить массы следующим образом:
- 45 + 20 + 95 + 70 + 80 = 310 фунтов
Все ваши коробки в сумме составляют 310 фунтов. Это намного меньше 600 фунтов, поэтому вы можете безопасно использовать этот лифт, чтобы перевезти коробки на третий этаж.
Вот еще пример.
Ваш напарник-инженер работает над новой игрушкой — электрической собакой, которая может слышать простые команды, такие как «приходи» и «сидеть», и подчиняться им. Эта электронная собака требует множества электрических компонентов.Один такой компонент питается от двух источников питания. Вашему напарнику необходимо вычислить общий заряд, который получает этот компонент. Один источник питания посылает заряд 2 вольта, в то время как другой источник питания посылает заряд 3 вольта. Вы можете помочь своему другу?
Вы непременно сможете помочь своему другу! На самом деле это очень простая проблема: вы понимаете, что заряд — это скалярная величина, поэтому вы можете использовать скалярное сложение с этими двумя величинами.
И готово. Этот конкретный компонент получает в общей сложности 5 вольт.
Краткое содержание урока
Прямое сложение чисел называется скалярным сложением . При скалярном сложении все, что вам нужно сделать, это сложить свои значения вместе. Вам не о чем больше беспокоиться.
Вам не о чем больше беспокоиться.
В физике и масса , и заряд являются скалярными величинами, поэтому вы можете использовать скалярное сложение с обоими из них. Это означает, что все, что вам нужно сделать, это добавить значения для каждого объекта, и вы найдете общую сумму.
Другими примерами скалярных величин являются скорость и высота.
В дополнение к скорости, что еще мы должны знать в порядке порядка 11 класса физики CBSE
Подсказка: Физические величины, которые участвуют в скорости изменения скоростей, все, что нам нужно, чтобы правильно предсказать положение движущегося тела. Мы также можем написать формулу одного из уравнений из законов движения, которое дает пройденное расстояние. Полный ответ:
В данном вопросе нам предоставлены следующие данные:
Нам дано движущееся тело.2} \]
Где
\ [S \] указывает расстояние, на которое перемещается тело.
\ [u \] указывает начальную скорость тела.
\ [t \] указывает время, необходимое для преодоления необходимого расстояния.
\ [a \] указывает ускорение движущегося тела.
Итак, из приведенного выше уравнения очень ясно, что для прогнозирования положения движущегося тела нам потребуются направление, время и ускорение движущегося тела. Все эти физические величины будут правильно определять положение движущегося тела с большой точностью. .
Дополнительная информация:
Ускорение — это физическая величина, которая говорит нам о скорости изменения скорости. Ускорение тела положительное, когда тело ускоряется, а ускорение отрицательное, когда тело замедляется. Скорость или скорость — это скорость изменения смещения расстояния. Скорость — это векторная величина, а скорость — это скалярная величина.
Примечание: Отвечая на этот вопрос, мы должны знать, что скорость не может сама по себе определять положение тела.Если определенное тело связано только со скоростью, то оно будет продолжать движение по прямой траектории бесконечное время.
 )
) Под каким углом к выбранному направлению оси ОУ и с какой скоростью относительно поверхности воды гребец держит курс, если скорость течения реки 5 км/ч? (Ответ: 0,22 м/с.)
Под каким углом к выбранному направлению оси ОУ и с какой скоростью относительно поверхности воды гребец держит курс, если скорость течения реки 5 км/ч? (Ответ: 0,22 м/с.)
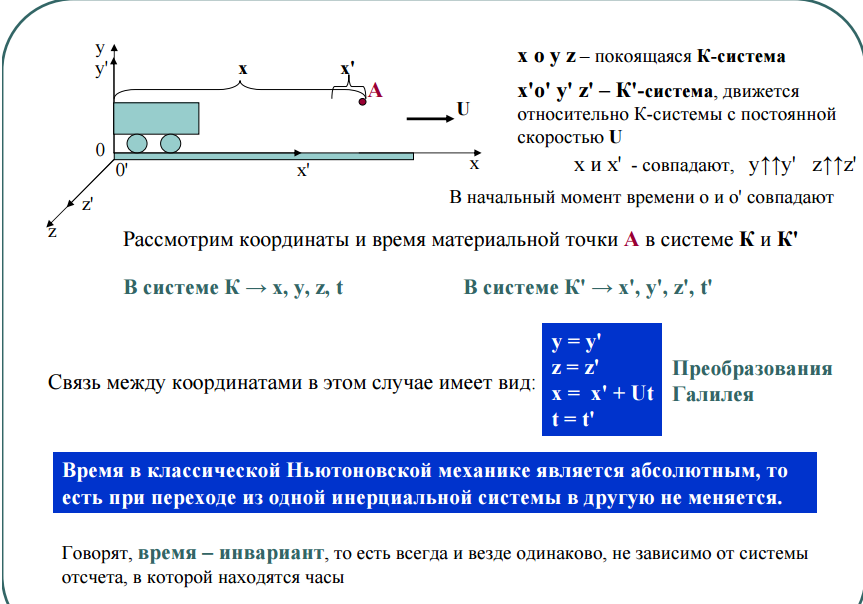

 Определите результирующее смещение Эрика.
Определите результирующее смещение Эрика. Обозначьте этот вектор как Resultant или просто R .
Обозначьте этот вектор как Resultant или просто R .