Урок 14. статика. равновесие абсолютно твердых тел — Физика — 10 класс
Физика, 10 класс
Урок 14. Статика. Равновесие абсолютно твёрдых тел
Перечень вопросов, рассматриваемых на уроке:
1.Условия равновесия тела
2.Момент силы
3.Плечо силы
4. Центр тяжести
Глоссарий по теме
Статика – раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой
Абсолютно твердое тело – модельное понятие классической механики, обозначающее совокупность точек, расстояния между текущими положениями которых не изменяются.
Центр тяжести – центром тяжести тела называют точку, через которую при любом положении тела в пространстве проходит равнодействующая сил тяжести, действующих на все частицы тела.
Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.
Устойчивое равновесие — это равновесие, при котором тело, выведенное из состояния устойчивого равновесия, стремится вернуться в начальное положение.
Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, будет еще больше отклоняться от положения равновесия.
Безразличное равновесие системы — равновесие, при котором после устранения причин, вызвавших малые отклонения, система остается в покое в этом отклоненном состоянии
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017.– С. 165 – 169.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009.
Степанова Г.Н. Сборник задач по физике. 10-11 класс. — М.: Просвещение. 1999 г. С.48- 50.
Теоретический материал для самостоятельного изучения
Равновесие – это состояние покоя, т. е. если тело покоится относительно инерциальной системы отсчета, то говорят, что оно находится в равновесии. Вопросы равновесия интересуют строителей, альпинистов, артистов цирка и многих-многих других людей. Любому человеку приходилось сталкиваться с проблемой сохранения равновесия. Почему одни тела, выведенные из состояния равновесия, падают, а другие – нет? Выясним, при каком условии тело будет находиться в состоянии равновесия.
е. если тело покоится относительно инерциальной системы отсчета, то говорят, что оно находится в равновесии. Вопросы равновесия интересуют строителей, альпинистов, артистов цирка и многих-многих других людей. Любому человеку приходилось сталкиваться с проблемой сохранения равновесия. Почему одни тела, выведенные из состояния равновесия, падают, а другие – нет? Выясним, при каком условии тело будет находиться в состоянии равновесия.
Раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой. Статика является частным случаем динамики. В статике твердое тело рассматривается как абсолютно твердое, т.е. недеформируемое тело. Это означает, что деформация так мала, что её можно не учитывать.
Центр тяжести существует у любого тела. Эта точка может находиться и вне тела. Как же подвесить или подпереть тело, чтобы оно находилось в равновесии.
Подобную задачу в свое время решил Архимед. Им же были введены понятие плеча силы и момента силы.
Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.
После своих исследований Архимед сформулировал условие равновесия рычага и вывел формулу:
Это правило является следствием 2-го закона Ньютона.
Первое условие равновесия
Для равновесия тела необходимо, чтобы сумма всех сил, приложенных к телу была равна нулю.
формула должна быть в векторном виде и стоять знак суммы
Второе условие равновесия
При равновесии твердого тела сумма моментов вcех внешних сил, действующих на него относительно любой оси, равна нулю.
Не менее важен случай, когда тело имеет площадь опоры. Тело, имеющее площадь опоры, находится в равновесии, когда вертикальная прямая, проходящая через центр тяжести тела, не выходит за пределы площади опоры этого тела. Известно, что в городе Пизе в Италии существует наклонная башня. Несмотря на то, что башня наклонена, она не опрокидывается, хотя ее часто называют падающей. Очевидно, что при том наклоне, которого башня достигла к настоящему времени, вертикаль, проведенная из центра тяжести башни, все еще проходит внутри ее площади опоры.
Очевидно, что при том наклоне, которого башня достигла к настоящему времени, вертикаль, проведенная из центра тяжести башни, все еще проходит внутри ее площади опоры.
В практике большую роль играет не только выполнение условия равновесия тел, но и качественная характеристика равновесия, называемая устойчивостью.
Различают 3 вида равновесия: устойчивое, неустойчивое, безразличное.
Если при отклонении тела от положения равновесия, возникают силы или моменты сил, стремящиеся вернуть тело в положение равновесия, то такое равновесие называется устойчивым.
Неустойчивое равновесие — это противоположный случай. При отклонении тела от положения равновесия, возникают силы или моменты сил, которые стремятся увеличить это отклонение.
Наконец, если при малом отклонении от положения равновесия тело все равно остается в равновесии, то такое равновесие называется безразличным.
Чаще всего необходимо, чтобы равновесие было устойчивым. Когда равновесие нарушается, то сооружение становится опасным, если его размеры велики.
Примеры и разбор решения заданий
1. Чему равен момент силы тяжести груза массой 40 кг, подвешенного на кронштейне АВС, относительно оси, проходящей через точку В, если АВ=0,5 м и угол α=450
Решение:
Момент силы – это величина равная произведению модуля силы на её плечо.
Сначала найдём плечо силы, для этого нам надо опустить перпендикуляр из точки опоры на линию действия силы. Плечо силы тяжести равно расстоянию АС. Так как угол равен 45°, то мы видим, что АС=АВ
Модуль силы тяжести находим по формуле:
После подстановки числовых значений величин мы получим:
F=40×9,8 =400 Н, М= 400 ×0,5=200 Н м.
Ответ: М=200 Н м.
2. Приложив вертикальную силу F, груз массой М — 100 кг удерживают на месте с помощью рычага (см. рис.). Рычаг состоит из шарнира без трения и однородного массивного стержня длиной L=8 м. Расстояние от оси шарнира до точки подвеса груза равно b=2 м. Чему равен модуль силы F, если масса рычага равна 40 кг.
Решение:
По условию задачи рычаг находится в равновесии. Напишем второе условие равновесия для рычага:
.
После подстановки числовых значений величин получим
F= (100×9,8 ×2 + 0,5×40×9,8×8)/8=450 Н
Ответ: 450 Н.
1.3.2 Условия равновесия твердого тела в ИСО
Видеоурок: Равновесие телЛекция: Равновесие тел
Под равновесием понимают такое состояние тела, при котором оно остается неподвижным относительно выбранной ИСО.
Раздел физики, который изучает равновесие, называется статикой.
Условия равновесия
Существует два основных условия равновесия тел:
1. Исходя из известного нам II закона Ньютона, чтобы тело оставалось неподвижным, суммарная (равнодействующая) сила должна быть равна нулю. То есть, чтобы определить условие, при котором тело будет находиться в равновесии, сумму проекций сил на любую ось, следует приравнять к нулю:
То есть, чтобы определить условие, при котором тело будет находиться в равновесии, сумму проекций сил на любую ось, следует приравнять к нулю:
2. Второе условие касается моментов сил:
Чтобы тело находилось в равновесии, сумма моментов на все оси тоже должна равняться нулю.
Для определения знака момента следует помнить правило:
Если момент вращает тело против часовой стрелки, то он отрицательный, если по часовой стрелке — положительный.
Следует запомнить некоторое уточнение: Если тело находится в равновесии, это еще не значит, что оно покоится.
Общие рекомендации по решению задач на статику
В основе каждого алгоритма лежит два основных условия равновесия, которые следует записать в первую очередь в проекциях с учетом знаков.
Для тела, двигающегося поступательно без вращений, следует:
1. Сделать схематический рисунок условия задачи. На данном рисунке следует обозначить все силы, указывая направления и точки приложения.
2. На рисунке следует указать направления осей. Они выбираются произвольно с учетом удобства нахождения проекций.
3. Записать условия равновесия. Если количество сил не превышает трёх, то для удобства их следует объединить в один треугольник, в котором можно воспользоваться теоремой синусов, косинусов, Пифагора для определения неизвестных величин.
Решение задач для тел, имеющих ось вращения:
1. На рисунке указать все силы, плечи, направление моментов.
2. Составить уравнения равновесия относительно оси. Если ось не задана, то установить её в неподвижной точке тела. Относительно данной оси следует определить знаки моментов.
3. Составить систему уравнений равновесия и решить её относительно неизвестной величины.
Условия равновесия твердых тел
На прошлом уроке мы уже выяснили, что для равновесия необходимо, чтобы сумма всех внешних и внутренних сил, приложенных к телу, была равна нулю.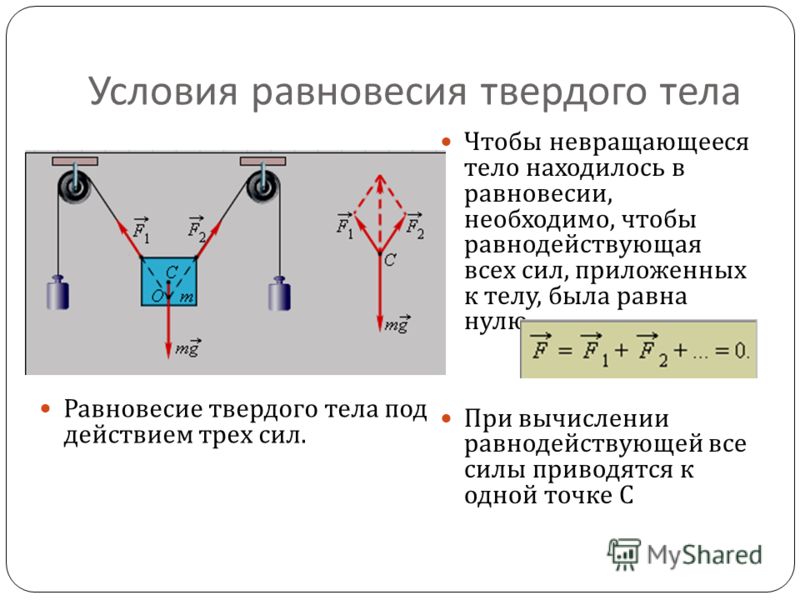
Но сумма всех внутренних сил любого тела равна нулю, исходя из третьего закона Ньютона. Поэтому, первое условие равновесия таково: сумма всех внешних сил, действующих на тело, должна быть равна нулю:
Самой очевидной внешней силой является сила тяжести, которая действует на все тела, находящиеся на Земле. Но эту силу, как мы помним, могут уравновешивать другие внешние силы. В этих случаях, возникает равновесие твердых тел.
Однако, даже если сумма всех внешних сил, действующих на тело, равна нулю — этого еще не достаточно, чтобы утверждать, что тело находится в равновесии. Дело в том, что тело может вращаться. Скажем, вы можете приложить к противоположным краям линейки силы, равные по модулю и противоположные по направлению. В этом случае, равнодействующая этих сил будет равна нулю. Несмотря на это, линейка начнет вращаться.
Значит, нужно найти еще
одно условие, равновесия тела. Проведем простой опыт: попытайтесь положить
линейку на ластик, так, чтоб ни один из краёв линейки не касался стола. Вам
удастся сделать это только тогда, когда ластик будет точно посередине линейки.
Теперь, давайте разберемся, почему так происходит. На каждый конец линейки
действует сила тяжести. Кроме того, на ту часть линейки, которая соприкасается
с ластиком, действует реакция опоры. Очевидно, что сила тяжести, действующая на
оба конца линейки, не меняется из-за того, что вы двигаете линейку.
Проведем простой опыт: попытайтесь положить
линейку на ластик, так, чтоб ни один из краёв линейки не касался стола. Вам
удастся сделать это только тогда, когда ластик будет точно посередине линейки.
Теперь, давайте разберемся, почему так происходит. На каждый конец линейки
действует сила тяжести. Кроме того, на ту часть линейки, которая соприкасается
с ластиком, действует реакция опоры. Очевидно, что сила тяжести, действующая на
оба конца линейки, не меняется из-за того, что вы двигаете линейку.
Значит, играет роль расстояние от каждого из концов до точки приложения силы реакции опоры.
Рассмотрим случай очень маленького отклонения линейки от положения равновесия. В этом случае, линейка повернётся на очень малый угол α.
Если линейка пришла в движение, значит, увеличилась её кинетическая энергия. А для того, чтобы изменить кинетическую энергию, необходимо совершить работу. Давайте подсчитаем работу сил:
Работа силы, как мы помним, равна произведению модулей силы, перемещения, и косинуса угла между их направлениями:
Формально, в описанной
ситуации концы линейки будут двигаться криволинейно. Но мы оговорили в самом
начале, что угол поворота очень маленький, поэтому, перемещения концов линейки
можно считать прямолинейными. В этом случае:
Но мы оговорили в самом
начале, что угол поворота очень маленький, поэтому, перемещения концов линейки
можно считать прямолинейными. В этом случае:
Очевидно, что ось вращения проходит через середину линейки. Плечо силы — это кратчайшее расстояние от оси вращения до линии действия силы. Произведения силы на её плечо, называется моментом силы.
Исходя из этого, мы можем сформулировать второе условие равновесия тел: сумма моментов внешних сил, действующих на тело относительно оси вращения, должна быть равна нулю:
Условимся считать момент силы положительным, если эта сила стремится повернуть тело против часовой стрелки. И наоборот, момент силы будем считать отрицательным, если эта сила стремится повернуть тело по часовой стрелке.
Итак, для того, чтобы твердое тело находилось в равновесии, сумма внешних сил должна быть равна нулю и сумма моментов внешних сил должна быть равна нулю:
Например, качаясь
на качелях, можно найти положение равновесия. Если оба человека обладают одной
и той же массой, то самое простое — это сесть обоим на самый край. Если же
массы не равны, то человек с наименьшей массой должен сесть на самый край, а
второй человек должен подсаживаться все ближе и ближе к оси вращения (то есть к
середине качели).
Если оба человека обладают одной
и той же массой, то самое простое — это сесть обоим на самый край. Если же
массы не равны, то человек с наименьшей массой должен сесть на самый край, а
второй человек должен подсаживаться все ближе и ближе к оси вращения (то есть к
середине качели).
В какой-то момент, расстояние от второго человека до середины качели будет меньше, чем расстояние от первого человека до середины качели, ровно во столько раз, во сколько масса второго человека, больше, чем масса первого человека. Это и будет означать, что сумма моментов внешних сил равна нулю, поэтому, качели окажутся в равновесии.
Вы знаете, что качаясь на таких качелях, нужно постоянно отталкиваться от земли.
Давайте разберемся, что
происходит в этот момент. Обозначим на рисунке силы, действующие на каждого
человека. Будем считать, что и тот, и другой человек сидит на краю качели, то
есть расстояние от каждого из них до середины качели одинаково. Итак,
представим, что один край качели, на котором сидит человек, обладающий большей
массой, только что опустился. Качели не сдвинутся с места до тех пор, пока
человек не оттолкнется от земли. Дело в том, что момент М1
> M2.
Действительно, поскольку расстояние d1
= d2,
момент силы будет больше при большей силе. Чтобы начать качаться, нужно сделать
так, чтобы момент M1
стал меньше M2.
То есть, в нашем случае, нужно сделать силу F1
меньше, чем F2.
Итак,
представим, что один край качели, на котором сидит человек, обладающий большей
массой, только что опустился. Качели не сдвинутся с места до тех пор, пока
человек не оттолкнется от земли. Дело в том, что момент М1
> M2.
Действительно, поскольку расстояние d1
= d2,
момент силы будет больше при большей силе. Чтобы начать качаться, нужно сделать
так, чтобы момент M1
стал меньше M2.
То есть, в нашем случае, нужно сделать силу F1
меньше, чем F2.
На первый взгляд, это
кажется невозможным, поскольку изменить силу тяжести можно только изменив
массу. Но, мы имеем дело не с силой тяжести, а с весом. Вспомните, ведь именно
вес определяется как сила, действующая на опору. До тех пор, пока человек не
предпринимает никаких действий, сила тяжести уравновешивается реакцией опоры. То
есть, в данном случае, вес равен силе тяжести. Рассмотрим теперь, что
произойдет, если человек, оттолкнётся от земли. Мышцы ног приложат некоторую
силу, направленную вертикально вниз, к поверхности земли. При этом по третьему
закону Ньютона, поверхность земли подействует на человека с силой, равной по
модулю, но противоположной по направлению. То есть, эта сила будет направлена
вертикально вверх. Тогда, по второму закону Ньютона, сила тяжести будет равна
сумме силы реакции опоры и силы, с которой человек оттолкнётся от земли. Таким
образом, вес человека (равный реакции опоры N1) будет равен
разности между силой тяжести и силой F.
Теперь, если выражение F1
– F2
меньше, чем F2,
то качели начнут двигаться. Как правило, достаточно приложить сравнительно
небольшую силу, поскольку чаще всего, на таких качелях качаются люди с
приблизительно одинаковой массой.
То
есть, в данном случае, вес равен силе тяжести. Рассмотрим теперь, что
произойдет, если человек, оттолкнётся от земли. Мышцы ног приложат некоторую
силу, направленную вертикально вниз, к поверхности земли. При этом по третьему
закону Ньютона, поверхность земли подействует на человека с силой, равной по
модулю, но противоположной по направлению. То есть, эта сила будет направлена
вертикально вверх. Тогда, по второму закону Ньютона, сила тяжести будет равна
сумме силы реакции опоры и силы, с которой человек оттолкнётся от земли. Таким
образом, вес человека (равный реакции опоры N1) будет равен
разности между силой тяжести и силой F.
Теперь, если выражение F1
– F2
меньше, чем F2,
то качели начнут двигаться. Как правило, достаточно приложить сравнительно
небольшую силу, поскольку чаще всего, на таких качелях качаются люди с
приблизительно одинаковой массой. Однако, очевидно, что человек, обладающий
меньшей массой, должен будет прикладывать бо́льшую силу, чтобы нормально
качаться. Или же, человек, обладающий большей массой, должен будет
пододвинуться поближе к середине качели.
Однако, очевидно, что человек, обладающий
меньшей массой, должен будет прикладывать бо́льшую силу, чтобы нормально
качаться. Или же, человек, обладающий большей массой, должен будет
пододвинуться поближе к середине качели.
Все выше сказанное, скорее всего, знал каждый из вас. Теперь же, вы можете описать это с точки зрения физики и объяснить, почему так происходит.
Пример решения задачи.
Задача. На двух веревках подвешен груз, так, как показано на рисунке. Если масса груза 20 кг, то каковы силы натяжения веревок?
Равновесие абсолютно твёрдого тела
Мы с вами уже долгое время изучаем различные взаимодействия
тел, основным признаком которых является появление у тел ускорений. Но бывают
случаи, когда нам необходимо знать, при каких условиях тело, на которое
действуют несколько сил одновременно, движется прямолинейно и равномерно или же
находится в состоянии покоя. Конечно же, в последнем случае мы всегда можем
выбрать другую инерциальную систему отсчёта, в которой тело будет покоиться. В
этом случае говорят, что тело находится в равновесии. Поэтому в дальнейшем мы с
вами будем изучать условия равновесия покоящихся тел. Задача эта имеет огромное
практическое значение для машиностроения, строительного дела и других областей
техники.
Конечно же, в последнем случае мы всегда можем
выбрать другую инерциальную систему отсчёта, в которой тело будет покоиться. В
этом случае говорят, что тело находится в равновесии. Поэтому в дальнейшем мы с
вами будем изучать условия равновесия покоящихся тел. Задача эта имеет огромное
практическое значение для машиностроения, строительного дела и других областей
техники.
Но прежде чем приступить к изучению этих условий, нам с вами необходимо вспомнить понятие абсолютно твёрдого тела. Итак, абсолютно твёрдое тело — это тело, размеры и форму которого можно считать неизменными при любых взаимодействиях тела. В дальнейшем для краткости абсолютно твёрдое тело мы с вами будем называть твёрдым телом или просто телом.
Раздел механики, в котором изучают условия равновесия
абсолютно твёрдых тел, называется статикой. Её главным отличием от
кинематики и динамики является то, что в ней необходимо учитывать не только
размеры и форму тел, но и точки приложения сил.
Изучая законы Ньютона, мы с вами говорили о том, что если на тело действуют одновременно несколько сил, но при этом оно покоится или движется прямолинейно и равномерно, то из второго закона Ньютона следует, что векторная сумма всех сил, приложенных к телу, равна нулю:
Это следствие из второго закона Ньютона называют первым условием равновесия тела. Из него следует, что и сумма проекций всех сил на любое направление тоже должна быть равна нулю. И несмотря на то, что последние три уравнения эквивалентны одному векторному равенству, с их помощью достаточно просто решать задачи.
Первое условие равновесия тела является необходимым, но не
является достаточным. Убедимся в этом. Для этого рассмотрим простой пример. Вот
у нас есть деревянный брусок. Что произойдёт, если мы к его концам приложим две
равные по модулю, но противоположные по направлению силы? Правильно, он начнёт
вращаться, несмотря на то, что геометрическая сумма действующих на него сил
равна нулю. Точно так же две одинаковые по модулю и противоположно направленные
силы поворачивают руль велосипеда или автомобиля.
Точно так же две одинаковые по модулю и противоположно направленные
силы поворачивают руль велосипеда или автомобиля.
Следовательно, необходимо ещё одно условие, при котором твёрдое тело может находиться в равновесии. Для его поиска рассмотрим тело с закреплённой осью вращения. Этот простой механизм известен нам ещё с седьмого класса как рычаг первого рода.
Итак, пусть на концы рычага действуют две силы F1 и F2, направленные в одну сторону. Кроме этих двух сил на рычаг будет действовать и сила нормальной реакции со стороны оси рычага. Очевидно, что при равновесии рычага геометрическая сумма этих трёх сил равна нулю:
Теперь предположим, что под действием внешних сил рычаг
повернулся на очень малый угол φ. При этом точки приложения внешних сил пройдут
некоторые пути, которые, в силу малости угла поворота, можно считать прямыми
отрезками. А раз точки приложения сил совершили перемещения, то сами силы
совершили работу. При этом сила F1
совершила положительную работу, так как точка В перемещалась по
направлению действия силы. А работа силы F2
отрицательна, поскольку точка С двигалась в сторону, противоположную
направлению силы. Сила же F3 работу
не совершала, так как точка её приложения не двигалась.
При этом сила F1
совершила положительную работу, так как точка В перемещалась по
направлению действия силы. А работа силы F2
отрицательна, поскольку точка С двигалась в сторону, противоположную
направлению силы. Сила же F3 работу
не совершала, так как точка её приложения не двигалась.
Пройденные точками В и С пути мы можем выразить из прямоугольных треугольников через угол поворота, измеренного в радианах:
А теперь давайте вспомним, что кратчайшее расстояние от оси вращения до линии действия силы называется плечом силы. Обозначив плечи сил F1 и F2 через d1 и d2 соответственно, перепишем уравнения для работ сил с учётом введённых нами обозначений:
Обратите внимание на вот эти множители. Ещё в седьмом классе
мы с вами говорили о том, что произведение модуля силы на её плечо
называется моментом силы относительно оси вращения.
Сразу же условимся считать момент силы положительным, если сила стремится повернуть тело по ходу часовой стрелки, а отрицательным — если против хода часовой стрелки (но никто вам не запрещает считать наоборот).
Тогда можно записать, что работа каждой из сил равна произведению момента силы на угол поворота рычага:
А суммарная работа, совершаемая внешними силами, — это сумма работ, совершаемых каждой из сил в отдельности:
С другой стороны, эту же работу мы могли бы найти и на основании теоремы о кинетической энергии:
Но при равновесии скорость не изменяется. А это значит, что изменение кинетической энергии тела равно нулю. Поэтому и работа внешних сил равна нулю. А так как угол поворота рычага отличен от нуля, то тогда должна быть равна нулю сумма моментов внешних сил:
Отсюда следует, что тело, имеющее неподвижную ось вращения,
находится в равновесии, если алгебраическая сумма моментов сил, приложенных к
телу, относительно этой оси́ равна нулю. Это и есть второе условие
равновесия твёрдого тела.
Это и есть второе условие
равновесия твёрдого тела.
Таким образом, в общем случае тело будет находится в равновесии, если геометрическая сумма приложенных к телу сил и алгебраическая сумма моментов этих сил относительно любой оси равны нулю.
Обратим ваше внимание на то, что эти условия равновесия применимы только для абсолютно твёрдых тел. Покажем это. Предположим, что у нас есть кусок резинового шнура. Приложим к его концам две одинаковые по модулю, но направленные вдоль шнура в противоположные стороны силы.
Их геометрическая сумма равна нулю? Равна. А сумма моментов этих сил? Тоже равна нулю, причём относительно оси́, проходящей через любую точку шнура. Но шнур при этом не находится в равновесии — он растягивается.
В механике очень часто необходимо знать, в каких случаях тело
может сколь угодно долго оставаться в равновесии, если оно находилось в покое в
начальный момент времени. Конечно же, должны выполняться условия равновесия,
рассмотренные нами ранее. Однако не во всяком равновесии тело, находящееся в
начальный момент времени в покое, будет покоится и в последующие моменты
времени. Ведь в реальных условиях оно испытывает и случайные неучитываемые нами
воздействия.
Конечно же, должны выполняться условия равновесия,
рассмотренные нами ранее. Однако не во всяком равновесии тело, находящееся в
начальный момент времени в покое, будет покоится и в последующие моменты
времени. Ведь в реальных условиях оно испытывает и случайные неучитываемые нами
воздействия.
Поэтому в механике принято различать три вида равновесий: устойчивое, неустойчивое и безразличное.
Рассмотрим их на таком примере. Пусть у нас есть игрушечная машинка, находящаяся в равновесии на некой выпуклой поверхности, и в начальный момент времени действующие на неё сила тяжести и сила нормальной реакции опоры уравновешивают друг друга.
Слегка толкнём машинку — она отклонится от своего
первоначального положения. Теперь силы тяжести и нормальной реакции опоры уже
не могут уравновесить друг друга. А их равнодействующая, как видно из рисунка,
направлена от положения равновесия и вызывает дальнейшее отклонение игрушки.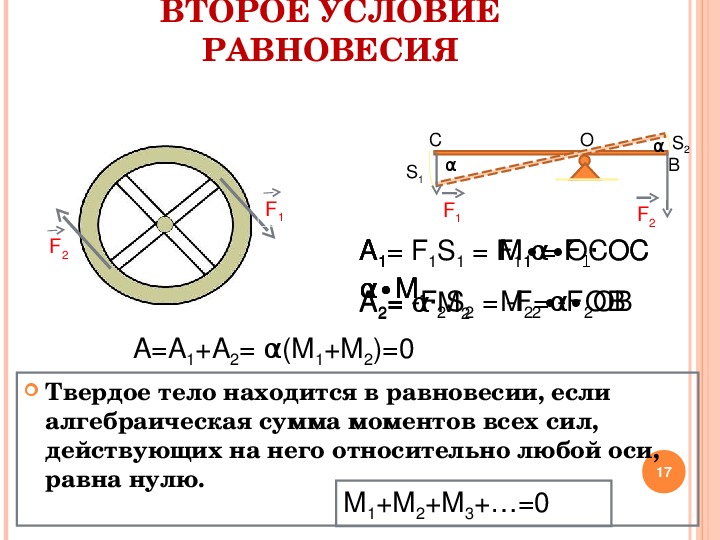 Такое равновесие тела называется неустойчивым.
Такое равновесие тела называется неустойчивым.
Итак, наша чудо машинка скатилась с горки и попала на абсолютно ровную и гладкую поверхность.
Теперь вновь сила тяжести и сила нормальной реакции опоры уравновешивают друг друга. При этом смещение машинки в любом направлении не изменяет действующих на неё сил и её равновесие сохраняется. Такое состояние тела называют безразличным равновесием.
Но вот горизонтальный участок пути закончился, и наша машинка попадает в ямку. Сила тяжести и сила нормальной реакции опоры уже не могут уравновесить друг друга, а их равнодействующая направлена к центру ямы. Достигнув дна, силы тяжести и нормальной реакции вновь направлены вдоль одной прямой в противоположные стороны.
Следовательно, в этом положении машинка находится в
равновесии. Дальше наша игрушка, согласно закону инерции, продолжит движение и
начнёт подниматься вверх. Равновесие нарушается. Но посмотрите: возникающая
равнодействующая сила направлена к положению равновесия, пытаясь вернуть туда
машинку. Таким образом, если при отклонении тела от положения равновесия
возникают силы, возвращающие его в это положение, то равновесие тела называется
устойчивым.
Но посмотрите: возникающая
равнодействующая сила направлена к положению равновесия, пытаясь вернуть туда
машинку. Таким образом, если при отклонении тела от положения равновесия
возникают силы, возвращающие его в это положение, то равновесие тела называется
устойчивым.
Статика (материалы для учителя)
Хочу предложить вашему внимания авторскую презентацию по теме «Статика». Презентация рассматривает общие условия равновесия тел; равновесие тел, имеющих площадь опоры; равновесие тел на плоскости. К каждому разделу прилагаются задания для закрепления темы. В дополнение к презентации предлагаю план распределения слайдов презентации по урокам темы, описание слайдов. Презентация «Статика»
Описание презентации
Ι. Равновесие телСлайд 3
- Раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой.

- Равновесие тела – это состояние покоя этого тела.
Вокруг нас нет ни одного тела, на которое не действовали бы силы. Под действием этих сил тела деформируются.
При выяснении условий равновесия деформированных тел необходимо учитывать величину и характер деформации, что усложняет выдвинутую задачу. Поэтому для выяснения основных законов равновесия удобно ввести понятие абсолютно твердого тела.
- Абсолютно твердое тело – тело, у которого деформации, возникающие под действием приложенных к нему сил, пренебрежимо малы.
Рассмотрим условия равновесия абсолютно твердых тел.
Слайд 4
(вывод первого условия равновесия с динамическим рисунком)
Все элементы тела взаимодействуют между собой. Силы, с которыми они действуют друг на друга, называются внутренними. В соответствии с первым законом Ньютона сумма внешних и внутренних сил, действующих на каждый элемент, равна нулю. Сложим все силы, действующие на все элементы тела. По третьему закону Ньютона силы, с которыми два элемента действуют друг на друга, равны по величине и противоположно направлены, а, следовательно их сумма будет равна нулю. После преобразования выражения приходим к выводу, что… .
Сложим все силы, действующие на все элементы тела. По третьему закону Ньютона силы, с которыми два элемента действуют друг на друга, равны по величине и противоположно направлены, а, следовательно их сумма будет равна нулю. После преобразования выражения приходим к выводу, что… .
- Твердое тело находится в равновесии, если геометрическая сумма всех сил, приложенных к нему, равна нулю.
(переход на скрытые слайды – задачи на применение первого условия равновесия)
Задача 1
Электрическая лампа подвешена на шнуре на кронштейне. Найти силы упругости в балках кронштейна, если масса лампы равна 1 кг, а угол α = 60°.
Задача 2
К концу двухметрового стержня АС, укрепленного шарнирно одним концом к стене, а с другого конца поддерживаемого тросом ВС длиной 2,5 м, подвешен груз массой 120 кг. Найти силы, действующие на трос и стержень.
Задача 3
На бельевой веревке длиной 10м висит костюм, вес которого 20 Н. Вешалка расположена посередине веревки, и эта точка провисает на 10 см ниже горизонтали, проведенной через точки закрепления веревки. Чему равна сила натяжения веревки?
Вешалка расположена посередине веревки, и эта точка провисает на 10 см ниже горизонтали, проведенной через точки закрепления веревки. Чему равна сила натяжения веревки?
Задача 4
Найти силы, действующие на подкос ВС и тягу АС, если АВ = 1,5 м, АС = 3 м, ВС = 4 м, а масса груза 200 кг.
В этом состоит первое условие равновесия. Это условие необходимо, но недостаточно.
ΙΙ. Момент силы. Правило моментов.Слайд 14
Вспомним основные понятия равновесия.
Слайд 15
- Что такое равновесие?
- Как читается условие равновесия абсолютно твердого тела?
Данное условие равновесия необходимо, но недостаточно. Рассмотрим условия равновесия тел, способных вращаться вокруг некоторой оси.
Слайд16
(второе условие равновесия с динамическим рисунком)
Рассмотрим пример с колесом. Если силы, действующие на колесо равны, противоположно направлены и действуют по одной прямой, то равнодействующая сил будет равна нулю и колесо будет в покое. Если те же самые силы будут действовать в противоположных направлениях, но не вдоль одной прямой, то колесо будет поворачиваться.
Если те же самые силы будут действовать в противоположных направлениях, но не вдоль одной прямой, то колесо будет поворачиваться.
Найдем условие равновесия стержня способного поворачиваться вокруг некоторой оси.
Каждая из сил, действующих на стержень, стремится повернуть его в свою сторону.
Определим работу, которую совершают внешние силы при повороте рычага на малый угол.
Для вывода второго условия равновесия необходимо ввести два новых понятия: плечо силы, момент силы.
Кратчайшее расстояние от оси вращения до линии действия силы называется плечом силы. (ссылка на слайд 17)
Слайд 17
(скрытый – задачи на определение плеча силы)
- Однородный куб опирается одним ребром о пол, другим – о вертикальную стену. Плечо силы трения относительно т.О равно… (см рис.)
- На рисунке схематически изображена лестница АВ, опирающаяся на стену. Определите плечо…
а) силы трения относительно точек А, О, В, D.
б) силы реакции опоры относительно точек А, О, В, D.
б) силы тяжести относительно точек А, О, В, D.
Работа силы зависит от произведения силы на ее плечо. (возврат на слайд 17)
Произведение силы на ее плечо называется моментом силы.
Слайд 18
(скрытый – определение момента силы)
- Чему равен момент силы F1 относительно точки О? (см. рис.)
- Наклонная плоскость длиной 0,6м составляет 600 с поверхностью стола. Чему равен момент силы тяжести бруска массой 0,1 кг, находящегося на середине наклонной плоскости относительно точки О?
Вернемся ко второму условию равновесия.
Слайд 19
(вывод второго условия равновесия)
Следовательно, работа каждой силы пропорциональна моменту данной силы. Полная работа всех сил определяется суммой моментов.
Если рычаг находится в равновесии, то работа всех сил равна нулю, и, соответственно, сумма моментов всех сил равна нулю.
Таким образом, второе условие равновесия можно сформулировать так:
- Твердое тело находится в равновесии, если алгебраическая сумма моментов всех сил, действующих на него относительно любой оси, равна нулю.
При этом договорились считать моменты сил, поворачивающих тело по часовой стрелке, положительными, а моменты сил, поворачивающих тело против часовой стрелки, отрицательными.
Подведем итог.
Слайд 20
(объединение условий равновесия)
- Твердое тело находится в равновесии, если геометрическая сумма всех сил, приложенных к нему, равна нулю.
- Твердое тело находится в равновесии, если алгебраическая сумма моментов всех сил, действующих на него относительно любой оси, равна нулю.
Слайд 21
(слайды 11-12 – скрытые – задачи на применение правила моментов сил)
Задача 1
Электрическая лампа подвешена на шнуре на кронштейне. Найти силы упругости в балках кронштейна, если масса лампы равна 1 кг, а угол α = 60°.
Найти силы упругости в балках кронштейна, если масса лампы равна 1 кг, а угол α = 60°.
(3-ий способ – решение – слайд 23)
Слайд 22
Задача 2
К балке массой 200кг и длиной 5м подвешен груз массой 250кг на расстоянии 3м от одного из концов. Балка своими концами лежит на опорах. Каковы силы давления на каждую из опор?
(решение – слайд 24)
Равновесие бывает разным.
ΙΙΙ. Виды равновесия.Слайд 25
Прежде, чем будем рассматривать виды равновесия, ответьте на вопросы…
Слайд 26
- Что такое равновесие?
- При каком условии твердое тело будет находиться в состоянии равновесия?
- При каком условии твердое тело способное вращаться будет находиться в состоянии равновесия?
Слайд 27
(виды равновесия – рисунки)
Рассмотрим условия различных видов равновесия тел, находящихся на плоскости.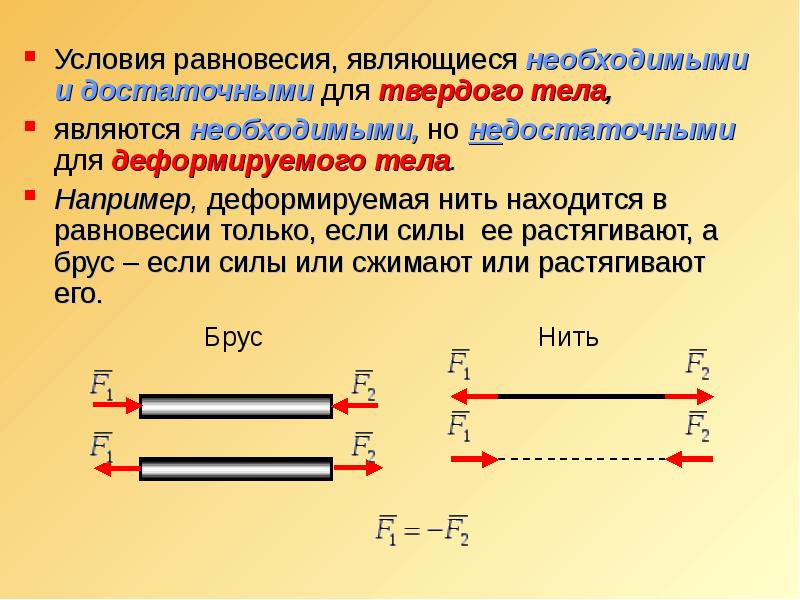 Тело находится в состоянии устойчивого равновесия, если при малейшем отклонении тела от положения равновесия возникает сила, возвращающая тело в положение равновесия.
Тело находится в состоянии устойчивого равновесия, если при малейшем отклонении тела от положения равновесия возникает сила, возвращающая тело в положение равновесия.
Тело находится в состоянии неустойчивого равновесия, если при малейшем отклонении тела от положения равновесия возникает сила, удаляющая тело от положения равновесия.
Тело находится в состоянии безразличного равновесия, если при малейшем отклонении тела от положения равновесия не возникает сил, изменяющих положение тела.
Рассмотрим условия различных видов равновесия тел, имеющих ось вращения.
Слайд 28
(виды равновесия тел, имеющих ось вращения – динамические рисунки)
Тело находится в состоянии устойчивого равновесия, если при малейшем отклонении тела от положения равновесия возникает момент сил, возвращающих тело в положение равновесия.
Тело находится в состоянии безразличного равновесия, если при малейшем отклонении тела от положения равновесия не возникает момента сил, изменяющих положение тела.
Тело находится в состоянии неустойчивого равновесия, если при малейшем отклонении тела от положения равновесия возникает момент сил, удаляющих тело от положения равновесия.
Обобщим условия устойчивости равновесия.
Слайд 29
(обобщение условий равновесия)
- Тела находятся в состоянии устойчивого равновесия, если при малейшем отклонении от положения равновесия возникает сила или момент силы, возвращающие тело в положение равновесия.
- Тела находятся в состоянии неустойчивого равновесия, если при малейшем отклонении от положения равновесия возникает сила или момент силы, удаляющие тело от положения равновесия.
- Тела находятся в состоянии безразличного равновесия, если при малейшем отклонении от положения равновесия не возникает ни сила, ни момент силы, изменяющие положение тела.
Условия устойчивого равновесия широко используются в игрушках, в устройствах, которые должны возвращаться в состояние равновесия при отклонениях.
Слайд 30
(рисунки игрушек, шахматных фигурок и т.д.)
Для тел, имеющих площадь опоры, существует дополнительное условие равновесия.
Слайд 31
(динамические рисунки равновесия тел, имеющих площадь опоры)
Рассмотрим, как изменяется положение линии действия силы тяжести по отношению к оси вращения тела при наклоне тела имеющего площадь опоры.
- Тело, имеющее площадь опоры, будет находиться в равновесии до тех пор, пока линия действия силы тяжести будет проходить через площадь опоры.
Кроме того, обратите внимание, что при повороте тела положение центра тяжести изменяется. А любая система всегда стремится к понижению положения центра тяжести. Так наклоненные тела будут находиться в состоянии устойчивого равновесия, пока линия действия силы тяжести будет проходить через площадь опоры.
Слайд 32
(наклонная башня, телебашня, движение человека)
Покачивание или наклон тела человека при ходьбе также объясняется стремлением сохранить устойчивое положение. Площадь опоры определяется площадью внутри линии, проведенной вокруг крайних точек касания телом опоры. когда человек стоит. Линия действия силы тяжести проходит через опору. Когда человек поднимает ногу, то, чтобы сохранить равновесие, он наклоняется перенося линию действия силы тяжести в новое положение таким образом, чтобы она вновь проходила через площадь опоры.
Площадь опоры определяется площадью внутри линии, проведенной вокруг крайних точек касания телом опоры. когда человек стоит. Линия действия силы тяжести проходит через опору. Когда человек поднимает ногу, то, чтобы сохранить равновесие, он наклоняется перенося линию действия силы тяжести в новое положение таким образом, чтобы она вновь проходила через площадь опоры.
Для устойчивости различных сооружений увеличивают площадь опоры или понижают положение центра тяжести сооружения, изготавливая мощную опору, или и увеличивают площадь опоры и, одновременно, понижают центр тяжести сооружения.
Устойчивость транспорта определяется теми же условиями.
Слайд 33
(наклон машины и автобуса)
Так, из двух видов транспорта автомобиля и автобуса на наклонной дороге более устойчив автомобиль.
При одинаковом наклоне данных видов транспорта у автобуса линия силы тяжести проходит ближе к краю площади опоры.
Приложение 1
Условия равновесия твердого тел — Энциклопедия по машиностроению XXL
На основании принципа отвердевания система сил, действующи на такую конструкцию, должна при равновесии удовлетворять условиям равновесия твердого тела. Но эти условия, как указывалось, будучи необходимыми, не будут являться достаточными поэтому из них нельзя определить все неизвестные величины. Для решения задачи необходимо дополнительно рассмотреть равновесие какой-нибудь одной или нескольких частей конструкции.
[c.53]
Но эти условия, как указывалось, будучи необходимыми, не будут являться достаточными поэтому из них нельзя определить все неизвестные величины. Для решения задачи необходимо дополнительно рассмотреть равновесие какой-нибудь одной или нескольких частей конструкции.
[c.53]
Равенства (51) выражают одновременно условия равновесия твердого тела, находящегося под действием любой пространственной системы сил. [c.80]
Равенства (12) служат для определения реакции R, а равенства (13) являются условиями равновесия тела. Следовательно, условия равновесия твердого тела, имеющего неподвижную точку, состоят в том, что суммы моментов всех действующих сил относительно каждой из трех взаимно перпендикулярных осей, проходящих через неподвижную точку, должны равняться нулю. [c.256]
Рассматривая условия равновесия твердого тела как звена механической системы, оперируют внешними силами, называемыми нагрузками, действующими на тело. Все внешние силы, действующие на тела, подразделяют на активные силы
[c.53]
Все внешние силы, действующие на тела, подразделяют на активные силы
[c.53]
Стол остается в равновесии на гладком горизонтальном полу под действием силы тяжести и четырех неизвестных вертикальных реакций опоры. Для определения этих реакций имеется лишь три условия равновесия твердого тела, что делает задачу нахождения реакций статически неопределимой. [c.358]
Необходимо ли выполнение условий равновесия твердого тела в положениях равновесия сосуда, наполовину наполненного водой [c.375]
Пусть условия равновесия твердого тела выполнены для сосуда, наполненного водой частично. Можно ли на этом основании утверждать, что такая система находится в равновесии [c.375]
Что можно сказать о равновесии системы, если для нее условия равновесия твердого тела не выполнены [c.375]
Теорема 6.3.1. Еслп ось вращения служит главной и центральной осью инерции тела, то уравнения для определения реакций Ri, R2, R[, R 2 совпадают с уравнениями, получающимися из условий равновесия твердого тела. [c.456]
[c.456]
В настоящем издании сделаны некоторые изменения и добавления. Прежде всего изменена (с целью упрощения) последовательность изложения сначала рассматривается закон сохранения импульса, а затем закон сохранения энергии (в предыдуш,их изданиях было наоборот). В связи с такой перестановкой обе главы пришлось довольно существенно переработать. Добавлены новые примеры и задачи на закон сохранения импульса, более подробно рассмотрен вопрос о потенциальной энергии системы частиц, введено понятие о полной механической энергии системы, находящейся во внешнем иоле, даны условия равновесия твердого тела, приведен ряд примеров на кинематику специальной теории относительности и др. [c.5]
Условия равновесия твердого тела. Тело будет оставаться в состоянии покоя, если нет причин, вызывающих его движение. Согласно уравнениям (5.26), для этого необходимо и достаточно выполнение двух условий [c.150]
Условия равновесия твердого тела с одной неподвижной точкой
[c. 291]
291]
УСЛОВИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА [c.115]
Уравнение (И. 5)—известное условие равновесия твердого тела с неподвижной осью ( 68 т. 1). [c.116]
Полученные таким способом условия равновесия твердого тела являются необходимыми, но не достаточными условиями его неподвижности. [c.402]
Приведенный только что вывод условий равновесия твердого тела (58) отличается от изложенного в первом отделе геометрического вывода Пуансо использованием Рис. 357, кинематического представления о перемещениях твердого тела и динамического понятия работы сил. Подчеркнем особенности этих двух различных подходов на простом примере определения реакций балки, лежащей на двух опорах (рис. 357). [c.325]
Всякое реальное тело природы вследствие взаимодействия с другими материальными объектами, будет ли оно оставаться в покое или приходить в определенное движение, изменяет свою форму (деформируется). При этом величины этих деформаций зависят от материала тела, его геометрической формы и размеров, а также от действующих на тело сил. Учет этих деформаций имеет существенное значение при расчете прочности частей (деталей) различных инженерных сооружений или машин . При этом для обеспечения необходимой прочности той или иной конструкции материал и размеры ее частей подбирают так, чтобы деформации при действующих силах были достаточно малы. Поэтому при изучении общих законов механического движения и общих условий равновесия твердых тел можно пренебрегать малыми деформациями этих тел и рассматривать их как недеформируемые, или абсолютно твердые. Абсолютно твердым телом называют такое тело, расстояние между двумя любыми точками которого всегда остается неизменным. В дальнейшем при изучении теоретической механики будем рассматривать все тела как абсолютно твердые.
[c.8]
При этом величины этих деформаций зависят от материала тела, его геометрической формы и размеров, а также от действующих на тело сил. Учет этих деформаций имеет существенное значение при расчете прочности частей (деталей) различных инженерных сооружений или машин . При этом для обеспечения необходимой прочности той или иной конструкции материал и размеры ее частей подбирают так, чтобы деформации при действующих силах были достаточно малы. Поэтому при изучении общих законов механического движения и общих условий равновесия твердых тел можно пренебрегать малыми деформациями этих тел и рассматривать их как недеформируемые, или абсолютно твердые. Абсолютно твердым телом называют такое тело, расстояние между двумя любыми точками которого всегда остается неизменным. В дальнейшем при изучении теоретической механики будем рассматривать все тела как абсолютно твердые.
[c.8]
Сложение сходящихся сил, равнодействующая. Статика как учение о равновесии твердых тел под действием приложенных к ним сил содержит д в е основные задачи I) замен i данной системы сил ей эквивалентной и 2) вывод общих условий равновесия твердых тел. Рассмотрение этих задач начнем с наиболее простого случая — системы сходящихся сил.
[c.34]
Рассмотрение этих задач начнем с наиболее простого случая — системы сходящихся сил.
[c.34]
В общем виде мы воспользуемся уравнениями (13.24) и (13.25) только для определения условий равновесия твердого тела. Но прежде приведем некоторые соображения, прямо вытекающие из вида этих уравне))ий. Если мы будем переносить силы вдоль их направления, т. е. заменим силы fi, Fg и т. д. силами F, F l, F s и т. д. (рис. 199), то не изменятся ни компоненты сил Fx, Fy, F , ни компоненты моментов сил Мх1 Му, Мг (так как плечи сил останутся прежними) следовательно, не изменится и движение тела. Поэтому точки приложения сил, действующих на твердое тело, можно переносить вдоль направления сил, — прием, которым постоянно пользуются. Это можно делать именно потому, что уравнения (13.24) и (13.25), определяющие движение тела, при этом не изменяются. [c.412]
При исследовании давления в различных точках покоящихся жидкости и газа мы можем применять условия равновесия твердого тела к любому конечному объему, выделенному из жидкости или газа.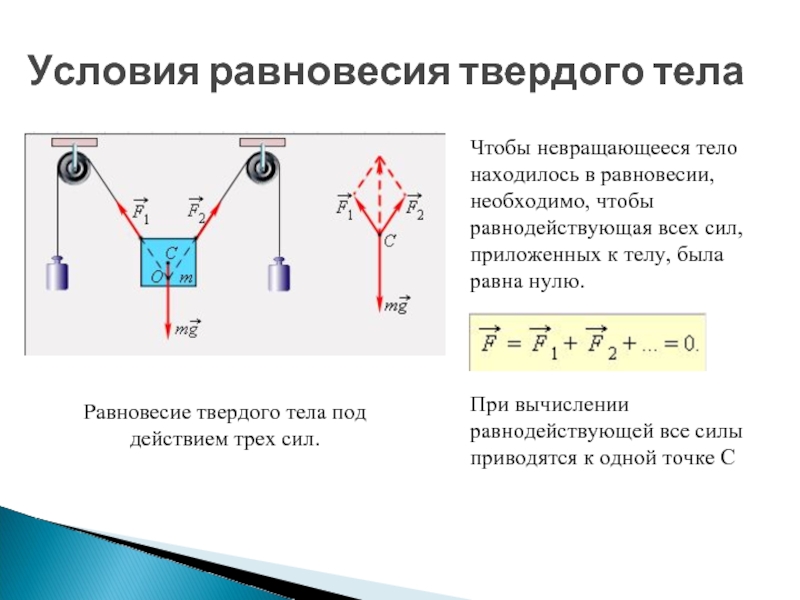 Но в этом случае уже нельзя пренебрегать массовыми силами, например силой тяжести, как мы это делали, рассматривая очень малый объем.
[c.504]
Но в этом случае уже нельзя пренебрегать массовыми силами, например силой тяжести, как мы это делали, рассматривая очень малый объем.
[c.504]
На основании некоторых следствий из этих аксиом выведем необходимые и достаточные (общие) условия равновесия твердого тела. [c.55]
Обратная формулировка принципа в общем случае несправедлива. Если твердое тело находится в равновесии, то, превратившись в нетвердое, оно может и не быть в равновесии. Это означает, что условия равновесия твердого тела являются необходимыми, но не достаточными для равновесия нетвердого тела и требуются дополнительные условия, учитывающие те или иные физические свойства тел. Так, например, при растяжении гибкой невесомой нити необходимо обеспечить условия равновесия двух сил, но нужно помнить, что нить может сопротивляться растяжению, но не может сопротивляться сжатию (дополнительное условие равновесия гибкой нити). [c.19]
Как было указано в начале гл.
 VI, статикой называется раздел кинетики, в котором изучаются операции преобразования систем сил в эквивалентные им и условия равновесия механических систем под действием приложенных к ним сил. Поскольку задача о преобразовании систем сил была решена в гл. IX, здесь мы будем рассматривать только условия равновесия твердого тела по отношению к инерциальной системе отсчета.
[c.244]
VI, статикой называется раздел кинетики, в котором изучаются операции преобразования систем сил в эквивалентные им и условия равновесия механических систем под действием приложенных к ним сил. Поскольку задача о преобразовании систем сил была решена в гл. IX, здесь мы будем рассматривать только условия равновесия твердого тела по отношению к инерциальной системе отсчета.
[c.244]Сформулируйте необходимые и достаточные условия равновесия твердого тела относительно инерциальной системы координат. [c.264]
Установите условия равновесия твердого тела при действии на него системы пар сил. [c.264]
Об этом можно составить себе представление на основании следующих рассуждений, основанных на идее затвердевания если система находится в равновесии, то последнее, очевидно, сохранится, если все точки станут неизменно связанными между собой, т. е. если система затвердеет. Внешние силы должны уравновешиваться для полученного таким образом твердого тела и, следовательно, они удовлетворяют общим условиям равновесия твердого тела. Эти необходимые условия не будут, вообще говоря, достаточными. Мы применим эти рассуждения к некоторым изменяемым системам.
[c.152]
Эти необходимые условия не будут, вообще говоря, достаточными. Мы применим эти рассуждения к некоторым изменяемым системам.
[c.152]
Приложение к условиям равновесия твердого тела. [c.241]
Задача Майера для случая внутренних сил. Допустим, что все силы системы являются внутренними, т. е. что они происходят исключительно от действий одних точек системы на другие. Становясь на очень общую точку зрения, Майер не предполагает, как мы делали во всем этом курсе, что внутренние силы происходят исключительно от попарных взаимодействий точек, т. е., что эти силы попарно равны и противоположны друг другу, а допускает только, что все внутренние силы в каждый момент времени удовлетворяют шести условиям равновесия твердого тела [c.396]
Постулат.— Яе изменяя ничего в условиях равновесия твердого тела, можно прибавить или отбросить две равные и прямо противоположные силы, приложенные к двум его точкам.
[c. 232]
232]
Не нарушая условий равновесия твердого тела, можно перенести точку приложения силы в произвольную точку ее линии действия, лишь бы эта новая точка была связана с телом. [c.232]
Условие равновесия твердого тела выводится отсюда непосредственно. Единственное перемещение, совместимое со связями, есть произвольное вращение о)8/ вокруг неподвижной точки. Условие (1) предыдущего п°, выражающее то обстоятельство, что сумма элементарных работ активных сил равна нулю, приводится к виду [c.293]
Основным принципом, на котором основано рассмотрение условий равновесия твердого тела так же, как и всех других вопросов теории равновесия, является принцип виртуальной работы. Он является частным случаем принципа Даламбера, из которого его можно получить, отбрасывая силы инерции. В связи с этим рассуждения, приводимые в настоящем параграфе, являются непосредственным следствием закона движения центра тяжести и закона площадей, разобранных в 13. Следует также отметить, что рассмотренные там виртуальные перемещения (параллельный перенос и поворот), очевидно, не противоречат неизменяемости формы твердого тела и соответствуют рассмотренным в предыдущем параграфе поступательному движению и вращению — двум составным частям произвольного движения твердого тела.
[c.167]
Следует также отметить, что рассмотренные там виртуальные перемещения (параллельный перенос и поворот), очевидно, не противоречат неизменяемости формы твердого тела и соответствуют рассмотренным в предыдущем параграфе поступательному движению и вращению — двум составным частям произвольного движения твердого тела.
[c.167]
Таким образом, отбрасывая силы инерции, мы получаем из (13.3) и (13.9) общие условия равновесия твердого тела [c.168]
Мы получили таким образом второе условие равновесия твердого тела. Так как произвольное виртуальное перемещение твердого тела всегда можно представить в виде суперпозиции бесконечно малых параллельного переноса и поворота, условия (3.2.3) и (3.2.8) совместно определяют равновесие тела. [c.102]
Формулы (29) выражают следующие аналитические условия равновесия для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лезкащеео в плоскости действия сил, были равны нулю. Одновременно равенства (29) выражают условия равновесия твердого тела, находящегося под действием плоской системы сил.
[c.46]
Одновременно равенства (29) выражают условия равновесия твердого тела, находящегося под действием плоской системы сил.
[c.46]
Итак, необходимые и достаточные условия равновесия твердого тела, находящегося под действием совокупности сходящихся сил, сводятся к равенству нулю алгебраических сумм проекций на оси координат всех приложенных сил. Число уравнений равновесия равно трем в случае пространственной совокупности сил и двулс — для плоской совокупности. [c.33]
Если (F , F2,. .., Fft) —система внешних сил, приложенных к твердому телу, а х,, jji, Zi — координаты точек приложения силы F( (г = 1, 2,. .., А ) в декартовой прямоугольной системе координат с началом в нолюсе О, то необходимые и достаточные условия равновесия твердого тела (1) запишутся в скалярной форме в виде следующих шести равенств [c.102]
В иекоторик задачах встречаются криволинейные нвЕесог.ые стержни. Реакции таких стержней направляются вдоль линии, соединяющей оси шарниров. Это следует из условия равновесия твердого тела под действием системы из двух сил, приложенных в шарнирах.
[c.48]
Это следует из условия равновесия твердого тела под действием системы из двух сил, приложенных в шарнирах.
[c.48]
Y h Уравнение (22.14) выражало бы в этом случгы-условие равновесия твердого тела. Динамической (дополнительной) реакцией опоры называется разность реакции опоры при вращении и реакции в покое (статической реакции) [c.402]
Рассмотренные условия равновесия твердого тела применимы и для исследования равновесия механическо системы, состоящей из п твердых тел, соединенных между собой (сочлененных) с помощью различных связей шарниров, нитей, соприкасающихся поверхностей и т. д. Такие связи, называются внутренними в отличие от внешних связей, которые связывают рассматриваемую систему с телами, в нее не входящими. [c.259]
Однако условия равновесия твердого тела справедливы и для равновесия систелгы сочлененных тел, что вытекает из свойства внутренних сил системы.
 Действительно, после освобождения каждого тела системы от наложенных на него внешних и внутренних связей и замены их соответствующими реакциями на тело будут действовать часть внешних сил системы (Г , ] = 1, 2,. . .. . т) и часть внутренних сил (F], / = 1,2,. . ., р), образующих уравновешенную систелху сил. Представим главный вектор и главный момент относительно точки
[c.260]
Действительно, после освобождения каждого тела системы от наложенных на него внешних и внутренних связей и замены их соответствующими реакциями на тело будут действовать часть внешних сил системы (Г , ] = 1, 2,. . .. . т) и часть внутренних сил (F], / = 1,2,. . ., р), образующих уравновешенную систелху сил. Представим главный вектор и главный момент относительно точки
[c.260]Условие равновесия тела, имеющего опорную плоскость
Содержание:
Условие равновесия тела, имеющего опорную плоскость
- Равновесным состоянием объекта с опорной поверхностью считается твердое тело, например, подпорная стенка. 8.3) покоится на бесконечно жестком основании. Со стороны грунта на подпорную стенку действует горизонтальная сила F, наклон для поворота ее (опрокидывания) вокруг ребра, а также вертикальная сила тяжести G,
которая прикладывается к центру тяжести. Сторона основания на подпорной стенке для того чтобы подействовать нормальная реакция/?так как активные силы F и G находятся в одной плоскости, то они образуют систему сходящихся
сил, и их результат можно найти по правилам параллелограмма.В первом случае Людмила Фирмаль
результирующий момент относительно точки В будет положительным (вращение подпорной стенки по часовой стрелке), во втором-отрицательным. Результирующий момент равен сумме моментов сил, составляющих его, так что неравенство достигается необходимое и достаточное для равновесия тела — +(8.5) Здесь b и bi-это плечи сил G и F относительно точек B или точек соответственно. ГБ>Фбт. (8.6) Продукты GB называются моментами удержания, а
продукты Fbi-моментами трансформации. В качестве критерия устойчивости принимается значение коэффициента устойчивости, который определяется как отношение момента удержания и момента опрокидывания к точке В. Ku=7iu d/L4o p R=Gb / Fbl. (8.7) О величине коэффициента устойчивости можно судить по степени устойчивости организма под действием- 76.3 8.3 Рис 8.4 По этой причине
- определение его стоимости является очень важной задачей, особенно при строительстве высотных зданий,таких как водонапорные башни, дымовые трубы и опоры ЛЭП.
 2+L1z=15,3+3,3. Итак, K u=M V1UD/A? ОПР=132.1 / 18.6=7.1>1.15.
2+L1z=15,3+3,3. Итак, K u=M V1UD/A? ОПР=132.1 / 18.6=7.1>1.15.Смотрите также:
Предмет техническая механика
3.6: Анализ равновесия для твердого тела
Для твердого тела в статическом равновесии, т. е. недеформируемого тела, в котором силы не действуют одновременно, сумма сил и моментов , действующих на тело должно быть равно нулю. Добавление моментов (в отличие от частиц, где мы рассматривали только силы) добавляет еще один набор возможных уравнений равновесия, позволяя нам решать больше неизвестных по сравнению с проблемами частиц.
Моменты, как и силы, являются векторами. Это означает, что наше векторное уравнение необходимо разбить на скалярные компоненты, прежде чем мы сможем решить уравнения равновесия. В двумерной задаче тело может вращаться только по часовой стрелке или против часовой стрелки (что соответствует вращению вокруг оси \(z\)). Это означает, что твердое тело в двумерной задаче имеет три возможных уравнения равновесия; то есть сумма составляющих силы в направлениях \(x\) и \(y\) и моментов относительно оси \(z\).
 Сумма каждого из них будет равна нулю.
Сумма каждого из них будет равна нулю.Для двумерной задачи мы разобьем наше уравнение одной векторной силы на два уравнения скалярных компонент. \[ \сумма \vec{F} \, = \, 0 \]
\[ \сумма F_x \, = \, 0\, ; \,\, \sum F_y \, = \, 0 \] Одномоментное векторное уравнение становится одномоментным скалярным уравнением. \[ \сумма \vec{M} \, = \, 0 \]
\[ \сумма M_z \, = \, 0 \]
Если мы рассмотрим трехмерную задачу, мы увеличим количество возможных уравнений равновесия до шести.Имеются три уравнения равновесия для силы, где сумма компонентов в направлениях \(x\), \(y\) и \(z\) должна быть равна нулю. Тело также может иметь моменты относительно каждой из трех осей. Второй набор из трех уравнений равновесия утверждает, что сумма компонентов момента относительно осей \(x\), \(y\) и \(z\) также должна быть равна нулю.
Разобьем силы на три составляющие уравнения. \[ \сумма \vec{F} \, = \, 0 \]
\[ \сумма F_x \, = \, 0 \, ; \,\, \сумма F_y \, = \, 0 \, ; \,\, \сумма F_z \, = \, 0 \]
Затем также разбиваем моменты на три составляющие уравнения.
 \[ \сумма \vec{M} \, = \, 0 \]
\[ \сумма \vec{M} \, = \, 0 \]\[ \сумма M_x \, = \, 0 \, ; \,\, \сумма M_y \, = \, 0 \, ; \,\, \сумма M_z \, = \, 0 \]
Нахождение уравнений равновесия
Как и в случае с частицами, первым шагом в поиске уравнений равновесия является построение диаграммы свободного тела анализируемого тела. На этой диаграмме должны быть показаны все векторы сил, действующих на тело. На диаграмме свободного тела задайте значения для любых известных величин, направлений и точек приложения векторов силы и задайте имена переменных для любых неизвестных (величин, направлений или расстояний).
Далее вам нужно будет выбрать оси \(x\), \(y\) и \(z\). Эти оси должны быть перпендикулярны друг другу, но они не обязательно должны быть горизонтальными или вертикальными. Если вы выберете координатные оси, которые совпадают с некоторыми из ваших векторов силы, вы упростите последующий анализ.
После того, как вы выбрали оси, вам необходимо разбить все векторы сил на составляющие вдоль направлений \(x\), \(y\) и \(z\) (подробнее см.
 страницу векторов в Приложении 1). подробности этого процесса).Ваше первое уравнение будет суммой величин компонентов в направлении \(x\), равных нулю, второе уравнение будет суммой величин компонентов в направлении \(y\), равных ноль, а третья (если у вас трехмерная задача) будет равна сумме величин в направлении \(z\), равной нулю.
страницу векторов в Приложении 1). подробности этого процесса).Ваше первое уравнение будет суммой величин компонентов в направлении \(x\), равных нулю, второе уравнение будет суммой величин компонентов в направлении \(y\), равных ноль, а третья (если у вас трехмерная задача) будет равна сумме величин в направлении \(z\), равной нулю.Далее вам нужно будет составить уравнения моментов. Для этого вам нужно будет выбрать точку, о которой будут сниматься моменты. Подойдет любая точка, но обычно выгоднее выбрать точку, которая уменьшит количество неизвестных в уравнении.Помните, что любой вектор силы, проходящий через данную точку, не будет иметь никакого момента относительно этой точки. Чтобы записать уравнения моментов, просто суммируйте моменты, создаваемые каждой силой (добавляя чистые моменты, показанные на диаграмме) относительно данной точки и данной оси, и приравняйте эту сумму к нулю. Все моменты будут относиться к оси \(z\) для двумерных задач, хотя моменты могут относиться к осям \(x\), \(y\) и \(z\) для трехмерных задач.

Когда у вас есть уравнения равновесия, вы можете решить эти формулы для неизвестных.Количество неизвестных, которые вы сможете решить, снова будет количеством уравнений, которые у вас есть.
Видеолекция по этому разделу, прочитанная доктором Джейкобом Муром. Источник YouTube: https://youtu.be/OiJ2xbMIixY.Пример \(\PageIndex{1}\)
Автомобиль ниже имеет вес 1500 фунтов с центром масс в 4 футах позади передних колес автомобиля. Каковы нормальные силы, действующие на переднее и заднее колеса автомобиля?
Рисунок \(\PageIndex{1}\): схема проблемы для примера \(\PageIndex{1}\).Адаптировано из общедоступного изображения Ebaychatter0.- Раствор
- Видео \(\PageIndex{2}\): Рабочее решение примера проблемы \(\PageIndex{1}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/1LD5QW-70PA.
Пример \(\PageIndex{2}\)
Балка длиной 5 м имеет неподвижное соединение со стеной в точке А и силу, действующую, как показано, в точке В.
Рисунок \(\PageIndex{2}\): схема проблемы для примера \(\PageIndex{2}\).На горизонтальную балку, прикрепленную одним концом к стене, действует сила, приложенная к ее свободному концу. Какие силы реакции действуют на балку в точке А?
Какие силы реакции действуют на балку в точке А?- Раствор
- Видео \(\PageIndex{3}\): Рабочее решение примера проблемы \(\PageIndex{2}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/JrVV7k1aQEk.
Пример \(\PageIndex{3}\)
Лестница незначительной массы поддерживает человека весом 120 фунтов, как показано ниже. Если точка контакта в точке А не имеет трения, а точка контакта в точке В представляет собой шероховатое соединение, определите силы, действующие в точках контакта А и В.
Рисунок \(\PageIndex{3}\): схема проблемы для примера \(\PageIndex{3}\). Лестница своим основанием на шершавом полу прислонена к стене без трения, а человек стоит на лестнице наполовину вверх.- Раствор
- Видео \(\PageIndex{4}\): Рабочее решение примера проблемы \(\PageIndex{3}\), предоставленное доктором Джейкобом Муром.
 Источник на YouTube: https://youtu.be/WzkAnPdhao4.
Источник на YouTube: https://youtu.be/WzkAnPdhao4.
Пример \(\PageIndex{4}\)
Элемент ABC имеет длину 6 метров, а точка B находится в его середине.Определить все силы, действующие на элемент ABC.
Рисунок \(\PageIndex{4}\): схема проблемы для примера \(\PageIndex{4}\). Диагональный элемент конструкции прикреплен к стене одним концом, соединен со стеной тросом в средней точке и выдерживает нагрузку 300 кг на своем свободном конце.- Раствор
- Видео \(\PageIndex{5}\): Рабочее решение примера проблемы \(\PageIndex{4}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/sMQrjwUMpSQ.
Пример \(\PageIndex{5}\)
Сидя на стуле, человек прикладывает силы, показанные на схеме ниже.Определите все силы, действующие на стул в точках A и B. (Предположим, что A не имеет трения, а B — шероховатая поверхность).
Рисунок \(\PageIndex{5}\): схема проблемы для примера \(\PageIndex{5}\). Стул стоит на плоской поверхности, при этом предполагается, что эта поверхность не имеет трения в месте контакта с передней ножкой стула (точка А) и создает трение в месте контакта с задней ножкой (точка В).
Стул стоит на плоской поверхности, при этом предполагается, что эта поверхность не имеет трения в месте контакта с передней ножкой стула (точка А) и создает трение в месте контакта с задней ножкой (точка В).- Раствор
- Видео \(\PageIndex{6}\): Рабочее решение примера проблемы \(\PageIndex{5}\), предоставленное Dr.Джейкоб Мур. Источник YouTube: https://youtu.be/nSOxK1ZMggA.
Пример \(\PageIndex{6}\)
Прицеп, показанный ниже, состоит из платформы весом 250 фунтов на оси с колесами весом 350 фунтов. Предположим, что силы веса действуют в центре каждого компонента. Если мы хотим, чтобы вес сцепки (\(F_T\)) незагруженного прицепа составлял 50 фунтов, на каком расстоянии \(d\) от передней части мы должны поместить ось?
Рисунок \(\PageIndex{6}\): схема проблемы для примера \(\PageIndex{6}\).Прицеп состоит из плоского прямоугольного настила поверх двух колес на оси.- Раствор
- Видео \(\PageIndex{7}\): Рабочее решение примера проблемы \(\PageIndex{6}\), предоставленное доктором Джейкобом Муром.
 Источник YouTube: https://youtu.be/wpEBuitLD5s.
Источник YouTube: https://youtu.be/wpEBuitLD5s.
Пример \(\PageIndex{7}\)
Плоский стальной знак размером 12 на 24 дюйма поддерживается двумя тросами, каждый на расстоянии 6 дюймов от края знака. Знак имеет вес 10 фунтов, и ветер заставляет знак располагаться под углом 10 градусов к вертикали (ось \(y\)).Если мы рассматриваем ветер как точечную силу, действующую в отрицательном направлении \(z\) на центр знака, насколько сильной должна быть сила ветра, чтобы вызвать этот угол в десять градусов?
Рисунок \(\PageIndex{7}\): схема проблемы для примера \(\PageIndex{7}\). На висящий знак действует ветер, направление которого указывает на экран, в результате чего знак образует угол 10 ° с плоскостью экрана.- Раствор
- Видео \(\PageIndex{8}\): Рабочее решение примера проблемы \(\PageIndex{7}\), предоставленное Dr.Джейкоб Мур. Источник на YouTube: https://youtu.be/pR-0xbj8wF0.
Пример \(\PageIndex{8}\)
Шестидесятикилограммовая акустическая панель подвешена на трех тросах, как показано ниже.
Рисунок \(\PageIndex{8}\): схема проблемы для примера \(\PageIndex{8}\). Однородная прямоугольная панель подвешена сверху на 3 тросах, расположенных в разных точках по ее краям. Предполагая, что панель имеет равномерно распределенный вес, каково натяжение каждого из тросов?
Предполагая, что панель имеет равномерно распределенный вес, каково натяжение каждого из тросов?- Раствор
- Видео \(\PageIndex{9}\): Рабочее решение примера проблемы \(\PageIndex{8}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/Kbsc1m0f9pQ.
Объяснение урока: Равновесие твердого тела под действием параллельных сил
В этом объяснителе мы научимся решать задачи о равновесии тела под действием параллельных копланарных сил.
Если тело жесткое, силы, действующие на тело, не могут вызвать деформацию.Силы имеют только два возможных воздействия на тело. Этими эффектами являются линейное ускорение тела и вращение тела вокруг точки.
Если силы, действующие на твердое тело, не вызывают результирующего линейного ускорения тела, то тело находится в поступательном равновесии.
 Для этого сумма сил, действующих на тело, должна быть равна нулю.
Для этого сумма сил, действующих на тело, должна быть равна нулю.Если силы, действующие на твердое тело, не вызывают чистого вращения тела, то тело находится в равновесии вращения.Для этого сумма моментов тела должна быть равна нулю.
Если сумма сил и сумма моментов на твердом теле равны нулю, тело находится в равновесии.
Определим условия равновесия твердого тела.
Определение: Условия равновесия твердого тела
Твердое тело находится в равновесии, если сумма сил и сумма моментов, действующих на тело, равны нулю.
Определим также момент силы.
Определение: Момент силы
Момент силы относительно точки 𝑃 — это расстояние 𝑑 от 𝑃 до точки, где действует сила, умноженная на составляющую силы, перпендикулярную направлению линия, пересекающая 𝑃 и точку, в которой действует сила. Это можно записать как 𝜏=𝐹⋅𝑑𝜃, грех где 𝐹 — сила, а 𝜃 — угол между направлением силы и направление линии, пересекающей 𝑃 и точку, в которой действует сила.

Этот пояснитель специально рассматривает примеры, когда силы, действующие на твердое тело, параллельны и компланарны.
Чтобы твердое тело находилось в равновесии, когда на него действуют параллельные силы, должно выполняться одно из двух условий.
Первое условие — это тривиальное условие, что линии действия всех сил параллельны длине тела и пересекающих центр масс тела. Линия действия таких сил показана на следующем рисунке.
Никакой момент не создается ни одной из сил в любой точке по длине тела, действующих вдоль этой линии.
Второе условие: линии действия всех сил должны быть перпендикулярны длине тела. Возможная линия действия таких сил показана на следующем рисунке.
Угол 𝜃 для сил вдоль этой линии действия или для любой линии, параллельной этой линии, должен быть 90∘.
Как грех(90)=1, расчет моментов в этих примерах требует только использования формулы 𝜏=𝐹⋅𝑑.
Давайте рассмотрим такой пример.

Пример 1. Нахождение реакций опор стержня, находящегося в равновесии
Однородный стержень весом 35 Н опирается горизонтально на две опоры 𝐴 и 𝐵 на его концах, где расстояние между опорами 48 см. Если груз массой 24 Н подвешен на точка, удаленная на 38 см от 𝐴, определите реакции двух опор 𝑅 и 𝑅.
Ответ
Существуют две неизвестные силы реакции. Стержень покоится, значит, сумма этих сил должна равняться сумме веса стержня и груза, подвешенного к стержню; следовательно, 𝑅+𝑅=35+24=59.NNN
Можно определить моменты, действующие относительно 𝐴 или 𝐵. Возьмем моменты про 𝐵.
Стержень находится в равновесии, поэтому моменты по часовой стрелке и против часовой стрелки относительно 𝐵 равны.
На следующем рисунке показаны силы, действующие на стержень.Стержень однородный, поэтому его вес действует на его середину. Расстояния в сантиметрах конвертируются в расстояния в метрах.

Единственный момент по часовой стрелке около 𝐵 обусловлен 𝑅. Моменты против часовой стрелки около 𝐵 возникают из-за веса стержня и веса, подвешенного к стержню.
Приравнивание моментов о 𝐵 дает (0,24×35)+((0,48−0,38)×24)=0,48×𝑅.
Это можно упростить следующим образом: 𝑅=(0,24×35)+((0,48−0,38)×24)0,48𝑅=8,4+2.40,48=22,5.N
Как было сказано ранее, 𝑅+𝑅=35+24=59,NNN и так, 𝑅 задается 𝑅=59−𝑅𝑅=36,5.N
Рассмотрим другой такой пример, на этот раз с неоднородным телом.
Пример 2. Нахождение точки, в которой вес действует на неоднородный стержень, путем нахождения равнодействующих сил и определения моментов
Неоднородный стержень 𝐴𝐵 весом 40 Н и длиной 80 см подвешен вертикально к его середина легкой струной, и он становится в равновесии в горизонтальном положении, когда вес величины 29 Н подвешен к его концу 𝐴.Определить расстояние 𝑥 между точкой, в которой вес стержня является действующим и концевым 𝐴.
 После снятия груза в точке 𝐴 определите величину вертикальной силы, которая потребуется, чтобы удерживать стержень в вертикальном положении.
равновесие в горизонтальном положении, когда он действует на конце 𝐵.
После снятия груза в точке 𝐴 определите величину вертикальной силы, которая потребуется, чтобы удерживать стержень в вертикальном положении.
равновесие в горизонтальном положении, когда он действует на конце 𝐵.Ответ
В этом примере неизвестна только направленная вертикально вверх сила, действующая на струну. Струна легкая, то есть имеет незначительный вес, поэтому сила, направленная вниз из-за веса струны, незначительна.
Восходящая сила, действующая на стержень, равна сумме направленных вниз сил. Следовательно, натяжение струны определяется выражением 𝑇=40+29=69.NNN
Стержень неоднороден, поэтому положение центра масс стержня неизвестно, кроме того, что он не находится в середине стержня.
Когда груз подвешен к стержню в точке 𝐴, стержень находится в равновесии. Если моменты по и против часовой стрелки взяты относительно точки 𝑃, где струна подвешивает стержень, сила струны создает нулевые моменты относительно 𝑃.
 Единственные моменты на стержне около 𝑃 связаны с весом, подвешенным в 𝐴.
и вес стержня, действующий в центре масс стержня. Поскольку стержень находится в равновесии, эти моменты должны быть равны.
Единственные моменты на стержне около 𝑃 связаны с весом, подвешенным в 𝐴.
и вес стержня, действующий в центре масс стержня. Поскольку стержень находится в равновесии, эти моменты должны быть равны.Нам дано, что длина стержня 80 см, поэтому расстояние от 𝑃 до 𝐴 составляет 40 см. Следовательно, моменты относительно 𝑃 задаются формулой 29×40=40𝑑, где 𝑑 — расстояние от 𝑃 до центра масс стержня. Решение уравнения для 𝑑 дает 𝑑=29×4040=29.см
Центр масс находится на расстоянии 29 см от середины стержня. Середина находится в 40 см от 𝐴, поэтому расстояние от 𝐴 к центру масс стержня 29+40=69 см
Когда груз, подвешенный в 𝐴, удаляется, стержень перестает находиться в равновесии до тех пор, пока вертикальная сила ⃑𝐹 действует в 𝐵.
Снова взяв моменты около 𝑃, отметим, что момент от веса стержня, который находится справа от 𝑃 действует по часовой стрелке.
 Сила, действующая на 𝐵, находится правее 𝑃,
поэтому сила, действующая на 𝐵, должна действовать в направлении, противоположном весу стержня.
Сила, действующая на 𝐵, находится правее 𝑃,
поэтому сила, действующая на 𝐵, должна действовать в направлении, противоположном весу стержня.Моменты про 𝑃 теперь даны 40×29=𝐹×40.Ncmcm
Решение уравнения для 𝐹 дает 𝐹=40×2940=29.N
Интересно отметить, что в предыдущем примере не было необходимости рассматривать условия поступательного равновесия для стержня, чтобы определить неизвестные величины, которые необходимо найти, только условия вращательного равновесия для стержня.
Давайте рассмотрим другой пример, связанный с натяжением струн, поддерживающих тело. Этот пример включает в себя больше сил, действующих на стержень, чем в предыдущих примерах, но решается таким же образом.
Пример 3. Нахождение напряжений в задаче о равновесии
Однородный стержень 𝐴𝐵 весит 70 Н и имеет длину 95 см. Он подвешен к концам на двух вертикальных нитях, где 𝑇 натяжение струны в точке 𝐴 а 𝑇 — натяжение струны в точке 𝐵.
 Вес 100 Н
подвешен на стержне, 30 см
подальше от 𝐴,
и весом 93 Н
подвешен к стержню, 20 см
подальше от 𝐵. Определите значения 𝑇 и 𝑇.
Вес 100 Н
подвешен на стержне, 30 см
подальше от 𝐴,
и весом 93 Н
подвешен к стержню, 20 см
подальше от 𝐵. Определите значения 𝑇 и 𝑇.Ответ
Существуют две неизвестные силы натяжения. Стержень покоится, поэтому сумма этих сил должен равняться сумме веса стержня и двух грузов, подвешенных к стержню; следовательно, 𝑇+𝑇=70+100+93=263.NNNN
Моменты, действующие либо на 𝐴, либо на 𝐵 можно определить.Возьмем моменты про 𝐴.
Стержень находится в равновесии, поэтому моменты по часовой и против часовой стрелки составляют примерно 𝐴 равны.
Поскольку 𝑇 действует в 𝐴, он производит ноль моментов относительно 𝐴. 𝑇 действует вверх, а все остальные силы на стержень действуют вниз, поэтому момент 𝑇 равно сумме остальных моментов, 95×𝑇=(30×100)+952×70+((95−20)×93)95×𝑇=3000+3325+6975=13300𝑇=1330095=140.N
Как указано ранее , 𝑇+𝑇=263,Н так 𝑇=263−140=123.
 N
NНекоторые силы, действующие на тела, обычно не считаются переменными. Например, обычно считается, что вес тела не изменяется. Технически, если тело переместилось на значительную расстояние от Земли, то он будет различаться по весу. Также, если тело раздроблено, то вес осколков извлекаемая из тела, будет вычтена из массы тела. Подобные ситуации не рассматриваются в этом объяснителе.
Однако, когда на протяженное твердое тело действуют множественные силы реакции или силы натяжения, величины этих сил могут изменяться только из-за положения точки на теле, в которой на него действует приложенная сила.
Рассмотрим силы, действующие на однородное тело на следующем рисунке.
На тело действуют две силы реакции. Чтобы тело находилось в поступательном равновесии, сумма сил реакции должна быть равна вес тела 𝑊 и приложенная вниз сила ⃑𝐹. Это должно быть верно везде, откуда действует ⃑𝐹.
Чтобы тело находилось в вращательном равновесии, если ⃑𝐹 действует в центре масс тела, ⃑𝑅 должно быть не равно ⃑𝑅.
 Если точка, в которой действует ⃑𝐹, меняется, ⃑𝑅
и ⃑𝑅 будут различаться.Чем больше расстояние ⃑𝐹
от 𝐴, тем меньше величина ⃑𝑅
должно быть и тем больше должна быть величина ⃑𝑅, чтобы тело находилось во вращательном равновесии.
Если точка, в которой действует ⃑𝐹, меняется, ⃑𝑅
и ⃑𝑅 будут различаться.Чем больше расстояние ⃑𝐹
от 𝐴, тем меньше величина ⃑𝑅
должно быть и тем больше должна быть величина ⃑𝑅, чтобы тело находилось во вращательном равновесии.Варьируя положение точки, в которой сила действует на тело, и сравнивая моменты относительно точки на тела при действии на него силы в разных точках можно определить положение точки при котором действует вес тела, а также величина веса.
Теперь рассмотрим пример, когда сила, приложенная к телу, действует в разных точках.
Пример 4: Уравновешенные моменты
𝐴𝐵 — неоднородный стержень длиной 77 см в горизонтальном положении на одной опоре, который находится на расстоянии 26 см от конца 𝐴. Он поддерживается в равновесии за счет подвешивания груз 16 Н на его конце 𝐴 и груз 2 Н в конце 𝐵. Если расстояние между опорой и концом 𝐴 изменено на 23 см, стержень будет сохранен в равновесии, подвешивая груз массой 18 Н только за конец 𝐴.
 Найдите величину
веса стержня 𝑊 и расстояния 𝑥 между его линией действия и точкой 𝐴. Округлите ваши ответы до ближайших двух знаков после запятой.
Найдите величину
веса стержня 𝑊 и расстояния 𝑥 между его линией действия и точкой 𝐴. Округлите ваши ответы до ближайших двух знаков после запятой.Ответ
То, что описано в вопросе, может быть кратко представлено следующим рисунком, который показывает два расположения стержня. Стержень находится в равновесии в обоих положениях.
В точке, где действует сила реакции, реакция определяется выражением 𝑅=18+𝑊, но 𝑊 неизвестно, как и 𝑥.Эти два неизвестных не могут быть однозначно определены рассмотрение любого из устройств стержня в отдельности, только путем сравнения обоих устройств.
В обоих случаях стержень находится в равновесии, поэтому суммарный момент относительно любой точки стержня равен нулю для обоих вариантов. Рассмотрим чистый момент относительно 𝐴 для обеих компоновок.
Для устройства с силами, действующими как на 𝐴, так и на 𝐵, моменты относительно 𝐴 определяются выражением (26(18+𝑊))−𝑥𝑊−2(77)=0.
 Это можно переставить как
468+26𝑊=𝑥𝑊+154314=𝑥𝑊−26𝑊.
Это можно переставить как
468+26𝑊=𝑥𝑊+154314=𝑥𝑊−26𝑊.Для устройства с силой, действующей только в точке 𝐴, моменты относительно 𝐴 определяются выражением (23(18+𝑊))−𝑥𝑊=0.
Можно изменить как 414=𝑥𝑊−23𝑊.
Поскольку чистые моменты относительно 𝐴 для обеих компоновок равны нулю, они также должны быть равны друг другу, поэтому 314+26𝑊−𝑥𝑊=414+23𝑊−𝑥𝑊.
Это можно изменить, чтобы сделать 𝑊 предметом уравнения следующим образом.
Вычтите −𝑥𝑊 из обеих частей уравнения, чтобы получить 314+26𝑊=414+23𝑊.
Вычтите 314 из обеих частей уравнения, чтобы получить 26𝑊=100+23𝑊.
Вычтите 23𝑊 из обеих частей уравнения, чтобы получить 3𝑊=100𝑊=1003.N
До двух знаков после запятой, 𝑊=33.33.N
В вопросе указано, что для устройства с силой, действующей только на 𝐴. Расстояние между местом действия веса стержня и концом 𝐴 равно 𝑥 в обеих конфигурациях.
 Чтобы определить 𝑥, можно взять моменты относительно точки, в которой действует сила реакции. Расстояние между этой точкой и точкой, на которую действует вес стержня, равно 𝑑 и определяется выражением
(23×18)=𝑑1003414=𝑑10034143100=𝑑=12,42.см
Чтобы определить 𝑥, можно взять моменты относительно точки, в которой действует сила реакции. Расстояние между этой точкой и точкой, на которую действует вес стержня, равно 𝑑 и определяется выражением
(23×18)=𝑑1003414=𝑑10034143100=𝑑=12,42.смРасстояние от 𝐴 до точки, в которой действует вес стержня, определяется выражением 𝑥=23+12,42=35,42.см
Мы закончим примером, где к твердому телу приложены силы до тех пор, пока оно не начнет вращаться.
Пример 5. Определение веса, прикрепленного к концу стержня, который заставляет его вращаться
Длина стержня 𝐴𝐵 составляет 111 см, а его вес составляет 95 ньютонов, который действует в его средней точке. Стержень опирается горизонтально на две опоры, где один из них находится в конце 𝐴, а другой в точке 𝐶, что составляет 30 см подальше от 𝐵. Груз массой 71 ньютон подвешен к стержню в точке, 9 см от 𝐵.
 Найдите модуль веса 𝑤, который должен быть
подвешен к концу 𝐵 так, что стержень собирается вращаться, и определить значение приложенной вниз силы 𝑃
на 𝐶 в этой ситуации.
Найдите модуль веса 𝑤, который должен быть
подвешен к концу 𝐵 так, что стержень собирается вращаться, и определить значение приложенной вниз силы 𝑃
на 𝐶 в этой ситуации.Ответ
Начнем с того, что нарисуем схему устройства, описанного в вопросе, как показано ниже.
Стержень опирается горизонтально на две опоры в точках 𝐴 и 𝐶; он собирается вращаться, но еще не начал вращаться. Следовательно, сумма сил и сумма моментов равны нулю, поэтому тело находится в равновесии.
Поскольку результирующая сила в любом направлении равна нулю, разрешение по вертикали дает 𝑅+𝑅=95+71+𝑤𝑅+𝑅=166+𝑤, где 𝑤 пока неизвестно.Однако, поскольку груз 𝑤 подвешен к концу 𝐵, это означает, что стержень собирается вращаться по часовой стрелке вокруг опоры в 𝐶. Следовательно, он вот-вот потеряет связь с техподдержкой на 𝐴, откуда следует, что 𝑅=0. Это дает 𝑅=166+𝑤.
Кроме того, суммарный момент относительно любой точки стержня равен нулю, поэтому, в частности, моменты по часовой стрелке и против часовой стрелки относительно 𝐶 равны.
 Записав все длины в метрах, мы имеем
(1,11−0,3)𝑅+(1,11−0,09)71+0.3𝑤=1,112−0,3950,81𝑅+14,91+0,3𝑤=24,225.
Записав все длины в метрах, мы имеем
(1,11−0,3)𝑅+(1,11−0,09)71+0.3𝑤=1,112−0,3950,81𝑅+14,91+0,3𝑤=24,225.Вспоминая, что 𝑅=0, и вычитая из обеих частей по 14,91, получаем 0,3𝑤=9,315.
Наконец, деление обеих частей на 0,3 означает, что 𝑤=31.05.
Мы заключаем, что величина веса 𝑤 равна 31,05 Н.
Чтобы определить значение силы 𝑃, направленной вниз, действующей на 𝐶 в этой ситуации, заметим, что она будет равна по величине, но в обратном направлении, к 𝑅. Поэтому, возвращаясь к нашему первому уравнению, имеем 𝑃=𝑅=166+𝑤=166+31.05=197.05.N
Ключевые моменты
- Параллельные силы, действующие на твердое тело в состоянии равновесия, должны либо действовать параллельно длине тела, либо пересекающих его центр масс, или действуют перпендикулярно этому направлению.
- Суммарная сила и результирующий момент от параллельных сил должны быть равны нулю, чтобы тело находилось в равновесии.

- Значения множественных сил растяжения или реакции, действующих на твердое тело в равновесии, зависят на соответствующих расстояниях от центра масс тела.
12.1 Условия статического равновесия – University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Определите физические условия статического равновесия.
- Нарисуйте диаграмму свободного тела для твердого тела, на которое действуют силы.
- Объясните, как условия равновесия позволяют нам решать задачи статики.
Мы говорим, что твердое тело находится в равновесии , когда его линейное и угловое ускорения равны нулю относительно инерциальной системы отсчета.Это означает, что тело, находящееся в равновесии, может двигаться, но в этом случае его линейная и угловая скорости должны быть постоянными. Мы говорим, что твердое тело находится в статическом равновесии , когда оно находится в покое в выбранной нами системе отсчета .
 Обратите внимание, что различие между состоянием покоя и состоянием равномерного движения является искусственным, то есть объект может находиться в состоянии покоя в выбранной нами системе отсчета, но для наблюдателя, движущегося с постоянной скоростью относительно нашей системы отсчета, тот же самый объект находится в равномерном движении с постоянной скоростью.Поскольку движение относительно , то, что для нас находится в статическом равновесии, находится в динамическом равновесии для движущегося наблюдателя, и наоборот. Поскольку законы физики одинаковы для всех инерциальных систем отсчета, в инерциальной системе отсчета нет различия между статическим равновесием и равновесием.
Обратите внимание, что различие между состоянием покоя и состоянием равномерного движения является искусственным, то есть объект может находиться в состоянии покоя в выбранной нами системе отсчета, но для наблюдателя, движущегося с постоянной скоростью относительно нашей системы отсчета, тот же самый объект находится в равномерном движении с постоянной скоростью.Поскольку движение относительно , то, что для нас находится в статическом равновесии, находится в динамическом равновесии для движущегося наблюдателя, и наоборот. Поскольку законы физики одинаковы для всех инерциальных систем отсчета, в инерциальной системе отсчета нет различия между статическим равновесием и равновесием.Согласно второму закону Ньютона линейное ускорение твердого тела вызвано действующей на него результирующей силой, или
[латекс] \ sum _ {k} {\ mathbf {\ overset {\ to} {F}}} _ {k} = m {\ mathbf {\ overset {\ to} {a}}} _ {\ text {СМ}}.[/латекс]
Здесь сумма всех внешних сил, действующих на тело, где м — его масса и [латекс]{\mathbf{\overset{\to }{a}}}_{\text{CM}}[ /латекс] — это линейное ускорение его центра масс (концепция, которую мы обсуждали в разделе «Линейный импульс и столкновения» о линейном импульсе и столкновениях).
 В состоянии равновесия линейное ускорение равно нулю. Если мы установим ускорение равным нулю на рисунке, мы получим следующее уравнение:
В состоянии равновесия линейное ускорение равно нулю. Если мы установим ускорение равным нулю на рисунке, мы получим следующее уравнение:Первое состояние равновесия
Первое условие равновесия статического равновесия твердого тела выражает поступательное равновесие:
[латекс] \ сумма _ {к} {\ mathbf {\ overset {\ to {F}}} _ {k} = \ mathbf {\ overset {\ to {0}}.[/латекс]
Первое условие равновесия, рис., — это условие равновесия сил, с которым мы столкнулись при изучении приложений законов Ньютона.
Это векторное уравнение эквивалентно следующим трем скалярным уравнениям для компонентов результирующей силы:
[латекс]\sum _{k}{F}_{kx}=0,\quad \sum _{k}{F}_{ky}=0,\quad \sum _{k}{F}_ {кз}=0.[/латекс]
Аналогично рисунку, мы можем утверждать, что вращательное ускорение [латекс]\mathbf{\overset{\to }{\альфа}}[/латекс] твердого тела вокруг фиксированной оси вращения вызывается чистым крутящим моментом, действующим на корпусе или
[латекс] \ sum _ {k} {\ mathbf {\ overset {\ to } {\ tau}}} _ {k} = I \ mathbf {\ overset {\ to } {\ alpha}}.
 [/латекс]
[/латекс]Здесь [латекс]I[/латекс] — инерция вращения тела при вращении вокруг этой оси, а сумма равна всем крутящим моментам [латекс]{\mathbf{\overset{\to }{\tau}}} _{k}[/latex] внешних сил на рис. В состоянии равновесия ускорение вращения равно нулю. Приравняв к нулю правую часть рисунка, мы получим второе условие равновесия:
Второе условие равновесия
Второе условие равновесия статического равновесия твердого тела выражает вращательное равновесие:
[латекс] \sum _ {k} {\ mathbf {\ overset {\ to } {\ tau}}} _ {k} = \ mathbf {\ overset {\ to {0}}.[/латекс]
Второе условие равновесия, рис., — это условие равновесия крутящих моментов, с которым мы столкнулись при изучении динамики вращения. Стоит отметить, что это уравнение равновесия обычно справедливо для вращательного равновесия вокруг любой оси вращения (фиксированной или иной). Опять же, это векторное уравнение эквивалентно трем скалярным уравнениям для векторных составляющих чистого крутящего момента:
[латекс]\sum _{k}{\tau }_{kx}=0,\quad \sum _{k}{\tau }_{ky}=0,\quad \sum _{k}{\ тау}_{kz}=0.
 [/латекс]
[/латекс]Второе условие равновесия означает, что в равновесии нет чистого внешнего крутящего момента, вызывающего вращение вокруг какой-либо оси.
Первое и второе условия равновесия указаны в конкретной системе отсчета. Первое условие включает только силы и, следовательно, не зависит от начала системы отсчета. Однако второе условие включает крутящий момент, который определяется как перекрестное произведение, {r}}}_{k}\times {\mathbf{\overset{\to}}{F}}}_{k},[/latex], где вектор положения [латекс]{\mathbf{\overset{\ в {r}}}_{k}[/latex] относительно оси вращения точки приложения силы входит в уравнение.Следовательно, крутящий момент зависит от положения оси в системе отсчета. Однако, когда условия вращательного и поступательного равновесия выполняются одновременно в одной системе отсчета, то они также выполняются в любой другой инерциальной системе отсчета, так что чистый крутящий момент относительно любой оси вращения по-прежнему равен нулю. Объяснение этому довольно простое.

Предположим, что вектор [latex]\mathbf{\overset{\to }{R}}[/latex] является положением начала новой инерциальной системы отсчета [latex]S\prime[/latex] в старой инерциальной системе отсчета. система отсчета S .{\ простое число}} _ {k} \ times {\ mathbf {\ overset {\ to} {F}}} _ {k} = \ sum _ {k} ({\ mathbf {\ overset {\ to} {r }}} _ {k} — \ mathbf {\ overset {\ to {R}}) \ times {\ mathbf {\ overset {\ to {F}}} _ {k} = \ sum _ {k} {\ mathbf {\ overset {\ to} {r}}} _ {k} \ times {\ mathbf {\ overset {\ to} {F}}} _ {k} — \ sum _ {k} \ mathbf { \ overset {\ to {R}} \ times {\ mathbf {\ overset {\ to {F}}} _ {k} = \ sum _ {k} {\ mathbf {\ overset {\ to} {\ тау }}} _ {k} — \ mathbf {\ overset {\ to {R}} \ times \ sum _ {k} {\ mathbf {\ overset {\ to {F}}} _ {k} = \mathbf{\overset{\to }{0}}.[/latex]
На последнем этапе этой цепочки рассуждений мы использовали тот факт, что в равновесии в старой системе отсчета S первый член исчезает из-за фигуры, а второй член исчезает из-за фигуры.
 Отсюда мы видим, что чистый крутящий момент в любой инерциальной системе отсчета [латекс]S\prime[/латекс] равен нулю, при условии, что оба условия равновесия выполняются в инерциальной системе отсчета S .
Отсюда мы видим, что чистый крутящий момент в любой инерциальной системе отсчета [латекс]S\prime[/латекс] равен нулю, при условии, что оба условия равновесия выполняются в инерциальной системе отсчета S .Практическим следствием этого является то, что при применении условий равновесия для твердого тела мы можем выбрать любую точку в качестве начала системы отсчета. Наш выбор системы отсчета продиктован физическими особенностями решаемой задачи. В одной системе отсчета математическая форма условий равновесия может быть довольно сложной, тогда как в другой системе те же самые условия могут иметь более простую математическую форму, которую легко решить.Начало выбранной системы отсчета называется точкой вращения .
В самом общем случае условия равновесия выражаются шестью скалярными уравнениями (рисунок и рисунок). Для плоских задач равновесия с вращением вокруг неподвижной оси, которые мы рассматриваем в этой главе, количество уравнений можно сократить до трех.
 Стандартная процедура заключается в принятии системы отсчета, где ось z является осью вращения. При таком выборе оси чистый крутящий момент имеет только z -компоненту, все силы, имеющие ненулевые крутящие моменты, лежат в xy -плоскости, поэтому вклад в чистый крутящий момент поступает только от x – и и — компоненты внешних сил.Таким образом, для плоских задач с осью вращения, перпендикулярной xy -плоскости, мы имеем следующие три условия равновесия сил и моментов:
Стандартная процедура заключается в принятии системы отсчета, где ось z является осью вращения. При таком выборе оси чистый крутящий момент имеет только z -компоненту, все силы, имеющие ненулевые крутящие моменты, лежат в xy -плоскости, поэтому вклад в чистый крутящий момент поступает только от x – и и — компоненты внешних сил.Таким образом, для плоских задач с осью вращения, перпендикулярной xy -плоскости, мы имеем следующие три условия равновесия сил и моментов:[латекс]{F}_{1x}+{F}_{2x}+\cdots+{F}_{Nx}=0[/латекс]
[латекс]{F}_{1y}+{F}_{2y}+\cdots+{F}_{Ny}=0[/латекс]
[латекс] {\ тау} _ {1} + {\ тау } _ {2} + \ cdots + {\ тау} _ {N} = 0 [/латекс]
где суммируется по всем N внешним силам, действующим на тело, и по их моментам. На рисунке мы упростили обозначения, опустив нижний индекс z , но здесь мы понимаем, что суммирование производится по всем вкладам вдоль оси z , которая является осью вращения.
 На рисунке z -компонента крутящего момента [латекс]{\mathbf{\overset{\to }{\тау}}}_{k}[/латекс] от силы [латекс]{\mathbf{\overset {\to}{F}}}_{k}[/латекс] равно
На рисунке z -компонента крутящего момента [латекс]{\mathbf{\overset{\to }{\тау}}}_{k}[/латекс] от силы [латекс]{\mathbf{\overset {\to}{F}}}_{k}[/латекс] равно[латекс] {\ тау} _ {к} = {г} _ {к} {F} _ {к} \ текст {грех} \, \ тета [/латекс]
, где [латекс]{r}_{k}[/латекс] — длина плеча рычага силы, а [латекс] {F}_{k}[/латекс] — величина силы (как вы видел в режиме вращения с фиксированной осью). Угол [латекс]\тета[/латекс] — это угол между векторами [латекс]{\mathbf{\overset{\to}}{r}}}_{k}[/латекс] и [латекс]{\mathbf{ \overset{\to }{F}}}_{k},[/latex] измеряет из вектора [latex]{\mathbf{\overset{\to }{r}}}_{k}[/latex ] в вектор [латекс] {\ mathbf {\ overset {\ to } {F}}} _ {k} [/латекс] в направлении против часовой стрелки (рисунок).При использовании рисунка мы часто вычисляем величину крутящего момента и присваиваем его смысл как положительный [латекс](+)[/латекс] или отрицательный [латекс](-),[/латекс] в зависимости от направления вращения, вызванного этим крутящий момент один.
Рисунок 12.2 Крутящий момент силы: (a) Когда крутящий момент силы вызывает вращение против часовой стрелки вокруг оси вращения, мы говорим, что его направление положительное, что означает, что вектор крутящего момента параллелен оси вращения. (b) Когда крутящий момент силы вызывает вращение по часовой стрелке вокруг оси, мы говорим, что его направление отрицательно, что означает, что вектор крутящего момента антипараллелен оси вращения. На рисунке чистый крутящий момент представляет собой сумму членов, причем каждый член вычисляется из рисунка, и каждый член должен иметь правильный смысл . Точно так же на рисунке мы назначаем знак [латекс]+[/латекс] компонентам в направлении [латекс]+[/латекс] x , а знак [латекс]-[/латекс] — компонентам в направлении [латекс]-[/латекс] x -направление.Этому же правилу необходимо последовательно следовать на рисунке при вычислении составляющих силы вдоль оси y .
На рисунке чистый крутящий момент представляет собой сумму членов, причем каждый член вычисляется из рисунка, и каждый член должен иметь правильный смысл . Точно так же на рисунке мы назначаем знак [латекс]+[/латекс] компонентам в направлении [латекс]+[/латекс] x , а знак [латекс]-[/латекс] — компонентам в направлении [латекс]-[/латекс] x -направление.Этому же правилу необходимо последовательно следовать на рисунке при вычислении составляющих силы вдоль оси y .Во многих равновесных ситуациях одной из сил, действующих на тело, является его вес.
 На диаграммах свободного тела вектор веса привязан к центру тяжести тела. Для всех практических целей центр тяжести идентичен центру масс, как вы узнали из линейного импульса и столкновений о линейном импульсе и столкновениях. Только в тех случаях, когда тело имеет большую пространственную протяженность, так что гравитационное поле неоднородно по всему его объему, центр тяжести и центр масс находятся в разных точках.{2}.[/latex] В этих ситуациях центр тяжести идентичен центру масс. Поэтому на протяжении всей этой главы мы используем центр масс (ЦМ) как точку, к которой прикрепляется весовой вектор. Напомним, что ЦМ имеет особый физический смысл: при приложении внешней силы к телу точно в его ЦМ тело в целом совершает поступательное движение и такая сила не вызывает вращения.
На диаграммах свободного тела вектор веса привязан к центру тяжести тела. Для всех практических целей центр тяжести идентичен центру масс, как вы узнали из линейного импульса и столкновений о линейном импульсе и столкновениях. Только в тех случаях, когда тело имеет большую пространственную протяженность, так что гравитационное поле неоднородно по всему его объему, центр тяжести и центр масс находятся в разных точках.{2}.[/latex] В этих ситуациях центр тяжести идентичен центру масс. Поэтому на протяжении всей этой главы мы используем центр масс (ЦМ) как точку, к которой прикрепляется весовой вектор. Напомним, что ЦМ имеет особый физический смысл: при приложении внешней силы к телу точно в его ЦМ тело в целом совершает поступательное движение и такая сила не вызывает вращения.Когда ЦМ находится вне оси вращения, на объекте возникает чистый гравитационный момент .Гравитационный крутящий момент — это крутящий момент, вызванный весом. Этот гравитационный момент может вращать объект, если нет поддержки для его уравновешивания.
Рисунок 12.3 Распределение массы влияет на положение центра масс (ЦМ), к которому присоединен весовой вектор [латекс]\mathbf{\overset{\to }{w}}[/латекс]. Если центр тяжести находится в пределах области опоры, грузовик возвращается в исходное положение после опрокидывания [см. левую панель в (b)]. Но если центр тяжести находится вне области опоры, грузовик переворачивается [см. правую панель в (b)].Оба транспортных средства в (b) находятся вне равновесия. Обратите внимание, что автомобиль в (а) находится в равновесии: низкое расположение его центра тяжести затрудняет его опрокидывание. Величина гравитационного момента зависит от того, насколько далеко от точки вращения находится ЦМ. Например, в случае самосвала (рисунок) ось расположена на линии, где шины соприкасаются с поверхностью дороги. Если ЦМ расположен высоко над поверхностью дороги, гравитационный момент может быть достаточно большим, чтобы перевернуть грузовик.Легковые автомобили с низко расположенным КМ, близко к тротуару, более устойчивы к опрокидыванию, чем грузовые.
Величина гравитационного момента зависит от того, насколько далеко от точки вращения находится ЦМ. Например, в случае самосвала (рисунок) ось расположена на линии, где шины соприкасаются с поверхностью дороги. Если ЦМ расположен высоко над поверхностью дороги, гравитационный момент может быть достаточно большим, чтобы перевернуть грузовик.Легковые автомобили с низко расположенным КМ, близко к тротуару, более устойчивы к опрокидыванию, чем грузовые.
Пример
Центр тяжести автомобиля
У легкового автомобиля с колесной базой 2,5 м 52 % веса приходится на передние колеса на ровной поверхности, как показано на рисунке. Где находится ЦМ этого автомобиля относительно задней оси?
Рисунок 12.4 Распределение веса между осями автомобиля.Где находится центр тяжести?Стратегия
Мы не знаем вес w автомобиля. Все, что мы знаем, это то, что когда автомобиль стоит на ровной поверхности, 0,52 w давит на поверхность в точках контакта передних колес и 0,48 w давит на поверхность в точках контакта задних колес. Кроме того, точки контакта разнесены друг от друга на расстояние [латекс]d=2,5\,\text{м}.[/latex] В этих точках контакта автомобиль испытывает нормальные силы реакции с величинами [латекс]{F} _{\текст{F}}=0.52 Вт[/латекс] и [латекс]{F}_{\text{R}}=0,48 Вт[/латекс] на передней и задней осях соответственно. Мы также знаем, что автомобиль является примером твердого тела, находящегося в равновесии, весь вес которого w действует на его ЦМ.
Рисунок 12.5 Диаграмма свободного тела автомобиля четко указывает векторы сил, действующих на автомобиль, и расстояния до центра масс (ЦМ). Когда в качестве точки поворота выбрана CM, эти расстояния являются плечами нормальных сил реакции. Обратите внимание, что векторные величины и плечи рычагов не обязательно изображать в масштабе, но все релевантные величины должны быть четко обозначены. ЦМ находится где-то между точками действия нормальных сил реакции, где-то на расстоянии х от точки действия [латекс]{F}_{R}[/латекс]. Наша задача найти х . Таким образом, мы выделяем три силы, действующие на тело (автомобиль), и можем нарисовать диаграмму свободного тела для протяженного твердого тела, как показано на рисунке.
ЦМ находится где-то между точками действия нормальных сил реакции, где-то на расстоянии х от точки действия [латекс]{F}_{R}[/латекс]. Наша задача найти х . Таким образом, мы выделяем три силы, действующие на тело (автомобиль), и можем нарисовать диаграмму свободного тела для протяженного твердого тела, как показано на рисунке.Мы почти готовы записать условия равновесия с рисунка на рисунок для автомобиля, но сначала мы должны определиться с системой отсчета.Предположим, мы выбираем ось x по длине автомобиля, ось y по вертикали и ось z перпендикулярно этой плоскости xy .
 При таком выборе нам нужно написать только Figure и Figure, потому что все компоненты и тождественно равны нулю. Теперь нам нужно определиться с расположением опорной точки. Мы можем выбрать любую точку в качестве местоположения оси вращения ( z -ось). Предположим, мы поместили ось вращения в CM, как показано на диаграмме свободного тела для автомобиля.Теперь мы готовы записать условия равновесия автомобиля.
При таком выборе нам нужно написать только Figure и Figure, потому что все компоненты и тождественно равны нулю. Теперь нам нужно определиться с расположением опорной точки. Мы можем выбрать любую точку в качестве местоположения оси вращения ( z -ось). Предположим, мы поместили ось вращения в CM, как показано на диаграмме свободного тела для автомобиля.Теперь мы готовы записать условия равновесия автомобиля.Решение
Каждое условие равновесия содержит только три члена, потому что на автомобиль действует [латекс]N=3[/латекс] сил. Первое условие равновесия, рисунок, читается как
.[латекс]+{F}_{\text{F}}-w+{F}_{\text{R}}=0.[/латекс]
Это условие тривиально выполняется, потому что, когда мы подставляем данные, Figure становится [латекс]+0,52w-w+0,48w=0.[/latex] Второе условие равновесия, Figure, читается как
.[латекс] {\ тау} _ {\ текст {F}} + {\ тау} _ {ш} + {\ тау} _ {\ текст {R}} = 0 [/латекс]
, где [латекс] {\ тау } _ {\ текст {F}} [/латекс] — момент силы [латекс] {F} _ {\ текст {F}}, \, {\ тау } _ {w }[/latex] — гравитационный момент силы w , а [latex]{\tau}_{\text{R}}[/latex] — момент силы [латекс]{F}_{\text {Р}}.
 [/latex] Когда точка вращения расположена в ЦМ, гравитационный момент тождественно равен нулю, потому что плечо рычага веса по отношению к оси, проходящей через ЦМ, равно нулю. Линии действия обеих нормальных сил реакции перпендикулярны плечам их рычагов, поэтому на рисунке мы имеем [латекс]|\,\текст{sin}\,\theta |=1[/латекс] для обеих сил. Из диаграммы свободного тела мы читаем, что крутящий момент [латекс] {\ тау} _ {\ текст {F}} [/латекс] вызывает вращение по часовой стрелке вокруг оси в СМ, поэтому его смысл отрицательный; а крутящий момент [латекс] {\ тау } _ {\ текст {R}} [/ латекс] вызывает вращение против часовой стрелки вокруг оси в СМ, поэтому его смысл положительный.С этой информацией мы запишем второе условие равновесия как
[/latex] Когда точка вращения расположена в ЦМ, гравитационный момент тождественно равен нулю, потому что плечо рычага веса по отношению к оси, проходящей через ЦМ, равно нулю. Линии действия обеих нормальных сил реакции перпендикулярны плечам их рычагов, поэтому на рисунке мы имеем [латекс]|\,\текст{sin}\,\theta |=1[/латекс] для обеих сил. Из диаграммы свободного тела мы читаем, что крутящий момент [латекс] {\ тау} _ {\ текст {F}} [/латекс] вызывает вращение по часовой стрелке вокруг оси в СМ, поэтому его смысл отрицательный; а крутящий момент [латекс] {\ тау } _ {\ текст {R}} [/ латекс] вызывает вращение против часовой стрелки вокруг оси в СМ, поэтому его смысл положительный.С этой информацией мы запишем второе условие равновесия как[латекс] \ text {−} {r} _ {\ text {F}} {F} _ {\ text {F}} + {r} _ {\ text {R}} {F} _ {\ text {R}}=0.[/латекс]
С помощью диаграммы свободного тела мы определяем величины сил [латекс]{F}_{\text{R}}=0,48w[/латекс] и [латекс]{F}_{\text{F }}=0,52w,[/latex] и соответствующие им плечи рычага [латекс]{r}_{\text{R}}=x[/латекс] и [латекс]{r}_{\text{F}} =dx.
 [/latex] Теперь мы можем записать второе условие равновесия, Figure, в явном виде через неизвестное расстояние x :
[/latex] Теперь мы можем записать второе условие равновесия, Figure, в явном виде через неизвестное расстояние x :[латекс]-0.52(dx)w+0.48xw=0.[/латекс]
Здесь вес w сокращается, и мы можем решить уравнение для неизвестного положения x ЦМ. Ответ: [латекс]x=0,52d=0,52(2,5\,\текст{м})=1,3\,\текст{м}\текст{.}[/латекс]
Решение
Выбор точки поворота в положении переднего моста не меняет результат. Диаграмма свободного тела для этого положения поворота представлена на рисунке. Для этого выбора точки разворота второе условие равновесия равно
.[латекс]\текст{−}{r}_{w}w+{r}_{\text{R}}{F}_{\text{R}}=0.[/латекс]
Подставляя величины, указанные на схеме, получаем
[латекс]\текст{−}(d-x)w+0.48dw=0.[/латекс]
Ответ, полученный при решении рисунка, снова равен [латекс]х=0,52d=1,3\,\текст{м}.[/латекс]
Рисунок 12.6 Эквивалентная диаграмма свободного кузова автомобиля; точка опоры четко обозначена.
Значение
Этот пример показывает, что при решении задач статического равновесия мы свободны в выборе точки опоры.Для разных вариантов точки разворота нам нужно решить разные наборы условий равновесия. Однако все варианты ведут к одному и тому же решению проблемы.
Проверьте свое понимание
Решите рисунок, выбрав точку опоры в месте расположения задней оси.
Показать решение[латекс]x=1,3\,\текст{м}[/латекс]
Проверьте свое понимание
Объясните, какая из следующих ситуаций удовлетворяет обоим условиям равновесия: (а) теннисный мяч, который не вращается при движении в воздухе; б) пеликан, парящий в воздухе с постоянной скоростью на одной высоте; или (c) коленчатый вал в двигателе припаркованного автомобиля.
Частный случай статического равновесия имеет место, когда все внешние силы, воздействующие на объект, действуют на или вдоль оси вращения или когда пространственным расширением объекта можно пренебречь.
 В таком случае объект можно эффективно рассматривать как точечную массу. В этом частном случае нам не нужно беспокоиться о втором условии равновесия, рис., поскольку все крутящие моменты тождественно равны нулю, а первое условие равновесия (для сил) является единственным условием, которое должно быть выполнено. Диаграмма свободного тела и стратегия решения проблем для этого особого случая были изложены в книге Ньютона «Законы движения и приложения законов Ньютона».В следующем примере вы увидите типичную ситуацию равновесия, включающую только первое условие равновесия.
В таком случае объект можно эффективно рассматривать как точечную массу. В этом частном случае нам не нужно беспокоиться о втором условии равновесия, рис., поскольку все крутящие моменты тождественно равны нулю, а первое условие равновесия (для сил) является единственным условием, которое должно быть выполнено. Диаграмма свободного тела и стратегия решения проблем для этого особого случая были изложены в книге Ньютона «Законы движения и приложения законов Ньютона».В следующем примере вы увидите типичную ситуацию равновесия, включающую только первое условие равновесия.Пример
Разрывное напряжение
Небольшая кастрюля массой 42,0 г поддерживается двумя нитями, как показано на рисунке. Максимальное натяжение, которое может выдержать струна, составляет 2,80 Н. Масса постепенно добавляется к чаше до тех пор, пока одна из струн не порвется. Какая это строка? Какое количество массы нужно добавить, чтобы это произошло?
Рисунок 12.7 Масса постепенно добавляется в чашу до тех пор, пока одна из нитей не порвется.
Стратегия
Эта механическая система, состоящая из струн, грузов и чаши, находится в статическом равновесии. В частности, узел, который связывает струны со сковородой, находится в статическом равновесии. Узел можно рассматривать как точку; поэтому нам нужно только первое условие равновесия. Три силы, тянущие узел, — это натяжение [латекс] {\ mathbf {\ overset {\ to} {T}}} _ {1} [/латекс] в 5,0-сантиметровой нити, натяжение [латекс] {\ mathbf{\overset{\to }{T}}}_{2}[/latex] в строке длиной 10,0 см, а вес [латекс]\mathbf{\overset{\to }{w}}[/latex ] кастрюли, удерживающей массы.Мы принимаем прямоугольную систему координат с осью y , направленной против направления силы тяжести, и рисуем диаграмму свободного тела для узла (см. рисунок). Чтобы найти компоненты натяжения, мы должны определить углы направления [латекс]{\альфа}_{1}[/латекс] и [латекс]{\альфа}_{2}[/латекс], которые струны образуют с горизонталью. направление, которое является осью x . Как вы можете видеть на рисунке, струны образуют две стороны прямоугольного треугольника.
Рисунок 12.8 Диаграмма свободного тела для узла на рисунке. Мы можем использовать теорему Пифагора, чтобы решить этот треугольник, показанный на рисунке, и найти синус и косинус углов [латекс] {\ альфа }_ {1} [/латекс] и [латекс] {\ альфа } _ {2 }.[/latex] Затем мы можем разложить натяжения на их прямоугольные компоненты, подставить в первое условие равновесия (рисунок и рисунок) и найти натяжения в струнах. Сначала порвется струна с большим натяжением.
Мы можем использовать теорему Пифагора, чтобы решить этот треугольник, показанный на рисунке, и найти синус и косинус углов [латекс] {\ альфа }_ {1} [/латекс] и [латекс] {\ альфа } _ {2 }.[/latex] Затем мы можем разложить натяжения на их прямоугольные компоненты, подставить в первое условие равновесия (рисунок и рисунок) и найти натяжения в струнах. Сначала порвется струна с большим натяжением.Решение
Вес w , тянущий узел, обусловлен массой M чаши и массой m , добавленной к чаше, или [латекс]w=(M+m)g.[/latex] С помощью диаграммы свободного тела на рисунке мы можем установить условия равновесия для узла:
[латекс]\begin{array}{ccccc}\text{в}\,x\текст{-направлении,}\hfill & & \hfill \text{−}{T}_{1x}+{T} _{2x}& =\hfill & 0\hfill \\ \text{в}\,y\text{-направлении,}\hfill & & \hfill \text{+}{T}_{1y}+{ T}_{2y}-w& =\hfill & 0.\hfill \end{массив}[/latex]
Из диаграммы свободного тела величины компонентов в этих уравнениях равны
[латекс]\begin{array}{ccc}{T}_{1x}={T}_{1}\text{cos}\,{\alpha}_{1}={T}_{1} \text{/}\sqrt{5},\hfill & & {T}_{1y}={T}_{1}\text{sin}\,{\alpha}_{1}=2{T} _{1}\text{/}\sqrt{5}\hfill \\ {T}_{2x}={T}_{2}\text{cos}\,{\alpha}_{2}=2 {T}_{2}\text{/}\sqrt{5},\hfill & & {T}_{2y}={T}_{2}\text{sin}\,{\alpha }_{ 2}={T}_{2}\текст{/}\sqrt{5}.
 \hfill \end{массив}[/латекс]
\hfill \end{массив}[/латекс]Подставляем эти компоненты в условия равновесия и упрощаем. Тогда мы получаем два уравнения равновесия для напряжений:
[латекс]\begin{array}{ccccc}\text{in}\,x\text{-направление,}\hfill & & \hfill {T}_{1}& =\hfill & 2{T}_ {2}\hfill \\ \text{in}\,y\text{-направление,}\hfill & & \hfill \frac{2{T}_{1}}{\sqrt{5}}+\frac {{T}_{2}}{\sqrt{5}}& =\hfill & (M+m)g.\hfill \end{массив}[/latex]
Уравнение равновесия для направления x говорит нам, что натяжение [латекс]{T}_{1}[/латекс] в 5.Нить длиной 0 см в два раза превышает натяжение [латекс]{T}_{2}[/латекс] нити длиной 10,0 см. Следовательно, более короткая струна порвется. Когда мы используем первое уравнение для исключения [латекса]{T}_{2}[/латекса] из второго уравнения, мы получаем связь между массой [латекса]m[/латекса] на поддоне и натяжением [латекса ]{T}_{1}[/latex] в более короткой строке:
[латекс]2.5{T}_{1}\text{/}\sqrt{5}=(M+m)g.[/latex]
Струна рвется, когда натяжение достигает критического значения [латекс]{T}_{1}=2.
 {2}}-0,042\,\text{кг}=0,277\,\text{кг}=277,0\,\text{г.}[/latex]
{2}}-0,042\,\text{кг}=0,277\,\text{кг}=277,0\,\text{г.}[/latex]Значение
Предположим, что механическая система, рассматриваемая в этом примере, прикреплена к потолку внутри поднимающегося лифта. Пока лифт движется вверх с постоянной скоростью, результат остается прежним, потому что вес [латекс]w[/латекс] не меняется. Если лифт движется вверх с ускорением, критическая масса меньше, потому что вес [латекс]М+м[/латекс] становится больше на кажущийся вес из-за ускорения лифта.Тем не менее, во всех случаях более короткая струна рвется первой.
Резюме
- Тело находится в равновесии, когда оно остается либо в равномерном движении (как поступательном, так и вращательном), либо в состоянии покоя. Когда тело в выбранной инерциальной системе отсчета не вращается и не совершает поступательного движения, говорят, что тело находится в статическом равновесии в этой системе отсчета.
- Условия равновесия требуют, чтобы сумма всех внешних сил, действующих на тело, была равна нулю (первое условие равновесия), а сумма всех внешних моментов от внешних сил равнялась нулю (второе условие равновесия).
 Эти два условия должны одновременно выполняться в равновесии. Если одно из них не выполняется, тело не находится в равновесии.
Эти два условия должны одновременно выполняться в равновесии. Если одно из них не выполняется, тело не находится в равновесии. - Диаграмма свободного тела для тела является полезным инструментом, который позволяет нам правильно подсчитать все вклады от всех внешних сил и крутящих моментов, действующих на тело. Диаграммы свободного тела для равновесия протяженного твердого тела должны указывать точку вращения и плечи рычагов действующих сил по отношению к оси вращения.
Концептуальные вопросы
Что вы можете сказать о скорости движущегося тела, находящегося в динамическом равновесии?
При каких условиях вращающееся тело может находиться в равновесии? Привести пример.
Какие три фактора влияют на крутящий момент, создаваемый силой относительно определенной точки поворота?
Показать решение: величину и направление силы, а также плечо рычага
.Механики иногда надевают кусок трубы на рукоятку гаечного ключа, когда пытаются выкрутить очень тугой болт.
 Как это помогает?
Как это помогает?В следующих четырех задачах оцените утверждение как верное или ложное и объясните свой ответ.
Если на объект действует только одна внешняя сила (или крутящий момент), он не может находиться в равновесии.
Показать решениеВерно, так как в этом случае сумма сил не может быть равна нулю, если только сама сила не равна нулю.
Если объект находится в равновесии, на него должно действовать четное число сил.
Если на объект действует нечетное количество сил, объект не может находиться в равновесии.
Показать решениеНеверно, при условии, что силы равны нулю как векторы, тогда равновесие может быть достигнуто.
Тело, движущееся по окружности с постоянной скоростью, находится в равновесии вращения.
Какой цели служит длинный и гибкий шест, который несут канатоходцы?
Показать решениеПомогает канатоходцу сохранять равновесие.
Проблемы
При затяжке болта ключ нажимают перпендикулярно с усилием 165 Н на расстоянии 0,140 м от центра болта.
 Какой крутящий момент вы прикладываете к центру болта?
Какой крутящий момент вы прикладываете к центру болта?Открывая дверь, вы нажимаете на нее перпендикулярно с силой 55.0 Н на расстоянии 0,850 м от шарниров. Какой крутящий момент вы прикладываете к петлям?
Показать решение[латекс]46.8\,\текст{N}\cdot \текст{м}[/латекс]
Найдите величину натяжения каждого несущего троса, показанного ниже. В каждом случае вес подвешенного тела равен 100,0 Н, а массы тросов пренебрежимо малы.
Какую силу необходимо приложить в точке P , чтобы удерживать показанную конструкцию в равновесии? Вес конструкции незначителен.
Можно ли приложить силу к P , чтобы удержать показанную структуру в равновесии? Вес конструкции незначителен.
Во время игры двое детей толкают противоположные стороны двери. Оба нажимают горизонтально и перпендикулярно двери. Один ребенок толкает с силой 17,5 Н на расстоянии 0,600 м от шарниров, а второй ребенок толкает на расстоянии 0,450 м.
 Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, что трением можно пренебречь.
Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, что трением можно пренебречь.Небольшой 1000-килограммовый внедорожник имеет колесную базу 3,0 м. Если 60 %, если его вес приходится на передние колеса, как далеко от передних колес находится центр масс вагона?
Униформа-качели сбалансированы в центре масс, как показано ниже. Меньший мальчик справа имеет массу 40,0 кг. Какова масса его друга?
Глоссарий
- центр тяжести
- точка, к которой присоединяется вектор весов
- равновесие
- тело находится в равновесии, когда его линейное и угловое ускорения равны нулю относительно инерциальной системы отсчета
- первое условие равновесия
- выражает поступательное равновесие; все внешние силы, действующие на тело, уравновешиваются и их векторная сумма равна нулю
- гравитационный момент
- крутящий момент на корпусе, вызванный его весом; возникает при расположении центра тяжести тела не на оси вращения
- второе условие равновесия
- выражает вращательное равновесие; все моменты от внешних сил, действующих на тело, уравновешиваются и их векторная сумма равна нулю
- статическое равновесие
- тело находится в статическом равновесии, когда оно находится в состоянии покоя в выбранной нами инерциальной системе отсчета
Статическое равновесие твердых тел
Трансляционное равновесие
Трансляция — это движение объекта влево или вправо, вперед или назад, вверх или вниз.
 Это движение всего объекта в определенном направлении. Говорят, что объект находится в поступательном равновесии, если силы уравновешены во всех направлениях: если направленные вверх силы равны силам, направленным вниз, силы, направленные влево, равны силам, направленным вправо, а силы, направленные вперед, равны силам, направленным назад. Силы равны, поэтому это называется равновесием.
Это движение всего объекта в определенном направлении. Говорят, что объект находится в поступательном равновесии, если силы уравновешены во всех направлениях: если направленные вверх силы равны силам, направленным вниз, силы, направленные влево, равны силам, направленным вправо, а силы, направленные вперед, равны силам, направленным назад. Силы равны, поэтому это называется равновесием.Равновесие включает в себя уравновешенные силы Например, вернемся к припаркованной машине.Он остается там, где он есть, потому что действующие на него силы уравновешены. Нисходящая сила тяжести уравновешивается тем, что земля давит на автомобиль. Если вы подходите к машине и толкаете ее, но машина не двигается, значит, ваша толкающая сила уравновешивается силой трения — силой, вызванной неровностями земли.
Вращательное равновесие
Но объекты не просто двигаются вверх и вниз, влево и вправо, вперед и назад.
 Есть еще один вид движения — вращательное движение.Вращательное движение — это когда объект остается на месте, но вращается вокруг точки вращения. Это похоже на то, как колесо вращается вокруг своей оси или как ветряная турбина вращается, когда ее толкает воздух.
Есть еще один вид движения — вращательное движение.Вращательное движение — это когда объект остается на месте, но вращается вокруг точки вращения. Это похоже на то, как колесо вращается вокруг своей оси или как ветряная турбина вращается, когда ее толкает воздух.Колесо обозрения является примером вращательного движения. Силы заставляют вещи вращаться так же, как они заставляют вещи двигаться. Но чтобы произошло вращение, сила должна быть не в центре. Если вы найдете качели в парке и толкнете их в самый центр, ничего не произойдет.Чтобы заставить качели двигаться вверх или вниз, вы должны нажать ближе к одному из краев. Мы называем эту силу на расстоянии от точки вращения крутящим моментом . Чем сильнее вы нажимаете, тем больше крутящий момент, и чем дальше от точки поворота вы нажимаете, тем больше крутящий момент.
Чтобы переместить качели, вы нажимаете на концы Вращательное равновесие — это когда крутящие моменты уравновешены — крутящие моменты по часовой стрелке уравновешиваются крутящими моментами против часовой стрелки.
 Если это произойдет для стационарного объекта, этот объект останется точно там, где он есть, и не будет вращаться.
Если это произойдет для стационарного объекта, этот объект останется точно там, где он есть, и не будет вращаться.Если объект находится в равновесии вращения, а также в равновесии поступательного движения, то выполняются два условия, и вместе говорят, что этот объект находится в полном статическом равновесии.
Краткий обзор урока
Статическое равновесие твердого тела — это состояние, в котором твердый объект не движется, потому что его воздействия уравновешены. Эти воздействия представляют собой силы и крутящие моменты. Чтобы объект находился в статическом равновесии, он должен находиться как в поступательном равновесии, так и в вращательном равновесии.
Поступательное равновесие – это когда силы вверх, влево и вперед равны силам вниз, вправо и назад. Поскольку все силы уравновешены, объект не будет ускоряться или замедляться, а стационарный объект в поступательном равновесии останется точно там, где он есть.
Равновесие при вращении – это когда крутящие моменты по часовой стрелке и против часовой стрелки (силы смещения от центра) уравновешены.
 Объект, находящийся в равновесии вращения, не начнет больше вращаться в любом направлении. Когда объект находится в поступательном и вращательном равновесии, то в целом он находится в статическом равновесии.Вот когда у вас есть действительно неподвижный объект.
Объект, находящийся в равновесии вращения, не начнет больше вращаться в любом направлении. Когда объект находится в поступательном и вращательном равновесии, то в целом он находится в статическом равновесии.Вот когда у вас есть действительно неподвижный объект.Условия равновесия твердого тела Вопросы и ответы
Этот набор вопросов и ответов с несколькими вариантами ответов (MCQ) по инженерной механике посвящен «Условиям равновесия твердого тела — 1».
1. Главное условие твердого тела состоит в том, что расстояние между различными частицами тела не меняется.
а) Верно
б) Ложно
Посмотреть ответОтвет: б
Пояснение: Главное условие твердого тела состоит в том, что расстояние между различными частицами тела не меняется.Если расстояние изменяется, то тело нельзя назвать твердым. Таким образом, фиксированное расстояние между частицами очень необходимо для равновесия твердого тела.2. Показанный здесь груз имеет массу 100 кг.
 Чего здесь не хватает на схеме?
Чего здесь не хватает на схеме?
а) Вес тела не указан
б) Момент силы не показан
в) Тело нельзя так удерживать
г) Диагональ тела не показана
Посмотреть ответОтвет: а
Объяснение: Нет.3. Что утверждает третий закон Ньютона?
а) Скорость изменения количества движения равна приложенной силе
б) На каждую реакцию существует противоположная реакция
в) Тело стремится повернуться, если сила приложена по касательной
г) Тело покоится до тех пор, пока приложена сила
View AnswerОтвет: b
Объяснение: Требование третьего закона важно для равновесия тела. Особенно твердые тела. Частицы твердого тела находятся в равновесии и, таким образом, сталкиваются с силами, и, чтобы быть в равновесии, они также реагируют и применяют противоположную силу и, следовательно, третий закон Ньютона.4. Определить горизонтальные составляющие реакции балки на штифт в точке P. Силу 60 Н умножить на 10, а затем приложить.

a) 424N
b) 24N
c) 44N
d) 441N
Посмотреть ответОтвет: a
Объяснение: Сумма сил должна быть равна нулю. Так же и сумма моментов должна равняться нулю. Но если говорить об углах, то они не нужны в ноль. Но силы, действующие под определенными углами, должны быть равны нулю.Основная потребность в силах, чтобы привести тело в равновесие.5. В случае равновесия результирующая сила, действующая на тело, равна нулю.
a) Верно
b) Неверно
Просмотреть ответОтвет: a
Объяснение: Равновесие достигается только в том случае, если результирующая сила, действующая на тело, стремится к нулю. Таким образом, силы уравновешиваются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии. Тело здесь твердое тело.6.Для равновесия суммарный момент, действующий на тело различными силами, равен нулю.
a) Верно
b) Неверно
Просмотреть ответОтвет: a
Объяснение: Равновесие достигается только в том случае, если суммарный момент тела стремится к нулю. Таким образом, моменты, вызванные различными силами, компенсируются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии. Тело здесь твердое тело.
Таким образом, моменты, вызванные различными силами, компенсируются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии. Тело здесь твердое тело.7. Определить вертикальные составляющие реакции балки на штифт в точке Q.Сила 60 Н умножается на 10 и затем прикладывается.
a) 319N
b) 445N
c) 45N
d) 40N
Посмотреть ответОтвет: a
Объяснение: Сумма сил должна быть равна нулю. Так же и сумма моментов должна равняться нулю. Но если говорить об углах, то они не нужны в ноль. Но силы, действующие под определенными углами, должны быть равны нулю. Основная потребность в силах, чтобы привести тело в равновесие.8.Суммарный момент тела равен нулю, что означает, что расстояние между силой и осью вращения равно нулю.
а) Первая часть утверждения ложна, а другая часть верна
б) Первая часть утверждения ложна, а другая часть ложна
в) Первая часть утверждения верна, а другая часть ложна
г) Первая часть утверждения верна, и другая часть тоже верна. равен нулю.Это означает, что моменты, вызванные различными силами, компенсируются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии.
равен нулю.Это означает, что моменты, вызванные различными силами, компенсируются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии.9. Определить горизонтальную составляющую реакции на балку, вызванную роликом на п.
a) 536N
b) 536cos30N
c) 536sin30N
d) 536tan30N
Посмотреть ответОтвет: c
Объяснение: Сумма сил должна быть равна нулю. Так же и сумма моментов должна равняться нулю.Но если говорить об углах, то они не нужны в ноль. Но силы, действующие под определенными углами, должны быть равны нулю. Основная потребность в силах, чтобы привести тело в равновесие.10. Суммарная сила тела равна нулю, что означает, что сила вообще не приложена к телу и, следовательно, тело находится в равновесии.
а) Первая часть утверждения ложна, а другая часть верна
б) Первая часть утверждения ложна, а другая часть ложна
в) Первая часть утверждения верна, а другая часть ложна
г) Первая часть утверждения верна, и другая часть тоже верна. вообще и, следовательно, тело находится в равновесии.Равновесие достигается только в том случае, если результирующая сила, действующая на тело, стремится к нулю. Таким образом, силы уравновешиваются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии.
вообще и, следовательно, тело находится в равновесии.Равновесие достигается только в том случае, если результирующая сила, действующая на тело, стремится к нулю. Таким образом, силы уравновешиваются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии.11. Что из следующего верно?
а) Применение условий равновесия тела действует только в 2D
б) Применение условий равновесия тела действует только в 3D
в) Применение условий Равновесие тела справедливо только в 1D
d) Применение условий равновесия тела справедливо на всем протяжении
View AnswerОтвет: d
Пояснение: Применение условий равновесия тела действует на протяжении всего.Это означает, что условия не зависят от размеров. Условия являются основными правилами, которые определяют равновесие тела и, таким образом, применимы в любом измерении реальной оси.12. Определить вертикальные составляющие реакции на балку, вызванные роликом на п.

a) 536N
b) 536cos30N
c) 536sin30N
d) 536tan30N
Посмотреть ответОтвет: b
Объяснение: Сумма сил должна быть равна нулю.Так же и сумма моментов должна равняться нулю. Но если говорить об углах, то они не нужны в ноль. Но силы, действующие под определенными углами, должны быть равны нулю. Основная потребность в силах, чтобы привести тело в равновесие.13. Для условий равновесия тела, т. е. твердого тела, только внешние силы определяют равновесие. Потому что внутренние силы компенсируются, поэтому их нельзя рассматривать.
а) Первая часть утверждения ложна, а другая часть верна
б) Первая часть утверждения ложна, а другая часть ложна
в) Первая часть утверждения верна, а другая часть ложна
г) Первая часть утверждения верна, и другая часть тоже верна.Не только внешние, но и внутренние силы, возникающие за счет внешних сил, оказывают тяготеющее действие на равновесие тела. Таким образом, внутренние силы не компенсируются.
14. Что из следующего необходимо обнулить для идеального равновесия?
а) ∑F=0, ∑M=0 и ∑θ = 0
б) ∑F=0, ∑M≠0 и ∑θ = 0
c) ∑F≠0, ∑M=0 и ∑θ = 0
d) ∑F=0, ∑M=0 и ∑θ≠0
Просмотреть ответОтвет: d
Объяснение: Сумма сил должна быть равна нулю.Так же и сумма моментов должна равняться нулю. Но если говорить об углах, то они не нужны в ноль. Но силы, действующие под определенными углами, должны быть равны нулю. Основная потребность в силах, чтобы привести тело в равновесие.15. Определить вертикальные составляющие реакции балки на штифт в точке P. Силу 60 Н умножить на 10, а затем приложить.
a) 405N
b) 445N
c) 45N
d) 40N
Посмотреть ответОтвет: a
Объяснение: Нет.Sanfoundry Global Education & Learning Series – Инженерная механика.
Чтобы практиковать все области инженерной механики, здесь полный набор из более чем 1000 вопросов и ответов с несколькими вариантами ответов .
Следующие шаги:
- Получите бесплатную грамоту в области инженерной механики
- Участие в конкурсе на получение сертификата инженерной механики
- Станьте лучшим специалистом в области инженерной механики
- Пройти тесты инженерной механики
- Практические тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
- Пробные тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Равновесие и статика
Когда все силы, действующие на объект, уравновешены, говорят, что объект находится в состоянии равновесия .Силы считаются уравновешенными , если силы, направленные вправо, уравновешиваются силами, направленными влево, а силы, направленные вверх, уравновешиваются силами, направленными вниз. Это, однако, не обязательно означает, что все силы равны друг другу. Рассмотрим два объекта, изображенных на силовой диаграмме, показанной ниже. Обратите внимание, что два объекта находятся в равновесии, потому что силы, действующие на них, уравновешены; однако отдельные силы не равны друг другу. Сила 50 Н не равна силе 30 Н.
Сила 50 Н не равна силе 30 Н.
Если объект находится в равновесии, то силы уравновешены. Сбалансированный — ключевое слово, которое используется для описания равновесных ситуаций. Таким образом, результирующая сила равна нулю, а ускорение равно 0 м/с/с. Объекты в равновесии должны иметь ускорение 0 м/с/с. Это следует из первого закона движения Ньютона. Но наличие ускорения 0 м/с/с не означает, что объект находится в состоянии покоя. Объект в равновесии либо …- в состоянии покоя и в состоянии покоя или
- в движении и продолжают движение с той же скоростью и направлением.
Это тоже следует из первого закона движения Ньютона.
Анализ ситуации статического равновесияЕсли объект покоится и находится в состоянии равновесия, то мы бы сказали, что объект находится в «статическом равновесии». «Статический» означает стационарный или в состоянии покоя .
 Обычная физическая лаборатория состоит в том, чтобы подвешивать объект на двух или более веревках и измерять силы, действующие под углом на объект, чтобы выдержать его вес.Состояние объекта анализируется с точки зрения сил, действующих на объект. Объект представляет собой точку на струне, на которую действовали три силы. См. схему справа. Если объект находится в равновесии, то результирующая сила, действующая на объект, должна быть равна 0 ньютонов. Таким образом, если все силы сложить как векторы, то результирующая сила (сумма векторов) должна быть равна 0 ньютонов. (Напомним, что результирующая сила — это «векторная сумма всех сил» или равнодействующая сложения всех отдельных сил «голова к хвосту».) Таким образом, можно построить точно нарисованную диаграмму сложения векторов для определения результата. Примеры данных для такой лаборатории показаны ниже.
Обычная физическая лаборатория состоит в том, чтобы подвешивать объект на двух или более веревках и измерять силы, действующие под углом на объект, чтобы выдержать его вес.Состояние объекта анализируется с точки зрения сил, действующих на объект. Объект представляет собой точку на струне, на которую действовали три силы. См. схему справа. Если объект находится в равновесии, то результирующая сила, действующая на объект, должна быть равна 0 ньютонов. Таким образом, если все силы сложить как векторы, то результирующая сила (сумма векторов) должна быть равна 0 ньютонов. (Напомним, что результирующая сила — это «векторная сумма всех сил» или равнодействующая сложения всех отдельных сил «голова к хвосту».) Таким образом, можно построить точно нарисованную диаграмму сложения векторов для определения результата. Примеры данных для такой лаборатории показаны ниже.Сила А Сила Б Сила С Величина
3.  4 Н
4 Н9,2 Н 9,8 Н Направление
161 град. 70 град. 270 градусов
Для большинства студентов результатом было 0 ньютонов (или, по крайней мере, очень близко к 0 Н).Это то, что мы ожидали — поскольку объект находился в равновесии, результирующая сила (векторная сумма всех сил) должна быть равна 0 Н.Другой способ определения результирующей силы (векторной суммы всех сил) заключается в использовании тригонометрических функций для разложения каждой силы на ее горизонтальную и вертикальную составляющие. Когда компоненты известны, их можно сравнить, чтобы увидеть, уравновешены ли вертикальные силы и уравновешены ли горизонтальные силы.На приведенной ниже диаграмме показаны векторы A, B и C и их соответствующие компоненты. Для векторов A и B вертикальные компоненты можно определить с помощью синуса угла, а горизонтальные компоненты можно проанализировать с помощью косинуса угла.
 Величина и направление каждого компонента для выборочных данных показаны в таблице под диаграммой.
Величина и направление каждого компонента для выборочных данных показаны в таблице под диаграммой.
Данные в таблице выше показывают, что силы 90 351 почти равны 90 352.Анализ горизонтальных составляющих показывает, что левая составляющая A почти уравновешивает правую составляющую B. Анализ вертикальных составляющих показывает, что сумма восходящих составляющих A + B почти уравновешивает нисходящую составляющую C , Векторная сумма всех сил ( почти ) равна 0 ньютонов. Но как быть с разницей в 0,1 Н между силами, направленными вправо и влево, и разницей в 0,2 Н между силами, направленными вверх и вниз? Почему составляющие силы только почти уравновешивают? Данные образца, используемые в этом анализе, являются результатом измеренных данных реальной экспериментальной установки.Разница между фактическими и ожидаемыми результатами связана с ошибкой, возникающей при измерении силы A и силы B. Мы должны были бы заключить, что этот низкий предел экспериментальной погрешности отражает эксперимент с отличными результатами. Мы могли бы сказать, что это «достаточно близко для работы правительства».
Мы могли бы сказать, что это «достаточно близко для работы правительства».
Анализ висящего знакаПриведенный выше анализ сил, действующих на объект, находящийся в равновесии, обычно используется для анализа ситуаций, связанных с объектами, находящимися в статическом равновесии.Наиболее распространенное приложение включает анализ сил, действующих на знак, который находится в состоянии покоя. Например, рассмотрим картину справа, которая висит на стене. Картина находится в состоянии равновесия, а значит, все силы, действующие на картину, должны быть уравновешены. То есть все горизонтальные компоненты должны составлять 0 ньютонов, а все вертикальные компоненты должны составлять 0 ньютонов. Натяжение троса A, направленное влево, должно уравновешивать натяжение троса B, направленного вправо, а сумма натяжения троса A и троса B вверх должна уравновешивать вес знака.
Предположим, что измеренное натяжение обоих тросов равно 50 Н, и известно, что угол, который каждый трос образует с горизонтом, равен 30 градусам.
 Каков вес знака? На этот вопрос можно ответить, проведя силовой анализ с использованием тригонометрических функций. Вес знака равен сумме восходящих составляющих натяжения двух тросов. Таким образом, для определения этой вертикальной составляющей можно использовать тригонометрическую функцию. Схема и сопутствующие работы показаны ниже.
Каков вес знака? На этот вопрос можно ответить, проведя силовой анализ с использованием тригонометрических функций. Вес знака равен сумме восходящих составляющих натяжения двух тросов. Таким образом, для определения этой вертикальной составляющей можно использовать тригонометрическую функцию. Схема и сопутствующие работы показаны ниже.Поскольку каждый трос тянет вверх с силой 25 Н, общая сила притяжения знака вверх составляет 50 Н. Следовательно, сила тяжести (также известная как вес) составляет 50 Н, направленная вниз. Знак весит 50 Н.
В приведенной выше задаче натяжение троса и угол , который трос образует с горизонталью, используются для определения веса знака.Идея состоит в том, что натяжение, угол и вес связаны. Если известны любые две из этих трех, то третью величину можно определить с помощью тригонометрических функций.
В качестве другого примера, иллюстрирующего эту идею, рассмотрим симметрично подвешенный знак, как показано справа.
 Если известно, что знак имеет массу 5 кг и если угол между двумя тросами составляет 100 градусов, то можно определить натяжение троса. Предполагая, что знак находится в равновесии (хорошее предположение, если он остается в покое), два троса должны создавать достаточную направленную вверх силу, чтобы уравновесить направленную вниз силу тяжести.Сила тяжести (также известная как вес) составляет 49 Н (Fgrav = m*g), поэтому каждый из двух тросов должен тянуться вверх с силой 24,5 Н. Поскольку угол между кабелями равен 100 градусам, каждый кабель должен составлять угол 50 градусов с вертикалью и угол 40 градусов с горизонталью. Эскиз этой ситуации (см. диаграмму ниже) показывает, что натяжение троса можно найти с помощью функции синуса. Треугольник ниже иллюстрирует эти отношения.
Если известно, что знак имеет массу 5 кг и если угол между двумя тросами составляет 100 градусов, то можно определить натяжение троса. Предполагая, что знак находится в равновесии (хорошее предположение, если он остается в покое), два троса должны создавать достаточную направленную вверх силу, чтобы уравновесить направленную вниз силу тяжести.Сила тяжести (также известная как вес) составляет 49 Н (Fgrav = m*g), поэтому каждый из двух тросов должен тянуться вверх с силой 24,5 Н. Поскольку угол между кабелями равен 100 градусам, каждый кабель должен составлять угол 50 градусов с вертикалью и угол 40 градусов с горизонталью. Эскиз этой ситуации (см. диаграмму ниже) показывает, что натяжение троса можно найти с помощью функции синуса. Треугольник ниже иллюстрирует эти отношения.
Концептуальное мышлениеСуществует важный принцип, вытекающий из некоторых из тригонометрических вычислений, выполненных выше.
 Принцип заключается в том, что по мере увеличения угла с горизонталью сила натяжения, необходимая для удержания знака в равновесии, уменьшается. Чтобы проиллюстрировать это, рассмотрим изображение силой 10 ньютонов, удерживаемое проводами с тремя разными ориентациями, как показано на диаграммах ниже. В каждом случае для поддержки изображения используются два провода; каждый провод должен выдерживать половину веса знака (5 Н). Угол, который провода образуют с горизонтом, варьируется от 60 до 15 градусов. Используйте эту информацию и приведенную ниже диаграмму, чтобы определить натяжение проволоки для каждой ориентации.Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
Принцип заключается в том, что по мере увеличения угла с горизонталью сила натяжения, необходимая для удержания знака в равновесии, уменьшается. Чтобы проиллюстрировать это, рассмотрим изображение силой 10 ньютонов, удерживаемое проводами с тремя разными ориентациями, как показано на диаграммах ниже. В каждом случае для поддержки изображения используются два провода; каждый провод должен выдерживать половину веса знака (5 Н). Угол, который провода образуют с горизонтом, варьируется от 60 до 15 градусов. Используйте эту информацию и приведенную ниже диаграмму, чтобы определить натяжение проволоки для каждой ориентации.Когда закончите, нажмите кнопку, чтобы просмотреть ответы.В заключение, равновесие – это состояние объекта, при котором все действующие на него силы уравновешены. В таких случаях результирующая сила равна 0 ньютонов. Зная силы, действующие на объект, можно использовать тригонометрические функции для определения горизонтальной и вертикальной составляющих каждой силы.
 Если в равновесии, то все вертикальные компоненты должны уравновешиваться, и все горизонтальные компоненты должны уравновешиваться.
Если в равновесии, то все вертикальные компоненты должны уравновешиваться, и все горизонтальные компоненты должны уравновешиваться.
Мы хотели бы предложить … Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей интерактивной игры Name That Vector, нашей интерактивной игры с добавлением вектора или нашей интерактивной игры с угадыванием вектора.Все три интерактива можно найти в разделе Physics Interactive на нашем веб-сайте, и они обеспечивают интерактивный опыт с возможностью добавления векторов.
Проверьте свое пониманиеСледующие вопросы предназначены для проверки вашего понимания равновесных ситуаций.
 Нажмите кнопку, чтобы просмотреть ответы на эти вопросы.
Нажмите кнопку, чтобы просмотреть ответы на эти вопросы.1.Следующая картина висит на стене. Используйте тригонометрические функции, чтобы определить вес изображения.
2. Нижеследующая табличка висит снаружи кабинета физики, рекламируя самую важную истину, которую можно найти внутри. Знак поддерживается диагональным тросом и жесткой горизонтальной перекладиной. Если знак имеет массу 50 кг, то определить натяжение диагонального троса, поддерживающего его вес.
3. Следующий знак можно найти в Гленвью. Знак имеет массу 50 кг. Определить натяжение тросов.
4. После последней доставки печально известный аист сообщает хорошие новости. Если знак имеет массу 10 кг, то какова сила натяжения в каждом тросе? Используйте тригонометрические функции и эскиз, чтобы помочь в решении.

5. Предположим, что студент тянет двумя большими силами (F 1 и F 2 ), чтобы поднять 1-килограммовую книгу двумя тросами. Если тросы образуют с горизонтом угол 1 градус, то чему равно натяжение троса?
РЕШЕНО:Зависит ли второе условие равновесия твердого тела от положение оси вращения?
Стенограмма видео
Итак, для этой задачи мы хотим исследовать вращательное равновесие.Итак, давайте посмотрим на колесо. Теперь мы знаем, если мы скажем, что к этому колесу прикреплен стержень, и мы приложим силу перпендикулярно. Итак, это прямо перпендикулярно этому колесу, а затем отсоедините этот столб. Это колесо начнет вращаться после приложения этой силы, перпендикулярной оси вращения. Вот, скажем, это вращается вокруг своего центра. Мы создадим угловую скорость и угловое ускорение, которые вместе дают нам рабочий городок.
. И это все векторы. Все зависит от направления.Если бы мы приложили силу в противоположном направлении, то это колесо закрутилось бы в другую сторону, которая обычно вращается. В физике вращения мы сокращаем направление вращения по часовой стрелке или против часовой стрелки. Итак, в этой ситуации мы движемся против часовой стрелки. против часовой стрелки. Итак, теперь мы хотим исследовать, как мы можем заставить эту систему находиться в равновесии, чтобы мы могли приравнять вращательный момент к стандартному медику. Итак, у нас есть сила в Кантоне Манниксе, Ньютоновская сила.Мы можем связать это с факелом. Вот что вызывает движение — это приложение силы. Мы знаем, что в статическом равновесии ко мне прилагается сила, а оно прикладывает ускорение. Это оба фактора. Масса — это масштабирование. Итак, мы применяем силу, которая применяет ускорение, которое изменяет скорость. Таким образом, сила — это то, что мы определили как ключевой фактор изменения равновесия. Если у нас есть система, находящаяся в равновесии, и мы приложим силу, она выведет ее за пределы этого равновесия.
И это все векторы. Все зависит от направления.Если бы мы приложили силу в противоположном направлении, то это колесо закрутилось бы в другую сторону, которая обычно вращается. В физике вращения мы сокращаем направление вращения по часовой стрелке или против часовой стрелки. Итак, в этой ситуации мы движемся против часовой стрелки. против часовой стрелки. Итак, теперь мы хотим исследовать, как мы можем заставить эту систему находиться в равновесии, чтобы мы могли приравнять вращательный момент к стандартному медику. Итак, у нас есть сила в Кантоне Манниксе, Ньютоновская сила.Мы можем связать это с факелом. Вот что вызывает движение — это приложение силы. Мы знаем, что в статическом равновесии ко мне прилагается сила, а оно прикладывает ускорение. Это оба фактора. Масса — это масштабирование. Итак, мы применяем силу, которая применяет ускорение, которое изменяет скорость. Таким образом, сила — это то, что мы определили как ключевой фактор изменения равновесия. Если у нас есть система, находящаяся в равновесии, и мы приложим силу, она выведет ее за пределы этого равновесия. Таким образом, этот крутящий момент также влияет. Теперь у нас есть уравнение для крутящего момента.Это оба уравнения суммирования. Мы сейчас рассмотрим только одну силу. Итак, если у нас есть крутящий момент, мы знаем, что он равен произведению инерционной женщины на угловое ускорение. Так что теперь мы можем Мы можем увидеть здесь тенденцию. Если крутящий момент подобен нашей силе, наши массы подобны нашей инерции, и это означает, что наше ускорение, угловое ускорение связаны, что также подразумевает, что у нас есть скорость, которая может быть получена из ускорения. У нас похожая угловая скорость, что тоже является фактором и что значит угловая скорость и чем она отличается от обычных скоростей.Угловая скорость — это скорость, с которой он вращается. Вот как быстро это вращается, Итак, объект. Посмотрите, не было ли это прикреплено. Что угодно может иметь как угловое ускорение вокруг. Извините, угловая скорость в поступательной скорости, так что вся эта система могла двигаться. Ярким примером ситуации является сама Земля, которая вращается вокруг Земли, но она также движется вокруг Солнца.
Таким образом, этот крутящий момент также влияет. Теперь у нас есть уравнение для крутящего момента.Это оба уравнения суммирования. Мы сейчас рассмотрим только одну силу. Итак, если у нас есть крутящий момент, мы знаем, что он равен произведению инерционной женщины на угловое ускорение. Так что теперь мы можем Мы можем увидеть здесь тенденцию. Если крутящий момент подобен нашей силе, наши массы подобны нашей инерции, и это означает, что наше ускорение, угловое ускорение связаны, что также подразумевает, что у нас есть скорость, которая может быть получена из ускорения. У нас похожая угловая скорость, что тоже является фактором и что значит угловая скорость и чем она отличается от обычных скоростей.Угловая скорость — это скорость, с которой он вращается. Вот как быстро это вращается, Итак, объект. Посмотрите, не было ли это прикреплено. Что угодно может иметь как угловое ускорение вокруг. Извините, угловая скорость в поступательной скорости, так что вся эта система могла двигаться. Ярким примером ситуации является сама Земля, которая вращается вокруг Земли, но она также движется вокруг Солнца. Итак, у нас есть оба сценария. У нас есть угловая скорость и поступательная скорость, поэтому мы можем приравнять эти два разных уравнения, которые у нас есть.Крутящий момент где-то силовой. У нас есть угловое ускорение, аналогичное возбуждению, а угловая скорость аналогична скорости. Таким образом, чтобы вывести систему из равновесия, мы должны приложить к ней силу. Таким образом, для того чтобы вращающееся тело находилось в равновесии, оно не должно иметь ни вращающихся сил, ни движения. Это крутящий момент равен нулю. На объект не действуют вращательные силы, поэтому то, что мы имеем, — две разные фамилии — это два разных, легко просматриваемых сценария. Для такого типа ситуаций у нас есть одно и то же колесо, и оно вообще не вращается.Нет ни угловой скорости, ни углового ускорения. С другой стороны, у нас также может быть система с постоянной скоростью вращения и постоянной угловой скоростью, так что, скажем, она вращается с постоянной скоростью. Еще раз против часовой стрелки, он по-прежнему не имеет никакого ускорения, поэтому он не ускоряется и не замедляется.
Итак, у нас есть оба сценария. У нас есть угловая скорость и поступательная скорость, поэтому мы можем приравнять эти два разных уравнения, которые у нас есть.Крутящий момент где-то силовой. У нас есть угловое ускорение, аналогичное возбуждению, а угловая скорость аналогична скорости. Таким образом, чтобы вывести систему из равновесия, мы должны приложить к ней силу. Таким образом, для того чтобы вращающееся тело находилось в равновесии, оно не должно иметь ни вращающихся сил, ни движения. Это крутящий момент равен нулю. На объект не действуют вращательные силы, поэтому то, что мы имеем, — две разные фамилии — это два разных, легко просматриваемых сценария. Для такого типа ситуаций у нас есть одно и то же колесо, и оно вообще не вращается.Нет ни угловой скорости, ни углового ускорения. С другой стороны, у нас также может быть система с постоянной скоростью вращения и постоянной угловой скоростью, так что, скажем, она вращается с постоянной скоростью. Еще раз против часовой стрелки, он по-прежнему не имеет никакого ускорения, поэтому он не ускоряется и не замедляется. Это немного сложнее интуитивно увидеть, потому что это не то, что мы видим в повседневной жизни, потому что у нас всегда есть какое-то трение, которое в конечном итоге замедляет объект.Но если бы не было трения, объект вращался бы до тех пор, пока на него не подействовала бы внешняя сила. Так что это еще одна форма равновесия, которую мы можем иметь. О, угловая скорость равна постоянной, но не может быть ускоряющей. Итак, если силы равны, здесь та же ситуация. Если крутящий момент равен нулю, то и наше ускорение тоже должно быть равно нулю. Так что это довольно универсальные ограничения для равновесия. Но самое главное, у нас не может быть крутящего момента. Если есть крутящий момент, он изменит вашу систему отсчета от равновесия.Он изменит свое состояние равновесия, поэтому крутящий момент должен быть равен нулю. На изолированную систему не должны воздействовать внешние силы
Это немного сложнее интуитивно увидеть, потому что это не то, что мы видим в повседневной жизни, потому что у нас всегда есть какое-то трение, которое в конечном итоге замедляет объект.Но если бы не было трения, объект вращался бы до тех пор, пока на него не подействовала бы внешняя сила. Так что это еще одна форма равновесия, которую мы можем иметь. О, угловая скорость равна постоянной, но не может быть ускоряющей. Итак, если силы равны, здесь та же ситуация. Если крутящий момент равен нулю, то и наше ускорение тоже должно быть равно нулю. Так что это довольно универсальные ограничения для равновесия. Но самое главное, у нас не может быть крутящего момента. Если есть крутящий момент, он изменит вашу систему отсчета от равновесия.Он изменит свое состояние равновесия, поэтому крутящий момент должен быть равен нулю. На изолированную систему не должны воздействовать внешние силы


 В первом случае Людмила Фирмаль
В первом случае Людмила Фирмаль 2+L1z=15,3+3,3. Итак, K u=M V1UD/A? ОПР=132.1 / 18.6=7.1>1.15.
2+L1z=15,3+3,3. Итак, K u=M V1UD/A? ОПР=132.1 / 18.6=7.1>1.15. Сумма каждого из них будет равна нулю.
Сумма каждого из них будет равна нулю. \[ \сумма \vec{M} \, = \, 0 \]
\[ \сумма \vec{M} \, = \, 0 \] страницу векторов в Приложении 1). подробности этого процесса).Ваше первое уравнение будет суммой величин компонентов в направлении \(x\), равных нулю, второе уравнение будет суммой величин компонентов в направлении \(y\), равных ноль, а третья (если у вас трехмерная задача) будет равна сумме величин в направлении \(z\), равной нулю.
страницу векторов в Приложении 1). подробности этого процесса).Ваше первое уравнение будет суммой величин компонентов в направлении \(x\), равных нулю, второе уравнение будет суммой величин компонентов в направлении \(y\), равных ноль, а третья (если у вас трехмерная задача) будет равна сумме величин в направлении \(z\), равной нулю.
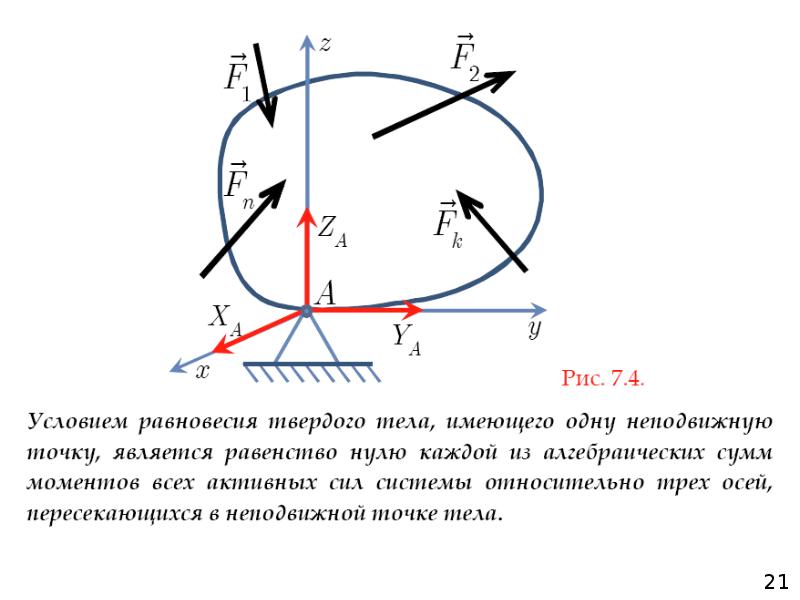 Какие силы реакции действуют на балку в точке А?
Какие силы реакции действуют на балку в точке А? Источник на YouTube: https://youtu.be/WzkAnPdhao4.
Источник на YouTube: https://youtu.be/WzkAnPdhao4. Стул стоит на плоской поверхности, при этом предполагается, что эта поверхность не имеет трения в месте контакта с передней ножкой стула (точка А) и создает трение в месте контакта с задней ножкой (точка В).
Стул стоит на плоской поверхности, при этом предполагается, что эта поверхность не имеет трения в месте контакта с передней ножкой стула (точка А) и создает трение в месте контакта с задней ножкой (точка В). Источник YouTube: https://youtu.be/wpEBuitLD5s.
Источник YouTube: https://youtu.be/wpEBuitLD5s. Предполагая, что панель имеет равномерно распределенный вес, каково натяжение каждого из тросов?
Предполагая, что панель имеет равномерно распределенный вес, каково натяжение каждого из тросов? Для этого сумма сил, действующих на тело, должна быть равна нулю.
Для этого сумма сил, действующих на тело, должна быть равна нулю.


 После снятия груза в точке 𝐴 определите величину вертикальной силы, которая потребуется, чтобы удерживать стержень в вертикальном положении.
равновесие в горизонтальном положении, когда он действует на конце 𝐵.
После снятия груза в точке 𝐴 определите величину вертикальной силы, которая потребуется, чтобы удерживать стержень в вертикальном положении.
равновесие в горизонтальном положении, когда он действует на конце 𝐵. Единственные моменты на стержне около 𝑃 связаны с весом, подвешенным в 𝐴.
и вес стержня, действующий в центре масс стержня. Поскольку стержень находится в равновесии, эти моменты должны быть равны.
Единственные моменты на стержне около 𝑃 связаны с весом, подвешенным в 𝐴.
и вес стержня, действующий в центре масс стержня. Поскольку стержень находится в равновесии, эти моменты должны быть равны. Сила, действующая на 𝐵, находится правее 𝑃,
поэтому сила, действующая на 𝐵, должна действовать в направлении, противоположном весу стержня.
Сила, действующая на 𝐵, находится правее 𝑃,
поэтому сила, действующая на 𝐵, должна действовать в направлении, противоположном весу стержня. Вес 100 Н
подвешен на стержне, 30 см
подальше от 𝐴,
и весом 93 Н
подвешен к стержню, 20 см
подальше от 𝐵. Определите значения 𝑇 и 𝑇.
Вес 100 Н
подвешен на стержне, 30 см
подальше от 𝐴,
и весом 93 Н
подвешен к стержню, 20 см
подальше от 𝐵. Определите значения 𝑇 и 𝑇. N
N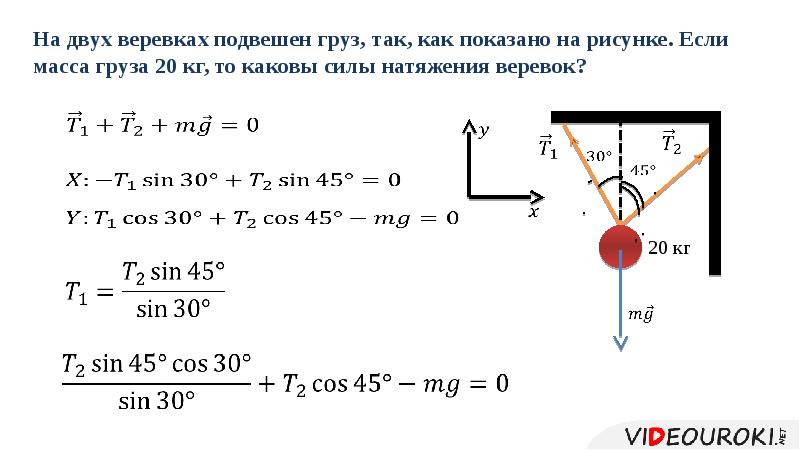 Если точка, в которой действует ⃑𝐹, меняется, ⃑𝑅
и ⃑𝑅 будут различаться.Чем больше расстояние ⃑𝐹
от 𝐴, тем меньше величина ⃑𝑅
должно быть и тем больше должна быть величина ⃑𝑅, чтобы тело находилось во вращательном равновесии.
Если точка, в которой действует ⃑𝐹, меняется, ⃑𝑅
и ⃑𝑅 будут различаться.Чем больше расстояние ⃑𝐹
от 𝐴, тем меньше величина ⃑𝑅
должно быть и тем больше должна быть величина ⃑𝑅, чтобы тело находилось во вращательном равновесии. Найдите величину
веса стержня 𝑊 и расстояния 𝑥 между его линией действия и точкой 𝐴. Округлите ваши ответы до ближайших двух знаков после запятой.
Найдите величину
веса стержня 𝑊 и расстояния 𝑥 между его линией действия и точкой 𝐴. Округлите ваши ответы до ближайших двух знаков после запятой. Это можно переставить как
468+26𝑊=𝑥𝑊+154314=𝑥𝑊−26𝑊.
Это можно переставить как
468+26𝑊=𝑥𝑊+154314=𝑥𝑊−26𝑊.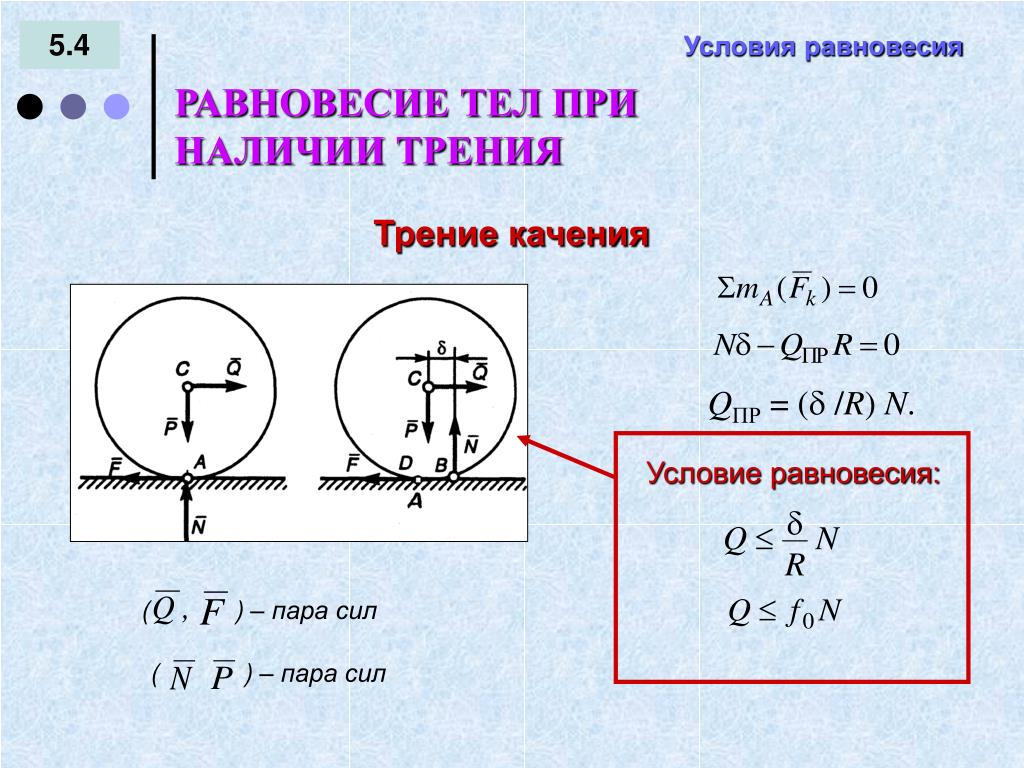 Чтобы определить 𝑥, можно взять моменты относительно точки, в которой действует сила реакции. Расстояние между этой точкой и точкой, на которую действует вес стержня, равно 𝑑 и определяется выражением
(23×18)=𝑑1003414=𝑑10034143100=𝑑=12,42.см
Чтобы определить 𝑥, можно взять моменты относительно точки, в которой действует сила реакции. Расстояние между этой точкой и точкой, на которую действует вес стержня, равно 𝑑 и определяется выражением
(23×18)=𝑑1003414=𝑑10034143100=𝑑=12,42.см Найдите модуль веса 𝑤, который должен быть
подвешен к концу 𝐵 так, что стержень собирается вращаться, и определить значение приложенной вниз силы 𝑃
на 𝐶 в этой ситуации.
Найдите модуль веса 𝑤, который должен быть
подвешен к концу 𝐵 так, что стержень собирается вращаться, и определить значение приложенной вниз силы 𝑃
на 𝐶 в этой ситуации. Записав все длины в метрах, мы имеем
(1,11−0,3)𝑅+(1,11−0,09)71+0.3𝑤=1,112−0,3950,81𝑅+14,91+0,3𝑤=24,225.
Записав все длины в метрах, мы имеем
(1,11−0,3)𝑅+(1,11−0,09)71+0.3𝑤=1,112−0,3950,81𝑅+14,91+0,3𝑤=24,225.
 Обратите внимание, что различие между состоянием покоя и состоянием равномерного движения является искусственным, то есть объект может находиться в состоянии покоя в выбранной нами системе отсчета, но для наблюдателя, движущегося с постоянной скоростью относительно нашей системы отсчета, тот же самый объект находится в равномерном движении с постоянной скоростью.Поскольку движение относительно , то, что для нас находится в статическом равновесии, находится в динамическом равновесии для движущегося наблюдателя, и наоборот. Поскольку законы физики одинаковы для всех инерциальных систем отсчета, в инерциальной системе отсчета нет различия между статическим равновесием и равновесием.
Обратите внимание, что различие между состоянием покоя и состоянием равномерного движения является искусственным, то есть объект может находиться в состоянии покоя в выбранной нами системе отсчета, но для наблюдателя, движущегося с постоянной скоростью относительно нашей системы отсчета, тот же самый объект находится в равномерном движении с постоянной скоростью.Поскольку движение относительно , то, что для нас находится в статическом равновесии, находится в динамическом равновесии для движущегося наблюдателя, и наоборот. Поскольку законы физики одинаковы для всех инерциальных систем отсчета, в инерциальной системе отсчета нет различия между статическим равновесием и равновесием. В состоянии равновесия линейное ускорение равно нулю. Если мы установим ускорение равным нулю на рисунке, мы получим следующее уравнение:
В состоянии равновесия линейное ускорение равно нулю. Если мы установим ускорение равным нулю на рисунке, мы получим следующее уравнение: [/латекс]
[/латекс] [/латекс]
[/латекс]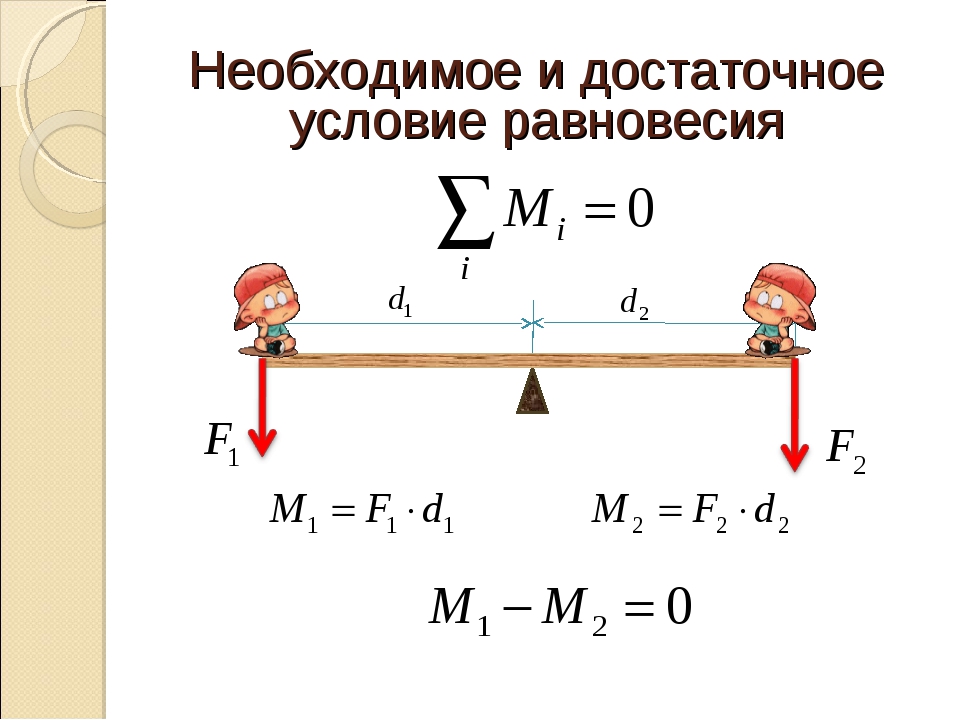
 Отсюда мы видим, что чистый крутящий момент в любой инерциальной системе отсчета [латекс]S\prime[/латекс] равен нулю, при условии, что оба условия равновесия выполняются в инерциальной системе отсчета S .
Отсюда мы видим, что чистый крутящий момент в любой инерциальной системе отсчета [латекс]S\prime[/латекс] равен нулю, при условии, что оба условия равновесия выполняются в инерциальной системе отсчета S . Стандартная процедура заключается в принятии системы отсчета, где ось z является осью вращения. При таком выборе оси чистый крутящий момент имеет только z -компоненту, все силы, имеющие ненулевые крутящие моменты, лежат в xy -плоскости, поэтому вклад в чистый крутящий момент поступает только от x – и и — компоненты внешних сил.Таким образом, для плоских задач с осью вращения, перпендикулярной xy -плоскости, мы имеем следующие три условия равновесия сил и моментов:
Стандартная процедура заключается в принятии системы отсчета, где ось z является осью вращения. При таком выборе оси чистый крутящий момент имеет только z -компоненту, все силы, имеющие ненулевые крутящие моменты, лежат в xy -плоскости, поэтому вклад в чистый крутящий момент поступает только от x – и и — компоненты внешних сил.Таким образом, для плоских задач с осью вращения, перпендикулярной xy -плоскости, мы имеем следующие три условия равновесия сил и моментов: На рисунке z -компонента крутящего момента [латекс]{\mathbf{\overset{\to }{\тау}}}_{k}[/латекс] от силы [латекс]{\mathbf{\overset {\to}{F}}}_{k}[/латекс] равно
На рисунке z -компонента крутящего момента [латекс]{\mathbf{\overset{\to }{\тау}}}_{k}[/латекс] от силы [латекс]{\mathbf{\overset {\to}{F}}}_{k}[/латекс] равно На рисунке чистый крутящий момент представляет собой сумму членов, причем каждый член вычисляется из рисунка, и каждый член должен иметь правильный смысл . Точно так же на рисунке мы назначаем знак [латекс]+[/латекс] компонентам в направлении [латекс]+[/латекс] x , а знак [латекс]-[/латекс] — компонентам в направлении [латекс]-[/латекс] x -направление.Этому же правилу необходимо последовательно следовать на рисунке при вычислении составляющих силы вдоль оси y .
На рисунке чистый крутящий момент представляет собой сумму членов, причем каждый член вычисляется из рисунка, и каждый член должен иметь правильный смысл . Точно так же на рисунке мы назначаем знак [латекс]+[/латекс] компонентам в направлении [латекс]+[/латекс] x , а знак [латекс]-[/латекс] — компонентам в направлении [латекс]-[/латекс] x -направление.Этому же правилу необходимо последовательно следовать на рисунке при вычислении составляющих силы вдоль оси y . На диаграммах свободного тела вектор веса привязан к центру тяжести тела. Для всех практических целей центр тяжести идентичен центру масс, как вы узнали из линейного импульса и столкновений о линейном импульсе и столкновениях. Только в тех случаях, когда тело имеет большую пространственную протяженность, так что гравитационное поле неоднородно по всему его объему, центр тяжести и центр масс находятся в разных точках.{2}.[/latex] В этих ситуациях центр тяжести идентичен центру масс. Поэтому на протяжении всей этой главы мы используем центр масс (ЦМ) как точку, к которой прикрепляется весовой вектор. Напомним, что ЦМ имеет особый физический смысл: при приложении внешней силы к телу точно в его ЦМ тело в целом совершает поступательное движение и такая сила не вызывает вращения.
На диаграммах свободного тела вектор веса привязан к центру тяжести тела. Для всех практических целей центр тяжести идентичен центру масс, как вы узнали из линейного импульса и столкновений о линейном импульсе и столкновениях. Только в тех случаях, когда тело имеет большую пространственную протяженность, так что гравитационное поле неоднородно по всему его объему, центр тяжести и центр масс находятся в разных точках.{2}.[/latex] В этих ситуациях центр тяжести идентичен центру масс. Поэтому на протяжении всей этой главы мы используем центр масс (ЦМ) как точку, к которой прикрепляется весовой вектор. Напомним, что ЦМ имеет особый физический смысл: при приложении внешней силы к телу точно в его ЦМ тело в целом совершает поступательное движение и такая сила не вызывает вращения. Величина гравитационного момента зависит от того, насколько далеко от точки вращения находится ЦМ. Например, в случае самосвала (рисунок) ось расположена на линии, где шины соприкасаются с поверхностью дороги. Если ЦМ расположен высоко над поверхностью дороги, гравитационный момент может быть достаточно большим, чтобы перевернуть грузовик.Легковые автомобили с низко расположенным КМ, близко к тротуару, более устойчивы к опрокидыванию, чем грузовые.
Величина гравитационного момента зависит от того, насколько далеко от точки вращения находится ЦМ. Например, в случае самосвала (рисунок) ось расположена на линии, где шины соприкасаются с поверхностью дороги. Если ЦМ расположен высоко над поверхностью дороги, гравитационный момент может быть достаточно большим, чтобы перевернуть грузовик.Легковые автомобили с низко расположенным КМ, близко к тротуару, более устойчивы к опрокидыванию, чем грузовые.
 ЦМ находится где-то между точками действия нормальных сил реакции, где-то на расстоянии х от точки действия [латекс]{F}_{R}[/латекс]. Наша задача найти х . Таким образом, мы выделяем три силы, действующие на тело (автомобиль), и можем нарисовать диаграмму свободного тела для протяженного твердого тела, как показано на рисунке.
ЦМ находится где-то между точками действия нормальных сил реакции, где-то на расстоянии х от точки действия [латекс]{F}_{R}[/латекс]. Наша задача найти х . Таким образом, мы выделяем три силы, действующие на тело (автомобиль), и можем нарисовать диаграмму свободного тела для протяженного твердого тела, как показано на рисунке. При таком выборе нам нужно написать только Figure и Figure, потому что все компоненты и тождественно равны нулю. Теперь нам нужно определиться с расположением опорной точки. Мы можем выбрать любую точку в качестве местоположения оси вращения ( z -ось). Предположим, мы поместили ось вращения в CM, как показано на диаграмме свободного тела для автомобиля.Теперь мы готовы записать условия равновесия автомобиля.
При таком выборе нам нужно написать только Figure и Figure, потому что все компоненты и тождественно равны нулю. Теперь нам нужно определиться с расположением опорной точки. Мы можем выбрать любую точку в качестве местоположения оси вращения ( z -ось). Предположим, мы поместили ось вращения в CM, как показано на диаграмме свободного тела для автомобиля.Теперь мы готовы записать условия равновесия автомобиля. [/latex] Когда точка вращения расположена в ЦМ, гравитационный момент тождественно равен нулю, потому что плечо рычага веса по отношению к оси, проходящей через ЦМ, равно нулю. Линии действия обеих нормальных сил реакции перпендикулярны плечам их рычагов, поэтому на рисунке мы имеем [латекс]|\,\текст{sin}\,\theta |=1[/латекс] для обеих сил. Из диаграммы свободного тела мы читаем, что крутящий момент [латекс] {\ тау} _ {\ текст {F}} [/латекс] вызывает вращение по часовой стрелке вокруг оси в СМ, поэтому его смысл отрицательный; а крутящий момент [латекс] {\ тау } _ {\ текст {R}} [/ латекс] вызывает вращение против часовой стрелки вокруг оси в СМ, поэтому его смысл положительный.С этой информацией мы запишем второе условие равновесия как
[/latex] Когда точка вращения расположена в ЦМ, гравитационный момент тождественно равен нулю, потому что плечо рычага веса по отношению к оси, проходящей через ЦМ, равно нулю. Линии действия обеих нормальных сил реакции перпендикулярны плечам их рычагов, поэтому на рисунке мы имеем [латекс]|\,\текст{sin}\,\theta |=1[/латекс] для обеих сил. Из диаграммы свободного тела мы читаем, что крутящий момент [латекс] {\ тау} _ {\ текст {F}} [/латекс] вызывает вращение по часовой стрелке вокруг оси в СМ, поэтому его смысл отрицательный; а крутящий момент [латекс] {\ тау } _ {\ текст {R}} [/ латекс] вызывает вращение против часовой стрелки вокруг оси в СМ, поэтому его смысл положительный.С этой информацией мы запишем второе условие равновесия как [/latex] Теперь мы можем записать второе условие равновесия, Figure, в явном виде через неизвестное расстояние x :
[/latex] Теперь мы можем записать второе условие равновесия, Figure, в явном виде через неизвестное расстояние x :
 В таком случае объект можно эффективно рассматривать как точечную массу. В этом частном случае нам не нужно беспокоиться о втором условии равновесия, рис., поскольку все крутящие моменты тождественно равны нулю, а первое условие равновесия (для сил) является единственным условием, которое должно быть выполнено. Диаграмма свободного тела и стратегия решения проблем для этого особого случая были изложены в книге Ньютона «Законы движения и приложения законов Ньютона».В следующем примере вы увидите типичную ситуацию равновесия, включающую только первое условие равновесия.
В таком случае объект можно эффективно рассматривать как точечную массу. В этом частном случае нам не нужно беспокоиться о втором условии равновесия, рис., поскольку все крутящие моменты тождественно равны нулю, а первое условие равновесия (для сил) является единственным условием, которое должно быть выполнено. Диаграмма свободного тела и стратегия решения проблем для этого особого случая были изложены в книге Ньютона «Законы движения и приложения законов Ньютона».В следующем примере вы увидите типичную ситуацию равновесия, включающую только первое условие равновесия.
 Мы можем использовать теорему Пифагора, чтобы решить этот треугольник, показанный на рисунке, и найти синус и косинус углов [латекс] {\ альфа }_ {1} [/латекс] и [латекс] {\ альфа } _ {2 }.[/latex] Затем мы можем разложить натяжения на их прямоугольные компоненты, подставить в первое условие равновесия (рисунок и рисунок) и найти натяжения в струнах. Сначала порвется струна с большим натяжением.
Мы можем использовать теорему Пифагора, чтобы решить этот треугольник, показанный на рисунке, и найти синус и косинус углов [латекс] {\ альфа }_ {1} [/латекс] и [латекс] {\ альфа } _ {2 }.[/latex] Затем мы можем разложить натяжения на их прямоугольные компоненты, подставить в первое условие равновесия (рисунок и рисунок) и найти натяжения в струнах. Сначала порвется струна с большим натяжением. \hfill \end{массив}[/латекс]
\hfill \end{массив}[/латекс] {2}}-0,042\,\text{кг}=0,277\,\text{кг}=277,0\,\text{г.}[/latex]
{2}}-0,042\,\text{кг}=0,277\,\text{кг}=277,0\,\text{г.}[/latex] Эти два условия должны одновременно выполняться в равновесии. Если одно из них не выполняется, тело не находится в равновесии.
Эти два условия должны одновременно выполняться в равновесии. Если одно из них не выполняется, тело не находится в равновесии. Как это помогает?
Как это помогает?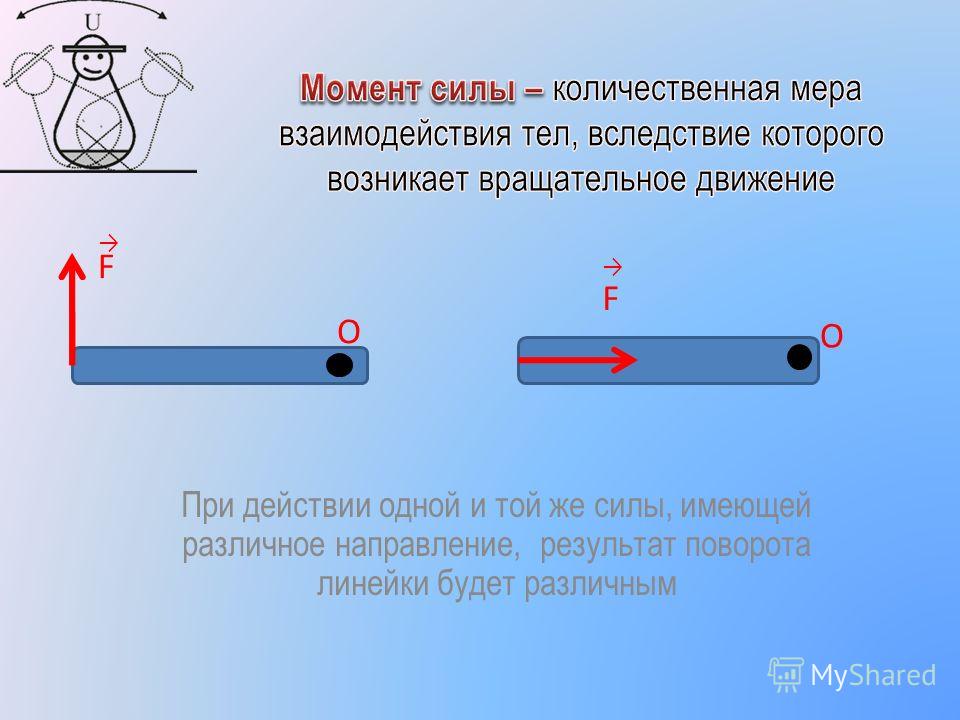 Какой крутящий момент вы прикладываете к центру болта?
Какой крутящий момент вы прикладываете к центру болта? Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, что трением можно пренебречь.
Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, что трением можно пренебречь.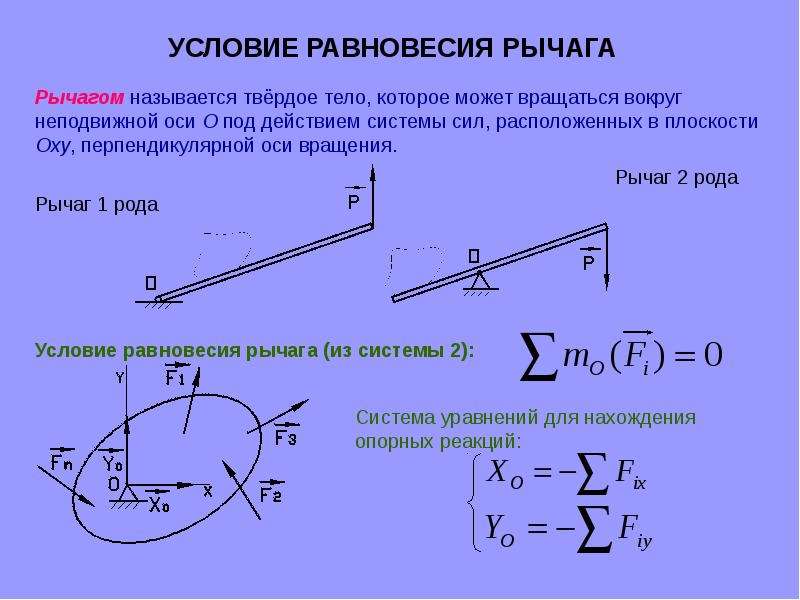 Это движение всего объекта в определенном направлении. Говорят, что объект находится в поступательном равновесии, если силы уравновешены во всех направлениях: если направленные вверх силы равны силам, направленным вниз, силы, направленные влево, равны силам, направленным вправо, а силы, направленные вперед, равны силам, направленным назад. Силы равны, поэтому это называется равновесием.
Это движение всего объекта в определенном направлении. Говорят, что объект находится в поступательном равновесии, если силы уравновешены во всех направлениях: если направленные вверх силы равны силам, направленным вниз, силы, направленные влево, равны силам, направленным вправо, а силы, направленные вперед, равны силам, направленным назад. Силы равны, поэтому это называется равновесием. Есть еще один вид движения — вращательное движение.Вращательное движение — это когда объект остается на месте, но вращается вокруг точки вращения. Это похоже на то, как колесо вращается вокруг своей оси или как ветряная турбина вращается, когда ее толкает воздух.
Есть еще один вид движения — вращательное движение.Вращательное движение — это когда объект остается на месте, но вращается вокруг точки вращения. Это похоже на то, как колесо вращается вокруг своей оси или как ветряная турбина вращается, когда ее толкает воздух. Если это произойдет для стационарного объекта, этот объект останется точно там, где он есть, и не будет вращаться.
Если это произойдет для стационарного объекта, этот объект останется точно там, где он есть, и не будет вращаться. Объект, находящийся в равновесии вращения, не начнет больше вращаться в любом направлении. Когда объект находится в поступательном и вращательном равновесии, то в целом он находится в статическом равновесии.Вот когда у вас есть действительно неподвижный объект.
Объект, находящийся в равновесии вращения, не начнет больше вращаться в любом направлении. Когда объект находится в поступательном и вращательном равновесии, то в целом он находится в статическом равновесии.Вот когда у вас есть действительно неподвижный объект. Чего здесь не хватает на схеме?
Чего здесь не хватает на схеме? 
 Таким образом, моменты, вызванные различными силами, компенсируются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии. Тело здесь твердое тело.
Таким образом, моменты, вызванные различными силами, компенсируются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии. Тело здесь твердое тело. равен нулю.Это означает, что моменты, вызванные различными силами, компенсируются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии.
равен нулю.Это означает, что моменты, вызванные различными силами, компенсируются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии. вообще и, следовательно, тело находится в равновесии.Равновесие достигается только в том случае, если результирующая сила, действующая на тело, стремится к нулю. Таким образом, силы уравновешиваются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии.
вообще и, следовательно, тело находится в равновесии.Равновесие достигается только в том случае, если результирующая сила, действующая на тело, стремится к нулю. Таким образом, силы уравновешиваются. Если это происходит, то тело не движется ни в каком направлении, и поэтому говорят, что тело находится в равновесии.


 Сила 50 Н не равна силе 30 Н.
Сила 50 Н не равна силе 30 Н. Обычная физическая лаборатория состоит в том, чтобы подвешивать объект на двух или более веревках и измерять силы, действующие под углом на объект, чтобы выдержать его вес.Состояние объекта анализируется с точки зрения сил, действующих на объект. Объект представляет собой точку на струне, на которую действовали три силы. См. схему справа. Если объект находится в равновесии, то результирующая сила, действующая на объект, должна быть равна 0 ньютонов. Таким образом, если все силы сложить как векторы, то результирующая сила (сумма векторов) должна быть равна 0 ньютонов. (Напомним, что результирующая сила — это «векторная сумма всех сил» или равнодействующая сложения всех отдельных сил «голова к хвосту».) Таким образом, можно построить точно нарисованную диаграмму сложения векторов для определения результата. Примеры данных для такой лаборатории показаны ниже.
Обычная физическая лаборатория состоит в том, чтобы подвешивать объект на двух или более веревках и измерять силы, действующие под углом на объект, чтобы выдержать его вес.Состояние объекта анализируется с точки зрения сил, действующих на объект. Объект представляет собой точку на струне, на которую действовали три силы. См. схему справа. Если объект находится в равновесии, то результирующая сила, действующая на объект, должна быть равна 0 ньютонов. Таким образом, если все силы сложить как векторы, то результирующая сила (сумма векторов) должна быть равна 0 ньютонов. (Напомним, что результирующая сила — это «векторная сумма всех сил» или равнодействующая сложения всех отдельных сил «голова к хвосту».) Таким образом, можно построить точно нарисованную диаграмму сложения векторов для определения результата. Примеры данных для такой лаборатории показаны ниже. 4 Н
4 Н Величина и направление каждого компонента для выборочных данных показаны в таблице под диаграммой.
Величина и направление каждого компонента для выборочных данных показаны в таблице под диаграммой. Мы могли бы сказать, что это «достаточно близко для работы правительства».
Мы могли бы сказать, что это «достаточно близко для работы правительства». Каков вес знака? На этот вопрос можно ответить, проведя силовой анализ с использованием тригонометрических функций. Вес знака равен сумме восходящих составляющих натяжения двух тросов. Таким образом, для определения этой вертикальной составляющей можно использовать тригонометрическую функцию. Схема и сопутствующие работы показаны ниже.
Каков вес знака? На этот вопрос можно ответить, проведя силовой анализ с использованием тригонометрических функций. Вес знака равен сумме восходящих составляющих натяжения двух тросов. Таким образом, для определения этой вертикальной составляющей можно использовать тригонометрическую функцию. Схема и сопутствующие работы показаны ниже. Если известно, что знак имеет массу 5 кг и если угол между двумя тросами составляет 100 градусов, то можно определить натяжение троса. Предполагая, что знак находится в равновесии (хорошее предположение, если он остается в покое), два троса должны создавать достаточную направленную вверх силу, чтобы уравновесить направленную вниз силу тяжести.Сила тяжести (также известная как вес) составляет 49 Н (Fgrav = m*g), поэтому каждый из двух тросов должен тянуться вверх с силой 24,5 Н. Поскольку угол между кабелями равен 100 градусам, каждый кабель должен составлять угол 50 градусов с вертикалью и угол 40 градусов с горизонталью. Эскиз этой ситуации (см. диаграмму ниже) показывает, что натяжение троса можно найти с помощью функции синуса. Треугольник ниже иллюстрирует эти отношения.
Если известно, что знак имеет массу 5 кг и если угол между двумя тросами составляет 100 градусов, то можно определить натяжение троса. Предполагая, что знак находится в равновесии (хорошее предположение, если он остается в покое), два троса должны создавать достаточную направленную вверх силу, чтобы уравновесить направленную вниз силу тяжести.Сила тяжести (также известная как вес) составляет 49 Н (Fgrav = m*g), поэтому каждый из двух тросов должен тянуться вверх с силой 24,5 Н. Поскольку угол между кабелями равен 100 градусам, каждый кабель должен составлять угол 50 градусов с вертикалью и угол 40 градусов с горизонталью. Эскиз этой ситуации (см. диаграмму ниже) показывает, что натяжение троса можно найти с помощью функции синуса. Треугольник ниже иллюстрирует эти отношения. Принцип заключается в том, что по мере увеличения угла с горизонталью сила натяжения, необходимая для удержания знака в равновесии, уменьшается. Чтобы проиллюстрировать это, рассмотрим изображение силой 10 ньютонов, удерживаемое проводами с тремя разными ориентациями, как показано на диаграммах ниже. В каждом случае для поддержки изображения используются два провода; каждый провод должен выдерживать половину веса знака (5 Н). Угол, который провода образуют с горизонтом, варьируется от 60 до 15 градусов. Используйте эту информацию и приведенную ниже диаграмму, чтобы определить натяжение проволоки для каждой ориентации.Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
Принцип заключается в том, что по мере увеличения угла с горизонталью сила натяжения, необходимая для удержания знака в равновесии, уменьшается. Чтобы проиллюстрировать это, рассмотрим изображение силой 10 ньютонов, удерживаемое проводами с тремя разными ориентациями, как показано на диаграммах ниже. В каждом случае для поддержки изображения используются два провода; каждый провод должен выдерживать половину веса знака (5 Н). Угол, который провода образуют с горизонтом, варьируется от 60 до 15 градусов. Используйте эту информацию и приведенную ниже диаграмму, чтобы определить натяжение проволоки для каждой ориентации.Когда закончите, нажмите кнопку, чтобы просмотреть ответы. Если в равновесии, то все вертикальные компоненты должны уравновешиваться, и все горизонтальные компоненты должны уравновешиваться.
Если в равновесии, то все вертикальные компоненты должны уравновешиваться, и все горизонтальные компоненты должны уравновешиваться.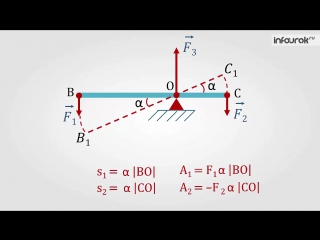 Нажмите кнопку, чтобы просмотреть ответы на эти вопросы.
Нажмите кнопку, чтобы просмотреть ответы на эти вопросы.
 И это все векторы. Все зависит от направления.Если бы мы приложили силу в противоположном направлении, то это колесо закрутилось бы в другую сторону, которая обычно вращается. В физике вращения мы сокращаем направление вращения по часовой стрелке или против часовой стрелки. Итак, в этой ситуации мы движемся против часовой стрелки. против часовой стрелки. Итак, теперь мы хотим исследовать, как мы можем заставить эту систему находиться в равновесии, чтобы мы могли приравнять вращательный момент к стандартному медику. Итак, у нас есть сила в Кантоне Манниксе, Ньютоновская сила.Мы можем связать это с факелом. Вот что вызывает движение — это приложение силы. Мы знаем, что в статическом равновесии ко мне прилагается сила, а оно прикладывает ускорение. Это оба фактора. Масса — это масштабирование. Итак, мы применяем силу, которая применяет ускорение, которое изменяет скорость. Таким образом, сила — это то, что мы определили как ключевой фактор изменения равновесия. Если у нас есть система, находящаяся в равновесии, и мы приложим силу, она выведет ее за пределы этого равновесия.
И это все векторы. Все зависит от направления.Если бы мы приложили силу в противоположном направлении, то это колесо закрутилось бы в другую сторону, которая обычно вращается. В физике вращения мы сокращаем направление вращения по часовой стрелке или против часовой стрелки. Итак, в этой ситуации мы движемся против часовой стрелки. против часовой стрелки. Итак, теперь мы хотим исследовать, как мы можем заставить эту систему находиться в равновесии, чтобы мы могли приравнять вращательный момент к стандартному медику. Итак, у нас есть сила в Кантоне Манниксе, Ньютоновская сила.Мы можем связать это с факелом. Вот что вызывает движение — это приложение силы. Мы знаем, что в статическом равновесии ко мне прилагается сила, а оно прикладывает ускорение. Это оба фактора. Масса — это масштабирование. Итак, мы применяем силу, которая применяет ускорение, которое изменяет скорость. Таким образом, сила — это то, что мы определили как ключевой фактор изменения равновесия. Если у нас есть система, находящаяся в равновесии, и мы приложим силу, она выведет ее за пределы этого равновесия. Таким образом, этот крутящий момент также влияет. Теперь у нас есть уравнение для крутящего момента.Это оба уравнения суммирования. Мы сейчас рассмотрим только одну силу. Итак, если у нас есть крутящий момент, мы знаем, что он равен произведению инерционной женщины на угловое ускорение. Так что теперь мы можем Мы можем увидеть здесь тенденцию. Если крутящий момент подобен нашей силе, наши массы подобны нашей инерции, и это означает, что наше ускорение, угловое ускорение связаны, что также подразумевает, что у нас есть скорость, которая может быть получена из ускорения. У нас похожая угловая скорость, что тоже является фактором и что значит угловая скорость и чем она отличается от обычных скоростей.Угловая скорость — это скорость, с которой он вращается. Вот как быстро это вращается, Итак, объект. Посмотрите, не было ли это прикреплено. Что угодно может иметь как угловое ускорение вокруг. Извините, угловая скорость в поступательной скорости, так что вся эта система могла двигаться. Ярким примером ситуации является сама Земля, которая вращается вокруг Земли, но она также движется вокруг Солнца.
Таким образом, этот крутящий момент также влияет. Теперь у нас есть уравнение для крутящего момента.Это оба уравнения суммирования. Мы сейчас рассмотрим только одну силу. Итак, если у нас есть крутящий момент, мы знаем, что он равен произведению инерционной женщины на угловое ускорение. Так что теперь мы можем Мы можем увидеть здесь тенденцию. Если крутящий момент подобен нашей силе, наши массы подобны нашей инерции, и это означает, что наше ускорение, угловое ускорение связаны, что также подразумевает, что у нас есть скорость, которая может быть получена из ускорения. У нас похожая угловая скорость, что тоже является фактором и что значит угловая скорость и чем она отличается от обычных скоростей.Угловая скорость — это скорость, с которой он вращается. Вот как быстро это вращается, Итак, объект. Посмотрите, не было ли это прикреплено. Что угодно может иметь как угловое ускорение вокруг. Извините, угловая скорость в поступательной скорости, так что вся эта система могла двигаться. Ярким примером ситуации является сама Земля, которая вращается вокруг Земли, но она также движется вокруг Солнца. Итак, у нас есть оба сценария. У нас есть угловая скорость и поступательная скорость, поэтому мы можем приравнять эти два разных уравнения, которые у нас есть.Крутящий момент где-то силовой. У нас есть угловое ускорение, аналогичное возбуждению, а угловая скорость аналогична скорости. Таким образом, чтобы вывести систему из равновесия, мы должны приложить к ней силу. Таким образом, для того чтобы вращающееся тело находилось в равновесии, оно не должно иметь ни вращающихся сил, ни движения. Это крутящий момент равен нулю. На объект не действуют вращательные силы, поэтому то, что мы имеем, — две разные фамилии — это два разных, легко просматриваемых сценария. Для такого типа ситуаций у нас есть одно и то же колесо, и оно вообще не вращается.Нет ни угловой скорости, ни углового ускорения. С другой стороны, у нас также может быть система с постоянной скоростью вращения и постоянной угловой скоростью, так что, скажем, она вращается с постоянной скоростью. Еще раз против часовой стрелки, он по-прежнему не имеет никакого ускорения, поэтому он не ускоряется и не замедляется.
Итак, у нас есть оба сценария. У нас есть угловая скорость и поступательная скорость, поэтому мы можем приравнять эти два разных уравнения, которые у нас есть.Крутящий момент где-то силовой. У нас есть угловое ускорение, аналогичное возбуждению, а угловая скорость аналогична скорости. Таким образом, чтобы вывести систему из равновесия, мы должны приложить к ней силу. Таким образом, для того чтобы вращающееся тело находилось в равновесии, оно не должно иметь ни вращающихся сил, ни движения. Это крутящий момент равен нулю. На объект не действуют вращательные силы, поэтому то, что мы имеем, — две разные фамилии — это два разных, легко просматриваемых сценария. Для такого типа ситуаций у нас есть одно и то же колесо, и оно вообще не вращается.Нет ни угловой скорости, ни углового ускорения. С другой стороны, у нас также может быть система с постоянной скоростью вращения и постоянной угловой скоростью, так что, скажем, она вращается с постоянной скоростью. Еще раз против часовой стрелки, он по-прежнему не имеет никакого ускорения, поэтому он не ускоряется и не замедляется. Это немного сложнее интуитивно увидеть, потому что это не то, что мы видим в повседневной жизни, потому что у нас всегда есть какое-то трение, которое в конечном итоге замедляет объект.Но если бы не было трения, объект вращался бы до тех пор, пока на него не подействовала бы внешняя сила. Так что это еще одна форма равновесия, которую мы можем иметь. О, угловая скорость равна постоянной, но не может быть ускоряющей. Итак, если силы равны, здесь та же ситуация. Если крутящий момент равен нулю, то и наше ускорение тоже должно быть равно нулю. Так что это довольно универсальные ограничения для равновесия. Но самое главное, у нас не может быть крутящего момента. Если есть крутящий момент, он изменит вашу систему отсчета от равновесия.Он изменит свое состояние равновесия, поэтому крутящий момент должен быть равен нулю. На изолированную систему не должны воздействовать внешние силы
Это немного сложнее интуитивно увидеть, потому что это не то, что мы видим в повседневной жизни, потому что у нас всегда есть какое-то трение, которое в конечном итоге замедляет объект.Но если бы не было трения, объект вращался бы до тех пор, пока на него не подействовала бы внешняя сила. Так что это еще одна форма равновесия, которую мы можем иметь. О, угловая скорость равна постоянной, но не может быть ускоряющей. Итак, если силы равны, здесь та же ситуация. Если крутящий момент равен нулю, то и наше ускорение тоже должно быть равно нулю. Так что это довольно универсальные ограничения для равновесия. Но самое главное, у нас не может быть крутящего момента. Если есть крутящий момент, он изменит вашу систему отсчета от равновесия.Он изменит свое состояние равновесия, поэтому крутящий момент должен быть равен нулю. На изолированную систему не должны воздействовать внешние силы