Что такое Угол? Определение, виды, как обозначают? Примеры

Определение угла

Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.

Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.

Если нам дана прямая a на плоскости, и на ней есть некоторая точку O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.

Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:

Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.

В математике существует специальный символ для обозначения угла, вот он: ∠.

Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.

Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре.

При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA.

Иногда можно встретить обозначение в виде цифр — так тоже можно.

Для наглядности — все способы обозначения углов:

Что такое вершина и стороны угла:

• Стороны угла — лучи, из которых состоит угол.
• Вершина угла — общее начало сторон угла.

Биссектриса — это луч, который исходит из вершины угла и делит его на два равных угла.

Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Единица измерения углов — градусы. Символ для обозначения градуса угла: °.

Определение смежных и вертикальных углов

Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Таким образом два смежных угла составляют развернутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.

Вертикальные углы — это пара углов, у которых есть общая вершина, при этом стороны одного угла составляют продолжение сторон другого угла.

При пересечении прямых получается четыре пары смежных и две пары вертикальных углов. Вот как это выглядит:

Виды углов

Есть разные типы углов и у каждого своё название:

• острый
• прямой
• тупой
• развернутый
• выпуклый
• полный

Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.

Острый угол — это угол, который меньше прямого угла, то есть < 90°.

Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен половине развернутого угла, то есть = 90°.

Если два смежных угла равны между собой, то каждый из них является прямым.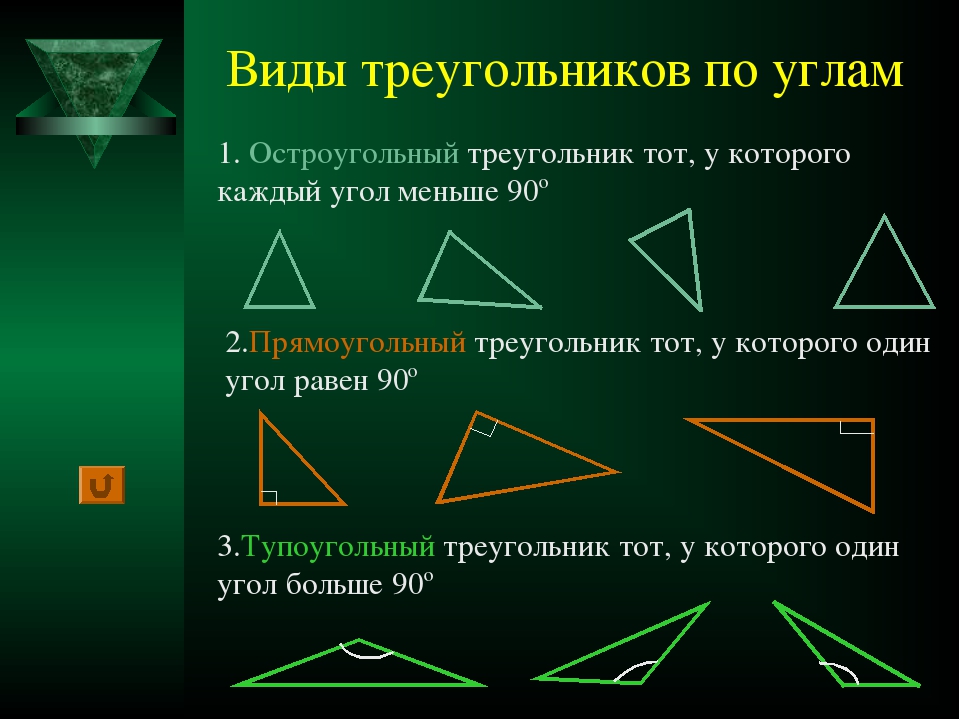 Для удобства прямой угол обозначается уголком. Вот так:

На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.

Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол показано на первой картинке.

Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.

Тупой угол — это угол, который больше прямого угла, но меньше развернутого:

90° < тупой угол < 180°.

Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.

Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.

Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.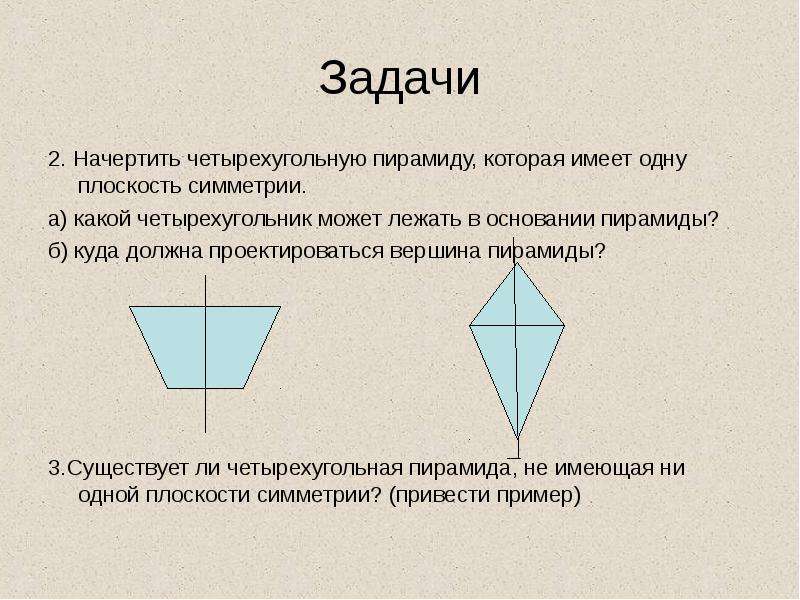

На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.

Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.

Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:

• ∠AOC = ∠AOB — ∠COB,
• ∠COB = ∠AOB — ∠AOC.

Сравнение углов

Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:

При этом развернутые углы всегда являются равными.

Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:

 

1. Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.


2. Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.

Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.

Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.

Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот, как он выглядит:

Как правильно измерять углы

Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Обозначается — 0.

Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.

Минута — 1/60 часть градуса. Обозначается — ´.

Секунда — 1/60 часть минуты. Обозначается — ´´.

Градус состоит из 3600 секунд, то есть: 1° = 60′ = 3600′.

Как происходит измерение угла: сначала измеряются стороны угла, а после его внутренняя область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.

Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.

На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠ A O B = ∠ A O C + ∠ D O B = 45° + 30° + 60° = 135 °.

Угол называется прямым, если он равен 90°, а острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол имеет 180°.

Равные углы имеют равную градусную меру.

Обозначение углов на чертеже

Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.

Задачи с углами могут быть разными и не всегда есть возможность правильно изобразить и отметить угол. Вот, что важно запомнить при обозначении лучей и углов:

• Равные углы обозначают одинаковым количеством дуг.
• Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
• Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.

На чертеже отмечены острые, равные и неравные углы.

Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом необязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.

Вникать во все тонкости математической вселенной комфортнее с внимательным наставником. Наши учителя объяснят сложную тему, ответят на неловкие вопросы и вдохновят ребенка учиться. А красочная платформа с увлекательными заданиями поможет заниматься современно и в удовольствие.

Запишите ребенка на бесплатный пробный урок в онлайн-школу Skysmart и попробуйте сами!

Урок 2. луч и угол — Геометрия — 7 класс

Геометрия

7 класс

Урок № 2

Луч и угол

Перечень рассматриваемых вопросов:

• Угол.
• Луч.
• Внутренняя и внешняя часть угла.
• Развёрнутый угол.

Тезаурус:

Луч – часть прямой, состоящая из всех точек, лежащих по одну сторону от заданной точки и той точки, которая является началом луча.

Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Угол также рассматривается как часть плоскости, ограниченная двумя лучами с общим началом.

Стороны угла – лучи, из которых состоит угол.

Основная литература:

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Дополнительная литература:

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Мы уже познакомились с некоторыми геометрическими понятиями: прямая, точка, отрезок. Сегодня мы рассмотрим ещё два понятия, часто встречающиеся в геометрии – это луч и угол.

Для начала, вспомним, как строятся и обозначаются лучи и углы.

Для этого проведём прямую а, отметим на ней точкуО, которая разделит прямую на две части. Эти части прямой называются лучами, исходящими из точки О. А сама точка О, называется началом каждого из лучей.

Луч принято обозначать как одной малой латинской буквой, например, а.

Или двумя большими латинскими буквами, например, ОА.

При этом стоит помнить, что первая буква всегда обозначает начало луча, а вторая– это любая точка на луче.

Теперь рассмотрим понятие угол.

Начнём с определения.

Угол – это часть плоскости, ограниченная двумя лучами с общим началом.

Лучи – это стороны угла.

В данном случае, это стороны ОА и ОВ.

Общее начало сторон, в данном случае О – это вершина угла.

Углы принято обозначать как двумя малыми латинскими буквами, по названию сторон угла, например, ∠hk,

так и тремя большими латинскими буквами, например, тот же угол можно обозначить ∠АОВ, где вершина угла будет стоять в середине обозначения угла.

Или одной большой латинской буквой, обозначающей вершину угла. Например, тот же угол можно обозначить буквой∠О, по вершине угла.

Далее введём понятия, связанные с углами.

Во-первых, рассмотрим угол, который называют развёрнутым, его обе стороны лежат на одной прямой. Например, ∠С– развёрнутый.

В дальнейшем будем рассматривать углы меньше развёрнутого.

Угол также рассматривается как часть плоскости, ограниченная двумя лучами с общим началом.

Во-вторых, плоскость, на которой изображён любой угол, кроме развёрнутого, делится на две области: внутреннюю и внешнюю.

В развёрнутом углу, любая часть считается внутренней.

Решим задачу.

На рисунке изображён угол. Какие из точек лежат внутри угла и вне его?

Решение:

Внутри угла лежат точки: М, Е, К.

Вне угла лежат точки: Р, D, N.

Отметим, что точкиВ и С лежат на сторонах углаО.

Продолжая изучать углы, отметим, что если внутри угла из его вершины провести луч, то он разделит угол на два угла.

Например, луч ОС делит ∠АОВ на два угла – ∠ВОС и ∠АОС.

Итак, сегодня мы повторили некоторые сведения о луче и углах; сформировали представления о внутренней и внешней областях угла, меньше развернутого, познакомились с различными обозначениями луча и угла.

Материал для углубленного изучения

Двугранный угол.

Мы разобрали понятие угол, связанное с планиметрией. Но как отмечалось ранее, у геометрии есть ещё один раздел – стереометрия, который изучается в старших классах. Этот раздел изучает пространственные фигуры, одна из таких фигур–двугранный угол. Дадим ему определение: двугранный угол – пространственнаягеометрическая фигура, образованная двумяполуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями. Двугранный угол имеет стороны (иначе их называют грани), это полуплоскости α и β, и ребро, в данном случае это прямая АВ. Как измерить такие углы и их разновидности, вы узнаете в курсе геометрии 10 класса.

Тренировочные задания.

№ 1. Какие из точек лежат на стороне угла?

Решение:

Посмотрите на рисунок. На нём изображён угол ВОС, соответственно точки B и C лежат на сторонах угла, других точек нет.

Ответ: B и C.

№ 2. Сколько углов изображено на рисунке?

Решение. Перечислим все углы, изображённые на рисунке.

СОВ, ВОА, АОD, DОС и развёрнутые углы СОА и DОВ. Получается 8 углов.

Ответ: 8 углов.

Что такое треугольник: определение, классификация, свойства

В данной публикации мы рассмотрим определение, классификацию и свойства одной из основных геометрических фигур – треугольника. Также разберем примеры решения задач для закрепления представленного материала.

Определение треугольника

Треугольник – это геометрическая фигура на плоскости, состоящая из трех сторон, которые образованы путем соединения трех точек, не лежащих на одной прямой. Для обозначения используется специальный символ – △.

• Точки A, B и C – вершины треугольника.
• Отрезки AB, BC и AC – стороны треугольника, которые часто обозначаются в виде одной латинской буквы. Например, AB = a, BC = b, AC = c.
• Внутренность треугольника – часть плоскости, ограниченная сторонами треугольника.

Стороны треугольника в вершинах образуют три угла, традиционно обозначающиеся греческими буквами – α, β, γ и т.д. Из-за этого треугольник еще называют многоугольником с тремя углами.

Углы можно, также, обозначать с помощью специального знака “∠“:

• α – ∠BAC или ∠CAB
• β – ∠ABC или ∠CBA
• γ – ∠ACB или ∠BCA

Классификация треугольников

В зависимости от величины углов или количества равных сторон выделяют следующие виды фигуры:

1. Остроугольный – треугольник, у которого все три угла острые, т. е. меньше 90°.

2. Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

3. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и AC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (BC).

4. Разносторонний – треугольник, у которого все стороны имеют разную длину.

5. Равнобедренный – треугольник, имеющие две равные стороны, которые называются боковыми (AB и BC). Третья сторона – это основание (AC). В данной фигуре углы при основании равны (∠BAC = ∠BCA).

6. Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

Свойства треугольника

1. Любая из сторон треугольника меньше двух оставшихся, но больше их разности. Для удобства примем стандартные обозначения сторон – a, b и с. Тогда:

b – c < a < b + c, при b > с

Это свойство применяется для проверки отрезков на предмет того, могут ли они образовывать треугольник.

2. Сумма углов любого треугольника равняется 180°. Из этого свойства следует, что в тупоугольном треугольнике два угла всегда являются острыми.

3. В любом треугольнике напротив большей стороны находится больший угол, и наоборот.

Примеры задач

Задание 1
В треугольнике известны два угла – 32° и 56°. Найдите значение третьего угла.

Решение
Примем известные углы за α (32°) и β (56°), а неизвестный – за γ.
Согласно свойству о сумме всех углов, α + β + γ = 180°.
Следовательно, γ = 180° – α – β = 180° – 32° – 56°  = 92°.

Задание 2
Даны три отрезка длиной 4, 8 и 11. Выясните, могут ли они образовать треугольник.

Решение
Составим неравенства для каждого из заданных отрезков, исходя из свойства, рассмотренного выше:
11 – 4 < 8 < 11 + 4
8 – 4 < 11 < 8 + 4
11 – 8 < 4 < 11 + 8

Все они верны, следовательно, данные отрезки могут быть сторонами треугольника.

Линии — геометрия и искусство

Кандинский систематизировал свои взгляды на живопись в книге «Точка и линия на плоскости» (1926). Изучая геометрические формы, художник нашёл, что с их помощью можно усиливать или ослаблять свойства цвета. Для  этой картины он использовал приглушённую палитру, смещённую к цветам, расположенным в одной части спектра.

Цитаты из книги:
ЛИНИЯ
Геометрическая линия – это невидимый объект. Она – след перемещающейся точки, то есть ее произведение. Она возникла из движения – а именно вследствие уничтожения высшего, замкнутого в себе покоя точки. Здесь произошел скачок из статики в динамику.
Таким образом, линия – величайшая противоположность живописного первоэлемента – точки. И она с предельной точностью может быть обозначена как вторичный элемент.

ВОЗНИКНОВЕНИЕ
Силы, приходящие извне, преобразовавшие точку в линию, могут быть различными. Разнообразие линий зависит от числа этих сил и их комбинаций.
В конце концов [происхождение] всех форм линий можно свести к двум случаям:
1. приложение одной силы и
2. приложение двух сил:
а) одно- или многократное поочередное воздействие обеих сил,
б) одновременное воздействие обеих сил.

ПРЯМАЯ
Если одна приходящая извне сила перемещает точку в каком-либо направлении, то возникает первый тип линии, причем выбранное направление остается неизменным, и сама линия стремится двигаться по прямому пути бесконечно.
Это – прямая, представляющая в своем напряжении самую сжатую форму бесконечной возможности движения.
…
Среди прямых мы выделяем три типа, по отношению к которым все прочие прямые – лишь отклонения.
1. Простейшая форма прямой – это горизонталь. В человеческом представлении она соответствует линии или поверхности, на которой человек стоит или передвигается. Итак, горизонталь – это холодная несущая основа, которая может быть продолжена на плоскости в различных направлениях. Холод и плоскостность – это основные звучания данной линии, она может быть определена как кратчайшая форма неограниченной холодной возможности движения.
2. Полностью противоположна этой линии и внешне, и внутренне стоящая к ней под прямым углом вертикаль, в которой плоскостность заменяется высотой, то есть холод – теплом. Таким образом, вертикаль является кратчайшей формой неограниченной теплой возможности движения.
3. Третий типичный вид прямой – это диагональ, которая схематичным образом под равным углом отклоняется от обеих вышеназванных и тем самым имеет к обеим равное тяготение, что и определяет ее внутреннее звучание, равномерное соединение холода и тепла. Итак: кратчайшая форма неограниченной тепло-холодной возможности движения. ..

Точки, прямые и отрезки — урок. Геометрия, 7 класс.

Введение в геометрию

 

Название нового предмета ГЕОМЕТРИЯ произошло от древнегреческих слов ЗЕМЛЯ и ИЗМЕРЕНИЕ.

Наука геометрия — одна из самых древних наук, и возникла в связи с практической необходимостью в измерениях, проведении границ, строительстве дорог и зданий, а сейчас мы знаем геометрию как науку, которая изучает свойства геометрических фигур.

 

В дальнейшем будут определения для разных фигур, кроме двух — точка и прямая. С помощью этих фигур мы определим все остальные геометрические фигуры, а точку и прямую можем попытаться только представить: точку — как что-то бесконечно малое, а прямую — как что-то бесконечно простирающееся в обе стороны.

 

Точки обозначаются большими латинскими буквами, прямые обозначаются малыми латинскими буквами. Словами описать взаимное расположение точек и прямой можно по разному:

            1.   точка находится (лежит) на прямой, или прямая проходит (проведена) через точку;

            2.  точка не находится (не лежит) на прямой, или прямая не проходит (не проведена) через точку.

 

В геометрии эти факты записываются символически:

            1. точки \(A\) и \(B\) находятся (лежат) на прямой \(a\), или

                прямая \(a\) проходит (проведена) через точки \(A\) и \(B\) — A∈a   и   B∈a;

            2. точки \(C\) и \(D\) не находятся (не лежат) на прямой \(a\),

                или прямая \(a\) не проходит (не проведена) через точки \(C\) и \(D\) — C∉a   и   D∉a.

Одно из самых важных предположений в геометрии — через любые две точки можно провести прямую, притом только одну.

Значит, иногда обозначить прямую можем и двумя большими латинскими буквами, например, прямая \(AB\), так как никакая другая прямая через эти две точки не может быть проведена.

 

Следовательно, две прямые могут иметь только одну общую точку и пересекаться или не иметь ни одной общей точки и никогда не пересекаться.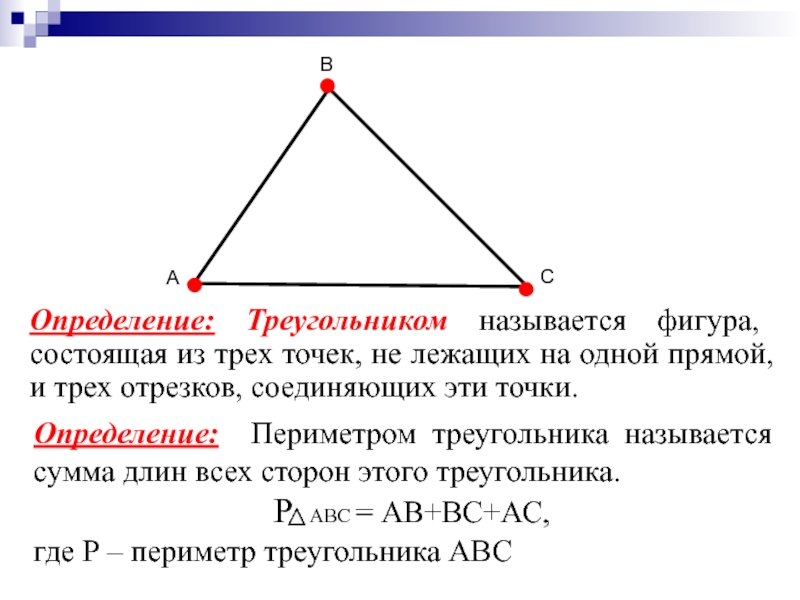

Символически записываем a∩b=A.

 

Символически записываем c&spar;d.

Часть прямой, ограниченная двумя точками, называется отрезком.

Символически записываем отрезок \(AB\).

 

Внимательно посмотри на рисунок!

 

Обрати внимание!

1) Отрезки \(AB\) и \(CD\) пересекаются, отрезки \(CD\) и \(DE\) имеют общий конец,

    отрезки \(AB\) и \(HF\), \(AB\) и \(DE\), \(CD\) и \(HF\) , \(HF\) и \(DE\) не пересекаются.

2) Все прямые — \(a\), \(b\) и \(c\) — пересекаются!

Так как мы представляем прямую как бесконечно простирающуюся в обе стороны, то рано или поздно эти прямые будут пересекаться, несмотря на то, что на рисунке этого не видно.

Мы можем нарисовать только часть бесконечных прямых.

определение угла, измерение углов, обозначения и примеры

Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.

Определение угла

Определение 1

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

Определение 2

Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.

Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Определение 3

Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Определение 4

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.

На рисунке ниже изображен развернутый угол.

Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.

Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .

Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.

Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Внутренняя область угла – элемент, служащий для второго определения угла.

Определение 5

Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.

Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.

Определение смежных и вертикальных углов

Определение 6

Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.

На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.

Определение 7

Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.

При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Сравнение углов

Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.

Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.

Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.

Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.

Развернутые углы являются равными.

Измерение углов

Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.

Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.

Чаще всего используют понятие градус.

Определение 8

Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.

Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.

Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.

Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .

Определение 9

Минутой называют одну шестидесятую часть градуса.

Определение 10

Секундой называют одну шестидесятую часть минуты.

Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:

1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,

а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .

Определение 11

Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.

Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.

Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».

В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.

Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.

Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .

Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.

Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.

Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.

Определение 12

Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.

На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.

Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.

Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.

На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.

Обозначение углов на чертеже

Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.

Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.

Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.

Что называется хордой окружности в математике и геометрии: определение, основные свойства

Хорда в переводе с греческого означает «струна». Это понятие широко применяется в разных областях науки — в математике, биологии и других.

В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Как построить геометрическую хорду

Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.

Это интересно: в геометрии луч — это что такое, основное понятие.

Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.

Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.

Свойства

Существует ряд закономерностей, связывающих между собой хорды и центр круга:

1. Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
2. Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.
3. Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности. И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
4. Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
5. Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга. Такая ось проходит через центр и делит её на две равные части.
6. Отрезок с наименьшей длиной представляет собой точку.
7. Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.

Это интересно: разность векторов, определение разности.

Взаимосвязь с радиусом и диаметром

Вышеуказанные математические понятия связаны между собой следующими закономерностями:

1. Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
2. С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
3. Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
4. Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
5. Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
6. Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.

Хорда и радиус

Между этими понятиями существуют следующие связи:

1. Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
2. Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
3. Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
4. Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
5. Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
6. Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.

Отношения со вписанными углами

Углы, вписанные в окружность, подчиняются следующим правилам:

1. Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
2. Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
3. Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
4. Вписанный угол, который опирается на диаметр круга, является прямым.
5. Равные между собой по размеру отрезки стягивают равные центральные углы.
6. Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
7. Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.

Взаимодействия с дугой

Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:

1. Две равные между собой хорды стягивают равные дуги.
2. Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
3. Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.

Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.

Определение геометрии Merriam-Webster

ge · om · e · попробовать | \ jē-ˈä-mə-trē \

1а : раздел математики, который занимается измерением, свойствами и взаимосвязями точек, линий, углов, поверхностей и твердых тел. широко : изучение свойств заданных элементов, которые остаются неизменными при заданных преобразованиях.

б : особый тип или система геометрии Евклидова геометрия

б : форма поверхности (механической части или кристалла)

3 : расположение предметов или частей, напоминающее геометрические фигуры. геометрия неоклассической архитектуры

Что такое геометрия? — Определение, факты и примеры

Учитесь с помощью полной программы обучения математике K-5

Что такое геометрия?

Геометрия — это раздел математики, изучающий размеры, формы, углы расположения и размеры предметов.

Плоские формы, такие как квадраты, круги и треугольники, являются частью плоской геометрии и называются 2D-фигурами. Эти формы имеют только 2 измерения: длину и ширину.

Примеры двумерных форм в плоской геометрии

Твердые объекты также известны как трехмерные объекты, имеющие третье измерение высоты или глубины.

Примеры трехмерных форм в твердой геометрии

Угол :

Вершина фигуры, в которой встречаются два ребра, образуют угол.Различные геометрические формы имеют разные размеры углов.

Например, :

• Треугольник — это 3-сторонняя форма, размеры трех внутренних углов которого равны 180 °.

• Квадрат, прямоугольник или четырехугольник имеют четырехугольную форму, а их внутренние углы измеряются 360 °.

• Другие многоугольники, такие как пятиугольник, шестиугольник, семиугольник, восьмиугольник, имеют соответственно 5, 6, 7, 8 сторон и разные углы.

Примеры различных многоугольников с их углами и сторонами

Мы изучаем различные аспекты форм, такие как измерение углов, длины сторон, площади, объема и т. Д. В геометрии.

Сходство и соответствие — два важных аспекта геометрии.

Сходство : Сходство — это когда две формы одинаковы, но их размеры могут различаться.

Конгруэнтность : Конгруэнтность — это когда две формы абсолютно одинаковы по форме и размеру.

Координатная плоскость :

• Координатная плоскость — это двумерная поверхность, образованная двумя числовыми линиями, пересекающими друг друга под прямым углом.

• Горизонтальная числовая линия — это ось x, а вертикальная числовая линия — ось y.

• Пересечение двух осей — координата (0,0).

• Используя координатную плоскость, мы наносим точки, линии и т. Д. Соединяя различные точки на координатной плоскости, мы можем создавать формы.

Мы используем формулу и теоремы для решения геометрических задач.

Формула — это математическое уравнение для решения геометрической задачи, а теорема — это утверждение, которое доказывается с использованием ранее известных фактов.

Например, « Теорема Пифагора » доказала, что a2 + b2 = c2 для прямоугольного треугольника, где a и b — стороны прямоугольного треугольника, а c — гипотенуза.

Однако a2 + b2 = c2 — это формула для определения гипотенузы прямоугольного треугольника.

Интересные факты

Написание хорошего определения — Концепция

В геометрии необходимо, чтобы вы
могли написать хорошее определение, потому что
поможет вам понять свойства
того, о чем вы говорите.

Три ключевых компонента хорошего разрешения.

Первый, он использует ранее
определенных терминов.
Итак, если вы уже определили, что такое параллельные линии
, вы можете использовать это, чтобы определить
параллелограмм.

Во-вторых, он классифицирует и количественно оценивает.
То есть, классифицируя
, получается многоугольник?
Это линия?
Что это?
И определяет количество.
Итак, если вы говорите о многоугольнике, вы,
, захотите сказать, сколько сторон.

И, наконец, нет контрпримера.
Но что такое контрпример?
Контрпример — это что-то, пример,
, который сделает определение или гипотезу
неверными.
Итак, если вы можете найти контрпример вашему определению
, значит, вы написали плохой пример.

Вкратце, допустим, у меня есть квадрат
, и я сказал, что квадрат — это четырехугольник
.
Это означает, что у него четыре стороны.
И я просто оставил свое определение таким.
Превратил его в мистера Макколла.

Ну, я собираюсь сказать четырехугольник, колодец
, который может быть трапецией, где
я мог бы нарисовать одной парой
параллельных сторон.
Это может быть воздушный змей, у которого есть две пары
одинаковых последовательных сторон.
Я мог нарисовать ромб.
Я мог нарисовать параллелограмм.
Я мог бы привести множество контрпримеров
, которые сделают это определение
неверным или не сделают его конкретным
, достаточным только для квадрата.

Давайте посмотрим на два других.
Скажем так,
не имеет прямого отношения к геометрии, скейтборд.
Скажем, я определяю скейтборд как что-то
с колесами, на которых вы катаетесь.
Ну, это не очень наглядно.
Это плохое определение.
В первую очередь потому, что я могу сказать
, что это может быть байк, потому что велосипед
— это то, что имеет колеса
, на которых вы ездите.

Как насчет хорошего разрешения?
Хорошее определение параллелограмма — это четырехугольник
с двумя парами параллельных
конгруэнтных сторон.
Обратите внимание, что мы используем слова
, которые мы, вероятно, уже определили.
Итак, четырехугольник, мы бы определили, прежде чем
мы начали определять параллелограмм.
Четырехугольник имеет четыре стороны.
Мы говорим, что параллельные линии никогда не пересекаются.
Две прямые в одной плоскости
, которые никогда не пересекаются.
И конгруэнтный означает, что
имеют одинаковый размер или одинаковую длину.

Обратите внимание, что я смог написать это определение
параллелограмма, используя три слова
, которые я уже определил ранее
, и нет другого контрпримера
, который я мог бы нарисовать или придумать, который
сделал бы это неприменимым к параллелограмм.

Так что имейте это в виду, когда вы пишете
хороших определений, и это поможет вам
даже в тесте и викторинах.

Aplusmath: геометрические термины

	Сегменты перпендикулярной линии	два линейных сегмента, которые пересекаются, образуя углы 90 градусов
	Прямой угол	угол 90 градусов
	Равносторонний треугольник	треугольник со всеми сторонами равными и всеми углами равными
	Чешуйчатый треугольник	треугольник с тремя неравными сторонами и углами
	Вершина	точка пересечения двух сторон плоской фигуры
	Прямой треугольник	треугольник с одним внутренним углом, равным 90 градусам
	Пентагон	многоугольник с 5 сторонами и 5 углами
	Квадрат	прямоугольник, у которого все четыре стороны равной длины
	Сегменты пересекающихся линий	отрезки пересекающиеся друг с другом
	Острый угол	угол меньше 90 градусов, но больше 0 градусов
	аккорд	отрезок линии между двумя точками на заданной кривой
	Радиус	прямая линия, проходящая от центра круга или сферы до окружности или поверхности
	Линейный сегмент	одна часть строки
	Строка	непрерывная протяженность
	Путевая точка	позиция в космосе
	Параллелограмм	четырехугольник, у которого обе пары противоположных сторон параллельны друг другу Примечание: квадраты и прямоугольники тоже четырехугольники
	Прямоугольник	параллелограмм с четырьмя прямыми углами Примечание: квадрат — это тоже прямоугольник
	Ромб	равносторонний параллелограмм с косыми углами
	Сегменты параллельной линии	отрезки линии, которые не пересекаются
	Четырехугольник	многоугольник с четырьмя сторонами Примечание: квадраты, прямоугольники и трапеции тоже четырехугольники
	восьмиугольник	многоугольник, имеющий восемь углов и восемь сторон
	Круг	замкнутая плоская кривая, состоящая из всех точек на заданном расстоянии от точки внутри нее, называемой центром
	Трапеция	четырехугольная плоская фигура, имеющая две параллельные и две непараллельные стороны
	Луч	часть прямой линии, которая, как считается, начинается в точке на линии и продолжается в одном направлении от этой точки
	Замкнутая кривая	кривая, которая является непрерывной и имеет концы, которые встречаются в одной точке
	Равнобедренный треугольник	треугольник, у которого две стороны равны
	Шестигранник	многоугольник с шестью сторонами и шестью углами
	Диаметр	прямая линия, проходящая через центр круга или сферы и встречающаяся с окружностью или поверхностью на каждом конце
	Тупой угол	угол больше 90 градусов, но меньше 180 градусов

определение геометрии Free Dictionary

Например, геометрия, которой вас учили в школе, основана на заблуждении.«Спасибо, я закончила с геометрией, изучением или преподаванием», — сказала Энн Ширли немного мстительно, когда она швырнула несколько потрепанный том Евклида в большой ящик с книгами, торжественно хлопнула крышкой и села глядя на Дайану Райт через чердак Зеленых Мезонинов серыми глазами, подобными утреннему небу. Вы знаете, что изучающие геометрию, арифметику и родственные науки предполагают четное и нечетное, а также числа и три вида углов и т.п. в их нескольких областях науки; это их гипотезы, которые они и все должны знать, и поэтому они не снисходят до того, чтобы давать какой-либо отчет о них ни себе, ни другим; но они начинают с них и продолжаются до тех пор, пока не придут, наконец, и последовательно, к своему заключению? Ибо в науках, использующих демонстрацию, есть то, что предшествует, и то, что является последующим по порядку; в геометрии элементы предшествуют предложениям; при чтении и письме буквы алфавита предшествуют слогам.Он сам взял на себя образование своей дочери и, чтобы развить в ней эти две основные добродетели, давал ей уроки алгебры и геометрии, пока ей не исполнилось двадцать, и устроил ее жизнь так, что все ее время было занято. Соответственно, видя, что наши чувства иногда обманывают нас, Я был готов предположить, что на самом деле ничего такого, как они нам преподнесли, не существовало; и поскольку некоторые люди ошибаются в рассуждениях и впадают в паралогизмы даже в простейших вопросах геометрии, я, убежденный, что я подвержен ошибкам, как и любой другой, отверг как ложные все рассуждения, которые я до сих пор принимал для демонстрации; и, наконец, когда я подумал, что те же самые мысли (представления), которые мы переживаем, когда бодрствуем, могут также испытываться, когда мы спим, хотя в то время ни одна из них не является истинной, я предположил, что все объекты (представления), которые когда-либо приходили мне в голову, когда бодрствовали, содержали в себе не больше правды, чем иллюзии моих снов.К концу семестра Энн и Гилберт были переведены в пятый класс и позволили начать изучение элементов «ветвей», под которыми подразумевались латынь, геометрия, французский язык и алгебра. — горшок с пекодом, вокруг которого старательно кружит мыльный камень, что меня первым косвенно поразил тот замечательный факт, что в геометрии все тела, скользящие по циклоиде, например, мой мыльный камень, будут спускаться из любой точки в одно и то же время К этому же принципу относятся геометрические максимы: «Целое больше своей части; одинаковые вещи равны друг другу; две прямые линии не могут окружать пространство; и все прямые углы равны друг другу.»Такую же природу имеют и другие максимы этики и политики, что не может быть следствия без причины; что средства должны быть соразмерны цели; что каждая сила должна быть соразмерна своему объекту; что должна быть не быть ограничением силы, предназначенной для достижения цели, которая сама по себе не может быть ограничена. Самый подлый математик в Космической стране с готовностью поверит мне, когда я буду утверждать, что проблемы жизни, которые возникают перед хорошо образованными, — когда они сами в движении, вращении, продвижении или отступлении, и в то же время попытки различить посредством зрения между несколькими многоугольниками высокого ранга, движущимися в разных направлениях, как, например, в бальном зале или в беседе, — должны иметь природа бросает вызов угловатости самых интеллектуальных и полностью оправдывает богатые способности ученых профессоров геометрии, как статической, так и кинетической, в прославленном университете Вентбриджа, где наука и Искусство распознавания зрения регулярно преподается в больших классах ЭЛИТЫ США.«Вы научились чему-нибудь в Редмонде, кроме мертвых языков, геометрии и всего такого мусора?» — спросила тетя Джемсина. В то время как Дедал, который силен, сдержан; в то время как Орфей, который является разумом, пел: — столб, который представляет собой букву; аркада, представляющая собой слог; пирамида, то есть слово, — все приводились в движение сразу по закону геометрии и по закону поэзии, сгруппировались, объединились, слились, спустились, поднялись, расположились бок о бок на земле, выстроились в ряд в рассказах в небе, пока они не написали под диктовку общей идеи эпохи, те чудесные книги, которые также были чудесными зданиями: Пагода Эклинга, Рамсейон Египта, Храм Соломона.

геометрических фигур (определение, примеры и видео) // Tutors.com

Геометрические фигуры (определение, характеристики, примеры и видео)

---

видео Определения Точка Линия Самолет Определенные термины

Весь этот урок посвящен трем мощным геометрическим элементам, которые не определены и составляют фундамент классической геометрии. Если вы научитесь понимать точку, линию и плоскость, вы сможете строить империи в своем уме.

Что вы узнаете:

Пройдя этот урок и видео, вы сможете:

• Напомните и опишите математические постулаты, относящиеся к геометрическим точкам, линиям и плоскостям
• Приведите характеристики этих трех неопределенных элементов
• Предоставьте реальные примеры в виде моделей точек, линий и плоскостей
• Определите термины «компланарный», «коллинеарный» и «неколлинеарный».

Постулат и неопределенный термин

В геометрии постулат (или аксиома) — это утверждение, принимаемое как истинное, принимаемое как истинное и не требующее доказательств.Вы можете думать об аксиоме или постулате как об определении вещи.

Неопределенный термин , напротив, не является определением геометрического элемента; это вместо этого его описание. Определение дает ощущение полноты: это то, что мы определили, а это — нет. Неопределенный термин — это то, что несет в себе существенную истину, и мы не можем точно определить его.

Три основные истины

Три элемента или термина в геометрии не определены:

1. точка
2. Строка
3. Самолет

Мы можем построить все остальное (многоугольники, твердые тела, косые линии, декартовы графы, круги — все) из этих трех членов.

Путевая точка

точка в геометрии описывается как место в пространстве, которое не имеет размера. Его можно пометить (Точка G), его можно расположить на координатном графике с использованием координат x, y (3, 5), а также обозначить на чертежах точкой.

Вы не можете сказать, что точка имеет ширину, длину, глубину или толщину. У него нет измеримого измерения.

Что трудно согласовать с этим описанием, так это то, что точки могут быть собраны вместе, чтобы образовать линию, или треугольник, или квадратную пирамиду, или что угодно.

Поскольку мы используем , описывающий точку, а не , определяющий ее, мы «позволяем» точке делать много вещей. Вам нужны только две точки, чтобы создать линию, соединив набор всех точек между двумя названными точками. Три точки способны определить самолет.

Если вы хотите быть абсурдистом, между любыми двумя точками на линии находится бесконечное количество других точек, но такой аргумент становится… бессмысленным.

Строка

Линия описывается как набор точек, продолжающихся бесконечно в двух направлениях.Он описывается как имеющий только одно измерение (длину), без какой-либо толщины или глубины.

Он обозначен и нарисован путем обозначения двух точек вдоль него и обозначения их заглавными буквами, а затем соединения их, ну, ну, ну, линии. Поместите стрелки на обоих концах нарисованной линии, и вы получите линию. Вы также можете использовать одну строчную букву для обозначения строки.

Евклид любил строчки. Он создал несколько постулатов о линиях, начиная со слов «две точки определяют линию» и опираясь на этот успех, чтобы показать, что сегмент линии может стать линией, а сегмент линии можно использовать для построения круга с одной конечной точкой в ​​качестве центра и другая конечная точка — как радиус.

Линии на плоскости могут быть параллельными или пересекающимися. Если они пересекаются под углом 90 °, они образуют прямой угол, что является еще одним постулатом Евклида. Он был без ума от реплик.

Более современный постулат о линиях состоит в том, что с их помощью можно установить взаимно однозначное соответствие с множеством всех целых чисел. Джордж Дэвид Биркофф назвал это предположением числовой линии .

Самолет

Плоскость — это теоретическая плоская поверхность, которая навсегда простирается в двух измерениях.Он не имеет толщины, но имеет бесконечную ширину и длину. Безразмерные точки могут лежать на (или «внутри») плоскостях.

Люди часто склонны думать о моделях самолетов как об игральных картах, бумаге для рисования или листах картона. Все они являются адекватными трехмерными моделями самолетов, но ни одна из них не обладает точностью, чтобы по-настоящему описать самолет.

Идеальный самолет существует только в вашей голове. Игральные карты кажутся хорошей заменой, но они заканчиваются краями и имеют небольшую толщину.Листы рисовальной бумаги начинаются как хорошие модели, но они хрупкие и деформируются. У них тоже есть некоторая толщина.

В уме вы должны представить идеально гладкую, непоколебимую поверхность, выходящую за пределы вашей способности видеть, только в двух направлениях. У самолета есть ширина и длина, но нет толщины. Когда две плоскости пересекаются, точки пересечения образуют линию.

Три определяемых термина

Три определенных термина происходят от трех неопределенных терминов.

Копланарный

В отличие от точки, линии и плоскости, можно определить компланарность.Точки и линии, лежащие в одной плоскости, копланарны. Это слово произносится как «co- plane -ar». Для существования плоскости необходимы три компланарные точки (и только одна плоскость может содержать эти три точки).

Копланарные объекты могут быть интересны только тогда, когда у нас их больше трех. Четыре точки не только определяют плоскость, но и компланарны, эта четвертая точка скрепляет сделку.

В заключение, копланарность имеет собственное определение: «находиться в одной плоскости».«

Коллинеарный

Точки коллинеарны, если совпадают. Для определения линии необходимы две точки; все точки, которые также попадают на эту линию, называются коллинеарными. Слово произносится как два слова: «co linear».

Подводя итог, слово «коллинеарность» имеет собственное определение: «лежать в одной строке».

Неколлинеарность

Точки неколлинеарны, если не все они лежат на прямой линии. Три точки должны быть неколлинеарными, чтобы создать плоскость, и каждая плоскость включает три неколлинеарных точки.Другими примерами неколлинеарных точек являются вершины любого и всех многоугольников.

Подводя итог, неколлинеарность имеет собственное определение: «не лежать в одной строке».

Краткое содержание урока

Теперь, когда вы внимательно изучили весь урок, вы можете вспомнить и описать математические постулаты, относящиеся к геометрическим точкам, линиям и плоскостям, указать характеристики этих трех неопределенных элементов и привести примеры из реальной жизни в качестве моделей точек, линии и плоскости.Вы также можете определить термины «копланарный», «коллинеарный» и «неколлинеарный».

Следующий урок:

Косые линии

Что такое вершина в геометрии? — Определение и примеры — Видео и стенограмма урока

Углы

Вершины обычно используются в геометрии при работе с углами. Угол — это мера между двумя линиями, лучами или сегментами, которые встречаются в вершине. Эти два отрезка образуют угол.Например, угол, который обычно встречается в геометрии, составляет 45 градусов. Градус — это мера 1/360 круга.

Полигоны

В полигонах также видны вершины. Полигоны — это двухмерные объекты, состоящие из отрезков прямых линий. Двумерные объекты имеют длину и ширину, но не имеют глубины. Примерами многоугольников являются квадраты, прямоугольники, треугольники и восьмиугольники. Сама по себе линия не будет считаться многоугольником, потому что многоугольники должны быть замкнуты, что означает, что каждый сегмент линии должен касаться концов двух других сегментов линии.Чтобы многоугольник был замкнутым, он должен иметь как минимум три линейных сегмента без промежутков между сегментами.

По своей природе многоугольники имеют несколько вершин. В многоугольниках эти отрезки часто называют сторонами. У квадрата четыре стороны и четыре вершины, по одной в каждом углу. У восьмиугольника восемь вершин на стыке каждой из сторон. У треугольника три вершины. Это также означает, что треугольник имеет три угла, которые можно измерять в градусах.

Трехмерные объекты

Трехмерные или трехмерные объекты также имеют вершины.Это объекты с длиной, шириной и глубиной, а не просто длиной и шириной, как двухмерные объекты. Примеры трехмерных объектов — кубы и сферы. Но помните, только объекты с прямыми линиями имеют вершины.

В трехмерных объектах вершина по-прежнему находится там, где встречаются два отрезка линии. Эти линейные сегменты часто называют ребрами в трехмерных объектах. У куба двенадцать ребер; эти двенадцать ребер пересекаются в восьми разных вершинах.