Урок геометрии в 8 классе Теорема Пифагора

Сахаров Алексей Павлович, учитель математики,

Частное общеобразовательное учреждение «Школа – интернат №3

среднего общего образования ОАО «РЖД» г. Ртищево Саратовской области

Конспект урока геометрии в 8 классе по теме: «Теорема Пифагора»

Тема урока: «Теорема Пифагора».

Цель урока: Дать понятие о теореме Пифагора, о многообразии способов ее доказательства, первичное применение теоремы для решения задач.

Задачи урока:

1. исследовать закономерности между сторонами прямоугольного треугольника; изучить теорему Пифагора; формировать умения применять теорему Пифагора при решении задач;

2. УУД:

• Познавательные: развивать основы логического и алгоритмического мышления; расширять кругозор учащихся; развивать интерес к математике.

• Регулятивные: развивать умения читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;

• Коммуникативные: строить высказывания, аргументировано доказывать свою точку зрения;

• Личностные: развивать навыки сотрудничества со сверстниками, внимания, памяти, воображения.

Тип урока: формирование новых знаний и умений.

Формы работы учащихся: фронтальная, индивидуальная, групповая.

Необходимое техническое оборудование: компьютер, проектор.

Дидактические средства: учебник, электронная презентация, раздаточный материал.

Методы и приемы: фронтальная работа, сочетающаяся с общеклассной; частично-поисковый метод; индивидуальная работа; работа в парах. 

Эпиграф урока: “Геометрия владеет двумя сокровищами, одно из них – …”. (слайд 1)

Иоганн Кеплер

План урока:

1. Организационный момент. (1 мин.)

2. Устная работа. (10 мин.)

3. Проблемная ситуация. (5 мин.)

4. Сообщение главной цели урока.

5. Исследовательская работа (в парах).

6. Изучение нового материала. (10 мин.)

7. Физминутка.

8. Закрепление изученного материала. ( решение задач) (10 мин.)

9. Применение теоремы Пифагора.

10. Подведение итога урока. (1 мин.)

11. Домашнее задание. (3 мин.)

12. Рефлексия.

Ход урока.

1. Организационный момент.

2. Устная работа.

Какая геометрическая фигура изображена на экране? (слайд 2).

Какой треугольник называется прямоугольным?

Сторона прямоугольного треугольника, лежащая против прямого угла, называется… (слайд 3).

Стороны, образующие прямой угол, называются…

Учитель. Сформулируйте свойства прямоугольных треугольников, которые мы уже знаем (слайд 4).

Продолжите предложения:

1. Сумма двух острых углов прямоугольного треугольника равна . (слайд 5).

По рисунку найдите угол 3 если сумма углов 1 и 2 равна 90⁰. (слайд 6).

2. Катет прямоугольного треугольника, лежащий против угла в

   , равен половине гипотенузы. (слайд 7).

— Один из углов прямоугольного треугольника равен 15°. Чему равны остальные углы?

— Один из углов из углов прямоугольного треугольника равен 30°, катет, противолежащий ему, равен 13 см. Чему равна гипотенуза?

— Катет прямоугольного треугольника равен 16 дм, гипотенуза – 32 дм. Найдите углы треугольника.

Учитель. — Сформулируйте признаки равенства прямоугольных треугольников

Сначала учащиеся формулируют признаки равенства прямоугольных треугольников, а затем переходим к решению задач на доказательство по готовым чертежам:

Докажите, что треугольники равны. (слайд 8).

Учитель. Посмотрим, что вы помните о свойствах площадей: (слайд 8).

— Равные многоугольники имеют … (слайд 9).

— Если многоугольник составлен из нескольких многоугольников, то его площадь равна … (слайд ).

— Площадь квадрата равна … (слайд 10).

— Сторона квадрата 14 см. Чему равна площадь квадрата?

— Площадь квадрата 225 м². Найдите его сторону.

— Площадь прямоугольного треугольника равна … (слайд 11).

— Катеты прямоугольного треугольника 4 см и 8 см. Найдите его площадь.

3. Проблемная ситуация.

А теперь давайте решим небольшую задачу. (слайд 12)

Задача 1. Велосипедист и пешеход отправились одновременно из одного населенного пункта в противоположных направлениях. Пешеход пошел на запад со скоростью 5 км/ч, а велосипедист поехал на восток со скоростью 12 км/ч. Какое расстояние будет между ними через час?

На каком предмете обычно решают такие задачи?

Задача 2. Велосипедист и пешеход отправились одновременно из одного населенного пункта в разных направлениях. Пешеход пошел на юг со скоростью 5 км/ч, а велосипедист поехал на восток со скоростью 12 км/ч. Какое расстояние будет между ними через час? (слайд 13)

Какая фигура получилась? Какие стороны известны? Что найти?

Тех знаний о прямоугольном треугольнике, которые мы имеем, не хватает. Последнюю задачу решить не можем.

Сформулируйте то, что мы должны знать, чтоб решить эту задачу? Это и будет целью нашего урока.

4. Сообщение главной цели урока.

Цель нашего урока как раз и заключается в том, чтобы выяснить, как связаны между собой стороны прямоугольного треугольника. (слайд 14)

5. Исследовательская работа (в парах).

Чтоб это выяснить, мы займемся исследовательской деятельностью. Работаем в парах.

1) Учащиеся, получившие бумажные треугольники, выполняют задание:

а) Измерьте стороны треугольников и заполните таблицу на доске:

№

a

b

c

a ²

b ²

c ²

a ² + b ²

1.

8

15

17

64

225

289

289

2.

7

24

25

49

576

625

625

3.

6

8

10

36

64

100

100

2) (дополнительное) Я вам раздам лист, на котором оранжевым цветом закрашен равнобедренный прямоугольный треугольник, на сторонах которого построены квадраты. Ответьте на два вопроса и сделайте вывод.

Вывод: Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Так изначально формулировалась теорема Пифагора.

1. Вычислите, чему равен квадрат гипотенузы.

2. Найдите сумму квадратов катетов.

3. Какой можно сделать вывод?

Ученик. Квадрат гипотенузы равен сумме квадратов катетов.

Можно ли из данных этой работы сделать такой вывод о связи катетов и гипотенузы всех прямоугольных треугольников? (Нет, т. к. из частных случаев не следуют общие заключения).

Учитель.

То, к чему мы пришли опытным путем, доказал древнегреческий ученый Пифагор в 6 в. до н. э. Он не открыл эту теорему (она была известна еще в Древнем Египте и Вавилоне), а нашел ее доказательство.

Итак, какова же тема нашего сегодняшнего урока? ( «Теорема Пифагора»). (слайд 15)

Эта теорема является основой решения множества геометрических задач и базой изучения теоретического материала в дальнейшем. Сама же теорема Пифагора замечательна тем, что она проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное практическое значение: она применяется в геометрии буквально на каждом шагу.

Докажем эту теорему и решим несколько задач с её применением.

Вероятно, факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников (слайд 16).

Предполагают, что во времена Пифагора теорема звучала так:

«Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».

Действительно, с² – площадь квадрата, построенного на гипотенузе, а² и b² – площади квадратов, построенных на катетах.

Квадрат, построенный на гипотенузе, содержит четыре треугольника. А на каждом катете построен квадрат, содержащий два треугольника. На рисунке вы видите, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.

В древние времена, доказывая эту теорему, чертили чертёж и просто говорили: «Смотри!».

Возникает вопрос, для любого ли прямоугольно треугольника справедливо это равенство или только для равнобедренного прямоугольного треугольника?

6. Изучение нового материала.

«Для того чтобы усовершенствовать ум, надо больше рассуждать, чем заучивать».

                                                                                                   Р. Декарт

Учитель.

— А кто из вас что-нибудь слышал об этой теореме? (Пифагоровы штаны на все стороны равны).

— Действительно, это шуточная формулировка теоремы. Почему так говорят, вы узнаете несколько позже, сейчас докажем теорему Пифагора в современной формулировке. Я хочу, чтобы вы попробовали доказать её сами, используя свойства площадей и метод, который мы использовали при введении формул сокращённого умножения, при выводе формул площадей некоторых фигур.

Теорема:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Выделите в данной теореме условие и заключение.

Ученик. Условие: в прямоугольном треугольнике. Заключение: квадрат гипотенузы равен сумме квадратов катетов.

Итак, нам дан прямоугольный треугольник с катетами a, b, гипотенузой с.

а

в

Запись на доске:

А

с

с

а

в

Дано:

с

в

∆АВС;

с

С=90;

с

а

а

в

С

В

АВ=с;

ВС=а;

а

в

АС=в;

Док-ть:

Учитель. Доказательство:

1. Достроим прямоугольный треугольник c катетами a, b, гипотенузой с до квадрата со стороной a+b. (Далее доказательство сопровождается пошаговой иллюстрацией производимых действий).

2. Площадь S этого квадрата равна

3. С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна, и квадрата со стороной , поэтому

4. Таким образом,

Теорема доказана.

Найдите формулировку теоремы в учебнике.

6. Физминутка.

Устали? Чтоб немного отдохнуть от умственной деятельности, давайте разомнемся!

Минута отдыха. Стихотворение, посвящённое теореме.

Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путём
К результату мы придём.

6. Закрепление изученного материала (решение задач).

Мы доказали с вами одну из важнейших теорем геометрии. Давайте попробуем решить с её помощью несколько задач по готовым чертежам устно (слайд 17).

Все задачи можно разделить на два типа

Задача 1

Замечание: Из курса алгебры известно, что уравнение АВ= 100 имеет два корня АВ = +. АВ = -10 не удовлетворяет условию задачи, так как длина стороны треугольника всегда положительна. Значит АВ = 10. В дальнейшем при решении уравнений в подобных задачах, мы будем находить только положительные корни, и не будем объяснять каждый раз почему отрицательные корни отбрасываются.

Задача №2

Мы с вами получили треугольник со сторонами 3, 4 и 5 единиц. Это единственный прямоугольный треугольник, стороны которого равны трём последовательным натуральным числам. Его часто называют египетским треугольником, так как он был известен ещё древним египтянам. Они использовали этот треугольник в «правиле верёвки» для построения прямых углов при закладке зданий, храмов, алтарей и т.п. Об этом мы поговорим подробнее на следующем уроке.

Вернёмся теперь к задаче про велосипедиста и пешехода, которую мы не смогли решить в начале урока. (слайд 18).

Теперь мы легко можем найти расстояние, которое будет между велосипедистом и пешеходом через 1 час.

Рассмотрим ещё две задачи не из школьного учебника.

Решение задачи индийского математика XII века Бхаскары (слайды 19 — 20)

и из учебника Леонтия Магницкого. (слайд 21).

6. Применение теоремы Пифагора.

Значение теоремы Пифагора состоит в том, что из нее или с ее помощью можно вывести множество теорем геометрии и решить много задач. (слайд 22)

ВИДЕО

Видеоролик мультяшной формы из интернета (1,5 мин.) (переход по гиперссылке к слайду 25).

6. Подведение итогов.

Итак, сегодня на уроке мы познакомились с одной из главных теорем геометрии — теоремой Пифагора и её доказательством, с некоторыми сведениями из жизни учёного, имя которого она носит, решили несколько простейших задач.

Теорема Пифагора замечательна и тем, что сама по себе она вовсе не очевидна, не смотря на внешнюю простоту.

Например, свойства равнобедренного треугольника можно видеть непосредственно на чертеже.

Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: c² = a² + b².

Кто уже запомнил формулировку теоремы Пифагора?

Пригодятся вам эти знания?

Популярность теоремы настолько велика, что доказательств очень-очень много. В некоторой литературе указывается, что их более 500. Может, вы сами захотите найти другие доказательства, больше узнать о Пифагоре. На следующем уроке мы рассмотрим некоторые из них.

6. Домашнее задание (слайд 23).

• п. 54. № 483, 484

• Почему теорему Пифагора называли «Теоремой невесты»?

• Найти какое-нибудь доказательство, отличное от рассмотренных на уроке (по желанию).

6. Рефлексия

Понравился вам урок?

Памятник Пифагору находится в порту города Пифагория на острове Самос и напоминает всем о теореме Пифагора, наиболее известном его открытии. Катет, лежащий в основании треугольника — мраморный, гипотенуза и фигура самого Пифагора в виде второго катета — медные. (слайд 24).

СПАСИБО ЗА УРОК!

Урок математики «Теорема Пифагора»

Муниципальное казенное общеобразовательное учреждение

средняя общеобразовательная школа №2

Методический проект урока

Геометрия

8 класс
Тема: Теорема Пифагора

Учитель:

Астафьева

Ирина Владиславовна

высшая квалификационная категория

г. Пласт

2014г.

Тема: Теорема Пифагора.

Цели урока:

1.Подвести учащихся к выводу теоремы Пифагора путём измерительных работ и логических рассуждений, доказать теорему Пифагора, формировать практические навыки применения данной теоремы.

2.Способствовать развитию гибкости мышления, умений анализировать, устанавливать связи ранее изученного материала с новым и осуществлять доказательные рассуждения .

3.Воспитывать культуру общения, умение вести дискуссию .Прививать устойчивый интерес к изучению математики , показывая красоту математических доказательств, их стройность, логичность. Создать условия для расширения общего кругозора учащихся, используя исторический материал.

Тип урока: урок изучения и первичного закрепления новых знаний .

Оборудование: ( мультимедийный проектор, компьютер, экран, презентация, портрет Пифагора).

ХОД УРОКА

1. Организационный момент.(3мин)

Ребята, я рада видеть вас на нашем уроке и предлагаю вам перенестись в Древнюю Грецию и стать учениками пифагорейской школы. Мне хотелось бы узнать с каким настроением, вы отправляетесь в путешествие. Мне приятно, что в основном у вас хорошее или отличное настроение, я обещаю, что к концу урока оно не испортится.

Презентация

На доске написана тема урока, портрет Пифагора, изображение пирамид и прямоугольных треугольников.

Учитель: Ребята, внимательно посмотрите на доску и ответьте на вопросы:

-Как вы думаете, что нам предстоит сделать сегодня на уроке?

-А для чего мы будем изучать эту теорему?

— Как вы думаете, почему она называется именно так? —

Кто-нибудь слышал имя этого ученого?

II. Вступительное слово учителя.

Таким образом подведем итог ваших размышлений. И так во время путешествия мы изучим одну из важнейших теорем геометрии – теорему Пифагора. Эта теорема является основой для решения многих геометрических задач и базой изучения теоретического материала в курсе геометрии 7-11класса.

III. Актуализация знаний.(10мин)

Учитель: Открыли рабочие тетради, записали число, классная работа, тема урока:

» Теорема Пифагора».

Для того чтобы наша работа была успешной, повторим некоторые геометрические факты.

—  Сформулируйте определение прямоугольного треугольника?

—  Как называются стороны прямоугольного треугольника?

—  Формула площади прямоугольного треугольника?

—  Формула площади квадрата?

-Свойство площадей?

Слайд 2– прямоугольный треугольник.
Слайд 3 – площадь квадрата.

Учитель: При решении геометрических задач нам приходится находить длины сторон прямоугольного треугольника, всегда ли это возможно? Постройте в тетради прямоугольный треугольник, катеты которого равны 3см и 4см. Можно ли вычислить длину гипотенузы? (учащиеся высказывают свои предположения, наверняка появится версия, что гипотенузу можно измерить, пользуясь линейкой).

Учитель: Т.о практическим путем мы установили , если катеты прямоугольного треугольника равны 3см и 4см, то гипотенуз равна 5см. В геометрии такой треугольник называют египетским треугольником.

Всегда ли можно пользоваться этим способом для нахождения гипотенузы?

Ученики: Этим способом можно пользоваться, только при малых длинах.

Учитель: По всей видимости надо установить закономерность между сторонами прямоугольного треугольника, для этого решим практическую задачу.

Практическая работа исследовательского характера.

(работа в парах)(Слайд 4).

Построить прямоугольные треугольники с катетами:

1 ряд	2 ряд	3 ряд
12см и 5см	6см и 8см	8см и 15см

Измерить гипотенузу, результаты занести в таблицу.

a	12	6	8
b	5	8	15
c	13	10	17

Учитель: Постараемся выразить формулой зависимость между длинами катетов и гипотенузой в прямоугольных треугольниках.

Ученики выдвигают свои гипотенузы, которые обсуждаются.

Учитель: Попытаемся установить соответствие между квадратами длин катетов и квадратом длины гипотенузы.( для всех трех условий аналогичные рассуждения)

	длины	квадраты длин
a	12	144
b	5	25
c	13	169

Учитель: Проанализируйте числовые значения в последнем столбике. Какую закономерность мы наблюдаем?

Ученики: «В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы».

Учитель: Аналогическую закономерность установил древнегреческий ученый Пифагор, его открытие назвали Теоремой Пифагора, существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.). Чуть позже мы рассмотрим одно из доказательств, приведенных в учебнике.

Слайд 5, 6.Сейчас послушаем рассказ о математике, именем которого она названа.

( сообщение ученика).( 3мин)

ПИФАГОР САМОССКИЙ (ок.580 – ок. 500г. до н.э.)

О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море, поэтому его называют Пифагором Самосским.
В молодости Пифагор был учеником Фалеса, побывал в Египте, где учился у жрецов.

В 530 г. до н.э. Пифагор основал так называемую пифагорейскую школу. Около сорока лет учёный посвятил себя, созданной им школе. Учеников школы называли пифагорейцами. Они занимались не только математикой, но и философией, естественными науками.
Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев.

Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя.

Физминутка(2мин)

IV. Этап усвоения новых знаний и способов действий. (10мин)

Работа над теоремой( на основе сотрудничества с учащимися).

Слайд 7 — «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов» с² = а² +b²(доказательство выполняют у доски).

Дано: Прямоугольный треугольник a, b – катеты, с — гипотенуза

Доказать:

c² = a² + b²

Доказательство.

Продолжим катеты прямоугольного треугольника: катет а — на длину b, катет b – на длину а.

— До какой фигуры можно достроить треугольник? Почему до квадрата? Чему будет равна сторона квадрата?

Достроим треугольник до квадрата со стороной: а + b.

— Как можно найти площадь этого квадрата?

Площадь квадрата равна

— Разобьем квадрат на части: 4 треугольника и квадрат со стороной с.

— Каким образом ещё можно найти площадь исходного квадрата?

— Почему равны получившиеся прямоугольные треугольники?

С другой стороны,

Приравняем получившиеся равенства:

Теорема доказана.

Учитель: Ребята, заучите формулировку теоремы.(спросить несколько человек, учитывая способности детей).

Слайд 8. — теорема Пифагора (в стихах).

VI. Этап первичной проверки понимания изученного. (12мин) Решение задач (презентация).

Учитель: Умение верно применять теорему Пифагора при решении задач различной степени сложности поможет нам успешно сдать экзамены в 9 и в11 классе.

Решим две задачи и сделаем вывод, что в них есть общего, а что отличного .

Слайд 9 — задача № 1.Найдите длину гипотенузы.(Учащиеся выполняют решение на доске, оформление решения, еще раз просматривают по презентации. Еще раз делают вывод, как найти длину гипотенузы).
Слайд 10,11 — задача №2. Найдите длину одного из катетов.( рассмотреть два способа решения, сформулировать правило, как найти квадрат неизвестного катета, использовать его в дальнейшем при решении задач).

VI I .Этап информирования учащихся о домашнем задании, инструктаж по его выполнению. (2мин)
Слайд 12 — разноуровневое домашнее задание Дети получают дифференцированное домашнее задание. Выбирают сами, в зависимости от того, какую оценку хотят получить. Записывают в дневник.

«5» -задача № 484(г, д ), 486(б, в)

«4» — задача № 484.№486(а)
«3» — задача № 483.

Выучить теорему с доказательством(стр. 130)

Творческая работа : найти и записать другие способы доказательства данной теоремы.(по желанию)

VIII. Этап рефлексии и оценивания. Подведение итогов урока.(3мин)

Рефлексия (по методу неоконченных предложений).Слайд 13.

• Сегодня на уроке я научился…

• Сегодня на уроке мне понравилось…

• Сегодня на уроке я повторил…

• Сегодня на уроке я поставил себе оценку…

• Что вызвало затруднения?

• Над чем следует еще поработать?

Оценивается работа класса в целом, выделяя отдельных учеников.

Ожидаемый результат:

1-й уровень: каждый ученик должен знать зависимость между сторонами прямоугольного треугольника, уметь применять теорему Пифагора для решения задач.

2-й уровень:

каждый ученик должен знать зависимость между сторонами прямоугольного треугольника, уметь доказывать теорему Пифагора, уметь применять теорему Пифагора для решения задач.

3-й уровень:

каждый ученик должен знать зависимость между сторонами прямоугольного треугольника, уметь доказывать теорему Пифагора, уметь применять теорему Пифагора для решения нестандартных задач.

СПАСИБО ЗА УРОК.

Урок по геометрии для 8 класса на тему «Теорема Пифагора»

Тема урока: “ТЕОРЕМА ПИФАГОРА”

Цели:

— расширить круг геометрических задач, решаемых школьниками; обучать учащихся применять полученные знания к решению прикладных задач;

-развивать познавательный интерес в изучении геометрии, при осуществлении межпредметной связи геометрии с алгеброй, географией, историей, литературой;

-формирование целостного отношения к окружающему миру посредством математики; воспитание чувства ответственности, умения работать в коллективе.

Ход урока:

1.Оргмомент. (1 мин)

Приветствие, настрой на работу, раздача конфет с разноцветными обертками.

2.Проверка домашнего задания.(1 мин)

— Ребята, в качестве д/з к этому уроку вы получили карточки с заданием:

Заполните таблицу, используя теорему Пифагора

№

a

b

c

Соответствующая ответу буква

1

6

8

2

1

1

3

12

15

4

11

20

5

3

4

6

1

7

1) И 11 2) Е √2 3) Н 3 4) И 279 5) В √5 6) Р 5√2

К 10 Ж 1 О 27 К 17 Г 25 С 50

Л 100 З 2√2 П 9 Л √279 Д 7 Т 25

М √10 И 2 Р 81 М 21 Е 5 У 5

Какое слово у вас получилось? Правильно! Молодцы! (Слайд 1) Иоганн Кеплер – нем.математик, астроном, механик, первооткрыватель законов движения планет Солнечной системы.

Иоганну Кеплеру принадлежат слова, которые я взяла в качестве эпиграфа к нашему уроку: «Геометрия владеет двумя сокровищами, одно из которых теорема Пифагора»

3.Сообщение темы и целей урока. (Слайд 2) (2 мин)

— Как же называется тема нашего урока.

-Правильно! Теорема Пифагора. Откройте тетради и запишите число, классная работа и тему урока.

-Ребята, вы уже изучили теорему Пифагора. Чем же мы займемся на уроке? Правильно, решением задач с использованием теоремы Пифагора и рассмотрим практические задачи.

4.Актуализация опорных знаний.(8 мин)

1) Один ученик подготовил презентацию о Пифагоре.

2) Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с его теоремой. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора это её простота, красота, значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о её широком применении.

3) Сформулируйте теорему Пифагора. (Слайд 4)

— Правильно! В современных учебниках она так и сформулирована. А во времена Пифагора она звучала так: площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

4) Устная работа «Теорема Пифагора в жизни» (Слайд 5)

Дом шириной 8 м надо покрыть крышей высотой 2 м. Какой длины нужны стропила?

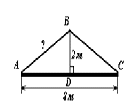
СТРОПИ́ЛО (др.-русск. стропъ — «крыша, потолок») — несущая, поддерживающая конструкция двускатной кровли.

5.Решение задач. (10 мин)

1)Задача из учебника Леонтия Магницкого «Арифметика», 18 век

Случися некоему человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготою 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.

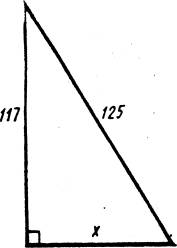
Решение:

x²+117²=125² x²=44² x=44 Ответ: 44 стопы

2) Задача №24 из демоверсии ОГЭ по математике 2015 года.

В прямоугольном треугольнике АВС угол С равен 90⁰, катеты АС=6, ВС=8. Найдите медиану СК этого треугольника.

6.Работа с кейсом «Помогла теорема Пифагора» (15 мин)

— Мы с вами рассмотрели много примеров применения теоремы Пифагора. Сейчас познакомимся с ещё одним. Я прошу разделиться на команды следующим образом: у кго красные конфеты – 1 группа, желтые – 2 группа, синие – 3 группа, зеленые – 4 группа.

Кейс «Помогла теорема Пифагора».

Действующие лица: — подозреваемый, следователь, потерпевший.

Цели:

-закрепить изучаемый материал.

-показать применение теоремы Пифагора в жизненной ситуации.

Проблемная ситуация: доказать с помощью теоремы Пифагора невиновность или виновность подозреваемого.

Этот эпизод взят из реальной следственной практики. Получив сообщение о краже, следователь выехал на место происшествия. Заявитель утверждал, что преступник проник в помещение, где хранились ценности, через окно. Осмотр показал, что подоконник находится на расстоянии 150 см от земли. Поверхность земли на расстоянии 200 см. от стены здания покрыта густой порослью, не имевшей никаких следов повреждений. При осмотре не было найдено никаких технических средств типа лестницы. Возникло предположение, что преступник проникал в помещение через окно каким-то образом преодолев расстояние между наружным краем поросли и подоконником. Оно было определено с помощью теоремы Пифагора. Следователь выдвинул версию об инсценировке кражи.

1. Проанализируйте ситуацию.

2. Выявите моменты, указывающие на возможность применения теоремы Пифагора.

3. На основании каких фактов следователь выдвинул версию о невиновности подозреваемого? Аргументируйте свой ответ.

4. Какие бы вы сделали выводы на месте следователя?

Решение:

   Расстояние от наружного края поросли до окна можно вычислить по т.Пифагора.

                                     S² = 124² + 180² = 47776 => S= 219cм.

 Вывод.

   Такое расстояние преодолеть без лестницы или другого технического средства невозможно. Поиски, какого-либо технического средства не дали результата.

 С учётом сказанного проникновение в комнату через окно невозможно.

7. Итоги урока. (5 мин)

1) Просмотр видеоролика «Ералаша» о теореме Пифагора.

2) -Найдите ошибку в данном сюжете.

3)Сформулируйте теорему Пифагора?

4)Где применяется теорема Пифагора?

8. Домашнее задание. (2 мин)

Оценка «3» — 1 задача

Оценка «4» — 1,2 задачи

Оценка «5» — 1-3 задачи

1. (Открытый банк заданий ОГЭ) От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода. Ответ дайте в метрах.

2. Пожарная лестница длиной 20 м стоит на машине, на высоте 2 м от земли и на расстоянии 5 м от здания. До какого этажа можно на ней добраться, если высота этажа 3 м?

3. Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?

9. Рефлексия (1 мин)

Оцените свои знания по данной теме: нарисуйте человечка на соответствующей ступени.

умею применять

при решении

практических задач

«5»

умею найти элементы

прямоугольного треугольника

«4»

умею найти

гипотенузу

«3»

знаю теорему

«2»

Ребята, мне очень понравилось работать с вами. От этого урока я получила огромное удовольствие. Спасибо за урок!

Теорема Пифагора — Математика — 8 класс

Открытый урок по теме «Теорема Пифагора»

8 класс

Цель: — Формирование у учащихся осознания теоремы Пифагора,

— Формирование умений воспроизводить содержание теоремы Пифагора,

— Развитие познавательного интереса учащихся, логического мышления, культуры математической речи.

Задачи: — Применение теоремы Пифагора для решения задач на нахождение неизвестных сторон прямоугольных треугольников;

— Проводить доказательные рассуждения.

Тип урока: изучение нового материала

Оборудование: карточки (Приложение №1), практическая работа (Приложение №2), презентация, проектор.

Ход урока:

1. Организация начала урока.

— Здравствуйте, садитесь. Рада всех приветствовать на открытом уроке. Хочу пожелать всем интересного и плодотворного занятия. Давайте начнем. И чтобы немножко размяться, подготовиться к работе, Ребята, давайте посчитаем. Сейчас каждой парте будет дана карточка, на которой записаны примеры, а рядом квадрат, в котором записаны ответы. Вам необходимо закрасить ответы на данные примеры, если вы все выполните верно, то у вас получится буква. Работать необходимо в паре. Ведь одна голова хорошо, а две лучше. Пожалуйста, приступайте. (ученики вычисляют значения выражений и закрашивают верные ответы, учитель ходит по классу контролирует процесс)

Приложение №1

16	5	64	36
3	8	12	4
144	20	17	100
9	28	24	25

Закрасьте ячейки таблицы, в которых

записаны значения выражений:

1) 4²; 2) 6²; 3) 3² ; 4) ;

5) 8²; 6) ; 7) 3²+4²; 8) ;

9) 12²; 10) 6²+8²

Учитель приглашает к доске учеников, которые первые сделали правильно. Каждая парта проверяет себя.

— Молодцы, ребята. Действительно получилась буква «П». А какие математические термины вы знаете на эту букву? (периметр, площадь, параллелограмм, прямоугольник). Хорошо, молодцы. Сегодня на нашем уроке буква «П» будет очень важна!

2. Мотивация учебной деятельности.

— Мы с вами размялись и готовы совершать открытия. А сейчас давайте попробуем решить некоторые задачки, при решении их многие сталкиваются с трудностями, посмотрим, удастся ли вам их решить? Вопрос: Какое расстояние будет между велосипедистом и пешеходом?

(С первой задачкой ребята справляются легко. Ответ:17 км. А вот во втором случае, что здесь будет расстоянием между велосипедистом и пешеходом?)

К сожалению, пока мы не можем найти данное расстояние, но я уверенна, что в конце урока у нас все с вами получится!!!

— А что за фигура здесь получилась? Давайте вспомни немного про прямоугольный треугольник. Верно или неверно? (Каверзные вопросы)

(Те ребята которые правильно отвечают, выходят к доске щелкают на квадратик и смотрят: верно или нет ответили, если верно, то кружок становится зеленого цвета)

3. Подготовка учеников к усвоению, актуализации учебных знаний

— А сейчас, давайте, исследуем прямоугольный треугольник и узнаем про него новое. Для этого разобьемся на три группы каждый ряд – это одна группа. Сойдитесь к центру. Каждой группе дается своя практическая работа, вам необходимо измерить катеты, гипотенузу данного треугольника и выполнить необходимые подсчеты (учитель подходит к каждой группе смотрит, что происходит подсказывает, подбадривает).

Приложение №2

Каждая команда выбирает одного ученика, который выйдет к доске объяснить, что у них получилось. (документ –камера включена, смотрим через неё)

У всех трех групп были разные треугольники, но вывод получился один. Сами того не подозревая ребята сформулировали знаменитую теорему.

4. Изучение нового материала.

Наконец, мы можем перейти к теме сегодняшнего урока! Откроем тетради, запишем теорема Пифагора (вот она важная буква П). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. (Чертеж + формула).

— Данная теорема будет вам большим помощником и в школе, и в жизни. Давайте, посмотрим небольшой ролик про данную теорему — это поможет вам лучше понять, где и как можно использовать данную теорему (Видеоролик)

5. Первичное закрепление знаний.

На представленных картинках ученики ищут прямоугольные треугольники и записывают для каждого теорему Пифагора.

(треугольники:

АОВ:

ВОС:

СОD:

AOD:)

6. Контроль и самопроверка.

Возвращаемся к задаче, с которой начали и находим расстояние между велосипедистом и пешеходом (По теореме Пифагора).

7. Подведение итогов. Рефлексия.

В конце урока давайте вспомним все, что было сегодня на уроке и запишем небольшое предложение 1 слово что запомнилось? Существительное 2 слово какой был урок? Прилагательное 3 слово что делали? Глагол

Ребята читают свои предложения.

8. Информация про домашнее задание

Спасибо большое за урок ребята. Вы отлично поработали, я очень рада, что для многих это был интересный урок. Давайте запишем домашнее задание: п. 63, № 2 (1,2) стр. 94

Спасибо за урок. До свидания

Проект по геометрии в 8-ом классе «Теорема Пифагора»

Проект учащихся 8 «А» и 8 «Б» классов МБОУСОШ

станицы Терской

«Теорема Пифагора».

«И ныне теорема Пифагора верна, как и в его далёкий век»

Шамиссо

Краткая аннотация проекта:

                Закон Архимеда, теорема Пифагора… Почему некоторые правила называют именами учёных? Справедливы ли такие названия? Почему теорему Пифагора назвали теоремой Пифагора?

Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о “пифагоровых штанах” — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость.

                Пифагор – едва ли не самый популярный учёный за всю историю человечества. Трудно найти человека, который бы не знал теорему Пифагора. Теорема Пифагора – одна из важнейших теорем геометрии, она имеет богатую историю. Но познакомиться с историей теоремы, фактами из жизни Пифагора, другими доказательствами теоремы  на уроках нет возможности из-за недостатка времени, а материал этот интересен учащимся. Поэтому я предложила им поучаствовать в этом проекте.

В результате реализации проекта учащиеся получили следующие дополнительные знания:

1. Познакомились с биографией Пифагора;

2. Узнали историю развития теоремы Пифагора;

3. Получили представление о различных доказательствах теоремы Пифагора;

4. Научились решать задачи с помощью теоремы Пифагора.

Ребята узнали некоторые тайны истории, и нашли ответ на вопрос «Почему теорема Пифагора называется его именем?»

Вопросы, направляющие проект

Основополагающий вопрос

Почему говорят, что все гениальное просто?

Проблемные вопросы

Оправдана ли популярность теоремы Пифагора?

Какова ценность теоремы Пифагора?

Почему в древние века так ценилось умение находить стороны прямоугольного треугольника?

В каких областях деятельности человека использует теорему Пифагора ?

Актуальна ли теорема Пифагора в современное время?

. Почему ревут 100 быков, заслыщав о теореме Пифагора?

Учебные вопросы

1. Какова формулировка теоремы Пифагора?

2. Какие доказательства теоремы Пифагора вы знаете?

3. Как теорема Пифагора применяется для решения треугольников?

4. Чем интересна биография Пифагора?

5. Какие исторические задачи решаются с помощью теоремы Пифагора?

Образовательные цели:

1. Ознакомление учащихся с историей развития теоремы Пифагора и фактами из жизни Пифагора;

2. Ознакомление со способами доказательства теоремы;

3. Развитие навыков решения задач с помощью теоремы Пифагора.

Развивающие цели:

1.Развитие познавательного интереса учащихся;

2.Развитие умение работать с информационными ресурсами;

3. Развитие самостоятельности в подборе материала по теме.

План проведения проекта:

1 этап: Постановка основополагающего и проблемных вопросов

2 этап: Ознакомление с основными этапами жизни и деятельности Пифагора

3 этап: Формулировка и доказательство теоремы Пифагора

4 этап: Способы доказательства теоремы.

5 этап: Использование теоремы Пифагора в жизни.

6 этап: Защита проекта.

Группа «Историки»

Наш проект называется «Теорема Пифагора». Это одна из основных теорем геометрии о свойствах сторон прямоугольного треугольника, поэтому Нина Петровна заранее дала нам задание, узнать, как строили прямой угол в древнем Египте, кто такой Пифагор, каковы его заслуги перед человечеством, почему эта теорема названа его именем, как он её доказал.

Вот что мы узнали в процессе работы над этим проектом.

Пифагор – древнегреческий математик, философ, религиозный и политический деятель. Он родился на острове Самос. Пифагор – это не имя, а прозвище, означающее «Убеждающий речью». С юных лет он стремился проникнуть в тайны великой природы. Первое образование он получил в храмах древней Греции. Но этих знаний ему было недостаточно. В возрасте 18 лет он отправился в поисках мудрости в Египет, где прожил 22года.

С группой пленников Пифагор попал из Египта в Вавилон, где продолжал своё образование ещё 12 лет. Приблизительно в 530 году до нашей эры он возвращается в Грецию, а затем переселяется в Южную Италию, в город Кротон. Там он прожил более 25 лет.

В Кротоне он основал пифагорейский союз, который одновременно был философской школой, политической партией и религиозным братством.

Обучение в школе продолжалось пятнадцать лет. Первые пять лет ученик должен был молчать: это приучало его к сосредоточенности. Вторые пять лет ученики могли только слушать речи учителя. Только последние пять лет ученики могли беседовать с учителем лицом к лицу.

Пифагорейская система знаний состояла из четырёх разделов:

1. Арифметика, наука о числах. 2.Геометрия, учение о фигурах. 3. Музыка.

4. Астрономия.

По утрам пифагорейцы молились и пели гимн восходящему солнцу. Школа Пифагора дала Греции много талантливых математиков, физиков и философов.

Главным пифагорейским символом здоровья и опознавательным знаком была пентаграмма или пифагорейская звезда. Пифагорейцы называли эту фигуру самой совершенной и считали, что она уберегает от нечистой силы. Пятиконечной звезде около 3000 лет, но и сегодня она реет на флагах очень многих государств.

Мы попробовали создать свои варианты пифагорейской звезды.

Пифагор впервые ввёл термин «Философ». Когда его спросили, кем он является, он ответил: «Я не мудрец, я любитель мудрости, то есть философ». До наших дней дошли афоризмы Пифагора, которые многому учат. Некоторые из них мы вывесили во время недели математики. Известен афоризм Пифагора «Пьянство – упражнение в безумии». В истории осталась любопытная придумка Пифагора – кружка жадности. Когда её наполняют до определённого уровня, то она такой и остаётся, но когда её переполняют, то всё содержимое вытекает, что объясняется гидростатическим давлением. Она и сейчас пользуется в Греции большим спросом как сувенир.

Наставления Пифагора всегда начинались словами: «Самое мудрое на свете – число, числа правят миром». До сих пор сохранились значения чисел по Пифагору. Именно Пифагор стал основателем мистического учения о числах. От Пифагора и его последователей и пошли всякие суеверия, связанные с числами.

Группа «Исследователи»

И всё-таки, самое главное, что досталось нам от Пифагора, это теорема, названная его именем: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Это свойство треугольника было известно и до Пифагора.

Уже древние египтяне знали, что если построить треугольник со сторонами 3, 4, 5, то один из углов будет прямым. Но они пришли к этому практическим путём, а доказать не могли. У них было такое правило: «Делай, как делается».

Мы так же, как египтяне, строили прямоугольный треугольник с помощью шнура, разделённого на 12 равных частей.

Так в чём же заслуга Пифагора, если задолго до него египтяне знали, что треугольник со сторонами 3, 4, 5 – прямоугольный? Пифагор доказал, что это свойство верно для любого прямоугольного треугольника. А произошло это так. К Пифагору пришли землемеры и попросили помочь им построить квадрат, площадь которого будет ровно в 2 раза больше площади первого квадрата. В результате неоднократных вычислений Пифагор пришёл к выводу, что если на гипотенузе равнобедренного треугольника построить квадрат, то его площадь будет равна сумме площадей квадратов, построенных на катетах. То есть, площадь большего квадрата в 2 раза больше площади малого квадрата. Так у него получился чертёж, который ученики до сих пор в шутку называют «Пифагоровы штаны во все стороны равны». А уже затем Пифагор доказал, что это свойство верно для любого прямоугольного треугольника.

Нам понравилось вот такое наглядное доказательство этой теоремы: Если на сторонах прямоугольного треугольника построить сообщающиеся сосуды и наполнить их водой, то легко убедиться, что ёмкость большего сосуда равна сумме ёмкостей двух меньших сосудов.

А вот ещё одно наглядное доказательство: Построим два равных квадрата со стороной (a+b) и разрежем их так, как показано на рисунке. Если от каждого квадрата отрезать по 4 равных треугольника, то видно, что от первого квадрата остаются два квадрата, в сумме равные остатку от второго квадрата. Вот ещё одно доказательство с анимацией.

Теорему Пифагора называют теоремой-рекордсменкой, потому что существует более 100 различных способов её доказательства. Это единственная теорема, в честь которой даже была выпущена почтовая марка.

Заслуга Пифагора и в том, что он вывел формулы, по которым легко найти тройку таких чисел, что с²=а²+в²

Группа «Практики».

Нужно взять два взаимно простых числа m >n и с помощью формул найти гипотенузу и катеты. Каждый из нас также нашёл свою тройку Пифагоровых чисел.

На уроках мы решали задачи с помощью теоремы Пифагора. Причём, не только из учебника, но и старинные задачи, которые мы нашли в интернете и сделали к ним рисунки и чертежи.

Задачи из учебника арифметики Магницкого, древнекитайская задача, древнеегипетская.

Теперь мы знаем, что

Если дан нам треугольник, и притом с прямым углом,

То квадрат гипотенузы мы всегда легко найдём:

Катеты в квадрат возводим, сумму степеней находим,

И таким простым путём к результату мы придём.

Спасибо за внимание!

Урок на тему «Теорема Пифагора»

Геометрия

8 класс

Тема урока: «Теорема Пифагора»

Учитель математики

ГБОУ ЛНР «Ровеньковская

общеобразовательная школа №5»

Василенко Л.И.

Уроки геометрии 1,2

Тема урока: Теорема Пифагора

Цель урока:

• формулированные системы знаний, связанной с понятием «Прямоугольный треугольник»;

• рассмотреть связь теоремы Пифагора с разными разделами геометрии;

• Формировать умения исследования свойств геометрических фигур с помощью доказанных теорем и известных аксиом;

• Развиваешь умения и навыки чтения и построения изображения геометрических фигур, вычисление основных элементов в прямоугольных треугольников и применять полученные знания и умения для пространственных тел:

• воспитывать интерес учащихся к общечеловеческим культурным и историческим ценностям на основе изучения биографии и научного наследия Пифагора

План уроков

1. Организационный этап

2. Мотивация учебной деятельности

3. Анализ опорных знаний

4. Изучение нового материала

5. Формирование умений и навыков

6. Подведение итогов урока

Оборудование урока: рабочие листы, мультимедийная презентация, рефераты учащихся

Типы уроков:

1) Урок усвоения новых знаний;

2) Применение знаний и формирование умений и навыков

Ход урока:

І. Организационный этап.

ІІ. Мотивация учебной деятельности (4 слайд)

1. После показа слайда 2 презентации поясните причину появления на экране таких фигур и объемных тел.

Пирамида, в основании которой лежит квадрат, две грани – прямоугольные треугольники.

Главный герой урока?

2. Учитель: Мы начинаем изучение великой теоремы, известной с древних времен, — теоремы Пифагора

1. Учащиеся делают небольшие доклады, связанные с биографией Пифагора, уделяют внимание различным научным фактам, связанным с именем Пифагора.

На экране демонстрируется слайд 3 презентации

2. Теорема Пифагора – основа эвклидовой геометрии (слайд 5)

Данные варианты применения теоремы Пифагора говорят о том, что это одна из главных теорем геометрии: с ее помощью можно вывести большинство теорем геометрии. Она чудесна тем, что сама по себе несложная

ІІІ. Актуализация опорных знаний.

Учащиеся в домашнем задании решали такую задачу ( слайд 6)

Задача

Дан равнобедренный треугольник АВС (АС=СВ=а) На каждом катете и на гипотенузе С вне этого треугольника построить квадраты. Найти С.

(по построению)

Слайд 7 поможет сформулировать теорему Пифагора (первичную формулировку)

IV.Изучение нового материала

1. Доказательство теоремы.

Одно из доказательств основывается на использовании равновеликих фигур ( доказательство Пифагора). Это доказательство предлагается рассмотреть одной группе учащихся. Необходимо найти зависимость между катетами а и в прямоугольного треугольника Бхаскари, которое может быть выражено словами «Смотри!»

Слайд 7

Доказательства Пифагора

Первая группа Вторая группа

Найдите зависимость между катетами а и в прямоугольного треугольника и его гипотенузой. Запишите в виде равенства. Сформулируйте вывод

Учитель формулирует теорему Пифагора, используя понятия «катет» и «гипотенуза». Что можно сказать о зависимости длин катета и гипотенузы?

Следствие: В прямоугольном треугольнике каждый из катетов меньше гипотенузы

Учитель: Какие элементы прямоугольного треугольника связывает теорема Пифагора? Предложите типы задач, которые требуют знания теоремы Пифагора.

Учащиеся предлагают основные типы задач, после получения формул объединяются в три группы

Слайд 8

Основные задачи, связанные с теоремой Пифагора

1. Нахождение гипотенузы прямоугольного треугольника по катетам

2. Нахождение катета прямоугольного треугольника по гипотенузе и второму катету

3. Заполните таблицу

V. Формирование умений и навыков. Слайд 9

1. Решение задач

Задача 1. Две стороны прямоугольного треугольника равны 9 см и 15 см. Найдите третью сторону

Задача 2. Найдите стороны ромба с диагоналями 12 см и 16 см.

Задача 3. Найдите высоту равнобедренной трапеции с основаниями 8 см и 10 см, боковой стороной, которая равна 6 см.

Задача 4. Найдите диагональ равнобедренной трапеции с основаниями 12 см и 6 см, боковой стороной, которая равна 5 см.

Слайд 10

Практическое применение теоремы Пифагора

Задача 5. На расстоянии 40 см одна от другой растут две сосны. Вы измеряли их высоту: одна высотой 31 м, другая – молодая – всего 6 м. Сможете ли вы вычислить расстояние между их верхушками?

Слайд 10

Слайд 11

2. Историческая справка

Учитель:

Рассмотрим удивительный треугольник с катетами 3 и 4. Оказывается 3² +4² = 5², т.е. гипотенуза равна 5.

Набор чисел 3, 4, 5 называют пифагоровы тройки, а треугольник – египетским так как он был известен еще древним египтянам. Для построения прямых углов египтяне поступали так: на веревке делали метки, делящие ее на 12 равных частей. Связывали концы веревки и растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4, 5. Тогда угол между сторонами, равными 3 и 4, оказывался прямым

Прямоугольными являются треугольники со сторонами

5, 12, 13

8, 15, 17

6, 8, 10

7, 24, 25

Объясните почему?

Слайд 12

Решение стереометрической задачи

Задача. Найдите неизвестные боковые ребра пирамиды, если высота МВ пирамиды МАВСД равна 4, а в основании пирамиды квадрат стороной 3.

АМ =?

МС=?

МД=?

VI. Подведение итогов урока: Слайд 13

1. Решение задач по готовым рисункам

Первая группа Вторая группа Третья группа

2. Формирование выводов для решения задач с применением теоремы Пифагора ( решенных задач)

Сформулируйте, как найти:

1. Сторону ромба по его диагоналям

2. Высоту равнобедренной трапеции по ее сторонам

3. Диагональ равнобедренной трапеции по ее сторонам.

4. Повторение основных фактов и определений, которые были использованы при решении задач и доказательстве теорем.

5. Оценивание результатов работы учащихся

VII. Домашнее задание: п.55, 56 № 483 ( а), 493

1. Найдите гипотенузу прямоугольного треугольника, если его катеты равны 12 см и 5 см

2. Сторона ромба равна 10 см, диагональ – 12 см. найдите вторую диагональ ромба

3. Катет прямоугольного треугольника равен 6 см, а медиана, проведенная к нему – 5 см. Найдите гипотенузу треугольника.

4. В пункте А две трассы пересекаются под прямым углом. Из этого пункта одновременно выехали автомобили со скоростью 80 км/час и 60 км/час. Какое расстояние между автомобилями будет через 3 часа?

Конспект урока «Практическое применение Теоремы Пифагора»

МБОУ Троицкая средняя общеобразовательная школа

Конспект открытого урока по геометрии

в 8 классе

«Практическое применение Теоремы Пифагора»

с использованием учебника Атанасяна Л.С. и др.

Разработала:

учитель математики

Зубова Анна

Николаевна

2015г

Конспект открытого урока по геометрии

Тема: «Практическое применение Теоремы Пифагора»

Место урока: (3 урок в теме «Теорема Пифагора»)

Тип урока: урок обобщения и закрепления полученных знаний.

Продолжительность: 45 минут

Цель урока: совершенствовать умения применять Теорему Пифагора при решении прикладных задач; показать учащимся на примерах ее практическое применение в повседневной жизни.

Задачи:

Образовательная: закрепить формулировку Теоремы Пифагора, выработать умение применять теорему для решения задач, закрепить знания при решении практических задач;

Развивающая: развивать математическое мышление и логическую речь учащихся; мотивацию к познанию социокультурной среды;

Воспитательная: формировать навыки самоконтроля; воспитывать чувство ответственности за качество и результата выполняемой работы;  воспитывать познавательную активность; повышать интерес к изучению математики.

Методы обучения: словесный, наглядный, проблемно – поисковый, репродуктивный.

Используемые формы организации познавательной деятельности учащихся: коллективная, индивидуальная, групповая работа.

Оборудование и основные источники информации: компьютер, проектор, экран, презентация к уроку, раздаточный материал.

ХОД УРОКА

1. Организационный момент.

Вступительное слово учителя: Девизом нашего урока является высказывание немецкого математика Феликса Хаусдорфа «Есть в математике нечто, вызывающее восторг…» так как на уроках геометрии очень важно уметь «смотреть» и «видеть», замечать и отличать различные особенности геометрических фигур.

На столах у каждого из вас лежит «Карта успешности». Подпишите их. В течении урока мы с вами будем выполнять задания и зарабатывать баллы.

2. Актуализация знаний.

Математический диктант с последующей взаимопроверкой

1. Прямоугольным треугольником называется треугольник, у которого один из

углов равен ________

2. Стороны треугольника, образующие прямой угол, называются ____________

3. Сторона треугольника, лежащая против прямого угла, называется_________

4. В прямоугольном треугольнике квадрат гипотенузы равен _______________

5. Сформулированное выше предложение носит название____________

6. Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон , то такой треугольник –__________

7. Найди х:

3. Активизация познавательной деятельности

«Учимся не для школы, а для жизни» – говорил Сенека Люций Анней (римский философ и поэт). При изучении математического материала ребята часто задают вопросы: «А зачем это нужно?», «Может ли мне пригодиться в реальной жизни?» (слайд 2)

Поэтому для начала предлагаю поиграть в игру.

Игра «Верите ли вы, что…»

• с Теоремой Пифагора вы сталкиваетесь каждый день?

• что Теорема Пифагора поможет стать востребованным в реальной жизни?

• что Теорема Пифагора применима многих сферах жизнедеятельности человека?

Я выслушала ваше мнение и в конце урока мы вернемся к этим вопросам.

4. Знакомство с областями применения теоремы Пифагора (слайд 3)

Строительство. При разметке фундамента. Очень легко можно воспроизвести способ построения «натягивателями веревок» прямых углов при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки.

При строительстве лестниц необходимо рассчитать длину, ширину каждой ступени, крутизну лестницы.( слайд 4)

При строительстве мостов, дорог рассчитывают подъемы и спуски. ( слайд 5)

Дизайн.

Ландшафтный дизайн. Дизайнер имеющимся на участке просчитывает расположение объектов, их высоту, форму, выводит прямые углы. ( слайд 6)

Дизайн одежды. При изготовлении выкройки модели необходимо в зависимости от полноты фигуры рассчитать ширину и глубину выточек. ( слайд 7)
Ориентирование. Расстояние до горизонта

На открытом пространстве расстояние до видимого горизонта зависит от высоты точки наблюдения над земной поверхностью. Ученые вывели

формулу расстояния до горизонта , где R – радиус земли, а h – высота объекта применяется. ( слайд 8)

Эта формула применима в следующих областях.

В космонавтике. 12 апреля 1961 года Ю.А. Гагарин на космическом корабле “Восток” был поднят над землёй на максимальную высоту 327 километров. Ученые смогли вычислить площадь увиденной им поверхности земли. ( слайд 9)

В мобильной связи. В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе. ( слайд 10)

TV, радиовещание, интернет. На определенную высоту от земной поверхности запускаются спутники, передающие ТV, радиовещания, интернета.

Геодезия, метеопрогноз. В геодезии , метеопрогнозе – фото поверхности земли из космоса, так же рассчитывают расстояние спутников от поверхности земли. ( слайд 11)

Суть истины вся в том, что нам она – навечно,

Когда хоть раз в прозрении её увидим свет,

И теорема Пифагора через столько лет

Для нас. Как для него, бесспорна, безупречна…

(Отрывок из стихотворения

А. Шамиссо фр.-нем. поэт, писатель)

( слайд 12)

V. Формирование умений и навыков.(Математическая игра). Класс делится на группы по рядам. За каждое верно выполненное задание, группа получает 1 балл.

«Сказка об Иване и Василисе»

В некотором царстве, в некотором государстве жил-был царь и была у него дочь Василиса — красоты неописуемой. Вот однажды прилетел Кощей Бессмертный и похитил Василису. Опечалился царь и издал указ: «Кто спасет мою дочь – тому отдам ее в жены и пол царства в придачу». А на краю того царства жил Иван- крестьянский сын. Решил он выручить из беды девицу-красавицу и отправился в путь.

Давайте поможем Ивану спасти Василису. ( слайд 13,14)

Вышел он в чисто поле, а то поле длиною 800м шириною – 600м. Как сократить путь Ивану? Чему равен короткий путь?

( слайд 15)

Решение:

1. (м)

Пришел он к Бабе Яге. Решила обмануть она Ивана, завести в лес густой. «Поди – говорит – 70 м за север, потом 15 м на запад, да еще 78 м на запад. Выйдешь к реке, а за ней дуб. На том дубу смерть кощеева в ларце на конце иглы». Как не заблудиться Ивану? Сколько метров составит путь Ивана?( слайд 16)

Решение:

1)78 – 70 =8 (м)

2) = 17 (м)

Ответ: 17 метров

Вышел Иван к реке, смотрит лодка привязана у другого берега. Сильное течение унесло ее вдоль берега на 2,4 м и на 1,8 от берега. Какова ширина реки?

Решение: = 3 (м)

Ответ: 3 метра

Перебрался он на другой берег, достал свой волшебный меч и одним махом срубил дерево на высоте метра от земли. Сколько метров надо пробежать Ивану до ларца, если высота дерева 3,6 м? ( слайд 18)

Решение:

1. 3,6 – 1 = 2,6 (м)

2) = 2,4 (м)

Ответ: 2,4 метр

Подбежал Иван к ларцу, открыл его, достал иглу и переломил ее. В тот же миг настала смерть Кощею. Видит перед ним дворец Кощея и ведет к его воротам лестница – загадка, длиною 7,5 м Сколько у нее ступенек, если длина каждой 40 см, а высота 30 см?

( слайд 19)

Решение:

1) = 50 (см) = 0,5(м)

2)7,5 : 0,5 = 15(с)

Ответ: 15 ступеней

Поднялся Иван по ступенькам, а двери дворца волшебные. Для того, чтобы они открылись надо произнести заветное слово – высоту дверей. Двери имеют форму равнобедренного треугольника с боковой стороной 250 см и основанием — 300 см. Какое число назовет Иван? ( слайд 20)

Решение: 1)300 : 2 = 150 (см)

2) = 200(см) Ответ: 200см

В знак победы своей поднял Иван флаг над королевством Кощеевым на высоту 4 м, закрепил трос в 3 м от флагштока. Какова длина троса? ( слайд 21)

Решение: = 5(м)

Ответ: 5 метров

Освободил Иван Василису Прекрасную, поженились они и стали жить поживать, да добра наживать. Тут и сказке конец, а кто помогал Ивану – Молодец! ( слайд 22)

Это интересно: Памятник Пифагору находится в порту города Пифагория и напоминает всем о теореме Пифагора, наиболее известном его открытии. Катет, лежащий в основании треугольника — мраморный , гипотенуза и фигура самого Пифагора в виде второго катета — медные. ( слайд 22)

VI. Итог урока. Оценивание.

Вернемся к игре «Верите ли вы, что…»

• с Теоремой Пифагора вы сталкиваетесь каждый день?

• что Теорема Пифагора поможет стать востребованным в реальной жизни?

• что Теорема Пифагора применима многих сферах жизнедеятельности человека?

Я надеюсь, что все полученные знания вам непременно пригодятся в дальнейшей жизни, например, когда решите построить свой дом.

Заполните свою карту успеха. Оцените свою работу на уроке и работу участников группы.

VII. Домашнее задание п. 54, 55 №489а), №493

VIII. Рефлексия. После того, как прозвенел звонок, учитель просит учащихся оставить на доске красный цветочек, синий квадрат или черную тучку.     

 — по окончании урока у меня замечательное настроение, потому что  все было понятно и интересно.

— настроение хорошее, но кое-что я не понял (а)

 -у меня плохое настроение, я ничего не понял(а), только время зря потратил(а)