1.5. Операции над векторами, заданными в координатной форме

Если векторы заданы в координатной форме, то операции сложения и вычитания векторов, умножения вектора на число можно заменить более простыми арифметическими операциями над координатами этих векторов по следующим правилам.

Правило 1. При сложении векторов их одноименные координаты складываются:

,,

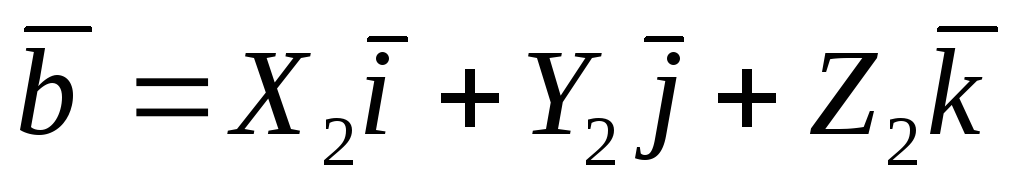(1.5.1)

Правило 2. Чтобы вычесть из вектора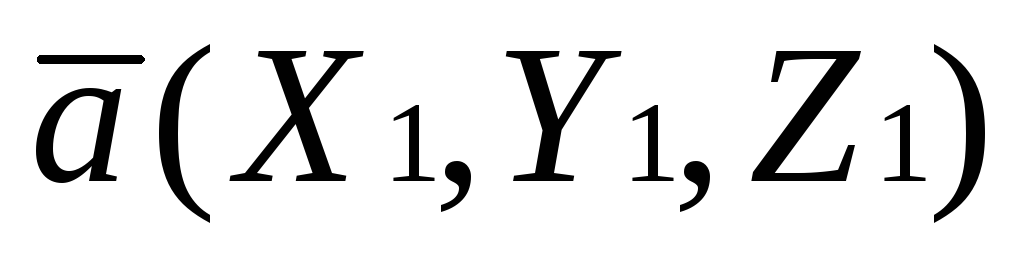

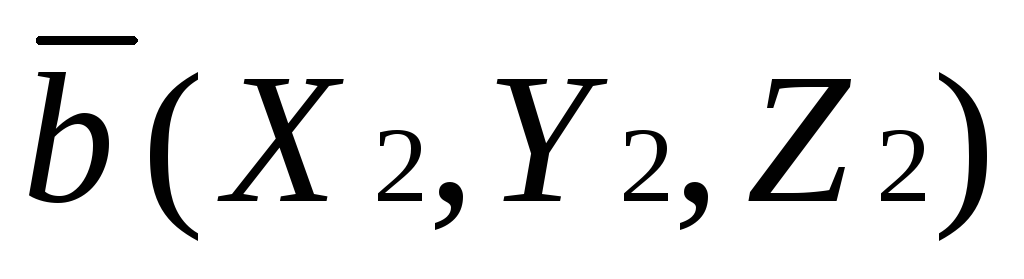вектор, нужно вычест координаты вектора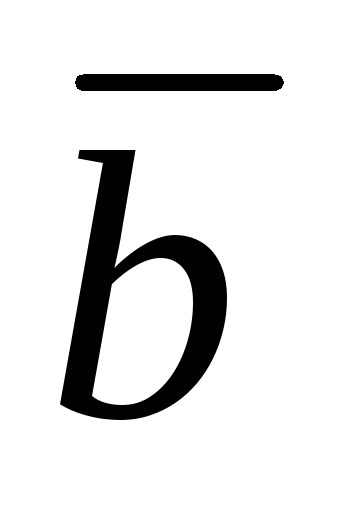из соответствующих координат вектора, т.е.

или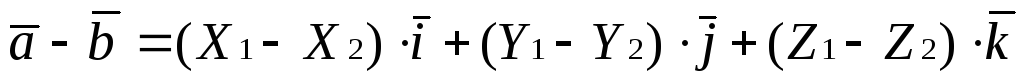(1.5.2)

Правило 3.Чтобы умножить векторна число, нужно умножить на это число его координаты , т.е. если

, то.

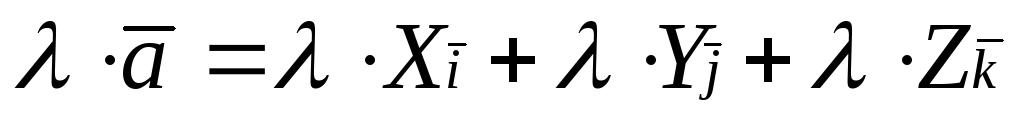1.6. Скалярное произведение векторов

Скалярным произведением двух векторов и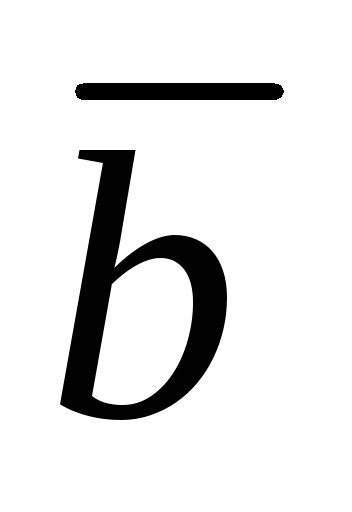называется число ,(обозначаемое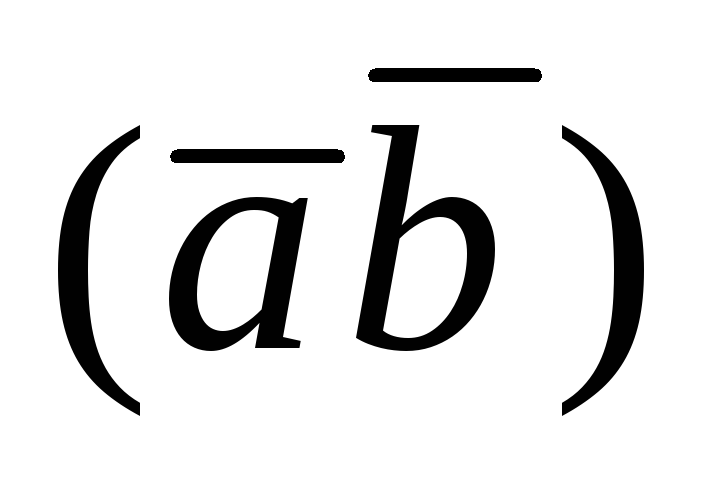) равное произведению длин векторов на косинус угла между ними:

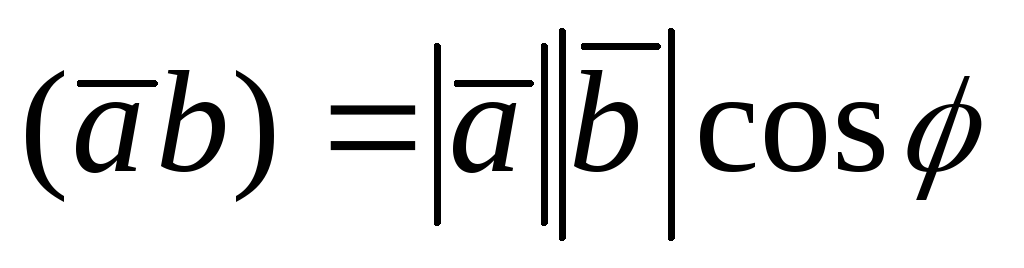, (1.6.1)

где — угол между векторамии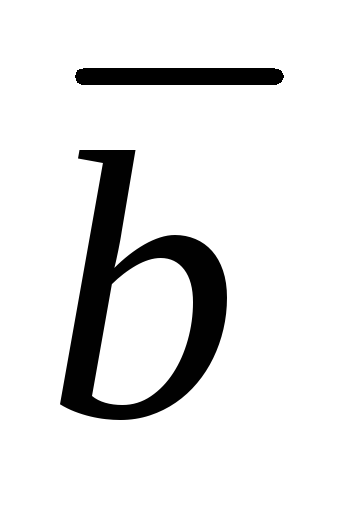

(рис.1.10).

Рис. 1.10

1.6.1. Свойства скалярного произведения:

1).

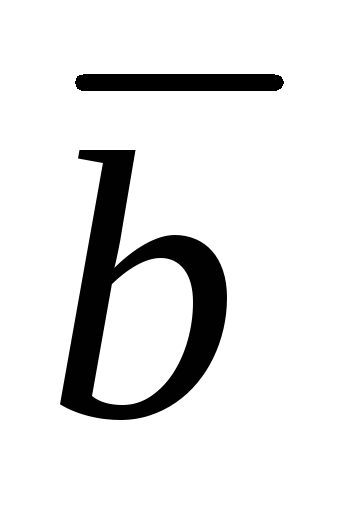2). иперпендикулярны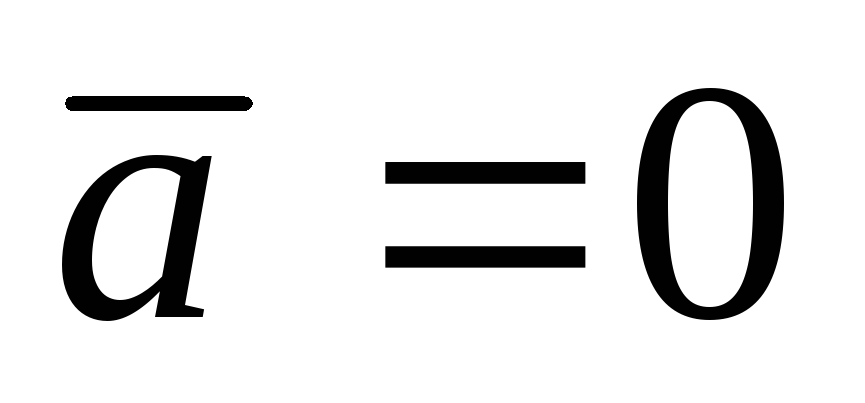; (или, или)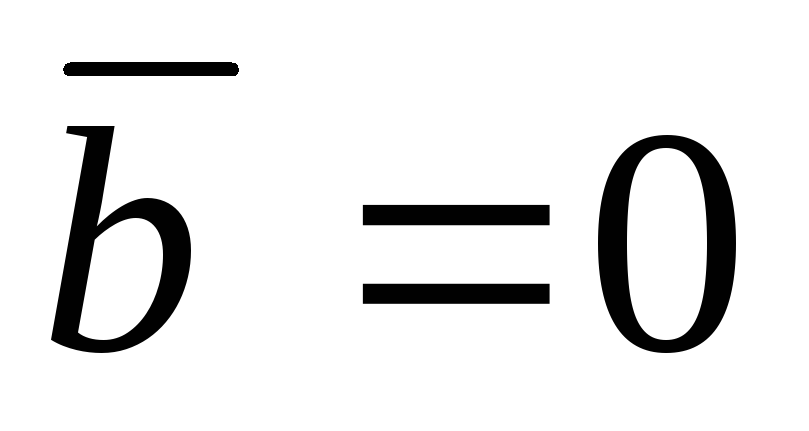

3).

4). 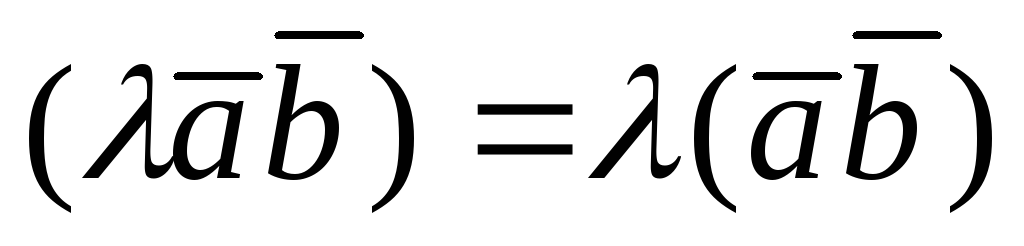, где

— число

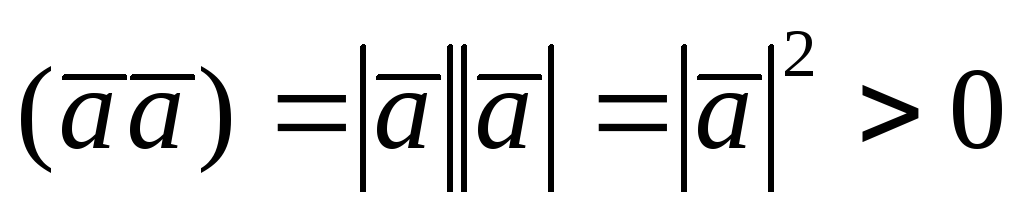5). , если

6).

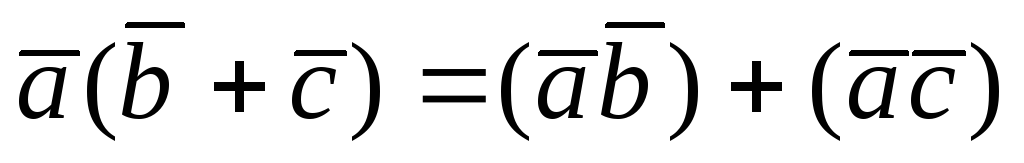
Докажем свойство 6. Имеем

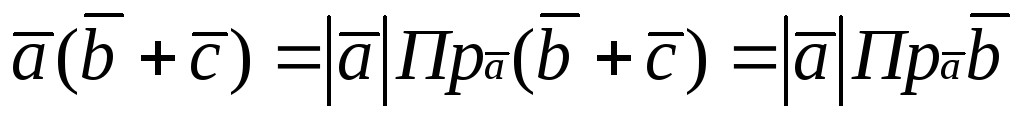
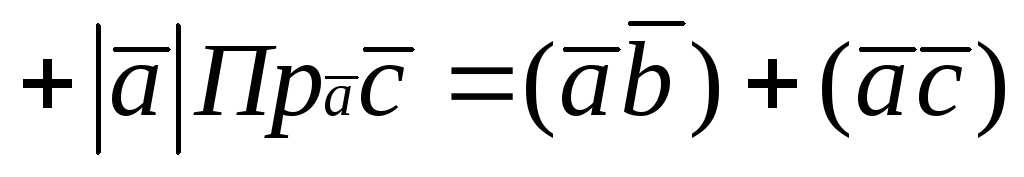
Замечание 1. Остальные свойства доказываются на основании определения.

Замечание 2. Свойства1, 3, 4, 6 дают право при скалярном умножении векторных многочленов выполнять действия так же, как при умножении алгебраических многочленов.

Замечание 3. Скалярное умножение не распространяется на три и большее число векторов. Произведение, например, трех векторовне является числом, оно будет вектором, коллинеарным вектору, который получается умножением векторана число.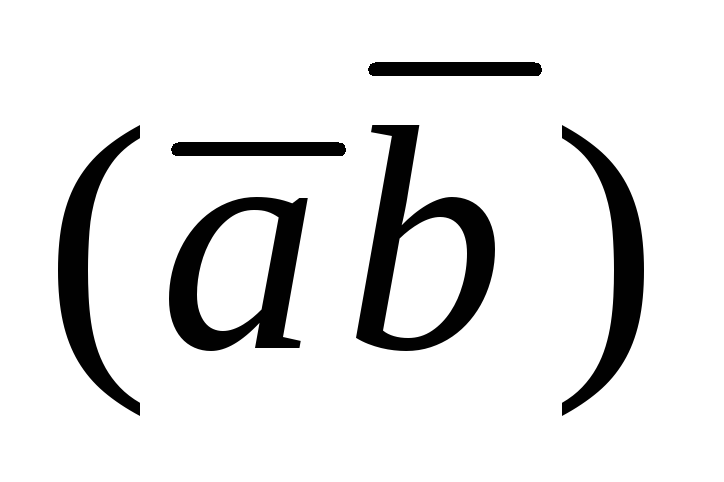

1.6.2. Скалярное произведение векторов, заданных координатами

Так как единичные векторы (орты) 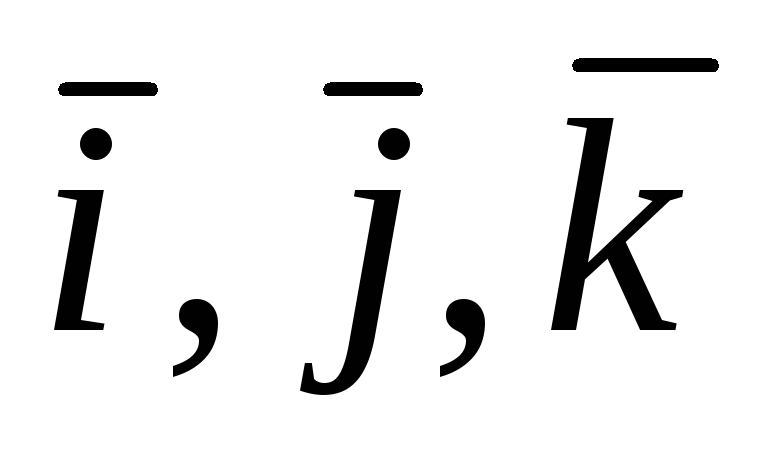осейOx, Oy, Oz прямоугольной системы координат взаимноперпендикулярны, то по формуле (1.6.1) получим :

,

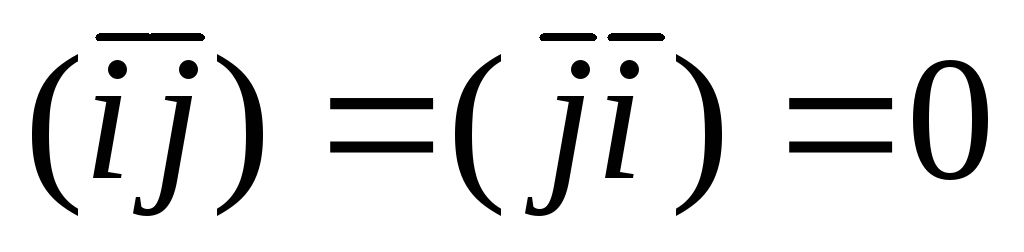,(1.6.2.1)

Далее, используя свойство скалярного произведения имеем:

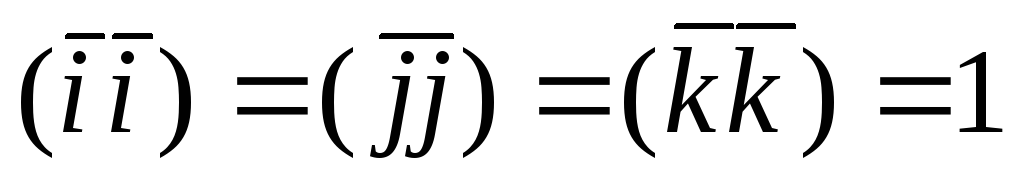(1.6.2.2)

Пусть, ,. Найдем произведение этих векторов (с учетом формул 1.6.2.1 и 1.6.2.2 ):

(1.6.2.3)

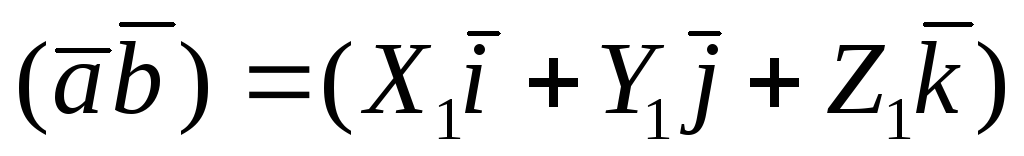
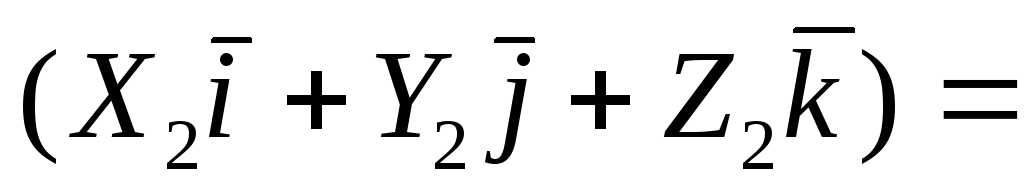
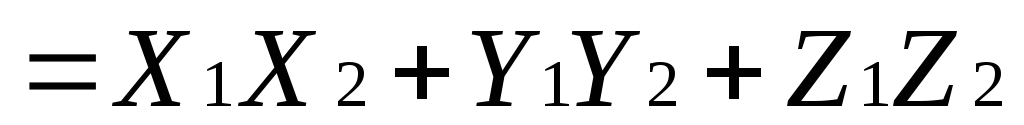
Таким образом, скалярное произведение двух векторов равно сумме произведений одноименных координат этих векторов.

Из равенства (1.6.2.3) и равенства векторов получим:

(1.6.2.4)

,

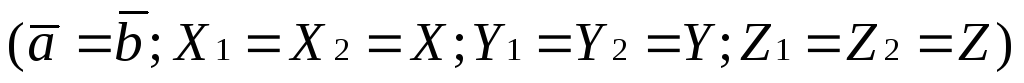т.е. квадрат длины вектора равен сумме его координат .

Из равенства (1.6.2.4) найдем длину вектора :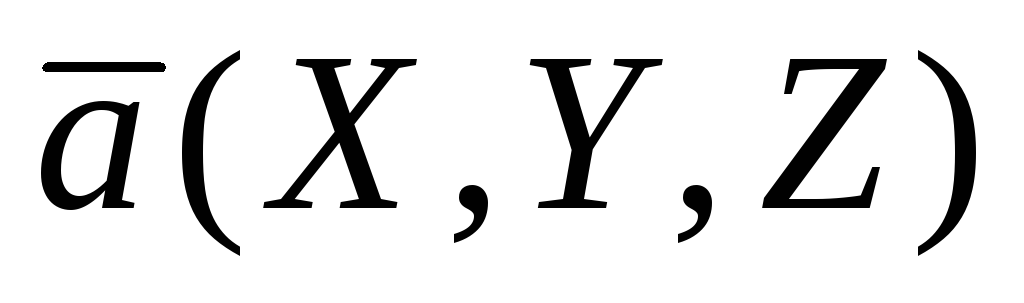

(1.6.2.5)

Длина вектора равна квадратному корню из суммы квадратов его координат.

1.6.3. Угол между векторами

Из определения скалярного произведения двух векторов следует, что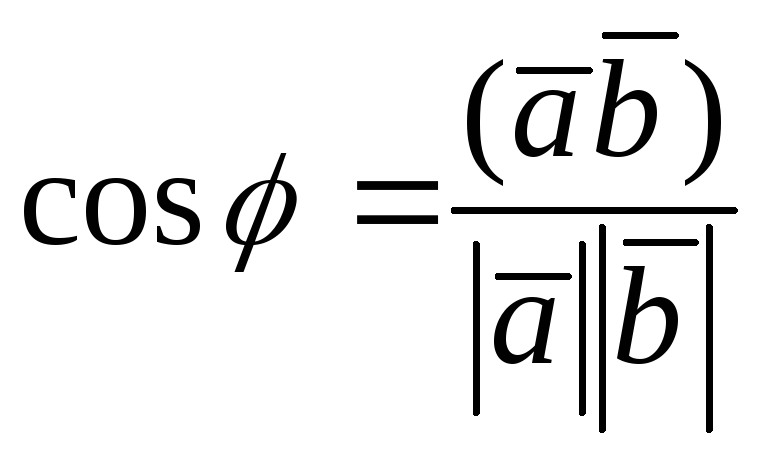

(1.6.3.1)

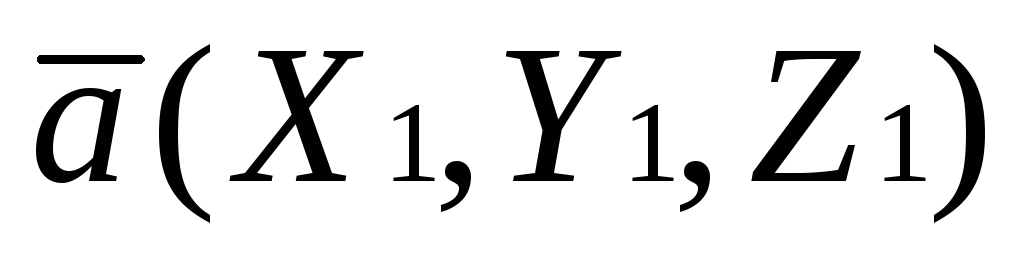Если векторы изаданы координатамии, то формула (1.6.3.1) запишется в виде:

(1.6.3.2)

1.6.4. Условия коллинеарности и перпендикулярности векторов

Как известно, необходимым и достаточным условием коллинеарности двух ненулевых векторов

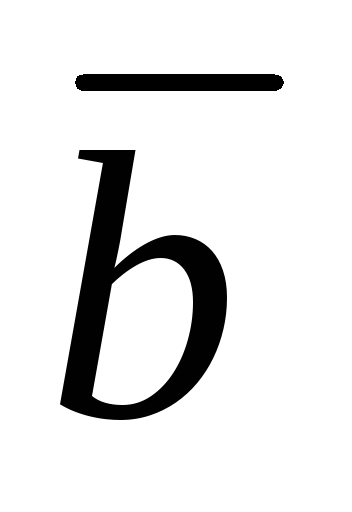иявляется равенство:

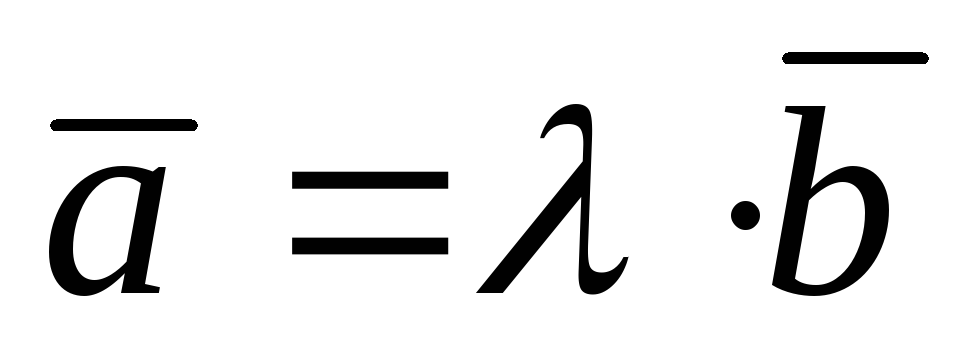, (1.6.4.1)

где скалярный множитель >0, если векторыиимеют одинаковые направления и<0 в противном случае.

Пусть заданны два вектора в координатной форме: 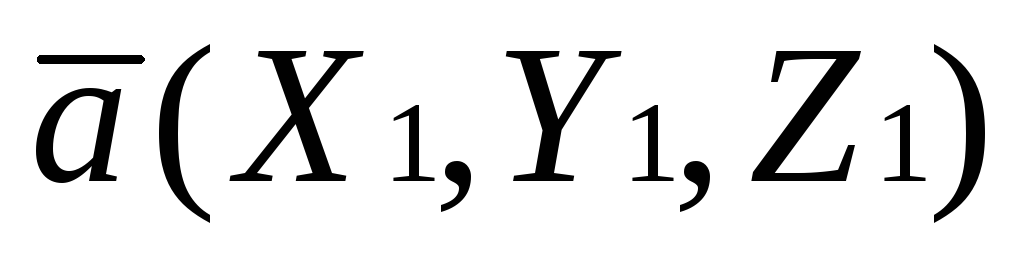и.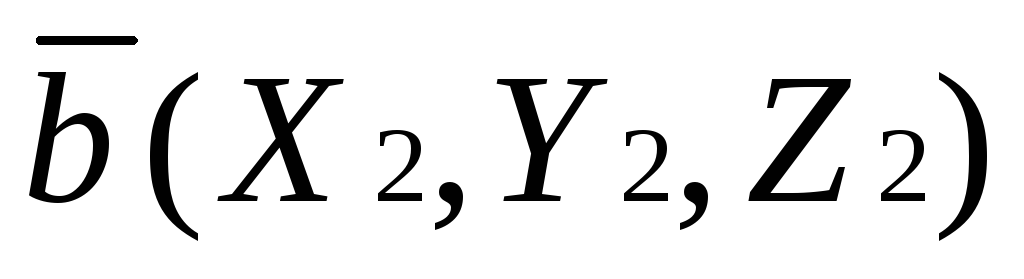

В этом случае из равенства (1.6.4.1) следует, что

, (1.6.4.2)

откуда 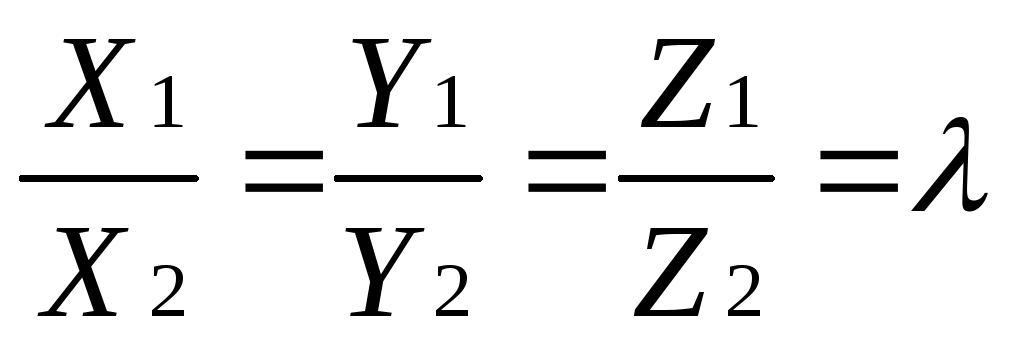(1.6.4.3)

Следовательно, если ненулевые векторы и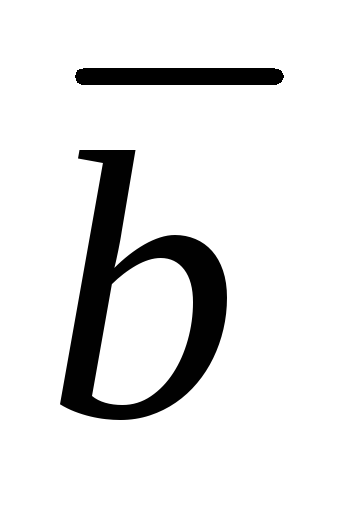коллинеарны, то и их одноименные координаты пропорциональны.

Необходимым и достаточным условием перпендикулярности векторов 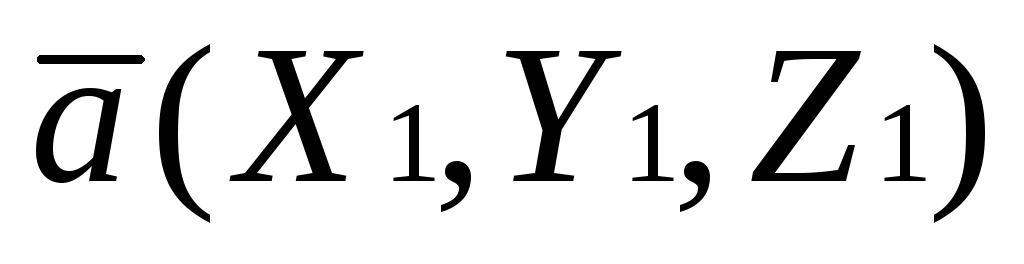иявляется равенство:

(1.6.4.4)

или в координатной форме условие (1.6.4.4) имеет вид:

(1.6.4.5)

1.7. Векторное произведение двух векторов

Векторным произведением вектора на вектор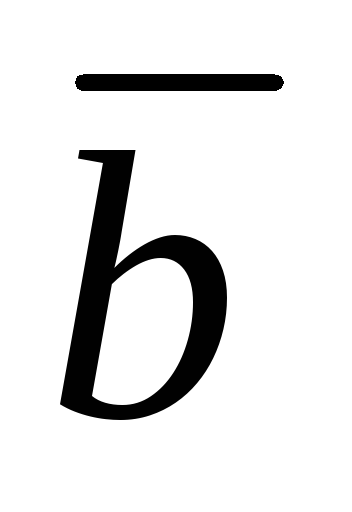называется новый вектор, обозначаемый символом

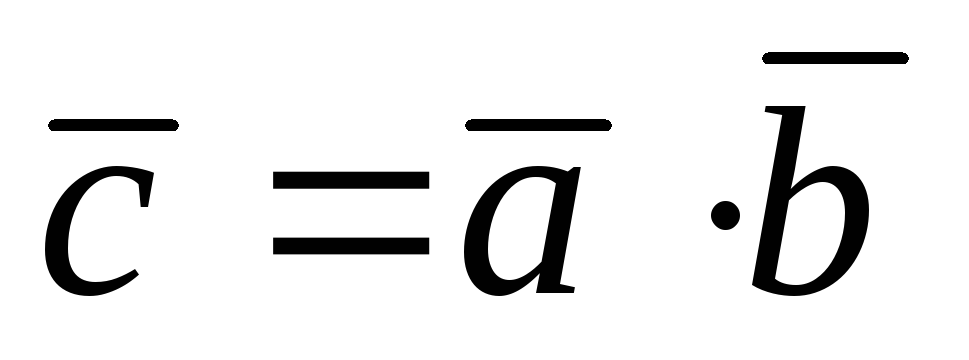или(1.7.1)

и определяемый следующими тремя условиями:

1) Модуль вектора равен площади параллелограмма, построенного на векторахи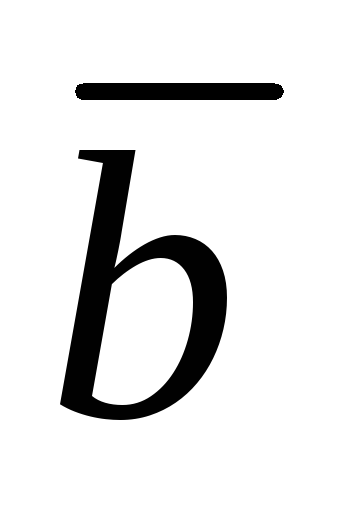(после совмещения их начал), т.е.

, (1.7.2)

где — угол между векторамии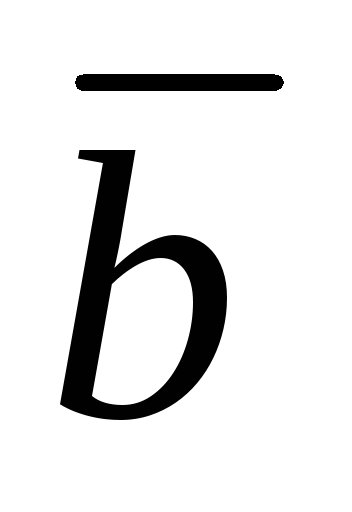(рис.1.11).

Рис.1.11

2). Вектор перпендикулярен к плоскости этого параллелограмма (т.е. перпендикулярен обоим векторами).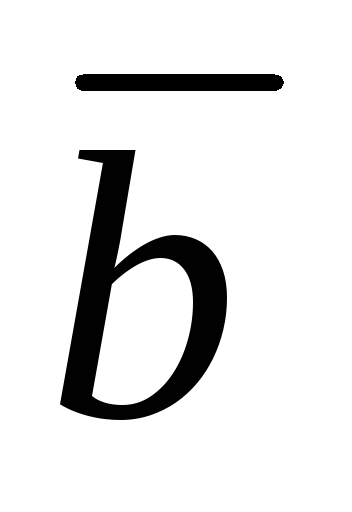

3). Вектор направлен в ту сторону от этой плоскости, что кратчайший поворот от векторак вектору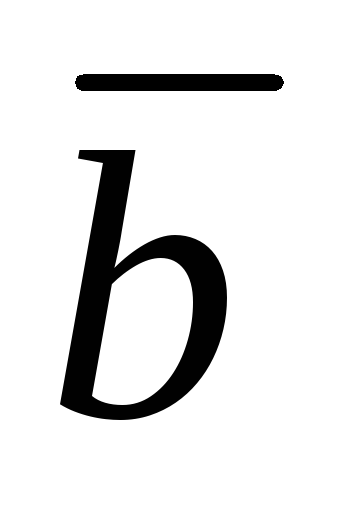вокруг вектора(после смещения начал всех трех векторов) кажется происходящим против часовой стрелки, если смотреть из конца вектора. Векторы,,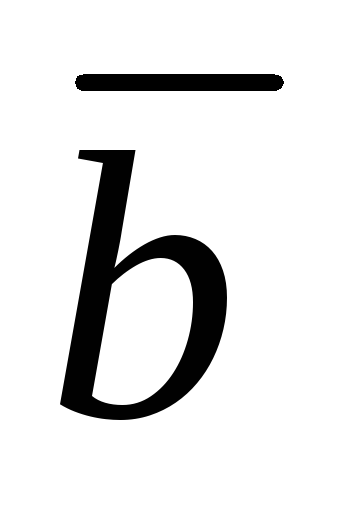образуют правую тройку векторов.

Замечание. Правую тройку образуют, например, большой, указательный, и средний пальцы правой руки; при пользовании левой системой координат в определении векторного произведения вместо правой берут левую тройку,,.

Своим прообразом произведение двух векторов имеет в механике операцию отыскания момента силы относительно точки. Именно, если в некоторой точке А приложена сила , то моментэтой силы относительно определенной точки О есть вектор, который в принятом нами обозначении (1.7.1) должен быть записан в виде, где— вектор, идущий из точки О в точку А.

Предложения со словосочетанием ЗАДАТЬ ВЕКТОР

Здесь задан вектор — не вверх (горы растаяли), а вниз. Тем самым был задан вектор дальнейшего развития самой культуры, предопределивший в какой-то степени её позднейшую самодостаточность при слабой способности материализоваться в развитую цивилизацию. Но на самом деле он необходим для создания определённой турбулентности и чтобы задать вектор физической силе, кинетической энергии, если угодно. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Намного проще держать в руке округлый предмет, чем пытаться одним пальцем задать вектор движения указателя по экрану.

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова закручивать (глагол), закручивая:

Кристально
понятно

Понятно
в общих чертах

Могу только
догадываться

Понятия не имею,
что это

Другое
Пропустить

И, если обстоятельства благоприятствуют, то можно задать вектор направления развития определённого сектора экономики или бизнеса на ближайшее время. Но самая большая опасность стригольничества заключалась не в конкретных инвективах, а в том, что «лиха беда — начало»: выступлением еретиков был задан вектор попятного движения к «истокам». Эти аспекты управления принципиально важны в деятельности и малой технологической компании, выводящей на рынок свой первый продукт, и крупной корпорации, долгие годы работающей в своей отрасли, и государства, которое стремится задать вектор и обеспечить темпы инновационного развития страны. Эпистемологически-философская рефлексия не задала вектора развития для науки, уже давно ищущей себя в огромном количестве публикаций и трудов: науки о пространстве. Но главное — он задал вектор развития города на много лет вперёд. Всё же империя играла положительную роль в развитии цивилизации, на долгие годы став примером для подражания и задав вектор развития для всего остального мира… Несмотря на то что эффективность методики невысока, она задавала вектор движения в определённом направлении: определение целей для каждого сотрудника и последующее концентрирование его деятельности для решения поставленных задач. Политическая экономия, как наука, задаёт вектор экономического развития. Они задают вектор движения политической системе, а через неё — всей системе культуры. Для научной философии спорт становится интересным не сам по себе, а в сопровождающем его социальном контексте, с позиции исследования того общего и исторически конкретного социального, которое воплощено в спорте как онтологическом объекте, задавая вектор его бытия — существования. Часто форма вопроса — это не только критерий правильности ответа, но и указатель, который задаёт вектор обсуждения. Определённый склад ума и потребности — задают вектор деятельности, характерный для того или иного человека. Кодируя себя определённым образом, руководитель тем самым не только задаёт вектор движения, но и определяет, какая реакция — «достижения успеха» или «избегания неудачи» — будет определяющей в его поведении и деятельности. Жители должны задавать вектор развития города, которому должны следовать органы местного самоуправления. На удивление, мне с первого раза удалось приподнять и зафиксировать труп над землёй, теперь необходимо задать вектор движения… Готово! Другими словами, этническая специфика всегда задавала вектор развития как духовной, так и материальной культуры, а также определяла (и во многом продолжает определять) облик различных цивилизаций. Потом в спокойном состоянии сказать что-то приятное вам — жене, тем самым задав вектор вашему дню. Этот подход на несколько столетий задал вектор исследования в категориях «объективного» познания. Само по себе наречение имени не является чем то фатальным и вряд ли задаёт вектор жизненного пути человека. Особо следует отметить, что мировые экономические процессы, опосредуемые глобализационными изменениями, задают вектор для развития межгосударственной интеграции, определяют правовые каналы её движения. По мнению автора, разработанная модель может быть использована при разработке внутривузовской системы непрерывного образования преподавателей и выполнять адаптационную (способствовать процессу адаптации преподавателя к профессиональной деятельности), целевую (задавать вектор развития профессиональных и личностных качеств преподавателя вуза), обучающую (дополнять и обогащать фундаментальную, предметную и развивать прикладную подготовку преподавателей), воспитывающую (оказывать влияние на продолжающийся в течение всей жизни процесс формирования личности преподавателя вуза), развивающую (формировать и развивать новые профессиональные качества преподавателя вуза), рефлексивную (предполагает анализ преподавателем собственной профессиональной подготовки, возможность проверки и корректировки уровня готовности), диагностическую (позволяет определять уровень готовности и недостатки подготовленности преподавателя к профессиональной деятельности) функции. Нам видится, что «проблема» понимается в методологии творчества концептов как «поле проблематики», включающее в себя ракурсы, с которых мы рассматриваем концепт, и серии вопросов, с помощью которых мы задаём вектор его конструирования. На первом месте стоит понимание смысла, цели, потому что именно это задаёт вектор и мотивацию движения, что означает способность не сбиваться с пути и двигаться в нужном направлении. Мечта задаёт вектор направления, без которого не горят глаза и отсутствует желание активно жить и светить в этом мире. Но сейчас мы обратимся к линейному мышлению, чтобы действовать и задать вектор развития результатов. Как максимум — неразумно, потому что план задаёт вектор движения в определённом направлении. Но именно вы должны задавать вектор, держать руку на пульсе, не давать изменениям слиться. Эта книга задала вектор моего поиска: я стал поглощать религиозную литературу в огромном количестве и днём, и ночью, где бы ни находился. Политика задаёт вектор движения и в самых общих чертах — его маршрут. Подходить к найму руководителя следует очень серьёзно, ведь именно он задаёт вектор развития отдела, организует работу максимально эффективно, обеспечивает реализацию планов и выполняет ряд других функций. Именно он должен служить примером для подчинённых, показывая, как правильно продавать, задавать вектор продаж и «дотягивать» план продаж. Осторожно отправила на неё книги и задала вектор. Во все времена любому предприятию нужен управляющий, тот, кто будет задавать вектор его развития. Ошибаться и вновь задавать вектор. Ну, задаёшь вектор движения, а он рассчитывает нужные коэффициенты, направление приложения сил и прочие важные вещи. Они задают вектор развития и обеспечивают процесс самоорганизации и воспроизводства социокультурного пространства отдельной российской территории. Благодаря финансовому плану на год (и его помощнику — плану на полгода) мы задаём вектор своего развития в вопросах аккумуляции денежных ресурсов. Всем главным героям нужно задать вектор развития характера, который будет прослеживаться в любом эпизоде. Задача правильного вуза — дать студентам необходимые теоретические знания и базовые практические навыки работы в выбранном направлении, помочь им реализовать свой творческий и научный потенциал, испытать свои силы в общественной деятельности, задать вектор трудоустройства и дальнейшего построения образовательной и карьерной траектории. Резко поднявшись с земли, я, не тратя времени на пафосные речи, раскинула руки в стороны и выпустила огонь, помноженный на воздух, стараясь задавать вектор так, чтобы моим валяющимся друзьям не досталось. Разумеется, прежде чем двигаться вперёд, надо задать вектор этого движения, то есть выбрать цель.

Неточные совпадения

Они, по сути, задали тот вектор развития человечества, который продолжается по сей день. Необходимо попытаться сделать её «живой» наукой, способной через анализ прошлого и настоящего не только указывать вектор исторического развития, но и активно способствовать движению в этом заданном направлении. Кто ему вектор задаст? Если это так, то ненаблюдаемая часть заработной платы в совокупности с доходами от собственности и предпринимательскими доходами может задать разнонаправленные векторы в динамике доходов и наблюдаемой части заработной платы. Концепция в области подготовки национальных кадров для зарубежных стран в российских образовательных учреждениях задала в общем виде основные векторы развития экспорта услуг российской системы образования. Мы выбрали именно эти лексические ареалы, оставив за пределами исследования множество других лексических групп, не в меньшей степени отражающих специфику французского менталитета, именно потому, что мы хотели прочертить таким образом основные оси нанизывания других понятий, задав своего рода смысловой и образный вектор для соотнесения. — Всё верно, — говорила девушка, — люди осознают свой потенциал на подсознательном уровне, но многие социальные факторы и неверно направленный вектор, заданный, скажем, родителями, не позволяет нам его реализовать. Создание общей системы целей и ценностей позволит задать общий вектор развития для всей организации. Так был задан определённый вектор, и явного осознанного отказа от него до сих пор не произошло. А не нашёл единомышленников на работе… Ищешь внешние силы, которые зададут твоему начальнику нужный вектор развития, да простят меня товарищи руководители. Наметим здесь параноидальный вектор, заданный шопенгауэровской мыслью. Что могут быть разные отклонения, что на какое-то время могут прийти к власти коммунисты, но вектор исторического развития задан такой, как во всём цивилизованном мире. Изменение времени даёт людям возможность задать необходимый вектор своего развития. Именно в этих науках складывался образ человека в терминах биосоциального детерминизма, декларировался подход к целям образования, вектор которого был направлен только от запросов общества и его институтов к образованию и не был задан ценностями индивидуальности образующегося человека. Если бы можно было, как киноплёнку отмотать время назад и, изменив вектор судьбы, задать ему другое направление, ситуация предстала бы в другом виде, а эти люди никогда бы не встретились.

Обсуждение:Вектор (математика) — Википедия

Мне так кажется, определение никуда не годится. А как же принцип «от простому к сложному»? Вектор — это изначально просто направленный отрезок. Уже потом вводят систему координат и доказывают, что каждый вектор (с точностью до параллельного переноса) однозначно задается своими координатами, и только в самом конце решают, что вектор — это и есть набор чисел-координат. —Aml 15:28, 14 июля 2006 (UTC)

В школьном курсе — да. А аксиоматика строится наоборот. Вводится понятие линейного пространства над полем, затем базиса, разложение вектора по базису. И как частный случай рассматривается пространство геометрических векторов — отрезков. Ery 15:31, 22 октября 2011 (UTC)

насколько я понял из статьи, исходное понятие вектора в математике -геометрический вектор, от него можно по-разному абстрагироваться, в одном направлении (в алгебре)- получается вектор в линейном пространстве(матрица, функция и тп), в другом — кортеж чисел или каких-то других объектов; но по-моему в обычном смысле под вектором понимается все-таки геометрический вектор anonim 6 дек 2011

Этот «кортеж чисел» — это частный случай линейное пространство — арифметическое линейное пространство. Я не совсем понимают, что вы имеет в виду «в обычном смысле»? Ery 17:00, 6 декабря 2011 (UTC)

по-моему,нет «кортеж чисел» — это еще не частный случай линейного пространства, тк линейное пространство предполагает наличие операций, а кортеж чисел сам по себе еще никаких операций не задает(точка-тоже может быть задана кортежем), а элемент ЛВП насколько я понял может быть и не кортежем — получается В этом смысле в понятии геометрического вектора есть 2 независимые составляющие — кортеж чисел и операции сложения и умножения на скаляр — как можно например задать функцию кортежем чисел?anonim 7 дек 2011

Есть понятие изоморфизма линейных пространств, поэтому любой геометрический вектор можно представить как арифметический, как матрицу, как полином, как функцию и так далее. Сам по себе картеж, если не определить над ним операции ещё не будет вектором. В понятие вектора как раз само множество векторов, в случае геометрических — это направленные отрезки и операции введены уже над ними. Картеж можно получить двумя путями: установить изоморфизм с арифметическим пространством или разложить вектор по базису. Поэтому я и строил так структуру статьи(как и аксиоматика) — с начало самое общее понятие: вектор в линейном пространстве, потом расширения линейного пространства — евклидово и нормированное, затем частный, но часто употребляемый случай — геометрические вектора. Определяется множество, определяются операции. Затем для него интерпретируется понятие ортогональности, нормы, скалярного произведения и угла. И получается привычные свойства и определения геометрических векторов, но уже как следствие аксиом более общего случая — линейного пространства. Ery 13:02, 7 декабря 2011 (UTC)

вектор можно представить матрицей, но как допустим можно матрицу задать арифм.вектором:) А арифметического вектора еще не достаточно чтобы задать геометрический, потому что геом.вектор может быть привязан к определенной точке-его наверное еще можно задать упорядоченной парой точки приложения и арифметического вектора, но не самим а.в.anonim 7 дек

матрицу можно задать арифм.вектором, если например первым элементом задать кол-во столбцов, а остальными — элементы матрицы, но можно кол-во столбцов задать и последним элементом, то есть все равно сам по себе вектор еще не задает конкретную матрицу-это насколько я себе представляю все равно разные объектыanonim 7 дек

Сдвинул обсуждение влево. Вот пример изоморфизма пространства матриц и арифметического вектора:

(a11a12a21a22)−>(a11,a12,a21,a22){\displaystyle {\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}}->(a_{11},a_{12},a_{21},a_{22})}. Частные случаи линейных пространств(как, например, пространство матриц) могут содержать дополнительные операции(умножение матриц). И если они нужны, то для них изоморфизм тоже необходимо устанавливать.
Вы видимо не совсем понимаете что значит изоморфизм или что даёт линейное пространство. Различные множество объектов могут попадать под определение линейного пространства, их путём изоморфизма можно свести к любому другому из пространств той же размерности, однако если над этим множеством установлены операции, то их надо переопределить в соответствии с теоремой об изоморфизме. Изоморфизм проводится между двумя пространствами. Множеств всех матриц не образует линейного пространства, а вот матриц фиксированной размерности образует и поэтому, если соотнести позиции элемента в матрице позицию элемента в арифметическом векторе, то получится изоморфизм и эту матрицу можно представить в виде вектора, пример я привёл выше. В случае геометрических векторов рассматривается обычно афинно-точечное пространство. Однако операции определены над векторами и любая точка характеризуется своим радиус-вектором. Поэтому определение положение вектора привязанного к точке можно определить с помощью двух векторов: радиус-вектора точки и вектора смешения. Ery 13:59, 7 декабря 2011 (UTC)

что дает линейное пространство понятно- формулировку части аксиом, а что дает изоморфизм для понятия г.вектора?, и все равно матрица(фикс.разм-те) и кортеж чисел разные объекты -об этом шла речь. тому же кортежу чисел опр.длины могут соответствовать матрицы разной фикс.разм-ти и понятие вектора в ЛП получается не равносильно геом.вектору -оно более широкоеa

Именно об этом я сразу и писал. Геометрические вектора — частный случай линейного пространства. И поэтому их определение надо давать, исходя из опредения линейного пространства. Изоморфизм даёт возможность переходить между пространствами, формулируя и доказывая теоремы и тождества в том пространстве, где это проще сделать и используя их там, где это необходимо. Ery 15:23, 7 декабря 2011 (UTC)

Итог[править код]

Подход, который заключается в том, что «Геометрические вектора — частный случай линейного пространства.» не может быть принят в Википедии, поскольку в Википедии должно описываться всё множество подходов к понятию вектора, а не какой-то один. Ничего не мешает начать с простого (невормального) определения вектора в аффинном пространстве, а уже потом придти к понятию вектора как элемента векторного пространства. Тем боле, что для статьи о векторе, как об элементе векторного пространства не нужна отдельная статья, потому что для векторного (линейного) пространства важнее система аксиом, а не, скажем, конкретное представление каждого вектора в заданном базисе. Статья, фактически, начинается с середины там, где идёт раздел «Геометрическая интерпретация». Вот я и предлагаю отбросить всю верхнюю часть и, ориентируясь, например, на статью en:Euclidean vector, сделать полноценную хорошую статью, даже лучше, чем английская. 🙂 —OZH 17:57, 7 декабря 2011 (UTC)

Вы сами себе противоречите. С начало пишете, что нужно описать все подходы, потом предлагаете описать только один. Ery 05:25, 8 декабря 2011 (UTC)

Не ищите противоречия, а просто посмотрите, что именно написано до раздела «Геометрическая интерпретация», а что описывается, начиная с этого раздела. Алгебраический подход можно сформулировать предельно просто: вектор — это элемент векторного (линейного) пространства. Но для этого существуют другие статьи. А здесь ответить на простой вопрос, что такое вектор, какие операции можно осуществлять над векторами, какие существуют представления векторов в координатах. И в этом статья en:Euclidean vector — хороший ориентир. Не пытайтесь описать всё на свете, опишите только самую суть и Вы опишите всё, что нужно. Только я предлагаю это всё сделать совместными усилиями, не растрачивая время и силы на искусственные противостояния. —OZH 16:03, 8 декабря 2011 (UTC)

Просто я считаю, что статья про вектор должна содержать наиболее полную информацию о векторе, как о математическом объекте. Собственно что идёт в части «вектор в линейном пространстве» и описывает представления вектора в координатах и операции над векторами. Т.е. как я предлагаю сделать — с начало кратко описать понятия в общем виде(с ссылками на соответствующие статьи), потом о геометрических векторах в прямоугольных координатах — интерпретировать абстрактные понятия, а затем описать изменения вектора при переходе в криволинейные координаты. Указываемая вами статья хорошая, не спорю, на неё можно ориентироваться, но помоему информация даётся там в слишком частных случаях. Поэтому предлагаю план статьи, который уже можно будет обсуждать:

1. Аксиоматическое определение вектора. Вектор в линейном пространстве: базис и координаты. Евклидовы и нормировочные пространства. — дать основные определения и кратко описать, возможно с примерами.
2. Геометрические вектора — основная часть статьи, здесь уже ориентируясь на en:Euclidean vector можно много чего написать, однако не ограничеваясь размерностью пространства. Дополнительные свойства трёхмерного и двумерного пространств(векторное и смешанное произведение итд)
3. Вектор в криволинейных координатах — здесь будет связь, между векторами при переходе к криволинейную систему координат и особенности такого перехода Ery 16:36, 8 декабря 2011 (UTC)

Евклидовые нормированные пространства нуждаются в полноценном и самостоятельном описании в Википедии (в отдельных статьях). Начинать надо с простых понятий, и такие простые понятия находятся в геометрии, а уже из геометрии — прямой путь в алгебру. (У меня сейчас возникнет пауза. К сожалению. Надеюсь, недолгая.) —OZH 08:12, 9 декабря 2011 (UTC)

Я считаю что начинать надо не с простых, а с общих понятий. Математика построена как множество теорий, теории излагаются от общего к частному. Значить в статьях на математические темы должна быть та же структура. Ery 12:22, 9 декабря 2011 (UTC)

Мнение двоечника[править код]

Мне мало что ясно с дискуссии, но аргументы OZH’а кажутся резонными, т.к. я, простой человек, НИЧЕГО не понял из статьи…никак не дополнил свое представление, а только напрягся от кучи формул и непонятных формулировок. Поел у няни, как говорится.

Убрать статьи двух-, трехмерный вектор[править код]

Предлагаю убрать эти статьи как малоинформационные, поставить редирект на основную — Evilmurmur 15:51, 8 ноября 2006 (UTC)

Привести структуру статей, связанных со словом вектор[править код]

Предлагается перенести содержание статей Вектор (значения) и Вектор в статью Вектор (математика) или Вектор (геометрия) или как-нибудь еще. А на странице Вектор (значения) оставить только список значений.

Я перевес это всё в вектор, это всётаки это сновное значение. Ещё бы нашёлся добрый человек который это всё перепишет… —Тоша 21:31, 9 мая 2006 (UTC)

Где постановляется, что основным значением считается математическое? Основным должно быть самое общее (вектор — упорядоченное множество элементов) и оно не должно относиться в раздел математики, где тип элементов ограничен числами. —javalenok 14:39, 2 ноября 2006 (UTC)

А общее определение разве не математическое? -«вектор-последовательность, кортеж) однородных элементов». —78.36.150.37 16:20, 28 ноября 2011 (UTC)

На самом деле, общее определение — это «вектор — направленный отрезок прямой. Характеризуется точкой приложения, длиной и направлением»! Всё остальное — абстракции на тему. —Nashev 15:40, 19 апреля 2013 (UTC)

Кто может объяснить разницу между вектором в геометрии и в алгебре? По-моему, уже давно это предмет алгебраической геометрии. Посему предлагаю объединить эти две статьи. infovarius 14:09, 12 августа 2008 (UTC)

Infovarius, я навверно поступил грубовато откатив всё, НО в геометрии рассматриваются также связанные и фиксированные вектора лучше не смешивать это всё в одной статье. Кроме того лучше там оставить всю геометрическую интерпретацию… Я не против обзединения в принципе, но пусть статьи дойдут до разумного вида — их легче править отдельно —Тоша 18:02, 19 июня 2009 (UTC)

Пусть все виды векторов, рассматриваемых в математике, будут в одном месте? infovarius 22:48, 19 июня 2009 (UTC)

Пусть, но надо это делать разумно — так чтоб читателю становилось легче читать, а не сложнее!

Иначе — не надо делать хуже, надо делать лучше. —Тоша 10:46, 20 июня 2009 (UTC)

На самом деле, разницы никакой нет. Просто в математике есть важное понятие изоморфизма: существуют аффинные и векторные пространства. Вот и всё. К сожалению, эта взаимосвязь в статье не отражена. (Или надо внимательно читать?) А без этого, ценность статьи сильно снижается. —OZH 14:01, 5 мая 2010 (UTC)

По тихоньку буду переписывать так, чтобы было всё. Не в один день, так что за оформление в течении процесса прошу не ругать. Ery 15:32, 22 октября 2011 (UTC) Сделал. Навёл логику в статье. Раньше было ощущение, что в геометрии вектор — это нечто совсем другое, не желе в линейной алгебре. Кстати, это, сохранив, информационную ценность, уменьшило объём статьи. Ery 12:19, 17 ноября 2011 (UTC)

Раздел «Понятие вектора в геометрическом n-мерном пространстве». Дублирует раздел «геометрическая интерпретация». Поэтому считаю нужным его удалить, а недостающую информацию перенести в указанный раздел. И, кстати, мне кажется, там такой информации нет. Ery 10:03, 6 декабря 2011 (UTC)

мне кажется, наоборот должен быть отдельный раздел именно геометрический вектор(и лучше в n-мерном пространстве)так сделано в английской википедии, а не геометрическая интерпретация, а вектор в линейной алгебре -другое понятие, более абстрактное. anonim6 декабря 2011

под геометрической интерпретацией вектора в линейной алгебре исходя из написанного может пониматься геометрическая интерпретация матрицы, функции и вообще геометрическая интерпретация чего имелась в виду?, поэтому и был добавлен раздел геометрический n-мерный вектор. а геометрическая интерпретация его не дублирует, это просто пример линейного вектораanonim

Геометрическая интерпритация вектора в линейном пространстве и есть обычный геометрический вектор. Частный случай линейного пространства — есть геометрическое пространство, элементами которого явл. геометрические вектора. Поэтому и происходит дублирование. Под геометрический интрпритацией имелась ввиду геометрическая интерпретация понятия «вектор». Ery 16:58, 6 декабря 2011 (UTC)

по-моему наоборот-интерпретации могут быть различные -функцию ведь тоже можно изобразить геометрически -она тоже может рассм. как вектор ЛВП насколько я понял из статьи? Вроде и сам г.вектор можно интерпретировать геометрически в виде другой фигуры, кстати=)anonim 7 дек

Само понятие геометрический вектор подразумевает направленный отрезок. И геометрический интерпретация — это множество геометрических ветров. Так называют, обозначают. Так прижилось. Ну а вообще вы правы — можно интерпретировать с помощью поверхности или кривой. Но говоря геометрические векторы имеют ввиду именно направленные отрезки. Ery 13:41, 7 декабря 2011 (UTC)

геометрическая интерпретация — это не обязательно множество геометрических векторов, если они определяется как напр.отрезки, может быть что угодно. по-моему интерпретация вообще -это отображение чего-то во что-то и поэтому должен быть раздел именно геометрический вектор, а если раздел геометрическая интерпретация там просто приводится какой-то пример интерпретации, на мой взгляд название раздела не совсем удачно для геом.вектораanonim 7 дек

Ладно, согласен, название раздела может и нужно сменить. Но это не отменят того, что было дописано позже и выше этого раздела дублирует то, что находится в нём и других разделах, причём в углублении на частные случаи(декартова система координат). Ery 15:01, 7 декабря 2011 (UTC)

• Статью и без того запутали. Даже не знаю, что делать. 🙁 —OZH 12:49, 6 декабря 2011 (UTC)

Итог[править код]

Не надо ничего дублировать. Если есть различные объекты, то их следует описывать в отдельных статьях и не боятся разделить материал. Лучше две небольшие, но ясные статьи, чем одна большая но без, собственно, предмета статьи. —OZH 17:38, 7 декабря 2011 (UTC)

Господа, поучаствуйте в Википедия:Обсуждение правил/Обозначения векторов, пожалуйста —Nashev 15:36, 19 апреля 2013 (UTC)

Начало «Пусть F=⟨F;+,∗⟩{\displaystyle {\mathfrak {F}}=\langle F;+,*\rangle }» даже прочесть нормально без подготовки нельзя. Эта кривуля из двух загогулин и точки после слова «Пусть» расшифровке не поддаётся. Обратите внимание на ВП:ПРОЩЕ, и поимейте совесть! —Nashev 15:50, 19 апреля 2013 (UTC)

По случаю, сегодня таки написал расшифровку.. —Nashev 13:57, 27 февраля 2019 (UTC)

Простите что вмещиваюсь в ваш сон, но мне тоже показалось, что в кирилической части интернета нет, определенно понятного объяснения вектора. здесь в вики конечно уместен подход от общего к частному, но не хватает Подчеркнутости и выделенности понятия «свободный вектор», с которым в большинстве случаев и приходится сталкиваться. Кроме того, я до сих пор не понимаю: есть кортеж <1,2,3> да, а теперь я таки скажу, что это точка, а не вектор (или наоборот) и кто мне помешает? и еще со школьной скамьи вдалбливали, вектор — направленный отрезок!! ппс вот у меня кортеж <1,2,3> ну и куда он направлен, налево от оси у, x и z ??????? —178.130.41.249 21:49, 11 июля 2013 (UTC)qssaka

Вы определитесь это точка либо вектор) Это два разных класса объектов и выбирается с каким работают, обозначают просто похоже(через координаты). Про объяснение — в интернете нет, в литературе есть, например в Гельфанде. Вопрос в том, чтобы нормально написать статью — это уже проблема из другой области. Ery 10:09, 12 июля 2013 (UTC)

Проекция вектора на вектор, формула и примеры

Определение и формула проекции вектора на вектор

Проекцией вектора на ось называется число, которое равно величине отрезка , принадлежащего указанной оси, где точки и – проекции точек и на рассматриваемую ось соответственно (рис. 1).

ОПРЕДЕЛЕНИЕ Проекцией вектора на направление вектора , называется число, которое равно величине проекции вектора на ось , проходящую через второй вектор (рис. 2).

Проекция вектора на направление вектора равна скалярному произведению этих векторов, деленному на длину вектора :

   

Примеры нахождения проекции вектора на вектор

ПРИМЕР

Задание	Найти проекцию вектора на вектор
Решение	Вычислим скалярное произведение заданных векторов. Оно равно сумме произведений соответствующих координат векторов-сомножителей     Модуль вектора равен корню квадратному из суммы квадратов координат, то есть     Тогда искомая проекция
Ответ

ПРИМЕР

Задание	Найти модуль вектора , если известно, что проекция вектора на него равна 2, а скалярное произведение этих векторов
Решение	Согласно формуле имеем, что     Тогда
Ответ

Значение слова ВЕКТОР. Что такое ВЕКТОР?

• ВЕ́КТОР, -а, м. Мат. Изображаемая отрезком прямой математическая величина, характеризующаяся численным значением и направлением.

  [От лат. vector — везущий, несущий]

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

• Ве́ктор (лат. vector — везущий, несущий).

Источник: Википедия

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: старатель — это что-то нейтральное, положительное или отрицательное?

Положительное

Отрицательное