Единичный вектор | matematicus.ru

Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.

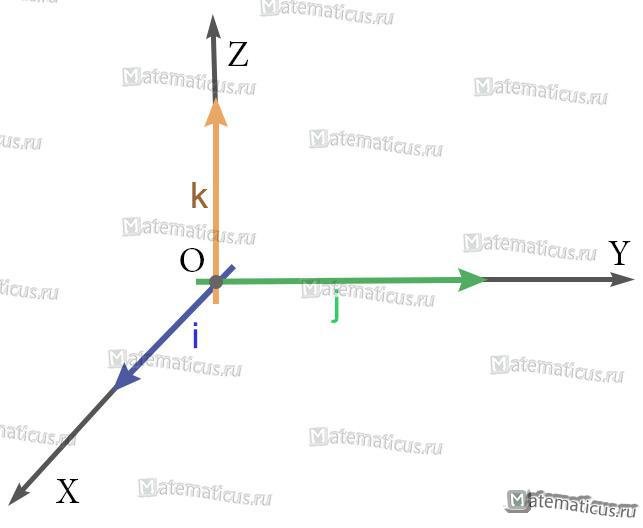
i — единичный вектор оси абсцисс;

j — единичный вектор оси ординат;

k — единичный вектор оси аппликат.

i⊥j⊥k,  i=j=k=1

В прямоугольной системе координат в пространстве координаты векторов равны:

i(1;0;0), j(0;1;0), k(0;0;1)

Замечание 1

Единичные векторы являются некомпланарными.

 

Замечание 2

Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.

a=xi+уj+zk

где x, y, z — координаты вектора проекции на соответствующие координатные оси.

Эта формула называется разложением вектора по ортам координатных осей.

Единичный вектор определяется по формуле:

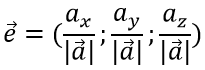
Пример

Дан вектор а = (1; 2; -2)

Требуется найти длину (модуль) и единичный вектор e направления вектора а

Решение

Находим длину вектора a

$\left| {\vec a} \right| = \sqrt {{1^2} + {2^2} + {{\left( { — 2} \right)}^2}}  = 3$

затем вычисляем единичный вектор e

$\vec e = \left( {\frac{1}{3};\frac{2}{3}; — \frac{2}{3}} \right)$

---

Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус». Смотрите схему 1.

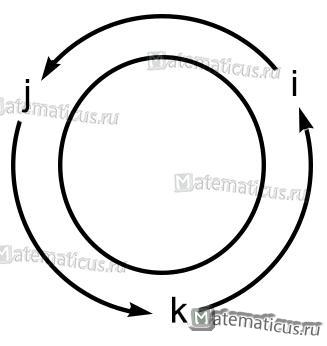
Схема 1

На основании схемы получаем таблицу векторного произведения единичных векторов

  i×i=0      i×j=k        i×k=-j 

  j×i=-k     j×j=0        j×k=i 

  k×i=j      k×j=-i       k×k=0

Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.

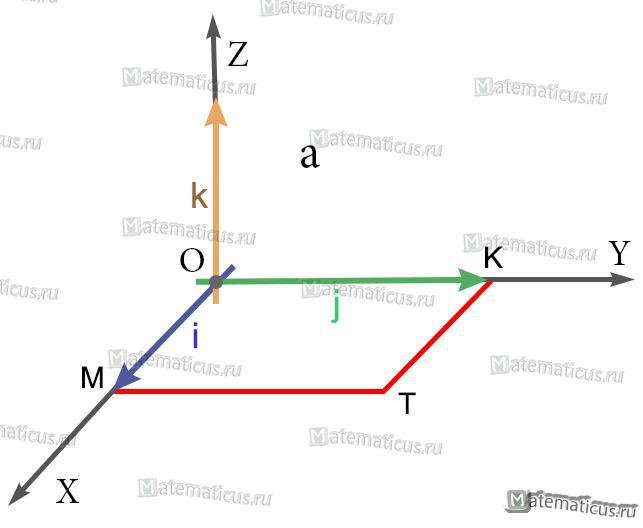
  Решение 
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2)  Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3)  Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).

iхj=k

---

Пример 2
Найти векторное произведение

jхi.

  Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k  -левую).
jхi = −k

www.matematicus.ru

6.2. Найти единичный вектор того же направления что и .

Единичный вектор находится: , где– модуль вектора.

Находим

тогда

Ответ: .

Примечание. Координаты единичного вектора должны быть не больше единицы.

6.3. Найти длину и направляющие косинусы вектора . Сравните с ответом в предыдущем пункте. Сделайте выводы.

Длина вектора – это есть его модуль:

, а направляющие косинусы мы можем найти по формуле одного из способов задания векторов:

Из полученного мы видим, что направляющие косинусы это и есть координаты единичного вектора.

Ответ: ,,,.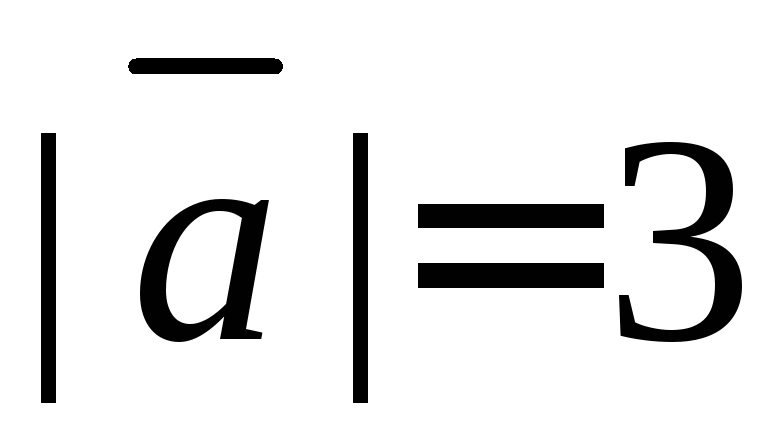

6.4. Найти .

Необходимо выполнить действия умножения вектора на число, сложения и модуль.

Почленно перемножаем координаты векторов на число.

Почленно складываем координаты векторов.

Находим модуль вектора.

Ответ: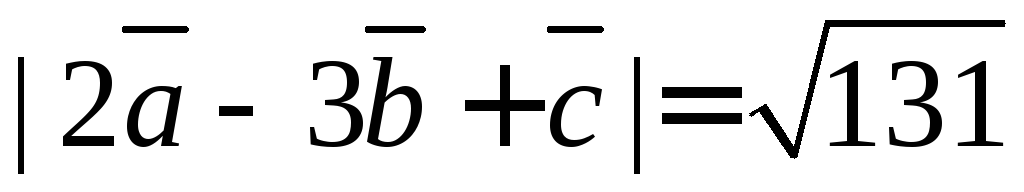

6.5. Определить координаты вектора , коллинеарного вектору, зная, что

и он направлен в сторону, противоположную вектору.

Вектор коллинеарен вектору, значит, его единичный вектор равен единичному векторутолько со знаком минус, т.к. направлен в противоположную сторону.

Единичный вектор имеет длину равную 1, значит, если его умножить на 5, то его длинна будет равна пяти.

Находим

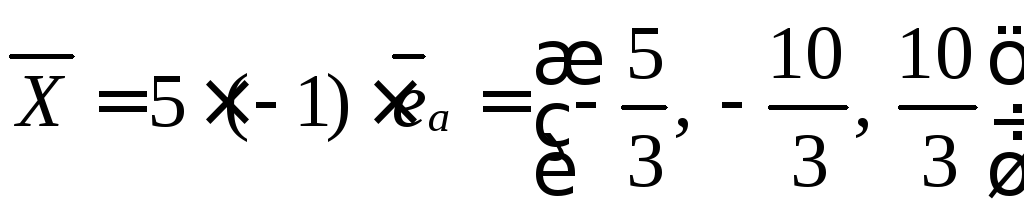
Ответ:

6.6. Вычислить скалярные произведения и. Перпендикулярны ли векторыи,имежду собой?

Выполним скалярное произведение векторов.

Если вектора перпендикулярны, их скалярное произведение равно нулю.

М

ы видим, что в нашем случае вектораи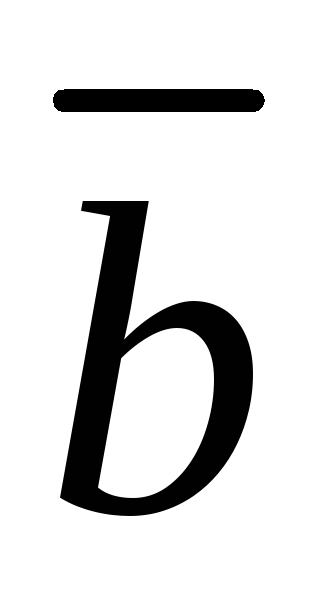перпендикулярны.

Ответ: ,, векторы не перпендикулярны.

Примечание. Геометрический смысл скалярного произведения малоприменим на практике, но все-таки существует. Результат такого действия можно изобразить и вычислить геометрически.

6.7. Найти работу, совершённую материальной точкой к которой приложена сила , при перемещении её из точки B в точку С.

Физический смысл скалярного произведения – это работа. Вектор силы здесь , вектор перемещения – это. А произведение этих векторов и будет искомой работой.

Находим работу

Ответ: -3.

6.8. Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC.

Из определения, скалярного произведения векторов получим формулу нахождения угла: .

Далее, нам нужно определить вектора, между которыми будем искать угол.

Внутренний угол будем искать как угол между векторами, выходящими из одной точки.

Для нахождения внешнего угла нужно совмещать вектора, таким образом, чтоб они выходили из одной точки. Рисунок это поясняет.

Стоит заметить, что , только имеют разные начальные координаты.

Находим необходимые вектора и углы

Ответ: внутренний угол при вершине А = , внешний угол при вершине В =.

6.9. Найти проекции векторов: и

Вспомним вектора-орты: ,,.

Проекция находится также из скалярного произведения

–проекция b на a.

Ранее полученные нами вектора

, ,

Находим проекцию

Находим вторую проекцию

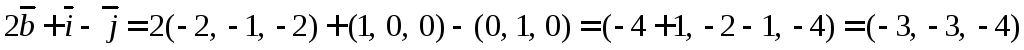
Ответ: ,

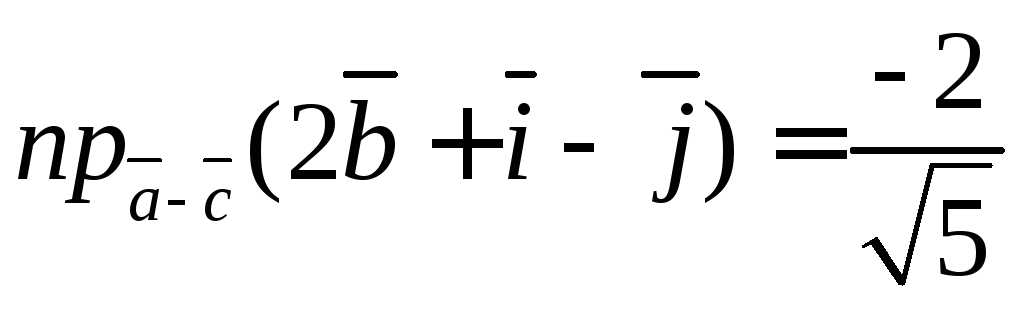
Примечание. Знак минуса при нахождении проекции означает то, что проекция опускается не на сам вектор, а в противоположную сторону, на линию на которой лежит этот вектор.

6.10. Вычислить .

Выполним векторное произведение векторов

Найдем модуль

Синус угла между векторами найдём из определения векторного произведения векторов

Ответ: ,,.

6.11. Найти площадь треугольника ABC и длину высоты, опушенной из точки С.

Геометрический смысл модуля векторного произведения состоит в том, что это площадь параллелограмма, образованного этими векторами. А площадь треугольника равна половине площади параллелограмма.

Площадь треугольника также можно найти как произведение высоты, на основание, делённое на два, из этого можно вывести формулу нахождения высоты.

Таким образом, найдём высоту

Ответ: ,.

6.12. Найти единичный вектор, перпендикулярный векторам и.

Результатом скалярного произведения есть вектор, который перпендикулярный двум исходным. А единичный вектор – это вектор, делённый на его длину.

Ранее, нами было найдено:

,

Ответ: .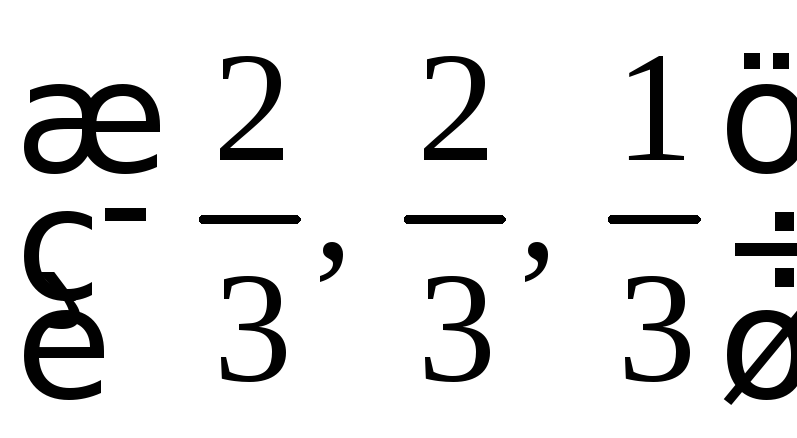

6.13. Определить величину и направляющие косинусы момента силы , приложенной к А относительно точки С.

Физический смысл векторного произведения – это момент силы. Приведём иллюстрацию к данному заданию.

Находим момент силы

Ответ: .

6.14. Лежат ли векторы ,ив одной плоскости? Могут ли эти векторы образовывать базис пространства? Почему? Если могут, разложите по этому базису вектор.

Чтобы проверить лежат ли вектора в одной плоскости необходимо выполнить смешанное произведение этих векторов.

Смешанное произведение не равно нулю, следовательно, вектора не лежат в одной плоскости (не компланарные) и могут образовывать базис. Разложим по этому базису.

Разложим по базису, решив уравнение

Ответ: Векторы ,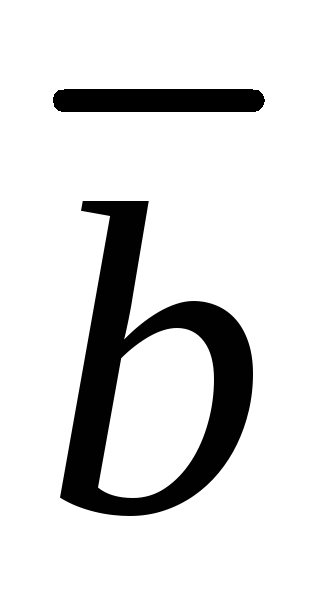ине лежат в одной плоскости..

6.15. Найти . Чему равен объём пирамиды с вершинами A, B, C, D и её высота, опущенная из точки A на основание BCD.

Геометрический смысл смешанного произведения в том, что это объём параллелепипеда образованного этими векторами.

Объём же пирамиды в шесть раз меньше объёма параллелепипеда.

Объём пирамиды, ещё можно найти так:

Получим формулу нахождения высоты

Находим

Находим высоту

Ответ: объём = 2.5, высота =.

6.16. Вычислить и.

–над этим заданием предлагаем вам подумать самим.

–выполним произведение.

Ранее было получено

Ответ: .

6.17. Вычислить

Выполним действия по частям

1)

2)

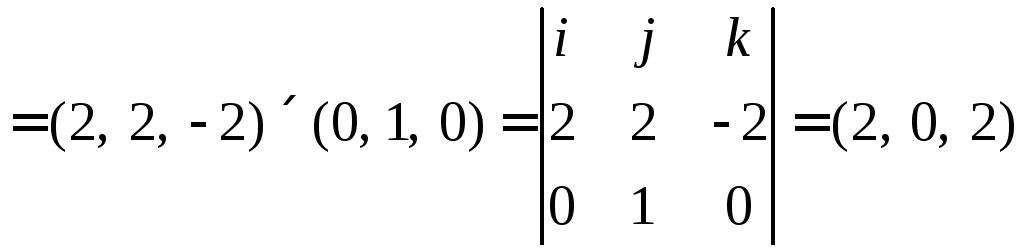
3)

4)

5)

Суммируем полученные значения

Ответ: .

6.18. Найти вектор , зная, что он перпендикулярен векторами, а его проекция на векторравна 5.

Разобьем данную задачу на две подзадачи

1) Найдём вектор, перпендикулярный векторам ипроизвольной длинны.

Перпендикулярный вектор мы получим в результате векторного произведения

Ранее, нами было найдено:

Искомый вектор отличается лишь длинной, от полученного

2) Найдем через уравнение

Ответ:

6.19. Найти вектор , удовлетворяющий условиям,,.

Рассмотрим более детально данные условия.

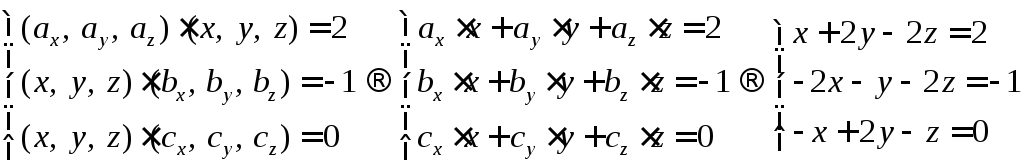
Это система линейных уравнений. Составим и решим данную систему.

Ответ: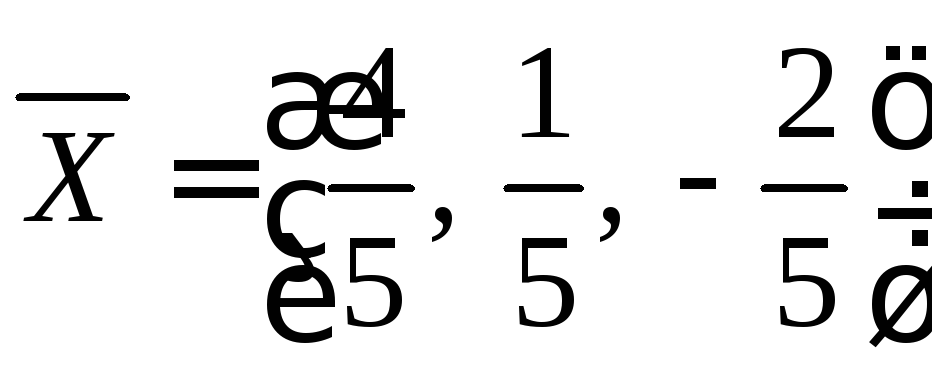

6.20. Определить координаты какого-либо вектора , компланарного с векторамии, и перпендикулярного вектору.

В данном задании два условия: компланарность векторов и перпендикулярность, выполним сначала первое условие, а потом второе.

1) Если вектора компланарны, значит их смешанное произведение равно нулю.

Отсюда получим некоторую зависимость координат вектора

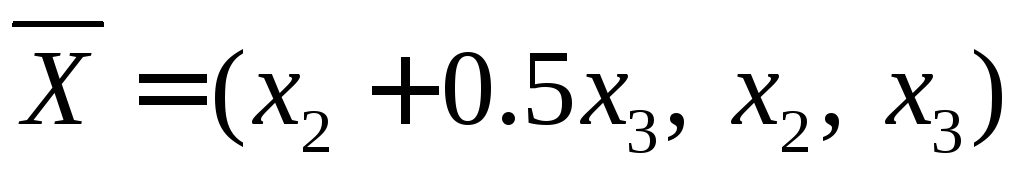
Найдем вектор .

2) Если вектора перпендикулярны, значит их скалярное произведение равно нулю

Мы получили вторую зависимость координат искомого вектора

Для любого значения вектор будет удовлетворять условиям. Подставим.

Ответ: .

Аналитическая геометрия

studfile.net

Алгебра векторов, страница 12

Решение. Пусть вектор d в базисе e₁, e₂, e₃ имеет координаты x, y, z. Тогда

d  = xe₁ + ye₂ + ze₃ , т.е. i + 5j — 2k  = x(2i – k) + y(3i + 3j) + z(2i + 3k),или (2х +3у)i + (3y + 2z)j +

+ (-x +3z)k =  i + 5j — 2k. Приравнивая коэффициенты при ортах i, j, k слева и справа, получим систему уравнений:

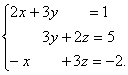
Решая систему уравнений, находим х = -4, у = 3, z = -2. Это и есть координаты вектора d в базисе e₁, e₂, e₃,  следовательно, d  = -4e₁ + 3e₂ — 2e₃.

Пример 4. Найти вектор а, коллинеарный вектору с = 3i — 6j + 2k, составляющий с осью Ох тупой угол, если |a| = 14.

            Решение. Искать вектор а будем исходя из формулы a = |a| a₀. Так как вектор a коллинеарен вектору c и образует тупой угол с осью Ох, а вектор c образует острый угол с осью Ох

(пр_i с = 3 > 0), то a₀ = — c₀. Следовательно, a = |a| (- с₀) = 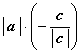. Найдем длину вектора с: 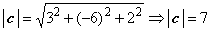, поэтому .

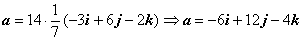Пример 5. Найти вектор с, направленный по биссектрисе угла, образованного векторами

а = 2i — 2j  — k  и b = -4 i + 7j – 4 k, если .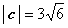

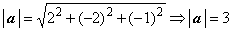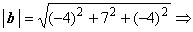
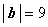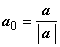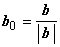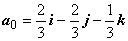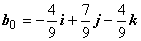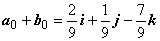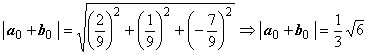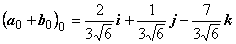Решение. Чтобы вектор c был направлен по биссектрисе, он должен быть диагональю ромба. Найдём модули векторов:  и   и орты  и :  и . Тогда вектор  направлен по биссектрисе. Найдем модуль вектора a₀ + b₀:  и орт . Находим вектор с = |с| (a₀ + b₀) 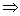 c = 2 i + j – 7 k.

Задачи для самостоятельной работы.

6. Найти координаты вектора 2a + b – 3c, если a = i — 2j, b = 3j – 2 k, c = i — j + k.

7. Разложить вектор d = 2 i – 6 j по векторам , , .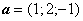

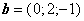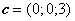vunivere.ru