Вес. Невесомость — Класс!ная физика
Вес. Невесомость
«Физика — 10 класс»
Вспомните определение силы тяжести. Может ли она исчезнуть?
Как мы знаем, силой тяжести называют силу, с которой Земля притягивает тело, находящееся на её поверхности или вблизи этой поверхности.
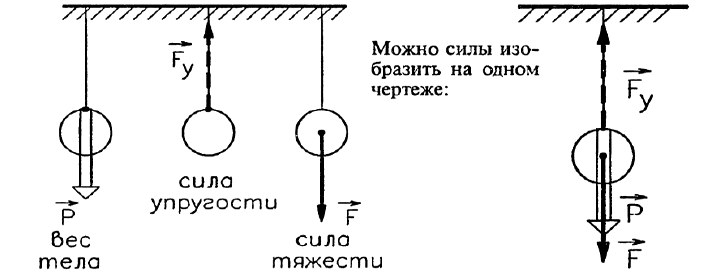
Весом тела называют силу, с которой это тело действует на горизонтальную опору или растягивает подвес.
Вес не является силой какой-то специфической природы. Это название присвоено частному случаю проявления силы упругости.
Вес действует непосредственно на чашку пружинных весов и растягивает пружину; под действием этой силы поворачивается коромысло рычажных весов.
Поясним сказанное простым примером.
Пусть тело А находится на горизонтальной опоре В (рис. 3.9), которой может служить чашка весов.
Силу тяжести обозначим через , а силу давления тела на опору (вес) — через 1.
Модуль силы реакции опоры равен модулю веса
Сила направлена в сторону, противоположную весу 1
Сила реакции опоры приложена не к опоре, а к находящемуся на ней телу.
В то время как сила тяжести обусловлена взаимодействием тела с Землёй, вес 1 появляется в результате совсем другого взаимодействия — взаимодействия тела А и опоры В.
Поэтому вес обладает особенностями, существенно отличающими его от силы тяжести.
Важнейшей особенностью веса является то, что его значение зависит от ускорения, с которым движется опора.
При перенесении тел с полюса на экватор их вес изменяется, так как вследствие суточного вращения Земли весы с телом имеют на экваторе центростремительное ускорение.
По второму закону Ньютона для тела, находящегося на экваторе, имеем
где N — сила реакции опоры, равная весу тела.
Отсюда
На полюсе вес тела равен силе тяготения. Очевидно, что на полюсе вес тела больше, чем на экваторе.
Остановимся на более простом случае.
Пусть тело находится на чашке пружинных весов в лифте, движущемся с ускорением .
Согласно второму закону Ньютона
m = +
где m — масса тела.
Координатную ось OY системы отсчёта, связанной с Землёй, направим вертикально вниз.
Запишем уравнение движения тела в проекции на эту ось:
mау = Fy + Nу.
Если ускорение направлено вниз, то, выражая проекции векторов через их модули, получаем mа = F — N. Так как N = F1, то mа = F — F1.
Отсюда ясно, что лишь при а = 0 вес равен силе, с которой тело притягивается к Земле (F1 = F). Если а ≠ 0, то F1 = F — mа = m(g — а).
Вес тела зависит от ускорения, с которым движется опора, и появление этого ускорения эквивалентно изменению ускорения свободного падения.
Наступление у тел состояния невесомости означает, что тела не давят на опору и, следовательно, на них не действует сила реакции опоры, они движутся только под действием силы притяжения к Земле.
Одинакова ли природа невесомости у тел, находящихся в лифте, и у тел, находящихся в спутнике?
Механическая сущность невесомости состоит в том, что в системе отсчёта, движущейся относительно Земли с ускорением свободного падения, исчезают все явления, которые на Земле обусловлены силой тяжести.
Многократно проводились опыты, в которых создавалось состояние невесомости. Например, самолёт разгоняется и начиная с некоторого момента движется строго по параболе, той, которая была бы в отсутствие воздуха.
В кабине при этом наблюдаются необыкновенные явления: маятник замирает в отклонённом положении, выплеснутая из стакана вода большой сферической каплей повисает в воздухе, и рядом с ней застывают, будто подвешенные на невидимых нитях, все остальные предметы независимо от их массы и формы.
То же самое происходит и в кабине космического корабля при движении его по орбите.
На большой высоте над Землёй почти нет воздуха, так что не надо его сопротивление компенсировать работой двигателей.
Да и полёт длится не минуту, а многие сутки.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Динамика — Физика, учебник для 10 класса — Класс!ная физика
Основное утверждение механики — Сила — Инертность тела. Масса. Единица массы — Первый закон Ньютона — Второй закон Ньютона — Принцип суперпозиции сил — Примеры решения задач по теме «Второй закон Ньютона» — Третий закон Ньютона — Геоцентрическая система отсчёта — Принцип относительности Галилея. Инвариантные и относительные величины — Силы в природе — Сила тяжести и сила всемирного тяготения — Сила тяжести на других планетах — Примеры решения задач по теме «Закон всемирного тяготения» — Первая космическая скорость — Примеры решения задач по теме «Первая космическая скорость» — Вес. Невесомость — Деформация и силы упругости. Закон Гука — Примеры решения задач по теме «Силы упругости. Закон Гука» — Силы трения — Примеры решения задач по теме «Силы трения» — Примеры решения задач по теме «Силы трения» (продолжение) —
Базовая физика. Чем отличаются вес и масса. Невесомость
N называется силой реакции опоры, уравновешивает силу тяжести (в данном случае равна по модулю тем же самым 10 Ньютонам), так что равнодействующая сила F (сумма всех сил) равна нулю: F = mg — N = 0.А то, что силы уравновешены, мы видим из второго закона Ньютона F = m*a, согласно которому если ускорение тела a равно нулю (то есть оно либо покоится, как в нашем случае, либо движется равномерно и прямолинейно), то равнодействующая сила F тоже равна нулю.
Вот теперь можно наконец сказать, что такое вес — это сила, с которой тело действует на подставку или подвес. Согласно третьему закону Ньютона эта сила противоположна силе N и равна ей по модулю. То есть в данном случае составляет те же 10 Н = 1 кгс. Вам, может быть, покажется, что всё это излишне сложно, и надо было сразу сказать, что вес и сила тяжести — одно и то же? Ведь они совпадают и по направлению, и по величине.
Нет, на самом деле они отличаются существенно. Сила тяжести действует постоянно. Вес меняется в зависимости от ускорения тела. Давайте приведём примеры.
1. Вы стартуете вверх на скоростном лифте (скоростном, чтобы фаза ускорения была эффектнее/заметнее). Ваша масса, скажем, 70 кг (вы можете пересчитать все числа ниже для вашей массы). Ваш вес в неподвижном лифте (перед стартом) равен 700 Н (или 70 кгс). В момент разгона вверх результирующая сила F направлена вверх (именно она вас и разгоняет), сила реакции N превышает силу тяжести mg, и поскольку ваш вес (сила, с которой вы действуете на пол лифта) по модулю совпадает с N, вы испытываете так называемую перегрузку. Если бы лифт разгонялся с ускорением g, то вы бы испытали вес 140 кгс, то есть перегрузку 2g, в 2 раза превышающую вес в состоянии покоя. На самом деле в штатном режиме таких перегрузок в лифтах не бывает, ускорение обычно не превышает 1 м/с2, что приводит к перегрузке всего 1.1g. Вес в нашем случае составит 77 кгс. Когда лифт разогнался до нужной скорости, ускорение равно нулю, вес возвращается к начальным 70 кгс. При замедлении вес, напротив, уменьшается, и если ускорение при этом по модулю равно 1 м/с2, то перегрузка составит 0.9g. При движении в обратную сторону (вниз) ситуация переворачивается: при разгоне вес уменьшается, на равномерном участке вес восстанавливается, при замедлении вес увеличивается.
2. Вы бежите, и ваш вес в состоянии покоя по-прежнему 70 кгс. В момент бега, когда вы отталкиваетесь от земли, ваш вес превышает 70 кгс. А пока вы летите (одна нога оторвалась от земли, другая — еще не коснулась), ваш вес равен нулю (поскольку вы не воздействуете ни на подставку, ни на подвес). Это — невесомость. Правда, совсем короткая. Таким образом, бег — это чередование перегрузок и невесомости.
Напомню, что сила тяжести во всех этих примерах никуда не девалась, не менялась, и составляла ваши «кровные» 70 кгс = 700 Н.
Теперь существенно удлиним фазу невесомости: представьте, что вы находитесь на МКС (международной космической станции). При этом мы не устранили силу тяжести — она по-прежнему действует на вас — но поскольку и вы, и станция находитесь в одинаковом орбитальном движении, то относительно МКС вы в невесомости. Можно представить себя где угодно в открытом космосе, просто МКС немного реалистичнее. )
Каким будет ваше взаимодействие с объектами? Ваша масса 70 кг, вы берёте в руку объект массой 1 кг, отбрасываете его от себя. В соответствии с законом сохранения импульса основную скорость получит 1-кг-объект, как менее массивный, и бросок будет примерно столь же «легким», как и на Земле. Но если вы попытаетесь оттолкнуться от объекта массой 1000 кг, то вы фактически оттолкнете себя от него, поскольку основную скорость в этом случае получите вы сами, и для разгона своих 70 кг придётся развить бОльшую силу. Чтобы примерно это представить, каково это, можете подойти сейчас к стене и оттолкнуться от неё руками.
Теперь вы вышли из станции в открытый космос и хотите поманипулировать каким-то массивным объектом. Пусть его масса будет пять тонн.
Честно сказать, я бы прямо очень поостерегся управляться с пятитонным объектом. Да, невесомость и все дела. Но достаточно лишь небольшой его скорости относительно МКС, чтобы прижать вам палец или чего-то посерьёзнее. Эти пять тонн сложно переместить: разогнать, остановить.
А уж представлять, как предложил один человек, себя между двумя объектами массой по 100 тонн и вовсе не хочется. Малейшее их встречное движение, и они вас с лёгкостью придавят. В полнейшей, что характерно, невесомости. )
Ну и наконец. Если вы будете весело лететь по МКС и ударитесь об стенку/переборку, то вам будет больно ровно так же, как если бы вы с той же скоростью бежали и ударились об стену/косяк в своей квартире. Потому что удар уменьшает вашу скорость (то есть сообщает вам ускорение со знаком минус), а ваша масса одинакова в обоих случаях. А значит по второму закону Ньютона и сила воздействия будет соразмерна.
Радует, что в фильмах про космос («Гравитация», «Интерстеллар», сериал «The Expanse») всё более реалистично (пусть и не без огрехов типа Джорджа Клуни, безнадёжно улетающего от Сандры Буллок) отображают базовые вещи, описанные в этом посте.
Резюмирую. Масса «неотчуждаема» от объекта. Если объект сложно разогнать на Земле (особенно если вы постарались минимизировать трение), то его так же сложно разогнать и в космосе. А что касается весов, то когда вы на них становитесь, они просто измеряют силу, с которой их сдавливают, и для удобства отображают эту силу не в Ньютонах, а в кгс. Не дописывая при этом букву «с», чтобы вас не смущать. )
Вес и невесомость
Известно, что в космических кораблях, самолётах и даже вблизи земли может наступать явление невесомости – отсутствие веса, то есть силы, с которой тело действует на опору или подвес (см. § 3-г).
Для выяснения причин невесомости познакомимся сначала с формулой для нахождения веса тела, движущегося с ускорением. Чтобы охватить множество различных направлений вектора ускорения тела по сравнению с вектором ускорения свободного падения, рассмотрим грузик на нити, который вращают в вертикальной плоскости (см. чертёж).
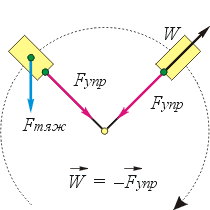
На грузик действуют два тела: нить и Земля, то есть действуют две силы: Fупр и Fтяж.
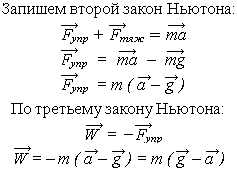
Выпишем начало и конец равенства в виде самостоятельной формулы для определения вектора веса тела, движущегося с ускорением:
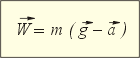 | W – модуль веса тела, Н g – модуль ускорения свободного падения, м/с2 a – модуль ускорения тела, м/с2 m – масса тела, кг |
Проанализируем формулу. Если ускорение тела a векторно равно g, разность в скобках обращается в ноль, и возникает невесомость.
Это может произойти, например, если нить оборвётся. Тогда грузик будет совершать свободное падение – движение только под действием силы тяжести. Так может быть не только с грузиком, но и с любым свободно падающим телом. Например, когда самолёт выключает двигатели и пикирует вниз, когда космический корабль выключает двигатели и движется вокруг Земли только под действием силы тяжести.
Примечание. Поскольку формула векторная, она будет справедлива в любой точке любой траектории, даже прямолинейной (см. задачу в § 13-г).
Военные лётчики и испытатели самолётов хорошо знают фигуру высшего пилотажа «петля Нестерова». Она заключается в том, что самолёт движется в небе также, как и рассмотренный грузик на нити – описывая окружность в вертикальной плоскости. При этом люди в самолёте испытывают перегрузку – многократное увеличение веса: как собственного, так и предметов вокруг. Значение перегрузки, то есть кратность увеличения веса, можно рассчитать по выведенной нами формуле. Рассмотрим пример.
Задача. Мальчик равномерно вращает грузик на нити в вертикальной плоскости так, что в верхней точке грузик совершенно не натягивает нить. Во сколько раз вес грузика в нижней точке превосходит обычный вес этого же грузика в состоянии покоя? Сделайте чертёж.
Решение. Если натяжение нити в верхней точке окружности равно нулю, следовательно, вес грузика равен нулю – он испытывает невесомость.
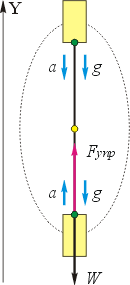
Используем формулу для определения вектора веса:
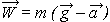
Запишем её в проекциях на ось Y для верхней и нижней точек траектории (левый и правый столбцы):
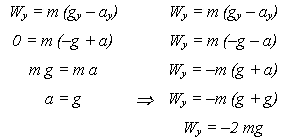
Последнее равенство означает, что вес грузика (то есть сила, с которой он тянет нить) в нижней точке траектории направлен противоположно оси Y, то есть вниз, и по модулю в два раза больше веса грузика при его покое. Поэтому говорят, что грузик испытывает двухкратную перегрузку. Напротив, в верхней точке грузик не натягивает нить, значит, он невесом.
13-е. Вес и невесомость
§ 13-е. Вес и невесомость
Известно, что в космических кораблях, самолётах и даже вблизи земли может наступать явление невесомости – отсутствие веса, то есть силы, с которой тело действует на опору или подвес (см. § 3-г).
Для выяснения причин невесомости познакомимся сначала с формулой для нахождения веса тела, движущегося с ускорением. Чтобы охватить множество различных направлений вектора ускорения тела по сравнению с вектором ускорения свободного падения, рассмотрим грузик на нити, который вращают в вертикальной плоскости (см. чертёж).
На грузик действуют два тела: нить и Земля, то есть действуют две силы: Fупр и Fтяж.
Выпишем начало и конец равенства в виде самостоятельной формулы для определения вектора веса тела, движущегося с ускорением:
Проанализируем формулу. Если ускорение тела a векторно равно g, разность в скобках обращается в ноль, и возникает невесомость.
Это может произойти, например, если нить оборвётся. Тогда грузик будет совершать свободное падение – движение только под действием силы тяжести. Так может быть не только с грузиком, но и с любым свободно падающим телом. Например, когда самолёт выключает двигатели и пикирует вниз, когда космический корабль выключает двигатели и движется вокруг Земли только под действием силы тяжести.
Примечание. Поскольку формула векторная, она будет справедлива в любой точке любой траектории, даже прямолинейной (см. задачу в § 13-г).
Военные лётчики и испытатели самолётов хорошо знают фигуру высшего пилотажа «петля Нестерова». Она заключается в том, что самолёт движется в небе также, как и рассмотренный грузик на нити – описывая окружность в вертикальной плоскости. При этом люди в самолёте испытывают перегрузку – многократное увеличение веса: как собственного, так и предметов вокруг. Значение перегрузки, то есть кратность увеличения веса, можно рассчитать по выведенной нами формуле. Рассмотрим пример.
Задача. Мальчик равномерно вращает грузик на нити в вертикальной плоскости так, что в верхней точке грузик совершенно не натягивает нить. Во сколько раз вес грузика в нижней точке превосходит обычный вес этого же грузика в состоянии покоя? Сделайте чертёж.
Решение. Если натяжение нити в верхней точке окружности равно нулю, следовательно, вес грузика равен нулю – он испытывает невесомость.
Используем формулу для определения вектора веса:
Запишем её в проекциях на ось Y для верхней и нижней точек траектории (левый и правый столбцы):
Последнее равенство означает, что вес грузика (то есть сила, с которой он тянет нить) в нижней точке траектории направлен противоположно оси Y, то есть вниз, и по модулю в два раза больше веса грузика при его покое. Поэтому говорят, что грузик испытывает двухкратную перегрузку. Напротив, в верхней точке грузик не натягивает нить, значит, он невесом.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Конспект урока по физике 7 класс «Вес и невесомость»
Тема урока: Вес тела. Невесомость.
Тип урока: урок «открытия» новых знаний
Базовый учебник: В. В. Белага Физика 7 класс.
Цель урока: сформировать представление о весе тела как силе, ввести понятие «невесомость».
Задачи: 1)сформировать понятие веса ела и невесомости
2)формировать умения различать понятие веса и массы тела, веса тела и силы тяжести
3)развивать наблюдательность, умение обобщать, сравнивать, анализировать
4)совершенствовать умение работать в группе, паре, самостоятельно
Планируемыеобразовательныерезультаты
Предметные: Определить понятия «вес тела» и «невесомость».
Личностные: воспитывать умение работать в микрогруппах, продолжить развитие культуры общения.
Метапредметные: развивать интеллектуальные умения: наблюдать, размышлять, сравнивать, делатьвыводы.
Универсальныеучебныедействия.
Личностные УУД: развитие познавательных интересов, учебных мотивов, оценка и самооценка.
РегулятивныеУУД: составляютпланиопределяютпоследовательностьдействий
КоммуникативныеУУД: описываютсодержаниесовершаемыхдействийвцеляхориентировкидеятельности.
ПознавательныеУУД: устанавливают причинно-следственные связи, осознанно и произвольно строить речевые высказывания.
.
ХОДУРОКА
Организационныймомент.1.
Каждый урок для вас – это новые знания и радость победы над неизвестным.
Есть такая легенда о греческом философе, который гулял в саду и разговаривал со своим учеником.
— Скажи мне, — спросил ученик, — почему тебя часто одолевают сомнения? Ты прожил долгую жизнь, у тебя богатый опыт. Так почему же для тебя осталось много неизвестного и вопросов без ответа?
Подумав, философ нарисовал на земле два шара: большой и маленький. – Твои знания – это маленький шар, а мои – большой. Чем больше шар, тем больше он касается неизвестным. Чем шире круг твоих знаний, тем большее его граница с тем, чего ты не знаешь. И дальше: чем больше ты будешь узнавать, тем больше будет возникать вопросов.
Сегодня мы попробуем расширить круг ваших знаний, чтобы в ваших головах рождались новые вопросы и появлялось желание находить на них ответы.
«Лучший способ изучить что-либо – это открыть самому» (Д. Пойа)
2.Актуализация знаний и фиксирование индивидуальных затруднений в пробной деятельности
1.Фронтальная работа с классом.
1. Что такое сила? Сила – мера взаимодействия тел.
2. Какой величиной является сила? Физическая и векторная.
3. От чего зависит результат действия силы на тело? От ее модуля, направления, точки приложения.
4. С какими видами сил вы познакомились? Сила тяжести, сила упругости
5. Какой буквой обозначается сила?F
6. Каким прибором измеряют силу? Динамометр
7. Назовите единицы измерения силы. Н, ньютон
8. Что стремиться сделать сила упругости? Вернуть тело в и сходное положение.
9. Продолжите предложение: «Сила тяжести – это…»Сила, с которой Земля притягивает к себе тело.
10. От какой величины зависит сила тяжести? От массы
2. Вы увидите неоконченные предложения или пропуски предложения Вам предстоит окончить или вставить в них пропущенные лова.
При любом виде деформации возникает … (сила упругости).
Сила упругости направлена …(противоположно деформации).
Точка приложения силы упругости — это…(точка соединения тела пружины).
Соотношение между силой упругости Fупр пружины и ее удлинением, k: … (формула) называют законом … (Гука) по имени его первооткрывателя
Коэффициент пропорциональности k в законе Гука называется…(жесткостью) пружины.
Жесткость тела зависит от:
Формы тела;
Размеров тела;
Материала, из которого изготовлено тело .Fупр
Назовите силы, изображенные на рисунке.
Формула силы тяжести: .Fтяж = gm Fтяж
Проверьте сами свои ответы и оцените себя.
Поднимите, пожалуйста, руки, кто выполнил работу на 5?4?
3. Выявление причины затруднения
Вопрос: Скажите, что мы измеряем в кабинете врача, встав на весы? Когда мы говорим, что худеем – что мы сбрасываем? Когда мы покупаем 3 кг блок – за что мы платим (Вес)
Правильно ли мы говорим, что наш вес составляет, например, 50 кг?
Поднимите руки те, кто считает, что говорим правильно.
А теперь те, кто считает, что говорим неправильно.
Мнения разделились. Не будем спорить, кто прав, а кто нет.
Разобраться в этом вам поможет новая тема. Сформулируйте её.
“Вес тела. Невесомость”
Как бы вы назвали в русском языке слова «вес» и «невесомость». О чем говорит частица не? Нет веса.
— Какой проблемный вопрос возник перед нами? Вес – это масса или … (сила)
4.Построение проекта выхода из затруднения (2 мин)
— Какую цель вы определили для себя на уроке? Выяснить:
Что такое вес и невесомость, составить характеристику по плану:
5.Релизация построенного проекта.
Опыт 1: У меня в руках грузик. Я выпускаю его из рук. Что с ним происходит? Он падает. Почему? (Грузик падает вниз под действием силы тяжести (притяжения земли? Как направлена сила тяжести?
Опыт 2: Этот же самый грузик подвешиваем к пружине, закреплённой в штативе. Скажите, сейчас на грузик действует сила тяжести? (Да.) А почему тогда грузик не падает? (Потому, что на него действует сила упругости пружины.) Куда она направлена?
Сегодня на уроке мы поговорим о силе, под действием которой произошло растяжение этой пружины..Скажите, в какой момент пружина, закреплённая в штативе, начала растягиваться? (Когда мы прикрепили к ней груз). Сила, с которой груз действует на пружину, вы давите на стул, я действую на пол и так далее, называется весом тела. Работа с текстом
Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.
Вес какая величина?
Итак, вес – это сила, а вовсе не масса, как мы привыкли говорить. Это сила, с которой тело действует, давит на опору или подвес.
План:
Имя:
Точка приложения: опора или подвес.
Вес действует на опору в точке соприкосновения тела и опоры или подвеса.
Направление: перпендикулярно опоре или подвесу.
Если с интеллигентного, скромного и тактичного физика требуют в магазине деньги за 2 кг колбасы, а он видит, что весы показывают всего 1 кг, то закричит ли физик на весь магазин: «Нет уж, простите, вес вашей колбасы не 2, а только 1 кг?»
Не закричит. Вежливый физик не станет так грубо выражаться, потому что помнит, что в килограммах измеряется только одна физическая величина (какая?) – масса, а вес измеряется в ньютонах.
Величина: Давайте подумаем, отчего зависит вес тела?
К первому грузу подвесим второй такой же груз. Пружина растянулась сильней, значит, вес двух грузов больше, чем вес одного груза Какой из этого можно сделать вывод? (Вес зависит от массы тела.) Чем больше масса тела, тем больше его вес. От чего ещё зависит вес? (Оказывается, что и на Земле вес одного и того же тела, в отличие от массы, может быть различным (про вес тела на экваторе и на полюсе). Доклад
Какой вывод можно сделать?
1.Представим себе такую ситуацию: Проводится чемпионат мира по тяжёлой атлетике сразу в двух точках Земли на полюсе и на экваторе. Два спортсмена подняли штангу одной и той же массы (400 кг). Кому бы из спортсменов вы присудили первое место? Оказывается, что первое место нужно присудить спортсмену с полюса, потому что на полюсе притяжение Земли больше, а следовательно и вес тела на полюсе больше, чем на экваторе.
2. Если вы подниметесь высоко в горы, то ваш вес тоже станет меньше, потому что расстояние до центра Земли в горах больше, чем у подножия горы, притяжение меньше и вес тоже уменьшается .
Итак, вес тела зависит от массы и ускорения свободного падения. Поэтому вес неподвижного тела или тела, движущегося с постоянной скоростью, определяется по формуле Р = mg (записывают в тетрадь). Вес направлен из центра соприкосновения тела и опоры или подвеса вертикально вниз.(Зарисовываем точку приложения и направление веса тела).
Итак, если опора неподвижна, то вес тела численно равен силе тяжести:
С помощью какого прибора можно измерить вес тела?
А что происходит, если тело не давит на опору? Оно не действует на опору или подвес, а значит, его вес равен 0. Это состояние называется невесомость.
Есть опора и подвес,
Это значит, есть и вес,
Нет опоры и подвеса,
Однозначно, нет и веса!
Запишите:
Невесомость – это состояние, когда тело не действует на опору или подвес.
Где возникает невесомость? В космосе притяжение к Земле ослабевает с увеличением расстояния, вес уменьшается, тело взмывает вверх и уже не действует на опору. Его вес равен 0.
Сейчас каждому из вас предоставляется уникальная возможность почувствовать себя космонавтом.
Физкультминутка. Подпрыгните 5 раз. Как ваше самочувствие? Ведь сейчас вы 5 раз были в состоянии невесомости. Когда вы находились в воздухе, вы не давили на опору, а, следовательно, ваш вес был равен 0.
Итак, мы с вами сейчас на короткое время почувствовали себя космонавтами – практически побывали в космосе.
А космос таит много загадок.
Представьте себя космонавтом. Скажите, а в космосе вы с такой же силой действовали бы на кресло космического корабля? А груз с такой же силой растягивал бы пружину? Правильно, нет. Так в чём же причина, что на Земле груз растягивает пружину, а в космосе нет? Почему тело может не иметь веса, т.е. находится в состоянии невесомости?
Космонавтам нужно тренироваться. А как вы думаете, где это можно сделать?
(Демонстрация опыта с водой). Вес тела в воде или в другой жидкости меньше, чем в воздухе). Давайте подумаем, где это может использоваться? Именно этот способ и используют для тренировки космонавтов.
.А может вес увеличиваться? Да. Это перегрузки!- учебник.
6.Первичное закрепление
Итак, вернемся к вопросам, заданным в начале урока.
Скажите, что мы измеряем в кабинете врача, встав на весы? Когда мы говорим, что худеем – что мы сбрасываем? Когда мы покупаем 3 кг яблок – за что м платим? Массу
Правильно ли мы говорим, что наш вес составляет, например, 50 кг?
Задача:- Найдите вес тела человека, масса которого равна 50 кг. Р = 50 кг ∙ 10 Н/кг = 500 Н .
7.Включениевсистемузнанийиповторение
— Давайте сделаем вывод:
В чем различие между силой тяжести и весом тела:
— в точке приложения,
— вес может быть равен 0 (невесомость) и может быть больше вычисленного по формуле Р = mg (перегрузки),а сила тяжести НИКОГДА не может быть равна 0!
Сказка: В одном сказочном физическом городе жила прекрасная девушка Масса. Всю свою сознательную жизнь она мечтала о прекрасном принце на белом коне, а влюбилась в обычного мальчишку с обычным физическим именем Вес. С утра до ночи мальчик Вес со своими друзьями гонял мяч во дворе. Так и пролетало бы его беззаботное детство, если бы его взгляд не привлекла эта очаровательная девушка Масса. Мальчик Вес собрал в себе все силы, подошёл к Массе и сказал: «Ты мне очень понравилась, давай с тобой дружить?» «Никакой дружбы у вас не получится!»- вдруг воскликнул мальчик по – имени Ж. Масса всегда постоянная, а ты, то больше, то меньше, а то тебя вообще нет. Я ей больше подхожу, я – ускорение свободного падения, практически не изменяюсь!
Очень сильно обиделся Вес на слова своего друга и пошёл он прочь со слезами на глазах. «Безвыходных ситуаций не бывает» — воскликнул самый умный ученик 7-го класса и посоветовал Весу, что нужно делать, чтобы не изменяться.
Задание: Придумайте продолжение сказки. Что посоветовал семиклассник мальчику Весу, чтобы всегда оставаться постоянным?
(Переселиться на планету шарообразной формы, у которой поверхность ровная, нет гор и морей. Жить на этой планете спокойно, без резких движений.)
Задание 1 : Продолжите предложение
Вес тела – это…
Формула для веса – …
Вес направлен…
Вес зависит от…
Составить синквейн со словом Вес
1.одно существительное, выражающее главную тему cинквейна.
2. два прилагательных, выражающих главную мысль.
3. два глагола, описывающие действия в рамках темы.
4. фраза, несущая определенный смысл.
Рефлексия. Какова была цель нашего урока? Достиг ли поставленной цели?
7. Подведениеитоговурока.
Завершить наш урок я бы хотела словами Конфуция:
«Три пути ведут к знанию: путь размышлений – это путь самый благородный,
Путь подражаний – это путь самый легкий, и путь опыта – это путь самый горький»
Неважно, каким путем человек получает знания, важен результат. И я надеюсь, что сегодня вы получили именно тот результат, которого ожидали.
На экране нарисованы лица, характеризующие состояние человека. Выберите то изображение, которое соответствует вашему состоянию после урока
Тест. Вес и невесомость.
Вес тела — это сила ..
А) с которой тело притягивается к Земле
Б) с которой тело вследствие притяжения к Земле действует на опору или подвес
В) с которой тело действует на другое тело, вызывающее деформацию
Г) возникающая при соприкосновении поверхностей двух тел и
препятствующая перемещению относительно друг друга
Укажите формулу, по какой можно вычислить вес тела?
А) Р= k∆l Б) Р = mg В) Р = Г) P =
Какие силы действуют на тело в состоянии невесомости?
А) Только сила тяжести
Б) Только вес тела
В) Сила тяжести и вес тела
Г) Никакие силы не действуют
Можно ли при помощи динамометра определить вес тела в невесомости?
А) нет
Б) да
В) нет, если тело находится на небольшой высоте
Г) да, если масса тела большая
5. В состоянии невесомости …
А) вес тела равен нулю
Б) на тело не действуют никакие силы
В) сила тяжести равна нулю
Г) масса тела равна нулю
Тест.
А) с которой тело притягивается к Земле
Б) с которой тело вследствие притяжения к Земле действует на опору или подвес
В) с которой тело действует на другое тело, вызывающее деформацию
Г) возникающая при соприкосновении поверхностей двух тел и
препятствующая перемещению относительно друг друга
Укажите формулу, по какой можно вычислить вес тела?
А) Р= k∆l Б) Р = mg В) Р = Г) P =
Какие силы действуют на тело в состоянии невесомости?
А) Только сила тяжести
Б) Только вес тела
В) Сила тяжести и вес тела
Г) Никакие силы не действуют
Можно ли при помощи динамометра определить вес тела в невесомости?
А) нет
Б) да
В) нет, если тело находится на небольшой высоте
Г) да, если масса тела большая
5. В состоянии невесомости …
А) вес тела равен нулю
Б) на тело не действуют никакие силы
В) сила тяжести равна нулю
Г) масса тела равна нулю
Ответы к тесту.
Вес тела.
Конечно, вам приходилось слышать такие выражения: штангист-тяжеловес, боксер наилегчайшей весовой категории. Или когда надо заполнить медицинскую карту, обязательно указывают вес человека. Нам необходимо знать вес различных предметов, чтобы перетащить их или поднять. Так что такое вес?
Вы скажете: надо положить тело на весы и взвесить его. Но ведь так мы лишь провели измерение того, что пока интуитивно считаем весом. Что же все-таки мы измеряем? Давайте-ка проведем мысленный опыт (нам часто придется прибегать к нему). «Выключим» притяжение Земли. Будут ли теперь тела весить? Очевидно, что если Земля перестала кого-то или что-то притягивать к себе, то «оно» не станет и давить на нее или на любую опору.
Значит, вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.
Если тело и опора неподвижны или движутся равномерно и прямолинейно, то вес тела по своему числовому значению равен силе тяжести. ().
Вес тела можно как увеличивать, так и уменьшать хоть до нуля.
Например, поднимая какие-то грузы, конструкторы должны учитывать, что во время резких рывков троса вес груза возрастает, и трос может не выдержать возможного напряжения. Или, стоя на платформе медицинских либо напольных домашних весов, мы заметим, как меняются их показания, если мы начнем приседать или двигать вверх-вниз руками.
Таким образом, вес испытывают те предметы, на которые что-то давит: пол, по которому мы ходим, стул, на котором сидим, веревка, за которую мы уцепились. Все эти тела выполняют одну функцию: мешают нам провалиться вниз или свалиться с чего-то, за что и «расплачиваются» принятой на себя нагрузкой.
Невесомость.
Как избавиться от веса? Если вес это давление на опору, то поступить просто: опору убрать.
Ах!.. В животике что-то обрывается, и мы летим вниз. Опоры нет, веса, значит, нет, что же это тогда? Ничего не остается, как назвать это невесомостью.
Невесомость – это состояние тела, когда его вес равен нулю и оно падает под действием силы тяжести.
Выходит, что любое падение приводит к невесомости? Конечно, нет. Только свободное падение, когда отсутствует воздух, например, в начале наших прыжков с парашютом или с вышки в бассейне. А уж тем более движение спутника вокруг Земли — свободное падение в чистом виде. Да, да, именно падение, ведь не будь притяжения Земли, спутник умчался бы по инерции вдоль нескончаемой прямой. А так и он, и все находящиеся в нем предметы, хоть и крутятся вокруг Земли, но все время одинаково падают, причем свободно. А раз падают вместе, то перестают давить друг на друга не весят.
Все это объясняет удивительные явления, наблюдаемые на орбитальной станции. Маятниковые часы замирают, капли воды не падают, а медленно «плавают» внутри кабины. Вообще исчезают понятия пола и потолка, «верха» и «низа».
.
Физика. Вес тела. Невесомость | Школа Онлайн. 7 класс
Конспект по физике для 7 класса «Вес тела. Невесомость». ВЫ УЗНАЕТЕ: Что такое вес тела. Чем отличается вес тела от силы тяжести. Чем отличается вес тела от массы. Что такое невесомость. ВСПОМНИТЕ:
Конспекты по физике Учебник физики Тесты по физике
Вес тела. Невесомость
В повседневной жизни мы очень часто используем слово «вес». Мы говорим: вес продуктов, вес нашего тела. При этом зачастую под словом «вес» подразумевается масса тела. В физике используют термины «вес», «масса» и «сила тяжести», и все они обозначают совершенно разные понятия.
ВЕС ТЕЛА
Рассмотрим тело, подвешенное к динамометру. На само тело действуют сила тяжести и сила упругости пружины. Именно поэтому тело находится в равновесии. Но и растянутая пружина также находится в равновесии, хотя сила упругости, возникающая в ней, стремится вернуть её в первоначальное состояние. То есть не только пружина действует на тело, но и тело действует на пружину с некоторой силой.
Силу, с которой тело, находящееся под действием силы тяжести, действует на опору или подвес, называют весом тела. Таким образом, на крючок динамометра действуют две силы: сила упругости пружины и вес тела.
Вес тела, как и любая сила, — векторная величина. Вес тела обозначают буквой Р. Сила упругости и вес тела имеют противоположные направления: сила упругости направлена вверх, а вес тела вниз. При этом модули этих сил равны: Р = Fупр.
Именно поэтому говорят, что динамометром можно измерять не только силу упругости, но и вес тела. Динамометр также называют пружинными весами.
ВЕС ТЕЛА И СИЛА ТЯЖЕСТИ
Вес возникает в результате притяжения Земли и зависит от состояния движения тела.
Если тело и опора находятся в покое или движутся равномерно и прямолинейно, то вес тела по своему числовому значению равен силе тяжести, действующей на тело: Р = Fтяж или Р = mg.
При этом важно помнить, что сила тяжести и вес тела не одно и то же, они имеют различную физическую природу: сила тяжести возникает вследствие взаимодействия тела и Земли, а вес — в результате взаимодействия тела и опоры. Именно поэтому сила тяжести приложена к телу, а вес приложен к опоре или подвесу.
ВЕС ТЕЛА И МАССА
Единицей веса тела, как и любой силы, является ньютон. Вес имеет числовое значение, направление и точку приложения.
Вес тела не следует путать с массой тела, которая измеряется в килограммах и является скалярной величиной, т. е. величиной, не имеющей направления и точки приложения. Так, ребёнок, имеющий массу 30 кг, имеет вес, равный 300 Н, если считать, что g = 10 Н/кг.
ЗАВИСИМОСТЬ ВЕСА ОТ УСЛОВИЙ, В КОТОРЫХ НАХОДИТСЯ ТЕЛО
Вес тела равен по своему числовому значению силе тяжести, если тело находится на неподвижной опоре или опора движется равномерно и прямолинейно. Если же опора вместе с телом движется неравномерно по линии действия силы, т. е. вверх или вниз, то тело действует на опору сильнее или слабее, чем при равномерном движении. В этом случае вес тела может быть больше силы тяжести, меньше се или равным нулю.
Поднимаясь на скоростном лифте, в самом начале движения мы ощущаем, как нас слегка прижимает к полу. А при спуске нас как будто слегка приподнимает. Дело в том, что при движении лифта вверх вес тела увеличивается, а при движении вниз — уменьшается. Этот факт можно проверить, если подняться или опуститься в лифте стоя на весах.
НЕВЕСОМОСТЬ
Проведем следующий опыт. Подвесим за нитку пружину, а к ней прикрепим груз. В результате пружина растянется. Теперь перережем нить и понаблюдаем за процессом падения пружины вместе с грузом. В течение всего времени падения пружина будет оставаться нерастянутой. Получается, что при падении груз не действует на пружину и, следовательно, его вес в этот момент равен нулю.
Таким образом, свободно падающее тело не действует на свободно падающую вместе с нам пружину. В этом случае вес тела равен нулю.
Про такое тело говорят, что оно находится в состоянии невесомости. При этом сила тяжести по-прежнему действует на тело и заставляет его падать.
Подобные явления наблюдаются и на спутнике, обращающемся вокруг Земли.
Сам спутник и все находящиеся в нем тела, включая космонавта, обращаясь вокруг Земли, как бы непрерывно свободно падают на Землю. Вследствие этот, все находящиеся на спутнике тела не действуют на опоры, а подвешенные к пружине не растягивают её. Все предметы находятся в состоянии невесомости. Однако при разгоне космического корабля, когда он выходит на орбиту, или при торможении во время посадки вес космонавта оказывается больше силы тяжести и он испытывает сильные перегрузки.
Вы смотрели Конспект по физике для 7 класса «Вес тела. Невесомость»: Что такое вес тела. Чем отличается вес тела от силы тяжести. Чем отличается вес тела от массы. Что такое невесомость.
Вернуться к Списку конспектов по физике (В оглавление).
Урок «Вес тела. Невесомость»
Муниципальное общеобразовательное учреждение
Донская средняя общеобразовательная школа
Открытыйурок
по физике в 10 классе
«Вес тела. Невесомость»
Учитель: Лохматова О.А.
Тема урока: Вес тела. Невесомость.
Цель урока:
Образовательная: Дать учащимся представление о понятии «вес тела». Раскрыть понятие невесомости и перегрузок.
Вывести формулы для веса тела движущегося с ускорением вертикально вверх и вниз.
Закрепить их на примерах из жизни.
Сформировать представления учащегося, где эти знания применяются.
Развивающая: развивать интерес к физике;
Воспитательная: воспитывать аккуратность.
Тип урока: комбинированный урок.
Оборудование: два бруска, металлическая планка, груз, штатив, пружина, динамометр, фильм «Невесомость», пружинные весы, диафильм «Явление тяготения».
Демонстрации:
1. Определение веса покоящегося тела;
2. Демонстрация состояния невесомости.
3. Определение веса тела, движущегося с ускорением.
План урока.
I. Мотивация.
Ребята, наш сегодняшний урок я хочу начать со слов К.Э.Циолковского: «Человечество не останется вечно на Земле, но в погоне за светом и пространством, сначала робко проникнет за пределы атмосферы, а затем завоюет себе все околосолнечное пространство».
На сегодняшний день люди сумели проникнуть за пределы атмосферы, но еще пока не завоевали все околосолнечное пространство. Какие были трудности и сложности в самом начале этого тернистого пути? Да и вообще нужно ли было человечеству осваивать космос? На эти вопросы нам предстоит ответить на уроке.
Итак, тема нашего урока: «Вес тела. Невесомость. Перегрузки».
II. Ход урока.
«Как это удивительно – обнаружить, что все явления природы управляются небольшим числом сил!» (М.Фарадей).
В механике выделяют силы тяготения, упругости, трения.
1. Актуализация знаний.
1)Сила упругости – Что ребята вы знаете о Fупр.?
План ответа:
а) что называется силой упругости.
б) когда возникает сила упругости.
в) куда направлена.
г) чему пропорциональна, формула.
2)Сила тяжести – Что ребята вы знаете о Fтяж.?
а) что называется?
б) куда направлена.
в) от чего зависит? Формула.
е) что такое g? g = ? Особенности g ?
ж) к чему прикладывается? Куда направлена?
3) Почему мяч, брошенный вертикально вверх, падает на землю?
4) Где больше сила тяжести, действующая на тело: на поверхности земли или на высоте 300км над землей? Почему?
5) Что общего между движением искусственных спутников земли и свободным падением тел в трубке, из которой откачан воздух?
2. Изучение нового материала.
А что такое вес тела?
В обиходе часто вес путают с массой, силой тяжести: «Сколько весит ведро воды?» или «Взвесьте 0,5 кг конфет». Чтобы в дальнейшем избежать путаницы, дадим определение понятия «вес тела»: сила, с которой тело, вследствие его притяжения к Земле действует на опору или подвес. Обратим внимание: вес действует на опору или подвес, а не на тело.
Фрагмент презентации.
Учитель:
Возникает неожиданный вопрос: а почему, собственно, тела действуют на опоры и подвесы?
Ученик I.
Обычный ответ: «Потому что тело притягивается к Земле». Согласны все?
Учитель:
Возражаю: действительно, тело притягивается к Земле с силой тяжести F = mg, но ведь это взаимодействие тела и Земли, при чем здесь опора?
Ученик I.
Другой аргумент: если бы не было опоры, то тело падало бы, а опора этому препятствует силой упругости, возникающей при её деформации.
Учитель:
Тоже верно, но это объясняет только действие опоры на тело, а не тела на опору, и вопрос остался открытым.
Ученик I.
Вспомним третий закон Ньютона: «Если опора действует на тело, то и тело должно действовать на опору с такой же по значению силой». Действие и противодействие — силы одной природы. Реакция опоры N есть сила упругости, значит, и вес тела возникает при деформации тела. Не только тело, падая, деформирует опору или подвес, но и опора деформирует тело. Да-да, все тела, стоящие сейчас на столе перед вами, слегка сжаты, настолько мало, что никто на это не обращает никакого внимания. И лично вы, встав с постели на пол ногами и деформируя пол, сами деформируетесь (сжимаетесь) на 2—3см.
Учитель.
И действительно, деформацию тела пронаблюдать трудно, а вот деформацию опоры и подвеса — пожалуйста.
Опыт:
1) Два бруска, металлическая планка, груз.
Под действием силы тяжести некоторое время груз будет двигаться вниз, прогибая доску, а затем, остановится, при этом возникает сила, с которой опора действует на тело. Деформируется не только опора, но и тело притягивается Землей.
2) Штатив, пружина, груз.
Пружина окажется деформированной, появится сила упругости пружины, но возникнет ещё одна сила — сила упругости деформированного тела.
Когда тело находится в покое или движется прямолинейно и равномерно относительно инерциальной системы отсчета, то вес тела по модулю равен силе тяжести.
Вес тела
а) что называется весом покоящегося тела?
б) какая природа этой силы?
в) на что действует? (к чему приложена)
г) формула. P = mg – если тело покоится или равномерно движется.
Б) P = mg и F = mg
– Одинаковы ли эти силы?
разная природа
действуют на разные тела
различны точки приложения.
В) работа на интерактивной доске
Вопросы:
Какая сила изображена?
Чем отличаются изображённые силы?
Г) От чего зависит
Fт ? — зависит от m – массы тела
Fу? — зависит от x-удлинения
P ? — от массы тела, при условии, что тело находится в покое или движется равномерно вместе с опорой (или подвесом)
. Выясним, что происходит с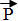 
(весом), когда тело движется по вертикали вниз.
Учащиеся самостоятельно проделывают опыт на столах и убеждаются в результате опыта.
Учитель проговаривает: а) учащиеся держат динамометр с грузом в руке
— Что происходит под действием груза?
— Какие силы возникают?
— Чему по модулю равен вес?
— Сравнить можно силы только … (одной природы)
— Что происходит со стрелкой динамометра, когда опускают динамометр с грузом вниз?
— Стрелка возвращается на «0» т.е. вес уменьшается.
— Докажем это.
С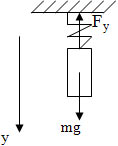
делаем рисунок, обозначим все действующие силы.
— Выберем ось по направлению ускорения.
— Какой закон описывает это движение?
— Какие силы действуют?
Вывод (сами учащиеся формируют):
Если тело вместе с опорой или подвесом движется с ускорением, которое направлено вниз, то его вес уменьшается по сравнению с весом покоящегося тела.
Рассмотрим второй способ движения.
Когда груз вместе с динамометром движется вверх. Учащиеся самостоятельно проделывают этот опыт и убеждаются, что стрелка отклоняется вниз.
— Что пронаблюдали?
Меняется Fy т. е. меняется и P – он увеличивается – докажем.
З
апишем II закон Ньютона – уравнение
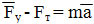
Оy: — Fy + mg = — ma
mg + ma = Fy , т.к. | Fy | = | P |, то
m (g + a) = P
Сравним P0= mg и P = m(g + a)
P0 < P т.к. g < (g + a)
Вывод (дети сами): Если тело движется с ускорением вверх, то его вес больше веса покоящегося тела.
— Может ли увеличиться вес тела, движущегося по окружности? (да)
— А в какой точке больше в верхней или в нижней?
Задача:
Рассчитать вес летчика массой m, выводящего самолёт из пикирования со скоростью v, и радиусом окружности r?
Учащиеся самостоятельно выполняют эту задачу, один у доски проговаривая каждый шаг.
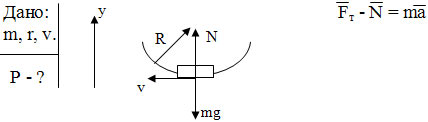
Оy: — mg + N = ma | N | = | P |
P = m (g + a) a = v2/R
Р = m(g + v2/R)
Вывод: вес лётчика увеличится.
Ребята, перегрузки влияют на организм человека, так как увеличивают свой вес внутренние органы летчика, увеличивается сила, с которой они действуют друг на друга и на самолет или кабину космического корабля. Это вызывает болезненные ощущения. Здоровый человек может без вреда выдерживать кратковременные трехкратные перегрузки, т. е. увеличение веса в три раза. Космонавтам при старте и посадке космического корабля приходится выдерживать многократные перегрузки. Чтобы это не нанесло ущерба здоровью космонавтов, их тренируют на земле с помощью специальных аппаратов.
Привести примеры перегрузки.
а) космонавт при старте ракеты – испытывает 10кратные перегрузки.
— Мы с вами на поверхности Земли можем испытывать перегрузку?
б) качели – «лопенги».
в) поднимаемся на 5-й, 9-й этажи.
г) прыгаем на физкультуре, подымаемся по шведской стенке.
Но эти перегрузки незначительны.
Рассмотрим ещё один вид движения.
Опыт (проделывают учащиеся самостоятельно и наблюдают):
Динамометр с грузом подняли и выпустили из рук. Что произошло со стрелкой?
— Она вернулась на «0»?
— Что это значит?
Нет Fy, Fу = 0 → P = 0 т. е. вес отсутствует.
Это явление называется невесомостью.
— При каком условии P = 0? При свободном падении, т. е. а = g
P = (g – g) = 0.
Вес исчез: груз, как говорят, стал невесомым. В чем состоит причина невесомости?
Ученик.
Невесомость объясняется тем, что сила всемирного тяготения, а значит и сила тяжести, сообщают всем телам одинаковое ускорение g. Поэтому всякое тело, на которое действует только сила тяжести или вообще сила всемирного тяготения, находится в состоянии невесомости. Но надо помнить, что если в нашем опыте стрелка весов стоит на нуле, то это не значит, что исчезла сила тяжести. Исчез вес, т.е. сила, с которой груз действует на подвес. Сила тяжести остается – она причина свободного падения.
Кратковременное состояние невесомости испытывал каждый. В таком состоянии находится прыгун с момента отрыва от Земли и до момента приземления; пловец, прыгающий с вышки, до соприкосновения с водой. Даже бегун в короткие промежутки времени между касаниями ногой земли. Длительное состояние невесомости возникает при свободном полете космического корабля.
(Фрагмент фильма «Невесомость»).
А все-таки невесомость – друг или враг? (Выслушиваю ответы учащихся).
Вывод: невесомость далеко не безобидна для человеческого организма, но для науки она открывает новые возможности. Можно, например, смешивать жидкости, которые на Земле невозможно перемешать; получать в 50—100 раз быстрее и в 10—20 раз чище, чем на Земле, вещества, необходимые для изготовления лекарств и полупроводников, и многое другое…
3. Итог урока
Весом тела называется сила, с которой тело, вследствие его притяжения к земле, давит на опору или растягивает подвес.
Вес покоящегося тела и тела, движущегося с постоянной скоростью, равен силе тяжести: Р = mg
Вес тела, движущегося с ускорением а, выражается формулой Р = m(g – a)
Тело находится в состоянии невесомости, если на него действует только сила тяжести.
Невесомость – это такое состояние тела, при котором в теле отсутствуют все внутренние напряжения, обусловленные силой тяжести.
4. Д/З. §33, подготовиться к самостоятельной работе.
Спасибо за урок.