Равновесие тел. Виды равновесия
Виды равновесия тел
Различают:
- устойчивое равновесие
- неустойчивое равновесие
- безразличное равновесие
Это происходит, если при небольшом смещении тела в любом направлении от первоначального положения равнодействующая сил, действующих на тело, становится отличной от нуля и направлена к положению равновесия. Например, шарик, лежащий на дне сферического углубления (рис.1 а).
В данном случае при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия. Примером может служить шарик, находящийся в верхней точке выпуклой сферической поверхности (ри.1 б).
В этом случае при небольших смещениях тела из первоначального положения равнодействующая приложенных к телу сил остается равной нулю. Например, шарик, лежащий на плоской поверхности (рис.1,в).
Рис.1. Различные типы равновесия тела на опоре: а) устойчивое равновесие; б) неустойчивое равновесие; в) безразличное равновесие.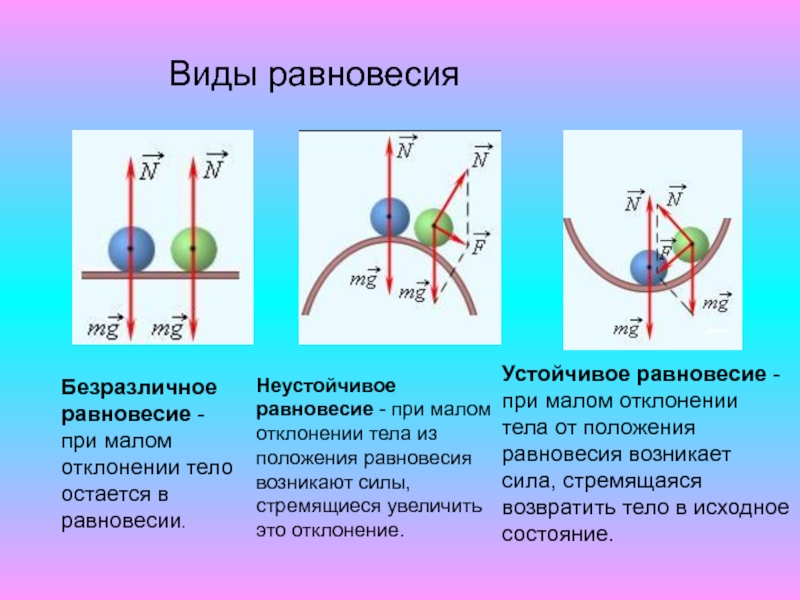
Статическое и динамическое равновесие тел
Если в результате действия сил тело не получает ускорения, оно может находиться в состоянии покоя или двигаться равномерно прямолинейно. Поэтому можно говорить о статическом и динамическом равновесии.
В состоянии статического равновесия находится подвешенный на тросах фонарь, любое строительное сооружение. В качестве примера динамического равновесия можно рассматривать колесо, которое катится по плоской поверхности при отсутствии сил трения.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Равновесие тел.
 Виды равновесия. 10-й класс Цели урока: Изучить состояние равновесия тел, познакомиться с различными видами равновесия; выяснить условия, при которых тело находится в равновесии.
Виды равновесия. 10-й класс Цели урока: Изучить состояние равновесия тел, познакомиться с различными видами равновесия; выяснить условия, при которых тело находится в равновесии.Задачи урока:
- Учебные: Изучить два условия равновесия, виды равновесия (устойчивое, неустойчивое, безразличное). Выяснить, при каких условиях тела более устойчивы.
- Развивающие: Способствовать развитию познавательного интереса к физике. Развитие навыков сравнивать, обобщать, выделять главное, делать выводы.
- Воспитательные: Воспитывать внимание, умения высказывать свою точку зрения и отстаивать её, развивать коммуникативные способности учащихся.
Тип урока: урок изучения нового материала с компьютерной поддержкой.
Оборудование:
- Диск «Движение и взаимодействие тел» из «Электронных уроков и тестов».

- Диск «Работа и мощность» из «Электронных уроков и тестов.
- Таблица «Условия равновесия».
- Призма наклоняющаяся с отвесом.
- Геометрические тела: цилиндр, куб, конус и т.д.
- Компьютер, мултимедиапроектор, интерактивная доска или экран.
- Презентация.
Ход урока
Сегодня на уроке мы узнаем, почему подъёмный кран не падает, почему игрушка «Ванька-встанька» всегда возвращается в исходное состояние, почему Пизанская башня не падает?
I. Повторение и актуализация знаний.
- Сформулировать первый закон Ньютона. О каком состоянии говорится в законе?
- На какой вопрос отвечает второй закон Ньютона? Формула и формулировка.
- На какой вопрос отвечает третий закон Ньютона? Формула и формулировка.
- Что называется равнодействующей силой? Как она находится?
- Из диска «Движение и взаимодействие тел» выполнить задание № 9 «Равнодействующая сил с разными направлениями» (правило сложения векторов (2, 3 упражнения)).

II. Изучение нового материала.
1. Что называется равновесием?
Равновесие – это состояние покоя.
2. Условия равновесия. (слайд 2)
а) Когда тело находится в покое? Из какого закона это следует?
Первое условие равновесия: Тело находится в равновесии, если геометрическая сумма внешних сил, приложенных к телу, равна нулю. ∑F = 0
б) Пусть на доску действуют две равные силы, как показано на рисунке.
Будет ли она находиться в равновесии? (Нет, она будет поворачиваться)
В покое находится только центральная точка, а остальные движутся. Значит, чтобы тело находилось в равновесии, необходимо, чтобы сумма всех сил, действующих на каждый элемент равнялась 0.
Второе условие равновесия: Сумма моментов сил, действующих по часовой стрелке, должна равняться сумме моментов сил, действующих против часовой стрелки.
∑ Mпо часовой = ∑ Mпротив часовой
Момент силы: M = F L
L – плечо силы – кратчайшее расстояние от точки опоры до линии действия силы.
3. Центр тяжести тела и его нахождение. (слайд 4)
Центр тяжести тела – это точка, через которую проходит равнодействующая всех параллельных сил тяжести, действующих на отдельные элементы тела (при любом положении тела в пространстве).
Найти центр тяжести следующих фигур:
4. Виды равновесия.
а) (слайды 5–8)
Вывод: Равновесие устойчиво, если при малом отклонении от положения равновесия есть сила, стремящаяся вернуть его в это положение.
Устойчиво то положение, в котором его потенциальная энергия минимальна. (слайд 9)
б) Устойчивость тел, находящихся на точке опоры или на линии опоры. (слайды 10–17)
(слайды 10–17)
Вывод: Для устойчивости тела, находящегося на одной точке или линии опоры необходимо, чтобы центр тяжести находился ниже точки (линии) опоры.
(слайд 18)
1) Поверхность опоры – это не всегда поверхность, которая соприкасается с телом (а та, которая ограниченна линиями, соединяющими ножки стола, треноги)
2) Разбор слайда из «Электронных уроков и тестов», диск «Работа и мощность», урок «Виды равновесия».
Рисунок 1.
- Чем различаются табуретки? (Площадью опоры)
- Какая из них более устойчивая? (С большей площадью)
- Чем различаются табуретки? (Расположением центра тяжести)
- Какая из них наиболее устойчива? (Укоторой центр тяжести ниже)
- Почему? (Т.к. её можно отклонить на больший угол без опрокидывания)
3) Опыт с призмой отклоняющейся
- Поставим на доску призму с отвесом и начнём её постепенно поднимать за один край.
 Что мы видим?
Что мы видим? - Пока линия отвеса пересекает поверхность, ограниченную опорой, равновесие сохраняется. Но как только вертикаль, проходящая через центр тяжести, начнёт выходить за границы поверхности опоры, этажерка опрокидывается.
Разбор слайдов 19–22.
Выводы:
- Устойчиво то тело, у которого площадь опоры больше.
- Из двух тел одинаковой площади устойчиво то тело, у которого центр тяжести расположен ниже, т.к. его можно отклонить без опрокидывания на большой угол.
Разбор слайдов 23–25.
Какие корабли наиболее устойчивы? Почему? (У которых груз расположен в трюмах, а не на палубе)
Какие автомобили наиболее устойчивы? Почему? (Чтобы увеличить устойчивость машин на поворотах, полотно дороги наклоняют в сторону поворота.)
Выводы:

III. Применение знаний об устойчивости тел.
- Каким специальностям наиболее необходимы знания о равновесии тел?
- Проектировщикам и конструкторам различных сооружений (высотных зданий, мостов, телевизионных башен и т.д.)
- Цирковым артистам.
- Водителям и другим специалистам.
(слайды 28–30)
- Почему «Ванька-встанька» возвращается в положение равновесия при любом наклоне игрушки?
- Почему Пизанская башня стоит под наклоном и не падает?
- Каким образом сохраняют равновесие велосипедисты и мотоциклисты?
Выводы из урока:
- Существует три вида равновесия: устойчивое, неустойчивое, безразличное.
- Устойчиво положение тела, в котором его потенциальная энергия минимальна.
- Устойчивость тел на плоской поверхности тем больше, чем больше площадь опоры и ниже центр тяжести.
Домашнее задание: § 54–56 (Г. Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский)
Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский)
Использованные источники и литература:
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н.Сотский. Физика. 10 класс.
- Диафильм «Устойчивость» 1976 г. (отсканирован мною на плёночном сканере).
- Диск «Движение и взаимодействие тел» из «Электронных уроков и тестов».
- Диск «Работа и мощность» из «Электронных уроков и тестов».
Равновесие тел. О Ваньке-встаньке, центре тяжести и сохранении равновесия :: Класс!ная физика
Если тело в покое, значит оно находится в состоянии равновесия. Тогда геометрическая сумма сил, а также сумма моментов, действующих на тело, равны нулю.
Большинство тел покоится на опорах, в том числе и человек. Стоящий предмет (тело на опоре), не опрокидывается, если вертикаль, проведенная через центр тяжести, пересекает площадь опоры тела.
Падающая башня в итальянском городе Пиза не падает, несмотря на свой наклон, т. к. отвесная линия, проведенная из центра тяжести, не выходит за пределы основания.
к. отвесная линия, проведенная из центра тяжести, не выходит за пределы основания.
Предел устойчивости тела, стоящего на наклонной плоскости удобно оценивать углом наклона. Предельный угол наклона можно определить геометрически: tag альфа = L / 2h
Чем больше L, тем ниже располагается центр тяжести тела (т.е. меньше h), и тем устойчивей тело на опоре.
Существуют три вида равновесия:
Безразличное равновесие.
И шар, и линейка, подвешенная на гвоздике, находятся в состоянии безразличного равновесия.
Лежащий на горизонтальной поверхности цельный однородный или полый шар сам по себе (без воздействия посторонних сил) с места не сдвинется, и расстояние от точки опоры до центра тяжести будет всегда одинаково.
Линейка, подвешенная на горизонтальной оси вращения в точке, где расположен её центр тяжести, будет висеть в любом положении, в каком её оставили, не стремясь повернуться.
Устойчивое равновесие.
Если попытаться вывести тело из состояния устойчивого равновесия, то обязательно возникнет сила, возвращающая его в исходное равновесное состояние.
Шарик на дне чаши находится в единственном состоянии устойчивого равновесия. В этом положении линия, соединяющая точку опоры и центр тяжести тела, вертикальна.
У неваляшки внутреннее устройство таково, что создает смещенный вниз центр тяжести. Поэтому такое положение равновесия является устойчивым: центр тяжести корпуса неваляшки и точка её опоры лежат на вертикали, причем расстояние между центром тяжести и точкой опоры всегда наименьшее.
Если тело подвешено на нити, то, как не изменяй его положение, оно будет стремиться занять положение устойчивого равновесия, когда линия, соединяющая центр тяжести тела и точку подвеса, принимает вертикальное положение. При этом центр тяжести всегда будет находиться ниже точки подвеса.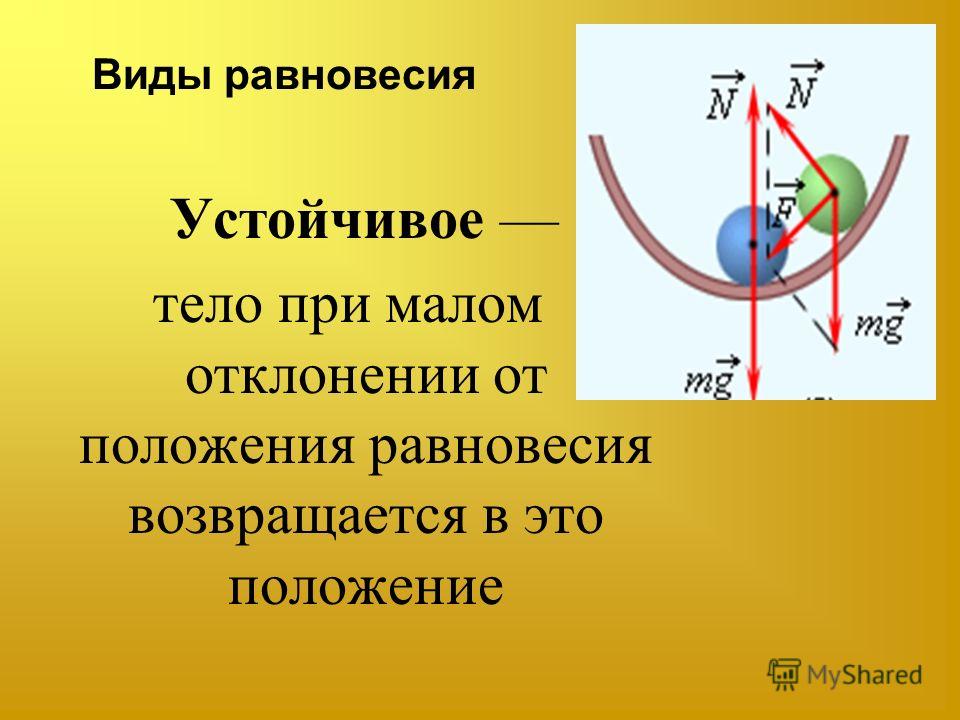 Создатели архитектурных сооружений стремятся, чтобы созданные ими конструкции находились в состоянии устойчивого равновесия. Эйфелева башня в Париже, телевышки во всех странах мира имеют расширение при основании и смещенный вниз центр тяжести. Так Александрийская колонна на Дворцовой площади Санкт-Петербурга при её огромной высоте не имеет врытого в землю фундамента, а спокойно стоит на земле. И это состояние устойчивого равновесия объяснимо: смещенный вниз центр тяжести колонны.
Создатели архитектурных сооружений стремятся, чтобы созданные ими конструкции находились в состоянии устойчивого равновесия. Эйфелева башня в Париже, телевышки во всех странах мира имеют расширение при основании и смещенный вниз центр тяжести. Так Александрийская колонна на Дворцовой площади Санкт-Петербурга при её огромной высоте не имеет врытого в землю фундамента, а спокойно стоит на земле. И это состояние устойчивого равновесия объяснимо: смещенный вниз центр тяжести колонны.
Неустойчивое равновесие.
Если чуть-чуть сдвинуть или отклонить тело, находящееся в состоянии неустойчивого равновесия, то возникает сила, стремящаяся ещё больше отклонить его от равновесного состояния.
В качестве примера можно привести шарик, лежащий на выпуклой поверхности или неваляшку, поставленную с «ног на голову».
Как надо положить книги, чтобы составить наклонную стопку?
Стопка книг не рассыплется, если расставлять их так, чтобы центр тяжести всех книг, находящихся выше некоторой произвольно выбранной книги, лежал на вертикали, проходящей через эту книгу. Это условие должно выполняться для любой книги в стопке.
Это условие должно выполняться для любой книги в стопке.
Опыты.
1. Невероятно, но держится!
Соединим поварёшку с ее подружкой — чумичкой — и установим новый рекорд равновесия: перевернутая тарелка будет лежать своим краем на краю графина в прочном, устойчивом положении.
2. Как в цирке!
Если стол совершенно горизонтален и прочно стоит на полу, ты сможешь выстроить эдакую фигуру из «доминошек».
Сперва поставь стоймя три косточки домино, — на них возвести такую хрупкую постройку легче, чем на одной кости. Потом, когда все будет построено, ты осторожно уберешь две крайние косточки, которые служили подпорками, и поставишь их на вершину своего непрочного здания. Равновесие здесь вполне возможно; нужно только, чтобы перпендикуляр, опущенный из центра тяжести всей конструкции, прошел через основание нижней косточки домино.
Для сохранения в неизменном положении предметов при движении их опоры уже много столетий применяется так называемый карданов подвес – устройство, в котором центр тяжести тела располагают ниже осей, вокруг которых оно может вращаться. В качестве примера можно рассмотреть корабельную керосиновую лампу. При любой качке на море благодаря вращающемуся карданову подвесу лампа всегда сохраняет вертикальное положение.
Включаем «соображалку»!
Поставьте неваляшку (Ваньку-встаньку) на шероховатую доску и слегка приподнимите один из концов доски. Как Вы думаете, в какую сторону отклонится голова игрушки при сохранении её равновесия?
Другие страницы о Ваньке-встаньке, центре тяжести и равновесии:
Центр тяжести
Равновесие тел
Человек и равновесие
Коварный центр тяжести
Ванька-встанька в цирке
FLIP, а по-русски Ванька-встанька
Тот, который переворачивает сам себя
Кто такой Чебурашка?
Ванька-встанька на воде
Фокус: яйцо «Ванька-встанька»
Балансирующее яйцо
Vanki-Vstanki Studio — интерактивная игра
Опыты по сохранению равновесия:
Тяжелое ведро. Зажги свечу. Давай поспорим!
Зажги свечу. Давай поспорим!
Вкусные опыты
Хитроумные изобретения:
А что же там внутри?
Вежливый Ванька-встанька
Ванька-встанька вверх ногами!
Ванька-встанька и магнитные поля
Ванька-не Ванька, но встанька!
Ванька-встанька и ферромагниты
Изменчивый Ванька-встанька
Руки, ноги, голова …хвост?
Рядом с физикой:
Поэты о ваньках — встаньках
Природный «Ванька -встанька»
Пирог «Ванька-встанька»
Условия равновесия: первое, второе. Виды равновесия: устойчивое, неустойчивое, безразличное, опрокидывание. Формулы, примеры
Тестирование онлайн
Равновесие
Состояние тела, которое не изменяется со временем. Например, тело длительно находится в покое или движется равномерно, или длительно вращается.
Первое условие равновесия
Векторная сумма всех действующих на тело сил равна нулю.
Рассмотрим на примере первое условие равновесия
Предмет будет находиться в равновесии, если векторная сумма всех сил (Fтр1, Fтр2, N1, N2, mg) равна нулю. То есть
То есть
Второе условие равновесия
Векторная сумма моментов сил равна нулю
Точку О выберем в точке пересечения Fтр2 и N2. Плечи этих сил равны нулю, значит и моменты этих сил равны нулю.
Определяем плечи сил Fтр1, N1 и mg и направление моментов сил (положительное или отрицательное).
Равновесие бывает устойчивым (тело возвращается в свое первоначальное положение), неустойчивым (тело не возвращается в свое первоначальное состояние), безразличное (тело остается в равновесии, несмотря на то, что на него подействовали (например переложили книгу из одного места на столе в другое). Тело стремится занять такое состояние, при котором его потенциальная энергия будет минимальной, центр масс стремиться быть ниже.
1 — безразличное равновесие, 2 — неустойчивое равновесие, 3 — устойчивое равновесие
На рисунке изображено условие опрокидывания тела.
Тело слева возвращается в исходное состояние. Тело справа опрокидывается.
Тело, имеющее площадь опоры, находится в состоянии устойчивого равновесия, если вертикаль, проведенная через центр масс этого тела, не выходит за рамки контура, ограниченного точками соприкосновения тела с опорой. Если же эта вертикаль проходит вне указанного контура, тело опрокидывается.
Урок по физике на тему «Центр тяжести. Виды равновесия» (9 класс)
Тема: Центр тяжести. Виды равновесия.
Класс: 9.
Цель урока: владение учащимися понятием центр тяжести, ознакомление с различными видами равновесия, выяснения условия, при которых тело находится в равновесии.
Задачи урока:
- Учебные: Изучить виды равновесия (устойчивое, неустойчивое, безразличное). Выяснить, при каких условиях тела более устойчивы.
- Развивающие: Способствовать
развитию познавательного интереса к физике. Развитие навыков сравнивать,
обобщать, выделять главное, делать выводы.

- Воспитательные: Воспитывать внимание, умения высказывать свою точку зрения и отстаивать её, развивать коммуникативные способности учащихся.
Тип урока: урок изучения нового материала.
Оборудование: компьютер, мултимедиапроектор, презентация, учебное пособие Л.А.Исаченкова «Физика 9 класс».
Ход урока
1. Организация класса. Создание ситуации успеха.
— Доброе утро ребята! Пусть оно действительно будет для нас добрым.
— Какое у вас настроение и как вы готовы на сегодняшнюю работу? Ваше настроение и готовность я предлагаю проверить с помощи небольшой ситуационной игры.
— Насчет раз два три предлагаю гостям и вам показать следующей: кулачки, открытые ладошки либо замок.
—
Итак, ребята, я вижу, что кто-то из вас показал кулачки ли замок, это означает,
что вы немного замкнуты на данный момент и присутствует волнение. Но
большинство из вас показали открытые ладошки – это означает, что вы открыты, вы
готовы к диалогу и к новым знаниям.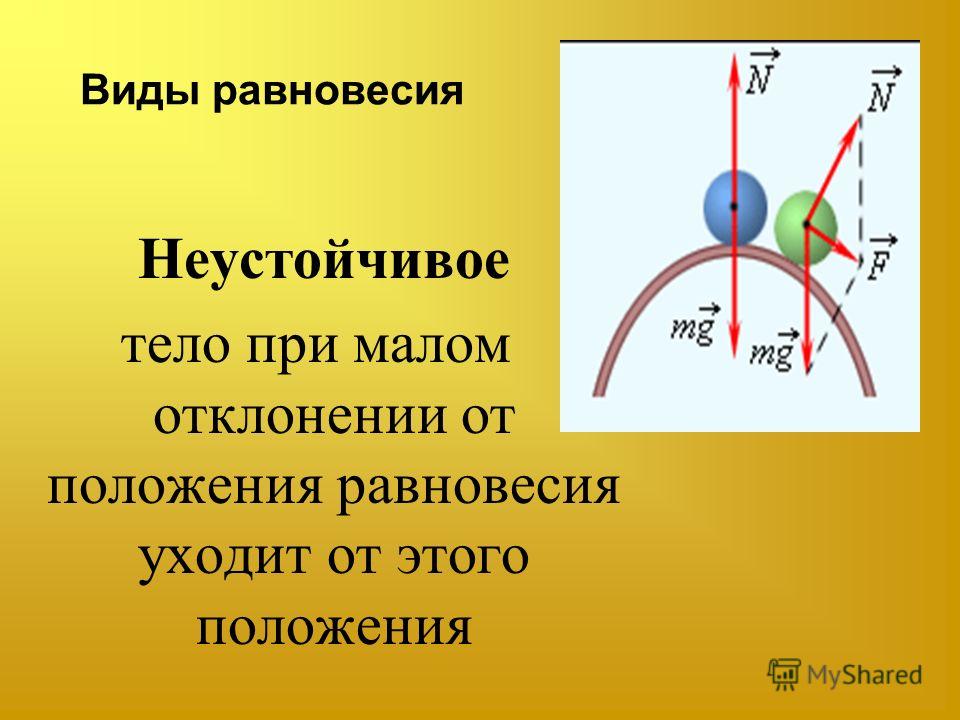 В чем я сегодня вам помогу.
В чем я сегодня вам помогу.
— А начнем мы наш урок с проверки домашнего задания и актуализации знаний.
2. Проверка домашнего задания. Актуализация знаний.
— Ответьте мне пожалуйста на вопросы.
1. Какое состояние тела называется состоянием механического равновесия?
(Состоянием механического равновесия называется состояние тела, при котором оно остается неподвижным относительно данной инерциальной системы отсчета.)
2. Сколько существует условий, при которых тела находятся в состоянии равновесия?
(2 условия)
3. Откуда следует первое условие равновесия?
(Второй закон Ньютона)
4. Что называют плечом силы?
(Расстояние от оси вращения до линии действия силы называют плечом силы.)
5. Что называют моментом силы?
(Произведение модуля силы и её плеча называют моментом силы.)
6. Единица момента силы в СИ?
(Ньютон × метр)
7.
Приведите
примеры простых механизмов.
(Рычаг, блок, винт, наклонная плоскость)
8. Какой выигрыш в силе дает подвижный блок?
(Подвижный блок дает выигрыш в силе приблизительно в 2 раза)
9. «Золотое правило механики»
(«Золотое правило механики» ни один механизм не дает выигрыша в работе.)
— Молодцы, мы с вами повторили то, что мы проходили на прошлых уроках.
3. Сообщение темы и цели урока.
— Совсем недавно моя сестра отдыхала в Италии. И вот какое фото она мне прислала. (Показать фото)
— Вы, наверное, знаете, что это за башня. (Пизанская башня)
— Верно, это Пизанская башня. Благодаря ей город Пиза стал известен целому миру. Тысячи туристов приезжают на нее посмотреть. По своей архитектуре, она как бы находится в состоянии падения.
— Так вот мне моя сестра задала вопрос почему же она не падает? Этот вопрос я сегодня переадресовываю вам. Может уже кто-то ответит на этот вопрос?
—
Но, ребята не совсем это верно. Но чтобы ответить на этот вопрос сегодня на уроке
мы изучим тему «Центр тяжести.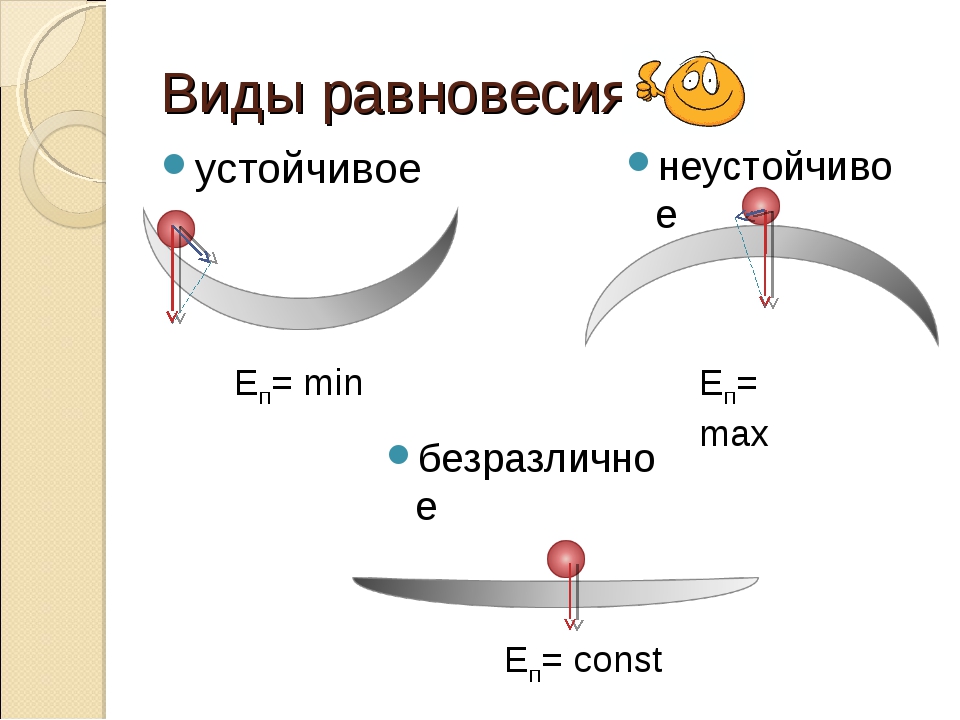 Виды равновесия»
Виды равновесия»
(Центр тяжести. Виды равновесия) (Тема на слайде и на доске)
— Давайте сформулируем цель нашего урока.
— Ребята, вы сегодня после урока сможете объяснить своим друзьям или родителям почему Пизанская башня не падает, вы узнаете о таком понятии как центр тяжести, познакомитесь с видами равновесия. А для этого нам с вами понадобится сплоченность, но и конечно такие качества как взаимопомощь и взаимоподдержка.
4. Изучение нового материла.
— И первое с чем мы с вами познакомимся с понятием центр тяжести.
— Ребята, что называется центром тяжести? А что бы ответить на этот вопрос я предлагаю обратиться вам к учебнику. Откройте учебник на странице 134 и найдите определение.
Центром тяжести тела называется точка приложения силы тяжести, действующей на него.
— У однородных тел правильной формы центр тяжести находится в геометрическом центре.
— Я предлагаю вам найти центр тяжести следующих фигур
(Самопроверка)
— А
как найти центр тяжести тела произвольной формы? Это можно сделать с помощью
простого опыта.
ОПЫТ
— И так можно повторить определение.
— Запишите себе определение в тетрадь.
— Давайте теперь вернемся к нашей Пизанскай башне. И почему же одни тела опрокидываются, а другие нет. Попробуем разобраться.
(Фрагмент видео)
— А теперь с помощью треугольной пирамиды. Ответьте на вопрос все ли вам было понятно на данном этапе. (Зеленая сторона – все понятно, желтая – Есть вопросы, красная – ничего не понятно)
— Хорошо, я вижу что всем все понятно.
— А что такое устойчивость? От чего она зависит?
Посмотрим опыт с шариком. (Видео)
Каждый случай соответствует одному из трех видов равновесия: устойчивое, неустойчивое и безразличное.
а) Если на тело, имеющее опору, действуют уравновешивающие силы, то тело находится в положении равновесия.
б)
При
отклонении тела от положения равновесия нарушается и равновесие сил. Если тело
под действием равнодействующей силы возвращается в исходное положение, то это — устойчивое равновесие.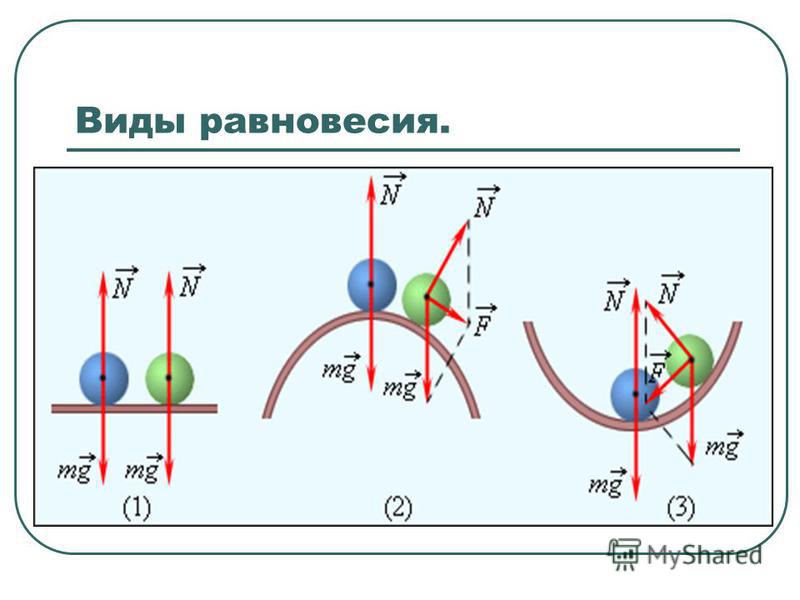
в) Если же тело под действием равнодействующей силы, ещё сильнее отклоняется от положения равновесия, то это — неустойчивое равновесие.
г) Возможен случай, когда при любом положении тела, равновесие сил сохраняется. Это состояние называется безразличным равновесием.
— Обратитесь к учебнику на стр.135 и найдите все определения видов равновесия и запишите их себе в тетрадь.
— Давайте еще раз их проговорим.
— Как вы считаете зависит ли положение тела от потенциальной энергии? А что бы ответить откройте стр. 135.
— Верно. Устойчиво то положение, в котором его потенциальная энергия минимальна.
— А теперь обратите внимание на слайды.
Какие корабли наиболее устойчивы? Почему? (У которых груз расположен в трюмах, а не на палубе)
Какие
автомобили наиболее устойчивы? Почему? (Чтобы увеличить устойчивость
машин на поворотах, полотно дороги наклоняют в сторону поворота. )
)
— Какие выводы вы можете сделать на данном этапе урока?
Выводы: Равновесие может быть устойчивым, неустойчивым, безразличным. Устойчивость тел тем больше, чем больше площадь опоры и ниже центр тяжести.
— А теперь с помощью треугольной пирамиды. Ответьте на вопрос все ли вам было понятно на данном этапе. (Зеленая сторона – все понятно, желтая – Есть вопросы, красная – ничего не понятно)
— Хорошо, я вижу что всем все понятно.
5. Физкультминутка.
6. Закрепление пройденного материала.
1. Каким специальностям наиболее необходимы знания о равновесии тел?
(Проектировщикам и конструкторам различных сооружений (высотных зданий, мостов, телевизионных башен и т.д.), цирковым артистам, водителям и другим специалистам.)
2. На примере каких детских игрушек нам демонстрируется равновесие?
Решение задач.
1. Какой шоколадный батончик легче разломать на две части – длинный или короткий? Почему?
(Легче-длинный. Потому что плечо рычага будет больше-соответственно прилагать усилий нужно
будет меньше.)
Потому что плечо рычага будет больше-соответственно прилагать усилий нужно
будет меньше.)
2. Почему дверные ручки укрепляют на самом краю двери?
(Чем больше длина рычага, тем меньше сил необходимо приложить для открытия двери. На краю двери самый длинный рычаг.)
3. В каком положении нога велосипедиста с большей силой действует на педаль? Почему?
(В
положении а) нога велосипедиста с большей силой действует на педаль, т.к. рычаг
силы больше.
)
4. На какую высоту с помощью подвижного блока массой 5 кг был поднят груз массой 100 кг? Если при этом выполнялась работа 210Дж. Найдите КПД блока. Силу сопротивления не учитывать.
7. Подведение итогов.
— Давайте вспомним тему нашего урока. Какую мы ставили цель перед собой? Достигли ли мы этой цели?
Выводы из урока:
1. Существует три вида равновесия: устойчивое, неустойчивое, безразличное.
2. Устойчиво
положение тела, в котором его потенциальная энергия минимальна.
3. Устойчивость тел на плоской поверхности тем больше, чем больше площадь опоры и ниже центр тяжести.
8. Выставление отметок.
9. Домашнее задание: § 28 (ответить на контрольные вопросы).
Творческое задание «Занимательное равновесие» (Вам необходимо из предметов воздушного шарика и груза подумать и на следующем уроке продемонстрировать как показать центр тяжести).
10.Рефлексия.
Пизанская башня.
— У вас перед глазами Пизанская башня и на партах лежат человечки.
Статика. Часть 2. Виды равновесия тела.
Рассмотрим в этой статье понятия центра тяжести, а также виды равновесия тела и решим несколько задач.
Итак, центр тяжести — это точка приложения силы тяжести. В однородном теле сила тяжести приложена к центру тела.
Видов равновесия тела всего три.
1. Устойчивое равновесие – это такое равновесие, когда при выведении тела из этого положения возникает результирующая сила, возвращающая это тело в исходное положение. Обратим внимание на то, что потенциальная энергия тела в положении устойчивого равновесия минимальна.
Обратим внимание на то, что потенциальная энергия тела в положении устойчивого равновесия минимальна.
2. Неустойчивое равновесие – это такое равновесие, когда при выведении тела из состояния покоя, возникает результирующая сила, направленная в противоположную сторону от положения, где тело покоилось. Потенциальная энергия тела в положении неустойчивого равновесия больше, чем в последующих положениях
3. Безразличное равновесие – это такое равновесие, когда при любом действии на тело, возникающая результирующая сила равна 0. Потенциальная энергия тела в таков виде равновесия не меняется.
Условие устойчивости тела, имеющего несколько точек опоры:
Отвесная линия, проведённая через центр тяжести данного тела, должна проходить внутри границ, проходящих через опоры данного тела.
Чем выше расположен центр тяжести данного тела, тем меньше предельный угол наклона, после которого равновесие этого тела уже не восстанавливается.
И по доброй традиции рассмотрим решение нескольких задач.
Задача 1.
На наклонной плоскости с углом наклона a находится тело массой m. Какую горизонтальную силу надо приложить, чтобы удержать это тело в покое, если сила трения равна 0?
Решение:
На тело в данной задаче действуют всего три силы: со стороны Земли – сила тяжести mg, со стороны поверхности, на которую давит тело – сила реакции опоры N и внешняя сила F, которую и необходимо найти.
Запишем условие равновесия для этого случая (II закон Ньютона) mg-> + N-> + F-> = 0.
Запишем теперь это уравнение в проекциях на оси c учётом знаков проекций
ОХ: -mgcos(90 – a) + Fcosа = 0 (1)
OY: -mgsin(90 – a) – Fsina + N = 0 (2)
В этом уравнении (при данном условии и вопросе) величина N для нас не имеет никакого значения. Поэтому при решении данной задачи решаем до конца только уравнение (1)
Поэтому при решении данной задачи решаем до конца только уравнение (1)
Fcosa = mgcos(90 – a), помним что cos(90 – a) = sina,
F = mg sina/cosa = mgtga
Ответ: F = mgtga
Задача 2.
Какую горизонтальную силу необходимо приложить, чтобы удержать брусок массой m на вертикальной поверхности, если коэффициент трения между стеной и бруском µ?
Решение:
На чертеже, как обычно, укажем все силы, действующие на тело: со стороны Земли – сила тяжести mg, со стороны опоры – вертикально сила трения Fтр и горизонтально – сила реакции опоры N, которая будет возникать, если тело прижимать к поверхности. Также на тело действует горизонтальная сила F, которую и необходимо найти.
Запишем условие равновесия для этого случая (II закон Ньютона) mg-> + Fтр-> + N-> + F-> = 0.
Запишем теперь это уравнение в проекциях на оси c учётом знаков проекций
ОХ: – F + N = 0 (1)
OY: – mg + Fтр = 0 (2)
помним, что /Fтр/ = /µN/ (3)
Из уравнения (1) = > N = F, а из (2) => µN = mg => N = mg/µ
Ответ: F = mg/µ
Остались вопросы? Не знаете, как решить задачу по физике?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Неустойчивое равновесие в физике. Т. Виды равновесия
Статикой называется раздел механики, изучающий условия равновесия тел.
Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс .
Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю .
На рис. 1.14.1 дан пример равновесия твердого тела под действием трех сил. Точка пересечения O линий действия сил и не совпадает с точкой приложения силы тяжести (центр масс C ), но при равновесии эти точки обязательно находятся на одной вертикали. При вычислении равнодействующей все силы приводятся к одной точке.
Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил .
Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения.
Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы .
Произведение модуля силы на плечо d называется моментом силы M . Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки (рис. 1.14.2).
Правило моментов : тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
В Международной системе единиц (СИ) моменты сил измеряются в Н ьютон — метрах (Н∙м ) .
В общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов сил.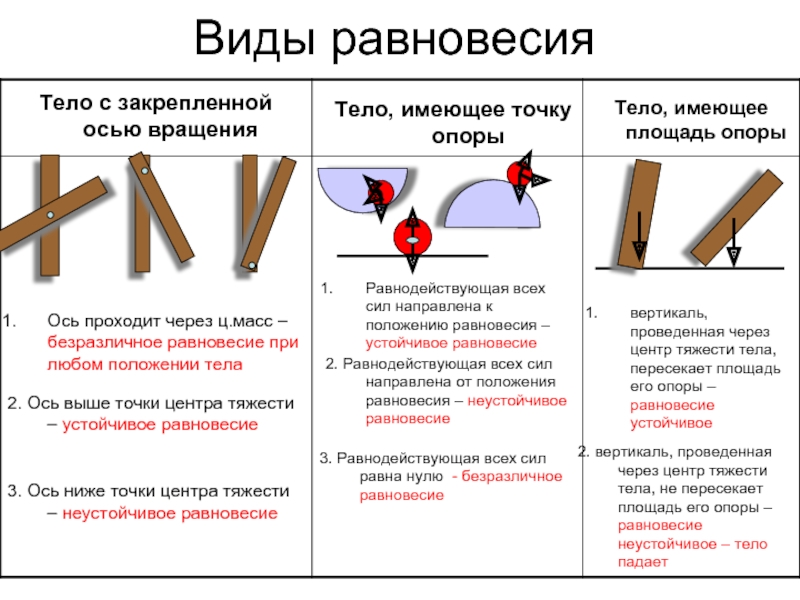
здесь скриншот игры про равновесие
Катящееся по горизонтальной поверхности колесо — пример безразличного равновесия (рис. 1.14.3). Если колесо остановить в любой точке, оно окажется в равновесном состоянии. Наряду с безразличным равновесием в механике различают состояния устойчивого и неустойчивого равновесия.
Состояние равновесия называется устойчивым, если при малых отклонениях тела от этого состояния возникают силы или моменты сил, стремящиеся возвратить тело в равновесное состояние.
При малом отклонении тела из состояния неустойчивого равновесия возникают силы или моменты сил, стремящиеся удалить тело от положения равновесия.
Шар, лежащий на плоской горизонтальной поверхности, находится в состоянии безразличного равновесия. Шар, находящийся в верхней точке сферического выступа, — пример неустойчивого равновесия. Наконец, шар на дне сферического углубления находится в состоянии устойчивого равновесия (рис. 1.14.4).
Для тела, имеющего неподвижную ось вращения, возможны все три вида равновесия. Безразличное равновесие возникает, когда ось вращения проходит через центр масс. При устойчивом и неустойчивом равновесии центр масс находится на вертикальной прямой, проходящей через ось вращения. При этом, если центр масс находится ниже оси вращения, состояние равновесия оказывается устойчивым. Если же центр масс расположен выше оси — состояние равновесия неустойчиво (рис. 1.14.5).
Безразличное равновесие возникает, когда ось вращения проходит через центр масс. При устойчивом и неустойчивом равновесии центр масс находится на вертикальной прямой, проходящей через ось вращения. При этом, если центр масс находится ниже оси вращения, состояние равновесия оказывается устойчивым. Если же центр масс расположен выше оси — состояние равновесия неустойчиво (рис. 1.14.5).
Особым случаем является равновесие тела на опоре. В этом случае упругая сила опоры приложена не к одной точке, а распределена по основанию тела. Тело находится в равновесии, если вертикальная линия, проведенная через центр масс тела, проходит через площадь опоры , т. е. внутри контура, образованного линиями, соединяющими точки опоры. Если же эта линия не пересекает площадь опоры, то тело опрокидывается. Интересным примером равновесия тела на опоре является падающая башня в итальянском городе Пиза (рис. 1.14.6), которую по преданию использовал Галилей при изучении законов свободного падения тел. Башня имеет форму цилиндра высотой 55 м и радиусом 7 м. Вершина башни отклонена от вертикали на 4,5 м.
Башня имеет форму цилиндра высотой 55 м и радиусом 7 м. Вершина башни отклонена от вертикали на 4,5 м.
Вертикальная линия, проведенная через центр масс башни, пересекает основание приблизительно в 2,3 м от его центра. Таким образом, башня находится в состоянии равновесия. Равновесие нарушится и башня упадет, когда отклонение ее вершины от вертикали достигнет 14 м. По-видимому, это произойдет очень нескоро.
Наглядной иллюстрацией устойчивого и неустойчивого равновесия служит поведения тяжелого шарика на гладкой поверхности (рис. 1.5). Интуиция и опыт подсказывают, что помещенный на вогнутую поверхность шарик останется на месте, а с выпуклой и седлообразной поверхностей он скатится. Положение шарика на вогнутой поверхности устойчиво, а положение шарика на выпуклой и седлообразной поверхностях неустойчиво. Аналогично два соединенных шарниром прямых стержня при растягивающей силе находятся в устойчивом положении равновесия, а при сжимающей силе — в неустойчивом (рис. 1.6).
Но интуиция может дать верный ответ только в простейших случаях; для более сложных систем одной интуиции оказывается недостаточно. Например, даже для сравнительно простой механической системы, изображенной на рис. 1.7, а, интуиция может лишь подсказать, что положение равновесия шарика на вершине при очень малой жесткости пружины будет неустойчивым, а с увеличением жесткости пружины оно должно стать устойчивым. Для изображенной на рис. 2.3, б системы стержней, соединенных шарнирами, на основе интуиции можно только сказать, что исходное положение равновесия этой системы устойчиво или неустойчиво в зависимости от соотношения между силой, жесткостью пружины и длиной стержней.
Например, даже для сравнительно простой механической системы, изображенной на рис. 1.7, а, интуиция может лишь подсказать, что положение равновесия шарика на вершине при очень малой жесткости пружины будет неустойчивым, а с увеличением жесткости пружины оно должно стать устойчивым. Для изображенной на рис. 2.3, б системы стержней, соединенных шарнирами, на основе интуиции можно только сказать, что исходное положение равновесия этой системы устойчиво или неустойчиво в зависимости от соотношения между силой, жесткостью пружины и длиной стержней.
Для того чтобы решить устойчиво или неустойчиво равновесие механической системы, необходимо использовать аналитические признаки устойчивости. Наиболее общим подходом к изучению устойчивости положения равновесия в механике является энергетический подход, основанный на исследовании изменения полной потенциальной энергии системы при отклонениях от положения равновесия.
В положении равновесия полная потенциальная энергия консервативной механической системы имеет стационарное значение, причем, согласно теореме Лагранжа, положение равновесия устойчиво, если это значение соответствует минимуму полной потенциальной энергии.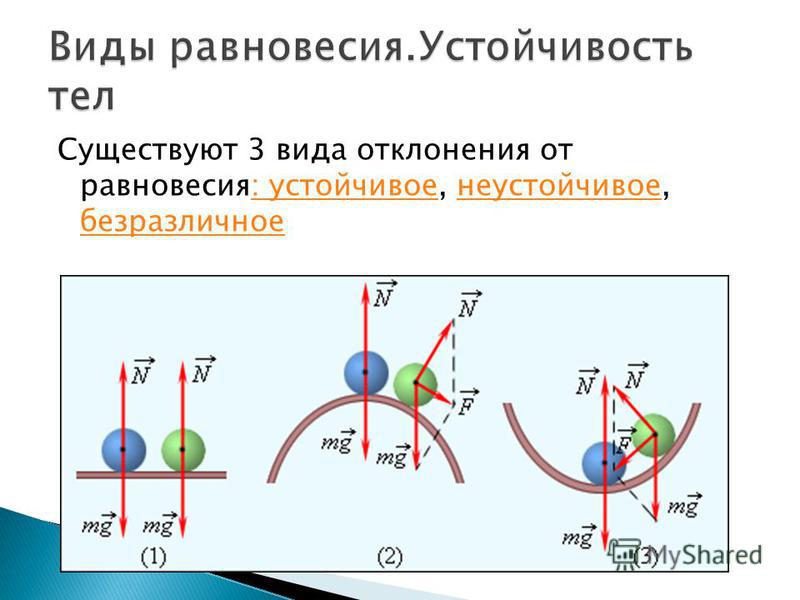 Не углубляясь в математические тонкости, поясним эти общие положения на простейших примерах.
Не углубляясь в математические тонкости, поясним эти общие положения на простейших примерах.
В системах, изображенных на рис. 1.5, полная потенциальная энергия изменяется пропорционально вертикальному смещению шарика. Когда шарик опускается, его потенциальная энергия, естественно, уменьшается. Если шарик поднимается, то потенциальная энергия возрастает. Поэтому нижняя точка вогнутой поверхности соответствует минимуму полной потенциальной энергии и положение равновесия шарика в этой точке устойчиво. Вершина выпуклой поверхности соответствует стационарному, но не минимальному значению полной потенциальной энергии (в данном случае — максимальному значению). Поэтому положение равновесия шарика здесь неустойчиво. Стационарная точка на седлообразной поверхности тоже не соответствует минимуму полной потенциальной энергии (это так называемая точка мини-макса) и положение равновесия шарика здесь неустойчиво. Последний случай весьма характерен. В неустойчивом состоянии равновесия потенциальная энергия вовсе не должна достигать максимального значения. Положение равновесия не будет устойчивым во всех случаях, когда полная потенциальная энергия имеет стационарное, но не минимальное значение.
Положение равновесия не будет устойчивым во всех случаях, когда полная потенциальная энергия имеет стационарное, но не минимальное значение.
Для изображенной на рис. 1.6 стержневой системы также нетрудно установить, что при растягивающей силе вертикальное неотклоненное положение стержней соответствует минимуму потенциальной энергии и поэтому является устойчивым. При сжимающей силе неотклоненное положение стержней соответствует максимуму потенциальной энергии и является неустойчивым.
Предоставив возможность читателю самому установить условия устойчивости систем, изображенных на рис. 1.7, вернемся к двум рассмотренным в предыдущем параграфе задачам.
Полная потенциальная энергия упругой системы (с точностью до постоянного слагаемого, которое опускаем) складывается из внутренней энергии деформации U и потенциала внешних сил :
Составим выражение для полной потенциальной энергии стержня с упругим шарниром, нагруженного вертикальной силой (см. рис. 1.1). Энергия деформации упругого шарнира . Потенциал внешних сил с точностью до постоянного слагаемого равен взятому с обратным знаком произведению силы на вертикальное перемещение точки ее приложения, т. е. . Следовательно, полная потенциальная энергия
Энергия деформации упругого шарнира . Потенциал внешних сил с точностью до постоянного слагаемого равен взятому с обратным знаком произведению силы на вертикальное перемещение точки ее приложения, т. е. . Следовательно, полная потенциальная энергия
Рассматриваемая система имеет одну степень свободы: ее деформированное состояние полностью описывается одним независимым параметром. В качестве такого параметра взят угол , поэтому для исследования устойчивости системы нужно найти производные полной потенциальной энергии по углу .
Дифференцируя выражение (1.6) по , получим
Приравнивая нулю первую производную полной потенциальной энергии, приходим к уравнению (1.1), которое раньше было получено непосредственно из условий равновесия стержня. Исследование знака второй производной позволяет установить, какие из найденных положений равновесия устойчивы.
Исследуем устойчивость положений равновесия стержня, соответствующих двум независимым решениям (1.2). Первое из них соответствует вертикальному неотклоненному положению стержня при .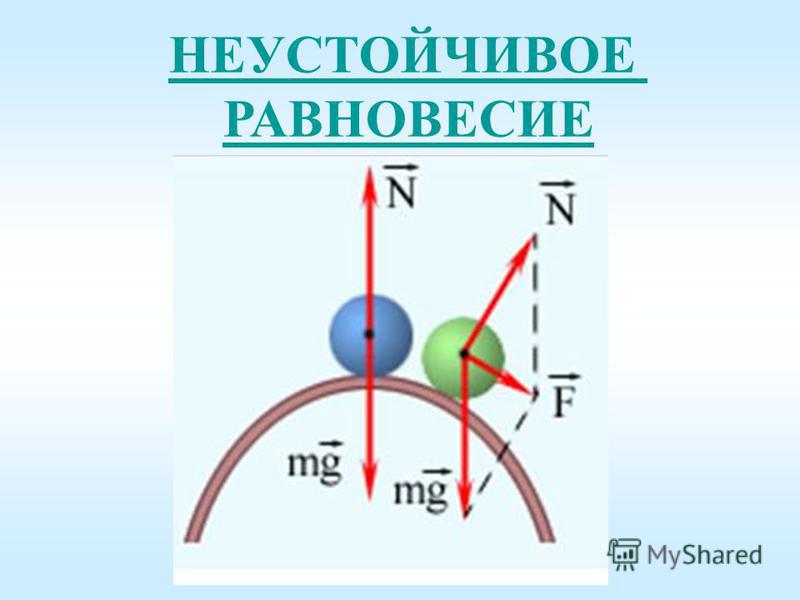
Согласно выражению (1.8) для этого положения равновесия
При полная потенциальная энергия минимальна и вертикальное положение стержня устойчиво, при полная потенциальная энергия максимальна и вертикальное положение стержня неустойчиво.
Для исследования устойчивости стержня в отклоненном положении подставим второе из решений (1.2) в выражение (1.8):
Если , то вторая производная полной энергии положительна, поскольку тогда , и отклоненное положение стержня, которое возможно при , всегда устойчиво.
Осталось еще не выясненным, устойчиво или неустойчиво положение равновесия, соответствующее точке пересечения двух решений при , поскольку в этой точке Вторая производная полной энергии равна нулю. Как известно из курса математического анализа, в таких случаях для исследования стационарной точки следует использовать высшие производные. Последовательно дифференцируя, находим
В исследуемой точке третья производная равна нулю, а четвертая положительна. Следовательно, в этой точке полная потенциальная энергия минимальна и неотклоненное положение равновесия стержня при устойчиво.
Следовательно, в этой точке полная потенциальная энергия минимальна и неотклоненное положение равновесия стержня при устойчиво.
Результаты проведенного исследования устойчивости различных положений равновесия стержня с упругим шарниром представлены на рис. 1.8. Там же показано изменение полной потенциальной энергии системы при . Точки соответствуют минимумам полной потенциальной энергии и устойчивым отклоненным положениям равновесия; точка Максимуму энергии и неустойчивому вертикальному положению равновесия стержня.
Составим выражение полной потенциальной энергии . представленной на рис. 1.2. При отклонении стержня на угол пружина удлиняется на величину , а энергия деформации пружины определяется выражением ., вторая производная полной потенциальной энергии равна
Таким образом, при вторая производная отрицательна и отклоненное положение равновесия стержневой системы неустойчиво.
Положения равновесия, соответствующие точкам пересечения двух решений (1.4), неустойчивы (например, неотклоненное положение стержня при ). В этом нетрудно убедиться, определяя в этих точках знаки высших производных.
В этом нетрудно убедиться, определяя в этих точках знаки высших производных.
На рис. 1.9 показаны результаты проведенного исследования и характерные кривые изменения полной потенциальной энергии при различных уровнях нагружения.
Продемонстрированный на простейших примерах путь исследования устойчивости положений статического равновесия упругих систем используют и в случае более сложных систем.
С усложнением упругой системы растут технические трудности его реализации, но принципиальная основа — условие минимума полной потенциальной энергии — полностью сохраняется.
Для того чтобы судить о поведении тела в реальных условиях, мало знать, что оно находится в равновесии. Надо еще оценить это равновесие. Различают устойчивое, неустойчивое и безразличное равновесие.
Равновесие тела называют устойчивым , если при отклонении от него возникают силы, возвращающие тело в положение равновесия (рис. 1, а, положение 2 ). В устойчивом равновесии центр тяжести тела занимает наинизшее из всех близких положений. Положение устойчивого равновесия связано с минимумом потенциальной энергии по отношению ко всем близким соседним положениям тела.
Положение устойчивого равновесия связано с минимумом потенциальной энергии по отношению ко всем близким соседним положениям тела.
Равновесие тела называют неустойчивым , если при самом незначительном отклонении от него равнодействующая действующих на тело сил вызывает дальнейшее отклонение тела от положения равновесия (рис. 1, а, положение 1 ). В положении неустойчивого равновесия высота центра тяжести максимальна и потенциальная энергия максимальна по отношению к другим близким положениям тела.
Равновесие, при котором смещение тела в любом направлении не вызывает изменения действующих на него сил и равновесие тела сохраняется, называют безразличным (рис. 1, а, положение 3 ).
Безразличное равновесие связано с неизменной потенциальной энергией всех близких состояний, и высота центра тяжести одинакова во всех достаточно близких положениях.
Тело, имеющее ось вращения (например, однородная линейка, которая может вращаться вокруг оси, проходящей через точку О , изображенная на рисунке 1, б), находится в равновесии, если вертикальная прямая, проходящая через центр тяжести тела, проходит через ось вращения. Причем если центр тяжести С выше оси вращения (рис. 1, б; 1 ), то при любом отклонении от положения равновесия потенциальная энергия уменьшается и момент силы тяжести относительно оси О отклоняет тело дальше от положения равновесия. Это неустойчивое положение равновесия. Если центр тяжести находится ниже оси вращения (рис. 1, б; 2 ), то равновесие устойчивое. Если центр тяжести и ось вращения совпадают (рис. 1, б; 3 ), то положение равновесия безразличное.
Причем если центр тяжести С выше оси вращения (рис. 1, б; 1 ), то при любом отклонении от положения равновесия потенциальная энергия уменьшается и момент силы тяжести относительно оси О отклоняет тело дальше от положения равновесия. Это неустойчивое положение равновесия. Если центр тяжести находится ниже оси вращения (рис. 1, б; 2 ), то равновесие устойчивое. Если центр тяжести и ось вращения совпадают (рис. 1, б; 3 ), то положение равновесия безразличное.
Тело, имеющее площадь опоры, находится в равновесии, если вертикальная прямая, проходящая через центр тяжести тела не выходит за пределы площади опоры этого тела, т.е. за пределы контура образованного точками соприкосновения тела с опорой Равновесие в этом случае зависит не только от расстояния между центром тяжести и опорой (т.е. от его потенциальной энергии в гравитационном поле Земли), но и от расположения и размеров площади опоры этого тела.
На рисунке 1, в изображено тело, имеющее форму цилиндра. Если его наклонить на малый угол, то оно возвратится в исходное положение 1 или 2 Если же его отклонить на угол β (положение 3 ), то тело опрокинется. При заданной массе и площади опоры устойчивость тела тем выше, чем ниже расположен его центр тяжести, т.е. чем меньше угол между прямой, соединяющей центр тяжести тела и крайнюю точку соприкосновения площади опоры с горизонтальной плоскостью.
Если его наклонить на малый угол, то оно возвратится в исходное положение 1 или 2 Если же его отклонить на угол β (положение 3 ), то тело опрокинется. При заданной массе и площади опоры устойчивость тела тем выше, чем ниже расположен его центр тяжести, т.е. чем меньше угол между прямой, соединяющей центр тяжести тела и крайнюю точку соприкосновения площади опоры с горизонтальной плоскостью.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 85-87.
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока: Изучить состояние равновесия тел, познакомиться с различными видами равновесия; выяснить условия, при которых тело находится в равновесии.
Задачи урока:
- Учебные: Изучить два условия равновесия, виды равновесия (устойчивое, неустойчивое, безразличное). Выяснить, при каких условиях тела более устойчивы.
- Развивающие: Способствовать развитию познавательного интереса к физике. Развитие навыков сравнивать, обобщать, выделять главное, делать выводы.
- Воспитательные: Воспитывать внимание, умения высказывать свою точку зрения и отстаивать её, развивать коммуникативные способности учащихся.
Тип урока: урок изучения нового материала с компьютерной поддержкой.
Оборудование:
- Диск «Работа и мощность» из «Электронных уроков и тестов.
- Таблица «Условия равновесия».
- Призма наклоняющаяся с отвесом.

- Геометрические тела: цилиндр, куб, конус и т.д.
- Компьютер, мултимедиапроектор, интерактивная доска или экран.
- Презентация.
Ход урока
Сегодня на уроке мы узнаем, почему подъёмный кран не падает, почему игрушка «Ванька-встанька» всегда возвращается в исходное состояние, почему Пизанская башня не падает?
I. Повторение и актуализация знаний.
- Сформулировать первый закон Ньютона. О каком состоянии говорится в законе?
- На какой вопрос отвечает второй закон Ньютона? Формула и формулировка.
- На какой вопрос отвечает третий закон Ньютона? Формула и формулировка.
- Что называется равнодействующей силой? Как она находится?
- Из диска «Движение и взаимодействие тел» выполнить задание № 9 «Равнодействующая сил с разными направлениями» (правило сложения векторов (2, 3 упражнения)).
II. Изучение нового материала.
1. Что называется равновесием?
Равновесие – это состояние покоя.
2. Условия равновесия. (слайд 2)
а) Когда тело находится в покое? Из какого закона это следует?
Первое условие равновесия: Тело находится в равновесии, если геометрическая сумма внешних сил, приложенных к телу, равна нулю. ∑F = 0
б) Пусть на доску действуют две равные силы, как показано на рисунке.
Будет ли она находиться в равновесии? (Нет, она будет поворачиваться)
В покое находится только центральная точка, а остальные движутся. Значит, чтобы тело находилось в равновесии, необходимо, чтобы сумма всех сил, действующих на каждый элемент равнялась 0.
Второе условие равновесия: Сумма моментов сил, действующих по часовой стрелке, должна равняться сумме моментов сил, действующих против часовой стрелки.
∑ M по часовой = ∑ M против часовой
Момент силы: M = F L
L – плечо силы – кратчайшее расстояние от точки опоры до линии действия силы.
3. Центр тяжести тела и его нахождение. (слайд 4)
(слайд 4)
Центр тяжести тела – это точка, через которую проходит равнодействующая всех параллельных сил тяжести, действующих на отдельные элементы тела (при любом положении тела в пространстве).
Найти центр тяжести следующих фигур:
4. Виды равновесия.
а) (слайды 5–8)
Вывод: Равновесие устойчиво, если при малом отклонении от положения равновесия есть сила, стремящаяся вернуть его в это положение.
Устойчиво то положение, в котором его потенциальная энергия минимальна. (слайд 9)
б) Устойчивость тел, находящихся на точке опоры или на линии опоры. (слайды 10–17)
Вывод: Для устойчивости тела, находящегося на одной точке или линии опоры необходимо, чтобы центр тяжести находился ниже точки (линии) опоры.
в) Устойчивость тел, находящихся на плоской поверхности.
(слайд 18)
1) Поверхность опоры – это не всегда поверхность, которая соприкасается с телом (а та, которая ограниченна линиями, соединяющими ножки стола, треноги)
2) Разбор слайда из «Электронных уроков и тестов», диск «Работа и мощность», урок «Виды равновесия».
Рисунок 1.
- Чем различаются табуретки? (Площадью опоры)
- Какая из них более устойчивая? (С большей площадью)
- Чем различаются табуретки? (Расположением центра тяжести)
- Какая из них наиболее устойчива? (Укоторой центр тяжести ниже)
- Почему? (Т.к. её можно отклонить на больший угол без опрокидывания)
3) Опыт с призмой отклоняющейся
- Поставим на доску призму с отвесом и начнём её постепенно поднимать за один край. Что мы видим?
- Пока линия отвеса пересекает поверхность, ограниченную опорой, равновесие сохраняется. Но как только вертикаль, проходящая через центр тяжести, начнёт выходить за границы поверхности опоры, этажерка опрокидывается.
Разбор слайдов 19–22 .
Выводы:
- Устойчиво то тело, у которого площадь опоры больше.
- Из двух тел одинаковой площади устойчиво то тело, у которого центр тяжести расположен ниже, т.
 к. его можно отклонить без опрокидывания на большой угол.
к. его можно отклонить без опрокидывания на большой угол.
Разбор слайдов 23–25.
Какие корабли наиболее устойчивы? Почему? (У которых груз расположен в трюмах, а не на палубе)
Какие автомобили наиболее устойчивы? Почему? (Чтобы увеличить устойчивость машин на поворотах, полотно дороги наклоняют в сторону поворота.)
Выводы: Равновесие может быть устойчивым, неустойчивым, безразличным. Устойчивость тел тем больше, чем больше площадь опоры и ниже центр тяжести.
III. Применение знаний об устойчивости тел.
- Каким специальностям наиболее необходимы знания о равновесии тел?
- Проектировщикам и конструкторам различных сооружений (высотных зданий, мостов, телевизионных башен и т.д.)
- Цирковым артистам.
- Водителям и другим специалистам.
(слайды 28–30)
- Почему «Ванька-встанька» возвращается в положение равновесия при любом наклоне игрушки?
- Почему Пизанская башня стоит под наклоном и не падает?
- Каким образом сохраняют равновесие велосипедисты и мотоциклисты?
Выводы из урока:
- Существует три вида равновесия: устойчивое, неустойчивое, безразличное.

- Устойчиво положение тела, в котором его потенциальная энергия минимальна.
- Устойчивость тел на плоской поверхности тем больше, чем больше площадь опоры и ниже центр тяжести.
Домашнее задание : § 54– 56 (Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский)
Использованные источники и литература:
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н.Сотский. Физика. 10 класс.
- Диафильм «Устойчивость» 1976 г. (отсканирован мною на плёночном сканере).
- Диск «Движение и взаимодействие тел» из «Электронных уроков и тестов».
- Диск «Работа и мощность» из «Электронных уроков и тестов».
Механическое равновесие
Механи́ческое равнове́сие — состояние механической системы , при котором сумма всех сил , действующих на каждую её частицу, равна нулю и сумма моментов всех сил, приложенных к телу относительно любой произвольно взятой оси вращения, также равна нулю.
В состоянии равновесия тело находится в покое (вектор скорости равен нулю) в выбранной системе отсчета либо движется равномерно прямолинейно или вращается без касательного ускорения.
Определение через энергию системы
Так как энергия и силы связаны фундаментальными зависимостями , это определение эквивалентно первому. Однако определение через энергию может быть расширено для того, чтобы получить информацию об устойчивости положения равновесия.
Виды равновесия
Приведём пример для системы с одной степенью свободы . В этом случае достаточным условием положения равновесия будет являться наличие локального экстремума в исследуемой точке. Как известно, условием локального экстремума дифференцируемой функции является равенство нулю её первой производной . Чтобы определить, когда эта точка является минимумом или максимумом, необходимо проанализировать её вторую производную. Устойчивость положения равновесия характеризуется следующими вариантами:
- неустойчивое равновесие;
- устойчивое равновесие;
- безразличное равновесие.
Неустойчивое равновесие
В случае, когда вторая производная отрицательна, потенциальная энергия системы находится в состоянии локального максимума. Это означает, что положение равновесия неустойчиво . Если система будет смещена на небольшое расстояние, то она продолжит своё движение за счёт сил, действующих на систему.
Это означает, что положение равновесия неустойчиво . Если система будет смещена на небольшое расстояние, то она продолжит своё движение за счёт сил, действующих на систему.
Устойчивое равновесие
Вторая производная > 0: потенциальная энергия в состоянии локального минимума, положение равновесия устойчиво (см. Теорема Лагранжа об устойчивости равновесия). Если систему сместить на небольшое расстояние, она вернётся назад в состояние равновесия. Равновесие устойчиво, если центр тяжести тела занимает наинизшее положение по сравнению со всеми возможными соседними положениями.
Безразличное равновесие
Вторая производная = 0: в этой области энергия не варьируется, а положение равновесия является безразличным . Если система будет смещена на небольшое расстояние, она останется в новом положении.
Устойчивость в системах с большим числом степеней свободы
Если система имеет несколько степеней свободы, то может оказаться, что в сдвигах одних направлениях равновесие устойчиво, а в других — неустойчиво. Простейшим примером такой ситуации является «седловина» или «перевал» (в этом месте хорошо бы разместить картинку).
Простейшим примером такой ситуации является «седловина» или «перевал» (в этом месте хорошо бы разместить картинку).
Равновесие системы с несколькими степенями свободы будет устойчивым только в том случае, если оно устойчиво во всех направлениях .
Wikimedia Foundation . 2010 .
Смотреть что такое «Механическое равновесие» в других словарях:
механическое равновесие — mechaninė pusiausvyra statusas T sritis fizika atitikmenys: angl. mechanical equilibrium vok. mechanisches Gleichgewicht, n rus. механическое равновесие, n pranc. équilibre mécanique, m … Fizikos terminų žodynas
— … Википедия
Фазовые переходы Статья я … Википедия
Состояние термодинамической системы, в которое она самопроизвольно приходит через достаточно большой промежуток времени в условиях изоляции от окружающей среды, после чего параметры состояния системы уже не меняются со временем. Изоляция… … Большая советская энциклопедия
РАВНОВЕСИЕ — (1) механическое состояние неподвижности тела, являющееся следствием Р. сил, действующих на него (когда сумма всех сил, действующих на тело, равна нулю, т. е. не сообщает ускорения). Различают Р.: а) устойчивое, когда при отклонении от… … Большая политехническая энциклопедия
сил, действующих на него (когда сумма всех сил, действующих на тело, равна нулю, т. е. не сообщает ускорения). Различают Р.: а) устойчивое, когда при отклонении от… … Большая политехническая энциклопедия
Состояние механич. системы, при к ром все её точки неподвижны по отношению к данной системе отсчёта. Если эта система отсчёта является инерциальной, то Р. м. наз. абсолютным, в противном случае относительным. В зависимости от поведения тела после … Большой энциклопедический политехнический словарь
Термодинамическое равновесие состояние изолированной термодинамической системы, при котором в каждой точке для всех химических, диффузионных, ядерных, и других процессов скорость прямой реакции равна скорости обратной. Термодинамическое… … Википедия
Равновесие — наиболее вероятное макросостояние вещества, когда переменные величины независимо от выбора остаются постоянными при полном описании системы. Различают равновесие: механическое, термодинамическое, химическое, фазовое и др. : Смотри… … Энциклопедический словарь по металлургии
: Смотри… … Энциклопедический словарь по металлургии
Содержание 1 Классическое определение 2 Определение через энергию системы 3 Виды равновесия … Википедия
Фазовые переходы Статья является частью серии «Термодинамика». Понятие фазы Равновесие фаз Квантовый фазовый переход Разделы термодинамики Начала термодинамики Уравнение состояния … Википедия
5.6: Типы равновесия — Physics LibreTexts
Stable Equilibrium
Если конструкция выталкивается из равновесия, мы говорим, что она вышла из равновесия. Если объект стремится вернуться к своему положению равновесия, то он должен находиться в области устойчивого равновесия , и сила, отталкивающая его назад, является восстанавливающей силой.
Мрамор на дне чаши — пример устойчивого равновесия. Кредит изображения:
Когда ваша рука свисает с плеча, она находится в стабильном равновесии.Если вашу руку поднять в сторону, а затем отпустить, она упадет обратно в положение для подвешивания. Подвесной рычаг находится в стабильном положении, потому что центр тяжести руки расположен ниже основания опоры, в данном случае плеча. При смещении (небольшом подъеме) сила тяжести, действующая на вашу руку, вызовет вращающий момент, который вернет вашу руку обратно в положение подвешивания. В таких случаях, когда объект смещается из положения равновесия и результирующие результирующие силы (или моменты, которые они вызывают) перемещают объект обратно в положение равновесия, эти силы называются восстанавливающими силами.Ленивец пользуется преимуществом стабильного равновесия, чтобы сэкономить энергию, которую люди тратят на то, чтобы оставаться в вертикальном положении. Если ленивец смещается в любом направлении, сила тяжести автоматически действует как восстанавливающая сила и возвращает прорезь в положение равновесия.
Подвесной рычаг находится в стабильном положении, потому что центр тяжести руки расположен ниже основания опоры, в данном случае плеча. При смещении (небольшом подъеме) сила тяжести, действующая на вашу руку, вызовет вращающий момент, который вернет вашу руку обратно в положение подвешивания. В таких случаях, когда объект смещается из положения равновесия и результирующие результирующие силы (или моменты, которые они вызывают) перемещают объект обратно в положение равновесия, эти силы называются восстанавливающими силами.Ленивец пользуется преимуществом стабильного равновесия, чтобы сэкономить энергию, которую люди тратят на то, чтобы оставаться в вертикальном положении. Если ленивец смещается в любом направлении, сила тяжести автоматически действует как восстанавливающая сила и возвращает прорезь в положение равновесия.
Двупалый ленивец висит на ногах в устойчивом положении равновесия. Кредит изображения: Клифф через Wikimedia Commons
Неустойчивое равновесие
Когда система в равновесии смещается и результирующая результирующая сила толкает объект еще дальше от положения равновесия, тогда он должен находиться в неустойчивом равновесии. Технически реальные системы не могут проводить время в точке нестабильного равновесия, потому что малейшая вибрация заставит их выйти из равновесия, не говоря уже о том, что вы никогда не могли бы идеально разместить их в первую очередь. Хороший пример — попытка уравновесить шарик на холме:
Технически реальные системы не могут проводить время в точке нестабильного равновесия, потому что малейшая вибрация заставит их выйти из равновесия, не говоря уже о том, что вы никогда не могли бы идеально разместить их в первую очередь. Хороший пример — попытка уравновесить шарик на холме:
Пример неустойчивого равновесия — шарик, поставленный на холм. Изображение предоставлено: «Нестабильное равновесие» Уруцега, через Wikimedia Commons.
Метастабильное равновесие
Человек в состоянии неустойчивого равновесия.Изображение предоставлено: Usien через Wikimedia Commons.
Некоторые конструкции, которые находятся в устойчивом равновесии, могут быть смещены относительно далеко, прежде чем они перестанут находиться в равновесии, по сравнению с другими структурами, которым требуется лишь небольшое смещение, чтобы выйти из равновесия. Мы часто называем эти системы стабильными и нестабильными, но это может вводить в заблуждение, потому что любая стоящая конструкция в некоторой степени стабильна, а действительно нестабильная структура не будет стоять на месте ни на какое время. Например, мы ожидаем, что большинство людей скажут, что человек, балансирующий на голове на изображении выше, нестабилен.Однако они активно корректируют форму своего тела, чтобы сместить центр тяжести и остаться в области устойчивого равновесия и не пройти переломный момент. Можно сказать, что этот человек находится в очень узком метастабильном равновесии. Удержание равновесия при стоянии, сидении или ходьбе — это акт поддержания метастабильного равновесия.
Например, мы ожидаем, что большинство людей скажут, что человек, балансирующий на голове на изображении выше, нестабилен.Однако они активно корректируют форму своего тела, чтобы сместить центр тяжести и остаться в области устойчивого равновесия и не пройти переломный момент. Можно сказать, что этот человек находится в очень узком метастабильном равновесии. Удержание равновесия при стоянии, сидении или ходьбе — это акт поддержания метастабильного равновесия.
Шарик находится в метастабильном равновесии до тех пор, пока он не выходит за пределы провала в центре. Пик на краю провала аналогичен точке опрокидывания конструкции; за пределами этой точки шарик не переместится обратно в положение равновесия.Изображение предоставлено: «Мета-стабильное равновесие» Уруцега через Wikimedia Commons
типов равновесия — что такое равновесие?
Загрузите лучшее приложение для подготовки к экзаменам в Индии
Класс 9-10, JEE и NEET
Скачать приложение eSaral Эй, вы хотите узнать о типах равновесия? Если так. Тогда вы попали в нужное место.
Тогда вы попали в нужное место.
Говорят, что тело находится в поступательном равновесии, если результирующая сила, действующая на тело, равна нулю, $ \ overrightarrow {\ mathrm {F}} _ {\ text {net}} = 0 $
Если сила консервативная, то $ \ mathrm {F} = — \ frac {\ mathrm {dU}} {\ mathrm {dr}} $
Для равновесия F = 0.
Итак, $ — \ frac {d U} {d r} = 0 $
или
$ \ frac {\ mathrm {dU}} {\ mathrm {dr}} = 0 $
В положении равновесия наклон графика U-r равен нулю или потенциальная энергия оптимальна (максимальная, минимальная или постоянная).
Типы равновесия.- Стабильное равновесие
- Неустойчивое равновесие
- Нейтральное равновесие
Стабильное равновесие:
Когда частица немного смещается из состояния равновесия и стремится вернуться в состояние равновесия, говорят, что она находится в стабильном равновесии
Неустойчивое равновесие:
Когда частица смещается из положения равновесия и стремится отклониться от положения равновесия, говорят, что она находится в неустойчивом состоянии равновесия
Нейтральное равновесие:
Когда частица выходит из состояния равновесия и на нее не действует никакая сила, считается, что равновесие является нейтральным равновесием.
Ситуация, когда F = 0 и $ \ frac {\ mathrm {d} \ mathrm {U}} {\ mathrm {dr}} = 0 $, может быть получена при трех условиях.
Три одинаковых шара уравновешиваются в положениях, показанных на рис. (а), (б) и (в) соответственно.
- Мяч помещен в гладкую сферическую оболочку. Этот шар находится в положении устойчивого равновесия .
- Мяч помещается над гладкой сферой. Это положение Неустойчивого равновесия .
- Мяч находится на ровной горизонтальной поверхности. Этот шар находится в положении Нейтрального равновесия .
Разница между стабильным, нестабильным и нейтральным равновесием
долларов США| S.no | Устойчивое равновесие | Неустойчивое равновесие | Нейтральное равновесие |
| 1 | Сила нетто равна нулю | Сила нетто равна нулю | Сила нетто равна нулю |
| 2 | $ \ frac {d U} {d r} = 0 $ или наклон графика $ U-r $ равен нулю | $ \ frac {\ mathrm {dU}} {\ mathrm {dr}} = 0 $ или наклон графика U-r равен нулю.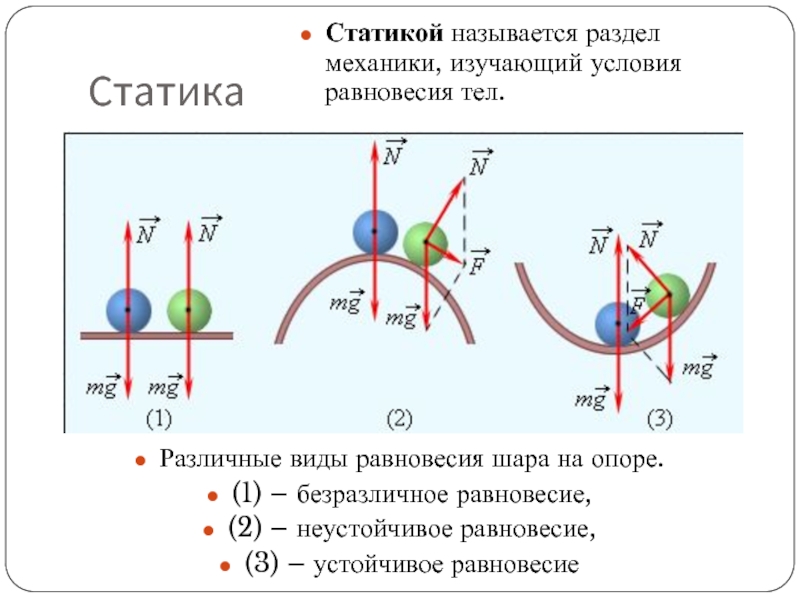 | $ \ frac {\ mathrm {dU}} {\ mathrm {dr}} = 0 $ или наклон графика U-r равен нулю. |
| 3 | При небольшом смещении из положения равновесия на тело начинает действовать результирующая восстанавливающая сила, которая имеет тенденцию возвращать тело в положение равновесия. | При небольшом смещении из положения равновесия на тело начинает действовать результирующая сила, которая перемещает тело в направлении смещения или от положения равновесия.{2}} = 0 | |
| 5 | При смещении из эквилирбиевого положения центр тяжести тела поднимается вверх. | При смещении из положения равновесия центр тяжести тела опускается вниз. | При смещении из положения равновесия центр тяжести тела остается на том же уровне. |
Итак, это все из статьи. Если вы нашли это «Разъяснение типов равновесия» полезным, поделитесь им со своими друзьями.
Для лучшего понимания этой главы, пожалуйста, ознакомьтесь с подробными примечаниями Рабочей Энергии и Мощности.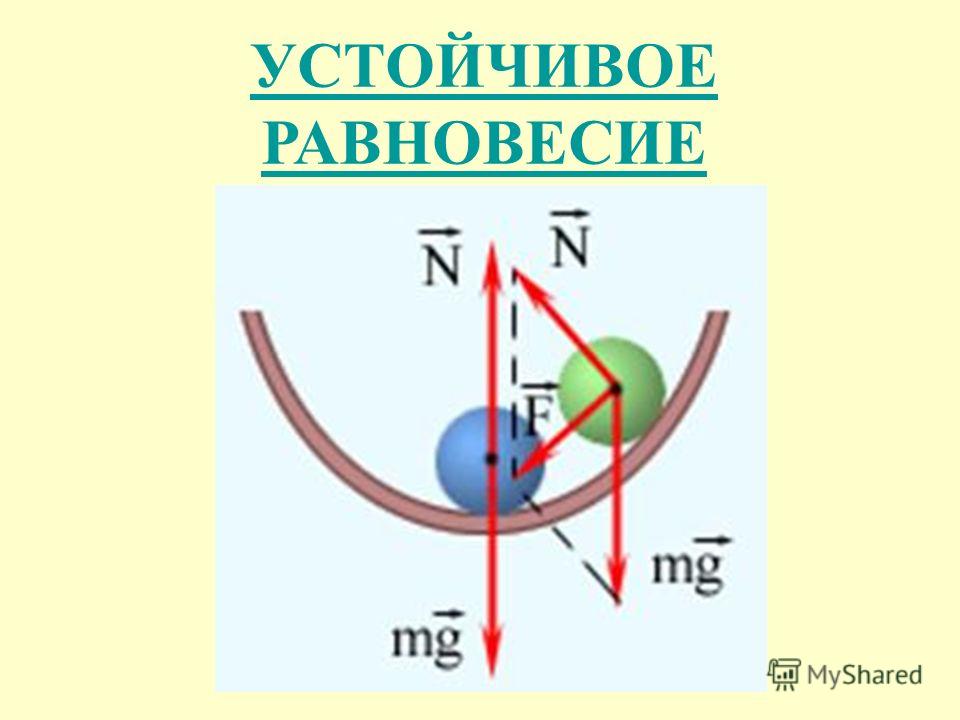 Для просмотра бесплатных обучающих видео по физике Саранша Гупты, сэр Установите приложение eSaral.
Для просмотра бесплатных обучающих видео по физике Саранша Гупты, сэр Установите приложение eSaral.
Загрузите лучшее приложение для подготовки к экзаменам в Индии
Класс 9-10, JEE и NEET
Скачать приложение eSaralравновесия | физика | Британника
равновесие , в физике, состояние системы, при котором ни ее состояние движения, ни ее внутреннее энергетическое состояние не имеют тенденции меняться со временем.Говорят, что простое механическое тело находится в равновесии, если оно не испытывает ни линейного, ни углового ускорения; если его не потревожит внешняя сила, он будет оставаться в этом состоянии бесконечно. Для отдельной частицы равновесие возникает, если векторная сумма всех сил, действующих на частицу, равна нулю. Твердое тело (по определению отличающееся от частицы свойством растяжения) считается находящимся в равновесии, если в дополнение к состояниям, перечисленным для частицы выше, векторная сумма всех крутящих моментов, действующих на тело, равна нулю, так что его состояние вращательного движения остается постоянным. Равновесие считается устойчивым, если небольшие вызванные извне смещения из этого состояния создают силы, которые стремятся противодействовать смещению и возвращать тело или частицу в состояние равновесия. Примеры включают груз, подвешенный на пружине, или кирпич, лежащий на ровной поверхности. Равновесие неустойчиво, если малейшее отклонение вызывает силы, которые увеличивают смещение. Примером может служить шарикоподшипник, балансирующий на краю лезвия бритвы.
Равновесие считается устойчивым, если небольшие вызванные извне смещения из этого состояния создают силы, которые стремятся противодействовать смещению и возвращать тело или частицу в состояние равновесия. Примеры включают груз, подвешенный на пружине, или кирпич, лежащий на ровной поверхности. Равновесие неустойчиво, если малейшее отклонение вызывает силы, которые увеличивают смещение. Примером может служить шарикоподшипник, балансирующий на краю лезвия бритвы.
В термодинамике понятие равновесия расширяется, чтобы включить возможные изменения внутреннего состояния системы, которое характеризуется ее температурой, давлением, плотностью и любыми другими величинами, необходимыми для полного определения ее состояния.При строгом термодинамическом равновесии температура системы однородна (в противном случае тепло текло бы), и любые градиенты в функциях состояния, таких как давление или плотность, уравновешиваются внешними силами, так что они остаются постоянными. Например, равновесное давление внизу столба воздуха выше, чем вверху из-за силы тяжести, а градиенты плотности в центрифуге уравновешиваются центробежной силой. Также полезно рассматривать квазиравновесные процессы, где, например, допускаются температурные градиенты, если скорость теплового потока слишком мала, чтобы быть значимой (адиабатические процессы), но в противном случае система находится в локальном термодинамическом равновесии.Например, адиабатическое расширение восходящего столба воздуха объясняет уменьшение температуры атмосферы с высотой.
Также полезно рассматривать квазиравновесные процессы, где, например, допускаются температурные градиенты, если скорость теплового потока слишком мала, чтобы быть значимой (адиабатические процессы), но в противном случае система находится в локальном термодинамическом равновесии.Например, адиабатическое расширение восходящего столба воздуха объясняет уменьшение температуры атмосферы с высотой.
Британская викторина
Физика и естественное право
Какая сила замедляет движение? Для каждого действия есть равное и противоположное что? В этой викторине по физике нет ничего E = mc square.
Эта статья была недавно отредактирована и обновлена Уильямом Л. Хошем.Равновесие — Определение и типы
Физика равновесия
Равновесие в физике относится к состоянию системы, когда ни ее состояние движения, ни ее внутреннее энергетическое состояние не меняются со временем.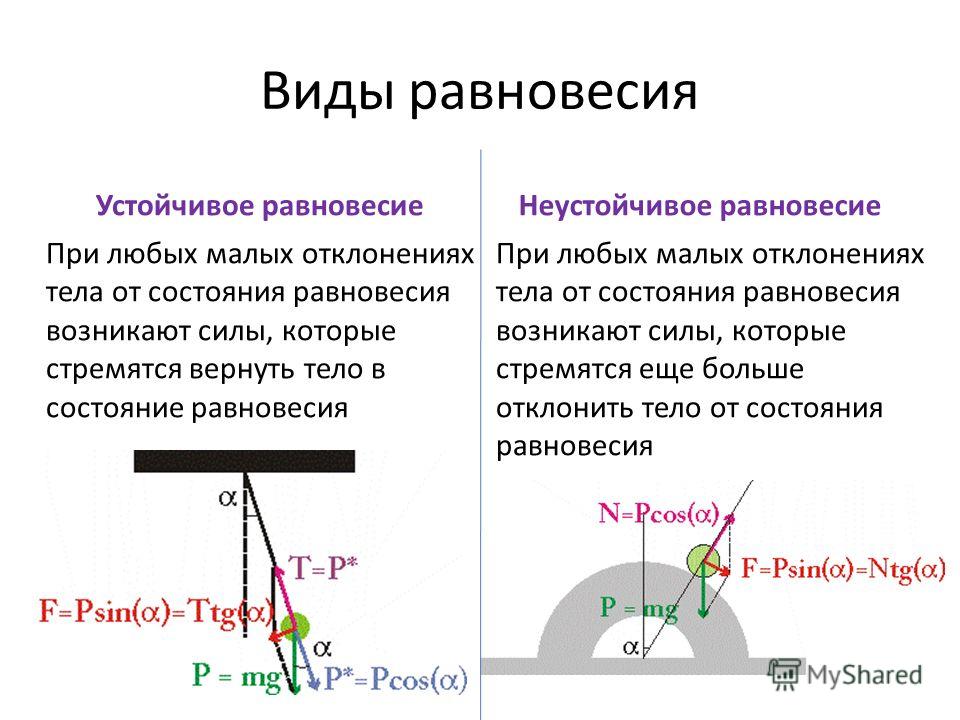 Известно, что простое механическое тело находится в состоянии равновесия, когда оно не испытывает ни линейного, ни углового ускорения. Если его не потревожила внешняя сила, он будет оставаться в этом конкретном состоянии бесконечно.Для одной-единственной частицы равновесие возникает, когда векторная сумма всех сил, действующих на частицу, равна нулю. Твердое тело, которое по определению отличается от частицы тем, что обладает свойством растяжения, считается находящимся в равновесии, когда в дополнение к состояниям, перечисленным для частицы выше, векторная сумма всех крутящих моментов, действующих на тело равно нулю, поэтому его состояние вращательного движения постоянно. Равновесие называется стабильным, если небольшие и вызванные извне смещения, из которых состояние порождает силы, стремятся противодействовать смещению и возвращают тело или частицу в состояние равновесия.Примеры: груз, подвешенный на пружине, или кирпич, лежащий на ровной поверхности. Равновесие считается неустойчивым, когда малейшее отклонение создает силы, которые стремятся увеличить смещение.
Известно, что простое механическое тело находится в состоянии равновесия, когда оно не испытывает ни линейного, ни углового ускорения. Если его не потревожила внешняя сила, он будет оставаться в этом конкретном состоянии бесконечно.Для одной-единственной частицы равновесие возникает, когда векторная сумма всех сил, действующих на частицу, равна нулю. Твердое тело, которое по определению отличается от частицы тем, что обладает свойством растяжения, считается находящимся в равновесии, когда в дополнение к состояниям, перечисленным для частицы выше, векторная сумма всех крутящих моментов, действующих на тело равно нулю, поэтому его состояние вращательного движения постоянно. Равновесие называется стабильным, если небольшие и вызванные извне смещения, из которых состояние порождает силы, стремятся противодействовать смещению и возвращают тело или частицу в состояние равновесия.Примеры: груз, подвешенный на пружине, или кирпич, лежащий на ровной поверхности. Равновесие считается неустойчивым, когда малейшее отклонение создает силы, которые стремятся увеличить смещение. Примером этого является шарикоподшипник, установленный на краю лезвия бритвы.
Примером этого является шарикоподшипник, установленный на краю лезвия бритвы.
Что такое равновесие в физике
Давайте узнаем о физике определения равновесия.
Когда вам нужно определить равновесие, самое простое определение — это точка, в которой чистая внешняя сила и крутящий момент, действующие на тело относительно COM или любой другой заданной точки, приводят к нулю.Но, если быть более точным, равновесие твердого тела означает как вращательное, так и поступательное равновесие. Рассмотрим следующие примеры равновесия твердого тела:
(Изображение будет добавлено в ближайшее время)
Типы равновесия
Равновесие классифицируется как динамическое или статическое равновесие. Возникает следующий вопрос: что такое статическое равновесие и чем оно отличается от динамического? Следовательно, когда тело находится в состоянии равновесия, но продолжает двигаться с неизвестной скоростью, это называется динамическим равновесием. Например, мяч движется с неизвестной скоростью. С другой стороны, когда тело находится в состоянии равновесия в состоянии покоя, это называется статическим равновесием.
Например, мяч движется с неизвестной скоростью. С другой стороны, когда тело находится в состоянии равновесия в состоянии покоя, это называется статическим равновесием.
Равновесие также классифицируется как стабильное, нестабильное и нейтральное. Давайте посмотрим, что означают все эти термины.
Устойчивое равновесие — это такое равновесие, при котором, когда тело смещается из своего состояния равновесия, оно имеет тенденцию двигаться к этой конкретной точке равновесия. Например, рассмотрим шар, который находится в нижней части полушария.В то время как в случае неустойчивого равновесия, когда оно перемещается из этой конкретной точки, тело удаляется от этой точки. Рассмотрим шар, который держится наверху сферы. Когда вы скользите по нему, мяч катится от самой верхней точки. Точно так же в случае нейтрального равновесия тело не движется к точке равновесия и не удаляется от нее. Например, слегка сместите мяч, который держится на горизонтальной поверхности.
(Изображение будет добавлено в ближайшее время)
Типы устойчивости — Физика тела: движение к метаболизму
Если конструкция выталкивается из равновесия, мы говорим, что она вышла из равновесия.Если объект стремится вернуться к своему положению равновесия, то он должен находиться в области устойчивого равновесия , и сила, отталкивающая его назад, является восстанавливающей силой.
Мрамор на дне чаши — пример устойчивого равновесия. Изображение предоставлено: «Стабильное равновесие» Уруцега, через Wikimedia Commons Когда ваша рука свисает с плеча, она находится в стабильном равновесии. Если вашу руку поднять в сторону, а затем отпустить, она упадет обратно в положение для подвешивания.Подвесной рычаг находится в стабильном положении, потому что центр тяжести руки расположен ниже основания опоры, в данном случае плеча. При смещении (небольшом подъеме) сила тяжести, действующая на вашу руку, вызовет вращающий момент, который вернет вашу руку обратно в положение подвешивания. В таких случаях, когда объект смещается из положения равновесия и результирующие результирующие силы (или моменты, которые они вызывают) перемещают объект обратно в положение равновесия, эти силы называются восстанавливающими силами.Ленивец пользуется преимуществом стабильного равновесия, чтобы сэкономить энергию, которую люди тратят на то, чтобы оставаться в вертикальном положении. Если ленивец смещается в любом направлении, сила тяжести автоматически действует как восстанавливающая сила и возвращает прорезь в положение равновесия.
В таких случаях, когда объект смещается из положения равновесия и результирующие результирующие силы (или моменты, которые они вызывают) перемещают объект обратно в положение равновесия, эти силы называются восстанавливающими силами.Ленивец пользуется преимуществом стабильного равновесия, чтобы сэкономить энергию, которую люди тратят на то, чтобы оставаться в вертикальном положении. Если ленивец смещается в любом направлении, сила тяжести автоматически действует как восстанавливающая сила и возвращает прорезь в положение равновесия.
Когда система в равновесии смещается и результирующая результирующая сила толкает объект еще дальше от положения равновесия, тогда он должен находиться в неустойчивом равновесии.Технически реальные системы не могут проводить время в точке нестабильного равновесия, потому что малейшая вибрация заставит их выйти из равновесия, не говоря уже о том, что вы никогда не могли бы идеально разместить их в первую очередь.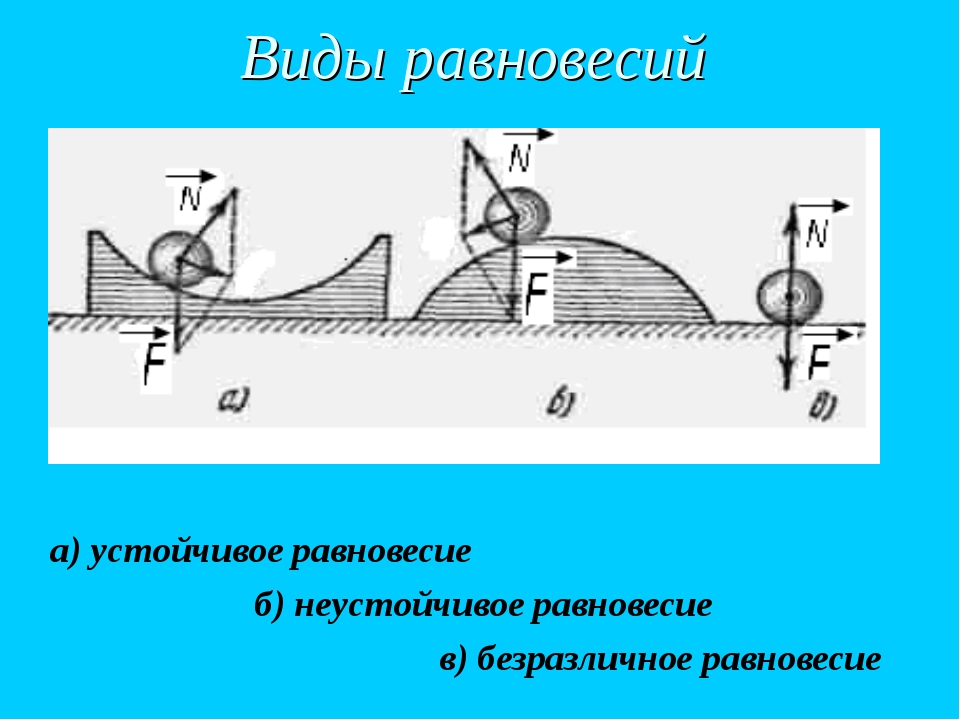 Хороший пример — попытка уравновесить шарик на холме:
Хороший пример — попытка уравновесить шарик на холме:
Некоторые структуры, которые находятся в устойчивом равновесии и могут быть перемещены относительно далеко, прежде чем они перестанут находиться в равновесии.Другие структуры структуры, которым требуется лишь небольшое смещение, чтобы выйти из равновесия (например, малыши). Мы часто называем эти системы стабильными и нестабильными, но это может вводить в заблуждение, потому что любая стоящая конструкция в некоторой степени стабильна, а действительно нестабильная структура не будет стоять на месте ни на какое время. Эти структуры, которые находятся в стабильной области, но могут быть вытолкнуты через критическую точку, как известно, находятся в метастабильном равновесии.
Мрамор находится в метастабильном равновесии до тех пор, пока он не выходит за пределы провала в центре. Пик на краю провала аналогичен точке опрокидывания конструкции; за пределами этой точки шарик не переместится обратно в положение равновесия. Изображение предоставлено: «Мета-стабильное равновесие» Уруцега через Wikimedia Commons
Пик на краю провала аналогичен точке опрокидывания конструкции; за пределами этой точки шарик не переместится обратно в положение равновесия. Изображение предоставлено: «Мета-стабильное равновесие» Уруцега через Wikimedia CommonsЧтобы сохранять равновесие, необходимо оставаться в устойчивой области метастабильного равновесия. Например, мы ожидаем, что большинство людей скажут, что человек, балансирующий на голове на следующем изображении, нестабилен, но это не совсем точно. Фактически, человек активно корректирует форму своего тела, чтобы сместить центр тяжести, чтобы оставаться в стабильной, хотя и узкой, области метастабильного равновесия.
Человек в едва устойчивом равновесии. Изображение предоставлено: Usien через Wikimedia Commons.12.1 Условия статического равновесия — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Определите физические условия статического равновесия.
- Нарисуйте диаграмму свободного тела для твердого тела, на которое действуют силы.

- Объясните, как условия равновесия позволяют нам решать задачи статики.
Мы говорим, что твердое тело находится в состоянии равновесия , когда его линейное и угловое ускорение равны нулю относительно инерциальной системы отсчета. Это означает, что тело в состоянии равновесия может двигаться, но в этом случае его линейная и угловая скорости должны быть постоянными. Мы говорим, что твердое тело находится в состоянии статического равновесия , когда оно находится в состоянии покоя в нашей выбранной системе отсчета . Обратите внимание, что различие между состоянием покоя и состоянием равномерного движения является искусственным — то есть объект может находиться в состоянии покоя в выбранной нами системе отсчета, но для наблюдателя, движущегося с постоянной скоростью относительно нашей системы координат, тот же объект кажется, находится в равномерном движении с постоянной скоростью.Поскольку движение составляет относительно , то, что для нас находится в статическом равновесии, находится в динамическом равновесии для движущегося наблюдателя, и наоборот. Поскольку законы физики идентичны для всех инерциальных систем отсчета, в инерциальной системе отсчета нет различия между статическим равновесием и равновесием.
Поскольку законы физики идентичны для всех инерциальных систем отсчета, в инерциальной системе отсчета нет различия между статическим равновесием и равновесием.
Согласно второму закону движения Ньютона, линейное ускорение твердого тела вызывается действующей на него чистой силой, или
Здесь сумма всех внешних сил, действующих на тело, где м, — его масса, а
— это линейное ускорение его центра масс (концепция, которую мы обсуждали в статьях «Линейный импульс и столкновения по импульсу и столкновениям»).В состоянии равновесия линейное ускорение равно нулю. Если установить нулевое ускорение на (рисунок), мы получим следующее уравнение:
Первое состояние равновесия
Первое условие равновесия для статического равновесия твердого тела выражает поступательное равновесие:
Первое условие равновесия (рисунок) — это условие равновесия сил, с которым мы столкнулись при изучении приложений законов Ньютона.
Это векторное уравнение эквивалентно следующим трем скалярным уравнениям для компонентов чистой силы:
Аналогично (рисунок) можно констатировать, что ускорение вращения
твердого тела вокруг фиксированной оси вращения вызывается чистым крутящим моментом, действующим на тело, или
Здесь
— это инерция вращения тела при вращении вокруг этой оси, а сумма составляет более всех крутящих моментов
внешних сил в (рисунок).В состоянии равновесия ускорение вращения равно нулю. Обнуляя правую часть (рисунок), мы получаем второе условие равновесия:
Второе состояние равновесия
Второе условие равновесия для статического равновесия твердого тела выражает вращательное равновесие:
Второе условие равновесия (рисунок) — это условие равновесия для крутящих моментов, с которым мы столкнулись при изучении динамики вращения.Стоит отметить, что это уравнение равновесия обычно справедливо для вращательного равновесия вокруг любой оси вращения (фиксированной или иной). Опять же, это векторное уравнение эквивалентно трем скалярным уравнениям для векторных компонентов чистого крутящего момента:
Опять же, это векторное уравнение эквивалентно трем скалярным уравнениям для векторных компонентов чистого крутящего момента:
Второе условие равновесия означает, что в равновесии нет чистого внешнего крутящего момента, вызывающего вращение вокруг любой оси.
Первое и второе условия равновесия указаны в конкретной системе отсчета.Первое условие включает только силы и поэтому не зависит от источника системы отсчета. Однако второе условие связано с крутящим моментом, который определяется как перекрестное произведение,
, где вектор положения
относительно оси вращения точки приложения силы входит в уравнение. Следовательно, крутящий момент зависит от положения оси в системе отсчета. Однако, когда условия вращательного и поступательного равновесия выполняются одновременно в одной системе отсчета, они также сохраняются в любой другой инерциальной системе отсчета, так что чистый крутящий момент вокруг любой оси вращения по-прежнему равен нулю.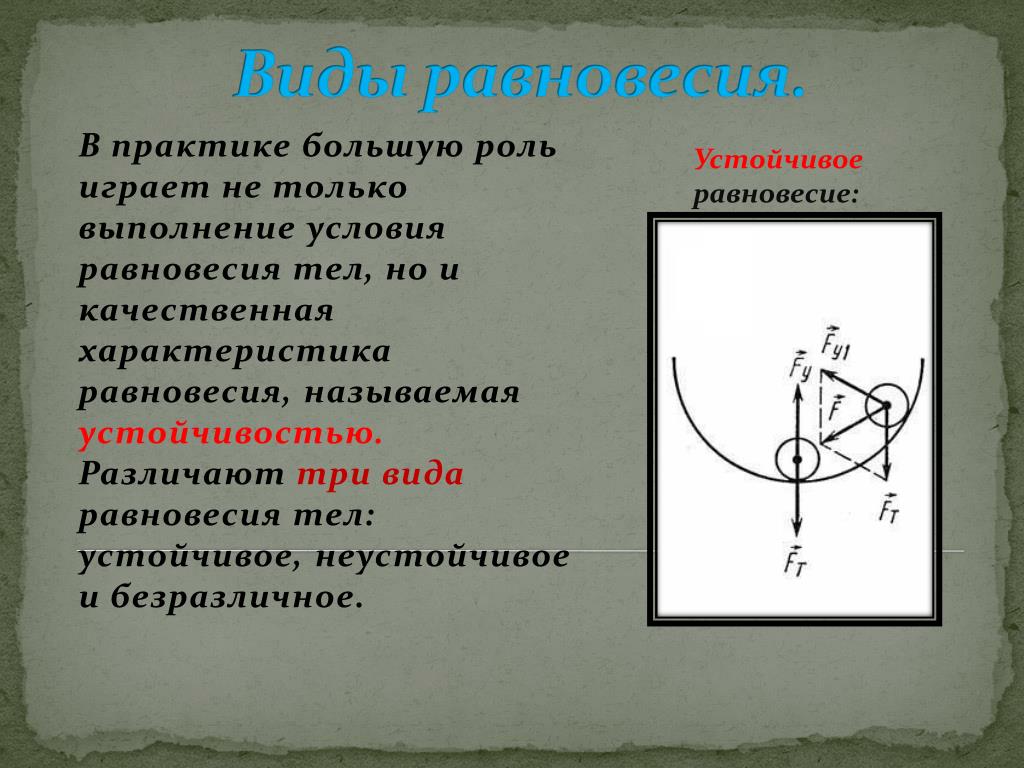 Объяснение этому довольно простое.
Объяснение этому довольно простое.
Предположим вектор
— позиция начала новой инерциальной системы отсчета
.в старой инерциальной системе отсчета S . Из нашего исследования относительного движения мы знаем, что в новой системе отсчета
вектор положения
точки, где действует сила
относится к
через уравнение
Теперь мы можем просуммировать все крутящие моменты
всех внешних сил в новой системе отсчета,
На последнем этапе этой цепочки рассуждений мы использовали тот факт, что в равновесии в старой системе отсчета, S , первый член исчезает из-за (Рисунок), а второй член исчезает из-за (Рисунок).Следовательно, мы видим, что чистый крутящий момент в любой инерциальной системе отсчета
равно нулю при условии, что оба условия равновесия сохраняются в инерциальной системе отсчета S .
Практическое значение этого состоит в том, что при применении условий равновесия для твердого тела мы можем выбрать любую точку в качестве начала отсчета системы отсчета. Наш выбор системы отсчета продиктован физическими особенностями решаемой проблемы. В одной системе отсчета математическая форма условий равновесия может быть довольно сложной, тогда как в другой системе координат те же условия могут иметь более простую математическую форму, которую легко решить.Начало выбранной системы отсчета называется точкой поворота .
В самом общем случае условия равновесия выражаются шестью скалярными уравнениями ((Рисунок) и (Рисунок)). Для плоских задач равновесия с вращением вокруг фиксированной оси, которые мы рассматриваем в этой главе, мы можем сократить количество уравнений до трех. Стандартная процедура состоит в том, чтобы принять систему отсчета, в которой ось z является осью вращения. При таком выборе оси чистый крутящий момент имеет только компонент z , все силы, которые имеют ненулевые крутящие моменты, лежат в плоскости xy , и, следовательно, вклад в чистый крутящий момент поступает только от x — и y — составляющие внешних сил. Таким образом, для плоских задач с осью вращения, перпендикулярной плоскости xy , мы имеем следующие три условия равновесия для сил и моментов:
Таким образом, для плоских задач с осью вращения, перпендикулярной плоскости xy , мы имеем следующие три условия равновесия для сил и моментов:
, где суммирование ведется по всем внешним силам Н, , действующим на тело, и их крутящим моментам. На (Рисунок) мы упростили обозначения, опустив нижний индекс z , но мы понимаем, что здесь суммирование ведется по всем вкладам вдоль оси z , которая является осью вращения.На (Рисунок) z -компонент крутящего момента
от силы
это
где
— длина плеча рычага силы и
— это величина силы (как вы видели в разделе «Вращение с фиксированной осью»). Уголок
— угол между векторами
и
измерение из вектора
в вектор
в направлении против часовой стрелки ((Рисунок)). При использовании (рисунок) мы часто вычисляем величину крутящего момента и присваиваем ее значение положительному значению
При использовании (рисунок) мы часто вычисляем величину крутящего момента и присваиваем ее значение положительному значению
или отрицательное
в зависимости от направления вращения, вызванного только этим крутящим моментом. На (Рисунок) чистый крутящий момент представляет собой сумму членов, каждый член вычисляется из (Рисунок), и каждый член должен иметь правильное значение , значение . Аналогичным образом на (Рисунок) мы назначаем
Знакдля принудительного включения компонентов в
x — направление и
знак компонентов в
x — направление.Это же правило должно последовательно соблюдаться на (Рисунок) при вычислении компонентов силы по оси y .
Рис. 12.2 Крутящий момент силы: (a) Когда крутящий момент силы вызывает вращение против часовой стрелки вокруг оси вращения, мы говорим, что его направление положительное, что означает, что вектор крутящего момента параллелен оси вращения. (b) Когда крутящий момент силы вызывает вращение вокруг оси по часовой стрелке, мы говорим, что его направление отрицательное, что означает, что вектор крутящего момента антипараллелен оси вращения.
(b) Когда крутящий момент силы вызывает вращение вокруг оси по часовой стрелке, мы говорим, что его направление отрицательное, что означает, что вектор крутящего момента антипараллелен оси вращения.Во многих ситуациях равновесия одной из сил, действующих на тело, является его вес. На диаграммах свободного тела вектор веса привязан к центру тяжести тела. Для всех практических целей центр тяжести идентичен центру масс, как вы узнали из статей «Линейный импульс» и «Столкновения» о линейном импульсе и столкновениях. Только в тех случаях, когда тело имеет большую пространственную протяженность, так что гравитационное поле неоднородно по всему его объему, центр тяжести и центр масс расположены в разных точках.Однако на практике даже такие большие объекты, как здания или круизные лайнеры, находятся в однородном гравитационном поле на поверхности Земли, где ускорение свободного падения имеет постоянную величину
. В этих ситуациях центр тяжести идентичен центру масс. Поэтому на протяжении всей главы мы используем центр масс (CM) как точку, к которой прикреплен вектор веса. Напомним, что ЦМ имеет особый физический смысл: когда внешняя сила приложена к телу точно в его ЦМ, тело в целом совершает поступательное движение, и такая сила не вызывает вращения.
Поэтому на протяжении всей главы мы используем центр масс (CM) как точку, к которой прикреплен вектор веса. Напомним, что ЦМ имеет особый физический смысл: когда внешняя сила приложена к телу точно в его ЦМ, тело в целом совершает поступательное движение, и такая сила не вызывает вращения.
Когда ЦМ расположен вне оси вращения, на объект возникает чистый гравитационный момент . Гравитационный момент — это крутящий момент, вызванный весом. Этот гравитационный момент может вращать объект, если нет опоры для его балансировки. Величина гравитационного момента зависит от того, как далеко от оси находится ЦМ. Например, в случае самосвала ((Рисунок)) ось поворота расположена на линии, где шины соприкасаются с поверхностью дороги.Если CM расположен высоко над поверхностью дороги, гравитационный момент может быть достаточно большим, чтобы перевернуть грузовик. Легковые автомобили с низко расположенной КМ, расположенной близко к тротуару, более устойчивы к опрокидыванию, чем грузовики.
прилагается. Если центр тяжести находится в зоне опоры, погрузчик возвращается в исходное положение после опрокидывания [см. Левую панель в (b)].Но если центр тяжести находится за пределами зоны опоры, грузовик перевернется [см. Правую панель в (b)]. Оба транспортных средства в (b) находятся вне равновесия. Обратите внимание, что автомобиль на (а) находится в равновесии: низкое расположение центра тяжести затрудняет опрокидывание.
Пример
Центр тяжести автомобиля
Легковой автомобиль с колесной базой 2,5 м имеет 52% веса на передние колеса на ровной поверхности, как показано на (Рисунок). Где находится ЦМ этого автомобиля по отношению к задней оси?
Рисунок 12.4 Распределение веса между осями автомобиля. Где находится центр тяжести?Стратегия
Нам неизвестен вес Вт автомобиля. Все, что мы знаем, это то, что когда автомобиль стоит на ровной поверхности, 0,52 w давит на поверхность в точках контакта передних колес и 0,48 w толкает вниз на поверхность в точках контакта задних колес. Также точки соприкосновения удалены друг от друга на расстояние
Все, что мы знаем, это то, что когда автомобиль стоит на ровной поверхности, 0,52 w давит на поверхность в точках контакта передних колес и 0,48 w толкает вниз на поверхность в точках контакта задних колес. Также точки соприкосновения удалены друг от друга на расстояние
В этих точках контакта автомобиль испытывает нормальные силы реакции с величиной
.и
на передней и задней оси соответственно.Мы также знаем, что автомобиль является примером твердого тела в равновесии, весь вес которого w действует на его CM. ЦМ находится где-то между точками действия нормальных сил реакции, где-то на расстоянии x от точки, где
акта. Наша задача найти х . Таким образом, мы идентифицируем три силы, действующие на тело (автомобиль), и можем нарисовать диаграмму свободного тела для расширенного твердого тела, как показано на (Рисунок).
Рисунок 12.5 На диаграмме свободного тела автомобиля четко указаны векторы сил, действующих на автомобиль, и расстояния до центра масс (CM). Когда CM выбран в качестве точки поворота, эти расстояния являются плечами рычагов нормальных сил реакции. Обратите внимание, что величины векторов и рычаги не нужно рисовать в масштабе, но все релевантные величины должны быть четко обозначены.
Когда CM выбран в качестве точки поворота, эти расстояния являются плечами рычагов нормальных сил реакции. Обратите внимание, что величины векторов и рычаги не нужно рисовать в масштабе, но все релевантные величины должны быть четко обозначены.Мы почти готовы записать условия равновесия (рисунок) — (рисунок) для автомобиля, но сначала мы должны определиться с системой отсчета.Предположим, мы выбрали ось x по длине кабины, ось y вертикальную и ось z , перпендикулярную плоскости xy . При таком выборе нам нужно только написать (рисунок) и (рисунок), потому что все компоненты y тождественно равны нулю. Теперь нам нужно определиться с расположением точки поворота. Мы можем выбрать любую точку в качестве местоположения оси вращения ( z -axis). Предположим, мы разместили ось вращения на CM, как показано на схеме свободного тела для автомобиля.На этом этапе мы готовы написать условия равновесия для автомобиля.
Решение
Каждое условие равновесия содержит только три члена, потому что их
силы, действующие на автомобиль. Первое условие равновесия (рисунок) читается как
Первое условие равновесия (рисунок) читается как
Это условие тривиально выполняется, потому что, когда мы подставляем данные, (рисунок) становится
.Второе условие равновесия (рисунок) читается как
.где
— момент силы
— это гравитационный момент силы w , а
— момент силы
Когда шарнир расположен в CM, гравитационный момент идентично нулю, потому что плечо рычага веса относительно оси, проходящей через CM, равно нулю.Линии действия обеих нормальных сил реакции перпендикулярны плечам их рычагов, поэтому на (Рисунок) мы имеем
для обеих сил. Из диаграммы свободного тела мы читаем, что крутящий момент
вызывает вращение по часовой стрелке вокруг оси CM, поэтому его направление отрицательное; и крутящий момент
вызывает вращение против часовой стрелки вокруг оси CM, поэтому его направление положительное.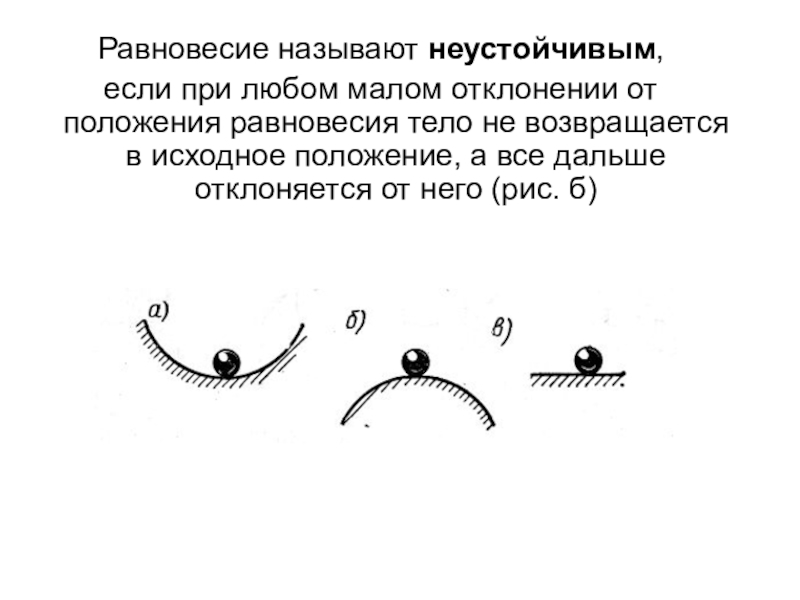 Имея эту информацию, запишем второе условие равновесия как
Имея эту информацию, запишем второе условие равновесия как
С помощью диаграммы свободного тела определяем величины силы
и
и соответствующие им рычаги
и
Теперь мы можем записать второе условие равновесия (рисунок) в явном виде в терминах неизвестного расстояния x :
Здесь вес w отменяется, и мы можем решить уравнение для неизвестного положения x CM.Ответ
Решение
Выбор шарнира в положении передней оси не меняет результата. Схема свободного тела для этой точки поворота представлена на (Рисунок). Для этого выбора точки поворота второе условие равновесия равно
.Когда мы подставляем числа, указанные на диаграмме, получаем
Ответ, полученный путем решения (рисунок), опять же:
. Рисунок 12.6 Эквивалентная диаграмма свободного тела для автомобиля; точка поворота четко обозначена.
Значение
Этот пример показывает, что при решении задач статического равновесия мы можем выбрать точку поворота. Для различных вариантов выбора точки поворота у нас есть разные наборы условий равновесия, которые необходимо решить. Однако любой выбор приводит к одному и тому же решению проблемы.
Проверьте свое понимание
Решите (рисунок), выбрав шарнир в месте расположения задней оси.
[показывать-ответ q = ”fs-id1163713143559 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1163713143559 ″]
[/ hidden-answer]
Проверьте свое понимание
Объясните, какая из следующих ситуаций удовлетворяет обоим условиям равновесия: (а) теннисный мяч, который не вращается при движении в воздухе; (б) пеликан, который парит в воздухе с постоянной скоростью на одной высоте; или (c) коленчатый вал двигателя припаркованного автомобиля.
[показывать-ответ q = ”fs-id1163709667984 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1163709667984 ″]
(б), (в)
[/ hidden-answer]
Особый случай статического равновесия возникает, когда все внешние силы на объект действуют на оси вращения или вдоль нее, или когда пространственное протяжение объекта можно не принимать во внимание.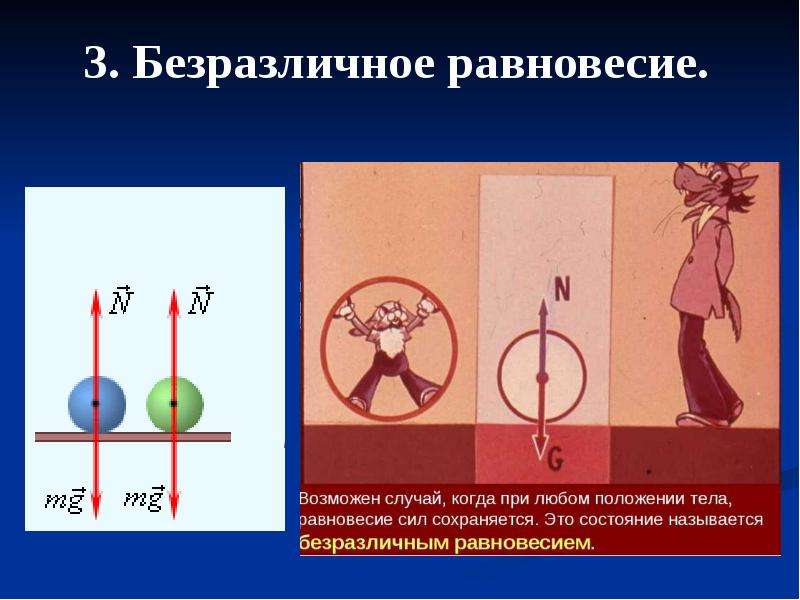 В таком случае объект можно эффективно рассматривать как точечную массу. В этом частном случае нам не нужно беспокоиться о втором условии равновесия (рисунок), потому что все крутящие моменты тождественно равны нулю, а первое условие равновесия (для сил) является единственным условием, которое должно выполняться.Диаграмма свободного тела и стратегия решения задач для этого особого случая были изложены в «Законах Ньютона» и «Приложениях законов Ньютона». В следующем примере вы увидите типичную ситуацию равновесия, включающую только первое условие равновесия.
В таком случае объект можно эффективно рассматривать как точечную массу. В этом частном случае нам не нужно беспокоиться о втором условии равновесия (рисунок), потому что все крутящие моменты тождественно равны нулю, а первое условие равновесия (для сил) является единственным условием, которое должно выполняться.Диаграмма свободного тела и стратегия решения задач для этого особого случая были изложены в «Законах Ньютона» и «Приложениях законов Ньютона». В следующем примере вы увидите типичную ситуацию равновесия, включающую только первое условие равновесия.
Пример
Разрывное напряжение
Маленькая кастрюля массой 42,0 г поддерживается двумя струнами, как показано на (Рисунок). Максимальное натяжение, которое может выдержать струна, составляет 2,80 Н. Масса постепенно добавляется к чаше, пока одна из струн не сломается.Какая это струна? Какую массу нужно добавить, чтобы это произошло?
Рис. 12.7. Постепенно добавляйте массу к кастрюле, пока одна из струн не сломается.
Стратегия
Эта механическая система, состоящая из струн, масс и сковороды, находится в статическом равновесии. В частности, узел, который привязывает струны к кастрюле, находится в статическом равновесии. Узел можно рассматривать как точку; следовательно, нам нужно только первое условие равновесия. Три силы, тянущие к узлу, — это натяжение
.в районе 5.Струна 0 см натяжение
в тетиве 10,0 см, а гиря
чаши, удерживающей массы. Мы принимаем прямоугольную систему координат с осью y , направленной противоположно направлению силы тяжести, и рисуем диаграмму свободного тела для узла (см. (Рисунок)). Чтобы найти компоненты натяжения, необходимо определить направления углов
и
, что струны образуют горизонтальное направление оси x .Как вы можете видеть на (Рисунок), струны составляют две стороны прямоугольного треугольника. Мы можем использовать теорему Пифагора, чтобы решить этот треугольник, показанный на (Рисунок), и найти синус и косинус углов
.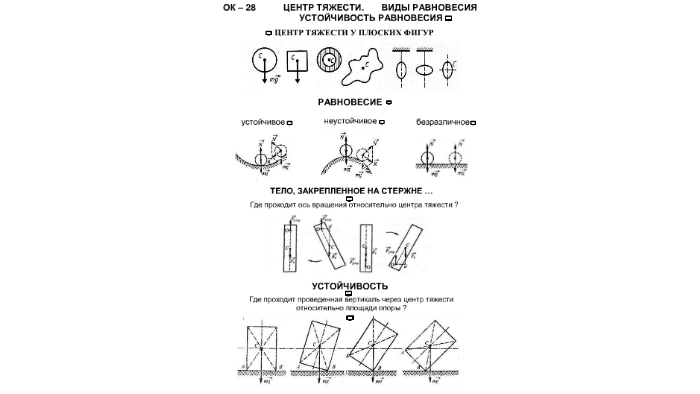
и
Затем мы можем разложить напряжения на их прямоугольные составляющие, подставить в первое условие для равновесия ((Рисунок) и (Рисунок)) и решить для напряжений в струнах. Первой порвется струна с большим натяжением.
Рис. 12.8 Схема свободного тела для узла на (Рис.).Решение
Вес w , тянущий за узел, обусловлен массой M кастрюли и массой m , добавленной к чаше, или
С помощью диаграммы свободного тела на (Рисунок), мы можем установить условия равновесия для узла:
Из диаграммы свободного тела, величины компонентов в этих уравнениях равны
.Подставляем эти компоненты в условия равновесия и упрощаем.Затем мы получаем два уравнения равновесия для натяжений:
Уравнение равновесия для направления x говорит нам, что натяжение
в 5,0-сантиметровой тетиве вдвое превышает натяжение
в тетиву 10,0 см.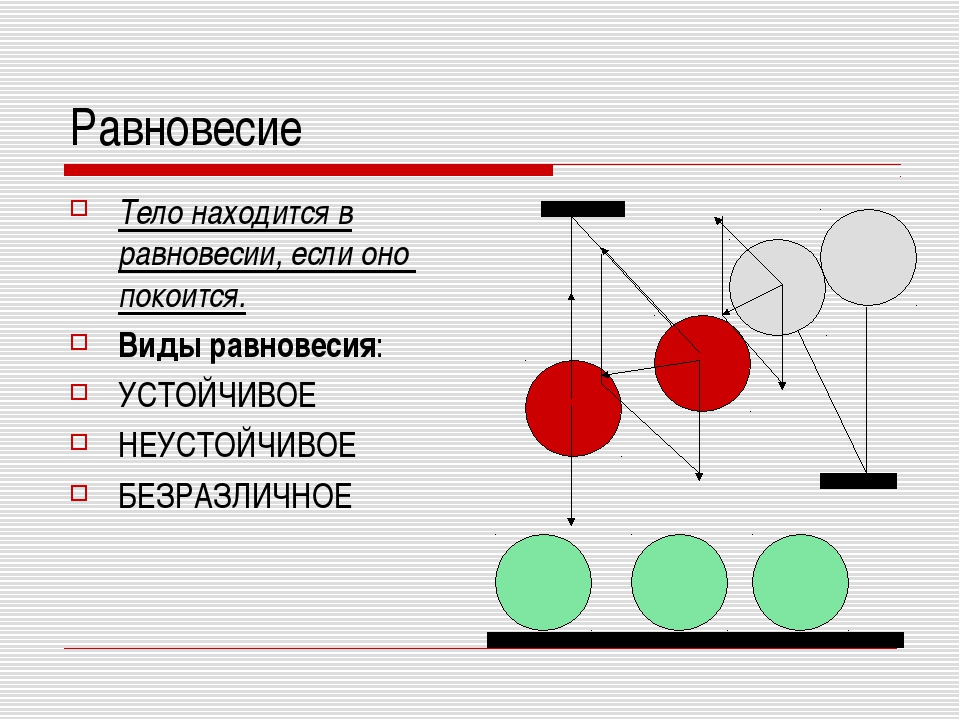 Таким образом, более короткая струна порвется. Когда мы используем первое уравнение для исключения
Таким образом, более короткая струна порвется. Когда мы используем первое уравнение для исключения
из второго уравнения, получаем связь между массой
на сковороде и натяжной
в более короткой строке:
Струна рвется, когда натяжение достигает критического значения
.Предыдущее уравнение может быть решено для критической массы м , которая разрывает струну:
Значение
Предположим, что механическая система, рассматриваемая в этом примере, прикреплена к потолку внутри лифта, поднимающегося вверх.Пока лифт движется вверх с постоянной скоростью, результат остается неизменным, потому что вес
не меняется. Если лифт движется вверх с ускорением, критическая масса меньше, потому что вес
становится больше на кажущуюся массу из-за ускорения лифта. Тем не менее, во всех случаях более короткая струна рвется первой.
Сводка
- Тело находится в равновесии, когда оно остается либо в равномерном движении (поступательном и вращательном), либо в состоянии покоя.
 Когда тело в выбранной инерциальной системе отсчета не вращается и не движется в поступательном движении, мы говорим, что тело находится в статическом равновесии в этой системе отсчета.
Когда тело в выбранной инерциальной системе отсчета не вращается и не движется в поступательном движении, мы говорим, что тело находится в статическом равновесии в этой системе отсчета. - Условия равновесия требуют, чтобы сумма всех внешних сил, действующих на тело, была равна нулю (первое условие равновесия), а сумма всех внешних моментов от внешних сил была равна нулю (второе условие равновесия). Эти два условия должны одновременно выполняться в состоянии равновесия. Если один из них не удовлетворен, тело не находится в равновесии.
- Диаграмма свободного тела для тела — полезный инструмент, который позволяет нам правильно подсчитать все вклады от всех внешних сил и моментов, действующих на тело. Диаграммы свободного тела для равновесия вытянутого твердого тела должны указывать точку поворота и плечи рычага действующих сил по отношению к оси.
Концептуальные вопросы
Что вы можете сказать о скорости движущегося тела, находящегося в динамическом равновесии?
[показывать-ответ q = ”fs-id1163713268541 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1163713268541 ″]
постоянная
[/ hidden-answer]
При каких условиях вращающееся тело может находиться в равновесии? Привести пример.
Какие три фактора влияют на крутящий момент, создаваемый силой относительно определенной точки поворота?
[показывать-ответ q = ”fs-id1163713358733 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1163713358733 ″]
Величина и направление силы, а ее плечо рычага
[/ hidden-answer]
Механики иногда кладут кусок трубы на рукоятку гаечного ключа, пытаясь открутить очень тугой болт. Как это помогает?
Для следующих четырех задач оцените утверждение как истинное или ложное и объясните свой ответ.
Если на объект действует только одна внешняя сила (или крутящий момент), он не может находиться в равновесии.
[показывать-ответ q = ”fs-id1163713282665 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1163713282665 ″]
Верно, поскольку в этом случае сумма сил не может быть равна нулю, если сама сила не равна нулю.
[/ hidden-answer]
Если объект находится в равновесии, на него должно действовать четное число сил.
Если на объект действует нечетное количество сил, объект не может находиться в равновесии.
[показывать-ответ q = ”fs-id1163709692362 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1163709692362 ″]
Ложно, если силы складываются в ноль как векторы, тогда может быть достигнуто равновесие.
[/ hidden-answer]
Тело, движущееся по окружности с постоянной скоростью, находится в равновесии вращения.
Для чего нужен длинный гибкий шест, который переносят канатоходцы?
[показывать-ответ q = ”fs-id1163713272740 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1163713272740 ″]
Помогает канатоходцу сохранять равновесие.
[/ hidden-answer]
Проблемы
При затяжке болта вы нажимаете гаечный ключ перпендикулярно с усилием 165 Н на расстоянии 0,140 м от центра болта. Какой крутящий момент вы прикладываете относительно центра болта?
При открытии двери вы нажимаете на нее перпендикулярно с усилием 55,0 Н на расстоянии 0,850 м от петель. Какой крутящий момент вы прилагаете к петлям?
Какой крутящий момент вы прилагаете к петлям?
[показывать-ответ q = ”fs-id1163713470139 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1163713470139 ″]
[/ hidden-answer]
Найдите величину натяжения каждого поддерживающего троса, показанного ниже.В каждом случае вес подвешенного тела составляет 100,0 Н, а массой кабелей можно пренебречь.
Какая сила должна быть приложена в точке P , чтобы удерживать показанную конструкцию в равновесии? Вес конструкции незначительный.
[show-answer q = ”264812 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 264812 ″] 153,4 ° [/ hidden-answer]
Можно ли приложить усилие на P , чтобы удерживать в равновесии показанную конструкцию? Вес конструкции незначительный.
Двое детей толкают противоположные стороны двери во время игры. Оба толкаются горизонтально и перпендикулярно двери. Один ребенок толкает с силой 17,5 Н на расстоянии 0,600 м от петель, а второй ребенок толкает на расстоянии 0,450 м. Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, трение незначительно.
Один ребенок толкает с силой 17,5 Н на расстоянии 0,600 м от петель, а второй ребенок толкает на расстоянии 0,450 м. Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, трение незначительно.
[показывать-ответ q = ”fs-id1163713183876 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1163713183876 ″]
23.3 N
[/ hidden-answer]
Небольшой внедорожник массой 1000 кг имеет колесную базу 3,0 м. Если 60%, если его вес приходится на передние колеса, как далеко позади передних колес находится центр масс фургона?
Унифицированные качели сбалансированы в центре масс, как показано ниже. Маленький мальчик справа имеет массу 40,0 кг. Какая масса у его друга?
[show-answer q = ”920895 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 920895 ″] 80.0 кг [/ hidden-answer]
Глоссарий
- центр тяжести
- точка, к которой прикреплен вектор весов
- равновесие Тело
- находится в равновесии, когда его линейное и угловое ускорения равны нулю относительно инерциальной системы отсчета
- первое условие равновесия
- выражает поступательное равновесие; все внешние силы, действующие на тело, уравновешиваются и их векторная сумма равна нулю
- гравитационный момент
- крутящий момент на корпусе от его веса; возникает, когда центр тяжести тела не расположен на оси вращения
- второе состояние равновесия
- выражает вращательное равновесие; все моменты из-за внешних сил, действующих на тело, уравновешиваются и их векторная сумма равна нулю
- статическое равновесие
- Тело находится в статическом равновесии, когда оно покоится в выбранной нами инерциальной системе отсчета
Равновесие: перевод и ротация — видео и стенограмма урока
Поступательное равновесие
Мы говорим, что объект находится в поступательном равновесии , когда сумма всех внешних сил, действующих на объект, равна нулю. Поскольку сила равна массе, умноженной на ускорение, другой способ взглянуть на это состоит в том, что объект находится в поступательном равновесии, когда он испытывает нулевое общее ускорение. Это может означать, что объект либо не движется, либо движется с постоянной скоростью.
Поскольку сила равна массе, умноженной на ускорение, другой способ взглянуть на это состоит в том, что объект находится в поступательном равновесии, когда он испытывает нулевое общее ускорение. Это может означать, что объект либо не движется, либо движется с постоянной скоростью.
Если мы можем сказать, что объект находится в поступательном равновесии, мы можем использовать это, чтобы помочь найти все силы, влияющие на этот объект. Представьте, что вы пытаетесь толкнуть 20-килограммовую коробку по полу. Вы толкаете с приложенной силой 200 Ньютонов, но коробка не сдвигается ни на дюйм.Поскольку наш ящик не движется, он должен находиться в поступательном равновесии. Используя предоставленную информацию, давайте найдем все силы, действующие на коробку.
В этом примере на ящик на самом деле действуют четыре силы: приложенная сила, исходящая от вас, сила трения, мешающая вам перемещать ящик, сила тяжести, толкающая вниз, и нормальная сила, исходящая от пола, толкающая вверх. коробка. Первое, что мы делаем, это используем массу нашего ящика и ускорение свободного падения, чтобы найти силу тяжести.
Первое, что мы делаем, это используем массу нашего ящика и ускорение свободного падения, чтобы найти силу тяжести.
Теперь нам просто нужно найти нормальные силы и силы трения. Для этого мы собираемся создать два отдельных уравнения. В 2D мы можем разделить наши силы на те, которые действуют в направлении x (горизонтально), и те, которые действуют в направлении y (вертикально). Сумма только горизонтальных сил и сумма только вертикальных сил должны равняться нулю, поскольку коробка находится в поступательном равновесии.
Наша приложенная сила и сила трения — это горизонтальные силы. Сила тяжести и нормальная сила — это вертикальные силы. Благодаря этому мы можем найти обе наши неизвестные силы. Начнем с определения силы трения.
Благодаря этому мы можем найти обе наши неизвестные силы. Начнем с определения силы трения.
Далее мы найдем нормальную силу.
Отрицательные знаки имеют смысл, потому что они показывают, что сила тяжести и сила трения действуют в противоположных направлениях от нормальной силы и приложенной силы соответственно.
Вращательное равновесие
Вращательное равновесие работает аналогично поступательному равновесию.Основное отличие состоит в том, что при вращении мы рассматриваем моменты, а не силы. Итак, как и в случае поступательного равновесия, мы говорим, что объект находится в вращательном равновесии , когда сумма всех внешних крутящих моментов, действующих на него, равна нулю. Опять же, мы обнаруживаем, что это должно означать, что объект либо неподвижен, либо движется с постоянной угловой скоростью. Таким образом, объект в состоянии вращательного равновесия не должен испытывать угловое ускорение.
Опять же, мы обнаруживаем, что это должно означать, что объект либо неподвижен, либо движется с постоянной угловой скоростью. Таким образом, объект в состоянии вращательного равновесия не должен испытывать угловое ускорение.
Когда объект находится в состоянии вращательного равновесия, мы можем использовать тот факт, что сумма крутящих моментов должна быть равна нулю, чтобы найти различные индивидуальные силы, действующие на этот объект.Одним из примеров этого является балансировка балки по центру на опоре с двумя грузами на каждом конце. Каждый груз создает крутящий момент на балке, который пытается вращать ее вокруг точки опоры. Балка не будет создавать крутящий момент сама по себе, пока она сбалансирована с центром масс на опоре. Таким образом, сумма крутящих моментов от веса 1 и веса 2 должна равняться нулю.
Используя то, что мы только что узнали, давайте попробуем найти силу гравитации, создаваемую грузом 2, действующим на балку.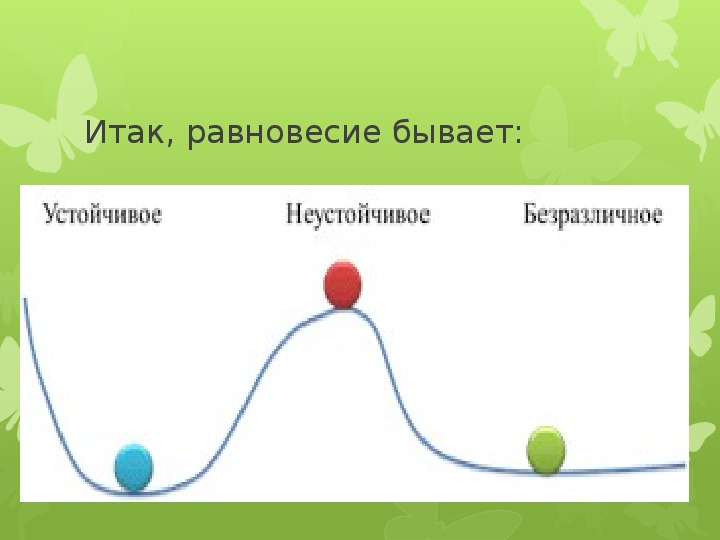 Вес 1 создает силу тяжести в 147 Ньютонов на балке и находится на расстоянии 2,4 метра от точки опоры. Вес 2 находится в 1,3 метра от точки опоры.
Вес 1 создает силу тяжести в 147 Ньютонов на балке и находится на расстоянии 2,4 метра от точки опоры. Вес 2 находится в 1,3 метра от точки опоры.
На изображении мы также можем видеть, что крутящий момент 1 пытается повернуть луч против часовой стрелки, а крутящий момент 2 пытается повернуть его по часовой стрелке. Чтобы показать направление вращения, мы задаем моменты, вращающие объект против часовой стрелки, как положительный знак, а вращающие моменты, вращающие объект по часовой стрелке, — как отрицательный знак.
Поскольку мы знаем, что крутящий момент — это сила, умноженная на расстояние, у нас есть достаточно информации, чтобы найти силу, создаваемую силой тяжести веса 2.
Краткое содержание урока
Поступательное и вращательное движение — два распространенных типа движения в физике. Поступательное движение происходит, когда тело перемещается из одной точки в другую, а вращательное движение происходит, когда твердое тело вращается вокруг оси. Оба эти типа движения имеют связанные с ними состояния равновесия.
Поступательное движение происходит, когда тело перемещается из одной точки в другую, а вращательное движение происходит, когда твердое тело вращается вокруг оси. Оба эти типа движения имеют связанные с ними состояния равновесия.
Объект находится в поступательном равновесии , когда сумма всех внешних сил, действующих на объект, равна нулю. Это также означает, что объект находится в поступательном равновесии, когда он испытывает нулевое общее ускорение.Следовательно, он либо не движется, либо движется с постоянной скоростью.
Подобно поступательному равновесию, объект находится в вращательном равновесии , когда сумма всех внешних крутящих моментов, действующих на него, равна нулю. Во вращательном равновесии объект либо не движется, либо движется с постоянной угловой скоростью. Это должно означать, что объект испытывает нулевое угловое ускорение.
Результаты обучения
После этого урока вы должны уметь делать следующее:
- Определить поступательное и вращательное движение
- Вспомните, когда объект находится в поступательном равновесии и когда объект находится в вращательном равновесии
- Объясните, как найти силы, действующие на объект как в поступательном, так и в вращательном равновесии.

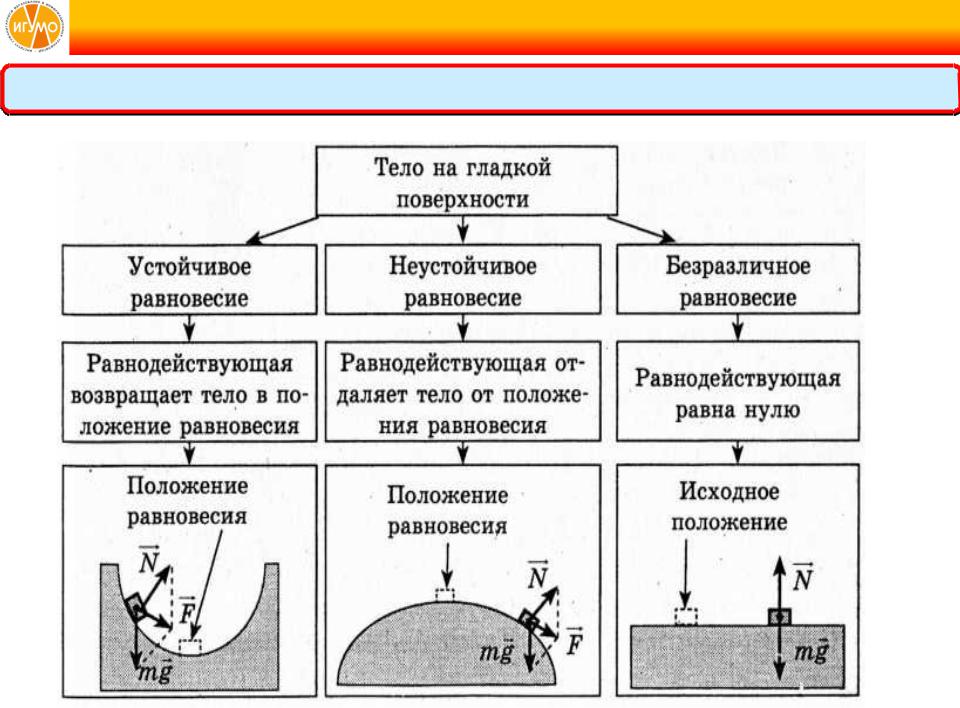
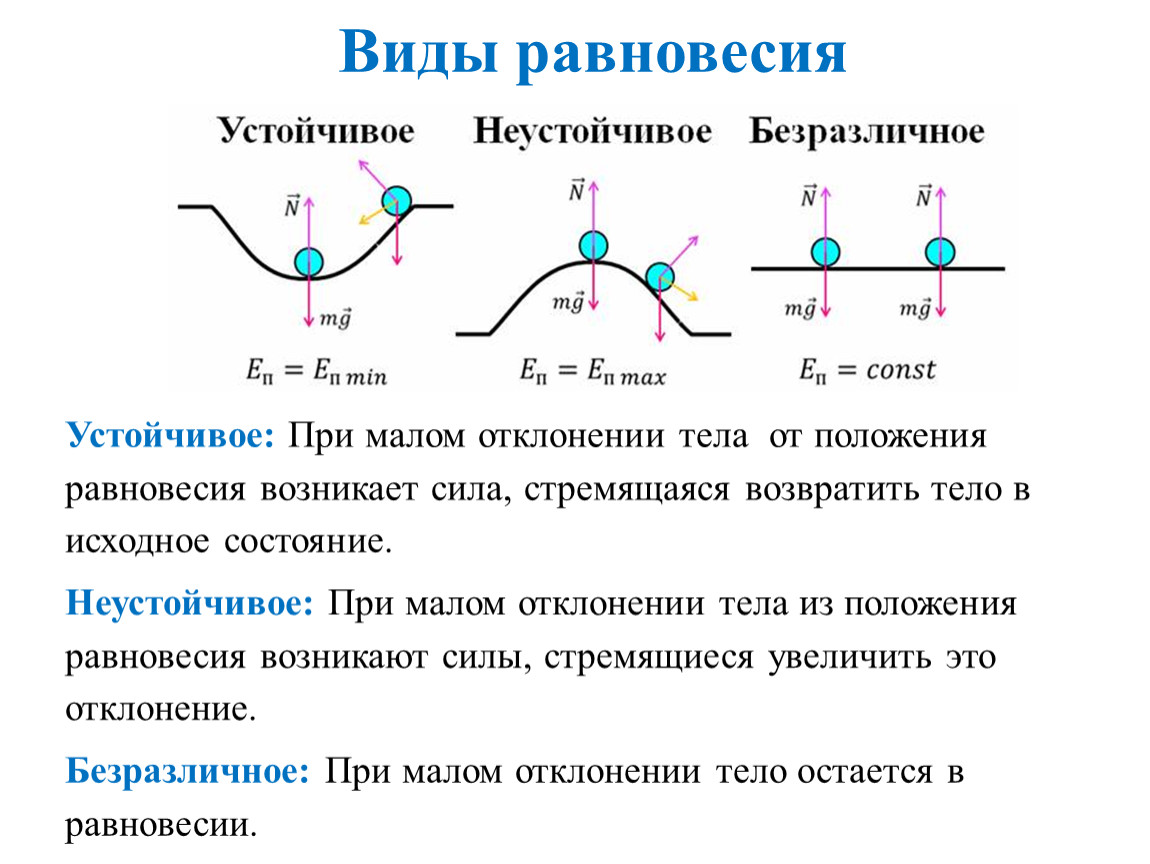
 Что мы видим?
Что мы видим?
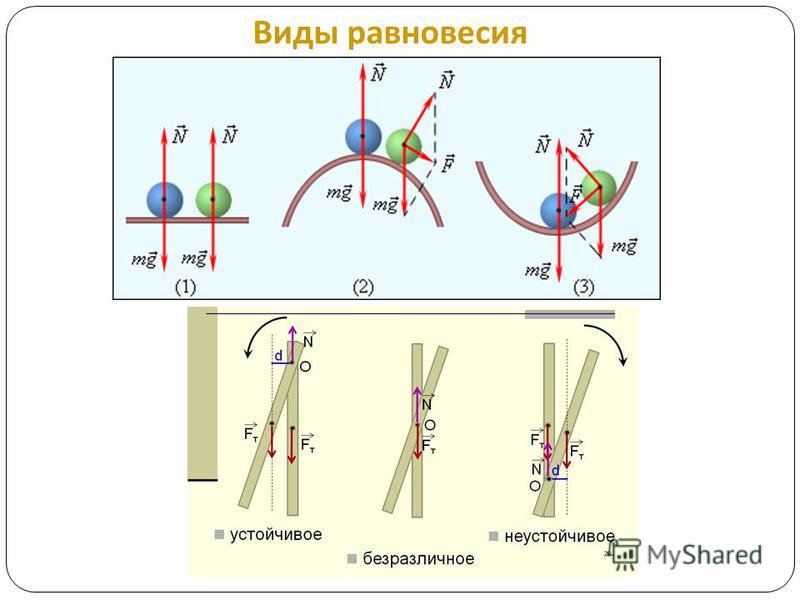
 к. его можно отклонить без опрокидывания на большой угол.
к. его можно отклонить без опрокидывания на большой угол.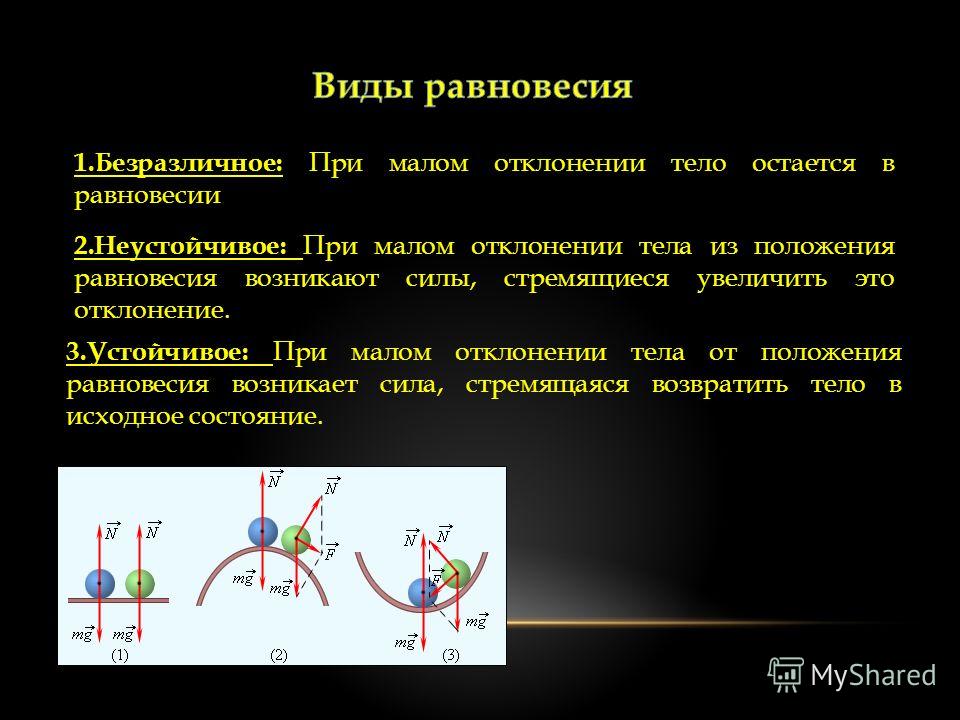

 Когда тело в выбранной инерциальной системе отсчета не вращается и не движется в поступательном движении, мы говорим, что тело находится в статическом равновесии в этой системе отсчета.
Когда тело в выбранной инерциальной системе отсчета не вращается и не движется в поступательном движении, мы говорим, что тело находится в статическом равновесии в этой системе отсчета.