Угол. Виды углов. Видеоурок. Математика 4 Класс

Ранее мы были ознакомлены с понятием «луч». Луч – это часть прямой, ограниченная с одной стороны точкой. На рисунке можно увидеть луч с началом в точке 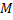 и луч с началом в точке  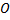(рис. 1).

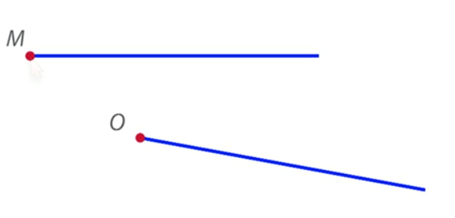
Рис. 1. Лучи

Фигура, образованная двумя лучами с одним и тем же началом, называется углом. Лучи, образующие угол, называются сторонами угла, а их общее начало – вершиной угла (рис. 2).

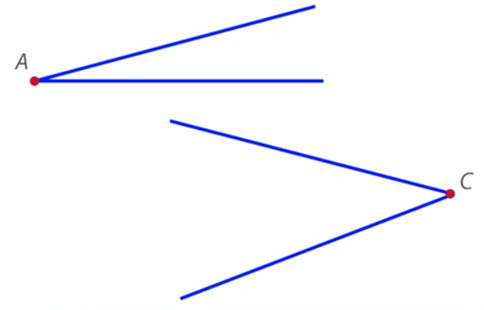
Рис. 2. Углы

Угол может быть назван одной заглавной латинской буквой по его вершине. На рис. 2 можно увидеть угол 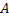 и угол 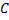. Но углы можно обозначить и другим способом.

Угол многоугольника обозначают тремя заглавными буквами. Называть угол начинают с буквы, стоящей у одной стороны, затем называют букву у вершины, а заканчивают буквой у другой стороны. Например, в треугольнике 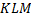, угол с вершиной  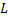является угол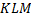

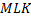 (рис. 3) или в обратном порядке – .

В треугольнике 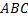 угол с вершиной  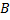– это угол  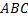или .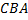

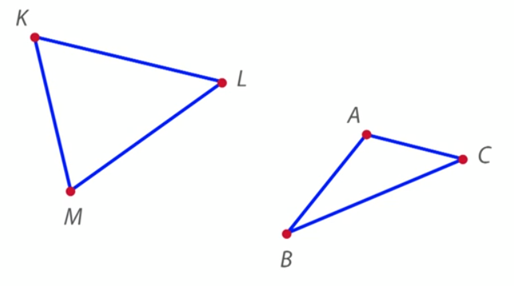
Рис. 3. Углы в треугольнике

Необходимо помнить, что в середине названия угла должна стоять та буква, которой обозначена вершина угла.

Иногда угол обозначают малой буквой или цифрой, ставя их внутри угла (рис. 4). Между сторонами угла проводят для ясности дужку.

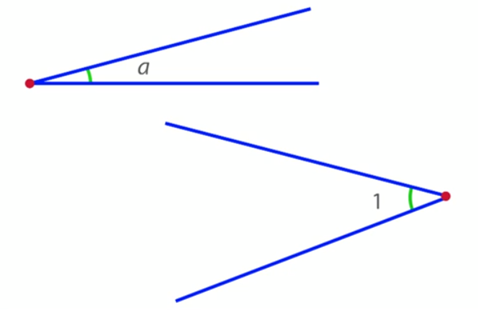
Рис. 4. Обозначение угла буквой или цифрой

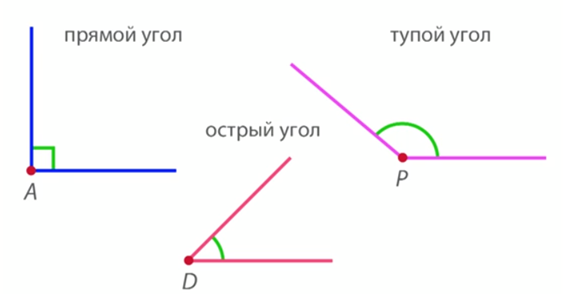
Рис. 5. Виды углов

Существуют различные виды углов.

1. Если стороны угла лежат на одной прямой, то такой угол называют развернутым. На рис. 6 угол М – развернутый (уместно сравнение с развернутым веером).

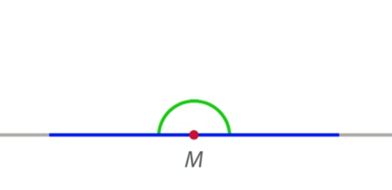
Рис. 6. Развернутый угол

2. Прямым углом называют тот угол, который составляет половину развернутого угла (рис. 7). Например, прямой угол можно получить путем складывания бумаги (если лист сложить дважды).

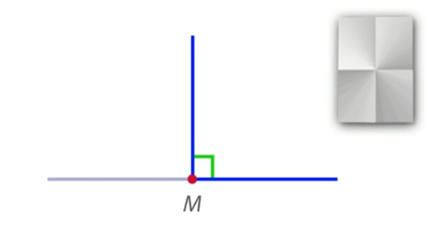
Рис. 7. Прямой угол

Для удобства определения, прямой угол или нет, есть особый инструмент – прямоугольный треугольник, у которого один из углов – прямой (рис. 8).

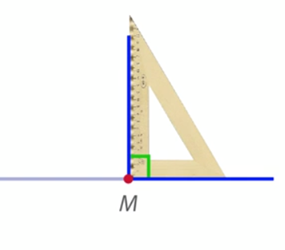
Рис. 8. Прямоугольный треугольник и его применение

3. Непрямые углы делятся на

тупые и острые.

Угол, который меньше прямого, – это острый угол (рис. 9).

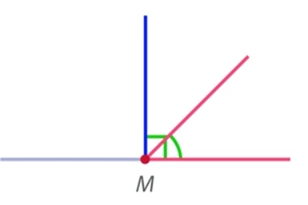
Рис. 9. Острый угол
Угол, который больше прямого, но меньше развернутого угла, – это тупой угол (рис. 10).

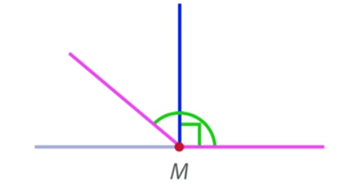
Рис. 10. Тупой угол

Найдите на чертеже прямые, тупые и острые углы (рис. 11).

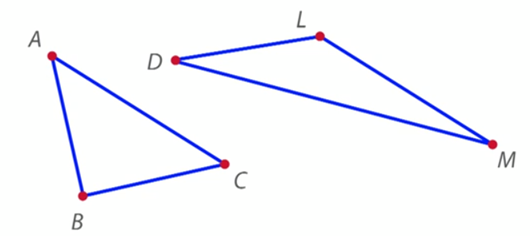
Рис. 11. Иллюстрация к заданию

В нахождении решения нам поможет инструмент – прямоугольный треугольник, который будет приложен к каждой из вершин треугольника путем совмещения одной из сторон. Если он будет совпадать с углом, то этот угол прямой. Если угол будет меньше прямого угла инструмента, то этот угол острый. А если же угол больше прямого угла инструмента – то это тупой угол.

Прямые углы:  

Тупые углы: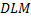

Острые углы: , ,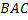

,

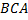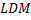
В построении 4 прямых углов с общей вершиной на нелинованной бумаге нам помогут циркуль и линейка.

Сначала необходимо провести прямую. Отложим на прямой произвольный отрезок 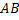. Проведем две окружности с центрами в точке  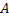и 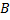 с радиусами, равными длине отрезка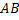

.

Обозначим точки пересечения окружносте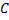й  и 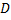. Проведем через точк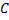и  и 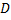 прямую. Точку пересечения прямых обозначим буквой .

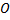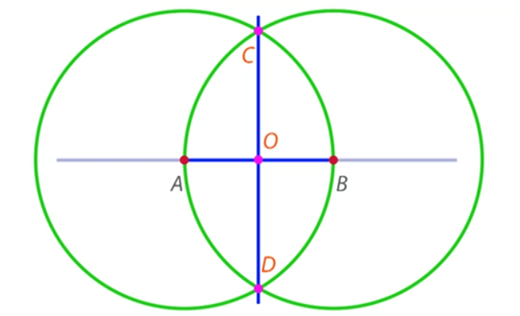
Рис. 12. Построение 4 прямых углов с общей вершиной на нелинованной бумаге

С помощью прямоугольного треугольника можно проверить, что все 4 угла с вершиной в точке 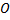 – прямые. При построении прямых углов на нелинованной бумаге вместо окружностей можно проводить дуги, то есть части окружности. Причем дуги могут быть любого радиуса, но больше, чем половина длины отрезка .

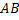На этом уроке мы познакомились с понятием угла и видами углов: развернутым углом, прямым углом, тупым углом и острым углом. Научились строить прямые углы на нелинованной бумаге с помощью циркуля и линейки.

 

Список литературы

1. Петерсон Л.Г. Математика 4 класс. Учебник в 3 частях, М.: 2013. Часть 1 96с., часть 2 128с., часть 3 96с.
2. Моро М.И., Бантова М.А., Бельтюкова Г.В., Волкова С.И., Степанова С.В.
   Учебник. – 8-е изд. – М.: Просвещение, 2011. – 112 с.: ил. – (Школа России). – ISBN 978–5–09–023769–7.
3. Математика. 4 класс. Учебник в 3 ч. Демидова Т.Е., Козлова С.А., Тонких А.П. 2-е изд., испр. – М.: 2013.; Ч.1 – 96 с., Ч.2 – 96 с., Ч.3 – 96 с.

 

Домашнее задание

1. Определите количество углов в квадрате. Ромбе.
2. Может ли быть в прямоугольном треугольнике тупой угол?

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Shkolo.ru (Источник).
2. Интернет-портал Festival.1september.ru (Источник).
3. Интернет-портал Math-prosto.ru (Источник).

interneturok.ru

Конспект «Угол. Смежные и вертикальные углы»

«Угол. Смежные и вертикальные углы»

Ключевые слова конспекта: углы, биссектриса, виды углов, измерение углов, смежные и вертикальные углы, свойства смежных и вертикальных углов, углы при пересечении двух прямых секущей.

---

---

Угол — фигура, образованная двумя лучами, которые выходят из одной точки (вершины).
Биссектриса — луч, который выходит из вершины угла и делит его пополам.

Виды углов. Измерение углов

• Развернутый угол — угoл, стороны которого лежат на одной прямой.
• Прямой угoл — угoл, который равен половине развернутого угла.
• Острый угол — угoл меньше прямого угла.
• Тупой угoл — угoл больше прямого, но меньше развернутого.

Единицы измерения углов:
Градус — величина (градусная мера) угла, равная части развернутого угла.
Минута — часть градуса.
Секунда — часть минуты.

Смежные и вертикальные углы

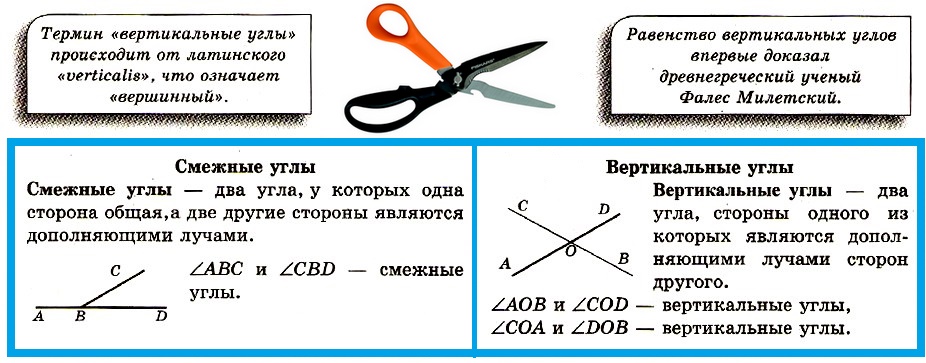
Смежные углы — два угла, у которых одна сторона общая,а две другие стороны являются дополняющими лучами.
Вертикальные углы — два угла, стороны одного из которых являются дополняющими лучами сторон другого.

Теорема. Сумма смежных углов равна 180°.

Теорема. Вертикальные углы равны.

---

Свойства смежных и вертикальных углов

 

Углы при пересечении двух прямых секущей

---

Это конспект по теме «Смежные и вертикальные углы». Выберите дальнейшие действия:

uchitel.pro

Угол. Виды углов / Основы геометрии / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Основы геометрии
5. Угол. Виды углов

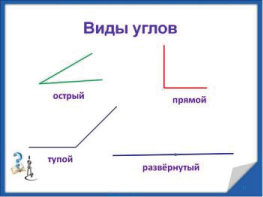
Мы узнаем, что углы бывают, острыми, прямыми и тупыми.

Вспомни, чтобы начертить угол, нужно поставить точку и из неё провести два луча в разные стороны.

Луч — это сторона угла.

Вершина — это точка, из которой выходят лучи.

---

Прямой угол

Прямой угол — это угол в 90^о (90 градусов). Его легко определять по треугольнику, например, такому:

---

Острый угол

Острый угол — это угол, который МЕНЬШЕ прямого угла, меньше 90^о.

м

---

Тупой угол

Острый угол — это угол, который БОЛЬШЕ прямого угла, больше 90^о.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Круг. Шар. Овал

Треугольники

Многоугольники

Обозначение геометрических фигур буквами

Периметр многоугольника

Площадь фигуры

Окружность

Основы геометрии

Правило встречается в следующих упражнениях:

2 класс

Страница 44. Вариант 1. № 2, Моро, Волкова, Проверочные работы

Страница 45. Вариант 2. № 2, Моро, Волкова, Проверочные работы

Страница 72. Вариант 1. Тест 3, Моро, Волкова, Проверочные работы

Страница 72. Вариант 2. Тест 3, Моро, Волкова, Проверочные работы

Страница 9, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 10, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 45, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 70, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 79, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 36, Моро, Волкова, Рабочая тетрадь, 2 часть

3 класс

Страница 16, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 43, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 27, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 35, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

4 класс

Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 34, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 38, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 40, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 49, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 93, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 95, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 18, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 24, Моро, Волкова, Рабочая тетрадь, 1 часть

---

© budu5.com, 2019

Пользовательское соглашение

Copyright

budu5.com

Геометрия. Урок 2. Углы — ЁП

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

 

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Стороны угла – лучи, которые образуют угол.

Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠AOB  или ∠BOA,  но ни в коем случае не ∠OAB,∠OBA,∠ABO,∠BAO.

Величину угла измеряют в градусах. ∠AOB=24°.

 

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.

Или

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

OD – биссектриса угла ∠AOB. Она делит этот угол на два равных угла.

∠AOD=∠BOD=∠AOB2

Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон OA и OB угла ∠AOB.

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.

Свойство: сумма смежных углов равна 180°.

Пример:

Пары углов

(1) и (3)
(2) и (4)

называются вертикальными.

По свойству вертикальных углов:

∠COD=∠AOB
∠BOD=∠AOC

Пары углов

(1) и (2)
(2) и (3)
(3) и (4)
(4) и (1)

называются смежными.

По свойству смежных углов:

∠COD+∠DOB=180°∠DOB+∠BOA=180°∠BOA+∠AOC=180°∠AOC+∠COD=180°

 

Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

Существует пять видов углов, которые образуются при пересечении двух прямых секущей.

Пары углов:

(1) и (5)
(2) и (6)
(3) и (7)
(4) и (8)

называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).

Пары углов:

(3) и (5)
(4) и (6)

называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).

Пары углов:

(1) и (7)
(2) и (8)

называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).

Пары углов:

(3) и (6)
(4) и (5)

называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).

Пары углов:

(1) и (8)
(2) и (7)

называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).

Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:

• Соответственные углы равны.
• Внутренние накрест лежащие углы равны.
• Внешние накрест лежащие углы равны.
• Сумма внутренних односторонних углов равна 180°.
• Сумма внешних односторонних углов равна 180°.

 

Сумма углов произвольного n-угольника вычисляется по формуле:

Sn=180°⋅(n−2)

где n – это количество углов в n-угольнике.

Пользуясь этой формулой, можно вычислить сумму углов для произвольного n-угольника.

Сумма углов треугольника: S3=180°⋅(3−2)=180°

Сумма углов четырехугольника: S4=180°⋅(4−2)=360°

Сумма углов пятиугольника: S5=180°⋅(5−2)=540°

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунках изображены примеры правильных многоугольников:

Чтобы найти величину угла правильного n-угольника, необходимо сумму углов этого многоугольника разделить на количество углов.

αn=180°⋅(n−2)n

 

Модуль геометрия: задания, связанные с углами

 

Скачать домашнее задание к уроку 2.

 

epmat.ru

Свойства углов, с примерами

ОПРЕДЕЛЕНИЕ

Углом называется геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Обозначают угол тремя буквами: , где – вершина угла, – стороны угла.

Величиной измерения угла является градус.

ОПРЕДЕЛЕНИЕ Углы бывают острые (если их градусная мера меньше ), прямые (если их градусная мера равна ) и тупые (если их градусная мера больше ).

Развернутый угол – это угол .

ОПРЕДЕЛЕНИЕ

Смежные углы – это углы, у которых одна сторона общая, а другие стороны лежат на одной прямой.

ОПРЕДЕЛЕНИЕ

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.

При пересечении двух параллельных прямых секущей образуются

– накрест лежащие углы: ;

– соответственные углы: ;

– односторонние углы: .

ОПРЕДЕЛЕНИЕ

Вписанный углом в окружность называется угол, вершина которого лежит на окружности, а стороны пересекают ее.

Сумма углов любого треугольника равна . Сумма углов любого n-угольника равна .

ОПРЕДЕЛЕНИЕ

Биссектрисой угла называется луч, который исходит из вершины угла и делит данный угол пополам.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

какой называется развернутым, сколько градусов в прямом и неразвернутом

С понятием угол учащиеся знакомятся еще в начальной школе. Но как геометрическую фигуру, имеющую определенные свойства, начинают изучать его с 7-го класса в геометрии. Кажется, довольно простая фигура, что о ней можно сказать. Но, приобретая новые знания, школьники всё больше понимают, что можно узнать о ней довольно интересные факты.

…

Вконтакте

Facebook

Twitter

Мой мир

Когда изучаются

Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию. В каждом из них немалое внимание уделяется углам:

• В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
• В стереометрии изучаются пространственные углы – двугранные и трехгранные.

Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии.

Определение и измерение

Приступая к изучению, первоначально определяют, что такое угол в планиметрии.

Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:

• вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита;
• стороны – полупрямые, проведенные из вершины.

Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части:

• внутренняя — в планиметрии не превышает 180 градусов;
• внешняя.

Принцип измерения углов в планиметрии объясняют на интуитивной основе. Для начала знакомят учащихся с понятием развернутый угол.

Важно! Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию. Неразвернутый угол это все остальные случаи.

Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.

Основные виды

Виды углов подразделяются по таким критериям, как градусная мера, характер их образования и представленные ниже категории.

По величине

Учитывая величину, углы разделяют на:

• развернутый;
• прямой;
• тупой;
• острый.

Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.

Его можно получить при делении развернутого на две равные части. В этом случае легко ответить на вопрос: прямой угол, сколько градусов составляет?

180 градусов развернутого делим на 2 и получаем, что прямой угол равен 90 градусам. Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.

Имеет она и свои особенности в обозначении. Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.

Это интересно! Легкие правила округления чисел после запятой

Углы, которые получаются при делении произвольным лучом прямого, называют острыми. По логике вещей следует, что острый угол меньше прямого, но его мера отлична от 0 градусов. То есть, он имеет величину от 0 до 90 градусов.

Тупой угол больше прямого, но меньше развернутого. Его градусная мера варьируется в интервале от 90 до 180 градусов.

Данный элемент можно разбить на разные виды рассматриваемых фигур, исключая развёрнутый.

Вне зависимости от того, как разбивается неразвернутый угол, всегда пользуются базовой аксиомой планиметрии — «основное свойство измерения».

При разделении угла одним лучом или несколькими, градусная мера данной фигуры равна сумме мер углов, на которые она разбита.

На уровне 7-го класса виды углов по их величине на этом заканчиваются. Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов.Их называют выпуклыми.

Фигуры при пересечении прямых

Следующие типы углов, с которыми знакомятся учащиеся – элементы, образованные при пересечении двух прямых. Фигуры, которые размещаются друг напротив друга, называют вертикальными. Их отличительное свойство – они равны.

Элементы, которые прилегают к одной и той же прямой, называют смежными. Теорема, отображающая их свойство, говорит о том, что смежные углы в сумме дают 180 градусов.

Это интересно! Чему равна и как найти площадь равностороннего треугольника

Элементы в треугольнике

Если рассматривать фигуру как элемент в треугольнике, то углы подразделяют на внутренний и внешний. Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними.

Если взять любой внутренний элемент при любой вершине и продлить любую сторону, то угол, который образовался и является смежным с внутренним, называется внешним. Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.

Пересечение двух прямых секущей

Пересечение прямых

При пересечении двух прямых секущей также образуются углы, которые принято распределять по парам. Каждая пара элементов имеет свое название. Выглядит это следующим образом:

• внутренние накрест лежащие:∟4 и ∟6, ∟3 и ∟5;
• внутренние односторонние: ∟4 и ∟5, ∟3 и ∟6;
• соответствующие: ∟1 и ∟5, ∟2 и ∟6, ∟4 и ∟8, ∟3 и ∟7.

В том случае, когда секущая пересекает две параллельные прямые, все эти пары углов имеют определённые свойства:

1. Внутренние накрест лежащие и соответственные фигуры между собой равны.
2. Внутренние односторонние элементы в сумме дают 180 градусов.

Изучаем углы в геометрии, их свойства

Виды углов в математике

Вывод

В этой статье представлены все основные виды углов, которые встречаются в планиметрии и изучаются в седьмом классе. Во всех последующих курсах свойства, касающихся всех рассмотренных элементов, являются основой для дальнейшего изучения геометрии. К примеру, изучая параллелограмм, необходимо будет вспомнить все свойства углов, образованных при пересечении двух параллельных прямых секущей. При изучении особенностей треугольников, необходимо вспомнить, что такое смежные углы. Перейдя в стереометрию, все объёмные фигуры будут изучаться и строиться, опираясь на планиметрические фигуры.

Это интересно! Изучение точного предмета: натуральные числа — это какие числа, примеры и свойства

uchim.guru

Угол, виды углов и их измерение

Определение. Угол — это часть плоскости, ограниченная двумя лучами, исходящими из одной точки, называемой вершиной угла.

Если плоскость круга разделить на 360 равных частей радиусами, то часть круга — это угловой градус, который обозначается знаком « ° » (читается — «градус»).

Следовательно, 1° = часть круга.

Круг составит * 360 = 1° * 360 = 360°.

Угол, равный плоскости круга, составляет 360° и называется полным углом.

Если плоскость круга разделить диаметром (двумя радиусами, расположенными на одной прямой линии) на две равные части, то плоскость полукруга составит угол в 360′: 2 = 180°.

Угол, равный полуплоскости круга, составляет 180° и называется развернутым углом.

Если плоскость круга разделить двумя диаметрами (горизонтальной и вертикальной линиями) на четыре равные части, то плоскость одной части составит угол в 360° : 4 = 90°.

Угол, равный четвертой части круга, составляет 90° и называется прямым углом.

Отвлекаясь от плоскости, в которой расположен круг, изобразим углы таким образом:

Углы равны, если равны их градусные меры или у них при наложении одного угла на другой совпадают вершины и соответствующие стороны углов.

Например, прямой угол (рис. 1) мы трижды развернули вокруг вершины угла, при этом на двух рисунках (рис. 2 и 4) мы передвинули вершину угла по плоскости листа.

Инструментом для измерения углов служит транспортир.

Для измерения угла следует совместить вершину угла и штрих с цифрой 0 на шкале транспортира. Одна сторона угла должна совпадать с прямой линией транспортира, на которой стоит 0, а вторая сторона угла пересекать шкалу транспортира (полуокружность с разметкой в угловых градусах).

На пересечении стороны угла и шкалы транспортира считывается градусная мера данного угла.

Мы рассмотрели полный, развернутый и прямой углы. Существует еще два типа углов: острые и тупые. Все острые углы имеют градусную меру в пределах: больше 0° и меньше 90°.

Например. острые углы:

Углы, градусная мера которых больше 90°, но меньше 180°*, называются тупыми углами.

Тупые углы (штриховой линией обозначен прямой угол в составе тупого угла) приведены на рис. 5, 6,7.

Чтобы построить заданный в градусной мере угол, необходимо иметь транспортир, линейку и карандаш.

shkolo.ru