Кинематика (основные понятия) — презентация онлайн
1. КИНЕМАТИКА (основные понятия)
КИНЕМАТИКА(ОСНОВНЫЕ ПОНЯТИЯ)
2. Краткая историческая справка
КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКАРазвитие кинематики как науки началось еще в древнем мире и
связано с таким именем как Галилей , который вводит понятие
ускорения . Развитие кинематики в XVIII в. связано с работами Эйлера,
заложившего основы кинематики твердого тела и создавшего
аналитические методы решения задач механики. Более глубокие
исследования геометрических свойств
Более глубокие исследования геометрических свойств движения тела
были вызваны развитием техники в начале XIX в. и, в частности,
быстрым развитием машиностроения.
Крупные исследования в области кинематики механизмов и машин
принадлежат и русским ученым: основоположнику русской школы
теории машин и механизмов П.Л. Чебышеву(1821-1894), Л.В. Ассуру
(1878-1920), Н.И. Мерцалову (1866-1948), Л.
 П.Котельникову (18651944) и другим ученым.
П.Котельникову (18651944) и другим ученым.3. Основные понятия кинематики:
ОСНОВНЫЕ ПОНЯТИЯКИНЕМАТИКИ:
Кинематика (с греч. κινειν — двигаться) раздел механики, в котором движение тел
рассматривается без выяснения причин
этого движения.
Основная задача кинематики:
зная закон движения данного тела,
определить все кинематические величины,
характеризующие как движение тела в целом,
так и движение каждой из его точек в
отдельности.
4. Кинематика — это описание движения тел с математическими ответами на вопросы:
КИНЕМАТИКА — ЭТО ОПИСАНИЕ ДВИЖЕНИЯ ТЕЛ СМАТЕМАТИЧЕСКИМИ ОТВЕТАМИ НА ВОПРОСЫ:
1.
Где?
?
?
?
?
2.
3.
Для получения ответов на
поставленные вопросы
необходимы следующие
понятия:
Когда?
Как?
?
t
a
v=
5. Основные понятия кинематики:
ОСНОВНЫЕ ПОНЯТИЯ КИНЕМАТИКИ:Механическое движение
Система отсчета
Материальная точка
Траектория
Путь
Перемещение
Скорость
Ускорение
6.
 Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением МЕХАНИЧЕСКИМ ДВИЖЕНИЕМ ТЕЛА
Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением МЕХАНИЧЕСКИМ ДВИЖЕНИЕМ ТЕЛА(ТОЧКИ) НАЗЫВАЕТСЯ ИЗМЕНЕНИЕ ЕГО
ПОЛОЖЕНИЯ В ПРОСТРАНСТВЕ ОТНОСИТЕЛЬНО
ДРУГИХ ТЕЛ С ТЕЧЕНИЕМ ВРЕМЕНИ.
Примеры механического
движения
ДВИЖЕНИЕ
РАВНОМЕРНОЕ
НЕРАВНОМЕРНОЕ
РАВНОУСКОРЕННОЕ
10 мин
1 км
10 мин
10 мин
10 мин
1 км
1 км
1 км
10 мин
10 мин
10 10 мин
1,3 км
1,6 км
0,4
км
Равномерное
движение
Неравномерное
движение
0,7 км
Прямолинейное равномерное движение –
движение, при котором тело за любые (!)
равные (!) промежутки времени проходит
одинаковые пути.
Характеристики:
1. Путь
Путь – длина траектории.
Обозначение пути:
[ ℓ] = м (метр)
ℓ=
vt
vℓ
t
—
ℓ
скорость;
– путь;
– время движения.
2. Скорость
Скорость равномерного движения – физ.
величина, равная отношению пути ко
времени, за который этот путь пройден:
=
ℓ
t
[
v] =
м
с
1 м/с – это такая скорость равномерного
движения, при которой тело за каждую
секунду преодолевает путь 1 метр.
При равномерном движении скорость тела
постоянна. При неравномерном движении
скорость тела меняется. Для описания этого
движения можно использовать среднюю скорость.
Средняя скорость равна
отношению всего (!) пройденного
телом пути, деленному на все (!)
время движения.
v
ср =
ℓ
t
v
ср
ℓ
t
—
средняя скорость;
– весь путь;
– все время движения.
3. Время
t=
[t]=c
ℓ
v
ℓ
t
ℓ=
v
v
=
t=
vt
ℓ
t
ℓ
v
Относительность движения означает,
что характеристики движения
(траектория, путь, скорость и др.)
зависят от выбора тела отсчета.
Тело отсчета – тело, относительно
которое рассматривают движение.

Материальная точка – тело, размерами
которого в данных условиях
пренебрегают. (масса тела
сосредоточена в этой точке)
18. Материальная точка
МАТЕРИАЛЬНАЯ ТОЧКАТело можно считать
материальной точкой, если:
1. расстояния, проходимые
телом, значительно больше
размеров этого тела;
2. тело движется
поступательно, т.е. все его
точки движутся одинаково в
любой момент времени.
19. Система отсчета:
СИСТЕМА ОТСЧЕТА:Тело отсчета
Система координат
Часы
Z
У
Х
Траектория – условная линия движения тела в пространстве;
Путь – длина траектории;
Перемещение – направленный отрезок
l,м
S
1
2
Примеры траекторий
22. Способы задания движения точки
СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИестественный
При этом способе задают: траекторию точки
и закон движения по этой траектории
координатный
Положение точки относительно некоторой
Уравнения движения точки в
прямоугольных координатах
x = f 1 (t ) , y = f 2 (t ) , z = f 3 (t )
Скорость:
векторная величина характеризует быстроту
движения, показывает, какое перемещение тело
совершает в единицу времени
Движение, при котором тело за любые равные промежутки времени совершает
одинаковые перемещения.
 называют ПРЯМОЛИНЕЙНЫМ РАВНОМЕРНЫМ.
называют ПРЯМОЛИНЕЙНЫМ РАВНОМЕРНЫМ.скорость равномерного движения –
s
v
t
[м/с]
Движение, при котором за равные промежутки времени тело совершает неравные
перемещения называют неравномерным
скорость неравномерного движения:
или переменным.
s
vср
Δt
Направление скорости при:
v2
прямолинейном движении –
неизменно
криволинейном движении – по
касательной к траектории в
данной точке
v1
v
v3
vv
4
24. Равномерное движение
РАВНОМЕРНОЕ ДВИЖЕНИЕ25. Равноускоренное движение
РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ26. Основные формулы кинематики
ОСНОВНЫЕ ФОРМУЛЫ КИНЕМАТИКИ2
at
S 0 t
2
0 at
Если a = 0, то
S 0 t
S 0 t
2
at
S 0 t
2
0 at
x 0 cos
y 0 sin
S x x t ( 0 cos ) t
gt 2
gt 2
Sy y t
( 0 sin ) t
2
2
y gt 0 sin gt
Ускорение величина, характеризующая изменение
скорости при неравномерном движении
тела.
Средним ускорением неравномерного
движения в интервале от t до t + ∆t
называется векторная величина, равная
отношению изменения скорости ∆v к
интервалу времени ∆t:
При свободном падении вблизи поверхности Земли
a g
g 9,8 м
с
2
Δv
a
Δt
, где
34. Равномерное Равноускоренное движение движение
РАВНОМЕРНОЕДВИЖЕНИЕ
РАВНОУСКОРЕННОЕ
ДВИЖЕНИЕ
0
Графиком перемещения будет
являться парабола
35. Равномерное Равноускоренное движение движение
РАВНОМЕРНОЕ0
РАВНОУСКОРЕННОЕ
ДВИЖЕНИЕ
36. Равномерное Равноускоренное движение движение
РАВНОМЕРНОЕДВИЖЕНИЕ
РАВНОУСКОРЕННОЕ
ДВИЖЕНИЕ
0
37. ЗАКРЕПЛЕНИЕ МАТЕРИАЛА
Какие из приведенных зависимостей отвремени пути S и модуля скорости V:
1) V=4+2t;
2) S=3+5t;
3) S=5t2;
4) S=3t+2t2;
5) V=2+3t+4t2
описывают прямолинейные равноускоренные
движения точки?
1) 1, 3, 4
2) 2, 3, 4
3)
3, 4, 5
4) 4, 5, 1
5) 5, 1, 2
На рис.
 изображена зависимость координаты тела х от
изображена зависимость координаты тела х отвремени t. Какое из следующих утверждений верно?
1) На участке 1 и 3 тело двигалось равноускоренно.
2) На участке 1 тело двигалось быстрее, чем на участке 3.
3) На участке 2 тело находилось в покое.
4) За время движения по участку 1 тело прошло меньше
расстояние, чем за время движения по участку 3.
На
рисунке
изображены
графики
зависимости скорости движения четырех
автомобилей от времени. Какой из
автомобилей — 1, 2, 3 или 4 ─ прошел
наибольший путь за первые 15 с движения?
1)1
2)2
3)3
4) 4
Уравнение движения материальной точки х =
5 + 6t — 3t2 (м). Координатой, в которой
скорость точки станет равна нулю, будет
1) 5 м
2) 6 м
3) 8 м
4) 11 м
Движение по окружности, угловая скорость, частота, период, центростремительное ускорение. Формулы, определения, пояснения
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
Найдем разницу векторов.
Разница векторов есть . Так как , получим
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Урок физики «Равномерное движение по окружности», 10 класс, ФГОС
10 класс Раздел «Кинематика»
Урок №
Тема урока: Равномерное движение по окружности
Цель урока: ознакомить учащихся с равномерным движением по окружности и физическими величинами, характеризующими это движение
Задачи урока: Образовательная — сформировать у учащихся представления о характеристиках равномерного движения по окружности.
Развивающие: формировать умение определять вид движения тела; сравнивать, анализировать, обобщать данные о движении тела; умение
развивать способность структурировать информацию в рамках поставленной задачи;
формировать умения использовать основные понятия, формулы и физические законы движения тела при движении по окружности;
развивать физическое мышление учащихся через практическую деятельность.
Воспитывающие: потребность познания окружающего мира, любознательность, внимательность и трудолюбие.
Планируемые результаты: Предметные: знать — определения и формулы периода, частоты, линейной и угловой скорости, центростремительного ускорения; уметь — применять формулы кинематики криволинейного движения при решении задач.
Личностные: формирование умений управлять своей учебной деятельностью, формирование интереса к физике при анализе явлений формирование мотивации постановкой познавательных задач.
Метапредметные: применять знания законов движения по окружности в повседневной жизни.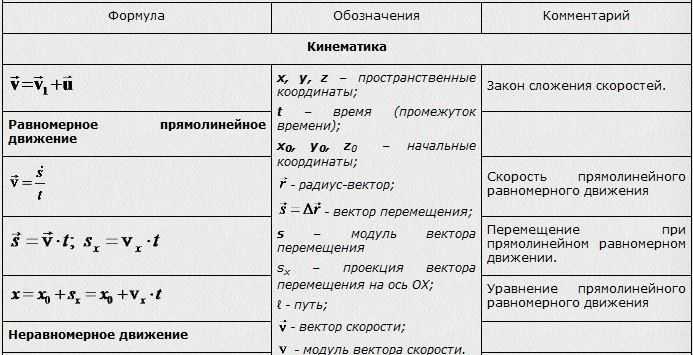
Тип урока: изучение нового материала
Ход урока
1.ОРГАНИЗАЦИОННЫЙ МОМЕНТ
Проверка наличия домашнего задания.
2. АКТУАЛИЗАЦИЯ ЗНАНИЙ А) и Б) выполняем одновременно.
А) В начале занятия давайте проведем физическую разминку в виде физического футбола по темам: «Равноускоренное прямолинейное движение. Свободное падение». Первый учащийся задаёт вопрос по теме и говорит кому направляет этот пас. Второй отвечает. Задает свой вопрос и т.д.
Б) написать формулы на доске по теме свободное падение. Дополнительный вопрос. С какого этажа дома упал предмет без начальной скорости, если он находился в полете 2 с?
3.ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Криволинейное движение в природе и технике более распространено, чем прямолинейное. Примеры: движение лыжника с горки на горку, движение человека на карусели, движение стержня ручки во время письма, движение частей станка при обработки детали(шлифование), полет волейбольного мяча после удара и тому подобное.
Любое криволинейное движение можно представить как последовательность движений по дугам окружностей различных радиусов.
Рассмотрим частный случай криволинейного движения — движение по окружности, которое в окружающем мире распространено: движение стрелки часов, движение искусственных спутники Земли, зубчатые колесики в велосипеде; движение автомобиля и поезда на выпуклых мостах.
Движение по окружности – это вращательное движение.
Демонстрация. Шарик на нити.
Вращательным движением тела называется такое движение, при котором все точки описывают окружности, центры которых находятся на одной прямой, называемой осью вращения.
Нарисуем окружность укажем в некоторых точках направление вектора мгновенной скорости.
Мгновенная скорость тела, движущегося по окружности, направлена по касательной к ней в этой точке.
Наблюдая движение брызг грязи из-под колес автомобиля, что буксует мы в этом можем убедиться.
(см. рис учебника). По касательной также разлетаются раскаленные частицы металла отрываются от стального резца, если коснуться им поверхности вращающегося точильного камня.
Величина | обозначение | Единица измерения | Формула |
Период | Т | с | Т=t/n; T=2πr/v |
Частота | υ | Гц | υ =n/t=1/Т |
Линейная скорость | v | м/с | v=2πr/T=ωr; v=Δl/Δt |
Угловая скорость | ω | рад/с | ω=v/r=2π/T= Δφ/Δt |
Ускорение | а | м/с2 | a=v2/r= ω2r |
Мы будем изучать движение точки по окружности с постоянной по модулю скоростью. Его называют равномерным движением по окружности.
Его называют равномерным движением по окружности.
Составим таблицу характеристик этого движения. Учащиеся по очереди выходят заполнять таблицу, руководствуясь учебником.
Скорость точки, движущейся по окружности, называют линейной скоростью.
Линейная скорость v — это физическая величина, характеризующая криволинейное движение и равна отношению пути Δl, пройденного телом по криволинейной траектории за малый промежуток времени Δt, к величине этого промежутка
Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за который тело совершает один полный оборот.
Период вращения Т — это физическая величина, равная времени одного полного оборота.
Единица периода вращения в СИ — секунда ([Т] = с).
Частота вращения — это физическая величина, численно равна числу полных оборотов за единицу времени.
Угловая скорость — это физическая величина, равная отношению угла поворота радиуса, проведенного к телу от центра круга, по которому движется тело, к промежутку времени, в течение которого этот поворот осуществлялся.
Основная задача механики для равномерного движения по окружности состоит так же в определении положения тела в любой момент времени.
Поскольку движение по кругу происходит в одной плоскости, то для описания движения можно воспользоваться двухмерной системой координат. Если связать точку начала координат с центром круга, по которому движется тело, а начальное положение тела соединить с точкой пересечения окружности и оси Ох, то координаты х и можно вычислить по формулам: х=Rсоsφ; y=Rsinφ.
Поскольку угол φ меняется с течением времени по закону φ = ωt, то уравнение координаты для равномерного движения по окружности имеет следующий вид: х=Rсоs ωt;y=Rsin ωt.
ЗАКРЕПЛЕНИЕ. РЕШЕНИЕ ЗАДАЧ У ДОСКИ. Вызываю 3 ученика.
1. Кабинка карусели движется по окружности радиусом 24 м. Период его вращения равен 30с. Чему равна скорость движения кабинки?
Дано:
R=24м
Т=30с v=2πR/T v=2*π*24м /30с=48 π /30м/с=5 м/с
v-? Ответ: 5 м/с
Вопрос к классу
Чему равен период вращения часовой стрелки часов? минутной? секундной?
Тм=1ч=3600с;
Тс=1мин=60с;
Тч=12ч=12*3600с=43200с.
2. Во сколько раз скорость конца минутной стрелки башенных часов Биг-Бен в Лондоне больше скорости конца минутной стрелки наручных часов, если длина стрелки башенных часов — 4,2 м, а длина стрелки наручных часов — 1,5 см?
Справка. Часы на башне Биг-Бен в Лондоне до настоящего времени являются самыми большими в мире. Диаметр циферблата – 7 метров. Длина стрелок – 2,7 и 4,2 метра. Часовой механизм считается эталоном надежности, общий вес его составляет 5 тонн.
Дано:
Rб=4,2м Тмб = Тмр =1ч=3600с v=2πr/T
Rр=1,5 см = 1,5*10-2 м vб/ vб =(2*π*4,2м / 3600с/)*(3600с/2*π*1,5*10-2 м )=280 раз
vб/ vб -? Ответ: 280 раз
3.Напишите уравнение движения материальной точки, движущейся по дуге радиусом 5 м с угловой скоростью π/4 рад/с. Какими будут координаты точки через 3 с после начала отсчета времени?
Дано:
R=5м х=Rсоs ωt; y=Rsin ωt
ω= π/4 рад/с
х(t)-? х=5соs π/4t; y=5sin π/4t
y (t)-?
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ. РАБОТА ПО КАРТОЧКЕ.
РАБОТА ПО КАРТОЧКЕ.
Детская карусель за одну минуту совершает 4 оборота. Найти период и частоту, с которой она вращается.
Дано:
N=4об
T=1мин 60с Т=t/N T=60с/4=15с υ=N/t υ=4/60=1/15=0.067Гц
T-?
υ -? Ответ: 15 с,15 Гц
РЕФЛЕКСИЯ
Что нового узнали? Сложно ли использовать формулы при решении задач?
ДОМАШНЕЕ ЗАДАНИЕ
1. Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский Физика 10 –М.: Просвещение, 2017.
§ 15,16 читать, учить определения, формулы. Выполнить с.61 А1-А4.
2.Проект в виде буклета «Равномерное движение по окружности» (по желанию)
Физика 9 класс. Законы, правила, формулы
Кинематика
Динамика
- Силы трения
- Трение покоя
Максимальная сила трения покоя (Fтр)max пропорциональна силе нормального давления (N) и зависит от характера взаимодействия соприкасающихся поверхностей тел, определяемого коэффициентом трения (μ)
(Fтр)max=μ×N
СИ: Н - Трение скольжения
Сила трения скольжения (Fтр) пропорциональна силе давления (N), коэффициенту трения (μ) и направлена противоположно направлению движения тела.
Fтр=μ×N
СИ: Н - Коэффициент трения
Коэффициент трения (μ) вычисляют как отношение модулей силы трения (Fтр) и силы давления (N).
μ=Fтр/N - Движение тела под действием силы трения
1) Путь (l), пройденный движущимся телом под действием силы трения до полной остановки (тормозной путь), прямо пропорционален квадрату начальной скорости (v0) и обратно пропорционален коэффициенту трения (μ): , (g — ускорение свободного падения).
2) Время (t) движения тела под действием силы трения до момента полной остановки (время торможения) прямо пропорционально начальной скорости (v0) и обратно пропорционально коэффициенту трения (μ):
СИ: м, с
- Движение тела под действием нескольких сил
- Условие равновесия тела (как материальной точки).

Тело находится в равновесии (в покое или движется равномерно и прямолинейно), если сумма проекций всех сил (), действующих на тело, на любую ось (ОХ, ОY, O, …) равна нулю.
;
;
СИ: Н - Движение тела по наклонной плоскости
Ускорение тела, скользящего вниз по наклонной плоскости с углом наклона (α) и коэффициентом трения тела о плоскость (μ), не зависит от массы тела и равно: , (g — ускорение свободного падения)
СИ: м/с2 - Движение связанных тел через неподвижный блок
Ускорение двух тел, массами m1 и m2, связанных нитью, перекинутой через неподвижный блок, равно:
, (g — ускорение свободного падения)
СИ: м/с2
- Законы сохранения в механике
- Импульс тела
Импульс тела () — векторная величина, равная произведению массы (m) тела на его скорость ().
СИ: (кг×м)/с - Импульс силы
Импульс силы ( — произведение силы на время t её действия) равен изменению импульса тела.
СИ: Н×с - Закон сохранения импульса
Геометрическая сумма импульсов тел (), составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.
СИ: Н×с - Механическая работа силы
Работа (А) постоянной силы равна произведению модулей векторов силы () и перемещения () на косинус угла между этими векторами.
СИ: Дж - Теорема о кинетической энергии
Работа (А) силы (или равнодействующей сил) равна изменению кинетической энергии (Ek1 и Ek2) движущегося тела.
,
где m — масса тела, v1, v2 — начальная и конечная скорости тела
СИ: Дж - Потенциальная энергия поднятого тела
Потенциальная энергия (ЕП) тела, поднятого на некоторую высоту (h) над нулевым уровнем, равна работе (А) силы тяжести (m×g) при падении тела с этой высоты до нулевого уровня.
A=ЕП=m×g×h
СИ: Дж - Работа силы тяжести
Работа (А) силы тяжести (mg) не зависит от пути, пройденного телом, а определяется разностью высот (Δh=h2-h1) положения тела в конце и в начале пути и равна разности его потенциальных энергий (EП2 и EП1).
A=-(EП2-EП1)=-m×g×Δh
СИ: Дж - Потенциальная энергия деформированного тела
Потенциальная энергия (ЕП) деформированного тела (пружины) равна работе силы упругости при переходе тела (пружины) в состояние, в котором его деформация равна нулю.
ЕП = ,
где k — жесткость; х — деформация пружины.
СИ: Дж - Закон сохранения полной механической энергии
Полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остается неизменной при любых движениях тел системы.
ЕК2+ЕП2=ЕК1+ЕП1=const
СИ: Дж
- Движение жидкостей и газов по трубам
- Закон Бернулли
Давление жидкости, текущей в трубе, больше в тех частях трубы, где скорость её движения меньше, и наоборот, в тех частях, где скорость больше, давление меньше.
,
где p1, v1, h1 — давление, скорость и вертикальная координата жидкости в одном сечении трубы; p2, v2, h2 — давление, скорость и вертикальная координата жидкости в другом сечении трубы;
ρ — плотность жидкости; g — ускорение свободного падения.
СИ: Па
Поделитесь с друзьями:
Подготовка к олимпиадам и ЕГЭ по физике: методические материалы
Мы занимаемся по специальным листкам, которые приведены ниже. Листки содержат:
В 7–8 классах мы готовимся к следующим олимпиадам:
Подготовка к этим олимпиадам осуществляется по листкам, приведённым ниже. Листки содержат:
Листки содержат:
Имеется моя книга: Физика. Полный курс подготовки к ЕГЭ (М: МЦНМО, 2016; второе издание). В ней вы сможете найти всю теорию, которую надо знать на ЕГЭ по физике. Ниже приводится весь курс школьной физики в отдельных статьях и пособиях. Материал распределён по темам, соответствующим кодификатору ЕГЭ.
На пересечении строки (ваш класс) и столбца (этап Всеросса) находятся ссылки на варианты. Цифры ссылки — год проведения финала олимпиады.
На основе классификации задач 1992–2017 годов составлены программы подготовки к региональному и заключительному этапам:
Примечания.
Примечания.
Здесь содержатся статьи, написанные мною в разное время и по разным поводам.
| ШЭ | МЭ | РЭ | ЗЭ | |
|---|---|---|---|---|
| 7 класс | 20,
19,
18,
17 16, 15, 14, 13 | 20,
19,
18,
17 16, 15, 14, 13 | 10, 09 | — |
| 8 класс | 20,
19,
18,
17 16, 15, 14, 13 | 20,
19,
18,
17 16, 15, 14, 13 | 10, 09, 07 | — |
| 9 класс | 20,
19,
18 17, 16, 15, 14 | 20,
19,
18 17, 16, 15, 14 | 21,
20,
19,
18,
17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 | 19,
18,
17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 |
| 10 класс | 20,
19,
18 17, 16, 15, 14 | 20,
19,
18 17, 16, 15, 14 | 21,
20,
19,
18,
17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 | 19,
18,
17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 |
| 11 класс | 20,
19,
18 17, 16, 15, 14 | 20,
19,
18 17, 16, 15, 14 | 21,
20,
19,
18,
17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 | 19,
18,
17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 |
| Нулевой тур | Первый тур | Второй тур | ||
| 7 класс | 21. 1,
21.2,
21.3 1,
21.2,
21.320.1, 20.2, 20.3 19.0, 19.1 18.0, 18.1 17.0, 17.1 16.0, 16.1 15.0, 15.1 14.0, 14.1, 14.2, 14.3, 14.4 | 19,
18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | 21,
20,
19 18, 17, 16, 15 | |
| 8 класс | 21.1,
21.2,
21.3 20.1, 20.2, 20.3 19.0, 19.1 18.0, 18.1 17.0, 17.1 16.0, 16.1 15.0, 15.1 14.0, 14.1, 14.2, 14.3, 14.4 | 19,
18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | 21,
20,
19,
18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | |
| 9 класс | 21.1,
21.2,
21.3 20.1, 20.2, 20.3 19.0, 19.1 18.0, 18.1 17.0, 17.1 16.0, 16.1 15.0, 15.1 14.0, 14.1, 14.2, 14.  3,
14.4 3,
14.4 | 19,
18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | 21,
20,
19,
18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | |
| 10 класс | 21.1,
21.2,
21.3 20.1, 20.2, 20.3 19.0, 19.1 18.0, 18.1 17.0, 17.1 16.0, 16.1 15.0, 15.1 14.0, 14.1, 14.2, 14.3, 14.4 | 19,
18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | 21,
20,
19,
18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | |
| 11 класс | 21.1,
21.2,
21.3 20.1, 20.2, 20.3 19.0, 19.1, 19.2, 19.T 18.0, 18.1, 18.2, 18.3 17.0, 17.1, 17.2, 17.3 16.0, 16.1, 16.2, 16.3 15.0, 15.1, 15.2, 15.3 14.0, 14.1, 14.2, 14.3, 14.4 | 21,
20,
19,
18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | 21,
20,
19,
18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | |
| 7 класс | 20,
19,
18,
17,
16 15, 14, 13, 12, 11 | |||
| 8 класс | 20.1,
20.2 19, 18, 17.1, 17.2 16, 15, 14, 13, 12, 11 | |||
| 9 класс | 20.1,
20.2,
20.3 19, 18, 17.1, 17.2 16, 15, 14, 13, 12, 11 | |||
| 10 класс | 20.1,
20.2,
20.3 19, 18, 17.1, 17.2 16, 15, 14, 13, 12, 11 | |||
| 11 класс | 20.1,
20.2,
20.3 19.1, 19.2, 19.3 18.1, 18.2, 18.3, 18.4 17.1, 17.2, 17.3, 17.4 16, 15, 14 13.1, 13.2, 13.3, 13.4, 13.5, 13.6 12.1, 12.2, 12.3, 12.4, 12.5 11.1, 11.2, 11.3, 11.4, 11.5 11.6 | |||
| 7 класс | 20, 19, 18, 17, 16, 15, 14 | |||
| 8 класс | 20, 19, 18, 17, 16, 15, 14 | |||
| 9 класс | 20, 19, 18, 17, 16, 15, 14 | |||
| 10 класс | 20, 19, 18, 17, 16, 15, 14 | |||
| 11 класс | 20, 19, 18, 17, 16, 15, 14 |
Сборник формул по физике для егэ. Формулы по физике, которые рекомендуется выучить и хорошо освоить для успешной сдачи ЕГЭ
Единый Государственный Экзамен охватывает информацию по всему курсу физики с 7 по 11 класс. Однако если некоторые формулы по физике для ЕГЭ неплохо запоминаются сами по себе, над другими приходится поработать. Мы рассмотрим некоторые формулы, которые полезны для решения различных задач.
Кинематика
Начнем традиционно с кинематики. Частая ошибка здесь – неверное вычисление средней скорости неравномерного прямолинейного движения. В данном случае задачи пытаются решать с помощью среднего арифметического. Однако все не так просто. Среднее арифметическое – только частный случай. А для нахождения средней скорости движения существует полезная формула:
где S – весь путь, пройденный телом за определенное время t.
Молекулярно-Кинетическая Теория (МКТ)
МКТ может поставить множество коварных «ловушек» для невнимательного школьника. Чтобы избежать этого, нужно свободно владеть формулами по физике для ЕГЭ в этой области.
Чтобы избежать этого, нужно свободно владеть формулами по физике для ЕГЭ в этой области.
Начнем с закона Менделеева-Клапейрона, использующегося для идеальных газов. Он звучит так:
где p –давление газа,
V – занимаемый им объем,
n – количество газа,
R – универсальная газовая постоянная,
T – температура.
Обратите внимание на примеры задач с применением этого закона.
Все представляют себе, что такое влажность. Значения относительной влажности ежедневно сообщаются в СМИ. На экзамене же пригодится формула: здесь ф – относительная влажность воздуха,
ρ – плотность водяного пара, находящегося в воздухе,
ρ0 – плотность насыщенного пара при конкретной температуре.
Эта последняя величина – табличное значение, поэтому оно должно быть в условии задачи.
Термодинамика
Термодинамика – отрасль, достаточно близкая к МКТ, поэтому многие понятия пересекаются. Термодинамика базируется на двух своих началах. Практически каждая задача этой области требует знание и применение первого начала термодинамики, выраженного формулой
Это формулируется следующим образом:
Количество теплоты Q, которое было получено системой, расходуется на совершение работы A над внешними телами и изменение ΔU внутренней энергии данной системы.
Сила Архимеда
Напоследок поговорим о поведении погруженных в жидкость тел. Очевидно, что на каждое из них действует сила тяжести, направленная вертикально вниз. Но в жидкости все тела весят меньше. Это обусловливается частичным компенсированием силы тяжести противоположно направленной силой Архимеда. Ее значение равно Таким образом, эта сила, старающаяся вытолкнуть тело из жидкости, зависит от плотности той самой жидкости и объема погруженной в нее части тела. Сила Архимеда действует и в газах, но вследствие ничтожности плотности газов ею обыкновенно пренебрегают.
ЕГЭ проверяет знания школьника в различных областях физики. Формулы для ЕГЭ по физике способствуют успешному решению задач (можно воспользоваться ) и общему пониманию основных физических процессов.
Абсолютно необходимы для того, чтобы человек, решивший изучать эту науку, вооружившись ими, мог чувствовать себя в мире физики как рыба в воде. Без знания формул немыслимо решение задач по физике. Но все формулы запомнить практически невозможно и важно знать, особенно для юного ума, где найти ту или иную формулу и когда ее применить.
Расположение физических формул в специализированных учебниках распределяется обычно по соответствующим разделам среди текстовой информации, поэтому их поиск там может отнять довольно-таки много времени, а тем более, если они вдруг понадобятся Вам срочно!
Представленные ниже шпаргалки по физике содержат все основные формулы из курса физики , которые будут полезны учащимся школ и вузов.
Все формулы школьного курса по физике с сайта http://4ege.ru
I. Кинематика скачать
1. Основные понятия
2. Законы сложения скоростей и ускорений
3. Нормальное и тангенциальное ускорения
4. Типы движений
4.1. Равномерное движение
4.1.1. Равномерное прямолинейное движение
4.1.2. Равномерное движение по окружности
4.2. Движение с постоянным ускорением
4.2.1. Равноускоренное движение
4.2.2. Равнозамедленное движение
4.3. Гармоническое движение
II. Динамика скачать
1. Второй закон Ньютона
2. Теорема о движении центра масс
3. Третий закон Ньютона
Третий закон Ньютона
4. Силы
5. Гравитационная сила
6. Силы, действующие через контакт
III. Законы сохранения. Работа и мощность скачать
1. Импульс материальной точки
2. Импульс системы материальных точек
3. Теорема об изменении импульса материальной точки
4. Теорема об изменении импульса системы материальных точек
5. Закон сохранения импульса
6. Работа силы
7. Мощность
8. Механическая энергия
9. Теорема о механической энергии
10. Закон сохранения механической энергии
11. Диссипативные силы
12. Методы вычисления работы
13. Средняя по времени сила
IV. Статика и гидростатика скачать
1. Условия равновесия
2. Вращающий момент
3. Неустойчивое равновесие, устойчивое равновесие, безразличное равновесие
4. Центр масс, центр тяжести
5. Сила гидростатического давления
6. Давлением жидкости
7. Давление в какой-либо точке жидкости
8, 9. Давление в однородной покоящейся жидкости
10. Архимедова сила
V. Тепловые явления скачать
Тепловые явления скачать
1. Уравнение Менделеева-Клапейрона
2. Закон Дальтона
3. Основное уравнение МКТ
4. Газовые законы
5. Первый закон термодинамики
6. Адиабатический процесс
7. КПД циклического процесса (теплового двигателя)
8. Насыщенный пар
VI. Электростатика скачать
1. Закон Кулона
2. Принцип суперпозиции
3. Электрическое поле
3.1. Напряженность и потенциал электрического поля, созданного одним точечным зарядом Q
3.2. Напряженность и потенциал электрического поля, созданного системой точечных зарядов Q1, Q2, …
3.3. Напряженность и потенциал электрического поля, созданного равномерно заряженным по поверхности шаром
3.4. Напряженность и потенциал однородного электрического поля, (созданного равномерно заряженной плоскотью или плоским конденсатором)
4. Потенциальная энергия системы электрических зарядов
5. Электроемкость
6. Свойства проводника в электрическом поле
VII. Постоянный ток скачать
1. Упорядоченная скорость
2. Сила тока
Сила тока
3. Плотность тока
4. Закон Ома для участка цепи, не содержащего ЭДС
5. Закон Ома для участка цепи, содержащего ЭДС
6. Закон Ома для полной (замкнутой) цепи
7. Последовательное соединение проводников
8. Параллельное соединение проводников
9. Работа и мощность электрического тока
10. КПД электрической цепи
11. Условие выделения максимальной мощности на нагрузке
12. Закон Фарадея для электролиза
VIII. Магнитные явления скачать
1. Магнитное поле
2. Движение зарядов в магнитном поле
3. Рамка с током в магнитном поле
4. Магнитные поля, создаваемые различными токами
5. Взаимодействие токов
6. Явление электромагнитной индукции
7. Явление самоиндукции
IX. Колебания и волны скачать
1. Колебания, определения
2. Гармонические колебания
3. Простейшие колебательные системы
4. Волна
X. Оптика скачать
1. Закон отражения
2. Закон преломления
3. Линза
4. Изображение
5. Возможные случаи расположения предмета
6. Интерференция
Интерференция
7. Дифракция
Большая шпаргалка по физике . Все формулы изложены в компактном виде с небольшими комментариями. Шпаргалка также содержит полезные константы и прочую информацию. Файл содержит следующие разделы физики:
Механика (кинематика, динамика и статика)
Молекулярная физика. Свойства газов и жидкостей
Термодинамика
Электрические и электромагнитные явления
Электродинамика. Постоянный ток
Электромагнетизм
Колебания и волны. Оптика. Акустика
Квантовая физика и теория относительности
Маленькая шпора по физике . Все самое необходимое для экзамена. Нарезка основных формул по физике на одной странице. Не очень эстетично, зато практично. 🙂
Размер: px
Начинать показ со страницы:
Транскрипт1
Формулы по физике, которые рекомендуется выучить и хорошо освоить для успешной сдачи ЕГЭ. Версия: 0.92 β. Составитель: Ваулин Д. Н. Литература: 1. Пёрышкин А.В. Физика 7 класс. Учебник для общеобразовательных учреждений. 13-е издание, стереотипное. Москва. Дрофа Пёрышкин А.В. Физика 8 класс. Учебник для общеобразовательных учреждений. 12-е издание, стереотипное. Москва. Дрофа Пёрышкин А.В., Гутник Е.М. Физика 9 класс. Учебник для общеобразовательных учреждений. 14-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я. и др. Физика. Механика 10 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 11-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Молекулярная физика. Термодинамика 10 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 13-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З., Слободсков Б.А. Физика. Электродинамика классы. Профильный уровень. Учебник для общеобразовательных учреждений. 11-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Колебания и волны 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений.
Н. Литература: 1. Пёрышкин А.В. Физика 7 класс. Учебник для общеобразовательных учреждений. 13-е издание, стереотипное. Москва. Дрофа Пёрышкин А.В. Физика 8 класс. Учебник для общеобразовательных учреждений. 12-е издание, стереотипное. Москва. Дрофа Пёрышкин А.В., Гутник Е.М. Физика 9 класс. Учебник для общеобразовательных учреждений. 14-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я. и др. Физика. Механика 10 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 11-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Молекулярная физика. Термодинамика 10 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 13-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З., Слободсков Б.А. Физика. Электродинамика классы. Профильный уровень. Учебник для общеобразовательных учреждений. 11-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Колебания и волны 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 9-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Оптика. Квантовая физика 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 9-е издание, стереотипное. Москва. Дрофа Жирным выделены формулы, которые стоит учить, когда уже отлично освоены не выделенные жирным формулы. 7 класс. 1. Средняя скорость: 2. Плотность: 3. Закон Гука: 4. Сила тяжести:
9-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Оптика. Квантовая физика 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 9-е издание, стереотипное. Москва. Дрофа Жирным выделены формулы, которые стоит учить, когда уже отлично освоены не выделенные жирным формулы. 7 класс. 1. Средняя скорость: 2. Плотность: 3. Закон Гука: 4. Сила тяжести:
2 5. Давление: 6. Давление столба жидкости: 7. Архимедова сила: 8. Механическая работа: 9. Мощность совершения работы: 10. Момент силы: 11. Коэффициент полезного действия (КПД) механизма: 12. Потенциальная энергия при постоянном: 13. Кинетическая энергия: 8 класс. 14. Количество теплоты необходимое для нагревания: 15. Количество теплоты, выделяемое при сгорании: 16. Количество теплоты необходимое для плавления:
3
17. Относительная влажность воздуха: 18. Количество теплоты необходимое для парообразования: 19. КПД теплового двигателя: 20. Полезная работа теплового двигателя: 21. Закон сохранения заряда: 22. Сила тока: 23. Напряжение: 24. Сопротивление: 25. Общее сопротивление последовательного соединения проводников: 26. Общее сопротивление параллельного соединения проводников: 27. Закон Ома для участка цепи:
Сила тока: 23. Напряжение: 24. Сопротивление: 25. Общее сопротивление последовательного соединения проводников: 26. Общее сопротивление параллельного соединения проводников: 27. Закон Ома для участка цепи:
4 28. Мощность электрического тока: 29. Закон Джоуля-Ленца: 30. Закон отражения света: 31. Закон преломления света: 32. Оптическая сила линзы: 9 класс. 33. Зависимость скорости от времени при равноускоренном движении: 34. Зависимость радиус вектора от времени при равноускоренном движении: 35. Второй закон Ньютона: 36. Третий закон Ньютона: 37. Закон всемирного тяготения:
5 38. Центростремительное ускорение: 39. Импульс: 40. Закон изменения энергии: 41. Связь периода и частоты: 42. Связь длинны волны и частоты: 43. Закон изменения импульса: 44. Закон Ампера: 45. Энергия магнитного поля тока: 46. Формула трансформатора: 47. Действующее значение тока: 48. Действующее значение напряжения:
6
49. Заряд конденсатора: 50. Электроёмкость плоского конденсатора: 51. Общая ёмкость параллельно соединённых конденсаторов: 52. Энергия электрического поля конденсатора: 53. Формула Томпсона: 54. Энергия фотона: 55. Поглощение фотона атомом: 56. Связь массы и энергии: 1. Поглощённая доза излучения: 2. Эквивалентная доза излучения:
Энергия электрического поля конденсатора: 53. Формула Томпсона: 54. Энергия фотона: 55. Поглощение фотона атомом: 56. Связь массы и энергии: 1. Поглощённая доза излучения: 2. Эквивалентная доза излучения:
7 57. Закон радиоактивного распада: 10 класс. 58. Угловая скорость: 59. Связь скорости с угловой: 60. Закон сложения скоростей: 61. Сила трения скольжения: 62. Сила трения покоя: 3. Сила сопротивления среды: [ 63. Потенциальная энергия растянутой пружины: 4. Радиус вектор центра масс:
8 64. Количество вещества: 65. Уравнение Менделеева-Клапейрона: 66. Основное уравнение молекулярно кинетической теории: 67. Концентрация частиц: 68. Связь между средней кинетической энергией частиц и температурой газа: 69. Внутренняя энергия газа: 70. Работа газа: 71. Первое начало термодинамики: 72. КПД машины Карно: 5. Тепловое линейное расширение: 6. Тепловое объёмное расширение:
9
73. Закон Кулона: 74. Напряжённость электрического поля: 75. Напряжённость электрического поля точечного заряда: 7. Поток напряжённости электрического поля: 8. Теорема Гаусса: 76. Потенциальная энергия заряда при постоянном: 77. Потенциальная энергия взаимодействия тел: 78. Потенциальная энергия взаимодействия зарядов: 79. Потенциал: 80. Разность потенциалов: 81. Связь напряжённости однородного электрического поля и напряжения:
Поток напряжённости электрического поля: 8. Теорема Гаусса: 76. Потенциальная энергия заряда при постоянном: 77. Потенциальная энергия взаимодействия тел: 78. Потенциальная энергия взаимодействия зарядов: 79. Потенциал: 80. Разность потенциалов: 81. Связь напряжённости однородного электрического поля и напряжения:
10 82. Общая электроёмкость последовательно соединённых конденсаторов: 83. Зависимость удельного сопротивления от температуры: 84. Первое правило Кирхгофа: 85. Закон Ома для полной цепи: 86. Второе правило Кирхгофа: 87. Закон Фарадея: 11 класс. 9. Закон Био-Савара-Лапласа: 10. Магнитная индукция бесконечного провода: 88. Сила Лоренца:
11
89. Магнитный поток: 90. Закон электромагнитной индукции: 91. Индуктивность: 92. Зависимость величины, изменяющейся по гармоническому закону от времени: 93. Зависимость скорости изменения величины, изменяющейся по гармоническому закону от времени: 94. Зависимость ускорения изменения величины, изменяющейся по гармоническому закону от времени: 95. Период колебаний нитяного маятника: 96. Период колебаний пружинного маятника: 11. Емкостное сопротивление: 12. Индуктивное сопротивление:
Период колебаний нитяного маятника: 96. Период колебаний пружинного маятника: 11. Емкостное сопротивление: 12. Индуктивное сопротивление:
12 13. Сопротивление для переменного тока: 97. Формула тонкой линзы: 98. Условие интерференционного максимума: 99. Условие интерференционного минимума: 14. Преобразования Лоренца координат: 15. Преобразования Лоренца времени: 16. Релятивистский закон сложения скоростей: 100. Зависимость массы тела от скорости: 17. Релятивистская связь между энергией и импульсом:
13 101. Уравнение фотоэффекта: 102. Красная граница фотоэффекта: 103. Длина волны Де Бройля:
Н.Е.Савченко ЗАДАЧИ ПО ФИЗИКЕ С АНАЛИЗОМ ИХ РЕШЕНИЯ В книге дана методика решения задач но физике с анализом типичных ошибок, допускаемых абитуриентами на вступительных экзаменах. Сборник рекомендуется
Аннотация к рабочей программе по физике.7-9 классы. Рабочая программа разработана на основе: 1. Примерной программы среднего общего образования по физике. 2. Программы основного общего образования по физике
2. Программы основного общего образования по физике
ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Государственный университет морского и речного
12.5.13. Физика Механические явления распознавать механические явления и объяснять на основе имеющихся знаний основные свойства или условия протекания этих явлений: равномерное и равноускоренное прямолинейное
АННОТАЦИЯ К РАБОЧЕЙ ПРОГРАММЕ УЧЕБНОЙ ДИСЦИПЛИНЫ «ФИЗИКА» (ПРОФИЛЬНЫЙ УРОВЕНЬ) Рабочая программа по математике составлена на основе федерального компонента государственного стандарта среднего (полного)
Рассмотрено на заседании МО Согласовано Утверждаю учителей математики и физики Зам. Директора по УВР Директор МБОУ СОШ с.ключи /Камалтдинова З.З./ /Селянина Ф.Ф./ /Селянина З.Р/ 2011 г. 2011 г. Приказ
2 Составитель: Куцов А.М., доцент кафедры естественнонаучных дисциплин, канд. геол.-минерал. наук Утверждена на заседании кафедры естественнонаучных дисциплин 03.02.2014 г., протокол 3 3 1. ПОЯСНИТЕЛЬНАЯ
геол.-минерал. наук Утверждена на заседании кафедры естественнонаучных дисциплин 03.02.2014 г., протокол 3 3 1. ПОЯСНИТЕЛЬНАЯ
Рабочая программа учебной дисциплины разработана на основе Федерального государственного образовательного стандарта (далее ФГОС) по специальности среднего профессионального образования 600«Технология молока
Министерство образования и науки Российской Федерации Федеральный институт развития образования ПРИМЕРНАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ ФИЗИКА для профессий начального профессионального образования и специальностей
2 3 ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Программа учебной дисциплины «Физика» предназначена для изучения физики в учреждениях среднего профессионального образования, реализующих образовательную программу среднего (полного)
ПЛАНИРУЕМ УЧЕБНУЮ ДЕЯТЕЛЬНОСТЬ ПОДГОТОВКА К ЕГЭ. 11 класс ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Базовый уровень изучения физики не рассчитан на подготовку учащихся к продолжению образования в вузах физико-технического
Муниципальное бюджетное общеобразовательное учреждение «Гатчинская средняя общеобразовательная школа 1» Приложение к образовательной программе среднего общего образования, утверждѐнной Приказом 80 от
Рабочая программа по предмету ФИЗИКА 0- классы (базовый уровень) Пояснительная записка Рабочая программа по физике составлена на основе федерального компонента государственного образовательного стандарта
Министерство образования и науки Государственное бюджетное профессиональное образовательное учреждение Республики Хакасия «Профессиональное училище 15» с. Бея РАССМОТРЕНО на заседании МО ОД (протокол от
Бея РАССМОТРЕНО на заседании МО ОД (протокол от
2.Пояснительная записка. Программа соответствует Федеральному компоненту государственного стандарта основного общего образования по физике (приказ Минобразования России от 05.03.2004 1089 «Об утверждении
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ ФИЗИКА (ПД.02) для специальности среднего профессионального образования 23.02.01 «Организация перевозок и управление на транспорте (по видам)»
Аннотация к рабочим программам по физике 10-11 класс 10 класс Рабочая программа по физике для учащихся 10 класса (профильного уровня) составлена на основе примерной программы среднего (полного) общего
3-7. На шелковых нитях длиной 50 см каждая, прикрепленных к одной точке, висят два одинаково заряженных шарика массой по 0,2 г каждый. Определить заряд каждого шарика, если они отошли друг от друга на
Формулы по физике для школьника сдающего ГИА по ФИЗИК (9 класс) Кинематика Линейная скорость [м/с]: L путевая: П средняя: мгновенная: () в проекции на ось Х: () () где _ Х x x направление: касательная
Рабочая программа по физике 11 класс (2 часа) 2013-2014 учебный год Пояснительная записка Рабочая общеобразовательная программа «Физика. 11 класс. Базовый уровень» составлена на основе Примерной программы
11 класс. Базовый уровень» составлена на основе Примерной программы
ЭЛЕКТРОСТАТИКА 1. Два рода электрических зарядов, их свойства. Способы зарядки тел. Наименьший неделимый электрический заряд. Единица электрического заряда. Закон сохранения электрических зарядов. Электростатика.
РАБОЧАЯ ПРОГРАММА ПО ФИЗИКЕ 11 КЛАСС (базовый уровень) 4 ЭЛЕКТРОДИНАМИКА 35 часов 4.1 Элементарный электрический заряд. 1 Знать: 4.2 Закон сохранения электрического заряда Закон Кулона 1 понятия: электрический
Программа элективного курса по физике класс. «Методы решения задач по физике повышенной сложности, класс» ч., час в неделю Составитель: Шмидт Е.Ф., учитель физики первой категории МОУ «Сосновская СОШ»
Пояснительная записка Рабочая программа по физике для 0- класса составлена на основе Программы общеобразовательных учреждений по физике для 0- классов, авторы программы П. Г. Саенко, В.С. Данюшенков, О.В.
Рабочая программа по физике составлена на основе федерального компонента государственного стандарта основного общего образования. Данная рабочая программа ориентирована на учащихся 11 класса и реализуется
Данная рабочая программа ориентирована на учащихся 11 класса и реализуется
Учебно-методический комплекс (УМК) Физика Аннотация к рабочей программе 7 класса А.В.Пѐрышкин. Физика 7 класс. Москва. Дрофа.2012г. А.В.Пѐрышкин. Сборник задач по физике 7-9. Москва Экзамен.2015 Учебный
Муниципальное автономное общеобразовательное учреждение лицей 102 г. Челябинска Рассмотрено на заседании НМС МАОУ лицея 102 2014 г. УТВЕРЖДАЮ директор МАОУ лицея 102 М.Л. Оксенчук 2014 г. РАБОЧАЯ ПРОГРАММА
ПРОГРАММА ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ ПО ФИЗИКЕ Настоящая программа составлена на основе действующих учебных программ для общеобразовательных учебных заведений. 1.1. Кинематика 1. МЕХАНИКА Механическое движение.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа по физике составлена на основе примерной программы среднего (полного) общего образования по физике базового уровня и соответствует федеральному государственному
Пояснительная записка Программа составлена в соответствии с:. Законом об образовании от 29.2.202 273-ФЗ «Закон об образовании в РФ»; 2. примерной программой среднего общего образования по физике. 0- классы.,
Законом об образовании от 29.2.202 273-ФЗ «Закон об образовании в РФ»; 2. примерной программой среднего общего образования по физике. 0- классы.,
«Согласовано» «Согласовано» на заседании методического объединения учителей Директор ГБОУ ОСОШ 88 биологии, физики, химии Маслова В.М. Протокол от 201 г. 201 г Руководитель МО учителей биологии, физики,
Муниципальное бюджетное общеобразовательное учреждение «Школа 41 «Гармония» с углубленным изучением отдельных предметов» городского округа Самара РАБОЧАЯ ПРОГРАММА Предмет физика Класс 9 Количество часов
Муниципальное бюджетное общеобразовательное учреждение гимназия 5 г. Ставрополя Рассмотрено: на заседании МО учителей естественных дисциплин МБОУ гимназии 5 Протокол 1 от «9» августа 014 г Согласовано:
Лицей автономной некоммерческой организации высшего профессионального образования академии «МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ В МОСКВЕ» «СОГЛАСОВАНО» «УТВЕРЖДАЮ» Руководитель МО Директор Лицея Полунина О. В. 201
В. 201
УТВЕРЖДАЮ Ректор ФГБОУ ВПО «МГУДТ» В.С.Белгородский 2015г. МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального
Приложение 5 Соответствие сроков прохождения тем по физике этапам Всероссийской олимпиады Комплекты заданий различных этапов олимпиад составляются по принципу «накопленного итога» и могут включать как
Инструктивно-методическое письмо о преподавании физики в 2015/16 учебном году Документы, необходимые для реализации учебного процесса по физике основного и среднего образования, а также в профильных классах:
ПРОГРАММА ПО ФИЗИКЕ Программа составлена на базе обязательного минимума содержания среднего (полного) общего образования. Экзаменационные задания по физике не выходят за рамки данной программы, но требуют
«Физика. 10 класс» и «Физика. 11 класс» базовый уровень стр.1 из 17 МОУ Киришская средняя общеобразовательная школа 8 Согласовано заместитель директора по УВР, Е. А. Королева «01» сентября 2014 г. Утверждена
А. Королева «01» сентября 2014 г. Утверждена
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ ОДБ.08 ФИЗИКА 2013 г Рабочая программа учебной дисциплины разработана на основе Федерального государственного образовательного стандарта (далее ФГОС) по профессии начального
Управление образования АМО ГО «Сыктывкар» Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа 9» (МОУ «СОШ 9») «9 -а Шӧр школа» муниципальнӧй велӧдан учреждение 02-01 Рекомендовано
Министерство физической культуры, спорта и молодежной политики Свердловской области Государственное автономное образовательное учреждение Среднего профессионального образования Свердловской области «Училище
Департамент образования и науки Кемеровской области Государственное образовательное учреждение среднего профессионального образования «Кемеровский коммунально-строительный техникум» имени В.И. Заузёлкова
Муниципальное бюджетное образовательное учреждение «Школа 13» города Сарова РАССМОТРЕНА на заседании школьного методического объединения учителей естественнонаучного цикла Протокол 1 от 29. 08.2016 СОГЛАСОВАНА
08.2016 СОГЛАСОВАНА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Национальный минерально-сырьевой университет
РАБОЧАЯ ПРОГРАММА ПО ФИЗИКЕ 0 КЛАСС БАЗОВЫЙ УРОВЕНЬ ПО УЧЕБНИКУ Г.Я.МЯКИШЕВ, Б.Б.БУХОВЦЕВ (36 часов 2 часа в неделю). ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа составлена на основе Федерального компонента
Средняя общеобразовательная школа с углубленным изучением иностранного языка при Посольстве России в Великобритании СОГЛАСОВАНО на заседании МС (Зубов С.Ю.) «10» сентября 2014 УТВЕРЖДАЮ директор школы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» «УТВЕРЖДАЮ» Ректор
Министерство образования и науки Челябинской области ГОУ СПО «Троицкий педагогический колледж» Рабочая программа учебной дисциплины ОДБ. 11 Физика по специальности 050146 Преподавание в начальных классах
11 Физика по специальности 050146 Преподавание в начальных классах
Экзамен в 8 классе общеобразовательной школы включает в себя проверку знаний теоретических (1 вопрос) и практических в виде навыков решения задач (1 задача). На экзамене можно пользоваться линейкой и калькулятором.
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа 14» г. Воркуты РАССМОТРЕНА школьным методическим объединением учителей естественно-математического цикла Протокол 1 от 30.08.2013
Государственное бюджетное общеобразовательное учреждение средняя общеобразовательная школа 18 с углубленным изучением математики Василеостровского района Санкт-Петербурга РАССМОТРЕНО на заседании МО протокол
Пояснительная записка При составлении программы были использованы следующие правовые документы федеральный компонент государственного стандарта среднего (полного) общего образования по физике, утвержденный
Автономное профессиональное образовательное учреждение Удмуртской Республики «Ижевский промышленно-экономический колледж» Учебно-программная документация ФИЗИКА (профильный уровень) РП. ОДП.16.СПО-01-2014
ОДП.16.СПО-01-2014
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа 39 имени Георгия Александровича Чернова» г.воркуты Рассмотрена на заседании ШМО учителей математики, физики и информатики
Аннотация к рабочей программе по предмету «Физика» 10-11 класс 10 класс Рабочая программа предназначена для работы в 10 классе общеобразовательной школы и составлена на основе: — федерального компонента
Анатация Рабочая программа учебной дисциплины «Физика» предназначена для изучения физики в учреждениях начального и среднего профессионального образования, реализующих образовательную программу среднего
II четверть 2.1. Название Основы динамики. Основные законы механики — законы Ньютона. НА УЧЕБНЫЙ ПЕРИОД 2015-2020 Сформировать понятия силы как количественной характеристики взаимодействия тел. Изучить
СОДЕРЖАНИЕ. Пояснительная записка 3 2. Содержание учебной программы 5 3. График практической части рабочей программы. 0 4. Календарно-тематический план…6 5. Список литературы для учащихся..33 6. Список
0 4. Календарно-тематический план…6 5. Список литературы для учащихся..33 6. Список
II четверть 2.1. Название Изменение агрегатных состояний вещества. НА УЧЕБНЫЙ ПЕРИОД 2015-2020 Продолжить формирование представлений о внутренней энергии. Изучить формулу для расчета количества теплоты,
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УЧЕБНЫЕ ПРОГРАММЫ ДЛЯ УЧРЕЖДЕНИЙ ОБЩЕГО СРЕДНЕГО ОБРАЗОВАНИЯ С РУССКИМ ЯЗЫКОМ ОБУЧЕНИЯ ФИЗИКА VI XI классы АСТРОНОМИЯ XI класс Утверждено Министерством образования
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Забайкальский государственный университет»
СИБИРСКИЙ УНИВЕРСИТЕТ ПОТРЕБИТЕЛЬСКОЙ КООПЕРАЦИИ ПРОГРАММА ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ ПО ПРЕДМЕТУ ФИЗИКА Новосибирск ВВЕДЕНИЕ Программа вступительного испытания по предмету физика составлена с учётом требований
1. ФИЗИКА 2. Кинематика. Система отсчета. Способы описания положения точки. Характеристики движения точки при различных способах описания положения. Уравнения движения. Кинематические сложения движений
Система отсчета. Способы описания положения точки. Характеристики движения точки при различных способах описания положения. Уравнения движения. Кинематические сложения движений
Тур 1 Вариант 1 1. Точка движется по оси х по закону х = 8 + 12t — 3t 2 (м). Определите величину скорости точки при t = 1 с. 2. Тело массой m = 1 кг движется по горизонтальной поверхности под действием
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Башантинский аграрный колледж им. Ф.Г. Попова (филиал) ГОУ ВПО «КАЛМЫЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ Физика
Государственное бюджетное общеобразовательное учреждение средняя общеобразовательная школа 13 с углубленным изучением английского языка Невского района Санкт-Петербурга Аннотация к рабочей программе по
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул.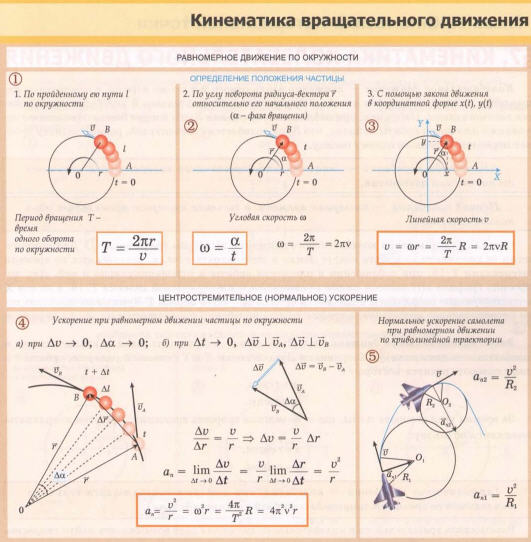 Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Шпаргалка с формулами по физике для ЕГЭ
Шпаргалка с формулами по физике для ЕГЭ
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
Шпаргалка с формулами по физике для ЕГЭ и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
А потом вордовский файл , который содержит все формулы чтобы их распечатать, которые находятся внизу статьи.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 —υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ —υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей — Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля — Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 — Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 — Т 2)/ Т 1
Электростатика и электродинамика — формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N 0 ∙2 — t / T
- Энергия связи атомных ядер
E CB =(Zm p +Nm n -Mя)∙c 2
СТО
- t=t 1 /√1-υ 2 /c 2
- ℓ=ℓ 0 ∙√1-υ 2 /c 2
- υ 2 =(υ 1 +υ)/1+ υ 1 ∙υ/c 2
- Е = mс 2
Задачи_10 класс.
 Механика
Механика 4. Автомобиль проходит первую половину пути со средней скоростью 70 км/ч, а вторую — со средней скоростью 30 км/ч. Определить среднюю скорость на всем пути.
6. При какой максимальной скорости самолеты могут приземляться на посадочную полосу аэродрома длиной 800 м при торможении с ускорением a1= −2,7 м/с2? a2= −5 м/с2? 7. 8. Луна движется вокруг Земли по окружности радиусом 384 000 км с периодом 27 сут 7 ч 43 мин. Какова линейная скорость Луны?
Каково центростремительное ускорение Луны к Земле? Механика. ДинамикаОсновная задача динамики материальной точки состоит в том, чтобы найти законы движения точки, зная приложенные к ней силы, или, наоборот, по известным законам движения определить силы, действующие на материальную точку. Общие правила решения задач по динамике Характерная особенность решения задач механики о движении материальной точки, требующих применения законов Ньютона, состоит в следующем:
—————————————————————————————————- 1. 2. Почему машинисту подъемного крана запрещается резко поднимать с места тяжелые грузы? 3. Вагонетка массой 500 кг движется под действием силы 100 Н. Определите ее ускорение. 4. Автобус массой 8000 кг едет по горизонтальному шоссе. Какая сила требуется 5. Два человека тянут за веревку в разные стороны с силой 90 Н каждый. Разорвется ли веревка, если она выдерживает натяжение до 120 Н? 6. На самолет, летящий в горизонтальном направлении, действует в направлении полета сила тяги двигателя F = 15000 Н, сила сопротивления воздуха FC = 11000 Н и сила давления бокового ветра FВ = 3000 H, направленная под углом α = 90° к курсу. Найти равнодействующую этих сил. Какие еще силы действуют на самолет в полете и чему равна их равнодействующая? 7. 8. Между всеми телами существует взаимное притяжение. Почему же мы наблюдаем притяжение тел к Земле и не замечаем взаимного тяготения окружающих нас предметов друг к другу? 9. Пружину детского пистолета сжали на 3 см. Определите возникшую в ней силу упругости, если жесткость пружины равна 700 Н/м. 10. Какой силой можно сдвинуть ящик массой 60 кг, если коэффициент трения между ним и полом равен 0,27? Сила действует под углом 30° к полу (горизонту). 11. Какую начальную скорость нужно сообщить сигнальной ракете, выпущенной под углом α = 45° к горизонту, чтобы она вспыхнула в наивысшей точке траектории, если запал ракеты горит t = 6 с? 12. Вычислить первую космическую скорость у поверхности Луны, если радиус Луны R= 1760 км, а ускорение свободного падения на Луне составляет 0,17 земного. Механика. Импульс, мощность, энергия1. Пуля массой 10 г, летящая горизонтально со скоростью 400 м/с, ударяется в преграду и останавливается. Чему равен импульс, полученный пулей от преграды? Куда он направлен? 2. Космический корабль массой 4800 кг двигался по орбите со скоростью 8000 м/с. При торможении из него тормозными двигателями было выброшено 500 кг продуктов сгорания со скоростью 800 м/с относительно его корпуса в направлении движения. Определите скорость корабля после торможения. 3. Снаряд, летевший горизонтально со скоростью 480 м/с, разорвался на два осколка равной массы. Один осколок полетел вертикально вверх со скоростью 400 м/с относительно Земли. Определите скорость второго осколка. 4. Охотник, плывя по озеру на легкой надувной лодке, стреляет в уток. 5. Стоящий на коньках человек массой 60 кг ловит мяч массой 500 грамм, летящий горизонтально со скоростью 72 км/ч, определите расстояние на которое откатится при этом человек, если коэффициент трения 0,05. Решение: 6. Самолет должен иметь для взлета скорость 25 м/с. Длина пробега по полосе аэродрома составляет 100 м. Какую мощность должны развивать двигатели при взлете, если масса самолета 1000 кг и сопротивление движению равно 200 Н? 7. Футбольный мяч массой 400 г падает на Землю с высоты 6 м и отскакивает на высоту 2,4 м. Какое количество механической энергии мяча превращается в другие виды энергии? 8. 9. Перед загрузкой в плавильную печь чугунный металлолом измельчают ударами падающего бойка молота массой 6000 кг. Определите полную энергию в нижней точке при падении бойка с высоты 9 м. Сравните ее с полной энергией, которую имеет боек, пройдя при падении 5 м. 10. Самолет массой 1000 кг летит горизонтально на высоте 1200 м со скоростью 50 м/с. При выключенном двигателе самолет планирует и приземляется со скоростью 25 м/с. Определите силу сопротивления воздуха при спуске, считая длину спуска равной 8 км. 11. Достаточна ли мощность электродвигателя токарного станка 1А62 (7,8 кВт) для обработки детали со скоростью резания 5 м/с, если сопротивление металла резанию составляет 600 Н? КПД станка 0,75. 12. Автомобиль, мощность двигателя которого 50 кВт, движется по горизонтальному шоссе. 13. При формировании железнодорожного состава происходят соударения вагонов буферами. Пружины двух буферов вагона сжались при ударе на 10 см каждая. Определите работу сжатия пружин, если коэффициент их жесткости равен 5·106 Н/м.
|
Уравнения кинематики и постоянное ускорение
В своих «Диалогах двух новых наук» Галилей вывел связь между пройденным расстоянием и временем, когда шары катятся по наклонной плоскости. Это часто называют законом падающих тел. Интересно, что доказательство Галилея использовало классическую евклидову геометрию (которая была бы незнакома современному изучающему геометрию из учебников) вместо алгебры, которую мы представим здесь. Продвинутые учащиеся могут вывести эти же уравнения с помощью исчисления.
В основе Закона падающих тел лежит то, что когда мяч катится по пандусу, он ускоряется. По мере того, как его скорость увеличивается, расстояние, которое он проходит в каждую единицу времени, увеличивается. Галилей определил это по тому, что катящийся шар срабатывает при вращении.
Процитировать Галилея в переводе:
По сути, Галилей представил, что не только ускорение вниз по рампе из-за постоянной гравитации, но и что скорость увеличивается линейно с временем . Он представил, что положение увеличивается с квадратом времени, что часто называют Законом Падающих Тел. Последний момент в этом отрывке, который он представил, заключается в том, что скорость увеличивается с квадратом расстояния вниз по рампе.
Он представил, что положение увеличивается с квадратом времени, что часто называют Законом Падающих Тел. Последний момент в этом отрывке, который он представил, заключается в том, что скорость увеличивается с квадратом расстояния вниз по рампе.
Опираясь на то, что вы уже узнали, и на то, что представил Галилей, у нас есть то, что мой учитель физики Гленн Глейзер любил называть пятью священными уравнениями кинематики для постоянного ускорения. В этих уравнениях v — это скорость, x — положение, t — время, а a — ускорение.Помните, Δ означает изменение.
1. или Δx = v среднее Δt
2. или v f = v o + aΔt или Δv= aΔt
3.
4. Δx = v o Δt + ½ a Δt 2
5. v f 2 =v o 2 +2aΔx
Первые два уравнения мы уже видели. Важно отметить, что первое уравнение использует среднюю скорость , тогда как второе уравнение использует изменение между исходной скоростью и конечной скоростью .Связь между ними представлена в третьем уравнении, которое представляет собой просто закон средних чисел. Средняя скорость – это среднее значение начальной и конечной скоростей.
Важно отметить, что первое уравнение использует среднюю скорость , тогда как второе уравнение использует изменение между исходной скоростью и конечной скоростью .Связь между ними представлена в третьем уравнении, которое представляет собой просто закон средних чисел. Средняя скорость – это среднее значение начальной и конечной скоростей.
Из этих трех основных определений мы можем вывести следующие два уравнения, используя либо геометрию, либо алгебру (или исчисление).
Используя алгебру, мы можем вывести уравнение №4.
Начиная с уравнения №1
Δx = v среднее Δt
Затем мы подставляем в определение среднюю скорость из уравнения №3.
Отсюда мы подставляем конечную скорость, полученную в уравнении № 2
Затем мы распределяем член Δt и упрощаем, комбинируя члены v o .
Мы упрощаем оставшиеся два члена, чтобы получить
.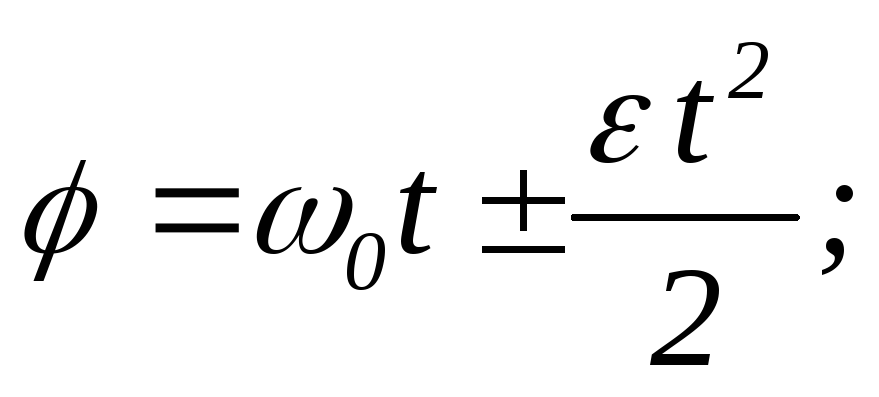
Стоит отметить, что происходит, когда исходная скорость v o, равна нулю. Это уравнение еще больше упрощается и становится равным
.Если мы предположим, что исходное положение и время равны нулю, мы можем уменьшить это число до
.Используя геометрию, мы можем исследовать площадь под кривой графика зависимости скорости от времени для движения с постоянным ускорением.
Если мы посмотрим на область под кривой, мы можем разбить ее на прямоугольник и треугольник. Красный прямоугольник — вклад исходной скорости объекта. Смещение из-за ускорения представлено зеленым треугольником. Треугольник имеет ширину Δt и высоту aΔt, которые мы знаем из уравнения № 2. Член ½ происходит от формулы площади треугольника.
Мы также можем использовать исчисление, чтобы вывести это уравнение, интегрируя удвоенное ускорение по времени.
Пятое священное уравнение может быть получено аналогичными заменами и останется в качестве домашнего задания.
Теперь давайте рассмотрим несколько примеров задач: Численное решение задач.
Пример 1
По легенде, Галилей уронил мяч с Пизанской башни. Если башня имеет высоту 55,9 м , и пренебрегая сопротивлением воздуха, сколько времени потребуется свинцовому шару, чтобы достичь земли?
Дано: a = g ≈ 10 м/с 2
Δx = 55.9 м
Неизвестно: t = ???
Уравнение, которое связывает эти переменные, является священным уравнением 4 th .
Δx = v o Δt + ½ a Δt 2
Как упоминалось ранее, поскольку начальная скорость равна нулю, уравнение упрощается.
Δx = v o Δt + ½ a Δt 2 = ½ a Δt 2
Поскольку мы хотим изолировать переменную для времени, мы пересекаем умножение, чтобы переместить ½ и ускорение в другую сторону.
Затем мы извлекаем квадратный корень из обеих частей.
В результате получается выражение для времени.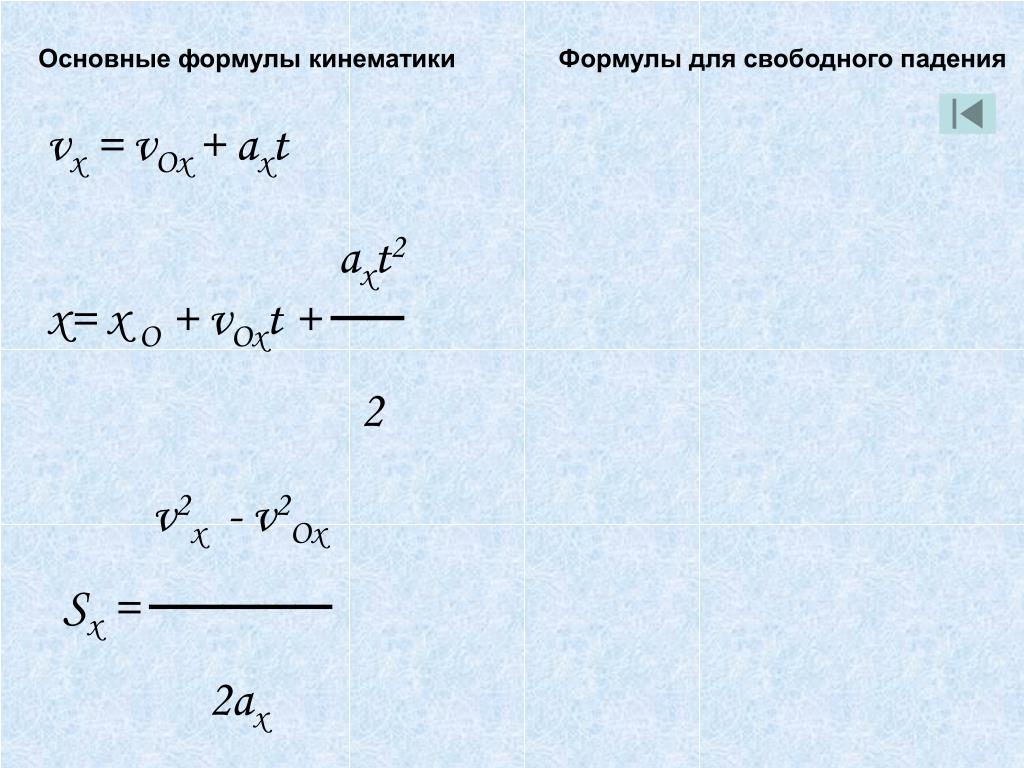 Обратите внимание, что я вставил несколько дополнительных наборов скобок, которые вам могут показаться ненужными.
Обратите внимание, что я вставил несколько дополнительных наборов скобок, которые вам могут показаться ненужными.
При подключении чисел довольно просто то, что мы называем «подключи и пыхти». Однако с юнитами нужно быть осторожным. Вы, наверное, догадались, что время будет измеряться в секундах. Тем не менее, вы должны иметь возможность отменить фактические единицы, чтобы получить секунды для времени.
Пример 2
Койот падает со скалы высотой 25 метров. С какой скоростью падает койот, когда ударяется о землю? Если проблема койота
Дано x = 25 м
а = g ≈ 10 м/с 2
Неизвестно: v = ???
Существует несколько способов решения этой проблемы. Можно было бы использовать комбинацию или Священные уравнения № 2 и № 4. Или вы можете напрямую использовать уравнение № 5.
Использование v f 2 =v o 2 + 2a∆x
Это упрощает, потому что начальная скорость v o, равна нулю.
Если мы возьмем квадратный корень из обеих частей уравнения
Обратите внимание, как вы извлекаете квадратный корень из единиц, чтобы получить м/с .
Мы оставим решение этой задачи с двумя уравнениями для домашнего задания.
Резюме по построению графиков и проблемам наклона и площади под кривыми
Изучив графики положения, скорости и ускорения, вы сможете рисовать их взаимозаменяемо.
Вчера в классе вы видели, что график движения тела с ускорением вниз по склону выглядит так:
В этом примере мы используем программное обеспечение для анализа изображений.Это пример с катящимся с горки мячом. Следует отметить, что график ускорения не говорит вам о фактической скорости, а только о том, как она меняется. Точно так же график скорости не показывает фактическое положение объекта, а только то, как оно меняется. Щелкнув по мячу и нажав кнопку отслеживания, вы увидите сгенерированный график положения и скорости.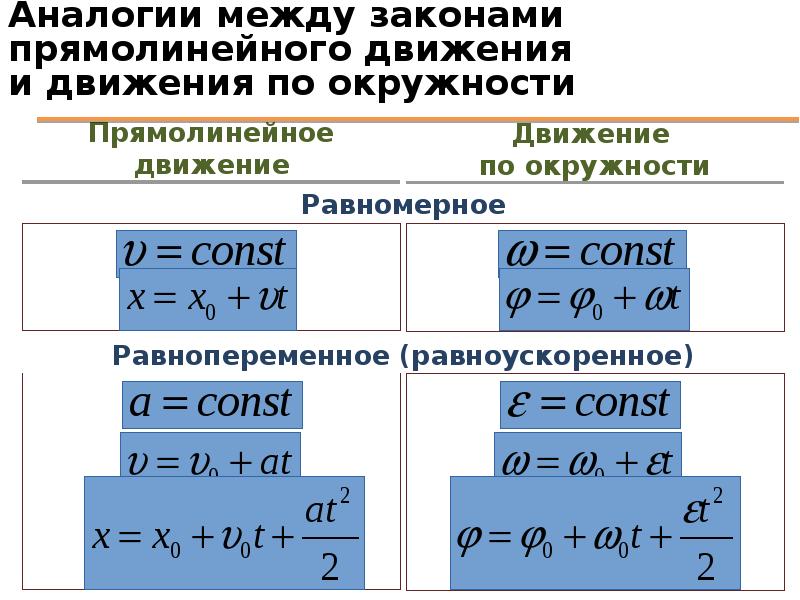
Здесь вы можете увидеть результаты построения графика движения. График положения представляет собой параболу, а график скорости — линейный.
Что такое кинематические формулы?
Кинематические уравнения: Целью этого первого раздела Класса физики было исследование различных средств, с помощью которых можно описать движение объектов. Разнообразие представлений, которые мы исследовали, включает словесные представления, графические представления, числовые представления и графические представления (графики положение-время и графики скорость-время).
В Уроке 6 мы исследуем использование уравнений для описания и представления движения объектов. Эти уравнения известны как кинематические уравнения. Существует множество величин, связанных с движением объектов: перемещение (и расстояние), скорость (и скорость), ускорение и время.
Что такое кинематические формулы? Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22.0 м/с, на север в течение 12,0 секунд для перемещения на север на 264 метра, то движение автомобиля полностью описано. И если известно, что второй автомобиль ускоряется из положения покоя с ускорением на восток 3,0 м/с 2 за время 8,0 секунд, обеспечивая конечную скорость 24 м/с, на восток и перемещение на восток на 96 метров , то движение этого автомобиля полностью описано.
Например, если известно, что автомобиль движется с постоянной скоростью 22.0 м/с, на север в течение 12,0 секунд для перемещения на север на 264 метра, то движение автомобиля полностью описано. И если известно, что второй автомобиль ускоряется из положения покоя с ускорением на восток 3,0 м/с 2 за время 8,0 секунд, обеспечивая конечную скорость 24 м/с, на восток и перемещение на восток на 96 метров , то движение этого автомобиля полностью описано.
Эти два утверждения обеспечивают полное описание движения объекта. Однако такая полнота не всегда известна.Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны. Например, приближаясь к светофору, вы можете знать, что скорость вашего автомобиля 22 м/с на восток и ускорение заноса 8,0 м/с 2 на запад.
Однако вы не знаете, какое смещение испытает ваша машина, если вы нажмете на тормоза и занесете до полной остановки; и вы не знаете время, необходимое для остановки. В таком случае неизвестные параметры могут быть определены с использованием принципов физики и математических уравнений (кинематических уравнений)
В таком случае неизвестные параметры могут быть определены с использованием принципов физики и математических уравнений (кинематических уравнений)
4 Кинематические уравнения
Кинематика — это изучение движущихся объектов и их взаимосвязей.Имеются четыре (4) кинематических уравнения, которые относятся к смещению D, скорости v, времени t и ускорению a.
а) D = v i t + 1/2 at 2 b) (v i +v f )/2 = D/t
C) A = (V F — V I ) / T D) 1 V F 2 = V I 2 + 2AD
D = рабочий объем
a = ускорение
t = время
v f = конечная скорость
v i = начальная скорость
Какие 3 кинематических уравнения?
Если мы знаем три из этих пяти кинематических переменных — Δ x , t , v 0 , v , a \Delta x, t, v_0, v, a Δx,t,v0,v,adelta, x, запятая , t, запятая, v, начальный индекс, 0, конечный индекс, запятая, v, запятая, a — для объекта с постоянным ускорением мы можем использовать кинематическую формулу, см. ниже, для решения одной из неизвестных переменных .
ниже, для решения одной из неизвестных переменных .
Сколько существует кинематических уравнений?
Четыре четырех кинематических уравнения , описывающих движение объекта: В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта.
Для чего используются кинематические уравнения?
Кинематические уравнения можно использовать для расчета различных аспектов движения, таких как скорость, ускорение, перемещение и время.
Список кинематических уравнений
Кинематические формулы представляют собой набор формул, относящихся к пяти перечисленным ниже кинематическим переменным.
Большой 1.
квадратный v=v0+at1
v=v0+at1,
точка, пробел, v, равно, v, начальный нижний индекс, 0, конечный нижний индекс, плюс, a, t
Большой 2.
четырехъядерный {\ Delta x} = (\ dfrac {v + v_0} {2}) t2
Δx=(2v+v0)t2,
точка, пробел, дельта, x, равенство, левая скобка, начальная дробь, v, плюс, v, начальный индекс, 0, конечный индекс, деление на, 2, конечная дробь, правая скобка, t
Большой 3.2+2а\Дельта х4.
v2=v02+2aΔx4,
точка, пробел, v, начальный верхний индекс, 2, конечный верхний индекс, равно, v, начальный нижний индекс, 0, конечный нижний индекс, начальный верхний индекс, 2, конечный верхний индекс, плюс, 2, a, дельта, x
Поскольку кинематические формулы точны только в том случае, если ускорение постоянно в течение рассматриваемого интервала времени, мы должны быть осторожны, чтобы не использовать их при изменении ускорения. Кроме того, кинематические формулы предполагают, что все переменные относятся к одному и тому же направлению: по горизонтали xxx, по вертикали yyy и т. д.2}g=9,81s2mg, равно, 9, точка, 81, начальная дробь, m, разделить на, s, начальный верхний индекс, 2, конечный верхний индекс, конечная дробь.
Кроме того, кинематические формулы предполагают, что все переменные относятся к одному и тому же направлению: по горизонтали xxx, по вертикали yyy и т. д.2}g=9,81s2mg, равно, 9, точка, 81, начальная дробь, m, разделить на, s, начальный верхний индекс, 2, конечный верхний индекс, конечная дробь.
Это и странно, и удачно, если подумать. Это странно, так как это означает, что большой валун будет двигаться вниз с таким же ускорением, как и маленький камешек, и если его уронить с той же высоты, то они ударятся о землю одновременно.
К счастью, нам не нужно знать массу снаряда при решении кинематических формул, так как свободно летящий объект будет иметь такое же ускорение, g=9.2}ay=−9.81s2ma, начальный нижний индекс, y, конечный нижний индекс, равно, минус, 9, точка, 81, начальная дробь, m, разделить на, s, начальный верхний индекс, 2, конечный верхний индекс, конечная дробь для снаряд, когда мы подключаемся к кинематическим формулам.
Физика Кинематические уравнения
Кинематические уравнения представляют собой набор из четырех уравнений, которые можно использовать для предсказания неизвестной информации о движении объекта, если известна другая информация. Уравнения можно использовать для любого движения, которое можно описать либо как движение с постоянной скоростью (ускорение 0 м/с/с), либо как движение с постоянным ускорением.Они никогда не могут быть использованы в течение какого-либо периода времени, в течение которого изменяется ускорение. Каждое из кинематических уравнений включает четыре переменные. Если известны значения трех из четырех переменных, то можно вычислить значение четвертой переменной. Таким образом, кинематические уравнения обеспечивают полезные средства прогнозирования информации о движении объекта, если известна другая информация.
Уравнения можно использовать для любого движения, которое можно описать либо как движение с постоянной скоростью (ускорение 0 м/с/с), либо как движение с постоянным ускорением.Они никогда не могут быть использованы в течение какого-либо периода времени, в течение которого изменяется ускорение. Каждое из кинематических уравнений включает четыре переменные. Если известны значения трех из четырех переменных, то можно вычислить значение четвертой переменной. Таким образом, кинематические уравнения обеспечивают полезные средства прогнозирования информации о движении объекта, если известна другая информация.
Например, если известно значение ускорения, а также значения начальной и конечной скорости скользящего автомобиля, то перемещение автомобиля и время можно предсказать с помощью кинематических уравнений.Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин движения объекта.
Четыре кинематических уравнения, описывающие движение объекта:
В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект перемещался. Символ обозначает ускорение объекта.А символ v обозначает скорость объекта; нижний индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а нижний индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект перемещался. Символ обозначает ускорение объекта.А символ v обозначает скорость объекта; нижний индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а нижний индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Каждое из этих четырех уравнений надлежащим образом описывает математическую связь между параметрами движения объекта. Таким образом, их можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация.В следующей части Урока 6 мы исследуем этот процесс.
Читайте также: Формула линейной интерполяции
Основные кинематические уравнения
Кинематика — это изучение движения объектов без учета сил, вызывающих движение. Эти знакомые уравнения позволяют учащимся анализировать и предсказывать движение объектов, и учащиеся будут продолжать использовать эти уравнения при изучении физики. Четкое понимание этих уравнений и того, как их использовать для решения задач, необходимо для успеха в физике.Эта статья представляет собой чисто математическое упражнение, предназначенное для быстрого обзора того, как уравнения кинематики выводятся с помощью алгебры.
Четкое понимание этих уравнений и того, как их использовать для решения задач, необходимо для успеха в физике.Эта статья представляет собой чисто математическое упражнение, предназначенное для быстрого обзора того, как уравнения кинематики выводятся с помощью алгебры.
В этом упражнении используется ссылка на диаграмму на рис. 1, на которой ось x представляет время, а ось y представляет скорость. Диагональная линия представляет движение объекта, скорость которого изменяется с постоянной скоростью. Заштрихованная область (A 1 + A 2 ) представляет собой смещение объекта за интервал времени между t 1 и t 2 , в течение которого скорость объекта увеличилась с v 1 до v 2 .
В этом документе будут использоваться следующие переменные:
v = величина скорости объекта (метры в секунду, м/с)
v 1 = величина начальной скорости (метры в секунду) секунда, м/с) (в некоторых текстах это vi или v 0 )
v 2 = модуль конечной скорости (метры в секунду, м/с) (в некоторых текстах это v f )
a = величина ускорения (в метрах в секунду в квадрате, м/с 2 )
s = вектор смещения, величина смещения равна расстоянию,
с = │ s │ = d (векторы выделены жирным шрифтом; тот же нежирный символ обозначает модуль вектора)
Δ обозначает изменение, например Δv = (v 2 –v 1 )
t = время
t 1 = начальное время
t 2 = окончательное время
Как решать задачи кинематики, часть 2
Эта статья является второй главой в серии статей о том, как понимать и подходить к задачам кинематики. В первой главе рассматривались положение, скорость и ускорение. Теперь, когда мы понимаем эти величины, мы собираемся использовать их для решения задач в одном измерении.
В первой главе рассматривались положение, скорость и ускорение. Теперь, когда мы понимаем эти величины, мы собираемся использовать их для решения задач в одном измерении.
Четыре всадника апокалипсиса кинематики это:
x f – x i = (v f – v i )*t/2
v f – v i = a*t
v f 2 = v i 2 + 2*a*(x f – x i )
x f = x i + v i *t + ½a*t 2
Примечание: маленькая цифра f означает окончательную (как в конечной скорости или положении), а маленькая цифра i означает начальную.
Примечание. Эти уравнения работают только для постоянного ускорения, но почти все задачи имеют постоянное ускорение.
Этапы решения одномерных задач Для каждой задачи одномерной кинематики шаги практически одинаковы.
- Запишите все величины, которые дает вам задача (начальное и конечное положение, начальная и конечная скорость, ускорение, время и т. д.)
- Запишите, какое количество вы пытаетесь найти
- Найдите кинематическое уравнение (или иногда два уравнения), чтобы связать эти величины.
- Решите алгебру.
Да, это действительно так просто. (На самом деле, большинство задач по физике работают одинаково. Подробнее об алгоритме решения задач по физике читайте в этой статье.)
Как избежать типичных ошибок: скрытые количества Иногда проблема может тайно сказать вам количество; вы можете даже не осознавать, что получили это. Например, если они сообщают вам смещение (как далеко что-то пройдено), но не позиции, вы можете рассматривать смещение как x f и установить x i равным 0.Точно так же, если в задаче ничего особенного не говорится об ускорении, то ускорение, вероятно, просто гравитационное, a = g = 9,8 м/с 2 .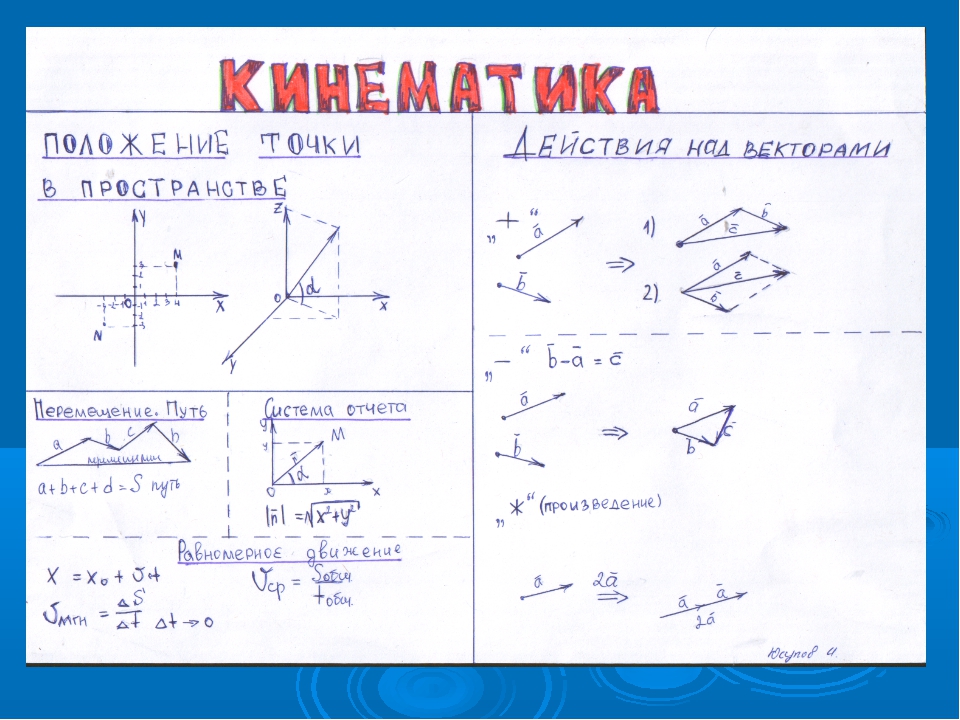 Эти скрытые количества так же действительны, как и обычные количества, просто их немного сложнее обнаружить.
Эти скрытые количества так же действительны, как и обычные количества, просто их немного сложнее обнаружить.
Особым примером скрытой величины является ситуация, когда вам говорят, что объект находится «на вершине своего полета/движения/траектории/и т. д.». Это означает, что они тайно сообщают вам, что v f равно 0, потому что объект, движущийся в одном измерении, всегда имеет скорость 0 в начале своего пути.Интересно, почему? Что ж, если бы скорость росла, то через миллисекунду объект был бы выше (и, следовательно, он не мог бы находиться в верхней части своего пути). Точно так же, если бы объект имел скорость, направленную вниз, то на миллисекунду раньше она была бы выше (поэтому он не может быть и наверху).
Как избежать распространенных ошибок: положительные и отрицательные числа Может быть сложно отслеживать негативы. Ключ — это направление; вниз всегда отрицательно. Итак, если объект падает, его скорость будет отрицательной.Если ускорение уменьшается (что почти всегда бывает), то ускорение отрицательное. И не забывайте из нашей первой главы, что возможно иметь положительную скорость и отрицательное ускорение одновременно!
Итак, если объект падает, его скорость будет отрицательной.Если ускорение уменьшается (что почти всегда бывает), то ускорение отрицательное. И не забывайте из нашей первой главы, что возможно иметь положительную скорость и отрицательное ускорение одновременно!
Женщина держит мяч на высоте 1 метр и бросает его вверх со скоростью 5 м/с. а) До какой высоты долетит мяч? б) Через какое время мяч упадет на землю? в) С какой скоростью движется мяч в момент удара о землю?
Давайте узнаем!
Часть A: Как высоко поднимается мяч?
Что мы знаем?
Начальное положение x i = 1 м
Начальная скорость v i = 5 м/с
Секретное количество: a = -9.8 м/с 2 (гравитация)
Секретное количество: В верхней части дуги мяча (т. е. когда она самая высокая) v f = 0 м/с
Что мы пытаемся найти?
Положение в верхней части броска, х f
Какое уравнение связывает эти величины?
Мы ищем уравнение, которое включает x f , x i , v f , v i и a
v f 2 = v i . *a*(x f – x i ) отлично подходит!
*a*(x f – x i ) отлично подходит!
Подключи и реши
v f 2 = v i 2 + 2*a*(x f – x i )
(0 м/с) 2 2 + 2*(-9.8 м/с 2 )*(x f – 1м)
0 = 25 (m 2 /с 2 ) – (19,6 м/с 2 )*(x f 900 )
(19,6 м/с 2 )*(x f – 1м) = 25 м 2 /с 2
x f –1м = (25 м 2 900) )/(19,6 м/с 2 )
x f –1 м = 1,28 м
x f = 2,28 м
Тада! Итоговая высота = 2,28 метра
Часть B: Через какое время мяч упадет на землю?
Что мы знаем?
Мы все еще знаем, что x i = 1 м, v i = 5 м/с и a = -9.8 м/с 2 но теперь мы также знаем, что x f = 0 м (поскольку высота земли равна 0 м)
Примечание. Так как мяч теперь находится на земле, а не в верхней части полета, v f ≠ 0, так что он не на столе.
Так как мяч теперь находится на земле, а не в верхней части полета, v f ≠ 0, так что он не на столе.
Что мы пытаемся найти?
Время, т
Какое уравнение связывает эти величины?
Мы ищем уравнение, которое включает x f , x i , v i , a и t
Похоже, нам понадобится x f = x i + v i *t + ½a*t 2
Подключи и реши
x f = x i + v i *t + ½a*t 2
0 м = 1 м + (5 м/с)*t + ½ (-9.8 м/с 2 )* t 2
-(4,9 м/с 2 )* t 2 + (5 м/с)*t + 1 м = 0
Это квадратное уравнение (ax 2 + bx + c = 0) и может быть решено с помощью квадратной формулы.
t =
t =
t = или t =
t = или t =
t = -,17 с или 1,2 с
Мы можем игнорировать t=-.17, потому что нам не разрешено иметь отрицательное время (мы называем это нефизическим ответом), что оставляет нам время = 1,2 секунды!
Часть C: Соберите все вместе.

Что мы знаем?
Мы все еще знаем, что x i = 1 м, v i = 5 м/с, a = -9,8 м/с 2 и x f = 0 м, но теперь мы также знаем t = 1,2 секунды, потому что мы только что решили это.
Что мы пытаемся найти?
Скорость, v f
Какое уравнение связывает эти величины?
У нас так много величин, что мы могли бы использовать любое из уравнений, но давайте возьмем v f — v i = a*t, потому что это просто, и мы еще не использовали его.
Подключи и реши
v f – v i = a*t
v f – 5 м/с = (-9,8 м/с 2 ) * 1,2 с
v f = 5 м/с – 11,8 м/с
v f = -6,8 м/с
Стрела, скорость в момент удара мяча о землю составляет 6,8 м/с вниз (поэтому знак минус).
Уравнения движения. Гиперучебник по физике
Обсуждение
постоянное ускорение
Для точности этот раздел следует назвать «Одномерные уравнения движения при постоянном ускорении». Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки. Эти уравнения движения действительны только тогда, когда ускорение постоянно, а движение ограничено прямой линией.
Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки. Эти уравнения движения действительны только тогда, когда ускорение постоянно, а движение ограничено прямой линией.
Учитывая, что мы живем в трехмерной вселенной, в которой единственной константой являются изменения, у вас может возникнуть соблазн сразу пропустить этот раздел. Было бы правильно сказать, что ни один объект никогда не двигался по прямой с постоянным ускорением где-либо во Вселенной в любое время — ни сегодня, ни вчера, ни завтра, ни пять миллиардов лет назад, ни тридцать миллиардов лет в будущем. , никогда.Это я могу сказать с абсолютной метафизической уверенностью.
Так что же хорошего в этом разделе? Что ж, во многих случаях полезно предположить, что объект двигался или будет двигаться по траектории, которая в основном является прямой, и с почти постоянным ускорением; то есть любое отклонение от идеального движения можно по существу игнорировать. Движение по криволинейной траектории можно считать эффективно одномерным, если для задействованных объектов имеется только одна степень свободы .Дорога может извиваться и поворачивать и исследовать всевозможные направления, но автомобили, движущиеся по ней, имеют только одну степень свободы — свободу двигаться в одном направлении или в противоположном направлении. (Вы не можете ехать по дороге по диагонали и надеяться, что продержитесь на ней долго.) В этом отношении это мало чем отличается от движения, ограниченного прямой линией. Аппроксимация реальных ситуаций моделями, основанными на идеальных ситуациях, не считается мошенничеством. Так дела обстоят в физике. Это настолько полезный метод, что мы будем использовать его снова и снова.
Движение по криволинейной траектории можно считать эффективно одномерным, если для задействованных объектов имеется только одна степень свободы .Дорога может извиваться и поворачивать и исследовать всевозможные направления, но автомобили, движущиеся по ней, имеют только одну степень свободы — свободу двигаться в одном направлении или в противоположном направлении. (Вы не можете ехать по дороге по диагонали и надеяться, что продержитесь на ней долго.) В этом отношении это мало чем отличается от движения, ограниченного прямой линией. Аппроксимация реальных ситуаций моделями, основанными на идеальных ситуациях, не считается мошенничеством. Так дела обстоят в физике. Это настолько полезный метод, что мы будем использовать его снова и снова.
Наша цель в этом разделе состоит в том, чтобы вывести новые уравнения, которые можно использовать для описания движения объекта с точки зрения его трех кинематических переменных: скорости ( v ), положения ( с ) и времени ().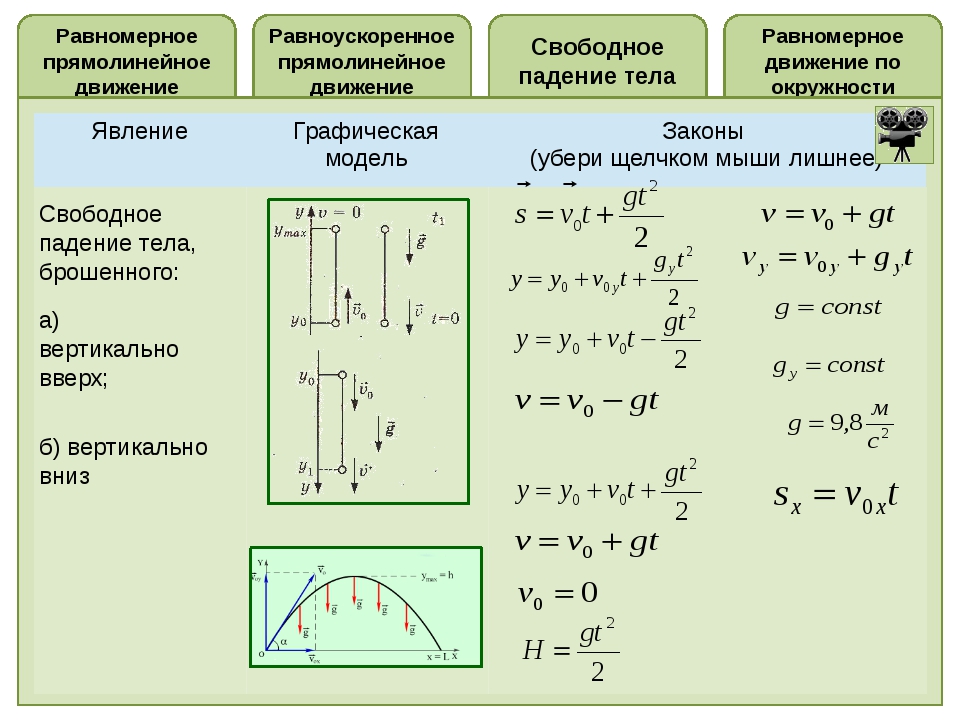 т ). Есть три способа их объединения: скорость-время, положение-время и скорость-положение. В таком порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин учить эти названия.
т ). Есть три способа их объединения: скорость-время, положение-время и скорость-положение. В таком порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин учить эти названия.
Поскольку мы имеем дело с прямолинейным движением, направление будет обозначаться знаком — положительные величины указывают в одну сторону, а отрицательные — в противоположную.Определение того, какое направление является положительным, а какое отрицательным, совершенно произвольно. Законы физики изотропны ; то есть они не зависят от ориентации системы координат. Однако некоторые проблемы легче понять и решить, когда одно направление предпочтительнее другого. Пока вы последовательны в решении проблемы, это не имеет значения.
скорость-время
Связь между скоростью и временем является простой при равноускоренном прямолинейном движении.Чем дольше ускорение, тем больше изменение скорости. Изменение скорости прямо пропорционально времени, если ускорение постоянно. Если скорость увеличивается на определенную величину за определенное время, она должна увеличиться вдвое на эту величину за удвоенное время. Если объект уже стартовал с определенной скоростью, то его новая скорость будет равна старой скорости плюс это изменение. Вы уже должны уметь видеть уравнение мысленным взором.
Если скорость увеличивается на определенную величину за определенное время, она должна увеличиться вдвое на эту величину за удвоенное время. Если объект уже стартовал с определенной скоростью, то его новая скорость будет равна старой скорости плюс это изменение. Вы уже должны уметь видеть уравнение мысленным взором.
Это самое простое из трех уравнений, которое можно вывести с помощью алгебры.Начните с определения ускорения.
Развернуть ∆ v до v − v 0 и сжать ∆ t до t .
Затем найдите v как функцию t .
v = v 0 + в [1]
Это первое уравнение движения . Он записывается как полином — постоянный член ( v 0 ), за которым следует член первого порядка ( на ).Поскольку высший порядок равен 1, правильнее называть его -линейной -функцией.
Символ v 0 [vee nought] называется начальной скоростью или скоростью a time t = 0. Ее часто считают «первой скоростью», но это довольно наивный способ Опишите это. Лучшим определением было бы сказать, что начальная скорость — это скорость, которую имеет движущийся объект, когда он впервые становится важным в задаче. Скажем, метеор был замечен глубоко в космосе, и задача состояла в том, чтобы определить его траекторию, тогда начальная скорость, вероятно, была бы скоростью, которую он имел при первом наблюдении.Но если проблема заключалась в том, что тот же самый метеор сгорает при входе в атмосферу, то начальная скорость, вероятно, будет равна скорости, с которой он вошел в атмосферу Земли. Ответ на вопрос «Какова начальная скорость?» это «это зависит». Оказывается, это ответ на многие вопросы.
Ее часто считают «первой скоростью», но это довольно наивный способ Опишите это. Лучшим определением было бы сказать, что начальная скорость — это скорость, которую имеет движущийся объект, когда он впервые становится важным в задаче. Скажем, метеор был замечен глубоко в космосе, и задача состояла в том, чтобы определить его траекторию, тогда начальная скорость, вероятно, была бы скоростью, которую он имел при первом наблюдении.Но если проблема заключалась в том, что тот же самый метеор сгорает при входе в атмосферу, то начальная скорость, вероятно, будет равна скорости, с которой он вошел в атмосферу Земли. Ответ на вопрос «Какова начальная скорость?» это «это зависит». Оказывается, это ответ на многие вопросы.
Символ v — это скорость через некоторое время t после начальной скорости. Ее часто называют конечной скоростью , но это не делает ее «последней скоростью» объекта. Возьмем случай с метеором.Какая скорость представлена символом v ? Если вы были внимательны, то должны были предвидеть ответ. По-разному. Это может быть скорость метеора при прохождении мимо Луны, при входе в атмосферу Земли или при ударе о поверхность Земли. Это также может быть скорость метеорита, когда он находится на дне кратера. (В этом случае v = 0 м/с.) Является ли какая-либо из этих скоростей конечной скоростью? Кто знает. Кто-то мог извлечь метеорит из отверстия в земле и увезти его с собой.Это актуально? Вероятно, нет, но это зависит. Для такого рода вещей нет правил. Вы должны разобрать текст задачи на наличие физических величин, а затем присвоить значение математическим символам.
По-разному. Это может быть скорость метеора при прохождении мимо Луны, при входе в атмосферу Земли или при ударе о поверхность Земли. Это также может быть скорость метеорита, когда он находится на дне кратера. (В этом случае v = 0 м/с.) Является ли какая-либо из этих скоростей конечной скоростью? Кто знает. Кто-то мог извлечь метеорит из отверстия в земле и увезти его с собой.Это актуально? Вероятно, нет, но это зависит. Для такого рода вещей нет правил. Вы должны разобрать текст задачи на наличие физических величин, а затем присвоить значение математическим символам.
Последняя часть этого уравнения по представляет собой изменение скорости по сравнению с начальным значением. Напомним, что 90 261 а 90 266 — скорость изменения скорости, а 90 261 t 90 266 — время после некоторого начального события 90 955 . Скорость раз время меняется. Если объект движется с ускорением 10 м/с 2 , через 5 с он будет двигаться на 50 м/с быстрее.Если бы он стартовал со скоростью 15 м/с, то его скорость через 5 с была бы…
15 м/с + 50 м/с = 65 м/с
позиция-время
Перемещение движущегося объекта прямо пропорционально скорости и времени. Двигайся быстрее. Иди дальше. Двигайтесь дольше (как в более длительное время). Иди дальше. Ускорение усложняет эту простую ситуацию, поскольку теперь скорость также прямо пропорциональна времени. Попробуйте сказать это словами, и это прозвучит смешно. «Перемещение прямо пропорционально времени и прямо пропорционально скорости, которая прямо пропорциональна времени.» Время — это удвоенный множитель, поэтому перемещение пропорционально квадрату времени. Автомобиль, ускоряющийся в течение двух секунд, преодолеет в четыре раза большее расстояние, чем автомобиль, ускоряющийся всего за одну секунду (2 2 = 4). Автомобиль, ускоряющийся за три секунд преодолели бы в девять раз большее расстояние (3 2 = 9).
Двигайся быстрее. Иди дальше. Двигайтесь дольше (как в более длительное время). Иди дальше. Ускорение усложняет эту простую ситуацию, поскольку теперь скорость также прямо пропорциональна времени. Попробуйте сказать это словами, и это прозвучит смешно. «Перемещение прямо пропорционально времени и прямо пропорционально скорости, которая прямо пропорциональна времени.» Время — это удвоенный множитель, поэтому перемещение пропорционально квадрату времени. Автомобиль, ускоряющийся в течение двух секунд, преодолеет в четыре раза большее расстояние, чем автомобиль, ускоряющийся всего за одну секунду (2 2 = 4). Автомобиль, ускоряющийся за три секунд преодолели бы в девять раз большее расстояние (3 2 = 9).
Если бы это было так просто. Этот пример работает только тогда, когда начальная скорость равна нулю. Перемещение пропорционально квадрату времени, когда ускорение постоянно, а начальная скорость равна нулю.Правильное общее утверждение должно было бы учитывать любую начальную скорость и то, как скорость изменялась. Это приводит к ужасно беспорядочному заявлению о пропорциональности. Смещение прямо пропорционально времени и пропорционально квадрату времени при постоянном ускорении. Функция, которая является одновременно линейной и квадратичной, называется квадратичной , что позволяет нам значительно сжать предыдущее утверждение. Перемещение является квадратичной функцией времени при постоянном ускорении
Это приводит к ужасно беспорядочному заявлению о пропорциональности. Смещение прямо пропорционально времени и пропорционально квадрату времени при постоянном ускорении. Функция, которая является одновременно линейной и квадратичной, называется квадратичной , что позволяет нам значительно сжать предыдущее утверждение. Перемещение является квадратичной функцией времени при постоянном ускорении
Заявления о пропорциональности полезны, но не так универсальны, как уравнения.Мы до сих пор не знаем, каковы константы пропорциональности для этой задачи. Один из способов выяснить их — использовать алгебру.
Начните с определения средней скорости.
Развернуть ∆ s до s − s 0 и сжать ∆ t до t .
Найдите положение.
с = с 0 + вт [а]
Чтобы продолжить, нам нужно прибегнуть к небольшому трюку, известному как теорема о средней скорости или правило Мертона . Я предпочитаю последнее, поскольку это правило можно применить к любой величине, изменяющейся с одинаковой скоростью, а не только к скорости. Правило Мертона было впервые опубликовано в 1335 году в Мертон-колледже в Оксфорде английским философом, математиком, логиком и вычислителем Уильямом Хейтсбери (1313–1372). Когда скорость изменения величины постоянна, ее среднее значение находится посередине между конечным и начальным значениями.
Я предпочитаю последнее, поскольку это правило можно применить к любой величине, изменяющейся с одинаковой скоростью, а не только к скорости. Правило Мертона было впервые опубликовано в 1335 году в Мертон-колледже в Оксфорде английским философом, математиком, логиком и вычислителем Уильямом Хейтсбери (1313–1372). Когда скорость изменения величины постоянна, ее среднее значение находится посередине между конечным и начальным значениями.
v = ½( v + v 0 ) [4]
Подставьте первое уравнение движения [1] в это уравнение [4] и упростите, чтобы исключить v .
| V = ½ [( V 0 + на ) + V 0 ] V = ½ (2 V 0 + в ) v = v 0 + ½ в [b] |
Теперь замените [b] на [a], чтобы исключить и [клиновидную черту].
s = s 0 + ( v 0 + ½ в ) t
И, наконец, найдите s как функцию t .
с = с 0 + v 0 t + ½ в 2 3 [0 ]
Это второе уравнение движения . Он записывается как многочлен — постоянный член ( s 0 ), за которым следует член первого порядка ( v 0 t ), за которым следует член второго порядка (½ в 6 2 2 ) ). Поскольку старший порядок равен 2, правильнее называть его квадратичным .
Символ s 0 [эсс ноль] часто рассматривается как начальная позиция . Символ s — это позиция через некоторое время t . Вы можете назвать это конечной позицией , если хотите. Изменение положения (∆ s ) называется перемещением или расстоянием (в зависимости от обстоятельств), и некоторые люди предпочитают писать второе уравнение движения так.
∆ s = v 0 t + ½ в 2 [2]
скорость-позиция
Первые два уравнения движения описывают одну кинематическую переменную как функцию времени. По сути…
По сути…
- Скорость прямо пропорциональна времени при постоянном ускорении ( v ∝ t ).
- Перемещение пропорционально квадрату времени при постоянном ускорении (∆ с ∝ t 2 ).
Объединение этих двух утверждений приводит к третьему — тому, что не зависит от времени. Подстановкой должно быть очевидно, что…
- Перемещение пропорционально квадрату скорости при постоянном ускорении (∆ с ∝ v 2 ).
Это утверждение особенно важно для безопасности вождения. Когда вы удваиваете скорость автомобиля, вам потребуется в четыре раза больше расстояния, чтобы его остановить. Утройте скорость, и вам понадобится в девять раз больше расстояния. Это хорошее практическое правило, которое следует запомнить.
Концептуальное введение завершено. Пришло время вывести формальное уравнение.
метод 1
Объедините первые два уравнения вместе таким образом, чтобы исключить время как переменную. Самый простой способ сделать это — начать с первого уравнения движения…
Самый простой способ сделать это — начать с первого уравнения движения…
v = v 0 + в [1]
решить на время…
и затем подставляем во второе уравнение движения…
с = с 0 + v 0 t + ½ в 2 3 [0 ]
вот так…
| с = | с 0 + v 0 | ⎛ ⎜ ⎝ | v − v 0 | ⎞ ⎟ ⎠ | + ½ и | ⎛ ⎜ ⎝ | v − v 0 | ⎞ 2 ⎟ ⎠ |
| и | и |
| с — с 0 = | vv 0 — v 0 2 | + | v 2 — 2 vv 0 + v 0 2 |
| и | 2 и |
| 2 | 2 A ( S — S 0 ) = 2 ( VV 0 — V 0 2 ) + ( V 2 — 2 vv 0 + v 0 2 ) | |
| 2 | 2 A ( S — S 0 ) = V 2 — V 0 2 | |
Сделайте квадрат скорости объекта, и все готово.
V 2 = V = V 0 2 + 2 A ( S — S 0 ) [3]
Это третье уравнение движения . Еще раз, символ s 0 [ess nought] – это начальная позиция , а s – позиция через какое-то время от до . Если хотите, вы можете написать уравнение, используя ∆ s — изменение положения , смещение или расстояние в зависимости от ситуации.
v 2 = v 0 2 + 2 a ∆ с [3]
метод 2
Более сложный способ вывести это уравнение — начать со второго уравнения движения в такой форме…
∆ s = v 0 t + ½ в 2 [2]
и решить его на время. Это непростая задача, так как уравнение квадратное. Переставьте термины вот так…
½ в 2 + v 0 t − ∆ s = 0
и сравните его с общей формой квадратного числа.
ax 2 + bx + c = 0
Решения этого уравнения дает знаменитое уравнение…
| x = | − b ± √( b 2 − 4 ac ) |
| 2 а |
Замените символы в общем уравнении эквивалентными символами из нашего перестроенного второго уравнения движения…
| т = | − v 0 ± √[ v 0 2 — 4(½ a )(-∆ с 8 ) |
| 2(½ и ) |
немного почистить…
| т = | − v 0 ± √( v 0 2 + 2 a ∆ s ) |
| и |
и подставить обратно в первое уравнение движения.
v = v 0 + в [1]
| v = v 0 + a | ⎛ ⎜ ⎝ | − v 0 ± √( v 0 2 + 2 a ∆ s ) | ⎞ ⎟ ⎠ |
| и |
Вещи отменяются, и мы получаем это…
v = ±√( v 0 2 + 2 a ∆ s )
Подровняйте обе стороны и готово.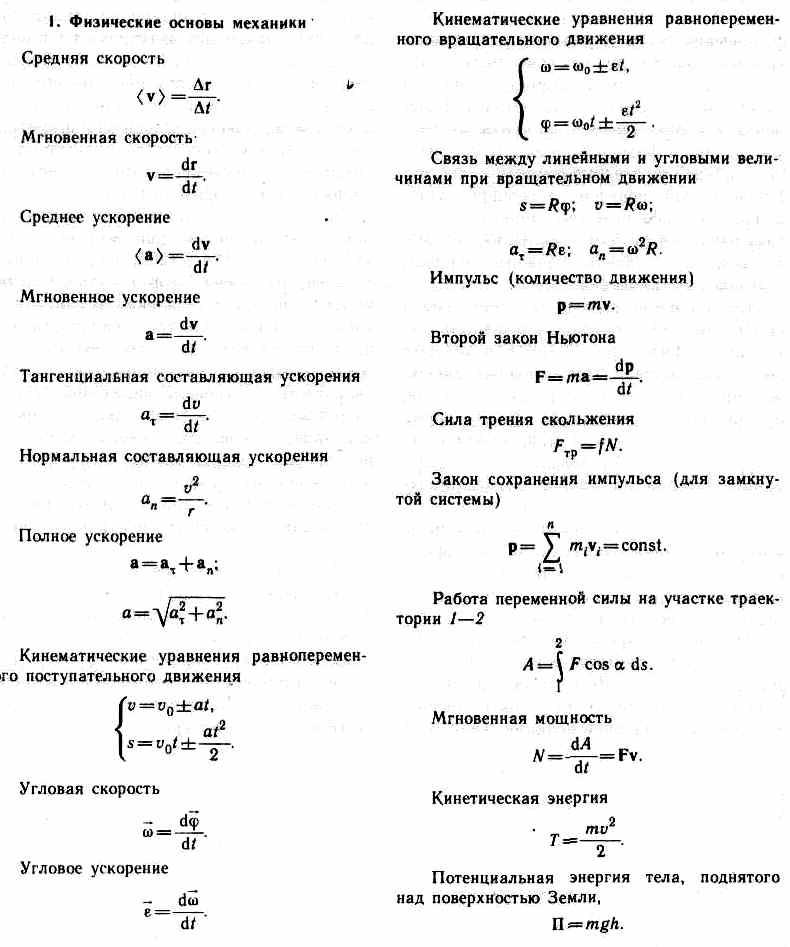
v 2 = v 0 2 + 2 a ∆ с [3]
Теперь это было не так уж плохо, не так ли?
математические выводы
Исчисление — сложная математическая тема, но оно значительно упрощает вывод двух из трех уравнений движения. По определению ускорение есть первая производная скорости по времени. Возьмите операцию в этом определении и отмените ее. Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость.Это дает нам уравнение скорость-время. Если предположить, что ускорение постоянно, мы получим так называемое первое уравнение движения [1].
| и | = | ||
| дв | = | а дт | |
| = | |||
| v − − v 0 | = | по телефону | |
| против | = | v 0 + в [1] | |
Опять же, по определению, скорость есть первая производная положения по времени. Отменить эту операцию. Вместо того, чтобы дифференцировать положение, чтобы найти скорость, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положение-время для постоянного ускорения, также известное как второе уравнение движения [2].
Отменить эту операцию. Вместо того, чтобы дифференцировать положение, чтобы найти скорость, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положение-время для постоянного ускорения, также известное как второе уравнение движения [2].
| против | = | |||||||||
| дс | = | v dt | ||||||||
| дс | = | ( v 0 + в ) dt | ||||||||
| = |
| |||||||||
| с — с 0 | = | v 0 t + ½ в 2 | ||||||||
| с | = | s 0 + v 0 t + ½ в 2 [2] | ||||||||
В отличие от первого и второго уравнений движения, нет очевидного способа вывести третье уравнение движения (которое связывает скорость с положением) с помощью вычислений. Мы не можем просто реконструировать это из определения. Нам нужно сыграть довольно изощренный трюк.
Мы не можем просто реконструировать это из определения. Нам нужно сыграть довольно изощренный трюк.
Первое уравнение движения связывает скорость со временем. По сути, мы вывели его из этой производной…
Второе уравнение движения связывает положение со временем. Оно произошло от этой производной…
Третье уравнение движения связывает скорость с положением. По логике это должно происходить от производной, которая выглядит так…
Но чему это равно? Ну ничего по определению, но, как и все величины, оно равно самому себе.Это также равно самому себе, умноженному на 1. Мы будем использовать специальную версию 1 ( dt dt ) и специальную версию алгебры (алгебра с бесконечно малыми). Посмотрите, что происходит, когда мы это делаем. Получаем одну производную, равную ускорению ( dv dt ) и другую производную, обратную скорости ( dt ds 9026 )
| дв | = | дв | 1 | |
| дс | дс | |||
| дв | = | дв | дт | |
| дс | дс | дт | ||
| дв | = | дв | дт | |
| дс | дт | дс | ||
| дв | = | и | 1 | |
| дс | против |
Следующий шаг, разделение переменных. Соберите похожие вещи и интегрируйте их. Вот что мы получаем при постоянном ускорении…
Соберите похожие вещи и интегрируйте их. Вот что мы получаем при постоянном ускорении…
| = | ||||
| в дв | = | и | ||
| = | ||||
| ½( v 2 — v 0 2 ) | = | a ( с — с 0 ) | ||
| v 2 | = | v 0 2 + 2 a ( s − s 0 ) [3] | ||
Определенно умное решение, и оно было не намного сложнее, чем первые два вывода. Однако на самом деле это работало только потому, что ускорение было постоянным — постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно сложным. Мы бы вернулись к использованию алгебры только для того, чтобы сохранить рассудок. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сохранить.
Однако на самом деле это работало только потому, что ускорение было постоянным — постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно сложным. Мы бы вернулись к использованию алгебры только для того, чтобы сохранить рассудок. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сохранить.
| v = | v 0 + в | [1] |
| + | ||
| с = | s 0 + v 0 t + ½ в 2 | [2] |
| = | ||
| v 2 = | v 0 2 + 2 a ( с — с 0 ) | [3] |
Уравнения кинематики, движения, перемещения, скорости, ускорения Множественный выбор ответов 11 класс Физика
Этот продукт содержит 17 страниц вопросов по физике с несколькими вариантами ответов на использование кинематических уравнений для определения расстояния, смещения, скорости, ускорения скорости или времени. Существуют проблемы с постоянным линейным ускорением и гравитационные проблемы. Эти вопросы с несколькими вариантами ответов подходят для тестов или викторин по физике для 11 класса.
Существуют проблемы с постоянным линейным ускорением и гравитационные проблемы. Эти вопросы с несколькими вариантами ответов подходят для тестов или викторин по физике для 11 класса.
Все вопросы с несколькими вариантами ответов набраны шрифтом 12, Times New Roman, без текстовых полей и сжаты до минимально возможного места. Все вопросы с несколькими вариантами ответов, вопросы с краткими ответами, Power Points, рабочие листы, викторины, лабораторные работы и тесты, которые я публикую, правильно отформатированы и готовы к печати. Они были проверены на ошибки и опечатки!
Меня зовут Даррин Мэтьюсон, и у меня есть докторская степень в области органической химии.Преподаю физику и химию более 15 лет.
В моем магазине продается более 140 баллов Power Points, 40 комплектов рабочих листов, 100 комплектов тестов, 100 комплектов с несколькими вариантами ответов и 70 комплектов с краткими ответами. У меня есть Power Points, тесты, викторины, вопросы с несколькими вариантами ответов, вопросы с краткими ответами и рабочие листы для каждой темы, охватываемой естественными науками для 10 класса, химией для 11 класса, физикой для 11 класса и химией для 12 класса!
ПОИСК ПО КЛЮЧЕВЫМ СЛОВАМ ДЛЯ НАВИГАЦИИ ПО МОЕМУ МАГАЗИНУ:
введите «11 класс по физике», чтобы просмотреть 11 класс по физике
введите «11 класс по химии», просмотрите 11 баллов по химии 10 очков силы науки», чтобы просмотреть очки силы науки 10 классавведите «тестовый пакет по физике для 11 класса» для просмотра тестов по физике для 11 класса
введите «тестовый пакет для 11 класса по химии» для просмотра тестов по химии для 11 класса естествознание для 10 класса», чтобы просмотреть тесты по естествознанию для 10 классавведите «worksheets 11 класс физика» чтобы посмотреть 11 класс физика
введите «worksheet 11 класс химия» чтобы посмотреть 11 класс химия
введите «worksheet 12 класс химия» чтобы посмотреть 12 класс химия
введите «worksheet 10 класс естествознание» просмотреть рабочие листы по естествознанию для 10 классавведите «краткий ответ по физике для 11 класса» чтобы просмотреть краткий ответ по физике для 11 класса
введите «краткий ответ по химии для 11 класса» посмотрите краткий ответ по химии для 11 класса ответить на 10 класс по науке», чтобы просмотреть краткий ответ 10 класса по наукетип «множественный выбор 11 класс физика» просмотреть 11 класс физика множественный выбор
тип «множественный выбор 10 класс естествознание» просмотреть 10 класс естествознание множественный выбор
тип «множественный выбор 11 класс химия» просмотреть 11 класс химия множественный
выбор
тип « множественный выбор химия 12 класс” посмотреть химию 12 класс множественный
выбор
IB Заметки по физике — 2.
 1 Кинематика
1 Кинематика Смещение
Смещение — это расстояние, пройденное в определенном направлении. Это векторная величина.
Единица СИ: м
Символ: с
Скорость
Скорость — скорость изменения смещения. Это векторная величина.
Скорость = (изменение смещения / изменение во времени)
Единица СИ: мс -1
Обозначение: v или u
Скорость
Скорость — это скорость изменения расстояния.Это скалярная величина.
Скорость = (изменение расстояния / изменение времени)
Единица СИ: мс -1
Обозначение: v или u
Обратите внимание, что скорость и скорость — это не одно и то же. Скорость имеет направление.
Скорость имеет направление.
Ускорение
Ускорение — это скорость изменения скорости. Это векторная величина.
Ускорение = (изменение скорости/изменение во времени)
Единица СИ: мс -2
Обозначение: a
Обратите внимание, что ускорение — это любое изменение скорости, то есть увеличение или уменьшение скорости или изменение направления.
Мгновенное
Мгновенное значение скорости, скорости или ускорения – это значение в определенный момент времени.
Среднее
Среднее значение скорости, скорости или ускорения — это значение, полученное за определенный период времени.
Уравнения равноускоренного движения могут быть только в условиях, когда ускорение постоянно.
Уравнения равноускоренного движения имеют вид:
| Переменная | Символ |
| т | затраченное время |
| с | пройденное расстояние |
| и | начальная скорость |
| против | конечная скорость |
| и | ускорение |
Таблица 1.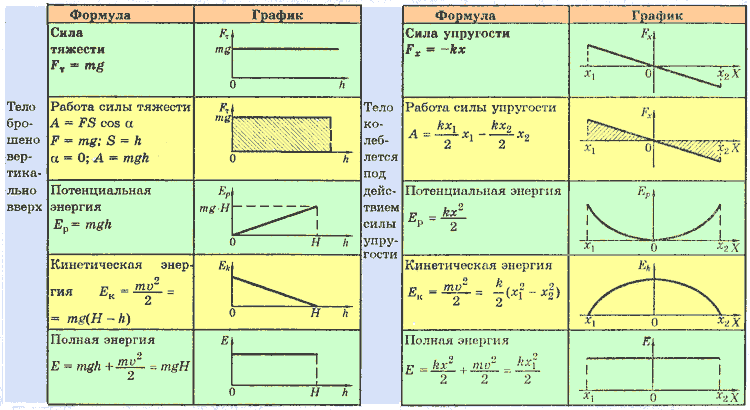 2.1 — Переменные, используемые в уравнениях равномерно ускоренного движения
2.1 — Переменные, используемые в уравнениях равномерно ускоренного движения
Другие уравнения могут быть получены из этих уравнений.
Когда мы игнорируем влияние сопротивления воздуха на объект, падающий на землю под действием силы тяжести, мы говорим, что объект находится в свободном падении. Свободное падение является примером равномерно ускоренного движения, поскольку единственная сила, действующая на объект, — это сила тяжести.
На поверхности земли ускорение объекта в свободном падении составляет около 9,81 мс -1 .Мы можем легко распознать равномерное ускорение на графиках перемещение-время, скорость-время и ускорение-время, как показано ниже:
Автомобиль равномерно ускоряется из состояния покоя. За 10 с он прошел 200 м.
Рассчитать:
Среднее ускорение
S = ut + 1/2 at²
200 = 0 x 10 + 1/2 x a x 10²
200 = 50а
а = 4 м с-2
Мгновенная скорость через 10 с
v² = u² + 2 как
= 0 + 2 х 4 х 10
= 80
В= 8.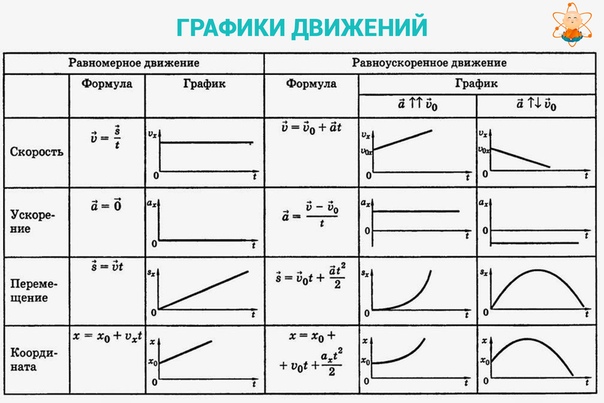 9 мс -1
9 мс -1
Сопротивление воздуха влияет на все движущиеся объекты. За счет эффекта сопротивления воздуха объекты могут достигать предельной скорости. Это точка, в которой скорость остается постоянной, а ускорение равно нулю.
При отсутствии сопротивления воздуха все объекты имеют одинаковое ускорение независимо от их массы.
Определение его скорости
Мы знаем, что градиент графика перемещение-время дает нам его скорость.Поэтому за первые 5 секунд скорость:
25/5 = 5 мс?¹
После первых 5 секунд объект неподвижен в течение 3 секунд. Для этих 3 с его скорость равна нулю.
Через 8 секунд объект начинает возвращаться с большей скоростью, чем раньше. Из графика находим скорость:
25/2 = 12,5 мс?¹
Рисунок 2.1.5 – График скорость-время
Определите его ускорение
Мы знаем, что градиент графика скорость-время дает нам его ускорение. Следовательно, за первые 5 с ускорение равно:
Следовательно, за первые 5 с ускорение равно:
50/5 =10 мс²
Когда объект движется с постоянной скоростью от 5 до 7 с, его ускорение равно нулю. В последнюю секунду пути объект замедляется на:
50/1 = 50 мс²
Определите его смещение
Площадь под графиком скорость-время представляет собой смещение. За первые 5 с объект прошел:
½ x 5 x 50 = 125 м
Определите изменение скорости
Площадь под графиком ускорение-время дает нам изменение скорости
Из графика находим, что изменение скорости составляет 10 x 3 = 30 мс?¹
Примечание. Градиент графика ускорение-время фактически представляет собой скорость изменения ускорения.Однако это не часто полезно.
Кинематика в двух измерениях
Представьте себе шар, катящийся по горизонтальной поверхности, освещенной стробоскопическим светом. На рис. (а) показано положение мяча через равные промежутки времени вдоль пунктирной траектории. Случай 1 показан в позициях с 1 по 3; величина и направление скорости не меняются (картинки расположены равномерно и по прямой линии), а значит, и ускорения нет.Случай 2 указан для позиций с 3 по 5; мяч имеет постоянную скорость, но меняет направление, поэтому существует ускорение. Рисунок (b) иллюстрирует вычитание v 3 и v 4 и результирующее ускорение по направлению к центру дуги. Случай 3 происходит с позиций с 5 по 7; направление скорости постоянно, но величина меняется. Ускорение на этом участке пути соответствует направлению движения. Мяч изгибается из положения 7 в положение 9, показывая случай 4; скорость меняет как направление, так и величину.В этом случае ускорение направлено почти вверх между 7 и 8 и имеет составляющую к центру дуги из-за изменения направления скорости и составляющую вдоль траектории из-за изменения величины скорости.
Случай 1 показан в позициях с 1 по 3; величина и направление скорости не меняются (картинки расположены равномерно и по прямой линии), а значит, и ускорения нет.Случай 2 указан для позиций с 3 по 5; мяч имеет постоянную скорость, но меняет направление, поэтому существует ускорение. Рисунок (b) иллюстрирует вычитание v 3 и v 4 и результирующее ускорение по направлению к центру дуги. Случай 3 происходит с позиций с 5 по 7; направление скорости постоянно, но величина меняется. Ускорение на этом участке пути соответствует направлению движения. Мяч изгибается из положения 7 в положение 9, показывая случай 4; скорость меняет как направление, так и величину.В этом случае ускорение направлено почти вверх между 7 и 8 и имеет составляющую к центру дуги из-за изменения направления скорости и составляющую вдоль траектории из-за изменения величины скорости.
Рисунок 7
(а) Путь мяча на столе. (b) Ускорение между точками 3 и 4.
Любой, кто наблюдал брошенный объект, например, бейсбольный мяч в полете, наблюдал движение снаряда . Для анализа этого распространенного типа движения делаются три основных предположения: (1) ускорение свободного падения постоянно и направлено вниз, (2) влияние сопротивления воздуха незначительно и (3) поверхность земли неподвижна. плоскости (то есть кривизна земной поверхности и вращение Земли пренебрежимо малы).
Для анализа этого распространенного типа движения делаются три основных предположения: (1) ускорение свободного падения постоянно и направлено вниз, (2) влияние сопротивления воздуха незначительно и (3) поверхность земли неподвижна. плоскости (то есть кривизна земной поверхности и вращение Земли пренебрежимо малы).
Для анализа движения разделите двухмерное движение на вертикальную и горизонтальную составляющие. Вертикально объект подвергается постоянному ускорению за счет силы тяжести.Горизонтально объект не испытывает ускорения и, следовательно, сохраняет постоянную скорость. Эта скорость показана на рисунке, где компоненты скорости изменяются в направлении y ; однако все они имеют одинаковую длину в направлении x (постоянная). Обратите внимание, что вектор скорости изменяется со временем из-за того, что меняется вертикальная составляющая.
Рисунок 8
Движение снаряда.
В этом примере частица покидает начало координат с начальной скоростью ( v o ) вверх под углом θ o . Оригинальный x И y компоненты скорости даны V
Оригинальный x И y компоненты скорости даны V
1 x0 = O и V и V
1 y0 = V O sin θ или .
Разделив движения на компоненты, можно проанализировать величины в направлениях x и y с помощью одномерных уравнений движения, индексированных для каждого направления: для горизонтального направления v x = v x0 и x = v x0 t ; Для вертикального направления, V Y = V Y0 — GT и Y = V
1 Y0 — (1/2) GT 2 , где х и y представляют расстояния в горизонтальном и вертикальном направлениях соответственно, а ускорение свободного падения (g ) равно 9. 8 м/с 2 . (Знак «минус» уже включен в уравнения.) Если объект выстреливается под углом, составляющая y начальной скорости отрицательна. Скорость снаряда в любой момент можно вычислить по составляющим в этот момент по теореме Пифагора, а направление найти по арктангенсу отношений составляющих:
8 м/с 2 . (Знак «минус» уже включен в уравнения.) Если объект выстреливается под углом, составляющая y начальной скорости отрицательна. Скорость снаряда в любой момент можно вычислить по составляющим в этот момент по теореме Пифагора, а направление найти по арктангенсу отношений составляющих:
Другая информация полезна при решении проблем со снарядами. Рассмотрим пример, показанный на рисунке, где снаряд выстреливается под углом к уровню земли и возвращается на тот же уровень.Время, за которое снаряд достигнет земли из высшей точки, равно времени падения свободно падающего предмета, падающего прямо вниз с той же высоты. Это равенство времени связано с тем, что горизонтальная составляющая начальной скорости снаряда влияет на то, как далеко снаряд перемещается по горизонтали, но не на время полета. Траектории снарядов параболические и, следовательно, симметричные. Также для этого случая объект достигает вершины своего подъема за половину общего времени (T) полета. На вершине подъема вертикальная скорость равна нулю. (Ускорение всегда равно g даже в верхней точке полета.) Эти факты можно использовать для определения дальности полета снаряда или расстояния, пройденного по горизонтали. На максимальной высоте v y = 0 и t = T /2; поэтому уравнение скорости в вертикальном направлении принимает вид 0 = v o sin θ − g T /2 или решение для T , T = (2 v sin θ)/ г .
На вершине подъема вертикальная скорость равна нулю. (Ускорение всегда равно g даже в верхней точке полета.) Эти факты можно использовать для определения дальности полета снаряда или расстояния, пройденного по горизонтали. На максимальной высоте v y = 0 и t = T /2; поэтому уравнение скорости в вертикальном направлении принимает вид 0 = v o sin θ − g T /2 или решение для T , T = (2 v sin θ)/ г .
Подстановка в уравнение горизонтального расстояния дает R = ( v o cos θ) T . Подставьте T в уравнение дальности и используйте тождество тригонометрии sin 2θ = 2 sin θ cos θ, чтобы получить выражение для дальности через начальную скорость и угол движения, R = ( v o 2 / г ) sin 2θ.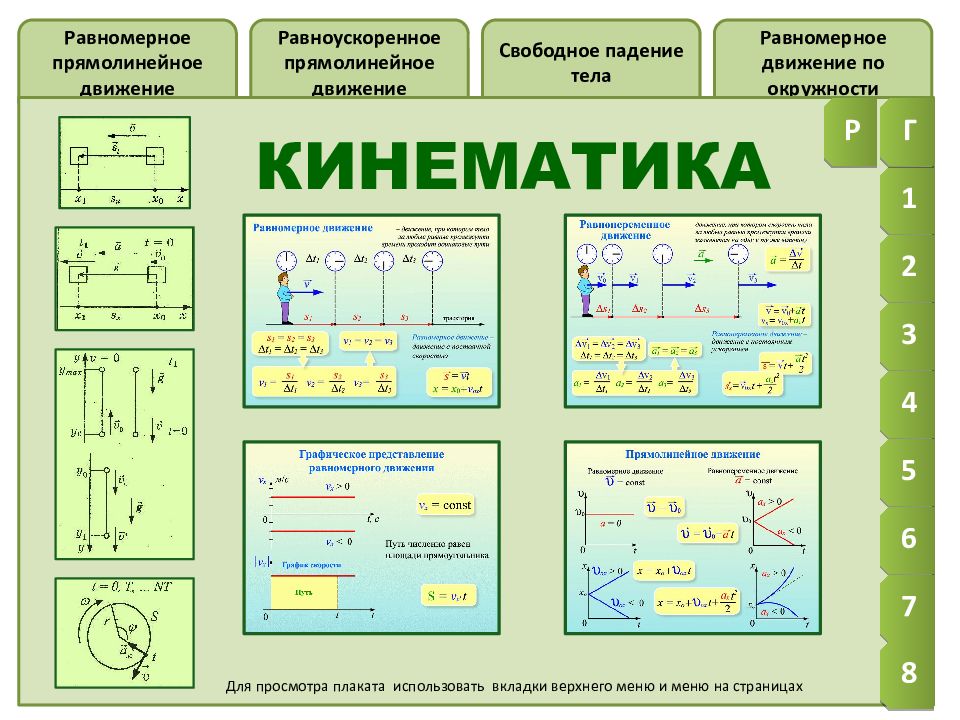 Как видно из этого выражения, максимальная дальность имеет место, когда θ = 45 градусов, потому что при этом значении θ максимальное значение sin 2θ равно 1.На рисунке изображены траектории снарядов, брошенных с одинаковой начальной скоростью под разными углами наклона.
Как видно из этого выражения, максимальная дальность имеет место, когда θ = 45 градусов, потому что при этом значении θ максимальное значение sin 2θ равно 1.На рисунке изображены траектории снарядов, брошенных с одинаковой начальной скоростью под разными углами наклона.
Рисунок 9
Набор снарядов, выпущенных под разными углами.
Для равномерного движения объекта по горизонтальной окружности радиусом (R) постоянная скорость определяется как одна революция.Время одного оборота (T) определяется как период . За один оборот головка вектора скорости описывает окружность окружности 2π v за один период; таким образом, величина ускорения равна a = 2π v / T . Объедините эти два уравнения, чтобы получить два дополнительных соотношения с другими переменными: a = v 2 / R и a = (4π 2 / T 2
2 )9004 Вектор смещения направлен наружу от центра круга движения.



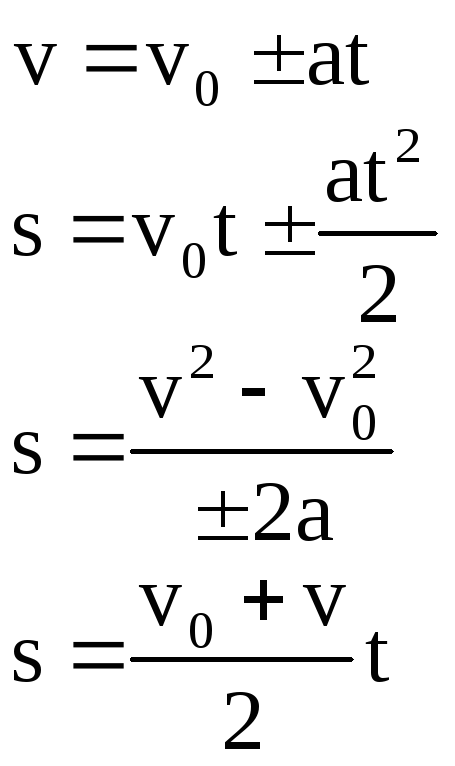

 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2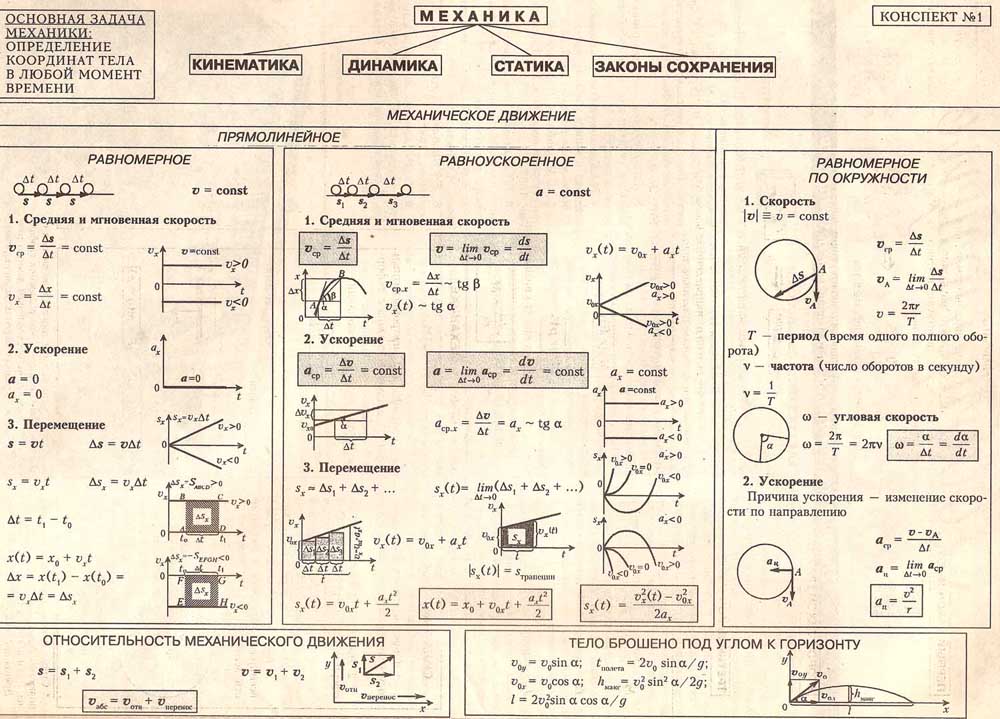 контура T=2π ∙√LC
контура T=2π ∙√LC Сигнальная ракета, запущенная вертикально вверх, вспыхнула через 6 с после запуска в наивысшей точке своей траектории.
На какую высоту поднялась ракета? С какой начальной скоростью ее запустили?
Сигнальная ракета, запущенная вертикально вверх, вспыхнула через 6 с после запуска в наивысшей точке своей траектории.
На какую высоту поднялась ракета? С какой начальной скоростью ее запустили?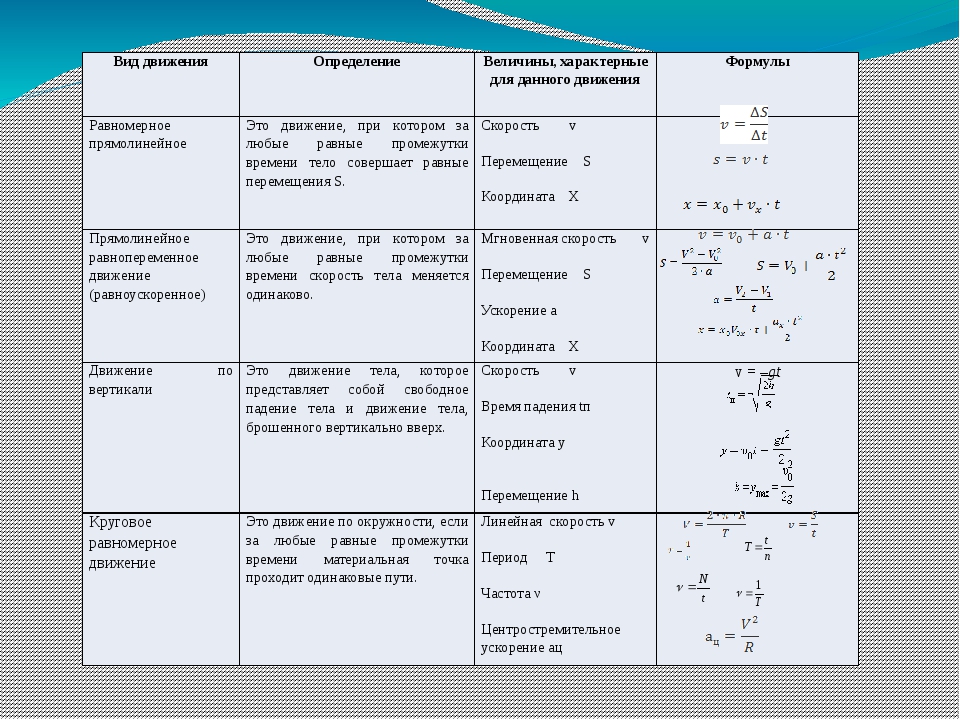 При этом, если возможно, обязательно проставить вектор ускорения.
При этом, если возможно, обязательно проставить вектор ускорения.
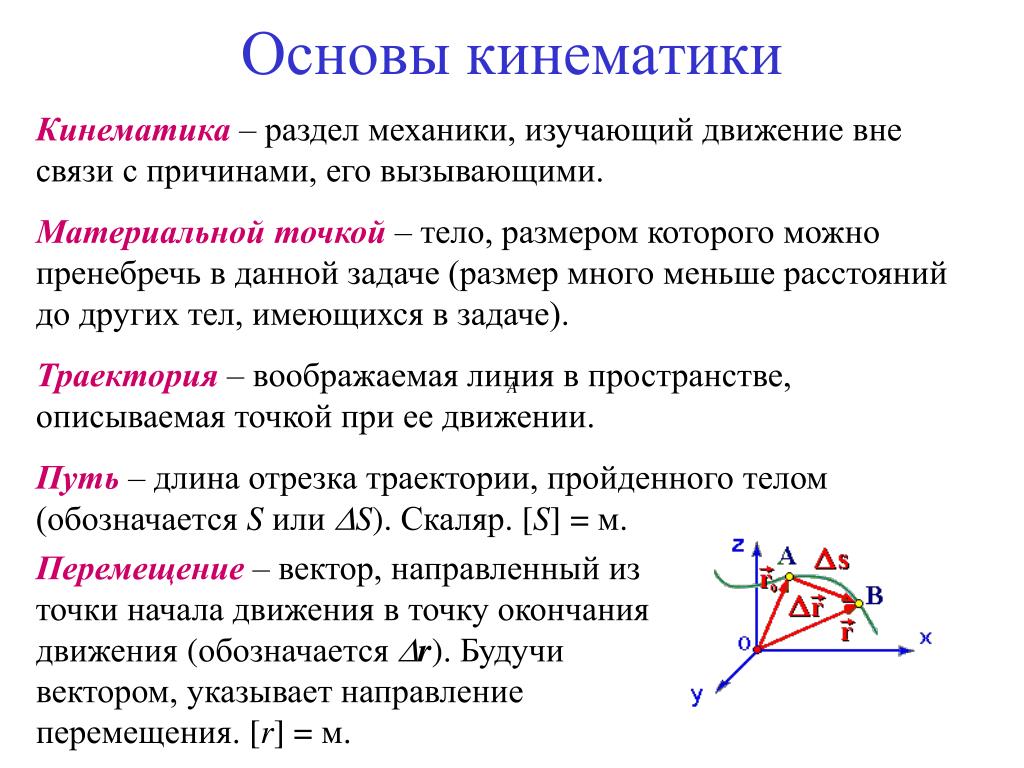 Для этого нужно разложить все силы, приложенные к частице, по линии скорости (касательной к траектории движения — оси ОХ) и по направлению, ей перпендикулярному (нормали к траектории — оси 0Y), найти проекции Fx и Fyсоставляющих сил по этим осям и затем составить основное уравнение динамики точки в проекциях:
Для этого нужно разложить все силы, приложенные к частице, по линии скорости (касательной к траектории движения — оси ОХ) и по направлению, ей перпендикулярному (нормали к траектории — оси 0Y), найти проекции Fx и Fyсоставляющих сил по этим осям и затем составить основное уравнение динамики точки в проекциях: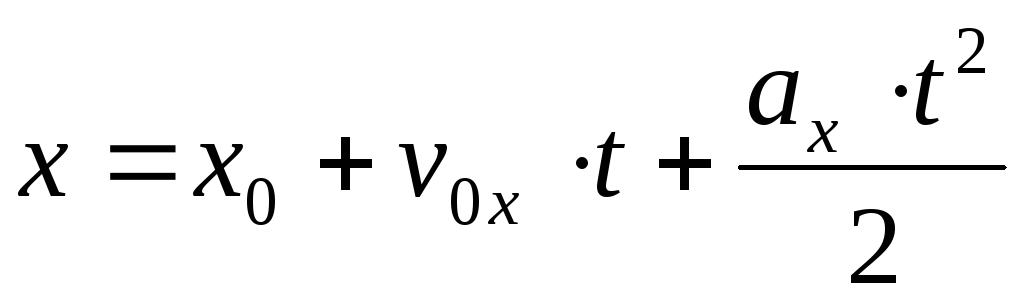
 В задачах динамики, особенно там, где ответ получается в виде сложной формулы, этого правила в начальной стадии обучения желательно придерживаться всегда, поскольку в этих задачах делают много ошибок.
В задачах динамики, особенно там, где ответ получается в виде сложной формулы, этого правила в начальной стадии обучения желательно придерживаться всегда, поскольку в этих задачах делают много ошибок. На опускающегося парашютиста действует сила земного притяжения. Объясните, почему он движется равномерно.
На опускающегося парашютиста действует сила земного притяжения. Объясните, почему он движется равномерно. Определите силу, с которой притягиваются друг к другу два корабля массой по 107 кг каждый, находящиеся на расстоянии 500 м друг от друга.
Определите силу, с которой притягиваются друг к другу два корабля массой по 107 кг каждый, находящиеся на расстоянии 500 м друг от друга.
 Какую скорость приобретает лодка в момент выстрела из двух стволов ружья (дуплетом)? Масса охотника с лодкой и ружьем 80 кг, масса пороха и дроби в одном патроне 40 г, начальная скорость дроби 320 м/с, ствол ружья во время выстрела направлен под углом 60° к горизонту.
Какую скорость приобретает лодка в момент выстрела из двух стволов ружья (дуплетом)? Масса охотника с лодкой и ружьем 80 кг, масса пороха и дроби в одном патроне 40 г, начальная скорость дроби 320 м/с, ствол ружья во время выстрела направлен под углом 60° к горизонту. Автомобиль массой 5000 кг при движении в горной местности поднялся на высоту 400 м над уровнем моря. Определите потенциальную энергию автомобиля относительно уровня моря.
Автомобиль массой 5000 кг при движении в горной местности поднялся на высоту 400 м над уровнем моря. Определите потенциальную энергию автомобиля относительно уровня моря. Масса автомобиля 1250 кг. Сопротивление движению равно 1225 Н. Какую максимальную скорость может развить автомобиль?
Масса автомобиля 1250 кг. Сопротивление движению равно 1225 Н. Какую максимальную скорость может развить автомобиль? спец. уч. заведений М., 1975.
спец. уч. заведений М., 1975.