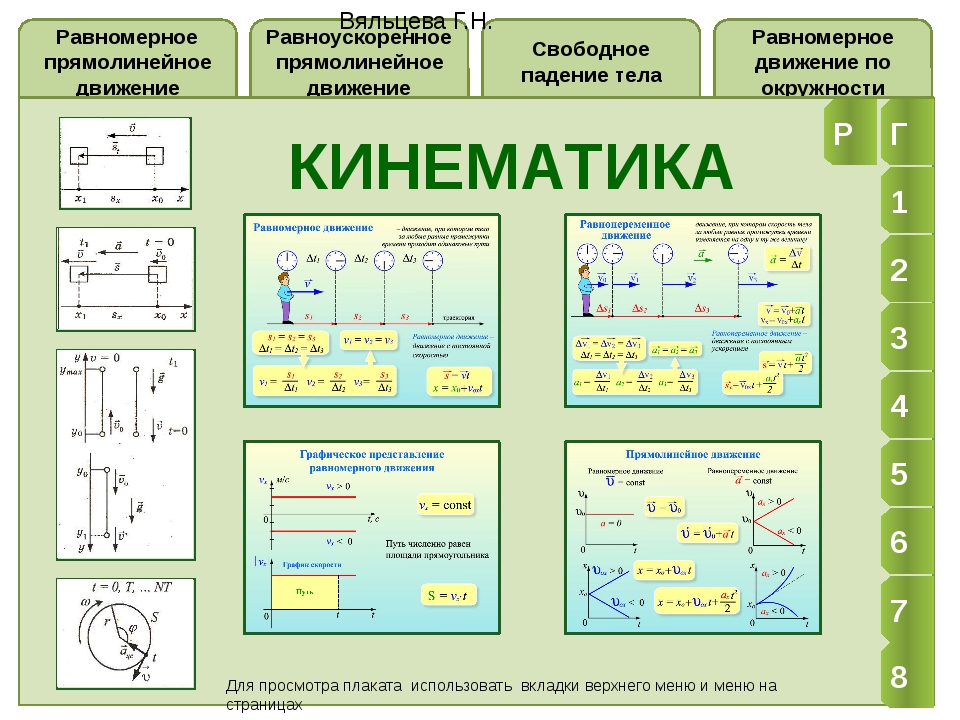
Кинематика. Формулы
Кинематика. Формулы| Номер | Название формулы | Запись формулы | Примечание |
| (1) | Закон равноускоренного криволинейного движения | vS0 — модуль начальной скорости; aS — ускорение | |
| (2) | Скорость равномерного прямолинейного движения | ||
| (3) | Скорость | ||
| (4) | Ускорение | ||
| (5) | Касательное ускорение | dv = dl/dt, т.е. путевая скорость вдоль рассматриваемой траектории | |
| (6) | Нормальное ускорение | ||
| (7) | Скорость свободного падения тела | ||
| (8) | Время тела при свободном падении | ||
| (9) | Время при равномерном движении по окружности | ||
| (10) | Скорость равномерного движения по окружности | ||
| (11) | Угловая (мгновенная) скорость равномерного движения по окружности | Единица измерения угловой скорости — радианы в секунду | |
| (12) | Скорость равноускоренного движения по окружности | ||
| (13) | Угловая (мгновенная) скорость равноускоренного движения по окружности |
— версия для печати
- Определение
- Кинематикой называется раздел физики, занимающийся исследованием законов движения идеальных тел
- Пояснение
- Под чертой вверху буквы подразумевается знак вектора.
Если у вас есть мысли или идеи по поводу данной таблицы или, например, вы считаете, что полезно было бы создать определенную
вспомогательную памятку, то мы обязательно рассмотрим ваше предложение, которое можно изложить по ссылке (где вы также можете поделиться с нами любыми мыслями по поводу сайта scolaire. ru).
Мы готовы устранить любые неудобства, связанные с использованием данной таблицы, или ей подобных, которые можно найти в разделе
«Физика». ru).
Мы готовы устранить любые неудобства, связанные с использованием данной таблицы, или ей подобных, которые можно найти в разделе
«Физика». |
© Школяр. Лингвистика (при поддержке «Ветвистого древа») 2009—2016
Формулы по кинематике, динамике, законам сохранения, молекулярной физике, электричеству, магнетизму, оптике. Тест
Формулы по кинематике, динамике, законам сохранения, молекулярной физике, электричеству, магнетизму, оптике. Тест — курсы по физике Skip navigation- Элементы математики
- действия с векторами
- выражение неизвестной
- Физические величины
- Единицы измерения
- Постоянные величины в физике
- плотность вещества
- предел прочности, модуль Юнга
- скорость звука
- удельная теплота
- диэлектрическая проницаемость
- удельное сопротивление
- электрохимический эквивалент
- Формулы
- I. Механика
- Кинематика
- равномерное движение
- относительность движения
- неравномерное движение
- равноускоренное движение
- ускорение свободного падения
- графики движения
- движение по окружности
- параболическое движение
- Динамика
- закон тяготения
- законы Ньютона
- силы в природе
- равнодействующая сила
- Законы сохранения
- импульс тела, импульс силы
- закон сохранения импульса
- работа и мощность
- кинетическая и потенциальная энергии
- закон сохранения энергии
- Статика
- плечо и момент силы
- условия равновесия
- центр тяжести, центр масс
- Колебания и волны
- колебательное движение
- гармонические колебания
- маятники
- превращение энергии при колебаниях
- упругие волны
- звуковые волны
- II.
 Молекулярная физика
Молекулярная физика - Молекулярная физика
- основные положения мкт
- давление
- основное уравнение мкт, температура
- уравнение идеального газа
- изопроцессы
- свойства жидкостей*
- свойства твердых тел
- Термодинамика
- количество теплоты
- работа, внутренняя энергия
- первый закон термодинамики
- второй закон термодинамики
- тепловые двигатели
- III. Основы электродинамики
- Электричество
- электрический заряд
- закон Кулона
- напряженность поля
- потенциал и работа поля
- диэлектрики, проводники
- электроемкость, конденсаторы
- энергия конденсатора
- Электрический ток
- электрический ток, сила и плотность
- закон Ома для участка цепи
- работа и мощность тока
- закон Ома для замкнутой цепи
- электрический ток в различных средах
- электрические явления
- Магнетизм
- магнитное поле
- сила Ампера
- сила Лоренца
- Электромагнетизм
- магнитный поток
- закон электромагнитной индукции
- самоиндукция, энергия поля
- электромагнитные колебания
- электромагнитные волны
- переменный ток
- трансформатор*
- IV. Оптика
- Волновая оптика
- свет как электромагнитные волны
- интерференция
- дифракция
- Геометрическая оптика
- законы распространения света
- линзы, оптические приборы
- V. Теория относительности
- Теория относительности
- постулаты теории относительности
- VI. Квантовая физика
- Световые кванты
- фотон
- фотоэффект
- квантовые постулаты Бора
- излучение и поглощение света
- Атомное ядро
- энергия связи ядра
- ядерные реакции
- закон радиоактивного распада
- элементарные частицы и их свойства
- Современная физика*
- физика элементарных частиц
- мир внутри атомного ядра
- время расщепляем на мгновения
- нанотехнологии и нанофизика
- вещество в экстремальных состояниях
формулы, определения, методы решения задач
Кинематика — это специальный раздел теоретической механики. Направление сформировалось несколько позднее, чем статика и динамика: во второй половине XIX столетия. Первые исследования в области кинематики были посвящены огнестрельному оружию. Ученые стремились понять процесс полета снаряда, производили расчет траектории его движения. В дальнейшем кинематика как научное направление получило широкое распространение и существенно повлияло на развитие технического прогресса.
Направление сформировалось несколько позднее, чем статика и динамика: во второй половине XIX столетия. Первые исследования в области кинематики были посвящены огнестрельному оружию. Ученые стремились понять процесс полета снаряда, производили расчет траектории его движения. В дальнейшем кинематика как научное направление получило широкое распространение и существенно повлияло на развитие технического прогресса.
Кинематика — описание
Кинематика является разделом механики, цель которого — изучение механического движения тел с пренебрежением к причинам, вызывающим это движение.
Механика представляет собой научную область физики, которой посвящены исследования механического движения тел. Основной целью данного направления служит определение точного положения тела в пространстве в любой момент времени. Важным понятием этого раздела является материальная точка в виде тела с определенной массой и размерами, которыми можно пренебречь для решения задачи при наличии следующих условий:
- Путь, который преодолевает тело, существенно больше, чем его размеры.
- Расстояние между телами значительно превышает их размеры.
- Объект совершает поступательное движение.
Движение тела рассматривают в системе отсчета, состоящей из системы координат и прибора, измеряющего время. Траекторией называют линию, которую объект описывает, совершая движение. Путь является скалярной величиной, определяемой как длина траектории. Перемещением обозначают вектор, который соединяет начальное и конечное положение тела, преодолеваемое им в течение определенного промежутка времени.
Совершая движение, тело может только увеличивать пройденный путь, при этом перемещение увеличивается или уменьшается. К примеру, уменьшение перемещения наблюдается во время обратного движения тела. Если объект движется прямолинейно в одном направлении, то путь определяется модулем перемещения. В случае криволинейного движения — путь превышает перемещение. При рассмотрении замкнутой траектории перемещение будет равно нулю.
При рассмотрении замкнутой траектории перемещение будет равно нулю.
Теория и формулы
Благодаря многолетним исследованиям в области кинематики ученым удалось вывести определенные закономерности движения тела. С помощью справедливых уравнений представляется возможным ответить на многие вопросы о разных характеристиках, которые изменяются либо остаются постоянными во время движения объектов.
Путь, время, скорость
Расстояние представляет собой удаленность одной точки положения тела от другой. Тело преодолевает путь, который представляет собой важную характеристику механического движения. Общепринятым обозначением пути является латинская буква s. Данный параметр измеряют метрами и километрами, если речь идет о больших расстояниях.
Скорость представляет собой путь, который тело преодолело в течение единицы времени. В качестве единицы времени часто используют 1 час, 1 минуту, 1 секунду. Для расчета скорости необходимо определить отношение пути к времени движения. В случае, когда в условиях задачи расстояние измеряется в метрах, а время пути — в секундах, то скорость следует рассчитывать в метрах в секунду (м/с). Для обозначения скорости используют латинскую букву \(v\).
Нередко требуется определить время пути. Данный параметр обозначают с помощью латинской буквы \(t\).
Важно отметить, что скорость, путь и время взаимосвязаны. При известных характеристиках скорости и времени можно определить расстояние, которое преодолело тело. Путь в данном случае равен произведению скорости и времени, рассчитывается по формуле:
\(s=v\times t\)
При известных величинах времени и расстояния достаточно просто определить скорость движения тела, руководствуясь следующим уравнением:
\(v=\frac{s}{t}\)
Равномерное движение
Равномерным движением называют движение тела, которое совершает равные перемещения в течение любых равных промежутков времени.
Скорость при равномерном движении определяется как отношение перемещения ко времени, в течение которого данное перемещение было совершено. Уравнение имеет следующий вид:
\(\vec{v}=\frac{\vec{s}}{t}\)
\(\vec{v}=const\)
Проекция вектора скорости на ось ОХ выглядит таким образом:
\(v_{x}=\frac{s_{x}}{t}\)
\(v_{x}=const\)
Если вектор скорости спроецировать на ось координат, то она будет равна быстроте изменения данной координаты:
\(v_{x}=\frac{x-x_{0}}{t}\)
Прямолинейное равноускоренное движение
Прямолинейным равноускоренным движением называют движение по прямой траектории, для которого характерно постоянное ускорение.
Ускорение для прямолинейного равноускоренного движения обозначают следующим образом:
\(\vec{a}=const\)
При таком движении можно наблюдать увеличение или уменьшение скорости. Чтобы определить скорость, необходимо выполнить следующий расчет:
\(\vec{v}=\vec{v}_{0}+\vec{a}t\)
Если тело разгоняется в проекции оси ОХ, то скорость можно определить по формуле:
\(v_{x}=v_{0x}+a_{x}t\)
a>0, движение является равноускоренным.
Источник: fizi4ka.ruВо время торможения в проекции на ось ОХ скорость рассчитывают следующим образом:
\(v_{x}=v_{0x}-a_{x}t\)
а<0, движение является равнозамедленным.
Источник: fizi4ka.ruГрафически зависимость ускорения от времени, то есть график ускорения во время равноускоренного движения тела, можно представить в виде:
Источник: fizi4ka.ruГрафик ускорения, характеризующий равноускоренное движение тела, представляет собой прямую, которая параллельна оси времени:
- график 1 находится над осью t, тело совершает разгон, ах>0;
- график 2 размещен под осью t, тело тормозит, ах<0.
Графически скорость или проекция скорости изображается в виде зависимости скорости от времени:
Источник: fizi4ka.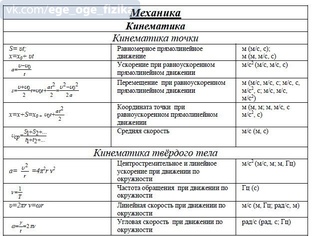 {2}}\)
{2}}\)Дальность полета тела соответствует уравнению:
\(l=v_{0x}t=v_{0x}\sqrt{\frac{2h_{0}}{g}}\)
Вычислить угол между вектором скорости и осью ОХ можно с помощью формулы:
\(\tan \beta =\frac{v_{y}}{v_{x}}=\frac{-gt}{v_{0x}}\)
Задачи по кинематике, их решение
Задача 1
Рассмотрим путь велосипедиста из одного населенного пункта в другой. Половина расстояния была преодолена со скоростью 12 км/ч (\(v_1\)). Далее половину оставшегося времени он ехал со скоростью 6 км/ч (\(v_2\)). Остаток расстояния путник преодолел пешком со скоростью 4км/ч (\(v_3\)). Необходимо рассчитать среднюю скорость на всем пути следования велосипедиста.
Решение
Данный пример относится к теме равномерного прямолинейного движения одного тела. Процесс можно изобразить схематично:
Источник: pandia.ru\(S = S_1 + S_2 + S_3\)
\(t = t_1 + t_2 + t_3\)
На каждый отрезок пути необходимо составить уравнение движения:
\(S_1 = v_1t_1\)
\(S_2 = v_2t_2\)
\(S_3 = v_3t_3\)
Далее можно представить дополнительные условия задачи:
\(S_1 = S_2 + S_3\)
\(t_2 = t_3\)
\(v_{sr}=\frac{S}{t}=\frac{S_{1}+S_{2}+S_{3}}{t_{1}+t_{2}+t_{3}}\)
Следует преобразить формулу и подставить числовые значения:
\(v_{sr}=\frac{2S_{1}}{\frac{S_{1}}{v_{1}}+\frac{2S_{1}}{v_{2}+v_{3}}}=\frac{2v_{1}\left(v_{2}+v_{3} \right)}{2v_{1}+v_{2}+v_{3}}\)
\(v_{sr}=\frac{2\times 12\left(6+4 \right)}{2\times 12+6+4}=7\)
Ответ: средняя скорость составляет \(7\) км/ч.
Задача 2
Тело подбросили вертикально вверх. Начальная скорость при этом составила 3,13 м/с (\(v_0\)). В момент, когда данное тело достигло максимальную высоту полета, из начального пункта подбросили второе тело с такой же начальной скоростью, как у первого. Необходимо определить на каком расстоянии от точки бросания встретятся тела. {2}}=\frac{9,81}{0,17}=57,7\)
{2}}=\frac{9,81}{0,17}=57,7\)
Ответ: камень упал с высоты \(57,7\) м.
Решение задач по кинематике основано на простых формулах. Успешность результата зависит от умения грамотно применять справедливые уравнения в том или ином случае. Бывают ситуации, когда в процессе изучения физики возникают некоторые трудности. Простым решением будет обратиться к порталу Феникс.Хелп.
Осн. формулы и метод. рекомендации по решению задач на кинематику МТ
Ближайшие темы будут посвящены решению задач на движение тел, без учета причин, вызвавших это движения, т.е. решению задач по кинематике.
Но для того, чтобы начать рассмотрение решений задач по данной теме, необходимо вспомнить основные формулы, связанные с этим разделом. Для удобства, сведём все формулы в таблицу.
Основные формулы равномерного прямолинейного движения
|
Формула |
Описание формулы |
|
Перемещение тела за промежуток времени t, где – скорость тела, sx, vx – проекции перемещения и скорость на ось Ох. |
|
|
Путь за промежуток времени t. |
|
|
Закон сложения скоростей в классической механике. |
|
|
Кинематическое уравнение равномерного движения, где х — координата тела в момент времени t, х0 — начальная координата тела. |
Основные формулы равноускоренного прямолинейного движения
|
Формула |
Описание формулы |
|
Скорость
тела в момент времени t, где –
ускорение тела, –
скорость тела в начальный момент времени. |
|
|
Перемещение тела за промежуток времени t. |
|
|
Кинематическое уравнение равноускоренного движения. |
Основные формулы движения тела по окружности с постоянной по модулю скоростью.
|
Формула |
Описание формулы |
|
Линейная скорость тела, где l — длина дуги окружности, пройденной телом за промежуток времени Δt. |
|
|
Угловая скорость тела, где Dj – угол поворота радиус-вектора движущегося по окружности тела за промежуток времени Dt. |
|
|
Связь линейной скорости с угловой, где R — радиус окружности. |
|
|
Период вращения, где N — число оборотов тела за промежуток времени Δt. |
|
|
Частота вращения. |
|
|
Связь между линейной скоростью, периодом вращения и частотой. |
|
|
Центростремительное ускорение. |
Известно, что для большей наглядности движение можно описывать с помощью графиков.
Давайте рассмотрим в сравнении графики для равномерного и
равноускоренного движения.
Известно, что при равномерном движении скорость тела не изменяется с течением времени. Поэтому графиком скорости, в этом случае, будет прямая линия, параллельная оси времени. При равноускоренном движении тела, неизменной величиной является ускорение. Поэтому графиком ускорения будет являться также прямая линия, параллельная оси времени.
По графику скорости для равномерного движения, можно определить путь, пройденный телом за некоторый промежуток времени. Для этого достаточно определить площадь прямоугольника, образованного графиком скорости и осью времени.
Известно, что перемещение тела при равномерном движении линейно зависит от времени, поэтому графиком перемещения является прямая линия вида
y = kx.
Наклон же графика к оси времени зависит от модуля скорости. При равноускоренном движении линейно зависимой величиной является скорость тела. Поэтому графиком скорости является прямая линия вида
y = kx +b.
Используя график скорости для равноускоренного движения можно определить перемещение тела за некоторый промежуток времени. Для этого необходимо определить площадь прямоугольной трапеции или прямоугольного треугольника, ограниченных графиком скорости и осью времени.
График зависимости координаты от времени при равномерном движении, то есть график движения, представлен на рисунке ниже. По этому графику можно определить: координату тела в любой момент времени, путь, пройденный телом за некоторый промежуток времени, кратчайшее расстояние между телами в любой момент времени, а также момент и место встречи тел.
А графиком перемещения при равноускоренном движении является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения. Так, если проекция ускорения отрицательна, то возможны следующие три вида графика перемещения:
– когда проекция начальной скороститела равна нулю;
– когда проекция начальной скорости тела меньше нуля;
– когда проекция начальной скорости тела больше нуля.
Если проекция ускорения положительна, то здесь также возможны три случая:
– когда начальная скорость тела равна нулю;
– когда проекция начальной скорости больше нуля;
– когда проекция начальной скорости меньше нуля.
Методические рекомендации по решению задач на кинематику материальной точки
1) Сделать схематический рисунок, который лучше всего представить в виде траектории движущейся точки с изображением векторов перемещения, скорости и ускорения.
2) Выбрать систему отсчета (то есть тело отсчета, связанную с ним систему координат и начало отсчета времени) на основании тщательного анализа условия задачи. Рациональный выбор системы отсчета, как правило, значительно упрощает решение задачи. При выборе положительных направлений координатных осей необходимо руководствоваться направлением движения (то есть направлением вектора скорости) или направлением вектора ускорения.
3) Составить на основании законов движения систему уравнений в векторном виде для всех тел, участвующих в движении. А затем в скалярной форме, спроецировав на координатные оси эти векторные уравнения движения. При записи этих уравнений не забыть привести в соответствие знаки проекций скорости и ускорения с направлением координатных осей. При необходимости дополнить систему уравнений соотношениями, составленными на основе данных задачи и конкретной ситуации, описанной в ней.
4) Решить полученную систему уравнений относительно искомых величин в общем виде, убедиться в соответствии единиц измерения и проделать числовые расчеты.
Следование этим простым рекомендациям позволит вам успешнее справляться с решением задач на кинематику материальной точки.
Законы кинематики формулы. Кинематика основные понятия, законы и формулы. Свободное падение по вертикали
Для того чтобы понять, что изучает механика, необходимо рассмотреть, что означает движение в самом общем смысле. Значение этого слова подразумевает под собой изменение чего-либо. Например, политическое движение выступает за равноправие разных слоев населения вне зависимости от их расовой принадлежности. Раньше его не было, затем что-то изменилось и теперь каждый человек имеет равные права. Это движение цивилизации вперед. Еще пример — экологическое. В прошлом, выбравшись на природу, никто не задумывался о том, что оставляет после себя мусор. Сегодня же любой цивилизованный человек соберет его за собой и отвезет в специально отведенное место для дальнейшей утилизации.
Значение этого слова подразумевает под собой изменение чего-либо. Например, политическое движение выступает за равноправие разных слоев населения вне зависимости от их расовой принадлежности. Раньше его не было, затем что-то изменилось и теперь каждый человек имеет равные права. Это движение цивилизации вперед. Еще пример — экологическое. В прошлом, выбравшись на природу, никто не задумывался о том, что оставляет после себя мусор. Сегодня же любой цивилизованный человек соберет его за собой и отвезет в специально отведенное место для дальнейшей утилизации.
Что-то подобное можно наблюдать и в механике. При механическом движении изменяется положение тела в пространстве относительно других предметов с течением времени. Основная задача механики — указать, где находится объект в любой момент, учитывая даже тот, который еще не наступил. То есть, предсказать положение тела в заданное время, а не только узнать, где именно в пространстве оно находилось в прошлом.
Кинематика — это раздел механики, который изучает движение тела, не анализируя его причины. Это значит, что она учит не объяснять, а описывать. То есть, придумать способ, с помощью которого можно было бы задать положение тела в любой момент времени. Основные понятия кинематики включают в себя скорость, ускорение, расстояние, время и перемещение.
Сложность в описании движения
Первая проблема, с которой сталкивается кинематика — это то, что у каждого тела есть определенный размер. Допустим, необходимо описать движение какого-нибудь предмета. Это значит научиться обозначать его положение в любой момент времени. Но каждый предмет занимает в пространстве какое-то место. То есть, что все части этого объекта в один и тот же момент времени занимают разное положение.
Какую точку в таком случае необходимо взять для описания нахождения всего предмета? Если учитывать каждую, то расчеты окажутся слишком сложными. Поэтому решение ответа на этот вопрос можно максимально упростить. Если все точки одного тела движутся в одинаковом направлении, то для описания движения достаточно одной такой, которую содержит это тело.
Виды движения в кинематике
Существует три типа:
- Поступательным называется движение, при котором любая прямая проведенная в теле остается параллельной самой себе. Например, автомобиль, который движется по шоссе, совершает такой вид движения.
- Вращательным называется такое движение тела при котором все его точки движутся по окружностям с центрами, лежащими на одной прямой, называемой осью вращения. Например, вращение Земли относительно своей оси.
- Колебательным называется движение, при котором тело повторяет свою траекторию через определенный отрезок времени. Например, движение маятника.
Основные понятия кинематики — материальная точка
Любое сложное движение можно описать как комбинацию двух простейших видов — поступательного и вращательного. Например колесо автомобиля или юла, стоящая на движущейся прямо платформе, участвуют одновременно в этих двух типах перемещения.
Но что делать, если движение тела нельзя представить в виде комбинации? Например, если автомобиль едет по ухабистой дороге, его положение будет меняться очень сложным образом. Если рассчитывать только то, что этот транспорт перемещается из одного города в другой, то в такой ситуации становится не важно какого размера тело движется из точки А в точку Б и им можно пренебречь. В данном случае важно только за какое время автомобиль прошел определенное расстояние и с какой скоростью двигался.
Однако следует учитывать, что пренебрежение размером допускается не в каждой задаче. Например, если рассчитывать движение при парковке автомобиля, то игнорирование величины данного тела, приведет к пагубным последствием. Поэтому, только в тех ситуациях, когда в рамках конкретной задачи, размерами движущегося объекта можно пренебречь, то такое тело принято называть материальной точкой.
Формулы кинематики
Числа, с помощью которых задается положение точки в пространстве, называются координатами. Чтобы определить его на прямой, достаточно одного числа, когда речь идет о поверхности, то двух, о пространстве — трех. Большего количества чисел в трехмерном мире (для описывания положения материальной точки) не требуется.
Большего количества чисел в трехмерном мире (для описывания положения материальной точки) не требуется.
Существует три основных уравнения для понятия кинематики, как раздела о движении тел:
- v = u + at.
- S = ut + 1/2at 2 .
- v 2 = u 2 + 2as.
v = конечная скорость,
u = Начальная скорость,
a = ускорение,
s = расстояние, пройденное телом,
Формулы кинематики в одномерном пространстве:
X — X o = V o t + 1/2a t2
V 2 = V o 1 + 2a (X — X o)
X — X o = 1\2 (V o + V) t
Где,
V — конечная скорость (м / с),
V o — начальная скорость (м / с),
a — ускорение (м / с 2),
t — время (с),
X — конечное положение (м),
Формулы кинематики в двумерном пространстве
Поскольку следующие уравнения используются для описания материальной точки на плоскости, стоит рассматривать ось X и Y.
Учитывая направление Х:
a x = constant
V fx = V i x + a x Δt
X f = X i + V i x Δt +1/2a x Δt 2
Δt = V fx -V ix /a x
V fx 2 = V ix 2 + 2ax Δx
X f = X i + 1/2 (V fx + V ix) Δ t .
И учитывая направление y:
a y = constant
V fy = V iy + a y Δt
y f = y i + V iy Δt + 1/2 a x Δt 2
Δt = V fy — V iy /a y
V fy 2 = V iy 2 + 2 ay Δ y
y f = y i +1/2 (V fy + V iy) Δt.
V f — конечная скорость (м / с),
V i — начальная скорость (м / с),
a — ускорение (m / с 2),
t — время (с),
X — конечное положение (м),
X 0 — начальное положение (м).
Перемещение брошенного снаряда — лучший пример для описания движения объекта в двух измерениях. Здесь тело перемещается, как в вертикальном положении У, так и в горизонтальном положении Х, поэтому можно сказать, что предмет имеет две скорости.
Примеры задач по кинематике
Задача 1 : Начальная скорость грузовика равна нулю. Изначально этот объект находится в состоянии покоя. На него начинает действовать равномерное ускорение в течение временного интервала 5,21 секунды. Расстояние, пройденное грузовиком, составляет 110 м. Найти ускорение.
Расстояние, пройденное грузовиком, составляет 110 м. Найти ускорение.
Решение:
Пройденное расстояние s = 110 м,
начальная скорость v i = 0,
время t = 5,21 с,
ускорение a =?
Используя основные понятие и формулы кинематики, можно заключить, что,
s = v i t + 1/2 a t 2 ,
110 м = (0) × (5.21) + 1/2 × a (5.21) 2 ,
a = 8,10 м / с 2 .
Задача 2: Точка движется вдоль оси х (в см), после t секунд путешествия, ее можно представить, используя уравнение x = 14t 2 — t + 10. Необходимо найти среднюю скорость точки, при условии, что t = 3s?
Решение:
Положение точки при t = 0, равно x = 10 см.
При t = 3s, x = 133 см.
Средняя скорость, V av = Δx/Δt = 133-10/3-0 = 41 см / с.
Что такое тело отсчета
О движении можно говорить только если существует что-то, относительно чего рассматривается изменение положения изучаемого объекта. Такой предмет называется телом отсчета и оно условно всегда принимается за неподвижное.
Если в задаче не указано в какой системе отчета движется материальная точка, то телом отсчета считается земля по умолчанию. Однако, это не означает, что за неподвижный в заданный момент времени объект, относительно которого совершается движение, нельзя принять любой другой удобный для расчета. Например, за тело отсчета можно взять движущийся поезд, поворачивающий автомобиль и так далее.
Система отсчета и ее значение в кинематике
Для описания движения необходимы три составляющие:
- Система координат.
- Тело отсчета.
- Прибор для измерения времени.
Тело отсчета, система координат, связанная с ним и прибор для измерения времени образуют систему отсчета. Бессмысленно говорить о движении, если ее не указывать. Правильно подобранная система отсчета, позволяет упростить описание перемещения и, наоборот, усложнить, если она выбрана неудачно.
Именно по этой причине, человечество долго считало, что Солнце движется вокруг Земли и что она находится в центре вселенной. Такое сложное движение светил, связанное с тем, что земные наблюдатели находятся в системе отсчета, которая очень замысловато движется. Земля вращается вокруг свое оси и одновременно вокруг Солнца. На самом деле, если сменить систему отсчета, то все движения небесных тел легко описываются. Это в свое время было сделано Коперником. Он предложил собственное описание мироустройства, в котором Солнце неподвижно. Относительно него описать движение планет гораздо проще, чем если телом отсчета будет являться Земля.
Такое сложное движение светил, связанное с тем, что земные наблюдатели находятся в системе отсчета, которая очень замысловато движется. Земля вращается вокруг свое оси и одновременно вокруг Солнца. На самом деле, если сменить систему отсчета, то все движения небесных тел легко описываются. Это в свое время было сделано Коперником. Он предложил собственное описание мироустройства, в котором Солнце неподвижно. Относительно него описать движение планет гораздо проще, чем если телом отсчета будет являться Земля.
Основные понятия кинематики — путь и траектория
Пусть некоторая точка первое время находилась в положении А, спустя некоторое время она оказалась в положении В. Между ними можно провести одну линию. Но для того, чтобы эта прямая несла больше информации о движении, то есть было понятно откуда и куда двигалось тело, это должен быть не просто отрезок, а направленный, обычно обозначающийся буквой S. Перемещением тела, называется вектор, проведенный из начального положения предмета в конечное.
Если тело изначально находилось в точке А, а затем оказалось в точке В, это не означает, что оно двигалось только по прямой. Из одного положения в другое можно попасть бесконечным количеством способов. Линия, вдоль которой движется тело, является еще одним основным понятием кинематики — траекторией. А ее длина называется путь, который обычно обозначается буквами L или l.
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Прежде всего, следует заметить, что речь будет идти о геометрической точке, то есть области пространства, не имеющей размеров. Именно для этого абстрактного образа (модели) и справедливы все представленные ниже определения и формулы. Однако для краткости я в дальнейшем буду часто говорить о движении тела , объекта или частицы . Это я делаю только для того, чтобы Вам легче было читать. Но всегда помните, что речь идет о геометрической точке.
Это я делаю только для того, чтобы Вам легче было читать. Но всегда помните, что речь идет о геометрической точке.
Радиус-вектор точки — это вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой. Радиус-вектор обозначается, как правило, буквой r . К сожалению некоторые авторы обозначают его буквой s . Настоятельно советую не использовать обозначение s для радиус-вектора. Дело в том, что подавляющее большинство авторов (как отечественных, так и зарубежных) используют букву s для обозначения пути, который является скаляром и к радиус-вектору, как правило, отношения не имеет. Если вы будете обозначать радиус-вектор как s , то легко можете запутаться. Еще раз, мы, как и все нормальные люди, будем использовать следующие обозначения: r — радиус-вектор точки, s — путь, пройденный точкой.
Вектор перемещения (часто говорят просто — перемещение ) — это вектор , начало которого совпадает с той точкой траектории, где было тело, когда мы начали изучать данное движение, а конец этого вектора совпадает с той точкой траектории, где мы это изучение закончили. Будем обозначать этот вектор как Δr . Использование символа Δ очевидно: Δr — это разность между радиус-вектором r конечной точки изучаемого отрезка траектории и радиус-вектором r 0 точки начала этого отрезка (рис. 1), то есть Δr = r − r 0 .
Траектория — это линия, вдоль которой движется тело.
Путь — это сумма длин всех участков траектории, последовательно проходимых телом при движения. Обозначается либо ΔS, если речь идет об участке траектории, либо S, если речь идет о всей траектории наблюдаемого движения. Иногда (редко) путь обозначают и другой буквой, например, L (только не обозначайте его как r, мы уже об этом говорили). Запомните! Путь — это положительный скаляр ! Путь в процессе движения может только увеличиваться .
Средняя скорость перемещения v ср
v ср = Δr /Δt.
Мгновенная скорость перемещения v — это вектор, определяемый выражением
v = dr /dt.
Средняя скорость пути v ср — это скаляр, определяемый выражением
V ср = Δs/Δt.
Часто встречаются и другие обозначения, например, .
Мгновенная скорость пути v — это скаляр, определяемый выражением
Модуль мгновенной скорости перемещения и мгновенная скорость пути — это одно и то же, поскольку dr = ds.
Среднее ускорение a
a ср = Δv /Δt.
Мгновенное ускорение (или просто, ускорение ) a — это вектор, определяемый выражением
a =dv /dt.
Касательное (тангенциальное) ускорение a τ (нижний индекс — это греческая строчная буква тау) — это вектор , являющийся векторной проекцией мгновенного ускорения на касательную ось .
Нормальное (центростремительное) ускорение a n — это вектор , являющийся векторной проекцией мгновенного ускорения на ось нормали .
Модуль касательного ускорения
| a τ | = dv/dt,
То есть это — производная модуля мгновенной скорости по времени.
Модуль нормального ускорения
| a n | = v 2 /r,
Где r — величина радиуса кривизны траектории в точке нахождения тела.
Важно! Хочу обратить внимание на следующее. Не путайтесь с обозначениями, касающимися касательного и нормального ускорений! Дело в том, что в литературе по этому поводу традиционно наблюдается полная чехарда.
Запомните!
a τ — это вектор касательного ускорения,
a n — это вектор нормального ускорения.
a τ и a n являются векторными проекциями полного ускорения а на касательную ось и ось нормали соответственно,
A τ — это проекция (скалярная!) касательного ускорения на касательную ось,
A n — это проекция (скалярная!) нормального ускорения на ось нормали,
| a τ |- это модуль вектора касательного ускорения,
| a n | — это модуль вектора нормального ускорения.
Особенно не удивляйтесь, если, читая в литературе о криволинейном (в частности, вращательном) движении, Вы обнаружите, что автор под a τ понимает и вектор, и его проекцию, и его модуль. То же самое относится и к a n . Все, как говорится, «в одном флаконе». И такое, к сожалению, сплошь и рядом. Даже учебники для высшей школы не являются исключением, во многих из них (поверьте — в большинстве!) царит полная неразбериха по этому поводу.
Вот так, не зная азов векторной алгебры или пренебрегая ими, очень легко полностью запутаться при изучении и анализе физических процессов. Поэтому знание векторной алгебры является наиглавнейшим условием успеха в изучении механики. И не только механики. В дальнейшем, при изучении других разделов физики, Вы неоднократно в этом убедитесь.
Мгновенная угловая скорость (или просто, угловая скорость ) ω — это вектор, определяемый выражением
ω = dφ /dt,
Где dφ — бесконечно малое изменение угловой координаты (dφ — вектор!).
Мгновенное угловое ускорение (или просто, угловое ускорение ) ε — это вектор, определяемый выражением
ε = dω /dt.
Связь между v , ω и r :
v = ω × r .
Связь между v, ω и r:
Связь между | a τ |, ε и r:
| a τ | = ε · r.
Теперь перейдем к кинематическим уравнениям конкретных видов движения. Эти уравнения надо выучить наизусть .
Кинематическое уравнение равномерного и прямолинейного движения имеет вид:
r = r 0 + v t,
Где r — радиус-вектор объекта в момент времени t, r 0 — то же в начальный момент времени t 0 (в момент начала наблюдений).
Кинематическое уравнение движения с постоянным ускорением имеет вид:
r = r 0 + v 0 t + a t 2 /2, где v 0 скорость объекта в момент t 0 .
Уравнение для скорости тела при движении с постоянным ускорением имеет вид:
v = v 0 + a t.
Кинематическое уравнение равномерного движения по окружности в полярных координатах имеет вид:
φ = φ 0 + ω z t,
Где φ — угловая координата тела в данный момент времени, φ 0 — угловая координата тела в момент начала наблюдения (в начальный момент времени), ω z — проекция угловой скорости ω на ось Z (обычно эта ось выбирается перпендикулярно плоскости вращения).
Кинематическое уравнение движения по окружности с постоянным ускорением в полярных координатах имеет вид:
φ = φ 0 + ω 0z t + ε z t 2 /2.
Кинематическое уравнение гармонических колебаний вдоль оси X имеет вид:
Х = А Cos (ω t + φ 0),
Где A — амплитуда колебаний, ω — циклическая частота, φ 0 — начальная фаза колебаний.
Проекция скорости точки, колеблющейся вдоль оси X, на эту ось равна:
V x = − ω · A · Sin (ω t + φ 0).
Проекция ускорения точки, колеблющейся вдоль оси X, на эту ось равна:
А x = − ω 2 · A · Cos (ω t + φ 0).
Связь между циклической частотой ω, обычной частотой ƒ и периодом колебаний T:
ω = 2 πƒ = 2 π/T (π = 3,14 — число пи).
Математический маятник имеет период колебаний T, определяемый выражением:
В числителе подкоренного выражения — длина нити маятника, в знаменателе — ускорение свободного падения
Связь между абсолютной v абс, относительной v отн и переносной v пер скоростями:
v абс = v отн + v пер.
Вот, пожалуй, и все определения и формулы, которые могут понадобиться при решении задач на кинематику. Приведенная информация носит только справочный характер и не может заменить электронную книгу, где доступно, подробно и, надеюсь, увлекательно изложена теория этого раздела механики.
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).

При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Путь и перемещение
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой . Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела .
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: L полн – весь путь, который прошло тело, t полн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v 0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t ).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей.
Свободное падение по вертикали
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х » писать «у ».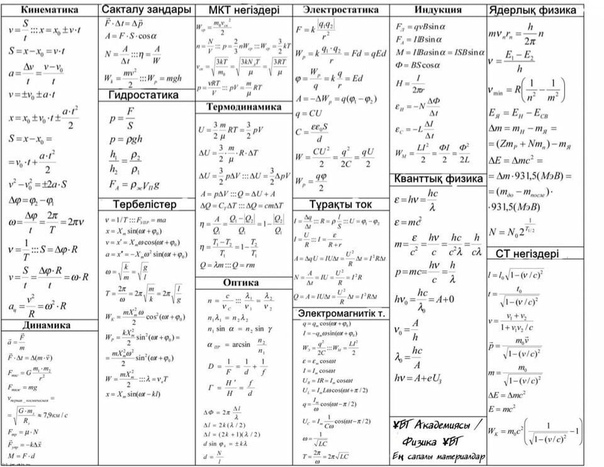 Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v 0 , время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
При горизонтальном броске с начальной скоростью v 0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна v x = v 0 . А вертикальная возрастает по законам ускоренного движения v y = gt . При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали . Тогда этот угол будет находиться из соотношения:
Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны.
Таким образом, покой и движение тела относительны.
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t . Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T . При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt . Очевидно, что за время равное периоду T тело пройдет угол равный 2π , следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω :
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением , так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
 Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов , позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Теоретическая механика и кинематика
Механика — это наука о простейших формах движения материи, которые сводятся к простым перемещениям или переходам физических тел с одного положения или состояния в пространстве и времени в другое, в результате взаимодействия между ними.
Теоретическая механика
Механика охватывает целый комплекс дисциплин, изучающих движение и взаимодействие различных материальных тел, например, прикладная механика, гидромеханика, аэромеханическая, небесная механика, биомеханика и др. Изучение наиболее общих свойств движения и взаимодействия всех тел является предметом специальной дисциплины, которую называют теоретическая механика.
Итак, теоретическая механика изучает наиболее общие законы движения и взаимодействия тел, считая своей главной задачей познания количественных и качественных закономерностей, наблюдаемых в природе. С определения теоретической механики следует, что она принадлежит к фундаментальным естественным наукам.
История развития теоретической механики убеждает в том, что она является одной из научных основ техники и технологии, поскольку существует взаимосвязь между проблемами теоретической механики, проблемами техники и технологии.
Теоретическая механика широко применяет такие методы:
- абстракции;
- обобщение;
- математические методы;
- методы формальной логики.
Критерием истинности наших знаний является опыт и практика. Таким образом, теоретическая механика имеет дело не с самими материальными объектами, а с их моделями.
Теоретическая механика — это важная наука для подготовки инженерных кадров. Она является основой для изучения таких дисциплин, как:
- теория колебаний, гидравлика;
- сопротивление материалов;
- теория машин, механизмов и тому подобное.
Знание законов теоретической механики, отражающие объективно существующие взаимосвязи, взаимообусловленности механических движений и преобразования энергии, позволяет научно предсказать ход процессов в новых задачах, возникающих при развитии науки, техники и технологии.
Замечание 1
Статикой называется раздел теоретической механики, в котором изучают методы преобразования одних систем сил в другие, эквивалентные им, а также условия равновесия различных систем сил, действующих на твердое тело.
Одним из основных понятий в статике, как и во всей механике, является понятие о силе. Величина, являющаяся мерой механического взаимодействия материальных тел, называется силой. Сила, действующая на тело, является вектором. Она характеризуется точкой приложения, направлением и величиной. В теоретической механике силу принято обозначать $\vec {F} $ cила, $A$- точка приложения силы, прямая $AB$ — линия действия силы.
Рисунок 1. Сила $\vec {F} $. Автор24 — интернет-биржа студенческих работ
В Международной системе единиц (СИ) за единицу силы принимают один ньютон (1Н). Ньютон — это такая сила, которая массе в 1 кг оказывает ускорение в 1 $мс_2$ (1Н = 1кг • м • с-2).
Основные понятия теоретической механики
К основным понятиям теоретической механики, прежде всего, относятся понятия материальной точки и абсолютно твердого тела. Они являются идеальными моделями материальных тел с той или иной степенью абстракции конкретных свойств реальных физических тел.
Они являются идеальными моделями материальных тел с той или иной степенью абстракции конкретных свойств реальных физических тел.
Определение 1
Материальной точкой называется геометрическая точка, которой приписана определенная масса.
Например, изучая движение планет вокруг Солнца, их рассматривают как материальные точки, в каждой из которых сосредоточена вся масса соответствующей планеты, абстрагируясь при этом от размеров планет.
С понятием материальной точки тесно связано понятие о системе материальных точек.
Определение 2
Абсолютно твердым телом называется тело, которое состоит из системы материальных точек, которые непрерывно заполняют определенную часть пространства таким образом, что расстояние между любыми двумя его точками остается неизменной.
Отметим, что абстракция абсолютно твердого тела позволяет изучать механическое движение тел, не связанных с существующим изменением их формы, в частности с деформацией. Изучение механических движений тел, зависит от их деформируемости, а также движения жидкости и газов, которые приводят к новой абстракции в виде понятие сплошной среды.
Раздел кинематика
Замечание 2
Кинематикой называется раздел теоретической механики, в котором изучается движение системы материальных точек с геометрической точки зрения. Кинематику называют также геометрией движения, поскольку в ней рассматриваются геометрические свойства движения.
Механические движения, что изучаются в кинематике, осуществляются в пространстве и времени. Отметим, что в теоретической механике пространство, в котором происходит движение тел, рассматривается как трехмерное, и все измерения выполняются на основании методов евклидовой геометрии. В механике время считается одинаковым в любых системах отсчета (системах координат) и не зависит от движения этих систем относительно друг друга. Время сказывается буквой $t$ и рассматривается как непрерывная переменная величина, которая применяется в качестве аргумента.
Изучая движение тела, всегда следует знать, в отношении какого другого тела, которое называется телом отсчета, рассматривается это движение. Совокупность тела отсчета, с которым связана система координат, и часов называют системой отсчета. Эта система может быть как подвижной, так и условно неподвижной. Точки тела, постоянно движущиеся, осуществляют в общем случае различные движения. Поэтому, в первую очередь, возникает необходимость изучить движение отдельных точек тела.
Поскольку движение геометрического образа тела будет известным, когда станет известен закон движения всех его точек, определение движения любого геометрического образа предшествует изучению движения одной его точки.
Эта логика лежит в основе разделения кинематики на такие разделы, как кинематика точки и кинематика твердого тела. Для определения положения точки в пространстве выбирают некоторую систему отсчета (систему координат).
Определение 3
Линия, которую описывает точка при своем движении, называется траекторией. Если траектория точки прямая линия, то движение точки называется прямолинейным, если траектория точки кривая, то — криволинейным.
Движение точки относительно выбранной системы отсчета считается заданным, если известно, с помощью которого способа можно определить положение точки в любой момент времени. Основными пространственно-временными (кинематическими) характеристиками движения точки является ее положение, скорость и ускорение.
Исходя из этого, основная задача кинематики точки заключается в нахождении способов задания ее положения и методов определения скорости и ускорения. Движение точки можно определить тремя способами: векторным, координатным и натуральным.
Векторный. Положение точки можно определить с помощью радиус-вектора $\vec {r}$, проведенного с некоторой заданной неподвижной точки $О$ в данную точку $М$. При движении точки радиус-вектор $\vec {r} $меняется по величине и направлению. Каждому моменту времени $t$ соответствует определенное значение $\vec {r}$. 2}$
2}$
Основные формулы по физике — МЕХАНИКА
Формулы механики. Механика делится на три раздела: кинематику, динамику и статику. В разделе кинематика рассматриваются такие кинематические характеристики движения, как перемещение, скорость, ускорение. Здесь необходимо использовать аппарат дифференциального и интегрального исчисления.
В основе классической динамики лежат три закона Ньютона. Здесь необходимо обратить внимание на векторный характер действующих на тела сил, входящих в эти законы.
Динамика охватывает такие вопросы, как закон сохранения импульса, закон сохранения полной механической энергии, работа силы.
При изучении кинематики и динамики вращательного движения следует обратить внимание на связь между угловыми и линейными характеристиками. Здесь вводятся понятия момента силы, момента инерции, момента импульса и рассматривается закон сохранения момента импульса.
Смотрите также основные формулы по термодинамике
Таблица основных формул по механике
|
Физические законы, формулы, переменные |
Формулы механики |
||||
|
Скорость мгновенная: где r — радиус-вектор материальной точки, t — время;
|
|||||
|
Модуль вектора скорости: где s — расстояние вдоль траектории движения (путь) |
|||||
|
Скорость средняя (модуль): |
|||||
|
Ускорение мгновенное: |
|||||
|
Модуль вектора ускорения при прямолинейном движении: |
|||||
|
Ускорение при криволинейном движении: 1) нормальное где R — радиус кривизны траектории, 2) тангенциальное 3) полное (вектор) 4) (модуль) |
|||||
|
Скорость и путь при движении: 1) равномерном 2) равнопеременном V0— начальная скорость; а > 0 при равноускоренном движении; а < 0 при равнозамедленном движении. |
|
||||
|
Угловая скорость: где φ — угловое перемещение. |
|||||
|
Угловое ускорение: |
|||||
|
Связь между линейными и угловыми величинами: |
|||||
|
Импульс материальной точки: где m — масса материальной точки. |
|||||
|
Основное уравнение динамики поступательного движения (II закон Ньютона): где F — результирующая сила, <> |
|||||
|
Формулы сил: тяжестиP где g — ускорение свободного падения трения Fтр где μ — коэффициент трения, N — сила нормального давления, упругости Fупр где k — коэффициент упругости (жесткости), Δх — деформация (изменение длины тела). |
|
||||
|
Закон сохранения импульса для замкнутой системы, состоящей из двух тел: где — скорости тел до взаимодействия; — скорости тел после взаимодействия. |
|||||
|
Потенциальная энергия тела: 1) поднятого над Землей на высоту h 2) упругодеформированного |
|
||||
|
Кинетическая энергия поступательного движения: |
|||||
|
Работа постоянной силы: где α — угол между направлением силы и направлением перемещения. |
|||||
|
Полная механическая энергия: |
|||||
|
Закон сохранения энергии: силы консервативны силы неконсервативны где W1 — энергия системы тел в начальном состоянии; W2 — энергия системы тел в конечном состоянии. |
|
||||
|
Момент инерции тел массой m относительно оси, проходящей через центр инерции (центр масс): 1) тонкостенного цилиндра (обруча) где R — радиус, 2) сплошного цилиндра (диска) 3) шара 4) стержня длиной l, если ось вращения перпендикулярна стержню и проходит через его середину |
|||||
|
Момент инерции тела относительно произвольной оси (теорема Штейнера): где — момент инерции тела относительно оси, проходящей через центр масс, d — расстояние между осями. |
|||||
|
Момент силы(модуль): где l — плечо силы. |
|||||
|
Основное уравнение динамики вращательного движения: где — угловое ускорение, — результирующий момент сил. |
|||||
|
Момент импульса: 1) материальной точки относительно неподвижной точки где r — плечо импульса, 2) твердого тела относительно неподвижной оси вращения |
|
||||
|
Закон сохранения момента импульса: где L1 — момент импульса системы в начальном состоянии, L2 — момент импульса системы в конечном состоянии. |
|||||
|
Кинетическая энергия вращательного движения: |
|||||
|
Работа при вращательном движении где Δφ — изменение угла поворота. |
Кинематические уравнения
Целью этого первого раздела «Класса физики» было исследование разнообразных средств, с помощью которых можно описать движение объектов. Разнообразие представлений, которые мы исследовали, включает словесные представления, графические представления, числовые представления и графические представления (графики положения-времени и графики скорости-времени). В Уроке 6 мы исследуем использование уравнений для описания и представления движения объектов.Эти уравнения известны как кинематические уравнения.
Есть множество величин, связанных с движением объектов — смещение (и расстояние), скорость (и скорость), ускорение и время. Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22,0 м / с, на север в течение 12,0 секунд для смещения на север на 264 метра, то движение автомобиля полностью описано.И если известно, что вторая машина ускоряется из положения покоя с ускорением на восток 3,0 м / с 2 в течение 8,0 секунд, обеспечивая конечную скорость 24 м / с, восток и смещение на восток 96 метров. , то полностью описывается движение этой машины. Эти два утверждения дают полное описание движения объекта. Однако не всегда такая полнота известна. Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны.Например, приближаясь к светофору, вы можете узнать, что ваша машина развивает скорость 22 м / с, восток и способна выдерживать заносное ускорение 8,0 м / с 2 , запад. Однако вы не знаете, какое смещение испытает ваша машина, если бы вы резко нажали на тормоз и занесло до полной остановки; и вы не знаете, сколько времени потребуется, чтобы остановиться. В таком случае неизвестные параметры могут быть определены с использованием физических принципов и математических уравнений (кинематических уравнений).
Однако вы не знаете, какое смещение испытает ваша машина, если бы вы резко нажали на тормоз и занесло до полной остановки; и вы не знаете, сколько времени потребуется, чтобы остановиться. В таком случае неизвестные параметры могут быть определены с использованием физических принципов и математических уравнений (кинематических уравнений).
БОЛЬШОЙ 4
Кинематические уравнения — это набор из четырех уравнений, которые можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. Уравнения можно использовать для любого движения, которое можно описать как движение с постоянной скоростью (ускорение 0 м / с / с) или движение с постоянным ускорением. Их нельзя использовать в течение какого-либо периода времени, в течение которого изменяется ускорение.Каждое из кинематических уравнений включает четыре переменные. Если известны значения трех из четырех переменных, то можно рассчитать значение четвертой переменной. Таким образом, кинематические уравнения предоставляют полезные средства прогнозирования информации о движении объекта, если известна другая информация. Например, если известно значение ускорения, а также начальное и конечное значения скорости буксирующего автомобиля, то смещение автомобиля и время можно предсказать с помощью кинематических уравнений.Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин для движения объекта.
Четыре кинематических уравнения, описывающие движение объекта:
В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект двигался.Символ a обозначает ускорение объекта. А символ v обозначает скорость объекта; индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Каждое из этих четырех уравнений надлежащим образом описывает математическую связь между параметрами движения объекта. Таким образом, они могут использоваться для прогнозирования неизвестной информации о движении объекта, если известна другая информация.В следующей части Урока 6 мы исследуем процесс этого.
Кинематические уравнения и решение проблем
Четыре кинематических уравнения, которые описывают математическую связь между параметрами, описывающими движение объекта, были введены в предыдущей части Урока 6. Четыре кинематических уравнения:
В приведенных выше уравнениях символ d обозначает смещение объекта.Символ t обозначает время, в течение которого объект двигался. Символ a обозначает ускорение объекта. А символ v обозначает мгновенную скорость объекта; индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Стратегия решения проблем
В этой части Урока 6 мы исследуем процесс использования уравнений для определения неизвестной информации о движении объекта.Процесс включает использование стратегии решения проблем, которая будет использоваться на протяжении всего курса. Стратегия предполагает следующие шаги:
- Постройте информативную диаграмму физической ситуации.
- Определите и перечислите данную информацию в переменной форме.
- Определите и перечислите неизвестную информацию в переменной форме.
- Определите и перечислите уравнение, которое будет использоваться для определения неизвестной информации из известной информации.
- Подставьте известные значения в уравнение и используйте соответствующие алгебраические шаги, чтобы найти неизвестную информацию.
- Проверьте свой ответ, чтобы убедиться, что он разумный и математически правильный.

Использование этой стратегии решения проблем при решении следующей проблемы смоделировано в примерах A и B ниже.
Пример задачи A
Има Харрин приближается к светофору, движущемуся со скоростью +30.0 м / с. Загорается желтый свет, и Има тормозит и останавливается. Если ускорение Има составляет -8,00 м / с 2 , то определите смещение автомобиля во время заноса. (Обратите внимание, что направление векторов скорости и ускорения обозначено знаками «+» и «-».)
Решение этой проблемы начинается с построения информативной диаграммы физической ситуации. Это показано ниже. Второй шаг включает идентификацию и перечисление известной информации в переменной форме.Обратите внимание, что значение v f может быть принято равным 0 м / с, поскольку машина Имы останавливается. Начальная скорость (v i ) кабины +30,0 м / с, так как это скорость в начале движения (заносное движение). А ускорение (а) автомобиля определяется как — 8,00 м / с 2 . (Всегда обращайте особое внимание на знаки + и — для данных количеств.) Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме.В этом случае проблема запрашивает информацию о перемещении автомобиля. Итак, d — неизвестная величина. Результаты первых трех шагов показаны в таблице ниже.
| Схема: | Дано: | Находка: |
|---|---|---|
| v i = +30,0 м / с v f = 0 м / с a = — 8,00 м / с 2 | d = ?? |
Следующий шаг стратегии включает определение кинематического уравнения, которое позволит вам определить неизвестную величину.На выбор предлагается четыре кинематических уравнения. В общем, вы всегда будете выбирать уравнение, которое содержит три известные и одну неизвестную переменные. В этом конкретном случае три известные переменные и одна неизвестная переменная: v f , v i , a и d. Таким образом, вы будете искать уравнение, в котором перечислены эти четыре переменные. Анализ четырех приведенных выше уравнений показывает, что уравнение в правом верхнем углу содержит все четыре переменные.
Таким образом, вы будете искать уравнение, в котором перечислены эти четыре переменные. Анализ четырех приведенных выше уравнений показывает, что уравнение в правом верхнем углу содержит все четыре переменные.
v f 2 = v i 2 + 2 • a • d
После того, как уравнение идентифицировано и записано, следующий шаг стратегии включает в себя замену известных значений в уравнение и использование соответствующих алгебраических шагов для поиска неизвестной информации.Этот шаг показан ниже.
(0 м / с) 2 = (30,0 м / с) 2 + 2 • (-8,00 м / с 2 ) • d
0 м 2 / с 2 = 900 м 2 / с 2 + (-16,0 м / с 2 ) • d
(16,0 м / с 2 ) • d = 900 м 2 / с 2 — 0 м 2 / с 2
(16,0 м / с 2 ) * d = 900 м 2 / с 2
d = (900 м 2 / с 2 ) / (16.0 м / с 2 )
d = (900 м 2 / с 2 ) / (16,0 м / с 2 )
d = 56,3 м
Решение, приведенное выше, показывает, что автомобиль заносит расстояние 56,3 метра. (Обратите внимание, что это значение округлено до третьей цифры.)
Последний шаг стратегии решения проблем включает проверку ответа, чтобы убедиться, что он является одновременно разумным и точным. Стоимость кажется достаточно разумной. Машине требуется значительное расстояние, чтобы занести из 30.0 м / с (примерно 65 миль / ч) до остановки. Расчетное расстояние составляет примерно половину футбольного поля, что делает его очень разумным расстоянием для заноса. Проверка точности включает подстановку вычисленного значения обратно в уравнение для смещения и обеспечение того, чтобы левая часть уравнения была равна правой части уравнения. В самом деле!
Пример задачи B
Бен Рушин ждет на светофоре. Когда он наконец стал зеленым, Бен ускорился из состояния покоя со скоростью 6,00 м / с 2 за время 4,10 секунды. Определите перемещение машины Бена за этот период времени.
Когда он наконец стал зеленым, Бен ускорился из состояния покоя со скоростью 6,00 м / с 2 за время 4,10 секунды. Определите перемещение машины Бена за этот период времени.
И снова решение этой проблемы начинается с построения информативной диаграммы физической ситуации. Это показано ниже. Второй шаг стратегии включает идентификацию и перечисление известной информации в переменной форме. Обратите внимание, что значение v i можно вывести как 0 м / с, поскольку машина Бена изначально находится в состоянии покоя.Ускорение (а) автомобиля составляет 6,00 м / с 2 . Время (t) равно 4,10 с. Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае проблема запрашивает информацию о перемещении автомобиля. Итак, d — неизвестная информация. Результаты первых трех шагов показаны в таблице ниже.
| Схема: | Дано: | Находка: |
|---|---|---|
| v i = 0 м / с т = 4.10 с a = 6,00 м / с 2 | d = ?? |
Следующий шаг стратегии включает определение кинематического уравнения, которое позволит вам определить неизвестную величину. На выбор предлагается четыре кинематических уравнения. Опять же, вы всегда будете искать уравнение, которое содержит три известные переменные и одну неизвестную переменную. В этом конкретном случае три известные переменные и одна неизвестная переменная — это t, v i , a и d.Анализ четырех приведенных выше уравнений показывает, что уравнение в левом верхнем углу содержит все четыре переменные.
d = v i • t + ½ • a • t 2
После того, как уравнение идентифицировано и записано, следующий шаг стратегии включает в себя замену известных значений в уравнение и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.
Этот шаг показан ниже.
d = (0 м / с) • (4.1 с) + ½ • (6,00 м / с 2 ) • (4,10 с) 2
d = (0 м) + ½ • (6,00 м / с 2 ) • (16,81 с 2 )
d = 0 м + 50,43 м
d = 50,4 м
Решение, приведенное выше, показывает, что автомобиль преодолеет расстояние 50,4 метра. (Обратите внимание, что это значение округлено до третьей цифры.)
Последний шаг стратегии решения проблем включает проверку ответа, чтобы убедиться, что он является одновременно разумным и точным.Стоимость кажется достаточно разумной. Автомобиль с ускорением 6,00 м / с / с достигнет скорости примерно 24 м / с (примерно 50 миль / ч) за 4,10 с. Расстояние, на которое такая машина будет перемещена в течение этого периода времени, будет примерно половиной футбольного поля, что делает это расстояние очень разумным. Проверка точности включает подстановку вычисленного значения обратно в уравнение для смещения и обеспечение того, чтобы левая часть уравнения была равна правой части уравнения.В самом деле!
Два приведенных выше примера задач иллюстрируют, как кинематические уравнения могут быть объединены с простой стратегией решения проблем для прогнозирования неизвестных параметров движения для движущегося объекта. Если известны три параметра движения, можно определить любое из оставшихся значений. В следующей части Урока 6 мы увидим, как эту стратегию можно применить к ситуациям свободного падения. Или, если интересно, вы можете попробовать несколько практических задач и сравнить свой ответ с данными решениями.
Решение проблем базовой кинематики | Безграничная физика
Приложения
Есть четыре кинематических уравнения, которые описывают движение объектов без учета его причин.
Цели обучения
Выберите, какое уравнение кинематики использовать в задачах, в которых начальное начальное положение равно нулю
Основные выводы
Ключевые моменты
- Четыре кинематических уравнения включают пять кинематических переменных: [latex] \ text {d} [/ latex], [latex] \ text {v} [/ latex], [latex] \ text {v} _0 [/ latex] , [латекс] \ text {a} [/ latex] и [латекс] \ text {t} [/ latex].

- Каждое уравнение содержит только четыре из пяти переменных, а другая отсутствует.
- Важно выбрать уравнение, которое содержит три известные переменные и одну неизвестную переменную для каждой конкретной ситуации.
Ключевые термины
- кинематика : Раздел физики, связанный с движущимися объектами.
Кинематика — это раздел классической механики, который описывает движение точек, тел (объектов) и систем тел (групп объектов) без учета причин движения.2 + 2 \ text {ad} [/ latex]
Обратите внимание, что четыре кинематических уравнения включают пять кинематических переменных: [latex] \ text {d} [/ latex] , [latex] \ text {v} [/ latex] , [latex] \ text {v } _0 [/ latex] , [латекс] \ text {a} [/ latex] и [латекс] \ text {t} [/ latex]. Каждое из этих уравнений содержит только четыре из пяти переменных, а другая отсутствует. Это говорит нам, что нам нужны значения трех переменных, чтобы получить значение четвертой, и нам нужно выбрать уравнение, которое содержит три известные переменные и одну неизвестную переменную для каждой конкретной ситуации.
Вот основные этапы решения проблем с использованием этих уравнений:
Шаг первый — Определите, что именно необходимо определить в проблеме (определите неизвестные).
Шаг второй. Найдите уравнение или систему уравнений, которые помогут вам решить проблему.
Шаг третий — Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численные решения вместе с единицами измерения.
Шаг четвертый. Проверьте ответ, чтобы узнать, разумен ли он: имеет ли он смысл?
Навыки решения проблем, безусловно, необходимы для успешного прохождения количественного курса физики.Что еще более важно, способность применять общие физические принципы, обычно представленные уравнениями, к конкретным ситуациям — очень мощная форма знания.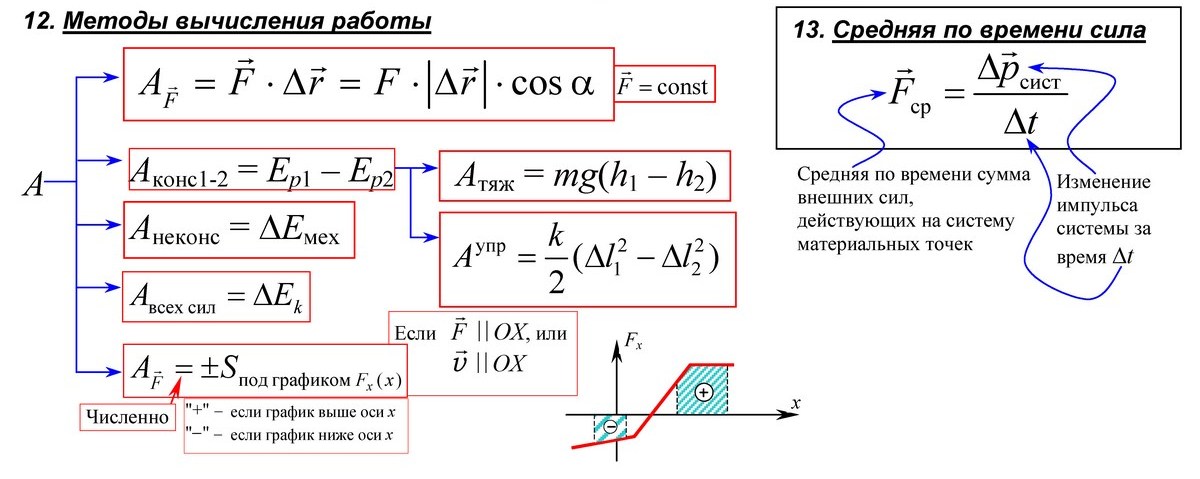 Это намного эффективнее, чем запоминание списка фактов. Аналитические навыки и способности решать проблемы могут быть применены к новым ситуациям, тогда как список фактов не может быть достаточно длинным, чтобы содержать все возможные обстоятельства. Такие аналитические навыки полезны как для решения задач на уроках физики, так и для применения физики в повседневной и профессиональной жизни.
Это намного эффективнее, чем запоминание списка фактов. Аналитические навыки и способности решать проблемы могут быть применены к новым ситуациям, тогда как список фактов не может быть достаточно длинным, чтобы содержать все возможные обстоятельства. Такие аналитические навыки полезны как для решения задач на уроках физики, так и для применения физики в повседневной и профессиональной жизни.
Диаграммы движения
Диаграмма движения — это графическое описание движения объекта, которое представляет положение объекта через равные промежутки времени.
Цели обучения
Построить диаграмму движения
Основные выводы
Ключевые моменты
- Диаграммы движения представляют движение объекта путем отображения его местоположения в разное время с равным интервалом на одной диаграмме.
- Диаграммы движения показывают начальное положение и скорость объекта, а также несколько точек в центре диаграммы.Эти пятна показывают состояние движения объекта.
- Диаграммы движения содержат информацию о положении объекта в определенные моменты времени и поэтому являются более информативными, чем диаграмма путей.
Ключевые термины
- стробоскопический : Относится к инструменту, который заставляет циклически движущийся объект казаться медленно движущимся или неподвижным.
- диаграмма : график или диаграмма.
- движение : изменение положения относительно времени.
Диаграмма движения — это графическое описание движения объекта. Он отображает местоположение объекта в разное время с равным интервалом на одной диаграмме; показывает начальное положение и скорость объекта; и представляет несколько точек в центре диаграммы. Эти пятна показывают, ускорился или замедлился объект. Для простоты объект представлен простой формой, например закрашенным кружком, который содержит информацию о положении объекта в определенные моменты времени. По этой причине диаграмма движения дает больше информации, чем диаграмма пути. Он также может отображать силы, действующие на объект в каждый момент времени.
По этой причине диаграмма движения дает больше информации, чем диаграмма пути. Он также может отображать силы, действующие на объект в каждый момент времени.
— диаграмма движения по простой траектории. Представьте себе объект в виде хоккейной шайбы, скользящей по льду. Обратите внимание, что шайба преодолевает одинаковое расстояние за единицу пути по траектории. Можно сделать вывод, что шайба движется с постоянной скоростью и, следовательно, во время движения нет ускорения или замедления.
Шайба, скользящая по льду : Диаграмма движения шайбы, скользящей по льду.Шайба движется с постоянной скоростью.
Одно из основных применений диаграмм движения — это представление фильма через серию кадров, снятых камерой; это иногда называют стробоскопической техникой (как показано на рисунке). Просмотр объекта на диаграмме движения позволяет определить, ускоряется или замедляется объект или находится в постоянном покое. Когда кадры сделаны, мы можем предположить, что объект находится в постоянном покое, если он занимает одно и то же положение с течением времени. Мы можем предположить, что объект ускоряется, если есть видимое увеличение пространства между объектами с течением времени, и что он замедляется, если есть видимое уменьшение пространства между объектами с течением времени.Объекты на кадре очень близко подходят друг к другу.
прыгающий мяч : прыгающий мяч, снятый с помощью стробоскопической вспышки со скоростью 25 изображений в секунду.
Формула кинематических уравнений
Кинематика — это исследование движущихся объектов и их взаимосвязей. Есть четыре (4) кинематических уравнения, которые относятся к смещению D, скорости v, времени t и ускорению a.
a) D = v i t + 1/2 при 2 b) (v i + v f ) / 2 = D / t
c) a = (v f — v i ) / t d) v f 2 = v i 2 + 2aD
D = смещение
a = ускорение
т = время
v f = конечная скорость
v i = начальная скорость
Формула кинематических уравнений.
1) Боб едет на велосипеде в магазин со скоростью 4 м / с, когда перед ним выбегает кошка. Он быстро тормозит до полной остановки, с ускорением — 2м / с 2 . Какое у него перемещение?
Ответ: Поскольку Боб остановлен, конечная скорость v f = 0. Его начальная скорость v i = 4 м / с. Ускорение, a = -2 м / с 2 . Время не указано, поэтому используйте уравнение (d) для смещения D, потому что оно не зависит от времени.
v f 2 = v i 2 + 2aD
(0) 2 = (4 м / с) 2 +2 (- 2 м / с 2 ) D
0 = 16 м 2 / с 2 + (- 4 м / с 2 ) D
-16 м 2 / с 2 = (- 4 м / с 2 ) D
16 м 2 / с 2 = 4 м / с 2 ) D
(16 м 2 / с 2 ) / (4 м / с 2 ) = D
Водоизмещение полное 4 м.
2) Вы путешествуете с постоянной скоростью 11 м / с в течение 5 минут. Как далеко ты проехал?
Ответ: При постоянной скорости v i = v f = 11 м / с. Время t = 5 мин или t = (60 сек / мин x 5 мин) = 300 сек. Теперь используйте уравнение (b), чтобы найти смещение D.
(v i + v f ) / 2 = D / t
D = [(v i + v f ) / 2] t
D = [(11 м / с + 11 м / с) / 2] x 300 с
D = (22 м / с) / 2 x 300 с
D = 11 м / с x 300 с
D = 3300 м Водоизмещение полное 3,300 м.
3) Каково ускорение автомобиля, который разгоняется с 11 до 40 м / с за 10 секунд?
Ответ: V i = 11 м / с. V f = 40 м / с. Время, t = 10 с. Используйте кинематическое уравнение c), чтобы найти ускорение.
a = (v f — v i ) / t
a = (40 м / с — 11 м / с) / 10 с
a = (29 м / с) / 10 с = 2,9 м / с 2
4) Если автомобиль разгоняется на 3. 0 м / с 2 от полной остановки, сколько времени потребуется, чтобы проехать 3000 м?
0 м / с 2 от полной остановки, сколько времени потребуется, чтобы проехать 3000 м?
Ответ: Ускорение a = 2,9 м / с 2 и перемещение D = 3000 м. Автомобиль был неподвижен, поэтому v i = 0. Используйте уравнение a), чтобы найти время.
D = v i t + 1/2 при 2
3000 м = 0т + 1/2 (3,0 м / с 2 ) т 2
3000 м = 1/2 (3,0 м / с 2 ) / т 2
3000 м / 1.5 м / с 2 = t 2
2000 с 2 = t 2
t = 44,72 сек
Каковы кинематические формулы?
Kinematic Equations: Целью этого первого раздела The Physics Classroom было исследование разнообразных средств, с помощью которых может быть описано движение объектов. Разнообразие представлений, которые мы исследовали, включает словесные представления, графические представления, числовые представления и графические представления (графики положения-времени и графики скорости-времени).
В Уроке 6 мы исследуем использование уравнений для описания и представления движения объектов. Эти уравнения известны как кинематические уравнения. Существует множество величин, связанных с движением объектов: смещение (и расстояние), скорость (и скорость), ускорение и время.
Что такое кинематические формулы?Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22.0 м / с, север в течение 12,0 секунд для смещения на север на 264 метра, затем движение автомобиля полностью описывается. И если известно, что вторая машина ускоряется из положения покоя с ускорением на восток 3,0 м / с 2 в течение 8,0 секунд, обеспечивая конечную скорость 24 м / с, восток и смещение на восток 96 метров. , то полностью описывается движение этой машины.
Эти два утверждения дают полное описание движения объекта.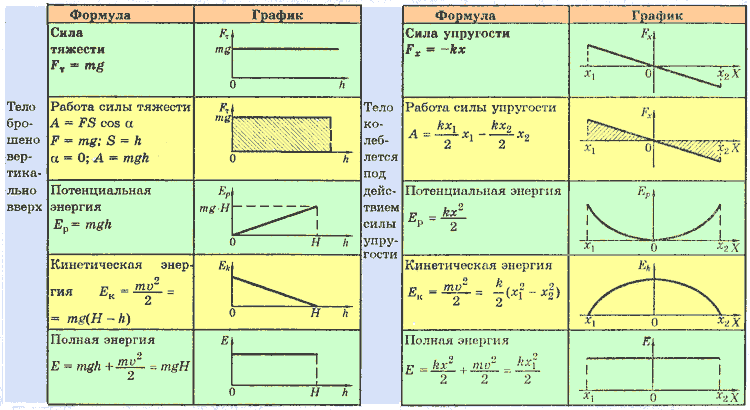 Однако не всегда такая полнота известна.Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны. Например, приближаясь к светофору, вы можете узнать, что ваша машина имеет скорость 22 м / с, восток, и способна к заносу 8,0 м / с 2 , запад.
Однако не всегда такая полнота известна.Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны. Например, приближаясь к светофору, вы можете узнать, что ваша машина имеет скорость 22 м / с, восток, и способна к заносу 8,0 м / с 2 , запад.
Однако вы не знаете, какое смещение испытает ваша машина, если бы вы резко нажали на тормоз и занесло до полной остановки; и вы не знаете, сколько времени потребуется, чтобы остановиться. В таком случае неизвестные параметры могут быть определены с использованием принципов физики и математических уравнений (кинематических уравнений)
4 кинематических уравнения
Кинематика — это изучение движущихся объектов и их взаимосвязей.Есть четыре (4) кинематических уравнения, которые относятся к смещению D, скорости v, времени t и ускорению a.
a) D = v i t + 1/2 при 2 b) (v i + v f ) / 2 = D / t
c) a = (v f — v i ) / t d) v f 2 = v i 2 + 2aD
D = смещение
a = ускорение
т = время
v f = конечная скорость
v i = начальная скорость
Какие 3 кинематических уравнения?
Если мы знаем три из этих пяти кинематических переменных — Δ x, t, v 0, v, a \ Delta x, t, v_0, v, a Δx, t, v0, v, adelta, x, запятая , t, запятая, v, начальный индекс, 0, конечный индекс, запятая, v, запятая, a — для объекта с постоянным ускорением мы можем использовать кинематическую формулу , см. ниже, чтобы найти одну из неизвестных переменных .
Сколько существует кинематических уравнений?
Четыре кинематических уравнения , которые описывают движение объекта: В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта.
Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта.
Для чего используются кинематические уравнения?
Кинематические уравнения могут быть использованы для вычисления различных аспектов движения, таких как скорость, ускорение, смещение и время.
Список кинематических уравнений
Кинематические формулы — это набор формул, которые относятся к пяти кинематическим переменным, перечисленным ниже.
Большой 1.
четырехъядерный v = v0 + at1
v = v0 + at1,
точка, пробел, v, равно, v, начальный индекс, 0, конечный индекс, плюс, a, t
Большой 2.
четырехугольник {\ Delta x} = (\ dfrac {v + v_0} {2}) t2
Δx = (2v + v0) t2,
точка, пробел, дельта, x, равно, левая скобка, начальная дробь, v, плюс, v, начальный нижний индекс, 0, конечный нижний индекс, деление на, 2, конечная дробь, правая скобка, t
Большой 3.2 + 2а \ Дельта x4.
v2 = v02 + 2aΔx4,
точка, пробел, v, начальный надстрочный индекс, 2, конечный надстрочный индекс, равно, v, начальный подстрочный индекс, 0, конечный подстрочный индекс, начальный надстрочный индекс, 2, конечный надстрочный индекс, плюс, 2, a, дельта, x
Поскольку кинематические формулы являются точными только в том случае, если ускорение является постоянным в течение рассматриваемого интервала времени, мы должны быть осторожны, чтобы не использовать их при изменении ускорения. Кроме того, кинематические формулы предполагают, что все переменные относятся к одному и тому же направлению: по горизонтали xxx, по вертикали yyy и т. Д.2} g = 9,81s2m g, равно, 9, точка, 81, начальная дробь, m, деленная на, s, начальный верхний индекс, 2, конечный верхний индекс, конечная дробь.
Это и странно, и удачно, если вдуматься. Это странно, так как это означает, что большой валун будет ускоряться вниз с таким же ускорением, как и небольшой камешек, и, если его уронить с той же высоты, он одновременно ударится о землю.
Это удачно, поскольку нам не нужно знать массу снаряда при решении кинематических формул, поскольку свободно летящий объект будет иметь такую же величину ускорения, g = 9.2} ay = −9,81s2m a, начальный индекс, y, конечный индекс, равно, минус, 9, точка, 81, начальная дробь, m, деленное на, s, начальный верхний индекс, 2, конечный верхний индекс, конечная дробь для снаряд, когда мы подставляем кинематические формулы.
Физика кинематических уравнений
Кинематические уравнения — это набор из четырех уравнений, которые можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. Уравнения можно использовать для любого движения, которое можно описать как движение с постоянной скоростью (ускорение 0 м / с / с) или движение с постоянным ускорением.Их нельзя использовать в течение какого-либо периода времени, в течение которого изменяется ускорение. Каждое из кинематических уравнений включает четыре переменные. Если известны значения трех из четырех переменных, то можно рассчитать значение четвертой переменной. Таким образом, кинематические уравнения предоставляют полезные средства прогнозирования информации о движении объекта, если известна другая информация.
Например, если значение ускорения, а также начальное и конечное значения скорости буксирующего автомобиля известны, то смещение автомобиля и время можно предсказать с помощью кинематических уравнений.Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин для движения объекта.
Четыре кинематических уравнения, описывающие движение объекта:
В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект двигался. Символ обозначает ускорение объекта.А символ v обозначает скорость объекта; индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект двигался. Символ обозначает ускорение объекта.А символ v обозначает скорость объекта; индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Каждое из этих четырех уравнений надлежащим образом описывает математическую связь между параметрами движения объекта. Таким образом, их можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация.В следующей части Урока 6 мы исследуем, как это сделать.
Читайте также: Формула линейной интерполяции
Основные кинематические уравнения
Кинематика — это исследование движения объектов без учета сил, вызывающих это движение. Эти знакомые уравнения позволяют студентам анализировать и предсказывать движение объектов, и студенты будут продолжать использовать эти уравнения на протяжении всего изучения физики. Твердое понимание этих уравнений и того, как их использовать для решения проблем, необходимо для успеха в физике.Эта статья представляет собой чисто математическое упражнение, предназначенное для быстрого обзора того, как уравнения кинематики выводятся с помощью алгебры.
Это упражнение ссылается на диаграмму на рис. 1, на которой ось x представляет время, а ось y представляет скорость. Диагональная линия представляет движение объекта, скорость которого изменяется с постоянной скоростью. Заштрихованная область (A 1 + A 2 ) представляет смещение объекта в течение интервала времени между t 1 и t 2 , в течение которого скорость объекта увеличилась с v 1 до v 2. .
В этом документе будут использоваться следующие переменные:
v = величина скорости объекта (метры в секунду, м / с)
v 1 = величина начальной скорости (метров на секунда, м / с) (в некоторых текстах это vi или v 0 )
v 2 = величина конечной скорости (метры в секунду, м / с) (в некоторых текстах это v f )
a = величина ускорения (в метрах в секунду в квадрате, м / с 2 )
с = вектор смещения, величина смещения — это расстояние,
с = │ s │ = d (векторы выделены жирным шрифтом; тот же символ, не выделенный жирным шрифтом, представляет величину вектора)
Δ указывает на изменение, например Δv = (v 2 –v 1 )
t = время
t 1 = начальное время
t 2 = Последний раз
Equations of Motion — The Physics Hypertextbook
Обсуждение
постоянное ускорение
Для точности этот раздел должен называться «Одномерные уравнения движения при постоянном ускорении». Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки. Эти уравнения движения действительны только тогда, когда ускорение постоянное и движение ограничено прямой линией.
Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки. Эти уравнения движения действительны только тогда, когда ускорение постоянное и движение ограничено прямой линией.
Учитывая, что мы живем в трехмерной вселенной, в которой единственная константа — это изменение, у вас может возникнуть соблазн сразу отказаться от этого раздела. Было бы правильно сказать, что ни один объект никогда не двигался по прямой с постоянным ускорением в любом месте Вселенной в любое время — ни сегодня, ни вчера, ни завтра, ни пять миллиардов лет назад, ни тридцать миллиардов лет в будущем. , никогда.Об этом я могу сказать с абсолютной метафизической уверенностью.
Так что же тогда хорошего в этом разделе? Что ж, во многих случаях полезно предположить, что объект двигался или будет двигаться по прямому пути с почти постоянным ускорением; то есть любое отклонение от идеального движения можно по существу игнорировать. Движение по криволинейной траектории можно считать фактически одномерным, если для задействованных объектов существует только одна степень свободы .Дорога может изгибаться и поворачиваться и исследовать всевозможные направления, но автомобили, движущиеся по ней, имеют только одну степень свободы — свободу двигаться в одном или противоположном направлении. (Вы не можете двигаться по дороге по диагонали и надеетесь остаться на ней надолго.) В этом отношении это мало чем отличается от движения, ограниченного прямой линией. Аппроксимация реальных ситуаций моделями, основанными на идеальных ситуациях, не считается обманом. Так поступают в физике. Это настолько полезный метод, что мы будем использовать его снова и снова.
Наша цель в этом разделе — вывести новые уравнения, которые можно использовать для описания движения объекта в терминах его трех кинематических переменных: скорости ( v ), положения ( с ) и времени ( т ). Есть три способа объединить их в пары: скорость-время, положение-время и скорость-положение. В этом порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин для изучения этих имен.
В этом порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин для изучения этих имен.
Поскольку мы имеем дело с движением по прямой линии, направление будет обозначено знаком — положительные величины указывают в одну сторону, а отрицательные величины указывают в противоположную сторону.Определение того, какое направление является положительным, а какое отрицательным, совершенно произвольно. Законы физики изотропны ; то есть они не зависят от ориентации системы координат. Однако некоторые проблемы легче понять и решить, если одно направление предпочтительнее другого. Пока вы последовательны в решении проблемы, это не имеет значения.
скорость-время
Связь между скоростью и временем проста при равномерно ускоренном прямолинейном движении.Чем дольше ускорение, тем больше изменение скорости. Изменение скорости прямо пропорционально времени, когда ускорение постоянно. Если скорость увеличивается на определенную величину за определенное время, она должна увеличиваться вдвое на эту величину в два раза быстрее. Если объект уже стартовал с определенной скоростью, то его новая скорость будет равна старой скорости плюс это изменение. Вы должны быть в состоянии увидеть уравнение уже мысленным взором.
Это самое простое из трех уравнений, которое можно вывести с помощью алгебры.Начнем с определения ускорения.
Расширить ∆ v до v — v 0 и сжать ∆ t до t .
Затем найдите v как функцию от t .
v = v 0 + at [1]
Это первое уравнение движения . Он записывается как полином — постоянный член ( v 0 ), за которым следует член первого порядка ( на ).Поскольку наивысший порядок равен 1, правильнее называть его линейной функцией 1.
Символ v 0 [vee naught] называется начальной скоростью или скоростью t = 0. Его часто называют «первой скоростью», но это довольно наивный способ Опишите это. Лучшее определение было бы сказать, что начальная скорость — это скорость, которую имеет движущийся объект, когда он впервые становится важным в проблеме. Скажем, метеор был замечен глубоко в космосе, и проблема заключалась в том, чтобы определить его траекторию, тогда начальная скорость, вероятно, будет той скоростью, которую он имел при первом наблюдении.Но если проблема заключалась в том, что тот же самый метеор сгорает при входе в атмосферу, то начальная скорость, вероятно, равна скорости, которую он имел при входе в атмосферу Земли. Ответ на вопрос «Какая начальная скорость?» «Это зависит от обстоятельств». Это оказывается ответом на множество вопросов.
Его часто называют «первой скоростью», но это довольно наивный способ Опишите это. Лучшее определение было бы сказать, что начальная скорость — это скорость, которую имеет движущийся объект, когда он впервые становится важным в проблеме. Скажем, метеор был замечен глубоко в космосе, и проблема заключалась в том, чтобы определить его траекторию, тогда начальная скорость, вероятно, будет той скоростью, которую он имел при первом наблюдении.Но если проблема заключалась в том, что тот же самый метеор сгорает при входе в атмосферу, то начальная скорость, вероятно, равна скорости, которую он имел при входе в атмосферу Земли. Ответ на вопрос «Какая начальная скорость?» «Это зависит от обстоятельств». Это оказывается ответом на множество вопросов.
Символ v — это скорость через некоторое время t после начальной скорости. Ее часто называют конечной скоростью , но это не делает ее «последней скоростью» объекта. Возьмем случай с метеором.Какая скорость обозначена символом v ? Если вы внимательно слушали, значит, вы должны были ожидать ответа. По-разному. Это может быть скорость метеора, когда он проходит мимо Луны, входит в атмосферу Земли или ударяется о поверхность Земли. Это также может быть скорость метеорита, находящегося на дне кратера. (В этом случае v = 0 м / с.) Является ли какое-либо из этих значений конечной скоростью? Кто знает. Кто-то мог извлечь метеорит из дыры в земле и уехать вместе с ним.Это актуально? Наверное, нет, но это зависит от обстоятельств. Для такого рода вещей нет правил. Вы должны проанализировать текст задачи на предмет физических величин, а затем присвоить значение математическим символам.
Последняя часть этого уравнения на — это изменение скорости от начального значения. Вспомните, что a — это скорость изменения скорости, а t — это время после некоторого начального события . Ставка раз время меняется. Учитывая, что объект ускоряется со скоростью 10 м / с 2 , через 5 с он будет двигаться на 50 м / с быстрее. Если бы он стартовал со скоростью 15 м / с, то его скорость через 5 с была бы…
Если бы он стартовал со скоростью 15 м / с, то его скорость через 5 с была бы…
15 м / с + 50 м / с = 65 м / с
время позиции
Смещение движущегося объекта прямо пропорционально скорости и времени. Двигайся быстрее. Иди дальше. Двигайтесь дольше (как и дольше). Иди дальше. Ускорение усугубляет эту простую ситуацию, поскольку скорость теперь также прямо пропорциональна времени. Попробуйте сказать это словами, и это прозвучит нелепо. «Смещение прямо пропорционально времени и прямо пропорционально скорости, которая прямо пропорциональна времени.»Время удваивается, поэтому смещение пропорционально квадрату времени. Автомобиль, разгоняющийся в течение двух секунд, преодолеет в четыре раза больше расстояния, чем автомобиль, ускоряющийся всего за одну секунду (2 2 = 4). Автомобиль, ускоряющийся в течение трех секунды покрыли бы расстояние в девять раз большее (3 2 = 9).
Если бы это было так просто. Этот пример работает, только когда начальная скорость равна нулю. Смещение пропорционально квадрату времени, когда ускорение постоянное, а начальная скорость равна нулю.Истинное общее утверждение должно учитывать любую начальную скорость и то, как она менялась. Это приводит к ужасно запутанному утверждению соразмерности. Смещение прямо пропорционально времени и пропорционально квадрату времени, когда ускорение постоянно. Функция, которая является одновременно линейной и квадратной, называется квадратичной функцией , что позволяет нам значительно сжать предыдущее утверждение. Перемещение является квадратичной функцией времени при постоянном ускорении
Формулировки пропорциональности полезны, но не столь общие, как уравнения.Мы до сих пор не знаем, каковы константы пропорциональности для этой проблемы. Один из способов понять их — использовать алгебру.
Начнем с определения средней скорости.
Расширить ∆ с до с — с 0 и сжать ∆ т до т .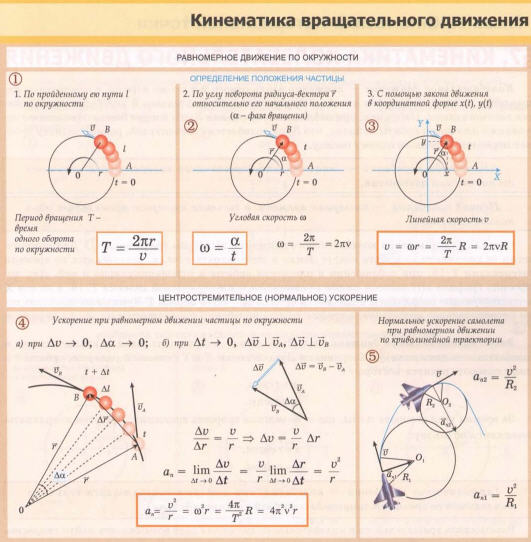
Найдите позицию.
с = с 0 + vt [a]
Чтобы продолжить, нам нужно прибегнуть к небольшому трюку, известному как теорема о средней скорости или правило Мертона .Я предпочитаю последнее, так как правило может применяться к любой величине, которая изменяется с одинаковой скоростью, а не только к скорости. Правило Мертона было впервые опубликовано в 1335 году в Мертон-колледже, Оксфорд, английским философом, математиком, логиком и калькулятором Уильямом Хейтсбери (1313–1372). Когда скорость изменения величины постоянна, ее среднее значение находится на полпути между ее конечным и начальным значениями.
v = ½ ( v + v 0 ) [4]
Подставьте первое уравнение движения [1] в это уравнение [4] и упростите его, исключив v .
| v = ½ [( v 0 + при ) + v 0 ] v = ½ (2 v 0 + при ) v = v 0 + ½ at [b] |
Теперь замените [b] на [a], чтобы исключить v [vee bar].
с = с 0 + ( v 0 + ½ при ) t
И наконец, найдите s как функцию от t .
с = с 0 + v 0 т + ½ при 2 [2]
Это второе уравнение движения . Он записывается как полином — постоянный член ( s 0 ), за которым следует член первого порядка ( v 0 t ), за которым следует член второго порядка (½ при 2 ). ). Поскольку старший порядок равен 2, правильнее называть его квадратичным .
Символ s 0 [ess naught] часто рассматривается как начальная позиция . Символ s — это позиция на t позже. Если хотите, вы можете называть ее конечной позицией . Изменение положения (∆ s ) называется смещением или расстоянием (в зависимости от обстоятельств), и некоторые люди предпочитают писать второе уравнение движения таким образом.
Символ s — это позиция на t позже. Если хотите, вы можете называть ее конечной позицией . Изменение положения (∆ s ) называется смещением или расстоянием (в зависимости от обстоятельств), и некоторые люди предпочитают писать второе уравнение движения таким образом.
∆ с = v 0 t + ½ при 2 [2]
скорость-позиция
Первые два уравнения движения описывают одну кинематическую переменную как функцию времени.По сути…
- Скорость прямо пропорциональна времени при постоянном ускорении ( v ∝ t ).
- Смещение пропорционально квадрату времени при постоянном ускорении (∆ с ∝ т 2 ).
Объединение этих двух утверждений приводит к третьему, не зависящему от времени. При замене должно быть очевидно, что…
- Смещение пропорционально квадрату скорости при постоянном ускорении (∆ s ∝ v 2 ).
Это утверждение особенно важно для безопасности вождения. Когда вы вдвое увеличиваете скорость автомобиля, требуется в четыре раза больше расстояния, чтобы его остановить. Увеличьте скорость втрое, и вам понадобится в девять раз больше расстояния. Это хорошее практическое правило, которое следует запомнить.
Концептуальное введение сделано. Пришло время вывести формальное уравнение.
способ 1
Объедините первые два уравнения вместе таким образом, чтобы исключить время как переменную. Самый простой способ сделать это — начать с первого уравнения движения…
v = v 0 + at [1]
решить на время…
, а затем подставим его во второе уравнение движения…
с = с 0 + v 0 т + ½ при 2 [2]
как это…
| с = | с 0 + в 0 | ⎛ ⎜ ⎝ | в — в 0 | ⎞ ⎟ ⎠ | + ½ a | ⎛ ⎜ ⎝ | в — в 0 | ⎞ 2 ⎟ 90 840 ⎠ |
| с — с 0 = | vv 0 — v 0 2 | + | v 2 -2 vv 0 + v 0 2 |
| 2 a |
| 2 a ( с — с 0 ) = 2 ( vv 0 — v 0 2 ) + ( v 2 — 2 vv 0 + v 0 2 ) | |
| 2 a ( с — с 0 ) = v 2 — v 0 2 | |
Возведите объект в квадрат скорости, и все готово.
v 2 = v 0 2 + 2 a ( s — s 0 ) [3]
Это третье уравнение движения . Еще раз, символ s 0 [ess naught] — это начальная позиция , а s — это позиция через некоторое время t позже. Если вы предпочитаете, вы можете написать уравнение, используя ∆ s — изменение в позиции , смещение или расстояние в зависимости от ситуации.
v 2 = v 0 2 + 2 a ∆ s [3]
метод 2
Более сложный способ вывести это уравнение — начать со второго уравнения движения в этой форме…
∆ с = v 0 t + ½ при 2 [2]
и решите ее на время. Это непростая работа, поскольку уравнение квадратично. Переставьте термины так…
½ при 2 + v 0 t — ∆ s = 0
и сравните его с общей формой квадратичного.
ось 2 + bx + c = 0
Решение этой задачи дает известное уравнение…
| x = | — b ± √ ( b 2 — 4 ac ) |
| 2 |
Замените символы в общем уравнении эквивалентными символами из нашего преобразованного второго уравнения движения…
| т = | — v 0 ± √ [ v 0 2 — 4 (½ a ) (∆ s )] |
| 2 (½ a ) |
почисти немного…
| т = | — в 0 ± √ ( в 0 2 -2 a ∆ с ) |
, а затем подставьте его обратно в первое уравнение движения.
v = v 0 + at [1]
| v = v 0 + a | ⎛ ⎜ ⎝ | — в 0 ± √ ( в 0 2 -2 a ∆ с ) | ⎞ ⎟ ⎠ |
Материал отменяется, и мы получаем это…
v = ± √ ( v 0 2 + 2 a ∆ s )
Выровняйте обе стороны, и все готово.
v 2 = v 0 2 + 2 a ∆ s [3]
Это было не так уж плохо, не так ли?
исчисления выводов
Исчисление — это сложная математическая тема, но она значительно упрощает вывод двух из трех уравнений движения. По определению, ускорение — это первая производная скорости по времени. Возьмите операцию в этом определении и отмените ее. Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость.Это дает нам уравнение скорость-время. Если предположить, что ускорение постоянное, мы получим так называемое первое уравнение движения [1].
| = | |||
| дв | = | a dt | |
| = | |||
| v — v 0 | = | при | |
| в | = | v 0 + at [1] | |
Опять же, по определению, скорость — это первая производная положения по времени. Выполните эту операцию в обратном порядке. Вместо того, чтобы различать положение для определения скорости, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положения-времени для постоянного ускорения, также известное как второе уравнение движения [2].
Выполните эту операцию в обратном порядке. Вместо того, чтобы различать положение для определения скорости, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положения-времени для постоянного ускорения, также известное как второе уравнение движения [2].
| в | = | |||||||||
| DS | = | в dt | ||||||||
| DS | = | ( v 0 + at ) dt | ||||||||
| = |
| |||||||||
| с — с 0 | = | v 0 t + ½ при 2 | ||||||||
| с | = | с 0 + v 0 t + ½ при 2 [2] | ||||||||
В отличие от первого и второго уравнений движения, нет очевидного способа вывести третье уравнение движения (то, которое связывает скорость с положением) с помощью расчетов.Мы не можем просто перепроектировать это по определению. Нам нужно разыграть довольно изощренный трюк.
Первое уравнение движения связывает скорость со временем. По сути, мы вывели его из этой производной…
Второе уравнение движения связывает положение со временем. Это произошло от этой производной…
Это произошло от этой производной…
Третье уравнение движения связывает скорость с положением. По логике, это должно происходить от производной, которая выглядит так…
Но что это значит? Ну, ничего по определению, но, как и все количества, оно равно самому себе.Он также равен самому себе, умноженному на 1. Мы будем использовать специальную версию 1 ( dt dt ) и специальную версию алгебры (алгебра с бесконечно малыми). Посмотрите, что происходит, когда мы это делаем. Мы получаем одну производную, равную ускорению ( dv dt ), и другую производную, равную обратной скорости ( dt ds ).
| дв | = | дв | 1 | |
| DS | DS | |||
| дв | = | дв | дт | |
| DS | DS | дт | ||
| дв | = | дв | дт | |
| DS | дт | DS | ||
| дв | = | a | 1 | |
| DS | в |
Следующий шаг, разделение переменных.Соберите вместе похожие вещи и интегрируйте их. Вот что мы получаем при постоянном ускорении…
| = | ||||
| в дв | = | и DS | ||
| = | ||||
| ½ ( v 2 — v 0 2 ) | = | a ( с — с 0 ) | ||
| в 2 | = | v 0 2 + 2 a ( с — с 0 ) [3] | ||
Безусловно, умное решение, и оно было не так уж сложно, чем первые два варианта. Однако на самом деле это сработало только потому, что ускорение было постоянным — постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно трудным. Мы вернемся к алгебре, чтобы спасти наше здравомыслие. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сэкономить.
Однако на самом деле это сработало только потому, что ускорение было постоянным — постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно трудным. Мы вернемся к алгебре, чтобы спасти наше здравомыслие. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сэкономить.
| v = | в 0 + в | [1] |
| + | ||
| с = | с 0 + v 0 t + ½ при 2 | [2] |
| = | ||
| v 2 = | в 0 2 + 2 a ( с — с 0 ) | [3] |
Кинематические уравнения и постоянное ускорение
В своих «Диалогах двух новых наук» Галилей вывел взаимосвязь между пройденным расстоянием и временем, когда шары катились по наклонной плоскости.Это часто называют законом падающих тел. Интересно, что в доказательстве Галилея вместо алгебры, которую мы представим здесь, использовалась классическая евклидова геометрия (которая была бы незнакома современному изучающему геометрию из учебников). Учащиеся продвинутого уровня могут получить те же уравнения, используя математический анализ.
Основа Закона падающих тел заключается в том, что по мере того, как мяч катится по рампе, он ускоряется. По мере увеличения его скорости увеличивается расстояние, которое он проходит за каждую единицу времени.Галилей определил это с помощью колокольчиков на спусковом крючке катящегося шарика.
Процитируем Галилея в переводе:
По сути, Галилей представил, что не только ускорение вниз по рампе из-за постоянной силы тяжести, но и что скорость увеличивается линейно с временем . Он представил, что положение увеличивается с квадратом времени, что часто называют Законом падающих тел. Последний пункт в этом отрывке, который он представил, заключается в том, что скорость увеличивается с квадратом расстояния вниз по рампе.
Он представил, что положение увеличивается с квадратом времени, что часто называют Законом падающих тел. Последний пункт в этом отрывке, который он представил, заключается в том, что скорость увеличивается с квадратом расстояния вниз по рампе.
Основываясь на том, что вы уже узнали и что представил Галилей, у нас есть то, что мой учитель физики, Гленн Глейзер, любил называть пятью священными уравнениями кинематики для постоянного ускорения. В этих уравнениях v — скорость, x — положение, t — время и a — ускорение. Помните, что Δ означает изменение.
1. или Δx = v ср. Δt
2. или v f = v o + aΔt или Δv = aΔt
3.
4. Δx = v o Δt + ½ a Δt 2
5. v f 2 = v o 2 + 2aΔx
Первые два уравнения, которые мы видели ранее. Важно отметить, что в первом уравнении используется средняя скорость , тогда как во втором уравнении используется изменение между исходной и конечной скоростью . Связь между ними представлена в третьем уравнении, которое представляет собой просто закон средних чисел.Средняя скорость — это среднее значение исходной и конечной скорости.
Из этих трех основных определений мы можем вывести следующие два уравнения, используя либо геометрию, либо алгебру (или исчисление).
Используя алгебру, мы можем вывести уравнение №4.
Исходя из уравнения № 1
Δx = v ср. Δt
Затем мы подставляем определение средней скорости из уравнения №3.
Отсюда мы подставляем окончательную скорость, полученную в уравнении № 2
Затем мы распределяем член Δt и упрощаем, комбинируя члены v o .
Мы упрощаем оставшиеся два члена, чтобы получить
Стоит отметить, что происходит, когда исходная скорость v o, равна нулю. Это уравнение еще больше упрощается и становится
Это уравнение еще больше упрощается и становится
Если мы предположим, что исходная позиция и время равны нулю, мы можем дополнительно уменьшить это до
Используя геометрию, мы можем исследовать область под кривой графика зависимости скорости от времени для движения с постоянным ускорением.
Если мы посмотрим на область под кривой, мы можем разбить ее на прямоугольник и треугольник. Красный прямоугольник — это вклад исходной скорости объекта. Смещение из-за ускорения представлено зеленым треугольником. Треугольник имеет ширину Δt и высоту aΔt, которые мы знаем из уравнения №2. Член ½ происходит от формулы площади треугольника.
Мы также можем использовать исчисление для вывода этого уравнения путем интегрирования удвоенного ускорения по времени.
Пятое священное уравнение может быть получено аналогичными заменами, и его оставят как домашнее задание.
Теперь давайте рассмотрим несколько примеров задач: Численное решение задач.
Пример 1
По легенде, Галилей уронил мяч из Пизанской башни. Если башня имеет высоту 55,9 м и пренебрегает сопротивлением воздуха, сколько времени потребуется свинцовому мячу, чтобы достичь земли?
Гивенс: a = g ≈ 10 м / с 2
Δx = 55.9 м
Неизвестно: t = ???
Уравнение, связывающее эти переменные, — это священное уравнение 4 th .
Δx = v o Δt + ½ a Δt 2
Как упоминалось ранее, поскольку начальная скорость равна нулю, уравнение упрощается.
Δx = v o Δt + ½ a Δt 2 = ½ a Δt 2
Поскольку мы хотим изолировать переменную для времени, мы пересекаем умножение, чтобы переместить ½ и член ускорения на другую сторону.
Затем извлекаем квадратный корень из обеих частей.
Это дает выражение для времени. Обратите внимание, что я вставил несколько дополнительных скобок, которые могут вам не понадобиться.
При подключении номеров это довольно просто то, что мы называем «подключи и забей». Однако с агрегатами нужно быть осторожным. Вы, наверное, догадались, что время будет измеряться в секундах. Однако у вас должна быть возможность отменить фактические единицы, чтобы получить время в секундах.
Пример 2
Койот падает со скалы высотой 25 метров. Как быстро койот падает, когда ударяется о землю? Если проблема койота
Дано x = 25 м
a = g ≈ 10 м / с 2
Неизвестно: v = ???
Эту проблему можно решить несколькими способами. Можно было использовать комбинацию или Священные уравнения №2 и №4. Или вы можете напрямую использовать уравнение №5.
Использование v f 2 = v o 2 + 2aΔx
Это упрощается, поскольку исходная скорость v o, равна нулю.
Если извлечь квадратный корень из обеих частей уравнения
Обратите внимание, как вы извлекаете квадратный корень из единиц, чтобы получить м / с .
Мы оставим решение этой задачи с двумя уравнениями для домашней задачи.
Краткое изложение проблем построения графиков, наклона и площади под кривыми
Изучая графики положения, скорости и ускорения, вы сможете рисовать их как взаимозаменяемые.
Вчера в классе вы видели, что график объекта, ускоряющегося вниз по склону, выглядит следующим образом:
В этом примере мы используем программное обеспечение для анализа изображений.Это пример с мячом, катящимся с холма. Следует отметить, что график ускорения не показывает фактическую скорость, а показывает только то, как она меняется. Точно так же график скорости не дает вам фактического положения объекта, а только того, как он изменяется. Щелкнув по мячу и нажав кнопку трека, вы увидите график положения и скорости.
Здесь вы можете увидеть результаты построения графика движения.
 Молекулярная физика
Молекулярная физика