НЕСОБСТВЕННЫЙ ИНТЕГРАЛ — это… Что такое НЕСОБСТВЕННЫЙ ИНТЕГРАЛ?
— интеграл от неограниченной функции или от функции по неограниченному множеству. Пусть функция f определена на конечном или бесконечном полуинтервале 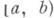 ,
,  и для любого
и для любого 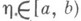 функция f интегрируема но Риману (по Лебегу) на отрезке
функция f интегрируема но Риману (по Лебегу) на отрезке  Тогда предел
Тогда предел 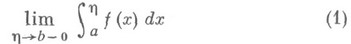
(в случае 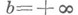 условие
условие  понимается как
понимается как  ) наз. несобственным интегралом
) наз. несобственным интегралом
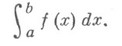
Если предел (1) существует, то говорят, что Н. и. сходится, если не существует — расходится. Напр., Н. и.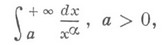 при
при  сходится, а при
сходится, а при  расходится.
Если же
расходится.
Если же  , то
, то 
сходится при 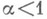 и расходится при
и расходится при  .
.
Если 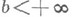
Аналогично при соответствующих предположениях определяют Н. и. по промежутку 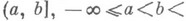
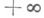
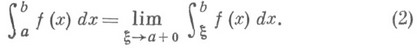
Если функция/ интегрируема по Риману (по Лебегу) на каждом отрезке 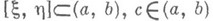 и существуют то Н. и.
и существуют то Н. и.
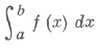
определяется как сумма
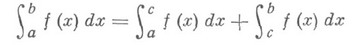
и не зависит от выбора точки с.
Если на интервале ( а, b
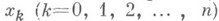 :
: 
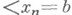 таких, что функция f интегрируема по Риману (по Лебегу) на каждом отрезке
таких, что функция f интегрируема по Риману (по Лебегу) на каждом отрезке  , не содержащем ни одной точки
, не содержащем ни одной точки 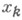 , и для каждого
, и для каждого  существуют Н. и.
существуют Н. и.

то Н. и.

Это определение не зависит от выбора точек 
На Н. и. переносятся общие свойства интегралов: линейность, аддитивность относительно промежутков, по к-рым производится интегрирование, правило интегрирования неравенств, теоремы о среднем, интегрирование по частям и замены переменного, формула Ньютона — Лейбница. Напр., если функция f почти всюду на [ а, b )совпадает с производной функции F, к-рая абсолютно непрерывна на каждом отрезке  то
то
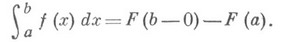
Для выяснения сходимости Н. и. от знакопостоянных функций применяется признак сравнения: напр., для Н. и. вида (1) при выполнении условия
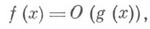
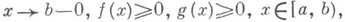 из сходимости Н. и.
из сходимости Н. и.
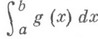
следует сходимость Н. и.
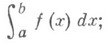
функция  наз. в этом случае функцией сравнения. В качестве функции сравнения для интегралов (1) в случае конечного предела интегрирования bчасто используются функции
наз. в этом случае функцией сравнения. В качестве функции сравнения для интегралов (1) в случае конечного предела интегрирования bчасто используются функции 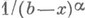 ; для интегралов вида (2) в случае конечности предела интегрирования а- функции
; для интегралов вида (2) в случае конечности предела интегрирования а- функции 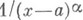 , при наличии одного или двух бесконечных пределов интегрирования — функции
, при наличии одного или двух бесконечных пределов интегрирования — функции 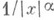 . Из признака сравнения следует, напр., если для неотрицательной функции f, определенной при
. Из признака сравнения следует, напр., если для неотрицательной функции f, определенной при 

то при  Н. и.
Н. и.
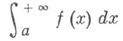
вида (1) сходится, а при  Н. и. расходится.
Н. и. расходится.
Необходимое и достаточное условие сходимости Н. и. дает критерий Коши. Так, Н. и. вида (1) сходится тогда и только тогда, когда для любого  существует такое
существует такое 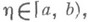 что для всех
что для всех 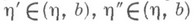 выполняется неравенство
выполняется неравенство
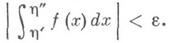
Н.
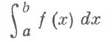
наз. абсолютно сходящимся, если сходится Н. и.

Если Н. и, абсолютно сходится, то он сходится и совпадает с интегралом Лебега. Существуют Н.
а для бесконечного:

Существуют различные признаки для установления сходимости Н. и. Так, если функции f и gопределены для  , функция f имеет на полуоси
, функция f имеет на полуоси 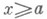
 то Н. и.
то Н. и.
сходится. Другой признак: если Н. и.
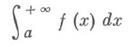
сходится, а функция gмонотонна и ограничена при  , то Н. и.
, то Н. и.
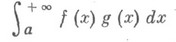
сходится.
Сходимость Н. и. можно выразить в терминах сходящихся рядов: напр., для того чтобы Н. и. (1) сходился, необходимо и достаточно, чтобы для любой последовательности  сходился ряд
сходился ряд
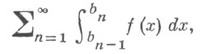
причем в случае его сходимости сумма ряда совпадает с Н. и. (1).
Понятие Н. и. обобщается для функций многих переменных. Пусть функция f определена на открытом (ограниченном или неограниченном) множестве G n -мерного евклидова пространства 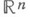 и интегрируема по Риману на любом измеримом по Жордану множестве
и интегрируема по Риману на любом измеримом по Жордану множестве  Функцию f наз. интегрируемой в несобственном смысле по множеству G, если для любой последовательности измеримых по Жордану множеств
Функцию f наз. интегрируемой в несобственном смысле по множеству G, если для любой последовательности измеримых по Жордану множеств  таких, что
таких, что 
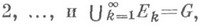
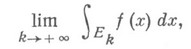
не зависящий от выбора указанной последовательности 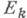 . Этот предел, если он существует, наз. Н. и.
. Этот предел, если он существует, наз. Н. и.
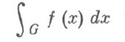
и, как в одномерном случае, говорят, что этот интеграл сходится. Он существует тогда и только тогда, когда существует интеграл

В этом случае Н. и.
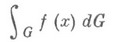
совпадает с интегралом Лебега. Это обстоятельство связано с тем, что при n=1 и данном выше определении Н. и. переход к пределу осуществлялся по весьма специальному классу измеримых по Жордану множеств, а именно по отрезкам. В качестве же 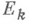
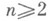 сделанное утверждение остается в силе и в том случае, когда в качестве множеств
сделанное утверждение остается в силе и в том случае, когда в качестве множеств 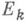 взяты только измеримые по Жордану области. Таким образом, в этом случае понятие Н. и. не приводит к новому понятию по сравнению с интегралом Лебега.
взяты только измеримые по Жордану области. Таким образом, в этом случае понятие Н. и. не приводит к новому понятию по сравнению с интегралом Лебега.Для Н. и. от функции многих переменных справедлив признак сравнения, аналогичный одномерному случаю. В качестве интегралов сравнения берут

где
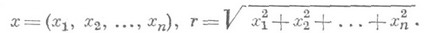
Первый сходится при  и расходится при
и расходится при  , второй сходится при
, второй сходится при 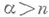 и расходится при
и расходится при  .
.
К Н. и. относятся интегралы в смысле главного значения. Пусть функция f определена на открытом множестве 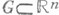 , кроме, быть может, точки
, кроме, быть может, точки  , и пусть для любого
, и пусть для любого 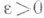 функция f интегрируема (по Риману или по Лебегу) на множестве
функция f интегрируема (по Риману или по Лебегу) на множестве 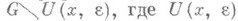 есть
есть  -окрестность точки х. Тогда если существует предел
-окрестность точки х. Тогда если существует предел 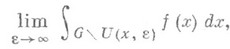
то его наз. интегралом в смысле главного значения и обозначают

Если интеграл
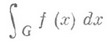
существует как Н. и., то он существует и в смысле главного значения. Обратное, вообще говоря, неверно. Напр., Н. и. расходится, а
расходится, а 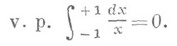
Аналогично определяют интегралы в смысле главного значения в бесконечно удаленной точке.
Лит.:[1] Ильин В. А., Позняк Э. Г., Основы математического анализа, т. 2, М., 1973; [2] Кудрявцев Л. Д., Курс математического анализа, т. 2, М., 1981; [3] Никольский С. М., Курс математического анализа, 2 изд., т. 2, М., 1975.
Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru
Несобственный интеграл — это… Что такое Несобственный интеграл?
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
- Предел a или b (или оба предела) являются бесконечными;
- Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].
Несобственные интегралы I рода
Пусть определена и непрерывна на множестве от и . Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае называется сходящимся.
- Если не существует конечного ( или ), то интеграл называется расходящимся к , или просто расходящимся.
Пусть определена и непрерывна на множестве от и . Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае называется сходящимся.
- Если не существует конечного ( или ), то интеграл называется расходящимся к , или просто расходящимся.
Если функция определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
, где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.
Примеры
Несобственные интегралы II рода
Пусть определена на , терпит бесконечный разрыв в точке x=a и . Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если или , то обозначение сохраняется, а называется расходящимся к , или просто расходящимся.
Пусть определена на , терпит бесконечный разрыв при x=b и . Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если или , то обозначение сохраняется, а называется расходящимся к , или просто расходящимся.
Если функция терпит разрыв во внутренней точке отрезка , то несобственный интеграл второго рода определяется формулой:
Геометрический смысл несобственных интегралов II рода
Несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции
Пример
Отдельный случай
Пусть функция определена на всей числовой оси и имеет разрыв в точках .
Тогда можно найти несобственный интеграл
Критерий Коши
1. Пусть определена на множестве от и .
- Тогда сходится
2. Пусть определена на и .
- Тогда сходится
Абсолютная сходимость
Интеграл называется абсолютно сходящимся, если сходится.
Если интеграл сходится абсолютно, то он сходится.
Условная сходимость
Интеграл называется условно сходящимся, если сходится, а расходится.
См. также
Список используемой литературы
Дмитрий Письменный Конспект лекций по высшей математике, часть 1. — Айрис Пресс, 2007. — С. 233-237.
dic.academic.ru
Несобственный интеграл — Википедия. Что такое Несобственный интеграл
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.
- Область интегрирования является бесконечной. Например, является бесконечным промежутком [a,+∞){\displaystyle [a,+\infty )}.
- Функция f(x){\displaystyle f(x)} является неограниченной в окрестности некоторых точек области интегрирования.
Если интервал [a,b]{\displaystyle [a,b]} конечный и функция интегрируема по Риману, то значение несобственного интеграла совпадает со значением определённого интеграла.
Несобственные интегралы I рода
![[a,b]](/800/600/https/upload.wikimedia.org/wikipedia/commons/thumb/d/d1/Improperintegral2.png/200px-Improperintegral2.png) Несобственный интеграл первого рода
Несобственный интеграл первого родаПусть f(x){\displaystyle f(x)} определена и непрерывна на интервале [a,+∞){\displaystyle [a,+\infty )} и ∀A>a ∃∫aAf(x)dx{\displaystyle \forall A>a\ \exists \int \limits _{a}^{A}f(x)dx}. Тогда:
- Если ∃limA→+∞∫aAf(x)dx=I∈R{\displaystyle \exists \lim _{A\to +\infty }\int \limits _{a}^{A}f(x)dx=I\in \mathbb {R} }, то используется обозначение I=∫a+∞f(x)dx{\displaystyle I=\int \limits _{a}^{+\infty }f(x)dx} и интеграл называется несобственным интегралом Римана первого рода. В этом случае I=∫a+∞f(x)dx{\displaystyle I=\int \limits _{a}^{+\infty }f(x)dx} называется сходящимся.
- Если не существует конечного limA→+∞∫aAf(x)dx{\displaystyle \lim _{A\to +\infty }\int \limits _{a}^{A}f(x)dx} (±∞{\displaystyle \pm \infty } или ∄{\displaystyle \nexists }), то интеграл ∫a+∞f(x)dx{\displaystyle \int \limits _{a}^{+\infty }f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Пусть f(x){\displaystyle f(x)} определена и непрерывна на множестве от (−∞,b]{\displaystyle (-\infty ,b]} и ∀B<b⇒∃∫Bbf(x)dx{\displaystyle \forall B<b\Rightarrow \exists \int \limits _{B}^{b}f(x)dx}. Тогда:
- Если ∃limB→−∞∫Bbf(x)dx=I∈R{\displaystyle \exists \lim _{B\to -\infty }\int \limits _{B}^{b}f(x)dx=I\in \mathbb {R} }, то используется обозначение I=∫−∞bf(x)dx{\displaystyle I=\int \limits _{-\infty }^{b}f(x)dx} и интеграл называется несобственным интегралом Римана первого рода. В этом случае I=∫−∞bf(x)dx{\displaystyle I=\int \limits _{-\infty }^{b}f(x)dx} называется сходящимся.
- Если не существует конечного limB→−∞∫Bbf(x)dx{\displaystyle \lim _{B\to -\infty }\int \limits _{B}^{b}f(x)dx} (±∞{\displaystyle \pm \infty } или ∄{\displaystyle \nexists }), то интеграл ∫−∞bf(x)dx{\displaystyle \int \limits _{-\infty }^{b}f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Если функция f(x){\displaystyle f(x)} определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
∫−∞+∞f(x)dx=∫−∞cf(x)dx+∫c+∞f(x)dx{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)dx=\int \limits _{-\infty }^{c}f(x)dx+\int \limits _{c}^{+\infty }f(x)dx}, где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
Примеры
∫−∞−11x2dx=lima→−∞∫a−11x2dx=lima→−∞−1x|a−1=1+lima→−∞1a=1+0=1{\displaystyle \int \limits _{-\infty }^{-1}{1 \over x^{2}}dx=\lim _{a\to -\infty }\int \limits _{a}^{-1}{1 \over x^{2}}dx=\lim _{a\to -\infty }{\Bigl .}-{\frac {1}{x}}{\Bigr |}_{a}^{-1}=1+\lim _{a\to -\infty }{\frac {1}{a}}=1+0=1}
Несобственные интегралы II рода
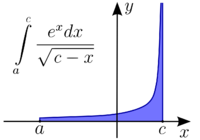 Несобственный интеграл Римана второго рода
Несобственный интеграл Римана второго родаПусть f(x){\displaystyle f(x)} определена на (a,b]{\displaystyle (a,b]}, терпит бесконечный разрыв в точке x = a и ∀δ>0⇒∃∫a+δbf(x)dx=I(δ){\displaystyle \forall \delta >0\Rightarrow \exists \int \limits _{a+\delta }^{b}f(x)dx={\mathcal {I}}(\delta )}. Тогда:
- Если ∃limδ→0+0I(δ)=I∈R{\displaystyle \exists \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=I\in \mathbb {R} }, то используется обозначение I=∫abf(x)dx{\displaystyle I=\int \limits _{a}^{b}f(x)dx} и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если limδ→0+0I(δ)=∞(±∞{\displaystyle \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=\infty \;(\pm \infty } или ∄){\displaystyle \nexists )}, то обозначение сохраняется, а I=∫abf(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{b}f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Пусть f(x){\displaystyle f(x)} определена на [a,b){\displaystyle [a,b)} , терпит бесконечный разрыв при x = b и ∀δ>0⇒∃∫ab−δf(x)dx=I(δ){\displaystyle \forall \delta >0\Rightarrow \exists \int \limits _{a}^{b-\delta }f(x)dx={\mathcal {I}}(\delta )}. Тогда:
- Если ∃limδ→0+0I(δ)=I∈R{\displaystyle \exists \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=I\in \mathbb {R} }, то используется обозначение I=∫abf(x)dx{\displaystyle I=\int \limits _{a}^{b}f(x)dx} и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если limδ→0+0I(δ)=∞(±∞{\displaystyle \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=\infty \;(\pm \infty } или ∄){\displaystyle \nexists )}, то обозначение сохраняется, а I=∫abf(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{b}f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Если функция f(x){\displaystyle f(x)} терпит разрыв во внутренней точке c{\displaystyle c} отрезка [a;b]{\displaystyle [a;b]}, то несобственный интеграл второго рода определяется формулой:
∫abf(x)dx=∫acf(x)dx+∫cbf(x)dx.{\displaystyle \int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{c}f(x)dx+\int \limits _{c}^{b}f(x)dx.}
Геометрический смысл несобственных интегралов II рода
Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции.
Пример
∫01dxx=limδ→0+0ln|x||0+δ1=0−limδ→0+0lnδ=+∞{\displaystyle \int \limits _{0}^{1}{dx \over x}=\lim _{\delta \to 0+0}{\Bigl .}\ln |x|{\Bigr |}_{0+\delta }^{1}=0-\lim _{\delta \to 0+0}\ln \delta =+\infty }
Отдельный случай
Пусть функция f(x){\displaystyle f(x)} определена на всей числовой оси и имеет разрыв в точках x1,x2,…,xk{\displaystyle x_{1},x_{2},\dots ,x_{k}}.
Тогда можно найти несобственный интеграл ∫−∞+∞f(x)dx=∫−∞x1f(x)dx+∑j=1k−1∫xjxj+1f(x)dx+∫xk+∞f(x)dx{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)dx=\int \limits _{-\infty }^{x_{1}}f(x)dx+\sum _{j=1}^{k-1}{\int \limits _{x_{j}}^{x_{j+1}}f(x)dx}+\int \limits _{x_{k}}^{+\infty }f(x)dx}
Критерий Коши́
1. Пусть f(x){\displaystyle f(x)} определена на множестве от [a,+∞){\displaystyle [a,+\infty )} и ∀A>a⇒∃∫aAf(x)dx=I{\displaystyle \forall A>a\Rightarrow \exists \int \limits _{a}^{A}f(x)dx={\mathcal {I}}}.
- Тогда I=∫a+∞f(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{+\infty }f(x)dx} сходится ⇔∀ε>0⇒∃A(ε)>a:∀(A2>A1>A)⇒|∫A1A2f(x)dx|<ε{\displaystyle \Leftrightarrow \forall \varepsilon >0\Rightarrow \exists A(\varepsilon )>a:\forall (A_{2}>A_{1}>A)\Rightarrow \left|\,\int \limits _{A_{1}}^{A_{2}}f(x)dx\right|<\varepsilon }
2. Пусть f(x){\displaystyle f(x)} определена на (a,b]{\displaystyle (a,b]} и ∀δ>0⇒∃∫a+δbf(x)dx=I{\displaystyle \forall \delta >0\Rightarrow \exists \int \limits _{a+\delta }^{b}f(x)dx={\mathcal {I}}}.
- Тогда I=∫abf(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{b}f(x)dx} сходится ⇔∀ε>0⇒∃δ(ε)>0:∀(0<δ1<δ2<δ)⇒|∫a+δ1a+δ2f(x)dx|<ε{\displaystyle \Leftrightarrow \forall \varepsilon >0\Rightarrow \exists \delta (\varepsilon )>0:\forall (0<\delta _{1}<\delta _{2}<\delta )\Rightarrow \left|\,\int \limits _{a+\delta _{1}}^{a+\delta _{2}}f(x)dx\right|<\varepsilon }
Абсолютная сходимость
Интеграл ∫a+∞f(x)dx (∫abf(x)dx){\displaystyle \int \limits _{a}^{+\infty }f(x)dx\ \ \left(\int \limits _{a}^{b}f(x)dx\right)} называется абсолютно сходящимся, если ∫a+∞|f(x)|dx (∫ab|f(x)|dx){\displaystyle \int \limits _{a}^{+\infty }|f(x)|dx\ \ \left(\int \limits _{a}^{b}|f(x)|dx\right)}сходится.
Если интеграл сходится абсолютно, то он сходится.
Условная сходимость
Интеграл ∫a+∞f(x)dx {\displaystyle \int \limits _{a}^{+\infty }f(x)dx\ \ } называется условно сходящимся, если ∫a+∞f(x)dx {\displaystyle \int \limits _{a}^{+\infty }f(x)dx\ \ } сходится, а ∫a+∞|f(x)|dx {\displaystyle \int \limits _{a}^{+\infty }|f(x)|dx\ \ } расходится.
См. также
Список используемой литературы
Дмитрий Письменный. Конспект лекций по высшей математике, часть 1. — Айрис Пресс, 2007. — С. 233-237.
wiki.sc
Несобственные интегралы — это… Что такое Несобственные интегралы?
обобщение классического понятия интеграла на случай неограниченных функций и функций, заданных на бесконечном промежутке интегрирования (см. Интеграл). Определённый интеграл как предел интегральных сумм Римана может существовать (иметь определённое конечное значение) лишь для ограниченных функций, заданных на конечном интервале. Поэтому, если интервал интегрирования или подынтегральная функция не ограничены, для определения интеграла требуется ещё один предельный переход: получающиеся при этом интегралы называются несобственными интегралами.Если функция f (x) интегрируема на любом конечном отрезке [a, N] и если существует

то его называют Н. п. функции f (x) на интервале [а, ∞] и обозначают

В этом случае говорят, что Н. и. сходится. Когда этот предел, а значит и Н. и., не существует, то иногда говорят, что Н. и. расходится. Например,

сходится при γ > 1 и расходится при γ ≤ 1. Аналогично определяют Н. и. на интервалах
[—∞, b] и [—∞, ∞].
Если функция f (x), заданная на отрезке [a, b], не ограничена в окрестности точки a, но интегрируема на любом отрезке [а + ε, b], 0 b — a и если существует

то его называют Н. и. функции f (x) на [а, b] и записывают обычным образом:

Аналогично поступают, если f (x) не ограничена в окрестности точки b.
Если существует Н. и.

или

то говорят, что Н. и.

или

абсолютно сходится: если же последние интегралы сходятся (но первые расходятся), то Н. и.

или

называются условно сходящимися.
Задачи, приводящие к Н. и., рассматривались в геометрической форме Э. Торричелли и П. Ферма в 1644. Точные определения Н. и. даны О. Коши в 1823. Различие условно и абсолютно сходящихся Н. и. установлено Дж. Стоксом и П. Г. Л. Дирихле (1854). Ряд работ математиков 19 в. посвящен вычислению Н. и. в случаях, когда соответствующая первообразная не выражается через элементарные функции. Основными приемами вычисления Н. и. являются дифференцирование и интегрирование по параметру, разложение в ряды, применение теории вычетов. Значения многих Н. и. приводятся в различных таблицах.Н. и. имеют важное значение во многих областях математического анализа и его приложений. В теории специальных функций (цилиндрических функций, ортогональных многочленов и др.) одним из основных способов изучения является изображение функций в виде Н. и., зависящих от параметра, например
 (см. Гамма-функция). К Н. и. относится и Фурье интеграл, а также интегралы, встречающиеся при др. интегральных преобразованиях. Решения краевых задач (См. Краевые задачи) математической физики записываются кратными Н. и. с неограниченной подинтегральной функцией. В теории вероятностей важное значение имеет Н. и.
(см. Гамма-функция). К Н. и. относится и Фурье интеграл, а также интегралы, встречающиеся при др. интегральных преобразованиях. Решения краевых задач (См. Краевые задачи) математической физики записываются кратными Н. и. с неограниченной подинтегральной функцией. В теории вероятностей важное значение имеет Н. и.

в теории диффракции света — Н. и.
 В ряде случаев расходящимся Н. и. можно приписать определённое значение (см. Суммирование). В частности, если интеграл
В ряде случаев расходящимся Н. и. можно приписать определённое значение (см. Суммирование). В частности, если интеграл

расходится, но существует

то А называется главным значением Н. и. и обозначают

Так,
 Аналогично вводится главное значение Н. и. от неограниченных функций. В работах Н. И. Мусхелишвили и его учеников построена теория интегральных уравнений, содержащих Н. и., понимаемые в смысле главного значения.
Аналогично вводится главное значение Н. и. от неограниченных функций. В работах Н. И. Мусхелишвили и его учеников построена теория интегральных уравнений, содержащих Н. и., понимаемые в смысле главного значения.Лит.: Смирнов В. И., Курс высшей математики, 20 изд., т. 2, М. — Л., 1967; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд. т. 2, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970.
partners.academic.ru
Несобственные интегралы
Пример. Сходится ли интеграл ∫1 | dx | ? | |
sin x | |||
0 |
| ||
Решение: |
|
|
Функция f(x) = sin1 x имеет на [0; 1] единственный разрыв в точке х = 0. Рассмотрим
функцию ϕ(х) = 1 . Интеграл x
1 | dx | = lim | 1 | dx | = limln x 1 = 0 − limlnε | ||||||||
0 | x | ε →0 | 0+ε | x | ε →0 | |ε | ε →0 | ||||||
∫ |
|
| ∫ |
|
|
| |||||||
расходится. И так как |
|
| |||||||||||
lim | f (x) | = lim |
|
| x | = 1, |
|
| |||||
|
|
|
|
|
| ||||||||
x→0 | ϕ (x) | x→0 sin x |
|
|
|
| |||||||
то интеграл ∫1 |
| dx |
| также расходится. | |||||||||
|
|
| |||||||||||
|
|
|
|
|
| 0 sin x |
|
|
| ||||
Геометрические приложения
Схемы применения определенного интеграла
Пусть требуется найти значение какой-либо геометрической или физической величины А (площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т.д.), связанной с отрезком [а; b] изменения независимой переменной х. Предполагается, что эта величина А аддитивна, т. е. такая, что при разбиении отрезка [а; b] точкой с (а; b) на части [а, с] и [с; b] значение величины А, соответствующее всему отрезку [a; b], равно сумме ее значений, соответствующих [а; с] и [с, b].
Для нахождения этой величины А можно руководствоваться одним из двух методов: методом интегральных сумм или методом дифференциала.
Первый метод базируется на определении определенного интеграла.
1 Точками x0 = a, x1, … xn = b разбить отрезок [а; b] на n частей. В соответствии с этим, интересующая нас величина А разобьется на n «элементарных слагаемых» Ai (i = 1, …, n): A = A1 + A2 + … + An.
2. Представить каждое «элементарное слагаемое» в виде произведения некоторой функции (определяемой из условия задачи), вычисленной в произвольной точке соответствующего отрезка на его длину: Ai ≈ f(ci) xi.
При нахождении приближенного значения Ai допустимы некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей ее концы; переменную скорость на малом участке можно приближенно считать постоянной и т.д.
Получим приближенное значение величины А в виде интегральной суммы:
n
A ≈ f(c1) x1 + … + f(cn) xn = ∑ f (ci ) xi .
i=1
3.Искомая величина А равна пределу интегральной суммы, т.е.
| n | b |
A = limn→∞ | ∑ f (ci ) | xi = ∫ f (x)dx. |
| i=1 | a |
Указанный «метод сумм», как видим, основан на представлении интеграла как о сумме бесконечно большого числа бесконечно малых слагаемых.
studfile.net
2.1. Несобственные интегралы для «чайников»
Это «родственник» определённого интеграла. …Нормальное такое определение :). И сразу возникает вопрос: чем отличается несобственный интеграл от «собрата»? Он может отличаться пределами интегрирования:
– то есть, один или даже оба предела бесконечны, при этом подынтегральная функция непрерывна на промежутке интегрирования.
Такие интегралы получили название несобственные интегралы первого рода.
Кроме того, несобственный интеграл может быть «внешне похож» на определённый интеграл и иметь вид . Но есть один нюанс. Подынтегральная функция не определена в точке или . Или на обоих концах. Или даже во внутренних точках отрезка .
Это так называемые несобственные интегралы второго рода.
Что значит решить несобственный интеграл? В отличие от определённого интеграла, тут есть три варианта. Решить несобственный интеграл – это значит найти конечное число, либо получить бесконечность, либо выяснить, что несобственного интеграла не существует.
1) Если несобственный интеграл равен конечному числу, то говорят, что он сходится. Число может быть как положительным, так и отрицательным. Или нулём.
2) Если несобственный интеграл равен бесконечности (со знаком «плюс» или «минус»), то говорят, он расходится.
3) И в ряде случаев несобственного интеграла может вовсе не существовать. Даже если подынтегральная функция непрерывна на промежутке интегрирования! (вспоминаем, что определённый интеграл при этом условии существует всегда).
Как решить несобственный интеграл? С помощью той же формулы Ньютона-Лейбница. С некоторыми особенностями.
И здесь вы должны понимать и уметь решать несложные пределы функций.
В чём смысл несобственного интеграла? Геометрически – это тоже площадь (если интеграл существует). Но площадь своеобразная. И с этим своеобразием мы познакомимся прямо на следующей странице:
2.2. Несобственный интеграл первого рода
1.11. А если подынтегральная функция нечётная?
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
mathprofi.com
§1. Несобственные интегралы 1-го рода
– 68–
Тема НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
В
теме «Определенный интеграл» было
рассмотрено понятие определенного
интеграла 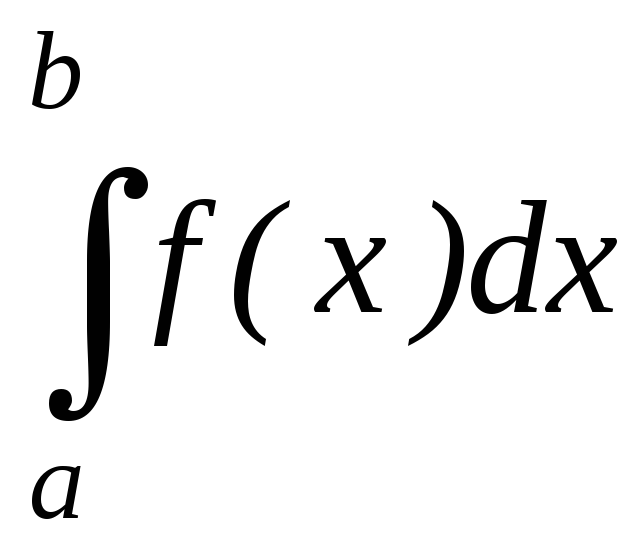 для случая конечного промежутка
для случая конечного промежутка и ограниченной функции
и ограниченной функции (см. теорему 1 из §3). Теперь займемся
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации.
(см. теорему 1 из §3). Теперь займемся
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации.
1.
Если, используя формулу для длины дуги,
попытаться вычислить длину четверти
окружности 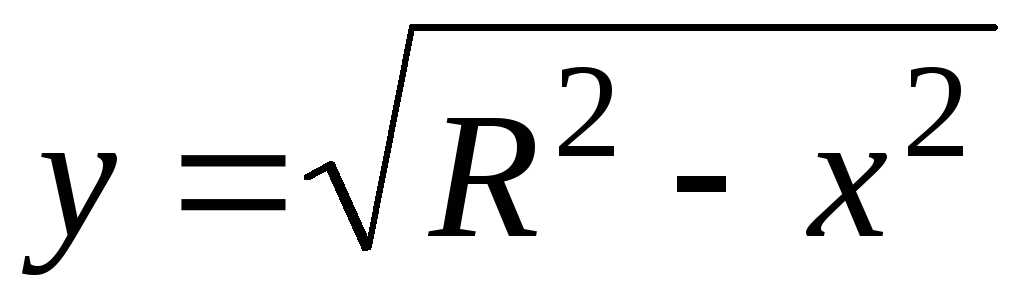 ,
,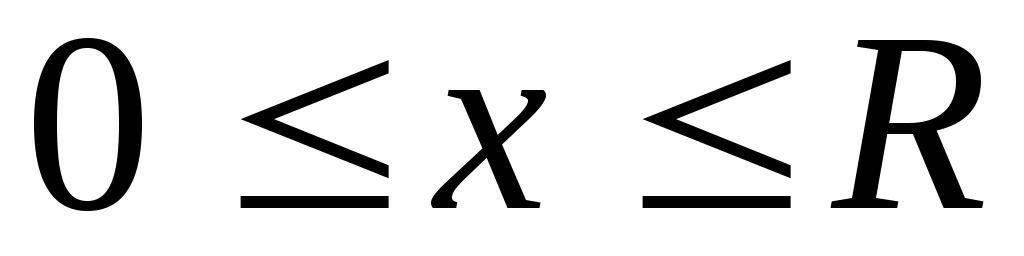 ,
то придем к интегралу от неограниченной
функции:
,
то придем к интегралу от неограниченной
функции:
 ,
где
,
где  .
.
2.
Пусть тело массой  движется
по инерции в среде с силой сопротивления
движется
по инерции в среде с силой сопротивления  ,
где
,
где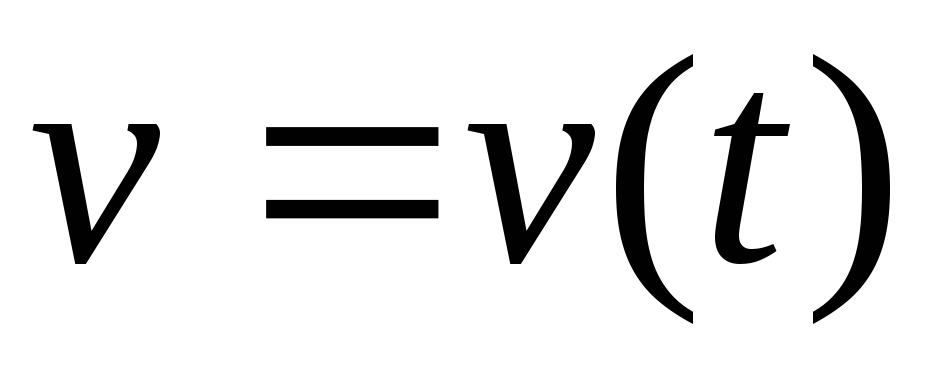 — скорость тела. Используя второй закон
Ньютона (
— скорость тела. Используя второй закон
Ньютона (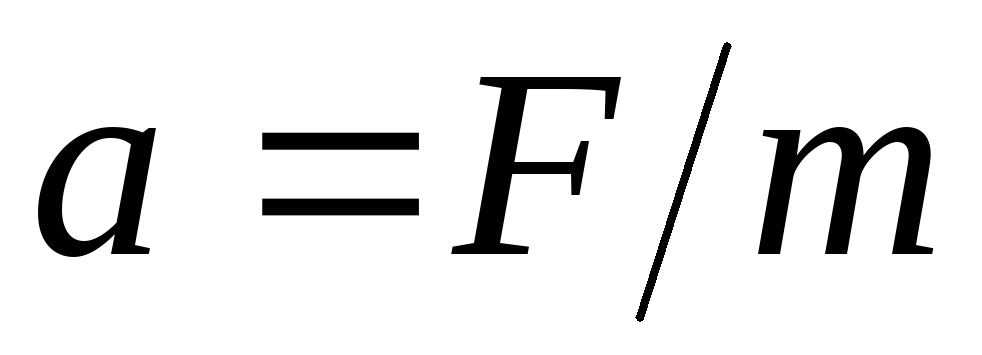 ,
где
,
где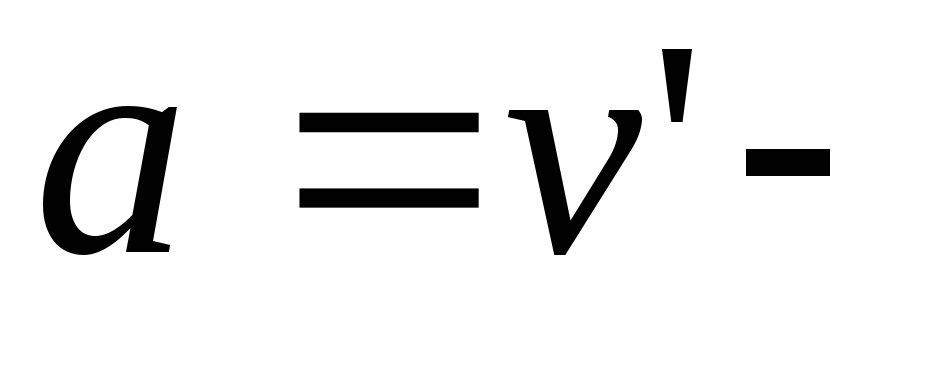 ускорение),
получим уравнение:
ускорение),
получим уравнение: ,
где
,
где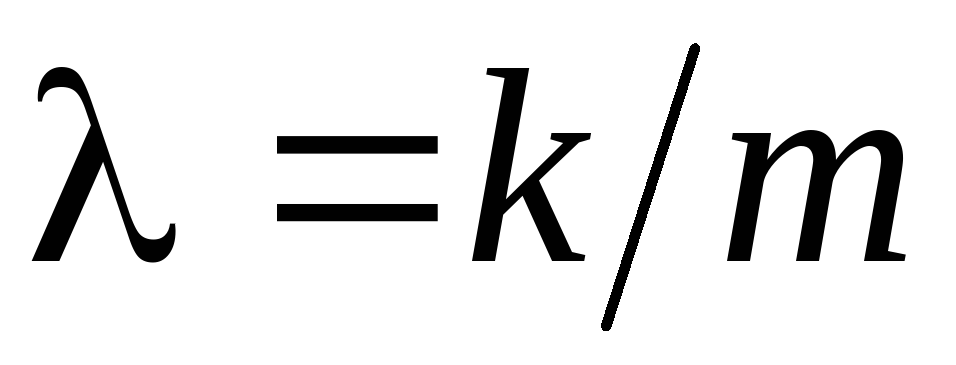 .
Нетрудно показать, что решением этого
(дифференциального!) уравнения является
функция
.
Нетрудно показать, что решением этого
(дифференциального!) уравнения является
функция Если
нам потребуется вычислить путь, пройденный
телом до полной остановки, т.е. до момента,
когда
Если
нам потребуется вычислить путь, пройденный
телом до полной остановки, т.е. до момента,
когда 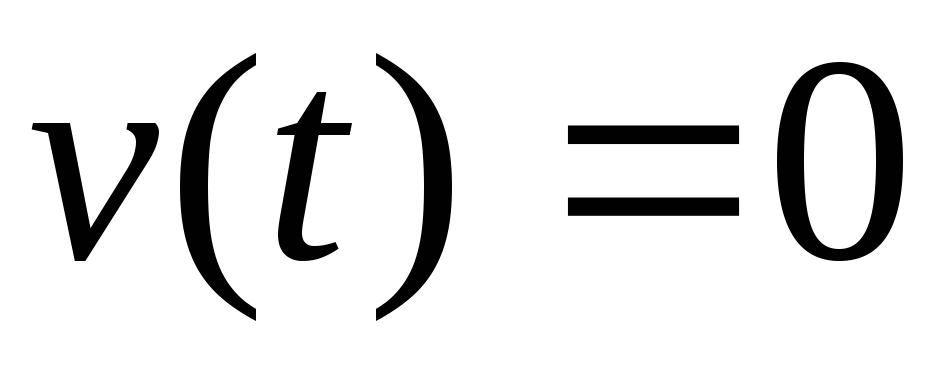 ,
то придем к интегралу по бесконечному
промежутку:
,
то придем к интегралу по бесконечному
промежутку:
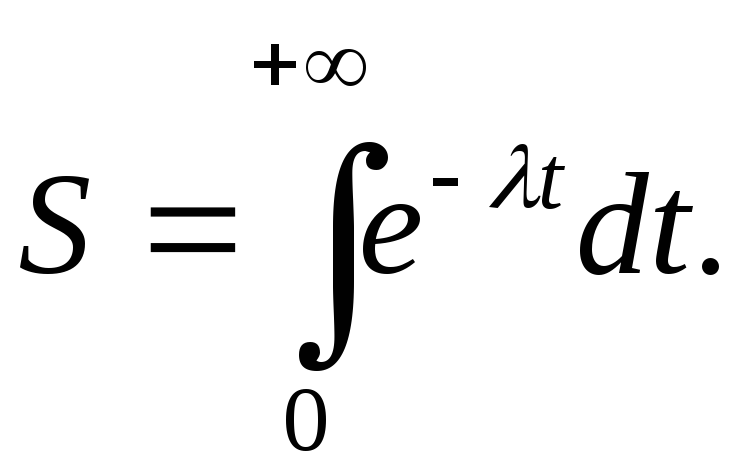
I Определение
Пусть
функция  определена и непрерывна на промежутке
определена и непрерывна на промежутке .
Тогда для любого
.
Тогда для любого она интегрируема на промежутке
она интегрируема на промежутке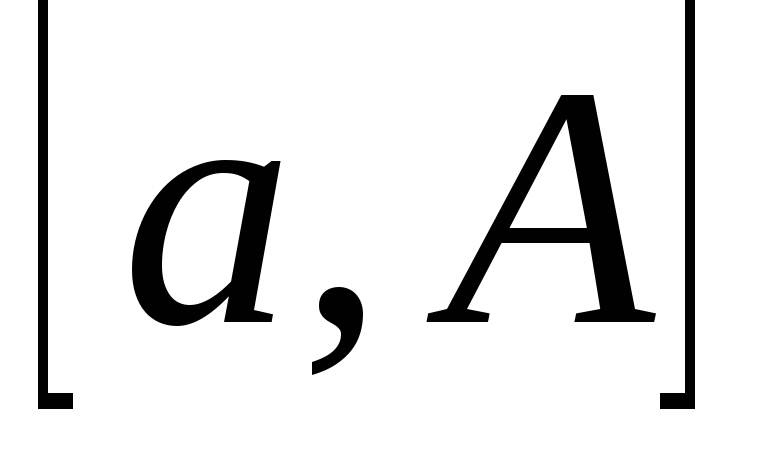 ,
то есть существует интеграл
,
то есть существует интеграл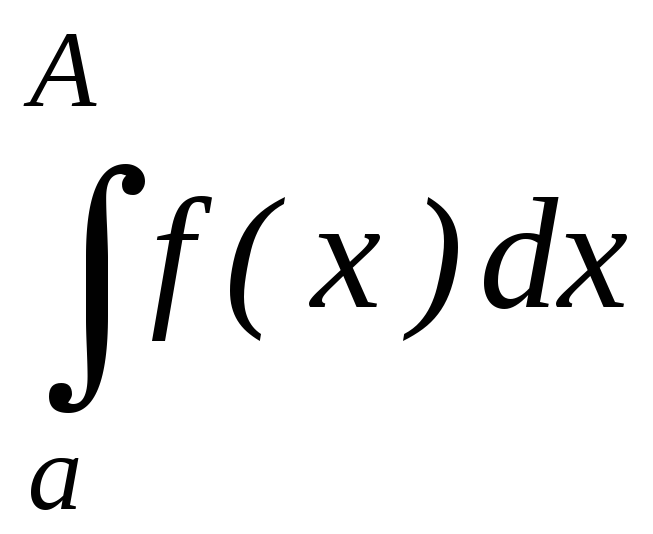 .
.
Определение
1.
Конечный или бесконечный предел этого
интеграла при  называют несобственным интегралом 1-го
рода от функции
называют несобственным интегралом 1-го
рода от функции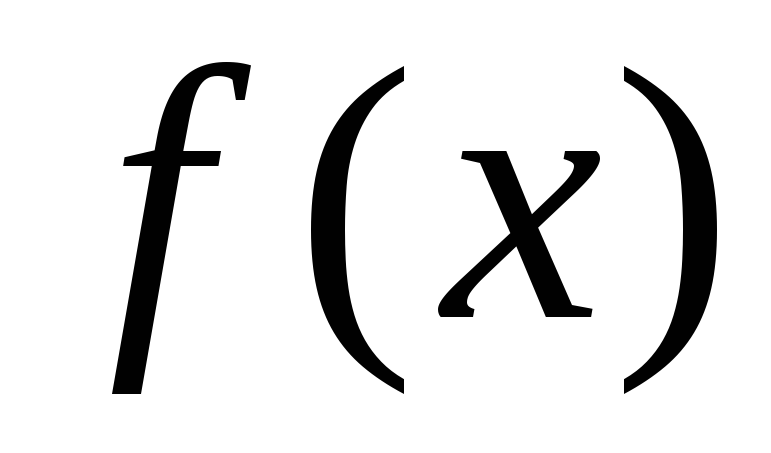 по промежутку
по промежутку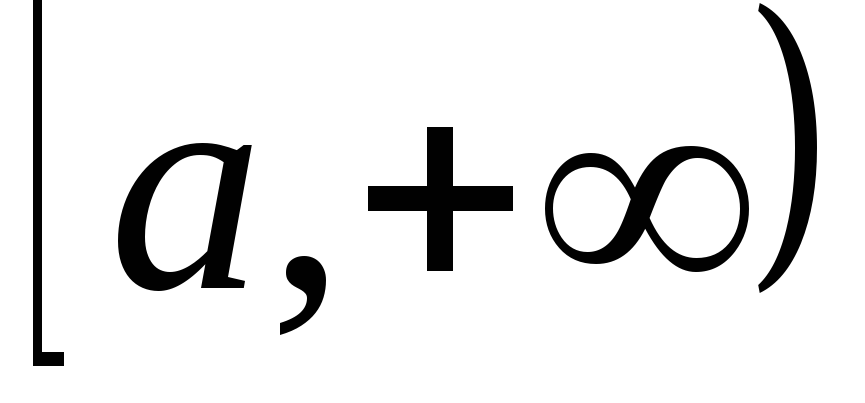 и обозначают символом
и обозначают символом .
При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае (
.
При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае ( или не существует ) – расходящимся.
или не существует ) – расходящимся.
Итак, по определению
| (1) |
Примеры
1.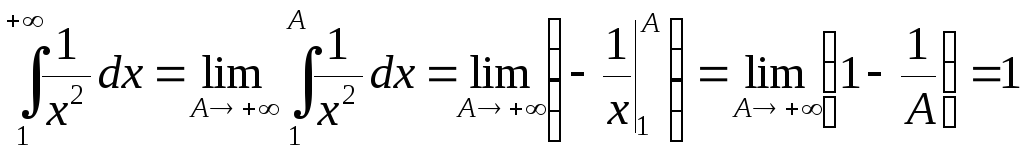 .
.
2. .
.
3. – не существует.
– не существует.
Несобственный интеграл из примера 1 сходится, в примерах 2 и 3 интегралы расходятся.
II Формула Ньютона – Лейбница для несобственного интеграла первого рода
Пусть 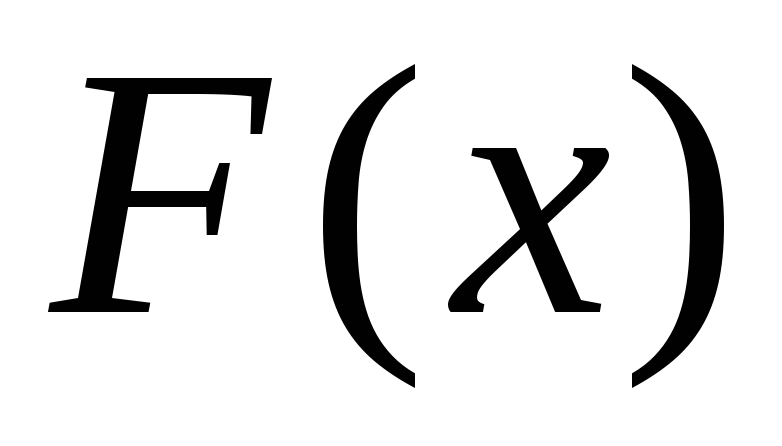 — некоторая первообразная для функции
— некоторая первообразная для функции (сущест-вует на
(сущест-вует на ,
т.к.
,
т.к. — непрерывна). Тогда
— непрерывна). Тогда

Отсюда
ясно, что сходимость несобственного
интеграла (1) равносильна существованию
конечного предела .
Если этот предел обозначить
.
Если этот предел обозначить ,
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
,
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
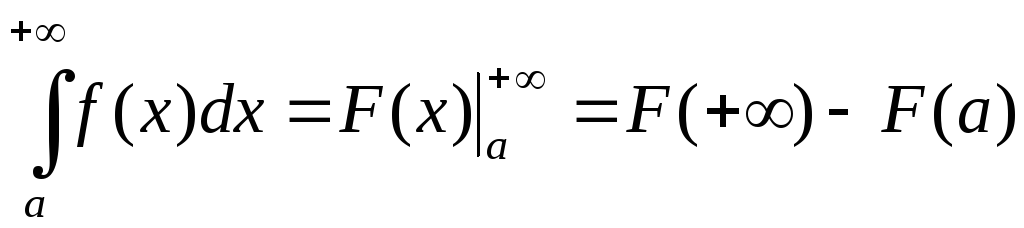 ,
где
,
где  .
.
Примеры.
4. 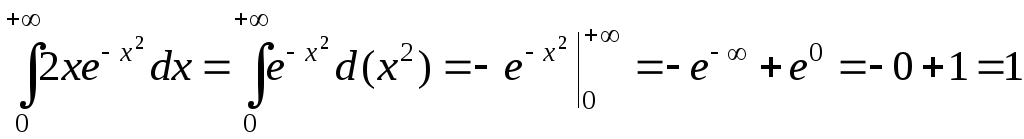 .
.
5.  .
.
6.
Более сложный пример: 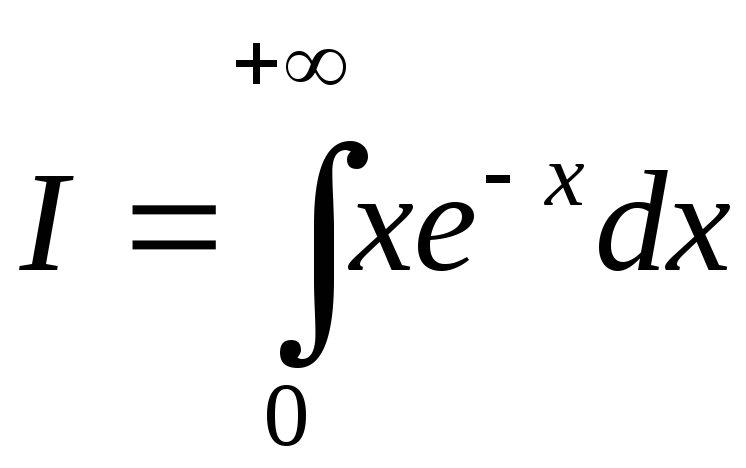 .
Сначала найдем первообразную:
.
Сначала найдем первообразную:
Теперь
можем найти интеграл 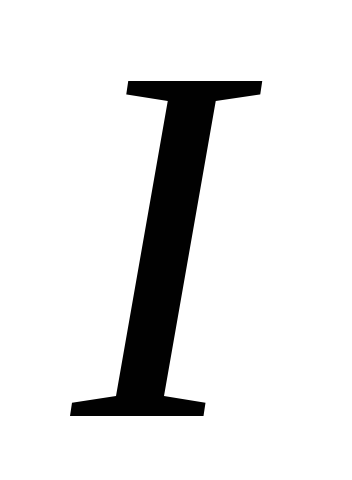 , учитывая,
что
, учитывая,
что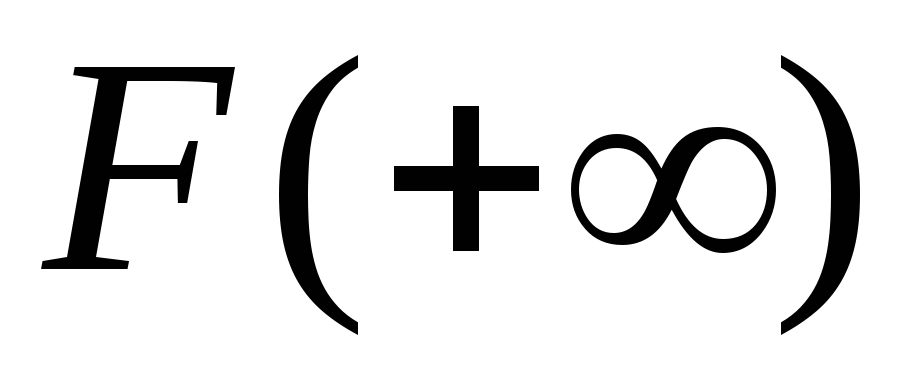
 :
:
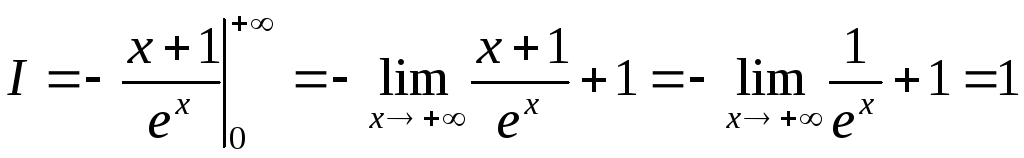 .
.
III Свойства
Приведем ряд свойств несобственного интеграла (1), которые вытекают из общих свойств пределов и определенного интеграла:
интегралы
 и
и
 сходятся или расходятся одновременно;
сходятся или расходятся одновременно;если
 ,
то интегралы
,
то интегралы и
и сходятся или рас-ходятся одновременно;
сходятся или рас-ходятся одновременно;если интеграл
 сходится, то
сходится, то .
.
IV Другие определения
Определение
2.
Если  непрерывна
на
непрерывна
на  ,
то
,
то
 .
.
Определение
3.
Если  непрерывна
на
непрерывна
на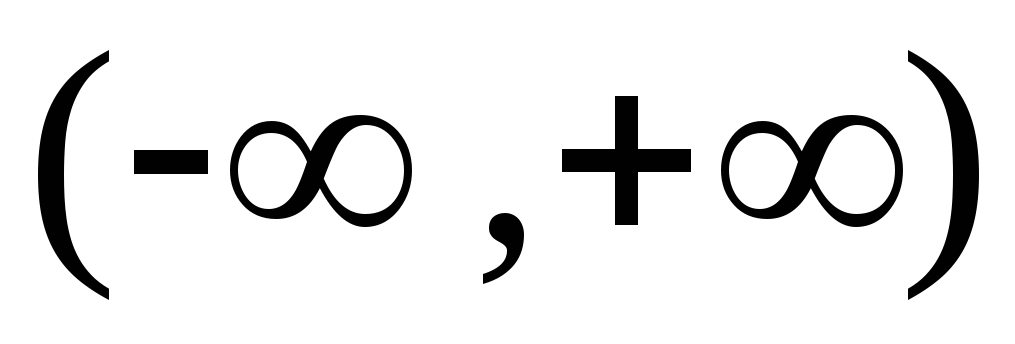 ,
то принимают по определению
,
то принимают по определению
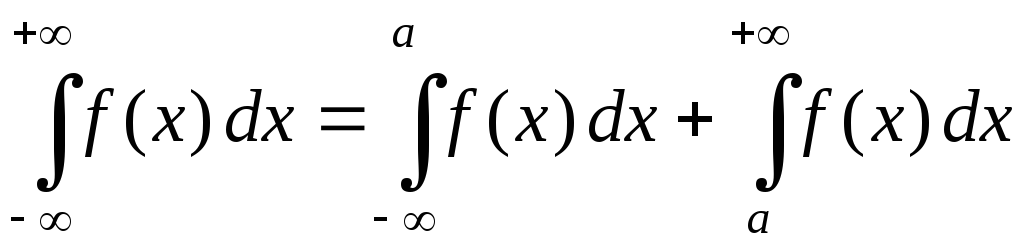 (
( –
произвольное),
–
произвольное),
причем несобственный интеграл в левой части сходится, если только оба ин-теграла в правой части сходятся.
Для этих интегралов, как и для интеграла (1) можно написать соответствующие формулы Ньютона – Лейбница.
Пример
7. 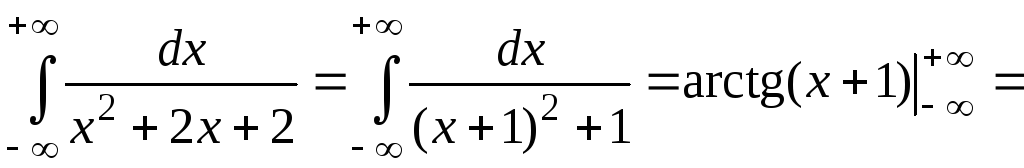

§2. Признаки сходимости несобственного интеграла 1-го рода
Чаще всего несобственный интеграл вычислить по определению не-возможно, поэтому используют приближенное равенство
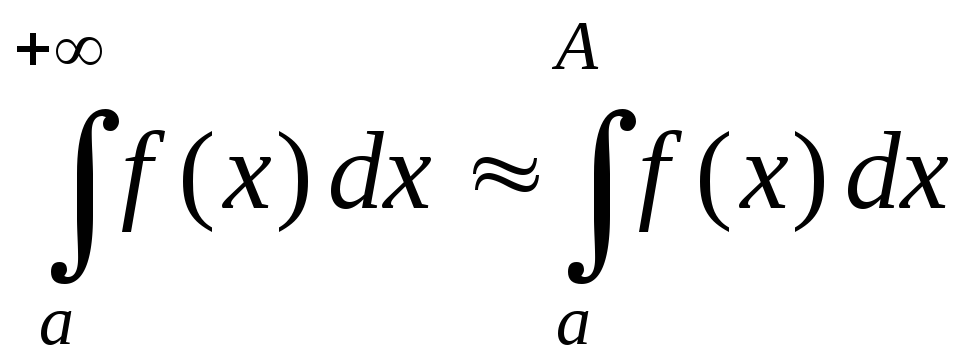 (для
больших
(для
больших  ).
).
Однако, это соотношение имеет смысл лишь для сходящихся интегралов. Необходимо иметь методы выяснения поведения интеграла минуя определение.
I Интегралы от положительных функций
Пусть 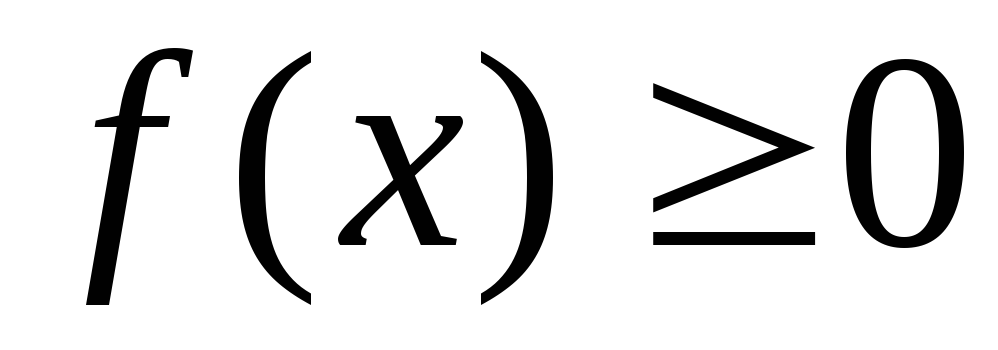 на
на  . Тогда определенный интеграл
. Тогда определенный интеграл  как функция верхнего предела есть
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
как функция верхнего предела есть
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
Теорема
1.
Несобственный интеграл 1го рода от неотрицательной функ-ции сходится
тогда и только тогда, когда функция 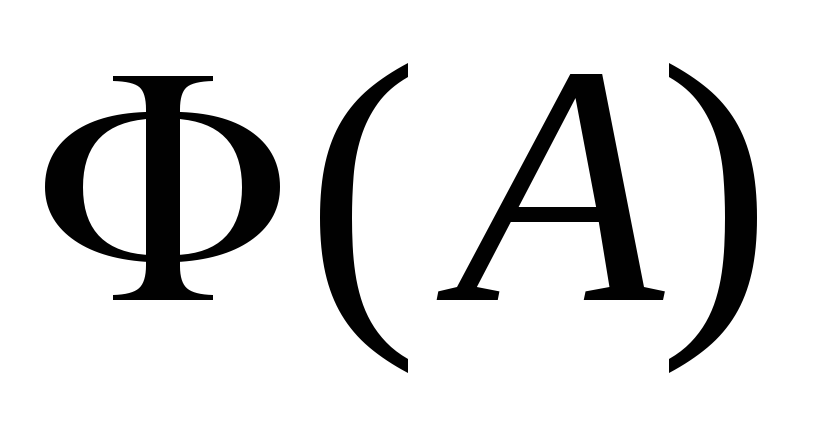 остается
ограниченной при увеличении
остается
ограниченной при увеличении .
.
Эта теорема – следствие общих свойств монотонных функций. Практического смысла теорема почти не имеет, но позволяет получить т.н. признаки сходимости.
Теорема
2 (1-й признак сравнения). Пусть функции  и
и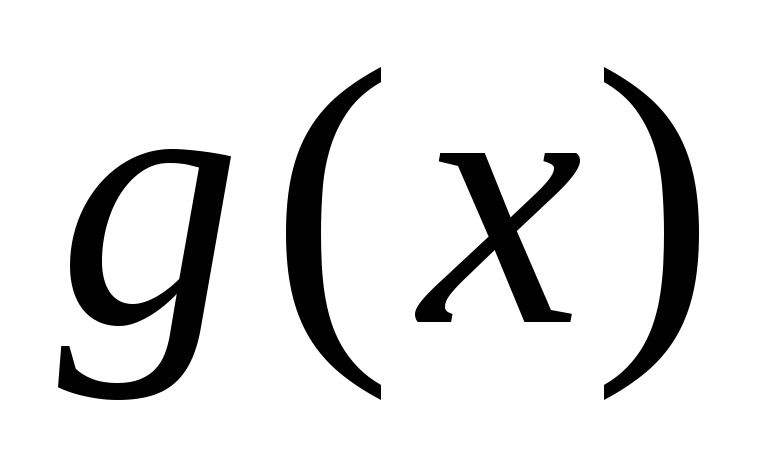 непре-рывны на
непре-рывны на и удовлетворяют неравенству
и удовлетворяют неравенству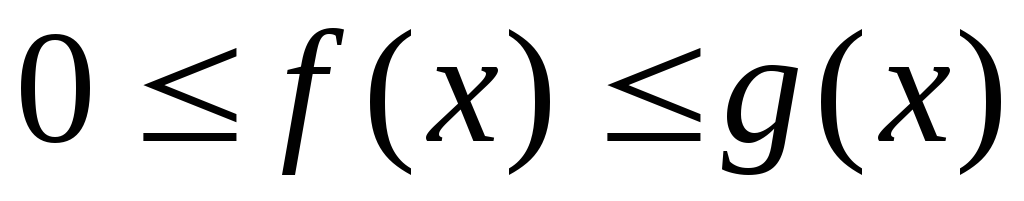 .
Тогда:
.
Тогда:
1)
если интеграл
сходится, то и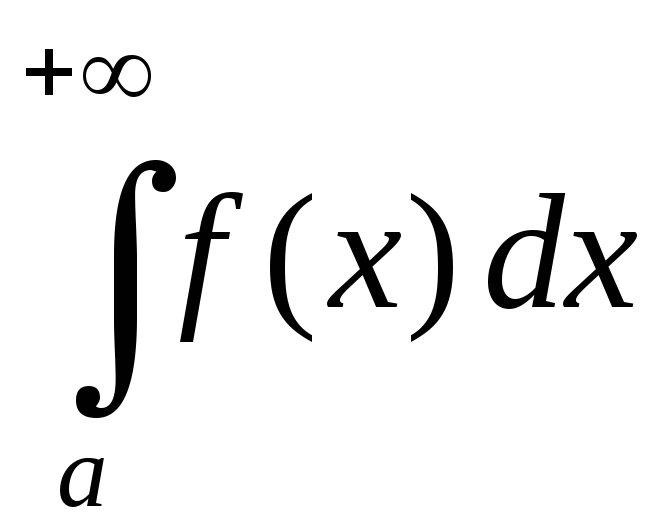 сходится;
сходится;
2)
если интеграл  расходится, то и
расходится, то и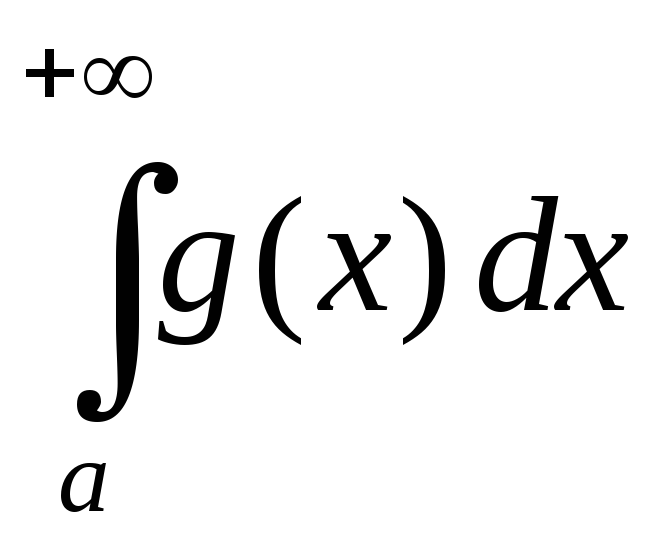 расходится.
расходится.
Доказательство.
Обозначим: 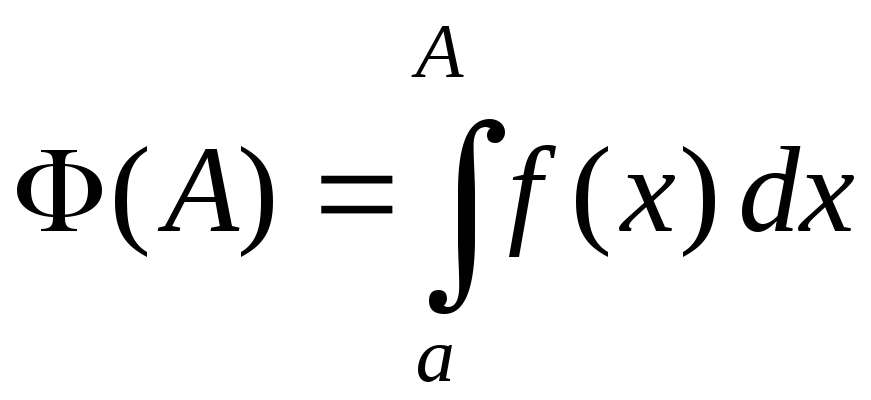 и
и .
Так как
.
Так как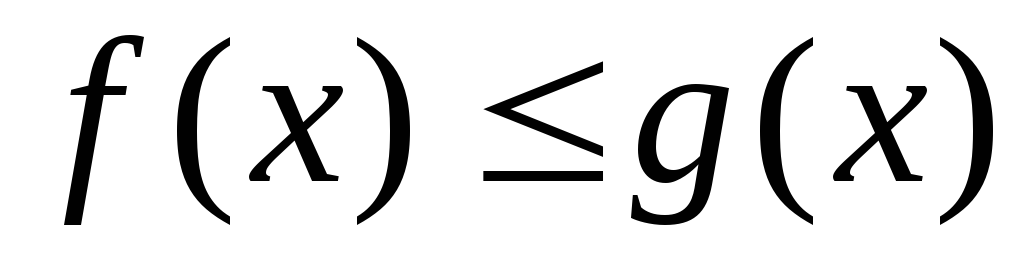 ,
то
,
то
 .
Пусть интеграл
.
Пусть интеграл сходится, тогда (в силу теоремы 1) функция
сходится, тогда (в силу теоремы 1) функция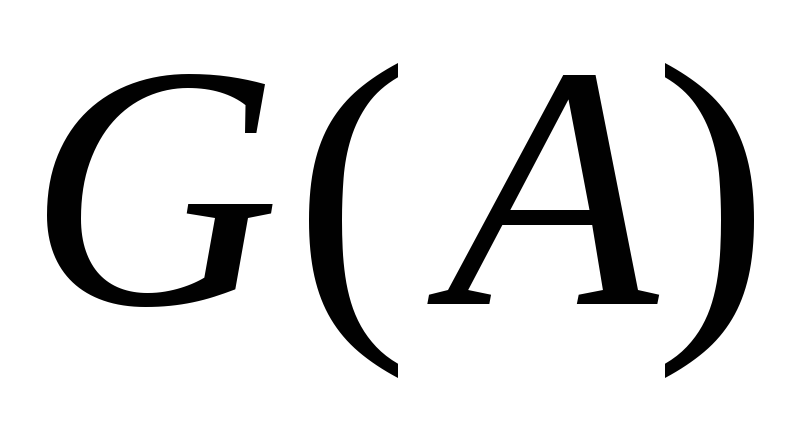 ‒ ограничена. Но тогда и
‒ ограничена. Но тогда и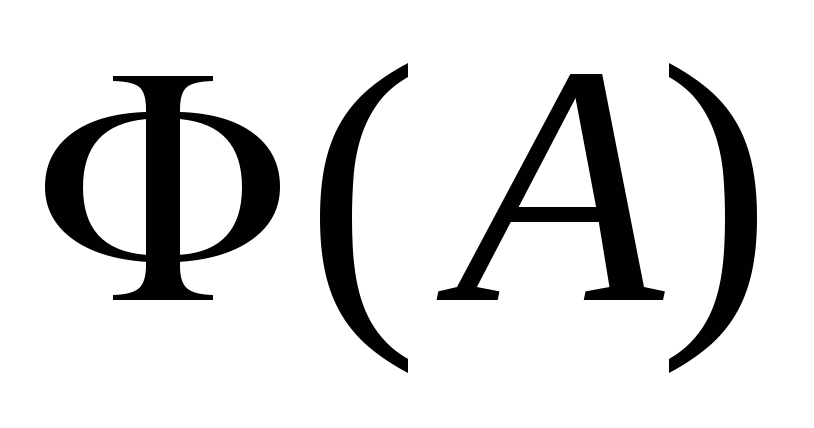 ограничена,
а значит, интеграл
ограничена,
а значит, интеграл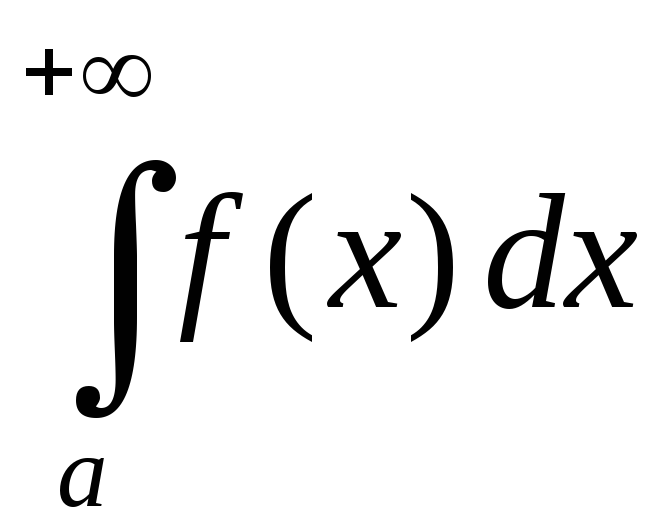 тоже сходится. Аналогично доказывается
и вторая часть теоремы.
тоже сходится. Аналогично доказывается
и вторая часть теоремы.
Этот
признак не применим в случае расходимости
интеграла от  или сходимости интеграла от
или сходимости интеграла от .
Этот недостаток отсутствует у 2-го
признака сравнения.
.
Этот недостаток отсутствует у 2-го
признака сравнения.
Теорема
3 (2-й признак сравнения). Пусть функции 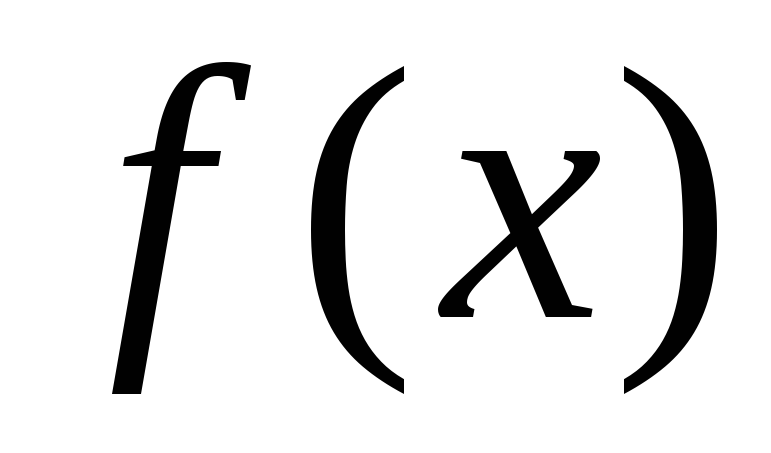 и
и непрерывны и неотрицательны на
непрерывны и неотрицательны на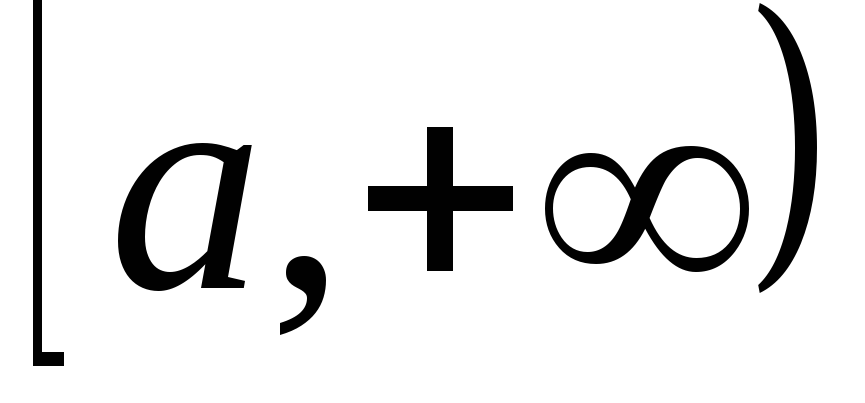 .
Тогда, если
.
Тогда, если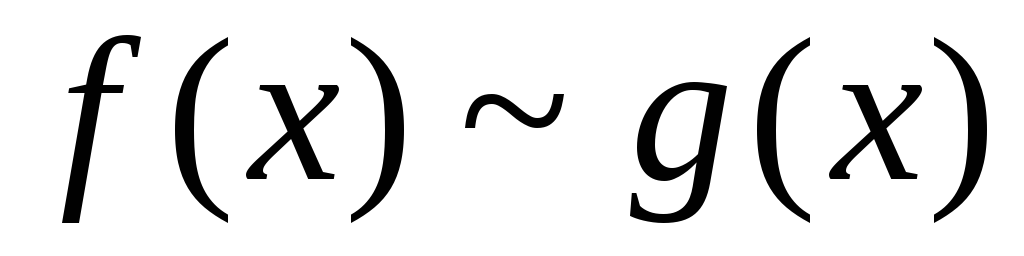 при
при ,
то несобственные интегралы
,
то несобственные интегралы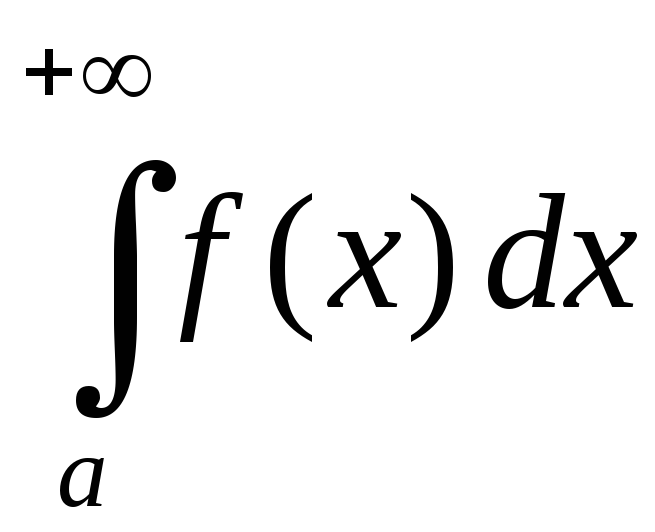 и
и сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Из условия теоремы получим такую цепочку равно-сильных утверждений:
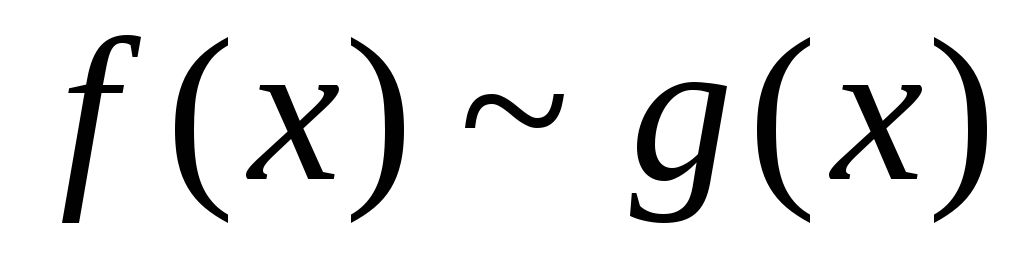 ,
, 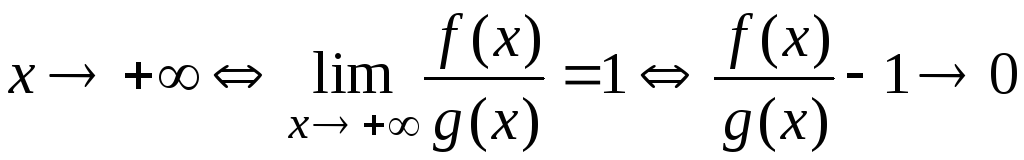 ,
,
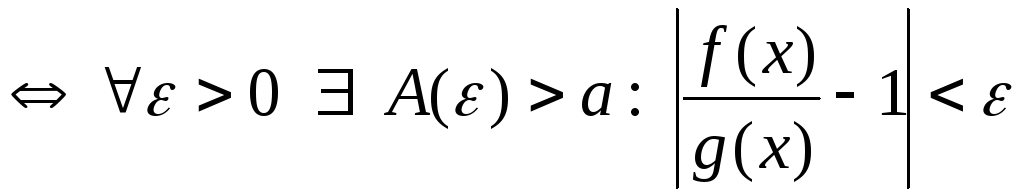
 .
.
Пусть,
например,  .
Тогда:
.
Тогда:
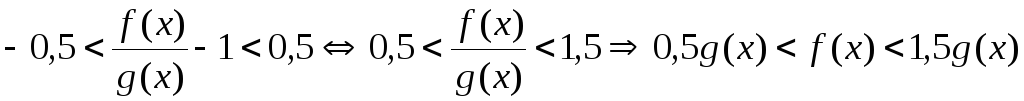 .
.
Применим теорему 2 и свойство 1) из §1 и получим утверждение теоремы 3.
В
качестве эталонной функции, с которой
сравнивают данную, высту-пает степенная
функция 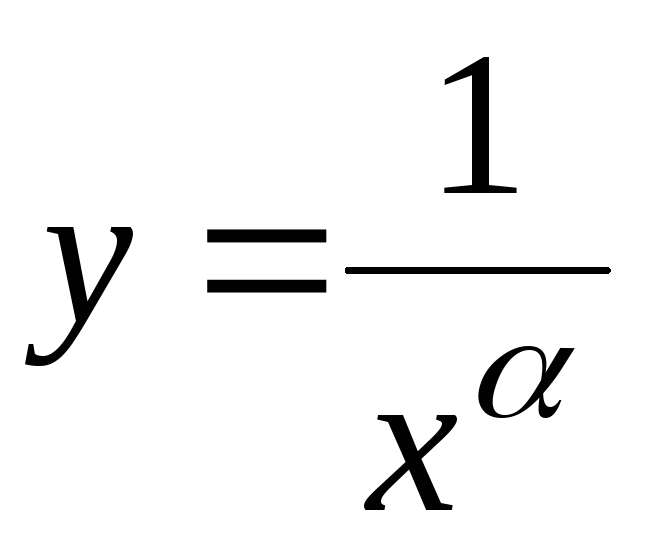 ,
, .
Предлагаем студентам самим доказать,
что интеграл
.
Предлагаем студентам самим доказать,
что интеграл

сходится
при 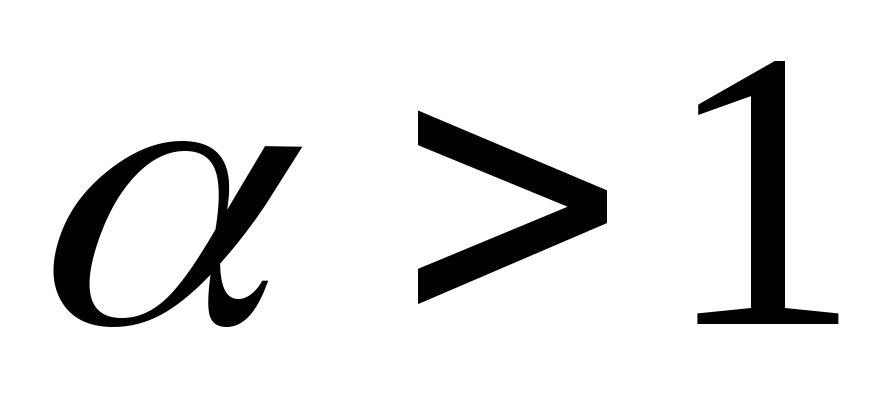 и расходится при
и расходится при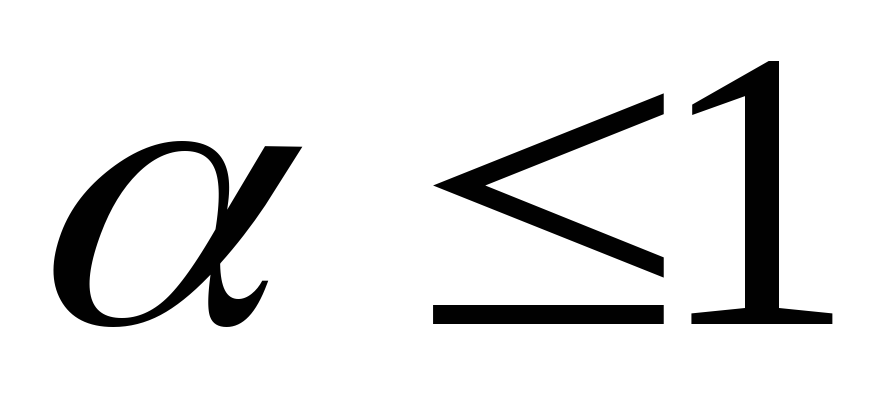 .
.
Примеры.
1.  .
.
Рассмотрим
подынтегральную функцию на промежутке 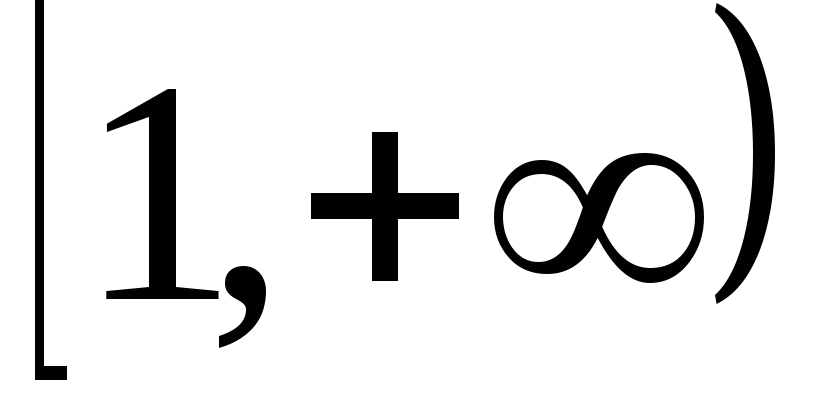 :
:
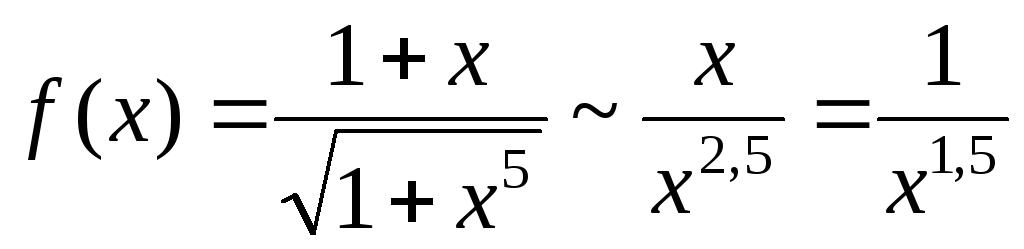 ,
,  .
.
Интеграл 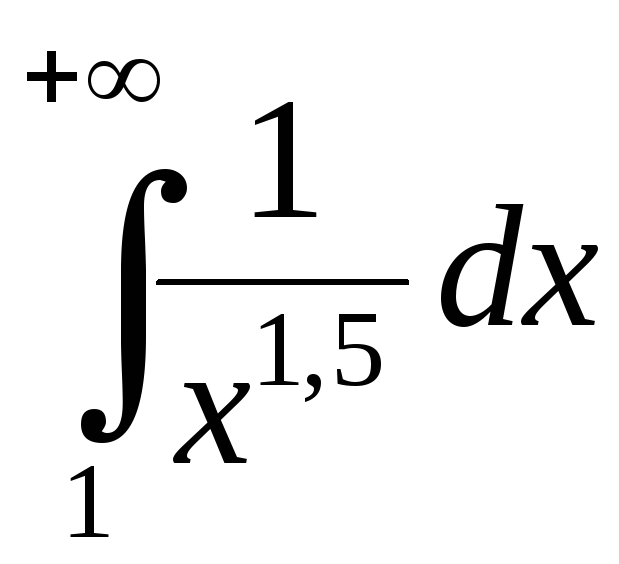 сходится, ибо
сходится, ибо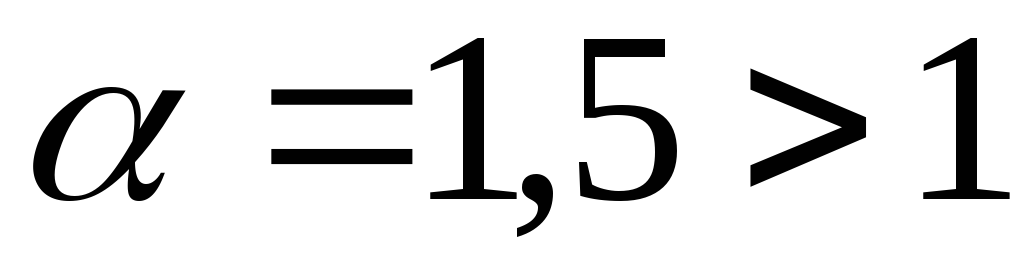 .
По 2-му признаку сравнения сходится и
интеграл
.
По 2-му признаку сравнения сходится и
интеграл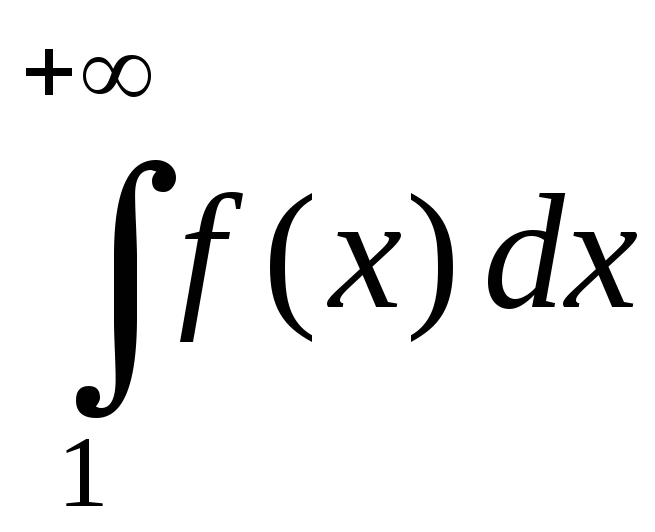 ,
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
,
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
2. .
.
Так
как 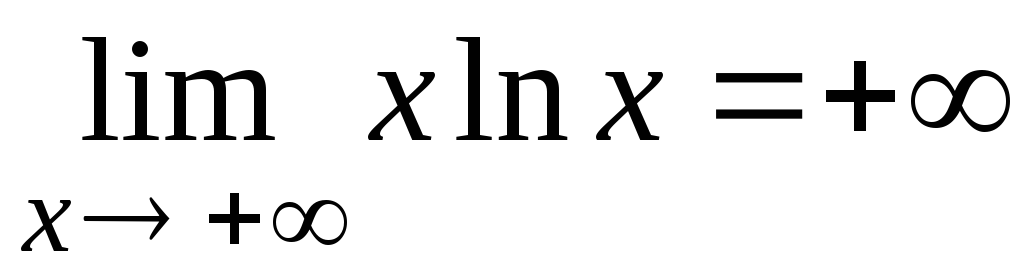 ,
тоcуществует
,
тоcуществует  такое, что при
такое, что при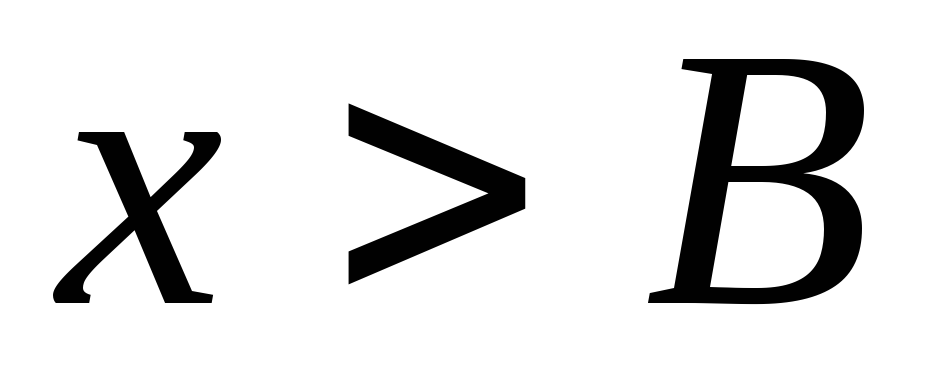
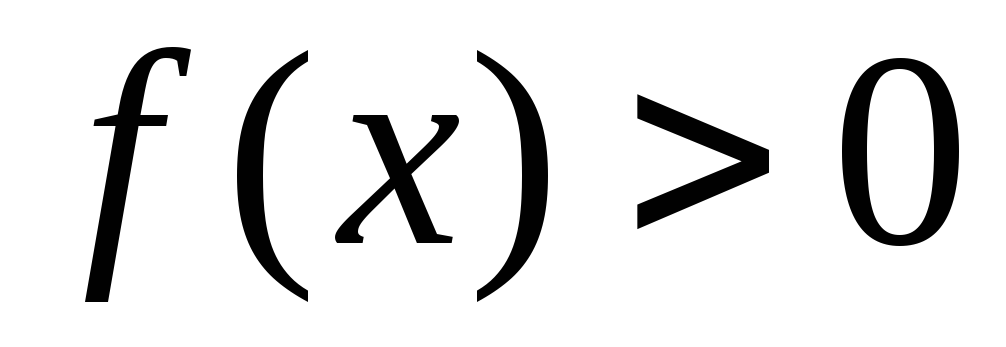 .
Для таких значений переменной:
.
Для таких значений переменной:
 .
.
Известно, что логарифмическая функция растет медленнее степенной, т.е.
 ,
,
а значит, начиная с некоторого значения переменной, эта дробь меньше 1. Поэтому
 .
.
Интеграл 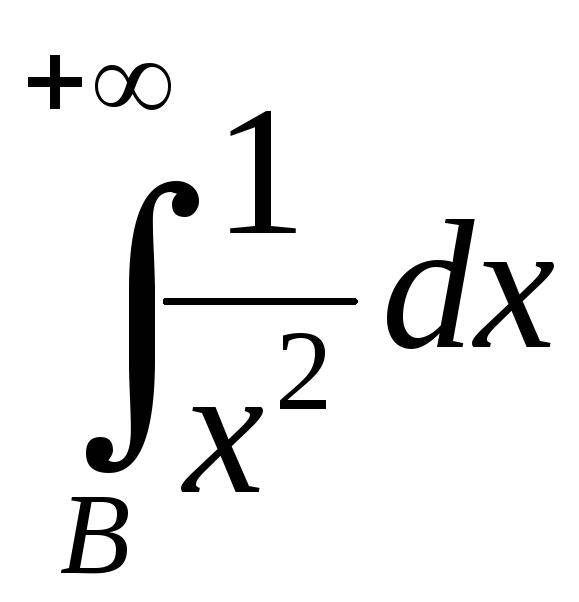 сходится как эталонный. В силу 1-го
признака сравнения сходится и
сходится как эталонный. В силу 1-го
признака сравнения сходится и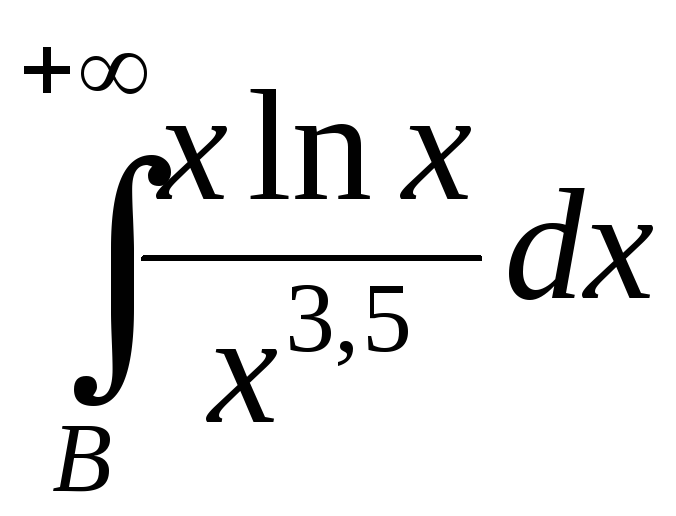 .
Применяя 2-й признак, получим, что и
интеграл
.
Применяя 2-й признак, получим, что и
интеграл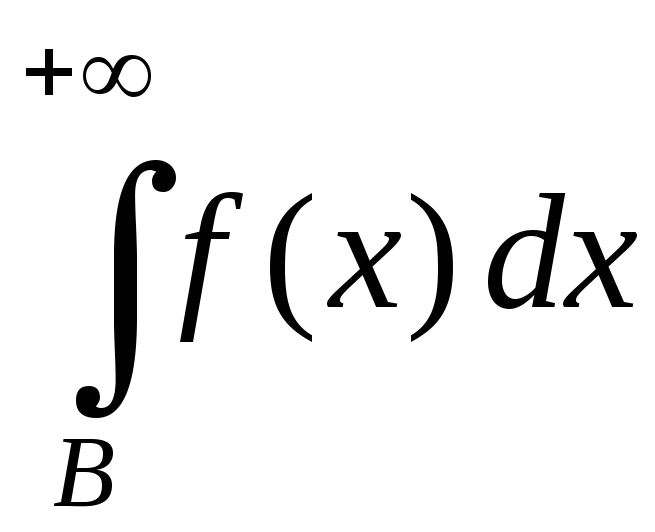 сходится. И снова свойство 2) из §1
доказывает сходимость исходного
интеграла.
сходится. И снова свойство 2) из §1
доказывает сходимость исходного
интеграла.
studfile.net
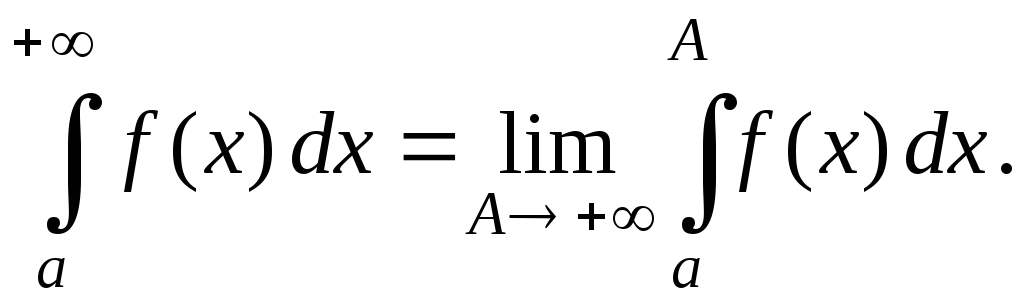
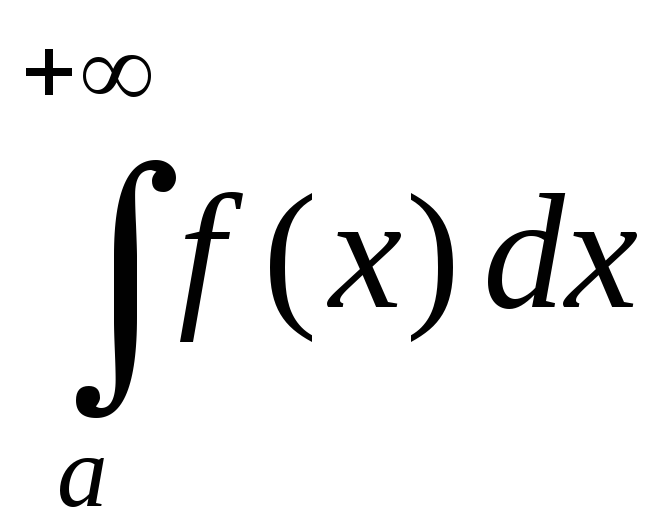 и
и
 сходятся или расходятся одновременно;
сходятся или расходятся одновременно; ,
то интегралы
,
то интегралы и
и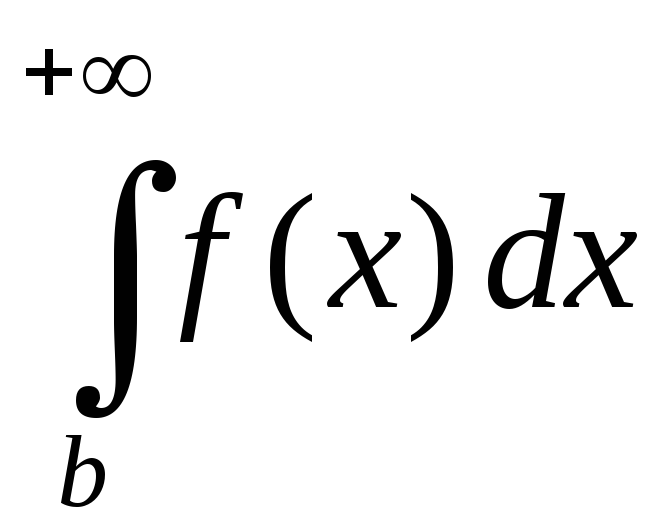 сходятся или рас-ходятся одновременно;
сходятся или рас-ходятся одновременно; сходится, то
сходится, то .
.