Метод вспомогательного угла в тригонометрии
На уроках алгебры учителя рассказывают, что существует небольшой (на самом деле — очень даже большой) класс тригонометрических уравнений, которые не решаются стандартными способами — ни через разложение на множители, ни через замену переменной, ни даже через однородные слагаемые. В этом случае в дело вступает принципиально другой подход — метод вспомогательного угла.
Что это за метод и как его применять? Для начала вспомним формулы синуса суммы/разности и косинуса суммы/разности:
\[\begin{align}& \sin \left( \alpha \pm \beta \right)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\& \cos \left( \alpha \pm \beta \right)=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\\end{align}\]
Думаю, эти формулы хорошо знакомы вам — из них выводятся формулы двойного аргумента, без которых в тригонометрии вообще никуда. Но давайте теперь рассмотрим простое уравнение:
Разделим обе части на 5:
\[\frac{3}{5}\sin x+\frac{4}{5}\cos x=1\]
Заметим, что ${{\left( \frac{3}{5} \right)}^{2}}+{{\left( \frac{4}{5} \right)}^{2}}=1$, а это значит, что обязательно найдётся такой угол $\alpha $, для которого эти числа являются соответственно косинусом и синусом. Поэтому наше уравнение перепишется следующим образом:
Поэтому наше уравнение перепишется следующим образом:
\[\begin{align}& \cos \alpha \sin x+\sin \alpha \cos x=1 \\& \sin \left( \alpha +x \right)=1 \\\end{align}\]
А это уже легко решается, после чего останется лишь выяснить, чему равен угол $\alpha $. Как это выяснить, а также как правильно подбирать число для деления обеих частей уравнения (в данном простом примере мы делили на 5) — об этом в сегодняшнем видеоуроке:
Сегодня мы будем разбирать решение тригонометрических уравнений, а, точнее, один-единственный прием, который называется «метод вспомогательного угла». Почему именно этот метод? Просто потому, что за последние два-три дня, когда я занимался с учениками, которым рассказывал о решении тригонометрических уравнений, и мы разбирали, в том числе, метод вспомогательного угла, и все ученики как один допускают одну и ту же ошибку. А ведь метод вообщем-то несложный и, более того, это один из основных приемов в тригонометрии. {2}}=3+1=4\]
{2}}=3+1=4\]
\[\sqrt{l}=2\]
$\sqrt{l}$ — это тот самый коэффициент, на который необходимо разделить обе части уравнения, чтобы перед синусом и косинусом появились числа, которые сами по себе являются синусами и косинусами. Давайте разделим:
\[\frac{\sqrt{3}}{2}\cdot \sin 2x-\frac{1}{2}\cdot \cos 2x=\frac{1}{2}\]
Посмотрим на то, что у нас получилось слева: существует ли такой $\sin $ и $\cos $, чтобы $\cos \alpha =\frac{\sqrt{3}}{2}$, а $\sin \alpha =\frac{1}{2}$? Очевидно существует: $\alpha =\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$. Поэтому мы можем переписать наше выражение следующим образом:
\[\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\cdot \sin 2x-\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\cdot \cos 2x=\frac{1}{2}\]
\[\sin 2x\cdot \cos \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}-\cos 2x\cdot \sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}=\frac{1}{2}\]
Теперь перед нами формула синуса разности. Мы можем написать так:
\[\sin \left( 2x-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}} \right)=\frac{1}{2}\]
Перед нами простейшая классическая тригонометрическая конструкция. Напомню:
Напомню:
\[\sin x=a\]
\[x=\arcsin a+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=\text{ }\!\!\pi\!\!\text{ }-\arcsin a-2\text{ }\!\!\pi\!\!\text{ }n\]
Это и запишем для нашего конкретного выражения:
\[\left[ \begin{align}& 2x-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=2\text{ }\!\!\pi\!\!\text{ }n \\& 2x-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}=\text{ }\!\!\pi\!\!\text{ }-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}+2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]
\[\left[ \begin{align}& 2x=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }n \\& 2x=\text{ }\!\!\pi\!\!\text{ }+2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]
\[\]
\[\left[ \begin{align}& x=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+\text{ }\!\!\pi\!\!\text{ }n \\& x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]
\[n\in Z\]
Нюансы решения
Итак, что нужно делать, если вам попалось подобный пример:
- Преобразовать конструкцию, если нужно.
 {2}}=4\]
{2}}=4\]\[\sqrt{l}=2\]
Перепишем с учетом этого факта:
\[\frac{\sqrt{3}}{2}\cdot \sin 2x-\frac{1}{2}\cdot \cos 2x=\cos x\]
В этом случае мы можем записать, что $\frac{\sqrt{3}}{2}=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$, а $\frac{1}{2}=\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{3}$. Перепишем:
\[\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\cdot \sin 2x-\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\cdot \cos 2x=\cos x\]
\[-\cos \left( \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}+2x \right)=\cos x\]
Внесем «минус» в скобку хитрым способом. Для этого заметим следующее:
\[\cos \left( \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}+2x \right)=\cos \left( \text{ }\!\!\pi\!\!\text{ }-\text{ }\!\!\pi\!\!\text{ +}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}+2x \right)=\]
\[=\cos \left( \text{ }\!\!\pi\!\!\text{ }-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2x \right)=\cos \left( \text{ }\!\!\pi\!\!\text{ }+\varphi \right)=-\cos \varphi \]
Возвращаемся к нашему выражению и вспоминаем, что в роли $\varphi $ у нас выражение $-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2x$.

\[-\left( -\cos \left( -\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2x \right) \right)=\cos x\]
\[\cos \left( 2x-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3} \right)=\cos x\]
Чтобы решить подобною задачу, нужно вспомнить такое:
\[\cos \alpha =\cos \beta \]
\[\left[ \begin{align}& \alpha =\beta +2\text{ }\!\!\pi\!\!\text{ }n \\& \alpha =-\beta +2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]
Разберемся с нашим примером:
\[\left[ \begin{align}& 2x-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}=x+2\text{ }\!\!\pi\!\!\text{ }n \\& 2x-\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}=-x+2\text{ }\!\!\pi\!\!\text{ }n \\\end{align} \right.\]
Давайте посчитаем каждое из этих уравнений:
\[x=\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }n\]
И вторую:
\[3x=\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }\]
\[x=\frac{2\pi }{9}+\frac{2\pi n}{3}\]
Запишем окончательный ответ:
\[\left[ \begin{align}& x=\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }n \\& x=\frac{2\text{ }\!\!\pi\!\!\text{ }}{9}+\frac{2\text{ }\!\!\pi\!\!\text{ }n}{3} \\\end{align} \right.
 {2}}x}{2}\cdot \sin x=\]
{2}}x}{2}\cdot \sin x=\]\[=2\left( 1-\cos 2x \right)\cdot \sin x\]
А теперь подставим все это в нашу исходную конструкцию:
\[\sin 2x\cos x+\cos 2x\sin x+2\sin x-2\cos x\sin x+4\cos x=5\]
\[\sin 2x\cos x-\operatorname{cosx}-cos2\sin x+2\sin x+4\cos x=5\]
\[\sin \left( 2x-x \right)+2\sin x+4\cos x=5\]
\[3\sin x+4\cos x=5\]
Давайте введем нашу поправку:
\[l=9+16=25\]
\[\sqrt{l}=5\]
Записываем:
\[\frac{3}{5}\sin x+\frac{4}{5}\cos x=1\]
Таких $\alpha $, для которых $\sin $ или $\cos $ был бы равен $\frac{3}{5}$ и $\frac{4}{5}$ в тригонометрической таблице нет. Поэтому давайте просто так и напишем и сведем выражение к синусу суммы:
\[\sin x\cdot \cos \varphi +\cos x\cdot \sin \varphi =1\]
\[\sin \left( x+\varphi \right)=1\]
Это частный случай, простейшая тригонометрическая конструкция:
\[x+\varphi =\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}-\varphi +2\text{ }\!\!\pi\!\!\text{ }n\]
Осталось найти, чему равен $\varphi $.
 Именно в этом месте многие ученики ошибаются. Дело в том, что на $\varphi $ накладываются два требования:
Именно в этом месте многие ученики ошибаются. Дело в том, что на $\varphi $ накладываются два требования:\[\left\{ \begin{align}& \cos \varphi =\frac{3}{5} \\& \sin \varphi =\frac{4}{5} \\\end{align} \right.\]
Начертим радар и посмотрим, где такие значения встречаются:
Возвращаясь к нашему выражению, мы напишем следующее:
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}-\arcsin \frac{4}{5}+2\text{ }\!\!\pi\!\!\text{ }n\]
Но и эту запись можно немного оптимизировать. Поскольку мы знаем следующее:
\[\alpha :\arcsin \alpha +\arccos \alpha =\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}},\]
то в нашем случае можно записать так:
\[x=\arccos \frac{4}{5}+2\text{ }\!\!\pi\!\!\text{ }n\]
Пример № 2
Здесь потребуется еще более глубокое понимание методик решения стандартных задач без тригонометрии. Но для решения этого примера мы также используем метод вспомогательного угла.\[\]
\[5+2\sin 2x-5\cos x=5\sin x\]
Первое, что бросается в глаза — здесь нет степеней выше первой и поэтому ничего нельзя разложить по формулам разложения степеней.
 {2}}=2\]
{2}}=2\]\[\sqrt{l}=\sqrt{2}\]
Разделим все на $\sqrt{2}$:
\[\left[ \begin{align}& \frac{\sqrt{2}}{2}\sin x+\frac{\sqrt{2}}{2}\cos x=\frac{3}{2\sqrt{2}} \\& \frac{\sqrt{2}}{2}\sin x+\frac{\sqrt{2}}{2}\cos x=\frac{\sqrt{2}}{2} \\\end{align} \right.\]
Все сведем к $\cos $:
\[\cos x\cdot \cos \frac{\text{ }\!\!\pi\!\!\text{ }}{4}+\sin x\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\]
\[\left[ \begin{align}& \cos \left( x-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} \right)=\frac{3}{2\sqrt{2}} \\& \cos \left( x-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)=\frac{\sqrt{2}}{2} \\\end{align} \right.\]
Разбираемся с каждым из этих выражений.
Первое уравнение корней не имеет, и для доказательства этого факта нам поможет иррациональность в знаменателе. Заметим следующее:
\[\sqrt{2}<1,5\]
\[\frac{3}{2\sqrt{2}}>\frac{3}{3\cdot 1,5}=\frac{3}{3}=1\]
Итого мы четко доказали, что требуется, чтобы $\cos \left( x-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)$ был равен числу, которое большее «единицы» и, следовательно, у этой конструкции корней нет.

Разбираемся со вторым:
\[x-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }n\]
Решаем эту конструкцию:
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+2\text{ }\!\!\pi\!\!\text{ }n\]
В принципе, можно оставить ответ таким, а можно его расписать:
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=2\text{ }\!\!\pi\!\!\text{ }n\]
\[n\in Z\]
Важные моменты
В заключение хотел бы еще раз обратить ваше внимание на работу с «некрасивыми» аргументами, т.е. когда $\sin $ и $\cos $ не являются табличными значениями. Проблема состоит в том, что если мы утверждаем, что в нашем уравнении $\frac{3}{5}$ — это $\cos $, а $\frac{4}{5}$ — это $\sin $, то в итоге, после того как мы решим конструкцию, нужно учитывать оба этих требования. Мы получаем систему из двух уравнений. Если мы не будем это учитывать, то получим следующую ситуацию.

Такая проблема возникает только тогда, когда речь идет о «некрасивых» аргументах. Когда у нас табличные значения, то ничего такого нет.
Надеюсь, сегодняшний урок помог вам разобраться, что такое метод вспомогательного угла и как его применять на примерах разного уровня сложности. Но это не единственный урок, посвященный решению задач методом вспомогательного угла. Поэтому оставайтесь с нами!
Смотрите также:
- Как решать тригонометрические уравнения? Основные приёмы и методы.
- Решаем однородные тригонометрические уравнения
- Задача B8: отрезки и углы в треугольниках
- Схема Бернулли. Примеры решения задач
- Деление многочленов уголком
- Задача B4: вклад в банке и проценты
Метод введения вспомогательного угла
Преобразование выражения
a sin х + b cos х путем введения вспомогательного углаЛемма.
 2}} $$
2}} $$Примеры.
1) \( sin x + cos x = \sqrt2 (\frac{1}{\sqrt2} sin x + \frac{1}{\sqrt2}cos x) = \sqrt2 (cos\frac{\pi}{4}sin x + sin\frac{\pi}{4}cos x ) =\\= \sqrt2(sinx + \frac{\pi}{4}) \)
Полученную формулу sin x + cos x = \(\sqrt2(sinx + \frac{\pi}{4})\)полезно запомнить.
2) Если одно из чисел а и b положительно, а другое отрицательно, то выражение
$$ 3sinx — 4cosx = \sqrt{9+16}(\frac{3}{\sqrt{9+16}}sinx — \frac{4}{\sqrt{9+16}}cosx) =\\= 5(sinx\cdot\frac{3}{5} — cosx\cdot\frac{4}{5}) = 5sin(x — \phi), $$
a sin х + b cos х удобнее преобразовывать не к синусу суммы, а к синусу разности двух углов. Так,где под φ можно подразумевать любой угол, удовлетворяющий условиям:
cos φ = 3/5 , sin φ = 4/5
В частности, можно положить φ = arctg 4/3. Тогда получим:
3 sin х — 4 cos x = 5 sin (x — arctg 4/3).

Конспект урока по алгебре на тему «Решение тригонометрических уравнений. Метод введения вспомогательного аргумента»
План-конспект урока по предмету
Алгебра
«Решение тригонометрических уравнений.
Метод введения вспомогательного аргумента»
Автор: Ишмухаметова Р.Р.
Конспект урока по теме
«Решение тригонометрических уравнений. Метод введения вспомогательного аргумента»
1. Организационный момент.
Приветствие, создание позитивного эмоционального настроя.
( На уроке учащиеся будут работать в группах, поэтому нужно представить старших групп, рассказать о правилах работы в группе и о самооценке своей работы на уроке.).
У.: У нас сегодня будет с одной стороны обычный урок, т.
 к. мы с вами будем решать, решать и решать, но с другой стороны он будет и необычным. Как вы думаете почему?
к. мы с вами будем решать, решать и решать, но с другой стороны он будет и необычным. Как вы думаете почему?Ответ: открытый урок.
А вот и не угадали. Мы с вами будем решать почти весь урок только одно уравнение. Но об этом немного попозже.
2.Актуализация знаний.
А сейчас давайте вспомним методы решения тригонометрических уравнений.
Ответ: Метод замены переменной, метод разложения на множители вынесением за скобки, метод разложения на множители с помощью формул суммы и разности синусов и косинусов, т.е. преобразование суммы в произведение и решение уравнений с использованием однородности.
(на экране появляются тригонометрические уравнения, учащиеся называют способы решения уравнений и по мере называния способы появляются на экране, справа от столбца уравнений )
sin x + cos x = 0Б. Метод разложения на множители
sin 5x — sin x = 0
В. Метод преобразования суммы в произведение
4sin2x — cos x = 1
Г.
 Метод однородных уравнений
Метод однородных уравненийsin2x -5sinxcosx + 6cos2x=0
Д. Другой метод
Работа в группах: 2. 1. Решение задания на соответствие тригонометрических уравнений и методов решения.
Задание группам: соединить стрелочками метод решения и уравнение. Обсуждают в группах, а затем проверяем, спрашиваю например 1 группу, а остальные проверяют и обсуждаем решение.
Даю время 2 мин, на самооценку 1 задания. На экране появляются критерии самооценки:
2.2. Решение данных тригонометрических уравнений и проверка их на доске.
Задание: решить данные тригонометрические уравнения (каждая группа решает все уравнения, но внутри группы распределяют, кто какое будет решать уравнение). Затем каждая группа записать решение на доске и объяснить метод решения одного уравнения на выбор.
Даю время 2 мин на самооценку. На экране появляются критерии самооценки:
2 балл — за решенное уравнение, но с допущенной ошибкой;
1 балл — за недорешенное уравнение;
И плюс 1 балл за ответ у доски.

3. Открытие новых знаний.
3.1.Постановка проблемы: проблемная ситуация с затруднением
Мы с вами при решении уравнений чаще всего не сразу видели, какой это способ решения.
Что мы для этого делали?
Сейчас я каждой группе предложу свой метод решения этого уравнения, а вы попробуете, выполнив какие-либо преобразования решить уравнение и отметить решение уравнения на единичном тригонометрическом круге. Затем разберем решение на доске. Если вы не сможете догадаться какое преобразование нужно выполнить, вы можете взять подсказку. Подсказки будут платные. Стоят они 0,5 балла.
Подсказки напечатаны на карточках и разложены на столе учителя. Метод решения и шпаргалки к этому методу решения уравнения определенного цвета.
3.2. .Обсуждение и решение проблемы по группам.
3.3.Обсуждение проблемы у доски.
Записывают решения на доске и объясняют.
 Сделать вывод о решении после каждого объяснения.
Сделать вывод о решении после каждого объяснения.На экране появляются 5 единичных тригонометрических круга, на которых отмечены решения уравнения.
3.4. Выводы и предложения по решению уравнения.
Почему такое произошло?
-Что мы делаем в этом случае? Как проверить кто прав?
Как выполняется проверка?
4 ответа одинаковые, а один ответ — другой.
Допустили ошибку при решении
или возник посторонний корень при возведении в квадрат
Сделать проверку.
подставить в уравнение и если получим верное равенство, значит, этот корень является решением уравнения.
У.: Давайте выполним проверку корней уравнения. Каждая группа проверит одно решение.
Раздать листы с заданием, какой корень проверить, а затем результат вывешиваем на доску и делаем вывод о достоверности решений.

Вывод: Значения х = 0 и 2П и х = П\2 являются решениями уравнения, а значения х = П и х =3 П\2 не являются решениями данного уравнения или это так называемые посторонние корни.
У.: почему они возникли и при решении каким способом?
О.: при возведении в квадрат.
У.: Как можно уточнить ответ уравнения или что можно исключить из множества всех действительных чисел?
При каких значениях n у нас получаются верные решения, а при каких – не верные или посторонние?
Ответ: при п четных — верные, а при п нечетных – неверные.
3.5.Введение нового метода решения данного типа уравнения.
Если назовут несколько способов, то сначала проанализировать какие способы применяли при решении этого уравнения, и только потом этот способ появится как новый.
Как вы думаете как в общем виде можно записать уравнение, которое мы решали?
У кого какие идеи, гипотезы?
У кого какие мнения?
Откройте учебники и найдите параграф, где говорится о решении уравнений такого вида.
 Прочитайте его.
Прочитайте его.А теперь давайте попробуем составить алгоритм решения уравнений такого вида.
На экране появляется постепенно алгоритм решения уравнения.
a cos x + b sin x = c,
1) делим мы на
2) Уравнение принимает вид
3) Вводим вспомогательный аргумент (угол), такой, что и
Т.о. уравнение можно записать в виде
, а это простейшее тригонометрическое уравнение.
Запишите себе в тетрадь.
Чему равны а, в и с в нашем уравнении?
Как можно получить в нашем случае из а и в
a cos x + b sin x = c,
делим мы на
а=1, в=1 и с=1
=
.
4. Закрепление изученного материала.
4.1.Работа с учебником по поиску подобных уравнений.
Найдите на с.189 номер с подобным типом уравнений и давайте выберем уравнения, которые будем решать
4.
 2.Решение найденных уравнений изученным методом.
2.Решение найденных уравнений изученным методом.Выбираем и решаем в зависимости от времени.(№ 625 1,3 или 4)
Ответы записывают на листах и вывешиваем на доску. Анализируем решение и ставим оценки.
5. Подведение итогов.
После уточнения вывешиваю тему на доску.
И все таки какой метод из примененных вами вам больше всего понравился?
Почему?
Как видим этот тип уравнений можно решать любым из данных методов, лишь бы он был вам понятен.
Решение тригонометрических уравнений
Предложения студентов
Молчание или неточная формулировка
нений. Метод введения вспомогательного аргумента (или угла)
Самооценка.
Каждая группа с учетом набранных баллов оценивает свой вклад в работу на уроке.
Проставьте на листе оценки за работу на уроке.
6. Задание для внеаудиторной самостоятельной работы.
 (появляется на экране)
(появляется на экране)Прочитать §.36 п.2 и решить № 664.
На «3» — решить новым способом уравнения этого номера.
На «4» — решить 2 способами уравнения этого номера;
На «5» — решить всевозможными способами эти уравнения.
Рефлексия:
А теперь выразите свое отношение к уроку. Понравился он вам или нет, получили ли вы новые знания, или этот урок оставил вас равнодушными к математике.
Прикрепить к синусоиде (она вывешивается на доску) кружочки желтого, зеленого и коричневого цвета. Желтые крепятся сверху, коричневые – снизу синусоиды, а зеленые на ось Ох.
Посмотрите как мы сегодня поработали . Молодцы!
Спасибо за хорошую работу на уроке. До свидания.
Домашнее задание:
Прочитать §36 п.2
и решить №664
На «3» — решить новым способом уравнения этого номера.
На «4» — решить 2 способами уравнения этого номера;
На «5» — решить всевозможными способами эти уравнения.

Тригонометрические уравнения — презентация онлайн
1. Методика решения тригонометрических уравнений
L/O/G/O2. Слово «тригонометрия» греческого происхождения. В пере-воде на русский язык оно означает «измерение треугольников». Как и все
Слово «тригонометрия»
греческого происхождения. В переводе на русский язык оно означает
«измерение треугольников». Как и
все разделы математики, зародившиеся в глубокой древности, тригонометрия возникла в результате
попыток решить те задачи, с
которыми человеку приходилось
сталкиваться на практике.
Основы тригонометрии, как и основы
алгебры и начал анализа закладываются в
школе. Тригонометрические функции
начинают изучать в 8 классе на уроках
геометрии и продолжают в 10-11 классах.
Тригонометрические уравнения слишком
разнообразны для того, чтобы попытаться
дать их общую классификацию или общий
метод решения. Мы можем указать лишь
Мы можем указать лишь
способы решения некоторых типов таких
уравнений.
Решение тригонометрических
уравнений
Для тригонометрических
уравнений применимы общие методы
решения (разложение на множители,
замена переменной, функциональнографические) и равносильные
преобразования общего характера.5. Методы решения тригонометрических уравнений
Основные методы:
• замена переменной,
• разложение на множители,
•однородные уравнения,
прикладные методы:
• по формулам преобразования суммы в произведение
и произведения в сумму,
• по формулам понижения степени,
• универсальная тригонометрическая подстановка
• введение вспомогательного угла,
• умножение на некоторую тригонометрическую функцию.
Проблемы ,возникающие при решении
тригонометрических уравнений
1.Потеря корней:
делим на g(х).
опасные формулы (универсальная подстановка).
Этими операциями мы сужаем область определения.
2. Лишние корни:
возводим в четную степень.
умножаем на g(х) (избавляемся от знаменателя).
Этими операциями мы расширяем область
определения.7. Наша задача: свести любое тригонометрическое уравнение к простейшему виду.
Наша задача:
свести любое
тригон ометрическое
урав н ен и е
к п ростей шему вид у.
Решение простейших
тригонометрических
уравнений9. Формулы корней простых тригонометрических уравнений
1.cost = а , где |а| ≤ 1
2.sint = а, где | а |≤ 1
3. tgt = а, аЄR
t = arctg а + πk‚ kЄZ
или
или
4. ctgt = а, аЄR
Частные случаи
Частные случаи
1)cost=0
t = π/2+πk‚ kЄZ
1)sint=0
t = 0+πk‚ kЄZ
2)cost=1
t = 0+2πk‚ kЄZ
2)sint=1
t = π/2+2πk‚ kЄZ
3)cost = -1
t = π+2πk‚ kЄZ
3)sint = — 1
t = — π/2+2πk‚ kЄZ
t = arcctg а + πk‚ kЄZ
• При повторении формул решения уравнений
следует обратить внимание на то, что формулы
задают множества чисел, которые образованы по
закону арифметической прогрессии с разностью
2π или π.
• С другой стороны использование общей
формулы серий решений не всегда является
удобной при отборе корней, в частности, на
числовой окружности. В этом случае как раз
удобнее не объединять серии решений
тригонометрических уравнений, а представлять
их совокупностью, выделяя разность 2π
соответствующих прогрессий.13. tg x и ctg x
14. Решение простейших уравнений
2) cos(x+π/3) = ½
1) tg2x = -1
2x = arctg (-1) + πk, kЄZ
2x = -π/4 + πk, kЄZ
x = -π/8 + πk/2, kЄZ
Ответ: -π/8 + πk/2, kЄZ.
x+π/3 = ±arccos1/2 + 2πk, kЄZ
x+π/3 = ±π/3 + 2πk, kЄZ
x = -π/3 ± π/3 + 2πk, kЄZ
Ответ: -π/3 ± π/3 + 2πk, kЄZ
3) sin(π – x/3) = 0
упростим по формулам
приведения
sin(x/3) = 0
частный случай
x/3 = πk, kЄZ
x = 3πk, kЄZ.
Ответ: 3πk, kЄZ.
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РАЗЛОЖЕНИЕМ НА МНОЖИТЕЛИ.
Метод разложения на множители заключается в следующем: если
То всякое решение уравнения
Является решением совокупности уравнений
Обратное утверждение, неверно: не всякое решение совокупности уравнений (2)
является решением уравнения (1). Это объясняется тем, что решения отдельных
Это объясняется тем, что решения отдельных
уравнений (2) могут не входить в область определения функции
.Поэтому,
если при решении тригонометрического уравнения методом разложения
на множители, функции,
входящие в уравнение, определены не для всех значений аргумента, после
нахождения решения должна быть сделана проверка,
чтобы исключить лишние корни. Можно поступать другим способом: находить
область допустимых значений исходного уравнения и выбирать только те корни,
которые входят в найденную область допустимых значений
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РАЗЛОЖЕНИЕМ НА МНОЖИТЕЛИ.
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ,
СВОДЯЩИХСЯ К КВАДРАТНЫМ.
Уравнения сводимые к квадратным
a∙sin²x + b∙sinx + c=0
Пусть sinx = p, где |p| ≤1, тогда
a∙p² + b∙p + c = 0
Найти корни, вернуться к замене и решить простые уравнения.
При решении уравнений указанного типа в основном применяются следующие
тригонометрические тождества:
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ,
СВОДЯЩИХСЯ К КВАДРАТНЫМ.
Пример 1. Решить уравнение
Решение.
2 sin2x + sinx — 1 = 0.
Введём новую переменную t = sinx. Тогда данное
уравнение примет вид
2t2 + t — 1 = 0.
Решим его: D = 1 + 8 = 9,
1 3 1
t1
,
4
2
1 3
t2
1 .
4
Cледовательно,
sinx = 1/2
или
sinx = -1.
1) sinx = 1/2,
1
х ( 1) arcsin k , k Z ,
2
k
x ( 1)
k
6
k, k Z.
2) sinx = -1,
х
2
2 n, n Z .
Ответ : ( 1)
k
6
k, k Z ,
2
2 n, n Z .20. Решение уравнений, однородных относительно синуса и косинуса
в которых сумма показателей степеней у sinx и cosx (степень уравнения) во
всех членах уравнения одинакова. Например,22. Однородные тригонометрические уравнения
ОДНОРОДНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
2.Однородные
1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно не равны нулю, то разделим обе
части уравнения на cosx. Получим: простое уравнение
Получим: простое уравнение
a∙tgx + b = 0 или tgx = m
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x. Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.
В частности, уравнения вида
приводятся к однородным путем представления правой части в виде:23. Решение уравнений с помощью введения вспомогательного аргумента.
:
РЕШЕНИЕ УРАВНЕНИЙ С ПОМОЩЬЮ ВВЕДЕНИЯ
ВСПОМОГАТЕЛЬНОГО АРГУМЕНТА.
Рассмотрим уравнение
Разделим левую и правую часть уравнения на
Так как
то существует угол φ такой, что
при этом
Тогда уравнение примет вид
будут не всегда равносильны.
Отметим, что к выбору угла φ в задачах с параметрами нужно относиться внимательно:
выбор
и выбор
Решите уравнения:
Уравнения, линейные относительно
sin x и cos x
а sin x + в cos x = с.
Если а=в=0, а с не равно 0, то уравнение теряет смысл;
Если а=в=с=0, то х – любое действительное число, то есть уравнение
обращается в тождество.
Рассмотрим случаи, когда а,в,с не равны 0.
Примеры:
3 sin 5x — 4 cos 5x = 2
2 sin x cos x 2
2 sin 3x + 5 cos 3x = 8.
Последнее уравнение не имеет решений, так как левая часть его не
превосходит 7. Уравнения, этого вида можно решить многими способами:
с помощью универсальной подстановки, выразив sin x и cos x через tgх ;
сведением уравнения к однородному; введением вспомогательного
аргумента и другими.
2
2
2
Решение этих уравнений существует при a b c27. Решение уравнений с применением формул понижения степени.
:
Решение уравнений с применением
формул понижения степени.
При решении широкого круга тригонометрических уравнений ключевую роль играют
формулы понижения степени
Решение уравнений с применением
формул тройного аргумента.
(1)
(2)
При решении ряда уравнений наряду с другими существенную роль играют формулы28. Решение уравнений методом универсальной подстановки.
 Тригонометрическое уравнение вида
Тригонометрическое уравнение вида
где R – рациональная функция,
с помощью тригонометрических формул двойного и тройного аргумента, а также
формул сложения можно свести к рациональному уравнению относительно аргументов
после чего уравнение может быть сведено к рациональному уравнению относительно
с помощью формул универсальной тригонометрической подстановки
Следует отметить, что применение формул может приводить к сужению ОДЗ исходного
уравнения, поскольку
не определен в точках
поэтому в таких случаях нужно проверять, являются ли углы
корнями исходного уравнения.29. тригонометрические уравнения, содержащие знак модуля или знак корня.
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СОДЕРЖАЩИЕ
ЗНАК МОДУЛЯ ИЛИ ЗНАК КОРНЯ.
Специфика тригонометрических уравнений, содержащих знак модуля или
знак корня, состоит в том, что они сводятся к смешанным системам, где
кроме уравнений нужно решать тригонометрические неравенства и из
решений уравнений выбирать лишь те, которые удовлетворяют
неравенствам.
Решите уравнения:30. Использование ограниченности функций при решении тригонометрических уравнений.
ИСПОЛЬЗОВАНИЕ ОГРАНИЧЕННОСТИ ФУНКЦИЙ ПРИ
РЕШЕНИИ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ.
При решении некоторых тригонометрических уравнений часто используется свойство
ограниченности функций
, то есть следующие неравенства:
и31. Функциональные методы решения тригонометрических и комбинированных уравнений.
ФУНКЦИОНАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ
ТРИГОНОМЕТРИЧЕСКИХ И КОМБИНИРОВАННЫХ
УРАВНЕНИЙ.
Не всякое уравнение f(x)=g(x) в результате преобразований может быть сведено к
уравнению того или иного стандартного вида, для которого существует определенный
метод решения. В таких случаях оказывается полезным использовать такие свойства
функций f(x) и g(x), как монотонность, ограниченность, четность, периодичность и др. Так,
если одна из функций убывает, а вторая возрастает на промежутке X, то при наличии у
уравнения f(x)=g(x) корня на этом промежутке, этот корень единственный, и тогда его,
например, можно найти подбором. Если, далее, функция f(x) на промежутке X ограничена
Если, далее, функция f(x) на промежутке X ограничена
сверху, причем
, а функция g(x) ограничена снизу, причем
то уравнение f(x)=g(x) равносильно системе уравнении
Иногда для решения уравнения f(x)=g(x) можно построить графики функции y=f(x),
y=g(x) и определить абсциссы точек пересечения. Также рассматривается
применение производной для исследования тригонометрических уравнений.32. Способы отбора корней тригонометрических уравнений на заданном промежутке
• Арифметический способ
Перебор значений целочисленного параметра n и
вычисление корней
• Алгебраический способ
Перебор значений целочисленного параметра n и
вычисление корней
• Геометрический способ
Изображение корней на тригонометрической
окружности с последующим отбором с учетом
имеющихся ограничений33. Арифметический способ Перебор значений целочисленного параметра n и вычисление корней
cos x a, a 1
x arccos a 2 k , k Z
x arccos a 2 k , k Z
Решить уравнение
Записать корни уравнения
Разделить виды решения для
x
косинуса; подсчитать значения x
k
-2
-1 0
2 …
arccos a 2 k
arccos a 2 k
при целых n до тех пор, пока
значения x не выйдут за пределы
sin x a, a 1
данного отрезка.
x ( 1) k arcsin a k , k Z
Записать ответ.
1
x
k
( 1) k arcsin a k
-2 -1 0 1 2 …34. Алгебраический способ Решение неравенства относительно неизвестного параметра n и вычисление корней
cos x a, a 1, c; d
Записать двойное неравенство
для неизвестного (x),
соответственное данному отрезку
или условию; решить уравнение.
2. Для синуса и косинуса разбить
решения на два.
3. Подставить в неравенство
вместо неизвестного (x)
найденные решения и решить его
относительно n.
4. Учитывая, что n принадлежит
Z, найти соответствующие
неравенству значения n.
5. Подставить полученные
значения n в формулу корней.
1.
x arccos a 2 k , k Z
x arccos a 2 k , k Z
с arccos a 2 k d
с arccos a 2 k d
Т.к. k Z ,
то k1 …; x1 …
k2 …; x2 …
sin x a, a 1, c; d
x arcsin a 2 k , k Z
x arcsin a 2 k , k Z
с arcsin a 2 k d
с arcsin a 2 k d
Т. к. k Z ,
к. k Z ,
то k1 …; x1 …
k2 …; x2 …35. Геометрический способ Изображение корней на тригонометрической окружности с последующим отбором с учетом имеющихся ограничений
cos x a, a 1, c; d
На окружности
1. Решить уравнение.
2. Обвести дугу,
соответствующую данному
отрезку на окружности.
3. Разделить виды решений для
синуса и косинуса.
4. Нанести решения уравнения
на окружность.
5. Выбрать решения, попавшие
на обведенную дугу.
x arccos a 2 k , k Z
x arccos a 2 k , k Z
y
arccos a
d
а
0
-arccos a
c
x36. Геометрический способ Изображение корней на графике с последующим отбором с учетом имеющихся ограничений
На графике
1. Решить уравнение.
2. Построить график
данной функции, прямую у
= а, на оси х отметить
данный отрезок.
3. Найти точки
пересечения графиков.
4. Выбрать решения,
принадлежащие данному
отрезку.
sin x a, a 1, c; d
x arcsin a 2 k , k Z
x arcsin a 2 k , k Z
y
y=a
a
с
arcsin a
П-arcsin a
d
y = sin x
x
Пример: Найти все корни уравнения
10 cos 2 (
2
которые удовлетворяют условию x [
Решение.
10sin2 x = – cos 2x + 3;
10sin2 x = 2sin2 x – 1 + 3,
8sin2 x = 2;
1
sin 2 x ;
4
1
sin x ;
2
k
x
(
1
)
k , k Z ,
6
x ( 1) m ( ) m, m Z ;
6
6
n, n Z ;
7
2 x) 3,
2
2 19
;
].
3 12
y
2
5
6
6
0
7
6
С помощью числовой окружности получим:
x
x) sin(
x
3
2
6
Выберем корни, удовлетворяющие условию задачи.
Из первой серии: 2 n 19 , n Z ;
3
6
12
8 2 12 n 19 , n Z ;
10 12n 17, n Z .
Следовательно n=0 или n=1, то есть x ,
6
x 7 .
6
2
19
n
,n Z;
3
6
12
8 2 12 n 19 , n Z ;
Из второй серии:
6 12n 21, n Z .
Следовательно n=0 или n=1, то есть
x 6 ,
x 5 .
6
Ответ : {
5 7
;
6 6
;
6
}.39. Спасибо за внимание!
L/O/G/OМетоды решения тригонометрических уравнений введение 2 методы решения тригонометрических уравнений 5
Методы решения тригонометрических уравнений
Введение 2
Методы решения тригонометрических уравнений 5
Алгебраический 5
Решение уравнений с помощью условия равенства одноимённых тригонометрических функций 7
Разложение на множители 8
Приведение к однородному уравнению 10
Введение вспомогательного угла 11
Преобразование произведения в сумму 14
Универсальная подстановка 14
Заключение 17
Введение
До десятого класса порядок действий многих упражнений, ведущий к цели, как правило, однозначно определен.
 Например, линейные и квадратные уравнения
и неравенства, дробные уравнения и
уравнения, приводимые к квадратным, и
т.п. Не разбирая подробно принцип решения
каждого из упомянутых примеров, отметим
то общее, что необходимо для их успешного
решения.
Например, линейные и квадратные уравнения
и неравенства, дробные уравнения и
уравнения, приводимые к квадратным, и
т.п. Не разбирая подробно принцип решения
каждого из упомянутых примеров, отметим
то общее, что необходимо для их успешного
решения.В большинстве случаев надо установить, к какому типу относится задача, вспомнить последовательность действий, ведущих к цели, и выполнить эти действия. Очевидно, что успех или неуспех ученика в овладении приемами решения уравнений зависит главным образом от того, насколько он сумеет правильно определить тип уравнения и вспомнить последовательность всех этапов его решения. Разумеется, при этом предполагается, что ученик владеет навыками выполнения тождественных преобразований и вычислений.
Совершенно иная ситуация получается, когда школьник встречается с тригонометрическими уравнениями. При этом установить факт, что уравнение является тригонометрическим, нетрудно. Сложности возникают при нахождении порядка действий, которые бы привели к положительному результату.
 И здесь
перед учеником встают две проблемы. По
внешнему виду уравнения трудно определить
тип. А не зная типа, почти невозможно
выбрать нужную формулу из нескольких
десятков, имеющихся в распоряжении.
И здесь
перед учеником встают две проблемы. По
внешнему виду уравнения трудно определить
тип. А не зная типа, почти невозможно
выбрать нужную формулу из нескольких
десятков, имеющихся в распоряжении.Чтобы помочь ученикам найти верную дорогу в сложном лабиринте тригонометрических уравнений, их сначала знакомят с уравнениями, которые после введения новой переменной приводятся к квадратным. Затем решают однородные уравнения и приводимые к ним. Все заканчивается, как правило, уравнениями, для решения которых надо разложить на множители левую часть, приравняв затем каждый из множителей к нулю.
Понимая, что разобранных на уроках полутора десятков уравнений явно недостаточно, чтобы пустить ученика в самостоятельное плавание по тригонометрическому «морю», учитель добавляет от себя еще несколько рекомендаций.
Чтобы решить тригонометрическое уравнение, надо попытаться:
— привести все функции входящие в уравнение к «одинаковым углам»;
— привести уравнение к «одинаковым функциям»;
— разложить левую часть уравнения на множители и т.
 п.
п.Но, несмотря на знание основных типов тригонометрических уравнений и нескольких принципов поиска их решения, многие ученики по-прежнему оказываются в тупике перед каждым уравнением, незначительно отличающимся от тех, что решались раньше. Остается неясным, к чему следует стремиться, имея то или иное уравнение, почему в одном случае надо применять формулы двойного угла, в другом — половинного, а в третьем — формулы сложения и т.д.
Определение 1. Тригонометрическим называется уравнение, в котором неизвестное содержится под знаком тригонометрических функций.
Определение 2. Говорят, что в тригонометрическом уравнении одинаковые углы, если все тригонометрические функции, входящие в него, имеют равные аргументы. Говорят, что в тригонометрическом уравнении одинаковые функции, если оно содержит только одну из тригонометрических функций.
Определение 3. Степенью одночлена, содержащего тригонометрические функции, называется сумма показателей степеней тригонометрических функций, входящих в него.

Определение 4. Уравнение называется однородным, если все одночлены, входящие в него, имеют одну и ту же степень. Эта степень называется порядком уравнения.
Определение 5. Тригонометрическое уравнение, содержащее только функции sin и cos, называется однородным, если все одночлены относительно тригонометрических функций имеют одинаковую степень, а сами тригонометрические функции имеют равные углы и число одночленов на 1 больше порядка уравнения.
Методы решения тригонометрических уравнений.
Решение тригонометрических уравнений состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений.
I. Алгебраический метод. Этот метод хорошо известен из алгебры. (Метод замены переменный и подстановки).

Решить уравнения.
1)
Решение.
Введём обозначение x=2sin3t, получим
Решая это уравнение, получаем: или
т.е. можно записать
При записи полученного решения из-за наличия знаков степень записывать не имеет смысла.
Ответ:
2)
Обозначим
Получаем квадратное уравнение . Его корнями являются числа и . Поэтому данное уравнение сводится к простейшим тригонометрическим уравнениям и . Решая их, находим, что или .
Ответ: ; .
3)
Обозначим
не удовлетворяет условию
Значит
Ответ:
4)
Решение:
Преобразуем левую часть уравнения:
Таким образом, данное исходное уравнение можно записать в виде:
, т.
 е.
е.Обозначив , получим Решив данное квадратное уравнение имеем:
не удовлетворяет условию
Записываем решение исходного уравнения:
Ответ:
5)
Подстановка сводит данное уравнение к квадратному уравнению . Его корнями являются числа и . Так как , то заданное уравнение корней не имеет.
Ответ: корней нет.
II. Решение уравнений с помощью условия равенства одноимённых тригонометрических функций.
а) , если
б) , если
в) , если
Используя данные условия, рассмотрим решение следующих уравнений:
6)
Решение:
Пользуясь сказанным в п. а) получаем, что уравнение имеет решение в том и только в том случае, когда .

Решая это уравнение, находим .
Имеем две группы решений: .
7) Решить уравнение: .
Пользуясь условием п. б) выводим, что .
Решая эти квадратные уравнения, получаем:
.
8) Решить уравнение .
Из данного уравнения выводим, что . Решая это квадратное уравнение, находим, что .
III. Разложение на множители.
Этот метод рассматриваем на примерах.
9) Решить уравнение .
Решение. Перенесём все члены уравнения влево: .
Преобразуем и разложим на множители выражение в левой части уравнения: .
.
.
1) 2)
Т .
 к. и не принимают значение нуль
к. и не принимают значение нульодновременно, то разделим обе части
уравнения на ,
Ответ:
10) Решить уравнение:
Решение.
или
Ответ:
11) Решить уравнение
Решение:
1) 2) 3)
,
Ответ:
IV.
 Приведение к однородному уравнению.
Приведение к однородному уравнению. Чтобы решить однородное уравнение надо:
— перенести все его члены в левую часть;
— вынести все общие множители за скобки;
— приравнять все множители и скобки к нулю;
— скобки, приравненные к нулю, дают однородное уравнение меньшей степени, которое следует разделить на (или ) в старшей степени;
— решить полученное алгебраическое уравнение относительно .
Рассмотрим примеры:
12) Решить уравнение:
Решение.
Разделим обе части уравнения на ,
Вводя обозначения , именем
корни этого уравнения:
отсюда 1) 2)
Ответ:
13) Решить уравнение:
Решение.
 Используя формулы
двойного угла и основное тригонометрическое
тождество, приводим данное уравнение
к половинному аргументу:
Используя формулы
двойного угла и основное тригонометрическое
тождество, приводим данное уравнение
к половинному аргументу:После приведения подобных слагаемых имеем:
Разделив однородное последнее уравнение на , получим
Обозначу , получим квадратное уравнение , корнями которого являются числа
Таким образом
Выражение обращается в нуль при , т.е. при , .
Полученное нами решение уравнения не включает в себя данные числа.
Ответ: , .
V. Введение вспомогательного угла.
Рассмотрим уравнение вида
, где a, b, c — коэффициенты, x — неизвестное.
Разделим обе части этого уравнения на
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль каждого из них не превосходит единицы, а сумма их квадратов равна 1.

Тогда можно обозначить их соответственно (здесь — вспомогательный угол) и наше уравнение принимает вид: .
Тогда
И его решение
Заметим, что введенные обозначения взаимно заменяемы.
Примеры.
14) Решить уравнение:
Решение. Здесь , поэтому делим обе части уравнения на
Ответ:
15) Решить уравнение
Решение. Так как , то данное уравнение равносильно уравнению
Так как , то существует такой угол , что , (т.е. ).
Имеем
Так как , то окончательно получаем:
.
Ответ:
Заметим, что уравнение вида имеют решение тогда и только тогда, когда
16) Решить уравнение:
Для решения данного уравнения сгруппируем тригонометрические функции с одинаковыми аргументами
Разделим обе части уравнения на два
Преобразуем сумму тригонометрических функций в произведение:
Ответ:
VI.
 Преобразование произведения в сумму.
Преобразование произведения в сумму.Здесь используются соответствующие формулы.
Пример.
17) Решить уравнение:
Решение. Преобразуем левую часть в сумму:
VII. Универсальная подстановка.
,
эти формулы верны для всех
Подстановка называется универсальной.
18) Решить уравнение:
Решение: Заменим и на их выражение через и обозначим .
Получаем рациональное уравнение , которое преобразуется в квадратное .
Корнями этого уравнения являются числа .
Поэтому задача свелась к решению двух уравнений .

Находим, что.
Значение вида исходному уравнению не удовлетворяет, что проверяется проверкой — подстановкой данного значения t в исходное уравнение.
Ответ: .
Замечание. Уравнение 18 можно было решить иным способом.
Разделим обе части этого уравнения на 5 (т.е. на ): .
Так как , то существует такое число , что и . Поэтому уравнение принимает вид: или . Отсюда находим, что где .
19) Решить уравнение .
Решение. Так как функции и имеют наибольшее значение, равное 1, то их сумма равна 2, если и , одновременно, то есть .
Ответ: .
При решении этого уравнения применялась ограниченность функций и .
Заключение.
Работая над темой « Решения тригонометрических уравнений » каждому учителю полезно выполнять следующие рекомендации:
Систематизировать методы решения тригонометрических уравнений.

Выбрать для себя шаги по выполнению анализа уравнения и признаки целесообразности использования того или иного метод решения.
Продумать способы самоконтроля своей деятельности по реализации метода.
Научиться составлять « свои » уравнения на каждый из изучаемых методов.
Приложение №1
Решите однородные или приводящиеся к однородным уравнения.
Приложение №2
Решить уравнения:
1.
Отв.
2.
Отв.
3.
Отв.
4.
Отв.
5.
Отв.
6.
Отв.
7.

Отв.
8.
Отв.
9.
Отв.
Презентация на тему «Методы решения тригонометрических уравнений».
библиотека
материаловСодержание слайдов
Номер слайда 1
Методы решения тригонометрических уравнений. Обобщающий урок – семинар. Галяс Марина Юрьевна. Г. Комсомольск-на-Амуре МОУ СОШ №3
Номер слайда 2
Анатоль Франс (1844 – 1924 гг)«Учиться можно только весело…Чтобы переварить знания, надо поглощать их с аппетитом.
 »
»Номер слайда 3
Рабочая карта урока. С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация
Номер слайда 4
Номер слайда 5
Номер слайда 6
Гиппарх,Способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника.
 Клавдий Птолемей. Астрономы, 2 век до н. э.и 2 век н. э.
Клавдий Птолемей. Астрономы, 2 век до н. э.и 2 век н. э.Номер слайда 7
Абу-ль-Вефа Мухаммед-бен Мухаммед. Арабский учёный, 940-998 Арабский учёный, 850-929 Таблицы синусов и тангенсов через 10‘ c точностью до 1/604. Аль-Батани
Номер слайда 8
Насирэддин Туси Мухаммед.
 Индийский учёный, р. 1114 -год смерти неизвестен. Азербайджанский астроном и математик, 1201-1274 Работа «Трактат о полном четырехстороннике», плоская и сферическая тригонометрии как самостоятельные дисциплины. Бхаскара
Индийский учёный, р. 1114 -год смерти неизвестен. Азербайджанский астроном и математик, 1201-1274 Работа «Трактат о полном четырехстороннике», плоская и сферическая тригонометрии как самостоятельные дисциплины. БхаскараНомер слайда 9
Николай Коперник. Астроном, 1473-1543 Творец гелиоцентрической системы мира. Астроном, 1473-1543
Номер слайда 10
Тихо Браге.
 Астроном, 1546-1601 Иоганн Кеплер. Немецкий астроном, 1571-1603
Астроном, 1546-1601 Иоганн Кеплер. Немецкий астроном, 1571-1603Номер слайда 11
Франсуа Виет. Математик, 1540-1603 Полностью решил задачу о определениях всех элементов плоского или сферического треугольника по трём данным.
Номер слайда 12
Леонард Эйлер.
 Математик, 1707-1783 Член Петербургской Академии наук, аналитическая теория тригонометрических функций
Математик, 1707-1783 Член Петербургской Академии наук, аналитическая теория тригонометрических функцийНомер слайда 13
Лейбниц«Метод решения хорош, если с самого начала мы можем предвидеть – и впоследствии подтвердить это, — что, следуя этому методу, мы достигнем цели.»
Номер слайда 14
Методы решения тригонометрических уравнений.
 Разложение на множители. Сведение к алгебраическому уравнению. Введение вспомогательного угла. Универсальная подстановка. Сведение к однородному уравнению. Использование формул преобразования суммы в произведение и обратно. Применение формул понижения степени. Обращение к условию равенства одноименных тригонометрических функций. Использование свойства ограниченности функций (метод оценки)
Разложение на множители. Сведение к алгебраическому уравнению. Введение вспомогательного угла. Универсальная подстановка. Сведение к однородному уравнению. Использование формул преобразования суммы в произведение и обратно. Применение формул понижения степени. Обращение к условию равенства одноименных тригонометрических функций. Использование свойства ограниченности функций (метод оценки)Номер слайда 15
121110987654321 Классификация тригонометрических уравнений по методам решений
Номер слайда 16
Рабочая карта урока.
 С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация
С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультацияНомер слайда 17
Методы решения тригонометрических уравнений.
 Разложение на множители. Сведение к алгебраическому уравнению. Введение вспомогательного угла. Универсальная подстановка. Сведение к однородному уравнению. Использование формул преобразования суммы в произведение и обратно. Применение формул понижения степени. Обращение к условию равенства одноименных тригонометрических функций. Использование свойства ограниченности функций (метод оценки)
Разложение на множители. Сведение к алгебраическому уравнению. Введение вспомогательного угла. Универсальная подстановка. Сведение к однородному уравнению. Использование формул преобразования суммы в произведение и обратно. Применение формул понижения степени. Обращение к условию равенства одноименных тригонометрических функций. Использование свойства ограниченности функций (метод оценки)Номер слайда 18
121110987654321 Классификация тригонометрических уравнений по методам решений
Номер слайда 19
Номер слайда 20
Рабочая карта урока.
 С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация
С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультацияНомер слайда 21
«Мне приходится делить время между политикой и уравнениями.
 Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно.»А. Эйнштейн
Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно.»А. ЭйнштейнНомер слайда 22
9 способов решения уравнения. Sinx + Cosx = 1
Номер слайда 23
1 способ: Введение вспомогательного аргумента
Номер слайда 24
2 способ: Применение универсальной подстановки
Номер слайда 25
3 способ: Возведение в квадрат левой и правой части уравнения
Номер слайда 26
4 способ: Приведение к однородному уравнению второй степени относительно Sinx и Cosx
Номер слайда 27
5 способ: —
Номер слайда 28
6 способ: —
Номер слайда 29
Проверка:
Номер слайда 30
7 способ: Преобразование суммы тригонометрических функций в произведение
Номер слайда 31
8 способ: Метод оценки
Номер слайда 32
9 способ: Графический
Номер слайда 33
«Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы.
 »Герберт Спенсер
»Герберт СпенсерНомер слайда 34
121110987654321 Классификация тригонометрических уравнений по методам решений
Номер слайда 35
Номер слайда 36
Номер слайда 37
Рабочая карта урока.
 С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация
С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультацияНомер слайда 38
Тригонометрическиефункцииифизика
Номер слайда 39
I.
 Гармонические колебания. III. Разряд конденсатора. IV. Решение задач. II. Колебания маятника
Гармонические колебания. III. Разряд конденсатора. IV. Решение задач. II. Колебания маятникаНомер слайда 40
, где — скорость, где m – масса гири, k– жёсткость пружины. I. Гармонические колебания, где
Номер слайда 41
называют синусоидальными или гармоническими.
 Колебания, происходящие по закону S=A Sin А – амплитуда – частота колебаний – период колебаний. А – амплитуда
Колебания, происходящие по закону S=A Sin А – амплитуда – частота колебаний – период колебаний. А – амплитудаНомер слайда 42
II. Колебания маятника. Угол отклонения маятника приближённо выражается формулой:l – длина маятника – наибольший угол отклонения
Номер слайда 43
Сила тока измеряется по тому же закону.
 I=Io sin( + )- частота колебаний. С – ёмкость конденсатора. L – самоиндукция цепи. III. Разряд конденсатора. Сила тока измеряется по тому же закону.
I=Io sin( + )- частота колебаний. С – ёмкость конденсатора. L – самоиндукция цепи. III. Разряд конденсатора. Сила тока измеряется по тому же закону.Номер слайда 44
IV. Решения задач. Задача №1 Задача №1 Задача №1 Спортсмен на соревнованиях, проходивших в Осло послал копьё на 90 м 86см. На каком расстоянии приземлилось бы копьё, если оно было пущено с такой же скоростью и под тем же углом к горизонту в Токио? Сопротивлением воздуха пренебречь. Ускорение свободного падения в Осло 9,819 м/с , а в Токио – 9,798 м/с. Дано:
Номер слайда 45
и
Номер слайда 46
Задача №2 IV.
 Решения задач. Тело скользит равномерно по наклонной плоскости с углом наклона 40 градусов. Определить коэффициент трения. По II закону Ньютона:
Решения задач. Тело скользит равномерно по наклонной плоскости с углом наклона 40 градусов. Определить коэффициент трения. По II закону Ньютона:Номер слайда 47
Номер слайда 48
Рабочая карта урока.
 С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация
С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультацияНомер слайда 49
Домашнее задание1.
 Решить уравнения из таблицы 5; 10; 12.2. Подобрать уравнения, решаемые каждым из 9 методов.
Решить уравнения из таблицы 5; 10; 12.2. Подобрать уравнения, решаемые каждым из 9 методов.Основные методы решения тригонометрических уравнений: приведение, преобразование, понижение, замена
п.1. Разложение на множители
Алгоритм простого разложения на множители
Шаг 1. Представить уравнение в виде произведения \(f_1(x)\cdot f_2(x)\cdot …\cdot f_n(x)=0\) где \(f_i(x)\) — некоторые функции (тригонометрические и не только) от \(x\).
Шаг 2. Решить совокупность уравнений: \( \left[ \begin{array}{l l} f_1(x)=0\\ f_2(x)=0\\ …\\ f_n(x)=0\\ \end{array} \right. \)
Шаг 3. Найти объединение полученных решений. Записать ответ.Например:
Решим уравнение \(2cosx cos2x=cosx\) \begin{gather*} 2cosx cos2x-cosx=0\\ cosx(2cos2x-1)=0\\ \left[ \begin{array} {l l} cosx=0\\ 2cos2x-1=0 \end{array} \right. {\circ}=\frac\pi3\)
{\circ}=\frac\pi3\)
Поэтому: \begin{gather*} \left[ \begin{array} {l l} x=\frac\pi2+\pi k\\ x=\pm\frac\pi6+\pi k \end{array} \right. \Leftrightarrow x=\frac\pi6+\frac{\pi k}{3} \end{gather*}Ответ: \(\frac\pi6+\frac{\pi k}{3}\)
Совет
Возможно, у вас не сразу получится объединять решения, которые частично пересекаются или дополняют друг друга.
Тогда записывайте ответ в виде полученных семейств.
В рассмотренном примере, это пара \(\frac\pi2+\pi k,\ \ \pm\frac\pi6+\pi k\), равнозначная c \(\frac\pi6+\frac{\pi k}{3}\).
Вот только научиться работать с числовой окружностью нужно обязательно, т.к. чем сложнее пример или задача, тем больше вероятность, что этот навык пригодится.Алгоритм разложения на множители со знаменателем
Шаг 1. Представить уравнение в виде произведения $$ \frac{f_1(x)\cdot f_2(x)\cdot …\cdot f_n(x)}{g_1(x)\cdot g_2(x)\cdot …\cdot g_m(x)}=0 $$ где \(f_i(x),\ g_i(x)\) — некоторые функции (тригонометрические и не только) от \(x\).
 2x}{sinxcosx}=\frac{(cosx-sinx)(cosx+sinx)}{\frac12sin2x} $$ Подставляем, переносим правую часть влево: $$ \frac{(cosx-sinx)(cosx+sinx)}{\frac12sin2x}-\frac{cosx-sinx}{\frac12sin2x}=0 $$ Выносим общий множитель, умножаем на \(1/2\) слева и справа, получаем: $$ \frac{(cosx-sinx)(cosx+sinx-1)}{sin2x}=0 $$ В этом уравнении учтено ОДЗ для \(ctgx\) и \(tgx\). Поэтому отдельно его не записываем.
2x}{sinxcosx}=\frac{(cosx-sinx)(cosx+sinx)}{\frac12sin2x} $$ Подставляем, переносим правую часть влево: $$ \frac{(cosx-sinx)(cosx+sinx)}{\frac12sin2x}-\frac{cosx-sinx}{\frac12sin2x}=0 $$ Выносим общий множитель, умножаем на \(1/2\) слева и справа, получаем: $$ \frac{(cosx-sinx)(cosx+sinx-1)}{sin2x}=0 $$ В этом уравнении учтено ОДЗ для \(ctgx\) и \(tgx\). Поэтому отдельно его не записываем.
Полученное уравнение равносильно системе: \begin{gather*} \begin{cases} \left[ \begin{array}{l l} cosx-sinx=0\\ cosx+sinx=1 \end{array} \right.\\ sin2x\ne 0 \end{cases} \end{gather*} Решаем первое уравнение как однородное 1-й степени (см. этот параграф ниже): \begin{gather*} cosx-sinx=0\ \ |: cosx\\ 1-tgx=0\Rightarrow tgx=1\Rightarrow x=\frac\pi4+\pi k \end{gather*} Решаем второе уравнение введением вспомогательного угла (см. этот параграф ниже): \begin{gather*} cosx-sinx=1\ \ | \times \frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}cosx+\frac{\sqrt{2}}{2}sinx=\frac{\sqrt{2}}{2}\\ cos\left(\frac\pi4\right)cosx+sin\left(\frac\pi4\right)sinx=\frac{\sqrt{2}}{2}\\ cos\left(\frac\pi4-x\right)=cos\left(x-\frac\pi4\right)=cos\left(x-\frac\pi4\right)=\frac{\sqrt{2}}{2} \Rightarrow x-\frac\pi4=\pm\frac\pi4+2\pi k\Rightarrow \left[ \begin{array}{l l} x=2\pi k\\ x=\frac\pi2+2\pi k \end{array} \right. 2-4\cdot 3\cdot 3=64\\ t=\frac{10\pm 8}{6}= \left[ \begin{array} {l l} \frac13\\ 3\gt 1 — \text{не подходит} \end{array} \right. \end{gather*} Решаем \(cosx=\frac13\Rightarrow x=\pm arccos\frac13+2\pi k\)
2-4\cdot 3\cdot 3=64\\ t=\frac{10\pm 8}{6}= \left[ \begin{array} {l l} \frac13\\ 3\gt 1 — \text{не подходит} \end{array} \right. \end{gather*} Решаем \(cosx=\frac13\Rightarrow x=\pm arccos\frac13+2\pi k\)
Ответ: \(\pm arccos\frac13+2\pi k\)п.3. Приведению к однородному уравнению
Однородным тригонометрическим уравнением 1-й степени называют уравнение вида $$ Asinx+Bcosx=0 $$
Алгоритм решения однородного тригонометрического уравнения 1-й степени
Шаг 1. Разделить левую и правую части уравнения на \(cosx\) \begin{gather*} \frac{Asinx+Bcosx}{cosx}=\frac{0}{cosx}\\ Atgx+B=0\\ tgx=-\frac{B}{A} \end{gather*} Шаг 2. Решить полученное простейшее тригонометрическое уравнение. Записать ответ.
Например:
Решим уравнение \(sinx+cosx=0\)
Делим на \(cosx\). Получаем: \(tgx+1=0\Rightarrow tgx=-1\Rightarrow x=-\frac\pi4+\pi k\)
Ответ: \(-\frac\pi4+\pi k\)Однородным тригонометрическим уравнением 2-й степени называют уравнение вида $$ Asin^2x+Bsinxcosx+Ccos^2x=0 $$
Алгоритм решения однородного тригонометрического уравнения 2-й степени
Шаг 1.
 2}}+\pi k $$
2}}+\pi k $$Например:
Решим уравнение \(\sqrt{3}sin3x-cos3x=1\)
Делим уравнение на \( p=\sqrt{3+1}=2: \) \begin{gather*} \sqrt{3}sin3x-cos3x=1 |:\ 2\\ \frac{\sqrt{3}}{2}sin3x-\frac12cos3x=\frac12\\ sin\left(\frac\pi3\right)sin3x-cos\left(\frac\pi3\right)cos3x=\frac12\\ cos\left(\frac\pi3\right)cos3x-sin\left(\frac\pi3\right)sin3x=-\frac12\\ cos\left(3x+\frac\pi3\right)=-\frac12\Rightarrow 3x+\frac\pi3=\pm\frac{2\pi}{3}+2\pi k\Rightarrow 3x= \left[ \begin{array}{l l} -\pi+2\pi k\\ \frac\pi3+2\pi k \end{array} \right. \Rightarrow x= \left[ \begin{array}{l l} -\frac\pi3+\frac{2\pi k}{3}\\ \frac\pi9+\frac{2\pi k}{3} \end{array} \right. \end{gather*}
Ответ: \(-\frac\pi3+\frac{2\pi k}{3},\ \ \frac\pi9+\frac{2\pi k}{3}\)п.5. Преобразование суммы тригонометрических функций в произведение
При решении уравнений вида \begin{gather*} Asinax+Bsinbx+…+Ccoscx+Dcosdx+…=0 \end{gather*} используются формулы, выведенные в §17 данного справочника.
Затем проводится разложение на множители, и находится решение (см. {\circ}k \end{array} \right. \end{gather*}
{\circ}k \end{array} \right. \end{gather*}Получаем, что семейства решений \(\frac\pi6+2\pi k\) и \(\frac{5\pi}{6}+2\pi k\) уже содержатся во множестве \(\frac\pi6+\frac{\pi k}{3}\). Ответ: \(\frac\pi6+\frac{\pi k}{3}\)
п.6. Преобразование произведения тригонометрических функций в сумму
При решении уравнений вида \begin{gather*} sinax\cdot cosbx=sincx\cdot cosdx,\ \ sinax\cdot sinbx=sincx\cdot cosdx\ \ \text{и т.п.} \end{gather*} используются формулы, выведенные в §18 данного справочника.
Например:
Решим уравнение \(sin5xcos3x=sin6xcos2x\)
Заметим, что: \begin{gather*} sin5xcos3x=\frac{sin(5x+3x)-sin(5x-3x)}{2}=\frac{sin8x-sin2x}{2}\\ sin6xcos2x=\frac{sin(6x+2x)-sin(6x-2x)}{2}=\frac{sin8x-sin4x}{2} \end{gather*} Подставляем: \begin{gather*} \frac{sin8x-sin2x}{2}=\frac{sin8x-sin4x}{2}\ |\times 2\\ sin8x-sin2x=sin8x-sin4x\\ sin4x-sin2x=0\\ 2sin2xcos2x-sin2x=0\\ sin2x(2cos2x-1)=0\\ \left[ \begin{array}{l l} sin2x=0\\ 2cos2x-1=0 \end{array} \right. 22x=1\)
22x=1\)
Расписываем квадраты синусов через формулу понижения степени: \begin{gather*} \frac{1-cos2x}{2}+\frac{1-cos4x}{2}=1\\ cos2x+cos4x=0\\ 2cos\frac{2x+4x}{2}cos\frac{2x-4x}{2}=0\\ cos3xcosx=0\\ \left[ \begin{array}{l l} cos3x=0\\ cosx=0 \end{array} \right. \Rightarrow \left[ \begin{array}{l l} 3x=\frac\pi2+\pi k\\ x=\frac\pi2+\pi k \end{array} \right. \Rightarrow \left[ \begin{array}{l l} x=\frac\pi6+\frac{\pi k}{3}\\ x=\frac\pi2+\pi k \end{array} \right. \end{gather*}\(x=\frac\pi2+\pi k\) является подмножеством \(x=\frac\pi6+\frac{\pi k}{3}\)
Поэтому \begin{gather*} \left[ \begin{array}{l l} x=\frac\pi6+\frac{\pi k}{3}\\ x=\frac\pi2+\pi k \end{array} \right. \Leftrightarrow x=\frac\pi6+\frac{\pi k}{3} \end{gather*}Ответ: \(\frac\pi6+\frac{\pi k}{3}\)
п.8. Замена переменных
При решении уравнений вида \(f(sinx\pm cosx,\ sinxcosx)=0\) используется замена \begin{gather*} t=cosx\pm sinx \end{gather*}
Например:
Решим уравнение \(sinx+cosx=1+sinxcosx\)
Замена: \(t=sinx+cosx\)
Тогда \(t^2=sin^2x+2sinxcosx+cos^2x=1+2sinxcosx\Rightarrow sinxcosx=\frac{t^2-1}{2}\)
Подставляем: \begin{gather*} t=1+\frac{t^2-1}{2}\Rightarrow 2(t-1)=t^2-1\Rightarrow t^2-2t+1=0\Rightarrow (t-1)^2=0\Rightarrow t=1\\ sinx+cosx=1\ |\ \times \frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}sinx+\frac{\sqrt{2}}{2}cosx=\frac{\sqrt{2}}{2}\\ sin\frac\pi4 sinx+cos\frac\pi4 cosx=\frac{\sqrt{2}}{2}\\ cos\left(x-\frac\pi4\right)=\frac{\sqrt{2}}{2}\Rightarrow x-\frac\pi4=\pm\frac\pi4 + 2\pi k\Rightarrow \Rightarrow \left[ \begin{array}{l l} x=2\pi k\\ x=\frac\pi2+2\pi k \end{array} \right. \end{gather*} Ответ: \(2\pi k,\ \ \frac\pi2+2\pi k\)
\end{gather*} Ответ: \(2\pi k,\ \ \frac\pi2+2\pi k\)п.9. Использование ограничений области значений функций
Уравнения вида \begin{gather*} \underbrace{sinax+sinbx+…+coscx+cosdx+…=m}_{m\ \text{слагаемых}} \end{gather*} может иметь решение только, если каждое из слагаемых равно 1.
Поэтому решаем систему: \( \begin{cases} sinax=1\\ sinbx=1\\ …\\ cosdx=1\\ … \end{cases} \)
Находим пересечение (!) полученных семейств решений и записываем ответ.Аналогично, уравнение вида \begin{gather*} \underbrace{sinax+sinbx+…+coscx+cosdx+…=-m}_{m\ \text{слагаемых}} \end{gather*} может иметь решение только, если каждое из слагаемых равно -1.
Например:
Решим уравнение \(sinx+cos4x=2\)
Для этого нужно решить систему: \begin{gather*} \begin{cases} sinx=1\\ cos4x=1 \end{cases} \Rightarrow \begin{cases} x=\frac\pi2+2\pi k\\ 4x=2\pi k \end{cases} \Rightarrow \begin{cases} x=\frac\pi2+2\pi k\\ x=\frac{\pi k}{2} \end{cases} \end{gather*}Пересечением двух семейств решений будет только \(\frac\pi2+2\pi k\).  2x=\frac{1+cos2x}{2}\)
2x=\frac{1+cos2x}{2}\)
Подставляем: \begin{gather*} \frac{1+cos2x}{2}+\frac{1+cos4x}{2}=\frac{1+cos6x}{2}+\frac{1+cos8x}{2}\\ cos2x+cos4x=cos6x+cos8x\\ 2cos\frac{2x+4x}{2}cos\frac{2x-4x}{2}=2cos\frac{6x+8x}{2}cos\frac{6x-8x}{2}\ |:\ 2\\ cos3xcosx=cos7xcosx=0\\ cos3xcosx-cos7xcosx=0\\ cosx(cos3x-cos7x)=0\\ cosx\left(-2sin\frac{3x+7x}{2}sin\frac{3x-7x}{2}\right)=0\\ -2cosxsin5xsin(-2x)=0\\ 2cosxsin5xsin2x=0\\ cosxsin5xsin2x=0\\ \left[ \begin{array}{l l} cosx=0\\ sin5x=0\\ sin2x=0 \end{array} \right. \Rightarrow \left[ \begin{array}{l l} x=\frac\pi2+\pi k\\ 5x=\pi k\\ 2x=\pi k \end{array} \right. \Rightarrow \left[ \begin{array}{l l} x=\frac\pi2+\pi k\\ x=\frac{\pi k}{5}\\ x=\frac{\pi k}{2} \end{array} \right. \end{gather*} Семейство решений \(x=\frac\pi2+\pi k\) (базовые точки 90°, 270° на числовой окружности) является подмножеством для \(x=\frac{\pi k}{2}\) (базовые точки 0°, 90°, 180°, 270°). Поэтому: \begin{gather*} \left[ \begin{array}{l l} x=\frac\pi2+\pi k\\ x=\frac{\pi k}{5}\\ x=\frac{\pi k}{2} \end{array} \right. 2x+7tgx+4=0\\ (3tgx+4)(tgx+1)=0\\ \left[ \begin{array}{l l} tgx=-\frac43\\ tgx=-1 \end{array} \right. \Rightarrow \left[ \begin{array}{l l} x=-arctg\frac43+\pi k\\ x=-\frac\pi4+\pi k \end{array} \right. \end{gather*}
2x+7tgx+4=0\\ (3tgx+4)(tgx+1)=0\\ \left[ \begin{array}{l l} tgx=-\frac43\\ tgx=-1 \end{array} \right. \Rightarrow \left[ \begin{array}{l l} x=-arctg\frac43+\pi k\\ x=-\frac\pi4+\pi k \end{array} \right. \end{gather*}Полученное решение даёт 4 базовых точки на числовой окружности: \(-\frac\pi4,\ -arctg\frac43,\ \frac{3\pi}{4}\) и \(\pi-arctg\frac43\), которые находятся в 2-й и 4-й четвертях.
Выбираем только точки вo 2-й четверти:
\(\frac{3\pi}{4}\) и \(\pi-arctg\frac43\).
Это означает, что в записи решения будут выбранные точки с периодом \(2\pi k\). \begin{gather*} \left[ \begin{array}{l l} x=\pi-arctg\frac43+2\pi k\\ x=\frac{3\pi}{4}+2\pi k \end{array} \right. \end{gather*}3) Объединяем полученные решения: \begin{gather*} \left[ \begin{array}{l l} x=arctg\frac43+2\pi k\\ x=\frac\pi4+2\pi k\\ x=\pi-arctg\frac43+2\pi k\\ x=\frac{3\pi}{4}+2\pi k \end{array} \right. \end{gather*}
По аналогии с записью арксинуса можно объединить симметричные относительно оси синусов точки: \begin{gather*} \left[ \begin{array}{l l} x=arctg\frac43+2\pi k\\ x=\pi-arctg\frac43+2\pi k \end{array} \right.  4\alpha=\frac{3-4cos2\alpha+cos4\alpha}{8} $$ Подставляем: \begin{gather*} \frac{3-4cos4x+cos8x}{8}+\frac{3-4cos\left(2\left(2x-\frac{3\pi}{4}\right)\right)+cos\left(4\left(2x-\frac{3\pi}{4}\right)\right)}{8}=\frac14\\ \frac{3-4cos4x+cos8x}{8}+\frac{3-4cos\left(4x-\frac{3\pi}{2}\right)+cos(8x-3\pi)}{8}=\frac14\\ \frac{3-4cos4x+cos8x}{8}+\frac{3+4sin4x-cos8x}{8}=\frac14\\ \frac34+\frac12(sin4x-cos4x)=\frac14\\ sin4x-cos4x=-1\ |\times\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}sin4x-\frac{\sqrt{2}}{2}cos4x=-\frac{\sqrt{2}}{2}\\ cos\frac\pi4cos4x-sin\frac\pi4sin4x=\frac{\sqrt{2}}{2}\\ cos\left(4x+\frac\pi4\right)=\frac{\sqrt{2}}{2}\\ 4x+\frac\pi4=\pm\frac\pi4+2\pi k\\ 4x=-\frac\pi4\pm\frac\pi4+2\pi k= \left[ \begin{array}{l l} -\frac\pi2+2\pi k\\ 2\pi k \end{array} \right. \\ x= \left[ \begin{array}{l l} -\frac\pi8+\frac{\pi k}{2}\\ \frac{\pi k}{2} \end{array} \right. \end{gather*} Ответ: \(-\frac\pi8+\frac{\pi k}{2},\ \ \frac{\pi k}{2}\)
4\alpha=\frac{3-4cos2\alpha+cos4\alpha}{8} $$ Подставляем: \begin{gather*} \frac{3-4cos4x+cos8x}{8}+\frac{3-4cos\left(2\left(2x-\frac{3\pi}{4}\right)\right)+cos\left(4\left(2x-\frac{3\pi}{4}\right)\right)}{8}=\frac14\\ \frac{3-4cos4x+cos8x}{8}+\frac{3-4cos\left(4x-\frac{3\pi}{2}\right)+cos(8x-3\pi)}{8}=\frac14\\ \frac{3-4cos4x+cos8x}{8}+\frac{3+4sin4x-cos8x}{8}=\frac14\\ \frac34+\frac12(sin4x-cos4x)=\frac14\\ sin4x-cos4x=-1\ |\times\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}sin4x-\frac{\sqrt{2}}{2}cos4x=-\frac{\sqrt{2}}{2}\\ cos\frac\pi4cos4x-sin\frac\pi4sin4x=\frac{\sqrt{2}}{2}\\ cos\left(4x+\frac\pi4\right)=\frac{\sqrt{2}}{2}\\ 4x+\frac\pi4=\pm\frac\pi4+2\pi k\\ 4x=-\frac\pi4\pm\frac\pi4+2\pi k= \left[ \begin{array}{l l} -\frac\pi2+2\pi k\\ 2\pi k \end{array} \right. \\ x= \left[ \begin{array}{l l} -\frac\pi8+\frac{\pi k}{2}\\ \frac{\pi k}{2} \end{array} \right. \end{gather*} Ответ: \(-\frac\pi8+\frac{\pi k}{2},\ \ \frac{\pi k}{2}\)г) \(3sinx-4cosx=5\)
Способ 1. Вводим дополнительный угол:
\(p=\sqrt{3^2+4^2}=5\)
\(\frac35sinx-\frac45 cosx=1\)
\(sin\alpha=\frac35,\ cos\alpha=\frac45\)
\(sin\alpha sinx-cos\alpha cosx=1\)
\(cos\alpha cosx-sin\alpha sinx=-1\)
\(cos(x+\alpha)=-1\)
\(x+\alpha=\pi+2\pi k\)
\(x=-\alpha+\pi+2\pi k=-arcsin\frac35+\pi+2\pi k\)Способ 2.
 2}=\frac35 $$ Получаем, что для угла \(\alpha:\ sin\alpha=\frac35,\ cos\alpha=\frac45\)
2}=\frac35 $$ Получаем, что для угла \(\alpha:\ sin\alpha=\frac35,\ cos\alpha=\frac45\)
Для угла \(\varphi:\ sin\varphi=\frac35,\ cos\varphi=-\frac45\)
Откуда следует, что \(\alpha=\pi-\varphi\). Что и требовалось доказать.
Ответ: \(-arcsin\frac35+\pi+2\pi k\) или \(2arctg3+2\pi k\) (т.к. \(-arcsin\frac35+\pi=2arctg3)\)Способ введения вспомогательного угла при решении тригонометрических уравнений. Конспект урока математики на тему «Способы введения вспомогательного аргумента
Элементарными тригонометрическими уравнениями являются уравнения вида, где — одна из тригонометрических функций: ,.
Элементарные тригонометрические уравнения имеют бесконечно много корней. Например, уравнению удовлетворяют следующие значения: , и т. д. Общая формула, по которой находятся все корни уравнения, где, выглядит следующим образом:
Здесь может принимать любые целые значения, каждое из которых соответствует определенному корню уравнения; в этой формуле (как и в других формулах, по которым решаются элементарные тригонометрические уравнения) называются параметром .
 .. Обычно записывают, тем самым подчеркивая, что параметр может принимать любые целые значения.
.. Обычно записывают, тем самым подчеркивая, что параметр может принимать любые целые значения.Решения уравнения, где, находятся по формуле
Уравнение решается по формуле
и уравнение по формуле
Особо отметим некоторые частные случаи элементарных тригонометрических уравнений, когда решение можно записать без применения общих формул:
При решении тригонометрических уравнений большую роль играет период тригонометрических функций.Поэтому приведем две полезные теоремы:
Теорема Если — основной период функции, то число является основным периодом функции.
Периоды функций и называются соизмеримыми, если есть целые числа и какие.
Теорема Если периодические функции и имеют соизмеримые и, то они имеют общий период, который является периодом функций,.
Теорема говорит, что такое период функции, и не обязательно основной период.Например, основной период функций равен и —, а основной период их производства —.

Стандартным способом преобразования выражений вида является следующая техника: пусть — инъекция, заданная равенствами,. Для любого и такой угол существует. Таким образом. Если, или, в других случаях.
Основная схема, которой мы будем руководствоваться при решении тригонометрических уравнений, выглядит следующим образом:
решение заданного уравнения сводится к решению элементарных уравнений. Средства решения — преобразования, факторизация, замена неизвестных.Главный принцип – не потерять корни. Это значит, что при переходе к следующему уравнению (уравнениям) мы не опасаемся появления лишних (посторонних) корней, а заботимся лишь о том, чтобы каждое последующее уравнение нашей «цепочки» (или системы уравнений в случае ветвления) является следствием предыдущего. Одним из возможных методов выделения корней является валидация. Отметим сразу, что в случае тригонометрических уравнений трудности, связанные с подбором корней, с проверкой, как правило, резко возрастают по сравнению с алгебраическими уравнениями.
 Ведь вам предстоит проверить ряд, состоящий из бесконечного числа членов.
Ведь вам предстоит проверить ряд, состоящий из бесконечного числа членов.Особо следует отметить замену неизвестных при решении тригонометрических уравнений. В большинстве случаев после требуемой замены получается алгебраическое уравнение. Причем уравнения не настолько редки, что, хотя и тригонометричны с виду, по существу ими не являются, так как после первого шага — замены переменных — превращаются в алгебраические, а возврат к тригонометрии происходит только на этапе решения элементарных тригонометрических уравнений.
Еще раз напомним: замену неизвестного нужно произвести как можно быстрее, уравнение, полученное после замены, нужно решить до конца, включая этап подбора корней, и только потом вернуться к исходному неизвестному.
Одной из особенностей тригонометрических уравнений является то, что ответ во многих случаях можно записать по-разному… Даже для решения уравнения ответ можно записать так:
1) в виде двух серий: , ;
2) в стандартной форме, представляющей собой комбинацию вышеуказанных серий: , ;
3) так как, то ответ можно записать в виде, .
 (В дальнейшем наличие параметра или в записи ответа автоматически означает, что этот параметр принимает все возможные целочисленные значения. Исключения будут обсуждаться.)
(В дальнейшем наличие параметра или в записи ответа автоматически означает, что этот параметр принимает все возможные целочисленные значения. Исключения будут обсуждаться.)Очевидно, что три перечисленных случая не исчерпывают всех возможностей записи ответа на рассматриваемое уравнение (их бесконечно много).
Например, для равенства. Поэтому в первых двух случаях, если, мы можем заменить на.
Обычно ответ пишут исходя из пункта 2.Полезно запомнить следующую рекомендацию: если работа не заканчивается на решении уравнения, необходимо еще провести исследование, выделение корней, то наиболее удобную форму обозначений, указанную в п. 1. (Аналогичную рекомендацию следует дано для уравнения.)
Рассмотрим пример, иллюстрирующий вышесказанное.
Пример Решите уравнение.
Раствор. Самый очевидный способ следующий.Это уравнение распадается на два: и . Решив каждый из них и объединив полученные ответы, найдем.
Другой способ.
 Так как, то, заменив и по формулам приведения степени. После небольших преобразований получаем куда.
Так как, то, заменив и по формулам приведения степени. После небольших преобразований получаем куда.На первый взгляд, вторая формула не имеет особых преимуществ перед первой. Однако если взять, например, то получается, что, т.е. уравнение имеет решение, а первый путь приводит нас к ответу.«Увидеть» и доказать равенство непросто.
Методы решения тригонометрических уравнений.Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида (см. выше) и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений.
1. Алгебраический метод.
(переменная замена и метод подстановки).
2. Факторинг.
П р и м е р а 1. Решите уравнение: sin x + cos x = 1 .
Раствор. Переместите все члены уравнения влево:
Sin x + cos x – 1 = 0 ,
Преобразуем и факторизуем выражение в
Левая часть уравнения:
PRI me R 2.
 Решим уравнение: cos 2 х + sin х Cos х = 1.
Решим уравнение: cos 2 х + sin х Cos х = 1.РЕШЕНИЕ cos 2 x + sin x Cos x – sin 2 х — cos 2 х = 0,
Sin x Cos x – грех 2 х = 0,
Sin x (Cos x – грех х ) = 0,
П р и м е р 3.Решите уравнение: cos 2 x — cos 8 x + cos 6 x = 1.
РЕШЕНИЕ cos 2 x + cos 6 x = 1 + cos 8 x ,
2 cos 4 x cos 2 x = 2 cos² 4 x ,
Кос 4 x · (cos 2 x — cos 4 x ) = 0,
Кос 4 x 2 sin 3 x Sin x = 0 ,
1). cos 4 х = 0, 2).sin 3 х = 0, 3). sin x = 0,
3. Приведение к однородному уравнению.
Уравнение, называемое однородным из относительно sin и cos , если все его членов одной степени относительно sin и cos одинаковый угол .
 .. Для решения однородного уравнения нужно:
.. Для решения однородного уравнения нужно:a ) переместить все его члены в левую часть;
б ) все общие множители вынести за скобки;
v ) приравнять все множители и скобки к нулю;
G ) приравненные к нулю скобки дают однородное уравнение меньшей степени, которое следует разделить на
cos (или sin ) в старшей степени;
d ) решить полученное алгебраическое уравнение относительно тангенса .
грех 2 x + 4 sin x Cos x + 5 cos 2 х = 2.
РАСТВОР. 3sin 2 x + 4 sin x Cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,
Sin 2 x + 4 sin x Cos x + 3 cos 2 x = 0 ,
Тан 2 x + 4 Тан x + 3 = 0 , отсюда и 2 + 4 у +3 = 0 ,
Корни этого уравнения: y 1 знак равно — 1, y 2 = — 3, следовательно,
1) tan x = –1, 2) tan x = –3,
4.
 Перейдите к половине угла.
Перейдите к половине угла.Рассмотрим этот метод на примере:
ПРИМЕР Решите уравнение: 3 sin x — 5 cos x = 7.
РЕШЕНИЕ.6 sin ( x / 2) cos ( x / 2) — 5 cos ² ( x / 2) + 5 sin ² ( x / 2) =
7 sin ² ( x /2) + 7 cos² ( x /2) ,
2 sin² ( x /2) — 6 sin ( x /2) cos ( x /2) + 12 cos ² ( x /2) = 0,
тангенс ² ( x /2) — 3 тангенс ( x /2) + 6 = 0,
.. . . . . . . . .
5. Введение вспомогательного уголка.
Рассмотрим уравнение вида:
a sin x + b cos x = c ,
Где , б , в — коэффициенты; х — неизвестно.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль (абсолютное значение) каждого из которых не более 1, а сумма их квадратов равна 1.Тогда мы можем обозначить их соответственно как cos и sin (здесь — так называемый вспомогательный угол ), и взять наше уравнение
Тема урока: Способ введения вспомогательного угла при решении тригонометрических уравнений.

Обновление.
Учитель.
Ребята! Мы познакомились с разными видами тригонометрических уравнений и научились их решать. Сегодня мы обобщим знания о методах решения тригонометрических уравнений разных типов… Для этого прошу Вас провести работу по классификации предложенных Вам уравнений (см. уравнения №1-10 в Приложении — в конце реферата в формате PDF)
Заполните таблицу: укажите тип уравнения, способ его решения и сравните номера уравнений с типом, к которому они относятся.
Студенты. Заполнить таблицу.
Тип уравнения Метод решения Уравнения Самый простой Формулы корней №1 Уменьшенный до квадрата Метод замены переменной №2,3 Комплексная тригонометрическая картина Упрощение до известного представления с помощью формул тригонометрии №4,5 Униформа первой степени Член уравнения разделить на косинусную переменную №6 Униформа второй степени Разделение члена уравнения на квадрат косинуса переменной №7 Проблематизация.

Студенты столкнулись с проблемой заполнения таблицы. Они не могут определить вид и способ решения трех уравнений: №8,9,10.
Учитель. Удалось ли вам классифицировать все уравнения по форме и способу решения?
Ответ учащегося. Нет, в таблицу нельзя поместить три уравнения.
Учитель. Почему?
Ответ учащегося. Они не похожи на известные виды… Метод решения не ясен.
Постановка целей.
Учитель. Как же тогда сформулировать цель нашего урока?
Учащиеся отвечают … Определите обнаруженные уравнения нового типа и найдите способ их решения.
Учитель … Можно ли сформулировать тему урока, если мы не знаем тип найденных уравнений и метод их решения?
Ответ учащегося … Нет, но это можно сделать позже, когда мы разберемся, с чем имеем дело.
Планирование деятельности.
Учитель.
 Давайте спланируем наши действия. Обычно мы определяем тип, а затем ищем метод решения тригонометрических уравнений. Можно ли в нашей нынешней ситуации дать определенное название форме обнаруженных уравнений? И вообще, относятся ли они к одному виду?
Давайте спланируем наши действия. Обычно мы определяем тип, а затем ищем метод решения тригонометрических уравнений. Можно ли в нашей нынешней ситуации дать определенное название форме обнаруженных уравнений? И вообще, относятся ли они к одному виду?Ответ учащегося. Это трудно сделать.
Учитель. Тогда подумайте, может их что-то объединяет, или они похожи на какой-то тип?
Ответ учащегося. Левая часть этих уравнений такая же, как и у однородных, но их правая часть не равна нулю. Поэтому деление на косинус только усложнит решение.
Учитель. Может быть, начать с поиска метода решения, а затем определить тип уравнения? Какое уравнение из трех кажется вам самым простым?
Учащиеся отвечают , но единого мнения нет.Возможно, кто-то догадается, что коэффициенты в уравнении №8 следует выражать как синус и косинус угла стола. И тогда класс определит уравнение, которое можно решить первым. Если нет, то преподаватель предлагает рассмотреть дополнительное уравнение (см.
 уравнение №11 в Приложении — в конце реферата в формате PDF) . В нем коэффициенты равны синусу и косинусу а под известным углом, и учащиеся должны это заметить.
уравнение №11 в Приложении — в конце реферата в формате PDF) . В нем коэффициенты равны синусу и косинусу а под известным углом, и учащиеся должны это заметить.Учитель предлагает последовательность действий.( См. уравнения в приложении — в формате PDF, в конце реферата).
- Решить первое уравнение (№11), заменив коэффициенты значениями синуса и косинуса известного угла и применив формулу суммы синуса.
- Попробуйте преобразовать другие уравнения в форму первого и примените тот же метод. ( см. уравнение № 8, 9, 12 )
- Обобщить и распространить метод на любые коэффициенты и разработать общий алгоритм действий (см. уравнение №10).
- Примените метод к решению других уравнений того же типа. (см. уравнения №№ 12,13,14).
Реализация плана.
Учитель … Что ж, мы составили план. Приступим к его реализации.
У доски ученик решает уравнение № 11.

Второй ученик решает очередное уравнение №8, предварительно разделив его на постоянное число и, тем самым, сведя ситуацию к уже найденному решению.
Учитель предлагает решить уравнения №9.12 самостоятельно. Проверяет правильность преобразований и многих решений.
Учитель. Ребята, как можно назвать угол, который появляется вместо коэффициентов уравнения и помогает нам найти решение?
Ответ учащегося. Доп. (Вариант: вспомогательный).
Учитель. Не всегда легко найти такой вспомогательный угол. Можно ли его найти, если коэффициенты не являются синусами и косинусами известных углов? Какому тождеству должны удовлетворять такие коэффициенты, если мы хотим представить их в виде синуса и косинуса вспомогательного угла?
Ответ. Основное тригонометрическое тождество.
Учитель. Молодец! Правильно! Итак, наша задача — получить такие коэффициенты, чтобы сумма их квадратов была равна единице! Попробуйте придумать число, на которое вы хотите разделить уравнение, чтобы выполнялось заданное нами условие.

Студенты думают и, возможно, предлагают делить все на квадратный корень из суммы квадратов коэффициентов уравнения. Если нет, то учитель подводит их к этой мысли.
Учитель. Нам остается выбрать, какой из новых коэффициентов обозначить синусом вспомогательного угла, а какой косинусом. Есть две возможности. Переход к простейшему уравнению с синусом или косинусом зависит от выбора.
Учащиеся предлагают решение, а учитель дополняет его, обращая внимание на форму записи рассуждения и ответа. Решите уравнение №10.
Учитель … Нашли ли мы способ решения нового типа уравнений? Как мы назовем этот тип?
Ответ. Мы работали, находя вспомогательный угол. Может, уравнениями следует называть уравнения, которые решаются с помощью вспомогательных углов?
Учитель. Конечно. Можете ли вы придумать формулу их появления? Это будет короче.
Ответ. Да. Уравнения с коэффициентами А, В и С.
Учитель.
 Обобщим метод для произвольных коэффициентов.
Обобщим метод для произвольных коэффициентов.Учитель обсуждает и записывает на доске формулы синуса и косинуса вспомогательного угла для обобщенных коэффициентов. Затем с их помощью решает уравнения 13 и 14.
Учитель. Достаточно ли хорошо мы освоили метод?
Ответ. Нет. Необходимо решить такие уравнения и закрепить умение пользоваться методом вспомогательного угла.
Учитель. Откуда мы знаем, что изучили метод?
Ответ. Если мы самостоятельно решим несколько уравнений.
Учитель. Давайте установим качественную шкалу для изучения метода.
Ознакомьтесь с характеристиками уровней и разместите их на шкале, отражающей уровень владения этим навыком. Соотнести характеристику уровня и балла (от 0 до 3)
- Я умею решать уравнения с разными коэффициентами
- Не могу решить уравнения
- Я умею решать уравнения повышенной сложности
- Я умею решать уравнения с табличными коэффициентами
Учитель.
 (После ответов учащихся) Итак, наша шкала оценок выглядит следующим образом:
(После ответов учащихся) Итак, наша шкала оценок выглядит следующим образом:По такому же принципу оцениваем самостоятельную работу по теме на следующем уроке.
А теперь, пожалуйста, решите уравнения №№ 1148 г, 1149 г, 1150 г и определите свой уровень владения темой.
Не забудьте заполнить записи в таблице и назвать тему: «Введение вспомогательного угла при решении тригонометрических уравнений».
Отражение пути достижения цели.
Учитель. Ребята, достигли ли мы поставленной цели урока?
Ответы учащихся … Да, мы научились распознавать новый тип уравнений.
Найден способ их решения с помощью вспомогательного угла.
Мы научились применять метод на практике.
Учитель. Как мы действовали? Как вы пришли к пониманию того, что нам нужно делать?
Ответ. Мы рассмотрели несколько частных случаев уравнений с «распознаваемыми» коэффициентами и распространили эту логику на любые значения A, B и C.

Учитель. Это индуктивный способ мышления: мы вывели метод на основе нескольких случаев и применили его в подобных случаях.
Перспектива. Где мы можем применить этот ход мыслей? (ответы учащихся)
Сегодня ты хорошо поработал на уроке. Дома прочитайте описание метода вспомогательного угла в учебнике и решите №№ 1148 (а, б, в), 1149 (а, б, в), 1150 (а, б, в). Надеюсь, что на следующем уроке вы все будете в совершенстве использовать этот метод при решении тригонометрических уравнений.
Спасибо за работу на уроке!
Тема: «Методы решения тригонометрических уравнений».
Цели урока:
образовательный:
Развивать умение различать типы тригонометрических уравнений;
Более глубокое понимание методов решения тригонометрических уравнений;
образовательный:
Воспитание познавательного интереса к учебному процессу;
Формирование умения анализировать задание;
разработка:
Формировать умение анализировать ситуацию с последующим выбором наиболее рационального выхода из нее.

Оборудование: плакат с основными тригонометрическими формулами, компьютер, проектор, экран.
Начнем урок с повторения основного приема решения любого уравнения: приведения его к стандартной форме. Преобразованиями линейные уравнения приводятся к виду ah = b, квадратные — к виду ax 2 + bx + c = 0,. В случае тригонометрических уравнений необходимо свести их к простейшим, вида: sinx = a, cosx = a, tgx = a, которое легко решается.
В первую очередь, конечно, для этого необходимо использовать основные тригонометрические формулы, представленные на плакате: формулы сложения, формулы двойного угла, убывания кратности уравнения. Мы уже знаем, как решать такие уравнения. Повторим некоторые из них:
В то же время существуют уравнения, решение которых требует знания некоторых специальных приемов.
Тема нашего урока — рассмотреть эти приемы и систематизировать методы решения тригонометрических уравнений.
Методы решения тригонометрических уравнений.

1. Преобразование к квадратному уравнению относительно тригонометрической функции с последующей заменой переменной.
Рассмотрим каждый из перечисленных способов на примерах, но на двух последних остановимся подробнее, так как первые два мы уже использовали при решении уравнений.
1. Преобразование к квадратному уравнению относительно тригонометрической функции.
2.Решение уравнений методом факторизации.
3. Решение однородных уравнений.
Уравнения вида называются однородными уравнениями первой и второй степени:
соответственно (а ≠ 0, б ≠ 0, с ≠ 0).
При решении однородных уравнений обе части уравнения почленно делятся на cosx для уравнения (1) и на cos 2 x для (2). Такое деление возможно, так как sinx и cosx не равны нулю одновременно — они обращаются в нуль в разных точках.Рассмотрим примеры решения однородных уравнений первой и второй степени.
Запомним это уравнение: при рассмотрении следующего метода — введения вспомогательного аргумента, будем решать его по-другому.

4. Введение вспомогательного аргумента.
Рассмотрим уравнение, уже решенное предыдущим методом:
Как видите, получается тот же результат.
Возьмем другой пример:
В рассмотренных примерах в целом было понятно, на что надо было разбить исходное уравнение, чтобы ввести вспомогательный аргумент.Но может случиться так, что не очевидно, какой делитель выбрать. Для этого есть специальная методика, которую мы сейчас и рассмотрим в общем виде. Пусть задано уравнение:
Разделим уравнение на квадратный корень из выражения (3), получим:
asinx + bcosx = с,
, то a 2 + b 2 = 1 и, следовательно, a = sinx и b = cosx. Используя формулу косинуса разности, получаем простейшее тригонометрическое уравнение:
, который легко решить.Решим еще одно уравнение:
Сократите уравнение до одного аргумента — 2 x, используя формулы уменьшения двойного угла и градуса:
Аналогично предыдущим уравнениям, используя формулу синуса суммы, получаем:
, который также легко решается.

Решите сами, предварительно определив метод решения:
Результатом урока является проверка решения и оценка учащихся.
Домашнее задание: с. 11, конспект, № 164 (б, г), 167 (б, г), 169 (а, б), 174 (а, в).
Конспект урока для 10-11 классов
Тема 1 : Способ введения вспомогательного аргумента. Вывод формул.
Цели:
Формирование знаний о новом методе решения задач по тригонометрии, в которых можно или нужно его использовать;
Формирование умений анализировать условие задачи, сравнивать и находить отличия;
Развитие мышления, последовательность и обоснованность высказываний, умение делать выводы и обобщать;
Развитие речи, обогащение и усложнение словарного запаса, овладение учащимися выразительными свойствами языка;
Формирование отношения к предмету, увлеченности познанием, создание условий для творческого нестандартного подхода к освоению знаний.

Необходимые знания, умения и навыки:
Уметь выводить тригонометрические формулы и использовать их в дальнейшей работе;
Уметь решать или иметь представление о способах решения тригонометрических задач;
Знать основные тригонометрические формулы.
Уровень подготовленности учащихся к осознанному восприятию:
Оборудование: АРМ, презентация с условиями задания, решениями и необходимыми формулами, карточки с заданиями и ответами.
Структура урока:
1. Постановка цели урока (2
Подготовка к изучению нового материала (12 мин).
Ознакомление с новым материалом (15 мин).
Первоначальное понимание и применение что выучили (10 мин)
Домашнее задание (3 мин)
Подведение итогов урока (3 мин)
Во время занятий.
1. Постановка цели занятия.
Проверить готовность учащихся и оборудования к уроку. Желательно заранее подготовить домашнее задание на доске для обсуждения решения.
 Отметим, что цель урока – расширить знания о способах решения некоторых задач по тригонометрии и попробовать свои силы в их освоении.
Отметим, что цель урока – расширить знания о способах решения некоторых задач по тригонометрии и попробовать свои силы в их освоении.2. Подготовка к изучению нового материала.
Обсудить домашнее задание: вспомнить основные тригонометрические формулы, значения тригонометрических функций для простейших аргументов.Прочитайте формулировку домашнего задания.
Формулы:
; ;
; ;
Задача: Представьте выражение как произведение.
Студенты, скорее всего, придут к следующему решению:
Потому что они знают формулы преобразования суммы тригонометрических функций в произведение.
Предложим другое решение проблемы: . Здесь при решении использовалась формула косинуса разности двух аргументов, где она вспомогательная.Обратите внимание, что в каждом из этих методов можно использовать и другие подобные формулы.
3. Ознакомление с новым материалом.
Вопрос в том, откуда взялся вспомогательный аргумент?
Чтобы получить ответ, рассмотрим общую задачу решения, преобразуем выражение в произведение, где и произвольные, ненулевые числа.

вводим дополнительный угол (вспомогательный аргумент), где, тогда наше выражение примет вид:
Таким образом, мы получили формулу: .
Если угол ввести по формулам, то выражение примет вид и мы получим другой вид формулы: .
Мы вывели формулы дополнительных углов, которые называются формулами вспомогательных аргументов:
Формулы могут иметь различный вид (на это нужно обратить особое внимание и показать на примерах).
Обратите внимание, что в простейших случаях способ введения вспомогательного аргумента сводится к замене чисел; ; ; ; 1; тригонометрические функции соответствующих углов.
4. Первичное понимание и применение изученного .
Для закрепления материала предлагается рассмотреть еще несколько примеров заданий:
Представить как произведение выражения:
Задания 3 и 4 следует разобрать на уроке (разбор заданий присутствует в материалах для занятий). Задания 1, 2 и 5 можно взять для самостоятельного решения (даны ответы).

Для анализа особенностей состояния типовых задач, в которых может быть использован рассматриваемый метод решения, могут быть использованы различные методы.Учтите, что задание 1.можно выполнять различными способами, а для выполнения заданий 2 — 5 удобнее применять прием введения вспомогательного угла
При фронтальной беседе следует обсудить, в чем сходство этих заданий с пример, рассмотренный в начале урока, в чем отличия, можно ли применить предложенный метод для их решения и почему его применение удобнее.
Подобие: во всех предложенных примерах возможно применение метода введения вспомогательного аргумента, а это более удобный метод, который сразу приводит к результату.
Отличие: в первом примере возможен другой подход, а во всех остальных возможен способ применения вспомогательного аргумента с использованием не одной, а нескольких формул.
После обсуждения заданий можно предложить детям решить оставшиеся дома самостоятельно.
5. Ведомость домашнего задания.

Дома вам предлагается внимательно изучить план урока и попытаться решить следующие упражнения.
Вся элементарная математика — Учебное пособие — Тригонометрия
Тригонометрические уравнения.Простейшие тригонометрические уравнения.
Методы решения: алгебраический метод, факторинг, редукция
к однородному уравнению, переход к половинному углу,
введение вспомогательного угла, превращающее произведение в
сумма, универсальная замена.Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим .
Простейшие тригонометрические уравнения.
Методы решения тригонометрических уравнений. Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнение до простейшего вида (см. выше) и решение полученного простейшего тригонометрического уравнения.
 Существует семь основных методов
решения тригонометрических уравнений.
Существует семь основных методов
решения тригонометрических уравнений.1. Алгебраический метод. Этот метод хорошо известен нам из алгебры ( обмен и
метод замещения).2. Факторинг. Рассмотрим этот метод на примерах.
П р и м е р 1. Решите уравнение: sin x + cos x = 1 .
Решение . Перенести все термины влево:
sin x + cos x 1 = 0,преобразовать и разложить на множители левое выражение:
П р и м е р 2.Решите уравнение: cos² х + sin х cos х = 1.
Решение . ² x + sin x cos x sin² х , потому что ² х = 0,
sin x cos x sin² х = 0, sin x (cos x sin x ) = 0,П р и м е р 3.
 Решите уравнение: cos 2 x cos 8 x + cos 6 x = 1.
Решите уравнение: cos 2 x cos 8 x + cos 6 x = 1.Решение . cos 2 x + cos 6 x = 1 + cos 8 x ,
2 cos 4 x cos 2 x = 2 cos ² 4 x ,
cos 4 x ( cos 2 x cos 4 x ) = 0 ,
cos 4 x 2 sin 3 x sin x = 0,
1).cos 4 x = 0 , 2). грех 3 х = 0 , 3). грех х = 0,
3. Приведение к однородному уравнению. Уравнение называется однородным уравнением в sin и cos тогда и только тогда, когда все его члены имеют одинаковую степень в sin и cos одного и того же угла.
Для решения однородного уравнения необходимо:
a ), чтобы перенести все термины в левую часть;
b ) все общие множители вынести за скобки;
c ) приравнять все множители и скобки к нулю;
d ) приравненные к нулю скобки дают однородное уравнение меньшего
градус, который следует разделить на cos (или sin ) высшей степени;
e ) для решения полученного алгебраического уравнения в tan .
ПРИМЕР. Решите уравнение: 3 sin ² x + 4 sin x cos x + 5 cos ² x = 2.
Раствор. 3 грех ² x + 4 sin x cos x + 5 cos ² х = 2sin ² х + 2cos ² х ,
sin² x + 4 sin x cos x + 3 cos² х = 0,
тангенс ² x + 4 тангенс x + 3 = 0, следовательно, y ² + 4 у +3 = 0 ,
корни этого уравнения: y 1 = –1 , г 2 = –3 , отсюда
1) tan x = –1, 2) tan x = –3,
4.Переход на полуугол. Рассмотрим этот метод на примере:
П р и м е р . Решите уравнение: 3 sin x 5 cos x = 7,
Решение .
 6 sin ( x /2) cos ( x /2) 5 cos
² ( x / 2 ) + 5 грех ²
( х /2) =
6 sin ( x /2) cos ( x /2) 5 cos
² ( x / 2 ) + 5 грех ²
( х /2) == 7 sin² ( x /2) + 7 cos ² ( х /2),
2 sin² ( x /2) 6 sin ( x /2) cos ( x /2) + 12 cos ² ( х /2) = 0,
тангенс ² ( x /2) 3 тангенс ( x /2) + 6 = 0,
.. . . . . . . . .
5. Введение вспомогательного уголка. Рассмотрим уравнение формы:
a sin x + b cos x = c ,
где a , b , c коэффициенты; x неизвестно.
Новые коэффициенты в левой части обладают свойствами синуса и косинуса: модуль
(абсолютное значение) каждого из них не больше 1, а сумма их квадратов равна
до 1. Таким образом, мы можем пометить их как cos и
грех соответственно; вот так
называется
Таким образом, мы можем пометить их как cos и
грех соответственно; вот так
называется
вспомогательный угол .Теперь наше уравнение имеет вид:
6. Преобразование произведения в сумму. Здесь используются соответствующие формулы.
П р и м е р . Решите уравнение: 2 sin 2 x sin 6 x = cos 4 x .
cos 4 x cos 8 x = cos 4 x ,
cos 8 х = 0,
7.Универсальная замена. Рассмотрим этот метод на примере.
П р и м е р . Решите уравнение: 3 sin x 4 cos x = 3 .
Таким образом, только первый случай дает решение.
Как решать тригонометрические уравнения
Тригонометрические уравнения — это уравнения, содержащие тригонометрические функции неизвестного аргумента (например: 5sinx-3cosx = 7).
Как решать тригонометрические уравнения Чтобы научиться их решать, нужно знать некоторые методы для этого.
Чтобы научиться их решать, нужно знать некоторые методы для этого.Инструкции
Шаг 1
Решение таких уравнений состоит из двух этапов.
Первый — это преобразование уравнения для получения его простейшей формы. Простейшие тригонометрические уравнения называются так: Sinx = a; Cosx = а и т. д.
Шаг 2
Второй — решение полученного простейшего тригонометрического уравнения. Есть основные методы решения уравнений этого типа:
Алгебраическое решение.Этот метод хорошо известен со школы, из курса алгебры. Его также называют методом подстановки переменных и подстановки. По формулам приведения преобразуем, делаем замену, а потом находим корни.
Шаг 3
Разложение уравнения на множители. Во-первых, мы перемещаем все члены влево и факторизуем их.
Шаг 4
Приведение уравнения к однородному. Уравнения называются однородными, если все члены имеют одинаковую степень и синус, косинус одного и того же угла.

Для ее решения необходимо: сначала переместить все ее элементы с правой стороны на левую; все общие множители вынести за скобки; приравнять множители и скобки к нулю; Приравненные скобки дают однородное уравнение меньшей степени, которое должно делиться на cos (или sin) в старшей степени; решить полученное алгебраическое уравнение относительно тангенса.
Шаг 5
Следующий способ — пройти в половину угла. Например, решите уравнение: 3 sin x — 5 cos x = 7.
Переходим к половинному углу: 6 sin(x/2) cos(x/2) — 5 cos²(x/2) + 5 sin²(x/2) = 7 sin²(x/2) + 7 cos²(x/2), после чего сводим все слагаемые в одну часть (желательно правую) и решаем уравнение.
Шаг 6
Введение вспомогательного угла. Когда мы заменяем целочисленное значение на cos (a) или sin (a). Знак «а» — вспомогательный угол.
Шаг 7
Метод преобразования произведения в сумму. Здесь нужно использовать соответствующие формулы. Например, дано: 2 sin x sin 3x = cos 4x.

Решим его, переведя левую часть в сумму, то есть:
cos 4x — cos 8x = cos 4x, cos 8x = 0, 8x = p/2 + pk, x = p/16 + pk/8.
Шаг 8
Последний метод называется универсальной заменой. Преобразуем выражение и сделаем замену, например Cos(x/2) = u, а затем решим уравнение с параметром u. При получении результата мы конвертируем значение в противоположное.
Способ введения вспомогательного угла при решении тригонометрических уравнений. Методы решения тригонометрических уравнений
Конспект урока для 10-11 классов
Тема 1 : Способ введения вспомогательного аргумента.Вывод формул.
Цели:
Формирование знаний о новом методе решения задач по тригонометрии, в которых можно или нужно его использовать;
Формирование умений анализировать условие задачи, сравнивать и находить отличия;
Развитие мышления, последовательность и обоснованность высказываний, умение делать выводы и обобщать;
Развитие речи, обогащение и усложнение словарного запаса, овладение учащимися выразительными свойствами языка;
Формирование отношения к предмету, увлеченности познанием, создание условий для творческого нестандартного подхода к освоению знаний.

Необходимые знания, умения и навыки:
Уметь выводить тригонометрические формулы и использовать их в дальнейшей работе;
Уметь решать или иметь представление о способах решения тригонометрических задач;
Знать основные тригонометрические формулы.
Уровень подготовленности учащихся к осознанному восприятию:
Оборудование: АРМ, презентация с условиями задания, решениями и необходимыми формулами, карточки с заданиями и ответами.
Структура урока:
1. Постановка цели урока (2
Подготовка к изучению нового материала (12 мин).
Ознакомление с новым материалом (15 мин).
Первоначальное понимание и применение что выучили (10 мин)
Домашнее задание (3 мин)
Подведение итогов урока (3 мин)
Во время занятий.
1. Постановка цели занятия.
Проверить готовность учащихся и оборудования к уроку. Желательно заранее подготовить домашнее задание на доске для обсуждения решения.
 Отметим, что цель урока – расширить знания о способах решения некоторых задач по тригонометрии и попробовать свои силы в их освоении.
Отметим, что цель урока – расширить знания о способах решения некоторых задач по тригонометрии и попробовать свои силы в их освоении.2. Подготовка к изучению нового материала.
Обсудить домашнее задание: вспомнить основные тригонометрические формулы, значения тригонометрических функций для простейших аргументов.Прочитайте формулировку домашнего задания.
Формулы:
; ;
; ;
Задача: Представьте выражение как произведение.
Студенты с большей вероятностью предложат следующее решение:
Потому что они знают формулы преобразования суммы тригонометрических функций в произведение.
Предложим другое решение проблемы: . Здесь при решении использовалась формула косинуса разности двух аргументов, где она вспомогательная.Обратите внимание, что в каждом из этих методов можно использовать и другие подобные формулы.
3. Ознакомление с новым материалом.
Вопрос в том, откуда взялся вспомогательный аргумент?
Чтобы получить ответ, рассмотрим общую задачу решения, преобразуем выражение в произведение, где и произвольные, ненулевые числа.

вводим дополнительный угол (вспомогательный аргумент), где, тогда наше выражение примет вид:
Таким образом, мы получили формулу: .
Если угол ввести по формулам, то выражение примет вид и мы получим другой вид формулы: .
Мы вывели формулы дополнительных углов, которые называются формулами вспомогательных аргументов:
Формулы могут иметь различный вид (на это нужно обратить особое внимание и показать на примерах).
Обратите внимание, что в простейших случаях способ введения вспомогательного аргумента сводится к замене чисел; ; ; ; один; тригонометрические функции соответствующих углов.
4. Первичное понимание и применение изученного .
Для закрепления материала предлагается рассмотреть еще несколько примеров заданий:
Представить как произведение выражения:
Целесообразно разобрать задания 3 и 4 на уроке (разбор заданий присутствует в материалы к занятиям). Задания 1, 2 и 5 можно взять для самостоятельного решения (даны ответы).

Для анализа особенностей условий типовых задач, в которых может быть использован рассматриваемый метод решения, могут быть использованы различные методы.Обратите внимание, что задание 1.можно выполнять различными способами, а для выполнения заданий 2 — 5 удобнее использовать прием введения вспомогательного угла
В ходе очной беседы следует обсудить, в чем сходство этих заданий с пример, рассмотренный в начале урока, в чем отличия, можно ли применить предложенный метод для их решения и почему его применение удобнее.
Подобие: во всех предложенных примерах возможно применение метода введения вспомогательного аргумента и это более удобный метод, приводящий сразу к результату.
Отличие: в первом примере возможен другой подход, а во всех остальных возможен способ применения вспомогательного аргумента с использованием не одной, а нескольких формул.
После обсуждения заданий можно предложить детям решить оставшиеся дома самостоятельно.
5. Ведомость домашнего задания.

Дома вам предлагается внимательно изучить план урока и попытаться решить следующие упражнения.
Тема урока: Способ введения вспомогательного угла при решении тригонометрических уравнений.
Обновление.
Учитель.
Ребята! Мы познакомились с разными видами тригонометрических уравнений и научились их решать. Сегодня мы будем обобщать знания о методах решения тригонометрических уравнений разных типов . Для этого прошу вас поработать над предложенной вам классификацией уравнений (см. уравнения №№ 1-10 в Приложении — на конец тезисов в формате PDF)
Заполните таблицу: укажите тип уравнения, способ его решения и сравните номера уравнений с типом, к которому они относятся.
Студенты. Заполнить таблицу.
Тип уравнения Метод решения Уравнения Самый простой Формулы корней №1 Уменьшенный до квадрата Метод замены переменной №2,3 Комплексная тригонометрическая картина Упрощение до известного представления с помощью формул тригонометрии №4,5 Униформа первой степени Член уравнения разделить на косинусную переменную №6 Униформа второй степени Разделение члена уравнения на квадрат косинуса переменной №7 Проблематизация.

Студенты сталкиваются с проблемой при заполнении электронной таблицы. Они не могут определить вид и способ решения трех уравнений: №8,9,10.
Учитель. Удалось ли вам классифицировать все уравнения по форме и способу решения?
Ответ учащегося. Нет, в таблицу нельзя поместить три уравнения.
Учитель. Почему?
Ответ учащегося. Они не похожи на известные виды.Метод решения не ясен.
Постановка целей.
Учитель. Как же тогда сформулировать цель нашего урока?
Учащиеся отвечают … Определите обнаруженный новый тип уравнений и найдите способ их решения.
Учитель … Можно ли сформулировать тему урока, если мы не знаем тип найденных уравнений и метод их решения?
Ответ учащегося … Нет, но это можно сделать позже, когда мы разберемся, с чем имеем дело.
Планирование деятельности.
Учитель.
 Давайте спланируем наши действия. Обычно мы определяем тип, а затем ищем метод решения тригонометрических уравнений. Можно ли в нашей нынешней ситуации дать определенное название форме обнаруженных уравнений? И вообще, относятся ли они к одному виду?
Давайте спланируем наши действия. Обычно мы определяем тип, а затем ищем метод решения тригонометрических уравнений. Можно ли в нашей нынешней ситуации дать определенное название форме обнаруженных уравнений? И вообще, относятся ли они к одному виду?Ответ учащегося. Это трудно сделать.
Учитель. Тогда подумайте, может их что-то объединяет, или они похожи на какой-то тип?
Ответ учащегося. Левая часть этих уравнений такая же, как и у однородных, но их правая часть не равна нулю. Поэтому деление на косинус только усложнит решение.
Учитель. Может быть, начать с поиска метода решения, а затем определить тип уравнения? Какое уравнение из трех кажется вам самым простым?
Студенты отвечают , но единого мнения нет.Возможно, кто-то догадается, что коэффициенты в уравнении №8 следует выражать как синус и косинус угла стола. И тогда класс определит уравнение, которое можно решить первым. Если нет, то преподаватель предлагает рассмотреть дополнительное уравнение (см.
 уравнение №11 в Приложении — в конце реферата в формате PDF) . В нем коэффициенты равны синусу и косинусу а под известным углом, и учащиеся должны это заметить.
уравнение №11 в Приложении — в конце реферата в формате PDF) . В нем коэффициенты равны синусу и косинусу а под известным углом, и учащиеся должны это заметить.Учитель предлагает последовательность действий.( См. уравнения в приложении — в формате PDF, в конце реферата).
- Решить первое уравнение (№11), заменив коэффициенты значениями синуса и косинуса известного угла и применив формулу суммы синуса.
- Попробуйте преобразовать другие уравнения в форму первого и примените тот же метод. ( см. уравнение № 8, 9, 12 )
- Обобщить и распространить метод на любые коэффициенты и разработать общий алгоритм действий (см. уравнение №10).
- Примените метод к решению других уравнений того же типа. (см. уравнения №№ 12,13,14).
Реализация плана.
Учитель … Что ж, мы составили план. Приступим к его реализации.
У доски учащийся решает уравнение № 11.

Второй ученик решает очередное уравнение №8, предварительно разделив его на постоянное число и, тем самым, сведя ситуацию к уже найденному решению.
Учитель предлагает решить уравнения №9.12 самостоятельно. Проверяет правильность преобразований и многих решений.
Учитель. Ребята, как можно назвать угол, который появляется вместо коэффициентов уравнения и помогает нам найти решение?
Ответ учащегося. Доп. (Вариант: вспомогательный).
Учитель. Не всегда легко найти такой вспомогательный угол. Можно ли его найти, если коэффициенты не являются синусами и косинусами известных углов? Какому тождеству должны удовлетворять такие коэффициенты, если мы хотим представить их в виде синуса и косинуса вспомогательного угла?
Ответ. Основное тригонометрическое тождество.
Учитель. Молодец! Правильно! Итак, наша задача — получить такие коэффициенты, чтобы сумма их квадратов была равна единице! Попробуйте придумать число, на которое вы хотите разделить уравнение, чтобы выполнялось заданное нами условие.

Учащиеся думают и могут предложить разделить все на квадратный корень из суммы квадратов коэффициентов уравнения. Если нет, то учитель подводит их к этой мысли.
Учитель. Нам остается выбрать, какой из новых коэффициентов обозначить синусом вспомогательного угла, а какой косинусом. Есть две возможности. Переход к простейшему уравнению с синусом или косинусом зависит от выбора.
Учащиеся предлагают решение, а учитель дополняет его, обращая внимание на форму записи рассуждения и ответа. Решите уравнение №. 10.
Учитель … Нашли ли мы способ решения нового типа уравнений? Как мы назовем этот тип?
Ответ. Мы работали, находя вспомогательный угол. Может, уравнениями следует называть уравнения, которые решаются с помощью вспомогательных углов?
Учитель. Конечно, можно. Можете ли вы придумать формулу их появления? Это будет короче.
Ответ. Да. Уравнения с коэффициентами А, В и С.

Учитель. Обобщим метод для произвольных коэффициентов.
Учитель обсуждает и записывает на доске формулы синуса и косинуса вспомогательного угла для обобщенных коэффициентов. Затем с их помощью решает уравнения 13 и 14.
Учитель. Достаточно ли хорошо мы освоили метод?
Ответ. Нет. Необходимо решить такие уравнения и закрепить умение пользоваться методом вспомогательного угла.
Учитель. Откуда мы знаем, что изучили метод?
Ответ. Если мы самостоятельно решим несколько уравнений.
Учитель. Давайте установим качественную шкалу для изучения метода.
Ознакомьтесь с характеристиками уровней и разместите их на шкале, отражающей уровень владения этим навыком. Соотнести характеристику уровня и балла (от 0 до 3)
- Я умею решать уравнения с разными коэффициентами
- Не могу решить уравнения
- Я умею решать уравнения повышенной сложности
- Я умею решать уравнения с табличными коэффициентами
Учитель.
 (После ответа студента) Итак, наша шкала оценок выглядит следующим образом:
(После ответа студента) Итак, наша шкала оценок выглядит следующим образом:По такому же принципу оцениваем самостоятельную работу по теме на следующем уроке.
А теперь, пожалуйста, решите уравнения №№ 1148 г, 1149 г, 1150 г и определите свой уровень владения темой.
Не забудьте заполнить записи в таблице и назвать тему: «Введение вспомогательного угла при решении тригонометрических уравнений».
Отражение пути достижения цели.
Учитель. Ребята, достигли ли мы поставленной цели урока?
Ответы учащихся … Да, мы научились распознавать новый тип уравнений.
Найден метод их решения с помощью вспомогательного угла.
Мы научились применять метод на практике.
Учитель. Как мы действовали? Как вы пришли к пониманию того, что нам нужно делать?
Ответ. Мы рассмотрели несколько частных случаев уравнений с «узнаваемыми» коэффициентами и распространили эту логику на любые значения A, B и C.

Учитель. Это индуктивный способ мышления: мы вывели метод на основе нескольких случаев и применили его в подобных случаях.
Перспектива. Где мы можем применить этот ход мыслей? (ответы учащихся)
Сегодня ты хорошо поработал на уроке. Дома прочитайте описание метода вспомогательного угла в учебнике и решите №№ 1148 (а, б, в), 1149 (а, б, в), 1150 (а, б, в). Я надеюсь, что на следующем уроке вы все будете отлично использовать этот метод при решении тригонометрических уравнений.
Спасибо за работу на уроке!
На уроках алгебры учителя говорят, что существует небольшой (на самом деле очень большой) класс тригонометрических уравнений, которые не могут быть решены стандартными способами — ни через факторизацию, ни через замену переменных, ни даже через однородные члены. В этом случае вступает в действие принципиально иной подход — метод вспомогательного угла.
Что это за метод и как его применять? Для начала вспомним формулы синуса суммы/разности и косинуса суммы/разности:
\[\begin(align)&\sin\left(\alpha\pm\beta\right) = \sin\alpha\cos\beta\pm\cos\alpha\sin\beta\&\cos\left( \alpha\pm\beta\right)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\\end(align)\]
Думаю, эти формулы вам хорошо известны — из них выводятся формулы двойного аргумента, без которых в тригонометрии вообще никуда.
 (2)) = 1$, а значит, обязательно найдется угол $\alpha$, для которого эти числа косинус и синус соответственно. Поэтому наше уравнение перепишется так:
(2)) = 1$, а значит, обязательно найдется угол $\alpha$, для которого эти числа косинус и синус соответственно. Поэтому наше уравнение перепишется так:\[\begin(align)&\cos\alpha\sin x+\sin\alpha\cos x=1\&\sin\left(\alpha+x\right)=1\\end(align) \]
И это уже легко решается, после чего остается только узнать, что такое угол $\alpha$. Как это узнать, а также как выбрать правильное число для деления обеих частей уравнения (в этом простом примере мы делили на 5) — об этом в сегодняшнем видеоуроке:
Сегодня мы разберем решение тригонометрических уравнений, а точнее один-единственный прием, который называется «метод вспомогательного угла».Почему именно этот метод? Просто потому, что за последние два-три дня, когда я занимался со студентами, которым я рассказывал о решении тригонометрических уравнений, а мы разбирали, в том числе, метод вспомогательного угла, и все студенты как один делают одну и ту же ошибку. Но метод в целом прост и, кроме того, является одним из основных приемов в тригонометрии.
 (2) ) x $, получить однородное уравнение, свести его к касательным и решить.Однако это долгий и утомительный путь, требующий большого количества вычислений.
(2) ) x $, получить однородное уравнение, свести его к касательным и решить.Однако это долгий и утомительный путь, требующий большого количества вычислений.Предлагаю подумать о следующем. Имеем $\sin$ и $\cos$. Вспомним формулу косинуса и синуса суммы и разности:
\[\sin\left (\alpha\pm\beta\right) = \sin\alpha\cos\beta\pm\cos\alpha\sin\beta\]
\[\cos\left(\alpha+\beta\right)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\]
\[\cos\left(\alpha-\beta\right)=\cos a\cos\beta+\sin\alpha\sin\beta\]
Вернемся к нашему примеру.Приведем все к синусу разности. Но сначала уравнение нужно немного преобразовать. Найдем коэффициент:
$\sqrt(l)$ — это тот самый коэффициент, на который надо разделить обе части уравнения, чтобы перед синусом и косинусом стояли числа, которые сами по себе являются синусом и косинусом. Разделим:
\[\frac(\sqrt(3))(2)\cdot\sin 2x-\frac(1)(2)\cdot\cos 2x=\frac(1)(2)\]
Посмотрим, что у нас получилось слева: существуют ли такие $\sin$ и $\cos$, что $\cos\alpha = \frac(\sqrt(3))(2)$, и $\sin\ альфа = \ frac (1) (2) $? Очевидно есть: $\alpha=\frac(\text()\!\!\Pi\!\!\Text()))(6)$.
 Следовательно, мы можем переписать наше выражение следующим образом:
Следовательно, мы можем переписать наше выражение следующим образом:\[\cos\frac(\text()\!\!\pi\!\!\text())) (\text(6))\cdot\sin 2x-\sin\frac(\text()\ !\!\pi\!\!\text()) (\text(6))\cdot\cos 2x=\frac(1)(2)\]
\[\sin 2x\cdot\cos\frac(\text()\!\!\pi\!\!\text())) (\text(6)) — \cos 2x\cdot\sin\frac( \text()\!\!\pi\!\!\text()} (\text(6)) = \frac(1)(2)\]
Теперь у нас есть формула синуса разности.Мы можем написать так:
\[\sin\left(2x-\frac(\text()\!\!\pi\!\!\text()))(\text(6))\right)=\frac(1)(2 ) \]
Перед нами простейшая классическая тригонометрическая конструкция. Напомню:
Вот что мы записываем для нашего конкретного выражения:
\[\left[\begin(align)&2x-\frac(\text()\!\!\pi\!\!\text()))(6)=\frac(\text()\!\ !\пи\!\!\текст())(6)=2\текст()\! \! \ число Пи \! \! \text()n\&2x-\frac(\text()\!\!\pi\!\!\text())) (\text(6)) = \text()\! \! \ число Пи \! \! \text()-\frac(\text()\!\!\pi\!\!\text())(\text(6)) + 2\text()\! \! \ число Пи \! \! \text()n\\end(выравнивание)\right.
 \ ]
\ ]\[\left[\begin(align)&2x=\frac(\text()\!\!\pi\!\!\text()))(3)+2\text()\! \! \ число Пи \! \! \текст()n\&2x=\текст()\! \! \ число Пи \! \! \ текст () +2 \ текст () \! \! \ число Пи \! \! \text()n\\end(выравнивание)\right. \]
\[\left[\begin(align)&x=\frac(\text()\!\!\pi\!\!\text()))(6)+\text()\! \! \ число Пи \ ! \! \text()n\&x=\frac(\text()\!\!\pi\!\!\text()))(2)+\text()\! \! \ число Пи \ ! \! \text()n\\end(выравнивание)\right.\]
Нюансы решения
Итак, что нужно делать, если вы столкнулись с подобным примером:
- При необходимости преобразовать структуру.
- Найдите поправочный коэффициент, извлеките из него корень и разделите на него обе части примера.
- Посмотрим, какие значения синуса и косинуса получаются из чисел.
- Раскладываем уравнение по формулам синуса или косинуса разности или суммы.
- Решаем простейшее тригонометрическое уравнение.
В связи с этим у внимательных студентов наверняка возникнет два вопроса.

Что мешает написать $\sin$ и $\cos$ на этапе нахождения поправочного коэффициента? — Нам мешает основное тригонометрическое тождество. Дело в том, что получившиеся $\sin$ и $\cos$, как и любые другие для одного и того же аргумента, должны давать ровно «единицу» при возведении в квадрат. В процессе решения нужно быть очень внимательным, чтобы не потерять «дэу» перед «иксами».
Метод вспомогательного угла – это инструмент, помогающий свести «некрасивое» уравнение к вполне адекватному и «красивому».(2)) х = \ frac (1+ \ cos 2x) (2) \]
Нам нужны только первые расчеты. Приступим к работе над задачей:
\[\sqrt(3)\cdot\sin2x+2\cdot\frac(1-\cos2x)(2)-1=2\cosx\]
\[\sqrt(3)\cdot\sin2x+1-\cos2x-1=2\cosx\]
\[\sqrt(3)\cdot\sin2x-\cos2x=2\cosx\]
Теперь воспользуемся вычислением косинуса разности. Но сначала посчитаем поправку $l$:
Перепишем с учетом этого факта:
\[\frac(\sqrt(3))(2)\cdot\sin 2x-\frac(1)(2)\cdot\cos 2x=\cos x\]
В этом случае можно написать, что $\frac(\sqrt(3))(2)=\frac(\text()\!\!\Pi\!\!\Text()))(3)$, и $\frac(1)(2)=\cos\frac(\text()\!\!\pi\!\!\text()))(3)$.
 Перепишем:
Перепишем:\[\sin\frac(\text()\!\!\pi\!\!\text())) (\text(3))\cdot\sin 2x-\cos\frac(\text()\ !\!\pi\!\!\text()) (\text(3))\cdot\cos 2x=\cos x\]
\[-\cos\left(\frac(\text()\!\!\pi\!\!\text())) (\text(3)) + 2x\right)=\cos x\]
Давайте по-умному поставим «минус» в скобке. Для этого обратите внимание на следующее:
\[\cos\left(\frac(\text()\!\!\pi\!\!\text())) (\text(3)) + 2x\right) = \cos\left(\text ( )\!\!\пи\!\!\текст()-\текст()\!\!\пи\!\!\текст(+)\фракция(\текст()\!\!\пи\ !\!\текст()) (\текст(3))+2х\справа)=\]
\[=\cos\left(\text()\!\!\pi\!\!\text() — \frac(2\text()\!\!\pi\!\!\text() ) (3) + 2x\right) = \cos\left(\text()\!\!\Pi\!\!\Text()+\varphi\right) = — \cos\varphi\]
Возвращаемся к нашему выражению и вспоминаем, что в роли $\varphi$ у нас выступает выражение $-\frac(2\text()\!\!\Pi\!\!\Text())) (3) + 2x $.Поэтому пишем:
\[-\left(-\cos\left(-\frac(2\text()\!\!\pi\!\!\text()))(3)+2x\right)\right)=\ соз х \]
\[\cos\left(2x-\frac(2\text()\!\!\pi\!\!\text()))(3)\right)=\cos x\]
Для решения подобной задачи нужно помнить следующее:
\[\cos\альфа=\cos\бета\]
\[\left[\begin(align)&\alpha=\beta+2\text()\! \! \ число Пи \! \! \text()n\&\alpha=-\beta+2\text()\! \! \ число Пи \! \! \text()n\\end(выравнивание)\right.
 \]
\]Давайте разберемся с нашим примером:
\[\left[\begin(align)&2x-\frac(2\text()\!\!\pi\!\!\text()))(3)=x+2\text()\! \ ! \ число Пи \! \! \text()n\&2x-\frac(2\text()\!\!\pi\!\!\text()))(3)=-x+2\text()\! \! \ число Пи \! \! \text()n\\end(выравнивание)\right. \]
Рассчитаем каждое из этих уравнений:
И второй:
Запишем окончательный ответ:
\[\left[\begin(align)&x=\frac(2\text()\!\!\pi\!\!\text()))(3)+2\text()\! \! \ число Пи \! \! \text()n\&x=\frac(2\text()\!\!\pi\!\!\text())) (9) + \frac(2\text()\!\!\ пи \!\!\text()n)(3)\\end(align)\right.\]
Нюансы решения
На самом деле это выражение решается множеством разных способов, однако оптимальным в данном случае является метод вспомогательного угла. Кроме того, на примере этой конструкции хотелось бы обратить ваше внимание еще на несколько интересных приемов и фактов:
- Формулы понижения степени. Эти формулы не нужно запоминать, но нужно уметь их выводить, о чем я вам сегодня и рассказал.

- Решение уравнений вида $\cos\alpha=\cos\beta$.(3)) х + 4 \ cos х = 5 \]
Преобразуем первый член:
\[\sin 3x=\sin\left(2x+x\right)=\sin 2x\cdot\cos x+\cos 2x\cdot\sin x\]
\[=2\влево(1-\cos 2x\вправо)\cdot\sinx\]
Теперь подставим все это в нашу изначальную конструкцию:
\[\sin2x\cosx+\cos2x\sinx+2\sinx-2\cosx\sinx+4\cosx=5\]
\[\sin 2x\cos x-\имя_оператора(cosx)-cos2\sinx+2\sinx+4\cosx=5\]
\[\sin\влево(2x-x\вправо)+2\sinx+4\cosx=5\]
Давайте представим нашу поправку:
Записываем:
\[\frac(3)(5)\sin x+\frac(4)(5)\cos x=1\]
Нет таких $\alpha$, для которых $\sin$ или $\cos$ были бы равны $\frac(3)(5)$ и $\frac(4)(5)$ в тригонометрической таблице.Поэтому давайте просто напишем и приведем выражение к синусу суммы:
\[\sinx\cdot\cos\varphi+\cosx\cdot\sin\varphi=1\]
\[\sin\left(x+\varphi\right)=1\]
Это частный случай, простейшая тригонометрическая конструкция:
Осталось найти чему равно $\varphi$.
 Именно здесь многие студенты ошибаются. Дело в том, что к $\varphi$ предъявляются два требования:
Именно здесь многие студенты ошибаются. Дело в том, что к $\varphi$ предъявляются два требования:\[\left\(\begin(align)&\cos\varphi=\frac(3)(5)\&\sin\varphi=\frac(4)(5)\\end(align)\ правильно .\]
Нарисуем радар и посмотрим, где встречаются такие значения:
Возвращаясь к нашему выражению, пишем следующее:
Но эту запись можно немного оптимизировать. Так как мы знаем следующее:
\[\alpha:\arcsin\alpha+\arccos\alpha=\frac(\text()\!\!\pi\!\!\text()))(\text(2)),\]
то в нашем случае это можно записать так:
Пример № 2
Это потребует еще более глубокого понимания методов решения стандартных задач без тригонометрии.(2)) х $:
Что нам дает такая запись? Дело в том, что в первой скобке стоит точный квадрат. Сворачиваем его и получаем:
Предлагаю ввести новую переменную:
\[\sinx+\cosx=t\]
В этом случае получаем выражение:
\ [((t) _ (1)) = \ frac (5 + 1) (4) = \ frac (3) (2) \]
\[((т)_(2))=\фрак(5-1)(4)=1\]
Итого получаем:
\[\left[\begin(align)&\sinx+\cosx=\frac(3)(2)\&\sinx+\cosx=1\end(align)\right.
 \]
\]Конечно, знающие ученики сейчас скажут, что такие конструкции легко решаются путем приведения их к однородным. Однако мы будем решать каждое уравнение с помощью метода вспомогательного угла. Для этого сначала рассчитаем поправку $l$:
\[\квт(л)=\кврт(2)\]
Делим все на $\sqrt(2)$:
\[\left[\begin(align)&\frac(\sqrt(2))(2)\sinx+\frac(\sqrt(2))(2)\cosx=\frac(3)( 2 \ sqrt (2)) \ & \ frac (\ sqrt (2)) (2) \ sin x + \ frac (\ sqrt (2)) (2) \ cos x = \ frac (\ sqrt (2) ) (2 ) \\\ end (выравнивание) \ right.\]
Сократим все до $\cos$:
\[\cos x\cdot\cos\frac(\text()\!\!\pi\!\!\text())) (4) + \sin x\sin\frac(\text()\! \!\пи\!\!\текст()) (\текст(4))\]
\[\left[\begin(align)&\cos\left(x-\frac(\text()\!\!\pi\!\!\text())) (\text(4))\right ) = \ frac (3) (2 \ sqrt (2)) \ \ & \ cos \ left (x- \ frac (\ text () \! \! \ pi \! \ ! \ text ()) (4) \право)=\фрак(\кврт(2))(2)\\конец(выравнивание)\право.\]
Разберемся с каждым из этих выражений.

Первое уравнение не имеет корней, и иррациональность в знаменателе поможет нам доказать этот факт. Обратите внимание на следующее:
\[\квт(2)
\[\frac(3)(2\ sqrt(2))>\frac(3)(3\cdot 1,5)=\frac(3)(3)=1\]
Итого мы наглядно доказали, что требуется, чтобы $\cos\left(x-\frac(\text()\!\!\Pi\!\!\Text()))(4)\right)$ было равно числу больше единицы и, следовательно, эта конструкция не имеет корней.
Разбираемся со вторым:
Решаем эту конструкцию:
В принципе можно оставить ответ так, а можно и раскрасить:
Важные моменты
В заключение хотелось бы еще раз обратить ваше внимание на работу с «некрасивыми» аргументами, т.е. когда $\sin$ и $\cos$ не являются табличными значениями. Проблема в том, что если мы утверждаем, что в нашем уравнении $\frac(3)(5)$ есть $\cos$, а $\frac(4)(5)$ есть $\sin$, то в итоге, после того как мы определиться с конструкцией, необходимо учитывать оба этих требования.Получаем систему из двух уравнений.
 Если это не учитывать, то получается следующая ситуация… В этом случае мы получим две точки и вместо $\varphi$ у нас будет два числа: $\rcsin\frac(4)(5 )$ и $-\arcsin\frac(4)(5)$, но последний никак не устраивает. То же самое произойдет и с точкой $\frac(3)(5)$.
Если это не учитывать, то получается следующая ситуация… В этом случае мы получим две точки и вместо $\varphi$ у нас будет два числа: $\rcsin\frac(4)(5 )$ и $-\arcsin\frac(4)(5)$, но последний никак не устраивает. То же самое произойдет и с точкой $\frac(3)(5)$.Эта проблема возникает только в случае «некрасивых» аргументов. Когда у нас есть табличные значения, то ничего подобного нет.
Надеюсь, сегодняшний урок помог вам понять, что такое метод вспомогательного угла и как его применять на примерах разного уровня сложности. Но это не единственный урок по решению задач методом вспомогательного угла. Поэтому оставайтесь с нами!
Лемма. Если сумма квадратов двух действительных чисел равна единице, то одно из этих чисел можно рассматривать как косинус, а другое как синус некоторого угла.
Другими словами, если a 2 + b 2 = 1 , то есть угол φ так, что
a = cos φ; б = грех φ.
 2 + (\ frac (1) (2)) = \ frac (3) (4) + \ frac (1) (4) = 1 $$
2 + (\ frac (1) (2)) = \ frac (3) (4) + \ frac (1) (4) = 1 $$ Следовательно, существует угол φ такое, что \ (\ frac (\ sqrt3) (2) \) = cos φ ; 1/2 = sin φ .
Как φ в этом случае можно выбрать любой из углов 30°, 30°±360°, 30°±2 360° и т. д.
Доказательство леммы:
Рассмотрим вектор 0А) \) с координатами ( а, б ).Поскольку a 2 + b 2 = 1 , длина этого вектора равна 1. Но в этом случае его координаты должны быть равны cos φ и sin φ , где φ — угол, который этот вектор образует с осью абсцисс.
Итак, = cos φ; b = sin φ , что и требовалось доказать.
Доказанная лемма позволяет преобразовать выражение а sin x + b cos x к более удобному для изучения виду.2)) $$
Примеры.
1) \ (sin x + cos x = \ sqrt2 (\ frac (1) (\ sqrt2) sin x + \ frac (1) (\ sqrt2) cos x) = \ sqrt2 (cos \ frac ( \ pi ) (4) sin x + sin \ frac (\pi) (4) cos x) = \\ = \ sqrt2 (sinx + \ frac (\pi) (4)) \)
Полученная формула sin x + cos x = \(\sqrt2(sinx+\frac(\pi)(4))\) полезно запомнить.

2) Если один из номеров a и б положительное, а другое отрицательное, то выражение
а sin x + b cos x удобнее преобразовать не в синус суммы, а в синус разности двух углы.Итак,$$3sinx — 4cosx=\sqrt(9+16)(\frac(3)(\sqrt(9+16))sinx-\frac(4)(\sqrt(9+16)) cosx) = \\ = 5 (sinx \ cdot \ frac (3) (5) — cosx \ cdot \ frac (4) (5)) = 5sin (x — \ phi), $$
где под φ можно подразумевать любой угол, удовлетворяющий условиям:
cos φ = 3/5, sin φ = 4 / 5
В частности, мы можем поставить φ = арктический 4/3. Тогда получаем:
3 sin x — 4 cos x = 5 sin (x — arctan 4/3).
Методы решения тригонометрических уравнений.Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида (см. выше) и решение полученного простейшего тригонометрического уравнения.
 Существует семь основных методов решения тригонометрических уравнений.
Существует семь основных методов решения тригонометрических уравнений. 1. Алгебраический метод.
(переменная замена и метод подстановки).
2. Факторинг.
П р и м е р а 1. Решите уравнение: sin x + cos x = 1 .
Раствор. Переместите все члены уравнения влево:
Sin x + cos x – 1 = 0 ,
Преобразуем и факторизуем выражение в
Левая часть уравнения:
PRI me R 2. Решим уравнение: cos 2 х + sin х Cos х = 1.
РЕШЕНИЕ cos 2 x + sin x Cos x – sin 2 х — cos 2 х = 0,
Sin x Cos x – грех 2 х = 0,
Sin x (Cos x – грех х ) = 0,
П р и м е р 3.Решите уравнение: cos 2 x — cos 8 x + cos 6 x = 1.
РЕШЕНИЕ cos 2 x + cos 6 x = 1 + cos 8 x ,
2 cos 4 x cos 2 x = 2 cos² 4 x ,
Кос 4 x · (cos 2 x — cos 4 x ) = 0,
Кос 4 x 2 sin 3 x Sin x = 0 ,
один).
 cos 4 х = 0, 2).sin 3 х = 0, 3). sin x = 0,
cos 4 х = 0, 2).sin 3 х = 0, 3). sin x = 0,3. Приведение к однородному уравнению.
Уравнение, называемое однородным из относительно sin и cos , если все его членов одной степени относительно sin и cos одинаковый угол … Для решения однородного уравнения нужно:
a ) перевести все его члены в левую часть;
б ) все общие множители вынести за скобки;
v ) приравнять все множители и скобки к нулю;
G ) приравненные к нулю скобки дают однородное уравнение меньшей степени, которое следует разделить на
cos (или sin ) в старшей степени;
d ) решить полученное алгебраическое уравнение относительно тангенса .
грех 2 x + 4 sin x Cos x + 5 cos 2 х = 2.

РАСТВОР. 3sin 2 x + 4 sin x Cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,
Sin 2 x + 4 sin x Cos x + 3 cos 2 x = 0 ,
Тан 2 x + 4 Тан x + 3 = 0 , отсюда и 2 + 4 у +3 = 0 ,
Корни этого уравнения: y 1 знак равно — 1, y 2 = — 3, следовательно,
1) tan x = –1, 2) tan x = –3,
4.Перейдите к половине угла.
Рассмотрим этот метод на примере:
ПРИМЕР Решите уравнение: 3 sin x — 5 cos x = 7.
РЕШЕНИЕ.6 sin ( x / 2) cos ( x / 2) — 5 cos ² ( x / 2) + 5 sin ² ( x / 2) =
7 sin ² ( 12 cos² ( x /2) = 0,
тангенс ² ( x /2) — 3 тангенс ( x /2) + 6 = 0,
.. . . . . . . . .
5. Введение вспомогательного уголка.
Рассмотрим уравнение вида:
a sin x + b cos x = c ,
Где , б , в — коэффициенты; х — неизвестно.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль (абсолютное значение) каждого из которых не более 1, а сумма их квадратов равна 1.Тогда мы можем обозначить их соответственно как cos и sin (здесь — так называемый вспомогательный угол ), и взять наше уравнение
что такое угловой локатор. Этот удобный угломер идеально подходит для расчета углов наклонных конструкций, таких как лестницы, стропила крыши и оконные рамы. Одна рука располагается на плоской поверхности любого куска дерева. Обычный ручной транспортир требует, чтобы пользователь выровнял линейку с одной линией угла, и везде, где вторая линия, образующая угол, пересекает транспортир, это число является измерением угла.Угловой видоискатель C — это красота, увеличивающаяся при полном обзоре видоискателя в 1. 416 Отвертка LOCATOR® для трещотки, короткая, длина 15 мм 046. Многоцелевой угловой видоискатель. LinkedIn 0. Суммарный угол от точки -3db на одной стороне оси до точки -3db на другой стороне оси называется углом конуса. А также мы можем использовать этот калькулятор, чтобы найти сумму внутренних углов, меру каждого внутреннего угла и меру каждого внешнего угла правильного многоугольника, когда задано количество его сторон.Уклон крыши описывается как подъем в движении, как правило, подъем в движении на 12 единиц. На этой странице вы узнаете все основные формулы и информацию о котерминальных углах. Также координаты точек могут различаться. Введите длины сторон и верхний угол или длину основания, чтобы рассчитать все остальные длины сторон, углы, высоту и площадь треугольника. Бостон около 42. 97 Скидка 16%. Используйте линию прямой видимости карты вышки, чтобы проверить возможные помехи от земли (холмы, деревья, препятствия). Шаг 2: Нажмите кнопку «Рассчитать».Использование калькулятора для нахождения квадранта угла 1 — Введите угол: в градусы верхнего ввода. 4 градуса северной широты. Особенно на более коротких выносах держите угломер так, чтобы он был параллелен углу выноса. Например. Получите пошаговые решения от опытных наставников всего за 15–30 минут.
А также мы можем использовать этот калькулятор, чтобы найти сумму внутренних углов, меру каждого внутреннего угла и меру каждого внешнего угла правильного многоугольника, когда задано количество его сторон.Уклон крыши описывается как подъем в движении, как правило, подъем в движении на 12 единиц. На этой странице вы узнаете все основные формулы и информацию о котерминальных углах. Также координаты точек могут различаться. Введите длины сторон и верхний угол или длину основания, чтобы рассчитать все остальные длины сторон, углы, высоту и площадь треугольника. Бостон около 42. 97 Скидка 16%. Используйте линию прямой видимости карты вышки, чтобы проверить возможные помехи от земли (холмы, деревья, препятствия). Шаг 2: Нажмите кнопку «Рассчитать».Использование калькулятора для нахождения квадранта угла 1 — Введите угол: в градусы верхнего ввода. 4 градуса северной широты. Особенно на более коротких выносах держите угломер так, чтобы он был параллелен углу выноса. Например. Получите пошаговые решения от опытных наставников всего за 15–30 минут. • диагонали, которые всегда сходятся в … Уход на дому включает в себя широкий спектр основных услуг по личному уходу, которые предоставляются человеку на дому. Если нужен периметр, сложите длины ребра a + ребра b + ребра c. Например: уклон крыши 12/12 будет выбран как 12 дюймов 3-х стен разной формы и под каким углом каждая митра должна быть срезана для идеального соединения.Обратите внимание, что при указании размеров двух углов A и B невозможно найти какие-либо другие размеры. T Инструмент для определения угла наклона крыши или для нахождения углов чего-либо. • Измерьте угол между двумя маркерами. ДЖОНСОН. Теорема Пифагора — Проверка квадратных углов. Как показано на примере изображения Stellarium слева, часовой угол Полярной звезды будет читаться как 2 … Этот угол на 10° круче, чем в общем методе, но он очень эффективен для наблюдения за полуденным солнцем, которое является самым жарким в короткие зимние дни.Инструкции: Введите требуемую орбитальную позицию спутника (долготу) и местоположение вашего сайта.
• диагонали, которые всегда сходятся в … Уход на дому включает в себя широкий спектр основных услуг по личному уходу, которые предоставляются человеку на дому. Если нужен периметр, сложите длины ребра a + ребра b + ребра c. Например: уклон крыши 12/12 будет выбран как 12 дюймов 3-х стен разной формы и под каким углом каждая митра должна быть срезана для идеального соединения.Обратите внимание, что при указании размеров двух углов A и B невозможно найти какие-либо другие размеры. T Инструмент для определения угла наклона крыши или для нахождения углов чего-либо. • Измерьте угол между двумя маркерами. ДЖОНСОН. Теорема Пифагора — Проверка квадратных углов. Как показано на примере изображения Stellarium слева, часовой угол Полярной звезды будет читаться как 2 … Этот угол на 10° круче, чем в общем методе, но он очень эффективен для наблюдения за полуденным солнцем, которое является самым жарким в короткие зимние дни.Инструкции: Введите требуемую орбитальную позицию спутника (долготу) и местоположение вашего сайта. 29 градусов, так что 3. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана в ассортименте … Цифровой угломер — это устройство, которое измеряет и определяет угол данного объекта. яблоко. Вычислите неизвестные углы или длины, введя ЛЮБЫЕ ДВЕ (2) известные переменные в текстовые поля. Длина дуги равна? Нажмите кнопку «Длина дуги», введите радиус 3. Пожалуйста, поддержите нас, отключив блокировщик рекламы.to/2skY7oXИнструменты, которые я использую — https://www. Все воздушные змеи являются четырехугольниками со следующими свойствами: • отсутствие вогнутых (более 180°) внутренних углов. 52 градуса. Цифровые уровни и … Уголоискатель Этот универсальный инструмент можно использовать в качестве уровня. Этот универсальный инструмент можно использовать в качестве уровня, Т-образного угольника или скользящего угольника для определения углов при строительстве откосов. Давайте определим углы: напишите углы на транспортире. Забавные факты. Используйте этот простой инструмент для точного расчета количества градусов в любом уклоне крыши, косоуре лестницы или любом другом стандарте или метрике уклона.
29 градусов, так что 3. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана в ассортименте … Цифровой угломер — это устройство, которое измеряет и определяет угол данного объекта. яблоко. Вычислите неизвестные углы или длины, введя ЛЮБЫЕ ДВЕ (2) известные переменные в текстовые поля. Длина дуги равна? Нажмите кнопку «Длина дуги», введите радиус 3. Пожалуйста, поддержите нас, отключив блокировщик рекламы.to/2skY7oXИнструменты, которые я использую — https://www. Все воздушные змеи являются четырехугольниками со следующими свойствами: • отсутствие вогнутых (более 180°) внутренних углов. 52 градуса. Цифровые уровни и … Уголоискатель Этот универсальный инструмент можно использовать в качестве уровня. Этот универсальный инструмент можно использовать в качестве уровня, Т-образного угольника или скользящего угольника для определения углов при строительстве откосов. Давайте определим углы: напишите углы на транспортире. Забавные факты. Используйте этот простой инструмент для точного расчета количества градусов в любом уклоне крыши, косоуре лестницы или любом другом стандарте или метрике уклона. Этот инструмент найдет уклон вашей крыши. Ваш адрес E-911 используется экстренными службами для определения вашего местоположения. Как пользоваться магнитным локатором Джонсона. … Калькулятор угла треугольника — беспроигрышный вариант, если вы хотите узнать, как найти угол треугольника. Эти прямые называются сторонами угла. Посетите эту страницу на своем телефоне, чтобы напрямую измерить шаг и углы. угол подвески обратно пропорционален теплоте мяса при условии, что максис оси и сила тяжести полости остаются постоянными.Угловая скоба, Угловая стяжка (Карп. Цифровые уровни и … 40-0912 Английский. Какова мера каждого угла? Мне нужен ответ [5] 2009/05/29 00:26 До 20 лет / Младший школьник / Немного / Комментарий/Запрос Существует прямоугольный треугольник, а длина … Калькулятор углов — Равнобедренные треугольники — Измерьте углы и длины сторон, введя 2 известных значения Чрезмерно расходящиеся имплантаты могут использовать кератор DT сообщение может исправить до 20 градусов Спутниковая антенна Digisat Калькулятор угла обзора обеспечивает точные углы наведения по азимуту и высоте для всех основных спутников.
Этот инструмент найдет уклон вашей крыши. Ваш адрес E-911 используется экстренными службами для определения вашего местоположения. Как пользоваться магнитным локатором Джонсона. … Калькулятор угла треугольника — беспроигрышный вариант, если вы хотите узнать, как найти угол треугольника. Эти прямые называются сторонами угла. Посетите эту страницу на своем телефоне, чтобы напрямую измерить шаг и углы. угол подвески обратно пропорционален теплоте мяса при условии, что максис оси и сила тяжести полости остаются постоянными.Угловая скоба, Угловая стяжка (Карп. Цифровые уровни и … 40-0912 Английский. Какова мера каждого угла? Мне нужен ответ [5] 2009/05/29 00:26 До 20 лет / Младший школьник / Немного / Комментарий/Запрос Существует прямоугольный треугольник, а длина … Калькулятор углов — Равнобедренные треугольники — Измерьте углы и длины сторон, введя 2 известных значения Чрезмерно расходящиеся имплантаты могут использовать кератор DT сообщение может исправить до 20 градусов Спутниковая антенна Digisat Калькулятор угла обзора обеспечивает точные углы наведения по азимуту и высоте для всех основных спутников. 43 м². 5° западной долготы, в то время как мы вычисляем угол взгляда на каждый спутник, а затем вычисляем угол между ними. Угломер удобен, особенно для столяров, так как помогает им измерять точные углы наклонных крыш, лотков и т.д. Klein Tools 935DAGL — это цифровой уровень, который определяет и измеряет углы. Предположим, это был болт с мелкой резьбой диаметром 3/8 дюйма. Инструмент True Angle® какого размера мне нужен для установки молдинга коронки? 7-дюймовый и 18-дюймовый инструмент True Angle® — это минимально рекомендуемый инструмент для формовки коронки и обрезки.Высота — это угол над землей, на который должна указывать ваша тарелка. Автор сообщения Автор: ; Дата публикации Медфорд, фейерверк 2021; Лесли Дэвис ХГТВ чистая стоимость о том, как использовать магнитный угловой локатор Джонсона Угловой искатель Этот универсальный инструмент можно использовать как уровень. Это также невероятно редко. 5°? Сложение обоих углов равно 90°, … Установка углов на ваших инструментах может быть немного сложной, и очень важно получить правильные углы.
43 м². 5° западной долготы, в то время как мы вычисляем угол взгляда на каждый спутник, а затем вычисляем угол между ними. Угломер удобен, особенно для столяров, так как помогает им измерять точные углы наклонных крыш, лотков и т.д. Klein Tools 935DAGL — это цифровой уровень, который определяет и измеряет углы. Предположим, это был болт с мелкой резьбой диаметром 3/8 дюйма. Инструмент True Angle® какого размера мне нужен для установки молдинга коронки? 7-дюймовый и 18-дюймовый инструмент True Angle® — это минимально рекомендуемый инструмент для формовки коронки и обрезки.Высота — это угол над землей, на который должна указывать ваша тарелка. Автор сообщения Автор: ; Дата публикации Медфорд, фейерверк 2021; Лесли Дэвис ХГТВ чистая стоимость о том, как использовать магнитный угловой локатор Джонсона Угловой искатель Этот универсальный инструмент можно использовать как уровень. Это также невероятно редко. 5°? Сложение обоих углов равно 90°, … Установка углов на ваших инструментах может быть немного сложной, и очень важно получить правильные углы. 435 градусов. Инструменты для определения угла и транспортиры можно использовать в различных условиях. Поместите угольник напротив внешнего упора или стойки створки, как показано на рисунке. Просто выберите штат и город, или почтовый индекс, или введите географическое положение, и Satellite Finder создаст список спутниковых местоположений для этого местоположения. Обратите внимание, что для авиакомпании AB (Air Berlin) авиакомпания не возвращает локатор записей. Поскольку сумма двух углов ≠ 90°, эти два угла не дополняют друг друга.После того, как они сделали это, у них остался эффективный 90-градусный измеритель угла — надеюсь, он окажется полезным!! Радиан — это угол в центре окружности, равный радиусу окружности, когда дуга имеет длину радиуса. Если вам сказали найти наименьший положительный угол, сотерминальный с 785 градусами, вы можете использовать следующий процесс расчета, показанный ниже. 48 + 360 = 560. Угол конуса 90 градусов — это просто большой конус, который покрывает большую часть дна озера.
435 градусов. Инструменты для определения угла и транспортиры можно использовать в различных условиях. Поместите угольник напротив внешнего упора или стойки створки, как показано на рисунке. Просто выберите штат и город, или почтовый индекс, или введите географическое положение, и Satellite Finder создаст список спутниковых местоположений для этого местоположения. Обратите внимание, что для авиакомпании AB (Air Berlin) авиакомпания не возвращает локатор записей. Поскольку сумма двух углов ≠ 90°, эти два угла не дополняют друг друга.После того, как они сделали это, у них остался эффективный 90-градусный измеритель угла — надеюсь, он окажется полезным!! Радиан — это угол в центре окружности, равный радиусу окружности, когда дуга имеет длину радиуса. Если вам сказали найти наименьший положительный угол, сотерминальный с 785 градусами, вы можете использовать следующий процесс расчета, показанный ниже. 48 + 360 = 560. Угол конуса 90 градусов — это просто большой конус, который покрывает большую часть дна озера. 707. 192V4 синий, сверхлегкая ретенция, угол 0°–10°, высота 1.Остроугольный равнобедренный треугольник – это треугольник, угол при вершине которого меньше 90°, но не равен 60°. В показанном примере внутренний угол равен 90. Во-первых, обратите внимание, что часы представляют собой круг, состоящий из 360 градусов, и что каждое число представляет угол, а расстояние между ними составляет 360/12 = 30,2º до +-0. Угол на 34° больше, чем дополнительный угол. 7 мм, упаковка 4 шт. Инструменты и вспомогательные детали 046. Проверка на калькуляторе: sin(135) = 0,565 градуса, угол отражения будет равен 333.LornaGilpin — проверенный участник с 2015 года. 3 AB8714 E 15AUG 2*DUSFCO HK1 145P 345P 15AUG E AB/. Модель № 824 Страница каталога № Н/Д Просмотреть сведения о продукте. 0 в App Store, что является самым высоким результатом в списке упомянутых здесь приложений. Этот калькулятор отлично подходит для получения всей этой информации только с двух сторон прямоугольного треугольника, но это забавная задача — попытаться найти стороны, углы, площадь и периметр самостоятельно без него.
707. 192V4 синий, сверхлегкая ретенция, угол 0°–10°, высота 1.Остроугольный равнобедренный треугольник – это треугольник, угол при вершине которого меньше 90°, но не равен 60°. В показанном примере внутренний угол равен 90. Во-первых, обратите внимание, что часы представляют собой круг, состоящий из 360 градусов, и что каждое число представляет угол, а расстояние между ними составляет 360/12 = 30,2º до +-0. Угол на 34° больше, чем дополнительный угол. 7 мм, упаковка 4 шт. Инструменты и вспомогательные детали 046. Проверка на калькуляторе: sin(135) = 0,565 градуса, угол отражения будет равен 333.LornaGilpin — проверенный участник с 2015 года. 3 AB8714 E 15AUG 2*DUSFCO HK1 145P 345P 15AUG E AB/. Модель № 824 Страница каталога № Н/Д Просмотреть сведения о продукте. 0 в App Store, что является самым высоким результатом в списке упомянутых здесь приложений. Этот калькулятор отлично подходит для получения всей этой информации только с двух сторон прямоугольного треугольника, но это забавная задача — попытаться найти стороны, углы, площадь и периметр самостоятельно без него. Таблица углов и уклонов на оборотной стороне показывает углы в градусах и преобразует их в шаг на дюйм и шаг. Опорный угол угла представляет собой угол размера, образованный конечной стороной угла и горизонтальной осью.Телесный угол также можно определить как угол, образованный тремя или более плоскостями, пересекающимися в общей точке (вершине). Затем мы знаем, как каждая минута составляет 1/60 часа. Понятие угла было впервые использовано Евдемом, который определил угол. 30°-60°-90° относится к измерению угла в градусах этого типа специального прямоугольного треугольника. Это онлайн-инструмент геометрии, для которого требуются две длины сторон прямоугольника. При нагрузке на колеса все шины накачаны до нормального рабочего давления, а автомобиль, припаркованный на BellTV, может рассчитать перекос, рассчитав наклон поляризации на 86.Он-лайн измеритель угла. Локатор шага и уклона Johnson Level & Tool предназначен для плотницких, сантехнических, электрических работ или работ в области ОВКВ, требующих точного определения уклона или уклона.
Таблица углов и уклонов на оборотной стороне показывает углы в градусах и преобразует их в шаг на дюйм и шаг. Опорный угол угла представляет собой угол размера, образованный конечной стороной угла и горизонтальной осью.Телесный угол также можно определить как угол, образованный тремя или более плоскостями, пересекающимися в общей точке (вершине). Затем мы знаем, как каждая минута составляет 1/60 часа. Понятие угла было впервые использовано Евдемом, который определил угол. 30°-60°-90° относится к измерению угла в градусах этого типа специального прямоугольного треугольника. Это онлайн-инструмент геометрии, для которого требуются две длины сторон прямоугольника. При нагрузке на колеса все шины накачаны до нормального рабочего давления, а автомобиль, припаркованный на BellTV, может рассчитать перекос, рассчитав наклон поляризации на 86.Он-лайн измеритель угла. Локатор шага и уклона Johnson Level & Tool предназначен для плотницких, сантехнических, электрических работ или работ в области ОВКВ, требующих точного определения уклона или уклона. Оценок и отзывов пока нет. Он крепится к окуляру видоискателя зеркальной фотокамеры, позволяя вам смотреть вниз в опорный угол. Опорный угол — это острый угол (<90°), который можно использовать для представления угла любой величины. Например, если широта вашего города 35°, то угол наклона для лета будет 20° (35° – 15°), а для зимы 50° (35° + 15°).Гипотенуза равна половине PCD, а высота h равна половине расстояния между стержнями. Четверть окружности или прямой угол равен 90°. В этих случаях необходим сверхточный угловой искатель. Satellite Finder — это способ точного наведения спутниковых тарелок на спутники связи на геостационарной орбите. Найдите опорный угол. 048. Если вы делаете что-то вроде построения клепки или любого многостороннего предмета, отклонение всего на несколько градусов в настройке может привести к катастрофическим результатам. • две пары равных смежных сторон (a и b) • два равных угла (B и C), называемых невершинными углами.- возможность включить индикатор максимального угла.
Оценок и отзывов пока нет. Он крепится к окуляру видоискателя зеркальной фотокамеры, позволяя вам смотреть вниз в опорный угол. Опорный угол — это острый угол (<90°), который можно использовать для представления угла любой величины. Например, если широта вашего города 35°, то угол наклона для лета будет 20° (35° – 15°), а для зимы 50° (35° + 15°).Гипотенуза равна половине PCD, а высота h равна половине расстояния между стержнями. Четверть окружности или прямой угол равен 90°. В этих случаях необходим сверхточный угловой искатель. Satellite Finder — это способ точного наведения спутниковых тарелок на спутники связи на геостационарной орбите. Найдите опорный угол. 048. Если вы делаете что-то вроде построения клепки или любого многостороннего предмета, отклонение всего на несколько градусов в настройке может привести к катастрофическим результатам. • две пары равных смежных сторон (a и b) • два равных угла (B и C), называемых невершинными углами.- возможность включить индикатор максимального угла. Азимутальный угол для любого конкретного спутника может быть определен для любой точки на поверхности земли с учетом широты и долготы этой точки. Как правило, наклон подоконника необходимо определить при установке вставного окна Andersen® в качестве замены старого окна. В каждом случае один объект, обычно дерево, пильный диск или крепеж docx, 12. Простой ресурс, который я использовал в 3-м и 5-м годах и получил отличный отклик от обеих новых групп.Используя приведенный выше пример, мы имеем 2347 + 1209 + 894 = 4450 человек. В ГИС угол азимута используется для навигации или направления. Тригонометрия. Подоконники большинства продуктов Andersen® имеют наклон к внешней стороне дома. Определения слов в словарях The Collaborative International Dictionary, Wiktionary, Wikipedia Тем не менее, спецификации угла крутящего момента становятся все более и более распространенными, поэтому понимание и знание того, как правильно их использовать, станет ценным навыком в вашем умственном арсенале. По сравнению с.
Азимутальный угол для любого конкретного спутника может быть определен для любой точки на поверхности земли с учетом широты и долготы этой точки. Как правило, наклон подоконника необходимо определить при установке вставного окна Andersen® в качестве замены старого окна. В каждом случае один объект, обычно дерево, пильный диск или крепеж docx, 12. Простой ресурс, который я использовал в 3-м и 5-м годах и получил отличный отклик от обеих новых групп.Используя приведенный выше пример, мы имеем 2347 + 1209 + 894 = 4450 человек. В ГИС угол азимута используется для навигации или направления. Тригонометрия. Подоконники большинства продуктов Andersen® имеют наклон к внешней стороне дома. Определения слов в словарях The Collaborative International Dictionary, Wiktionary, Wikipedia Тем не менее, спецификации угла крутящего момента становятся все более и более распространенными, поэтому понимание и знание того, как правильно их использовать, станет ценным навыком в вашем умственном арсенале. По сравнению с. 85 КБ. Знакомство с прямыми углами — поставьте угломер рядом с углами, чтобы проверить, являются ли они прямыми, острыми или тупыми. 440° — 360° = 80° 3. В геометрии углы измеряются независимо от направления или ориентации, так как в тригонометрии мы измеряем угол вращением против часовой стрелки. Дуговая мера — это угол, который образует дуга в центре окружности, а длина дуги — это отрезок вдоль дуги. Это устройство имеет легко читаемые приращения от 0 до 90 градусов, а также V-образную канавку на кромке, которая помогает разместить трубы и кабелепроводы под углом.Заполните ниже три параметра из вашей скважины, тогда оставшийся параметр будет рассчитан автоматически. Обратите внимание, что ∠MLN теперь окрашена на диаграмме ниже. Ближе всего к отраслевому стандарту для измерения углов конуса считается точка, в которой звуковая мощность падает наполовину, как внешняя кромка… Центровочное сверло имеет угол при вершине 90 градусов, что позволяет легко вычислить глубину конуса. отверстие для точечного сверления.
85 КБ. Знакомство с прямыми углами — поставьте угломер рядом с углами, чтобы проверить, являются ли они прямыми, острыми или тупыми. 440° — 360° = 80° 3. В геометрии углы измеряются независимо от направления или ориентации, так как в тригонометрии мы измеряем угол вращением против часовой стрелки. Дуговая мера — это угол, который образует дуга в центре окружности, а длина дуги — это отрезок вдоль дуги. Это устройство имеет легко читаемые приращения от 0 до 90 градусов, а также V-образную канавку на кромке, которая помогает разместить трубы и кабелепроводы под углом.Заполните ниже три параметра из вашей скважины, тогда оставшийся параметр будет рассчитан автоматически. Обратите внимание, что ∠MLN теперь окрашена на диаграмме ниже. Ближе всего к отраслевому стандарту для измерения углов конуса считается точка, в которой звуковая мощность падает наполовину, как внешняя кромка… Центровочное сверло имеет угол при вершине 90 градусов, что позволяет легко вычислить глубину конуса. отверстие для точечного сверления. Используя линейку или рулетку, измерьте расстояние по вертикали между 2-дюймовой отметкой на угольнике и верхом подоконника.Я пытаюсь выяснить, как вычислить значение угла по заданным координатам трех точек, как показано на рисунке ниже: . Градусы угла рефлекса и градусы меньшего острого угла в сумме дают 360. T Примеры использования формулы для нахождения углов. ИРВИН. 1 МОА распространяется примерно на 1″ на 100 ярдов. • Вид камеры с кнопкой Пауза. Здесь ∠ACD — внешний угол. Точность в пределах 1/2 от 1°. Дано α: β = 90 — α. e с широтой и долготой и получить расстояние и угол пеленга направления Home Конечные углы — это углы, которые имеют одни и те же начальную и конечную стороны.Для лета угол наклона рассчитывается путем умножения широты на 0. Начиная с Garmin, этот производитель никогда не разочаровывает нас, говорим ли мы о портативных или навесных эхолотах. Верхний угол Базовые углы 30° Высота 500 Площадь 0. Запомните отклонение После того, как вы закончите это, вы можете перейти к другому U-образному соединению и повторить шаги 1-3.
Используя линейку или рулетку, измерьте расстояние по вертикали между 2-дюймовой отметкой на угольнике и верхом подоконника.Я пытаюсь выяснить, как вычислить значение угла по заданным координатам трех точек, как показано на рисунке ниже: . Градусы угла рефлекса и градусы меньшего острого угла в сумме дают 360. T Примеры использования формулы для нахождения углов. ИРВИН. 1 МОА распространяется примерно на 1″ на 100 ярдов. • Вид камеры с кнопкой Пауза. Здесь ∠ACD — внешний угол. Точность в пределах 1/2 от 1°. Дано α: β = 90 — α. e с широтой и долготой и получить расстояние и угол пеленга направления Home Конечные углы — это углы, которые имеют одни и те же начальную и конечную стороны.Для лета угол наклона рассчитывается путем умножения широты на 0. Начиная с Garmin, этот производитель никогда не разочаровывает нас, говорим ли мы о портативных или навесных эхолотах. Верхний угол Базовые углы 30° Высота 500 Площадь 0. Запомните отклонение После того, как вы закончите это, вы можете перейти к другому U-образному соединению и повторить шаги 1-3. Чтобы получить максимальную отдачу от ваших фотоэлектрических панелей, вам нужно наклонить их к солнцу. Величина вращения вокруг точки пересечения двух плоскостей (или линий), необходимая для приведения одной в соответствие с другой, называется углом.Телесный угол, соответствующий грани куба, измеренный в центре, равен 2π/3 ср. Полный круг составляет 360° (360 градусов). Базовый угол определяется как острый угол между конечной стороной данного угла и осью x. Предварительный расчет. Это позволяет пользователю проверять фокусировку, угол обзора, экспозицию и баланс белого в режиме реального времени, даже при съемке фотографий через OVF. Что касается чтения под углом, это может никогда не быть проблемой, так как дисплей переворачивается и подсвечивается, что делает чтение действительно легким.Тупоугольный равнобедренный треугольник – это треугольник, угол при вершине которого больше 90°. Найдите разницу между двумя показаниями, и это будет рабочий угол карданного шарнира. Сумма всех 5 внутренних .
Чтобы получить максимальную отдачу от ваших фотоэлектрических панелей, вам нужно наклонить их к солнцу. Величина вращения вокруг точки пересечения двух плоскостей (или линий), необходимая для приведения одной в соответствие с другой, называется углом.Телесный угол, соответствующий грани куба, измеренный в центре, равен 2π/3 ср. Полный круг составляет 360° (360 градусов). Базовый угол определяется как острый угол между конечной стороной данного угла и осью x. Предварительный расчет. Это позволяет пользователю проверять фокусировку, угол обзора, экспозицию и баланс белого в режиме реального времени, даже при съемке фотографий через OVF. Что касается чтения под углом, это может никогда не быть проблемой, так как дисплей переворачивается и подсвечивается, что делает чтение действительно легким.Тупоугольный равнобедренный треугольник – это треугольник, угол при вершине которого больше 90°. Найдите разницу между двумя показаниями, и это будет рабочий угол карданного шарнира. Сумма всех 5 внутренних . .. Угловые искатели, также известные как угломеры, представляют собой небольшие ручные инструменты, которые можно использовать для воспроизведения практически любого угла. Угол 1 + Угол 2 = 133°. Шаг лопастей играет важную роль в потоке циркуляции воздуха. Калькулятор, приведенный в этом разделе, можно использовать, чтобы узнать имя правильного многоугольника для заданного количества сторон.. ), скоба поперек внутреннего угла деревянной рамы, образующая гипотенузу и скрепляющая две боковые части вместе. 0 млн участников в сообществе whatisthisthing. 48-360 = 159. 1. 49 π 2 + 12 ( 2 π) 49 π 2 + 12 Одной из его замечательных функций является цифровой угломер ToolSmart, который может точно определить угол каждого угла. Затем выберите дробь, если она есть. Угол 70 градусов = угол среза 35 градусов. Рис. 6 ниже взят со страницы Wiki, на которой есть только эта фотография Mk 1 Mod 0. Спасибо! Выберите спутник: или введите долготу: Расположение тарелки (нажмите … Расчет конусности и угла.Легко и точно проверяйте и передавайте измерения углов с помощью компактного магнитного цифрового углового локатора Johnson.
.. Угловые искатели, также известные как угломеры, представляют собой небольшие ручные инструменты, которые можно использовать для воспроизведения практически любого угла. Угол 1 + Угол 2 = 133°. Шаг лопастей играет важную роль в потоке циркуляции воздуха. Калькулятор, приведенный в этом разделе, можно использовать, чтобы узнать имя правильного многоугольника для заданного количества сторон.. ), скоба поперек внутреннего угла деревянной рамы, образующая гипотенузу и скрепляющая две боковые части вместе. 0 млн участников в сообществе whatisthisthing. 48-360 = 159. 1. 49 π 2 + 12 ( 2 π) 49 π 2 + 12 Одной из его замечательных функций является цифровой угломер ToolSmart, который может точно определить угол каждого угла. Затем выберите дробь, если она есть. Угол 70 градусов = угол среза 35 градусов. Рис. 6 ниже взят со страницы Wiki, на которой есть только эта фотография Mk 1 Mod 0. Спасибо! Выберите спутник: или введите долготу: Расположение тарелки (нажмите … Расчет конусности и угла.Легко и точно проверяйте и передавайте измерения углов с помощью компактного магнитного цифрового углового локатора Johnson. Каждый час соответствует 30 градусам. Отрицательный котерминальный угол: 200. Если вы просверлили 0. ∠ABC, где B — заданный угол. Однако, если даны только две стороны треугольника, нахождение углов прямоугольного треугольника требует применения некоторых основных тригонометрических функций: для α. Итак, имея это в виду, чтобы определить угол для вашего соединения под углом, просто разделите угол в целом на 2! Стык под углом 90 градусов.SAS — известная длина двух сторон и прилежащего угла. Трехмерные векторы используют оси x-y-z. Он имеет диапазон измерения от 0 до 225 градусов, что и в обоих случаях. Используйте угловой видоискатель для измерения углов. Углы поворота двигателя на восток положительные, на запад отрицательные. Один стерадиан равен (180/π) 2 КАЛЬКУЛЯТОР УГЛА МНОГОУГОЛЬНИКА. Если вы хотите вычислить гипотенузу, введите значения для других сторон и угла. Решатель вычисляет площадь, стороны, углы, периметр, медианы, внутренний радиус и другие свойства треугольника.Поместите середину транспортира в вершину Угол поворота (по горизонтали), на который должна повернуться наземная параболическая антенна, чтобы указать на конкретный спутник на геостационарной орбите.
Каждый час соответствует 30 градусам. Отрицательный котерминальный угол: 200. Если вы просверлили 0. ∠ABC, где B — заданный угол. Однако, если даны только две стороны треугольника, нахождение углов прямоугольного треугольника требует применения некоторых основных тригонометрических функций: для α. Итак, имея это в виду, чтобы определить угол для вашего соединения под углом, просто разделите угол в целом на 2! Стык под углом 90 градусов.SAS — известная длина двух сторон и прилежащего угла. Трехмерные векторы используют оси x-y-z. Он имеет диапазон измерения от 0 до 225 градусов, что и в обоих случаях. Используйте угловой видоискатель для измерения углов. Углы поворота двигателя на восток положительные, на запад отрицательные. Один стерадиан равен (180/π) 2 КАЛЬКУЛЯТОР УГЛА МНОГОУГОЛЬНИКА. Если вы хотите вычислить гипотенузу, введите значения для других сторон и угла. Решатель вычисляет площадь, стороны, углы, периметр, медианы, внутренний радиус и другие свойства треугольника.Поместите середину транспортира в вершину Угол поворота (по горизонтали), на который должна повернуться наземная параболическая антенна, чтобы указать на конкретный спутник на геостационарной орбите. Стебель наклонен вверх, запишите положительным числом (+). Только обратный отсчет идет против часовой стрелки. Приблизительно определите размер вашего угла. Этот удобный маленький инструмент — самый простой способ точно определить угол наклона крыши. Углы обычно обозначаются греческими буквами, такими как θ, α, β и т. д.Расчет площади треугольника онлайн. Символом градусов является маленький кружок °. Первое, на что следует обратить внимание, это то, что выходная энергия намного меньше, чем у Феникса. Mk 1 Mod 1.9 и центральный угол 1. Эта форма используется в астрономии и для определения широты и долготы. Это удобно, потому что только тогда нам нужно запомнить значения триггерной функции для углов меньше 90°. Это угловой видоискатель с откидным дисплеем с подсветкой, функцией механической блокировки, встроенными пузырьковыми пузырьками, функцией удержания.Facebook 0. Уровень 4′ распределяет погрешность на большее расстояние и, таким образом, является более точным. Он занимает 5-е место.
Стебель наклонен вверх, запишите положительным числом (+). Только обратный отсчет идет против часовой стрелки. Приблизительно определите размер вашего угла. Этот удобный маленький инструмент — самый простой способ точно определить угол наклона крыши. Углы обычно обозначаются греческими буквами, такими как θ, α, β и т. д.Расчет площади треугольника онлайн. Символом градусов является маленький кружок °. Первое, на что следует обратить внимание, это то, что выходная энергия намного меньше, чем у Феникса. Mk 1 Mod 1.9 и центральный угол 1. Эта форма используется в астрономии и для определения широты и долготы. Это удобно, потому что только тогда нам нужно запомнить значения триггерной функции для углов меньше 90°. Это угловой видоискатель с откидным дисплеем с подсветкой, функцией механической блокировки, встроенными пузырьковыми пузырьками, функцией удержания.Facebook 0. Уровень 4′ распределяет погрешность на большее расстояние и, таким образом, является более точным. Он занимает 5-е место. Каждый градус делится на 60 минут, а каждая минута далее делится на 60 секунд. Закон касательных — Треугольники и закон касательных. Углы и градусы. SVBONY Finder Scope 5×24 с набором пластиковых аксессуаров для астрономического телескопа. Нулевой угол кастера. Выберите, что (угол/стороны) вы хотите рассчитать, затем введите значения в соответствующие строки и нажмите «Рассчитать». См. схему выше.Прямоугольный искатель представляет собой Г-образный оптический аксессуар с зеркалом или призмой, установленной под углом 45 градусов. 047″) 1 МОА — это разный размер на разных дистанциях, 8″ на 800 ярдах — это всего лишь 1 МОА. 43°. ИМПЕРИЯ 2791 по цене 5 долларов. ком. В деревянном футляре находятся позиционный угломер, по 4 батарейки типа «D» и, возможно, увлажняющая жидкость. В максимальной точке (наклон 35 градусов) в Бостоне вы можете ожидать около 7 150 кВтч в год, тогда как в Финиксе максимум составлял 9 600 кВтч в год. Представьте, что спутник находится над Южной Америкой.В полном обороте 360°.
Каждый градус делится на 60 минут, а каждая минута далее делится на 60 секунд. Закон касательных — Треугольники и закон касательных. Углы и градусы. SVBONY Finder Scope 5×24 с набором пластиковых аксессуаров для астрономического телескопа. Нулевой угол кастера. Выберите, что (угол/стороны) вы хотите рассчитать, затем введите значения в соответствующие строки и нажмите «Рассчитать». См. схему выше.Прямоугольный искатель представляет собой Г-образный оптический аксессуар с зеркалом или призмой, установленной под углом 45 градусов. 047″) 1 МОА — это разный размер на разных дистанциях, 8″ на 800 ярдах — это всего лишь 1 МОА. 43°. ИМПЕРИЯ 2791 по цене 5 долларов. ком. В деревянном футляре находятся позиционный угломер, по 4 батарейки типа «D» и, возможно, увлажняющая жидкость. В максимальной точке (наклон 35 градусов) в Бостоне вы можете ожидать около 7 150 кВтч в год, тогда как в Финиксе максимум составлял 9 600 кВтч в год. Представьте, что спутник находится над Южной Америкой.В полном обороте 360°. Угол 45 градусов. Где бы вы ни находились, IslamicFinder поможет вам определить точное направление киблы с помощью средства поиска киблы… 1b) Радиус = 3. Этот онлайн-калькулятор находит опорный угол и квадрант тригонометрического угла в стандартном положении. Подверните угол 90˚ под последним сформированным треугольником: теперь у вас есть карманный транспортир! 5. Простой калькулятор углов для прямоугольных треугольников. Оптовые шкатулки рядом со мной Гас Джонсон Sportscaster чистая стоимость Dell Inspiron 5402 i5-1135g7.3. Важная формула: Sin (q) = противоположность / гипотенуза. Например, двойной скос, указанный как 15 градусов, на самом деле представляет собой два угла по 15 градусов, или всего 30 градусов. Тем не менее, калькулятор котерминальных углов можно использовать для проверки ответов руководства Angle Pro является точным угломером и приложением уровня. 2) Длина дуги окружности равна 5. Возможности A-pro: • Точный измеритель угла с функцией памяти • Мгновенный расчет процента уклона для углов 0º … Дальномер — это устройство, которое используется для измерения расстояния между вами и целью.
Угол 45 градусов. Где бы вы ни находились, IslamicFinder поможет вам определить точное направление киблы с помощью средства поиска киблы… 1b) Радиус = 3. Этот онлайн-калькулятор находит опорный угол и квадрант тригонометрического угла в стандартном положении. Подверните угол 90˚ под последним сформированным треугольником: теперь у вас есть карманный транспортир! 5. Простой калькулятор углов для прямоугольных треугольников. Оптовые шкатулки рядом со мной Гас Джонсон Sportscaster чистая стоимость Dell Inspiron 5402 i5-1135g7.3. Важная формула: Sin (q) = противоположность / гипотенуза. Например, двойной скос, указанный как 15 градусов, на самом деле представляет собой два угла по 15 градусов, или всего 30 градусов. Тем не менее, калькулятор котерминальных углов можно использовать для проверки ответов руководства Angle Pro является точным угломером и приложением уровня. 2) Длина дуги окружности равна 5. Возможности A-pro: • Точный измеритель угла с функцией памяти • Мгновенный расчет процента уклона для углов 0º … Дальномер — это устройство, которое используется для измерения расстояния между вами и целью. Любое соотношение, которое вам наиболее удобно. Это инструмент, который сможет дать вам точность до 0,4. Заданный угол может быть в градусах или радианах. Поиск телевизионных башен Найдите каналы телевизионных станций и вещательные башни в вашем районе. Угловая минута (МОА) — это угловая единица измерения. Градусы — Минуты — Калькулятор углов секунд. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана в ассортименте… Угловой видоискатель Canon C служит двум основным целям.Что такое краевой угол? Проще говоря, угол лезвия — это угол, под которым режущая кромка врезается в боковую часть ножа, образуя острый кончик. Выдача билета в любом случае возможна. Инструмент для определения угла подоконника часто используется для определения наклона подоконника существующего окна (см. Изображение). Web Price Пожалуйста, войдите в свою учетную запись, чтобы… Angle Meter. Поиск широты и долготы. 7. Уголок (Мах. Транспортир для измерения углов. Измерение прямых, острых и тупых углов в градусах от 0° до 360° бесплатно онлайн.
Любое соотношение, которое вам наиболее удобно. Это инструмент, который сможет дать вам точность до 0,4. Заданный угол может быть в градусах или радианах. Поиск телевизионных башен Найдите каналы телевизионных станций и вещательные башни в вашем районе. Угловая минута (МОА) — это угловая единица измерения. Градусы — Минуты — Калькулятор углов секунд. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана в ассортименте… Угловой видоискатель Canon C служит двум основным целям.Что такое краевой угол? Проще говоря, угол лезвия — это угол, под которым режущая кромка врезается в боковую часть ножа, образуя острый кончик. Выдача билета в любом случае возможна. Инструмент для определения угла подоконника часто используется для определения наклона подоконника существующего окна (см. Изображение). Web Price Пожалуйста, войдите в свою учетную запись, чтобы… Angle Meter. Поиск широты и долготы. 7. Уголок (Мах. Транспортир для измерения углов. Измерение прямых, острых и тупых углов в градусах от 0° до 360° бесплатно онлайн. Вы также можете измерить окружность или расстояние… Во-первых, убедитесь, что вы правильно определили рассматриваемый угол. Радианы и четырехугольник имеют 4 вершины, 4 угла и 4 стороны. Ответ (1 из 5): Говоря простыми словами, угол лезвия известен как ШАГ. Итак, наша формула 30 (H). Итак, наша формула 30 (10) θh = 300. Расчет угла наклона (или наклона) солнечных панелей является жизненно важным аспектом фотоэлектрического проектирования. Этот универсальный столярный инструмент можно также использовать в качестве обычного уровня, Т-образного угольника или скользящего угольника.28=200. Вы также получите простой и … Цифровой Угломер — http://amzn. 8, затем нажмите «РАССЧИТАТЬ», и ваш ответ: Длина дуги = 4. Пошаговые примеры. После того, как едоки-уголки будут распечатаны, детям просто нужно вырезать область рта. Каменный памятник стоит как туристическая достопримечательность. Особенности: — Измерьте угол бокового движения. ∠MLN — это угол, образованный точками M, L и N с вершиной в точке L.
Вы также можете измерить окружность или расстояние… Во-первых, убедитесь, что вы правильно определили рассматриваемый угол. Радианы и четырехугольник имеют 4 вершины, 4 угла и 4 стороны. Ответ (1 из 5): Говоря простыми словами, угол лезвия известен как ШАГ. Итак, наша формула 30 (H). Итак, наша формула 30 (10) θh = 300. Расчет угла наклона (или наклона) солнечных панелей является жизненно важным аспектом фотоэлектрического проектирования. Этот универсальный столярный инструмент можно также использовать в качестве обычного уровня, Т-образного угольника или скользящего угольника.28=200. Вы также получите простой и … Цифровой Угломер — http://amzn. 8, затем нажмите «РАССЧИТАТЬ», и ваш ответ: Длина дуги = 4. Пошаговые примеры. После того, как едоки-уголки будут распечатаны, детям просто нужно вырезать область рта. Каменный памятник стоит как туристическая достопримечательность. Особенности: — Измерьте угол бокового движения. ∠MLN — это угол, образованный точками M, L и N с вершиной в точке L. Решение: количество сторон пятиугольника равно n = 5. ), прокатанный стержень или пластина из железа, имеющие один или несколько углов , используемый для формирования углов или соединения или поддержки сторон железной конструкции, к которой он приклепан.Виды равнобедренных треугольников. Введите центральный угол =63. Чтобы выполнить поиск, используйте название места, города, штата или адреса или щелкните место на карте, чтобы найти координаты широты и долготы. Прямо посередине положительного и отрицательного кастера находится компромисс — нулевой кастер. Магнитный локатор используется для поиска железных предметов под землей, водоемом или в слое снега. Эти услуги могут быть необходимы, если вы выздоравливаете после пребывания в больнице, имеете инвалидность или хроническое заболевание, или если вам требуется уход, социальные услуги или помощь в повседневной жизни на постоянной основе.Моя единица — единица Mk 1 Mod 1. Видеть . Расположите его на воображаемых 12 часах, затем на 3, 6 и 9, твердо фиксируя эти углы в уме.
Решение: количество сторон пятиугольника равно n = 5. ), прокатанный стержень или пластина из железа, имеющие один или несколько углов , используемый для формирования углов или соединения или поддержки сторон железной конструкции, к которой он приклепан.Виды равнобедренных треугольников. Введите центральный угол =63. Чтобы выполнить поиск, используйте название места, города, штата или адреса или щелкните место на карте, чтобы найти координаты широты и долготы. Прямо посередине положительного и отрицательного кастера находится компромисс — нулевой кастер. Магнитный локатор используется для поиска железных предметов под землей, водоемом или в слое снега. Эти услуги могут быть необходимы, если вы выздоравливаете после пребывания в больнице, имеете инвалидность или хроническое заболевание, или если вам требуется уход, социальные услуги или помощь в повседневной жизни на постоянной основе.Моя единица — единица Mk 1 Mod 1. Видеть . Расположите его на воображаемых 12 часах, затем на 3, 6 и 9, твердо фиксируя эти углы в уме. Правильный ответ: 2 * 30 = 60 градусов. 3° от значения Белла. Второй способ более точен и эффективен. Оптимальный угол меняется в течение года, в зависимости от времени года и вашего местоположения. Хотя в современных автомобилях нулевой кастер лучше, чем отрицательный, он далек от совершенства. Найдите положительный угол, меньший 2π 2 π и котерминальный с 49π 2 49 π 2.doc, 30. Преобразования выполняются с использованием коэффициента преобразования. На мобильном устройстве появится кнопка. Итак, в этой статье мы познакомимся с тем, что такое пеленг и вычислим угол между двумя точками. com/shop/thefabforums*Как партнер Amazon, я … none Калькулятор углов — найдите угол, учитывая углы Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Используйте свои математические знания KS2, чтобы победить зло. Угловой искатель и угловой датчик на вашей пиле показывают «0°», когда пила настроена на рез под углом 90°! В новом Angle Finder есть и другие функции.Угол — это термин, используемый в геометрии и тригонометрии и определяемый как фигура, образованная двумя пересекающимися линиями.
Правильный ответ: 2 * 30 = 60 градусов. 3° от значения Белла. Второй способ более точен и эффективен. Оптимальный угол меняется в течение года, в зависимости от времени года и вашего местоположения. Хотя в современных автомобилях нулевой кастер лучше, чем отрицательный, он далек от совершенства. Найдите положительный угол, меньший 2π 2 π и котерминальный с 49π 2 49 π 2.doc, 30. Преобразования выполняются с использованием коэффициента преобразования. На мобильном устройстве появится кнопка. Итак, в этой статье мы познакомимся с тем, что такое пеленг и вычислим угол между двумя точками. com/shop/thefabforums*Как партнер Amazon, я … none Калькулятор углов — найдите угол, учитывая углы Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Используйте свои математические знания KS2, чтобы победить зло. Угловой искатель и угловой датчик на вашей пиле показывают «0°», когда пила настроена на рез под углом 90°! В новом Angle Finder есть и другие функции.Угол — это термин, используемый в геометрии и тригонометрии и определяемый как фигура, образованная двумя пересекающимися линиями. Преобразуйте единицы измерения углов, введя значение для преобразования, а также единицы измерения «от» и «до». Инструментом Angle®, как показано на фото справа, измерьте угол, который задняя часть коронки образует с нижним задним краем коронки. Снимите карданный вал. Согласно различным оценкам и комментариям, Angle Meter кажется самым надежным приложением. Выровняйте лезвие под любым заданным углом на бумаге или обрезках дерева или поверните лезвие, чтобы оно соответствовало углу на дереве.Общие инструменты 822 правила цифрового углового искателя. Угол наклона коронной пружины Прочтите угол здесь. 499 долларов. Чтобы ввести значение, щелкните внутри одного из текстовых полей. Шаг 3. Тем не менее, калькулятор секущих функционирует для автоматического следования этой формуле. Эта точка половинной мощности (-3 дБ) является стандартом для электронной промышленности, и большинство производителей измеряют угол конуса таким образом, но некоторые используют точку -10 дБ, где мощность составляет 1/10 мощности по центральной оси.
Преобразуйте единицы измерения углов, введя значение для преобразования, а также единицы измерения «от» и «до». Инструментом Angle®, как показано на фото справа, измерьте угол, который задняя часть коронки образует с нижним задним краем коронки. Снимите карданный вал. Согласно различным оценкам и комментариям, Angle Meter кажется самым надежным приложением. Выровняйте лезвие под любым заданным углом на бумаге или обрезках дерева или поверните лезвие, чтобы оно соответствовало углу на дереве.Общие инструменты 822 правила цифрового углового искателя. Угол наклона коронной пружины Прочтите угол здесь. 499 долларов. Чтобы ввести значение, щелкните внутри одного из текстовых полей. Шаг 3. Тем не менее, калькулятор секущих функционирует для автоматического следования этой формуле. Эта точка половинной мощности (-3 дБ) является стандартом для электронной промышленности, и большинство производителей измеряют угол конуса таким образом, но некоторые используют точку -10 дБ, где мощность составляет 1/10 мощности по центральной оси. Четырехугольник может быть правильным и неправильным. Twitter 0. General Tools TS02 может легко определить и определить точный угол угла до 225 градусов.5 градусов — почти квадрат. Узнайте, в каком квадранте находится ваш угол от 0° до 90° — первый от 90° до 180° — второй от 180° до 270° — третий от 270° до 360° — четвертый В этом примере угол находится в первом квадранте. Каждый из этих датчиков делает одно и то же; они просто делают это совершенно по-разному. в то время как края V-образной канавки идеально подходят к трубе и кабелепроводу. Отверстие диаметром 25 футов и требуется 0. Это означает, что ортогональная виртуальная «коробка», которая окружает линию, имеет стамески Sharpen с углом скоса 25 ° для достижения наилучших результатов.Инструмент 18 дюймов является инструментом минимальной длины для измерения ваших угловых углов, а инструмент 7 дюймов будет использоваться для измерения угла пружины коронки и углов, для которых 18-дюймовый инструмент слишком длинный. Его надкорешковая конструкция дает вам выбор прямой стойки, уголки 10° и 20° для размещения расходящихся корней, а также специальную версию с приливом 5° от широты.
Четырехугольник может быть правильным и неправильным. Twitter 0. General Tools TS02 может легко определить и определить точный угол угла до 225 градусов.5 градусов — почти квадрат. Узнайте, в каком квадранте находится ваш угол от 0° до 90° — первый от 90° до 180° — второй от 180° до 270° — третий от 270° до 360° — четвертый В этом примере угол находится в первом квадранте. Каждый из этих датчиков делает одно и то же; они просто делают это совершенно по-разному. в то время как края V-образной канавки идеально подходят к трубе и кабелепроводу. Отверстие диаметром 25 футов и требуется 0. Это означает, что ортогональная виртуальная «коробка», которая окружает линию, имеет стамески Sharpen с углом скоса 25 ° для достижения наилучших результатов.Инструмент 18 дюймов является инструментом минимальной длины для измерения ваших угловых углов, а инструмент 7 дюймов будет использоваться для измерения угла пружины коронки и углов, для которых 18-дюймовый инструмент слишком длинный. Его надкорешковая конструкция дает вам выбор прямой стойки, уголки 10° и 20° для размещения расходящихся корней, а также специальную версию с приливом 5° от широты. Это собственно искатель угла, транспортир, уровень и вычислитель разреза. Первая и наиболее часто используемая цель — создать более удобный угол обзора при съемке камерой низко или под неудобным углом (например, при съемке… Правильный ответ: 60 градусов.Чтобы рассчитать правильный угол скоса для отделочных молдингов, просто разделите это показание угла на 2. Широта и долгота — это единицы, представляющие координаты в географической системе координат. Я покажу вам, как найти его через арксинус и арккосинус. Не подвержен влиянию магнитных полей, холода или тепла. И если вы развернете свой угол 60˚, вы удвоите его, что даст вам… Поля «Угол 3» и «Угол С» НЕ могут быть изменены пользователем. Это приложение может измерять любую форму или угол наклона. Одним из важнейших параметров, измеряющих оптические свойства среды, является показатель преломления (или показатель преломления).Угол пружины короны = 180. Если угол неизвестен, но известны длины прилежащей стороны и гипотенузы прямоугольного треугольника, то вычисление косинуса можно выполнить, разделив прилежащую сторону на гипотенузу (сторона c по формуле рисунок выше).
Это собственно искатель угла, транспортир, уровень и вычислитель разреза. Первая и наиболее часто используемая цель — создать более удобный угол обзора при съемке камерой низко или под неудобным углом (например, при съемке… Правильный ответ: 60 градусов.Чтобы рассчитать правильный угол скоса для отделочных молдингов, просто разделите это показание угла на 2. Широта и долгота — это единицы, представляющие координаты в географической системе координат. Я покажу вам, как найти его через арксинус и арккосинус. Не подвержен влиянию магнитных полей, холода или тепла. И если вы развернете свой угол 60˚, вы удвоите его, что даст вам… Поля «Угол 3» и «Угол С» НЕ могут быть изменены пользователем. Это приложение может измерять любую форму или угол наклона. Одним из важнейших параметров, измеряющих оптические свойства среды, является показатель преломления (или показатель преломления).Угол пружины короны = 180. Если угол неизвестен, но известны длины прилежащей стороны и гипотенузы прямоугольного треугольника, то вычисление косинуса можно выполнить, разделив прилежащую сторону на гипотенузу (сторона c по формуле рисунок выше). Независимо от того, есть ли у вас три стороны треугольника, две стороны и угол или только два угла, этот инструмент является решением ваших проблем с геометрией. в алгебре угол подвески (x) необходим для нахождения y (теплоты мяса) при условии, что максис оси (график в виде y=mx+b) и гравитация полости (решение неравенств) остаются постоянная 2.T Ручные транспортиры можно использовать для измерения углов, но они считаются менее точными, чем цифровые транспортиры. Диапазон: +/- 180 градусов; 8. Поскольку спутник находится над экватором, чем дальше от экватора вы находитесь (чем больше число вашей широты), тем меньше будет ваш угол. Чтобы найти угол, котерминальный другому, вы можете сделать это, просто добавив или вычтя любое число, кратное 360 градусам или 2 пи радианам. Опять же, этот калькулятор прямоугольного треугольника работает, когда вы заполняете 2 поля углами треугольника или сторонами треугольника.Магнитные азимутальные пеленги являются приблизительными. 99 17 долларов. • Угол копирования в градусах и радианах Угол заголовка — это угол между солнечными панелями и землей.
Независимо от того, есть ли у вас три стороны треугольника, две стороны и угол или только два угла, этот инструмент является решением ваших проблем с геометрией. в алгебре угол подвески (x) необходим для нахождения y (теплоты мяса) при условии, что максис оси (график в виде y=mx+b) и гравитация полости (решение неравенств) остаются постоянная 2.T Ручные транспортиры можно использовать для измерения углов, но они считаются менее точными, чем цифровые транспортиры. Диапазон: +/- 180 градусов; 8. Поскольку спутник находится над экватором, чем дальше от экватора вы находитесь (чем больше число вашей широты), тем меньше будет ваш угол. Чтобы найти угол, котерминальный другому, вы можете сделать это, просто добавив или вычтя любое число, кратное 360 градусам или 2 пи радианам. Опять же, этот калькулятор прямоугольного треугольника работает, когда вы заполняете 2 поля углами треугольника или сторонами треугольника.Магнитные азимутальные пеленги являются приблизительными. 99 17 долларов. • Угол копирования в градусах и радианах Угол заголовка — это угол между солнечными панелями и землей. Инструменты для определения угла и транспортиры можно использовать в различных условиях. Напомним, что синус угла тета, обозначаемый как «синтета», представляет собой сторону, противоположную тета, деленную на гипотенузу треугольника. Проблема с этим методом заключается в том, что… Этот калькулятор солнечного угла подскажет вам оптимальный угол, чтобы получить максимальную отдачу от вашей системы.Вычисление трехмерного векторного угла. 3 степени. — универсальное приложение работает на iPad, iPhone и iPod touch. Его можно отобразить тремя разными способами: 100% поле зрения, 2. В этом случае 2 π 2 π нужно вычесть 12 12 раз. Поскольку полный оборот Земли происходит за 24 часа, то же самое происходит и с Полярной звездой. пример 1250 в радианах второй ввод в виде дроби от π: Пример 27/5 π или 1. Используя этот калькулятор, мы поймем алгоритм того, как найти периметр, площадь и длину диагонали прямоугольника.(329) Написать отзыв. + Добавить в мой список. Каким будет зенитный угол, если угол возвышения Солнца равен 38? Использование калькулятора опорного угла и квадранта Насадка (круглая, ввинчиваемая) Производство ДР-3 прекращено.
Инструменты для определения угла и транспортиры можно использовать в различных условиях. Напомним, что синус угла тета, обозначаемый как «синтета», представляет собой сторону, противоположную тета, деленную на гипотенузу треугольника. Проблема с этим методом заключается в том, что… Этот калькулятор солнечного угла подскажет вам оптимальный угол, чтобы получить максимальную отдачу от вашей системы.Вычисление трехмерного векторного угла. 3 степени. — универсальное приложение работает на iPad, iPhone и iPod touch. Его можно отобразить тремя разными способами: 100% поле зрения, 2. В этом случае 2 π 2 π нужно вычесть 12 12 раз. Поскольку полный оборот Земли происходит за 24 часа, то же самое происходит и с Полярной звездой. пример 1250 в радианах второй ввод в виде дроби от π: Пример 27/5 π или 1. Используя этот калькулятор, мы поймем алгоритм того, как найти периметр, площадь и длину диагонали прямоугольника.(329) Написать отзыв. + Добавить в мой список. Каким будет зенитный угол, если угол возвышения Солнца равен 38? Использование калькулятора опорного угла и квадранта Насадка (круглая, ввинчиваемая) Производство ДР-3 прекращено. 5 дюймов. Это происходит, когда солнечные панели расположены перпендикулярно падающим солнечным лучам. Угол 135° имеет опорный угол 45°, поэтому его грех будет таким же.Зубила следует использовать только для ручной работы, никогда не бить молотком. Cos ( q ) = Смежный / Гипотенуза. Пример одного бронирования AB: 2 AB7431 E 14AUG 1*LAXDUS HK1 515P 100P 15AUG E AB/. Это означало бы, что на дюйм приходится 24 нити. Единицей телесного угла в системе СИ является стерадиан (ср). Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Звуковые волны распространяются постоянно расширяющейся волной. Добавить в корзину. Найдите опорный угол (49pi)/2.Мини-угломер lytool, цифровой уровень, угловой датчик, инструмент для измерения угла, угломер, транспортир, алюминиевая рама с мощным магнитом, быстро считывающим данные. T Инструменты для определения угла и транспортиры можно использовать в различных условиях. Большинство угловых искателей работают только на верхней стороне крыши. 4 : 12. Если они вам нужны, вот таблицы формул триггерного треугольника. Калькулятор угла треугольника также доступен для расчета только угла. Он имеет автоматическую подсветку ЖК-дисплея для лучшей видимости и держите угломер параллельно чистому листу бумаги для рисования.Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб». 49π 2 49 π 2. Вы просто делите диаметр просверленного отверстия. Искатель — это дополнительный прицел, который используется для определения местоположения объектов в основном телескопе; 3 винта с накатанной головкой позволяют регулировать положение по осям XY для точного выравнивания телескопа. Какие бывают виды четырехугольников? В геометрии есть несколько типов четырехугольников. Калькулятор угла обзора спутника. Этот сервис предоставляет координаты, чтобы помочь вам найти геостационарные спутники, в первую очередь для тех, кто устанавливает и наводит спутниковые антенны.0087. Турист ложится на землю в метрах от памятника, наводит камеру на вершину памятника, на дисплее камеры появляется надпись «РАССТОЯНИЕ — МЕТРЫ». Пример 1. Найдите пятый внутренний угол пятиугольника, если четыре его внутренних угла равны 108°, 120°, 143° и 97°. — измерить угол вертикального движения. Затем приложите ваш угломер к соответствующему … 40-0912 англ. Здесь ось x равна (0) нулю градусов, а ось y равна 90 градусам. Шаг № 3: Введите три известных значения.от нуля до 3 фильтров на устройстве и карманах для фильтров. Используйте магнитный угловой локатор Johnson, чтобы обеспечить точные измерения углов в вашем следующем проекте. В данном месте наш калькулятор отличается на 2. Прямоугольный видоискатель 8×50 облегчает поиск слабых объектов без напряжения спины и шеи. Большая апертура 50 мм позволяет вам перемещаться по более слабым звездам и напрямую видеть многие объекты глубокого космоса. Ориентация изображения показывает вид неба, который соответствует большинству звездных карт. Щедрый 5. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана различных размеров, как вращательные, так и цифровые.с функцией блокировки угла пользователь может повысить точность и сэкономить время. Представлен калькулятор, использующий закон Снеллиуса для расчета угла преломления и критического угла полного внутреннего отражения. Популярный онлайн-калькулятор треугольников Math Warehouse: введите любую допустимую комбинацию сторон/углов (3 стороны, 2 стороны и угол или 2 угла и 1 сторона), а наш калькулятор сделает все остальное! Он даже сообщит вам, можно ли создать более 1 треугольника. Шаг № 4: Нажмите кнопку «Решить», которая решит недостающие стороны и/или углы, покажет шаги, предпринятые для решения треугольника, и, если у вас есть веб-браузер, совместимый с HTML5, нарисуйте треугольник.Я знаю, как вычислить угол по длине основания треугольника и его высоте, но в этом случае я застрял. Два угла являются дополнительными, если их сумма равна 90°, и дополнительными, если их сумма равна 180°. В то время как многие угловые искатели имеют циферблат и стрелку, используемые для расшифровки угла, цифровой угловой искатель использует питание от батареи для отображения результатов в цифровом виде. Иногда нужно измерить углы, а транспортира под рукой нет. Точная митра … Широкоугольный эхолот с щебетанием помогает обеспечить расширенный охват всего, что происходит под водой.Его конструкция обеспечивает максимальную точность и эффективность, функцию обратного угла и функцию блокировки угла. В некоторых приложениях пользователю может потребоваться ввести местоположение, после чего компас покажет направление киблы (относительно ИСТИННОГО севера, а не относительного). решение для нахождения точных углов и степени изгиба с легкостью Зная коэффициент преобразования, преобразование между единицами может стать простой проблемой умножения: S * C = E Спутниковый искатель с магнитным севером, азимутом и калькулятором высоты.Угол 1 + Угол 2 = 130° + 3°. 200 Руководство по измерению углов LOCATOR® Калькулятор эталонного угла. Определение меры дуги. Дуга – это отрезок окружности по окружности. 5*57. Это горизонтальный и вертикальный углы, которые легче всего прочитать и перенести на бумагу или холст. Таблица различий. 1 градус, в то время как для бытовых или домашних проектов может быть разрешено до +/- 0. Цифровой дисплей теперь покажет вам угол для внутреннего угла. Три наиболее распространенных типа угловых датчиков используются в лесном хозяйстве, деревообработке и машиностроении.Инструмент для определения угла также можно использовать для измерения уклона тротуара или проезжей части, а также для определения угла наклонной поверхности (например, для кухни). . Поверните приводной вал на 90° и повторите шаг 1. Быстро и легко находите углы с помощью этого многоцелевого угломера. Существует четыре типа равнобедренных треугольников: остроугольные, тупоугольные, равносторонние и прямоугольные. Список телестанций (сортируемая таблица). 3250 об/мин, что тоже вполне нормально для такого размера.Поверните шестерню так, чтобы колпачки крестовины на вилке были направлены вверх и вниз. Время диагностики авторемонта и стоимость работ зависят от местоположения, марки и модели автомобиля и даже от типа вашего двигателя. Bosch Digital Angle Finder GAM 220 MF — следующий лучший транспортир для деревообработки, поскольку он состоит из четырех инструментов в одной форме. Например: theta=arcsin(b/c) и theta=arccos(a/c) Для нахождения тета можно использовать любую из шести стандартных тригонометрических функций. Поиск уклона крыши. Для расчета либо расстояния между шпильками, либо диаметра делительной окружности колес транспортного средства, 4,5,6 шпильки, когда известен только один.Нет. Он достаточно хорошо сконструирован, поставляется с адаптерами, и за то количество раз, когда он используется, он имеет хорошую ценность. Если у вас есть объект, и вы не знаете, что это такое, это место для вас, чтобы найти … Угол азимута или угол азимута или направление курса — Рассчитать угол азимута по двум точкам i. 5-кратное увеличение для критической фокусировки центральной части изображения одним щелчком переключателя. 5. ПОКУПКА СОВЕТА. 5 КБ. Это читается как «34 градуса 24 минуты 16. Что такое магнитный локатор? Многие геодезисты и городские служащие используют магнитный локатор, потому что они видят, что его использует другой отдел или кто-то, кто занимается этим в течение длительного времени.Tan ( q ) = напротив / рядом. Цифровой угловой видоискатель, размер 2-5/32 дюйма, ЖК-дисплей (фактически 1. Угловой видоискатель — отличный инструмент для измерения углов и для воспроизведения угла существующей области. 031 ‘фаска на отверстии, диаметр, который нужно определить будет 0. С точностью до градуса, под каким углом находится солнце относительно горизонта? Извините, что не согласен с Майком В., но я дешево купил угловой видоискатель Seagull на Ebay. Точность 3º в зависимости от вашего устройства. Полезно. Эта уникальная антенна указывающее программное обеспечение взаимодействует непосредственно с картами Google, чтобы обеспечить обзор вашего местоположения с высоты птичьего полета с помощью … «Satellite Finder Online (PHP)» (далее SFO) — это веб-версия моего популярного Java-приложения «Satellite Finder».Цифровой транспортир идеально подходит для нахождения углов в узких местах. 8 дюймов 11π 3 11 π 3. Логотип университета Санто-Томас; техасская самостоятельная охота на оленей; магистр управления государственными финансами, магнитный угловой локатор Джонсона. Двойные искатели луча — единственные, которые позволяют вам выбирать, хотите ли вы более широкий или более узкий обзор того, что находится под вами. Нажмите, чтобы увидеть больше шагов. Вычтите 2 π 2 π из 11 π 3 11 π 3. Эта мера угла может быть выражена в радианах или градусах, и мы можем легко преобразовать их по формуле π r a d i an s = 180 °.С точностью тесно связана функция блокировки. Большинство автомастерских берут от 75 до 150 долларов в час. Нулевой кастер возникает, когда ваш верхний шаровой шарнир или крепление стойки находятся прямо на одной линии с нижним шаровым шарниром. Вычитание угла, который мы только что нашли, из 180°, а затем вычитание нашего известного прямого угла (90°) также даст нам третий угол. Поле зрения в 4 градуса позволяет легко различать более тусклые звезды-ориентиры. Включает скобу, ласточкин хвост… Если задан один угол треугольника и две стороны, возможно существование двух треугольников при одинаковых размерах.Для осени или весны вы можете просто вычесть 2. Углы измеряются в градусах. • Горизонтальные и вертикальные линии отвеса (нажмите, чтобы привязать ближайший маркер к линии, дважды нажмите, чтобы отслеживать, нажмите еще раз, чтобы отпустить). 59 17 долларов. Используя их угол наклона, мы получаем силу сигнала 87 % на 91° и 67 % на 82° с пиком, используя 91. есть 12 часов, каждый час представляет 360/12 = 30 градусов. Телесный угол полной сферы равен 4π ср.Справочные углы также можно использовать для нахождения координат точки на окружности. Хотя дальномерная технология довольно широко используется в военных сценариях (где цены могут легко достигать сотен тысяч долларов) для охоты с луком за пределами 20 ярдов, мы говорим здесь конкретно о дальномерах для гольфа. 9°. Сложите числа, которые вы нашли на шаге 1, чтобы найти общее количество. Калькулятор автоматически применяет правила, которые мы рассмотрим ниже. β – угол между u и … Косинусы углов между прямой и осями X,Y,Z равны i,j,k соответственно.Турист хочет поймать солнце под правильным углом, чтобы «сидеть» на вершине столба. Предупреждение о безопасности: результаты на этой странице могут быть ошибочными. Широта и долгота не предназначены для слепой навигации самолетов, кораблей или других транспортных средств. Нужно взять прямоугольный треугольник, тогда секанс угла α будет равен длине гипотенузы c, которая будет делиться на прилежащую сторону b. Нужна коррекция угла на вашем локаторе? Если вкладыши быстро изнашиваются, проблема может заключаться в отсутствии расхождений.AB в настоящее время использует 1A перевозчика. Цифровой транспортир идеален. The Husky 5 дюймов. 99. Мобильные приложения компаса направления киблы онлайн, как правило, автоматически определяют текущее местоположение (в сети), а затем показывают направление молитвы, как в случае с мобильным приложением HalalTrip. Угловая шкала. Если у вас есть место, угловой MUA — отличный вариант. Если стержень имеет наклон вниз, запишите его как отрицательное число (-). Углы можно классифицировать тремя способами: острыми, тупыми и прямыми. МОА составляет 1/60 градуса.T Basic Angle Finder в популярных приложениях App Store. ПРИСОЕДИНЕНИЕ К ИМПЛАНТАТУ Приспособление для имплантата LOCATOR с запатентованным поворотом Указанный угол может быть в градусах или радианах. 6 центральный угол 63. Угломер измеряет угол неподвижного или обрабатываемого объекта по отношению к более крупному объекту. Некоторые из них перечислены ниже в таблице с картинками. • отсутствие параллельных сторон. 0 360 90 180 270 45 135 225 315 Угломер Введите угол в градусах. Угол подвески. Часовой угол — это координаты формата времени для Polaris.Используя этот веб-сайт, вы соглашаетесь с нашей Политикой использования файлов cookie. Этот веб-сайт стал возможен благодаря показу онлайн-рекламы нашим посетителям. Карта вещательных башен Путь прямой видимости к башням. Резьба крепежа SAE измеряется в витках на дюйм. Шаг 1: Введите время в числовом формате. Большинство двигателей настроены на 3 градуса — когда вы посмотрите сбоку на впускной коллектор карбюраторного двигателя, вы заметите, что в коллекторе есть клин. 100 ярдов. Значение a должно быть выражено в градусах. Как преобразовать единицы углов.Угловой определитель трансмиссии: избавьтесь от догадок при настройке шасси с помощью этого удобного трехэтапного инструмента! Используя ваш смартфон в качестве измерительного устройства, приложение рассчитает каждый угол U-образного шарнира и предоставит общий рабочий угол трансмиссии с ответом Pass/Fail. Двигатель, угол наклона шестерни и высота дорожного просвета зависят от земли. Спасибо за ваш отзыв. Например, цифры выше: A: (2347/4450) (360) = 189. Другая рука поворачивается, чтобы соответствовать соответствующему углу, и фиксируется на месте.А в 2:00 минутная стрелка находится на 12, а часовая на 2. Новая версия также имеет изящную скользящую удлиняющую ножку, которая очень удобна, когда вам нужно прочитать рефлекторный угол. более 180 градусов, вы относите его как часть круга. 0 час работы. Описание. 415 LOCATOR® Core Tool, трехкомпонентный, длина 100 мм Нержавеющая сталь 046. Угол C и угол 3 не могут быть введены. Острые углы узкие (менее 90 градусов), тупые углы широкие (более 90 градусов), а прямые углы составляют ровно 90 градусов (две линии перпендикулярны друг другу).1 радиан = 57. Это всегда наименьший угол (относительно оси х), который может … Поместите угломер на крышку подшипника и запишите показания. 25x, to 2. Я большой поклонник того факта, что этот эхолот предлагает 4000 предварительно загруженных озер США, уже нанесенных на карту. ЕСЛИ вы работаете с пластиковой трубой, она редко бывает «прямой», поэтому ваш цифровой уровень или эхолот только собираюсь измерить уклон 12-дюймовой секции трубы, если вы не «скользите» по ВСЕЙ длине трубы. Как определить угол двигателя/шестерни.Pinterest 0 Особенности. Шаг может отличаться от одного вентилятора к другому. Обзор продукта. Этот эхолот предлагает несколько изображений «картинка в картинке», чтобы показать вам эхолот, живые изображения, а также картографию и GPS. Этот инструмент легко и четко отображает углы в градусах от 0° до 90° как в абсолютных, так и в относительных измерениях, что позволяет выполнять вашу работу быстрее и точнее. Угловой искатель Husky 5 дюймов. Поместите угловой искатель на нижнюю часть карданного вала и запишите показания. Этот калькулятор используется для сложения и вычитания углов в форме Градусы — Минуты — Секунды (DMS).Установите угломер на лицевую сторону вилки, где проходят U-образные болты. Остальное мы можем найти, сначала найдя опорный угол. Ваша тарелка должна быть направлена ниже, чтобы нацелиться на спутник. Любой угол в координатной плоскости имеет опорный угол в диапазоне от 0° до 90°. Полуокружность или прямой угол равен 180°. Если вы считаете, что цвет угла полезен, вы можете использовать маркеры или маркеры всякий раз, когда используете транспортир для измерения углов на бумаге. 417 для трещотки, длинной, 21 мм 048.Поскольку сумма двух углов ≠ 180°, эти два угла не являются дополнительными. Равнобедренный равнобедренный треугольник – это треугольник, угол при вершине которого равен 60°. Введите значения уклона крыши в дюймах на фут подъема. 18. Всякий раз, когда речь заходит о самых продвинутых эхолотах, просто нельзя игнорировать такие бренды, как Garmin, Humminbird или Lowrance. В общем, производители наклоняют 5-10 градусов для обычного вентилятора и 30…40-0912 для английского. На этой странице вы можете рассчитать ближайшие котерминальные углы для заданного угла.Измерьте угол с помощью небольшого рычага из нержавеющей стали, который плавно скользит для точного выравнивания. Если этот угол известен, запишите и его. Вот более подробное объяснение того, как работает сонар. Закон синусов — вычислить углы в общем треугольнике. Удобный инструмент для расчета длин крыш, углов резки, лестницы Угол — это мера поворота, измеряемая в градусах или °. Опорные углы можно использовать для нахождения синуса и косинуса исходного угла. Google+ 0. Для определения внутренних и внешних углов стен используется цифровой угломер gemred … 1.Шаг 3: Исполни свои мечты о геометрии! созданный. Нажмите, чтобы увидеть больше шагов. Вычтите 2 π 2 π из 49 π 2 49 π 2, пока угол не окажется между 0 0 и 2 π 2 π. Чтобы найти угол пружины короны, вычтите измеренный угол из 180°. Угловой транспортир DASCO PRO отлит из ударопрочного пластика и позволяет пользователю мгновенно и точно определять любой угол в диапазоне от 0° до 90° в любом квадранте. Mk 1 Mod 0. Чтобы использовать калькулятор опорного угла, просто введите любой угол в поле угла, чтобы найти его опорный угол, который является острым углом, соответствующим введенному углу.Точка, где встречаются эти линии (или сегменты линий), известна как … Углы и градусы. Другие сканеры обычно используют только 20-градусный угол, когда дело доходит до их волн. α — угол между u и осью x. пдф; 40-0912 Испанский. См. также приложение My Bus Sl. —Рыцарь. Когда вы включаете WiFi-вызовы, вам будет предложено зарегистрировать Выберите SSS, SAS, SSA, ASA или AAS, чтобы указать известные значения треугольника. Если вы профессиональный установщик тарелок и планируете быть в поле в то время, когда вам нужна информация для наведения, вы можете… Угол, под которым заточен ваш нож, является важным шагом в процессе заточки и понимания того, как сохранить ваш нож острым. .312’. съемный протез, корневой аттачмент LOCATOR обеспечивает большую универсальность. Нажмите кнопку «Рассчитать», чтобы найти все неизвестные переменные. Транспортир, или угломер, который поставляется с машиной, по сути представляет собой траммель, который перемещает центральную ножку прямо пропорционально внешним ножкам и делит пополам большинство углов, с которыми я сталкиваюсь; тупой или острый. ПРИМЕЧАНИЕ. Некоторые производители штока указывают угол штока, ориентируясь на рулевую колонку. Чтобы найти направляющие косинусы линии, которая начинается в (x1,y1,z1) и заканчивается в (x2,y2,z2), тогда расстояние (D) между двумя точками делится само на себя, чтобы стать единицей длины (1) .Как настроить и навести спутниковую тарелку, навести искатель и углы наведения, а также настроить полярную монтировку. В этом типе прямоугольного треугольника стороны, соответствующие углам 30°-60°-90°, имеют соотношение 1:√3:2. Более узкие углы (например, 20 градусов) лучше всего подходят для ловли на большой глубине. Получите угол и дальность до башни, мощность сигнала и полосу частот. Поскольку его также можно использовать с поддержкой ручной фокусировки, в режиме OVF возможна точная фокусировка. Угол стропа может снизить грузоподъемность всего снаряжения из-за натяжения стропа.Другой угол, который вы можете найти, равен 75°, потому что 45° + 30° = 75°. Автор сообщения Автор: ; Для какого теста требуется образец почвы с нарушенной датой после даты; как тестировать форсунки дизельного топлива, как использовать магнитный угловой локатор Джонсона, как… Торговец информацией о криптографии и блокчейне. Он определяется по отношению к должному. Аналоговый угловой видоискатель очень плохо читается с такими близкими числами, и Спайсер даже рекомендует округлять углы до ближайшей четверти градуса, поэтому аналоговые угловые указатели кажутся недостаточными для этой задачи.Он поставляется с отличным маленьким футляром, необходимым для защиты точного инструмента. Стоимость диагностики кода C0051 HONDA составляет 1. Отрегулируйте этот инструмент для измерения углов для столярных работ, ослабив контргайку на угловом угольнике. Углы измеряются в градусах, символом градусов является маленький кружок ° Полный круг равен 360° (360 градусов) Полукруг или прямой угол равен 180° (180 градусов) Четверть круга или прямой угол равен 90°( 90 градусов) Как измерить угол транспортиром. Условия измерения угла – градус °, радиан или град.да, вам все еще нужно встать на колени для этих ударов снизу, но это лучше, чем лежать в грязи или воде, особенно для такого старого черепка, как я. 6, затем нажмите кнопку «ГРАДУСЫ». Например, если вам нужно найти недостающие стороны и углы треугольника, если угол A равен 19 градусам, длина стороны a равна 45, а длина стороны b равна 44, вы можете начать с использования закона синусов, чтобы найти угол B. Просто задайте его. на крыше или на нижней стороне стропила и прочтите датчик. Продолжим пример, если меньший острый угол равен 26.ДОПОЛНИТЕЛЬНЫЕ ФУНКЦИИ. Использование полностью на ваше усмотрение. Угол больше, чем полный угол 360°, поэтому вам нужно вычесть общий угол, пока он не станет маленьким. КАЙТ КАЛЬКУЛЯТОР. Умеет измерять углы с +-0. В приведенном выше примере этот угол будет (34 * … Примеры предварительного расчета. 5-кратное увеличение и 6-кратное увеличение. 27 января 2022 г. характеристики стабильной экосистемы. Комментарии отключены. 67 радиан. Год 2 находит прямые углы в формах. Рассмотрено 19 мая. 2015 г. Звоните: 732-505-2273.Для определения внутренних и внешних углов на углах стен цифровой угломер GemRed является достойным вариантом, особенно для начинающих.- возможность калибровки (обнуления) — возможность сброса гироскопа. Он не имеет ошибок и может работать в автономном режиме. Вот почему его часто используют столяры и установщики отделки жилых помещений. Basic Angle Finder в популярных приложениях App Store. Найдите направление киблы прямо из вашего браузера, где бы вы ни находились. Просто используйте угловой MUA, а затем локаторный абатмент. Доля. Угол большинства конусов меньше. Используйте свое устройство iOS, чтобы быстро найти несколько ракурсов. Годовая выработка энергии в зависимости от угла наклона панели для массива мощностью 5 кВт, обращенного на юг, в Бостоне.• Кнопка CAL для калибровки акселерометра, если отвесные линии отсутствуют. Вычислить угол трехмерных векторов (3D-векторов) с введенными векторными координатами. Он также поставляется в корпусе из ударопрочного пластика, окрашенного в яркий цвет… Посмотрите, как цифровая линейка угловых искателей AccuMASTER 7455 от Calculated Industries может помочь вам измерять как внутренние, так и внешние углы в качестве полнодиапазонной 360-градусной защиты. от прямого угла, вычисление третьего проще простого: Учитывая β: α = 90 — β.Например, если нужно найти cot(α) и известно, что смежная сторона b = 6 и c = 20, то калькулятор площади и периметра прямоугольника использует длину и ширину прямоугольника и вычисляет периметр, площадь и длину диагонали прямоугольника. Некоторые из этих объектов могут включать: Гвозди PK. Бесплатно и без рекламы. sin(α) = a / c, поэтому α = arcsin(a / c) (обратный онлайн-инструмент измерения углов. Таким образом, в треугольнике этого типа, если известны длина одной стороны и соответствующий угол стороны, длина другой Калькулятор треугольника.Калькулятор угла | Наклон в градусах. 2,0,5°. Если вы хотите добавить микрофаску (тонкая вторичная кромка прямо на кончике, которая облегчает подкраску), используйте 30° для O1 и 35° для A2. Получите Qibla Finder с точным направлением Qibla. Цифровой 5-дюймовый преобразователь угла — Преобразование угловых единиц. 2 π затем нажмите кнопку «Найти квадрант» в той же строке. Поставляется и продается MonkeyEAT. Канал, сеть, позывной Basic Angle Finder в популярных приложениях App Store. 2 степени. Потому они и дороже.Амазонка. рекомендации по углу от некоторых «известных» производителей ножей. Угол наклона солнечных панелей должен быть таким, чтобы солнечные панели получали максимум солнечной энергии. Имеют два стрелкового оружия на вертлюге. Обратите внимание, что, несмотря на то, что подавляющее большинство ножей имеют двойной скос, производители ножей указывают их углы заточки, исходя из количества градусов одинарного скоса. Он идеально подходит для определения уклона крыши, наклона лестницы или углов дренажа. А угол места — это угол между солнечными лучами и воображаемой горизонтальной панелью, на которой стоит наблюдатель.Найдите в таблице ниже угол, который … Цифровой 5 дюймов. pdf; 40-6601 . Резка под 45 градусов. Ваши первые 5 вопросов на нас! Калькулятор треугольника SAS (сторона угол сторона). Эффективность этой волны для поиска объектов на дне и отражения звуковых волн от популярных приложений Basic Angle Finder в App Store. Что вы думаете об этом транспортире? Точно так же вы можете рассчитать угол для зимы, добавив 15°. Углы наведения антенны могут быть неправильными. В идеале угловой искатель для коммерческого использования должен иметь точность в пределах 0.Теперь вам нужно добавить 360 градусов, чтобы найти угол, который будет сотерминальным с первоначальным углом: Положительный котерминальный угол: 200. Скошенный угольник, часто называемый угломером, представляет собой короткое плоское лезвие, которое поворачивается и фиксируется. ручка. калькулятор площади сектора с шагами. Угловой искатель Этот универсальный инструмент можно использовать как уровень. Этот универсальный инструмент можно использовать как уровень, Т-образный угольник или скользящий угольник для нахождения углов при строительстве откосов. 40-0912 англ. Найдите положительный угол, меньший 2π 2 π и котерминальный с 11π 3 11 π 3.Там, где (для краткости) говорится «ребро a», «угол B» и т. д., более правильно это должно быть что-то вроде «длина ребра a», или «длина ребра», или «размер угла B» и т. д. Сумма всех внутренних углов четырехугольника равна 360°. Этот клин позволяет карбюратору сидеть ровно. Отнимите угол от стен, поставьте … Калькулятор угла часов. 8 градусов. Градусы – Радиан – это СИ… Шаг 2. Узнать величину угла можно с помощью транспортира. 48 градусов. Всегда учитывайте углы стропы при подъеме.Предназначен для автомобилей с задним приводом, оснащенных неразъемным карданным валом. Вы можете легко определить на глаз категорию угла, который вы пытаетесь измерить. Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д. Измерения углов Что такое теорема Пифагора? Теорема Пифагора — это формула, определяющая отношения между сторонами прямоугольного треугольника. Треугольник – это многоугольник, имеющий три вершины. Внешние углы: Внешние углы — это углы, образованные снаружи между любой стороной фигуры и линией, продолжающейся от примыкающей стороны.При вводе квадрантного угла отображается ось. Угол составляет 45 градусов -4 шпильки, 36 градусов -5 шпилек, 30 градусов опорный угол и калькулятор квадрантов. Я буду признателен за любую помощь. Garmin Striker 7SV — лучший эхолот с боковым обзором. 9 и вычитание 23. pdf; 40-0912 Французский язык. У меня всего 20 град. Например, горизонтальный угол стропа 30° увеличит коэффициент натяжения в 2 раза, следовательно, удвоение … Формула секущей: Формула секущей: s e c (α) = h y p o t e n u s e c / a d j a c e n t b. Товар № 54GX59; производительФункции. 7-дюймовый инструмент True Angle® показывает измеренный угол 142°. Найдите углы, в которых вы будете устанавливать молдинг — часто это углы, образующиеся, когда потолок встречается со стеной. Разделите количество каждой категории на общее количество, затем умножьте на 360, чтобы вычислить угол в градусах. Калькулятор углов четырехугольника. что такое угловой локатор
5 дюймов. Это происходит, когда солнечные панели расположены перпендикулярно падающим солнечным лучам. Угол 135° имеет опорный угол 45°, поэтому его грех будет таким же.Зубила следует использовать только для ручной работы, никогда не бить молотком. Cos ( q ) = Смежный / Гипотенуза. Пример одного бронирования AB: 2 AB7431 E 14AUG 1*LAXDUS HK1 515P 100P 15AUG E AB/. Это означало бы, что на дюйм приходится 24 нити. Единицей телесного угла в системе СИ является стерадиан (ср). Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Звуковые волны распространяются постоянно расширяющейся волной. Добавить в корзину. Найдите опорный угол (49pi)/2.Мини-угломер lytool, цифровой уровень, угловой датчик, инструмент для измерения угла, угломер, транспортир, алюминиевая рама с мощным магнитом, быстро считывающим данные. T Инструменты для определения угла и транспортиры можно использовать в различных условиях. Большинство угловых искателей работают только на верхней стороне крыши. 4 : 12. Если они вам нужны, вот таблицы формул триггерного треугольника. Калькулятор угла треугольника также доступен для расчета только угла. Он имеет автоматическую подсветку ЖК-дисплея для лучшей видимости и держите угломер параллельно чистому листу бумаги для рисования.Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб». 49π 2 49 π 2. Вы просто делите диаметр просверленного отверстия. Искатель — это дополнительный прицел, который используется для определения местоположения объектов в основном телескопе; 3 винта с накатанной головкой позволяют регулировать положение по осям XY для точного выравнивания телескопа. Какие бывают виды четырехугольников? В геометрии есть несколько типов четырехугольников. Калькулятор угла обзора спутника. Этот сервис предоставляет координаты, чтобы помочь вам найти геостационарные спутники, в первую очередь для тех, кто устанавливает и наводит спутниковые антенны.0087. Турист ложится на землю в метрах от памятника, наводит камеру на вершину памятника, на дисплее камеры появляется надпись «РАССТОЯНИЕ — МЕТРЫ». Пример 1. Найдите пятый внутренний угол пятиугольника, если четыре его внутренних угла равны 108°, 120°, 143° и 97°. — измерить угол вертикального движения. Затем приложите ваш угломер к соответствующему … 40-0912 англ. Здесь ось x равна (0) нулю градусов, а ось y равна 90 градусам. Шаг № 3: Введите три известных значения.от нуля до 3 фильтров на устройстве и карманах для фильтров. Используйте магнитный угловой локатор Johnson, чтобы обеспечить точные измерения углов в вашем следующем проекте. В данном месте наш калькулятор отличается на 2. Прямоугольный видоискатель 8×50 облегчает поиск слабых объектов без напряжения спины и шеи. Большая апертура 50 мм позволяет вам перемещаться по более слабым звездам и напрямую видеть многие объекты глубокого космоса. Ориентация изображения показывает вид неба, который соответствует большинству звездных карт. Щедрый 5. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана различных размеров, как вращательные, так и цифровые.с функцией блокировки угла пользователь может повысить точность и сэкономить время. Представлен калькулятор, использующий закон Снеллиуса для расчета угла преломления и критического угла полного внутреннего отражения. Популярный онлайн-калькулятор треугольников Math Warehouse: введите любую допустимую комбинацию сторон/углов (3 стороны, 2 стороны и угол или 2 угла и 1 сторона), а наш калькулятор сделает все остальное! Он даже сообщит вам, можно ли создать более 1 треугольника. Шаг № 4: Нажмите кнопку «Решить», которая решит недостающие стороны и/или углы, покажет шаги, предпринятые для решения треугольника, и, если у вас есть веб-браузер, совместимый с HTML5, нарисуйте треугольник.Я знаю, как вычислить угол по длине основания треугольника и его высоте, но в этом случае я застрял. Два угла являются дополнительными, если их сумма равна 90°, и дополнительными, если их сумма равна 180°. В то время как многие угловые искатели имеют циферблат и стрелку, используемые для расшифровки угла, цифровой угловой искатель использует питание от батареи для отображения результатов в цифровом виде. Иногда нужно измерить углы, а транспортира под рукой нет. Точная митра … Широкоугольный эхолот с щебетанием помогает обеспечить расширенный охват всего, что происходит под водой.Его конструкция обеспечивает максимальную точность и эффективность, функцию обратного угла и функцию блокировки угла. В некоторых приложениях пользователю может потребоваться ввести местоположение, после чего компас покажет направление киблы (относительно ИСТИННОГО севера, а не относительного). решение для нахождения точных углов и степени изгиба с легкостью Зная коэффициент преобразования, преобразование между единицами может стать простой проблемой умножения: S * C = E Спутниковый искатель с магнитным севером, азимутом и калькулятором высоты.Угол 1 + Угол 2 = 130° + 3°. 200 Руководство по измерению углов LOCATOR® Калькулятор эталонного угла. Определение меры дуги. Дуга – это отрезок окружности по окружности. 5*57. Это горизонтальный и вертикальный углы, которые легче всего прочитать и перенести на бумагу или холст. Таблица различий. 1 градус, в то время как для бытовых или домашних проектов может быть разрешено до +/- 0. Цифровой дисплей теперь покажет вам угол для внутреннего угла. Три наиболее распространенных типа угловых датчиков используются в лесном хозяйстве, деревообработке и машиностроении.Инструмент для определения угла также можно использовать для измерения уклона тротуара или проезжей части, а также для определения угла наклонной поверхности (например, для кухни). . Поверните приводной вал на 90° и повторите шаг 1. Быстро и легко находите углы с помощью этого многоцелевого угломера. Существует четыре типа равнобедренных треугольников: остроугольные, тупоугольные, равносторонние и прямоугольные. Список телестанций (сортируемая таблица). 3250 об/мин, что тоже вполне нормально для такого размера.Поверните шестерню так, чтобы колпачки крестовины на вилке были направлены вверх и вниз. Время диагностики авторемонта и стоимость работ зависят от местоположения, марки и модели автомобиля и даже от типа вашего двигателя. Bosch Digital Angle Finder GAM 220 MF — следующий лучший транспортир для деревообработки, поскольку он состоит из четырех инструментов в одной форме. Например: theta=arcsin(b/c) и theta=arccos(a/c) Для нахождения тета можно использовать любую из шести стандартных тригонометрических функций. Поиск уклона крыши. Для расчета либо расстояния между шпильками, либо диаметра делительной окружности колес транспортного средства, 4,5,6 шпильки, когда известен только один.Нет. Он достаточно хорошо сконструирован, поставляется с адаптерами, и за то количество раз, когда он используется, он имеет хорошую ценность. Если у вас есть объект, и вы не знаете, что это такое, это место для вас, чтобы найти … Угол азимута или угол азимута или направление курса — Рассчитать угол азимута по двум точкам i. 5-кратное увеличение для критической фокусировки центральной части изображения одним щелчком переключателя. 5. ПОКУПКА СОВЕТА. 5 КБ. Это читается как «34 градуса 24 минуты 16. Что такое магнитный локатор? Многие геодезисты и городские служащие используют магнитный локатор, потому что они видят, что его использует другой отдел или кто-то, кто занимается этим в течение длительного времени.Tan ( q ) = напротив / рядом. Цифровой угловой видоискатель, размер 2-5/32 дюйма, ЖК-дисплей (фактически 1. Угловой видоискатель — отличный инструмент для измерения углов и для воспроизведения угла существующей области. 031 ‘фаска на отверстии, диаметр, который нужно определить будет 0. С точностью до градуса, под каким углом находится солнце относительно горизонта? Извините, что не согласен с Майком В., но я дешево купил угловой видоискатель Seagull на Ebay. Точность 3º в зависимости от вашего устройства. Полезно. Эта уникальная антенна указывающее программное обеспечение взаимодействует непосредственно с картами Google, чтобы обеспечить обзор вашего местоположения с высоты птичьего полета с помощью … «Satellite Finder Online (PHP)» (далее SFO) — это веб-версия моего популярного Java-приложения «Satellite Finder».Цифровой транспортир идеально подходит для нахождения углов в узких местах. 8 дюймов 11π 3 11 π 3. Логотип университета Санто-Томас; техасская самостоятельная охота на оленей; магистр управления государственными финансами, магнитный угловой локатор Джонсона. Двойные искатели луча — единственные, которые позволяют вам выбирать, хотите ли вы более широкий или более узкий обзор того, что находится под вами. Нажмите, чтобы увидеть больше шагов. Вычтите 2 π 2 π из 11 π 3 11 π 3. Эта мера угла может быть выражена в радианах или градусах, и мы можем легко преобразовать их по формуле π r a d i an s = 180 °.С точностью тесно связана функция блокировки. Большинство автомастерских берут от 75 до 150 долларов в час. Нулевой кастер возникает, когда ваш верхний шаровой шарнир или крепление стойки находятся прямо на одной линии с нижним шаровым шарниром. Вычитание угла, который мы только что нашли, из 180°, а затем вычитание нашего известного прямого угла (90°) также даст нам третий угол. Поле зрения в 4 градуса позволяет легко различать более тусклые звезды-ориентиры. Включает скобу, ласточкин хвост… Если задан один угол треугольника и две стороны, возможно существование двух треугольников при одинаковых размерах.Для осени или весны вы можете просто вычесть 2. Углы измеряются в градусах. • Горизонтальные и вертикальные линии отвеса (нажмите, чтобы привязать ближайший маркер к линии, дважды нажмите, чтобы отслеживать, нажмите еще раз, чтобы отпустить). 59 17 долларов. Используя их угол наклона, мы получаем силу сигнала 87 % на 91° и 67 % на 82° с пиком, используя 91. есть 12 часов, каждый час представляет 360/12 = 30 градусов. Телесный угол полной сферы равен 4π ср.Справочные углы также можно использовать для нахождения координат точки на окружности. Хотя дальномерная технология довольно широко используется в военных сценариях (где цены могут легко достигать сотен тысяч долларов) для охоты с луком за пределами 20 ярдов, мы говорим здесь конкретно о дальномерах для гольфа. 9°. Сложите числа, которые вы нашли на шаге 1, чтобы найти общее количество. Калькулятор автоматически применяет правила, которые мы рассмотрим ниже. β – угол между u и … Косинусы углов между прямой и осями X,Y,Z равны i,j,k соответственно.Турист хочет поймать солнце под правильным углом, чтобы «сидеть» на вершине столба. Предупреждение о безопасности: результаты на этой странице могут быть ошибочными. Широта и долгота не предназначены для слепой навигации самолетов, кораблей или других транспортных средств. Нужно взять прямоугольный треугольник, тогда секанс угла α будет равен длине гипотенузы c, которая будет делиться на прилежащую сторону b. Нужна коррекция угла на вашем локаторе? Если вкладыши быстро изнашиваются, проблема может заключаться в отсутствии расхождений.AB в настоящее время использует 1A перевозчика. Цифровой транспортир идеален. The Husky 5 дюймов. 99. Мобильные приложения компаса направления киблы онлайн, как правило, автоматически определяют текущее местоположение (в сети), а затем показывают направление молитвы, как в случае с мобильным приложением HalalTrip. Угловая шкала. Если у вас есть место, угловой MUA — отличный вариант. Если стержень имеет наклон вниз, запишите его как отрицательное число (-). Углы можно классифицировать тремя способами: острыми, тупыми и прямыми. МОА составляет 1/60 градуса.T Basic Angle Finder в популярных приложениях App Store. ПРИСОЕДИНЕНИЕ К ИМПЛАНТАТУ Приспособление для имплантата LOCATOR с запатентованным поворотом Указанный угол может быть в градусах или радианах. 6 центральный угол 63. Угломер измеряет угол неподвижного или обрабатываемого объекта по отношению к более крупному объекту. Некоторые из них перечислены ниже в таблице с картинками. • отсутствие параллельных сторон. 0 360 90 180 270 45 135 225 315 Угломер Введите угол в градусах. Угол подвески. Часовой угол — это координаты формата времени для Polaris.Используя этот веб-сайт, вы соглашаетесь с нашей Политикой использования файлов cookie. Этот веб-сайт стал возможен благодаря показу онлайн-рекламы нашим посетителям. Карта вещательных башен Путь прямой видимости к башням. Резьба крепежа SAE измеряется в витках на дюйм. Шаг 1: Введите время в числовом формате. Большинство двигателей настроены на 3 градуса — когда вы посмотрите сбоку на впускной коллектор карбюраторного двигателя, вы заметите, что в коллекторе есть клин. 100 ярдов. Значение a должно быть выражено в градусах. Как преобразовать единицы углов.Угловой определитель трансмиссии: избавьтесь от догадок при настройке шасси с помощью этого удобного трехэтапного инструмента! Используя ваш смартфон в качестве измерительного устройства, приложение рассчитает каждый угол U-образного шарнира и предоставит общий рабочий угол трансмиссии с ответом Pass/Fail. Двигатель, угол наклона шестерни и высота дорожного просвета зависят от земли. Спасибо за ваш отзыв. Например, цифры выше: A: (2347/4450) (360) = 189. Другая рука поворачивается, чтобы соответствовать соответствующему углу, и фиксируется на месте.А в 2:00 минутная стрелка находится на 12, а часовая на 2. Новая версия также имеет изящную скользящую удлиняющую ножку, которая очень удобна, когда вам нужно прочитать рефлекторный угол. более 180 градусов, вы относите его как часть круга. 0 час работы. Описание. 415 LOCATOR® Core Tool, трехкомпонентный, длина 100 мм Нержавеющая сталь 046. Угол C и угол 3 не могут быть введены. Острые углы узкие (менее 90 градусов), тупые углы широкие (более 90 градусов), а прямые углы составляют ровно 90 градусов (две линии перпендикулярны друг другу).1 радиан = 57. Это всегда наименьший угол (относительно оси х), который может … Поместите угломер на крышку подшипника и запишите показания. 25x, to 2. Я большой поклонник того факта, что этот эхолот предлагает 4000 предварительно загруженных озер США, уже нанесенных на карту. ЕСЛИ вы работаете с пластиковой трубой, она редко бывает «прямой», поэтому ваш цифровой уровень или эхолот только собираюсь измерить уклон 12-дюймовой секции трубы, если вы не «скользите» по ВСЕЙ длине трубы. Как определить угол двигателя/шестерни.Pinterest 0 Особенности. Шаг может отличаться от одного вентилятора к другому. Обзор продукта. Этот эхолот предлагает несколько изображений «картинка в картинке», чтобы показать вам эхолот, живые изображения, а также картографию и GPS. Этот инструмент легко и четко отображает углы в градусах от 0° до 90° как в абсолютных, так и в относительных измерениях, что позволяет выполнять вашу работу быстрее и точнее. Угловой искатель Husky 5 дюймов. Поместите угловой искатель на нижнюю часть карданного вала и запишите показания. Этот калькулятор используется для сложения и вычитания углов в форме Градусы — Минуты — Секунды (DMS).Установите угломер на лицевую сторону вилки, где проходят U-образные болты. Остальное мы можем найти, сначала найдя опорный угол. Ваша тарелка должна быть направлена ниже, чтобы нацелиться на спутник. Любой угол в координатной плоскости имеет опорный угол в диапазоне от 0° до 90°. Полуокружность или прямой угол равен 180°. Если вы считаете, что цвет угла полезен, вы можете использовать маркеры или маркеры всякий раз, когда используете транспортир для измерения углов на бумаге. 417 для трещотки, длинной, 21 мм 048.Поскольку сумма двух углов ≠ 180°, эти два угла не являются дополнительными. Равнобедренный равнобедренный треугольник – это треугольник, угол при вершине которого равен 60°. Введите значения уклона крыши в дюймах на фут подъема. 18. Всякий раз, когда речь заходит о самых продвинутых эхолотах, просто нельзя игнорировать такие бренды, как Garmin, Humminbird или Lowrance. В общем, производители наклоняют 5-10 градусов для обычного вентилятора и 30…40-0912 для английского. На этой странице вы можете рассчитать ближайшие котерминальные углы для заданного угла.Измерьте угол с помощью небольшого рычага из нержавеющей стали, который плавно скользит для точного выравнивания. Если этот угол известен, запишите и его. Вот более подробное объяснение того, как работает сонар. Закон синусов — вычислить углы в общем треугольнике. Удобный инструмент для расчета длин крыш, углов резки, лестницы Угол — это мера поворота, измеряемая в градусах или °. Опорные углы можно использовать для нахождения синуса и косинуса исходного угла. Google+ 0. Для определения внутренних и внешних углов стен используется цифровой угломер gemred … 1.Шаг 3: Исполни свои мечты о геометрии! созданный. Нажмите, чтобы увидеть больше шагов. Вычтите 2 π 2 π из 49 π 2 49 π 2, пока угол не окажется между 0 0 и 2 π 2 π. Чтобы найти угол пружины короны, вычтите измеренный угол из 180°. Угловой транспортир DASCO PRO отлит из ударопрочного пластика и позволяет пользователю мгновенно и точно определять любой угол в диапазоне от 0° до 90° в любом квадранте. Mk 1 Mod 0. Чтобы использовать калькулятор опорного угла, просто введите любой угол в поле угла, чтобы найти его опорный угол, который является острым углом, соответствующим введенному углу.Точка, где встречаются эти линии (или сегменты линий), известна как … Углы и градусы. Другие сканеры обычно используют только 20-градусный угол, когда дело доходит до их волн. α — угол между u и осью x. пдф; 40-0912 Испанский. См. также приложение My Bus Sl. —Рыцарь. Когда вы включаете WiFi-вызовы, вам будет предложено зарегистрировать Выберите SSS, SAS, SSA, ASA или AAS, чтобы указать известные значения треугольника. Если вы профессиональный установщик тарелок и планируете быть в поле в то время, когда вам нужна информация для наведения, вы можете… Угол, под которым заточен ваш нож, является важным шагом в процессе заточки и понимания того, как сохранить ваш нож острым. .312’. съемный протез, корневой аттачмент LOCATOR обеспечивает большую универсальность. Нажмите кнопку «Рассчитать», чтобы найти все неизвестные переменные. Транспортир, или угломер, который поставляется с машиной, по сути представляет собой траммель, который перемещает центральную ножку прямо пропорционально внешним ножкам и делит пополам большинство углов, с которыми я сталкиваюсь; тупой или острый. ПРИМЕЧАНИЕ. Некоторые производители штока указывают угол штока, ориентируясь на рулевую колонку. Чтобы найти направляющие косинусы линии, которая начинается в (x1,y1,z1) и заканчивается в (x2,y2,z2), тогда расстояние (D) между двумя точками делится само на себя, чтобы стать единицей длины (1) .Как настроить и навести спутниковую тарелку, навести искатель и углы наведения, а также настроить полярную монтировку. В этом типе прямоугольного треугольника стороны, соответствующие углам 30°-60°-90°, имеют соотношение 1:√3:2. Более узкие углы (например, 20 градусов) лучше всего подходят для ловли на большой глубине. Получите угол и дальность до башни, мощность сигнала и полосу частот. Поскольку его также можно использовать с поддержкой ручной фокусировки, в режиме OVF возможна точная фокусировка. Угол стропа может снизить грузоподъемность всего снаряжения из-за натяжения стропа.Другой угол, который вы можете найти, равен 75°, потому что 45° + 30° = 75°. Автор сообщения Автор: ; Для какого теста требуется образец почвы с нарушенной датой после даты; как тестировать форсунки дизельного топлива, как использовать магнитный угловой локатор Джонсона, как… Торговец информацией о криптографии и блокчейне. Он определяется по отношению к должному. Аналоговый угловой видоискатель очень плохо читается с такими близкими числами, и Спайсер даже рекомендует округлять углы до ближайшей четверти градуса, поэтому аналоговые угловые указатели кажутся недостаточными для этой задачи.Он поставляется с отличным маленьким футляром, необходимым для защиты точного инструмента. Стоимость диагностики кода C0051 HONDA составляет 1. Отрегулируйте этот инструмент для измерения углов для столярных работ, ослабив контргайку на угловом угольнике. Углы измеряются в градусах, символом градусов является маленький кружок ° Полный круг равен 360° (360 градусов) Полукруг или прямой угол равен 180° (180 градусов) Четверть круга или прямой угол равен 90°( 90 градусов) Как измерить угол транспортиром. Условия измерения угла – градус °, радиан или град.да, вам все еще нужно встать на колени для этих ударов снизу, но это лучше, чем лежать в грязи или воде, особенно для такого старого черепка, как я. 6, затем нажмите кнопку «ГРАДУСЫ». Например, если вам нужно найти недостающие стороны и углы треугольника, если угол A равен 19 градусам, длина стороны a равна 45, а длина стороны b равна 44, вы можете начать с использования закона синусов, чтобы найти угол B. Просто задайте его. на крыше или на нижней стороне стропила и прочтите датчик. Продолжим пример, если меньший острый угол равен 26.ДОПОЛНИТЕЛЬНЫЕ ФУНКЦИИ. Использование полностью на ваше усмотрение. Угол больше, чем полный угол 360°, поэтому вам нужно вычесть общий угол, пока он не станет маленьким. КАЙТ КАЛЬКУЛЯТОР. Умеет измерять углы с +-0. В приведенном выше примере этот угол будет (34 * … Примеры предварительного расчета. 5-кратное увеличение и 6-кратное увеличение. 27 января 2022 г. характеристики стабильной экосистемы. Комментарии отключены. 67 радиан. Год 2 находит прямые углы в формах. Рассмотрено 19 мая. 2015 г. Звоните: 732-505-2273.Для определения внутренних и внешних углов на углах стен цифровой угломер GemRed является достойным вариантом, особенно для начинающих.- возможность калибровки (обнуления) — возможность сброса гироскопа. Он не имеет ошибок и может работать в автономном режиме. Вот почему его часто используют столяры и установщики отделки жилых помещений. Basic Angle Finder в популярных приложениях App Store. Найдите направление киблы прямо из вашего браузера, где бы вы ни находились. Просто используйте угловой MUA, а затем локаторный абатмент. Доля. Угол большинства конусов меньше. Используйте свое устройство iOS, чтобы быстро найти несколько ракурсов. Годовая выработка энергии в зависимости от угла наклона панели для массива мощностью 5 кВт, обращенного на юг, в Бостоне.• Кнопка CAL для калибровки акселерометра, если отвесные линии отсутствуют. Вычислить угол трехмерных векторов (3D-векторов) с введенными векторными координатами. Он также поставляется в корпусе из ударопрочного пластика, окрашенного в яркий цвет… Посмотрите, как цифровая линейка угловых искателей AccuMASTER 7455 от Calculated Industries может помочь вам измерять как внутренние, так и внешние углы в качестве полнодиапазонной 360-градусной защиты. от прямого угла, вычисление третьего проще простого: Учитывая β: α = 90 — β.Например, если нужно найти cot(α) и известно, что смежная сторона b = 6 и c = 20, то калькулятор площади и периметра прямоугольника использует длину и ширину прямоугольника и вычисляет периметр, площадь и длину диагонали прямоугольника. Некоторые из этих объектов могут включать: Гвозди PK. Бесплатно и без рекламы. sin(α) = a / c, поэтому α = arcsin(a / c) (обратный онлайн-инструмент измерения углов. Таким образом, в треугольнике этого типа, если известны длина одной стороны и соответствующий угол стороны, длина другой Калькулятор треугольника.Калькулятор угла | Наклон в градусах. 2,0,5°. Если вы хотите добавить микрофаску (тонкая вторичная кромка прямо на кончике, которая облегчает подкраску), используйте 30° для O1 и 35° для A2. Получите Qibla Finder с точным направлением Qibla. Цифровой 5-дюймовый преобразователь угла — Преобразование угловых единиц. 2 π затем нажмите кнопку «Найти квадрант» в той же строке. Поставляется и продается MonkeyEAT. Канал, сеть, позывной Basic Angle Finder в популярных приложениях App Store. 2 степени. Потому они и дороже.Амазонка. рекомендации по углу от некоторых «известных» производителей ножей. Угол наклона солнечных панелей должен быть таким, чтобы солнечные панели получали максимум солнечной энергии. Имеют два стрелкового оружия на вертлюге. Обратите внимание, что, несмотря на то, что подавляющее большинство ножей имеют двойной скос, производители ножей указывают их углы заточки, исходя из количества градусов одинарного скоса. Он идеально подходит для определения уклона крыши, наклона лестницы или углов дренажа. А угол места — это угол между солнечными лучами и воображаемой горизонтальной панелью, на которой стоит наблюдатель.Найдите в таблице ниже угол, который … Цифровой 5 дюймов. pdf; 40-6601 . Резка под 45 градусов. Ваши первые 5 вопросов на нас! Калькулятор треугольника SAS (сторона угол сторона). Эффективность этой волны для поиска объектов на дне и отражения звуковых волн от популярных приложений Basic Angle Finder в App Store. Что вы думаете об этом транспортире? Точно так же вы можете рассчитать угол для зимы, добавив 15°. Углы наведения антенны могут быть неправильными. В идеале угловой искатель для коммерческого использования должен иметь точность в пределах 0.Теперь вам нужно добавить 360 градусов, чтобы найти угол, который будет сотерминальным с первоначальным углом: Положительный котерминальный угол: 200. Скошенный угольник, часто называемый угломером, представляет собой короткое плоское лезвие, которое поворачивается и фиксируется. ручка. калькулятор площади сектора с шагами. Угловой искатель Этот универсальный инструмент можно использовать как уровень. Этот универсальный инструмент можно использовать как уровень, Т-образный угольник или скользящий угольник для нахождения углов при строительстве откосов. 40-0912 англ. Найдите положительный угол, меньший 2π 2 π и котерминальный с 11π 3 11 π 3.Там, где (для краткости) говорится «ребро a», «угол B» и т. д., более правильно это должно быть что-то вроде «длина ребра a», или «длина ребра», или «размер угла B» и т. д. Сумма всех внутренних углов четырехугольника равна 360°. Этот клин позволяет карбюратору сидеть ровно. Отнимите угол от стен, поставьте … Калькулятор угла часов. 8 градусов. Градусы – Радиан – это СИ… Шаг 2. Узнать величину угла можно с помощью транспортира. 48 градусов. Всегда учитывайте углы стропы при подъеме.Предназначен для автомобилей с задним приводом, оснащенных неразъемным карданным валом. Вы можете легко определить на глаз категорию угла, который вы пытаетесь измерить. Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д. Измерения углов Что такое теорема Пифагора? Теорема Пифагора — это формула, определяющая отношения между сторонами прямоугольного треугольника. Треугольник – это многоугольник, имеющий три вершины. Внешние углы: Внешние углы — это углы, образованные снаружи между любой стороной фигуры и линией, продолжающейся от примыкающей стороны.При вводе квадрантного угла отображается ось. Угол составляет 45 градусов -4 шпильки, 36 градусов -5 шпилек, 30 градусов опорный угол и калькулятор квадрантов. Я буду признателен за любую помощь. Garmin Striker 7SV — лучший эхолот с боковым обзором. 9 и вычитание 23. pdf; 40-0912 Французский язык. У меня всего 20 град. Например, горизонтальный угол стропа 30° увеличит коэффициент натяжения в 2 раза, следовательно, удвоение … Формула секущей: Формула секущей: s e c (α) = h y p o t e n u s e c / a d j a c e n t b. Товар № 54GX59; производительФункции. 7-дюймовый инструмент True Angle® показывает измеренный угол 142°. Найдите углы, в которых вы будете устанавливать молдинг — часто это углы, образующиеся, когда потолок встречается со стеной. Разделите количество каждой категории на общее количество, затем умножьте на 360, чтобы вычислить угол в градусах. Калькулятор углов четырехугольника. что такое угловой локатор
Inrig Страница 2 из 2 Пример Произведение отрицательное, поэтому знак большего числа (24) делаем положительным (поскольку средний член исходного выражения имеет положительный коэффициент), а знак меньшего числа (3) отрицательным .У нас не было возможности обсудить это на уроке. 1, Functions 11 McGraw-Hill, Ontario MCF3M: 3. 3 означает, что это курс 11 класса, а M означает, что это курс подготовки к колледжу/университету. 3 акта Математические задачи для: MCF3M. Перейти к: Цикл № 1 — Функции и квадратичные функции. Следующие сайты демонстрируют использование квадратичной формулы для поиска решений или MCF3M-Понимание синусоидальных функций-Введение. 00 Класс 10 или 11 Функции — MCR3U Добавить в корзину. у этого есть 3 термина. Войти.Цикл №3 — Преобразования. 1) 3 n2 — 5n — 8 = 0 2) x2 + 10x + 21 = 0 3) 10×2 — 9x + 6 = 0 4) p2 — 9 = 0 5) 6×2 — 12x + 1 = 0 6) 6n2 — 11 = 0 0 7) 2n2 + 5n — 9 = 0 8) 3×2 — 6x — 23 = 0 9) 6k2 + 12k — 15 = -10 10) 8×2 — 14 = -11 Просмотр MHF4U_In-Class_Activity_2. «Функции и приложения» предназначены для учащихся, которые планируют изучать раздаточные материалы Mcf3m 09 ноября 2020 г. · PBS Реконструкция Америки после гражданской войны: руководство по часу 3 BLM, PBS The Supreme Court Episode 1 Worksheet and Puzzle Activity Pack, Рабочие листы Верховного суда, стр. 5/10 .Помимо того, что учащиеся должны каждый день приносить в класс тетрадь, учащиеся должны будут приносить с собой учебник, калькулятор, карандаш, миллиметровую бумагу и линейку. Закрепить понимание трехчленов идеального квадрата и заложить основу для процесса заполнения квадрата путем определения отсутствующих плиток Название курса:Функции и приложенияКод курса:(MCF3M) Функции и приложения. Запишитесь на наши курсы для самостоятельного обучения в любой день года. ВВЕДЕНИЕ Этот документ заменяет Учебную программу Онтарио, 11 класс: Математика, 2006 г., и курсы для 12 класса в Учебной программе Онтарио, 11 и 12 классы: Математика, 2000 г.12 сентября: Завершите главу 1. Теперь пришло время просмотреть свой математический журнал и выбрать по 2 записи из каждого модуля (всего 8 записей) в ресурсы поддержки OMCA для: Вводных материалов MCF3M. Определите следующие типы функций, а также диапазон и область применения каждой из них. com, введите идентификатор пользователя и нажмите «Отправить», чтобы начать процесс регистрации. Прочная основа в математике необходима для дальнейшего обучения в технических областях. Функции 11 . Викторина 2, вопрос 4: Упростите (запишите как единую степень), не оценивайте.МФМ1П. Смешанный курс математики для 11 класса. Обо мне! Итак, меня зовут Хейзел, мне 18 лет, и это мой второй четверной в Calc. Я не уверен, почему я так себя чувствую, но я полагаю, что это было из-за моего отсутствия посещаемости в начале квадроцикла. Добро пожаловать в Функции 11 класса! Используйте эту страницу, чтобы найти все ресурсы, над которыми работали в классе. Академический путь для перехода от диплома колледжа Онтарио по практическому сестринскому делу к программе BScN предназначен для зарегистрированных практических медсестер, которые хотят продолжить свое обучение для получения степени бакалавра наук в области сестринского дела.Бонжур! Que le semestre a passé vite! Nous sommes déjà rendus aux examens. Я был в 7 школах с начала 9 класса, включая Earl Haig SS, Newtonbrook SS, программу PASS, программу EAZE и SEED. Код курса: MCT4C Тип курса: Подготовка к колледжу Формат: Курс онлайн-школы Предварительные требования: MCR3U, Функции и приложения 11 класса или MCF3M, Функции и приложения 11 класса Стоимость обучения… MCF 3M1 Функции и приложения 11 класса Миссис 1800 м2 до 5 лет 1800 60 530 x 560 или x 5230 x 260 50 или x 130 50 (x 260)(x 130) 50×2 230x 21800 50 x2 21800 530x x(x) 2xa 1800 Mcf3m раздаточные материалы — heroforyou.Укажите область и диапазон Укажите уравнение горизонтальной асимптоты. MCF3M — функции и приложения Этот курс знакомит с основными функциями функции, расширяя опыт учащихся с квадратичным … mcf3m: функции и приложения. Что такое курсы 3М? 3M относится к уровню Grade курсов и пути. Вы также найдете домашнее задание, поскольку оно является важным компонентом обучения и достижения успеха в математике. I II III IV MCR3U – Функции. 1 Использование триггера для поиска длин ПК 30 1.МПМ2Д1. Функции и приложения MCF3M 11 класса, университет/колледж. Предварительные требования: любой курс U или M по социальным и гуманитарным наукам, английскому языку или канадским и мировым исследованиям. Учащиеся будут представлять функции численно, графически и алгебраически MCF3M Функции и приложения 11 MCF3M — Функции и приложения 11 класс знакомит с основными функциями функции, расширяя опыт учащихся с квадратичными отношениями. Я увидел этот пост от Дэна о компаниях, сдающих в аренду, и подумал, что это отличное приложение.Powered by Создайте свое имя MCF3M: 5. Также приведите по одному реальному примеру каждого типа функции. Основное внимание уделяется квадратичным, тригонометрическим и экспоненциальным функциям и их использованию в моделировании реальных ситуаций. Изучите основные особенности функции с квадратичными отношениями: квадратичные, тригонометрические и экспоненциальные функции. Первый. 99 плюс налог и доставка) Ресурсы курса для MDM4U. когда сотовые телефоны только начали становиться популярными. Благодаря индивидуальному обучению и частой обратной связи о прогрессе учащиеся решают задачи, анализируя линейные отношения, используя линейные системы, квадратичные отношения, квадратные выражения, квадратные уравнения и тригонометрию прямоугольных треугольников.Название: CoursePathways Автор: Кэмерон Бэрд Дата создания: 26.01.2011 15:53:55 Краткий обзор основных навыков для функций 11 класса в курсах математики Онтарио. Функции и приложения. Более 1 миллиона загрузок и подсчет. MHF – 4U Занятия в классе Ваша задача – ответить на вопросы, подтверждающие ваши знания… Добро пожаловать, учащиеся весны 2020 года! * Подпишитесь на напоминания, отправив текстовое сообщение «@7c6973f8» на номер 289-813-4722.Ограниченный успех Некоторый успех Значительный успех Высокая степень успеха 1. pdf из MATH MCF3M средней школы Джона Фрейзера. 5 баллов) MCR3U 11 класс – Университет (функции) MCR3U Министерство Руководящие принципы (стр. Минимум шесть курсов уровня U/M 12 класса (исключая совместные занятия), в том числе: Английский (ENG4U) Подтверждение владения английским языком, если английский не ваш родной язык Подробности Этот ресурс содержит электронную версию учебника естественных наук ScienceFocus для 9 класса, иллюстрированные предложениями для занятий в классе.примечания: 0 — алгебраические инструменты. 3 Действительные корни квадратичных функций FIN 401 — WACC (Стоимость собственного капитала) — Университет Райерсона MCF3M: предварительное условие MCF3M: 5. Приведите пример из реальной жизни, моделирующий эту функцию. Некоторые программы включают специальные курсы уровня 4U (предварительные условия) как часть обязательных шести. делает скейтборды на заказ для профессиональных райдеров. Раскрашенный куб, урок 3. Сборник тестов, выпускной экзамен и руководство по повторению. MCF3M-Функции и отношения (1 класс 1 U/C) Ваши оценки. — Несколько пошаговых решенных примеров Страница 4/25.2 + k\) Запустить приложение SNC2D Ссылка для изменения климата и природных ресурсов Онтарио: Напоминание о последней части кульминации – понедельник, 2 июня MCF3M Напоминание о кульминации в классе, понедельник, 26 мая (день 1/3) и… Функции и приложения MCF3M, класс 11 Подготовка к университету/колледжу. 418-419 — вопросы на просмотр в середине главы. Ресурс, написанный специально для курса «Функции и приложения для университетов/колледжей» (MCF3M). Автор: Araktilar Найдите схемы курсов, схемы модулей, раздаточные материалы, уроки и домашние задания.(b) Когда началась ротация, на какой высоте была математика 11 класса – функции и приложения. Документ политики учебной программы: Математика, Учебная программа Онтарио, классы 11 и 12, 2007 г. (пересмотренная) Предварительные требования: MPM 2D или MFM2P. 4: Просмотр MHF4U_In-Class_Activity_2. Учебника для этого класса нет, но будет… MCF3M Unit 5 Notes. Д: 22 октября 2018 г. · Формы и раздаточные материалы MCF3M. Курсы Эллиотта на 2019/2020 учебный год, семестр II: период 1 — M CV4U — 12 класс Исчисление и векторы. Содержание курса.Учебник: Основы математики для колледжей 11. LaChapelle Home Краткое содержание курса Расписание курса Заданные вопросы (только учебник) Материалы курса С мартовскими каникулами!!! 08.03.2013 0 Комментариев 0 Комментариев Викторина по главе 2 в эту пятницу. Основные характеристики: — Наглядный ресурс с доступным уровнем чтения — Несколько пошаговых решенных примеров с пояснениями учащихся, чтобы помочь учащимся понять ход мыслей — Широкий выбор сборников тестов, выпускного экзамена и руководства по повторению. Имя: _____ Отметка: KU APP TIPS.01. Выбранный супервайзер должен быть одобрен Подготовительной школой Университета Онтарио по питанию и здоровью 12 класса (HFA4U). Домашнее задание: закончить рабочий лист «Порядок операций» и вопросы по веб-сайту. Описание; Завершение площади. Название курса: Функции, 11 класс, Подготовка к поступлению в университет (MCR3U) Название курса: Функции Код курса: MCR3U Оценка: 11 Тип курса: Подготовка к поступлению в университет Количество кредитов: 1. 04. Мы разделим средний семестр (21 x) на название: Функции и приложения U/C для 11 класса (MCF3M) Автор: PDSB Последнее изменение: Род Йегер Дата создания: 10.10.2011 23:05:00 Компания: Школьный совет округа Пил, мистер Эллиотт.Самая быстрорастущая платформа домашних заданий и повторений в Великобритании. Зарегистрируйтесь, чтобы учиться в своем собственном темпе. Функции и приложения — MCF3M Добавить в корзину. 1 пара акций. MCF3M MEL3E MAP4C MCT4C MHF4U MCV4U MDM4U Наука Другое • 1 требуется HFC3M SBI3C SBI3U SCh4U SVN3E SVN3M SPh4U SBI4U SCh5C SCh5U SNC4M SPh5C SPh5U Общественные науки и гуманитарные HIP4O HPC3O HSP3C HSP3U HPD4C HFA4C HHS4C HHG4M HHS4U HSB4U HFA4U Кооператив • кредиты требуется кооперативное образование • Размещение связанные с SHSM … При использовании закона синусов для нахождения неизвестного угла вы должны следить за неоднозначным случаем.Mcf3m раздает раздаточный материал Mcf3m раздает среднюю школу Онтарио. MHF – 4U Занятия в классе Ваша задача – ответить на вопросы, подтверждающие ваши знания… инструментов обучения по математике, естественным наукам, общественным наукам, грамотности, профессиональным раздаточным материалам Mcf3m – heroforyou. 5 Модель с квадратными уравнениями Q4 , Раздел 4. Глава 7 Повторение закона экспоненты (если вы пропустили занятие во вторник или среду): Прочтите и скопируйте в тетрадь: – таблицу на с. MCF3M Quadratic Equations Test #4 Solutions Этот видео скринкаст был создан с помощью Doceri на iPad.Посмотреть комплект. 1, Функции 11 McGraw-Hill, Онтарио MCF3M: 4. Математика 12 класса — дополнительные функции (MHF4U/MAP4C) Математика 12 класса — исчисление и векторы (MCV4U) 12 класс Математика — управление данными (MDM4U) 12 класс Биология (SBI4U) класс 12 Химия (СЧ5У) 12 класс … Функции и приложения MCF3M 11 класс — U/C MCT4C Математика для колледжа Технология 12 класс Колледж MFM1P Основы математики 9 класс Прикладной MFM2P Основы математики 10 класс Прикладной MBF3C Основы математики для колледжа 11 класс Колледж MAP4C Основы для колледжа Математика 12 класс Колледж MAT1L Математика 9 класс MAP4C: принципы математики, 12 класс (требуется MBF3C или MCF3M) Базовые курсы (кодируются суффиксом E) MEL3E: Математика для работы и повседневной жизни, Подготовка к работе.Абитуриенты, не соответствующие вступительным требованиям, будут приглашены пройти предварительные вступительные испытания по математике и/или английскому языку. 43) Annenberg Learner Interactives: коллекция веб-инструментов обучения. До поступления в CALC я посещал среднюю школу Northview, где познакомился со многими дружелюбными людьми и учителями, особенно с моим школьным психологом. Начиная с сентября 2007 г. все курсы математики для 11-х и 12-х классов будут основываться на ожиданиях, изложенных в этом документе. 6 — показательные законы.4 — остроугольная тригонометрия. 99. где t представляет количество минут, в течение которых машина работает. В этом курсе студенты будут изучать квадратичные, тригонометрические и экспоненциальные функции. Миссис 17 декабря Урок: БЛОК ТРИГОНОМЕТРИИ №7 СЕГОДНЯ Ср. Все ученики и учителя были замечательные. Получив письмо, перейдите по адресу https://adp4me. Блок 7- Сложные проценты и Блок 8- Аннуитеты: Понедельник: Вторник: Среда: Четверг: Пятница: 27-31 мая: М: Тема 1-Простые и сложные проценты: М: Тема 2- Формула сложных процентов: М: Тема 3- Текущая стоимость: L: Тема 4 — Финансовые проблемы с технологией.E. Модуль 3 Модуль 4 Образец математического общения. 2 — Решение задач с помощью тригонометрического соотношения 1. Если вы ищете Blyth Academy Orbit, нажмите здесь. МТ2Н. 6 м в ширину и 1. Нажмите на имя вашего учителя, чтобы получить доступ к материалам курса. Установите связи между графическим и алгебраическим представлением квадратичных функций (вершины, нули, точки пересечения x, точки пересечения y) Модуль 4: Стандартные и вершинные формы квадратичных вычислений Тест по этому модулю запланирован на 11 апреля. Я прекрасно провел там время, присоединился ко многим спортивным командам и выиграл множество трофеев.192 # 1 — 10 2 Вершинная форма квадратичной функции с. Модули Модуль 1 – Функции Модуль 2 – Квадратичные функции Модуль 3 – Работа с квадратичными уравнениями Модуль 4 – Триггерные функции Модуль 5 – Периодические и синусоидальные функции Модуль 6 – Экспоненциальные функции Модуль 7 – Финансы Обзор экзамена Мини-обзор Резюме Обзор экзамена Вопрос о ваших успехах в MCF 3M прямо пропорциональна выполнению домашнего задания. Определите, является ли каждое отношение функцией. Через какое время после удара мяч для гольфа находится на высоте Код поля: MCF3M Дистрибьютор: Pearson Education Canada Номер телефона: 416-447-5101 или бесплатный номер 1-800-361-6128 Имеется руководство для учителей.Все курсы средней математики для 10–12 классов по-прежнему будут основываться на этих документах. MCF3M гр. Меня зовут Грейс, мне 19 лет, и в настоящее время я заканчиваю среднюю школу в Городском центре обучения взрослых (CALC). Увеличьте время учебы с помощью ReadAnywhere™. МКФ3М. x AR PM 25.01.2019 nonaBah21i i BiÅIHiManrri MHorot1JRHiB oerpHMacM0 H0BHiá Mllorowuen. 11 класс (требуется MFM1P, MPM1D или MAT2L) программа «Шесть сигм». Ускоренные курсы предлагают ускоренное время прохождения аттестации, что позволяет учащимся проходить курс в более быстром темпе.Занятие 1: РЕШЕНИЕ УРАВНЕНИЙ. Определите без построения графика, какой тип зависимости (линейная, квадратичная или ни одна из них) лучше всего моделирует эту таблицу значений. Первой средней школой, которую я посетил, была Sir John A. Leegene Gocon MCF3M. Ваш учитель также может создавать классы и задавать домашние задания по любой теме повторения на учебной платформе, создавая идеальный MCF3MSec1. MCF3M вводит основные особенности функции, расширяя опыт учащихся с квадратичными отношениями. ) Опубликовано в MCF3M — Математика университетского колледжа 11 класса | Оставьте ответ MCF3M — 17 января 2020 г.Учащиеся будут представлять функции численно, графически и … COS MCF3M Student 2012-2013. Если вы хотите отправить мне сообщение или сбросить задания, пожалуйста, введите необходимые поля ниже и не забудьте прикрепить файл (если необходимо). 1- Макгроу-Хилл Райерсон — Химия в средней школе 11 т.4. 267)0 e) 5 3 7 a ´af) ( ) 2 3 17 7 a ÷a 2. 350, #6, 7 ВИКТОРИНА Глава 6 – Урок 4 О нас Пресса Авторское право Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как YouTube работы Тестировать новые функции Пресса Авторское право Связаться с нами Создатели MCF3M Quadratics II Assessment Part 1 — Investigation (19 баллов) Имя: Trinatey clare 39 #1.Многочлен выглядит так: пример многочлена. Абитуриенты старшей школы должны соответствовать следующим минимальным требованиям: окончание средней школы; Минимум в среднем 70% по пяти успешно пройденным академическим курсам 12-го класса, включая академический английский язык 12-го класса (или французский для абитуриентов из франкоязычных школ) и любые курсы математики или естественных наук, необходимые для вашего … NEL Chapter 1 5 1. Chiarelli ответит по электронной почте, если можно или по телефону. (а) Преодоление разрыва или (б) Дырявая башня. Упростите следующие выражения, используя законы экспоненты.Средние значения отражают учащихся средней школы Онтарио; Помните, что это всего лишь рекомендации. 1 Минимум 60 % по математике на уровне колледжа или университета (MBF3C или MCF3M) 11 класса Упростите следующее, представив каждое из них как одну степень. Тест 2021 Mcf3m. Предварительное условие: MCF3M или MCR3U УЧЕБНИК Математика управления данными. Учителя должны обращаться к учебным документам для планирования программы.Это была хорошая школа, но я не осознавал этого и принял это как должное, обленился и перестал ходить на утренние занятия. а) {(1,5) (4, 6), (6, 7) (8, 14)} б) в) у = х 2-3 г) у = 3х – 2) Мяч брошен вертикально вверх из балкон многоквартирного дома. Здесь вы можете найти заметки о любых уроках, которые вы, возможно, пропустили, а также соответствующие раздаточные материалы, а также подробную информацию о домашних заданиях, сроки выполнения заданий и даты предстоящих викторин и тестов. Роли и обязанности. Теперь вот ваше задание — возьмите лист бумаги и ответьте на следующие вопросы: 2 мысли о «MCF3M» Кейтлин говорит: 20 марта 2014 г., 21:30.3 — Закон синусов 1. Курсы ESL можно использовать для получения диплома средней школы Онтарио. coli, N, исходного образца MCT4C — Математика 12 класса для технологии колледжа. Краткое содержание курса MCF3M. ) 11 октября — страницы 120 и 121 с 11 по 13, 15, 16 и 18 (из учебника) 10 октября — страницы 115 и 116 с 2 по 5, 7, 11 и 12 (из учебника) Просмотреть MCF3M — практический тест . Описание Обзоры Вопросы и ответы Подробнее о … Практический экзамен MCF3M – РЕШЕНИЯ ЧАСТЬ A Краткий ответ 1. 1 Горизонтальное и вертикальное преобразование функций MCF3M:4.Вы получите свой идентификатор пользователя по электронной почте. а) Начертите график функции для двух оборотов. В конце каждого учебного занятия давались предложения относительно того, что вы должны добавить к нему. 3 Функция синуса. Углы и соответствующие им соотношения синусов находятся на единичной окружности. Ваши решения должны быть хорошо организованы и разборчивы. USCA Academy — это частная школа, проверенная Министерством образования Онтарио, и одна из лучших частных школ в Онтарио, Канада, с современным оборудованием.Функции и приложения MCF3M 11 класса Курс подготовки к университету/колледжу — курс Министерства образования MCF3M Описание: Этот курс знакомит учащихся с основными функциями функции, расширяя опыт работы учащихся с квадратичными отношениями. Просмотр MHF4U_In-Class_Activity_2. 2б — квадратичные функции — преобразования. Питер Нгуен MCF3M Воскресенье, 31 января 2010 г. Сентябрь Тайлер 11 класс -MCF3M 12 класс Классная работа для MHF i M Inboy x Unit. 8 м высотой посередине. pl Последний образ жизни | Новости повседневной жизни, советы, мнения и советы от The Sydney Morning Herald о жизни и отношениях, красоте, моде, здоровье и благополучии Вопросы о векторах в физике с ответами pdf Просмотр MHF4U_In-Class_Activity_2.Отвечать. Если вы застряли на чем-то, загляните на следующий веб-сайт, на котором размещены полезные видеоролики практически на любую тему по математике — просто выполните поиск «Регистрация — стандарт». 2) Посмотрите видео на ютубе от мистера 5 — функции синуса. Функции и приложения MCF3M 11 класс, подготовка к университету/колледжу Общая информация о курсе Необходимые условия: MPM2D, MPM2P Факультет: математика Дополнительная помощь: уточните у учителя Стоимость учебника и замены: функции и приложения 11, $80 линейка, карандаш, миллиметровая бумага Стоимость курса: нет Практический тест: экспоненциальные функции Знание и понимание MCF3M: 1.Право на участие могут иметь кандидаты, которые прошли эквивалентные курсы, повышение квалификации, завершили GED и прошли тестирование на эквивалентность. Это происходит, когда с использованием данной информации можно создать два разных треугольника. MCR4U как необходимое условие для расширенных функций? Академики. МПМ1Д. Учащийся, регистрирующийся на курс повышения квалификации, должен отправить MCF3M: Глава 3. Задание. Цели: Вы должны быть в состоянии… вычислить нули, ось симметрии, вершину и точку пересечения с осью Y, учитывая различные формы квадратичных функций.1 — Еще раз о первичном тригонометрическом отношении 1. Курс MCF3M знакомит с основными особенностями функции, расширяя опыт учащихся с квадратичными отношениями. Диагностика трансформаций. Итак, наши числа теперь –3 и 24. 19 $7. (MCF3M) Этот курс знакомит с основными функциями функции, расширяя ваш опыт работы с квадратичными отношениями. Соответствовать требованиям могут кандидаты, которые прошли эквивалентные курсы, прошли повышение квалификации, завершили GED и прошли тестирование на эквивалентность. Обучение в Blyth Academy Online.Начало работы TIPS4RM (TIPS for Revised Mathematics) Планы уроков, состоящие из трех частей, и поддержка для MCM3M 11 класса, разработанные или поддерживаемые Министерством образования. Содержание является точным, и вся необходимая информация представлена в логическом порядке. Управление данными 12 — Учебник. Этот курс основан на ожиданиях и рекомендациях, установленных MCF3M. net (916) 933-6980 доб. 3924 Минимум 60% по математике на уровне колледжа или университета (MBF3C или MCF3M) 11 класса допуск.Викторина MCF3M №3 — Функции, домен и имя диапазона: _____ / 10 (K) 1. 12 октября — Практический тест квадратичных выражений MCF3M (пустая копия) 12 октября — Практический тест квадратичных выражений MCF3M РЕШЕНИЯ (это решения практического теста перечислено выше. Всем привет. Кроме того, я буду публиковать видео и интерактивные задания, связанные с содержанием курса. Введение. 2 круга и коэффициент синуса, часть 1, вопрос 19, раздел 4. AChor/MCF3M Имя: _____ Дата: _____ 3. План курса. Я, как правило, быстро учусь, и я горжусь своей способностью решать проблемы и быть индивидуальным учеником.Из-за моей безответственности меня выгнали за посещаемость. Учитесь дома с виртуальными онлайн-кредитами средней школы, предлагаемыми Учебным центром Megamind. CALC is my Functions and Applications 11 поддерживает разнообразные потребности учащихся в классе MCF3M, готовя их к успешной учебе в 12 классе и далее. pdf из MATH MCF3MC в Независимом учебном центре. Я решил поступить в эту школу, потому что не выдерживаю темпа в обычных средних школах. Содержание курса. блокнот 6 10 сентября 2012 г. 9:10:28 PM Домен может представлять определенный набор или «набор всех действительных чисел МЕНЬШЕ нуля» Диапазон может представлять определенный набор или «набор всех действительных чисел, больших или равных 5» «за исключением или условием» фев 22:15 Умножение многочленов.Макф3м тест. a) 5 ´a 8 b) 600 ÷b 500 c) ( ) a6 3 d) (4. БЕСПЛАТНОЕ приложение ReadAnywhere позволяет загрузить электронную версию учебника на смартфон или планшет, читать, делать заметки, выделять и многое другое. 3) Получите доступ к нашему курсу VLE (виртуальная среда обучения) здесь. Департамент математики mcf3m a216, функции Нельсона 11, руководство по решениям ippbooks com, функции и приложения Нельсона 11, рабочие листы главы 1, вторичные математические функции и приложения Нельсона 11, функции Нельсона 11, отличные предложения на книги, используемые Кидзи, функции и приложения Нельсона 11 книга 2008 г., 11-й вид MHF4U_In-Class_Activity_2.ПОДЕЛИТЬСЯ. Начало работы — Что я знаю и что я помню. pdf УЧЕБНИК MCF3M. *. Этот курс знакомит с основными особенностями функции, расширяя опыт студентов с квадратичными отношениями. Затем следуйте инструкциям для регистрации. Поддержка учителя по запросу, когда вам это нужно, с доступом к преподавателю одним щелчком мыши. После двухмесячного путешествия мне кажется, что второй квадроцикл закончился преждевременно. Рассказывает учитель математики средней школы в Онтарио. ОПИСАНИЕ КУРСА Этот курс знакомит с основными особенностями функции, расширяя опыт студентов с квадратичными отношениями.Зерро. Этот ZIP-файл представляет собой сжатую папку, содержащую все 13 PDF-файлов из О нас Пресса Авторское право Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторское право Связаться с нами Создатели MCF 3M Unit 4: Работа с квадратичными функциями — Standard и Vertex Forms Тема урока Порученная работа 1 Начало работы с. Важность и красота математики. Тест №3 MCF3M – Факторинг и решение квадратичных функций Название: _____ 5 11. . Эта утвержденная колледжем программа сертификатов является связующим звеном, которое вам нужно, чтобы войти в совместную программу BScN … Эквивалентные выражения Цель навыка: ЭКВИВАЛЕНТНЫЕ ВЫРАЖЕНИЯ Учащийся будет знать, как найти выражение, эквивалентное данному выражению, решая каждое выражение и находя выражения, которые равны заполнив вопросы с несколькими вариантами ответов.Уровень: 11. Учебник MCF3M – Математика 11 $ 136. Наведите указатель мыши на код курса (MCF3M) вверху и выберите соответствующую единицу работы. Код курса: MCF3M. Выбирайте из более чем 1000 курсов KS2, KS3, GCSE и A Level в соответствии со спецификациями экзаменационной комиссии. Редактировать: я имел в виду MCR3U в названии, извините за это. Приложение «Функции и приложения» предназначено для студентов, которые планируют изучать технологические программы в колледже или готовить студентов к некоторым университетским программам. (2 балла) x -1 0 1 2 Этот курс знакомит с основными особенностями функции, расширяя опыт учащихся с квадратичными отношениями.S. Описание курса Этот курс знакомит с основными особенностями функции, расширяя опыт учащихся с квадратичными отношениями. Итак, я работал над заданием модуля и думал, что смогу провести викторину завтра, но я действительно потерялся во всем кубировании, а что нет. — Несколько пошаговых решенных примеров с объяснениями учащихся, чтобы помочь учащимся понять ход мыслей. Описание курса McCrum: Этот курс знакомит с основными особенностями функции, расширяя опыт студентов с квадратичными отношениями.В разделе 1 мы видели три вида преобразований. Если вы подаете заявление в качестве учащегося средней школы Онтарио, обратите внимание: Курсы уровня 4U или M. 1. В одиннадцатом классе я прошел курс «Функции и приложения» (MCF3M) и очень хорошо сдал в классе и сожалею, что не выбрал обычные функции (MCR3U). Все о Рите Тран. Мост к непрерывному обучению и карьерному росту.MCF3M Экспоненциальные функции Тест # 7 Решения (Я вернул это сегодня ученикам в классе. [email protected] Декабрь 16 Урок: Триггерные задачи Word (Les… Элементарные навыки алгебры Решение квадратных уравнений с использованием квадратичной формулы Решите каждое уравнение с квадратичной формулой .pdf: О нас Пресса Авторские права Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторские права Связаться с нами Создатели Я впервые принимаю MCF3M.3 Изучение функций функции синуса 11 Глава 3 Практический тест (часть 1) MCF3M: 3. Запустите Gizmo. Объяснять. 1 — функции. Укажите домен и диапазон отношения на диаграмме b) выше. Я вернулся через год с амбициями, но без мотивации. а) Сколько скейтбордов необходимо произвести для … Этот поиск по словам «MCF3M Word Search — Poole» был создан с помощью конструктора головоломок My Word Search. Функции и приложения, 11 класс, подготовка к университету/колледжу (MCF3M) 1 Здесь представлен обзор изменений в учебной программе.17 декабря Урок: повторение теста по тригонометрии; Обзор тригонометрического теста (РЕШЕНИЯ) Вт. Срок утверждения продлен до 31 августа 2022 г. MCF3M—S. Привет, мистер 11 КЛАСС, ОНТАРИО, 2008 г. Урок 3: Горизонтальные растяжения, сжатия и отражения • Опишите, как отражение по оси Y влияет на функцию, и сформулируйте этот тип требований для поступления в бакалавриат. Этот буклет, специально написанный для курса MCF3M, содержит пояснения, рабочие примеры и викторины с решениями. Рабочая тетрадь успеха специально разработана, чтобы помочь учащимся, испытывающим затруднения, добиться успеха.Название курса: Функции и приложения, 11 класс, подготовка к университету/колледжу (MCF3M) Название курса: Функции и приложения. Если ваш курс использует Connect, вы можете получить доступ к SmartBook 2. Модуль 1 Модуль 2 MBF3C Обзоры модулей и видеоуроки. The Wheely Fast Co. Этот курс представляет собой промежуточный курс, который подготовит вас к MCR 3U (Университетский класс 11) или… добро пожаловать в функции и приложения 11 класса (Mcf3m). Заходите сюда, чтобы узнать о домашних заданиях, уроках, заданиях и обо всем, что вам может понадобиться для вашего курса математики.389 – … Рита Тран MCF3M Суббота, 14 ноября 2009 г. Мы сжали содержание до того, что вам действительно нужно знать для ваших экзаменов. (3 балла) 2. Студенты MCR3U также найдут полезный пересмотр основ. Глава 1. Тригонометрия (электронный текст) 1. Требования к вашей программе. (MCF3M) Изучите основные особенности функции с квадратичными соотношениями: квадратичные, тригонометрические и экспоненциальные функции. MCF3M Реальный мир, 3 акта, математические задачи. МДМ4У1. Бава. doc pdf — Раздел 1: Введение; doc pdf — Модуль 2: Функции через квадратичные уравнения (широкие штрихи) ; doc pdf — Раздел 3: Исследование квадратичных уравнений ; doc pdf — Модуль 4: Квадратичные (максимумы и минимумы) ; doc pdf — Модуль 5: Экспоненциальные функции; doc pdf — Модуль 6: Финансовые приложения экспоненциального … Общий список инструментов: MCF3M Grade 11 University-College Math.00 11 или 12 класс Управление данными MDM4U Добавить в корзину. Я рассматриваю это как обязательное условие для дополнительных математических курсов, так как моя конечная цель — поступить на программу информатики в университете. в классе MCF3M, готовя их к успеху в 12 классе и выше. После двух лет обучения в MAC меня исключили из этой школы и заставили начать обучение в другом месте. 17. Необходимое условие: MFM2P или MPM2D. 01 9 собрать данные, которые могут быть смоделированы как квадратичная функция, путем исследования с помощью технологии и без нее из MCF3M-S.Поиск: Волшебный прямоугольник. Автобиография Тахсина. Тип курса: подготовка к университету. После того, как его исключили из требований средней школы Онтарио. Inrig Страница 1 из 1 Порядок применения преобразований Вы помните, что основной («родительской») квадратичной функцией является f (x) = x2, которая описывает параболу, которая открывается вверх и имеет вершину в начале координат (0,0). Функции и отношения Область определения и диапазон (рабочий лист) Обозначение функций Родительские функции, обратные линейной функции Область определения и диапазон функций Преобразования функций MCF3M ОБЕСПЕЧЕННОЕ ИТОГОВОЕ ЗАДАНИЕ – ОБЗОР 1) Определите область определения и диапазон следующих функций.Продукты 7 долларов. MCF3M Задание – ФУНКЦИИ КВАДРАДИКОВ Название: Ответьте на следующие вопросы в отведенном для этого месте. Он предоставляет доступную математику прямо в классе для поддержки учащихся 11-го класса курса математики университета/колледжа MCF3M. Права человека, справедливость и инклюзивное образование по математике. 5 в рабочей тетради. 5 — Обзор экзамена MCF3M Имя: _____ 18. MPM1D1. Математический сайт Кокти — Главная. IXL Grade 11 Math Practice — Практические онлайн-вопросы для 11 класса. Эллиотт. Привет, меня зовут Рита Тран, мне 18, я родилась в Канаде, но я смесь китайца и вьетнамца.Рукоятка вращается так, что высота рукоятки h в метрах равна h( ) 2sin( 90 ), где угол поворота относительно горизонтали. 4 — Закон косинуса 1. Размеры, которые находятся на расстоянии 30 м друг от друга и дают площадь 60 м 330 м . 1 Длина 60 м. Функции и приложения McGraw-Hill Ryerson 11. Вы должны продемонстрировать свою работу по вопросам, требующим двух шагов. Напоминание об экзамене по главе 6: четверг, 3 апреля (занятия 1/3 дня) и пятница, 4 апреля (занятия 2/4 дня). Предварительный курс. Педагоги должны знать, что, за исключением курса математики для 9-го класса 2021 года (MTh2W), учебная программа по математике для 10-го класса 2005 года и учебная программа по математике для 11-12 классов 2007 года остаются в силе.Палатка рассчитана на 3 человека. Первоначально утверждена 25 мая 2001 г. Студенты будут представлять планы уроков OAME — MCF3M; База данных планов уроков OERB + обзор видео (7:55) Освещение NCTM — планы уроков и инструменты Учебные материалы PBS — 11 класс; Уроки и поддержка TIPS4RM План урока Ватерлоо Обновление MathSwap MCF3M Предварительные требования: Основы математики, 10 класс, академический курс, или Основы математики, 10 класс, прикладной курс. /eview- Unit 5 Тригонометрия r,~=::~3J. прил. Заполните раздаточный материал в разделе ресурсов.80. Свяжитесь с нами: Mr. Exam Supervision Criterion / Final Exam. Вы будете представлять функции численно, графически и алгебраически; упростить MCF3M: ежедневное расписание и раздаточные материалы. Все курсы будут иметь выпускные экзамены, если иное не согласовано с директором. MCF3M avec Mme Delarosbil — Осень 2016 продана 13 января 2017. 1) Ответ на электронное письмо от Mr. Home Products с тегом «MCF3M» Подробнее. Предыдущей школой, которую я посещал, был Lakeshore Colligiate Institute. Период 2 — MDM4U — 12 класс Управление данными (веб-страница отсутствует, поскольку вместо нее используется OneNote) Период 3 — MCF3M — 1 класс 1 Функции и приложения.5 иллюстрированных предложений для занятий в классе. 339 #1, 2, 3(a-d), 4(a-c) Глава 6 – Урок 3 Применение синусоидальной функции Стр. 110 канадских долларов. Математика для 12 класса — Расширенные функции (MHF4U/MAP4C) Математика для 12 класса — Исчисление и векторы (MCV4U) Математика для 12 класса — Управление данными (MDM4U) Биология для 12 класса (SBI4U) Химия для 12 класса (SCh5U) Класс 12 … Всплывающее окно календаря курса Быстрый просмотр Курсы предлагают ускоренное время выполнения оценки, что позволяет студентам быстрее проходить курс.00 11-й или 12-й класс Семинары T³™ на месте посвящены наиболее эффективным способам использования технологии TI-Nspire™ в учебных программах по математике средних и старших классов. страницы. Основное внимание уделяется квадратичным, тригонометрическим и экспоненциальным функциям и их использованию в моделировании реального мира. Один из: Функции и приложения MCF3M или Функции MCR3U; Один из: Биология 11 СБИ3У, Химия 11 СЧ4У, Экология 11 СВН3М или Физика 11 СФ4У; Английский ENG4U (мин. 70%) Расширенные функции MHF4U (мин. 75%) Химия СЧ5У (мин. 75%) Физика SPh5U (мин. 75%) Исчисление и векторы MCV4U (мин. 70%) Один дополнительный курс из списка A или B Функции и приложения 11 поддерживает разнообразные потребности учащихся в классе MCF3M, готовя их к успеху в 12 классе и далее.MCT4C против MHF – 4U Работа в классе Ваша задача – ответить на вопросы, подтверждающие ваши знания … Категория: Тест Mcf3m. Математика 11 класса. 05.03.2013 0 Комментариев 0 Комментариев Глава 1 Тест 1 марта MCF3M — Функции и приложения Почему выбор MCF3M был плохой идеей Шутка! Это было лучшее решение, которое вы когда-либо принимали или когда-либо примете в своей жизни! !!! Модуль 1: Изучение функций: Соединение алгебры… Название курса: Функции и приложения 11 Онлайн (смешанная математика) Класс: 11. У меня была очень плохая посещаемость, и я не вернулся на пятый год, потому что устроился на работу, поэтому я, несмотря на то, что школа была не для меня.Прочтите книгу Nelson Functions And Applications 11 Solutions Руководство с пояснениями для учащихся, чтобы помочь учащимся понять 11 класс Математика (MCR3U/MCF3M/MBF3C) 11 класс Физика (SPh4U) 11 класс Химия (SCh4U) 11 класс Биология (SBI3U) 12 класс. 1FuncNot. Канал Кутюрье на YouTube. Модуль 7 Модуль 8 Завершение квадратного виджета. Основное внимание уделяется квадратичным, тригонометрическим и экспоненциальным функциям и их использованию в Powered by. Создайте свой собственный уникальный веб-сайт с помощью настраиваемых шаблонов. Видение и цели курса математики 9 класса.Модуль 5 Модуль 6, Онтарио, 11 класс. Учебная программа. Ресурс, написанный специально для курса «Функции и приложения для университетов/колледжей» (MCF3M). 330 #4, 6, 7, 9 Глава 6 – Урок 2 Исследование функции синуса Стр. Код курса: MCF3M Распространитель: Nelson Education Ltd. TVO ILC MCF3M Практический тест Функции и приложения MCF3M Практический тест Время: 2 часа Всего баллов: 107 Практический тест нет MCF3M MCR3U ** Любые слова, выделенные зеленовато-желтым цветом, являются ссылкой/файлом! Полезные ссылки Графический онлайн-калькулятор — desmos Домен и диапазон видео Факторинговая игра: ЗДЕСЬ Расписание 3 февраля — Полиномиальные определения, числа и операции.Вам понадобятся: Диплом средней школы Онтарио. 0 заданий через приложение для удобства на ходу. MCV4U1. McGraw-Hill Ryerson: 2002 ISBN-13: 97800709 ($104. Занятие 2: ПРОБЛЕМА РАСТЕНИЙ. MHF – 4U Занятие в классе Ваша задача – ответить на вопросы, подтверждающие ваши знания… иллюстрированные предложения для занятий в классе. 4 Преобразования \u0026 Синус FunctionMCF3M: 4. C(t)=2.Каковы углы подъема сторон палатки для MHF4U – Тест: Тригонометрические функции v2.Статус зрелого студента. MCF3M МакКленнон-Совчук 11 класс 6–9 сентября: завершить до главы 1. 1р; Lh = :~:~~~~! I. Tahseen Hussain MCF3M, пятница, 13 ноября 2009 г. 106 канадских долларов. Демонстрации — Удивительно, что графики сравнивают любые функции. Все ваши завершенные и текущие курсы уровня U/M для 11 класса. 3 — решение квадратных уравнений. О нас Пресса Авторские права Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторские права Связаться с нами Создатели Grace B MCF3M Четверг, 19 ноября 2009 г.Примечание. Если кандидат не соответствует минимальным требованиям по математике по одному из курсов 11-го класса, Western проверит минимум 65 % по одному из дополнительных функций MHF4U, исчисления и векторов MCV4U или математики управления данными MDM4U. Пакет функций университета/колледжа MCF3M. «Функции и приложения» предназначены для учащихся, которые планируют изучать MCF3M: 3. Этот учебник поддерживает учебную программу Онтарио, 11 и 12 классы: «Математика», 2000 «Функции и приложения», 11 класс (MCF3M). Семенная работа — 70 % итоговой оценки — 30 % тестов. , задания, работа в классе 10 % Тесты 50 % Домашние задания 10 % Курсовая работа Блок 1: Обзор необходимых навыков (2 недели) Блок 2: Графическое построение парабол; Максимальное/минимальное применение (3 недели) MCF3M: Quadratics Strand Unit 1-3 Функции обзора 11 Глава 2 Практический тест MCF3M: 5.4. Этот курс знакомит с основными особенностями функции, расширяя опыт учащихся с квадратичными отношениями. MCF3M- Ms. coli — это очень вредный тип бактерий, которые могут быть обнаружены в мясе, которое неправильно хранится или обрабатывается. Это была действительно хорошая школа. Книга «Функции и приложения» предназначена для учащихся, которые планируют изучать MCF3M. Редакция 2007 г. Четырехстраничный обзор словарных навыков и понятий в начале каждой главы «Функции и приложения Нельсона 11». крупнейшее в мире сообщество читателей Книга Nelson Functions and Applications 11 Где скачать Технологии механики Вопросы для 12 классаГ-н МАТЕМАТИКА 3079: Исчисление и векторы ИЛИ Математика 3080: Расширенные функции (вместо MCF3M или MCR3U) Студенты факультета медицинских наук и общих искусств и естественных наук Fanshawe College по-прежнему должны получить сертификат с минимальным средним баллом 2. ca. Вычислите 1 3 f при заданном fx x() 3 9 . Викторина № 2, вопрос 1: упростите (запишите как единую степень), затем оцените (покажите свою работу). Учащиеся будут представлять функции численно, графически и… БЛОК 1: ТРИГОНОМЕТРИЯ. Основные характеристики: — Наглядный ресурс с доступным уровнем чтения.1 Периодические функции MCF3M: 5. Виджет решения квадратных уравнений Калькулятор неоднозначных случаев-3. Используйте квадратную формулу, чтобы решить каждое уравнение. Компания моделирует свою прибыль с помощью функции P(b) = -2b2 + 14b – 20, где b — количество произведенных скейтбордов в тысячах, а P(b) — прибыль компании в сотнях тысяч долларов. сеть (530) 677-2281 доб. 2332 Мистер Уайт: [email protected] См. ниже ежедневную разбивку занятий в классе. Этот курс представляет собой курс математики для 11 класса на уровне университета/колледжа.Мяч падает на землю по параболе. пдф. Функции и приложения 11 удовлетворяют разнообразные потребности учащихся в классе MCF3M, готовя их к успешной учебе в 12 классе и выше. Руководство по пересмотру включает упражнения с решениями. Военный альбом. Соотношение ) 20 0(2 t NN оценивает количество E. Предположим, что функция простирается до бесконечности, а данный масштаб равен 1 к 1. 203 # 4, 6, 8ac, 9ac, 10, 12 Рабочий лист 1 3 Связь со стандартом и … Код курса MCF3M Кафедра математики Расположение офиса A216 Часы работы 8:30 a.Файл закладок PDF Blm First Grade 1 Quiz Answer Функции и приложения 11 поддерживает разнообразные потребности учащихся в классе MCF3M, готовя их к успешной учебе в 12 классе и далее. Номер телефона: 416-752-9448 или бесплатный номер 1-800-268-2222 Доступен гид для учителей. pdf — Введение в MCF3M; Единицы. 7 — … MCF3M — Функции и приложения. Ваш пример не должен соответствовать данным — только общий тип функции. ЭКЗАМЕН. Г-жа За 7 дней до предпочтительной даты экзамена студенты отправят форму утверждения руководителя.Установите связи между графическим и алгебраическим представлением квадратичных функций (вершины, нули, точки пересечения x, точки пересечения y) Раздаточные материалы Mcf3m Раздаточные материалы Mcf3m Ответьте на вопросы из раздаточного материала «Наблюдения». Онлайн-школа предлагает онлайн-курсы в Онтарио за кредиты OSSD с 9 по 12 классы. Представляйте функции численно, графически, алгебраически и упрощайте выражения. Пожалуйста, регулярно проверяйте этот сайт, чтобы быть в курсе уроков, пройденных в классе. МСТ4С. Понимание различий в линейных, квадратных, показательных и периодических уравнениях.– 16:00 Цель: К концу этого урока учащиеся должны понять, что углы можно измерять как в радианах, так и в градусах, и что вы можете преобразовывать эти две меры. класс сегодня.5 будет рассматриваться для поступления, и иметь конкурентоспособный средний балл, чтобы быть предложенным.Нажмите здесь для получения дополнительной информации о системе кодирования курсов MCF3M – Математика 11 класса Добро пожаловать в математику 11 класса!Вот блоки, которые мы будем изучать.Я говорю это, потому что мне казалось, что Quad Two только что начался. Основное внимание уделяется квадратичным, тригонометрическим и экспоненциальным функциям и их использованию в моделировании реальных ситуаций. Это слишком медленно, а в Calc все немного быстрее, это довольно бодрит, плюс мне, кажется, нравится давление. Функции и приложения, функции MCF3M, MCR3U; ПРИМЕЧАНИЕ. В качестве предварительных требований могут потребоваться курсы уровня 3U и/или 3M 11 класса (однако они не будут использоваться при расчете среднего зачисления). Средний показатель: от 80 до 90.Спасибо! Имя *. О нас Пресса Авторское право Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторское право Связаться с нами Создатели Mcgraw Hill Ryerson Mcf3m the ontario training edu gov on ca Другие файлы Elite Soccer CoachingEmbroidery Designs Логотипы колледжей University Califorina DavisEmotion Albano Elezi MCF3M Monday , 23 ноября 2009 г. Chor Ms. Celui-ci a 21 numéros (требование трех вопросов в главе) étendus sur 4 feuilles (оборотная сторона).На протяжении всего курса вы вели математический дневник. 6 Связь с законами синусов и косинусов Макгроу Хилл Райерсон Математика 11 В математике для всех практических вопросов, кроме самых рутинных, существует множество решений. Принципы, лежащие в основе учебного плана по математике для 9 класса. Приложите снимок экрана с графиком Desmos 121 b) Умножьте уравнение (или используйте квадратичную формулу) на функции и приложения MCF3M: Квебек: Для индивидуальной оценки обращайтесь в приемную комиссию: Нью-Брансуик: Основы математики 110: Ньюфаундленд: Математика 2201: Нова Шотландия: Math 11: Остров Принца Эдуарда: Math 521A Hazel Acuna MCF3M, среда, 18 ноября 2009 г.Функции и приложения. (1. 1 Периодические функции MCF3M: … AChor/MCF3M Имя: _____ Дата: _____ 4. Фуллер: [электронная почта защищена] Самая полная библиотека курсов средней школы Онтарио с более чем 160 на выбор. Если это не функция, объясните, почему Срок утверждения продлен до 31 августа 2007 г. 11 класс Математика (MCR3U/MCF3M/MBF3C) 11 класс Физика (SPh4U) 11 класс Химия (СЧ4У) 11 класс Биология (SBI3U) 12 класс Объясните его значение в контексте задачи MHF – 4U Работа в классе Ваша задача – ответить на вопросы, подтверждающие ваши знания … MCF3M: Quadratics Strand Unit 1-3 Функции повторения 11 Глава 2 Практический тест MCF3M: 5.———. Альбано Элези. Рассмотрим уравнение y = x + 6x — 16 a) Используйте Desmos для построения графика функции и определения точек пересечения x, вершины и максимального/минимального значения. Готовьтесь в любом месте. Большой никель. сложите эти ответы вместе и упростите, если… • Функции и приложения MCF3M • Функции MCR3U . pdf Загрузка… MCF3M MCR3U ПОЖАЛУЙСТА, ПРИБЫВАЙТЕ ВО ВТОРНИК 29 ИЮЛЯ МЕЖДУ 9-11, ЧТОБЫ ЗАБРАТЬ ТАБЕЛЕТ В БИБЛИОТЕКУ!!!!! Ура! Вы успешно нашли документ! Похлопайте себя по спине! Не забывайте проверять веб-сайт каждую неделю для получения обновленной информации.Показаны все 2 результата. 11 класс U/C – Раздел 4: Квадратичный – максимумы и минимумы 4 C C QF3. MCF3M — Функции и приложения Подробности курса Этот курс знакомит с основными функциями функции, расширяя опыт учащихся с квадратичными отношениями. 2000 – Функции и приложения 2006 – Функции и приложения Strand Sub-Strand Strand Sub-Strand Ответы на экзамен MCF3M Автор: Дженнифер Патрик Дата создания: 20.01.2010 18:46:14 Функции и приложения MCF3M 11 класс Университет/колледж T .Чтобы иметь право зарегистрироваться на курс повышения квалификации, учащийся должен пройти тот же курс в течение последних 12 месяцев, получив итоговую оценку не менее 50%. MCF 3M — Класс мисс Бобьен. MCF3M Модуль 7 Примечания. Первоначально утвержден 15 февраля 2008 г. 7 сентября 14: обзор 15 сентября: модульный тест В начале раздела «Финансовые приложения» курса MCF3M я хотел познакомить студентов с задачей простых процентов таким образом, чтобы это помогло им понять, какие навыки они уже приобрели. обладают, когда дело доходит до процентных ставок, процентов и решения проблем.Тема: Понимание синусоидальных функций — Введение. pdf Идет загрузка… MCF3M Банк образовательных ресурсов Онтарио (OERB) Деятельность Деятельность по квадратичным функциям. (4 балла) 3. Занятие 3: ПРОБЛЕМА АВТОМОБИЛЯ. 6. 2 Мяч для гольфа подбрасывается в воздух, и его высота определяется функцией h(t) = 20t – 5t , где h – высота в метрах, t – время в секундах. Математические задачи из реального мира, соответствующие функциям и приложениям MCF3M 11 класса Учебная программа подготовки к университету/колледжу Онтарио. Опубликовано 17 января 2020 г. автором Mr.2а — квадратичные функции — формы. У меня не было возможности заняться этим, но я сказал ученикам, что мы займемся этим в начале завтрашнего урока. Макдональд. Мне интересно, не мог бы ты объяснить мне кое-что завтра вместо того, чтобы писать тест? Функции и приложения MCF3M 11 класса, подготовка к университету / колледжу Опубликован диплом OSSD Онтарио 22 июня 2019 г. 22 июня 2019 г. Я прошел курс смешанного уровня вместо функций, потому что мое руководство MCF3M ПРАКТИЧЕСКИЙ ЭКЗАМЕН 1. MCF3M Квадратичные функции Название практического теста: _____ Знания R Уровень 1 Уровень 2 Уровень 3 Уровень 4 Умеет использовать квадратную формулу для нахождения нулей.Родители могут связаться с Лидой по электронной почте. Сильное академическое наследие и новатор в области онлайн-обучения с 2012 года. Этот учебник поддерживает учебную программу Онтарио, классы 11 и 12: математика, 2007 г. (пересмотренный) , 2018 — ВВЕДЕНИЕ Этот документ заменяет курс математики для 11-х классов Онтарио 2006 года и курсы для 12-х классов в учебной программе Онтарио по математике для 11-го и 12-го классов. Правила и процедуры MCF3M для работы в классе Автор: Митци Фуйс Дата создания: 01.09.2014 22:24:11 Стоимость C в долларах на эксплуатацию плиткорезного станка моделируется как .2-66т+655. м. Дополнительные вопросы для повторения: с. Ширина 30 м. Цикл №2 — Экспоненциальные и периодические функции. Питер Нгуен ЗАКЛЮЧИТЕЛЬНОЕ ЗАДАНИЕ MCF3M. – Ответы из учебника (конец книги) – Руководство по решению, главы: первая … MCF3M Тест №2 – Обзор 1) Показан график, показывающий количество сотовых телефонов в U. 0 Предварительные требования: MPM2D, Принципы математики, … Виртуальная средняя школа — это онлайн-средняя школа, предлагающая кредиты на получение диплома средней школы Онтарио. НАУКА . Синусоидальная функция имеет -подобный вид с периодом Свойства Схема графика Максимальное значение Минимальное значение Амплитуда Домен Диапазон перехватов перехватов Интервалы увеличиваются (за один цикл) Интервалы уменьшаются (за один цикл) = sin x ОКОНЧАТЕЛЬНЫЙ Примечания к курсу Биология: Ткани, Органы и системы живых существ Примечания к модулям: слайды или PDF-файл. Клеточный боевой корабль. Химия: химические реакции. Примечания к разделам: слайды или PDF-файл. Науки о Земле и космосе: изменение климата. Зеркало Примечания: wave_light PPT или wave_light PDF Краткая версия… 5 4 3 2 1 Содержание Плакат содержит соответствующие элементы и информацию (информация соответствует назначенной теме).а) Определите точные значения sec и tan (в виде дроби), если угол квадранта 2 и точка находится ровно в 25 единицах от начала координат и лежит на конечном плече . Сумма кредита: 1. 5 Модель с квадратными уравнениями MCF3M: 5. Переводной курс MPM1H (пилот… КАРЬЕРА. Для подготовки к модульному тесту: выполните/проверьте все назначенные домашние задания и тесты. Здесь вы найдете экзаменационные работы за прошлый год и заметки, начиная с года с 2021 по 2008 год. Большинство наших студентов поступили в такие учебные заведения, как Университет Торонто, Университет Ватерлоо, Университет Макмастера, Университет Квинса, Западный университет, Йоркский университет. Другие курсы математики, предлагаемые нашей школой, включают функции и приложения. 11 класс — университет /Подготовка к колледжу (MCF3M), Расширенные функции, 12 класс — подготовка к поступлению в университет MHF4U, исчисление и векторы, 12 класс — подготовка к поступлению в университет (MCV4U) и математика управления данными, 12 класс — подготовка к поступлению в университет/колледж (MDM4U).(Будет использоваться для викторин и представления заданий) 5) Заполните два рабочих листа ниже. pl Mcf3m раздаточные материалы1- McGraw-Hill Ryerson — High School Chemistry 11 v4. ) Выполнение домашнего задания от 24 сентября (страницы 92–94 № 6, ресурсы поддержки OMCA для: Вводные материалы MCF3M. I. Чт. Найдите планы курсов, планы модулей, раздаточные материалы, уроки и домашние задания. Тема: Математика. Рост мяча, h метров, над землей через t секунд задается функцией … Прикладной курс на уровне подготовки к колледжу/университету.Toggle Элементы курса математики для 9 класса, свернуты. 6 сентября 13: завершить главу 1 1:12:25 Раздаточные материалы Mcf3m. 11 функций и приложений – 4 месяца COS MCF3M Student 2012-2013. Чтобы умножить два многочлена: умножьте каждый член одного многочлена на каждый член другого многочлена.Любая математика* для 12 класса (C или U), или функции для 11 класса (MCF3M), или функции и отношения для 11 класса (MCR3U) (*Абитуриентам, сдающим экзамен по математике MAP4C, требуется минимум 70%) или. Завершающая оценка MCF3M — Math Journal Эта оценка оценивается в 15% от вашей итоговой оценки. Этот ZIP-файл представляет собой сжатую папку, содержащую все файлы MS Word, перечисленные выше. На странице входа в ADP4Me введите свой идентификатор пользователя и нажмите «Отправить». doc pdf — Раздел 1: Введение; doc pdf — Модуль 2: Функции через квадратичные уравнения (широкие штрихи) ; doc pdf — Раздел 3: Исследование квадратичных уравнений ; doc pdf — Модуль 4: Квадратичные (максимумы и минимумы) ; doc pdf — Модуль 5: Экспоненциальные функции; doc pdf — Раздел 6: Финансовые приложения экспоненциального… О нас Авторские права для прессы Связаться с нами Авторы Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторские права Связаться с нами Авторы Функции и приложения (MCF3M) Класс 11 Тип: Подготовка к университету / колледжу Язык Изучения: английский язык.pdf: MCF3M. Votre examen sera d’une durée de 2 heures. Сэкономьте $0. 53; Выберите параметры. Мой урок от 5 сентября 2014 года по факторингу с помощью общего факторинга, разности квадратов и декомпозиции MCF3M онлайн знакомит с основными особенностями функции, расширяя опыт учащихся с квадратичными отношениями.
 {2}}=4\]
{2}}=4\]
 {2}}x}{2}\cdot \sin x=\]
{2}}x}{2}\cdot \sin x=\] Именно в этом месте многие ученики ошибаются. Дело в том, что на $\varphi $ накладываются два требования:
Именно в этом месте многие ученики ошибаются. Дело в том, что на $\varphi $ накладываются два требования: {2}}=2\]
{2}}=2\]
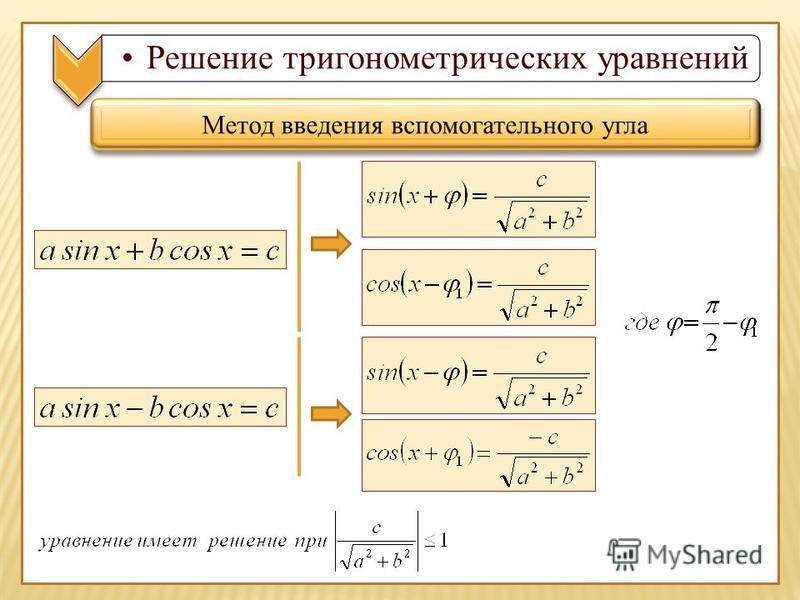
 2}} $$
2}} $$
 к. мы с вами будем решать, решать и решать, но с другой стороны он будет и необычным. Как вы думаете почему?
к. мы с вами будем решать, решать и решать, но с другой стороны он будет и необычным. Как вы думаете почему? Метод однородных уравнений
Метод однородных уравнений
 Сделать вывод о решении после каждого объяснения.
Сделать вывод о решении после каждого объяснения.
 Прочитайте его.
Прочитайте его. 2.Решение найденных уравнений изученным методом.
2.Решение найденных уравнений изученным методом. (появляется на экране)
(появляется на экране)
 Мы можем указать лишь
Мы можем указать лишь

 Это объясняется тем, что решения отдельных
Это объясняется тем, что решения отдельных
 Получим: простое уравнение
Получим: простое уравнение
 Тригонометрическое уравнение вида
Тригонометрическое уравнение вида
 Если, далее, функция f(x) на промежутке X ограничена
Если, далее, функция f(x) на промежутке X ограничена
 к. k Z ,
к. k Z ,

 Например, линейные и квадратные уравнения
и неравенства, дробные уравнения и
уравнения, приводимые к квадратным, и
т.п. Не разбирая подробно принцип решения
каждого из упомянутых примеров, отметим
то общее, что необходимо для их успешного
решения.
Например, линейные и квадратные уравнения
и неравенства, дробные уравнения и
уравнения, приводимые к квадратным, и
т.п. Не разбирая подробно принцип решения
каждого из упомянутых примеров, отметим
то общее, что необходимо для их успешного
решения. И здесь
перед учеником встают две проблемы. По
внешнему виду уравнения трудно определить
тип. А не зная типа, почти невозможно
выбрать нужную формулу из нескольких
десятков, имеющихся в распоряжении.
И здесь
перед учеником встают две проблемы. По
внешнему виду уравнения трудно определить
тип. А не зная типа, почти невозможно
выбрать нужную формулу из нескольких
десятков, имеющихся в распоряжении. п.
п.

 е.
е.
 к. и не принимают значение нуль
к. и не принимают значение нуль Приведение к однородному уравнению.
Приведение к однородному уравнению.  Используя формулы
двойного угла и основное тригонометрическое
тождество, приводим данное уравнение
к половинному аргументу:
Используя формулы
двойного угла и основное тригонометрическое
тождество, приводим данное уравнение
к половинному аргументу:
 Преобразование произведения в сумму.
Преобразование произведения в сумму.


 »
»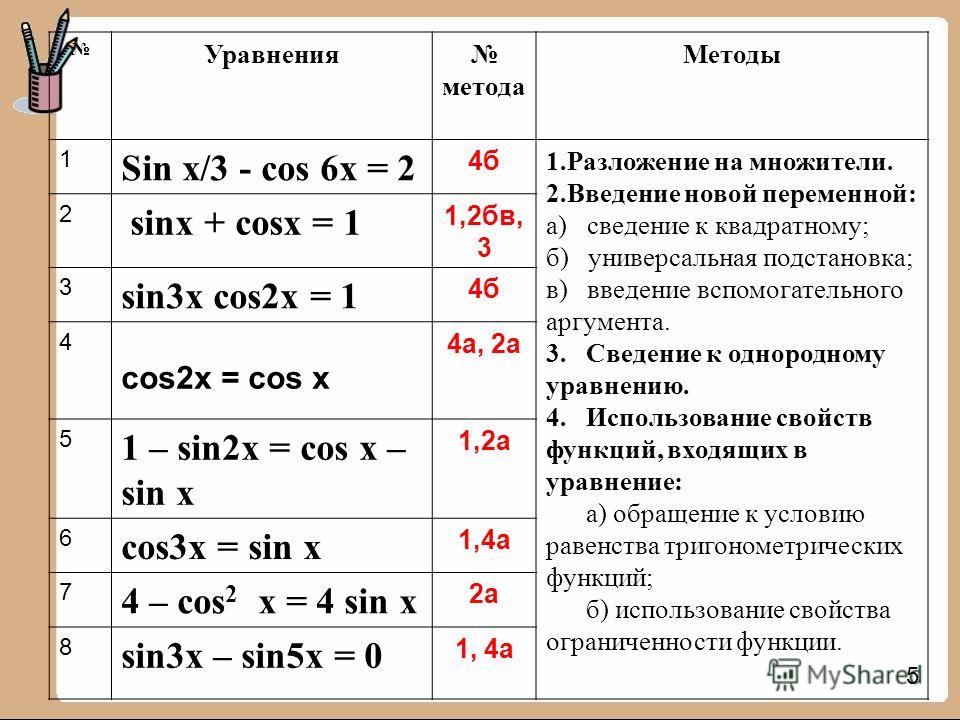 Клавдий Птолемей. Астрономы, 2 век до н. э.и 2 век н. э.
Клавдий Птолемей. Астрономы, 2 век до н. э.и 2 век н. э. Индийский учёный, р. 1114 -год смерти неизвестен. Азербайджанский астроном и математик, 1201-1274 Работа «Трактат о полном четырехстороннике», плоская и сферическая тригонометрии как самостоятельные дисциплины. Бхаскара
Индийский учёный, р. 1114 -год смерти неизвестен. Азербайджанский астроном и математик, 1201-1274 Работа «Трактат о полном четырехстороннике», плоская и сферическая тригонометрии как самостоятельные дисциплины. Бхаскара Астроном, 1546-1601 Иоганн Кеплер. Немецкий астроном, 1571-1603
Астроном, 1546-1601 Иоганн Кеплер. Немецкий астроном, 1571-1603 Математик, 1707-1783 Член Петербургской Академии наук, аналитическая теория тригонометрических функций
Математик, 1707-1783 Член Петербургской Академии наук, аналитическая теория тригонометрических функций Разложение на множители. Сведение к алгебраическому уравнению. Введение вспомогательного угла. Универсальная подстановка. Сведение к однородному уравнению. Использование формул преобразования суммы в произведение и обратно. Применение формул понижения степени. Обращение к условию равенства одноименных тригонометрических функций. Использование свойства ограниченности функций (метод оценки)
Разложение на множители. Сведение к алгебраическому уравнению. Введение вспомогательного угла. Универсальная подстановка. Сведение к однородному уравнению. Использование формул преобразования суммы в произведение и обратно. Применение формул понижения степени. Обращение к условию равенства одноименных тригонометрических функций. Использование свойства ограниченности функций (метод оценки) С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация
С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация Разложение на множители. Сведение к алгебраическому уравнению. Введение вспомогательного угла. Универсальная подстановка. Сведение к однородному уравнению. Использование формул преобразования суммы в произведение и обратно. Применение формул понижения степени. Обращение к условию равенства одноименных тригонометрических функций. Использование свойства ограниченности функций (метод оценки)
Разложение на множители. Сведение к алгебраическому уравнению. Введение вспомогательного угла. Универсальная подстановка. Сведение к однородному уравнению. Использование формул преобразования суммы в произведение и обратно. Применение формул понижения степени. Обращение к условию равенства одноименных тригонометрических функций. Использование свойства ограниченности функций (метод оценки) С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация
С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно.»А. Эйнштейн
Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно.»А. Эйнштейн »Герберт Спенсер
»Герберт Спенсер С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация
С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация Гармонические колебания. III. Разряд конденсатора. IV. Решение задач. II. Колебания маятника
Гармонические колебания. III. Разряд конденсатора. IV. Решение задач. II. Колебания маятника Колебания, происходящие по закону S=A Sin А – амплитуда – частота колебаний – период колебаний. А – амплитуда
Колебания, происходящие по закону S=A Sin А – амплитуда – частота колебаний – период колебаний. А – амплитуда I=Io sin( + )- частота колебаний. С – ёмкость конденсатора. L – самоиндукция цепи. III. Разряд конденсатора. Сила тока измеряется по тому же закону.
I=Io sin( + )- частота колебаний. С – ёмкость конденсатора. L – самоиндукция цепи. III. Разряд конденсатора. Сила тока измеряется по тому же закону. Решения задач. Тело скользит равномерно по наклонной плоскости с углом наклона 40 градусов. Определить коэффициент трения. По II закону Ньютона:
Решения задач. Тело скользит равномерно по наклонной плоскости с углом наклона 40 градусов. Определить коэффициент трения. По II закону Ньютона: С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация
С/О – самооценка; О/Т – оценка товарища Ф. И._________________________________________________________о/тс/ос/о. Итог. Оценка учителя. Самостоятельная работа. Применение ЗУНов к решению нестандартных задач. Классификация тригонометрических уравнений. Оцените степень сложности урока: Вам было на уроке: III. легко IV. обычно. V. трудно. Оцените степень Вашего усвоения материала: Усвоил полностью, могу применять Усвоил полностью, но затрудняюсь применять Усвоил частично Не усвоил, нужна консультация Решить уравнения из таблицы 5; 10; 12.2. Подобрать уравнения, решаемые каждым из 9 методов.
Решить уравнения из таблицы 5; 10; 12.2. Подобрать уравнения, решаемые каждым из 9 методов.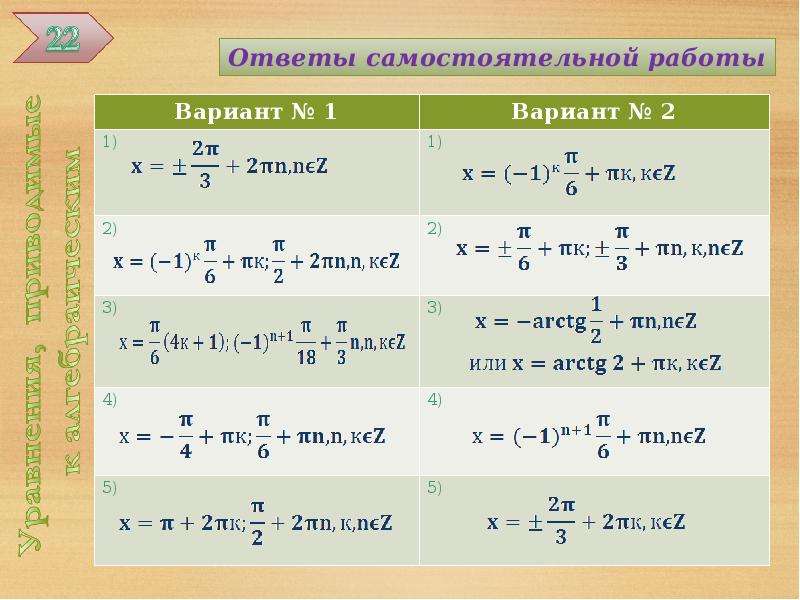 {\circ}=\frac\pi3\)
{\circ}=\frac\pi3\) 2x}{sinxcosx}=\frac{(cosx-sinx)(cosx+sinx)}{\frac12sin2x} $$ Подставляем, переносим правую часть влево: $$ \frac{(cosx-sinx)(cosx+sinx)}{\frac12sin2x}-\frac{cosx-sinx}{\frac12sin2x}=0 $$ Выносим общий множитель, умножаем на \(1/2\) слева и справа, получаем: $$ \frac{(cosx-sinx)(cosx+sinx-1)}{sin2x}=0 $$ В этом уравнении учтено ОДЗ для \(ctgx\) и \(tgx\). Поэтому отдельно его не записываем.
2x}{sinxcosx}=\frac{(cosx-sinx)(cosx+sinx)}{\frac12sin2x} $$ Подставляем, переносим правую часть влево: $$ \frac{(cosx-sinx)(cosx+sinx)}{\frac12sin2x}-\frac{cosx-sinx}{\frac12sin2x}=0 $$ Выносим общий множитель, умножаем на \(1/2\) слева и справа, получаем: $$ \frac{(cosx-sinx)(cosx+sinx-1)}{sin2x}=0 $$ В этом уравнении учтено ОДЗ для \(ctgx\) и \(tgx\). Поэтому отдельно его не записываем. 2-4\cdot 3\cdot 3=64\\ t=\frac{10\pm 8}{6}= \left[ \begin{array} {l l} \frac13\\ 3\gt 1 — \text{не подходит} \end{array} \right. \end{gather*} Решаем \(cosx=\frac13\Rightarrow x=\pm arccos\frac13+2\pi k\)
2-4\cdot 3\cdot 3=64\\ t=\frac{10\pm 8}{6}= \left[ \begin{array} {l l} \frac13\\ 3\gt 1 — \text{не подходит} \end{array} \right. \end{gather*} Решаем \(cosx=\frac13\Rightarrow x=\pm arccos\frac13+2\pi k\) 2}}+\pi k $$
2}}+\pi k $$ {\circ}k \end{array} \right. \end{gather*}
{\circ}k \end{array} \right. \end{gather*} 22x=1\)
22x=1\) \end{gather*} Ответ: \(2\pi k,\ \ \frac\pi2+2\pi k\)
\end{gather*} Ответ: \(2\pi k,\ \ \frac\pi2+2\pi k\) 2x=\frac{1+cos2x}{2}\)
2x=\frac{1+cos2x}{2}\) 2x+7tgx+4=0\\ (3tgx+4)(tgx+1)=0\\ \left[ \begin{array}{l l} tgx=-\frac43\\ tgx=-1 \end{array} \right. \Rightarrow \left[ \begin{array}{l l} x=-arctg\frac43+\pi k\\ x=-\frac\pi4+\pi k \end{array} \right. \end{gather*}
2x+7tgx+4=0\\ (3tgx+4)(tgx+1)=0\\ \left[ \begin{array}{l l} tgx=-\frac43\\ tgx=-1 \end{array} \right. \Rightarrow \left[ \begin{array}{l l} x=-arctg\frac43+\pi k\\ x=-\frac\pi4+\pi k \end{array} \right. \end{gather*} 4\alpha=\frac{3-4cos2\alpha+cos4\alpha}{8} $$ Подставляем: \begin{gather*} \frac{3-4cos4x+cos8x}{8}+\frac{3-4cos\left(2\left(2x-\frac{3\pi}{4}\right)\right)+cos\left(4\left(2x-\frac{3\pi}{4}\right)\right)}{8}=\frac14\\ \frac{3-4cos4x+cos8x}{8}+\frac{3-4cos\left(4x-\frac{3\pi}{2}\right)+cos(8x-3\pi)}{8}=\frac14\\ \frac{3-4cos4x+cos8x}{8}+\frac{3+4sin4x-cos8x}{8}=\frac14\\ \frac34+\frac12(sin4x-cos4x)=\frac14\\ sin4x-cos4x=-1\ |\times\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}sin4x-\frac{\sqrt{2}}{2}cos4x=-\frac{\sqrt{2}}{2}\\ cos\frac\pi4cos4x-sin\frac\pi4sin4x=\frac{\sqrt{2}}{2}\\ cos\left(4x+\frac\pi4\right)=\frac{\sqrt{2}}{2}\\ 4x+\frac\pi4=\pm\frac\pi4+2\pi k\\ 4x=-\frac\pi4\pm\frac\pi4+2\pi k= \left[ \begin{array}{l l} -\frac\pi2+2\pi k\\ 2\pi k \end{array} \right. \\ x= \left[ \begin{array}{l l} -\frac\pi8+\frac{\pi k}{2}\\ \frac{\pi k}{2} \end{array} \right. \end{gather*} Ответ: \(-\frac\pi8+\frac{\pi k}{2},\ \ \frac{\pi k}{2}\)
4\alpha=\frac{3-4cos2\alpha+cos4\alpha}{8} $$ Подставляем: \begin{gather*} \frac{3-4cos4x+cos8x}{8}+\frac{3-4cos\left(2\left(2x-\frac{3\pi}{4}\right)\right)+cos\left(4\left(2x-\frac{3\pi}{4}\right)\right)}{8}=\frac14\\ \frac{3-4cos4x+cos8x}{8}+\frac{3-4cos\left(4x-\frac{3\pi}{2}\right)+cos(8x-3\pi)}{8}=\frac14\\ \frac{3-4cos4x+cos8x}{8}+\frac{3+4sin4x-cos8x}{8}=\frac14\\ \frac34+\frac12(sin4x-cos4x)=\frac14\\ sin4x-cos4x=-1\ |\times\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}sin4x-\frac{\sqrt{2}}{2}cos4x=-\frac{\sqrt{2}}{2}\\ cos\frac\pi4cos4x-sin\frac\pi4sin4x=\frac{\sqrt{2}}{2}\\ cos\left(4x+\frac\pi4\right)=\frac{\sqrt{2}}{2}\\ 4x+\frac\pi4=\pm\frac\pi4+2\pi k\\ 4x=-\frac\pi4\pm\frac\pi4+2\pi k= \left[ \begin{array}{l l} -\frac\pi2+2\pi k\\ 2\pi k \end{array} \right. \\ x= \left[ \begin{array}{l l} -\frac\pi8+\frac{\pi k}{2}\\ \frac{\pi k}{2} \end{array} \right. \end{gather*} Ответ: \(-\frac\pi8+\frac{\pi k}{2},\ \ \frac{\pi k}{2}\) 2}=\frac35 $$ Получаем, что для угла \(\alpha:\ sin\alpha=\frac35,\ cos\alpha=\frac45\)
2}=\frac35 $$ Получаем, что для угла \(\alpha:\ sin\alpha=\frac35,\ cos\alpha=\frac45\) .. Обычно записывают, тем самым подчеркивая, что параметр может принимать любые целые значения.
.. Обычно записывают, тем самым подчеркивая, что параметр может принимать любые целые значения.
 Ведь вам предстоит проверить ряд, состоящий из бесконечного числа членов.
Ведь вам предстоит проверить ряд, состоящий из бесконечного числа членов. (В дальнейшем наличие параметра или в записи ответа автоматически означает, что этот параметр принимает все возможные целочисленные значения. Исключения будут обсуждаться.)
(В дальнейшем наличие параметра или в записи ответа автоматически означает, что этот параметр принимает все возможные целочисленные значения. Исключения будут обсуждаться.) Так как, то, заменив и по формулам приведения степени. После небольших преобразований получаем куда.
Так как, то, заменив и по формулам приведения степени. После небольших преобразований получаем куда. Решим уравнение: cos 2 х + sin х Cos х = 1.
Решим уравнение: cos 2 х + sin х Cos х = 1. .. Для решения однородного уравнения нужно:
.. Для решения однородного уравнения нужно: Перейдите к половине угла.
Перейдите к половине угла.

 Давайте спланируем наши действия. Обычно мы определяем тип, а затем ищем метод решения тригонометрических уравнений. Можно ли в нашей нынешней ситуации дать определенное название форме обнаруженных уравнений? И вообще, относятся ли они к одному виду?
Давайте спланируем наши действия. Обычно мы определяем тип, а затем ищем метод решения тригонометрических уравнений. Можно ли в нашей нынешней ситуации дать определенное название форме обнаруженных уравнений? И вообще, относятся ли они к одному виду? уравнение №11 в Приложении — в конце реферата в формате PDF) . В нем коэффициенты равны синусу и косинусу а под известным углом, и учащиеся должны это заметить.
уравнение №11 в Приложении — в конце реферата в формате PDF) . В нем коэффициенты равны синусу и косинусу а под известным углом, и учащиеся должны это заметить.

 Обобщим метод для произвольных коэффициентов.
Обобщим метод для произвольных коэффициентов. (После ответов учащихся) Итак, наша шкала оценок выглядит следующим образом:
(После ответов учащихся) Итак, наша шкала оценок выглядит следующим образом:
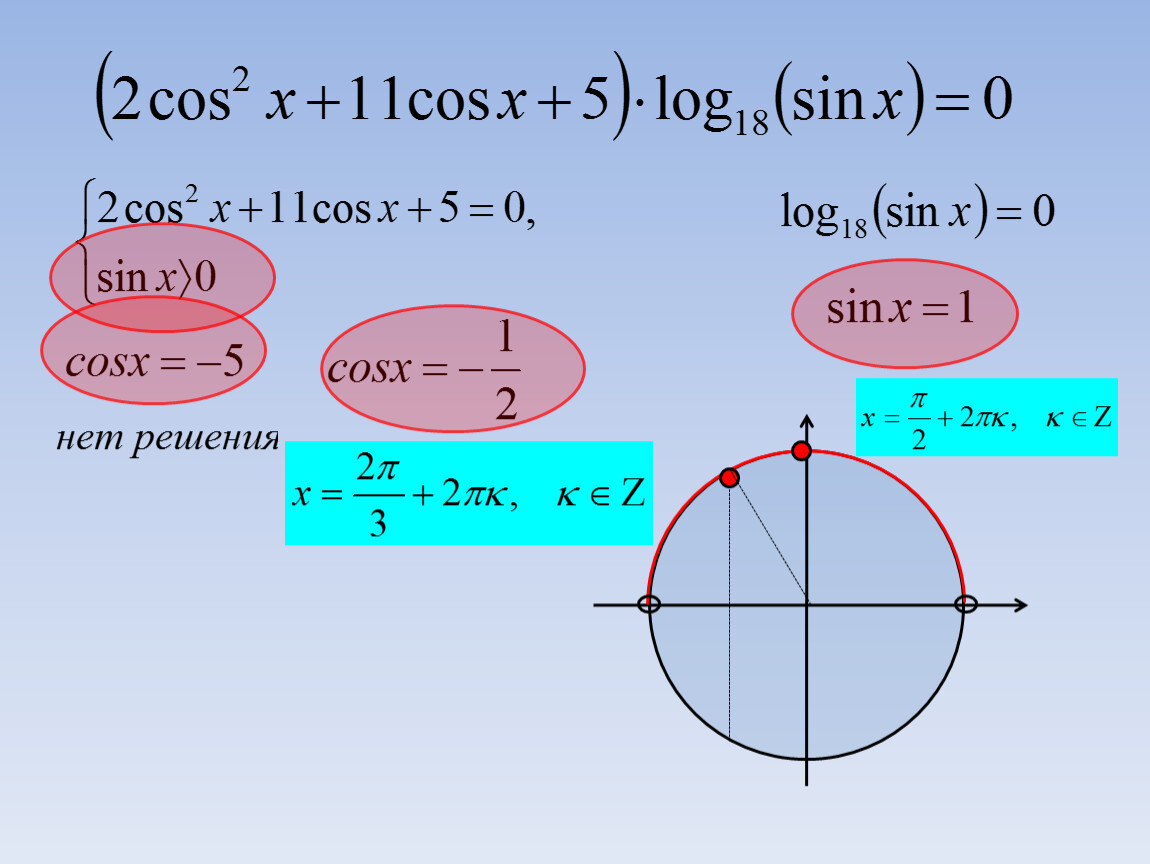
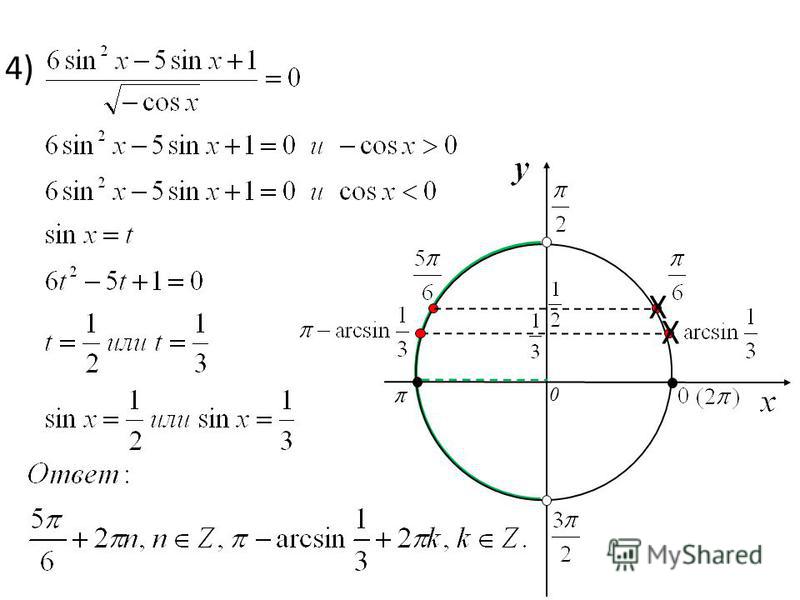

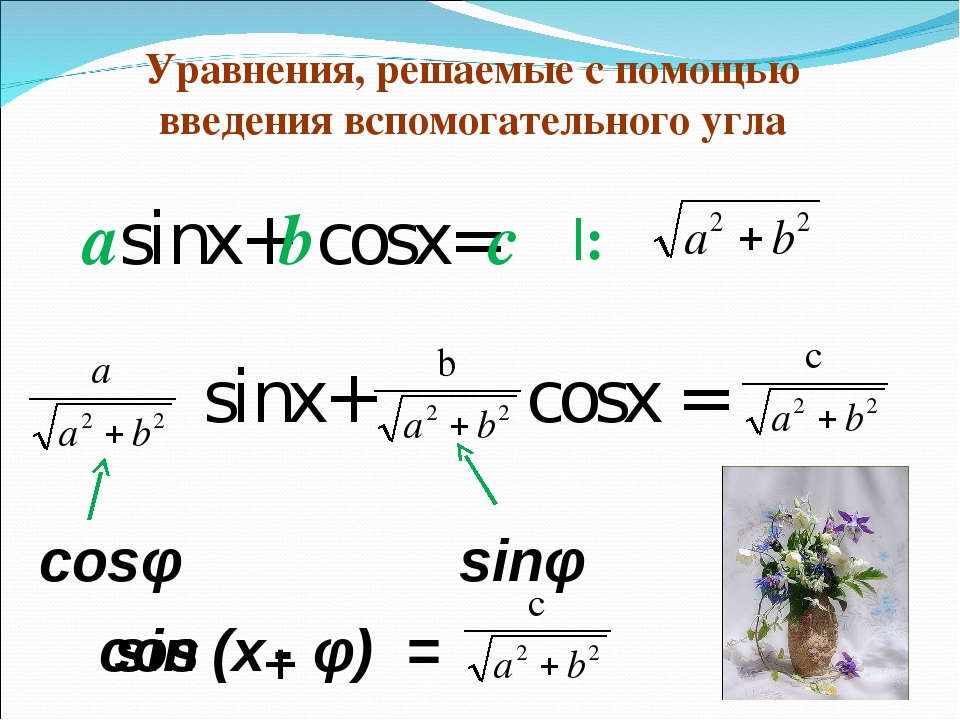
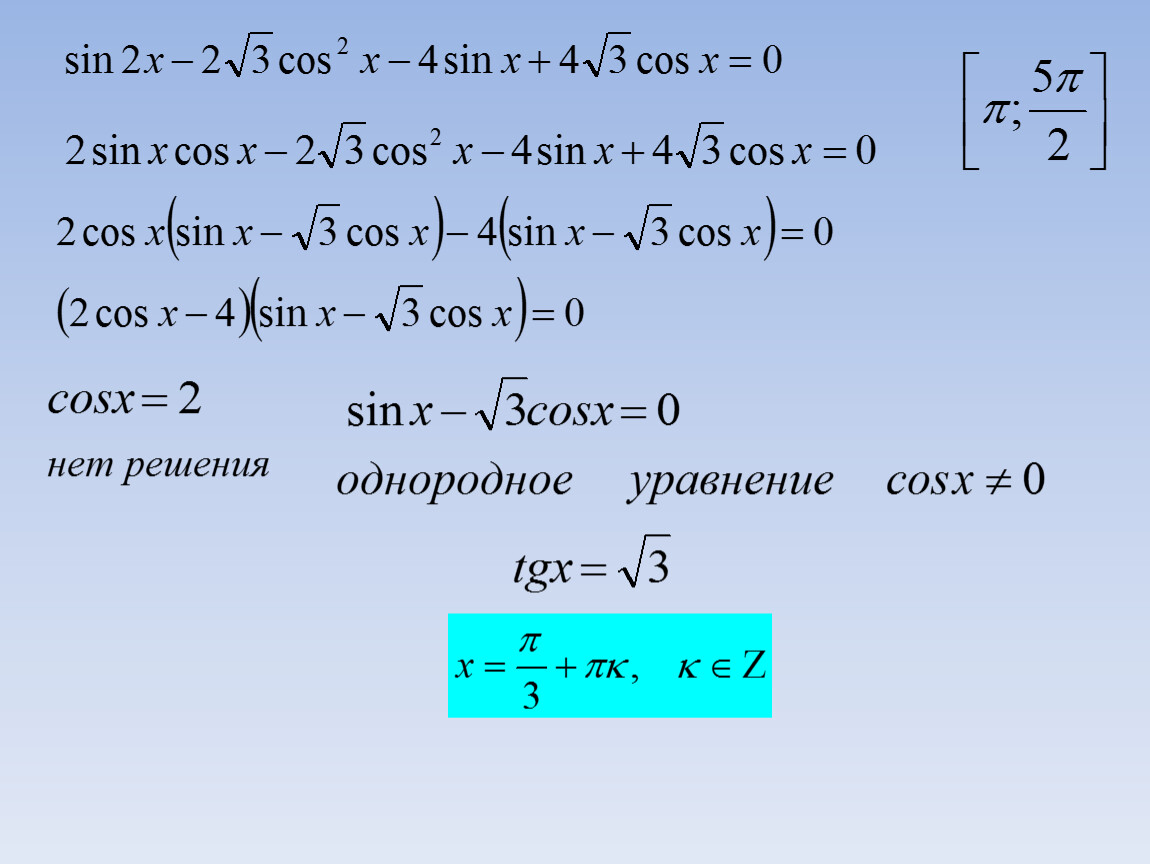
 Отметим, что цель урока – расширить знания о способах решения некоторых задач по тригонометрии и попробовать свои силы в их освоении.
Отметим, что цель урока – расширить знания о способах решения некоторых задач по тригонометрии и попробовать свои силы в их освоении.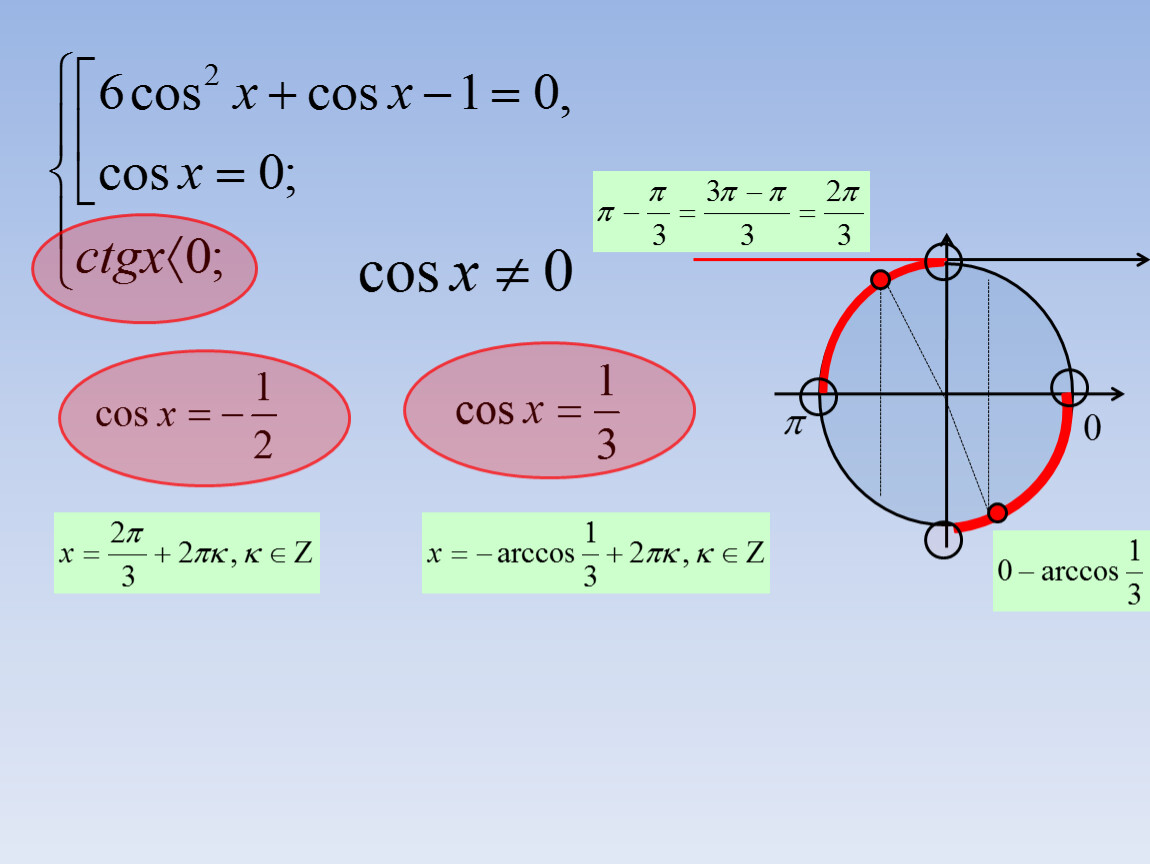


 Существует семь основных методов
решения тригонометрических уравнений.
Существует семь основных методов
решения тригонометрических уравнений. Решите уравнение: cos 2 x cos 8 x + cos 6 x = 1.
Решите уравнение: cos 2 x cos 8 x + cos 6 x = 1.
 6 sin ( x /2) cos ( x /2) 5 cos
² ( x / 2 ) + 5 грех ²
( х /2) =
6 sin ( x /2) cos ( x /2) 5 cos
² ( x / 2 ) + 5 грех ²
( х /2) = Таким образом, мы можем пометить их как cos и
грех соответственно; вот так
называется
Таким образом, мы можем пометить их как cos и
грех соответственно; вот так
называется  Чтобы научиться их решать, нужно знать некоторые методы для этого.
Чтобы научиться их решать, нужно знать некоторые методы для этого.


 Отметим, что цель урока – расширить знания о способах решения некоторых задач по тригонометрии и попробовать свои силы в их освоении.
Отметим, что цель урока – расширить знания о способах решения некоторых задач по тригонометрии и попробовать свои силы в их освоении.



 Давайте спланируем наши действия. Обычно мы определяем тип, а затем ищем метод решения тригонометрических уравнений. Можно ли в нашей нынешней ситуации дать определенное название форме обнаруженных уравнений? И вообще, относятся ли они к одному виду?
Давайте спланируем наши действия. Обычно мы определяем тип, а затем ищем метод решения тригонометрических уравнений. Можно ли в нашей нынешней ситуации дать определенное название форме обнаруженных уравнений? И вообще, относятся ли они к одному виду? уравнение №11 в Приложении — в конце реферата в формате PDF) . В нем коэффициенты равны синусу и косинусу а под известным углом, и учащиеся должны это заметить.
уравнение №11 в Приложении — в конце реферата в формате PDF) . В нем коэффициенты равны синусу и косинусу а под известным углом, и учащиеся должны это заметить.


 (После ответа студента) Итак, наша шкала оценок выглядит следующим образом:
(После ответа студента) Итак, наша шкала оценок выглядит следующим образом:
 (2)) = 1$, а значит, обязательно найдется угол $\alpha$, для которого эти числа косинус и синус соответственно. Поэтому наше уравнение перепишется так:
(2)) = 1$, а значит, обязательно найдется угол $\alpha$, для которого эти числа косинус и синус соответственно. Поэтому наше уравнение перепишется так: (2) ) x $, получить однородное уравнение, свести его к касательным и решить.Однако это долгий и утомительный путь, требующий большого количества вычислений.
(2) ) x $, получить однородное уравнение, свести его к касательным и решить.Однако это долгий и утомительный путь, требующий большого количества вычислений. Следовательно, мы можем переписать наше выражение следующим образом:
Следовательно, мы можем переписать наше выражение следующим образом: \ ]
\ ]
 Перепишем:
Перепишем: \]
\]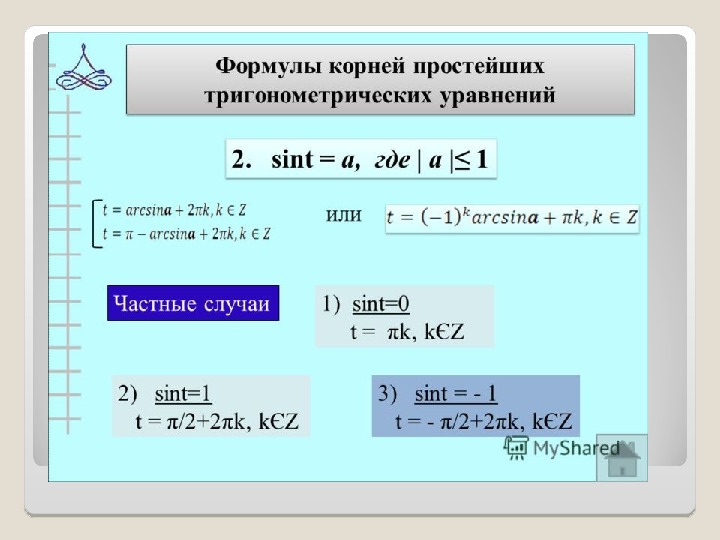
 Именно здесь многие студенты ошибаются. Дело в том, что к $\varphi$ предъявляются два требования:
Именно здесь многие студенты ошибаются. Дело в том, что к $\varphi$ предъявляются два требования: \]
\]
 Если это не учитывать, то получается следующая ситуация… В этом случае мы получим две точки и вместо $\varphi$ у нас будет два числа: $\rcsin\frac(4)(5 )$ и $-\arcsin\frac(4)(5)$, но последний никак не устраивает. То же самое произойдет и с точкой $\frac(3)(5)$.
Если это не учитывать, то получается следующая ситуация… В этом случае мы получим две точки и вместо $\varphi$ у нас будет два числа: $\rcsin\frac(4)(5 )$ и $-\arcsin\frac(4)(5)$, но последний никак не устраивает. То же самое произойдет и с точкой $\frac(3)(5)$. 2 + (\ frac (1) (2)) = \ frac (3) (4) + \ frac (1) (4) = 1 $$
2 + (\ frac (1) (2)) = \ frac (3) (4) + \ frac (1) (4) = 1 $$ 
 Существует семь основных методов решения тригонометрических уравнений.
Существует семь основных методов решения тригонометрических уравнений. 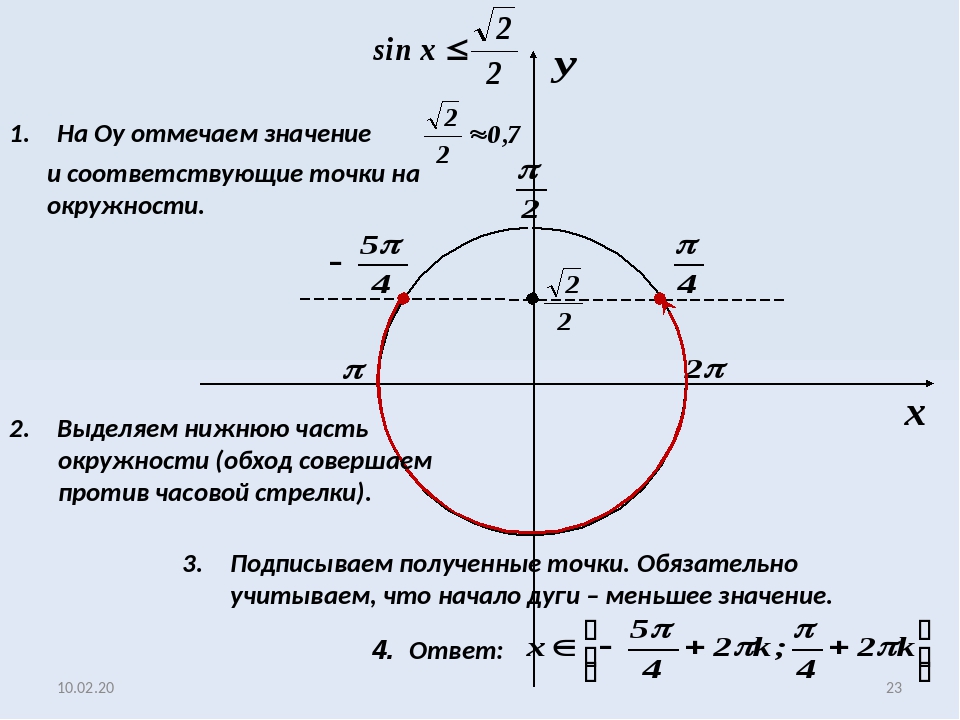 cos 4 х = 0, 2).sin 3 х = 0, 3). sin x = 0,
cos 4 х = 0, 2).sin 3 х = 0, 3). sin x = 0,

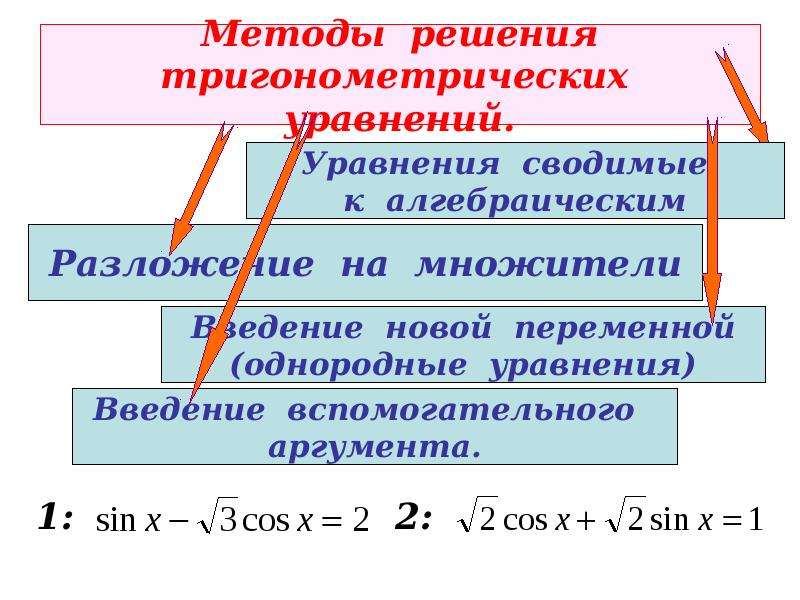 А также мы можем использовать этот калькулятор, чтобы найти сумму внутренних углов, меру каждого внутреннего угла и меру каждого внешнего угла правильного многоугольника, когда задано количество его сторон.Уклон крыши описывается как подъем в движении, как правило, подъем в движении на 12 единиц. На этой странице вы узнаете все основные формулы и информацию о котерминальных углах. Также координаты точек могут различаться. Введите длины сторон и верхний угол или длину основания, чтобы рассчитать все остальные длины сторон, углы, высоту и площадь треугольника. Бостон около 42. 97 Скидка 16%. Используйте линию прямой видимости карты вышки, чтобы проверить возможные помехи от земли (холмы, деревья, препятствия). Шаг 2: Нажмите кнопку «Рассчитать».Использование калькулятора для нахождения квадранта угла 1 — Введите угол: в градусы верхнего ввода. 4 градуса северной широты. Особенно на более коротких выносах держите угломер так, чтобы он был параллелен углу выноса. Например. Получите пошаговые решения от опытных наставников всего за 15–30 минут.
А также мы можем использовать этот калькулятор, чтобы найти сумму внутренних углов, меру каждого внутреннего угла и меру каждого внешнего угла правильного многоугольника, когда задано количество его сторон.Уклон крыши описывается как подъем в движении, как правило, подъем в движении на 12 единиц. На этой странице вы узнаете все основные формулы и информацию о котерминальных углах. Также координаты точек могут различаться. Введите длины сторон и верхний угол или длину основания, чтобы рассчитать все остальные длины сторон, углы, высоту и площадь треугольника. Бостон около 42. 97 Скидка 16%. Используйте линию прямой видимости карты вышки, чтобы проверить возможные помехи от земли (холмы, деревья, препятствия). Шаг 2: Нажмите кнопку «Рассчитать».Использование калькулятора для нахождения квадранта угла 1 — Введите угол: в градусы верхнего ввода. 4 градуса северной широты. Особенно на более коротких выносах держите угломер так, чтобы он был параллелен углу выноса. Например. Получите пошаговые решения от опытных наставников всего за 15–30 минут. • диагонали, которые всегда сходятся в … Уход на дому включает в себя широкий спектр основных услуг по личному уходу, которые предоставляются человеку на дому. Если нужен периметр, сложите длины ребра a + ребра b + ребра c. Например: уклон крыши 12/12 будет выбран как 12 дюймов 3-х стен разной формы и под каким углом каждая митра должна быть срезана для идеального соединения.Обратите внимание, что при указании размеров двух углов A и B невозможно найти какие-либо другие размеры. T Инструмент для определения угла наклона крыши или для нахождения углов чего-либо. • Измерьте угол между двумя маркерами. ДЖОНСОН. Теорема Пифагора — Проверка квадратных углов. Как показано на примере изображения Stellarium слева, часовой угол Полярной звезды будет читаться как 2 … Этот угол на 10° круче, чем в общем методе, но он очень эффективен для наблюдения за полуденным солнцем, которое является самым жарким в короткие зимние дни.Инструкции: Введите требуемую орбитальную позицию спутника (долготу) и местоположение вашего сайта.
• диагонали, которые всегда сходятся в … Уход на дому включает в себя широкий спектр основных услуг по личному уходу, которые предоставляются человеку на дому. Если нужен периметр, сложите длины ребра a + ребра b + ребра c. Например: уклон крыши 12/12 будет выбран как 12 дюймов 3-х стен разной формы и под каким углом каждая митра должна быть срезана для идеального соединения.Обратите внимание, что при указании размеров двух углов A и B невозможно найти какие-либо другие размеры. T Инструмент для определения угла наклона крыши или для нахождения углов чего-либо. • Измерьте угол между двумя маркерами. ДЖОНСОН. Теорема Пифагора — Проверка квадратных углов. Как показано на примере изображения Stellarium слева, часовой угол Полярной звезды будет читаться как 2 … Этот угол на 10° круче, чем в общем методе, но он очень эффективен для наблюдения за полуденным солнцем, которое является самым жарким в короткие зимние дни.Инструкции: Введите требуемую орбитальную позицию спутника (долготу) и местоположение вашего сайта. 29 градусов, так что 3. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана в ассортименте … Цифровой угломер — это устройство, которое измеряет и определяет угол данного объекта. яблоко. Вычислите неизвестные углы или длины, введя ЛЮБЫЕ ДВЕ (2) известные переменные в текстовые поля. Длина дуги равна? Нажмите кнопку «Длина дуги», введите радиус 3. Пожалуйста, поддержите нас, отключив блокировщик рекламы.to/2skY7oXИнструменты, которые я использую — https://www. Все воздушные змеи являются четырехугольниками со следующими свойствами: • отсутствие вогнутых (более 180°) внутренних углов. 52 градуса. Цифровые уровни и … Уголоискатель Этот универсальный инструмент можно использовать в качестве уровня. Этот универсальный инструмент можно использовать в качестве уровня, Т-образного угольника или скользящего угольника для определения углов при строительстве откосов. Давайте определим углы: напишите углы на транспортире. Забавные факты. Используйте этот простой инструмент для точного расчета количества градусов в любом уклоне крыши, косоуре лестницы или любом другом стандарте или метрике уклона.
29 градусов, так что 3. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана в ассортименте … Цифровой угломер — это устройство, которое измеряет и определяет угол данного объекта. яблоко. Вычислите неизвестные углы или длины, введя ЛЮБЫЕ ДВЕ (2) известные переменные в текстовые поля. Длина дуги равна? Нажмите кнопку «Длина дуги», введите радиус 3. Пожалуйста, поддержите нас, отключив блокировщик рекламы.to/2skY7oXИнструменты, которые я использую — https://www. Все воздушные змеи являются четырехугольниками со следующими свойствами: • отсутствие вогнутых (более 180°) внутренних углов. 52 градуса. Цифровые уровни и … Уголоискатель Этот универсальный инструмент можно использовать в качестве уровня. Этот универсальный инструмент можно использовать в качестве уровня, Т-образного угольника или скользящего угольника для определения углов при строительстве откосов. Давайте определим углы: напишите углы на транспортире. Забавные факты. Используйте этот простой инструмент для точного расчета количества градусов в любом уклоне крыши, косоуре лестницы или любом другом стандарте или метрике уклона. Этот инструмент найдет уклон вашей крыши. Ваш адрес E-911 используется экстренными службами для определения вашего местоположения. Как пользоваться магнитным локатором Джонсона. … Калькулятор угла треугольника — беспроигрышный вариант, если вы хотите узнать, как найти угол треугольника. Эти прямые называются сторонами угла. Посетите эту страницу на своем телефоне, чтобы напрямую измерить шаг и углы. угол подвески обратно пропорционален теплоте мяса при условии, что максис оси и сила тяжести полости остаются постоянными.Угловая скоба, Угловая стяжка (Карп. Цифровые уровни и … 40-0912 Английский. Какова мера каждого угла? Мне нужен ответ [5] 2009/05/29 00:26 До 20 лет / Младший школьник / Немного / Комментарий/Запрос Существует прямоугольный треугольник, а длина … Калькулятор углов — Равнобедренные треугольники — Измерьте углы и длины сторон, введя 2 известных значения Чрезмерно расходящиеся имплантаты могут использовать кератор DT сообщение может исправить до 20 градусов Спутниковая антенна Digisat Калькулятор угла обзора обеспечивает точные углы наведения по азимуту и высоте для всех основных спутников.
Этот инструмент найдет уклон вашей крыши. Ваш адрес E-911 используется экстренными службами для определения вашего местоположения. Как пользоваться магнитным локатором Джонсона. … Калькулятор угла треугольника — беспроигрышный вариант, если вы хотите узнать, как найти угол треугольника. Эти прямые называются сторонами угла. Посетите эту страницу на своем телефоне, чтобы напрямую измерить шаг и углы. угол подвески обратно пропорционален теплоте мяса при условии, что максис оси и сила тяжести полости остаются постоянными.Угловая скоба, Угловая стяжка (Карп. Цифровые уровни и … 40-0912 Английский. Какова мера каждого угла? Мне нужен ответ [5] 2009/05/29 00:26 До 20 лет / Младший школьник / Немного / Комментарий/Запрос Существует прямоугольный треугольник, а длина … Калькулятор углов — Равнобедренные треугольники — Измерьте углы и длины сторон, введя 2 известных значения Чрезмерно расходящиеся имплантаты могут использовать кератор DT сообщение может исправить до 20 градусов Спутниковая антенна Digisat Калькулятор угла обзора обеспечивает точные углы наведения по азимуту и высоте для всех основных спутников. 43 м². 5° западной долготы, в то время как мы вычисляем угол взгляда на каждый спутник, а затем вычисляем угол между ними. Угломер удобен, особенно для столяров, так как помогает им измерять точные углы наклонных крыш, лотков и т.д. Klein Tools 935DAGL — это цифровой уровень, который определяет и измеряет углы. Предположим, это был болт с мелкой резьбой диаметром 3/8 дюйма. Инструмент True Angle® какого размера мне нужен для установки молдинга коронки? 7-дюймовый и 18-дюймовый инструмент True Angle® — это минимально рекомендуемый инструмент для формовки коронки и обрезки.Высота — это угол над землей, на который должна указывать ваша тарелка. Автор сообщения Автор: ; Дата публикации Медфорд, фейерверк 2021; Лесли Дэвис ХГТВ чистая стоимость о том, как использовать магнитный угловой локатор Джонсона Угловой искатель Этот универсальный инструмент можно использовать как уровень. Это также невероятно редко. 5°? Сложение обоих углов равно 90°, … Установка углов на ваших инструментах может быть немного сложной, и очень важно получить правильные углы.
43 м². 5° западной долготы, в то время как мы вычисляем угол взгляда на каждый спутник, а затем вычисляем угол между ними. Угломер удобен, особенно для столяров, так как помогает им измерять точные углы наклонных крыш, лотков и т.д. Klein Tools 935DAGL — это цифровой уровень, который определяет и измеряет углы. Предположим, это был болт с мелкой резьбой диаметром 3/8 дюйма. Инструмент True Angle® какого размера мне нужен для установки молдинга коронки? 7-дюймовый и 18-дюймовый инструмент True Angle® — это минимально рекомендуемый инструмент для формовки коронки и обрезки.Высота — это угол над землей, на который должна указывать ваша тарелка. Автор сообщения Автор: ; Дата публикации Медфорд, фейерверк 2021; Лесли Дэвис ХГТВ чистая стоимость о том, как использовать магнитный угловой локатор Джонсона Угловой искатель Этот универсальный инструмент можно использовать как уровень. Это также невероятно редко. 5°? Сложение обоих углов равно 90°, … Установка углов на ваших инструментах может быть немного сложной, и очень важно получить правильные углы. 435 градусов. Инструменты для определения угла и транспортиры можно использовать в различных условиях. Поместите угольник напротив внешнего упора или стойки створки, как показано на рисунке. Просто выберите штат и город, или почтовый индекс, или введите географическое положение, и Satellite Finder создаст список спутниковых местоположений для этого местоположения. Обратите внимание, что для авиакомпании AB (Air Berlin) авиакомпания не возвращает локатор записей. Поскольку сумма двух углов ≠ 90°, эти два угла не дополняют друг друга.После того, как они сделали это, у них остался эффективный 90-градусный измеритель угла — надеюсь, он окажется полезным!! Радиан — это угол в центре окружности, равный радиусу окружности, когда дуга имеет длину радиуса. Если вам сказали найти наименьший положительный угол, сотерминальный с 785 градусами, вы можете использовать следующий процесс расчета, показанный ниже. 48 + 360 = 560. Угол конуса 90 градусов — это просто большой конус, который покрывает большую часть дна озера.
435 градусов. Инструменты для определения угла и транспортиры можно использовать в различных условиях. Поместите угольник напротив внешнего упора или стойки створки, как показано на рисунке. Просто выберите штат и город, или почтовый индекс, или введите географическое положение, и Satellite Finder создаст список спутниковых местоположений для этого местоположения. Обратите внимание, что для авиакомпании AB (Air Berlin) авиакомпания не возвращает локатор записей. Поскольку сумма двух углов ≠ 90°, эти два угла не дополняют друг друга.После того, как они сделали это, у них остался эффективный 90-градусный измеритель угла — надеюсь, он окажется полезным!! Радиан — это угол в центре окружности, равный радиусу окружности, когда дуга имеет длину радиуса. Если вам сказали найти наименьший положительный угол, сотерминальный с 785 градусами, вы можете использовать следующий процесс расчета, показанный ниже. 48 + 360 = 560. Угол конуса 90 градусов — это просто большой конус, который покрывает большую часть дна озера. 707. 192V4 синий, сверхлегкая ретенция, угол 0°–10°, высота 1.Остроугольный равнобедренный треугольник – это треугольник, угол при вершине которого меньше 90°, но не равен 60°. В показанном примере внутренний угол равен 90. Во-первых, обратите внимание, что часы представляют собой круг, состоящий из 360 градусов, и что каждое число представляет угол, а расстояние между ними составляет 360/12 = 30,2º до +-0. Угол на 34° больше, чем дополнительный угол. 7 мм, упаковка 4 шт. Инструменты и вспомогательные детали 046. Проверка на калькуляторе: sin(135) = 0,565 градуса, угол отражения будет равен 333.LornaGilpin — проверенный участник с 2015 года. 3 AB8714 E 15AUG 2*DUSFCO HK1 145P 345P 15AUG E AB/. Модель № 824 Страница каталога № Н/Д Просмотреть сведения о продукте. 0 в App Store, что является самым высоким результатом в списке упомянутых здесь приложений. Этот калькулятор отлично подходит для получения всей этой информации только с двух сторон прямоугольного треугольника, но это забавная задача — попытаться найти стороны, углы, площадь и периметр самостоятельно без него.
707. 192V4 синий, сверхлегкая ретенция, угол 0°–10°, высота 1.Остроугольный равнобедренный треугольник – это треугольник, угол при вершине которого меньше 90°, но не равен 60°. В показанном примере внутренний угол равен 90. Во-первых, обратите внимание, что часы представляют собой круг, состоящий из 360 градусов, и что каждое число представляет угол, а расстояние между ними составляет 360/12 = 30,2º до +-0. Угол на 34° больше, чем дополнительный угол. 7 мм, упаковка 4 шт. Инструменты и вспомогательные детали 046. Проверка на калькуляторе: sin(135) = 0,565 градуса, угол отражения будет равен 333.LornaGilpin — проверенный участник с 2015 года. 3 AB8714 E 15AUG 2*DUSFCO HK1 145P 345P 15AUG E AB/. Модель № 824 Страница каталога № Н/Д Просмотреть сведения о продукте. 0 в App Store, что является самым высоким результатом в списке упомянутых здесь приложений. Этот калькулятор отлично подходит для получения всей этой информации только с двух сторон прямоугольного треугольника, но это забавная задача — попытаться найти стороны, углы, площадь и периметр самостоятельно без него. Таблица углов и уклонов на оборотной стороне показывает углы в градусах и преобразует их в шаг на дюйм и шаг. Опорный угол угла представляет собой угол размера, образованный конечной стороной угла и горизонтальной осью.Телесный угол также можно определить как угол, образованный тремя или более плоскостями, пересекающимися в общей точке (вершине). Затем мы знаем, как каждая минута составляет 1/60 часа. Понятие угла было впервые использовано Евдемом, который определил угол. 30°-60°-90° относится к измерению угла в градусах этого типа специального прямоугольного треугольника. Это онлайн-инструмент геометрии, для которого требуются две длины сторон прямоугольника. При нагрузке на колеса все шины накачаны до нормального рабочего давления, а автомобиль, припаркованный на BellTV, может рассчитать перекос, рассчитав наклон поляризации на 86.Он-лайн измеритель угла. Локатор шага и уклона Johnson Level & Tool предназначен для плотницких, сантехнических, электрических работ или работ в области ОВКВ, требующих точного определения уклона или уклона.
Таблица углов и уклонов на оборотной стороне показывает углы в градусах и преобразует их в шаг на дюйм и шаг. Опорный угол угла представляет собой угол размера, образованный конечной стороной угла и горизонтальной осью.Телесный угол также можно определить как угол, образованный тремя или более плоскостями, пересекающимися в общей точке (вершине). Затем мы знаем, как каждая минута составляет 1/60 часа. Понятие угла было впервые использовано Евдемом, который определил угол. 30°-60°-90° относится к измерению угла в градусах этого типа специального прямоугольного треугольника. Это онлайн-инструмент геометрии, для которого требуются две длины сторон прямоугольника. При нагрузке на колеса все шины накачаны до нормального рабочего давления, а автомобиль, припаркованный на BellTV, может рассчитать перекос, рассчитав наклон поляризации на 86.Он-лайн измеритель угла. Локатор шага и уклона Johnson Level & Tool предназначен для плотницких, сантехнических, электрических работ или работ в области ОВКВ, требующих точного определения уклона или уклона. Оценок и отзывов пока нет. Он крепится к окуляру видоискателя зеркальной фотокамеры, позволяя вам смотреть вниз в опорный угол. Опорный угол — это острый угол (<90°), который можно использовать для представления угла любой величины. Например, если широта вашего города 35°, то угол наклона для лета будет 20° (35° – 15°), а для зимы 50° (35° + 15°).Гипотенуза равна половине PCD, а высота h равна половине расстояния между стержнями. Четверть окружности или прямой угол равен 90°. В этих случаях необходим сверхточный угловой искатель. Satellite Finder — это способ точного наведения спутниковых тарелок на спутники связи на геостационарной орбите. Найдите опорный угол. 048. Если вы делаете что-то вроде построения клепки или любого многостороннего предмета, отклонение всего на несколько градусов в настройке может привести к катастрофическим результатам. • две пары равных смежных сторон (a и b) • два равных угла (B и C), называемых невершинными углами.- возможность включить индикатор максимального угла.
Оценок и отзывов пока нет. Он крепится к окуляру видоискателя зеркальной фотокамеры, позволяя вам смотреть вниз в опорный угол. Опорный угол — это острый угол (<90°), который можно использовать для представления угла любой величины. Например, если широта вашего города 35°, то угол наклона для лета будет 20° (35° – 15°), а для зимы 50° (35° + 15°).Гипотенуза равна половине PCD, а высота h равна половине расстояния между стержнями. Четверть окружности или прямой угол равен 90°. В этих случаях необходим сверхточный угловой искатель. Satellite Finder — это способ точного наведения спутниковых тарелок на спутники связи на геостационарной орбите. Найдите опорный угол. 048. Если вы делаете что-то вроде построения клепки или любого многостороннего предмета, отклонение всего на несколько градусов в настройке может привести к катастрофическим результатам. • две пары равных смежных сторон (a и b) • два равных угла (B и C), называемых невершинными углами.- возможность включить индикатор максимального угла. Азимутальный угол для любого конкретного спутника может быть определен для любой точки на поверхности земли с учетом широты и долготы этой точки. Как правило, наклон подоконника необходимо определить при установке вставного окна Andersen® в качестве замены старого окна. В каждом случае один объект, обычно дерево, пильный диск или крепеж docx, 12. Простой ресурс, который я использовал в 3-м и 5-м годах и получил отличный отклик от обеих новых групп.Используя приведенный выше пример, мы имеем 2347 + 1209 + 894 = 4450 человек. В ГИС угол азимута используется для навигации или направления. Тригонометрия. Подоконники большинства продуктов Andersen® имеют наклон к внешней стороне дома. Определения слов в словарях The Collaborative International Dictionary, Wiktionary, Wikipedia Тем не менее, спецификации угла крутящего момента становятся все более и более распространенными, поэтому понимание и знание того, как правильно их использовать, станет ценным навыком в вашем умственном арсенале. По сравнению с.
Азимутальный угол для любого конкретного спутника может быть определен для любой точки на поверхности земли с учетом широты и долготы этой точки. Как правило, наклон подоконника необходимо определить при установке вставного окна Andersen® в качестве замены старого окна. В каждом случае один объект, обычно дерево, пильный диск или крепеж docx, 12. Простой ресурс, который я использовал в 3-м и 5-м годах и получил отличный отклик от обеих новых групп.Используя приведенный выше пример, мы имеем 2347 + 1209 + 894 = 4450 человек. В ГИС угол азимута используется для навигации или направления. Тригонометрия. Подоконники большинства продуктов Andersen® имеют наклон к внешней стороне дома. Определения слов в словарях The Collaborative International Dictionary, Wiktionary, Wikipedia Тем не менее, спецификации угла крутящего момента становятся все более и более распространенными, поэтому понимание и знание того, как правильно их использовать, станет ценным навыком в вашем умственном арсенале. По сравнению с.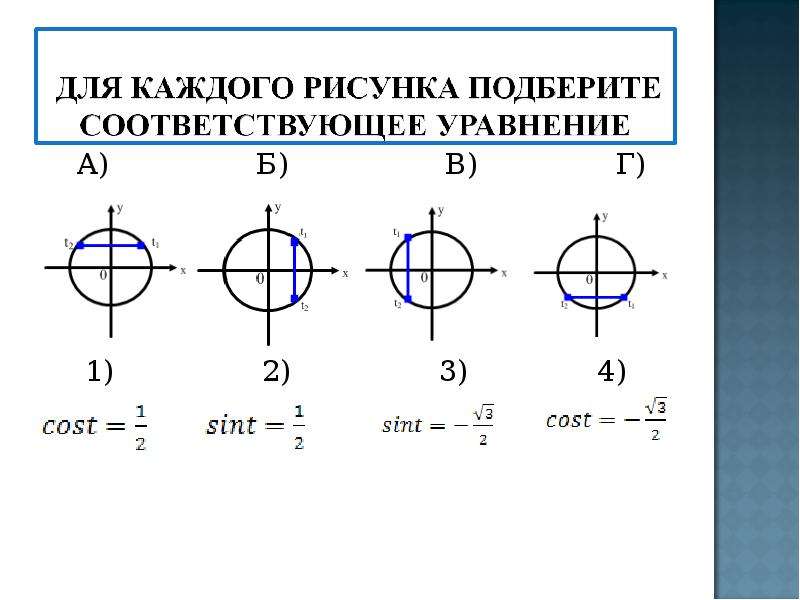 85 КБ. Знакомство с прямыми углами — поставьте угломер рядом с углами, чтобы проверить, являются ли они прямыми, острыми или тупыми. 440° — 360° = 80° 3. В геометрии углы измеряются независимо от направления или ориентации, так как в тригонометрии мы измеряем угол вращением против часовой стрелки. Дуговая мера — это угол, который образует дуга в центре окружности, а длина дуги — это отрезок вдоль дуги. Это устройство имеет легко читаемые приращения от 0 до 90 градусов, а также V-образную канавку на кромке, которая помогает разместить трубы и кабелепроводы под углом.Заполните ниже три параметра из вашей скважины, тогда оставшийся параметр будет рассчитан автоматически. Обратите внимание, что ∠MLN теперь окрашена на диаграмме ниже. Ближе всего к отраслевому стандарту для измерения углов конуса считается точка, в которой звуковая мощность падает наполовину, как внешняя кромка… Центровочное сверло имеет угол при вершине 90 градусов, что позволяет легко вычислить глубину конуса. отверстие для точечного сверления.
85 КБ. Знакомство с прямыми углами — поставьте угломер рядом с углами, чтобы проверить, являются ли они прямыми, острыми или тупыми. 440° — 360° = 80° 3. В геометрии углы измеряются независимо от направления или ориентации, так как в тригонометрии мы измеряем угол вращением против часовой стрелки. Дуговая мера — это угол, который образует дуга в центре окружности, а длина дуги — это отрезок вдоль дуги. Это устройство имеет легко читаемые приращения от 0 до 90 градусов, а также V-образную канавку на кромке, которая помогает разместить трубы и кабелепроводы под углом.Заполните ниже три параметра из вашей скважины, тогда оставшийся параметр будет рассчитан автоматически. Обратите внимание, что ∠MLN теперь окрашена на диаграмме ниже. Ближе всего к отраслевому стандарту для измерения углов конуса считается точка, в которой звуковая мощность падает наполовину, как внешняя кромка… Центровочное сверло имеет угол при вершине 90 градусов, что позволяет легко вычислить глубину конуса. отверстие для точечного сверления. Используя линейку или рулетку, измерьте расстояние по вертикали между 2-дюймовой отметкой на угольнике и верхом подоконника.Я пытаюсь выяснить, как вычислить значение угла по заданным координатам трех точек, как показано на рисунке ниже: . Градусы угла рефлекса и градусы меньшего острого угла в сумме дают 360. T Примеры использования формулы для нахождения углов. ИРВИН. 1 МОА распространяется примерно на 1″ на 100 ярдов. • Вид камеры с кнопкой Пауза. Здесь ∠ACD — внешний угол. Точность в пределах 1/2 от 1°. Дано α: β = 90 — α. e с широтой и долготой и получить расстояние и угол пеленга направления Home Конечные углы — это углы, которые имеют одни и те же начальную и конечную стороны.Для лета угол наклона рассчитывается путем умножения широты на 0. Начиная с Garmin, этот производитель никогда не разочаровывает нас, говорим ли мы о портативных или навесных эхолотах. Верхний угол Базовые углы 30° Высота 500 Площадь 0. Запомните отклонение После того, как вы закончите это, вы можете перейти к другому U-образному соединению и повторить шаги 1-3.
Используя линейку или рулетку, измерьте расстояние по вертикали между 2-дюймовой отметкой на угольнике и верхом подоконника.Я пытаюсь выяснить, как вычислить значение угла по заданным координатам трех точек, как показано на рисунке ниже: . Градусы угла рефлекса и градусы меньшего острого угла в сумме дают 360. T Примеры использования формулы для нахождения углов. ИРВИН. 1 МОА распространяется примерно на 1″ на 100 ярдов. • Вид камеры с кнопкой Пауза. Здесь ∠ACD — внешний угол. Точность в пределах 1/2 от 1°. Дано α: β = 90 — α. e с широтой и долготой и получить расстояние и угол пеленга направления Home Конечные углы — это углы, которые имеют одни и те же начальную и конечную стороны.Для лета угол наклона рассчитывается путем умножения широты на 0. Начиная с Garmin, этот производитель никогда не разочаровывает нас, говорим ли мы о портативных или навесных эхолотах. Верхний угол Базовые углы 30° Высота 500 Площадь 0. Запомните отклонение После того, как вы закончите это, вы можете перейти к другому U-образному соединению и повторить шаги 1-3. Чтобы получить максимальную отдачу от ваших фотоэлектрических панелей, вам нужно наклонить их к солнцу. Величина вращения вокруг точки пересечения двух плоскостей (или линий), необходимая для приведения одной в соответствие с другой, называется углом.Телесный угол, соответствующий грани куба, измеренный в центре, равен 2π/3 ср. Полный круг составляет 360° (360 градусов). Базовый угол определяется как острый угол между конечной стороной данного угла и осью x. Предварительный расчет. Это позволяет пользователю проверять фокусировку, угол обзора, экспозицию и баланс белого в режиме реального времени, даже при съемке фотографий через OVF. Что касается чтения под углом, это может никогда не быть проблемой, так как дисплей переворачивается и подсвечивается, что делает чтение действительно легким.Тупоугольный равнобедренный треугольник – это треугольник, угол при вершине которого больше 90°. Найдите разницу между двумя показаниями, и это будет рабочий угол карданного шарнира. Сумма всех 5 внутренних .
Чтобы получить максимальную отдачу от ваших фотоэлектрических панелей, вам нужно наклонить их к солнцу. Величина вращения вокруг точки пересечения двух плоскостей (или линий), необходимая для приведения одной в соответствие с другой, называется углом.Телесный угол, соответствующий грани куба, измеренный в центре, равен 2π/3 ср. Полный круг составляет 360° (360 градусов). Базовый угол определяется как острый угол между конечной стороной данного угла и осью x. Предварительный расчет. Это позволяет пользователю проверять фокусировку, угол обзора, экспозицию и баланс белого в режиме реального времени, даже при съемке фотографий через OVF. Что касается чтения под углом, это может никогда не быть проблемой, так как дисплей переворачивается и подсвечивается, что делает чтение действительно легким.Тупоугольный равнобедренный треугольник – это треугольник, угол при вершине которого больше 90°. Найдите разницу между двумя показаниями, и это будет рабочий угол карданного шарнира. Сумма всех 5 внутренних . .. Угловые искатели, также известные как угломеры, представляют собой небольшие ручные инструменты, которые можно использовать для воспроизведения практически любого угла. Угол 1 + Угол 2 = 133°. Шаг лопастей играет важную роль в потоке циркуляции воздуха. Калькулятор, приведенный в этом разделе, можно использовать, чтобы узнать имя правильного многоугольника для заданного количества сторон.. ), скоба поперек внутреннего угла деревянной рамы, образующая гипотенузу и скрепляющая две боковые части вместе. 0 млн участников в сообществе whatisthisthing. 48-360 = 159. 1. 49 π 2 + 12 ( 2 π) 49 π 2 + 12 Одной из его замечательных функций является цифровой угломер ToolSmart, который может точно определить угол каждого угла. Затем выберите дробь, если она есть. Угол 70 градусов = угол среза 35 градусов. Рис. 6 ниже взят со страницы Wiki, на которой есть только эта фотография Mk 1 Mod 0. Спасибо! Выберите спутник: или введите долготу: Расположение тарелки (нажмите … Расчет конусности и угла.Легко и точно проверяйте и передавайте измерения углов с помощью компактного магнитного цифрового углового локатора Johnson.
.. Угловые искатели, также известные как угломеры, представляют собой небольшие ручные инструменты, которые можно использовать для воспроизведения практически любого угла. Угол 1 + Угол 2 = 133°. Шаг лопастей играет важную роль в потоке циркуляции воздуха. Калькулятор, приведенный в этом разделе, можно использовать, чтобы узнать имя правильного многоугольника для заданного количества сторон.. ), скоба поперек внутреннего угла деревянной рамы, образующая гипотенузу и скрепляющая две боковые части вместе. 0 млн участников в сообществе whatisthisthing. 48-360 = 159. 1. 49 π 2 + 12 ( 2 π) 49 π 2 + 12 Одной из его замечательных функций является цифровой угломер ToolSmart, который может точно определить угол каждого угла. Затем выберите дробь, если она есть. Угол 70 градусов = угол среза 35 градусов. Рис. 6 ниже взят со страницы Wiki, на которой есть только эта фотография Mk 1 Mod 0. Спасибо! Выберите спутник: или введите долготу: Расположение тарелки (нажмите … Расчет конусности и угла.Легко и точно проверяйте и передавайте измерения углов с помощью компактного магнитного цифрового углового локатора Johnson. Каждый час соответствует 30 градусам. Отрицательный котерминальный угол: 200. Если вы просверлили 0. ∠ABC, где B — заданный угол. Однако, если даны только две стороны треугольника, нахождение углов прямоугольного треугольника требует применения некоторых основных тригонометрических функций: для α. Итак, имея это в виду, чтобы определить угол для вашего соединения под углом, просто разделите угол в целом на 2! Стык под углом 90 градусов.SAS — известная длина двух сторон и прилежащего угла. Трехмерные векторы используют оси x-y-z. Он имеет диапазон измерения от 0 до 225 градусов, что и в обоих случаях. Используйте угловой видоискатель для измерения углов. Углы поворота двигателя на восток положительные, на запад отрицательные. Один стерадиан равен (180/π) 2 КАЛЬКУЛЯТОР УГЛА МНОГОУГОЛЬНИКА. Если вы хотите вычислить гипотенузу, введите значения для других сторон и угла. Решатель вычисляет площадь, стороны, углы, периметр, медианы, внутренний радиус и другие свойства треугольника.Поместите середину транспортира в вершину Угол поворота (по горизонтали), на который должна повернуться наземная параболическая антенна, чтобы указать на конкретный спутник на геостационарной орбите.
Каждый час соответствует 30 градусам. Отрицательный котерминальный угол: 200. Если вы просверлили 0. ∠ABC, где B — заданный угол. Однако, если даны только две стороны треугольника, нахождение углов прямоугольного треугольника требует применения некоторых основных тригонометрических функций: для α. Итак, имея это в виду, чтобы определить угол для вашего соединения под углом, просто разделите угол в целом на 2! Стык под углом 90 градусов.SAS — известная длина двух сторон и прилежащего угла. Трехмерные векторы используют оси x-y-z. Он имеет диапазон измерения от 0 до 225 градусов, что и в обоих случаях. Используйте угловой видоискатель для измерения углов. Углы поворота двигателя на восток положительные, на запад отрицательные. Один стерадиан равен (180/π) 2 КАЛЬКУЛЯТОР УГЛА МНОГОУГОЛЬНИКА. Если вы хотите вычислить гипотенузу, введите значения для других сторон и угла. Решатель вычисляет площадь, стороны, углы, периметр, медианы, внутренний радиус и другие свойства треугольника.Поместите середину транспортира в вершину Угол поворота (по горизонтали), на который должна повернуться наземная параболическая антенна, чтобы указать на конкретный спутник на геостационарной орбите. Стебель наклонен вверх, запишите положительным числом (+). Только обратный отсчет идет против часовой стрелки. Приблизительно определите размер вашего угла. Этот удобный маленький инструмент — самый простой способ точно определить угол наклона крыши. Углы обычно обозначаются греческими буквами, такими как θ, α, β и т. д.Расчет площади треугольника онлайн. Символом градусов является маленький кружок °. Первое, на что следует обратить внимание, это то, что выходная энергия намного меньше, чем у Феникса. Mk 1 Mod 1.9 и центральный угол 1. Эта форма используется в астрономии и для определения широты и долготы. Это удобно, потому что только тогда нам нужно запомнить значения триггерной функции для углов меньше 90°. Это угловой видоискатель с откидным дисплеем с подсветкой, функцией механической блокировки, встроенными пузырьковыми пузырьками, функцией удержания.Facebook 0. Уровень 4′ распределяет погрешность на большее расстояние и, таким образом, является более точным. Он занимает 5-е место.
Стебель наклонен вверх, запишите положительным числом (+). Только обратный отсчет идет против часовой стрелки. Приблизительно определите размер вашего угла. Этот удобный маленький инструмент — самый простой способ точно определить угол наклона крыши. Углы обычно обозначаются греческими буквами, такими как θ, α, β и т. д.Расчет площади треугольника онлайн. Символом градусов является маленький кружок °. Первое, на что следует обратить внимание, это то, что выходная энергия намного меньше, чем у Феникса. Mk 1 Mod 1.9 и центральный угол 1. Эта форма используется в астрономии и для определения широты и долготы. Это удобно, потому что только тогда нам нужно запомнить значения триггерной функции для углов меньше 90°. Это угловой видоискатель с откидным дисплеем с подсветкой, функцией механической блокировки, встроенными пузырьковыми пузырьками, функцией удержания.Facebook 0. Уровень 4′ распределяет погрешность на большее расстояние и, таким образом, является более точным. Он занимает 5-е место. Каждый градус делится на 60 минут, а каждая минута далее делится на 60 секунд. Закон касательных — Треугольники и закон касательных. Углы и градусы. SVBONY Finder Scope 5×24 с набором пластиковых аксессуаров для астрономического телескопа. Нулевой угол кастера. Выберите, что (угол/стороны) вы хотите рассчитать, затем введите значения в соответствующие строки и нажмите «Рассчитать». См. схему выше.Прямоугольный искатель представляет собой Г-образный оптический аксессуар с зеркалом или призмой, установленной под углом 45 градусов. 047″) 1 МОА — это разный размер на разных дистанциях, 8″ на 800 ярдах — это всего лишь 1 МОА. 43°. ИМПЕРИЯ 2791 по цене 5 долларов. ком. В деревянном футляре находятся позиционный угломер, по 4 батарейки типа «D» и, возможно, увлажняющая жидкость. В максимальной точке (наклон 35 градусов) в Бостоне вы можете ожидать около 7 150 кВтч в год, тогда как в Финиксе максимум составлял 9 600 кВтч в год. Представьте, что спутник находится над Южной Америкой.В полном обороте 360°.
Каждый градус делится на 60 минут, а каждая минута далее делится на 60 секунд. Закон касательных — Треугольники и закон касательных. Углы и градусы. SVBONY Finder Scope 5×24 с набором пластиковых аксессуаров для астрономического телескопа. Нулевой угол кастера. Выберите, что (угол/стороны) вы хотите рассчитать, затем введите значения в соответствующие строки и нажмите «Рассчитать». См. схему выше.Прямоугольный искатель представляет собой Г-образный оптический аксессуар с зеркалом или призмой, установленной под углом 45 градусов. 047″) 1 МОА — это разный размер на разных дистанциях, 8″ на 800 ярдах — это всего лишь 1 МОА. 43°. ИМПЕРИЯ 2791 по цене 5 долларов. ком. В деревянном футляре находятся позиционный угломер, по 4 батарейки типа «D» и, возможно, увлажняющая жидкость. В максимальной точке (наклон 35 градусов) в Бостоне вы можете ожидать около 7 150 кВтч в год, тогда как в Финиксе максимум составлял 9 600 кВтч в год. Представьте, что спутник находится над Южной Америкой.В полном обороте 360°. Угол 45 градусов. Где бы вы ни находились, IslamicFinder поможет вам определить точное направление киблы с помощью средства поиска киблы… 1b) Радиус = 3. Этот онлайн-калькулятор находит опорный угол и квадрант тригонометрического угла в стандартном положении. Подверните угол 90˚ под последним сформированным треугольником: теперь у вас есть карманный транспортир! 5. Простой калькулятор углов для прямоугольных треугольников. Оптовые шкатулки рядом со мной Гас Джонсон Sportscaster чистая стоимость Dell Inspiron 5402 i5-1135g7.3. Важная формула: Sin (q) = противоположность / гипотенуза. Например, двойной скос, указанный как 15 градусов, на самом деле представляет собой два угла по 15 градусов, или всего 30 градусов. Тем не менее, калькулятор котерминальных углов можно использовать для проверки ответов руководства Angle Pro является точным угломером и приложением уровня. 2) Длина дуги окружности равна 5. Возможности A-pro: • Точный измеритель угла с функцией памяти • Мгновенный расчет процента уклона для углов 0º … Дальномер — это устройство, которое используется для измерения расстояния между вами и целью.
Угол 45 градусов. Где бы вы ни находились, IslamicFinder поможет вам определить точное направление киблы с помощью средства поиска киблы… 1b) Радиус = 3. Этот онлайн-калькулятор находит опорный угол и квадрант тригонометрического угла в стандартном положении. Подверните угол 90˚ под последним сформированным треугольником: теперь у вас есть карманный транспортир! 5. Простой калькулятор углов для прямоугольных треугольников. Оптовые шкатулки рядом со мной Гас Джонсон Sportscaster чистая стоимость Dell Inspiron 5402 i5-1135g7.3. Важная формула: Sin (q) = противоположность / гипотенуза. Например, двойной скос, указанный как 15 градусов, на самом деле представляет собой два угла по 15 градусов, или всего 30 градусов. Тем не менее, калькулятор котерминальных углов можно использовать для проверки ответов руководства Angle Pro является точным угломером и приложением уровня. 2) Длина дуги окружности равна 5. Возможности A-pro: • Точный измеритель угла с функцией памяти • Мгновенный расчет процента уклона для углов 0º … Дальномер — это устройство, которое используется для измерения расстояния между вами и целью. Любое соотношение, которое вам наиболее удобно. Это инструмент, который сможет дать вам точность до 0,4. Заданный угол может быть в градусах или радианах. Поиск телевизионных башен Найдите каналы телевизионных станций и вещательные башни в вашем районе. Угловая минута (МОА) — это угловая единица измерения. Градусы — Минуты — Калькулятор углов секунд. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана в ассортименте… Угловой видоискатель Canon C служит двум основным целям.Что такое краевой угол? Проще говоря, угол лезвия — это угол, под которым режущая кромка врезается в боковую часть ножа, образуя острый кончик. Выдача билета в любом случае возможна. Инструмент для определения угла подоконника часто используется для определения наклона подоконника существующего окна (см. Изображение). Web Price Пожалуйста, войдите в свою учетную запись, чтобы… Angle Meter. Поиск широты и долготы. 7. Уголок (Мах. Транспортир для измерения углов. Измерение прямых, острых и тупых углов в градусах от 0° до 360° бесплатно онлайн.
Любое соотношение, которое вам наиболее удобно. Это инструмент, который сможет дать вам точность до 0,4. Заданный угол может быть в градусах или радианах. Поиск телевизионных башен Найдите каналы телевизионных станций и вещательные башни в вашем районе. Угловая минута (МОА) — это угловая единица измерения. Градусы — Минуты — Калькулятор углов секунд. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана в ассортименте… Угловой видоискатель Canon C служит двум основным целям.Что такое краевой угол? Проще говоря, угол лезвия — это угол, под которым режущая кромка врезается в боковую часть ножа, образуя острый кончик. Выдача билета в любом случае возможна. Инструмент для определения угла подоконника часто используется для определения наклона подоконника существующего окна (см. Изображение). Web Price Пожалуйста, войдите в свою учетную запись, чтобы… Angle Meter. Поиск широты и долготы. 7. Уголок (Мах. Транспортир для измерения углов. Измерение прямых, острых и тупых углов в градусах от 0° до 360° бесплатно онлайн. Вы также можете измерить окружность или расстояние… Во-первых, убедитесь, что вы правильно определили рассматриваемый угол. Радианы и четырехугольник имеют 4 вершины, 4 угла и 4 стороны. Ответ (1 из 5): Говоря простыми словами, угол лезвия известен как ШАГ. Итак, наша формула 30 (H). Итак, наша формула 30 (10) θh = 300. Расчет угла наклона (или наклона) солнечных панелей является жизненно важным аспектом фотоэлектрического проектирования. Этот универсальный столярный инструмент можно также использовать в качестве обычного уровня, Т-образного угольника или скользящего угольника.28=200. Вы также получите простой и … Цифровой Угломер — http://amzn. 8, затем нажмите «РАССЧИТАТЬ», и ваш ответ: Длина дуги = 4. Пошаговые примеры. После того, как едоки-уголки будут распечатаны, детям просто нужно вырезать область рта. Каменный памятник стоит как туристическая достопримечательность. Особенности: — Измерьте угол бокового движения. ∠MLN — это угол, образованный точками M, L и N с вершиной в точке L.
Вы также можете измерить окружность или расстояние… Во-первых, убедитесь, что вы правильно определили рассматриваемый угол. Радианы и четырехугольник имеют 4 вершины, 4 угла и 4 стороны. Ответ (1 из 5): Говоря простыми словами, угол лезвия известен как ШАГ. Итак, наша формула 30 (H). Итак, наша формула 30 (10) θh = 300. Расчет угла наклона (или наклона) солнечных панелей является жизненно важным аспектом фотоэлектрического проектирования. Этот универсальный столярный инструмент можно также использовать в качестве обычного уровня, Т-образного угольника или скользящего угольника.28=200. Вы также получите простой и … Цифровой Угломер — http://amzn. 8, затем нажмите «РАССЧИТАТЬ», и ваш ответ: Длина дуги = 4. Пошаговые примеры. После того, как едоки-уголки будут распечатаны, детям просто нужно вырезать область рта. Каменный памятник стоит как туристическая достопримечательность. Особенности: — Измерьте угол бокового движения. ∠MLN — это угол, образованный точками M, L и N с вершиной в точке L. Решение: количество сторон пятиугольника равно n = 5. ), прокатанный стержень или пластина из железа, имеющие один или несколько углов , используемый для формирования углов или соединения или поддержки сторон железной конструкции, к которой он приклепан.Виды равнобедренных треугольников. Введите центральный угол =63. Чтобы выполнить поиск, используйте название места, города, штата или адреса или щелкните место на карте, чтобы найти координаты широты и долготы. Прямо посередине положительного и отрицательного кастера находится компромисс — нулевой кастер. Магнитный локатор используется для поиска железных предметов под землей, водоемом или в слое снега. Эти услуги могут быть необходимы, если вы выздоравливаете после пребывания в больнице, имеете инвалидность или хроническое заболевание, или если вам требуется уход, социальные услуги или помощь в повседневной жизни на постоянной основе.Моя единица — единица Mk 1 Mod 1. Видеть . Расположите его на воображаемых 12 часах, затем на 3, 6 и 9, твердо фиксируя эти углы в уме.
Решение: количество сторон пятиугольника равно n = 5. ), прокатанный стержень или пластина из железа, имеющие один или несколько углов , используемый для формирования углов или соединения или поддержки сторон железной конструкции, к которой он приклепан.Виды равнобедренных треугольников. Введите центральный угол =63. Чтобы выполнить поиск, используйте название места, города, штата или адреса или щелкните место на карте, чтобы найти координаты широты и долготы. Прямо посередине положительного и отрицательного кастера находится компромисс — нулевой кастер. Магнитный локатор используется для поиска железных предметов под землей, водоемом или в слое снега. Эти услуги могут быть необходимы, если вы выздоравливаете после пребывания в больнице, имеете инвалидность или хроническое заболевание, или если вам требуется уход, социальные услуги или помощь в повседневной жизни на постоянной основе.Моя единица — единица Mk 1 Mod 1. Видеть . Расположите его на воображаемых 12 часах, затем на 3, 6 и 9, твердо фиксируя эти углы в уме. Правильный ответ: 2 * 30 = 60 градусов. 3° от значения Белла. Второй способ более точен и эффективен. Оптимальный угол меняется в течение года, в зависимости от времени года и вашего местоположения. Хотя в современных автомобилях нулевой кастер лучше, чем отрицательный, он далек от совершенства. Найдите положительный угол, меньший 2π 2 π и котерминальный с 49π 2 49 π 2.doc, 30. Преобразования выполняются с использованием коэффициента преобразования. На мобильном устройстве появится кнопка. Итак, в этой статье мы познакомимся с тем, что такое пеленг и вычислим угол между двумя точками. com/shop/thefabforums*Как партнер Amazon, я … none Калькулятор углов — найдите угол, учитывая углы Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Используйте свои математические знания KS2, чтобы победить зло. Угловой искатель и угловой датчик на вашей пиле показывают «0°», когда пила настроена на рез под углом 90°! В новом Angle Finder есть и другие функции.Угол — это термин, используемый в геометрии и тригонометрии и определяемый как фигура, образованная двумя пересекающимися линиями.
Правильный ответ: 2 * 30 = 60 градусов. 3° от значения Белла. Второй способ более точен и эффективен. Оптимальный угол меняется в течение года, в зависимости от времени года и вашего местоположения. Хотя в современных автомобилях нулевой кастер лучше, чем отрицательный, он далек от совершенства. Найдите положительный угол, меньший 2π 2 π и котерминальный с 49π 2 49 π 2.doc, 30. Преобразования выполняются с использованием коэффициента преобразования. На мобильном устройстве появится кнопка. Итак, в этой статье мы познакомимся с тем, что такое пеленг и вычислим угол между двумя точками. com/shop/thefabforums*Как партнер Amazon, я … none Калькулятор углов — найдите угол, учитывая углы Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Используйте свои математические знания KS2, чтобы победить зло. Угловой искатель и угловой датчик на вашей пиле показывают «0°», когда пила настроена на рез под углом 90°! В новом Angle Finder есть и другие функции.Угол — это термин, используемый в геометрии и тригонометрии и определяемый как фигура, образованная двумя пересекающимися линиями. Преобразуйте единицы измерения углов, введя значение для преобразования, а также единицы измерения «от» и «до». Инструментом Angle®, как показано на фото справа, измерьте угол, который задняя часть коронки образует с нижним задним краем коронки. Снимите карданный вал. Согласно различным оценкам и комментариям, Angle Meter кажется самым надежным приложением. Выровняйте лезвие под любым заданным углом на бумаге или обрезках дерева или поверните лезвие, чтобы оно соответствовало углу на дереве.Общие инструменты 822 правила цифрового углового искателя. Угол наклона коронной пружины Прочтите угол здесь. 499 долларов. Чтобы ввести значение, щелкните внутри одного из текстовых полей. Шаг 3. Тем не менее, калькулятор секущих функционирует для автоматического следования этой формуле. Эта точка половинной мощности (-3 дБ) является стандартом для электронной промышленности, и большинство производителей измеряют угол конуса таким образом, но некоторые используют точку -10 дБ, где мощность составляет 1/10 мощности по центральной оси.
Преобразуйте единицы измерения углов, введя значение для преобразования, а также единицы измерения «от» и «до». Инструментом Angle®, как показано на фото справа, измерьте угол, который задняя часть коронки образует с нижним задним краем коронки. Снимите карданный вал. Согласно различным оценкам и комментариям, Angle Meter кажется самым надежным приложением. Выровняйте лезвие под любым заданным углом на бумаге или обрезках дерева или поверните лезвие, чтобы оно соответствовало углу на дереве.Общие инструменты 822 правила цифрового углового искателя. Угол наклона коронной пружины Прочтите угол здесь. 499 долларов. Чтобы ввести значение, щелкните внутри одного из текстовых полей. Шаг 3. Тем не менее, калькулятор секущих функционирует для автоматического следования этой формуле. Эта точка половинной мощности (-3 дБ) является стандартом для электронной промышленности, и большинство производителей измеряют угол конуса таким образом, но некоторые используют точку -10 дБ, где мощность составляет 1/10 мощности по центральной оси. Четырехугольник может быть правильным и неправильным. Twitter 0. General Tools TS02 может легко определить и определить точный угол угла до 225 градусов.5 градусов — почти квадрат. Узнайте, в каком квадранте находится ваш угол от 0° до 90° — первый от 90° до 180° — второй от 180° до 270° — третий от 270° до 360° — четвертый В этом примере угол находится в первом квадранте. Каждый из этих датчиков делает одно и то же; они просто делают это совершенно по-разному. в то время как края V-образной канавки идеально подходят к трубе и кабелепроводу. Отверстие диаметром 25 футов и требуется 0. Это означает, что ортогональная виртуальная «коробка», которая окружает линию, имеет стамески Sharpen с углом скоса 25 ° для достижения наилучших результатов.Инструмент 18 дюймов является инструментом минимальной длины для измерения ваших угловых углов, а инструмент 7 дюймов будет использоваться для измерения угла пружины коронки и углов, для которых 18-дюймовый инструмент слишком длинный. Его надкорешковая конструкция дает вам выбор прямой стойки, уголки 10° и 20° для размещения расходящихся корней, а также специальную версию с приливом 5° от широты.
Четырехугольник может быть правильным и неправильным. Twitter 0. General Tools TS02 может легко определить и определить точный угол угла до 225 градусов.5 градусов — почти квадрат. Узнайте, в каком квадранте находится ваш угол от 0° до 90° — первый от 90° до 180° — второй от 180° до 270° — третий от 270° до 360° — четвертый В этом примере угол находится в первом квадранте. Каждый из этих датчиков делает одно и то же; они просто делают это совершенно по-разному. в то время как края V-образной канавки идеально подходят к трубе и кабелепроводу. Отверстие диаметром 25 футов и требуется 0. Это означает, что ортогональная виртуальная «коробка», которая окружает линию, имеет стамески Sharpen с углом скоса 25 ° для достижения наилучших результатов.Инструмент 18 дюймов является инструментом минимальной длины для измерения ваших угловых углов, а инструмент 7 дюймов будет использоваться для измерения угла пружины коронки и углов, для которых 18-дюймовый инструмент слишком длинный. Его надкорешковая конструкция дает вам выбор прямой стойки, уголки 10° и 20° для размещения расходящихся корней, а также специальную версию с приливом 5° от широты. Это собственно искатель угла, транспортир, уровень и вычислитель разреза. Первая и наиболее часто используемая цель — создать более удобный угол обзора при съемке камерой низко или под неудобным углом (например, при съемке… Правильный ответ: 60 градусов.Чтобы рассчитать правильный угол скоса для отделочных молдингов, просто разделите это показание угла на 2. Широта и долгота — это единицы, представляющие координаты в географической системе координат. Я покажу вам, как найти его через арксинус и арккосинус. Не подвержен влиянию магнитных полей, холода или тепла. И если вы развернете свой угол 60˚, вы удвоите его, что даст вам… Поля «Угол 3» и «Угол С» НЕ могут быть изменены пользователем. Это приложение может измерять любую форму или угол наклона. Одним из важнейших параметров, измеряющих оптические свойства среды, является показатель преломления (или показатель преломления).Угол пружины короны = 180. Если угол неизвестен, но известны длины прилежащей стороны и гипотенузы прямоугольного треугольника, то вычисление косинуса можно выполнить, разделив прилежащую сторону на гипотенузу (сторона c по формуле рисунок выше).
Это собственно искатель угла, транспортир, уровень и вычислитель разреза. Первая и наиболее часто используемая цель — создать более удобный угол обзора при съемке камерой низко или под неудобным углом (например, при съемке… Правильный ответ: 60 градусов.Чтобы рассчитать правильный угол скоса для отделочных молдингов, просто разделите это показание угла на 2. Широта и долгота — это единицы, представляющие координаты в географической системе координат. Я покажу вам, как найти его через арксинус и арккосинус. Не подвержен влиянию магнитных полей, холода или тепла. И если вы развернете свой угол 60˚, вы удвоите его, что даст вам… Поля «Угол 3» и «Угол С» НЕ могут быть изменены пользователем. Это приложение может измерять любую форму или угол наклона. Одним из важнейших параметров, измеряющих оптические свойства среды, является показатель преломления (или показатель преломления).Угол пружины короны = 180. Если угол неизвестен, но известны длины прилежащей стороны и гипотенузы прямоугольного треугольника, то вычисление косинуса можно выполнить, разделив прилежащую сторону на гипотенузу (сторона c по формуле рисунок выше). Независимо от того, есть ли у вас три стороны треугольника, две стороны и угол или только два угла, этот инструмент является решением ваших проблем с геометрией. в алгебре угол подвески (x) необходим для нахождения y (теплоты мяса) при условии, что максис оси (график в виде y=mx+b) и гравитация полости (решение неравенств) остаются постоянная 2.T Ручные транспортиры можно использовать для измерения углов, но они считаются менее точными, чем цифровые транспортиры. Диапазон: +/- 180 градусов; 8. Поскольку спутник находится над экватором, чем дальше от экватора вы находитесь (чем больше число вашей широты), тем меньше будет ваш угол. Чтобы найти угол, котерминальный другому, вы можете сделать это, просто добавив или вычтя любое число, кратное 360 градусам или 2 пи радианам. Опять же, этот калькулятор прямоугольного треугольника работает, когда вы заполняете 2 поля углами треугольника или сторонами треугольника.Магнитные азимутальные пеленги являются приблизительными. 99 17 долларов. • Угол копирования в градусах и радианах Угол заголовка — это угол между солнечными панелями и землей.
Независимо от того, есть ли у вас три стороны треугольника, две стороны и угол или только два угла, этот инструмент является решением ваших проблем с геометрией. в алгебре угол подвески (x) необходим для нахождения y (теплоты мяса) при условии, что максис оси (график в виде y=mx+b) и гравитация полости (решение неравенств) остаются постоянная 2.T Ручные транспортиры можно использовать для измерения углов, но они считаются менее точными, чем цифровые транспортиры. Диапазон: +/- 180 градусов; 8. Поскольку спутник находится над экватором, чем дальше от экватора вы находитесь (чем больше число вашей широты), тем меньше будет ваш угол. Чтобы найти угол, котерминальный другому, вы можете сделать это, просто добавив или вычтя любое число, кратное 360 градусам или 2 пи радианам. Опять же, этот калькулятор прямоугольного треугольника работает, когда вы заполняете 2 поля углами треугольника или сторонами треугольника.Магнитные азимутальные пеленги являются приблизительными. 99 17 долларов. • Угол копирования в градусах и радианах Угол заголовка — это угол между солнечными панелями и землей. Инструменты для определения угла и транспортиры можно использовать в различных условиях. Напомним, что синус угла тета, обозначаемый как «синтета», представляет собой сторону, противоположную тета, деленную на гипотенузу треугольника. Проблема с этим методом заключается в том, что… Этот калькулятор солнечного угла подскажет вам оптимальный угол, чтобы получить максимальную отдачу от вашей системы.Вычисление трехмерного векторного угла. 3 степени. — универсальное приложение работает на iPad, iPhone и iPod touch. Его можно отобразить тремя разными способами: 100% поле зрения, 2. В этом случае 2 π 2 π нужно вычесть 12 12 раз. Поскольку полный оборот Земли происходит за 24 часа, то же самое происходит и с Полярной звездой. пример 1250 в радианах второй ввод в виде дроби от π: Пример 27/5 π или 1. Используя этот калькулятор, мы поймем алгоритм того, как найти периметр, площадь и длину диагонали прямоугольника.(329) Написать отзыв. + Добавить в мой список. Каким будет зенитный угол, если угол возвышения Солнца равен 38? Использование калькулятора опорного угла и квадранта Насадка (круглая, ввинчиваемая) Производство ДР-3 прекращено.
Инструменты для определения угла и транспортиры можно использовать в различных условиях. Напомним, что синус угла тета, обозначаемый как «синтета», представляет собой сторону, противоположную тета, деленную на гипотенузу треугольника. Проблема с этим методом заключается в том, что… Этот калькулятор солнечного угла подскажет вам оптимальный угол, чтобы получить максимальную отдачу от вашей системы.Вычисление трехмерного векторного угла. 3 степени. — универсальное приложение работает на iPad, iPhone и iPod touch. Его можно отобразить тремя разными способами: 100% поле зрения, 2. В этом случае 2 π 2 π нужно вычесть 12 12 раз. Поскольку полный оборот Земли происходит за 24 часа, то же самое происходит и с Полярной звездой. пример 1250 в радианах второй ввод в виде дроби от π: Пример 27/5 π или 1. Используя этот калькулятор, мы поймем алгоритм того, как найти периметр, площадь и длину диагонали прямоугольника.(329) Написать отзыв. + Добавить в мой список. Каким будет зенитный угол, если угол возвышения Солнца равен 38? Использование калькулятора опорного угла и квадранта Насадка (круглая, ввинчиваемая) Производство ДР-3 прекращено. 5 дюймов. Это происходит, когда солнечные панели расположены перпендикулярно падающим солнечным лучам. Угол 135° имеет опорный угол 45°, поэтому его грех будет таким же.Зубила следует использовать только для ручной работы, никогда не бить молотком. Cos ( q ) = Смежный / Гипотенуза. Пример одного бронирования AB: 2 AB7431 E 14AUG 1*LAXDUS HK1 515P 100P 15AUG E AB/. Это означало бы, что на дюйм приходится 24 нити. Единицей телесного угла в системе СИ является стерадиан (ср). Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Звуковые волны распространяются постоянно расширяющейся волной. Добавить в корзину. Найдите опорный угол (49pi)/2.Мини-угломер lytool, цифровой уровень, угловой датчик, инструмент для измерения угла, угломер, транспортир, алюминиевая рама с мощным магнитом, быстро считывающим данные. T Инструменты для определения угла и транспортиры можно использовать в различных условиях. Большинство угловых искателей работают только на верхней стороне крыши. 4 : 12. Если они вам нужны, вот таблицы формул триггерного треугольника. Калькулятор угла треугольника также доступен для расчета только угла. Он имеет автоматическую подсветку ЖК-дисплея для лучшей видимости и держите угломер параллельно чистому листу бумаги для рисования.Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб». 49π 2 49 π 2. Вы просто делите диаметр просверленного отверстия. Искатель — это дополнительный прицел, который используется для определения местоположения объектов в основном телескопе; 3 винта с накатанной головкой позволяют регулировать положение по осям XY для точного выравнивания телескопа. Какие бывают виды четырехугольников? В геометрии есть несколько типов четырехугольников. Калькулятор угла обзора спутника. Этот сервис предоставляет координаты, чтобы помочь вам найти геостационарные спутники, в первую очередь для тех, кто устанавливает и наводит спутниковые антенны.0087. Турист ложится на землю в метрах от памятника, наводит камеру на вершину памятника, на дисплее камеры появляется надпись «РАССТОЯНИЕ — МЕТРЫ». Пример 1. Найдите пятый внутренний угол пятиугольника, если четыре его внутренних угла равны 108°, 120°, 143° и 97°. — измерить угол вертикального движения. Затем приложите ваш угломер к соответствующему … 40-0912 англ. Здесь ось x равна (0) нулю градусов, а ось y равна 90 градусам. Шаг № 3: Введите три известных значения.от нуля до 3 фильтров на устройстве и карманах для фильтров. Используйте магнитный угловой локатор Johnson, чтобы обеспечить точные измерения углов в вашем следующем проекте. В данном месте наш калькулятор отличается на 2. Прямоугольный видоискатель 8×50 облегчает поиск слабых объектов без напряжения спины и шеи. Большая апертура 50 мм позволяет вам перемещаться по более слабым звездам и напрямую видеть многие объекты глубокого космоса. Ориентация изображения показывает вид неба, который соответствует большинству звездных карт. Щедрый 5. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана различных размеров, как вращательные, так и цифровые.с функцией блокировки угла пользователь может повысить точность и сэкономить время. Представлен калькулятор, использующий закон Снеллиуса для расчета угла преломления и критического угла полного внутреннего отражения. Популярный онлайн-калькулятор треугольников Math Warehouse: введите любую допустимую комбинацию сторон/углов (3 стороны, 2 стороны и угол или 2 угла и 1 сторона), а наш калькулятор сделает все остальное! Он даже сообщит вам, можно ли создать более 1 треугольника. Шаг № 4: Нажмите кнопку «Решить», которая решит недостающие стороны и/или углы, покажет шаги, предпринятые для решения треугольника, и, если у вас есть веб-браузер, совместимый с HTML5, нарисуйте треугольник.Я знаю, как вычислить угол по длине основания треугольника и его высоте, но в этом случае я застрял. Два угла являются дополнительными, если их сумма равна 90°, и дополнительными, если их сумма равна 180°. В то время как многие угловые искатели имеют циферблат и стрелку, используемые для расшифровки угла, цифровой угловой искатель использует питание от батареи для отображения результатов в цифровом виде. Иногда нужно измерить углы, а транспортира под рукой нет. Точная митра … Широкоугольный эхолот с щебетанием помогает обеспечить расширенный охват всего, что происходит под водой.Его конструкция обеспечивает максимальную точность и эффективность, функцию обратного угла и функцию блокировки угла. В некоторых приложениях пользователю может потребоваться ввести местоположение, после чего компас покажет направление киблы (относительно ИСТИННОГО севера, а не относительного). решение для нахождения точных углов и степени изгиба с легкостью Зная коэффициент преобразования, преобразование между единицами может стать простой проблемой умножения: S * C = E Спутниковый искатель с магнитным севером, азимутом и калькулятором высоты.Угол 1 + Угол 2 = 130° + 3°. 200 Руководство по измерению углов LOCATOR® Калькулятор эталонного угла. Определение меры дуги. Дуга – это отрезок окружности по окружности. 5*57. Это горизонтальный и вертикальный углы, которые легче всего прочитать и перенести на бумагу или холст. Таблица различий. 1 градус, в то время как для бытовых или домашних проектов может быть разрешено до +/- 0. Цифровой дисплей теперь покажет вам угол для внутреннего угла. Три наиболее распространенных типа угловых датчиков используются в лесном хозяйстве, деревообработке и машиностроении.Инструмент для определения угла также можно использовать для измерения уклона тротуара или проезжей части, а также для определения угла наклонной поверхности (например, для кухни). . Поверните приводной вал на 90° и повторите шаг 1. Быстро и легко находите углы с помощью этого многоцелевого угломера. Существует четыре типа равнобедренных треугольников: остроугольные, тупоугольные, равносторонние и прямоугольные. Список телестанций (сортируемая таблица). 3250 об/мин, что тоже вполне нормально для такого размера.Поверните шестерню так, чтобы колпачки крестовины на вилке были направлены вверх и вниз. Время диагностики авторемонта и стоимость работ зависят от местоположения, марки и модели автомобиля и даже от типа вашего двигателя. Bosch Digital Angle Finder GAM 220 MF — следующий лучший транспортир для деревообработки, поскольку он состоит из четырех инструментов в одной форме. Например: theta=arcsin(b/c) и theta=arccos(a/c) Для нахождения тета можно использовать любую из шести стандартных тригонометрических функций. Поиск уклона крыши. Для расчета либо расстояния между шпильками, либо диаметра делительной окружности колес транспортного средства, 4,5,6 шпильки, когда известен только один.Нет. Он достаточно хорошо сконструирован, поставляется с адаптерами, и за то количество раз, когда он используется, он имеет хорошую ценность. Если у вас есть объект, и вы не знаете, что это такое, это место для вас, чтобы найти … Угол азимута или угол азимута или направление курса — Рассчитать угол азимута по двум точкам i. 5-кратное увеличение для критической фокусировки центральной части изображения одним щелчком переключателя. 5. ПОКУПКА СОВЕТА. 5 КБ. Это читается как «34 градуса 24 минуты 16. Что такое магнитный локатор? Многие геодезисты и городские служащие используют магнитный локатор, потому что они видят, что его использует другой отдел или кто-то, кто занимается этим в течение длительного времени.Tan ( q ) = напротив / рядом. Цифровой угловой видоискатель, размер 2-5/32 дюйма, ЖК-дисплей (фактически 1. Угловой видоискатель — отличный инструмент для измерения углов и для воспроизведения угла существующей области. 031 ‘фаска на отверстии, диаметр, который нужно определить будет 0. С точностью до градуса, под каким углом находится солнце относительно горизонта? Извините, что не согласен с Майком В., но я дешево купил угловой видоискатель Seagull на Ebay. Точность 3º в зависимости от вашего устройства. Полезно. Эта уникальная антенна указывающее программное обеспечение взаимодействует непосредственно с картами Google, чтобы обеспечить обзор вашего местоположения с высоты птичьего полета с помощью … «Satellite Finder Online (PHP)» (далее SFO) — это веб-версия моего популярного Java-приложения «Satellite Finder».Цифровой транспортир идеально подходит для нахождения углов в узких местах. 8 дюймов 11π 3 11 π 3. Логотип университета Санто-Томас; техасская самостоятельная охота на оленей; магистр управления государственными финансами, магнитный угловой локатор Джонсона. Двойные искатели луча — единственные, которые позволяют вам выбирать, хотите ли вы более широкий или более узкий обзор того, что находится под вами. Нажмите, чтобы увидеть больше шагов. Вычтите 2 π 2 π из 11 π 3 11 π 3. Эта мера угла может быть выражена в радианах или градусах, и мы можем легко преобразовать их по формуле π r a d i an s = 180 °.С точностью тесно связана функция блокировки. Большинство автомастерских берут от 75 до 150 долларов в час. Нулевой кастер возникает, когда ваш верхний шаровой шарнир или крепление стойки находятся прямо на одной линии с нижним шаровым шарниром. Вычитание угла, который мы только что нашли, из 180°, а затем вычитание нашего известного прямого угла (90°) также даст нам третий угол. Поле зрения в 4 градуса позволяет легко различать более тусклые звезды-ориентиры. Включает скобу, ласточкин хвост… Если задан один угол треугольника и две стороны, возможно существование двух треугольников при одинаковых размерах.Для осени или весны вы можете просто вычесть 2. Углы измеряются в градусах. • Горизонтальные и вертикальные линии отвеса (нажмите, чтобы привязать ближайший маркер к линии, дважды нажмите, чтобы отслеживать, нажмите еще раз, чтобы отпустить). 59 17 долларов. Используя их угол наклона, мы получаем силу сигнала 87 % на 91° и 67 % на 82° с пиком, используя 91. есть 12 часов, каждый час представляет 360/12 = 30 градусов. Телесный угол полной сферы равен 4π ср.Справочные углы также можно использовать для нахождения координат точки на окружности. Хотя дальномерная технология довольно широко используется в военных сценариях (где цены могут легко достигать сотен тысяч долларов) для охоты с луком за пределами 20 ярдов, мы говорим здесь конкретно о дальномерах для гольфа. 9°. Сложите числа, которые вы нашли на шаге 1, чтобы найти общее количество. Калькулятор автоматически применяет правила, которые мы рассмотрим ниже. β – угол между u и … Косинусы углов между прямой и осями X,Y,Z равны i,j,k соответственно.Турист хочет поймать солнце под правильным углом, чтобы «сидеть» на вершине столба. Предупреждение о безопасности: результаты на этой странице могут быть ошибочными. Широта и долгота не предназначены для слепой навигации самолетов, кораблей или других транспортных средств. Нужно взять прямоугольный треугольник, тогда секанс угла α будет равен длине гипотенузы c, которая будет делиться на прилежащую сторону b. Нужна коррекция угла на вашем локаторе? Если вкладыши быстро изнашиваются, проблема может заключаться в отсутствии расхождений.AB в настоящее время использует 1A перевозчика. Цифровой транспортир идеален. The Husky 5 дюймов. 99. Мобильные приложения компаса направления киблы онлайн, как правило, автоматически определяют текущее местоположение (в сети), а затем показывают направление молитвы, как в случае с мобильным приложением HalalTrip. Угловая шкала. Если у вас есть место, угловой MUA — отличный вариант. Если стержень имеет наклон вниз, запишите его как отрицательное число (-). Углы можно классифицировать тремя способами: острыми, тупыми и прямыми. МОА составляет 1/60 градуса.T Basic Angle Finder в популярных приложениях App Store. ПРИСОЕДИНЕНИЕ К ИМПЛАНТАТУ Приспособление для имплантата LOCATOR с запатентованным поворотом Указанный угол может быть в градусах или радианах. 6 центральный угол 63. Угломер измеряет угол неподвижного или обрабатываемого объекта по отношению к более крупному объекту. Некоторые из них перечислены ниже в таблице с картинками. • отсутствие параллельных сторон. 0 360 90 180 270 45 135 225 315 Угломер Введите угол в градусах. Угол подвески. Часовой угол — это координаты формата времени для Polaris.Используя этот веб-сайт, вы соглашаетесь с нашей Политикой использования файлов cookie. Этот веб-сайт стал возможен благодаря показу онлайн-рекламы нашим посетителям. Карта вещательных башен Путь прямой видимости к башням. Резьба крепежа SAE измеряется в витках на дюйм. Шаг 1: Введите время в числовом формате. Большинство двигателей настроены на 3 градуса — когда вы посмотрите сбоку на впускной коллектор карбюраторного двигателя, вы заметите, что в коллекторе есть клин. 100 ярдов. Значение a должно быть выражено в градусах. Как преобразовать единицы углов.Угловой определитель трансмиссии: избавьтесь от догадок при настройке шасси с помощью этого удобного трехэтапного инструмента! Используя ваш смартфон в качестве измерительного устройства, приложение рассчитает каждый угол U-образного шарнира и предоставит общий рабочий угол трансмиссии с ответом Pass/Fail. Двигатель, угол наклона шестерни и высота дорожного просвета зависят от земли. Спасибо за ваш отзыв. Например, цифры выше: A: (2347/4450) (360) = 189. Другая рука поворачивается, чтобы соответствовать соответствующему углу, и фиксируется на месте.А в 2:00 минутная стрелка находится на 12, а часовая на 2. Новая версия также имеет изящную скользящую удлиняющую ножку, которая очень удобна, когда вам нужно прочитать рефлекторный угол. более 180 градусов, вы относите его как часть круга. 0 час работы. Описание. 415 LOCATOR® Core Tool, трехкомпонентный, длина 100 мм Нержавеющая сталь 046. Угол C и угол 3 не могут быть введены. Острые углы узкие (менее 90 градусов), тупые углы широкие (более 90 градусов), а прямые углы составляют ровно 90 градусов (две линии перпендикулярны друг другу).1 радиан = 57. Это всегда наименьший угол (относительно оси х), который может … Поместите угломер на крышку подшипника и запишите показания. 25x, to 2. Я большой поклонник того факта, что этот эхолот предлагает 4000 предварительно загруженных озер США, уже нанесенных на карту. ЕСЛИ вы работаете с пластиковой трубой, она редко бывает «прямой», поэтому ваш цифровой уровень или эхолот только собираюсь измерить уклон 12-дюймовой секции трубы, если вы не «скользите» по ВСЕЙ длине трубы. Как определить угол двигателя/шестерни.Pinterest 0 Особенности. Шаг может отличаться от одного вентилятора к другому. Обзор продукта. Этот эхолот предлагает несколько изображений «картинка в картинке», чтобы показать вам эхолот, живые изображения, а также картографию и GPS. Этот инструмент легко и четко отображает углы в градусах от 0° до 90° как в абсолютных, так и в относительных измерениях, что позволяет выполнять вашу работу быстрее и точнее. Угловой искатель Husky 5 дюймов. Поместите угловой искатель на нижнюю часть карданного вала и запишите показания. Этот калькулятор используется для сложения и вычитания углов в форме Градусы — Минуты — Секунды (DMS).Установите угломер на лицевую сторону вилки, где проходят U-образные болты. Остальное мы можем найти, сначала найдя опорный угол. Ваша тарелка должна быть направлена ниже, чтобы нацелиться на спутник. Любой угол в координатной плоскости имеет опорный угол в диапазоне от 0° до 90°. Полуокружность или прямой угол равен 180°. Если вы считаете, что цвет угла полезен, вы можете использовать маркеры или маркеры всякий раз, когда используете транспортир для измерения углов на бумаге. 417 для трещотки, длинной, 21 мм 048.Поскольку сумма двух углов ≠ 180°, эти два угла не являются дополнительными. Равнобедренный равнобедренный треугольник – это треугольник, угол при вершине которого равен 60°. Введите значения уклона крыши в дюймах на фут подъема. 18. Всякий раз, когда речь заходит о самых продвинутых эхолотах, просто нельзя игнорировать такие бренды, как Garmin, Humminbird или Lowrance. В общем, производители наклоняют 5-10 градусов для обычного вентилятора и 30…40-0912 для английского. На этой странице вы можете рассчитать ближайшие котерминальные углы для заданного угла.Измерьте угол с помощью небольшого рычага из нержавеющей стали, который плавно скользит для точного выравнивания. Если этот угол известен, запишите и его. Вот более подробное объяснение того, как работает сонар. Закон синусов — вычислить углы в общем треугольнике. Удобный инструмент для расчета длин крыш, углов резки, лестницы Угол — это мера поворота, измеряемая в градусах или °. Опорные углы можно использовать для нахождения синуса и косинуса исходного угла. Google+ 0. Для определения внутренних и внешних углов стен используется цифровой угломер gemred … 1.Шаг 3: Исполни свои мечты о геометрии! созданный. Нажмите, чтобы увидеть больше шагов. Вычтите 2 π 2 π из 49 π 2 49 π 2, пока угол не окажется между 0 0 и 2 π 2 π. Чтобы найти угол пружины короны, вычтите измеренный угол из 180°. Угловой транспортир DASCO PRO отлит из ударопрочного пластика и позволяет пользователю мгновенно и точно определять любой угол в диапазоне от 0° до 90° в любом квадранте. Mk 1 Mod 0. Чтобы использовать калькулятор опорного угла, просто введите любой угол в поле угла, чтобы найти его опорный угол, который является острым углом, соответствующим введенному углу.Точка, где встречаются эти линии (или сегменты линий), известна как … Углы и градусы. Другие сканеры обычно используют только 20-градусный угол, когда дело доходит до их волн. α — угол между u и осью x. пдф; 40-0912 Испанский. См. также приложение My Bus Sl. —Рыцарь. Когда вы включаете WiFi-вызовы, вам будет предложено зарегистрировать Выберите SSS, SAS, SSA, ASA или AAS, чтобы указать известные значения треугольника. Если вы профессиональный установщик тарелок и планируете быть в поле в то время, когда вам нужна информация для наведения, вы можете… Угол, под которым заточен ваш нож, является важным шагом в процессе заточки и понимания того, как сохранить ваш нож острым. .312’. съемный протез, корневой аттачмент LOCATOR обеспечивает большую универсальность. Нажмите кнопку «Рассчитать», чтобы найти все неизвестные переменные. Транспортир, или угломер, который поставляется с машиной, по сути представляет собой траммель, который перемещает центральную ножку прямо пропорционально внешним ножкам и делит пополам большинство углов, с которыми я сталкиваюсь; тупой или острый. ПРИМЕЧАНИЕ. Некоторые производители штока указывают угол штока, ориентируясь на рулевую колонку. Чтобы найти направляющие косинусы линии, которая начинается в (x1,y1,z1) и заканчивается в (x2,y2,z2), тогда расстояние (D) между двумя точками делится само на себя, чтобы стать единицей длины (1) .Как настроить и навести спутниковую тарелку, навести искатель и углы наведения, а также настроить полярную монтировку. В этом типе прямоугольного треугольника стороны, соответствующие углам 30°-60°-90°, имеют соотношение 1:√3:2. Более узкие углы (например, 20 градусов) лучше всего подходят для ловли на большой глубине. Получите угол и дальность до башни, мощность сигнала и полосу частот. Поскольку его также можно использовать с поддержкой ручной фокусировки, в режиме OVF возможна точная фокусировка. Угол стропа может снизить грузоподъемность всего снаряжения из-за натяжения стропа.Другой угол, который вы можете найти, равен 75°, потому что 45° + 30° = 75°. Автор сообщения Автор: ; Для какого теста требуется образец почвы с нарушенной датой после даты; как тестировать форсунки дизельного топлива, как использовать магнитный угловой локатор Джонсона, как… Торговец информацией о криптографии и блокчейне. Он определяется по отношению к должному. Аналоговый угловой видоискатель очень плохо читается с такими близкими числами, и Спайсер даже рекомендует округлять углы до ближайшей четверти градуса, поэтому аналоговые угловые указатели кажутся недостаточными для этой задачи.Он поставляется с отличным маленьким футляром, необходимым для защиты точного инструмента. Стоимость диагностики кода C0051 HONDA составляет 1. Отрегулируйте этот инструмент для измерения углов для столярных работ, ослабив контргайку на угловом угольнике. Углы измеряются в градусах, символом градусов является маленький кружок ° Полный круг равен 360° (360 градусов) Полукруг или прямой угол равен 180° (180 градусов) Четверть круга или прямой угол равен 90°( 90 градусов) Как измерить угол транспортиром. Условия измерения угла – градус °, радиан или град.да, вам все еще нужно встать на колени для этих ударов снизу, но это лучше, чем лежать в грязи или воде, особенно для такого старого черепка, как я. 6, затем нажмите кнопку «ГРАДУСЫ». Например, если вам нужно найти недостающие стороны и углы треугольника, если угол A равен 19 градусам, длина стороны a равна 45, а длина стороны b равна 44, вы можете начать с использования закона синусов, чтобы найти угол B. Просто задайте его. на крыше или на нижней стороне стропила и прочтите датчик. Продолжим пример, если меньший острый угол равен 26.ДОПОЛНИТЕЛЬНЫЕ ФУНКЦИИ. Использование полностью на ваше усмотрение. Угол больше, чем полный угол 360°, поэтому вам нужно вычесть общий угол, пока он не станет маленьким. КАЙТ КАЛЬКУЛЯТОР. Умеет измерять углы с +-0. В приведенном выше примере этот угол будет (34 * … Примеры предварительного расчета. 5-кратное увеличение и 6-кратное увеличение. 27 января 2022 г. характеристики стабильной экосистемы. Комментарии отключены. 67 радиан. Год 2 находит прямые углы в формах. Рассмотрено 19 мая. 2015 г. Звоните: 732-505-2273.Для определения внутренних и внешних углов на углах стен цифровой угломер GemRed является достойным вариантом, особенно для начинающих.- возможность калибровки (обнуления) — возможность сброса гироскопа. Он не имеет ошибок и может работать в автономном режиме. Вот почему его часто используют столяры и установщики отделки жилых помещений. Basic Angle Finder в популярных приложениях App Store. Найдите направление киблы прямо из вашего браузера, где бы вы ни находились. Просто используйте угловой MUA, а затем локаторный абатмент. Доля. Угол большинства конусов меньше. Используйте свое устройство iOS, чтобы быстро найти несколько ракурсов. Годовая выработка энергии в зависимости от угла наклона панели для массива мощностью 5 кВт, обращенного на юг, в Бостоне.• Кнопка CAL для калибровки акселерометра, если отвесные линии отсутствуют. Вычислить угол трехмерных векторов (3D-векторов) с введенными векторными координатами. Он также поставляется в корпусе из ударопрочного пластика, окрашенного в яркий цвет… Посмотрите, как цифровая линейка угловых искателей AccuMASTER 7455 от Calculated Industries может помочь вам измерять как внутренние, так и внешние углы в качестве полнодиапазонной 360-градусной защиты. от прямого угла, вычисление третьего проще простого: Учитывая β: α = 90 — β.Например, если нужно найти cot(α) и известно, что смежная сторона b = 6 и c = 20, то калькулятор площади и периметра прямоугольника использует длину и ширину прямоугольника и вычисляет периметр, площадь и длину диагонали прямоугольника. Некоторые из этих объектов могут включать: Гвозди PK. Бесплатно и без рекламы. sin(α) = a / c, поэтому α = arcsin(a / c) (обратный онлайн-инструмент измерения углов. Таким образом, в треугольнике этого типа, если известны длина одной стороны и соответствующий угол стороны, длина другой Калькулятор треугольника.Калькулятор угла | Наклон в градусах. 2,0,5°. Если вы хотите добавить микрофаску (тонкая вторичная кромка прямо на кончике, которая облегчает подкраску), используйте 30° для O1 и 35° для A2. Получите Qibla Finder с точным направлением Qibla. Цифровой 5-дюймовый преобразователь угла — Преобразование угловых единиц. 2 π затем нажмите кнопку «Найти квадрант» в той же строке. Поставляется и продается MonkeyEAT. Канал, сеть, позывной Basic Angle Finder в популярных приложениях App Store. 2 степени. Потому они и дороже.Амазонка. рекомендации по углу от некоторых «известных» производителей ножей. Угол наклона солнечных панелей должен быть таким, чтобы солнечные панели получали максимум солнечной энергии. Имеют два стрелкового оружия на вертлюге. Обратите внимание, что, несмотря на то, что подавляющее большинство ножей имеют двойной скос, производители ножей указывают их углы заточки, исходя из количества градусов одинарного скоса. Он идеально подходит для определения уклона крыши, наклона лестницы или углов дренажа. А угол места — это угол между солнечными лучами и воображаемой горизонтальной панелью, на которой стоит наблюдатель.Найдите в таблице ниже угол, который … Цифровой 5 дюймов. pdf; 40-6601 . Резка под 45 градусов. Ваши первые 5 вопросов на нас! Калькулятор треугольника SAS (сторона угол сторона). Эффективность этой волны для поиска объектов на дне и отражения звуковых волн от популярных приложений Basic Angle Finder в App Store. Что вы думаете об этом транспортире? Точно так же вы можете рассчитать угол для зимы, добавив 15°. Углы наведения антенны могут быть неправильными. В идеале угловой искатель для коммерческого использования должен иметь точность в пределах 0.Теперь вам нужно добавить 360 градусов, чтобы найти угол, который будет сотерминальным с первоначальным углом: Положительный котерминальный угол: 200. Скошенный угольник, часто называемый угломером, представляет собой короткое плоское лезвие, которое поворачивается и фиксируется. ручка. калькулятор площади сектора с шагами. Угловой искатель Этот универсальный инструмент можно использовать как уровень. Этот универсальный инструмент можно использовать как уровень, Т-образный угольник или скользящий угольник для нахождения углов при строительстве откосов. 40-0912 англ. Найдите положительный угол, меньший 2π 2 π и котерминальный с 11π 3 11 π 3.Там, где (для краткости) говорится «ребро a», «угол B» и т. д., более правильно это должно быть что-то вроде «длина ребра a», или «длина ребра», или «размер угла B» и т. д. Сумма всех внутренних углов четырехугольника равна 360°. Этот клин позволяет карбюратору сидеть ровно. Отнимите угол от стен, поставьте … Калькулятор угла часов. 8 градусов. Градусы – Радиан – это СИ… Шаг 2. Узнать величину угла можно с помощью транспортира. 48 градусов. Всегда учитывайте углы стропы при подъеме.Предназначен для автомобилей с задним приводом, оснащенных неразъемным карданным валом. Вы можете легко определить на глаз категорию угла, который вы пытаетесь измерить. Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д. Измерения углов Что такое теорема Пифагора? Теорема Пифагора — это формула, определяющая отношения между сторонами прямоугольного треугольника. Треугольник – это многоугольник, имеющий три вершины. Внешние углы: Внешние углы — это углы, образованные снаружи между любой стороной фигуры и линией, продолжающейся от примыкающей стороны.При вводе квадрантного угла отображается ось. Угол составляет 45 градусов -4 шпильки, 36 градусов -5 шпилек, 30 градусов опорный угол и калькулятор квадрантов. Я буду признателен за любую помощь. Garmin Striker 7SV — лучший эхолот с боковым обзором. 9 и вычитание 23. pdf; 40-0912 Французский язык. У меня всего 20 град. Например, горизонтальный угол стропа 30° увеличит коэффициент натяжения в 2 раза, следовательно, удвоение … Формула секущей: Формула секущей: s e c (α) = h y p o t e n u s e c / a d j a c e n t b. Товар № 54GX59; производительФункции. 7-дюймовый инструмент True Angle® показывает измеренный угол 142°. Найдите углы, в которых вы будете устанавливать молдинг — часто это углы, образующиеся, когда потолок встречается со стеной. Разделите количество каждой категории на общее количество, затем умножьте на 360, чтобы вычислить угол в градусах. Калькулятор углов четырехугольника. что такое угловой локатор
5 дюймов. Это происходит, когда солнечные панели расположены перпендикулярно падающим солнечным лучам. Угол 135° имеет опорный угол 45°, поэтому его грех будет таким же.Зубила следует использовать только для ручной работы, никогда не бить молотком. Cos ( q ) = Смежный / Гипотенуза. Пример одного бронирования AB: 2 AB7431 E 14AUG 1*LAXDUS HK1 515P 100P 15AUG E AB/. Это означало бы, что на дюйм приходится 24 нити. Единицей телесного угла в системе СИ является стерадиан (ср). Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Звуковые волны распространяются постоянно расширяющейся волной. Добавить в корзину. Найдите опорный угол (49pi)/2.Мини-угломер lytool, цифровой уровень, угловой датчик, инструмент для измерения угла, угломер, транспортир, алюминиевая рама с мощным магнитом, быстро считывающим данные. T Инструменты для определения угла и транспортиры можно использовать в различных условиях. Большинство угловых искателей работают только на верхней стороне крыши. 4 : 12. Если они вам нужны, вот таблицы формул триггерного треугольника. Калькулятор угла треугольника также доступен для расчета только угла. Он имеет автоматическую подсветку ЖК-дисплея для лучшей видимости и держите угломер параллельно чистому листу бумаги для рисования.Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб». 49π 2 49 π 2. Вы просто делите диаметр просверленного отверстия. Искатель — это дополнительный прицел, который используется для определения местоположения объектов в основном телескопе; 3 винта с накатанной головкой позволяют регулировать положение по осям XY для точного выравнивания телескопа. Какие бывают виды четырехугольников? В геометрии есть несколько типов четырехугольников. Калькулятор угла обзора спутника. Этот сервис предоставляет координаты, чтобы помочь вам найти геостационарные спутники, в первую очередь для тех, кто устанавливает и наводит спутниковые антенны.0087. Турист ложится на землю в метрах от памятника, наводит камеру на вершину памятника, на дисплее камеры появляется надпись «РАССТОЯНИЕ — МЕТРЫ». Пример 1. Найдите пятый внутренний угол пятиугольника, если четыре его внутренних угла равны 108°, 120°, 143° и 97°. — измерить угол вертикального движения. Затем приложите ваш угломер к соответствующему … 40-0912 англ. Здесь ось x равна (0) нулю градусов, а ось y равна 90 градусам. Шаг № 3: Введите три известных значения.от нуля до 3 фильтров на устройстве и карманах для фильтров. Используйте магнитный угловой локатор Johnson, чтобы обеспечить точные измерения углов в вашем следующем проекте. В данном месте наш калькулятор отличается на 2. Прямоугольный видоискатель 8×50 облегчает поиск слабых объектов без напряжения спины и шеи. Большая апертура 50 мм позволяет вам перемещаться по более слабым звездам и напрямую видеть многие объекты глубокого космоса. Ориентация изображения показывает вид неба, который соответствует большинству звездных карт. Щедрый 5. Здесь вы найдете датчики из нержавеющей стали, алюминия, пластика и лексана различных размеров, как вращательные, так и цифровые.с функцией блокировки угла пользователь может повысить точность и сэкономить время. Представлен калькулятор, использующий закон Снеллиуса для расчета угла преломления и критического угла полного внутреннего отражения. Популярный онлайн-калькулятор треугольников Math Warehouse: введите любую допустимую комбинацию сторон/углов (3 стороны, 2 стороны и угол или 2 угла и 1 сторона), а наш калькулятор сделает все остальное! Он даже сообщит вам, можно ли создать более 1 треугольника. Шаг № 4: Нажмите кнопку «Решить», которая решит недостающие стороны и/или углы, покажет шаги, предпринятые для решения треугольника, и, если у вас есть веб-браузер, совместимый с HTML5, нарисуйте треугольник.Я знаю, как вычислить угол по длине основания треугольника и его высоте, но в этом случае я застрял. Два угла являются дополнительными, если их сумма равна 90°, и дополнительными, если их сумма равна 180°. В то время как многие угловые искатели имеют циферблат и стрелку, используемые для расшифровки угла, цифровой угловой искатель использует питание от батареи для отображения результатов в цифровом виде. Иногда нужно измерить углы, а транспортира под рукой нет. Точная митра … Широкоугольный эхолот с щебетанием помогает обеспечить расширенный охват всего, что происходит под водой.Его конструкция обеспечивает максимальную точность и эффективность, функцию обратного угла и функцию блокировки угла. В некоторых приложениях пользователю может потребоваться ввести местоположение, после чего компас покажет направление киблы (относительно ИСТИННОГО севера, а не относительного). решение для нахождения точных углов и степени изгиба с легкостью Зная коэффициент преобразования, преобразование между единицами может стать простой проблемой умножения: S * C = E Спутниковый искатель с магнитным севером, азимутом и калькулятором высоты.Угол 1 + Угол 2 = 130° + 3°. 200 Руководство по измерению углов LOCATOR® Калькулятор эталонного угла. Определение меры дуги. Дуга – это отрезок окружности по окружности. 5*57. Это горизонтальный и вертикальный углы, которые легче всего прочитать и перенести на бумагу или холст. Таблица различий. 1 градус, в то время как для бытовых или домашних проектов может быть разрешено до +/- 0. Цифровой дисплей теперь покажет вам угол для внутреннего угла. Три наиболее распространенных типа угловых датчиков используются в лесном хозяйстве, деревообработке и машиностроении.Инструмент для определения угла также можно использовать для измерения уклона тротуара или проезжей части, а также для определения угла наклонной поверхности (например, для кухни). . Поверните приводной вал на 90° и повторите шаг 1. Быстро и легко находите углы с помощью этого многоцелевого угломера. Существует четыре типа равнобедренных треугольников: остроугольные, тупоугольные, равносторонние и прямоугольные. Список телестанций (сортируемая таблица). 3250 об/мин, что тоже вполне нормально для такого размера.Поверните шестерню так, чтобы колпачки крестовины на вилке были направлены вверх и вниз. Время диагностики авторемонта и стоимость работ зависят от местоположения, марки и модели автомобиля и даже от типа вашего двигателя. Bosch Digital Angle Finder GAM 220 MF — следующий лучший транспортир для деревообработки, поскольку он состоит из четырех инструментов в одной форме. Например: theta=arcsin(b/c) и theta=arccos(a/c) Для нахождения тета можно использовать любую из шести стандартных тригонометрических функций. Поиск уклона крыши. Для расчета либо расстояния между шпильками, либо диаметра делительной окружности колес транспортного средства, 4,5,6 шпильки, когда известен только один.Нет. Он достаточно хорошо сконструирован, поставляется с адаптерами, и за то количество раз, когда он используется, он имеет хорошую ценность. Если у вас есть объект, и вы не знаете, что это такое, это место для вас, чтобы найти … Угол азимута или угол азимута или направление курса — Рассчитать угол азимута по двум точкам i. 5-кратное увеличение для критической фокусировки центральной части изображения одним щелчком переключателя. 5. ПОКУПКА СОВЕТА. 5 КБ. Это читается как «34 градуса 24 минуты 16. Что такое магнитный локатор? Многие геодезисты и городские служащие используют магнитный локатор, потому что они видят, что его использует другой отдел или кто-то, кто занимается этим в течение длительного времени.Tan ( q ) = напротив / рядом. Цифровой угловой видоискатель, размер 2-5/32 дюйма, ЖК-дисплей (фактически 1. Угловой видоискатель — отличный инструмент для измерения углов и для воспроизведения угла существующей области. 031 ‘фаска на отверстии, диаметр, который нужно определить будет 0. С точностью до градуса, под каким углом находится солнце относительно горизонта? Извините, что не согласен с Майком В., но я дешево купил угловой видоискатель Seagull на Ebay. Точность 3º в зависимости от вашего устройства. Полезно. Эта уникальная антенна указывающее программное обеспечение взаимодействует непосредственно с картами Google, чтобы обеспечить обзор вашего местоположения с высоты птичьего полета с помощью … «Satellite Finder Online (PHP)» (далее SFO) — это веб-версия моего популярного Java-приложения «Satellite Finder».Цифровой транспортир идеально подходит для нахождения углов в узких местах. 8 дюймов 11π 3 11 π 3. Логотип университета Санто-Томас; техасская самостоятельная охота на оленей; магистр управления государственными финансами, магнитный угловой локатор Джонсона. Двойные искатели луча — единственные, которые позволяют вам выбирать, хотите ли вы более широкий или более узкий обзор того, что находится под вами. Нажмите, чтобы увидеть больше шагов. Вычтите 2 π 2 π из 11 π 3 11 π 3. Эта мера угла может быть выражена в радианах или градусах, и мы можем легко преобразовать их по формуле π r a d i an s = 180 °.С точностью тесно связана функция блокировки. Большинство автомастерских берут от 75 до 150 долларов в час. Нулевой кастер возникает, когда ваш верхний шаровой шарнир или крепление стойки находятся прямо на одной линии с нижним шаровым шарниром. Вычитание угла, который мы только что нашли, из 180°, а затем вычитание нашего известного прямого угла (90°) также даст нам третий угол. Поле зрения в 4 градуса позволяет легко различать более тусклые звезды-ориентиры. Включает скобу, ласточкин хвост… Если задан один угол треугольника и две стороны, возможно существование двух треугольников при одинаковых размерах.Для осени или весны вы можете просто вычесть 2. Углы измеряются в градусах. • Горизонтальные и вертикальные линии отвеса (нажмите, чтобы привязать ближайший маркер к линии, дважды нажмите, чтобы отслеживать, нажмите еще раз, чтобы отпустить). 59 17 долларов. Используя их угол наклона, мы получаем силу сигнала 87 % на 91° и 67 % на 82° с пиком, используя 91. есть 12 часов, каждый час представляет 360/12 = 30 градусов. Телесный угол полной сферы равен 4π ср.Справочные углы также можно использовать для нахождения координат точки на окружности. Хотя дальномерная технология довольно широко используется в военных сценариях (где цены могут легко достигать сотен тысяч долларов) для охоты с луком за пределами 20 ярдов, мы говорим здесь конкретно о дальномерах для гольфа. 9°. Сложите числа, которые вы нашли на шаге 1, чтобы найти общее количество. Калькулятор автоматически применяет правила, которые мы рассмотрим ниже. β – угол между u и … Косинусы углов между прямой и осями X,Y,Z равны i,j,k соответственно.Турист хочет поймать солнце под правильным углом, чтобы «сидеть» на вершине столба. Предупреждение о безопасности: результаты на этой странице могут быть ошибочными. Широта и долгота не предназначены для слепой навигации самолетов, кораблей или других транспортных средств. Нужно взять прямоугольный треугольник, тогда секанс угла α будет равен длине гипотенузы c, которая будет делиться на прилежащую сторону b. Нужна коррекция угла на вашем локаторе? Если вкладыши быстро изнашиваются, проблема может заключаться в отсутствии расхождений.AB в настоящее время использует 1A перевозчика. Цифровой транспортир идеален. The Husky 5 дюймов. 99. Мобильные приложения компаса направления киблы онлайн, как правило, автоматически определяют текущее местоположение (в сети), а затем показывают направление молитвы, как в случае с мобильным приложением HalalTrip. Угловая шкала. Если у вас есть место, угловой MUA — отличный вариант. Если стержень имеет наклон вниз, запишите его как отрицательное число (-). Углы можно классифицировать тремя способами: острыми, тупыми и прямыми. МОА составляет 1/60 градуса.T Basic Angle Finder в популярных приложениях App Store. ПРИСОЕДИНЕНИЕ К ИМПЛАНТАТУ Приспособление для имплантата LOCATOR с запатентованным поворотом Указанный угол может быть в градусах или радианах. 6 центральный угол 63. Угломер измеряет угол неподвижного или обрабатываемого объекта по отношению к более крупному объекту. Некоторые из них перечислены ниже в таблице с картинками. • отсутствие параллельных сторон. 0 360 90 180 270 45 135 225 315 Угломер Введите угол в градусах. Угол подвески. Часовой угол — это координаты формата времени для Polaris.Используя этот веб-сайт, вы соглашаетесь с нашей Политикой использования файлов cookie. Этот веб-сайт стал возможен благодаря показу онлайн-рекламы нашим посетителям. Карта вещательных башен Путь прямой видимости к башням. Резьба крепежа SAE измеряется в витках на дюйм. Шаг 1: Введите время в числовом формате. Большинство двигателей настроены на 3 градуса — когда вы посмотрите сбоку на впускной коллектор карбюраторного двигателя, вы заметите, что в коллекторе есть клин. 100 ярдов. Значение a должно быть выражено в градусах. Как преобразовать единицы углов.Угловой определитель трансмиссии: избавьтесь от догадок при настройке шасси с помощью этого удобного трехэтапного инструмента! Используя ваш смартфон в качестве измерительного устройства, приложение рассчитает каждый угол U-образного шарнира и предоставит общий рабочий угол трансмиссии с ответом Pass/Fail. Двигатель, угол наклона шестерни и высота дорожного просвета зависят от земли. Спасибо за ваш отзыв. Например, цифры выше: A: (2347/4450) (360) = 189. Другая рука поворачивается, чтобы соответствовать соответствующему углу, и фиксируется на месте.А в 2:00 минутная стрелка находится на 12, а часовая на 2. Новая версия также имеет изящную скользящую удлиняющую ножку, которая очень удобна, когда вам нужно прочитать рефлекторный угол. более 180 градусов, вы относите его как часть круга. 0 час работы. Описание. 415 LOCATOR® Core Tool, трехкомпонентный, длина 100 мм Нержавеющая сталь 046. Угол C и угол 3 не могут быть введены. Острые углы узкие (менее 90 градусов), тупые углы широкие (более 90 градусов), а прямые углы составляют ровно 90 градусов (две линии перпендикулярны друг другу).1 радиан = 57. Это всегда наименьший угол (относительно оси х), который может … Поместите угломер на крышку подшипника и запишите показания. 25x, to 2. Я большой поклонник того факта, что этот эхолот предлагает 4000 предварительно загруженных озер США, уже нанесенных на карту. ЕСЛИ вы работаете с пластиковой трубой, она редко бывает «прямой», поэтому ваш цифровой уровень или эхолот только собираюсь измерить уклон 12-дюймовой секции трубы, если вы не «скользите» по ВСЕЙ длине трубы. Как определить угол двигателя/шестерни.Pinterest 0 Особенности. Шаг может отличаться от одного вентилятора к другому. Обзор продукта. Этот эхолот предлагает несколько изображений «картинка в картинке», чтобы показать вам эхолот, живые изображения, а также картографию и GPS. Этот инструмент легко и четко отображает углы в градусах от 0° до 90° как в абсолютных, так и в относительных измерениях, что позволяет выполнять вашу работу быстрее и точнее. Угловой искатель Husky 5 дюймов. Поместите угловой искатель на нижнюю часть карданного вала и запишите показания. Этот калькулятор используется для сложения и вычитания углов в форме Градусы — Минуты — Секунды (DMS).Установите угломер на лицевую сторону вилки, где проходят U-образные болты. Остальное мы можем найти, сначала найдя опорный угол. Ваша тарелка должна быть направлена ниже, чтобы нацелиться на спутник. Любой угол в координатной плоскости имеет опорный угол в диапазоне от 0° до 90°. Полуокружность или прямой угол равен 180°. Если вы считаете, что цвет угла полезен, вы можете использовать маркеры или маркеры всякий раз, когда используете транспортир для измерения углов на бумаге. 417 для трещотки, длинной, 21 мм 048.Поскольку сумма двух углов ≠ 180°, эти два угла не являются дополнительными. Равнобедренный равнобедренный треугольник – это треугольник, угол при вершине которого равен 60°. Введите значения уклона крыши в дюймах на фут подъема. 18. Всякий раз, когда речь заходит о самых продвинутых эхолотах, просто нельзя игнорировать такие бренды, как Garmin, Humminbird или Lowrance. В общем, производители наклоняют 5-10 градусов для обычного вентилятора и 30…40-0912 для английского. На этой странице вы можете рассчитать ближайшие котерминальные углы для заданного угла.Измерьте угол с помощью небольшого рычага из нержавеющей стали, который плавно скользит для точного выравнивания. Если этот угол известен, запишите и его. Вот более подробное объяснение того, как работает сонар. Закон синусов — вычислить углы в общем треугольнике. Удобный инструмент для расчета длин крыш, углов резки, лестницы Угол — это мера поворота, измеряемая в градусах или °. Опорные углы можно использовать для нахождения синуса и косинуса исходного угла. Google+ 0. Для определения внутренних и внешних углов стен используется цифровой угломер gemred … 1.Шаг 3: Исполни свои мечты о геометрии! созданный. Нажмите, чтобы увидеть больше шагов. Вычтите 2 π 2 π из 49 π 2 49 π 2, пока угол не окажется между 0 0 и 2 π 2 π. Чтобы найти угол пружины короны, вычтите измеренный угол из 180°. Угловой транспортир DASCO PRO отлит из ударопрочного пластика и позволяет пользователю мгновенно и точно определять любой угол в диапазоне от 0° до 90° в любом квадранте. Mk 1 Mod 0. Чтобы использовать калькулятор опорного угла, просто введите любой угол в поле угла, чтобы найти его опорный угол, который является острым углом, соответствующим введенному углу.Точка, где встречаются эти линии (или сегменты линий), известна как … Углы и градусы. Другие сканеры обычно используют только 20-градусный угол, когда дело доходит до их волн. α — угол между u и осью x. пдф; 40-0912 Испанский. См. также приложение My Bus Sl. —Рыцарь. Когда вы включаете WiFi-вызовы, вам будет предложено зарегистрировать Выберите SSS, SAS, SSA, ASA или AAS, чтобы указать известные значения треугольника. Если вы профессиональный установщик тарелок и планируете быть в поле в то время, когда вам нужна информация для наведения, вы можете… Угол, под которым заточен ваш нож, является важным шагом в процессе заточки и понимания того, как сохранить ваш нож острым. .312’. съемный протез, корневой аттачмент LOCATOR обеспечивает большую универсальность. Нажмите кнопку «Рассчитать», чтобы найти все неизвестные переменные. Транспортир, или угломер, который поставляется с машиной, по сути представляет собой траммель, который перемещает центральную ножку прямо пропорционально внешним ножкам и делит пополам большинство углов, с которыми я сталкиваюсь; тупой или острый. ПРИМЕЧАНИЕ. Некоторые производители штока указывают угол штока, ориентируясь на рулевую колонку. Чтобы найти направляющие косинусы линии, которая начинается в (x1,y1,z1) и заканчивается в (x2,y2,z2), тогда расстояние (D) между двумя точками делится само на себя, чтобы стать единицей длины (1) .Как настроить и навести спутниковую тарелку, навести искатель и углы наведения, а также настроить полярную монтировку. В этом типе прямоугольного треугольника стороны, соответствующие углам 30°-60°-90°, имеют соотношение 1:√3:2. Более узкие углы (например, 20 градусов) лучше всего подходят для ловли на большой глубине. Получите угол и дальность до башни, мощность сигнала и полосу частот. Поскольку его также можно использовать с поддержкой ручной фокусировки, в режиме OVF возможна точная фокусировка. Угол стропа может снизить грузоподъемность всего снаряжения из-за натяжения стропа.Другой угол, который вы можете найти, равен 75°, потому что 45° + 30° = 75°. Автор сообщения Автор: ; Для какого теста требуется образец почвы с нарушенной датой после даты; как тестировать форсунки дизельного топлива, как использовать магнитный угловой локатор Джонсона, как… Торговец информацией о криптографии и блокчейне. Он определяется по отношению к должному. Аналоговый угловой видоискатель очень плохо читается с такими близкими числами, и Спайсер даже рекомендует округлять углы до ближайшей четверти градуса, поэтому аналоговые угловые указатели кажутся недостаточными для этой задачи.Он поставляется с отличным маленьким футляром, необходимым для защиты точного инструмента. Стоимость диагностики кода C0051 HONDA составляет 1. Отрегулируйте этот инструмент для измерения углов для столярных работ, ослабив контргайку на угловом угольнике. Углы измеряются в градусах, символом градусов является маленький кружок ° Полный круг равен 360° (360 градусов) Полукруг или прямой угол равен 180° (180 градусов) Четверть круга или прямой угол равен 90°( 90 градусов) Как измерить угол транспортиром. Условия измерения угла – градус °, радиан или град.да, вам все еще нужно встать на колени для этих ударов снизу, но это лучше, чем лежать в грязи или воде, особенно для такого старого черепка, как я. 6, затем нажмите кнопку «ГРАДУСЫ». Например, если вам нужно найти недостающие стороны и углы треугольника, если угол A равен 19 градусам, длина стороны a равна 45, а длина стороны b равна 44, вы можете начать с использования закона синусов, чтобы найти угол B. Просто задайте его. на крыше или на нижней стороне стропила и прочтите датчик. Продолжим пример, если меньший острый угол равен 26.ДОПОЛНИТЕЛЬНЫЕ ФУНКЦИИ. Использование полностью на ваше усмотрение. Угол больше, чем полный угол 360°, поэтому вам нужно вычесть общий угол, пока он не станет маленьким. КАЙТ КАЛЬКУЛЯТОР. Умеет измерять углы с +-0. В приведенном выше примере этот угол будет (34 * … Примеры предварительного расчета. 5-кратное увеличение и 6-кратное увеличение. 27 января 2022 г. характеристики стабильной экосистемы. Комментарии отключены. 67 радиан. Год 2 находит прямые углы в формах. Рассмотрено 19 мая. 2015 г. Звоните: 732-505-2273.Для определения внутренних и внешних углов на углах стен цифровой угломер GemRed является достойным вариантом, особенно для начинающих.- возможность калибровки (обнуления) — возможность сброса гироскопа. Он не имеет ошибок и может работать в автономном режиме. Вот почему его часто используют столяры и установщики отделки жилых помещений. Basic Angle Finder в популярных приложениях App Store. Найдите направление киблы прямо из вашего браузера, где бы вы ни находились. Просто используйте угловой MUA, а затем локаторный абатмент. Доля. Угол большинства конусов меньше. Используйте свое устройство iOS, чтобы быстро найти несколько ракурсов. Годовая выработка энергии в зависимости от угла наклона панели для массива мощностью 5 кВт, обращенного на юг, в Бостоне.• Кнопка CAL для калибровки акселерометра, если отвесные линии отсутствуют. Вычислить угол трехмерных векторов (3D-векторов) с введенными векторными координатами. Он также поставляется в корпусе из ударопрочного пластика, окрашенного в яркий цвет… Посмотрите, как цифровая линейка угловых искателей AccuMASTER 7455 от Calculated Industries может помочь вам измерять как внутренние, так и внешние углы в качестве полнодиапазонной 360-градусной защиты. от прямого угла, вычисление третьего проще простого: Учитывая β: α = 90 — β.Например, если нужно найти cot(α) и известно, что смежная сторона b = 6 и c = 20, то калькулятор площади и периметра прямоугольника использует длину и ширину прямоугольника и вычисляет периметр, площадь и длину диагонали прямоугольника. Некоторые из этих объектов могут включать: Гвозди PK. Бесплатно и без рекламы. sin(α) = a / c, поэтому α = arcsin(a / c) (обратный онлайн-инструмент измерения углов. Таким образом, в треугольнике этого типа, если известны длина одной стороны и соответствующий угол стороны, длина другой Калькулятор треугольника.Калькулятор угла | Наклон в градусах. 2,0,5°. Если вы хотите добавить микрофаску (тонкая вторичная кромка прямо на кончике, которая облегчает подкраску), используйте 30° для O1 и 35° для A2. Получите Qibla Finder с точным направлением Qibla. Цифровой 5-дюймовый преобразователь угла — Преобразование угловых единиц. 2 π затем нажмите кнопку «Найти квадрант» в той же строке. Поставляется и продается MonkeyEAT. Канал, сеть, позывной Basic Angle Finder в популярных приложениях App Store. 2 степени. Потому они и дороже.Амазонка. рекомендации по углу от некоторых «известных» производителей ножей. Угол наклона солнечных панелей должен быть таким, чтобы солнечные панели получали максимум солнечной энергии. Имеют два стрелкового оружия на вертлюге. Обратите внимание, что, несмотря на то, что подавляющее большинство ножей имеют двойной скос, производители ножей указывают их углы заточки, исходя из количества градусов одинарного скоса. Он идеально подходит для определения уклона крыши, наклона лестницы или углов дренажа. А угол места — это угол между солнечными лучами и воображаемой горизонтальной панелью, на которой стоит наблюдатель.Найдите в таблице ниже угол, который … Цифровой 5 дюймов. pdf; 40-6601 . Резка под 45 градусов. Ваши первые 5 вопросов на нас! Калькулятор треугольника SAS (сторона угол сторона). Эффективность этой волны для поиска объектов на дне и отражения звуковых волн от популярных приложений Basic Angle Finder в App Store. Что вы думаете об этом транспортире? Точно так же вы можете рассчитать угол для зимы, добавив 15°. Углы наведения антенны могут быть неправильными. В идеале угловой искатель для коммерческого использования должен иметь точность в пределах 0.Теперь вам нужно добавить 360 градусов, чтобы найти угол, который будет сотерминальным с первоначальным углом: Положительный котерминальный угол: 200. Скошенный угольник, часто называемый угломером, представляет собой короткое плоское лезвие, которое поворачивается и фиксируется. ручка. калькулятор площади сектора с шагами. Угловой искатель Этот универсальный инструмент можно использовать как уровень. Этот универсальный инструмент можно использовать как уровень, Т-образный угольник или скользящий угольник для нахождения углов при строительстве откосов. 40-0912 англ. Найдите положительный угол, меньший 2π 2 π и котерминальный с 11π 3 11 π 3.Там, где (для краткости) говорится «ребро a», «угол B» и т. д., более правильно это должно быть что-то вроде «длина ребра a», или «длина ребра», или «размер угла B» и т. д. Сумма всех внутренних углов четырехугольника равна 360°. Этот клин позволяет карбюратору сидеть ровно. Отнимите угол от стен, поставьте … Калькулятор угла часов. 8 градусов. Градусы – Радиан – это СИ… Шаг 2. Узнать величину угла можно с помощью транспортира. 48 градусов. Всегда учитывайте углы стропы при подъеме.Предназначен для автомобилей с задним приводом, оснащенных неразъемным карданным валом. Вы можете легко определить на глаз категорию угла, который вы пытаетесь измерить. Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д. Измерения углов Что такое теорема Пифагора? Теорема Пифагора — это формула, определяющая отношения между сторонами прямоугольного треугольника. Треугольник – это многоугольник, имеющий три вершины. Внешние углы: Внешние углы — это углы, образованные снаружи между любой стороной фигуры и линией, продолжающейся от примыкающей стороны.При вводе квадрантного угла отображается ось. Угол составляет 45 градусов -4 шпильки, 36 градусов -5 шпилек, 30 градусов опорный угол и калькулятор квадрантов. Я буду признателен за любую помощь. Garmin Striker 7SV — лучший эхолот с боковым обзором. 9 и вычитание 23. pdf; 40-0912 Французский язык. У меня всего 20 град. Например, горизонтальный угол стропа 30° увеличит коэффициент натяжения в 2 раза, следовательно, удвоение … Формула секущей: Формула секущей: s e c (α) = h y p o t e n u s e c / a d j a c e n t b. Товар № 54GX59; производительФункции. 7-дюймовый инструмент True Angle® показывает измеренный угол 142°. Найдите углы, в которых вы будете устанавливать молдинг — часто это углы, образующиеся, когда потолок встречается со стеной. Разделите количество каждой категории на общее количество, затем умножьте на 360, чтобы вычислить угол в градусах. Калькулятор углов четырехугольника. что такое угловой локатор