Определенный интеграл. Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Задание 7
В этой статье мы будем учиться решать задачи на нахождение площади криволинейной трапеции.
Как всегда, начнем с теории. Как вы помните, неопределенный интеграл от функции  — это множество всех первообразных
— это множество всех первообразных  :
:
∫
В неопределенном интеграле не заданы границы интегрирования, и в результате нахождения неопределенного интеграла от функции 
Если заданы границы интегрирования, то мы получаем определенный интеграл:

Здесь число  — нижний предел интегрирования, число
— нижний предел интегрирования, число  — верхний предел интегрирования. Определенный интеграл — это ЧИСЛО, значение которого вычисляется по формуле Ньютона — Лейбница:
— верхний предел интегрирования. Определенный интеграл — это ЧИСЛО, значение которого вычисляется по формуле Ньютона — Лейбница:

 — это значение первообразной функции
— это значение первообразной функции  в точке
в точке  , и, соответственно,
, и, соответственно,  — это значение первообразной функции
— это значение первообразной функции 
 .
.Для нас с точки зрения решения задач важное значение имеет геометрический смысл определенного интеграла.
Рассмотрим фигуру, изображенную на рисунке:

Зеленая фигура, ограниченая сверху графиком функции  , слева прямой
, слева прямой  , справа прямой
, справа прямой 
Геометрический смысл определенного интеграла:
Определенный интеграл  — это число, равное площади криволинейной трапеции — фигуры, ограниченой сверху графиком положительной на отрезке
— это число, равное площади криволинейной трапеции — фигуры, ограниченой сверху графиком положительной на отрезке ![[a;b] [a;b]](/800/600/https/ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980.5_4fd6467dde9f264696b4c9a924e29717.png) функции
функции  , слева прямой
, слева прямой 
 , и снизу осью ОХ.
, и снизу осью ОХ.Решим задачу из Открытого банка заданий для подготовки к ЕГЭ по математике.
Прототип Задания 7 (№ 323080)
На рисунке изображён график некоторой функции  . Функция
. Функция  — одна из первообразных функции
— одна из первообразных функции  . Найдите площадь закрашенной фигуры.
. Найдите площадь закрашенной фигуры.

Закрашенная фигура представляет собой криволинейную трапецию, ограниченную сверху графиком функции  , слева прямой
, слева прямой  , справа прямой
, справа прямой  , и снизу осью ОХ.
, и снизу осью ОХ.
Площадь этой криволинейной трапеции вычисляется по формуле:
 , где
, где  — первообразная функции
— первообразная функции  .
.
По условию задачи  , поэтому, чтобы найти площадь фигуры, нам нужно найти значение первообразной в точке -8, в точке -10, и затем из первого вычесть второе.
, поэтому, чтобы найти площадь фигуры, нам нужно найти значение первообразной в точке -8, в точке -10, и затем из первого вычесть второе.
Замечу, что в этих задачах очень часто возникают ошибки именно в вычислениях, поэтому советую аккуратно и подробно их записывать, и ничего не считать «в уме».
 =
=
 =
=

Ответ: 4
Посмотрите небольшую видеолекцию, в которой решены все типы задач на первообразную:
И.В. Фельдман, репетитор по математике.


ege-ok.ru
Урок-лекция по теме «Интеграл. Площадь криволинейной трапеции»
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Ключевые слова: интеграл, криволинейная трапеция, площадь фигур, ограниченных лилиями
Оборудование: маркерная доска, компьютер, мультимедиа-проектор
Тип урока: урок-лекция
Цели урока:
- воспитательные: формировать культуру умственного труда, создавать для каждого ученика ситуацию успеха, формировать положительную мотивацию к учению; развивать умение говорить и слушать других.
- развивающие: формирование самостоятельности мышления ученика по применению знаний в различных ситуациях, умения анализировать и делать выводы, развитие логики, развитие умения правильно ставить вопросы и находить на них ответы. Совершенствование формирования вычислительных, расчётных навыков, развитие мышления учащихся в ходе выполнения предложенных заданий, развитие алгоритмической культуры.
- образовательные: сформировать понятия о криволинейной трапеции, об интеграле, овладеть навыками вычисления площадей плоских фигур
Метод обучения: объяснительно-иллюстративный.
Ход урока
В предыдущих классах мы научились вычислять площади фигур, границами которых являются ломаные. В математике существуют методы, позволяющие вычислять площади фигур, ограниченных кривыми. Такие фигуры называются криволинейными трапециями, и вычисляют их площадь с помощью первообразных.
Криволинейная трапеция (слайд 1)
Криволинейной трапецией называется фигура, ограниченная графиком функции , (щ.м.), прямыми x = a и x = b и осью абсцисс
Различные виды криволинейных трапеций (слайд 2)
Рассматриваем различные виды криволинейных трапеций и замечаем: одна из прямых вырождена в точку, роль ограничивающей функции играет прямая
Площадь криволинейной трапеции (слайд 3)
Зафиксируем левый конец промежутка а, а правый х будем менять, т. е., мы двигаем правую стенку криволинейной трапеции и получаем меняющуюся фигуру. Площадь переменной криволинейной трапеции, ограниченной графиком функции , является первообразной F для функции f
И на отрезке [a; b] площадь криволинейной трапеции, образованной функцией f, равна приращению первообразной этой функции:
S к. т.
Задание 1:
Найти площадь криволинейной трапеции, ограниченной графиком функции: f(x) = х2 и прямыми у = 0, х = 1, х = 2.
Решение: (по алгоритму слайд 3)
Начертим график функции и прямые
Найдём одну из первообразных функции f(x) = х2 :
F(x) = ,
Значит
Самопроверка по слайду
Интеграл
Рассмотрим криволинейную трапецию, заданную функцией f на отрезке [a; b]. Разобьём этот отрезок на несколько частей. Площадь всей трапеции разобьётся на сумму площадей более мелких криволинейных трапеций. (слайд 5). Каждую такую трапецию можно приближённо считать прямоугольником. Сумма площадей этих прямоугольников даёт приближённое представление о всей площади криволинейной трапеции. Чем мельче мы разобьём отрезок [a; b], тем точнее вычислим площадь.
Запишем эти рассуждения в виде формул.
Разделим отрезок [a; b] на n частей точками х0 =а, х1,… ,хn = b. Длину k-го обозначим через хk = xk – xk-1. Составим сумму
Геометрически эта сумма представляет собой площадь фигуры, заштрихованной на рисунке (щ.м.)
Суммы вида называются интегральными суммами для функции f. (щ.м.)
Интегральные суммы дают приближённое значение площади. Точное значение получается при помощи предельного перехода. Представим, что мы измельчаем разбиение отрезка [a; b] так, что длины всех маленьких отрезков стремятся к нулю. Тогда площадь составленной фигуры будет приближаться к площади криволинейной трапеции. Можно сказать, что площадь криволинейной трапеции равна пределу интегральных сумм, Sк.т. (щ.м.) или интегралу, т. е.,
Определение:
Интегралом функции f (х) от a до b называется предел интегральных сумм
= (щ.м.)
Формула Ньютона- Лейбница.
Помним, что предел интегральных сумм равен площади криволинейной трапеции, значит можно записать:
Sк.т. =(щ.м.)
С другой стороны, площадь криволинейной трапеции вычисляется по формуле
S к. т.(щ.м.)
Сравнивая эти формулы, получим:
= (щ.м.)Это равенство называется формулой Ньютона- Лейбница.
Для удобства вычислений формулу записывают в виде:
= =Задания: (щ.м.)
1. Вычислить интеграл по формуле Ньютона- Лейбница: (проверяем по слайду 5)
2. Составить интегралы по чертежу (проверяем по слайду 6)
3. Найти площадь фигуры, ограниченной линиями: у = х3, у = 0, х = 1, х = 2. (Слайд 7)
Нахождение площадей плоских фигур (слайд 8)
Как найти площадь фигур, которые не являются криволинейными трапециями?
Пусть даны две функции, графики которых вы видите на слайде. (щ.м.) Необходимо найти площадь закрашенной фигуры. (щ.м.). Фигура, о которой идёт речь, является криволинейной трапецией? А как можно найти её площадь, пользуясь свойством аддитивности площади? Рассмотреть две криволинейные трапеции и из площади одной из них вычесть площадь другой (щ.м.)
Составим алгоритм нахождения площади по анимации на слайде:
- Построить графики функций
- Спроецировать точки пересечения графиков на ось абсцисс
- Заштриховать фигуру, полученную при пересечении графиков
- Найти криволинейные трапеции, пересечение или объединение которых есть данная фигура.
- Вычислить площадь каждой из них
- Найти разность или сумму площадей
Устное задание: Как получить площадь заштрихованной фигуры (рассказать при помощи анимации, слайд 8 и 9)
Домашнее задание: Проработать конспект, №353 (а), № 364 (а).
Список литературы
- Алгебра и начала анализа: учебник для 9-11 классов вечерней (сменной) школы/ под ред. Г.Д. Глейзера. - М: Просвещение, 1983.
- Башмаков М.И. Алгебра и начала анализа: учебное пособие для 10-11 кл.сред.шк./ Башмаков М.И. — М: Просвещение, 1991.
- Башмаков М.И. Математика: учебник для учреждений нач. и сред. проф. образования/ М.И. Башмаков. — М: Академия, 2010.
- Колмогоров А.Н. Алгебра и начала анализа: учебник для 10-11 кл. общеобразовательных учреждений/ А.Н.Колмогоров. — М: Просвещение, 2010.
- Островский С.Л. Как сделать презентацию к уроку?/ C.Л. Островский. – М.: Первое сентября, 2010.
urok.1sept.ru
11.1.9.2. Площадь криволинейной трапеции. Примеры математика-повторение
Площадь криволинейной трапеции, ограниченной сверху графиком функции y=f (x), снизу — осью Ох, слева и справа прямыми х=a, x=b, находят по формуле Ньютона-Лейбница (ф. Н-Л):
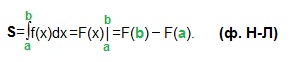
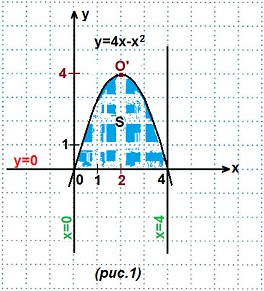 Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=4x-x²; y=0; x=0; x=4.
Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=4x-x²; y=0; x=0; x=4.
Решение. Строим графики данных линий. (рис. 1).
1) y=4x-x² — парабола (вида y=ax²+bx+c). Запишем данное уравнение в общем виде: y=-x²+4x. Ветви этой параболы направлены вниз, так как первый коэффициент а=-1<0.
Вершина параболы находится
в точке O′(m; n), где

О′(2; 4). Нули функции (точки пересечения графика с осью Ох) найдем из уравнения:
4х-х²=0.
Выносим х за скобки, получаем: х(4-х)=0. Отсюда, х=0 или х=4. Абсциссы точек найдены, ордината равна нулю — искомые точки:
2) y=0 — это ось Ох; 3) х=0 — это ось Оy; 4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных отрезка вправо.
Площадь построенной криволинейной трапеции находим по (ф. Н-Л). У нас f (x)=4x-x², a=0, b=4.
Кстати, если Вы подсчитаете все целые заштрихованные клетки и добавите к ним половину всех остальных клеток заштрихованной фигуры, то получите приближенное значение искомой площади. Действительно, если единичный отрезок равен одной клетке, то площадь квадратика со стороной, равной 1 клетке, равна 1·1=1 (кв. ед.). Сколько квадратиков — столько квадратных единиц и составляет площадь фигуры.
Пример 2. Найти площадь криволинейной трапеции, ограниченной линиями:
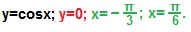
Решение. Строим графики данных линий. (рис. 2).

Площадь данной криволинейной трапеции:

Запись имеет метки: криволинейная трапеция
www.mathematics-repetition.com
Интеграл. Площадь криволинейной трапеции. 12-й класс
(Алгебра и начала анализа: Учебник для 10-11кл. общеобразовательных учреждений/ А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под ред. А.Н. Колмогорова, М.: Просвещение, 2010г.)
Цели:
- Подвести итоги к.р. по теме «Первообразная». Ввести понятие криволинейной трапеции, доказательство теоремы о площади криволинейной трапеции.
- Развивать логическое мышление учащихся через установление причинно-следственных связей.
- Побудить интерес к изучению темы.
Задачи:
- Закрепить навыки по нахождению первообразных функций. Определить криволинейную трапецию, научить использовать формулу для вычисления о площади криволинейной трапеции.
- Развитие познавательного интереса и логического мышления.
- Закрепление изученного.
План занятия
| Содержание этапов урока | Виды и формы работы |
| Урок №1 | |
| 1. Организационный момент | Приветствие, готовность |
| 2. Мотивационное начало | Постановка целей |
| 3. Итоги контрольной работы по пройденной теме «Первообразная» | Анализ ошибок, работа с карточками, работа в рабочих тетрадях |
| 4. Объяснение нового материала: определение криволинейной трапеции | Презентация, работа в рабочих тетрадях |
| Урок №2 | |
| 5. Объяснение нового материала: доказательство теоремы | Презентация, работа в тетрадях |
| 6. Закрепление: решение заданий | Презентация, письменная работа в рабочих тетрадях |
| 7. Подведение итогов урока | Презентация, устный опрос |
Ход занятия
Урок №1
I Организационный момент
Приветствие, готовность к уроку.
II Мотивационное начало занятия
Постановка целей, показ презентации (первый слайд).
III Итоги и анализ контрольной работы по пройденной теме «Первообразная»
Оценки за контрольную работу. Анализ работ учителем. Учащиеся получают индивидуальные карточки (приложение №1), под руководством учителя разбираются ошибки. Рассматриваются примеры первого задания по готовому решению. Предлагается решить задания второго задания (у каждого отмечен пример).
IV Объяснение нового материала: определение криволинейной трапеции
1 Ввести определение криволинейной трапеции (приложение №2, при объяснении используется презентация).
Определение:
Пусть на отрезке оси задана непрерывная функция , не меняющая на нем знака. Фигура, ограниченная графиком этой функции, отрезком и прямыми и называется криволинейной трапецией.
Примеры приведены на рисунках 1-4 (слайды 2-5).
2 Рассматриваем рисунки. Выясняем, какие из предложенных фигур являются криволинейными трапециями.
Урок №2
V Объяснение нового материала: доказательство теоремы
Теорема:
Если - непрерывная и неотрицательная на отрезке функция, а — её первообразная на этом отрезке, то площадь соответствующей криволинейной трапеции равна приращению первообразной на отрезке , т.е.
Доказательство.
Рассмотрим функцию , определенную на отрезке . Если , то — площадь той части криволинейной трапеции, которая расположена левее вертикальной прямой, проходящей через точку (рисунок 4).
Если , то ;
Если , то , где — площадь криволинейной трапеции.
Докажем, что
По определению производной надо доказать, что
.
Выясним геометрический смысл числителя . Для простоты рассмотрим случай . Поскольку , то - площадь фигуры, заштрихованной на рисунке 5. Возьмем теперь прямоугольник той же площади , опирающийся на отрезок (рисунок 5).
В силу непрерывности функции верхняя сторона прямоугольника пересекает график функции в некоторой точке с абсциссой (в противном случае этот прямоугольник либо содержится в части криволинейной трапеции над отрезком , либо содержит ее; соответственно его площадь будет меньше или больше площади ). Высота прямоугольника равна . По формуле площади прямоугольника имеем , откуда . (Эта формула верна и при ) Поскольку точка лежит между и , то стремится к при . Так как функция непрерывна, при . Итак, при .
Формула (2) доказана.
Мы получили, что есть первообразная для . Поэтому в силу основного свойства первообразных для всех имеем: ,
где - некоторая постоянная, а — одна из первообразных для функции . Для нахождения подставим :
, откуда . Следовательно,
Поскольку площадь криволинейной трапеции равна , подставляя в формулу (4), получим: .
VI Закрепление изученного материала
№ 353 (а, б, г).
Вычислите площадь фигуры, ограниченной линиями.
а) .
б) .
г) .
VII Итоги урока
Используется презентация. Проговариваем цели, определение, теорему, формулу. Отмечаются активность и понимание, объявляется благодарность классу и персонально.
urok.1sept.ru
Учебно-методическое пособие по математике (11 класс) на тему: Практическое занятие по теме Вычисление площади криволинейной трапеции
Практическое занятие
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР С ПОМОЩЬЮ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Цель практического занятия: приобрести навыки и умения вычисления площадей фигур.
- Краткие сведения из теории
Геометрический смысл определенного интеграла.
Если интегрируемая на отрезке функция f(x) неотрицательна, то определенный интеграл численно равен площади S криволинейной трапеции aABb, ограниченной графиком функции y = f(x), осью абсцисс 0х и прямыми х = а и х = b, т.е.
(1)
- Если функция на , то площадь вычисляется по формуле (1) от абсолютной величины подынтегральной функции
или
- Если надо вычислить площадь фигуры, ограниченной двумя кривыми и , при условии, что , то искомую площадь найдем как разность площадей двух криволинейных трапеций
(2)
Для нахождения пределов интегрирования надо найти абсциссы точек А и В пересечения кривых, решив уравнение .
- Найдите площадь фигуры, ограниченной данными линиями,
в соответствии с номером варианта:
№ варианта | Уравнения линий | Уравнения линий | Уравнения линий |
1 | |||
2 | |||
3 | |||
4 | |||
5 | |||
6 |
| ||
7 | |||
8 | |||
9 | |||
10 |
- Решение типовых примеров:
Пример 1. Вычислить площадь фигуры, ограниченной линиями
Решение.
Находим точки пересечения заданных линий. Для этого решаем систему уравнений:
Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:
или .
Находим: x1 = -2, x2 = 4.
Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A(-2; 0), B(4; 6).
Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:
По формуле Ньютона-Лейбница находим:
Ответ:
Пример 2. Вычислить площадь фигуры, ограниченную линиями .
Решение.
Находим точки пересечения заданных линий. Для этого решаем систему уравнений:
Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:
Находим:
Искомую площадь криволинейной трапеции найдем по формуле:
Ответ:
Пример 3. Вычислить площадь, ограниченную линиями
.
Решение.
Искомую площадь криволинейной трапеции найдем по формуле:
Ответ:
Пример 4.Вычислить площадь, ограниченную линиями и .
Решение.
Решая систему уравнений и , найдем координаты точек пересечения параболы и прямой: .
Искомая площадь равна разности площадей
двух криволинейных трапеций:
Ответ:
Пример 4.Вычислить площадь фигуры, ограниченной кривыми , , ,
Ответ:
Пример 5.Найти площадь фигуры, ограниченной линиями y=sinx, y=2sinx, x=0,
Решение: Построим графики функций y=sinx, y=2sinx
Ответ:
Пример 6..
Вычислить площадь фигуры, ограниченной параболой , осями координат и прямой .
В рассматриваемом случае функция на отрезке [0; 2] меняет знак, а именно на отрезке [0; 1] и на отрезке [1; 2] .
Для нахождения искомой площади воспользуемся формулой (3):
(кв. ед.).
Ответ:
nsportal.ru
Криволинейная трапеция и ее площадь
№____ Дата________
Тема: Криволинейная трапеция и ее площадь
Цели урока: Дать определения криволинейной трапеции и ее площади, научиться вычислять площадь криволинейной трапеции.
ХОД УРОКА
1. Организационный момент.
Приветствие учащихся, проверка готовности класса к уроку, организация внимания учащихся, раскрытие общих целей урока и плана его проведения.
2. Этап проверки домашнего задания.
Задачи: Установить правильность, полноту и осознанность выполнения д/з всеми учащимися, выявить пробелы в знаниях и способах деятельности учащихся. Определить причины возникновения затруднений, устранить обнаруженные пробелы.
3.Этап актуализации.
Задачи: обеспечение мотивации учения школьников, включение в совместную деятельность по определению целей урока. Актуализировать субъективный опыт учащихся.
Вспомним основные понятия и формулы.
Определение. Функция y=f(x), x(a,b), называется первообразной для функции y=f(x), x(a,b), если для каждого x(a,b) выполняется равенство
F(x)=f(x).
Замечание. Если f(x) есть первообразная для функции f(x), то при любой константе С, F(x)+C также является первообразной для f(x).
Задача нахождения всех первообразных функции f(x) называется интегрированием, а множество всех первообразных называется неопределенным интегралом для функции f(x) по dx и обозначается
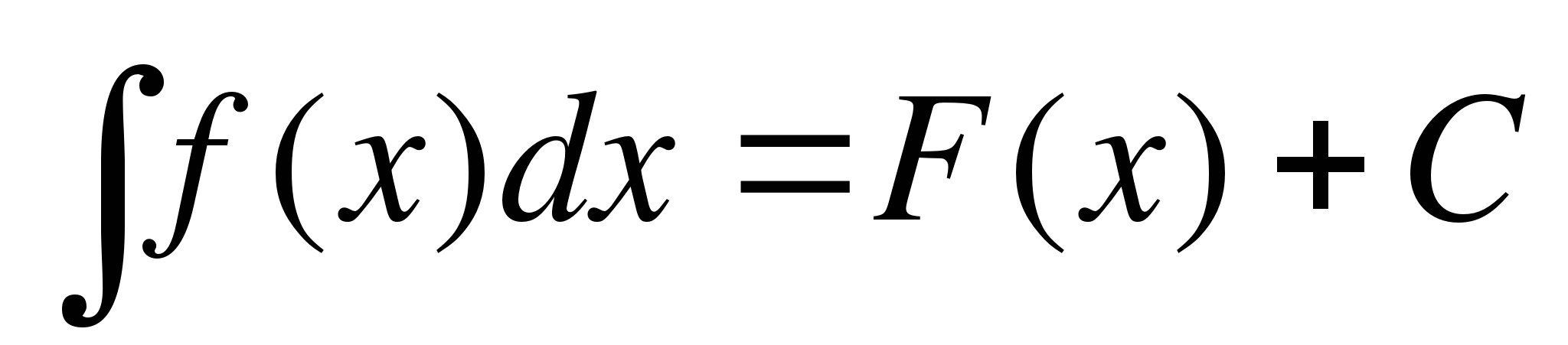 .
.
Имеют место свойства:
1. 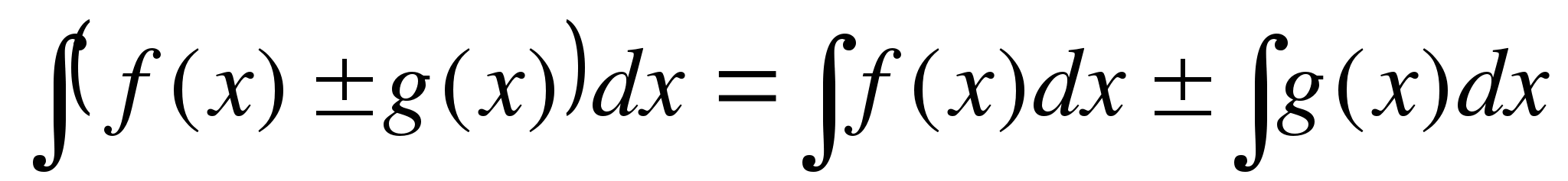 ;
;
2. Если С=Const, то 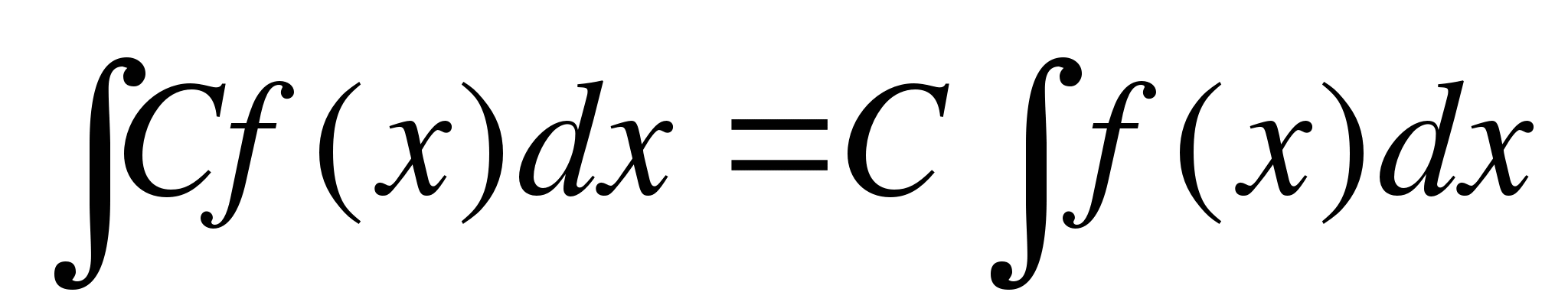 ;
;
3. 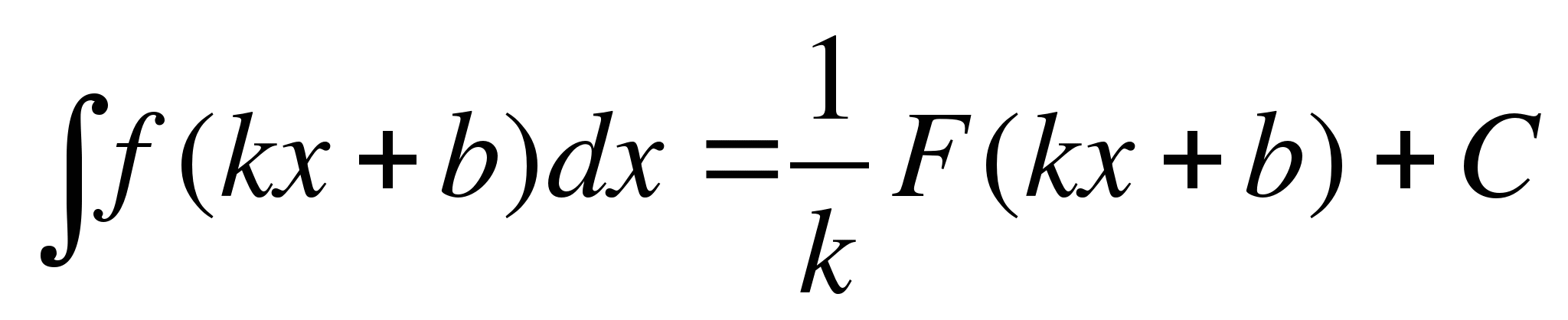 .
.
Замечание. В школьном курсе математики не употребляется термин «неопределенный интеграл», вместо этого говорят «множество всех первообразных».
Приведем таблицу неопределенных интегралов.
 ;
; ;
; ;
; ; в частности,
; в частности,  ;
; ;
; ;
; ;
; .
.
Пример 1. Найти первообразную для функции 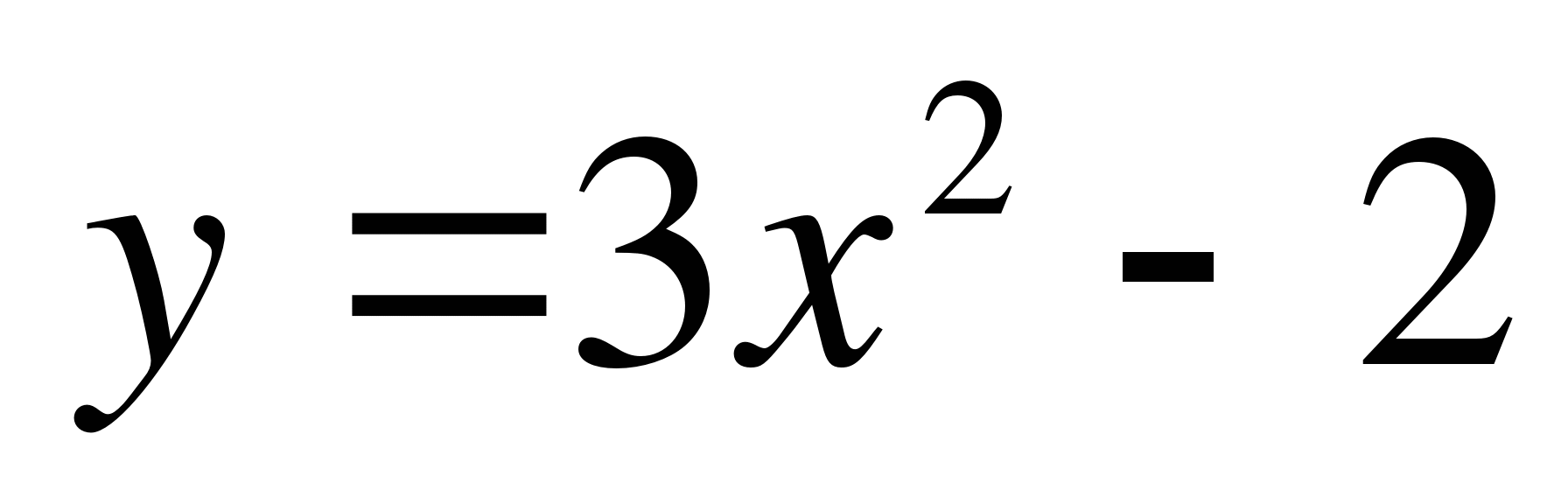 , проходящую через точку М(2;4).
, проходящую через точку М(2;4).
Решение. Множество всех первообразных функции 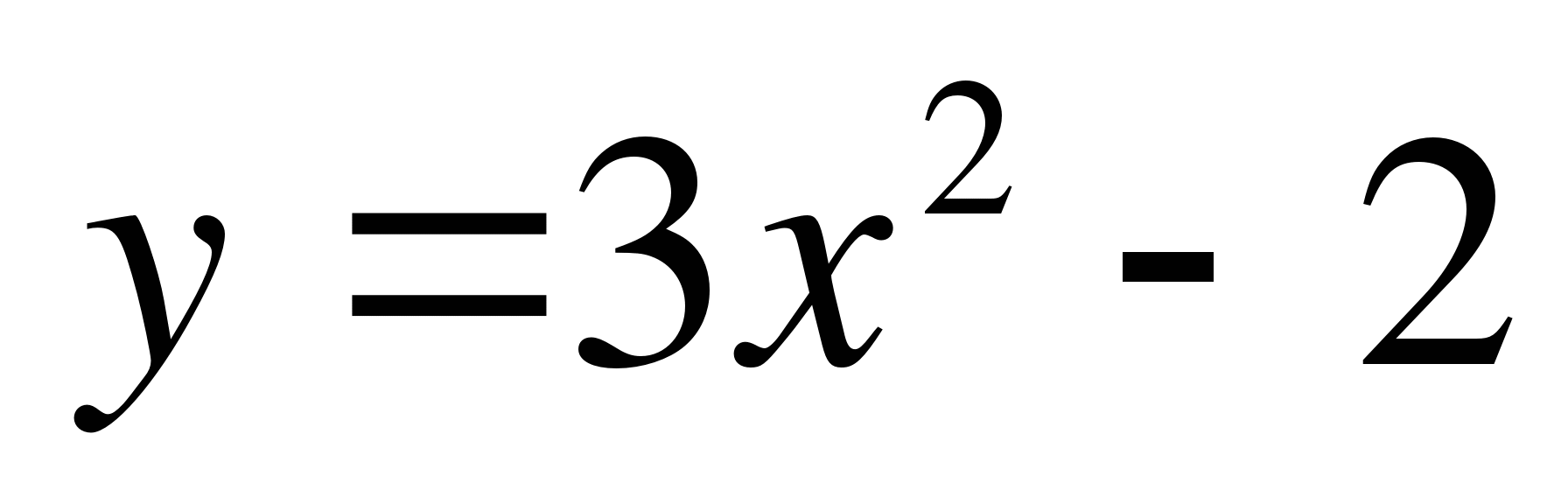 есть неопределенный интеграл
есть неопределенный интеграл  . Вычислим его, используя свойства интеграла 1 и 2. Имеем:
. Вычислим его, используя свойства интеграла 1 и 2. Имеем:
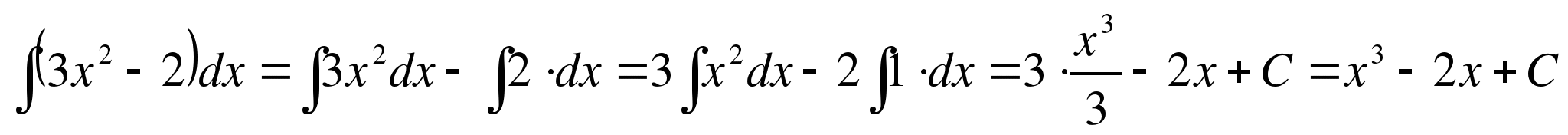 .
.
Получили, что множество всех первообразных задается семейством функций y=F(x)+C, то есть y=x3–2x+C, где С – произвольная постоянная.
Зная, что первообразная проходит через точку М(2;4), подставим ее координаты в предыдущее выражение и найдем С.
4=23–22+С С=4–8+4; С=0.
Ответ: F(x)=x3—2x – искомая первообразная.
4. Формирование новых понятий и способов действия.
Задачи: Обеспечить восприятие, осмысление и запоминание учащимися изучаемого материала. Обеспечить усвоение учащимися методики воспроизведения изученного материала, содействовать философскому осмыслению усваиваемых понятий, законов, правил, формул. Установить правильность и осознанность учащимися изученного материала, выявить пробелы первичного осмысления, провести коррекцию. Обеспечить соотнесение учащимися своего субъективного опыта с признаками научного знания .
Нахождение площадей плоских фигур
Задача нахождения площади плоской фигуры тесно связана с задачей нахождения первообразных (интегрированием). А именно: площадь криволинейной трапеции ограниченной графиком функции y=f(x) (f(x)>0) прямыми x=a; x=b; y=0, равна разности значений первообразной для функции y=f(x) в точках b и a:
S=F(b)–F(a)
Дадим определение определенного интеграла.
О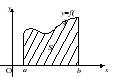
пределение. Пусть функция y=f(x) определена и интегрируема на отрезке [a,b] и пусть F(x) – некоторая ее первообразная. Тогда число F(b)–F(a) называется интегралом от а до b функции f(x) и обозначается
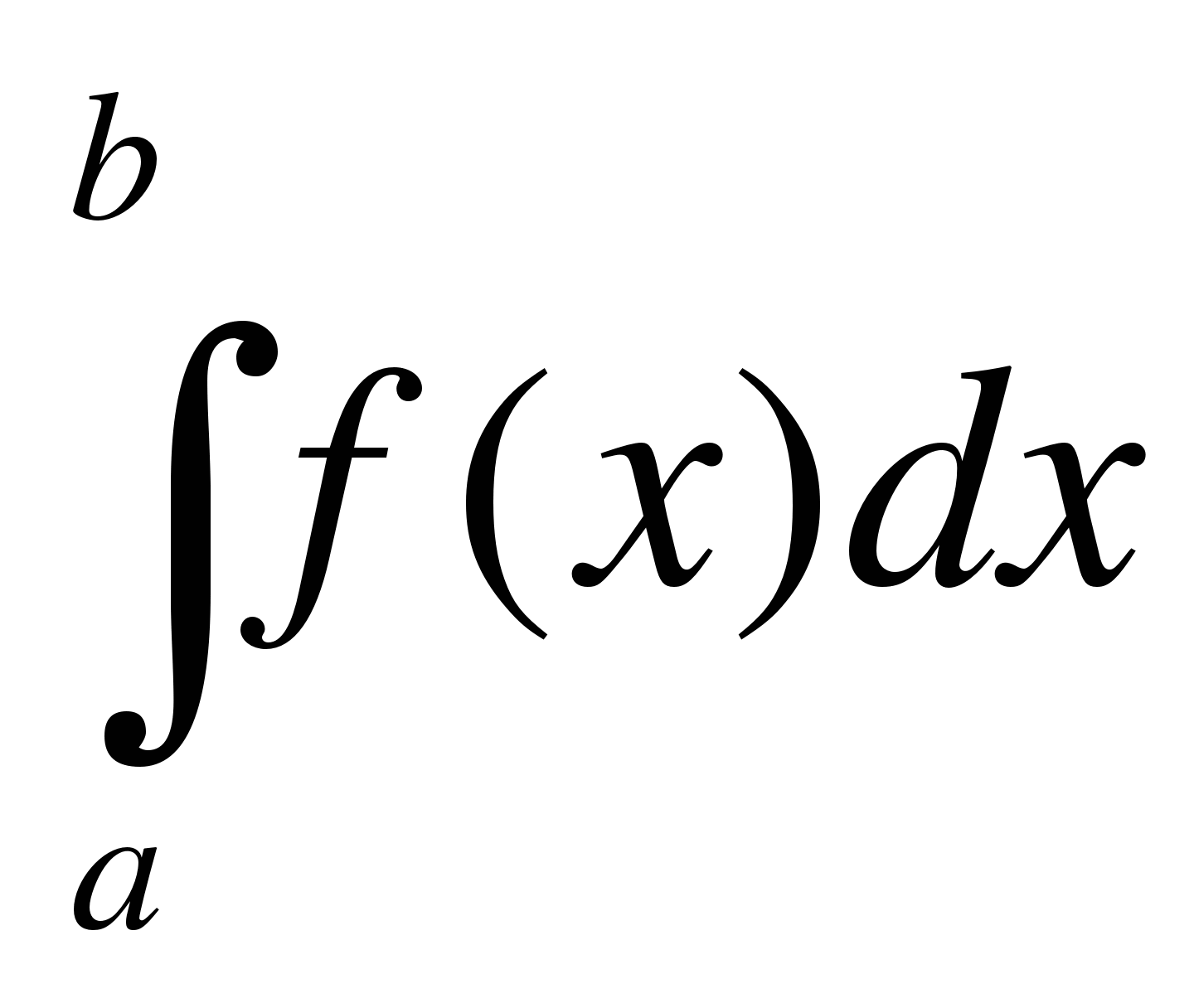 .
.
Равенство 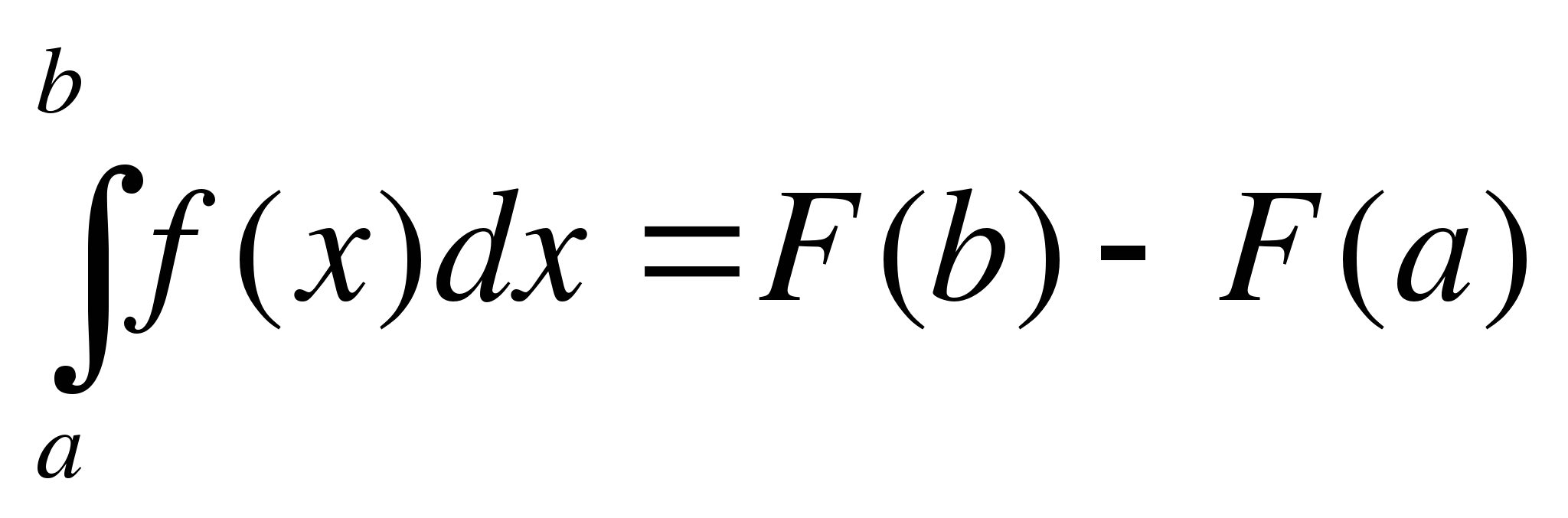 называется формулой Ньютона–Лейбница.
называется формулой Ньютона–Лейбница.
Э та формула связывает задачу нахождения площади плоской фигуры с интегралом.
та формула связывает задачу нахождения площади плоской фигуры с интегралом.
В общем случае, если фигура ограничена графиками функций y=f(x); y=g(x) (f(x)>g(x)) и прямыми x=a; x=b, то ее площадь равна:
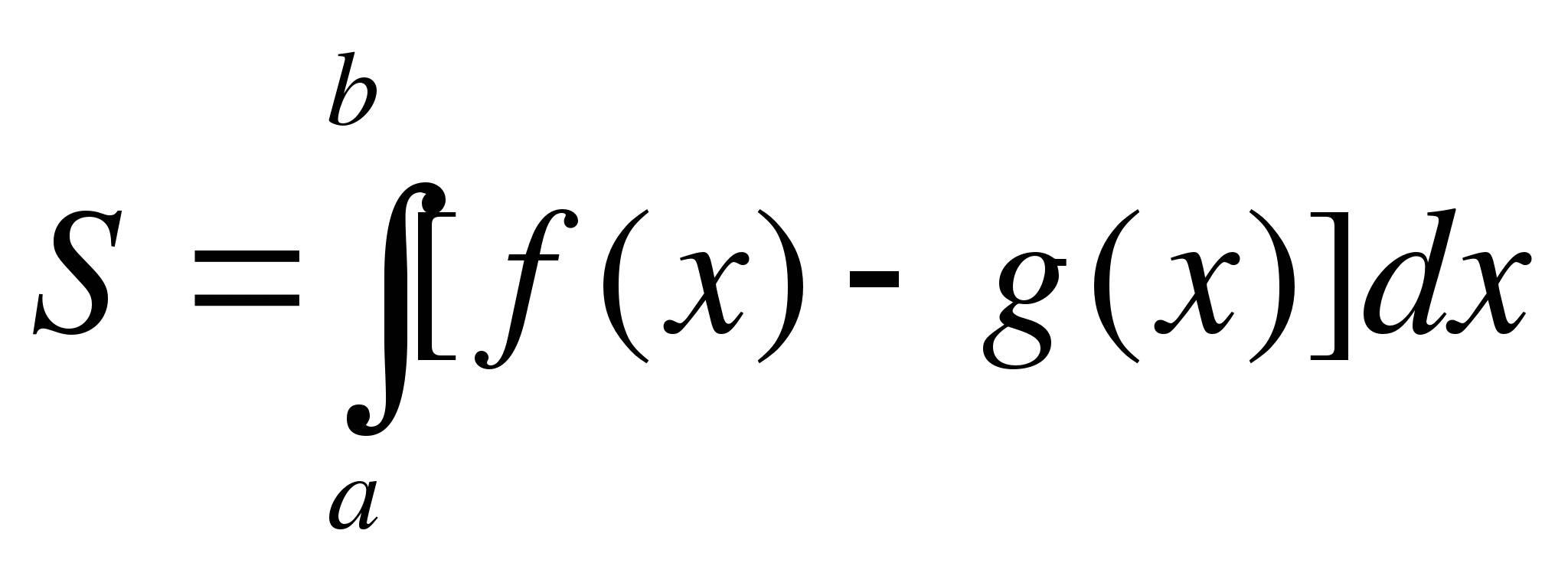 .
.
Пример2. В какой точке графика функции y=x2+1 надо провести касательную, чтобы она отсекала от фигуры, образованной графиком этой функции и прямыми y=0, x=0, x=1 трапецию наибольшей площади?
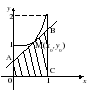 Решение. Пусть M0(x0,y0) – точка графика функции y=x2+1, в которой проведена искомая касательная.
Решение. Пусть M0(x0,y0) – точка графика функции y=x2+1, в которой проведена искомая касательная.
Найдем уравнение касательной y=y0+f(x0)(x–x0).
Имеем: 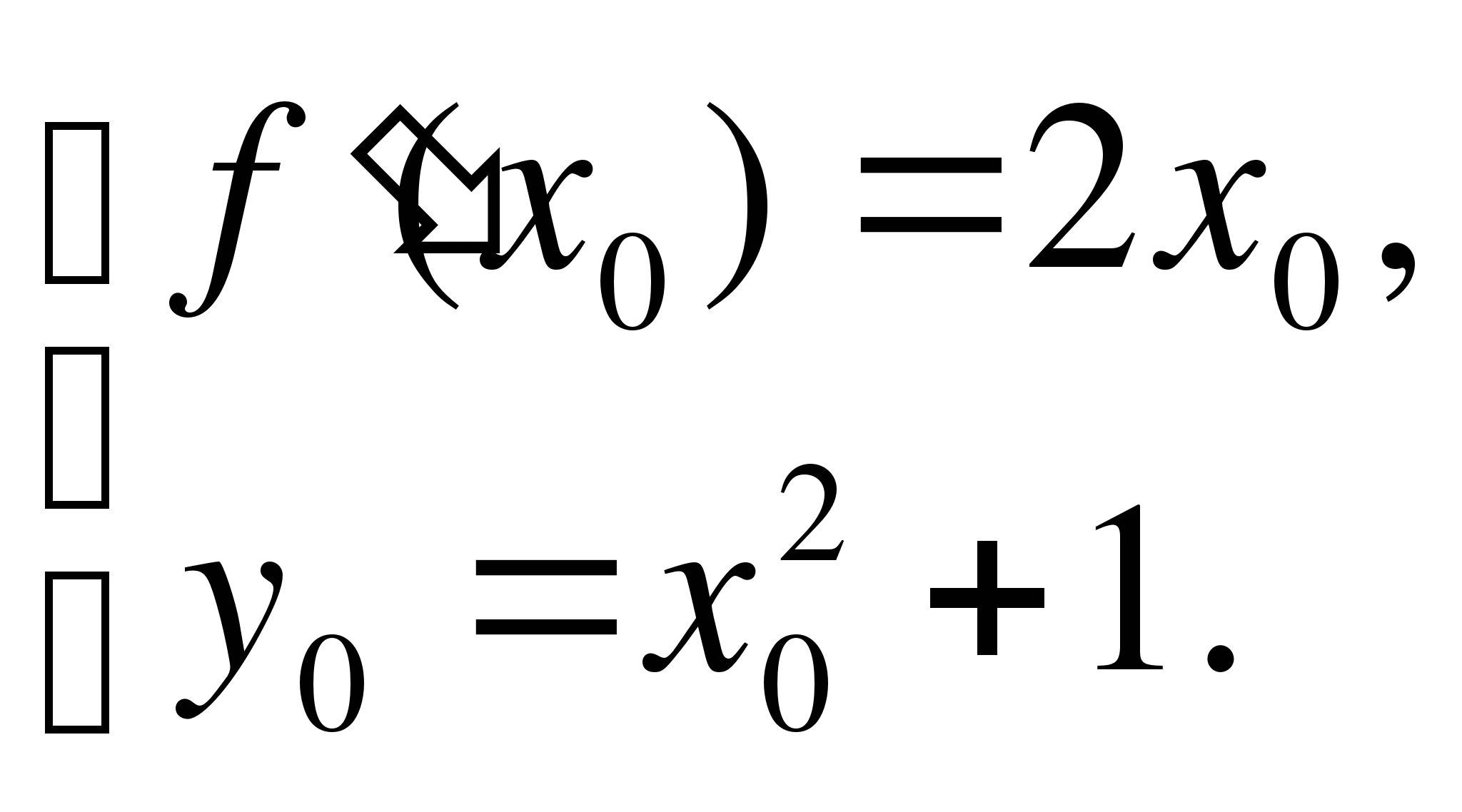
Поэтому 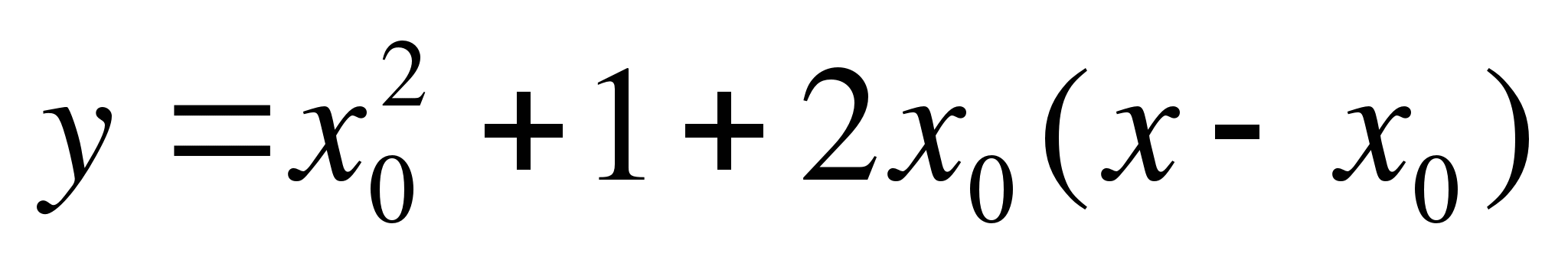
 .
.
Найдем площадь трапеции ОАВС.
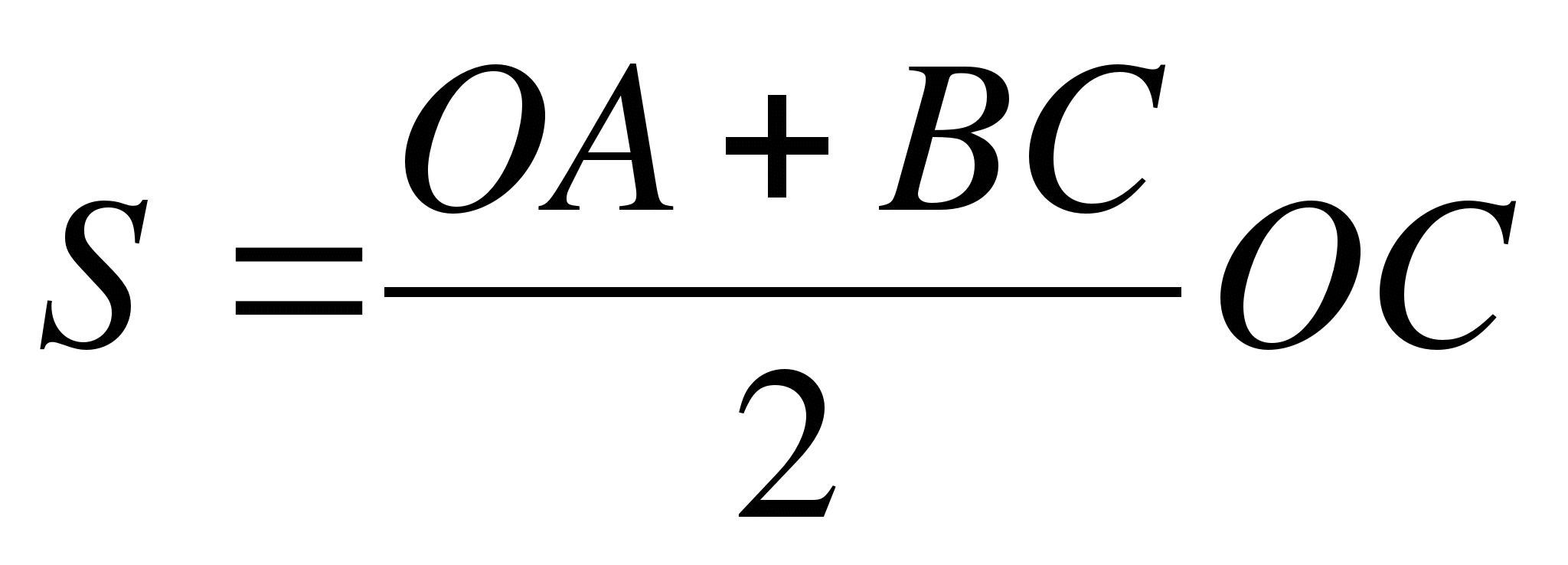 .
.
Далее, А – точка пересечения касательной с осью Oy, поэтому
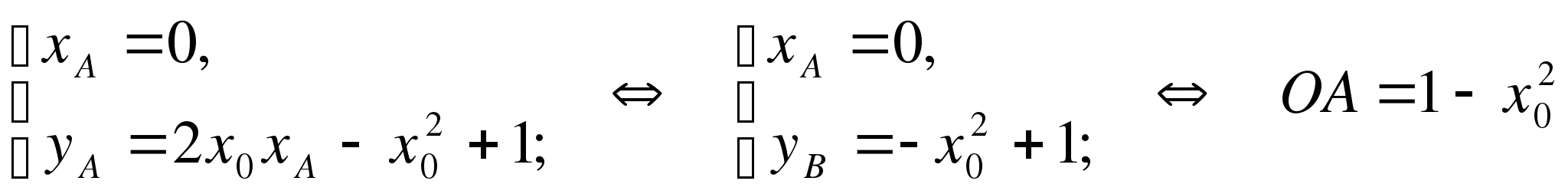 .
.
B – точка пересечения касательной с прямой x=1
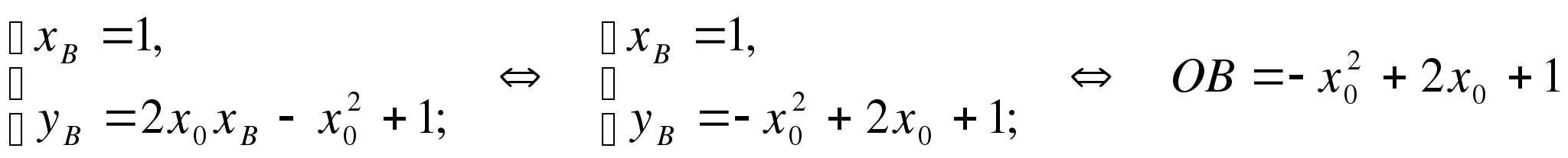 .
.
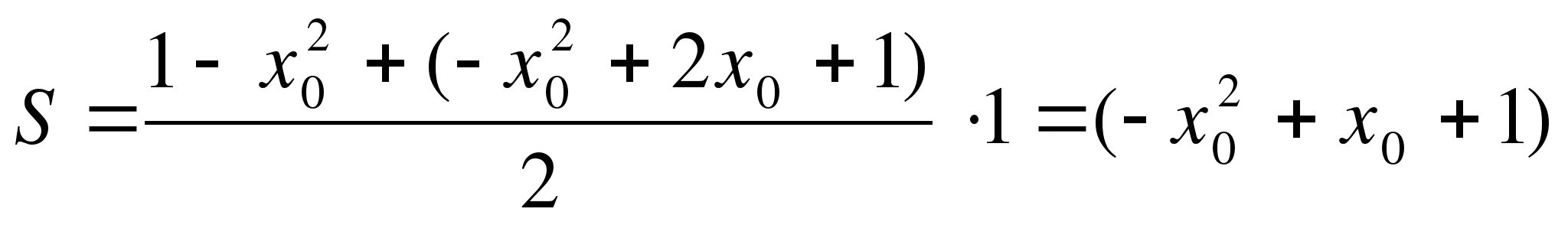 .
.
Задача свелась к нахождению наибольшего значения функции
S(x)=–x2+x+1 на отрезке [0;1]. Найдем S(x)=–2x+1. Найдем критическую точку из условия S(x)=0 x=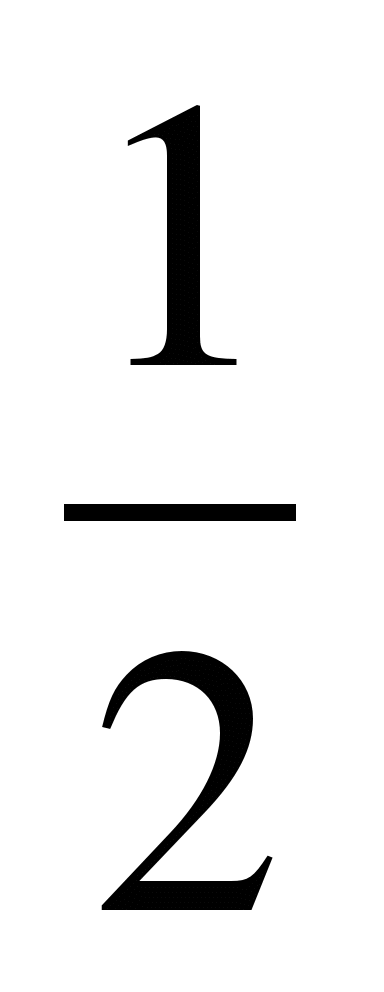 .
.
Найдем 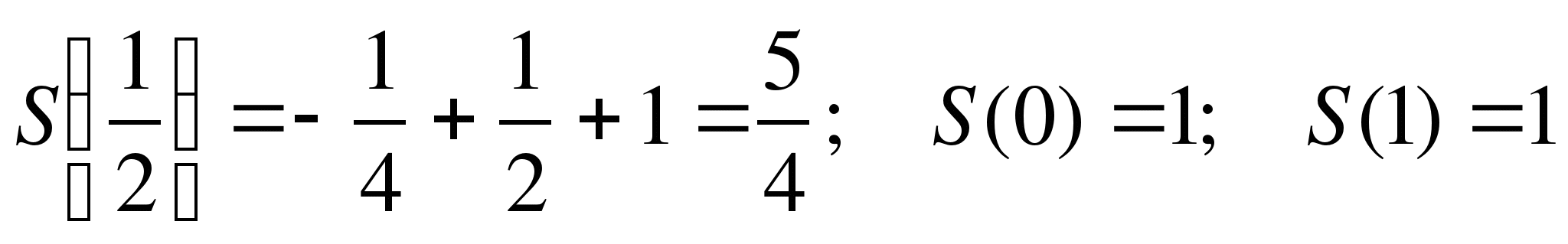 .
.
Видим, что функция достигает наибольшего значения при x=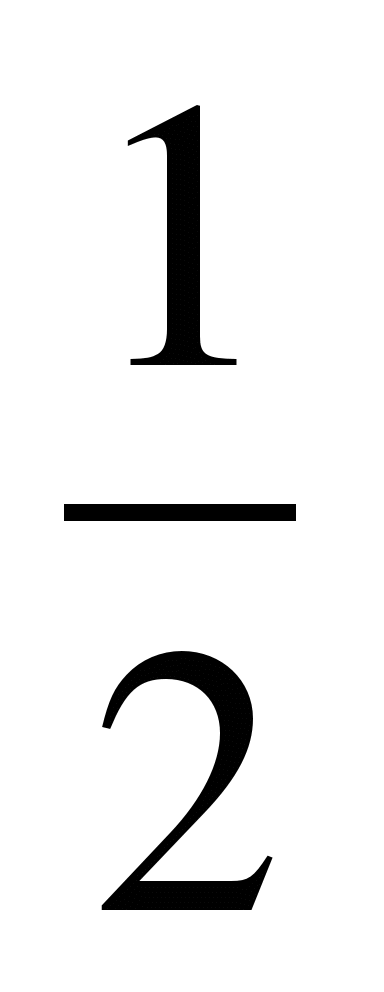 . Найдем
. Найдем 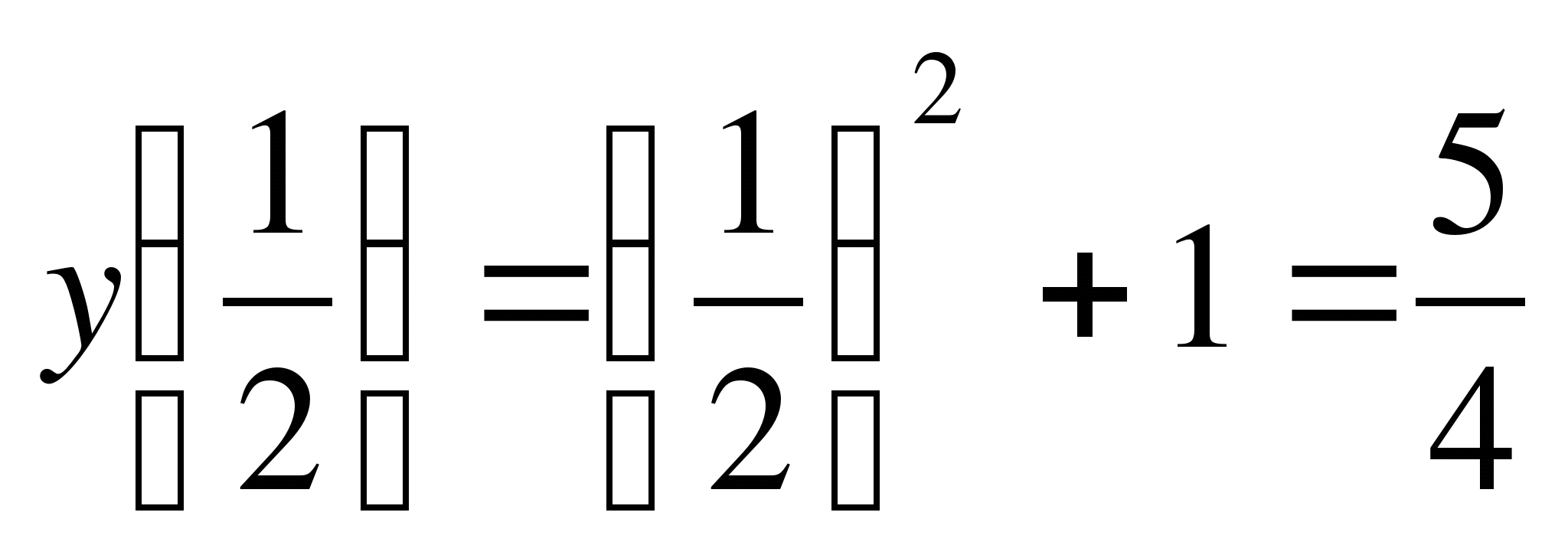 .
.
Ответ: касательную надо провести в точке  .
.
Отметим, что часто встречается задача нахождения интеграла, исходя из его геометрического смысла. Покажем на примере, как решается такая задача.
Пример 4. Используя геометрический смысл интеграла вычислить
а )
) 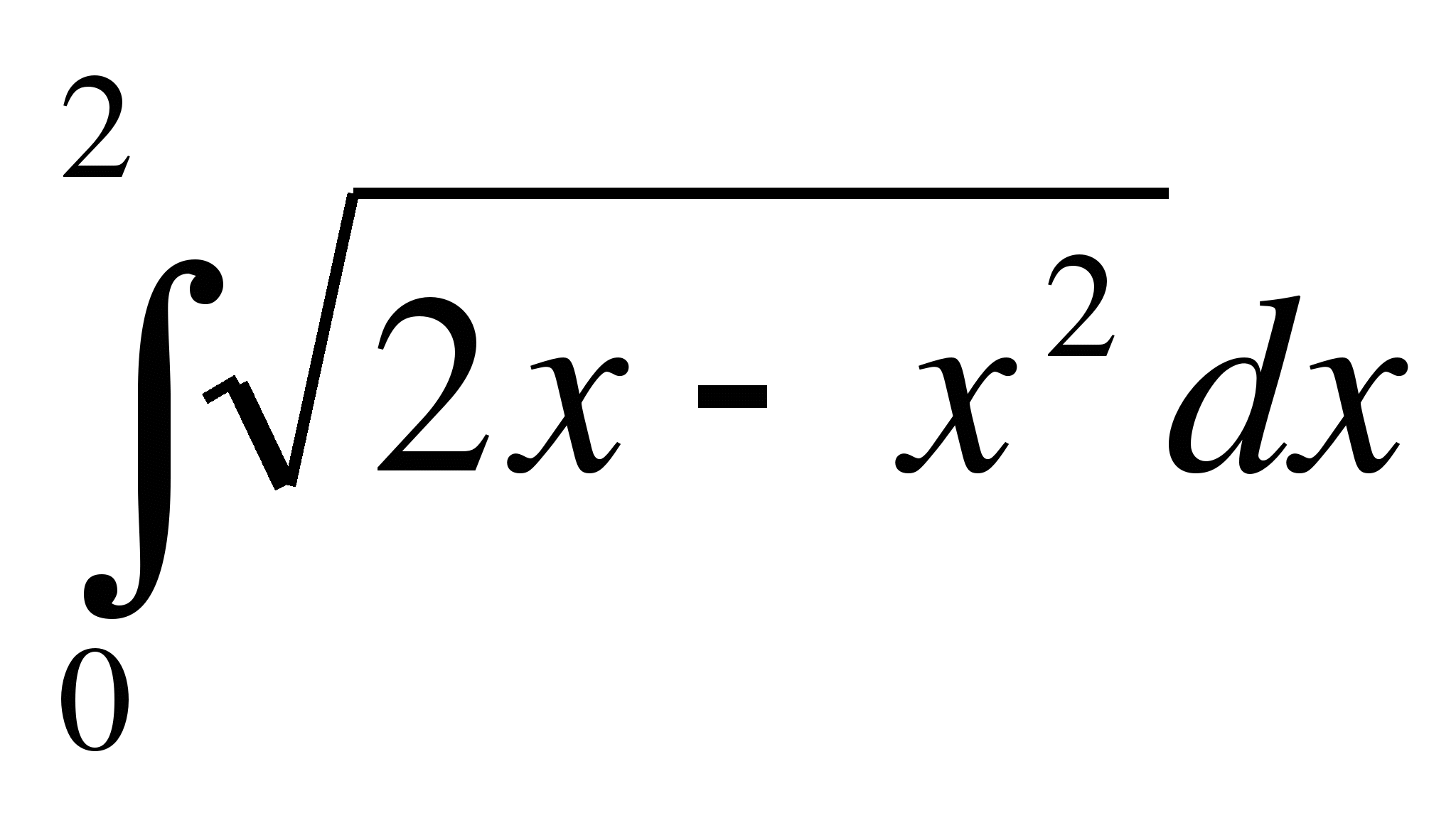 ; б)
; б)  .
.
Решение.
а) 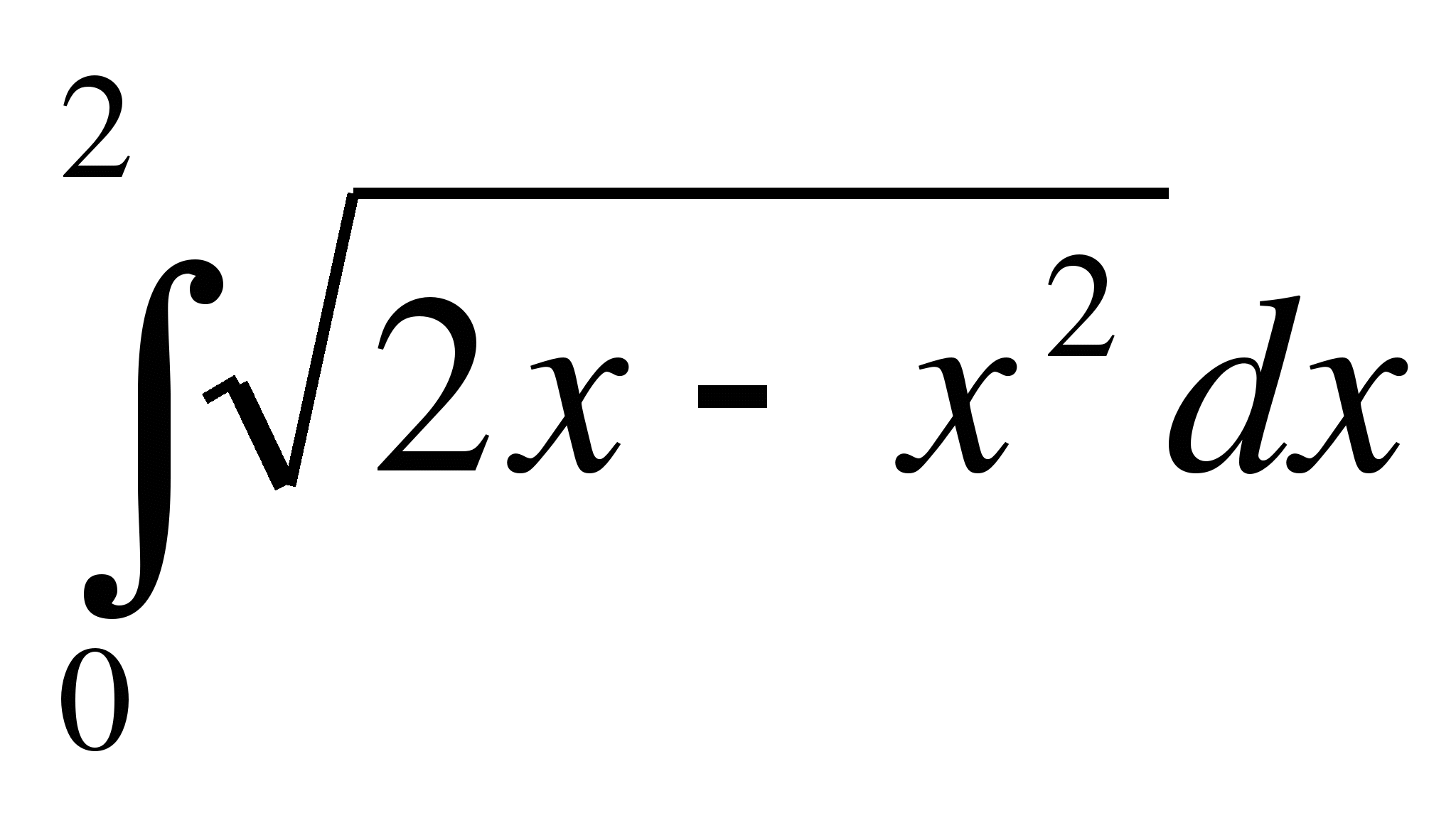 – равен площади криволинейной трапеции, ограниченной линиями
– равен площади криволинейной трапеции, ограниченной линиями 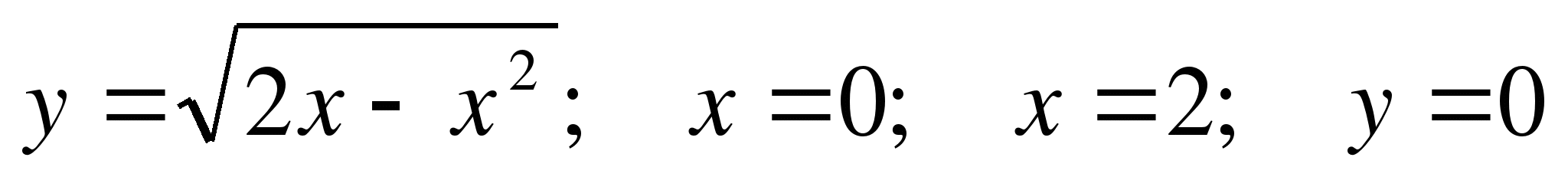 .
.
П реобразуем
реобразуем 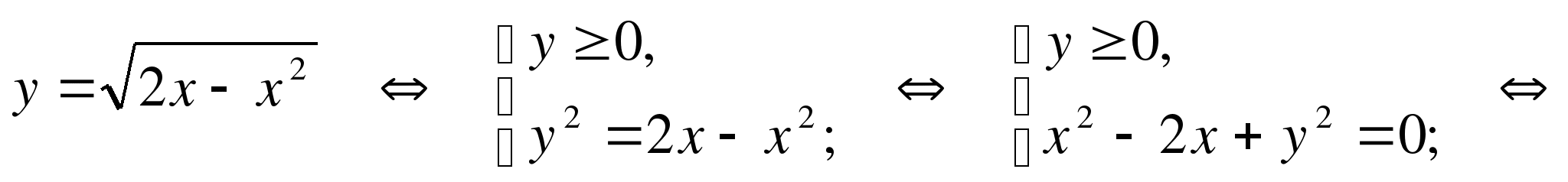
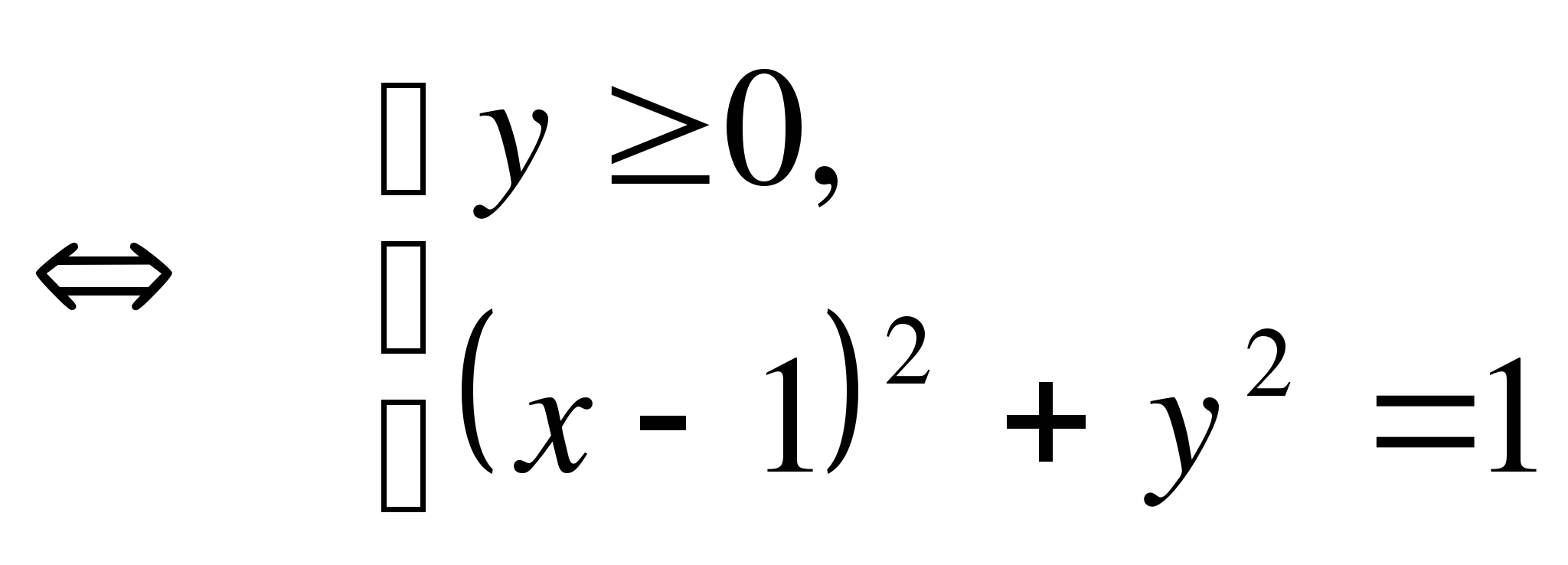 – верхняя половина окружности с центром Р(1;0) и радиусом R=1.
– верхняя половина окружности с центром Р(1;0) и радиусом R=1.
Поэтому 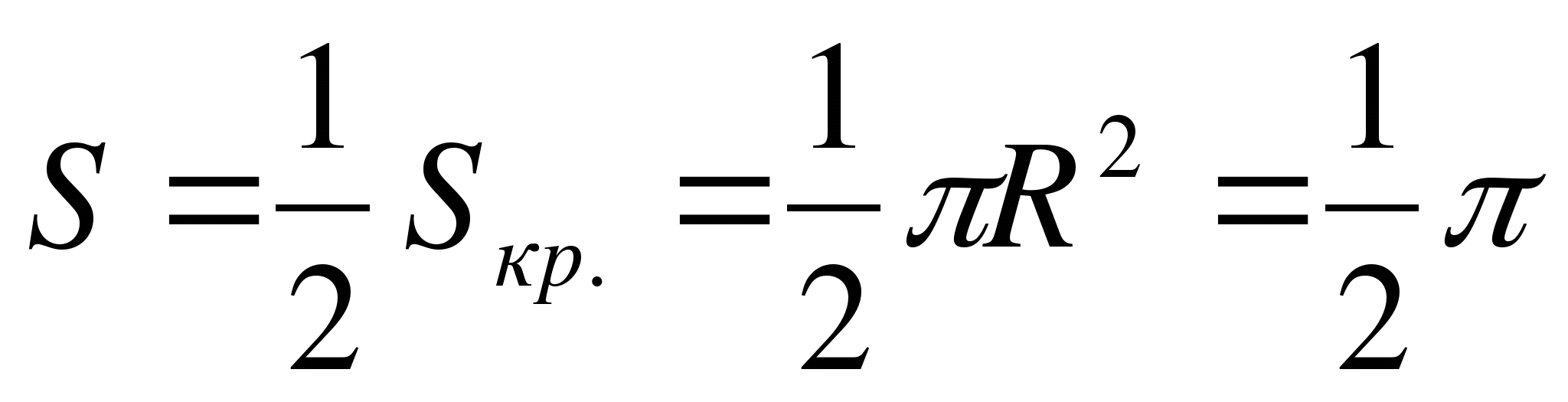 .
.
Ответ: 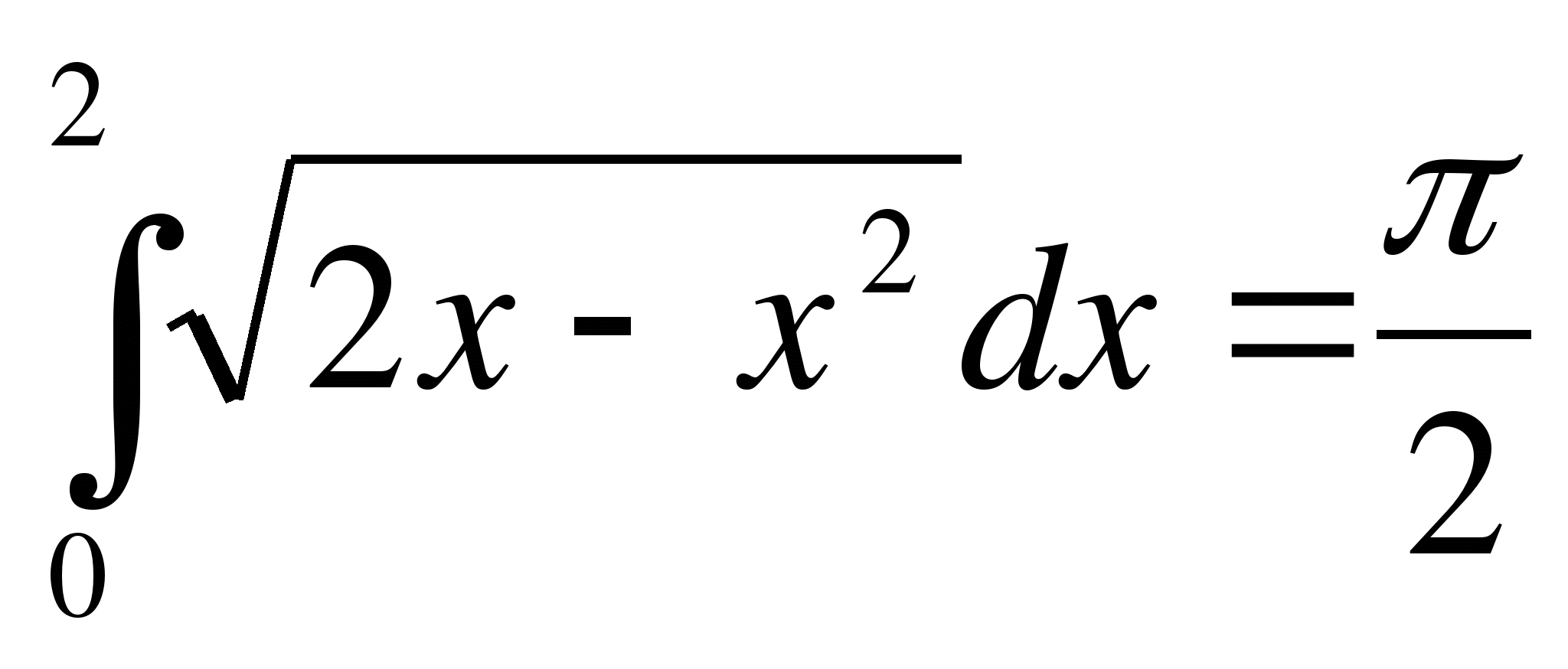 .
.
б) Рассуждая аналогично, построим область, ограниченную графиками 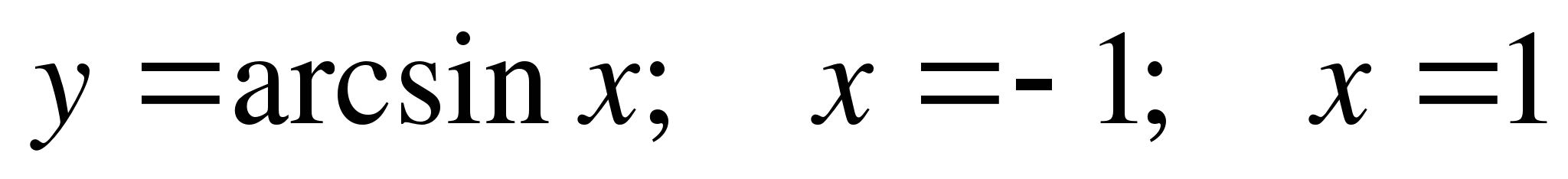 .
.
Имеем: 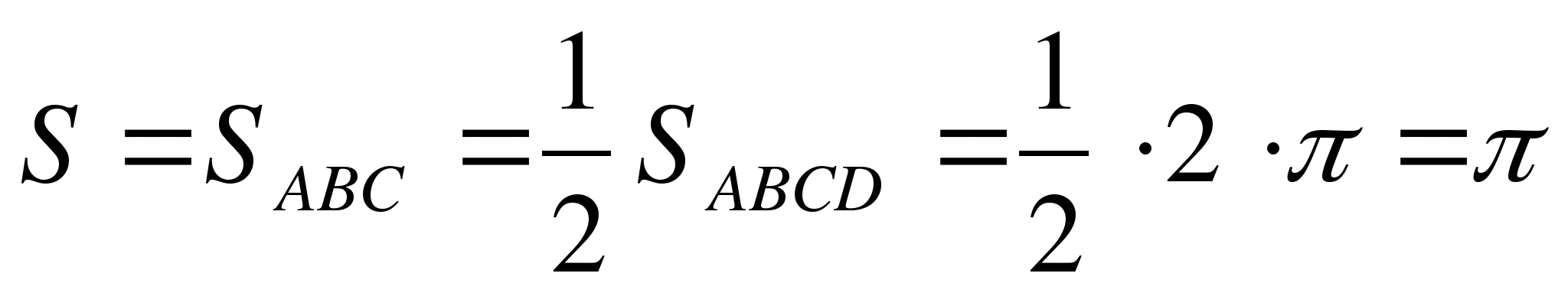 .
.
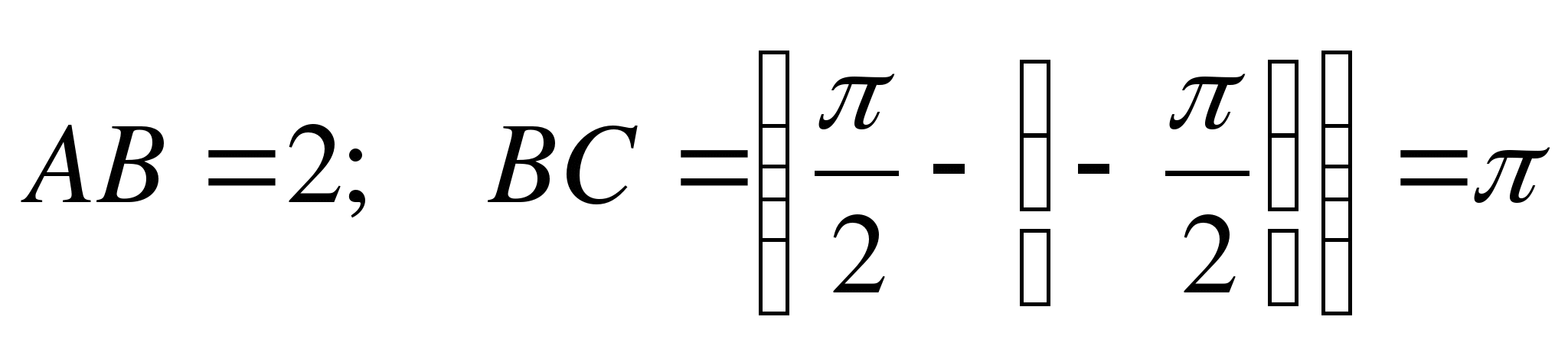 .
.
Ответ: 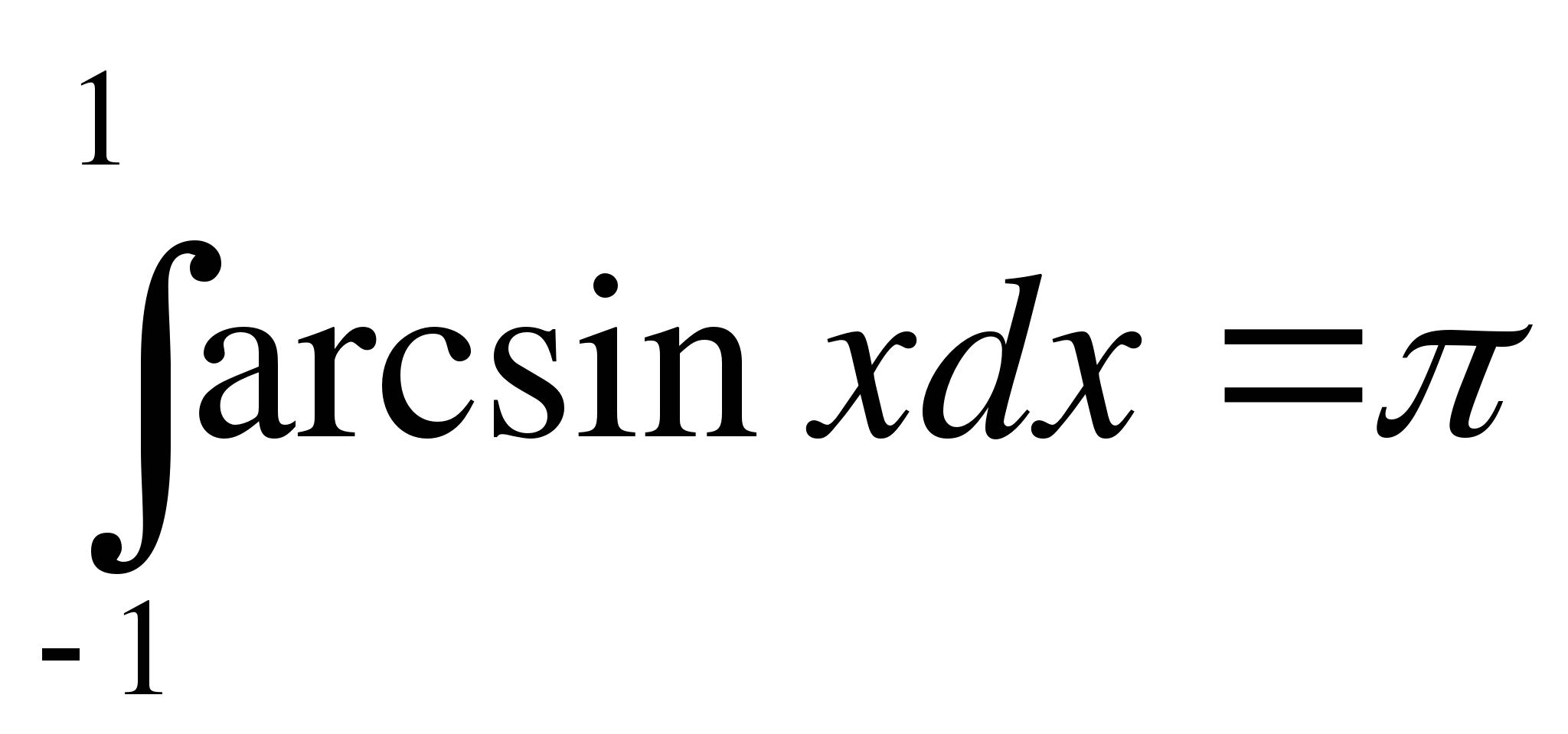 .
.
5. Применение. Формирование умений и навыков.
Задачи: Обеспечить применение учащимися знаний и способов действий, которые им необходимы для СР, создать условия для выявления школьниками индивидуальных способов применения изученного.
Контрольное задание
Ниже приводятся тексты заданий для самостоятельного решения. Вам необходимо решить эти задачи, оформить решения отдельно от решений по другим предметам и выслать в адрес Хабаровской краевой заочной физико-математической школы.
Найти первообразную функции y=f(x), проходящую через точку M0(x0,y0).
f(x)=1+cosx+cos2x, M0(0;1)
f(x)=3cosx–2sinx, M0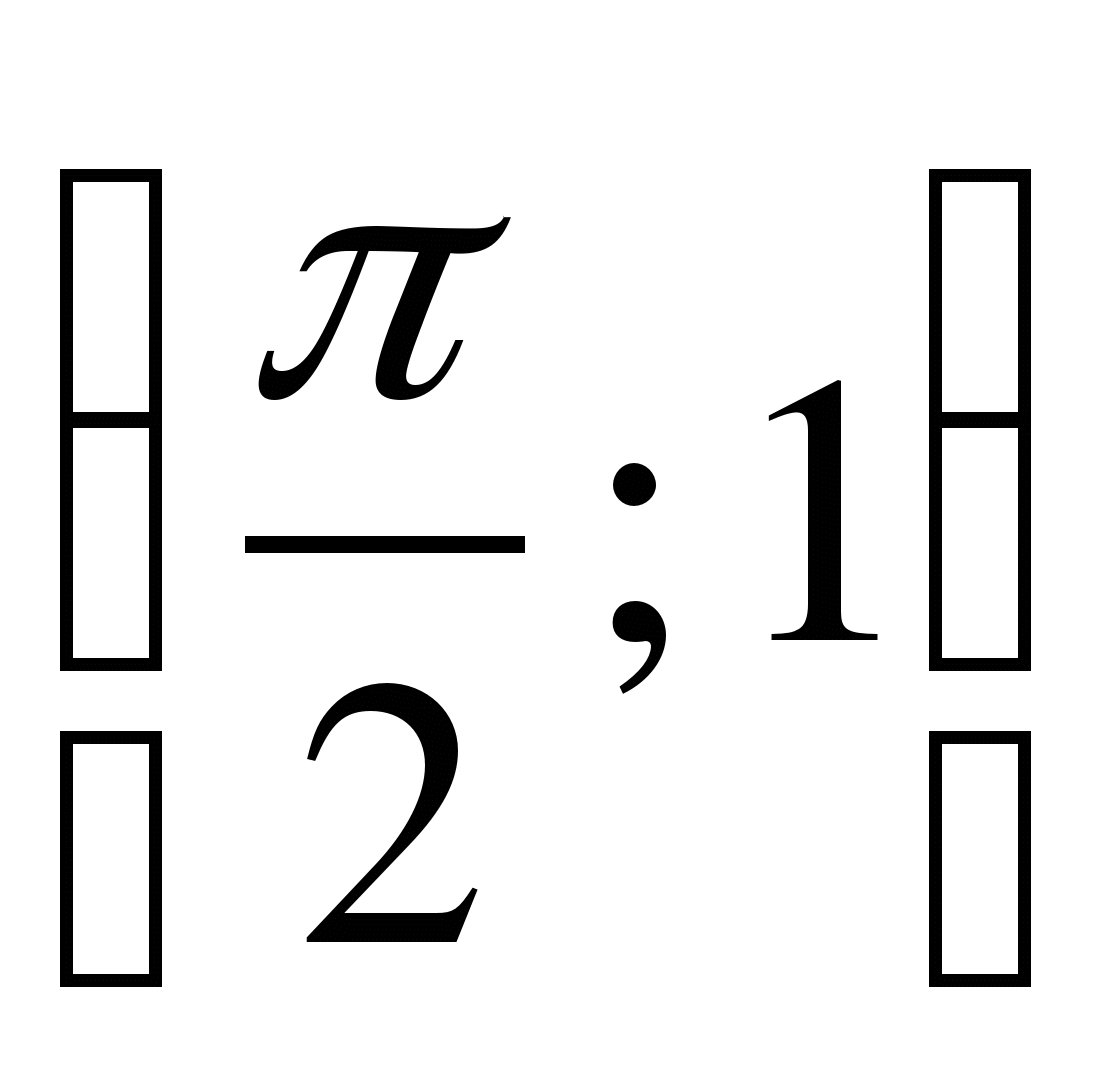
f(x)= , M0(0;3)
, M0(0;3)
Найти площадь фигуры. Ограниченной линиями
y=–3x2–2, x=1, x=2, y=–1
y=4x–x2, y=0
y=x2–2x+3, x+y=5
y=x2, y=x
y=0,5x2–2x+2, касательными к ней в точках A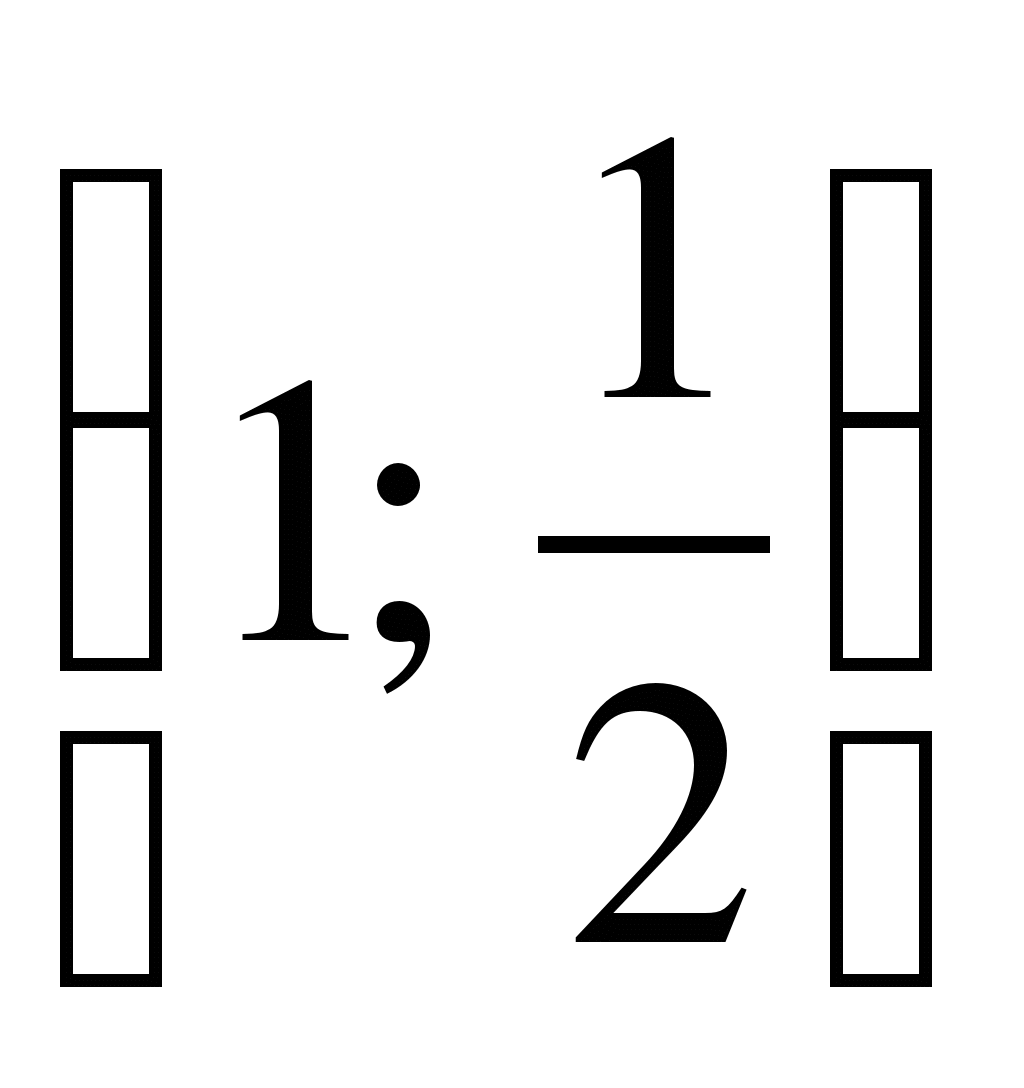 , B(4;2)
, B(4;2)
y=–9x–59, параболой y=3x2+ax+1, если известно, что касательная к параболе в точке x=–2 составляет с осью Ox угол величиной arctg6.
Найти а, если известно, что площадь криволинейной трапеции, ограниченной линиями y=3x3+2x, x=a, y=0, равна единице.
Найти наименьшее значение площади фигуры, ограниченной параболой y=x2+2x–3 и прямой y=kx+1.
6.Этап информации о домашнем задании.
Задачи: Обеспечить понимание учащимися цели, содержания и способов выполнения домашнего задания.№18, 19,20,21 нечетные
7.Подведение итогов урока.
Задача: Дать качественную оценку работы класса и отдельных учащихся.
infourok.ru
Вычисление площади криволинейной трапеции методами приближенного вычисления в среде MS Excel
Задачи урока:
Образовательные:
- Совершенствовать навыки работы в ЭТ.
- Углублять и систематизировать знания работы с Мастером диаграмм.
Развивающие:
- Способствовать развитию мышления, умения применять полученные знания при решении задач различной направленности.
- Способствовать развитию представлений учащихся о прикладном значении программ MS-Office.
Воспитательные:
- Воспитывать ответственность, коллективизм, взаимопомощь.
- Воспитывать познавательный интерес к предмету.
Тип урока: Урок совершенствование знаний, умений и навыков на основе полученных знаний в курсе “Алгебра и начала анализа”.
Материально техническое оснащение:
- Компьютеры с операционной системой Windows XP.
- Программное обеспечение Microsoft Office Excel XP (2003,2007).
- Мультимедийный проектор. Экран.
- Листы с вопросами по домашнему заданию – 14 шт.
- Магнитная доска, маркеры, магниты.
ХОД УРОКА
1. Организационный момент.
Тема сегодняшнего урока: “Вычисление площади криволинейной трапеции методами приближенного вычисления в среде MS Excel”.
На предыдущих уроках мы изучили функции ЭТ, составляли таблицы, строили диаграммы. Сегодня на уроке, используя возможности ЭТ, мы рассмотрим три метода приближенного вычисления площади криволинейной трапеции:
- метод прямоугольников с недостатком;
- метод прямоугольников с избытком;
- метод трапеций.
Наша цель не дублирование и не повторение пройденной темы по алгебре, а углубление понятий, связанных с интегральным исчислением.
Вспомним немного истории: интегральное исчисление было предложено в XVII в. И.Ньютоном и Г. Лейбницем. Интегрирование – нахождение интеграла, через который выражаются площади плоских фигур, длины кривых, объемы и поверхности тел и т.д.
Сам знак возник из первой буквы S латинского слова Summa. Но ведь при Евдоксе и Архимеде (400 г до н.э.) не было интегралов. Как же находили площади нестандартных фигур?
Представим себе, что мы рыболовы … Как найти площадь пойманной рыбы?
Демонстрируются рисунки через проектор на экран.
Рисунок 1
Возможные ответы учащихся …
Учитель: Я предлагаю вам следующее. Разделим рыбу на несколько равных частей.
Рисунок 2
Введем систему координат
Рисунок 3
Посмотрим на закрашенную фигуру. Что она нам напоминает?
— Отдаленно криволинейную трапецию.
Вопрос классу: Давайте вспомним: Что называют криволинейной трапецией?
Криволинейной трапецией называется фигура, ограниченная отрезком [a; b], графиком непрерывной функции не изменяющая своего знака на заданном отрезке и прямыми х=а и x=b.
(На доске через проектор)
Рисунок 4
Вычислим площадь криволинейной трапеции приближенными способами.
1. Метод прямоугольников.
Рисунок 5
2. Метод трапеций.
Рисунок 6
S1трап = (F(x0) + F(x1)) / 2 * dx
S2трап = (F(x1) + F(x2)) / 2 * dx
…
Si трап = (F(xn-1) + F(xn)) / 2 * dx
Реализуем все методы через электронную таблицу.
Что нам необходимо знать?
- Функцию.
- Пределы интегрирования.
- Шаг интегрирования (разбиения).
Рассмотрим на примере:
1. Функция Y= , ограниченная прямыми y = 0, x = 1, x = 2.
2. Пределы интегрирования [1,2].
3. Шаг интегрирования dx = 0.1.
Ресурсы ЭТ
- Заголовочная часть.
- Начальное и конечное значения аргумента (пределы интегрирования).
- Шаг разбиения.
Заполним ЭТ в соответствии с тремя рассмотренными способами, при этом учтем следующее:
- Вспомним, что обозначает “??????” при работе с формулами или с числами? (Не хватает места для записи чисел или формул, следовательно необходимо увеличить ширину колонки)
- Можно ли заносить в одну ячейку числовую и текстовую информацию? (Нельзя)
- Какую команду следует использовать для облегчения многократного ввода и идентичного вычисления данных? (Копирование)
Вычисление площади криволинейной трапеции
(Учитель показывает начало заполнения таблицы, далее вызывает контрольный пример и проводит объяснение с демонстрацией через проектор)
Замечание
1. Особенности вычисления площади криволинейной трапеции методом прямоугольников с недостатком и с избытком.
Функция возрастающая Функция убывающая.
Рисунок 7
При убывающей функции – формулы для вычисления соответствующих площадей криволинейных трапеций методом прямоугольников с недостатком и с избытком взаимо поменяются.
2. Поменяем шаг интегрирования с dx = 0,1 на dx = 0,5 следовательно изменится количество значений аргумента и соответствующих им значений функций, поэтому применяя команду копирования необходимо взять заведомо большее количество значений аргумента.
3. Рассмотрим графическое представление данной функции при различных dx.
Приложение 1, Приложение 2
Задание:
- Найти площадь криволинейной трапеции, заданной функцией Y= всеми тремя способами. Сначала с шагом интегрирования dx = 0,1, а затем с шагом dx = 0,5.
- Сравнить результаты вычислений, полученных при вычислении через электронную таблицу с найденным значением интеграл данной функции
= 0,5 кв. ед
Сравнив все полученные результаты, какой вывод можно сделать?
- От чего зависит точность вычисления площади криволинейной трапеции?
- Какой из способов дает более точное значение? Как вы думаете, почему?
Итак, подведем итог:
- Точность вычисления площади криволинейной трапеции зависит от шага разбиения.
- От вида функции: монотонно-возрастающая или монотонно-убывающая.
- От метода, применяемого к функции.
urok.1sept.ru
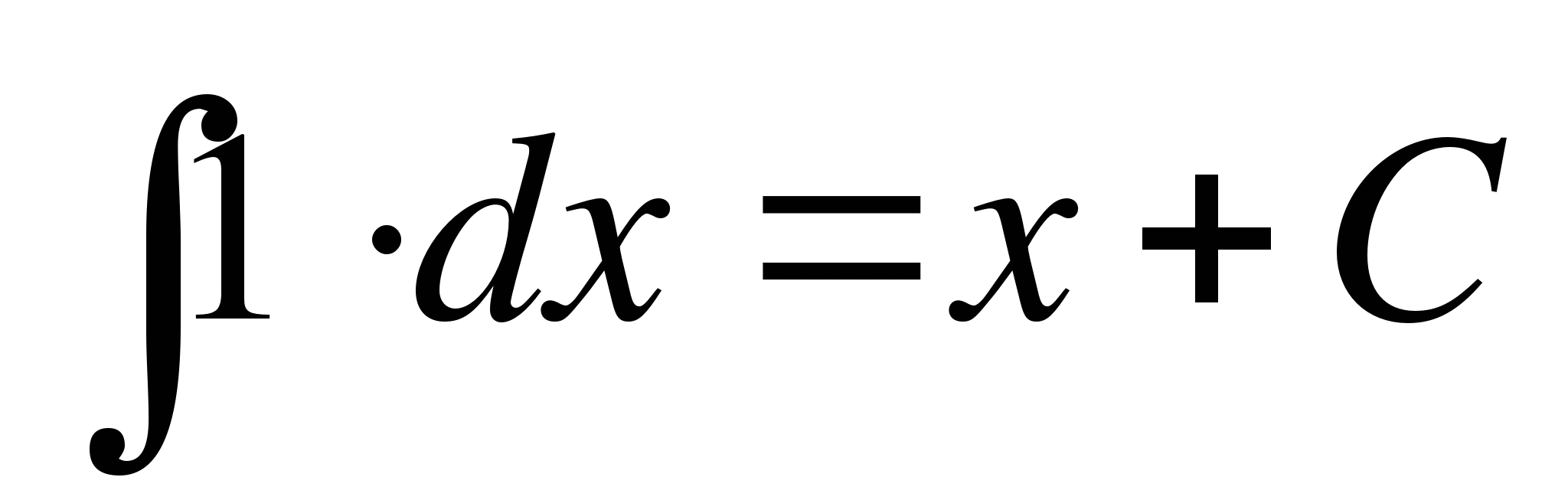 ;
; ;
;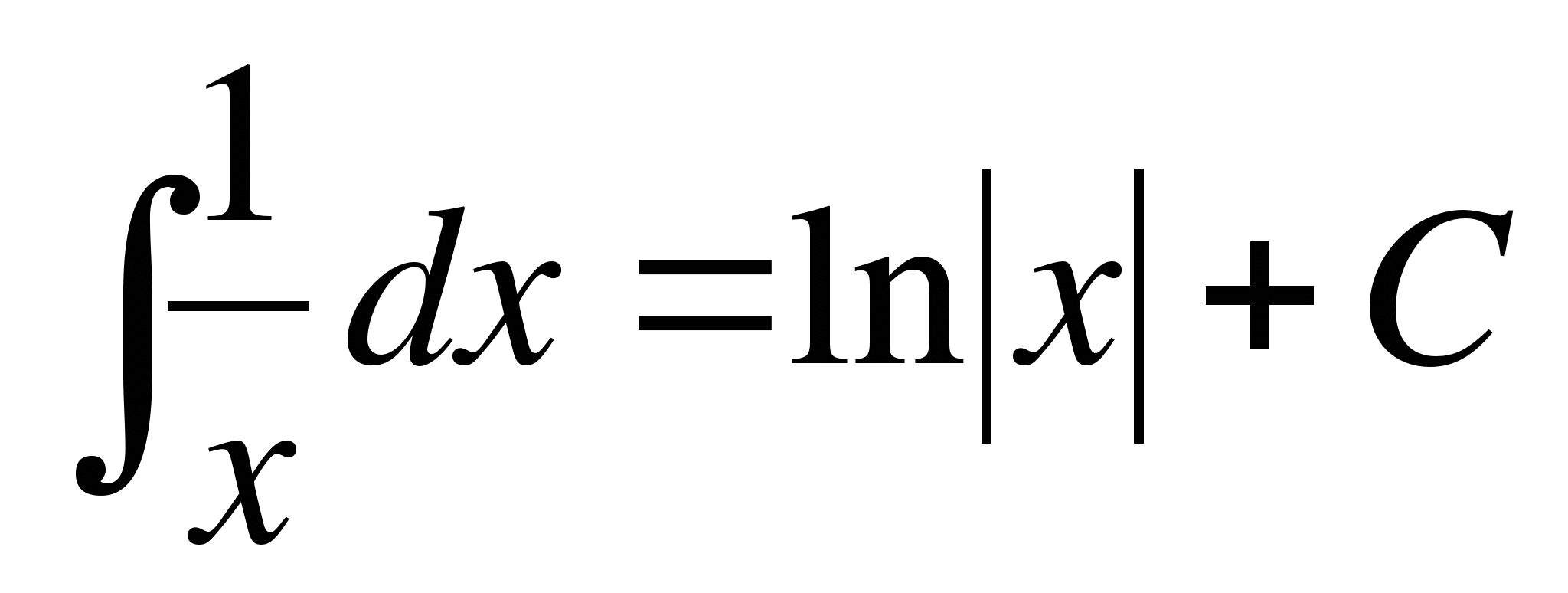 ;
;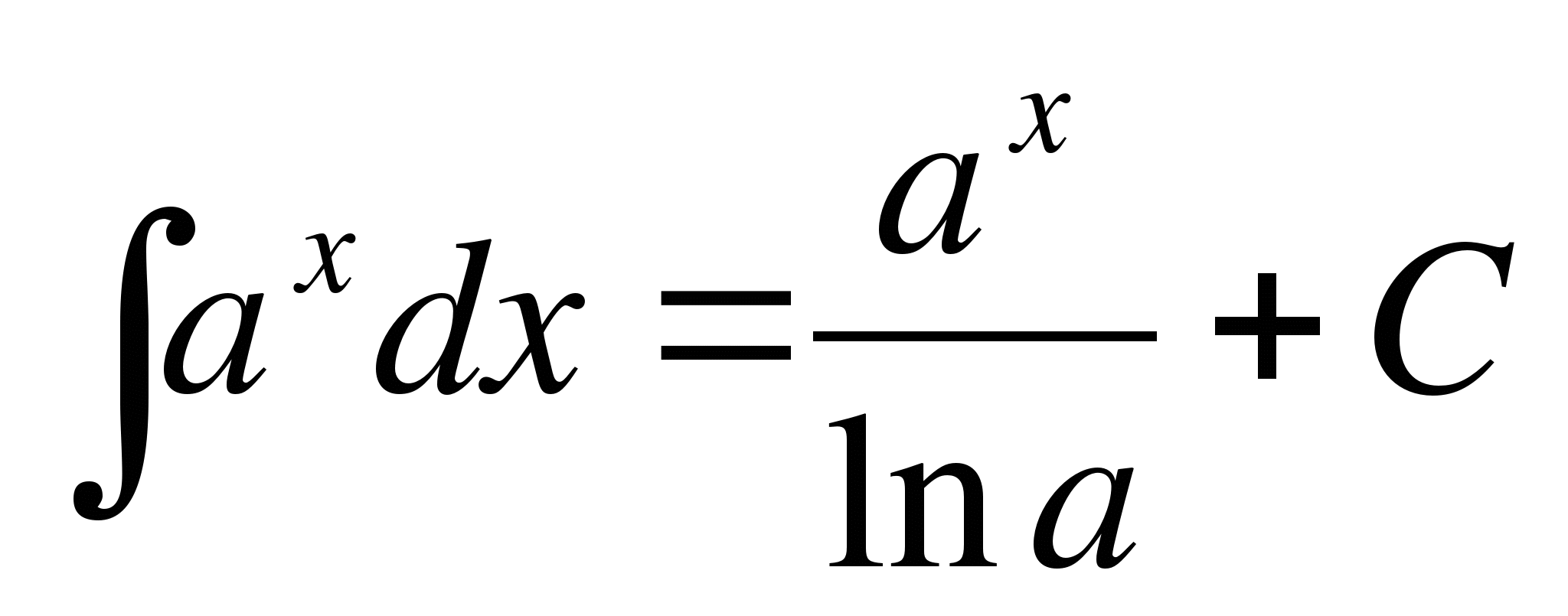 ; в частности,
; в частности, 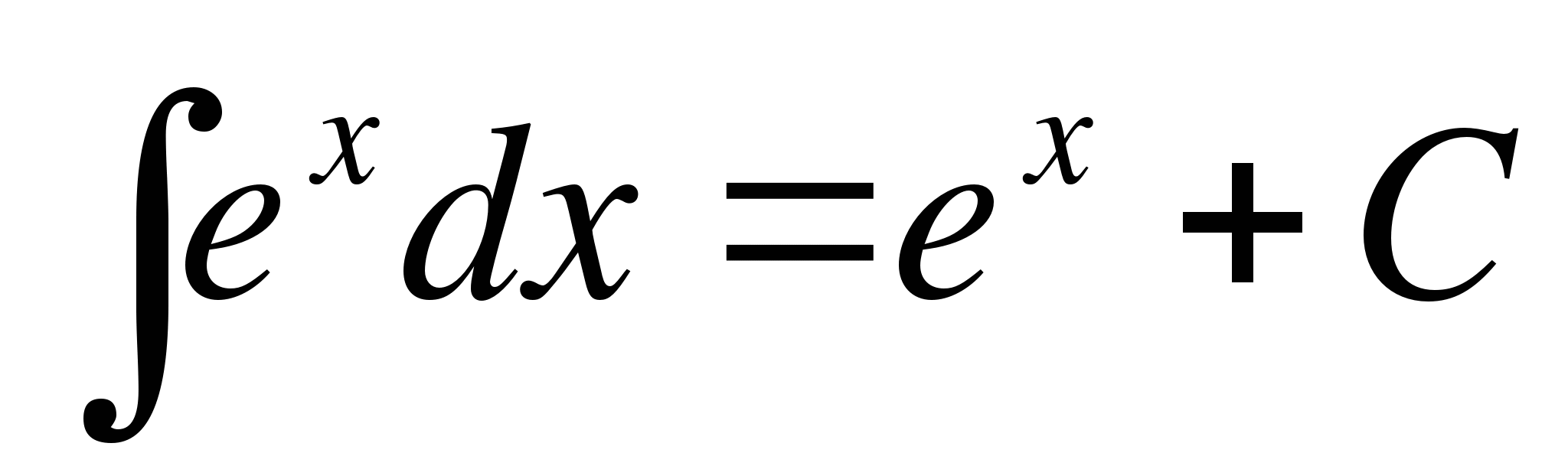 ;
;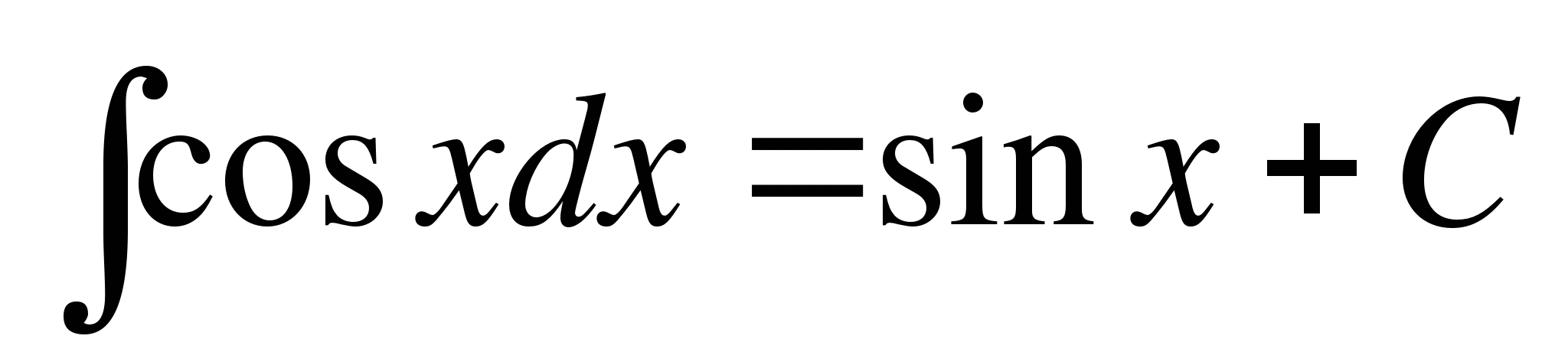 ;
; ;
;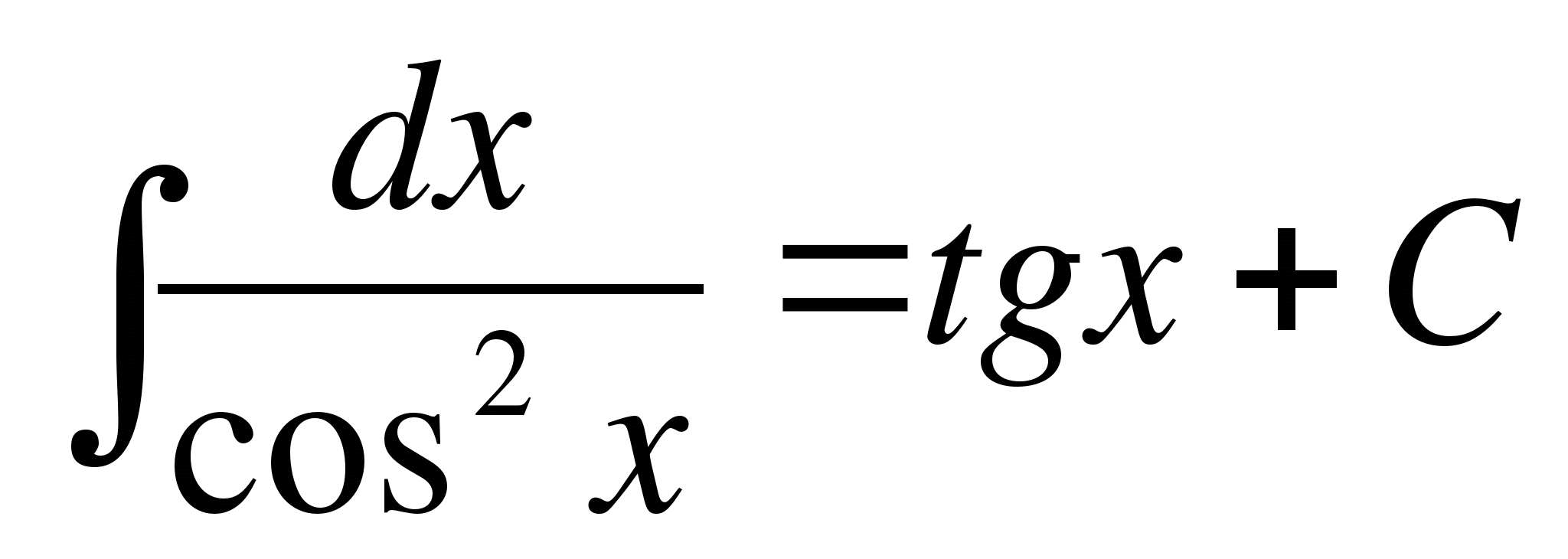 ;
;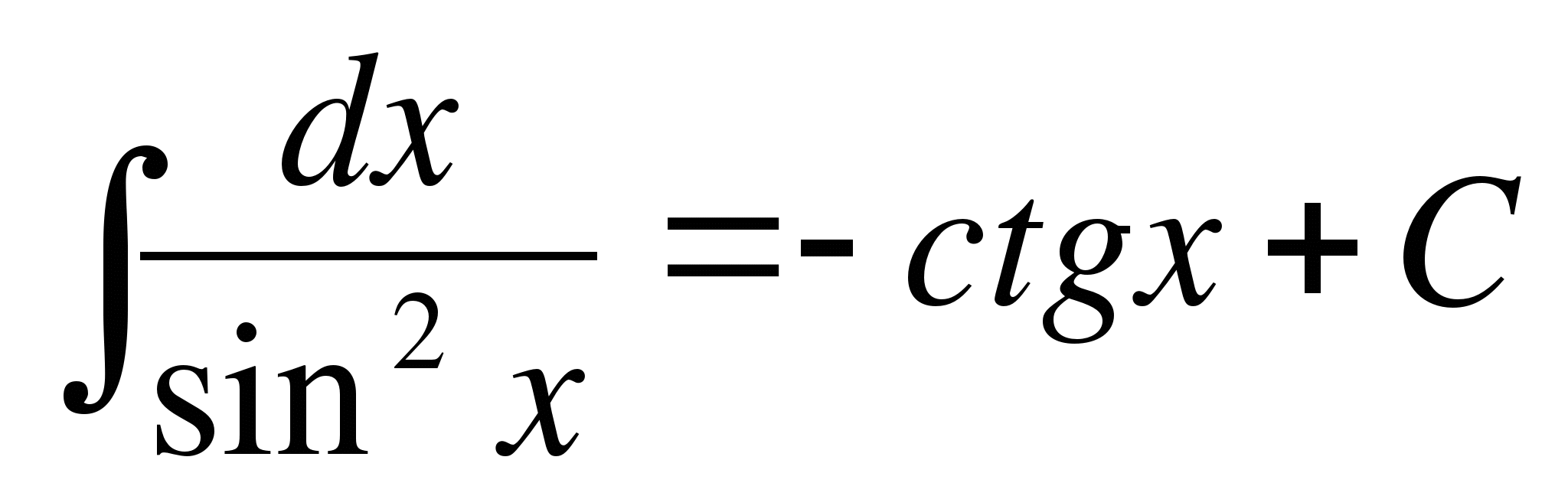 .
.