Натуральный логарифм — Википедия

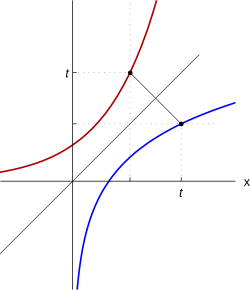Функция натурального логарифма (синяя кривая) обратна к экспоненте (красная кривая) 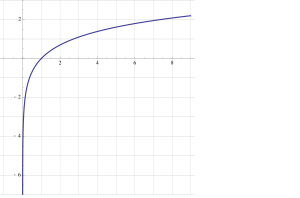График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0

Натуральный логарифм — это логарифм по основанию e, где e{\displaystyle e} — иррациональная константа, равная приблизительно 2,72. Он обозначается как ln⁡x{\displaystyle \ln x}, loge⁡x{\displaystyle \log _{e}x} или иногда просто log⁡x{\displaystyle \log x}, если основание e{\displaystyle e} подразумевается^[1]. Обычно число x{\displaystyle x} под знаком логарифма вещественное, но можно расширить это понятие и на комплексные числа.

Из определения следует, что логарифмическая зависимость есть обратная функция для экспоненты y=ex{\displaystyle y=e^{x}}, поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (см. рисунок справа). Как и экспонента, логарифмическая функция относится к категории трансцендентных функций.

Натуральные логарифмы полезны для решения алгебраических уравнений, в которых неизвестная присутствует в качестве показателя степени, они незаменимы в математическом анализе. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада радиоактивного вещества. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения различных задач, (например, нахождение сложных процентов).

Натуральный логарифм числа x — это показатель степени, в которую нужно возвести число e, чтобы получить x. Другими словами, натуральный логарифм ln⁡a{\displaystyle \ln a} есть решение x{\displaystyle x} уравнения ex=a.{\displaystyle e^{x}=a.}

Примеры:

ln⁡e=1{\displaystyle \ln e=1}, потому что e1=e{\displaystyle e^{1}=e};

ln⁡1=0{\displaystyle \ln 1=0}, потому что e0=1{\displaystyle e^{0}=1}.

Натуральный логарифм ln⁡a{\displaystyle \ln a} для вещественного числа a{\displaystyle a} определён и однозначен для любого положительного числа a.{\displaystyle a.}

Натуральный логарифм может быть также определён геометрически для любого положительного вещественного числа a как площадь под кривой y=1x{\displaystyle y={\frac {1}{x}}} на промежутке [1;a]{\displaystyle [1;a]}. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется данный логарифм, объясняет происхождение названия «натуральный».

Свойства[править | править код]

Из определения логарифма следует основное логарифмическое тождество^[2]:

eln⁡a=a{\displaystyle e^{\ln a}=a}

Приведём сводку формул в предположении, что все значения положительны^[3]:

Другие свойства:

• Из равенства двух вещественных логарифмов следует равенство логарифмируемых выражений.
• С возрастанием аргумента возрастает и логарифм: если 0<x<y,{\displaystyle 0<x<y,} то ln⁡x<ln⁡y.{\displaystyle \ln x<\ln y.}
• h2+h⩽ln⁡(1+h)⩽h,{\displaystyle {\frac {h}{1+h}}\leqslant \ln(1+h)\leqslant h,} если h>−1.{\displaystyle h>-1.}

Связь с логарифмами по другому основанию[править | править код]

Логарифм может быть определён для любого положительного основания, отличного от 1{\displaystyle 1}, а не только для e{\displaystyle e}, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем.

Логарифм loga⁡b{\displaystyle \log _{a}b} по основанию a{\displaystyle a} можно преобразовать^[4] в натуральный логарифм и обратно:

ln⁡b=loga⁡bloga⁡e=loga⁡b⋅ln⁡a{\displaystyle \ln b={\frac {\log _{a}b}{\log _{a}e}}=\log _{a}b\cdot \ln a}

loga⁡b=ln⁡bln⁡a{\displaystyle \log _{a}b={\frac {\ln b}{\ln a}}}

Связь десятичного (lg⁡x{\displaystyle \lg x}) и натурального логарифмов^[5]:

ln⁡x≈2,30259 lg⁡x;lg⁡x≈0,43429 ln⁡x{\displaystyle \ln x\approx 2{,}30259\ \lg x;\quad \lg x\approx 0{,}43429\ \ln x}

Связь двоичного (lb⁡x{\displaystyle \operatorname {lb} x}) и натурального логарифмов:

ln⁡x≈0,693147lb⁡x;lb⁡x≈1,442695ln⁡x{\displaystyle \ln x\approx 0,693147\operatorname {lb} x;\quad \operatorname {lb} x\approx 1{,}442695\ln x}

Логарифмическая функция[править | править код]

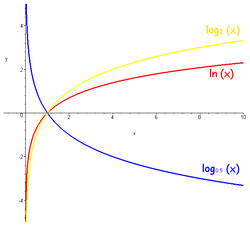Графики логарифмических функций; красная кривая — натуральный логарифм

Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию

y=ln⁡x{\displaystyle y=\ln x}. Она определена при x>0{\displaystyle x>0}. Область значений: E(y)=(−∞;+∞){\displaystyle E(y)=(-\infty ;+\infty )}. Эта кривая часто называется логарифмикой^[6]. Из формулы замены основания логарифма видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси y{\displaystyle y}; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.

Функция является строго возрастающей, она непрерывна и неограниченно дифференцируема всюду в своей области определения.

Ось ординат (x=0{\displaystyle x=0}) является вертикальной асимптотой, поскольку:

limx→0+0ln⁡x=−∞{\displaystyle \lim _{x\to 0+0}\ln x=-\infty }

Производная натуральной логарифмической функции равна:

ddxln⁡x=1x{\displaystyle {\frac {d}{dx}}\ln x={\frac {1}{x}}}

Простота этой формулы — одна из причин широкого использования именно натурального логарифма в анализе и при решении дифференциальных уравнений.

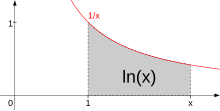
Проинтегрировав формулу для производной в интервале от x=1{\displaystyle x=1} до x=b{\displaystyle x=b}, мы получаем:

ln⁡b=∫1bdxx{\displaystyle \ln b=\int \limits _{1}^{b}{\frac {dx}{x}}}

Другими словами, натуральный логарифм равен площади под гиперболой y=1x{\displaystyle y={\frac {1}{x}}} для указанного интервала x.

С точки зрения общей алгебры, логарифмическая функция осуществляет (единственно возможный) изоморфизм мультипликативной группы положительных вещественных чисел и аддитивной группы всех вещественных чисел. Другими словами, логарифмическая функция есть единственное (определённое для всех положительных значений аргумента) непрерывное решение функционального уравнения^[7]:

f(xy)=f(x)+f(y){\displaystyle f(xy)=f(x)+f(y)}

Аналитические свойства функции[править | править код]

Из формулы для производной натурального логарифма следует, что первообразная для гиперболы y=1/x{\displaystyle y=1/x} имеет вид:

∫dxx=ln⁡|x|+C,{\displaystyle \int {dx \over x}=\ln |x|+C,}

где C{\displaystyle C} — произвольная константа интегрирования. Поскольку функция y=1/x{\displaystyle y=1/x} состоит из двух ветвей (одна для положительных, другая для отрицательных x{\displaystyle x}), семейство первообразных для y=1/x{\displaystyle y=1/x} тоже состоит из двух подсемейств, причём константы интегрирования у них независимы одна от другой.

Неопределённый интеграл от натурального логарифма легко найти интегрированием по частям:

∫ln⁡xdx=xln⁡x−x+C{\displaystyle \int {\ln x\,\mathrm {d} x}=x\ln x-x+C}

В математическом анализе и теории дифференциальных уравнений большую роль играет понятие логарифмической производной функции f(x){\displaystyle f(x)}:

ddxln⁡(f(x))=f′(x)f(x){\displaystyle {\frac {d}{dx}}\ln(f(x))={\frac {f'(x)}{f(x)}}}

Методы вычисления логарифма[править | править код]

Разложим натуральный логарифм в ряд Тейлора вблизи единицы:

ln⁡(1+x)=x−x22+x33−x44+…{\displaystyle \ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\dots }

(Ряд 1)

Этот ряд, называемый «рядом Меркатора», сходится при −1<x⩽1{\displaystyle -1<x\leqslant 1}. В частности:

ln⁡2=1−12+13−14+…{\displaystyle \ln 2=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\dots }

Формула ряда 1 непригодна для практического расчёта логарифмов из-за того, что ряд сходится очень медленно и только в узком интервале. Однако нетрудно получить из неё более удобную формулу:

ln⁡(1+x1−x)=2(x+x33+x55+x77+…){\displaystyle \ln \left({\frac {1+x}{1-x}}\right)=2\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\dots \right)}

(Ряд 2)

Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа. Данный алгоритм уже пригоден для реальных численных расчётов значений логарифмов, однако не является наилучшим с точки зрения трудоёмкости; см. следующий раздел.

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула:^[8][9]:

ln⁡x≈π2M(1,4/s)−mln⁡2{\displaystyle \ln x\approx {\frac {\pi }{2M(1,4/s)}}-m\ln 2}

где M{\displaystyle M} обозначает арифметико-геометрическое среднее 1 и 4/s, и

s=x2m>2p/2,{\displaystyle s=x\,2^{m}>2^{p/2},}

m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.

Полезные пределы[править | править код]

Приведём несколько полезных пределов, связанных с логарифмами^[10]:

limx→0ln⁡(1+x)x=1{\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1}

limx→0+xbln⁡x=0(b>0){\displaystyle \lim _{x\to 0^{+}}x^{b}\ln x=0\quad (b>0)}

limx→∞ln⁡xxb=0(b>0){\displaystyle \lim _{x\to \infty }{\frac {\ln x}{x^{b}}}=0\quad (b>0)}

ln⁡x=limn→∞n(xn−1)=limn→∞n(1−1xn

Логарифмы и их свойства | umath.ru

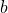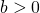Логарифмом числа , где , по основанию , где 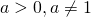(обозначается 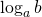), называется показатель степени, в которую нужно возвести число , чтобы получить число 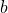, т.е.

   

Это равенство называют основным логарифмическим тождеством.

Логарифм числа по основанию 10 называют десятичным и обозначают 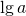, а логарифм числа по основанию называют натуральным и обозначают .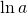

Свойства логарифмов

Если 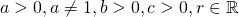, то

   

   

   

Формула перехода к новому основанию.

Если 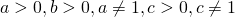, то

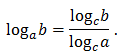Эта формула называется формулой перехода от логарифма по основанию к логарифму по основанию . Частные случаи формулы перехода: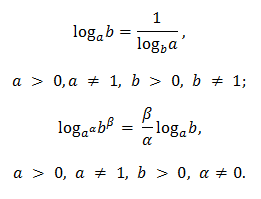

Десятичный логарифм — Википедия

График десятичного логарифма

Десятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа b{\displaystyle b} есть решение уравнения 10x=b.{\displaystyle 10^{x}=b.}

Вещественный десятичный логарифм числа b{\displaystyle b} существует, если b>0{\displaystyle b>0} (комплексный десятичный логарифм существует для всех b≠0{\displaystyle b\neq 0}). Международный стандарт ISO 31-11 обозначает его lgb{\displaystyle \lg \,b}. Примеры:

lg1=0;lg10=1;lg100=2{\displaystyle \lg \,1=0;\,\lg \,10=1;\,\lg \,100=2}

lg1000000=6;lg0,1=−1;lg0,001=−3{\displaystyle \lg \,1000000=6;\,\lg \,0{,}1=-1;\,\lg \,0{,}001=-3}

В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: log,Log,Log10{\displaystyle \operatorname {log} ,\operatorname {Log} ,\operatorname {Log10} }, причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.

В нижеследующей таблице предполагается, что все значения положительны^[1]:

Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные переменные, например:

lg⁡|xy|=lg⁡(|x|)+lg⁡(|y|),{\displaystyle \lg |xy|=\lg(|x|)+\lg(|y|),}

lg|xy|=lg⁡(|x|)−lg⁡(|y|),{\displaystyle \lg \!\left|{\frac {x}{y}}\right|=\lg(|x|)-\lg(|y|),}

Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:

lg⁡(x1x2…xn)=lg⁡(x1)+lg⁡(x2)+⋯+lg⁡(xn){\displaystyle \lg(x_{1}x_{2}\dots x_{n})=\lg(x_{1})+\lg(x_{2})+\dots +\lg(x_{n})}

Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел x,y{\displaystyle x,y} с помощью логарифмических таблиц^[⇨] производилось по следующему алгоритму:

1. Найти в таблицах логарифмы чисел x,y{\displaystyle x,y}.
2. Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения x⋅y{\displaystyle x\cdot y}.
3. По логарифму произведения найти в таблицах само произведение.

Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.

Связь десятичного и натурального логарифмов^[2]:

ln⁡x≈2,30259 lg⁡x;lg⁡x≈0,43429 ln⁡x{\displaystyle \ln x\approx 2{,}30259\ \lg x;\quad \lg x\approx 0{,}43429\ \ln x}

Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. Пример:

lg0,012=lg(10−2×1,2)=−2+lg1,2≈−2+0,079181=−1,920819{\displaystyle \lg \,0{,}012=\lg \,(10^{-2}\times 1{,}2)=-2+\lg \,1{,}2\approx -2+0{,}079181=-1{,}920819}

Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (характеристика) надчёркивалась сверху:

lg0,012≈−2+0,079181=2¯,079181{\displaystyle \lg \,0{,}012\approx -2+0{,}079181={\bar {2}}{,}079181}

Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.

Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: y=lgx.{\displaystyle y=\lg \,x.} Она определена при всех x>0.{\displaystyle x>0.} Область значений: E(y)=(−∞;+∞){\displaystyle E(y)=(-\infty ;+\infty )}. График этой кривой часто называется логарифмикой^[3].

Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:

ddxlgx=lgex{\displaystyle {\frac {d}{dx}}\lg \,x={\frac {\lg \,e}{x}}}

Ось ординат (x=0){\displaystyle (x=0)} является вертикальной асимптотой, поскольку:

limx→0+0lgx=−∞{\displaystyle \lim _{x\to 0+0}\lg \,x=-\infty }

Логарифмы по основанию 10 до изобретения в 1970-е годы компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа x{\displaystyle x} (характеристику логарифма) [lg⁡x]{\displaystyle [\lg x]} легко определить.

• Если x⩾1{\displaystyle x\geqslant 1}, то [lg⁡x]{\displaystyle [\lg x]} на 1 меньше числа цифр в целой части числа x{\displaystyle x}. Например, сразу очевидно, что lg⁡345{\displaystyle \lg 345} находится в промежутке (2,3){\displaystyle (2,3)}.
• Если 0<x<1{\displaystyle 0<x<1}, то ближайшее к lg⁡x{\displaystyle \lg x} целое в меньшую сторону равно общему числу нулей в x{\displaystyle x} перед первой ненулевой цифрой (включая ноль перед запятой), взятому со знаком минус. Например, lg⁡0,0014{\displaystyle \lg 0{,}0014} находится в интервале (−3,−2){\displaystyle (-3,-2)}.

Кроме того, при переносе десятичной запятой в числе на n{\displaystyle n} разрядов значение десятичного логарифма этого числа изменяется на n.{\displaystyle n.} Например:

lg⁡8314,63=lg⁡8,31463+3{\displaystyle \lg 8314{,}63=\lg 8{,}31463+3}

Отсюда следует, что для вычисления десятичных логарифмов достаточно составить таблицу логарифмов для чисел в диапазоне от 1{\displaystyle 1} до 10{\displaystyle 10}^[4]. Такие таблицы, начиная с XVII века, выпускались большим тиражом и служили незаменимым расчётным инструментом учёных и инженеров.

Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным^[5]. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.

Десятичные логарифмы для чисел вида 5 × 10^C

Число	Логарифм	Характеристика	Мантисса	Запись
n	lg(n)	C	M = lg(n) − C
5 000 000	6.698 970…	6	0.698 970…	6.698 970…
50	1.698 970…	1	0.698 970…	1.698 970…
5	0.698 970…	0	0.698 970…	0.698 970…
0.5	−0.301 029…	−1	0.698 970…	1.698 970…
0.000 005	−5.301 029…	−6	0.698 970…	6.698 970…

Обратите внимание, что у всех приведенных в таблице чисел n{\displaystyle n} одна и та же мантисса M{\displaystyle M}, поскольку:

lg⁡(n)=lg⁡(x×10C)=lg⁡(x)+lg⁡(10C)=lg⁡(x)+C{\displaystyle \lg(n)=\lg \left(x\times 10^{C}\right)=\lg(x)+\lg \left(10^{C}\right)=\lg(x)+C},

где 1<x<10{\displaystyle 1<x<10} — значащая часть числа n{\displaystyle n}.

Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми. Но в этих и в последующих изданиях таблиц обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1852 году в Берлине (таблицы Бремикера)^[6].

В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого^[7]. В СССР выпускались несколько сборников таблиц логарифмов^[8]:

1. Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
2. Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.

Теория логарифмов

История логарифмов

• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. I. Арифметика. Алгебра. Анализ. — 432 с.
• Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
• Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
• Успенский Я. В. Очерк истории логарифмов. — Петроград: Научное книгоиздательство, 1923. — 78 с.

1. ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187..
2. ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189..
3. ↑ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
4. ↑ Элементарная математика, 1976, с. 94—100.
5. ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 406..
6. ↑ История математики, том II, 1970, с. 62..
7. ↑ Гнеденко Б. В. Очерки по истории математики в России, издание 2-е.. — М.: КомКнига, 2005. — С. 66.. — 296 с. — ISBN 5-484-00123-4.
8. ↑ Логарифмические таблицы //Большая советская энциклопедия.