y x 2 y 0 x 2 найти площадь
Вы искали y x 2 y 0 x 2 найти площадь? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить площадь фигуры ограниченной линиями x 2 y 2, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «y x 2 y 0 x 2 найти площадь».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y x 2 y 0 x 2 найти площадь,вычислить площадь фигуры ограниченной линиями x 2 y 2,найдите площадь фигуры ограниченной линиями y 2 x 2,найдите площадь фигуры ограниченной линиями y x 2 y 0 x 2,найдите площадь фигуры ограниченной линиями y x 2 y 0 x 3,найдите площадь фигуры ограниченной линиями y x 3 y 0 x 2,найдите площадь фигуры ограниченной линиями y x 3 y 0 y 2,найти площадь фигуры ограниченной линиями y 2 x 2,найти площадь фигуры ограниченной линиями y x 2 x y 2,найти площадь фигуры ограниченной линиями y x 2 y 0 x 2,найти площадь фигуры ограниченной линиями y x 2 y x.
Где можно решить любую задачу по математике, а так же y x 2 y 0 x 2 найти площадь Онлайн?
Решить задачу y x 2 y 0 x 2 найти площадь вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Площадь фигуры ограниченной кривыми в прямоугольных координатах
Площадь фигуры между двумя кривыми в прямоугольных координатах определяется интегралом
от разницы кривых, где одна из них всегда принимает не меньшие значения чем другая , а также кривые непрерывны.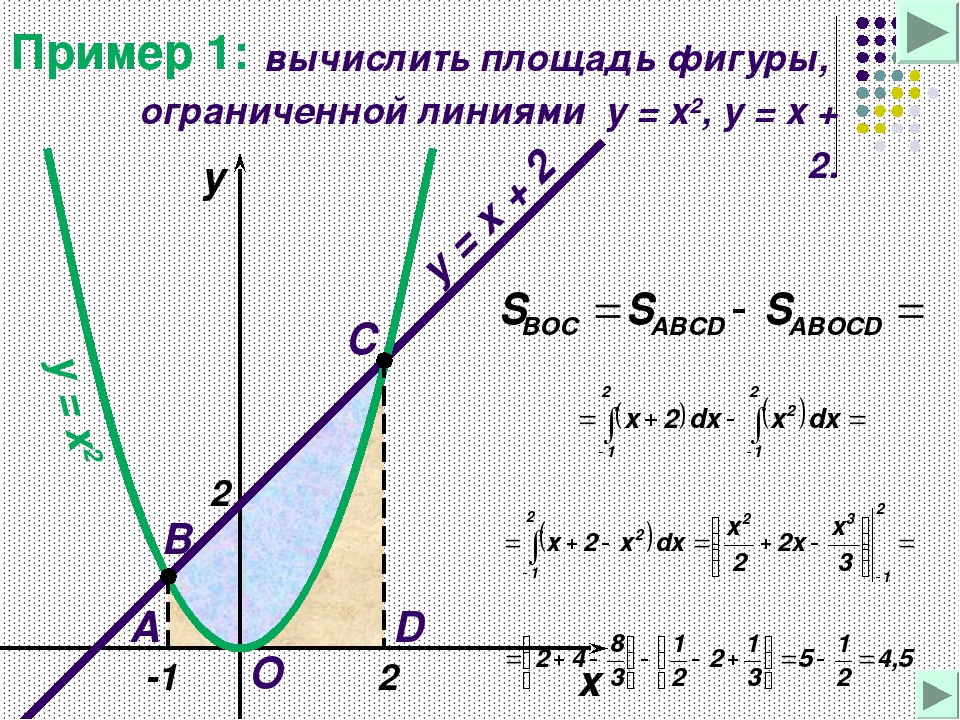
Пределы интегрирования — прямые x1=a, x2=b — ограничивают фигуру (a<b чаще всего это точки пересечения заданных кривых).
Данный цикл задач в первую очередь подойдет студентам мех-мата Львовского национального университета имени Ивана Франко для прохождения практикума из математического анализа.
Студенты других Вузов могут набираться практики на подобных интегралах, и изучать методику вычисления.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
Пример 2.81 (2397). Найти площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах ax=y2, ay=x2,(a>0).
Вычисление: Построим графики функций, которые ограничивают искомую площадь фигуры:
На графике они будут иметь следующий вид
Площадь между кривыми и нужно найти.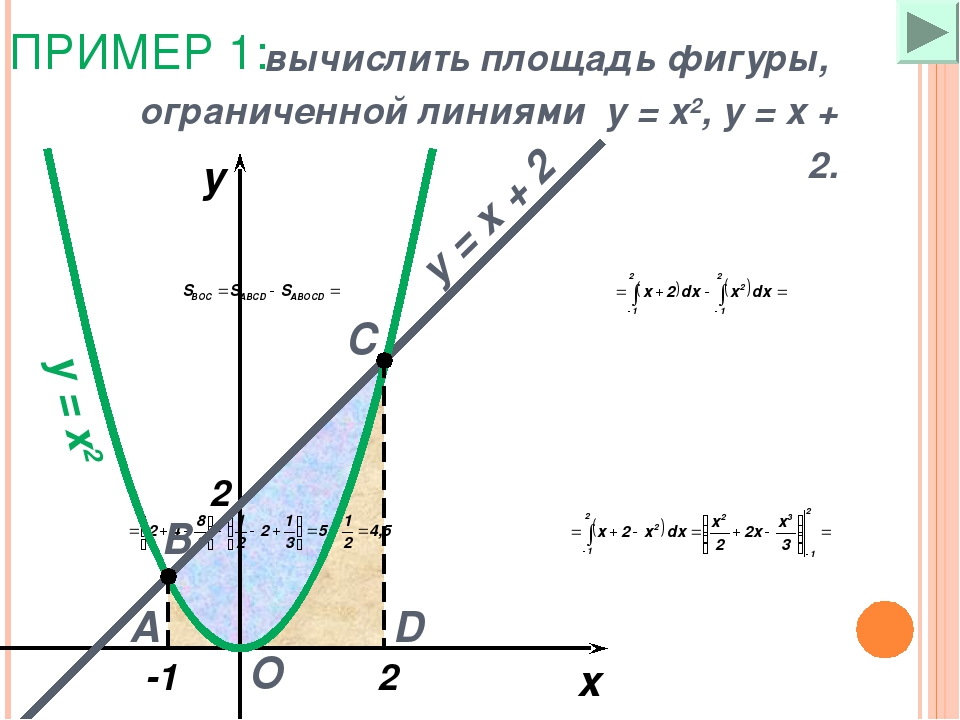 Как правило, Вам редко будет известно сам график, поэтому в заданиях где не заданы области на которой находить площадь в первую очередь необходимо найти точки пересечения кривых.
Как правило, Вам редко будет известно сам график, поэтому в заданиях где не заданы области на которой находить площадь в первую очередь необходимо найти точки пересечения кривых.
Найдем пределы интегрирования, то есть точки абсцисс пересечения заданных функций y1(x)=y2(x):
Как видите таким условием есть условие равенства функций.
Из последнего уравнения получим две точки x1=0, x2=a.
Дальше, когда Вы не видите графика функций необходимо установить какая из кривых принимает большие значения. Это нужно лишь для того, чтобы с первого раза получить положительное значение площади фигуры. Поскольку площадь всегда больше нуля, а интеграл может принимать произвольные значения, то без проверки следующего условия для нахождения площади интеграл нужно брать за модулем.
Выбираем произвольную точку из отрезка интегрирования [0;a] и убеждаемся в правильности неравенства , то есть проверяем которая из кривых принимает большее значения .
Как отмечалось выше, это нужно для того, чтобы после интегрирования получить положительную площадь фигуры между кривыми.
Вычисляем площадь фигуры, которая ограничена заданными кривыми интегрированиям:
Здесь мы имели достаточно простые функции, поэтому возведя их к табличным интегралам найти площадь достаточно легко. Следующие примеры будут содержать все более тяжелые функции, для интегрирования которых нужно применять знание практически всех формул интегрирования.
Следует заметить: значения площадей (во всех заданиях) измеряются в квадратных единицах (кв. од.), об этом Вы должны помнить, однако для экономии места и времени здесь будут приведены лишь значения определенных интегралов.
Пример 2.82 (2398) Вычислить площадь фигуры, ограниченной кривыми y=x2, x+y=2.
Вычисление: По методике записываем уравнение кривых, которые ограничивают площадь фигуры:
y1(x)=x2, y2(x)=2-x.
Здесь функции выразить достаточно просто.
Вычислим пределы интегрирования, приравняв между собой функции y1(x)=y2(x):
x2=2-x.
Переносим переменные по одну сторону от знака равенства и решаем квадратное уравнение
x2+x-2=0;
(x+2)(x-1)=0.
Следовательно, корни уравнения x1=-2, x2=1.
Сам график кривых и фигуры, площадь которой ищем, приведен на рисунку
Подстановкой любой точки из промежутка [-2;1], например x=0 в функции убеждаемся, что выполняется неравенство
, поэтому .
Площадь фигуры вычисляем интегрированием разницы кривых в найденных пределах:
Площадь равна S=4,5 квадратных единиц.
По физическому содержанию площадь фигуры равна разнице площадей двух криволинейных трапеций. Первая отвечает за верхний график y2(x), нижняя криволинейная трапеция за функцию, которая принимает меньшие значения y2(x). Разница заключается в том, что здесь еще нужно определять пределы интегрирования.
Пример 2.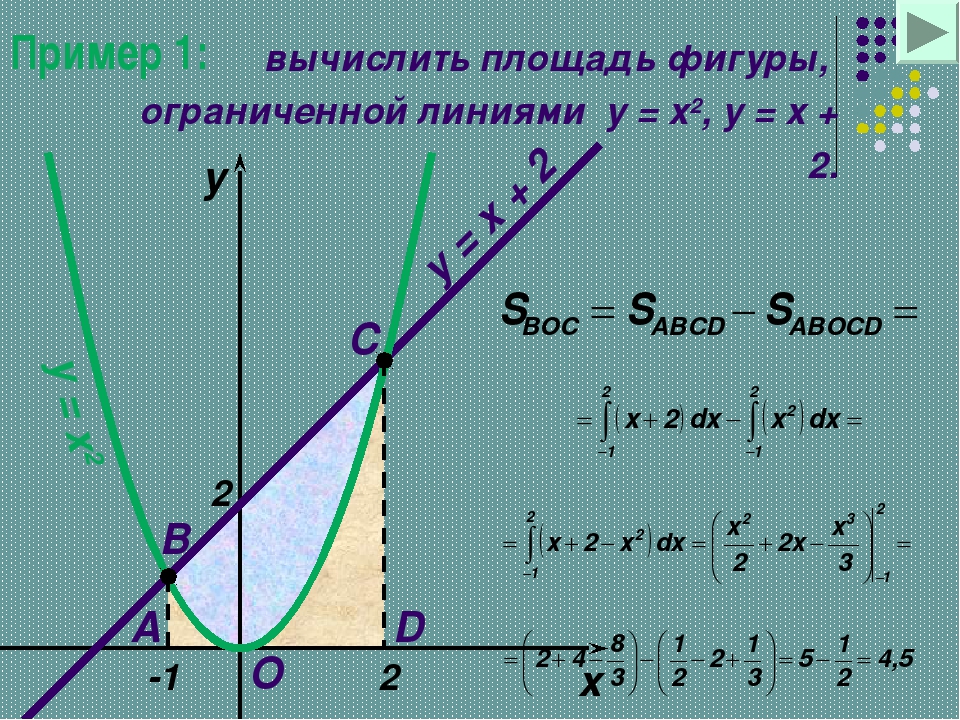 83 (2399) Найти площадь фигуры, ограниченной кривыми y=2x-x2, x+y=0.
83 (2399) Найти площадь фигуры, ограниченной кривыми y=2x-x2, x+y=0.
Вычисление: Запишем уравнение кривых, которые ограничивают искомую фигуру:
y1(x)=-x, y2(x)=2x-x2.
Из условия равенства функций y1(x)=y2(x) найдем пределы интегрирования:
2x-x2=-x;
x2-3x=0;
x (x-3) =0.
Следовательно, x1=0, x2=3.
Подстановкой единицы видим, что на промежутке [0;3] исполняется неравенство
, то есть .
Находим площадь фигуры ограниченной заданными кривыми:
Под интегралом простая квадратичная функция, поэтому само интегрирование не сложно.
Следующие функции будут более сложными в плане интегрирования, однако используя табличные интегралы площадь найти удается.
Пример 2.84 (2400) Найти площадь фигуры, ограниченной кривыми y=2x, y=2, x=0.
Вычисление: Запишем подынтегральные функции:
y1(x)=2x, y2(x)=2, а также прямую x1=0 (ограничивает фигуру по оси абсцисс).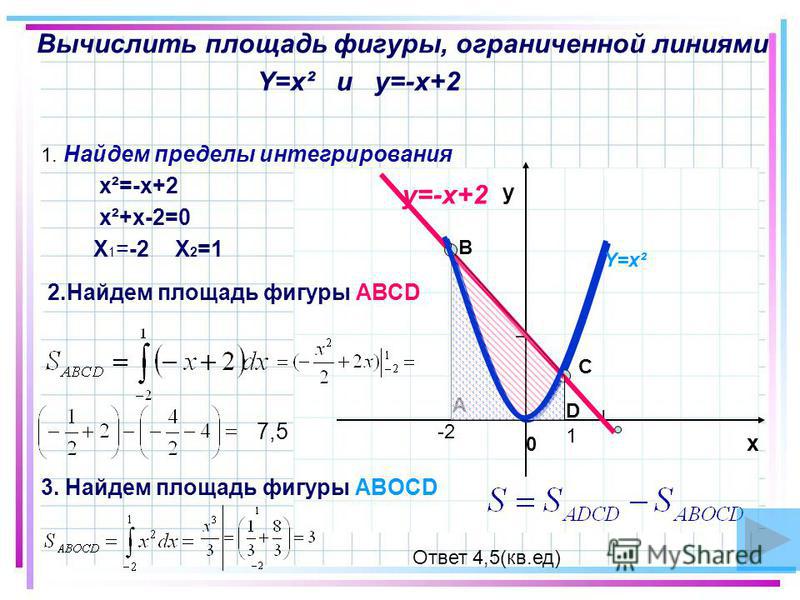
Найдем вторую границу интегрирования из условия равенства функций y1(x)=y2(x):
2x=2, 2x=21, отсюда имеем вторую точку x1=1.
На промежутке [0;1] исполняется неравенство , поэтому .
График степенной функции и прямой приведен ниже.
Площадь фигуры, которая ограничена кривыми равна интегралу:
При интегрировании получим логарифм.
На калькуляторах можете проверить, что площадь положительна.
Пример 2.85 (2401) Вычислить площадь фигуры, ограниченной кривыми y=x, y=x+sin2x, .
Вычисление: Запишем уравнение кривых, которые ограничивают площадь фигуры:
y1(x)=x, y2(x)=x+sin2x.
Дальше пределы интегрирования:
x1=0, x2=Pi (это известно нам по условию).
На промежутке справедливо неравенство
, поэтому .
Если бы существовала дополнительная точка пересечения, то площадь была бы равна сумме двух интегралов.
Площадь фигуры вычисляем интегрированием: квадрат синуса под интегралом понижаем и выражаем с помощью косинуса двойного угла, а дальше за классической формулой интегрирования
Площадь равна Pi/2, что приблизительно равно 1,5708.
Пример 2.86 (2402) Найти площадь фигуры, ограниченной кривыми
Вычисление: Переписываем функции
Найдем пределы интегрирования, то есть точки абсцисс пересечения заданных функций из условия y1(x)=y2(x):
Поскольку функция парная
то найдем половину площади и результат умножим на двойку.
Из условия находим
что пределы равны плюс, минус бесконечности.
Чтобы легко представить, что мы интегрируем наведем график подынтегральных функций
Учитывая четность функции интегрировать будем от 0 к бесконечности , а полученное значение умножим на двойку.
Получим несвойственный интеграл первого рода (детальнее о нем в части ІІІ).
Площадь фигуры вычисляем через предел интеграла:
В результате интегрирования получим арктангенс, который в предельном случае стремится к Pi/2.
Конечная формула достаточно компактна и удобна для расчетов, хотя с таким типом интегралов Вы знакомитесь впервые.
Пример 2.87 (2403) Вычислить площадь фигуры, ограниченной кривыми
Вычисление: Все Вы должны знать, что такой формулой задается уравнение эллипса.
Так как оси эллипса в канонической системе координат являются его осями симметрии, то эти оси делят эллипс на 4 равные части. Поэтому будем рассматривать часть эллипса, который находится в первом квадранте канонической (прямоугольной) системы координат.
Выражаем уравнение функции, которая ограничивает искомую площадь (четверть эллипса):
Запишем пределы интегрирования: из аналитической геометрии известно, что четверть эллипса ограничена прямыми x1=0, x2=a.
Для вычисления площади эллипса в самом интеграле необходимо выполнить замену переменных, что в свою очередь ведет к изменению пределов интегрирование. При этом придем к квадрату косинуса, который понижаем через косинус двойного угла.
В конце манипуляций приходим к табличным интегралам, которые легко интегрируем и подставляем пределы:
Получили классическую формулу площади эллипса S=Pi*a*b .
Видим, если эллипс вырождается в круг при (a=b=R), тогда формула площади круга S=Pi*R2.
Пример 2.88 (2404) Вычислить площадь фигуры, ограниченной кривыми y2=x2(a2-x2).
Вычисление: Так как все переменные в заданном уравнении входят в квадратах, то оси прямоугольной системы координат являются осями симметрии фигуры, которая ограничена этой линией, потому эти оси делят заданную фигуру на 4 равных части. Достаточно рассмотреть часть фигуры, которая заходиться в первом квадранте прямоугольной системы координат.
Построим график функции, которая ограничивает искомую площадь четвертины фигуры:
График неизвестной фигуры подобен на крылья бабочки.
При y=0 имеем два корня уравнения x1=0 и x2=a.
Площадь фигуры равна 4 умножить на интеграл с найденными пределами.
Во время интегрирования выполняем замену переменных и пределов интегрирования
Это позволяет перейти к показательной функции, которая легко интегрируется.
Всегда помните, что замена переменных под интегралом ведет к изменению пределов интегрирования.
Пример 2.89 Найти площадь фигуры, ограниченную линиями
Вычисление: Запишем графику функций, которые ограничивают искомую площадь фигуры:
Определим пределы интегрирования из условия y1(x)=y2(x):
отсюда x1=0 и x2=1.
Между функциями справедлива зависимость на [0;1], поэтому .
График функций, что анализируем следующий
Площадь фигуры через определенный интеграл равна 1/3 (сравните 2.81 при a=1) :
Пример 2.90 Вычислить площадь фигуры, ограниченной кривыми
Вычисление: Вычислим пределы интегрирования из условия равенства функций y1(x)=y2(x):
Из биквадратного уравнения получим значение точек пересечения:
x1=-1 и x2=1.
Сами же функции в прямоугольных координатах будут иметь вид
Интегрированием находим площадь фигуры (смотри рисунок и образец 2.89) :
Первый интеграл даст арктангенс, запомните хорошо эту формулу.
Пример 2.91 Вычислить площадь фигуры, ограниченной кривыми y=ex, y=e-x,x=1.
Вычисление: Из условия, которое Вы из-за повторяемости должны выучить y1(x)=y2(x) находим точки пересечения кривых:
ex=e-x,x=-x, 2x=0, следовательно, x1=0.
x2=1 (известно за условием).
График функций следующий
Экспоненту интегрировать не трудно, а площадь фигуры выражается формулой (смотри рисунок и образец 2.84) :
Пример 2.92 Найти площадь фигуры, ограниченной кривыми y=ln(x), y=ln2(x).
Вычисление: Пределы интегрирования из условия равенства функций y=ln(x), y=ln2(x) равны x1=1 и x2=e.
Интегрированием логарифмов находим площадь фигуры (смотри рисунок):
Здесь надо проинтегрировать по частям, положив ln(x) =u, (ln2(x)=u) и dx=dv. Попробуйте промежуточные действия провести самостоятельно.
Пример 2.93 Вычислить площадь фигуры, ограниченной кривыми
y=ln(x), y=ln(a), y=ln(b), x=0, где 0<a<b.
Вычисление: Построим графики функций, которые ограничивают искомую площадь фигуры:
x (y) =ey (то есть обратная функция к заданной функции y(x)=ln(x)) .
Такой прием применяют, когда пределы интегрирования параллельны оси Оx, то есть y=const.
Запишем пределы интегрирования:
y1=ln(a), y2=ln(b) (берем из начального условия).
График искомой фигуры следующий
Площадь фигуры, которая ограничена заданными кривыми:
Пример 2.94 Найти площадь фигуры, ограниченной кривыми
Вычисление: Пределы интегрирования в формуле площади находим из условия y1(x)=y2(x):
ln(x)/(4x)=x*ln(x).
Упростив на логарифм (если он больше нуля), получим
1=4x2; 4x2-1=0, x1=1/2.
Из условия на логарифм (=0) получим
ln(x) =0; x2=1.
ОДЗ: x>0.
График фигуры в прямоугольных координатах следующий
Площадь фигуры между кривыми (на [0,5;1]) находим интегрированием:
для вычисления интегралов используем метод замены переменных
Вычисление не так просты, поэтому с превращениями попробуйте разобраться самостоятельно.
Пример 2.95 Вычислить площадь фигуры, ограниченной кривыми y=arcsin(x), y=arccos(x), y=0.
Вычисление: Находим точки пересечения кривых из равенства x1(y)=x2(y):
sin(x)=cos(y), отсюда y1=0 (известно за условием) и y1=Pi/4 (образец 2.93).
На графике это выглядит следующим образом
Учитывая справедливость неравенства вычисляем площадь фигуры:
Думаю, что с такими заданиями на экзамене или модулях Вы справитесь.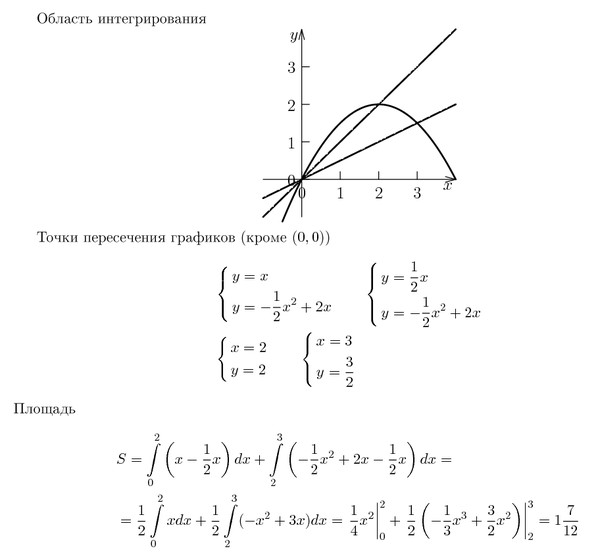
Пример 2.96 Найти площадь фигуры, ограниченной кривыми y=tg(x), y=2/3*cos(x), x=0.
Вычисление: Найдем пределы интегрирования, то есть абсциссы точек пересечения заданных функций y1(x)=y2(x):
tg(x)=2/3*cos(x), отсюда
(вторая точка известна за условием).
Кривые на плоскости имеют вид
Площадь фигуры, которая ограничена заданными кривыми () равна интегралу:
Пример 2.97 (2400) Вычислить площадь фигуры, ограниченной кривыми y=|ln(x)|, y=0, x=0,1; x=10.
Вычисление: Выписываем пределы интегрирования x1=0,1; x2=10 из начального условия.
Как строить модуль от логарифма Вы, по-видимому, еще не забыли
Площадь фигуры равна сумме двух интегралов, причем первый берем со знаком минус ():
Во время интегрирования использовали интегрирование частями.
Пример 2.98 (2400) Найти площадь фигуры, ограниченной кривыми y=(x+1)2, x=sin(Pi*y), y=0 .
Вычисление: Построим график функций, которые ограничивают искомую площадь фигуры:
(здесь взяли обратную функцию к заданной y1(x)=(x+1)2), x2=sin(Pi*y).
Выпишем пределы интегрирования:
y1=0; y2=1 (известно за условием).
График функций приведен ниже
Неизвестную площадь фигуры вычисляем интегрированием ():
Пример 2.99 Вычислить площадь фигуры, ограниченной кривыми y=sin(x), y=cos(x), y=0
Вычисление: Из рисунку видно, что площадь S лучше разбить на две части: S=S1+S2.
Запишем уравнение функций, которые ограничивают искомую площадь фигуры:
Интегрируем синус и косинус функции и находим площадь.
Второй вариант заключается в интегрировании разницы обратных функций по y.
Пример 2407 Найти площадь фигуры, ограниченной кривыми (циссоида Диокла) x=2a (a>0).
Вычисление: Поскольку график функции симметричен относительно оси Ox, то будем рассматривать половину площади фигуры (над осью Ox) и результат умножим на 2.
В точке x=2a функция не определена, поэтому будем иметь интеграл второго рода (детальнее смотрите часть ІІІ), он совпадает и, следовательно, площадь будет выражена числом.
Запишем пределы интегрирования:
x1=0 (потому что ) x2=2a (за условием).
График функций следующий
Площадь фигуры, что ограниченна заданной кривой находится достаточно непростым интегрированием
Здесь пришлось трижды выполнять замену переменных, чтобы прийти к правильному ответу.
Еще раз внимательно разберите интеграл.
Пример 2408 Вычислить площадь фигуры, ограниченной кривыми (трактриса), y=0.
Вычисление: Трактриса — кривая, по которой двигается объект, когда его тянуть по горизонтальной плоскости за бечевку фиксированной длины, если направление движения тягача является ортогональным к начальному положению бечевки и скорость тягача бесконечно малая величина.
Очевидно, что (смотри рисунок).
Принимая к сведению, что положительному приросту x отвечает отрицательный прирост y, и что фигура не квадрируема (в общем понимании), допускаем
где дифференциал за x находим через производную
Площадь фигуры через определенный интеграл равна
Следующим идет материал из которого Вы научитесь находить площадь фигуры, ограниченной кривыми заданными параметрически.
Урок 24. вычисление площадей с помощью интегралов — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №24. Вычисление площадей с помощью интегралов.
Перечень вопросов, рассматриваемых в теме
1) Нахождение площади фигуры, ограниченной графиками функций с помощью определенного интеграла.
2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница
3) Решение задач, с помощью формулы Ньютона – Лейбница
Формула Ньютона – Лейбница
Основная литература:
Колягин Ю. М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].
Отрезок [a;b] называют основанием этой криволинейной трапеции
формула Ньютона – Лейбница
Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым. ( зависит от расположения криволинейной трапеции)
Примеры и разбор решения заданий тренировочного модуля
№1 Вычислите площадь фигуры, ограниченной линиями y= x, y = 5 – x, x = 1, x = 2, используя определенный интеграл.
Решение. Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b).
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) — F(а) , это и будет ответ
Решение: Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) — F(а) , это и будет ответ.
Решение. S=SOAB +SABC
№3. Найти площадь криволинейной трапеции (х-1)2, ограниченной линиями х=2 и х=1, осью 0х
Решение:
Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) — F(а), это и будет ответ.
Урок алгебры в 11-м классе на тему: «Вычисление площадей фигур»
Цели урока:
1) Повторить, закрепить и расширить знания по заданной теме.
2) Уметь самостоятельно применять полученные знания по теме к решению задач.
3) Уметь рационально решать задачи.
4) Творчески подходить к решению конкретной задачи.
1. Повторение теоретического материала
Фронтальный опрос (по таблице “Площади фигур”)
Вопрос: Как найти площади изображенных фигур?
Ответ:
2. Разминка (на 3 мин. , в тетрадях только
решение)
, в тетрадях только
решение)
Задача. Найти площади изображенных фигур. Ответы с комментариями.
3. Программированный контроль
Задания |
Ответы |
||||
Вычислить площадь фигуры, ограниченной линиями: |
|||||
I вариант |
II вариант |
1 |
2 |
3 |
4 |
y=x2+2, y=x+2 |
y=-x2+4, y=-x+4 |
7 |
1/6 |
2/3 |
1/3 |
y=sin2x,y=0 x=0, x=/4 |
y=cos2x, y=0 x=-/4, x=/4 |
2 |
-1 |
1/2 |
1 |
y=-2/х, y=2 x=-4, x=-1 |
y=-1/х, y=1 x=-3, x=-1 |
6-4ln2 | 2-ln3 |
2ln2 |
2-3ln2 |
Верные ответы: I вариант: 2,3,1 II вариант: 2,4,2
4. Решение задач на закрепление (с проверкой у
доски)
Решение задач на закрепление (с проверкой у
доски)
1) Найти площадь фигуры, ограниченной линиями
2) Фигура, ограниченная линиями y=x+6, x=1, y=0 делится параболой y=x2+2x+4 на две части. Найти площадь каждой части.
3) Найти ту первообразную F(x) функции f(x)=2x+4, график которой касается прямой у=6х+3. Вычислить площадь фигуры, ограниченной графиком найденной первообразной и прямыми у=6х+3 и у=0.
4) Составить формулы для нахождения площадей фигур, изображенных на таблице:
Ответы с комментариями:
5) Интересная задача. Найти сумму площадей бесконечного количества фигур, заштрихованных на рисунках:
(Аргумент каждой следующей функции увеличивается в 2 раза)
Указания к решению: sin nx=0 ; x=/n;
где n=1,2,4,8,16…;
S=2+1+1/2+1/4+1/8+…=2/(1-1/2)=4
Ответ: 4.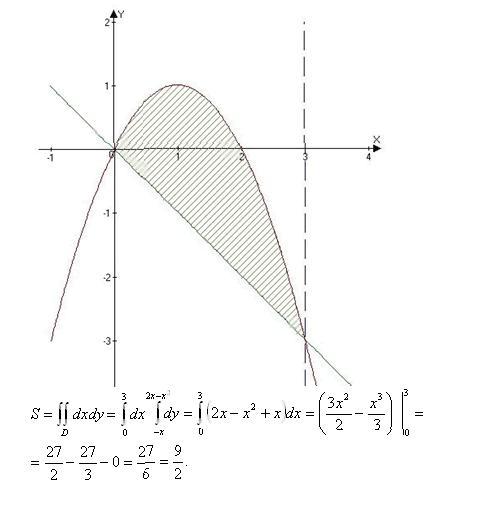
5. Задачи с индивидуальным подходом
Задачи, которые прокомментируют сейчас ученики, имеют индивидуальный подход. Поэтому, прежде чем приступить к их решению, надо проанализировать заданную ситуацию. Решения этих задач в тетрадях не пишутся, дома же вы их решите, по возможности, несколькими способами.
1) Найти площадь фигуры, ограниченной линиями y=x2-4x+8 и y=3x2-x3, если х[-2;3]
Решение:
- Если не рисовать графиков данных функций, то надо узнать имеют ли эти графики общие точки на (-2;3).Для этого надо решить уравнение:
3x2-x3= x2-4x+8. Итак, х=2 и х=-2. 2(-2;3).
Не зная, график какой из функций находится выше другого на (-2;2) и (2;3], площадь фигуры находится так
- Если же нарисовать графики данных функций (что очень не сложно), то замечаем, что всюду на [-2;3] выполняется неравенство: х2-4x+83х2-х3
Сравнивая формулы, полученные для вычисления
площади S, видим, что в данном примере значительно
легче искать площадь после того, как нарисованы
графики функций. А можно ли всё-таки решить
задачу, не делая рисунка? Найдите ещё один способ
решения! Но есть задачи, в которых построение
графиков затруднено.
А можно ли всё-таки решить
задачу, не делая рисунка? Найдите ещё один способ
решения! Но есть задачи, в которых построение
графиков затруднено.
2) Найти площадь фигуры, ограниченную линиями: y=x2-4x+sin2x/2 и y=-3-cos2x/2, если х[2;3].
Решение:
Так как графики данных функций построить трудно, то можно выяснить соотношение между функциями, не используя графиков. Исследуем разность данных функций:
x2-4x+sin2x/2-(-3-cos2x/2)=x2-4x+4=(х-2)2 0
Следовательно, x2-4x+sin2x/2>-3-cos2x/2 на [2;3], а, значит, график первой функции лежит выше графика второй функции и
3) Вычислить площадь фигуры, ограниченной данными линиями:y=x2 при x0, y=1, y=4, x=0
Решение:
Данная фигура симметрична криволинейной
трапеции, ограниченной прямыми х=1, х=4, у=0,
графиком функции , обратной у=х2, x0. Поэтому эти фигуры имеют равные
площади и .
Поэтому эти фигуры имеют равные
площади и .
А всегда ли рационально использовать интеграл при нахождении площади фигуры?
4) Найти площадь фигуры, ограниченной прямыми у=3х+1, у=9-х, у=х+1.
Решение:
Вершины полученного ABC имеют координаты: А(0;1), В(2;7), С(4;5).
Можно заметить, что ABC — прямоугольный (произведение угловых коэффициентов прямых у=х+и у=9-х равно -1). Поэтому применение интеграла для вычисления S(ABC) не рационально. Её всегда можно найти как разность площадей треугольников, у которых известны высота и основание или же можно использовать координатный метод.
6. Домашнее задание
Найти площади фигур, ограниченных линиями (1-7)
- у=х2 (х0), у=1, у=4, х=0
- у=х2-4х+8, 3х2-х3, если если х[-2;3]
- у=х2-4х+sin2(x/2), y=-3-cos2(x/2), если х[2;3]
- у=3х+1, у=9-х, у=х+1
- у=|x-2|,
- x|y|=2;x=1;x=3
- y= arcsin x; у=0; x=0,5; x=1
- При каком значении а прямая х=а делит площадь фигуры, ограниченной линиями у=2/х; х=1; х=3 в отношении 1:3?
- Вычислить
исходя из его геометрического смысла.

Составить карточку (можно несколько) для зачета, в которой должны быть:
- Теоретический вопрос: (определение, свойств без доказательства)
- Теоретический вопрос: (с доказательством)
- Пример на вычисление неопределенного интеграла (одним из методов)
- Пример на вычисление определённого интеграла.
- Пример на нахождение первообразной сложной функции.
- Пример на нахождение площади фигуры.
7. Итог урока
Страница не найдена — Саранский политехнический техникум
Это выглядит, как будто ничего не было найдено в этом месте. Может быть, попробовать поиск или один из приведенных ниже ссылок?
Архивы Выберите месяц Май 2021 Апрель 2021 Март 2021 Февраль 2021 Январь 2021 Декабрь 2020 Ноябрь 2020 Октябрь 2020 Сентябрь 2020 Август 2020 Июль 2020 Июнь 2020 Май 2020 Апрель 2020 Март 2020 Февраль 2020 Январь 2020 Декабрь 2019 Ноябрь 2019 Октябрь 2019 Сентябрь 2019 Август 2019 Июль 2019 Июнь 2019 Май 2019 Апрель 2019 Март 2019 Февраль 2019 Январь 2019 Декабрь 2018 Ноябрь 2018 Октябрь 2018 Сентябрь 2018 Август 2018 Июль 2018 Июнь 2018 Май 2018 Апрель 2018 Март 2018 Февраль 2018 Январь 2018 Декабрь 2017 Ноябрь 2017 Октябрь 2017 Сентябрь 2017 Август 2017 Июль 2017 Июнь 2017 Май 2017 Январь 2017 Декабрь 2016 Ноябрь 2016 Октябрь 2016 Сентябрь 2016 Август 2016 Июль 2016
РубрикиВыберите рубрикуБез рубрики
- «Моя малая родина Ардатов!»
- «Один день из жизни студента»
- 205,206,301,302,303,304 группа
- 305, 306, 401, 402, 403, 404 группа
- 75 лет техникуму
- Abilympics Russia
- I Республиканская заочная интернет-конференция
- II Региональный чемпионат «Абилимпикс»
- II Республиканская заочная интернет-конференция » Педагогическая деятельность в системе образования XXI века: от теории к практике»
- III Региональный чемпионат «Абилимпикс»
- III Региональный чемпионат «Абилимпикс» в Республике Мордовия по компетенции «Поварское дело»
- IX Межрегиональная Интернет-конференция
- WorldSkills Russia
- АБИЛИМПИКС
- Абитуриентам
- Акимова Анастасия Николаевна
- Акция «Безопасные окна»
- Беседа ГБПОУ РМ «Саранский политехнический техникум»
- Бойцова Наталья Сергеевна
- Бусаров Максим Михайлович
- Василькина Татьяна Николаевна
- Видео о техникуме
- ВНИМАНИЕ ГРИПП!
- Волонтерский отряд «Открытое сердце»
- Всероссийская акция «Стоп ВИЧ/СПИД»
- Всероссийский интернет-семинар «Современное профессиональное образование: опыт, проблемы, перспективы»
- Выпускникам
- Герои войны – ровесники мои.

- Главная
- ГОЛИКОВ МИХАИЛ ЕГОРОВИЧ
- ГОЛИКОВСКИЕ ЧТЕНИЯ
- Голиковские чтения
- Голиковские чтения 2020
- ГОСТИНИЧНОЕ ДЕЛО
- ГОСТИНИЧНЫЙ СЕРВИС МФЦ СПТ
- ГРАФИК СОБЕСЕДОВАНИЙ
- График учебного процесса
- ГРАФИК УЧЕБНОГО ПРОЦЕССА(РУЗАЕВСКОЕ ОТДЕЛЕНИЕ)
- Демонстрационный экзамен
- День знаний — подробности
- Детский телефон доверия
- ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
- Документы
- Дополнительное профессиональное образование
- Доступная среда
- Дуальное образование
- Жизнь техникума
- Замены
- Замены в расписании
- Заочная научно — практическая конференция «Межведомственное взаимодействие ССУЗ с органами системы профилактики по предупреждению асоциальных проявлений среди молодежи»
- Заочная научно — практическая конференция «Межведомственное взаимодействие ССУЗ с органами системы профилактики по предупреждению асоциальных проявлений среди молодежи» Положение о Конференции
- Заочная научно — практическая конференция «Межведомственное взаимодействие ССУЗ с органами системы профилактики по предупреждению асоциальных проявлений среди молодежи» СЕРТИФИКАТЫ
- Зверева Елизавета Алексеевна
- ИНФОРМАЦИОННЫЕ СИСТЕМЫ И ПРОГРАММИРОВАНИЕ
- Информация для лиц с ограниченными возможностями
- ИНФОРМАЦИЯ ДЛЯ РОДИТЕЛЕЙ
- История техникума
- ИТОГИ КОНКУРСА
- ИТОГИ КОНКУРСА
- Калашников Денис Игоревич
- Караваева Мария Михайловна
- Кокнаева Владислава Юрьевна
- Контакты
- Корецкая Елена Александровна
- Королев Дмитрий Вячеславович
- Кузьминова Алина Сергеевна
- Медпункт
- Международное сотрудничество
- Межрегиональный заочный конкурс интегрированных уроков по дисциплинам гуманитарного цикла
- Методическая копилка
- Методическая копилка
- Методическая копилка
- Методическая копилка
- Методическая копилка
- Многофункциональный центр
- Мы памяти этой свято верны!
- Навигатор ВУЗ абитуриента 2017
- НАСТАВНИЧЕСТВО
- Наставничество
- Научно-методическая работа
- Научно-методическая работа
- Наша гордость
- О техникуме
- Обмен педагогическим опытом
- ОБОБЩЕНИЕ ОПЫТА
- Обобщение опыта Судуткина
- Обратная связь
- Оксин Даниил Владимирович
- Олимпиады профессионального мастерства
- Онлайн подача документов
- Оператор станков с программным управлением
- Организация и проведение безопасного отдыха в 2018 году
- ПАРИКМАХЕР
- Партнеры
- Педагогический опыт
- Повышение квалификации
- ПОРЯДОК ПРИЕМА 2017
- Прием 2016
- ПРИЕМ 2021
- ПРИЕМНАЯ КОМИССИЯ 2017
- ПРИКАЗ ОБ АППЕЛЯЦИОННОЙ КОМИССИИ
- ПРИКАЗ О ПРИЕМНОЙ КОМИССИИ
- Пример страницы
- Программа развития ГБПОУ РМ «Саранский политехнический техникум» на 2018-2024 годы
- Производственная практика
- Промышленно-технологический центр СПТ
- Профилактика гриппа и ОРВИ
- РАСПИСАНИЕ ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНОВ
- Результаты испытаний
- РЕЗУЛЬТАТЫ ИСПЫТАНИЙ
- Результаты независимой оценки качества оказания услуг организациями
- Реорганизации структуры техникума
- Республиканские предметные олимпиады среди ССУЗ РМ по предметам общеобразовательного цикла
- Республиканский заочный конкурс исследовательских работ, посвященный 75 – летию Победы в Великой Отечественной войне 1941 – 1945 гг.
 , «Герои войны – ровесники мои»
, «Герои войны – ровесники мои» - Республиканский заочный конкурс презентаций, буклетов, плакатов «75 лет со дня Победы в Великой Отечественной войне»
- Рузаевское отделение
- РУЗАЕВСКОЕ ОТДЕЛЕНИЕ
- РУЗАЕВСКОЕ ОТДЕЛЕНИЕ
- С Днем весны, мира и труда!
- Сведения об образовательной организации
- Сивов Дмитрий Николаевич
- Символика техникума
- Символика техникума
- Системы ротаций баннеров
- Согласие на обработку персональных данных
- Сорокина Татьяна Михайловна
- Специальности
- Списки абитуриентов
- СТАЖИРОВКА
- Студентам
- График учебного процесса
- ПРАВИЛА ПОВЕДЕНИЯ И ОБЯЗАННОСТИ СТУДЕНТА
- Расписание занятий
- 1 курс
- 1 курс
- 101, 102, 103, 104, 105, 106 группа
- 107,108,201,202,203,204 группа
- 2 курс
- Расписание звонков
- Студендческий совет
- ТЕХНОЛОГИЯ МЕТАЛЛООБРАБАТЫВАЮЩЕГО ПРОИЗВОДСТВА
- ТЕХНОЛОГИЯ ПАРИКМАХЕРСКОГО ИСКУССТВА
- Урекина Татьяна Владимировна
- Учебно-воспитательная деятельность
- Что нужно знать о коррупции
- Щербакова Ольга Владимировна
- Это важно знать!
, где \ (F \ left (x \ right) \) — любая первообразная от \ (f \ left (x \ right).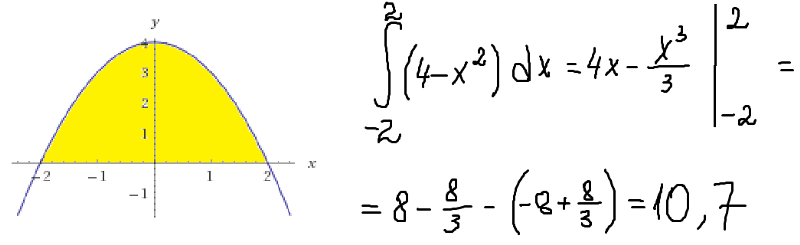 b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx}.b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx}} = {F \ left (b \ right) — G \ left (b \ right) — F \ left (a \ right) + G \ left (a \ right),} \]
b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx}.b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx}} = {F \ left (b \ right) — G \ left (b \ right) — F \ left (a \ right) + G \ left (a \ right),} \]
, где \ (F \ left (x \ right) \) и \ (G \ left (x \ right) \) — первообразные функций \ (f \ left (x \ right) \) и \ (g \ left (x \ right), \) соответственно.
Обратите внимание, что эта область всегда будет неотрицательной как \ (f \ left (x \ right) — g \ left (x \ right) \ ge 0 \) для всех \ (x \ in \ left [{a, b } \ right]. \)
Если есть точки пересечения, мы должны разбить интервал на несколько подинтервалов и определить, какая кривая больше на каждом подынтервале.\ prime \ left (t \ right), \) \ (y \ left (t \ right) \) здесь предполагается непрерывными на интервале \ (\ left [{a, b} \ right]. \) Кроме того то есть функция \ (x \ left (t \ right), \) должна быть монотонной на этом интервале.
Рис. 5. Если \ (x = x \ left (t \ right), \) \ (y = y \ left (t \ right), \) \ (0 \ le t \ le T \) являются параметрическими уравнениями гладкая кусочно замкнутая кривая \ (C \), пересеченная против часовой стрелки и ограничивающая область слева (рис.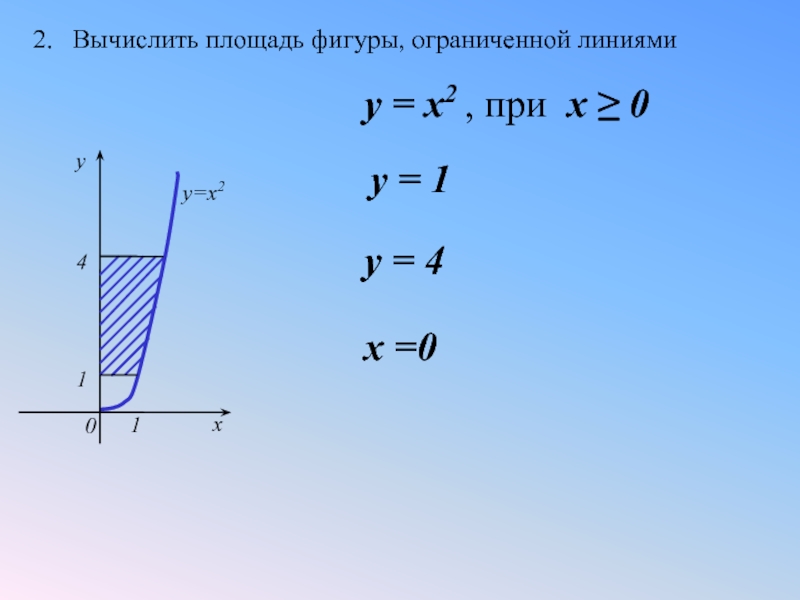 \ prime \ left (t \ right) y \ left (t \ right)} \ right] dt}.2} \) на интервале \ (\ left [{1, b} \ right] \) равно \ (1? \)
\ prime \ left (t \ right) y \ left (t \ right)} \ right] dt}.2} \) на интервале \ (\ left [{1, b} \ right] \) равно \ (1? \)
Пример 3
Найдите координату точки \ (a \), которая разделяет область под корневой функцией \ (y = \ sqrt {x} \) на интервале \ (\ left [{0,4} \ right] \) на равные части.Пример 4
Область ограничена вертикальными линиями \ (x = t \), \ (x = t + \ large {\ frac {\ pi} {2}} \ normalsize \), осью \ (x — \) и кривая \ (y = a + \ cos x, \), где \ (a \ ge 1. \). Определите значение \ (t \), при котором область имеет наибольшую площадь.{t + \ frac {\ pi} {2}}} = {a \ left ({t + \ frac {\ pi} {2}} \ right) + \ sin \ left ({t + \ frac {\ pi } {2}} \ right)} — {at — \ sin t} = {\ cancel {at} + \ frac {{a \ pi}} {2} + \ sin \ left ({t + \ frac {\ pi} {2}} \ right)} — {\ cancel {at} — \ sin t} = {\ frac {{a \ pi}} {2} + \ sin \ left ({t + \ frac {\ pi } {2}} \ right) — \ sin t.} \]Использование тождества разницы синусов
\ [{\ sin \ alpha — \ sin \ beta} = {2 \ cos \ frac {{\ alpha + \ beta}} {2} \ sin \ frac {{\ alpha — \ beta}} {2}, } \]
получаем
\ [{A = \ frac {{a \ pi}} {2}} + {2 \ cos \ frac {{t + \ frac {\ pi} {2} + t}} {2} \ sin \ frac {{\ cancel {t} + \ frac {\ pi} {2} — \ cancel {t}}} {2}} = {\ frac {{a \ pi}} {2} + 2 \ cos \ left ( {t + \ frac {\ pi} {4}} \ right) \ sin \ frac {\ pi} {4}} = {\ frac {{a \ pi}} {2} + 2 \ cos \ left ({ t + \ frac {\ pi} {4}} \ right) \ cdot \ frac {{\ sqrt 2}} {2}} = {\ frac {{a \ pi}} {2} + \ sqrt 2 \ cos \ left ({t + \ frac {\ pi} {4}} \ right). } \]
} \]
Область имеет наибольшую площадь, когда \ (\ cos \ left ({t + \ large {\ frac {\ pi} {4}} \ normalsize} \ right) = -1. \)
Решая это уравнение, находим
\ [{\ cos \ left ({t + \ frac {\ pi} {4}} \ right) = — 1,} \; \; \ Rightarrow {t + \ frac {\ pi} {4} = \ pi + 2 \ pi n,} \; \; \ Rightarrow {t = \ frac {{3 \ pi}} {4} + 2 \ pi n, \, n \ in \ mathbb {Z}.} \]
Пример 5.
Найдите площадь области, заключенной между кривой \ (y = \ sqrt {x + 1} \) и прямой \ (y = x + 1. \)Решение.0} = {\ left ({\ frac {2} {3} — 0 — 0} \ right) — \ left ({0 — \ frac {1} {2} + 1} \ right)} = {\ frac {2} {3} — \ frac {1} {2}} = {\ frac {1} {6}.} \]
Пример 6.
Найдите площадь области, заключенной между корневой кривой \ (y = \ sqrt {x} \) и прямой \ (y = kx, \), где \ (k \ gt 0. \)Решение.
Сначала находим точки пересечения обеих кривых:
\ [{\ sqrt x = kx,} \; \; \ Rightarrow {\ sqrt x — kx = 0,} \; \; \ Rightarrow {\ sqrt x \ left ({1 — k \ sqrt x} \ right) = 0,} \; \; \ Rightarrow {{x_1} = 0, \;} \ kern0pt {{x_2} = \ frac {1} {{{k ^ 2}}}. {2 \ pi} {\ left ({3 + 4 \ cos \ theta + \ cos 2 \ theta} \ right) d \ theta}} = {\ frac {1} {4} \ left.{2 \ pi}} = {\ frac {3} {{16}} \ cdot 2 \ pi} = {\ frac {{3 \ pi}} {8}} \]
{2 \ pi} {\ left ({3 + 4 \ cos \ theta + \ cos 2 \ theta} \ right) d \ theta}} = {\ frac {1} {4} \ left.{2 \ pi}} = {\ frac {3} {{16}} \ cdot 2 \ pi} = {\ frac {{3 \ pi}} {8}} \]
Исчисление I — площадь между кривыми
Показать мобильное уведомление Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон).Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 6-2: Площадь между кривыми
В этом разделе мы собираемся найти область между двумя кривыми. На самом деле есть два случая, которые мы собираемся рассмотреть.
На самом деле есть два случая, которые мы собираемся рассмотреть.
В первом случае мы хотим определить область между \ (y = f \ left (x \ right) \) и \ (y = g \ left (x \ right) \) на интервале \ (\ left [{ яркий]\). Мы также будем предполагать, что \ (f \ left (x \ right) \ ge g \ left (x \ right) \). Взгляните на следующий рисунок, чтобы понять, на что мы изначально будем смотреть.
В разделе «Формулы площади и объема» главы «Дополнительно» мы вывели следующую формулу для площади в данном случае.{{\, d}} {{f \ left (y \ right) — g \ left (y \ right) \, dy}} \ label {eq: eq2} \ end {уравнение} \]
Теперь \ (\ eqref {eq: eq1} \) и \ (\ eqref {eq: eq2} \) — совершенно удобные формулы, однако иногда легко забыть, что они всегда требуют, чтобы первая функция была большей из две функции. Поэтому вместо этих формул мы будем использовать следующие «словесные» формулы, чтобы убедиться, что мы помним, что площадь всегда является «большей» функцией минус «меньшей» функцией.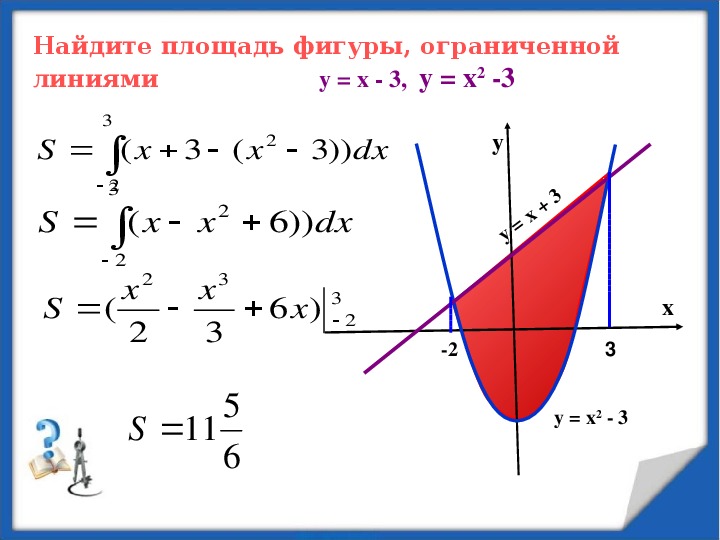 2} \) и \ (y = \ sqrt x \).Показать решение
2} \) и \ (y = \ sqrt x \).Показать решение
Прежде всего, что мы подразумеваем под «замкнутой территорией». Это означает, что интересующая нас область должна иметь одну из двух кривых на каждой границе области. Итак, вот график двух функций с заштрихованной областью.
Обратите внимание, что мы не берем какую-либо часть области справа от точки пересечения этих двух графиков. В этой области нет границы с правой стороны, поэтому она не является частью замкнутой области.2} \) является верхней функцией, и они будут правильными для подавляющего большинства \ (x \) ‘s. Однако в данном случае это младшая из двух функций.
Пределы интегрирования для этого будут точками пересечения двух кривых. В этом случае довольно легко увидеть, что они будут пересекаться в точках \ (x = 0 \) и \ (x = 1 \), так что это пределы интегрирования.
Итак, интеграл, который нам потребуется вычислить, чтобы найти площадь, равен
. 2} \, dx}} \\ & = \ left.1 \\ & = \ frac {1} {3} \ end {align *} \]
2} \, dx}} \\ & = \ left.1 \\ & = \ frac {1} {3} \ end {align *} \]Прежде чем перейти к следующему примеру, следует отметить несколько важных моментов.
Во-первых, почти во всех этих задачах граф требуется. Часто ограничивающую область, которая дает пределы интегрирования, трудно определить без графика.
Кроме того, без графика часто бывает сложно определить, какая из функций является верхней, а какая нижней функцией.Это особенно верно в случаях, подобных последнему примеру, где ответ на этот вопрос фактически зависел от диапазона значений \ (x \), которые мы использовали.
Наконец, в отличие от площади под кривой, которую мы рассматривали в предыдущей главе, площадь между двумя кривыми всегда будет положительной. Если мы получим отрицательное число или ноль, мы можем быть уверены, что где-то допустили ошибку, и нам нужно будет вернуться и найти ее.
Также обратите внимание, что иногда вместо того, чтобы говорить регион, заключенный в, мы говорим регион, ограниченный. 2}}} \), \ (y = x + 1 \), \ (x = 2 \) и ось \ (y \) -.
Показать решение
2}}} \), \ (y = x + 1 \), \ (x = 2 \) и ось \ (y \) -.
Показать решение
В этом случае последние две части информации, \ (x = 2 \) и ось \ (y \), сообщают нам правую и левую границы области. Также напомним, что ось \ (y \) задается линией \ (x = 0 \). Вот график с заштрихованной областью.
Здесь, в отличие от первого примера, две кривые не пересекаются. Вместо этого мы полагаемся на две вертикальные линии, чтобы ограничить левую и правую стороны области, как мы отметили выше
Вот интеграл, который даст площадь.2} + 10 \) и \ (y = 4x + 16 \). Показать решение
В этом случае точки пересечения (которые нам в конечном итоге понадобятся) будет нелегко идентифицировать по графику, поэтому давайте займемся их получением. Обратите внимание, что для большинства этих проблем вы не сможете точно определить точки пересечения на графике, поэтому вам нужно будет определить их вручную. 2} — 4x — 6 & = 0 \\ 2 \ left ({x + 1} \ right) \ left ({x — 3} \ right) & = 0 \ end {align *} \]
2} — 4x — 6 & = 0 \\ 2 \ left ({x + 1} \ right) \ left ({x — 3} \ right) & = 0 \ end {align *} \]
Итак, похоже, что две кривые пересекутся в точках \ (x = — 1 \) и \ (x = 3 \).Если они нам нужны, мы можем получить значения \ (y \), соответствующие каждому из них, вставив значения обратно в любое из уравнений. Мы предоставим вам проверить, что координаты двух точек пересечения на графике равны \ (\ left ({- 1,12} \ right) \) и \ (\ left ({3,28} \ right) ) \).
Также обратите внимание, что если вы не умеете строить графики, знание точек пересечения может помочь хотя бы в начале построения графика. Вот график региона.
Теперь с помощью графика мы можем определить верхнюю и нижнюю функцию, и теперь мы можем найти замкнутую область.2} + 10 \), \ (y = 4x + 16 \), \ (x = — 2 \) и \ (x = 5 \). Показать решение
Итак, функции, используемые в этой задаче, идентичны функциям из первой задачи.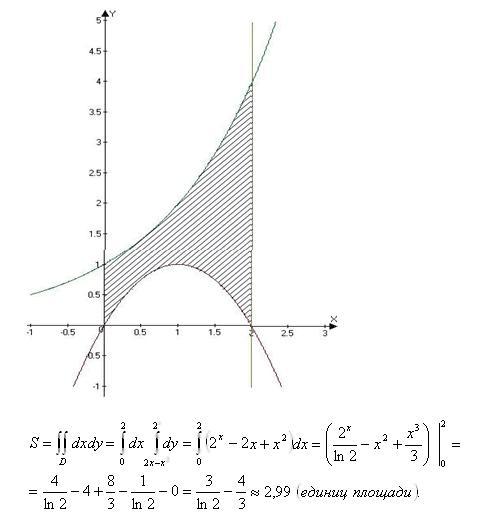 Разница в том, что мы расширили ограниченную область за пределы точек пересечения. Поскольку это те же функции, которые мы использовали в предыдущем примере, мы больше не будем утруждать себя поиском точек пересечения.
Разница в том, что мы расширили ограниченную область за пределы точек пересечения. Поскольку это те же функции, которые мы использовали в предыдущем примере, мы больше не будем утруждать себя поиском точек пересечения.
Вот график этого региона.
Хорошо, у нас тут небольшая проблема.Наша формула требует, чтобы одна функция всегда была верхней функцией, а другая функция всегда была нижней функцией, а здесь этого явно нет. Однако на самом деле проблема не в этом, как может показаться на первый взгляд. Есть три области, в которых одна функция всегда является верхней функцией, а другая всегда является нижней функцией. Итак, все, что нам нужно сделать, это найти площадь каждой из трех областей, что мы можем сделать, а затем сложить их все.
Вот площадь.5 \\ & = \ frac {{14}} {3} + \ frac {{64}} {3} + \ frac {{64}} {3} \\ & = \ frac {{142}} {3 } \ end {align *} \]
Пример 5 Определите площадь области, заключенной в \ (y = \ sin x \), \ (y = \ cos x \), \ (x = \ frac {\ pi} {2} \) и \ ( у \) — ось.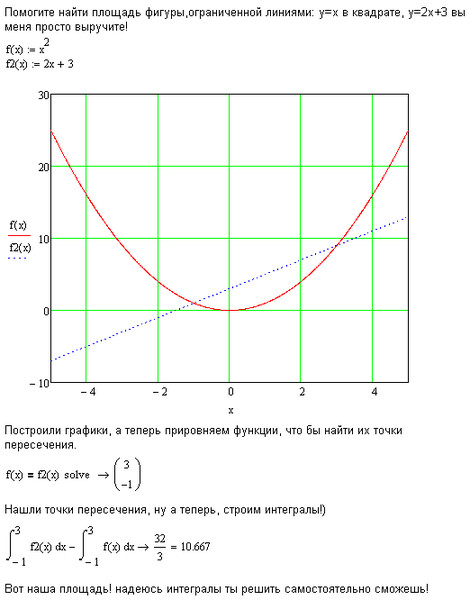 2} — 2y — 8 \\ 0 & = \ left ({y — 4} \ right) \ left ({y + 2} \ right) \ end {align *} \]
2} — 2y — 8 \\ 0 & = \ left ({y — 4} \ right) \ left ({y + 2} \ right) \ end {align *} \]
Итак, похоже, что две кривые пересекутся в точках \ (y = — 2 \) и \ (y = 4 \), или, если нам нужны полные координаты, они будут: \ (\ left ({- 1, — 2 } \ right) \) и \ (\ left ({5,4} \ right) \).
Вот эскиз двух кривых.
Теперь у нас будет серьезная проблема, если мы не будем осторожны. До сих пор мы использовали верхнюю функцию и нижнюю функцию. Для этого обратите внимание, что на самом деле есть две части региона, которые будут выполнять разные нижние функции. В диапазоне \ (\ left [{- 3, — 1} \ right] \) парабола фактически является как верхней, так и нижней функцией.
Чтобы использовать формулу, которую мы использовали до сих пор, нам нужно решить параболу для \ (y \).Это дает,
\ [y = \ pm \ sqrt {2x + 6} \], где «+» означает верхнюю часть параболы, а «-» — нижнюю часть. {{\, 5}} {{- x + 1 \, dx}} \\ & = \ left.{{\, d}} {{\ left (\ begin {array} {c} {\ mbox {right}} \\ {\ mbox {function}} \ end {array} \ right) — \ left (\ begin {array} {c} {\ mbox {left}} \\ {\ mbox {function}} \ end {array} \ right) \, dy}}, \ hspace {0,5 дюйма} c \ le y \ le d \ ]
{{\, 5}} {{- x + 1 \, dx}} \\ & = \ left.{{\, d}} {{\ left (\ begin {array} {c} {\ mbox {right}} \\ {\ mbox {function}} \ end {array} \ right) — \ left (\ begin {array} {c} {\ mbox {left}} \\ {\ mbox {function}} \ end {array} \ right) \, dy}}, \ hspace {0,5 дюйма} c \ le y \ le d \ ]
, и в нашем случае у нас есть одна функция, которая всегда слева, а другая всегда справа. Так что в данном случае это определенно правильный путь. Обратите внимание, что нам нужно будет переписать уравнение линии, поскольку оно должно быть в форме \ (x = f \ left (y \ right) \), но это достаточно легко сделать.4 \\ & = 18 \ end {align *} \]
Это то же самое, что мы получили, используя первую формулу, и это было определенно проще, чем первый метод.
Итак, в этом последнем примере мы видели случай, когда мы могли использовать любую формулу для определения площади. Однако второе было определенно легче.
Студенты часто приходят в класс по математике с мыслью, что единственный простой способ работать с функциями — использовать их в форме \ (y = f \ left (x \ right) \). 2} + 4y + 6 \, dy} } \\ & = \ left.3 = \ frac {{64}} {3} \ end {align *} \]
2} + 4y + 6 \, dy} } \\ & = \ left.3 = \ frac {{64}} {3} \ end {align *} \]
1.1: Площадь между двумя кривыми
- Последнее обновление
- Сохранить как PDF
- Площадь, ограниченная двумя функциями от \ (y \)
- Приложение
- Участники и атрибуты
Напомним, что площадь под кривой и над осью x может быть вычислена с помощью определенного интеграла.1 \\ & = \ big (- \ dfrac {3} {4} + \ dfrac {3} {2} \ big) — \ big (\ dfrac {3} {4} — \ dfrac {3} {2} \ big) \\ & = \ dfrac {3} {2} \ end {align *}. \]
Приложение
Пусть \ (y = f (x) \) будет функцией спроса на продукт, а \ (y = g (x) \) будет функцией предложения. Затем мы определяем точку равновесия как пересечение двух кривых. Излишек потребителя определяется площадью выше равновесного значения и ниже кривой спроса, в то время как излишек производителя определяется площадью ниже равновесного значения и выше кривой предложения.х \) и \ (у = 2х +1 \).
Затем мы определяем точку равновесия как пересечение двух кривых. Излишек потребителя определяется площадью выше равновесного значения и ниже кривой спроса, в то время как излишек производителя определяется площадью ниже равновесного значения и выше кривой предложения.х \) и \ (у = 2х +1 \).
Авторы и авторство
MathScene — Интеграция — Урок 3
MathScene — Интеграция — Урок 3| 2010 Rasmus ehf и Джанн Сак | Интеграция |
Урок 3
.Области между графиками функции
Области, ограниченные графиками функций, можно найти интегрированием.Для
Например, мы найдем площадь, ограниченную двумя графиками f (x) = x 2 + 5x 3
и y = x.
Это площадь, показанная в калькуляторе:
Начнем с найти точки пересечения двух графиков, чтобы дать нам границы площади:
х 2 + 5х 3 = х
х 2 + 4х 3 = 0 Упрощать.
(x 2 4x + 3) = 0 Взять 1 из кронштейна.
(x 1) (x 3) = 0 Факторизация .
(x 2 4x + 3) = 0
(х 1) (х 3) = 0
Точки пересечения — x = 1 и x = 3.Они лежат на прямой y = x, поэтому координаты y такие же, как координаты x, то есть (1, 1) и (3, 3).
Нам нужно только используйте координаты x для вычисления площади между каждой кривой и осью x.
Интеграл дает площадь между осью x и функцией f (x) = x 2 + 5x 3 на интервале от 1 до 3.
Это заштрихованная область графика ниже
Таким же образом это область между y = x и x — на том же интервале.На графике снова показана площадь нашел.
Если мы сложим эти два графика вместе, мы увидим, что область, которую мы хотим найти, — это разница между двумя выше.
Итак, мы просто
нужно взять разницу между двумя интегралами, чтобы найти площадь, которую мы
требовать.
|
Новое уравнение параболы будет f (x) = x 2 + 5x 3 2 = x 2 + 5x 5 и прямой y = x 2. На диаграмме показана новая ситуация.
Точки пересечения остаются такими же, поскольку мы добавили 2 к обеим сторонам уравнение. Ниже приведены расчеты, если вы не уверены!
х 2 + 5х 5 = х 2
х 2 + 4х 3 = 0 Упростим .
(х 2 4x + 3) = 0
(x 1) (x 3) = 0 Факторизация.
Снова решения x = 1 и x = 3. Интегрируя таким же образом, вы видите, что 2
снова упрощается, поэтому мы получаем тот же результат, что и раньше.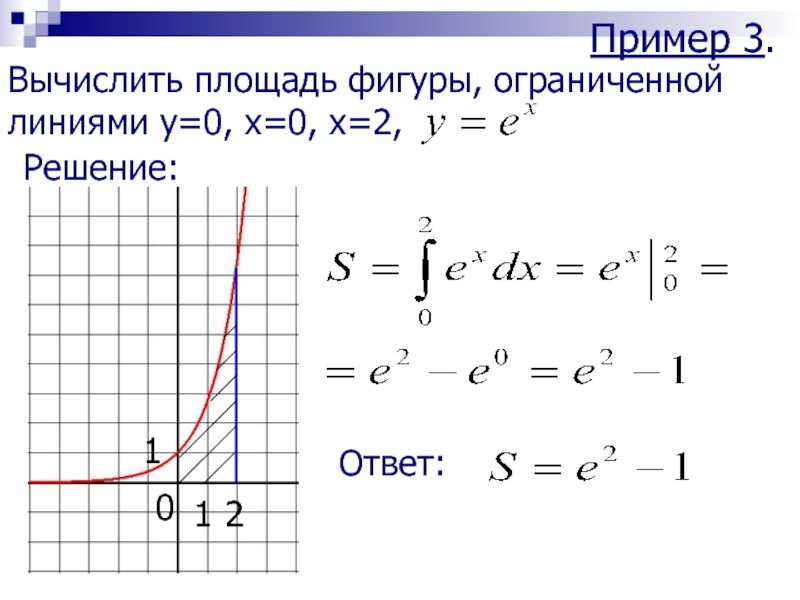
Это означает что при расчете площади между кривыми нам не нужно беспокоиться о независимо от того, находится ли область выше или ниже оси x, метод всегда один и тот же.
Площадь ограниченный сверху графиком f (x) а ниже по графику g (x) составляет: Границы х = а и х = b являются решениями уравнения е (х) = г (х) |
Пример 1
Найдите площадь между параболами f (x) = x 2 4 и прямая y = x 2.
Начнем с решение уравнения x 2 4 = x 2 найти район границы
х 2 4 = х 2
х 2 4 х + 2 = 0
х 2 х 2 = 0
(х + 1) (х 2) = 0
Решения x = 1 и x = 2.
Хорошая идея — посмотреть на график и область, вовлеченную в
калькулятор.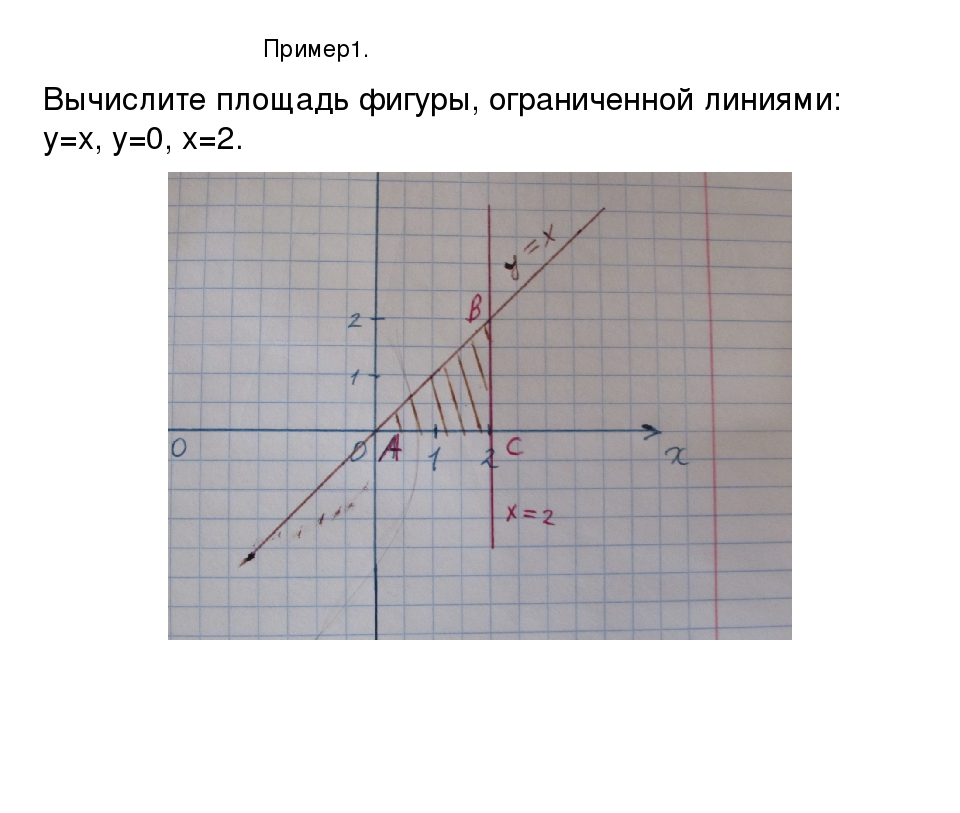
Мы видим, что линия ограничивает область выше, поэтому мы вычитаем интеграл от парабола от линии.
Пример 2
Найдите площадь, заключенную между графиками f (x) = sin x и g (x) = cos x
на интервале 0 ≤ x <2p
Калькулятор показывает нам область, которую мы собираемся найти.
Снова мы должны начните с поиска точек пересечения двух графиков.
Решение уравнения грех х = соз х.
грех х / соз х = 1 Разделить на cos x
загар х = 1
х = загар 1 1 = / 4 + п
Это означает что x = / 4 и х = 5/4 на интервале 0 ≤ x <2
График f (x) = sin x лежит над графиком g (x) = cos x на всех интервал между точками пересечения, поэтому расчет площади выполняется как следует:
Сейчас потому что / 4 = грех / 4 знак равно и cos 5/4 = грех 5/4 знак равно
Таким образом, точная стоимость площади составляет
.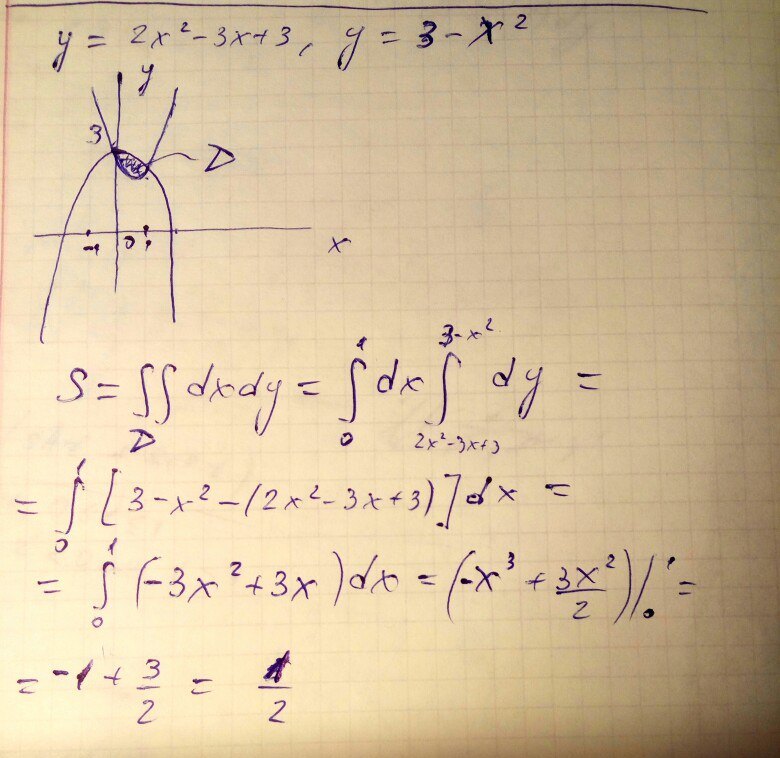
Пример 3
Найдите площадь, ограниченную графиками прямой y = 3x + 1 и многочлен f (x) = ⅓ x 3 2x 2 + 3x + 1.
Сначала граф нарисован с помощью калькулятора. Следующие значения окна должны работать
Вот график:
Теперь вычислите точки пересечения.
⅓ x 3 2x 2 + 3x + 1 = 3x + 1
⅓ x 3 2x 2 = 0
х 2 (⅓ х 2) = 0
Решения x = 0 и x = 6 необходимых нам границ. Линия верхняя функция.
Вы можете проверить свой ответ в калькуляторе (с помощью RUN, OPTN, F4 и F4).
Практика затем эти методы проходят тест 3 на интеграцию.
Запомните контрольный список !!
Глава 8 Применение Integral.
 pmd
pmd% PDF-1.3 % 250 0 объект >>>] / ON [301 0 R] / Order [] / RBGroups [] >> / OCGs [301 0 R] >> / Pages 242 0 R / Type / Catalog >> эндобдж 251 0 объект > / Шрифт >>> / Поля 238 0 R >> эндобдж 247 0 объект > поток приложение / pdf
4a.
 Объем Solid of Revolution путем интеграции (дисковый метод)
Объем Solid of Revolution путем интеграции (дисковый метод)М. Борна
Токарный станок
Многие твердые объекты, особенно сделанные на токарном станке , имеют круглое поперечное сечение и изогнутые стороны. На этой странице мы видим, как найти том таких объектов с помощью интеграции.
Предметы, сделанные на токарном станке …
Пример 1
Рассмотрим область, ограниченную прямой y = 3x, осью x и x = 1:
График y = 3x с заштрихованной областью под «кривой» от x = 0 до x = 1.
Когда заштрихованная область поворачивается на 360 ° вокруг оси «x», создается объем.
Получившееся твердое тело представляет собой конус:
Область под кривой `y = 3x` от` x = 0` до `x = 1`, повернутой вокруг оси` x`, показывая типичный диск.
Дисковый метод для поиска томов
Чтобы найти этот объем, мы могли бы взять срезы (темно-зеленый диск , показанный выше, является типичным срезом), каждый шириной `dx` и радиусом` y`:
Типичный диск, показанный с его размерами, радиусом `= y` и« высотой »` = dx`. 3` (Проверяет ОК.2] dx`
3` (Проверяет ОК.2] dx`
На следующем общем графике y_2 выше y_1. Нижний и верхний пределы для области, которая должна быть повернута, обозначены вертикальными линиями в точках «x = a» и «x = b».
Площадь, ограниченная кривыми y_1 и y_2 и линиями x = a и x = b, включая типичный прямоугольник .xyab`y_2`
`y_1`
Площадь, ограниченная кривыми `y_1` и` y_2` и линиями `x = a` и` x = b`.
Когда мы вращаем такую фигуру вокруг оси и делаем срезы, в результате получается шайба формы (с круглым отверстием посередине).2` (нижняя кривая), `y = x + 1` (линия вверху) и` x = 0`, показывая типичный прямоугольник.
Нижний предел интегрирования равен «x = 0» (поскольку в вопросе указано «x ≥ 0»).
Затем нам нужно найти место пересечения кривых, чтобы мы знали верхний предел интегрирования.
Приравнивая 2 выражения и решая:
2 x 2 = x + 1
2 x 2 — x — 1 = 0
(2 x + 1) ( x — 1) = 0
x = 1 (поскольку нам нужно учитывать только x ≥ 0.
3`
`~~ 8.2 = 4` в квадранте I, повернутом вокруг оси `y`.
Ответ
Мы понимаем, что это эллипс. Вопрос говорит нам, что интересующая нас область находится только в первом квадранте.
Эллипс x 2 + 4 y 2 = 4, показывающий часть, ограниченную кривой, x = 0, x = 2 и ось x .
Из диаграммы видно, что пределы ограниченной области составляют y = 0 и y = 1.3`
Приложения
1. Объем винной бочки
Винная бочка имеет радиус в верхней части 30 см и радиус в середине 40 см. Высота бочки 1 м. Каков объем бочки (в л), если предположить, что форма сторон параболическая?
Ответ
Положим бочку набок, чтобы облегчить алгебру:
Парабола с вершиной в точке `(0, 40)` и проходящая через `(50, 30)`.
Нам нужно найти уравнение параболы с вершиной в точке `(0, 40)` и проходящей через `(50, 30)`.2) / (250) + 40`
Нам нужно найти объем бочки, который образуется, когда мы вращаем эту параболу между x = -50 и x = 50 вокруг оси x .2ч.
Интересно, что Архимед (тот, кто, как известно, выпрыгнул из ванны и побежал по улице с криком «Эврика! Я понял») использовал этот подход, чтобы найти объемы сфер около 200 г. до н.э. Этот метод был почти забыт до начала 1700-х годов, когда исчисление было разработано Ньютоном и Лейбницем.
Мы видим, как решить проблему, используя оба подхода.
Объем историческим методом:
Ответ
Поскольку дыня симметрична, мы можем вычислить объем одной половины дыни, а затем удвоить наш ответ.3` или `9.161 \» L «`. Это примерно то же самое, что мы получили, нарезав арбуз и увеличив объем ломтиков.
[См. Также Архимед и площадь параболического сегмента.]
AC Использование определенных интегралов для определения площади и длины
В начале нашей работы с определенным интегралом мы узнали, что для объекта, движущегося вдоль оси, площадь под неотрицательной функцией скорости \ (v \) между \ ( a \) и \ (b \) говорят нам расстояние, которое объект прошел за этот интервал времени, и эта площадь задается точно определенным интегралом \ (\ int_a ^ bv (t) \, dt \ text {.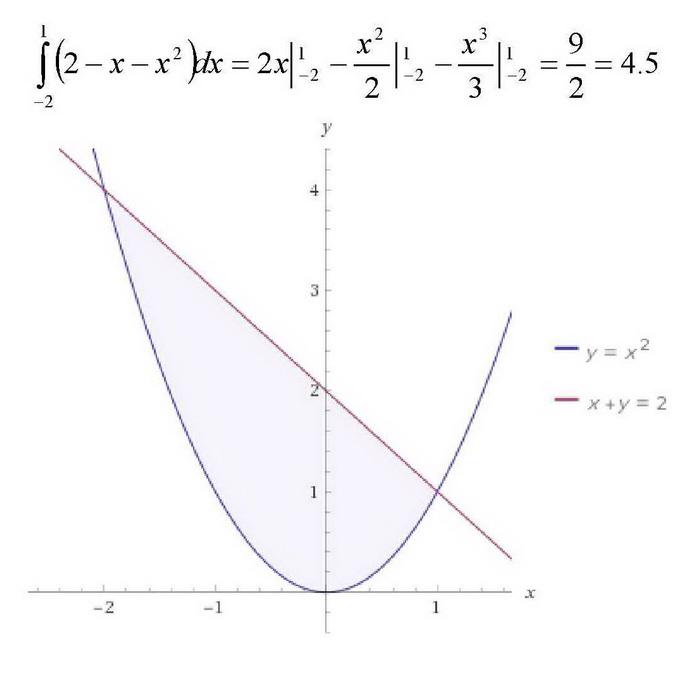 2 \) и \ (g (x) = 4-x \ text {.} \)
2 \) и \ (g (x) = 4-x \ text {.} \)
Используйте алгебру, чтобы найти точки пересечения графиков \ (f \) и \ (g \).
Нарисуйте точный график \ (f \) и \ (g \) на предусмотренных осях, пометив кривые по имени и точки пересечения упорядоченными парами.
Найдите и точно вычислите интегральное выражение, которое представляет область между \ (y = f (x) \) и осью \ (x \) на интервале между точками пересечения \ (f \) и \ (g \текст{.} \)
Найдите и точно вычислите интегральное выражение, которое представляет площадь между \ (y = g (x) \) и осью \ (x \) на интервале между точками пересечения \ (f \) и \ (g \ text {.} \)
Какова точная площадь между \ (f \) и \ (g \) между их точками пересечения? Почему?
Подраздел 6.1.1 Площадь между двумя кривыми
В действии предварительного просмотра 6. 2 + 1] \, dx = \ frac {21} {2} — 6 = \ frac {9} {2} \ text {.} \ Label {wfW} \ tag {6.1.1}
\ end {уравнение}
2 + 1] \, dx = \ frac {21} {2} — 6 = \ frac {9} {2} \ text {.} \ Label {wfW} \ tag {6.1.1}
\ end {уравнение}
Мы также можем думать о площади таким образом: если мы разрежем область между двумя кривыми на тонкие вертикальные прямоугольники (в том же духе, в котором мы изначально нарезали область между одной кривой и осью \ (x \) в разделе 4.2), мы видим (как показано на рисунке 6.1.4), что высота типичного прямоугольника определяется разницей между двумя функциями: \ (g (x) — f (x) \ text {,} \) и его ширина равна \ (\ Delta x \ text {.3 (g (x) — f (x)) \, dx \ text {.} \ Label {oBx} \ tag {6.1.2} \ end {уравнение}
Во многих приложениях с определенным интегралом нам будет полезно подумать о «репрезентативном срезе» и использовать определенный интеграл для добавления этих срезов. Здесь интеграл суммирует площади тонких прямоугольников.
Наконец, не имеет значения, думаем ли мы о площади между двумя кривыми как о разнице между площадью, ограниченной отдельными кривыми (как в (6.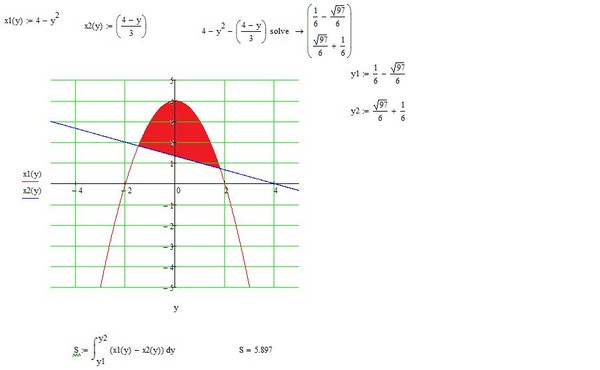 1.1)), или как о пределе римановой суммы площадей тонких прямоугольники между кривыми (как в (6.б (д (х) — е (х)) \, dx \ text {.} \)
1.1)), или как о пределе римановой суммы площадей тонких прямоугольники между кривыми (как в (6.б (д (х) — е (х)) \, dx \ text {.} \)
Мероприятие 6.1.2.
В каждой из следующих задач наша цель — определить площадь описываемого региона. Для каждой области (i) определить точки пересечения кривых, (ii) нарисуйте область, область которой находится, (iii) нарисуйте и пометьте репрезентативный срез и (iv) укажите площадь репрезентативного среза. Затем укажите определенный интеграл, значение которого является точной площадью области, и оцените интеграл, чтобы найти числовое значение площади области.2 — y — 2 = 0 \ text {.} \) Таким образом, мы находим \ (y = -1 \) или \ (y = 2 \ text {,} \), поэтому точки пересечения двух кривых равны \ ( (0, -1) \) и \ ((3,2) \ text {.} \)
Если мы попытаемся использовать вертикальные прямоугольники, чтобы разрезать область (как на центральном графике на рис. 6.1.6), мы увидим, что от \ (x = -1 \) до \ (x = 0 \) кривые, ограничивающие верх и низ прямоугольника — одно и то же.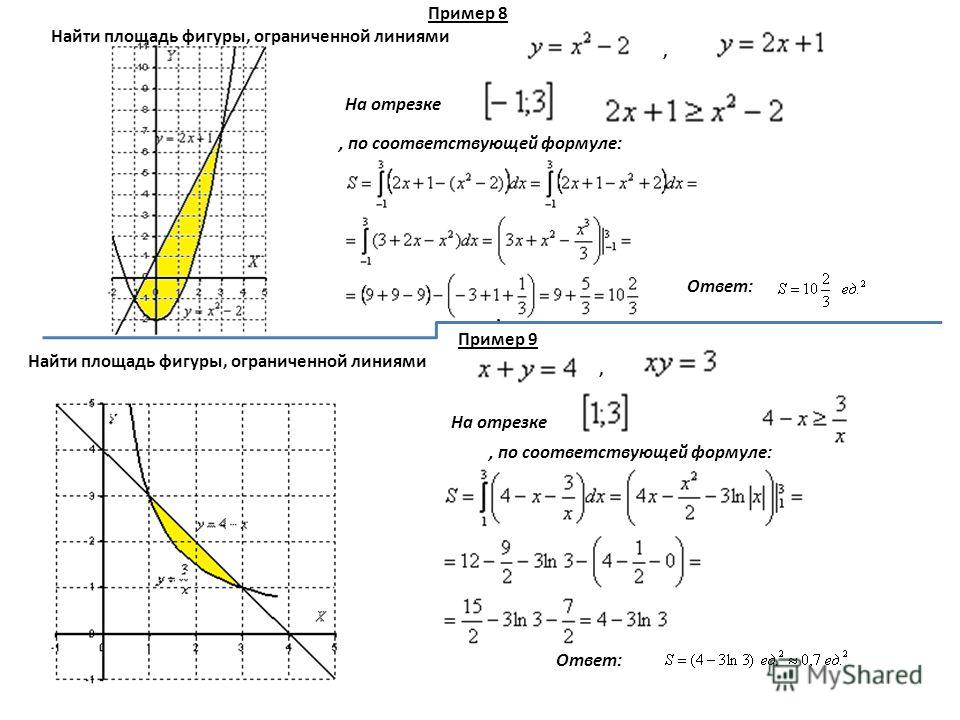 Это предполагает, как показано на крайнем правом графике на рисунке, что мы попробуем использовать горизонтальные прямоугольники.
Это предполагает, как показано на крайнем правом графике на рисунке, что мы попробуем использовать горизонтальные прямоугольники.
Обратите внимание, что ширина горизонтального прямоугольника зависит от \ (y \ text {.2-1)] \, dy \ text {.} \ Label {Neh} \ tag {6.1.3} \ end {уравнение}
Мы подчеркиваем, что мы интегрируем относительно \ (y \ text {;} \), потому что мы решили использовать горизонтальные прямоугольники, ширина которых зависит от \ (y \), а толщина обозначена \ (\ Delta y \ text {.} \) Это несложное упражнение — вычислить интеграл в уравнении (6.1.3) и найти, что \ (A = \ frac {9} {2} \ text {.} \)
Так же, как и с использованием вертикальных прямоугольников толщиной \ (\ Delta x \ text {,} \), у нас есть общий принцип нахождения площади между двумя кривыми, который мы формулируем следующим образом.{y = d} (g (y) — f (y)) \, dy \ text {.} \ end {уравнение *}
Мероприятие 6.1.3.
В каждой из следующих задач наша цель — определить площадь описываемого региона.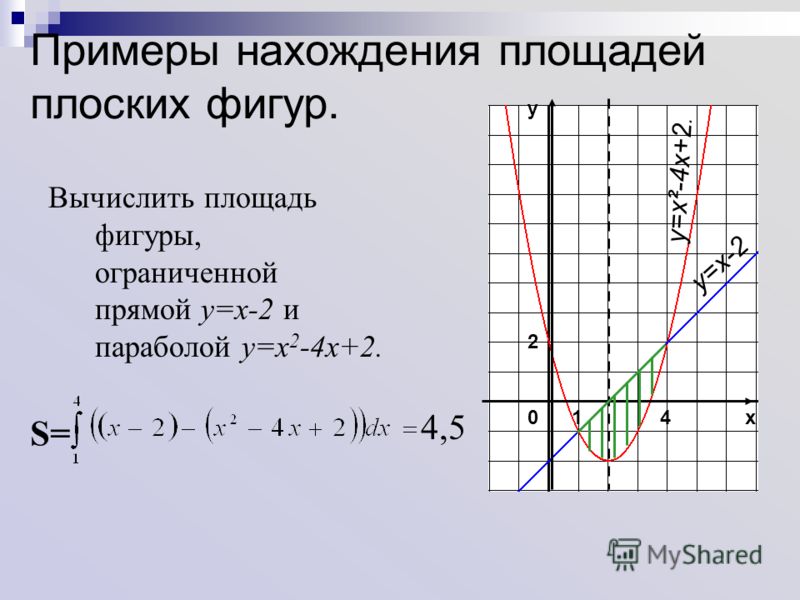 Для каждой области (i) определить точки пересечения кривых, (ii) нарисуйте область, область которой находится, (iii) нарисуйте и пометьте репрезентативный срез и (iv) укажите площадь репрезентативного среза. Затем укажите определенный интеграл, значение которого является точной площадью области, и оцените интеграл, чтобы найти числовое значение площади области.2-2y \) и \ (y = x \ text {.} \)
Для каждой области (i) определить точки пересечения кривых, (ii) нарисуйте область, область которой находится, (iii) нарисуйте и пометьте репрезентативный срез и (iv) укажите площадь репрезентативного среза. Затем укажите определенный интеграл, значение которого является точной площадью области, и оцените интеграл, чтобы найти числовое значение площади области.2-2y \) и \ (y = x \ text {.} \)
Подраздел 6.1.3 Определение длины кривой
Мы также можем использовать определенный интеграл, чтобы найти длину участка кривой. Мы используем тот же фундаментальный принцип: мы разрезаем кривую на небольшие части, длину которых мы можем легко приблизительно определить. В частности, мы подразделяем кривую на небольшие аппроксимирующие отрезки прямых, как показано слева на рисунке 6.1.7.
Рисунок 6.1.7. Слева непрерывная функция \ (y = f (x) \), длину которой мы ищем на интервале от \ (a = x_0 \) до \ (b = x_3 \ text {.} \) Справа — увеличенный вид части кривой.
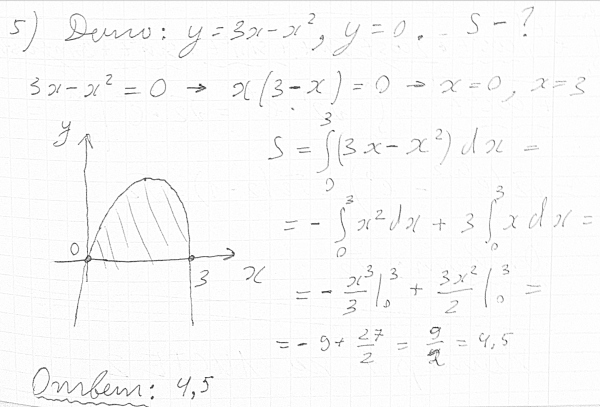

 , «Герои войны – ровесники мои»
, «Герои войны – ровесники мои» 3`
3` 2) / (250) + 40`
2) / (250) + 40`