Метод решения несобственного интеграла с бесконечным нижним пределом
Данный раздел предназначен для тех, кто хорошо разобрался с уроком Несобственные интегралы. Примеры решения, или, по крайне мере, понял бОльшую его часть.
Речь пойдет о несобственных интегралах первого рода с бесконечным нижним пределом:
.
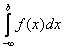Пример 7
Вычислить несобственный интеграл или установить его расходимость
.
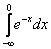Чем отличается данный интеграл от «обычного» несобственного интеграла с бесконечным верхним пределом? По технике решения практически ничем. Так же нужно найти первообразную (неопределенный интеграл), так же нужно использовать предел при вычислении интеграла. Отличие состоит в том, что необходимо устремить нижний предел интегрирования к «минус бесконечности»:
.
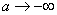Из вышесказанного следует очевидная формула для вычисления такого несобственного интеграла:
.
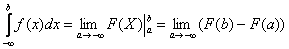В данном примере, подынтегральная функция непрерывна на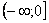 
и:
,
то есть, несобственный интеграл расходится.
Вот тут, главное, быть аккуратным в знаках и не забывать, что 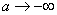. Нужно внимательно разобраться, что куда стремится.
Пример 8
Вычислить несобственный интеграл или установить его расходимость
.
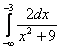Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Метод решения несобственного интеграла с бесконечными пределами интегрирования
Очень интересный случай. Несобственный интеграл первого рода с двумя бесконечными пределами интегрирования имеет следующий вид:
.
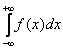Как его решать? Его нужно представить в виде суммы двух несобственных интегралов:
.
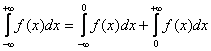Примечание: вместо ноля может быть любое число, но ноль обычно удобнее всего.
Если обаинтеграла правой части сходятся, то сходится и сам интеграл
Если хотя бы один из интегралов правой части расходится, то расходится и интеграл
.
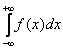Пример 9
Вычислить несобственный интеграл или установить его расходимость.
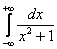
Мы специально подобрали простой пример, чтобы проиллюстрировать другой важный момент применения метода.
Подынтегральная функция непрерывна на всей числовой прямой.
Согласно правилу, интеграл следует представить в виде суммы интегралов:
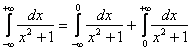
Интеграл будет сходиться, если будут сходиться оба интеграла правой части. Проверяем:
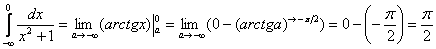
– сходится.
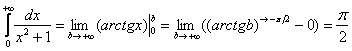
– сходится.
Оба интеграла сходятся, значит, сходится и весь интеграл:
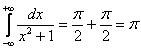
Теперь обратим внимание на подынтегральную функцию. Она является чётной.
В несобственных интегралах с (двумя) бесконечными пределами, а, значит, симметричными интервалами интегрирования, чётностью пользоваться МОЖНО.Аналогично определенному интегралу, интервал интегрирования можно разделить, а результат – удвоить. То есть, решение допустимо записать короче:
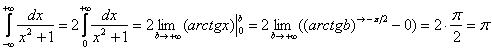
Почему такое возможно?
График подынтегральной чётной функции симметричен относительно оси OY. Следовательно, если половина площади конечна (интеграл сходится) – то симметричная половина площади тоже конечна.
Если же половина площади бесконечна (интеграл расходится), следовательно, симметричная половина тоже будет расходиться.
Пример 10
Вычислить несобственный интеграл или установить его расходимость.
.
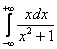Подынтегральная функция непрерывна на всей числовой прямой. Согласно правилу, интеграл нужно представить в виде суммы двух интегралов:
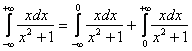
Проверяем сходимость интегралов правой части:
.
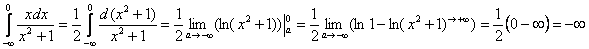Первый интеграл расходится. Знак «минус» говорит о том, что бесконечная криволинейная трапеция расположена ниже оси абсцисс.
Не нужно проверять сходимость второго интеграла правой части, поскольку для того, чтобы интеграл
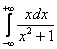
сходился, необходимо чтобы сходились обаинтеграла правой части.
Ответ:несобственный интеграл
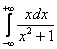
расходится.
А сейчас очень важный момент: подынтегральная функция
В несобственных интегралах с бесконечными пределами (т. е. симметричными интервалами интегрирования) нечётностью пользоваться НЕ СЛЕДУЕТ!!!
В этом состоит отличие от определенного интеграла. Там всегда можно смело записать:
,
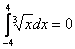а здесь так поступать – не следует. Почему? Потому что в ряде случаев, как, например, в рассмотренном примере, получится нонсенс (бессмыслица). Если считать, что
,
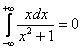то интеграл будет сходящимся (поскольку получено конечное число), но в то же время его часть:
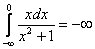
– расходится (как мы только что показали в решении). Тонкость же состоит в том, что несобственный интеграл равен своему значению только в предельном смысле. Интеграл
от нечетной функции f(x), в принципе, может стремиться (а не равняться) к нулю, но нельзя сразу записывать, что
.
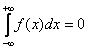Всегда представляем интеграл в виде двух интегралови выполняем проверку на сходимость по стандартному алгоритму.
Пример 11
Вычислить несобственный интеграл или установить его расходимость
.
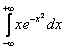Полное решение и ответ в конце урока.
2.5. Несобственные интегралы второго рода
Это интегралы от неограниченных (сверху и / или снизу) функций. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: . Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв: 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или разрывы даже есть внутри.
На практике гораздо чаще и одинаково часто встречаются первые два варианта, и сейчас я подброшу монетку… так, начинаем, со Случая 1, когда подынтегральной функции не существует в точке .
Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле нет – это несобственный интеграл второго рода: если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Проверим заодно и верхний предел: . Здесь всё хорошо. И вообще, обязательно анализируем весь знаменатель, а то, может статься, точки разрыва есть и внутри отрезка (и это не выдумки). В нашем примере знаменатель обращается в ноль в единственной точке, а значит, вопрос закрыт.
Принципиально этот случай выглядит так:
И здесь почти всё так же, как в интеграле первого рода. Если интеграл существует, то он численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо он равен конечному числу (площадь бесконечной фигуры – конечна!).
Осталось модифицировать формулу Ньютона-Лейбница, я приведу упрощённый по сравнению с учебниками вариант, без лишних букв:
«Добавка» символизирует тот факт, что к точке разрыва мы приближаемся
Разделаемся с демонстрационным интегралом:
Пример 35
Вычислить несобственный интеграл или установить его расходимость.
Во-первых, ПИСЬМЕННО констатируем тот факт, что подынтегральная функция терпит бесконечный разрыв в точке . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
И приём стар, как чешуя динозавра: сначала всегда можно найти неопределённый интеграл.
Особенно, если пример не прост и особенно в кубе, если вы «чайник».
Проведём замену: , откуда выражаем оставшийся кусок исходного интеграла, сиротливый дифференциал:
Проверка:
, в чём мы и хотели убедиться.
Теперь вычислим несобственный интеграл, сначала решение, затем комментарии:
(1) Используем формулу
(2) и её продолжение , где при подстановке нижнего предела интегрирования вместо «икс» мы формально подставляем «икс».
(3) Но самое главное: как выяснить, куда стремится , если ? Всё просто. Мысленно либо на черновике подставляем под корень и проводим упрощения: – в результате получено бесконечно малое положительное значение, поэтому .
Результат получился отрицательным, и в этом нет криминала, просто соответствующая криволинейная трапеция расположена под осью .
Решение можно оформить и по-другому. Например, провести ту же замену прямо в несобственном интеграле с пересчётом новых пределов интегрирования. Ну и совсем шикарно обыденно – это с ходу подвести под знак дифференциала:
А сейчас два интеграла для самостоятельного решения:
Пример 36
Вычислить несобственные интегралы или установить их расходимость
а) , б)
В образце я привёл прямое решение с подведением под знак дифференциала и подробно закомментировал что, к чему и почему стремится. Обязательно разберитесь!
Случай 2. Если подынтегральной функции не существует в точке .
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит так:
Здесь всё так же, за исключением того, что предел у нас стремится к значению слева:
Такой предел называют левосторонним, и бесконечно малая отрицательная «добавка» означает, что к точке «бэ» мы подбираемся по оси именно слева.
Пример 37
Вычислить несобственный интеграл или установить его расходимость.
Очевидно, что подынтегральная функция терпит бесконечный разрыв в точке , но не пренебрегаем и проверяем, что больше разрывов нет! – по той причине, что знаменатель обращается в ноль в единственной точке.
Интеграл решим методом подведения под знак дифференциала:
(1) Берём интеграл и используем формулу . Наверное, вы обратили внимание, что саму формулу на чистовик записывать не обязательно. Все эти формулы носят частный характер и не предназначены даже для запоминания – самое главное, ПОНИМАТЬ, что происходит в том или ином интеграле, в том или ином случае. Не забываем быстренько выполнить черновую проверку:
, ОК.
(2) Представляем первообразную в более удобном виде.
(3) Подставляем в неё пределы интегрирования: , формально считая, что вместо «икс» мы подставляем «икс».
Как выяснить, что при дробь ? Приём тот же самый: мысленно либо на черновике подставляем под корень и проводим упрощения:
, а единица, делённая на бесконечно малое и положительное значение – это «плюс» бесконечность: .
И на завершающем шаге бесконечность меняет знак:
Будьте очень внимательны в знаках! Да, конечно, несобственный интеграл расходится, но и – это две разные вещи, и если вы недосмотрите за знаками, то допустите серьезную ошибку.
Следующие интегралы для самостоятельного рассмотрения:
Пример 38
Вычислить несобственные интегралы или установить их расходимость.
а) , б)
В образце решения я опять использовал «быстрый» способ, но если вам трудно, то, конечно, сначала лучше найти неопредёленный интеграл.
И в заключение курса коротко о более редких случаях:
2.6. Когда разрывы на обоих концах и / или внутри отрезка интегрирования
2.4. Что делать, если оба предела интегрирования бесконечны?
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее
2.2. Несобственный интеграл первого рода
Это интеграл с бесконечным (и) пределом интегрирования, и самый популярный на практике вариант таков: . При этом подынтегральная функция непрерывна на промежутке , и этот важный факт следует всегда проверять, и проверять в первую очередь! Ибо если есть разрывы, то это уже особый случай.
Для определённости положим, что , и тогда типичная криволинейная трапеция будет выглядеть так:
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади.
И первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может. И такой интеграл называют расходящимся (как отмечалось выше). Но. Как это ни парадоксально, площадь бесконечной фигуры может равняться… конечному числу! Например, . Такие интегралы называют сходящимися.
Если криволинейная трапеция лежит под осью , то получится «минус» бесконечность либо отрицательное конечное число, т.е. со знаками всё как у «собрата».
И для решения рассматриваемого интеграла нужно немного модифицировать формулу Ньютона-Лейбница – с поправкой, что , а это, как вы догадываетесь, попахивает применением теории пределов:
В чем отличие от определённого интеграла? Да ни в чём особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела.
Следует отметить, что строгое определение несобственного интеграла даётся именно через предел, и иногда его не существует.
Классический пример: . Несмотря на то, что косинус непрерывен на промежутке , этого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела.
Обратите внимание, что вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что другая буква ничем не хуже стандартного «икса». Ну, может, только не такая харизматичная 🙂
Теперь перейдём к «обычным» задачам и начнём с двух хрестоматийных примеров:
Пример 26
Вычислить несобственный интеграл или установить его расходимость.
В таких заданиях чертежей строить не нужно, но понимания ради:
Подынтегральная функция непрерывна на промежутке , а значит, перед нами несобственный интеграл 1-рода (не забываем, что есть и другие!). Используем формулу :
– таким образом, несобственный интеграл расходится, т.е. площадь криволинейной трапеции бесконечна.
Не забываем пометить, что . Все поняли, почему? Ещё раз откройте Приложение Графики функций и взгляните на график логарифма: при неограниченном увеличении аргумента ветка логарифма уходит вверх на «плюс» бесконечность.
Таким образом, чтобы не было «затыков» с простейшими пределами,
важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания может выглядеть так:
“
Подынтегральная функция непрерывна на
Таким образом, несобственный интеграл расходится.
“
! При оформлении примера всегда указываем, что происходит с подынтегральной функцией – непрерывна она или нет. Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Пример 27
Вычислить несобственный интеграл или установить его расходимость.
Здесь ситуация вроде бы похожа:
Но: – интеграл сходится, и площадь бесконечной криволинейной трапеции равна конечному числу!
Надеюсь ни у кого не возникло проблем с табличным интегралом и пониманием того, что при ветка гиперболы .
Чистовое оформление примера может быть ещё лаконичнее:
“
Подынтегральная функция непрерывна на , таким образом:
“
Тут даже без послесловия обошлось, ибо и так понятно, что интеграл сходится. И, что особенно приятно, никаких чертежей! По условию же не требуется.
Рассмотрим более содержательный пример:
Пример 28
Вычислить несобственный интеграл или установить его расходимость.
Со знаменателем всё хорошо и подынтегральная функция непрерывна на . Но интеграл не так прост, особенно для «чайника». Что делать, если интеграл кажется не самым простым или не сразу понятно как его решать?
В этом случае целесообразно применить тот же алгоритм, что и для определённого интеграла,… вы точно наклеили его на стену? …Ай-яй-яй – а ведь давно пора организовать дома красный угол высшей математики!
1) Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.
И тут прямо напрашивается навести под корнем порядок, проведём замену и навесим на обе части дифференциалы:
, откуда выразим нужный кусок:
2) Проверим найденную первообразную дифференцированием:
– в результате получена исходная подынтегральная функция, что и требовалось проверить.
3) И теперь с несобственным интегралом никаких проблем, по формуле :
Точно так же, как и у «собрата», в несобственном интеграле допустима замена переменной с вычислением новых пределов интегрирования, и поэтому решение можно оформить другим способом:
Подынтегральная функция непрерывна на , проведём замену .
Вычислим новые пределы интегрирования:
Но самый продвинутый и быстрый способ – это подвести функцию под знак дифференциала, в этом случае решение будет выглядеть примерно так:
Подынтегральная функция непрерывна на , таким образом:
Кому как нравится, кому как удобнее! И, конечно, тут нужно учитывать целесообразность того или иного способа – в зависимости от того, простой интеграл попался или посложнее.
А сейчас два типовых примера для самостоятельного решения:
Пример 29
Исследовать сходимость несобственных интегралов
а) , б)
В пункте «а» используем метод выделения полного квадрата. И об
Вычислить несобственный интеграл
Для того, чтобы вычислить несобственный интеграл, необходимо разбираться в вычислении неопределенных интегралов, определенных интегралов, вычислять площадь фигуры, применяя определенный интеграл, знать основы вычисления простых пределов и графики элементарных функций.
Геометрический смысл несобственного интеграла состоит в том, что вычисление несобственного интеграла сводится к нахождению числа (результата интеграла) или показать, что интеграл расходится (в результате получить бесконечность, а не число).
Решим пример.
Пример.
Вычислим несобственный интеграл или установим его расходимость
Решение.
Подынтегральная функция является непрерывной на интервале . Следовательно, несобственный интеграл можно вычислить обычным способом.
Применим формулу Ньютона-Лейбница и вычислим несобственный интеграл:
Воспользуемся таблицами Брадиса и найдем приближенное значение ln 3:
В результате получаем, что несобственный интеграл расходится, а соответствующая ему площадь криволинейной трапеции стремится к бесконечности.
Ответ. Несобственный интеграл расходится.
В рассмотренном задании, как и при вычислении определенного интеграла, применяется формула Ньютона-Лейбница, только под знаком предела.