Приближённые вычисления определённых интегралов с помощью рядов. Первая часть.

Пусть требуется вычислить определенный интеграл $\int\limits_{a}^{b}f(x)dx$ с некоторой наперёд заданной точностью $\varepsilon$. Если непосредственное нахождение первообразной подынтегральной функции $f(x)$ чересчур громоздко, или же интеграл $\int f(x)dx$ вообще не берётся, то в этих случаях можно использовать функциональные ряды. В частности, применяются ряды Маклорена, с помощью которых получают разложение в степенной ряд подынтегральной функции $f(x)$. Именно поэтому в работе нам будет нужен документ с рядами Маклорена.

Степенные ряды, которые мы и станем использовать, сходятся равномерно, поэтому их можно почленно интегрировать по любому отрезку, лежащему внутри интервала сходимости. Схема решения подобных задач на вычисление интегралов с помощью рядов проста:

1. Разложить подынтегральную функцию в функциональный ряд (обычно в ряд Маклорена).
2. Произвести почленное интегрирование членов записанного в первом пункте функционального ряда.
3. Вычислить сумму полученного во втором пункте числового ряда с заданной точностью $\varepsilon$.

Задачи на вычисление интегралов с помощью рядов популярны у составителей типовых расчётов по высшей математике. Поэтому в данной теме мы разберём пять примеров, в каждом из которых требуется вычислить определенный интеграл с точностью $\varepsilon$.

Пример №1

Вычислить $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx$ с точностью до $\varepsilon=10^{-3}$.

Решение

Сразу отметим, что интеграл $\int e^{-x^2}dx$ не берётся, т.е. первообразная подынтегральной функции не выражается через конечную комбинацию элементарных функций. Иными словами, стандартными способами (подстановка, интегрирование по частям и т.д.) первообразную функции $e^{-x^2}$ найти не удастся.

Для таких задач есть два варианта оформления, поэтому рассмотрим их отдельно. Условно их можно назвать «развёрнутый» и «сокращённый» варианты.

Развёрнутый вариант оформления

Запишем разложение функции $e^x$ в ряд Маклорена:

$$e^x=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\ldots$$

Данное разложение верно при всех $x\in{R}$. Подставим $-x^2$ вместо $x$:

$$e^{-x^2}=1-x^2+\frac{\left(-x^2\right)^2}{2}+\frac{\left(-x^2\right)^3}{6}+\ldots=1-x^2+\frac{x^4}{2}-\frac{x^6}{6}+\ldots$$

Интегрируем полученное разложение на отрезке $\left[0;\frac{1}{2}\right]$:

$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx=\int\limits_{0}^{\frac{1}{2}}\left(1-x^2+\frac{x^4}{2}-\frac{x^6}{6}+\ldots\right)dx=\\ =\left.\left(x-\frac{x^3}{3}+\frac{x^5}{10}-\frac{x^7}{42}+\ldots\right)\right|_{0}^{1/2}= \frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}-\frac{1}{42\cdot{2^7}}+\ldots$$

Получили сходящийся знакочередующийся ряд. Это значит, что если для вычисления приближенного значения заданного интеграла взять $k$ членов полученного ряда, то погрешность не превысит модуля $(k+1)$-го члена ряда.

Согласно условию, точность $\varepsilon=10^{-3}$. Так как $\frac{1}{42\cdot{2^7}}=\frac{1}{5376}<10^{-3}$, то для достижения требуемой точности достаточно ограничиться первыми тремя членами знакочередующегося ряда:

$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx\frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}=\frac{443}{960}.$$

Погрешность полученного равенства не превышает $\frac{1}{5376}$.

Однако суммировать обычные дроби – дело утомительное, поэтому чаще всего расчёты ведут в десятичных дробях:

$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx\frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}\approx{0{,}5}-0{,}0417+0{,}0031\approx{0{,}461}.$$

Разумеется, в этом случае нужно учитывать погрешность округления. Первое слагаемое (т.е. $0{,}5$) было рассчитано точно, поэтому никакой погрешности округления там нет. Второе и третье слагаемые брались с округлением до четвёртого знака после запятой, посему погрешность округления для каждого из них не превысит $0,0001$. Итоговая погрешность округления не превысит $0+0{,}0001+0{,}0001=0{,}0002$.

Следовательно, суммарная погрешность равенства $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx{0{,}461}$ не превысит $0{,}0002+\frac{1}{5376}<10^{-3}$, т.е. значение интеграла вычислено с требуемой точностью.

Отмечу, что большинство авторов методичек и учебных пособий не учитывают погрешность округления, хоть это и не совсем корректно. В дальнейших примерах данной темы я буду упоминать про эту погрешность, если она возникнет.

Сокращённый вариант оформления

Запишем разложение функции $e^x$ в ряд Маклорена:

$$e^x=\sum\limits_{n=0}^{\infty}\frac{x^n}{n!}$$

Данное разложение верно при всех $x\in{R}$. Подставим $-x^2$ вместо $x$:

$$e^{-x^2}=\sum\limits_{n=0}^{\infty}\frac{\left(-x^2\right)^n}{n!}=\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{x}^{2n}}{n!}$$

Интегрируем полученный ряд на отрезке $\left[0;\frac{1}{2}\right]$:

$$\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx=\int\limits_{0}^{\frac{1}{2}}\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{x}^{2n}}{n!}dx= \sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!}\int\limits_{0}^{\frac{1}{2}}x^{2n}dx=\\ =\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!}\left.\frac{x^{2n+1}}{2n+1}\right|_{0}^{1/2}= \sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot\left(\frac{1}{2}\right)^{2n+1}}{n!\cdot(2n+1)}= \sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!\cdot(2n+1)\cdot{2^{2n+1}}}$$

Получили знакочередующийся ряд. Запишем несколько первых членов этого ряда (до тех пор, пока записанный член не станет меньше $\varepsilon$):

$$\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{n!\cdot(2n+1)\cdot{2^{2n+1}}}=\frac{1}{2}-\frac{1}{24}+\frac{1}{320}-\frac{1}{5376}+\ldots$$

Все рассуждения, что были сделаны относительно погрешностей в развёрнутом варианте оформления остаются в силе, т.е. $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx\frac{1}{2}-\frac{1}{3\cdot{2^3}}+\frac{1}{10\cdot{2^5}}\approx{0{,}461}$.

Чем сокращённый вариант записи лучше развёрнутого?

Во-первых, нам не нужно угадывать, сколько членов ряда взять в изначальном разложении, чтобы вычислить определенный интеграл с заданной точностью. Например, мы записали в самом начале решения:

$$e^{-x^2}=1-x^2+\frac{x^4}{2}-\frac{x^6}{6}+\ldots$$

Однако почему мы решили, что нужно взять именно четыре члена ряда? А вдруг нужно взять два члена ряда или пять, или сто? Если бы только шестой член ряда оказался меньше чем $\varepsilon$, – что тогда? А тогда пришлось бы возвращаться в самое начало решения, добавлять ещё пару членов ряда и интегрировать их. А если и этого не хватит, то проделать эту процедуру ещё раз.

Сокращённый вид записи таким недостатком не страдает. Мы получаем числовой ряд, записанный в общем виде, поэтому можем брать столько его членов, сколько потребуется.

Далее, при интегрировании в развёрнутом способе записи мы находили первообразную четыре раза. При интегрировании в сокращённом способе записи, по сути, мы нашли лишь первообразную для $x^{2n}$.

Исходя из вышеперечисленных причин, я предпочитаю именно сокращённый способ записи. В дальнейнем все решения в этой теме будут оформлены в сокращённой форме.

Ответ: $\int\limits_{0}^{\frac{1}{2}}e^{-x^2}dx\approx{0{,}461}$.

Пример №2

Вычислить определённый интеграл $\int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx$ с точностью до $\varepsilon=10^{-3}$, разложив подынтегральную функцию в ряд Маклорена и проинтегрировав почленно.

Решение

Начнём с разложения подынтегральной функции $\frac{1-\cos\frac{5x}{3}}{x}$ в ряд Маклорена. Запишем разложение функции $\cos{x}$ в ряд Маклорена:

$$\cos{x}=\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{x}^{2n}}{(2n)!}$$

Данное разложение верно при всех $x\in{R}$. Подставим вместо $x$ дробь $\frac{5x}{3}$:

$$\cos{\frac{5x}{3}}=\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{\left(\frac{5x}{3}\right)}^{2n}}{(2n)!}= \sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}.$$

Теперь разложим $1-\cos\frac{5x}{3}$:

$$ 1-\cos\frac{5x}{3}=1-\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}} $$

Забирая из суммы $\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}$ первый член, получим: $\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}=1+\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}$. Следовательно:

$$ 1-\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}=1-\left(1+\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}\right)=\\ =-\sum\limits_{n=1}^{\infty}\frac{(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}} =\sum\limits_{n=1}^{\infty}\frac{-(-1)^n\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}=\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}. $$

Последнее, что остаётся – это разделить на $x$:

$$ \frac{1-\cos\frac{5x}{3}}{x}=\frac{1}{x}\cdot\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n}}{3^{2n}\cdot{(2n)!}}= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n-1}}{3^{2n}\cdot{(2n)!}}. $$

Интегрируем данное разложение на отрезке $\left[0;\frac{1}{5}\right]$:

$$ \int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx=\int\limits_{0}^{\frac{1}{5}}\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}\cdot{x}^{2n-1}}{3^{2n}\cdot{(2n)!}}dx= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}}{3^{2n}\cdot{(2n)!}}\int\limits_{0}^{\frac{1}{5}}{x}^{2n-1}dx=\\ =\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot{5^{2n}}}{3^{2n}\cdot{(2n)!}}\cdot\left.\frac{x^{2n}}{2n}\right|_{0}^{1/5}= \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{{2n}\cdot 3^{2n}\cdot{(2n)!}} $$

Получили знакочередующийся ряд. Запишем несколько первых членов этого ряда (до тех пор, пока записанный член не станет меньше $\varepsilon$):

$$\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{{2n}\cdot 3^{2n}\cdot{(2n)!}}=\frac{1}{36}-\frac{1}{7776}+\ldots$$

Так как $\frac{1}{7776}<\varepsilon$, то для вычисления интеграла с точностью $\varepsilon$ достаточно первого члена полученного числового ряда:

$$\int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx\approx\frac{1}{36}\approx{0{,}028}.$$

Ответ: $\int\limits_{0}^{0{,}2}\frac{1-\cos\frac{5x}{3}}{x}dx\approx{0{,}028}$.

Продолжение темы вычисления интегралов с помощью рядов Маклорена продолжим во второй части.

math1.ru

Вычисление определенных интегралов с помощью рядов.

 |   |   |   |   |   |   |   |   |   |   |   |  Вычисление определенных интегралов с помощью рядов.  | 

Рассмотрим несколько примеров:

Пример 1:

С помощью разложения подынтегральной функции в ряд вычислить определенный интеграл с точностью до  e=0,001.

.

Решение.

Воспользуемся разложением подынтегральной функции в ряд. Используем формулу:

.

Получаем:

 

Тогда заданный интеграл:

Т.к. второй член разложения , то для достижения заданной точности ( e=0,001) согласно признаку Лейбница, можем ограничиться только первым членом ряда. Имеем:

Пример  2:

С помощью разложения подынтегральной функции в ряд вычислить определенный интеграл  с точностью до  e=0,001.

Решение.

Воспользуемся разложением функции    в степенной ряд:

Тогда

Интегрируя ряд почленно от 0 до 0,4, получим:

 

Так как четвёртый член ряда по модулю меньше 0,001, то, ограничившись первыми тремя его членами, сделаем ошибку менее 0,001:

 

Ответ: 0,367

 

primer.by

Приближённые вычисления определённых интегралов с помощью рядов. Вторая часть.

Продолжим тему вычисления определённых интегралов с помощью функциональных рядов, начатую в первой части. Как и в первой части нам понадобится документ с рядами Маклорена. Схема решения остаётся неизменной: разложить подынтегральную функцию в ряд (чаще всего – ряд Маклорена) и проинтегрировать почленно.

Пример №3

Вычислить интеграл $\int\limits_{0}^{1}\frac{1}{\sqrt[3]{8+x^3}}dx$ с точностью до $\varepsilon=0{,}001$.

Решение

Чтобы вычислить интеграл с точностью $\varepsilon$, как и ранее, будем использовать ряды Маклорена. С целью разложения подынтегральной функции в ряд Маклорена применим формулу разложения функции $(1+x)^\alpha$. Для начала подгоним подынтегральную функцию под вид $(1+x)^\alpha$:

$$\frac{1}{\sqrt[3]{8+x^3}}=\frac{1}{\sqrt[3]{8\left(1+\frac{x^3}{8}\right)}}=\frac{1}{2\sqrt[3]{1+\frac{x^3}{8}}}=\frac{1}{2}\cdot\left(1+\frac{x^3}{8}\right)^{-\frac{1}{3}}$$

Разложение для $(1+x)^\alpha$ верно при условии $-1<x<1$. Т.е. чтобы применить формулу разложения для $(1+x)^\alpha$ с целью разложить выражение $\frac{1}{2}\cdot\left(1+\frac{x^3}{8}\right)^{-\frac{1}{3}}$, потребуется выполнение условия $-1<\frac{x^3}{8}<1$, $-2<x<2$. Отрезок интегрирования, т.е. $[0;1]$, лежит внутри интервала $(-2;2)$, поэтому можем применять почленное интегрирование. В примерах первой части данное замечание не требовалось, так как использованные там разложения были верны при $x\in{R}$.

Нам надо получить разложение подынтегральной функции $\frac{1}{2}\cdot\left(1+\frac{x^3}{8}\right)^{-\frac{1}{3}}$ в ряд Маклорена. Запишем для начала разложение функции $(1+x)^{-1/3}$ в ряд Маклорена. Здесь сокращённый вариант записи будет несколько неудобен, поэтому запишем развёрнуто:

$$(1+x)^{-1/3}=1+\frac{-\frac{1}{3}}{1!}x+\frac{-\frac{1}{3}\cdot\left(-\frac{1}{3}-1\right)}{2!}x^2+\ldots= 1-\frac{1}{3}x+\frac{2}{9}x^2-\ldots $$

Подставим вместо $x$ дробь $\frac{x^3}{8}$:

$$ \left(1+\frac{x^3}{8}\right)^{-\frac{1}{3}}=1-\frac{1}{3}\cdot\frac{x^3}{8}+\frac{2}{9}\cdot\left(\frac{x^3}{8}\right)^2-\ldots= 1-\frac{x^3}{24}+\frac{x^6}{288}-\ldots $$

Домножая на $\frac{1}{2}$ получим разложение подынтегральной функции:

$$ \frac{1}{2}\cdot\left(1+\frac{x^3}{8}\right)^{-\frac{1}{3}}=\frac{1}{2}-\frac{x^3}{48}+\frac{x^6}{576}-\ldots $$

Интегрируем полученный ряд на отрезке $[0;1]$:

$$\int\limits_{0}^{1}\frac{1}{\sqrt[3]{8+x^3}}dx=\int\limits_{0}^{1}\left(\frac{1}{2}-\frac{x^3}{48}+\frac{x^6}{576}-\ldots\right)dx=\\ =\left.\left(\frac{x}{2}-\frac{x^4}{192}+\frac{x^7}{4032}-\ldots\right)\right|_{0}^{1}=\frac{1}{2}-\frac{1}{192}+\frac{1}{4032}-\ldots$$

Так как $\frac{1}{4032}<\varepsilon$, то для вычисления интеграла с точностью $\varepsilon$ достаточно первых двух членов полученного числового ряда:

$$\int\limits_{0}^{1}\frac{1}{\sqrt[3]{8+x^3}}dx\approx\frac{1}{2}-\frac{1}{192}=\frac{95}{192}\approx{0{,}495}.$$

Ответ: $\int\limits_{0}^{1}\frac{1}{\sqrt[3]{8+x^3}}dx\approx{0{,}495}$.

Пример №4

Вычислить интеграл $\int\limits_{0}^{1/8}\sin\sqrt[3]{x}dx$ с точностью до $\varepsilon=0{,}001$.

Решение

Иногда перед тем, как разложить подынтегральную функцию в ряд Маклорена, удобно осуществить предварительную замену переменной. Чтобы избавиться от корня сделаем замену $t=\sqrt[3]{x}$. При этом получим:

$$ \int\limits_{0}^{1/8}\sin\sqrt[3]{x}dx=\left|\begin{aligned}& t=\sqrt[3]{x};\;x=t^3;\;dx=3t^2dt.\\ &\begin{array}{c|c|c}x&0&1/8\\\hline{t}&0&1/2\end{array}\end{aligned}\right|=\int\limits_{0}^{1/2}3t^2\sin{t}dt$$.

Дальнейшяя схема решения ранее разобрана подробно, поэтому я лишь кратко запишу основные этапы. Так как $\sin{x}=\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{x^{2n+1}}}{(2n+1)!}$, то:

$$ 3t^2\sin{t}=3t^2\cdot\sum\limits_{n=0}^{\infty}\frac{(-1)^n\cdot{t^{2n+1}}}{(2n+1)!}=\sum\limits_{n=0}^{\infty}\frac{3\cdot(-1)^n\cdot{t^{2n+3}}}{(2n+1)!} $$

Подставляем полученное разложение в интеграл:

$$ \int\limits_{0}^{1/2}3t^2\sin{t}dt=\int\limits_{0}^{1/2}\sum\limits_{n=0}^{\infty}\frac{3\cdot(-1)^n\cdot{t^{2n+3}}}{(2n+1)!}dt= \sum\limits_{n=0}^{\infty}\frac{3\cdot(-1)^n}{(2n+1)!}\int\limits_{0}^{1/2}t^{2n+3}dt=\\ =\sum\limits_{n=0}^{\infty}\frac{3\cdot(-1)^n}{(2n+1)!}\cdot\left.\frac{t^{2n+4}}{2n+4}\right|_{0}^{1/2}= \sum\limits_{n=0}^{\infty}\frac{3\cdot(-1)^n}{(2n+1)!\cdot(2n+4)\cdot{2^{2n+4}}}=\frac{3}{64}-\frac{1}{768}+\frac{1}{81920}-\ldots $$

Так как $\frac{1}{81920}<\varepsilon$, то для требуемой точности достаточно ограничиться первыми двумя членами ряда:

$$\int\limits_{0}^{1/2}3t^2\sin{t}dt\approx\frac{3}{64}-\frac{1}{768}\approx{0{,}0469}-0{,}0013\approx{0{,}046}.$$

Замечания по поводу погрешности округления, высказанные при решении примера №1 первой части остаются в силе. Погрешность округления двух слагаемых до четвертого знака после запятой не превысит $0{,}0001+0{,}0001=0{,}0002$. Суммарная погрешность равенства $\int\limits_{0}^{1/2}3t^2\sin{t}dt\approx{0{,}046}$ не превысит $\frac{1}{81920}+0{,}0002<0{,}001$, т.е. не превысит $\varepsilon=0{,}001$.

Ответ: $\int\limits_{0}^{1/8}\sin\sqrt[3]{x}dx\approx{0{,}046}$.

Пример №5

Вычислить интеграл $\int\limits_{10}^{100}\frac{\ln(1+x)}{x}dx$ с точностью до $\varepsilon=0{,}001$.

Решение

В рядах Маклорена нетрудно найти разложение для функции $\ln(1+x)$:

$$\ln(1+x)=\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}\cdot{x^n}}{n}$$

Однако стоит учесть, что записанное разложение имеет место при $x\in(-1;1]$, а для нашего интеграла отрезок интегрирования таков: $[10;100]$. Поэтому непосредственное применение формулы $\ln(1+x)=\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}\cdot{x^n}}{n}$ невозможно. Подынтегральную функцию нужно немного преобразовать:

$$\int\limits_{10}^{100}\frac{\ln(1+x)}{x}dx=\int\limits_{10}^{100}\frac{\ln\left(x\cdot\left(1+\frac{1}{x}\right)\right)}{x}dx= \int\limits_{10}^{100}\frac{\ln{x}+\ln\left(1+\frac{1}{x}\right)}{x}dx=\\ =\int\limits_{10}^{100}\left(\frac{\ln{x}}{x}+\frac{\ln\left(1+\frac{1}{x}\right)}{x}\right)dx= \int\limits_{10}^{100}\frac{\ln{x}}{x}dx+\int\limits_{10}^{100}\frac{\ln\left(1+\frac{1}{x}\right)}{x}dx=\\ =\int\limits_{10}^{100}\ln{x}d\left(\ln{x}\right)+\int\limits_{10}^{100}\frac{\ln\left(1+\frac{1}{x}\right)}{x}dx= \left.\frac{\ln^2{x}}{2}\right|_{10}^{100}+\int\limits_{10}^{100}\frac{\ln\left(1+\frac{1}{x}\right)}{x}dx=\frac{3\ln^2{10}}{2}+\int\limits_{10}^{100}\frac{1}{x}\ln\left(1+\frac{1}{x}\right)dx$$

Так как $x\in[10;100]$, то $\frac{1}{100}≤\frac{1}{x}≤\frac{1}{10}$. Следовательно, мы можем использовать формулу $\ln(1+x)=\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}\cdot{x^n}}{n}$, подставив $\frac{1}{x}$ вместо $x$:

\begin{aligned}&\ln\left(1+\frac{1}{x}\right)=\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}\cdot{\left(\frac{1}{x}\right)^n}}{n}=\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}}{n\cdot{x^n}};\\ &\frac{1}{x}\cdot\ln\left(1+\frac{1}{x}\right)=\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}}{n\cdot{x^{n+1}}}. \end{aligned}

Кстати сказать, полученный нами ряд не является рядом Маклорена. Подставляя полученное разложение в интеграл, получим:

$$ \frac{3\ln^2{10}}{2}+\int\limits_{10}^{100}\frac{1}{x}\ln\left(1+\frac{1}{x}\right)dx=\frac{3\ln^2{10}}{2}+\int\limits_{10}^{100}\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}}{n\cdot{x^{n+1}}}dx=\frac{3\ln^2{10}}{2}+\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}\int\limits_{10}^{100}x^{-(n+1)}dx=\\ =\frac{3\ln^2{10}}{2}+\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}\cdot\left.\frac{x^{-n}}{-n}\right|_{10}^{100}= \frac{3\ln^2{10}}{2}+\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}}{n^2}\left(1-\frac{1}{10^n}\right) $$

Так как при всех $n\in{N}$ имеем $1-\frac{1}{10^n}>0$, то ряд $\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}}{n^2}\left(1-\frac{1}{10^n}\right)$ является знакочередующимся.

$$ \frac{3\ln^2{10}}{2}+\sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}}{n^2}\left(1-\frac{1}{10^n}\right)=\frac{3\ln^2{10}}{2}+\frac{9}{100}-\frac{99}{40000}+\frac{111}{1000000}-\ldots\approx\\ \approx\frac{3\ln^2{10}}{2}+\frac{9}{100}-\frac{99}{40000}\approx{7{,}95285}+0{,}09-0{,}002475\approx{8{,}040}. $$

Ответ: $\int\limits_{10}^{100}\frac{\ln(1+x)}{x}dx\approx{8{,}040}$.

math1.ru

Разложение в ряд — Калькулятор Онлайн

Чтобы посчитать сумму ряда онлайн выполните следующие действия:

• ввести выражение, для которого нужно вычислить ряд
• указать параметр, по которому будет считать сумма
• указать значение параметра, до которого нужно подсчитать (для бесконечного ряда указываем бесконечность)

Перейти: Найти «сумму числового ряда» →

Разложение в ряд Тейлора (степенной ряд)

Это он-лайн сервис в три шага:

• Ввести функцию, которую необходимо разложить
• Ввести точку, в окрестности которой необходимо разложить
• Указать до какого члена раскладывать

Перейти: Онлайн «Разложение функции в ряд Тейлора» →

Разложение в ряд Фурье

Это он-лайн сервис в два шага:

• Ввести функцию, которую необходимо разложить
• Ввести отрезок, на котором необходимо разложить

Перейти: Онлайн «Разложение функции в ряд Фурье» →

Чтобы посчитать произведение ряда онлайн выполните следующие действия:

• ввести выражение, для которого нужно вычислить произведение ряда
• указать параметр, по которому считать произведение
• указать значение параметра, до которого нужно подсчитать (для бесконечного ряда указываем бесконечность oo)

Перейти: Найти «произведение числового ряда» →

www.kontrolnaya-rabota.ru

Приближенное вычисление определенного интеграла

Пусть требуется найти определенный интеграл , причем функция считается непрерывной на отрезке . Если от подынтегральной функции первообразная находится легко, то значение рассматриваемого интеграла находится по формуле Ньютона-Лейбница:

   

Но не в каждом случае отыскание первообразной для подынтегральной функции является достаточно простым, а также не для всякой непрерывной функции существует первообразная, выражающаяся через элементарные функции. В подобных случаях применяют приближенные формулы, которые позволяют вычислить определенный интеграл с любой степенью точности.

Наиболее часто используются три формулы приближенного вычисления определенного интеграла – формула прямоугольников, формула трапеций и формулу парабол или формула Симпсона, основанные на геометрическом смысле определенного интеграла: если функция непрерывна и положительна на отрезке , то определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями , , и (рис. 1).

1. Формула прямоугольников

Пусть на отрезке задана непрерывная функция . Вычислим численно определенный интеграл , который равен площади криволинейной трапеции.

Разобьем основание этой трапеции (отрезок ) на равных частей-отрезков длины

   

Величину будем называть шагом разбиения. В результате получим точки

   

Можно записать, что

   

В середине каждого такого элементарного отрезка отметим точку . Приняв ординату этой точки за высоту, построим прямоугольник с площадью (рис. 2).

Тогда сумма площадей всех прямоугольников равна площади ступенчатой фигуры, которая представляет собой приближенное значение искомого определенного интеграла :

   

Полученная формула называется формулой прямоугольников.

Абсолютная погрешность последнего приближенного равенства удовлетворяет следующей оценке:

   

где – наибольшее значение на рассматриваемом отрезке .

2. Формула трапеций

Эту формулу получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.

Пусть необходимо вычислить определенный интеграл . Разобьем отрезок интегрирования на равных частей длины . В результате получим точки (рис. 3). Пусть – соответствующие им ординаты функции. Тогда можно записать, что

   

Заменим кривую ломаной линией, звенья которой соединяют концы ординат и . Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями , и высотой , то есть

   

   

Записанная формула называется формулой трапеций.

Абсолютная погрешность

   

где .

3. Формула парабол (Симпсона)

Если заменить график функции на каждом отрезке , которые получены после разбиения отрезка интегрирования на равных частей, не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную формулу приближенного вычисления определенного интеграла .

Как было сказано выше, разобьем отрезок на равных частей (отрезков) длиной точками

   

причем , . В точках разбиения находим значения подынтегральной функции

   

то есть (рис. 4).

Заменяем каждую пару соседних элементарных криволинейных трапеций с основаниями одной элементарной параболической трапецией с основанием . Тогда, например, на частичном отрезке парабола проходит через три точки , , и так далее.

Расчетная формула парабол (или Симпсона) для этого метода имеет вид:

   

   

Абсолютная погрешность вычисления по этой формуле оценивается соотношением

   

где .

ru.solverbook.com

5.6. Вычисление интегралов с заданной точностью

Программная реализация формул Рунге или Эйткена позволяет вычислить определенные интегралы с заданной точностью, когда выбор необходимого числа разбиений интервала интегрирования осуществляется автоматически. При этом, конечно, можно использовать многократное обращение к подпрограммам соответствующих методов интегрирования, не изменяя алгоритмов самих методов. Однако для методов, использующих равноотстоящие узлы, удается модифицировать алгоритмы и уменьшить вдвое количеств вычислений подынтегральной функции за счет использования интегральных сумм, накопленных при предыдущих кратных разбиениях интервала интегрирования.

Так, два приближенных значения S_k и S_k-1 интеграла

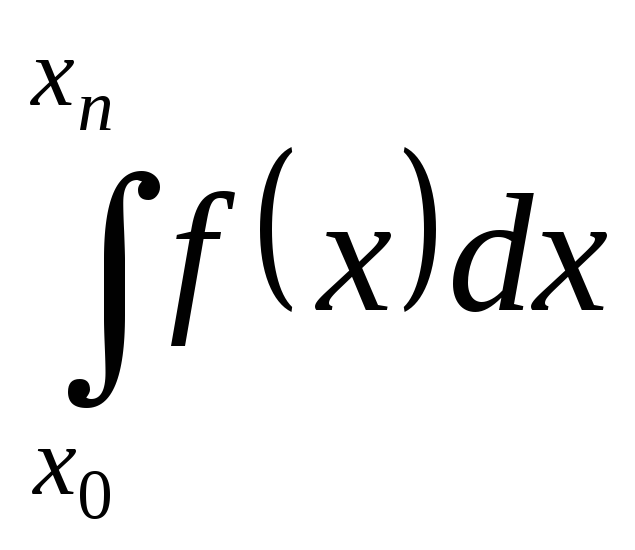(5.36)

вычисляемые по методу трапеций с шагами h_k и h_k-1 связаны соотношением

(5.37)

где

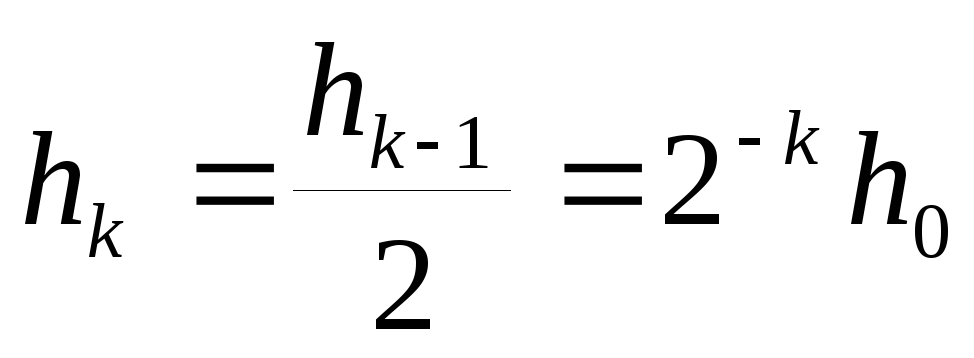
Формула (5.37) получена методом математической индукции. Если выбрать начальный шаг интегрирования

h_o = х_n — x_о, то приближенное значение интеграла (5.36) по методу трапеций запишется в виде

(5.38)

где

При уменьшении шага h₀ вдвое получим приближенное значение того же интеграла

(5.39)

где

Сравнение формул (5.38) и (5.39) позволяет записать соотношение между значениями S_o и

S₁

которое позволяет получать приближенное значение интеграла S₁ с шагом h₁, вычислив подынтегральную функцию только в одном дополнительном узле х_n/2. Продолжая процесс уменьшения шага интегрирования вдвое, приходим к формуле (5.37), по которой каждое новое приближенное значение интеграла (5.36) получаем, вычислив дополнительно подынтегральную функцию только в 2^k-1 узле. Обращение же к подпрограмме метода трапеций по­требовало бы вычисления функции в (2^k+1) узле.

Аналогичным способом получены соотношения между двумя прибли­женными значениями S_k и S_k-1 интеграла (5.36), вычисляемые по методу Симпсона с шагами

h_k и h_k-1

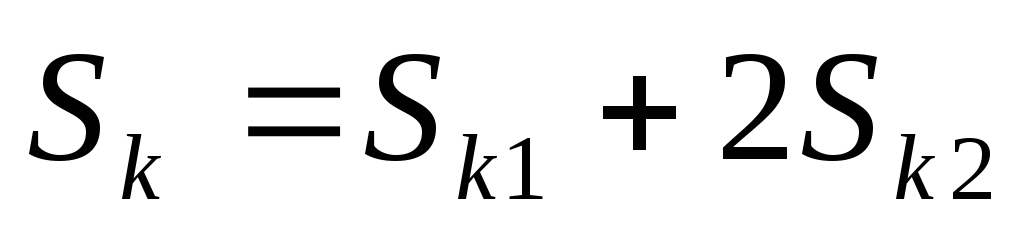(5.40)

где

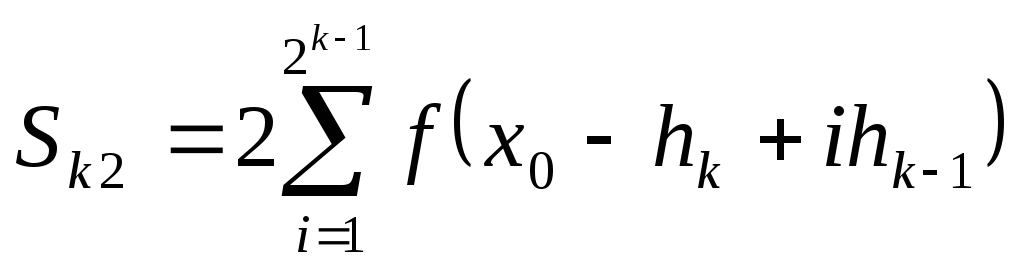
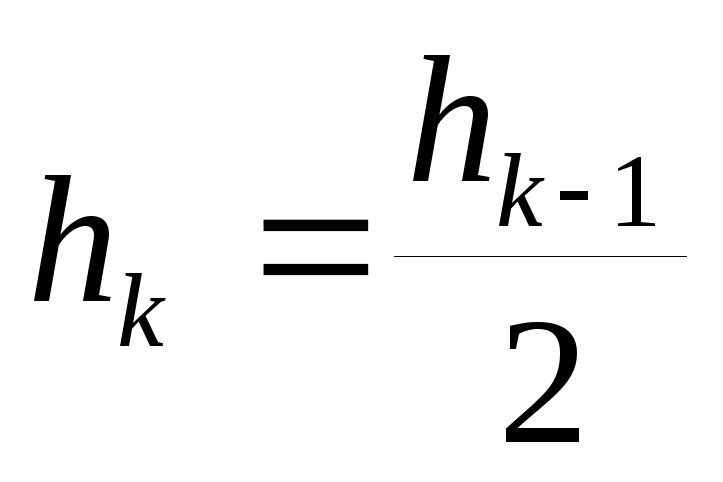
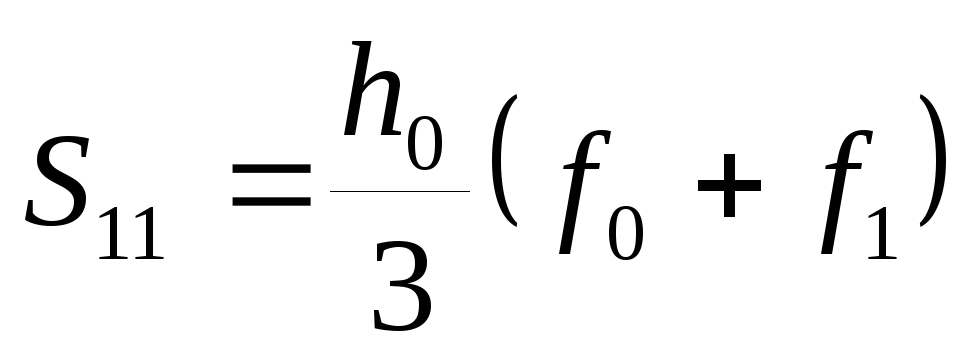
5.7. Применение сплайнов для численного интегрирования

В п. 3.6 рассмотрена интерполяция кубическими сплайнами, коэффициенты которых определяются из условий Лагранжа, условий непрерывности первой и второй производных в узлах и условий на концах интервала. Вследствие этого коэффициенты всех сплайнов оказываются связанными системой линейных алгебраических уравнений с трехдиагональной матрицей. Рассмотрим применение сплайнов для вычисления определенных интегралов или так называемую сплайн-квадратуру [19]. Пусть необходимо вычислить интеграл вида

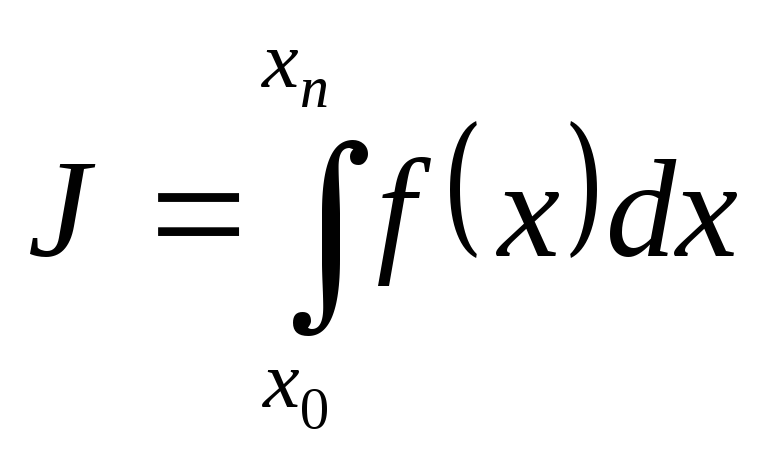(5.41)

Разобьем интервал [x₀, x_n] на участки

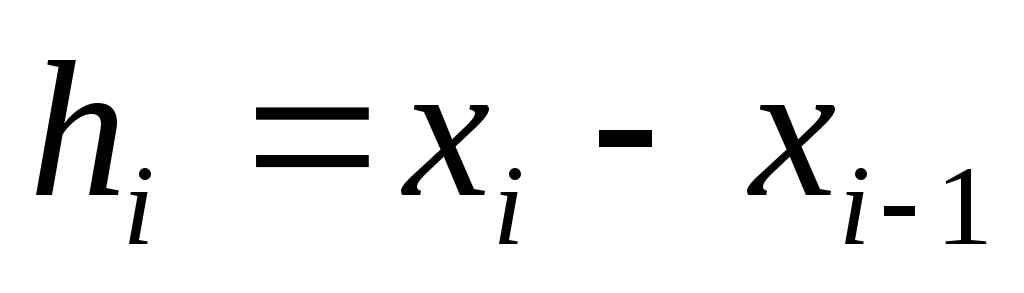
i=1,…n, на каждом из которых подынтегральную функцию f(x) заменим кубическим сплайном _j(х):

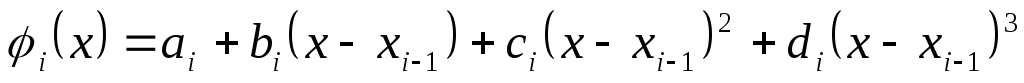
где

Тогда интеграл (5.41) запишется как сумма интегралов от сплайнов:

Последняя формула упрощается при подстановке в нее выражений (3.26), (3.34) и (3.35) для коэффициентов а_j, b_j, и d_j.

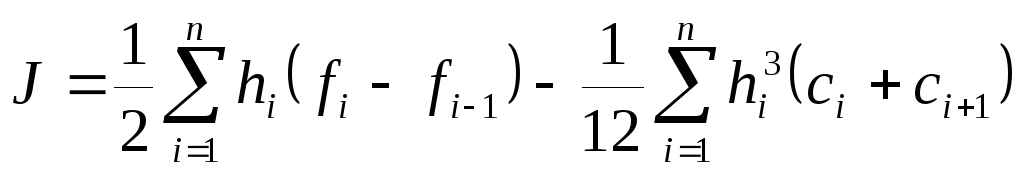(5.42)

Нетрудно видеть, что первая сумма в формуле (5.42) есть формула трапеций, а вторая сумма — поправочное слагаемое для формулы трапеций, примененной к сплайнам, так как при малых значениях h, коэффициенты с_j и с_j+1 близки по величине, коэффициент, следовательно,

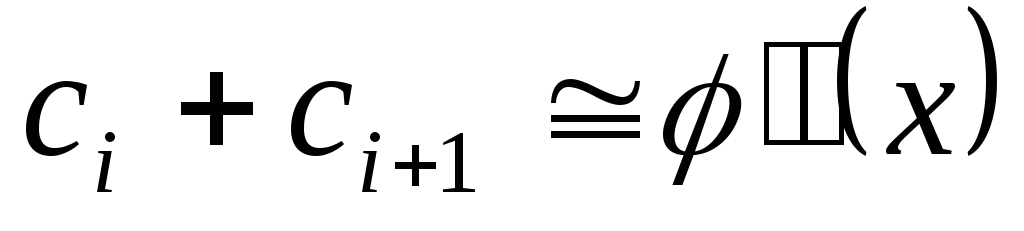
Значит, погрешность сплайн-квадратуры меньше, чем погрешность метода трапеций. Однако алгоритм интегрирования с помощью сплайнов сложнее алгоритмов методов трапеций и Симпсона за счет необходимости решения системы линейных уравнений для определения коэффициентов сплайнов с_j. Поэтому рационально использовать сплайн-квадратуры в комплексе, когда сплайны применяются для сглаживания зависимостей, обработки экспериментальных данных и т. п.

studfile.net