Вычисление выражений для заданных значений переменных

Данный калькулятор вычисляет значение выражения, подставляя туда значения переменных из таблицы. Удобно для проверки домашних заданий типа «Найдите значение выражения при a = 0.1, b = 2». Обозначения переменных в выражении должны совпадать с именами переменных в таблице. Если не совпадет — замены не будет и подсчитает неправильно, так что следите.

Вычисление выражений для заданных значений переменных

addimport_exportmode_editdelete

Переменные

Размер страницы: chevron_leftchevron_right

Переменные

Сохранить Отменить

Импортировать данныеОшибка импорта

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: Lorem ipsum;Lorem ipsum

Импортировать Назад Отменить Точность вычисления

Знаков после запятой: 2

Формула после подстановки

 

Результат расчета

 

save Сохранить share Поделиться extension Виджет

Для расчета после подстановки значений переменных используется Математический калькулятор.
Таким образом, аналогично указанному калькулятору, здесь также в математическом выражении допускается использование числа пи (pi), экспоненты (e), следующих математических операторов:

• / — деление
• ^ — возведение в степень

и следующих функций:

• sqrt — квадратный корень
• rootp — корень степени p, например root3(x) — кубический корень
• exp — e в указанной степени
• lb — логарифм по основанию 2
• lg — логарифм по основанию 10
• ln — натуральный логарифм (по основанию e)
• logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
• sin — синус
• cos — косинус
• tg — тангенс
• ctg — котангенс
• sec — секанс
• cosec — косеканс
• arcsin — арксинус
• arccos — арккосинус
• arctg — арктангенс
• arcctg — арккотангенс
• arcsec — арксеканс
• arccosec — арккосеканс
• versin — версинус
• vercos — коверсинус
• haversin — гаверсинус
• exsec — экссеканс
• excsc — экскосеканс
• sh — гиперболический синус
• ch — гиперболический косинус
• th — гиперболический тангенс
• cth — гиперболический котангенс
• sech — гиперболический секанс
• csch — гиперболический косеканс
• abs — абсолютное значение (модуль)
• sgn — сигнум (знак)

Вычисление сложных арифметических выражений

Excelобладает мощными вычислительными возможностями. Кроме привычных математических операций сложения (+), вычитания (-), умножения (*), деления (/) и возведения в степень (^),Excelрасполагает встроенной библиотекой всевозможных функций, в том числе математических, алгебраических и тригонометрических.

Для вычисления выражения, в ячейке сначала необходимо поставить знак =, а затем набрать формулу. Все исправления в формулу вносятся в строке редактирования.

Формула состоит их констант, имён функций и ссылок на значения.

Например, математическая формула

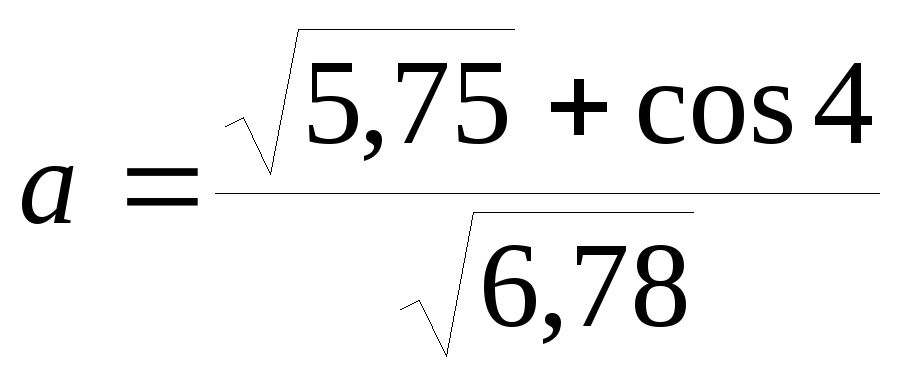
В Excelбудет иметь вид

Или 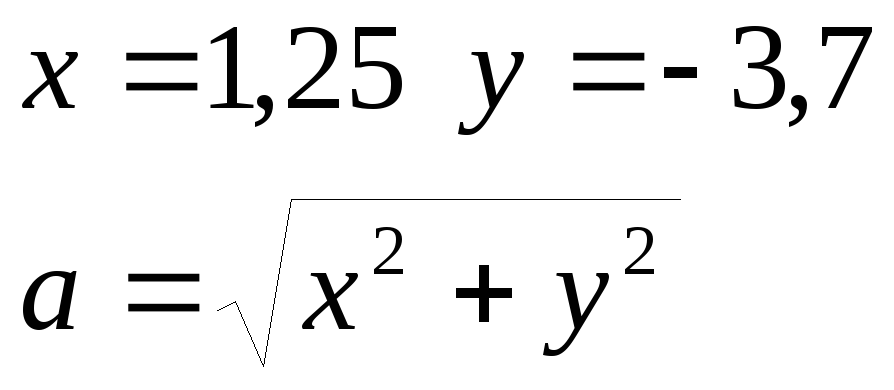ВExcelимеет вид :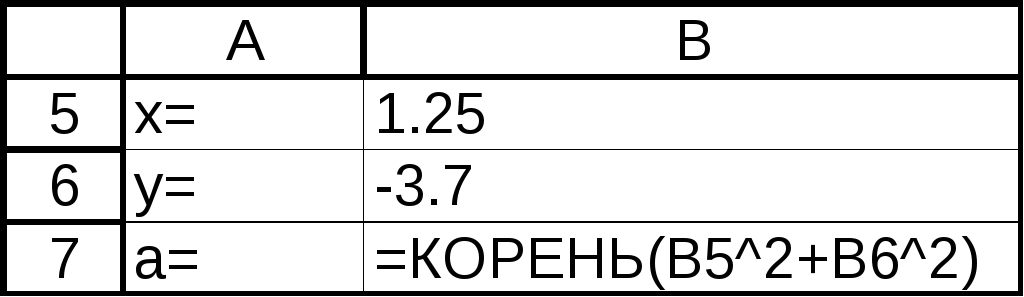

Для использования функций в формулах запускается мастер функций командой Вставка, Функция, либо кнопкой-пиктограммойfx

Пример

Вычисление сложных арифметических выражений

Вычислить выражения

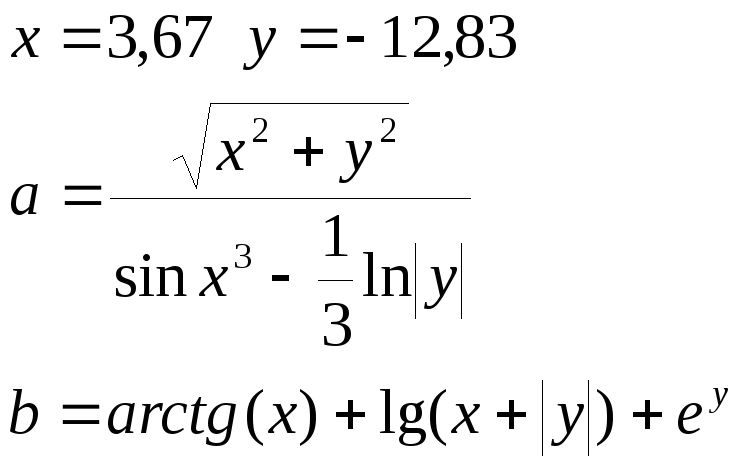
Режим значений

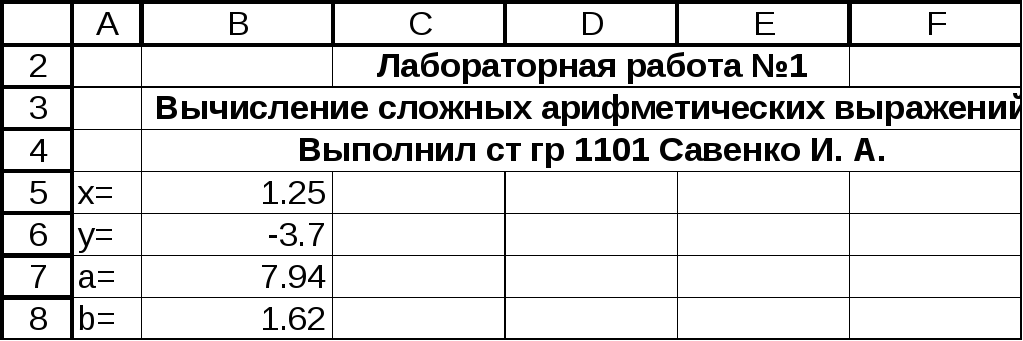
Режим формул

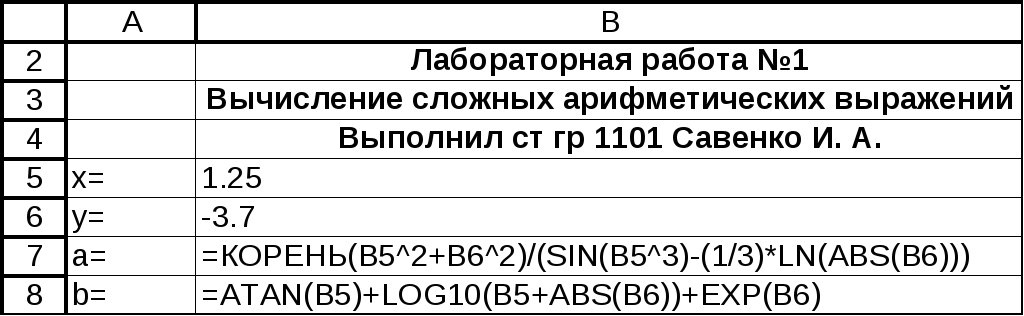
Вычисления в EXCEL

Очень часто в математических задачах требуется вычислить то или иное выражение в зависимости от значений переменных, входящих в формулу выражения

Например,

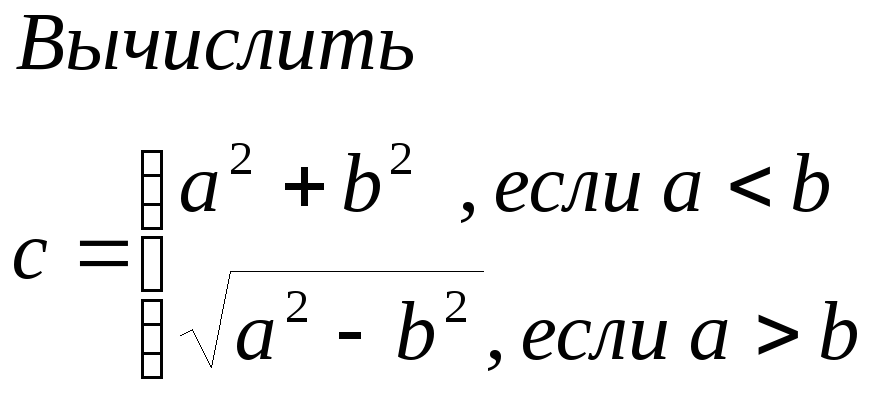
В Excelдля вычисления условных выражений используется функция

ЕСЛИ()

Для приведённого примера фрагмент рабочего листа Excel

Табулирование функции одной переменной и построение её графика

Табулирование функции – это получение таблицы значений функции при заданных значениях аргумента. Например, функция F(X)=X²

X	F(X)
-1	1
-0,5	0,25
0	0
0,5	0,25
1	1
1,5	2,25
2	4

Для вычисления значений функции рекомендуется использовать инструмент автозаполнения.

Автозаполнение– копирование ячеек, при котором относительные адреса ячеек в формулах автоматически изменяются, абсолютные же остаются без изменения.

.Как выполнить автозаполнение? Установитерабочий курсорв ячейку, которую необходимо скопировать. Установитекурсор мыши

в нижний правый угол выделенной ячейки так, чтобы он принял формукурсора автозаполнения (+).Не отпуская левой клавиши мыши, протащите курсор автозаполнения доN-й ячейки, гдеN– номер конечной ячейки для копирования. В данной лабораторной работе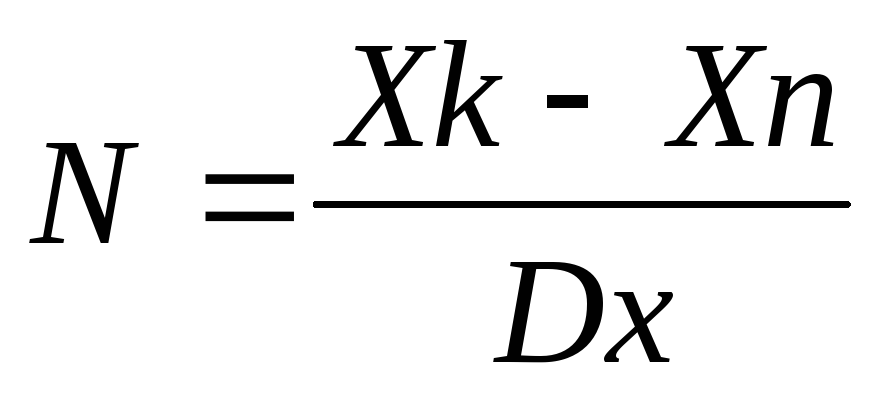

.Фрагмент рабочего листа с решением задачи табулирования функции 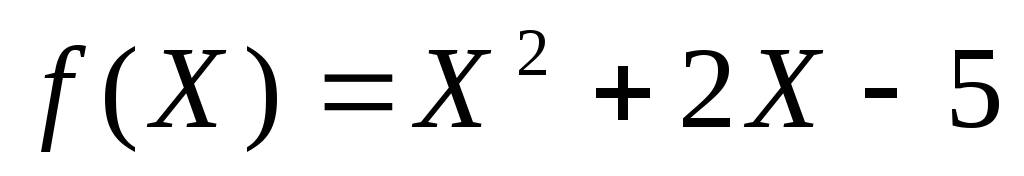приведён ниже

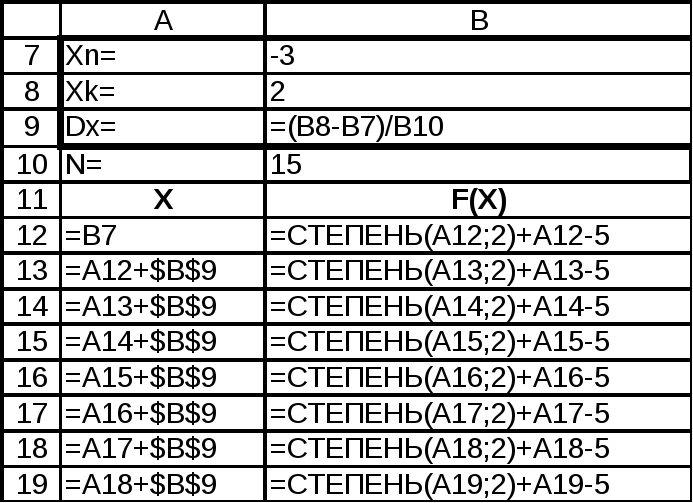
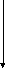
С этой ячейки начинается автозаполнение для значений аргумента X. Для значений функции автозаполнение начинается с ячейки В12.

Как построить диаграмму (график) функции F(

X)?

Построить диаграмму в ExcelпоможетМастер диаграмм. Чтобы его запустить, выполните команду менюВставка, Диаграммаили нажмите на панели инструментов кнопку. Мастер работает в пошаговом режиме и на каждом шаге предлагает выполнить то или иное действие. Мастер позволяет вернуться на шаг или несколько шагов назад и отредактировать построенную диаграмму.

1 шаг

Задайте вид диаграммы и нажмите кнопку Далее

Для данного примера: График, Непрерывный

2 шаг

На вкладке Диапазонданных в окнеДиапазонзадайте интервал, содержащий только значения функции без заголовка,(в данной лабораторной работе это диапазон В12:В19) и установите флажокРяды в столбцах. Чтобы задать диапазон значений, щёлкните на первой ячейке диапазона и не отпуская левую клавишу мыши протяните курсор до последней ячейки диапазона

Щёлкните по вкладке Ряд.

В окне Подписи по оси Хзадайте диапазон значений для Х (А12: А19).

В окне РядыИмязадайте адрес ячейки заголовка функции (В8), нажмите кнопкуДалее

3 шаг

Окно Параметры диаграммы: Здесь нужно задатьНадпись диаграммы,Надписи осейуказать расположение легенды (Название графиков), на вкладкеПодписи данныхможно включить флажокзначения, тогда на графике будут указаны значения функции в точках диапазона. На вкладкеЛегендаможно изменить положение легенды на диаграмме или совсем убрать её с диаграммы.

4шаг

Укажите, где построить диаграмму: на текущем или отдельном листе и нажмите кнопку

Готово.

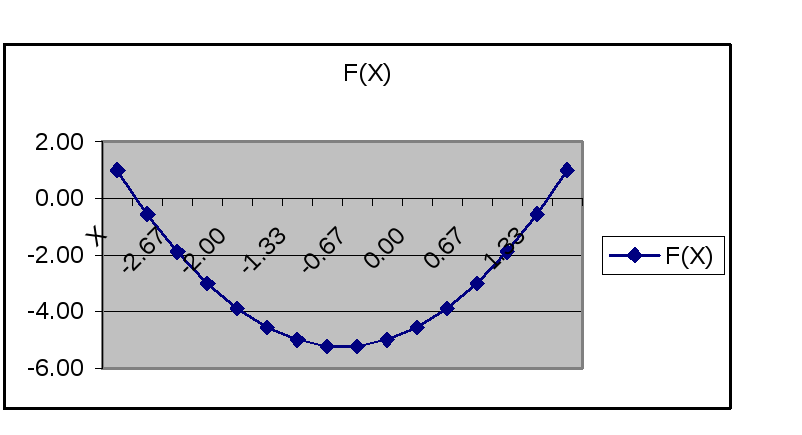
Рисунок 1 График функции

Построенную диаграмму можно отредактировать. Для этого нужно установить курсор мыши на нужный объект диаграммы и щелкнуть правой кнопкой, в контекстном меню выбрать ту или иную опцию. Например, чтобы изменить вид линии графика, выбираем опцию Формат рядов данных

В Excel, кроме абсолютных ссылок на значения, можно использоватьимена ячеекПрисвойте ячейкам, содержащим значенияXn,Xk,Dxимена.

Как присвоить имя ячейке? Выполните команду менюВставка, Имя, Присвоить — в открывшемся окне укажите имя переменной и адрес её значения (окно Формула), после этого нажмите кнопкуДобавить.

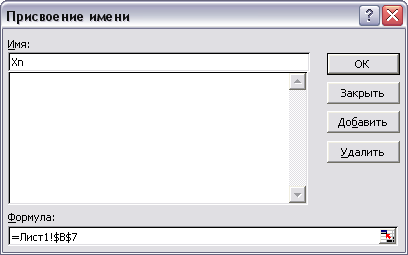
Рисунок 2 Окно Присвоение имени

Измените формулы в таблице и заполните таблицу заново. Формулы в столбце Xизменятся следующим образом.

=A12+Dx

=A13+Dx

…

=A18+Dx

Если в формуле для функции присутствуют константы, то ячейкам, содержащим их значения тоже присвойте имена и измените формулу для вычисления функции, заменив ссылки на значения констант на имена

Пример отчёта по лабораторной работе находится на следующей странице

Калькулятор онлайн — Сложение, сокращение, умножение, деление, вычитание неправильных числовых дробей (с подробным решением)

С помощью данного калькулятора онлайн вы можете умножить, вычесть, поделить, сложить и сократить числовые дроби с разными знаменателями.

Программа работает с правильными, неправильными и смешанными числовыми дробями.

Данная программа (калькулятор онлайн) умеет:
— выполнять сложение смешанных дробей с разными знаменателями

— выполнять вычетание смешанных дробей с разными знаменателями
— выполнять деление смешанных дробей с разными знаменателями
— выполнять умножение смешанных дробей с разными знаменателями
— приводить дроби к общему знаменателю
— преобразовывать смешанные дроби в неправильные
— сокращать дроби

Также можно ввести не выражение с дробями, а одну единственную дробь.
В этом случае дробь будет сокращена и из результата выделена целая часть.

Калькулятор онлайн для вычисления выражений с числовыми дробями не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс нахождения решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода выражений с числовыми дробями, рекомендуем с ними ознакомиться.

Правила ввода выражений с числовыми дробями

В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3 + 7/5
Результат: \( -\frac{2}{3} + \frac{7}{5} \)

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&2/3 * 5&8/3
Результат: \( -1\frac{2}{3} \cdot 5\frac{8}{3} \)

Деление дробей вводится знаком двоеточие: :
Ввод: -9&37/12 : -3&5/14
Результат: \( -9\frac{37}{12} : \left( -3\frac{5}{14} \right) \)
Помните, что на ноль делить нельзя!

При вводе выражений с числовыми дробями можно использовать скобки.
Ввод: -2/3 * (6&1/2-5/9) : 2&1/4 + 1/3
Результат: \( -\frac{2}{3} \cdot \left( 6 \frac{1}{2} — \frac{5}{9} \right) : 2\frac{1}{4} + \frac{1}{3} \)

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Обыкновенные дроби. Деление с остатком

Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления. В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).

Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель. Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток. В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.

Остаток всегда меньше делителя.

Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать так: 64 = 32 * 2.

Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление. Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».

Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а знаменатель п — делитель:
\( m:n = \frac{m}{n} \)

Верны следующие правила:

Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n.

Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)

Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a : m}{b : m} \)
Это свойство называют основным свойством дроби.

Два последних преобразования называют сокращением дроби.

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю.

Правильные и неправильные дроби. Смешанные числа

Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют неправильными дробями. Остальные дроби, т. е. дроби, у которых числитель меньше знаменателя, называют правильными дробями.

Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.

Если число состоит из целой части и дроби, то такие дроби называются смешанными.

Например:
\( 5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \( \frac{2}{3} \) — дробная часть.

Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель разделить на это число:
\( \large \frac{a}{b} : n = \frac{a:n}{b} \)

Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её знаменатель умножить на это число:
\( \large \frac{a}{b} : n = \frac{a}{bn} \)

Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.

Действия с дробями. Сложение дробей.

С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \). Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)

Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.

Сложение смешанных дробей

Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».

При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)

Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть.

Вычитание дробей (дробных чисел)

Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит найти такое число, которое при сложении со вторым дает первое. Например:
\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)

Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель оставить прежним.

С помощью букв это правило записывается так:
\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)

Умножение дробей

Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.

С помощью букв правило умножения дробей можно записать так:
\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)

Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.

Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.

Деление дробей

Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \). Эту дробь называют обратной дроби \( \frac{2}{3} \).

Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как \( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.

Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).

С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)

Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)

Используя взаимно обратные дроби, можно деление дробей свести к умножению.

Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.

Используя буквы, правило деления дробей можно записать так:
\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)

Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.

Калькулятор комлексных чисел | Вычисление выражений, содержащих комплексные числа

Калькулятор комплексных чисел позволяет вычислять арифметические выражения, содержащие комплексные числа, знаки арифметических действий (+, -, *, /, ^), а также некоторые математические функции.

Калькулятор комплексных чисел

7

8

9

+

—

*

/

^

4

5

6

i

(

)

π

e

1

2

3

sin

cos

tg

ctg

ln

.

0

√

sh

ch

th

cth

abs

Скрыть клавиатуру

Вычислено выражений: 43332

Как пользоваться калькулятором

1. Введите в поле ввода выражение с комплексными числами
2. Укажите, требуется ли вывод решения переключателем «С решением»
3. Нажмите на кнопку «Построить»

Ввод комплексных чисел

комплексные числа можно вводить в следующих трёх форматах:

• Только действительная часть: 2, 2.5, -6.7, 12.25
• Только мнимая часть: i, -i, 2i, -5i, 2.16i, -12.5i
• Действительная и мнимая части: 2+i, -5+15i, -7+2.5i, -6+i
• Математические константы: π, e

Поддерживаемые операции и математические функции

• Арифметические операции: +, -, *, /, ^
• Получение абсолютного значения числа: abs
• Базовые математические функции: exp, ln, sqrt
• Получение действительной и мнимой частей: re, im
• Тригонометрические функции: sin, cos, tg, ctg
• Гиперболические функции: sh, ch, th, cth
• Обратные тригонометрические функции: arcsin, arccos, arctg, arcctg
• Обратные гиперболические функции: arsh, arch, arth, arcth

Примеры корректных выражений

• (2+3i)*(5-7i)
• sh(i)
• (4+i) / (3 — 4i)
• sqrt(2i)
• (-3+4i)*2i / exp(2i + (15 — 8i)/4 — 3.75)

Комплексные числа

Комплексные числа — это числа вида x+iy, где x, y — вещественные числа, а i — мнимая единица (специальное число, квадрат которого равен -1, то есть i2 = -1).
Так же, как и для вещественных чисел, для комплексных чисел определены операции сложения, разности, умножения и деления, однако комплексные числа нельзя сравнивать.

Примеры комплексных чисел

• 4+3i — действительная часть = 4, мнимая = 3
• -2+i — действительная часть = -2, мнимая = 1
• i — действительная часть = 0, мнимая = 1
• -i — действительная часть = 0, мнимая = -1
• 10 — действительная часть = 10, мнимая = 0

Основные действия с комплексными числами

Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:

• сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
• вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
• умножение: (a + bi) · (c + di) = ac + bci + adi + bdi² = (ac — bd) + (bc + ad)i
• деление: = = + i

Примеры

Найти сумму чисел 5+7i и 5.5-2i:
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом:5+7i + 5.5-2i = 10.5 + 5i

Найти разность чисел 12-i и -2i:
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом:12-i — (-2i) = 12 + i

Найти произведение чисел 2+3i и 5-7i:
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом:2+3i * (5-7i) = 31 + i

Найти отношение чисел 75-50i и 3+4i:
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом:75-50i / (3+4i) = 1 - 18i

Другие действия над комплексными числами

Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:

• Получение действительной части числа: Re(z) = a
• Получение мнимой части числа: Im(z) = b
• Модуль числа: |z| = √(a2 + b2)
• Аргумент числа: arg z = arctg(b / a)
• Экспонента: ez = ea·cos(b) + i·ea·sin(b)
• Логарифм: Ln(z) = ln |z| + i·arg(z)
• Тригонометрические функции: sin z, cos z, tg z, ctg z
• Гиперболические функции: sh z, ch z, th z, cth z
• Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
• Обратные гиперболические функции: arsh z, arch z, arth z, arcth z

Примеры

Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3
|z| = √(4² + (-3)²) = √25 = 5

Формы представления комплексных чисел

Комплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.

• Алгебраическая форма — наиболее часто используемая форма комплексного числа, запись числа в виде суммы действительной и мнимой частей: x+iy, где x — действительная часть, а y — мнимая часть
• Тригонометричкая форма — запись вида r·(cos φ + isin φ), где r — модуль комплексного числа (r = |z|), а φ — аргумент этого числа (φ = arg(z))
• Показательная форма — запись вида r·eiφ, где r — модуль комплексного числа (r = |z|), e — число Эйлера, а φ — аргумент комплексного числа (φ = arg(z))

Пример:

Переведите число 1+i в тригонометрическую и показательную формы:

Решение:

• Найдём радиус (модуль) комплексного числа r: r = √(1² + 1²) = √2
• Найдём аргумент числа: φ = arctan() = = 45°
• Запишем результат в тригонометрической форме: √2·(cos(45°) + isin(45°))
• Запишем результат в показательной форме: √2·eπi/4

Онлайн калькулятор: Запись математических выражений

Достаточно много калькуляторов на нашем сайте используют математические выражения см. Математический калькулятор, Производная функции, Нахождение предела функции в точке по правилу Лопиталя, Производные любого порядка, и т. п. В комментариях практически ко всем таким калькуляторам постоянно возникают вопросы о том, как правильно записать то или иное выражение. Эта статья призвана закрыть вопрос раз и навсегда (ну, по крайней мере, я в это очень верю :).
Далее предлагаю вашему вниманию калькулятор-шпаргалку по математическим выражениям для функций с одной переменной:

Синтаксис записи математических формул

Математическое выражениеАрккосеканс иксАрккосинус иксАрксеканс иксАрксинус иксАрктангенс иксВерсинус иксВычитание — икс минус дваГаверсинус иксГиперболический косеканс иксГиперболический косинус иксГиперболический котангенс иксГиперболический секанс иксГиперболический синусГиперболический тангенс иксДеление — икс пополамДесятичный логарифм от иксЗнак иксИкс в кубеКоверсинус иксКонстанта — E (основание натурального логарифма)Константа — дробноеКонстанта — дробное в виде мантисса, порядокКонстанта — целоеКонстанта — число ПИКорень из иксКорень из косинуса в третьей степени от 5 икс минус 7Корень пятой степени из xКосеканс иксКосинус иксКосинус пи на четыре икс в пятой степениКотангенс иксКубический корень из xЛогарифм по основанию 2 от иксЛогарифм по основанию 7 от иксМодуль иксНатуральный логарифм от xПеременная иксСеканс иксСинус в кубе от семи иксСинус иксСложение — икс плюс 2Тангенс иксТри в степени иксУмножение — два иксЭкскосеканс иксЭкссеканс икс

Пример математических выражений

Математическая запись

 

save Сохранить share Поделиться extension Виджет

А вот тут все функции в одной таблице с примерами:

Таблица синтаксиса математических выражений

ГруппаКонстанты и переменныеОперацииТригонометрические функцииОбратные тригонометрические функцииГиперболические функции

save Сохранить share Поделиться extension Виджет