Урок 24. вычисление площадей с помощью интегралов — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №24. Вычисление площадей с помощью интегралов.
Перечень вопросов, рассматриваемых в теме
1) Нахождение площади фигуры, ограниченной графиками функций с помощью определенного интеграла.
2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница
3) Решение задач, с помощью формулы Ньютона – Лейбница
Формула Ньютона – Лейбница
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.
Теоретический материал для самостоятельного изучения
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].
Отрезок [a;b] называют основанием этой криволинейной трапеции
формула Ньютона – Лейбница
Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым. ( зависит от расположения криволинейной трапеции)
Примеры и разбор решения заданий тренировочного модуля
№1 Вычислите площадь фигуры, ограниченной линиями y= x, y = 5 – x, x = 1, x = 2, используя определенный интеграл.
Решение. Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b).
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) — F(а) , это и будет ответ
№2. Найти площадь фигуры, ограниченной линиями у=4-х2,у=3х, у=0 и находящейся в 1-й четверти.
Решение: Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) — F(а) , это и будет ответ.
Решение. S=SOAB +SABC
№3. Найти площадь криволинейной трапеции (х-1)2, ограниченной линиями х=2 и х=1, осью 0х
Решение:
Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .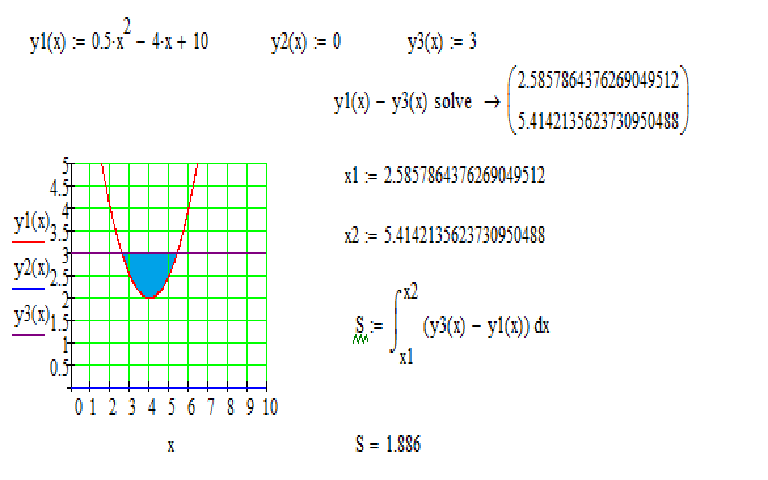
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) — F(а), это и будет ответ.
Комбинированный урок математики «Вычисление площадей плоских фигур с помощью определенного интеграла»
Тип урока: комбинированный.
Цель урока:
- закрепить умение выделять криволинейные трапеции из ряда геометрических фигур и отработать навык вычислений площадей криволинейных трапеций;
- познакомиться с понятием плоской фигуры;
- научиться вычислять площадь плоских фигур;
- способствовать развитию логического мышления, грамотной математической речи, аккуратности при построении чертежей;
- воспитывать интерес к предмету, к оперированию математическими понятиями и образами, воспитать волю, самостоятельность, настойчивость при достижении конечного результата.
Структура урока:
- Организационный момент.
- Повторение ранее изученного материала.
- Изучение нового материала.
- Закрепление изученного материала.
- Подведение итога урока.
- Постановка домашнего задания.
Приветствие класса. Сообщение учащимся целей урока.
II. Повторение ранее изученного материала- На прошлом уроке мы познакомились с понятием криволинейной трапеции и научились вычислять площадь этой фигуры. Давайте вспомним, какая фигура называется криволинейной трапецией?
- Криволинейной трапецией называется фигура, ограниченная осью ОХ, прямыми x = a,
- Какую формулу можно использовать для вычислений площади криволинейной трапеции?
- Формулу Ньютона-Лейбница.
- Формулу вывели английский физик Исаака Ньютона (1643–1727) и немецкий философ Готфрида Лейбница (1646–1716). И это не удивительно, ведь математика – язык, на котором говорит сама природа.
- Для того чтобы вспомнить основные моменты ранее изученного материала, выполним тест по теме: «Первообразная. Площадь криволинейной трапеции» (Приложение 1). (Для применения теста, ознакомьтесь, пожалуйста, с инструкцией.)
Тема нашего урока: «Вычисление площадей плоских фигур с помощью определенного интеграла». (Слайд 1)
- Обратите внимание на экран. Что изображено на первом рисунке? (Слайд 2)
- Криволинейная трапеция.
- Что изображено на втором рисунке? Является ли эта фигура криволинейной трапецией?
- На рисунке представлена плоская фигура. Рассмотрим ее более подробно. (Слайд 3)
- Плоская фигура — это фигура ограниченная прямыми x = a, x = b и графиками непрерывных функций y = f(x), y = g(x), причем на отрезке [a; b] выполняется неравенство g(x) f(x).
- Как можно вычислить площадь этой фигуры?
(Слайд 4)
Итак, площадь S фигуры, ограниченной прямыми x = a, x = b и графиками функций y = f(x), y = g(x), непрерывных на отрезке [a; b] и таких, что для всех х из отрезка [a; b]выполняется неравенство
Рассмотрим, как при решении практических заданий используется эта формула.
(Слайд 5)
Пример 1: Вычислить площадь фигуры, ограниченной линиями y = x, y = 5 – x, x = 1, x = 2.
Решение: Построим на координатной плоскости графики функций y = x, y = 5 – x, x = 1, x = 2. Заштрихуем площадь фигуры, площадь которой надо найти.
Воспользовавшись формулой , получим
Ответ: S = 2.
(Слайд 6)
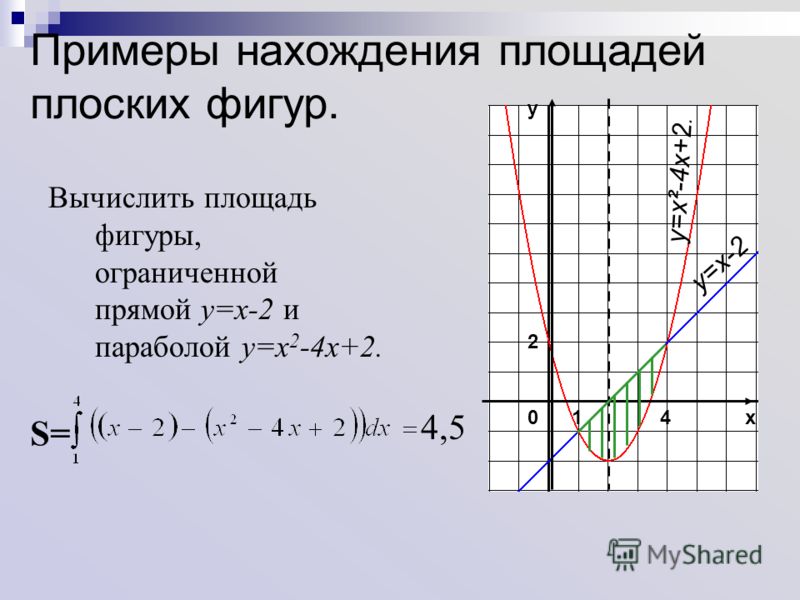
Пример 2: Вычислить площадь фигуры, ограниченной прямойy = x – 2 и параболой y = x2 – 4x + 2.
Решение:
Построим прямую y = x – 2 по точкам, например (2; 0) и (0; -2).
Для построения параболы найдем координаты вершины по формулам ; yв = y(xв). Имеем:
;.
Значит, вершиной параболы служит точка (2; -2). Возьмем пару дополнительных точек, например (0; 2), (4; 2) и построим график данной квадратичной функции.
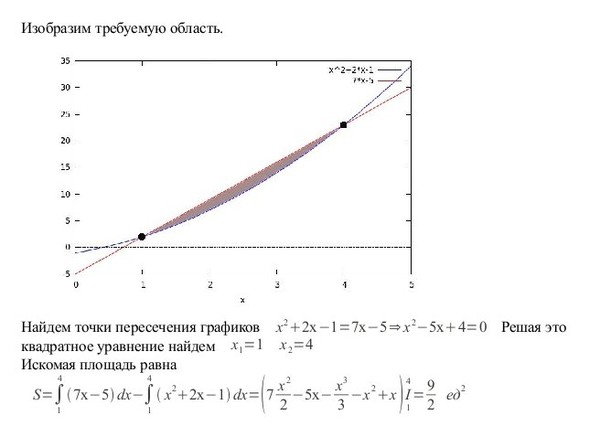
Найдем абсциссы точек пересечения прямой и параболы, для чего решим уравнение
х2 – 4х + 2 = х – 2
Находим последовательно: х2 – 5х + 4 = 0;
х1 = 1; х2 = 4.
Фигура, площадь которой надо найти, ограничена линиями y = x2 – 4x + 2 (снизу) и y = x – 2 (сверху). С боков эта фигура ограничена прямыми х = 1 и х = 4.
(Слайд 7)
Для вычисления площади фигуры можно применить изученную сегодня формулу.
Ответ: S = 4,5.
IV. Закрепление изученного материалаЗадания решаются самостоятельно с проверкой у доски.
(Слайд 8)
Задание 1: Вычислите площадь фигуры, ограниченной прямыми:
а) y = x, y = -0,5x + 5, x = -1, x = 3;
б) y = 1 – x, y = 3 – 2x, x = 0.
(Слайд 9)
Задание 2: Вычислите площадь фигуры, ограниченной графиками функций:
V. Подведение итога урокаа) y = 1 – x2, y = -x – 1;
б) y = x2 – 3x + 2, y = x – 1;
в) y = x2 + 2x-3, y = -x2 + 2x +5;
г) y = cos x, y = -x, x = 0, x = ;
д) y = sin 2x, y = x — , x = 0.
Что сегодня изучили на уроке?
Чем отличается плоская фигура от криволинейной трапеции?
Как вычисляется площадь плоской фигуры?
Сформулируйте основные шаги вычисления площади криволинейной трапеции и плоской фигуры.
(Слайд 10)
Домашнее задание:
Вычислите (предварительно сделав рисунок) площадь фигуры, ограниченной линиями:
а) y = x3, y = 8, y = 1;
б) y = 4x – x2, y = 4 – x;
в) y = x2 – 2x + 2, y = 2+ 6x – x2;
г) y = sin x, y = , .
Спасибо за урок! До свидания.
Подготовка к ЕГЭ по теме «Первообразная»
Подготовка к ЕГЭ по теме «Первообразная»
Задания уровня В.
1. Вычислите площадь фигуры, ограниченной линиями у = , у = 0,5х
Ответ:
2. Первообразная функции f(х) = 3х2 + 2х при х = 1 принимает значение В1. Найдите ее значение при х = -1
Ответ: 79
3. Вычислите площадь фигуры, ограниченной линиями у=2, у=3–х, х = 0
Ответ:
4.
Первообразная функции f(х) = 4х3+2х
при = 1 принимает значение 25. Найдите ее значение при х = 2
Ответ: 43
5. Найдите площадь фигуры, ограниченной линиями у = 2х2, у = 4х
Ответ: 8/3
6. Найдите площадь фигуры, ограниченной линиями у = х2, у = -2х
Ответ: 4/3
7. Найдите площадь фигуры, ограниченной линиями у= 9х2–6х+1, у = 0, х= 0
Ответ:
8. Найдите площадь фигуры, ограниченной линиями у = 4х2 + 12х + 9, у = 0, х = 0
Ответ: 4,5
9. найдите площадь фигуры, ограниченной линиями у = 1–х, у = 0 и у=(х+1)2, где х ≥ -1
Ответ: 5/6
10. Найдите площадь фигуры, ограниченной линиями у = х – 1, у = 0 и у=(х-3)2, где х ≤ 3
Ответ: 5/6
11. Найдите площадь фигуры, ограниченной графиком функции у = -х2+х-4 и осями координат.
Ответ: 8/3
12.
Найдите площадь фигуры, ограниченной
графиком функции у=х2+6х+9 и осями координат
Ответ: 9
13. Вычислите площадь фигуры, ограниченной графиком функции у=х2 -4х-4 и прямой у=-х
Ответ: 125/6
14. Найдите площадь фигуры, ограниченной графиком функции у=3-х2 и прямой у=2х
Ответ: 32/3
15. Найдите площадь фигуры, ограниченной линиями у=х2-4х+4, у=0 и х=0
Ответ: 8/3
16. Найдите площадь фигуры, ограниченной линиями у= и у=
Ответ: 4/3
17. Найдите площадь фигуры, ограниченной линиями у-х2=0 и у2-х=0
Ответ:
18. Найдите площадь фигуры, ограниченной линиями у=(1-х) (х-5), у=4 и х=1
Ответ: 2
19. Найдите площадь фигуры, ограниченной линиями у-х2=0 и у2+х=0
Ответ:
20. Найти площадь фигуры, ограниченной линиями у=(х+1) (3-х), у=4 и х=3
Ответ: 2
21.
Найти площадь фигуры, ограниченной
графиком функции у=sinх, касательной к
графику в его точке с абсциссой х0=π и прямой х=0,5π
Ответ:-1
22. Найдите площадь фигуры, ограниченной графиком функции у=cosх, касательной к нему в его точке с абсциссой х0=1,5π и прямой х=2π
Ответ: S=-1
23. Найдите площадь фигуры, ограниченной графиком функции у=sin х, определенной на отрезке [о;π], и прямой, проходящей через точки М(π/2;1) и N (π; 0)
Ответ: 1
24. Найти площадь фигуры, ограниченной графиком функции у=cosх, определенной на отрезке [-π/2; π/2] и прямой, проходящей через точки А(-π/2; 0) и В (0; 1)
Ответ: 1
25. Найти площадь фигуры, ограниченной графиком функций у=х3/4 и у=
Ответ: 1
26. Найти площадь фигуры, ограниченной графиками функций у=х3/9 и у=
Ответ: 3,75
27. Найдите площадь фигуры, ограниченной линиями у=, у=6-х, у=0
Ответ: 7
28.
Найдите площадь фигуры, ограниченной
линиями у=, у=х-6, у=0
Ответ: 18
Задания уровня С
1. Составьте уравнение касательной, проведенной к графику функции f(х)=-х2+4 параллельно прямой у=-2х+6. Вычислите площадь фигуры, ограниченной графиком данной функции, этой касательной и осью ординат.
Ответ: у=5-2х; S=.
2. Составьте уравнение касательной, проведенной к графику функции f(х)=-х2+4х параллельно прямой у=2х+3. Вычислите площадь фигуры, ограниченной графиком данной функции, этой касательной и осью ординат.
Ответ: у=2х+1; S=.
3. Вычислите площадь фигуры, ограниченной графиком функции у=- х2+3 и двумя касательными к этому графику, проходящими через точку на оси ОУ и образующими между собой угол 90º
Ответ:
4. Вычислите площадь фигуры, ограниченной
графиком функции у=х2+2,5 и двумя
касательными к этому графику, проходящими через точку на оси ОУ и образующими
между собой угол 90º.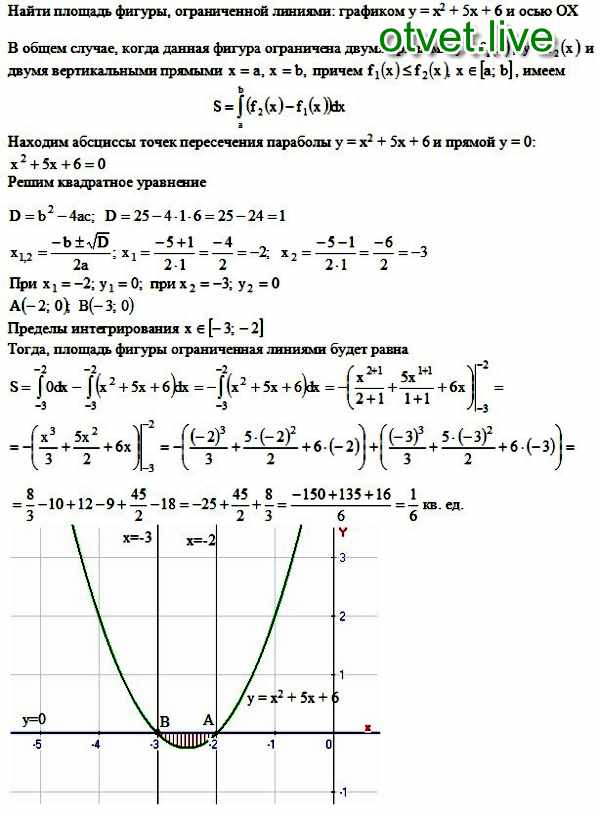
Ответ:
5. Вычислите площадь фигуры, ограниченной графиком функции у= — х2+1 и касательными, проведенными к этому графику в точках пересечения его с осью абсцесс
Ответ: 4/3
6. Вычислите площадь фигуры, ограниченной графиком функции у=-х2+4х и касательными, проведенными к этому графику в точках пересечения его с осью абсцисс
Ответ: 16/3
7. Найдите площадь фигуры, ограниченной графиком функции f(х)=2х-2 и графиком ее первообразной F(х), зная, что F(0)=1
Ответ:
8. Функция F является первообразной для функции f(х)=2х-4. Найдите площадь фигуры ограниченной графиками функций f и F, зная, что график функции F проходит через точку А(0; 4)
Ответ: 4/3
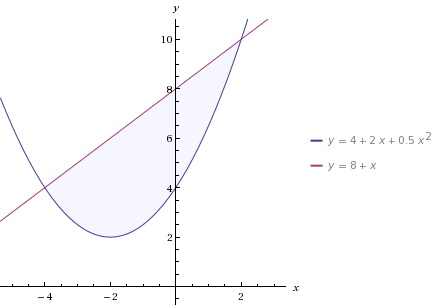
9. Вычислите площадь фигуры, ограниченной параболой у=4х-х2 и прямой, проходящей через точки (4; 0) и (0; 4)
Ответ:
10. Вычислите площадь фигуры, ограниченной параболой у=3х2(х≤0), прямой у=0 и прямой, проходящей через точки (-3; 0) и (0; 4,5)
Ответ: 4
11.
Составьте уравнение касательной к
графику функции у=-3х2+6х+1 в точке пересечения этого графика с осью
ординат. Вычислите площадь фигуры, ограниченной графиком данной функции,
найденной касательной и прямой х=2
Ответ: у=6х+1; 8
12. Составьте уравнение касательной к графику функции у=-2х2+4х+1 в точке пересечения этого графика с осью ординат. Вычислите площадь фигуры, ограниченной графиком данной функции, найденной касательной и прямой х=2
Ответ: у=4х+1;
13. Найдите площадь фигуры, ограниченной графиком функции и прямой у=1,5
Ответ: 4/3
14. Найдите площадь фигуры, ограниченной графиком функции у= S 3t2dt и прямой у=1
Ответ: 0,5
15. Найдите площадь фигуры, ограниченной графиком функции у= — и прямыми у=0, х= — 5, х = -2,5. Не пользуясь микрокалькулятором, сравните полученное значение площади с числом 2
Ответ: S=ln4, S<2
16.
Найдите площадь фигуры, ограниченной
графиком функции у=ех+1 и прямыми х= -2, х= -1, у=0. Не пользуясь
микрокалькулятором, сравните полученное значение площади с числом 0,5
Ответ: S=1-е-1; S>0,5
17. Для каждого а>0 найдите площадь фигуры, ограниченной графиком функции у= -х3+ах2 и осью абсцисс. При каких значениях, а эта площадь равна 4/3?
Ответ: S=а4/12; S=4/3 при а=2
18. Для каждого а<0 найдите площадь фигуры, ограниченной прямыми х=2а, х=а, у=0 и графиком функции у= -3/х. Сравните полученное значение площади с числом 3.
Ответ: S=3ln; S<3
19. В каком отношении делится площадь четырехугольника ОВСД, где 0(0;0), В(1; 2) С(4; 2), Д(4; 0), параболой у=(2-х)2+1
Ответ: 17; 4 (или 4,25; возможен ответ 4; 17)
20. Найдите площадь фигуры, ограниченной линиями у= х3, у=3-х, у= -4х
Ответ: 5
21. Найдите площадь фигуры, ограниченной линиями у=- х3, у=х+4, у=5х
Ответ: 7
22.
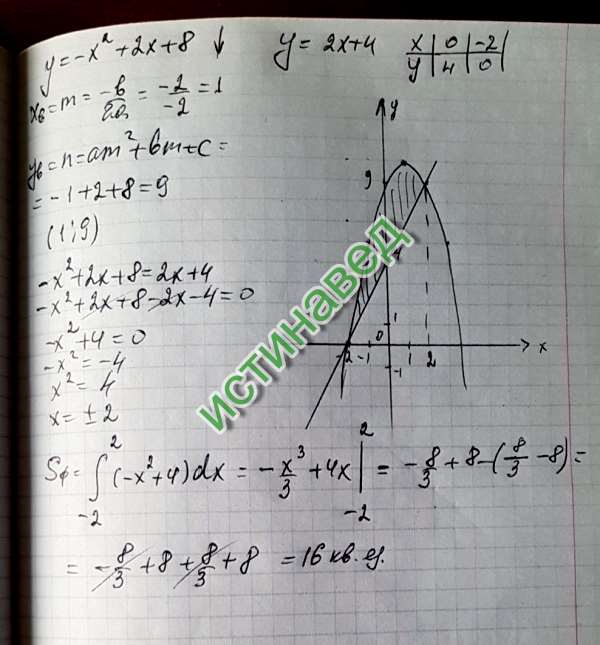Найдите площадь фигуры, ограниченной
линиями х · [у]=2, х=1, х=3
Ответ: 4ln 3
24. Найдите площадь фигуры, ограниченной линиями х [у]=3, х=1, х=2
Ответ: 6ln 2
25. Докажите, что площадь фигуры, ограниченной графиком функции у=2е2х и прямыми у=0, х= -0,5; х=t (при t< -0,5), меньше 1
26. Найдите ту первообразную функции f(х)=2х+4, график которой касается прямой у=6х+3. Вычислите площадь фигуры, ограниченной графиком найденной первообразной и прямыми у=6х+3 и у=0
Ответ: Первообразная у=х2+4х+4, площадь 2,25
27. Найдите ту первообразную функции f(х)=2х-2, график которой касается прямой у= -4х. Вычислите площадь фигуры, ограниченной графиком найденной первообразной и прямыми у= -4х, у=0
Ответ: Первообразная у=х2-2х+1, площадь 2/3
28. Фигура ограничена линиями у= х2 и у=х.
Отрезок наибольшей длины, заключенный внутри этой фигуры и принадлежащий прямой
х=а, делит фигуру на две части.
Докажите, что площади этих частей равны.
29. Фигура ограничена линиями у= х2 и у=-3х. Отрезок наибольшей длины, заключённый внутри этой фигуры и принадлежащей прямой х=а, делит фигуру на две части. Докажите, что площади этих частей равны.
30. Найдите площадь фигуры, ограниченной графиком функции у=х2-2х+3, касательной к графику в его точке с абсциссой 2 и прямой х=-1.
Ответ: 9
31. Найдите площадь фигуры, ограниченной графиком функции у=3+2х-х2, касательной к графику в его точке с абсциссой 3 и прямой х=0.
Ответ: 9
32. Найдите площадь фигуры, ограниченной линиями у=(х-2)(2х-3) и у=0
Ответ:
33. Найдите площадь фигуры, ограниченной линиями у=(3х+2)(х-1) и у=0
Ответ: 125/54
34. Найдите площадь фигуры, ограниченной линиями у= и у= х
Ответ:
35. Найдите площадь фигуры, ограниченной линиями у= , у=х и х=е.
Ответ: 0,5(е2-3)
36.
Найдите площадь фигуры, ограниченной
линиями у= и у=6-х.
37. Найдите площадь фигуры, ограниченной параболой у= 4х-х2 и прямой, проходящей через вершину параболы и начало координат.
Ответ: 12-5ln5
38. Найдите площадь фигуры, ограниченной параболой у=х2-6х и прямой, проходящей через вершину параболы и начало координат.
Ответ: 4/3
39. Найдите площадь фигуры, ограниченной графиком функции у= -х3-2х2-х+3 и касательной к нему, проведённой в точке графика с абсциссой -1
Ответ:
40. Найдите площадь фигуры, ограниченной графиком функции у=х3-4х2+4х-5 и касательной к нему, проведённой в точке графика с абсциссой 2.
Ответ: 4/3
41. Найдите площадь фигуры, ограниченной параболами у-х2-2х и у= х2.
Ответ: 16/3
42. Найдите площадь фигуры, ограниченной
параболами у-4х-х2 и у= х2.
Ответ: 6
43. Найдите площадь фигуры, ограниченной графиками функций у= и у=3-х
Ответ:
44. Найдите площадь фигуры, ограниченной графиками функций у=х2 и у=2х-х2.
Ответ: 16/3
45. Укажите все первообразные функции g(х)=3х2+2х-2, графики которых имеют ровно две общие точки с графиком функции , графики которых имеют ровно две общие точки с графиком функции g(х).
Ответ: G1(х)=х3+х2-2х-3; G2(х)=х3+х2-2х+6
46. Укажите все первообразные функции f(х)=5+2х-3х2, графики которых имеют с графиком функции f(х) ровно две общие точки.
Ответ: F1(х)= -х3+х2+5х-13; F2(х)=-х3+х2+5х+5
27. Найдите площадь фигуры, ограниченной линиями у=(3-х)3, у=0,5х, у=0.
Ответ: 1,25
28. Найдите площадь фигуры, ограниченной графиком функции у=х2-4х+4 и касательными к этому графику, проходящими через начало координат
Ответ: 16/3
29.
Найдите площадь фигуры, ограниченной
графиком функции у=х2+6х+9 и касательными к этому графику,
проходящими через начало координат.
Ответ:18
30. Найдите площадь фигуры, ограниченной линиями у= -4(х+3)3, у+х=0, у=2х.
Ответ: 12
31. Найдите площадь фигуры, ограниченной линиями у=3(х-2)3, у+3х=0, у=х
Ответ: 6
32. Фигура ограничена линиями: у=0; у= -х2+2х+3. Найдите отношение площадей фигур, на которые данная фигура делится графиком функции у=(х+1)2
Ответ: 2: 8= или 3 : 1
33. Фигура ограничена линиями у=0 и у=-х2+6х-5. Найдите отношение площадей фигур, на которые данная фигура делится графиком функции у=(х-5)2
Ответ: 3 (или 1/3)
34. Найдите площадь фигуры, ограниченной линиями у=, у=(х+2)3, у=1 и у=0
Ответ: 1
35. Найдите площадь фигуры, ограниченной линиями у= у=2-(х+3)3 и у=3
Ответ: 8
36.
Найдите площадь фигуры, ограниченной
линиями у=, у=2+(х-4)3 и
у=3
Ответ: 8
Сложные задания
1. Вычислите площадь фигуры, ограниченной линиями у = и у= .
Ответ: — ln3
2. Вычислите площадь фигуры, ограниченной линиями у= и у=
Ответ: — ln2
3. Вычислите площадь фигуры, ограниченной гиперболой у= -1/х, касательной к этой кривой, проведённой в точке с абсциссой х=1, и прямой х=2.
Ответ: ln2-0,5
4. Вычислите площадь фигуры, ограниченной графиком функции у=, касательной к этой кривой, проведённой в точке с абсциссой х=1, и прямой х=-1.
Ответ: ln3
5. Вычислите площадь фигуры, ограниченной линиями у=, у=3- .
Ответ: 6,5- ln2
6. Вычислите площадь фигуры, ограниченной линиями у= и у=2+4.
Ответ: 32
7. Вычислите площадь фигуры, ограниченной
линиями х=1, у=е, у=-е, х=0, а
также отрезком прямой х=1 при -1≤ у ≤ 1.
Ответ: 4
8. Вычислите площадь фигуры, ограниченной линиями ху2=1, у= -1, у=1, х=0, х=0, а также отрезком прямой х=2 при — ≤ у ≤
Ответ: 2
9. Вычислите площадь фигуры, ограниченной линиями у=х2-2х, у= -4х-1 и у=4х-9
Ответ: 16/3
10. Вычислите площадь фигуры, ограниченной линиями у=-х2+6х-9, у=2х-5 и у= -2х+7
Ответ: 2/3
11. Пользуясь геометрической интерпретацией определённого интеграла, вычислите S dх.
Ответ: +
12. Пользуясь геометрической интерпретацией определённого интеграла, вычислите dх.
Ответ: —
13. Найдите все такие точки М графика функции у=х2-4х, что площадь фигуры. Ограниченной этим графиком, касательной к графику, проходящей через точку М, и осью ординат, равна 72
Ответ: (6; 60) и (6; 12)
14. Найдите все такие точки М графика функции у=6х-х2, что площадь фигуры, ограниченной графиком этой функции, касательной к графику, проходящей через точку №, и осью ординат равна 41
Ответ: (1/5; 5) и (-5; -55)
15.
Докажите, что при всех к > 0
площадь фигуры, ограниченной графиком функции у=к2х5-кх2
и осью абсцисс, не зависит от к.
Ответ: Sор= и не зависит от к.
16. Докажите, что при всех к > 0 площадь фигуры, ограниченной графиком функции у= х4— х9 и осью абсцисс, не зависит от к.
Ответ: ; COS???<0
17. Докажите, что площади фигур, каждая из которых ограничена графиком функции у=х3-6х2+1 и одной из касательных к этому графику, параллельных оси абсцисс, равны.
Ответ: Sор=1/10
18. Докажите, что площадь фигуры, ограниченной осью ординат, графиком функции у=4х-х2 и касательной к этому графику в точке с абсциссой х0 ≠ 0, равна площади фигуры, ограниченной графиком той же функции, касательной к графику в точке с абсциссой (-х0) и осью ординат.
Ответ:
19. Вычислите площадь фигуры, ограниченной
графиками функций у=0,5х2-2х-1 и у=6,5-1,5×.
Ответ: 25,5
20. Вычислите площадь фигуры, ограниченной графиками функций у=-0,5х2+х+7,5 и у=1,5()-1.
Ответ: 25,5
21. При каком t площадь фигуры, ограниченной графиком функции у=х4+2х2, касательной к нему, проведённой в точке графика с абсциссой t, и прямой х=t-1, наименьшая?
Ответ: t=0,25
22. Найдите такое р, чтобы площадь фигуры, ограниченной графиком функции у=х-х4, касательной к нему, проведённой в точке графика с абсциссой р, и прямой х=р+2, была наименьшей.
Ответ: р=-0,5
23. Найдите площадь фигуры, ограниченной линиями у=х+1, у=1- х и у=1-(х-2)3.
Ответ: 2
24. Найдите площадь фигуры, ограниченной линиями у=(х+2)3+3, у=-4х и у=- х.
Ответ: 5
25. Найдите площадь фигуры, ограниченной линиями у=4+, у=-0,6х+2,8 и х=.
Ответ: 12,5
26. Найдите площадь фигуры, ограниченной
линиями х+=0, у=+4 и у= х+ .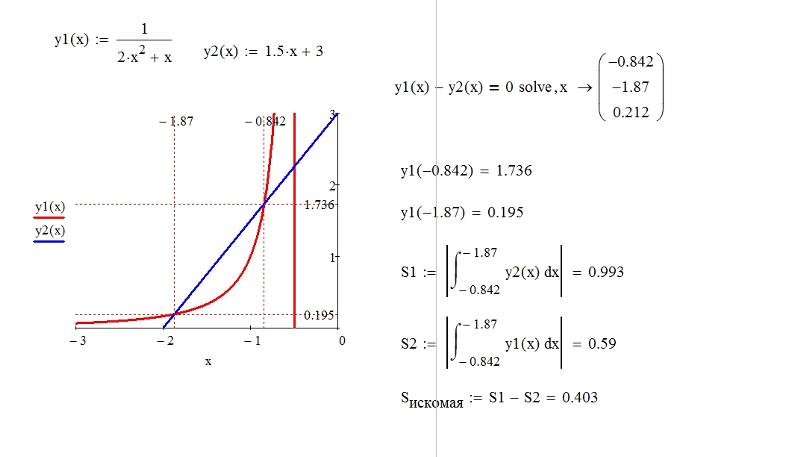
Ответ: 38/3
2\кр &={16\более4}-{64\более3}+28-4-({1\более4}-{8\более3}+7-2)\кр &=23-{56\over3}-{1\over4}={49\over12}.\cr }$$ $\квадрат$
Стоит рассмотреть эту проблему немного подробнее. Мы видели один из способов посмотрите на него, рассматривая желаемую область как большую область минус маленькую площади, что естественным образом приводит к различию между двумя интегралы. Но поучительно рассмотреть, как мы могли бы найти желаемая область напрямую. Мы можем аппроксимировать площадь, разделив площадь на тонкие срезы и аппроксимируя площадь каждого среза на прямоугольник, как показано на рисунок 9.2 = 1$. Обратите внимание: $t$ фиксировано, плоскость $x$-$y$.
Пример 9.1.15 Докажите, что площадь $R$ равна $t$.
MathScene — Интеграция — Урок 3
MathScene — Интеграция — Урок 3| 2010 Расмус Эф и Джанн Сак | Интеграция |
Урок 3
Области между графиками функции
Области, ограниченные графиками функций, можно найти интегрированием.
За
Например, мы найдем площадь, ограниченную двумя графиками f(x) = x 2 + 5x 3
и у = х.
Это площадь, показанная в калькуляторе:
Начнем с нахождение точек пересечения двух графиков, чтобы дать нам границы площади:
х 2 + 5х 3 = х
х 2 + 4х 3 = 0 Упрощать.
(x 2 4x + 3) = 0 1 из-за скобки.
(x 1)(x 3) = 0 Факторизация .
(x 2 4x + 3) = 0
(x 1)(x 3) = 0
Точками пересечения являются x = 1 и x = 3.Они лежат на прямой y = x, поэтому координаты y совпадают с координатами x, то есть (1, 1) и (3, 3).
Нам нужно только
используйте координаты x для вычисления площади между каждой кривой и осью x.
Интеграл дает площадь между осью x и функцией f(x) = x 2 + 5x 3 на интервале от 1 до 3.
Это заштрихованная область графика ниже
Таким же образом это площадь между y = x и x — на одном интервале.Снова на графике показана площадь нашел.
Если мы соединим эти два графика, мы увидим, что область, которую мы хотим найти, является разница между двумя вышеперечисленными.
Итак, мы просто нужно взять разницу между двумя интегралами, чтобы найти площадь, которую мы требовать.
|
Новое уравнение
параболы будет f(x) = x 2 + 5x 3 2
= x 2 + 5x 5 и линии y = x
2.
На диаграмме показана новая ситуация.
Точки пересечения остаются прежними, так как мы добавили 2 к обеим сторонам уравнение. Ниже приведены расчеты, если вы не уверены!
x 2 + 5x 5 = x 2
х 2 + 4х 3 = 0 Упростить .
(x 2 4x + 3) = 0
(x 1)(x 3) = 0 Факторизация.
И снова решения x = 1 и x = 3. Интегрируя таким же образом, вы можете видеть, что 2 снова упрощается, поэтому мы имеем тот же результат, что и раньше.
Это означает что при вычислении площади между кривыми нам не нужно беспокоиться о независимо от того, находится ли область выше или ниже оси x, метод всегда один и тот же.
Площадь ограничен сверху графиком е(х) и ниже по графику g(x): Границы х = а и х = б являются решениями уравнения f(x) = g(x) |
Пример 1
Найдите площадь между параболой f(x) = x 2 4 и линия у = х 2.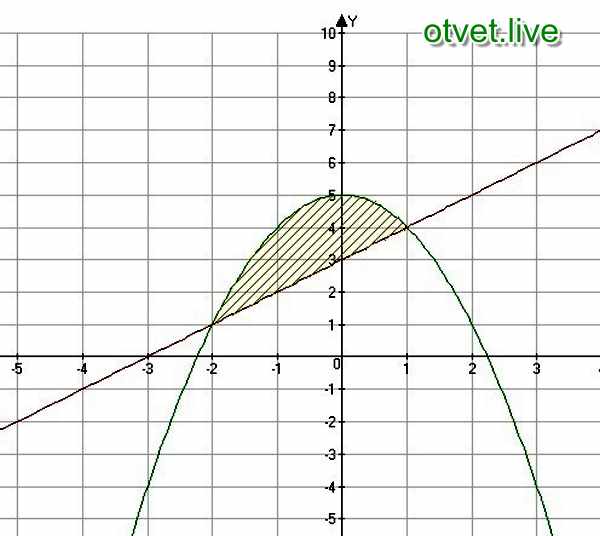
Начнем с решение уравнения x 2 4 = x 2 найти площадь границы
х 2 4 = х 2
x 2 4 х + 2 = 0
х 2 х 2 = 0
(х + 1)(х 2) = 0
Решения: х = 1 х = 2,
Это хорошая идея, чтобы посмотреть на график и область, вовлеченную в калькулятор.
Мы видим, что линия ограничивает область выше, поэтому мы вычитаем интеграл от парабола от линии.
Пример 2
Найдите площадь, заключенную между графиками f(x) = sin x и g(x) = cos x.
на интервале 0 ≤ x < 2p
Калькулятор показывает нам площадь, которую мы собираемся найти.
Мы снова должны начнем с поиска точек пересечения двух графиков.
Решение уравнения
грех х = потому что х.
sin x/cos x = 1 Разделить на cos х
тангенс х = 1
х = коричневый 1 1 = /4 + номер
Это означает что х = /4 и х = 5/4 на интервале 0 ≤ x < 2
График f(x) = sin x лежит над графиком g(x) = cos x на всех интервал между точками пересечения, поэтому расчеты площади выглядят как следует:
Сейчас потому что /4 = грех / 4 знак равно и cos 5/4 = грех 5/4 знак равно
Таким образом, точное значение площади равно
.Пример 3
Найдите площадь, ограниченную графиками прямой y = 3x + 1 и многочлен f(x) = ⅓ x 3 2x 2 + 3x + 1.
Сначала график рисуется с помощью калькулятора. Следующие значения окна должны работать
Вот график:
Теперь вычисляем точки пересечения.
⅓ x 3 2x 2 + 3x + 1 = 3x + 1
⅓ x 3 2x 2 = 0
х 2 (⅓ х 2) = 0
Решения x = 0 и x = 6 нужные нам границы. Линия является верхней функция.
Вы можете проверить свой ответ в калькуляторе (с помощью RUN, OPTN, F4 и F4).
Практика затем эти методы проходят тест 3 на интеграцию.
Помните контрольный список!!
AC Использование определенных интегралов для нахождения объема
Рисунок 6.2.4. Ориентирование пирамиды по оси \(x\)Есть много способов «ориентировать» пирамиду вдоль оси \(х\); Рисунок 6.2.4 дает один такой способ, с заостренной вершиной пирамиды в начале координат и осью \(х\), проходящей через центр основания.
Мы разрезаем тело на вертикальные срезы толщиной \(\Delta x\) между \(x = 0\) и \(x = 5\text{.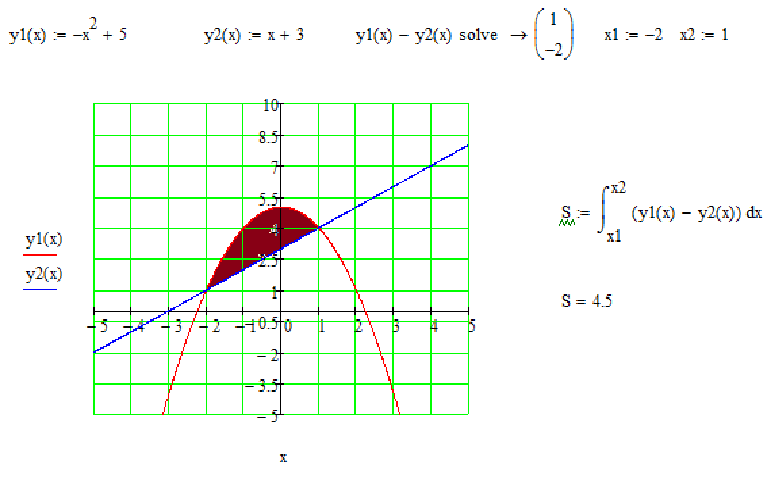
2.3.
\конец{выравнивание*}
Мы можем проверить нашу работу, обратившись к общему уравнению для объема пирамиды:
\begin{уравнение*} V = \frac{1}{3} \times \text{ площадь основания } \times \text{высота.} \end{уравнение*}
Конечно, использование этой формулы из геометрии быстрее, чем наш новый метод, но метод, основанный на исчислении, можно применять не только к пирамидам или конусам.
томов твердых тел революции
Тома твердых тел вращения
Вы также можете использовать определенный интеграл, чтобы найти объем твердого тела, полученного путем вращения плоской области вокруг горизонтальной или вертикальной линии, не проходящей через плоскость.Этот тип твердого тела будет состоять из одного из трех типов элементов — дисков, шайб или цилиндрических оболочек, — каждый из которых требует своего подхода к составлению определенного интеграла для определения его объема.Дисковый метод
Если ось вращения является границей плоской области, а поперечные сечения взяты перпендикулярно оси вращения, то для нахождения объема твердого тела используется дисковый метод .
Поскольку поперечное сечение диска представляет собой круг с площадью π r 2 , объем каждого диска равен его площади, умноженной на его толщину.Если диск перпендикулярен оси x , то его радиус должен быть выражен как функция x . Если диск перпендикулярен оси y , то его радиус должен быть выражен как функция y .
Объем ( V ) твердого тела, образованного вращением области, ограниченной y = f(x ) и осью x на интервале [ a, b ] вокруг x -ось
Если область, ограниченная x = f(y ) и осью y на [ a, b ], вращается вокруг оси y , то ее объем ( V ) равен
Обратите внимание, что f(x ) и f(y ) представляют радиусы дисков или расстояние от точки на кривой до оси вращения.
Пример 1: Найдите объем твердого тела, образованного вращением области, ограниченной y = x 2 и осью x на [−2,3] вокруг оси x .
Поскольку ось x является границей области, вы можете использовать дисковый метод (см. рис. 1).
Рисунок 1 Схема для примера 1.
Объем ( V ) твердого тела равен
Метод шайбы
Если ось вращения не является границей плоской области, а поперечные сечения взяты перпендикулярно оси вращения, для нахождения объема твердого тела используется метод шайбы .Думайте о шайбе как о «диске с отверстием в нем» или как о «диске с удаленным от центра диском». Если R – радиус внешнего диска, а r – радиус внутреннего диска, то площадь шайбы равна π R 2 – π r 2 , а ее объем будет быть его площадь, умноженная на его толщину. Как отмечалось при обсуждении дискового метода, если шайба перпендикулярна оси 90 518 x 90 519, то внутренний и внешний радиусы должны быть выражены как функции 90 518 x 90 519.
Если шайба перпендикулярна оси y , то радиусы должны быть выражены как функции y .
Если область ограничена x = f(y ) и x = g(y ) на [ a, b ], где f(y ) ≥ g(y 9 ) вращается вокруг оси y , то его объем ( V ) равен
Еще раз обратите внимание, что f(x ) и g(x ) и f(y ) и g(y ) представляют собой внешний и внутренний радиусы шайб или расстояние между точками на каждой кривой до ось вращения.
Пример 2: Найдите объем твердого тела, образованного вращением области, ограниченной y = x 2 + 2 и y = x + 4 вокруг оси x 90.
Поскольку y = x 2 + 2 и y = x + 4, вы находите, что
Графики будут пересекаться в точках (–1,3) и (2,6) с x + 4 ≥ x 2 + 2 на [–1,2] (рис.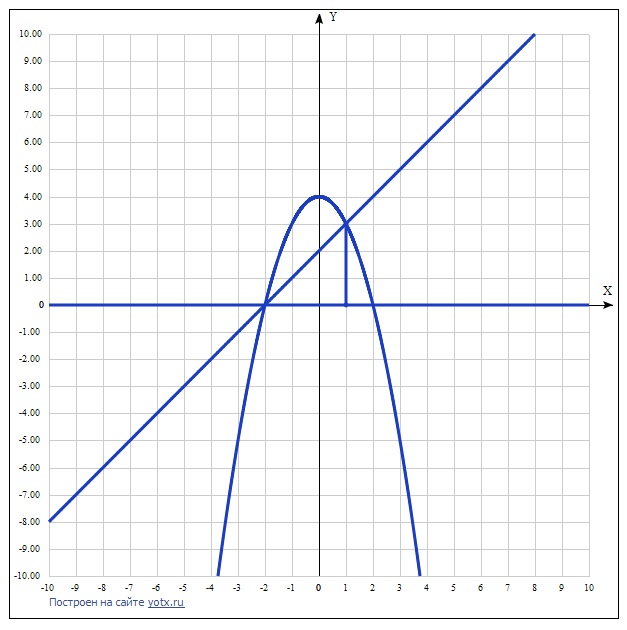
2).
Рисунок 2 Схема для примера 2.
Поскольку ось x не является границей области, вы можете использовать метод шайбы, а объем ( V ) твердого тела равен
Метод цилиндрической оболочки
Если поперечные сечения твердого тела взяты параллельно оси вращения, то для нахождения объема твердого тела будет использован метод цилиндрической оболочки .Если цилиндрическая оболочка имеет радиус 90 518 r 90 519 и высоту 90 518 h, 90 519, то ее объем будет в 2π 90 518 rh 90 519 умножить на толщину. Думайте о первой части этого произведения (2π rh ) как о площади прямоугольника, образованного путем разрезания оболочки перпендикулярно ее радиусу и плоской укладки. Если ось вращения вертикальна, то радиус и высота должны быть выражены в терминах x . Если же ось вращения горизонтальна, то радиус и высота должны быть выражены через y .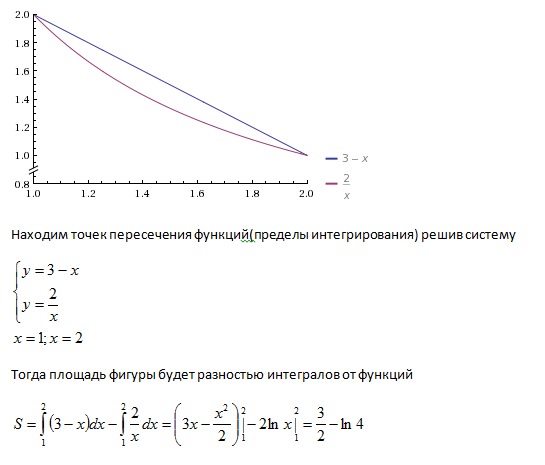
Объем ( V ) твердого тела, образованного вращением области, ограниченной y = f(x ) и осью x на интервале [ a,b ], где f( x ) ≥ 0, относительно оси y ‐
Если область, ограниченная x = f(y ) и осью y на интервале [ a,b ], где f(y ) ≥ 0, вращается вокруг x ‐ось, то его объем ( V ) равен
Обратите внимание, что x и y в подынтегральных выражениях представляют радиусы цилиндрических оболочек или расстояние между цилиндрической оболочкой и осью вращения.Коэффициенты f(x ) и f(y ) представляют высоты цилиндрических оболочек.
Пример 3: Найдите объем твердого тела, образованного вращением области, ограниченной y = x 2 и осью x [1,3] вокруг оси y .
При использовании метода цилиндрической оболочки интеграл должен быть выражен через x , поскольку ось вращения вертикальна.