Объем усеченной пирамиды, зная стороны оснований и боковое ребро, можно найти через высоту и площади оснований, найденные по указанным выше формулам. V=1/3 h(S_осн1+S_осн2+√(S_осн1 S_осн2 ))
Объем усеченной пирамиды четырехугольной формула. Онлайн-калькулятор для расчета площади поверхности усеченной пирамиды
Пирамидой называется многогранник, одна из граней которого многоугольник (основание ), а все остальные грани – треугольники с общей вершиной (боковые грани ) (рис. 15). Пирамида называется правильной , если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис. 16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром .
Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию Высотой пирамиды называется расстояние от ее вершины до плоскости основания.
Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.
Теоремы
1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности описанной около основания.
2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности описанной около основания.
3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности вписанной в основание.
Для вычисления объема произвольной пирамиды верна формула:
где V – объем;
S осн – площадь основания;
H – высота пирамиды.
Для правильной пирамиды верны формулы:
где p – периметр основания;
h а – апофема;
H – высота;
S полн
S бок
S осн – площадь основания;
V – объем правильной пирамиды.
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.
Основания усеченной пирамиды – подобные многоугольники.
 Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.Для усеченной пирамиды справедливы формулы:
(4)
где S 1 , S 2 – площади верхнего и нижнего оснований;
S полн – площадь полной поверхности;
S бок – площадь боковой поверхности;
H – высота;
V – объем усеченной пирамиды.
Для правильной усеченной пирамиды верна формула:
где p 1 , p 2 – периметры оснований;
h а – апофема правильной усеченной пирамиды.Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.
Решение. Сделаем рисунок (рис. 18).
18).
Пирамида правильная, значит в основании равносторонний треугольник и все боковые грани равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: и т.е. Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС ). Угол наклона бокового ребра (например SB ) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол
Ответ:
Пример 2. Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота 4 см.
Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (4). Чтобы найти площади оснований необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит площади оснований и Подставив все данные в формулу, вычислим объем усеченной пирамиды:
Ответ: 112 см 3 .
Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды 2 см.
Решение. Сделаем рисунок (рис. 19).
Боковая грань данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из где А 1 Е перпендикуляр из точки А 1 на плоскость нижнего основания, A 1 D – перпендикуляр из А 1 на АС . А 1 Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:
Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:
MK = DE .
По теореме Пифагора из
Площадь боковой грани:
Ответ:
Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b ). Каждая боковая грань образует с плоскостью основания пирамиды угол равный j . Найти площадь полной поверхности пирамиды.
Решение. Сделаем рисунок (рис. 21). Площадь полной поверхности пирамиды SABCD равна сумме площадей и площади трапеции ABCD .
Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:
Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:
Аналогично и значит Таким образом задача свелась к нахождению площади трапеции АВСD . Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.
Так как в трапецию можно вписать окружность, то или Из по теореме Пифагора имеем
Многогранник, у которого одна из граней – многоугольник, а все остальные грани – треугольники с общей вершиной, называется пирамидой.
Эти треугольники, из которых составлена пирамида, называют боковыми гранями , а оставшийся многоугольник – основанием пирамиды.
В основании пирамиды лежит геометрическая фигура – n-угольник. В таком случае пирамиду называют еще n-угольной .
Треугольную пирамиду, все ребра которой равны, называют тетраэдром.
Ребра пирамиды, которые не принадлежат основанию, называются боковыми , а их общая точка – это вершина
Пирамиду называют правильной , если у нее в основании лежит правильный многоугольник, а все боковые ребра равны между собой.
Расстояние от вершины пирамиды до плоскости основания называется высотой пирамиды. Можно сказать, что высота пирамиды есть отрезок, перпендикулярный основанию, концы которого находятся в вершине пирамиды и на плоскости основания.
Для любой пирамиды имеют место следующие формулы:
1) S полн = S бок + S осн , где
S полн – площадь полной поверхности пирамиды;
S бок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней пирамиды;
S осн – площадь основания пирамиды.
2) V = 1/3 S осн · Н , где
V – объем пирамиды;
Н – высота пирамиды.
Для правильной пирамиды имеет место:
S бок = 1/2 P осн h , где
P осн – периметр основания пирамиды;
h – длина апофемы, то есть длина высоты боковой грани, опущенной из вершины пирамиды.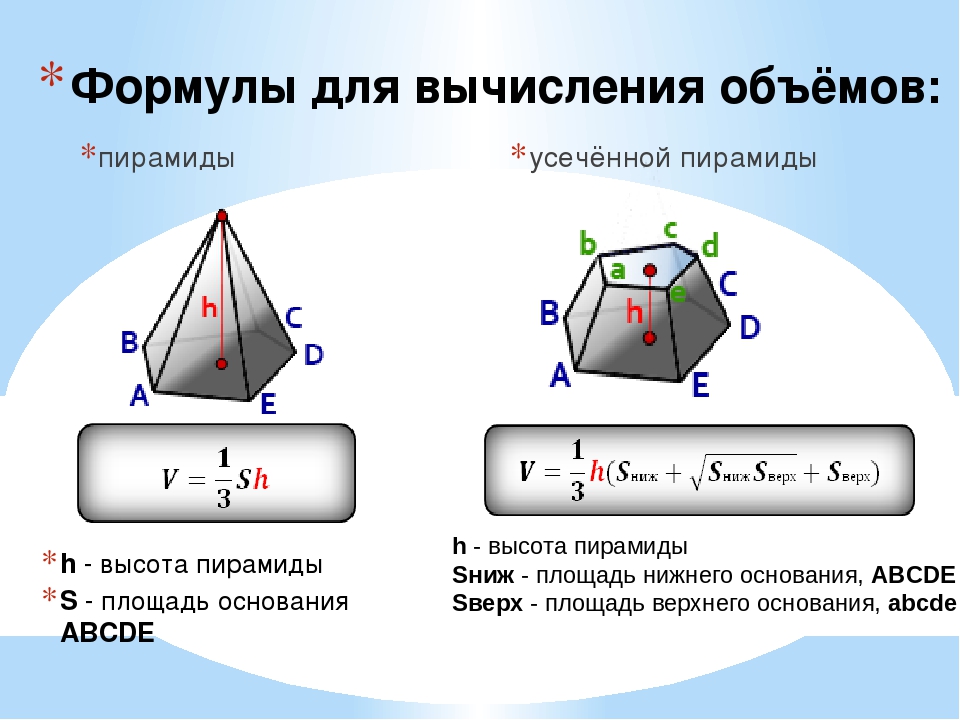
Часть пирамиды, заключенная между двумя плоскостями – плоскостью основания и секущей плоскостью, проведенной параллельно основанию, называют усеченной пирамидой .
Основание пирамиды и сечение пирамиды параллельной плоскостью называются основаниями усеченной пирамиды. Остальные грани называют боковыми . Расстояние между плоскостями оснований называют высотой усеченной пирамиды. Ребра, которые не принадлежат основаниям, называются боковыми .
Кроме того, основания усеченной пирамиды подобные n-угольники . Если основания усеченной пирамиды – правильные многоугольники, а все боковые ребра равны между собой, то такая усеченная пирамида называется правильной .
Для произвольной усеченной пирамиды имеют место следующие формулы:
1) S полн = S бок + S 1 + S 2
S полн – площадь полной поверхности;
S бок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней усеченной пирамиды, которые представляют собой трапеции;
S 1 , S 2 – площади оснований;
2) V = 1/3(S 1 + S 2 + √(S 1 · S 2))H , где
V – объем усеченной пирамиды;
H – высота усеченной пирамиды.
Для правильной усеченной пирамиды также имеем:
S бок = 1/2(P 1 + P 2) · h, где
P 1 , P 2 – периметры оснований;
h – апофема (высота боковой грани, представляющей собой трапецию).
Рассмотрим несколько задач на усеченную пирамиду.
Задача 1.
В треугольной усеченной пирамиде с высотой, равной 10, стороны одного из оснований равны 27, 29 и 52. Определите объем усеченной пирамиды, если периметр другого основания равен 72.
Решение.
Рассмотрим усеченную пирамиду АВСА 1 В 1 С 1 , изображенную на рисунке1.
1. Объем усеченной пирамиды может быть найден по формуле
V = 1/3H · (S 1 + S 2 + √(S 1 · S 2)), где S 1 – площадь одного из оснований, можно найти по формуле Герона
S = √(p(p – a)(p – b)(p – c)),
т.к. в задаче даны длины трех сторон треугольника.
Имеем: p 1 = (27 + 29 + 52)/2 = 54.
S 1 = √(54(54 – 27)(54 – 29)(54 – 52)) = √(54 · 27 · 25 · 2) = 270.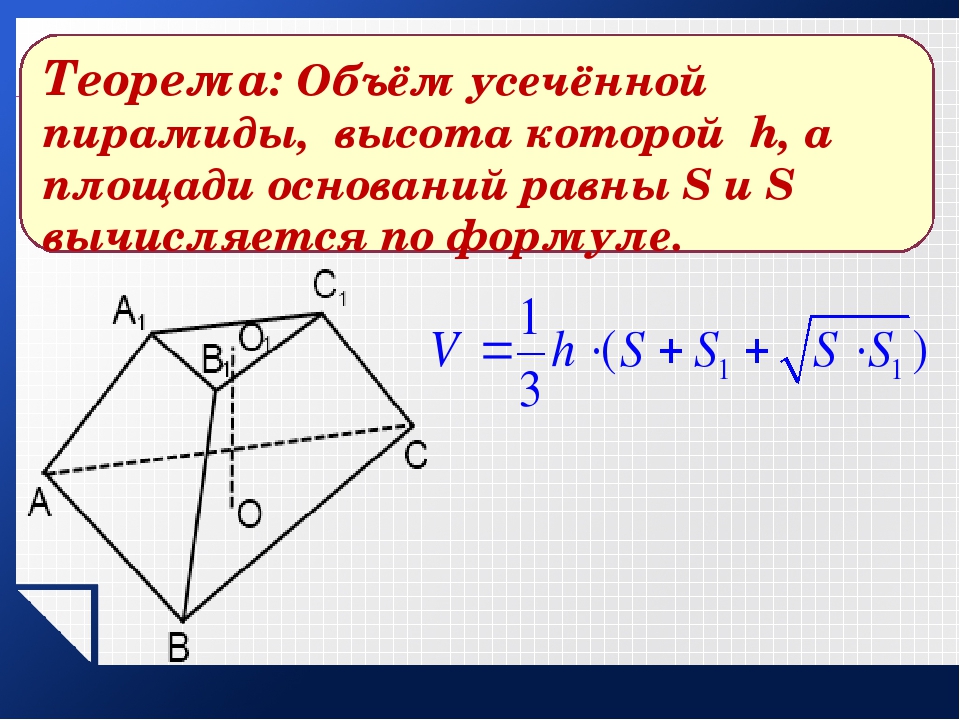
2. Пирамида усеченная, а значит, в основаниях лежат подобные многоугольники. В нашем случае треугольник АВС подобен треугольнику А 1 В 1 С 1 . Кроме того, коэффициент подобия можно найти как отношение периметров рассматриваемых треугольников, а отношение их площадей будет равно квадрату коэффициента подобия. Таким образом, имеем:
S 1 /S 2 = (P 1) 2 /(P 2) 2 = 108 2 /72 2 = 9/4. Отсюда S 2 = 4S 1 /9 = 4 · 270/9 = 120.
Итак, V = 1/3 · 10(270 + 120 + √(270 · 120)) = 1900.
Ответ: 1900.
Задача 2.
В треугольной усеченной пирамиде через сторону верхнего основания проведена плоскость параллельно противоположному боковому ребру. В каком отношении разделился объем усеченной пирамиды, если соответственные стороны оснований относятся как 1: 2?
Решение.
Рассмотрим АВСА 1 В 1 С 1 – усеченную пирамиду, изображенную на рис. 2.
Так как в основаниях стороны относятся как 1: 2, то площади оснований относятся как 1: 4 (треугольник АВС подобен треугольнику А 1 В 1 С 1).
Тогда объем усеченной пирамиды равен:
V = 1/3h · (S 1 + S 2 + √(S 1 · S 2)) = 1/3h · (4S 2 + S 2 + 2S 2) = 7/3 · h · S 2 , где S 2 – площадь верхнего основания, h – высота.
Но объем призмы АDEA 1 B 1 C 1 составляет V 1 = S 2 · h и, значит,
V 2 = V – V 1 = 7/3 · h · S 2 — h · S 2 = 4/3 · h · S 2 .
Итак, V 2: V 1 = 3: 4.
Ответ: 3: 4.
Задача 3.
Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 и 1, а высота равна 3. Через точку пересечения диагоналей пирамиды параллельно основаниям пирамиды проведена плоскость, делящая пирамиду на две части. Найти объем каждой из них.
Решение.
Рассмотрим усеченную пирамиду АВСDА 1 В 1 С 1 D 1 , изображенную на рис. 3.
Обозначим О 1 О 2 = х, тогда ОО₂ = О 1 О – О 1 О 2 = 3 – х.
Рассмотрим треугольник В 1 О 2 D 1 и треугольник ВО 2 D:
угол В 1 О 2 D 1 равен углу ВО 2 D как вертикальные;
угол ВDO 2 равен углу D 1 B 1 O 2 и угол O 2 ВD равен углу B 1 D 1 O 2 как накрест лежащие при B 1 D 1 || BD и секущих B₁D и BD₁ соответственно.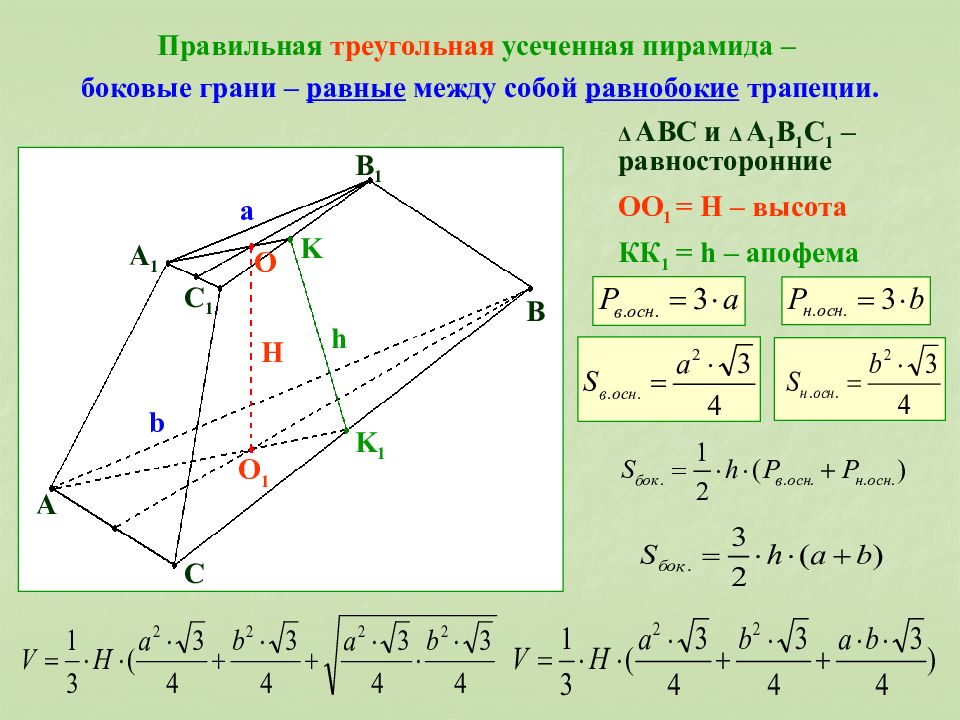
Следовательно, треугольник В 1 О 2 D 1 подобен треугольнику ВО 2 D и имеет место отношение сторон:
В1D 1 /ВD = О 1 О 2 /ОО 2 или 1/2 = х/(х – 3), откуда х = 1.
Рассмотрим треугольник В 1 D 1 В и треугольник LО 2 B: угол В – общий, а так же имеется пара односторонних углов при B 1 D 1 || LM, значит, треугольник В 1 D 1 В подобен треугольнику LО 2 B, откуда В 1 D: LO 2 = OO 1: OO 2 = 3: 2, т.е.
LO 2 = 2/3 · B 1 D 1 , LN = 4/3 · B 1 D 1 .
Тогда S KLMN = 16/9 · S A 1 B 1 C 1 D 1 = 16/9.
Итак, V 1 = 1/3 · 2(4 + 16/9 + 8/3) = 152/27.
V 2 = 1/3 · 1 · (16/9 + 1 + 4/3) = 37/27.
Ответ: 152/27; 37/27.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
– это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств:
- Боковые грани пирамиды являются трапециями;
- Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
- Основания являются подобными многоугольниками;
- В правильной усеченной пирамиде, грани представляют собой одинаковые равнобедренные трапеции, площадь которых равна.
 Также они наклонены к основанию под одним углом.
Также они наклонены к основанию под одним углом.
Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон:
Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции . Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.
Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:
Давайте рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l = 5 см, длина грани в большом основании равна a = 6 см, а грань в меньшем основании b = 4 см. Рассчитайте площадь усеченной пирамиды.
Рассчитайте площадь усеченной пирамиды.
Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:
Таким же образом находим периметр меньшего основания:
Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу:
Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.
Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований .
Давайте рассмотрим пример расчета. Помним, что данная формула применяется только для правильной усеченной пирамиды.
Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.
Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата . Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:
Теперь используем найденные значения для расчета площади боковой поверхности.
Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.
Умение вычислять объем пространственных фигур является важным при решение ряда практических задач по геометрии. Одной из распространенных фигур является пирамида. В данной статье рассмотрим пирамиды как полной, так и усеченной.
Пирамида как объемная фигура
Каждый знает о египетских пирамидах, поэтому хорошо представляет, о какой фигуре пойдет речь. Тем не менее египетские каменные сооружения являются лишь частным случаем огромного класса пирамид.
Рассматриваемый геометрический объект в общем случае представляет собой многоугольное основание, каждая вершина которого соединена с некоторой точкой в пространстве, не принадлежащей плоскости основания. Данное определение приводит к фигуре, состоящей из одного n-угольника и n треугольников.
Любая пирамида состоит из n+1 граней, 2*n ребер и n+1 вершины. Поскольку рассматриваемая фигура является совершенным полиэдром, то числа отмеченных элементов подчиняются равенству Эйлера:
2*n = (n+1) + (n+1) — 2.
Многоугольник, находящийся в основании, дает название пирамиды, например, треугольная, пятиугольная и так далее. Набор пирамид с разными основаниями приведен на фото ниже.
Точка, в которой n треугольников фигуры соединяются, называется вершиной пирамиды. Если из нее опустить на основание перпендикуляр и он пересечет его в геометрическом центре, тогда такая фигура будет называться прямой. Если это условие не выполняется, то имеет место наклонная пирамида.
Прямая фигура, основание которой образовано равносторонним (равноугольным) n-угольником, называется правильной.
Формула объема пирамиды
Для вычисления объема пирамиды воспользуемся интегральным исчислением. Для этого разобьем фигуру параллельными основанию секущими плоскостями на бесконечное число тонких слоев. Рисунок ниже показывает четырехугольную пирамиду высотой h и длиной стороны L, в которой четырехугольником отмечен тонкий слой сечения.
Площадь каждого такого слоя можно вычислить по формуле:
A(z) = A 0 *(h-z) 2 /h 2 .
Здесь A 0 — площадь основания, z — значение вертикальной координаты. Видно, что если z = 0, то формула дает значение A 0 .
Чтобы получить формулу объема пирамиды, следует вычислить интеграл по всей высоте фигуры, то есть:
V = ∫ h 0 (A(z)*dz).
Подставляя зависимость A(z) и вычисляя первообразную, приходим к выражению:
V = -A 0 *(h-z) 3 /(3*h 2)| h 0 = 1/3*A 0 *h.
Мы получили формулу объема пирамиды. Чтобы найти величину V, достаточно умножить высоту фигуры на площадь основания, а затем результат поделить на три.
Заметим, что полученное выражение справедливо для вычисления объема пирамиды произвольного типа. То есть она может быть наклонной, а ее основание представлять собой произвольный n-угольник.
и ее объем
Полученную в пункте выше общую формулу для объема можно уточнить в случае пирамиды с правильным основанием. Площадь такого основания вычисляется по следующей формуле:
A 0 = n/4*L 2 *ctg(pi/n).
Здесь L является длиной стороны правильного многоугольника с n вершинами. Символ pi — это число пи.
Подставляя выражение для A 0 в общую формулу, получаем объем правильной пирамиды:
V n = 1/3*n/4*L 2 *h*ctg(pi/n) = n/12*L 2 *h*ctg(pi/n).
Например, для треугольной пирамиды эта формула приводит к следующему выражению:
V 3 = 3/12*L 2 *h*ctg(60 o) = √3/12*L 2 *h.
Для правильной четырехугольной пирамиды формула объема приобретает вид:
V 4 = 4/12*L 2 *h*ctg(45 o) = 1/3*L 2 *h.
Определение объемов правильных пирамид требует знания стороны их основания и высоты фигуры.
Пирамида усеченная
Предположим, что мы взяли произвольную пирамиду и отсекли у нее часть боковой поверхности, содержащей вершину. Оставшаяся фигура называется усеченной пирамидой. Она состоит уже из двух n-угольных оснований и n трапеций, которые их соединяют. Если секущая плоскость была параллельна основанию фигуры, тогда образуется усеченная пирамида с параллельными подобными основаниями. То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.
Рисунок выше демонстрирует усеченную правильную Видно, что верхнее основание ее так же, как и нижнее, образовано правильным шестиугольником.
Формула которую можно вывести, используя подобное приведенному интегральное исчисление, имеет вид:
V = 1/3*h*(A 0 + A 1 + √(A 0 *A 1)).
Где A 0 и A 1 — площади нижнего (большого) и верхнего (маленького) оснований соответственно. Переменной h обозначается высота усеченной пирамиды.
Объем пирамиды Хеопса
Любопытно решить задачу на определение объема, который заключает внутри себя самая большая египетская пирамида.
В 1984 году британские египтологи Марк Легнер (Mark Lehner) и Джон Гудман (Jon Goodman) установили точные размеры пирамиды Хеопса. Ее первоначальная высота равнялась 146,50 метра (в настоящее время около 137 метров). Средняя длина каждой из четырех сторон сооружения составила 230,363 метра. Основание пирамиды с высокой точностью является квадратным.
Воспользуемся приведенными цифрами для определения объема этого каменного гиганта. Поскольку пирамида является правильной четырехугольной, тогда для нее справедлива формула:
Подставляем цифры, получаем:
V 4 = 1/3*(230,363) 2 *146,5 ≈ 2591444 м 3 .
Объем пирамиды Хеопса равен практически 2,6 млн м 3 . Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м 3 . То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!
Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м 3 . То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!
Объем усеченной четырехугольной пирамиды. Площадь боковой поверхности усеченной пирамиды
- 09.10.2014
Показанный на рисунке предварительный усилитель предназначен для использования с 4-я видами источников звука, например микрофон, CD-проигрыватель, магнитола и др. При этом у предварительно усилителя один вход, который может менять чувствительность от 50 мВ до 500мВ. выходное напряжение усилителя 1000мВ. Подключая разные источники сигнала при переключении переключателя SA1, мы всегда получим …
- 20.09.2014
БП рассчитан на нагрузку мощностью 15…20 Вт. Источник выполнен по схеме однотактного импульсного высокочастотного преобразователя. На транзисторе собран автогенератор, работающий на частоте 20…40кГц. Частота настраивается емкостью С5. Элементы VD5,VD6 и С6 образуют цепь запуска автогенератора.
 Во вторичной цепи после мостового выпрямителя стоит обычный линейный стабилизатор на микросхеме, что позволяет иметь …
Во вторичной цепи после мостового выпрямителя стоит обычный линейный стабилизатор на микросхеме, что позволяет иметь … - 28.09.2014
На рисунке представлен генератор на микросхеме К174ХА11, частота которого управляется напряжением. При изменении емкости С1 от 560 до 4700пФ можно получить широкий диапазон частот, при этом настройка частоты производится изменением сопротивления R4. Так например автор выяснил что, при С1=560пФ частоту генератора можно изменять при помощи R4 от 600Гц до 200кГц, …
- 03.10.2014
Блок предназначен для питания мощного УНЧ, он рассчитан на выходное напряжение ±27В и так нагрузки до 3А на каждое плече. БП двух полярный, выполнен на комплектарных составных транзисторах КТ825-КТ827. Оба плеча стабилизатора выполнены по одной схеме, но в другом плече (он не показан) изменена полярность конденсаторов и использованы транзисторы другой …
Умение вычислять объем пространственных фигур является важным при решение ряда практических задач по геометрии.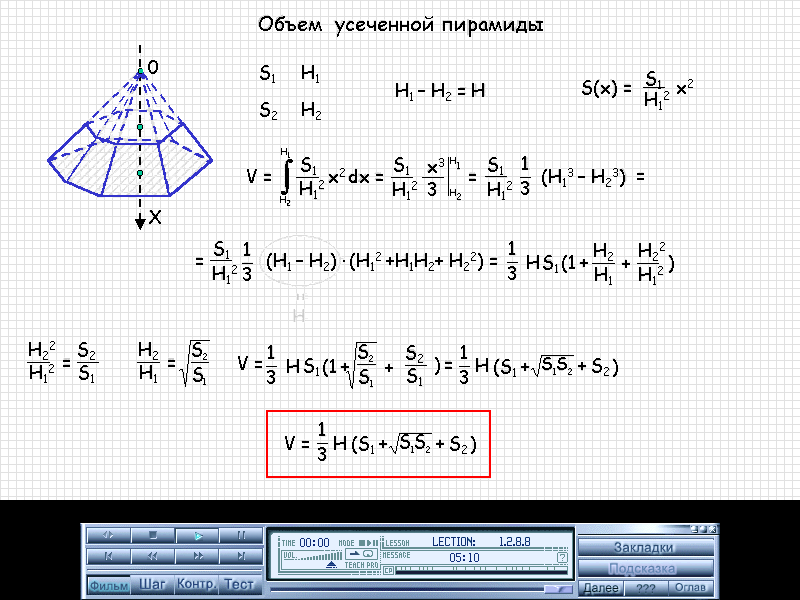 Одной из распространенных фигур является пирамида. В данной статье рассмотрим пирамиды как полной, так и усеченной.
Одной из распространенных фигур является пирамида. В данной статье рассмотрим пирамиды как полной, так и усеченной.
Пирамида как объемная фигура
Каждый знает о египетских пирамидах, поэтому хорошо представляет, о какой фигуре пойдет речь. Тем не менее египетские каменные сооружения являются лишь частным случаем огромного класса пирамид.
Рассматриваемый геометрический объект в общем случае представляет собой многоугольное основание, каждая вершина которого соединена с некоторой точкой в пространстве, не принадлежащей плоскости основания. Данное определение приводит к фигуре, состоящей из одного n-угольника и n треугольников.
Любая пирамида состоит из n+1 граней, 2*n ребер и n+1 вершины. Поскольку рассматриваемая фигура является совершенным полиэдром, то числа отмеченных элементов подчиняются равенству Эйлера:
2*n = (n+1) + (n+1) — 2.
Многоугольник, находящийся в основании, дает название пирамиды, например, треугольная, пятиугольная и так далее.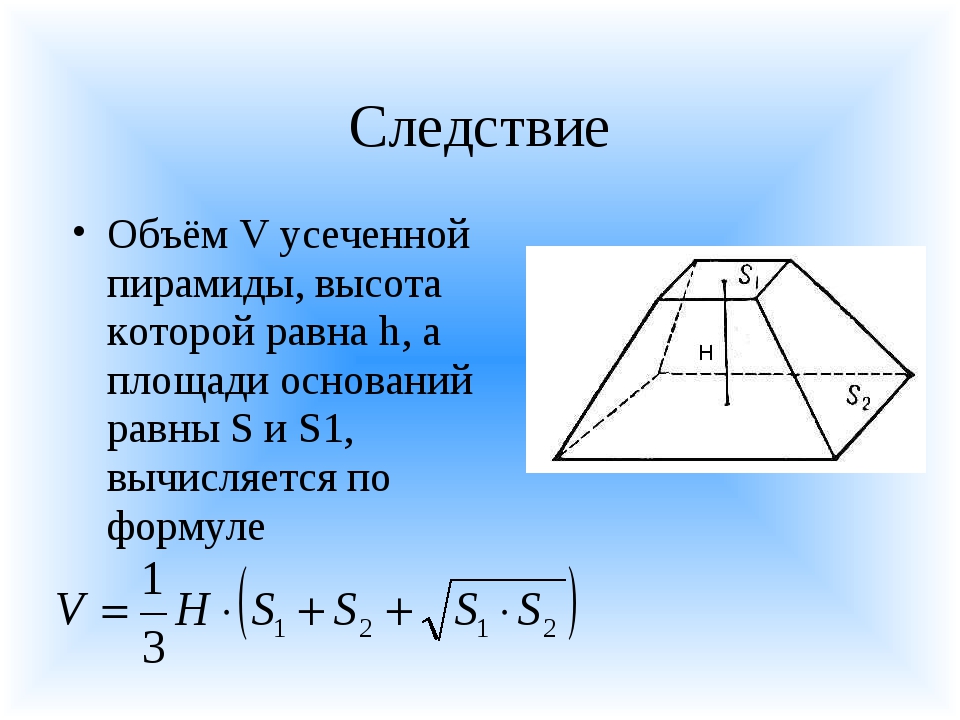 Набор пирамид с разными основаниями приведен на фото ниже.
Набор пирамид с разными основаниями приведен на фото ниже.
Точка, в которой n треугольников фигуры соединяются, называется вершиной пирамиды. Если из нее опустить на основание перпендикуляр и он пересечет его в геометрическом центре, тогда такая фигура будет называться прямой. Если это условие не выполняется, то имеет место наклонная пирамида.
Прямая фигура, основание которой образовано равносторонним (равноугольным) n-угольником, называется правильной.
Формула объема пирамиды
Для вычисления объема пирамиды воспользуемся интегральным исчислением. Для этого разобьем фигуру параллельными основанию секущими плоскостями на бесконечное число тонких слоев. Рисунок ниже показывает четырехугольную пирамиду высотой h и длиной стороны L, в которой четырехугольником отмечен тонкий слой сечения.
Площадь каждого такого слоя можно вычислить по формуле:
A(z) = A 0 *(h-z) 2 /h 2 .
Здесь A 0 — площадь основания, z — значение вертикальной координаты. Видно, что если z = 0, то формула дает значение A 0 .
Видно, что если z = 0, то формула дает значение A 0 .
Чтобы получить формулу объема пирамиды, следует вычислить интеграл по всей высоте фигуры, то есть:
V = ∫ h 0 (A(z)*dz).
Подставляя зависимость A(z) и вычисляя первообразную, приходим к выражению:
V = -A 0 *(h-z) 3 /(3*h 2)| h 0 = 1/3*A 0 *h.
Мы получили формулу объема пирамиды. Чтобы найти величину V, достаточно умножить высоту фигуры на площадь основания, а затем результат поделить на три.
Заметим, что полученное выражение справедливо для вычисления объема пирамиды произвольного типа. То есть она может быть наклонной, а ее основание представлять собой произвольный n-угольник.
и ее объем
Полученную в пункте выше общую формулу для объема можно уточнить в случае пирамиды с правильным основанием. Площадь такого основания вычисляется по следующей формуле:
A 0 = n/4*L 2 *ctg(pi/n).
Здесь L является длиной стороны правильного многоугольника с n вершинами. Символ pi — это число пи.
Символ pi — это число пи.
Подставляя выражение для A 0 в общую формулу, получаем объем правильной пирамиды:
V n = 1/3*n/4*L 2 *h*ctg(pi/n) = n/12*L 2 *h*ctg(pi/n).
Например, для треугольной пирамиды эта формула приводит к следующему выражению:
V 3 = 3/12*L 2 *h*ctg(60 o) = √3/12*L 2 *h.
Для правильной четырехугольной пирамиды формула объема приобретает вид:
V 4 = 4/12*L 2 *h*ctg(45 o) = 1/3*L 2 *h.
Определение объемов правильных пирамид требует знания стороны их основания и высоты фигуры.
Пирамида усеченная
Предположим, что мы взяли произвольную пирамиду и отсекли у нее часть боковой поверхности, содержащей вершину. Оставшаяся фигура называется усеченной пирамидой. Она состоит уже из двух n-угольных оснований и n трапеций, которые их соединяют. Если секущая плоскость была параллельна основанию фигуры, тогда образуется усеченная пирамида с параллельными подобными основаниями. То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.
То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.
Рисунок выше демонстрирует усеченную правильную Видно, что верхнее основание ее так же, как и нижнее, образовано правильным шестиугольником.
Формула которую можно вывести, используя подобное приведенному интегральное исчисление, имеет вид:
V = 1/3*h*(A 0 + A 1 + √(A 0 *A 1)).
Где A 0 и A 1 — площади нижнего (большого) и верхнего (маленького) оснований соответственно. Переменной h обозначается высота усеченной пирамиды.
Объем пирамиды Хеопса
Любопытно решить задачу на определение объема, который заключает внутри себя самая большая египетская пирамида.
В 1984 году британские египтологи Марк Легнер (Mark Lehner) и Джон Гудман (Jon Goodman) установили точные размеры пирамиды Хеопса. Ее первоначальная высота равнялась 146,50 метра (в настоящее время около 137 метров). Средняя длина каждой из четырех сторон сооружения составила 230,363 метра.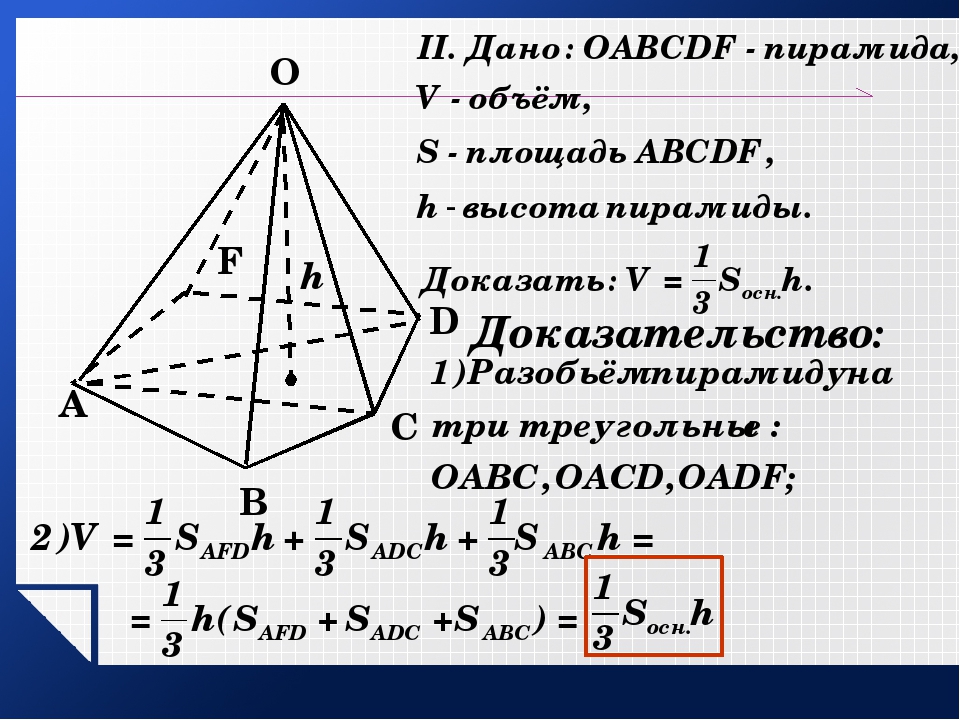 Основание пирамиды с высокой точностью является квадратным.
Основание пирамиды с высокой точностью является квадратным.
Воспользуемся приведенными цифрами для определения объема этого каменного гиганта. Поскольку пирамида является правильной четырехугольной, тогда для нее справедлива формула:
Подставляем цифры, получаем:
V 4 = 1/3*(230,363) 2 *146,5 ≈ 2591444 м 3 .
Объем пирамиды Хеопса равен практически 2,6 млн м 3 . Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м 3 . То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!
Пирамидой называется многогранник, одна из граней которого многоугольник (основание ), а все остальные грани – треугольники с общей вершиной (боковые грани ) (рис. 15). Пирамида называется правильной , если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис. 16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром .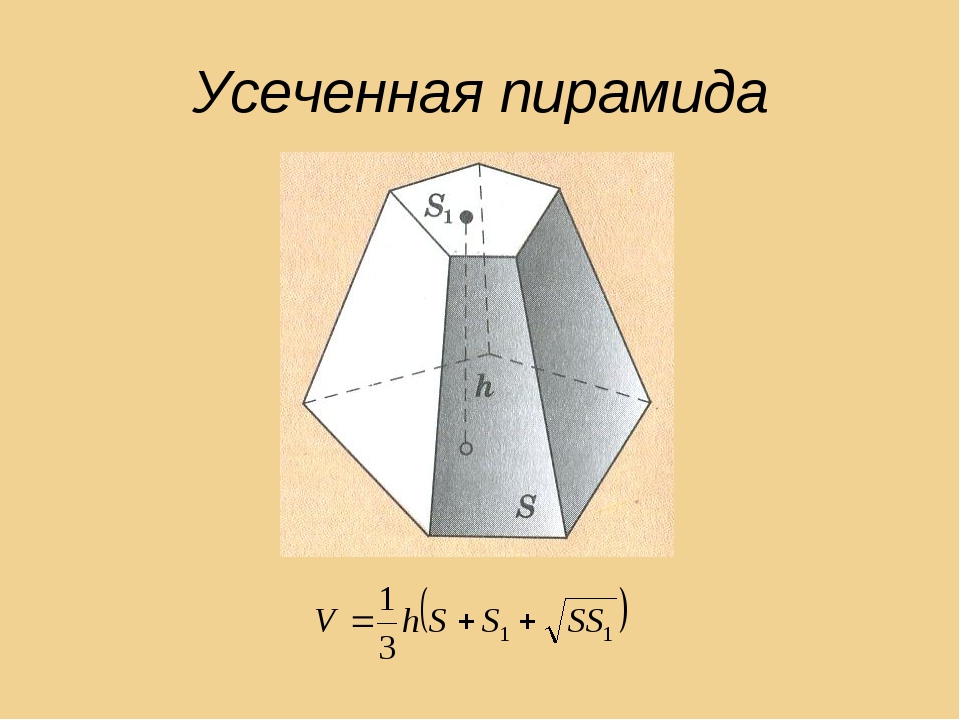
Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию Высотой пирамиды называется расстояние от ее вершины до плоскости основания. Все боковые ребра правильной пирамиды равны между собой, все боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой . Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.
Теоремы
1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности описанной около основания.
2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности описанной около основания.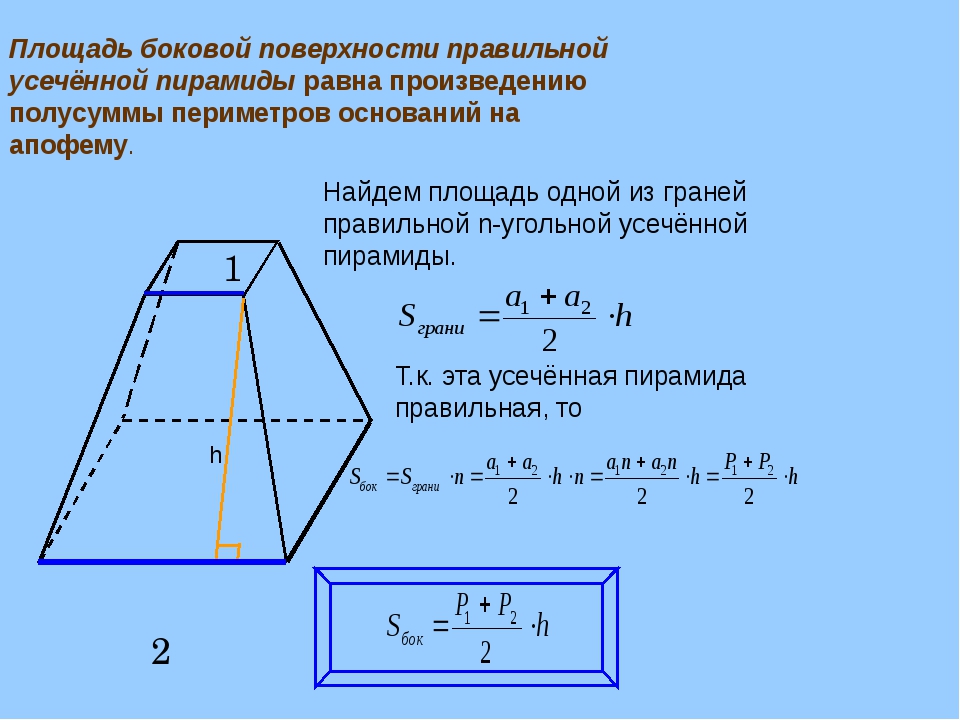
3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности вписанной в основание.
Для вычисления объема произвольной пирамиды верна формула:
где V – объем;
S осн – площадь основания;
H – высота пирамиды.
Для правильной пирамиды верны формулы:
где p – периметр основания;
h а – апофема;
H – высота;
S полн
S бок
S осн – площадь основания;
V – объем правильной пирамиды.
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.
Основания усеченной пирамиды – подобные многоугольники. Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Для усеченной пирамиды справедливы формулы:
(4)
где S 1 , S 2 – площади верхнего и нижнего оснований;
S полн – площадь полной поверхности;
S бок – площадь боковой поверхности;
H – высота;
V – объем усеченной пирамиды.
Для правильной усеченной пирамиды верна формула:
где p 1 , p 2 – периметры оснований;
h а – апофема правильной усеченной пирамиды.
Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.
Найти тангенс угла наклона бокового ребра к плоскости основания.
Решение. Сделаем рисунок (рис. 18).
Пирамида правильная, значит в основании равносторонний треугольник и все боковые грани равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: и т.е. Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС ). Угол наклона бокового ребра (например SB ) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD . Чтобы найти тангенс необходимо знать катеты SO и OB . Пусть длина отрезка BD равна 3а . Точкой О отрезок BD делится на части: и Из находим SO : Из находим:
Ответ:
Пример 2. Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота 4 см.
Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота 4 см.
Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (4). Чтобы найти площади оснований необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит площади оснований и Подставив все данные в формулу, вычислим объем усеченной пирамиды:
Ответ: 112 см 3 .
Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды 2 см.
Решение. Сделаем рисунок (рис. 19).
Боковая грань данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из где А 1 Е перпендикуляр из точки А 1 на плоскость нижнего основания, A 1 D – перпендикуляр из А 1 на АС . А 1 Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:
А 1 Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:
MK = DE .
По теореме Пифагора из
Площадь боковой грани:
Ответ:
Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b ). Каждая боковая грань образует с плоскостью основания пирамиды угол равный j . Найти площадь полной поверхности пирамиды.
Решение. Сделаем рисунок (рис. 21). Площадь полной поверхности пирамиды SABCD равна сумме площадей и площади трапеции ABCD .
Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:
Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:
Аналогично и значит Таким образом задача свелась к нахождению площади трапеции АВСD . Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.
Так как в трапецию можно вписать окружность, то или Из по теореме Пифагора имеем
– это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств:
- Боковые грани пирамиды являются трапециями;
- Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
- Основания являются подобными многоугольниками;
- В правильной усеченной пирамиде, грани представляют собой одинаковые равнобедренные трапеции, площадь которых равна.
 Также они наклонены к основанию под одним углом.
Также они наклонены к основанию под одним углом.
Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон:
Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции . Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.
Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:
Давайте рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l = 5 см, длина грани в большом основании равна a = 6 см, а грань в меньшем основании b = 4 см. Рассчитайте площадь усеченной пирамиды.
Рассчитайте площадь усеченной пирамиды.
Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:
Таким же образом находим периметр меньшего основания:
Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу:
Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.
Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований .
Давайте рассмотрим пример расчета. Помним, что данная формула применяется только для правильной усеченной пирамиды.
Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.
Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата . Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:
Теперь используем найденные значения для расчета площади боковой поверхности.
Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.
Объём усечённой пирамиды
[музыка] здравствуйте уважаемые ученики начинаем наш сегодняшний урок и наша тема усеченный конус усеченная пирамида их объем и сегодня мы рассмотрим сами усеченный конус усеченную пирамиду рассмотрим формула объема данных фигур а также порешаем задачи что касается усеченного конуса с этим предметам мы встречаются в жизни практически каждый день посмотрите на это ведро или перевернутое ведро если мы заполним ведро водой заморозим затем перевернем вы берём ведро то получим усеченный конус мы с вами уже рассматривали конус это тело вращения а также объем конуса имеют следующий вид 1 3 площадь основания конуса площадь круга 1 драть умноженное на высоту конусом что касается усеченного конуса это когда мы проводим параллельную плоскость к плоскости основания конуса сверху у нас тоже получается конус если уберем этот верхний конус то у нас получится усеченный конус основании круг меньшее основание имеет меньшую соответственно больше оснований мид польши радиус и высота усеченный конус это расстояние между центрами оснований или кругов ну и конечно же как наверно мы уже поняли объем усеченного конуса и то есть объем полного конуса минус объем верхнего конуса если мы все роста на свои места и правильно вычислен то у нас получится следующую форму формула когда не объемы для усеченного конуса давайте теперь рассмотрим усеченную пирамиду и перед нами четыре угольные усеченные пирамиды и треугольное усеченная пирамида точно так же как и для конуса формула объема для усеченной пирамиды равняется одной трети аж и у нас в скобочках с 1 это площадь основания меньшего основания пирамиды с 2 это площадь большего основания и под корнем s1 и s2 все это в сумме нажатием на высоту с коэффициентом 1 3 получаем объем усеченной пирамиды давайте теперь порешаем задачи в треугольной усеченной пирамиде большим основанием служит равносторонний треугольник значит меньше основание также является равносторонним треугольником высота этого равносторонний треугольник a равна 18 а высота меньшего основания равна 6 определите объем усеченные пирамиды есть ли его высота то есть высота пирамиды равна 10 сантиметрам записали сразу форму объема усеченная пирамида на 3 умножить на высоту высота у нас имеется и мы должны найти величины которые находятся у нас скобках то есть площади верхнего и нижнего основания давайте отдельно рассмотрим треугольники то есть треугольник который расположен нас в нижнем основании то есть равносторонний треугольник высота известно равна 18 сантиметров так как это равносторонний треугольник все углы тоже равны и они равны 60 градусам здесь у нас и высота и медианы и биссектрисы значит вы владелец попала на значит этот угол равен 30 градусам давайте запишем и так данную вы у нас половина 60 лет 30 градусов и рассмотрим прямоугольный треугольник расположенные здесь с правой стороны нашего право стороны треугольника и мы знаем теорему а катите и нам известно теорема о том что катит лежащий напротив 30 градусов прямоугольный треугольник a равняется половине гипотенузы то есть вот у нас гипотенуза этот катет равняется половине то есть если мы его обозначим как а то гипотенуза будет два раза больше 2 а тогда потерями форм можем вычислить значение а а затем найти площадь нашего равностороннего треугольника ну давайте построим теоремы пифагора для такого прямоугольных треугольника возведем в квадрат гипотенузу 2 а если возвести в квадрат после 4а в квадрате возведем в квадрат меньший катет и вычтем от квадрату гипотенузы 4 а в квадрате минус а в квадрате это будет равно больше и котят нашем случае высота 18 в квадрате 4а в квадрате минус а в квадрате 3 а в квадрате равно в 18 квадрате давайте запишем как 18 умножить на 18 и разделим на 3 с двух сторон получим а в квадрате равно 18 лет на 3 будет 6 умножить на 18 ну 8 нас я могу разложить на множители как 6 умножить на 3 это а в квадрате если вам нужно эти значения извлечем корень и а будет равно 6 корней из 3 как видите а это половина основания данного треугольника значит здесь 2 половин тоже равна 6 корней из 3 либо сторона равна струн только равна двум а по нашим обозначениям и мы получаем 2 у нужно 6 корней из 3 основным будет равна 12 корней из 3 если мы помним формулу площади для равностороннего треугольника то мы можем сразу подставить значение стороны и найти по данной формуле либо можно использовать классическую форму нахождения площади треугольника то есть умножить высоту на основании и взять половину данной величины то есть 18 умножить на 12 корней из 3 и разделим на 2 давайте запишем сюда это у нас площадь нашего треугольника что произойдет конечно можем сократить 18 едва к примеру идей пир нужно 12 корней из 3 тогда мы получим 108 корней из 3 это у нас площадь большего основания нашей усеченной пирамидой что касается площади меньшего основания смотрите мы имеем два подобных треугольников вспомним подобие фигур если коэффициент подобия равняется к кассе подобие это отношения соответствующих сторон или отрезков в двух треугольник например здесь если высота равна 18 здесь высота равна 6 мы понимаем что это высота в три раза больше чем данная высота сторона этого треугольника в три раза больше чем в сторона этого треугольника но мы так же знаем что если известен коэффициент подобие то отношения площадей это и будет квадрат данного коллекция на подобе то есть мы видим что высота в 3 раза больше тогда площадь будет больше в 9 раз то есть 3 в квадрате мы можем разделить на 9 найденную площадь большого треугольника тогда у нас получится получить меньшего треугольника здесь мы использовали именно подобие треугольник вы могли аналогичным образом потери им пифагора вычислить сторону через высоту и точно также как здесь вычислить площадь но я хочу показать вам другой способ через подобие 108 разделим на день получим 12 корней из 3 это площадь меньшего основания теперь мы должны расставить формула объема то есть рассмотреть суммы площадей 108 корней из 3 + 2 носками из 3 мм 120 корней из 3 и т с одним из 2 а также под корень и должны перемножить их площади что значит переносит под корнем эти две величины 12 корней из 3 какой же ответит получилось когда 108 разделили на 9 значит 108 можно записать как 9 умножить на 12 камней в 3 это площадь большого треугольника умножен на 12 камней есть люк это площадь меньшего треугольника и все это под корень что означает мы ищем величину s1 можно с 2 под общим корни как видите когда два одинаковых число умножается и все это берет под корень мы берем это число без кормит а с 12 кому из трех и корень из 9 будет 33 умноженного на скамью строф получим 36 корней из 3 это у нас корень из s 1 умножить на s 2 суммы с одним с 2 мы получили 120 корней из 3 120 сложим 36 хормейстера получим 150 6 корней из 3 это и есть все что у нас скобках учителем диппер объем 1 3 умножить на высоту на 10 и на то что у нас получилось скобках то есть 108 кратеров вблизи nascar метров плюс 3 6 корней из 3 получаем 156 вы можете сократить 156 и 3 получить 52 корней из 3 умножить на 10 у вас просят 520 корней из 3 кубических сантиметров это будет объем нашей усеченной пирамиды давайте теперь рассмотрим задачу на нахождение объема усеченного конуса определите объем истину конца есть ли его высота равна 8-ми сантиметрам радиус верхнего основания равен четырем сантиметрам образующая равна 10 сантиметров записали все числовой величины и давайте решим формула объема усеченного конуса выглядит следующим образом меньший радиус нам известен он равен 4 но нет большего радиуса радиуса основания как мы вычислили смотрите рассмотрим такой прямоугольник у прямоугольника противоположной стороны равны если здесь 4 то нижний тоже будет равна 4 если здесь 8 то эта сторона справа в данном прямоугольника тоже будет равна 8 теперь рассмотрим данный прямоугольный треугольник потерям пифагора мы можем вычислить вот этот вот катит который обозначен времена за микс так как гипотенуза у нас равна 10 больше катет равен 8 тогда потерями пифагора мы получаем x квадрате будет равно 10 в квадрате гипотенуза квадрате минус 8 в квадрате и получим 100 минус 436 это x в квадрате 36 значит x будет равен 6 запишем сюда вместо из 6 тогда радиус большего основания нашего усеченного конуса будет равна 6 плюс 4 либо 10 итак у нас имеются радиусы имеется высота то есть мы можем вычислить объем v объем равен 1 3 умноженное на пи умноженное на высоту h что равняется 8 а теперь скобки напишем r в квадрате больший радиус квадрат 10 в квадрате давайте сразу запишем результат 100 + r на r радиус больше оснований умножить на радиус меньше основание 10 на 4 у нас получается 40 и + r в квадрате либо радиус меньшего основания 4 в квадрате будут 16 ну рассмотрим сумму 100 + 40 + 40 + 16 156 получаем 1 3 на пи на 8 и на 156 конечно теперь можно сократить 156 и 3 как в предыдущей задаче у нас получится 5252 умножим на 8 почему 416 и оставим пи кубических сантиметров вот такой объем у данного усеченного конуса уважаемые ученики на этом мы завершаем наш сегодняшний урок желаю вам всем полезных знаний спасибо до свидания [музыка]
Задачи на усеченную пирамиду
Многогранник, у которого одна из граней – многоугольник, а все остальные грани – треугольники с общей вершиной, называется пирамидой.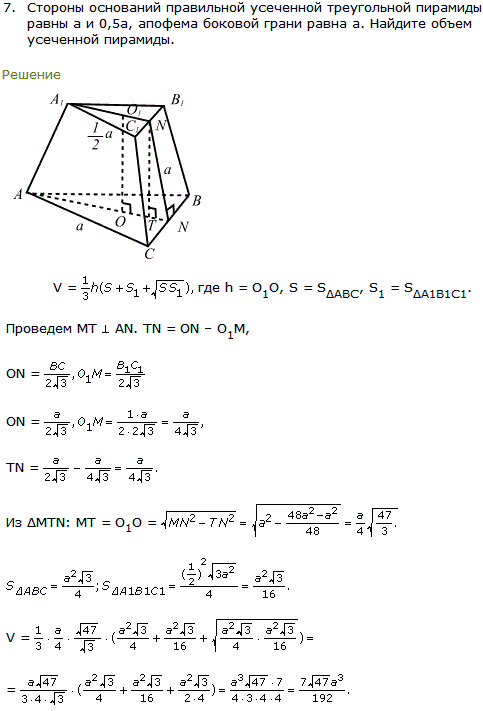
Эти треугольники, из которых составлена пирамида, называют боковыми гранями, а оставшийся многоугольник – основанием пирамиды.
В основании пирамиды лежит геометрическая фигура – n-угольник. В таком случае пирамиду называют еще n-угольной.
Треугольную пирамиду, все ребра которой равны, называют тетраэдром.
Ребра пирамиды, которые не принадлежат основанию, называются боковыми, а их общая точка – это вершина пирамиды. Другие ребра пирамиды обычно называют сторонами основания.
Пирамиду называют правильной, если у нее в основании лежит правильный многоугольник, а все боковые ребра равны между собой.
Расстояние от вершины пирамиды до плоскости основания называется высотой пирамиды. Можно сказать, что высота пирамиды есть отрезок, перпендикулярный основанию, концы которого находятся в вершине пирамиды и на плоскости основания.
Для любой пирамиды имеют место следующие формулы:
1) Sполн = S бок + Sосн, где
Sполн – площадь полной поверхности пирамиды;
Sбок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней пирамиды;
S осн – площадь основания пирамиды.
2) V = 1/3 Sосн · Н, где
V – объем пирамиды;
Н – высота пирамиды.
Для правильной пирамиды имеет место:
Sбок = 1/2 Pосн h, где
Pосн – периметр основания пирамиды;
h – длина апофемы, то есть длина высоты боковой грани, опущенной из вершины пирамиды.
Часть пирамиды, заключенная между двумя плоскостями – плоскостью основания и секущей плоскостью, проведенной параллельно основанию, называют усеченной пирамидой.
Основание пирамиды и сечение пирамиды параллельной плоскостью называются основаниями усеченной пирамиды. Остальные грани называют боковыми. Расстояние между плоскостями оснований называют высотой усеченной пирамиды. Ребра, которые не принадлежат основаниям, называются боковыми.
Остальные грани называют боковыми. Расстояние между плоскостями оснований называют высотой усеченной пирамиды. Ребра, которые не принадлежат основаниям, называются боковыми.
Кроме того, основания усеченной пирамиды подобные n-угольники. Если основания усеченной пирамиды – правильные многоугольники, а все боковые ребра равны между собой, то такая усеченная пирамида называется правильной.
Для произвольной усеченной пирамиды имеют место следующие формулы:
1) Sполн = Sбок + S1 + S2, где
Sполн – площадь полной поверхности;
Sбок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней усеченной пирамиды, которые представляют собой трапеции;
S1, S2 – площади оснований;
2) V = 1/3( S1 + S2 + √(S1 · S2 ))H, где
V – объем усеченной пирамиды;
H – высота усеченной пирамиды.
Для правильной усеченной пирамиды также имеем:
Sбок = 1/2(P1 + P2) · h, где
P1 , P2 – периметры оснований;
h – апофема (высота боковой грани, представляющей собой трапецию).
Рассмотрим несколько задач на усеченную пирамиду.
Задача 1.
В треугольной усеченной пирамиде с высотой, равной 10, стороны одного из оснований равны 27, 29 и 52. Определите объем усеченной пирамиды, если периметр другого основания равен 72.
Решение.
Рассмотрим усеченную пирамиду АВСА1В1С1, изображенную на рисунке1.
1. Объем усеченной пирамиды может быть найден по формуле
V = 1/3H · (S1 + S2 + √(S1 · S2)), где S1 – площадь одного из оснований, можно найти по формуле Герона
S = √(p(p – a)(p – b)(p – c)),
т. к. в задаче даны длины трех сторон треугольника.
к. в задаче даны длины трех сторон треугольника.
Имеем: p1 = (27 + 29 + 52)/2 = 54.
S1 = √(54(54 – 27)(54 – 29)(54 – 52)) = √(54 · 27 · 25 · 2) = 270.
2. Пирамида усеченная, а значит, в основаниях лежат подобные многоугольники. В нашем случае треугольник АВС подобен треугольнику А1В1С1. Кроме того, коэффициент подобия можно найти как отношение периметров рассматриваемых треугольников, а отношение их площадей будет равно квадрату коэффициента подобия. Таким образом, имеем:
S1/S2 = (P1)2/(P2)2 = 1082/722 = 9/4. Отсюда S2 = 4S1/9 = 4 · 270/9 = 120.
Итак, V = 1/3 · 10(270 + 120 + √(270 · 120)) = 1900.
Ответ: 1900.
Задача 2.
В треугольной усеченной пирамиде через сторону верхнего основания проведена плоскость параллельно противоположному боковому ребру. В каком отношении разделился объем усеченной пирамиды, если соответственные стороны оснований относятся как 1 : 2?
В каком отношении разделился объем усеченной пирамиды, если соответственные стороны оснований относятся как 1 : 2?
Решение.
Рассмотрим АВСА1В1С1 – усеченную пирамиду, изображенную на рис. 2.
Так как в основаниях стороны относятся как 1 : 2, то площади оснований относятся как 1 : 4 (треугольник АВС подобен треугольнику А1В1С1).
Тогда объем усеченной пирамиды равен:
V = 1/3h · (S1 + S2 + √(S1 · S2)) = 1/3h · (4S2 + S2 + 2S2) = 7/3 · h · S2, где S2 – площадь верхнего основания, h – высота.
Но объем призмы АDEA1B1C1 составляет V1 = S2 · h и, значит,
V2 = V – V1 = 7/3 · h · S2 — h · S2 = 4/3 · h · S2.
Итак, V2 : V1 = 3 : 4.
Ответ: 3 : 4.
Задача 3.
Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 и 1, а высота равна 3. Через точку пересечения диагоналей пирамиды параллельно основаниям пирамиды проведена плоскость, делящая пирамиду на две части. Найти объем каждой из них.
Решение.
Рассмотрим усеченную пирамиду АВСDА1В1С1D1, изображенную на рис. 3.
Обозначим О1О2 = х, тогда ОО₂ = О1О – О1О2 = 3 – х.
Рассмотрим треугольник В1О2D1 и треугольник ВО2D:
угол В1О2D1 равен углу ВО2D как вертикальные;
угол ВDO2 равен углу D1B1O2 и угол O2ВD равен углу B1D1O2 как накрест лежащие при B1D1 || BD и секущих B₁D и BD₁ соответственно.
Следовательно, треугольник В1О2D1 подобен треугольнику ВО2D и имеет место отношение сторон:
В1D1/ВD = О1О2/ОО2 или 1/2 = х/(х – 3), откуда х = 1.
Рассмотрим треугольник В1D1В и треугольник LО2B: угол В – общий, а так же имеется пара односторонних углов при B1D1 || LM, значит, треугольник В1D1В подобен треугольнику LО2B, откуда В1D : LO2 = OO1 : OO2 = 3 : 2, т.е.
LO2 = 2/3 · B1D1, LN = 4/3 · B1D1.
Тогда SKLMN = 16/9 · SA1B1C1D1 = 16/9.
Итак, V1 = 1/3 · 2(4 + 16/9 + 8/3) = 152/27.
V2 = 1/3 · 1 · (16/9 + 1 + 4/3) = 37/27.
Ответ: 152/27; 37/27.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Урок геометрии в 11-м классе: «Объём пирамиды»
Цели и задачи урока:
- вывести формулы: объема пирамиды с использованием основной формулы объема тел и объема усеченной пирамиды.
- систематизировать теоретические знания по теме нахождения объема пирамиды.
- сформировать навык нахождения объема пирамиды, у которой вершина проецируется в центр вписанной или описанной около основания окружности.
- выработать навыки решения типовых задач на применение формул объемов пирамиды и усеченной пирамиды.
Ход урока
I. Объяснение нового материала.
Доказательство теоремы выполняется с помощью мультимедийного проектора
Докажем теорему: объем пирамиды равен одной трети, произведения площади основания на высоту.
Рис. 1
Доказательство:
Сначала докажем теорему для треугольной пирамиды, затем для произвольной.
1. Рассмотрим треугольную пирамиду ОАВС с объемом V, площадью основания S и высотой h . Проведем ось ох (ОМ2— высота), рассмотрим сечение А1В1С1пирамиды плоскостью, перпендикулярной к оси ох и, значит, параллельной плоскости основания. Обозначим через х абсциссу точки М1пересечения этой плоскости с осью ох, а через S{x) — площадь сечения. Выразим S(x) через S, h и х . Заметим, что
В самом деле , следовательно, .
Прямоугольные треугольники , тоже подобны (они имеют общий острый угол с вершиной О).
Применим теперь основную формулу для вычисления объемов тел при a = 0, b = h получаем
Pис. 2
2
2. Докажем теперь теорему для произвольной пирамиды с высотой h и площадью основания S . Такую пирамиду можно разбить на треугольные пирамиды с общей высотой h. Выразим объем каждой треугольной пирамиды по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель , получим в скобках сумму оснований треугольных пирамид, т.е. площадь S оснований исходной пирамиды.
Таким образом, объем исходной пирамиды равен . Теорема доказана.
II. решить задачи по готовым чертежам .
Задача 1. (рис. 3)
Дано: АВСD – правильная пирамида, АВ =3; AD= . Найти: а)Sосн; б) АО; в) DO г) V.
Задача 2. (рис. 4)
4)
Дано: АВСDF – правильная пирамида, .
Задача 3. (рис. 5)
Дано : АВСDEKF – правильная пирамида,
Найти: а) Sосн; б) V.
Задача 4. (рис. 6)
Найти: V.
Проверка задач выполняется с помощью мультимедийного проектора с подробным анализом поэтапного решения.
Задача 1. (рис. 3)
Решение:
а) (используется формула для вычисления площади правильного треугольника)
АВ = = 3, имеем
б) (формула радиуса описанной окружности через сторону правильного треугольника) .
Задача 2. (рис. 4)
4)
Решение:
1) Рассмотрим следовательно,
– равнобедренный, ОС = FО = 2.
Задача 3. (рис. 5)
Решение:
Задача 4. (рис. 6)
Решение:
III. Проверка вывода формулы для вычисления объема усеченной пирамиды (сообщение ученика у доски выполняется с помощью мультимедийного проектора)
Ответ ученика:
Объем усеченной пирамиды рассматриваем как разность объемов полной пирамиды и той, что отсечена от нее плоскостью, параллельной основанию (рис. 1).
Подставим это выражение для х в первую формулу,
Pабота в форме теста, с проверкой через мультимедийный проектор.
1.В наклонной призме боковое ребро равно 7 см, перпендикулярное сечение — прямоугольный треугольник с катетами: 4 см и 3 см. найдите объем призмы.
а) 10 см3, б) 42 см3, в) 60 см3, г) 30 см3.
2. В правильной шестиугольной пирамиде сторона ее основания 2 см. Объем пирамиды равен 6 см3. Чему равна высота?
3. Объем пирамиды равен 56 см3, площадь основания 14 см2. Чему равна высота?
а) 14 см, б) 12 см, в) 16 см.
4. В правильной треугольной пирамиде высота равна 5 см, стороны основания 3 см. Чему равен объем пирамиды?
5. В правильной четырехугольной пирамиде высота равна 9 см. Сторона основания 4 см. найдите объем пирамиды.
а) 50 см3, б) 48 см3, в) 16 см3.
6. Объем правильной четырехугольной пирамиды равен 27 см3, высота 9 см. найти сторону основания.
а)12 см, б) 9 см, в) 3 см.
7. Объем усеченной пирамиды равен 210 см3, площадь нижнего основания 36 см2, верхнего 9 см2. Найдите высоту пирамиды.
Найдите высоту пирамиды.
а) 1см, б) 15 см, в) 10см.
8. Равновеликие призма и правильная четырехугольная пирамида имеют равные высоты. Чему равна сторона основания пирамиды, если площадь основания призмы равна S?
Таблица ответов.
| Задача | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Ответ | б | а | б | а | б | в | в | в |
Домашняя работа: 1. Решить задачи №695в, №697, №690
2. Рассмотреть базовые задачи
Задача 1.
Докажите, что если боковые ребра пирамиды равны (или составляют равные углы с плоскостью основания), то вершина пирамиды проецируется в центр окружности, описанной около основания.
Pис. 2
Задача 2.
Докажите, что если двугранные углы при основании пирамиды равны (или равны высоты боковых граней, проведенные из вершины пирамиды), то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.
Pис. 3
Формула расчета объема усеченной пирамиды четырехгранной. Формулы объема пирамиды полной и усеченной. Объем пирамиды Хеопса. Формулы для усеченной пирамиды
и секущей плоскостью, которая параллельна ее основанию.
Или другими словами: усеченная пирамида — это такой многогранник, который образован пирамидой и ее сечением, параллельным основанию.
Сечение, которое параллельно основанию пирамиды делит пирамиду на 2 части. Часть пирамиды меж ее основанием и сечением — это усеченная пирамида .
Часть пирамиды меж ее основанием и сечением — это усеченная пирамида .
Это сечение для усеченной пирамиды оказывается 1-ним из оснований этой пирамиды.
Расстояние меж основаниями усеченной пирамиды является высотой усеченной пирамиды .
Усеченная пирамида будет правильной , когда пирамида, из которой она была получена, тоже была правильной.
Высота трапеции боковой грани правильной усеченной пирамиды является апофемой правильной усеченной пирамиды.
Свойства усеченной пирамиды.
1. Каждая боковая грань правильной усеченной пирамиды является равнобокими трапециями одной величины.
2. Основания усеченной пирамиды являются подобными многоугольниками.
3. Боковые ребра правильной усеченной пирамиды имеют равную величину и один наклонен по отношению к основанию пирамиды.
4. Боковые грани усеченной пирамиды являются трапециями.
5. Двугранные углы при боковых ребрах правильной усеченной пирамиды имеют равную величину.
6. Отношение площадей оснований: S 2 /S 1 = k 2 .
Формулы для усеченной пирамиды.
Для произвольной пирамиды:
Объем усеченной пирамиды равен 1/3 произведения высоты h (OS ) на сумму площадей верхнего основания S 1 (abcde ), нижнего основания усеченной пирамиды S 2 (ABCDE ) и средней пропорциональной между ними.
Объем пирамиды:
где S 1 , S 2 — площади оснований,
h — высота усеченной пирамиды.
Площадь боковой поверхности равняется сумме площадей боковых граней усеченной пирамиды.
Для правильной усеченной пирамиды:
Правильная усеченная пирамида — многогранник, который образован правильной пирамидой и ее сечением, которое параллельно основанию.
Площадь боковой поверхности правильной усеченной пирамиды равна ½ произведения суммы периметров ее оснований и апофемы.
где S 1 , S 2 — площади оснований,
φ — двугранный угол у основания пирамиды.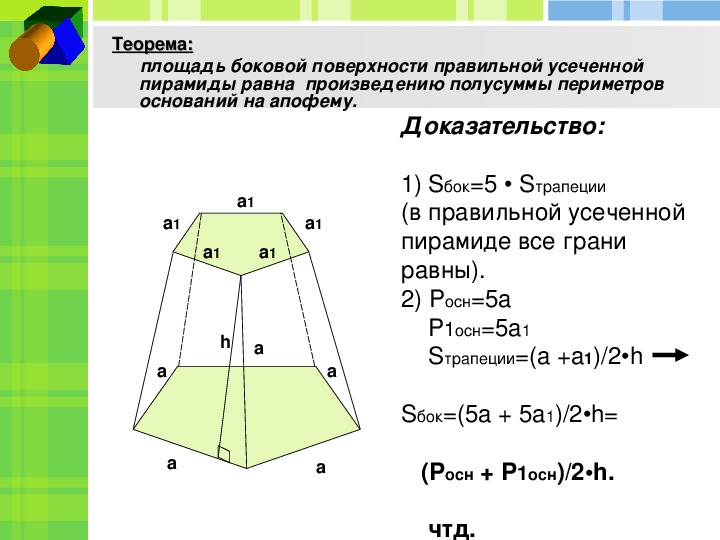
CH является высотой усеченной пирамиды, P 1 и P 2 — периметрами оснований, S 1 и S 2 — площадями оснований, S бок — площадью боковой поверхности, S полн — площадью полной поверхности:
Сечение пирамиды плоскостью, параллельной основанию.
Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) разделяет высоту и боковые ребра пирамиды на пропорциональные отрезки.
Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) — это многоугольник, который подобен основанию пирамиды, при этом коэффициент подобия этих многоугольников соответствует отношению их расстояний от вершины пирамиды.
Площади сечений, которые параллельны основанию пирамиды, относятся как квадраты их расстояний от вершины пирамиды.
Умение вычислять объем пространственных фигур является важным при решение ряда практических задач по геометрии. Одной из распространенных фигур является пирамида. В данной статье рассмотрим пирамиды как полной, так и усеченной.
В данной статье рассмотрим пирамиды как полной, так и усеченной.
Пирамида как объемная фигура
Каждый знает о египетских пирамидах, поэтому хорошо представляет, о какой фигуре пойдет речь. Тем не менее египетские каменные сооружения являются лишь частным случаем огромного класса пирамид.
Рассматриваемый геометрический объект в общем случае представляет собой многоугольное основание, каждая вершина которого соединена с некоторой точкой в пространстве, не принадлежащей плоскости основания. Данное определение приводит к фигуре, состоящей из одного n-угольника и n треугольников.
Любая пирамида состоит из n+1 граней, 2*n ребер и n+1 вершины. Поскольку рассматриваемая фигура является совершенным полиэдром, то числа отмеченных элементов подчиняются равенству Эйлера:
2*n = (n+1) + (n+1) — 2.
Многоугольник, находящийся в основании, дает название пирамиды, например, треугольная, пятиугольная и так далее. Набор пирамид с разными основаниями приведен на фото ниже.
Точка, в которой n треугольников фигуры соединяются, называется вершиной пирамиды. Если из нее опустить на основание перпендикуляр и он пересечет его в геометрическом центре, тогда такая фигура будет называться прямой. Если это условие не выполняется, то имеет место наклонная пирамида.
Прямая фигура, основание которой образовано равносторонним (равноугольным) n-угольником, называется правильной.
Формула объема пирамиды
Для вычисления объема пирамиды воспользуемся интегральным исчислением. Для этого разобьем фигуру параллельными основанию секущими плоскостями на бесконечное число тонких слоев. Рисунок ниже показывает четырехугольную пирамиду высотой h и длиной стороны L, в которой четырехугольником отмечен тонкий слой сечения.
Площадь каждого такого слоя можно вычислить по формуле:
A(z) = A 0 *(h-z) 2 /h 2 .
Здесь A 0 — площадь основания, z — значение вертикальной координаты. Видно, что если z = 0, то формула дает значение A 0 .
Чтобы получить формулу объема пирамиды, следует вычислить интеграл по всей высоте фигуры, то есть:
V = ∫ h 0 (A(z)*dz).
Подставляя зависимость A(z) и вычисляя первообразную, приходим к выражению:
V = -A 0 *(h-z) 3 /(3*h 2)| h 0 = 1/3*A 0 *h.
Мы получили формулу объема пирамиды. Чтобы найти величину V, достаточно умножить высоту фигуры на площадь основания, а затем результат поделить на три.
Заметим, что полученное выражение справедливо для вычисления объема пирамиды произвольного типа. То есть она может быть наклонной, а ее основание представлять собой произвольный n-угольник.
и ее объем
Полученную в пункте выше общую формулу для объема можно уточнить в случае пирамиды с правильным основанием. Площадь такого основания вычисляется по следующей формуле:
A 0 = n/4*L 2 *ctg(pi/n).
Здесь L является длиной стороны правильного многоугольника с n вершинами. Символ pi — это число пи.
Символ pi — это число пи.
Подставляя выражение для A 0 в общую формулу, получаем объем правильной пирамиды:
V n = 1/3*n/4*L 2 *h*ctg(pi/n) = n/12*L 2 *h*ctg(pi/n).
Например, для треугольной пирамиды эта формула приводит к следующему выражению:
V 3 = 3/12*L 2 *h*ctg(60 o) = √3/12*L 2 *h.
Для правильной четырехугольной пирамиды формула объема приобретает вид:
V 4 = 4/12*L 2 *h*ctg(45 o) = 1/3*L 2 *h.
Определение объемов правильных пирамид требует знания стороны их основания и высоты фигуры.
Пирамида усеченная
Предположим, что мы взяли произвольную пирамиду и отсекли у нее часть боковой поверхности, содержащей вершину. Оставшаяся фигура называется усеченной пирамидой. Она состоит уже из двух n-угольных оснований и n трапеций, которые их соединяют. Если секущая плоскость была параллельна основанию фигуры, тогда образуется усеченная пирамида с параллельными подобными основаниями. То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.
То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.
Рисунок выше демонстрирует усеченную правильную Видно, что верхнее основание ее так же, как и нижнее, образовано правильным шестиугольником.
Формула которую можно вывести, используя подобное приведенному интегральное исчисление, имеет вид:
V = 1/3*h*(A 0 + A 1 + √(A 0 *A 1)).
Где A 0 и A 1 — площади нижнего (большого) и верхнего (маленького) оснований соответственно. Переменной h обозначается высота усеченной пирамиды.
Объем пирамиды Хеопса
Любопытно решить задачу на определение объема, который заключает внутри себя самая большая египетская пирамида.
В 1984 году британские египтологи Марк Легнер (Mark Lehner) и Джон Гудман (Jon Goodman) установили точные размеры пирамиды Хеопса. Ее первоначальная высота равнялась 146,50 метра (в настоящее время около 137 метров). Средняя длина каждой из четырех сторон сооружения составила 230,363 метра. Основание пирамиды с высокой точностью является квадратным.
Основание пирамиды с высокой точностью является квадратным.
Воспользуемся приведенными цифрами для определения объема этого каменного гиганта. Поскольку пирамида является правильной четырехугольной, тогда для нее справедлива формула:
Подставляем цифры, получаем:
V 4 = 1/3*(230,363) 2 *146,5 ≈ 2591444 м 3 .
Объем пирамиды Хеопса равен практически 2,6 млн м 3 . Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м 3 . То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!
Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания и вершины ее сечения плоскостью, параллельной основанию.
Свойства усеченной пирамиды:
- Основания усеченной пирамиды — подобные многоугольники.
- Боковые грани усеченной пирамиды — трапеции.
- Боковые ребра правильной усеченной пирамиды равны и одинаково
наклонены к основанию пирамиды.

- Боковые грани правильной усеченной пирамиды — равные между собой равнобедренные трапеции и одинаково наклонены к основанию пирамиды.
- Двугранные углы при боковых ребрах правильной усеченной пирамиды равны.
Площадь поверхности и объём усеченной пирамиды
Пусть — высота усеченной пирамиды, и — периметры оснований усеченной пирамиды, и — площади оснований усеченной пирамиды, — площадь боковой поверхности усеченной пирамиды, — площадь полной поверхности усеченной пирамиды, — объем усеченной пирамиды. Тогда имеют место следующие соотношения:
.
Если все двугранные углы при основании усеченной пирамиды равны , а высоты всех боковых граней пирамиды равны , то
Пирамидой называется многогранник, одна из граней которого многоугольник (основание ), а все остальные грани – треугольники с общей вершиной (боковые грани ) (рис. 15). Пирамида называется правильной , если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис. 16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром .
16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром .
Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию Высотой пирамиды называется расстояние от ее вершины до плоскости основания. Все боковые ребра правильной пирамиды равны между собой, все боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой . Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.
Теоремы
1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности описанной около основания.
2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности описанной около основания.
3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности вписанной в основание.
Для вычисления объема произвольной пирамиды верна формула:
где V – объем;
S осн – площадь основания;
H – высота пирамиды.
Для правильной пирамиды верны формулы:
где p – периметр основания;
h а – апофема;
H – высота;
S полн
S бок
S осн – площадь основания;
V – объем правильной пирамиды.
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.
Основания усеченной пирамиды – подобные многоугольники. Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Для усеченной пирамиды справедливы формулы:
(4)
где S 1 , S 2 – площади верхнего и нижнего оснований;
S полн – площадь полной поверхности;
S бок – площадь боковой поверхности;
H – высота;
V – объем усеченной пирамиды.
Для правильной усеченной пирамиды верна формула:
где p 1 , p 2 – периметры оснований;
h а – апофема правильной усеченной пирамиды.
Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.
Решение. Сделаем рисунок (рис. 18).
Пирамида правильная, значит в основании равносторонний треугольник и все боковые грани равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: и т.е. Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС ). Угол наклона бокового ребра (например SB ) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD . Чтобы найти тангенс необходимо знать катеты SO и OB . Пусть длина отрезка BD равна 3а . Точкой О отрезок BD делится на части: и Из находим SO : Из находим:
Точкой О отрезок BD делится на части: и Из находим SO : Из находим:
Ответ:
Пример 2. Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота 4 см.
Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (4). Чтобы найти площади оснований необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит площади оснований и Подставив все данные в формулу, вычислим объем усеченной пирамиды:
Ответ: 112 см 3 .
Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды 2 см.
Решение. Сделаем рисунок (рис. 19).
Боковая грань данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из где А 1 Е перпендикуляр из точки А 1 на плоскость нижнего основания, A 1 D – перпендикуляр из А 1 на АС . А 1 Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:
Ее найдем из где А 1 Е перпендикуляр из точки А 1 на плоскость нижнего основания, A 1 D – перпендикуляр из А 1 на АС . А 1 Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:
MK = DE .
По теореме Пифагора из
Площадь боковой грани:
Ответ:
Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b ). Каждая боковая грань образует с плоскостью основания пирамиды угол равный j . Найти площадь полной поверхности пирамиды.
Решение. Сделаем рисунок (рис. 21). Площадь полной поверхности пирамиды SABCD равна сумме площадей и площади трапеции ABCD .
Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:
Аналогично и значит Таким образом задача свелась к нахождению площади трапеции АВСD . Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.
Так как в трапецию можно вписать окружность, то или Из по теореме Пифагора имеем
Пирамидой называют многогранник, у которого основание представлено произвольным многоугольником, а остальные грани – треугольниками с общей вершиной, которая соответствует вершине пирамиды.
Если в пирамиде провести параллельное основанию сечение, то оно разделить фигуру на две части. Пространство межу нижним основанием и сечением, ограниченное гранями, называется усеченной пирамидой .
Пространство межу нижним основанием и сечением, ограниченное гранями, называется усеченной пирамидой .
Формула объема усеченной пирамиды представляет собой одну треть произведения высоты на сумму площадей верхнего и нижнего основания с их средним пропорциональным:
Рассмотрим пример расчета объема усеченной пирамиды.
Задача: Дана треугольная усеченная пирамида. Ее высота h
= 10 см, стороны одного из оснований равны a
= 27 см, b
= 29 см, c
= 52 см. Периметр второго основания равняется P2
=72 см. Найдите объем пирамиды.
Для расчета объема нам потребуется площадь оснований. Зная длины сторон одного треугольника, мы можем рассчитать >. Для этого потребуется найти полупериметр:
Теперь найдем S2:
Зная, что пирамида усеченная, делаем вывод, что треугольники, лежащие в основаниях подобны. Коэффициент подобия этих треугольников можно найти из соотношения периметров. Отношение площадей треугольников будет равно квадрату этого коэффициента:
Теперь, когда мы нашли площади оснований усеченной пирамиды, можем легко рассчитать ее объем:
Таким образом, вычислив коэффициент подобия и рассчитав площадь оснований, мы нашли объем заданной усеченной пирамиды.
Объем усеченной пирамиды
Объем усеченной пирамиды равен емкости усеченной пирамиды. Пирамида — это многогранник, представляющий собой объемную трехмерную фигуру с многоугольным основанием и вершиной, называемой вершиной. Когда пирамиду разрезают вдоль ее поперечного сечения, получают меньшую пирамиду и усеченную пирамиду. В этом разделе мы узнаем об объеме усеченной пирамиды. Оставайтесь с нами, чтобы узнать больше!!!
Каков объем усеченной пирамиды?
Объем усеченной пирамиды — это количество кубических единиц, которые может вместить усеченная пирамида.Пирамида имеет вершину и только одну грань основания, тогда как усеченная пирамида не имеет вершины и имеет две грани основания, одну вверху и одну внизу. Только основание пирамиды — многоугольник, остальные грани — треугольники. Пирамида может быть «правой», в которой ее вершина находится прямо над центром тяжести над ее основанием, или же пирамида может быть «наклонной», что в основном является неправильными пирамидами.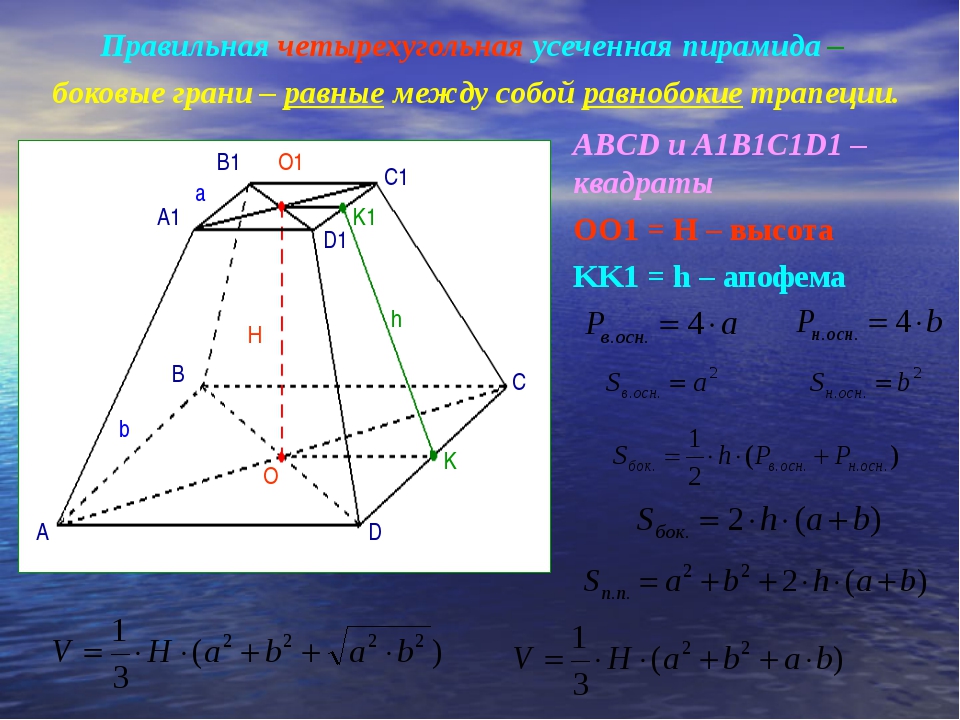 Пирамиды названы в честь их оснований, например, пирамида с треугольным основанием называется треугольным основанием, пирамида с квадратным основанием называется квадратной пирамидой, пирамида с восьмиугольным основанием называется восьмиугольной пирамидой и так далее.Пирамида с n-сторонним основанием имеет n+1 вершин, n+1 граней и 2n ребер. В случае усеченной пирамиды обе грани основания должны иметь равные стороны, поэтому усеченная пирамида с n-сторонними гранями основания имеет «2n» вершин, «n+2» граней и «3n» ребер. Например, это может быть выражено как m 3 , cm 3 , in 3 и т. д. в зависимости от заданных единиц.
Пирамиды названы в честь их оснований, например, пирамида с треугольным основанием называется треугольным основанием, пирамида с квадратным основанием называется квадратной пирамидой, пирамида с восьмиугольным основанием называется восьмиугольной пирамидой и так далее.Пирамида с n-сторонним основанием имеет n+1 вершин, n+1 граней и 2n ребер. В случае усеченной пирамиды обе грани основания должны иметь равные стороны, поэтому усеченная пирамида с n-сторонними гранями основания имеет «2n» вершин, «n+2» граней и «3n» ребер. Например, это может быть выражено как m 3 , cm 3 , in 3 и т. д. в зависимости от заданных единиц.
Формула объема усеченной пирамиды
Поскольку мы знаем, что усеченная пирамида образуется путем разрезания пирамиды вдоль ее поперечного сечения, это понятие поможет нам понять формулу объема усеченной пирамиды.
Следовательно, объем усеченной пирамиды = объем всей пирамиды — объем малой пирамиды.
Таким образом, формула объема усеченной пирамиды V = 1/3 × h × (a 2 + b 2 + ab), где «V», «h», «a» и «b» равны объем усеченной пирамиды, высота усеченной пирамиды, длина стороны основания всей пирамиды и длина стороны основания меньшей пирамиды.
Определение объема усеченной пирамиды
Теперь найдем формулу объема усеченной пирамиды.
Предположим, что основание всей пирамиды представляет собой квадрат со стороной «а» единиц, а основание маленькой пирамиды наверху — квадрат со стороной «b» единиц. Также примем высоту всей пирамиды за «H» единиц, высоту усеченной пирамиды за «h» единиц, следовательно, высоту малой пирамиды за «H-h» единиц.
Объем усеченной пирамиды, V = Объем всей пирамиды — Объем малой пирамиды.
⇒ V = (1/3 × площадь основания всей пирамиды × высота всей пирамиды) — (1/3 × площадь основания маленькой пирамиды × высота маленькой пирамиды)
⇒ V = (1/3 × a 2 × H) — (1/3 × b 2 × (H — h)
⇒ V = 1/3 × (а 2 H — b 2 (H — h))
⇒ V = 1/3 × (a 2 H — b 2 H + b 2 h)
⇒ V = 1/3 × ((a 2 — b 2 )H + b 2 h) . ..(1)
..(1)
Теперь отношение между высотами всей пирамиды и маленькой пирамиды, H:(H — h) = a:b. Следовательно, отношение всей пирамиды к усеченной пирамиде будет H:h = a:(a — b)
. ⇒ Н/ч = а/(а — б)
⇒ H = (a/(a — b)) × h … (2)
Подставляя значение «H» из уравнения (2) в уравнение (1), получаем:
⇒ V = 1/3 × ((a 2 — b 2 )(a/(a — b)) × h) + b 2 h))
⇒ V = 1/3 × (((a + b)(a — b) × a)/(a — b)) × h + b 2 ч
⇒ V = 1/3 × (a + b) × a × h + b 2 ч
⇒ V = 1/3 × h × (а 2 + b 2 + ab)
Таким образом, объем усеченной пирамиды определяется как V = 1/3 × h × (a 2 + b 2 + ab).
Как найти объем усеченной пирамиды?
Мы можем найти объем усеченной пирамиды, используя следующие шаги:
- Шаг 1: Определите данные размеры как высоту усеченной пирамиды, длину стороны основания всей пирамиды и длину стороны меньшей пирамиды.

- Шаг 2: Подставьте значения в формулу V = 1/3 × h × (a 2 + b 2 + ab), чтобы определить значение объема усеченной пирамиды.
- Шаг 3: Запишите полученный ответ в кубических единицах.
Пример: Найдите объем усеченной пирамиды, высота которой равна 9 единицам, если длина стороны основания всей пирамиды равна 5 единицам, а длина стороны основания меньшей пирамиды равна 3 единицам.
Решение: Учитывая, что h = 9 единиц, a = 5 единиц и b = 3 единицы.
Объем усеченной пирамиды, V = 1/3 × h × (a 2 + b 2 + ab)
⇒ V = 1/3 × 9 × (5 2 + 3 2 + 15)
⇒ V = 3 × 49 = 147 кубических единиц
Таким образом, объем усеченной пирамиды равен 147 кубических единиц.
Часто задаваемые вопросы об объеме усеченной пирамиды
Каков объем усеченной пирамиды?
Объем усеченной пирамиды определяется как вместимость усеченной пирамиды. Усеченная пирамида получается, когда мы разрезаем пирамиду вдоль ее поперечного сечения. Таким образом, объем усеченной пирамиды получается, если из объема всей пирамиды вычесть объем меньшей пирамиды.
Усеченная пирамида получается, когда мы разрезаем пирамиду вдоль ее поперечного сечения. Таким образом, объем усеченной пирамиды получается, если из объема всей пирамиды вычесть объем меньшей пирамиды.
Какова формула объема усеченной пирамиды?
Объем усеченной пирамиды определяется по формуле V = 1/3 × h × (a 2 + b 2 + ab), где «V», «h», «a» и «b» объем усеченной пирамиды, высота усеченной пирамиды, длина стороны основания всей пирамиды и длина стороны основания меньшей пирамиды.
Какие единицы измерения используются при нахождении объема усеченной пирамиды?
Единицей объема усеченной пирамиды являются «кубические единицы». Например, это может быть выражено как m 3 , cm 3 , in 3 и т. д. в зависимости от заданных единиц.
Как найти объем усеченной пирамиды?
Мы можем найти объем усеченной пирамиды, используя следующие шаги:
- Шаг 1: Обозначьте заданные размеры как «h», «a» и «b».

- Шаг 2: Теперь определим значение объема усеченной пирамиды, подставив значения в формулу V = 1/3 × h × (a 2 + b 2 + ab).
- Шаг 3: Представить полученный ответ в кубических единицах.
Как найти объем усеченной пирамиды, если известны объемы всей пирамиды и меньшей пирамиды?
Мы можем найти объем усеченной пирамиды, если объемы всей пирамиды и меньшей пирамиды даны с помощью следующих шагов:
- Шаг 1: Определите заданные размеры как объемы всей пирамиды и меньшей пирамиды.
- Шаг 2: Теперь определим значение объема усеченной пирамиды, подставив значения в формулу V = Объем всей пирамиды — Объем малой пирамиды.
- Шаг 3: Представить полученный ответ в кубических единицах.
Что произойдет с объемом усеченной пирамиды, если высоту пирамиды увеличить вдвое?
Объем усеченной пирамиды удваивается, если высота пирамиды удваивается, поскольку «h» заменяется на «2h», что дает формулу V = 1/3 × h × (a 2 + b 2 + ab) = 1/3 × (2h) × (a 2 + b 2 + ab) = 2(1/3 × h × (a 2 + b 2 + ab)), что дает в два раза больше первоначального значения объема.
Что произойдет с объемом усеченной пирамиды, если высоту пирамиды уменьшить вдвое?
Объем усеченной пирамиды уменьшится вдвое, если высота пирамиды уменьшится вдвое, поскольку «h» заменяется на «h/2», что дает формулу V = 1/3 × h × (a 2 + b 2 + ab) = 1/3 × (h/2) × (a 2 + b 2 + ab) = (1/2) × (1/3 × h × (a 2 + b) 2 + ab)) что дает половину первоначального значения объема.
Объем усеченной квадратной пирамиды Калькулятор
- Назначение
- Расчет объема цветочного горшка
[1] 26.10.2021 19:11 30-летний уровень / Инженер / Очень /
- Назначение
- Нахождение объема
- Комментарий/Запрос
- Подскажите пожалуйста формулу объема усеченной прямоугольной пирамиды
[3] 10.07.2020 11:40 30-летний уровень / Инженер / Очень /
- Цель использования
- помощь в проверке уравнений для домашнего задания по математике
[] 10.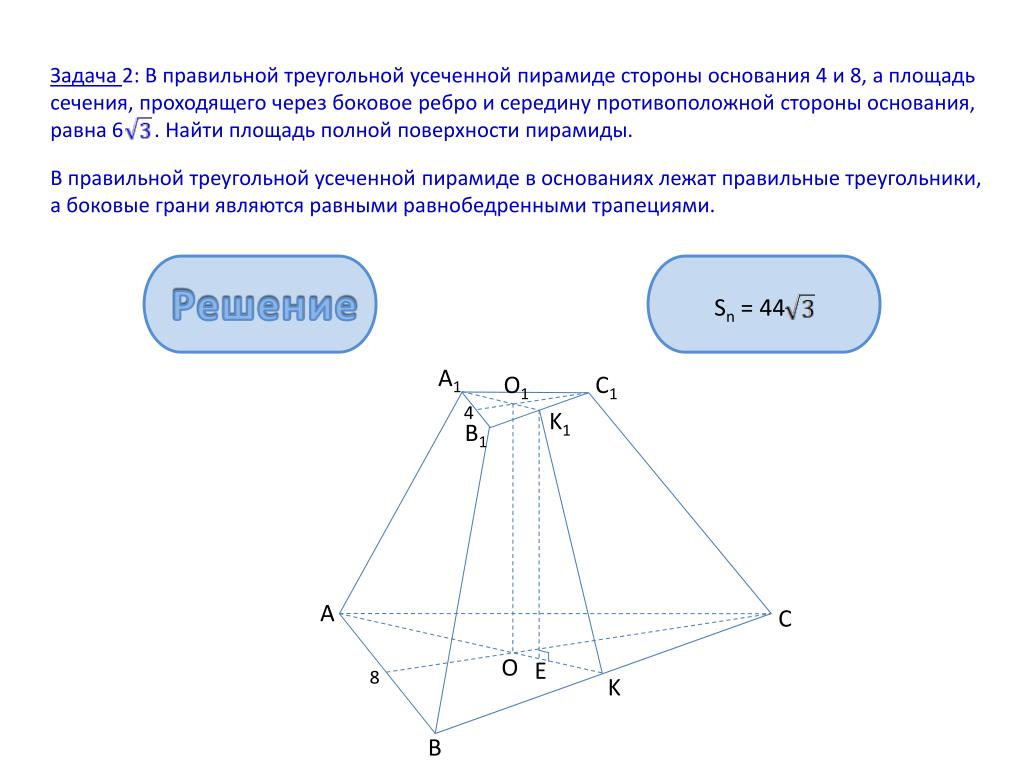 02.2020 20:52 Младше 20 лет / Начальная школа/ Учащийся средней школы / Очень /
02.2020 20:52 Младше 20 лет / Начальная школа/ Учащийся средней школы / Очень /
- Назначение
- Расчет объема склада для хранения вынутого грунта на строительной площадке
[5] 2020/01/15 20 :00 20-летний уровень / Инженер / В. ery /
- Назначение
- Проектирование метрономной акустической системы.
[6] 2020/01/04 14:24 30-летний уровень / Инженер / Очень /
- Цель использования
- Двойная проверка расчетов объема
- Комментарий/Запрос
- объем и скорость потока, полученные из уравнения сохранения массы. Это оказалось отличным ресурсом.
[7] 21.10.2019 12:53 30-летний уровень / Инженер / Очень /
- Назначение
- расчет объема бетона, необходимого для заполнения формы
[8] 2019/07/02 13:44 50-летний уровень / Инженер / Очень /
- Цель использования
- Расчет объема стального слитка, произведенного на заводе по переработке расплава радиоактивного металла в Швеции.

[9] 6 /24 16:17 30-летний уровень / Инженер / Очень /
- Назначение
- расчет конструкции
[10] 17.06.2019 08:54 20 лет уровень / Инженер / Очень /
Объем усеченного прямоугольного пирамидального пруда
В октябре 2017 года Реза обнаружил ошибку в нашем предыдущем ответе на этот вопрос. Ниже исправленная версия. Спасибо за это Резе. Я всегда благодарен, что когда кто-то находит ошибку на одной из наших страниц, они берут на себя труд сообщить нам об этом.
Харлей
Привет Пол,
Сайт Wolfram MathWorld дает объем $V$ усеченной пирамиды на
\[V = \frac13 h \left( A_1 + A_2 + \sqrt{A_1 A_2} \right)\]
, где $h$ — высота, $A_1$ — нижняя область, а $A_2$ — верхняя область.
Я перерисовал диаграмму с сайта Wolfram, чтобы она больше соответствовала вашей ситуации.
Прямоугольник у основания пруда имеет длину $L_2$ единиц и ширину $W_2$, прямоугольник наверху пруда имеет длину $L_1$ единиц и ширину $W_1$ единиц, размер пруда составляет $h$ единиц глубина, а глубина воды в пруду составляет $H$ единиц, $P$ – середина верхнего прямоугольника, $Q$ – середина нижнего прямоугольника, а $R$ и $S$ – середины соответствующих сторон. .Пусть прямоугольник, образованный поверхностью воды, имеет длину $L_3$ и ширину $W_3$ единиц.
.Пусть прямоугольник, образованный поверхностью воды, имеет длину $L_3$ и ширину $W_3$ единиц.
Рассмотрим двухмерную фигуру $PQRS.$
Расширьте стороны $PQ$ и $SR$, чтобы они встретились в точке $V.$
\[|QR| = \frac{L_2}{2}, |TU| = \frac{L_3}{2}, |PS| = \frac{L_1}{2}, |PT| = h — H\mbox{ и } |TQ| = Х.\]
Пусть расстояние от $P$ до $V$ равно $x$ футов.
Треугольники $QRV, TUV$ и $PSV$ подобны, поэтому
\[\frac{|PS|}{|PV|}= \frac{|TU|}{|TV|} = \frac{|QR|}{|QV|}\]
и, следовательно,
\[\ frac{\ frac {L_1} {2}} {h + x} = \ frac {\ frac {L_3} {2}} {H + x} = \ frac {\ frac {L_2} {2} }{Икс}.\]
Решить
\[\frac{\frac{L_1}{2}}{h+x} = \frac{\frac{L_2}{2}}{x}\]
вместо $x,$ заменить на
\[\frac{\frac{L_1}{2}}{h+x} = \frac{\frac{L_3}{2}}{H+x}\]
и упростить, чтобы получить
\[L_3 = \frac{H L_1 + (h-H)L_2}{h}.\]
Аналогично
\[W_3 = \frac{H W_1 + (h-H)W_2}{h}. \]
\]
Теперь, когда вы знаете размеры прямоугольника, образованного поверхностью воды, вы можете использовать выражение с сайта Wolfram для расчета объема воды в пруду.
Надеюсь, это поможет,
Харлей
Объем пирамиды – объяснение и примеры
Пирамида представляет собой трехмерную диаграмму , многоугольное основание которой соединено с вершиной треугольными гранями в геометрии. Треугольные грани пирамиды известны как боковые грани, а перпендикулярное расстояние от вершины (вершины) до основания пирамиды известно как высота.
Пирамиды названы в честь формы их оснований. Например, прямоугольная пирамида имеет прямоугольное основание, треугольная пирамида имеет треугольное основание, пятиугольная пирамида имеет пятиугольное основание и т. д.
Как найти объем пирамиды?
В этой статье мы обсудим , как найти объем пирамиды с различными типами оснований и решить текстовые задачи, связанные с объемом пирамиды.
Объем пирамиды определяется как количество кубических единиц, занимаемых пирамидой. Как указывалось ранее, название пирамиды происходит от формы ее основания. Следовательно, объем пирамиды также зависит от формы основания.
Чтобы найти объем пирамиды, вам нужны только размеры основания и высоты.
Формула объема пирамиды
Общий объем формулы пирамиды определяется как:
Объем пирамиды = 1/3 x площадь основания x высота.
V= 1/3 A b h
Где A b = площадь основания многоугольника, а h = высота пирамиды.
Примечание: Объем пирамиды немного меняется в зависимости от многоугольного основания.
Пример 1
Вычислите объем прямоугольной пирамиды, основание которой 8 см на 6 см, а высота 10 см.
Решение
Для прямоугольной пирамиды основание представляет собой прямоугольник.
Площадь прямоугольника = Д x Ш
= 8 x 6
= 48 см 2 .
А по формуле объема пирамиды имеем:
Объем пирамиды = 1/3A b h
= 1/3 x 48 см 2 x 10 см
= 160 см 3 .
Пример 2
Объем пирамиды 80 мм 3 .Найдите высоту пирамиды, если основание пирамиды представляет собой прямоугольник длиной 8 мм и шириной 6 мм.
Решение
Объем пирамиды = 1/3A b h
⇒ 80 = 1/3 x (8 x 6) xh
⇒ 80 = 15,9h
получаем,h = 5
Таким образом, высота пирамиды 5 мм.
Объем квадратной пирамиды
Чтобы получить формулу объема квадратной пирамиды, заменим площадь основания (A b ) на площадь квадрата (Площадь квадрата = a 2 )
Таким образом, объем квадратной пирамиды определяется как:
Объем квадратной пирамиды = 1/3 xa 2 xh
V = 1/3 a 2 h
90 длина стороны основания (квадрата) и h = высота пирамиды.
Пример 3
Квадратная пирамида имеет длину основания 13 см и высоту 20 см. Найдите объем пирамиды.
Решение
Дано:
Длина основания, a = 13 см
Высота = 20 см
Объем квадратной пирамиды = 1/3 a
Объем = 1/3 x 13 x 13 x 20
= 1126,7 см 3
Если высота пирамиды 10 футов, каковы размеры основания пирамиды?
Раствор
Дано:
Объем = 625 кубических футов.
Высота = 10 футов
по объему квадратной формулы,
⇒ 625 = 1/3 A 2 H
⇒ 625 = 1/3 xa 2 x 10
⇒ 625 = 3.3a 2
⇒ a 2 = 187,5
⇒ a = = √187,5
a = 13,7 футов
Таким образом, размеры основания будут равны 13.7 футов на 13,7 футов.
Пример 5
Длина основания квадратной пирамиды вдвое больше высоты пирамиды. Найдите размеры пирамиды, если ее объем 48 куб.
Найдите размеры пирамиды, если ее объем 48 куб.
Решение
Пусть высота пирамиды = x
длина = 3x
объем = 48 куб. .
⇒ 48 = 1/3 (3x) 2 (x)
⇒ 48 = 1/3 (9x 3 )
⇒ 48 = 3x 3
⇒ х 3 = 16
⇒ х = 3 √16
х = 2.52
Следовательно, высота пирамиды = x ⇒ 2,53 ярда,
и каждая сторона основания равна 7,56 ярда
Объем трапециевидной пирамиды
Трапециевидная пирамида – это пирамида, основанием которой является трапеция или трапеция .
Поскольку мы знаем, площадь трапеции = h 1 (b 1 + b 2 )/2
Где h = высота трапеции
b 1 9043 и длины двух параллельных сторон трапеции.
Зная общую формулу объема пирамиды, мы можем вывести формулу объема трапециевидной пирамиды как:
Объем трапециевидной пирамиды = 1/6 [h 1 (b 1 + b 2 )] H
Примечание: При использовании этой формулы всегда помните, что h — высота основания трапеции, а H — высота пирамиды.
Пример 6
Основанием пирамиды является трапеция с параллельными сторонами длиной 5 м и 8 м и высотой 6 м.Найдите объем пирамиды, если высота пирамиды 15 м.
Решение
Дано;
h = 6 м, H = 15 м, b 1 = 5 м и b 2 = 8 м
Объем трапециевидной пирамиды = 1/6 [h 1 (b 1 + b 2 )] h
= 1/6 x 6 x 15 (5 + 8)
= 15 x 13
= 195 м 3 .
Объем треугольной пирамиды
Как известно, площадь треугольника;
Площадь треугольника = 1/2 b h
Объем треугольной пирамиды = 1/3 (1/2 b h) H
Где b и h — длина основания и высота треугольника.Н — высота пирамиды.
Пример 70113 . 2
H = 18 в.
Объем треугольной пирамиды = 1/3 (1/2 BH) H
= 1/3 x 144 x 18071
Калькулятор квадратной пирамидыКвадратная форма пирамиды
ч = высота
с = наклонная высота
а = длина стороны
P = периметр основания
e = длина боковой кромки
г = а/2
В = объем
L = площадь боковой поверхности
B = площадь базовой поверхности
A = общая площадь поверхности
Использование калькулятора
Этот онлайн-калькулятор рассчитает различные свойства квадратной пирамиды с учетом двух известных переменных. Квадратная пирамида — это частный случай пирамиды, основание которой квадратное. Это правильная пирамида с квадратным основанием.
Квадратная пирамида — это частный случай пирамиды, основание которой квадратное. Это правильная пирамида с квадратным основанием.
Единицы: Обратите внимание, что единицы измерения показаны для удобства, но не влияют на расчеты. Единицы используются для обозначения порядка результатов, таких как футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты приведут к s в мм, V в мм 3 , L в мм 2 , B в мм 2 и A в мм мм 2 .
NAN: означает не число. Это проявится в результате, если вы используете значения, которые просто не имеют смысла в качестве разумных значений для пирамиды.
Ниже приведены стандартные формулы пирамиды. Расчеты основаны на алгебраических манипуляциях с этими стандартными формулами.
Квадратная пирамида Формулы, полученные через длину стороны a и высоту h:
- Объем квадратной пирамиды:
- Наклонная высота квадратной пирамиды :
- По теореме Пифагора мы знаем, что
- с 2 = г 2 + ч 2
- , так как r = а/2
- с 2 = (1/4)a 2 + h 2 и
- с = √(ч 2 + (1/4)а 2 )
- Это также высота стороны треугольника
- Площадь боковой поверхности квадратной пирамиды (4 равнобедренных треугольника):
- Для равнобедренного треугольника Площадь = (1/2) Основание x Высота.
 Наше основание — это длина стороны a, а для этого расчета наша высота треугольника равна наклонной высоте s. С 4 сторонами нам нужно умножить на 4.
Наше основание — это длина стороны a, а для этого расчета наша высота треугольника равна наклонной высоте s. С 4 сторонами нам нужно умножить на 4. - L = 4 x (1/2)as = 2as = 2a√(h 2 + (1/4)a 2 )
- Возведение числа 2 в квадрат, чтобы вернуть его внутрь радикала,
- L = а√(а 2 + 4ч 2 )
- Для равнобедренного треугольника Площадь = (1/2) Основание x Высота.
- Площадь основания квадратной пирамиды (квадрат):
- Общая площадь поверхности квадратной пирамиды :
- А = L + В = а 2 + а√(а 2 + 4h 2 ))
- А = а(а + √(а 2 + 4h 2 ))
Квадратная пирамида Вычисления:
Другие формулы для расчетов получены из приведенных выше формул.
Ссылки
Вайсштейн, Эрик В. «Квадратная пирамида». Из MathWorld — веб-ресурса Wolfram. Квадратная пирамида.
ΑΡΙΘΜΟΣ: 3D-аналог трапеции (часть 2): усеченная пирамида
С тех пор, как я написал пост под названием «Трехмерный аналог трапеции», я узнал, что люди уже что-то имеют в виду, когда вводят термины на этот счет.Их интересует усеченная пирамида. В вышеупомянутом посте я описал фигуру, а именно призму неправильной треугольной формы, аналогичную трапеции по формуле объема (доказательство находится здесь). Теперь рассмотрим фигуру, аналогичную трапеции по внешнему виду, но имеющую лишь приблизительно аналогичную формулу объема.Первое наблюдение, которое мы могли бы сделать, состоит в том, что пирамиды на самом деле не очень отличаются от конусов с точки зрения объема. Простая формула объема для обоих задается как
, где B — площадь основания, а h — высота конуса.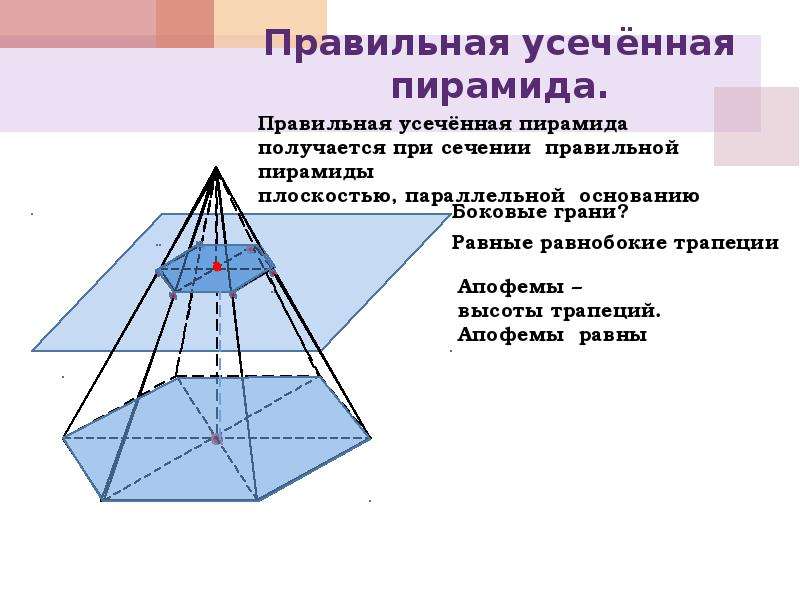 Это верно независимо от формы основания. Единственное требование состоит в том, что одна и та же форма должна продолжаться до самого пика. Говоря более техническим языком, поперечное сечение пирамиды на расстоянии b ниже вершины должно быть аналогично основанию , а соответствующие линейные размеры должны быть в соотношении b : h . Таким образом, при заданном размере длины d в основании соответствующий размер в поперечном сечении b ниже вершины должен иметь длину d(b/h) .Это часть определения пирамиды. На этом этапе может оказаться полезной хорошо известная причудливая теорема.
Это верно независимо от формы основания. Единственное требование состоит в том, что одна и та же форма должна продолжаться до самого пика. Говоря более техническим языком, поперечное сечение пирамиды на расстоянии b ниже вершины должно быть аналогично основанию , а соответствующие линейные размеры должны быть в соотношении b : h . Таким образом, при заданном размере длины d в основании соответствующий размер в поперечном сечении b ниже вершины должен иметь длину d(b/h) .Это часть определения пирамиды. На этом этапе может оказаться полезной хорошо известная причудливая теорема.
Теорема . Пусть A и B — подобные (двумерные) фигуры. Тогда
соответствующих линейных размеров имеют отношение a : b тогда и только тогда, когда площади A и B (или соответствующие подплощади) находятся в отношении a 2 : b 2 .
В форме теоремы может показаться, что это из космоса, но обратите внимание, как просто это работает с квадратами и кругами. Например, если один квадрат имеет сторону a , а другой — b , то их площади равны a 2 и b 2 соответственно. Обратное тоже, очевидно, верно, и оно нам и понадобится.
Например, если один квадрат имеет сторону a , а другой — b , то их площади равны a 2 и b 2 соответственно. Обратное тоже, очевидно, верно, и оно нам и понадобится.
Предположим, мы принимаем площадь верхней поверхности равной B 1 , а площадь нижней поверхности равной B 2 . Также примем a за высоту удаленной части пирамиды, а h за высоту усеченной пирамиды.Вот передний ортографский вид на пирамиду с отрезной частью, добавленной назад к вершине:
Наша теорема затем говорит нам, что
, если мы решаем на A , мы получаем
объем объема Наша усеченная пирамида — это просто объем полной пирамиды минус объема части, которая была отрезана (усечена выключена):
. Примечательно, что мы могли бы рассчитать A без вычисления областей В 1 или В 2 . Но нам нужно знать соотношение между парой соответствующих сторон, скажем, d 1 и d 2 (см. диаграмму ниже).
Но нам нужно знать соотношение между парой соответствующих сторон, скажем, d 1 и d 2 (см. диаграмму ниже).
Мы бы рассчитали A согласно
, что дает
нашей формулы объема будет выглядеть немного приятнее:
R = D 2 / D 1 , получаем
Первая формула объема имеет некоторую аналогию с формулой площади трапеции: мы берем среднее (среднее арифметическое)
- площади основания,
- верхняя базовая зона и
- среднее геометрическое верхней и нижней областей
Как найти объем трапециевидной пирамиды? — Ответы на все
Как найти объем трапециевидной пирамиды?
Формула объема трапециевидной призмы. Если длина призмы равна L, ширина основания трапеции B, ширина вершины трапеции A и высота трапеции H, то объем призмы определяется формулой с четырьмя переменными: V(L, B, A, H) = LH( А+В)/2. Другими словами, умножьте длину, высоту и среднее значение A и B.
Если длина призмы равна L, ширина основания трапеции B, ширина вершины трапеции A и высота трапеции H, то объем призмы определяется формулой с четырьмя переменными: V(L, B, A, H) = LH( А+В)/2. Другими словами, умножьте длину, высоту и среднее значение A и B.
Как найти площадь поверхности трапециевидной пирамиды?
Чтобы найти площадь поверхности, объем пространства снаружи твердого тела трапециевидной призмы, вам нужно найти площадь основания трапеции и умножить ее на два. Затем вы добавите площадь четырех прямоугольников к площади двух оснований.
Как называется пирамида со срезанной вершиной?
Математическое название фигуры — усеченная квадратная пирамида. Это часть пирамиды со срезанной вершиной.
Почему пирамида составляет 1/3 призмы?
Чтобы показать, что этот куб имеет объем, в три раза превышающий объем пирамиды, вы можете создать три новые пирамиды такого же объема, как исходная. Соберите эти три пирамиды, чтобы сформировать куб.
Что такое усеченная пирамида?
Усеченная пирамида получается в результате разрезания пирамиды плоскостью, параллельной основанию, и отделения части, содержащей вершину. Боковые грани усеченной пирамиды – трапеции. Высота усеченной пирамиды – это перпендикулярное расстояние между основаниями.2)/4ч). Это даст вам угол пирамиды от вершины до края основания.
Как найти высоту прямоугольной пирамиды?
Извлеките формулу высоты прямоугольной пирамиды, используя свои знания по алгебре. H = V / (L x W) / 3. Например, V = 60 куб. см, L = 4 см и W = 6 см. Замените формулу данными числами.
Какова формула треугольной пирамиды?
Формула объема треугольной пирамиды Объем треугольной пирамиды можно найти по формуле V = 1/3AH, где A = площадь основания треугольника, а H = высота пирамиды или расстояние от основания пирамиды до вершины. .
Как выглядит прямоугольная пирамида?
Прямоугольная пирамида. Прямоугольная пирамида представляет собой трехмерный объект с прямоугольником в основании и треугольной гранью, соответствующей каждой стороне основания. Треугольные грани, которые не являются прямоугольным основанием, называются боковыми гранями и встречаются в точке, называемой вершиной или вершиной.
Треугольные грани, которые не являются прямоугольным основанием, называются боковыми гранями и встречаются в точке, называемой вершиной или вершиной.
Как выглядит треугольная пирамида?
Многогранник или трехмерная фигура, имеющая не менее трех сторон и многоугольное основание.Треугольная пирамида — это пирамида с треугольником в основании и тремя треугольными гранями. Он имеет четыре вершины или точки и шесть ребер. Существуют также прямоугольные, пятиугольные, квадратные и шестиугольные пирамиды.
Существует ли трехсторонняя пирамида?
«Трехгранная пирамида» называется тетраэдром.
Как называется трехгранная пирамида?
В геометрии тетраэдр (множественное число: тетраэдры или тетраэдры), также известный как треугольная пирамида, представляет собой многогранник, состоящий из четырех треугольных граней, шести прямых ребер и четырех вершинных углов.
Пирамида состоит из равносторонних треугольников?
Когда основание представляет собой треугольник, пирамида является треугольной пирамидой. Он также известен как тетраэдр, поскольку, включая основание, имеет четыре грани. Когда эти грани представляют собой равносторонние треугольники, это квадратная пирамида с квадратом в основании. Чаще всего встречаются «правильные» пирамиды.
Он также известен как тетраэдр, поскольку, включая основание, имеет четыре грани. Когда эти грани представляют собой равносторонние треугольники, это квадратная пирамида с квадратом в основании. Чаще всего встречаются «правильные» пирамиды.
Сколько сторон у пирамиды?
Что бы вы ни думали об этом древнем сооружении, Великая пирамида представляет собой восьмигранную, а не четырехгранную фигуру.Каждая из четырех сторон пирамиды равномерно разделена от основания до вершины очень тонкими вогнутыми углублениями.
Является ли пирамида треугольником?
Пирамида – это многогранник, у которого основание – многоугольник, а все боковые грани – треугольники.
Сколько вершин у пирамиды?
5 вершин
Сколько вершин у пирамиды с 10 гранями?
Пирамида, имеющая 9-гранное основание, также имеет десять граней, но имеет десять вершин. Но формула Эйлера говорит нам, что ни один простой многогранник не имеет ровно десяти граней и семнадцати вершин. Рисунок 6: Оба этих многогранника имеют десять граней, но ни один из них не имеет семнадцати вершин.
Рисунок 6: Оба этих многогранника имеют десять граней, но ни один из них не имеет семнадцати вершин.
Сколько сторон и вершин у пирамиды?
5 граней
Сколько вершин имеет ответы треугольной пирамиды?
4 вершины
Может ли пирамида иметь 5 сторон?
В геометрии пятиугольная пирамида — это пирамида с пятиугольным основанием, на котором возвышаются пять треугольных граней, сходящихся в одной точке (вершине). Как и всякая пирамида, она самодвойственна.Правильная пятиугольная пирамида имеет основание, являющееся правильным пятиугольником, и боковые грани, являющиеся равносторонними треугольниками.
Сколько вершин у прямоугольной пирамиды?
5
Сколько граней в треугольной пирамиде?
4
Сколько плоскостей в пирамиде?
Равносторонняя призма с треугольным основанием имеет четыре плоскости симметрии. Пирамида с прямоугольным основанием имеет 2 плоскости симметрии. Пирамида с квадратным основанием имеет 4 плоскости симметрии.
Сколько существует типов пирамид?
четыре разных типа
Сколько плоскостей в треугольной пирамиде?
Правильная треугольная пирамида имеет на всех гранях равносторонние треугольники. Имеет 6 плоскостей симметрии.
Сколько граней у пирамиды?
5 граней
Сколько вершин у пятиугольной пирамиды?
6
Какая трехмерная фигура имеет 6 вершин, 6 граней и 10 ребер?
Шестигранник (множественное число: гексаэдры) — это любой многогранник с шестью гранями.Куб, например, представляет собой правильный шестигранник со всеми квадратными гранями и тремя квадратами вокруг каждой вершины… Шестигранник.
| Вогнутая | ||
|---|---|---|
| 4.4.3.3.3.3 Стороны 10 E, 6 В | 5.5.3.3.3.3 Лица 11 E, 7 В | 6.6.3.3.3.3 Лица 12 E, 8 В |

 Также они наклонены к основанию под одним углом.
Также они наклонены к основанию под одним углом.


 Во вторичной цепи после мостового выпрямителя стоит обычный линейный стабилизатор на микросхеме, что позволяет иметь …
Во вторичной цепи после мостового выпрямителя стоит обычный линейный стабилизатор на микросхеме, что позволяет иметь … Также они наклонены к основанию под одним углом.
Также они наклонены к основанию под одним углом.


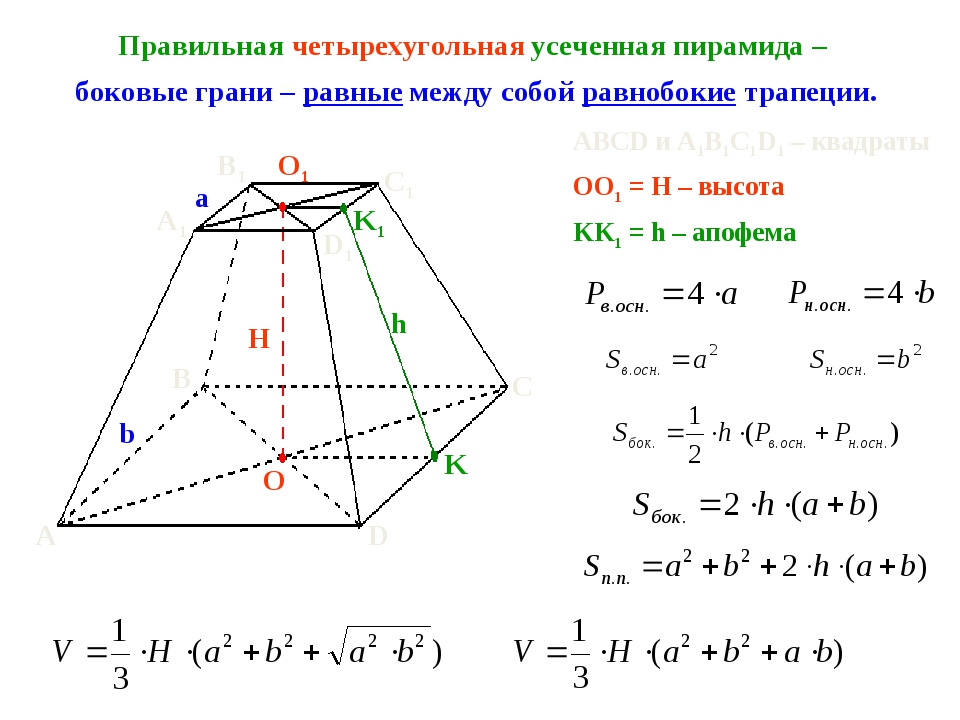
 Наше основание — это длина стороны a, а для этого расчета наша высота треугольника равна наклонной высоте s. С 4 сторонами нам нужно умножить на 4.
Наше основание — это длина стороны a, а для этого расчета наша высота треугольника равна наклонной высоте s. С 4 сторонами нам нужно умножить на 4.