Выражение с переменной что такое: Выражения с переменными. Буквенные равенства и неравенства.

Posted on by alexxlab

Содержание

Выражения с переменными. Буквенные равенства и неравенства.

Выражениями с переменными называются выражения содержащие переменные.

В качестве переменных в выражениях используются буквы, поэтому их также называют буквенными выражениями. Буквенные выражения могут содержать как несколько букв, так и одну букву.

Например:

 

 

В задачах и примерах буквенные выражения используются для вычисления выражений с заданными переменными. То есть вместо букв надо подставить заданные значения:

Вычислить выражение

Подставляем в выражение значения вместо букв:

Произведения с переменными записывают без знака умножения (·):

Если в выражениях участвует деление, такие выражения записывают в виде дроби:

Соответственно выражение в предыдущем примере можно записать следующим образом:

Давайте рассмотрим ещё один пример:

при x = 2

Если в выражении встречается несколько раз одна и та же буква (переменная), то ей соответствует одно и то же значение.

В таком случае решение будет следующим:

 

Буквенными равенствами или равенствами с переменными называют выражения, которые содержат буквы (переменные).

В предыдущей статье мы рассматривали свойства числовых равенств и приводили выражение:

Это и есть пример буквенного равенства.

Буквенные равенства применяют, например, для записи различных физических или математических формул:

 

Например, вычисление периметра треугольника:

При подстановке численных значений переменных получаются верные или неверные числовые равенства.

Пример:

Это равенство верно при y = 4. А при y = 5 это равенство неверно.

Буквенные равенства обладают теми же свойствами, что и числовые.

Буквенными неравенствами называют неравенства с переменными.

Пример:

Это равенство будет верно при n = 10, и неверным при n = 2.

Спасибо, что Вы с нами!

 

 

Понравилась статья — поделитесь с друзьями:

Оставляйте пожалуйста комментарии в форме ниже

Выражения с переменными

Вопросы занятия:

·  ввести понятие «выражение с переменными»;

·  ввести понятие «область определения выражения».

Материал урока

Вспомним, что на прошлом уроке мы говорили о числовых выражениях и значениях числовых выражений.

Числовым выражением называется запись, составленная из чисел, знаков арифметических действий и скобок, указывающих на порядок выполнения действий.

Значением числового выражения называется число, которое получается при выполнении всех действий числового выражения.

Определение.

Буквенным выражением называется запись, состоящая из чисел, букв, знаков арифметических действий и скобок, указывающих на порядок выполнения действий.

Строчные буквы латинского алфавита чаще всего используют при записи буквенных выражений.

Следует также знать, что и одна буква является буквенным выражением.

Давайте решим задачу.

Велосипедист двигается со скорость 15 километров в час. Какой путь он проедет за время t?

Известно, что путь можно найти скорость умножив на время. Тогда путь, который проедет велосипедист, будет равен 15t.

Теперь, если нам нужно будет узнать, какое расстояние проехал велосипедист, например, за 3 часа, мы подставим в выражение 15 ∙ t вместо буквы t число 3, то есть найдём значение выражения при t = 3, и получим 45 километров.

В нашем случае буква t называется переменой, а само выражение – выражением с переменной.

То есть, переменная – это буква, входящая в буквенное выражение, которая может принимать различные значения.

Например,

Если мы в выражение с переменной вместо переменной подставим число, то получим числовое выражение.

Например,

Теперь, прежде, чем перейти к решению упражнений, вернёмся к выражению 15t, которое мы получили при решении первой задачи. Здесь переменная t может принимать только положительные значения, так как время не может быть отрицательным, и это множество значений называется

областью определения выражения 15t.

Таким образом, важно помнить, что в область определения любого выражения могут входить только те значения переменных, при которых получается числовое равенство, имеющее смысл.

А сейчас давайте решим некоторые упражнения.

Пример.

Следующее упражнение.

Пример.

И последнее упражнение.

Пример.

Урок 40. выражение с двумя переменными — Математика — 3 класс

Математика, 3 класс

Урок № 40. Выражение с двумя переменными

Перечень вопросов, рассматриваемых в теме:

  1. Что такое переменная?
  2. В каких выражениях может быть две переменных?
  3. Как находить значение переменной?
  4. Как изменяется результат при изменении одного из компонентов?

Глоссарий по теме:

Выражение – это запись одно или нескольких математических действий (сложение, вычитание, умножение, деление) при помощи цифр и знаков.

Переменная – это буквенное обозначение.

Обязательная литературы и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 11.

2. Математика. 3 класс. Часть 2. / Л. Г. Петерсон. – М.: Ювента, 2013 – 96 с.: ил. с. 65-69.

Теоретический материал для самостоятельного изучения

В начале урока учитель сказал: «К доске пойдёт Петя».

В середине урока учитель сказал: «К доске пойдёт Серёжа». А незадолго до конца урока он сказал: «К доске пойдёт Таня».

Во всех этих предложениях меняется только имя ученика. Имя здесь переменное. Если обозначить имя буквой х, можно записать предложение: «К доске пойдёт

х». Вместо х можно подставить имя любого ученика класса.

Под переменной будем понимать буквенное обозначение.

Имена Петя, Серёжа, Таня являются значениями переменной.

Рассмотрим задачи.

1) У Тани 3 розы и 5 пионов. Сколько цветов у Тани?

2) У Тани 3 розы и 4 пионов. Сколько цветов у Тани?

3) У Тани 3 розы и 2 пионов. Сколько цветов у Тани?

Эти задачи можно объединить в одну:

У Тани 3 розы и п пионов. Сколько цветов у Тани?

Выражение 3 + п является решением задачи, в которой п = 5, 4, 2.

п – это переменная

Буквенные выражения называют выражения с переменной потому, что буква принимает разные значения.

Буквенное выражение может содержать две и более переменных.

Буквенные обозначения используются в формулах, например формула площади прямоугольника:

S = a ∙ b

Формула периметра прямоугольника

Р = ( a + b) ∙ 2

Формула периметра треугольника

Р = a + b + c

Разбор тренировочных заданий

№1. Найдите значение выражения:

а + b, если а = 56, b = 37

Ответ: 56 + 37 = 93

№2. Вставьте в таблицу пропущенные числа:

Значение переменной

с

Значение выражения

с ∙ 4

12

13

14

Таблица должна быть с числами:

Значение переменной

с

Значение выражения

с ∙ 4

12

48

13

52

14

56

№3. Найдите и выделите цветом по вертикали и горизонтали в филворде название компонента, которым является переменная

  1. 67 – а;
  2. с + 43;
  3. 17 ∙ d;
  4. 81 : b.

В таблице нужно выделить слова: вычитаемое; слагаемое; множитель; делитель.

№4. Сравните выражения и подчеркните правильное высказывание:

1. 16 ∙ х (больше, меньше, равно) 16 + х

2. у + у + у + у + у (больше, меньше, равно) у ∙ 5

Ответ: больше; равно.

Выражения с переменными. 7-й класс

Цели урока: познакомить с понятиями выражение с переменными, значение выражения с переменными, формула, учить различать выражения, которые не имеют смысла.

Вид урока: комбинированный урок.

Оборудование: карточки для индивидуального опроса, карточки для игры «Математическое лото», презентация.

Ход урока

I. Инициация.

А) Проверка готовности к уроку.

Б) Приветствие.

II. Домашнее задание.

с.7 № 25, 31, 44.

III. Актуализация знаний.

А) Проверка домашнего задания.

№ 25

840=23*3*5*7; 1260=22*3*5*31

НОД (840, 1260)=23*3*5*7*31=26040.

Ответ: 26040.

№ 28

120=23*3*5

280=23*5*7

320=26*5

НОД (120, 280, 320)=23*5=40

40>30, 40 (уч.) – в первом классе.

Ответ: 40 учащихся.

№ 8

1 способ

х=3,2*200/1000; х=0,64.

0,64 (%) – жира

х=2,5*200/1000; х=0,5.

0,5 (%) – белка

х=4,7*200/1000; х=0,94.

0,94 (%) – углеводов

2 способ

1л=1000г

1000/200=5 (раз) – уменьшился объем молока

  1. 3,2:5=0,64 (%) – жира
  2. 2,5:5=0,5 (%) – белка
  3. 4,7:5=0,94 (%) – углеводов

Ответ: 0,64 %,0,5 %, 0,94 %.

№ 18

а) 28+15; б) 6*3; в) 3-8,7; г) 0,8:0,4.

Б) Индивидуальные карточки.

К-1.

  1. Найти НОД чисел 24 и 34.
  2. Найти значение выражения: а) 69,95+27,8; б) 54,5-6,98.

К-2.

  1. Найти НОД чисел 27 и 19.
  2. Вычислить: а) 85-98,04; б) 65,7*13,4.

К-3.

  1. Найти НОД чисел 17 и 36.
  2. Вычислить: а) 0,48*5,6; б) 67,89-23,3.

В) Математическое лото.

Выполнить действия и получить изображение.

8,5-7,3 5,6+0,9 2,5-(3,2+1,8)
4,7*12,3 2*9,5+14 6,1*(8,4:4)
65:1,3 (10-2,7):5 (6,4+7):2

1,2 6,5 -2,5
57,81 33 12,81
50 1,46 6,7

IV. Формирование новых понятий и убеждений.

1. Новый материал.

Выражения с переменными

Двигаясь со скоростью 70 км/ч, автомобиль за 3 ч пройдет 70*3 км, за 4 ч – 70*4 км, за 5 ч – 70*5 км, за 5,5 ч – 70*5,5 км.

– А какое расстояние пройдет автомобиль за t часов? Вообще за t ч он пройдет 70t км. Изменяя значение t, мы можем с помощью выражения 70t находить путь, пройденный автомобилем за разные промежутки времени. Для этого достаточно вместо буквы t подставить ее значение и выполнить умножение. Букву t в выражении 70t называют переменной, а само выражение 70t – выражением с переменной.

Приведем еще пример. Пусть длины сторон прямоугольника равны а см и в см. Тогда его площадь равна ав см2. Выражение ав содержит две переменные а и в. Оно показывает, как находить площадь прямоугольника при различных значениях а и в. Например:

если а = 8 и в = 11, то ав = 8-11 = 88;

если а = 25 и в = 4, то ав = 25-4=100.

Если в выражение с переменными подставить вместо каждой переменной какое-либо ее значение, то получится числовое выражение. Его значение называют значением выражения с переменными при выбранных значениях переменных.

Так, число 88 есть значение выражения ab при а = 8 и 6=11, чис­ло 100 есть значение этого выражения при а = 25 и 6 = 4.

Некоторые выражения не имеют смысл при некоторых значениях переменной, а другие имеют смысл при всех значениях перемен­ных. Примерами могут служить выражения

х(х + 1), ау – 4.

Выражения с переменными используются для записи формул. Рассмотрим примеры.

Любое четное число m можно представить в виде произведения числа 2 и целого числа n, т. е. m=2n.

Если в эту формулу вместо n подставлять целые числа, то значе­ниями переменной m будут четные числа. Формулу m= 2n называют формулой четного числа.

Формулу m= 2n + 1, где n – целое число, называют формулой не­четного числа.

Аналогично формуле четного числа можно записать формулу чис­ла, кратного любому другому натуральному числу.

Например, формулу числа, кратного 3, можно записать так: m=3n, где n – целое число.

V. Применение полученных знаний на практике.

Выполнение №№ 19-24 по учебнику.

Резерв №26.

VI. Рефлексия.
  1. Что называется выражением c переменными?
  2. Что такое значение выражения с переменной?
  3. Приведите примеры выражения с переменными.

Let statement (VBA) | Microsoft Docs

  • Статья
  • Чтение занимает 2 мин
Были ли сведения на этой странице полезными?

Оцените свои впечатления

Да Нет

Хотите оставить дополнительный отзыв?

Отзывы будут отправляться в корпорацию Майкрософт. Нажав кнопку «Отправить», вы разрешаете использовать свой отзыв для улучшения продуктов и служб Майкрософт. Политика конфиденциальности.

Отправить

В этой статье

Назначает значение выраженияпеременной или свойству.

Синтаксис

[ Пусть ] varname = выражение

Синтаксис оператора Let состоит из следующих частей:

PartОписание
LetНеобязательное. Явное использование ключевого слова Let — это вопрос стиля, но обычно он опущен.
varnameОбязательный. Имя переменной или свойства, соответствует стандартным соглашениям об именовании переменных.
выражениеОбязательная часть. Значение, назначаемое переменной или свойству.

Примечания

Выражение значения может быть назначено переменной или свойству, только если его тип данных совместим с переменной. Нельзя назначить строковые выражения числовым переменным, и нельзя назначить числовые выражения строковым переменным. Нарушение этого запрета вызовет ошибку во время компиляции.

Переменные вариантов могут быть назначены строке или числу выражений. Но обратное не всегда верно. Строковой переменной может быть назначено любое значение Variant, кроме Null, но числовой переменной может быть назначено только значение Variant, которое может быть интерпретировано как число. Используйте функцию IsNumeric, чтобы определить, можно ли преобразовать значение Variant в число.

Назначение выражения одного числового типа переменной другого числового типа приводит значение выражения к числовому типу конечной переменной.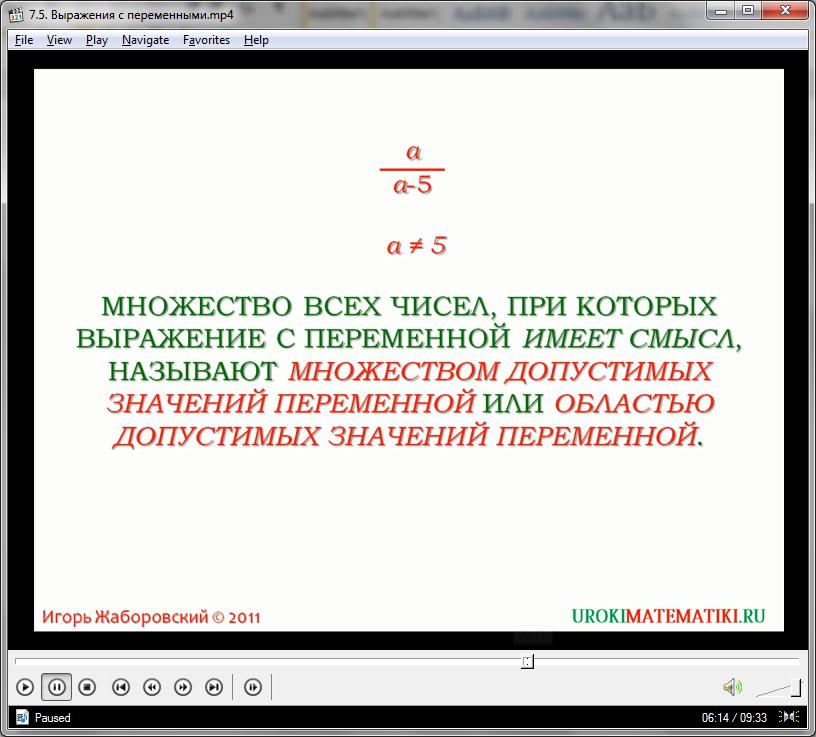

Операторы Let можно использовать, чтобы назначить одну переменную записи другой, только если обе переменные относятся к одному и тому же пользовательскому типу. Используйте заявление LSet для назначения переменных записей различных типов, определенных пользователем. Используйте заявление Set для назначения ссылок объектов на переменные.

Пример

В этом примере значения выражений назначаются переменным с помощью явного утверждения Let.

Dim MyStr, MyInt 
' The following variable assignments use the Let statement. 
Let MyStr = "Hello World" 
Let MyInt = 5

Ниже показаны те же назначения без оператора Let.

Dim MyStr, MyInt 
MyStr = "Hello World" 
MyInt = 5

См. также

Поддержка и обратная связь

Есть вопросы или отзывы, касающиеся Office VBA или этой статьи? Руководство по другим способам получения поддержки и отправки отзывов см. в статье Поддержка Office VBA и обратная связь.

Числовые выражения. Выражения с переменной. Уравнения. Математическая модель

1. Урок-обобщение

Автор Цыбикова Сэндэма
Дугаровна
учитель СОСОШ№2»
С.Сосново-Озёрское

2. «Умение мыслить математически – одна из благороднейших способностей человека.» Бернард Шоу

ирландский драматург, философ и прозаик
«Умение мыслить математически –
одна из благороднейших
способностей человека.»
Бернард Шоу
Ирландский драматург,
философ и прозаик

3. « Вычислительная культура находит повсеместное применение, является фундаментом изучения математики Характеризуется

правильностью,
осознанностью, рациональностью,
обобщенностью, автоматизмом,
прочностью»
Ройтман П.Б
Умение решать задачи есть искусство,
приобретающееся практикой, подобно, скажем,
плаванию.
Джордж Пойа.

5. «Теория без практики (упражнения) и практика без теории есть ничто»

Протаго́р (др. -греч. Πρωταγόρας, ок. 490 до
н. э. — ок. 420 до н. э.) из Абдер —
древнегреческий философ, виднейший
представитель

6. Сформулируйте цель урока

• Повысить вычислительную культуру
• Развить способность решать задачи,
составлять математическую модель
• Развивать теоретическое мышление

8. Устные упражнения:

9. Проверка домашнего задания

143 5) 6)7)
5) (60а -30 ):5=18 6)92+56:(14 -в)=100
7) (с:9)∙15-47=28
Проверка
Вопросы Оценки
207 Для столовой закупают на неделю n
батонов хлеба .Сколько батонов хлеба
надо закупить на 4 дня при постоянном
расходе хлеба в день?(n=280) Вопросы
Оценки
Опросный лист. Числовые выражения. Выражения с переменной. Уравнения. Математическая модель.
Вопросы
Ответы
1.Что называется числовым выражением?
Запись, которая состоит из чисел, знаков арифметических действий и
скобок, называется числовым выражением. Следует понимать, что
одно число тоже будет являться числовым выражением
2. Что называется значением числового
выражения?
Результат выполнения действий над числами в числовом
выражении называется значением числового выражения.
3.Что называется выражением с
переменной?
Выражением называется запись, состоящая из чисел, букв,
знаков арифметических действий и скобок, указывающих на
порядок выполнения действий.
4.Что называется уравнением?
5.Что называется корнем уравнения?
Равенство с переменной
Значение переменной, при котором уравнение обращается в верное
равенство
6.Что называется математической
моделью?
Перевод условия задачи на математический язык
7.Какая связь существует между
понятиями: «Числовые выражения.»
«Выражения с переменной.» «Уравнения.»
«Математическая модель.»
8.Что значить упростить числовое и
буквенное выражения?
Числовые выражения. Выражения с
переменной. Уравнения. Математическая
модель.
Сформируем понятийный
аппарат.
Проанализируй, установи
связь между этими понятиями
докажи
1)(1652:28+410)∙700
2)57120:102∙10-5590
3)36108:354+80∙137
Установите связь
4)3х+5х+6х +3, при х=5
5)(715-х)∙83=49 883
6)19 698:(m+6)=98
7)При испытании авиамоделей одна из них
летела со скоростью а м/c и продержалась в
воздухе 40 секунд.Скорость второй была на 2
м/c , но продержалась в воздухе в секунд.На
сколько метров первая модель пролетела
больше,чем вторая?(а=4, в=25)
1)(1652:28+410)∙700
2)57120:102∙10-5590
3)36108:354+80∙137
Установите связь
4)3х+5х+6х +3, при х=5
5)(715-х)∙83=49 883
6)19 698:(m+6)=98
7)При испытании авиамоделей одна из них
летела со скоростью а м/c и продержалась в
воздухе 40 секунд.Скорость второй была на 2
м/c , но продержалась в воздухе в секунд.На
сколько метров первая модель пролетела
больше,чем вторая?(а=4, в=25)
Опросный лист. Числовые выражения. Выражения с переменной. Уравнения. Математическая модель.
Вопросы
Ответы
1.Что называется числовым выражением?
Запись, которая состоит из чисел, знаков арифметических действий и
скобок, называется числовым выражением. Следует понимать, что
одно число тоже будет являться числовым выражением
2.Что называется значением числового
выражения?
Результат выполнения действий над числами в числовом
выражении называется значением числового выражения.
3.Что называется выражением с
переменной?
Выражением называется запись, состоящая из чисел, букв,
знаков арифметических действий и скобок, указывающих на
порядок выполнения действий.
4.Что называется уравнением?
5.Что называется корнем уравнения?
Равенство с переменной
Значение переменной, при котором уравнение обращается в верное
равенство
6.Что называется математической
моделью?
Перевод условия задачи на математический язык
7.Какая связь существует между
понятиями: «Числовые выражения. »
«Выражения с переменной.» «Уравнения.»
«Математическая модель.»
Если вместо переменной подставить число, то выражение с
переменной обращается в числовое выражение.
Выражение с переменной может представлять правую или
левую часть уравнения.
Значение числового выражения может представлять правую
или левую часть уравнения.
Проверка уравнения приводит к нахождению значения
числового выражения.
Математическая модель представляет собой выражение с
переменной
8.Что значить упростить числовое и
буквенное выражения?
Применить переместительные свойства сложения и умножения,
сочетательные свойства сложения и
умножения,распределительное свойство
Физкультминутка
Самостоятельная работа
Проверь.
Определи своё настроение
Рефлексия
отличное
я был(а) уверен(а) в себе
мне было трудно
я устал(а)
Спасибо за урок!

Выражения с переменными — I четверть

ЦЕЛЬ УРОКА: Углубление и систематизация сведений о выражениях с переменными: понятие переменной, выражение с переменной, значение выражения с переменной.

ПЛАН УРОКА:

№

Этап урока

Содержание

Время (мин)

1

Организационный момент

Нацелить учащихся на урок

1

2

Проверка домашнего задания

Коррекция ошибок

5

3

Устная работа

Актуализация опорных знаний

5

4

Восприятие и первичное осознание материала

Углубление и систематизация знаний о выражениях с переменными

5

5

Комментированные упражнения на формирование понятия значения выражения с переменной

Формирование соответствующих умений

9

6

Упражнения на формирование умений составлять выражение с переменной по условию задачи

Формирование соответствующих умений

8

7

Самостоятельная работа

Коррекция знаний

8

8

Подведение итогов урока

Обобщить теоретические сведения, полученные на уроке

2

9

Сообщение домашнего задания

Разъяснить содержание домашнего задания

2

ХОД УРОКА

I. Организационный момент.

II. Проверка домашнего задания.

III. Актуализация опорных знаний.

Устно:

1) Пароход шел по течению реки 9 ч со скоростью а км/ч, а против течения — 6 ч со скоростью b км/ч.

Как записать в виде выражения:

а) общее время движения парохода;

б) путь, пройденный по течению;

в) путь, пройденный против течения;

г) весь путь, пройденный пароходом?

2) Найти значение выражения:

а) 4х + 5 при х = -8; х = -1/4; х = 0,1.

б) а3 при а = -1; а = -4; а = 5.

IV. Восприятие и первичное осознание материала.

Работа с учебником, п. 2. Учащиеся самостоятельно читают п. 2 учебника и выполняют задания учителя:

1) Привести примеры выражений с переменными.

а) Почему эти выражения так называются?

б) Что называют значением выражения с переменной?

2) Привести примеры формул.

3) Может ли выражение с переменной состоять из одной буквы?

4) Какие числа могут обозначать буквы в следующих выражениях:

а) продолжительность перемены n минут;

б) в вашем классе у учеников;

в) в VIII классе х учебных предметов;

г) в месяце k дней;

д) g/p = p?

V. Комментированные упражнения на формирование понятия значения выражения с переменной.

№ 19 — с записью на доске;

№ 20 — письменно без записи на доске;

№ 27 — устно;

№ 39 — обсуждение устное, запись ответа.

VI. Упражнения на формирование умений составлять выражение с переменной по условию задачи.

№№ 33, 34 — решаются коллективно с записью на доске;

№ 41 — комментирование.

VII. Самостоятельная работа.

(под контролем учителя №№ 23, 29)

VIII. Итог урока.

IX. Домашнее задание.

п .2 №№ 21, 24, 30.

выражений переменных | Определение, решаемые примеры, вопросы

Содержание


Мы в Cuemath считаем, что математика — это жизненный навык. Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что». Студенты могут изучить огромное количество интерактивных листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.

Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня! и поучаствуйте в онлайн-классе Cuemath LIVE вместе со своим ребенком.

Введение в выражения переменных

Джеймс и Натали играли спичками, и они подумали о том, чтобы с помощью спичек сформировать схемы чисел.

Джеймс взял 4 спички и образовал число \ (4 \)

.

Натали добавила еще 3 спичечных палочки, чтобы сформировать узор из двух \ (4 \).

Затем Джеймс снова добавил еще 3 спичечных палочки, чтобы сформировать узор из трех \ (4 \).

Внезапно у Натали возникло сомнение: сколько спичечных палочек нужно, чтобы сделать узор из десяти \ (4 \) сек?

Они поняли из существующего шаблона, что им нужно \ (4+ 9 (3) \) палочек, чтобы сделать это, поскольку они хотят шаблон с десятью \ (4 \) s.

Из этого они пришли к выводу, что им нужно \ (4+ (n-1) 3 \) палочек, как правило, чтобы сделать узор с \ (n \) числом \ (4 \) s.

Здесь \ (4+ (n-1) 3 \) называется алгебраическим выражением.

Определение переменной, константы, члена и коэффициента

  • Символ, не имеющий фиксированного значения, в Math называется переменной.Может принимать любое значение.

В приведенном выше примере \ (n \) — это переменная, и здесь она может принимать значения \ (1,2,3, … \)

Примеры переменных в математике: \ (a, b, x, y, z, m, \) и т. Д.

  • Символ, имеющий фиксированное числовое значение, называется константой.

Все числа постоянные.

Примеры констант: \ (3, 6, \ dfrac {-1} {2}, \ sqrt {5} \) и т. Д.

  • Термин — это одна переменная (или) одна константа (или) он может быть комбинацией переменных и констант посредством операции умножения или деления.2, \ dfrac {-2} {3} y, \ sqrt {5m}, \) и т. Д.

    Здесь числами, которые умножают переменные, являются \ (3, \ dfrac {-2} {3} \) и \ (5 \), которые называются коэффициентами .

    CLUEless по математике? Узнайте, как учителя CUEMATH объяснят вашему ребенку Variable Expressions , используя интерактивное моделирование и рабочие листы, чтобы им больше никогда не приходилось запоминать что-либо по математике!

    Изучите живые, интерактивные и персонализированные онлайн-классы Cuemath, чтобы сделать своего ребенка экспертом по математике. Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня!

    Выражение переменной (алгебраическое выражение)

    Выражение переменной (или) алгебраическое выражение — это комбинация терминов с помощью таких операций, как сложение, вычитание, умножение, деление и т. Д.

    Пример выражения переменной

    Пример выражения переменной (или) алгебраического выражения: \ (5x + 7 \)

    Вычисление переменной выражения

    Чтобы оценить выражение переменной по заданному значению, мы просто подставляем это значение в выражение и упрощаем его. {- 1} + 2y + 3z \)

    Аналитический центр

    1. Каждый ли многочлен многочлен?
    2. Является ли каждый многочлен многочленом?

    Действия по вычислению выражений переменных

    Вот упражнение с выражениями переменных.

    Отсюда вы можете выбрать одно из заданных выражений переменных и указать значение (я) его переменной (й).

    Затем вы можете оценить и ввести значение решения выражения переменной в соответствии с заданными вами значениями.

    Не беспокойтесь, если вы введете неправильный ответ для выражения.

    Он покажет вам пошаговое объяснение правильного ответа.

    Помогите своему ребенку набрать больше баллов с помощью запатентованного БЕСПЛАТНОГО диагностического теста Cuemath.Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Попытайтесь пройти тест сейчас.

    Решенные примеры

    В сумке \ (25 \) апельсинов. Напишите переменное выражение (алгебраическое выражение) для количества апельсинов в \ (x \) количестве мешков.

    Решение:

    Количество апельсинов в одном пакете = \ (25 \)

    Количество мешков = \ (x \)

    Итак, количество апельсинов в \ (x \) пакетах = \ (25x \)

    Выражение обязательной переменной \ (= 25x \)

    Вычислить данное выражение переменной для \ (a = 7; b = -3 \) и \ (c = 2 \)

    \ [6ab + 7bc + 9ca \]

    Решение:

    Дано алгебраическое выражение \ (6ab + 7bc + 9ca \)

    Подставьте следующие значения в приведенное выше выражение:

    \ (а = 7; \; b = -3; \; c = 2 \)

    \ [\ begin {align} 6ab \! + \! 7bc \! + \! 9ca & \! = \! 6 (7) (- 3) \! + \! 7 (-3) (2) \! + \! 9 (2) (7) \\ [0.3 см] & \! = \! \! — \! 126 \! — \! 42 \! + \! 126 \\ [0,3 см] & \! = \! \! — \! 42 \ end {align} \ ]

    \ [6ab + 7bc + 9ca = — 42 \]

    Определите правильный вариант (-ы).

    \ (4x + 5 \) — это …

    (а) Моном

    (б) Биномиальный

    (c) Трехчлен

    (d) Полином

    Решение:

    \ (4x + 2 \) имеет два одночлена \ (4x \) и \ (5 \) и, следовательно, является двучленом.2-3x + 2 \) при \ (x = 2 \)

    • Практические вопросы

    Важные темы

    Ниже приведен список тем, которые тесно связаны с выражениями переменных. Эти темы также дадут вам представление о том, как такие концепции рассматриваются в Cuemath.

    Образцы материалов олимпиады по математике

    IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, который ежегодно проводится для школьников.Он побуждает детей развивать свои навыки решения математических задач с точки зрения соревнований.

    Вы можете БЕСПЛАТНО скачать образцы работ по оценкам ниже:

    Чтобы узнать больше об олимпиаде по математике щелкните здесь

    Часто задаваемые вопросы (FAQ)

    1. Как написать переменное выражение?

    Выражение переменной зависит от условия.

    Например, «\ (3 \) больше, чем \ (x \)» можно записать как выражение переменной \ (x + 3 \)

    «\ (7 \) меньше суммы \ (a \) и \ (b \)» можно записать как выражение переменной \ (a + b-7 \)

    2.Что такое переменный пример?

    Символ, не имеющий фиксированного значения, в Math называется переменной. Может принимать любое значение.

    Примеры переменных в математике: \ (a, b, x, y, z, m, \) и т. Д.

    Дополнительную информацию можно найти в разделе «Определение переменной, константы, члена и коэффициента» на этой странице.

    3. Какие бывают 3 типа переменных?

    3 типа переменных:

    1. Независимые переменные
    2. Зависимые переменные
    3. Управляемые переменные

    4.

    Всегда ли в выражениях должна быть переменная?

    Нет, в выражении не обязательно должна быть переменная.

    Например, такие константы, как \ (2, -3, \ dfrac {-3} {4} \), также называются выражениями.

    5. Как определить переменную?

    Символ, не имеющий фиксированного значения, в Math называется переменной. Может принимать любое значение.

    Примеры переменных в математике: \ (a, b, x, y, z, m, \) и т. Д.

    6. Что такое переменная? Привести пример.

    Символ, не имеющий фиксированного значения, в Math называется переменной. Может принимать любое значение.

    Примеры переменных в математике: \ (a, b, x, y, z, m, \) и т. Д.


    Начальная алгебра
    Урок 4: Введение в выражения и уравнения переменных

    Цели обучения

    По завершении этого руководства вы сможете:
    1. Вычислить экспоненциальное выражение.
    2. Упростите выражение, используя порядок операций.
    3. Вычислить выражение.
    4. Знайте, когда число является решением уравнения или нет.
    5. Перевести английское выражение в математическое выражение.
    6. Переведите английское выражение в математическое уравнение.

    Введение


    В этом руководстве будут рассмотрены некоторые ключевые определения и фразы, используемые, когда специально работая с алгебраическими выражениями, а также оценивая их. Также коснемся порядка операций. Это очень ВАЖНЫЙ что вы понимаете математический жаргон, который используется в алгебре класс, в противном случае вам все это может показаться греческим. Зная термины и концепции на этой странице определенно помогут вам построить понимание того, что такое переменная, и вам будет удобнее работать с их. Переменные — ОГРОМНАЯ часть алгебры, поэтому для вас это очень важно. к чувствовать себя комфортно рядом с ними, чтобы добиться успеха в алгебре.Так Давайте приступим и поможем вам встать на путь переменчивой смекалки.

    Учебник




    Показатель показывает, сколько раз вы пишете база в ИЗДЕЛИЕ .

    Другими словами, экспоненты — это еще один способ записать УМНОЖЕНИЕ.

    Давайте проиллюстрируем эту концепцию, переписав продукт (4) (4) (4) с использованием экспоненциальной записи:

    В этом примере 4 представляет собой основание, а 3 — показатель степени. Поскольку в продукте 4 было написано три раза, наша экспонента равна 3. Мы всегда пишем нашу экспоненту в виде меньшего скрипта, который находится вверху справа. угол основания.

    Вы можете применить эту идею в другом направлении. Скажем вы запишите его в экспоненциальной записи, и вам нужно его оценить. экспонента скажет вам, сколько раз вы выписываете базу в продукт. Например, если у вас было 7 в качестве основы и 2 в качестве показателя степени, и вы хотел для оценки вы можете написать это так:




    Пример 1: Вычислить

    В этой задаче какая база?

    Если вы сказали 5, вы правы!

    Что такое показатель степени?

    Если вы сказали 4, вы правы!

    Давайте перепишем это как умножение и посмотрим, что мы получите за ответ:



    * Перепишите основание 5 четыре раза в продукт
    * Умножить





    Пример 2: Вычислить

    В этой задаче какая база?

    Если вы сказали 7, вы правы!

    Что такое показатель степени?

    Если вы сказали 1, вы правы!

    Давайте перепишем это как умножение и посмотрим, что мы получите за ответ:


    * Перепишите основание 7, один раз в продукте




    Пример 3: Вычислить

    В этой задаче какая база?

    Если вы сказали 1/3, вы правы!

    Что такое показатель степени?

    Если вы сказали 2, вы правы!

    Давайте перепишем это как умножение и посмотрим, что мы получите за ответ:


    * Перепишем базу 1/3, два раз в продукте

    * умножить


    Обратите внимание, что когда у вас есть 2 в качестве экспоненты, также известен как квадрат основания. В этой задаче можно сказать, что мы Ищу за 1/3 кв.


    Порядок действий

    Пожалуйста, скобки или символы группировки
    Извините Показатели (и радикалы)
    Дорогие мои умножение / деление слева направо
    Тетя Салли Сложение / Вычитание слева направо


    Если у вас есть более одной математической операции, тебе надо используйте порядок операций, указанный выше.Вы, возможно, уже слышали поговорки «Пожалуйста, извините мою дорогую тетю Салли». Это просто способ чтобы помочь вам запомнить порядок, в котором вам нужно идти при применении приказ операций.




    Пример 4: Упростить.


    * умножить
    * сложить
    * вычесть



    Пример 5: Упростить


    * Внутри ()

    * экспонента
    * умножить
    * сложить




    Пример 6: Упростить.

    Обратите внимание, что символ абсолютного значения | | является причудливая группировка символ. По порядку действий это было бы в том числе в первой строке в скобках.

    Итак, в этой задаче первое, что нам нужно сделать, это работать изнутри абсолютного значения. А потом идите оттуда.


    * Внутри | |

    * Показатель

    * Добавьте кол. и вычесть в ден.





    Переменная — это буква, которая представляет номер.

    Не позволяйте тому факту, что это письмо, вас сбивает. С это представляет число, вы относитесь к нему так же, как и к числу, когда вы делаете различные математический операции с переменными.

    x — очень распространенный переменная, которая используется в алгебре, но вы можете использовать любую букву ( a , b , c , d , ….) быть переменной.




    Алгебраическое выражение — число, переменная или комбинация из двух, связанных некоторой математической операцией, например сложением, вычитание умножение, деление, экспоненты и / или корни.

    2 x + y , a /5, и 10 — r являются примерами алгебраических выражения.



    Вы оцениваете выражение , заменяя переменная с заданный номер и выполнение указанной операции.




    Когда вас попросят найти значение выражение, что означает, что вы ищете результат, который получаете, когда оцениваете выражение.


    Так что имейте в виду, что разные способы изменения — a переменная позволяет выражение может принимать разные значения в зависимости от ситуации .

    Например, площадь прямоугольника равна длине, умноженной на ширина. Что ж, не каждый прямоугольник будет иметь одинаковую длину и ширину, поэтому мы может используйте алгебраическое выражение с переменными для представления площади и тогда вставьте соответствующие числа, чтобы оценить его.Итак, если мы позволим длина будет переменной l и ширина будет w , мы можем использовать выражение lw . Если данный прямоугольник имеет длину 4 и ширину 3, мы оценили бы выражение путем замены l на 4 и w на 3 и умножения, чтобы получить значение 4 умноженное на 3 или 12.

    Давайте рассмотрим несколько примеров, которые помогут проиллюстрировать эти идеи.



    Пример 7: Вычислить выражение когда x = 4, y = 6, z = 8.

    Вставка соответствующего значения для каждого переменная, а затем оценка выражение получаем:



    * Заглушка в 4 для x , 6 для y и 8 для z

    * экспонента
    * умножить
    * сложить
    * вычесть



    Пример 8: Вычислить выражение когда x = 3, y = 5 и z = 7.

    Вставка соответствующего значения для каждого переменная, а затем оценка выражение получаем:


    * Вставка 3 для x , 5 для y и 7 для z
    * Показатель степени

    * умножить

    * прибавить



    Уравнение

    Два выражения равны друг другу.


    Решение

    Значение, такое, что при замене переменной на it,
    это делает уравнение верно.

    (левая сторона выходит равной правой)


    Набор решений

    Комплект всех решений.


    Пример 9: Является ли 2 решением проблемы?


    Замена x на 2 получаем:



    * Вставьте 2 для x
    * Оцените обе стороны


    2 — решение?

    Поскольку мы получили утверждение ИСТИНА (7 на самом деле равно 7), тогда 2 является решением этого уравнения.




    Пример 10: 5 — это решение?


    Замена x на 5 получаем:


    * Вставка 5 для x
    * Оценка с обеих сторон


    5 — это решение?

    Поскольку мы получили оператор FALSE (16 не равно 14), тогда 5 это не решение.




    Перевод
    английской фразы в
    Алгебраическое выражение


    Иногда вам приходится выписывать собственный алгебраический выражение, основанное на формулировке проблемы.

    В этой ситуации вы хотите

    1. внимательно прочтите задачу,
    2. выбирают ключевые слова и фразы и определяют их эквиваленты математический значение,
    3. заменяет все неизвестные на переменные, а
    4. собрал все это в алгебраическое выражение.
    Ниже приведены некоторые ключевые слова и фразы и их переводы:

    Дополнение: сумма, плюс, прибавить более чем увеличилось на, всего


    Вычитание: разницы из, минус, вычтено из, меньше, уменьшено на, меньше


    Умножение: произведение, раз, умножить, дважды, из


    Деление: частное разделить на, передаточное число




    Пример 11: Запишите фразу как алгебраический выражение.

    Сумма числа и 10.


    В этом примере мы не оцениваем выражение, так что мы не будем придумать ценность. Однако мы хотим его переписать. как алгебраическое выражение.

    Похоже, единственная ссылка на математический операция сумма слов. Итак, какая операция у нас будет в этом выражение?

    Если вы сказали сложение, вы правы !!!

    Фраза «число» указывает на то, что это неизвестное номер. Ему не придавалось особой ценности. Так что заменим фраза «число» с переменной x . Мы хотим, чтобы наша переменная представляла любое неизвестное число

    Собрав все вместе, мы можем перевести данная английская фраза со следующим алгебраическим выражением:


    Сумма числа и 10


    * ‘сумма’ = +
    * ‘число’ = переменная x



    Пример 12: Запишите фразу как алгебраический выражение.

    Произведение 5 и числа.


    Опять же, мы хотим переписать это как алгебраический выражение, а не оцените это.

    На этот раз фраза, которая соответствует нашему операция — это «продукт» — так какую операцию мы будем выполнять на этот раз? Если вы сказали умножение , вы правы.

    Опять же, у нас есть фраза «число», которая снова будет заменен с переменной, так как мы не знаем, что это за число.

    Давайте посмотрим, что мы получим в ответ:


    Произведение 5 и числа


    * ‘продукт’ = умножение
    * ‘число’ = переменная x




    Перевод приговора в Уравнение

    Поскольку уравнение состоит из двух выражений, равных каждому другое, мы будем использовать те же математические переводы, что и выше. В разница у нас будет знак равенства между двумя выражениями.

    Ниже приведены некоторые ключевые слова и фразы что переводится в знак равенства (=):


    Знак равенства (=): равно, дает, есть, урожайность, составляет, такая же, как




    Пример 13: Запишите предложение как уравнение. Пусть x представляют неизвестное номер.

    Частное 3 и числа равно ½.


    Вы помните, что означает частное ? в? Если Вы сказали подразделение , у вас все отлично.

    «Is» будет заменено символом =.

    Соберем все слева направо:


    Частное от 3 и числа составляет ½




    Пример 14: Запишите предложение как уравнение. Пусть x представляет неизвестное число.

    Число меньше чем в 3 раза совпадает с 0.


    Вы помните, что меньше чем переводит в? Если вы сказали вычитание , у вас все отлично.

    Вы помните, что раз переводит в? если ты сказал умножение , вы правы.

    «То же, что и» будет заменено символом =.

    Соберем все слева направо:


    7, меньшее трехкратного числа, равно 0.



    Практические задачи

    Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Математика работает так же, как что-либо иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться Это. Даже лучшим спортсменам и музыкантам помогали на протяжении всего пути. практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики.

    Чтобы получить от них максимальную отдачу, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, щелкнув ссылку для ответ / обсуждение для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.

    Практика Задачи 1a — 1b: Оценить.

    Практика Задачи 2a — 2b: Упростите каждое выражение.

    Практика Задача 3a: Вычислить выражение, если x = 1, y = 2, и z = 3.

    Практика Задачи 4a — 4b: Определите, является ли данное число решение данное уравнение.

    Практика Задачи 5a — 5b: Запишите каждую фразу как алгебраическую выражение. Пусть x представляет неизвестное число.

    Практика Задачи 6a — 6b: Запишите каждое предложение как уравнение. Пусть x представляют неизвестный номер.


    Нужна дополнительная помощь по этим темам?



    Последний раз редактировал Ким Сьюард 42 июля 2011 г.
    Авторские права на все содержимое (C) 2001 — 2011, WTAMU и Kim Seward. Все права защищены.

    Переменные и алгебраические выражения

    Переменные и алгебраические выражения

    Прежде чем приступить к решению уравнений, вы должны иметь общее представление о переменных, а также о переводе и оценке алгебраических выражений.
    Переменные

    Переменная — это буква, обозначающая число.Буквы x , y , z , a , b , c , m и n , вероятно, являются наиболее часто используемыми переменными. Буквы e и i имеют специальные значения в алгебре и обычно не используются в качестве переменных. Буква o обычно не используется, поскольку ее можно принять за 0 (ноль).

    Алгебраические выражения

    Переменные используются для преобразования словесных выражений в алгебраические выражения, то есть выражения, состоящие из букв, обозначающих числа.Ключевые слова, которые могут помочь вам переводить слова в буквы и цифры, включают:

    • На сложение: сумма, больше, больше, прибавка
    • Для вычитания: минус, меньше, меньше, уменьшение
    • Для умножения: раз, произведение, умноженное на, из
    • Для деления: делить пополам на, соотношение.
    Пример 1

    Приведите алгебраические выражения для каждого из следующих утверждений.

    1. сумма числа и 5

    2. число минус 4

    3. шесть умноженное на число

    4 . x разделить на 7

    5. на три больше, чем произведение 2 и x

    1. сумма числа и 5: x + 5 или 5 + x

    2. число минус 4: x — 4

    3. шесть умноженное на число: 6 x

    4. x разделить на 7: или

    5.на три больше, чем произведение 2 и x : 2 x + 3

    Вычисление выражений

    Чтобы оценить выражение, просто замените переменные символами группировки, вставьте значения, заданные для переменных, и выполните арифметические действия. Не забудьте соблюдать порядок операций: скобки, показатели степени, умножение / деление, сложение / вычитание.

    Пример 2

    Оцените каждое из следующих действий.

    1. x + 2 y , если x = 2 и y = 5

    2. a + bc — 3, если a = 4, b = 5 и c = 6

    3. м 2 + 4 n + 1, если m = 3 и n = 2

    4. если a = 2, b = 3 и c = 4

    5. –5 xy + z , если x = 6, y = 7 и z = 1

    1.

    2.

    3.

    4.

    5.

    Алгебра — Определения

    Это может помочь вам сначала прочитать Введение в алгебру

    Что такое уравнение

    Уравнение говорит, что две вещи равны. У него будет знак равенства «=», например:

    .

    Это уравнение говорит: то, что слева (x + 2) равно тому, что справа (6)

    Таким образом, уравнение похоже на выражение «, это равно , что »

    Части уравнения

    Так люди могут говорить об уравнениях, существует имен для разных частей (лучше, чем говорить «вот эта штука»!)

    Здесь мы есть уравнение, в котором 4x — 7 равно 5, и все его части:

    A Переменная — это символ числа, которое мы еще не знаем. Обычно это буква типа x или y.

    Число называется константой .

    A Коэффициент — это число, используемое для умножения переменной ( 4x означает 4 умножить на x , поэтому 4 — коэффициент)

    Переменные сами по себе (без номера рядом с ними) фактически имеют коэффициент 1 ( x на самом деле 1x )

    Иногда коэффициент представляет собой букву типа a или b вместо числа:

    Пример: ax

    2 + bx + c
    • x — переменная
    • a и b — коэффициенты
    • c — постоянная

    Оператор — это символ (например, +, × и т. Д.), Который показывает операцию (т. Е. Мы хотим что-то сделать со значениями).

    A Член — это либо одно число, либо переменная, либо числа и переменные, умноженные вместе.

    Выражение — это группа терминов (термины разделены знаками + или -)

    Итак, теперь мы можем сказать такие вещи, как «это выражение имеет только два члена», или «второй член является константой», или даже «вы уверены, что коэффициент действительно равен 4?»

    Экспоненты

    Показатель степени (например, 2 в x 2 ) говорит , сколько раз использовать значение при умножении.

    Примеры:

    8 2 = 8 × 8 = 64

    y 3 = y × y × y

    y 2 z = y × y × z

    Показатели упрощают запись и использование множества умножений

    Пример: y 4 z 2 проще, чем y × y × y × y × z × z

    Полином

    Пример полинома: 3x 2 + x — 2

    Многочлен может иметь константу , переменную и степень 0,1,2,3 ,…

    Но в нем никогда не бывает деления на переменную.

    Моном, бином, трехчлен

    Существуют специальные названия многочленов с 1, 2 или 3 членами:

    Понятия «Нравится»

    подобных терминов — это термин , переменные которых (и их показатели, такие как 2 в x 2 ) одинаковы.

    Другими словами, термины, которые «похожи» друг на друга. (Примечание: коэффициенты могут быть разными)

    Пример:

    Все ли похожи на термины , потому что все переменные xy 2

    переменных, выражений и уравнений

    Обзор

    Алгебра — это решение математических задач с использованием уравнений .Уравнение (в контексте алгебры) — это утверждение, которое говорит, что два выражения равны друг другу по значению. Выражение (кроме, разумеется, половины уравнения) представляет собой математическую строку, которая может состоять из одного числа или переменной, или набора чисел, переменных и математических операторов, упорядоченных таким образом, что это может быть оценивается для получения некоторого результата. Переменная — это то, что используется для представления неизвестной величины в уравнении.Если смотреть с несколько иной точки зрения, числа, переменные и операторы являются основными строительными блоками, из которых строятся алгебраические выражения и, следовательно, уравнения. В следующих разделах каждый из этих терминов объясняется более подробно и приводится несколько примеров, которые, мы надеемся, прояснят их значение.

    Переменные

    Переменная представляет собой заполнитель , представляющий число или количество, значение которых изначально неизвестно.В алгебре буквы x и y обычно используются в качестве имен переменных, хотя можно использовать любой символ или символ. Имя, выбранное для переменной, часто зависит от типа решаемой проблемы. Например, в уравнении, описывающем процесс, который происходит в течение некоторого (неизвестного) периода времени, мы могли бы использовать букву t для представления значения прошедшего времени в секундах. В более сложных уравнениях вполне могут быть две или более переменных одного типа.Мы могли бы, например, захотеть найти время, которое прошло в течение двух отдельных этапов одного и того же процесса. В этой ситуации мы могли бы использовать имена переменных t 1 и t 2 для представления двух периодов времени (обратите внимание на использование чисел с индексами).

    Имя переменной подразумевает, что неизвестная величина, к которой относится переменная, может варьироваться. Хотя это часто верно (например, для координат x и y , которые описывают точки на графике), существует множество примеров уравнений, в которых значение неизвестной величины не изменяется, независимо от других задействованных значений. .В этом отношении переменная фактически может рассматриваться как константа (величина, имеющая постоянное значение). Мы используем термин переменная здесь больше для обозначения того факта, что мы можем присвоить переменной разные значения, даже если уравнение будет истинным только для одного из этих значений (или в некоторых случаях для двух, но мы вернемся к что в другом месте). Термин константа обычно зарезервирован для хорошо известных постоянных значений, таких как Pi. Эта греческая буква, представленная символом «π», используется для обозначения отношения длины окружности к ее диаметру и имеет приблизительное значение 3.14159 (с точностью до пяти знаков после запятой).

    Рассмотрим следующие простые уравнения:

    5 x + 3 = 28

    y = x + 2

    В первом из этих уравнений числа пять , три и двадцать восемь (5, 3 и 28) являются константами, и есть только одно возможное значение для x (= 5), которое делает уравнение верно.Подставьте любое другое значение в уравнение для x , и уравнение будет просто неверным. Однако во втором уравнении у нас есть две переменные: x и y . Это означает, что потенциально существует неопределенное количество возможных значений для x и y , которые удовлетворяют уравнению (т. е. делают его истинным), хотя для любого заданного значения x может быть только одно значение y. , и наоборот. На графике ниже показаны значения x и y , нанесенные на график для значений x в диапазоне от минус десяти до плюс десять (от -10 до +10).Обратите внимание, что значения попадают на прямую линию, которая может быть продолжена в любом направлении до бесконечности («До бесконечности и дальше!», Как сказал бы Базз Лайтер!).


    График y = x + 2


    Другой способ выразить взаимосвязь между x и y — сказать, что y — это результат функции ƒ ( x ) = x + 2.Другими словами, функция ƒ имеет x в качестве входа , а ее выход ( y ) всегда будет равен x + 2. Идея функции будет снова подхвачена в другом месте. На данный момент достаточно понять, что термин переменная , когда он используется в контексте алгебры, может использоваться для обозначения как статических значений (как в первом примере выше), так и значений, которые могут изменяться динамически (как во втором примере). ).

    Выражения

    Выражение может состоять из одного постоянного значения (т.е.е. число или символьная константа) или переменная, но чаще состоит из двух или более переменных и / или постоянных значений плюс арифметические операторы (например, операторы, обозначающие сложение , вычитание , умножение , деление и т. д.), индексов и радикалов . Выражение может дополнительно включать синтаксические объекты, такие как круглые скобки (скобки). Ниже приведены некоторые примеры алгебраических выражений.

    2π r

    2 x + y

    x 2 + 3 x — 17

    Значение выражения будет зависеть от значения переменных и констант, которые оно содержит (термины ), и от операций, которые выполняются над ними. Вычисление алгебраического выражения подчиняется тем же правилам относительно порядка операций, которые применяются к вычислению арифметических выражений (см. Страницу под названием «BODMAS» в разделе арифметики, если вы не знакомы с этой концепцией). Выражения появляются в уравнениях и часто меняются или упрощаются как часть процесса решения уравнения (это будет вскоре обсуждаться в контексте уравнений).

    Обратите внимание, что термины в алгебраических выражениях обычно рассматриваются как элементы, разделенные операторами плюс («+») или минус («-«).В приведенных выше выражениях члены состоят из 2π r , 2 x , y , x 2 , 3 x и 17. В более широком математическом контексте член 2π r может считаться выражением, состоящим из трех отдельных членов, все из которых являются множителями в выражении. Также обратите внимание, что из-за частого использования буквы x для представления неизвестного значения в алгебраических уравнениях оператор умножения («×») либо вообще опускается, либо заменяется средней точкой или промежуточной точкой (» · «). Первый из показанных выше членов, 2π r , может быть записан в риторической форме как «два, умноженные на Pi, умноженные на r» или в более традиционной математической записи как «2 × π × r ». Для целей этих страниц мы, где это возможно, будем обозначать умножение в алгебраических выражениях, используя простое сопоставление значений (то есть записывая их рядом друг с другом, без пробелов между ними).

    Довольно часто от нас требуется создать алгебраическое выражение на основе текстового описания решаемой задачи.Обычно это не так уж сложно, хотя может потребоваться немного практики, чтобы сделать это правильно. В качестве примера того, что обычно возникает на экзаменах, представьте себе ситуацию, когда автомобиль движется по дороге с заданной скоростью. Ожидается, что мы получим выражение для расстояния, которое транспортное средство пройдет через определенное количество часов, ч , при движении с постоянной скоростью (скажем) сорок пять миль в час. Поскольку расстояние равно скорости, умноженной на время, полученное нами выражение может быть таким:

    45 ч

    Мы могли бы так же легко написать «45 × h », но сопоставление значений для обозначения умножения чаще используется в алгебраической записи, чтобы избежать путаницы.Символ x часто используется в качестве имени переменной в алгебраических выражениях, и его можно спутать с оператором умножения («×»). Если ответ, который мы ищем, — это не расстояние, а время (в часах), которое пройдет после того, как транспортное средство проехало расстояние d , тогда (поскольку время равно расстоянию над скоростью) выражение может быть таким:


    Обратите внимание, что мы могли бы также записать это как « d ÷ 45», но оператор деления («÷») только изредка используется в алгебраических выражениях.Аналогичным образом, предположим, что у нас есть топливный бак заправочной станции, в котором содержится тысяча галлонов топлива. Автоцистерна начинает наполнять бак со скоростью двести галлонов в минуту. Нас могут попросить найти выражение для количества топлива в галлонах, которое будет вмещаться в баке через м минут. Это, конечно, будет количество прошедших минут ( м ), умноженное на скорость, с которой мы заполняем бак (двести галлонов в минуту), плюс количество топлива, уже находящегося в баке (тысяча галлонов ).Мы могли бы написать это как:

    200 кв.м + 1,000

    Когда у нас есть значения для всех переменных, используемых в выражении, мы можем оценить выражение, заменив переменные фактическими значениями. Выражение тогда по существу становится арифметическим выражением, а не алгебраическим. Если мы знаем, например, что танкер в приведенном выше примере заправляет топливный бак ровно пятнадцать минут, мы можем заменить число пятнадцать в нашем выражении, чтобы получить:

    200 х 15 + 1000 = 3000 + 1000 = 4000

    Уравнения

    Уравнение — это, по сути, утверждение, в котором говорится, что два выражения равны друг другу. Эти два утверждения пишутся одно за другим, разделенные знаком равенства («=»). Мы используем уравнения, чтобы найти значение одной или нескольких неизвестных величин. Мы делаем это, переупорядочивая и упрощая члены в уравнении, чтобы неизвестные величины могли быть выражены в терминах известных значений, чтобы мы могли вычислить их значение. Мы называем это решением уравнения. Если мы пытаемся найти значение определенной переменной в уравнении, мы говорим, что ищем решение для этой переменной.Итак, если переменная, для которой мы хотим получить значение, называется x , мы говорим, что мы решаем для x . В зависимости от типа проблемы, с которой мы имеем дело, не всегда удается решить уравнение. К счастью, уравнения, не имеющие решения, обычно не появляются на экзаменах, но они часто встречаются в реальном мире, потому что очень часто у нас просто нет всей необходимой информации. Если бы это было не так, мы бы наверняка уже нашли ответ на жизнь, вселенную и все остальное (извинения Дугласу Адамсу). Во всяком случае, вот несколько примеров уравнений:

    5 + 18 = 23

    x = 9

    y + 15 = 24

    2 x + 18 = 42

    3 x 2 + 5 x + 17 = 0

    Как видно из вышеизложенного, уравнения различаются по формату и сложности. Первый пример (5 + 18 = 23) на самом деле вообще не является алгебраическим уравнением, поскольку он просто утверждает, что сложение пяти и восемнадцати дает результат двадцать три.Второй пример ( x = 9) тоже не является уравнением как таковым, поскольку в нем просто указано, что значение x равно девяти. Следующие два уравнения можно решить относительно легко, поскольку мы можем переупорядочить и упростить их, чтобы получить ответы:

    y + 15 = 24 ⇒ y = 24-15 = 9

    2 x + 18 = 42 ⇒ 2 x = 42-18 = 24 ⇒ x = 24/2 = 12

    Последнее уравнение (3 x 2 + 5 x + 17 = 0) — это то, что называется квадратным уравнением (потому что оно содержит член, возведенный в квадрат). Это уравнение не так просто решить, и мы не будем здесь приводить отработанное решение. Достаточно сказать, что такого рода уравнения действительно возникают на экзаменах, их можно решить без особых усилий, и мы рассмотрим квадратные уравнения более подробно на отдельной странице.

    Типы уравнения

    Как вы, наверное, уже поняли, алгебраические уравнения бывают разных видов.Хотя невозможно аккуратно классифицировать все типы уравнений, с которыми мы можем когда-либо столкнуться, мы можем классифицировать уравнения по ряду общих критериев. Метка, которую мы наклеиваем на уравнение, будет зависеть от таких факторов, как количество и размещение переменных, типы задействованных операторов и форма, которую мы получим, если построим график значений, удовлетворяющих уравнению. Одно из различий, проводимых при попытке определить тип уравнения, на которое мы смотрим, — это количество терминов, задействованных в . Мономиальное уравнение имеет только один член, а биномиальное уравнение имеет два члена. Нет призов за то, чтобы угадать, сколько членов имеет трехчленное уравнение . Фактически, любое уравнение с более чем одним членом можно назвать полиномиальным уравнением .

    Еще одно различие относится к мономиальным и полиномиальным уравнениям, а именно: все члены должны иметь показатель степени (то есть степень), который является целым числом.Обратите внимание, что это будет автоматически включать члены без экспоненты, поскольку любое число в степени единицы является само по себе (если показатель степени равен один , мы не утруждаемся записывать его как показатель степени, потому что в действительности нет смысла). Помимо этого, многочлен также классифицируется в соответствии со значением наибольшего показателя любого из его членов. Многочлен, ни один из членов которого не имеет показателя больше единицы, называется linear , что отражает тот факт, что если мы нанесем на график значения, удовлетворяющие уравнению, мы получим прямую линию. Мы уже видели пример графика, созданного линейным уравнением y = x + 2 (см. Выше).

    Многочлен, член высшего порядка которого имеет показатель степени два, называется квадратным уравнением, а многочлен с членом высшего порядка с показателем степени три называется кубическим уравнением. Вы будете часто сталкиваться с квадратными уравнениями во многих областях техники и науки. Когда значения переменных, которые удовлетворяют квадратному уравнению, нанесены на график, они образуют характеристическую кривую, известную как парабола .Рассмотрим следующее квадратное уравнение:

    y = x 2 + 3 x + 2

    Вот график y = x 2 + 3 x + 2 для значений x в диапазоне от минус один (-1) до плюс четыре (+4):


    График y = x 2 + 3 x + 2 для значений x между -1 и +4


    Другие типы уравнений, с которыми мы можем столкнуться, включают экспоненциальные уравнения. Эти уравнения отличаются от полиномов тем, что в уравнении будет хотя бы один член, в котором показатель степени является переменной. График экспоненциальной функции ƒ ( x ) = e x показан ниже и удовлетворяет экспоненциальному уравнению y = e x . Экспоненциальные уравнения часто можно использовать для моделирования экспоненциального роста (например, распространения инфекционного заболевания), если показатель степени положительный, или экспоненциального распада (например, распада радиоактивного изотопа), если показатель степени отрицательный.


    График экспоненциальной функции ƒ ( x ) = e x


    Другой тип уравнения, тесно связанный с экспоненциальным уравнением, — это логарифмическое уравнение . Логарифмические функции являются обратными экспоненциальным функциям, поэтому логарифмическое уравнение y = log 10 ( x ) является обратным экспоненциальному уравнению y = 10 x . Логарифмические уравнения часто используются для расчета значений характеристик природных явлений, которые могут изменяться экспоненциально. В 1935 году Чарльз Рихтер определил магнитуду землетрясения M , используя логарифмическое уравнение: M = log I / S , где I представляет собой амплитуду сейсмических волн, измеренных в сто километров. от эпицентра землетрясения, а S — амплитуда сейсмических волн, создаваемых «стандартным землетрясением» (один микрон, или 10 -6 метров).Уравнение магнитуды стандартного землетрясения:

    M = журнал S / S = Log1 = 0

    Таким образом, по определению, сила стандартного землетрясения составляет ноль (0) баллов по шкале Рихтера. Сильнейшее землетрясение, измеренное Рихтером за многие годы его исследований, имело магнитуду восемь баллов (8.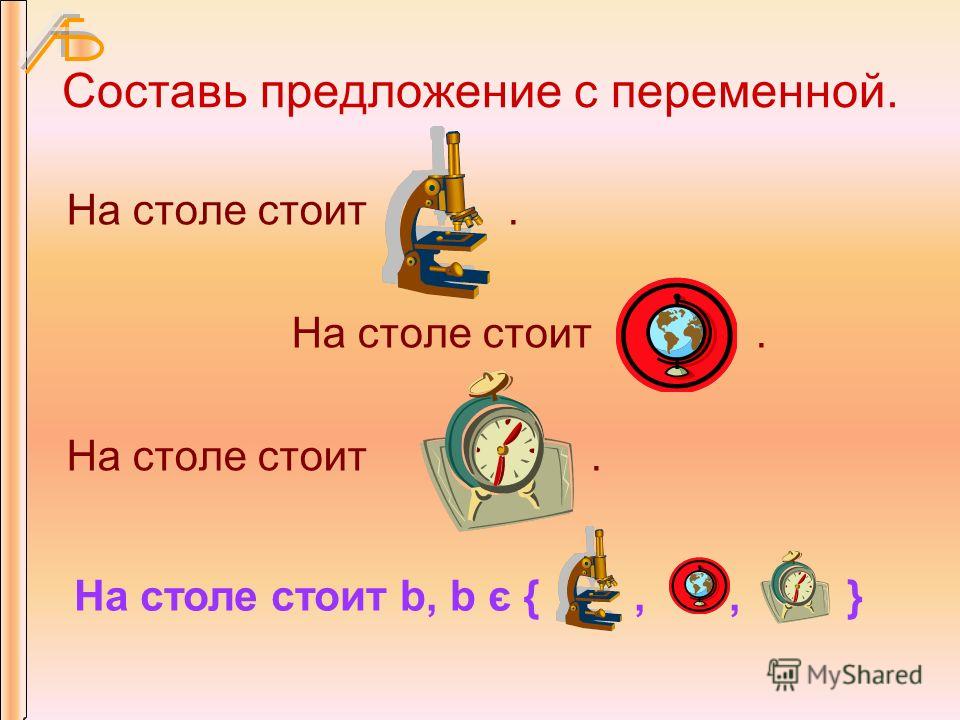 9) по шкале Рихтера. Это представляет собой амплитуду сейсмической волны, которая почти в восемьсот миллионов (800000000) раз превышает размер сейсмической волны, создаваемой стандартным землетрясением! Поэтому неудивительно, что относительная сила землетрясений описывается с использованием логарифмической шкалы, а не шкалы, включающей абсолютные значения.


    Темы алгебры: чтение алгебраических выражений

    Урок 5: Чтение алгебраических выражений

    / ru / algebra-themes / reciprocals-and-inverse-numbers / content /

    Введение

    Если вы новичок в алгебре — или не задумывались об этом некоторое время, — первое, что вы можете заметить, это то, что задачи алгебры немного отличаются от простых арифметических задач.Возьмем, например, выражение ниже:

    x + 4x ⋅ 2 2 — (3 / x)

    Это не так сложно решить, если вы знаете, как это сделать, но оно включает в себя несколько символов, которые являются общими в алгебре, но не в более базовой математике. То, как вы пишете алгебраические выражения, называется алгебраической нотацией . Хотя сначала это может показаться сложным, алгебраические обозначения не так уж и сложны.

    Алгебраическая нотация включает пять основных компонентов: переменных , коэффициентов , операторов , показателей и скобок .Вы можете увидеть все пять из них в приведенном ниже выражении:

    Мы рассмотрим их один за другим.

    Переменные

    Переменная — это буква, которая используется для представления числа . Например, в этой задаче переменная x представляет собой неизвестное число, которое будет равно 5 при добавлении к 2 .

    2 + х = 5

    Другими словами, это выражение задает вопрос: «Какое число вы можете добавить к 2 , чтобы получить 5 ?» Мы написали x , потому что сначала не знали, какое это число, но мы можем его вычислить. Поскольку мы знаем, что 2 + 3 = 5 , наша переменная должна быть равна 3 . Другими словами, x = 3 .

    Хотя это была простая задача сложения, тот факт, что она включала переменную, превратил ее в проблему алгебры. Фактически, поиск значения неизвестного числа часто является целью алгебры.

    В то время как x является наиболее часто используемой переменной, любая буква может быть переменной. Задача алгебры может иметь одну или несколько переменных.Если переменная используется более одного раза в одной и той же задаче, каждый раз она будет иметь одно и то же число. Возьмите это уравнение:

    х + х + у = 20

    Каждое значение x в этом выражении равно одной и той же сумме. Другая переменная, y , может иметь другую величину.

    Тот факт, что вы нашли значение переменной в одной задаче, не означает, что переменная будет иметь то же значение в другой задаче. Например, хотя x было равно 3 в нашей первой задаче, оно не обязательно равно 3 в любом другом выражении.

    Коэффициенты

    Иногда вы видите переменную с другим числом перед ней, например:

    2x

    В этом примере 2 — это коэффициент . Коэффициенты — это способ сгруппировать переменных. Например, 2 x — это просто еще один способ записать x + x . Не могли бы вы использовать коэффициенты, чтобы переписать это выражение?

    х + х + х + х + у + у + у

    Поскольку имеется четыре x и три y , вы можете записать это как 4 x + 3 y .Не зная, чему равны x и y , мы не можем упростить его еще больше, но его намного проще читать:

    4x + 3 года

    Вам может быть интересно, почему мы не можем еще больше упростить это до 7xy. Это потому, что вы можете только складывать или вычитать переменные, которые являются одинаковыми — поэтому вы можете складывать x + x или y + y , но никогда не x + y . Для получения дополнительной информации о добавлении и вычитании переменных ознакомьтесь с нашим уроком «Упрощение выражений».

    Операторы

    Операторы — это символы, которые говорят нам, что делать в математических задачах. Вы их всех уже видели:

    + — ÷ x

    Эти символы позволяют узнать, как вычислить выражение — например, когда вы видите знак плюс , вы знаете, что нужно сложить два числа, а когда вы видите знак минус , вы умеете вычитать. Знаки плюс и минус в алгебре одинаковы, но умножение и деление могут быть записаны немного по-другому.

    Умножение

    В арифметике умножение обычно записывается так:

    2 х 6

    Однако в алгебре символ умножения пишется немного иначе. Это потому, что x похоже на переменную x . По этой причине многие люди используют этот символ точек , чтобы показать умножение: ⋅ (это то, что вы увидите в наших уроках). В алгебре задача умножения записывается так:

    2 ⋅ 6

    Есть еще несколько способов показать умножение в алгебре. Как вы видели, когда мы умножали коэффициенты, вы можете просто написать переменные рядом друг с другом, чтобы умножить их. Если вы хотите умножить x и y , вы можете просто написать xy .

    xy

    Дивизия

    Есть несколько способов показать деление в алгебре. Вы, вероятно, наиболее знакомы с задачами деления, которые выглядят так:

    4 ÷ 2

    Вы увидите, что деление в алгебре написано таким образом. Однако вы также увидите, что это написано так (особенно на наших уроках):

    4/2

    Если вы разделяете группы чисел, вы также можете отобразить деление горизонтальной линией.Например, посмотрите на эту задачу:

    Здесь все, что находится выше линии, делится на все, что находится под ней, поэтому вы разделите 3 x — 12 y + 18 на 3.

    Другие части алгебраических выражений

    Круглые скобки

    Вы, вероятно, привыкли использовать круглые скобки в письменной форме, чаще всего с несущественной частью предложения (хотя они также могут использоваться для других целей). В алгебре круглые скобки используются немного иначе.Скобки используются для группировки частей алгебраического выражения. Когда вы видите часть задачи по алгебре, заключенную в круглые скобки, вам нужно решить эту часть, прежде чем приступать к остальной части задачи.

    7 + (40 / x) = 15

    В этой задаче вы должны сначала решить все, что указано в скобках; тогда вы решите все остальное.

    Интересно, почему вы сначала решаете часть в круглых скобках? Ознакомьтесь с нашим уроком о порядке работы.

    Что произойдет, если два набора скобок расположены рядом друг с другом без каких-либо операторов между ними?

    (3) (5)

    Если вы вспомнили, что две переменные рядом друг с другом равны , умноженному на , вы можете предположить, что вам нужно умножить на два набора скобок, стоящих рядом.Таким образом, (3) (5) равно 3 ⋅ 5 , что равно 15.

    Экспоненты

    Показатели — это числа, которые были умножены сами на себя. Например, давайте посмотрим на показатель 10 3 .

    10 3

    10 3 — это просто еще один способ сказать, что 10 было умножено само на себя 3 раз. Другими словами, это 10 ⋅ 10 ⋅ 10. Вы можете узнать больше в нашем уроке экспонентов.

    / ru / algebra-themes / написание-алгебраических-выражений / содержание /

    Оценка

    : оценка выражений и многочленов

    Purplemath

    «Оценка» в основном означает «упрощение выражения до одного числового значения».Иногда вам будет предложено числовое выражение, и все, что вам нужно сделать, это упростить; это скорее вопрос порядка действий. В этом уроке я сконцентрируюсь на аспекте оценки «включил и нажал»: вставлял значения для переменных и «пробирался» к упрощенному ответу.

    (Кстати, да, «plug-n-chug» — довольно стандартная терминология. Это не «технический» термин, поэтому вы, вероятно, не увидите его в своем учебнике, но наверняка услышите его от других студенты, а также, возможно, ваш инструктор.)

    MathHelp.com

    Обычно единственной сложной задачей при оценке является отслеживание знаков «минус».Я настоятельно рекомендую вам широко использовать круглые скобки, особенно когда вы только начинаете.

    • Вычислить
      a 2 b для a = –2, b = 3, c = –4 и d = 4.

    Чтобы найти ответ, я просто вставляю указанные значения, стараясь использовать круглые скобки, особенно вокруг знаков «минус». Если я только начинаю, может быть полезно сначала нарисовать круглые скобки:

    а 2 б

    () 2 ()

    (–2) 2 (3)

    (4) (3)

    12

    Обратите внимание, как использование круглых скобок помогло мне отследить знак «минус» на значении a .Это было важно, потому что в противном случае я мог бы возвести в квадрат только 2, получив в итоге –4, что было бы неправильно.

    Кстати, оказалось, что нам не нужны значения переменных c и d . Когда вам дается большой набор выражений для оценки, вы должны ожидать, что часто будут те или иные переменные, которые не будут включены в какое-либо конкретное упражнение из набора.

    • Вычислить
      a — cd для a = –2, b = 3, c = –4 и d = 4.

    В этом упражнении они дали мне дополнительную информацию. В выражении, которое они хотят, чтобы я оценил, нет b , поэтому я могу игнорировать это значение в своей работе:

    (–2) — (–4) (4)

    –2 — (–16)

    –2 + 16

    16–2

    14

    • Вычислить (
      b + d ) 2 для a = –2, b = 3, c = –4 и d = 4.

    Я должен позаботиться о том, чтобы не пытаться «распределить» показатель степени через круглые скобки. Экспоненты НЕ распределяются сверх сложения! Я никогда не должен пытаться сказать, что ( b + d ) 2 совпадает с b 2 + d 2 . Это НЕ одно и то же! Я должен оценить выражение в его нынешнем виде:

    • Вычислить
      b 2 + d 2 для a = –2, b = 3, c = –4 и d = 4.

    В этом выражении возведение в квадрат выполняется отдельно для каждой из переменных.

    Обратите внимание, что этот последний ответ выше не совпадает с ответом на предыдущую оценку. Это прямо демонстрирует тот факт, что показатели не распределяются сверх сложения, как это происходит при умножении.

    Вы должны ожидать хотя бы упражнения, аналогичные двум предыдущим, в следующем тесте, а также на заключительном экзамене.Эта тенденция пытаться распределить показатель степени (а не умножение) над сложением — распространенная ошибка студентов, и ваш преподаватель почти наверняка захочет напоминать вам — часто! — разницы между возведением суммы в квадрат и суммированием двух квадратов. Не путайте их!

    • Вычислить
      bc 3 — ad для a = –2, b = 3, c = –4 и d = 4.

    В этом упражнении мне нужно использовать значения всех четырех переменных. Но мне нужно быть осторожным при размещении, потому что это выражение не использует переменные в алфавитном порядке.

    (3) (- 4) 3 — (–2) (4)

    (3) (- 64) — (–8)

    –192 + 8

    –184

    Партнер

    Самым распространенным типом «выражения», которое вам, вероятно, потребуется вычислить, будут полиномы. Чтобы оценить многочлен, вы берете этот многочлен и подставляете в качестве переменной (обычно x ) любое число, которое они вам дали.

    • Вычислить
      x 4 + 3 x 3 — x 2 + 6 для x = –3.

    Это мой первый многочлен, который нужно вычислить, поэтому я начну снова с пустых скобок, показывая мне, где нужно поместить значение переменной.

    x 4 + 3 x 3 — x 2 + 6

    () 4 + 3 () 3 — () 2 + 6

    (–3) 4 + 3 (–3) 3 — (–3) 2 + 6

    81 + 3 (–27) — (9) + 6

    81 — 81 — 9 + 6

    –3

    • Вычислить 3
      x 2 — 12 x + 4 для x = –2.

    Я рад, что попрактиковался в использовании скобок, чтобы сделать свои замены более понятными. В этом случае эти круглые скобки помогут мне отслеживать знаки «минус».

    3 (–2) 2 — 12 (–2) + 4

    3 (4) + 24 + 4

    12 + 24 + 4

    40

    • Вычислить
      y = 4 x — 3 при x = –1.

    Это другое. Они дали мне уравнение с двумя переменными, но дали мне значение только для одной из переменных. Думаю, они хотят, чтобы я подключил x и вычислил результирующее значение для y .

    Тогда мой ответ — уравнение:

    Примечание. В этом последнем упражнении выше мы подставляли значение для одной из переменных и упрощали поиск значения другой переменной.Кроме того, для той части, к которой мы подключались, было присвоено имя y . Из-за этого мы не просто оценивали выражение; мы фактически вычисляли полиномиальную функцию. Результат нашего plug-n-chug означает, что точка ( x , y ) = (–1, –7) находится на линии y = 4 x — 3; то есть эта точка находится на графике полиномиальной функции.

    Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении выражений для заданных значений переменных.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или перейдите к следующей странице этого урока.)

    (Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *