| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет) Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Все, что нужно знать о свойствах четырехугольников
В этой статье мы рассмотрим все основные свойства и признаки четырехугольников.
Для начала я расположу все виды четырехугольников в виде такой сводной схемы:
Схема замечательна тем, что четырехугольники, стоящие в каждой строке обладают ВСЕМИ СВОЙСТВАМИ ЧЕТЫРЕХУГОЛЬНИКОВ, РАСПОЛОЖЕННЫХ НАД НИМИ. Поэтому запоминать надо совсем немного.
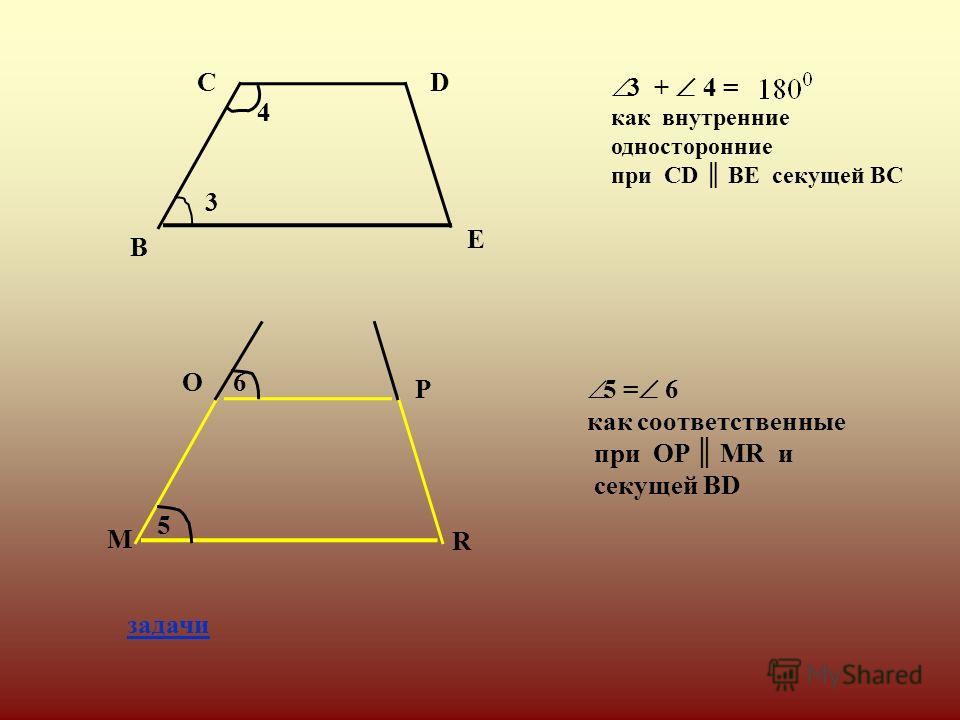
Трапеция — это четырехугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами.
1. В трапеции сумма углов, прилежащих к боковой стороне равна 180°: А+В=180°, C+D=180°
2. Биссектриса любого угла трапеции отсекает на ее основании отрезок, равный боковой стороне:
3. Биссектрисы смежных углов трапеции пересекаются под прямым углом.
4.Трапеция называется равнобедренной
В равнобедренной трапеции
- углы при основании равны,
- проекции боковых сторон на основание равны: .

5. Площадь трапеции равна произведению полусуммы оснований на высоту:
Параллелограм — это четырехугольник, у которого противоположные стороны попарно параллельны: В параллелограмме:
- противоположные стороны и противоположные углы равны
- диагонали параллелограмма делятся точкой пересечения пополам:
Соответственно, если четырехугольник обладает этими свойствами, то он является параллелограммом.
Площадь параллелограмма равна произведению основания на высоту:
или произведению сторон на синус угла между ними:
:
Ромб — это параллелограмм, у которого все стороны равны:
В ромбе:
- противоположные углы равны
- диагонали точкой пересечения делятся пополам
- диагонали взаимно перпендикулярны
- диагонали ромба являются биссектрисами углов
Площадь ромба равна половине произведения диагоналей:
или произведению квадрата стороны на синус угла между сторонами:
Прямоугольник — это параллелограмм, у которого все углы прямые:
- Диагонали прямоугольника равны.

- Диагонали точкой пересечения делятся пополам.
Площадь прямоугольника равна произведению его сторон:
.
Квадрат — это прямоугольник, у которого все стороны равны
или
Квадрат — это ромб, у которого все углы прямые.
Соответственно: квадрат обладает свойствами ромба и прямоугольника:
В квадрате:
- все углы равны 90 градусов
- диагонали точкой пересечения делятся пополам
- диагонали взаимно перпендикулярны
- диагонали являются биссектрисами углов
- диагонали равны
Площадь квадрата равна квадрату его стороны.
Площадь квадрата равна половине произведения диагоналей.
И.В. Фельдман, репетитор по математике.
Параллелограмм и трапеция
Многоугольник — часть плоскости, ограниченная замкнутой ломаной линией. Углы у многоугольника обозначаются точками вершин ломаной. Вершины углов многоугольника и вершины многоугольника — это совпадающие точки.
Определение. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны.
Свойства параллелограмма
1. Противолежащие стороны равны.
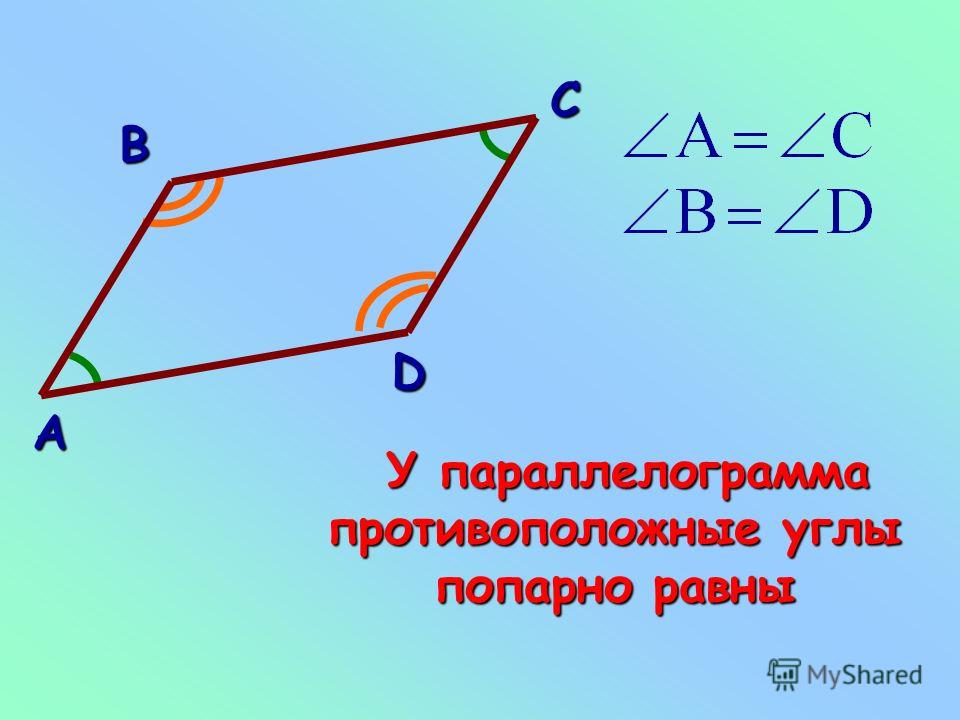
2. Противолежащие углы равны (два острых и два тупых угла).
На рис. 11 ∠A = ∠C; ∠B = ∠D.
3 Диагонали (отрезки прямой, соединяющие две противолежащие вершины) пересекаются и точкой пересечения делятся пополам.
На рис. 11 отрезки AO = OC; BO = OD.
Определение. Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие — нет.
Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
Виды трапеций
1. Трапеция, у которой боковые стороны не равны,
называется разносторонней (рис. 12).
12).
2. Трапеция, у которой боковые стороны равны, называется равнобокой (рис. 13).
3. Трапеция, у которой одна боковая сторона составляет прямой угол с основаниями, называется прямоугольной (рис. 14).
Отрезок, соединяющий середины боковых сторон трапеции (рис. 15), называется средней линией трапеции (MN). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Трапецию можно назвать усеченным треугольником (рис. 17), поэтому и названия трапеций сходны с названиями треугольников (треугольники бывают разносторонние, равнобедренные, прямоугольные).
Площадь параллелограмма и трапеции
Правило. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Правило. Площадь трапеции равна произведению полусуммы ее оснований на высоту (рис. 17).
У прямоугольной трапеции (рис. 14) высотой служит боковая сторона, перпендикулярная основаниям. Вместо полусуммы оснований трапеции можно взять длину средней линии трапеции (на рис. 15 отрезок MN).
Вместо полусуммы оснований трапеции можно взять длину средней линии трапеции (на рис. 15 отрезок MN).
|
Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон. Сумма углов выпуклого четырёхугольника равна 360°: ∠A+∠B+∠C+∠D=360°. Не существует четырёхугольников, у которых все углы острые или все углы тупые. Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов: ∠A < ∠B+∠C+∠D, ∠B < ∠A+∠C+∠D, ∠C < ∠A+∠B+∠D, ∠D < ∠A+∠B+∠D. Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон: a < b+c+d, b < a+c+d, c < a+b+d, d < a+b+c. Площадь произвольного выпуклого четырёхугольника равна: |
||
|
Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины. Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет. Площадь произвольного выпуклого четырёхугольника: |
||
|
Если M, N, P, Q – середины сторон выпуклого четырёхугольника ABCD, а R, S – середины его диагоналей, то четырёхугольники MNPQ, MRPS, NSQR являются параллелограммами и называются параллелограммами Вариньона. Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD. SABCD = 2SMNPQ . |
||
|
Отрезки MP, NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника. В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Для других четырёхугольников средние линии – отрезки. Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам: MG=GP, NG=GQ, RG=GS . Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей: MP2+ NQ2+ RS 2 = ¼(AB2+BC2+CD2+AD2+AC2+BD2). Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь: SABCD = MP·NQ·sinβ. |
||
|
|
||
|
Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости. |
||
|
Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной. Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны: a+c = b+d. Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно: a+c ≥ 4r, b+d ≥ 4r. Площадь описанного четырёхугольника: S = pr, где r – радиус вписанной окружности, p – полупериметр четырёхугольника. Площадь описанного четырёхугольника: |
||
|
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника. Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника: AK=AN, BK=BL, CL=CM, DM=DN. Если O – центр окружности, вписанной в четырёхугольник ABCD, то ∠AOB+∠COD=∠BOC+∠AOD=180°. Для описанного четырёхугольника ABCD со сторонами AB=a, BC=b, CD=c и AD=d верны соотношения: |
||
|
Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника. Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°: ∠A+∠C=∠B+∠D=180°. Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника. |
||
|
Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство: Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство: Радиус окружности, описанной около четырёхугольника: Площадь вписанного четырёхугольника: |
||
|
Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами. Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов. У вписанного четырёхугольника любые два связанных угла равны. |
||
|
Если четырёхугольник одновременно является описанным и вписанным, то его площадь: Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение: |
||
|
Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны: AB||CD, BC||AD. У параллелограмма противолежащие стороны равны и противолежащие углы равны: AB=CD, BC=AD; ∠A=∠C, ∠B=∠D. Сумма любых двух соседних углов параллелограмма равна 180°: ∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°. |
||
|
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам: AO=OC; BO=OD. Каждая диагональ делит параллелограмм на два равных треугольника: ∠ABC=∠CDA; ∠ABD=∠CDB. Две диагонали параллелограмма делят его на четыре равновеликих треугольника: SΔABO=SΔBCO=SΔCDO=SΔADO. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: e2+f2 = a2+b2+a2+b2 = 2(a2+b2). |
||
|
Признаки параллелограмма:
|
||
|
Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне: ha = b·sin γ; hb = a·sin γ. Площадь параллелограмма можно определить:
S = aha = bhb;
S = ab·sin γ. |
||
|
Ромбом называется параллелограмм, у которого все стороны равны: AB=BC=CD=AD. Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов: AC⊥BD; ∠ABD=∠CBD=∠ADB=∠CDB; ∠BAC=∠DAC=∠BCA=∠DCA. |
||
|
В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности, вписанной в ромб, можно вычислить:
Площадь ромба можно определить:
|
||
|
Прямоугольником называется параллелограмм, у которого все углы прямые: ∠A=∠B=∠C=∠D=90°. |
||
|
Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка: AC=BD; AO=BO=CO=DO. Площадь прямоугольника можно определить:
S = ab;
S = ½d²·sin γ. |
||
|
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали: BD = 2R. |
||
|
Квадрат – это прямоугольник, у которого все стороны равны: ∠A=∠B=∠C=∠D=90°, AB=BC=CD=AD. |
||
|
Диагонали квадрата равны и перпендикулярны. Сторона и диагональ квадрата связаны соотношениями: Площадь квадрата: |
||
|
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей. Радиус описанной окружности: Радиус вписанной окружности: |
||
|
Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны: AD||BC. Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами. Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции. |
||
|
Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции: AK=KB; CL=LD. Средняя линия трапеции параллельна её основаниям и равна их полусумме: KL||AD; KL||BC; KL = ½(AD+BC). |
||
|
При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ: ΔAED∼ΔBEC, k=AD/BC. Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ: ΔAОD∼ΔCОВ, k=AD/BC. Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны: SΔABO = SΔCDO. |
||
|
Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон: O∈KL; E∈KL. Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности: RS||AD; RS||BC; RS = ½(AD–BC). |
||
|
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон: AD+BC=AB+CD. Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции. В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств: Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом: ∠AOB=∠COD=90°. Радиус вписанной в трапецию окружности можно определить:
|
||
|
Равнобокой называется трапеция, у которой боковые стороны равны: AB=CD. У равнобокой трапеции:
AC=BD;
∠A=∠D, ∠B=∠C;
∠A+∠C=∠B+∠D=180°. Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая. Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c². |
||
|
Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям. |
||
|
Площадь трапеции можно определить:
|
||
|
Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон. Дельтоид может быть выпуклым или невыпуклым. Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом. В любом дельтоиде углы между соседними неравными сторонами равны. Площадь любого дельтоида можно определить:
S = ab·sin α . |
||
|
В любой выпуклый дельтоид можно вписать окружность. Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида. Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины. |
||
|
Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°. Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:
|
||
|
Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом. Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий:
|
||
|
Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности: a²+c² = b²+d² = 4R². |
||
|
Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны: ac = bd. Если ABCD – ортодиагональный четырёхугольник, описанный около окружности с центром в точке О, то верны соотношения: |
||
Внеклассный урок — Четырехугольники
ЧетырехугольникиЧетырехугольник – это фигура, состоящая из четырех точек, которые последовательно соединены четырьмя отрезками. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Данные точки называются вершинами четырехугольника, а соединяющие их отрезки – сторонами четырехугольника.
Параллелограмм.
Параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны (рис.1).
Теорема:
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Свойства параллелограмма:
1) У параллелограмма противолежащие стороны равны, противолежащие углы равны.
2) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
3) Сумма квадратов диагоналей равна удвоенной сумме квадратов его двух смежных сторон:
d12 + d22 = 2(a2 + b2),
где d1 и d2 – диагонали параллелограмма, a и b – смежные стороны.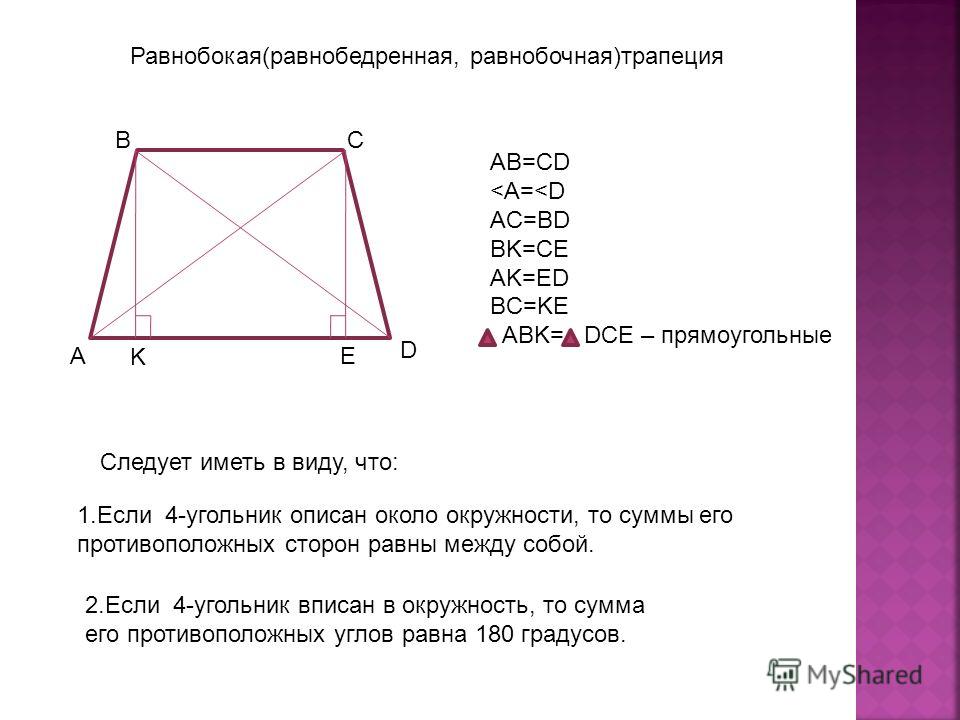
Прямоугольник.
Прямоугольник – это параллелограмм, у которого все углы прямые (рис.2).
Теорема:
Диагонали прямоугольника равны.
Ромб.
Ромб – это параллелограмм, у которого все стороны равны (рис.3).
Теорема:
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.
Квадрат.
Квадрат – это прямоугольник, у которого все стороны равны (рис.4).
Квадрат обладает свойствами прямоугольника и ромба.
Свойства квадрата:
1.У квадрата все углы прямые.
2.Диагонали квадрата равны.
3.Диагонали квадрата пересекаются под прямым углом и являются биссектрисами его углов.
Трапеция.
Трапеция – это четырехугольник, у которого только две противолежащие стороны параллельны (рис.5).
Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.
Две другие стороны называются боковыми сторонами.
Трапеция, у которой боковые стороны равны, называется равнобокой.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Теорема:
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Виды четырехугольников.
Тестирование онлайн
Параллелограмм и трапеция
Прямоугольник, ромб, квадрат
Параллелограмм
Определение. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
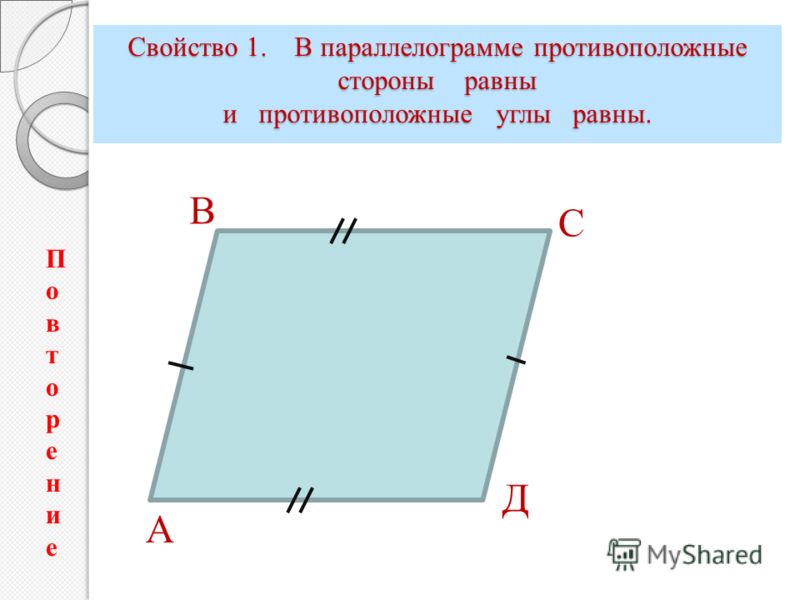
Свойство. В параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство. Диагонали параллелограмма точкой пересечения делятся пополам.
1 признак параллелограмма. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
2 признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
3 признак параллелограмма. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Трапеция
Определение. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны называются основаниями.
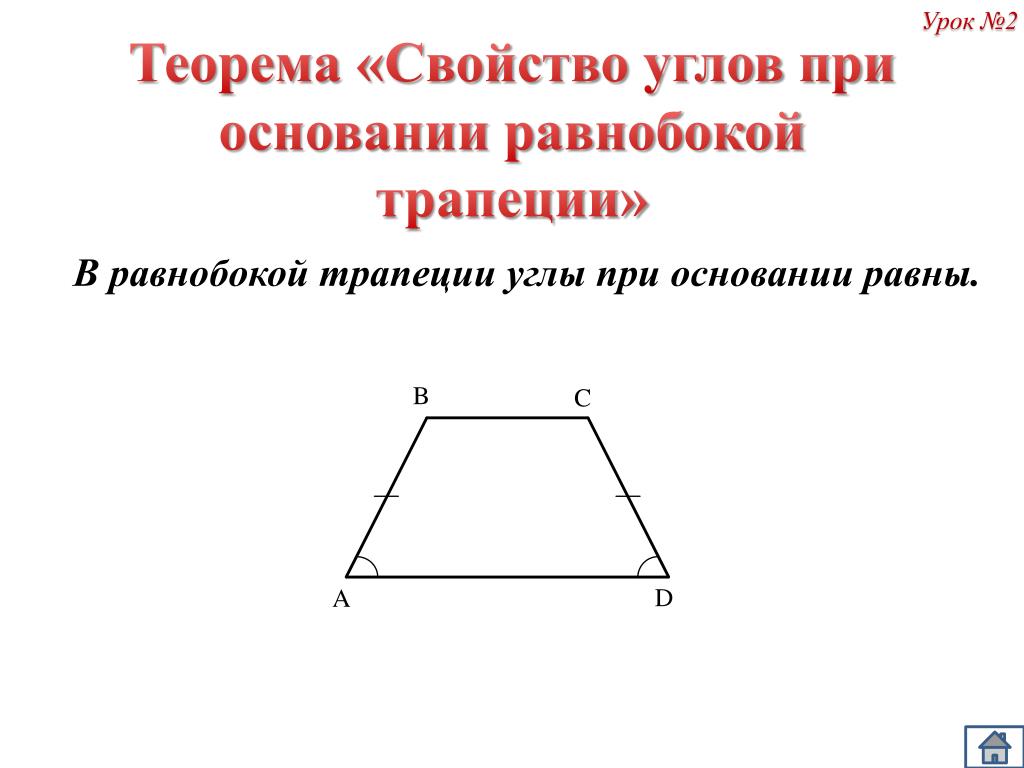
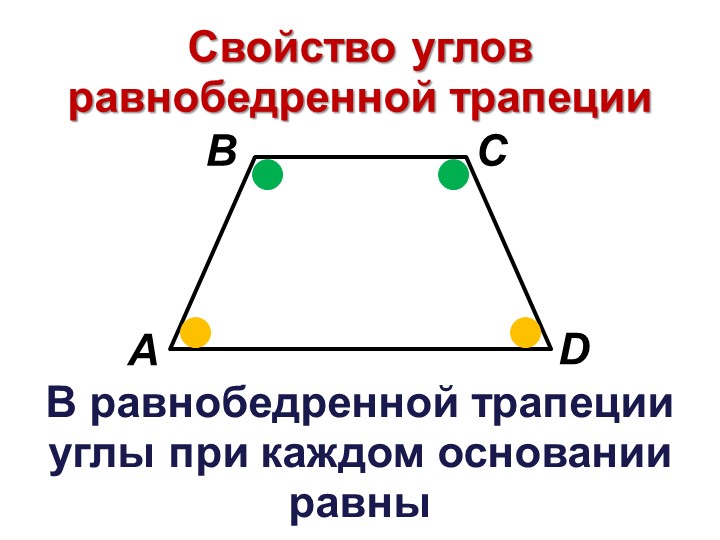
Трапеция называется равнобедренной (равнобочной), если ее боковые стороны равны. В равнобедренной трапеции углы при основаниях равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Средняя линия параллельна основаниям и равна их полусумме.
Прямоугольник
Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойство. Диагонали прямоугольника равны.
Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Ромб
Определение. Ромбом называется параллелограмм, у которого все стороны равны.
Свойство. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Квадрат есть частный вид прямоугольника, а также частный вид ромба. Поэтому он имеет все их свойства.
Свойства:
1. Все углы квадрата прямые
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Четырехугольники 8 класс — online presentation
Геометрия 8 класс1
Раздел І:
Четырехугольники
Учитель математики
МОУ “Оленовская школа №2
Волновахского района”
Прохоренко Ирина Ивановна
Четырехугольник, его елементы
Четырехугольник — фигура, состоящая из четырёх
точек и четырёх отрезков, соединяющих их
последовательно;
1.
 На одной прямой должно
На одной прямой должнолежать не больше двух точек.
2. Отрезки, соединяющие
точки, не должны
пересекаться.
Точки чотырехугольника
называются вершинами,
а отрезки, соединяющие их , — сторонами.
Соседние вершины — вершины
четырехугольника, которые
являются концами одной из его
сторон.
Противоположные вершины—
вершины четырехугольника,
которые не являются соседними.
Диагональ — отрезок, соединяющий
противоположные вершины.
Соседние стороны— стороны
четырехугольника, которые выходят из одной
вершины.
Противолежащие
стороны — стороны
четырехугольника,
которые не имеют
общего конца.
Периметр — сумма всех
сторон четырехугольника.
Четырехугольник называется указанием его
вершин, при этом вершины называют
последовательно.
В
А
С
Четырехугольник
АВСД
Д
У каждого
четырехугольника
4 вершины,
4 стороны,
2 диагонали.
.jpg)
Сумма углов четырехугольника
Если в четырехугольнике провести одну диагональ, то
четырехугольник разбивается на два треугольника.
Сумма углов заданного четырехугольника будет равняться
сумме углов обоих полученных треугольников.
Учитывая, что сумма углов любого треугольника равна
1800, то сумма углов заданного четырехугольника равна
360°.
1800
Запомните!
Сумма углов любого
четырехугольника равна
3600.
1800
Параллелограмм и его свойства.
Признаки параллелограмма.
Четырехугольник, у которого противолежащие
стороны параллельны, называется параллелограммом.
А
В
АВ ││СД
Д
С
АД ││ВС
Высотою параллелограмма называется
отрезок, перпендикулярный к прямой,
содержащую противоположную сторону.
У параллелограмма из каждой его вершины
можно провести по две высоты.
А
Д
В
С
Высоты, проведенные из вершин тупых углов
параллелограмма, лежат в параллелограмме;
Высоты, проведенные из
острых углов
параллелограмма, лежат вне
параллелограмма.

Свойства параллелограмма
У параллелограмма противоположные стороны равны.
АД=ВС
А
АВ=СД
В
У параллелограмма противоположные углы равны.
Д
С
У параллелограмма сумма углов, прилежащих к одной стороне,
равна 180°.
Диагонали параллелограмма пересекаются и
точкой пересечения делятся пополам.
АО=ОС
А
ВО=ОД
В
О
Д
Диагонали параллелограмма делят его
на два равных треугольника.
А
Д
В
С
АВС= АДС
С
Признаки параллелограмма
Если диагонали четырехугольника пересекаются
и точкой пересечения делятся пополам, то этот
четырехугольник параллелограмм.
А
В
О
Д
Если АВ=ДС и
АВ//ДС , то
АВСД параллелограмм
С
Если АО=ОС и ВО=ОД , то
АВСД — параллелограмм
Если в четырехугольнике две
противолежащие стороны
параллельны и равны, то этот
четырехугольник параллелограмм.
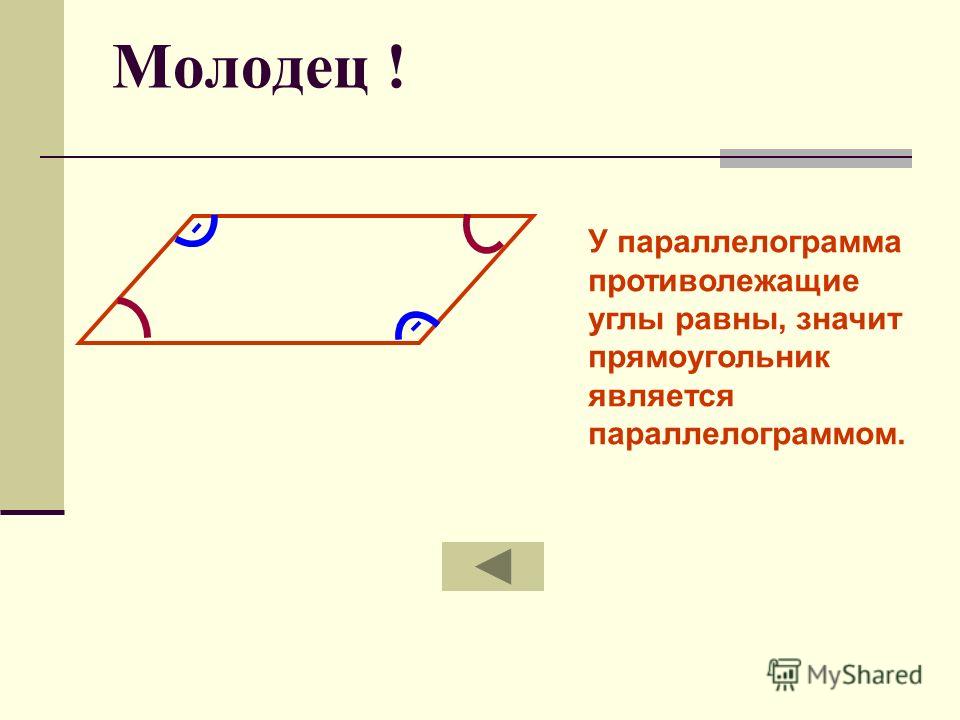
Если в четырехугольнике
противолежащие стороны попарно
равны, то этот четырехугольник
параллелограмм.
А
Д
То есть , если АВ=СД и АД=ВС ,
то АВСД — параллелограмм
Если в четырехугольнике противоположные углы
попарно равны, то этот четырехугольник
параллелограмм.
То есть , если
то АВСД — параллелограмм
В
С
Свойство диагоналей параллелограмма:
Диагонали параллелограмма
пересекаются и точкой
пересечения делятся пополам.
А
Д
АО=ОС і ВО=ОД
Свойство противоположных сторон и углов
параллелограмма:
У параллелограмма
АВ=СД
АД=ВС
противоположные стороны
и углы равны.
В
О
С
Это интересно.
Если провести биссектрисы двух противолежащих
углов параллелограмма, то они будут
параллельны или совпадут.
Е
А
В
ВК//ДЕ
Д
Если провести биссектрисы двух
углов, прилежащих к одной стороне
параллелограмма, то они будут
перпендикулярными.

С
К
ВК
СЕ
Прямоугольник, его свойства
Представитель класса параллелограммов прямоугольник.
Параллелограмм, у которого все углы
прямые, называются прямоугольником.
Свойства прямоугольника
Противолежащие стороны прямоугольника равны.
А
В
Д
С
АВ=СД
АД=ВС
Все углы прямоугольника равны.
Диагонали прямоугольника равны.
АС=ВД
Диагонали прямоугольника
пересекаются и точкою пересечения
делятся пополам.
АО=ОС и ВО=ОД
Диагонали прямоугольника делят его
на два равных треугольника.
А
Д
В
О
С
А
В
Д
С
АВС= АДС
В прямоугольнике сумма углов,
прилежащих к одной стороне, равна 180°.
Признаки прямоугольника
Если в параллелограмме все углы равны, то
этот параллелограмм — прямоугольник.
Если
АВСД — прямоугольник
А
В Если в параллелограмме один угол прямой,
то этот параллелограмм — прямоугольник.
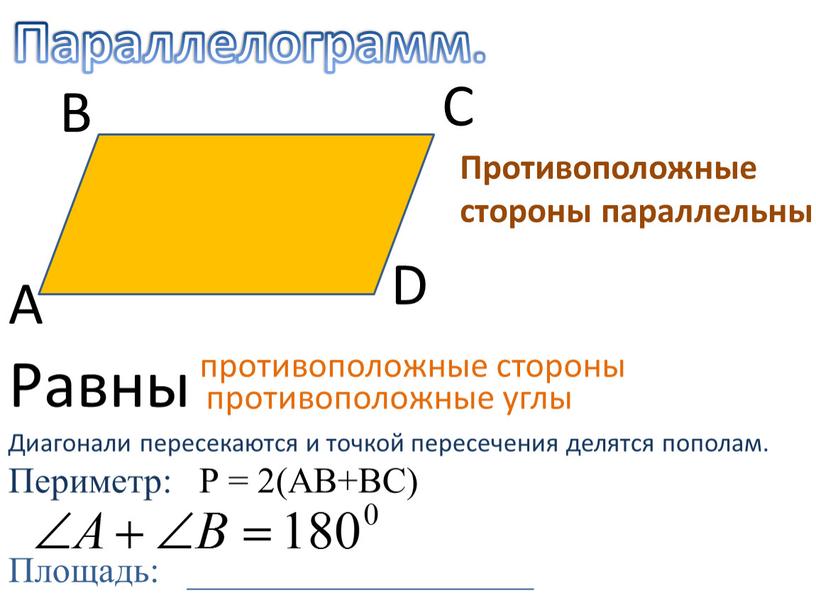
Если
Д
С
Если в параллелограмме диагонали равны,
Если АС=ВД, то
то этот параллелограмм — прямоугольник.
АВСД — прямоугольник
Если в четырехугольнике три угла прямые,
то этот четырехугольник — прямоугольник.
Если
АВСД — прямоугольник
Это интересно.
Если в прямоугольнике с неравными смежными
сторонами провести биссектрисы его углов, то при
их пересечении образуется прямоугольник.
Обратите внимание!
Если в прямоугольнике проведена биссектриса,
пересекающую одну из сторон, то она
отсекает от прямоугольника равнобедренный
треугольник.
Ромб, его свойства.
Параллелограмм, у
которого все стороны
равны,
называется ромбом.
Свойства ромба
Противолежащие углы ромба равны.
У ромба сумма углов, прилежащих к
одной стороне, равна 1800
А
В
Диагонали ромба пересекаются под прямым углом.
АС ВД
Диагонали ромба являются биссектрисами его углов.
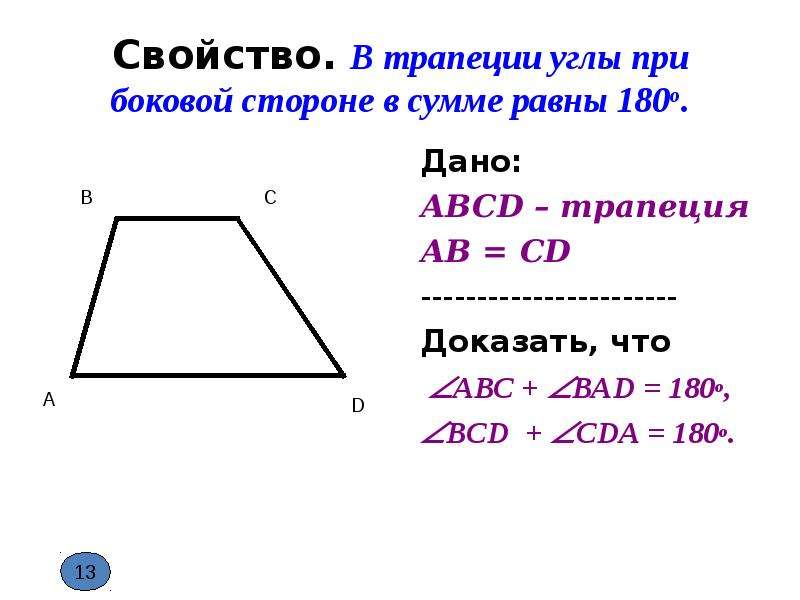
Диагонали ромба пересекаются и точкою пересечения
делятся пополам.
АО=ОС и ВО=ОД
Д
О
С
Признаки ромба
Если в параллелограмме диагонали пересекаются под
прямым углом, то этот параллелограмм — ромб.
Если в параллелограмме диагонали являются
биссектрисами его углов, то этот параллелограмм — ромб.
Если в параллелограмме две смежные стороны равны, то
этот параллелограмм — ромб.
Если в четырехугольнике все стороны равны, то этот
четырехугольник — ромб.
Если в параллелограмме одна из диагоналей является
биссектрисою его угла, то этот параллелограмм — ромб.
Если в четырехугольнике диагонали являются
биссектрисами его углов и пересекаются под прямым углом,
то этот четырехугольник — ромб.
Это интересно.
Если соединить отрезками средины сторон прямоугольника, то
получим ромб.
Если соединить отрезками средины сторон
ромба, то получим прямоугольник.
Если у параллелограмма все высоты
равны, то этот параллелограмм — ромб.
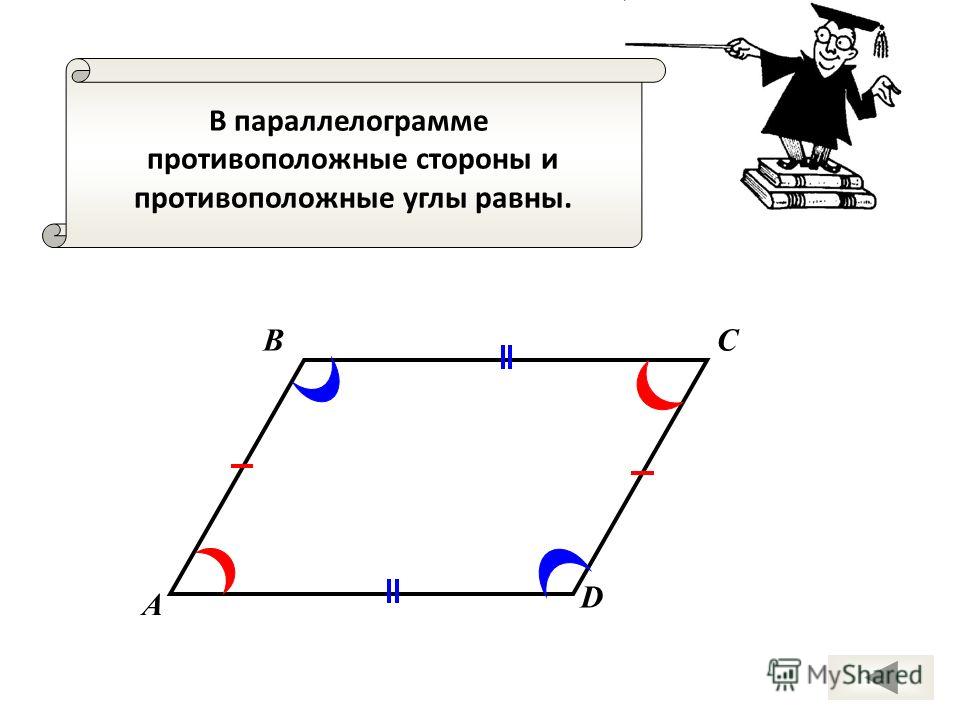
Квадрат, его свойства
Прямоугольник, у которого все стороны равны,
называются квадратом.
Свойства квадрата
Все углы квадрата — прямые.
А
В
О
Д
Диагонали квадрата пересекаются и точкою пересечения
делятся пополам.
АО=ОС и ВО=ОД
Диагонали квадрата равны.
АС=ВД
Диагонали квадрата пересекаются под
прямым углом.
Диагонали квадрата являются биссектрисами его углов.
С
Признаки квадрата
Если в прямоугольнике диагонали
пересекаются под прямым углом, то
этот прямоугольник — квадрат.
Если у ромба диагонали равны, то
этот ромб — квадрат.
Если в четырехугольнике все стороны
равны и все углы равны, то этот
четырехугольник — квадрат.
Трапеция, её свойства
Четырехугольник, у которого только две противоположные
стороны параллельны, называется трапецией.
Основы трапеции —
две параллельные стороны;
боковые стороны — две другие.
Высотою трапеции называется отрезок,
перпендикулярный к прямым, содержащим
основы трапеции, и с концами на этих
основах.

А
Равнобедренная трапеция — это
трапеция, у которой боковые
стороны равны.
В
Д
С
Прямоугольная трапеция — это трапеция,
одна боковая сторона которой
перпендикулярна её основам.
В прямоугольной трапеции
два угла прямые, один острый
и один тупой.
Боковая сторона трапеции, перпендикулярна к
её основам, является меньшею боковою
стороною и равна высоте трапеции.
АД = h
Свойства трапеции
Сумма углов трапеции,
прилежащих к одной боковой
стороне, равна 180°.
А
Д
В
С
В равнобедренной трапеции углы при каждой основе равны
А
Д
В
С
В равнобедренной трапеции диагонали
равны и наклонены к основанию под
одинаковыми углами. АС=ВД
Признаки равнобедренной трапеции
Если в трапеции углы при основании
равны, то трапеция равнобедренная.
Если в трапеции диагонали равны,
то трапеция равнобедренная.
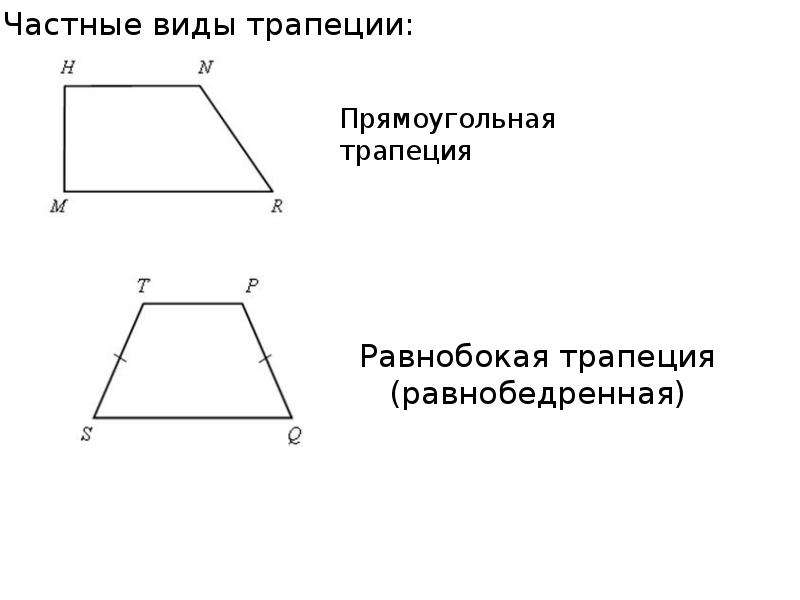
Если в трапеции диагонали
образуют с основаниями равные углы,
то трапеция равнобедренная.
Это интересно.
Если средины сторон равнобедренной
трапеции соединить отрезками, то
получим ромб.
Иллюстративная математика
Комментарий IM
Цель этого задания — дать учащимся определение трапеции. Есть два конкурирующих определения слова «трапеция»:
Исключительное определение трапеции гласит, что трапеция имеет ровно одну пару параллельных противоположных сторон.
Включенное определение гласит, что трапеция имеет по крайней мере одну пару параллельных противоположных сторон.
Иногда люди говорят, что у трапеций «одна пара противоположных сторон параллельна», поэтому остается неясным, может быть их больше одной или нет.Вторая часть задания подталкивает учащихся к четкому пониманию того, какую версию они намереваются. Из-за того, что студенты должны внимательно относиться к определениям, эта задача в значительной степени опирается на MP6, «Заботьтесь о точности».
После того, как учащиеся сформулировали определения для себя или с партнером, класс должен обсудить определение вместе. Класс должен выбрать одно определение, с которым все согласны, поскольку смысл четко сформулированных определений состоит в том, что мы все знаем, что говорим об одном и том же.Хотя оба определения законны, преимущество инклюзивного определения состоит в том, что любая теорема, верная для трапеции, верна и для параллелограмма. Кроме того, в своем исследовании Классификация четырехугольников (Information Age Publishing, 2008) Usiskin et al. заключение,
Преобладание преимуществ всеобъемлющего определения трапеции привело к тому, что все статьи, которые мы могли найти по этому предмету, и большинство книг по геометрии, выпускаемых колледжем, отдали предпочтение всеобъемлющему определению.
Инклюзивное определение устанавливает взаимосвязь между параллелограммами и трапециями, которая в точности аналогична взаимосвязи между квадратами и прямоугольниками; определение прямоугольников включает квадраты так же, как включающее определение трапеций включает параллелограммы.
Дополнительную информацию об этих проблемах см. В документе K-6 Geometry Progressions: http://commoncoretools.me/wp-content/uploads/2012/06/ccss_progression_g_k6_2012_06_27.pdf.
Решение
- Трапеция — это четырехугольник, у которого одна пара противоположных сторон параллельна. Он может иметь прямые углы (прямая трапеция) и равнобедренные стороны, но это не обязательно.
- Иногда люди определяют трапеции, чтобы иметь по крайней мере одну пару противоположных сторон, параллельных, а иногда говорят, что существует одна и только одна пара противоположных сторон, параллельных. Параллелограмм соответствует «по крайней мере одному» варианту определения, поскольку у него две пары противоположных сторон, параллельных друг другу, поэтому он попадает в категорию как трапеции, так и параллелограмма.Параллелограмм не подходит под «один-единственный» вариант определения. То, как студенты ответят на этот вопрос, зависит от их определения.
Примечание: если учащиеся дают разные определения, это нормально. Однако, чтобы иметь возможность обсуждать математические идеи в будущем, класс должен остановиться на одной из этих версий и двигаться дальше. См. Примечание в комментарии, поощряющее версию определения, включающую параллелограммы.
Однако, чтобы иметь возможность обсуждать математические идеи в будущем, класс должен остановиться на одной из этих версий и двигаться дальше. См. Примечание в комментарии, поощряющее версию определения, включающую параллелограммы.
Урок трапеции — Бесплатная справка по математике
Определение трапеции
Трапеция — четырехугольник с одной парой параллельных сторон.Как показано на рисунке ниже, параллельные стороны трапеции ABCD называются основаниями , а стороны, которые не параллельны, называются ножками .
Факты о трапециях
Сумма четырех углов в градусах дает 360 градусов . На самом деле это верно для любого четырехугольника. Пусть строчные буквы a, b, c и d представляют углы трапеции ABCD.
Тогда: a + b + c + d = 360 градусов.
Соответствующие пары углов основания, такие как A и B или C и D, являются дополнительными (в сумме составляют 180 градусов).
угол a + угол b = 180 градусов
угол c + угол d = 180 градусов
Равнобедренная трапеция
Существует особый вид трапеции, называемый равнобедренной трапецией и . Равнобедренная трапеция — это трапеция, у которой ноги равны по длине. Помните, что ноги — это непараллельные стороны , в отличие от параллельных оснований. Вы заметите, что в первой трапеции этого урока (выше) ноги НЕ равны.
Это равнобедренная трапеция, называемая ABCD:
.Имеет следующие характеристики:
Два нижних базовых угла имеют одинаковую меру, а два верхних базовых угла имеют одинаковую меру.
угол a = угол d
угол b = угол c
Диагонали одинаковой длины.
диагональ AC = диагональ BD
Пример проблемы
В равнобедренной трапеции MATH сторона HT параллельна стороне MA, отрезок MH конгруэнтен отрезку AT.Градусная мера угла MHT = 60 градусов. Каковы размеры остальных трех углов?
Решение:
Мы знаем, что две ноги совпадают, поэтому это равнобедренная трапеция. Учитывая это, мы знаем, что два основных угла (T, H) имеют одинаковую меру. Поскольку нам задан угол H равным 60, мы также можем сказать, что
Учитывая это, мы знаем, что два основных угла (T, H) имеют одинаковую меру. Поскольку нам задан угол H равным 60, мы также можем сказать, что
Поскольку верхний и нижний углы являются дополнительными, мы знаем, что
Угол M = 180-60
Угол M = 120
По той же логике, угол A = 120 градусов.
Урок, проводимый г-ном Фелизом
Свойства, типы, определение и примеры
Согласно евклидовой геометрии, четырехугольник, у которого есть одна пара параллельных противоположных сторон, известен как трапеция. Слово трапеция произошло от греческого слова «трапеция», что означает стол. В этом уроке мы узнаем больше о свойствах трапеции на примерах.
Что такое трапеция?
Трапеция — это двухмерный четырехугольник (так как он состоит из четырех прямых линий), имеющий пару параллельных противоположных сторон.Противоположные параллельные стороны называются основанием, а непараллельные стороны называются ножками трапеции. Это замкнутая плоская форма, имеющая четыре стороны и четыре угла. Форма трапеции представлена как:
Это замкнутая плоская форма, имеющая четыре стороны и четыре угла. Форма трапеции представлена как:
На рисунке выше XY и WZ — это основания, а XW и YZ — ножки трапеции. Форму трапеции можно наблюдать в окружающих нас объектах, например:
Виды трапеций
Ниже представлены три основных типа трапеций:
- Равнобедренная трапеция
- Скален трапеция
- Трапеция правая
Трапеции классифицируются на основе длины ног или измерения их углов.Определение каждого типа трапеции вместе с ее формой дано ниже.
Свойства трапеции
У каждого четырехугольника есть свои особенности, которые делают его узнаваемым и отличным от остальных. Эти свойства позволяют лучше понять геометрическое построение формы. Характеристики трапеции перечислены ниже:
- Это двухмерная форма.
- Основания трапеции параллельны друг другу.
- Длина обеих диагоналей одинакова.

- Диагонали трапеции всегда пересекаются.
- Сумма соседних внутренних углов составляет 180 °.
- Сумма всех внутренних углов трапеции всегда равна 360 °.
Площадь и периметр трапеции
Возьмем трапецию, имеющую длину параллельных сторон a, b единиц соответственно и высоту «h».
Площадь трапеции определяется путем вычисления среднего значения оснований и умножения его результата на высоту.Следовательно, площадь трапеции = ((AB + DC) / 2) × AM = ((a + b) / 2) × h, где AB, CD показывают основания, а AM — высоту.
Периметр трапеции определяется суммой всех ее сторон. Следовательно, периметр трапеции ABCD = AB + BC + CD + AD.
Темы, связанные с Trapezium
Ознакомьтесь с этими интересными статьями, относящимися к концепции формы трапеции в геометрии.
Часто задаваемые вопросы о Trapezium
Что такое форма трапеции?
Двумерный четырехугольник, который имеет пару несмежных параллельных сторон и пару непараллельных сторон, называется формой трапеции. Похоже на вырезанный сверху треугольник.
Похоже на вырезанный сверху треугольник.
Как определить площадь трапеции?
Площадь трапеции можно найти, вычислив среднее значение оснований и умножив результат на высоту, то есть ((a + b) / 2) × h, где a и b — длины параллельных сторон, а h — высота трапеции.
Трапеция — четырехугольник?
Да, трапеция четырехугольная. У него четыре стороны, четыре вершины и четыре угла. Сумма всех четырех внутренних углов трапеции составляет 360 градусов.
Есть ли у трапеции параллельные стороны?
Да, у трапеции есть пара параллельных сторон, которые называются основаниями.
Может ли трапеция иметь прямой угол?
Да, трапеция может иметь прямой угол. Трапеция с парой прямых углов известна как прямая трапеция.
Каковы свойства трапеции?
Свойства трапеции приведены ниже:
- Основания всегда параллельны друг другу.
- Обе диагонали всегда пересекают друг друга.
- Сумма прилегающих внутренних углов трапеции 180 °.

- Сумма внутренних углов трапеции всегда составляет 360 °.
Какова формула площади трапеции?
Если ‘h’ — высота, а a и b — длины параллельных сторон трапеции, формула площади трапеции задается как квадратные единицы 1/2 × (a + b) × h.
Что такое равнобедренная трапеция?
Равнобедренная трапеция — это трапеция, у которой обе ноги или непараллельные стороны равны друг другу.Углы, противоположные этим двум равным сторонам, также равны.
В чем разница между трапецией и трапецией?
Трапеция и трапеция означают одно и то же. Они относятся к четырехстороннему многоугольнику, имеющему пару несмежных параллельных сторон и пару несмежных непараллельных сторон. Как правило, трапеция соответствует британскому английскому языку, а трапеция — это общий термин в американском английском.
Четырехугольники — объяснения и примеры
Различные типы форм отличаются друг от друга сторонами или углами.Многие формы имеют 4 стороны, но разница в углах их сторон делает их уникальными. Мы называем эти 4-сторонние формы четырехугольниками.
Мы называем эти 4-сторонние формы четырехугольниками.
Из этой статьи вы узнаете:
- Что такое четырехугольник.
- Как выглядят разные виды четырехугольников.
- Свойства четырехугольника.
Что такое четырехугольник?
Как следует из этого слова, « Quad » означает четыре, а « lateral » означает боковой.Следовательно, четырехугольник — это замкнутый двумерный многоугольник , состоящий из 4-линейных сегментов . Проще говоря, четырехугольник — это фигура с четырьмя сторонами .
Четырехугольники везде! Из книг, диаграмм, компьютерных ключей, телевизоров и мобильных экранов. Список реальных примеров четырехугольников бесконечен.
Типы четырехугольников
Имеется шесть четырехугольников в геометрии . Некоторые из четырехугольников наверняка вам знакомы, а другие могут быть не так знакомы.
Давайте посмотрим.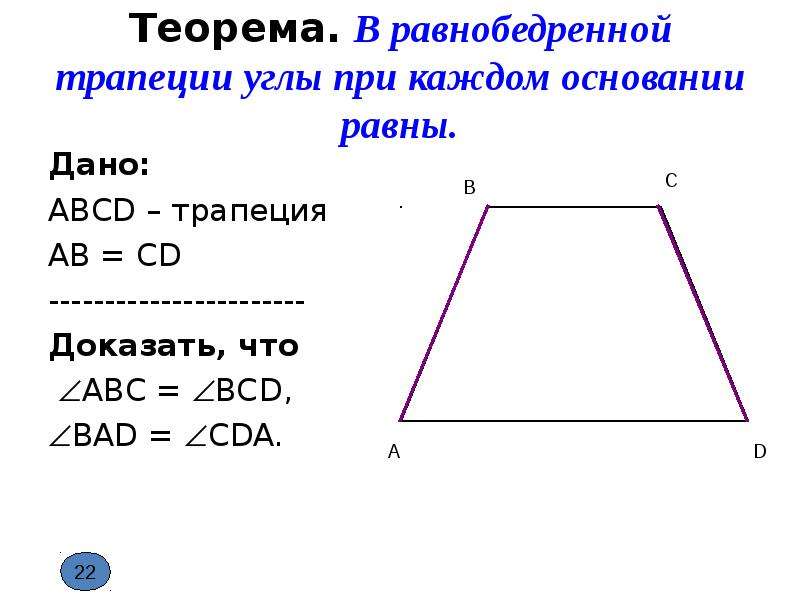
- Прямоугольник
- Квадраты
- Трапеция
- Параллелограмм
- Ромб
- Воздушный змей
Прямоугольник
Прямоугольник — это четырехугольник с 4 прямыми углами (90 °). В прямоугольнике обе пары противоположных сторон параллельны и равны по длине.
Свойства прямоугольников:
- Все углы прямые.
- Диагонали совпадают.
Прямоугольники очень удобно носить с собой. Например, коробки для обуви, разделочные доски, листы бумаги, рамы для картин и т. Д. Имеют прямоугольную форму.
Прямоугольники легко складывать, поскольку у них две пары параллельных сторон. Их прямые углы гарантируют, что построенные объекты, такие как дома, офисные здания, школы и т. Д., Будут стоять прямо и высоко.
Квадрат
Квадрат — это четырехугольник с 4 прямыми углами (90 °). В квадрате обе пары противоположных сторон параллельны и равны по длине.
Свойства квадрата:
- Все стороны квадрата равны.
- Все углы по определению прямые.
Реальные примеры квадратов включают компьютеры, ключи, подставки, пробелы на шахматной доске и т. Д.
Параллелограмм
Параллелограмм — это четырехугольник с двумя парами параллельных противоположных и равных сторон. Точно так же противоположные углы в параллелограмме равны по меру.
В параллелограмме PQRS сторона PQ параллельна стороне SR, и сторона PS параллельна стороне QR. Точка M — это середина двух диагоналей параллелограмма.
Следовательно, длина PM = MR, и длина SM = MQ
Ромб
Ромб — это четырехугольник, все четыре стороны которого имеют одинаковую длину. Противоположные стороны ромба равны и параллельны, а противоположные углы одинаковы.
ABCD представляет собой ромб, в котором AB параллельны и равны DC и AD также параллельны и равны BC.
Диагонали AC = BD, и M — это точка пересечения двух диагоналей.
Трапеция
Трапеция или трапеция является равносторонней с одной парой противоположных параллельных сторон. Стороны трапеции называются основаниями, а перпендикулярная линия от любой вершины трапеции к основанию называется высотой.
ABCD — это трапеция, у которой сторона BD параллельна стороне CA. Перпендикулярная линия DM — это высота ( h ) трапеции, а BD и CA — основания.
Воздушный змей
Воздушный змей представляет собой четырехугольник с двумя парами длин сторон, которые примыкают друг к другу.
Свойства ромба
- Все стороны совпадают по определению.
- Диагонали делят углы пополам.
- Диагонали воздушного змея пересекают друг друга под прямым углом.
Свойства четырехугольника
Свойства четырехугольника включают:
- Каждый четырехугольник имеет 4 стороны, 4 вершины и 4 угла.
 4
4 - Суммарная величина всех четырех внутренних углов четырехугольника равна всегда равен 360 градусам.
- Сумма внутренних углов четырехугольника соответствует формуле многоугольника i.е.
Сумма внутренних углов = 180 ° * (n — 2), где n равно количеству сторон многоугольника
- Прямоугольники, ромб и квадраты — это все типы параллелограммов.
- Квадрат — это одновременно ромб и прямоугольник.
- Прямоугольник и ромб не квадратные.
- Параллелограмм — это трапеция.
- Трапеция не параллелограмм.
- Воздушный змей — это не параллелограмм.
Классификация четырехугольников
Четырехугольники подразделяются на два основных типа:
- Выпуклые четырехугольники: это четырехугольники с внутренними углами менее 180 градусов, и две диагонали находятся внутри четырехугольников.К ним относятся трапеция, параллелограмм, ромб, прямоугольник, квадрат, воздушный змей и т. Д.
- Вогнутые четырехугольники: это четырехугольники с по крайней мере одним внутренним углом больше 180 градусов, и по крайней мере одна из двух диагоналей находится за пределами четырехугольника.
 Дротик — это вогнутый четырехугольник.
Дротик — это вогнутый четырехугольник.
Есть еще один менее распространенный тип четырехугольников, называемый сложными четырехугольниками. Это скрещенные фигуры. Например, скрещенная трапеция, скрещенный прямоугольник, скрещенный квадрат и т. Д.
Давайте поработаем над несколькими примерами задач о четырехугольниках.
Пример 1
Внутренние углы неправильного четырехугольника равны; x °, 80 °, 2x ° и 70 °. Рассчитайте значение x.
Решение
По свойству четырехугольника (сумма внутренних углов = 360 °), мы имеем
⇒ x ° + 80 ° + 2x ° + 70 ° = 360 °
Упростите.
⇒ 3x + 150 ° = 360 °
Вычтите 150 ° с обеих сторон.
⇒ 3x + 150 ° — 150 ° = 360 ° — 150 °
⇒ 3x = 210 °
Разделите обе стороны на 3, чтобы получить;
⇒ x = 70 °
Следовательно, значение x равно 70 °
А углы четырехугольников равны; 70 °, 80 °, 140 ° и 70 °.
Пример 2
Внутренние углы четырехугольника равны; 82 °, (25x — 2) °, (20x — 1) ° и (25x + 1) °. Найдите углы четырехугольника.
Найдите углы четырехугольника.
Решение
Общая сумма внутренних углов в четырехугольнике = 360 °
⇒ 82 ° + (25x — 2) ° + (20x — 1) ° + (25x + 1) ° = 360 °
⇒ 82 + 25x — 2 + 20x — 1 + 25x + 1 = 360
Упростить.
⇒ 70x + 80 = 360
Вычтите обе стороны на 80, чтобы получить;
⇒ 70x = 280
Разделим обе части на 70.
⇒ x = 4
Путем подстановки
⇒ (25x — 2) = 98 °
⇒ (20x — 1) = 79 °
⇒ (25x + 1) = 101 °
Следовательно, углы четырехугольника равны; 82 °, 98 °, 79 ° и 101 °.
Практические вопросы- Рассмотрим параллелограмм PQRS, где
- Найдите 4 внутренних угла ромба, стороны которого и одна из диагоналей равны.
Ответы
- 60 °, 60 °, 120 ° и ° 120.
Радиус описанной окружности равнобедренной трапеции с учетом сторон и диагонали Калькулятор
Радиус описанной окружности равнобедренной трапеции с учетом сторон и диагонали Формула
радиус = (сторона A * основание A * диагональ) / sqrt ((сторона A + диагональ + основание A) * (диагональ A + основание A, сторона A) * (сторона A + диагональ-основание A) * (сторона A + основание A-диагональ A))
r = (S a * B a * d) / sqrt ((S a + d + B a ) * (da + B a -S a ) * (S a + дБ a ) * (S a + B a -da))
Что такое трапеция.
 .?
.?Трапеция, также известная как трапеция, представляет собой плоскую замкнутую форму, имеющую 4 прямые стороны с одной парой параллельных сторон. Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ножками. У трапеции тоже могут быть параллельные ножки. Параллельные стороны могут быть горизонтальными, вертикальными или наклонными. Расстояние по перпендикуляру между параллельными сторонами называется высотой. Трапеция называется параллелограммом, если обе пары ее противоположных сторон параллельны.Трапеция считается квадратом, если обе пары ее противоположных сторон параллельны; все его стороны равной длины и расположены под прямым углом друг к другу.
Как рассчитать радиус описанной окружности равнобедренной трапеции с учетом сторон и диагонали?
Радиус описанной окружности равнобедренной трапеции с учетом сторон и диагонали калькулятор использует радиус = (сторона A * основание A * диагональ) / sqrt ((сторона A + диагональ + основание A) * (диагональ A + основание A-сторона A) * (сторона A + диагональ-основание A) * (сторона A + основание A-диагональ A)) для вычисления радиуса, Радиус описанной окружности равнобедренной трапеции с заданными сторонами и диагональной формулой определяется как радиус окружности, описывающей равнобедренную трапецию, когда дано значение меньшей стороны и диагонали. Радиус обозначается символом r .
Радиус обозначается символом r .
Как рассчитать радиус описанной окружности равнобедренной трапеции по сторонам и диагонали с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для вычисления радиуса описанной окружности равнобедренной трапеции с учетом сторон и диагонали, введите Сторона A (S a ) , основание A (B a ) , диагональ (d) и диагональ A (da) и нажмите кнопку расчета. Вот как Радиус описанной окружности равнобедренной трапеции с учетом сторон и расчета диагонали можно объяснить с заданными входными значениями -> 537.1517 = (8 * 10 * 8) / sqrt ((8 + 8 + 10) * (5 + 10-8) * (8 + 8-10) * (8 + 10-5)) .
Что такое четырехугольник? [Определение, факты и пример]
Что такое четырехугольник?Многоугольник состоит из четырех вершин или углов.
Мы можем найти форму четырехугольников в различных предметах вокруг нас, например, в шахматной доске, колоде карт, воздушном змеи, кадке с попкорном, вывеске и стрелке.
- Четырехугольник имеет 4 стороны, 4 угла и 4 вершины.
- Четырехугольник может быть правильным или неправильным.
- Сумма всех внутренних углов четырехугольника составляет 360 °.
Четырехугольники можно разделить на параллелограммы, квадраты, прямоугольники и ромбы. Квадрат, Прямоугольник и Ромб тоже параллелограммы.
Вот список типов четырехугольников с их названиями, изображениями и свойствами:
| Название четырехугольника: | Изображение четырехугольника: | Свойства четырехугольника: |
| Параллелограмм | Противоположные стороны параллельны. Противоположные стороны равны. Противоположные углы равны. | |
| Квадрат | Все стороны равны. Все углы равны и составляют 90 °. | |
| Прямоугольник | Противоположные стороны параллельны. Противоположные стороны равны. Все углы равны и составляют 90 °. | |
Ромб | Все стороны равны. Противоположные углы равны. | |
| Трапеция | Противоположные стороны параллельны. Смежные углы в сумме составляют 180 °. |
Интересные факты
|
Четыре стороны и четыре углы тоже,
Найдите четырехугольник на полу в ванной.
Другой вы можете увидеть в деревянной двери,
Или в лодке и веслах, у самого берега моря !!
Давайте сделаем это!Вместо того, чтобы раздавать своим детям четырехугольные листы-раскраски, попросите их наблюдать и отмечать предметы в форме правильных и неправильных четырехугольников, например, в телевизоре, ноутбуке, книге или воздушном змее. Далее вы можете обсудить и показать видео, чтобы рассмотреть свойства разных четырехугольников.
Связанный математический словарьполигонов — четырехугольники — в глубину
Есть много разные виды четырехугольников, но все они имеют несколько общих черт: все они имеют четыре стороны, компланарны, имеют две диагонали, а сумма их четырех внутренних углов равняется 360 градусам. Вот как они похожи, но что их отличает?
Мы знаем многих
четырехугольники по их особой форме и свойствам, как квадраты. Помните,
если вы видите слово четырехугольник, это не обязательно означает фигуру с
особые свойства, такие как квадрат или прямоугольник! В словесных задачах будьте осторожны
не предполагать, что у четырехугольника есть параллельные или равные стороны, если только
что заявлено.
Помните,
если вы видите слово четырехугольник, это не обязательно означает фигуру с
особые свойства, такие как квадрат или прямоугольник! В словесных задачах будьте осторожны
не предполагать, что у четырехугольника есть параллельные или равные стороны, если только
что заявлено.
Специальные четырехугольники
ср может использовать диаграмму Венна, чтобы помочь нам сгруппировать типы четырехугольников.
Диаграмма Венна использует перекрывающиеся круги, чтобы показать отношения между группами объектов.Все «четырехугольники» можно разделить на три подгруппы: общие четырехугольники, параллелограммы и трапеции.
— это прямоугольник
всегда ромб? Нет, потому что все четыре стороны прямоугольника не обязательно
быть равным. Однако наборы прямоугольников и ромбов пересекаются, и
их пересечение — это множество квадратов — все квадраты представляют собой прямоугольник
и ромб.
Можем поставить квадраты на пересечении двух кругов.
Из этой диаграммы, вы можете видеть, что квадрат — это четырехугольник, параллелограмм, прямоугольник, и ромб!
— это трапеция параллелограмм? Нет, потому что у трапеции только одна пара параллельных сторон. Поэтому мы должны показать набор трапеций отдельным кружком на Диаграмма Венна.
А как насчет воздушных змеев? Воздушные змеи — это четырехугольники, которые могут быть параллелограммами . Если их две пары сторон равны, он становится ромбом, а если их углы равны, он становится квадратом.
Ссылки по теме:
Формулы площади
Формулы периметра
назад наверх
.
 Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции.
Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции.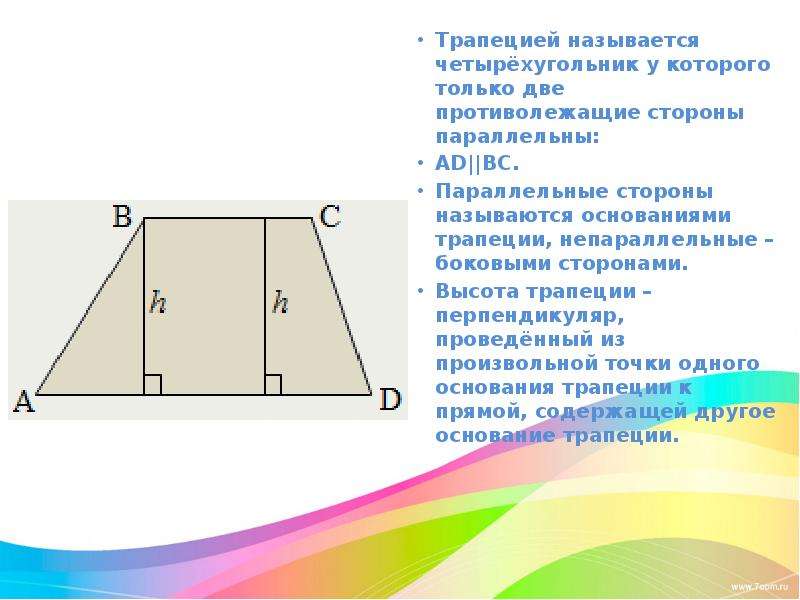
 Введите свой запрос:
Введите свой запрос:


 Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны;
Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны;








 4
4 Дротик — это вогнутый четырехугольник.
Дротик — это вогнутый четырехугольник.