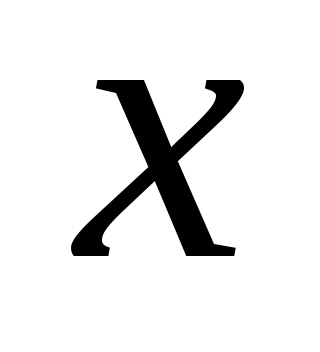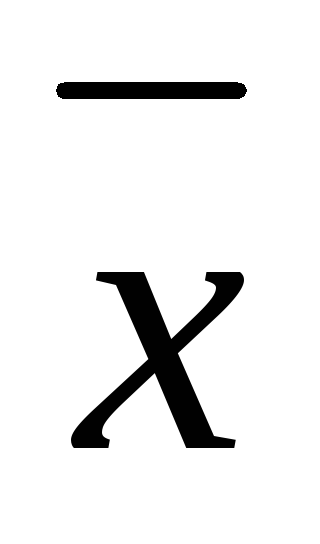Урок математики по теме «Выражения». 1-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели: учить составлять простые задачи и выражения по рисункам; закреплять навыки счета в пределах семи, сложение и вычитания чисел на числовом отрезке, закрепить сравнение чисел с помощью составления пар, умения находить взаимосвязь между частью и целым, суммой и разностью.
Оборудование: карточки с цифрами, материал для счета.
Ход урока
I. Организационное начало.
Ребята, сегодня у нас гости. Повернитесь к ним и поздоровайтесь. Спасибо. Садитесь. Давайте настроимся на работу. Облокотитесь на спинку стула. Закрыли глазки и повторяйте за мной про себя слова.
Я все умею.
Я все могу.
Я спокоен.
Я уверен в себе.
Я сосредоточен.
Открываем глазки. Что ж я вам желаю хорошо поработать, а вы мне пожелайте удачи.
II. Актуализация опорных знаний.
1. Работа со смарт доской.
Ребята, посмотрите на доску.
Белочки грибы сушили,
Ну а посчитать забыли
Кто ответит быстро, детки,
Хватит ли грибов всем белкам? (Хватит)
Cлайд 1
Как вы узнали? (Грибов 7, а белок 6)
Докажите? Как вы будете доказывать? (Составим пары. Знаки соответствия)
Сколько белок? (6)
Каким числом обозначим?(6)
Сколько грибов? (7)
Каким числом обозначим? (7)
Какой вывод можно сделать? 7>6
Прочитайте, что нам говорят белки.
Cлайд 2
А скажите мне, как же образовалось число семь в числовом ряду? (К 6 +1)
Молодцы!
Cлайд 3
Кто догадался, что нужно выполнить? (Поставить все числа по порядку)
Давайте попробуем!
Что интересного заметили? (Образовался натуральный ряд)
Какую закономерность вы видите? (Каждое число увеличится на 1)
2. Работа в тетрадях.
Математический диктант.
Открыли свои тетради. Нашли точку. В этой клеточки начинам работу. Внимание.
- Чему равна сумма чисел 6 и 1? (6+1=7)
- Уменьшаемое 7, вычитаемое 2. Чему равна разность? (7-2=5)
- Первое слагаемое 2, второе 5. Найдите сумму? (2+5=7)
- Чему равна разность чисел 7 и 3? (7-3=4)
Хорошо, давайте проверим.
6+1=7
7-2=5
2+5=7
7-3=4
Посмотрите на следующее задание. Что нужно сделать?
Cлайд 4
Молодцы!
Физминутка
А теперь все дружно встали
Ножками потопали
Ручками похлопали
Покружились, повертелись
И за парты все уселись
Глазки крепко закрываем
Дружно до пяти считаем
Открываем. Поморгали.
Продолжаем работу.
III. Открытие нового.
Ребят, а может кто-нибудь знает как называется эти записи? (Выражение) если дети не отвечают, я сама говорю, что такая запись в математике называется “выражение” и тема нашего урока “Выражения”.
А вот что такое выражения мы сейчас узнаем.
При помощи веера ответьте мне на мой вопрос.
На полянке у дубка
Еж увидел два грибка
Походил вокруг осин
И нашел еще один
Ну-ка кто считать готов
Сколько еж нашел грибов?
Сколько всего грибов стало? (3)
Каким действием узнали? (Сложением)
Почему вы использовали это действие?
Этот математический рассказ можно проиллюстрировать.
Cлайд 5
Сколько еж встретил сначало грибов? (2)
Каким числом обозначим? (2)
Покажите карточку с соответствующим числом.
Что произошло дальше? (Он увидел еще один)
Каким числом обозначим? (1)
Покажите карточку с соответствующим числом
Какой знак нужно поставить между числами? (+)
Почему? (Грибы объединились, их стало больше)
2+1 – вот такая запись называется выражением.
«Выражение» показывает, какое действие выполнили.
IV. Закрепление первичных знаний.
Cлайд 6
Найдите здесь выражения.
Что такое выражение? (Запись действия, которое произошло)
1. Работа по учебнику.
Открываем учебники на с.6. №1
Дети в учебники и одновременно на доске.
Рассмотрите, что изменилось? Запишите недостающие числа и выражения.
Cлайд 7
Почему на картинке записано число 2? (Было 2 котенка)
Почему над стрелочкой отмечено +3? (Прибежало еще 3)
Что обозначает выражение? (Было 2 котенка, к ним прибежало еще 3)
Сколько яблок на картинке? (7)
Каким числом обозначим? (7)
Что обозначает -1? (одно съели)
Какое выражение надо записать? (7-1)
И т.д.
№ 2. Кто догадался что нужно сделать?
Cлайд 8
Посмотрите на выражение
Прочитайте его. 1+6
Что заметили? (Сливы разбили на группы. В одну группу 1 сливу в другую группу 5 слив)
Б) Прочитайте выражение 2+5
Как нужно разбить данную совокупность?
В) самостоятельно запишите выражение.
Физминутка для глаз
Cлайд 9
V. Закрепление нового материала.
2. Работа со смарт доской.
Рассмотрите рисунок.
Как называется это дерево?
Почему вы так решили?
Как называются данные записи?
Прочитайте первое выражение.
Cлайд 10
Что обозначает число 3? (Яблоки на земле)
— Что обозначает число 4? (Яблоки на дереве)
Что можем узнать?
Каким действием?
Так что же обозначает все выражение?
Кто прокомментирует третье выражение?
Что мы найдем в четвертом выражении?
Составьте с помощью выражения математические рассказы по рисунку.
I вариант по первому выражению.
II вариант по третьему выражению.
VI. Самостоятельная работа.
Cлайд 11
А теперь составьте выражения и запишите их в тетрадь. Вы должны составить еще один столбик. Внимание на доску. Отступаем от записи в сторону три клеточки ставим точку и начинаем записывать.
Проверяем
Cлайд 12
VII. Итог урока.
Cлайд 13
Посмотрите на ваши столбики. В каком столбике записаны выражения? (Во втором)
А что такое выражение? (Математическая запись, которая показывает действие)
Молодцы всем спасибо!
Cлайд 14
Примечание.
Слайды 1-4, 10-14 выполнены в программе SmartBoard, но для наглядности они же переконвертированы в PowerPoint.
urok.1sept.ru
Названия математических выражений
Именование выражений
Если в алгебраическом выражении последнее по порядку действие является сложением, то выражение называется суммой. Например, выражения:
a + b, ab + 5, a2 + b2, a + b(x + y)
это суммы.
Если последним действием является вычитание, то выражение называется разностью. Например, выражения:
27 — a, a2 — b2, a — b(x + y)
это разности.
Если в выражении последним действием является умножение, то такое выражение называется произведением. Например, выражения:
ab, (a — b)c, a3b3
это произведения.
Произведение, составленное из нескольких букв, принято записывать с соблюдением алфавитного порядка. Например, вместо b4a3c2 пишут a3b4c2.
Если в выражении последним действием является деление, то такое выражение называется частным. Например, выражения:

это частные.
Если в выражении последним действием является возведение в степень, то такое выражение называется степенью. Например, выражения:
a3, (a — b)2, (ab)4это степени.
Если последним действием является возведение во вторую степень, то выражение называется квадратным, а если в третью, то кубом.
Полные словесные формулировки
- a2 + b2 — сумма квадратов чисел a и b
- (a + b)2 — квадрат суммы чисел a и b
- (a + b)(a — b) — произведение суммы чисел a и b на их разность
- a3 — b3 — разность кубов чисел a и b
- (a — b)3 — куб разности чисел a и b
- (a + b)n — n-я степень суммы чисел a и b

- 3a2b — утроенное произведение квадрата числа a на число b
Обратите внимание на то, что полное название выражения a2 + b2 мы начали со слова «сумма», потому что в этом выражении последним действием является сложение. Полное название выражения (a + b)2 мы начали со слова «квадрат», потому что в этом выражении последним действием является возведение в квадрат. Полное название выражения
a2 — b2 мы должны начинать со слова «разность», а выражение a2b2 — со слова «произведение».
Если бы последним действием было бы деление, то мы должны были бы начинать формулировку со слова «частное».
naobumium.info
Выражения в математике. | Александр Будников
Числовые и алгебраические выражения и их преобразования.
Как работать с математическими выражениями?
Допустим, перед вами пример. Хоть простой, хоть суперсложный (уравнение, неравенство, интеграл, производная и т.д….). Допустими, вы не Витя Перестукин и с математикой на «ты». Сможете, глядя на пример, сразу дать ответ?
В 99% случаев – нет. Если вы не гений математической мысли, конечно.)
Почему? А потому, что вам, так или иначе, придётся решать этот пример. Что значит «решать»? Это значит, последовательно, шаг за шагом, этот пример упрощать, добираясь до окончательного ответа. Или, по-другому, преобразовывать. Естественно, все эти фокусы (т.е. преобразования) надо проделывать по определённым правилам математики. Вот насколько успешно вы проведёте эти самые преобразования, настолько вы и сильны в математике.)
Так вот, имейте в виду: если вы не умеете делать правильные преобразования выражений, в математике вы не сможете сделать НИЧЕГО. Вообще ничего. Грустная перспектива? Вот и я так думаю.
Чтобы нас с вами не постигла столь печальная участь, имеет смысл разобраться в этой теме. Тем более тема достаточно простая. Разберёмся?:)
Что такое выражение в математике?
Выражение в математике (или – математическое выражение) – это, фактически, язык, на котором говорит вся математика. Да-да! Какую бы задачу мы с вами ни решали (хоть простую, хоть сложную), без математических выражений – никак. Любые формулы, дроби, уравнения, неравенства, синусы, логарифмы, функции, производные, интегралы и т.д. – это всё состоит из математических выражений. Намёк понятен?)
2+3 – это математическое выражение. a2 – b2 – это математическое выражение. И здоровенная дробь, и интеграл, и даже одно число или одна буковка – это всё математические выражения.
Например, уравнение:
3x+1 = 2x-5
состоит из двух математических выражений, соединённых знаком равенства «=» (равно).
Неравенство:
x2-4x+4≤0 – это тоже два математических выражения, соединённых знаком «≤» (меньше либо равно).
Короче говоря, термин «математическое выражение» применяется, чаще всего, чтобы не мычать, как корова и не кукарекать, как петух…
Спросят у вас, к примеру, что такое разность квадратов двух выражений. Первый вариант ответа: «Это ммммм… такая фиговина… Может, я лучше напишу разность? Вам какую?»
А человек в теме уверенно и с блеском в глазах ответит: «Разность квадратов двух выражений – это математическое выражение, представляющее собой произведение разности этих выражений и их суммы»!
Или: что такое квадратный корень? Квадратный корень – это математическое выражение, состоящее из подкоренного выражения и знака корня (радикала).
Согласитесь, второй вариант ответа выглядит куда более солидно и научно.)
Вот в таких вопросах фраза «математическое выражение» очень и очень удобна. Чтобы не объясняться на пальцах, как иностранные туристы в экзотической стране.
Гораздо сложнее – это конкретные математические выражения и работа с ними. Это совершенно другое дело.
Дело всё в том, что у каждого вида математических выражений имеется свой набор правил и приёмов, которому необходимо следовать при работе с ними.
У чисел – свой набор, у буквенных выражений – свой, у дробей – свой, у всяких там синусов, логарифмов, производных, интегралов – свои наборы действий. В каких-то наборах эти правила похожи или даже совпадают, а где-то – кардинально отличаются. Но пугаться этих жутких слов не надо. Эти страшные понятия мы с вами обязательно освоим в соответствующих разделах. А здесь мы с вами поработаем только с двумя видами математических выражений. А именно – с числовыми выражениями и с алгебраическими выражениями.
Что такое числовое выражение?
Что такое числовое выражение? Всё проще пареной репы.) Числовое выражение – это какое-то выражение с числами. Да-да, всего-навсего. Математическое выражение, составленное из цифр, знаков действий, скобок, знаков равенства/неравенства – это всё числовые выражения.
Например:
10-6 – числовое выражение,
(3-2,1)·0,5 – числовое выражение.
Или даже вот эти монстры:
это всё числовые выражения.
Да, в последнем примере появились специальные математические символы – радикал, значок логарифма и значок синуса. Но в этом выражении тоже нет букв. Только числа! Это самое главное.
Короче говоря, любые числа, дроби, примеры на вычисление без иксов, игреков и прочих буковок – это всё числовые выражения. Намёк понятен?)
В чём главный признак числового выражения? В том, что в нём нет букв. Вообще никаких. Математические значки (если надо) – пожалуйста. А вот букв – нету. Это ключевой признак.)
Что же можно делать с числовыми выражениями? Числовые выражения, как правило, можно (и нужно) считать. Для этого, бывает, приходится менять знаки, раскрывать скобки (или наоборот, заключать в скобки), сокращать, выносить общий множитель, раскладывать на множители т.д. То есть, делать преобразования числовых выражений. Но о преобразованиях выражений – чуть позже. Терпение, друзья.)
А здесь мы с вами разберёмся с одним забавным случаем, когда с числовым выражением делать ничего не надо. Совсем! Эта приятная операция (ничего не делать)) производится, когда числовое выражение не имеет смысла.
Понятное дело, что если мы с вами напишем какую-то белиберду типа 4+)-(=), то делать ничего и не будем. Ибо непонятно, что с этим делать. Ну, разве посчитать количество скобочек.)
Однако, попадаются в математике и внешне вполне себе благопристойные выражения.
Например, такое:
Однако это числовое выражение тоже не имеет смысла. Почему? А потому, что если выписать отдельно знаменатель дроби да посчитать, получается ноль. На который делить нельзя. Нет такой операции в математике!
Или вот такое:
И это выражение тоже не имеет смысла! Догадались? А вы посчитайте, что под корнем получится.) Минус единичка там получится. А извлекать квадратный корень из отрицательных чисел в средней школе не учат (а вот в ВУЗе — пожалуйста). Это тоже запретное действие в (школьной) математике.
Конечно, чтобы сделать такое умозаключение, пришлось потрудиться и посчитать, что в знаменателе да под корнем получится. А в примерах может быть такого понаворочено, что… Тут уж ничего не поделаешь.)
Короче говоря, числовое выражение не имеет смысла тогда, когда в результате преобразований этого самого выражение получается запретное действие. Запретных действий в математике не так уж много: это деление на ноль, извлечение корня чётной степени из отрицательного числа, ограничения в логарифмах, в тригонометрии и в арках. Это обсуждается в соответствующих темах.
Итак, что такое числовое выражение – вникли (надеюсь).
Когда числовое выражение не имеет смысла – осознали.
Пора двигаться на следующий уровень.)
Что такое алгебраическое выражение?
Если в игру дополнительно вступают буквы, то выражение становится… Да! Оно становится алгебраическим выражением!
Например:
a+6, x+y, 2a/b, c2 + 9, x2+2x+1
В общем, вы поняли…
Понятие алгебраическое выражение – более широкое, чем числовое. Почему? Потому, что в понятие алгебраические выражения входят и все числовые тоже. То есть, любое числовое выражение – это и алгебраическое выражение. Только без букв. Типа всякий русский – россиянин, но не всякий россиянин – русский.)
Такие выражения ещё называют выражениями с переменными. Или просто буквенными выражениями. Почему буквенное – ясно, надеюсь. Ну, раз буквы есть.) Фраза «выражение с переменными» тоже не требует особого умственного напряжения. Если, конечно, понимать, что под буквами могут скрываться различные числа. Всякие могут скрываться: и 5, и -30 – всё что угодно. То есть, букву в алгебраическом выражении можно заменять на разные числа. Какие хотим.
В выражении х+6, например, буква икс – переменная величина. Или коротко – переменная. В отличие от шестёрки, которая – величина постоянная. Или коротко – постоянная.
Что означает термин «алгебраическое выражение»? Он означает, что, в отличие от арифметики, (которая, как известно, работает только с числами), мы должны использовать законы и правила алгебры. Непонятно? Поясняю на несложном примере:
2·3 = 3·2
Что можно сделать? Посчитать и всего делов-то.) Слева шестёрка и справа тоже. А для каких-нибудь других чисел такое выполняется? Тоже можно посчитать и сравнить. Но чисел в математике – бесконечное количество. И что же? Каждый раз считать и сравнивать?!
А вот если мы шагнём из арифметики в алгебру и распишем данное равенство через алгебраические выражения:
ab = ba,
то мы сразу решим все вопросы! Для всех чисел махом! Мощная штука – алгебра.)
А когда алгебраическое выражение не имеет смысла? Что такое ОДЗ?
С числовыми выражениями всё ясно. Там на ноль делить нельзя да корни извлекать из отрицательных чисел, ну и некоторые другие логарифмические/тригонометрические фишки. А тут как узнаешь, на что делим или из чего извлекаем…
Очень просто! Точно так же!
Возьмём, к примеру, алгебраическое выражение:
Имеет ли оно смысл? Бэ-то любое число… Любое-то любое… Но есть среди этого бесконечного набора чисел такое значение b, при котором это выражение точно не имеет смысла. Догадались? Да! Это единичка (b=1). Если в знаменателе дроби заменить переменную b (как по-школьному говорят «подставить») на единичку, то в знаменателе нолик получится. На который делить нельзя. Вот и получается, что наше выражение имеет смысл при любом b, кроме единички.
А остальные b подставлять можно? Конечно! Хоть 5 возьмите, хоть -100 – наше выражение иметь смысл будет. В таких случаях говорят, что выражение имеет смысл при любом b , кроме 1.
И вот этот самый весь остальной набор чисел, которые можно подставлять в данное выражение, и который не приводит к запретному действию, в математике называется областью допустимых значений (ОДЗ) выражения. В нашем примере областью допустимых значений (ОДЗ) служат все числа, кроме единички.
Другой пример:
Видим квадратный корень. Сразу соображаем (из теории, т.е. основ), что корень квадратный извлекается только из положительных чисел и нуля. А вот из отрицательных – ни в какую!
Вот и обезопасим себя вот такой записью:
x-2≥0
x≥2
Таким образом, данный хитрое выражение имеет смысл лишь при иксах, больших (или равных) двойке. Число, скажем, 3, вполне себе прокатит, а вот ноль — никак нет: он меньше двойки. ОДЗ — штука жёсткая!
Уловили принцип? Внимательно смотрим на выражение с переменными, ищем опасные места и смотрим, при каких переменных получается запретная операция. И исключаем эти значения из ОДЗ.
А потом внимательно читаем задание. Чего хотят-то? Внимательное чтение никто не отменял, да… Если в задании спрашивают, при каких значениях переменной выражение имеет смысл, то ответом будут служить все значения, кроме запретных.
Или наоборот: при каких значениях переменных выражение не имеет смысла? Тогда найденные запретные значения и будут служить ответом к заданию. Почувствуйте разницу, что называется.)
А теперь вопрос к размышлению. А зачем нам смысл выражения? Есть он, нет его… Какая разница? Дело всё в том, что это понятие становится крайне важным в старших классах! Да и в ВУЗе тоже. Без этого важного понятия вы не сможете проделывать такие простые операции, как нахождение области определения функции, ОДЗ уравнений, неравенств. Что неизбежно будет приводить к полному провалу и непониманию всех этих серьёзных тем. Увы.)
Итак, самое главное из сегодняшнего урока:
1. Числовое выражение — это выражение с числами (т.е. без букв).
2. Если, помимо чисел, в выражении есть буквы, то оно называется алгебраическим выражением.
3. Как числовое, так и алгебраическое выражение, может иметь смысл, а может и не иметь. При встрече с алгебраическим выражением первым делом ищем его ОДЗ.
4. Все допустимые значения переменной (переменных), не приводящих к запретному действию, составляют Область Допустимых Значений (ОДЗ) алгебраического выражения. При необходимости ищем её!
Ну а в различных видах преобразований выражений мы с вами подробненько разберёмся и плотно поработаем в следующих уроках этого раздела.)
abudnikov.ru
Урок по математике в начальной школе «Числовые выражения», 2-й класс
В формировании многих качеств, необходимых успешному современному человеку, может большую роль сыграть школьная дисциплина – математика. На уроках математики школьники учатся рассуждать, доказывать, находить рациональные пути выполнения заданий, делать соответствующие выводы. Общепризнанно, что «математика – самый короткий путь к самостоятельному мышлению», «математика ум в порядок приводит» как отмечал М.В. Ломоносов.
Деятельностный подход был разработан в трудах Алексея Николаевича Леонтьева, Даниила Борисовича Эльконина, Петра Яковлевича Гальперина, Александра Владимировича Запорожца в середине 20 века.
Педагогическая практика показывает, что формирование универсальных учебных действий, то есть действий, обеспечивающих умение учиться, самостоятельно искать, находить и усваивать знание – самый прогрессивный путь организации обучения.
Основу концепции деятельностного подхода к обучению составляет положение: усвоение содержания обучения и развитие ученика происходит в процессе его собственной деятельности.
Любое усвоение знаний строится на усвоении учеником учебных действий, овладев которыми, ученик смог бы усваивать знания самостоятельно, пользуясь различными источниками информации. Научить учиться (усваивать информацию) – главный тезис деятельностного подхода.
Цель: познакомить с понятием «числовое выражение», учить говорить на математическом языке.
Задачи:
- учить распознавать числовые выражения, правильно их читать, находить их значения;
- развивать логическое мышление, умение анализировать, делать выводы, развивать речь детей;
- воспитывать самостоятельность, упорство в достижении цели.
ХОД УРОКА
I. Оргмомент
– Сегодня у нас не совсем обычный урок. На уроке
присутствуют гости. Повернитесь и
поздоровайтесь с нашими гостями.
– Повернитесь ко мне.
С добрым утром начат день.
Первым делом гоним лень.
На уроке не зевать,
А работать и считать!
– Ребята, а что вы уже умеете делать? (Ответы
детей) Что уже знаете?
(На доске карточки с названием тем: «Во сколько
раз больше или меньше?» «Умножение и деление.
Часть числа.» «Решение задач на уменьшение и
увеличение в несколько раз» «Нахождение числа по
нескольким долям» «Нахождение нескольких долей
числа» «Название чисел в записях действий»)
– Начинаем урок математики.
II. Актуализация знаний
– На прошлом уроке математики вы учились
читать разные примеры, используя названия
компонентов и результата действия.
– Прочитайте по-разному примеры на доске: 8 + 2
(появляется карточка: «слагаемое +
слагаемое = сумма»)
8 – 2 (уменьшаемое – вычитаемое = разность)
8 * 2 (первый множитель • второй множитель = произведение)
8 : 2 (делимое : делитель = частное)
III. Постановка проблемы
На доске:
25 + 4 33 + а в – 7 6 • 8 с • 5 (15 – 7) + 4 18 : 3 • 6 – 3
– Разделите записи на карточках на две группы. (Ученик
у доски делит записи на группы) (Рассматриваются
несколько вариантов группировки)
– Какая запись оказалась лишней?
– Почему?
– Дайте общее название группе. А как ещё можно
назвать эти записи? (Выражения))
– Я предлагаю сыграть в игру «Как вы думаете?».
Мне нужны две пары.
Каждая пара получает лист – игровое поле и набор
карточек. (Играют на доске)
| ? | Числовые выражения | Нет |
4 > 40
7 = 7
x + 5 > 8
13 – 9
(16 – 9) • 2
63 : 9
– Карточки, на которых, по вашему мнению,
записаны числовые выражения, положите на сектор
«числовые выражения». Уверены, что на карточке не
числовые выражения – сектор «нет», сомневаетесь
– сектор «?».
(Выполняют)
– Как вы думаете, правильно или неправильно
ребята выполнили задание?
– Как бы вы определили тему нашего урока?
– Чему будем учиться на уроке?
– Откройте учебник на странице 68.
– Прочитайте тему урока вверху страницы.
– Рассмотрите страницу учебника и подумайте, о
чём вы хотели бы меня спросить по этой теме?
(На доске карточки-помощницы: Что…? Почему…?
Зачем…?)
(Если вопросов нет: «Наверное, вопросы у вас
появятся потом»)
IV. «Открытие» нового знания
– Что вы видите на стр. 68? (Таблицу)
– Прочитайте названия столбиков в таблице.
– Это четыре вопроса, в которых нам надо
разобраться.
– Что общего во всех записях 1-й колонки?
– Из чего состоит 1-я запись? (Из двух цифр, и
знака «+» между числами)
– Что они обозначают? (Числа)
(Аналогично рассматривается запись 2, 3 и 4)
– Что общего? Что в числовом выражении очень
важно?(Состоят из чисел)
На доске: 1. Числа
– Какие числа в первой записи? (во 2-й, 3-й, 4-й)
На доске: 1.
Числа
5;4
6;7
15;8
48;6
– Что ещё есть в записи кроме чисел? (Знаки
действий)
На доске: 1.
Числа
5;4
6;7
15;8
48;6
2. знаки действий
– Какой знак в первой записи? (второй, третьей, четвёртой)
На доске: 1.
Числа
5;4
6;7
15;8
48;6
2. знаки действий
+
•
–
:
– Работайте в парах: составьте новые
числовые выражения, используя те же числа и знаки
действий. Докажите.
(Работа в парах. Проверка.)
– Как называется вторая колонка? (Название
выражения)
– У каждого выражения есть имя. Кто догадался,
как определить название выражения?
– Поработайте в паре: обсудите, какое выражение
мы будем называть суммой? Произведением?
Разностью? Частным? (Обсуждение)
– Какое выражение мы будем называть суммой? (Выражение,
в котором числа соединены знаком « + »)
(Аналогично остальные)
На доске: 1.
Числа
5; 4
6;
7
15; 8
48; 6
2. знаки действий
+ – сумма
• – произведение
– – разность
: – частное
– Прочитайте выражения.
– Как называется 3-й столбик? (Вычисление)
– О чём рассказывает этот столбик? (Что с
выражением можно выполнить действия (вычислить,
найти ответ, сосчитать), решить)
– Можно выполнить действия, вычисления с
любым выражением.
– Всю ли таблицу рассмотрели?
– Как называется четвёртый столбик? (Значение
выражения)
– Кто догадался, что такое значение выражения?
Как бы вы объяснили, что такое значение
выражения? (Это число)
– Какое число?
– Как вы понимаете задание «вычислить значение
выражения»? (Выполнить вычисления, найти
результат, число)
На доске: 1.
Числа
5; 4
6; 7
15; 8
48; 6
2. знаки
действий +
– сумма
• – произведение
– – разность
: –
частное
есть значение выражения (его можно найти)
– Что же вы можете рассказать о выражении?
Физминутка
Мы немножко отдохнём.
Встанем, глубоко вздохнём.
Руки в стороны, вперёд.
Дети по лесу гуляли,
За природой наблюдали.
Вверх на солнце посмотрели –
И их всех лучи согрели.
Чудеса у нас на свете:
Стали карликами дети.
А потом все дружно встали,
Великанами мы стали.
Дружно хлопаем,
Ногами топаем!
Хорошо мы погуляли
И немножечко устали!
– Числа в выражении имеют своё название, а
значение выражения не имеет?
– Это справедливо?
– Посмотрите на стр. 68 учебника. О чём вели
разговор Волк и Заяц?
– Оказывается, название выражения и его значение
называются одинаково.
– Чему учились?
V. Комментирование решения типовых задач
– Потренируемся в применении наших знаний.
– Откройте тетрадь на стр. 41 № 129.
– Как будем рассуждать, является ли эта запись
выражением?
(Карточка пооперационного контроля:
Записи |
72 : 8 |
83 – 17 |
46 + |
1 + 0 = |
3 • 5 = 15 |
0 : 42 |
| Числа | ||||||
| Знаки действий | ||||||
| Вывод |
– Прочитай первую запись. Работаем на карточке
пооперационного контроля и делаем вывод.
(Работают над каждой записью при помощи
карточки)
– Кто понял, что такое числовое выражение?
– Чему учились?
– Откройте стр. 42 № 131 (1-я таблица).
– Заполним первую таблицу вместе.
– Что вы видите в таблице?
– Что мы должны сделать?
(Комментируют заполнение 1-й таблицы)
– Чему учились?
– Мне кажется, вы всё хорошо понимаете. А как вы
думаете, а эту запись – (15 – 7) + 4
– можно назвать числовым выражением?
– Почему?
– С такими выражениями мы ещё будем знакомиться
на уроках математики.
VI. Самостоятельная работа с самопроверкой в классе
– Откройте учебник на стр. 69. Найдите № 3.
– Прочитайте, что надо сделать.
– Кто не понял, что надо сделать, поднимите руки.
(Если не поняли, вернуться к табл. на стр. 68,
третья графа, ещё раз выяснить, что вычислить –
это сосчитать, решить, а значение выражения – это
число, значит, вычислить значение выражения –
значит решить выражение, найти число)
1 вар. – вычислить значения суммы и произведения,
2 вар. – разности и частного (запись задания на
доске)
(На доске появляется карточка самоконтроля:
1 вар.: 36 + 20 = 56 6 • 8 = 48
2 вар.: 60 – 3 = 57 21 : 7 = 3)
VII. Формирование системы знаний
– Что же такое числовое выражение?
– Нам много ещё чему надо учиться (если есть
время – можно рассмотреть № 1, 2 в учебнике)
– Поучимся вычислять выражения.
(Игра для повторения таблицы умножения «Лотерея
«Спринт»)
– Внимательно слушайте задание, делайте устные
вычисления и в таблице-заготовке вычёркивайте
ответ.
Задания к набору:
1. 5 : 5 5. 21 : 7 9. 4 • 3
2. 49 : 7 6. 27 : 3 10. 3 • 5
3. 3 • 6 7. 32 : 8 11. 18 : 9
4. 4 • 4 8. 48 : 6 12. 8 • 2 + 1
(Ответ: в результате из вычеркнутых чисел в таблице получается «5»: )
– Если у вас получилась оценка «5» из
зачёркнутых ответов, то вы справились с заданием
на отлично, если же нет – значит вы где-то
ошиблись, а значит, надо повторить таблицу
умножения и деления.
– Решите задачу. Запишите решение задачи
выражением.
Шарики воздушные –
Такие непослушные!
Было всех их семью восемь.
Девять в небо унеслись.
Сколько здесь их – разберись.
(Решение: 7 • 8 – 9 = 47 (ш.))
– Запишите решение задачи на доске.
VIII. Рефлексия
– Наш урок подходит к концу. Был ли он
интересен? Полезен?
– Узнали ли вы что-либо новое?
– Что же такое числовое выражение?
– Что повторили?
– На какой ступеньке знаний нашей лестницы вы
сейчас находитесь? Закрасьте на этой ступеньке
солнышко.
Хочу знать больше
Хорошо, но могу лучше
Пока испытываю трудности
IX. Домашнее задание
– Придумайт
urok.1sept.ru
Онлайн урок: Числовые и буквенные выражения по предмету Математика 5 класс
Числовые выражения вам уже хорошо знакомы.
В начальных классах на уроках математики, решая задачи и примеры, вы составляли и записывали числовые выражения и находили значения этих выражений.
Числовое выражение- это запись, состоящая из чисел, арифметических операций, скобок и иных специальных математических символов.

Числовым выражением можно назвать только такую запись, которая является осмысленной и составлена согласно математическим правилам.
Рассмотрим примеры числовых выражений.
4 — является числовым выражением.
2 + 17 — является числовым выражением.
247 + 13 — 3 — является числовым выражением.
84 + (273 — 16) — является числовым выражением.
Не каждую математическую запись из символов и знаков можно считать числовым выражением.
Числовое выражение всегда ориентировано на то, чтобы операции, входящие в него, могли быть выполнены.
Если числовое выражение невозможно вычислить, то оно не имеет смысла.
Пример.
45 + ( — + 1 — не является числовым выражением, данная запись представляет собой бессмысленный набор символов и знаков.
Существуют такие математические записи, которые на первый взгляд можно принять за числовые выражения, но вычислить их невозможно.
Пример.
15 : (37 — 22 — 15)
Число 15 необходимо разделить на результат операции в скобках, а он равен нулю.
Так как деление на нуль в математике запрещено, данную математическую операцию совершить невозможно, следовательно, запись 15 : (37 — 22 — 15) не вычислить, она не является числовым выражением.
Математические равенства и неравенства выражениями не являются, но равенства и неравенства состоят из математических выражений.
Два числовых выражения, соединенные знаком равно «=», называют числовым равенством.
Два числовых выражения, соединенные знаками больше «>» или меньше «<», называют неравенством.
Несмотря на то, что в записи равенств и неравенств присутствуют математически верно построенные комбинации из чисел и арифметических операций, они не являются математическими выражениями.
Например,
Запись вида 26 — 5 > 4 не является числовым выражением, это неравенство.
Запись вида 24 — 6 = 18 также не является числовым выражением, данная запись является равенством.
Смысл решения любой задачи, любого примера заключается в том, чтобы найти значение выражения, которое превращает его в верное равенство.
Число, которое получается после выполнения всех арифметических операций, называют значением числового выражения.
Следовательно, чтобы найти значение числового выражения, необходимо выполнить в определенном порядке все арифметические операции, указанные в выражении.
У числового выражения значение только одно.
Например, значение числового выражения (45 — 3) + (12 + 2) всегда равно 56, и только это значение является единственно верным.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Важно уметь не только верно записывать числовые выражения, но и уметь их правильно читать.
Чтобы прочитать числовое выражение нужно определить, какая арифметическая операция является последней при вычислении значения этого выражения.
Так, например, если последнее по порядку действие было сложение, то выражение называют «суммой».
Если последним действием является вычитание, то выражение называют «разностью».
Следовательно, если последним действием является умножение, то выражение называют «произведением», если деление- «частным».
Например, выражение (10 — 3) + (6 — 4) читается так: «Сумма разности чисел 10 и 3 и разности чисел 6 и 4».
Выражение (10 — 3)∙(6 — 4) читается так: «Произведение разности чисел 10 и 3 и разности чисел 6 и 4».
Умение составлять математические выражения и находить их значение используют при решении как простых, так и составных задач.
Рассмотрим пример решения составной задачи и выясним особенности процесса составления числовых выражений.
Известно, что любая составная задача содержит несколько простых.
Существуют различные способы оформления решения текстовых задач.
Чаще всего используют такие формы записи решения задач:
1. По действиям с пояснениями.
2. Выражением.
При решении составных задач важно выделить главное, сделать краткую запись, разделить задачу на простые, составить план решения.
Задача 1.
В первый день собрали 12 кг клубники, а во второй день на 2 кг больше.
Сколько килограммов клубники собрали за эти два дня?

Решение:
Запишем кратко условие задачи:
В I день — 12 кг клубники.
Во II день — на 2 кг больше, чем в I день.
Общее количество клубники в I и во II день- ?
Изобразим к задаче рисунок в виде схемы.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Чтобы определить, сколько собрали клубники за два дня, необходимо знать, какое количество клубники было собрано в первый и во второй день.
Из условия задачи известно количество клубники, собранной в первый день.
Неизвестно количество клубники, собранной во второй день.
Когда будет известно сколько собрали клубники во второй день, можно узнать какое количество ягод собрали за два дня.
Задачу решаем в два действия (каждое действие поясним).
1. Выясним сколько килограммов ягод собрали во второй день.
Известно, что в первый день собрали 12 кг клубники. Так как во второй день собрали на 2 кг больше, то во второй день собрали столько же, как в первый, и еще 2 кг.
Выполним сложение чисел 12 и 2, получим выражение 12 + 2.
Найдем значение данного числового выражения:
12 + 2 = 14 (кг) клубники собрали во второй день.
2. Вторым действием определим общее количество ягод, собранных за два дня.
Необходимо сложить все ягоды, который собрали в первый и во второй день, получим следующее выражение: 12 + 14.
Найдем значение данного числового выражения:
12 + 14 = 26 (кг) клубники собрали за два дня.
Ответ: 26 кг.
Как нам уже известно, решение задачи можно записать не только по действиям, но и в форме выражения.
Запись решения составной задачи с помощью составления по ней итогового числового выражения позволяет увидеть ход решения в целом, и такая запись сокращает время оформления задачи.
Составим числовое выражение для решения нашей задачи.
Согласно рассуждениям, изложенным выше, имеем следующие данные:
12 кг — клубники собрали в первый день.
12 + 2 кг — клубники собрали во второй день.
Определим общее количество ягод, собранных за два дня.
Сложив все ягоды, собранные в первый и во второй день, получим следующее числовое выражение:
12 + (12 + 2).
Вычислим значение данного выражения, выполнив последовательно все действия в нем.
Тогда запись решения задачи будет выглядеть так:
12 + (12 + 2) = 12 + 14 = 26 (кг) клубники собрали за два дня.
Ответ: 26 кг.
Попробуем решить вторую задачу.
Задача 2.
В первый день собрали 12 кг клубники, а во второй день на 5 кг больше.
Сколько килограммов клубники собрали за эти два дня?
Скорее всего вы заметили, что первая и вторая задачи отличаются только одним числом, а именно число 2 заменено на число 5.
Остальные условия задачи остались прежние.
Все логические рассуждения во второй задаче аналогичны рассуждениям первой.
Таким образом, имеем следующие данные:
12 кг — клубники собрали в первый день.
12 + 5 кг — клубники собрали во второй день.
Определим общее количество ягод, собранных за два дня.
Сложив все ягоды, собранные в первый и во второй день, получим следующее выражение:
12 + (12 + 5).
Вычислим значение данного выражения, выполнив последовательно все действия в нем.
Тогда запись решения задачи будет выглядеть так:
12 + (12 + 5) = 12 + 17 = 29 (кг) клубники собрали за два дня.
Ответ: 29 кг.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
ladle.ru
Математическая логика Высказывания и операции над высказываниями.
Высказыванием называется повествовательное предложение, о котором можно сказать истинно оно или ложно.
Москва — столица России.
Если студент учится на отлично, то он получит красный диплом.
Осадки — это снег или дождь.
Курица – не птица.
Пейте томатный сок.
Я лгу.
23<5
Высказываниями являются 1, 2, 3,4 и 7 предложения. Предложение 5 не является высказыванием, так как про него нельзя сказать истинно оно или ложно. Предложение 6 является логическим парадоксом.
Элементарным высказыванием называется высказывание, которое содержит одно утверждение (предложения 1,7).
Сложное (составное) высказывание состоит из элементарных высказываний связанных с помощью следующих предлогов и частиц: И, НЕ, ИЛИ, ЕСЛИ — ТО, ТОГДА И ТОЛЬКО ТОГДА и другие. Предложения 2,3,4 являются сложными высказываниями.
Операции над высказываниями.
Отрицанием высказывания х называется новое высказывание, которое истинно, если высказывание ложное и наоборот. Таблица истинности операции отрицания имеет вид:
|
|
0 | 1 |
1 | 0 |
Дизъюнкцией двух высказываний x и y (логическое «или»)называется новое высказывание, которое будет истинным тогда когда, когда хотя бы одно из высказываний будет истинным.
Конъюнкцией
двух высказываний x и y (логическое
«и»)называется
новое высказывание, которое будет
истинным тогда когда, когда оба
высказывания истины. Обозначение
операции конъюнкция — &(
Импликацией двух высказываний x и y («если – то») называется новое высказывание, которое ложно тогда, когда х (предпосылка) истинно, а у (следствие) ложно.
Эквивалентностью двух высказываний x и y («тогда и только тогда») называется новое высказывание, которое будет истинно , если высказывания х и у будут одновременно истинны или ложны.
Неодназночностью (суммой по модулю два) двух высказываний x и y («тогда и только тогда») называется новое высказывание, которое будет истинно тогда когда одно из высказываний х или у истинно, а другое ложно.
Штрих Шеффера (логическое «и — не») высказываний x и y — это новое высказывание, которое будет ложно тогда и только тогда когда оба высказывания истинны.
Стрелка Пирса (логическое «или — не») высказываний x и y — это новое высказывание, которое будет истинно тогда и только тогда когда оба высказывания ложны.
Для операций справедливы следующие приоритеты:, &, , , .
studfile.net
Что такое числовые выражения 🚩 выражения математика 🚩 Математика
Отличительной особенностью выражения является наличие математических действий. Оно обозначаются определенными знаками (умножения, деления, вычитания или сложения). Последовательность выполнения математических действий при необходимости корректируется скобками. Выполнить математические действия – значит найти значение выражения.Не всякую математическую запись можно отнести к числу выражений.
Равенства не являются выражениями. Присутствуют при этом в равенстве математические действия или нет, не имеет значения. Например, a=5 – это равенство, а не выражение, но и 8+6*2=20 тоже нельзя считать выражением, хотя в нем и присутствуют умножение и сложение. Этот пример тоже принадлежит к категории равенств.
Понятия выражения и равенства не являются взаимоисключающими, первое входят в состав второго. Знак равенства соединяет два выражения:
5+7=24:2
Можно это равенство упростить:
5+7=12
Выражение всегда предполагает, что представленные в нем математические действия могут быть выполнены. 9+:-7 – это не выражение, хотя здесь есть знаки математических действий, ведь выполнить эти действия невозможно.
Существуют и такие математические примеры, которые формально являются выражениями, но не имеют смысла. Пример такого выражения:
46:(5-2-3)
Число 46 необходимо разделить на результат действий в скобках, а он равен нулю. На нуль же делить нельзя, такое действие в математике считается запретным.
Существует два вида математических выражений.
Если выражение содержит только числа и знаки математических действий, такое выражение называется числовым. Если же в выражении наряду с числами присутствуют переменные, обозначаемые буквами, или чисел нет вообще, выражение состоит только из переменных и знаков математических действий, оно называется алгебраическим.
Принципиальное отличие числового значения от алгебраического состоит в том, что у числового выражения значение только одно. Например, значение числового выражения 56–2*3 всегда будет равно 50, ничего изменить нельзя. У алгебраического же выражения значений может быть много, ведь вместо буквы можно подставить любое число. Так, если в выражении b–7 вместо b подставить 9, значение выражения будет равно 2, а если 200 – оно будет составлять 193.
www.kakprosto.ru