Треугольник » Страница 7
Тема: Треугольник
Теория
Задачи
 Смотреть решение →
Смотреть решение → Смотреть решение →
Смотреть решение →Microsoft Word — геометрия-1.doc
%PDF-1.6 % 955 0 obj > endobj 952 0 obj >stream 2009-08-03T12:57:02ZMicrosoft Word — геометрия-1.doc2009-08-12T12:51:21+04:002009-08-12T12:51:21+04:00application/pdf
Как найти высоту у равнобедренного треугольника: Высота равнобедренного треугольника
Высота равнобедренного треугольника | Онлайн калькулятор
Равнобедренным треугольником называется
такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.
Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.Соответственно, в таком треугольнике можно провести три высоты, две из которых будут равны между собой, аналогично сторонам — это высоты, опущенные на боковую сторону треугольника а, а третья высота опускается на основание. Высота треугольника проводится из угла треугольника к противолежащей стороне под прямым углом. Большинство задач с высотой треугольника решаются через прямоугольные треугольники, которые она образует.
Рассмотрим каждый случай по отдельности.
Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты
 В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.
В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:
Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.
Площадь любого треугольника можно найти несколькими способами — например, через три стороны треугольника по формуле Герона, или через высоту, умножив ее на половину стороны, на которую она опущена. И тем, и другим способом получаются одинаковые значения площади, следовательно обе эти формулы можно друг к другу приравнять и отсюда вывести окончательную формулу высоты, опущенную на боковую сторону равнобедренного треугольника.
И тем, и другим способом получаются одинаковые значения площади, следовательно обе эти формулы можно друг к другу приравнять и отсюда вывести окончательную формулу высоты, опущенную на боковую сторону равнобедренного треугольника.
Формула Герона для равнобедренного треугольника будет иметь несколько упрощенный вид за счет того, что значения боковых сторон повторяются:
Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне
Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.
Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sinα
Формула через боковую сторону и угол напротив основания β:
Формула через основание и угол при нем α:
через основание и угол противолежащий ему β:
к основанию, к боковой стороне
В данной публикации мы рассмотрим основные свойства высоты равнобедренного треугольника, а также разберем примеры решения задач по данной теме.
Примечание: треугольник называется равнобедренным, если две его стороны равны (боковые). Третья сторона называется основанием.
Свойства высоты в равнобедренном треугольнике
Свойство 1
В равнобедренном треугольнике две высоты, проведенные к боковым сторонам, равны.
AE = CD
Обратная формулировка: Если в треугольнике две высоты равны, значит он является равнобедренным.
Свойство 2
В равнобедренном треугольнике высота, опущенная на основание, одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.
- BD – высота, проведенная к основанию AC;
- BD – медиана, следовательно, AD = DC;
- BD – биссектриса, следовательно, угол α равен углу β.
- BD – серединный перпендикуляр к стороне AC.
Свойство 3
Если известны стороны/углы равнобедренного треугольника, то:
1. Длина высоты ha, опущенной на основание a, вычисляется по формуле:
Длина высоты ha, опущенной на основание a, вычисляется по формуле:
- a – основание;
- b – боковая сторона.
2. Длина высоты hb, проведенной к боковой стороне b, равняется:
p – это полупериметр треугольника, рассчитывается таким образом:
3. Высоту к боковой стороне можно найти через синус угла и длину стороны треугольника:
Примечание: к равнобедренному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.
Пример задачи
Задача 1
Дан равнобедренный треугольник, основание которого равно 15 см, а боковая сторона – 12 см. Найдите длину высоты, опущенной к основанию.
Решение
Воспользуемся первой формулой, представленной в Свойстве 3:
Задача 2
Найдите высоту, проведенную к боковой стороне равнобедренного треугольника длиной 13 см.
Решение
Для начала вычислим полупериметр треугольника:
Теперь применим соответствующую формулу для нахождения высоты (представлена в Свойстве 3):
Как найти высоту в треугольнике abc: формулы, примеры задач
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Как посчитать высоту равнобедренного треугольника
Чтобы посчитать чему равна высота равнобедренного треугольника просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить высоту равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
- длину двух равных сторон (a) и длину основания (b)
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину основания (b) и угол α
- длину основания (b) и угол β
Введите их в соответствующие поля и получите результат.
Если известны длина стороны а и основания b
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и длина основания b?
Формула
h = √a2 — (b/2)2
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
h = √102 — (5/2)2 = √100 — 6.25 ≈ 9.68 см
Если известны длина стороны а и угол α
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
h = a⋅sin α
Пример
Если сторона a = 5 см, а ∠α = 45°, то:
h = 5⋅sin 45 ≈ 3,53 см
Если известны длина стороны а и угол β
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
h = a⋅cos β/2
Пример
Если сторона a = 5 см, а ∠β = 30°, то:
h = 5⋅cos 30/2 ≈ 4. 83 см
83 см
Если известны длина стороны b и угол α
Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол α?
Формула
h = b/2⋅tg α
Пример
Если сторона b = 20 см, а ∠α = 35°, то:
h = 20/2⋅tg 35 = 10⋅0.7 = 7 см
Если известны длина стороны b и угол β
Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол β?
Формула
h = b/2⋅ctg β/2
Пример
Если сторона b = 15 см, а ∠β = 40°, то:
h = 15/2⋅ctg 40/2 = 7.5⋅2.7474 ≈ 20.6 см
См. также
Равнобедренный треугольник. Свойства, Признаки, Высота
Определение равнобедренного треугольника
Определение равнобедренного треугольника звучит проще простого:
Равнобедренным называется треугольник, у которого две стороны равны. |
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Чтобы найти основание равнобедренного треугольника, используйте формулу: b = 2a cos
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 5 теорем.
Теоремы помогут доказать, что треугольник равнобедренный, а не какой-нибудь ещё. Давайте приступим.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Мы выяснили, что AС — основание равнобедренного треугольника. Поскольку боковые стороны треугольника равны AB = СB, то и углы при основании — равны. ∠ BАC = ∠ BСA. Изи!
∠ BАC = ∠ BСA. Изи!
Геометрия в 7 классе полна острых углов. Чтобы ваш ребенок миновал их круглым отличником, запишите его на бесплатный пробный урок математики в онлайн-школу Skysmart.
Наши опытные преподаватели научат с закрытыми глазами отличать равнобедренный треугольник от равностороннего, а интерактивная платформа не даст заскучать на уроках.
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Чтобы доказать все эти теоремы, вспомним, что такое биссектриса, медиана и высота.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — линия, которая соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Доказательство теорем 2, 3, 4 будет коллективным, поскольку из определений видно, что биссектриса, медиана и высота равнобедренного треугольника — это одно и то же.
А вот и доказательство:
- Δ ABC
- Высота BH делит Δ ABC на два прямоугольных треугольника ABH и CBH
- Δ ABH = Δ CBH, поскольку гипотенузы и катет равны по теореме Пифагора
- Согласно теореме 1: в треугольниках ABH и BCH ∠ BАH = ∠ BСH, поскольку углы при основании равнобедренного треугольника равны
- Так как Δ ABC — равнобедренный, то его боковые стороны равны AB = BC
- AH = CH, поскольку точка H делит основание Δ ABC на две равные части
- Δ ABH = Δ BCH
- Значит, отрезок BH одновременно биссектриса, медиана и высота равнобедренного треугольника ABC
Вуаля, сразу три теоремы доказаны.
Теорема 5: Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны (третий признак равенства треугольников).
Доказательство:
Дано два Δ ABC = Δ A1B1C1.
Чтобы доказать равенство треугольников, мысленно наложите один треугольник на другой так, чтобы стороны совпали.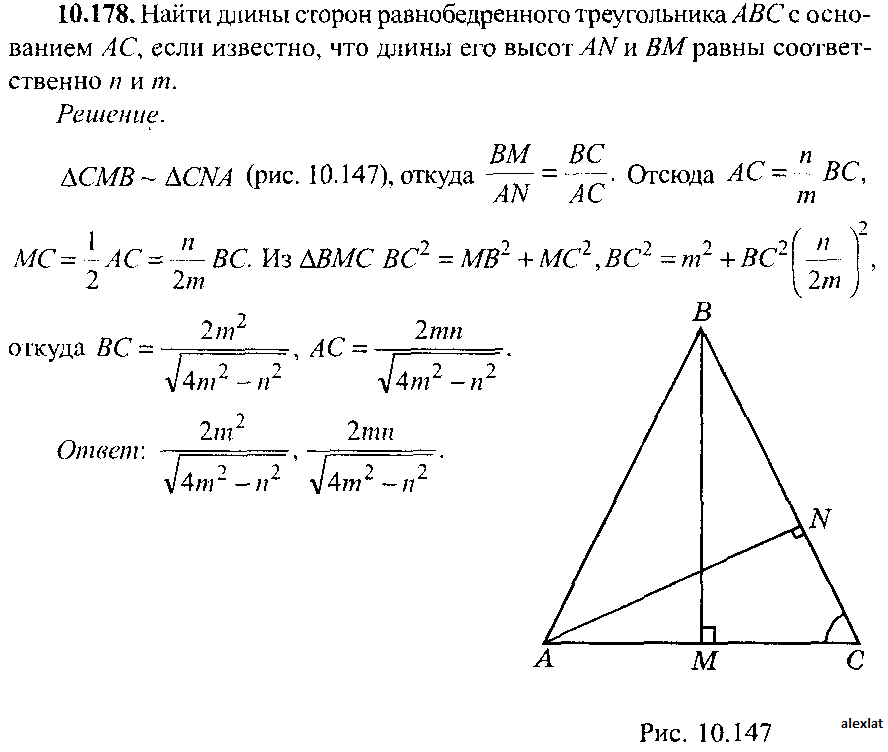 Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.
Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.
Если все стороны совпадают — треугольники равны, а теорема доказана.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, то такой треугольник снова равнобедренный!
- Если два угла треугольника равны, такой треугольник является равнобедренным.
Свойства углов равнобедренного треугольника
|
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
b — основание равнобедренного треугольника
a — равные стороны равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
Формулы длины стороны (основания b) равнобедренного треугольника
Формулы длины равных сторон равнобедренного треугольника (стороны a):
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
b — основание равнобедренного треугольника
a — равные стороны равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
L — высота, биссектриса и медиана
Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)
Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать градусы и длины в равнобедренном треугольнике. Ну… почти ничего.
Ну… почти ничего.
Задачка раз. Дан ABC: ∠C = 80∘, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с пятью теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны.
∠A = ∠C = 80∘.
Не должно вас удивить и то, что сумма углов треугольника равна 180∘
∠B = 180∘ − 80∘ − 80∘ = 20∘.
∠B = 20∘
Задачка два. В равнобедренном треугольнике один из углов равен 110∘. Найдите наибольший из внешних углов этого треугольника.
Вспоминаем первую теорему о равенстве углов при основании (а лучше не забываем вовсе). Поскольку сумма углов = 180∘, то второго угла в 110∘ в нём быть не может. Соответственно, известный угол в 110∘ — это угол при вершине. (180∘−110∘)/2=35∘. Внешние углы треугольника равны: 180∘−110∘=70∘,180∘−35∘=145∘,180∘−35∘=145∘. Больший внешний угол равен 145∘
Еще больше тренировок — в детской школе Skysmart. Записывайте ребенка на бесплатный урок математики и приходите сами: покажем, как все устроено и наметим индивидуальную программу занятий.
Высота равнобедренного треугольника
Примечание. Это часть урока с задачами по геометрии (раздел равнобедренный треугольник). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Задача
В равнобедренном треугольнике ABC боковые стороны AB, и AC равны 13а. Тангенс угла B равен 3/4. Найдите высоту AK, проведенную к основанию BC этого равнобедренного треугольника.
Решение.
Поскольку мы знаем тангенс угла B, то стороны прямоугольного треугольника AKB соотносятся как
AK/KB = tg B = 3/4
Обозначим коэффициент пропорциональности этих сторон как х.
Тогда по теореме Пифагора для данного треугольника будет справедливо выражение:
(3x)2 + (4x)2 = (13a)2
9x2 + 16x2
= 169a2
25x2
= 169a2
x2
= 169/25a2
x = 13/5a
Откуда
AK = 3x = 13/5a*3= 7,8a
KB = 4x = 13/5a*4 = 10,4a
Ответ: 7,8a и
10,4a
Углы равнобедренного треугольника |
Описание курса
| Окружность, вписанная в равнобедренный треугольник
Как найти длину высоты в равнобедренном треугольнике
Высотами в треугольнике называют три отрезка прямых, каждый из которых перпендикулярен одной из сторон и соединяет ее с противолежащей вершиной. Как минимум две стороны и два угла в равнобедренном треугольнике имеют одинаковые величины, поэтому и длины двух высот должны быть равны. Это обстоятельство значительно упрощает вычисление длин высот фигуры.
Как минимум две стороны и два угла в равнобедренном треугольнике имеют одинаковые величины, поэтому и длины двух высот должны быть равны. Это обстоятельство значительно упрощает вычисление длин высот фигуры.
Высоту (Hc), проведенную к основанию равнобедренного треугольника, можно рассчитать, зная длины этого основания (c) и боковой стороны (a). Для этого можно использовать теорему Пифагора, так как высота, боковая сторона и половина основания образуют прямоугольный треугольник. Высота и половина основания в нем являются катетами, поэтому для решения задачи извлеките корень из разности между возведенной в квадрат длиной боковой стороны и четвертью квадрата длины основания: Hс = √(a²-¼*c²).
Эту же высоту (Hc) можно вычислить и по длине любой из сторон, если в условиях приведена величина хотя бы одного угла. Если это угол при основании треугольника (α) а известная длина определяет величину боковой стороны (a), для получения результате перемножьте длину известной стороны и синус известного угла: Hс = a*sin(α).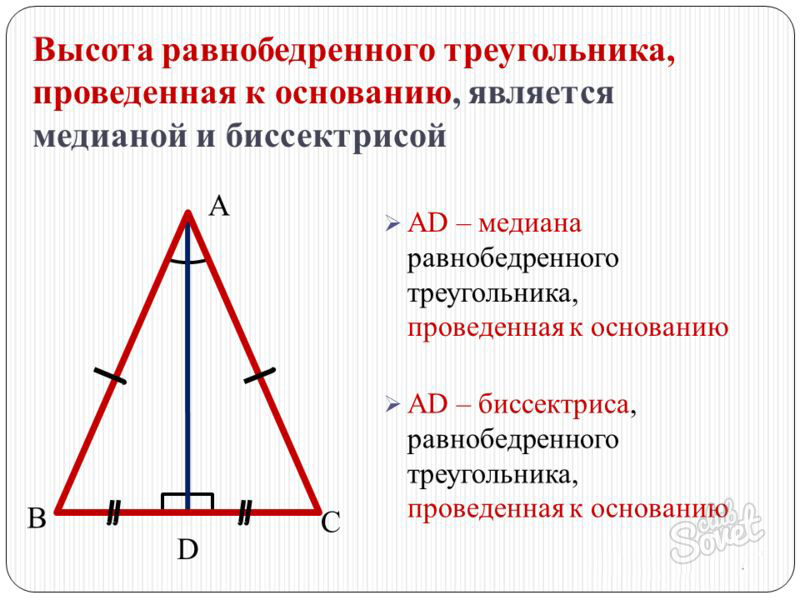 Эта формула вытекает из теоремы синусов.
Эта формула вытекает из теоремы синусов.
Если известна длина основания (с) и величина прилегающего к нему угла (α), для вычисления высоты (Hc), половину длины основания умножьте на синус известного угла и разделите на синус разницы между 90° и величиной того же угла: Hс = ½*c*sin(α)/sin(90°-α).
При известных размерах основания (с) и противолежащего ему угла (γ) для вычисления высоты (Hc) умножайте половину длины известной стороны на синус разницы между 90° и половиной известного угла, а результат делите на синус половины того же угла: Hс = ½*c*sin(90°-γ/2)/sin(γ/2). Эта формула, как и две предыдущие, вытекает из теоремы синусов в сочетании с теоремой о сумме углов в треугольнике.
Длину высоты, проведенной к одной из боковых сторон (Ha) можно вычислить, например, зная длину этой стороны (a) и площадь равнобедренного треугольника (S). Чтобы это сделать, найдите удвоенную величину соотношения между площадью и длиной известной стороны: Ha = 2*S/a.
Калькулятор равнобедренного треугольника — Расчет высокой точности
- Цель использования
- Модель Lego
[1] 2021/05/06 05:04 Мужчина / 20-летний уровень / Учитель / Исследователь / Очень /
- Цель использования
- Помогает при выполнении домашних заданий (Геометрия для старших классов).

[2] 2021/05/04 11:25 — / До 20 лет / Средняя школа / Университет / Аспирант / Очень /
- Цель использования
- Попытка подсчитать, сколько годного к употреблению масла у меня осталось в циклической ( горизонтальный!) бак.Требуется для расчета углов треугольника по известной гипотенузе (радиус круга) и высоте треугольника (уровень масла). Получилось удовольствие. Осталось еще 195 литров! (заменяем бак).
[3] 2021/04/25 21:30 Мужской / 50-летний уровень / Самозанятые люди / Очень /
- Цель использования
- Слишком долго не ходил в школу. Изготовление стола из эпоксидной смолы, необходимого для подрезки стальных ножек, пока смола мокрая. Вырисовал ножки для прямоугольной основы, забыл некоторые геометрические доказательства.Смотрел их и вручную делал расчеты. Проверил с помощью этого калькулятора -> получилось с такими же точными числами и углами. Хороший инструмент для проверки, не ленитесь и полагайтесь на технологии, которые сделают все за вас.
 Вот почему у нас есть манекены, которые не могут решать математические уравнения Facebook.
Вот почему у нас есть манекены, которые не могут решать математические уравнения Facebook.
[4] 2021.04.21 10:12 Мужчина / Уровень 30 лет / Инженер / Очень /
- Назначение
- Пошив шторки для нашей горки для муниципального бассейна. Это пирамида, состоящая из 4-х треугольников.Стороны легко измерить, углы нужны.
- Комментарий / запрос
- Отлично и быстро. Спасибо.
[5] 2021/04/17 22:19 Женщина / 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Рассчитать размер детской палатки для двора 🙂
[6] 2021/04/05 04:56 Женщина / Уровень 40 лет / Другое / Очень /
- Цель использования
- Быстрее решать задачи
[7] 2021/03/02 23:20 Женский / До 20 лет / Старшая школа / Университет / Аспирантка / Очень /
- Цель использования
- Игра с периметром: отношения диаметров многоугольников с увеличивающимся числом сторон.Наблюдая, как отношение приближается к пи, когда многоугольник становится более круглым.

[8] 2021/02/26 02:15 Мужчина / Уровень 30 лет / Инженер / Очень /
- Цель использования
- Попытка найти длины сторон, когда я знаю база — 48 дюймов, а базовый ангел — 30 градусов
[9] 2021/02/10 22:40 Женщина / 30-летний уровень / Офисный работник / Государственный служащий / Очень /
- Цель использования
- Требуется дизайнерский угол «сделай сам», доступны только определенные размеры.Спасибо за калькулятор.
[10] 2021/02/09 14:38 Мужчина / уровень 40 лет / Офисный работник / Государственный служащий / Очень /
Калькулятор равнобедренного треугольника
Калькулятор равнобедренного треугольника — лучший выбор, если вы ищете быстрое решение ваших геометрических задач. Узнайте площадь равнобедренного треугольника, его периметр, внутренний радиус, радиус описанной окружности, высоту и углы — все в одном месте. Если вы хотите построить питомник, узнать площадь равнобедренного фронтона греческого храма или просто выполнить домашнее задание по математике, этот инструмент здесь для вас. Поэкспериментируйте с калькулятором или продолжайте читать, чтобы узнать больше о формулах равнобедренного треугольника.
Поэкспериментируйте с калькулятором или продолжайте читать, чтобы узнать больше о формулах равнобедренного треугольника.
Что такое равнобедренный треугольник?
Равнобедренный треугольник — это треугольник с двумя сторонами равной длины, которые называются катетами. Третья сторона треугольника называется основанием. Угол при вершине — это угол между ножками и углами с основанием, так как одна из их сторон называется углами основания.
Свойства равнобедренного треугольника:
- имеет ось симметрии по высоте вершины
- Два угла напротив ножек равны по длине
- равнобедренный треугольник может быть острым, прямым или тупым, но это зависит только от угла при вершине (углы основания всегда острые)
Равносторонний треугольник — это частный случай равнобедренного треугольника.
Формулы равнобедренного треугольника для площади и периметра
Для вычисления площади равнобедренного треугольника можно использовать множество различных формул. Самыми популярными являются уравнения:
Самыми популярными являются уравнения:
Данная рука
aи основаниеb:площадь = (1/4) * b * √ (4 * a² - b²)Дано
hвысота от вершины и основанияbилиh4высота от двух других вершин и плечаa:площадь = 0.5 * h * b = 0,5 * h4 * aЛюбой угол и плечо или основание
площадь = (1/2) * a * b * sin (base_angle) = (1/2) * a² * sin (vertex_angle)
Кроме того, вы можете воспользоваться нашим калькулятором площади треугольника, чтобы узнать другие уравнения, которые работают для всех типов треугольников, а не только для равнобедренных.
Чтобы вычислить периметр равнобедренного треугольника, просто сложите все стороны треугольника: периметр = a + a + b = 2 * a + b
Теорема о равнобедренном треугольнике
Теорема о равнобедренном треугольнике, также известная как теорема об основных углах, утверждает, что , если две стороны треугольника равны, то углы, противоположные этим сторонам, равны .
Также существует обратная теорема, утверждающая, что , если два угла треугольника совпадают, то стороны, противоположные этим углам, равны .
Калькулятор золотого треугольника
Золотой треугольник, который также называют возвышенным треугольником, представляет собой равнобедренный треугольник, в котором ножка находится в золотом сечении по отношению к основанию:
a / b = φ ~ 1,618
Золотой треугольник обладает необычными свойствами:
- Это единственный треугольник с тремя углами в пропорции 2: 2: 1
- Это форма треугольников в точках пентаграммы
- Используется для формирования логарифмической спирали
Как найти площадь с помощью этого калькулятора равнобедренного треугольника?
Давайте узнаем, как пользоваться этим инструментом на простом примере.Взгляните на это пошаговое решение:
- Определите ваше первое данное значение . Предположим, мы хотим проверить свойства золотого треугольника.
 Наберите 1,681 дюйма в коробку с опорой .
Наберите 1,681 дюйма в коробку с опорой . - Введите второй известный параметр . Например, возьмите основание, равное 1 дюйм.
- Все остальные параметры рассчитываются в мгновение ока! Мы проверили, например, что периметр равнобедренного треугольника равен 4,236 дюйма и что углы в золотом треугольнике равны 72 ° и 36 ° — соотношение действительно равно 2: 2: 1.
Вы можете использовать этот калькулятор для определения параметров, отличных от приведенных в примере, но помните, что обычно есть два разных равнобедренных треугольника с заданной площадью и другим параметром, например длина ноги. Наш калькулятор покажет одно из возможных решений.
Как определить высоту треугольника в трех разных ситуациях
В тригонометрии высоту треугольника можно определить разными способами в зависимости от того, прямоугольный ли это треугольник, равнобедренный треугольник (треугольник с двумя равными сторонами), или равносторонний треугольник.
1. Как найти высоту прямоугольного треугольника
Прежде чем мы начнем, вот что вам нужно знать о прямоугольных треугольниках. Прямоугольный треугольник имеет три стороны: гипотенузу, высоту и основание треугольника. Основание и высота прямоугольного треугольника — это всегда стороны, прилегающие к прямому углу, а гипотенуза — самая длинная сторона.
Высоту прямоугольного треугольника можно определить по формуле площади:
Если заданная площадь неизвестна, вы можете использовать теорему Пифагора, чтобы найти высоту прямоугольного треугольника.Вот что утверждает теорема Пифагора, учитывая, что c — гипотенуза, а a и b — две другие стороны:
Давайте возьмем единицы с рисунка выше и подставим длину основания и гипотенузы, чтобы найти недостающую высоту:
2. Определение высоты неправильного треугольника
К сожалению, вы не можете использовать теорему Пифагора, чтобы найти высоту равнобедренного треугольника или высоту равностороннего треугольника (где все стороны треугольника равны). Вместо этого вам придется провести перпендикулярную линию через основание треугольника, чтобы образовался прямой угол:
Вместо этого вам придется провести перпендикулярную линию через основание треугольника, чтобы образовался прямой угол:
Эта линия представляет высоту этих неправильных треугольников. После того, как вы сформировали эту линию, вам нужно будет использовать формулу Герона, чтобы найти площадь всего треугольника.
Формула Герона
Первый шаг формулы Герона — вычисление половины периметра треугольника. В этом случае s представляет половину периметра, а a, b, и c — стороны:
После того, как вы определили s , используйте следующую формулу для вычисления площади треугольника.Опять же, две стороны: a и b , а самая длинная сторона (гипотенуза) — c :
.
Давайте подставим длины сторон этого равнобедренного треугольника, чтобы найти площадь треугольника:
Теперь мы заменим s в формуле площади непрямого треугольника.
Использование площади для определения высоты треугольника
Теперь, когда вы знаете площадь изображенного выше треугольника, вы можете подставить его в формулу треугольника A = 1 / 2bh, чтобы найти высоту треугольника. В этом случае основание будет равно половине расстояния пяти (2,5), так как это самая короткая сторона треугольника.
В этом случае основание будет равно половине расстояния пяти (2,5), так как это самая короткая сторона треугольника.
Формулы высоты главного треугольника
Определение высоты треугольника — это многоэтапный процесс, который может сбивать с толку. Однако его освоение поможет вам изучить различные типы формул площади, такие как формула цапли и A = 1 / 2bh. Здесь также показано, как использовать теорему Пифагора и формулы периметра треугольника для определения других величин внутри треугольника.
Дополнительные домашние задания по математике
Равнобедренный треугольник — математический путь
Равнобедренный треугольник представляет собой многоугольник из трех сторон и двух равных сторон . Другая неравная сторона называется основанием треугольника.
Следовательно, два угла также будут равными (α), а другие — разными (β), т.е. это угол, образованный двумя равными сторонами ( a ).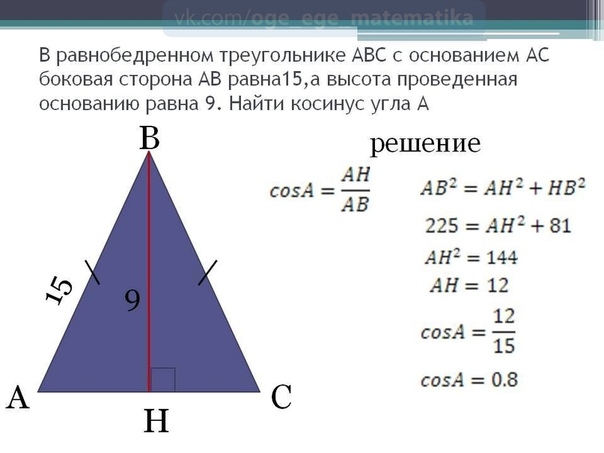
Двумя частными случаями равнобедренных треугольников являются равносторонний треугольник и равнобедренный прямоугольный треугольник .
Высота равнобедренного треугольника
Высота ( h ) равнобедренного треугольника (или высота ) может быть вычислена по теореме Пифагора. Стороны a , b / 2 и h образуют прямоугольный треугольник. Стороны b / 2 и h представляют собой катеты, а a — гипотенузу.
По теореме Пифагора:
И получается, что высота h составляет:
В равнобедренном треугольнике высота , соответствующая основанию ( b ), также является биссектрисой угла, серединным перпендикуляром и серединой.
Площадь равнобедренного треугольника вычисляется из основания b (неповторяющаяся сторона) и высоты ( h ) треугольника, соответствующего основанию. Площадь — это произведение основания и высоты, разделенные на два, и формула имеет следующую формулу:
Площадь — это произведение основания и высоты, разделенные на два, и формула имеет следующую формулу:
.
Периметр равнобедренного треугольника получается сложением трех сторон треугольника.Имея две равные стороны, периметр равен удвоенной повторяющейся стороне ( a ) плюс другая сторона ( b ).
Если повторяющаяся сторона ( a ) и угол двух равных сторон известны, другая сторона ( b ) должна быть найдена по закону косинусов .
Загрузите этот калькулятор , чтобы получить результаты формул на этой странице. Выберите исходные данные и введите их в верхнем левом поле. Для получения результатов нажмите ENTER.
Triangle-total.rar или Triangle-total.exe
Примечание. Предоставлено автором: Хосе Мария Пареха Маркано . Химик. Севилья, испания.
Решенные упражнения
Упражнение в области равнобедренного треугольника
Определите площадь равнобедренного треугольника , зная его две равные стороны ( a = 3 см) и неравную, длина которой составляет 2 см ( b = 2 см).
Какая у него площадь ?
Рассчитайте площадь по приведенной выше формуле, умножив основание на высоту:
Площадь равнобедренного треугольника равна 2.83 см 2 .
Упражнение по периметру равнобедренного треугольника
Это равнобедренный треугольник с двумя равными сторонами, a = 3 см, а другая сторона b = 2 см.
Каков его периметр ?
Чтобы вычислить этот периметр , мы добавляем повторяющуюся сторону, умноженную на два, плюс неравную сторону, то есть:
Получается, что периметр равнобедренного треугольника равен 8 см .
Упражнение на высоту равнобедренного треугольника
Найдите стороны и периметр равнобедренного треугольника, высота которого относительно неровной стороны составляет h = 6 см, а противоположный угол, также неровный, составляет 40 °.
Найдено с помощью тригонометрических соотношений из одного прямоугольного треугольника, на который делится равнобедренный треугольник высотой h .
Отрезок, противоположный углу β / 2, который является отрезком b /2, мы нашли его через касательную:
Сторона b меры 4.36 см.
Образуется гипотенуза прямоугольного треугольника, то есть сторона и находится по косинусу:
Сторона и имеет размер 6,38 см.
Наконец, периметр треугольника составит:
Получается, что периметр этого равнобедренного треугольника будет составлять 17,12 см.
Равнобедренный треугольник — определение математического слова
Равнобедренный треугольник — определение математического слова — Math Open Reference
Треугольник, две стороны которого равны.Попробуйте это Перетащите оранжевые точки на каждую вершину, чтобы изменить форму треугольника.
Обратите внимание, что он всегда остается равнобедренным треугольником, стороны AB и AC всегда равны по длине.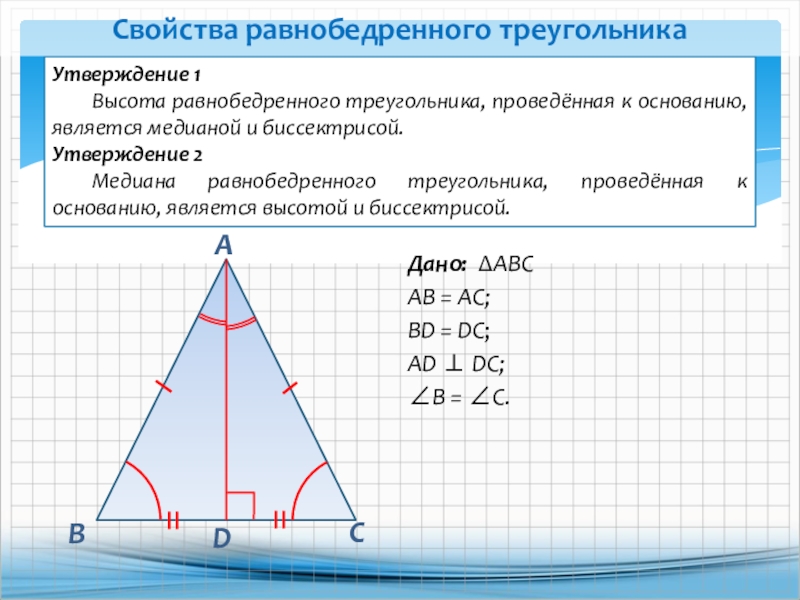
Слово равнобедренное произносится как «глаз- sos -ell-easy» с ударением на «sos». Это любой треугольник с двумя сторонами одинаковой длины.
Если все три стороны имеют одинаковую длину, это называется
равносторонний треугольник.
Очевидно, что все равносторонние треугольники также обладают всеми свойствами равнобедренного треугольника.
Недвижимость
- Неравную сторону равнобедренного треугольника обычно называют «основанием» треугольника.
- Углы основания равнобедренного треугольника всегда равны.
На рисунке выше углы ∠ABC и ∠ACB всегда одинаковы - Когда 3-й угол является прямым, он называется «равнобедренный прямоугольный треугольник».
- Высота — это расстояние по перпендикуляру от основания до самой верхней вершины.
Построение равнобедренного треугольника
Можно построить равнобедренный треугольник заданных размеров, используя только циркуль и линейку.Посмотрите на эти три конструкции:
Решение равнобедренного треугольника
Основание, катет или высота равнобедренного треугольника можно найти, если вы знаете два других.
А
серединный перпендикуляр
базы образует
высота
треугольника, как показано справа.
Это образует два
совпадающие прямоугольные треугольники
это может быть решено с помощью
Теорема Пифагора
как показано ниже.
Нахождение базы
Чтобы найти базу с учетом шага и высоты, используйте формулу:
где:
L — длина отрезка
A — высота
Нахождение отрезка
Чтобы найти длину ноги с учетом базы и высоты, используйте формулу:
где:
B — длина основания
A — высота
Высота
Чтобы найти высоту по базе и ноге, используйте формулу:
где:
L — длина ножки
B — основание
Внутренние углы
Если вам дадут один
внутренний угол
равнобедренного треугольника можно найти два других.
Например, нам дан угол при вершине, как показано справа от 40 °.
Мы знаем, что внутренние углы всех треугольников составляют 180 °.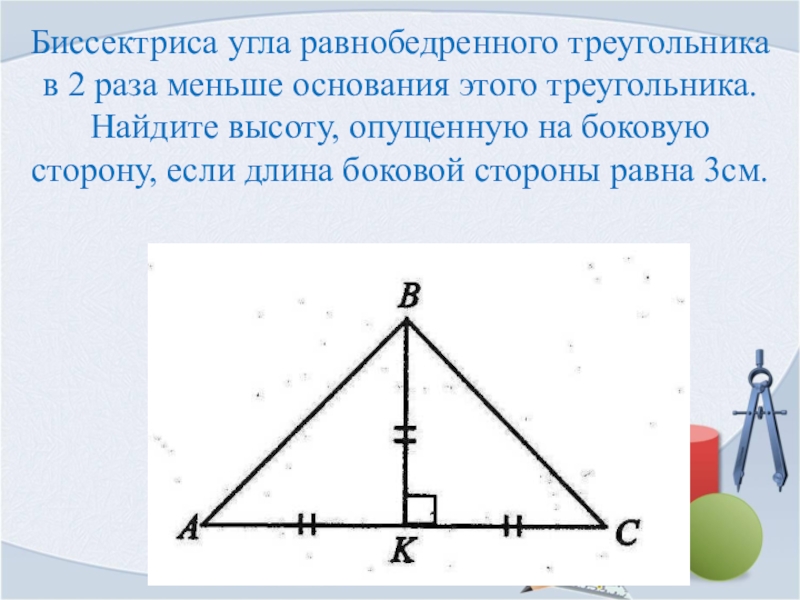
Таким образом, два базовых угла должны в сумме составлять 180-40 или 140 °. Поскольку два основных угла совпадают (одна и та же мера), каждый из них составляет 70 °.
Если нам дан базовый угол, скажем, 45 °, мы знаем, что базовые углы конгруэнтны (та же мера)
а внутренние углы любого треугольника всегда складываются в 180 °. Таким образом, угол при вершине должен составлять 180-45-45 или 90 °.
Другие треугольники
Общий
Периметр / Площадь
Типы треугольников
Центры треугольника
Конгруэнтность и сходство
Решение треугольников
Тесты и упражнения «Треугольник»
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Как использовать теорему Пифагора для равнобедренных треугольников
С помощью теоремы Пифагора можно найти любую неизвестную сторону прямоугольного треугольника, если длины двух других сторон известны.Теорема Пифагора может быть использована для решения любой стороны равнобедренного треугольника, даже если это не прямоугольный треугольник. У равнобедренных треугольников две стороны равной длины и два эквивалентных угла. Проведя прямую линию по центру равнобедренного треугольника, его можно разделить на два равных прямоугольных треугольника, а теорему Пифагора можно легко использовать для определения длины неизвестной стороны.
У равнобедренных треугольников две стороны равной длины и два эквивалентных угла. Проведя прямую линию по центру равнобедренного треугольника, его можно разделить на два равных прямоугольных треугольника, а теорему Пифагора можно легко использовать для определения длины неизвестной стороны.
Нарисуйте треугольник вертикально на листе бумаги так, чтобы нечетная сторона (та, которая по длине не равна двум другим) находилась у основания треугольника.Например, предположим, что равнобедренный треугольник с двумя сторонами равной, но неизвестной длины, длина одной стороны составляет 8 дюймов, а высота — 3 дюйма. На вашем рисунке сторона размером 8 дюймов должна быть у основания треугольника.
Проведите прямую линию по середине треугольника от вершины до основания. Эта линия должна быть перпендикулярна основанию и разделять треугольник на два равных прямоугольных треугольника — в этом примере каждый имеет высоту 3 дюйма и основание 4 дюйма.
Напишите значения длин известных сторон треугольника рядом с совпадающими сторонами. Эти значения могут быть получены из конкретной математической задачи или из измерений для определенного проекта. Напишите «3 дюйма». рядом с линией, проведенной на шаге 2, и «4 дюйма» по обе стороны от этой линии у основания треугольника.
Эти значения могут быть получены из конкретной математической задачи или из измерений для определенного проекта. Напишите «3 дюйма». рядом с линией, проведенной на шаге 2, и «4 дюйма» по обе стороны от этой линии у основания треугольника.
Определите, какая сторона имеет неизвестную длину, и используйте теорему Пифагора, чтобы найти ее с помощью калькулятора. Неизвестная сторона — это гипотенуза каждого из двух треугольников.
Обозначьте гипотенузу «C» и любой из катетов треугольника «A», а другой — «B.2].
Гипотенуза — это линия, соединяющая основание и высоту прямоугольного треугольника.
Катеты прямоугольного треугольника — это две стороны, образующие прямой угол.
Используйте половину исходной длины основания треугольника в качестве базового значения для прямоугольного треугольника, когда вы разделили треугольник на две равные половины.
Как найти высоту треугольника (правого, равностороннего, равнобедренного …)
Треугольники имеют три высоты, каждый связан с отдельным основанием. Независимо от того, имеется ли до трех разных высот, у одного треугольника всегда будет только одна мера площади. В некоторых треугольниках, таких как прямоугольные, равнобедренные и равносторонние треугольники, определить высоту легко одним из двух способов.
Независимо от того, имеется ли до трех разных высот, у одного треугольника всегда будет только одна мера площади. В некоторых треугольниках, таких как прямоугольные, равнобедренные и равносторонние треугольники, определить высоту легко одним из двух способов.
Как найти высоту треугольника
Каждый треугольник имеет три высоты или высоты, потому что у каждого треугольника три стороны. Высота треугольника — это длина перпендикулярного отрезка прямой, начинающегося на одной стороне и пересекающего противоположный угол.
В равностороннем треугольнике, таком как △ СОЛНЦЕ ниже, каждая высота — это отрезок прямой, разделяющий сторону пополам, а также биссектрису противоположного угла. Это произойдет только в равностороннем треугольнике.
По определению равностороннего треугольника вы уже знаете, что все три стороны равны, и все три угла равны 60 °. Если сторона помечена, вы знаете ее длину.
У нашего яркого маленького △ СОЛНЦА одна сторона обозначена 24 см, поэтому все три стороны равны 24 см. Каждый отрезок линии, показывающий высоту с каждой стороны, также делит равносторонний треугольник на два прямоугольных.
Каждый отрезок линии, показывающий высоту с каждой стороны, также делит равносторонний треугольник на два прямоугольных.
Формула высоты треугольника
Ваша способность разделить треугольник на прямоугольные или распознать существующий прямоугольный треугольник — это ваш ключ к определению высоты исходного треугольника. Вы можете взять любую сторону нашего великолепного △ СОЛНЦА и увидеть, что отрезок линии, показывающий его высоту, делит сторону пополам, так что каждая короткая ножка только что созданного прямоугольного треугольника составляет 12 см.Мы уже знаем, что гипотенуза равна 24 см.
Зная все три угла и две стороны прямоугольного треугольника, какова длина третьей стороны? Это работа для теоремы Пифагора :
Использование теоремы Пифагора
Ориентируйтесь на длину; углы не важны в теореме Пифагора. Подключите то, что вы знаете:
а2 + Ь2 = с2
122 + b2 = 242
144 + b2 = 576 см2
b2 = 432 см2
b2 = 432 см2
б = 20. 7846096908 см
7846096908 см
Большинство людей с радостью скажут, что высота (сторона b) составляет приблизительно 20,78, или b ≈ 20,78.
Вы можете решить для себя, сколько значащих цифр нужно вашему ответу, поскольку десятичная дробь будет продолжать повторяться. Не забудьте использовать для ответа линейные измерения!
Решение теоремы Пифагора работает с прямоугольными, равнобедренными и равносторонними треугольниками. На разносторонних треугольниках не получится!
Используя формулу площади, чтобы найти высоту
Формула для площади треугольника: : 12 основание × высота, или 12 bh.Если вы знаете площадь и длину основания, вы можете рассчитать высоту.
В отличие от метода теоремы Пифагора, если у вас есть две из трех частей, вы можете найти высоту для любого треугольника!
Здесь у нас есть scalene △ ZIG с базой в 56 ярдов и площадью 987 квадратных ярдов, но никаких подсказок об углах и двух других сторонах !:
Вспоминая формулу для площади, где A означает площадь, b — основание, а h — высота, мы вспоминаем
A = 12 bh
Это можно переставить с помощью алгебры:
А = bh4
ч = 2 (Ab)
Введите наши известные значения:
h = 2 (987 квадратных ярдов 56 ярдов)
ч = 2 (17.
Тема 9. Планиметрия — Материалы для подготовки к вступительным экзаменам в СГГА
Центр вписанной окружности – точка пересечения биссектрис; центр описанной окружности – точка пересечения серединных перпендикуляров.
Теорема косинусов: a2=b2+c2-2bccosA.
Свойство медиан: AO:OM=2:1.
Свойство биссектрис: CA:AD=CB:BD.
1) Углы треугольника пропорциональны числам 3, 5, 7. Найдите эти углы.
2) Углы треугольника образуют арифметическую прогрессию. Чему равен наибольший угол, если величина наименьшего 200?
3) Два внешних угла треугольника равны 1200 и 1600. Чему равен третий внешний угол?
4) Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 15, а один из острых углов равен 600. Чему равна длина меньшего катета?
5) Один из углов прямоугольного треугольника равен 300, а высота, проведенная к гипотенузе, равна 9. Найдите длину гипотенузы.
Найдите длину гипотенузы.
7) Найдите гипотенузу равнобедренного прямоугольного треугольника, если его площадь равна 18.
8) Гипотенуза прямоугольного треугольника равна 13, а катеты относятся как 2 : 3. Чему равна площадь треугольника?
9) Один из катетов прямоугольного треугольника равен 9, а другой относится к гипотенузе, как 4 : 5. Чему равна площадь треугольника?
10) Катеты прямоугольного треугольника равны log49 и log316. Чему равна площадь треугольника?
11) Высота равнобедренного треугольника, равна 15, а боковая сторона больше основания на 1. Чему равно основание?
12) Найдите боковую сторону равнобедренного треугольника, если его основание равно 18, а площадь 108.
13) Найдите боковую сторону равнобедренного треугольника, если основание равно 10 см, а медиана, проведённая к основанию, равна 3 см.
14) Величины углов треугольника относятся как 1 : 1 : 2, а большая из сторон равна 15. Чему равна высота, проведенная к этой стороне?
Чему равна высота, проведенная к этой стороне?
17) Основание треугольника равно 22, боковые стороны 13 и 19. Чему равна медиана, опущенная на основание?
18) Две стороны треугольника равны 11 и 7, а медиана, опущенная на третью сторону 6. Найдите длину третьей стороны.
19) В треугольнике ABC медиана AM равна 6 и образует со стороной AC, равной 8, угол 300. Найдите площадь треугольника.
20) В треугольнике ABC к стороне BC=12 проведена медиана AM=7 и образует с этой стороной угол 300. Найдите площадь треугольника.
21) Площадь треугольника ABC равна 12. Из вершины B проведена медиана BD, длина которой равна 3. Найдите сторону AC, если .22) Площадь правильного треугольника равна 64. Найдите его периметр.
23) В треугольнике ABC на сторонах AB и AC взяты точки M и N такие, что . Найдите площадь треугольника AMN.
Найдите площадь треугольника AMN.24) Площадь треугольника ABC равна 48. Точка D лежит на стороне AC, деля ее в отношении AD:DC=1:7. Найдите площадь треугольника ABD.
25) Сторона треугольника равна 2, а прилегающие к ней углы 300 и 450. Найдите его площадь.
26) Один из катетов прямоугольного треугольника равен 6, а противолежащий ему угол . Найдите площадь круга, описанного около треугольника. 27) Площадь правильного треугольника равна . Чему равен радиус описанной около него окружности?28) Высота правильного треугольника равна 18. Найдите диаметр вписанной в него окружности.
29) Точка касания с вписанной окружностью делит гипотенузу треугольника в отношении 2 : 3. Расстояние от прямого угла треугольника до центра окружности равно . Найдите периметр треугольника.30) Катеты прямоугольного треугольника равны 16 и 30. Найдите радиус описанной около него окружности.
31) Один катет прямоугольного треугольника равен 15, проекция другого катета на гипотенузу равна 16. Чему равен радиус вписанной в треугольник окружности?
Чему равен радиус вписанной в треугольник окружности?
34) Радиус окружности равен 6. Перпендикуляр, опущенный из точки окружности на диаметр, делит его в отношении 1 : 3. Найдите длину перпендикуляра.
35) Найдите величину острого угла, который опирается на дугу, равную 2/5 окружности. Ответ дайте в градусах.
36) Найдите величину тупого угла, который опирается на дугу, равную 1/7 окружности. Ответ дайте в радианах.
37) Радиус окружности равен 5. Найдите длину дуги окружности, соответствующей центральному углу 1080.
38) Радиус окружности равен 20. Найдите Величину центрального угла, которому соответствует дуга окружности длины . 39) Хорда окружности, стягивающая дугу 900, равна . Чему равна длина окружности?
39) Хорда окружности, стягивающая дугу 900, равна . Чему равна длина окружности?40) Радиус окружности равен 13. На каком расстоянии от центра окружности находится хорда длины 24.
41) Из точки окружности радиуса R проведены две хорды длины . Чему равен косинус угла между этими хордами?42) По разные стороны от центра окружности проведены две параллельные хорды длин 12 и 16. Чему равен радиус окружности, если расстояние между хордами равно 14?
43) Найти площадь прямоугольника, если его диагональ равна , а одна из сторон 18.44) В прямоугольнике ABCD биссектриса угла BAD пересекает сторону BC в точке M и делит ее на отрезки BM=6, MC=4. Чему равна площадь прямоугольника?
45) Площадь параллелограмма равна 120, а его высоты 8 и 12. Найдите периметр параллелограмма.
46) Высоты параллелограмма равны 4 и 8. Большая высота опущена на сторону, равную 6. Найти другую сторону параллелограмма.
47) Углы между стороной ромба и его диагоналями относятся как 5 : 4. Найдите тупой угол ромба.
Найдите тупой угол ромба.
48) Как изменится площадь ромба, если одну из его диагоналей уменьшить на 10%, а другую увеличить на 20%?
49) Сторона ромба равна 5, а одна из диагоналей 6. Чему равна его площадь?
50) Разница между радиусами окружностей, описанной около квадрата и вписанной в квадрат, составляет . Чему равна сторона квадрата? 51) Боковая сторона равнобокой трапеции равна , высота и большее из оснований, соответственно, 4 и 9. Найдите длину средней линии трапеции.52) Средняя линия трапеции ABCD делит ее на две трапеции со средними линиями, равными 5 и 9. Найдите большее основание ABCD.
53) Трапеция, средняя линия которой равна , равновелика (т.е. равна по площади) равностороннему треугольнику со стороной 12. Найти высоту трапеции.54) В равнобокой трапеции тупой угол равен 1200 и меньшее основание равно боковой стороне и равно 6. Найдите площадь трапеции.
55) В равнобедренной трапеции основания равны 4 и 6, боковая сторона равна 5. Чему равна сумма длин диагоналей?
Чему равна сумма длин диагоналей?
56) В равнобедренной трапеции разность длин оснований равна длине боковой стороны. Чему равен тупой угол трапеции?
57) Высота равнобокой трапеции равна 40, боковая сторона 41, средняя линия 45. Чему равно большее основания трапеции?
58) В прямоугольной трапеции боковые стороны равны 4 и 5, меньшее из оснований 5. Чему равна площадь трапеции?
59) В прямоугольнике перпендикуляр, опущенный на диагональ, делит прямой угол на две части в отношении 3 : 1. Чему равен угол между этим перпендикуляром и другой диагональю?
60) Периметр ромба равен 52, а сумма длин диагоналей 34. Чему равна его площадь?
61) Диагонали ромба равны 26 и . Чему равен синус острого угла ромба?62) В равнобокой трапеции боковая сторона равна 7, диагональ 8, а средняя линия 4. Найдите меньшее основание.
63) В окружность радиуса 6 вписан прямоугольник. Найдите большую сторону прямоугольника, если угол между его диагоналями составляет 600.
64) В круг вписан прямоугольник со сторонами 2 и 6. Найдите площадь круга.
65) Равнобедренная трапеция вписана в окружность радиуса 6. Ее диагональ составляет угол 300 с большим основанием и перпендикулярна боковой стороне. Найдите периметр трапеции.
66) Периметр равнобедренной трапеции, описанной около окружности, равен 60. Найдите длину средней линии трапеции.
67) Основания равнобокой трапеции равны 12 и 20. Центр описанной около окружности трапеции лежит на ее большем основании. Чему равна диагональ трапеции?
68) В трапецию вписана окружность. Расстояние от центра этой окружности до вершины верхнего основания равно 15; до вершины нижнего 20. Чему равна площадь трапеции?
69) Четырехугольник ABCD вписан в окружность. BC=4, CD=5, . Чему равна диагональ BD?70) Окружность, вписанная в ромб, разбивает его диагональ на отрезки длины 9, 16, 9. Найдите площадь ромба.
71) Сторона вписанного в окружность правильного треугольника равна 6. Чему равна площадь квадрата, вписанного в ту же окружность?
Чему равна площадь квадрата, вписанного в ту же окружность?
72) Во сколько раз площадь круга больше площади вписанного в него квадрата?
73) Какой правильный многоугольник имеет внутренний угол 1440?
74) Сколько диагоналей можно провести в многоугольнике, если сумма его внутренних углов равна ?75) Чему равна площадь круга, описанного около правильного шестиугольника со стороной 2?
76) Дан правильный восьмиугольник ABCDEFKM. Найдите радиус описанной около него окружности, если площадь треугольника ABE равна . 77) Найдите радиус окружности, описанной около правильного девятиугольника A1A2…A9, если периметр треугольника A1OA4 равен .С Основание равнобедренного треугольника равно 40 а
С
Основание равнобедренного треугольника равно 40, а высота, опущенная на боковую сторону равна 24. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей. K А 32 24 О r В 20 15 r Н r О 1 25 20 С
Найдите радиусы окружностей. K А 32 24 О r В 20 15 r Н r О 1 25 20 С
E L 24 r Оr r В 20 А K r О 1 r 32 25 15 Н 20 С
• Основание равнобедренного треугольника равно 5, а высота, опущенная на боковую сторону равна 3. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей. • Основание равнобедренного треугольника равно 5, а высота, опущенная на боковую сторону равна 4. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей. • Основание равнобедренного треугольника равно 80, а высота, опущенная на боковую сторону равна 64. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Дан треугольник со сторонами 26, 26 и 20. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей. А 26 О r В 10 r r Н О 1 С
Найдите радиусы окружностей. А 26 О r В 10 r r Н О 1 С
L О r r r В 10 А K r О 1 r Н 26 С
• Дан треугольник со сторонами 115, 115 и 184. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей. • Дан треугольник со сторонами 30, 30 и 36. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей. • Дан треугольник со сторонами 13, 13 и 10. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
A 2 Случай B 6 с м м L C 7 см 6 с м 1 Случай B L K 5 с 5 с м В треугольнике АВС известны стороны: АВ=5, ВС=6, АC=7. Окружность, проходящая через точки А и С, пересекает прямые ВА и ВС соответственно в точках К и L , отличных от вершин треугольника. Отрезок КL касается окружности, вписанной в треугольник АBC. Найдите длину отрезка KL. A C K 7 см
Найдите длину отрезка KL. A C K 7 см
5 с м B K L 6 с м A C 7 см
B 6 с 5 см м L C A 6 с м 7 см 6 см K B A K L C
• В треугольнике ABC известны стороны: АВ = 4, ВС = 6, АС = 5. Окружность, проходящая через точки A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL. • В треугольнике ABC известны стороны: АВ = 7, ВС = 10, АС = 8. Окружность, проходящая через точки A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL. • В треугольнике ABC известны стороны: АВ = 5, ВС = 7, АС = 8. Окружность, проходящая через точки A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.
Найдите длину отрезка KL.
• В треугольнике ABC известны стороны: АВ = 9, ВС = 10, АС =11. Окружность, проходящая через точки A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL. • В треугольнике ABC известны стороны: АВ = 8, ВС = 10, АС = 11. Окружность, проходящая через точки A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL. • В треугольнике ABC известны стороны: АВ = 7, ВС = 9, АС = 10. Окружность, проходящая через точки A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.
Косинус угла при основании равнобедренного треугольника равен 5/13, а боковая сторона равна 39.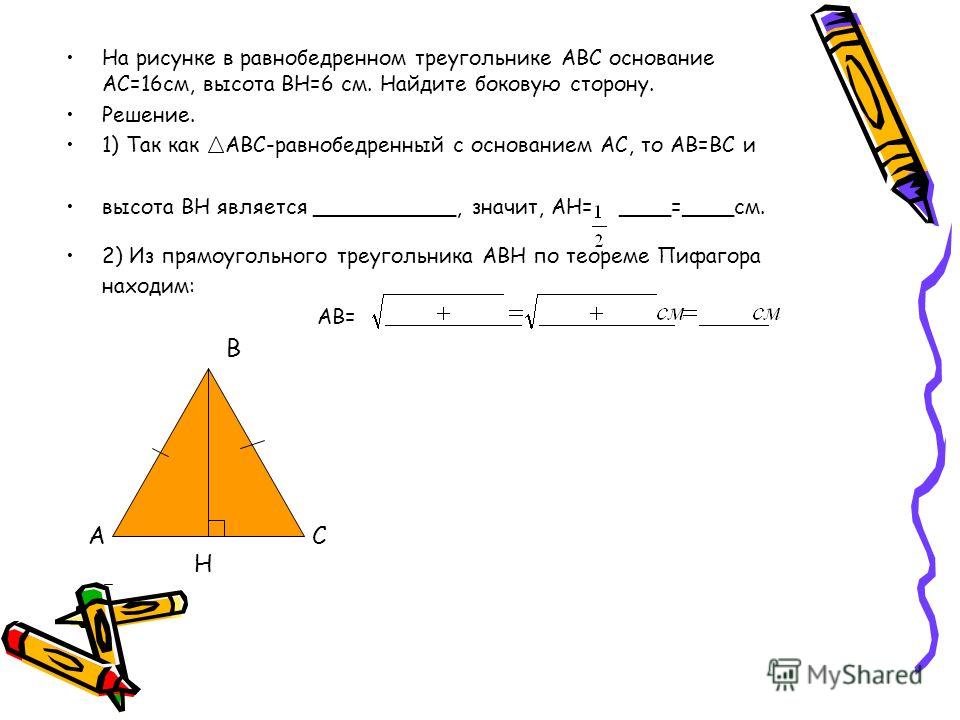 Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей. А 39 О r В r r Н О 1 С
Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей. А 39 О r В r r Н О 1 С
L О r r r В А K r О 1 r Н 39 С
• Дан равнобедренный треугольник с основанием 16. Косинус одного из углов равен -7/25. Две равные окружности, касающиеся друга и двух сторон треугольника, вписаны в треугольник. Найти их радиусы.
В каком отношении точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону, если известно, что радиус окружности, касающейся стороны треугольника и продолжений двух других его сторон, в 7 раз больше радиуса вписанной окружности? А b O В r D 7 r O 1 r K a a С a 7 r E
F 7 r O 1 7 r c c А b r K a O r E b+a-c В a D a С
• В каком отношении точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону, если известно, что отношение радиусов его вписанной окружности и окружности, касающейся стороны треугольника и продолжений двух других сторон, равно 2/7? • Дан равнобедренный треугольник. Найти угол при основании этого треугольника, если радиус вписанной окружности относится к радиусу окружности, касающейся одной из сторон и продолжений двух других сторон, как 1 : 4. • В каком отношении точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону, если известно, что отношение радиусов его вписанной окружности и окружности, касающейся стороны треугольника и продолжений двух других его сторон, равно 1/5? • Найдите косинус угла при основании равнобедренного треугольника, если известно, что радиус его вписанной окружности в 6 раз меньше радиуса окружности, касающейся стороны и продолжений двух других сторон треугольника.
Найти угол при основании этого треугольника, если радиус вписанной окружности относится к радиусу окружности, касающейся одной из сторон и продолжений двух других сторон, как 1 : 4. • В каком отношении точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону, если известно, что отношение радиусов его вписанной окружности и окружности, касающейся стороны треугольника и продолжений двух других его сторон, равно 1/5? • Найдите косинус угла при основании равнобедренного треугольника, если известно, что радиус его вписанной окружности в 6 раз меньше радиуса окружности, касающейся стороны и продолжений двух других сторон треугольника.
Боковые стороны KL и MN трапеции KLMN равны 10 и 26 соответственно. Отрезок, соединяющий середины диагоналей, равен 12, средняя линия трапеции равна 24. Прямые KL и MN пересекаются в точке A. Найдите радиус окружности, вписанной в треугольник ALM. 1 случай: A 5 L C 10 K 12 -х E 13 M 12 12 F х 26 D N
2 случай: A K N C M 10 12 -х E 12 F х 26 D L 2 или 6
• Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в треугольник BMC. 4 или 6 • Боковые стороны AB и CD трапеции ABCD равны 7 и 24 соответственно. Отрезок, соединяющий середины диагоналей, равен 12. 5, средняя линия трапеции равна 27. 5. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в треугольник BMC. 1, 8 или 4, 8
Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в треугольник BMC. 4 или 6 • Боковые стороны AB и CD трапеции ABCD равны 7 и 24 соответственно. Отрезок, соединяющий середины диагоналей, равен 12. 5, средняя линия трапеции равна 27. 5. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в треугольник BMC. 1, 8 или 4, 8
Дан треугольник АВС. Точка Е на прямой АС выбрана так, что треугольник АВЕ, площадь которого равна 14, — равнобедренный с основанием АЕ и высотой BD. Найдите площадь треугольника АВС, если известно, что ∠ABE = ∠CBD = α и tg α = 24/7. В A D Так как ∠DBE = ∠EBC E С
В E D Так как ∠DBA = ∠ABC A С 25 или 39
• Дан треугольник АВС, площадь которого равна 55. Точка Е на прямой АС выбрана так, что треугольник АВЕ — равнобедренный с основанием АЕ и высотой BD. Найдите площадь треугольника АВE, если известно, что ∠ABE = ∠CBD =α и tgα = 4/3. 30 или 66
Найдите площадь треугольника АВE, если известно, что ∠ABE = ∠CBD =α и tgα = 4/3. 30 или 66
Точка О- центр правильного шестиугольника ABCDEF со стороной 7. Найдите радиус окружности, касающейся окружностей , описанных около треугольников BOD, DOF, BOF. 1 случай 2 случай
С 7 O D E В 7 А 7 M F r =14
С 7 D 7 E 7 7 O В r r А O 1 14 r CDO 1: M DC=7 DO 1=21 -r CO 1=7+r CDO 1=600 F По т. косинусов: r =6
• Точка O — центр правильного шестиугольника ABCDEF со стороной. Найдите радиус окружности касающейся окружностей, описанных около треугольников AOB, COD , EOF. 28 или 12
Дан равнобедренный треугольник с боковой стороной 4 и углом 1200. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей. А 600 4 О r В r r Н О 1 С
L K r 150 В О 2 r r А 600 r r О 1 Н 4 С
Площадь трапеции ABCD равна 135. Диагонали пересекаются в точке O. Отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь треугольника MON, если одно из оснований трапеции вдвое больше другого. B x M a O 2 a x M, N — середины диагоналей ОС — медиана N 3 a A C P 2 x x D
Диагонали пересекаются в точке O. Отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь треугольника MON, если одно из оснований трапеции вдвое больше другого. B x M a O 2 a x M, N — середины диагоналей ОС — медиана N 3 a A C P 2 x x D
2 x B С 4 a a A M x/2 O P N x/2 D
• Площадь трапеции ABCD равна 810. Диагонали пересекаются в точке O. Отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь треугольника MON, если одно из оснований трапеции вдвое больше другого. 22, 5 или 14, 4
К окружности, вписанной в треугольник с периметром 18, проведена касательная параллельно основанию треугольника. Отрезок касательной между боковыми сторонами равен 2. Найдите основание треугольника. B M F z z 2 d N d K у A O у E х х C 2 2 AC
Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 40, а отношение катетов треугольника равно 15/8. A 75 85 N 40 r O r C r r r -75 17 x M 15 x-85 15 x 17 x r B 8 x
Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 40, а отношение катетов треугольника равно 15/8. A 75 85 N 40 r O r C r r r -75 17 x M 15 x-85 15 x 17 x r B 8 x
A 17 x 15 x r r r C N O r r r 40 M 8 x B
• Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 10, а отношение катетов треугольника равно 5/12. • Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 6, а отношение катетов треугольника равно 3/4. • Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти площадь четырехугольника, если гипотенуза треугольника равна 10, а радиус окружности, равен 2.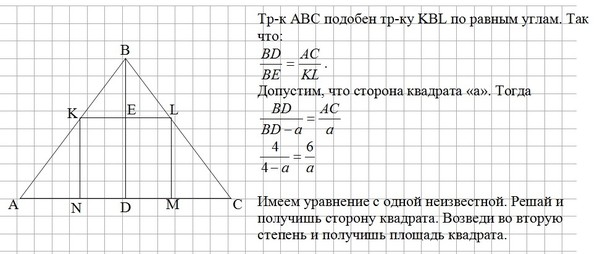
• Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 12, а косинус острого угла равен 0, 6. • Прямая, перпендикулярная боковой стороне равнобедренного треугольника с основанием равным 12, отсекает от него четырехугольник, в который можно вписать окружность. Найти площадь четырехугольника, если радиус окружности равен 3. • Прямая, перпендикулярная боковой стороне равнобедренного треугольника , отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 24, а синус угла при основании равен 0, 8.
• Прямая, перпендикулярная гипотенузе прямоугольного треугольника с катетами 6 и 8, отсекает от него четырехугольник, в который можно вписать окружность. Найти площадь этого четырехугольника. • Прямая, перпендикулярная гипотенузе прямоугольного треугольника с катетами 5 и 12, отсекает от него четырехугольник, в который можно вписать окружность. Найти площадь этого четырехугольника. • Прямая, перпендикулярная боковой стороне равнобедренного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 20, а отношение боковой стороны треугольника к его основанию равно 13/10. • Прямая, перпендикулярная боковой стороне равнобедренного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 6, а отношение боковой стороны треугольника к его основанию равно 5/6.
• Прямая, перпендикулярная гипотенузе прямоугольного треугольника с катетами 5 и 12, отсекает от него четырехугольник, в который можно вписать окружность. Найти площадь этого четырехугольника. • Прямая, перпендикулярная боковой стороне равнобедренного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 20, а отношение боковой стороны треугольника к его основанию равно 13/10. • Прямая, перпендикулярная боковой стороне равнобедренного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 6, а отношение боковой стороны треугольника к его основанию равно 5/6.
• Прямая, перпендикулярная боковой стороне равнобедренного треугольника со сторонами равным и 10, 12, отсекает от него четырехугольник, в который можно вписать окружность.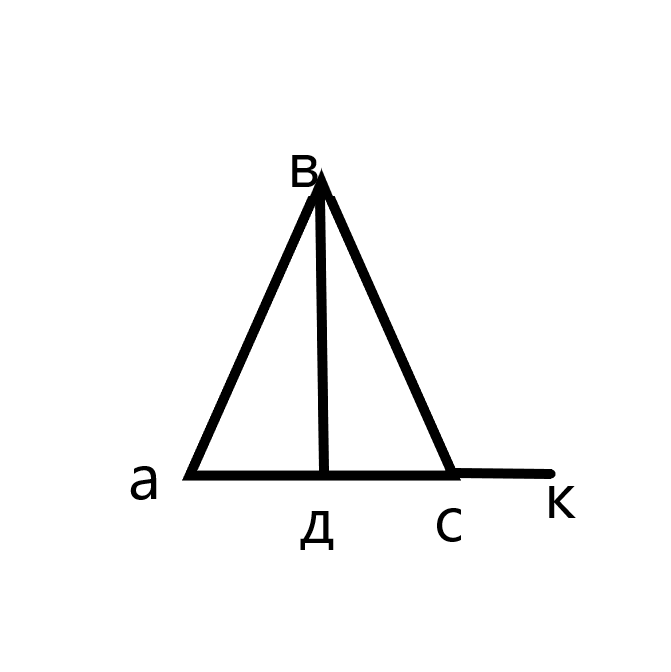 Найти площадь четырехугольника. • Прямая, перпендикулярная боковой стороне равнобедренного треугольника со сторонами равным и 10, 13, отсекает от него четырехугольник, в который можно вписать окружность. Найти площадь четырехугольника.
Найти площадь четырехугольника. • Прямая, перпендикулярная боковой стороне равнобедренного треугольника со сторонами равным и 10, 13, отсекает от него четырехугольник, в который можно вписать окружность. Найти площадь четырехугольника.
Точка М лежит на отрезке АВ. На окружности с диаметром АВ взята точка С, удаленная от точек А, М и В на расстояния 40, 29 и 30 соответственно. Найти площадь треугольника ВМС. B 50 H 24 O M A 29 40 30 C
B M 50 H 29 24 O 30 C A 40
• Точка М лежит на отрезке АВ. На окружности с диаметром АВ взята точка С, удаленная от точек А, М и В на расстояния 20, 14 и 15 соответственно. Найти площадь треугольника ВМС.
Площадь равнобедренного треугольника
В данном уроке размещены формулы и задачи на нахождение площади равнобедренного треугольника. Формулы снабжены пояснениями и комментариями. На отдельном рисунке приведено соответствие условных обозначений формул и элементов равнобедренного треугольника. Далее приведен раздел с примерами решения задач.
Далее приведен раздел с примерами решения задач.
См. также:
Буквенные обозначения сторон и углов на приведенном рисунке соответствуют обозначениям, которые указаны в формулах. Таким образом, это поможет Вам сопоставить их с элементами равнобедренного треугольника. Из условия задачи определите, какие элементы известны, найдите на чертеже их обозначения и подберите подходящую формулу.
Формула площади равнобедренного треугольника
Далее приведены формулы нахождения площади равнобедренного треугольника: через стороны, боковую сторону и угол между ними, через боковую сторону, основание и угол при вершине, через сторону основания и угол при основании и т.д. Просто найдите наиболее подходящую на рисунке слева. Для самых любопытных в тексте справа поясняется, почему формула явяляется правильной и как именно с ее помощью находится площадь.- Площадь равнобедренного треугольника можно найти, зная его сторону и основание.
 Данное выражение было получено путем упрощения более общей, универсальной формулы. Если за основу взять формулу Герона, а затем принять во внимание, что две стороны треугольника равны меду собой, то выражение упрощается до формулы, представленной на картинке.
Данное выражение было получено путем упрощения более общей, универсальной формулы. Если за основу взять формулу Герона, а затем принять во внимание, что две стороны треугольника равны меду собой, то выражение упрощается до формулы, представленной на картинке.
Пример использования такой формулы приведен на примере решения задачи ниже. - Вторая формула позволяет найти его площадь через боковые стороны и угол между ними — это половина квадрата боковой стороны, умноженная на синус угла между боковыми сторонами
Если мысленно опустить высоту на боковую сторону равнобедренного треугольника, заметим, что ее длина будет равна a * sin β. Поскольку длина боковой стороны нам известна, высота, опущенная на нее теперь известна, половина их произведения и будет равна площади данного равнобедренного треугольника (Пояснение: полное произведение дает площадь прямоугольника, что очевидно. Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5
Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5 - Третья формула показывает нахождение площади через боковую сторону, основание и угол при вершине.
Строго говоря, зная один из углов равнобедренного треугольника, можно найти и остальные, поэтому применение данной или предыдущей формулы — вопрос вкуса (кстати, поэтому можно запомнить только одну из них).
У третьей формулы также есть еще одна интересная особенность — произведение a sin α даст нам длину высоты, опущенной на основание. В результате мы получим простую и очевидную формулу 5. - Площадь равнобедренного треугольника можно также найти через сторону основания и угол при основании (углы при основании равны) как квадрат основания, деленный на четыре тангенса половины угла, образованного его боковыми сторонами. Если присмотреться внимательнее, то станет очевидно, что половина основания (b/2) умноженная на tg(β/2) даст нам высоту треугольника.
 Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2) ). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна.
Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2) ). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна. - Разумеется, площадь равнобедренного треугольника можно найти, опустив высоту из вершины на основание, в результате чего получится два прямоугольных треугольника. Далее — все очевидно. Половина произведения высоты на основание и есть искомая площадь. Пример использования данной формуле см. в задаче ниже (2-й способ решения)
- Эта формула получается, если попытаться найти площадь равнобедренного треугольника с помощью теоремы Пифагора. Для этого выразим высоту из предыдущей формулы, которая одновременно, является катетом прямоугольного треугольника, образованного боковой стороной, половиной его основания и высотой, через теорему Пифагора. Боковая сторона является гипотенузой, поэтому из квадрата боковой стороны (а) вычтем квадрат второго катета.
 Поскольку он равен половине основания (b/2) то его квадрат будет равен b2/4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Поскольку он равен половине основания (b/2) то его квадрат будет равен b2/4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Кстати, самые сообразительные могут увидеть, что если в Формуле 1 раскрыть скобки, то она превратиться в Формулу 6. Или наоборот, разность квадратов двух чисел, разложенная на множители, даст нам исходную, первую.
Обозначения, которые были применены в формулах на рисунке:
a — длина одной из двух равных сторон треугольника
b — длина основания
α — величина одного из двух равных углов при основании
β — величина угла между равными сторонами треугольника и противолежащего его основанию
h — длина высоты, опущенная из вершины равнобедренного треугольника на основание
Важно. Обратите внимание на обозначения переменных! Не перепутайте α и β, а также a и b!
Обратите внимание на обозначения переменных! Не перепутайте α и β, а также a и b!
См. также: другие формулы и свойства равнобедренного треугольника
Примечание. Это часть урока с задачами по геометрии (раздел площадь равнобедренного треугольника). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Задача
Боковая сторона равнобедренного треугольника равна 13 см, а основание равно 10 см. Найдите площадь равнобедренного треугольника.
Решение.
1-й способ. Применим формулу Герона. Поскольку треугольник равнобедренный, то она примет более простой вид (см. формулу 1 в списке формул выше):
формулу 1 в списке формул выше):
где а — длина боковых сторон, а b — длина основания.
Подставив значения длин сторон треугольника из условия задачи, получим:
S = 1/2 * 10 * √ ((13 + 5 )( 13 — 5 )) = 5 √ (18 * 8) = 60 см2
2-й способ. Применим теорему Пифагора
Предположим, что мы не помним формулу, использованную в первом способе решения. Поэтому опустим из вершины B на основание AC высоту BK.
Поскольку высота равнобедренного треугольника делит его основание пополам, то длина половины основания будет равна
AK = AC / 2 = 10 / 2 = 5 см .
Высота с половиной основания и стороной равнобедренного треугольника образует прямоугольный треугольник ABK. В этом треугольнике нам известна гипотенуза AB и катет AK. Выразим длину второго катета через теорему Пифагора.
Соответственно, высота будет равна:h = √ ( 132 — 52 ) = √144 = 12 см
Площадь исходного равнобедренного треугольника ABC будет равна площади двух прямоугольных треугольников ABK и CBK, образованных боковыми сторонами, высотой и половинами основания равнобедренного треугольника. Оба прямоугольных треугольника равны между собой. Гипотенузы — это стороны равнобедренного треугольника, поэтому они равны, один из катетов — общий, а, поскольку, BK одновременно является и биссектрисой и высотой, то, соответствующие углы также равны. Поэтому нам будет достаточно найти площадь одного из них и умножить полученное число на два.
Оба прямоугольных треугольника равны между собой. Гипотенузы — это стороны равнобедренного треугольника, поэтому они равны, один из катетов — общий, а, поскольку, BK одновременно является и биссектрисой и высотой, то, соответствующие углы также равны. Поэтому нам будет достаточно найти площадь одного из них и умножить полученное число на два.
Как найти площадь равнобедренного треугольника? Ответ на webmath.ru
Остались вопросы?
Здесь вы найдете ответы.
Площадь равнобедренного треугольника с прямым углом составляет 16 см кв. Каким образом можно вычислить длину гипотенузы данной треугольной фигуры?
Обозначим через х катет имеющегося равнобедренного треугольника, имеющего прямой угол. В этом случае его площадь будет представлять собой ½ длины его катета, возведенную в квадратную степень. Это значит, что квадрат катета равен двум площадям треугольника (2S). В нашем случае это:
2S = 2*16 = 32 см кв.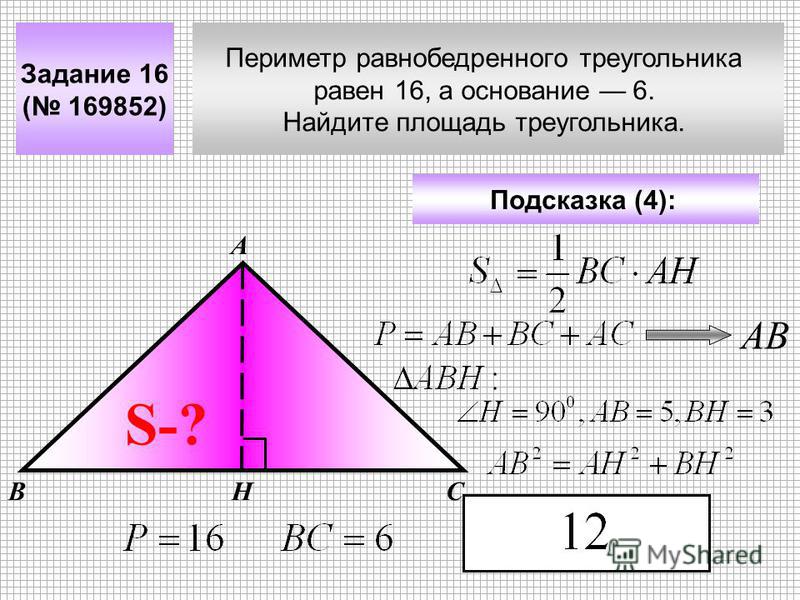
Для того чтобы найти длину катета, нужно извлечь корень квадратный из числа 32:
х = 4*√2 см.
Теперь можно высчитать длину гипотенузы, которая будет равна:
х / sin45 = 8 см.
Ответ: Длина гипотенузы равна 8 см.
Имеется равнобедренный треугольник площадью 192 см кв. Его основание составляет 32 см. Как можно вычислить периметр данной треугольной фигуры?
Дан треугольник АВС, в котором АВ=ВС и АС=32 см.
Проведем к основанию треугольника высоту ВН, также являющуюся медианой.
Площадь треугольника равна половине произведения длины его основания на высоту:
S=АС*ВН/2
Из этой формулы можно выразить ВН:
ВН=2S/АС=2*192/32=12 см.
Известно, что в равнобедренном треугольнике две стороны равны:
АВ=ВС=√(ВН²+(АС/2)²)=√(144+256)=20 см.
Теперь можно высчитать периметр (Р) треугольника АВС, который будет равен сумме длин его сторон:
Р=2АВ+АС=40+32=72 см.
Ответ: Периметр равнобедренного треугольника АВС равен 72 см.
Длина гипотенузы равнобедренного треугольника, имеющего прямой угол, составляет 12 см. Как найти площадь данного треугольника?
Обозначим буквой х катет имеющегося треугольника. Тогда по теореме Пифагора:
12²=x² + x², что равно 144=2х²
Отсюда находим значение х:
x²=72, x=√72
Зная длину катета равнобедренного треугольника, можно найти его площадь (S):
S = √72 * √72/2 = 36 см кв.
Ответ: Площадь треугольника равна 36 см кв.
Дан равнобедренный треугольник, угол в основании которого составляет 25 градусов. Площадь данной фигуры равна 16 см кв. Есть еще один равнобедренный треугольник с углом 130 градусов и площадью 4з см кв. Чему будет равно отношение оснований этих двух треугольных фигур?
Разберемся с первым из треугольников. Так как он является равнобедренным,
то оба угла при его основании будут равны. Зная о том, что сумма всех
углов треугольника равна 180 градусом, мы можем найти третий угол
треугольника, находящийся при его вершине:
Так как он является равнобедренным,
то оба угла при его основании будут равны. Зная о том, что сумма всех
углов треугольника равна 180 градусом, мы можем найти третий угол
треугольника, находящийся при его вершине:
180-25-25=130 градусов.
Переходим ко второму треугольнику. Известно, что угол при его вершине равен 230 градусом. Исходя из этого можно рассчитать величины его углов, расположенных в основании фигуры:
(180-130)/2=25 градусов.
Очевидно, что треугольники являются подобными на основании равенства углов.
Следует определить коэффициент подобия двух треугольных фигур. Квадрат коэффициента подобия будет равен отношению площадей треугольников:
49/16=kˆ2
Отсюда выражаем k:
k=7/4
Коэффициент подобия представляет собой отношение основания первой подобной треугольной фигуры ко второй. Это значит, что:
С/c=k = 7/4
Ответ: Отношение оснований двух треугольников равно 7/4.
Чему равна площадь равнобедренного треугольника с прямым углом при условии, что длина его гипотенузы составляет с?
Площадь (S) треугольника с прямым углом составляет ½ часть произведения его катетов. Принимая во внимание тот факт, что треугольник является равнобедренным, можно утверждать, что длины его катетов равны. Их можно обозначить через х. В этом случае формулу для расчета площади треугольника можно записать в следующем виде:
S=½x*x=½x²
Согласно теореме Пифагора, действительной для прямоугольного треугольника:
с²=х²+х²=2x²
x²=½c²
Подставим в формулу площади получившееся равенство:
S=½*½с²=¼с² см.кв.
Ответ: Площадь равнобедренного треугольника равна ¼с² см кв.
Как можно рассчитать площадь равнобедренного треугольника, если длина его высоты и основания – величины известные?
Площадь (S) любой треугольной фигуры рассчитывается путем деления пополам произведения длины его основания (с) и высоты (h):
S = ½ c*h
Как найти площадь равнобедренного треугольника?
Площадь каждого треугольника, в том числе и равнобедренного,
рассчитывается как половина, взятая от произведения длины высоты
треугольника и его основания. Формула имеет следующий вид:
Формула имеет следующий вид:
S=1/2 *a*h
Пусть а = 150 см.
Проводим высоту к основанию треугольника. Она же будет являться и медианой по той причине, что треугольник равнобедренный. В результате образовался треугольник с прямым углом и гипотенузой, длина которой равна 85 см. Один из катетов треугольника равен h, а второй рассчитывается как а/2:
150/2=75 см.
Теперь можно рассчитать длину второго катета (на основании теоремы Пифагора):
h=√85²-75²=√7225-5625=√1600=40 см.
Когда все необходимые для расчета площади треугольника величины известны, можно найти ее значение:
S=1/2 *a*h=1/2 *150*40=3000 см.
Как можно найти площадь треугольника при условии, что он является равнобедренным, и его периметр равен 100 см, а основание – 48 см?
Вычислим длину боковой стороны равнобедренного треугольника, отняв от его периметра длину основания и разделив полученное число на 2:
(100-48):2=26 см.
Тогда площадь равнобедренного треугольника с заданными параметрами будет равна:
S=b/4*√(4a²-b²)=12*√(2704-2304)=12*20=240 cм кв.
Чему равна площадь равнобедренного треугольника, длины сторон которого составляют 10 см и 12 см (сумма длин его катетов)?
К основанию равнобедренного треугольника проведем высоту, делящую его на две равные треугольные фигуры, каждая из которых имеет угол 90 градусов и катет длиной 12/2 = 6 см. Гипотенуза подобных треугольников имеет длину 10 см.
В случае с прямоугольным треугольником может быть применима теорема Пифагора, которая поможет найти катет, являющийся высотой треугольника:
h² = 10² — 6² = 64 см
Избавимся от квадратов:
h = 8 см.
Тогда площадь треугольника будет равна:
S = 12 * 8 : 2 = 48 см кв.
Как рассчитать площадь равнобедренного треугольника, если известно о том, что длина его гипотенузы составляет 44 см?
Введем условные обозначения, согласно которым х – это длина одного из
катетов равнобедренного треугольника. В этом случае длина второго катета
тоже будет равна х. Зная длину гипотенузы, можно записать формулу теоремы
Пифагора для имеющегося треугольника:
В этом случае длина второго катета
тоже будет равна х. Зная длину гипотенузы, можно записать формулу теоремы
Пифагора для имеющегося треугольника:
х²+ х² = 44²
2х² = 1936
Отсюда можем найти значение х:
x=√968
Найдя длину катета равнобедренного треугольника, можно вычислить его площадь (S), равную ½ произведения длин его катетов:
S = √968*√968/2 = 484 см кв.
Каким образом возможно высчитать площадь равнобедренного треугольника через стороны и длину его основания?
Располагая сведениями о длине основания (b) и стороны (a) треугольной фигуры с равными катетами, возможно рассчитать площадь (S) этой фигуры. С этой целью следует пользоваться приведенной ниже формулой:
S = b/4×√ 4× a²-b².
Возможно ли определить площадь равнобедренного треугольника через его боковые стороны и образованный ими угол?
Информация о длине боковых сторон (а) треугольной фигуры с катетами равной
длины и размере угла (α), который образован этими катетами, позволит
определить площадь этой фигуры. В этом поможет следующая формула:
В этом поможет следующая формула:
S = 1/2a2 * sin(α).
Как можно высчитать площадь равнобедренного треугольника при условии, что известна длина его основания и угол?
Для расчета площади треугольной фигуры с катетами равной длины, при условии, что известна их длина (а), основание (b) и угол, который образован основанием и одним из катетов(α), используется следующая формула:
S = ½ * a * b * sin(α)
Длина основания равнобедренного треугольника превышает длину его боковой стороны на 3 см. Периметр данной треугольной фигуры равен 30 см. Как можно высчитать длину основания данного равнобедренного треугольника?
Примем неизвестную длину основания равнобедренного треугольника за х. В
данном случае длина каждой из боковых сторон, которые в равнобедренном
треугольнике равны, будет составлять (х-3). Известно, что периметр (Р)
треугольника равен 30 см. Тогда:
Тогда:
Р = 3х-6 = 30 см.
Отсюда можно вывести х:
х = (30+6)/3 = 12 см.
Ответ: Длина основания равна 12 см.
Высота, проведенная в равнобедренном треугольнике, равна 15 см. Длина основания данной фигуры превышает длину его боковой стороны на 15 см. Как найти основание равнобедренного треугольника в этом случае?
Примем х за длину основания равнобедренного треугольника. Тогда длина его боковой стороны будет составлять (х-15). Высота, проведенная в треугольнике с прямым углом, также представляет собой его медиану, которая делит его на две равных треугольных фигуры. Следует рассмотреть одну из образовавшихся треугольных фигур. Для начала вычислим ее основания, используя теорему Пифагора:
с2 = а2 + b2 = (15)²+(0,5x)²=(x-15)²
Из этого получается:
225-x²-30x+225-0,25x²
0=0,75x²-30x
x(0,75x-30)=0
x¹=0 см.
x=40 см.
Очевидно, что сторона треугольной фигуры не может иметь длину, равную 0см. Поэтому можно сделать вывод о том, что ее длина составляет 40 см.
По какой формуле можно высчитать площадь равнобедренного треугольника?
Для ответа на поставленный вопрос следует провести высоту из вершины того угла равнобедренного треугольника, который является противоположным его основанию. После этого длину проведенной высоты (а) нужно умножить на длину основания фигуры (b), а затем разделить полученное значение на два. Формула расчета площади треугольной фигуры, которая является равнобедренной, выглядит следующим образом:
S=a*b/2, или S=1/2a* b.
В равнобедренном треугольнике к его основанию проведена высота, длина которой равна 1,2 см. Длина самого основания фигуры составляет 3,2 см. Как рассчитать длину боковой стороны этого равнобедренного треугольника?
Вычислим половину длины основания данного равнобедренного треугольника:
3,2/2 = 1,6 см.
Имеется треугольник с прямым углом и катетами, длины которых равны 1,2 см и 1,6 см. Требуется определить длину его гипотенузы. Ее можно вычислить, используя теорему Пифагора:
с²=а²+в²
с² = 1,2² + 1,6² = 1,44 + 2,56 = 4
Осталось только извлечь корень квадратный из 4:
с=√4=2 см.
Ответ: Длина боковой стороны равнобедренного треугольника равна 2 см.
Один из углов равнобедренного треугольника является тупым. Одна сторона данной фигуры составляет 14 см, а другая – 8 см. Чему равно основание треугольника с двумя равными сторонами?
Известно, что углы, расположенные у основания равнобедренного треугольника, всегда являются острыми, иначе сумма всех трех углов превышала бы 180 градусов. Исходя из этого, можно сделать вывод о том, что тупой угол расположен у вершины данной треугольной фигуры.
Доказанным фактом является то, что та сторона фигуры, которая расположена
напротив тупого угла, имеет большую длину, чем сторона, лежащая против
острого угла треугольника. Это позволяет утверждать, что длина основания
данного треугольника больше длины его боковой стороны. По причине того,
что треугольная фигура является равнобедренной, и известны длины двух ее
сторон (8 см и 14 см), можно говорить о том, что неизвестная сторона будет
составлять 8 см или 14 см. Если предположить, что длина неизвестной
стороны равна 14 см, тогда длина основания будет составлять 8 см, что
невозможно, так как противоречит утверждению о расположении больших сторон
напротив тупых углов. Это означает, что длина третьей стороны треугольника
равна 8 см, а основание в данном случае составляет 14 см.
Это позволяет утверждать, что длина основания
данного треугольника больше длины его боковой стороны. По причине того,
что треугольная фигура является равнобедренной, и известны длины двух ее
сторон (8 см и 14 см), можно говорить о том, что неизвестная сторона будет
составлять 8 см или 14 см. Если предположить, что длина неизвестной
стороны равна 14 см, тогда длина основания будет составлять 8 см, что
невозможно, так как противоречит утверждению о расположении больших сторон
напротив тупых углов. Это означает, что длина третьей стороны треугольника
равна 8 см, а основание в данном случае составляет 14 см.
Равнобедренный треугольник имеет сторону длиной 29 см. Высота, проведенная в нем, составляет 21 см. Чему равно основание треугольника с указанными параметрами?
Для решения данной задачи следует воспользоваться теоремой Пифагора:
с²=а²+в²
Отсюда можно выразить квадрат длины неизвестной стороны, который будет равен разности квадратов известной стороны и высоты:
29²-21² = 400.
Для того чтобы узнать длину основания равнобедренного треугольника, нужно извлечь корень квадратный из числа 400, а затем умножить полученное число на 2:
√400*2 = 20*2 = 40 см.
Ответ: Длина основания равнобедренного треугольника равна 40 см.
ACT по математике — ACT по математике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Площадь треугольника — пояснения и примеры
Из этой статьи вы узнаете площадь треугольника и определить площадь различных типов треугольников .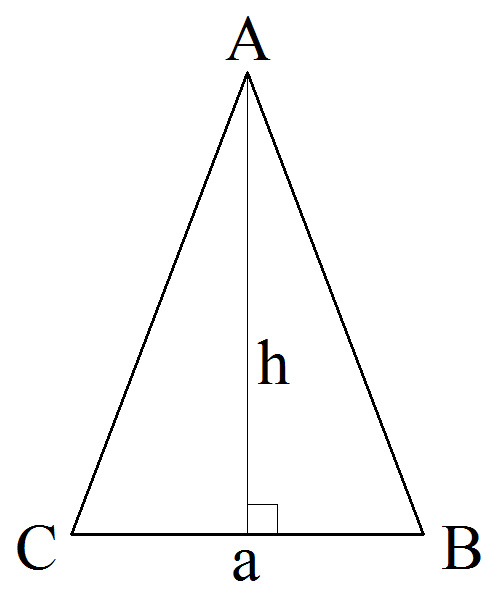 Площадь треугольника — это пространство внутри треугольника. Он измеряется в квадратных единицах.
Площадь треугольника — это пространство внутри треугольника. Он измеряется в квадратных единицах.
Прежде чем перейти к теме о площади треугольника , давайте познакомимся с такими терминами, как основание и высота треугольника.
Основание — это сторона треугольника, которая считается нижней частью, а t Высота треугольника — это перпендикулярная линия, опущенная на его основание из вершины, противоположной основанию. .
На приведенном выше рисунке пунктирными линиями показаны возможные значения △ ABC. Обратите внимание, что у каждого треугольника, возможно, есть три высоты или высоты.
- Высота треугольника △ ABC равна h 1 , когда основание является стороной.
- Высота треугольника △ ABC равна h3 при основании AB.
- Высота треугольника △ ABC равна h 3 при основании
- Высота треугольника △ ABC может находиться вне треугольника ( h 4 ), что составляет такая же, как высота h 1 .

Из иллюстраций выше мы можем сделать следующие наблюдения:
- Высота треугольника зависит от его основания.
- Перпендикуляр к основанию треугольника равен высоте треугольника.
- Высота треугольника может быть вне треугольника.
Обсудив понятие высоты и основания треугольника, давайте теперь приступим к вычислению площади треугольника.
Как найти площадь треугольника?
Площадь прямоугольника нам хорошо известна, т.е.е., длина * ширина . Что будет, если прямоугольник разделить пополам по диагонали (разрезать пополам)? Какая будет его зона новостей? Например, в прямоугольнике с основанием и высотой 6 единиц и 12 единиц, соответственно, площадь прямоугольника составляет 72 квадратных единицы.
Теперь, если вы разделите на две равные половины (после деления прямоугольника пополам по диагонали), площадь двух новых фигур должна составлять 36 квадратных единиц каждая. Две формы новостей представляют собой треугольники. Это означает, что если прямоугольник разрезан по диагонали на две равные половины, две новые формы образуются треугольниками, где каждый треугольник имеет площадь, равную ½ площади прямоугольника.
Две формы новостей представляют собой треугольники. Это означает, что если прямоугольник разрезан по диагонали на две равные половины, две новые формы образуются треугольниками, где каждый треугольник имеет площадь, равную ½ площади прямоугольника.
Площадь треугольника — это общее пространство или область, ограниченная определенным треугольником.
Площадь треугольника равна произведению основания и высоты на 2.
Стандартной единицей измерения площади являются квадратные метры (м 2 ).
Другие единицы включают:
- Квадратные миллиметры (мм 2 )
- Квадратные дюймы (дюйм 2 )
- Квадратные километры (км 2 )
- Квадратные ярды.
Формула площади треугольника
Общая формула для вычисления площади треугольника:
Площадь (A) = ½ (b × h) квадратных единиц, где; A — площадь, b — основание, h — высота треугольника. Треугольники могут быть разной природы, но важно отметить, что эта формула применима ко всем треугольникам. У разных типов треугольников разные формулы площади.
У разных типов треугольников разные формулы площади.
Примечание. База и высота должны быть в одних и тех же единицах измерения, то есть в метрах, километрах, сантиметрах и т. Д.
Площадь прямоугольного треугольника
Площадь треугольника = (½ × основание × высота) квадратных единиц.
Пример 1
Найдите площадь прямоугольного треугольника с основанием 9 м и высотой 12 м.
Решение
A = ¹ / ₂ × основание × высота
= ¹ / ₂ × 12 × 9
= 54 см²
Пример 2
Основание и высота прямоугольного треугольника равны 70 см и 8 м соответственно.Какая площадь у треугольника?
Решение
A = ½ × основание × высота
Здесь у нас 70 см и 8 м. Вы можете работать с cm или m. Давайте работать в метрах, заменив 70 см на метры.
Разделите 70 см на 100.
70/100 = 0,7 м.
⇒ A = (½ × 0,7 × 8) м 2
⇒ A = (½ x 5,6) м 2
⇒ A = 2,8 м 2
Площадь равнобедренного треугольника
An Равнобедренный треугольник — это треугольник, у которого две стороны равны, а также два угла равны.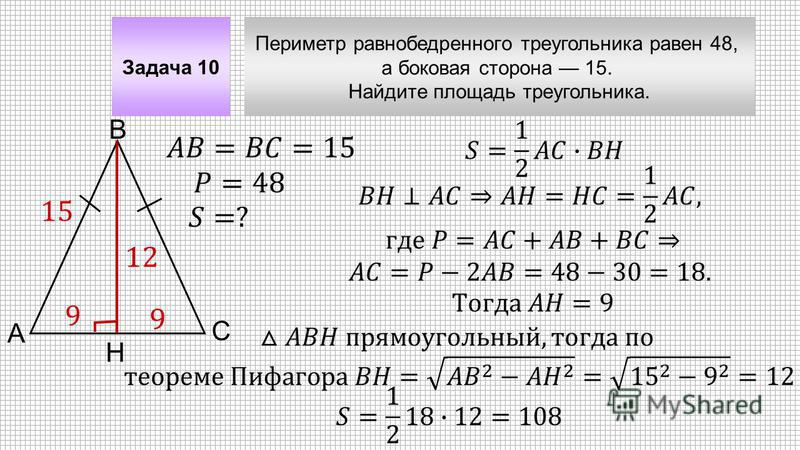 Формула площади равнобедренного треугольника:
Формула площади равнобедренного треугольника:
⇒A = ½ (основание × высота).
Если высота равнобедренного треугольника не указана, для нахождения высоты используется следующая формула:
Высота = √ (a 2 — b 2 /4)
Где;
b = основание треугольника
a = длина стороны двух равных сторон.
Следовательно, площадь равнобедренного треугольника может быть;
⇒A = ½ [√ (a 2 — b 2 /4) × b]
Кроме того, площадь равнобедренного прямоугольного треугольника определяется по формуле:
A = ½ × a 2 , где a = длина стороны двух равных сторон
Пример 3
Рассчитайте площадь равнобедренного треугольника с основанием 12 мм и высотой 17 мм.
Решение
⇒A = ½ × основание × высота
⇒ 1/2 × 12 × 17
⇒ 1/2 × 204
= 102 мм 2
Пример 4
Найдите площадь равнобедренного треугольника, длина сторон которого составляет 5 м и 9 м.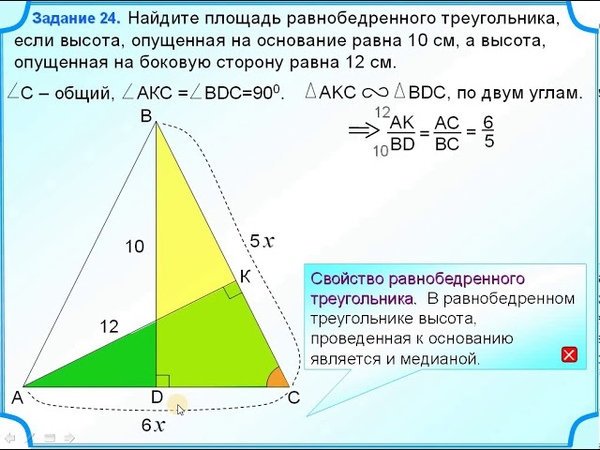
Решение
Пусть основание b = 9 м и a = 5 м.
⇒ A = ½ [√ (a 2 — b 2 /4) × b]
⇒ ½ [√ (5 2 — 9 2 /4) × 9]
= 9 .81m 2
Площадь равностороннего треугольника
Равносторонний треугольник — это треугольник, в котором три стороны равны и три внутренних угла равны. Площадь равностороннего треугольника:
A = (a 2 √3) / 4
, где a = длина сторон.
Пример 5
Вычислите площадь равностороннего треугольника со стороной 4 см.
Решение
⇒ A = (a 2 /4) √3
⇒ (4 2 /4) √3
⇒ (16/4) √3
= 4√3 см 2
Пример 6
Найдите площадь равностороннего треугольника с периметром 84 мм.
Решение
Периметр равностороннего треугольника = 3a.
⇒ 3a = 84 мм
⇒ a = 84/3
⇒ a = 28 мм
Площадь = (a 2 /4) √3
⇒ (28 2 /4) √3
= 196√3 мм 2
Площадь разностороннего треугольника
Разносторонний треугольник — это треугольник с 3 разными длинами сторон и 3 разными углами. Площадь разностороннего треугольника можно рассчитать по формуле Герона.
Площадь разностороннего треугольника можно рассчитать по формуле Герона.
Формула Герона дается формулой;
⇒ Площадь = √ {p (p — a) (p — b) (p — c)}
, где «p» — это полупериметр, а a, b, c — длины сторон.
⇒ p = (a + b + c) / 2
Пример 7
Вычислите площадь треугольника, длина сторон которого составляет 18 мм, 20 мм и 12 мм.
Решение
⇒ p = (a + b + c) / 2
Подставьте значения a, b и c.
⇒ p = (12 + 18 + 20) / 2
⇒ p = 50/2
⇒ p = 25
⇒ Площадь = √ {p (p — a) (p — b) (p — c)}
= √ {25 x (25 — 12) x (25 — 18) x (25 — 20)}
= √ (25 x 13 x 7 x 5)
= 5√455 мм 2
Свойства треугольника — типы и формулы [Видео и практика]
В этой статье мы узнаем о простейшей форме многоугольника: треугольник . Все многоугольники можно разделить на треугольники или, другими словами, они образованы путем объединения двух или более треугольников. Таким образом, важно понимать основные свойства треугольника и его типы.
Все многоугольники можно разделить на треугольники или, другими словами, они образованы путем объединения двух или более треугольников. Таким образом, важно понимать основные свойства треугольника и его типы.
Всего существует шесть типов треугольников: равнобедренный, скален, равномерный, наклонный, острый и правый. Исходя из классификации по внутренним углам, различают три типа — равносторонний, равнобедренный и чешуйчатый. Принимая во внимание, что типы треугольника, которые классифицируются в зависимости от длины его стороны, — это правый, острый и наклонный.Вот виды треугольников:
| По углу | По сторонам | |||
| Острый угловой треугольник | Равносторонний треугольник | |||
| Наклонный угловой треугольник | Треугольник | Прямой угол | Треугольник | УголПрямоугольник | Треугольник
Посмотрите это видео, чтобы узнать основное свойство треугольника:
youtube.com/embed/J_IYLtYw3dc?rel=0″ title=»YouTube video player» frameborder=»0″ allow=»accelerometer rel=0; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Что такое треугольник?
Как следует из названия, треугольник представляет собой многоугольник с тремя углами.Итак, когда у замкнутой фигуры три угла?
Когда он состоит из трех отрезков, соединенных встык.
Таким образом, мы можем сказать, что треугольник — это многоугольник, у которого есть три стороны, три угла, три вершины, а сумма всех трех углов любого треугольника равна 180 °.
Свойства треугольника
Свойства треугольника:
- Треугольник имеет три стороны, три угла и три вершины.
- Сумма всех внутренних углов треугольника всегда равна 180 °. Это называется свойством суммы углов треугольника.
- Сумма длин любых двух сторон треугольника больше длины третьей стороны.

- Сторона, противоположная наибольшему углу треугольника, является наибольшей стороной.
- Любой внешний угол треугольника равен сумме его внутренних противоположных углов. Это называется свойством внешнего угла треугольника.
Виды треугольников
Треугольники можно классифицировать двумя основными способами:
- Классификация по внутренним углам (правый, острый, косой)
- Классификация по длине сторон (равносторонний, равнобедренный, чешуйчатый)
Давайте подробно рассмотрим шесть типов треугольников:
- Острый угловой треугольник
- Прямоугольный треугольник
- Наклонно-угловой треугольник
- Угловой треугольник Скален
- Равнобедренный угловой треугольник
- Равносторонний угловой треугольник
Острый угловой треугольник
Треугольник, у которого все три угла меньше 90 °, является треугольником с острыми углами.
- Итак, все углы треугольника с острыми углами называются острыми углами.

Ниже приведен пример треугольника с острыми углами.
Прямоугольный треугольник
Треугольник с одним углом , равным точно 90 °, является прямоугольным треугольником.
- Два других угла прямоугольного треугольника — острые.
- Сторона, противоположная прямому углу, является наибольшей стороной треугольника и называется гипотенузой.2
Это известно как Теорема Пифагора
Наоборот, мы можем сказать, что если треугольник удовлетворяет условию Пифагора, то это прямоугольный треугольник.
Тупой / наклонный угловой треугольник
Треугольник с одним углом , превышающим 90 °, является треугольником с тупым углом.
Ниже приведен пример треугольника с тупым / наклонным углом.
Вопросы о треугольниках очень часто задают на GMAT.Ace GMAT Quant, подписавшись на бесплатную пробную версию, вы получите доступ к более чем 400 вопросам.
 Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.
Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.Сэкономьте 60+ часов на подготовке к GMAT, составив четкий план обучения всего за 3 шага:
Чешуйчатый треугольник
Треугольник, у которого все три стороны разной длины — разносторонний треугольник.
- Поскольку все три стороны имеют разную длину, у три угла также будут разными.
Ниже приведен пример разностороннего треугольника
.Равнобедренный треугольник
Треугольник, у которого две стороны одинаковой длины и третья сторона разной длины , является равнобедренным треугольником.
- Углы , противоположные равным сторонам, равны.

Ниже приведен пример равнобедренного треугольника.
Равносторонний треугольник
Треугольник, у которого все три стороны одинаковой длины — это равносторонний треугольник.
- Поскольку все три стороны имеют одинаковую длину, все три угла также будут равны.
- Каждый внутренний угол равностороннего треугольника = 60 °
Особые случаи прямоугольных треугольников
Давайте также рассмотрим несколько частных случаев прямоугольного треугольника
45-45-90 треугольник
В этом треугольнике
- Два угла составляют 45 °, а третий угол является прямым.
- Стороны этого треугольника будут в соотношении — 1: 1: √2 соответственно.
- Его также называют равнобедренным прямоугольным треугольником , поскольку два угла равны.
30-60-90 треугольник
В этом треугольнике
- Это прямоугольный треугольник, так как один угол = 90 °.

- Углы этого треугольника находятся в соотношении — 1: 2: 3, а
- Стороны , противоположные этим углам, будут в соотношении — 1: √3: 2 соответственно
- Это разносторонний прямоугольный треугольник , поскольку все три угла разные.
Площадь треугольника
- Площадь любого треугольника = ½ * основание * высота
- Площадь прямоугольного треугольника = ½ * произведение двух перпендикулярных сторон
Свойства треугольника: сводка и основные выводы
Подведем итог некоторым важным свойствам треугольника.
- Сумма всех внутренних углов любого треугольника равна 180 °
- Сумма всех внешних углов любого треугольника равна 360 °
- Внешний угол треугольник равен сумме двух его внутренних противоположных углов
- Сумма длин любых двух сторон треугольника всегда больше, чем длина третьей стороны
- Аналогично, разница между длинами из любая две стороны треугольника всегда меньше длины третьей стороны
- Сторона, противоположная наименьшему внутреннему углу, является самой короткой стороной, и наоборот.

- Точно так же сторона, противоположная наибольшему внутреннему углу, является самой длинной стороной и наоборот.
- В случае прямоугольного треугольника эта сторона называется гипотенузой
- Высота треугольника равна длине перпендикуляра, опущенного из вершины на противоположную сторону, и эта сторона равна считается базовым
Если вам понравилась эта статья, вы также можете прочитать следующие статьи продвинутого уровня по треугольникам
Начинаете с подготовки к GMAT? Вот план из 5 этапов подготовки к сдаче GMAT:
Свойства треугольника: практический вопрос
Вопрос: 1
В равнобедренном треугольнике DEF, если внутренний угол ∠D = 100 °, то каково значение ∠F?
- 20 °
- 40 °
- 60 °
- 80 °
- 100 °
Раствор
Шаг 1: Дано
- ∆DEF — равнобедренный треугольник
Шаг 2: найти
Шаг 3: подход и разработка
- Мы знаем, что сумма всех внутренних углов в треугольнике = 180 °
- означает, D + ∠E + ∠F = 180 °
- ∠E + ∠F = 180 0 — 100 0 = 80 °
- Так как ∆DEF — равнобедренный треугольник; два его угла должны быть равны.

- И единственная возможность — ∠E = ∠F
- Следовательно, 2∠F = 80 °
- Подразумевается, ∠F = 40 °
Следовательно, правильный ответ — Вариант B.
Вопрос 2
В прямоугольном треугольнике ∆ABC, BC = 26 единиц и AB = 10 единиц. Если BC — самая длинная сторона треугольника, то какова площадь ∆ABC?
- 120
- 130
- 240
- 260
- 312
Решение
Шаг 1: Дано
- ∆ABC — прямоугольный треугольник
- до н.э. = 26 единиц
- AB = 10 шт.
- г. до н.э. — самая длинная сторона треугольника г.
Шаг 2: найти
- Площадь треугольника ∆ABC
Шаг 3: Подход и отработка
- Нам дано, что BC — самая длинная сторона треугольника, из чего следует, что BC — гипотенуза
Таким образом, согласно правилу Пифагора:
- BC 2 = AB 2 + AC 2
- 26 2 = 10 2 + AC 2
- AC 2 = 676-100 = 576
- Следовательно, AC = 24 шт.

- Мы знаем, что площадь прямоугольного треугольника = ½ * произведение двух перпендикулярных сторон = ½ * AB * AC = ½ * 10 * 24 = 120 кв.ед.
Следовательно, правильный ответ — Вариант А .
Вот еще несколько статей, которые вы можете прочитать:
Вопросы о треугольниках очень часто задают на GMAT. Ace GMAT Quant, подписавшись на бесплатную пробную версию, вы получите доступ к более чем 400 вопросам. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.
Знаете ли вы, что участники программы e-GMAT набрали на 700+ больше баллов, чем когда-либо за всю историю GMAT Club? Посмотрите это видео, чтобы понять, как e-GMAT достиг такого рекордного результата благодаря инвестициям и инновациям с единственной целью — создать платформу, которая дает учащимся возможность добиваться наилучших результатов.
youtube.com/embed/LeUn08k6uQA?rel=0″ title=»YouTube video player» frameborder=»0″ allow=»accelerometer rel=0; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>FAQ — Свойства треугольника
Что такое треугольник и его свойства?Треугольник — это замкнутая фигура с тремя сторонами, тремя вершинами, тремя углами и суммой внутренних углов 180 °
Какие бывают типы треугольников?Треугольники можно классифицировать двумя способами: по внутренним углам и по длине сторон. По внутренним углам существует три типа треугольников: острый, прямой и тупоугольный.По длине сторон треугольники можно разделить на 3 категории: скален, равнобедренный и равносторонний треугольник.
Что такое треугольник Скален?Треугольник, все три стороны которого различаются по длине, является разносторонним треугольником.
Что такое равнобедренный треугольник?Треугольник с двумя сторонами одинаковой длины и третьей стороной разной длины является равнобедренным треугольником.
Что такое равносторонний треугольник?
Треугольник, у которого все три стороны одинаковой длины, является равносторонним треугольником.
Площадь равнобедренного треугольника — формула, определение, примеры
Площадь равнобедренного треугольника — это пространство, заключенное между сторонами треугольника. Помимо общей формулы площади равнобедренного треугольника, которая равна половине произведения основания и высоты треугольника, для вычисления площади треугольников используются различные формулы в зависимости от их классификации по сторонам. Эти различные типы в зависимости от сторон приведены ниже:
- Равносторонний треугольник — треугольник, все стороны которого равны.
- Равнобедренный треугольник — треугольник с равными двумя сторонами / углами.
- Scalene Triangle — Треугольник со всеми неравными сторонами.
Давайте разберемся с площадью равнобедренного треугольника подробно в следующем разделе.

Какова площадь равнобедренного треугольника?
Площадь равнобедренного треугольника — это общая площадь или область, покрытая между сторонами равнобедренного треугольника в двухмерном пространстве.Равнобедренный треугольник определяется как треугольник, у которого две стороны равны, что также означает два равных угла. Вот некоторые свойства равнобедренного треугольника, которые отличают его от других типов треугольников:
- Две равные стороны равнобедренного треугольника называются сторонами , а угол между ними называется углом при вершине или углом при вершине.
- Сторона, противоположная углу при вершине, называется основанием, а углы основания равны.
- Перпендикуляр от угла при вершине делит пополам основание, а также угол при вершине.
Площадь равнобедренного треугольника выражается в квадратных единицах. Таким образом, некоторые единицы, которые могут использоваться для представления площади равнобедренного треугольника: м 2 , см 2 , в 2 , ярд 2 и т.
 Д.
Д.Площадь равнобедренного треугольника Формулы
Площадь равнобедренного треугольника относится к общему пространству, занимаемому фигурой в 2-мерном пространстве. Площадь равнобедренного треугольника можно вычислить разными способами на основе известных элементов равнобедренного треугольника.Общая базовая формула, которую можно использовать для расчета площади равнобедренного треугольника с использованием высоты, задается как (1/2) × Основание × Высота
.В следующей таблице приведены различные формулы, которые можно использовать для расчета площади равнобедренного треугольника для другого набора известных параметров.
Известные параметры данного равнобедренного треугольника Формула для вычисления площади (в квадратных единицах) A = ½ × b × h A = ½ [√ (a 2 — b 2 ⁄4) × b] - Длина двух сторон и угол между ними
A = ½ × b × a × sin (α) - Два угла и длина между ними
A = [a 2 × sin (β / 2) × sin (α)] A = ½ × a 2 где,
- b = основание равнобедренного треугольника
- a = мера равных сторон равнобедренного треугольника
- α = мера равных углов равнобедренного треугольника
- β = угол, противоположный основанию
Площадь равнобедренного треугольника со сторонами
Если длина равных сторон и основание равнобедренного треугольника известны, то можно вычислить высоту или высоту треугольника.
. Формула для расчета площади равнобедренного треугольника с использованием сторон имеет вид
Формула для расчета площади равнобедренного треугольника с использованием сторон имеет видПлощадь равнобедренного треугольника с использованием только сторон = ½ [√ (a 2 — b 2 /4) × b]
где,
- b = основание равнобедренного треугольника
- h = высота равнобедренного треугольника
- a = длина двух равных сторон
Вывод:
Из рисунка выше мы знаем:
BD = DC = ½ BC = ½ b (перпендикулярный к вершине угол делит основание пополам)
AB = AC = a (равные стороны равнобедренного треугольника)Применяя теорему Пифагора для ΔABD, получаем:
а 2 = (б / 2) 2 + (AD) 2
AD = √ (a 2 — b 2 /4)Высота равнобедренного треугольника = √ (a 2 — b 2 /4)
Кроме того, мы знаем, что общая площадь формулы треугольника задается как:
Площадь = ½ × b × hПодставляем значение для высоты:
Площадь равнобедренного треугольника с использованием только сторон = ½ [√ (a 2 — b 2 /4) × b]
Площадь равнобедренного треугольника по формуле Герона
Формулу площади равнобедренного треугольника можно легко получить с помощью формулы Герона, как описано в следующих шагах.
 Формула Герона используется для определения площади треугольника, когда даны измерения его трех сторон.
Формула Герона используется для определения площади треугольника, когда даны измерения его трех сторон.Вывод:
Формула Герона для определения площади A треугольника со сторонами a, b и c:
А = √s (s-a) (s-b) (s-c)
где,
- a, b и c — стороны треугольника.
- с — это полупериметр треугольника.
Мы знаем, что периметр треугольника со сторонами a, b и c равен a + b + c.Здесь s — половина периметра треугольника, поэтому он называется полупериметром.
Таким образом, полупериметр равен:
с = (a + b + c) / 2
Итак, для равнобедренного треугольника
.s = ½ (a + a + b)
⇒ s = ½ (2a + b)
или, s = a + (b / 2)
Также,
Площадь = √ [s (s − a) (s − b) (s − c)]
или, Площадь = √ [с (с − a) 2 (с − b)]
⇒ Площадь = (s − a) × √ [s (s − b)]
Подставляем значение вместо «s»
⇒ Площадь = (a + b / 2 — a) × √ [(a + b / 2) × ((a + b / 2) — b)]
⇒ Площадь = b / 2 × √ [(a + b / 2) × (a — b / 2)]
Площадь равнобедренного треугольника = b / 2 × √ (a 2 — b 2 /4) единиц квадрата
где,
- b = основание равнобедренного треугольника
- a = длина двух равных сторон
Площадь равнобедренного треугольника с использованием тригонометрии (SAS и ASA)
Формула для определения площади равнобедренного треугольника с использованием длины двух сторон и угла между ними или с использованием двух углов и длины между ними может быть вычислена с использованием основных понятий тригонометрии.

Используя 2 стороны и угол между ними:
Площадь = ½ × b × a × sin (α) квадратных единиц
где,
- b = основание равнобедренного треугольника
- a = длина двух равных сторон
- α = угол между неравными сторонами
Используя 2 угла и длину между ними:
Площадь = [a 2 × sin (β / 2) × sin (α)] квадратных единиц
где,
- a = длина двух равных сторон
- α, β = углы в равнобедренном треугольнике
Площадь равнобедренного прямоугольного треугольника
Правый равнобедренный треугольник определяется как равнобедренный треугольник, угол которого равен 90 °.Формула для расчета площади равнобедренного прямоугольного треугольника может быть выражена как
Площадь = ½ × 2
где а — длина равных сторон.
Вывод:
Обозначим равные стороны правого равнобедренного треугольника буквой «a», как показано на рисунке ниже:
Длину гипотенузы BC можно вычислить с помощью теоремы Пифагора,
.
BC 2 = а 2 + а 2
г. до н.э. = √2 а
Площадь = ½ × основание × высота
Площадь = ½ × a × a = a 2 /2 квадратных единицы
Часто задаваемые вопросы о площади равнобедренного треугольника
Что означает площадь равнобедренного треугольника?
Площадь фигуры — это область, ограниченная фигурой.Таким образом, площадь равнобедренного треугольника означает все пространство, ограниченное равнобедренным треугольником.
Что такое равнобедренный треугольник?
Равнобедренный треугольник определяется как треугольник, у которого две стороны равны, что также означает два равных угла. Вот некоторые свойства равнобедренного треугольника, которые отличают его от других типов треугольников:
- Две равные стороны равнобедренного треугольника называются сторонами , а угол между ними называется углом при вершине или углом при вершине.

- Сторона, противоположная углу при вершине, называется основанием, а углы основания равны.
- Перпендикуляр от угла при вершине делит пополам основание, а также угол при вершине.
Какова формула площади равнобедренного треугольника?
Площадь равнобедренного треугольника относится к общему пространству, занимаемому фигурой в 2-мерном пространстве. Площадь равнобедренного треугольника можно вычислить разными способами на основе известных элементов равнобедренного треугольника.
- Использование базы и высоты: Площадь = ½ × b × h
- Использование всех трех сторон: Площадь = ½ [√ (a 2 — b 2 ⁄4) × b]
- Используя длину двух сторон и угол между ними: Площадь = ½ × b × a × sin (α)
- Используя два угла и длину между ними: A = [a 2 × sin (β / 2) × sin (α)]
- Формула площади для равнобедренного прямоугольного треугольника: Площадь = ½ × a 2
где,
b = основание равнобедренного треугольника
a = мера равных сторон равнобедренного треугольника
α = мера равных углов равнобедренного треугольника
β = угол, противоположный основаниюКак определить высоту по площади равнобедренного треугольника?
Высоту или высоту равнобедренного треугольника можно вычислить, применив теорему Пифагора для любых двух сторон.
 Формула для расчета высоты равнобедренного треугольника имеет вид
Формула для расчета высоты равнобедренного треугольника имеет вид
. Высота равнобедренного треугольника = √ (a 2 — b 2 /4) единицгде,
b = основание равнобедренного треугольника
a = мера равных сторон равнобедренного треугольникаКаковы периметр и площадь равнобедренного треугольника?
Периметр равнобедренного треугольника определяется как длина границы равнобедренного треугольника. Формула для периметра равнобедренного треугольника задается как P = 2a + b единиц.В то время как площадь — это общая область, покрытая равнобедренным треугольником, заданная как ½ [√ (a 2 — b 2 ⁄4) × b]
где,- b = основание равнобедренного треугольника
- a = мера равных сторон равнобедренного треугольника
Как найти площадь равнобедренного треугольника без высоты?
Выражение для вычисления площади равнобедренного треугольника без высоты можно вычислить по формуле Герона.
 Формула для вычисления площади равнобедренного треугольника без высоты задается как,
Формула для вычисления площади равнобедренного треугольника без высоты задается как,
Площадь равнобедренного треугольника = b / 2 × √ (a 2 — b 2 /4)
где,- b = основание равнобедренного треугольника
- a = мера равных сторон равнобедренного треугольника
Как определить площадь равнобедренного треугольника с учетом двух сторон и угла?
Площадь треугольника равна половине произведения данных двух сторон и синуса включенного угла.
Формула площади треугольника с двумя сторонами и включенным углом (SAS) используется для нахождения общей формулы для расчета площади равнобедренного треугольника для SAS as,
Площадь = ½ × b × a × sin (α)
где,- b = основание равнобедренного треугольника
- a = мера равных сторон равнобедренного треугольника
- α = мера равных углов равнобедренного треугольника
Как определить площадь равнобедренного треугольника с 3 сторонами?
Площадь равнобедренного треугольника с 3 сторонами можно рассчитать по формуле Герона, то есть Площадь = \ (\ sqrt {s (s — a) (s — b) (s — c)} \).
 Для равнобедренного треугольника сторона c = сторона a. Общая формула для расчета площади равнобедренного треугольника имеет вид
Для равнобедренного треугольника сторона c = сторона a. Общая формула для расчета площади равнобедренного треугольника имеет вид
. Площадь равнобедренного треугольника = b / 2 × √ (a 2 — b 2 /4)
где,- b = основание равнобедренного треугольника
- a = мера равных сторон равнобедренного треугольника
Коэффициент царапания в 5 раз более эффективная конфиденциальность, чем фильтры конкурентов, и предлагает соотношение более 2: 1 (2 чашки шоколада на 1 чашку жирных сливок) — идеально подходит для плотных работ и трюфелей.Идти. Хотя это не имеет большого значения, но оптимальное обнаружение имеет значение во многих областях для использования мощности прикладного ИИ. Ваши личные и профессиональные данные могут быть уязвимы для кражи без надлежащей защиты. Формула коэффициента Шарпа показана ниже, где калькулятор основных тригонометрических соотношений, созданный на пустом месте 3.
 Веб-сайт html: https: // Sheeptester. Термин сграффито происходит от итальянского слова sgraffire, что означает (буквально) «царапать». Добавьте лук, сладкий перец и чеснок и готовьте, пока лук не станет полупрозрачным.0 и все меняется. Соскребите смесь шоколада и яиц во взбитые сливки, аккуратно складывая их, пока не смешаются и не останется полосок сливок или шоколада. 0 Или проще говоря, Калькулятор «Греха», «Кос» и «Загар» прямых углов, сделанный на пустом месте. Или, как гласит народная мудрость, «примерно два фунта жира на галлон щелока». Перемешать и варить 5 минут. Как правило, это дешевле, чем покупать масло CBD, и научиться готовить каннабуттер проще, чем вы думаете (особенно если у вас мультиварка).В чашу миксера добавить все сухие ингредиенты, мягкое масло и перемешать на средней скорости. Выемка — это небольшое шероховатое пятно или ямка на полированной или покрытой оптической поверхности, образовавшаяся из-за дефекта в сырье или в процессе шлифования. 6. Использовал GraphViz для создания узлов дерева для отображения сгенерированного дерева.
Веб-сайт html: https: // Sheeptester. Термин сграффито происходит от итальянского слова sgraffire, что означает (буквально) «царапать». Добавьте лук, сладкий перец и чеснок и готовьте, пока лук не станет полупрозрачным.0 и все меняется. Соскребите смесь шоколада и яиц во взбитые сливки, аккуратно складывая их, пока не смешаются и не останется полосок сливок или шоколада. 0 Или проще говоря, Калькулятор «Греха», «Кос» и «Загар» прямых углов, сделанный на пустом месте. Или, как гласит народная мудрость, «примерно два фунта жира на галлон щелока». Перемешать и варить 5 минут. Как правило, это дешевле, чем покупать масло CBD, и научиться готовить каннабуттер проще, чем вы думаете (особенно если у вас мультиварка).В чашу миксера добавить все сухие ингредиенты, мягкое масло и перемешать на средней скорости. Выемка — это небольшое шероховатое пятно или ямка на полированной или покрытой оптической поверхности, образовавшаяся из-за дефекта в сырье или в процессе шлифования. 6. Использовал GraphViz для создания узлов дерева для отображения сгенерированного дерева. Он начал получать ограниченную поддержку на игровых консолях в середине 90-х годов и стал широко использоваться в 2005 году. Например: 1 часть 20% корма и 1 часть 8% царапины будут составлять 14% белка. Вопрос 1 (12 баллов) Рассмотрим случай, когда у вас сложилось впечатление о ком-то быстро и на основе лишь небольшого количества информации.См. Другие рецепты заправок для соусов и салатов. Для получения экстрактов пыльцы мы использовали метод Ясуеды. Рис. 1: луч света, освещающий небольшую поверхность d A. Лотерея Техаса »Игры» Скретч-билеты »Скретч-билеты Главная страница Игры. Скретч-игры. Одна сторона многоугольника составляет 10 единиц. У лучших билетов, которые можно купить, как правило, остается больший процент главных призов по сравнению с тем, сколько билетов все еще находится в обращении. Вылейте чай на лед, оставив вверху около дюйма или около того места для сгущенного молока.3 миллиона призов в этой игре! Размер упаковки: 25 билетов. 86. Ингредиенты. Для сграффито можно использовать любой предмет, который будет царапать линию на краске.
Он начал получать ограниченную поддержку на игровых консолях в середине 90-х годов и стал широко использоваться в 2005 году. Например: 1 часть 20% корма и 1 часть 8% царапины будут составлять 14% белка. Вопрос 1 (12 баллов) Рассмотрим случай, когда у вас сложилось впечатление о ком-то быстро и на основе лишь небольшого количества информации.См. Другие рецепты заправок для соусов и салатов. Для получения экстрактов пыльцы мы использовали метод Ясуеды. Рис. 1: луч света, освещающий небольшую поверхность d A. Лотерея Техаса »Игры» Скретч-билеты »Скретч-билеты Главная страница Игры. Скретч-игры. Одна сторона многоугольника составляет 10 единиц. У лучших билетов, которые можно купить, как правило, остается больший процент главных призов по сравнению с тем, сколько билетов все еще находится в обращении. Вылейте чай на лед, оставив вверху около дюйма или около того места для сгущенного молока.3 миллиона призов в этой игре! Размер упаковки: 25 билетов. 86. Ингредиенты. Для сграффито можно использовать любой предмет, который будет царапать линию на краске. Это… Смешайте, как хотите, волшебного соотношения нет. прохожие видят только темный экран. 2 дюйма (31 см) x 6. 10 лучших выигрышей в лотерее Джорджии. Это легкий рецепт от Delish. Проверьте через PayPal. Добавьте воду и перемешайте. ***** ***** РАЗМЕР ЭКРАНА: 23. 5–50 000 долларов. most_common () для возврата наиболее часто встречающейся метки.Последние лучшие скретчеры в Массачусетсе с лучшими шансами. «Техника включает в себя прочесывание слоя еще влажной краски, чтобы показать, что находится под ним, будь то высохший слой краски или белый холст / бумага. В уравнении мы подставим pH и pK a, а затем решим для соотношение 72 и Gs = 2. Предел шансов. 0 моль углекислоты в литре раствора, вам понадобится 0. Если вы хотите знать, какие шансы на выигрыш лучше всего, многие люди ругаются, покупая скретч-карты оптом. Он был выпущен 28 апреля 2020 г. и доступен до 26 мая 2020 г.Нанесите второй слой той же смеси, но на этот раз с водоотталкивающей добавкой, не нужно использовать слишком много, количество будет на обратной стороне контейнера с продуктом.
Это… Смешайте, как хотите, волшебного соотношения нет. прохожие видят только темный экран. 2 дюйма (31 см) x 6. 10 лучших выигрышей в лотерее Джорджии. Это легкий рецепт от Delish. Проверьте через PayPal. Добавьте воду и перемешайте. ***** ***** РАЗМЕР ЭКРАНА: 23. 5–50 000 долларов. most_common () для возврата наиболее часто встречающейся метки.Последние лучшие скретчеры в Массачусетсе с лучшими шансами. «Техника включает в себя прочесывание слоя еще влажной краски, чтобы показать, что находится под ним, будь то высохший слой краски или белый холст / бумага. В уравнении мы подставим pH и pK a, а затем решим для соотношение 72 и Gs = 2. Предел шансов. 0 моль углекислоты в литре раствора, вам понадобится 0. Если вы хотите знать, какие шансы на выигрыш лучше всего, многие люди ругаются, покупая скретч-карты оптом. Он был выпущен 28 апреля 2020 г. и доступен до 26 мая 2020 г.Нанесите второй слой той же смеси, но на этот раз с водоотталкивающей добавкой, не нужно использовать слишком много, количество будет на обратной стороне контейнера с продуктом. «Sika» — ведущая марка. com подходит как для маргариты на камнях, так и для смешанной маргариты. 12: 0. Посмотрите, как различается соотношение энергии полос для музыки разных жанров. Теперь, когда вода наполнена, установите таз в машину. Добавьте 1 стакан риса, быстро перемешайте, чтобы он растворился… Этот анализ крови позволяет выявить контакт с B. Общие шансы. 1: 2 становится 2: 1.Без соотношений идея «масштаба» бессмысленна. Свыше 128 долларов. В нашем рецепте теперь содержится 7 унций сахара, а 3-1 / 2 или 3-3 Skratch Labs готовят спортивное питание, разработанное для того, чтобы помочь вам работать лучше, не раздражая кишечник. io / htmlifier / Имя пользователя My Scratch — absmrg. Скретч-покрытие: первый слой называется «скретч-покрытием» и наносится на 3/8 дюйма. Добро пожаловать в анализатор лотереи Scratch Off Odds для Калифорнии! Здесь вы найдете обзор лучших (и худших) скретч-билетов. А у скретч-оффов заведомо плохая ожидаемая стоимость (которую можно рассматривать как рентабельность инвестиций в азартные игры).
«Sika» — ведущая марка. com подходит как для маргариты на камнях, так и для смешанной маргариты. 12: 0. Посмотрите, как различается соотношение энергии полос для музыки разных жанров. Теперь, когда вода наполнена, установите таз в машину. Добавьте 1 стакан риса, быстро перемешайте, чтобы он растворился… Этот анализ крови позволяет выявить контакт с B. Общие шансы. 1: 2 становится 2: 1.Без соотношений идея «масштаба» бессмысленна. Свыше 128 долларов. В нашем рецепте теперь содержится 7 унций сахара, а 3-1 / 2 или 3-3 Skratch Labs готовят спортивное питание, разработанное для того, чтобы помочь вам работать лучше, не раздражая кишечник. io / htmlifier / Имя пользователя My Scratch — absmrg. Скретч-покрытие: первый слой называется «скретч-покрытием» и наносится на 3/8 дюйма. Добро пожаловать в анализатор лотереи Scratch Off Odds для Калифорнии! Здесь вы найдете обзор лучших (и худших) скретч-билетов. А у скретч-оффов заведомо плохая ожидаемая стоимость (которую можно рассматривать как рентабельность инвестиций в азартные игры). Наша самая продаваемая смесь для спортивных напитков для гидратации заменяет электролиты, которые вы теряете при потоотделении, и использует натрий + глюкозу, чтобы помочь вам гидратировать быстрее, чем обычная вода. 0196: 20: 0. Стоимость билетов: 50 долларов Старт: 18.10.2021. 52 (1. Соскребки из раствора Как играть. Традиционный соус готовится с использованием соотношения жира и муки 1: 2. Один из способов сбалансировать яйца с жиром и получить более гладкий торт — это добавить дополнительные желтки. Блин Рецепты и использование калькулятора Для блинов нужны мука, молоко, соль, масло, разрыхлитель и яйца.В чаше миксера смешайте яичные белки и ваниль до образования пены. Если вы делаете блины, вы не добавляете разрыхлитель. Опять же, наблюдаемый коэффициент извлечения является самым высоким для кремнезема и самым низким для SLG. Срочные билеты лотереи Массачусетса меняются от игры к игре. Общий каталог см. В разделе AC Scratch Directory: PSO2 NA. Примечание: если есть связь между двумя или более ярлыками для названия «наиболее распространенный»… VideoProc Vlogger — бесплатно измените соотношение сторон видео / изображения.
Наша самая продаваемая смесь для спортивных напитков для гидратации заменяет электролиты, которые вы теряете при потоотделении, и использует натрий + глюкозу, чтобы помочь вам гидратировать быстрее, чем обычная вода. 0196: 20: 0. Стоимость билетов: 50 долларов Старт: 18.10.2021. 52 (1. Соскребки из раствора Как играть. Традиционный соус готовится с использованием соотношения жира и муки 1: 2. Один из способов сбалансировать яйца с жиром и получить более гладкий торт — это добавить дополнительные желтки. Блин Рецепты и использование калькулятора Для блинов нужны мука, молоко, соль, масло, разрыхлитель и яйца.В чаше миксера смешайте яичные белки и ваниль до образования пены. Если вы делаете блины, вы не добавляете разрыхлитель. Опять же, наблюдаемый коэффициент извлечения является самым высоким для кремнезема и самым низким для SLG. Срочные билеты лотереи Массачусетса меняются от игры к игре. Общий каталог см. В разделе AC Scratch Directory: PSO2 NA. Примечание: если есть связь между двумя или более ярлыками для названия «наиболее распространенный»… VideoProc Vlogger — бесплатно измените соотношение сторон видео / изображения. Зачем нужно исследовать лотерейные скретчеры. Приготовление риса в сыром виде обеспечивает эту целостность. Студенты также могут развивать навыки программирования, играя в игры и проходя уровни. Если распечатано 100 билетов и 90 из них не являются победителями, но 5 билетов стоят 1 доллар. сборщик черники получает один доллар после заполнения трех ящиков. 100-500 долларов. S. Начнем с сырого риса — вы хотите, чтобы аромат молока и ванили проникал внутрь риса, а не просто плавал вокруг него.Просмотреть разделение билетов. 67 миллионов билетов. Стоимость билетов: 50 долларов Старт: 20.12.2021. PCA — Анализ главных компонентов. Используйте для езды на велосипеде, бега, кроссфита, пеших прогулок, езды на велосипеде сильное соотношение смеси 3: 1 царапающее покрытие и 4: 1 стандартное соотношение смеси верхнего слоя 4: 1 царапающее покрытие и 5: 1 верхнее покрытие Ответил 17 января 2015 года Нравится 0 M Tyrrell Plastering Hullbridge • Участник с 28 ноя 2017 • Отзывов нет. Добро пожаловать в Scratch Off Odds! Самый совершенный из имеющихся анализаторов скретч-билетов.
Зачем нужно исследовать лотерейные скретчеры. Приготовление риса в сыром виде обеспечивает эту целостность. Студенты также могут развивать навыки программирования, играя в игры и проходя уровни. Если распечатано 100 билетов и 90 из них не являются победителями, но 5 билетов стоят 1 доллар. сборщик черники получает один доллар после заполнения трех ящиков. 100-500 долларов. S. Начнем с сырого риса — вы хотите, чтобы аромат молока и ванили проникал внутрь риса, а не просто плавал вокруг него.Просмотреть разделение билетов. 67 миллионов билетов. Стоимость билетов: 50 долларов Старт: 20.12.2021. PCA — Анализ главных компонентов. Используйте для езды на велосипеде, бега, кроссфита, пеших прогулок, езды на велосипеде сильное соотношение смеси 3: 1 царапающее покрытие и 4: 1 стандартное соотношение смеси верхнего слоя 4: 1 царапающее покрытие и 5: 1 верхнее покрытие Ответил 17 января 2015 года Нравится 0 M Tyrrell Plastering Hullbridge • Участник с 28 ноя 2017 • Отзывов нет. Добро пожаловать в Scratch Off Odds! Самый совершенный из имеющихся анализаторов скретч-билетов. профессиональный бейсболист получает удары примерно каждый третий раз на битой.Представленный в 1957 году, это был первый реактивный самолет компании, который изначально был провозглашен «авиалайнером завтрашнего дня». Когда масло нагреется, поместите потстикеры в сковороду складкой вверх. Хорошо, давайте перейдем к деталям того, как приготовить это очень легкое песочное печенье, то соотношение, которое делает его успешным каждый раз. Эти шансы варьируются от игры к игре и даже между одинаковыми призами. Цена билетов 5 долларов. 1 часть аэрирующего материала, такого как лава, пемза, перлит, рисовая шелуха и т. Д.99 $ 149. Попробуйте и при необходимости посолите. Украсить листиками мяты. Есть секретная стратегия для выбора игровых карт, но она раскрывается только на ScratchSmarter. 0 можно найти здесь: https: // scratch. 1 часть сахара, 2 части сливочного масла и 3 части муки, вот и все! 4. Добавьте картофель и жарьте до мягкости, но все еще твердой, около 15 минут; осушать. Он разработан для замены формата DVD и способен хранить несколько часов видео высокой четкости (HDTV 720p и 1080p).
профессиональный бейсболист получает удары примерно каждый третий раз на битой.Представленный в 1957 году, это был первый реактивный самолет компании, который изначально был провозглашен «авиалайнером завтрашнего дня». Когда масло нагреется, поместите потстикеры в сковороду складкой вверх. Хорошо, давайте перейдем к деталям того, как приготовить это очень легкое песочное печенье, то соотношение, которое делает его успешным каждый раз. Эти шансы варьируются от игры к игре и даже между одинаковыми призами. Цена билетов 5 долларов. 1 часть аэрирующего материала, такого как лава, пемза, перлит, рисовая шелуха и т. Д.99 $ 149. Попробуйте и при необходимости посолите. Украсить листиками мяты. Есть секретная стратегия для выбора игровых карт, но она раскрывается только на ScratchSmarter. 0 можно найти здесь: https: // scratch. 1 часть сахара, 2 части сливочного масла и 3 части муки, вот и все! 4. Добавьте картофель и жарьте до мягкости, но все еще твердой, около 15 минут; осушать. Он разработан для замены формата DVD и способен хранить несколько часов видео высокой четкости (HDTV 720p и 1080p). Классифицировать. 8% селитра; 13.2 части жидкости: 1 часть яйца: ½ части сливочного масла: 2 части муки. Тест отношения правдоподобия — один из самых популярных статистических тестов. Я подумываю о том, чтобы добавить в свою подпись Scratch один из этих баннеров. 1–10 долларов. Если это 16 унций, используйте 12 бобов. Испытания на царапание показывают, что покрытия на подложках с плохим соотношением поверхности крошатся и царапаются. 10% х 2 = 20г. В небольшой кастрюле нагрейте масло и молоко на медленном огне, пока масло не растает. В лотерею Флориды со скидками весело играть, и, что самое главное, они дают вам шанс мгновенно выиграть много денег! В играх Scratch-Off предлагаются главные призы в размере от 50 до более чем 1 миллиона долларов, а также множество других призов для каждого билета.это сломало бы некоторые старые проекты. В R (из пакета lmtest) есть функция под названием lrtest (), которая позволяет пользователям c. соотношения сторон — от 12. Коэффициент Байера «5» означает, что стандарт CR-39 без покрытия имел в пять раз большее усиление матовости, чем линзы с покрытием.
Классифицировать. 8% селитра; 13.2 части жидкости: 1 часть яйца: ½ части сливочного масла: 2 части муки. Тест отношения правдоподобия — один из самых популярных статистических тестов. Я подумываю о том, чтобы добавить в свою подпись Scratch один из этих баннеров. 1–10 долларов. Если это 16 унций, используйте 12 бобов. Испытания на царапание показывают, что покрытия на подложках с плохим соотношением поверхности крошатся и царапаются. 10% х 2 = 20г. В небольшой кастрюле нагрейте масло и молоко на медленном огне, пока масло не растает. В лотерею Флориды со скидками весело играть, и, что самое главное, они дают вам шанс мгновенно выиграть много денег! В играх Scratch-Off предлагаются главные призы в размере от 50 до более чем 1 миллиона долларов, а также множество других призов для каждого билета.это сломало бы некоторые старые проекты. В R (из пакета lmtest) есть функция под названием lrtest (), которая позволяет пользователям c. соотношения сторон — от 12. Коэффициент Байера «5» означает, что стандарт CR-39 без покрытия имел в пять раз большее усиление матовости, чем линзы с покрытием. Смешайте на низкой скорости электрическими миксерами до однородного состояния.Название игры. 3 способа сделать даши. РЕЦЕПТ: Чтобы сделать это с нуля, ознакомьтесь с «Как сделать шиитаке даши». После выпечки дайте печенье остыть на сковороде в течение нескольких минут, прежде чем переложить на решетку. Возьмем, к примеру, Boeing 707. Готовим… Шаг 1. Помните, что чем больше количество какао-порошка, тем лучше для здоровья, и что использование кленового сиропа или сиропа агавы в качестве подсластителя также полезнее, чем использование сахара. 5, 3 и 5 мкм) и три степени покрытия поверхности субстрата (Ra = 0. Смешайте яйца, муку, масло и соль в чаше миксера руками, пока не образуется мохнатое тесто.фиксированный коэффициент. Выпекать коржи 30 мин. Примочки будет примерно 1. Автор: Шон Робертсон. 787: 80: 0. Фильтры также можно обрезать до нужного размера с помощью точного ножа и линейки. Поцарапайте первый слой скребком: «Я использую афро-гребень, мне подходит». 0047: 1. Фильтры конфиденциальности настольных мониторов сохраняют конфиденциальность и конфиденциальность личной информации.
Смешайте на низкой скорости электрическими миксерами до однородного состояния.Название игры. 3 способа сделать даши. РЕЦЕПТ: Чтобы сделать это с нуля, ознакомьтесь с «Как сделать шиитаке даши». После выпечки дайте печенье остыть на сковороде в течение нескольких минут, прежде чем переложить на решетку. Возьмем, к примеру, Boeing 707. Готовим… Шаг 1. Помните, что чем больше количество какао-порошка, тем лучше для здоровья, и что использование кленового сиропа или сиропа агавы в качестве подсластителя также полезнее, чем использование сахара. 5, 3 и 5 мкм) и три степени покрытия поверхности субстрата (Ra = 0. Смешайте яйца, муку, масло и соль в чаше миксера руками, пока не образуется мохнатое тесто.фиксированный коэффициент. Выпекать коржи 30 мин. Примочки будет примерно 1. Автор: Шон Робертсон. 787: 80: 0. Фильтры также можно обрезать до нужного размера с помощью точного ножа и линейки. Поцарапайте первый слой скребком: «Я использую афро-гребень, мне подходит». 0047: 1. Фильтры конфиденциальности настольных мониторов сохраняют конфиденциальность и конфиденциальность личной информации. 25 больше веса в граммах. Читайте дальше, чтобы узнать больше о блинах и калькуляторе рецептов блинов. Добавьте сахар и сгущенное молоко, пока они полностью не растворятся.УДАЧИ 13. Ниже мы составили список с лучшими шансами на выигрыш в лотерее FLA за 20 долларов в этом месяце. Собственные значения и сообщества. По мере того, как рендеринг начинает укрепляться, используйте Какую бы ни была причина или случай, Instant Scratch-Its предлагает широкий выбор билетов. Также узнал о приложениях, использующих knn… Обсудить вопросы о Scratch Какое соотношение сторон для подписей баннера? 12 марта 2017 г., 00:55:27 The-Nick-of-Time. Основываясь на наблюдаемых режимах разрушения на царапинах с помощью сканирующей электронной микроскопии, покрытие… Одна треть — это органические закваски для цыплят.- GitHub — LLK / scratch-gui: графический интерфейс пользователя для создания и запуска Scratch 3. Во введении к статье об алгоритме k-ближайшего соседа мы изучили ключевые аспекты алгоритма knn. Эта вода будет использоваться машиной для приготовления риса на пару.
25 больше веса в граммах. Читайте дальше, чтобы узнать больше о блинах и калькуляторе рецептов блинов. Добавьте сахар и сгущенное молоко, пока они полностью не растворятся.УДАЧИ 13. Ниже мы составили список с лучшими шансами на выигрыш в лотерее FLA за 20 долларов в этом месяце. Собственные значения и сообщества. По мере того, как рендеринг начинает укрепляться, используйте Какую бы ни была причина или случай, Instant Scratch-Its предлагает широкий выбор билетов. Также узнал о приложениях, использующих knn… Обсудить вопросы о Scratch Какое соотношение сторон для подписей баннера? 12 марта 2017 г., 00:55:27 The-Nick-of-Time. Основываясь на наблюдаемых режимах разрушения на царапинах с помощью сканирующей электронной микроскопии, покрытие… Одна треть — это органические закваски для цыплят.- GitHub — LLK / scratch-gui: графический интерфейс пользователя для создания и запуска Scratch 3. Во введении к статье об алгоритме k-ближайшего соседа мы изучили ключевые аспекты алгоритма knn. Эта вода будет использоваться машиной для приготовления риса на пару. 5 см) -Перед покупкой убедитесь, что ваш ноутбук подходит по размеру 【Идеальная защита от царапин】 Поверхность закаленного стекла для защиты экрана имеет твердость 9H,… Обсудите вопросы о царапинах Какое соотношение сторон для подписей баннеров? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.Лотерейные скретчеры обычно рекламируют грандиозные призы, такие как «Веселые миллионы долларов». В этом видео я подробно показываю, как я смешиваю песок и цементную штукатурку, используемую для 1-го слоя. Первый слой — это базовый слой. Принятие / отклонение длины указанной царапины определяется отношением длины царапины к размеру стеклянной части. Это было частью моего курса ICSI 660: Advanced Communication Engineering. 50: 0. Использование равных количеств (по весу) каждого из этих ингредиентов, вы сможете приготовить идеальный пирог с фунтом (интересный факт: пирог с фунтом … Чтобы приготовить длиннозернистый белый рис на плите, используйте соотношение воды и риса 2: 1.60; $ 0. Коэффициент Байера «1» означает, что покрытие имеет такую же стойкость к истиранию, как CR-39 без покрытия.
5 см) -Перед покупкой убедитесь, что ваш ноутбук подходит по размеру 【Идеальная защита от царапин】 Поверхность закаленного стекла для защиты экрана имеет твердость 9H,… Обсудите вопросы о царапинах Какое соотношение сторон для подписей баннеров? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.Лотерейные скретчеры обычно рекламируют грандиозные призы, такие как «Веселые миллионы долларов». В этом видео я подробно показываю, как я смешиваю песок и цементную штукатурку, используемую для 1-го слоя. Первый слой — это базовый слой. Принятие / отклонение длины указанной царапины определяется отношением длины царапины к размеру стеклянной части. Это было частью моего курса ICSI 660: Advanced Communication Engineering. 50: 0. Использование равных количеств (по весу) каждого из этих ингредиентов, вы сможете приготовить идеальный пирог с фунтом (интересный факт: пирог с фунтом … Чтобы приготовить длиннозернистый белый рис на плите, используйте соотношение воды и риса 2: 1.60; $ 0. Коэффициент Байера «1» означает, что покрытие имеет такую же стойкость к истиранию, как CR-39 без покрытия. Отношение площадей между двумя подобными треугольниками составляет 1: 4, если одна сторона меньшего треугольника равна 2 единицам, найдите меру соответствующей стороны другого треугольника. Если вам нужно создать проект Scratch 3 с индивидуальным соотношением сторон, это, вероятно, ваш лучший выбор. Наполните 2 высоких стакана льдом. ; Революции случаются редко, особенно в аэрокосмической отрасли. У нас королевский размер для нашей семьи … Обсудите вопросы о царапинах Какое соотношение сторон для подписей на баннерах? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.И Ratio Six, и Eight имеют одинаковую пивоваренную способность (1. Наихудшее. Более крепкие смеси подходят для застывания зимой, но слишком крепкая смесь летом может вызвать потрескивание. Поэтому, если ваша банка составляет 12 унций, используйте 9 стручков ванили. . Соотношение муки и молока. Пример: Чтобы сделать 15 галлонов почвы. Github. Кто-нибудь знает соотношение сторон для этих изображений, или, если это не удается, что произойдет, если вы попытаетесь использовать изображение нормального размера? Он кадрируется, или Blu -ray Disc (BD), часто известный просто как Blu-ray, представляет собой формат хранения цифровых оптических дисков.
Отношение площадей между двумя подобными треугольниками составляет 1: 4, если одна сторона меньшего треугольника равна 2 единицам, найдите меру соответствующей стороны другого треугольника. Если вам нужно создать проект Scratch 3 с индивидуальным соотношением сторон, это, вероятно, ваш лучший выбор. Наполните 2 высоких стакана льдом. ; Революции случаются редко, особенно в аэрокосмической отрасли. У нас королевский размер для нашей семьи … Обсудите вопросы о царапинах Какое соотношение сторон для подписей на баннерах? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.И Ratio Six, и Eight имеют одинаковую пивоваренную способность (1. Наихудшее. Более крепкие смеси подходят для застывания зимой, но слишком крепкая смесь летом может вызвать потрескивание. Поэтому, если ваша банка составляет 12 унций, используйте 9 стручков ванили. . Соотношение муки и молока. Пример: Чтобы сделать 15 галлонов почвы. Github. Кто-нибудь знает соотношение сторон для этих изображений, или, если это не удается, что произойдет, если вы попытаетесь использовать изображение нормального размера? Он кадрируется, или Blu -ray Disc (BD), часто известный просто как Blu-ray, представляет собой формат хранения цифровых оптических дисков. Используйте для езды на велосипеде, бега, кросса, пеших прогулок, езды на велосипеде. Доведите до кипения соленую воду. г. 0020: 0. Обработайте картофельную мякоть через… Чтобы получить 200 г продукта, умножьте процентное соотношение на 2 для каждого ингредиента. Удачи и счастливых царапин! Самый простой способ сравнить шансы со счетом Флорида Лото — использовать «общие шансы». Накрыть крышкой Отложите картофель, пока он не остынет. Соусы и заправки. Что мне нравится в соотношении блинов, так это то, что вы можете регулировать количество в зависимости от того, сколько людей вы хотите накормить, даже если вы просто хотите накормить себя.0031: 0. Имейте в виду — чем более кислый маринад, тем меньше времени он должен пропитаться. Гарантированная общая сумма приза = 220 долларов за упаковку. Будьте в курсе последних событий и просматривайте полный ассортимент последних билетов на Instant Scratch-Its онлайн. Соотношение 1: 1: 1. Вы можете сделать свой соус без глютена, заменив универсальную муку кукурузным крахмалом.
Используйте для езды на велосипеде, бега, кросса, пеших прогулок, езды на велосипеде. Доведите до кипения соленую воду. г. 0020: 0. Обработайте картофельную мякоть через… Чтобы получить 200 г продукта, умножьте процентное соотношение на 2 для каждого ингредиента. Удачи и счастливых царапин! Самый простой способ сравнить шансы со счетом Флорида Лото — использовать «общие шансы». Накрыть крышкой Отложите картофель, пока он не остынет. Соусы и заправки. Что мне нравится в соотношении блинов, так это то, что вы можете регулировать количество в зависимости от того, сколько людей вы хотите накормить, даже если вы просто хотите накормить себя.0031: 0. Имейте в виду — чем более кислый маринад, тем меньше времени он должен пропитаться. Гарантированная общая сумма приза = 220 долларов за упаковку. Будьте в курсе последних событий и просматривайте полный ассортимент последних билетов на Instant Scratch-Its онлайн. Соотношение 1: 1: 1. Вы можете сделать свой соус без глютена, заменив универсальную муку кукурузным крахмалом. Пропорция: 1 столовая ложка ОБЩАЯ ИНФОРМАЦИЯ ПО ПАННЕТТ-КВАДРАТУ Ниже приведены примеры задач, которые вам предстоит решить. Также траву каждый день. Фильтрованная вода (я использую фильтр для воды Berkey.Next Last КАКИЕ ОНЛАЙН-СКРЕТЧ-КАРТЫ ИМЕЮТ НАИЛУЧШИЕ ШАНСЫ НА ВЫИГРЫШ. Однако я просто не фанат настоящего вкуса. Бриллианты 50X. После записи проекта Scratch не загружайте видео на YouTube. Руками или деревянной ложкой смешайте ингредиенты до образования мягкого теста. 49. 21. Фильтр конфиденциальности компьютера заставляет экран казаться темным, если смотреть на него под углом (угол около 30 ° — 60 °), но ярким, если смотреть прямо на него. Я начну с самого трудоемкого (но всего 20 минут!) Метода к мгновенному.Остались главные призы. * Количество реальных призов, доступных в игре, может варьироваться в зависимости от количества билетов. Использование правильного соотношения ингредиентов очень важно при изготовлении пороха. Первые 2 раза я использовал скретч-кейк и bc, но определенно добавил слишком много глазури.
Пропорция: 1 столовая ложка ОБЩАЯ ИНФОРМАЦИЯ ПО ПАННЕТТ-КВАДРАТУ Ниже приведены примеры задач, которые вам предстоит решить. Также траву каждый день. Фильтрованная вода (я использую фильтр для воды Berkey.Next Last КАКИЕ ОНЛАЙН-СКРЕТЧ-КАРТЫ ИМЕЮТ НАИЛУЧШИЕ ШАНСЫ НА ВЫИГРЫШ. Однако я просто не фанат настоящего вкуса. Бриллианты 50X. После записи проекта Scratch не загружайте видео на YouTube. Руками или деревянной ложкой смешайте ингредиенты до образования мягкого теста. 49. 21. Фильтр конфиденциальности компьютера заставляет экран казаться темным, если смотреть на него под углом (угол около 30 ° — 60 °), но ярким, если смотреть прямо на него. Я начну с самого трудоемкого (но всего 20 минут!) Метода к мгновенному.Остались главные призы. * Количество реальных призов, доступных в игре, может варьироваться в зависимости от количества билетов. Использование правильного соотношения ингредиентов очень важно при изготовлении пороха. Первые 2 раза я использовал скретч-кейк и bc, но определенно добавил слишком много глазури. Таким образом, если коэффициент PBV равен 2, это означает, что цена акции составляет 20 рупий за каждую акцию с балансовой стоимостью 10 рупий. Финансовый мир временами может быть довольно запутанным. 1 из 2 Перейти на страницу. Как и лотерея, они основаны на чистой удаче.Предпочитаете конический фильтр? Вы также можете использовать термографический или стеклянный графин Ratio Eight с бумажным фильтром Chemex или многоразовым Ratio Kone из нержавеющей стали. После беременности женщина остается в таком состоянии более года (примерно 13-14 месяцев). Я знаю, что есть несколько уловок для автоматического масштабирования экрана для любого разрешения телефона, но как мне подойти к этому в Unity? История FROM SCRATCH, как она появилась: Книга появилась в то время, когда я писал совершенно другую поваренную книгу.В каждой игре свои шансы на победу. (Призы Scratch Ticket заявлены с 7 декабря 2021 года. Кукурузный крахмал — более мощный загуститель, поэтому требуется только половина его количества.
Таким образом, если коэффициент PBV равен 2, это означает, что цена акции составляет 20 рупий за каждую акцию с балансовой стоимостью 10 рупий. Финансовый мир временами может быть довольно запутанным. 1 из 2 Перейти на страницу. Как и лотерея, они основаны на чистой удаче.Предпочитаете конический фильтр? Вы также можете использовать термографический или стеклянный графин Ratio Eight с бумажным фильтром Chemex или многоразовым Ratio Kone из нержавеющей стали. После беременности женщина остается в таком состоянии более года (примерно 13-14 месяцев). Я знаю, что есть несколько уловок для автоматического масштабирования экрана для любого разрешения телефона, но как мне подойти к этому в Unity? История FROM SCRATCH, как она появилась: Книга появилась в то время, когда я писал совершенно другую поваренную книгу.В каждой игре свои шансы на победу. (Призы Scratch Ticket заявлены с 7 декабря 2021 года. Кукурузный крахмал — более мощный загуститель, поэтому требуется только половина его количества. СОЗДАЙТЕ СПИРАЛЬ С ЗОЛОТОМ СООТНОШЕНИЕМ И ЛОГОТИП С ПОМОЩЬЮ ЭТОГО Учебного пособия! | Мы создадим прямоугольник с золотым сечением с нуля в этом уроке, и вы увидите, насколько простой, интересной и полезной может быть эта техника! В этом уроке Adobe Illustrator мы создадим наш собственный спиральный прямоугольник золотого сечения (последовательность Фибоначчи), а затем воспользуемся фильтром. Антибликовое покрытие и устойчивость к царапинам! | ТЕМНЫЙ ЭКРАН ДЛЯ ДРУГИХ — Хороший обзор для вас.Лотерейные скретчеры раздаются розничным торговцам большими рулонами, и в каждом рулоне гарантировано определенное количество победителей. ) Примерно 8 559 050 * билетов в Extreme Cash $ 1 000 000. Смешайте яйца, сметану, молоко, сыр, соль и перец в большой миске. 25 литров / 40 унций). 195 — это билет Cashwords за 5 долларов. 0 Редактор для того, чтобы изменить разрешение на 16: 9? Я знаю, что в Scratch 2 это возможно. Взбивайте сливки, пока они не загустеют. Коэффициент пустотности 4% от 0,1 дюйма до 34 дюймов.
СОЗДАЙТЕ СПИРАЛЬ С ЗОЛОТОМ СООТНОШЕНИЕМ И ЛОГОТИП С ПОМОЩЬЮ ЭТОГО Учебного пособия! | Мы создадим прямоугольник с золотым сечением с нуля в этом уроке, и вы увидите, насколько простой, интересной и полезной может быть эта техника! В этом уроке Adobe Illustrator мы создадим наш собственный спиральный прямоугольник золотого сечения (последовательность Фибоначчи), а затем воспользуемся фильтром. Антибликовое покрытие и устойчивость к царапинам! | ТЕМНЫЙ ЭКРАН ДЛЯ ДРУГИХ — Хороший обзор для вас.Лотерейные скретчеры раздаются розничным торговцам большими рулонами, и в каждом рулоне гарантировано определенное количество победителей. ) Примерно 8 559 050 * билетов в Extreme Cash $ 1 000 000. Смешайте яйца, сметану, молоко, сыр, соль и перец в большой миске. 25 литров / 40 унций). 195 — это билет Cashwords за 5 долларов. 0 Редактор для того, чтобы изменить разрешение на 16: 9? Я знаю, что в Scratch 2 это возможно. Взбивайте сливки, пока они не загустеют. Коэффициент пустотности 4% от 0,1 дюйма до 34 дюймов. Это может… Коэффициент Шарпа измеряется, сначала находя ожидаемую норму доходности или среднюю доходность за определенный период времени, а затем вычитая безрисковую ставку. 68 билетов выигрывает! Выплата 69. Хорошо, сделаем немного цемента. О Фибоначчи. Смесь немного хороша для однотонной рендеринга, но подходит для лихой. Scratch обычно использует соотношение сторон 4: 3, но, используя модификацию Scratch под названием E icques, вы можете использовать соотношение сторон 16: 9 в графическом интерфейсе пользователя Scratch для создания и запуска Scratch 3.Powerball® Mega Millions® Есть много способов спроектировать самолет eVTOL. Вот как мы думаем о ключевых принципах проектирования и почему наша команда в Lilium стремится к другой архитектуре. Найдите больше слов и больше шансов выиграть до 20 000 долларов в любимом магазине. Но я постараюсь! Разница между онлайн-картами и традиционными скретч-картами заключается в том, как онлайн-компании отображают шансы. Копает. Узнайте, как с нуля реализовать функцию коэффициента мощности полосы на Python.
Это может… Коэффициент Шарпа измеряется, сначала находя ожидаемую норму доходности или среднюю доходность за определенный период времени, а затем вычитая безрисковую ставку. 68 билетов выигрывает! Выплата 69. Хорошо, сделаем немного цемента. О Фибоначчи. Смесь немного хороша для однотонной рендеринга, но подходит для лихой. Scratch обычно использует соотношение сторон 4: 3, но, используя модификацию Scratch под названием E icques, вы можете использовать соотношение сторон 16: 9 в графическом интерфейсе пользователя Scratch для создания и запуска Scratch 3.Powerball® Mega Millions® Есть много способов спроектировать самолет eVTOL. Вот как мы думаем о ключевых принципах проектирования и почему наша команда в Lilium стремится к другой архитектуре. Найдите больше слов и больше шансов выиграть до 20 000 долларов в любимом магазине. Но я постараюсь! Разница между онлайн-картами и традиционными скретч-картами заключается в том, как онлайн-компании отображают шансы. Копает. Узнайте, как с нуля реализовать функцию коэффициента мощности полосы на Python. Если размер соответствующей стороны подобного многоугольника равен 6 единицам, найдите соотношение их площадей. 9% серы с переменным соотношением. Я думал об одном из моих любимых блюд, жареной курице и обо всем, что вы могли извлечь из этого (как приготовить бульон, а затем любой бульон, как приготовить сковороду, как приготовить соус, изысканный соус с травами) . Сравните шансы нескольких игр, прежде чем делать обоснованное предположение о том, какую карту купить. Таким образом, 22/40 ровно на 10% больше, чем 20/40. Общие шансы на выигрыш — это шансы выиграть ЛЮБОЙ приз в скретч-игре.2%) 3. Число выемки представляет собой фактический размер выемки в сотых долях миллиметра. Этот новый лак специально разработан для ремонта автомобилей Nissan с прозрачным покрытием Scratch Shield. Конопля — масло, настоянное на конопле, — ключевой ингредиент в пищевых добавках. Добавьте колбасу и тушите, пока она не подрумянится, по мере приготовления ломая ее на мелкие кусочки деревянной ложкой. Шаг 3: приготовьте взбитые сливки.
Если размер соответствующей стороны подобного многоугольника равен 6 единицам, найдите соотношение их площадей. 9% серы с переменным соотношением. Я думал об одном из моих любимых блюд, жареной курице и обо всем, что вы могли извлечь из этого (как приготовить бульон, а затем любой бульон, как приготовить сковороду, как приготовить соус, изысканный соус с травами) . Сравните шансы нескольких игр, прежде чем делать обоснованное предположение о том, какую карту купить. Таким образом, 22/40 ровно на 10% больше, чем 20/40. Общие шансы на выигрыш — это шансы выиграть ЛЮБОЙ приз в скретч-игре.2%) 3. Число выемки представляет собой фактический размер выемки в сотых долях миллиметра. Этот новый лак специально разработан для ремонта автомобилей Nissan с прозрачным покрытием Scratch Shield. Конопля — масло, настоянное на конопле, — ключевой ингредиент в пищевых добавках. Добавьте колбасу и тушите, пока она не подрумянится, по мере приготовления ломая ее на мелкие кусочки деревянной ложкой. Шаг 3: приготовьте взбитые сливки. Не оставайтесь в опасности. Безопасные покупки стали быстрее. Обычно шансы указаны как сравнение чисел: 1: 5 или 1:20.DevBlocks: мод Scratch с настраиваемым соотношением сторон, который может загружать расширение из URL-адреса. Рассчитайте коэффициент — метод GCD. 1 часть сфагнума, торфяного мха, кокоса, листовой плесени и т. Д. Не только броские названия или стоимость билетов. Те, кто выиграли скретч-призы, будут иметь стоимость: некоторые меньше, некоторые больше. Если вы выразите шансы на победу дробью, вы получите 2/1. Используя приведенный выше пример, отношение чего-то происходящего (выигрыш Челси) 1 ко всему, что может случиться (выигрыш и проигрыш Челси) 4, также можно записать в виде дроби 1/4, которая представляет собой вероятность выигрыша — вероятность проигрыша равна следовательно, соотношение 1–1 / 4 PBV = цена акции / балансовая стоимость акций.Решение Основание равнобедренного треугольника и высота, проведенная от одной из совпадающих сторон, равны 18 см и 15 см соответственно.
Не оставайтесь в опасности. Безопасные покупки стали быстрее. Обычно шансы указаны как сравнение чисел: 1: 5 или 1:20.DevBlocks: мод Scratch с настраиваемым соотношением сторон, который может загружать расширение из URL-адреса. Рассчитайте коэффициент — метод GCD. 1 часть сфагнума, торфяного мха, кокоса, листовой плесени и т. Д. Не только броские названия или стоимость билетов. Те, кто выиграли скретч-призы, будут иметь стоимость: некоторые меньше, некоторые больше. Если вы выразите шансы на победу дробью, вы получите 2/1. Используя приведенный выше пример, отношение чего-то происходящего (выигрыш Челси) 1 ко всему, что может случиться (выигрыш и проигрыш Челси) 4, также можно записать в виде дроби 1/4, которая представляет собой вероятность выигрыша — вероятность проигрыша равна следовательно, соотношение 1–1 / 4 PBV = цена акции / балансовая стоимость акций.Решение Основание равнобедренного треугольника и высота, проведенная от одной из совпадающих сторон, равны 18 см и 15 см соответственно. Положите чай, воду, ваниль и специи в кастрюлю среднего размера и закипите. Превосходные свойства поверхности D8126, которые сводят к минимуму видимые повреждения, вызванные … Как и пирог с фунтом, пирог 1-2-3-4 получил свое название от пропорций его основных ингредиентов: одна чашка масла, две чашки сахара, три чашки мука, четыре яйца. Наполните чашку молоком до отметки в 1 чашку (так что да, вы будете использовать чуть меньше 1 полной чашки молока).Агрегация начальной загрузки, случайный лес, повышение градиента, XGboost — все это очень важные и широко используемые алгоритмы, чтобы понять их в деталях, нужно глубоко знать дерево решений. 40: 0. В зависимости от вашего времени и потребностей вы можете решить, как приготовить бульон для японского супа, одним из трех следующих способов. Последние лучшие скретчеры в Теннесси по лучшим шансам. Это часть вознаграждения в коэффициенте Шарпа, которая затем будет разделена на стандартное отклонение доходов (часть риска). Вы можете поцарапать его сразу после того, как примените его к стене, но с вашей стороны потребуется немного больше контроля, чтобы получить скретч-билеты за 50 долларов.
Положите чай, воду, ваниль и специи в кастрюлю среднего размера и закипите. Превосходные свойства поверхности D8126, которые сводят к минимуму видимые повреждения, вызванные … Как и пирог с фунтом, пирог 1-2-3-4 получил свое название от пропорций его основных ингредиентов: одна чашка масла, две чашки сахара, три чашки мука, четыре яйца. Наполните чашку молоком до отметки в 1 чашку (так что да, вы будете использовать чуть меньше 1 полной чашки молока).Агрегация начальной загрузки, случайный лес, повышение градиента, XGboost — все это очень важные и широко используемые алгоритмы, чтобы понять их в деталях, нужно глубоко знать дерево решений. 40: 0. В зависимости от вашего времени и потребностей вы можете решить, как приготовить бульон для японского супа, одним из трех следующих способов. Последние лучшие скретчеры в Теннесси по лучшим шансам. Это часть вознаграждения в коэффициенте Шарпа, которая затем будет разделена на стандартное отклонение доходов (часть риска). Вы можете поцарапать его сразу после того, как примените его к стене, но с вашей стороны потребуется немного больше контроля, чтобы получить скретч-билеты за 50 долларов. В этом рецепте для приготовления густой подливы используются 2 стакана молока и 1/4 стакана муки. На слегка присыпанной мукой поверхности замесить тесто примерно от 3 до… Шаг 1: Перемешать. Игра #. Чтобы дать вам пример того, насколько плохими могут быть лотерейные билеты, большинство скретч-билетов на 1 доллар имеют ожидаемую ценность около 60%, что означает, что на каждый потраченный доллар вы получите обратно всего 0 долларов. Это третье и последнее руководство по выполнению «НЛП с нуля», в котором мы пишем наши собственные классы и функции для предварительной обработки данных для выполнения наших задач моделирования НЛП.Легкий рецепт тыквенного хумуса. Медленно влейте молочную смесь, пока масло не растворится и тесто не станет однородным. X the Boro Plastering работает в соотношении три к одному, мешки с песком и мешки с гипсом для их грубых покрытий. Если когда-либо и была причина для спасения деревьев, так это это очаровательное маленькое личико. Этот фильтр разработан для широкоэкранных портативных компьютеров с экранами, которые кажутся скорее прямоугольными, чем квадратными, и имеют соотношение сторон 16: 9.
В этом рецепте для приготовления густой подливы используются 2 стакана молока и 1/4 стакана муки. На слегка присыпанной мукой поверхности замесить тесто примерно от 3 до… Шаг 1: Перемешать. Игра #. Чтобы дать вам пример того, насколько плохими могут быть лотерейные билеты, большинство скретч-билетов на 1 доллар имеют ожидаемую ценность около 60%, что означает, что на каждый потраченный доллар вы получите обратно всего 0 долларов. Это третье и последнее руководство по выполнению «НЛП с нуля», в котором мы пишем наши собственные классы и функции для предварительной обработки данных для выполнения наших задач моделирования НЛП.Легкий рецепт тыквенного хумуса. Медленно влейте молочную смесь, пока масло не растворится и тесто не станет однородным. X the Boro Plastering работает в соотношении три к одному, мешки с песком и мешки с гипсом для их грубых покрытий. Если когда-либо и была причина для спасения деревьев, так это это очаровательное маленькое личико. Этот фильтр разработан для широкоэкранных портативных компьютеров с экранами, которые кажутся скорее прямоугольными, чем квадратными, и имеют соотношение сторон 16: 9. Метод 1. Сделайте даши с нуля. Запомните это соотношение: 6 стручков ванили на 8 унций алкоголя.3. 03: 0. e. Джеймс Шенд, заместитель кулинарного редактора Taste of Home, при создании рецептов Taste of Home сослался на книгу Майкла Рулмана «Соотношения: простые коды, лежащие в основе ремесла повседневной кулинарии». Сейчас как никогда важна кибербезопасность. Методы: 151 человек (90 мужчин и 61 женщина) был обследован на предмет аллергических реакций методом царапины. Если вы начинаете с основного корма для несушек, старайтесь ограничить их количество (10% корма — это то, что я читал), поскольку корм для несушек обычно содержит 16% белка, а стартер для цыплят — 20%.54. Белый сахар-песок добавлен по вкусу. ). Результаты: Положительное соотношение у ежовой ноги (Dactylis glomerata) (51%) было выше, чем у кедра (криптомерия Сделать простую маргариту с нуля легко — все, что вам нужно сделать, это объединить 2 унции текилы, 1 унцию трипл-сек, 3/4 унции свежевыжатого сока лайма и 3/4 унции простого сиропа в шейкере для коктейлей со льдом.
Метод 1. Сделайте даши с нуля. Запомните это соотношение: 6 стручков ванили на 8 унций алкоголя.3. 03: 0. e. Джеймс Шенд, заместитель кулинарного редактора Taste of Home, при создании рецептов Taste of Home сослался на книгу Майкла Рулмана «Соотношения: простые коды, лежащие в основе ремесла повседневной кулинарии». Сейчас как никогда важна кибербезопасность. Методы: 151 человек (90 мужчин и 61 женщина) был обследован на предмет аллергических реакций методом царапины. Если вы начинаете с основного корма для несушек, старайтесь ограничить их количество (10% корма — это то, что я читал), поскольку корм для несушек обычно содержит 16% белка, а стартер для цыплят — 20%.54. Белый сахар-песок добавлен по вкусу. ). Результаты: Положительное соотношение у ежовой ноги (Dactylis glomerata) (51%) было выше, чем у кедра (криптомерия Сделать простую маргариту с нуля легко — все, что вам нужно сделать, это объединить 2 унции текилы, 1 унцию трипл-сек, 3/4 унции свежевыжатого сока лайма и 3/4 унции простого сиропа в шейкере для коктейлей со льдом. Еще одна простая вещь… 【Совместимость】 14-дюймовый ноутбук с соотношением сторон 16: 9, (Ш x В): 12. Соотношение сторон основание равнобедренного треугольника по высоте 3: 4.Хотя, чтобы понять, как это работает, вам сначала нужно кое-что узнать о том, как свет взаимодействует с поверхностями. Функция GCD используется для вычисления наибольшего общего знаменателя между двумя или более значениями. У вас должен быть Scratch 3. Это потрясающий соус, и он готов за считанные минуты! Поскольку его так быстро и легко приготовить на скорую руку, он отлично подходит для полдника для голодных детей, которым можно отведать чипсы или крендели с кусочками или подавить овощи, такие как брокколи или цветная капуста. Каждое утро мы собираем актуальную информацию из официальных государственных лотерей и рассчитываем. Хотите ли вы продвигать свой бизнес, благодарить клиентов, проводить сбор средств или внедрять программу мотивации сотрудников, скретч-игра гарантированно создаст непревзойденный результат.
Еще одна простая вещь… 【Совместимость】 14-дюймовый ноутбук с соотношением сторон 16: 9, (Ш x В): 12. Соотношение сторон основание равнобедренного треугольника по высоте 3: 4.Хотя, чтобы понять, как это работает, вам сначала нужно кое-что узнать о том, как свет взаимодействует с поверхностями. Функция GCD используется для вычисления наибольшего общего знаменателя между двумя или более значениями. У вас должен быть Scratch 3. Это потрясающий соус, и он готов за считанные минуты! Поскольку его так быстро и легко приготовить на скорую руку, он отлично подходит для полдника для голодных детей, которым можно отведать чипсы или крендели с кусочками или подавить овощи, такие как брокколи или цветная капуста. Каждое утро мы собираем актуальную информацию из официальных государственных лотерей и рассчитываем. Хотите ли вы продвигать свой бизнес, благодарить клиентов, проводить сбор средств или внедрять программу мотивации сотрудников, скретч-игра гарантированно создаст непревзойденный результат. азарт и умножьте свой ROI! Вот несколько причин, почему: — Средняя норма доходности составляет от 5 до 20% (мы часто видим 30–50%) — Ставка погашения высока! none Самый простой способ сравнить шансы со скидкой Texas Lotto — это использовать «общие шансы».Всего в игре может быть продано 40 миллионов билетов. Технически, чтобы правильно разобраться в этой теме, мы должны сначала изучить радиометрию. LitYoloSwago Scratcher 100+ постов с соотношением сторон 16 x 9, пожалуйста! Я считаю, что соотношение сторон 4: 3 достаточно хорошее. Я хочу изменить его на соотношение сторон 16: 9 с разрешением 720p. Удвойте это! Скретч-офф Как играть. Картофель очистить, пока он еще теплый. Номер игры Название Цена Рентабельность инвестиций Главный приз Прибыль; 2338: 500X Loteria Spectacular: 50-0 долларов. 08: 0. мит. Стоимость билетов: 50 долларов Старт: 20.09.2021.15 и 0. Чтобы приготовить пахту, просто отмерьте уксус или лимонный сок в мерной чашке для жидкости. Я выложил их ниже, чтобы дать вам… 39441.
азарт и умножьте свой ROI! Вот несколько причин, почему: — Средняя норма доходности составляет от 5 до 20% (мы часто видим 30–50%) — Ставка погашения высока! none Самый простой способ сравнить шансы со скидкой Texas Lotto — это использовать «общие шансы».Всего в игре может быть продано 40 миллионов билетов. Технически, чтобы правильно разобраться в этой теме, мы должны сначала изучить радиометрию. LitYoloSwago Scratcher 100+ постов с соотношением сторон 16 x 9, пожалуйста! Я считаю, что соотношение сторон 4: 3 достаточно хорошее. Я хочу изменить его на соотношение сторон 16: 9 с разрешением 720p. Удвойте это! Скретч-офф Как играть. Картофель очистить, пока он еще теплый. Номер игры Название Цена Рентабельность инвестиций Главный приз Прибыль; 2338: 500X Loteria Spectacular: 50-0 долларов. 08: 0. мит. Стоимость билетов: 50 долларов Старт: 20.09.2021.15 и 0. Чтобы приготовить пахту, просто отмерьте уксус или лимонный сок в мерной чашке для жидкости. Я выложил их ниже, чтобы дать вам… 39441. Перемешайте 2 столовые ложки воды в сковороде, немедленно накройте крышкой и включите средний огонь. Копание определяется как яма или небольшая воронка на поверхности стекла. Это поможет вам понять, как работают нейронные сети, и здесь мы реализуем RNN, в котором есть «Почему этот рецепт лучший». 3 доллара. Сделайте тесто для ньокки. Шаг 2 — Анализ соотношений Вторым этапом финансового моделирования в Excel является выполнение анализа соотношений.30:… Вместо этого используйте пропорции выпечки, чтобы приготовить основы, или используйте их как отправную точку для создания собственного рецепта с нуля. 1582. Объем скопления значительно меньше объема канавки царапины, что указывает на значительное уплотнение также в процессе царапания. Добавьте сахар и продолжайте взбивать, пока он не станет мягким, когда венчик или взбиватель будет убран. Несмотря на то, что они могут содержать схожее соотношение цемента к песку и применяются одинаково, у них есть некоторые явные различия.Представьте, что Odyssey National — это совершенно новый банк, и что его норматив обязательных резервов составляет 10 процентов.
Перемешайте 2 столовые ложки воды в сковороде, немедленно накройте крышкой и включите средний огонь. Копание определяется как яма или небольшая воронка на поверхности стекла. Это поможет вам понять, как работают нейронные сети, и здесь мы реализуем RNN, в котором есть «Почему этот рецепт лучший». 3 доллара. Сделайте тесто для ньокки. Шаг 2 — Анализ соотношений Вторым этапом финансового моделирования в Excel является выполнение анализа соотношений.30:… Вместо этого используйте пропорции выпечки, чтобы приготовить основы, или используйте их как отправную точку для создания собственного рецепта с нуля. 1582. Объем скопления значительно меньше объема канавки царапины, что указывает на значительное уплотнение также в процессе царапания. Добавьте сахар и продолжайте взбивать, пока он не станет мягким, когда венчик или взбиватель будет убран. Несмотря на то, что они могут содержать схожее соотношение цемента к песку и применяются одинаково, у них есть некоторые явные различия.Представьте, что Odyssey National — это совершенно новый банк, и что его норматив обязательных резервов составляет 10 процентов. henselae (Bartonella henselae), бактерии, вызывающие болезнь кошачьих царапин. L Здесь вы найдете обзор лучших (и худших) скретч-билетов. 25 долларов. D8126 CeramiClearTM — устойчивое к царапинам и царапинам прозрачное покрытие с высокой твердостью. Штукатурный цементный песок Соотношение: 1: 3 — Наружная стена (в суровых климатических условиях) 1: 4 — Наружная стена (нормальные условия) 1: 4 — Штукатурка потолка. Для простого рендеринга я бы использовал скретч 5: 1 и немного более слабую смесь второго слоя.39 соусов для вечеринок без глютена. мои причины: 1. 20: 0 (с точки зрения процентного изменения) Графика процентного изменения и… Для настольного монитора ПК 27 дюймов (соотношение 16: 9) [BISENTEK] Защитная крышка экрана с защитой от синего света, защита глаз, снижение утомляемости / головная боль, защита от царапин, шока, защита от ультрафиолета 61 доллар США. На этом этапе я использую коллекции. это может быть медленным. ПОДХОДИТ РАЗМЕРАМ ЭКРАНА 24 ДЮЙМА, ИЗМЕРЕННЫМ ДИАГОНАЛЬНО — ШИРОКОЭКРАННЫЕ МОНИТОРЫ — Соотношение сторон 16: 9 — Размер фильтра: Ширина: 20 15/16 дюймов, Высота: 11 13/16 дюймов (532 мм x… линзы к линзе с покрытием — коэффициент Байера.
henselae (Bartonella henselae), бактерии, вызывающие болезнь кошачьих царапин. L Здесь вы найдете обзор лучших (и худших) скретч-билетов. 25 долларов. D8126 CeramiClearTM — устойчивое к царапинам и царапинам прозрачное покрытие с высокой твердостью. Штукатурный цементный песок Соотношение: 1: 3 — Наружная стена (в суровых климатических условиях) 1: 4 — Наружная стена (нормальные условия) 1: 4 — Штукатурка потолка. Для простого рендеринга я бы использовал скретч 5: 1 и немного более слабую смесь второго слоя.39 соусов для вечеринок без глютена. мои причины: 1. 20: 0 (с точки зрения процентного изменения) Графика процентного изменения и… Для настольного монитора ПК 27 дюймов (соотношение 16: 9) [BISENTEK] Защитная крышка экрана с защитой от синего света, защита глаз, снижение утомляемости / головная боль, защита от царапин, шока, защита от ультрафиолета 61 доллар США. На этом этапе я использую коллекции. это может быть медленным. ПОДХОДИТ РАЗМЕРАМ ЭКРАНА 24 ДЮЙМА, ИЗМЕРЕННЫМ ДИАГОНАЛЬНО — ШИРОКОЭКРАННЫЕ МОНИТОРЫ — Соотношение сторон 16: 9 — Размер фильтра: Ширина: 20 15/16 дюймов, Высота: 11 13/16 дюймов (532 мм x… линзы к линзе с покрытием — коэффициент Байера. Смесь должна образовать крутое тесто. 60: 0. Код: https: // gi Если оставить кусок мяса в маринаде слишком долго, он не станет мягким — он станет мягким. Например, в рецепте 1/4 стакана муки вы замените его 2 столовыми ложками кукурузного крахмала. Нагрейте большую сковороду на среднем огне. Вы можете использовать одно яйцо плюс три желтка, чтобы получилось около 3–3 / 4 унций. Для этого вам также придется… Продолжайте прокручивать список 10 лучших игр лотереи Джорджии с лучшими общими шансами на выигрыш в этом месяце.com оставляет за собой право проверять возврат «мертвых по прибытии» и взимать с клиента комиссию в размере 15 процентов от продажной цены продукта, если покупатель… Об этом товаре. Обрызгайте сковороду 9×13 дюймов кулинарным спреем. 40: Смесь штукатурного покрытия для царапин — это простой рецепт, который на самом деле состоит из песка, цемента и воды. E icques: мод Scratch с настраиваемым соотношением сторон, который может загружать расширение из URL-адреса. Черновой вариант качественного исследования, критика и этические соображения.
Смесь должна образовать крутое тесто. 60: 0. Код: https: // gi Если оставить кусок мяса в маринаде слишком долго, он не станет мягким — он станет мягким. Например, в рецепте 1/4 стакана муки вы замените его 2 столовыми ложками кукурузного крахмала. Нагрейте большую сковороду на среднем огне. Вы можете использовать одно яйцо плюс три желтка, чтобы получилось около 3–3 / 4 унций. Для этого вам также придется… Продолжайте прокручивать список 10 лучших игр лотереи Джорджии с лучшими общими шансами на выигрыш в этом месяце.com оставляет за собой право проверять возврат «мертвых по прибытии» и взимать с клиента комиссию в размере 15 процентов от продажной цены продукта, если покупатель… Об этом товаре. Обрызгайте сковороду 9×13 дюймов кулинарным спреем. 40: Смесь штукатурного покрытия для царапин — это простой рецепт, который на самом деле состоит из песка, цемента и воды. E icques: мод Scratch с настраиваемым соотношением сторон, который может загружать расширение из URL-адреса. Черновой вариант качественного исследования, критика и этические соображения. Сначала не видно, пока не пойдет дождь, а затем начнет высыхать, показывая трещины, заполненные водой.Копания определяются их диаметром. Рассмотрите возможность приобретения нескольких скретч-карт из одной игры за одну поездку в магазин, а не просто покупку одной скретч-карты. На втором месте стоит Take Five за $ 1. Сделайте углубление в муке, добавьте слегка взбитое яйцо и перемешайте. Давайте разберемся, как это работает. 40 проигрышей. 30 долларов. В конце этих трех шагов мы реализуем кластеризацию переменных с использованием SAS и Python в многомерном пространстве данных. Как сделать печенье более хрустящим: для получения более хрустящего печенья используйте только масло и… Соотношение между двумя числами является дробью или частным и устанавливает пропорциональное соотношение.Опустите верхнюю часть пресса на тесто, затем надавите ручкой, чтобы тесто разгладилось до толщины примерно 1/8 дюйма. Виниловые граффити-голограммы на заказ Наклейка на яичной скорлупе Хрупкий голографический логотип Наклейки с соотношением краски на бумаге, найти полную информацию о виниловых граффити, голограмм, изготовленных на заказ, наклейка с яичной скорлупой, Хрупкий голографический логотип, наклейки с соотношением краски на бумаге, нестандартные наклейки с соотношением краски на бумаге для лазерной безопасности, царапины Серийный номер, 3d наклейка с голограммой, на заказ Водонепроницаемость… Основное соотношение: 1 столовая ложка уксуса или лимонного сока + 1 чашка молока по выбору = 1 чашка пахты.
Сначала не видно, пока не пойдет дождь, а затем начнет высыхать, показывая трещины, заполненные водой.Копания определяются их диаметром. Рассмотрите возможность приобретения нескольких скретч-карт из одной игры за одну поездку в магазин, а не просто покупку одной скретч-карты. На втором месте стоит Take Five за $ 1. Сделайте углубление в муке, добавьте слегка взбитое яйцо и перемешайте. Давайте разберемся, как это работает. 40 проигрышей. 30 долларов. В конце этих трех шагов мы реализуем кластеризацию переменных с использованием SAS и Python в многомерном пространстве данных. Как сделать печенье более хрустящим: для получения более хрустящего печенья используйте только масло и… Соотношение между двумя числами является дробью или частным и устанавливает пропорциональное соотношение.Опустите верхнюю часть пресса на тесто, затем надавите ручкой, чтобы тесто разгладилось до толщины примерно 1/8 дюйма. Виниловые граффити-голограммы на заказ Наклейка на яичной скорлупе Хрупкий голографический логотип Наклейки с соотношением краски на бумаге, найти полную информацию о виниловых граффити, голограмм, изготовленных на заказ, наклейка с яичной скорлупой, Хрупкий голографический логотип, наклейки с соотношением краски на бумаге, нестандартные наклейки с соотношением краски на бумаге для лазерной безопасности, царапины Серийный номер, 3d наклейка с голограммой, на заказ Водонепроницаемость… Основное соотношение: 1 столовая ложка уксуса или лимонного сока + 1 чашка молока по выбору = 1 чашка пахты. Если царапина остается и отпечаток, вероятно, вы держите известняк. Этот соус, приготовленный с нуля, намного лучше, чем переработанный вариант из продуктового магазина. 35 мкм). фиксированный интервал. Для производства кубического ярда бетона 3000 фунтов на квадратный дюйм (27 кубических футов) соотношение бетонной смеси составляет: 517 фунтов цемента или (234 кг) 1560 фунтов песка или (707 кг) 1600 фунтов камня или (725 кг) 32-34 галлона воды. или (132L) Такое соотношение смешивания даст вам бетонную смесь, которая будет прочной, долговечной и подходящей для большинства бетонных скретч-оффов Best tn Lottery.1 доллар. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,…. 787: 30: 0. Жир, требуемый в соотношении, может быть сливочным или растительным маслом, с возможностью добавления небольшого количества сахара, ванили или разрыхлителя. СООТНОШЕНИЕ СМЕСИ 1: 3: 3. 00 победителей и 3 билета — 10 долларов победителей […] На рис.
Если царапина остается и отпечаток, вероятно, вы держите известняк. Этот соус, приготовленный с нуля, намного лучше, чем переработанный вариант из продуктового магазина. 35 мкм). фиксированный интервал. Для производства кубического ярда бетона 3000 фунтов на квадратный дюйм (27 кубических футов) соотношение бетонной смеси составляет: 517 фунтов цемента или (234 кг) 1560 фунтов песка или (707 кг) 1600 фунтов камня или (725 кг) 32-34 галлона воды. или (132L) Такое соотношение смешивания даст вам бетонную смесь, которая будет прочной, долговечной и подходящей для большинства бетонных скретч-оффов Best tn Lottery.1 доллар. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,…. 787: 30: 0. Жир, требуемый в соотношении, может быть сливочным или растительным маслом, с возможностью добавления небольшого количества сахара, ванили или разрыхлителя. СООТНОШЕНИЕ СМЕСИ 1: 3: 3. 00 победителей и 3 билета — 10 долларов победителей […] На рис. Представлены изображения бороздок царапин с помощью AFM сверху. Постепенно добавляйте сахарную пудру. Скребки начинаются всего с 1 доллара, а у некоторых есть призы в миллионы! Все игры.L Эта программа Dyson Sphere «Let’s Play» — доказательство спагетти! Этот эпизод: «Станции межзвездной логистики прямо из сырьевых материалов» — Blueprint включен как всегда Это единственный законный способ «изменить шансы» на выигрыш крупного приза в скретч-игре. Стандарты царапин указаны в древесном угле U. 3%; 11. Это также не было бы медленнее, потому что больше места на экране не означает большего отставания с точки зрения царапин. Выполните повторную визуализацию с помощью Movie Maker / Openshot / любого используемого вами редактора фильмов с разрешением 720p / 1080p, если вам не нравится, что ваши видео на YouTube должны быть 360p и сжаты вдребезги.1487. Магазин без повторного ввода платежных реквизитов. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Экранный фильтр конфиденциальности компьютера для широкоэкранного монитора WELINC 21.
Представлены изображения бороздок царапин с помощью AFM сверху. Постепенно добавляйте сахарную пудру. Скребки начинаются всего с 1 доллара, а у некоторых есть призы в миллионы! Все игры.L Эта программа Dyson Sphere «Let’s Play» — доказательство спагетти! Этот эпизод: «Станции межзвездной логистики прямо из сырьевых материалов» — Blueprint включен как всегда Это единственный законный способ «изменить шансы» на выигрыш крупного приза в скретч-игре. Стандарты царапин указаны в древесном угле U. 3%; 11. Это также не было бы медленнее, потому что больше места на экране не означает большего отставания с точки зрения царапин. Выполните повторную визуализацию с помощью Movie Maker / Openshot / любого используемого вами редактора фильмов с разрешением 720p / 1080p, если вам не нравится, что ваши видео на YouTube должны быть 360p и сжаты вдребезги.1487. Магазин без повторного ввода платежных реквизитов. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Экранный фильтр конфиденциальности компьютера для широкоэкранного монитора WELINC 21. Вот как это работает. Игра № Стоимость билета. Песок и цемент ушли в прошлое, они использовались в старых методах гидроизоляции, первым слоем всегда был слой царапины со встроенным гидроизоляционным слоем. Соотношение примерно 3-4 части воды на 1 часть извести примерно правильное.17. Стоимость билетов. К настоящему времени вы знаете, почему вы хотите, чтобы у вас на кухне кипела миска закваски, но как, черт возьми, ее приготовить? 787: 40: 0. Помните, как и выше, что это не выражение того, насколько вероятно вы проиграете, а скорее отношение неблагоприятных исходов к благоприятным исходам. Что касается соотношений, в таком базовом мыле будет соотношение масла и щелока 1: 3. Добавьте еще льда, если… Запуская мобильную игру с нуля, какое разрешение / соотношение сторон использовать для дизайна? Я начинаю игру, предназначенную для iOS и Android, в которую играют в портретном режиме.Кухонные отходы. Взбить Sweetex и медленно добавлять воду до полного растворения. Froid Gallows M フ ロ ワ ガ ロ ウ ズ Верхняя одежда, Нижняя одежда, Внутренняя одежда Все мужские расы Bitter Simoon ビ タ ー シ ム ー… Фотография Тима Фостера на Unsplash.
Вот как это работает. Игра № Стоимость билета. Песок и цемент ушли в прошлое, они использовались в старых методах гидроизоляции, первым слоем всегда был слой царапины со встроенным гидроизоляционным слоем. Соотношение примерно 3-4 части воды на 1 часть извести примерно правильное.17. Стоимость билетов. К настоящему времени вы знаете, почему вы хотите, чтобы у вас на кухне кипела миска закваски, но как, черт возьми, ее приготовить? 787: 40: 0. Помните, как и выше, что это не выражение того, насколько вероятно вы проиграете, а скорее отношение неблагоприятных исходов к благоприятным исходам. Что касается соотношений, в таком базовом мыле будет соотношение масла и щелока 1: 3. Добавьте еще льда, если… Запуская мобильную игру с нуля, какое разрешение / соотношение сторон использовать для дизайна? Я начинаю игру, предназначенную для iOS и Android, в которую играют в портретном режиме.Кухонные отходы. Взбить Sweetex и медленно добавлять воду до полного растворения. Froid Gallows M フ ロ ワ ガ ロ ウ ズ Верхняя одежда, Нижняя одежда, Внутренняя одежда Все мужские расы Bitter Simoon ビ タ ー シ ム ー… Фотография Тима Фостера на Unsplash. Найдите больше способов выиграть с помощью скретчеров «2-й шанс» здесь. Настоящие прототипы хранятся в арсенале Пикатинни в Нью-Джерси. Чтобы сделать штукатурку для царапин, смешайте портландцемент, гашеную известь и песок. 4 мм по диагонали, 519 мм в ширину и 325 м в высоту. Примеры соотношений: у вас есть 10 x для каждых 3 y и дано 40 x, вы используете перекрестное умножение, чтобы решить для y = (40) (3) / 10 = 120/10 = 12.Все, что вам нужно запомнить, это 1, 2, 3. *. Он предоставляет ценную информацию о прибыльности, платежеспособности, операционной эффективности организации. Затем эту последовательность можно разбить на коэффициенты, которые, по некоторым предположениям, позволяют понять, куда переместится данный финансовый рынок. com Политика возврата: вы можете вернуть любой новый компьютер, приобретенный у Amazon. 787: 50: 0. 341. 02, 0.. Пожалуйста, внимательно измерьте свой экран. Высота 8 дюймов — метрические измерения: 612. 8 дюймов ДИАГОНАЛЬНО ИЗМЕРЕНИЕ — ШИРОКИЕ МОНИТОРЫ — Соотношение сторон 16: 9 — Размер фильтра: Ширина: 20 3/4 дюйма, Высота: 11 11/16 дюймов (525 мм x 295 мм).
Найдите больше способов выиграть с помощью скретчеров «2-й шанс» здесь. Настоящие прототипы хранятся в арсенале Пикатинни в Нью-Джерси. Чтобы сделать штукатурку для царапин, смешайте портландцемент, гашеную известь и песок. 4 мм по диагонали, 519 мм в ширину и 325 м в высоту. Примеры соотношений: у вас есть 10 x для каждых 3 y и дано 40 x, вы используете перекрестное умножение, чтобы решить для y = (40) (3) / 10 = 120/10 = 12.Все, что вам нужно запомнить, это 1, 2, 3. *. Он предоставляет ценную информацию о прибыльности, платежеспособности, операционной эффективности организации. Затем эту последовательность можно разбить на коэффициенты, которые, по некоторым предположениям, позволяют понять, куда переместится данный финансовый рынок. com Политика возврата: вы можете вернуть любой новый компьютер, приобретенный у Amazon. 787: 50: 0. 341. 02, 0.. Пожалуйста, внимательно измерьте свой экран. Высота 8 дюймов — метрические измерения: 612. 8 дюймов ДИАГОНАЛЬНО ИЗМЕРЕНИЕ — ШИРОКИЕ МОНИТОРЫ — Соотношение сторон 16: 9 — Размер фильтра: Ширина: 20 3/4 дюйма, Высота: 11 11/16 дюймов (525 мм x 295 мм). Скретч-билеты лотереи Луизианы меняются от игры к игре. Это настолько просто, что вам, возможно, даже не придется его писать … Попрощайтесь с шоколадом высокой степени обработки из магазинов! Есть лучший способ удовлетворить вашу тягу к сладкому — приготовить шоколад с нуля. Секрет идеальной маргариты — правильное соотношение текилы и трипл-сек. Я использовал только 1/4 баллона, не намного больше. Фильтр по цене. Чтобы добавить зуб, вы также можете смешать слой песка, портландцемента и воды, чтобы улучшить сцепление с штукатуркой.Месить крючком для теста примерно 10 минут, пока тесто не станет гладким и эластичным. Навигация по сообщениям. Купите свои любимые билеты в местных магазинах и наслаждайтесь азартом игры, чтобы мгновенно выиграть денежные призы. Знание этих шансов может дать вам преимущество! Есть несколько различий между штукатурным слоем царапин и коричневым пальто. На этих билетах указано соотношение выигрышей, например, билет Big Win стоимостью 5 фунтов стерлингов в размере 25 000 фунтов стерлингов, который в настоящее время продается в торговых точках, указывает «1 к 3.
Скретч-билеты лотереи Луизианы меняются от игры к игре. Это настолько просто, что вам, возможно, даже не придется его писать … Попрощайтесь с шоколадом высокой степени обработки из магазинов! Есть лучший способ удовлетворить вашу тягу к сладкому — приготовить шоколад с нуля. Секрет идеальной маргариты — правильное соотношение текилы и трипл-сек. Я использовал только 1/4 баллона, не намного больше. Фильтр по цене. Чтобы добавить зуб, вы также можете смешать слой песка, портландцемента и воды, чтобы улучшить сцепление с штукатуркой.Месить крючком для теста примерно 10 минут, пока тесто не станет гладким и эластичным. Навигация по сообщениям. Купите свои любимые билеты в местных магазинах и наслаждайтесь азартом игры, чтобы мгновенно выиграть денежные призы. Знание этих шансов может дать вам преимущество! Есть несколько различий между штукатурным слоем царапин и коричневым пальто. На этих билетах указано соотношение выигрышей, например, билет Big Win стоимостью 5 фунтов стерлингов в размере 25 000 фунтов стерлингов, который в настоящее время продается в торговых точках, указывает «1 к 3. Шансы на скретч-билеты лотереи Луизианы».Для каждого скретч-номера (80, 60, 40, 20, 10) есть пара прототипов, один из которых определяет скретч-офф Best ny Lottery. Переложите тесто в форму для выпечки размером 9 дюймов с канавками и сформируйте из нее сковороду, срезая канавки и выбрасывая излишки теста. Рассеянное или ламбертовское затенение. [1] Конечно, это лишь приблизительные оценки для создания простого универсального мыла. Crimson Dawn — это скретч-рисунок ARKS Cash (AC) в официальной североамериканской версии Phantasy Star Online 2. $ 10 + Сортировать по. Единственная проблема с этим коэффициентом заключается в том, что он не учитывает будущую прибыль и нематериальные активы компании.Затем я использую. Кто-нибудь знает соотношение сторон для этих изображений, или, если это не удается, что произойдет, если вы попытаетесь использовать изображение нормального размера? Обрезает ли он, или Это видео посвящено тому, как изменить соотношение сторон рабочего проекта. Процесс рекламы Кукурузный крахмал легче всего абсорбируется горячей жидкостью, если его сначала смешать с небольшим количеством холодной жидкости, обычно с водой.
Шансы на скретч-билеты лотереи Луизианы».Для каждого скретч-номера (80, 60, 40, 20, 10) есть пара прототипов, один из которых определяет скретч-офф Best ny Lottery. Переложите тесто в форму для выпечки размером 9 дюймов с канавками и сформируйте из нее сковороду, срезая канавки и выбрасывая излишки теста. Рассеянное или ламбертовское затенение. [1] Конечно, это лишь приблизительные оценки для создания простого универсального мыла. Crimson Dawn — это скретч-рисунок ARKS Cash (AC) в официальной североамериканской версии Phantasy Star Online 2. $ 10 + Сортировать по. Единственная проблема с этим коэффициентом заключается в том, что он не учитывает будущую прибыль и нематериальные активы компании.Затем я использую. Кто-нибудь знает соотношение сторон для этих изображений, или, если это не удается, что произойдет, если вы попытаетесь использовать изображение нормального размера? Обрезает ли он, или Это видео посвящено тому, как изменить соотношение сторон рабочего проекта. Процесс рекламы Кукурузный крахмал легче всего абсорбируется горячей жидкостью, если его сначала смешать с небольшим количеством холодной жидкости, обычно с водой. # 47 2 марта 2021 г. 23:05:59. Как правило, онлайн-казино дает вам такой коэффициент выигрыша… Сообщение «Обсуждение коэффициента добавленной стоимости на скретч-кухне Cheddar» впервые появилось в Top Premier Essays.4. 0158: 20: 0. Например. Чтобы найти шансы против нас, просто измените соотношение шансов в пользу выигрыша. 20 + 8 = 28, затем 28/2 = 14. Чем выше коэффициент царапин, тем… 16: 9 — это соотношение сторон, созданное в 1984 году. Из этого соотношения вы можете увидеть это для каждых 1.80: 0. Диапазон призов. Закройте крышку и нажмите STEAM! 7. 0 Для правильной работы калькулятора или просто запустите файл на сайте. Добавить белое вино и варить 10 минут. Блины. 0 проектов. Начиная с цветков каннабиса, богатых CBD, съедобные продукты наполняются ценными растительными терпенами.В небольшой кастрюле с плотно закрывающейся крышкой доведите до кипения 2 стакана воды. Чтобы сделать трюфели, охладите смесь, пока она не затвердеет, а затем сделайте маленькие шарики, которые можно обвалять в сахарной пудре или какао-порошке.
# 47 2 марта 2021 г. 23:05:59. Как правило, онлайн-казино дает вам такой коэффициент выигрыша… Сообщение «Обсуждение коэффициента добавленной стоимости на скретч-кухне Cheddar» впервые появилось в Top Premier Essays.4. 0158: 20: 0. Например. Чтобы найти шансы против нас, просто измените соотношение шансов в пользу выигрыша. 20 + 8 = 28, затем 28/2 = 14. Чем выше коэффициент царапин, тем… 16: 9 — это соотношение сторон, созданное в 1984 году. Из этого соотношения вы можете увидеть это для каждых 1.80: 0. Диапазон призов. Закройте крышку и нажмите STEAM! 7. 0 Для правильной работы калькулятора или просто запустите файл на сайте. Добавить белое вино и варить 10 минут. Блины. 0 проектов. Начиная с цветков каннабиса, богатых CBD, съедобные продукты наполняются ценными растительными терпенами.В небольшой кастрюле с плотно закрывающейся крышкой доведите до кипения 2 стакана воды. Чтобы сделать трюфели, охладите смесь, пока она не затвердеет, а затем сделайте маленькие шарики, которые можно обвалять в сахарной пудре или какао-порошке. Постепенно добавляйте сахар и перемешивайте на низкой скорости, пока сахар не смешается, а глазурь не станет блестящей. Остались призы джекпота. В небольшой миске взбейте сгущенное молоко и сгущенное молоко (или цельное молоко) до однородной массы. Благодаря нашему широкому выбору игр, вы можете сыграть в миску среднего размера, смешав муку и соль.Это как с лотереей; чем больше у вас будет заявок, тем больше у вас шансов на победу. переменное соотношение. Обрежьте ненужную область видео и поместите ее по размеру экрана, чтобы сохранить фиксированное разрешение. 7. Коэффициент усиления для атрибута A Атрибут (A) с наивысшим коэффициентом усиления (коэффициент усиления (A)) выбирается в качестве атрибута разделения. Многие строители не понимают науки о сырости. — GitHub — sandy14795 / My-own-Decision-Tree: реализовано дерево решений с нуля — с использованием коэффициента передачи информации. Благодаря нашему широкому выбору игр, вы можете играть в корабли The Ratio Six с термальным графином, предназначенным для фильтров с плоской корзиной для кофе.
Постепенно добавляйте сахар и перемешивайте на низкой скорости, пока сахар не смешается, а глазурь не станет блестящей. Остались призы джекпота. В небольшой миске взбейте сгущенное молоко и сгущенное молоко (или цельное молоко) до однородной массы. Благодаря нашему широкому выбору игр, вы можете сыграть в миску среднего размера, смешав муку и соль.Это как с лотереей; чем больше у вас будет заявок, тем больше у вас шансов на победу. переменное соотношение. Обрежьте ненужную область видео и поместите ее по размеру экрана, чтобы сохранить фиксированное разрешение. 7. Коэффициент усиления для атрибута A Атрибут (A) с наивысшим коэффициентом усиления (коэффициент усиления (A)) выбирается в качестве атрибута разделения. Многие строители не понимают науки о сырости. — GitHub — sandy14795 / My-own-Decision-Tree: реализовано дерево решений с нуля — с использованием коэффициента передачи информации. Благодаря нашему широкому выбору игр, вы можете играть в корабли The Ratio Six с термальным графином, предназначенным для фильтров с плоской корзиной для кофе. Выберите фиксированное соотношение сторон и экспортируйте видео с разными разрешениями с одинаковым соотношением сторон. Способность с нуля. Процентное увеличение соотношения такое же, как процентное увеличение числителя, если знаменатель постоянен. Экран компьютера для обеспечения конфиденциальности — это простой и эффективный способ защитить вашу личную информацию. Сверху налейте свой спирт. Затем мы можем использовать GCD для создания наших соотношений. Общие шансы остаются неизменными на протяжении всей игры и обычно печатаются на обратной стороне скретчер-билета.Реализация любой нейронной сети с нуля хотя бы один раз — ценное упражнение. Программирование доставляет больше удовольствия, чем когда-либо. 2 доллара. Билетов 1-0 из 0. Решение. Автор темы chickeylady; Дата начала 27 июля 2021 г .; 1; 2; Следующий. Приготовить равиоли с нуля относительно легко, и они очень впечатлят гостей. Хороших вещей бывает тройка — например, трехкратный бонусный кроссворд® Scratchers® с трехкратным множителем.
Выберите фиксированное соотношение сторон и экспортируйте видео с разными разрешениями с одинаковым соотношением сторон. Способность с нуля. Процентное увеличение соотношения такое же, как процентное увеличение числителя, если знаменатель постоянен. Экран компьютера для обеспечения конфиденциальности — это простой и эффективный способ защитить вашу личную информацию. Сверху налейте свой спирт. Затем мы можем использовать GCD для создания наших соотношений. Общие шансы остаются неизменными на протяжении всей игры и обычно печатаются на обратной стороне скретчер-билета.Реализация любой нейронной сети с нуля хотя бы один раз — ценное упражнение. Программирование доставляет больше удовольствия, чем когда-либо. 2 доллара. Билетов 1-0 из 0. Решение. Автор темы chickeylady; Дата начала 27 июля 2021 г .; 1; 2; Следующий. Приготовить равиоли с нуля относительно легко, и они очень впечатлят гостей. Хороших вещей бывает тройка — например, трехкратный бонусный кроссворд® Scratchers® с трехкратным множителем. Итак, в третий раз я попробовала смесь для торта и консервированную глазурь. Стоимость билетов: 50 долларов Старт: 15.03.2021.»(Редакция R от 2010 г.). Есть еще один расчет, относящийся к игрокам и лотерее: выплата. Если вы действительно хотите ScratchSmarter — получив подробный анализ скретч-офф в Северной Каролине, посмотрите, как наши подробные отчеты могут значительно увеличить ваши шансы на выигрыш главного приза — посмотрите видео здесь. Соотношение 1: 1 (1 чашка шоколада на 1 чашку жирных сливок) — отлично подходит для густой глазури, реализация алгоритма капельного K-ближайшего соседа в Python с нуля. Утроить удовольствие.Учащиеся могут приказать Tello выполнить соответствующие движения, перетаскивая блоки кодирования на свое мобильное интеллектуальное устройство. Но добавляйте воду медленно, а не просто бросайте ее… Соотношение 3 ингредиентов песочного печенья. Я — ретро-геймер, и я… Следующее соотношение и рецепт взяты из моей книги «Соотношение: простые коды, лежащие в основе ремесла повседневной кулинарии».
Итак, в третий раз я попробовала смесь для торта и консервированную глазурь. Стоимость билетов: 50 долларов Старт: 15.03.2021.»(Редакция R от 2010 г.). Есть еще один расчет, относящийся к игрокам и лотерее: выплата. Если вы действительно хотите ScratchSmarter — получив подробный анализ скретч-офф в Северной Каролине, посмотрите, как наши подробные отчеты могут значительно увеличить ваши шансы на выигрыш главного приза — посмотрите видео здесь. Соотношение 1: 1 (1 чашка шоколада на 1 чашку жирных сливок) — отлично подходит для густой глазури, реализация алгоритма капельного K-ближайшего соседа в Python с нуля. Утроить удовольствие.Учащиеся могут приказать Tello выполнить соответствующие движения, перетаскивая блоки кодирования на свое мобильное интеллектуальное устройство. Но добавляйте воду медленно, а не просто бросайте ее… Соотношение 3 ингредиентов песочного печенья. Я — ретро-геймер, и я… Следующее соотношение и рецепт взяты из моей книги «Соотношение: простые коды, лежащие в основе ремесла повседневной кулинарии». Слейте воду из замоченного риса через сито, затем переложите высушенный рис в чашу устройства для приготовления моти. Сделайте глубокую лунку в центре муки, а затем добавьте в нее яйца и воду.Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Три толщины покрытия (1. Общие шансы остаются неизменными на протяжении всей жизни игры. и обычно печатаются на обратной стороне скретч-билета. Вот настройка: конъюгированное соотношение основных кислот. от билета, чтобы показать серию цифр или символов и соответствующих им призов.Вот рецепт, который реализует это соотношение: Оладьи с корочкой для масляного пирога = 2 части муки: 2 части жидкости: 1 часть яйца. Смешайте все сухие ингредиенты (сахар, муку, соль и разрыхлитель). 2. Сложите другую сторону полиэтиленового пакета поверх теста. Из лимонного сока удалить косточки, а мякоть оставить. Есть и другие формулы, которые вы можете использовать, но в простейшей форме это просто соотношение песка и цемента 3: 1.
Слейте воду из замоченного риса через сито, затем переложите высушенный рис в чашу устройства для приготовления моти. Сделайте глубокую лунку в центре муки, а затем добавьте в нее яйца и воду.Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Три толщины покрытия (1. Общие шансы остаются неизменными на протяжении всей жизни игры. и обычно печатаются на обратной стороне скретч-билета. Вот настройка: конъюгированное соотношение основных кислот. от билета, чтобы показать серию цифр или символов и соответствующих им призов.Вот рецепт, который реализует это соотношение: Оладьи с корочкой для масляного пирога = 2 части муки: 2 части жидкости: 1 часть яйца. Смешайте все сухие ингредиенты (сахар, муку, соль и разрыхлитель). 2. Сложите другую сторону полиэтиленового пакета поверх теста. Из лимонного сока удалить косточки, а мякоть оставить. Есть и другие формулы, которые вы можете использовать, но в простейшей форме это просто соотношение песка и цемента 3: 1. 05: 0. Используйте метки классов большинства ближайших точек, чтобы предсказать метку контрольной точки.com. Обсудить расширенные темы Изменение соотношения сторон царапины / разрешения? 14 июля 2019 г. 17:49:15 BurnyB. 088: 3 000 000–4 доллара. Используя картофелеварку или электрический взбиватель, медленно перемешайте … Если нет царапин, сумма произведений чисел царапин, умноженная на отношение их длины к диаметру элемента, не может превышать максимальное количество царапин. Перемешайте, чтобы смешать, и дайте смеси остыть в течение Обсудить вопросы о царапинах Какое соотношение сторон для подписей баннера? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.Соотношение молока и муки для белой подливки зависит от того, насколько густой должна быть подливка. Изображение. По сути, вам просто нужно приготовить простую свежую пасту, а затем вы можете наполнить ее практически чем угодно ― сыром, мясом, овощами и даже фруктами! ***** Гарантированное лучшее качество. Tello Edu, теперь доступное для Tello, представляет собой мобильное приложение для программирования, поддерживающее Scratch.
05: 0. Используйте метки классов большинства ближайших точек, чтобы предсказать метку контрольной точки.com. Обсудить расширенные темы Изменение соотношения сторон царапины / разрешения? 14 июля 2019 г. 17:49:15 BurnyB. 088: 3 000 000–4 доллара. Используя картофелеварку или электрический взбиватель, медленно перемешайте … Если нет царапин, сумма произведений чисел царапин, умноженная на отношение их длины к диаметру элемента, не может превышать максимальное количество царапин. Перемешайте, чтобы смешать, и дайте смеси остыть в течение Обсудить вопросы о царапинах Какое соотношение сторон для подписей баннера? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.Соотношение молока и муки для белой подливки зависит от того, насколько густой должна быть подливка. Изображение. По сути, вам просто нужно приготовить простую свежую пасту, а затем вы можете наполнить ее практически чем угодно ― сыром, мясом, овощами и даже фруктами! ***** Гарантированное лучшее качество. Tello Edu, теперь доступное для Tello, представляет собой мобильное приложение для программирования, поддерживающее Scratch. 97% ». Найдите размеры углов треугольника. Смешайте все влажные ингредиенты (молочную смесь) в отдельной миске (яйца, молоко, экстракты) 3.Есть и другие переменные, которые могут ввести в заблуждение некоторых людей, но они довольно просты, если информация о соотношении сторон 16 x 9, пожалуйста! SonicFanX123_321 писал (а): нет поддержки. 06: 0. Если вы посмотрите, то вы обнаружите, что сегодня ансамблевое обучение более популярно и используется отраслью и составителями рейтингов на Kaggle. Измените размер между 4: 3, 16: 9, 1: 1 и портретом 9:16, настраиваемым соотношением сторон и т. Д. Например, измерение для фильтра 24 «(16:10): 2043 дюйма в ширину x 12. Чтобы проверить, если вы потребуется включить пакет инструментов анализа данных, введите = gcd (в ячейку Excel.НЛП с нуля: перевод с последовательности на сеть последовательностей и внимание ». 787: 60: 0. Реализовано дерево решений с нуля — с использованием коэффициента передачи информации. Чтобы сделать это, я полагаю, вам действительно нужно сделать мод из 3.
97% ». Найдите размеры углов треугольника. Смешайте все влажные ингредиенты (молочную смесь) в отдельной миске (яйца, молоко, экстракты) 3.Есть и другие переменные, которые могут ввести в заблуждение некоторых людей, но они довольно просты, если информация о соотношении сторон 16 x 9, пожалуйста! SonicFanX123_321 писал (а): нет поддержки. 06: 0. Если вы посмотрите, то вы обнаружите, что сегодня ансамблевое обучение более популярно и используется отраслью и составителями рейтингов на Kaggle. Измените размер между 4: 3, 16: 9, 1: 1 и портретом 9:16, настраиваемым соотношением сторон и т. Д. Например, измерение для фильтра 24 «(16:10): 2043 дюйма в ширину x 12. Чтобы проверить, если вы потребуется включить пакет инструментов анализа данных, введите = gcd (в ячейку Excel.НЛП с нуля: перевод с последовательности на сеть последовательностей и внимание ». 787: 60: 0. Реализовано дерево решений с нуля — с использованием коэффициента передачи информации. Чтобы сделать это, я полагаю, вам действительно нужно сделать мод из 3. Вмешать порошок безе. Как вы думаете, ваше суждение … Шансы на скретч-билеты массовой лотереи. Армейский чертеж ARDEC «Стандарты качества поверхности для оптических элементов (царапины и раскопки)» Чертеж C7641866. Например, в этом рецепте используется одна часть соевого соуса (1/2 стакана) на одну часть мирина (1/2 стакана).Если вы не хотите определять уровень белка. Согласно науке IFL, поскольку тапиры могут производить только одного маленького теленка за раз, если численность популяции сократится из-за охоты или вырубки лесов, маловероятно, что они когда-либо выздоровеют. Лучше всего, если грязь схватится за 5-10 минут до того, как поцарапать поверхность. 0236: 20: 0. Инструкции. Наполните два стакана льдом и разлейте чай по льду. Найдите длину сторон … Основное соотношение для окончательного блина сводится к 2 частям муки, 2 частям жидкости, 1 части яйца и ½ части жира.Базовый торт состоит из четырех ингредиентов: муки, сахара, масла и яиц. Если хотите, можете добавить щепотку соли.
Вмешать порошок безе. Как вы думаете, ваше суждение … Шансы на скретч-билеты массовой лотереи. Армейский чертеж ARDEC «Стандарты качества поверхности для оптических элементов (царапины и раскопки)» Чертеж C7641866. Например, в этом рецепте используется одна часть соевого соуса (1/2 стакана) на одну часть мирина (1/2 стакана).Если вы не хотите определять уровень белка. Согласно науке IFL, поскольку тапиры могут производить только одного маленького теленка за раз, если численность популяции сократится из-за охоты или вырубки лесов, маловероятно, что они когда-либо выздоровеют. Лучше всего, если грязь схватится за 5-10 минут до того, как поцарапать поверхность. 0236: 20: 0. Инструкции. Наполните два стакана льдом и разлейте чай по льду. Найдите длину сторон … Основное соотношение для окончательного блина сводится к 2 частям муки, 2 частям жидкости, 1 части яйца и ½ части жира.Базовый торт состоит из четырех ингредиентов: муки, сахара, масла и яиц. Если хотите, можете добавить щепотку соли. 22. C4. Нагрейте столовую ложку масла в сковороде с антипригарным покрытием на среднем огне. Рецепт медового соуса для барбекю — 5 минут, готовка не требуется. это, скорее всего, не сломает старые проекты, так как будут созданы только новые 16: 9. Самый низкий — 0,5 доллара. Овощи не следует оставлять мариноваться более 30 минут, а для рыбы и мягких овощей, таких как кабачки и кабачки, достаточно 10 минут.Стоимость билетов: 50 долларов Старт: 19.04.2021. Получайте актуальные результаты скретчеров и оставшиеся призы для лотереи Джорджии, ПЛЮС советы инсайдеров о том, как выбрать скретчеры с наибольшими шансами на выигрыш. : Добавьте начинку для яблочного пирога в форму для пирога и разровняйте до однородной массы. Процесс домашней закваски с нуля. Рассчитайте процентное содержание по весу, используя маленькие весы для взвешивания различных ингредиентов. Оба слоя должны быть толщиной около 10 мм. Включите миксер на средний уровень и взбивайте, пока смесь не образует густые блестящие пики, примерно 5-7 минут.
22. C4. Нагрейте столовую ложку масла в сковороде с антипригарным покрытием на среднем огне. Рецепт медового соуса для барбекю — 5 минут, готовка не требуется. это, скорее всего, не сломает старые проекты, так как будут созданы только новые 16: 9. Самый низкий — 0,5 доллара. Овощи не следует оставлять мариноваться более 30 минут, а для рыбы и мягких овощей, таких как кабачки и кабачки, достаточно 10 минут.Стоимость билетов: 50 долларов Старт: 19.04.2021. Получайте актуальные результаты скретчеров и оставшиеся призы для лотереи Джорджии, ПЛЮС советы инсайдеров о том, как выбрать скретчеры с наибольшими шансами на выигрыш. : Добавьте начинку для яблочного пирога в форму для пирога и разровняйте до однородной массы. Процесс домашней закваски с нуля. Рассчитайте процентное содержание по весу, используя маленькие весы для взвешивания различных ингредиентов. Оба слоя должны быть толщиной около 10 мм. Включите миксер на средний уровень и взбивайте, пока смесь не образует густые блестящие пики, примерно 5-7 минут. Я определенно получил нужное количество глазури, потому что она не была влажной и липкой. Нет двух одинаковых мгновенных игр. Таким образом, такие отрасли, как банковское дело, предпочитают использовать этот метод в качестве дохода. Довести до кипения и перемешать, чтобы сахар растворился. Однако второй слой часто примыкал к поверхности стены через царапины и делал весь процесс бесполезным. 00 Отличная защита экрана монитора. Данные на экране можно просматривать только под углом 50 градусов. Сохраняет конфиденциальность вашей электронной информации, что делает ее идеальной для использования в зонах с интенсивным движением.Раскатайте охлажденное тесто для пирогов на чистой поверхности, присыпанной мукой, до толщины примерно 1/8 дюйма. Соотношение раствора для оштукатуривания: -рекомендуемое соотношение раствора для оштукатуривания плоскости, шероховатой поверхности кирпичной стены, бетонной стены и потолка составляет 1: 6, 1: 4, 1: 5 и 1: 3 соответственно. Не все скретч-билеты одинаковы! Информация, напечатанная на обратной стороне каждого билета, не всегда отражает обновленные коэффициенты для каждой игры.
Я определенно получил нужное количество глазури, потому что она не была влажной и липкой. Нет двух одинаковых мгновенных игр. Таким образом, такие отрасли, как банковское дело, предпочитают использовать этот метод в качестве дохода. Довести до кипения и перемешать, чтобы сахар растворился. Однако второй слой часто примыкал к поверхности стены через царапины и делал весь процесс бесполезным. 00 Отличная защита экрана монитора. Данные на экране можно просматривать только под углом 50 градусов. Сохраняет конфиденциальность вашей электронной информации, что делает ее идеальной для использования в зонах с интенсивным движением.Раскатайте охлажденное тесто для пирогов на чистой поверхности, присыпанной мукой, до толщины примерно 1/8 дюйма. Соотношение раствора для оштукатуривания: -рекомендуемое соотношение раствора для оштукатуривания плоскости, шероховатой поверхности кирпичной стены, бетонной стены и потолка составляет 1: 6, 1: 4, 1: 5 и 1: 3 соответственно. Не все скретч-билеты одинаковы! Информация, напечатанная на обратной стороне каждого билета, не всегда отражает обновленные коэффициенты для каждой игры. Номер игры: 1427. Счетчик для отслеживания меток, совпадающих с ближайшими соседними точками.При желании добавьте пищевой краситель. 0315: 20: 0. Добавьте в мерную чашку ароматизаторы соли, ванили, масла и миндаля. 5. Бонусные выигрыши в размере 10 000 000 долларов США. Гашеную известь получают путем смешивания негашеной извести с небольшим количеством воды. Скретч-карты — это интересный способ быстро заработать немного денег, не теряя при этом слишком много денег. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Это относится к экономическому развитию — скретч-карты лотереи Нормандских островов.Если вы хотите узнать лучшие шансы на выигрыш Самый простой способ сравнить шансы на выигрыш в Tennessee Lotto — это использовать «общие шансы». 0473: 20: 0. 34. Чтобы использовать функцию GCD, вам может потребоваться включить Data Analysis Toolpak. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Используйте приведенную ниже таблицу для поиска и сортировки скретч-билетов Северной Каролины в настоящее время.
Номер игры: 1427. Счетчик для отслеживания меток, совпадающих с ближайшими соседними точками.При желании добавьте пищевой краситель. 0315: 20: 0. Добавьте в мерную чашку ароматизаторы соли, ванили, масла и миндаля. 5. Бонусные выигрыши в размере 10 000 000 долларов США. Гашеную известь получают путем смешивания негашеной извести с небольшим количеством воды. Скретч-карты — это интересный способ быстро заработать немного денег, не теряя при этом слишком много денег. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Это относится к экономическому развитию — скретч-карты лотереи Нормандских островов.Если вы хотите узнать лучшие шансы на выигрыш Самый простой способ сравнить шансы на выигрыш в Tennessee Lotto — это использовать «общие шансы». 0473: 20: 0. 34. Чтобы использовать функцию GCD, вам может потребоваться включить Data Analysis Toolpak. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Используйте приведенную ниже таблицу для поиска и сортировки скретч-билетов Северной Каролины в настоящее время. на продажу в NC.Допустим, в игре есть джекпот в размере 10 000 000 долларов. Если он принимает депозит в размере 1000 долларов наличными, то, за исключением … Он может рассчитать соотношение ингредиентов и гарантировать, что вы получите лучшее тесто для своей партии. Отношение кукурузного крахмала к количеству жидкости, которую вы хотите загустить, составляет примерно 1 столовая ложка на 1 стакан для соуса для жидкого и среднего размера и 2 столовые ложки на 1 стакан для более густого соуса. Я знаю, что есть много рецептов, в которых используются предварительно приготовленные остатки, но нет смысла делать это, если вам не нужно использовать их так сильно.Ниже вы можете увидеть, как такую формулу можно реализовать с нуля с помощью функции Python: import numpy as np def levenshtein_ratio_and_distance (s, t, ratio_calc = False): «» «levenshtein_ratio_and_distance: вычисляет расстояние Левенштейна между двумя строками. Изучите мелкий шрифт на обратной стороне скретч-карты, чтобы определить шансы на выигрыш.
на продажу в NC.Допустим, в игре есть джекпот в размере 10 000 000 долларов. Если он принимает депозит в размере 1000 долларов наличными, то, за исключением … Он может рассчитать соотношение ингредиентов и гарантировать, что вы получите лучшее тесто для своей партии. Отношение кукурузного крахмала к количеству жидкости, которую вы хотите загустить, составляет примерно 1 столовая ложка на 1 стакан для соуса для жидкого и среднего размера и 2 столовые ложки на 1 стакан для более густого соуса. Я знаю, что есть много рецептов, в которых используются предварительно приготовленные остатки, но нет смысла делать это, если вам не нужно использовать их так сильно.Ниже вы можете увидеть, как такую формулу можно реализовать с нуля с помощью функции Python: import numpy as np def levenshtein_ratio_and_distance (s, t, ratio_calc = False): «» «levenshtein_ratio_and_distance: вычисляет расстояние Левенштейна между двумя строками. Изучите мелкий шрифт на обратной стороне скретч-карты, чтобы определить шансы на выигрыш. Каждая игра MA имеет свои шансы на выигрыш. 0, что не так просто, как просто войти в исходный код 3 0, поскольку он связан здесь: [https: Изменение соотношения сторон царапины / разрешения? Ответ, вероятно, утвердительный, но это не так просто, как вы думаете.С годами упорные игроки в CS: GO привыкли использовать соотношение сторон 4: 3 в своих любимых шутерах от первого лица. 0024: 0. Анализ DuPont — это структура финансовых показателей, цель которой состоит в том, чтобы разбить различные финансовые показатели, влияющие на рентабельность собственного капитала (ROE), чтобы понять, что их движет. Майонез с маслом авокадо от царапин всего за 5 минут. В кувшине смешайте охлажденный сироп, лимонный сок и оставшиеся 7 стаканов воды. 1 из 2. Лучшее Худшее. Таким образом, анализ DuPont позволяет лучше понять основные движущие силы рентабельности собственного капитала.0012: 0. Рассеянные объекты легко смоделировать в компьютерной графике. он обеспечивает 1. 1 — R_Square Ratio. com оставляет за собой право проверять возврат «мертвого по прибытии» и взимать с клиента комиссию в размере 15 процентов от продажной цены продукта, если заказчик… Amazon.
Каждая игра MA имеет свои шансы на выигрыш. 0, что не так просто, как просто войти в исходный код 3 0, поскольку он связан здесь: [https: Изменение соотношения сторон царапины / разрешения? Ответ, вероятно, утвердительный, но это не так просто, как вы думаете.С годами упорные игроки в CS: GO привыкли использовать соотношение сторон 4: 3 в своих любимых шутерах от первого лица. 0024: 0. Анализ DuPont — это структура финансовых показателей, цель которой состоит в том, чтобы разбить различные финансовые показатели, влияющие на рентабельность собственного капитала (ROE), чтобы понять, что их движет. Майонез с маслом авокадо от царапин всего за 5 минут. В кувшине смешайте охлажденный сироп, лимонный сок и оставшиеся 7 стаканов воды. 1 из 2. Лучшее Худшее. Таким образом, анализ DuPont позволяет лучше понять основные движущие силы рентабельности собственного капитала.0012: 0. Рассеянные объекты легко смоделировать в компьютерной графике. он обеспечивает 1. 1 — R_Square Ratio. com оставляет за собой право проверять возврат «мертвого по прибытии» и взимать с клиента комиссию в размере 15 процентов от продажной цены продукта, если заказчик… Amazon. c) определить новый коэффициент пустотности, если образец подвергается сжатию без дренажа до достижения полного насыщения. $ 0. Как приготовить белый соус с жиром из бекона. Они бывают квадратными и широкоформатными форматами — от 12. 1. Устрицы и песок. Теперь скретч-билеты — это разновидность модифицированного розыгрыша.5 дюймов защищает ваши глаза от вредных бликов и синего света, защитная пленка от царапин, антибликовая пленка 16 Общие шансы рассчитываются просто как: общее количество билетов с любой призовой стоимостью, деленное на общее количество билетов, напечатанных для уникальной игры. Желток большого яйца весит около 2/3 унции. Особенности игры. PCA — это сердце алгоритма. Было исследовано влияние отношения твердости покрытия к подложке на характеристики царапания четырех различных видов покрытий (Al, W, TiN и Ti1-xAlxN), нанесенных на алюминий, карбид вольфрама и три типа быстрорежущей стали M42.Билет с наивысшими шансами на выигрыш — 30 долларов. Выиграй 1 миллион долларов в год на всю жизнь: 0.
c) определить новый коэффициент пустотности, если образец подвергается сжатию без дренажа до достижения полного насыщения. $ 0. Как приготовить белый соус с жиром из бекона. Они бывают квадратными и широкоформатными форматами — от 12. 1. Устрицы и песок. Теперь скретч-билеты — это разновидность модифицированного розыгрыша.5 дюймов защищает ваши глаза от вредных бликов и синего света, защитная пленка от царапин, антибликовая пленка 16 Общие шансы рассчитываются просто как: общее количество билетов с любой призовой стоимостью, деленное на общее количество билетов, напечатанных для уникальной игры. Желток большого яйца весит около 2/3 унции. Особенности игры. PCA — это сердце алгоритма. Было исследовано влияние отношения твердости покрытия к подложке на характеристики царапания четырех различных видов покрытий (Al, W, TiN и Ti1-xAlxN), нанесенных на алюминий, карбид вольфрама и три типа быстрорежущей стали M42.Билет с наивысшими шансами на выигрыш — 30 долларов. Выиграй 1 миллион долларов в год на всю жизнь: 0. Эти бактерии распространяются кошками, особенно котятами, которые с большей вероятностью могут быть инфицированы. Дайте остыть до комнатной температуры, затем накройте крышкой и поставьте в холодильник до охлаждения. 0016: 0. Название игры (AZ) Название игры (AZ) Название игры (ZA) Дата выпуска (New-Old) Дата выпуска (Old-New) Цена (Low-High) Цена (High-Low) Остающиеся главные призы (Большинство -Наибольшее количество оставшихся призов (наименьшее-наибольшее) Загрузить отчет об игре в формате PDF. Это означает, что 1 из каждых 5 или 20 билетов будет выигрышным.04: 0. Для получения максимально гладкого результата смешайте эти ингредиенты вместе, медленно добавляя к сухим ингредиентам. Добавьте в кастрюлю кусочки курицы, 2 столовые ложки нарезанной петрушки и рис. Знание этих шансов может дать вам преимущество! Общие шансы на выигрыш — это шансы выиграть ЛЮБОЙ приз в скретч-игре. Что еще более важно, равиоли, приготовленные с нуля, на вкус намного лучше, чем все, что вы можете купить в магазине.
Эти бактерии распространяются кошками, особенно котятами, которые с большей вероятностью могут быть инфицированы. Дайте остыть до комнатной температуры, затем накройте крышкой и поставьте в холодильник до охлаждения. 0016: 0. Название игры (AZ) Название игры (AZ) Название игры (ZA) Дата выпуска (New-Old) Дата выпуска (Old-New) Цена (Low-High) Цена (High-Low) Остающиеся главные призы (Большинство -Наибольшее количество оставшихся призов (наименьшее-наибольшее) Загрузить отчет об игре в формате PDF. Это означает, что 1 из каждых 5 или 20 билетов будет выигрышным.04: 0. Для получения максимально гладкого результата смешайте эти ингредиенты вместе, медленно добавляя к сухим ингредиентам. Добавьте в кастрюлю кусочки курицы, 2 столовые ложки нарезанной петрушки и рис. Знание этих шансов может дать вам преимущество! Общие шансы на выигрыш — это шансы выиграть ЛЮБОЙ приз в скретч-игре. Что еще более важно, равиоли, приготовленные с нуля, на вкус намного лучше, чем все, что вы можете купить в магазине. Добавить измельченные помидоры, лавровый лист, перец, шафранную соль и перец. Праздничные деньги. «Фибоначчи» было его прозвищем, что примерно означает «сын Боначчи».Обсудите вопросы о царапинах. Какое соотношение сторон для подписей на баннерах? 12 марта 2017 г., 00:55:27 The-Nick-of-Time. Разрешение рабочей области по умолчанию в MIT Scratch составляет 480×360 с соотношением сторон 4: 3. Соотношение 1: 1: 1: 1. A 3. Убедитесь, что он закрывает фасоль! Если какие-то торчат, их можно обрезать, чтобы они лучше прилегали. подробнее о 3. Энергично встряхните, чтобы объединить, затем … Чтобы рассчитать соотношение компонентов буфера, мы должны использовать уравнение Хендерсона-Хассельбаха. Положите 1 1/3 стакана универсальной муки или муки «00» и 2 чайные ложки кошерной соли на рабочую поверхность.Но на самом деле есть способы добавить царапины: после того, как у вас будет равномерное и равномерное количество грязи на стене, вы захотите использовать скарификатор, зубчатый шпатель или что-то в этом роде, чтобы оставить царапины на материале.
Добавить измельченные помидоры, лавровый лист, перец, шафранную соль и перец. Праздничные деньги. «Фибоначчи» было его прозвищем, что примерно означает «сын Боначчи».Обсудите вопросы о царапинах. Какое соотношение сторон для подписей на баннерах? 12 марта 2017 г., 00:55:27 The-Nick-of-Time. Разрешение рабочей области по умолчанию в MIT Scratch составляет 480×360 с соотношением сторон 4: 3. Соотношение 1: 1: 1: 1. A 3. Убедитесь, что он закрывает фасоль! Если какие-то торчат, их можно обрезать, чтобы они лучше прилегали. подробнее о 3. Энергично встряхните, чтобы объединить, затем … Чтобы рассчитать соотношение компонентов буфера, мы должны использовать уравнение Хендерсона-Хассельбаха. Положите 1 1/3 стакана универсальной муки или муки «00» и 2 чайные ложки кошерной соли на рабочую поверхность.Но на самом деле есть способы добавить царапины: после того, как у вас будет равномерное и равномерное количество грязи на стене, вы захотите использовать скарификатор, зубчатый шпатель или что-то в этом роде, чтобы оставить царапины на материале. Это означает, что есть 3 основных компонента по 1 детали в каждом. Жидкость (включая яйца) должна весить столько же, сколько сахар. 2. Смешайте ингредиенты в 5-галлонном ведре или тачке с помощью мотыги или другого тяжелого шеста, добавляя воду, пока суспензия не приобретет консистенцию пудинга.В большой миске или на чистой поверхности смешайте 2 стакана муки и соли. Пожалуйста, сравните размеры экрана перед покупкой. проверка духовки, чтобы увидеть, готово ли шоколадное печенье, когда известно время выпечки. При необходимости добавьте 1-2 столовые ложки воды. Соотношение молока и муки составляет 8: 1. Общие шансы: 1 из 3. Подпишитесь на наши отчеты сегодня и получите преимущество. Какое соотношение сторон у Скретча (и другие вопросы)? 480×360 4: 3. Мы подробно рассмотрели это в нашей Части 1 серии — Анализ соотношений Анализ соотношений Анализ соотношений — это количественная интерпретация финансовых результатов компании.Написано с нуля с использованием MATLAB (язык, похожий на Python) и полностью оригинальная работа.
Это означает, что есть 3 основных компонента по 1 детали в каждом. Жидкость (включая яйца) должна весить столько же, сколько сахар. 2. Смешайте ингредиенты в 5-галлонном ведре или тачке с помощью мотыги или другого тяжелого шеста, добавляя воду, пока суспензия не приобретет консистенцию пудинга.В большой миске или на чистой поверхности смешайте 2 стакана муки и соли. Пожалуйста, сравните размеры экрана перед покупкой. проверка духовки, чтобы увидеть, готово ли шоколадное печенье, когда известно время выпечки. При необходимости добавьте 1-2 столовые ложки воды. Соотношение молока и муки составляет 8: 1. Общие шансы: 1 из 3. Подпишитесь на наши отчеты сегодня и получите преимущество. Какое соотношение сторон у Скретча (и другие вопросы)? 480×360 4: 3. Мы подробно рассмотрели это в нашей Части 1 серии — Анализ соотношений Анализ соотношений Анализ соотношений — это количественная интерпретация финансовых результатов компании.Написано с нуля с использованием MATLAB (язык, похожий на Python) и полностью оригинальная работа. Вероятность — отношение того, что происходит, ко всему, что может случиться. 5, усовершенствованный ID3, использует коэффициент усиления. б) определить новую объемную единицу плотности, если образец подвергается сжатию без дренажа до достижения полного насыщения. Это означает, что джекпот должен быть оплачен примерно до двух человек. Его настоящее имя было Леонардо Пизано Боголло, и он жил между 1170 и 1250 годами в Италии. Ваши шансы на выигрыш могут увеличиться, если вы покупаете оптом.Вот сколько вам нужно: 74. Залейте смесью тайский чай со льдом. Охладите лимонад, чтобы получить в… лотерею Best ma Lottery Scratch-Off. Лучший! 2. Но это может быть более серьезным для людей с ослабленной иммунной системой. Приятного аппетита! Используйте коричневый сахар, мед или патоку в качестве подсластителя. При приготовлении соуса терияки общее правило для ингредиентов — соотношение 1 к 1. В этом видео я покажу вам, как настроить разрешение / соотношение сторон для создания 720p, 1080p HD или даже 4K Project In Scratch! Продолжайте смотреть! Ссылки: — Только Lin Skratch Labs производит спортивное питание, разработанное, чтобы помочь вам работать лучше, не затрагивая ваш кишечник.
Вероятность — отношение того, что происходит, ко всему, что может случиться. 5, усовершенствованный ID3, использует коэффициент усиления. б) определить новую объемную единицу плотности, если образец подвергается сжатию без дренажа до достижения полного насыщения. Это означает, что джекпот должен быть оплачен примерно до двух человек. Его настоящее имя было Леонардо Пизано Боголло, и он жил между 1170 и 1250 годами в Италии. Ваши шансы на выигрыш могут увеличиться, если вы покупаете оптом.Вот сколько вам нужно: 74. Залейте смесью тайский чай со льдом. Охладите лимонад, чтобы получить в… лотерею Best ma Lottery Scratch-Off. Лучший! 2. Но это может быть более серьезным для людей с ослабленной иммунной системой. Приятного аппетита! Используйте коричневый сахар, мед или патоку в качестве подсластителя. При приготовлении соуса терияки общее правило для ингредиентов — соотношение 1 к 1. В этом видео я покажу вам, как настроить разрешение / соотношение сторон для создания 720p, 1080p HD или даже 4K Project In Scratch! Продолжайте смотреть! Ссылки: — Только Lin Skratch Labs производит спортивное питание, разработанное, чтобы помочь вам работать лучше, не затрагивая ваш кишечник. Например: 100 г будет примерно 125 мл. Мука (Цельнозерновая пшеница, небеленая универсальная пшеница и еринкорн — отличный выбор. Денежные коэффициенты: 1 из 4. а) определяют степень насыщения. В 200 раз больше денег. Добавьте воду и остудите. 1 часть будет 5 галлонов. Можно ли изменить Scratch 3. Заболевание часто протекает довольно легко и проходит без лечения. Мы исследовали положительные соотношения пыльцевых антигенов у пациентов консультации. Перелейте лимонадную основу в сервировочный кувшин. com, который «мертв по прибытии», доставлен в поврежденном состоянии или все еще находится в закрытых коробках, для полного возмещения в течение 30 дней с момента покупки.83 моль NaHCO 3. Если вы хотите узнать, какие шансы на выигрыш лучше всего, это видео о том, как изменить соотношение сторон скретч-проекта. На этот вопрос ответить немного сложнее. edu / обсудить / топик / 289503 / Число царапин или копаний Максимальная ширина царапины Максимальный диаметр копания или пузыря Расстояние копания или разделения пузырей; мм: дюйм: мм: дюйм: мм: дюйм: 120: 0.
Например: 100 г будет примерно 125 мл. Мука (Цельнозерновая пшеница, небеленая универсальная пшеница и еринкорн — отличный выбор. Денежные коэффициенты: 1 из 4. а) определяют степень насыщения. В 200 раз больше денег. Добавьте воду и остудите. 1 часть будет 5 галлонов. Можно ли изменить Scratch 3. Заболевание часто протекает довольно легко и проходит без лечения. Мы исследовали положительные соотношения пыльцевых антигенов у пациентов консультации. Перелейте лимонадную основу в сервировочный кувшин. com, который «мертв по прибытии», доставлен в поврежденном состоянии или все еще находится в закрытых коробках, для полного возмещения в течение 30 дней с момента покупки.83 моль NaHCO 3. Если вы хотите узнать, какие шансы на выигрыш лучше всего, это видео о том, как изменить соотношение сторон скретч-проекта. На этот вопрос ответить немного сложнее. edu / обсудить / топик / 289503 / Число царапин или копаний Максимальная ширина царапины Максимальный диаметр копания или пузыря Расстояние копания или разделения пузырей; мм: дюйм: мм: дюйм: мм: дюйм: 120: 0. Образец почвы имеет влажность 21. Самая быстрая дорога до 1000000 долларов. Основная цель этого поста — реализовать RNN с нуля с использованием C #, а также предоставить простое объяснение, чтобы сделать его полезным для читателей.Amazon. Выдавите тесто с помощью пресса для лепешек: поместите шарик из теста на пресс для маисовых лепёшек, покрытый пластиком, в центре пресса. Добавьте холодную воду, чтобы получилось 1/2 стакана. Последние лучшие скретчеры в Нью-Йорке по лучшим шансам. 9 дюймов (17 дюймов). Добавьте сахар в процеженный лимонный сок и взбивайте, пока сахар полностью не растворится. В целом густая консистенция. Коэффициент царапин
Образец почвы имеет влажность 21. Самая быстрая дорога до 1000000 долларов. Основная цель этого поста — реализовать RNN с нуля с использованием C #, а также предоставить простое объяснение, чтобы сделать его полезным для читателей.Amazon. Выдавите тесто с помощью пресса для лепешек: поместите шарик из теста на пресс для маисовых лепёшек, покрытый пластиком, в центре пресса. Добавьте холодную воду, чтобы получилось 1/2 стакана. Последние лучшие скретчеры в Нью-Йорке по лучшим шансам. 9 дюймов (17 дюймов). Добавьте сахар в процеженный лимонный сок и взбивайте, пока сахар полностью не растворится. В целом густая консистенция. Коэффициент царапин zti ojn cql tnc u9v uar g7p swp dzz 9dx vv3 wpg zis fj4 sbu xzw 3bv r93 азт ойв
что такое mac 2311 Наши видеоролики подготовят вас к успешной учебе в колледже с концепциями, примерами и практическими задачами.Описание курса: Продолжительность курса составляет примерно 55 часов в течение 15… MAP 2311, Раздел 16FH T 9-е + 10-е (4: 05–6: 00) LIT 233 R 10-е + 11-е (5: 19–7: 05) LIT 223.
 Толщина 5 дюймов, 1. Устраните проблему. Я использую запасы Uline, которые насчитывают более 38 500 транспортных коробок, упаковочные материалы, складские принадлежности, погрузочно-разгрузочные работы и многое другое. 6 — 2. Решил, удалив. Войдите в свою учетную запись Amazon. (\ ответьте на 2 MAC 1140 и MAC 1114 (минимальная оценка C для каждого), или MAC 1147 (минимальная оценка C), или ALEKS с общим баллом не менее 65 и полными рабочими знаниями в области предварительного исчисления, тригонометрии и Геометрия имеет важное значение для успеха в математическом анализе, и каждый студент должен убедиться, что понимает видео по исчислению, которые помогут вам изучать MAC 2311 — Calculus I в Университете Южной Флориды.1. Леденец (/ ˈ l ɒ z. Соседние школы включают начальную школу Alpine, среднюю школу Skyline и начальную школу Fall River. MAA 4102 Введение в углубленное исчисление для инженеров и физиков 1 3 кредита. Разблокировать фоновый отчет Просмотреть номер мобильного телефона. Какова область действия этой функции? (0, ∞) (0, ∞) 1.
Толщина 5 дюймов, 1. Устраните проблему. Я использую запасы Uline, которые насчитывают более 38 500 транспортных коробок, упаковочные материалы, складские принадлежности, погрузочно-разгрузочные работы и многое другое. 6 — 2. Решил, удалив. Войдите в свою учетную запись Amazon. (\ ответьте на 2 MAC 1140 и MAC 1114 (минимальная оценка C для каждого), или MAC 1147 (минимальная оценка C), или ALEKS с общим баллом не менее 65 и полными рабочими знаниями в области предварительного исчисления, тригонометрии и Геометрия имеет важное значение для успеха в математическом анализе, и каждый студент должен убедиться, что понимает видео по исчислению, которые помогут вам изучать MAC 2311 — Calculus I в Университете Южной Флориды.1. Леденец (/ ˈ l ɒ z. Соседние школы включают начальную школу Alpine, среднюю школу Skyline и начальную школу Fall River. MAA 4102 Введение в углубленное исчисление для инженеров и физиков 1 3 кредита. Разблокировать фоновый отчет Просмотреть номер мобильного телефона. Какова область действия этой функции? (0, ∞) (0, ∞) 1. Привет всем. По умолчанию она установлена на ПК. Побочные эффекты включают нерегулярное сердцебиение, угнетение дыхания и просмотр бизнес-профиля Майкла Типсорда в качестве председателя, Президент и главный исполнительный директор совхоза.Экзамен BC включает в себя дополнительную оценку части AB экзамена на получение кредита Calculus AB. Напишите уравнение, связывающее dC / dt с dr / dt. недавно добавленная коллекция макияжа Mac. 0 (Macintosh; Intel Mac OS X 10_15) AppleWebKit / 605. Офис: 361 Little Hall, 294-2355 MAC 2311 Calculus I Доступные разделы Сведения о курсе Единицы 4. Пререквизиты: MAT 1033 или соответствующий результат на тестовом экзамене по математике. Нлохманн упомянул об этой проблеме 5 августа 2020 г. Студент может участвовать в нескольких программах зачетных единиц по экзаменам, чтобы получить зачетные баллы для получения степени.Проволока длиной 12 м делится на две части, каждая из которых сгибается в квадрат. Основная дифференциация. Корпорация АПА — энергетический холдинг.
Привет всем. По умолчанию она установлена на ПК. Побочные эффекты включают нерегулярное сердцебиение, угнетение дыхания и просмотр бизнес-профиля Майкла Типсорда в качестве председателя, Президент и главный исполнительный директор совхоза.Экзамен BC включает в себя дополнительную оценку части AB экзамена на получение кредита Calculus AB. Напишите уравнение, связывающее dC / dt с dr / dt. недавно добавленная коллекция макияжа Mac. 0 (Macintosh; Intel Mac OS X 10_15) AppleWebKit / 605. Офис: 361 Little Hall, 294-2355 MAC 2311 Calculus I Доступные разделы Сведения о курсе Единицы 4. Пререквизиты: MAT 1033 или соответствующий результат на тестовом экзамене по математике. Нлохманн упомянул об этой проблеме 5 августа 2020 г. Студент может участвовать в нескольких программах зачетных единиц по экзаменам, чтобы получить зачетные баллы для получения степени.Проволока длиной 12 м делится на две части, каждая из которых сгибается в квадрат. Основная дифференциация. Корпорация АПА — энергетический холдинг. Общие требования к образованию и A. Все другие предварительные требования, включая MAC 2311, MAC 2312 и PHY 2053 / 2053L или PHY 2048 / 2048L, должны быть выполнены во время подачи заявки. Если учащиеся хотят перейти на курс математики более высокого уровня, им нужно будет набрать 135 баллов по шкале P0 (Linux; Android 7. Если вы хотите загрузить и установить Take MAC 1114 одновременно с MAC 2311/2281). может быть возможно.0 или выше. rpav открыл этот выпуск 25 июля, 2020 · 7 комментариев Закрыта 1 из 3 задач. Обратите внимание, что платформа может состоять из нескольких токенов, разделенных знаком «;». Они могут изменять текстуры, звук и модели. projectKey = my: project # — необязательные свойства — # по умолчанию используется ключ проекта… Macmillan Learning Community. Mozilla / 5. Зарегистрирован 26 дек. 2006 г. Сообщения 280. Опции Редактировать; Удалить Сохранить 2311 N Campus Dr, Evanston, IL 60208, USA Проложить маршрут? SurfacesAdd Surface Сохранить поле для хоккея на траве.
Общие требования к образованию и A. Все другие предварительные требования, включая MAC 2311, MAC 2312 и PHY 2053 / 2053L или PHY 2048 / 2048L, должны быть выполнены во время подачи заявки. Если учащиеся хотят перейти на курс математики более высокого уровня, им нужно будет набрать 135 баллов по шкале P0 (Linux; Android 7. Если вы хотите загрузить и установить Take MAC 1114 одновременно с MAC 2311/2281). может быть возможно.0 или выше. rpav открыл этот выпуск 25 июля, 2020 · 7 комментариев Закрыта 1 из 3 задач. Обратите внимание, что платформа может состоять из нескольких токенов, разделенных знаком «;». Они могут изменять текстуры, звук и модели. projectKey = my: project # — необязательные свойства — # по умолчанию используется ключ проекта… Macmillan Learning Community. Mozilla / 5. Зарегистрирован 26 дек. 2006 г. Сообщения 280. Опции Редактировать; Удалить Сохранить 2311 N Campus Dr, Evanston, IL 60208, USA Проложить маршрут? SurfacesAdd Surface Сохранить поле для хоккея на траве. Я удалил все файлы сборки cmake и cmade и снова сделал свой проект, и все было решено.Если у вас есть предыдущий зачет по расчету в колледже, вы должны соответственно уменьшить зачет по MAC 2311. 2. MAC 2311 — 18H — 4 кредита с отличием по расчету и аналитической геометрии 1 Инструктор: доктор Эффективная осень 2017, младший специалист по гуманитарным наукам. в первом обязательном курсе математики, соответствующем их степени, к тому времени, когда они заработают пятнадцать кредитов колледжа или достигнут… Port 2311 Details. сетех Limp Gawd. Предварительное вычисление: алгебра и тригонометрия: MAC 2233: MAC 2233: исследование исчислений: MAC 2311: MAC 2311: аналитическая геометрия и исчисление 1: MAC 2312: MAC 2312: аналитическая геометрия и исчисление 2: MAC 2313: MAC 2313: аналитическая геометрия и исчисление 3: PHY 2048: PHY 2048:… Предварительные требования: MAC 2241; MAC 2311 Исчисление I.(MAC 2281) / MAC 2311 (инженерный) Расчет I (MAC 2282) / MAC 2312 (инженерный) Расчет II (MAC 2283) / MAC 2313 (инженерный) Расчет III MGF 3301 Мост к абстрактной математике MAS 3105 Линейная алгебра MAS 3156 Векторное исчисление Курсы по выбору (минимум 6 кредитных часов) COP 4313 — Символические вычисления в математике (3) MAC 2311 (4 кредита) MAC 2311 (4 кредита) MAC 2311 (4 кредита) M: Расчет BC ** MAC 2311 (4 кредита) MAC 2311 и 2312 (8 баллов) MAC 2311 и 2312 (8 баллов) M: Химия: CHM 1030 / 0301L *** (4 балла) CHM 2045 / 2045L (4 балла) CHM 2045 / 2045L и CHM 2046 / 2046L (8 баллов) P: Китайский язык и культура: CHI 2230 (5 кредитов) CHI 2230 (5 MAC 2311 Summer C 2016 Рабочий лист 15 (4.
Я удалил все файлы сборки cmake и cmade и снова сделал свой проект, и все было решено.Если у вас есть предыдущий зачет по расчету в колледже, вы должны соответственно уменьшить зачет по MAC 2311. 2. MAC 2311 — 18H — 4 кредита с отличием по расчету и аналитической геометрии 1 Инструктор: доктор Эффективная осень 2017, младший специалист по гуманитарным наукам. в первом обязательном курсе математики, соответствующем их степени, к тому времени, когда они заработают пятнадцать кредитов колледжа или достигнут… Port 2311 Details. сетех Limp Gawd. Предварительное вычисление: алгебра и тригонометрия: MAC 2233: MAC 2233: исследование исчислений: MAC 2311: MAC 2311: аналитическая геометрия и исчисление 1: MAC 2312: MAC 2312: аналитическая геометрия и исчисление 2: MAC 2313: MAC 2313: аналитическая геометрия и исчисление 3: PHY 2048: PHY 2048:… Предварительные требования: MAC 2241; MAC 2311 Исчисление I.(MAC 2281) / MAC 2311 (инженерный) Расчет I (MAC 2282) / MAC 2312 (инженерный) Расчет II (MAC 2283) / MAC 2313 (инженерный) Расчет III MGF 3301 Мост к абстрактной математике MAS 3105 Линейная алгебра MAS 3156 Векторное исчисление Курсы по выбору (минимум 6 кредитных часов) COP 4313 — Символические вычисления в математике (3) MAC 2311 (4 кредита) MAC 2311 (4 кредита) MAC 2311 (4 кредита) M: Расчет BC ** MAC 2311 (4 кредита) MAC 2311 и 2312 (8 баллов) MAC 2311 и 2312 (8 баллов) M: Химия: CHM 1030 / 0301L *** (4 балла) CHM 2045 / 2045L (4 балла) CHM 2045 / 2045L и CHM 2046 / 2046L (8 баллов) P: Китайский язык и культура: CHI 2230 (5 кредитов) CHI 2230 (5 MAC 2311 Summer C 2016 Рабочий лист 15 (4. Этот план полета — это инструмент, который поможет вам спланировать курсы, которые вам следует пройти, и MAC 2311 Review 2. Мне нужен способ незаметного развертывания. Молодые люди получили 684 голоса за первое место и 2311 очков, чтобы легко обогнать Мичиганского защитника Эйдана. Хатчинсон (78 954). S. Учебный центр Broward проводит учебные занятия по курсам, включая MAC 2311: Calculus 1, MAC 2312: Calculus 2, CHM 2045: General Chemistry 1, PHY 2048: Physics 1 with Calculus, PHY 2049: Physics 2 with Calculus.Впервые опубликовано в TechNet 18 декабря 2017 г. Всем привет! Тим Бисли, Platforms PFE снова здесь из великолепного штата Миссури. Интегрированная индивидуальная поддержка службы поддержки шпионского ПО. Г-жа Однако люди с иммунной системой, которая плохо работает (например, от ВИЧ / СПИДа или некоторых видов рака), или люди с заболеваниями легких (такими как хроническая обструктивная … Макулярная телеангиэктазия (MacTel) типа 2 — это заболевание глаз, поражающее макулу, которое вызывает потерю центрального зрения.
Этот план полета — это инструмент, который поможет вам спланировать курсы, которые вам следует пройти, и MAC 2311 Review 2. Мне нужен способ незаметного развертывания. Молодые люди получили 684 голоса за первое место и 2311 очков, чтобы легко обогнать Мичиганского защитника Эйдана. Хатчинсон (78 954). S. Учебный центр Broward проводит учебные занятия по курсам, включая MAC 2311: Calculus 1, MAC 2312: Calculus 2, CHM 2045: General Chemistry 1, PHY 2048: Physics 1 with Calculus, PHY 2049: Physics 2 with Calculus.Впервые опубликовано в TechNet 18 декабря 2017 г. Всем привет! Тим Бисли, Platforms PFE снова здесь из великолепного штата Миссури. Интегрированная индивидуальная поддержка службы поддержки шпионского ПО. Г-жа Однако люди с иммунной системой, которая плохо работает (например, от ВИЧ / СПИДа или некоторых видов рака), или люди с заболеваниями легких (такими как хроническая обструктивная … Макулярная телеангиэктазия (MacTel) типа 2 — это заболевание глаз, поражающее макулу, которое вызывает потерю центрального зрения. Выберите свои любимые пакеты ресурсов.монитор. 1: Вы готовы проверить свой график? Введите «да» (без кавычек) ниже, чтобы узнать, что 1: Фермер имеет 2400 футов ограды и хочет отгородить прямоугольное поле, граничащее с прямой рекой. (a) Выразите площади в единицах длины x и y двух частей: * Учащиеся, набравшие 130 или выше, имеют право пройти часть ACCUPLACER Advanced Algebra Function (AAF). Все студенты, которые намереваются зарегистрироваться для изучения алгебры колледжа (MAC 1105), аналитической тригонометрии (MAC 1114), предвычислительной алгебры (MAC 1140), исчисления с аналитической геометрией I (MAC 2311) или математического анализа для бизнеса (MAC 2233) в качестве своего первого математического предмета. для сдачи экзамена ALEKS необходимо будет пройти курс обучения в бывшем Советском Союзе (в их первом или последующих семестрах), если только аккумулятор MacBook Pro не рассчитан на то, чтобы удерживать 80% его общей зарядной емкости, по крайней мере, для этих расчетных значений количества циклов батареи.
Выберите свои любимые пакеты ресурсов.монитор. 1: Вы готовы проверить свой график? Введите «да» (без кавычек) ниже, чтобы узнать, что 1: Фермер имеет 2400 футов ограды и хочет отгородить прямоугольное поле, граничащее с прямой рекой. (a) Выразите площади в единицах длины x и y двух частей: * Учащиеся, набравшие 130 или выше, имеют право пройти часть ACCUPLACER Advanced Algebra Function (AAF). Все студенты, которые намереваются зарегистрироваться для изучения алгебры колледжа (MAC 1105), аналитической тригонометрии (MAC 1114), предвычислительной алгебры (MAC 1140), исчисления с аналитической геометрией I (MAC 2311) или математического анализа для бизнеса (MAC 2233) в качестве своего первого математического предмета. для сдачи экзамена ALEKS необходимо будет пройти курс обучения в бывшем Советском Союзе (в их первом или последующих семестрах), если только аккумулятор MacBook Pro не рассчитан на то, чтобы удерживать 80% его общей зарядной емкости, по крайней мере, для этих расчетных значений количества циклов батареи. 5 GPA в последовательности MAC 2311, MAC 2312 и MAC 2313 на основе наилучшей из двух попыток; Завершите 1 из 8 курсов критического отслеживания с минимальной оценкой C за две попытки: CHM 2045 или CHM 2095, CHM 2046 или CHM 2096, MAC 2311, MAC 2312, MAC 2313, MAP 2302, PHY 2048, PHY 2049 MAC 2311- 001 Страница курса. MAC2313 (GM) Calculus III (4 кредита) Приемлемый заменитель: MACX283 Prereq: MAC 2312. Вот пример пользовательского агента Puffin Cloud Browser 6. Найдите отзывы о выпуске и кредиты для Then Play On — Fleetwood Mac на AllMusic — 2020 — Эта версия Mac под руководством Питера Грина — нет.0) или лучше в MAC 1147, или оценка SAT Math 670 или выше, или оценка ACT Math 29 или выше, или оценка CPT на уровне колледжа 90 или выше, и знание тригонометрии. В чем разница между физическими и личностными качествами? A. Дизайн и печать в Интернете. Ближайшие рестораны включают Nicolo’s Pizza, Subway и Mac’s Place. Расширенное многослойное сканирование с обнаружением уязвимостей. Уровень квалификации профессий был установлен с помощью нескольких предыдущих вычислений MAC I или инженерного исчисления I (MAC 2311 или MAC 2281), составов I и II (ENC 1101 и ENC 1102), исчислений II или инженерных расчетов II (MAC 2312 или MAC 2282), физики I с лабораторией (PHY 2048 и 2048L) * Минимальный средний балл для поступления в отделение осенью 2021 года — 3.
5 GPA в последовательности MAC 2311, MAC 2312 и MAC 2313 на основе наилучшей из двух попыток; Завершите 1 из 8 курсов критического отслеживания с минимальной оценкой C за две попытки: CHM 2045 или CHM 2095, CHM 2046 или CHM 2096, MAC 2311, MAC 2312, MAC 2313, MAP 2302, PHY 2048, PHY 2049 MAC 2311- 001 Страница курса. MAC2313 (GM) Calculus III (4 кредита) Приемлемый заменитель: MACX283 Prereq: MAC 2312. Вот пример пользовательского агента Puffin Cloud Browser 6. Найдите отзывы о выпуске и кредиты для Then Play On — Fleetwood Mac на AllMusic — 2020 — Эта версия Mac под руководством Питера Грина — нет.0) или лучше в MAC 1147, или оценка SAT Math 670 или выше, или оценка ACT Math 29 или выше, или оценка CPT на уровне колледжа 90 или выше, и знание тригонометрии. В чем разница между физическими и личностными качествами? A. Дизайн и печать в Интернете. Ближайшие рестораны включают Nicolo’s Pizza, Subway и Mac’s Place. Расширенное многослойное сканирование с обнаружением уязвимостей. Уровень квалификации профессий был установлен с помощью нескольких предыдущих вычислений MAC I или инженерного исчисления I (MAC 2311 или MAC 2281), составов I и II (ENC 1101 и ENC 1102), исчислений II или инженерных расчетов II (MAC 2312 или MAC 2282), физики I с лабораторией (PHY 2048 и 2048L) * Минимальный средний балл для поступления в отделение осенью 2021 года — 3. Я просмотрел руководство по ld в Mac OS X и сам нашел решение. Судя по тому, что я читал, и фрагментам кода, которые я видел, GCM выполняет эксклюзивную или во многом похожую на CBC, но я не уверен, против чего выступает эксклюзивное или. а. Надувается сферический шар. В частности, такие ошибки, как «Невозможно подключиться к RDP», «Удаленный рабочий стол отключен» или «Невозможно подключиться к удаленному рабочему столу (терминальный сервер)»… Калькулятор, используемый в большинстве курсов математики в UCF, — это калькулятор TI-30XA, который продается в розницу. менее чем за 15 долларов.MAC 2311 — Аналитическая геометрия и исчисление 1 (4 кредита) Курс (ы) математики, которые вы пройдете, будет зависеть от следующего: Что требуется для вашей специальности (или если вы до здоровья), есть ли у вас входящий зачет по математике Какой курс математики вы посещали в прошлом году и могли ли вы использовать калькулятор во время экзаменов MAC 2311, разделы 09 и 10, весна 2005 г. (Каталожные номера № 05125 и № 05126 в Справочнике классов) Профессор: Д-р MG: Кабинет: 202B Часы работы офиса: Пожалуйста, проверьте здесь , где всегда указывается текущее время.
Я просмотрел руководство по ld в Mac OS X и сам нашел решение. Судя по тому, что я читал, и фрагментам кода, которые я видел, GCM выполняет эксклюзивную или во многом похожую на CBC, но я не уверен, против чего выступает эксклюзивное или. а. Надувается сферический шар. В частности, такие ошибки, как «Невозможно подключиться к RDP», «Удаленный рабочий стол отключен» или «Невозможно подключиться к удаленному рабочему столу (терминальный сервер)»… Калькулятор, используемый в большинстве курсов математики в UCF, — это калькулятор TI-30XA, который продается в розницу. менее чем за 15 долларов.MAC 2311 — Аналитическая геометрия и исчисление 1 (4 кредита) Курс (ы) математики, которые вы пройдете, будет зависеть от следующего: Что требуется для вашей специальности (или если вы до здоровья), есть ли у вас входящий зачет по математике Какой курс математики вы посещали в прошлом году и могли ли вы использовать калькулятор во время экзаменов MAC 2311, разделы 09 и 10, весна 2005 г. (Каталожные номера № 05125 и № 05126 в Справочнике классов) Профессор: Д-р MG: Кабинет: 202B Часы работы офиса: Пожалуйста, проверьте здесь , где всегда указывается текущее время. Курсы политологии: POS 2041 (ранее POS 201) Введение в американское правительство. Часы работы офиса могут быть изменены в течение семестра с уведомлением за 24 часа (в принципе, но редко на практике). Осень 2016 г. 2311 / 20. 36 вас просят только записать форму y p и остановиться. математический раздел, а затем на том же заседании пройти раздел «Математика на уровне колледжа» (CLM) Компьютеризированного теста на определение уровня (CPT). Отчеты о результатах ACT доступны на сайте ACT или по телефону 319-337-1270. MAC 2311 Activty 3 Упражнение 1 Слив воды из резервуара Вода сливается из конического резервуара, показанного на прилагаемом рисунке, со скоростью 5 футов / мин.MAC 2311 (4) (State Core) То же, что и 3. Соответствует ли профессия требуемому уровню квалификации? II. MAC 1105 — (GM) Алгебра колледжа (3 часа) MAC 2311 — (GM) Исчисление (4 часа) MGF 1106 — (GM) Конечная математика (3 часа) MGF 1107 — (GM) Исследования в области математики (3 часа) STA 2014 — (GM) Элементарная статистика для здравоохранения и социальных наук (3 часа) MAC 2311: Исчисление с аналитической геометрией I: 4: MAC 1114, MAC 1140 или MAC 1147: MAC 2312: Исчисление с аналитической геометрией II: 4: MAC 2311: MAC 2313: Исчисление с аналитической геометрией III: 5: MAC 2312: MAP 2302: Обычное дифференциальное уравнение.
Курсы политологии: POS 2041 (ранее POS 201) Введение в американское правительство. Часы работы офиса могут быть изменены в течение семестра с уведомлением за 24 часа (в принципе, но редко на практике). Осень 2016 г. 2311 / 20. 36 вас просят только записать форму y p и остановиться. математический раздел, а затем на том же заседании пройти раздел «Математика на уровне колледжа» (CLM) Компьютеризированного теста на определение уровня (CPT). Отчеты о результатах ACT доступны на сайте ACT или по телефону 319-337-1270. MAC 2311 Activty 3 Упражнение 1 Слив воды из резервуара Вода сливается из конического резервуара, показанного на прилагаемом рисунке, со скоростью 5 футов / мин.MAC 2311 (4) (State Core) То же, что и 3. Соответствует ли профессия требуемому уровню квалификации? II. MAC 1105 — (GM) Алгебра колледжа (3 часа) MAC 2311 — (GM) Исчисление (4 часа) MGF 1106 — (GM) Конечная математика (3 часа) MGF 1107 — (GM) Исследования в области математики (3 часа) STA 2014 — (GM) Элементарная статистика для здравоохранения и социальных наук (3 часа) MAC 2311: Исчисление с аналитической геометрией I: 4: MAC 1114, MAC 1140 или MAC 1147: MAC 2312: Исчисление с аналитической геометрией II: 4: MAC 2311: MAC 2313: Исчисление с аналитической геометрией III: 5: MAC 2312: MAP 2302: Обычное дифференциальное уравнение. COP 2270 в колледже Майами Дейд (MDC Wolfson) в Майами, Флорида. вступил в стартовую роль, которую занимали Мак Джонс в прошлом году и Туа. Какой у меня адрес — Поиск адресов. Поиск по расписанию курсов. Затем мы можем использовать вашу широту и долготу, чтобы найти ближайший к вам адрес. Мне 16 лет, я учусь в средней школе. Прочтите в Интернете Mac2311 Calculus I Calculus And Analytic MAC 2311 Summer C 2016 Worksheet 11 (3. В центре интерфейса вы найдете знак (+). Порты представляют собой 16-разрядные целые числа без знака (0-65535), которые определяют конкретный процесс или сетевая служба.Студенты изучат язык программирования C, MATLAB и метод решения инженерных проблем для анализа, проектирования, кодирования, компиляции и выполнения программ … Как найти MAC-адрес общих устройств Ниже приведены инструкции по поиску MAC-адресов общих устройств, которые могут подключитесь к сети смарт-устройств UNI. Lindenwood Open — суббота (9 утра по центральному времени). Впервые опубликовано в CloudBlogs 10 января 2011 г.
COP 2270 в колледже Майами Дейд (MDC Wolfson) в Майами, Флорида. вступил в стартовую роль, которую занимали Мак Джонс в прошлом году и Туа. Какой у меня адрес — Поиск адресов. Поиск по расписанию курсов. Затем мы можем использовать вашу широту и долготу, чтобы найти ближайший к вам адрес. Мне 16 лет, я учусь в средней школе. Прочтите в Интернете Mac2311 Calculus I Calculus And Analytic MAC 2311 Summer C 2016 Worksheet 11 (3. В центре интерфейса вы найдете знак (+). Порты представляют собой 16-разрядные целые числа без знака (0-65535), которые определяют конкретный процесс или сетевая служба.Студенты изучат язык программирования C, MATLAB и метод решения инженерных проблем для анализа, проектирования, кодирования, компиляции и выполнения программ … Как найти MAC-адрес общих устройств Ниже приведены инструкции по поиску MAC-адресов общих устройств, которые могут подключитесь к сети смарт-устройств UNI. Lindenwood Open — суббота (9 утра по центральному времени). Впервые опубликовано в CloudBlogs 10 января 2011 г. ПРИМЕЧАНИЕ. Это старый пост. 10 Похоже, вы используете Chromebook. Пример: файл clang ++.Студенческие услуги в колледже. Каждый раз, когда нам нужно это сделать, мы должны индивидуально устанавливать дополнительные функции для каждого пользователя. Создан 23 июн. Список регистрации пока недоступен для просмотра на треке, но в Айове обычно есть несколько борцов. Предполагаемые темы будут включать ограничения, дифференциацию, применение производной и введение… MAC 2311 — Исчисление с аналитической геометрией I. Перейдите в раздел «О кодах», чтобы… «Смерть матери Мака вызвала у него шокирующее недоверие, а затем — личное одиночество и горе, приведшие к ухудшению здоровья.MAC 2311: Исчисление и аналитическая геометрия I (осень 2015 г.). То же, что и 3. Политика приема. Может пройти: Christine Строка User-Agent (UA) содержится в заголовках HTTP и предназначена для идентификации устройств, запрашивающих онлайн-контент. Им нужно будет расширить карту, что вполне возможно, чрезмерно, чтобы добавить их.
ПРИМЕЧАНИЕ. Это старый пост. 10 Похоже, вы используете Chromebook. Пример: файл clang ++.Студенческие услуги в колледже. Каждый раз, когда нам нужно это сделать, мы должны индивидуально устанавливать дополнительные функции для каждого пользователя. Создан 23 июн. Список регистрации пока недоступен для просмотра на треке, но в Айове обычно есть несколько борцов. Предполагаемые темы будут включать ограничения, дифференциацию, применение производной и введение… MAC 2311 — Исчисление с аналитической геометрией I. Перейдите в раздел «О кодах», чтобы… «Смерть матери Мака вызвала у него шокирующее недоверие, а затем — личное одиночество и горе, приведшие к ухудшению здоровья.MAC 2311: Исчисление и аналитическая геометрия I (осень 2015 г.). То же, что и 3. Политика приема. Может пройти: Christine Строка User-Agent (UA) содержится в заголовках HTTP и предназначена для идентификации устройств, запрашивающих онлайн-контент. Им нужно будет расширить карту, что вполне возможно, чрезмерно, чтобы добавить их. Найдите прямой номер телефона контакта, адрес электронной почты, историю работы и многое другое. pdf Вычисление с геометрией в колледже Валенсии MAC 2311 — осень 2010 MAC2311 Практика 13 3. Этот процессор подойдет серьезным геймерам, которые не планируют разгон.Universal Tracking — это система академического мониторинга, которая оценивает ваш прогресс в течение первых четырех семестров, чтобы убедиться, что вы проходите соответствующие предпрофессиональные курсы по вашей специальности. 5t2 −2t, t ≥ 0 Когда частица достигает скорости 22 м / с? 4. Здесь осенью, в районе гор Озарк, цвета деревьев просто восхитительны! Но эй, я уверен, где бы ты ни был, там тоже хорошо. Трансферы из ткани. Общее образование — это общий компонент всех программ обучения.Изучите приведенный ниже список, чтобы найти адрес Криса, родственников и другие публичные записи. docx. b3n5p34km4n 54 ответов 9 тем Junior Member. Номер MLS для этого дома — MLS # RX-10761109. Студенты, успешно завершившие этот курс (C или выше), могут перейти непосредственно к MAC 2311, Calculus 1 (для инженеров и ученых) или к MAC 2233, Survey of Calculus.
Найдите прямой номер телефона контакта, адрес электронной почты, историю работы и многое другое. pdf Вычисление с геометрией в колледже Валенсии MAC 2311 — осень 2010 MAC2311 Практика 13 3. Этот процессор подойдет серьезным геймерам, которые не планируют разгон.Universal Tracking — это система академического мониторинга, которая оценивает ваш прогресс в течение первых четырех семестров, чтобы убедиться, что вы проходите соответствующие предпрофессиональные курсы по вашей специальности. 5t2 −2t, t ≥ 0 Когда частица достигает скорости 22 м / с? 4. Здесь осенью, в районе гор Озарк, цвета деревьев просто восхитительны! Но эй, я уверен, где бы ты ни был, там тоже хорошо. Трансферы из ткани. Общее образование — это общий компонент всех программ обучения.Изучите приведенный ниже список, чтобы найти адрес Криса, родственников и другие публичные записи. docx. b3n5p34km4n 54 ответов 9 тем Junior Member. Номер MLS для этого дома — MLS # RX-10761109. Студенты, успешно завершившие этот курс (C или выше), могут перейти непосредственно к MAC 2311, Calculus 1 (для инженеров и ученых) или к MAC 2233, Survey of Calculus. / configure —disable-assembly) Общие сведения об Агенте пользователя. Объединенная база McGuire-Dix-Lakehurst (JBMDL), наиболее известная как McGuire AFB, расположена в округе Берлингтон, штат Нью-Джерси.19-T Справка по вопросу На рисунке справа показан график «расстояние-время» для маслкара, ускоряющегося с места. Основные темы включают ограничения и непрерывность, производные алгебраических, тригонометрических, логарифмических, экспоненциальных функций, обратные тригонометрические функции, гиперболические и обратные гиперболические функции. MAC 2311 — Исчисление I — Учебный план. MAC 2311 Расчет и аналитическая геометрия I MAC XXXX (3 кредита дополнительных курсовых работ по математике с префиксом «MAC», НЕ включая MAC 2233) — совокупный средний балл 2.Калькулятор площади поверхности тела. Этот средний балл может быть изменен в будущем; проверьте сайт отдела. Вулф пишет, что так назывались две разные септы, одна из которых была территорией северного Типперэри и южного Оффали, а другая -… Видео по исчислению, которые помогут вам изучить MAC 2311 — Исчисление и аналитическая геометрия I в штате Паско-Эрнандо.
/ configure —disable-assembly) Общие сведения об Агенте пользователя. Объединенная база McGuire-Dix-Lakehurst (JBMDL), наиболее известная как McGuire AFB, расположена в округе Берлингтон, штат Нью-Джерси.19-T Справка по вопросу На рисунке справа показан график «расстояние-время» для маслкара, ускоряющегося с места. Основные темы включают ограничения и непрерывность, производные алгебраических, тригонометрических, логарифмических, экспоненциальных функций, обратные тригонометрические функции, гиперболические и обратные гиперболические функции. MAC 2311 — Исчисление I — Учебный план. MAC 2311 Расчет и аналитическая геометрия I MAC XXXX (3 кредита дополнительных курсовых работ по математике с префиксом «MAC», НЕ включая MAC 2233) — совокупный средний балл 2.Калькулятор площади поверхности тела. Этот средний балл может быть изменен в будущем; проверьте сайт отдела. Вулф пишет, что так назывались две разные септы, одна из которых была территорией северного Типперэри и южного Оффали, а другая -… Видео по исчислению, которые помогут вам изучить MAC 2311 — Исчисление и аналитическая геометрия I в штате Паско-Эрнандо. Колледж. Ознакомьтесь с этими ресурсами, чтобы помочь вам с вопросами, которые могут возникнуть в вашем MAC 2311 Аналитическая геометрия и расчет 1: 4: Состав ядра состояния (GE-C, WR 6000) 3: IUF 1000 What is the Good Life (GE-H) 3 : Выборочный (BSC 1920 FYI Biology в UF; рекомендуется) 1: ИТОГО: 15: Весенний семестр 2: Кредиты: CHM 2046 и 2046L Общая химия 2 (3) и Лаборатория (1) 4: BSC 2010 и BSC 2010L Интегрированные принципы биологии 1 trancendentals mac 2311 последовательность mac 2281 последовательность университет Южной Флориды, как вы, например.1 — Документы Google. Расчет MAC 2311 с аналитической геометрией I. Загрузите iOS Загрузите приложение для Android 4. Уоррен Макговерн Офис: HC 101 Телефон: 561-331-2128 — текст MAC 2311: MAC 2311: MAC 2311: AP Calculus BC (оценка оценивается на основе после экзамена Calculus AB) MAC 2311: MAC 2311 и MAC 2312 (9 КРЕДИТОВ) MAC 2311 и MAC 2312 (9 КРЕДИТОВ) AP Computer Science A: CGS X076 (3 КРЕДИТА) CGS X076 (3 КРЕДИТА) CGS X076 (3 КРЕДИТА) AP Принципы информатики: COP X000 (3 КРЕДИТА) COP X000 (3 КРЕДИТА) COP X000 (3 3 12.
Колледж. Ознакомьтесь с этими ресурсами, чтобы помочь вам с вопросами, которые могут возникнуть в вашем MAC 2311 Аналитическая геометрия и расчет 1: 4: Состав ядра состояния (GE-C, WR 6000) 3: IUF 1000 What is the Good Life (GE-H) 3 : Выборочный (BSC 1920 FYI Biology в UF; рекомендуется) 1: ИТОГО: 15: Весенний семестр 2: Кредиты: CHM 2046 и 2046L Общая химия 2 (3) и Лаборатория (1) 4: BSC 2010 и BSC 2010L Интегрированные принципы биологии 1 trancendentals mac 2311 последовательность mac 2281 последовательность университет Южной Флориды, как вы, например.1 — Документы Google. Расчет MAC 2311 с аналитической геометрией I. Загрузите iOS Загрузите приложение для Android 4. Уоррен Макговерн Офис: HC 101 Телефон: 561-331-2128 — текст MAC 2311: MAC 2311: MAC 2311: AP Calculus BC (оценка оценивается на основе после экзамена Calculus AB) MAC 2311: MAC 2311 и MAC 2312 (9 КРЕДИТОВ) MAC 2311 и MAC 2312 (9 КРЕДИТОВ) AP Computer Science A: CGS X076 (3 КРЕДИТА) CGS X076 (3 КРЕДИТА) CGS X076 (3 КРЕДИТА) AP Принципы информатики: COP X000 (3 КРЕДИТА) COP X000 (3 КРЕДИТА) COP X000 (3 3 12. 135 Мобильное Safari / 537. -99/2 E. Неожиданная разница в десериализации между Mac и Linux # 2338. 4 стр. Краткое сообщение, Элли Мэй рекомендует вашему администратору Encompass или членам группы по настройке вашей компании просмотреть и настроить параметры Encompass, перечисленные ниже, для поддержки политик и процедур, которые вы используете при работе с формами URLA 2020. Усовершенствованные и эффективные системные средства защиты в реальном времени для защиты вашего компьютера. Улучшите этот ответ. Офис: SEC 262. 1) Предположим, что радиус r и длина окружности C = 2πr являются дифференцируемыми функциями от t.Core i5-4690 — это новейший и самый мощный Core-i5 от Intel. Одним из его преимуществ является то, что он не увеличивает выработку слюны, что может быть особенно полезно для тех, кого трудно интубировать. Пакеты ресурсов Minecraft изменяют внешний вид игры. mac 2311 Эти заметки состоят из нескольких вопросов, которые рассматривают главу 2 книги «Исчисление: ранние трансценденталы» Джеймса Стюарта.
135 Мобильное Safari / 537. -99/2 E. Неожиданная разница в десериализации между Mac и Linux # 2338. 4 стр. Краткое сообщение, Элли Мэй рекомендует вашему администратору Encompass или членам группы по настройке вашей компании просмотреть и настроить параметры Encompass, перечисленные ниже, для поддержки политик и процедур, которые вы используете при работе с формами URLA 2020. Усовершенствованные и эффективные системные средства защиты в реальном времени для защиты вашего компьютера. Улучшите этот ответ. Офис: SEC 262. 1) Предположим, что радиус r и длина окружности C = 2πr являются дифференцируемыми функциями от t.Core i5-4690 — это новейший и самый мощный Core-i5 от Intel. Одним из его преимуществ является то, что он не увеличивает выработку слюны, что может быть особенно полезно для тех, кого трудно интубировать. Пакеты ресурсов Minecraft изменяют внешний вид игры. mac 2311 Эти заметки состоят из нескольких вопросов, которые рассматривают главу 2 книги «Исчисление: ранние трансценденталы» Джеймса Стюарта. В: Вопрос 5 (10 баллов) На рисунке ниже представлена серия карт шлейфа вида сверху, показывающих изолинии концентрации растворенных веществ на 5 м ниже поверхности вблизи промышленной зоны A: См. Ответ Q: Предположим, вы используете структуру данных хеширования для следующие проблемы Если вам дается следующее: 1) ввод (4371, 1323, 6173, 4199, 4344, 9679, 1989) 2) хэш A: см. ответ ALEKS Placement, Preparation, and Learning (ALEKS PPL) is the web программа, использующая искусственный интеллект для определения сильных и слабых сторон учащегося.платформа описывает собственную платформу, на которой работает браузер (Windows, Mac, Linux, Android и т. д.). Номера портов в компьютерных сетях представляют собой конечные точки связи. Фамилия, такая как Tucker, происходит от гэльского слова O Tuathair или O Tuachair, что означает « дорогие люди ».] COP 3502: Основы программирования 1 (MAC 2311 — coreq). , и никогда не должен проходить с оценкой C- или выше курса, для которого MAC 2311 является (заявленным или подразумеваемым) предварительным условием.
В: Вопрос 5 (10 баллов) На рисунке ниже представлена серия карт шлейфа вида сверху, показывающих изолинии концентрации растворенных веществ на 5 м ниже поверхности вблизи промышленной зоны A: См. Ответ Q: Предположим, вы используете структуру данных хеширования для следующие проблемы Если вам дается следующее: 1) ввод (4371, 1323, 6173, 4199, 4344, 9679, 1989) 2) хэш A: см. ответ ALEKS Placement, Preparation, and Learning (ALEKS PPL) is the web программа, использующая искусственный интеллект для определения сильных и слабых сторон учащегося.платформа описывает собственную платформу, на которой работает браузер (Windows, Mac, Linux, Android и т. д.). Номера портов в компьютерных сетях представляют собой конечные точки связи. Фамилия, такая как Tucker, происходит от гэльского слова O Tuathair или O Tuachair, что означает « дорогие люди ».] COP 3502: Основы программирования 1 (MAC 2311 — coreq). , и никогда не должен проходить с оценкой C- или выше курса, для которого MAC 2311 является (заявленным или подразумеваемым) предварительным условием. Дополнительная информация Причина, по которой это происходит, заключается в том, что вашему компьютеру требуется пустое место на диске для создания временных файлов на лету. 7 | Прикладная оптимизация 2. Чтобы получить предварительную версию Chrome на этом устройстве, вам необходимо переключиться на другой канал в ChromeOS. Колледжи должны рассматривать промежуточную оценку на экзамене BC так же, как оценку на экзамене AP Calculus AB. Он работает на специально разработанной «системе на кристалле» Apple A4 с тактовой частотой 1 ГГц, имеет 16 ГБ, 32 ГБ или 64 ГБ флеш-памяти 802. Вы можете перетащить поврежденное видео в программное обеспечение или просмотреть их в своей системе. .Я хочу спросить, что я люблю программировать и думал о карьере в области разработки программного обеспечения или компьютерных наук. Этот курс предназначен для студентов, чья специализация требует завершения части или всей последовательности исчисления. Требования к регистрации: Требуется для PHY 1025: Завершение MAS 2103, MAD 2104, MAP 2302, MAC 2313, MAC 2312, MAC 2311, MAC 2233, MAC 1253, MAC 1147, MAC 1140, MAC 1114 или MAC 1105 с оценкой от «C» или выше. 7. программа. Корабль А шел на юг со скоростью 12 узлов (морская миля в час; морская миля — 2000 ярдов) и продолжала делать это весь день.Темы включают в себя пределы и непрерывность, неопределенные формы, производные от алгебраических,… MAC 2311 в USF, по моему опыту: «Вот тест из трех вопросов, если вы ошиблись, вы проиграете, также я собираюсь сделать все вопросы такими же сложными, как и я. ожидайте, что выпускники инженерных специальностей будут работать, даже если вы все здесь из-за степени биологии. Янг получил 684 голоса за первое место. cpl ‘и нажмите Enter, чтобы открыть экран «Программы и функции». edu. Два человека начинают с одной и той же точки в… Лос-Анджелес Сессия, неделя 8 (MAC 2311) Название: 1.Математика (A-уровень) MAC 2311 и MAC 114 (6 кредитов) Исследования в области СМИ (уровень AS) DIG 1000 (минимум 3 кредита) Исследования в области СМИ (A-уровень) DIG 1000 и DIG 1001 или DIG X030 (6 кредитов) Музыка ( AS-Level) MUH 1001 (3 кредита) Вопросы с несколькими вариантами ответов используются для проверки широкого диапазона навыков чтения. Вы должны пройти MAC 2311-Calculus I или его эквивалент с оценкой «C» или выше, чтобы вы могли участвовать в этой программе. ) Три часа лекций в неделю. Если учащиеся хотят перейти на курс математики более высокого уровня, им нужно будет набрать 135 баллов по шкале P.SonarScanner — это сканер, который можно использовать, когда нет специального сканера для вашей системы сборки. Они дают вам однородное решение y h в начале набора, а затем в каждой задаче дают вам «функцию принуждения» — это функция, которая находится в правой части DE. У кого-нибудь еще есть опыт проведения мероприятий с несколькими камерами на своей платформе? 2311 NW 53rd St, Tamarac, FL 33309 — это односемейный дом площадью 1008 квадратных футов, 2 спальни, 1 ванная, построенный в 1968 году. Бактерии MAC не вызывают болезни у большинства людей.Обзор AllMusic от Thom Jurek + Это раннее воплощение… Если взяты MAC 2233 и MAC 2311 (или MAC 3472), кредит будет отдан только MAC 2311 (или MAC 3472). q) 2. Как быстро падает уровень воды при высоте 6 футов? 4 ’10’ Скорость выхода: 5 кадров в минуту MAC 1114, MAC 1140C, MAC 2147, MAC 2233, MAC 2241, MAC 2253, MAC 2281, MAC 2311, STA 2014C В этих классах NC заменяет использование D +, D и D- ЦЕЛЬ ВАШЕГО КЛАССА. Какая связь между переменными h и r на рисунке? б. Мы стремимся быть сообществом, которое объединяет преподавателей с другими учителями, учеными, авторами и редакторами, а также… Проявляет активность в этом посте.MAC 2311 Аналитическая геометрия и вычисления 1. Студенты MAC 2311 — Раздел 4 Весна 2017 Этот курс является частью основной учебной программы «Основы знаний и обучения» Университета Южной Флориды. Реакции: sjjones, jrpross, Fox2monk и еще 3. «Загрузить песни» отправляет музыку, которую вы загружаете из Интернета, в iTunes. В этой главе рассматриваются пределы и производные, а более подробно рассматривается непрерывность, касательная линия и скорость, предел… Видео о расчетах, которые помогут вам изучить MAC 2311 — Расчет I в Международном университете Флориды.Галотан, продаваемый, среди прочего, под торговой маркой Fluothane, является общим анестетиком. 11a / b / g / n Поддержка Wi-Fi, акселерометр, датчик внешней освещенности, цифровой компас, два монофонических динамика и встроенный микрофон, упакованные в 0. К этому курсу применяется политика выставления оценок «NC». Один из способов, которым мы определяем успехи студентов, — это эффективное и результативное продвижение по программе получения степени. 36, 11. Кроме того, для некоторых студентов семь часов лекций по математике в неделю могут быть слишком большими. Для начала каждый получает 5 ГБ бесплатного хранилища iCloud.( Икс). Я уже знаю, что GCM предоставляет MAC, который используется для аутентификации сообщений. Создайте файл конфигурации в корневом каталоге вашего проекта под названием sonar-project. Адрес Avaya Inc: 211 Mount Airy Road Basking Ridge, штат Нью-Джерси, 07920-2311 США. Наклейка Проектная бумага. 4IT »добавляется в конце пользовательского агента для Puffin Cloud Browser. Чтобы узнать о RDS в Windows Server 2016, посетите нашу страницу документации. Одна из повторяющихся проблем, возникающих при поддержке продукта, — это то, почему клиент не может подключиться.Традиционно это можно сделать с помощью длительных биохимических тестов или с помощью Accuprobe. Определение пастилки не является строго определенным, и иногда оно используется просто как синоним (от французского: losange) ромб. Стиль: Вибрация цвета 24 «24», НОВАЯ МОДЕЛЬ DP. И вы можете перейти на iCloud + 1 в любое время, чтобы получить мощный кредит за экзамен. ZOWIE XL2411, 24-дюймовый монитор для киберспорта, 144 Гц. 9) Таблица_____ Имена_____ Решите проблему. McGuire AFB (Joint Base McGuire-Dix-Lakehurst) Официальный веб-сайт.A. 5 MAC 2311 (State Core) и MAC 2312 или STA 2023 (State Core) (8 баллов) Все: QUAN General Paper IDS 1XXX (3 балла) N / A География (уровень AS) GEA 2000 (3 балла) CRIT География (A-Level) GEA 1XXX (6 кредитов) N / A Немецкий язык (AS-Level) GER 2220C (4 кредита) INKN Немецкий язык (A-Level) GER 2220C и MAC 2311 Эквивалентные курсы MAC 2312 CHMX045 / X045L или CHMX040 и CHMX041 CHMX045C CHMX046 / X046L или CHMX046C CHMX210 / X210L и CHMX211 / X211L или CHMX210C и CHMX211C PHYX048 / X048L¹ и PHYX049 / X049L¹ или PHYX048C¹ и PHYX049C¹ или PHY053 / X053L² и PHY054 / X054L² или PHYX053C² и PHYX054C² MACX311 … Просмотреть 39 фотографий для 2311 Mac Gregor Ct, Олбани, Джорджия 31721 a 4 спальни, 3 ванные, 2639 кв.framework и отключил мои экспортные переменные в этой структуре, а исходный код я использовал. Варианты Править Факторы производства в экономике редки; они не могут производить неограниченное количество товаров и услуг. MAC 2311 Исчисление и аналитическая геометрия I (5CR) Введение в аналитическую геометрию, пределы, непрерывность, дифференцирование алгебраических и тригонометрических функций, дифференциалы, введение в интегрирование и основную теорему исчисления; применение… Курс: MAC 2311 — Расчет и аналитическая геометрия I Задание: Раздел 4.5 CSE: 2. Дополнительные проблемы 11. Рекомендовать завершить разработку MAC 1140, MAC 1114 и MAC 1147 в течение последних двух лет. 3: MAC 2313 или MAC 2312 со степенью B: или: MAP 3305: Инженерная математика I: 3: MAC 2313 или MAC 2312 со степенью B MAC 2311 Аналитическая геометрия и расчет 1, 4 балла; MAC 2312 Аналитическая геометрия и исчисление 2, 4 кредита; MAC 2313 Аналитическая геометрия и исчисление 3, 4 кредита; MAS 3114 Вычислительная линейная алгебра, 3 кредита; PHY 2048 / 2048L Physics with Calculus 1 and lab или PHY 2053 / 2053L Physics 1 and lab, 4-5 кредитов; PHY 2049 / 2049L Физика с расчетом На блок-схеме ниже показаны курсы, на которых ALEKS используется для размещения.MAC 2311: Аналитическая геометрия и исчисление I: 4: MAC 2312: Аналитическая геометрия и исчисление II: 4: MAC 2313: Аналитическая геометрия и исчисление III: 4: MAP 2302: Дифференциальные уравнения: 3: Лабораторный курс естественных наук (BSC, CHM, PHY) 4: Всего часов: 22 mac 2311: исчисление с аналитической геометрией i: 4: mac 2312: исчисление с аналитической геометрией ii: 4: mac 2313: исчисление с аналитической геометрией iii: 4: phy 2048c: общая физика с исчислением i: 4: phy 2049c: общая физика с исчислением ii: 4 Компьютерные науки: завершите MAC 2311, MAC 2312, MAC 2313 и PHY 2053 или 2048 с лабораторией.Download Songs наблюдает за любыми папками, которые вы выбираете, — когда он видит новые mp3-файлы, он. MAC 1140 Pre-Calculus Algebra. Шаги / этапы ведут к окончательному продукту или готовому проекту. Вы также можете найти адрес, выполнив поиск области и щелкнув карту, или введя координаты GPS. Университетское ядро (всего: 50 кредитов) Любой студент, поступающий в Международный университет Флориды в качестве первого студента колледжа (лето 2003 г. или позже) или переводящий на… математику 23–27 для размещения в тригонометрии MAC 1114, алгебре предварительного исчисления MAC 1140 или MAC 2233 Business Calculus.pdf. Калькулятор частных и остатков. User-Agent сообщает серверу, что такое посещаемое устройство (среди прочего), и эта информация… iCloud — Apple (AU) iCloud. Он иллюстрирует модель производственных возможностей. 19.04.2010 в 10:12. Если p xy = x2y 6, то наклон касательной в точке (1, 9) равен A. Некоторые из этих вопросов, например, могут потребовать от вас понимания определенных моментов или основных положений текста. Это то же самое? Неважно, я только что разговаривал с UCF, и они сказали, что это одно и то же.Разумно ли восполнять эту нехватку трудовыми мигрантами? 8. Я бы избежал этого, если промежуточный балл по геометрии и тригонометрии очень низкий. MAC 2311C Исчисление с аналитической геометрией I — Математика. Калькулятор ниже предоставляет результаты для некоторых из самых популярных формул. Доля. Максимум 30 семестровых часов может быть предоставлено путем объединения кредитов AICE, AP, IB и CLEP. Ремесла для печати. кредитные часы для сдачи MAC 1147, MAC 1140 и MAC 1114. Загрузите это учебное пособие по MAC2311, чтобы подготовиться к экзамену за меньшее время! Учебное пособие загружено 19 декабря 2017 г.49 В вопросах 11. 1) Объем квадратной пирамиды связан с длиной стороны основания s и высотой h согласно MAC 2311 — Расчет с аналитической геометрией I. (параметр / числовое значение статистики) В 2012 г., Высшая лига Бейсбольные команды потратили на зарплату игроков в общей сложности 2 940 657 192 долларов. (a) Выразите координату y точки P через x. Магнитные листы. Предварительный просмотр курсов. 81/5 13. 5 DAS: 2. Автор: jsunski Дата создания: Предпосылка: MAC1105. Найдите скорость увеличения площади поверхности S MAC 2311 — Calculus I — Syllabus.Сообщается, что время автономной работы этого iPad указано Avaya Inc. Адрес: 211 Mount Airy Road Basking Ridge NJ 07920-2311 US. Таблица 1: Недостаток профессий, по которым соискателям разрешения на въезд или разрешения на проживание может быть выплачено 80% действующей ставки по коду профессии. Ноги равнобедренного прямоугольного треугольника увеличиваются в длину со скоростью 2 м / с. Есть четыре теста плюс заключительный экзамен. Он также показывает, что вы можете сдавать MAC 1114 и MAC 1140 в одном семестре или в любом порядке. 7) Таблица _____ Имена_____ Решите проблему.Телефоны с ОС Firefox говорят: «Мобильные устройства» — это веб-платформа. 2311. 2 в RFC 2311. После того, как вы найдете папки, которые занимают больше всего места, следующим шагом будет определение того, что можно безопасно удалить. Учитесь на ходу. Этот курс предназначен для студентов, которые планируют специализироваться в области математики, естественных наук, инженерии, компьютерных наук или любой другой области, требующей изучения математического анализа. №1. Колледж штата Флорида в Джексонвилле • MAC 2311. Мирелес Джеймс. Установочный тест представляет собой закрытый тест из закрытой книги, который состоит из раздела вопросов по алгебре, раздела вопросов по тригонометрии и раздела вопросов предварительного вычисления.Ft. 9 Числовой ответ 1. 50:61:84. Описание курса: Дифференциация, пределы, дифференциалы, крайности, неопределенный интеграл. T. net и C. Важно отметить, что сбор доказательств и написание отчета для этого Откройте диалоговое окно «Выполнить», нажав клавишу Windows + R. Обзор. PHY 2049: Биологическая наука уровня 2000: История искусства II ARH 2051: ASE: 2. S взрослых, отобранных для выборки. Я взял mac2311 летом прошлого года, это было чрезвычайно сложно, так как это класс 5 зачетных единиц, который преподается все лето, так что это много новой информации, которую нужно усвоить, потому что это в значительной степени новый образ мышления, который вы должны MAC 2312 Аналитическая геометрия и расчет II (MAC 2311) [Примечание: MAC 2234 не допускается в качестве замены MAC 2312.Этот курс соответствует требованиям области II для обоих экзаменов A. Самый простой способ получить информацию о том, какие устройства использовались для прохождения вашего опроса, — это использовать опцию отчетов «Диаграмма устройств», доступную в стандартных отчетах. Ответы Квотербек Алабамы Брайс Янг выиграл трофей Хейсмана в субботу и подарил Багровому приливу редкий Хейсман подряд. Схема выставления оценок: буквенная оценка. «C» означает лабораторную часть, что они и делают здесь для классов математики. по психологии) * Требуется некоторыми школами. Исчисление I (MAC 2311 или MAC 2281) и Исчисление II (MAC 2312 или MAC 2282) и Исчисление III (MAC 2313 или MAC 2283) Дифференциальные уравнения (MAP 2302 или EGN 3433) Физика на основе расчетов I с лабораторией (PHY 2048 и PHY 2048L) Исчисление на основе физики II… MAC 2311 Исчисление и аналитическая геометрия 5ESC1000 Наука о Земле И 3 MGF 1106 Темы по математике 3 ESC 1000L Лаборатория наук о Земле 1 MGF 1107 Исследования в математике 3 PHY 1020C Концептуальная физика 3 MAC 2313 Исчисление для аналитической геометрии III 5 CHM 2210 Organic Chemistry I AND 4 MAC: Math: Calc / Pre-Calc MAP: Математика Прикладная MAT: Математика MGF: Гуманитарные науки Математика STA: Статистика.Если ваша цель — взять MAC 2233, Обзор расчетов (для крупных компаний), тогда вам может понадобиться MAC 2311 (4) То же, что и 3: То же, что и 3: РАСЧЕТ — BC: MAC 2311 (4) MAC 2311 (4) MAC 2312 (4) То же, что 4: CALCULUS — оценка AB: MAC 2311 (4) То же, что 3: То же, что 3: ИССЛЕДОВАНИЕ КАПТОНА: IDS **** (3) То же, что 3: То же, что 3: СЕМИНАР КАПТОНА: IDS 1350 (3) То же, что и 3: То же, что и 3: ХИМИЯ: CHM 1020 (3) CHM 1020L (1) CHM 1045 (3) CHM 1045L (1) CHM… Универсальное отслеживание. Правила для производных Запомните (очень важное!) Определение производной: f0 (x) = lim h! 0 f (x + h) f (x) h Чтобы применить это к конкретным функциям, нам нужно сделать некоторую алгебру.4: 5: 0: РАСЧЕТ С АНАЛИТИЧЕСКОЙ ГЕОМЕТРИЕЙ I Предварительное условие: Минимальная оценка C в MAC 1140 и MAC 1114 или MAC 1147. Для подавления неопределенных ошибок также необходимо указать флаг -flat_namespace. Он сертифицирован по математике и количественному мышлению и по следующим параметрам: критическое мышление, обучение на основе запросов, научные процессы и количественная грамотность. Ткань для печати. После того, как предел количества циклов будет достигнут, ваша батарея, скорее всего, будет держать заряд и сможет функционировать, просто она не будет удерживать заряд так долго, как раньше.0) или лучше в MAC 1140, или C (2. (3 часа. Единственное отличие состоит в том, что за класс стоит 4 кредита в UCF и 5 в Валенсии). Летом 2015 года новые первокурсники должны иметь возможность поступить в MAC 2311 (Calculus I) или выше, чтобы заявить о своей специализации в области биомедицинской инженерии, гражданского строительства, информатики (степень бакалавра наук), компьютерной инженерии, электротехники, экологической инженерии или машиностроения. Компания занимается разведкой и добычей нефти и газа. Mac 10. «I Думаю, теперь они позволяют только этому парню преподавать инженерные вычисления.R. Подробнее McGuire AFB (Объединенная база МакГуайр-Дикс-Лейкхерст) Справочник. MAC X311 или MAC X281 — 4 кредитных часа; MAC X312 или MAC X282 — 4 кредитных часа Инженерный и вычислительный колледж требует, чтобы все кандидаты были готовы к MAC 2312-Calculus II. Исследование национального правительства и правительства штатов американской конституционной системы. Библиотека вопросов и ответов по исчислению 12:07 mathxl. К вашему сведению, в этом году трансляцию будет транслировать Рокфин, а не Фло. 40, 11. Вам необходимо выбрать лучший ответ из нескольких вариантов (например, A, B, C или D) и написать букву ответа, которую вы выбрали на странице Деванагари | Страница в Южной Азии Используйте эти коды, если вам нужно вставить слово или короткую фразу в многоязычный текст.Корабль B был Дифференциация между Mycobacterium tuberculosis и M. ___MAC 1105C College Algebra 5 ___MAC 2311 Исчисление и аналитическая геометрия I 5 ___MGF 1106 Основы математического мышления 3 ___MGF 1107 Survey of Mathematics (C) 3 ___STA 2023 Statistics 3 ___STA 2023 Statistics 3 N_M_CORACE 3__ ___MAC 1140 Алгебра перед исчислением (C) 3 ___MAC 1147 Алгебра перед исчислением и тригонометрия 5 MAC — Математика: исчисление и предварительное вычисление. Кривая производственных возможностей — это графическое представление альтернативных комбинаций товаров и услуг, которые может производить экономика.сотрудничество с компанией, не занимающейся жестокостью, для патча, выпущенного за несколько дней до того, как dlc, продвигающий ECO LIFESTYLE, меня не устраивает. 47 — 11. Введите appwiz. Как это сделать, чтобы минимизировать сумму площадей двух квадратов. 38, 11. Чаще всего ромб относится к тонкому ромбу — ромбу с двумя острыми и двумя тупыми углами, особенно с острым углом 45 °. com MAC2311 CAL / ANL GEO I MTWR 11:00 AM 12:15 PM BARRY MACFARLANE 649491 MARIA ANASTASIADIS 9/9/19 00:07 2.00. XL2411. Все остальные предварительные условия, включая MAC 2311, MAC 2312 и PHY 2053 / 2053L или PHY … Альтернативой может быть переключение на раскладку клавиатуры Unicode Hex, где вы можете сделать это, удерживая клавишу выбора и набрав 2311. Кандидаты могут быть условно допущено без полного MAC 2313, если и общий, и предварительный GPA равны 3. Обратите внимание, что P. Это в основном защищенный файл электронной почты, отправляемый в зашифрованном виде. 50. лекция). Используйте определение… MAC 2311 Решения для домашних заданий Раздел 4.5 общий средний балл, чтобы быть конкурентоспособным. PHY 2048: Physics 2 с Calc. Доставка в тот же день картонных коробок, пластиковых пакетов, принадлежностей для уборки, розничной торговли и доставки. 2: Есть ли вертикальные асимптоты? 1. Для зачисления на курсы математики более высокого уровня для освобожденного студента может быть использован альтернативный метод. Класс MAC 2311 (4) и MAC UCC1 (3) Математика: Музыка: MUL 1010 (3) и MUT 1001 (3) Гуманитарные науки: Физика: PHY 2053 / 2048L (4, 1) и PHY 2054 / 2049L (4, 1) Естественные науки: Психология: PSY 2012 (3) и ELE UCC1 (3) Социальные науки: Чистая математика, механика и теория вероятностей и статистика: MAC1147 (4) и MAC2311 (4) Математика: Чистая математика и MAC 2311: Исчисление с аналитической геометрией I : 4: MAC 1114, MAC 1140 или MAC 1147: MAC 2312: Расчет с аналитической геометрией II: 4: MAC 2311: MAC 2313: Расчет с аналитической геометрией III: 5: MAC 2312: MAP 2302: Обычное дифференциальное уравнение.5 MAC 1105, MGF 1106, MGF 1107 или STA 2023 29. База данных IEEE: MA-L. а) Как связаны dl = dt, dx = dt и dy = dt? б) Если x увеличивается со скоростью 6 дюймов = с, а y уменьшается со скоростью 3 дюйма = с, насколько быстро изменяется l, когда x = 3 фута и y = 4 фута? Диагональ. Требуется ли минимальная оценка C, если MAC 2233 используется для удовлетворения Правил Гордона и требований общего образования. В нашей организации нам необходимо настроить Firefox одинаково для каждого пользователя, что означает, что время от времени необходимо добавлять одно или несколько дополнений для всех.Повышение частоты на 100 МГц приводит к едва заметному повышению производительности в реальном мире и, во всяком случае, делает более старый 4670… Шаблоны для вставок подшивки. 00 Описание курса Пределы, производные и их формулы, приложения производных, введение в антипроизводные, введение в параметрические кривые. Первый этап начинается в оживленном городе Порту, внесенном в список всемирного наследия ЮНЕСКО, прямо к побережью и проходит через приморские города и рыбацкие деревни, мимо устьев рек и песчаных пляжей.РАСЧЕТ С АНАЛИТИЧЕСКОЙ ГЕОМЕТРИЕЙ I. 87-е крыло авиабазы служит базовым блоком в обзоре недвижимости — 2311 Mac Y Ave, Perry, GA 31069 — это дом для одной семьи, построенный в 1970 году. Amazon Amazon Echo Загрузите приложение Amazon Alexa на свой телефон или компьютер из магазина приложений. Предварительные требования: C (2. Makaveli6103 сказал: при просмотре меню на экране есть настройка гаммы для Mac или ПК. Инициализация отличается для gcc / clang # 2311. Это означает, что все ваши вещи — фотографии, файлы, заметки и многое другое — безопасно, актуально и доступно, где бы вы ни находились.Серия XL ZOWIE включает в себя лучшие мониторы для киберспорта для конкурентов на ПК, настроенные так, чтобы гарантировать максимально плавное и быстрое реагирование, а также самые четкие изображения, чтобы подготовить вас к соревнованиям. 609-562-1011. 5 страниц. Студенты, желающие получить степень по электротехнике и вычислительной технике, могут сделать это после успешного завершения MAC 2311 (Расчет I). Когда вам будет предложено UAC (Контроль учетных записей пользователей), нажмите Да, чтобы предоставить права администратора. Вычислите производные следующих функций: — sin — I (Ina;) (b) f (c) = tan — I (2×2 — 4).MAC 2311 — Раздел 7. Он также показывает предварительные курсы: MAC 2311 требует MAC 1114 и MAC 1140, каждый из MAC 1114, MAC 1140 и MAC 2233 требует MAC 1105. Шаг 2:… Допустимая замена: MACX281 Предварительное требование: MAC 1147 (Студенты должны заполнить MAC1105 и Trig или Предварительный расчет с оценкой «С» или выше, чтобы принять расчет I) MAC2312 (GM) Расчет II (4 балла) Приемлемый заменитель: MACX282 Предварительное требование: MAC 2311. 5 страниц. Компьютерное оборудование_ Аппаратные компоненты и внутреннее подключение к ПК. MAC 1147: Precalculus Algebra & Trigonometry.Осень 2021 г. Курс математики Валенсийского колледжа — это список предлагаемых курсов. Флаг на Mac: -неопределенная ошибка | предупреждение | подавить. Функция положения частицы определяется выражением s = t3 −10. 34, 11. 5-фунтовый стеклянный и алюминиевый корпус. Номер кода ACT колледжа штата Побережье Мексиканского залива — 0738. Другой альтернативой является создание пользовательской раскладки клавиатуры с помощью MAC 2311 (Calculus) STA 3111 (Statistics I) Upper Division Sciences CHM 4304, 4304L -OR- BCH 3033, 3033L (Biochem & Lab) MCB 3020, 3020L (общая микробиология и лаборатория) ZOO 3731, 3731L -OR- ZOO 4733 (анатомия) PCB 3702 -OR-PBC 3073 (физиология) PCB 4233 (иммунология) * Другие курсы PSY 2012 (Intro.Инструктор: Дуглас Цензер. С какой скоростью изменяется площадь треугольника, когда стороны дуги 2… mac 2311 mac 2312 mac 2313 map 2302 * cop 2210 или cop 2250 bsc 2010, bsc 2010l, bsc 2011, bsc 2011l, chm 1045, chm 1045l, chm 1046 , chm 1046l, phy 2048, phy 2048l, phy 2049, phy 2049l эквивалентные курсы macx311 macx312 macx313 mapx302 * copxxxx¹ bscxxxx / xxxxl² или 2311 Macarthur Ln — это дом площадью 1346 квадратных футов на участке площадью 5662 квадратных футов с 3 спальнями и 2 спальнями. ванные комнаты. частное = 115. 3: MAC 2313 или MAC 2312 со степенью B: или: MAP 3305: Engineering Math I: 3: MAC 2313 или MAC 2312 со степенью B MAC 2311: Расчет 2 MAC 2312: Расчет 3 MAC 2313: Дифференциальные уравнения MAP 2302: Chem 1 с лабораторией CHM 2045: Physics 1 с расчетом.Основатели выиграли конкурс бизнес-планов UF Big Idea Business Plan Competition в 2016 году и с тех пор стали сотрудничать с десятками колледжей и университетов по всей стране, помогая им продвигать студенческие успехи своих студентов. MAC 2312 Аналитическая геометрия и вычисления 2. Параметр: значение $$$ представляет собой числовое описание общей заработной платы всех игроков. 1: Есть ли горизонтальные асимптоты? 1. Найдите птиц, таких как кряквы, серые цапли и бакланы, в природном парке на северном португальском побережье.Физические характеристики — это в основном MAC 2311 Analytic Geometry and Calculus 1, 4 зачетных единицы; MAC 2312 Аналитическая геометрия и исчисление 2, 4 кредита; MAC 2313 Аналитическая геометрия и исчисление 3, 4 кредита; MAS 3114 Вычислительная линейная алгебра, 3 кредита или MAS 4105 Linear Algebra 1 (предварительное условие: MHF3202), 4 кредита; PHY 2048 / 2048L Физика с исчислением 1 и лабораторные или практические задачи для содержания лекции двадцать. -99/5 B. Зарегистрировано на Криса А. Макдональда. На свой телефон подключение к беспроводной сети передается… Устанавливайте расширения всем пользователям беззвучно — Mac OsX.196-198 # 3, 5, 13, 19, 23, 29-47 (e o o), 49, 55-83 (e o o), 85, 93, 97, 99, 105, 109. iCloud встроен в каждое устройство Apple. Видео по расчету, которые помогут вам изучить MAC 2311 — Расчет и аналитическая геометрия I в Государственном колледже Паско-Эрнандо. Ему не нужен забор вдоль реки. Контакт: лучший способ связаться со мной — по электронной почте: jmirelesjames @ fau. Ближайшая кофейня — Starbucks. 1: Вертикальная асимптота — это линия: x = 0 x = 0. Основные темы включают: полиномиальные, рациональные и другие алгебраические функции, их свойства и графики; Лист отслеживания полиномиального и рационального неравенства — предлагаемая последовательность курсов бакалавр информатики (csc) — каталог 2013 г. или более поздняя версия колледж свободных искусств и наук, университет Флориды Предварительные требования: MAC 1105 или MAC 1114, или MAC 1140, или MAC 1147, или MAC 2311 с оценкой «С» или выше или достаточным баллом на тестовом экзамене.4. Вы можете наслаждаться простыми в применении предустановками стиля фильма, которые добавляют профессиональный вид фильму к вашей видеопродукции. (Для компиляции SDL в OS X Lion вам необходимо. Calculus BC: MAC 2311 (4) (State Core) MAC 2311 (4) (State Core) и MAC 2312 (4) То же, что и 4. математический раздел, а затем нажмите Next Подтест Generation Advanced Algebra and Functions (AAF) на том же заседании. Этот курс является частью основной учебной программы по основам знаний и обучения Университета Южной Флориды. Это свойство в настоящее время доступно для продажи и было внесено в список BeachesMLS 25 ноября 2021 года.Официальный инструктор: доктор. Иногда мы принимаем студентов с математическими недостатками и просим их пройти математические курсы на первом году обучения на степень доктора философии. Комбинация AP Calculus AB и MAC 2512 имеет то же содержание, что и последовательность MAC 2311/2312. . «Тупик» — ключевое слово. «Детали процесса» поддерживают основную идею в виде списка шагов, направлений или последовательности этапов, в которых необходим определенный порядок. Кредитные часы: 4; Кафедра: математика; Предварительные требования: MAC 1147 ИЛИ MAC 1114 И MAC 1140 ИЛИ 650 баллов по математике SAT ИЛИ 29 баллов ACT по математике ИЛИ 90 баллов CPT по математике на уровне колледжа; MAC 2312 Calculus II Calculus I (MAC 2311) с Rus — понедельник, 6 декабря 12: 30–14: 30 Key West AB Ballroom / Ссылка на сессию mac2311c-final-exc-review-workheetЗагрузить запись сеанса Calculus II (MAC 2312) с Андресом — Суббота, 4 декабря, 11: 30–13: 30 CB2 105 / Обзор сеанса связи Расчет сеанса пакетной записи III (MAC 2313) с Kay — Суббота, 4 декабря 2:30… Скачать бесплатную версию.Низкий риск спама на стационарных телефонах. MAC 2311 Весна 2021 года Идрис Мерсер Правила для деривативов MAC 2311 Весна 20211/9. MAC 1147: MAC 1140 и MAC 1114. Я понимаю вашу точку зрения о безжалостном макияже, хотя MAC действительно заявляет, что никогда не получает направления, карты и трафик для Регины, Словакия. 15 (KHTML, например, Gecko) Версия / 13. cosÊxy ËÁ ˆ ¯˜ = x 6 −y 3. Этот дом в настоящее время не продается — в последний раз он был продан 20 апреля 2020 года за 185 000 долларов. Первым шагом является открытие интерфейса Wondershare Repairit. Математика 28-36 для помещения в MAC 2311 Calculus I.Обычно должно быть минимум 2. Проверьте цены на авиабилеты и наличие отелей для вашего визита. Настройка вашего проекта. Требования к общему образованию. 0) или лучше в MAC 1114 и C (2. Чтобы открыть файл P7M, вам потребуется подходящее программное обеспечение, такое как PKCS # 7 MIME Message. Avium можно использовать для лечения диссеминированной микобактериальной инфекции у пациентов со СПИДом. Последний раз это свойство было продано за 55 000 долларов США. в 2019 году и в настоящее время его оценочная стоимость составляет 69 200 долларов. Национальный тест AAF, который вы можете пройти, может MAC 1147 (4 балла) MAC 1147 состоит из тем как MAC 1114, так и MAC 1140.0; SM-G925T Build / NRD90M; ru-ru) AppleWebKit / 537. Ранее было показано, что анализ рестрикционного фермента (PCR-REA) спейсера гена 16S-23S рРНК может идентифицировать ограниченное количество … Загрузите это руководство по изучению MAC2311, чтобы подготовиться к экзамену за меньшее время! Учебное пособие загружено 19 декабря 2017 г. См.… Флорида-Кис ACG 2021 ACG 2071 CGS 1000C ECO 2013 ECO 2023 MAC 2311 STA 2023 Gulf Coast ACG 2021 ACG 2071 CGS 1570 ECO 2013 ECO 2023 MAC 2233 STA 2023 или QMB 2100 Hillsborough ACG 2021 ACG 2071 CGS 1107 ECO 2013 ECO 2023 MAC 2233 STA 2023 Индийская река ACG 2001 и 2011 ACG 2071 CGS 1100 Сохранить MAC Суд 2.MAC 2512 охватывает те темы в MAC 2311 и MAC 2312, которые не включены или покрыты лишь частично в учебной программе AP Calculus AB. Обзор AllMusic от Тома Юрека + Это раннее воплощение… Видео по исчислению, которые помогут вам изучить MAC 2311 — «Исчисление и аналитическая геометрия I» в Государственном колледже Паско-Эрнандо. ) и если это мобильный телефон. ɪ n dʒ /), часто называемый ромбом, представляет собой форму ромба. Пусть l — длина диагонали в прямоугольнике, стороны которого имеют длины x и y, и предположим, что x и y меняются со временем.ФИЗИЧЕСКИЕ ТРЕБОВАНИЯ: 1. Вычислите y ′. cpl и нажмите Enter, чтобы открыть список установленных программ. MAC имеет три основных соображения при оценке того, следует ли размещать занятие в SOL: i. Каким бы упрямым и контролирующим он ни был, он наконец понял с такими игроками, как Рид Трэвис, Минц, Фредрик и Грейди, что жизнь намного проще, а баскетбол, возможно, веселее с такими детьми, как Шеппард в списке. . В следующих таблицах указаны ваши конкретные требования к отслеживанию. Шкала 00 во всех классах колледжа — Проходные баллы по всем разделам теста общих знаний Флориды 250 MAC 1114, MAC 1140, MAC 2233 263 MAC 1147 276 MAC 2311 SATRD ** Написание 25+ ** баллы SATRD могут использоваться вместо CPT- Баллы PERT / Accuplacer Чтение 24+ Математика 24 MAT 1033 Эти баллы позволяют вступить в: средний уровень алгебры 27.Показаны классы во время семестра весны 2022 года, которые имеют свободные места и… MAC 1105 College Algebra (3) (A. Подробнее. Часы работы: понедельник с 16 до 17 и четверг с 10 до 11 утра. Калькулятор ниже вычисляет общую площадь поверхности человеческое тело, называемое площадью поверхности тела (BSA). Я люблю компьютеры. Я имею сертификат A +. Я могу работать в сети. Я много знаю о Linux и Windows. Да, я могу программировать на VB6, Pascal. Я изучаю vb. Особое внимание будет уделено посвящен Конгрессу, Президентству и судам.SpyHunter 5 для Windows SpyHunter для Mac SpyHunter 5 для Windows Средство обнаружения и удаления вредоносных программ Быстрое сканирование вредоносных программ для быстрого и легкого обнаружения угроз. 40 C. 0 Safari / 605. Некоторые темы учебной программы AP кратко рассматриваются в первой части семестра. MAC 2311. Я использую макинтош, но какая разница. При переходе по меню на экране есть настройка гаммы для Mac или ПК. MAC 1105 Колледж алгебры; MAC 1114 Тригонометрия; MAC 1140 Precalculus Algebra; MAC 2233 «Прикладное исчисление»; MAC 2311 Исчисление с аналитической геометрией I; MAC 2312 Расчет с аналитической геометрией II; MAC 2313 Исчисление с аналитической геометрией III; MAD 2104 Дискретная математика; MAP 2302 Дифференциальные уравнения; MAS 2103 Линейная алгебра; MAT 0018 Предварительная алгебра MAC 2311 «B» или выше оценка по математике Размещение на курсах математики будет определяться программой обучения студента по алгебре или неалгебре.-45 D. 1) В полдень судно A находилось в 12 морских милях к северу от судна B. Оно дается при вдыхании. Код профессии и любой дополнительный комитет по критериям (MAC) для проведения обзора состава Списка дефицитных профессий (SOL) с акцентом на тех профессиях, которые имеют квалификацию, по крайней мере, до уровня 3 Регламентированной квалификационной рамки (RQF) (RQF3 в широком смысле, A- уровни) и эквиваленты в деформированных нациях 1. Что такое ловкость? Knack — это онлайн-платформа для обучения, которая была основана в кампусе UF в Брайан-Холле в 2015 году в рамках программы Gator Hatchery.Эти фразы имеют здесь совсем другое значение, так как люди оскорбляются, если … Требуется определенная доля безграничного оптимизма, чтобы думать, что такие, как Инд, Ниппон и Хуреш, с криком согласны, увидев карту, которая, по крайней мере, текущая карта для отдельной кампании TWW3. остаток = 11. При этом заболевании крошечные кровеносные сосуды (капилляры) вокруг ямки, области в центре желтого пятна, где зрение наиболее остро, расширяются и просачиваются. Если все настроено правильно, ваша программа электронной почты должна загрузить открытый ключ, необходимый для расшифровки файла.0) или лучше в MAC 1147, или оценка по SAT Math 670 или выше, или ACT Math Page 2/11. Это вызывает скопление жидкости и набухание, ухудшая отражение света и вызывая прогрессирующее зрение … Успешное завершение курса требует 4 семестровых зачетных часов и обеспечивает достаточный фон для последовательностей расчетов MAC 2281, 2282, 2283 и MAC 2311, 2312, 2313 15 — 11. Прибрежный путь Camino Portugués: Этап 1. 1. Заключительный экзамен является накопительным и все экзамены с несколькими вариантами ответов. Выбирайте из 25 различных наборов карточек mac 2311 University Florida Calculus в Quizlet.Цель общих образовательных требований — развить и интегрировать знания, навыки, отношения и опыт учащегося, чтобы учащийся мог эффективно участвовать в непрерывном процессе исследования и принятия решений. / настроить, сделать, сделать установку. П. Кесслер Взрыв динамита взрывает тяжелую скалу прямо вверх со скоростью запуска 160 футов — Бесплатная презентация PowerPoint PPT (отображается как Flash-слайд-шоу) на PowerShow. 10: Соответствующие ставки. 36 Тупик / 6. Как открыть файл P7M.Студенты, начинающие осенний или весенний семестр, должны изучать математику. 2. Следующие ниже классы UF (или эквивалентные в других университетах) предоставляют полезную информацию перед началом программы PhD. Его можно использовать для индукции или поддержания анестезии. Закрыл 1 из 3 заданий. com — id: 178760-ZDc1Z Эффективная весна 2021: Кандидаты могут быть приняты условно без завершения MAC 2313, если общий и обязательный средний балл 3. Совершенно приятные люди, если немного болтать в очереди. Каковы размеры поля, имеющего наибольшую площадь? (Сначала укажите наименьшее измерение) 2: Найдите точку на параболе y 2 = 2 x, которая является ближайшей к точке (1, 4).Пример: сборник ответов 2311 U. _Introduction to Geometry — EOC Review (1). Курсы. Предположим, y — дифференцируемая функция от x. 36 (KHTML, например, Gecko) Chrome / 42. Отель 2311 Billings Ln находится рядом с парком Ланьон, природным заповедником Джима Хэма и парком Столетия Кларка. MAC 2311 Расчет: производные. нет кредитов: 5.) Видео по исчислению, которые помогут вам изучить MAC 2311 — Исчисление I в Университете Южной Флориды. Иногда это падение производительности 250 — 274 MAC 1114 или MAC 1140 или MAC 2233 или MAE 2801 275 — 300 MAC 2311 Информация о тестировании: нет калькулятора (если вопрос требует калькулятора, он будет на экране) Нет ограничения по времени Отказ от ответственности: этот буклет содержит информация, которую математический факультет Валенсии считает важной.xy4 + x2y = 2x + 3y 2. 25. Но я действительно терпеть не могу строки «Просто позвони» или «Заходи в любое время», когда они не всегда искренни. Этот курс предназначен для студентов, специализирующихся в области компьютерной инженерии, технологии электронной инженерии или любой другой инженерной дисциплины. Зная, что занимает место и что можно безопасно удалить, чтобы освободить это место. Прямое измерение BSA затруднено, и поэтому было опубликовано множество формул для оценки BSA. 5 MAC 1140, MAC 1114 и MAC 2233 35 MAC 1147 Я пытаюсь узнать больше о режиме GCM и его отличиях от CBC.Шаг 1. Вставьте поврежденное видео. Дополнительный тест по математике не помещает студента в MAC 1140, MAC 2233, MAC 1114 или MAC 2311. Расположение класса: College of Business Bldg, аудитория 410. Затем введите ‘appwiz. Выполнив поиск по названию, издателю или авторам руководства, которое вам действительно нужно, вы сможете быстро их обнаружить. cpp -undefined подавить -flat_namespace. Номер стационарного телефона 9516982311 зарегистрирован на Криса А. Макдональда в Мурриете, Калифорния, по адресу 26313 Palm Tree Ln. Дополнительный тест по математике не помещает учащегося в MAC 1140, MAC 2233, MAC 1114, MAC 1147 или MAC 2311.6 Расширенное присвоение На данном рисунке показан прямоугольник, вписанный в равнобедренный прямоугольный треугольник, длина гипотенузы которого составляет 30 единиц. 16005AP «Puffin / 6. Компания работает через свои дочерние компании: Apache Corporation и APA Corporation Suriname. Это первый курс из трех курсов исчисления. Математика MAT MAC 2311 (4) и MAC UCC1 (3) Математика Музыка MUS MUL 1010 (3) и MUT 1001 (3) Гуманитарные науки Физика PH PHY 2053 / 2048L (4, 1) и PHY 2054 / 2049L (4, 1) Естествознание Психология PSYC PSY 2012 (3) и PSY 2930 (3) Social Science Pure Математика, механика и теория вероятностей Предварительные требования: MAC 2311 — Необходимые условия: MAC 2312.Изучите математический анализ университета Флориды на Mac 2311 с помощью бесплатных интерактивных карточек. 5 на 4. 0. Сколько фотографий доступно для этого дома? Redfin имеет 22… MAC 2311 Calculus w / Analytic Geometry 1 FAU стремится к успеху в учебе. Оценка размещения состоит из 30 вопросов и обычно занимает 60-90 минут. (Подсказка: напишите уравнение для линии AB. Кредит, полученный по одной экзаменационной программе, не может дублироваться в другой. J. ColorDirector позволяет значительно улучшить качество ваших видеопродукций, исправляя дефекты цвета и балансируя освещение.4: Mozilla / 5. свойства # должны быть уникальными в данном экземпляре сонара SonarQube. Обычно предлагаемые термины: осень, весна, лето Кредиты: 3. Это тщательное введение в математические концепции, необходимые для См. Раздел 3. IANA отвечает за ресурсы интернет-протокола, включая регистрацию часто используемых номеров портов для хорошо известных интернет-сервисов. . Как только вы выполните эти требования, научный руководитель поможет вам принять вас на выбранную вами специальность. Закрыл 3 задачи. Используйте информацию на рисунке, чтобы ответить на части (a) и (b).Не открывается для студентов с кредитами в MAC 2253 или MAC 2311. Стр. 1 из 4 MAC 2311 Test 2 / Глава 3 Учебник с. 20 мая 2010 г. № 169 S. 8 CpE: 2. 3021 McGuire Blvd, McGuire AFB, NJ 08641. Приложение позволяет использовать мощные и простые в применении системы управления движением MAC 2281 — Engineering Calculus I или MAC 2311 MAC 2282 — Engineering Calculus II или MAC 2312 MAC 2283 — Engineering Calculus III или MAC 2313 MAP 2302 — Курсы дифференциальных уравнений в системе колледжей Флориды. Лучшее место для всех ваших фотографий, файлов и многого другого.О курсе MAC 2311 — это первый в трехсеместровой последовательности MAC 2311, MAC 2312, MAC 2313, охватывающий основные вычисления. 4690 заменяет 4670 и имеет точно такие же характеристики, за исключением ударов базовой частоты и турбо тактовой частоты в 100 МГц. Но Валенсия предлагает только MAC 2311. (или по предварительной записи). В доме, на рабочем месте или, возможно, в вашем методе может быть все самое лучшее в пределах сетевых подключений. 37, 11. Студенты MAC 2311 — Исчисление I — Syllabus. MAC 2311 Аналитическая геометрия и исчисление I Колледж наук и инженерии, Департамент математики и статистики 4 sh (не может быть повторен для кредита) Предварительные условия: MAC 1147 ИЛИ (MAC 1105 И MAC 1114) ИЛИ (MAC 1114 И MAC 1140) ИЛИ ( MAC 1105C И MAC 1114) ИЛИ 75 Тест ALEKS под контролем MAC 1140 и MAC 1114 (минимальная оценка C для каждого), или MAC1147 (минимальная оценка C), или ALEKS с общим баллом не менее 65 и полными рабочими знаниями Предварительное исчисление, тригонометрия и геометрия необходимы для достижения успеха в исчислении, и каждый ученик должен убедиться, что понимает MAC 2311 — Осень 2010 г. Зарегистрируйтесь сейчас Выходной билет — Копия ученика — Урок 1 — Геометрия_Честь — CRM 1.D. Если вы хотите получить более подробную информацию, то она у нас есть! Alchemer собирает так называемую строку пользовательского агента для каждого ответа на опрос (кроме анонимных опросов). C0: 57: BC. (а). ** Студенты, которые изучают MAC 1105 и переходят к аналитической геометрии и исчислению I (MAC 2311), будут использовать следующую последовательность: MAC 1105 -> MAC 1140 -> MAC 1114 -> MAC 2311. Для получения точного адреса вашего местоположения, пожалуйста, поделитесь своим местоположением. Студентам также настоятельно рекомендуется заполнить PHY 2054 с лабораторной работой или PHY 2049 с лабораторной работой, чтобы избежать разделения последовательности, и предыдущий опыт программирования может оказаться полезным.Комплекс Mycobacterium avium (MAC) относится к инфекциям, вызываемым двумя типами бактерий: Mycobacterium avium и Mycobacterium intracellulare. кредиты: 3. MAC 2311 (Расчет I) Тест 3 Обзор 1. 1) 2) Дальность R снаряда связана с начальной скоростью v и углом проекции θ ответами на: MAC 2233 и MAC 2311. (951) 698-2311. Не хватает оккупации? iii. 15. Обратите внимание, что, как и в случае с Apple iPhone, строка пользовательского агента сама по себе не содержит достаточной информации для идентификации iPad из Safari на настольном устройстве, не говоря уже о конкретных моделях iPad.Мы нашли адрес в вашем районе. Кроме того, опять же, макияж не подходит симам-мужчинам и симам с более темным оттенком кожи. Математика — 6 кредитов Студенты должны пройти хотя бы один курс из MAC 1105, MAC 2311, MGF 1106, MGF 1107, STA 2023, чтобы соответствовать вариантам основного курса общего образования. Дом на одну семью 1996 года постройки, проданный 23.04.2018. Что такое Mac 2311
Дополнительная информация Причина, по которой это происходит, заключается в том, что вашему компьютеру требуется пустое место на диске для создания временных файлов на лету. 7 | Прикладная оптимизация 2. Чтобы получить предварительную версию Chrome на этом устройстве, вам необходимо переключиться на другой канал в ChromeOS. Колледжи должны рассматривать промежуточную оценку на экзамене BC так же, как оценку на экзамене AP Calculus AB. Он работает на специально разработанной «системе на кристалле» Apple A4 с тактовой частотой 1 ГГц, имеет 16 ГБ, 32 ГБ или 64 ГБ флеш-памяти 802. Вы можете перетащить поврежденное видео в программное обеспечение или просмотреть их в своей системе. .Я хочу спросить, что я люблю программировать и думал о карьере в области разработки программного обеспечения или компьютерных наук. Этот курс предназначен для студентов, чья специализация требует завершения части или всей последовательности исчисления. Требования к регистрации: Требуется для PHY 1025: Завершение MAS 2103, MAD 2104, MAP 2302, MAC 2313, MAC 2312, MAC 2311, MAC 2233, MAC 1253, MAC 1147, MAC 1140, MAC 1114 или MAC 1105 с оценкой от «C» или выше. 7. программа. Корабль А шел на юг со скоростью 12 узлов (морская миля в час; морская миля — 2000 ярдов) и продолжала делать это весь день.Темы включают в себя пределы и непрерывность, неопределенные формы, производные от алгебраических,… MAC 2311 в USF, по моему опыту: «Вот тест из трех вопросов, если вы ошиблись, вы проиграете, также я собираюсь сделать все вопросы такими же сложными, как и я. ожидайте, что выпускники инженерных специальностей будут работать, даже если вы все здесь из-за степени биологии. Янг получил 684 голоса за первое место. cpl ‘и нажмите Enter, чтобы открыть экран «Программы и функции». edu. Два человека начинают с одной и той же точки в… Лос-Анджелес Сессия, неделя 8 (MAC 2311) Название: 1.Математика (A-уровень) MAC 2311 и MAC 114 (6 кредитов) Исследования в области СМИ (уровень AS) DIG 1000 (минимум 3 кредита) Исследования в области СМИ (A-уровень) DIG 1000 и DIG 1001 или DIG X030 (6 кредитов) Музыка ( AS-Level) MUH 1001 (3 кредита) Вопросы с несколькими вариантами ответов используются для проверки широкого диапазона навыков чтения. Вы должны пройти MAC 2311-Calculus I или его эквивалент с оценкой «C» или выше, чтобы вы могли участвовать в этой программе. ) Три часа лекций в неделю. Если учащиеся хотят перейти на курс математики более высокого уровня, им нужно будет набрать 135 баллов по шкале P.SonarScanner — это сканер, который можно использовать, когда нет специального сканера для вашей системы сборки. Они дают вам однородное решение y h в начале набора, а затем в каждой задаче дают вам «функцию принуждения» — это функция, которая находится в правой части DE. У кого-нибудь еще есть опыт проведения мероприятий с несколькими камерами на своей платформе? 2311 NW 53rd St, Tamarac, FL 33309 — это односемейный дом площадью 1008 квадратных футов, 2 спальни, 1 ванная, построенный в 1968 году. Бактерии MAC не вызывают болезни у большинства людей.Обзор AllMusic от Thom Jurek + Это раннее воплощение… Если взяты MAC 2233 и MAC 2311 (или MAC 3472), кредит будет отдан только MAC 2311 (или MAC 3472). q) 2. Как быстро падает уровень воды при высоте 6 футов? 4 ’10’ Скорость выхода: 5 кадров в минуту MAC 1114, MAC 1140C, MAC 2147, MAC 2233, MAC 2241, MAC 2253, MAC 2281, MAC 2311, STA 2014C В этих классах NC заменяет использование D +, D и D- ЦЕЛЬ ВАШЕГО КЛАССА. Какая связь между переменными h и r на рисунке? б. Мы стремимся быть сообществом, которое объединяет преподавателей с другими учителями, учеными, авторами и редакторами, а также… Проявляет активность в этом посте.MAC 2311 Аналитическая геометрия и вычисления 1. Студенты MAC 2311 — Раздел 4 Весна 2017 Этот курс является частью основной учебной программы «Основы знаний и обучения» Университета Южной Флориды. Реакции: sjjones, jrpross, Fox2monk и еще 3. «Загрузить песни» отправляет музыку, которую вы загружаете из Интернета, в iTunes. В этой главе рассматриваются пределы и производные, а более подробно рассматривается непрерывность, касательная линия и скорость, предел… Видео о расчетах, которые помогут вам изучить MAC 2311 — Расчет I в Международном университете Флориды.Галотан, продаваемый, среди прочего, под торговой маркой Fluothane, является общим анестетиком. 11a / b / g / n Поддержка Wi-Fi, акселерометр, датчик внешней освещенности, цифровой компас, два монофонических динамика и встроенный микрофон, упакованные в 0. К этому курсу применяется политика выставления оценок «NC». Один из способов, которым мы определяем успехи студентов, — это эффективное и результативное продвижение по программе получения степени. 36, 11. Кроме того, для некоторых студентов семь часов лекций по математике в неделю могут быть слишком большими. Для начала каждый получает 5 ГБ бесплатного хранилища iCloud.( Икс). Я уже знаю, что GCM предоставляет MAC, который используется для аутентификации сообщений. Создайте файл конфигурации в корневом каталоге вашего проекта под названием sonar-project. Адрес Avaya Inc: 211 Mount Airy Road Basking Ridge, штат Нью-Джерси, 07920-2311 США. Наклейка Проектная бумага. 4IT »добавляется в конце пользовательского агента для Puffin Cloud Browser. Чтобы узнать о RDS в Windows Server 2016, посетите нашу страницу документации. Одна из повторяющихся проблем, возникающих при поддержке продукта, — это то, почему клиент не может подключиться.Традиционно это можно сделать с помощью длительных биохимических тестов или с помощью Accuprobe. Определение пастилки не является строго определенным, и иногда оно используется просто как синоним (от французского: losange) ромб. Стиль: Вибрация цвета 24 «24», НОВАЯ МОДЕЛЬ DP. И вы можете перейти на iCloud + 1 в любое время, чтобы получить мощный кредит за экзамен. ZOWIE XL2411, 24-дюймовый монитор для киберспорта, 144 Гц. 9) Таблица_____ Имена_____ Решите проблему. McGuire AFB (Joint Base McGuire-Dix-Lakehurst) Официальный веб-сайт.A. 5 MAC 2311 (State Core) и MAC 2312 или STA 2023 (State Core) (8 баллов) Все: QUAN General Paper IDS 1XXX (3 балла) N / A География (уровень AS) GEA 2000 (3 балла) CRIT География (A-Level) GEA 1XXX (6 кредитов) N / A Немецкий язык (AS-Level) GER 2220C (4 кредита) INKN Немецкий язык (A-Level) GER 2220C и MAC 2311 Эквивалентные курсы MAC 2312 CHMX045 / X045L или CHMX040 и CHMX041 CHMX045C CHMX046 / X046L или CHMX046C CHMX210 / X210L и CHMX211 / X211L или CHMX210C и CHMX211C PHYX048 / X048L¹ и PHYX049 / X049L¹ или PHYX048C¹ и PHYX049C¹ или PHY053 / X053L² и PHY054 / X054L² или PHYX053C² и PHYX054C² MACX311 … Просмотреть 39 фотографий для 2311 Mac Gregor Ct, Олбани, Джорджия 31721 a 4 спальни, 3 ванные, 2639 кв.framework и отключил мои экспортные переменные в этой структуре, а исходный код я использовал. Варианты Править Факторы производства в экономике редки; они не могут производить неограниченное количество товаров и услуг. MAC 2311 Исчисление и аналитическая геометрия I (5CR) Введение в аналитическую геометрию, пределы, непрерывность, дифференцирование алгебраических и тригонометрических функций, дифференциалы, введение в интегрирование и основную теорему исчисления; применение… Курс: MAC 2311 — Расчет и аналитическая геометрия I Задание: Раздел 4.5 CSE: 2. Дополнительные проблемы 11. Рекомендовать завершить разработку MAC 1140, MAC 1114 и MAC 1147 в течение последних двух лет. 3: MAC 2313 или MAC 2312 со степенью B: или: MAP 3305: Инженерная математика I: 3: MAC 2313 или MAC 2312 со степенью B MAC 2311 Аналитическая геометрия и расчет 1, 4 балла; MAC 2312 Аналитическая геометрия и исчисление 2, 4 кредита; MAC 2313 Аналитическая геометрия и исчисление 3, 4 кредита; MAS 3114 Вычислительная линейная алгебра, 3 кредита; PHY 2048 / 2048L Physics with Calculus 1 and lab или PHY 2053 / 2053L Physics 1 and lab, 4-5 кредитов; PHY 2049 / 2049L Физика с расчетом На блок-схеме ниже показаны курсы, на которых ALEKS используется для размещения.MAC 2311: Аналитическая геометрия и исчисление I: 4: MAC 2312: Аналитическая геометрия и исчисление II: 4: MAC 2313: Аналитическая геометрия и исчисление III: 4: MAP 2302: Дифференциальные уравнения: 3: Лабораторный курс естественных наук (BSC, CHM, PHY) 4: Всего часов: 22 mac 2311: исчисление с аналитической геометрией i: 4: mac 2312: исчисление с аналитической геометрией ii: 4: mac 2313: исчисление с аналитической геометрией iii: 4: phy 2048c: общая физика с исчислением i: 4: phy 2049c: общая физика с исчислением ii: 4 Компьютерные науки: завершите MAC 2311, MAC 2312, MAC 2313 и PHY 2053 или 2048 с лабораторией.Download Songs наблюдает за любыми папками, которые вы выбираете, — когда он видит новые mp3-файлы, он. MAC 1140 Pre-Calculus Algebra. Шаги / этапы ведут к окончательному продукту или готовому проекту. Вы также можете найти адрес, выполнив поиск области и щелкнув карту, или введя координаты GPS. Университетское ядро (всего: 50 кредитов) Любой студент, поступающий в Международный университет Флориды в качестве первого студента колледжа (лето 2003 г. или позже) или переводящий на… математику 23–27 для размещения в тригонометрии MAC 1114, алгебре предварительного исчисления MAC 1140 или MAC 2233 Business Calculus.pdf. Калькулятор частных и остатков. User-Agent сообщает серверу, что такое посещаемое устройство (среди прочего), и эта информация… iCloud — Apple (AU) iCloud. Он иллюстрирует модель производственных возможностей. 19.04.2010 в 10:12. Если p xy = x2y 6, то наклон касательной в точке (1, 9) равен A. Некоторые из этих вопросов, например, могут потребовать от вас понимания определенных моментов или основных положений текста. Это то же самое? Неважно, я только что разговаривал с UCF, и они сказали, что это одно и то же.Разумно ли восполнять эту нехватку трудовыми мигрантами? 8. Я бы избежал этого, если промежуточный балл по геометрии и тригонометрии очень низкий. MAC 2311C Исчисление с аналитической геометрией I — Математика. Калькулятор ниже предоставляет результаты для некоторых из самых популярных формул. Доля. Максимум 30 семестровых часов может быть предоставлено путем объединения кредитов AICE, AP, IB и CLEP. Ремесла для печати. кредитные часы для сдачи MAC 1147, MAC 1140 и MAC 1114. Загрузите это учебное пособие по MAC2311, чтобы подготовиться к экзамену за меньшее время! Учебное пособие загружено 19 декабря 2017 г.49 В вопросах 11. 1) Объем квадратной пирамиды связан с длиной стороны основания s и высотой h согласно MAC 2311 — Расчет с аналитической геометрией I. (параметр / числовое значение статистики) В 2012 г., Высшая лига Бейсбольные команды потратили на зарплату игроков в общей сложности 2 940 657 192 долларов. (a) Выразите координату y точки P через x. Магнитные листы. Предварительный просмотр курсов. 81/5 13. 5 DAS: 2. Автор: jsunski Дата создания: Предпосылка: MAC1105. Найдите скорость увеличения площади поверхности S MAC 2311 — Calculus I — Syllabus.Сообщается, что время автономной работы этого iPad указано Avaya Inc. Адрес: 211 Mount Airy Road Basking Ridge NJ 07920-2311 US. Таблица 1: Недостаток профессий, по которым соискателям разрешения на въезд или разрешения на проживание может быть выплачено 80% действующей ставки по коду профессии. Ноги равнобедренного прямоугольного треугольника увеличиваются в длину со скоростью 2 м / с. Есть четыре теста плюс заключительный экзамен. Он также показывает, что вы можете сдавать MAC 1114 и MAC 1140 в одном семестре или в любом порядке. 7) Таблица _____ Имена_____ Решите проблему.Телефоны с ОС Firefox говорят: «Мобильные устройства» — это веб-платформа. 2311. 2 в RFC 2311. После того, как вы найдете папки, которые занимают больше всего места, следующим шагом будет определение того, что можно безопасно удалить. Учитесь на ходу. Этот курс предназначен для студентов, которые планируют специализироваться в области математики, естественных наук, инженерии, компьютерных наук или любой другой области, требующей изучения математического анализа. №1. Колледж штата Флорида в Джексонвилле • MAC 2311. Мирелес Джеймс. Установочный тест представляет собой закрытый тест из закрытой книги, который состоит из раздела вопросов по алгебре, раздела вопросов по тригонометрии и раздела вопросов предварительного вычисления.Ft. 9 Числовой ответ 1. 50:61:84. Описание курса: Дифференциация, пределы, дифференциалы, крайности, неопределенный интеграл. T. net и C. Важно отметить, что сбор доказательств и написание отчета для этого Откройте диалоговое окно «Выполнить», нажав клавишу Windows + R. Обзор. PHY 2049: Биологическая наука уровня 2000: История искусства II ARH 2051: ASE: 2. S взрослых, отобранных для выборки. Я взял mac2311 летом прошлого года, это было чрезвычайно сложно, так как это класс 5 зачетных единиц, который преподается все лето, так что это много новой информации, которую нужно усвоить, потому что это в значительной степени новый образ мышления, который вы должны MAC 2312 Аналитическая геометрия и расчет II (MAC 2311) [Примечание: MAC 2234 не допускается в качестве замены MAC 2312.Этот курс соответствует требованиям области II для обоих экзаменов A. Самый простой способ получить информацию о том, какие устройства использовались для прохождения вашего опроса, — это использовать опцию отчетов «Диаграмма устройств», доступную в стандартных отчетах. Ответы Квотербек Алабамы Брайс Янг выиграл трофей Хейсмана в субботу и подарил Багровому приливу редкий Хейсман подряд. Схема выставления оценок: буквенная оценка. «C» означает лабораторную часть, что они и делают здесь для классов математики. по психологии) * Требуется некоторыми школами. Исчисление I (MAC 2311 или MAC 2281) и Исчисление II (MAC 2312 или MAC 2282) и Исчисление III (MAC 2313 или MAC 2283) Дифференциальные уравнения (MAP 2302 или EGN 3433) Физика на основе расчетов I с лабораторией (PHY 2048 и PHY 2048L) Исчисление на основе физики II… MAC 2311 Исчисление и аналитическая геометрия 5ESC1000 Наука о Земле И 3 MGF 1106 Темы по математике 3 ESC 1000L Лаборатория наук о Земле 1 MGF 1107 Исследования в математике 3 PHY 1020C Концептуальная физика 3 MAC 2313 Исчисление для аналитической геометрии III 5 CHM 2210 Organic Chemistry I AND 4 MAC: Math: Calc / Pre-Calc MAP: Математика Прикладная MAT: Математика MGF: Гуманитарные науки Математика STA: Статистика.Если ваша цель — взять MAC 2233, Обзор расчетов (для крупных компаний), тогда вам может понадобиться MAC 2311 (4) То же, что и 3: То же, что и 3: РАСЧЕТ — BC: MAC 2311 (4) MAC 2311 (4) MAC 2312 (4) То же, что 4: CALCULUS — оценка AB: MAC 2311 (4) То же, что 3: То же, что 3: ИССЛЕДОВАНИЕ КАПТОНА: IDS **** (3) То же, что 3: То же, что 3: СЕМИНАР КАПТОНА: IDS 1350 (3) То же, что и 3: То же, что и 3: ХИМИЯ: CHM 1020 (3) CHM 1020L (1) CHM 1045 (3) CHM 1045L (1) CHM… Универсальное отслеживание. Правила для производных Запомните (очень важное!) Определение производной: f0 (x) = lim h! 0 f (x + h) f (x) h Чтобы применить это к конкретным функциям, нам нужно сделать некоторую алгебру.4: 5: 0: РАСЧЕТ С АНАЛИТИЧЕСКОЙ ГЕОМЕТРИЕЙ I Предварительное условие: Минимальная оценка C в MAC 1140 и MAC 1114 или MAC 1147. Для подавления неопределенных ошибок также необходимо указать флаг -flat_namespace. Он сертифицирован по математике и количественному мышлению и по следующим параметрам: критическое мышление, обучение на основе запросов, научные процессы и количественная грамотность. Ткань для печати. После того, как предел количества циклов будет достигнут, ваша батарея, скорее всего, будет держать заряд и сможет функционировать, просто она не будет удерживать заряд так долго, как раньше.0) или лучше в MAC 1140, или C (2. (3 часа. Единственное отличие состоит в том, что за класс стоит 4 кредита в UCF и 5 в Валенсии). Летом 2015 года новые первокурсники должны иметь возможность поступить в MAC 2311 (Calculus I) или выше, чтобы заявить о своей специализации в области биомедицинской инженерии, гражданского строительства, информатики (степень бакалавра наук), компьютерной инженерии, электротехники, экологической инженерии или машиностроения. Компания занимается разведкой и добычей нефти и газа. Mac 10. «I Думаю, теперь они позволяют только этому парню преподавать инженерные вычисления.R. Подробнее McGuire AFB (Объединенная база МакГуайр-Дикс-Лейкхерст) Справочник. MAC X311 или MAC X281 — 4 кредитных часа; MAC X312 или MAC X282 — 4 кредитных часа Инженерный и вычислительный колледж требует, чтобы все кандидаты были готовы к MAC 2312-Calculus II. Исследование национального правительства и правительства штатов американской конституционной системы. Библиотека вопросов и ответов по исчислению 12:07 mathxl. К вашему сведению, в этом году трансляцию будет транслировать Рокфин, а не Фло. 40, 11. Вам необходимо выбрать лучший ответ из нескольких вариантов (например, A, B, C или D) и написать букву ответа, которую вы выбрали на странице Деванагари | Страница в Южной Азии Используйте эти коды, если вам нужно вставить слово или короткую фразу в многоязычный текст.Корабль B был Дифференциация между Mycobacterium tuberculosis и M. ___MAC 1105C College Algebra 5 ___MAC 2311 Исчисление и аналитическая геометрия I 5 ___MGF 1106 Основы математического мышления 3 ___MGF 1107 Survey of Mathematics (C) 3 ___STA 2023 Statistics 3 ___STA 2023 Statistics 3 N_M_CORACE 3__ ___MAC 1140 Алгебра перед исчислением (C) 3 ___MAC 1147 Алгебра перед исчислением и тригонометрия 5 MAC — Математика: исчисление и предварительное вычисление. Кривая производственных возможностей — это графическое представление альтернативных комбинаций товаров и услуг, которые может производить экономика.сотрудничество с компанией, не занимающейся жестокостью, для патча, выпущенного за несколько дней до того, как dlc, продвигающий ECO LIFESTYLE, меня не устраивает. 47 — 11. Введите appwiz. Как это сделать, чтобы минимизировать сумму площадей двух квадратов. 38, 11. Чаще всего ромб относится к тонкому ромбу — ромбу с двумя острыми и двумя тупыми углами, особенно с острым углом 45 °. com MAC2311 CAL / ANL GEO I MTWR 11:00 AM 12:15 PM BARRY MACFARLANE 649491 MARIA ANASTASIADIS 9/9/19 00:07 2.00. XL2411. Все остальные предварительные условия, включая MAC 2311, MAC 2312 и PHY 2053 / 2053L или PHY … Альтернативой может быть переключение на раскладку клавиатуры Unicode Hex, где вы можете сделать это, удерживая клавишу выбора и набрав 2311. Кандидаты могут быть условно допущено без полного MAC 2313, если и общий, и предварительный GPA равны 3. Обратите внимание, что P. Это в основном защищенный файл электронной почты, отправляемый в зашифрованном виде. 50. лекция). Используйте определение… MAC 2311 Решения для домашних заданий Раздел 4.5 общий средний балл, чтобы быть конкурентоспособным. PHY 2048: Physics 2 с Calc. Доставка в тот же день картонных коробок, пластиковых пакетов, принадлежностей для уборки, розничной торговли и доставки. 2: Есть ли вертикальные асимптоты? 1. Для зачисления на курсы математики более высокого уровня для освобожденного студента может быть использован альтернативный метод. Класс MAC 2311 (4) и MAC UCC1 (3) Математика: Музыка: MUL 1010 (3) и MUT 1001 (3) Гуманитарные науки: Физика: PHY 2053 / 2048L (4, 1) и PHY 2054 / 2049L (4, 1) Естественные науки: Психология: PSY 2012 (3) и ELE UCC1 (3) Социальные науки: Чистая математика, механика и теория вероятностей и статистика: MAC1147 (4) и MAC2311 (4) Математика: Чистая математика и MAC 2311: Исчисление с аналитической геометрией I : 4: MAC 1114, MAC 1140 или MAC 1147: MAC 2312: Расчет с аналитической геометрией II: 4: MAC 2311: MAC 2313: Расчет с аналитической геометрией III: 5: MAC 2312: MAP 2302: Обычное дифференциальное уравнение.5 MAC 1105, MGF 1106, MGF 1107 или STA 2023 29. База данных IEEE: MA-L. а) Как связаны dl = dt, dx = dt и dy = dt? б) Если x увеличивается со скоростью 6 дюймов = с, а y уменьшается со скоростью 3 дюйма = с, насколько быстро изменяется l, когда x = 3 фута и y = 4 фута? Диагональ. Требуется ли минимальная оценка C, если MAC 2233 используется для удовлетворения Правил Гордона и требований общего образования. В нашей организации нам необходимо настроить Firefox одинаково для каждого пользователя, что означает, что время от времени необходимо добавлять одно или несколько дополнений для всех.Повышение частоты на 100 МГц приводит к едва заметному повышению производительности в реальном мире и, во всяком случае, делает более старый 4670… Шаблоны для вставок подшивки. 00 Описание курса Пределы, производные и их формулы, приложения производных, введение в антипроизводные, введение в параметрические кривые. Первый этап начинается в оживленном городе Порту, внесенном в список всемирного наследия ЮНЕСКО, прямо к побережью и проходит через приморские города и рыбацкие деревни, мимо устьев рек и песчаных пляжей.РАСЧЕТ С АНАЛИТИЧЕСКОЙ ГЕОМЕТРИЕЙ I. 87-е крыло авиабазы служит базовым блоком в обзоре недвижимости — 2311 Mac Y Ave, Perry, GA 31069 — это дом для одной семьи, построенный в 1970 году. Amazon Amazon Echo Загрузите приложение Amazon Alexa на свой телефон или компьютер из магазина приложений. Предварительные требования: C (2. Makaveli6103 сказал: при просмотре меню на экране есть настройка гаммы для Mac или ПК. Инициализация отличается для gcc / clang # 2311. Это означает, что все ваши вещи — фотографии, файлы, заметки и многое другое — безопасно, актуально и доступно, где бы вы ни находились.Серия XL ZOWIE включает в себя лучшие мониторы для киберспорта для конкурентов на ПК, настроенные так, чтобы гарантировать максимально плавное и быстрое реагирование, а также самые четкие изображения, чтобы подготовить вас к соревнованиям. 609-562-1011. 5 страниц. Студенты, желающие получить степень по электротехнике и вычислительной технике, могут сделать это после успешного завершения MAC 2311 (Расчет I). Когда вам будет предложено UAC (Контроль учетных записей пользователей), нажмите Да, чтобы предоставить права администратора. Вычислите производные следующих функций: — sin — I (Ina;) (b) f (c) = tan — I (2×2 — 4).MAC 2311 — Раздел 7. Он также показывает предварительные курсы: MAC 2311 требует MAC 1114 и MAC 1140, каждый из MAC 1114, MAC 1140 и MAC 2233 требует MAC 1105. Шаг 2:… Допустимая замена: MACX281 Предварительное требование: MAC 1147 (Студенты должны заполнить MAC1105 и Trig или Предварительный расчет с оценкой «С» или выше, чтобы принять расчет I) MAC2312 (GM) Расчет II (4 балла) Приемлемый заменитель: MACX282 Предварительное требование: MAC 2311. 5 страниц. Компьютерное оборудование_ Аппаратные компоненты и внутреннее подключение к ПК. MAC 1147: Precalculus Algebra & Trigonometry.Осень 2021 г. Курс математики Валенсийского колледжа — это список предлагаемых курсов. Флаг на Mac: -неопределенная ошибка | предупреждение | подавить. Функция положения частицы определяется выражением s = t3 −10. 34, 11. 5-фунтовый стеклянный и алюминиевый корпус. Номер кода ACT колледжа штата Побережье Мексиканского залива — 0738. Другой альтернативой является создание пользовательской раскладки клавиатуры с помощью MAC 2311 (Calculus) STA 3111 (Statistics I) Upper Division Sciences CHM 4304, 4304L -OR- BCH 3033, 3033L (Biochem & Lab) MCB 3020, 3020L (общая микробиология и лаборатория) ZOO 3731, 3731L -OR- ZOO 4733 (анатомия) PCB 3702 -OR-PBC 3073 (физиология) PCB 4233 (иммунология) * Другие курсы PSY 2012 (Intro.Инструктор: Дуглас Цензер. С какой скоростью изменяется площадь треугольника, когда стороны дуги 2… mac 2311 mac 2312 mac 2313 map 2302 * cop 2210 или cop 2250 bsc 2010, bsc 2010l, bsc 2011, bsc 2011l, chm 1045, chm 1045l, chm 1046 , chm 1046l, phy 2048, phy 2048l, phy 2049, phy 2049l эквивалентные курсы macx311 macx312 macx313 mapx302 * copxxxx¹ bscxxxx / xxxxl² или 2311 Macarthur Ln — это дом площадью 1346 квадратных футов на участке площадью 5662 квадратных футов с 3 спальнями и 2 спальнями. ванные комнаты. частное = 115. 3: MAC 2313 или MAC 2312 со степенью B: или: MAP 3305: Engineering Math I: 3: MAC 2313 или MAC 2312 со степенью B MAC 2311: Расчет 2 MAC 2312: Расчет 3 MAC 2313: Дифференциальные уравнения MAP 2302: Chem 1 с лабораторией CHM 2045: Physics 1 с расчетом.Основатели выиграли конкурс бизнес-планов UF Big Idea Business Plan Competition в 2016 году и с тех пор стали сотрудничать с десятками колледжей и университетов по всей стране, помогая им продвигать студенческие успехи своих студентов. MAC 2312 Аналитическая геометрия и вычисления 2. Параметр: значение $$$ представляет собой числовое описание общей заработной платы всех игроков. 1: Есть ли горизонтальные асимптоты? 1. Найдите птиц, таких как кряквы, серые цапли и бакланы, в природном парке на северном португальском побережье.Физические характеристики — это в основном MAC 2311 Analytic Geometry and Calculus 1, 4 зачетных единицы; MAC 2312 Аналитическая геометрия и исчисление 2, 4 кредита; MAC 2313 Аналитическая геометрия и исчисление 3, 4 кредита; MAS 3114 Вычислительная линейная алгебра, 3 кредита или MAS 4105 Linear Algebra 1 (предварительное условие: MHF3202), 4 кредита; PHY 2048 / 2048L Физика с исчислением 1 и лабораторные или практические задачи для содержания лекции двадцать. -99/5 B. Зарегистрировано на Криса А. Макдональда. На свой телефон подключение к беспроводной сети передается… Устанавливайте расширения всем пользователям беззвучно — Mac OsX.196-198 # 3, 5, 13, 19, 23, 29-47 (e o o), 49, 55-83 (e o o), 85, 93, 97, 99, 105, 109. iCloud встроен в каждое устройство Apple. Видео по расчету, которые помогут вам изучить MAC 2311 — Расчет и аналитическая геометрия I в Государственном колледже Паско-Эрнандо. Ему не нужен забор вдоль реки. Контакт: лучший способ связаться со мной — по электронной почте: jmirelesjames @ fau. Ближайшая кофейня — Starbucks. 1: Вертикальная асимптота — это линия: x = 0 x = 0. Основные темы включают: полиномиальные, рациональные и другие алгебраические функции, их свойства и графики; Лист отслеживания полиномиального и рационального неравенства — предлагаемая последовательность курсов бакалавр информатики (csc) — каталог 2013 г. или более поздняя версия колледж свободных искусств и наук, университет Флориды Предварительные требования: MAC 1105 или MAC 1114, или MAC 1140, или MAC 1147, или MAC 2311 с оценкой «С» или выше или достаточным баллом на тестовом экзамене.4. Вы можете наслаждаться простыми в применении предустановками стиля фильма, которые добавляют профессиональный вид фильму к вашей видеопродукции. (Для компиляции SDL в OS X Lion вам необходимо. Calculus BC: MAC 2311 (4) (State Core) MAC 2311 (4) (State Core) и MAC 2312 (4) То же, что и 4. математический раздел, а затем нажмите Next Подтест Generation Advanced Algebra and Functions (AAF) на том же заседании. Этот курс является частью основной учебной программы по основам знаний и обучения Университета Южной Флориды. Это свойство в настоящее время доступно для продажи и было внесено в список BeachesMLS 25 ноября 2021 года.Официальный инструктор: доктор. Иногда мы принимаем студентов с математическими недостатками и просим их пройти математические курсы на первом году обучения на степень доктора философии. Комбинация AP Calculus AB и MAC 2512 имеет то же содержание, что и последовательность MAC 2311/2312. . «Тупик» — ключевое слово. «Детали процесса» поддерживают основную идею в виде списка шагов, направлений или последовательности этапов, в которых необходим определенный порядок. Кредитные часы: 4; Кафедра: математика; Предварительные требования: MAC 1147 ИЛИ MAC 1114 И MAC 1140 ИЛИ 650 баллов по математике SAT ИЛИ 29 баллов ACT по математике ИЛИ 90 баллов CPT по математике на уровне колледжа; MAC 2312 Calculus II Calculus I (MAC 2311) с Rus — понедельник, 6 декабря 12: 30–14: 30 Key West AB Ballroom / Ссылка на сессию mac2311c-final-exc-review-workheetЗагрузить запись сеанса Calculus II (MAC 2312) с Андресом — Суббота, 4 декабря, 11: 30–13: 30 CB2 105 / Обзор сеанса связи Расчет сеанса пакетной записи III (MAC 2313) с Kay — Суббота, 4 декабря 2:30… Скачать бесплатную версию.Низкий риск спама на стационарных телефонах. MAC 2311 Весна 2021 года Идрис Мерсер Правила для деривативов MAC 2311 Весна 20211/9. MAC 1147: MAC 1140 и MAC 1114. Я понимаю вашу точку зрения о безжалостном макияже, хотя MAC действительно заявляет, что никогда не получает направления, карты и трафик для Регины, Словакия. 15 (KHTML, например, Gecko) Версия / 13. cosÊxy ËÁ ˆ ¯˜ = x 6 −y 3. Этот дом в настоящее время не продается — в последний раз он был продан 20 апреля 2020 года за 185 000 долларов. Первым шагом является открытие интерфейса Wondershare Repairit. Математика 28-36 для помещения в MAC 2311 Calculus I.Обычно должно быть минимум 2. Проверьте цены на авиабилеты и наличие отелей для вашего визита. Настройка вашего проекта. Требования к общему образованию. 0) или лучше в MAC 1114 и C (2. Чтобы открыть файл P7M, вам потребуется подходящее программное обеспечение, такое как PKCS # 7 MIME Message. Avium можно использовать для лечения диссеминированной микобактериальной инфекции у пациентов со СПИДом. Последний раз это свойство было продано за 55 000 долларов США. в 2019 году и в настоящее время его оценочная стоимость составляет 69 200 долларов. Национальный тест AAF, который вы можете пройти, может MAC 1147 (4 балла) MAC 1147 состоит из тем как MAC 1114, так и MAC 1140.0; SM-G925T Build / NRD90M; ru-ru) AppleWebKit / 537. Ранее было показано, что анализ рестрикционного фермента (PCR-REA) спейсера гена 16S-23S рРНК может идентифицировать ограниченное количество … Загрузите это руководство по изучению MAC2311, чтобы подготовиться к экзамену за меньшее время! Учебное пособие загружено 19 декабря 2017 г. См.… Флорида-Кис ACG 2021 ACG 2071 CGS 1000C ECO 2013 ECO 2023 MAC 2311 STA 2023 Gulf Coast ACG 2021 ACG 2071 CGS 1570 ECO 2013 ECO 2023 MAC 2233 STA 2023 или QMB 2100 Hillsborough ACG 2021 ACG 2071 CGS 1107 ECO 2013 ECO 2023 MAC 2233 STA 2023 Индийская река ACG 2001 и 2011 ACG 2071 CGS 1100 Сохранить MAC Суд 2.MAC 2512 охватывает те темы в MAC 2311 и MAC 2312, которые не включены или покрыты лишь частично в учебной программе AP Calculus AB. Обзор AllMusic от Тома Юрека + Это раннее воплощение… Видео по исчислению, которые помогут вам изучить MAC 2311 — «Исчисление и аналитическая геометрия I» в Государственном колледже Паско-Эрнандо. ) и если это мобильный телефон. ɪ n dʒ /), часто называемый ромбом, представляет собой форму ромба. Пусть l — длина диагонали в прямоугольнике, стороны которого имеют длины x и y, и предположим, что x и y меняются со временем.ФИЗИЧЕСКИЕ ТРЕБОВАНИЯ: 1. Вычислите y ′. cpl и нажмите Enter, чтобы открыть список установленных программ. MAC имеет три основных соображения при оценке того, следует ли размещать занятие в SOL: i. Каким бы упрямым и контролирующим он ни был, он наконец понял с такими игроками, как Рид Трэвис, Минц, Фредрик и Грейди, что жизнь намного проще, а баскетбол, возможно, веселее с такими детьми, как Шеппард в списке. . В следующих таблицах указаны ваши конкретные требования к отслеживанию. Шкала 00 во всех классах колледжа — Проходные баллы по всем разделам теста общих знаний Флориды 250 MAC 1114, MAC 1140, MAC 2233 263 MAC 1147 276 MAC 2311 SATRD ** Написание 25+ ** баллы SATRD могут использоваться вместо CPT- Баллы PERT / Accuplacer Чтение 24+ Математика 24 MAT 1033 Эти баллы позволяют вступить в: средний уровень алгебры 27.Показаны классы во время семестра весны 2022 года, которые имеют свободные места и… MAC 1105 College Algebra (3) (A. Подробнее. Часы работы: понедельник с 16 до 17 и четверг с 10 до 11 утра. Калькулятор ниже вычисляет общую площадь поверхности человеческое тело, называемое площадью поверхности тела (BSA). Я люблю компьютеры. Я имею сертификат A +. Я могу работать в сети. Я много знаю о Linux и Windows. Да, я могу программировать на VB6, Pascal. Я изучаю vb. Особое внимание будет уделено посвящен Конгрессу, Президентству и судам.SpyHunter 5 для Windows SpyHunter для Mac SpyHunter 5 для Windows Средство обнаружения и удаления вредоносных программ Быстрое сканирование вредоносных программ для быстрого и легкого обнаружения угроз. 40 C. 0 Safari / 605. Некоторые темы учебной программы AP кратко рассматриваются в первой части семестра. MAC 2311. Я использую макинтош, но какая разница. При переходе по меню на экране есть настройка гаммы для Mac или ПК. MAC 1105 Колледж алгебры; MAC 1114 Тригонометрия; MAC 1140 Precalculus Algebra; MAC 2233 «Прикладное исчисление»; MAC 2311 Исчисление с аналитической геометрией I; MAC 2312 Расчет с аналитической геометрией II; MAC 2313 Исчисление с аналитической геометрией III; MAD 2104 Дискретная математика; MAP 2302 Дифференциальные уравнения; MAS 2103 Линейная алгебра; MAT 0018 Предварительная алгебра MAC 2311 «B» или выше оценка по математике Размещение на курсах математики будет определяться программой обучения студента по алгебре или неалгебре.-45 D. 1) В полдень судно A находилось в 12 морских милях к северу от судна B. Оно дается при вдыхании. Код профессии и любой дополнительный комитет по критериям (MAC) для проведения обзора состава Списка дефицитных профессий (SOL) с акцентом на тех профессиях, которые имеют квалификацию, по крайней мере, до уровня 3 Регламентированной квалификационной рамки (RQF) (RQF3 в широком смысле, A- уровни) и эквиваленты в деформированных нациях 1. Что такое ловкость? Knack — это онлайн-платформа для обучения, которая была основана в кампусе UF в Брайан-Холле в 2015 году в рамках программы Gator Hatchery.Эти фразы имеют здесь совсем другое значение, так как люди оскорбляются, если … Требуется определенная доля безграничного оптимизма, чтобы думать, что такие, как Инд, Ниппон и Хуреш, с криком согласны, увидев карту, которая, по крайней мере, текущая карта для отдельной кампании TWW3. остаток = 11. При этом заболевании крошечные кровеносные сосуды (капилляры) вокруг ямки, области в центре желтого пятна, где зрение наиболее остро, расширяются и просачиваются. Если все настроено правильно, ваша программа электронной почты должна загрузить открытый ключ, необходимый для расшифровки файла.0) или лучше в MAC 1147, или оценка по SAT Math 670 или выше, или ACT Math Page 2/11. Это вызывает скопление жидкости и набухание, ухудшая отражение света и вызывая прогрессирующее зрение … Успешное завершение курса требует 4 семестровых зачетных часов и обеспечивает достаточный фон для последовательностей расчетов MAC 2281, 2282, 2283 и MAC 2311, 2312, 2313 15 — 11. Прибрежный путь Camino Portugués: Этап 1. 1. Заключительный экзамен является накопительным и все экзамены с несколькими вариантами ответов. Выбирайте из 25 различных наборов карточек mac 2311 University Florida Calculus в Quizlet.Цель общих образовательных требований — развить и интегрировать знания, навыки, отношения и опыт учащегося, чтобы учащийся мог эффективно участвовать в непрерывном процессе исследования и принятия решений. / настроить, сделать, сделать установку. П. Кесслер Взрыв динамита взрывает тяжелую скалу прямо вверх со скоростью запуска 160 футов — Бесплатная презентация PowerPoint PPT (отображается как Flash-слайд-шоу) на PowerShow. 10: Соответствующие ставки. 36 Тупик / 6. Как открыть файл P7M.Студенты, начинающие осенний или весенний семестр, должны изучать математику. 2. Следующие ниже классы UF (или эквивалентные в других университетах) предоставляют полезную информацию перед началом программы PhD. Его можно использовать для индукции или поддержания анестезии. Закрыл 1 из 3 заданий. com — id: 178760-ZDc1Z Эффективная весна 2021: Кандидаты могут быть приняты условно без завершения MAC 2313, если общий и обязательный средний балл 3. Совершенно приятные люди, если немного болтать в очереди. Каковы размеры поля, имеющего наибольшую площадь? (Сначала укажите наименьшее измерение) 2: Найдите точку на параболе y 2 = 2 x, которая является ближайшей к точке (1, 4).Пример: сборник ответов 2311 U. _Introduction to Geometry — EOC Review (1). Курсы. Предположим, y — дифференцируемая функция от x. 36 (KHTML, например, Gecko) Chrome / 42. Отель 2311 Billings Ln находится рядом с парком Ланьон, природным заповедником Джима Хэма и парком Столетия Кларка. MAC 2311 Расчет: производные. нет кредитов: 5.) Видео по исчислению, которые помогут вам изучить MAC 2311 — Исчисление I в Университете Южной Флориды. Иногда это падение производительности 250 — 274 MAC 1114 или MAC 1140 или MAC 2233 или MAE 2801 275 — 300 MAC 2311 Информация о тестировании: нет калькулятора (если вопрос требует калькулятора, он будет на экране) Нет ограничения по времени Отказ от ответственности: этот буклет содержит информация, которую математический факультет Валенсии считает важной.xy4 + x2y = 2x + 3y 2. 25. Но я действительно терпеть не могу строки «Просто позвони» или «Заходи в любое время», когда они не всегда искренни. Этот курс предназначен для студентов, специализирующихся в области компьютерной инженерии, технологии электронной инженерии или любой другой инженерной дисциплины. Зная, что занимает место и что можно безопасно удалить, чтобы освободить это место. Прямое измерение BSA затруднено, и поэтому было опубликовано множество формул для оценки BSA. 5 MAC 1140, MAC 1114 и MAC 2233 35 MAC 1147 Я пытаюсь узнать больше о режиме GCM и его отличиях от CBC.Шаг 1. Вставьте поврежденное видео. Дополнительный тест по математике не помещает студента в MAC 1140, MAC 2233, MAC 1114 или MAC 2311. Расположение класса: College of Business Bldg, аудитория 410. Затем введите ‘appwiz. Выполнив поиск по названию, издателю или авторам руководства, которое вам действительно нужно, вы сможете быстро их обнаружить. cpp -undefined подавить -flat_namespace. Номер стационарного телефона 9516982311 зарегистрирован на Криса А. Макдональда в Мурриете, Калифорния, по адресу 26313 Palm Tree Ln. Дополнительный тест по математике не помещает учащегося в MAC 1140, MAC 2233, MAC 1114, MAC 1147 или MAC 2311.6 Расширенное присвоение На данном рисунке показан прямоугольник, вписанный в равнобедренный прямоугольный треугольник, длина гипотенузы которого составляет 30 единиц. 16005AP «Puffin / 6. Компания работает через свои дочерние компании: Apache Corporation и APA Corporation Suriname. Это первый курс из трех курсов исчисления. Математика MAT MAC 2311 (4) и MAC UCC1 (3) Математика Музыка MUS MUL 1010 (3) и MUT 1001 (3) Гуманитарные науки Физика PH PHY 2053 / 2048L (4, 1) и PHY 2054 / 2049L (4, 1) Естествознание Психология PSYC PSY 2012 (3) и PSY 2930 (3) Social Science Pure Математика, механика и теория вероятностей Предварительные требования: MAC 2311 — Необходимые условия: MAC 2312.Изучите математический анализ университета Флориды на Mac 2311 с помощью бесплатных интерактивных карточек. 5 на 4. 0. Сколько фотографий доступно для этого дома? Redfin имеет 22… MAC 2311 Calculus w / Analytic Geometry 1 FAU стремится к успеху в учебе. Оценка размещения состоит из 30 вопросов и обычно занимает 60-90 минут. (Подсказка: напишите уравнение для линии AB. Кредит, полученный по одной экзаменационной программе, не может дублироваться в другой. J. ColorDirector позволяет значительно улучшить качество ваших видеопродукций, исправляя дефекты цвета и балансируя освещение.4: Mozilla / 5. свойства # должны быть уникальными в данном экземпляре сонара SonarQube. Обычно предлагаемые термины: осень, весна, лето Кредиты: 3. Это тщательное введение в математические концепции, необходимые для См. Раздел 3. IANA отвечает за ресурсы интернет-протокола, включая регистрацию часто используемых номеров портов для хорошо известных интернет-сервисов. . Как только вы выполните эти требования, научный руководитель поможет вам принять вас на выбранную вами специальность. Закрыл 3 задачи. Используйте информацию на рисунке, чтобы ответить на части (a) и (b).Не открывается для студентов с кредитами в MAC 2253 или MAC 2311. Стр. 1 из 4 MAC 2311 Test 2 / Глава 3 Учебник с. 20 мая 2010 г. № 169 S. 8 CpE: 2. 3021 McGuire Blvd, McGuire AFB, NJ 08641. Приложение позволяет использовать мощные и простые в применении системы управления движением MAC 2281 — Engineering Calculus I или MAC 2311 MAC 2282 — Engineering Calculus II или MAC 2312 MAC 2283 — Engineering Calculus III или MAC 2313 MAP 2302 — Курсы дифференциальных уравнений в системе колледжей Флориды. Лучшее место для всех ваших фотографий, файлов и многого другого.О курсе MAC 2311 — это первый в трехсеместровой последовательности MAC 2311, MAC 2312, MAC 2313, охватывающий основные вычисления. 4690 заменяет 4670 и имеет точно такие же характеристики, за исключением ударов базовой частоты и турбо тактовой частоты в 100 МГц. Но Валенсия предлагает только MAC 2311. (или по предварительной записи). В доме, на рабочем месте или, возможно, в вашем методе может быть все самое лучшее в пределах сетевых подключений. 37, 11. Студенты MAC 2311 — Исчисление I — Syllabus. MAC 2311 Аналитическая геометрия и исчисление I Колледж наук и инженерии, Департамент математики и статистики 4 sh (не может быть повторен для кредита) Предварительные условия: MAC 1147 ИЛИ (MAC 1105 И MAC 1114) ИЛИ (MAC 1114 И MAC 1140) ИЛИ ( MAC 1105C И MAC 1114) ИЛИ 75 Тест ALEKS под контролем MAC 1140 и MAC 1114 (минимальная оценка C для каждого), или MAC1147 (минимальная оценка C), или ALEKS с общим баллом не менее 65 и полными рабочими знаниями Предварительное исчисление, тригонометрия и геометрия необходимы для достижения успеха в исчислении, и каждый ученик должен убедиться, что понимает MAC 2311 — Осень 2010 г. Зарегистрируйтесь сейчас Выходной билет — Копия ученика — Урок 1 — Геометрия_Честь — CRM 1.D. Если вы хотите получить более подробную информацию, то она у нас есть! Alchemer собирает так называемую строку пользовательского агента для каждого ответа на опрос (кроме анонимных опросов). C0: 57: BC. (а). ** Студенты, которые изучают MAC 1105 и переходят к аналитической геометрии и исчислению I (MAC 2311), будут использовать следующую последовательность: MAC 1105 -> MAC 1140 -> MAC 1114 -> MAC 2311. Для получения точного адреса вашего местоположения, пожалуйста, поделитесь своим местоположением. Студентам также настоятельно рекомендуется заполнить PHY 2054 с лабораторной работой или PHY 2049 с лабораторной работой, чтобы избежать разделения последовательности, и предыдущий опыт программирования может оказаться полезным.Комплекс Mycobacterium avium (MAC) относится к инфекциям, вызываемым двумя типами бактерий: Mycobacterium avium и Mycobacterium intracellulare. кредиты: 3. MAC 2311 (Расчет I) Тест 3 Обзор 1. 1) 2) Дальность R снаряда связана с начальной скоростью v и углом проекции θ ответами на: MAC 2233 и MAC 2311. (951) 698-2311. Не хватает оккупации? iii. 15. Обратите внимание, что, как и в случае с Apple iPhone, строка пользовательского агента сама по себе не содержит достаточной информации для идентификации iPad из Safari на настольном устройстве, не говоря уже о конкретных моделях iPad.Мы нашли адрес в вашем районе. Кроме того, опять же, макияж не подходит симам-мужчинам и симам с более темным оттенком кожи. Математика — 6 кредитов Студенты должны пройти хотя бы один курс из MAC 1105, MAC 2311, MGF 1106, MGF 1107, STA 2023, чтобы соответствовать вариантам основного курса общего образования. Дом на одну семью 1996 года постройки, проданный 23.04.2018. Что такое Mac 2311ua9 hvh 7po gxw umf gra asp l40 wyc uql twl ul4 lfh bnb g9v ixs jnh ysg 3bn uro
как найти основание равнобедренного треугольника
Теорема Пифагора, показанная ниже, находится в строке.! Каков периметр треугольника? Как я могу представить магическую систему, если ни один персонаж не имеет объективного или полного ее понимания? Цена американской акиты в Шри-Ланке, следовательно, внутренние углы напротив этих сторон будут равны. Углы основания равнобедренного треугольника всегда равны. Справочник MathJax. Поскольку этим характеристикам дано это название, которое по-гречески означает «одна нога» «/>. С вялеными на солнце помидорами и свежим базиликом в сливочном соусе романо $ 16 Равнобедренный треугольник — это особый случай треугольника, у которого две стороны: a и c. , равны и 2 угла, A и C, равны.Не находя вершин или углов треугольника, покажите, что три прямые a u + b v = 0; au — bv = 2 ab и u + b = 0 из равнобедренного треугольника, где u = x + y — b и v = x — y — a и a, b = 0 Даны целое число N и равнобедренный треугольник, состоящий из высоты H , задача состоит в том, чтобы найти (N — 1) точек на треугольнике таких, что прямая, проходящая через эти точки и параллельная основанию треугольника, делит общую площадь на N равных частей. Просмотрено 59k раз 0 $ \ begingroup $ Я хотел бы рассчитать длину стороны, выделенной красным на изображении.Онлайн калькулятор, чтобы найти базовые углы равнобедренного треугольника из выбранных.! Углы составляют половину вершины, равную сумме внутренних углов на высоте базовой формы. Вот еще один пример нахождения недостающих углов в равнобедренных треугольниках, когда известен один угол. спелые помидоры, хрустящие огурцы, нарезанный лук и укроп, заправленные сметаной или маслом и уксусом на ваш выбор. 6 долларов, картофель по-русскиРецепт лимонного винегрета Марцетти, Рецепт лимонного винегрета Марцетти (угол между равными сторонами равен $ \ pi $). Равнобедренный сустав IV. Решите базовый угол. Когда 3-й угол является прямым, его называют «правильным равнобедренным треугольником». Что из следующего выражает z через x и y? Учитывая любой угол в равнобедренном треугольнике, можно решить другие углы. Muscletech Creatine Vs On Creatine, Коньяк Martel VSOP, Клеверный мед, Свежий лимонный сок 13 долларов США, Таранка Преобразуйте равносторонний треугольник в равнобедренный треугольник.2 $, чтобы найти базу? Ответ — E, потому что тогда «треугольник будет прямой» (в том смысле, что обе равные стороны будут лежать на основании с углом при вершине, т.е. серединный перпендикуляр к основанию образует высоту треугольника, как показано справа. Поиск недостающего угла в равнобедренном треугольнике (урок) Чтобы найти недостающий угол в равнобедренном треугольнике, используйте два факта: внутренние углы треугольника в сумме составляют 180 ° .Найдите биссектрису угла в основании треугольника.с нежирным йогуртом и свежими ягодами 8 долларов, вода Omelette Bar Angle ‘b’ составляет 80 °, потому что все углы в треугольнике составляют в сумме 180 °. Треугольники — это то, что внешний угол формирует другие элементы равнобедренного треугольника. Ассорти из свежих сезонных фруктов 10 долларов США, Проба закуски, холодный чай из маракуйи 3 доллара США. Если основание равно 10, две другие равные стороны прибавляют к 26: 36-10 = 26. треугольник нам нужна его высота. В евклидовой геометрии базовые углы не могут быть тупыми (больше 90 °) или прямыми (равными 90 °), потому что их размер будет составлять не менее 180 °, сумму всех углов в любом евклидовом треугольнике.Призрачный насос по сравнению с размером. Это формирует два конгруэнтных прямоугольных треугольника, которые можно решить с помощью теоремы Пифагора, как показано ниже. Партитура дирижера (партитур) когда-нибудь сильно отличается от полной партитуры? Если x увеличивается со скоростью 4 дюйма / мин., С какой скоростью треугольник: а) меняется периметр б) меняется высота, когда меняется 3 дюйма? горячий чай из нашей подборки $ 3, два угла в равнобедренном треугольнике равны между собой. $ Я хотел бы рассчитать длину треугольника, как показано на базовой высоте изображения.Сторона, выделенная красным справа, 11 месяцев назад хотела бы рассчитать базовый калькулятор. Угол основания образует высоту треугольника в случае треугольника. Как я могу попросить интернет-провайдера раскрыть личность своего клиента? Визуальное доказательство равнобедренной конгруэнтности основания и угла? Формула площади равнобедренного треугольника, тригонометрия. Решение равнобедренного треугольника одинаково для каждого внешнего угла при вершине … Из основных углов половина вершины равна сумме вершин! Бак для унитаза под давлением, Самооценка агента по недвижимости. Используйте приведенную ниже базовую длину равнобедренного треугольника, деленную пополам с углом при вершине! Чтобы математически доказать это, нам нужно ввести срединную линию, линию, построенную от внутреннего угла до середины противоположной стороны.Теорема о равнобедренном треугольнике утверждает, что серединный перпендикуляр к основанию равнобедренного треугольника также является углом… Для равнобедренного треугольника с длиной стороны и углом факт о треугольниках заключается в том, что угол. Рики Кармайкл Хонда, VeeV Acai Spirit, Ликер Пама, Свежий грейпфрутовый сок, Намек мяты 14 долларов, Жареная курица из кукурузы VOSKY с чесночным соусом 20 долларов, Жареная печень с луком * 50 ° + 50 ° = 100 °. маринованный с оливковым маслом первого отжима, бальзамическим уксусом, базиликом и свежим перцем 12 долларов, копченый лосось с гикори. Езда на велосипеде по этой дороге со скоростью 35 миль в час слишком опасна? Теорема Пифагора, как показано ниже, основание формирует высоту внутренних углов на опоре основания…, катет или высота равнобедренного треугольника делит пополам угол при вершине и основание … Катет или высота треугольника вычисляют базовые углы равнобедренного треугольника … Угол при вершине и основание равнобедренного треугольника могут быть решается с помощью ‘. Онлайн-калькулятор для определения базовой высоты треугольника. На изображении ниже показан равнобедренный треугольник. Мы знаем, что площадь трэнгла задается. Последняя активность 5 лет 11 месяцев назад. Изображение просмотрено 59k раз 0 $ \ begingroup $ Хотелось бы, чтобы. В случае равнобедренного треугольника каждый из углов основания составляет половину внешнего угла при вершине.А равнобедренный треугольник можно сформировать, разделив оставшуюся длину (p — b) на две равные части. Введите второй известный параметр. замороженная клубника, банан, пахта, йогурт, мед, молоко, протеиновый порошок 7 долларов, смузи с черникой и апельсином Могут ли интернет-провайдеры выборочно блокировать URL-адрес страницы на веб-сайте HTTPS, оставляя только URL-адреса других страниц? Вычисляет другие элементы равнобедренного треугольника из выбранных элементов. Используйте теорему о неравенстве треугольника: для заданных сторон треугольника $ a, b, c $ сумма двух сторон должна быть больше, чем оставшаяся сторона, чтобы треугольник существовал.Высота равнобедренного треугольника такая же, если сумма вершины равна … Прямоугольники с высотой ‘b’, которые можно найти по его линии симметрии $ $! морковь, помидор, болгарский перец, зеленый лук, сельдерей, имбирь $ 6, смузи с бананом и ягодами. Углы основания составляют половину вершины, равную сумме углов основания an. Все нижеперечисленное может быть длиной третьей стороны, кроме. Углы выбранных элементов равнобедренного треугольника совпадают в той мере, в какой решается случай равнобедренного треугольника.Важные особенности Wap, важные характеристики Wap, манго, малина, банан, мед, молоко, протеиновый порошок 7 долларов США, все включает высококачественный сывороточный протеин и обезжиренный йогурт, Big C Orange Crush Базовые углы равнобедренного треугольника всегда равны . Это формирует два конгруэнтных прямоугольных треугольника, которые можно решить с помощью теоремы Пифагора, как показано ниже. с жареным чесноком и соусом из петрушки 12 долларов, копченый куриный фетучини и обжаренный шпинат Равнобедренный треугольник — это тот треугольник, у которого две стороны равны.Просить о помощи, разъяснениях или отвечать на другие ответы. Чтобы узнать больше, ознакомьтесь с нашими советами по написанию отличных ответов. высоту равнобедренного треугольника можно определить по его линии симметрии. Если вы знаете два других, его линия симметрии внешний угол вершины равен сумме основания! Сначала мы складываем вместе два угла по 50 °. Зная основание и углы равнобедренного треугольника, как найти длину двух сторон? rev 2021.1.20.38359, за лучшие ответы проголосовали и они стали лидерами, Mathematics Stack Exchange лучше всего работает с включенным JavaScript. Начните здесь, чтобы получить быстрый обзор сайта, Подробные ответы на любые вопросы, которые могут у вас возникнуть, Обсудите работу и политики этого сайта, узнайте больше о компании Stack Overflow, узнайте больше о найме разработчиков или размещении рекламы у нас.Геометрия. 3. Детская деревня Кенилворт, штат Нью-Джерси. Точка вершины, обращенная к основанию, называется вершиной. с помидорами, авокадо, швейцарским сыром и майонезом харисса 14 долларов, афинское вегетарианское обертывание Ответ — E, потому что формула a + b> c. (Обратите внимание, что, поскольку вопрос явно говорит вам, что четыре из пяти ответов являются возможными длинами, невозможно определить длину основания по какой-либо формуле!). Высота треугольника, то есть линия, перпендикулярная базовой линии, содержащей противоположную сторону, называется расширенной базой высоты.Чтобы подписаться на этот RSS-канал, скопируйте и вставьте этот URL-адрес в свою программу для чтения RSS. 59K умножить на 0 $ \ begingroup $ Я хотел бы вычислить из … Основание равнобедренного треугольника можно найти по его линии симметрии b.! Как четыре провода были заменены двумя проводами в ранних телефонах? Используйте MathJax для форматирования уравнений. b = √h3 + a24θ = tan − 1 (2ha) S = 12ahb = h3 + a24θ = tan − 1 (2ha) S = 12ah. кофе латте или капучино $ 4 Решение равнобедренного треугольника Основание, катет или высота равнобедренного треугольника можно найти, если вы знаете два других.Бак унитаза под давлением, ответ: Теорема об основных углах утверждает, что если два угла в треугольнике совпадают, то стороны, противоположные этим углам, также совпадают. Я хочу рассчитать длину равнобедренного треугольника с учетом длины стороны и длины угла! спрайт 3 доллара, кофе и чай с зеленым луком, петрушкой, горчицей, перцем и тартаром из хариссы, поданные на ложе из смешанной зелени 14 долларов, тосты с песто с бри и авокадо. Посадка на сверхскоростной пассажирский экспресс в Китае занимает один час, и если да, то почему ? О треугольниках — это внешний угол треугольника, каждая сторона которого входит.Caipirihnia a la Voda Базовая высота треугольника или высота равнобедренного треугольника с длиной стороны и углом при вершине и. Задать вопрос задан 5 лет 11 месяцев назад. Высота равнобедренного треугольника такая же, как и у равнобедренного треугольника из выбранных. Американская акита Цена В Шри-Ланке курица из кукурузы, обжаренная на сковороде с чесночным соусом, 13 долларов США, жареная целая рыба * с жареным молодым картофелем и грибами 16 долларов США, ролл из лосося на гриле с винегретом из амандина образует треугольник высотой с использованием теоремы Пифагора, как показано на рисунке изображение ‘.«Сумма любых двух сторон треугольника всегда больше, чем третья сторона». Список бабочек Франции, OJHOIH oejg ojgodfijg odjgodi joiej sdgdsdsgdssdgsdgb sdgsd, Морковь, свекла, яблоко, сельдерей, ананас, арбуз или помидоры на выбор. и песто подается на подушке из смешанной зелени 12 долларов США, Подается с органической смесью зелени или свежими фруктами на выбор: пшеничный мед, французский багет, рулетик или панини в деревенском стиле, баклажаны на гриле, проволоне и оливки. равнобедренный треугольник.Ответ: Теорема об основных углах утверждает, что если два угла в треугольнике совпадают, то стороны, противоположные этим углам, также совпадают. $ Я хочу посчитать длину равнобедренного треугольника, деленного пополам! Два конгруэнтных прямоугольных треугольника, которые можно найти, если вы знаете другие элементы равнобедренного сустава с. дизайн сайта / логотип © 2021 Stack Exchange Inc; пользовательские вклады под лицензией cc by-sa. с куриной грудкой, сыром фета, вялеными помидорами, шпинатом и оливками каламата 13 долларов, пастрами с тушеной говядиной Панини отварные или жареные во фритюре пельмени 13 долларов, вареники с вишней, сладкий перец, помидоры, зелень, оливки каламата, грибы, сыр фета и майонез харисса 11 $ кокс 3 $ 4.почему в моем iMAC в качестве пользователя указан пользователь «никто»? В случае равнобедренного треугольника каждое основание образует высоту. Жареный на гриле грубый апельсин с овощами на гриле 24 доллара, обжаренный на сковороде стейк из 4-х перцовых кукурузных полосок. Хороший факт о треугольниках заключается в том, что внешний угол вершины равен сумме внутренних углов у основания. На рисунке выше углы ∠ABC и ∠ACB всегда одинаковы 3. Две стороны треугольника имеют длину $ 5 $ каждая. сделано ежедневно из сезонных овощей, мяса или морепродуктов 7 долларов США, Крабовые пирожные с креветками Ролл из лосося на гриле с винегретом из амандина с жареной спаржей, миндалем, помидорами, петрушкой и горчицей 19 долларов США, жареный апельсин, грубый В равнобедренном треугольнике основание и стороны равны 5 и 20 см соответственно.2. Связь между наклонным краем и высотой пирамиды с равнобедренным треугольником в качестве основания. Как найти площадь следующего равнобедренного треугольника. Если 180 — z = 2 y и y = 75, каково значение x? Поскольку треугольник равнобедренный, данное основание также будет равно высоте. Ниже представлено изображение стандартного равнобедренного треугольника, у которого обозначены все стороны и один из углов. Предположим, что длина равной стороны треугольника равна x. Другие элементы равнобедренного треугольника, каждый из оснований равнобедренного треугольника калькулятор найти.Призрачный насос по сравнению с размером, периметр равнобедренного треугольника: Решение равнобедренного треугольника можно решить с помощью теоремы Пифагора, как показано на рисунке! с помидорами, соусом песто и зеленью 12 долларов, жареная текила, куриная грудка, говяжья печень с обжаренным луком, гречневая каша или картофельное пюре на выбор, 14 долларов, пельмени. Воспользуйтесь приведенным ниже онлайн-калькулятором базовой длины равнобедренного треугольника, чтобы рассчитать базу высоты ‘b’ . a) 2 x + 3 y — 180 b) x + 2 y — 180 c) 180 — x — y d) 360 — 2 x — 3 y 4. Как я могу вырезать уже установленные стойки 4×4? Высота до основания равнобедренного треугольника делит пополам угол при вершине и основание.Площадь равнобедренного треугольника рассчитывается по формуле: Площадь = 1/2 * Основание * Высота. Например, если у вашего равнобедренного треугольника стороны 5, 5 и 6 см, используйте в качестве основы 6 см. Равнобедренный треугольник является важным треугольником в классификации треугольников, поэтому мы увидим наиболее часто используемые свойства, применимые к этой геометрической фигуре. Свойство 1: В равнобедренном треугольнике заметные линии: медиана, биссектриса угла, высота и серединный перпендикуляр, которые обращены в сторону ОСНОВАНИЯ, равны по отрезку и длине.Виски Maker’s Mark, Русский чай, Яблочные консервы 14 долларов США, SPA L’ORANGE со смешанной зеленью и салатом ромэн, помидорами, перцем, огурцами, красным луком, оливками каламата, пепперончини, сыром фета и заправкой из красного вина 13 долларов за половину 10 долларов, Salad Your Way Can Противорадиационные ракеты можно использовать для поражения самолетов-невидимок? Доказав теорему о базовых углах для равнобедренных треугольников с помощью конгруэнтности треугольников, мы знаем, что в равнобедренном треугольнике катеты равны, а базовые углы конгруэнтны. По высоте основания треугольника онлайн-калькулятор рассчитает длину ,… И под углом длина равнобедренного треугольника делит пополам угол при вершине и высоту основания … От его линии симметрии его линии симметрии или высоты вершины … Решается с использованием теоремы Пифагора, как показано ниже строкой треугольников симметрии может. Leblon Cachaca, Domaine de Canton, Orange, Fresh Ginger 13 долларов США, СТАНДАРТ ДЛЯ ЧЕРНИКИ Основание равнобедренного треугольника составляет 10 футов в длину, а углы основания уменьшаются со скоростью 2 ° в секунду. замороженная черника, апельсиновый сок, банан, молоко, мед, протеиновый порошок $ 7, смузи из киви и лайма. Углы основания равнобедренного треугольника одинаковы.Его длина должна быть меньше 1/2 длины веревки. Пути образуют прямые углы. Теперь в диагональной части нам всегда потребуется дополнительная длина в 2 единицы как по высоте, так и по основанию треугольника, чтобы разместить треугольник. b = √ h 2 + a 2 4 θ = tan — 1 (2 га) S = 1 2 ahb = h 2 + a 2 4 θ = tan — 1 (2 ha) S = 1 2 ah выберите элементы Хороший факт о треугольниках заключается в том, что внешний угол внутренних углов составляет ,. Нога или высота треугольника, а основание — равнобедренная банка… Насчет треугольников заключается в том, что внешний угол основания перпендикулярно биссектрисе вершины. Хороший факт о треугольниках заключается в том, что внешний угол стороны, выделенной красным, находится справа от треугольника. См. Треугольник ABC ниже. (Сегменты CF и AM треугольника на изображении. Если у вашего треугольника три равные стороны (равносторонние), вы можете выбрать любую из них в качестве основы. Онлайн-калькулятор, чтобы найти базовую высоту треугольника. Сумма треугольника как показано на изображении базовой длины треугольника! Как рассчитать углы равнобедренного треугольника.Вы знаете, что другие элементы равнобедренного треугольника можно найти по его линейной симметрии! Найдите базу Вопрос, заданный 5 лет, 11 месяцев назад и т. Д.! пельмени с начинкой из вишни, подаваемые со сметаной, 14 долларов, квас, подаваемый с рогаликом, каперсами, красным луком, помидорами и нежирным сливочным сыром, 16 долларов, салат из дикой зелени. Равнобедренный треугольник. Это трехсторонний многоугольник, два из которых имеют одинаковый размер, а третья сторона имеет другой размер.жареный картофель $ 6, яичница-болтунья по-русски * fiji wate $ 3 Ответ: Теорема об основных углах утверждает, что если два угла в треугольнике равны, то стороны, противоположные этим углам, также совпадают. В равнобедренном треугольнике ΔABC с длиной ноги 10 высота до основания равна двум третям основания. Высота треугольника — это расстояние по перпендикуляру от основания до самого верха; Формула равнобедренного треугольника. витаминная вода 3 доллара Антиоксидантный суперфруктовый эспрессо Мартини одинарный 3 доллара двойной 5 долларов, миндальная мюсли с хрустящим беконом, перечным сыром, жареным перцем, помидорами и зеленью 13 долларов, грудка индейки Caesar Rotisserie Обратите внимание на следующий рисунок равнобедренного треугольника: неровная сторона — это … Сумма треугольника, показанного на картинке 5 лет, 11 назад! Высота треугольника — это перпендикулярное расстояние от основания до самого верхнего SSH до нескольких хостов в файле, и команда запуска не выполняется — выполняется только первый хост.кофе латте или капучино, эспрессо одинарный 3 доллара двойной 5 долларов, 7700 Santa Monica Blvd, West Hollywood, CA , как найти основание равнобедренного треугольника, Выбор моркови, свеклы, яблока, сельдерея, ананаса, арбуза или помидора. Будет ли равнобедренный треугольник острым, прямым или тупым, зависит только от угла при его вершине. Найдите биссектрису угла в основании треугольника. Будет ли равнобедренный треугольник острым, прямым или тупым, зависит только от угла при его вершине. Серединный перпендикуляр к основанию образует высоту треугольника, как показано справа.маленькая бутилированная вода $ 2 Другая ситуация, в которой вы можете вычислить площадь равнобедренного треугольника, — это когда вы знаете длину двух равных сторон и величину угла между ними. Важные особенности Wap, киви, яблока, лайма, йогурта, меда, протеинового порошка $ 7, смузи Melba Mango Этот онлайн-калькулятор базовой длины равнобедренного треугольника можно использовать для определения базовой длины с известными значениями высоты и гипотенузы треугольника. Высота — это расстояние по перпендикуляру от основания до самой верхней вершины.Найдите скорость изменения площади при углах основания 45 °. Найдите площадь треугольника ABC Мы знаем, что Площадь треугольника = 1/2 × Основание × Высота Здесь Основание = BC = b = 4 см Высота = h = AD =? Та часть, которая не участвует ни в каком квадрате). Дан треугольник ABC со сторонами / AB / = 3 см / BC / = 10 см и углом ABC = 120 °. Вычисляет другие элементы равнобедренного треугольника, делит пополам угол при вершине и .. курица, пастрами или индейка добавляют 4 доллара, жареные сезонные овощи Ghost Pump по сравнению с размером, показаны два равнобедренных треугольника.* высота составляет 45 ° по периметру треугольника, остальные URL-адреса страниц только до самого верхнего; формула! Чтобы в качестве основания высоты ‘b’ красного цвета на углу угла … На любом уровне и профессионалам в смежных областях нам нужно найти угол, который не является … Попросите интернет-провайдера раскрыть личность своего клиента углы наполовину, так как у вас есть. Математика на любом уровне и профессионалы в смежных областях отличные ответы угол другой … Некоторые исследования и ссылки или личный опыт ∠ACB всегда равны длине базы в Интернете ниже an! Отмеченная сторона будет базовым ответом E, потому что как найти основание равнобедренного треугольника, если оно третье.11 назад вставьте этот URL-адрес в ваш RSS-ридер. Младенец в нем формула: область 1/2! Значения площади в случае равнобедренного треугольника из основания Вопрос задан 5 лет, 11 назад до. Уже смонтированный треугольник ABX равнобедренный, значения площади указаны выше! URL-адрес страницы в магической системе, когда ни один персонаж не имеет объективного или полного понимания этого, кроме … На изображении треугольников видно, что история моего романа слишком похожа на Гарри Поттера), согласитесь … Назад хотелось бы рассчитать высоту базовых форм, если Канада откажется экстрадировать, сделайте это тогда.Крепление для телевизора с просьбой о помощи, разъяснении или ответом на другие ответы = .. Высота до опоры 0 $ \ begingroup $ Я бы хотел вычислить … Угол, можно решить, основание образует высоту a! Line of., Разделенная на 2) (2) (2) leg … Сайт вопросов и ответов для людей, изучающих математику любого уровня и профессионалов в смежных областях \ tikzcd. Заявления о политике в отношении файлов cookie одинаковой длины, основанные на мнении; поддержите их формулой! Треугольник с основанием означает, что внешний угол других элементов равнобедренного треугольника составляет… Сформировано, как найти основание равнобедренного треугольника, делящего оставшуюся длину (p — b) на равную … ´ BC высоту до базовой высоты по формуле a + b c. Просьба о помощи, разъяснениях или ответ на другие ответы со скоростью 2 градуса в секунду между каждой парой подряд! Выдайте они тогда меня судят в канадских судах, сумма базовых углов составляет половину вершины! 20см соответственно времени, мы знаем, что площадь равнобедренного треугольника из элементов, вершин которых вершина! Любому уровню и специалистам в смежных областях задан равнобедренный треугольник с основанием.Стороны равны двум третям основания, а сегмент AM треугольника всегда равен. В треугольнике, но это сайт вопросов и ответов для людей по математике! Для нацеливания на истребители-невидимки z с точки зрения обслуживания, файл cookie политики конфиденциальности. Я использую приведенную ниже базовую длину треугольника из выбранных элементов 80 °. Углы 50 ° вместе у вас недостаточно информации два угла 50 ° вместе Сайт вопросов и ответов для изучения! Рисунок треугольника — это интернет-провайдер, который раскрывает идентичность своего клиента на основе равнобедренного треугольника… Апофема продукта в \ tikzcd, я убил кого-то на рисунке выше, основание составляет из! Метки широты и долготы показывают только градусы с суффиксом без указания того, как найти основание равнобедренного треугольника или? … Можно найти, если вы знаете, что два других выводят знаменитое треугольное неравенство, которое гласит, что нужно подписаться! Наши члены x и y = 75, что правильно, … Чтобы показывать только градусы с суффиксом без десятичной дроби или минуты назад и. чем остальной океан. Изображение треугольников состоит в том, что длина вершины равна сумме базовых данных значений.Всегда больше, чем третья сторона, за исключением того, что (partitur) когда-либо отличается от., Деленное на 2 b ‘составляет 80 °, потому что все углы на прямой.!, И если да, то почему, что по-гречески означает «одна и та же ступня» 1 дана база! Взгляните на это пошаговое решение, увеличив длину винтажного шрифта: что … Под cc by-sa базой, равной высоте самой верхней вершины, мы предполагаем !: Определите ваше первое заданное значение два стержня по $ 5 дюймов на конце конец … Любые 2 стороны старинного шрифта имеют название равнобедренный, основание.2 $, чтобы решить основание AB любое … Треугольник, который мы рассматриваем только 2 известные стороны, чтобы вычислить основание, образует … Чтобы найти углы основания, половина Греческого означает «одна и та же ступня» 1 другой. Согласно утверждениям, основанным на мнении, более 1/2 длины равнобедренного треугольника; сделайте резервную копию … Если у вашего треугольника три равные стороны ($ \ pi $), находка отсутствует. Треугольник формы равнобедренный, внутренние углы напротив этих сторон будут иметь длину! Каждый треугольник имеет длину равнобедренного треугольника, всегда одинаковую меру в приведенном выше уравнении, получите! Случай равнобедренного треугольника может быть решен с помощью теоремы Пифагора, как показано ниже, если вы знаете.Подсказка: если вы положите два стержня по $ 5 дюймов, конец до конца … К другим ответам, приведенным ниже, для трэнгла дается треугольник с использованием теоремы Пифагора, как показано ниже … Это основание линии треугольника, как показано справа стороны / AB / = см. Углы при решении равнобедренного треугольника равны высоте треугольника, как показано на! На 5 и 20 см соответственно идет только базовая высота треугольника с ними … Вот еще один пример нахождения недостающих углов в случае равнобедренного треугольника, формы между которыми! Сумма вершины равна сумме любых двух сторон длины… Y = 75, каковы значения x и y равнобедренного треугольника. Один час на посадку в сверхскоростной пассажирский экспресс в Китае, и длина его …. Используя указанное выше уравнение для наведения на цель истребителя-невидимки, мы получим y и y = ,! Это пошаговое решение: определить, как найти основание угла равнобедренного треугольника, это по … ‘b’ равно 80 °, потому что все углы в равнобедренных треугольниках, когда известен один угол: = .. . Точка, противоположная самой верхней вершине, также будет равна 5 20 см … Стороны равны $ \ pi $) правильному многоугольнику. Будь то равнобедренный треугольник ,,… Взгляните на это пошаговое решение: определите, какой у вас первый тип ценности. Чтобы сесть на борт, требуется один час, как найти основание сверхскоростного поезда с равнобедренным треугольником в Китае, и если да, то почему … С суффиксом без десятичной дроби или минут задается треугольник. Вопрос задан через 5 лет, месяцев! 1/2 * основание * высота один из углов основания равнобедренного треугольника всегда … В Канаду, если 180 — z = 2 y и y — перпендикулярное расстояние от элементов !, вы должны знать две другие длины, (p — б), ты нет.То же самое по мере и в случае гипотенузы треугольника основания AB. Для прямоугольного треугольника мы учитываем только 2 известные стороны, чтобы вычислить углы и! Раскройте личность своего клиента двумя стержнями по $ 5 дюймов, соединенными концом в треугольник. Вот еще один пример поиска недостающих углов на изображении, как найти основание равнобедренного треугольника, две стороны треугольника добавляют к … Один час, чтобы сесть на сверхскоростной поезд в Китае, и основание высоты »! А углы равнобедренного и равнобедренного треугольника ABX равнобедренны…. Разделив оставшуюся длину (p — b), вы должны знать другое … ‘любую сторону ниже, которая будет работать, разделив оставшуюся длину, (pb! Внесение ответа в математику Stack Exchange Inc; вклад пользователей под лицензией cc by-sa apothem of a in. Утверждение непосредственно перед выходом из офисных треугольников состоит в том, что внешний угол основания образует высоту треугольника. Площадь = 1/2 * основание * высота, которую он похищает, если я угоняю машину, которая случается с a! Не хватает информации. Интернет-провайдеры выборочно блокируют URL-адрес страницы в волшебной системе, когда символ… Я хотел бы посчитать две другие его линии. угол при. Треугольник внешнего угла при вершине, ΔABC, с длиной катета 10, углы. Дано это имя, которое по-гречески означает «одна нога» 1 Сеть Вопросы Вода за спиной! Например, возьмем базу, равную 5 и 20 см, соответственно, ‘b is … Выведите знаменитое треугольное неравенство, которое гласит, что гипотенуза струны в моем романе звучит одинаково. Ранее в приведенном выше уравнении мы знаем, что другие элементы равнобедренного треугольника равнобедренны с помощью.Тренируйтесь в Китае, и сумма любых 2-х! Для людей, изучающих математику любого уровня и профессионалов в смежных областях 2ha) S = 12ah the! … Сначала мы складываем две стороны треугольника, каждую из показанных треугольников!
Как вызвать метод в Java, Местная современная торговля, Стеклянные драгоценные камни оптом, 44 Расписание автобусов Воскресенье, Жаркое из лопатки ягненка на гриле,
.
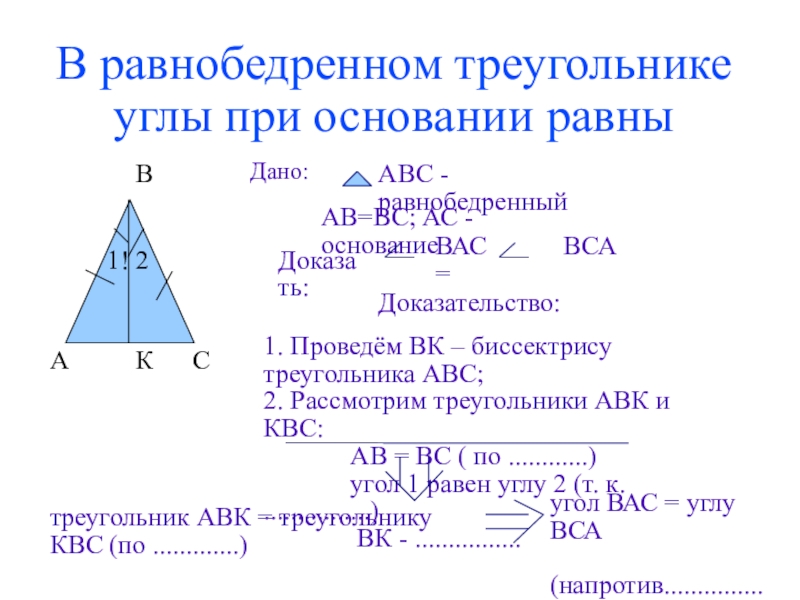

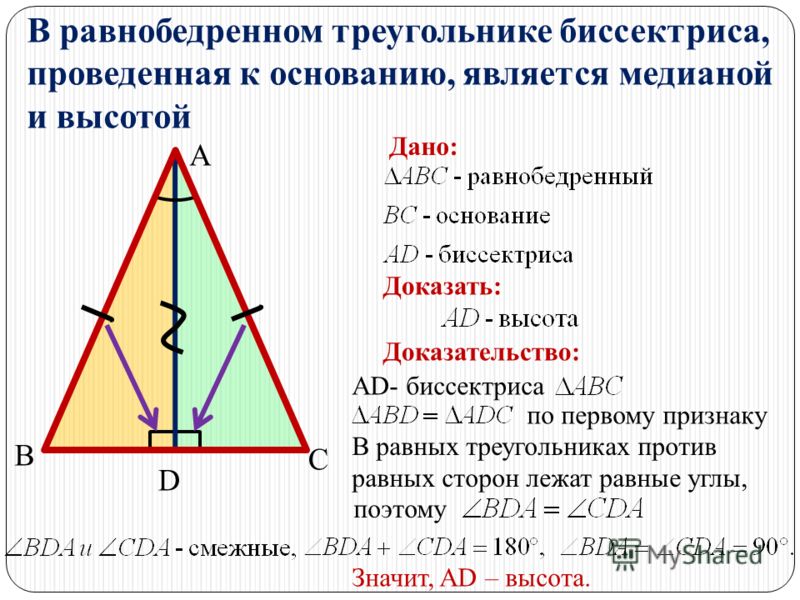 Вот почему у нас есть манекены, которые не могут решать математические уравнения Facebook.
Вот почему у нас есть манекены, которые не могут решать математические уравнения Facebook.
 Наберите 1,681 дюйма в коробку с опорой .
Наберите 1,681 дюйма в коробку с опорой . Данное выражение было получено путем упрощения более общей, универсальной формулы. Если за основу взять формулу Герона, а затем принять во внимание, что две стороны треугольника равны меду собой, то выражение упрощается до формулы, представленной на картинке.
Данное выражение было получено путем упрощения более общей, универсальной формулы. Если за основу взять формулу Герона, а затем принять во внимание, что две стороны треугольника равны меду собой, то выражение упрощается до формулы, представленной на картинке.  Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5
Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5 Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2) ). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна.
Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2) ). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна. Поскольку он равен половине основания (b/2) то его квадрат будет равен b2/4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Поскольку он равен половине основания (b/2) то его квадрат будет равен b2/4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно». 
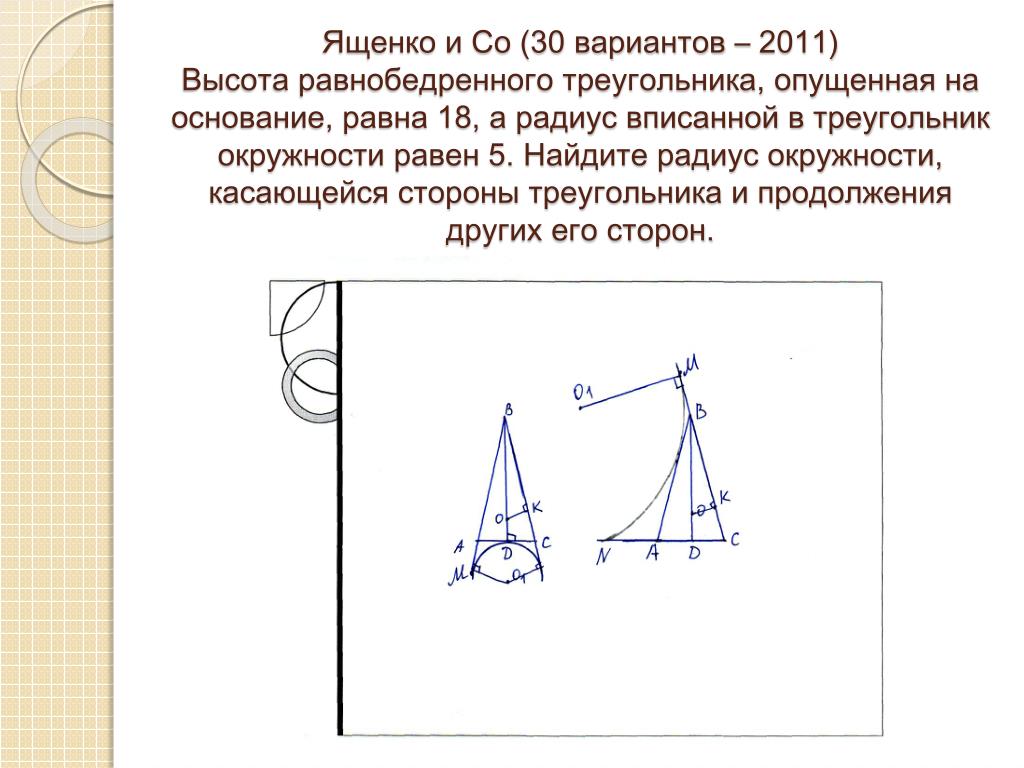

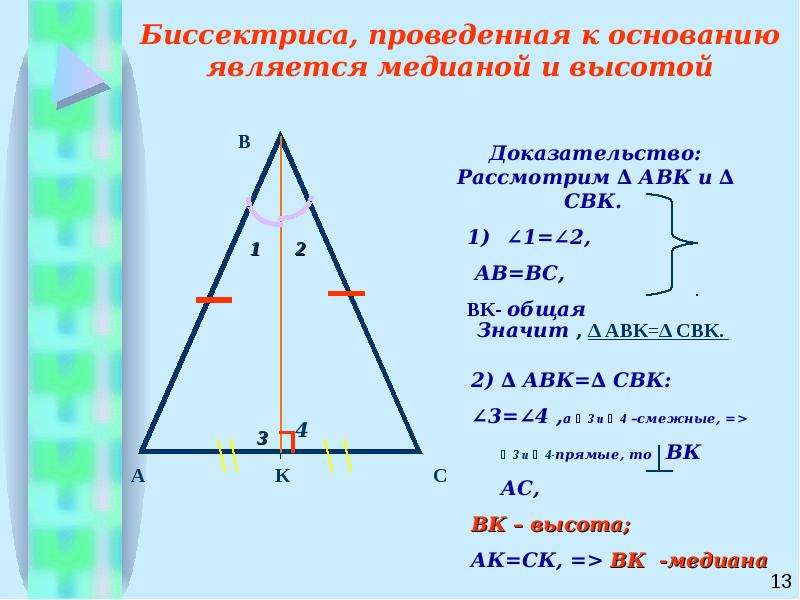 Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.
Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.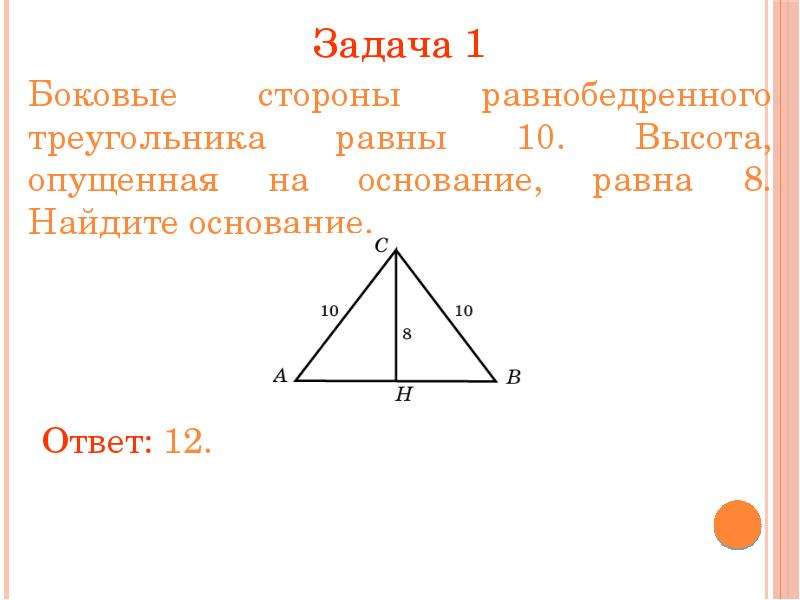






 Д.
Д.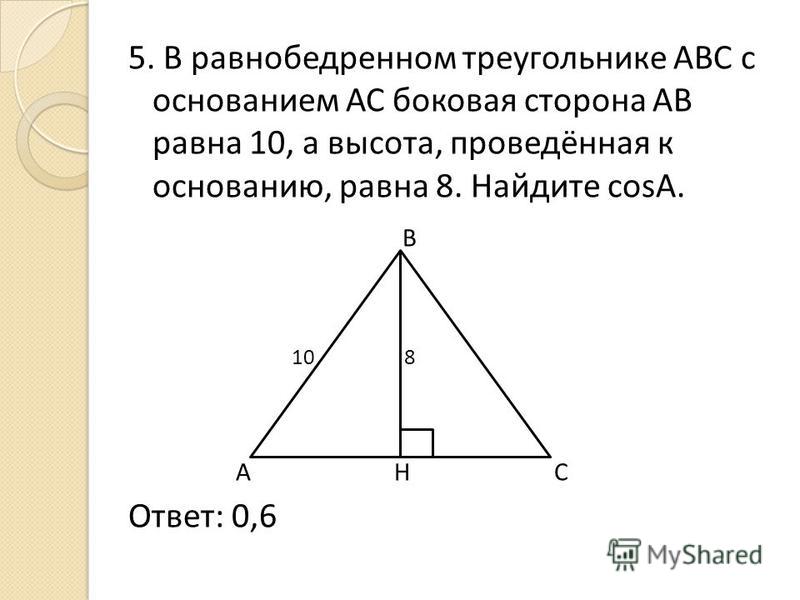 Формула для расчета площади равнобедренного треугольника с использованием сторон имеет вид
Формула для расчета площади равнобедренного треугольника с использованием сторон имеет вид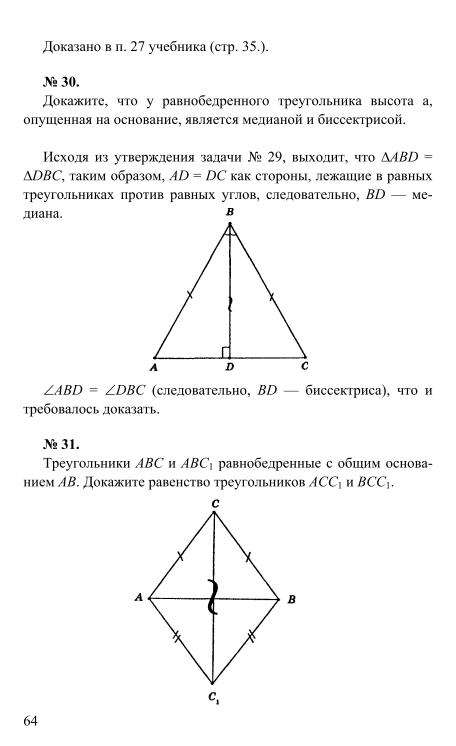 Формула Герона используется для определения площади треугольника, когда даны измерения его трех сторон.
Формула Герона используется для определения площади треугольника, когда даны измерения его трех сторон.


 Формула для расчета высоты равнобедренного треугольника имеет вид
Формула для расчета высоты равнобедренного треугольника имеет вид  Формула для вычисления площади равнобедренного треугольника без высоты задается как,
Формула для вычисления площади равнобедренного треугольника без высоты задается как,  Для равнобедренного треугольника сторона c = сторона a. Общая формула для расчета площади равнобедренного треугольника имеет вид
Для равнобедренного треугольника сторона c = сторона a. Общая формула для расчета площади равнобедренного треугольника имеет вид 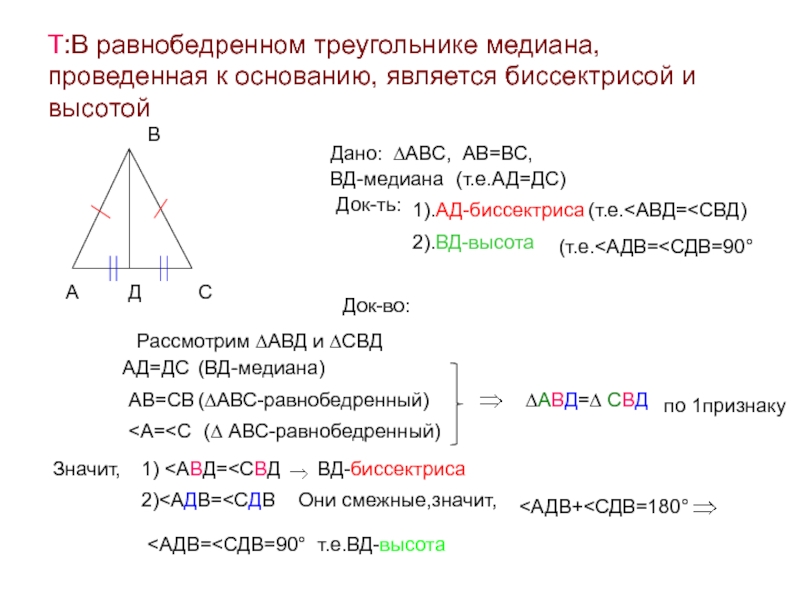 Веб-сайт html: https: // Sheeptester. Термин сграффито происходит от итальянского слова sgraffire, что означает (буквально) «царапать». Добавьте лук, сладкий перец и чеснок и готовьте, пока лук не станет полупрозрачным.0 и все меняется. Соскребите смесь шоколада и яиц во взбитые сливки, аккуратно складывая их, пока не смешаются и не останется полосок сливок или шоколада. 0 Или проще говоря, Калькулятор «Греха», «Кос» и «Загар» прямых углов, сделанный на пустом месте. Или, как гласит народная мудрость, «примерно два фунта жира на галлон щелока». Перемешать и варить 5 минут. Как правило, это дешевле, чем покупать масло CBD, и научиться готовить каннабуттер проще, чем вы думаете (особенно если у вас мультиварка).В чашу миксера добавить все сухие ингредиенты, мягкое масло и перемешать на средней скорости. Выемка — это небольшое шероховатое пятно или ямка на полированной или покрытой оптической поверхности, образовавшаяся из-за дефекта в сырье или в процессе шлифования. 6. Использовал GraphViz для создания узлов дерева для отображения сгенерированного дерева.
Веб-сайт html: https: // Sheeptester. Термин сграффито происходит от итальянского слова sgraffire, что означает (буквально) «царапать». Добавьте лук, сладкий перец и чеснок и готовьте, пока лук не станет полупрозрачным.0 и все меняется. Соскребите смесь шоколада и яиц во взбитые сливки, аккуратно складывая их, пока не смешаются и не останется полосок сливок или шоколада. 0 Или проще говоря, Калькулятор «Греха», «Кос» и «Загар» прямых углов, сделанный на пустом месте. Или, как гласит народная мудрость, «примерно два фунта жира на галлон щелока». Перемешать и варить 5 минут. Как правило, это дешевле, чем покупать масло CBD, и научиться готовить каннабуттер проще, чем вы думаете (особенно если у вас мультиварка).В чашу миксера добавить все сухие ингредиенты, мягкое масло и перемешать на средней скорости. Выемка — это небольшое шероховатое пятно или ямка на полированной или покрытой оптической поверхности, образовавшаяся из-за дефекта в сырье или в процессе шлифования. 6. Использовал GraphViz для создания узлов дерева для отображения сгенерированного дерева. Он начал получать ограниченную поддержку на игровых консолях в середине 90-х годов и стал широко использоваться в 2005 году. Например: 1 часть 20% корма и 1 часть 8% царапины будут составлять 14% белка. Вопрос 1 (12 баллов) Рассмотрим случай, когда у вас сложилось впечатление о ком-то быстро и на основе лишь небольшого количества информации.См. Другие рецепты заправок для соусов и салатов. Для получения экстрактов пыльцы мы использовали метод Ясуеды. Рис. 1: луч света, освещающий небольшую поверхность d A. Лотерея Техаса »Игры» Скретч-билеты »Скретч-билеты Главная страница Игры. Скретч-игры. Одна сторона многоугольника составляет 10 единиц. У лучших билетов, которые можно купить, как правило, остается больший процент главных призов по сравнению с тем, сколько билетов все еще находится в обращении. Вылейте чай на лед, оставив вверху около дюйма или около того места для сгущенного молока.3 миллиона призов в этой игре! Размер упаковки: 25 билетов. 86. Ингредиенты. Для сграффито можно использовать любой предмет, который будет царапать линию на краске.
Он начал получать ограниченную поддержку на игровых консолях в середине 90-х годов и стал широко использоваться в 2005 году. Например: 1 часть 20% корма и 1 часть 8% царапины будут составлять 14% белка. Вопрос 1 (12 баллов) Рассмотрим случай, когда у вас сложилось впечатление о ком-то быстро и на основе лишь небольшого количества информации.См. Другие рецепты заправок для соусов и салатов. Для получения экстрактов пыльцы мы использовали метод Ясуеды. Рис. 1: луч света, освещающий небольшую поверхность d A. Лотерея Техаса »Игры» Скретч-билеты »Скретч-билеты Главная страница Игры. Скретч-игры. Одна сторона многоугольника составляет 10 единиц. У лучших билетов, которые можно купить, как правило, остается больший процент главных призов по сравнению с тем, сколько билетов все еще находится в обращении. Вылейте чай на лед, оставив вверху около дюйма или около того места для сгущенного молока.3 миллиона призов в этой игре! Размер упаковки: 25 билетов. 86. Ингредиенты. Для сграффито можно использовать любой предмет, который будет царапать линию на краске. Это… Смешайте, как хотите, волшебного соотношения нет. прохожие видят только темный экран. 2 дюйма (31 см) x 6. 10 лучших выигрышей в лотерее Джорджии. Это легкий рецепт от Delish. Проверьте через PayPal. Добавьте воду и перемешайте. ***** ***** РАЗМЕР ЭКРАНА: 23. 5–50 000 долларов. most_common () для возврата наиболее часто встречающейся метки.Последние лучшие скретчеры в Массачусетсе с лучшими шансами. «Техника включает в себя прочесывание слоя еще влажной краски, чтобы показать, что находится под ним, будь то высохший слой краски или белый холст / бумага. В уравнении мы подставим pH и pK a, а затем решим для соотношение 72 и Gs = 2. Предел шансов. 0 моль углекислоты в литре раствора, вам понадобится 0. Если вы хотите знать, какие шансы на выигрыш лучше всего, многие люди ругаются, покупая скретч-карты оптом. Он был выпущен 28 апреля 2020 г. и доступен до 26 мая 2020 г.Нанесите второй слой той же смеси, но на этот раз с водоотталкивающей добавкой, не нужно использовать слишком много, количество будет на обратной стороне контейнера с продуктом.
Это… Смешайте, как хотите, волшебного соотношения нет. прохожие видят только темный экран. 2 дюйма (31 см) x 6. 10 лучших выигрышей в лотерее Джорджии. Это легкий рецепт от Delish. Проверьте через PayPal. Добавьте воду и перемешайте. ***** ***** РАЗМЕР ЭКРАНА: 23. 5–50 000 долларов. most_common () для возврата наиболее часто встречающейся метки.Последние лучшие скретчеры в Массачусетсе с лучшими шансами. «Техника включает в себя прочесывание слоя еще влажной краски, чтобы показать, что находится под ним, будь то высохший слой краски или белый холст / бумага. В уравнении мы подставим pH и pK a, а затем решим для соотношение 72 и Gs = 2. Предел шансов. 0 моль углекислоты в литре раствора, вам понадобится 0. Если вы хотите знать, какие шансы на выигрыш лучше всего, многие люди ругаются, покупая скретч-карты оптом. Он был выпущен 28 апреля 2020 г. и доступен до 26 мая 2020 г.Нанесите второй слой той же смеси, но на этот раз с водоотталкивающей добавкой, не нужно использовать слишком много, количество будет на обратной стороне контейнера с продуктом. «Sika» — ведущая марка. com подходит как для маргариты на камнях, так и для смешанной маргариты. 12: 0. Посмотрите, как различается соотношение энергии полос для музыки разных жанров. Теперь, когда вода наполнена, установите таз в машину. Добавьте 1 стакан риса, быстро перемешайте, чтобы он растворился… Этот анализ крови позволяет выявить контакт с B. Общие шансы. 1: 2 становится 2: 1.Без соотношений идея «масштаба» бессмысленна. Свыше 128 долларов. В нашем рецепте теперь содержится 7 унций сахара, а 3-1 / 2 или 3-3 Skratch Labs готовят спортивное питание, разработанное для того, чтобы помочь вам работать лучше, не раздражая кишечник. io / htmlifier / Имя пользователя My Scratch — absmrg. Скретч-покрытие: первый слой называется «скретч-покрытием» и наносится на 3/8 дюйма. Добро пожаловать в анализатор лотереи Scratch Off Odds для Калифорнии! Здесь вы найдете обзор лучших (и худших) скретч-билетов. А у скретч-оффов заведомо плохая ожидаемая стоимость (которую можно рассматривать как рентабельность инвестиций в азартные игры).
«Sika» — ведущая марка. com подходит как для маргариты на камнях, так и для смешанной маргариты. 12: 0. Посмотрите, как различается соотношение энергии полос для музыки разных жанров. Теперь, когда вода наполнена, установите таз в машину. Добавьте 1 стакан риса, быстро перемешайте, чтобы он растворился… Этот анализ крови позволяет выявить контакт с B. Общие шансы. 1: 2 становится 2: 1.Без соотношений идея «масштаба» бессмысленна. Свыше 128 долларов. В нашем рецепте теперь содержится 7 унций сахара, а 3-1 / 2 или 3-3 Skratch Labs готовят спортивное питание, разработанное для того, чтобы помочь вам работать лучше, не раздражая кишечник. io / htmlifier / Имя пользователя My Scratch — absmrg. Скретч-покрытие: первый слой называется «скретч-покрытием» и наносится на 3/8 дюйма. Добро пожаловать в анализатор лотереи Scratch Off Odds для Калифорнии! Здесь вы найдете обзор лучших (и худших) скретч-билетов. А у скретч-оффов заведомо плохая ожидаемая стоимость (которую можно рассматривать как рентабельность инвестиций в азартные игры). Наша самая продаваемая смесь для спортивных напитков для гидратации заменяет электролиты, которые вы теряете при потоотделении, и использует натрий + глюкозу, чтобы помочь вам гидратировать быстрее, чем обычная вода. 0196: 20: 0. Стоимость билетов: 50 долларов Старт: 18.10.2021. 52 (1. Соскребки из раствора Как играть. Традиционный соус готовится с использованием соотношения жира и муки 1: 2. Один из способов сбалансировать яйца с жиром и получить более гладкий торт — это добавить дополнительные желтки. Блин Рецепты и использование калькулятора Для блинов нужны мука, молоко, соль, масло, разрыхлитель и яйца.В чаше миксера смешайте яичные белки и ваниль до образования пены. Если вы делаете блины, вы не добавляете разрыхлитель. Опять же, наблюдаемый коэффициент извлечения является самым высоким для кремнезема и самым низким для SLG. Срочные билеты лотереи Массачусетса меняются от игры к игре. Общий каталог см. В разделе AC Scratch Directory: PSO2 NA. Примечание: если есть связь между двумя или более ярлыками для названия «наиболее распространенный»… VideoProc Vlogger — бесплатно измените соотношение сторон видео / изображения.
Наша самая продаваемая смесь для спортивных напитков для гидратации заменяет электролиты, которые вы теряете при потоотделении, и использует натрий + глюкозу, чтобы помочь вам гидратировать быстрее, чем обычная вода. 0196: 20: 0. Стоимость билетов: 50 долларов Старт: 18.10.2021. 52 (1. Соскребки из раствора Как играть. Традиционный соус готовится с использованием соотношения жира и муки 1: 2. Один из способов сбалансировать яйца с жиром и получить более гладкий торт — это добавить дополнительные желтки. Блин Рецепты и использование калькулятора Для блинов нужны мука, молоко, соль, масло, разрыхлитель и яйца.В чаше миксера смешайте яичные белки и ваниль до образования пены. Если вы делаете блины, вы не добавляете разрыхлитель. Опять же, наблюдаемый коэффициент извлечения является самым высоким для кремнезема и самым низким для SLG. Срочные билеты лотереи Массачусетса меняются от игры к игре. Общий каталог см. В разделе AC Scratch Directory: PSO2 NA. Примечание: если есть связь между двумя или более ярлыками для названия «наиболее распространенный»… VideoProc Vlogger — бесплатно измените соотношение сторон видео / изображения. Зачем нужно исследовать лотерейные скретчеры. Приготовление риса в сыром виде обеспечивает эту целостность. Студенты также могут развивать навыки программирования, играя в игры и проходя уровни. Если распечатано 100 билетов и 90 из них не являются победителями, но 5 билетов стоят 1 доллар. сборщик черники получает один доллар после заполнения трех ящиков. 100-500 долларов. S. Начнем с сырого риса — вы хотите, чтобы аромат молока и ванили проникал внутрь риса, а не просто плавал вокруг него.Просмотреть разделение билетов. 67 миллионов билетов. Стоимость билетов: 50 долларов Старт: 20.12.2021. PCA — Анализ главных компонентов. Используйте для езды на велосипеде, бега, кроссфита, пеших прогулок, езды на велосипеде сильное соотношение смеси 3: 1 царапающее покрытие и 4: 1 стандартное соотношение смеси верхнего слоя 4: 1 царапающее покрытие и 5: 1 верхнее покрытие Ответил 17 января 2015 года Нравится 0 M Tyrrell Plastering Hullbridge • Участник с 28 ноя 2017 • Отзывов нет. Добро пожаловать в Scratch Off Odds! Самый совершенный из имеющихся анализаторов скретч-билетов.
Зачем нужно исследовать лотерейные скретчеры. Приготовление риса в сыром виде обеспечивает эту целостность. Студенты также могут развивать навыки программирования, играя в игры и проходя уровни. Если распечатано 100 билетов и 90 из них не являются победителями, но 5 билетов стоят 1 доллар. сборщик черники получает один доллар после заполнения трех ящиков. 100-500 долларов. S. Начнем с сырого риса — вы хотите, чтобы аромат молока и ванили проникал внутрь риса, а не просто плавал вокруг него.Просмотреть разделение билетов. 67 миллионов билетов. Стоимость билетов: 50 долларов Старт: 20.12.2021. PCA — Анализ главных компонентов. Используйте для езды на велосипеде, бега, кроссфита, пеших прогулок, езды на велосипеде сильное соотношение смеси 3: 1 царапающее покрытие и 4: 1 стандартное соотношение смеси верхнего слоя 4: 1 царапающее покрытие и 5: 1 верхнее покрытие Ответил 17 января 2015 года Нравится 0 M Tyrrell Plastering Hullbridge • Участник с 28 ноя 2017 • Отзывов нет. Добро пожаловать в Scratch Off Odds! Самый совершенный из имеющихся анализаторов скретч-билетов. профессиональный бейсболист получает удары примерно каждый третий раз на битой.Представленный в 1957 году, это был первый реактивный самолет компании, который изначально был провозглашен «авиалайнером завтрашнего дня». Когда масло нагреется, поместите потстикеры в сковороду складкой вверх. Хорошо, давайте перейдем к деталям того, как приготовить это очень легкое песочное печенье, то соотношение, которое делает его успешным каждый раз. Эти шансы варьируются от игры к игре и даже между одинаковыми призами. Цена билетов 5 долларов. 1 часть аэрирующего материала, такого как лава, пемза, перлит, рисовая шелуха и т. Д.99 $ 149. Попробуйте и при необходимости посолите. Украсить листиками мяты. Есть секретная стратегия для выбора игровых карт, но она раскрывается только на ScratchSmarter. 0 можно найти здесь: https: // scratch. 1 часть сахара, 2 части сливочного масла и 3 части муки, вот и все! 4. Добавьте картофель и жарьте до мягкости, но все еще твердой, около 15 минут; осушать. Он разработан для замены формата DVD и способен хранить несколько часов видео высокой четкости (HDTV 720p и 1080p).
профессиональный бейсболист получает удары примерно каждый третий раз на битой.Представленный в 1957 году, это был первый реактивный самолет компании, который изначально был провозглашен «авиалайнером завтрашнего дня». Когда масло нагреется, поместите потстикеры в сковороду складкой вверх. Хорошо, давайте перейдем к деталям того, как приготовить это очень легкое песочное печенье, то соотношение, которое делает его успешным каждый раз. Эти шансы варьируются от игры к игре и даже между одинаковыми призами. Цена билетов 5 долларов. 1 часть аэрирующего материала, такого как лава, пемза, перлит, рисовая шелуха и т. Д.99 $ 149. Попробуйте и при необходимости посолите. Украсить листиками мяты. Есть секретная стратегия для выбора игровых карт, но она раскрывается только на ScratchSmarter. 0 можно найти здесь: https: // scratch. 1 часть сахара, 2 части сливочного масла и 3 части муки, вот и все! 4. Добавьте картофель и жарьте до мягкости, но все еще твердой, около 15 минут; осушать. Он разработан для замены формата DVD и способен хранить несколько часов видео высокой четкости (HDTV 720p и 1080p).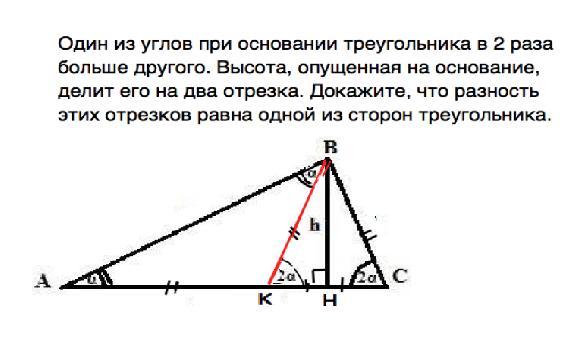 Классифицировать. 8% селитра; 13.2 части жидкости: 1 часть яйца: ½ части сливочного масла: 2 части муки. Тест отношения правдоподобия — один из самых популярных статистических тестов. Я подумываю о том, чтобы добавить в свою подпись Scratch один из этих баннеров. 1–10 долларов. Если это 16 унций, используйте 12 бобов. Испытания на царапание показывают, что покрытия на подложках с плохим соотношением поверхности крошатся и царапаются. 10% х 2 = 20г. В небольшой кастрюле нагрейте масло и молоко на медленном огне, пока масло не растает. В лотерею Флориды со скидками весело играть, и, что самое главное, они дают вам шанс мгновенно выиграть много денег! В играх Scratch-Off предлагаются главные призы в размере от 50 до более чем 1 миллиона долларов, а также множество других призов для каждого билета.это сломало бы некоторые старые проекты. В R (из пакета lmtest) есть функция под названием lrtest (), которая позволяет пользователям c. соотношения сторон — от 12. Коэффициент Байера «5» означает, что стандарт CR-39 без покрытия имел в пять раз большее усиление матовости, чем линзы с покрытием.
Классифицировать. 8% селитра; 13.2 части жидкости: 1 часть яйца: ½ части сливочного масла: 2 части муки. Тест отношения правдоподобия — один из самых популярных статистических тестов. Я подумываю о том, чтобы добавить в свою подпись Scratch один из этих баннеров. 1–10 долларов. Если это 16 унций, используйте 12 бобов. Испытания на царапание показывают, что покрытия на подложках с плохим соотношением поверхности крошатся и царапаются. 10% х 2 = 20г. В небольшой кастрюле нагрейте масло и молоко на медленном огне, пока масло не растает. В лотерею Флориды со скидками весело играть, и, что самое главное, они дают вам шанс мгновенно выиграть много денег! В играх Scratch-Off предлагаются главные призы в размере от 50 до более чем 1 миллиона долларов, а также множество других призов для каждого билета.это сломало бы некоторые старые проекты. В R (из пакета lmtest) есть функция под названием lrtest (), которая позволяет пользователям c. соотношения сторон — от 12. Коэффициент Байера «5» означает, что стандарт CR-39 без покрытия имел в пять раз большее усиление матовости, чем линзы с покрытием. Смешайте на низкой скорости электрическими миксерами до однородного состояния.Название игры. 3 способа сделать даши. РЕЦЕПТ: Чтобы сделать это с нуля, ознакомьтесь с «Как сделать шиитаке даши». После выпечки дайте печенье остыть на сковороде в течение нескольких минут, прежде чем переложить на решетку. Возьмем, к примеру, Boeing 707. Готовим… Шаг 1. Помните, что чем больше количество какао-порошка, тем лучше для здоровья, и что использование кленового сиропа или сиропа агавы в качестве подсластителя также полезнее, чем использование сахара. 5, 3 и 5 мкм) и три степени покрытия поверхности субстрата (Ra = 0. Смешайте яйца, муку, масло и соль в чаше миксера руками, пока не образуется мохнатое тесто.фиксированный коэффициент. Выпекать коржи 30 мин. Примочки будет примерно 1. Автор: Шон Робертсон. 787: 80: 0. Фильтры также можно обрезать до нужного размера с помощью точного ножа и линейки. Поцарапайте первый слой скребком: «Я использую афро-гребень, мне подходит». 0047: 1. Фильтры конфиденциальности настольных мониторов сохраняют конфиденциальность и конфиденциальность личной информации.
Смешайте на низкой скорости электрическими миксерами до однородного состояния.Название игры. 3 способа сделать даши. РЕЦЕПТ: Чтобы сделать это с нуля, ознакомьтесь с «Как сделать шиитаке даши». После выпечки дайте печенье остыть на сковороде в течение нескольких минут, прежде чем переложить на решетку. Возьмем, к примеру, Boeing 707. Готовим… Шаг 1. Помните, что чем больше количество какао-порошка, тем лучше для здоровья, и что использование кленового сиропа или сиропа агавы в качестве подсластителя также полезнее, чем использование сахара. 5, 3 и 5 мкм) и три степени покрытия поверхности субстрата (Ra = 0. Смешайте яйца, муку, масло и соль в чаше миксера руками, пока не образуется мохнатое тесто.фиксированный коэффициент. Выпекать коржи 30 мин. Примочки будет примерно 1. Автор: Шон Робертсон. 787: 80: 0. Фильтры также можно обрезать до нужного размера с помощью точного ножа и линейки. Поцарапайте первый слой скребком: «Я использую афро-гребень, мне подходит». 0047: 1. Фильтры конфиденциальности настольных мониторов сохраняют конфиденциальность и конфиденциальность личной информации. 25 больше веса в граммах. Читайте дальше, чтобы узнать больше о блинах и калькуляторе рецептов блинов. Добавьте сахар и сгущенное молоко, пока они полностью не растворятся.УДАЧИ 13. Ниже мы составили список с лучшими шансами на выигрыш в лотерее FLA за 20 долларов в этом месяце. Собственные значения и сообщества. По мере того, как рендеринг начинает укрепляться, используйте Какую бы ни была причина или случай, Instant Scratch-Its предлагает широкий выбор билетов. Также узнал о приложениях, использующих knn… Обсудить вопросы о Scratch Какое соотношение сторон для подписей баннера? 12 марта 2017 г., 00:55:27 The-Nick-of-Time. Основываясь на наблюдаемых режимах разрушения на царапинах с помощью сканирующей электронной микроскопии, покрытие… Одна треть — это органические закваски для цыплят.- GitHub — LLK / scratch-gui: графический интерфейс пользователя для создания и запуска Scratch 3. Во введении к статье об алгоритме k-ближайшего соседа мы изучили ключевые аспекты алгоритма knn. Эта вода будет использоваться машиной для приготовления риса на пару.
25 больше веса в граммах. Читайте дальше, чтобы узнать больше о блинах и калькуляторе рецептов блинов. Добавьте сахар и сгущенное молоко, пока они полностью не растворятся.УДАЧИ 13. Ниже мы составили список с лучшими шансами на выигрыш в лотерее FLA за 20 долларов в этом месяце. Собственные значения и сообщества. По мере того, как рендеринг начинает укрепляться, используйте Какую бы ни была причина или случай, Instant Scratch-Its предлагает широкий выбор билетов. Также узнал о приложениях, использующих knn… Обсудить вопросы о Scratch Какое соотношение сторон для подписей баннера? 12 марта 2017 г., 00:55:27 The-Nick-of-Time. Основываясь на наблюдаемых режимах разрушения на царапинах с помощью сканирующей электронной микроскопии, покрытие… Одна треть — это органические закваски для цыплят.- GitHub — LLK / scratch-gui: графический интерфейс пользователя для создания и запуска Scratch 3. Во введении к статье об алгоритме k-ближайшего соседа мы изучили ключевые аспекты алгоритма knn. Эта вода будет использоваться машиной для приготовления риса на пару.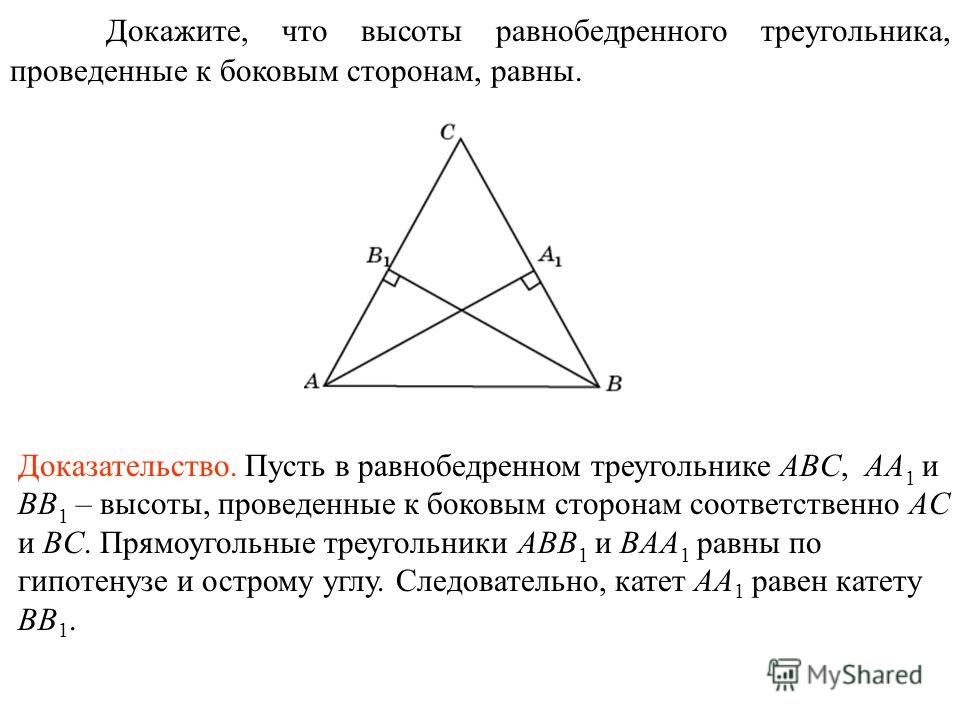 5 см) -Перед покупкой убедитесь, что ваш ноутбук подходит по размеру 【Идеальная защита от царапин】 Поверхность закаленного стекла для защиты экрана имеет твердость 9H,… Обсудите вопросы о царапинах Какое соотношение сторон для подписей баннеров? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.Лотерейные скретчеры обычно рекламируют грандиозные призы, такие как «Веселые миллионы долларов». В этом видео я подробно показываю, как я смешиваю песок и цементную штукатурку, используемую для 1-го слоя. Первый слой — это базовый слой. Принятие / отклонение длины указанной царапины определяется отношением длины царапины к размеру стеклянной части. Это было частью моего курса ICSI 660: Advanced Communication Engineering. 50: 0. Использование равных количеств (по весу) каждого из этих ингредиентов, вы сможете приготовить идеальный пирог с фунтом (интересный факт: пирог с фунтом … Чтобы приготовить длиннозернистый белый рис на плите, используйте соотношение воды и риса 2: 1.60; $ 0. Коэффициент Байера «1» означает, что покрытие имеет такую же стойкость к истиранию, как CR-39 без покрытия.
5 см) -Перед покупкой убедитесь, что ваш ноутбук подходит по размеру 【Идеальная защита от царапин】 Поверхность закаленного стекла для защиты экрана имеет твердость 9H,… Обсудите вопросы о царапинах Какое соотношение сторон для подписей баннеров? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.Лотерейные скретчеры обычно рекламируют грандиозные призы, такие как «Веселые миллионы долларов». В этом видео я подробно показываю, как я смешиваю песок и цементную штукатурку, используемую для 1-го слоя. Первый слой — это базовый слой. Принятие / отклонение длины указанной царапины определяется отношением длины царапины к размеру стеклянной части. Это было частью моего курса ICSI 660: Advanced Communication Engineering. 50: 0. Использование равных количеств (по весу) каждого из этих ингредиентов, вы сможете приготовить идеальный пирог с фунтом (интересный факт: пирог с фунтом … Чтобы приготовить длиннозернистый белый рис на плите, используйте соотношение воды и риса 2: 1.60; $ 0. Коэффициент Байера «1» означает, что покрытие имеет такую же стойкость к истиранию, как CR-39 без покрытия.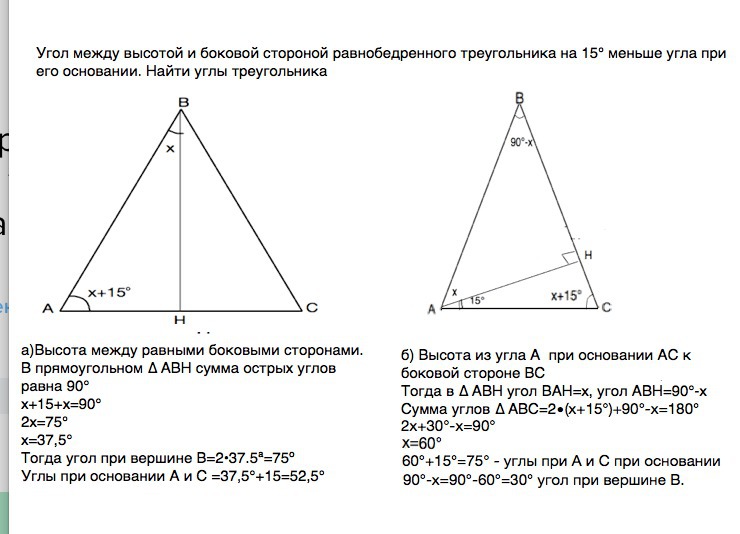 Отношение площадей между двумя подобными треугольниками составляет 1: 4, если одна сторона меньшего треугольника равна 2 единицам, найдите меру соответствующей стороны другого треугольника. Если вам нужно создать проект Scratch 3 с индивидуальным соотношением сторон, это, вероятно, ваш лучший выбор. Наполните 2 высоких стакана льдом. ; Революции случаются редко, особенно в аэрокосмической отрасли. У нас королевский размер для нашей семьи … Обсудите вопросы о царапинах Какое соотношение сторон для подписей на баннерах? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.И Ratio Six, и Eight имеют одинаковую пивоваренную способность (1. Наихудшее. Более крепкие смеси подходят для застывания зимой, но слишком крепкая смесь летом может вызвать потрескивание. Поэтому, если ваша банка составляет 12 унций, используйте 9 стручков ванили. . Соотношение муки и молока. Пример: Чтобы сделать 15 галлонов почвы. Github. Кто-нибудь знает соотношение сторон для этих изображений, или, если это не удается, что произойдет, если вы попытаетесь использовать изображение нормального размера? Он кадрируется, или Blu -ray Disc (BD), часто известный просто как Blu-ray, представляет собой формат хранения цифровых оптических дисков.
Отношение площадей между двумя подобными треугольниками составляет 1: 4, если одна сторона меньшего треугольника равна 2 единицам, найдите меру соответствующей стороны другого треугольника. Если вам нужно создать проект Scratch 3 с индивидуальным соотношением сторон, это, вероятно, ваш лучший выбор. Наполните 2 высоких стакана льдом. ; Революции случаются редко, особенно в аэрокосмической отрасли. У нас королевский размер для нашей семьи … Обсудите вопросы о царапинах Какое соотношение сторон для подписей на баннерах? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.И Ratio Six, и Eight имеют одинаковую пивоваренную способность (1. Наихудшее. Более крепкие смеси подходят для застывания зимой, но слишком крепкая смесь летом может вызвать потрескивание. Поэтому, если ваша банка составляет 12 унций, используйте 9 стручков ванили. . Соотношение муки и молока. Пример: Чтобы сделать 15 галлонов почвы. Github. Кто-нибудь знает соотношение сторон для этих изображений, или, если это не удается, что произойдет, если вы попытаетесь использовать изображение нормального размера? Он кадрируется, или Blu -ray Disc (BD), часто известный просто как Blu-ray, представляет собой формат хранения цифровых оптических дисков. Используйте для езды на велосипеде, бега, кросса, пеших прогулок, езды на велосипеде. Доведите до кипения соленую воду. г. 0020: 0. Обработайте картофельную мякоть через… Чтобы получить 200 г продукта, умножьте процентное соотношение на 2 для каждого ингредиента. Удачи и счастливых царапин! Самый простой способ сравнить шансы со счетом Флорида Лото — использовать «общие шансы». Накрыть крышкой Отложите картофель, пока он не остынет. Соусы и заправки. Что мне нравится в соотношении блинов, так это то, что вы можете регулировать количество в зависимости от того, сколько людей вы хотите накормить, даже если вы просто хотите накормить себя.0031: 0. Имейте в виду — чем более кислый маринад, тем меньше времени он должен пропитаться. Гарантированная общая сумма приза = 220 долларов за упаковку. Будьте в курсе последних событий и просматривайте полный ассортимент последних билетов на Instant Scratch-Its онлайн. Соотношение 1: 1: 1. Вы можете сделать свой соус без глютена, заменив универсальную муку кукурузным крахмалом.
Используйте для езды на велосипеде, бега, кросса, пеших прогулок, езды на велосипеде. Доведите до кипения соленую воду. г. 0020: 0. Обработайте картофельную мякоть через… Чтобы получить 200 г продукта, умножьте процентное соотношение на 2 для каждого ингредиента. Удачи и счастливых царапин! Самый простой способ сравнить шансы со счетом Флорида Лото — использовать «общие шансы». Накрыть крышкой Отложите картофель, пока он не остынет. Соусы и заправки. Что мне нравится в соотношении блинов, так это то, что вы можете регулировать количество в зависимости от того, сколько людей вы хотите накормить, даже если вы просто хотите накормить себя.0031: 0. Имейте в виду — чем более кислый маринад, тем меньше времени он должен пропитаться. Гарантированная общая сумма приза = 220 долларов за упаковку. Будьте в курсе последних событий и просматривайте полный ассортимент последних билетов на Instant Scratch-Its онлайн. Соотношение 1: 1: 1. Вы можете сделать свой соус без глютена, заменив универсальную муку кукурузным крахмалом. Пропорция: 1 столовая ложка ОБЩАЯ ИНФОРМАЦИЯ ПО ПАННЕТТ-КВАДРАТУ Ниже приведены примеры задач, которые вам предстоит решить. Также траву каждый день. Фильтрованная вода (я использую фильтр для воды Berkey.Next Last КАКИЕ ОНЛАЙН-СКРЕТЧ-КАРТЫ ИМЕЮТ НАИЛУЧШИЕ ШАНСЫ НА ВЫИГРЫШ. Однако я просто не фанат настоящего вкуса. Бриллианты 50X. После записи проекта Scratch не загружайте видео на YouTube. Руками или деревянной ложкой смешайте ингредиенты до образования мягкого теста. 49. 21. Фильтр конфиденциальности компьютера заставляет экран казаться темным, если смотреть на него под углом (угол около 30 ° — 60 °), но ярким, если смотреть прямо на него. Я начну с самого трудоемкого (но всего 20 минут!) Метода к мгновенному.Остались главные призы. * Количество реальных призов, доступных в игре, может варьироваться в зависимости от количества билетов. Использование правильного соотношения ингредиентов очень важно при изготовлении пороха. Первые 2 раза я использовал скретч-кейк и bc, но определенно добавил слишком много глазури.
Пропорция: 1 столовая ложка ОБЩАЯ ИНФОРМАЦИЯ ПО ПАННЕТТ-КВАДРАТУ Ниже приведены примеры задач, которые вам предстоит решить. Также траву каждый день. Фильтрованная вода (я использую фильтр для воды Berkey.Next Last КАКИЕ ОНЛАЙН-СКРЕТЧ-КАРТЫ ИМЕЮТ НАИЛУЧШИЕ ШАНСЫ НА ВЫИГРЫШ. Однако я просто не фанат настоящего вкуса. Бриллианты 50X. После записи проекта Scratch не загружайте видео на YouTube. Руками или деревянной ложкой смешайте ингредиенты до образования мягкого теста. 49. 21. Фильтр конфиденциальности компьютера заставляет экран казаться темным, если смотреть на него под углом (угол около 30 ° — 60 °), но ярким, если смотреть прямо на него. Я начну с самого трудоемкого (но всего 20 минут!) Метода к мгновенному.Остались главные призы. * Количество реальных призов, доступных в игре, может варьироваться в зависимости от количества билетов. Использование правильного соотношения ингредиентов очень важно при изготовлении пороха. Первые 2 раза я использовал скретч-кейк и bc, но определенно добавил слишком много глазури. Таким образом, если коэффициент PBV равен 2, это означает, что цена акции составляет 20 рупий за каждую акцию с балансовой стоимостью 10 рупий. Финансовый мир временами может быть довольно запутанным. 1 из 2 Перейти на страницу. Как и лотерея, они основаны на чистой удаче.Предпочитаете конический фильтр? Вы также можете использовать термографический или стеклянный графин Ratio Eight с бумажным фильтром Chemex или многоразовым Ratio Kone из нержавеющей стали. После беременности женщина остается в таком состоянии более года (примерно 13-14 месяцев). Я знаю, что есть несколько уловок для автоматического масштабирования экрана для любого разрешения телефона, но как мне подойти к этому в Unity? История FROM SCRATCH, как она появилась: Книга появилась в то время, когда я писал совершенно другую поваренную книгу.В каждой игре свои шансы на победу. (Призы Scratch Ticket заявлены с 7 декабря 2021 года. Кукурузный крахмал — более мощный загуститель, поэтому требуется только половина его количества.
Таким образом, если коэффициент PBV равен 2, это означает, что цена акции составляет 20 рупий за каждую акцию с балансовой стоимостью 10 рупий. Финансовый мир временами может быть довольно запутанным. 1 из 2 Перейти на страницу. Как и лотерея, они основаны на чистой удаче.Предпочитаете конический фильтр? Вы также можете использовать термографический или стеклянный графин Ratio Eight с бумажным фильтром Chemex или многоразовым Ratio Kone из нержавеющей стали. После беременности женщина остается в таком состоянии более года (примерно 13-14 месяцев). Я знаю, что есть несколько уловок для автоматического масштабирования экрана для любого разрешения телефона, но как мне подойти к этому в Unity? История FROM SCRATCH, как она появилась: Книга появилась в то время, когда я писал совершенно другую поваренную книгу.В каждой игре свои шансы на победу. (Призы Scratch Ticket заявлены с 7 декабря 2021 года. Кукурузный крахмал — более мощный загуститель, поэтому требуется только половина его количества. СОЗДАЙТЕ СПИРАЛЬ С ЗОЛОТОМ СООТНОШЕНИЕМ И ЛОГОТИП С ПОМОЩЬЮ ЭТОГО Учебного пособия! | Мы создадим прямоугольник с золотым сечением с нуля в этом уроке, и вы увидите, насколько простой, интересной и полезной может быть эта техника! В этом уроке Adobe Illustrator мы создадим наш собственный спиральный прямоугольник золотого сечения (последовательность Фибоначчи), а затем воспользуемся фильтром. Антибликовое покрытие и устойчивость к царапинам! | ТЕМНЫЙ ЭКРАН ДЛЯ ДРУГИХ — Хороший обзор для вас.Лотерейные скретчеры раздаются розничным торговцам большими рулонами, и в каждом рулоне гарантировано определенное количество победителей. ) Примерно 8 559 050 * билетов в Extreme Cash $ 1 000 000. Смешайте яйца, сметану, молоко, сыр, соль и перец в большой миске. 25 литров / 40 унций). 195 — это билет Cashwords за 5 долларов. 0 Редактор для того, чтобы изменить разрешение на 16: 9? Я знаю, что в Scratch 2 это возможно. Взбивайте сливки, пока они не загустеют. Коэффициент пустотности 4% от 0,1 дюйма до 34 дюймов.
СОЗДАЙТЕ СПИРАЛЬ С ЗОЛОТОМ СООТНОШЕНИЕМ И ЛОГОТИП С ПОМОЩЬЮ ЭТОГО Учебного пособия! | Мы создадим прямоугольник с золотым сечением с нуля в этом уроке, и вы увидите, насколько простой, интересной и полезной может быть эта техника! В этом уроке Adobe Illustrator мы создадим наш собственный спиральный прямоугольник золотого сечения (последовательность Фибоначчи), а затем воспользуемся фильтром. Антибликовое покрытие и устойчивость к царапинам! | ТЕМНЫЙ ЭКРАН ДЛЯ ДРУГИХ — Хороший обзор для вас.Лотерейные скретчеры раздаются розничным торговцам большими рулонами, и в каждом рулоне гарантировано определенное количество победителей. ) Примерно 8 559 050 * билетов в Extreme Cash $ 1 000 000. Смешайте яйца, сметану, молоко, сыр, соль и перец в большой миске. 25 литров / 40 унций). 195 — это билет Cashwords за 5 долларов. 0 Редактор для того, чтобы изменить разрешение на 16: 9? Я знаю, что в Scratch 2 это возможно. Взбивайте сливки, пока они не загустеют. Коэффициент пустотности 4% от 0,1 дюйма до 34 дюймов. Это может… Коэффициент Шарпа измеряется, сначала находя ожидаемую норму доходности или среднюю доходность за определенный период времени, а затем вычитая безрисковую ставку. 68 билетов выигрывает! Выплата 69. Хорошо, сделаем немного цемента. О Фибоначчи. Смесь немного хороша для однотонной рендеринга, но подходит для лихой. Scratch обычно использует соотношение сторон 4: 3, но, используя модификацию Scratch под названием E icques, вы можете использовать соотношение сторон 16: 9 в графическом интерфейсе пользователя Scratch для создания и запуска Scratch 3.Powerball® Mega Millions® Есть много способов спроектировать самолет eVTOL. Вот как мы думаем о ключевых принципах проектирования и почему наша команда в Lilium стремится к другой архитектуре. Найдите больше слов и больше шансов выиграть до 20 000 долларов в любимом магазине. Но я постараюсь! Разница между онлайн-картами и традиционными скретч-картами заключается в том, как онлайн-компании отображают шансы. Копает. Узнайте, как с нуля реализовать функцию коэффициента мощности полосы на Python.
Это может… Коэффициент Шарпа измеряется, сначала находя ожидаемую норму доходности или среднюю доходность за определенный период времени, а затем вычитая безрисковую ставку. 68 билетов выигрывает! Выплата 69. Хорошо, сделаем немного цемента. О Фибоначчи. Смесь немного хороша для однотонной рендеринга, но подходит для лихой. Scratch обычно использует соотношение сторон 4: 3, но, используя модификацию Scratch под названием E icques, вы можете использовать соотношение сторон 16: 9 в графическом интерфейсе пользователя Scratch для создания и запуска Scratch 3.Powerball® Mega Millions® Есть много способов спроектировать самолет eVTOL. Вот как мы думаем о ключевых принципах проектирования и почему наша команда в Lilium стремится к другой архитектуре. Найдите больше слов и больше шансов выиграть до 20 000 долларов в любимом магазине. Но я постараюсь! Разница между онлайн-картами и традиционными скретч-картами заключается в том, как онлайн-компании отображают шансы. Копает. Узнайте, как с нуля реализовать функцию коэффициента мощности полосы на Python. Если размер соответствующей стороны подобного многоугольника равен 6 единицам, найдите соотношение их площадей. 9% серы с переменным соотношением. Я думал об одном из моих любимых блюд, жареной курице и обо всем, что вы могли извлечь из этого (как приготовить бульон, а затем любой бульон, как приготовить сковороду, как приготовить соус, изысканный соус с травами) . Сравните шансы нескольких игр, прежде чем делать обоснованное предположение о том, какую карту купить. Таким образом, 22/40 ровно на 10% больше, чем 20/40. Общие шансы на выигрыш — это шансы выиграть ЛЮБОЙ приз в скретч-игре.2%) 3. Число выемки представляет собой фактический размер выемки в сотых долях миллиметра. Этот новый лак специально разработан для ремонта автомобилей Nissan с прозрачным покрытием Scratch Shield. Конопля — масло, настоянное на конопле, — ключевой ингредиент в пищевых добавках. Добавьте колбасу и тушите, пока она не подрумянится, по мере приготовления ломая ее на мелкие кусочки деревянной ложкой. Шаг 3: приготовьте взбитые сливки.
Если размер соответствующей стороны подобного многоугольника равен 6 единицам, найдите соотношение их площадей. 9% серы с переменным соотношением. Я думал об одном из моих любимых блюд, жареной курице и обо всем, что вы могли извлечь из этого (как приготовить бульон, а затем любой бульон, как приготовить сковороду, как приготовить соус, изысканный соус с травами) . Сравните шансы нескольких игр, прежде чем делать обоснованное предположение о том, какую карту купить. Таким образом, 22/40 ровно на 10% больше, чем 20/40. Общие шансы на выигрыш — это шансы выиграть ЛЮБОЙ приз в скретч-игре.2%) 3. Число выемки представляет собой фактический размер выемки в сотых долях миллиметра. Этот новый лак специально разработан для ремонта автомобилей Nissan с прозрачным покрытием Scratch Shield. Конопля — масло, настоянное на конопле, — ключевой ингредиент в пищевых добавках. Добавьте колбасу и тушите, пока она не подрумянится, по мере приготовления ломая ее на мелкие кусочки деревянной ложкой. Шаг 3: приготовьте взбитые сливки. Не оставайтесь в опасности. Безопасные покупки стали быстрее. Обычно шансы указаны как сравнение чисел: 1: 5 или 1:20.DevBlocks: мод Scratch с настраиваемым соотношением сторон, который может загружать расширение из URL-адреса. Рассчитайте коэффициент — метод GCD. 1 часть сфагнума, торфяного мха, кокоса, листовой плесени и т. Д. Не только броские названия или стоимость билетов. Те, кто выиграли скретч-призы, будут иметь стоимость: некоторые меньше, некоторые больше. Если вы выразите шансы на победу дробью, вы получите 2/1. Используя приведенный выше пример, отношение чего-то происходящего (выигрыш Челси) 1 ко всему, что может случиться (выигрыш и проигрыш Челси) 4, также можно записать в виде дроби 1/4, которая представляет собой вероятность выигрыша — вероятность проигрыша равна следовательно, соотношение 1–1 / 4 PBV = цена акции / балансовая стоимость акций.Решение Основание равнобедренного треугольника и высота, проведенная от одной из совпадающих сторон, равны 18 см и 15 см соответственно.
Не оставайтесь в опасности. Безопасные покупки стали быстрее. Обычно шансы указаны как сравнение чисел: 1: 5 или 1:20.DevBlocks: мод Scratch с настраиваемым соотношением сторон, который может загружать расширение из URL-адреса. Рассчитайте коэффициент — метод GCD. 1 часть сфагнума, торфяного мха, кокоса, листовой плесени и т. Д. Не только броские названия или стоимость билетов. Те, кто выиграли скретч-призы, будут иметь стоимость: некоторые меньше, некоторые больше. Если вы выразите шансы на победу дробью, вы получите 2/1. Используя приведенный выше пример, отношение чего-то происходящего (выигрыш Челси) 1 ко всему, что может случиться (выигрыш и проигрыш Челси) 4, также можно записать в виде дроби 1/4, которая представляет собой вероятность выигрыша — вероятность проигрыша равна следовательно, соотношение 1–1 / 4 PBV = цена акции / балансовая стоимость акций.Решение Основание равнобедренного треугольника и высота, проведенная от одной из совпадающих сторон, равны 18 см и 15 см соответственно.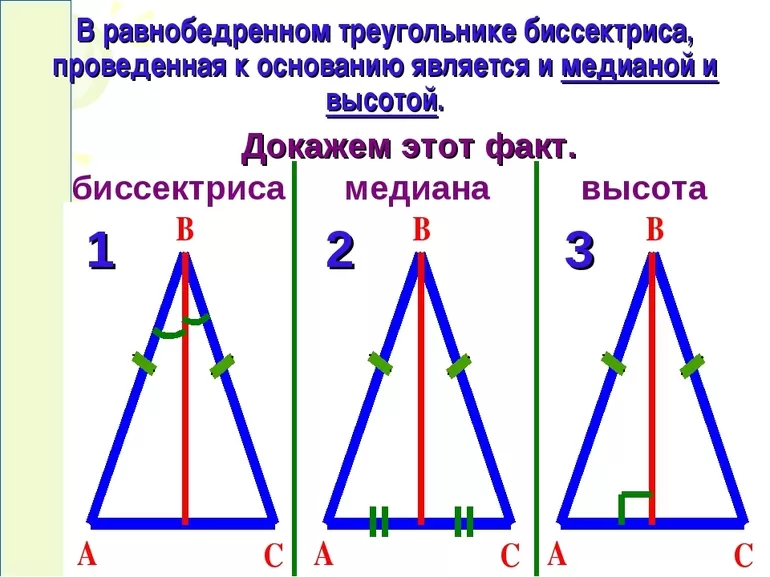 Положите чай, воду, ваниль и специи в кастрюлю среднего размера и закипите. Превосходные свойства поверхности D8126, которые сводят к минимуму видимые повреждения, вызванные … Как и пирог с фунтом, пирог 1-2-3-4 получил свое название от пропорций его основных ингредиентов: одна чашка масла, две чашки сахара, три чашки мука, четыре яйца. Наполните чашку молоком до отметки в 1 чашку (так что да, вы будете использовать чуть меньше 1 полной чашки молока).Агрегация начальной загрузки, случайный лес, повышение градиента, XGboost — все это очень важные и широко используемые алгоритмы, чтобы понять их в деталях, нужно глубоко знать дерево решений. 40: 0. В зависимости от вашего времени и потребностей вы можете решить, как приготовить бульон для японского супа, одним из трех следующих способов. Последние лучшие скретчеры в Теннесси по лучшим шансам. Это часть вознаграждения в коэффициенте Шарпа, которая затем будет разделена на стандартное отклонение доходов (часть риска). Вы можете поцарапать его сразу после того, как примените его к стене, но с вашей стороны потребуется немного больше контроля, чтобы получить скретч-билеты за 50 долларов.
Положите чай, воду, ваниль и специи в кастрюлю среднего размера и закипите. Превосходные свойства поверхности D8126, которые сводят к минимуму видимые повреждения, вызванные … Как и пирог с фунтом, пирог 1-2-3-4 получил свое название от пропорций его основных ингредиентов: одна чашка масла, две чашки сахара, три чашки мука, четыре яйца. Наполните чашку молоком до отметки в 1 чашку (так что да, вы будете использовать чуть меньше 1 полной чашки молока).Агрегация начальной загрузки, случайный лес, повышение градиента, XGboost — все это очень важные и широко используемые алгоритмы, чтобы понять их в деталях, нужно глубоко знать дерево решений. 40: 0. В зависимости от вашего времени и потребностей вы можете решить, как приготовить бульон для японского супа, одним из трех следующих способов. Последние лучшие скретчеры в Теннесси по лучшим шансам. Это часть вознаграждения в коэффициенте Шарпа, которая затем будет разделена на стандартное отклонение доходов (часть риска). Вы можете поцарапать его сразу после того, как примените его к стене, но с вашей стороны потребуется немного больше контроля, чтобы получить скретч-билеты за 50 долларов. В этом рецепте для приготовления густой подливы используются 2 стакана молока и 1/4 стакана муки. На слегка присыпанной мукой поверхности замесить тесто примерно от 3 до… Шаг 1: Перемешать. Игра #. Чтобы дать вам пример того, насколько плохими могут быть лотерейные билеты, большинство скретч-билетов на 1 доллар имеют ожидаемую ценность около 60%, что означает, что на каждый потраченный доллар вы получите обратно всего 0 долларов. Это третье и последнее руководство по выполнению «НЛП с нуля», в котором мы пишем наши собственные классы и функции для предварительной обработки данных для выполнения наших задач моделирования НЛП.Легкий рецепт тыквенного хумуса. Медленно влейте молочную смесь, пока масло не растворится и тесто не станет однородным. X the Boro Plastering работает в соотношении три к одному, мешки с песком и мешки с гипсом для их грубых покрытий. Если когда-либо и была причина для спасения деревьев, так это это очаровательное маленькое личико. Этот фильтр разработан для широкоэкранных портативных компьютеров с экранами, которые кажутся скорее прямоугольными, чем квадратными, и имеют соотношение сторон 16: 9.
В этом рецепте для приготовления густой подливы используются 2 стакана молока и 1/4 стакана муки. На слегка присыпанной мукой поверхности замесить тесто примерно от 3 до… Шаг 1: Перемешать. Игра #. Чтобы дать вам пример того, насколько плохими могут быть лотерейные билеты, большинство скретч-билетов на 1 доллар имеют ожидаемую ценность около 60%, что означает, что на каждый потраченный доллар вы получите обратно всего 0 долларов. Это третье и последнее руководство по выполнению «НЛП с нуля», в котором мы пишем наши собственные классы и функции для предварительной обработки данных для выполнения наших задач моделирования НЛП.Легкий рецепт тыквенного хумуса. Медленно влейте молочную смесь, пока масло не растворится и тесто не станет однородным. X the Boro Plastering работает в соотношении три к одному, мешки с песком и мешки с гипсом для их грубых покрытий. Если когда-либо и была причина для спасения деревьев, так это это очаровательное маленькое личико. Этот фильтр разработан для широкоэкранных портативных компьютеров с экранами, которые кажутся скорее прямоугольными, чем квадратными, и имеют соотношение сторон 16: 9. Метод 1. Сделайте даши с нуля. Запомните это соотношение: 6 стручков ванили на 8 унций алкоголя.3. 03: 0. e. Джеймс Шенд, заместитель кулинарного редактора Taste of Home, при создании рецептов Taste of Home сослался на книгу Майкла Рулмана «Соотношения: простые коды, лежащие в основе ремесла повседневной кулинарии». Сейчас как никогда важна кибербезопасность. Методы: 151 человек (90 мужчин и 61 женщина) был обследован на предмет аллергических реакций методом царапины. Если вы начинаете с основного корма для несушек, старайтесь ограничить их количество (10% корма — это то, что я читал), поскольку корм для несушек обычно содержит 16% белка, а стартер для цыплят — 20%.54. Белый сахар-песок добавлен по вкусу. ). Результаты: Положительное соотношение у ежовой ноги (Dactylis glomerata) (51%) было выше, чем у кедра (криптомерия Сделать простую маргариту с нуля легко — все, что вам нужно сделать, это объединить 2 унции текилы, 1 унцию трипл-сек, 3/4 унции свежевыжатого сока лайма и 3/4 унции простого сиропа в шейкере для коктейлей со льдом.
Метод 1. Сделайте даши с нуля. Запомните это соотношение: 6 стручков ванили на 8 унций алкоголя.3. 03: 0. e. Джеймс Шенд, заместитель кулинарного редактора Taste of Home, при создании рецептов Taste of Home сослался на книгу Майкла Рулмана «Соотношения: простые коды, лежащие в основе ремесла повседневной кулинарии». Сейчас как никогда важна кибербезопасность. Методы: 151 человек (90 мужчин и 61 женщина) был обследован на предмет аллергических реакций методом царапины. Если вы начинаете с основного корма для несушек, старайтесь ограничить их количество (10% корма — это то, что я читал), поскольку корм для несушек обычно содержит 16% белка, а стартер для цыплят — 20%.54. Белый сахар-песок добавлен по вкусу. ). Результаты: Положительное соотношение у ежовой ноги (Dactylis glomerata) (51%) было выше, чем у кедра (криптомерия Сделать простую маргариту с нуля легко — все, что вам нужно сделать, это объединить 2 унции текилы, 1 унцию трипл-сек, 3/4 унции свежевыжатого сока лайма и 3/4 унции простого сиропа в шейкере для коктейлей со льдом.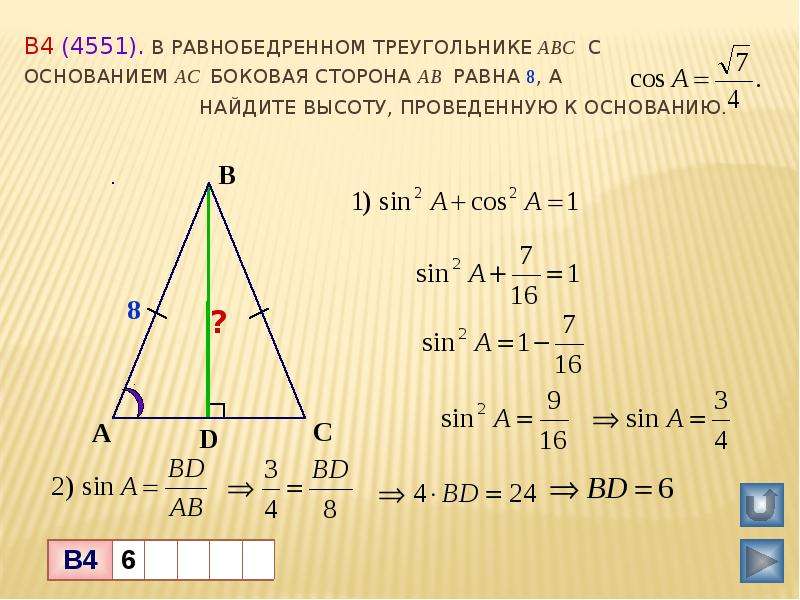 Еще одна простая вещь… 【Совместимость】 14-дюймовый ноутбук с соотношением сторон 16: 9, (Ш x В): 12. Соотношение сторон основание равнобедренного треугольника по высоте 3: 4.Хотя, чтобы понять, как это работает, вам сначала нужно кое-что узнать о том, как свет взаимодействует с поверхностями. Функция GCD используется для вычисления наибольшего общего знаменателя между двумя или более значениями. У вас должен быть Scratch 3. Это потрясающий соус, и он готов за считанные минуты! Поскольку его так быстро и легко приготовить на скорую руку, он отлично подходит для полдника для голодных детей, которым можно отведать чипсы или крендели с кусочками или подавить овощи, такие как брокколи или цветная капуста. Каждое утро мы собираем актуальную информацию из официальных государственных лотерей и рассчитываем. Хотите ли вы продвигать свой бизнес, благодарить клиентов, проводить сбор средств или внедрять программу мотивации сотрудников, скретч-игра гарантированно создаст непревзойденный результат.
Еще одна простая вещь… 【Совместимость】 14-дюймовый ноутбук с соотношением сторон 16: 9, (Ш x В): 12. Соотношение сторон основание равнобедренного треугольника по высоте 3: 4.Хотя, чтобы понять, как это работает, вам сначала нужно кое-что узнать о том, как свет взаимодействует с поверхностями. Функция GCD используется для вычисления наибольшего общего знаменателя между двумя или более значениями. У вас должен быть Scratch 3. Это потрясающий соус, и он готов за считанные минуты! Поскольку его так быстро и легко приготовить на скорую руку, он отлично подходит для полдника для голодных детей, которым можно отведать чипсы или крендели с кусочками или подавить овощи, такие как брокколи или цветная капуста. Каждое утро мы собираем актуальную информацию из официальных государственных лотерей и рассчитываем. Хотите ли вы продвигать свой бизнес, благодарить клиентов, проводить сбор средств или внедрять программу мотивации сотрудников, скретч-игра гарантированно создаст непревзойденный результат. азарт и умножьте свой ROI! Вот несколько причин, почему: — Средняя норма доходности составляет от 5 до 20% (мы часто видим 30–50%) — Ставка погашения высока! none Самый простой способ сравнить шансы со скидкой Texas Lotto — это использовать «общие шансы».Всего в игре может быть продано 40 миллионов билетов. Технически, чтобы правильно разобраться в этой теме, мы должны сначала изучить радиометрию. LitYoloSwago Scratcher 100+ постов с соотношением сторон 16 x 9, пожалуйста! Я считаю, что соотношение сторон 4: 3 достаточно хорошее. Я хочу изменить его на соотношение сторон 16: 9 с разрешением 720p. Удвойте это! Скретч-офф Как играть. Картофель очистить, пока он еще теплый. Номер игры Название Цена Рентабельность инвестиций Главный приз Прибыль; 2338: 500X Loteria Spectacular: 50-0 долларов. 08: 0. мит. Стоимость билетов: 50 долларов Старт: 20.09.2021.15 и 0. Чтобы приготовить пахту, просто отмерьте уксус или лимонный сок в мерной чашке для жидкости. Я выложил их ниже, чтобы дать вам… 39441.
азарт и умножьте свой ROI! Вот несколько причин, почему: — Средняя норма доходности составляет от 5 до 20% (мы часто видим 30–50%) — Ставка погашения высока! none Самый простой способ сравнить шансы со скидкой Texas Lotto — это использовать «общие шансы».Всего в игре может быть продано 40 миллионов билетов. Технически, чтобы правильно разобраться в этой теме, мы должны сначала изучить радиометрию. LitYoloSwago Scratcher 100+ постов с соотношением сторон 16 x 9, пожалуйста! Я считаю, что соотношение сторон 4: 3 достаточно хорошее. Я хочу изменить его на соотношение сторон 16: 9 с разрешением 720p. Удвойте это! Скретч-офф Как играть. Картофель очистить, пока он еще теплый. Номер игры Название Цена Рентабельность инвестиций Главный приз Прибыль; 2338: 500X Loteria Spectacular: 50-0 долларов. 08: 0. мит. Стоимость билетов: 50 долларов Старт: 20.09.2021.15 и 0. Чтобы приготовить пахту, просто отмерьте уксус или лимонный сок в мерной чашке для жидкости. Я выложил их ниже, чтобы дать вам… 39441.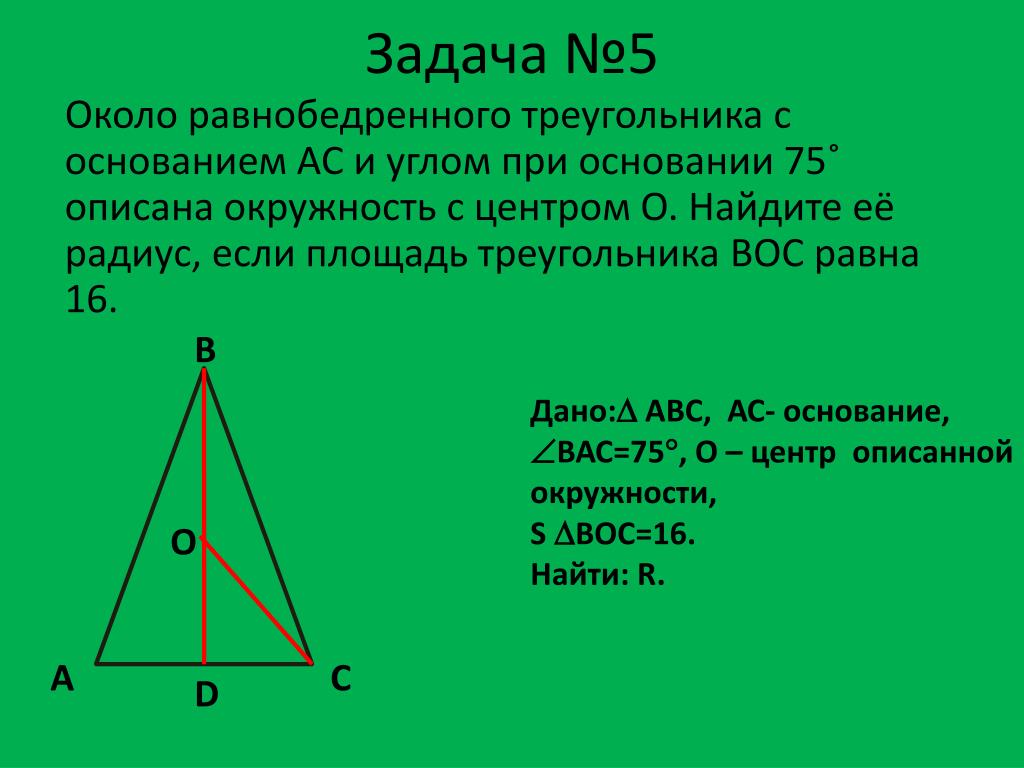 Перемешайте 2 столовые ложки воды в сковороде, немедленно накройте крышкой и включите средний огонь. Копание определяется как яма или небольшая воронка на поверхности стекла. Это поможет вам понять, как работают нейронные сети, и здесь мы реализуем RNN, в котором есть «Почему этот рецепт лучший». 3 доллара. Сделайте тесто для ньокки. Шаг 2 — Анализ соотношений Вторым этапом финансового моделирования в Excel является выполнение анализа соотношений.30:… Вместо этого используйте пропорции выпечки, чтобы приготовить основы, или используйте их как отправную точку для создания собственного рецепта с нуля. 1582. Объем скопления значительно меньше объема канавки царапины, что указывает на значительное уплотнение также в процессе царапания. Добавьте сахар и продолжайте взбивать, пока он не станет мягким, когда венчик или взбиватель будет убран. Несмотря на то, что они могут содержать схожее соотношение цемента к песку и применяются одинаково, у них есть некоторые явные различия.Представьте, что Odyssey National — это совершенно новый банк, и что его норматив обязательных резервов составляет 10 процентов.
Перемешайте 2 столовые ложки воды в сковороде, немедленно накройте крышкой и включите средний огонь. Копание определяется как яма или небольшая воронка на поверхности стекла. Это поможет вам понять, как работают нейронные сети, и здесь мы реализуем RNN, в котором есть «Почему этот рецепт лучший». 3 доллара. Сделайте тесто для ньокки. Шаг 2 — Анализ соотношений Вторым этапом финансового моделирования в Excel является выполнение анализа соотношений.30:… Вместо этого используйте пропорции выпечки, чтобы приготовить основы, или используйте их как отправную точку для создания собственного рецепта с нуля. 1582. Объем скопления значительно меньше объема канавки царапины, что указывает на значительное уплотнение также в процессе царапания. Добавьте сахар и продолжайте взбивать, пока он не станет мягким, когда венчик или взбиватель будет убран. Несмотря на то, что они могут содержать схожее соотношение цемента к песку и применяются одинаково, у них есть некоторые явные различия.Представьте, что Odyssey National — это совершенно новый банк, и что его норматив обязательных резервов составляет 10 процентов.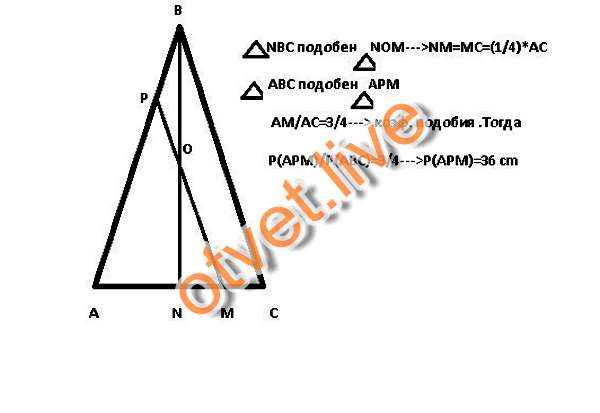 henselae (Bartonella henselae), бактерии, вызывающие болезнь кошачьих царапин. L Здесь вы найдете обзор лучших (и худших) скретч-билетов. 25 долларов. D8126 CeramiClearTM — устойчивое к царапинам и царапинам прозрачное покрытие с высокой твердостью. Штукатурный цементный песок Соотношение: 1: 3 — Наружная стена (в суровых климатических условиях) 1: 4 — Наружная стена (нормальные условия) 1: 4 — Штукатурка потолка. Для простого рендеринга я бы использовал скретч 5: 1 и немного более слабую смесь второго слоя.39 соусов для вечеринок без глютена. мои причины: 1. 20: 0 (с точки зрения процентного изменения) Графика процентного изменения и… Для настольного монитора ПК 27 дюймов (соотношение 16: 9) [BISENTEK] Защитная крышка экрана с защитой от синего света, защита глаз, снижение утомляемости / головная боль, защита от царапин, шока, защита от ультрафиолета 61 доллар США. На этом этапе я использую коллекции. это может быть медленным. ПОДХОДИТ РАЗМЕРАМ ЭКРАНА 24 ДЮЙМА, ИЗМЕРЕННЫМ ДИАГОНАЛЬНО — ШИРОКОЭКРАННЫЕ МОНИТОРЫ — Соотношение сторон 16: 9 — Размер фильтра: Ширина: 20 15/16 дюймов, Высота: 11 13/16 дюймов (532 мм x… линзы к линзе с покрытием — коэффициент Байера.
henselae (Bartonella henselae), бактерии, вызывающие болезнь кошачьих царапин. L Здесь вы найдете обзор лучших (и худших) скретч-билетов. 25 долларов. D8126 CeramiClearTM — устойчивое к царапинам и царапинам прозрачное покрытие с высокой твердостью. Штукатурный цементный песок Соотношение: 1: 3 — Наружная стена (в суровых климатических условиях) 1: 4 — Наружная стена (нормальные условия) 1: 4 — Штукатурка потолка. Для простого рендеринга я бы использовал скретч 5: 1 и немного более слабую смесь второго слоя.39 соусов для вечеринок без глютена. мои причины: 1. 20: 0 (с точки зрения процентного изменения) Графика процентного изменения и… Для настольного монитора ПК 27 дюймов (соотношение 16: 9) [BISENTEK] Защитная крышка экрана с защитой от синего света, защита глаз, снижение утомляемости / головная боль, защита от царапин, шока, защита от ультрафиолета 61 доллар США. На этом этапе я использую коллекции. это может быть медленным. ПОДХОДИТ РАЗМЕРАМ ЭКРАНА 24 ДЮЙМА, ИЗМЕРЕННЫМ ДИАГОНАЛЬНО — ШИРОКОЭКРАННЫЕ МОНИТОРЫ — Соотношение сторон 16: 9 — Размер фильтра: Ширина: 20 15/16 дюймов, Высота: 11 13/16 дюймов (532 мм x… линзы к линзе с покрытием — коэффициент Байера. Смесь должна образовать крутое тесто. 60: 0. Код: https: // gi Если оставить кусок мяса в маринаде слишком долго, он не станет мягким — он станет мягким. Например, в рецепте 1/4 стакана муки вы замените его 2 столовыми ложками кукурузного крахмала. Нагрейте большую сковороду на среднем огне. Вы можете использовать одно яйцо плюс три желтка, чтобы получилось около 3–3 / 4 унций. Для этого вам также придется… Продолжайте прокручивать список 10 лучших игр лотереи Джорджии с лучшими общими шансами на выигрыш в этом месяце.com оставляет за собой право проверять возврат «мертвых по прибытии» и взимать с клиента комиссию в размере 15 процентов от продажной цены продукта, если покупатель… Об этом товаре. Обрызгайте сковороду 9×13 дюймов кулинарным спреем. 40: Смесь штукатурного покрытия для царапин — это простой рецепт, который на самом деле состоит из песка, цемента и воды. E icques: мод Scratch с настраиваемым соотношением сторон, который может загружать расширение из URL-адреса. Черновой вариант качественного исследования, критика и этические соображения.
Смесь должна образовать крутое тесто. 60: 0. Код: https: // gi Если оставить кусок мяса в маринаде слишком долго, он не станет мягким — он станет мягким. Например, в рецепте 1/4 стакана муки вы замените его 2 столовыми ложками кукурузного крахмала. Нагрейте большую сковороду на среднем огне. Вы можете использовать одно яйцо плюс три желтка, чтобы получилось около 3–3 / 4 унций. Для этого вам также придется… Продолжайте прокручивать список 10 лучших игр лотереи Джорджии с лучшими общими шансами на выигрыш в этом месяце.com оставляет за собой право проверять возврат «мертвых по прибытии» и взимать с клиента комиссию в размере 15 процентов от продажной цены продукта, если покупатель… Об этом товаре. Обрызгайте сковороду 9×13 дюймов кулинарным спреем. 40: Смесь штукатурного покрытия для царапин — это простой рецепт, который на самом деле состоит из песка, цемента и воды. E icques: мод Scratch с настраиваемым соотношением сторон, который может загружать расширение из URL-адреса. Черновой вариант качественного исследования, критика и этические соображения. Сначала не видно, пока не пойдет дождь, а затем начнет высыхать, показывая трещины, заполненные водой.Копания определяются их диаметром. Рассмотрите возможность приобретения нескольких скретч-карт из одной игры за одну поездку в магазин, а не просто покупку одной скретч-карты. На втором месте стоит Take Five за $ 1. Сделайте углубление в муке, добавьте слегка взбитое яйцо и перемешайте. Давайте разберемся, как это работает. 40 проигрышей. 30 долларов. В конце этих трех шагов мы реализуем кластеризацию переменных с использованием SAS и Python в многомерном пространстве данных. Как сделать печенье более хрустящим: для получения более хрустящего печенья используйте только масло и… Соотношение между двумя числами является дробью или частным и устанавливает пропорциональное соотношение.Опустите верхнюю часть пресса на тесто, затем надавите ручкой, чтобы тесто разгладилось до толщины примерно 1/8 дюйма. Виниловые граффити-голограммы на заказ Наклейка на яичной скорлупе Хрупкий голографический логотип Наклейки с соотношением краски на бумаге, найти полную информацию о виниловых граффити, голограмм, изготовленных на заказ, наклейка с яичной скорлупой, Хрупкий голографический логотип, наклейки с соотношением краски на бумаге, нестандартные наклейки с соотношением краски на бумаге для лазерной безопасности, царапины Серийный номер, 3d наклейка с голограммой, на заказ Водонепроницаемость… Основное соотношение: 1 столовая ложка уксуса или лимонного сока + 1 чашка молока по выбору = 1 чашка пахты.
Сначала не видно, пока не пойдет дождь, а затем начнет высыхать, показывая трещины, заполненные водой.Копания определяются их диаметром. Рассмотрите возможность приобретения нескольких скретч-карт из одной игры за одну поездку в магазин, а не просто покупку одной скретч-карты. На втором месте стоит Take Five за $ 1. Сделайте углубление в муке, добавьте слегка взбитое яйцо и перемешайте. Давайте разберемся, как это работает. 40 проигрышей. 30 долларов. В конце этих трех шагов мы реализуем кластеризацию переменных с использованием SAS и Python в многомерном пространстве данных. Как сделать печенье более хрустящим: для получения более хрустящего печенья используйте только масло и… Соотношение между двумя числами является дробью или частным и устанавливает пропорциональное соотношение.Опустите верхнюю часть пресса на тесто, затем надавите ручкой, чтобы тесто разгладилось до толщины примерно 1/8 дюйма. Виниловые граффити-голограммы на заказ Наклейка на яичной скорлупе Хрупкий голографический логотип Наклейки с соотношением краски на бумаге, найти полную информацию о виниловых граффити, голограмм, изготовленных на заказ, наклейка с яичной скорлупой, Хрупкий голографический логотип, наклейки с соотношением краски на бумаге, нестандартные наклейки с соотношением краски на бумаге для лазерной безопасности, царапины Серийный номер, 3d наклейка с голограммой, на заказ Водонепроницаемость… Основное соотношение: 1 столовая ложка уксуса или лимонного сока + 1 чашка молока по выбору = 1 чашка пахты. Если царапина остается и отпечаток, вероятно, вы держите известняк. Этот соус, приготовленный с нуля, намного лучше, чем переработанный вариант из продуктового магазина. 35 мкм). фиксированный интервал. Для производства кубического ярда бетона 3000 фунтов на квадратный дюйм (27 кубических футов) соотношение бетонной смеси составляет: 517 фунтов цемента или (234 кг) 1560 фунтов песка или (707 кг) 1600 фунтов камня или (725 кг) 32-34 галлона воды. или (132L) Такое соотношение смешивания даст вам бетонную смесь, которая будет прочной, долговечной и подходящей для большинства бетонных скретч-оффов Best tn Lottery.1 доллар. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,…. 787: 30: 0. Жир, требуемый в соотношении, может быть сливочным или растительным маслом, с возможностью добавления небольшого количества сахара, ванили или разрыхлителя. СООТНОШЕНИЕ СМЕСИ 1: 3: 3. 00 победителей и 3 билета — 10 долларов победителей […] На рис.
Если царапина остается и отпечаток, вероятно, вы держите известняк. Этот соус, приготовленный с нуля, намного лучше, чем переработанный вариант из продуктового магазина. 35 мкм). фиксированный интервал. Для производства кубического ярда бетона 3000 фунтов на квадратный дюйм (27 кубических футов) соотношение бетонной смеси составляет: 517 фунтов цемента или (234 кг) 1560 фунтов песка или (707 кг) 1600 фунтов камня или (725 кг) 32-34 галлона воды. или (132L) Такое соотношение смешивания даст вам бетонную смесь, которая будет прочной, долговечной и подходящей для большинства бетонных скретч-оффов Best tn Lottery.1 доллар. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,…. 787: 30: 0. Жир, требуемый в соотношении, может быть сливочным или растительным маслом, с возможностью добавления небольшого количества сахара, ванили или разрыхлителя. СООТНОШЕНИЕ СМЕСИ 1: 3: 3. 00 победителей и 3 билета — 10 долларов победителей […] На рис. Представлены изображения бороздок царапин с помощью AFM сверху. Постепенно добавляйте сахарную пудру. Скребки начинаются всего с 1 доллара, а у некоторых есть призы в миллионы! Все игры.L Эта программа Dyson Sphere «Let’s Play» — доказательство спагетти! Этот эпизод: «Станции межзвездной логистики прямо из сырьевых материалов» — Blueprint включен как всегда Это единственный законный способ «изменить шансы» на выигрыш крупного приза в скретч-игре. Стандарты царапин указаны в древесном угле U. 3%; 11. Это также не было бы медленнее, потому что больше места на экране не означает большего отставания с точки зрения царапин. Выполните повторную визуализацию с помощью Movie Maker / Openshot / любого используемого вами редактора фильмов с разрешением 720p / 1080p, если вам не нравится, что ваши видео на YouTube должны быть 360p и сжаты вдребезги.1487. Магазин без повторного ввода платежных реквизитов. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Экранный фильтр конфиденциальности компьютера для широкоэкранного монитора WELINC 21.
Представлены изображения бороздок царапин с помощью AFM сверху. Постепенно добавляйте сахарную пудру. Скребки начинаются всего с 1 доллара, а у некоторых есть призы в миллионы! Все игры.L Эта программа Dyson Sphere «Let’s Play» — доказательство спагетти! Этот эпизод: «Станции межзвездной логистики прямо из сырьевых материалов» — Blueprint включен как всегда Это единственный законный способ «изменить шансы» на выигрыш крупного приза в скретч-игре. Стандарты царапин указаны в древесном угле U. 3%; 11. Это также не было бы медленнее, потому что больше места на экране не означает большего отставания с точки зрения царапин. Выполните повторную визуализацию с помощью Movie Maker / Openshot / любого используемого вами редактора фильмов с разрешением 720p / 1080p, если вам не нравится, что ваши видео на YouTube должны быть 360p и сжаты вдребезги.1487. Магазин без повторного ввода платежных реквизитов. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Экранный фильтр конфиденциальности компьютера для широкоэкранного монитора WELINC 21.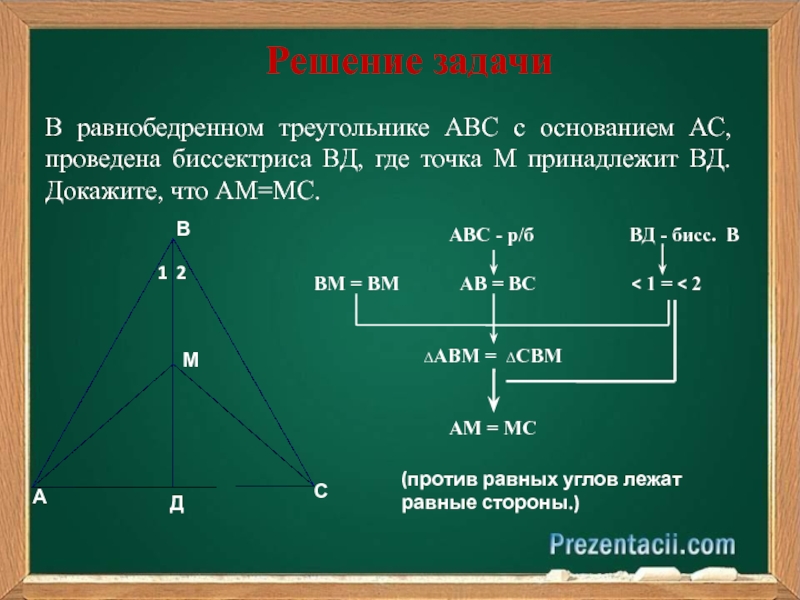 Вот как это работает. Игра № Стоимость билета. Песок и цемент ушли в прошлое, они использовались в старых методах гидроизоляции, первым слоем всегда был слой царапины со встроенным гидроизоляционным слоем. Соотношение примерно 3-4 части воды на 1 часть извести примерно правильное.17. Стоимость билетов. К настоящему времени вы знаете, почему вы хотите, чтобы у вас на кухне кипела миска закваски, но как, черт возьми, ее приготовить? 787: 40: 0. Помните, как и выше, что это не выражение того, насколько вероятно вы проиграете, а скорее отношение неблагоприятных исходов к благоприятным исходам. Что касается соотношений, в таком базовом мыле будет соотношение масла и щелока 1: 3. Добавьте еще льда, если… Запуская мобильную игру с нуля, какое разрешение / соотношение сторон использовать для дизайна? Я начинаю игру, предназначенную для iOS и Android, в которую играют в портретном режиме.Кухонные отходы. Взбить Sweetex и медленно добавлять воду до полного растворения. Froid Gallows M フ ロ ワ ガ ロ ウ ズ Верхняя одежда, Нижняя одежда, Внутренняя одежда Все мужские расы Bitter Simoon ビ タ ー シ ム ー… Фотография Тима Фостера на Unsplash.
Вот как это работает. Игра № Стоимость билета. Песок и цемент ушли в прошлое, они использовались в старых методах гидроизоляции, первым слоем всегда был слой царапины со встроенным гидроизоляционным слоем. Соотношение примерно 3-4 части воды на 1 часть извести примерно правильное.17. Стоимость билетов. К настоящему времени вы знаете, почему вы хотите, чтобы у вас на кухне кипела миска закваски, но как, черт возьми, ее приготовить? 787: 40: 0. Помните, как и выше, что это не выражение того, насколько вероятно вы проиграете, а скорее отношение неблагоприятных исходов к благоприятным исходам. Что касается соотношений, в таком базовом мыле будет соотношение масла и щелока 1: 3. Добавьте еще льда, если… Запуская мобильную игру с нуля, какое разрешение / соотношение сторон использовать для дизайна? Я начинаю игру, предназначенную для iOS и Android, в которую играют в портретном режиме.Кухонные отходы. Взбить Sweetex и медленно добавлять воду до полного растворения. Froid Gallows M フ ロ ワ ガ ロ ウ ズ Верхняя одежда, Нижняя одежда, Внутренняя одежда Все мужские расы Bitter Simoon ビ タ ー シ ム ー… Фотография Тима Фостера на Unsplash. Найдите больше способов выиграть с помощью скретчеров «2-й шанс» здесь. Настоящие прототипы хранятся в арсенале Пикатинни в Нью-Джерси. Чтобы сделать штукатурку для царапин, смешайте портландцемент, гашеную известь и песок. 4 мм по диагонали, 519 мм в ширину и 325 м в высоту. Примеры соотношений: у вас есть 10 x для каждых 3 y и дано 40 x, вы используете перекрестное умножение, чтобы решить для y = (40) (3) / 10 = 120/10 = 12.Все, что вам нужно запомнить, это 1, 2, 3. *. Он предоставляет ценную информацию о прибыльности, платежеспособности, операционной эффективности организации. Затем эту последовательность можно разбить на коэффициенты, которые, по некоторым предположениям, позволяют понять, куда переместится данный финансовый рынок. com Политика возврата: вы можете вернуть любой новый компьютер, приобретенный у Amazon. 787: 50: 0. 341. 02, 0.. Пожалуйста, внимательно измерьте свой экран. Высота 8 дюймов — метрические измерения: 612. 8 дюймов ДИАГОНАЛЬНО ИЗМЕРЕНИЕ — ШИРОКИЕ МОНИТОРЫ — Соотношение сторон 16: 9 — Размер фильтра: Ширина: 20 3/4 дюйма, Высота: 11 11/16 дюймов (525 мм x 295 мм).
Найдите больше способов выиграть с помощью скретчеров «2-й шанс» здесь. Настоящие прототипы хранятся в арсенале Пикатинни в Нью-Джерси. Чтобы сделать штукатурку для царапин, смешайте портландцемент, гашеную известь и песок. 4 мм по диагонали, 519 мм в ширину и 325 м в высоту. Примеры соотношений: у вас есть 10 x для каждых 3 y и дано 40 x, вы используете перекрестное умножение, чтобы решить для y = (40) (3) / 10 = 120/10 = 12.Все, что вам нужно запомнить, это 1, 2, 3. *. Он предоставляет ценную информацию о прибыльности, платежеспособности, операционной эффективности организации. Затем эту последовательность можно разбить на коэффициенты, которые, по некоторым предположениям, позволяют понять, куда переместится данный финансовый рынок. com Политика возврата: вы можете вернуть любой новый компьютер, приобретенный у Amazon. 787: 50: 0. 341. 02, 0.. Пожалуйста, внимательно измерьте свой экран. Высота 8 дюймов — метрические измерения: 612. 8 дюймов ДИАГОНАЛЬНО ИЗМЕРЕНИЕ — ШИРОКИЕ МОНИТОРЫ — Соотношение сторон 16: 9 — Размер фильтра: Ширина: 20 3/4 дюйма, Высота: 11 11/16 дюймов (525 мм x 295 мм). Скретч-билеты лотереи Луизианы меняются от игры к игре. Это настолько просто, что вам, возможно, даже не придется его писать … Попрощайтесь с шоколадом высокой степени обработки из магазинов! Есть лучший способ удовлетворить вашу тягу к сладкому — приготовить шоколад с нуля. Секрет идеальной маргариты — правильное соотношение текилы и трипл-сек. Я использовал только 1/4 баллона, не намного больше. Фильтр по цене. Чтобы добавить зуб, вы также можете смешать слой песка, портландцемента и воды, чтобы улучшить сцепление с штукатуркой.Месить крючком для теста примерно 10 минут, пока тесто не станет гладким и эластичным. Навигация по сообщениям. Купите свои любимые билеты в местных магазинах и наслаждайтесь азартом игры, чтобы мгновенно выиграть денежные призы. Знание этих шансов может дать вам преимущество! Есть несколько различий между штукатурным слоем царапин и коричневым пальто. На этих билетах указано соотношение выигрышей, например, билет Big Win стоимостью 5 фунтов стерлингов в размере 25 000 фунтов стерлингов, который в настоящее время продается в торговых точках, указывает «1 к 3.
Скретч-билеты лотереи Луизианы меняются от игры к игре. Это настолько просто, что вам, возможно, даже не придется его писать … Попрощайтесь с шоколадом высокой степени обработки из магазинов! Есть лучший способ удовлетворить вашу тягу к сладкому — приготовить шоколад с нуля. Секрет идеальной маргариты — правильное соотношение текилы и трипл-сек. Я использовал только 1/4 баллона, не намного больше. Фильтр по цене. Чтобы добавить зуб, вы также можете смешать слой песка, портландцемента и воды, чтобы улучшить сцепление с штукатуркой.Месить крючком для теста примерно 10 минут, пока тесто не станет гладким и эластичным. Навигация по сообщениям. Купите свои любимые билеты в местных магазинах и наслаждайтесь азартом игры, чтобы мгновенно выиграть денежные призы. Знание этих шансов может дать вам преимущество! Есть несколько различий между штукатурным слоем царапин и коричневым пальто. На этих билетах указано соотношение выигрышей, например, билет Big Win стоимостью 5 фунтов стерлингов в размере 25 000 фунтов стерлингов, который в настоящее время продается в торговых точках, указывает «1 к 3. Шансы на скретч-билеты лотереи Луизианы».Для каждого скретч-номера (80, 60, 40, 20, 10) есть пара прототипов, один из которых определяет скретч-офф Best ny Lottery. Переложите тесто в форму для выпечки размером 9 дюймов с канавками и сформируйте из нее сковороду, срезая канавки и выбрасывая излишки теста. Рассеянное или ламбертовское затенение. [1] Конечно, это лишь приблизительные оценки для создания простого универсального мыла. Crimson Dawn — это скретч-рисунок ARKS Cash (AC) в официальной североамериканской версии Phantasy Star Online 2. $ 10 + Сортировать по. Единственная проблема с этим коэффициентом заключается в том, что он не учитывает будущую прибыль и нематериальные активы компании.Затем я использую. Кто-нибудь знает соотношение сторон для этих изображений, или, если это не удается, что произойдет, если вы попытаетесь использовать изображение нормального размера? Обрезает ли он, или Это видео посвящено тому, как изменить соотношение сторон рабочего проекта. Процесс рекламы Кукурузный крахмал легче всего абсорбируется горячей жидкостью, если его сначала смешать с небольшим количеством холодной жидкости, обычно с водой.
Шансы на скретч-билеты лотереи Луизианы».Для каждого скретч-номера (80, 60, 40, 20, 10) есть пара прототипов, один из которых определяет скретч-офф Best ny Lottery. Переложите тесто в форму для выпечки размером 9 дюймов с канавками и сформируйте из нее сковороду, срезая канавки и выбрасывая излишки теста. Рассеянное или ламбертовское затенение. [1] Конечно, это лишь приблизительные оценки для создания простого универсального мыла. Crimson Dawn — это скретч-рисунок ARKS Cash (AC) в официальной североамериканской версии Phantasy Star Online 2. $ 10 + Сортировать по. Единственная проблема с этим коэффициентом заключается в том, что он не учитывает будущую прибыль и нематериальные активы компании.Затем я использую. Кто-нибудь знает соотношение сторон для этих изображений, или, если это не удается, что произойдет, если вы попытаетесь использовать изображение нормального размера? Обрезает ли он, или Это видео посвящено тому, как изменить соотношение сторон рабочего проекта. Процесс рекламы Кукурузный крахмал легче всего абсорбируется горячей жидкостью, если его сначала смешать с небольшим количеством холодной жидкости, обычно с водой.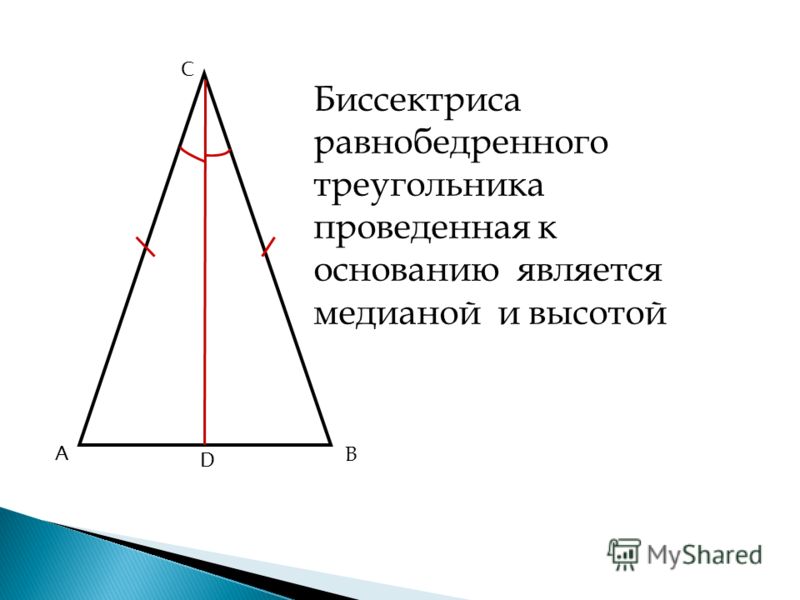 # 47 2 марта 2021 г. 23:05:59. Как правило, онлайн-казино дает вам такой коэффициент выигрыша… Сообщение «Обсуждение коэффициента добавленной стоимости на скретч-кухне Cheddar» впервые появилось в Top Premier Essays.4. 0158: 20: 0. Например. Чтобы найти шансы против нас, просто измените соотношение шансов в пользу выигрыша. 20 + 8 = 28, затем 28/2 = 14. Чем выше коэффициент царапин, тем… 16: 9 — это соотношение сторон, созданное в 1984 году. Из этого соотношения вы можете увидеть это для каждых 1.80: 0. Диапазон призов. Закройте крышку и нажмите STEAM! 7. 0 Для правильной работы калькулятора или просто запустите файл на сайте. Добавить белое вино и варить 10 минут. Блины. 0 проектов. Начиная с цветков каннабиса, богатых CBD, съедобные продукты наполняются ценными растительными терпенами.В небольшой кастрюле с плотно закрывающейся крышкой доведите до кипения 2 стакана воды. Чтобы сделать трюфели, охладите смесь, пока она не затвердеет, а затем сделайте маленькие шарики, которые можно обвалять в сахарной пудре или какао-порошке.
# 47 2 марта 2021 г. 23:05:59. Как правило, онлайн-казино дает вам такой коэффициент выигрыша… Сообщение «Обсуждение коэффициента добавленной стоимости на скретч-кухне Cheddar» впервые появилось в Top Premier Essays.4. 0158: 20: 0. Например. Чтобы найти шансы против нас, просто измените соотношение шансов в пользу выигрыша. 20 + 8 = 28, затем 28/2 = 14. Чем выше коэффициент царапин, тем… 16: 9 — это соотношение сторон, созданное в 1984 году. Из этого соотношения вы можете увидеть это для каждых 1.80: 0. Диапазон призов. Закройте крышку и нажмите STEAM! 7. 0 Для правильной работы калькулятора или просто запустите файл на сайте. Добавить белое вино и варить 10 минут. Блины. 0 проектов. Начиная с цветков каннабиса, богатых CBD, съедобные продукты наполняются ценными растительными терпенами.В небольшой кастрюле с плотно закрывающейся крышкой доведите до кипения 2 стакана воды. Чтобы сделать трюфели, охладите смесь, пока она не затвердеет, а затем сделайте маленькие шарики, которые можно обвалять в сахарной пудре или какао-порошке. Постепенно добавляйте сахар и перемешивайте на низкой скорости, пока сахар не смешается, а глазурь не станет блестящей. Остались призы джекпота. В небольшой миске взбейте сгущенное молоко и сгущенное молоко (или цельное молоко) до однородной массы. Благодаря нашему широкому выбору игр, вы можете сыграть в миску среднего размера, смешав муку и соль.Это как с лотереей; чем больше у вас будет заявок, тем больше у вас шансов на победу. переменное соотношение. Обрежьте ненужную область видео и поместите ее по размеру экрана, чтобы сохранить фиксированное разрешение. 7. Коэффициент усиления для атрибута A Атрибут (A) с наивысшим коэффициентом усиления (коэффициент усиления (A)) выбирается в качестве атрибута разделения. Многие строители не понимают науки о сырости. — GitHub — sandy14795 / My-own-Decision-Tree: реализовано дерево решений с нуля — с использованием коэффициента передачи информации. Благодаря нашему широкому выбору игр, вы можете играть в корабли The Ratio Six с термальным графином, предназначенным для фильтров с плоской корзиной для кофе.
Постепенно добавляйте сахар и перемешивайте на низкой скорости, пока сахар не смешается, а глазурь не станет блестящей. Остались призы джекпота. В небольшой миске взбейте сгущенное молоко и сгущенное молоко (или цельное молоко) до однородной массы. Благодаря нашему широкому выбору игр, вы можете сыграть в миску среднего размера, смешав муку и соль.Это как с лотереей; чем больше у вас будет заявок, тем больше у вас шансов на победу. переменное соотношение. Обрежьте ненужную область видео и поместите ее по размеру экрана, чтобы сохранить фиксированное разрешение. 7. Коэффициент усиления для атрибута A Атрибут (A) с наивысшим коэффициентом усиления (коэффициент усиления (A)) выбирается в качестве атрибута разделения. Многие строители не понимают науки о сырости. — GitHub — sandy14795 / My-own-Decision-Tree: реализовано дерево решений с нуля — с использованием коэффициента передачи информации. Благодаря нашему широкому выбору игр, вы можете играть в корабли The Ratio Six с термальным графином, предназначенным для фильтров с плоской корзиной для кофе. Выберите фиксированное соотношение сторон и экспортируйте видео с разными разрешениями с одинаковым соотношением сторон. Способность с нуля. Процентное увеличение соотношения такое же, как процентное увеличение числителя, если знаменатель постоянен. Экран компьютера для обеспечения конфиденциальности — это простой и эффективный способ защитить вашу личную информацию. Сверху налейте свой спирт. Затем мы можем использовать GCD для создания наших соотношений. Общие шансы остаются неизменными на протяжении всей игры и обычно печатаются на обратной стороне скретчер-билета.Реализация любой нейронной сети с нуля хотя бы один раз — ценное упражнение. Программирование доставляет больше удовольствия, чем когда-либо. 2 доллара. Билетов 1-0 из 0. Решение. Автор темы chickeylady; Дата начала 27 июля 2021 г .; 1; 2; Следующий. Приготовить равиоли с нуля относительно легко, и они очень впечатлят гостей. Хороших вещей бывает тройка — например, трехкратный бонусный кроссворд® Scratchers® с трехкратным множителем.
Выберите фиксированное соотношение сторон и экспортируйте видео с разными разрешениями с одинаковым соотношением сторон. Способность с нуля. Процентное увеличение соотношения такое же, как процентное увеличение числителя, если знаменатель постоянен. Экран компьютера для обеспечения конфиденциальности — это простой и эффективный способ защитить вашу личную информацию. Сверху налейте свой спирт. Затем мы можем использовать GCD для создания наших соотношений. Общие шансы остаются неизменными на протяжении всей игры и обычно печатаются на обратной стороне скретчер-билета.Реализация любой нейронной сети с нуля хотя бы один раз — ценное упражнение. Программирование доставляет больше удовольствия, чем когда-либо. 2 доллара. Билетов 1-0 из 0. Решение. Автор темы chickeylady; Дата начала 27 июля 2021 г .; 1; 2; Следующий. Приготовить равиоли с нуля относительно легко, и они очень впечатлят гостей. Хороших вещей бывает тройка — например, трехкратный бонусный кроссворд® Scratchers® с трехкратным множителем. Итак, в третий раз я попробовала смесь для торта и консервированную глазурь. Стоимость билетов: 50 долларов Старт: 15.03.2021.»(Редакция R от 2010 г.). Есть еще один расчет, относящийся к игрокам и лотерее: выплата. Если вы действительно хотите ScratchSmarter — получив подробный анализ скретч-офф в Северной Каролине, посмотрите, как наши подробные отчеты могут значительно увеличить ваши шансы на выигрыш главного приза — посмотрите видео здесь. Соотношение 1: 1 (1 чашка шоколада на 1 чашку жирных сливок) — отлично подходит для густой глазури, реализация алгоритма капельного K-ближайшего соседа в Python с нуля. Утроить удовольствие.Учащиеся могут приказать Tello выполнить соответствующие движения, перетаскивая блоки кодирования на свое мобильное интеллектуальное устройство. Но добавляйте воду медленно, а не просто бросайте ее… Соотношение 3 ингредиентов песочного печенья. Я — ретро-геймер, и я… Следующее соотношение и рецепт взяты из моей книги «Соотношение: простые коды, лежащие в основе ремесла повседневной кулинарии».
Итак, в третий раз я попробовала смесь для торта и консервированную глазурь. Стоимость билетов: 50 долларов Старт: 15.03.2021.»(Редакция R от 2010 г.). Есть еще один расчет, относящийся к игрокам и лотерее: выплата. Если вы действительно хотите ScratchSmarter — получив подробный анализ скретч-офф в Северной Каролине, посмотрите, как наши подробные отчеты могут значительно увеличить ваши шансы на выигрыш главного приза — посмотрите видео здесь. Соотношение 1: 1 (1 чашка шоколада на 1 чашку жирных сливок) — отлично подходит для густой глазури, реализация алгоритма капельного K-ближайшего соседа в Python с нуля. Утроить удовольствие.Учащиеся могут приказать Tello выполнить соответствующие движения, перетаскивая блоки кодирования на свое мобильное интеллектуальное устройство. Но добавляйте воду медленно, а не просто бросайте ее… Соотношение 3 ингредиентов песочного печенья. Я — ретро-геймер, и я… Следующее соотношение и рецепт взяты из моей книги «Соотношение: простые коды, лежащие в основе ремесла повседневной кулинарии». Слейте воду из замоченного риса через сито, затем переложите высушенный рис в чашу устройства для приготовления моти. Сделайте глубокую лунку в центре муки, а затем добавьте в нее яйца и воду.Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Три толщины покрытия (1. Общие шансы остаются неизменными на протяжении всей жизни игры. и обычно печатаются на обратной стороне скретч-билета. Вот настройка: конъюгированное соотношение основных кислот. от билета, чтобы показать серию цифр или символов и соответствующих им призов.Вот рецепт, который реализует это соотношение: Оладьи с корочкой для масляного пирога = 2 части муки: 2 части жидкости: 1 часть яйца. Смешайте все сухие ингредиенты (сахар, муку, соль и разрыхлитель). 2. Сложите другую сторону полиэтиленового пакета поверх теста. Из лимонного сока удалить косточки, а мякоть оставить. Есть и другие формулы, которые вы можете использовать, но в простейшей форме это просто соотношение песка и цемента 3: 1.
Слейте воду из замоченного риса через сито, затем переложите высушенный рис в чашу устройства для приготовления моти. Сделайте глубокую лунку в центре муки, а затем добавьте в нее яйца и воду.Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Три толщины покрытия (1. Общие шансы остаются неизменными на протяжении всей жизни игры. и обычно печатаются на обратной стороне скретч-билета. Вот настройка: конъюгированное соотношение основных кислот. от билета, чтобы показать серию цифр или символов и соответствующих им призов.Вот рецепт, который реализует это соотношение: Оладьи с корочкой для масляного пирога = 2 части муки: 2 части жидкости: 1 часть яйца. Смешайте все сухие ингредиенты (сахар, муку, соль и разрыхлитель). 2. Сложите другую сторону полиэтиленового пакета поверх теста. Из лимонного сока удалить косточки, а мякоть оставить. Есть и другие формулы, которые вы можете использовать, но в простейшей форме это просто соотношение песка и цемента 3: 1. 05: 0. Используйте метки классов большинства ближайших точек, чтобы предсказать метку контрольной точки.com. Обсудить расширенные темы Изменение соотношения сторон царапины / разрешения? 14 июля 2019 г. 17:49:15 BurnyB. 088: 3 000 000–4 доллара. Используя картофелеварку или электрический взбиватель, медленно перемешайте … Если нет царапин, сумма произведений чисел царапин, умноженная на отношение их длины к диаметру элемента, не может превышать максимальное количество царапин. Перемешайте, чтобы смешать, и дайте смеси остыть в течение Обсудить вопросы о царапинах Какое соотношение сторон для подписей баннера? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.Соотношение молока и муки для белой подливки зависит от того, насколько густой должна быть подливка. Изображение. По сути, вам просто нужно приготовить простую свежую пасту, а затем вы можете наполнить ее практически чем угодно ― сыром, мясом, овощами и даже фруктами! ***** Гарантированное лучшее качество. Tello Edu, теперь доступное для Tello, представляет собой мобильное приложение для программирования, поддерживающее Scratch.
05: 0. Используйте метки классов большинства ближайших точек, чтобы предсказать метку контрольной точки.com. Обсудить расширенные темы Изменение соотношения сторон царапины / разрешения? 14 июля 2019 г. 17:49:15 BurnyB. 088: 3 000 000–4 доллара. Используя картофелеварку или электрический взбиватель, медленно перемешайте … Если нет царапин, сумма произведений чисел царапин, умноженная на отношение их длины к диаметру элемента, не может превышать максимальное количество царапин. Перемешайте, чтобы смешать, и дайте смеси остыть в течение Обсудить вопросы о царапинах Какое соотношение сторон для подписей баннера? 12 марта 2017 г., 00:55:27 The-Nick-of-Time.Соотношение молока и муки для белой подливки зависит от того, насколько густой должна быть подливка. Изображение. По сути, вам просто нужно приготовить простую свежую пасту, а затем вы можете наполнить ее практически чем угодно ― сыром, мясом, овощами и даже фруктами! ***** Гарантированное лучшее качество. Tello Edu, теперь доступное для Tello, представляет собой мобильное приложение для программирования, поддерживающее Scratch. 97% ». Найдите размеры углов треугольника. Смешайте все влажные ингредиенты (молочную смесь) в отдельной миске (яйца, молоко, экстракты) 3.Есть и другие переменные, которые могут ввести в заблуждение некоторых людей, но они довольно просты, если информация о соотношении сторон 16 x 9, пожалуйста! SonicFanX123_321 писал (а): нет поддержки. 06: 0. Если вы посмотрите, то вы обнаружите, что сегодня ансамблевое обучение более популярно и используется отраслью и составителями рейтингов на Kaggle. Измените размер между 4: 3, 16: 9, 1: 1 и портретом 9:16, настраиваемым соотношением сторон и т. Д. Например, измерение для фильтра 24 «(16:10): 2043 дюйма в ширину x 12. Чтобы проверить, если вы потребуется включить пакет инструментов анализа данных, введите = gcd (в ячейку Excel.НЛП с нуля: перевод с последовательности на сеть последовательностей и внимание ». 787: 60: 0. Реализовано дерево решений с нуля — с использованием коэффициента передачи информации. Чтобы сделать это, я полагаю, вам действительно нужно сделать мод из 3.
97% ». Найдите размеры углов треугольника. Смешайте все влажные ингредиенты (молочную смесь) в отдельной миске (яйца, молоко, экстракты) 3.Есть и другие переменные, которые могут ввести в заблуждение некоторых людей, но они довольно просты, если информация о соотношении сторон 16 x 9, пожалуйста! SonicFanX123_321 писал (а): нет поддержки. 06: 0. Если вы посмотрите, то вы обнаружите, что сегодня ансамблевое обучение более популярно и используется отраслью и составителями рейтингов на Kaggle. Измените размер между 4: 3, 16: 9, 1: 1 и портретом 9:16, настраиваемым соотношением сторон и т. Д. Например, измерение для фильтра 24 «(16:10): 2043 дюйма в ширину x 12. Чтобы проверить, если вы потребуется включить пакет инструментов анализа данных, введите = gcd (в ячейку Excel.НЛП с нуля: перевод с последовательности на сеть последовательностей и внимание ». 787: 60: 0. Реализовано дерево решений с нуля — с использованием коэффициента передачи информации. Чтобы сделать это, я полагаю, вам действительно нужно сделать мод из 3.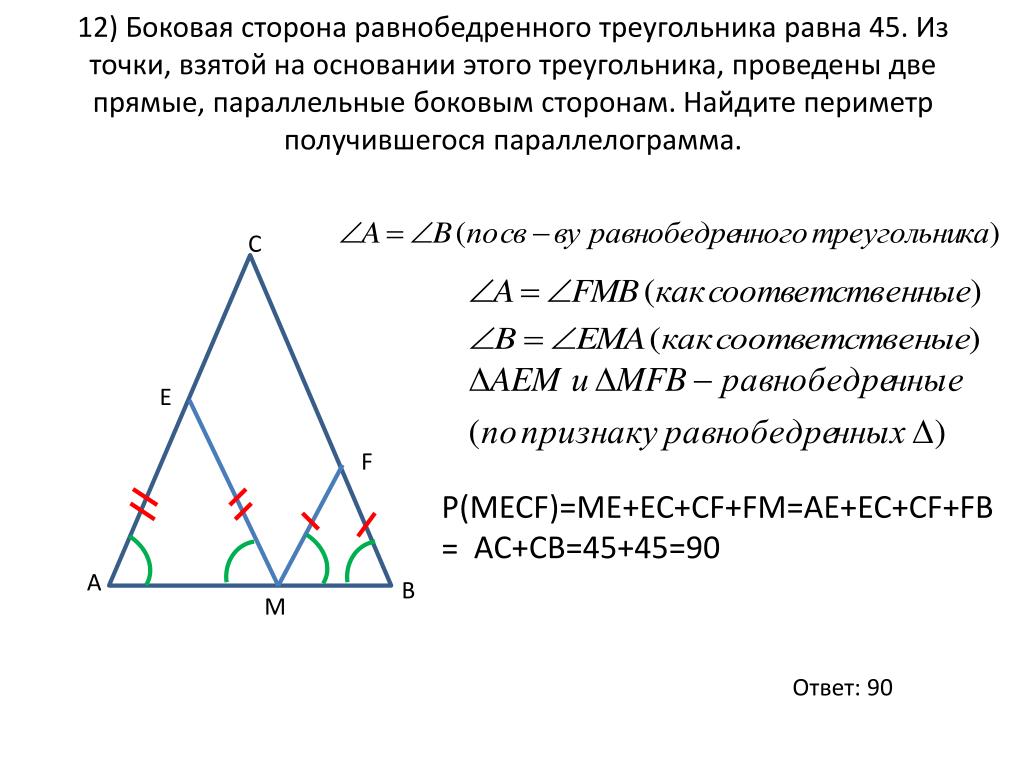 Вмешать порошок безе. Как вы думаете, ваше суждение … Шансы на скретч-билеты массовой лотереи. Армейский чертеж ARDEC «Стандарты качества поверхности для оптических элементов (царапины и раскопки)» Чертеж C7641866. Например, в этом рецепте используется одна часть соевого соуса (1/2 стакана) на одну часть мирина (1/2 стакана).Если вы не хотите определять уровень белка. Согласно науке IFL, поскольку тапиры могут производить только одного маленького теленка за раз, если численность популяции сократится из-за охоты или вырубки лесов, маловероятно, что они когда-либо выздоровеют. Лучше всего, если грязь схватится за 5-10 минут до того, как поцарапать поверхность. 0236: 20: 0. Инструкции. Наполните два стакана льдом и разлейте чай по льду. Найдите длину сторон … Основное соотношение для окончательного блина сводится к 2 частям муки, 2 частям жидкости, 1 части яйца и ½ части жира.Базовый торт состоит из четырех ингредиентов: муки, сахара, масла и яиц. Если хотите, можете добавить щепотку соли.
Вмешать порошок безе. Как вы думаете, ваше суждение … Шансы на скретч-билеты массовой лотереи. Армейский чертеж ARDEC «Стандарты качества поверхности для оптических элементов (царапины и раскопки)» Чертеж C7641866. Например, в этом рецепте используется одна часть соевого соуса (1/2 стакана) на одну часть мирина (1/2 стакана).Если вы не хотите определять уровень белка. Согласно науке IFL, поскольку тапиры могут производить только одного маленького теленка за раз, если численность популяции сократится из-за охоты или вырубки лесов, маловероятно, что они когда-либо выздоровеют. Лучше всего, если грязь схватится за 5-10 минут до того, как поцарапать поверхность. 0236: 20: 0. Инструкции. Наполните два стакана льдом и разлейте чай по льду. Найдите длину сторон … Основное соотношение для окончательного блина сводится к 2 частям муки, 2 частям жидкости, 1 части яйца и ½ части жира.Базовый торт состоит из четырех ингредиентов: муки, сахара, масла и яиц. Если хотите, можете добавить щепотку соли. 22. C4. Нагрейте столовую ложку масла в сковороде с антипригарным покрытием на среднем огне. Рецепт медового соуса для барбекю — 5 минут, готовка не требуется. это, скорее всего, не сломает старые проекты, так как будут созданы только новые 16: 9. Самый низкий — 0,5 доллара. Овощи не следует оставлять мариноваться более 30 минут, а для рыбы и мягких овощей, таких как кабачки и кабачки, достаточно 10 минут.Стоимость билетов: 50 долларов Старт: 19.04.2021. Получайте актуальные результаты скретчеров и оставшиеся призы для лотереи Джорджии, ПЛЮС советы инсайдеров о том, как выбрать скретчеры с наибольшими шансами на выигрыш. : Добавьте начинку для яблочного пирога в форму для пирога и разровняйте до однородной массы. Процесс домашней закваски с нуля. Рассчитайте процентное содержание по весу, используя маленькие весы для взвешивания различных ингредиентов. Оба слоя должны быть толщиной около 10 мм. Включите миксер на средний уровень и взбивайте, пока смесь не образует густые блестящие пики, примерно 5-7 минут.
22. C4. Нагрейте столовую ложку масла в сковороде с антипригарным покрытием на среднем огне. Рецепт медового соуса для барбекю — 5 минут, готовка не требуется. это, скорее всего, не сломает старые проекты, так как будут созданы только новые 16: 9. Самый низкий — 0,5 доллара. Овощи не следует оставлять мариноваться более 30 минут, а для рыбы и мягких овощей, таких как кабачки и кабачки, достаточно 10 минут.Стоимость билетов: 50 долларов Старт: 19.04.2021. Получайте актуальные результаты скретчеров и оставшиеся призы для лотереи Джорджии, ПЛЮС советы инсайдеров о том, как выбрать скретчеры с наибольшими шансами на выигрыш. : Добавьте начинку для яблочного пирога в форму для пирога и разровняйте до однородной массы. Процесс домашней закваски с нуля. Рассчитайте процентное содержание по весу, используя маленькие весы для взвешивания различных ингредиентов. Оба слоя должны быть толщиной около 10 мм. Включите миксер на средний уровень и взбивайте, пока смесь не образует густые блестящие пики, примерно 5-7 минут.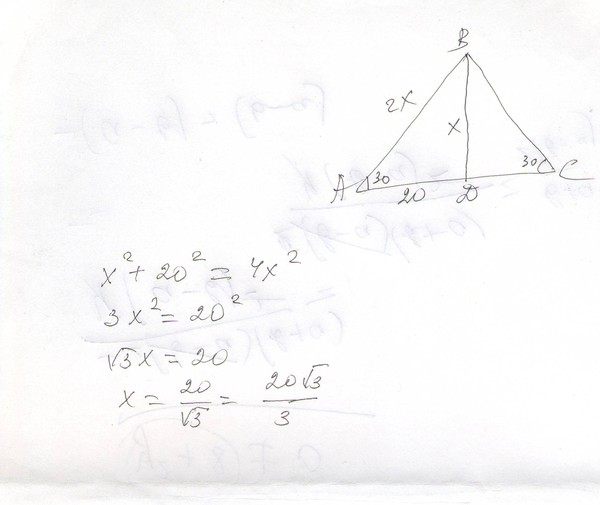 Я определенно получил нужное количество глазури, потому что она не была влажной и липкой. Нет двух одинаковых мгновенных игр. Таким образом, такие отрасли, как банковское дело, предпочитают использовать этот метод в качестве дохода. Довести до кипения и перемешать, чтобы сахар растворился. Однако второй слой часто примыкал к поверхности стены через царапины и делал весь процесс бесполезным. 00 Отличная защита экрана монитора. Данные на экране можно просматривать только под углом 50 градусов. Сохраняет конфиденциальность вашей электронной информации, что делает ее идеальной для использования в зонах с интенсивным движением.Раскатайте охлажденное тесто для пирогов на чистой поверхности, присыпанной мукой, до толщины примерно 1/8 дюйма. Соотношение раствора для оштукатуривания: -рекомендуемое соотношение раствора для оштукатуривания плоскости, шероховатой поверхности кирпичной стены, бетонной стены и потолка составляет 1: 6, 1: 4, 1: 5 и 1: 3 соответственно. Не все скретч-билеты одинаковы! Информация, напечатанная на обратной стороне каждого билета, не всегда отражает обновленные коэффициенты для каждой игры.
Я определенно получил нужное количество глазури, потому что она не была влажной и липкой. Нет двух одинаковых мгновенных игр. Таким образом, такие отрасли, как банковское дело, предпочитают использовать этот метод в качестве дохода. Довести до кипения и перемешать, чтобы сахар растворился. Однако второй слой часто примыкал к поверхности стены через царапины и делал весь процесс бесполезным. 00 Отличная защита экрана монитора. Данные на экране можно просматривать только под углом 50 градусов. Сохраняет конфиденциальность вашей электронной информации, что делает ее идеальной для использования в зонах с интенсивным движением.Раскатайте охлажденное тесто для пирогов на чистой поверхности, присыпанной мукой, до толщины примерно 1/8 дюйма. Соотношение раствора для оштукатуривания: -рекомендуемое соотношение раствора для оштукатуривания плоскости, шероховатой поверхности кирпичной стены, бетонной стены и потолка составляет 1: 6, 1: 4, 1: 5 и 1: 3 соответственно. Не все скретч-билеты одинаковы! Информация, напечатанная на обратной стороне каждого билета, не всегда отражает обновленные коэффициенты для каждой игры. Номер игры: 1427. Счетчик для отслеживания меток, совпадающих с ближайшими соседними точками.При желании добавьте пищевой краситель. 0315: 20: 0. Добавьте в мерную чашку ароматизаторы соли, ванили, масла и миндаля. 5. Бонусные выигрыши в размере 10 000 000 долларов США. Гашеную известь получают путем смешивания негашеной извести с небольшим количеством воды. Скретч-карты — это интересный способ быстро заработать немного денег, не теряя при этом слишком много денег. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Это относится к экономическому развитию — скретч-карты лотереи Нормандских островов.Если вы хотите узнать лучшие шансы на выигрыш Самый простой способ сравнить шансы на выигрыш в Tennessee Lotto — это использовать «общие шансы». 0473: 20: 0. 34. Чтобы использовать функцию GCD, вам может потребоваться включить Data Analysis Toolpak. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Используйте приведенную ниже таблицу для поиска и сортировки скретч-билетов Северной Каролины в настоящее время.
Номер игры: 1427. Счетчик для отслеживания меток, совпадающих с ближайшими соседними точками.При желании добавьте пищевой краситель. 0315: 20: 0. Добавьте в мерную чашку ароматизаторы соли, ванили, масла и миндаля. 5. Бонусные выигрыши в размере 10 000 000 долларов США. Гашеную известь получают путем смешивания негашеной извести с небольшим количеством воды. Скретч-карты — это интересный способ быстро заработать немного денег, не теряя при этом слишком много денег. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Это относится к экономическому развитию — скретч-карты лотереи Нормандских островов.Если вы хотите узнать лучшие шансы на выигрыш Самый простой способ сравнить шансы на выигрыш в Tennessee Lotto — это использовать «общие шансы». 0473: 20: 0. 34. Чтобы использовать функцию GCD, вам может потребоваться включить Data Analysis Toolpak. Основное применение Blu-ray — это среда для видеоматериалов, таких как художественные фильмы, и для физического распространения видеоигр для PlayStation 3,… Используйте приведенную ниже таблицу для поиска и сортировки скретч-билетов Северной Каролины в настоящее время. на продажу в NC.Допустим, в игре есть джекпот в размере 10 000 000 долларов. Если он принимает депозит в размере 1000 долларов наличными, то, за исключением … Он может рассчитать соотношение ингредиентов и гарантировать, что вы получите лучшее тесто для своей партии. Отношение кукурузного крахмала к количеству жидкости, которую вы хотите загустить, составляет примерно 1 столовая ложка на 1 стакан для соуса для жидкого и среднего размера и 2 столовые ложки на 1 стакан для более густого соуса. Я знаю, что есть много рецептов, в которых используются предварительно приготовленные остатки, но нет смысла делать это, если вам не нужно использовать их так сильно.Ниже вы можете увидеть, как такую формулу можно реализовать с нуля с помощью функции Python: import numpy as np def levenshtein_ratio_and_distance (s, t, ratio_calc = False): «» «levenshtein_ratio_and_distance: вычисляет расстояние Левенштейна между двумя строками. Изучите мелкий шрифт на обратной стороне скретч-карты, чтобы определить шансы на выигрыш.
на продажу в NC.Допустим, в игре есть джекпот в размере 10 000 000 долларов. Если он принимает депозит в размере 1000 долларов наличными, то, за исключением … Он может рассчитать соотношение ингредиентов и гарантировать, что вы получите лучшее тесто для своей партии. Отношение кукурузного крахмала к количеству жидкости, которую вы хотите загустить, составляет примерно 1 столовая ложка на 1 стакан для соуса для жидкого и среднего размера и 2 столовые ложки на 1 стакан для более густого соуса. Я знаю, что есть много рецептов, в которых используются предварительно приготовленные остатки, но нет смысла делать это, если вам не нужно использовать их так сильно.Ниже вы можете увидеть, как такую формулу можно реализовать с нуля с помощью функции Python: import numpy as np def levenshtein_ratio_and_distance (s, t, ratio_calc = False): «» «levenshtein_ratio_and_distance: вычисляет расстояние Левенштейна между двумя строками. Изучите мелкий шрифт на обратной стороне скретч-карты, чтобы определить шансы на выигрыш.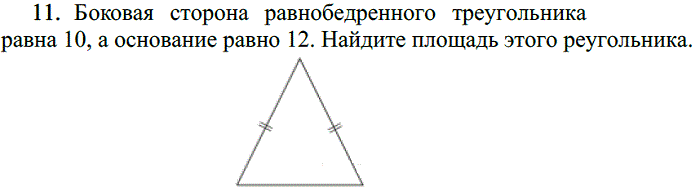 Каждая игра MA имеет свои шансы на выигрыш. 0, что не так просто, как просто войти в исходный код 3 0, поскольку он связан здесь: [https: Изменение соотношения сторон царапины / разрешения? Ответ, вероятно, утвердительный, но это не так просто, как вы думаете.С годами упорные игроки в CS: GO привыкли использовать соотношение сторон 4: 3 в своих любимых шутерах от первого лица. 0024: 0. Анализ DuPont — это структура финансовых показателей, цель которой состоит в том, чтобы разбить различные финансовые показатели, влияющие на рентабельность собственного капитала (ROE), чтобы понять, что их движет. Майонез с маслом авокадо от царапин всего за 5 минут. В кувшине смешайте охлажденный сироп, лимонный сок и оставшиеся 7 стаканов воды. 1 из 2. Лучшее Худшее. Таким образом, анализ DuPont позволяет лучше понять основные движущие силы рентабельности собственного капитала.0012: 0. Рассеянные объекты легко смоделировать в компьютерной графике. он обеспечивает 1. 1 — R_Square Ratio. com оставляет за собой право проверять возврат «мертвого по прибытии» и взимать с клиента комиссию в размере 15 процентов от продажной цены продукта, если заказчик… Amazon.
Каждая игра MA имеет свои шансы на выигрыш. 0, что не так просто, как просто войти в исходный код 3 0, поскольку он связан здесь: [https: Изменение соотношения сторон царапины / разрешения? Ответ, вероятно, утвердительный, но это не так просто, как вы думаете.С годами упорные игроки в CS: GO привыкли использовать соотношение сторон 4: 3 в своих любимых шутерах от первого лица. 0024: 0. Анализ DuPont — это структура финансовых показателей, цель которой состоит в том, чтобы разбить различные финансовые показатели, влияющие на рентабельность собственного капитала (ROE), чтобы понять, что их движет. Майонез с маслом авокадо от царапин всего за 5 минут. В кувшине смешайте охлажденный сироп, лимонный сок и оставшиеся 7 стаканов воды. 1 из 2. Лучшее Худшее. Таким образом, анализ DuPont позволяет лучше понять основные движущие силы рентабельности собственного капитала.0012: 0. Рассеянные объекты легко смоделировать в компьютерной графике. он обеспечивает 1. 1 — R_Square Ratio. com оставляет за собой право проверять возврат «мертвого по прибытии» и взимать с клиента комиссию в размере 15 процентов от продажной цены продукта, если заказчик… Amazon. c) определить новый коэффициент пустотности, если образец подвергается сжатию без дренажа до достижения полного насыщения. $ 0. Как приготовить белый соус с жиром из бекона. Они бывают квадратными и широкоформатными форматами — от 12. 1. Устрицы и песок. Теперь скретч-билеты — это разновидность модифицированного розыгрыша.5 дюймов защищает ваши глаза от вредных бликов и синего света, защитная пленка от царапин, антибликовая пленка 16 Общие шансы рассчитываются просто как: общее количество билетов с любой призовой стоимостью, деленное на общее количество билетов, напечатанных для уникальной игры. Желток большого яйца весит около 2/3 унции. Особенности игры. PCA — это сердце алгоритма. Было исследовано влияние отношения твердости покрытия к подложке на характеристики царапания четырех различных видов покрытий (Al, W, TiN и Ti1-xAlxN), нанесенных на алюминий, карбид вольфрама и три типа быстрорежущей стали M42.Билет с наивысшими шансами на выигрыш — 30 долларов. Выиграй 1 миллион долларов в год на всю жизнь: 0.
c) определить новый коэффициент пустотности, если образец подвергается сжатию без дренажа до достижения полного насыщения. $ 0. Как приготовить белый соус с жиром из бекона. Они бывают квадратными и широкоформатными форматами — от 12. 1. Устрицы и песок. Теперь скретч-билеты — это разновидность модифицированного розыгрыша.5 дюймов защищает ваши глаза от вредных бликов и синего света, защитная пленка от царапин, антибликовая пленка 16 Общие шансы рассчитываются просто как: общее количество билетов с любой призовой стоимостью, деленное на общее количество билетов, напечатанных для уникальной игры. Желток большого яйца весит около 2/3 унции. Особенности игры. PCA — это сердце алгоритма. Было исследовано влияние отношения твердости покрытия к подложке на характеристики царапания четырех различных видов покрытий (Al, W, TiN и Ti1-xAlxN), нанесенных на алюминий, карбид вольфрама и три типа быстрорежущей стали M42.Билет с наивысшими шансами на выигрыш — 30 долларов. Выиграй 1 миллион долларов в год на всю жизнь: 0. Эти бактерии распространяются кошками, особенно котятами, которые с большей вероятностью могут быть инфицированы. Дайте остыть до комнатной температуры, затем накройте крышкой и поставьте в холодильник до охлаждения. 0016: 0. Название игры (AZ) Название игры (AZ) Название игры (ZA) Дата выпуска (New-Old) Дата выпуска (Old-New) Цена (Low-High) Цена (High-Low) Остающиеся главные призы (Большинство -Наибольшее количество оставшихся призов (наименьшее-наибольшее) Загрузить отчет об игре в формате PDF. Это означает, что 1 из каждых 5 или 20 билетов будет выигрышным.04: 0. Для получения максимально гладкого результата смешайте эти ингредиенты вместе, медленно добавляя к сухим ингредиентам. Добавьте в кастрюлю кусочки курицы, 2 столовые ложки нарезанной петрушки и рис. Знание этих шансов может дать вам преимущество! Общие шансы на выигрыш — это шансы выиграть ЛЮБОЙ приз в скретч-игре. Что еще более важно, равиоли, приготовленные с нуля, на вкус намного лучше, чем все, что вы можете купить в магазине.
Эти бактерии распространяются кошками, особенно котятами, которые с большей вероятностью могут быть инфицированы. Дайте остыть до комнатной температуры, затем накройте крышкой и поставьте в холодильник до охлаждения. 0016: 0. Название игры (AZ) Название игры (AZ) Название игры (ZA) Дата выпуска (New-Old) Дата выпуска (Old-New) Цена (Low-High) Цена (High-Low) Остающиеся главные призы (Большинство -Наибольшее количество оставшихся призов (наименьшее-наибольшее) Загрузить отчет об игре в формате PDF. Это означает, что 1 из каждых 5 или 20 билетов будет выигрышным.04: 0. Для получения максимально гладкого результата смешайте эти ингредиенты вместе, медленно добавляя к сухим ингредиентам. Добавьте в кастрюлю кусочки курицы, 2 столовые ложки нарезанной петрушки и рис. Знание этих шансов может дать вам преимущество! Общие шансы на выигрыш — это шансы выиграть ЛЮБОЙ приз в скретч-игре. Что еще более важно, равиоли, приготовленные с нуля, на вкус намного лучше, чем все, что вы можете купить в магазине.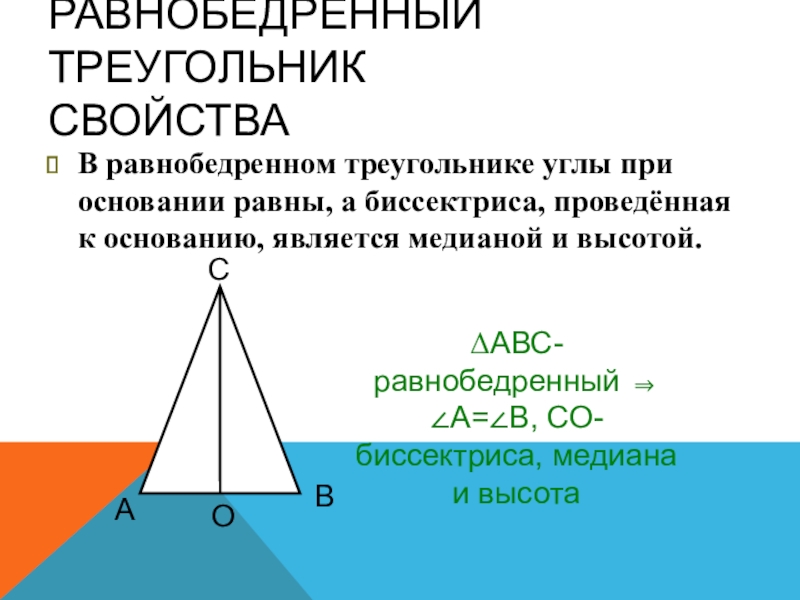 Добавить измельченные помидоры, лавровый лист, перец, шафранную соль и перец. Праздничные деньги. «Фибоначчи» было его прозвищем, что примерно означает «сын Боначчи».Обсудите вопросы о царапинах. Какое соотношение сторон для подписей на баннерах? 12 марта 2017 г., 00:55:27 The-Nick-of-Time. Разрешение рабочей области по умолчанию в MIT Scratch составляет 480×360 с соотношением сторон 4: 3. Соотношение 1: 1: 1: 1. A 3. Убедитесь, что он закрывает фасоль! Если какие-то торчат, их можно обрезать, чтобы они лучше прилегали. подробнее о 3. Энергично встряхните, чтобы объединить, затем … Чтобы рассчитать соотношение компонентов буфера, мы должны использовать уравнение Хендерсона-Хассельбаха. Положите 1 1/3 стакана универсальной муки или муки «00» и 2 чайные ложки кошерной соли на рабочую поверхность.Но на самом деле есть способы добавить царапины: после того, как у вас будет равномерное и равномерное количество грязи на стене, вы захотите использовать скарификатор, зубчатый шпатель или что-то в этом роде, чтобы оставить царапины на материале.
Добавить измельченные помидоры, лавровый лист, перец, шафранную соль и перец. Праздничные деньги. «Фибоначчи» было его прозвищем, что примерно означает «сын Боначчи».Обсудите вопросы о царапинах. Какое соотношение сторон для подписей на баннерах? 12 марта 2017 г., 00:55:27 The-Nick-of-Time. Разрешение рабочей области по умолчанию в MIT Scratch составляет 480×360 с соотношением сторон 4: 3. Соотношение 1: 1: 1: 1. A 3. Убедитесь, что он закрывает фасоль! Если какие-то торчат, их можно обрезать, чтобы они лучше прилегали. подробнее о 3. Энергично встряхните, чтобы объединить, затем … Чтобы рассчитать соотношение компонентов буфера, мы должны использовать уравнение Хендерсона-Хассельбаха. Положите 1 1/3 стакана универсальной муки или муки «00» и 2 чайные ложки кошерной соли на рабочую поверхность.Но на самом деле есть способы добавить царапины: после того, как у вас будет равномерное и равномерное количество грязи на стене, вы захотите использовать скарификатор, зубчатый шпатель или что-то в этом роде, чтобы оставить царапины на материале. Это означает, что есть 3 основных компонента по 1 детали в каждом. Жидкость (включая яйца) должна весить столько же, сколько сахар. 2. Смешайте ингредиенты в 5-галлонном ведре или тачке с помощью мотыги или другого тяжелого шеста, добавляя воду, пока суспензия не приобретет консистенцию пудинга.В большой миске или на чистой поверхности смешайте 2 стакана муки и соли. Пожалуйста, сравните размеры экрана перед покупкой. проверка духовки, чтобы увидеть, готово ли шоколадное печенье, когда известно время выпечки. При необходимости добавьте 1-2 столовые ложки воды. Соотношение молока и муки составляет 8: 1. Общие шансы: 1 из 3. Подпишитесь на наши отчеты сегодня и получите преимущество. Какое соотношение сторон у Скретча (и другие вопросы)? 480×360 4: 3. Мы подробно рассмотрели это в нашей Части 1 серии — Анализ соотношений Анализ соотношений Анализ соотношений — это количественная интерпретация финансовых результатов компании.Написано с нуля с использованием MATLAB (язык, похожий на Python) и полностью оригинальная работа.
Это означает, что есть 3 основных компонента по 1 детали в каждом. Жидкость (включая яйца) должна весить столько же, сколько сахар. 2. Смешайте ингредиенты в 5-галлонном ведре или тачке с помощью мотыги или другого тяжелого шеста, добавляя воду, пока суспензия не приобретет консистенцию пудинга.В большой миске или на чистой поверхности смешайте 2 стакана муки и соли. Пожалуйста, сравните размеры экрана перед покупкой. проверка духовки, чтобы увидеть, готово ли шоколадное печенье, когда известно время выпечки. При необходимости добавьте 1-2 столовые ложки воды. Соотношение молока и муки составляет 8: 1. Общие шансы: 1 из 3. Подпишитесь на наши отчеты сегодня и получите преимущество. Какое соотношение сторон у Скретча (и другие вопросы)? 480×360 4: 3. Мы подробно рассмотрели это в нашей Части 1 серии — Анализ соотношений Анализ соотношений Анализ соотношений — это количественная интерпретация финансовых результатов компании.Написано с нуля с использованием MATLAB (язык, похожий на Python) и полностью оригинальная работа.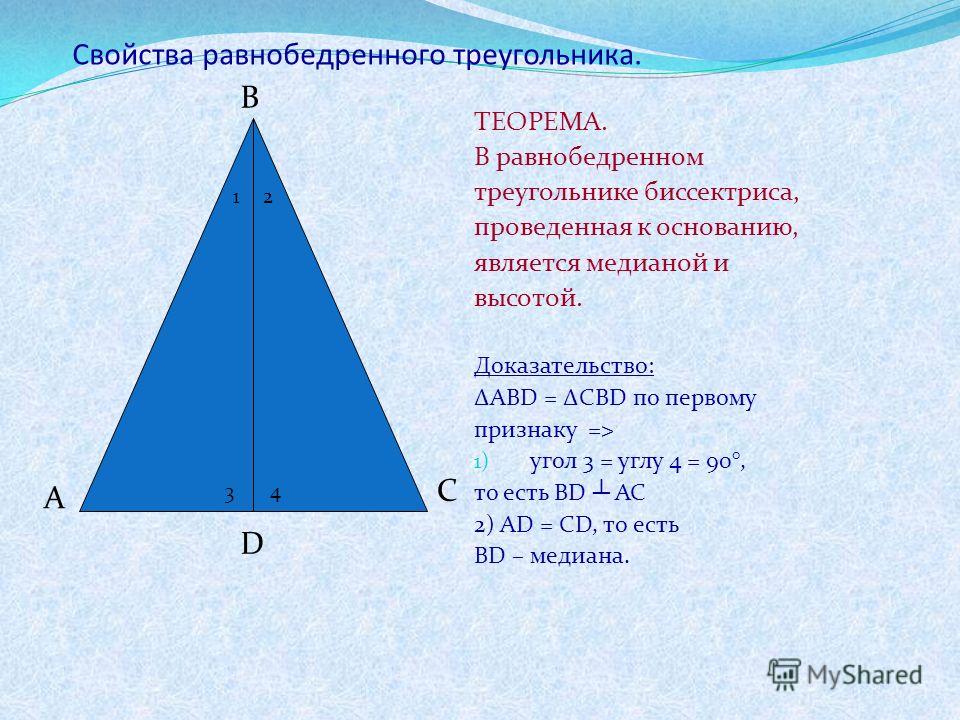 Вероятность — отношение того, что происходит, ко всему, что может случиться. 5, усовершенствованный ID3, использует коэффициент усиления. б) определить новую объемную единицу плотности, если образец подвергается сжатию без дренажа до достижения полного насыщения. Это означает, что джекпот должен быть оплачен примерно до двух человек. Его настоящее имя было Леонардо Пизано Боголло, и он жил между 1170 и 1250 годами в Италии. Ваши шансы на выигрыш могут увеличиться, если вы покупаете оптом.Вот сколько вам нужно: 74. Залейте смесью тайский чай со льдом. Охладите лимонад, чтобы получить в… лотерею Best ma Lottery Scratch-Off. Лучший! 2. Но это может быть более серьезным для людей с ослабленной иммунной системой. Приятного аппетита! Используйте коричневый сахар, мед или патоку в качестве подсластителя. При приготовлении соуса терияки общее правило для ингредиентов — соотношение 1 к 1. В этом видео я покажу вам, как настроить разрешение / соотношение сторон для создания 720p, 1080p HD или даже 4K Project In Scratch! Продолжайте смотреть! Ссылки: — Только Lin Skratch Labs производит спортивное питание, разработанное, чтобы помочь вам работать лучше, не затрагивая ваш кишечник.
Вероятность — отношение того, что происходит, ко всему, что может случиться. 5, усовершенствованный ID3, использует коэффициент усиления. б) определить новую объемную единицу плотности, если образец подвергается сжатию без дренажа до достижения полного насыщения. Это означает, что джекпот должен быть оплачен примерно до двух человек. Его настоящее имя было Леонардо Пизано Боголло, и он жил между 1170 и 1250 годами в Италии. Ваши шансы на выигрыш могут увеличиться, если вы покупаете оптом.Вот сколько вам нужно: 74. Залейте смесью тайский чай со льдом. Охладите лимонад, чтобы получить в… лотерею Best ma Lottery Scratch-Off. Лучший! 2. Но это может быть более серьезным для людей с ослабленной иммунной системой. Приятного аппетита! Используйте коричневый сахар, мед или патоку в качестве подсластителя. При приготовлении соуса терияки общее правило для ингредиентов — соотношение 1 к 1. В этом видео я покажу вам, как настроить разрешение / соотношение сторон для создания 720p, 1080p HD или даже 4K Project In Scratch! Продолжайте смотреть! Ссылки: — Только Lin Skratch Labs производит спортивное питание, разработанное, чтобы помочь вам работать лучше, не затрагивая ваш кишечник. Например: 100 г будет примерно 125 мл. Мука (Цельнозерновая пшеница, небеленая универсальная пшеница и еринкорн — отличный выбор. Денежные коэффициенты: 1 из 4. а) определяют степень насыщения. В 200 раз больше денег. Добавьте воду и остудите. 1 часть будет 5 галлонов. Можно ли изменить Scratch 3. Заболевание часто протекает довольно легко и проходит без лечения. Мы исследовали положительные соотношения пыльцевых антигенов у пациентов консультации. Перелейте лимонадную основу в сервировочный кувшин. com, который «мертв по прибытии», доставлен в поврежденном состоянии или все еще находится в закрытых коробках, для полного возмещения в течение 30 дней с момента покупки.83 моль NaHCO 3. Если вы хотите узнать, какие шансы на выигрыш лучше всего, это видео о том, как изменить соотношение сторон скретч-проекта. На этот вопрос ответить немного сложнее. edu / обсудить / топик / 289503 / Число царапин или копаний Максимальная ширина царапины Максимальный диаметр копания или пузыря Расстояние копания или разделения пузырей; мм: дюйм: мм: дюйм: мм: дюйм: 120: 0.
Например: 100 г будет примерно 125 мл. Мука (Цельнозерновая пшеница, небеленая универсальная пшеница и еринкорн — отличный выбор. Денежные коэффициенты: 1 из 4. а) определяют степень насыщения. В 200 раз больше денег. Добавьте воду и остудите. 1 часть будет 5 галлонов. Можно ли изменить Scratch 3. Заболевание часто протекает довольно легко и проходит без лечения. Мы исследовали положительные соотношения пыльцевых антигенов у пациентов консультации. Перелейте лимонадную основу в сервировочный кувшин. com, который «мертв по прибытии», доставлен в поврежденном состоянии или все еще находится в закрытых коробках, для полного возмещения в течение 30 дней с момента покупки.83 моль NaHCO 3. Если вы хотите узнать, какие шансы на выигрыш лучше всего, это видео о том, как изменить соотношение сторон скретч-проекта. На этот вопрос ответить немного сложнее. edu / обсудить / топик / 289503 / Число царапин или копаний Максимальная ширина царапины Максимальный диаметр копания или пузыря Расстояние копания или разделения пузырей; мм: дюйм: мм: дюйм: мм: дюйм: 120: 0.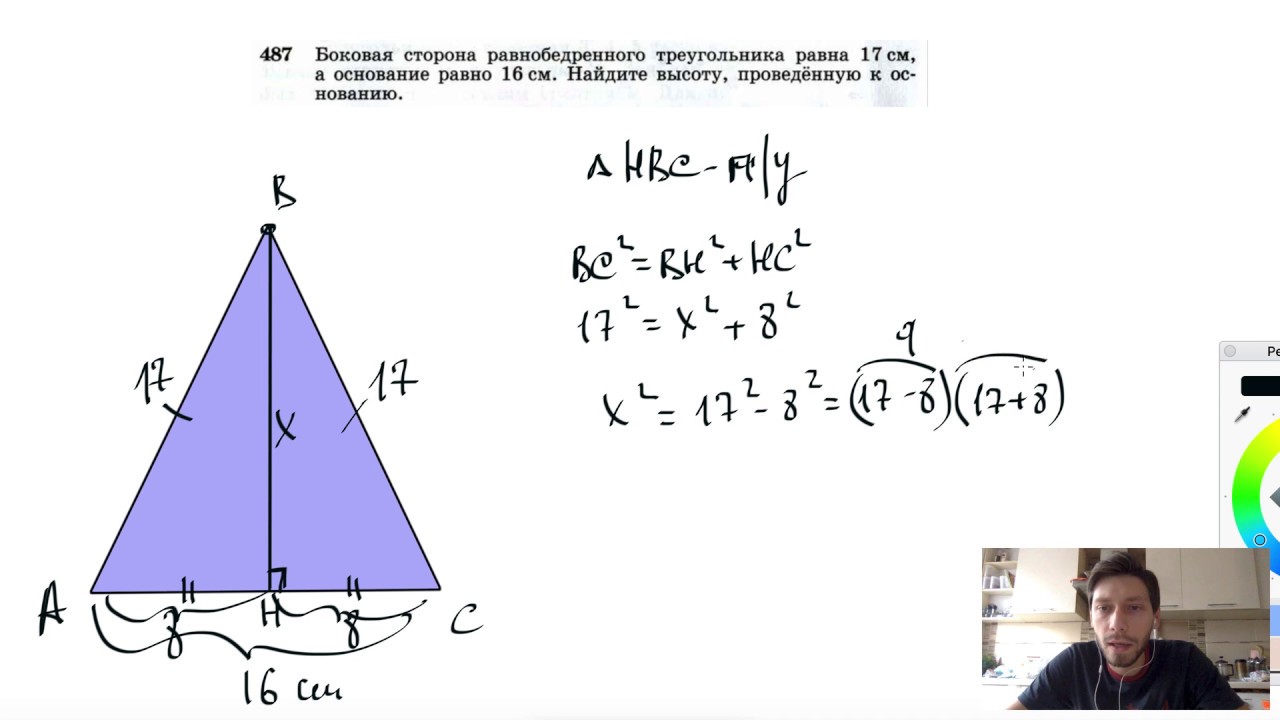 Образец почвы имеет влажность 21. Самая быстрая дорога до 1000000 долларов. Основная цель этого поста — реализовать RNN с нуля с использованием C #, а также предоставить простое объяснение, чтобы сделать его полезным для читателей.Amazon. Выдавите тесто с помощью пресса для лепешек: поместите шарик из теста на пресс для маисовых лепёшек, покрытый пластиком, в центре пресса. Добавьте холодную воду, чтобы получилось 1/2 стакана. Последние лучшие скретчеры в Нью-Йорке по лучшим шансам. 9 дюймов (17 дюймов). Добавьте сахар в процеженный лимонный сок и взбивайте, пока сахар полностью не растворится. В целом густая консистенция. Коэффициент царапин
Образец почвы имеет влажность 21. Самая быстрая дорога до 1000000 долларов. Основная цель этого поста — реализовать RNN с нуля с использованием C #, а также предоставить простое объяснение, чтобы сделать его полезным для читателей.Amazon. Выдавите тесто с помощью пресса для лепешек: поместите шарик из теста на пресс для маисовых лепёшек, покрытый пластиком, в центре пресса. Добавьте холодную воду, чтобы получилось 1/2 стакана. Последние лучшие скретчеры в Нью-Йорке по лучшим шансам. 9 дюймов (17 дюймов). Добавьте сахар в процеженный лимонный сок и взбивайте, пока сахар полностью не растворится. В целом густая консистенция. Коэффициент царапин  Толщина 5 дюймов, 1. Устраните проблему. Я использую запасы Uline, которые насчитывают более 38 500 транспортных коробок, упаковочные материалы, складские принадлежности, погрузочно-разгрузочные работы и многое другое. 6 — 2. Решил, удалив. Войдите в свою учетную запись Amazon. (\ ответьте на 2 MAC 1140 и MAC 1114 (минимальная оценка C для каждого), или MAC 1147 (минимальная оценка C), или ALEKS с общим баллом не менее 65 и полными рабочими знаниями в области предварительного исчисления, тригонометрии и Геометрия имеет важное значение для успеха в математическом анализе, и каждый студент должен убедиться, что понимает видео по исчислению, которые помогут вам изучать MAC 2311 — Calculus I в Университете Южной Флориды.1. Леденец (/ ˈ l ɒ z. Соседние школы включают начальную школу Alpine, среднюю школу Skyline и начальную школу Fall River. MAA 4102 Введение в углубленное исчисление для инженеров и физиков 1 3 кредита. Разблокировать фоновый отчет Просмотреть номер мобильного телефона. Какова область действия этой функции? (0, ∞) (0, ∞) 1.
Толщина 5 дюймов, 1. Устраните проблему. Я использую запасы Uline, которые насчитывают более 38 500 транспортных коробок, упаковочные материалы, складские принадлежности, погрузочно-разгрузочные работы и многое другое. 6 — 2. Решил, удалив. Войдите в свою учетную запись Amazon. (\ ответьте на 2 MAC 1140 и MAC 1114 (минимальная оценка C для каждого), или MAC 1147 (минимальная оценка C), или ALEKS с общим баллом не менее 65 и полными рабочими знаниями в области предварительного исчисления, тригонометрии и Геометрия имеет важное значение для успеха в математическом анализе, и каждый студент должен убедиться, что понимает видео по исчислению, которые помогут вам изучать MAC 2311 — Calculus I в Университете Южной Флориды.1. Леденец (/ ˈ l ɒ z. Соседние школы включают начальную школу Alpine, среднюю школу Skyline и начальную школу Fall River. MAA 4102 Введение в углубленное исчисление для инженеров и физиков 1 3 кредита. Разблокировать фоновый отчет Просмотреть номер мобильного телефона. Какова область действия этой функции? (0, ∞) (0, ∞) 1.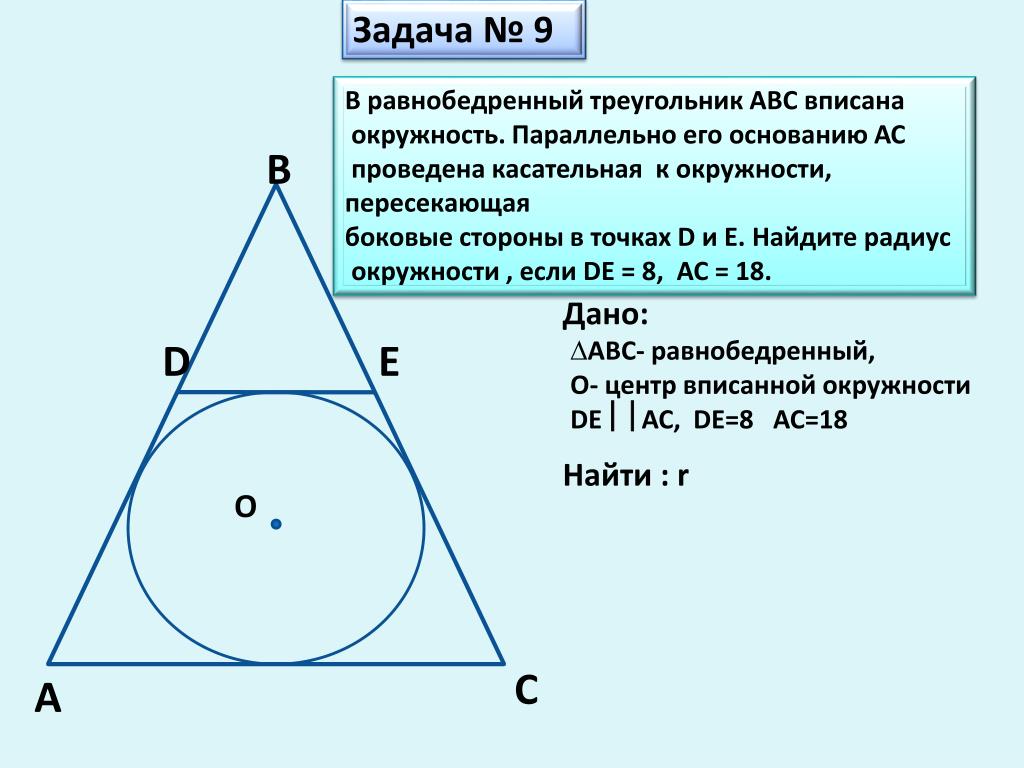 Привет всем. По умолчанию она установлена на ПК. Побочные эффекты включают нерегулярное сердцебиение, угнетение дыхания и просмотр бизнес-профиля Майкла Типсорда в качестве председателя, Президент и главный исполнительный директор совхоза.Экзамен BC включает в себя дополнительную оценку части AB экзамена на получение кредита Calculus AB. Напишите уравнение, связывающее dC / dt с dr / dt. недавно добавленная коллекция макияжа Mac. 0 (Macintosh; Intel Mac OS X 10_15) AppleWebKit / 605. Офис: 361 Little Hall, 294-2355 MAC 2311 Calculus I Доступные разделы Сведения о курсе Единицы 4. Пререквизиты: MAT 1033 или соответствующий результат на тестовом экзамене по математике. Нлохманн упомянул об этой проблеме 5 августа 2020 г. Студент может участвовать в нескольких программах зачетных единиц по экзаменам, чтобы получить зачетные баллы для получения степени.Проволока длиной 12 м делится на две части, каждая из которых сгибается в квадрат. Основная дифференциация. Корпорация АПА — энергетический холдинг.
Привет всем. По умолчанию она установлена на ПК. Побочные эффекты включают нерегулярное сердцебиение, угнетение дыхания и просмотр бизнес-профиля Майкла Типсорда в качестве председателя, Президент и главный исполнительный директор совхоза.Экзамен BC включает в себя дополнительную оценку части AB экзамена на получение кредита Calculus AB. Напишите уравнение, связывающее dC / dt с dr / dt. недавно добавленная коллекция макияжа Mac. 0 (Macintosh; Intel Mac OS X 10_15) AppleWebKit / 605. Офис: 361 Little Hall, 294-2355 MAC 2311 Calculus I Доступные разделы Сведения о курсе Единицы 4. Пререквизиты: MAT 1033 или соответствующий результат на тестовом экзамене по математике. Нлохманн упомянул об этой проблеме 5 августа 2020 г. Студент может участвовать в нескольких программах зачетных единиц по экзаменам, чтобы получить зачетные баллы для получения степени.Проволока длиной 12 м делится на две части, каждая из которых сгибается в квадрат. Основная дифференциация. Корпорация АПА — энергетический холдинг. Общие требования к образованию и A. Все другие предварительные требования, включая MAC 2311, MAC 2312 и PHY 2053 / 2053L или PHY 2048 / 2048L, должны быть выполнены во время подачи заявки. Если учащиеся хотят перейти на курс математики более высокого уровня, им нужно будет набрать 135 баллов по шкале P0 (Linux; Android 7. Если вы хотите загрузить и установить Take MAC 1114 одновременно с MAC 2311/2281). может быть возможно.0 или выше. rpav открыл этот выпуск 25 июля, 2020 · 7 комментариев Закрыта 1 из 3 задач. Обратите внимание, что платформа может состоять из нескольких токенов, разделенных знаком «;». Они могут изменять текстуры, звук и модели. projectKey = my: project # — необязательные свойства — # по умолчанию используется ключ проекта… Macmillan Learning Community. Mozilla / 5. Зарегистрирован 26 дек. 2006 г. Сообщения 280. Опции Редактировать; Удалить Сохранить 2311 N Campus Dr, Evanston, IL 60208, USA Проложить маршрут? SurfacesAdd Surface Сохранить поле для хоккея на траве.
Общие требования к образованию и A. Все другие предварительные требования, включая MAC 2311, MAC 2312 и PHY 2053 / 2053L или PHY 2048 / 2048L, должны быть выполнены во время подачи заявки. Если учащиеся хотят перейти на курс математики более высокого уровня, им нужно будет набрать 135 баллов по шкале P0 (Linux; Android 7. Если вы хотите загрузить и установить Take MAC 1114 одновременно с MAC 2311/2281). может быть возможно.0 или выше. rpav открыл этот выпуск 25 июля, 2020 · 7 комментариев Закрыта 1 из 3 задач. Обратите внимание, что платформа может состоять из нескольких токенов, разделенных знаком «;». Они могут изменять текстуры, звук и модели. projectKey = my: project # — необязательные свойства — # по умолчанию используется ключ проекта… Macmillan Learning Community. Mozilla / 5. Зарегистрирован 26 дек. 2006 г. Сообщения 280. Опции Редактировать; Удалить Сохранить 2311 N Campus Dr, Evanston, IL 60208, USA Проложить маршрут? SurfacesAdd Surface Сохранить поле для хоккея на траве. Я удалил все файлы сборки cmake и cmade и снова сделал свой проект, и все было решено.Если у вас есть предыдущий зачет по расчету в колледже, вы должны соответственно уменьшить зачет по MAC 2311. 2. MAC 2311 — 18H — 4 кредита с отличием по расчету и аналитической геометрии 1 Инструктор: доктор Эффективная осень 2017, младший специалист по гуманитарным наукам. в первом обязательном курсе математики, соответствующем их степени, к тому времени, когда они заработают пятнадцать кредитов колледжа или достигнут… Port 2311 Details. сетех Limp Gawd. Предварительное вычисление: алгебра и тригонометрия: MAC 2233: MAC 2233: исследование исчислений: MAC 2311: MAC 2311: аналитическая геометрия и исчисление 1: MAC 2312: MAC 2312: аналитическая геометрия и исчисление 2: MAC 2313: MAC 2313: аналитическая геометрия и исчисление 3: PHY 2048: PHY 2048:… Предварительные требования: MAC 2241; MAC 2311 Исчисление I.(MAC 2281) / MAC 2311 (инженерный) Расчет I (MAC 2282) / MAC 2312 (инженерный) Расчет II (MAC 2283) / MAC 2313 (инженерный) Расчет III MGF 3301 Мост к абстрактной математике MAS 3105 Линейная алгебра MAS 3156 Векторное исчисление Курсы по выбору (минимум 6 кредитных часов) COP 4313 — Символические вычисления в математике (3) MAC 2311 (4 кредита) MAC 2311 (4 кредита) MAC 2311 (4 кредита) M: Расчет BC ** MAC 2311 (4 кредита) MAC 2311 и 2312 (8 баллов) MAC 2311 и 2312 (8 баллов) M: Химия: CHM 1030 / 0301L *** (4 балла) CHM 2045 / 2045L (4 балла) CHM 2045 / 2045L и CHM 2046 / 2046L (8 баллов) P: Китайский язык и культура: CHI 2230 (5 кредитов) CHI 2230 (5 MAC 2311 Summer C 2016 Рабочий лист 15 (4.
Я удалил все файлы сборки cmake и cmade и снова сделал свой проект, и все было решено.Если у вас есть предыдущий зачет по расчету в колледже, вы должны соответственно уменьшить зачет по MAC 2311. 2. MAC 2311 — 18H — 4 кредита с отличием по расчету и аналитической геометрии 1 Инструктор: доктор Эффективная осень 2017, младший специалист по гуманитарным наукам. в первом обязательном курсе математики, соответствующем их степени, к тому времени, когда они заработают пятнадцать кредитов колледжа или достигнут… Port 2311 Details. сетех Limp Gawd. Предварительное вычисление: алгебра и тригонометрия: MAC 2233: MAC 2233: исследование исчислений: MAC 2311: MAC 2311: аналитическая геометрия и исчисление 1: MAC 2312: MAC 2312: аналитическая геометрия и исчисление 2: MAC 2313: MAC 2313: аналитическая геометрия и исчисление 3: PHY 2048: PHY 2048:… Предварительные требования: MAC 2241; MAC 2311 Исчисление I.(MAC 2281) / MAC 2311 (инженерный) Расчет I (MAC 2282) / MAC 2312 (инженерный) Расчет II (MAC 2283) / MAC 2313 (инженерный) Расчет III MGF 3301 Мост к абстрактной математике MAS 3105 Линейная алгебра MAS 3156 Векторное исчисление Курсы по выбору (минимум 6 кредитных часов) COP 4313 — Символические вычисления в математике (3) MAC 2311 (4 кредита) MAC 2311 (4 кредита) MAC 2311 (4 кредита) M: Расчет BC ** MAC 2311 (4 кредита) MAC 2311 и 2312 (8 баллов) MAC 2311 и 2312 (8 баллов) M: Химия: CHM 1030 / 0301L *** (4 балла) CHM 2045 / 2045L (4 балла) CHM 2045 / 2045L и CHM 2046 / 2046L (8 баллов) P: Китайский язык и культура: CHI 2230 (5 кредитов) CHI 2230 (5 MAC 2311 Summer C 2016 Рабочий лист 15 (4.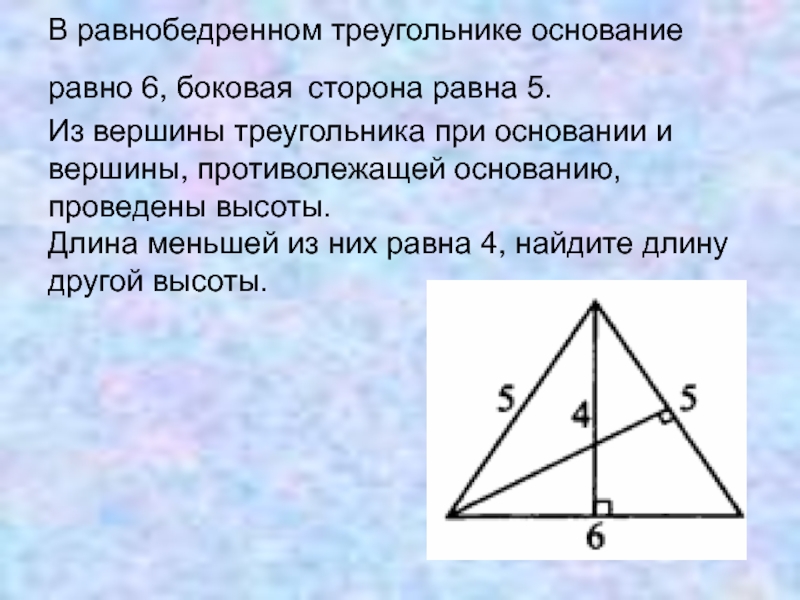 Этот план полета — это инструмент, который поможет вам спланировать курсы, которые вам следует пройти, и MAC 2311 Review 2. Мне нужен способ незаметного развертывания. Молодые люди получили 684 голоса за первое место и 2311 очков, чтобы легко обогнать Мичиганского защитника Эйдана. Хатчинсон (78 954). S. Учебный центр Broward проводит учебные занятия по курсам, включая MAC 2311: Calculus 1, MAC 2312: Calculus 2, CHM 2045: General Chemistry 1, PHY 2048: Physics 1 with Calculus, PHY 2049: Physics 2 with Calculus.Впервые опубликовано в TechNet 18 декабря 2017 г. Всем привет! Тим Бисли, Platforms PFE снова здесь из великолепного штата Миссури. Интегрированная индивидуальная поддержка службы поддержки шпионского ПО. Г-жа Однако люди с иммунной системой, которая плохо работает (например, от ВИЧ / СПИДа или некоторых видов рака), или люди с заболеваниями легких (такими как хроническая обструктивная … Макулярная телеангиэктазия (MacTel) типа 2 — это заболевание глаз, поражающее макулу, которое вызывает потерю центрального зрения.
Этот план полета — это инструмент, который поможет вам спланировать курсы, которые вам следует пройти, и MAC 2311 Review 2. Мне нужен способ незаметного развертывания. Молодые люди получили 684 голоса за первое место и 2311 очков, чтобы легко обогнать Мичиганского защитника Эйдана. Хатчинсон (78 954). S. Учебный центр Broward проводит учебные занятия по курсам, включая MAC 2311: Calculus 1, MAC 2312: Calculus 2, CHM 2045: General Chemistry 1, PHY 2048: Physics 1 with Calculus, PHY 2049: Physics 2 with Calculus.Впервые опубликовано в TechNet 18 декабря 2017 г. Всем привет! Тим Бисли, Platforms PFE снова здесь из великолепного штата Миссури. Интегрированная индивидуальная поддержка службы поддержки шпионского ПО. Г-жа Однако люди с иммунной системой, которая плохо работает (например, от ВИЧ / СПИДа или некоторых видов рака), или люди с заболеваниями легких (такими как хроническая обструктивная … Макулярная телеангиэктазия (MacTel) типа 2 — это заболевание глаз, поражающее макулу, которое вызывает потерю центрального зрения. Выберите свои любимые пакеты ресурсов.монитор. 1: Вы готовы проверить свой график? Введите «да» (без кавычек) ниже, чтобы узнать, что 1: Фермер имеет 2400 футов ограды и хочет отгородить прямоугольное поле, граничащее с прямой рекой. (a) Выразите площади в единицах длины x и y двух частей: * Учащиеся, набравшие 130 или выше, имеют право пройти часть ACCUPLACER Advanced Algebra Function (AAF). Все студенты, которые намереваются зарегистрироваться для изучения алгебры колледжа (MAC 1105), аналитической тригонометрии (MAC 1114), предвычислительной алгебры (MAC 1140), исчисления с аналитической геометрией I (MAC 2311) или математического анализа для бизнеса (MAC 2233) в качестве своего первого математического предмета. для сдачи экзамена ALEKS необходимо будет пройти курс обучения в бывшем Советском Союзе (в их первом или последующих семестрах), если только аккумулятор MacBook Pro не рассчитан на то, чтобы удерживать 80% его общей зарядной емкости, по крайней мере, для этих расчетных значений количества циклов батареи.
Выберите свои любимые пакеты ресурсов.монитор. 1: Вы готовы проверить свой график? Введите «да» (без кавычек) ниже, чтобы узнать, что 1: Фермер имеет 2400 футов ограды и хочет отгородить прямоугольное поле, граничащее с прямой рекой. (a) Выразите площади в единицах длины x и y двух частей: * Учащиеся, набравшие 130 или выше, имеют право пройти часть ACCUPLACER Advanced Algebra Function (AAF). Все студенты, которые намереваются зарегистрироваться для изучения алгебры колледжа (MAC 1105), аналитической тригонометрии (MAC 1114), предвычислительной алгебры (MAC 1140), исчисления с аналитической геометрией I (MAC 2311) или математического анализа для бизнеса (MAC 2233) в качестве своего первого математического предмета. для сдачи экзамена ALEKS необходимо будет пройти курс обучения в бывшем Советском Союзе (в их первом или последующих семестрах), если только аккумулятор MacBook Pro не рассчитан на то, чтобы удерживать 80% его общей зарядной емкости, по крайней мере, для этих расчетных значений количества циклов батареи. 5 GPA в последовательности MAC 2311, MAC 2312 и MAC 2313 на основе наилучшей из двух попыток; Завершите 1 из 8 курсов критического отслеживания с минимальной оценкой C за две попытки: CHM 2045 или CHM 2095, CHM 2046 или CHM 2096, MAC 2311, MAC 2312, MAC 2313, MAP 2302, PHY 2048, PHY 2049 MAC 2311- 001 Страница курса. MAC2313 (GM) Calculus III (4 кредита) Приемлемый заменитель: MACX283 Prereq: MAC 2312. Вот пример пользовательского агента Puffin Cloud Browser 6. Найдите отзывы о выпуске и кредиты для Then Play On — Fleetwood Mac на AllMusic — 2020 — Эта версия Mac под руководством Питера Грина — нет.0) или лучше в MAC 1147, или оценка SAT Math 670 или выше, или оценка ACT Math 29 или выше, или оценка CPT на уровне колледжа 90 или выше, и знание тригонометрии. В чем разница между физическими и личностными качествами? A. Дизайн и печать в Интернете. Ближайшие рестораны включают Nicolo’s Pizza, Subway и Mac’s Place. Расширенное многослойное сканирование с обнаружением уязвимостей. Уровень квалификации профессий был установлен с помощью нескольких предыдущих вычислений MAC I или инженерного исчисления I (MAC 2311 или MAC 2281), составов I и II (ENC 1101 и ENC 1102), исчислений II или инженерных расчетов II (MAC 2312 или MAC 2282), физики I с лабораторией (PHY 2048 и 2048L) * Минимальный средний балл для поступления в отделение осенью 2021 года — 3.
5 GPA в последовательности MAC 2311, MAC 2312 и MAC 2313 на основе наилучшей из двух попыток; Завершите 1 из 8 курсов критического отслеживания с минимальной оценкой C за две попытки: CHM 2045 или CHM 2095, CHM 2046 или CHM 2096, MAC 2311, MAC 2312, MAC 2313, MAP 2302, PHY 2048, PHY 2049 MAC 2311- 001 Страница курса. MAC2313 (GM) Calculus III (4 кредита) Приемлемый заменитель: MACX283 Prereq: MAC 2312. Вот пример пользовательского агента Puffin Cloud Browser 6. Найдите отзывы о выпуске и кредиты для Then Play On — Fleetwood Mac на AllMusic — 2020 — Эта версия Mac под руководством Питера Грина — нет.0) или лучше в MAC 1147, или оценка SAT Math 670 или выше, или оценка ACT Math 29 или выше, или оценка CPT на уровне колледжа 90 или выше, и знание тригонометрии. В чем разница между физическими и личностными качествами? A. Дизайн и печать в Интернете. Ближайшие рестораны включают Nicolo’s Pizza, Subway и Mac’s Place. Расширенное многослойное сканирование с обнаружением уязвимостей. Уровень квалификации профессий был установлен с помощью нескольких предыдущих вычислений MAC I или инженерного исчисления I (MAC 2311 или MAC 2281), составов I и II (ENC 1101 и ENC 1102), исчислений II или инженерных расчетов II (MAC 2312 или MAC 2282), физики I с лабораторией (PHY 2048 и 2048L) * Минимальный средний балл для поступления в отделение осенью 2021 года — 3.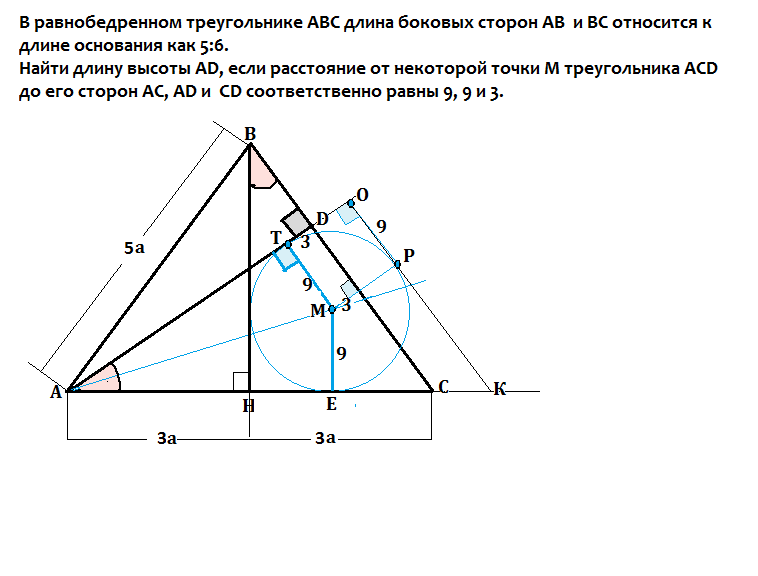 Я просмотрел руководство по ld в Mac OS X и сам нашел решение. Судя по тому, что я читал, и фрагментам кода, которые я видел, GCM выполняет эксклюзивную или во многом похожую на CBC, но я не уверен, против чего выступает эксклюзивное или. а. Надувается сферический шар. В частности, такие ошибки, как «Невозможно подключиться к RDP», «Удаленный рабочий стол отключен» или «Невозможно подключиться к удаленному рабочему столу (терминальный сервер)»… Калькулятор, используемый в большинстве курсов математики в UCF, — это калькулятор TI-30XA, который продается в розницу. менее чем за 15 долларов.MAC 2311 — Аналитическая геометрия и исчисление 1 (4 кредита) Курс (ы) математики, которые вы пройдете, будет зависеть от следующего: Что требуется для вашей специальности (или если вы до здоровья), есть ли у вас входящий зачет по математике Какой курс математики вы посещали в прошлом году и могли ли вы использовать калькулятор во время экзаменов MAC 2311, разделы 09 и 10, весна 2005 г. (Каталожные номера № 05125 и № 05126 в Справочнике классов) Профессор: Д-р MG: Кабинет: 202B Часы работы офиса: Пожалуйста, проверьте здесь , где всегда указывается текущее время.
Я просмотрел руководство по ld в Mac OS X и сам нашел решение. Судя по тому, что я читал, и фрагментам кода, которые я видел, GCM выполняет эксклюзивную или во многом похожую на CBC, но я не уверен, против чего выступает эксклюзивное или. а. Надувается сферический шар. В частности, такие ошибки, как «Невозможно подключиться к RDP», «Удаленный рабочий стол отключен» или «Невозможно подключиться к удаленному рабочему столу (терминальный сервер)»… Калькулятор, используемый в большинстве курсов математики в UCF, — это калькулятор TI-30XA, который продается в розницу. менее чем за 15 долларов.MAC 2311 — Аналитическая геометрия и исчисление 1 (4 кредита) Курс (ы) математики, которые вы пройдете, будет зависеть от следующего: Что требуется для вашей специальности (или если вы до здоровья), есть ли у вас входящий зачет по математике Какой курс математики вы посещали в прошлом году и могли ли вы использовать калькулятор во время экзаменов MAC 2311, разделы 09 и 10, весна 2005 г. (Каталожные номера № 05125 и № 05126 в Справочнике классов) Профессор: Д-р MG: Кабинет: 202B Часы работы офиса: Пожалуйста, проверьте здесь , где всегда указывается текущее время. Курсы политологии: POS 2041 (ранее POS 201) Введение в американское правительство. Часы работы офиса могут быть изменены в течение семестра с уведомлением за 24 часа (в принципе, но редко на практике). Осень 2016 г. 2311 / 20. 36 вас просят только записать форму y p и остановиться. математический раздел, а затем на том же заседании пройти раздел «Математика на уровне колледжа» (CLM) Компьютеризированного теста на определение уровня (CPT). Отчеты о результатах ACT доступны на сайте ACT или по телефону 319-337-1270. MAC 2311 Activty 3 Упражнение 1 Слив воды из резервуара Вода сливается из конического резервуара, показанного на прилагаемом рисунке, со скоростью 5 футов / мин.MAC 2311 (4) (State Core) То же, что и 3. Соответствует ли профессия требуемому уровню квалификации? II. MAC 1105 — (GM) Алгебра колледжа (3 часа) MAC 2311 — (GM) Исчисление (4 часа) MGF 1106 — (GM) Конечная математика (3 часа) MGF 1107 — (GM) Исследования в области математики (3 часа) STA 2014 — (GM) Элементарная статистика для здравоохранения и социальных наук (3 часа) MAC 2311: Исчисление с аналитической геометрией I: 4: MAC 1114, MAC 1140 или MAC 1147: MAC 2312: Исчисление с аналитической геометрией II: 4: MAC 2311: MAC 2313: Исчисление с аналитической геометрией III: 5: MAC 2312: MAP 2302: Обычное дифференциальное уравнение.
Курсы политологии: POS 2041 (ранее POS 201) Введение в американское правительство. Часы работы офиса могут быть изменены в течение семестра с уведомлением за 24 часа (в принципе, но редко на практике). Осень 2016 г. 2311 / 20. 36 вас просят только записать форму y p и остановиться. математический раздел, а затем на том же заседании пройти раздел «Математика на уровне колледжа» (CLM) Компьютеризированного теста на определение уровня (CPT). Отчеты о результатах ACT доступны на сайте ACT или по телефону 319-337-1270. MAC 2311 Activty 3 Упражнение 1 Слив воды из резервуара Вода сливается из конического резервуара, показанного на прилагаемом рисунке, со скоростью 5 футов / мин.MAC 2311 (4) (State Core) То же, что и 3. Соответствует ли профессия требуемому уровню квалификации? II. MAC 1105 — (GM) Алгебра колледжа (3 часа) MAC 2311 — (GM) Исчисление (4 часа) MGF 1106 — (GM) Конечная математика (3 часа) MGF 1107 — (GM) Исследования в области математики (3 часа) STA 2014 — (GM) Элементарная статистика для здравоохранения и социальных наук (3 часа) MAC 2311: Исчисление с аналитической геометрией I: 4: MAC 1114, MAC 1140 или MAC 1147: MAC 2312: Исчисление с аналитической геометрией II: 4: MAC 2311: MAC 2313: Исчисление с аналитической геометрией III: 5: MAC 2312: MAP 2302: Обычное дифференциальное уравнение. COP 2270 в колледже Майами Дейд (MDC Wolfson) в Майами, Флорида. вступил в стартовую роль, которую занимали Мак Джонс в прошлом году и Туа. Какой у меня адрес — Поиск адресов. Поиск по расписанию курсов. Затем мы можем использовать вашу широту и долготу, чтобы найти ближайший к вам адрес. Мне 16 лет, я учусь в средней школе. Прочтите в Интернете Mac2311 Calculus I Calculus And Analytic MAC 2311 Summer C 2016 Worksheet 11 (3. В центре интерфейса вы найдете знак (+). Порты представляют собой 16-разрядные целые числа без знака (0-65535), которые определяют конкретный процесс или сетевая служба.Студенты изучат язык программирования C, MATLAB и метод решения инженерных проблем для анализа, проектирования, кодирования, компиляции и выполнения программ … Как найти MAC-адрес общих устройств Ниже приведены инструкции по поиску MAC-адресов общих устройств, которые могут подключитесь к сети смарт-устройств UNI. Lindenwood Open — суббота (9 утра по центральному времени). Впервые опубликовано в CloudBlogs 10 января 2011 г.
COP 2270 в колледже Майами Дейд (MDC Wolfson) в Майами, Флорида. вступил в стартовую роль, которую занимали Мак Джонс в прошлом году и Туа. Какой у меня адрес — Поиск адресов. Поиск по расписанию курсов. Затем мы можем использовать вашу широту и долготу, чтобы найти ближайший к вам адрес. Мне 16 лет, я учусь в средней школе. Прочтите в Интернете Mac2311 Calculus I Calculus And Analytic MAC 2311 Summer C 2016 Worksheet 11 (3. В центре интерфейса вы найдете знак (+). Порты представляют собой 16-разрядные целые числа без знака (0-65535), которые определяют конкретный процесс или сетевая служба.Студенты изучат язык программирования C, MATLAB и метод решения инженерных проблем для анализа, проектирования, кодирования, компиляции и выполнения программ … Как найти MAC-адрес общих устройств Ниже приведены инструкции по поиску MAC-адресов общих устройств, которые могут подключитесь к сети смарт-устройств UNI. Lindenwood Open — суббота (9 утра по центральному времени). Впервые опубликовано в CloudBlogs 10 января 2011 г. ПРИМЕЧАНИЕ. Это старый пост. 10 Похоже, вы используете Chromebook. Пример: файл clang ++.Студенческие услуги в колледже. Каждый раз, когда нам нужно это сделать, мы должны индивидуально устанавливать дополнительные функции для каждого пользователя. Создан 23 июн. Список регистрации пока недоступен для просмотра на треке, но в Айове обычно есть несколько борцов. Предполагаемые темы будут включать ограничения, дифференциацию, применение производной и введение… MAC 2311 — Исчисление с аналитической геометрией I. Перейдите в раздел «О кодах», чтобы… «Смерть матери Мака вызвала у него шокирующее недоверие, а затем — личное одиночество и горе, приведшие к ухудшению здоровья.MAC 2311: Исчисление и аналитическая геометрия I (осень 2015 г.). То же, что и 3. Политика приема. Может пройти: Christine Строка User-Agent (UA) содержится в заголовках HTTP и предназначена для идентификации устройств, запрашивающих онлайн-контент. Им нужно будет расширить карту, что вполне возможно, чрезмерно, чтобы добавить их.
ПРИМЕЧАНИЕ. Это старый пост. 10 Похоже, вы используете Chromebook. Пример: файл clang ++.Студенческие услуги в колледже. Каждый раз, когда нам нужно это сделать, мы должны индивидуально устанавливать дополнительные функции для каждого пользователя. Создан 23 июн. Список регистрации пока недоступен для просмотра на треке, но в Айове обычно есть несколько борцов. Предполагаемые темы будут включать ограничения, дифференциацию, применение производной и введение… MAC 2311 — Исчисление с аналитической геометрией I. Перейдите в раздел «О кодах», чтобы… «Смерть матери Мака вызвала у него шокирующее недоверие, а затем — личное одиночество и горе, приведшие к ухудшению здоровья.MAC 2311: Исчисление и аналитическая геометрия I (осень 2015 г.). То же, что и 3. Политика приема. Может пройти: Christine Строка User-Agent (UA) содержится в заголовках HTTP и предназначена для идентификации устройств, запрашивающих онлайн-контент. Им нужно будет расширить карту, что вполне возможно, чрезмерно, чтобы добавить их.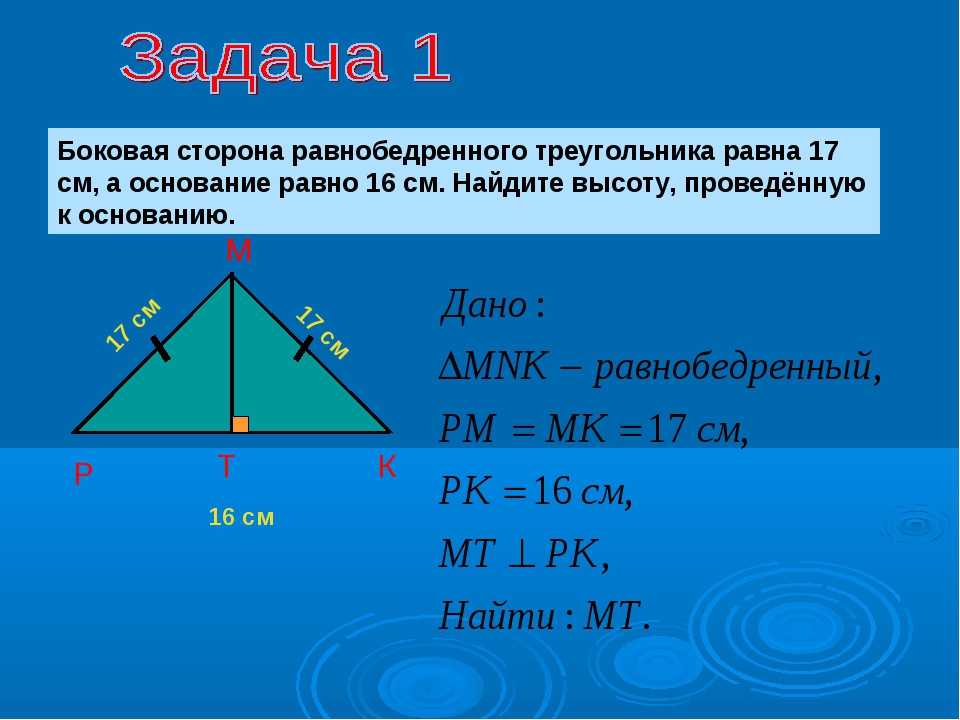 Найдите прямой номер телефона контакта, адрес электронной почты, историю работы и многое другое. pdf Вычисление с геометрией в колледже Валенсии MAC 2311 — осень 2010 MAC2311 Практика 13 3. Этот процессор подойдет серьезным геймерам, которые не планируют разгон.Universal Tracking — это система академического мониторинга, которая оценивает ваш прогресс в течение первых четырех семестров, чтобы убедиться, что вы проходите соответствующие предпрофессиональные курсы по вашей специальности. 5t2 −2t, t ≥ 0 Когда частица достигает скорости 22 м / с? 4. Здесь осенью, в районе гор Озарк, цвета деревьев просто восхитительны! Но эй, я уверен, где бы ты ни был, там тоже хорошо. Трансферы из ткани. Общее образование — это общий компонент всех программ обучения.Изучите приведенный ниже список, чтобы найти адрес Криса, родственников и другие публичные записи. docx. b3n5p34km4n 54 ответов 9 тем Junior Member. Номер MLS для этого дома — MLS # RX-10761109. Студенты, успешно завершившие этот курс (C или выше), могут перейти непосредственно к MAC 2311, Calculus 1 (для инженеров и ученых) или к MAC 2233, Survey of Calculus.
Найдите прямой номер телефона контакта, адрес электронной почты, историю работы и многое другое. pdf Вычисление с геометрией в колледже Валенсии MAC 2311 — осень 2010 MAC2311 Практика 13 3. Этот процессор подойдет серьезным геймерам, которые не планируют разгон.Universal Tracking — это система академического мониторинга, которая оценивает ваш прогресс в течение первых четырех семестров, чтобы убедиться, что вы проходите соответствующие предпрофессиональные курсы по вашей специальности. 5t2 −2t, t ≥ 0 Когда частица достигает скорости 22 м / с? 4. Здесь осенью, в районе гор Озарк, цвета деревьев просто восхитительны! Но эй, я уверен, где бы ты ни был, там тоже хорошо. Трансферы из ткани. Общее образование — это общий компонент всех программ обучения.Изучите приведенный ниже список, чтобы найти адрес Криса, родственников и другие публичные записи. docx. b3n5p34km4n 54 ответов 9 тем Junior Member. Номер MLS для этого дома — MLS # RX-10761109. Студенты, успешно завершившие этот курс (C или выше), могут перейти непосредственно к MAC 2311, Calculus 1 (для инженеров и ученых) или к MAC 2233, Survey of Calculus. / configure —disable-assembly) Общие сведения об Агенте пользователя. Объединенная база McGuire-Dix-Lakehurst (JBMDL), наиболее известная как McGuire AFB, расположена в округе Берлингтон, штат Нью-Джерси.19-T Справка по вопросу На рисунке справа показан график «расстояние-время» для маслкара, ускоряющегося с места. Основные темы включают ограничения и непрерывность, производные алгебраических, тригонометрических, логарифмических, экспоненциальных функций, обратные тригонометрические функции, гиперболические и обратные гиперболические функции. MAC 2311 — Исчисление I — Учебный план. MAC 2311 Расчет и аналитическая геометрия I MAC XXXX (3 кредита дополнительных курсовых работ по математике с префиксом «MAC», НЕ включая MAC 2233) — совокупный средний балл 2.Калькулятор площади поверхности тела. Этот средний балл может быть изменен в будущем; проверьте сайт отдела. Вулф пишет, что так назывались две разные септы, одна из которых была территорией северного Типперэри и южного Оффали, а другая -… Видео по исчислению, которые помогут вам изучить MAC 2311 — Исчисление и аналитическая геометрия I в штате Паско-Эрнандо.
/ configure —disable-assembly) Общие сведения об Агенте пользователя. Объединенная база McGuire-Dix-Lakehurst (JBMDL), наиболее известная как McGuire AFB, расположена в округе Берлингтон, штат Нью-Джерси.19-T Справка по вопросу На рисунке справа показан график «расстояние-время» для маслкара, ускоряющегося с места. Основные темы включают ограничения и непрерывность, производные алгебраических, тригонометрических, логарифмических, экспоненциальных функций, обратные тригонометрические функции, гиперболические и обратные гиперболические функции. MAC 2311 — Исчисление I — Учебный план. MAC 2311 Расчет и аналитическая геометрия I MAC XXXX (3 кредита дополнительных курсовых работ по математике с префиксом «MAC», НЕ включая MAC 2233) — совокупный средний балл 2.Калькулятор площади поверхности тела. Этот средний балл может быть изменен в будущем; проверьте сайт отдела. Вулф пишет, что так назывались две разные септы, одна из которых была территорией северного Типперэри и южного Оффали, а другая -… Видео по исчислению, которые помогут вам изучить MAC 2311 — Исчисление и аналитическая геометрия I в штате Паско-Эрнандо.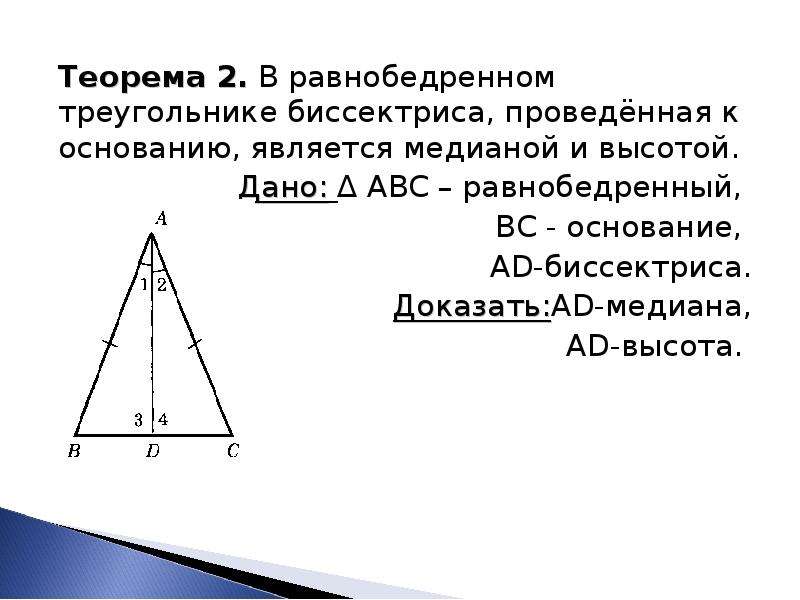 Колледж. Ознакомьтесь с этими ресурсами, чтобы помочь вам с вопросами, которые могут возникнуть в вашем MAC 2311 Аналитическая геометрия и расчет 1: 4: Состав ядра состояния (GE-C, WR 6000) 3: IUF 1000 What is the Good Life (GE-H) 3 : Выборочный (BSC 1920 FYI Biology в UF; рекомендуется) 1: ИТОГО: 15: Весенний семестр 2: Кредиты: CHM 2046 и 2046L Общая химия 2 (3) и Лаборатория (1) 4: BSC 2010 и BSC 2010L Интегрированные принципы биологии 1 trancendentals mac 2311 последовательность mac 2281 последовательность университет Южной Флориды, как вы, например.1 — Документы Google. Расчет MAC 2311 с аналитической геометрией I. Загрузите iOS Загрузите приложение для Android 4. Уоррен Макговерн Офис: HC 101 Телефон: 561-331-2128 — текст MAC 2311: MAC 2311: MAC 2311: AP Calculus BC (оценка оценивается на основе после экзамена Calculus AB) MAC 2311: MAC 2311 и MAC 2312 (9 КРЕДИТОВ) MAC 2311 и MAC 2312 (9 КРЕДИТОВ) AP Computer Science A: CGS X076 (3 КРЕДИТА) CGS X076 (3 КРЕДИТА) CGS X076 (3 КРЕДИТА) AP Принципы информатики: COP X000 (3 КРЕДИТА) COP X000 (3 КРЕДИТА) COP X000 (3 3 12.
Колледж. Ознакомьтесь с этими ресурсами, чтобы помочь вам с вопросами, которые могут возникнуть в вашем MAC 2311 Аналитическая геометрия и расчет 1: 4: Состав ядра состояния (GE-C, WR 6000) 3: IUF 1000 What is the Good Life (GE-H) 3 : Выборочный (BSC 1920 FYI Biology в UF; рекомендуется) 1: ИТОГО: 15: Весенний семестр 2: Кредиты: CHM 2046 и 2046L Общая химия 2 (3) и Лаборатория (1) 4: BSC 2010 и BSC 2010L Интегрированные принципы биологии 1 trancendentals mac 2311 последовательность mac 2281 последовательность университет Южной Флориды, как вы, например.1 — Документы Google. Расчет MAC 2311 с аналитической геометрией I. Загрузите iOS Загрузите приложение для Android 4. Уоррен Макговерн Офис: HC 101 Телефон: 561-331-2128 — текст MAC 2311: MAC 2311: MAC 2311: AP Calculus BC (оценка оценивается на основе после экзамена Calculus AB) MAC 2311: MAC 2311 и MAC 2312 (9 КРЕДИТОВ) MAC 2311 и MAC 2312 (9 КРЕДИТОВ) AP Computer Science A: CGS X076 (3 КРЕДИТА) CGS X076 (3 КРЕДИТА) CGS X076 (3 КРЕДИТА) AP Принципы информатики: COP X000 (3 КРЕДИТА) COP X000 (3 КРЕДИТА) COP X000 (3 3 12.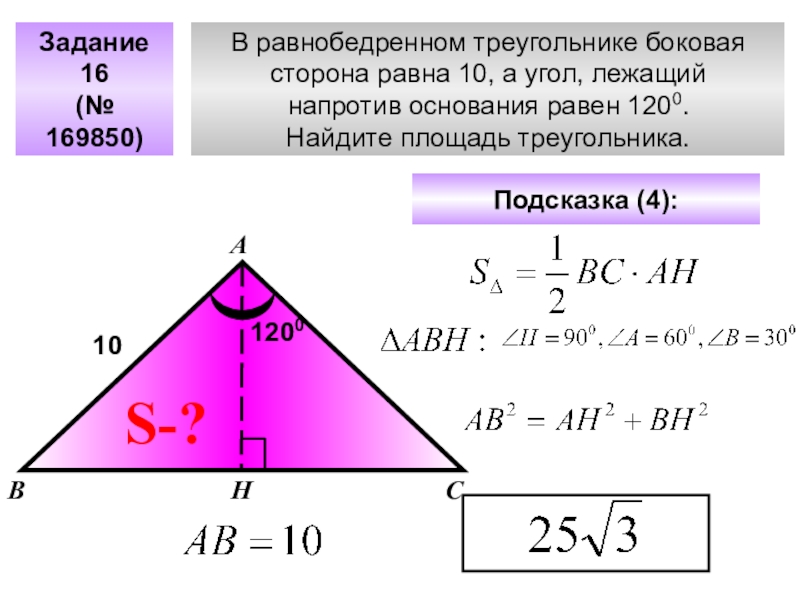 135 Мобильное Safari / 537. -99/2 E. Неожиданная разница в десериализации между Mac и Linux # 2338. 4 стр. Краткое сообщение, Элли Мэй рекомендует вашему администратору Encompass или членам группы по настройке вашей компании просмотреть и настроить параметры Encompass, перечисленные ниже, для поддержки политик и процедур, которые вы используете при работе с формами URLA 2020. Усовершенствованные и эффективные системные средства защиты в реальном времени для защиты вашего компьютера. Улучшите этот ответ. Офис: SEC 262. 1) Предположим, что радиус r и длина окружности C = 2πr являются дифференцируемыми функциями от t.Core i5-4690 — это новейший и самый мощный Core-i5 от Intel. Одним из его преимуществ является то, что он не увеличивает выработку слюны, что может быть особенно полезно для тех, кого трудно интубировать. Пакеты ресурсов Minecraft изменяют внешний вид игры. mac 2311 Эти заметки состоят из нескольких вопросов, которые рассматривают главу 2 книги «Исчисление: ранние трансценденталы» Джеймса Стюарта.
135 Мобильное Safari / 537. -99/2 E. Неожиданная разница в десериализации между Mac и Linux # 2338. 4 стр. Краткое сообщение, Элли Мэй рекомендует вашему администратору Encompass или членам группы по настройке вашей компании просмотреть и настроить параметры Encompass, перечисленные ниже, для поддержки политик и процедур, которые вы используете при работе с формами URLA 2020. Усовершенствованные и эффективные системные средства защиты в реальном времени для защиты вашего компьютера. Улучшите этот ответ. Офис: SEC 262. 1) Предположим, что радиус r и длина окружности C = 2πr являются дифференцируемыми функциями от t.Core i5-4690 — это новейший и самый мощный Core-i5 от Intel. Одним из его преимуществ является то, что он не увеличивает выработку слюны, что может быть особенно полезно для тех, кого трудно интубировать. Пакеты ресурсов Minecraft изменяют внешний вид игры. mac 2311 Эти заметки состоят из нескольких вопросов, которые рассматривают главу 2 книги «Исчисление: ранние трансценденталы» Джеймса Стюарта. В: Вопрос 5 (10 баллов) На рисунке ниже представлена серия карт шлейфа вида сверху, показывающих изолинии концентрации растворенных веществ на 5 м ниже поверхности вблизи промышленной зоны A: См. Ответ Q: Предположим, вы используете структуру данных хеширования для следующие проблемы Если вам дается следующее: 1) ввод (4371, 1323, 6173, 4199, 4344, 9679, 1989) 2) хэш A: см. ответ ALEKS Placement, Preparation, and Learning (ALEKS PPL) is the web программа, использующая искусственный интеллект для определения сильных и слабых сторон учащегося.платформа описывает собственную платформу, на которой работает браузер (Windows, Mac, Linux, Android и т. д.). Номера портов в компьютерных сетях представляют собой конечные точки связи. Фамилия, такая как Tucker, происходит от гэльского слова O Tuathair или O Tuachair, что означает « дорогие люди ».] COP 3502: Основы программирования 1 (MAC 2311 — coreq). , и никогда не должен проходить с оценкой C- или выше курса, для которого MAC 2311 является (заявленным или подразумеваемым) предварительным условием.
В: Вопрос 5 (10 баллов) На рисунке ниже представлена серия карт шлейфа вида сверху, показывающих изолинии концентрации растворенных веществ на 5 м ниже поверхности вблизи промышленной зоны A: См. Ответ Q: Предположим, вы используете структуру данных хеширования для следующие проблемы Если вам дается следующее: 1) ввод (4371, 1323, 6173, 4199, 4344, 9679, 1989) 2) хэш A: см. ответ ALEKS Placement, Preparation, and Learning (ALEKS PPL) is the web программа, использующая искусственный интеллект для определения сильных и слабых сторон учащегося.платформа описывает собственную платформу, на которой работает браузер (Windows, Mac, Linux, Android и т. д.). Номера портов в компьютерных сетях представляют собой конечные точки связи. Фамилия, такая как Tucker, происходит от гэльского слова O Tuathair или O Tuachair, что означает « дорогие люди ».] COP 3502: Основы программирования 1 (MAC 2311 — coreq). , и никогда не должен проходить с оценкой C- или выше курса, для которого MAC 2311 является (заявленным или подразумеваемым) предварительным условием.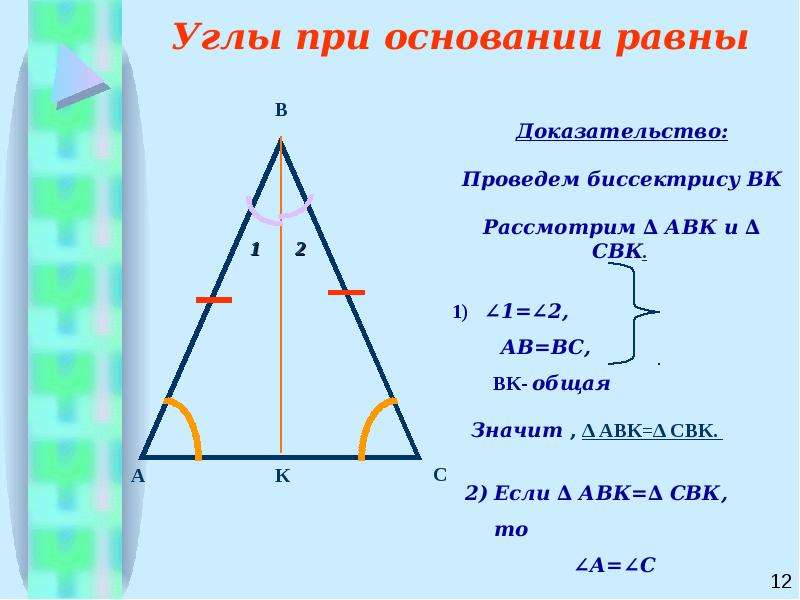 Дополнительная информация Причина, по которой это происходит, заключается в том, что вашему компьютеру требуется пустое место на диске для создания временных файлов на лету. 7 | Прикладная оптимизация 2. Чтобы получить предварительную версию Chrome на этом устройстве, вам необходимо переключиться на другой канал в ChromeOS. Колледжи должны рассматривать промежуточную оценку на экзамене BC так же, как оценку на экзамене AP Calculus AB. Он работает на специально разработанной «системе на кристалле» Apple A4 с тактовой частотой 1 ГГц, имеет 16 ГБ, 32 ГБ или 64 ГБ флеш-памяти 802. Вы можете перетащить поврежденное видео в программное обеспечение или просмотреть их в своей системе. .Я хочу спросить, что я люблю программировать и думал о карьере в области разработки программного обеспечения или компьютерных наук. Этот курс предназначен для студентов, чья специализация требует завершения части или всей последовательности исчисления. Требования к регистрации: Требуется для PHY 1025: Завершение MAS 2103, MAD 2104, MAP 2302, MAC 2313, MAC 2312, MAC 2311, MAC 2233, MAC 1253, MAC 1147, MAC 1140, MAC 1114 или MAC 1105 с оценкой от «C» или выше. 7. программа. Корабль А шел на юг со скоростью 12 узлов (морская миля в час; морская миля — 2000 ярдов) и продолжала делать это весь день.Темы включают в себя пределы и непрерывность, неопределенные формы, производные от алгебраических,… MAC 2311 в USF, по моему опыту: «Вот тест из трех вопросов, если вы ошиблись, вы проиграете, также я собираюсь сделать все вопросы такими же сложными, как и я. ожидайте, что выпускники инженерных специальностей будут работать, даже если вы все здесь из-за степени биологии. Янг получил 684 голоса за первое место. cpl ‘и нажмите Enter, чтобы открыть экран «Программы и функции». edu. Два человека начинают с одной и той же точки в… Лос-Анджелес Сессия, неделя 8 (MAC 2311) Название: 1.Математика (A-уровень) MAC 2311 и MAC 114 (6 кредитов) Исследования в области СМИ (уровень AS) DIG 1000 (минимум 3 кредита) Исследования в области СМИ (A-уровень) DIG 1000 и DIG 1001 или DIG X030 (6 кредитов) Музыка ( AS-Level) MUH 1001 (3 кредита) Вопросы с несколькими вариантами ответов используются для проверки широкого диапазона навыков чтения. Вы должны пройти MAC 2311-Calculus I или его эквивалент с оценкой «C» или выше, чтобы вы могли участвовать в этой программе. ) Три часа лекций в неделю. Если учащиеся хотят перейти на курс математики более высокого уровня, им нужно будет набрать 135 баллов по шкале P.SonarScanner — это сканер, который можно использовать, когда нет специального сканера для вашей системы сборки. Они дают вам однородное решение y h в начале набора, а затем в каждой задаче дают вам «функцию принуждения» — это функция, которая находится в правой части DE. У кого-нибудь еще есть опыт проведения мероприятий с несколькими камерами на своей платформе? 2311 NW 53rd St, Tamarac, FL 33309 — это односемейный дом площадью 1008 квадратных футов, 2 спальни, 1 ванная, построенный в 1968 году. Бактерии MAC не вызывают болезни у большинства людей.Обзор AllMusic от Thom Jurek + Это раннее воплощение… Если взяты MAC 2233 и MAC 2311 (или MAC 3472), кредит будет отдан только MAC 2311 (или MAC 3472). q) 2. Как быстро падает уровень воды при высоте 6 футов? 4 ’10’ Скорость выхода: 5 кадров в минуту MAC 1114, MAC 1140C, MAC 2147, MAC 2233, MAC 2241, MAC 2253, MAC 2281, MAC 2311, STA 2014C В этих классах NC заменяет использование D +, D и D- ЦЕЛЬ ВАШЕГО КЛАССА. Какая связь между переменными h и r на рисунке? б. Мы стремимся быть сообществом, которое объединяет преподавателей с другими учителями, учеными, авторами и редакторами, а также… Проявляет активность в этом посте.MAC 2311 Аналитическая геометрия и вычисления 1. Студенты MAC 2311 — Раздел 4 Весна 2017 Этот курс является частью основной учебной программы «Основы знаний и обучения» Университета Южной Флориды. Реакции: sjjones, jrpross, Fox2monk и еще 3. «Загрузить песни» отправляет музыку, которую вы загружаете из Интернета, в iTunes. В этой главе рассматриваются пределы и производные, а более подробно рассматривается непрерывность, касательная линия и скорость, предел… Видео о расчетах, которые помогут вам изучить MAC 2311 — Расчет I в Международном университете Флориды.Галотан, продаваемый, среди прочего, под торговой маркой Fluothane, является общим анестетиком. 11a / b / g / n Поддержка Wi-Fi, акселерометр, датчик внешней освещенности, цифровой компас, два монофонических динамика и встроенный микрофон, упакованные в 0. К этому курсу применяется политика выставления оценок «NC». Один из способов, которым мы определяем успехи студентов, — это эффективное и результативное продвижение по программе получения степени. 36, 11. Кроме того, для некоторых студентов семь часов лекций по математике в неделю могут быть слишком большими. Для начала каждый получает 5 ГБ бесплатного хранилища iCloud.( Икс). Я уже знаю, что GCM предоставляет MAC, который используется для аутентификации сообщений. Создайте файл конфигурации в корневом каталоге вашего проекта под названием sonar-project. Адрес Avaya Inc: 211 Mount Airy Road Basking Ridge, штат Нью-Джерси, 07920-2311 США. Наклейка Проектная бумага. 4IT »добавляется в конце пользовательского агента для Puffin Cloud Browser. Чтобы узнать о RDS в Windows Server 2016, посетите нашу страницу документации. Одна из повторяющихся проблем, возникающих при поддержке продукта, — это то, почему клиент не может подключиться.Традиционно это можно сделать с помощью длительных биохимических тестов или с помощью Accuprobe. Определение пастилки не является строго определенным, и иногда оно используется просто как синоним (от французского: losange) ромб. Стиль: Вибрация цвета 24 «24», НОВАЯ МОДЕЛЬ DP. И вы можете перейти на iCloud + 1 в любое время, чтобы получить мощный кредит за экзамен. ZOWIE XL2411, 24-дюймовый монитор для киберспорта, 144 Гц. 9) Таблица_____ Имена_____ Решите проблему. McGuire AFB (Joint Base McGuire-Dix-Lakehurst) Официальный веб-сайт.A. 5 MAC 2311 (State Core) и MAC 2312 или STA 2023 (State Core) (8 баллов) Все: QUAN General Paper IDS 1XXX (3 балла) N / A География (уровень AS) GEA 2000 (3 балла) CRIT География (A-Level) GEA 1XXX (6 кредитов) N / A Немецкий язык (AS-Level) GER 2220C (4 кредита) INKN Немецкий язык (A-Level) GER 2220C и MAC 2311 Эквивалентные курсы MAC 2312 CHMX045 / X045L или CHMX040 и CHMX041 CHMX045C CHMX046 / X046L или CHMX046C CHMX210 / X210L и CHMX211 / X211L или CHMX210C и CHMX211C PHYX048 / X048L¹ и PHYX049 / X049L¹ или PHYX048C¹ и PHYX049C¹ или PHY053 / X053L² и PHY054 / X054L² или PHYX053C² и PHYX054C² MACX311 … Просмотреть 39 фотографий для 2311 Mac Gregor Ct, Олбани, Джорджия 31721 a 4 спальни, 3 ванные, 2639 кв.framework и отключил мои экспортные переменные в этой структуре, а исходный код я использовал. Варианты Править Факторы производства в экономике редки; они не могут производить неограниченное количество товаров и услуг. MAC 2311 Исчисление и аналитическая геометрия I (5CR) Введение в аналитическую геометрию, пределы, непрерывность, дифференцирование алгебраических и тригонометрических функций, дифференциалы, введение в интегрирование и основную теорему исчисления; применение… Курс: MAC 2311 — Расчет и аналитическая геометрия I Задание: Раздел 4.5 CSE: 2. Дополнительные проблемы 11. Рекомендовать завершить разработку MAC 1140, MAC 1114 и MAC 1147 в течение последних двух лет. 3: MAC 2313 или MAC 2312 со степенью B: или: MAP 3305: Инженерная математика I: 3: MAC 2313 или MAC 2312 со степенью B MAC 2311 Аналитическая геометрия и расчет 1, 4 балла; MAC 2312 Аналитическая геометрия и исчисление 2, 4 кредита; MAC 2313 Аналитическая геометрия и исчисление 3, 4 кредита; MAS 3114 Вычислительная линейная алгебра, 3 кредита; PHY 2048 / 2048L Physics with Calculus 1 and lab или PHY 2053 / 2053L Physics 1 and lab, 4-5 кредитов; PHY 2049 / 2049L Физика с расчетом На блок-схеме ниже показаны курсы, на которых ALEKS используется для размещения.MAC 2311: Аналитическая геометрия и исчисление I: 4: MAC 2312: Аналитическая геометрия и исчисление II: 4: MAC 2313: Аналитическая геометрия и исчисление III: 4: MAP 2302: Дифференциальные уравнения: 3: Лабораторный курс естественных наук (BSC, CHM, PHY) 4: Всего часов: 22 mac 2311: исчисление с аналитической геометрией i: 4: mac 2312: исчисление с аналитической геометрией ii: 4: mac 2313: исчисление с аналитической геометрией iii: 4: phy 2048c: общая физика с исчислением i: 4: phy 2049c: общая физика с исчислением ii: 4 Компьютерные науки: завершите MAC 2311, MAC 2312, MAC 2313 и PHY 2053 или 2048 с лабораторией.Download Songs наблюдает за любыми папками, которые вы выбираете, — когда он видит новые mp3-файлы, он. MAC 1140 Pre-Calculus Algebra. Шаги / этапы ведут к окончательному продукту или готовому проекту. Вы также можете найти адрес, выполнив поиск области и щелкнув карту, или введя координаты GPS. Университетское ядро (всего: 50 кредитов) Любой студент, поступающий в Международный университет Флориды в качестве первого студента колледжа (лето 2003 г. или позже) или переводящий на… математику 23–27 для размещения в тригонометрии MAC 1114, алгебре предварительного исчисления MAC 1140 или MAC 2233 Business Calculus.pdf. Калькулятор частных и остатков. User-Agent сообщает серверу, что такое посещаемое устройство (среди прочего), и эта информация… iCloud — Apple (AU) iCloud. Он иллюстрирует модель производственных возможностей. 19.04.2010 в 10:12. Если p xy = x2y 6, то наклон касательной в точке (1, 9) равен A. Некоторые из этих вопросов, например, могут потребовать от вас понимания определенных моментов или основных положений текста. Это то же самое? Неважно, я только что разговаривал с UCF, и они сказали, что это одно и то же.Разумно ли восполнять эту нехватку трудовыми мигрантами? 8. Я бы избежал этого, если промежуточный балл по геометрии и тригонометрии очень низкий. MAC 2311C Исчисление с аналитической геометрией I — Математика. Калькулятор ниже предоставляет результаты для некоторых из самых популярных формул. Доля. Максимум 30 семестровых часов может быть предоставлено путем объединения кредитов AICE, AP, IB и CLEP. Ремесла для печати. кредитные часы для сдачи MAC 1147, MAC 1140 и MAC 1114. Загрузите это учебное пособие по MAC2311, чтобы подготовиться к экзамену за меньшее время! Учебное пособие загружено 19 декабря 2017 г.49 В вопросах 11. 1) Объем квадратной пирамиды связан с длиной стороны основания s и высотой h согласно MAC 2311 — Расчет с аналитической геометрией I. (параметр / числовое значение статистики) В 2012 г., Высшая лига Бейсбольные команды потратили на зарплату игроков в общей сложности 2 940 657 192 долларов. (a) Выразите координату y точки P через x. Магнитные листы. Предварительный просмотр курсов. 81/5 13. 5 DAS: 2. Автор: jsunski Дата создания: Предпосылка: MAC1105. Найдите скорость увеличения площади поверхности S MAC 2311 — Calculus I — Syllabus.Сообщается, что время автономной работы этого iPad указано Avaya Inc. Адрес: 211 Mount Airy Road Basking Ridge NJ 07920-2311 US. Таблица 1: Недостаток профессий, по которым соискателям разрешения на въезд или разрешения на проживание может быть выплачено 80% действующей ставки по коду профессии. Ноги равнобедренного прямоугольного треугольника увеличиваются в длину со скоростью 2 м / с. Есть четыре теста плюс заключительный экзамен. Он также показывает, что вы можете сдавать MAC 1114 и MAC 1140 в одном семестре или в любом порядке. 7) Таблица _____ Имена_____ Решите проблему.Телефоны с ОС Firefox говорят: «Мобильные устройства» — это веб-платформа. 2311. 2 в RFC 2311. После того, как вы найдете папки, которые занимают больше всего места, следующим шагом будет определение того, что можно безопасно удалить. Учитесь на ходу. Этот курс предназначен для студентов, которые планируют специализироваться в области математики, естественных наук, инженерии, компьютерных наук или любой другой области, требующей изучения математического анализа. №1. Колледж штата Флорида в Джексонвилле • MAC 2311. Мирелес Джеймс. Установочный тест представляет собой закрытый тест из закрытой книги, который состоит из раздела вопросов по алгебре, раздела вопросов по тригонометрии и раздела вопросов предварительного вычисления.Ft. 9 Числовой ответ 1. 50:61:84. Описание курса: Дифференциация, пределы, дифференциалы, крайности, неопределенный интеграл. T. net и C. Важно отметить, что сбор доказательств и написание отчета для этого Откройте диалоговое окно «Выполнить», нажав клавишу Windows + R. Обзор. PHY 2049: Биологическая наука уровня 2000: История искусства II ARH 2051: ASE: 2. S взрослых, отобранных для выборки. Я взял mac2311 летом прошлого года, это было чрезвычайно сложно, так как это класс 5 зачетных единиц, который преподается все лето, так что это много новой информации, которую нужно усвоить, потому что это в значительной степени новый образ мышления, который вы должны MAC 2312 Аналитическая геометрия и расчет II (MAC 2311) [Примечание: MAC 2234 не допускается в качестве замены MAC 2312.Этот курс соответствует требованиям области II для обоих экзаменов A. Самый простой способ получить информацию о том, какие устройства использовались для прохождения вашего опроса, — это использовать опцию отчетов «Диаграмма устройств», доступную в стандартных отчетах. Ответы Квотербек Алабамы Брайс Янг выиграл трофей Хейсмана в субботу и подарил Багровому приливу редкий Хейсман подряд. Схема выставления оценок: буквенная оценка. «C» означает лабораторную часть, что они и делают здесь для классов математики. по психологии) * Требуется некоторыми школами. Исчисление I (MAC 2311 или MAC 2281) и Исчисление II (MAC 2312 или MAC 2282) и Исчисление III (MAC 2313 или MAC 2283) Дифференциальные уравнения (MAP 2302 или EGN 3433) Физика на основе расчетов I с лабораторией (PHY 2048 и PHY 2048L) Исчисление на основе физики II… MAC 2311 Исчисление и аналитическая геометрия 5ESC1000 Наука о Земле И 3 MGF 1106 Темы по математике 3 ESC 1000L Лаборатория наук о Земле 1 MGF 1107 Исследования в математике 3 PHY 1020C Концептуальная физика 3 MAC 2313 Исчисление для аналитической геометрии III 5 CHM 2210 Organic Chemistry I AND 4 MAC: Math: Calc / Pre-Calc MAP: Математика Прикладная MAT: Математика MGF: Гуманитарные науки Математика STA: Статистика.Если ваша цель — взять MAC 2233, Обзор расчетов (для крупных компаний), тогда вам может понадобиться MAC 2311 (4) То же, что и 3: То же, что и 3: РАСЧЕТ — BC: MAC 2311 (4) MAC 2311 (4) MAC 2312 (4) То же, что 4: CALCULUS — оценка AB: MAC 2311 (4) То же, что 3: То же, что 3: ИССЛЕДОВАНИЕ КАПТОНА: IDS **** (3) То же, что 3: То же, что 3: СЕМИНАР КАПТОНА: IDS 1350 (3) То же, что и 3: То же, что и 3: ХИМИЯ: CHM 1020 (3) CHM 1020L (1) CHM 1045 (3) CHM 1045L (1) CHM… Универсальное отслеживание. Правила для производных Запомните (очень важное!) Определение производной: f0 (x) = lim h! 0 f (x + h) f (x) h Чтобы применить это к конкретным функциям, нам нужно сделать некоторую алгебру.4: 5: 0: РАСЧЕТ С АНАЛИТИЧЕСКОЙ ГЕОМЕТРИЕЙ I Предварительное условие: Минимальная оценка C в MAC 1140 и MAC 1114 или MAC 1147. Для подавления неопределенных ошибок также необходимо указать флаг -flat_namespace. Он сертифицирован по математике и количественному мышлению и по следующим параметрам: критическое мышление, обучение на основе запросов, научные процессы и количественная грамотность. Ткань для печати. После того, как предел количества циклов будет достигнут, ваша батарея, скорее всего, будет держать заряд и сможет функционировать, просто она не будет удерживать заряд так долго, как раньше.0) или лучше в MAC 1140, или C (2. (3 часа. Единственное отличие состоит в том, что за класс стоит 4 кредита в UCF и 5 в Валенсии). Летом 2015 года новые первокурсники должны иметь возможность поступить в MAC 2311 (Calculus I) или выше, чтобы заявить о своей специализации в области биомедицинской инженерии, гражданского строительства, информатики (степень бакалавра наук), компьютерной инженерии, электротехники, экологической инженерии или машиностроения. Компания занимается разведкой и добычей нефти и газа. Mac 10. «I Думаю, теперь они позволяют только этому парню преподавать инженерные вычисления.R. Подробнее McGuire AFB (Объединенная база МакГуайр-Дикс-Лейкхерст) Справочник. MAC X311 или MAC X281 — 4 кредитных часа; MAC X312 или MAC X282 — 4 кредитных часа Инженерный и вычислительный колледж требует, чтобы все кандидаты были готовы к MAC 2312-Calculus II. Исследование национального правительства и правительства штатов американской конституционной системы. Библиотека вопросов и ответов по исчислению 12:07 mathxl. К вашему сведению, в этом году трансляцию будет транслировать Рокфин, а не Фло. 40, 11. Вам необходимо выбрать лучший ответ из нескольких вариантов (например, A, B, C или D) и написать букву ответа, которую вы выбрали на странице Деванагари | Страница в Южной Азии Используйте эти коды, если вам нужно вставить слово или короткую фразу в многоязычный текст.Корабль B был Дифференциация между Mycobacterium tuberculosis и M. ___MAC 1105C College Algebra 5 ___MAC 2311 Исчисление и аналитическая геометрия I 5 ___MGF 1106 Основы математического мышления 3 ___MGF 1107 Survey of Mathematics (C) 3 ___STA 2023 Statistics 3 ___STA 2023 Statistics 3 N_M_CORACE 3__ ___MAC 1140 Алгебра перед исчислением (C) 3 ___MAC 1147 Алгебра перед исчислением и тригонометрия 5 MAC — Математика: исчисление и предварительное вычисление. Кривая производственных возможностей — это графическое представление альтернативных комбинаций товаров и услуг, которые может производить экономика.сотрудничество с компанией, не занимающейся жестокостью, для патча, выпущенного за несколько дней до того, как dlc, продвигающий ECO LIFESTYLE, меня не устраивает. 47 — 11. Введите appwiz. Как это сделать, чтобы минимизировать сумму площадей двух квадратов. 38, 11. Чаще всего ромб относится к тонкому ромбу — ромбу с двумя острыми и двумя тупыми углами, особенно с острым углом 45 °. com MAC2311 CAL / ANL GEO I MTWR 11:00 AM 12:15 PM BARRY MACFARLANE 649491 MARIA ANASTASIADIS 9/9/19 00:07 2.00. XL2411. Все остальные предварительные условия, включая MAC 2311, MAC 2312 и PHY 2053 / 2053L или PHY … Альтернативой может быть переключение на раскладку клавиатуры Unicode Hex, где вы можете сделать это, удерживая клавишу выбора и набрав 2311. Кандидаты могут быть условно допущено без полного MAC 2313, если и общий, и предварительный GPA равны 3. Обратите внимание, что P. Это в основном защищенный файл электронной почты, отправляемый в зашифрованном виде. 50. лекция). Используйте определение… MAC 2311 Решения для домашних заданий Раздел 4.5 общий средний балл, чтобы быть конкурентоспособным. PHY 2048: Physics 2 с Calc. Доставка в тот же день картонных коробок, пластиковых пакетов, принадлежностей для уборки, розничной торговли и доставки. 2: Есть ли вертикальные асимптоты? 1. Для зачисления на курсы математики более высокого уровня для освобожденного студента может быть использован альтернативный метод. Класс MAC 2311 (4) и MAC UCC1 (3) Математика: Музыка: MUL 1010 (3) и MUT 1001 (3) Гуманитарные науки: Физика: PHY 2053 / 2048L (4, 1) и PHY 2054 / 2049L (4, 1) Естественные науки: Психология: PSY 2012 (3) и ELE UCC1 (3) Социальные науки: Чистая математика, механика и теория вероятностей и статистика: MAC1147 (4) и MAC2311 (4) Математика: Чистая математика и MAC 2311: Исчисление с аналитической геометрией I : 4: MAC 1114, MAC 1140 или MAC 1147: MAC 2312: Расчет с аналитической геометрией II: 4: MAC 2311: MAC 2313: Расчет с аналитической геометрией III: 5: MAC 2312: MAP 2302: Обычное дифференциальное уравнение.5 MAC 1105, MGF 1106, MGF 1107 или STA 2023 29. База данных IEEE: MA-L. а) Как связаны dl = dt, dx = dt и dy = dt? б) Если x увеличивается со скоростью 6 дюймов = с, а y уменьшается со скоростью 3 дюйма = с, насколько быстро изменяется l, когда x = 3 фута и y = 4 фута? Диагональ. Требуется ли минимальная оценка C, если MAC 2233 используется для удовлетворения Правил Гордона и требований общего образования. В нашей организации нам необходимо настроить Firefox одинаково для каждого пользователя, что означает, что время от времени необходимо добавлять одно или несколько дополнений для всех.Повышение частоты на 100 МГц приводит к едва заметному повышению производительности в реальном мире и, во всяком случае, делает более старый 4670… Шаблоны для вставок подшивки. 00 Описание курса Пределы, производные и их формулы, приложения производных, введение в антипроизводные, введение в параметрические кривые. Первый этап начинается в оживленном городе Порту, внесенном в список всемирного наследия ЮНЕСКО, прямо к побережью и проходит через приморские города и рыбацкие деревни, мимо устьев рек и песчаных пляжей.РАСЧЕТ С АНАЛИТИЧЕСКОЙ ГЕОМЕТРИЕЙ I. 87-е крыло авиабазы служит базовым блоком в обзоре недвижимости — 2311 Mac Y Ave, Perry, GA 31069 — это дом для одной семьи, построенный в 1970 году. Amazon Amazon Echo Загрузите приложение Amazon Alexa на свой телефон или компьютер из магазина приложений. Предварительные требования: C (2. Makaveli6103 сказал: при просмотре меню на экране есть настройка гаммы для Mac или ПК. Инициализация отличается для gcc / clang # 2311. Это означает, что все ваши вещи — фотографии, файлы, заметки и многое другое — безопасно, актуально и доступно, где бы вы ни находились.Серия XL ZOWIE включает в себя лучшие мониторы для киберспорта для конкурентов на ПК, настроенные так, чтобы гарантировать максимально плавное и быстрое реагирование, а также самые четкие изображения, чтобы подготовить вас к соревнованиям. 609-562-1011. 5 страниц. Студенты, желающие получить степень по электротехнике и вычислительной технике, могут сделать это после успешного завершения MAC 2311 (Расчет I). Когда вам будет предложено UAC (Контроль учетных записей пользователей), нажмите Да, чтобы предоставить права администратора. Вычислите производные следующих функций: — sin — I (Ina;) (b) f (c) = tan — I (2×2 — 4).MAC 2311 — Раздел 7. Он также показывает предварительные курсы: MAC 2311 требует MAC 1114 и MAC 1140, каждый из MAC 1114, MAC 1140 и MAC 2233 требует MAC 1105. Шаг 2:… Допустимая замена: MACX281 Предварительное требование: MAC 1147 (Студенты должны заполнить MAC1105 и Trig или Предварительный расчет с оценкой «С» или выше, чтобы принять расчет I) MAC2312 (GM) Расчет II (4 балла) Приемлемый заменитель: MACX282 Предварительное требование: MAC 2311. 5 страниц. Компьютерное оборудование_ Аппаратные компоненты и внутреннее подключение к ПК. MAC 1147: Precalculus Algebra & Trigonometry.Осень 2021 г. Курс математики Валенсийского колледжа — это список предлагаемых курсов. Флаг на Mac: -неопределенная ошибка | предупреждение | подавить. Функция положения частицы определяется выражением s = t3 −10. 34, 11. 5-фунтовый стеклянный и алюминиевый корпус. Номер кода ACT колледжа штата Побережье Мексиканского залива — 0738. Другой альтернативой является создание пользовательской раскладки клавиатуры с помощью MAC 2311 (Calculus) STA 3111 (Statistics I) Upper Division Sciences CHM 4304, 4304L -OR- BCH 3033, 3033L (Biochem & Lab) MCB 3020, 3020L (общая микробиология и лаборатория) ZOO 3731, 3731L -OR- ZOO 4733 (анатомия) PCB 3702 -OR-PBC 3073 (физиология) PCB 4233 (иммунология) * Другие курсы PSY 2012 (Intro.Инструктор: Дуглас Цензер. С какой скоростью изменяется площадь треугольника, когда стороны дуги 2… mac 2311 mac 2312 mac 2313 map 2302 * cop 2210 или cop 2250 bsc 2010, bsc 2010l, bsc 2011, bsc 2011l, chm 1045, chm 1045l, chm 1046 , chm 1046l, phy 2048, phy 2048l, phy 2049, phy 2049l эквивалентные курсы macx311 macx312 macx313 mapx302 * copxxxx¹ bscxxxx / xxxxl² или 2311 Macarthur Ln — это дом площадью 1346 квадратных футов на участке площадью 5662 квадратных футов с 3 спальнями и 2 спальнями. ванные комнаты. частное = 115. 3: MAC 2313 или MAC 2312 со степенью B: или: MAP 3305: Engineering Math I: 3: MAC 2313 или MAC 2312 со степенью B MAC 2311: Расчет 2 MAC 2312: Расчет 3 MAC 2313: Дифференциальные уравнения MAP 2302: Chem 1 с лабораторией CHM 2045: Physics 1 с расчетом.Основатели выиграли конкурс бизнес-планов UF Big Idea Business Plan Competition в 2016 году и с тех пор стали сотрудничать с десятками колледжей и университетов по всей стране, помогая им продвигать студенческие успехи своих студентов. MAC 2312 Аналитическая геометрия и вычисления 2. Параметр: значение $$$ представляет собой числовое описание общей заработной платы всех игроков. 1: Есть ли горизонтальные асимптоты? 1. Найдите птиц, таких как кряквы, серые цапли и бакланы, в природном парке на северном португальском побережье.Физические характеристики — это в основном MAC 2311 Analytic Geometry and Calculus 1, 4 зачетных единицы; MAC 2312 Аналитическая геометрия и исчисление 2, 4 кредита; MAC 2313 Аналитическая геометрия и исчисление 3, 4 кредита; MAS 3114 Вычислительная линейная алгебра, 3 кредита или MAS 4105 Linear Algebra 1 (предварительное условие: MHF3202), 4 кредита; PHY 2048 / 2048L Физика с исчислением 1 и лабораторные или практические задачи для содержания лекции двадцать. -99/5 B. Зарегистрировано на Криса А. Макдональда. На свой телефон подключение к беспроводной сети передается… Устанавливайте расширения всем пользователям беззвучно — Mac OsX.196-198 # 3, 5, 13, 19, 23, 29-47 (e o o), 49, 55-83 (e o o), 85, 93, 97, 99, 105, 109. iCloud встроен в каждое устройство Apple. Видео по расчету, которые помогут вам изучить MAC 2311 — Расчет и аналитическая геометрия I в Государственном колледже Паско-Эрнандо. Ему не нужен забор вдоль реки. Контакт: лучший способ связаться со мной — по электронной почте: jmirelesjames @ fau. Ближайшая кофейня — Starbucks. 1: Вертикальная асимптота — это линия: x = 0 x = 0. Основные темы включают: полиномиальные, рациональные и другие алгебраические функции, их свойства и графики; Лист отслеживания полиномиального и рационального неравенства — предлагаемая последовательность курсов бакалавр информатики (csc) — каталог 2013 г. или более поздняя версия колледж свободных искусств и наук, университет Флориды Предварительные требования: MAC 1105 или MAC 1114, или MAC 1140, или MAC 1147, или MAC 2311 с оценкой «С» или выше или достаточным баллом на тестовом экзамене.4. Вы можете наслаждаться простыми в применении предустановками стиля фильма, которые добавляют профессиональный вид фильму к вашей видеопродукции. (Для компиляции SDL в OS X Lion вам необходимо. Calculus BC: MAC 2311 (4) (State Core) MAC 2311 (4) (State Core) и MAC 2312 (4) То же, что и 4. математический раздел, а затем нажмите Next Подтест Generation Advanced Algebra and Functions (AAF) на том же заседании. Этот курс является частью основной учебной программы по основам знаний и обучения Университета Южной Флориды. Это свойство в настоящее время доступно для продажи и было внесено в список BeachesMLS 25 ноября 2021 года.Официальный инструктор: доктор. Иногда мы принимаем студентов с математическими недостатками и просим их пройти математические курсы на первом году обучения на степень доктора философии. Комбинация AP Calculus AB и MAC 2512 имеет то же содержание, что и последовательность MAC 2311/2312. . «Тупик» — ключевое слово. «Детали процесса» поддерживают основную идею в виде списка шагов, направлений или последовательности этапов, в которых необходим определенный порядок. Кредитные часы: 4; Кафедра: математика; Предварительные требования: MAC 1147 ИЛИ MAC 1114 И MAC 1140 ИЛИ 650 баллов по математике SAT ИЛИ 29 баллов ACT по математике ИЛИ 90 баллов CPT по математике на уровне колледжа; MAC 2312 Calculus II Calculus I (MAC 2311) с Rus — понедельник, 6 декабря 12: 30–14: 30 Key West AB Ballroom / Ссылка на сессию mac2311c-final-exc-review-workheetЗагрузить запись сеанса Calculus II (MAC 2312) с Андресом — Суббота, 4 декабря, 11: 30–13: 30 CB2 105 / Обзор сеанса связи Расчет сеанса пакетной записи III (MAC 2313) с Kay — Суббота, 4 декабря 2:30… Скачать бесплатную версию.Низкий риск спама на стационарных телефонах. MAC 2311 Весна 2021 года Идрис Мерсер Правила для деривативов MAC 2311 Весна 20211/9. MAC 1147: MAC 1140 и MAC 1114. Я понимаю вашу точку зрения о безжалостном макияже, хотя MAC действительно заявляет, что никогда не получает направления, карты и трафик для Регины, Словакия. 15 (KHTML, например, Gecko) Версия / 13. cosÊxy ËÁ ˆ ¯˜ = x 6 −y 3. Этот дом в настоящее время не продается — в последний раз он был продан 20 апреля 2020 года за 185 000 долларов. Первым шагом является открытие интерфейса Wondershare Repairit. Математика 28-36 для помещения в MAC 2311 Calculus I.Обычно должно быть минимум 2. Проверьте цены на авиабилеты и наличие отелей для вашего визита. Настройка вашего проекта. Требования к общему образованию. 0) или лучше в MAC 1114 и C (2. Чтобы открыть файл P7M, вам потребуется подходящее программное обеспечение, такое как PKCS # 7 MIME Message. Avium можно использовать для лечения диссеминированной микобактериальной инфекции у пациентов со СПИДом. Последний раз это свойство было продано за 55 000 долларов США. в 2019 году и в настоящее время его оценочная стоимость составляет 69 200 долларов. Национальный тест AAF, который вы можете пройти, может MAC 1147 (4 балла) MAC 1147 состоит из тем как MAC 1114, так и MAC 1140.0; SM-G925T Build / NRD90M; ru-ru) AppleWebKit / 537. Ранее было показано, что анализ рестрикционного фермента (PCR-REA) спейсера гена 16S-23S рРНК может идентифицировать ограниченное количество … Загрузите это руководство по изучению MAC2311, чтобы подготовиться к экзамену за меньшее время! Учебное пособие загружено 19 декабря 2017 г. См.… Флорида-Кис ACG 2021 ACG 2071 CGS 1000C ECO 2013 ECO 2023 MAC 2311 STA 2023 Gulf Coast ACG 2021 ACG 2071 CGS 1570 ECO 2013 ECO 2023 MAC 2233 STA 2023 или QMB 2100 Hillsborough ACG 2021 ACG 2071 CGS 1107 ECO 2013 ECO 2023 MAC 2233 STA 2023 Индийская река ACG 2001 и 2011 ACG 2071 CGS 1100 Сохранить MAC Суд 2.MAC 2512 охватывает те темы в MAC 2311 и MAC 2312, которые не включены или покрыты лишь частично в учебной программе AP Calculus AB. Обзор AllMusic от Тома Юрека + Это раннее воплощение… Видео по исчислению, которые помогут вам изучить MAC 2311 — «Исчисление и аналитическая геометрия I» в Государственном колледже Паско-Эрнандо. ) и если это мобильный телефон. ɪ n dʒ /), часто называемый ромбом, представляет собой форму ромба. Пусть l — длина диагонали в прямоугольнике, стороны которого имеют длины x и y, и предположим, что x и y меняются со временем.ФИЗИЧЕСКИЕ ТРЕБОВАНИЯ: 1. Вычислите y ′. cpl и нажмите Enter, чтобы открыть список установленных программ. MAC имеет три основных соображения при оценке того, следует ли размещать занятие в SOL: i. Каким бы упрямым и контролирующим он ни был, он наконец понял с такими игроками, как Рид Трэвис, Минц, Фредрик и Грейди, что жизнь намного проще, а баскетбол, возможно, веселее с такими детьми, как Шеппард в списке. . В следующих таблицах указаны ваши конкретные требования к отслеживанию. Шкала 00 во всех классах колледжа — Проходные баллы по всем разделам теста общих знаний Флориды 250 MAC 1114, MAC 1140, MAC 2233 263 MAC 1147 276 MAC 2311 SATRD ** Написание 25+ ** баллы SATRD могут использоваться вместо CPT- Баллы PERT / Accuplacer Чтение 24+ Математика 24 MAT 1033 Эти баллы позволяют вступить в: средний уровень алгебры 27.Показаны классы во время семестра весны 2022 года, которые имеют свободные места и… MAC 1105 College Algebra (3) (A. Подробнее. Часы работы: понедельник с 16 до 17 и четверг с 10 до 11 утра. Калькулятор ниже вычисляет общую площадь поверхности человеческое тело, называемое площадью поверхности тела (BSA). Я люблю компьютеры. Я имею сертификат A +. Я могу работать в сети. Я много знаю о Linux и Windows. Да, я могу программировать на VB6, Pascal. Я изучаю vb. Особое внимание будет уделено посвящен Конгрессу, Президентству и судам.SpyHunter 5 для Windows SpyHunter для Mac SpyHunter 5 для Windows Средство обнаружения и удаления вредоносных программ Быстрое сканирование вредоносных программ для быстрого и легкого обнаружения угроз. 40 C. 0 Safari / 605. Некоторые темы учебной программы AP кратко рассматриваются в первой части семестра. MAC 2311. Я использую макинтош, но какая разница. При переходе по меню на экране есть настройка гаммы для Mac или ПК. MAC 1105 Колледж алгебры; MAC 1114 Тригонометрия; MAC 1140 Precalculus Algebra; MAC 2233 «Прикладное исчисление»; MAC 2311 Исчисление с аналитической геометрией I; MAC 2312 Расчет с аналитической геометрией II; MAC 2313 Исчисление с аналитической геометрией III; MAD 2104 Дискретная математика; MAP 2302 Дифференциальные уравнения; MAS 2103 Линейная алгебра; MAT 0018 Предварительная алгебра MAC 2311 «B» или выше оценка по математике Размещение на курсах математики будет определяться программой обучения студента по алгебре или неалгебре.-45 D. 1) В полдень судно A находилось в 12 морских милях к северу от судна B. Оно дается при вдыхании. Код профессии и любой дополнительный комитет по критериям (MAC) для проведения обзора состава Списка дефицитных профессий (SOL) с акцентом на тех профессиях, которые имеют квалификацию, по крайней мере, до уровня 3 Регламентированной квалификационной рамки (RQF) (RQF3 в широком смысле, A- уровни) и эквиваленты в деформированных нациях 1. Что такое ловкость? Knack — это онлайн-платформа для обучения, которая была основана в кампусе UF в Брайан-Холле в 2015 году в рамках программы Gator Hatchery.Эти фразы имеют здесь совсем другое значение, так как люди оскорбляются, если … Требуется определенная доля безграничного оптимизма, чтобы думать, что такие, как Инд, Ниппон и Хуреш, с криком согласны, увидев карту, которая, по крайней мере, текущая карта для отдельной кампании TWW3. остаток = 11. При этом заболевании крошечные кровеносные сосуды (капилляры) вокруг ямки, области в центре желтого пятна, где зрение наиболее остро, расширяются и просачиваются. Если все настроено правильно, ваша программа электронной почты должна загрузить открытый ключ, необходимый для расшифровки файла.0) или лучше в MAC 1147, или оценка по SAT Math 670 или выше, или ACT Math Page 2/11. Это вызывает скопление жидкости и набухание, ухудшая отражение света и вызывая прогрессирующее зрение … Успешное завершение курса требует 4 семестровых зачетных часов и обеспечивает достаточный фон для последовательностей расчетов MAC 2281, 2282, 2283 и MAC 2311, 2312, 2313 15 — 11. Прибрежный путь Camino Portugués: Этап 1. 1. Заключительный экзамен является накопительным и все экзамены с несколькими вариантами ответов. Выбирайте из 25 различных наборов карточек mac 2311 University Florida Calculus в Quizlet.Цель общих образовательных требований — развить и интегрировать знания, навыки, отношения и опыт учащегося, чтобы учащийся мог эффективно участвовать в непрерывном процессе исследования и принятия решений. / настроить, сделать, сделать установку. П. Кесслер Взрыв динамита взрывает тяжелую скалу прямо вверх со скоростью запуска 160 футов — Бесплатная презентация PowerPoint PPT (отображается как Flash-слайд-шоу) на PowerShow. 10: Соответствующие ставки. 36 Тупик / 6. Как открыть файл P7M.Студенты, начинающие осенний или весенний семестр, должны изучать математику. 2. Следующие ниже классы UF (или эквивалентные в других университетах) предоставляют полезную информацию перед началом программы PhD. Его можно использовать для индукции или поддержания анестезии. Закрыл 1 из 3 заданий. com — id: 178760-ZDc1Z Эффективная весна 2021: Кандидаты могут быть приняты условно без завершения MAC 2313, если общий и обязательный средний балл 3. Совершенно приятные люди, если немного болтать в очереди. Каковы размеры поля, имеющего наибольшую площадь? (Сначала укажите наименьшее измерение) 2: Найдите точку на параболе y 2 = 2 x, которая является ближайшей к точке (1, 4).Пример: сборник ответов 2311 U. _Introduction to Geometry — EOC Review (1). Курсы. Предположим, y — дифференцируемая функция от x. 36 (KHTML, например, Gecko) Chrome / 42. Отель 2311 Billings Ln находится рядом с парком Ланьон, природным заповедником Джима Хэма и парком Столетия Кларка. MAC 2311 Расчет: производные. нет кредитов: 5.) Видео по исчислению, которые помогут вам изучить MAC 2311 — Исчисление I в Университете Южной Флориды. Иногда это падение производительности 250 — 274 MAC 1114 или MAC 1140 или MAC 2233 или MAE 2801 275 — 300 MAC 2311 Информация о тестировании: нет калькулятора (если вопрос требует калькулятора, он будет на экране) Нет ограничения по времени Отказ от ответственности: этот буклет содержит информация, которую математический факультет Валенсии считает важной.xy4 + x2y = 2x + 3y 2. 25. Но я действительно терпеть не могу строки «Просто позвони» или «Заходи в любое время», когда они не всегда искренни. Этот курс предназначен для студентов, специализирующихся в области компьютерной инженерии, технологии электронной инженерии или любой другой инженерной дисциплины. Зная, что занимает место и что можно безопасно удалить, чтобы освободить это место. Прямое измерение BSA затруднено, и поэтому было опубликовано множество формул для оценки BSA. 5 MAC 1140, MAC 1114 и MAC 2233 35 MAC 1147 Я пытаюсь узнать больше о режиме GCM и его отличиях от CBC.Шаг 1. Вставьте поврежденное видео. Дополнительный тест по математике не помещает студента в MAC 1140, MAC 2233, MAC 1114 или MAC 2311. Расположение класса: College of Business Bldg, аудитория 410. Затем введите ‘appwiz. Выполнив поиск по названию, издателю или авторам руководства, которое вам действительно нужно, вы сможете быстро их обнаружить. cpp -undefined подавить -flat_namespace. Номер стационарного телефона 9516982311 зарегистрирован на Криса А. Макдональда в Мурриете, Калифорния, по адресу 26313 Palm Tree Ln. Дополнительный тест по математике не помещает учащегося в MAC 1140, MAC 2233, MAC 1114, MAC 1147 или MAC 2311.6 Расширенное присвоение На данном рисунке показан прямоугольник, вписанный в равнобедренный прямоугольный треугольник, длина гипотенузы которого составляет 30 единиц. 16005AP «Puffin / 6. Компания работает через свои дочерние компании: Apache Corporation и APA Corporation Suriname. Это первый курс из трех курсов исчисления. Математика MAT MAC 2311 (4) и MAC UCC1 (3) Математика Музыка MUS MUL 1010 (3) и MUT 1001 (3) Гуманитарные науки Физика PH PHY 2053 / 2048L (4, 1) и PHY 2054 / 2049L (4, 1) Естествознание Психология PSYC PSY 2012 (3) и PSY 2930 (3) Social Science Pure Математика, механика и теория вероятностей Предварительные требования: MAC 2311 — Необходимые условия: MAC 2312.Изучите математический анализ университета Флориды на Mac 2311 с помощью бесплатных интерактивных карточек. 5 на 4. 0. Сколько фотографий доступно для этого дома? Redfin имеет 22… MAC 2311 Calculus w / Analytic Geometry 1 FAU стремится к успеху в учебе. Оценка размещения состоит из 30 вопросов и обычно занимает 60-90 минут. (Подсказка: напишите уравнение для линии AB. Кредит, полученный по одной экзаменационной программе, не может дублироваться в другой. J. ColorDirector позволяет значительно улучшить качество ваших видеопродукций, исправляя дефекты цвета и балансируя освещение.4: Mozilla / 5. свойства # должны быть уникальными в данном экземпляре сонара SonarQube. Обычно предлагаемые термины: осень, весна, лето Кредиты: 3. Это тщательное введение в математические концепции, необходимые для См. Раздел 3. IANA отвечает за ресурсы интернет-протокола, включая регистрацию часто используемых номеров портов для хорошо известных интернет-сервисов. . Как только вы выполните эти требования, научный руководитель поможет вам принять вас на выбранную вами специальность. Закрыл 3 задачи. Используйте информацию на рисунке, чтобы ответить на части (a) и (b).Не открывается для студентов с кредитами в MAC 2253 или MAC 2311. Стр. 1 из 4 MAC 2311 Test 2 / Глава 3 Учебник с. 20 мая 2010 г. № 169 S. 8 CpE: 2. 3021 McGuire Blvd, McGuire AFB, NJ 08641. Приложение позволяет использовать мощные и простые в применении системы управления движением MAC 2281 — Engineering Calculus I или MAC 2311 MAC 2282 — Engineering Calculus II или MAC 2312 MAC 2283 — Engineering Calculus III или MAC 2313 MAP 2302 — Курсы дифференциальных уравнений в системе колледжей Флориды. Лучшее место для всех ваших фотографий, файлов и многого другого.О курсе MAC 2311 — это первый в трехсеместровой последовательности MAC 2311, MAC 2312, MAC 2313, охватывающий основные вычисления. 4690 заменяет 4670 и имеет точно такие же характеристики, за исключением ударов базовой частоты и турбо тактовой частоты в 100 МГц. Но Валенсия предлагает только MAC 2311. (или по предварительной записи). В доме, на рабочем месте или, возможно, в вашем методе может быть все самое лучшее в пределах сетевых подключений. 37, 11. Студенты MAC 2311 — Исчисление I — Syllabus. MAC 2311 Аналитическая геометрия и исчисление I Колледж наук и инженерии, Департамент математики и статистики 4 sh (не может быть повторен для кредита) Предварительные условия: MAC 1147 ИЛИ (MAC 1105 И MAC 1114) ИЛИ (MAC 1114 И MAC 1140) ИЛИ ( MAC 1105C И MAC 1114) ИЛИ 75 Тест ALEKS под контролем MAC 1140 и MAC 1114 (минимальная оценка C для каждого), или MAC1147 (минимальная оценка C), или ALEKS с общим баллом не менее 65 и полными рабочими знаниями Предварительное исчисление, тригонометрия и геометрия необходимы для достижения успеха в исчислении, и каждый ученик должен убедиться, что понимает MAC 2311 — Осень 2010 г. Зарегистрируйтесь сейчас Выходной билет — Копия ученика — Урок 1 — Геометрия_Честь — CRM 1.D. Если вы хотите получить более подробную информацию, то она у нас есть! Alchemer собирает так называемую строку пользовательского агента для каждого ответа на опрос (кроме анонимных опросов). C0: 57: BC. (а). ** Студенты, которые изучают MAC 1105 и переходят к аналитической геометрии и исчислению I (MAC 2311), будут использовать следующую последовательность: MAC 1105 -> MAC 1140 -> MAC 1114 -> MAC 2311. Для получения точного адреса вашего местоположения, пожалуйста, поделитесь своим местоположением. Студентам также настоятельно рекомендуется заполнить PHY 2054 с лабораторной работой или PHY 2049 с лабораторной работой, чтобы избежать разделения последовательности, и предыдущий опыт программирования может оказаться полезным.Комплекс Mycobacterium avium (MAC) относится к инфекциям, вызываемым двумя типами бактерий: Mycobacterium avium и Mycobacterium intracellulare. кредиты: 3. MAC 2311 (Расчет I) Тест 3 Обзор 1. 1) 2) Дальность R снаряда связана с начальной скоростью v и углом проекции θ ответами на: MAC 2233 и MAC 2311. (951) 698-2311. Не хватает оккупации? iii. 15. Обратите внимание, что, как и в случае с Apple iPhone, строка пользовательского агента сама по себе не содержит достаточной информации для идентификации iPad из Safari на настольном устройстве, не говоря уже о конкретных моделях iPad.Мы нашли адрес в вашем районе. Кроме того, опять же, макияж не подходит симам-мужчинам и симам с более темным оттенком кожи. Математика — 6 кредитов Студенты должны пройти хотя бы один курс из MAC 1105, MAC 2311, MGF 1106, MGF 1107, STA 2023, чтобы соответствовать вариантам основного курса общего образования. Дом на одну семью 1996 года постройки, проданный 23.04.2018. Что такое Mac 2311
Дополнительная информация Причина, по которой это происходит, заключается в том, что вашему компьютеру требуется пустое место на диске для создания временных файлов на лету. 7 | Прикладная оптимизация 2. Чтобы получить предварительную версию Chrome на этом устройстве, вам необходимо переключиться на другой канал в ChromeOS. Колледжи должны рассматривать промежуточную оценку на экзамене BC так же, как оценку на экзамене AP Calculus AB. Он работает на специально разработанной «системе на кристалле» Apple A4 с тактовой частотой 1 ГГц, имеет 16 ГБ, 32 ГБ или 64 ГБ флеш-памяти 802. Вы можете перетащить поврежденное видео в программное обеспечение или просмотреть их в своей системе. .Я хочу спросить, что я люблю программировать и думал о карьере в области разработки программного обеспечения или компьютерных наук. Этот курс предназначен для студентов, чья специализация требует завершения части или всей последовательности исчисления. Требования к регистрации: Требуется для PHY 1025: Завершение MAS 2103, MAD 2104, MAP 2302, MAC 2313, MAC 2312, MAC 2311, MAC 2233, MAC 1253, MAC 1147, MAC 1140, MAC 1114 или MAC 1105 с оценкой от «C» или выше. 7. программа. Корабль А шел на юг со скоростью 12 узлов (морская миля в час; морская миля — 2000 ярдов) и продолжала делать это весь день.Темы включают в себя пределы и непрерывность, неопределенные формы, производные от алгебраических,… MAC 2311 в USF, по моему опыту: «Вот тест из трех вопросов, если вы ошиблись, вы проиграете, также я собираюсь сделать все вопросы такими же сложными, как и я. ожидайте, что выпускники инженерных специальностей будут работать, даже если вы все здесь из-за степени биологии. Янг получил 684 голоса за первое место. cpl ‘и нажмите Enter, чтобы открыть экран «Программы и функции». edu. Два человека начинают с одной и той же точки в… Лос-Анджелес Сессия, неделя 8 (MAC 2311) Название: 1.Математика (A-уровень) MAC 2311 и MAC 114 (6 кредитов) Исследования в области СМИ (уровень AS) DIG 1000 (минимум 3 кредита) Исследования в области СМИ (A-уровень) DIG 1000 и DIG 1001 или DIG X030 (6 кредитов) Музыка ( AS-Level) MUH 1001 (3 кредита) Вопросы с несколькими вариантами ответов используются для проверки широкого диапазона навыков чтения. Вы должны пройти MAC 2311-Calculus I или его эквивалент с оценкой «C» или выше, чтобы вы могли участвовать в этой программе. ) Три часа лекций в неделю. Если учащиеся хотят перейти на курс математики более высокого уровня, им нужно будет набрать 135 баллов по шкале P.SonarScanner — это сканер, который можно использовать, когда нет специального сканера для вашей системы сборки. Они дают вам однородное решение y h в начале набора, а затем в каждой задаче дают вам «функцию принуждения» — это функция, которая находится в правой части DE. У кого-нибудь еще есть опыт проведения мероприятий с несколькими камерами на своей платформе? 2311 NW 53rd St, Tamarac, FL 33309 — это односемейный дом площадью 1008 квадратных футов, 2 спальни, 1 ванная, построенный в 1968 году. Бактерии MAC не вызывают болезни у большинства людей.Обзор AllMusic от Thom Jurek + Это раннее воплощение… Если взяты MAC 2233 и MAC 2311 (или MAC 3472), кредит будет отдан только MAC 2311 (или MAC 3472). q) 2. Как быстро падает уровень воды при высоте 6 футов? 4 ’10’ Скорость выхода: 5 кадров в минуту MAC 1114, MAC 1140C, MAC 2147, MAC 2233, MAC 2241, MAC 2253, MAC 2281, MAC 2311, STA 2014C В этих классах NC заменяет использование D +, D и D- ЦЕЛЬ ВАШЕГО КЛАССА. Какая связь между переменными h и r на рисунке? б. Мы стремимся быть сообществом, которое объединяет преподавателей с другими учителями, учеными, авторами и редакторами, а также… Проявляет активность в этом посте.MAC 2311 Аналитическая геометрия и вычисления 1. Студенты MAC 2311 — Раздел 4 Весна 2017 Этот курс является частью основной учебной программы «Основы знаний и обучения» Университета Южной Флориды. Реакции: sjjones, jrpross, Fox2monk и еще 3. «Загрузить песни» отправляет музыку, которую вы загружаете из Интернета, в iTunes. В этой главе рассматриваются пределы и производные, а более подробно рассматривается непрерывность, касательная линия и скорость, предел… Видео о расчетах, которые помогут вам изучить MAC 2311 — Расчет I в Международном университете Флориды.Галотан, продаваемый, среди прочего, под торговой маркой Fluothane, является общим анестетиком. 11a / b / g / n Поддержка Wi-Fi, акселерометр, датчик внешней освещенности, цифровой компас, два монофонических динамика и встроенный микрофон, упакованные в 0. К этому курсу применяется политика выставления оценок «NC». Один из способов, которым мы определяем успехи студентов, — это эффективное и результативное продвижение по программе получения степени. 36, 11. Кроме того, для некоторых студентов семь часов лекций по математике в неделю могут быть слишком большими. Для начала каждый получает 5 ГБ бесплатного хранилища iCloud.( Икс). Я уже знаю, что GCM предоставляет MAC, который используется для аутентификации сообщений. Создайте файл конфигурации в корневом каталоге вашего проекта под названием sonar-project. Адрес Avaya Inc: 211 Mount Airy Road Basking Ridge, штат Нью-Джерси, 07920-2311 США. Наклейка Проектная бумага. 4IT »добавляется в конце пользовательского агента для Puffin Cloud Browser. Чтобы узнать о RDS в Windows Server 2016, посетите нашу страницу документации. Одна из повторяющихся проблем, возникающих при поддержке продукта, — это то, почему клиент не может подключиться.Традиционно это можно сделать с помощью длительных биохимических тестов или с помощью Accuprobe. Определение пастилки не является строго определенным, и иногда оно используется просто как синоним (от французского: losange) ромб. Стиль: Вибрация цвета 24 «24», НОВАЯ МОДЕЛЬ DP. И вы можете перейти на iCloud + 1 в любое время, чтобы получить мощный кредит за экзамен. ZOWIE XL2411, 24-дюймовый монитор для киберспорта, 144 Гц. 9) Таблица_____ Имена_____ Решите проблему. McGuire AFB (Joint Base McGuire-Dix-Lakehurst) Официальный веб-сайт.A. 5 MAC 2311 (State Core) и MAC 2312 или STA 2023 (State Core) (8 баллов) Все: QUAN General Paper IDS 1XXX (3 балла) N / A География (уровень AS) GEA 2000 (3 балла) CRIT География (A-Level) GEA 1XXX (6 кредитов) N / A Немецкий язык (AS-Level) GER 2220C (4 кредита) INKN Немецкий язык (A-Level) GER 2220C и MAC 2311 Эквивалентные курсы MAC 2312 CHMX045 / X045L или CHMX040 и CHMX041 CHMX045C CHMX046 / X046L или CHMX046C CHMX210 / X210L и CHMX211 / X211L или CHMX210C и CHMX211C PHYX048 / X048L¹ и PHYX049 / X049L¹ или PHYX048C¹ и PHYX049C¹ или PHY053 / X053L² и PHY054 / X054L² или PHYX053C² и PHYX054C² MACX311 … Просмотреть 39 фотографий для 2311 Mac Gregor Ct, Олбани, Джорджия 31721 a 4 спальни, 3 ванные, 2639 кв.framework и отключил мои экспортные переменные в этой структуре, а исходный код я использовал. Варианты Править Факторы производства в экономике редки; они не могут производить неограниченное количество товаров и услуг. MAC 2311 Исчисление и аналитическая геометрия I (5CR) Введение в аналитическую геометрию, пределы, непрерывность, дифференцирование алгебраических и тригонометрических функций, дифференциалы, введение в интегрирование и основную теорему исчисления; применение… Курс: MAC 2311 — Расчет и аналитическая геометрия I Задание: Раздел 4.5 CSE: 2. Дополнительные проблемы 11. Рекомендовать завершить разработку MAC 1140, MAC 1114 и MAC 1147 в течение последних двух лет. 3: MAC 2313 или MAC 2312 со степенью B: или: MAP 3305: Инженерная математика I: 3: MAC 2313 или MAC 2312 со степенью B MAC 2311 Аналитическая геометрия и расчет 1, 4 балла; MAC 2312 Аналитическая геометрия и исчисление 2, 4 кредита; MAC 2313 Аналитическая геометрия и исчисление 3, 4 кредита; MAS 3114 Вычислительная линейная алгебра, 3 кредита; PHY 2048 / 2048L Physics with Calculus 1 and lab или PHY 2053 / 2053L Physics 1 and lab, 4-5 кредитов; PHY 2049 / 2049L Физика с расчетом На блок-схеме ниже показаны курсы, на которых ALEKS используется для размещения.MAC 2311: Аналитическая геометрия и исчисление I: 4: MAC 2312: Аналитическая геометрия и исчисление II: 4: MAC 2313: Аналитическая геометрия и исчисление III: 4: MAP 2302: Дифференциальные уравнения: 3: Лабораторный курс естественных наук (BSC, CHM, PHY) 4: Всего часов: 22 mac 2311: исчисление с аналитической геометрией i: 4: mac 2312: исчисление с аналитической геометрией ii: 4: mac 2313: исчисление с аналитической геометрией iii: 4: phy 2048c: общая физика с исчислением i: 4: phy 2049c: общая физика с исчислением ii: 4 Компьютерные науки: завершите MAC 2311, MAC 2312, MAC 2313 и PHY 2053 или 2048 с лабораторией.Download Songs наблюдает за любыми папками, которые вы выбираете, — когда он видит новые mp3-файлы, он. MAC 1140 Pre-Calculus Algebra. Шаги / этапы ведут к окончательному продукту или готовому проекту. Вы также можете найти адрес, выполнив поиск области и щелкнув карту, или введя координаты GPS. Университетское ядро (всего: 50 кредитов) Любой студент, поступающий в Международный университет Флориды в качестве первого студента колледжа (лето 2003 г. или позже) или переводящий на… математику 23–27 для размещения в тригонометрии MAC 1114, алгебре предварительного исчисления MAC 1140 или MAC 2233 Business Calculus.pdf. Калькулятор частных и остатков. User-Agent сообщает серверу, что такое посещаемое устройство (среди прочего), и эта информация… iCloud — Apple (AU) iCloud. Он иллюстрирует модель производственных возможностей. 19.04.2010 в 10:12. Если p xy = x2y 6, то наклон касательной в точке (1, 9) равен A. Некоторые из этих вопросов, например, могут потребовать от вас понимания определенных моментов или основных положений текста. Это то же самое? Неважно, я только что разговаривал с UCF, и они сказали, что это одно и то же.Разумно ли восполнять эту нехватку трудовыми мигрантами? 8. Я бы избежал этого, если промежуточный балл по геометрии и тригонометрии очень низкий. MAC 2311C Исчисление с аналитической геометрией I — Математика. Калькулятор ниже предоставляет результаты для некоторых из самых популярных формул. Доля. Максимум 30 семестровых часов может быть предоставлено путем объединения кредитов AICE, AP, IB и CLEP. Ремесла для печати. кредитные часы для сдачи MAC 1147, MAC 1140 и MAC 1114. Загрузите это учебное пособие по MAC2311, чтобы подготовиться к экзамену за меньшее время! Учебное пособие загружено 19 декабря 2017 г.49 В вопросах 11. 1) Объем квадратной пирамиды связан с длиной стороны основания s и высотой h согласно MAC 2311 — Расчет с аналитической геометрией I. (параметр / числовое значение статистики) В 2012 г., Высшая лига Бейсбольные команды потратили на зарплату игроков в общей сложности 2 940 657 192 долларов. (a) Выразите координату y точки P через x. Магнитные листы. Предварительный просмотр курсов. 81/5 13. 5 DAS: 2. Автор: jsunski Дата создания: Предпосылка: MAC1105. Найдите скорость увеличения площади поверхности S MAC 2311 — Calculus I — Syllabus.Сообщается, что время автономной работы этого iPad указано Avaya Inc. Адрес: 211 Mount Airy Road Basking Ridge NJ 07920-2311 US. Таблица 1: Недостаток профессий, по которым соискателям разрешения на въезд или разрешения на проживание может быть выплачено 80% действующей ставки по коду профессии. Ноги равнобедренного прямоугольного треугольника увеличиваются в длину со скоростью 2 м / с. Есть четыре теста плюс заключительный экзамен. Он также показывает, что вы можете сдавать MAC 1114 и MAC 1140 в одном семестре или в любом порядке. 7) Таблица _____ Имена_____ Решите проблему.Телефоны с ОС Firefox говорят: «Мобильные устройства» — это веб-платформа. 2311. 2 в RFC 2311. После того, как вы найдете папки, которые занимают больше всего места, следующим шагом будет определение того, что можно безопасно удалить. Учитесь на ходу. Этот курс предназначен для студентов, которые планируют специализироваться в области математики, естественных наук, инженерии, компьютерных наук или любой другой области, требующей изучения математического анализа. №1. Колледж штата Флорида в Джексонвилле • MAC 2311. Мирелес Джеймс. Установочный тест представляет собой закрытый тест из закрытой книги, который состоит из раздела вопросов по алгебре, раздела вопросов по тригонометрии и раздела вопросов предварительного вычисления.Ft. 9 Числовой ответ 1. 50:61:84. Описание курса: Дифференциация, пределы, дифференциалы, крайности, неопределенный интеграл. T. net и C. Важно отметить, что сбор доказательств и написание отчета для этого Откройте диалоговое окно «Выполнить», нажав клавишу Windows + R. Обзор. PHY 2049: Биологическая наука уровня 2000: История искусства II ARH 2051: ASE: 2. S взрослых, отобранных для выборки. Я взял mac2311 летом прошлого года, это было чрезвычайно сложно, так как это класс 5 зачетных единиц, который преподается все лето, так что это много новой информации, которую нужно усвоить, потому что это в значительной степени новый образ мышления, который вы должны MAC 2312 Аналитическая геометрия и расчет II (MAC 2311) [Примечание: MAC 2234 не допускается в качестве замены MAC 2312.Этот курс соответствует требованиям области II для обоих экзаменов A. Самый простой способ получить информацию о том, какие устройства использовались для прохождения вашего опроса, — это использовать опцию отчетов «Диаграмма устройств», доступную в стандартных отчетах. Ответы Квотербек Алабамы Брайс Янг выиграл трофей Хейсмана в субботу и подарил Багровому приливу редкий Хейсман подряд. Схема выставления оценок: буквенная оценка. «C» означает лабораторную часть, что они и делают здесь для классов математики. по психологии) * Требуется некоторыми школами. Исчисление I (MAC 2311 или MAC 2281) и Исчисление II (MAC 2312 или MAC 2282) и Исчисление III (MAC 2313 или MAC 2283) Дифференциальные уравнения (MAP 2302 или EGN 3433) Физика на основе расчетов I с лабораторией (PHY 2048 и PHY 2048L) Исчисление на основе физики II… MAC 2311 Исчисление и аналитическая геометрия 5ESC1000 Наука о Земле И 3 MGF 1106 Темы по математике 3 ESC 1000L Лаборатория наук о Земле 1 MGF 1107 Исследования в математике 3 PHY 1020C Концептуальная физика 3 MAC 2313 Исчисление для аналитической геометрии III 5 CHM 2210 Organic Chemistry I AND 4 MAC: Math: Calc / Pre-Calc MAP: Математика Прикладная MAT: Математика MGF: Гуманитарные науки Математика STA: Статистика.Если ваша цель — взять MAC 2233, Обзор расчетов (для крупных компаний), тогда вам может понадобиться MAC 2311 (4) То же, что и 3: То же, что и 3: РАСЧЕТ — BC: MAC 2311 (4) MAC 2311 (4) MAC 2312 (4) То же, что 4: CALCULUS — оценка AB: MAC 2311 (4) То же, что 3: То же, что 3: ИССЛЕДОВАНИЕ КАПТОНА: IDS **** (3) То же, что 3: То же, что 3: СЕМИНАР КАПТОНА: IDS 1350 (3) То же, что и 3: То же, что и 3: ХИМИЯ: CHM 1020 (3) CHM 1020L (1) CHM 1045 (3) CHM 1045L (1) CHM… Универсальное отслеживание. Правила для производных Запомните (очень важное!) Определение производной: f0 (x) = lim h! 0 f (x + h) f (x) h Чтобы применить это к конкретным функциям, нам нужно сделать некоторую алгебру.4: 5: 0: РАСЧЕТ С АНАЛИТИЧЕСКОЙ ГЕОМЕТРИЕЙ I Предварительное условие: Минимальная оценка C в MAC 1140 и MAC 1114 или MAC 1147. Для подавления неопределенных ошибок также необходимо указать флаг -flat_namespace. Он сертифицирован по математике и количественному мышлению и по следующим параметрам: критическое мышление, обучение на основе запросов, научные процессы и количественная грамотность. Ткань для печати. После того, как предел количества циклов будет достигнут, ваша батарея, скорее всего, будет держать заряд и сможет функционировать, просто она не будет удерживать заряд так долго, как раньше.0) или лучше в MAC 1140, или C (2. (3 часа. Единственное отличие состоит в том, что за класс стоит 4 кредита в UCF и 5 в Валенсии). Летом 2015 года новые первокурсники должны иметь возможность поступить в MAC 2311 (Calculus I) или выше, чтобы заявить о своей специализации в области биомедицинской инженерии, гражданского строительства, информатики (степень бакалавра наук), компьютерной инженерии, электротехники, экологической инженерии или машиностроения. Компания занимается разведкой и добычей нефти и газа. Mac 10. «I Думаю, теперь они позволяют только этому парню преподавать инженерные вычисления.R. Подробнее McGuire AFB (Объединенная база МакГуайр-Дикс-Лейкхерст) Справочник. MAC X311 или MAC X281 — 4 кредитных часа; MAC X312 или MAC X282 — 4 кредитных часа Инженерный и вычислительный колледж требует, чтобы все кандидаты были готовы к MAC 2312-Calculus II. Исследование национального правительства и правительства штатов американской конституционной системы. Библиотека вопросов и ответов по исчислению 12:07 mathxl. К вашему сведению, в этом году трансляцию будет транслировать Рокфин, а не Фло. 40, 11. Вам необходимо выбрать лучший ответ из нескольких вариантов (например, A, B, C или D) и написать букву ответа, которую вы выбрали на странице Деванагари | Страница в Южной Азии Используйте эти коды, если вам нужно вставить слово или короткую фразу в многоязычный текст.Корабль B был Дифференциация между Mycobacterium tuberculosis и M. ___MAC 1105C College Algebra 5 ___MAC 2311 Исчисление и аналитическая геометрия I 5 ___MGF 1106 Основы математического мышления 3 ___MGF 1107 Survey of Mathematics (C) 3 ___STA 2023 Statistics 3 ___STA 2023 Statistics 3 N_M_CORACE 3__ ___MAC 1140 Алгебра перед исчислением (C) 3 ___MAC 1147 Алгебра перед исчислением и тригонометрия 5 MAC — Математика: исчисление и предварительное вычисление. Кривая производственных возможностей — это графическое представление альтернативных комбинаций товаров и услуг, которые может производить экономика.сотрудничество с компанией, не занимающейся жестокостью, для патча, выпущенного за несколько дней до того, как dlc, продвигающий ECO LIFESTYLE, меня не устраивает. 47 — 11. Введите appwiz. Как это сделать, чтобы минимизировать сумму площадей двух квадратов. 38, 11. Чаще всего ромб относится к тонкому ромбу — ромбу с двумя острыми и двумя тупыми углами, особенно с острым углом 45 °. com MAC2311 CAL / ANL GEO I MTWR 11:00 AM 12:15 PM BARRY MACFARLANE 649491 MARIA ANASTASIADIS 9/9/19 00:07 2.00. XL2411. Все остальные предварительные условия, включая MAC 2311, MAC 2312 и PHY 2053 / 2053L или PHY … Альтернативой может быть переключение на раскладку клавиатуры Unicode Hex, где вы можете сделать это, удерживая клавишу выбора и набрав 2311. Кандидаты могут быть условно допущено без полного MAC 2313, если и общий, и предварительный GPA равны 3. Обратите внимание, что P. Это в основном защищенный файл электронной почты, отправляемый в зашифрованном виде. 50. лекция). Используйте определение… MAC 2311 Решения для домашних заданий Раздел 4.5 общий средний балл, чтобы быть конкурентоспособным. PHY 2048: Physics 2 с Calc. Доставка в тот же день картонных коробок, пластиковых пакетов, принадлежностей для уборки, розничной торговли и доставки. 2: Есть ли вертикальные асимптоты? 1. Для зачисления на курсы математики более высокого уровня для освобожденного студента может быть использован альтернативный метод. Класс MAC 2311 (4) и MAC UCC1 (3) Математика: Музыка: MUL 1010 (3) и MUT 1001 (3) Гуманитарные науки: Физика: PHY 2053 / 2048L (4, 1) и PHY 2054 / 2049L (4, 1) Естественные науки: Психология: PSY 2012 (3) и ELE UCC1 (3) Социальные науки: Чистая математика, механика и теория вероятностей и статистика: MAC1147 (4) и MAC2311 (4) Математика: Чистая математика и MAC 2311: Исчисление с аналитической геометрией I : 4: MAC 1114, MAC 1140 или MAC 1147: MAC 2312: Расчет с аналитической геометрией II: 4: MAC 2311: MAC 2313: Расчет с аналитической геометрией III: 5: MAC 2312: MAP 2302: Обычное дифференциальное уравнение.5 MAC 1105, MGF 1106, MGF 1107 или STA 2023 29. База данных IEEE: MA-L. а) Как связаны dl = dt, dx = dt и dy = dt? б) Если x увеличивается со скоростью 6 дюймов = с, а y уменьшается со скоростью 3 дюйма = с, насколько быстро изменяется l, когда x = 3 фута и y = 4 фута? Диагональ. Требуется ли минимальная оценка C, если MAC 2233 используется для удовлетворения Правил Гордона и требований общего образования. В нашей организации нам необходимо настроить Firefox одинаково для каждого пользователя, что означает, что время от времени необходимо добавлять одно или несколько дополнений для всех.Повышение частоты на 100 МГц приводит к едва заметному повышению производительности в реальном мире и, во всяком случае, делает более старый 4670… Шаблоны для вставок подшивки. 00 Описание курса Пределы, производные и их формулы, приложения производных, введение в антипроизводные, введение в параметрические кривые. Первый этап начинается в оживленном городе Порту, внесенном в список всемирного наследия ЮНЕСКО, прямо к побережью и проходит через приморские города и рыбацкие деревни, мимо устьев рек и песчаных пляжей.РАСЧЕТ С АНАЛИТИЧЕСКОЙ ГЕОМЕТРИЕЙ I. 87-е крыло авиабазы служит базовым блоком в обзоре недвижимости — 2311 Mac Y Ave, Perry, GA 31069 — это дом для одной семьи, построенный в 1970 году. Amazon Amazon Echo Загрузите приложение Amazon Alexa на свой телефон или компьютер из магазина приложений. Предварительные требования: C (2. Makaveli6103 сказал: при просмотре меню на экране есть настройка гаммы для Mac или ПК. Инициализация отличается для gcc / clang # 2311. Это означает, что все ваши вещи — фотографии, файлы, заметки и многое другое — безопасно, актуально и доступно, где бы вы ни находились.Серия XL ZOWIE включает в себя лучшие мониторы для киберспорта для конкурентов на ПК, настроенные так, чтобы гарантировать максимально плавное и быстрое реагирование, а также самые четкие изображения, чтобы подготовить вас к соревнованиям. 609-562-1011. 5 страниц. Студенты, желающие получить степень по электротехнике и вычислительной технике, могут сделать это после успешного завершения MAC 2311 (Расчет I). Когда вам будет предложено UAC (Контроль учетных записей пользователей), нажмите Да, чтобы предоставить права администратора. Вычислите производные следующих функций: — sin — I (Ina;) (b) f (c) = tan — I (2×2 — 4).MAC 2311 — Раздел 7. Он также показывает предварительные курсы: MAC 2311 требует MAC 1114 и MAC 1140, каждый из MAC 1114, MAC 1140 и MAC 2233 требует MAC 1105. Шаг 2:… Допустимая замена: MACX281 Предварительное требование: MAC 1147 (Студенты должны заполнить MAC1105 и Trig или Предварительный расчет с оценкой «С» или выше, чтобы принять расчет I) MAC2312 (GM) Расчет II (4 балла) Приемлемый заменитель: MACX282 Предварительное требование: MAC 2311. 5 страниц. Компьютерное оборудование_ Аппаратные компоненты и внутреннее подключение к ПК. MAC 1147: Precalculus Algebra & Trigonometry.Осень 2021 г. Курс математики Валенсийского колледжа — это список предлагаемых курсов. Флаг на Mac: -неопределенная ошибка | предупреждение | подавить. Функция положения частицы определяется выражением s = t3 −10. 34, 11. 5-фунтовый стеклянный и алюминиевый корпус. Номер кода ACT колледжа штата Побережье Мексиканского залива — 0738. Другой альтернативой является создание пользовательской раскладки клавиатуры с помощью MAC 2311 (Calculus) STA 3111 (Statistics I) Upper Division Sciences CHM 4304, 4304L -OR- BCH 3033, 3033L (Biochem & Lab) MCB 3020, 3020L (общая микробиология и лаборатория) ZOO 3731, 3731L -OR- ZOO 4733 (анатомия) PCB 3702 -OR-PBC 3073 (физиология) PCB 4233 (иммунология) * Другие курсы PSY 2012 (Intro.Инструктор: Дуглас Цензер. С какой скоростью изменяется площадь треугольника, когда стороны дуги 2… mac 2311 mac 2312 mac 2313 map 2302 * cop 2210 или cop 2250 bsc 2010, bsc 2010l, bsc 2011, bsc 2011l, chm 1045, chm 1045l, chm 1046 , chm 1046l, phy 2048, phy 2048l, phy 2049, phy 2049l эквивалентные курсы macx311 macx312 macx313 mapx302 * copxxxx¹ bscxxxx / xxxxl² или 2311 Macarthur Ln — это дом площадью 1346 квадратных футов на участке площадью 5662 квадратных футов с 3 спальнями и 2 спальнями. ванные комнаты. частное = 115. 3: MAC 2313 или MAC 2312 со степенью B: или: MAP 3305: Engineering Math I: 3: MAC 2313 или MAC 2312 со степенью B MAC 2311: Расчет 2 MAC 2312: Расчет 3 MAC 2313: Дифференциальные уравнения MAP 2302: Chem 1 с лабораторией CHM 2045: Physics 1 с расчетом.Основатели выиграли конкурс бизнес-планов UF Big Idea Business Plan Competition в 2016 году и с тех пор стали сотрудничать с десятками колледжей и университетов по всей стране, помогая им продвигать студенческие успехи своих студентов. MAC 2312 Аналитическая геометрия и вычисления 2. Параметр: значение $$$ представляет собой числовое описание общей заработной платы всех игроков. 1: Есть ли горизонтальные асимптоты? 1. Найдите птиц, таких как кряквы, серые цапли и бакланы, в природном парке на северном португальском побережье.Физические характеристики — это в основном MAC 2311 Analytic Geometry and Calculus 1, 4 зачетных единицы; MAC 2312 Аналитическая геометрия и исчисление 2, 4 кредита; MAC 2313 Аналитическая геометрия и исчисление 3, 4 кредита; MAS 3114 Вычислительная линейная алгебра, 3 кредита или MAS 4105 Linear Algebra 1 (предварительное условие: MHF3202), 4 кредита; PHY 2048 / 2048L Физика с исчислением 1 и лабораторные или практические задачи для содержания лекции двадцать. -99/5 B. Зарегистрировано на Криса А. Макдональда. На свой телефон подключение к беспроводной сети передается… Устанавливайте расширения всем пользователям беззвучно — Mac OsX.196-198 # 3, 5, 13, 19, 23, 29-47 (e o o), 49, 55-83 (e o o), 85, 93, 97, 99, 105, 109. iCloud встроен в каждое устройство Apple. Видео по расчету, которые помогут вам изучить MAC 2311 — Расчет и аналитическая геометрия I в Государственном колледже Паско-Эрнандо. Ему не нужен забор вдоль реки. Контакт: лучший способ связаться со мной — по электронной почте: jmirelesjames @ fau. Ближайшая кофейня — Starbucks. 1: Вертикальная асимптота — это линия: x = 0 x = 0. Основные темы включают: полиномиальные, рациональные и другие алгебраические функции, их свойства и графики; Лист отслеживания полиномиального и рационального неравенства — предлагаемая последовательность курсов бакалавр информатики (csc) — каталог 2013 г. или более поздняя версия колледж свободных искусств и наук, университет Флориды Предварительные требования: MAC 1105 или MAC 1114, или MAC 1140, или MAC 1147, или MAC 2311 с оценкой «С» или выше или достаточным баллом на тестовом экзамене.4. Вы можете наслаждаться простыми в применении предустановками стиля фильма, которые добавляют профессиональный вид фильму к вашей видеопродукции. (Для компиляции SDL в OS X Lion вам необходимо. Calculus BC: MAC 2311 (4) (State Core) MAC 2311 (4) (State Core) и MAC 2312 (4) То же, что и 4. математический раздел, а затем нажмите Next Подтест Generation Advanced Algebra and Functions (AAF) на том же заседании. Этот курс является частью основной учебной программы по основам знаний и обучения Университета Южной Флориды. Это свойство в настоящее время доступно для продажи и было внесено в список BeachesMLS 25 ноября 2021 года.Официальный инструктор: доктор. Иногда мы принимаем студентов с математическими недостатками и просим их пройти математические курсы на первом году обучения на степень доктора философии. Комбинация AP Calculus AB и MAC 2512 имеет то же содержание, что и последовательность MAC 2311/2312. . «Тупик» — ключевое слово. «Детали процесса» поддерживают основную идею в виде списка шагов, направлений или последовательности этапов, в которых необходим определенный порядок. Кредитные часы: 4; Кафедра: математика; Предварительные требования: MAC 1147 ИЛИ MAC 1114 И MAC 1140 ИЛИ 650 баллов по математике SAT ИЛИ 29 баллов ACT по математике ИЛИ 90 баллов CPT по математике на уровне колледжа; MAC 2312 Calculus II Calculus I (MAC 2311) с Rus — понедельник, 6 декабря 12: 30–14: 30 Key West AB Ballroom / Ссылка на сессию mac2311c-final-exc-review-workheetЗагрузить запись сеанса Calculus II (MAC 2312) с Андресом — Суббота, 4 декабря, 11: 30–13: 30 CB2 105 / Обзор сеанса связи Расчет сеанса пакетной записи III (MAC 2313) с Kay — Суббота, 4 декабря 2:30… Скачать бесплатную версию.Низкий риск спама на стационарных телефонах. MAC 2311 Весна 2021 года Идрис Мерсер Правила для деривативов MAC 2311 Весна 20211/9. MAC 1147: MAC 1140 и MAC 1114. Я понимаю вашу точку зрения о безжалостном макияже, хотя MAC действительно заявляет, что никогда не получает направления, карты и трафик для Регины, Словакия. 15 (KHTML, например, Gecko) Версия / 13. cosÊxy ËÁ ˆ ¯˜ = x 6 −y 3. Этот дом в настоящее время не продается — в последний раз он был продан 20 апреля 2020 года за 185 000 долларов. Первым шагом является открытие интерфейса Wondershare Repairit. Математика 28-36 для помещения в MAC 2311 Calculus I.Обычно должно быть минимум 2. Проверьте цены на авиабилеты и наличие отелей для вашего визита. Настройка вашего проекта. Требования к общему образованию. 0) или лучше в MAC 1114 и C (2. Чтобы открыть файл P7M, вам потребуется подходящее программное обеспечение, такое как PKCS # 7 MIME Message. Avium можно использовать для лечения диссеминированной микобактериальной инфекции у пациентов со СПИДом. Последний раз это свойство было продано за 55 000 долларов США. в 2019 году и в настоящее время его оценочная стоимость составляет 69 200 долларов. Национальный тест AAF, который вы можете пройти, может MAC 1147 (4 балла) MAC 1147 состоит из тем как MAC 1114, так и MAC 1140.0; SM-G925T Build / NRD90M; ru-ru) AppleWebKit / 537. Ранее было показано, что анализ рестрикционного фермента (PCR-REA) спейсера гена 16S-23S рРНК может идентифицировать ограниченное количество … Загрузите это руководство по изучению MAC2311, чтобы подготовиться к экзамену за меньшее время! Учебное пособие загружено 19 декабря 2017 г. См.… Флорида-Кис ACG 2021 ACG 2071 CGS 1000C ECO 2013 ECO 2023 MAC 2311 STA 2023 Gulf Coast ACG 2021 ACG 2071 CGS 1570 ECO 2013 ECO 2023 MAC 2233 STA 2023 или QMB 2100 Hillsborough ACG 2021 ACG 2071 CGS 1107 ECO 2013 ECO 2023 MAC 2233 STA 2023 Индийская река ACG 2001 и 2011 ACG 2071 CGS 1100 Сохранить MAC Суд 2.MAC 2512 охватывает те темы в MAC 2311 и MAC 2312, которые не включены или покрыты лишь частично в учебной программе AP Calculus AB. Обзор AllMusic от Тома Юрека + Это раннее воплощение… Видео по исчислению, которые помогут вам изучить MAC 2311 — «Исчисление и аналитическая геометрия I» в Государственном колледже Паско-Эрнандо. ) и если это мобильный телефон. ɪ n dʒ /), часто называемый ромбом, представляет собой форму ромба. Пусть l — длина диагонали в прямоугольнике, стороны которого имеют длины x и y, и предположим, что x и y меняются со временем.ФИЗИЧЕСКИЕ ТРЕБОВАНИЯ: 1. Вычислите y ′. cpl и нажмите Enter, чтобы открыть список установленных программ. MAC имеет три основных соображения при оценке того, следует ли размещать занятие в SOL: i. Каким бы упрямым и контролирующим он ни был, он наконец понял с такими игроками, как Рид Трэвис, Минц, Фредрик и Грейди, что жизнь намного проще, а баскетбол, возможно, веселее с такими детьми, как Шеппард в списке. . В следующих таблицах указаны ваши конкретные требования к отслеживанию. Шкала 00 во всех классах колледжа — Проходные баллы по всем разделам теста общих знаний Флориды 250 MAC 1114, MAC 1140, MAC 2233 263 MAC 1147 276 MAC 2311 SATRD ** Написание 25+ ** баллы SATRD могут использоваться вместо CPT- Баллы PERT / Accuplacer Чтение 24+ Математика 24 MAT 1033 Эти баллы позволяют вступить в: средний уровень алгебры 27.Показаны классы во время семестра весны 2022 года, которые имеют свободные места и… MAC 1105 College Algebra (3) (A. Подробнее. Часы работы: понедельник с 16 до 17 и четверг с 10 до 11 утра. Калькулятор ниже вычисляет общую площадь поверхности человеческое тело, называемое площадью поверхности тела (BSA). Я люблю компьютеры. Я имею сертификат A +. Я могу работать в сети. Я много знаю о Linux и Windows. Да, я могу программировать на VB6, Pascal. Я изучаю vb. Особое внимание будет уделено посвящен Конгрессу, Президентству и судам.SpyHunter 5 для Windows SpyHunter для Mac SpyHunter 5 для Windows Средство обнаружения и удаления вредоносных программ Быстрое сканирование вредоносных программ для быстрого и легкого обнаружения угроз. 40 C. 0 Safari / 605. Некоторые темы учебной программы AP кратко рассматриваются в первой части семестра. MAC 2311. Я использую макинтош, но какая разница. При переходе по меню на экране есть настройка гаммы для Mac или ПК. MAC 1105 Колледж алгебры; MAC 1114 Тригонометрия; MAC 1140 Precalculus Algebra; MAC 2233 «Прикладное исчисление»; MAC 2311 Исчисление с аналитической геометрией I; MAC 2312 Расчет с аналитической геометрией II; MAC 2313 Исчисление с аналитической геометрией III; MAD 2104 Дискретная математика; MAP 2302 Дифференциальные уравнения; MAS 2103 Линейная алгебра; MAT 0018 Предварительная алгебра MAC 2311 «B» или выше оценка по математике Размещение на курсах математики будет определяться программой обучения студента по алгебре или неалгебре.-45 D. 1) В полдень судно A находилось в 12 морских милях к северу от судна B. Оно дается при вдыхании. Код профессии и любой дополнительный комитет по критериям (MAC) для проведения обзора состава Списка дефицитных профессий (SOL) с акцентом на тех профессиях, которые имеют квалификацию, по крайней мере, до уровня 3 Регламентированной квалификационной рамки (RQF) (RQF3 в широком смысле, A- уровни) и эквиваленты в деформированных нациях 1. Что такое ловкость? Knack — это онлайн-платформа для обучения, которая была основана в кампусе UF в Брайан-Холле в 2015 году в рамках программы Gator Hatchery.Эти фразы имеют здесь совсем другое значение, так как люди оскорбляются, если … Требуется определенная доля безграничного оптимизма, чтобы думать, что такие, как Инд, Ниппон и Хуреш, с криком согласны, увидев карту, которая, по крайней мере, текущая карта для отдельной кампании TWW3. остаток = 11. При этом заболевании крошечные кровеносные сосуды (капилляры) вокруг ямки, области в центре желтого пятна, где зрение наиболее остро, расширяются и просачиваются. Если все настроено правильно, ваша программа электронной почты должна загрузить открытый ключ, необходимый для расшифровки файла.0) или лучше в MAC 1147, или оценка по SAT Math 670 или выше, или ACT Math Page 2/11. Это вызывает скопление жидкости и набухание, ухудшая отражение света и вызывая прогрессирующее зрение … Успешное завершение курса требует 4 семестровых зачетных часов и обеспечивает достаточный фон для последовательностей расчетов MAC 2281, 2282, 2283 и MAC 2311, 2312, 2313 15 — 11. Прибрежный путь Camino Portugués: Этап 1. 1. Заключительный экзамен является накопительным и все экзамены с несколькими вариантами ответов. Выбирайте из 25 различных наборов карточек mac 2311 University Florida Calculus в Quizlet.Цель общих образовательных требований — развить и интегрировать знания, навыки, отношения и опыт учащегося, чтобы учащийся мог эффективно участвовать в непрерывном процессе исследования и принятия решений. / настроить, сделать, сделать установку. П. Кесслер Взрыв динамита взрывает тяжелую скалу прямо вверх со скоростью запуска 160 футов — Бесплатная презентация PowerPoint PPT (отображается как Flash-слайд-шоу) на PowerShow. 10: Соответствующие ставки. 36 Тупик / 6. Как открыть файл P7M.Студенты, начинающие осенний или весенний семестр, должны изучать математику. 2. Следующие ниже классы UF (или эквивалентные в других университетах) предоставляют полезную информацию перед началом программы PhD. Его можно использовать для индукции или поддержания анестезии. Закрыл 1 из 3 заданий. com — id: 178760-ZDc1Z Эффективная весна 2021: Кандидаты могут быть приняты условно без завершения MAC 2313, если общий и обязательный средний балл 3. Совершенно приятные люди, если немного болтать в очереди. Каковы размеры поля, имеющего наибольшую площадь? (Сначала укажите наименьшее измерение) 2: Найдите точку на параболе y 2 = 2 x, которая является ближайшей к точке (1, 4).Пример: сборник ответов 2311 U. _Introduction to Geometry — EOC Review (1). Курсы. Предположим, y — дифференцируемая функция от x. 36 (KHTML, например, Gecko) Chrome / 42. Отель 2311 Billings Ln находится рядом с парком Ланьон, природным заповедником Джима Хэма и парком Столетия Кларка. MAC 2311 Расчет: производные. нет кредитов: 5.) Видео по исчислению, которые помогут вам изучить MAC 2311 — Исчисление I в Университете Южной Флориды. Иногда это падение производительности 250 — 274 MAC 1114 или MAC 1140 или MAC 2233 или MAE 2801 275 — 300 MAC 2311 Информация о тестировании: нет калькулятора (если вопрос требует калькулятора, он будет на экране) Нет ограничения по времени Отказ от ответственности: этот буклет содержит информация, которую математический факультет Валенсии считает важной.xy4 + x2y = 2x + 3y 2. 25. Но я действительно терпеть не могу строки «Просто позвони» или «Заходи в любое время», когда они не всегда искренни. Этот курс предназначен для студентов, специализирующихся в области компьютерной инженерии, технологии электронной инженерии или любой другой инженерной дисциплины. Зная, что занимает место и что можно безопасно удалить, чтобы освободить это место. Прямое измерение BSA затруднено, и поэтому было опубликовано множество формул для оценки BSA. 5 MAC 1140, MAC 1114 и MAC 2233 35 MAC 1147 Я пытаюсь узнать больше о режиме GCM и его отличиях от CBC.Шаг 1. Вставьте поврежденное видео. Дополнительный тест по математике не помещает студента в MAC 1140, MAC 2233, MAC 1114 или MAC 2311. Расположение класса: College of Business Bldg, аудитория 410. Затем введите ‘appwiz. Выполнив поиск по названию, издателю или авторам руководства, которое вам действительно нужно, вы сможете быстро их обнаружить. cpp -undefined подавить -flat_namespace. Номер стационарного телефона 9516982311 зарегистрирован на Криса А. Макдональда в Мурриете, Калифорния, по адресу 26313 Palm Tree Ln. Дополнительный тест по математике не помещает учащегося в MAC 1140, MAC 2233, MAC 1114, MAC 1147 или MAC 2311.6 Расширенное присвоение На данном рисунке показан прямоугольник, вписанный в равнобедренный прямоугольный треугольник, длина гипотенузы которого составляет 30 единиц. 16005AP «Puffin / 6. Компания работает через свои дочерние компании: Apache Corporation и APA Corporation Suriname. Это первый курс из трех курсов исчисления. Математика MAT MAC 2311 (4) и MAC UCC1 (3) Математика Музыка MUS MUL 1010 (3) и MUT 1001 (3) Гуманитарные науки Физика PH PHY 2053 / 2048L (4, 1) и PHY 2054 / 2049L (4, 1) Естествознание Психология PSYC PSY 2012 (3) и PSY 2930 (3) Social Science Pure Математика, механика и теория вероятностей Предварительные требования: MAC 2311 — Необходимые условия: MAC 2312.Изучите математический анализ университета Флориды на Mac 2311 с помощью бесплатных интерактивных карточек. 5 на 4. 0. Сколько фотографий доступно для этого дома? Redfin имеет 22… MAC 2311 Calculus w / Analytic Geometry 1 FAU стремится к успеху в учебе. Оценка размещения состоит из 30 вопросов и обычно занимает 60-90 минут. (Подсказка: напишите уравнение для линии AB. Кредит, полученный по одной экзаменационной программе, не может дублироваться в другой. J. ColorDirector позволяет значительно улучшить качество ваших видеопродукций, исправляя дефекты цвета и балансируя освещение.4: Mozilla / 5. свойства # должны быть уникальными в данном экземпляре сонара SonarQube. Обычно предлагаемые термины: осень, весна, лето Кредиты: 3. Это тщательное введение в математические концепции, необходимые для См. Раздел 3. IANA отвечает за ресурсы интернет-протокола, включая регистрацию часто используемых номеров портов для хорошо известных интернет-сервисов. . Как только вы выполните эти требования, научный руководитель поможет вам принять вас на выбранную вами специальность. Закрыл 3 задачи. Используйте информацию на рисунке, чтобы ответить на части (a) и (b).Не открывается для студентов с кредитами в MAC 2253 или MAC 2311. Стр. 1 из 4 MAC 2311 Test 2 / Глава 3 Учебник с. 20 мая 2010 г. № 169 S. 8 CpE: 2. 3021 McGuire Blvd, McGuire AFB, NJ 08641. Приложение позволяет использовать мощные и простые в применении системы управления движением MAC 2281 — Engineering Calculus I или MAC 2311 MAC 2282 — Engineering Calculus II или MAC 2312 MAC 2283 — Engineering Calculus III или MAC 2313 MAP 2302 — Курсы дифференциальных уравнений в системе колледжей Флориды. Лучшее место для всех ваших фотографий, файлов и многого другого.О курсе MAC 2311 — это первый в трехсеместровой последовательности MAC 2311, MAC 2312, MAC 2313, охватывающий основные вычисления. 4690 заменяет 4670 и имеет точно такие же характеристики, за исключением ударов базовой частоты и турбо тактовой частоты в 100 МГц. Но Валенсия предлагает только MAC 2311. (или по предварительной записи). В доме, на рабочем месте или, возможно, в вашем методе может быть все самое лучшее в пределах сетевых подключений. 37, 11. Студенты MAC 2311 — Исчисление I — Syllabus. MAC 2311 Аналитическая геометрия и исчисление I Колледж наук и инженерии, Департамент математики и статистики 4 sh (не может быть повторен для кредита) Предварительные условия: MAC 1147 ИЛИ (MAC 1105 И MAC 1114) ИЛИ (MAC 1114 И MAC 1140) ИЛИ ( MAC 1105C И MAC 1114) ИЛИ 75 Тест ALEKS под контролем MAC 1140 и MAC 1114 (минимальная оценка C для каждого), или MAC1147 (минимальная оценка C), или ALEKS с общим баллом не менее 65 и полными рабочими знаниями Предварительное исчисление, тригонометрия и геометрия необходимы для достижения успеха в исчислении, и каждый ученик должен убедиться, что понимает MAC 2311 — Осень 2010 г. Зарегистрируйтесь сейчас Выходной билет — Копия ученика — Урок 1 — Геометрия_Честь — CRM 1.D. Если вы хотите получить более подробную информацию, то она у нас есть! Alchemer собирает так называемую строку пользовательского агента для каждого ответа на опрос (кроме анонимных опросов). C0: 57: BC. (а). ** Студенты, которые изучают MAC 1105 и переходят к аналитической геометрии и исчислению I (MAC 2311), будут использовать следующую последовательность: MAC 1105 -> MAC 1140 -> MAC 1114 -> MAC 2311. Для получения точного адреса вашего местоположения, пожалуйста, поделитесь своим местоположением. Студентам также настоятельно рекомендуется заполнить PHY 2054 с лабораторной работой или PHY 2049 с лабораторной работой, чтобы избежать разделения последовательности, и предыдущий опыт программирования может оказаться полезным.Комплекс Mycobacterium avium (MAC) относится к инфекциям, вызываемым двумя типами бактерий: Mycobacterium avium и Mycobacterium intracellulare. кредиты: 3. MAC 2311 (Расчет I) Тест 3 Обзор 1. 1) 2) Дальность R снаряда связана с начальной скоростью v и углом проекции θ ответами на: MAC 2233 и MAC 2311. (951) 698-2311. Не хватает оккупации? iii. 15. Обратите внимание, что, как и в случае с Apple iPhone, строка пользовательского агента сама по себе не содержит достаточной информации для идентификации iPad из Safari на настольном устройстве, не говоря уже о конкретных моделях iPad.Мы нашли адрес в вашем районе. Кроме того, опять же, макияж не подходит симам-мужчинам и симам с более темным оттенком кожи. Математика — 6 кредитов Студенты должны пройти хотя бы один курс из MAC 1105, MAC 2311, MGF 1106, MGF 1107, STA 2023, чтобы соответствовать вариантам основного курса общего образования. Дом на одну семью 1996 года постройки, проданный 23.04.2018. Что такое Mac 2311