X 2 1 х: Решите неравенство x^2 — Детская игровая комната «Волшебный лес»

Posted on 03.01.197021.06.2021 by alexxlab

Содержание

Урок 12. решение алгебраических уравнений разложением на множители — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №12. Решение алгебраических уравнений разложением на множители.

Перечень вопросов, рассматриваемых в теме

1) типы алгебраических уравнений;

2) решение алгебраические уравнения методом разложения на множители;

3) методы решения алгебраических уравнений.

Глоссарий по теме

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0, где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнение над множеством F.

Степенью алгебраического уравнения называют степень многочлена P.

Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Биквадратными называются уравнения вида ах⁴ + bх² + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.

Симметрическим уравнением 3-ей степени называют уравнение вида: ax³ + bx² + bx + a = 0, где a, b – заданные числа.

Уравнение вида aⁿxⁿ₊a^n-1x^n-1+…+a¹x+a⁰=0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. a^n-1=a^k, при k=0, 1, …, n.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М. И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Давайте вспомним, что такое алгебраическое уравнение?

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0, где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого поля F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнение над полем F.

Степенью алгебраического уравнения называют степень многочлена P.

Например, уравнение

является алгебраическим уравнением седьмой степени от трёх переменных (с тремя неизвестными) над полем вещественных чисел.

Связанные определения. Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Примеры и разбор решения заданий тренировочного модуля

Алгебраические уравнения, решаемые разложением на множители:

Пример 1.

x³ – 3x – 2 = 0.

Решение: I способ

D(–2) : ,

Можно догадаться, что число х₁ = –1 является корнем этого уравнения, так как –1 + 3 – 2 = 0.

(х + 1)( х² –х–2) = 0;

х + 1 = 0 или х² –х–2 = 0;

х₁= –1 х

2,3 = ;

х_2,3 = ;

х₂= –1, х₃ = 2

Ответ: –1; 2.

II способ

x³ + х² – х²– х – 2x – 2 = 0;

(x³ + х²) – (х² + х) – 2(x + 1) = 0;

х²(х + 1) – х(х + 1) – 2(х + 1) = 0;

(х + 1) (х² –х–2) = 0;

(х + 1) (х + 1) (х –2) = 0;

(х –2) = 0;

х₁= –1, х₂ = 2

Ответ: –1; 2.

Уравнения, сводящиеся к алгебраическим
1. Биквадратные уравнения

На прошлом уроке мы познакомились с данным видом уравнений

Определение. Биквадратными называются уравнения вида ах⁴ + bх² + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.

Метод решения

Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки у=х².

Новое квадратное уравнение относительно переменной у: ay²+by+c=0.

Решая это уравнение, мы получаем корни квадратного уравнения

y₁ и y₂.

Решая эти два уравнения (y₁=x₁² и y₂=x₁²) относительно переменной x, мы получаем корни данного биквадратного уравнения.

Порядок действий при решении биквадратных уравнений

Ввести новую переменную у=х²
Подставить данную переменную в исходное уравнение
Решить квадратное уравнение относительно новой переменной
После нахождения корней (y₁; y₂) подставить их в нашу переменную у=х² и найти исходные корни биквадратного уравнения

Пример 2.

х⁴ – 8х² – 9 = 0.

Решение: Пусть у = х², где у 0; у² – 8у – 9 = 0;

По формулам Виета:

у₁ = –1; у₂ = 9;

Первое решение отбрасываем ( у 0),

а из второго находим х₁ = –3; х₂ = 3.

Ответ: х₁ = –3; х₂ = 3.

2 Симметрические уравнения

Решение симметрических уравнений рассмотрим на примере симметрических уравнений третьей степени.

Симметрическим уравнением 3-ей степени называют уравнение вида ax³ + bx² + bx + a = 0, где a, b – заданные числа.

Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства симметрических уравнений:

1⁰. У любого симметрического уравнения нечетной степени всегда есть корень, равный -1.

Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х³ + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т. е.

(х + 1)(ах² + (b – а)x + а) = 0, поэтому,
х + 1 = 0 или ах² + (b – а)x + а = 0,

первое уравнение и доказывает интересующее нас утверждение.

2⁰. У симметрического уравнения корней, равных нулю, нет.

3⁰. При делении многочлена нечетной степени на (х + 1) частное является снова симметрическим многочленом.

Пример 3.

х³ + 2x² + 2х + 1 = 0.

Решение: У исходного уравнения обязательно есть корень х = –1.

Разлагая далее левую часть на множители, получим

(х + 1)(x² + х + 1) = 0.

Квадратное уравнение

2 + х + 1 = 0 не имеет корней.

Ответ: –1.

2 Возвратные уравнения

Уравнение вида aⁿxⁿ₊a^n-1x^n-1+…+a¹x+a⁰=0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т. е. a^n-1=a^k, при k=0, 1, …, n.

Рассмотрим возвратное уравнение четвёртой степени вида

ax⁴ + bx³ + cx² + bx + a = 0, где a, b и c — некоторые числа, причём a ≠ 0. Оно является частным случаем уравнения ax⁴ + bx³ + cx² + kbx + k²a = 0 при k = 1.

Порядок действий при решении возвратных уравнений вида ax⁴ + bx³ + cx² + bx + a = 0:

разделить левую и правую части уравнения на . При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;
группировкой привести полученное уравнение к виду

ввести новую переменную , тогда выполнено
, то есть ;

в новых переменных рассматриваемое уравнение является квадратным: at² +bt+c–2a=0;

решить его относительно t, возвратиться к исходной переменной.

Пример 4

2x⁴ – 3x³ – 7x² –15x + 50 = 0.

Решение: Разделим на x², получим:

Введем замену:
Пусть

тогда 2t² – 3t – 27 = 0

t=-3

x2+3x+5=0

D<0

2×2-9x+10=0

x=2; x=2,5

Ответ: .

12. Уравнения, содержащие модуль. Рациональные уравнения

МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ

Уравнения, содержащие модуль

Если в уравнении некоторые выражения, содержащие неизвестное, стоят по знаком модуля, то решение исходного уравнения ищется отдельно на каждом из промежутков знакопостоянства этих выражений.

Пример 1
Решить уравнение |3x-6|=x+2.
Решение:
Рассмотрим первый случай: 3х-6≥0, тогда 3х-6=х+2, 2х=8, х=4.
Рассмотрим второй случай: 3х-6<0, тогда 3х-6=-(х+2), 4х=4, х=1.
Ответ: 1; 4.
Пример 2
Решить уравнение |x-2| — 3|x-1| + 4|x-3| = 5.

Отметим на координатной прямой точки:

х-2=0 х-1=0 х-3=0
х=2 х=1 х=3

Рассмотрим решения уравнения на промежутках (-∞; 1]; (1; 2]; (2; 3] и (3; +∞).

При х≤1: -(х-2) + 3(х-1) -4(х-3)=5, -х+2+3х-3-4х+12=5, -2х=-6, х=3. Ответ не принадлежит промежутку, следовательно нет решений.
При 1<х≤2: -(х-2) — 3(х-1) -4(х-3)=5, -х+2-3х+3-4х+12=5, -8х=-12, х=1,5. Ответ принадлежит промежутку.
При 2<х≤3: х-2 — 3(х-1) -4(х-3)=5, х-2-3х+3-4х+12=5, -6х=-8, х=4/3. Ответ не принадлежит промежутку, следовательно нет решений.
При х>3: х-2 — 3(х-1) +4(х-3)=5, х-2-3х+3+4х-12=5, 2х=16, х=8. Ответ принадлежит промежутку.
Ответ: 1,5; 8.

Рациональные уравнения Рациональным уравнением называется уравнение вида

где P(x), Q(x) — многочлены.

Решение уравнения сводится к решению системы:

Пример

Решить уравнение

Решение:

x²-4=0, х-2≠0,

x²=4, х≠ 2.

х=-2 или х=2.

Число 2 не может быть корнем.

Ответ: -2.

УПРАЖНЕНИЯ 1. Из данных уравнений выберите те, которые не имеют корней:

а) |x|+4=1; |x-5|=2; |x+3|=-6. б) |1+x|=3; |1-x|=-4; 8+|x|=2.

Решение:
а) |x|+4=1 не имеет корней, т.к. |x|=-3 и модуль не может быть отрицательным числом; |x-5|=2 имеет корни; |x+3|=-6 не имеет корней, т.к. модуль не может быть отрицательным числом.
Ответ: |x|+4=1; |x+3|=-6.

2. Решите уравнение:

а) |5x|=15; б) |2x|=16.

Решение:
а) |5x|=15;
|5||x|=15;
5|x|=15;
|x|=3;
x=3 или x=-3.

3. Решите уравнение:

а) |5x+1|=5; б) |2x-1|=10.

Решение:
а) |5x+1|=5;
Ответ: -1,2; 0,8.

4. Решите уравнение:

а) |5x²+3x-1|=-x²-36; б) |3x²-5x-4|=-4x²-23.

Решение:
а) |5x²+3x-1|=-x²-36. Рассмотрим выражение -x²-36, оно принимает отрицательные значения при любых значениях х, следовательно уравнение |5x²+3x-1|=-x²-36 не имеет корней.
Ответ: нет корней

5. Решите уравнение:

Решение:
Ответ: -1/3.

6. Решите уравнение:
Решение:
14х²-5x-1=0,

7. Решите уравнение:
Решение:

8. Решите уравнение:

Решение:

х ≠3.
Ответ: -4; 1.

9. Найдите, при каком значении переменной значение выражения
равно: а) -6; б) 6. Решение:

10. Решите уравнение:

Решение:
а) Разложим знаменатели на множители:
х²-36=(x-6)(x+6).
108-24x+х²=(x-6)(x-18).
2x-36=2(x-18).

11. Решите уравнение:

а) х²-6|x|=0; б) х²+4|x|=0.

Решение:
а) х²-6|x|=0;
х≥0: х²-6x=0; х(х-6)=0, x1=0, x2=6.

x<0: х²+6x=0; х(х+6)=0, x1=0, x2=-6.

Ответ: -6; 0; 6.

12.Решите уравнение:

а) х²-3|x|+2=0; б) х²-2|x|+1=0.

Решение:
а) х²-3|x|+2=0.
х≥0: х²-3x+2=0; D=9-8=1, x1=2, x2=1.
x<0: х²+3x+2=0; D=9-8=1, x1=-2, x2=-1.
Ответ: -2; -1; 1; 2.

13. Решите уравнение:

а) |x-2|+|x-4|=5; б) |x-1|-|x-4|=6.

Решение:
а) |x-2|+|x-4|=5.
x≤2: -(x-2)-(x-4)=5, -x+2-x+4=5, x=0,5.
2<x≤4: x+2-(x-4)=5, x-2-x+4=5, 2=5 — нет решений.
x>4: x-2+x-4=5, 2x=11, x=5,5.

Ответ: 0,5; 5,5.

14.Решите уравнение:

а) |3- |4- |x|||=5; б) 8-|2 -|x|||=3.

Решение:
а) |3- |4- |x|||=5;
3- |4- |x||=5 или 3- |4- |x||=-5;
|4-|x||=-2 — нет решений |4-|x||=8
4-|x|=8 или 4-|x|=-8
|x|=-4 — нет решений |x|=12
х=12 или х=-12.
Ответ: -12; 12.

15. Решите уравнение:
Решение:
а)
3x-7≥0: х²-3x+10=0; D=9-40=-31<0 — нет корней.

3x-7<0: х²-3x-10=0; D=9+40=49, x1=5, x2=-2.
3x-7≠0, x≠7/3.
Ответ: -2; 5.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Какие из чисел -4; -1; 2; 1,5; 2,5 являются корнями уравнения:

а) |3x-1|=5; б) |4-2x|=1?

2. Решите уравнение:

а) |3x|=21; б) |2x|=-12.

3. Решите уравнение:

а) |2x-5|=1; б) |3x+6|=18.

4. Решите уравнение:

5. Решите уравнение:

6. Решите уравнение:

7. Решите уравнение:

8. Решите уравнение:

9. Решите уравнение:

а) 3(x-1) = |2x-1|; б) |5-2x|=|x+4|.

10. Решите уравнение:

а) |х²+x|=12; б) |х²-3x|=10.

Проверь себя

Aquashine BTX 1 x 2 мл Биоревитализант

Aquashine BTX 1 x 2 мл Микрорелаксант

Многоуровневый универсальный препарат с возможностью мультивведения. Уникальный препарат оказывающий эффект выраженного биолифитинга. Благодаря пептидному комплексу и ГК, препарат активно стимулирует синтез нового коллагена и препятствует его разрушению, что приводит к быстрому увеличению плотности и эластичности кожи, мышц и фасций. Максимальный лифтинг-эффект наступает через 2 недели после процедуры. Дополнительные компоненты, такие как витамины, аминокислоты, минералы и коэнзимы обеспечивают коже антиоксидантную защиту.

Aquashine BTX увлажняет, повышает тургор кожи и укрепляет каркас. Восстанавливает внутрикожный баланс. Можно использовать на веках (вплоть до ресничного края). Не вызывает отечности и покраснения.

Прекрасно работает в сочетании с препаратами Aquashine Soft Filler и Aquashine BR.

Aquashine BTX содержит:

Гиалуроновую кислоту (1,5 %)
Витамины (А; C, Е, В6, В1, В2, В7, В8, В3, В12,В9,К1)
Аминокислоты (аланин, аминобутировая кислота, аргинин, аспарагин, аспарагиновая кислота, цистин, глутаминовая кислота, глутамин, глицин, гистидин, гидроксипролин, изолейцин, лейцин, лизин, метионин, орнитин, фенилаланин, пролин, серин, таурин, треонин, триптофан, тирозин, валин)
Минералы и коэнзимы (кальция хлорид, магния сульфат, натрия хлорид, натрия фосфат, тиамин дифосфат, коэнзим А, флавинадениндинуклеотид, никотинамидадениндинуклеотид)
Нуклеиновые кислоты (аденозин фосфат, цитозин, гуанозин, тимин)
Пептиды (Олигопептид-29, Олигопептид-62, Ацетил Декапептид-3, Олигопептид-24, Олигопептид-51)

Показания:

Anti-aging терапия и профилактика инволюционных изменений кожи (коррекция овала лица, мелкие морщины, мимические морщины в периорбитальной области, мимические и статические морщины лба, кисетные морщины верхней губы и т. д.)
Постакне и другие рубцовые деформации кожи (атрофические рубцы пост-акне, пост-операционные рубцы, подготовка к шлифовке кожи)
Пролонгация действия ботулинотерапии и миорелаксация при резистентности к ботулинотерапии

Способ применения:

Препарат используется в качестве биоревитализанта.

Стандартный курс

3 процедуры через каждые 4 недели рекомендуются для достижения оптимального эффекта.
Затем 2-3 процедуры в течение года для поддержания эффекта

Интенсивный курс

6 процедур с интервалом в 2 недели и 5-6 процедур в течение года для оптимального поддержания результатов.

О производителе:

Уникальные препараты гаммы Revofil Aquashine для биоревитализации разработаны южно-корейским фармацевтическим концерном Caregen Co.LTD, находящимся в Сеуле. Компания была основана в 2001 году и занимается исследованиями и продажей космецевтики, фармацевтических препаратов, биомиметических пептидов и факторов роста, а также других сопутствующих товаров.

X2 0 решение. Уравнения онлайн. Тождественные преобразования уравнений

Цели:

Систематизировать и обобщить знания и умения по теме: Решения уравнений третьей и четвертой степени.
Углубить знания, выполнив ряд заданий, часть из которых не знакома или по своему типу, или способу решения.
Формирование интереса к математике через изучение новых глав математики, воспитание графической культуры через построение графиков уравнений.

Тип урока : комбинированный.

Оборудование: графопроектор.

Наглядность: таблица «Теорема Виета».

Ход урока

1. Устный счет

а) Чему равен остаток от деления многочлена р n (х) = а n х n + а n-1 х n-1 + … + а 1 х 1 + a 0 на двучлен х-а?

б) Сколько корней может иметь кубическое уравнение?

в) С помощью чего мы решаем уравнение третьей и четвертой степени?

г) Если b четное число в квадратном уравнение, то чему равен Д и х 1 ;х 2

2. Самостоятельная работа (в группах)

Составить уравнение, если известны корни (ответы к заданиям закодированы) Используется «Теорема Виета»

1 группа

Корни: х 1 = 1; х 2 = -2; х 3 = -3; х 4 = 6

Составить уравнение:

B=1 -2-3+6=2; b=-2

с=-2-3+6+6-12-18= -23; с= -23

d=6-12+36-18=12; d= -12

е=1(-2)(-3)6=36

х 4 — 2 х 3 — 23х 2 — 12 х + 36 = 0 (это уравнение решает потом 2 группа на доске)

Решение . Целые корни ищем среди делителей числа 36.

р = ±1;±2;±3;±4;±6…

р 4 (1)=1-2-23-12+36=0 Число 1 удовлетворяет уравнению, следовательно, =1 корень уравнения. По схеме Горнера

р 3 (x) = х 3 -х 2 -24x -36

р 3 (-2) = -8 -4 +48 -36=0, х 2 =-2

р 2 (x) = х 2 -3х -18=0

х 3 =-3, х 4 =6

Ответ: 1;-2;-3;6 сумма корней 2 (П)

2 группа

Корни: х 1 = -1; х 2 = х 3 =2; х 4 =5

Составить уравнение:

B=-1+2+2+5-8; b= -8

с=2(-1)+4+10-2-5+10=15; с=15

D=-4-10+20-10= -4; d=4

е=2(-1)2*5=-20;е=-20

8+15+4х-20=0 (это уравнение решает на доске 3 группа)

р = ±1;±2;±4;±5;±10;±20.

р 4 (1)=1-8+15+4-20=-8

р 4 (-1)=1+8+15-4-20=0

р 3 (x) = х 3 -9х 2 +24x -20

р 3 (2) = 8 -36+48 -20=0

р 2 (x) = х 2 -7х +10=0 х 1 =2; х 2 =5

Ответ: -1;2;2;5 сумма корней 8(Р)

3 группа

Корни: х 1 = -1; х 2 =1; х 3 =-2; х 4 =3

Составить уравнение:

В=-1+1-2+3=1;в=-1

с=-1+2-3-2+3-6=-7;с=-7

D=2+6-3-6=-1; d=1

е=-1*1*(-2)*3=6

х 4 — х 3 — 7х 2 + х + 6 = 0 (это уравнение решает потом на доске 4 группа)

Решение. Целые корни ищем среди делителей числа 6.

р = ±1;±2;±3;±6

р 4 (1)=1-1-7+1+6=0

р 3 (x) = х 3 — 7x -6

р 3 (-1) = -1+7-6=0

р 2 (x) = х 2 -х -6=0; х 1 =-2; х 2 =3

Ответ:-1;1;-2;3 Сумма корней 1(О)

4 группа

Корни: х 1 = -2; х 2 =-2; х 3 =-3; х 4 =-3

Составить уравнение:

B=-2-2-3+3=-4; b=4

с=4+6-6+6-6-9=-5; с=-5

D=-12+12+18+18=36; d=-36

е=-2*(-2)*(-3)*3=-36;е=-36

х 4 + 4х 3 – 5х 2 – 36х -36 = 0 (это уравнение решает потом 5 группа на доске)

Решение. Целые корни ищем среди делителей числа -36

р = ±1;±2;±3…

р(1)= 1 + 4-5-36-36 = -72

р 4 (-2) = 16 -32 -20 + 72 -36 = 0

р 3 (х) = х 3 +2х 2 -9х-18 = 0

р 3 (-2)= -8 + 8 + 18-18 = 0

р 2 (х) = х 2 -9 = 0; x=±3

Ответ: -2; -2; -3; 3 Сумма корней-4 (Ф)

5 группа

Корни: х 1 = -1; х 2 =-2; х 3 =-3; х 4 =-4

Составить уравнение

х 4 + 10х 3 + 35х 2 + 50х + 24 = 0 (это уравнение решает потом 6группа на доске)

Решение . Целые корни ищем среди делителей числа 24.

р = ±1;±2;±3

р 4 (-1) = 1 -10 + 35 -50 + 24 = 0

р 3 (х) = x- 3 + 9х 2 + 26x+ 24 = 0

p 3 (-2) = -8 + 36-52 + 24 = О

р 2 (х) = x 2 + 7x+ 12 = 0

Ответ:-1;-2;-3;-4 сумма-10 (И)

6 группа

Корни: х 1 = 1; х 2 = 1; х 3 = -3; х 4 = 8

Составить уравнение

B=1+1-3+8=7;b=-7

с=1 -3+8-3+8-24= -13

D=-3-24+8-24= -43; d=43

х 4 — 7х 3 — 13х 2 + 43 x — 24 = 0 (это уравнение решает потом 1 группа на доске)

Решение . Целые корни ищем среди делителей числа -24.

р 4 (1)=1-7-13+43-24=0

р 3 (1)=1-6-19+24=0

р 2 (x)= х 2 -5x — 24 = 0

х 3 =-3, х 4 =8

Ответ: 1;1;-3;8 сумма 7 (Л)

3. Решение уравнений с параметром

1. Решить уравнение х 3 + 3х 2 + mх — 15 = 0; если один из корней равен (-1)

Ответ записать в порядке возрастания

R=Р 3 (-1)=-1+3-m-15=0

х 3 + 3х 2 -13х — 15 = 0; -1+3+13-15=0

По условию х 1 = — 1; Д=1+15=16

Р 2 (х) = х 2 +2х-15 = 0

х 2 =-1-4 = -5;

х 3 =-1 + 4 = 3;

Ответ:- 1;-5; 3

В порядке возрастания: -5;-1;3. (Ь Н Ы)

2. Найти все корни многочлена х 3 — 3х 2 + ах — 2а + 6, если остатки от его деления на двучлены х-1 и х +2 равны.

Решение: R=Р 3 (1) = Р 3 (-2)

Р 3 (1) = 1-3 + а- 2а + 6 = 4-а

Р 3 (-2) = -8-12-2а-2а + 6 = -14-4а

x 3 -Зх 2 -6х + 12 + 6 = х 3 -Зх 2 -6х + 18

x 2 (x-3)-6(x-3) = 0

(х-3)(х 2 -6) = 0

Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из этих множителей равен нулю, а другой при этом имеет смысл. n} \)

7) a n > 1, если a > 1, n > 0

8) a n 1, n
9) a n > a m , если 0

В практике часто используются функции вида y = a x , где a — заданное положительное число, x — переменная. Такие функции называют показательными . Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \(a \neq 1\)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \(a \neq 1\), не имеет корней, если \(b \leq 0\), и имеет корень при любом b > 0.

3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 Это следует из свойств степени (8) и (9)

Построим графики показательных функций у = a x при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = a x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a x при 0 Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \(a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \(a \neq 1\) равны тогда и только тогда, когда равны их показатели. {x-2} = 1 \)
x — 2 = 0
Ответ х = 2

Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \(3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен.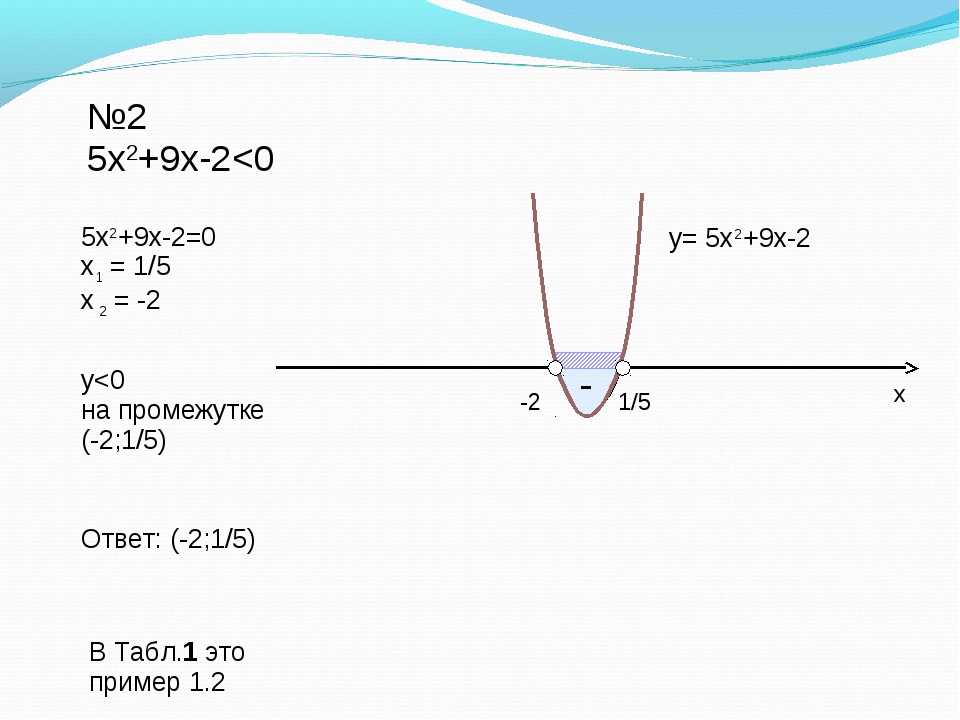 Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:
x 2 − 8x + 12 = 0;
5x 2 + 3x + 7 = 0;
x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня.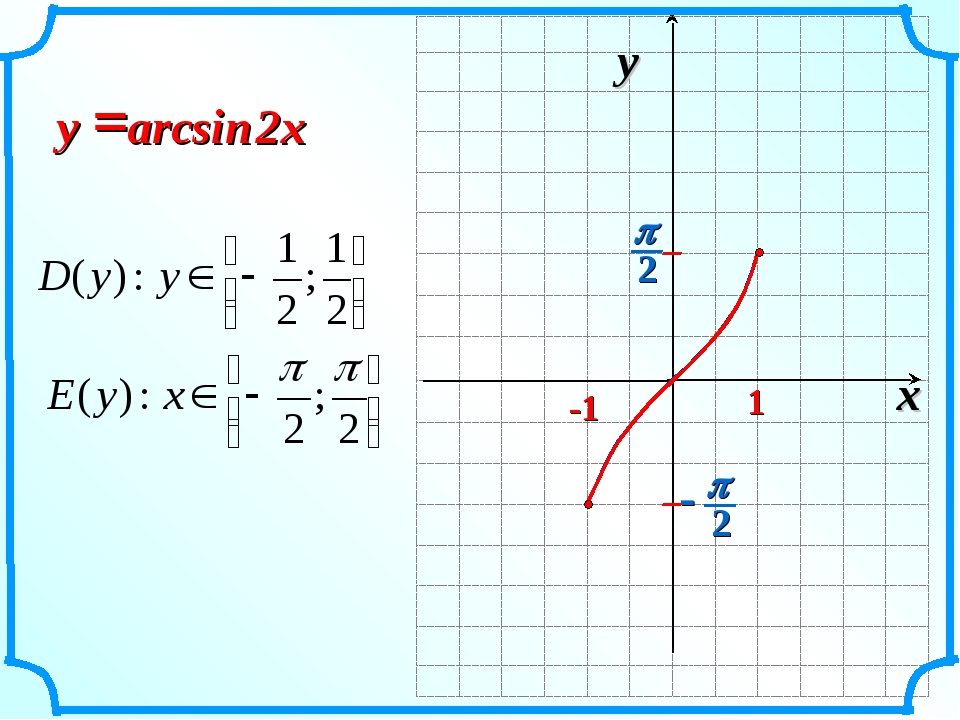 Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

x 2 − 2x − 3 = 0;
15 − 2x − x 2 = 0;
x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

x 2 + 9x = 0;
x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:
x 2 − 7x = 0;
5x 2 + 30 = 0;
4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

I. Линейные уравнения

II. Квадратные уравнения

ax 2 + bx + c = 0, a ≠ 0, иначе уравнение становится линейным

Корни квадратного уравнения можно вычислять различными способами, например:

Мы хорошо умеем решать квадратные уравнения. Многие уравнения более высоких степеней можно привести к квадратным.

III. Уравнения, приводимые к квадратным.

замена переменной: а) биквадратное уравнение ax 2n + bx n + c = 0, a ≠ 0, n ≥ 2

2) симметрическое уравнение 3 степени – уравнение вида

3) симметрическое уравнение 4 степени – уравнение вида

ax 4 + bx 3 + cx 2 + bx + a = 0, a ≠ 0, коэффициенты a b c b a или

ax 4 + bx 3 + cx 2 – bx + a = 0, a ≠ 0, коэффициенты a b c (–b) a

Т.к. x = 0 не является корнем уравнения, то возможно деление обеих частей уравнения на x 2 , тогда получаем: .

Произведя замену решаем квадратное уравнение a (t 2 – 2) + bt + c = 0

Например, решим уравнение x 4 – 2x 3 – x 2 – 2x + 1 = 0, делим обе части на x 2 ,

, после замены получаем уравнение t 2 – 2t – 3 = 0

– уравнение не имеет корней.

4) Уравнение вида (x – a )(x – b )(x – c )(x – d ) = Ax 2 , коэффициенты ab = cd

Например, (x + 2 )(x +3 )(x + 8 )(x + 12 ) = 4x 2 . Перемножив 1–4 и 2–3 скобки, получим (x 2 + 14x + 24)(x 2 +11x + 24) = 4x 2 , разделим обе части уравнения на x 2 , получим:

Имеем (t + 14)(t + 11) = 4.

5) Однородное уравнение 2 степени – уравнение вида Р(х,у) = 0, где Р(х,у) – многочлен, каждое слагаемое которого имеет степень 2.

Ответ: -2; -0,5; 0

IV. Все приведенные уравнения узнаваемы и типичны, а как быть с уравнениями произвольного вида?

Пусть дан многочлен P n (x ) = a n x n + a n-1 x n-1 + …+a 1 x + a 0 , где a n ≠ 0

Рассмотрим метод понижения степени уравнения.

Известно, что, если коэффициенты a являются целыми числами и a n = 1 , то целые корни уравнения P n (x ) = 0 находятся среди делителей свободного члена a 0 . Например, x 4 + 2x 3 – 2x 2 – 6x + 5 = 0, делителями числа 5 являются числа 5; –5; 1; –1. Тогда P 4 (1) = 0, т.е. x = 1 является корнем уравнения. Понизим степень уравнения P 4 (x ) = 0 с помощью деления “уголком” многочлена на множитель х –1, получаем

P 4 (x ) = (x – 1)(x 3 + 3x 2 + x – 5).

Аналогично, P 3 (1) = 0, тогда P 4 (x ) = (x – 1)(x – 1)(x 2 + 4x +5), т.е. уравнение P 4 (x) = 0 имеет корни x 1 = x 2 = 1. Покажем более короткое решение этого уравнения (с помощью схемы Горнера).

	1	2	–2	–6	5
1	1	3	1	–5	0
1	1	4	5	0

значит, x 1 = 1 значит, x 2 = 1.

Итак, (x – 1) 2 (x 2 + 4x + 5) = 0

Что мы делали? Понижали степень уравнения.

V. Рассмотрим симметрические уравнения 3 и 5 степени.

а) ax 3 + bx 2 + bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень уравнения до двух.

б) ax 5 + bx 4 + cx 3 + cx 2 + bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень уравнения до двух.

Например, покажем решение уравнения 2x 5 + 3x 4 – 5x 3 – 5x 2 + 3x + = 0

	2	3	–5	–5	3	2
–1	2	1	–6	1	2	0
1	2	3	–3	–2	0
1	2	5	2	0

x = –1

Получаем (x – 1) 2 (x + 1)(2x 2 + 5x + 2) = 0. Значит, корни уравнения: 1; 1; –1; –2; –0,5.

VI. Приведем список различных уравнений для решения в классе и дома.

Предлагаю читателю самому решить уравнения 1–7 и получить ответы…

для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.

3.Уравнения-следствия и равносильные преобразования уравнений

Объяснение и обоснование

1. Понятие уравнения и его корней. Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной x записывают так: f (x) = g (x).

Часто уравнения определяют короче — как равенство с переменной.

Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни (и обосновать, что других корней нет) или доказать, что корней нет.

Например, уравнение 2x = —1 имеет единственный корень x = -1, а уравнение | x | = —1 не имеет корней, поскольку значение | x | не может быть отрицательным числом.

2. Область допустимых значений (ОДЗ) уравнения. Если задано уравнение f (x) = g (x), то общая область определения для функций f (x) и g (x) называется областью допустимых значений этого уравнения. (Иногда используются также термины «область определения уравнения» или «множество допустимых значений уравнения».) Например, для уравнения х² = х областью допустимых значений являются все действительные числа. Это можно записать, например, так. ОДЗ: R, поскольку функции f (x) = x² и g (x) = x имеют области определения R.

Понятно, что каждый корень данного уравнения принадлежит как области определения функции f (x), так и области определения функции g (x) (иначе мы не сможем получить верное числовое равенство). Поэтому каждый корень уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет в некоторых случаях применить анализ ОДЗ уравнения при его решении.

Например, в уравнении л/x — 2 + \/1 — x = x функция g (x) = x определена при всех действительных значениях x, а функция f (x) = л/x — 2 + VT — x ко при условии, что под знаком квадратного корня будут стоять неотрицательные выражения. Следовательно, ОДЗ этого уравнения задается систе-

lx — 210, lx 12,

мой -! из которой получаем систему -! не имеющую решений.

[1 — x 10, [x < 1,

Таким образом, ОДЗ данного уравнения не содержит ни одного числа, и поэтому это уравнение не имеет корней.

Нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.

3. Методы решения уравнений. Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5—6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств;

6 класс. Математика. Никольский. Учебник. Ответы к стр. 122

Рациональные числа

Уравнения

Ответы к стр. 122

618. Является ли число 2 корнем уравнения:
а) x – 2 = 0; б) x + 4 = 0; в) 2x = 4;
г) 3x – 4 = x; д) x + 3 = 2x + 1; е) 3x + 4 = 6x – 2?

Подставим в уравнение вместо х число 2.
а) 2 – 2 = 0,
0 = 0 – является;

б) 2 + 4 = 0,
6 ≠ 0 – не является;

в) 2 • 2 = 4,
4 = 4 – является;

г) 3 • 2 – 4 = 2,
2 = 2 – является;

д) 2 + 3 = 2 • 2 + 1,
5 = 5 – является;

е) 3 • 2 + 4 = 6 • 2 – 2,
10 = 10 – является.

Решите уравнение (619-629):

619. а) х – 2 = 0; б) х + 4 = 0; в) 100 + х = 0; г) х – 5 = 6;
д) х + 2 = 5; е) х – 11 = -7; ж) 12 + х = 17; з) х + 7 = 7.

а) х – 2 = 0,
х = 0 + 2,
х = 2;

б) х + 4 = 0,
х = 0 – 4,
х = -4;

в) 100 + х = 0,
х = 0 – 100,
х = -100;

г) х – 5 = 6,
х = 6 + 5,
х = 11;

д) х + 2 = 5,
х = 5 – 2,
х = 3;

е) х – 11 = -7,
х = -7 + 11,
х = 4;

ж) 12 + х = 17,
х = 17 – 12,
х = 5;

з) х + 7 = 7,
х = 7 – 7,
х = 0.

620. а) 5 + x = 3; б) -7 + x = -2; в) x + 3 = -6;
г) 12 + x = -8; д) x + 18 = 18; е) -13 + x = -5;
ж) x – ¹/₅ = 2; з) x – 2 = ¹/₂; и) x – 4 = 1 ¹/₃.

а) 5 + x = 3,
x = 3 – 5,
x = -2;

б) -7 + x = -2,
x = -2 + 7,
x = 5;

в) x + 3 = -6,
x = -6 – 3,
x = -9;

г) 12 + x = -8,
x = -8 – 12,
x = -20;

д) x + 18 = 18,
x = 18 – 18,
x = 0;

е) -13 + x = -5,
x = -5 + 13,
x = 8;

ж) x – ¹/₅ = 2,
x = 2 + ¹/₅,
x = 2 ¹/₅;

з) x – 2 = ¹/₂,
x = ¹/₂ + 2,
x = 2 ¹/₂;

и) x – 4 = 1 ¹/₃,
x = 1 ¹/₃ + 4,
x = 5 ¹/₃.

621. а) x – ¹/₂ = ¹/₂; б) x – ¹/₃ = ¹/₄; в) x – ¹/₁₈ = ¹/₁₂;
г) x – 1 = – ¹/₃; д) ¹/₇ + x = 11; е) 1 ¹/₅ + x = 1;
ж) x – 6 ¹/₃ = -3 ²/₃; з) ⁷/₉ + x = 2 ¹/₂; и) x – 2 ¹/₂ = -1 ³/₅.

а) x – ¹/₂ = ¹/₂,
x = ¹/₂ + ¹/₂,
x = ²/₂,
х = 1;

б) x – ¹/₃ = ¹/₄,
x = ¹/₄ + ¹/₃,
x = ³⁺⁴/₁₂,
х = ⁷/₁₂;

в) x – ¹/₁₈ = ¹/₁₂,
x = ¹/₁₂ + ¹/₁₈,
x = ³⁺²/₃₆,
х = ⁵/₃₆;

г) x – 1 = – ¹/₃,
x = – ¹/₃ + 1,
x = ²/₃;

д) ¹/₇ + x = 11,
x = 11 – ¹/₇,
x = 10 ⁶/₇;

е) 1 ¹/₅ + x = 1,
x = 1 – 1 ¹/₅,
x = – ¹/₅;

ж) x – 6 ¹/₃ = -3 ²/₃,
x = -3 ²/₃ + 6 ¹/₃,
x = 2 ²/₃;

з) ⁷/₉ + x = 2 ¹/₂,
x = 2 ¹/₂ – ⁷/₉,
x = 2 ⁹/₁₈ – ¹⁴/₁₈,
х = 1 ²⁷/₁₈ – ¹⁴/₁₈,
х = 1 ¹³/₁₈;

и) x – 2 ¹/₂ = -1 ³/₅,
x = -1 ³/₅ + 2 ¹/₂,
x = -1 ⁶/₁₀ + 2 ⁵/₁₀,
х = 1 ¹⁵/₁₀ – 1 ⁶/₁₀,
х = ⁹/₁₀.

622. а) 2x = 4; б) 6x = 24; в) 7x = -14;
г) -5x = 100; д) -2x = -8; е) 12x = -36.

а) 2x = 4,
x = 4 : 2,
х = 2;

б) 6x = 24,
x = 24 : 6,
х = 4;

в) 7x = -14,
x = -14 : 7,
х = -2;

г) -5x = 100,
x = -100 : 5,
х = -20;

д) -2x = -8,
x = -8 : (-2),
х = 4;

е) 12x = -36,
x = -36 : 12,
х = -3.

623. а) 3x = 2; б) 6x = -7; в) -2x = -13; г) 2x = 0;
д) -5x = 0; е) –x = 2; ж) –x = 0; з) –x = -5.

а) 3x = 2,
x = ²/₃;

б) 6x = -7,
x = – ⁷/₆,
х = -1 ¹/₆;

в) -2x = -13,
x = ^-13/_-2,
х = 6 ¹/₂;

г) 2x = 0,
x = 0 : 2,
х = 0;

д) -5x = 0,
x = 0 : (-5),
х = 0;

е) –x = 2,
x = 2 : (-1),
х = -2;

ж) –x = 0,
x = 0 : (-1),
х = 0;

з) –x = -5,
x = -5 : (-1),
х = 5.

624. а) 2x = ¹/₂; б) 3x = – ¹/₄; в) -2x = ¹/₄;
г) ¹/₂x = 3; д) ³/₄x = 1; е) – ¹/₃x = -3;
ж) – ²/₇x = 0; з) -4x = ⁸/₂₅; и) 2x = 1 ¹/₃.

а) 2x = ¹/₂,
x = ¹/₂ : 2,
х = ¹/₂ • ¹/₂,
х = ¹/₄;

б) 3x = – ¹/₄,
x = – ¹/₄: 3,
х = – ¹/₄• ¹/₃,
х = – ¹/₁₂;

в) -2x = ¹/₄,
x = ¹/₄: (-2),
х = ¹/₄ • (- ¹/₂),
х = – ¹/₈;

г) ¹/₂x = 3,
x = 3 : 12,
х = 3 • 2,
х = 6;

д) ³/₄x = 1,
x = 1 : ³/₄,
х = 1 • ⁴/₃,
х = ⁴/₃,
х = 1 ¹/₃;

е) – ¹/₃x = -3,
x = -3 : (- ¹/₃),
х = -3 • (- ³/₁),
х = ⁹/₁,
х = 9;

ж) – ²/₇x = 0,
x = 0 : (- ²/₇),
х = 0;

з) -4x = ⁸/₂₅,
x = ⁸/₂₅: (-4),
х = ⁸/₂₅ • (- ¹/₄),
х = – ^2•1/_25•1,
х = – ²/₂₅;

и) 2x = 1 ¹/₃,
x = 1 ¹/₃: 2,
х = ⁴/₃ • ¹/₂,
х = ^2•1/_3•1,
х = ²/₃.

625. а) 2x – 6 = 0; б) 12 + 3x = 0; в) –x + 7 = 0; г) 15 – 3x = 0;
д) 3x + 1 = 7; е) 5 – 2x = 1; ж) 5x – 2 = 1; з) -5x – 2 = -12.

а) 2x – 6 = 0,
2x = 0 + 6,
х = 6 : 2,
х = 3;

б) 12 + 3x = 0,
3x = 0 – 12,
х = -12 : 3,
х = -4;

в) –x + 7 = 0,
–x = 0 – 7,
х = -7 : (-1),
х = 7;

г) 15 – 3x = 0,
-3x = 0 – 15,
х = -15 : (- 3),
х = 5;

д) 3x + 1 = 7,
3x = 7 – 1,
х = 6 : 3,
х = 2;

е) 5 – 2x = 1,
-2x = 1 – 5,
-2х = -4,
x = -4 : (-2),
х = 2;

ж) 5x – 2 = 1,
5x = 1 + 2,
x = ³/₅;

з) -5x – 2 = -12,
-5x = -12 + 2,
х = -10 : (-5),
х = 2.

626. а) 3x + 2x = 10; б) 5x + x = 6; в) 4x + 2x – 7 = 5;
г) 7x + x + 3 = 19; д) 5 = 4x – 3x; е) 8 = 3x – x;
ж) 3x – 1 = 2x; з) 3x – 6 = x.

а) 3x + 2x = 10,
(3 + 2)х = 10,
5x = 10,
x = 10 : 5,
х = 2;

б) 5x + x = 6,
(5 + 1)х = 6,
6x = 6,
x = 6 : 6,
х = 1;

в) 4x + 2x – 7 = 5,
(4 + 2)х = 5 + 7,
6x = 12,
x = 12 : 6,
х = 2;

г) 7x + x + 3 = 19,
(7 + 1)х = 19 – 3,
8x = 16,
x = 16 : 8,
х = 2;

д) 5 = 4x – 3x,
5 = (4 – 3)х,
x = 5;

е) 8 = 3x – x,
8 = (3 – 1)х,
8 = 2x,
x = 8 : 2,
х = 4;

ж) 3x – 1 = 2x,
3x – 2x = 1,
(3 – 2)х = 1,
x = 1;

з) 3x – 6 = x,
3x – x = 6,
(3 – 1)х = 6,
2x = 6,
x = 6 : 2,
х = 3.

627. а) x + 3 = 3x – 7; б) 3 – x = 1 + x; в) 7x + 2 = 3x – 10;
г) 5x – 8 = 3x – 8; д) ¹/₂x – 3 = 2 – ¹/₃x; е) 5x – 2 ¹/₄ = ¹/₂x;
ж) ²/₅x – 1 = ³/₄x – 6; з) 2x – ³/₅ = ³/₄x – ¹/₂.

а) x + 3 = 3x – 7,
3 + 7 = 3x – x,
10 = (3 – 1)х,
10 = 2х,
х = 10 : 2,
х = 5;

б) 3 – x = 1 + x,
3 – 1 = x + x,
2 = (1 + 1)х,
2 = 2х,
х = 2 : 2,
х = 1;

в) 7x + 2 = 3x – 10,
7x – 3x = -10 – 2,
(7 – 3)х = -12,
4x = -12,
x = -12 : 4,
x = -3;

г) 5x – 8 = 3x – 8,
5x – 3x = -8 + 8,
(5 – 3)х = 0,
2х = 0,
х = 0 : 2,
х = 0;

д) ¹/₂x – 3 = 2 – ¹/₃x,
¹/₂x + ¹/₃x = 2 + 3,
³/₆x + ²/₆x = 5,
⁵/₆x = 5,
x = 5 : ⁵/₆,
х = 5 • ⁶/₅,
х = 6;

е) 5x – 2 ¹/₄ = ¹/₂x,
5x – ¹/₂x = 2 ¹/₄,
(5 – ¹/₂)х = 2 ¹/₄,
4 ¹/₂x = 2 ¹/₄,
x = 2 ¹/₄: 4 ¹/₂,
х = ⁹/₄ • ²/₉,
х = ¹/₂;

ж) ²/₅x – 1 = ³/₄x – 6,
²/₅x – ³/₄x = -6 + 1,
(⁸/₂₀ – ¹⁵/₂₀)х = -5,
– ⁷/₂₀х = -5,
х = -5 : (- ⁷/₂₀),
х = -5 • (- ²⁰/₇),
х = ¹⁰⁰/₇,
х = 14 ²/₇;

з) 2x – ³/₅ = ³/₄x – ¹/₂,
2x – ³/₄x = – ¹/₂ + ³/₅,
(2 – ³/₄)x = – ⁵/₁₀ + ⁶/₁₀,
1 ¹/₄x = ¹/₁₀,
х = ¹/₁₀: ⁵/₄,
х = ¹/₁₀ • ⁴/₅,
х = ^1•2/_5•5,
х = ²/₂₅.

628. а) 2(x – 5) = 9; б) 12 + 3(x – 1) = 0; в) -(x + 8) = 3;
г) 1 – 5(2 – 3x) = 6; д) 7 – 3(x + 1) = 6; е) 5 – 2(3 – x) = 11;
ж) 2x – (7 + x) = 2; з) -3 – 3(3 – 2x) = 1.

а) 2(x – 5) = 9,
2x – 10 = 9,
2x = 9 + 10,
x = ¹⁹/₂,
х = 9 ¹/₂;

б) 12 + 3(x – 1) = 0,
12 + 3x – 3 = 0,
3x = 0 – 12 + 3,
x = -9 : 3,
х = -3;

в) -(x + 8) = 3,
–x – 8 = 3,
–x = 3 + 8,
x = 11 : (-1),
х = -11;

г) 1 – 5(2 – 3x) = 6,
1 – 10 + 15x = 6,
15x = 6 – 1 + 10,
x = 15 : 15,
х = 1;

д) 7 – 3(x + 1) = 6,
7 – 3x – 3 = 6,
-3x = 6 – 7 + 3,
x = 2 : (-3),
х = – ²/₃;

е) 5 – 2(3 – x) = 11,
5 – 6 + 2x = 11,
2x = 11 – 5 + 6,
x = 12 : 2,
х = 6;

ж) 2x – (7 + x) = 2,
2x – 7 – x = 2,
(2 – 1)x = 2 + 7,
х = 9;

з) -3 – 3(3 – 2x) = 1,
-3 – 9 + 6x = 1,
6x = 1 + 3 + 9,
x = ¹³/₆,
х = 2 ¹/₆.

Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.

Математика. 6 класс

Понравилось? Оцени!

Различные методы решения уравнений

I. Линейные уравнения

II. Квадратные уравнения

ax² + bx + c = 0, a ≠ 0, иначе уравнение становится линейным

Корни квадратного уравнения можно вычислять различными способами, например:

III. Уравнения, приводимые к квадратным.

замена переменной: а) биквадратное уравнение ax²ⁿ+ bxⁿ + c = 0, a ≠ 0, n ≥ 2

2) симметрическое уравнение 3 степени – уравнение вида

3) симметрическое уравнение 4 степени – уравнение вида

ax⁴ + bx³ + cx² + bx + a = 0, a ≠ 0, коэффициенты a b c b a или

ax⁴ + bx³ + cx² – bx + a = 0, a ≠ 0, коэффициенты a b c (–b) a

Т.к. x = 0 не является корнем уравнения, то возможно деление обеих частей уравнения на x², тогда получаем: .

Произведя замену решаем квадратное уравнение a(t² – 2) + bt + c = 0

Например, решим уравнение x⁴ – 2x³ – x² – 2x + 1 = 0, делим обе части на x²,

, после замены получаем уравнение t² – 2t – 3 = 0

– уравнение не имеет корней.

Ответ:

4) Уравнение вида (x – a)(x – b)(x – c)(x – d) = Ax², коэффициенты ab = cd

Например, (x + 2)(x +3)(x + 8)(x + 12) = 4x². Перемножив 1–4 и 2–3 скобки, получим (x² + 14x + 24)(x² +11x + 24) = 4x², разделим обе части уравнения на x², получим:

имеем (t + 14)(t + 11 ) = 4.

Ответ: -2; -0,5; 0

IV. Все приведенные уравнения узнаваемы и типичны, а как быть с уравнениями произвольного вида?

Пусть дан многочлен P_n(x) = a_nxⁿ + a_n-1x^n-1 + …+a₁x + a₀ , где a_n≠ 0

Рассмотрим метод понижения степени уравнения.

Известно, что, если коэффициенты a являются целыми числами и a_n = 1 , то целые корни уравнения P_n(x) = 0 находятся среди делителей свободного члена a₀. Например, x⁴+ 2x³ – 2x² – 6x + 5 = 0, делителями числа 5 являются числа 5; –5; 1; –1. Тогда P₄(1) = 0, т.е. x = 1 является корнем уравнения. Понизим степень уравнения P₄(x) = 0 с помощью деления “уголком” многочлена на множитель х –1, получаем

P₄(x) = (x – 1)(x³ + 3x² + x – 5).

Аналогично, P₃(1) = 0, тогда P₄(x) = (x – 1)(x – 1)(x² + 4x +5), т.е. уравнение P₄(x) = 0 имеет корни x₁ = x₂ = 1. Покажем более короткое решение этого уравнения (с помощью схемы Горнера).

	1	2	–2	–6	5
1	1	3	1	–5	0
1	1	4	5	0

значит, x₁ = 1 значит, x₂ = 1.

Итак, (x – 1)²(x² + 4x + 5) = 0

Что мы делали? Понижали степень уравнения.

V. Рассмотрим симметрические уравнения 3 и 5 степени.

а) ax³ + bx² + bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень уравнения до двух.

б) ax⁵+ bx⁴ + cx³ + cx²+ bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень уравнения до двух.

Например, покажем решение уравнения 2x⁵ + 3x⁴ – 5x³– 5x²+ 3x + = 0

	2	3	–5	–5	3	2
–1	2	1	–6	1	2	0
1	2	3	–3	–2	0
1	2	5	2	0

x = –1

x = 1

Получаем (x – 1)²(x + 1)(2x² + 5x + 2) = 0. Значит, корни уравнения: 1; 1; –1; –2; –0,5.

VI. Приведем список различных уравнений для решения в классе и дома.

Предлагаю читателю самому решить уравнения 1–7 и получить ответы…

3 6 Решить для? cos (x) = 1/2 7 Решить относительно x sin (x) = — 1/2 8 Преобразование из градусов в радианы 225 9 Решить для? cos (x) = (квадратный корень из 2) / 2 10 Решить относительно x cos (x) = (квадратный корень из 3) / 2 11 Решить относительно x sin (x) = (квадратный корень из 3) / 2 12 График г (x) = 3/4 * корень пятой степени x 13 Найдите центр и радиус х ^ 2 + у ^ 2 = 9 14 Преобразование из градусов в радианы 120 градусов 15 Преобразование из градусов в радианы 180 16 Найдите точное значение коричневый (195) 17 Найдите степень е (х) = 2x ^ 2 (x-1) (x + 2) ^ 3 (x ^ 2 + 1) ^ 2 18 Решить для? тангенс (x) = квадратный корень из 3 19 Решить для? sin (x) = (квадратный корень из 2) / 2 20 Найдите центр и радиус х ^ 2 + у ^ 2 = 25 21 Найдите центр и радиус х ^ 2 + у ^ 2 = 4 22 Решить относительно x 2cos (x) -1 = 0 23 Решить относительно x 6x ^ 2 + 12x + 7 = 0 24 Найдите домен х ^ 2 25 Найдите домен е (х) = х ^ 2 26 Преобразование из градусов в радианы 330 градусов 27 Разверните логарифмическое выражение натуральный логарифм (x ^ 4 (x-4) ^ 2) / (квадратный корень из x ^ 2 + 1) 28 Упростить ((3x ^ 2) ^ 2y ^ 4) / (3y ^ 2) 29 Упростить (csc (x) детская кроватка (x)) / (sec (x)) 30 Решить для? тангенс (х) = 0 31 Решить относительно x х ^ 4-3x ^ 3-х ^ 2 + 3x = 0 32 Решить относительно x cos (x) = sin (x) 33 Найдите точки пересечения x и y х ^ 2 + у ^ 2 + 6х-6у-46 = 0 34 Решить относительно x квадратный корень из x + 30 = x 35 Упростить детская кроватка (x) коричневый (x) 36 Найдите домен у = х ^ 2 37 Найдите домен квадратный корень из x ^ 2-4 38 Найдите точное значение грех (255) 39 Оценить, основание журнала 27 из 36 40 преобразовать из радианов в градусы 2п 41 Упростить (F (x + h) -Fx) / час 42 Решить для? 2sin (x) ^ 2-3sin (x) + 1 = 0 43 Решить относительно x tan (x) + квадратный корень из 3 = 0 44 Решить относительно x грех (2х) + соз (х) = 0 45 Упростить (1-соз (х)) (1 + соз (х)) 46 Найдите домен х ^ 4 47 Решить для? 2sin (x) + 1 = 0 48 Решить относительно x х ^ 4-4x ^ 3-х ^ 2 + 4x = 0 49 Упростить 9 / (х ^ 2) + 9 / (х ^ 3) 50 Упростить (детская кроватка (x)) / (csc (x)) 51 Упростить 1 / (с ^ (3/5)) 52 Упростить квадратный корень из 9a ^ 3 + квадратный корень из 53 Найдите точное значение желто-коричневый (285) 54 Найдите точное значение cos (255) 55 Преобразовать в логарифмическую форму 12 ^ (x / 6) = 18 56 Расширьте логарифмическое выражение (основание 27 из 36) (основание 36 из 49) (основание 49 из 81) 57 Недвижимость х ^ 2 = 12 лет 58 Недвижимость х ^ 2 + у ^ 2 = 25 59 График f (x) = — натуральный логарифм x-1 + 3 60 Найдите значение, используя единичную окружность арксин (-1/2) 61 Найдите домен квадратный корень из 36-4x ^ 2 62 Упростить (корень квадратный из x-5) ^ 2 + 3 63 Решить относительно x х ^ 4-2x ^ 3-х ^ 2 + 2x = 0 64 Решить относительно x у = (5-х) / (7х + 11) 65 Решить относительно x х ^ 5-5x ^ 2 = 0 66 Решить относительно x cos (2x) = (квадратный корень из 2) / 2 67 График г = 3 68 График f (x) = — логарифм по основанию 3 из x-1 + 3 69 Найдите корни (нули) f (x) = 3x ^ 3-12x ^ 2-15x 70 Найдите степень 2x ^ 2 (x-1) (x + 2) ^ 3 (x ^ 2 + 1) ^ 2 71 Решить относительно x квадратный корень из x + 4 + квадратный корень из x-1 = 5 72 Решить для? cos (2x) = — 1/2 73 Решить относительно x логарифм по основанию x 16 = 4 74 Упростить е ^ х 75 Упростить (соз (х)) / (1-грех (х)) + (1-грех (х)) / (соз (х)) 76 Упростить сек (x) sin (x) 77 Упростить кубический корень из 24 кубический корень из 18 78 Найдите домен квадратный корень из 16-x ^ 2 79 Найдите домен квадратный корень из 1-x 80 Найдите домен у = грех (х) 81 Упростить корень квадратный из 25x ^ 2 + 25 82 Определить, нечетно ли, четно или нет е (х) = х ^ 3 83 Найдите домен и диапазон f (x) = квадратный корень из x + 3 84 Недвижимость х ^ 2 = 4г 85 Недвижимость (x ^ 2) / 25 + (y ^ 2) / 9 = 1 86 Найдите точное значение cos (-210) 87 Упростить кубический корень из 54x ^ 17 88 Упростить квадратный корень из квадратного корня 256x ^ 4 89 Найдите домен е (х) = 3 / (х ^ 2-2x-15) 90 Найдите домен квадратный корень из 4-x ^ 2 91 Найдите домен квадратный корень из x ^ 2-9 92 Найдите домен е (х) = х ^ 3 93 Решить относительно x е ^ х-6е ^ (- х) -1 = 0 94 Решить относительно x 6 ^ (5x) = 3000 95 Решить относительно x 4cos (x-1) ^ 2 = 0 96 Решить относительно x 3x + 2 = (5x-11) / (8лет) 97 Решить для? грех (2x) = — 1/2 98 Решить относительно x (2x-1) / (x + 2) = 4/5 99 Решить относительно x сек (4x) = 2 100 Решите для n (4n + 8) / (n ^ 2 + n-72) + 8 / (n ^ 2 + n-72) = 1 / (n + 9)

Упростить 1 / x-1-2 / x ^ 2 = 0 Tiger Algebra Solver

Пошаговое решение:

Шаг 1:

 2
 Упростить ——
            x ²

Уравнение в конце шага 1:

 1 2
  (- - 1) - —— = 0
   x x ²

Шаг 2:

 1
 Упростить -
            Икс

Уравнение в конце шага 2:

 1 2
  (- - 1) - —— = 0
   x x ²

Шаг 3:

Переписывание целого как эквивалентной дроби:

3.1 Вычитание целого из дроби

Перепишем целое как дробь, используя x в качестве знаменателя:

 1 1 • x
    1 = - = —————
         1 х

Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое

Общий знаменатель: Эквивалентная дробь и другая дробь, участвующие в вычислении, имеют один и тот же знаменатель

   Сложение дробей с общим знаменателем: 
    3.2 Сложение двух эквивалентных дробей 
 Сложите две эквивалентные дроби, которые теперь имеют общий знаменатель 
  Объедините числители вместе, сложите сумму или разность над общим знаменателем, затем уменьшите до наименьших членов, если возможно: 
  1 - (x) 1 - х
 знак равно
    х х
 
 Уравнение в конце шага 3: 
 (1 - x) 2
  ——————— - —— = 0
     x x ² 
 Шаг 4: 
  Вычисление наименьшего общего кратного: 
  4.1 Найдите наименьшее общее кратное 
  Левый знаменатель: x 
  Правый знаменатель: x ² 
 
   Сколько раз каждый алгебраический множитель 
 появляется при факторизации:     Алгебраический фактор 
  Левый 
 Знаменатель   Правый 
 Знаменатель   НОК = Макс 
 {Левый, Правый}  
   x   1   2   2  
 
 
  
 
 909 9 Множественный 909 
  Расчет множителей: 
  4.2 Вычислить множители для двух дробей 
  Обозначить наименьшее общее кратное LCM 
 Обозначить левый множитель Left_M 
 Обозначить правый множитель Right_M 
 Обозначить левый знаменатель L_Deno 
 Обозначить правый множитель R_Deno 
 = LCM  Left_M L_Deno = x 
  Right_M = LCM / R_Deno = 1 
  Получение эквивалентных дробей: 
    4.3 Перепишите две дроби в эквивалентные дроби 
  Две дроби называются эквивалентными, если они имеют одинаковое числовое значение.
  Например: 1/2 и 2/4 эквивалентны, y / (y + 1) ² и (y ² + y) / (y + 1) ³ также эквивалентны. 
  Чтобы вычислить эквивалентную дробь, умножьте числитель каждой дроби на соответствующий ей множитель. 
  L. Mult. • L. Num. (1-х) • х
   знак равно
         L.C.M x ²
   R. Mult. • R. Num. 2
   знак равно
         L.C.M x ² 
 Сложение дробей с общим знаменателем: 
  4.4 Сложение двух эквивалентных дробей 
 
  (1-x) • x - (2) -x ² + x - 2
 знак равно
       x ² x ² 
 Шаг 5: 
  Вытягивание как термины: 
   5.1 Вытягивание как факторы: 
  -x ² + x — 2 = -1 • (x ² — x + 2) 
 
   Попытка разложить на множители путем разделения среднего члена 
   5.2 Факторинг x ² — x + 2 
  Первый член x ², его коэффициент равен 1. 
 Средний член, -x, его коэффициент -1. 
 Последний член, «константа», равен +2 
  Шаг-1: Умножьте коэффициент первого члена на константу 1 • 2 = 2 
  Шаг-2: Найдите два множителя 2, сумма которых равна коэффициенту среднего члена, который равен -1. 
 
 — 900      -2   +  -1   =  -3   
    -1   +  -2   = 
    1   +   2   =   3   
     2   +   1   =   3  90 900 два таких фактора: можно найти !! 
 Вывод: трехчлен не может быть разложен на множители 
   Уравнение в конце шага 5: 
   -x ² + x - 2
  ——————————— = 0
      x ² 
 Шаг 6: 
  Когда дробь равна нулю: 
   6.1 Когда дробь равна нулю ... 
 Если дробь равна нулю, ее числитель, часть, которая находится над чертой дроби, должна быть равна нулю.
 Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
 Вот как:
 -x ² + x-2
  ——————— • x ² = 0 • x ²
    x ² 
 Теперь, с левой стороны, x ² отменяет знаменатель, в то время как с правой стороны ноль, умноженный на что-либо, по-прежнему равно нулю.
 Уравнение теперь принимает форму: 
 -x ² + x-2 = 0
   Парабола, поиск вершины: 
   6.2 Найдите вершину y = -x ² + x-2 
  Параболы имеют наивысшую или низшую точку, называемую Вершиной. Наша парабола открывается вниз и, соответственно, имеет наивысшую точку (также известную как абсолютный максимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, -1, отрицателен (меньше нуля). 
  Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину.Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения. 
  Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
  Для любой параболы Ax ² + Bx + C координата x вершины задается как -B / (2A). В нашем случае координата x равна 0,5000 
  Подставив в формулу параболы 0,5000 для x, мы можем вычислить координату y: 
 y = -1,0 * 0,50 * 0,50 + 1,0 * 0,50 — 2,0 
 или y = -1,750 
   Парабола, графическая вершина и пересечения по оси X: 
  Корневой график для: y = -x ² + x-2 
 Ось симметрии (пунктирная линия) {x} = {0.50} 
 Vertex at {x, y} = { 0.50, -1.75} 
 Функция не имеет действительных корней 
  Решите квадратное уравнение, заполнив квадрат 
  6.3 Решение -x ² + x-2 = 0, заполнив квадрат. 
  Умножьте обе части уравнения на (-1), чтобы получить положительный коэффициент для первого члена: 
 x ² -x + 2 = 0 Вычтите 2 из обеих частей уравнения: 
 x ² -x = -2 
  А теперь хитрый момент: возьмите коэффициент при x, равный 1, разделите его на два, получив 1/2, и возведите его в квадрат, получив 1/4 
  Добавьте 1/4 к обеим сторонам уравнения: 
 В правой части имеем: 
 -2 + 1/4 или, (-2/1) + (1/4) 
 Общий знаменатель двух дробей равен 4 Сложение (-8/4) + (1 / 4) дает -7/4 
 Таким образом, прибавляя к обеим сторонам, мы, наконец, получаем: 
 x ² -x + (1/4) = -7/4 
  Добавление 1/4 завершило левую часть в виде идеального квадрата. : 
 x ² -x + (1/4) = 
 (x- (1/2)) • (x- (1/2)) = 
 (x- (1/2)) ² 
 Вещи которые равны одному и тому же, также равны друг другу.Поскольку 
 x ² -x + (1/4) = -7/4 и 
 x ² -x + (1/4) = (x- (1/2)) ² 
, то согласно закон транзитивности, 
 (x- (1/2)) ² = -7/4 
  Мы будем называть это уравнение уравнением. # 6.3.1 
  Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны. 
  Обратите внимание, что квадратный корень из 
 (x- (1/2)) ² равен 
 (x- (1/2)) ^2/2 = 
 (x- (1/2)) ¹ = 
 x- (1/2) 
  Теперь, применяя принцип квадратного корня к уравнению.# 6.3.1 получаем: 
 x- (1/2) = √ -7/4 
  Добавьте 1/2 к обеим сторонам, чтобы получить: 
 x = 1/2 + √ -7/4 
 В математике, i называется мнимой единицей. Он удовлетворяет i ² = -1. Оба i и -i являются квадратными корнями из -1 
  Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное 
 x ² — x + 2 = 0 
 имеет два решения: 
 x = 1/2 + √ 7/4 • i 
 или 
 x = 1/2 — √ 7/4 • i 
  Обратите внимание, что √ 7/4 можно записать как 
 √ 7 / √ 4, что равно √ 7/2 
 
   Решите квадратное уравнение через квадратную формулу 
    6.4 Решение -x ² + x-2 = 0 по квадратичной формуле. 
  Согласно квадратичной формуле, x, решение для Ax ² + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как: 
   
 — B ± √ B ² -4AC 
 x = ———————— 
 2A 
  В нашем случае A = -1 
 B = 1 
 C = -2 
  Соответственно B ² — 4AC = 
 1 — 8 = 
 -7 
  Применение формулы корней квадратного уравнения: 
  -1 ± √ -7 
 x = ————— 
 -2 
  В наборе действительных чисел отрицательные числа не имеют квадратных корней.Был изобретен новый набор чисел, названный комплексным, чтобы отрицательные числа имели квадратный корень. Эти числа записываются (a + b * i) 
  Оба i и -i являются квадратными корнями из минус 1 
  Соответственно √ -7 = 
 √ 7 • (-1) = 
 √ 7 • √ -1 = 
 ± √ 7 • i 
  √ 7, округленное до 4 десятичных цифр, составляет 2,6458 
 Итак, теперь мы смотрим на: 
 x = (-1 ± 2,646 i) / -2 
  Два мнимых решения: 
 
  x = (- 1 + √-7) / - 2 = (1-i√ 7) / 2 = 0.5000 + 1.3229i
или: 
 x = (- 1-√-7) / - 2 = (1 + i√ 7) / 2 = 0,5000–1,3229i
 
 
 Было найдено два решения: 
 x = (- 1-√-7) / — 2 = (1 + i√ 7) / 2 = 0.5000-1.3229i
 x = (- 1 + √-7 ) / — 2 = (1-i√ 7) / 2 = 0,5000 + 1,3229i
 Ввод математических задач на этом сайте 
 Быстро! Мне нужна помощь с:
 Выберите элемент справки по математике … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesLines Theotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансовМатематика, Практика полиномов по математике, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание чисел Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они из себя представляют, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, РазделениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Прямоугольные треугольники, ветряк, фигура
 Вычислить sin (x-1) / (x ^ 2 -1), когда предел x стремится к 1 
 Угол прямоугольного треугольника выражается как $ x-1 $.2-1} $ $ = $ $ \ Large \ displaystyle \ lim_ {x \ to 1} \ normalsize \ dfrac {\ sin (x-1)} {(x-1) (x + 1)} $
 Шаг: 2 
 Разделите соотношение функций как два множителя.
 $ = \ Large \ displaystyle \ lim_ {x \ to 1} \ normalsize \ Bigg [\ dfrac {\ sin (x-1)} {(x-1)} \ times \ dfrac {1} {(x + 1 )} \ Bigg] $
 $ = \ Large \ displaystyle \ lim_ {x \ to 1} \ normalsize \ Bigg [\ dfrac {\ sin (x-1)} {(x-1)} \ Bigg] \ times \ Bigg [\ dfrac {1 } {(x + 1)} \ Bigg]
 долларов США Шаг: 3 
 Примените ограничение к обеим функциям умножения правилом произведения.
 $ = \ Large \ displaystyle \ lim_ {x \ to 1} \ normalsize \ Bigg [\ dfrac {\ sin (x-1)} {(x-1)} \ Bigg] $ $ \ times $ $ \ Large \ displaystyle \ lim_ {x \ to 1} \ normalsize \ Bigg [\ dfrac {1} {(x + 1)} \ Bigg] $
 Шаг: 4 
 Первый множитель представляет отношение синуса угла к углу, и это то же самое, что предел x стремится к правилу 0 sinx / x. Согласно этому тождеству отношение синуса угла к углу равно единице, когда $ x $ приближается к нулю. Итак, попробуем скорректировать первый множитель.
 Если $ x $ стремится к 1 $, то $ x-1 $ стремится к 0 $. Итак, измените предельное значение $ x \ to 1 $ на $ x-1 \ на 0 $, но только для первой функции умножения.
 $ = \ Large \ displaystyle \ lim_ {x-1 \ to 0} \ normalsize \ Bigg [\ dfrac {\ sin (x-1)} {(x-1)} \ Bigg] $ $ \ times $ $ \ Большой \ displaystyle \ lim_ {x \ to 1} \ normalsize \ Bigg [\ dfrac {1} {(x + 1)} \ Bigg] $
 Следовательно, значение первого множителя составляет $ 1 $, и подставьте $ x = 1 $ во второй множитель, чтобы получить требуемое решение.2 -1} = \ dfrac {1} {2}
 долларов США Купите стальную квадратную трубу онлайн! 
  Т11218   1/2 X 1/2 X 18 GA (стена 0,049)  
 A513 Квадратная стальная труба
 Т11218
  1/2 X 1/2 X 18 GA (.049 стенка)  
 A513 Квадратная стальная труба
 0,31 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  0,31 фунта / фут
 Добавить в корзину    Т11216   1/2 X 1/2 X 16 GA (.065 стена)  
 A513 Квадратная стальная труба
 Т11216
  1/2 X 1/2 X 16 GA (стена 0,065)  
 A513 Квадратная стальная труба
 0,39 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  0.39 фунтов / фут
 Добавить в корзину    Т15816   5/8 x 5/8 x 16GA (стена 0,065)  
 A513 Квадратная стальная труба
 T15816
  5/8 x 5/8 x 16GA (.065 стенка)  
 A513 Квадратная стальная труба
 0,50 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  0,50 фунта / фут
 Добавить в корзину    Т13416   3/4 X 3/4 X 16 GA (.065 стена)  
 A513 Квадратная стальная труба
 T13416
  3/4 X 3/4 X 16 GA (стена 0,065)  
 A513 Квадратная стальная труба
 0,60 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  0.60 фунтов / фут
 Добавить в корзину    Т13414   3/4 X 3/4 X 14 GA (стена 0,083)  
 A513 Квадратная стальная труба
 T13414
  3/4 X 3/4 X 14 GA (.083 стенка)  
 A513 Квадратная стальная труба
 0,75 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  0,75 фунта / фут
 Добавить в корзину    Т13411   3/4 X 3/4 X 11 GA (.120 стенка)  
 A513 Квадратная стальная труба
 T13411
  3/4 X 3/4 X 11 GA (стенка 0,120)  
 A513 Квадратная стальная труба
 1,03 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  1.03 фунт / фут
 Добавить в корзину    Т17816   7/8 X 7/8 X 16GA (стена 0,065)  
 A513 Квадратная стальная труба
 T17816
  7/8 X 7/8 X 16GA (.065 стенка)  
 A513 Квадратная стальная труба
 0,72 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  0,72 фунта / фут
 Добавить в корзину    Т11116   1 X 1 X 16GA (.065 стена)  
 A513 Квадратная стальная труба
 Т11116
  1 X 1 X 16GA (стена 0,065)  
 A513 Квадратная стальная труба
 0,82 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  0.82 фунт / фут
 Добавить в корзину    Т11114   1 X 1 X 14 GA (стена 0,083)  
 A513 Квадратная стальная труба
 Т11114
  1 X 1 X 14 GA (.083 стенка)  
 A513 Квадратная стальная труба
 1,04 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  1,04 фунта / фут
 Добавить в корзину    Т11112   1 X 1 X 12 GA (.105 стенка)  
 A513 Квадратная стальная труба
 Т11112
  1 X 1 X 12 GA (стенка .105)  
 A513 Квадратная стальная труба
 1,32 фунта
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  1,32 фунта / фут
 Добавить в корзину    Т11111   1 X 1 X 11 GA (.120 стенка)  
 A513 Квадратная стальная труба
 Т11111
  1 X 1 X 11 GA (стена 0,120)  
 A513 Квадратная стальная труба
 1,44 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  1.44 фунт / фут
 Добавить в корзину    т111416   1-1 / 4 X 1-1 / 4 X 16GA (стена 0,065)  
 A513 Квадратная стальная труба
 Т111416
  1-1 / 4 X 1-1 / 4 X 16GA (.065 стенка)  
 A513 Квадратная стальная труба
 1,04 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  1,04 фунта / фут
 Добавить в корзину    Т111414   1-1 / 4 x 1-1 / 4 x 14 GA (.083 стена)  
 A513 Квадратная стальная труба
 Т111414
  1-1 / 4 x 1-1 / 4 x 14 GA (стена 0,083)  
 A513 Квадратная стальная труба
 1,32 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  1.32 фунт / фут
 Добавить в корзину    Т111412   1-1 / 4 X 1-1 / 4 X 12 GA (стенка .109)  
 A513 Квадратная стальная труба
 Т111412
  1-1 / 4 X 1-1 / 4 X 12 GA (.109 стенка)  
 A513 Квадратная стальная труба
 1,70 фунта
 Выберите … 4 фута 6 футов 8 футов 12 футов 24 фута или обрезать до размера
  Вес:  1,70 фунт / фут
 Добавить в корзину    Т111411   1-1 / 4 X 1-1 / 4 X 11 GA (.120 стенка)  
 A513 Квадратная стальная труба
 Т111411
  1-1 / 4 X 1-1 / 4 X 11 GA (стена 0,120)  
 A513 Квадратная стальная труба
 1,80 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  1.80 фунтов / фут
 Добавить в корзину    т1114316   1-1 / 4 X 1-1 / 4 X 3/16 стенка  
 Стальная квадратная труба A500
 Т1114316
  1-1 / 4 X 1-1 / 4 X 3/16 стенка  
 Стальная квадратная труба A500
 2.40 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  2,40 фунта / фут
 Добавить в корзину    т111216   1-1 / 2 X 1-1 / 2 X 16GA (.065 стена)  
 A513 Квадратная стальная труба
 Т111216
  1-1 / 2 X 1-1 / 2 X 16GA (стена 0,065)  
 A513 Квадратная стальная труба
 1,26 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  1.26 фунтов / фут
 Добавить в корзину    Т111214   1-1 / 2 X 1-1 / 2 X 14 GA (стена 0,083)  
 A513 Квадратная стальная труба
 Т111214
  1-1 / 2 X 1-1 / 2 X 14 GA (.083 стенка)  
 A513 Квадратная стальная труба
 1,67 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  1,67 фунт / фут
 Добавить в корзину    Т111212   1-1 / 2 X 1-1 / 2 X 12 GA (.109 стена)  
 A513 Квадратная стальная труба
 Т111212
  1-1 / 2 X 1-1 / 2 X 12 GA (стенка .109)  
 A513 Квадратная стальная труба
 2,07 фунта
 Выберите … 4 фута 6 футов 8 футов 12 футов 24 фута или обрезать до размера
  Вес:  2.07 фунт / фут
 Добавить в корзину    Т111211   1-1 / 2 X 1-1 / 2 X 11 GA (стена 0,120)  
 A513 Квадратная стальная труба
 Т111211
  1-1 / 2 X 1-1 / 2 X 11 GA (.120 стенка)  
 A513 Квадратная стальная труба
 2,22 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  2,22 фунта / фут
 Добавить в корзину    т1112316   1-1 / 2 X 1-1 / 2 X 3/16 стенка  
 Стальная квадратная труба A500
 Т1112316
  1-1 / 2 X 1-1 / 2 X 3/16 стенка  
 Стальная квадратная труба A500
 3.04 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  3,04 фунта / фут
 Добавить в корзину    Т1112250   1-1 / 2 X 1-1 / 2 X 1/4 стенки  
 Стальная квадратная труба A500
 Т1112250
  1-1 / 2 X 1-1 / 2 X 1/4 стенки  
 Стальная квадратная труба A500
 4.07 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  4,07 фунта / фут
 Добавить в корзину    Т113414   1-3 / 4 X 1-3 / 4 X 14 GA (.083 стена)  
 A513 Квадратная стальная труба
 Т113414
  1-3 / 4 X 1-3 / 4 X 14 GA (стена 0,083)  
 A513 Квадратная стальная труба
 1,88 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  1.88 фунтов / фут
 Добавить в корзину    Т113411   1-3 / 4 X 1-3 / 4 X 11 GA (стенка 0,120)  
 A513 Квадратная стальная труба
 Т113411
  1-3 / 4 X 1-3 / 4 X 11 GA (.120 стенка)  
 A513 Квадратная стальная труба
 2,58 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  2,58 фунт / фут
 Добавить в корзину    т1134316   1-3 / 4 X 1-3 / 4 X 3/16 стенка  
 Стальная квадратная труба A500
 Т1134316
  1-3 / 4 X 1-3 / 4 X 3/16 стенки  
 Стальная квадратная труба A500
 3.68 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  3,68 фунта / фут
 Добавить в корзину    Т12216   2 X 2 X 16GA (.065 стена)  
 A513 Квадратная стальная труба
 T12216
  2 X 2 X 16GA (стена 0,065)  
 A513 Квадратная стальная труба
 1,71 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  1.71 фунт / фут
 Добавить в корзину    Т12214   2 X 2 X 14 GA (стена 0,083)  
 A513 Квадратная стальная труба
 T12214
  2 X 2 X 14 GA (.083 стенка)  
 A513 Квадратная стальная труба
 2,14 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  2,14 фунта / фут
 Добавить в корзину    Т12212   2 X 2 X 12 GA (.109 стена)  
 A513 Квадратная стальная труба
 T12212
  2 X 2 X 12 GA (стенка .109)  
 A513 Квадратная стальная труба
 2,81 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  2.81 фунт / фут
 Добавить в корзину    Т12211   2 X 2 X 11 GA (стена 0,120)  
 Стальная квадратная труба A500
 T12211
  2 X 2 X 11 GA (.120 стенка)  
 A500 Квадратная стальная труба
 2,94 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  2,94 фунта / фут
 Добавить в корзину    Т122316   2 X 2 X 3/16 стенки  
 Стальная квадратная труба A500
 T122316
  2 X 2 X 3/16 стенки  
 Стальная квадратная труба A500
 4.32 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  4,32 фунта / фут
 Добавить в корзину    Т122250   2 X 2 X 1/4 стенки  
 Стальная квадратная труба A500
 T122250
  2 X 2 X 1/4 стенки  
 Стальная квадратная труба A500
 5.41 фунт
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  5,41 фунт / фут
 Добавить в корзину    Т121414   2-1 / 4 X 2-1 / 4 X 1/4 стенки  
 Стальная квадратная труба A500
 T121414
  2-1 / 4 X 2-1 / 4 X 1/4 стенки  
 Стальная квадратная труба A500
 6.26 фунтов
 Выберите … 4 фута 6 футов 8 футов 12 футов 24 фута или обрезать до размера
  Вес:  6,26 фунт / фут
 Добавить в корзину    Т121214   2-1 / 2 X 2-1 / 2 X 14 GA (.083 стенка)  
 A500 Квадратная стальная труба
 Т121214
  2-1 / 2 X 2-1 / 2 X 14 GA (стена 0,083)  
 A500 Стальная квадратная труба
 2,73 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  2.73 фунт / фут
 Добавить в корзину    Т121211   2-1 / 2 X 2-1 / 2 X 11 GA (стена 0,120)  
 A500 Стальная квадратная труба
 Т121211
  2-1 / 2 X 2-1 / 2 X 11 GA (.120 стенка)  
 A500 Квадратная стальная труба
 3,90 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  3,90 фунта / фут
 Добавить в корзину    Т1212316   2-1 / 2 X 2-1 / 2 X 3/16 стенка  
 Стальная квадратная труба A500
 Т1212316
  2-1 / 2 X 2-1 / 2 X 3/16 стенки  
 Стальная квадратная труба A500
 5.59 фунтов
 Выберите … 1 фут 2 фут 4 фут 6 фут 8 фут 12 фут 24 фут или Отрезать до размера
  Вес:  5,59 фунт / фут
 Добавить в корзину    Т1212250   2-1 / 2 X 2-1 / 2 X 1/4 стенки  
 Стальная квадратная труба A500
 Т1212250
  2-1 / 2 X 2-1 / 2 X 1/4 стенки  
 Стальная квадратная труба A500
 7.50 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  7,50 фунт / фут
 Добавить в корзину    т133083   3 X 3 X 14 GA (.083) стенка  
 A500 Квадратная стальная труба
 T133083
  Стенка 3 X 3 X 14 GA (0,083)  
 Стальная квадратная труба A500
 3,24 фунта
 Выберите … 4 фута 6 футов 8 футов 12 футов 24 фута или обрезать до размера
  Вес:  3,24 фунта / фут
 Добавить в корзину    Т13318   3 X 3 X 11GA (.120 стенка)  
 A500 Квадратная стальная труба
 T13318
  3 X 3 X 11GA (стена 0,120)  
 Стальная квадратная труба A500
 4,58 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  4.58 фунтов / фут
 Добавить в корзину    Т133316   3 X 3 X 3/16 стенки  
 Стальная квадратная труба A500
 T133316
  3 X 3 X 3/16 стенки  
 Стальная квадратная труба A500
 6.87 фунтов
 Выберите … 1 фут 2 фут 4 фут 6 фут 8 фут 12 фут 24 фут или Отрезать до размера
  Вес:  6,87 фунт / фут
 Добавить в корзину    Т13314   3 X 3 X 1/4 стены  
 Стальная квадратная труба A500
 T13314
  3 X 3 X 1/4 стенки  
 Стальная квадратная труба A500
 8.81 фунт
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  8,81 фунт / фут
 Добавить в корзину    Т13338   3 X 3 X 3/8 стены  
 Стальная квадратная труба A500
 T13338
  3 X 3 X 3/8 стенки  
 Стальная квадратная труба A500
 12.17 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  12,17 фунт / фут
 Добавить в корзину    т131218   3-1 / 2 X 3-1 / 2 X 11GA (.120 стенка)  
 A500 Квадратная стальная труба
 Т131218
  3-1 / 2 X 3-1 / 2 X 11GA (стена 0,120)  
 Стальная квадратная труба A500
 5,68 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  5.68 фунтов / фут
 Добавить в корзину    т1312316   3-1 / 2 X 3-1 / 2 X 3/16 стенка  
 Стальная квадратная труба A500
 Т1312316
  3-1 / 2 X 3-1 / 2 X 3/16 стенка  
 Стальная квадратная труба A500
 8.15 фунтов
 Выберите … 1 фут 2 фута 4 фута 6 футов 8 футов 10 футов 20 футов или Отрежьте до размера
  Вес:  8,15 фунт / фут
 Добавить в корзину    т131214   3-1 / 2 X 3-1 / 2 X 1/4 стенки  
 Стальная квадратная труба A500
 T131214
  3-1 / 2 X 3-1 / 2 X 1/4 стенки  
 A500 Стальная квадратная труба
 10.51 фунт
 Выберите … 1 фут 2 фут 4 фут 6 фут 8 фут 12 фут 24 фут или Отрезать до размера
  Вес:  10,51 фунт / фут
 Добавить в корзину    т131238   3-1 / 2 X 3-1 / 2 X 3/8 стенки  
 Стальная квадратная труба A500
 T131238
  3-1 / 2 X 3-1 / 2 X 3/8 стенки  
 Стальная квадратная труба A500
 14.72 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  14,72 фунт / фут
 Добавить в корзину    Т144083   4 X 4 X 14 GA (.083) стенка  
 A500 Квадратная стальная труба
 T144083
  Стенка 4 X 4 X 14 GA (0,083)  
 Стальная квадратная труба A500
 4,32 фунта
 Выберите … 4 фута 6 футов 8 футов 12 футов 24 фута или обрезать до размера
  Вес:  4,32 фунта / фут
 Добавить в корзину    Т14418   4 X 4 X 11GA (.120 стенка)  
 A500 Квадратная стальная труба
 T14418
  4 X 4 X 11GA (стена 0,120)  
 Стальная квадратная труба A500
 6,22 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  6.22 фунт / фут
 Добавить в корзину    Т144316   4 X 4 X 3/16 стенки  
 Стальная квадратная труба A500
 T144316
  4 X 4 X 3/16 стенки  
 Стальная квадратная труба A500
 9.42 фунтов
 Выберите … 1 фут 2 фут 4 фут 6 фут 8 фут 12 фут 24 фут или Отрезать до размера
  Вес:  9,42 фунта / фут
 Добавить в корзину    Т14414   4 X 4 X 1/4 стены  
 Стальная квадратная труба A500
 T14414
  4 X 4 X 1/4 стенки  
 Стальная квадратная труба A500
 12.21 фунт
 Выберите … 1 фут 2 фут 4 фут 6 фут 8 фут 12 фут 24 фут или Отрезать до размера
  Вес:  12,21 фунт / фут
 Добавить в корзину    Т14438   4 X 4 X 3/8 стены  
 Стальная квадратная труба A500
 T14438
  4 X 4 X 3/8 стены  
 Стальная квадратная труба A500
 17.27 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  17,27 фунт / фут
 Добавить в корзину    Т14412   4 X 4 X 1/2 стены  
 Стальная квадратная труба A500
 T14412
  4 X 4 X 1/2 стенки  
 Стальная квадратная труба A500
 21.63 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  21,63 фунт / фут
 Добавить в корзину    т1412316   4-1 / 2 X 4-1 / 2 X 3/16 стенка  
 Стальная квадратная труба A500
 T1412316
  4-1 / 2 X 4-1 / 2 X 3/16 стенки  
 Стальная квадратная труба A500
 10.70 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  10,70 фунт / фут
 Добавить в корзину    Т141214   4-1 / 2 X 4-1 / 2 X 1/4 стенки  
 Стальная квадратная труба A500
 T141214
  4-1 / 2 X 4-1 / 2 X 1/4 стенки  
 Стальная квадратная труба A500
 14.00 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 12 фута 24 фута или Вырезать до размера
  Вес:  14,00 фунт / фут
 Добавить в корзину    Т15511   5 X 5 X 11GA (.120) стенка  
 A500 Стальная квадратная труба
 T15511
  Стенка 5 X 5 X 11GA (.120)  
 Стальная квадратная труба A500
 8,16 фунтов
 Выберите … 4 фута 6 футов 8 футов 12 футов 24 фута или обрезать до размера
  Вес:  8,16 фунт / фут
 Добавить в корзину    T155316   5 X 5 X 3/16 стенка  
 Стальная квадратная труба A500
 T155316
  Стенка 5 X 5 X 3/16  
 Стальная квадратная труба A500
 11.97 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  11,97 фунт / фут
 Добавить в корзину    Т15514   5 X 5 X 1/4 стены  
 Стальная квадратная труба A500
 T15514
  5 X 5 X 1/4 стенки  
 Стальная квадратная труба A500
 15.62 фунтов
 Выберите … 1 фут 2 фута 4 фута 6 футов 8 футов 10 футов 20 футов или Отрежьте до размера
  Вес:  15,62 фунт / фут
 Добавить в корзину    Т15538   5 X 5 X 3/8 стены  
 Стальная квадратная труба A500
 T15538
  5 X 5 X 3/8 стены  
 Стальная квадратная труба A500
 23.12 фунтов
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  23,12 фунта / фут
 Добавить в корзину    Т15512   5 X 5 X 1/2 стены  
 Стальная квадратная труба A500
 T15512
  5 X 5 X 1/2 стены  
 Стальная квадратная труба A500
 28.43 фунтов
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  28,43 фунта / фут
 Добавить в корзину    Т16611   6 X 6 X 11ga (1/8 «) стенка  
 Стальная квадратная труба A500
 T16611
  Стенка 6 X 6 X 11ga (1/8 «)  
 Стальная квадратная труба A500
 9.85 фунтов
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  9,85 фунт / фут
 Добавить в корзину    Т166316   6 X 6 X 3/16 стенка  
 Стальная квадратная труба A500
 T166316
  6 X 6 X 3/16 стенки  
 Стальная квадратная труба A500
 14.65 фунтов
 Выберите … 1 фут 2 фута 4 фута 6 футов 8 футов 10 футов 20 футов или Отрежьте до размера
  Вес:  14,65 фунт / фут
 Добавить в корзину    Т16614   6 X 6 X 1/4 стены  
 Стальная квадратная труба A500
 T16614
  6 X 6 X 1/4 стенки  
 Стальная квадратная труба A500
 19.02 фунтов
 Выберите … 1 фут 2 фут 4 фут 6 фут 8 фут 12 фут 24 фут или Отрезать до размера
  Вес:  19,02 фунт / фут
 Добавить в корзину    T16638   6 X 6 X 3/8 стены  
 Стальная квадратная труба A500
 T16638
  6 X 6 X 3/8 стены  
 Стальная квадратная труба A500
 27.48 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  27,48 фунт / фут
 Добавить в корзину    Т16612   6 X 6 X 1/2 стены  
 Стальная квадратная труба A500
 T16612
  6 X 6 X 1/2 стенки  
 Стальная квадратная труба A500
 35.24 фунта
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  35,24 фунта / фут
 Добавить в корзину    Т17714   7 x 7 x 1/4 стенки  
 Стальная квадратная труба A500
 T17714
  7 x 7 x 1/4 стенки  
 Стальная квадратная труба A500
 22.42 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  22,42 фунта / фут
 Добавить в корзину    Т17738   7 X 7 X 3/8 стены  
 Стальная квадратная труба A500
 T17738
  7 X 7 X 3/8 стены  
 Стальная квадратная труба A500
 32.58 фунтов
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  32,58 фунт / фут
 Добавить в корзину    Т17712   7 X 7 X 1/2 стены  
 Стальная квадратная труба A500
 T17712
  7 X 7 X 1/2 стенки  
 Стальная квадратная труба A500
 42.05 фунтов
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  42,05 фунт / фут
 Добавить в корзину    Т188316   8 X 8 X 3/16 стены  
 Стальная квадратная труба A500
 T188316
  8 X 8 X 3/16 стенки  
 Стальная квадратная труба A500
 19.63 фунтов
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  19,63 фунт / фут
 Добавить в корзину    Т18814   8 x 8 x 1/4 стенки  
 Стальная квадратная труба A500
 T18814
  8 x 8 x 1/4 стенки  
 Стальная квадратная труба A500
 26.00 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  26,00 фунт / фут
 Добавить в корзину    Т18838   8 x 8 x 3/8 стенки  
 Стальная квадратная труба A500
 T18838
  8 x 8 x 3/8 стенки  
 Стальная квадратная труба A500
 37.70 фунтов
 Выберите … 1 фут 2 фута 4 фута 6 футов 8 футов 10 футов 20 футов или Отрежьте до размера
  Вес:  37,70 фунт / фут
 Добавить в корзину    Т18812   8 x 8 x 1/2 стенки  
 Стальная квадратная труба A500
 T18812
  8 x 8 x 1/2 стенки  
 Стальная квадратная труба A500
 49.00 фунтов
 Выберите … 2 фута 4 фута 6 фута 8 фута 10 фута 20 фута или Отрежьте до размера
  Вес:  49,00 фунт / фут
 Добавить в корзину    Т18858   8 X 8 X 5/8 стенка  
 Стальная квадратная труба A500
 T18858
  8 X 8 X 5/8 стенка  
 Стальная квадратная труба A500
 59.32 фунта
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  59,32 фунт / фут
 Добавить в корзину    Т110316   10 X 10 X 3/16 стены  
 Стальная квадратная труба A500
 Т110316
  10 X 10 X 3/16 стенка  
 Стальная квадратная труба A500
 24.73 фунтов
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  24,73 фунта / фут
 Добавить в корзину    Т11014   10 x 10 x 1/4 стенки  
 Стальная квадратная труба A500
 Т11014
  10 x 10 x 1/4 стенки  
 Стальная квадратная труба A500
 32.63 фунтов
 Выберите … 1 фут 2 фута 4 фута 6 футов 8 футов 10 футов 20 футов или Отрежьте до размера
  Вес:  32,63 фунта / фут
 Добавить в корзину    Т11038   10 X 10 X 3/8 стены  
 Стальная квадратная труба A500
 T11038
  10 X 10 X 3/8 стены  
 Стальная квадратная труба A500
 47.90 фунтов
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  47,90 фунт / фут
 Добавить в корзину    Т11012   10 X 10 X 1/2 стены  
 Стальная квадратная труба A500
 Т11012
  10 X 10 X 1/2 стенки  
 Стальная квадратная труба A500
 62.46 фунтов
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  62,46 фунт / фут
 Добавить в корзину    Т11058   10 X 10 X 5/8 стенка  
 Стальная квадратная труба A500
 T11058
  10 X 10 X 5/8 стенка  
 Стальная квадратная труба A500
 76.33 фунтов
 Выберите … 10 Ft.20 Ft.
  Вес:  76,33 фунта / фут
 Добавить в корзину    Т11214   12 x 12 x 1/4 стенки  
 Стальная квадратная труба A500
 Т11214
  12 x 12 x 1/4 стенки  
 Стальная квадратная труба A500
 39.45 фунтов
 Выберите … 1 фут 2 фута 4 фута 6 футов 8 футов 10 футов 20 футов или Отрежьте до размера
  Вес:  39,45 фунт / фут
 Добавить в корзину    Т11238   12 X 12 X 3/8 стены  
 Стальная квадратная труба A500
 Т11238
  12 X 12 X 3/8 стены  
 Стальная квадратная труба A500
 58.10 фунтов
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  58,10 фунт / фут
 Добавить в корзину    Т11212   12 X 12 X 1/2 стены  
 Стальная квадратная труба A500
 Т11212
  12 X 12 X 1/2 стенки  
 Стальная квадратная труба A500
 76.07 фунтов
 Выберите … 10 Ft.20 Ft.
  Вес:  76,07 фунт / фут
 Добавить в корзину    Т11258   12 X 12 X 5/8 стенка  
 Стальная квадратная труба A500
 Т11258
  12 X 12 X 5/8 стенка  
 Стальная квадратная труба A500
 93.34 фунтов
 Выберите … 4 фута 6 футов 8 футов 10 футов 20 футов или Отрезать до размера
  Вес:  93,34 фунта / фут
 Добавить в корзину   Пр. 4.2, 12 — Показать | 1 x x2 x2 1 x x x2 1 | = (1 — x3) 2 
 Последнее обновление: 22 января 2020 г., автор: Teachoo
 Выписка
 Пр. 4.2, 12
Используя свойства определителей, покажите, что:
 | ■ 8 (1 & x & x2 @ x2 & 1 & x @ x & x2 & 1) | = (1 — x3) 2  Решение L.H.S
 | ■ 8 (1 & x & x2 @ x2 & 1 & x @ x & x2 & 1) |
Применение R1 → R1 + R2 + R3
= | ■ 8 (𝟏 + 𝐱𝟐 + 𝐱 & 𝐱 + 𝟏 + 𝐱𝟐 & 𝐱𝟐 + 𝐱 + 𝟏 @ x2 & 1 & x @ x & x2 & 1) |
Взяв (1 + x + x2) обыкновенный из 1-го ряда 
= (𝟏 + 𝐱 + 𝐱𝟐) | ■ 8 (1 & 1 & 1 @ x2 & 1 & x @ x & x2 & 1) |
Применение C1 → C1 — C2
 = (1 + x + x2) | ■ 8 (𝟏 − 𝟏 & 1 & 1 @ x2−1 & 1 & x @ x − x2 & x2 & 1) |
= (1 + x + x2) | ■ 8 (0 & 1 & 1 @ x2−1 & 1 & x @ x (1 − x) & x2 & 1) |
= (1 + x + x2) | ■ 8 (𝟎 & 1 & 1 @ (𝐱 − 𝟏) (𝑥 + 1) & 1 & x @ −x (𝐱 − 𝟏) & x2 & 1) |
Взяв (x — 1) общее из C1
= (x — 1) (1 + x + x2) | ■ 8 (0 & 1 & 1 @ (x + 1) & 1 & x @ −x & x2 & 1) |
Применение C2 → C2 — C3
= (x — 1) (1 + x + x2) | ■ 8 (0 & 𝟏 − 𝟏 & 1 @ x + 1 & 1 − x & x @ −x & x2−1 & 1) |
= (x — 1) (1 + x + x2) | ■ 8 (0 & 𝟎 & 1 @ x + 1 & — (𝒙 − 𝟏) & x @ −x & (x + 1) (𝐱 − 𝟏) & 1) |  Взяв (x — 1) общее из 2-го столбца
= (x — 1) (1 + x + x2) (x — 1) | ■ 8 (0 & 0 & 1 @ x + 1 & −1 & x @ −x & 𝑥 + 1 & 1) |  = (x — 1) 2 (1 + x + x2) | ■ 8 (0 & 0 & 1 @ x + 1 & −1 & x @ −x & 𝑥 + 1 & 1) |
Расширение определителя по R1
= (x — 1) 2 (1 + x + x2) (0 | ■ 8 (−1 & 𝑥 @ 𝑥 + 1 & 1) | −0 | ■ 8 (𝑥 + 1 & x @ −𝑥 & 1) | +1 | ■ 8 (𝑥 + 1 & −1 @ −x & 𝑥 + 1) |)
= (x — 1) 2 (1 + x + x2) (0−0 + 1 | ■ 8 (𝑥 + 1 & −1 @ −x & 𝑥 + 1) |)
= (x — 1) 2 (1 + x + x2) (0−0 + 1 ((𝑥 + 1) 2 − 𝑥))
= (х — 1) 2 (1 + х + х2) ((𝑥 + 1) ^ 2 − 𝑥)
= (x — 1) 2 (1 + x + x2) ((x2 + 1 + 2x) — x)
= (х — 1) 2 (1 + х + х2) (1 + х + х2)  = (х — 1) 2 (1 + х + х2) 2
= ((х — 1) (1 + х + х2)) 2
= (- (1 — х) (1 + х + х2)) 2
= ((1 — х) (1 + х + х2)) 2  = (13 — x3) 2
= (1 — x3) 2
= R.H.S
 Следовательно, доказано  = (х — 1) 2 (1 + х + х2) 2
= ((х — 1) (1 + х + х2)) 2
= (- (1 — х) (1 + х + х2)) 2
= ((1 — х) (1 + х + х2)) 2  = (13 — x3) 2
= (1 — x3) 2
= R.H.S
 Следовательно, доказано  Мы знаем это
a3 — b3 = (a — b) (a2 + b2 + ab)
Здесь a = 1, b = x
 Показать больше Инверсия функции — объяснение и примеры 
 Что такое обратная функция? 
  В математике обратная функция — это функция, отменяющая действие другой функции.
  Например, , сложение и умножение являются инверсией соответственно вычитания и деления.
 Обратную функцию можно рассматривать как отражение исходной функции по линии y = x. Проще говоря, обратная функция получается заменой (x, y) исходной функции на (y, x).
 Мы используем символ f ^{— 1} для обозначения обратной функции. Например, если f (x) и g (x) противоположны друг другу, то мы можем символически представить это утверждение как:
 g (x) = f ^{— 1} (x) или f (x) = g ⁻¹ (x)
 Об обратной функции следует отметить то, что обратная функция — это не то же самое, что и обратная функция, т.е.е., f ^{— 1} (x) ≠ 1 / f (x). В этой статье мы обсудим, как найти обратную функцию.
 Поскольку не все функции имеют инверсию, важно проверить, есть ли у функции инверсия, прежде чем приступать к определению инверсии.
 Мы проверяем, есть ли у функции инверсия, чтобы не тратить время на поиск чего-то несуществующего.
 Индивидуальные функции 
  Итак, как мы докажем, что данная функция имеет обратную? Функции, у которых есть обратные, называются взаимно однозначными функциями.
 Функция называется взаимно однозначной, если для каждого числа y в диапазоне f существует ровно одно число x в области определения f такое, что f (x) = y.
  Другими словами, домен и диапазон однозначной функции имеют следующие отношения: 
 Область f ^-1 = Диапазон f.
 Диапазон f ^-1 = Область f.
 Например, чтобы проверить, является ли f (x) = 3x + 5 однозначно заданной функцией, f (a) = 3a + 5 и f (b) = 3b + 5.
 ⟹ 3a + 5 = 3b + 5
 ⟹ 3a = 3b
 ⟹ а = б.
 Следовательно, f (x) является взаимно однозначной функцией, потому что a = b.
 Рассмотрим другой случай, когда функция f задается формулой f = {(7, 3), (8, –5), (–2, 11), (–6, 4)}. Эта функция взаимно однозначна, потому что ни одно из ее значений y не встречается более одного раза.
 А как насчет этой другой функции h = {(–3, 8), (–11, –9), (5, 4), (6, –9)}? Функция h не является взаимно однозначной, потому что значение y, равное –9, встречается более одного раза.
 Вы также можете графически проверить взаимно однозначную функцию, проведя вертикальную и горизонтальную линии через график функции. Функция взаимно однозначна, если и горизонтальная, и вертикальная линии проходят через график один раз.
 Как найти обратную функцию? 
 Нахождение обратной функции — простой процесс, хотя нам действительно нужно быть осторожными с парой шагов. В этой статье мы будем предполагать, что все функции, с которыми мы будем иметь дело, относятся друг к другу.
  Вот процедура нахождения обратной функции f (x): 
 Заменить обозначение функции f (x) на y.
 Поменять местами x на y и наоборот.
 Начиная с шага 2, решите уравнение относительно y. Будьте осторожны с этим шагом.
 Наконец, заменим y на f ⁻¹ (x). Это обратная функция.
 Вы можете проверить свой ответ, проверив, верны ли следующие два утверждения:
 ⟹ (f ∘ f ⁻¹) (x) = x
 ⟹ (f ⁻¹ ∘ f) (x) = x
 Давайте поработаем пару примеров.
   Пример 1  
 Дана функция f (x) = 3x — 2, найдите обратную ей.
  Решение 
 f (x) = 3x — 2
 Замените f (x) на y.
 ⟹ y = 3x — 2
 Поменять местами x на y
 ⟹ x = 3y — 2
 Решить для y
 х + 2 = 3 года
 Разделим на 3, чтобы получить;
 1/3 (x + 2) = y
 х / 3 + 2/3 = у
 Наконец, заменим y на f ⁻¹ (x).
 f ⁻¹ (x) = x / 3 + 2/3
 Проверить (f ∘ f ⁻¹) (x) = x
 (f ∘ f ⁻¹) (x) = f [f ⁻¹ (x)]
 = е (х / 3 + 2/3)
 ⟹ 3 (х / 3 + 2/3) — 2
 ⟹ x + 2–2
 = х
 Следовательно, f ⁻¹ (x) = x / 3 + 2/3 — правильный ответ.
   Пример 2  
 Дано f (x) = 2x + 3, найдите f ⁻¹ (x).
  Решение 
 f (x) = y = 2x + 3
 2x + 3 = y
 Поменять местами x и y
 ⟹2y + 3 = х
 Теперь решите для y
 ⟹2y = х — 3
 ⟹ y = x / 2 — 3/2
 Наконец, заменим y на f ⁻¹ (x)
 ⟹ f ⁻¹ (x) = (x– 3) / 2
   Пример 3  
 Задайте функцию f (x) = log ₁₀ (x), найдите f ⁻¹ (x).
  Решение 
 f (x) = log₁₀ (x)
 Заменен f (x) на y
 ⟹ y = журнал ₁₀ (x) ⟹ 10 ^y = x
 Теперь поменяйте местами x на y, чтобы получить;
 ⟹ y = 10 ^x
 Наконец, заменим y на f ⁻¹ (x).
 f ^-1 (x) = 10 ^x
 Следовательно, обратное значение f (x) = log ₁₀ (x) равно f ^-1 (x) = 10 ^x
   Пример 4  
 Найдите обратную функцию к следующей функции g (x) = (x + 4) / (2x -5)
  Решение 
 г (x) = (x + 4) / (2x -5) ⟹ y = (x + 4) / (2x -5)
 Поменять местами y с x и наоборот
 y = (x + 4) / (2x -5) ⟹ x = (y + 4) / (2y -5)
 ⟹ х (2y − 5) = y + 4
 ⟹ 2xy — 5x = y + 4
 ⟹ 2xy — y = 4 + 5x
 ⟹ (2x — 1) y = 4 + 5x
 Разделите обе части уравнения на (2x — 1).
 ⟹ у = (4 + 5x) / (2x — 1)
 Заменить y на g ^-1 (x)
 = г ^{— 1} (x) = (4 + 5x) / (2x — 1)
 Проба:
 (г г ^-1) (x) = г [г ^-1 (x)]
 = г [(4 + 5x) / (2x — 1)]
 = [(4 + 5x) / (2x — 1) + 4] / [2 (4 + 5x) / (2x — 1) — 5]
 Умножьте числитель и знаменатель на (2x — 1).
 ⟹ (2x — 1) [(4 + 5x) / (2x — 1) + 4] / [2 (4 + 5x) / (2x — 1) — 5] (2x — 1).
 ⟹ [4 + 5x + 4 (2x — 1)] / [2 (4 + 5x) — 5 (2x — 1)]
 ⟹ [4 + 5x + 8x − 4] / [8 + 10x — 10x + 5]
 ⟹13x / 13 = x 
 Следовательно, g ^{— 1} (x) = (4 + 5x) / (2x — 1)
   Пример 5  
 Определите значение, обратное следующей функции f (x) = 2x — 5
  Решение 
 Замените f (x) на y.
 f (x) = 2x — 5⟹ y = 2x — 5
 Переключите x и y, чтобы получить;
 ⟹ x = 2y — 5
 Изолировать переменную y.
 2у = х + 5
 ⟹ у = х / 2 + 5/2
 Измените y обратно на f ^–1 (x).
 ⟹ f ^–1 (x) = (x + 5) / 2
   Пример 6  
 Найти обратную функцию к функции h (x) = (x — 2) ³.
  Решение 
 Измените h (x) на y, чтобы получить;
 h (x) = (x — 2) ³ ⟹ y = (x — 2) ³
 Поменять местами x и y
 ⟹ х = (у — 2) ³
 Изолятор ул.
 y ³ = x + 2 ³
 Найдите кубический корень из обеих частей уравнения.
 ³ √y ³ = ³ √x ³ + ³ √2 ³
 y = ³ √ (2 ³) + 2
 Заменить y на h ^-1 (x)
 ч ^{— 1} (x) = ³ √ (2 ³) + 2
   Пример 7  
 Найдите обратное к h (x) = (4x + 3) / (2x + 5)
  Решение 
 Замените h (x) на y.
 h (x) = (4x + 3) / (2x + 5) ⟹ y = (4x + 3) / (2x + 5)
 Поменять местами x и y.
 ⟹ х = (4у + 3) / (2у + 5).
 Решите относительно y в приведенном выше уравнении следующим образом:
 ⟹ х = (4у + 3) / (2у + 5)
 Умножаем обе стороны на (2y + 5)
 ⟹ х (2у + 5) = 4у + 3
 Распределить x
 ⟹ 2xy + 5x = 4y + 3
 Изолятор ул.
 ⟹ 2xy — 4y = 3 — 5x
 ⟹ y (2x — 4) = 3-5x
 Разделим на 2x — 4, чтобы получить;
 ⟹ y = (3 — 5x) / (2x — 4)
 Наконец, замените y на h ^{— 1} (x).
 Posted in Разное
Навигация по записям
Поделки елки своими руками из шишек: Новогодние поделки ИЗ ШИШЕК (45 идей для детей).
Решение системы уравнений методом: Разбираемся в линейных уравнениях раз и навсегда
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя * 
Email * 
Сайт 
  
  Найти:   
Рубрики
Воспитание
Детям
Идеи
Полезно
Родителям
Советы
Разное
 2015-2019 © Игровая комната «Волшебный лес», Челябинск
 тел.:+7 351 724-05-51, +7 351 777-22-55 игровая комната челябинск, праздник детям челябинск