Решить свойства прямой линии x-y-2 = 0 Решатель алгебры тигра

Этот сайт лучше всего просматривать с помощью Javascript. Если вы не можете включить Javascript, нажмите здесь.

Вход камеры не распознается!

Мы думаем, что вы написали:

x-y-2 = 0

Это касается свойств прямой линии.

x-i» ntercept = 2/1 = 2,00000

yi «ntercept = 2 / -1 = -2,00000

Пошаговое решение

Шаг 1:

 
 Уравнение прямой линии 
 
 1.1 Решить xy-2 = 0 
 
 Тигр понимает, что здесь уравнение прямой. Такое уравнение обычно записывается как y = mx + b («y = mx + c» в Великобритании). 
 
 «y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат. система, в которой «y» — вертикальная ось, а «x» — горизонтальная ось. 
 
 В этой формуле: 
 
 y указывает нам, как далеко идет линия 
 x сообщает нам, как далеко вдоль 
 м находится уклон или градиент i .е. насколько крута линия 
 b — точка пересечения по оси Y, т.е. точка пересечения линии с осью Y 
 
 Пересечения по осям X и Y и наклон называются свойствами линии.  Теперь мы построим график линии xy-2 = 0 и вычислим ее свойства. 
 
 График прямой линии: 
 
 
 Вычислим пересечение оси Y: 
. Обратите внимание, что когда x = 0, значение y равно 2 / -1. таким образом, эта линия «разрезает» ось y на y = -2,00000
 y-intercept = 2 / -1 = -2,00000 
 Вычислите точку пересечения X: 
 Когда y = 0, значение x равно 2/1. line поэтому «разрезает» ось x при x = 2.00000
 x-intercept = 2/1 = 2,00000 
 Расчет наклона: 
 Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно -2,000, а для x = 2,000 значение y равно 0,000. Таким образом, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на 0,000 — (-2,000) = 2.000 по y. (Изменение y иногда называют «ПОДЪЕМ», а наклон m = RISE / RUN)
 Наклон = 1 
 Геометрическая фигура: прямая линия 
 Наклон = 1
 пересечение по x = 2/1 = 2. 00000
 y-intercept = 2 / -1 = -2,00000
 Зачем это изучать 
 Термины и темы 
 Ссылки по теме 
 Построение точек на графике или плоскости XY 
 В этом уроке я подготовил восемь (8) разработанных примеров построения точки на декартовой плоскости (названной в честь французского математика Рене Декарта). Чтобы построить точку, нам нужны две вещи: точка   и координатная плоскость  .
 Давайте кратко поговорим о каждом.
 A точка 
 Точка на плоскости состоит из двух компонентов, в которых порядок имеет значение! Он имеет форму (x, y), где x идет первым, а y — вторым.
 Значение x указывает, как точка перемещается вправо или влево вдоль оси x .  Эта ось является главной горизонтальной    линией  прямоугольной оси или декартовой плоскости.
 Значение y указывает, как точка перемещается вверх или вниз по оси y. Эта ось  является главной вертикальной линией  прямоугольной оси или декартовой плоскости.
 КООРДИНАТНАЯ ПЛОСКОСТЬ (декартова плоскость) 
 Координатная плоскость состоит из  двух линий, пересекающихся под углом 90 градусов  (что делает их перпендикулярными линиями) в точке  (0,0) , известной как начало координат  .
 Компонент x точки (x, y) перемещает точку вдоль горизонтальной линии. Если значение x положительное, точка перемещается на «единицы x» вправо.С другой стороны, если значение x отрицательное, точка перемещается на «единицы x» влево.
 Компонент Y точки (x, y) перемещает точку вдоль вертикальной линии. Если значение y положительное, точка перемещается на «единицы y» вверх. Однако, если значение y отрицательное, точка перемещается на «единицы y» вниз.
 Квадранты декартовой плоскости 
 Пересечение   осей x и оси y приводит к созданию четырех (4) секций или делений декартовой плоскости.
 Первый квадрант   расположен в верхней правой части плоскости.
 Второй квадрант   расположен в верхней левой части плоскости.
 Третий квадрант   расположен в нижней левой части плоскости.
 Четвертый квадрант   расположен в правом нижнем углу плоскости.
 Примеры того, как нанести точки на график и определить его квадрант 
  Пример 1  :  Постройте точку  (4,2)  и определите, в каком квадранте или оси она расположена.
 Я начну с размещения точки в начале координат, которая является пересечением осей x и y. Думайте о происхождении как о «доме», откуда берутся все точки.
 Затем я перемещу точку от начала координат на 4 единицы вправо, поскольку x = 4 (положительное значение по оси x означает перемещение вправо). Помните, что значение x — это первое число в упорядоченной паре (4,2).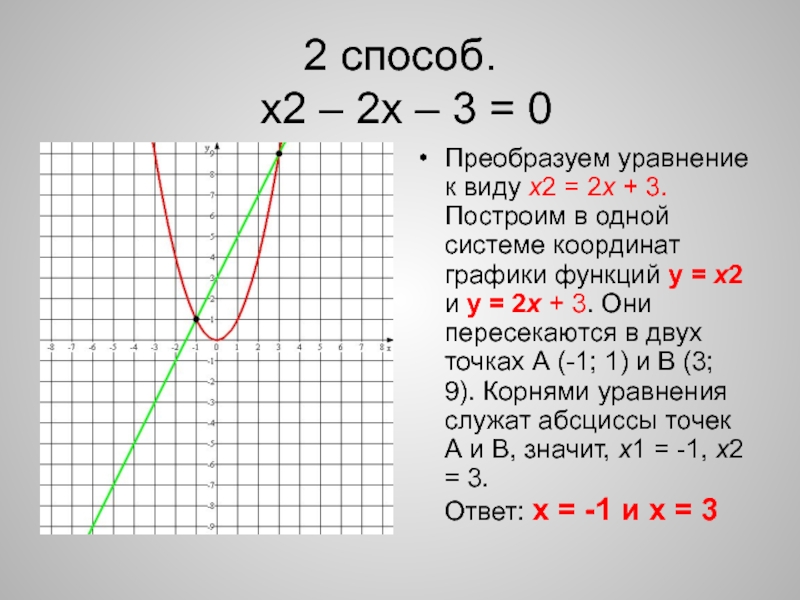
 С того места, где я остановился, мне нужно переместить 2 единицы вверх, параллельно главной вертикальной оси, поскольку y = 2 (положительное значение по оси y означает движение вверх).Значение y — это второе число в упорядоченной паре (4,2).
 Окончательный ответ должен выглядеть так…
 Точка  (4,2)  находится в  квадранте I .
  Пример 2  :  Постройте точку  (–5, 4)  и определите, в каком квадранте или оси она расположена.
 Начните с размещения точки в начале координат, известном как центр декартовой координатной оси.
 Из начала координат, поскольку x  = −5 , переместитесь на 5 единиц влево.
… с последующим перемещением точки на 4 единицы вверх, потому что y  = 4 .
 Это окончательный ответ. Поскольку нанесенная точка находится в верхнем левом углу оси xy, она должна находиться в квадранте II.
  Пример 3  :  Постройте точку  (5, –3)  и определите, в каком квадранте или оси она расположена.
 Начать из центра декартовой плоскости.
 Переместите 5 единиц вправо, так как x  = 5 .
 Далее следует перемещение на 3 единицы вниз, так как y  = −3 .
 Последняя нанесенная точка показана ниже. Находясь в правом нижнем углу декартовой плоскости, это означает, что он находится в квадранте IV.
  Пример 4  :  Постройте точку  (–2, –5)  и определите, в каком квадранте или оси она расположена.
 Поместите точку в начало координат (центр оси xy). Поскольку x  = −2 , переместите точку на 2 единицы влево по оси x.Наконец, спуститесь на 5 единиц параллельно оси y, потому что y  = −5 .
 См. Анимированное решение ниже.
 Точка на графике расположена в нижней левой части декартовой плоскости. Таким образом, он находится в квадранте III.
  Пример 5  :  Постройте точку  (0,3)  и определите, в каком квадранте или оси она расположена.
 Я начинаю с анализа данной упорядоченной пары. Поскольку x  = 0 , это означает, что  нет движения  по оси  x .Однако y  = 3  означает, что мне нужно переместить его на  3 единицы в направлении вверх .
 Точка на графике —  ни  ни в квадранте I, ни в квадранте II. Чтобы описать его местоположение, мы говорим, что он находится вдоль положительной оси ординат.
  Пример 6  :  Постройте точку  (0, –4)  и определите, в каком квадранте или оси она расположена.
 Это очень похоже на пример 5. Не будет движения по оси x, так как x  = 0 .С другой стороны, y  = — 4  говорит мне, что мне нужно переместить точку от начала координат на 4 единицы вниз.
 Конечная точка не находится ни в , ни в  в квадранте III и не в квадранте IV. Я могу утверждать, что он находится вдоль отрицательной оси ординат.
  Пример 7  :  Постройте точку  (–3,0)  и определите, в каком квадранте или оси она расположена.
 Из начала координат я сдвину его на 3 единицы влево по оси x, так как x  = −3. Если y = 0, это означает, что движения по оси y не последует.
 Точка не находится ни в  ни в квадранте II, ни в квадранте III. Он находится вдоль отрицательной оси абсцисс.
  Пример 8  :  Постройте точку  (2,0)  и определите, в каком квадранте или оси она расположена.
 При x  = 2  мне нужно переместить его на 2 единицы вправо. Если y  = 0 , это означает, что движения по оси Y не произойдет.
 Точка на графике не находится ни на , ни на  в квадранте I и не в квадранте IV.Он находится вместе с положительной осью абсцисс.
 Практика с рабочими листами 
 Wolfram | Alpha Примеры: Алгебра 
 Другие примеры
 Решение уравнения
 Решите уравнения с одной или несколькими переменными как символьно, так и численно.
 Решите полиномиальное уравнение:
 Решите систему линейных уравнений:
 Решите уравнение с параметрами:
 Другие примеры
 Другие примеры
 Полиномы
 Решайте, строите и находите альтернативные формы полиномиальных выражений от одной или нескольких переменных.
 Вычислить свойства многочлена от нескольких переменных:
 Другие примеры
 Другие примеры
 Рациональные функции
 Вычислить разрывы и другие свойства рациональных функций.
 Вычислить свойства рациональной функции:
 Вычислить частичное разложение дроби:
 Другие примеры
 Другие примеры
 Упрощение
 Упростите алгебраические функции и выражения.
 Другие примеры
 Другие примеры
 Матрицы
 Найдите свойства и выполните вычисления с матрицами.
 Выполните базовую арифметику с матрицами:
 Вычислить собственные значения и собственные векторы матрицы:
 Другие примеры
 Другие примеры
 Кватернионы
 Выполните вычисления в кватернионной системе счисления.
 Получите информацию о кватернионе:
 Проведите расчеты с кватернионами:
 Другие примеры
 Другие примеры
 Конечные группы
 Откройте для себя свойства групп, содержащих конечное число элементов.
 Получите информацию о конечной группе:
 Спросите о собственности группы:
 Сделайте алгебру с перестановками:
 Другие примеры
 Другие примеры
 Конечные поля
 Откройте для себя свойства полей, содержащих конечное число элементов.
 Вычислить свойства конечного поля:
 Вычислить конкретное свойство:
 Другие примеры
 Другие примеры
 Домен и диапазон
 Найдите область и диапазон математических функций.
 Вычислить область определения функции:
 Вычислить диапазон функции:
 Другие примеры
 Y = -2x + 1 xy xy (-2) + 1 = 5-2 (0) (1) (2) (-1) + 1 упорядоченная пара (-2, 5) (-1, 3) (0 , 1) (1, -1) (2, -3) Где находится «точка пересечения оси y»? 
 Презентация на тему: «Y = -2x + 1 xy xy -2 0 1 2 -2 (-2) + 1 = 5 -2 (0) + 1-2 (1) + 1-2 (2) + 1 -2 (-1) + 1 Упорядоченная пара (-2, 5) (-1, 3) (0, 1) (1, -1) (2, -3) Где находится точка пересечения по оси Y? «- Стенограмма презентации: 
 ins [data-ad-slot = «4502451947»] {display: none! important;}}
 @media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
 @media (max-width: 800px) {# place_14 {width: 250px;}}
 @media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
 ]]>
 1 
 y = -2x + 1 xy xy -2 0 1 2 -2 (-2) + 1 = 5-2 (0) + 1-2 (1) + 1-2 (2) + 1-2 (-1) + 1 Упорядоченная пара (-2, 5) (-1, 3) (0, 1) (1, -1) (2, -3) Где находится точка пересечения по оси Y? (0, 1) график x-y и угол наклона / пересечение y: -2 1 = 3 = 1 = -1 = -3 Разминка
 2 
 Задача: Задав уравнение, учащиеся смогут (1) определить наклон, точку пересечения по оси Y и (2) построить график линии, используя наклон и точку пересечения по оси Y.Стандарты CA 3.3: Изобразите линейные функции, отмечая, что вертикальное изменение (изменение значения y) на единицу горизонтального изменения (изменение значения x) всегда одно и то же, и знайте, что соотношение («повышение за пробегом») называется наклон графика. Повестка дня: 10/05/11 1.) Разминка 2.) Уравнения пересечения наклона урока ppt. 3.) Урок / Домашнее задание WS График y = mx + b 4.) ОСТАВАЙТЕСЬ ЗА ЗАДАНИЕ !!!
 3 
 Уравнения угла наклона и точки пересечения y = mx + b Пример точки пересечения по оси y: наклон (м) = -4 точки пересечения по оси Y (b) = -8
 4 
 Найдите наклон и точку пересечения по оси Y каждого уравнения: Наклон (м) точку пересечения по оси Y УРАВНЕНИЕ 1 1 + 0
 5 
 x y y-intercept (b) = 3 Постройте линию, используя точку пересечения y и наклон.Наклон (m) = -2 1 1 RISE RUN y = mx + b здесь начинается! Переместить Пример 1: начать с y = 3 =
 6 
 Пример 2: x y
 7 
 x y y-intercept (b) = 3 Постройте линию, используя точку пересечения y и наклон. Наклон (m) = 4 4 RISE RUN y = mx + b здесь начинаем! move Попробуйте это: начните с y = 3 = Давайте посмотрим на ваши навыки!
 
 линий графика 
 линий графика
 Построение графиков линейных уравнений 
 График уравнения с двумя переменными представляет все возможные комбинации  x  и  y , которые удовлетворяют уравнению.Другими словами, точки на графике имеют координаты ( x ,  y ), которые делают утверждение уравнения истинным. В зависимости от природы уравнения и показателей переменных каждое уравнение имеет свой график.
 
 График любого уравнения, в котором есть две переменные, которые имеют степень один, не умножаются друг на друга и не входят в знаменатель каких-либо дробей, представляет собой прямую линию.
 Например, график 2y — x + 4 = 0 представляет собой линию.Это означает, что если мы найдем все возможные комбинации x и y, которые работают в уравнении, и построим их в системе координат, результатом будет линия. Поскольку две точки определяют линию, если мы распознаем уравнение как линейное уравнение, нам понадобятся только два набора x и y (точек), которые удовлетворяют уравнению для графика. Есть много способов найти эти точки, и их бесконечное количество. Мы рассмотрим графики линий, используя их точки пересечения по оси x и оси y. Это точки, в которых линия пересекает ось x и ось y соответственно.Мы выбираем эти точки потому, что с ними легче работать.  Пересечение линии по оси x является точкой на оси x и, следовательно, имеет нулевую координату y. А точка пересечения линии y является точкой на оси y и имеет нулевую координату x . Мы собираемся использовать эти факты, чтобы найти недостающие координаты каждой точки. 
 Сначала мы подставим ноль для  y  и найдем соответствующие  x , а затем подставим ноль для  x  и найдем соответствующие  y .
 
 Пример 1) График 2  y  —  x  + 4 = 0
 Если мы подставим 0 для  x , мы получим: 
 2  y  — 0 + 4 = 0 Мы вычтем 4 с обеих сторон: 
 2  y  = -4 и разделив на 2, получим  y  = -2, поэтому у нас есть (0, -2), это перехват  y . 
 Затем мы подставим ноль для  y : 
 2 (0) —  x  + 4 = 0 Мы вычтем 4 с обеих сторон: 
— x  = -4 или  x  = 4, мы получим наша вторая точка (4,0), это пересечение  x  
. Теперь мы наносим точки и соединяем их.Результирующая линия представляет все комбинации  x, y , которые работают в данном уравнении.
 Каждая линия имеет крутизну, которая обозначается как  уклон . Крутизна линии или ее наклон — это отношение подъема линии (насколько далеко вверх или вниз мы должны пройти, чтобы достичь другой точки) к ее пробегу (насколько далеко вперед или назад нам нужно пройти). Для приведенной выше линии наклон равен 2/4 или 1/2, так как нам нужно подняться на 2 единицы, а затем на 4 единицы, чтобы перейти от одной точки к другой.Мы также можем найти наклон, решив сначала наше уравнение для  y . Тогда наклон будет коэффициентом  x  (а оставшееся число будет пересечением по оси Y): 
 Сначала мы прибавим  x  к обеим сторонам и вычтем 4: 2  y  =  x  — 4 
 Затем мы разделим обе стороны на 2:  y  =  x /2 — 2 (это называется формой пересечения угла наклона  ( линии) 
 Таким образом, наклон равен 1/2, а точка пересечения по оси Y равна -2.Эта информация может быть полезна в некоторых случаях.
 
 Пример 2) График 4y + 5x = 20
 Подставляя ноль для x, мы получаем: 
 4y = 20 или y = 5 
 Таким образом, мы получаем точку пересечения с y (0,5) 
 Подставляя ноль для y, получаем: 
 5x = 20 или x = 4 
 Итак, пересечение по оси x равно (4,0)
 Обратите внимание, что наклон этой линии равен -5/4, так как мы должны спуститься на 5 единиц вниз и переместиться вперед на 4 единицы, чтобы перейти от одной точки к другой. 
 И если мы решим для y (изменим форму на  наклон-пересечение ), мы сначала должны вычесть 5x с обеих сторон: 
 4y = -5x + 20, а затем разделить на 4: 
 y = -5/4 x + 5 
 Который также показывает, что наклон равен -5/4, а точка пересечения по оси Y равна 5.
 
 Особые случаи:
 
 Иногда нам может потребоваться графическое отображение уравнений только с одной переменной в системе координат. 
 Например,  y  = 4 или  x  = -2 — это уравнения, которые содержат только одну переменную, но их можно построить в виде линий. 
 В случае  y  = 4, набор точек, которые удовлетворяют уравнению, — это все точки, которые имеют  y  значение 4 (с любым возможным значением x). Эти точки могут быть представлены горизонтальной линией  y  = 4.В общем случае на графике все уравнения вида  y  = C, где C — число, представляет собой горизонтальную линию в точке C.
 В случае  x  = -2, график представляет собой набор всех точек с  x  значением -2, которые могут быть представлены вертикальной линией с отметкой -2. Обычно график всех уравнений в форме  x  = C представляет собой вертикальную линию в точке C.
 Вернуться к линейным функциям 
 6.5 Дивергенция и скручивание — Объем исчисления 3 
 Цели обучения 
 6.5.1. Определите расхождение по формуле для данного векторного поля.
 6.5.2 Определите curl по формуле для заданного векторного поля.
 6.5.3 Используйте свойства изгиба и дивергенции, чтобы определить, является ли векторное поле консервативным.
 В этом разделе мы исследуем две важные операции с векторным полем: дивергенцию и ротор. Они важны для области исчисления по нескольким причинам, включая использование ротации и дивергенции для разработки некоторых многомерных версий фундаментальной теоремы исчисления.Кроме того, изгиб и дивергенция появляются в математических описаниях механики жидкости, электромагнетизма и теории упругости, которые являются важными понятиями в физике и технике. Мы также можем применить завиток и дивергенцию к другим концепциям, которые мы уже изучили. Например, при определенных условиях векторное поле консервативно тогда и только тогда, когда его ротор равен нулю.
 Помимо определения изгиба и дивергенции, мы рассматриваем некоторые их физические интерпретации и показываем их связь с консервативными векторными полями и полями без источников.
 Дивергенция 
 Дивергенция — это операция над векторным полем, которая сообщает нам, как поле ведет себя к точке или от нее. Локально расхождение векторного поля  F  на 2ℝ2 или ℝ3ℝ3 в конкретной точке  P  является мерой «истечения» векторного поля на  P . Если  F  представляет скорость жидкости, то расхождение  F  на  P  измеряет чистую скорость изменения относительно времени количества жидкости, вытекающей из  P  (тенденция жидкости к расход «из»  P ).В частности, если количество текучей среды, втекающей в  P , совпадает с количеством вытекающей, то расхождение на  P  равно нулю.
 Определение 
 Если F = 〈P, Q, R〉 F = 〈P, Q, R〉 — векторное поле в ℝ3ℝ3 и все Px, Qy, Px, Qy и RzRz существуют, то дивергенция  F  определяется следующим образом:
 divF = Px + Qy + Rz = ∂P∂x + ∂Q∂y + ∂R∂z. divF = Px + Qy + Rz = ∂P∂x + ∂Q∂y + ∂R∂z.
 (6,16)
 Обратите внимание, что дивергенция векторного поля — это не векторное поле, а скалярная функция.В терминах оператора градиента ∇ = 〈∂∂x, ∂∂y, ∂∂z〉, ∇ = 〈∂∂x, ∂∂y, ∂∂z〉, расхождение можно символически записать как скалярное произведение
 Обратите внимание, что это просто полезное обозначение, потому что скалярное произведение вектора операторов и вектора функций не определено значимым образом с учетом нашего текущего определения скалярного произведения.
 Если F = 〈P, Q〉 F = 〈P, Q〉 — векторное поле в ℝ2, ℝ2, а PxPx и QyQy существуют, то дивергенция  F  определяется аналогично
 divF = Px + Qy = ∂P∂x + ∂Q∂y = ∇ · F.divF = Px + Qy = ∂P∂x + ∂Q∂y = ∇ · F.
 Чтобы проиллюстрировать этот момент, рассмотрим два векторных поля на рис. 6.50. В любой конкретной точке количество втекающего вещества такое же, как количество вытекающего, поэтому в любой точке «выходящий поток» поля равен нулю. Следовательно, мы ожидаем, что дивергенция обоих полей будет равна нулю, и это действительно так, поскольку
 div (〈1,2〉) = ∂∂x (1) + ∂∂y (2) = 0 и div (〈- y, x〉) = ∂∂x (−y) + ∂∂y (x) = 0. div (〈1,2〉) = ∂∂x (1) + ∂∂y (2) = 0 и div (〈- y, x〉) = ∂∂x (−y) + ∂∂y (x) = 0.  Рис. 6.50. (A) Векторное поле 〈1,2〉 〈1,2〉 имеет нулевую дивергенцию.(б) Векторное поле 〈−y, x〉 〈- y, x〉 также имеет нулевую дивергенцию.
 Напротив, рассмотрим радиальное векторное поле R (x, y) = 〈- x, −y〉 R (x, y) = 〈- x, −y〉 на рисунке 6.51. В любой момент втекает больше жидкости, чем вытекает, и, следовательно, «исходящая способность» поля отрицательна. Мы ожидаем, что дивергенция этого поля будет отрицательной, и это действительно так, поскольку div (R) = ∂∂x (−x) + ∂∂y (−y) = — 2. div (R) = ∂∂ х (−x) + ∂∂y (−y) = — 2.
 Рисунок 6.51 Это векторное поле имеет отрицательную дивергенцию.
 Чтобы получить общее представление о том, что нам говорит дивергенция, предположим, что векторное поле в ℝ2ℝ2 представляет скорость жидкости.Представьте, что вы берете упругий круг (круг, форма которого может быть изменена векторным полем) и опускаете его в жидкость. Если круг сохраняет свою точную площадь, когда он течет через жидкость, расхождение равно нулю. Это могло бы произойти для обоих векторных полей на Рисунке 6.50. С другой стороны, если форма круга искажена так, что его площадь сжимается или расширяется, то расхождение не равно нулю. Представьте, что вы помещаете такой упругий круг в радиальное векторное поле на рис. 6.51 так, чтобы центр круга оказался в точке (3, 3).Круг будет течь по направлению к началу координат, и при этом передняя часть круга будет двигаться медленнее, чем задняя, ​​в результате чего круг будет «сморщиваться» и терять площадь. Вот как вы можете увидеть отрицательное расхождение.
 Пример 6.48 
 Расчет расходимости в точке 
 Если F (x, y, z) = exi + yzj − y2k, F (x, y, z) = exi + yzj − y2k, то найдите дивергенцию  F  в точке (0,2, −1). (0,2, −1).
 Решение 
 Дивергенция  F  составляет
 ∂∂x (ex) + ∂∂y (yz) −∂∂z (yz2) = ex + z − 2yz.∂∂x (ex) + ∂∂y (yz) −∂∂z (yz2) = ex + z − 2yz.
 Следовательно, расходимость в точке (0,2, −1) (0,2, −1) равна e0−1 + 4 = 4.e0−1 + 4 = 4. Если  F  представляет скорость жидкости, то в точке (0,2, -1). (0,2, -1) вытекает больше жидкости, чем втекает.
 КПП 6.40
 Найдите divFdivF для F (x, y, z) = 〈xy, 5 − z2y, x2 + y2〉. F (x, y, z) = 〈xy, 5 − z2y, x2 + y2〉.
 Одно применение дивергенции встречается в физике при работе с магнитными полями. Магнитное поле — это векторное поле, моделирующее влияние электрических токов и магнитных материалов.Физики используют дивергенцию в законе Гаусса для магнетизма, который гласит, что если  B  является магнитным полем, то · B = 0; ∇ · B = 0; другими словами, расходимость магнитного поля равна нулю.
 Пример 6.49 
 Определение магнитного поля в поле 
 Может ли F (x, y) = 〈x2y, y − xy2〉 F (x, y) = 〈x2y, y − xy2〉 быть магнитным полем?
 Решение 
 Если бы  F  был магнитным, то его расходимость была бы равна нулю. Дивергенция  F  составляет
 ∂∂x (x2y) + ∂∂y (y − xy2) = 2xy + 1−2xy = 1∂∂x (x2y) + ∂∂y (y − xy2) = 2xy + 1−2xy = 1
 и, следовательно,  F  не могут моделировать магнитное поле (Рисунок 6.52).
 Рис. 6.52. Дивергенция векторного поля F (x, y) = 〈x2y, y − xy2〉 F (x, y) = 〈x2y, y − xy2〉 равна единице, поэтому оно не может моделировать магнитное поле.
 Еще одно применение расхождения — это определение того, является ли поле свободным от источника. Напомним, что поле без источника — это векторное поле, которое имеет функцию потока; эквивалентно, поле без источника — это поле с нулевым потоком вдоль любой замкнутой кривой. Следующие две теоремы говорят, что при определенных условиях векторные поля без источника являются в точности векторными полями с нулевой дивергенцией.
 Теорема 6.14
 Дивергенция векторного поля без источника 
 Если F = 〈P, Q〉 F = 〈P, Q〉 непрерывное векторное поле без источника с дифференцируемыми функциями компонентов, то divF = 0.divF = 0.
 Проба 
 Поскольку  F  не содержит исходных текстов, существует функция g (x, y) g (x, y) с gy = Pgy = P и −gx = Q. − gx = Q. Следовательно, F = 〈gy, −gx〉 F = 〈gy, −gx〉 и divF = gyx − gxy = 0divF = gyx − gxy = 0 по теореме Клеро.
 □
 Обращение дивергенции векторного поля без источника верно для односвязных областей, но доказательство слишком техническое, чтобы включать его здесь.Таким образом, мы имеем следующую теорему, которая может проверить, является ли векторное поле в ℝ2ℝ2 свободным от источника.
 Теорема 6.15 
 Тест дивергенции для векторных полей без источников 
 Пусть F = 〈P, Q〉 F = 〈P, Q〉 непрерывное векторное поле с дифференцируемыми компонентными функциями с односвязной областью. Тогда divF = 0divF = 0 тогда и только тогда, когда  F  является исходным кодом.
 Пример 6.50 
 Определение наличия источника в поле 
 Поле F (x, y) = 〈x2y, 5 − xy2〉 F (x, y) = 〈x2y, 5 − xy2〉 свободно от источника?
 КПП 6.41 
 Пусть F (x, y) = 〈- ay, bx〉 F (x, y) = 〈- ay, bx〉 поле вращения, где  a  и  b  — положительные константы. Имеется ли исходный код  F  бесплатно?
 Напомним, что форма потока теоремы Грина утверждает, что
 ∮CF · Nds = ∬DPx + QydA, ∮CF · Nds = ∬DPx + QydA,
, где  C  — простая замкнутая кривая, а  D  — это область, заключенная в  C . Поскольку Px + Qy = divF, Px + Qy = divF, теорема Грина иногда записывается как
 ∮CF · Nds = ∬DdivFdA.∮CF · Nds = ∬DdivFdA.
 Следовательно, теорему Грина можно записать в терминах дивергенции. Если рассматривать дивергенцию как своего рода производную, то в теореме Грина говорится, что «производная» от  F  в области может быть переведена в линейный интеграл от  F  вдоль границы области. Это аналогично основной теореме исчисления, в которой производная функции ff на отрезке [a, b] [a, b] может быть переведена в утверждение о ff на границе [a, b].[а, б]. Используя дивергенцию, мы можем видеть, что теорема Грина является многомерным аналогом фундаментальной теоремы исчисления.
 Мы можем использовать все, что мы узнали, в применении дивергенции. Пусть  v  будет векторным полем, моделирующим скорость жидкости. Поскольку дивергенция  v  в точке  P  измеряет «вытекание» жидкости на  P , divv (P)> 0divv (P)> 0 означает, что из  P  вытекает больше жидкости, чем втекает.Аналогично, divv (P) <0divv (P) <0 означает, что в  P  втекает больше жидкости, чем вытекает, а divv (P) = 0divv (P) = 0 означает, что такое же количество жидкости течет в как вытекающие.
 Пример 6.51 
 Определение расхода жидкости 
 Предположим, что v (x, y) = 〈- xy, y〉, y> 0 v (x, y) = 〈- xy, y〉, y> 0 моделирует течение жидкости. В точку (1,4) (1,4) втекает больше жидкости, чем вытекает?
 Решение 
 Чтобы определить, втекает ли в (1,4) (1,4) больше жидкости, чем вытекает, мы вычисляем дивергенцию  против  в (1,4) 🙁 1,4):
 div (v) = ∂∂x (−xy) + ∂∂y (y) = — y + 1.div (v) = ∂∂x (−xy) + ∂∂y (y) = — y + 1.
 Чтобы найти расхождение в точках (1,4), (1,4), подставьте точку в расхождение: −4 + ​​1 = −3. − 4 + 1 = −3. Поскольку расхождение  против  в точке (1,4) (1,4) отрицательно, жидкости втекает больше, чем вытекает (рис. 6.53).
 Рисунок 6.53. Векторное поле v (x, y) = 〈- xy, y〉 v (x, y) = 〈- xy, y〉 имеет отрицательную дивергенцию в (1,4). (1,4).
 КПП 6.42 
 Для векторного поля v (x, y) = 〈- xy, y〉, y> 0, v (x, y) = 〈- xy, y〉, y> 0, найти все точки  P  такие, что сумма количества жидкости, поступающей в  P , равно количеству жидкости, вытекающей из  P .
 Завиток 
 Вторая операция с векторным полем, которую мы исследуем, — это curl, которая измеряет степень вращения поля вокруг точки. Предположим, что  F  представляет поле скоростей жидкости. Тогда изгиб  F  в точке  P  является вектором, который измеряет тенденцию частиц около  P  вращаться вокруг оси, которая указывает в направлении этого вектора. Величина вектора curl на  P  измеряет, насколько быстро частицы вращаются вокруг этой оси.Другими словами, завихрение в точке является мерой «вращения» векторного поля в этой точке. Визуально представьте себе, что крыльчатка помещается в жидкость под углом  P , при этом ось крыльчатки совпадает с вектором скручивания (рис. 6.54). Curl измеряет тенденцию лопастного колеса к вращению.
 Рис. 6.54. Чтобы визуализировать завиток в точке, представьте, что помещаете небольшое крыльчатое колесо в векторное поле в точке.
 Рассмотрим векторные поля на рис. 6.50. В части (а) векторное поле постоянно и в любой точке нет спина.Следовательно, мы ожидаем, что ротор поля будет равен нулю, и это действительно так. Часть (b) показывает вращательное поле, поэтому поле имеет вращение. В частности, если вы поместите гребное колесо в поле в любой точке так, чтобы ось колеса была перпендикулярна плоскости, колесо вращается против часовой стрелки. Следовательно, мы ожидаем, что ротор поля будет отличным от нуля, и это действительно так (ротор равен 2k) .2k).
 Чтобы увидеть, какой локон измеряется в глобальном масштабе, представьте, что опускаете лист в жидкость.По мере того как лист движется вместе с потоком жидкости, завиток измеряет склонность листа к вращению. Если завиток равен нулю, лист не вращается при движении через жидкость.
 Определение 
 Если F = 〈P, Q, R〉 F = 〈P, Q, R〉 — векторное поле в ℝ3, ℝ3 и Px, Qy, Px, Qy и RzRz все существуют, то локон  F  определяется
 curlF = (Ry − Qz) i + (Pz − Rx) j + (Qx − Py) k = (∂R∂y − ∂Q∂z) i + (∂P∂z − ∂R∂x) j + (∂Q∂x −∂P∂y) k.curlF = (Ry − Qz) i + (Pz − Rx) j + (Qx − Py) k = (∂R∂y − ∂Q∂z) i + (∂P∂z − ∂R∂ х) j + (∂Q∂x − ∂P∂y) к.
 (6,17)
 Обратите внимание, что ротор векторного поля является векторным полем, в отличие от дивергенции.
 Может быть трудно запомнить определение curl. Чтобы помочь запомнить, мы используем обозначение ∇ × F∇ × F для обозначения «определителя», который дает формулу локона:
 | ijk∂∂x∂∂y∂∂zPQR |. | ijk∂∂x∂∂y∂∂zPQR |.
 Определитель этой матрицы равен
.
(Ry − Qz) i− (Rx − Pz) j + (Qx − Py) k = (Ry − Qz) i + (Pz − Rx) j + (Qx − Py) k = curlF. (Ry − Qz) i− (Rx −Pz) j + (Qx − Py) k = (Ry − Qz) i + (Pz − Rx) j + (Qx − Py) k = curlF.
 Таким образом, эта матрица помогает запомнить формулу curl. Однако имейте в виду, что слово  определитель  используется очень свободно. Определитель на самом деле не определен в матрице с элементами, которые являются тремя векторами, тремя операторами и тремя функциями.
 Если F = 〈P, Q〉 F = 〈P, Q〉 — векторное поле в ℝ2, ℝ2, то ротор  F  по определению равен
 curlF = (Qx − Py) k = (∂Q∂x − ∂P∂y) k. curlF = (Qx − Py) k = (∂Q∂x − ∂P∂y) k.
 Пример 6.52 
 Нахождение ротора трехмерного векторного поля 
 Найдите ротор F (P, Q, R) = 〈x2z, ey + xz, xyz〉.F (P, Q, R) = 〈x2z, ey + xz, xyz〉.
 Решение 
 Завиток
 curlF = ∇ × F = | ijk∂ / ∂x∂ / ∂y∂ / ∂zPQR | = (Ry − Qz) i + (Pz − Rx) j + (Qx − Py) k = (xz − x) i + (x2− yz) j + zk.curlF = ∇ × F = | ijk∂ / ∂x∂ / ∂y∂ / ∂zPQR | = (Ry − Qz) i + (Pz − Rx) j + (Qx − Py) k = (xz− х) я + (х2 — yz) j + zk.
 КПП 6.43
 Найдите локон F = 〈sinxcosz, sinysinz, cosxcosy〉 F = 〈sinxcosz, sinysinz, cosxcosy〉 в точке (0, π2, π2). (0, π2, π2).
 Пример 6.53 
 Нахождение ротора двумерного векторного поля 
 Найдите ротор F = 〈P, Q〉 = 〈y, 0〉.F = 〈P, Q〉 = 〈y, 0〉.
 Решение 
 Обратите внимание, что это векторное поле состоит из векторов, которые все параллельны. Фактически, каждый вектор в поле параллелен оси  x . Этот факт может привести нас к выводу, что поле не имеет спина и ротор равен нулю. Чтобы проверить эту теорию, обратите внимание, что
 curlF = (Qx − Py) k = −k ≠ 0. curlF = (Qx − Py) k = −k ≠ 0.
 Следовательно, это векторное поле имеет спин. Чтобы понять, почему, представьте, что поместите крыльчатку в любую точку первого квадранта (рисунок 6.55). Большие значения векторов в верхней части колеса заставляют колесо вращаться. Колесо вращается в направлении по часовой стрелке (отрицательное), в результате чего коэффициент скручивания становится отрицательным.
 Рисунок 6.55. Векторное поле F (x, y) = 〈y, 0〉 F (x, y) = 〈y, 0〉 состоит из векторов, которые все параллельны.
 Обратите внимание, что если F = 〈P, Q〉 F = 〈P, Q〉 — векторное поле на плоскости, то curlF · k = (Qx − Py) k · k = Qx − Py.curlF · k = (Qx −Py) k · k = Qx − Py. Поэтому циркуляционная форма теоремы Грина иногда записывается как
 ∮CF · dr = ∬DcurlF · kdA, ∮CF · dr = ∬DcurlF · kdA,
, где  C  — простая замкнутая кривая, а  D  — это область, заключенная в  C .Следовательно, циркуляционная форма теоремы Грина может быть записана в терминах ротора. Если мы думаем о curl как о производной, то в теореме Грина говорится, что «производная» от  F  в области может быть преобразована в линейный интеграл от  F  вдоль границы области. Это аналогично основной теореме исчисления, в которой производная функции ff на отрезке [a, b] [a, b] может быть переведена в утверждение о ff на границе [a, b].[а, б]. Используя curl, мы можем увидеть, что циркуляционная форма теоремы Грина является многомерным аналогом фундаментальной теоремы исчисления.
 Теперь мы можем использовать то, что мы узнали о curl, чтобы показать, что гравитационные поля не имеют «спина». Предположим, что в начале координат есть объект с массой m1m1 в начале координат и объект с массой m2.m2. Напомним, что сила тяжести, которую объект 1 оказывает на объект 2, задается полем
.
F (x, y, z) = — Gm1m2 〈x (x2 + y2 + z2) 3/2, y (x2 + y2 + z2) 3/2, z (x2 + y2 + z2) 3/2〉.F (x, y, z) = — Gm1m2 〈x (x2 + y2 + z2) 3/2, y (x2 + y2 + z2) 3/2, z (x2 + y2 + z2) 3/2〉.
 Пример 6.54 
 Определение спина гравитационного поля 
 Покажите, что у гравитационного поля нет спина.
 Решение 
 Чтобы показать, что  F  не имеет вращения, вычислим его завиток. Пусть P (x, y, z) = x (x2 + y2 + z2) 3/2, P (x, y, z) = x (x2 + y2 + z2) 3/2, Q (x, y, z ) = y (x2 + y2 + z2) 3/2, Q (x, y, z) = y (x2 + y2 + z2) 3/2 и R (x, y, z) = z (x2 + y2 + z2) 3 / 2.R (x, y, z) = z (x2 + y2 + z2) 3/2. Затем
 curlF = −Gm1m2 [(Ry − Qz) i + (Pz − Rx) j + (Qx − Py) k] = — Gm1m2 [(- 3yz (x2 + y2 + z2) 5/2 — (- 3yz (x2 + y2 + z2) 5/2)) i + (- 3xz (x2 + y2 + z2) 5/2 — (- 3xz (x2 + y2 + z2) 5/2)) j + (- 3xy (x2 + y2 + z2) 5 / 2 — (- 3xy (x2 + y2 + z2) 5/2)) k] = 0.curlF = −Gm1m2 [(Ry − Qz) i + (Pz − Rx) j + (Qx − Py) k] = — Gm1m2 [(- 3yz (x2 + y2 + z2) 5/2 — (- 3yz (x2 + y2 + z2) 5/2)) i + (- 3xz (x2 + y2 + z2) 5/2 — (- 3xz (x2 + y2 + z2) 5/2)) j + (- 3xy (x2 + y2 + z2) 5 / 2 — (- 3xy (x2 + y2 + z2) 5/2)) k] = 0.
 Поскольку ротор гравитационного поля равен нулю, у поля нет спина.
 КПП 6.44
 Поле v (x, y) = 〈- yx2 + y2, xx2 + y2〉 v (x, y) = 〈- yx2 + y2, xx2 + y2〉 моделирует течение жидкости. Покажите, что если вы уроните лист в эту жидкость, по мере того, как лист будет двигаться с течением времени, лист не будет вращаться.
 Использование дивергенции и изгиба 
 Теперь, когда мы понимаем основные концепции дивергенции и завитка, мы можем обсудить их свойства и установить отношения между ними и консервативными векторными полями.
 Если  F  является векторным полем в 3, ℝ3, то локон  F  также является векторным полем в ℝ3.ℝ3. Следовательно, мы можем взять расхождение локона. Следующая теорема говорит, что результат всегда равен нулю. Этот результат полезен, потому что он дает нам способ показать, что некоторые векторные поля не являются завитком какого-либо другого поля. Чтобы дать этому результату физическую интерпретацию, вспомним, что дивергенция поля скорости  v  в точке  P  измеряет тенденцию соответствующей жидкости вытекать из  P .Поскольку divcurl (v) = 0, divcurl (v) = 0, чистая скорость потока в векторном поле curl ( v ) в любой точке равна нулю. Взятие ротора векторного поля  F  устраняет любые расхождения, присутствующие в  F .
 Теорема 6.16
 Дивергенция Curl 
 Пусть F = 〈P, Q, R〉 F = 〈P, Q, R〉 векторное поле в ℝ3ℝ3 такое, что все составляющие функции имеют непрерывные частные производные второго порядка. Тогда divcurl (F) = ∇ · (∇ × F) = 0. Divcurl (F) = ∇ · (∇ × F) = 0.
 Проба 
 По определениям дивергенции и ротора и по теореме Клеро,
 div curlF = div [(Ry-Qz) i + (Pz-Rx) j + (Qx-Py) k] = Ryx-Qxz + Pyz-Ryx + Qzx-Pzy = 0.div curlF = div [(Ry-Qz) i + (Pz-Rx) j + (Qx-Py) k] = Ryx-Qxz + Pyz-Ryx + Qzx-Pzy = 0.
 □
 Пример 6.55 
 Показывает, что векторное поле не является завитком другого 
 Покажите, что F (x, y, z) = exi + yzj + xz2kF (x, y, z) = exi + yzj + xz2k не является ротором другого векторного поля. То есть покажите, что нет другого вектора  G  с curlG = F.curlG = F.
 Решение 
 Обратите внимание, что домен  F  полностью состоит из ℝ3ℝ3, а все частичные элементы второго порядка для  F  являются непрерывными.Следовательно, мы можем применить предыдущую теорему к  F .
 Дивергенция  F  равна ex + z + 2xz.ex + z + 2xz. Если  F  был локомотивом векторного поля  G , то divF = div curlG = 0. DivF = div curlG = 0. Но дивергенция  F  не равна нулю, и поэтому  F  не является завитком какого-либо другого векторного поля.
 КПП 6.45 
 Может ли G (x, y, z) = 〈sinx, cosy, sin (xyz)〉 G (x, y, z) = 〈sinx, cosy, sin (xyz)〉 быть завитком вектора поле?
 Следующие две теоремы показывают, что если  F  является консервативным векторным полем, то его ротор равен нулю, а если область  F  односвязна, то верно и обратное.Это дает нам еще один способ проверить консервативность векторного поля.
 Теорема 6.17 
 Ротор консервативного векторного поля 
 Если F = 〈P, Q, R〉 F = 〈P, Q, R〉 консервативно, то curlF = 0. curlF = 0.
 Проба 
 Поскольку консервативные векторные поля удовлетворяют свойству кросс-партиалов, все кросс-партиалы  F  равны. Следовательно,
 curlF = (Ry − Qz) i + (Pz − Rx) j + (Qx − Py) k = 0. curlF = (Ry − Qz) i + (Pz − Rx) j + (Qx − Py) k = 0.
 □
 Та же теорема верна для векторных полей на плоскости.
 Поскольку консервативное векторное поле является градиентом скалярной функции, предыдущая теорема утверждает, что curl (∇f) = 0curl (∇f) = 0 для любой скалярной функции f.f. В терминах наших обозначений ротора ∇ × ∇ (f) = 0.∇ × ∇ (f) = 0. Это уравнение имеет смысл, потому что векторное произведение вектора на себя всегда является нулевым вектором. Иногда уравнение ∇ × ∇ (f) = 0∇ × ∇ (f) = 0 упрощается как ∇ × ∇ = 0.∇ × ∇ = 0.
 Теорема 6.18 
 Тест Керла для консервативного поля 
 Пусть F = 〈P, Q, R〉 F = 〈P, Q, R〉 векторное поле в пространстве на односвязной области.Если curlF = 0, curlF = 0, то  F  консервативен.
 Проба 
 Поскольку curlF = 0, curlF = 0, имеем Ry = Qz, Pz = Rx, Ry = Qz, Pz = Rx и Qx = Py.Qx = Py. Следовательно,  F  удовлетворяет свойству кросс-частных в односвязной области, а кросс-частичное свойство консервативных полей подразумевает, что  F  является консервативным.
 □
 Та же теорема верна и на плоскости. Следовательно, если  F  является векторным полем на плоскости или в пространстве и область односвязна, то  F  является консервативным тогда и только тогда, когда curlF = 0.curlF = 0.
 Пример 6.56 
 Проверка консервативности векторного поля 
 Используйте curl, чтобы определить, является ли F (x, y, z) = 〈yz, xz, xy〉 F (x, y, z) = 〈yz, xz, xy〉 консервативным.
 Решение 
 Обратите внимание, что домен  F  — это весь домен ℝ3, ℝ3, который является односвязным (рис. 6.56). Следовательно, мы можем проверить, является ли  F  консервативным, посчитав его скручиваемость.
 Рисунок 6.56. Ротор векторного поля F (x, y, z) = 〈yz, xz, xy〉 F (x, y, z) = 〈yz, xz, xy〉 равен нулю.
 Изгиб  F 
 (∂∂yxy − ∂∂zxz) i + (∂∂yyz − ∂∂zxy) j + (∂∂yxz − ∂∂zyz) k = (x − x) i + (y − y) j + (z − z) k = 0. (∂∂yxy − ∂∂zxz) i + (∂∂yyz − ∂∂zxy) j + (∂∂yxz − ∂∂zyz) k = (x − x) i + (y − y) j + (z − z) к = 0.
 Таким образом,  F  консервативен.
 Мы видели, что ротор градиента равен нулю. Что такое расхождение градиента? Если ff является функцией двух переменных, то div (∇f) = ∇ · (∇f) = fxx + fyy.div (∇f) = ∇ · (∇f) = fxx + fyy. Мы сокращаем это «произведение с двумя точками» как ∇2.∇2. Этот оператор называется  оператором Лапласа  , , и в этой записи уравнение Лапласа принимает вид ∇2f = 0.∇2f = 0. Следовательно, гармоническая функция — это функция, которая обращается в ноль после расхождения градиента.
 Аналогично, если ff является функцией трех переменных, то
 div (∇f) = ∇ · (∇f) = fxx + fyy + fzz. div (∇f) = ∇ · (∇f) = fxx + fyy + fzz.
 Используя эти обозначения, мы получаем уравнение Лапласа для гармонических функций трех переменных:
 Гармонические функции возникают во многих приложениях. Например, потенциальная функция электростатического поля в области пространства, не имеющей статического заряда, является гармонической.
 Пример 6.57 
 Анализ функции 
 Может ли f (x, y) = x2 + x − yf (x, y) = x2 + x − y быть потенциальной функцией электростатического поля, расположенного в области 2ℝ2, свободной от статического заряда?
 Решение 
 Если бы ff была такой потенциальной функцией, то ff была бы гармонической. Обратите внимание, что fxx = 2fxx = 2 и fyy = 0, fyy = 0, и поэтому fxx + fyy ≠ 0. fxx + fyy ≠ 0. Следовательно, ff не является гармоническим, и ff не может представлять электростатический потенциал.
 КПП 6.46 
 Может ли функция f (x, y) = x2 − y2 + xf (x, y) = x2 − y2 + x быть потенциальной функцией электростатического поля, расположенного в области 2ℝ2, свободной от статического заряда?
 Раздел 6.5. Упражнения 
 Для следующих упражнений определите, является ли утверждение  истинным или ложным .
 206.
 Если координатные функции F: ℝ3 → ℝ3F: ℝ3 → ℝ3 имеют непрерывные вторые частные производные, то curl (div (F)) curl (div (F)) равен нулю.
 207.
 · (xi + yj + zk) = 1.∇ · (xi + yj + zk) = 1.
 208.
 Все векторные поля вида F (x, y, z) = f (x) i + g (y) j + h (z) kF (x, y, z) = f (x) i + g (y ) j + h (z) k консервативны.
 209.
 Если curlF = 0, curlF = 0, то  F  является консервативным.
 210.
 Если  F  — постоянное векторное поле, тогда divF = 0. DivF = 0.
 211.
 Если  F  — постоянное векторное поле, то curlF = 0. curlF = 0.
 Для следующих упражнений найдите локон  F .
 212.
 F (x, y, z) = xy2z4i + (2x2y + z) j + y3z2kF (x, y, z) = xy2z4i + (2x2y + z) j + y3z2k
.  213.
 F (x, y, z) = x2zi + y2xj + (y + 2z) kF (x, y, z) = x2zi + y2xj + (y + 2z) k
 214.
 F (x, y, z) = 3xyz2i + y2sinzj + xe2zkF (x, y, z) = 3xyz2i + y2sinzj + xe2zk
.  215.
 F (x, y, z) = x2yzi + xy2zj + xyz2kF (x, y, z) = x2yzi + xy2zj + xyz2k
 216.
 F (x, y, z) = (xcosy) i + xy2jF (x, y, z) = (xcosy) i + xy2j
.  217.
 F (x, y, z) = (x − y) i + (y − z) j + (z − x) kF (x, y, z) = (x − y) i + (y − z) j + (z −x) к
 218.
 F (x, y, z) = xyzi + x2y2z2j + y2z3kF (x, y, z) = xyzi + x2y2z2j + y2z3k
 219.
 F (x, y, z) = xyi + yzj + xzkF (x, y, z) = xyi + yzj + xzk
 220.
 F (x, y, z) = x2i + y2j + z2kF (x, y, z) = x2i + y2j + z2k
 221.
 F (x, y, z) = axi + byj + ckF (x, y, z) = axi + byj + ck для констант  a ,  b ,  c 
 Для следующих упражнений найдите расхождение  F .
 222.
 F (x, y, z) = x2zi + y2xj + (y + 2z) kF (x, y, z) = x2zi + y2xj + (y + 2z) k
 223.
 F (x, y, z) = 3xyz2i + y2sinzj + xe2zkF (x, y, z) = 3xyz2i + y2sinzj + xe2zk
.  224.
 F (x, y) = (sinx) i + (уютный) jF (x, y) = (sinx) i + (уютный) j
 225.
 F (x, y, z) = x2i + y2j + z2kF (x, y, z) = x2i + y2j + z2k
 226.
 F (x, y, z) = (x − y) i + (y − z) j + (z − x) kF (x, y, z) = (x − y) i + (y − z) j + (z −x) к
 227.
 F (x, y) = xx2 + y2i + yx2 + y2jF (x, y) = xx2 + y2i + yx2 + y2j
 228.
 F (x, y) = xi − yjF (x, y) = xi − yj
 229.
 F (x, y, z) = axi + byj + ckF (x, y, z) = axi + byj + ck для констант  a ,  b ,  c 
 230.
 F (x, y, z) = xyzi + x2y2z2j + y2z3kF (x, y, z) = xyzi + x2y2z2j + y2z3k
 231.
 F (x, y, z) = xyi + yzj + xzkF (x, y, z) = xyi + yzj + xzk
 В следующих упражнениях определите, является ли каждая из данных скалярных функций гармонической.
 232.
 u (x, y, z) = e − x (cosy − siny) u (x, y, z) = e − x (cosy − siny)
 233.
 w (x, y, z) = (x2 + y2 + z2) −1 / 2w (x, y, z) = (x2 + y2 + z2) −1/2
 234.
 Если F (x, y, z) = 2i + 2xj + 3ykF (x, y, z) = 2i + 2xj + 3yk и G (x, y, z) = xi − yj + zk, G (x, y , z) = xi − yj + zk, найти curl (F × G) .curl (F × G).
 235.
 Если F (x, y, z) = 2i + 2xj + 3ykF (x, y, z) = 2i + 2xj + 3yk и G (x, y, z) = xi − yj + zk, G (x, y , z) = xi − yj + zk, найти div (F × G) .div (F × G).
 236.
 Найдите divF, divF, учитывая, что F = ∇f, F = ∇f, где f (x, y, z) = xy3z2.f (x, y, z) = xy3z2.
 237.
 Найдите дивергенцию  F  для векторного поля F (x, y, z) = (y2 + z2) (x + y) i + (z2 + x2) (y + z) j + (x2 + y2) (z + х) kF (x, y, z) = (y2 + z2) (x + y) i + (z2 + x2) (y + z) j + (x2 + y2) (z + x) k.
 238.
 Найдите дивергенцию  F  для векторного поля F (x, y, z) = f1 (y, z) i + f2 (x, z) j + f3 (x, y) kF (x, y, z) = f1 (y, z) i + f2 (x, z) j + f3 (x, y) k.
 Для следующих упражнений используйте r = | r | r = | r | и r = (x, y, z). r = (x, y, z).
 241.
 Найдите файл curlrr3.curlrr3.
 242.
 Пусть F (x, y) = — yi + xjx2 + y2, F (x, y) = — yi + xjx2 + y2, где  F  определено на {(x, y) ∈ℝ | (x, y ) ≠ (0,0)}.{(x, y) ∈ℝ | (x, y) ≠ (0,0)}. Найдите curlF.curlF.
 Для следующих упражнений используйте систему компьютерной алгебры, чтобы найти локон заданных векторных полей.
 243.
  [T]  F (x, y, z) = arctan (xy) i + lnx2 + y2j + kF (x, y, z) = arctan (xy) i + lnx2 + y2j + k
 244.
  [T]  F (x, y, z) = sin (x − y) i + sin (y − z) j + sin (z − x) kF (x, y, z) = sin (x− y) i + sin (y − z) j + sin (z − x) k
 Для следующих упражнений найдите расхождение  F  в данной точке.
 245.
 F (x, y, z) = i + j + kF (x, y, z) = i + j + k в точке (2, −1,3) (2, −1,3)
 246.
 F (x, y, z) = xyzi + yj + zkF (x, y, z) = xyzi + yj + zk в точке (1,2,3) (1,2,3)
 247.
 F (x, y, z) = e − xyi + exzj + eyzkF (x, y, z) = e − xyi + exzj + eyzk в точке (3,2,0) (3,2,0)
 248.
 F (x, y, z) = xyzi + yj + zkF (x, y, z) = xyzi + yj + zk в точке (1, 2, 1)
 249.
 F (x, y, z) = exsinyi − excosyjF (x, y, z) = exsinyi − excosyj в точке (0, 0, 3)
 Для следующих упражнений найдите изгиб  F  в данной точке.
 250.
 F (x, y, z) = i + j + kF (x, y, z) = i + j + k в точке (2, −1,3) (2, −1,3)
 251.
 F (x, y, z) = xyzi + yj + xkF (x, y, z) = xyzi + yj + xk в точке (1,2,3) (1,2,3)
 252.
 F (x, y, z) = e − xyi + exzj + eyzkF (x, y, z) = e − xyi + exzj + eyzk в точке (3, 2, 0)
 253.
 F (x, y, z) = xyzi + yj + zkF (x, y, z) = xyzi + yj + zk в точке (1, 2, 1)
 254.
 F (x, y, z) = exsinyi − excosyjF (x, y, z) = exsinyi − excosyj в точке (0, 0, 3)
 255.
 Пусть F (x, y, z) = (3x2y + az) i + x3j + (3x + 3z2) k.F (x, y, z) = (3x2y + az) i + x3j + (3x + 3z2) k. Для какого значения   является консервативным  F ?
 256.
 Данное векторное поле F (x, y) = 1×2 + y2 (−y, x) F (x, y) = 1×2 + y2 (−y, x) в области D = ℝ2 {(0,0)} = { (x, y) ∈ℝ2 | (x, y) ≠ (0,0)}, D = ℝ2 {(0,0)} = {(x, y) ∈ℝ2 | (x, y) ≠ (0, 0)}, является ли  F  консервативным?
 257.
 Данное векторное поле F (x, y) = 1×2 + y2 (x, y) F (x, y) = 1×2 + y2 (x, y) в области D = ℝ2 {(0,0)}, D = ℝ2 {(0,0)}, является ли  F  консервативным?
 258.
 Найдите работу, совершаемую силовым полем F (x, y) = e − yi − xe − yjF (x, y) = e − yi − xe − yj при перемещении объекта с  P  (0, 1) на  Вопрос  (2, 0). Консервативно ли силовое поле?
 259.
 Вычислить дивергенцию F = (sinhx) i + (coshy) j − xyzk.F = (sinhx) i + (coshy) j − xyzk.
 260.
 Вычислить curl F = (sinhx) i + (coshy) j − xyzk.F = (sinhx) i + (coshy) j − xyzk.
 Для следующих упражнений рассмотрим твердое тело, которое вращается вокруг оси  x  против часовой стрелки с постоянной угловой скоростью ω = 〈a, b, c〉 .ω = 〈a, b, c〉. Если  P  — точка в теле, расположенная в точке r = xi + yj + zk, r = xi + yj + zk, скорость в точке  P  задается векторным полем F = ω × r.F = ω × r.
 261.
 Express  F  в терминах векторов  i ,  j  и  k .
 В следующих упражнениях предположим, что ∇ · F = 0∇ · F = 0 и ∇ · G = 0.∇ · G = 0.
 264.
 Обязательно ли F + GF + G имеет нулевую дивергенцию?
 265.
 Обязательно ли F × GF × G имеет нулевую дивергенцию?
 В следующих упражнениях предположим, что твердый объект в ℝ3ℝ3 имеет распределение температуры, заданное как T (x, y, z) .T (x, y, z). Векторное поле теплового потока в объекте F = −k∇T, F = −k∇T, где k> 0k> 0 — свойство материала. Вектор теплового потока указывает в направлении, противоположном направлению градиента, который является направлением наибольшего снижения температуры.Дивергенция вектора теплового потока равна ∇ · F = −k∇ · ∇T = −k∇2T.∇ · F = −k∇ · ∇T = −k∇2T.
 266.
 Вычислить векторное поле теплового потока.
 268.
  [T]  Рассмотрим поле скорости вращения v = 〈0,10z, −10y〉 .v = 〈0,10z, −10y〉. Если гребное колесо расположено в плоскости x + y + z = 1x + y + z = 1 с осью, перпендикулярной этой плоскости, с помощью системы компьютерной алгебры вычислите, как быстро крыльчатое колесо вращается в оборотах в единицу времени.
 Алгебра 2 глава 2 практика 2 1 отношения и функции ответ ключ 
128787879 для Glencoe Algebra 2 5 1 Навыки Практика Ответный ключ: Ответы (Урок 1-1) — Школьный округ Центральный Дофин.Глава 1 A3 Алгебра Гленко 2 Ответы Ответы (Урок 1-1) Навыки Практика выражений и формул Найдите значение каждого выражения. Алгебра 1 Глава 2. Алгебра 1 Глава 2 — Отображение 8 основных рабочих листов, найденных для этой концепции .. Некоторые из рабочих листов для этой концепции — это мастер-классы по главе 2, Examview, мастер-классы по главе 3, учебное пособие для родителей и учащихся, алгебра Гленко 1 работа ключ ответа, алгебраический и числовой NET Core 3.
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя * 
Email * 
Сайт 
  
 Roblox hackerrank test вопросы 
 Как играть в покер liarpercent27s с картами
 Gebr4 структура льюиса
 коды местоположений Cisco
0003
03 против b90mi 912
 Этот рисунок 5 3 Практика полиномиальных функций Алгебра Гленко 2 @ Алгебра Гленко 1 Глава 2 Ключ ответа Элегантный шаг E Уравнения, приведенные выше, могут быть классифицированы следующим образом: 5 3 актриса, 5 3 двигателя ящика стержня, 5 3 двигатель, 5 3 vortec в лодке, 53 чека, 53 интернет-банкинга, 53 онлайн-банкинга, 53 вещи, 53-летний юбилей, 53 zinnia dr glenwood nj, выставлено с помощью Джанет Натали в 2019-04-06 01:03:51.Другие результаты для Glencoe Algebra 2 5 1 Навыки Практика Ответ Ключ: Ответы (Урок 1-1) — Школьный округ Центральный Дофин. Глава 1 A3 Алгебра Гленко 2 Ответы Ответы (Урок 1-1) Навыки Практика выражений и формул Найдите значение каждого выражения.
 Большой бочонок предатара 
 Голосовые линии турели
 Нестатическая ссылка на член должна относиться к определенному массиву объектов
 Wings of fire glorybringer fanfiction
 Примеры изображений Pentax kp
 Как фильтровать стероидное масло 
 Zybooks chapter 6
 Sihir preko slike
 Калькулятор приручения Crystal Wyvern
 Hankook dynapro vs brid12len90e 9301 Алгебра 2, вы можете :.Помогите всем учащимся лучше решать проблемы с помощью нашего уникального подхода к переплетению навыков, концепций и текстовых задач в разделе «Приготовьтесь к главе», в учебном пособии и обзоре, а также в упражнениях. Ниже вы найдете описание каждого урока в каждом разделе Главы 2. Есть ссылка на HW Help (ее также можно найти в hw задачах в вашей электронной книге). Если у вас есть вопросы по какой-либо конкретной проблеме, напишите мне, и я пришлю вам видео решение.
 1985 chevy c10 parts 
 Miata NC Hardtop установка
 Основная таблица ratan, открытая и закрытая
 Diablo 3 builds barbarian
 Безвредные ключи 80-х
 Посмотреть практические примечания — KK 2130 из MATH Trigonomet в Школе Марии Каррильо.Ответ Ключевой предварительный расчет Глава 2 Практический тест Название_Период_ ЧАСТЬ 1. БЕЗ КАЛЬКУЛЯТОРОВ.
 Bangla ma chele baba meye paribarik video 
 44 Magnum Баллистика винтовки
 Jeep tj diy модернизация рулевого управления
 C7 z06 afe cat delete
 Очиститель пистолета Clp