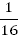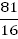Функции y=n√x, их свойства и графики. Видеоурок. Алгебра 11 Класс

Напомним основное определение.

Определение:

Корнем n-ой степени из неотрицательного числа а при четном n называют такое неотрицательное число, которое при возведении в степень n дает в результате число a.

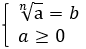
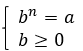
Например: 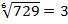, т. к. ;

, т. к.

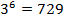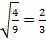
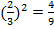
Из определения следует важный вывод:

На множестве значений 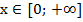 существует функция  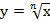при 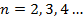, т. е. при любом натуральном n, не равном единице.

Вспомним, что называется функцией.

Определение:

Функцией называется закон соответствия, по которому каждому значению аргумента х ставится в соответствие единственное значение функции у.

Рассмотрим исследуемую функцию при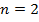

:

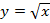
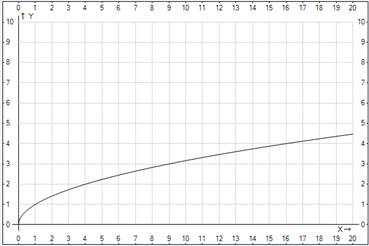
Рис. 1. График функции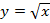

Очевидно, что представленный график (Рис. 1.) проходит через точки (1;1), (4;2), (9;3) и т. д.

Чтобы избавиться от корня, возведем функцию в квадрат, наложив условие на у:

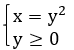
Рассмотрим две функции. Первая –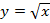

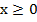 при , график ее – это часть параболы. Вторая функция –  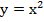при 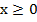, это также часть параболы. Данные ветви парабол симметричны относительно прямой 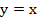. графики имеют две общие точки: (0;0) и (1;1). На ветви параболы

interneturok.ru

Число e. Функция y=e^x, ее свойства, график, дифференцирование

Напомним, что показательной называется функция вида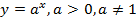

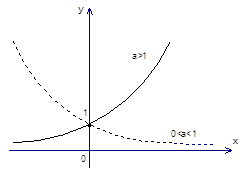
. График выглядит так:

Рис. 1. График показательной функции

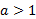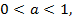График функции возрастает, если ; если основание  лежит в пределах то функция убывает.

Вспомним основные свойства.

1.     

. x может принимать любые действительные значения;

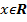
2. 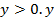      может принимать любые положительные значения;

3.       Графики всех функций при любом значении  проходят через эту точку;

4.      Функция возрастает, если ;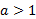

5.      Функция убывает, если .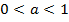

Итак, мы вспомнили, что такое показательная функция и каковы ее основные свойства.

Число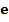

Рассмотрим две конкретные показательные функции с основанием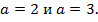

Вот график функции :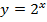

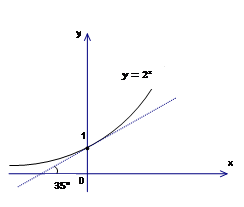
Рис. 2. График функции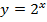

Вот график функции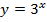

:

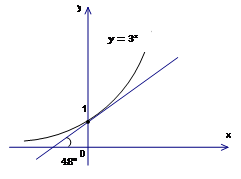
Рис. 3. График функции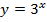

В точке 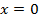, если проведем касательную к одному и второму графику, обнаружим, что касательная к первому графику наклонена к оси 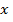примерно на 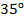(меньше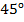

).

Во втором случае касательная наклонена к оси 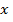примерно на 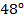(больше ).

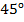Предполагаем, и вообще это доказано, что существует между основаниями 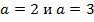 такое число 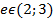, что график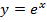

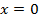 имеет касательную в точке , которая наклонена к оси 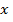ровно на .

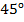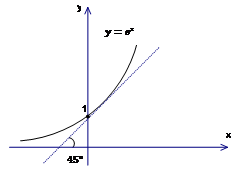
Рис. 4. Касательная к графику функции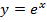

Итак, в первом случае касательная наклонена под углом меньше 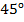, во втором случае касательная наклонена под углом больше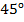

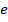. И, оказывается, есть такое число , что касательная в точке  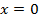наклонена к оси  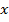под углом ровно  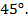Это число 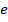, во-первых, расположено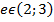 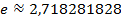 и, во-вторых, иррационально. Вот выписано несколько десятичных знаков этого числа: . Таким образом, мы ввели очень важное число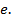

Теперь рассмотрим свойства показательной функции с основанием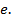

 

График функции выглядит так:

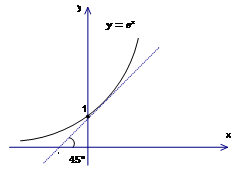
Рис. 5. График функции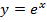

Свойства аналогичны свойствам функции с основанием: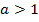

;

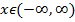Функция возрастает;

Функция не ограничена сверху, но ограничена снизу;

Не существует ни наибольшего  ни наименьшего 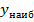 значений;

Функция непрерывна;

Принимает все значения, когда ;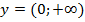

Функция выпукла вниз;

Функция дифференцируема. Что это значит практически? Что касательную к экспоненте можно провести в любой точке.

Таковы свойства данной функции.

Поговорим о производной этой функции. Что мы на данный момент о ней знаем и без доказательства понимаем?

Мы говорили, что функция 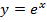 дифференцируема. Это значит, что касательная в любой точке существует, то есть производная существует в любой точке. Но как ее найти? Мы знаем, что производная в точке 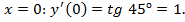Доказан важный факт:

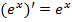 При любом действительном значении  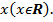То есть отсюда видна особенность числа 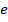. Производная, то есть скорость роста функции 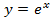в точке  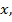равна значению функции в этой же точке. Это основная формула, которая позволит нам дифференцировать все показательные функции.

Теперь рассмотрим некоторые типовые задачи на производную функции

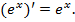
Пример 1.

Дано: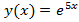

Найти: Производную

Решение.

Вот основная формула 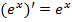, мы умеем дифференцировать сложную функцию.

Ответ:=

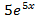
Пример 2.

Дано: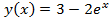

Найти: Производную

Решение.

По тем же правилам, по которым мы дифференцируем все функции, продифференцируем и эту.

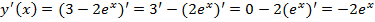
Ответ:=

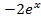
Итак, зная основную формулу 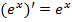, мы можем решать примеры на нахождение производных.

Следующая стандартная задача на касательную.

Пример 3.

Дано:, абсцисса точки касания;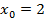

Найти: Уравнение касательной к данной кривой с абсциссой в .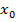

Решение.

Вспоминаем уравнение касательной и стандартную методику ее построения:

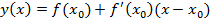
Какие действия нужно сделать, чтобы составить уравнение касательной?

Найти координаты точки касания:

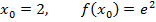
Итак, точка с координатами – это точка касания (рис. 6).

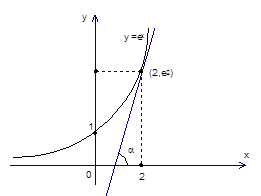
Рис. 6. Точка касания

Найти производную в любой точке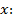

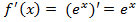
Найти конкретное значение производной в точке :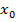

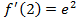
У нас все есть, чтобы заполнить уравнение касательной.

Заполняем, получаем:

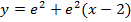
Ответ: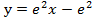

Небольшой анализ:

Тангенс угла наклона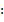

 

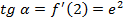
Ордината пересечения точки с осью :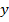

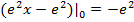
Задача решена.

Пример 4.

Найти наименьшее значение функции.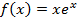

Решение.

Имеем производную произведения:

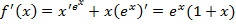
Приравниваем производную к нулю и убеждаемся, что 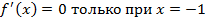, так как по свойству показательной функции 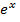всегда больше нуля.

Итак, имеем единственную критическую точку (рис. 7).

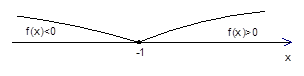
Рис. 7. Критическая точка

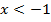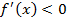Если , то и функция убывает. Если 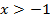, то .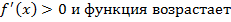

Мы уже говорили, что 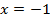 – единственная критическая точка. Посчитаем значение функции в ней:

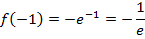
Рис. 8. Точка наименьшего значения функции

И получаем ответ: наименьшее значение функции достигается в точке 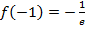. Рис. 8.

Ответ: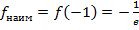

Итак, мы познакомились с числом 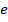, показательной функцией с основанием 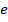. На следующем уроке мы рассмотрим логарифмическую функцию с основанием .

 

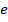Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Uztest.ru (Источник).
2. Schoolife.ru (Источник).
3. Terver.ru (Источник).

 

Домашнее задание

1. Найти производные функция в указанных точках:

а) ;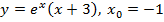

б) .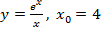

2. Найдите тангенс угла наклона касательной к графику функции 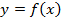 в точке с абсциссой :

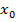а) ;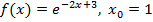

б) .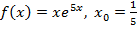

3. Алгебра и начала анализа, Мордкович А.Г.: № 1616, 1618, 1621, 1624.

 

interneturok.ru

Степенная функция y=x(-2n), ее свойства и график. Видеоурок. Алгебра 9 Класс

Тема: Числовые функции

Урок: Степенная функция 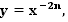её свойства и график

 

На этом уроке мы начнем рассматривать степенную функцию с отрицательным показателем.

Сначала мы познакомимся с функцией 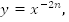т.е. с функциями вида:

Рассмотрим график функции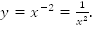

Можно воспользоваться таблицей, а можно проанализировать уже известные нам графики (рис. 1,2).

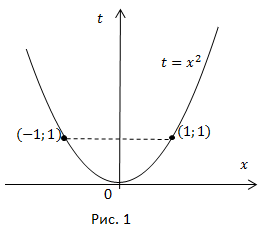
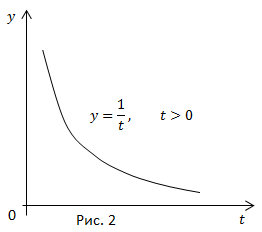
Изучая графики функций можно себе представить, как будет выглядеть график функции 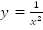 (рис. 3).

Функция четная, поэтому мы можем изучить и изобразить график на луче 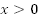и симметрично отобразить относительно оси y.

Если  xвозрастает, то и 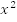возрастает, а 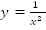убывает.

При 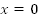 функция не существует.

 

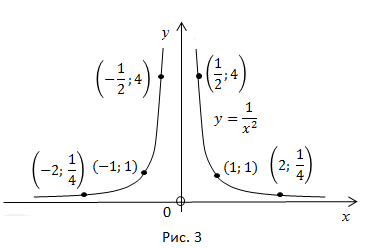
Прочтем график.

Если  то у возрастает,

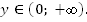
Если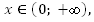 то у убывает,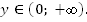

1.

2. Функция четная, 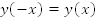График симметричен относительно оси y.

3. Функция убывает на луче 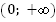 и возрастает на луче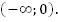

4. Функция ограничена снизу и не ограничена сверху.

5. Функция не имеет ни наибольшего, ни наименьшего значения.

6. Функция непрерывна на луче 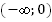 и на луче

interneturok.ru

Функция y=x^n

Определение:

Функцию, заданную формулой , называют степенной функцией с натуральным показателем, где x — независимая переменная, а n - натуральное число.

Например:

Существуют два случая степенной функции: с чётным показателем и с нечётным показателем.

Рассмотрим пример: найти на рисунке степенные функции с чётным показателем и с нечётным показателем.

С чётным показателем:

С нечётным показателем:

Определение:

Областью определения любой степенной функции с натуральным показателем является множество всех действительных чисел.

Рассмотрим случай, когда n - чётное число. График выглядит так:

Опишем свойства этой функции:

1.     Если x=0, то y=0.

2.     Если x≠0, то y>0, т.к. чётная степень как положительного, так и

отрицательного числа положительна.

3.     Противоположным значениям аргумента соответствуют равные значения функции.

4.     Функция возрастает и убывает на промежутке:

5.     При любых значения аргумента функция принимает неотрицательные значения. Областью значений является:

Рассмотрим случай, когда n - нечётное число (n>1).

График выглядит так:

Опишем свойства этой функции:

1.     Если x=0, то y=0. Ноль в любой степени равен нулю.

Если x>0, то y>0.

Если x<0, то y<0.

2.     Нечётная степень отрицательного числа отрицательна.

3.     Противоположным значениям аргумента соответствуют противоположные значения функции.

4.     Функция возрастает на всей области определения, принимая любые значения.

5.     Областью значений является:

Рассмотрим пример: сравнить значения выражений:

Показатель степени у обоих выражений одинаковые. Рассмотрим график степенной функции с нечётным показателем:

На рисунке изображен график степенной функции с нечётным показателем, функция возрастает на всей области определения. В данном случае при любых значениях аргумента из множества всех действительных чисел, т.е. большему значению аргумента соответствует большее значение функции.

Рассмотрим пример: сравнить значения выражений:

Показатель степени у обоих выражений нечётный, т.е большему значению аргумента соответствует большее значение функции.

Рассмотрим пример: сравнить значения выражений:

Рассмотрим график:

Показатель степени у обоих выражений чётный, т.е. большему значению аргумента соответствует меньшее значение функции.

Пример.

Сравнить значения выражений:

Данные значения принадлежат промежутку возрастания, то есть большему значению аргумента соответствует большее значение функции.

Пример.

Определить, принадлежат ли графику функции  точки А(2,16), В(3,9), С(-1,1).

Точка А.

Значит, точка А принадлежит графику функции.

Точка Б.

Значит, точка Б не принадлежит графику функции.

Точка С.

Значит, точка С принадлежит графику функции.

videouroki.net

линейная функция, квадратичная, кубическая и y=1/x

 

Степенной называется функция вида y=xⁿ (читается как y равно х в степени n), где n – некоторое заданное число. Частными случаями степенных функций является функции вида y=x, y=x², y=x³, y=1/x и многие другие. Расскажем подробнее о каждой из них.

Линейная функция y=x¹ (y=x)

График прямая линия, проходящая через точку (0;0) под углом 45 градусов к положительному направлению оси Ох.

График представлен ниже.

Основные свойства линейной функции:

• Функция возрастающая и определена на всей числовой оси. 
• Не имеет максимального и минимального значений. 

Квадратичная функция y=x²

Графиком квадратичной функции является парабола. 

Общий вид параболы представлен на рисунке ниже.

Основные свойства квадратичной функции:

• 1.  При х =0, у=0, и у>0 при х0
• 2. Минимальное значение  квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
• 3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;+∞). 
• 4. Противоположным значениям х соответствует одинаковые значения y. 

Кубическая функция y=x³

Графиком кубической функции называется кубическая парабола.

Общий вид параболы представлен на рисунке ниже.  

Основные свойства кубической функции:

• 1. При х =0, у=0. у>0 при х>0 и y
• 2. У кубической функции не существует не максимального ни минимального значения.
• 3. Кубическая функция возрастает на всей числовой оси (-∞;+∞).
• 4. Противоположным значениям х, соответствуют противоположные значения y.

Функция вида y=x^-1 (y=1/x)

Графиком функции y=1/x называется гипербола.

Общий вид гиперболы представлен на рисунке ниже.

Основные свойства функции y = 1/x:

• 1. Точка (0;0) центр симметрии гиперболы. 
• 2. Оси координат – асимптоты гиперболы.
• 3. Прямая y=x ось симметрии гиперболы.
• 4. Область определения функции все х, кроме х=0.
• 5. y>0 при x>0; y
• 6. Функция убывает как на промежутке (-∞;0), так и на промежутке (0;+∞).
• 7. Функция не ограничена ни снизу, ни сверху.
• 8. У функции нет ни наибольшего, ни наименьшего значений.
• 9. Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
• 10. Область значений функции два открытых промежутка (-∞;0) и (0;+∞).

Нужна помощь в учебе?

Предыдущая тема: Четные и нечетные функции: графики и свойства
Следующая тема:&nbsp&nbsp&nbspОпределение корня n-ой степени: извлечение корня

Все неприличные комментарии будут удаляться.

www.nado5.ru

Степенная функция с четным показателем степени y=x2n, ее свойства и график

Тема: Числовые функции

Урок: Степенная функция с четным показателем степени 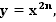 её свойства и график

Мы уже знакомы с функцией 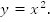 На этом уроке мы познакомимся со степенной функцией вида  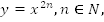изучим свойства и графики таких функций.

Рассмотрим функцию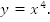

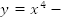 четная функция,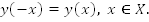

График симметричен относительно оси y.

Рассмотрим график функци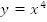и  при 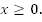 Построим график по таблице значений функции (Рис. 1).

x	0	1		2
y	0	1		16

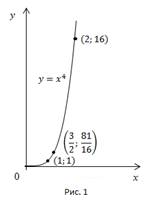
Симметрично отобразим график относительно оси y, и получим график функции 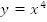  (Рис. 2).

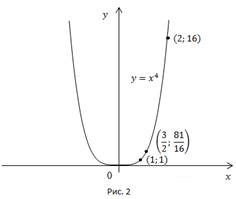
Прочтем полученный график.

1.

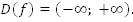
2. Функция четная.

3. Убывает при  возрастает при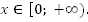

4. Функция ограничена снизу и не ограничена сверху.

5.

interneturok.ru

Функция

	Главная > Учебные материалы > Математика:  Функция
	1.Понятие функции. 2.Свойства функций. 3.Основные элементарные функции.
	1 2 3 4 5 6 7 8 9
	1. Понятие функции    Понятие «функция» является одним из основных понятий в математике. Под функцией понимают некий закон, по которому одна переменная величина зависит от другой. Согласно определению, если каждому значению переменной х множества Х ставится в соответствие одно определенное значение переменной у множества Y, то такое соответствие называется функцией. Исходя из этого, можно дать другую формулировку: однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией.    Переменая х называется независимой переменной или аргументом, y — зависимой переменной от x, буква f обозначает закон соответствия. Множество X называется областью определения функции, а множество Y, соответственно, областью значений функции.
	2. Cвойства функций    1.Четность и нечетность. Функция f(x) называется четной, если ее значения симметричны относительно оси OY, т.е. f(-x) = f(x). Функция f(x) называется нечетной, если  ее значение изменяется на противоположное при изменении переменной х на -х , т.е. f(-x) = -f(x). В противном случае функция называется функцией общего вида.    2.Монотонность. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции, т.е. при x1< (>) x2, f(x1) < (>) f(x2).    3.Периодичность. Если значение функции f(x) повторяется через определенный период Т, то функция называется периодической с периодом  Т ≠ 0 , т.е. f(x + T) = f(x). В противном случае непериодической.    4. Ограниченность. Функция f (x) называется ограниченной на промежутке Х, если существует такое положительное число М > 0 , что для любого x, принадлежащего промежутку Х, | f (x) | < M. В противном случае функция называется неограниченной.
	3. Основные элементарные функции Степенная функция    у = х  область определения (-∞,∞) область значений (-∞,∞) нечетная возрастает на (-∞,∞) непериодическая
	у = х²  область определения (-∞,∞) область значений (0,∞) четная возрастает на (0,∞) убывает на (-∞,0) непериодическая
	у = х³   область определения (-∞,∞) область значений (-∞,∞) нечетная возрастает на (-∞,∞) непериодическая
	у = 1/х область определения (-∞,0)U(0,∞) область значений (-∞,0)U(0,∞) нечетная убывает на (-∞;0) и на ( 0;∞) непериодическая
	у = 1/х²   область определения (-∞,0)U(0,∞) область значений (0,∞) четная возрастает на (-∞,0) и убывает на (0,∞) непериодическая
	область определения [0,∞) область значений [0,∞) общего вида, возрастает на [0; ∞) непериодическая
	область определения (-∞,∞) область значений (-∞,∞) нечетная возрастает на (-∞,∞) непериодическая
	Показательная функция    у = а ͯ      (a>0  a≠1) область определения (-∞,∞) область значений (0; ∞)  общего вида возрастает на (-∞,∞), если a>1; убывает на (-∞,∞), если 0<a<1 непериодическая
	Логарифмическая функция    у = log ₐ x    (a>0  a≠1) область определения (0,∞) область значений (-∞; ∞)  общего вида возрастает на (0,∞), если a>1; убывает на (0,∞), 0<a<1 непериодическая
	Тригонометрические функции    y = sin x область определения (-∞; ∞)  область значений [-1; 1]  нечетная возрастает на [-π/2 + 2πn, π/2 + 2πn]; убывает на [π/2 + 2πn, 3π/2 + 2πn], nϵZ; период  Т=2π
	y = cos x область определения (-∞; ∞)  область значений [-1; 1]  четная возрастает на [-π + 2πn, 2πn]; убывает на [2πn, π + 2πn], nϵZ; период  Т=2π
	y = tg x область определения (-π/2 + πn, π/2 + πn) nϵZ; область значений (-∞; ∞)  нечетная возрастает на (-π/2 + πn, π/2 + πn) nϵZ; период  Т=π
	y = ctg x область определения (πn, π + πn) nϵZ; область значений (-∞; ∞)  нечетная убывает на (πn, π + πn) nϵZ; период  Т=π
	y = arcsin x область определения [-1; 1] область значений [-π/2; π/2]  нечетная возрастает на [-1; 1]
	y = arccos x область определения [-1; 1] область значений [0; π]  функция центрально-симметрична относительно точки (0; π/2) убывает на [-1; 1]
	y = arctg x область определения (-∞; ∞) область значений [-π/2; π/2]  нечетная возрастает на (-∞; ∞)
	y = arcctg x область определения (-∞; ∞) область значений [0; π]  ни четная, ни нечетная убывает на (-∞; ∞)
	Пример 1. Найти область определения функции.
	Пример 2 Выяснить четность или нечетность функции.		График функции y=x³+2sin x
	Пример 3
	1 2 3 4 5 6 7 8 9

www.mathtask.ru