Вывод:
Надеюсь, из кода всё понятно, но немного поясню.
Поскольку |y| может быть только больше нуля, нам нужно выделить значения функции, которые >= 0 и нарисовать в основной части графика только их. Для этого мы делаем булевую маску для всех значений f(x) (в моём коде это значение обозначено как y, но мой y это не y из вашей формулы).
ind = y >= 0
Более понятно можно записать так:
ind = (y >= 0)
В ind у нас теперь булева маска, содержащая True на тех позициях, где y >= 0 и False, где y < 0.
Далее, мы отбираем по этой маске значения из наших массивов y:
x1 = x[ind]
y1 = y[ind]
А также мы отбираем остальные значения x и y, для чего инвертируем маску с помощью булевой операции инверсии ~ (где было True станет False и наоборот:
x2 = x[~ind]
y2 = y[~ind]
После этого мы рисуем основной график, причём два раза — один раз используя f(x), а другой раз -f(x) (по формуле |y| = f(x) получается, что у нас есть два графика: y = f(x) и y = -f(x)).
И затем рисуем псевдо-график там, где функция f(x) могла бы продолжаться, но из-за условия равенства модулю |y| она в этом месте прерывается.
постройте график функции y 2 x 2
Вы искали постройте график функции y 2 x 2? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и постройте график функции y 2x 2, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «постройте график функции y 2 x 2».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте.
Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как постройте график функции y 2 x 2,постройте график функции y 2x 2,постройте график функции y 2×2,постройте график функции y x2. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и постройте график функции y 2 x 2. Просто введите задачу в окошко и нажмите
«решить» здесь (например, постройте график функции y 2×2).
Где можно решить любую задачу по математике, а так же постройте график функции y 2 x 2 Онлайн?
Решить задачу постройте график функции y 2 x 2 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды.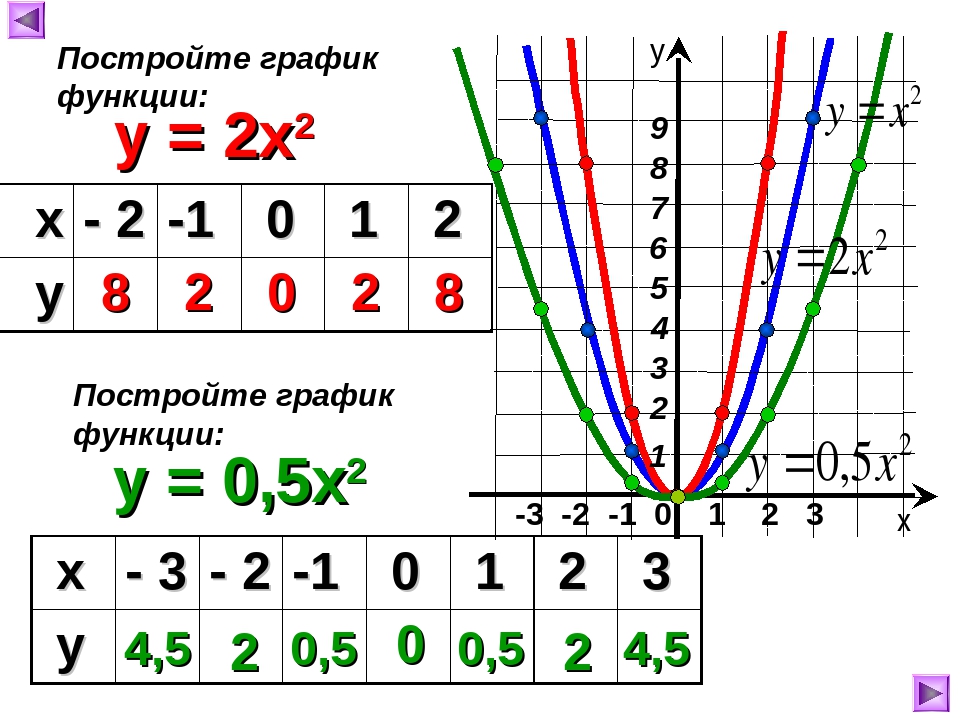
Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Урок 20. построение графиков функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №20. Построение графиков функций.
Перечень вопросов, рассматриваемых в теме
- Исследование функций;
- Построение графиков функций;
- Применение производной для решения графических задач.
Глоссарий по теме
Асимптота графика функции y = f(x) – прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1и х2, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Выпуклость вверх. Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка.
Выпуклость вниз. Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.
Максимум функции. Значение функции в точке максимума называют максимумом функции.
Минимум функции. Значение функции в точке минимума называют минимумом функции.
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Производная второго порядка (вторая производная).
Производная второго порядка есть первая производная от производной первого порядка.
Производную определяют, как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к 0, если такой предел существует.
Точка максимума функции. Точку х0называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .
Точка перегиба. Точки, в которых выпуклость вверх меняется на выпуклость вниз или наоборот, называются точками перегиба.
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y=f(x) убывает на интервале X, если для любых х1 и х2 , из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.
Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит вышепроведенного отрезка.
Полная схема построения графика функции:
- Найти область определения функции D(f).
- Исследовать функцию на четность (найти f(-x)).
- Найти асимптоты.
- Найти стационарные и критические точки.
- Найти промежутки монотонности.
- Найти интервалы выпуклости вверх и выпуклости вниз.
- Найти точки перегиба
- Составить таблицу значений функции для некоторых точек.
- По полученным данным построить график функции.
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Постройте график функции у = х3 – 3х + 3, используя краткую схему построения. схему построения.
Решение:
1) D(y) = (-∞; +∞)
2) Функция не является ни четной, ни нечетной, т. к.
3) Асимптот нет
4) f’(x) = 3x2 – 3, f’(x) = 0 при х = 1, х = -1.
х = 1, х = -1 – стационарные точки.
5) f’(x)>0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки возрастания.
f’(x)<0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки убывания.
6) Так как в точке х = -1 производная меняет знак с «+» на «-», то х = -1 – точка максимума.
Так как в точке х = 1 производная меняет знак с «-» на «+», то х = 1 – точка минимума.
7) Результаты исследования представим в виде таблицы.
x | (-∞; -1) | -1 | (-1; 1) | 1 | (1; +∞) |
f’(x) | + | 0 | — | 0 | + |
f(x) | 5 | 1 | |||
max | min |
8) Координаты некоторых точек:
9) По полученным данным строим график (рис. 1)
Рисунок 1 – график функции у = х3 – 3х + 3
Пример 2. Постройте график функции, используя подробную схему построения. схему построения.
Решение:
1)
2) Функция не является ни четной, ни нечетной, т.
к.
3) х = 1 – вертикальная асимптота
4) , f’(x) = 0 при х = 2, х = 0.
х = 2, х = 0 – стационарные точки.
5) f’(x)>0 при . Так как в точках х = 0, х = 2 функция непрерывна, то эти точки также включаются в промежутки возрастания.
f’(x)<0 при . Так как в точках х = 0, х = 2 функция непрерывна, то эти точки также включаются в промежутки убывания.
Так как в точке х = 0 производная меняет знак с «+» на «-», то х = 0 – точка максимума.
Так как в точке х = 2 производная меняет знак с «-» на «+», то х = 2 – точка минимума.
х = 1 – не является точкой экстремума
6) Найдем интервалы выпуклости функции.
; при функция выпукла вверх.
; при функция выпукла вниз.
7) Результаты исследования представим в виде таблицы.
x | (-∞; 0) | 0 | (0; 1) | 1 | (1; 2) | 2 | (2; +∞) |
f’(x) | + | 0 | — | Не сущ. | — | 0 | + |
f’’(x) | — | — | Не сущ. | + | + | ||
f(x) | -4 | Не сущ. | 0 | ||||
max | min |
8) Координаты некоторых точек:
x | -1 | 0,5 | 1,5 | 3 |
f(x) | -4,5 | -4,5 | 0,5 | 0,5 |
9) По полученным данным строим график (рис. 2)
Рисунок 2 – график функции
Сдвиги графиков функций
☰
Изменение значения k влияет на вид графика (степень крутизны в случае параболы), расположение ветвей в координатных четвертях и др. Однако точкой, через которую можно провести ось симметрии графиков, является точка O с координатами (0; 0).
Если же рассматривать функций, подобные перечисленным выше, у которых к переменной x или ко всей исходной функции прибавляется (или вычитается) какое-либо число, то графики этих функций остаются такими же как у исходных, однако смещаются относительно точки (0; 0).
Если обозначить исходные функции как y = f(x), то прибавление к x числа дает функции вида y = f(x+l), а прибавление ко всей исходной функции значения дает вид y = f(x) + m.
Например, если исходная функция y = 2x2, то примером первого типа будет функция y = 2(x+5)2, а второго — y = 2x2 + 5.
Для функций вида y = f(x+l) график смещается влево на l единиц, если l прибавляется. Если же l вычитается, то график смещается вправо. Действительно, представим параболу функции y = x2 и сравним ее с функцией y = (x+1)2. Когда x = 1, то для первой функции y = 1, а для второй — y = 4. Когда x = 0, для первой y = 0, для второй y = 1. Когда x = –1, для первой y = 1, для второй y = 0.
То есть график второй функции касается оси x в точке (–1; 0). Это значит, что график смещен влево по сравнению с исходным на 1.
Для функций вида y = f(x) + m график соответствующей функции y = f(x) смещается на m единиц, но уже по вертикальной оси (ось y). Здесь если m прибавляется, то график сдвигается вверх. Если m вычитается, то график сдвигается вниз.
Рассмотрим ту же параболу y = x2 и функцию y = x2 + 1. Когда x = 0, первая принимает значение 0, а у второй y = 1. Получить у второй функции значение y, которое равно 0, вообще невозможно. Это значит, что парабола имеет точку симметрии с координатами (0; 1), т. е. сдвинута от исходной вверх на 1.
«Смешанные» функции вида y = f(x + l) + m сдвигаются вдоль оси x и y. Вдоль оси x они сдвигаются на l, а вдоль y — на значение m.
2.Квадратичная функция y=x² — Функции и их графики
В уравнении квадратичной функции:
a – старший коэффициент
b – второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:
Точки, обозначенные зелеными кружками – это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:
Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.
График функции имеет вид:
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции.
На графике нули функции — это точки пересечения графика функции с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .
В случае квадратичной функции нужно решить квадратное уравнение .
В процессе решения квадратного уравнения находим дискриминант: , который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:
2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:
3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:
,
Если ,то график функции выглядит примерно так:
Следующий важный параметр графика квадратичной функции – координаты вершины параболы:
Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии паработы.
И еще один параметр, полезный при построении графика функции – точка пересечения параболы с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
| Преобразование y = f (x + c), где c – число | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Преобразование y = f (x) + c, где c – число | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Преобразование y = – f (x) | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: График функции y = f (x) симметрично отражается относительно оси Ox. Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Преобразование y = f ( – x) | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: График функции y = f (x) симметрично отражается относительно оси Oy. Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Преобразование y = f (kx), где k – число | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае k > 1 происходит сжатие графика функции y = f (x) в k раз к оси Oy. Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае k < – 1 происходит сжатие графика функции y = f (x) в | k | раз к оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Преобразование y = k f (x), где k – число | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в раз к оси Ox. Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: | |||||||||||||||||||||||||||||||||||||||||||||||||||
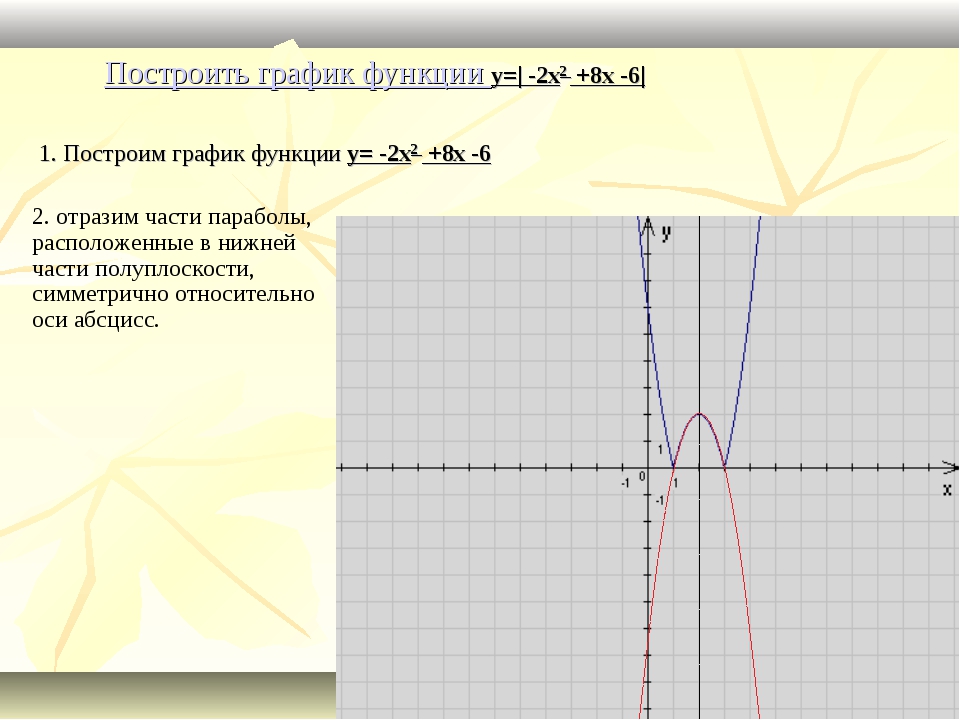
| Преобразование y = | f (x)| | |||||||||||||||||||||||||||||||||||||||||||||||||||
Описание: Часть графика функции y = f (x), расположенная в области , остаётся на месте. Квадратичная функцияРис 1. Общий вид параболы Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым. Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0). Основные свойства квадратичной функции1. При х =0, у=0, и у>0 при х0 2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует. Если график квадратичной функции был симметричен оси Оу, то график кубической параболы симметричен относительно начала координат, то есть точки (0;0). Свойства кубической функцииПеречислим основные свойства кубической функции
Нужна помощь в учебе?Предыдущая тема: Умножение одночленов и возведение одночлена в степень + примеры Следующая тема:   Абсолютная погрешность: понятие, как вычислить + примеры
Графические уравнения, система уравнений с программой «Пошаговое решение математических задач»ОписаниеКоманда plot генерирует график практически любой функции или отношения, обнаруживаемого в математике средней школы и колледжа.Он будет отображать функции, заданные в форме y = f (x), например y = x 2 или y = 3x + 1, а также отношения вида f (x, y) = g (x, y) , например x 2 + y 2 = 4. Чтобы использовать команду построения графика, просто перейдите к основному
страницу графика, введите свое уравнение (в терминах x и y), введите набор
значения x и y, для которых должен быть построен график, и нажмите «График»
кнопка. Параметры (только расширенная страница)Деления Значения: отмечен или не отмечен Если галочки отмечены, оси на графике будут показывать отметки и числовые шкалы. Линии сетки Значения: установлен или не установлен Если установлен флажок Линии сетки, на график будет наложена синяя сетка. Оси Значения: Нет или Автоматическая исходная точка или Исходная точка в (#, #) Параметр «Оси» управляет внешним видом и расположением осей на графике. Если отмечено «Нет», оси не будут отображаться вообще. Когда установлен флажок «Автоматическая исходная точка», будут отображаться оси. Две оси обычно пересекаются в точке (0,0), но иногда эта точка пересечения может быть расположена в другом месте. Соотношение сторон Значения: Один к одному или Золотое сечение или #: # Параметр Соотношение сторон управляет соотношением высоты графика к его ширине. Когда установлен флажок «Один к одному», соотношение составляет 1: 1, и масштабы на двух осях будут идентичными. Это гарантирует, что круги, например, действительно будут отображаться на экране круглыми. Когда выбрано золотое сечение, соотношение сторон составляет 1: 1 / г, где g — золотое сечение (приблизительно 1.6180). Это якобы дает соотношение высоты к ширине, которое особенно «приятно» для глаз. Когда выбрано #: # и введены два значения, будет применяться указанное соотношение сторон. Это полезно, если сюжет сильно сжат в одном или другом направлении и его нужно «растянуть», чтобы сделать его более четким. Цели обученияОписать свойства графиков экспоненциальных функций Основные выводыКлючевые моменты
Ключевые термины
ОпределенияНа самом базовом уровне экспоненциальная функция — это функция, в которой переменная появляется в экспоненте.x [/ latex], когда [latex] b> 1 [/ latex]. Один из способов построить график этой функции — выбрать значения для [latex] x [/ latex] и подставить их в уравнение для генерации значений для [latex] y [/ latex]. Таким образом мы можем получить следующие баллы: [латекс] (- 2, \ frac {1} {4}) [/ латекс], [латекс] (- 1, \ frac {1} {2}) [/ латекс], [латекс] (0,1 ) [/ латекс], [латекс] (1,2) [/ латекс] и [латекс] (2,4) [/ латекс] При соединении точек вы заметите плавную кривую, которая пересекает ось [latex] y [/ latex] в точке [latex] (0,1) [/ latex] и увеличивается как [latex] x [ / latex] принимает все большие и большие значения.x [/ latex], когда [latex] 0 [латекс] (- 2,4) [/ латекс], [латекс] (- 1,2) [/ латекс], [латекс] (0,1) [/ латекс], [латекс] (1, \ frac {1} {2}) [/ latex] и [latex] (2, \ frac {1} {4}) [/ latex] При соединении точек вы заметите плавную кривую, которая пересекает ось Y в точке [latex] (0,1) [/ latex] и уменьшается по мере того, как [latex] x [/ latex] принимает все больше и больше значения.х [/ латекс]. Поскольку [latex] 1 [/ latex] к любой мощности дает [latex] 1 [/ latex], функция эквивалентна [latex] y = 1 [/ latex], которая представляет собой горизонтальную линию, а не экспоненциальное уравнение. Если [latex] b [/ latex] отрицательное значение, то увеличение [latex] b [/ latex] до четной степени приводит к положительному значению для [latex] y [/ latex] при увеличении [latex] b [/ latex] ] с нечетной степенью приводит к отрицательному значению [latex] y [/ latex], что делает невозможным соединение полученных точек каким-либо значимым образом и, конечно, не таким образом, который генерирует кривую, как в приведенных выше примерах.x [/ latex] имеет ось [latex] x [/ latex] в качестве горизонтальной асимптоты, потому что кривая всегда будет приближаться к оси [latex] x [/ latex], когда [latex] x [/ latex] приближается к положительному или отрицательная бесконечность, но никогда не пересечет ось, так как никогда не будет равна нулю. Графики логарифмических функцийЛогарифмические функции могут быть построены вручную или в электронном виде с точками, обычно определяемыми с помощью калькулятора или таблицы. Цели обученияОписать свойства графиков логарифмических функций Основные выводыКлючевые моменты
Ключевые термины
Ниже приведены графики логарифмических функций с основаниями 2, [latex] e [/ latex] и 10. Логарифмические графики: После [latex] x = 1 [/ latex], где графики пересекают ось [latex] x [/ latex], [latex] \ log_2 (x) [/ latex] красное выше [latex] \ log_e (x) [/ latex] зеленого цвета, который выше [latex] \ log_ {10} (x) [/ latex] синего цвета.До этого момента порядок обратный. Все три логарифма имеют ось [latex] y [/ latex] в качестве вертикальной асимптоты и всегда увеличиваются. Все три логарифмических графика начинаются с крутого подъема после [latex] x = 0 [/ latex], но растягиваются все больше и больше по горизонтали, их наклон уменьшается по мере увеличения [latex] x [/ latex]. Все они пересекают ось [latex] x [/ latex] в [latex] x = 1 [/ latex]. Свойства графов логарифмических функцийОсобые очкиГрафик пересекает ось [latex] x [/ latex] в точке [latex] 1 [/ latex].у = 1 [/ латекс]. Поскольку [latex] b> 0 [/ latex], искомый показатель степени равен [latex] 1 [/ latex] независимо от значения [latex] b [/ latex]. Это означает, что точка [latex] (x, y) = (1,0) [/ latex] всегда будет на логарифмической функции этого типа. АсимптотыОсь [latex] y [/ latex] — это вертикальная асимптота графа. Это означает, что кривая приближается к оси [латекс] y [/ латекс], но не пересекает ее. Давайте посмотрим, что происходит, когда значение [latex] x [/ latex] приближается к нулю справа для уравнения, график которого показан выше.А именно [латекс] y = бревно {_b} x [/ латекс]. Мы можем сделать это, выбрав значения для [latex] x [/ latex], подставив их в уравнение и сгенерировав значения для [latex] y [/ latex]. Предположим, что [latex] b [/ latex] является положительным числом больше, чем [latex] 1 [/ latex], и давайте исследуем значения [latex] x [/ latex] между [latex] 0 [/ latex] ] и [латекс] 1 [/ латекс]. В этих условиях, если мы допустим [latex] x = \ frac {1} {b} [/ latex], уравнение станет [latex] y = log \ frac {1} {b} [/ latex]. Таким образом, мы ищем такой показатель степени, что [latex] b [/ latex], возведенный к этому показателю, дает [latex] \ frac {1} {b} [/ latex].{1000}}, — 1000) [/ латекс] Как видно, чем ближе значение [latex] x [/ latex] к [latex] 0 [/ latex], тем более отрицательным становится график. То есть, когда [latex] x [/ latex] приближается к нулю, график приближается к отрицательной бесконечности. Это означает, что ось [latex] y [/ latex] является вертикальной асимптотой функции. Домен и диапазонОбласть определения функции — все положительные числа. Это означает, что значение функции [latex] x [/ latex] всегда будет положительным.Давайте начнем с рассмотрения, почему значение кривой [latex] x [/ latex] никогда не равно [latex] 0 [/ latex]. Если бы значение [latex] x [/ latex] было равно нулю, функция считала бы [latex] y = log {_b} 0 [/ latex]. Здесь мы ищем такой показатель степени, что [latex] b [/ latex], возведенный в эту экспоненту, равен [latex] 0 [/ latex]. Поскольку [latex] b [/ latex] является положительным числом, не существует показателя степени, в который мы можем возвести [latex] b [/ latex], чтобы получить [latex] 0 [/ latex]. Фактически, поскольку [latex] b [/ latex] положительное значение, возведение его в степень всегда будет давать положительное число. Диапазон функции — все действительные числа. То есть график может принимать любое действительное число. Сравнение [latex] y = log {_x} [/ latex] и [latex] y = \ sqrt {x} [/ latex]На первый взгляд график логарифмической функции легко принять за график функции квадратного корня. График [latex] y = \ sqrt {x} [/ latex] : График функции квадратного корня напоминает график логарифмической функции, но не имеет вертикальной асимптоты. Как квадратный корень, так и логарифмические функции имеют домен, ограниченный значениями [latex] x [/ latex] больше, чем [latex] 0 [/ latex]. Однако у логарифмической функции есть вертикальная асимптота, убывающая в сторону [латекс] — \ infty [/ latex], когда [latex] x [/ latex] приближается к [latex] 0 [/ latex], тогда как квадратный корень достигает минимума [латекс] y [/ latex] -значение [latex] 0 [/ latex]. Диапазон функции квадратного корня — это все неотрицательные действительные числа, тогда как диапазон логарифмической функции — все действительные числа. Графические логарифмические функцииГрафические логарифмические функции могут быть выполнены путем определения точек на кривой вручную или с помощью калькулятора. При построении графиков без калькулятора мы используем тот факт, что обратная логарифмическая функция является экспоненциальной функцией. При построении графиков с помощью калькулятора мы используем тот факт, что калькулятор может вычислять только десятичные логарифмы (основание [латекс] 10 [/ latex]), натуральные логарифмы (основание [латекс] e [/ latex]) или двоичные логарифмы ( основа [латекс] 2 [/ латекс]). y = x [/ латекс] Теперь рассмотрим инверсию этой функции.х = у [/ латекс]. Однако, если мы поменяем местами координаты [latex] x [/ latex] и [latex] y [/ latex] каждой точки, мы фактически получим список точек исходной функции. Это: [латекс] (\ frac {1} {9}, — 2), (\ frac {1} {3}, — 1), (1,0), (3,1), (9, 2) [/ латекс] и [латекс] (27,3) [/ латекс]. Мы строим и соединяем эти точки, чтобы получить график функции [latex] y = log {_3} x [/ latex] ниже. График [latex] y = log {_3} x [/ latex]: График логарифмической функции с основанием [latex] 3 [/ latex] может быть сгенерирован с использованием обратного преобразования функции.Его форма такая же, как и у других логарифмических функций, только в другом масштабе. Графические логарифмические функции с основанием между [latex] 0 [/ latex] и [latex] 1 [/ latex]Итак, мы построили график логарифмических функций, основания которых больше [latex] 1 [/ latex]. Если вместо этого мы рассмотрим логарифмические функции с основанием [latex] b [/ latex], таким, что [latex] 0 Фактически, если [latex] b> 0 [/ latex], график [latex] y = log {_b} x [/ latex] и график [latex] y = log {_ \ frac {1} { b}} x [/ latex] симметричны по оси [latex] x [/ latex].Таким образом, если мы идентифицируем точку [latex] (x, y) [/ latex] на графике [latex] y = log {_b} x [/ latex], мы можем найти соответствующую точку на [latex] y = log {_ \ frac {1} {b}} x [/ latex], изменив знак координаты [latex] y [/ latex]. Соответствующая точка — [латекс] (x, -y) [/ latex]. Вот пример для [latex] b = 2 [/ latex]. Графики [latex] log {_2} x [/ latex] и [latex] log {_ \ frac {1} {2}} x [/ latex] : Графики [latex] log_2 x [/ latex ] И [latex] log {_ \ frac {1} {2}} x [/ latex] симметричны по оси x Решение задач с логарифмическими графамиНекоторые функции с быстро меняющейся формой лучше всего отображать в масштабе, который экспоненциально возрастает, например на логарифмическом графике. Цели обученияПреобразуйте задачи в логарифмические масштабы и обсудите преимущества этого Основные выводыКлючевые моменты
Ключевые термины
Зачем нужна логарифмическая шкала?Многие математические и физические зависимости функционально зависят от переменных высокого порядка. Это означает, что при небольших изменениях в независимой переменной происходят очень большие изменения в зависимой переменной. Таким образом, становится трудно построить график таких функций на стандартной оси. Рассмотрим, например, закон Стефана-Больцмана, который связывает мощность (j * ), излучаемую черным телом, с температурой (T).4 [/ латекс] На стандартном графике это уравнение может быть довольно громоздким. Зависимость четвертой степени от температуры означает, что мощность увеличивается чрезвычайно быстро. Тот факт, что скорость постоянно увеличивается (и очень круто), означает, что изменение масштаба (масштабирование осей на [латекс] 5 [/ латекс], [латекс] 10 [/ латекс] или даже [латекс] 100 [/ латекс]) ) мало помогает облегчить интерпретацию графика. Для очень крутых функций можно строить точки более плавно, сохраняя при этом целостность данных: можно использовать график с логарифмической шкалой, где вместо каждого пробела на графике, представляющего постоянное увеличение, он представляет экспоненциальное увеличение .Если нормальный (линейный) график может иметь равные интервалы, идущие от 1, 2, 3, 4, то в логарифмической шкале те же равные интервалы будут представлять 1, 10, 100, 1000. x, f (x) = x [/ latex] и [latex] f (x) = \ log x [/ latex] на четырех разные координатные участки.Слева вверху — линейная шкала, справа вверху и слева внизу — полулогарифмические шкалы, а справа внизу — логарифмическая шкала. Как вы можете видеть, когда обе оси использовали логарифмическую шкалу (внизу справа), график сохранил свойства исходного графика (вверху слева), где обе оси были масштабированы с использованием линейной шкалы. Это означает, что если мы хотим построить график функции, которая является громоздкой в линейном масштабе, мы можем использовать логарифмическую шкалу на каждой оси и сохранить свойства графика, в то же время облегчая построение графика. В полулогарифмических масштабах функции имеют формы, которые искажены относительно оригинала. Когда только ось [latex] x [/ latex] имеет логарифмический масштаб, логарифмическая кривая отображается в виде линии, а линейная и экспоненциальная кривые выглядят экспоненциально. Когда только ось [латекс] y [/ латекс] имеет логарифмический масштаб, экспоненциальная кривая отображается как линия, а линейная и логарифмическая кривые выглядят как логарифмические. Следует отметить, что примеры на графиках предназначены для иллюстрации точки и что изображенные на графике функции не обязательно были громоздкими на линейно масштабируемом наборе осей. Преобразование линейной шкалы в логарифмическуюОсновное различие между логарифмической и линейной шкалами состоит в том, что, хотя разница в значениях между линейными точками равного расстояния остается постоянной (то есть, если расстояние от [latex] 0 [/ latex] до [latex] 1 [/ latex] ] по шкале [латекс] 1 [/ латекс] см на странице, расстояние от [латекса] 1 [/ латекса] до [латекса] 2 [/ латекса], от [латекса] 2 [/ латекса] до [латекса ] 3 [/ latex] и т. Д. Будут одинаковыми) разница значений между точками по логарифмической шкале будет меняться экспоненциально.Логарифмическая шкала начинается с определенной степени [латекс] 10 [/ латекс], и с каждой единицей увеличивается на степень [латекс] 10 [/ латекс]. Таким образом, если кто-то хочет преобразовать линейную шкалу (со значениями [latex] 0-5 [/ latex] в логарифмическую шкалу, одним вариантом будет замена [latex] 1,2,3,4 [/ latex] и 5 с [латексом] 0,001,0,01,0,1,1,1,10 [/ латекс] и [латекс] 100 [/ латекс], соответственно. Между каждым основным значением на логарифмической шкале хэш-метки становятся все ближе друг к другу с увеличением значения.Например, в пространстве между [latex] 1 [/ latex] и [latex] 10 [/ latex], [latex] 8 [/ latex] и [latex] 9 [/ latex] расположены гораздо ближе друг к другу, чем [ латекс] 2 [/ латекс] и [латекс] 3 [/ латекс]. Использование логарифмической шкалы имеет два преимущества. Во-первых, это позволяет построить очень большой диапазон данных без потери формы графика. Во-вторых, он позволяет выполнять интерполяцию в любой точке графика, независимо от диапазона графика. Подобные данные в линейном масштабе менее ясны.b = (b) \ log (a) [/ латекс] Используя вышеизложенное, наше уравнение принимает следующий вид: [латекс] \ begin {align} \ log j & = 4 \ log {(\ sigma \ tau)} \\ & = 4 \ log {(\ sigma)} + 4 \ log {(\ tau)} \\ & = 4 \ log {(\ tau)} +4 \ log {(\ sigma)} \ end {align} [/ latex] Графические экспоненциальные функцииПростая экспоненциальная функция для построения графика: у знак равно 2 Икс .
Обратите внимание, что на графике Икс -ось как асимптота слева и очень быстро увеличивается справа. Изменение база изменяет форму графика. Замена Икс с участием — Икс отражает график по у -ось; замена у с участием — у отражает это через Икс -ось. Замена Икс с участием Икс + час переводит график час единиц слева. Замена у с участием у — k (что то же самое, что и добавление k вправо) переводит график k единиц вверх. Поверхности, часть 2Поверхности, часть 2Поверхности и контурные графикиЧасть 2: Квадрические поверхностиКвадрические поверхности — это графики квадратных уравнений с тремя декартовыми переменными. в космосе.Как и графики квадратиков на плоскости, их форма зависит от знаки различных коэффициентов в их квадратных уравнениях. Сферы и эллипсоиды Сфера — график уравнение вида x 2 + y 2 + z 2 = p 2 для какого-то реального числа р . Радиус сферы p (см. рисунок ниже). Эллипсоиды — это графики уравнений вида ax 2 + на 2 + c z 2 = p 2 , где a , b и c все положительны. В частности, сфера — это особый эллипсоид, для которого a , b и c все равны.
Параболоиды Поверхности, пересекающиеся с плоскости, перпендикулярные любым двум осям координат, являются параболами в тех самолеты называются параболоидами .Пример показан на рисунке ниже. — это график z = x 2 + y 2 .
The Поверхность на следующем рисунке представляет собой график z = x 2 — y 2 .В этом случае пересечения с плоскостями, перпендикулярными x — и y- осей по-прежнему являются параболами, но два набора парабол отличаются друг от друга направление, в котором они указывают. По причинам, которые мы увидим, эта поверхность называется гиперболический параболоид — и по понятным причинам его еще называют «седловая поверхность».
Гиперболоиды Гиперболоиды — поверхности в трехмерном пространстве аналогично гиперболам на плоскости. Их определяющие характерно то, что их пересечения с плоскостями, перпендикулярными любой две из координатных осей являются гиперболами.Есть два типа гиперболоидов — первый тип иллюстрируется графиком x 2 + y 2 — z 2 = 1, который показан на рисунке ниже. Как показано на рисунке справа, эта форма очень похожа на ту, которая обычно используется на атомных электростанциях. градирни. (Источник: EPA Реакция на инцидент на Три-Майл-Айленд.) Эта поверхность называется гиперболоидом . одного листа , потому что он все «связан» одним куском.(Мы будем перейдем к другому делу сейчас.)
Другой тип — гиперболоид . двух листов , и это иллюстрируется графиком x 2 — y 2 — z 2 = 1, показано ниже.
|
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
3 называется кубической функцией. Графиком кубической функции называется кубическая парабола. Общий вид параболы представлен на рисунке ниже. 
4 из 4) 
Также, если есть
если в функции больше одного экспоненциального члена, график может выглядеть иначе.
Ниже приведены несколько примеров, чтобы показать вам, как они работают.
Больной
присоединяйтесь к набранным пунктам и убедитесь, что я не забываю рисовать
график в виде кривой линии:
На этом этапе в
ваша математическая карьера, скорее всего, вы будете в основном иметь дело
со стандартной экспоненциальной формой. Так что убедитесь, что вам удобно
с его общей формой и поведением.
«Графические экспоненциальные функции: примеры». Пурпурная математика .
Доступно по номеру 
Ваше уравнение будет автоматически построено, и будет показан ответ.
в вашем браузере в течение нескольких секунд.2 = 1 от x = -2 до x = 2, y = -1,8 до y = 1,8
Когда установлен флажок «Исходная точка в (#, #)» и вводится точка, оси будут отображаться, и их точка пересечения будет принудительно находиться в указанной точке.
x [/ latex], где [latex] b> 0 [/ latex] — это функция, которая остается пропорциональной своему исходному значению при увеличении или уменьшении.