Построение и решение графиков Функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Чтобы ребенок разобрался в теории и чувствовал себя увереннее на школьных контрольных, запишите его на современные уроки математики в онлайн-школу Skysmart.
Интерактивные задания, математические комиксы и карта прогресса в личном кабинете — математика еще никогда не была таким увлекательным приключением!
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.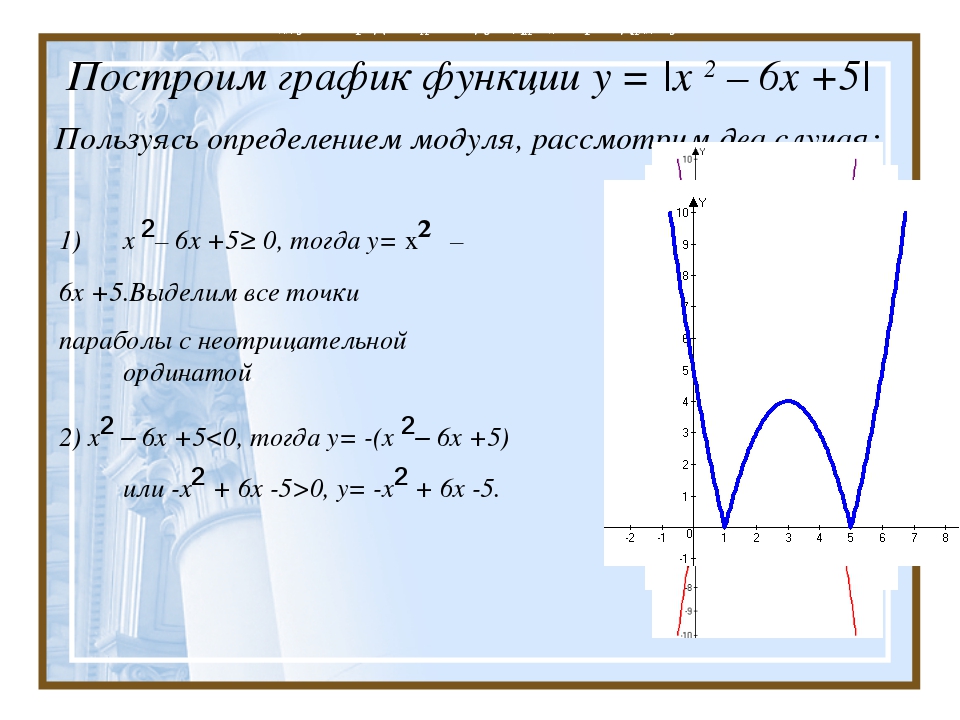
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Как решаем:
Упростим формулу функции:
Задача 2. Построим график функции
Как решаем:
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как решаем:
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 4.
Построить графики функций:
а) y = 3x — 1
б) y = -x + 2
в) y = 2x
г) y = -1
Как решаем:
Воспользуемся методом построения линейных функций «по точкам».
а) y = 3x — 1
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
б) y = -x + 2
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
в) y = 2x
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
г) y = -1
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Как решаем:
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1.
Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
а) y = x² + 1
б)
в) y = (x — 1)² + 2
г)
д)
Как решаем:
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
y = x²
Сдвигаем график вверх на 1:
y = x² + 1
б)
Преобразование в одно действие типа f(x — a).
y = √x
Сдвигаем график вправо на 1:
y = √x — 1
в) y = (x — 1)² + 2
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
y = x²
Сдвигаем график вправо на 1:
y = (x — 1)²
Сдвигаем график вверх на 2:
y = (x — 1)² + 2
г)
Преобразование в одно действие типа
y = cos(x)
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
В детской школе Skysmart учиники чертят графики на специальной онлайн-доске. Учитель видит, как размышляет ученик и может вовремя его направить в нужную сторону.
Запишитесь на бесплатный вводный урок математики и занимайтесь в современном формате и с поддержкой заботливых учителей.
y x 2 4x 5 построить график
Вы искали y x 2 4x 5 построить график? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y x 2 4x 5 построить график данной функции, не
исключение.
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y x 2 4x 5 построить график».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y x 2 4x 5 построить график,y x 2 4x 5 построить график данной функции,постройте график функции y x2 4x 5. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y x 2 4x 5 построить график.
Просто введите задачу в окошко и нажмите
«решить» здесь (например, постройте график функции y x2 4x 5).
Где можно решить любую задачу по математике, а так же y x 2 4x 5 построить график Онлайн?
Решить задачу y x 2 4x 5 построить график вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор онлайн — Построение графика квадратичной функции (с подробным решением)
Если вам нужно просто построить график любой функции, то для этого у нас есть отдельная программа.
Эта математическая программа для построения графика квадратичной функции сначала делает преобразование вида
\( y=ax^2+cx+b \;\; \rightarrow \;\; y=a(x+p)^2+q \)
а затем последовательно строит графики функций:
$$ y=ax^2 $$
$$ y=a(x+p)^2+q $$
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода квадратного многочлена, рекомендуем с ними ознакомиться.
В качестве переменной может выступать любая латинсая буква.Например: \( x, y, z, a, b, c, o, p, q \) и т.д.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
2+bx_в+с\)
Ось симметрии проходит через вершину параболы и параллельна оси \(y\) (ординат). \(x_1\) и \(x_2\) – нули функции. Их можно найти, приравняв формулу функции к нулю и решив соответствующее квадратное уравнение.
3 параметра позволяющих сопоставить формулу квадратичной функции и график:
|
1. |
\(a>0\) — ветви параболы направлены вверх |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(a<0\) — ветви параболы направлены вниз |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. |
\(c\) равна ординате точки пересечения |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. Ответ: Как построить график квадратичной функции (параболу)?Квадратичную функцию можно строить, как и все остальные, выбирая точки наугад (подробнее можно прочитать здесь). Но есть способ позволяющий строить параболу быстрее, выбирая точки осмысленно.
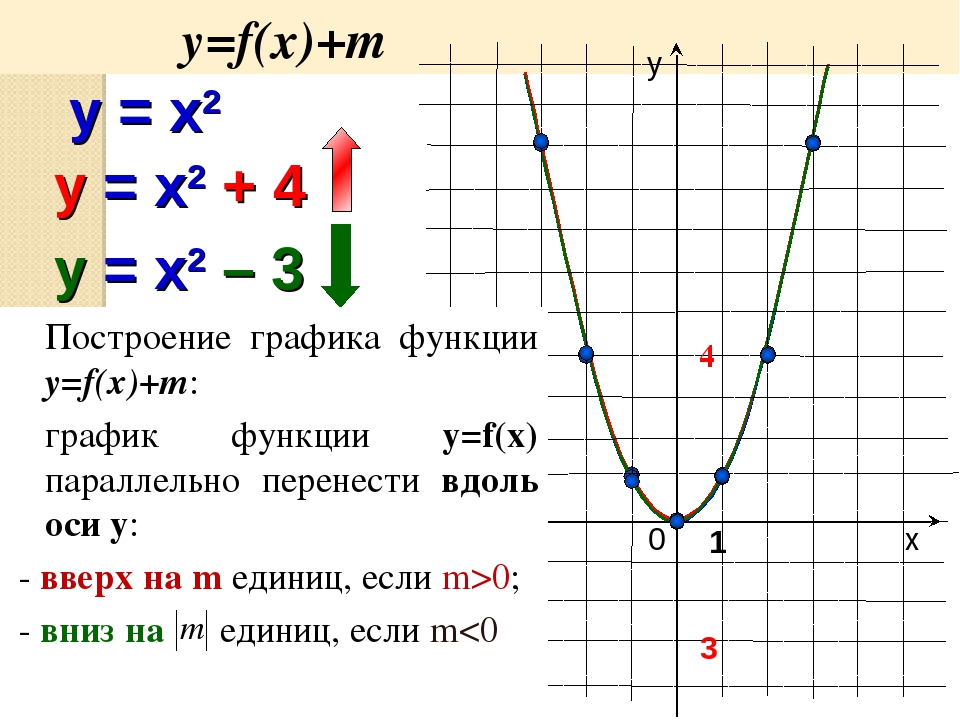
Отметим полученные точки на координатной плоскости и соединим их кривой: Полученный график называют параболой. Точка (0;0) — это вершина параболы. Вершина делит график на левую и правую части, которые называют ветвями параболы. Свойства параболы y=x²1. Область определения $x \in (- \infty;+ \infty)$ — все действительные числа. 2. Область значений $y \in [0;+ \infty)$ — все неотрицательные действительные числа. 3. Функция убывает при $x \lt 0$, функция возрастает при $x \gt 0$. 4. Наименьшее значение функции y = 0 — в вершине параболы при x = 0. Вершина параболы совпадает с началом координат. 5. Все точки на ветвях параболы лежат выше оси абсцисс, для них $y \gt 0$. 2.Квадратичная функция y=x² — Функции и их графикиВ уравнении квадратичной функции: a – старший коэффициент b – второй коэффициент с — свободный член. Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид: Точки, обозначенные зелеными кружками – это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу: Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов. График функции имеет вид: Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ. Итак, мы заметили: Если старший коэффициент a>0, то ветви параболы напрaвлены вверх. Если старший коэффициент a<0, то ветви параболы напрaвлены вниз. Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ. Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение . В случае квадратичной функции нужно решить квадратное уравнение . В процессе решения квадратного уравнения находим дискриминант: , который определяет число корней квадратного уравнения. И здесь возможны три случая: 1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так: 2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. 3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ: , Если ,то график функции выглядит примерно так: Следующий важный параметр графика квадратичной функции – координаты вершины параболы:
Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии паработы. И еще один параметр, полезный при построении графика функции – точка пересечения параболы с осью OY. Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: . То есть точка пересечения параболы с осью OY имеет координаты (0;c). Итак, основные параметры графика квадратичной функции показаны на рисунке: python — Библиотека matplotlib: построение графика функции |y| = x^2 — 2x — 3Примерно так: Вывод: Надеюсь, из кода всё понятно, но немного поясню. Поскольку Более понятно можно записать так: В Далее, мы отбираем по этой маске значения из наших массивов А также мы отбираем остальные значения После этого мы рисуем основной график, причём два раза — один раз используя И затем рисуем псевдо-график там, где функция Wolfram | Примеры альфа: построение и графикаФункции Изобразите функцию одной переменной в виде кривой на плоскости. Постройте функцию одной переменной: Укажите явный диапазон для переменной: Постройте функцию с действительным знаком: Постройте функцию в логарифмическом масштабе: График в логарифмическом масштабе: Другие примеры 3D графики Постройте функцию двух переменных как поверхность в трехмерном пространстве. Постройте функцию от двух переменных: Укажите явные диапазоны для переменных: Другие примеры Уравнения Постройте набор решений уравнения с двумя или тремя переменными. Постройте решение уравнения с двумя переменными: Другие примеры Неравенства Постройте набор решений неравенства или системы неравенств. Постройте область, удовлетворяющую неравенству двух переменных: Постройте область, удовлетворяющую множеству неравенств: Другие примеры Полярные графики Нарисуйте график точек или кривых в полярной системе координат. Укажите диапазон для переменной theta: Другие примеры Параметрические графики Графические параметрические уравнения в двух или трех измерениях. Укажите диапазон для параметра: Нарисуйте параметрическую кривую в трех измерениях: Нарисуйте параметрическую поверхность в трех измерениях: Другие примеры Другие примеры Числовые строкиНанесите набор чисел или значений на числовую линию. Визуализируйте набор действительных чисел на числовой строке: Показать несколько наборов в числовой строке: Другие примеры 3D поверхностный плоттер | Academo.orgЭта демонстрация позволяет вам ввести математическое выражение в терминах x и y. Когда вы нажмете кнопку «Рассчитать», демонстрация будет вычислить значение выражения в предоставленных диапазонах x и y, а затем отобразить результат в виде поверхности. График можно увеличивать, прокручивая мышью, и вращать, перетаскивая. Щелчок по графику покажет значения x, y и z в этой конкретной точке. В таблице ниже перечислены функции, которые можно вводить в поле выражения.
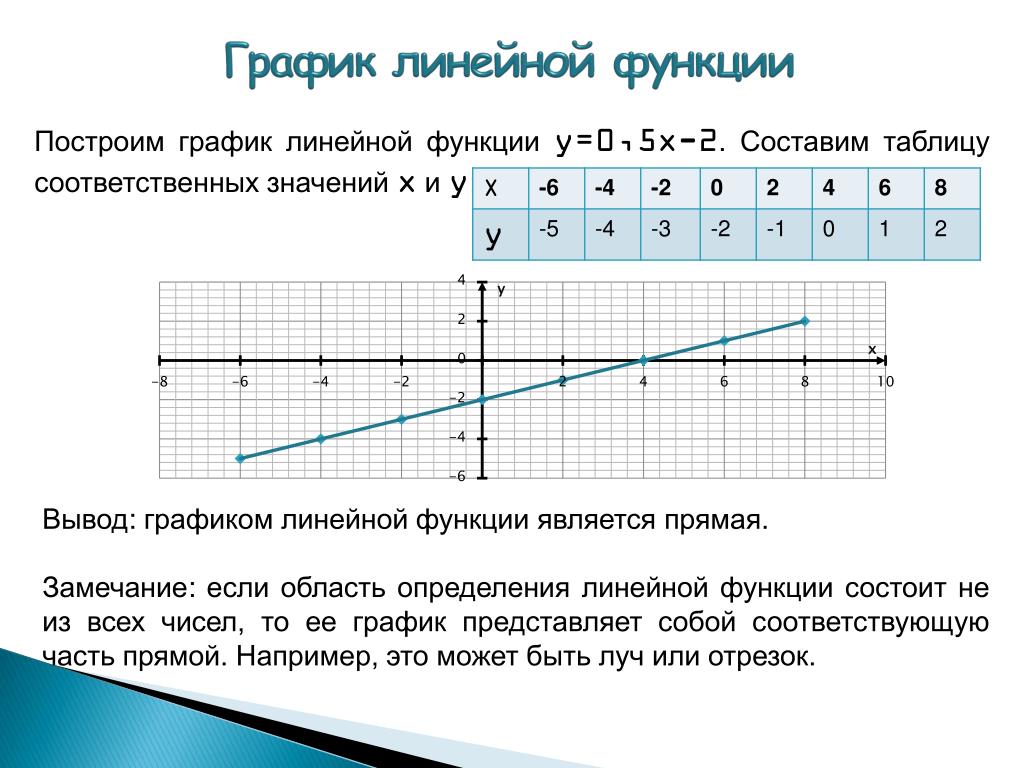
Вы также можете применить к графику определенные ограничения / неравенства.2 \) во всех областях, где \ (x \) больше, чем \ (y \), и \ (x \) во всех областях, где x равен , а не больше, чем y. Ползунок разрешения можно использовать для увеличения количества точек данных, отображаемых на графике, что дает более плавный конечный результат, но поскольку для этого требуется больше вычислительной мощности, вы можете заметить небольшое снижение частоты кадров при взаимодействии с графиком. Каждый раз, когда вы нажимаете кнопку «Рассчитать», URL-адрес обновляется с вашими текущими настройками, что означает, что вы можете поделиться ссылкой прямо на график по вашему выбору, не набирая значения в настройках. Обратите внимание: если ваша поверхность содержит комплексные числа, будет отображена только действительная часть. Пожалуйста, включите JavaScript, чтобы просматривать комментарии от Disqus.Линейные уравнения в координатной плоскости (предалгебра, построение графиков и функции) — MathplanetЛинейное уравнение — это уравнение с двумя переменными, график которого представляет собой линию. График линейного уравнения — это набор точек на координатной плоскости, которые все являются решениями уравнения. Если все переменные представляют собой действительные числа, можно изобразить уравнение, нанеся на график достаточно точек, чтобы распознать шаблон, а затем соединить точки, чтобы включить все точки. Если вы хотите построить график линейного уравнения, у вас должно быть как минимум две точки, но обычно рекомендуется использовать более двух точек. При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль. Пример Постройте функцию y = x + 2 Начните с выбора пары значений для x, например. -2, -1, 0, 1 и 2 и вычислите соответствующие значения y.
Теперь вы можете просто построить пять упорядоченных пар в координатной плоскости На данный момент это пример дискретной функции.Дискретная функция состоит из изолированных точек. Проведя линию через все точки и продолжая линию в обоих направлениях, мы получаем противоположность дискретной функции, непрерывную функцию, которая имеет непрерывный график. Если вы хотите использовать только две точки для определения вашей линии, вы можете использовать две точки, где график пересекает оси. Точка, в которой график пересекает ось x, называется отрезком x, а точка, в которой график пересекает ось y, называется отрезком y.Пересечение по оси x находится путем нахождения значения x, когда y = 0, (x, 0), а точка пересечения по оси y находится путем нахождения значения y, когда x = 0, (0, y). Видеоурок Найдите значения x и изобразите это уравнение на графике
Графические уравнения, система уравнений с программой «Пошаговое решение математических задач»ОписаниеКоманда plot генерирует график практически любой функции или отношения, обнаруживаемого в математике средней школы и колледжа.Он будет отображать функции, заданные в форме y = f (x), например y = x 2 или y = 3x + 1, а также отношения вида f (x, y) = g (x, y) , например x 2 + y 2 = 4. Чтобы использовать команду построения графика, просто перейдите к основному страницу графика, введите свое уравнение (в терминах x и y), введите набор значения x и y, для которых должен быть построен график, и нажмите «График» кнопка. Ваше уравнение будет автоматически построено, и будет показан ответ. в вашем браузере в течение нескольких секунд.2 = 1 от x = -2 до x = 2, y = -1,8 до y = 1,8 Опции (только расширенная страница)Деления Значения: отмечен или не отмечен Если установлен флажок Отметки, на осях графика будут отображаться отметки и числовые шкалы. Линии сетки Значения: установлен или не установлен Если установлен флажок Линии сетки, на график будет наложена синяя сетка. Оси Значения: Нет или Автоматическая исходная точка или Исходная точка в (#, #) Параметр «Оси» управляет внешним видом и расположением осей на графике. Если установлен флажок «Нет», оси вообще отображаться не будут. Когда установлен флажок «Автоматическое начало координат», будут отображаться оси. Две оси обычно пересекаются в точке (0,0), но иногда эта точка пересечения может быть расположена в другом месте. Когда установлен флажок «Исходная точка в (#, #)» и вводится точка, оси будут отображаться, и их точка пересечения будет принудительно находиться в указанной точке. Соотношение сторон Значения: Один к одному или Золотое сечение или #: # Параметр Соотношение сторон управляет соотношением высоты графика к его ширине. Когда установлен флажок «Один к одному», соотношение составляет 1: 1, и масштабы на двух осях будут идентичными. Это гарантирует, что круги, например, действительно будут отображаться на экране круглыми. Когда выбрано золотое сечение, соотношение сторон составляет 1: 1 / г, где g — золотое сечение (приблизительно 1.6180). Это якобы дает соотношение высоты к ширине, которое особенно «приятно» для глаз. Когда выбрано #: # и введены два значения, будет применяться указанное соотношение сторон. Это полезно, если сюжет сильно сжат в одном или другом направлении и его необходимо «растянуть», чтобы сделать его более четким. Графики линейных неравенствЭто график линейного неравенства: Вы можете увидеть линию y = x + 2, а заштрихованная область — это место, где y меньше или равно x + 2 Линейное неравенствоЛинейное неравенство похоже на линейное уравнение (например, y = 2x + 1 )… … но у него будет неравенство типа <,>, ≤ или ≥ вместо = . Как построить график линейного неравенстваСначала нарисуйте линию «равно», затем заштрихуйте нужную область. Есть три шага:
Попробуем несколько примеров: Пример: y≤2x-11. Неравенство уже имеет «y» слева и все остальное справа, поэтому нет необходимости переставлять 2. График y = 2x-1 (сплошная линия, потому что y≤ включает , равное ) 3. Закрасьте область ниже (поскольку y на меньше или равно) Пример: 2y — x ≤ 61.Нам нужно будет переставить это так, чтобы «y» находилось слева само по себе: Начать с: 2y — x ≤ 6 Добавьте x к обеим сторонам: 2y ≤ x + 6 Разделить все на 2: y ≤ x / 2 + 3 2. Теперь постройте график y = x / 2 + 3 (сплошная линия, потому что y≤ включает , равное ) 3. Закрасьте область ниже (поскольку y на меньше или равно) Пример: y / 2 + 2> x1.Нам нужно будет переставить это так, чтобы «y» находилось слева само по себе: Начать с: y / 2 + 2> x Вычтем 2 с обеих сторон: y / 2> x — 2 Умножить все на 2: y> 2x — 4 2. Теперь постройте график y = 2x — 4 (пунктирная линия, потому что y> не включает равное) 3. Закрасьте область выше (поскольку y на больше ) Пунктирная линия показывает, что неравенство не включает линию y = 2x-4 . Два особых случаяУ вас также может быть горизонтальная или вертикальная линия:
Узнайте, как построить график правила функции, построить график входов (x) и выходов (y)
В этом видео мы узнаем, как построить график функции.Чтобы построить график функции, вы должны выбрать значения x и вставить их в уравнение. Как только вы подставите эти значения в уравнение, вы получите значение y . Ваши значения x и y составляют ваши координаты для одной точки. Продолжайте вводить значения x, чтобы получить координаты для построения большего количества точек на графике, и тогда вы увидите свою графическую функцию, как только точки будут соединены. Обязательно пометьте свой график. После того, как вы закончите этот урок, просмотрите все наши уроки Алгебры 1 и попрактикуйтесь. Пример построения графика функции правила Стенограмма видеоурокаПример 1Давайте выберем значения x, а затем решим соответствующие им значения y. У нас есть значения x как. Наша функция. Итак, давайте заменим значения, чтобы получить значения. А теперь нарисуем координаты. Пример 2Давайте выберем значения x, а затем решим соответствующие им значения y. У нас есть значения x как. Наша функция. Итак, давайте заменим значения, чтобы получить значения. А теперь нарисуем координаты. Давайте рассмотрим график функции-правила. Например: Давайте выберем значения, а затем решим соответствующие им значения. У нас есть значения as. Наша функция. Итак, давайте заменим значения, чтобы получить значения. Если , затем так Если , затем т. Если , затем так Если , затем т. Если , затем т. Если , затем т. И, наконец, если , затем т. Давайте также напишем наши координаты и Теперь давайте изобразим это. После соединения точек важно поставить стрелки на обоих концах отрезка линии. Потому что мы знаем, что эти точки являются точками функции. Но дело не только в этом. Функция может перемещаться на обоих концах, обозначенных стрелками. |
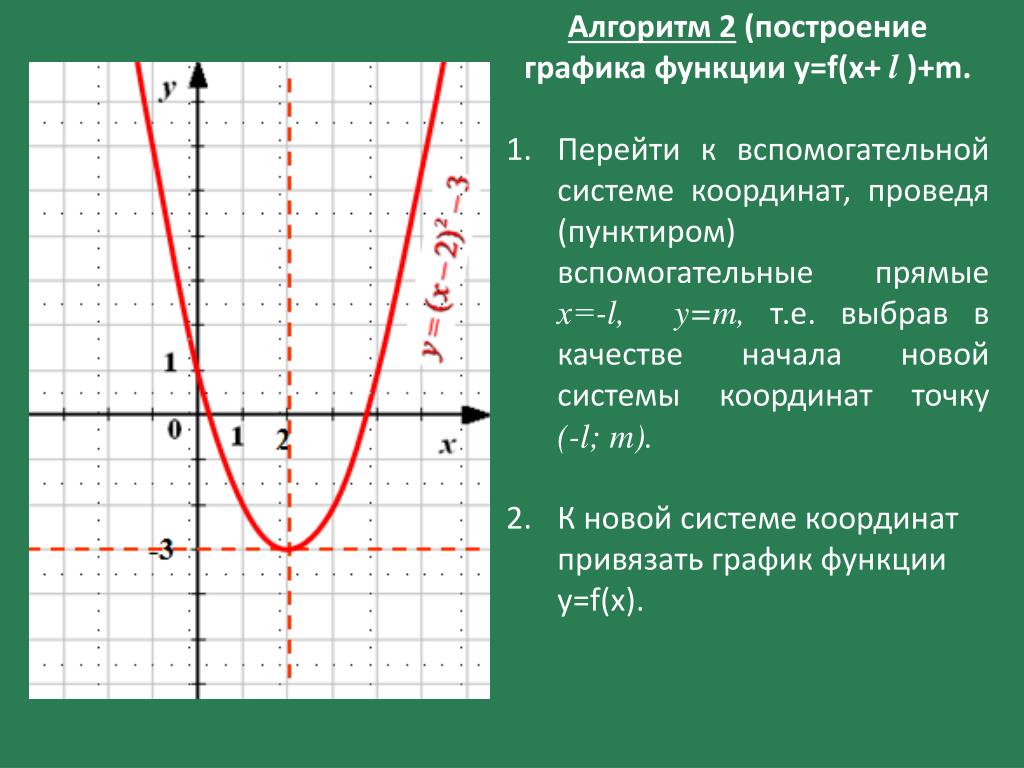2+5x+1\) \(x_в= \frac{-5}{2}=-2,5\) так же как на графике 3
2$
2$, кроме двух точек с $ x \neq \pm 1 $.
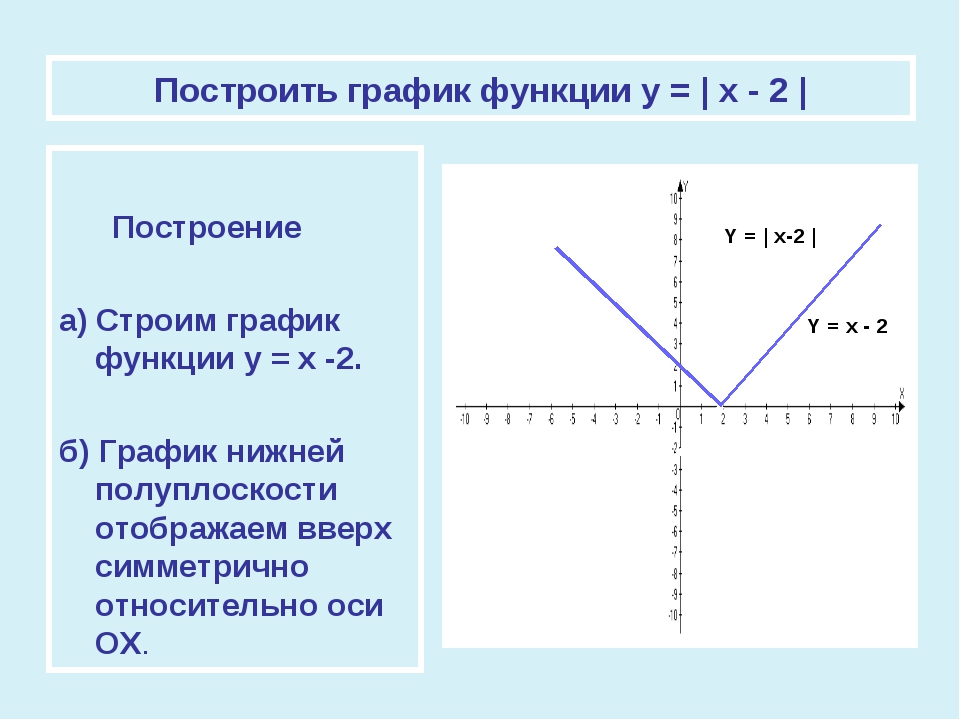Если ,то график функции выглядит примерно так:
2 - 2x - 3')
plt.ylabel('Ось y')
plt.xlabel('Ось x')
plt.grid()
plt.axis([-10, 16, -10, 10])
plt.scatter(x1, y1, s = 1, c = 'b')
plt.scatter(x1, -y1, s = 1, c= 'b')
plt.plot(x2, y2, 'r--')
plt.plot(x2, -y2, 'r--')
plt.show()
