Текстовые задачи на движение 5 класс
Краткое описание документа:
Задачи на движение.
1. Из двух поселков навстречу друг другу движутся два мотоциклиста. Скорость одного из них 45км/ч, а другого 55км/ч. Через сколько часов они встретятся, если расстояние между поселками 400 км?
2..Из двух поселков, расстояние между которыми 80 км, навстречу друг другу выехали два велосипедиста. Скорость одного 5км/ч, а скорость другого на 10км/ч больше. Через сколько часов велосипедисты встретятся?
3.Из двух пунктов навстречу друг другу выехали два лыжника. Скорость одного лыжника12км/ч, что в 2 раза больше, чем скорость второго. Чему равно расстояние между пунктами, если они встретились через 3 часа?
4.Из двух городов, расстояние между которыми 24 км, вышли навстречу друг другу велосипедист и пешеход. Их встреча произошла через 3 часа после выхода. Найдите скорость велосипедиста, если скорость пешехода 3км/ч.
5.Из двух пунктов, расстояние между которыми 30 км, в одном направлении выехали велосипедист и мотоциклист. Скорость мотоциклиста 20км/ч, скорость велосипедиста 5км/ч. Через сколько часов мотоциклист догонит велосипедиста?
6.Из двух городов, расстояние между которыми 40 км .Выехали грузовой и легковой автомобили в одном направлении. Скорость грузового 40 км/ч, скорость легкового 60км/ч.Догонит ли легковая машина грузовую за 2 часа?
7.Из двух деревень. расстояние между которыми 20км. в одном направлении вышли пешеход и велосипедист. Скорость пешехода 3км/ч. Найдите скорость велосипедиста, если он догнал пешехода за 4 часа.
8.Из двух городов, расстояние между которыми 45 км, в одном направлении выехали два мотоциклиста. Скорость одного из них 35км/ч. С какой скорость должен ехать другой мотоциклист, чтобы догнать первого через 3 часа?
9.Из одного пункта в противоположных направлениях выехали 2 автомашины. Скорость одной – 63км/ч, а другой 82 км/ч.
10.С одной станции в противоположных направлениях вышли два поезда. Через 3 часа расстояние между ними стало 315км. Найдите скорость второго поезда, если скорость первого 45км/ч.
11.Два велосипедиста выехали со стадиона в противоположных направлениях. Скорость одного 15км/ч, скорость другого 18км/ч. Через какое время расстояние между ними будет 132км.?
12.Поезд преодолевает расстояние в 300км, за тоже время, что и автомобиль преодолевает расстояние в 200км, двигаясь со скоростью 50км/ч. На сколько скорость поезда больше скорости автомобиля.?
13.Двигаясь на велосипеде со скоростью 12км/ч в течении 5 часов, можно преодолеть тоже расстояние, что и на мотоцикле за 2 часа. Найдите скорость мотоцикла.
14. Машина преодолевает расстояние в 250км , за тоже время, что и пешеход проходит 25км со скоростью 5км/ч. Во сколько раз скорость машины больше скорости пешехода?
15. От деревни до города велосипедист ехал4ч со скоростью 12км/ч. Сколько времени он потратит на обратный путь, если увеличит скорость на 4 км/ч?
От деревни до города велосипедист ехал4ч со скоростью 12км/ч. Сколько времени он потратит на обратный путь, если увеличит скорость на 4 км/ч?
73, 74, 75. Задачи на движение по воде
В задачах на движение по воде скорость реки считается постоянной и неизменной.
При движении по течению скорость реки прибавляется к собственной скорости плывущего тела, так как скорость реки помогает двигаться телу.
При движении против течения от собственной скорости вычитается скорость реки, так как в этом случае скорость реки мешает движущемуся телу.
Скорость плота считается равной скорости реки.Пример:
Пусть скорость движения лодки 5 км/ч, а скорость течения — 2 км/ч.
1) 5 + 2= 7 (км/ч) — скорость лодки по течению
2) 5 — 2 = 3 (км/ч) — скорость лодки против течения
Пусть наша лодка проплыла 2 часа по течению реки и 3 часа против течения реки. Найдем расстояние, которое проплывет лодка.
3) 7 ∙ 2 = 14 (км) — плыла лодка по течению
4) 3 ∙ 3 = 9 (км) — плыла лодка против течения
5) 14 + 9 = 23 (км) — все расстояние
Ответ: 23 км.
Видеоурок
Домашнее задание
К уроку 73 (на 16.12)П. 4.11
№ 1
Скорость катера в стоячей воде (собственная скорость) 12 км/ч, а скорость течения реки 3 км/ч. Определите:
1) скорость катера по течению и против течения реки;
3) путь катера против течения реки за 5 ч.
№ 2
Скорость катера против течения равна 23 км/ч, а скорость течения 4 км/ч. Найдите скорость катера по течению.№ 3
Скорость моторной лодки по течению реки равна 14 км/ч/ а скорость течения 3 км/ч. Найдите скорость лодки против теченияК уроку 74 (на 17.12)
П. 4.11
№ 5.
 302
302Расстояние между пристанями прогулочный теплоход проплывает по течению за 3 ч со скоростью 24 км/ч, а за 4 ч возвращается обратно. Какова скорость катера в стоячей воде и скорость течения реки?
№ 5.303
Путешественник спустился вниз по течению реки за 2 сут. на плоту, а обратно вернулся теплоходом за 2 ч. Найдите собственную скорость теплохода, если скорость течения реки равна 2 км/ч.
№ 5.304
Наша Таня громко плачет, уронила в речку мячик. Но проплакав 2 мин, Таня поплыла за мячиком и через 2 мин догнала его. С какой скоростью плыла Таня, если скорость течения реки равна 35 м/мин?
К уроку 75 (на 18.12)
П. 4.11
№ 5.306
Вниз по течению реки плывет моторная лодка, а навстречу ей катер. Через какое время после начала движения лодка и катер встретятся, если их собственные скорости равны 12 км/ч и 15 км/ч соответственно, скорость течения реки равна 2 км/ч; лодка и катер начали движение одновременно, находясь на расстоянии 54 км друг от друга?
№ 5. 297
297
Из поселка Веселково одновременно в противоположных направлениях отправились два рейсовых автобуса. Скорость одного автобуса равна 56 км/ч, другого — на 8 км/ч больше. Через сколько часов расстояние между автобусами будет равно 480 км?
Вариант № 1
1. Два автомобиля отъезжают от АЗС, расположенной на шоссе, в противоположных направлениях. Скорость одного из них 60 км/ч, другого 75 км/ч. Найдите расстояние, на котором будут находиться друг от друга автомобили через 3 часа. Решите задачу двумя способами. К каждому способу решения составьте выражение. 2. Из двух городов
навстречу друг другу выехали два автомобиля и встретились через 3 часа.
Скорость оного из них 80 км/ч, а скорость другого 70 км/ч. Найдите расстояние
между городами. Решите задачу двумя способами. К каждому способу решения составьте
выражение. 3. Два велосипедиста едут по шоссе навстречу друг другу. Расстояние между ними в данный момент 78 км. Скорость одного из них 12 км/ч, а скорость другого 14 км/ч. Через сколько часов они встретятся? Составьте выражение по условию задачи. | Вариант № 2
1. Два поезда отправляются от одной станции в противоположных направлениях. Скорость одного поезда 65 км/ч, а скорость другого – 80 км/ч. Найдите расстояние, на котором будут находиться друг от друга поезда через 3 часа. Решите задачу двумя способами. К каждому способу решения составьте выражение. 2. Два
велосипедиста едут по шоссе навстречу друг другу. Скорость одного из них 15
км/ч, а скорость другого 12 км/ч. Найдите расстояние, на котором находятся
друг от друга велосипедисты, если известно, что их встреча произойдет через 2
часа. Решите задачу двумя способами. К каждому способу решения составьте
выражение. 3. Два спортсмена бегут по аллее парка навстречу друг другу. Расстояние между ними в данный момент 440 м. Скорость одного из них 100 м/мин, а скорость другого 120 м/мин. Через сколько минут они встретятся? Составьте выражение по условию задачи.
|
Вариант № 3
1. Из города одновременно выехали автобус и автомобиль в противоположных направлениях. Скорость автобуса 45 км/ч, а скорость автомобиля 55 км/ч. Найдите расстояние, на котором будут находиться друг от друга автобус и автомобиль через 3 часа. Решите задачу двумя способами. К каждому способу решения составьте выражение. 2. Из двух сел
одновременно навстречу друг другу вышли два пешехода и встретились через 20
минут. Один шел со скоростью 80 м/мин, а другой – со скоростью 60 м/мин.
Какое расстояние было между ними в начале пути? Решите задачу двумя
способами. К каждому способу решения составьте выражение. 3. От двух пристаней одновременно навстречу друг другу отправляются два теплохода. Расстояние между пристанями 200 км. Скорость одного теплохода 24 км/ч, а скорость другого 26 км/ч. Через сколько часов они встретятся? Составьте выражение по условию задачи. |
Вариант № 4
1. Два поезда отправляются от одной станции в противоположных направлениях. Скорость оного поезда 43 км/ч, а скорость другого – 56 км/ч. Найдите расстояние, на котором будут находиться друг от друга поезда через 4 часа. Решите задачу двумя способами. К каждому способу решения составьте выражение. 2. От двух станций
одновременно навстречу друг другу отправляются два поезда. Скорость одного
поезда 45 км/ч, а скорость другого – 60 км/ч. Найдите расстояние между
станциями, если известно, что они встретились через 3 часа. Решите задачу
двумя способами. К каждому способу решения составьте выражение. 3. Из двух сел, расстояние между которыми 6000 м, одновременно навстречу друг другу вышли два пешехода. Один шел со скоростью 90 м/мин, а другой – со скоростью 60 м/мин. Через сколько минут они встретятся? Составьте выражение по условию задачи.
|
Решение задач на движение. 5 класс
2. Доброе утро!!! Предлагаю вам посмотреть презентацию по решению задач на движение. Чтобы картинки двигались нажимайте на кнопку
«посмотреть».Чтобы перейти к следующему кадру нажимайте
на стрелочку на самом слайде.
УДАЧИ!!!
Из двух пунктов, расстояние между которыми 50 км,
навстречу друг другу одновременно отправились пешеход и
велосипедист. Скорость велосипедиста
в 4 раза больше скорости пешехода. Найдите скорости
пешехода и велосипедиста, если известно, что они встретились
через 2ч30мин после своего выхода.
В
А
в 4 раза
>
tвстр =2ч30мин
40 км
Показать (2)
5.
 Решение Из двух пунктов, расстояние между которыми 210 км,
Решение Из двух пунктов, расстояние между которыми 210 км,вышли одновременно навстречу друг другу два поезда.
Скорость одного из них на 5 км/ч больше скорости
другого. Найдите скорость каждого поезда, если они
встретились через 2 ч после своего выхода.
Показать
tвстр =2 ч
7. Решение
Эта задача уже на уравниваниеНайдем скорость сближения
1) 210 :2=….(км/ч)
2) … — 5 =….(км/ч) обе скорости поровну
3) … : 2 = …(км/ч)- меньшая скорость
4) …. + 5= … (км/ч)- большая скорость
Ответ:
Показать
Из аэропорта вылетел самолет со скоростью 600 км/ч. Через
30 минут вслед за ним вылетел другой самолет со скоростью
750 км/ч. Через сколько часов второй самолет после своего
вылета будет впереди на 225 км?
Показать (2)
Из аэропорта вылетел самолет со скоростью 600 км/ч. Через
0,5 ч вслед за ним вылетел другой самолет со скоростью 750
км/ч. Через сколько часов второй самолет после своего
вылета будет впереди на 225 км?
Еще
2) 300способ
: (750 – 600) = 2(ч)
tвстр
(225+300)
:
(750
–
600)
=
3ч30минут
3) 225 : (750 – 600) = 1,5(ч)
1,5 ч потребуется на обгон на 225 км
750км/ч
600км/ч
вдогонку
300км
600км/ч
750км/ч
С отставанием
225км
Один человек идет в другой город и проходит в день 40 верст, а
другой человек идет навстречу ему из другого города и в день
проходит по 30 верст.
 Расстояние между городами 700 верст.
Расстояние между городами 700 верст.Через сколько дней путники встретятся, если вышли
одновременно.
Показать (2)
12. Дома: № 542, 546(б), 549, 551(а) Задачи из презентации и номера переслать завтра!!! Эти задания у вас на два дня
Текстовые задачи на движение по воде 10 класс онлайн-подготовка на Ростелеком Лицей
Текстовые задачи на движение по воде
Движение по течению реки → течение «помогает» движению → скорость течения и собственная скорость объекта складываются.
Движение против течения реки → течение препятствует движению объекта → скорость течения вычитается из собственной скорости объекта.
V=V0+Vтечения
V=V0−Vтечения
Задача №1.
Катер прошел 36 км по течению реки и вернулся обратно, затратив на весь путь 5 ч. Найдите скорость катера в стоячей воде, если известно, что скорость течения реки равна 3 км/ч.
Решение
|
Расстояние |
Скорость |
Время |
|
|
По течению |
36 |
x+3 |
36x+3 |
|
Против течения |
36 |
x-3 |
36x-3 |
36x+3+36x-3=5
36x-3+36x+3=5x+3x-3
36x-108+36x+108=5×2-45
5×2-72x-45=0
D=722-4∙5∙-45=5184+900=6084=782
x1=72+7810=15;
x2=72-7810=-0,6
Ответ: 15
Задача №2.
Расстояние между пристанями А и В равно 135 км. Из А в В по течению реки отправился плот, а через 2 часа вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 80 км. Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
Решение
|
Расстояние |
Скорость |
Время |
|
|
Лодка по течению |
135 |
x+4 |
135x+4 |
|
Лодка против течения |
135 |
x-4 |
135x-4 |
|
Плот |
80 |
4 |
80:4=20 |
Составим уравнение, где время пребывания лодки по воде складывается из времени движения по течению и времени движения против течения и на 2 часа меньше времени движения плота, т. к. лодка выдвинулась позже:
к. лодка выдвинулась позже:
135x+4+135x-4=20-2
135x-4+135x+4-18x-4x+4=0
135x-540+135x+540-18×2+18∙16=0
18×2-270x-288=0
x2-15x-16=0
По теореме Виета:
x1=-1; x2=16.
Поскольку скорость не может быть отрицательной величиной, собственная скорость лодки равна 16 км/ч.
Ответ: 16
Задачи на движение по реке | Шевкин.Ru
Развитием линии задач раздела 1.4 являются задачи на движение по реке, не вызывающие обычно каких-либо затруднений у пятиклассников. Опыт, полученный ими при решении задач 70–75 можно обобщить при работе с задачей 76, в которой возникают сложности только в последнем задании, где требуется определить скорость течения реки по двум скоростям — по течению и против течения реки. Для успешного усвоения этого материала следует показать, что скорости по течению и против течения — суть сумма и разность собственной скорости и скорости течения. Чтобы их найти, нужно применить освоенный ранее прием нахождения двух величин по их сумме и разности: разность скоростей по течению и против течения равна удвоенной скорости течения. Будет еще лучше, если к этому выводу учащиеся придут самостоятельно. Ведь ситуации, в которых школьники находят возможность для применения ранее полученных знаний, способствуют их развитию. Когда же отрицательные числа будут изучены, этот факт будет просто доказать:
Чтобы их найти, нужно применить освоенный ранее прием нахождения двух величин по их сумме и разности: разность скоростей по течению и против течения равна удвоенной скорости течения. Будет еще лучше, если к этому выводу учащиеся придут самостоятельно. Ведь ситуации, в которых школьники находят возможность для применения ранее полученных знаний, способствуют их развитию. Когда же отрицательные числа будут изучены, этот факт будет просто доказать:
vпо т. – vпр.т. = (vс. + vт.) – (vс. – vт.) = … = 2vт.
А пока можно обойтись ссылкой на уже известное правило нахождения двух чисел по их сумме и разности или на графическую иллюстрацию:
70.о 1) Мальчик заметил, что на путь по течению реки было затрачено меньше времени, чем на тот же путь против течения. Чем это можно объяснить, если мотор лодки работал одинаково хорошо во время всей поездки?
2) На путь из пункта А в пункт В теплоход затратил 1 ч 40 мин, а на обратный путь — 2 ч.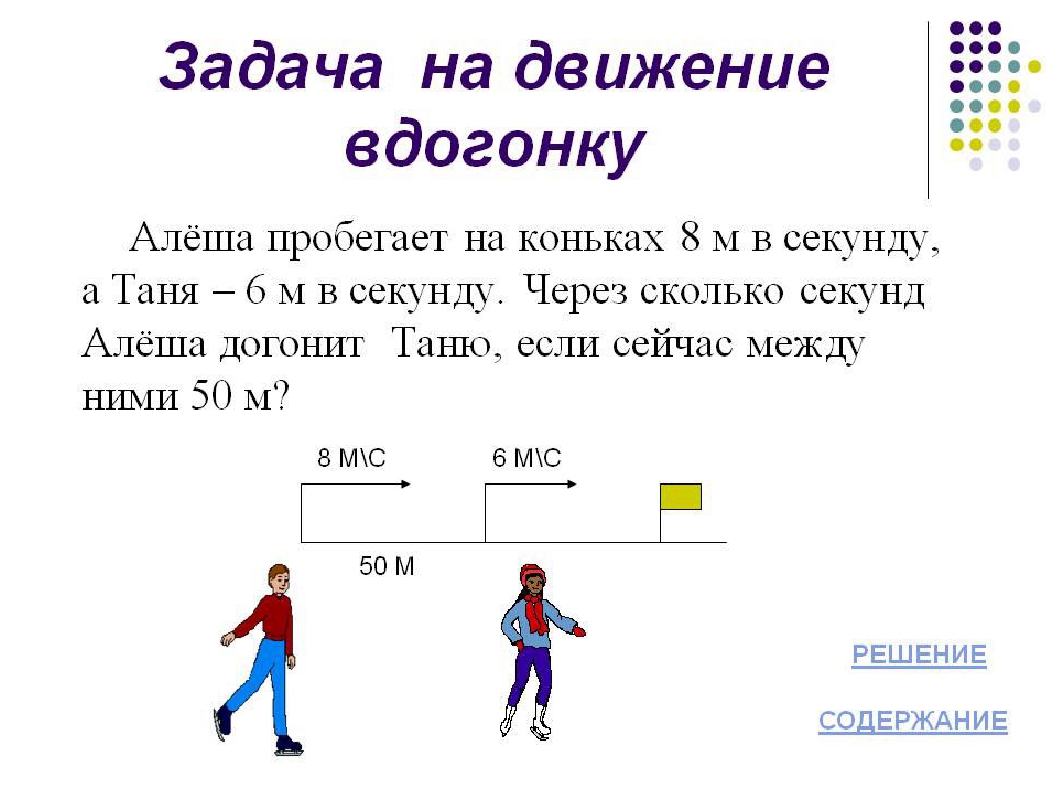 В каком направлении течет река?
В каком направлении течет река?
3) Скорость катера по озеру (в стоячей воде) 18 км/ч. Какой путь пройдет катер за 3 ч?
4) Скорость течения реки 2 км/ч. На сколько километров река относит любой предмет (плот, лодку) за 1 ч, за 5 ч?
71. Скорость катера в стоячей воде 18 км/ч. Скорость течения реки 2 км/ч. С какой скоростью будет двигаться катер по течению реки? Против течения?
72. Скорость катера в стоячей воде (собственная скорость) 12 км/ч, а скорость течения реки 3 км/ч. Определите:
1) скорость катера по течению и против течения реки;
2) путь катера по течению реки за 3 ч;
3) путь катера против течения реки за 5 ч.
73. 1) Собственная скорость теплохода 27 км/ч, скорость течения реки 3 км/ч. Сколько времени затратит теплоход на путь по течению реки между двумя причалами, если расстояние между ними равно 120 км?
2) Сколько времени потребуется для того, чтобы проплыть на моторной лодке 90 км против течения, если ее собственная скорость 20 км/ч, а скорость течения реки 2 км/ч?
74. Катер, имеющий собственную скорость 15 км/ч, плыл 2 ч по течению реки и 3 ч против течения. Какое расстояние он проплыл за все время, если скорость течения реки 2 км/ч?
Катер, имеющий собственную скорость 15 км/ч, плыл 2 ч по течению реки и 3 ч против течения. Какое расстояние он проплыл за все время, если скорость течения реки 2 км/ч?
75. а) Расстояние между двумя причалами 24 км. Сколько времени потратит моторная лодка на путь от одного причала до другого и обратно, если ее собственная скорость 10 км/ч, а скорость течения 2 км/ч?
б) Расстояние между двумя причалами 36 км. Сколько времени потратит на путь от одного причала до другого и обратно катер, если его собственная скорость 15 км/ч, а скорость течения реки 3 км/ч?
76. Определите скорости и заполните таблицу:
|
|
vс. |
vт. |
vпо т. |
vпр. т.
|
|
1. |
12 км/ч |
4 км/ч |
|
|
|
2. |
25 км/ч |
|
28 км/ч |
|
|
3. |
24 км/ч |
|
|
20 км/ч |
|
4. |
|
5 км/ч |
17 км/ч |
|
|
5. |
|
3 км/ч |
|
16 км/ч |
|
6. |
|
|
48 км/ч |
42 км/ч |
77.* Определите, какая скорость получится в результате:
1) vс. + vт. ; 4) vпр.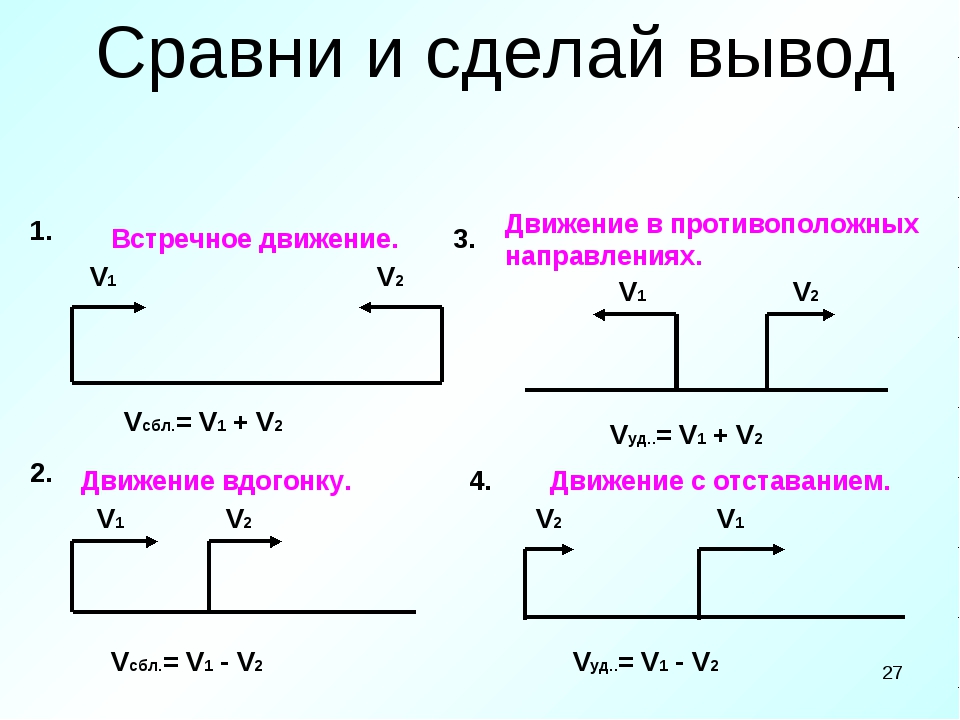 т. + 2vт. ;
т. + 2vт. ;
2) vс. – vт. ; 5) vпо т. – 2vт. ;
3) vпр. т. + vт. ; 6) vпо т. – vпр. т.
78. 1) Моторная лодка проплыла 48 км по течению за 3 ч, а против течения — за 4 ч. Найдите скорость течения.
2) Катер проплыл 72 км между пристанями по течению за 2 ч, а против течения за 3 ч. За сколько часов это расстояние проплывут плоты?
79. Скорость течения реки 3 км/ч. На сколько километров в час скорость катера по течению больше его скорости против течения?
Задача B14: движение навстречу
В этом видео вас ждут сразу две фишки:
- Собственно, решение задачи B14 про движение навстречу — помните, что скорости при таком движении складываются.

- По условию задачи, нам неизвестно общее расстояние. В смысле, вообще неизвестно — его нельзя найти ни из текста, ни из полученных уравнений.
Как работать с такими задачами? Смотрите урок — и берите на вооружение.:)
Мы продолжаем длинную серию уроков, посвященных текстовым задачам на движение. И сегодня настала очередь для задачи про движение навстречу.
Решаем реальные примеры
Задача:
Из города А в город Б навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город Б на 6 часов раньше, чем велосипедист приехал в А. Встретились они через 4 часа после выезда. Сколько часов затратил на путь из города Б в город А велосипедист?
Итак, решаем эту текстовую задачу. Решать мы ее будем, разумеется, с помощью таблиц. Но прежде чем переходить к решению таблицей, давайте вспомним, что такое скорость встречного движения.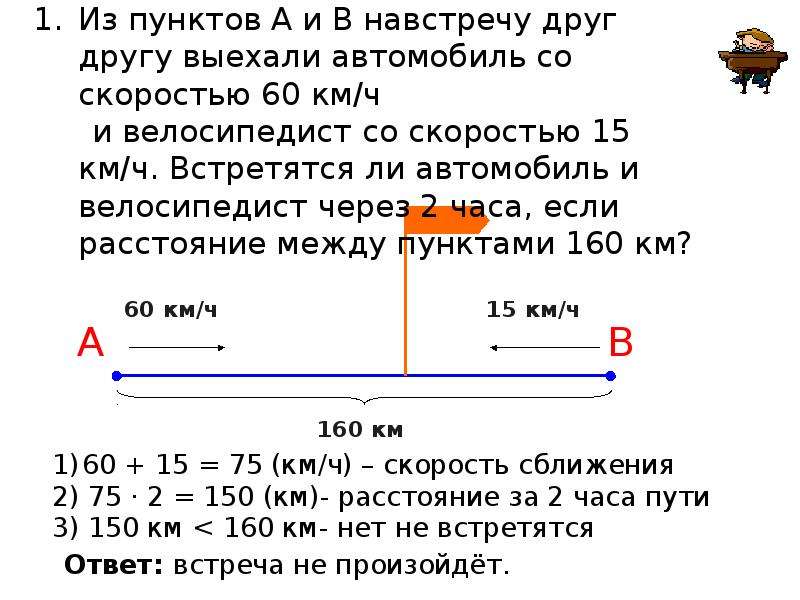 Допустим, у нас некий отрезок, соединяющий пункты А и Б. пусть тот, кто выезжает из пункта А, имеет скорость v1{{v}_{1}}, а второй персонаж —v2{{v}_{2}}:
Допустим, у нас некий отрезок, соединяющий пункты А и Б. пусть тот, кто выезжает из пункта А, имеет скорость v1{{v}_{1}}, а второй персонаж —v2{{v}_{2}}:
В этом случае они приближаются друг к другу со скоростью vv, равной сумме этих скоростей:
v=v1+v2
v={{v}_{1}}+{{v}_{2}}. Вот эта несложная формула называется суммарной формулой скорости при встреченном движении.
Итак:
Из А в Б навстречу друг другу одновременно выехали мотоциклист и велосипедист. Строим нашу стандартную таблицу. И тут к нам на помощь приходит основное правило: где нам в этой таблице поставить xx или переменную yy? Вспоминаем, что первой мы стараемся обозначить vv, затем, если vv нам прямо дана, стараемся обозначить tt, т. е. время — xx или yy. Наконец, если и время нам дано, нужно вводить в качестве переменных SS:
v→t→S
v\to t\to S
Разумеется, два последних шага нас не интересует, потому что в примере нам неизвестна vv ни одного из персонажей. Следовательно, давайте их обозначим за xx и yy. Но есть еще одна проблема: нигде в текстовой задаче нам не указано полное расстояние, которое предстоит проехать нашим персонажам. И вот тут мы поступаем точно также как в текстовых задачах на работу. Вспомните, если в задаче на работу полный объем работы неизвестен, то мы просто обозначаем его за единицу. Для текстовых задач на движение действует точно такое же правило. Если общее расстояние нам неизвестно, а в нашем примере так и происходит, мы обозначаем его за
Следовательно, давайте их обозначим за xx и yy. Но есть еще одна проблема: нигде в текстовой задаче нам не указано полное расстояние, которое предстоит проехать нашим персонажам. И вот тут мы поступаем точно также как в текстовых задачах на работу. Вспомните, если в задаче на работу полный объем работы неизвестен, то мы просто обозначаем его за единицу. Для текстовых задач на движение действует точно такое же правило. Если общее расстояние нам неизвестно, а в нашем примере так и происходит, мы обозначаем его за
S=100
S=100. Почему именно 100 км? Просто в тех текстовых задачах, которые попадаются на ЕГЭ, а также на пробниках и контрольных все расстояния крутятся именно вокруг 100 км — бывает чуть больше, бывает чуть меньше, но порядок величины именно такой. Следовательно, если мы предположим, что общее расстояние равно именно 100, то наши ответы и решения как минимум не потеряют своей достоверности, а то и окажутся именно такими, какими и задумали их авторы.
Еще раз: если в условии вообще ничего не сказано про расстояние, то мы смело приравниваем его к 100 км. Таким образом, получаем таблицу, в которой два столбца заполнены, и осталось найти третий столбец. Если
S=v⋅t
S=v\cdot t, то
t=Sv
t=\frac{S}{v}. Сосчитаем время для каждого персонажа:
| SS | vv | tt | |
| Мот. | 100 | xx | 100x \frac{100}{x} |
| Вел. | 100 | yy | 100y \frac{100}{y} |
Идем дальше. В задаче сказано, что мотоциклист приехал в город Б на 6 часов раньше, чем велосипедист приехал в А. Это значит что наши времена, которые мы только что нашли, ни в коем случае не складываются — они сравниваются друг с другом. Поэтому составляем первое уравнение:
100x=100y−6
\frac{100}{x}=\frac{100}{y}-6
И вот тут всегда возникает вопрос: почему именно -6, почему мы не написали это -6, например, слева или вообще почему перед 6 стоит минус? Общее правило здесь следующее:
Возвращаемся к нашему условию: по условию мотоциклист приехал раньше, т. е. его время
е. его время
100x
\frac{100}{x} —меньше. Оно должно быть равно времени второго участника движения, которое больше, а дальше то же самое ±6\pm 6. Но наша запись явно показывает, что должен стоять именно минус, потому что, чтобы получить меньшее число, нужно вычесть, а ни в коем случае не прибавить. Соответственно, наша конструкция записана корректно. Вот такое простое правило гарантировано избавит вас головной боли при решении задач на движение.
Однако одним выражением рассматриваемая сегодня задача на движение не ограничивается. Дело в том, что есть другое условие: встретились они через 4 часа после выезда. Следовательно, нужно составить еще одну таблицу. Время записываем согласно данным задачи, расстояние запишем как 100, а что касаетсяvv, воспользуемся следующей формулой:
v=v1+v2
v={{v}_{1}}+{{v}_{2}}, т. е.
v=x+y
v=x+y. Все три величины связаны известной нам формулой:
Все три величины связаны известной нам формулой:
S=v⋅t
S=v\cdot t
Запишем следующую конструкцию:
100=(+)⋅4|:4
100=\left( + \right)\cdot 4|:4
+=25
+=25
А теперь решаем систему уравнений. Запишем их вместе:
Erroneous nesting of equation structures
\begin{align}& \left\{ \left. \begin{align}& \frac{100}{x}=\frac{100}{y}-6 \\& x+y=25 \\\end{align} \right\} \right. \\& \\\end{align}
У нас получилось два уравнения и две переменных. Очевидно, что такая система должна решаться довольно просто. Но даже для такой системы можно приметь маленькую, но очень полезную хитрость. Давайте посмотрим, что требуется в условии задачи на движение. Спрашивают: сколько часов затратил на путь велосипедист? Другими словами, нас просят найти величину
100y
\frac{100}{y}, а мы найдем ее, если будем знать у. Именно yy является ключевой переменной, вокруг которой должно быть построено все решение. И вот тут применяем ту самую маленькую хитрость. Звучит она следующим образом:
Именно yy является ключевой переменной, вокруг которой должно быть построено все решение. И вот тут применяем ту самую маленькую хитрость. Звучит она следующим образом:
Если в системе уравнений требуется найти какую-то переменную, т. е. в данном случае у, то в процессе решения через нее нужно выразить все остальные.
Что это значит на практике? Давайте посмотрим на второе уравнение
+=25
+=25. Очевидно, отсюда можно найти и xx, и yy. Но согласно данному замечанию давайте выразим именно xx:
=25−˜
=25-˜
Полученное выражение подставим в первую конструкцию, и получим:
10025−y=100y−6
\frac{100}{25-y}=\frac{100}{y}-6
Что дает нам такая запись? Все очень просто. Взгляните еще раз: в нашем равенстве осталась единственная переменная yy, та самая, которую нам необходимо найти, чтобы получит ответ к текстовой задаче. {\text{2}}}}=25\cdot \text{5}=\text{125}
{\text{2}}}}=25\cdot \text{5}=\text{125}
Вот мы и нашли дискриминант —без всякого напряга, без всяких умножений столбиком и прочих непотребств. Все, что для этого потребовалось —разложить на множители каждый из слагаемых исходного выражения. Идем далее: считаем корни, т. е. yy:
y=175±1256
y=\frac{175\pm 125}{6}
y1=3006=50
{{y}_{1}}=\frac{300}{6}=50
y2=506=253
{{y}_{2}}=\frac{50}{6}=\frac{25}{3}
Итак, мы получили два варианта скорости: либо скорость второго участника движения равна 50 км/ч, либо
253
\frac{25}{3} км/ч. Как же узнать, какая из этих vv правильная. А все очень просто. Давайте вспомним про наше выражение скоростей: vv мотоциклиста равна 25 минус vv велосипедиста:
=25
=25. Так вот, если скорость второго участника будет равна 50 км/ч, это значит, что мотоциклист едет со скоростью
25−50=−25
25-50=-25 км/ч. Очевидно, это полный бред, vv не может быть отрицательной. Следовательно, vv велосипедиста на самом деле равна
Очевидно, это полный бред, vv не может быть отрицательной. Следовательно, vv велосипедиста на самом деле равна
253
\frac{25}{3} км/ч.
Переходим к последнему шагу и выясняем, что нам нужно. Для этого возвращаемся к условию текстовой задачи на движение, и видим, что от нас требуется найти, сколько часов затратил на путь из города Б в город А велосипедист. Другими словами, нам нужно найти величину
100y
\frac{100}{y} . Посчитаем ее:
100y=100253=100:253=100⋅325=12
\frac{100}{y}=\frac{\frac{100}{25}}{3}=100:\frac{25}{3}=100\cdot \frac{\text{3}}{\text{25}}=12
Все, мы нашли ответ: t=12t=12 ч.
Ключевые моменты
И путь вас не пугает большой объем вычислении и длина этой текстовой задачи. Давайте вернемся еще раз в начало и посмотрим ключевые моменты решения.
В первую очередь нужно правильно заполнить таблицу. Для этого помним, что переменные xx и yy мы в первую очередь стараемся ввести дляvv. Затем нас ждет вторая проблема: мы не знаем расстояние. Если расстояние в задаче прямо не указано, смело приравниваем его к 100. Затем воспользуемся формулой сложения скоростей, чтобы получить второе уравнение системы. Разумеется, в первом уравнении системы тоже не все так просто. Нужно грамотно определить, прибавлять или вычитать 6. В данном случае 6 нужно именно вычитать, в чем легко убедиться, если внимательно прочитать условие задачи на движение и заметить, что мотоциклист приехал раньше, т. е. его время меньше. Следовательно, чтобы получить меньшее число, нужно из большего числа вычесть 6. Такой способ самопроверки очень эффективен при решении любых текстовых задач на движение и избавит вас от глупых и обидных ошибок.
Для этого помним, что переменные xx и yy мы в первую очередь стараемся ввести дляvv. Затем нас ждет вторая проблема: мы не знаем расстояние. Если расстояние в задаче прямо не указано, смело приравниваем его к 100. Затем воспользуемся формулой сложения скоростей, чтобы получить второе уравнение системы. Разумеется, в первом уравнении системы тоже не все так просто. Нужно грамотно определить, прибавлять или вычитать 6. В данном случае 6 нужно именно вычитать, в чем легко убедиться, если внимательно прочитать условие задачи на движение и заметить, что мотоциклист приехал раньше, т. е. его время меньше. Следовательно, чтобы получить меньшее число, нужно из большего числа вычесть 6. Такой способ самопроверки очень эффективен при решении любых текстовых задач на движение и избавит вас от глупых и обидных ошибок.
Главный вывод из этого видео: если в текстовой задаче неизвестно общее расстояние, просто полагаем, что оно равно 100 км: S=100. Затем смело заполняем стандартную таблицу, составляем уравнение и решаем его.
Но будьте внимательны: данное правило работает только в тех задачах, где расстояние не вычисляется вообще никаким образом! В частности, вы можете обозначить расстояние просто переменной S — и при этом ответ получится тем же.
Смотрите также:
- Движение вдогонку и сравнение времени
- Особенности решения текстовых задач
- Тест на тему «Значащая часть числа»
- Сложные логарифмические неравенства
- Задача B5: площадь кольца
- Дробно-рациональные уравнения с модулем
5 способов сделать перерыв в движении в классе, помочь с поведением
Учителя, сколько физической активности ваши ученики получают каждый день? Предусмотрены ли в вашей школе перерывы в работе в классе?
Вы слышали о забавных способах, которыми учителя передовых школ включают упражнения в свой распорядок дня? И это упражнения, которые обычно связаны с трудотерапией!
Прошли те времена, когда в классных комнатах стояли парты в один ряд. Сейчас тенденция в организации классных комнат иная. Сегодняшняя классная комната предпочитает столы для группового обучения, тематические станции по комнате и даже уникальные варианты сидения.
Сейчас тенденция в организации классных комнат иная. Сегодняшняя классная комната предпочитает столы для группового обучения, тематические станции по комнате и даже уникальные варианты сидения.
Кроме того, учителя ищут все больше и больше способов включить столь необходимую физическую активность в распорядок дня своих учеников.
Неожиданный побочный эффект перерывов на движение в классе
То, что могло начаться как реакция на инклюзивные варианты для детей с особыми потребностями в обучении, теперь становится стандартной практикой.
Перерывы в движении в классе — во всем классе — кажется ответом. По сути, долгожданный ответ на озабоченность сегодняшней малоподвижной, экранозависимой молодежи.
В специализированных классах и кабинетах трудотерапии уже давно поняли, что перерывы в движении чрезвычайно важны.
Перерывы в классе дают детям с ШРЛ, СДВГ, тревогой, диспраксией и другими проблемами в классе, такими как ерзание, плохая концентрация и мечтательность, столь необходимую возможность перезагрузиться в течение дня.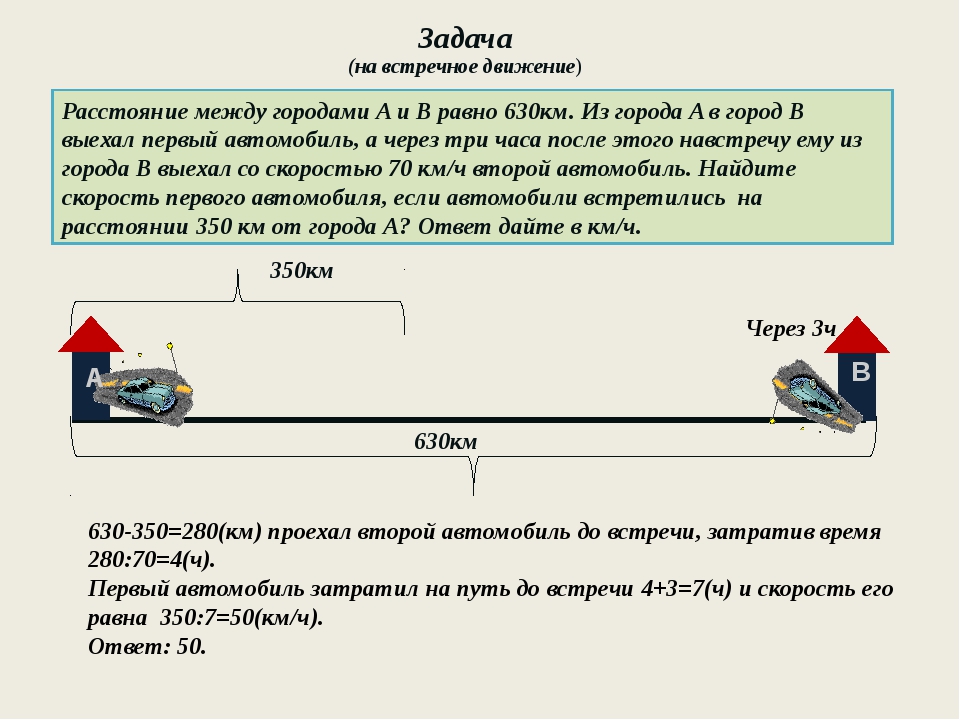 Более того, преимущества перерывов в классе распространяются на всех учащихся.
Более того, преимущества перерывов в классе распространяются на всех учащихся.
Перерывы в классе полезны не только для детей с особыми потребностями. Было показано, что перерывы в движении помогают повысить концентрацию и внимание.
Кроме того, было показано, что они приводят к повышению эффективности обучения в целом.
5 минут движения между уроками могут оказать огромное влияние на внимание и поведение вашего ученика.
Вот 5 примеров того, как перерывы в работе в классе приносят пользу учащимся в этих условиях:
1. Перерывы в движении делают обучение более эффективным.
Исследования показывают, что перерывы в движении делают обучение более эффективным. Потратив 5 минут на то, чтобы скрытое обучение вступило в силу, вы сможете усвоить предыдущий урок.
А также следующий урок, чтобы начать заново. Биологически говоря, гиппокамп головного мозга — это область, ответственная за создание новых воспоминаний.
Исследования показывают, что гиппокамп лучше функционирует при создании долговременных воспоминаний, когда между повторениями нового материала есть короткие перерывы.
Латентные периоды, по-видимому, усиливают способность мозга запоминать информацию. Таким образом, перерыв, например, перерыв на движение, — отличный способ закрепить новый учебный материал в классе.
2. Физическая активность увеличивает поступление кислорода в мозг.
Физическая активность также увеличивает поступление кислорода в мозг, что имеет решающее значение для внимания и обучения.Биологи предполагают, что 90% кислорода в нашем организме «несвежий» — некачественный.
Тем не менее, когда мы зеваем, делаем глубокие вдохи или встаем и двигаемся всем телом, в нашем организме циркулирует воздух, богатый кислородом. Это особенно важно в нашем мозгу для обучения!
Внимание и способность запоминать новый материал напрямую связаны с количеством кислорода в крови.
3.
 Перебои в движении прерывают негативные паттерны.
Перебои в движении прерывают негативные паттерны.Перерывы на движение также дают учащимся возможность регулировать или прерывать любое беспокойство или стресс.Если вы думаете, что наши дети младшего и среднего школьного возраста слишком малы для беспокойства и стресса, подумайте еще раз.
Мы говорим об обычных проблемах, связанных с поступлением в школу.
4. Перерывы в движении предлагают мини-перерыв.
Перерывы в движении предлагают детям умственную и сенсорную передышку. Это особенно важно для учащихся с расстройством сенсорной обработки (SPD), СДВГ, диспраксией или другими проблемами в классе.
5. Саморегуляция эмоций имеет шанс сработать.
Кроме того, они могут помочь с саморегуляцией эмоций в целом. В раннем детстве дети все еще учатся управлять своим поведением и эмоциями.
Саморегуляция имеет решающее значение для обучения и социального взаимодействия. Следование указаниям, сидение на месте, не выпалив или не выплескивая эмоции на каждом шагу, — все это коррелирует со способностью человека к саморегуляции.
Физические упражнения в целом положительно влияют на эмоциональную регуляцию как детей, так и взрослых.Кроме того, специальные упражнения, используемые в большинстве групповых перерывов в занятиях по трудотерапии, нацелены на связи между мозгом и телом, которые помогают детям физически лучше регулировать свои эмоции.
Даже всего 5 минут физических движений между уроками могут оказать огромное влияние на учебный день любого ребенка, независимо от того, есть ли у него расстройство сенсорной обработки, СДВ, СДВГ, РАС, диспраксия или нет!
Передовые школы разрешают перерывы в движении в течение дня
Некоторые школы проявляют творческий подход, разрешая индивидуальные перерывы в течение дня.Например, одна мама по имени Скайли говорит: «У учителя моего сына были бумажки на липучках с надписью «Мне нужен перерыв!» на столе каждого ребенка.
Им разрешили передать его учителю, чтобы заработать несколько минут, чтобы встать и передвигаться, когда им это нужно».
Например:
- двусторонние движения стимулируют активность обоих полушарий,
- баланс и ритм поддерживают концентрацию, а
- слуховой компонент побуждает слушать.
В целом, в 5-минутном перерыве основное внимание уделяется движениям тела, давая коре (мыслящему мозгу) передышку, чтобы освежиться и подготовиться к концентрации.
Тем не менее, упражнения доставляют удовольствие всем участвующим детям. Упражнения заставляют их мышцы двигаться, кислород поступает в мозг и не требуют от учителя дополнительного времени на подготовку.
Он или она просто запускает одно из онлайн-видео, а класс может следовать за ним.
Какие типы перерывов в классе лучше всего?
Знаете ли вы, что существуют определенные проверенные физические упражнения для улучшения концентрации внимания у школьников?
Исследования в области трудотерапии привели к созданию нескольких программ такого рода.
Это программы, которые показывают учителям специальные комплексы упражнений для улучшения концентрации внимания в классе. Эти программы идеально подходят для перерывов в движении.
Активность проприоцепции — это типы движений, которые устраняют любые пробелы в осознании тела в пространстве. Эти пробелы могут быть вызваны диспраксией, ШРЛ, РАС или некоторыми другими отклонениями в развитии.
Все дети получают пользу от проприоцептивной деятельности (иногда называемой «тяжелой работой»).Поэтому многие учителя включают эти движения в ежедневные части планов уроков.
Перерывы движения проприоцепции Учителя могут беспрепятственно интегрироваться в класс
Перемещение столов и стульев для разных мест в течение дня (подробнее об этом позже), переноска книг, толкание тележки, перенос стопки коробок для завтрака, перемещение ковриков или спортивного инвентаря, сшивание скобами и резка и т. д.
Учитель Эрика говорит,
«Одна вещь, которую я делаю, чтобы помочь ученикам переехать, это то, что я заставляю учеников делать почти все.
Они раздают припасы, сортируют припасы, собирают припасы. Цель состоит в том, чтобы у них всегда была какая-то двигательная задача».
Действия по вестибулярной стимуляции нацелены на вестибулярную систему во внутреннем ухе. Вестибулярная система может быть нарушена в связи с целым рядом проблем, связанных с развитием и сенсорной интеграцией.
Вестибулярный аппарат активируется движениями головы. Координацию, баланс, саморегуляцию эмоций и сосредоточенность на задачах можно укрепить с помощью практики вестибулярной стимуляции.
Типичный пример — наклониться в пояснице и снова выпрямиться. Итак, все, что двигает головой в совершенно разных направлениях.
Перерывы вестибулярных движений в классе, которые учителя могут беспрепятственно интегрировать
Упражнения, нацеленные на эту систему, можно легко включить в обучающие песни, такие как «Голова, плечи, колени и пальцы ног».
Или:
- Создайте подвижное упражнение, в котором учащиеся наклоняются, чтобы взять палочки от эскимо или кубики с цифрами и буквами, чтобы составлять слова или решать математические задачи.

- повесьте разные числа в каждом углу комнаты, называя простые числовые задачи и предлагая учащимся подпрыгнуть и повернуться лицом к углу с правильным ответом.
- просто храните канцтовары под детским стульчиком. Ребенок должен наклониться, чтобы взять карандаши, мелки, ластики и т. д.
Ознакомьтесь с программами перерывов для движения, созданными эрготерапевтами в CoordiKids специально для таких учителей, как вы!
19 забавных идей и ресурсов для изучения силы и движения
Обучайте силе и движению стильно, используя эксперименты, бесплатные распечатки и ресурсы, которые помогут оживить научные концепции.Этот сборник идей о силе и движении должен помочь вам охватить темы текстур, гравитации, наклона и некоторых простых механизмов .
Если вы ищете интересные идеи, начните с этого!
источник: librarianismchronicles.blogspot.com 1. Высота угла и текстура дорожки. Используйте основные учебные материалы, такие как книги, чтобы поэкспериментировать с высотой угла (наклоном) для разработки прогнозов. Используйте ту же настройку эксперимента, чтобы изменить переменную текстуры рампы, чтобы поэкспериментировать с трением.
Используйте ту же настройку эксперимента, чтобы изменить переменную текстуры рампы, чтобы поэкспериментировать с трением.
2. Элементарное исследование: трение. Используя линейки, деревянный брусок и несколько материалов, вы можете провести эксперимент, подобный описанному выше, чтобы увидеть, как учащиеся могут сравнить то, что они узнали о трении с помощью автомобиля и текстуры, и применить его к эта ситуация. Использование линеек позволит учащимся делиться точными измерениями наклона. {Бесплатная загрузка}
источник: mrsmathes.blogspot.com3. Мраморные гонки с уклоном. Чтобы создать некоторые основные представления о том, как наклон влияет на движение предметов, попробуйте создать несколько мраморных гонок.Позвольте учащимся экспериментировать и записывать свои выводы, используя простые материалы и предметы разной высоты, например книжную полку.
4. Силы в действии: игра. Этот интерактивный веб-сайт виртуально воссоздает аналогичный набор экспериментов и позволит учащимся регулировать наклон и добавлять парашюты для усиления сопротивления.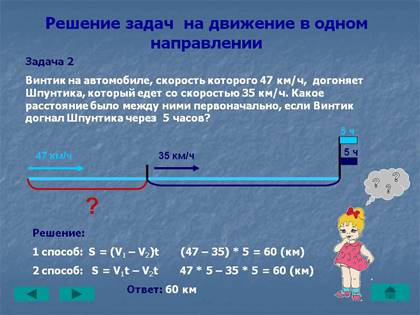 Какие концепции учащиеся могут закрепить с помощью прилагаемой таблицы на основе своих виртуальных экспериментов? Отлично подходит для умной доски для всей группы.
Какие концепции учащиеся могут закрепить с помощью прилагаемой таблицы на основе своих виртуальных экспериментов? Отлично подходит для умной доски для всей группы.
5. Автомобильные пандусы. Вот пример создания экспериментов, которые сталкиваются с несколькими проблемами и дают студентам время для поиска решений. Это более исследовательский подход, но он является хорошим введением в понимание того, как вещи движутся на склоне.
6. Силы в действии: план урока. Этот урок преследует четыре цели, включая понимание того, что трение (включая сопротивление воздуха) — это сила, которая замедляет движущиеся объекты. Прекрасно работает вместе с интерактивным сайтом, указанным выше под номером 4.
источник: tekyteach.blogspot.com 7. Стрельба из зефира. Когда вы обсуждаете толкание и тягу как силы и включаете измерения, вам следует включить в планы уроков стрельбу из зефира. В конечном итоге вы будете включать такие слова, как сила, расстояние и поиск способов измерения.
8. Гонки на воздушном шаре Лепрекона. Это был бы забавный эксперимент, когда вы пытаетесь исследовать трение другой поверхности – струны и исследовать трение воздуха. Какие виды силы может создавать воздушный шар, в котором также есть воздух? Вы видите, как студенты проникаются силой и движением этого?
источник: eia.gov9. Горка — это простая машина. Какая школьная игровая площадка не обходится без горки? Прервите свой урок естествознания на свежем воздухе, чтобы обсудить и изучить, как слайд работает как простой механизм. Это поможет изучить концепции, согласно которым наклонные плоскости облегчают подъем вещей, а машины облегчают работу. {Бесплатная загрузка}
10. Простые механизмы: рычаг. Вот еще одна идея, которая вырывается на игровую площадку, чтобы исследовать концепцию использования простых механизмов для исследования силы и движения.Начните с изучения пилы, а затем создайте свои собственные рычаги с помощью карандашей, мелкой ленты и линейки. {Бесплатная загрузка}
{Бесплатная загрузка}
11. Испытания с ловушками для мышей. Это отличное завершающее упражнение, которое учащиеся могут использовать при изучении блока силы и движения. Предложите учащимся создать собственную мышеловку! Используя бытовой «мусор», посмотрите, какие типы быстро движущихся творений они могут создать, используя то, что они узнали о движении, силе и трении. {Бесплатные загрузки}
источник: ideabyjivey.blogspot.com12. Оценка силы и движения (до/после) — вот одностраничное задание, которое вы можете использовать, чтобы увидеть, на каком уровне находятся ваши ученики, или дать в конце модуля, чтобы охватить словарный запас и основные понятия. силы и движения. {Бесплатная загрузка}
источник: sparklebox.co.uk13. Плакаты о силе и движении. Вы найдете карточки со словами, которые отлично подойдут для стены слов, рекламного баннера, справочного коврика со словами движения и плакатов с 6 типами сил. . {Бесплатная загрузка}
14. Рабочий лист «Силы в действии». Здесь представлен рабочий лист для тренировки названий сил, таких как гравитация, подъемная сила, толкание и притяжение.Вы также сможете попрактиковаться в демонстрации того, как действуют силы, а учащиеся смогут создать свои собственные примеры иллюстраций. {Бесплатная загрузка}
Рабочий лист «Силы в действии». Здесь представлен рабочий лист для тренировки названий сил, таких как гравитация, подъемная сила, толкание и притяжение.Вы также сможете попрактиковаться в демонстрации того, как действуют силы, а учащиеся смогут создать свои собственные примеры иллюстраций. {Бесплатная загрузка}
15. Песня о гравитации. Кому не нравится использовать песню для обучения концепции. В этой песне они не будут читать рэп, но она поможет изучить концепцию гравитации и поможет встроить словарный запас, просто прослушав ее один раз.
16. What is Friction – эта песня напомнит вам о том, что вы слушали, когда учились в школе, но она помогает привести некоторые основные примеры трения и словарного запаса.
What is Friction – эта песня напомнит вам о том, что вы слушали, когда учились в школе, но она помогает привести некоторые основные примеры трения и словарного запаса.
Это партнерские ссылки на полезные книги, которые вы наверняка захотите иметь под рукой!
17. Силы заставляют вещи двигаться. Эта книга иллюстрирует примеры сил, окружающих учащихся в течение обычного дня. Это помогает дать названия этим силам, и их легко разыгрывать в классе.
18. Силы и движение: от высокоскоростных реактивных двигателей до заводных игрушек. Эта книга лучше подходит для учащихся третьего класса и старше, но это отличный ресурс с 20 заданиями, которые вы можете с легкостью выполнить с учащимися, чтобы развить некоторые навыки. основные и твердые понятия.
19. И все кричали: «Тяни» — забавный способ привнести художественное произведение в исследование «тяни и тяни», присоединяйтесь к этим сельскохозяйственным животным, когда они отправляются на рынок. Отлично подходит для начальных классов.
А недавно я наткнулся на эту новую книгу, которую не мог не добавить в список!
20. Движение: толкай и тяни, быстро и медленно. В этой книге используются повседневные события, чтобы объяснить детям, что такое движение. Он охватывает инерцию, гравитацию и трение. Дети поймут, зачем нужны ремни безопасности — из-за инерции!
Я надеюсь, что вы сможете вдохновиться или использовать некоторые из этих идей в следующий раз, когда будете обучать силе и движению.Не слишком ли банально говорить что-то вроде «Да пребудет с тобой сила», когда вы преподаете эту концепцию? {ха!}
Нужно больше материалов для силы и движения? Вам понравятся эти 24 элементарных эксперимента с силой и движением.
Нужно больше практических научных идей? Я тебя прикрою. Ознакомьтесь с этими 8 быстрыми бесплатными ресурсами и мероприятиями по круговороту воды.
Больше науки
Teach Junkie
Лесли {она же первая Teach Junkie} любит узнавать новое, чтобы сделать обучение проще и эффективнее. Ей нравится творчески развлекаться в классе, когда она не создает рубашки для учителей, не составляет планы уроков в детском саду или не планирует следующую поездку своей семьи в Диснейуорлд.
Ей нравится творчески развлекаться в классе, когда она не создает рубашки для учителей, не составляет планы уроков в детском саду или не планирует следующую поездку своей семьи в Диснейуорлд.
Руководство по даче четких инструкций учащимся (которым они действительно будут следовать)
Учителя иногда с удивлением обнаруживают, насколько четкие инструкции могут повлиять на их успехи в классе. Получив эффективные указания, учащиеся могут более эффективно взаимодействовать с материалом и, в конечном итоге, получить более продуктивный опыт.
Учителя могут предпринять несколько шагов, чтобы убедиться, что их ученики понимают инструкции и могут с легкостью выполнять задания.
1. Используйте ясный и точный язык Тридцать три года назад Чилкоут и Шталь написали окончательную основу для предоставления четких указаний. Они посоветовали использовать короткие, полные предложения и точные, конкретные термины, чтобы учащиеся могли понять, что от них ожидается. Они также предложили использовать существительные вместо местоимений — особенно при обучении младших школьников — и избегать расплывчатых терминов, таких как «некоторые», «несколько» или «пара».»
Они также предложили использовать существительные вместо местоимений — особенно при обучении младших школьников — и избегать расплывчатых терминов, таких как «некоторые», «несколько» или «пара».»
Дополнительная литература: «Как сделать» для начинающих учителей.
Учителя также должны четко сформулировать ожидания от задания или задачи. Объяснение учащимся того, что они должны делать, как они должны это делать и к какому сроку они должны это сделать, может помочь им понять и следовать вашим указаниям. Предоставление строгой и подробной рубрики вместе с заданием также может сделать работу как учителя, так и ученика более ясной и легкой.
2. Повторите ваши указания Мы предполагаем, что наши студенты слушают, когда мы говорим, но любой, кто преподает более пяти минут, знает, что это не всегда так.Учитель может давать указания и обнаруживать, что их ученики не обращают внимания или что ученики понимают инструкции только наполовину. Быстрый осмотр комнаты, некоторое перенаправление и некоторое повторение могут гарантировать, что каждый ученик сосредоточится и поймет, что ему нужно делать. Я часто пишу инструкции к заданиям на доске, в листе заданий и на нашей компьютерной платформе, чтобы студенты могли обращаться к ним во время работы.
Я часто пишу инструкции к заданиям на доске, в листе заданий и на нашей компьютерной платформе, чтобы студенты могли обращаться к ним во время работы.
Когда вы объясняете учащимся, почему их просят выполнить задание, они лучше оценят полученный опыт.Связь задачи с имеющимися у учащихся знаниями, предыдущими уроками или пройденным материалом поможет учащимся чувствовать себя более уверенно при выполнении задачи.
4. Убедитесь, что ваши учащиеся понимаютДав им указания, попросите их повторить или перефразировать то, что от них ожидается. Задайте им конкретные вопросы о требованиях. Уточните все непонятные моменты. Предоставьте учащимся обратную связь, которая поможет им понять и выполнить задание.
5.Используйте соответствующий тон Это не просто то, что вы говорите; это также, как вы это говорите. Не кричи, не бормочи и не осуждай. Убедитесь, что темп подачи информации соответствует уровню обучения и способностям. Не спешите и не двигайтесь слишком медленно. Часто делайте паузы, чтобы дать учащимся время переварить информацию.
Не спешите и не двигайтесь слишком медленно. Часто делайте паузы, чтобы дать учащимся время переварить информацию.
Если задание требует определенных материалов или определенного формата, обязательно сообщите об этом учащимся. В моем классе, например, на каждый вопрос нужно отвечать полным предложением, а ответов в одно предложение обычно недостаточно, чтобы ответить на вопрос.Создание и четкое объяснение таких особенностей настраивает ваших учеников на успех.
7. Приведите примерыВ 1965 году (но я помню это, как будто это было вчера) мой учитель первого класса попросил нас создать буклет с алфавитом. Я был в восторге от задания и усердно работал над ним каждый день в течение недели. После того, как я сдал его, я понял, что многие из студентов сделали искусные обложки для своих буклетов. Поскольку у меня не было примера для отражения, я не включил обложку, и моя гордость за свою работу быстро угасла.
То, что я помню этот урок почти 55 лет спустя, подчеркивает важность использования примеров при даче инструкций. Как преподаватель сегодня, я почти всегда предоставляю своим ученикам примеры выдающихся работ прошлых лет, и в результате ученики четко понимают мои ожидания. Это также помогло мне наладить отношения с моими учениками.
Как преподаватель сегодня, я почти всегда предоставляю своим ученикам примеры выдающихся работ прошлых лет, и в результате ученики четко понимают мои ожидания. Это также помогло мне наладить отношения с моими учениками.
Если задание большое или многогранное, разделите его на более мелкие задачи, особенно если вы обучаете младших школьников, которые не могут справиться с длинным списком направлений.Разбивка заданий на выполнимые задачи может помочь учащимся чувствовать себя более уверенно в своей работе.
Дополнительная литература: 5 эффективных стратегий активного слушания
Предоставление учащимся четких инструкций может гарантировать, что они полностью понимают, что им нужно делать, чтобы добиться успеха в вашем классе. Это успокоит нервы учеников, успокоит их неуверенность и поможет им подтвердить ваши ожидания, чтобы они могли быть счастливыми и успешными в школе.
Как научить сложению | 7 простых шагов
Сложение — это первый большой математический шаг после того, как первоклассники освоят базовое чувство чисел.
И, как и все первые шаги, это может быть сложно сделать (и не менее сложно научить).
Но это не обязательно. Вот 7-этапный процесс обучения дополнению, который создает более простых планов уроков для вас и лучшего понимания для ваших учеников.
Познакомить с понятием, используя счетные манипуляции
Использование счетных манипуляторов (физических объектов) сделает сложение более конкретным и более понятным. Важно использовать разнообразие, чтобы учащиеся начали понимать концепцию независимо от того, что подсчитывается.
Счет на пальцах — наиболее интуитивно понятный способ начать, прежде чем переходить к жетонам, крышкам от бутылок или вырезкам из бумаги. Если вы хотите включить какое-то движение, разбейте учащихся на небольшие группы и попросите их объединиться, подсчитав общее количество участников еще раз.
Переход к визуальным эффектам
Начните переносить сложение на бумагу, используя проиллюстрированные суммы, или попросите учеников нарисовать предметы, которые они могут сосчитать.
Лучше всего, если вы поместите визуальные эффекты рядом с числами, чтобы способствовать ассоциации между ними.Рассмотрите возможность использования графического органайзера с суммой, написанной сверху, и местом для рисования под каждым числом.
Использовать числовую строку
На этом этапе большинство учеников будут по-прежнему складывать, считая каждое число в сумме, чтобы получить полное решение. Однако числовая строка избавляет от необходимости отсчитывать первое число в сумме.
Если сумма равна, например, 4 + 3, учащиеся могут сначала поставить палец на четверку, а затем подсчитать три разряда, чтобы получить 7.Им больше не нужно сначала отсчитывать 4, чтобы найти решение.
Подсчет
Как только учащиеся узнают, как использовать числовую прямую, вы захотите, чтобы они использовали ту же стратегию «подсчета» в уме.
Затем вы можете попросить их попрактиковаться, считая вслух на пальцах. Возьмем, к примеру, 4 + 3:
Возьмем, к примеру, 4 + 3:
- Учащиеся начинают со сжатым кулаком и говорят «4».
- Затем учащиеся считают «5, 6, 7», вытягивая три пальца по очереди.
- Учащиеся вытянули три пальца, но напомните им, что ответ не будет 3. Они начали с 4 в кулаке, а затем подсчитали, поэтому ответ равен 7.
Скачать ресурсы по математике для печати
В поисках десяти
Это математический трюк в уме , который поможет учащимся развить беглость выполнения процедур.
Вместо того, чтобы складывать два числа как есть, предложите учащимся сложить их до 10, а затем прибавить остаток к этим 10.Например, процесс для 7 + 5:
- 7 + 3 = 10
- Нам все еще нужно добавить еще 2, чтобы превратить 3 в 5.
- 10 + 2 = 12
Вы можете использовать манипуляции, чтобы помочь учащимся освоить этот навык. Нарисуйте два ряда по 10 коробок на листе бумаги, одну под другой, а затем попросите учеников поместить в них манипуляторы, чтобы представить сумму. Для 7+5 первая попытка может выглядеть так:
Для 7+5 первая попытка может выглядеть так:
Но затем вы можете показать учащимся, как становится легче, если вы переместите манипуляторы так, чтобы они заполнили один ряд из 10, сделав так:
Разговоры о числах также являются отличным способом сломать эту стратегию.Сначала смоделируйте его, а затем попросите учащихся таким же образом рассказать о своем подходе к вопросу.
Word проблемы
задачи Word побуждают учащихся определять задачи на сложение, даже если они четко не определены. Начните с того, что познакомьте их с языком сложения, например:
.- Х плюс у
- X дополнительный
- X добавлено к
- общая сумма
- всего
- всего
После того, как они освоят язык, начните с простых решений задач и логических рассуждений.
Запомните математические факты
В конечном счете, мы хотим, чтобы учащиеся могли быстро и точно складывать в уме. Эта процедурная беглость важна, поскольку они переходят к более сложным проблемам, и нет никакого способа добраться туда, не запоминая каждый факт сложения до одной цифры.
Эта процедурная беглость важна, поскольку они переходят к более сложным проблемам, и нет никакого способа добраться туда, не запоминая каждый факт сложения до одной цифры.
Вот несколько полезных стратегий:
Разбить его
Вся таблица дополнительных фактов может показаться слишком большой, поэтому просто сосредоточьтесь на отдельных разделах за раз. Например, вы можете сосредоточиться на + 1 и + 2 одну неделю, прежде чем перейти к парам, которые в сумме дают 10.
Геймифицируйте процесс
Викторины, групповые задания и награды сделают зубрежку более увлекательной. Просто убедитесь, что он не становится слишком конкурентным и не отпугивает учеников, у которых возникают трудности.
Найдите 10 простых способов геймифицировать свой класс здесь.
Используйте инструменты EdTech
Программы онлайн-обучения могут обучать сложению в увлекательной интерактивной виртуальной среде. А еще лучше, если вы выберете забавную программу, которую учащиеся могут использовать самостоятельно, они будут входить в систему дома для дополнительной практики.
А еще лучше, если вы выберете забавную программу, которую учащиеся могут использовать самостоятельно, они будут входить в систему дома для дополнительной практики.
Все это мы объединили в наших собственных отмеченных наградами программах Mathseeds и Mathletics. Нажмите на ссылку ниже, чтобы узнать больше!
Повысьте навыки сложения ваших учащихся с помощью наших программ обучения математике.
Исследуйте сейчасКатегории Математика, Стратегии обучения
Рабочие листы для учителей (K-12)
Эти готовые к использованию рабочие листы помогут вам закрепить понятия и проверить понимание ваших учеников.Есть рабочие листы по всем предметам, а также по праздникам, временам года, использованию технологий и многому другому! Многие рабочие листы требуют участия учащихся, поскольку содержат различные типы вопросов, такие как множественный выбор, заполнение пропусков, краткий ответ и сопоставление. Другие рабочие листы содержат план уроков дня или инструкции для предстоящей деятельности.
Просмотр рабочих листов Ресурсы
ГРАФИЧЕСКИЕ ОРГАНИЗАТОРЫ
Сочинение из пяти абзацев
Помогите учащимся написать эссе из пяти абзацев с помощью графического органайзера.Эта печатная форма настраивается. Адаптируйте PDF-файл к вашим…ОЦЕНКА
Критерий групповой деятельности
Оценивайте участие и эффективность учащихся в групповой деятельности с помощью этой настраиваемой рубрики. Адаптируйте PDF к своим…ГРАФИЧЕСКИЕ ОРГАНИЗАТОРЫ
Последовательность последовательностей чтения
Этот подробный графический органайзер помогает учащимся улучшить понимание прочитанного, определяя важные истории el…РАБОЧИЕ ТАБЛИЦЫ
Напишите свои собственные истории Mad Libs®
Используйте эту форму для печати, чтобы учащиеся могли создавать свои собственные истории Mad Libs®. Учащиеся вводят ключевые слова (существительные, прилагательные,…ГРАФИЧЕСКИЕ ОРГАНИЗАТОРЫ
Web для мозгового штурма
Используйте этот графический органайзер для мозгового штурма. Эту форму для печати можно настроить. Адаптируйте PDF-файл к вашим потребностям в обучении, набрав…
Эту форму для печати можно настроить. Адаптируйте PDF-файл к вашим потребностям в обучении, набрав…РАБОЧИЕ ТАБЛИЦЫ
30 Правила этикета в классе для учителей и учащихся
В целях создания вежливой и гармоничной атмосферы в классе в этом печатном листе содержатся советы по этикету для обоих учителей…ГРАФИЧЕСКИЕ ОРГАНИЗАТОРЫ
Графический органайзер причин и следствий
Необходимый графический органайзер для всех классов ELA! Учащихся просят определить причину и следствие рассказа с помощью этих…РАБОЧИЕ ТАБЛИЦЫ
Лимонадная война Руководство для учителя
Поощряйте развитие предпринимательских навыков учащихся с помощью занятий по экономике и математике в этом учебном…ИНСТРУМЕНТЫ ДЛЯ КЛАССА
Диаграмма в три столбца
РАБОЧИЕ ТАБЛИЦЫ
Разделение как совместное использование: подробный план урока
Этот урок содержит все, что вам нужно, чтобы познакомить учащихся с делением. Все, что вам нужно сделать, это загрузить,…
Все, что вам нужно сделать, это загрузить,…ОЦЕНКА
Критерий оценки: Резюме
Необходимый обязательный критерий для уроков словесности Организация, элементы резюме, грамматика, использование, меха…ПЛАНЫ УРОКОВ
Афро-американские ученые: комплексный проект по учету в социальных сетях
В этом проекте учащиеся исследуют известного афроамериканского ученого, а затем создают учетная запись в социальной сети для …РАБОЧИЕ ТАБЛИЦЫ
Завершите последовательность 1
РАБОЧИЕ ТАБЛИЦЫ
Написание мнений План урока: гендерное равенство
Этот раздел для 2-3 занятий включает планы уроков, графику для организаторов оценивания и рубрику. В блоке учащиеся…ОЦЕНКА
Критерии предварительного чтения и оценочный лист
ИНСТРУМЕНТЫ ДЛЯ КЛАССА
Заметка на выпускном: «Сова» Всегда помни тебя
Поздравление учащихся с окончанием школы или переходом в следующий класс школу с милой запиской, в которой говорится: «Поздравляем. ..
..ОЦЕНКА
Критерий совместной группы
Раздайте критерий, который позволит вам оценить работу учащихся над групповыми проектами. Используйте это руководство по подсчету очков вместе с «Мо…ГРАФИЧЕСКИЕ ОРГАНИЗАТОРЫ
Диаграмма KWL — Животные
Познакомьте учащихся с диаграммой KWL, которая является графическим органайзером для записи того, что учащиеся знают, хотят знать и чт…ИНСТРУМЕНТЫ ДЛЯ КЛАССА
Таблица размеров: от метрической до U.S. Customary
Преобразование метрических единиц измерения в единицы измерения, принятые в США! Вашим учащимся понравится, насколько полезен этот рабочий лист, когда…ГРАФИЧЕСКИЕ ОРГАНИЗАТОРЫ
Органайзер по алфавиту
Назначьте тему и попросите учащихся заполнить сетку как можно большим количеством слов, которые, по их мнению, поместятся в каждый квадрат таблицы. …РАБОЧИЕ ТАБЛИЦЫ
Способы отображения данных
В этом рабочем листе учащимся предлагается показать одни и те же данные тремя различными способами. Их также просят …
Их также просят …ИНСТРУМЕНТЫ ДЛЯ КЛАССА
Схема принятия решений
Проблемы, цели, плюсы, минусы и решения подробно описаны в графическом органайзере. Эта печатная форма настраивается. Tailor T…ГРАФИЧЕСКИЕ ОРГАНИЗАТОРЫ
Покрытия для животных
С помощью этого графического органайзера учащиеся наклеивают изображения животных на соответствующие внешние покрытия: мех, чешуйки, шкурки…
Национальные стандарты физического воспитания-SHAPE America Sets Стандарты
Пересмотр национальных стандартов
SHAPE America начала процесс пересмотра Национальных стандартов и результатов для школьных классов по физическому воспитанию K-12.Ниже вы найдете информацию и возможности для участия в процессе пересмотра.
Обновления Целевой группы по стандартам PE
Национальная рабочая группа по стандартам PE будет предоставлять обновленную информацию о ходе своей работы. Если у вас есть какие-либо вопросы или вы хотите оставить отзыв или внести свой вклад, пожалуйста, свяжитесь с Мишель Картер, mcarter@shapeamerica. org.
org.
Обновления от 23 июня 2021 г.
Целевая группа по национальным стандартам физического воспитания собирается еженедельно с 23 марта 2021 года.Целевая группа была особенно заинтересована в том, чтобы узнать точку зрения преподавателей/профессоров PETE, практикующих специалистов PreK-12 и учащихся PreK-12 посредством использования городских советов и опросов. Было много отзывов, касающихся результатов на уровне классов. Опрос студентов завершился 15 июня и собрал более 4600 ответов. Целевая группа потратила некоторое время на просмотр и обсуждение ответов и отзывов от этих заинтересованных сторон, чтобы помочь им сформировать свое мнение.
Кроме того, целевая группа была действительно сосредоточена на том, какова цель или цель физического воспитания, сейчас и в будущем.Было проведено много философских дискуссий и мероприятий, направленных на то, чтобы действительно сузить и отточить ключевые понятия. Целевая группа рассмотрела стандарты из других областей контента и других стран, включая Новую Зеландию и Австралию.
Целевая группа по национальным стандартам физического воспитания
- Салли Джонс, доктор философии, Председатель, консультант по физическому воспитанию/адаптированному физическому воспитанию, Департамент обучения Северной Каролины
- Аманда Амтманис, доктор медицинских наук, Учитель физкультуры, Государственные школы Миддлтауна
- Брэд Браммел, М.Эд., Координатор по физическому воспитанию, здоровью и взаимодействию, Государственные школы Спрингфилда
- Лэнгстон Кларк, доктор философии, Адъюнкт-профессор Техасского университета в Сан-Антонио
- Фрэн Клеланд, P.E.D., Профессор Вестчестерского университета
- Келли Корнетт, MS, Специалист в области здравоохранения, Центры по контролю и профилактике заболеваний
- Дэн ДеДжагер, MS, NBCT, Учитель физкультуры, Объединенный школьный округ Сан-Хуана
- Сюзанна Диллон, доктор философии, CAPE, Доцент Техасского женского университета
- Кори Диксон, доктор философии, Доцент, Университет Роуэна
- Роберт Доан, доктор философии, Помощник декана / доцент, Чарльстонский Южный университет
- Джонатан Джонс, MS, Учитель ресурсов по физическому воспитанию, государственные школы округа Принс-Джордж
- Ладонда Портер, MS, Учитель физкультуры, государственные школы округа Фейет
Стратегии опроса
Вопросы по планированию Эффективные вопросы в классе требуют предварительной подготовки. В то время как некоторые преподаватели могут быть опытными в импровизированных вопросах, многие обнаруживают, что такие вопросы имеют проблемы с формулировкой, не организованы в логической последовательности или не требуют от студентов использования желаемых навыков мышления.
В то время как некоторые преподаватели могут быть опытными в импровизированных вопросах, многие обнаруживают, что такие вопросы имеют проблемы с формулировкой, не организованы в логической последовательности или не требуют от студентов использования желаемых навыков мышления.
Уровни и типы вопросов
Вопросы следует использовать для достижения четко определенных целей. Преподаватель должен задавать вопросы, которые потребуют от студентов использования мыслительных навыков, которые он или она пытается развить. Таксономия Блума представляет собой иерархическую систему упорядочения мыслительных навыков от низшего к высшему, где каждый уровень требует от учащегося овладения нижележащими навыками.Не обязательно, чтобы инструктор мог классифицировать каждый вопрос на определенном уровне. Таксономия представлена как инструмент, полезный для определения типов мыслительных навыков, которые преподаватели ожидают от студентов, и для установления соответствия между целями преподавателя и вопросами, которые он или она задает.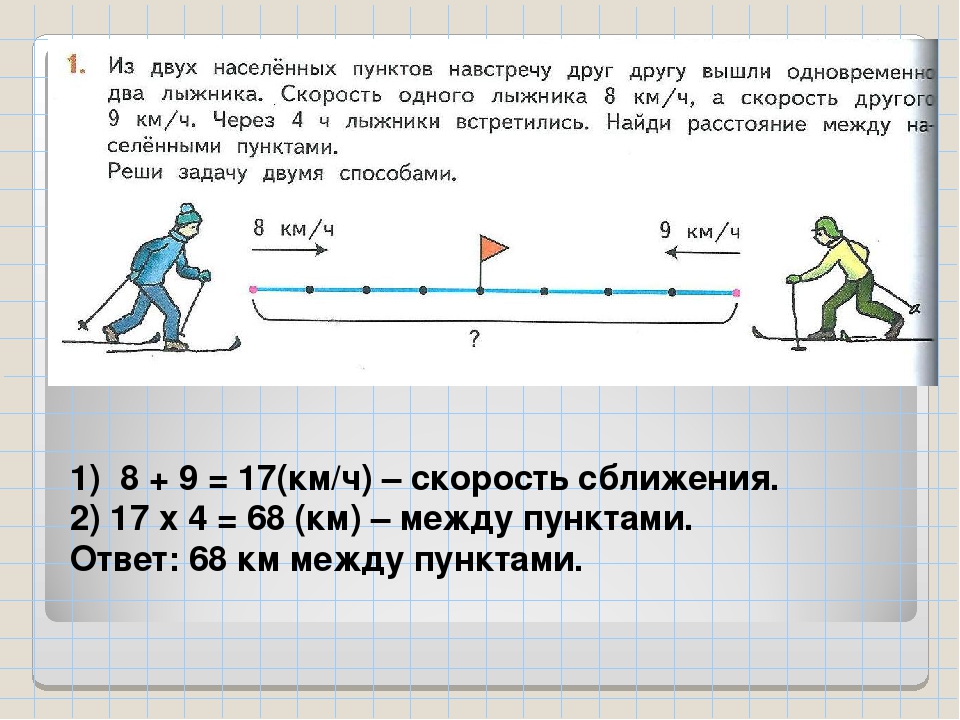
Люди часто ссылаются на «низкоуровневые» и «высокоуровневые» вопросы или действия, вместо того чтобы присваивать этим вопросам или поведению определенный уровень. Вопросы более низкого уровня обычно относятся к уровням запоминания, понимания и применения таксономии и наиболее подходят для:
- оценка подготовки и понимания учащихся
- диагностика сильных и слабых сторон учащихся
- просмотр и/или обобщение содержания
Вопросы более высокого уровня предполагают способность анализировать, оценивать или создавать и наиболее подходят для:
- поощрение учащихся к более глубокому и критическому мышлению
- решение проблем
- поощрение обсуждений
- стимулирование учащихся к самостоятельному поиску информации
Обычно инструктор меняет уровень вопросов в течение одного занятия.Например, преподаватель может задать вопрос более высокого уровня: «Как могут быть связаны стиль письма и тезис данного эссе?» Если она получает неадекватный или неправильный ответ ученика на этот вопрос, она может задать более низкие вопросы, чтобы проверить, знают ли и понимают ли ученики материал. Например, затем она может спросить: «Каково определение тезиса ?» или «Каковы некоторые характеристики различных стилей письма?»
Например, затем она может спросить: «Каково определение тезиса ?» или «Каковы некоторые характеристики различных стилей письма?»
В дополнение к вопросам на различных уровнях таксономии инструктор может учитывать, задает ли он закрытые или открытые вопросы.Закрытый вопрос — это вопрос, на который имеется ограниченное количество приемлемых ответов, большинство из которых обычно заранее предвидит преподаватель. Например, «Каково определение прилагательного?» Открытый вопрос — это вопрос, на который можно дать много приемлемых ответов, большинство из которых не предвидится инструктором. Например, «Что является примером прилагательного?»
Как открытые, так и закрытые вопросы могут использоваться на любом уровне таксономии:
| Нижний уровень | Высший уровень |
Закрыто | Какие стадии клеточного деления? | Учитывая имеющиеся у вас медицинские данные, можете ли вы сказать, что этот пациент находится в состоянии алкогольного опьянения или страдает диабетической реакцией? |
Открыть | Какой пример прилагательного? | Какими способами мы можем решить энергетический кризис? |
- Определитесь с целью задавать вопросы.
 Ваша цель должна помочь вам определить, какие уровни вопросов вы будете задавать.
Ваша цель должна помочь вам определить, какие уровни вопросов вы будете задавать. - Выберите контент для опроса. Выберите материал, который вы считаете важным, а не тривиальным. Студенты будут учиться и учиться на основе вопросов, которые вы задаете. Не вводите их в заблуждение, подчеркивая менее важный материал.
- Задавайте вопросы, требующие развернутого ответа или хотя бы «содержательного» ответа. Избегайте вопросов, на которые можно ответить «да» или «нет», если только вы не собираетесь задавать дополнительные вопросы для изучения рассуждений.
- Пока вы не освоите вопросы в классе, вы должны заранее написать свои основные вопросы. Это называется «скриптинг». Расположите свой список в некоторой логической последовательности (от общего к более низкому уровню, последовательности, связанной с содержанием). Если вы думаете о дополнительных или лучших вопросах в процессе опроса, вы можете проявить гибкость и добавить их или заменить ими некоторые из ваших запланированных вопросов.
 Однако наличие подготовленного списка вопросов поможет убедиться, что вы задаете вопросы, соответствующие вашим целям и представляющие важный материал.
Однако наличие подготовленного списка вопросов поможет убедиться, что вы задаете вопросы, соответствующие вашим целям и представляющие важный материал. - Сформулируйте вопросы так, чтобы задание было понятно учащимся. Такие вопросы, как «А как насчет иностранных дел?» не часто приводят к продуктивным ответам и обсуждению. «Что мы говорили о химической связи?» слишком общий, если вы не ищете только обзор любого материала, который учащиеся помнят.
- Ваши вопросы не должны содержать ответов. Избегайте вопросов с подразумеваемым ответом, если вы действительно хотите получить ответ от класса. Такой вопрос, как «Разве мы все не согласны с тем, что автор статьи преувеличил опасность оранжевого агента, чтобы укрепить свою точку зрения?» не будет стимулировать реакцию учащихся.
- При планировании вопросов старайтесь предвидеть возможные ответы учащихся. Предвосхищение ответов учащихся должно помочь вам в планировании, заставив вас подумать о том, насколько точны формулировки, сосредоточены ли вопросы на цели, которую вы имеете в виду, и достаточно ли у вас гибкости, чтобы позволить учащимся выражать идеи своими словами.
 Вы можете рассмотреть следующее:
Вы можете рассмотреть следующее:- Какие типичные заблуждения могут привести учащихся к неправильным ответам?
- Я задаю открытый или закрытый вопрос?
- Какой тип ответа я ожидаю от студентов, определение? Пример? Решение?
- Приму ли я ответ на языке учащихся или ожидаю слов из учебников или своих терминов?
- Какова будет моя стратегия обработки неправильных ответов?
- Что я буду делать, если ученики не ответят?
Обработка ответов учащихся на вопросы
Важным аспектом взаимодействия в классе является то, как преподаватель обрабатывает ответы учащихся.Когда преподаватель задает вопрос, учащиеся могут ответить, задать вопрос или не отвечать.
Обработка ответов учащихся на вопросы Важным аспектом взаимодействия в классе является то, как преподаватель обрабатывает ответы учащихся. Когда преподаватель задает вопрос, учащиеся могут ответить, задать вопрос или не отвечать.
Стратегии, используемые при ответах учащихся
- Поощрение: Преподаватель должен положительно подкреплять ответы и вопросы учащихся, чтобы поощрять их участие в будущем.Инструктор может подкрепить, делая позитивные утверждения и используя позитивную невербальную коммуникацию. Правильные невербальные реакции включают улыбку, кивание и поддержание зрительного контакта, в то время как неправильные невербальные реакции включают просмотр заметок во время разговора учащихся, взгляд на доску или перелистывание бумаги. Тип армирования определяется:
- Правильность ответа. Если учащийся дает неверный или неверный ответ, преподаватель может кратко подтвердить ответ, а затем подумать о том, как помочь учащемуся дать правильный ответ.Преподаватель может использовать такие стратегии, как зондирование, перефразирование или постановка вопроса по-другому.
- Сколько раз учащийся ответил. Преподаватели могут захотеть дать учащемуся, который никогда не отвечал в классе, больше поощрения, чем тому, кто отвечает часто.

Обязательно меняйте методы подкрепления между различными вербальными утверждениями и невербальными реакциями. Старайтесь не злоупотреблять подкреплением в классе, чрезмерно хваля каждый комментарий ученика.Студенты начинают сомневаться в искренности подкрепления, если каждый ответ подкрепляется в равной степени или одинаковым образом.
- Зондирование: Первоначальная реакция учащихся может быть поверхностной. Преподаватель должен использовать стратегию вопросов, называемую зондированием, чтобы заставить студентов изучить первоначальные комментарии. Зонды полезны для вовлечения учащихся в критический анализ собственных идей и идей других учащихся. Зонды можно использовать для:
- Проанализируйте заявление учащегося, познакомьте учащегося с лежащими в его основе предположениями, обосновайте или оцените утверждение. Инструктор : Какими способами мы можем решить энергетический кризис? Студент : Я хотел бы, чтобы коммунальные предприятия больше переходили на тарифы в период пиковой нагрузки.
 Преподаватель: Какие предположения вы делаете о поведении потребителей, когда предлагаете это решение?
Преподаватель: Какие предположения вы делаете о поведении потребителей, когда предлагаете это решение? - Помогите учащимся определить отношения. Преподаватели могут попросить студентов оценить последствия своих утверждений или сравнить и противопоставить концепции. Преподаватель : Каковы преимущества и недостатки выставления оценок за курсы? Учащийся 1 : Оценки могут мотивировать людей учиться. Ученик 2 : Слишком сильное давление на оценки приводит к тому, что некоторые ученики перестают учиться, замирают, теряют сознание. Преподаватель : Если оба эти утверждения верны, какие обобщения вы можете сделать о взаимосвязи между мотивацией и обучением?
- Попросите учащихся пояснить или уточнить свои комментарии, запросив дополнительную информацию. Преподаватель: Не могли бы вы развить свои идеи дальше? Можете ли вы привести пример этой концепции? Студент: Было очевидно, что команда сошла с ума.
 Инструктор : Какое юридическое определение безумия? Студент : Это было нарушение процессуальных норм. Преподаватель: Можете объяснить почему?
Инструктор : Какое юридическое определение безумия? Студент : Это было нарушение процессуальных норм. Преподаватель: Можете объяснить почему?
- Проанализируйте заявление учащегося, познакомьте учащегося с лежащими в его основе предположениями, обосновайте или оцените утверждение. Инструктор : Какими способами мы можем решить энергетический кризис? Студент : Я хотел бы, чтобы коммунальные предприятия больше переходили на тарифы в период пиковой нагрузки.
- Настройка/перефокусировка: Когда учащийся дает ответ, вырывающийся из контекста, преподаватель может перефокусировать внимание, чтобы побудить учащегося связать свой ответ с обсуждаемым содержанием.Этот прием также используется для переключения внимания на новую тему. Преподаватель: Что значит девальвировать доллар? Ученик: Гм… я не совсем уверен, но разве это не означает, что, гм, доллар не стоит так далеко, как раньше? Значит ли это, что он обесценился? Преподаватель: Что ж, давайте немного поговорим о другом понятии, и это инфляция. Как инфляция влияет на ваш доллар?
Стратегии ответов на вопросы учащихся
Преподаватель может отвечать на вопросы студентов разными способами. Однако все стратегии начинаются с этого важного шага: Выслушайте вопрос ученика . Убедившись, что вы поняли вопрос, убедитесь, что другие учащиеся услышали и поняли вопрос. Затем примените одну из следующих стратегий:
Однако все стратегии начинаются с этого важного шага: Выслушайте вопрос ученика . Убедившись, что вы поняли вопрос, убедитесь, что другие учащиеся услышали и поняли вопрос. Затем примените одну из следующих стратегий:
- Ответь на вопрос сам. Эта стратегия лучше всего подходит, когда у вас осталось мало времени на занятия. Недостатком этого подхода является то, что вы не поощряете взаимодействие между учениками или самостоятельное обучение.
- Перенаправить вопрос классу. Эта стратегия помогает стимулировать взаимодействие между учениками и уменьшить зависимость от преподавателя в отношении получения всей информации.
- Попытка помочь ученику ответить на его собственный вопрос. Для этого может потребоваться подсказка через напоминания о соответствующей ранее изученной информации. Или эта стратегия может потребовать, чтобы вы задали студенту вопрос более низкого уровня или связанный с ним вопрос, чтобы начать его мыслительный процесс. Преимущество этой стратегии, как и перенаправления, состоит в том, что учащийся может изучить процесс поиска ответов на свои собственные вопросы, а не полагаться на учителя.
 Риск заключается в том, что процесс может быть смущающим или настолько угрожающим, что учащийся будет слишком напуган, чтобы задавать вопросы в будущем. Очевидно, что при использовании этой стратегии требуется некоторое человеческое сострадание.
Риск заключается в том, что процесс может быть смущающим или настолько угрожающим, что учащийся будет слишком напуган, чтобы задавать вопросы в будущем. Очевидно, что при использовании этой стратегии требуется некоторое человеческое сострадание. - Попросите ученика остановиться после урока, чтобы обсудить вопрос. Эта стратегия наиболее уместна, когда учащийся задает сложные, второстепенные вопросы или когда учащийся, очевидно, единственный, кто не понимает какой-либо точки зрения, а простой ответ не проясняет ее для учащегося.Даже в этих ситуациях использование этой стратегии сопряжено с риском. Студенты могут бояться задавать вопросы в классе. Преподаватель может подумать, что только вопрошающий студент не понимает, когда на самом деле у нескольких студентов возникает одна и та же проблема.
- Направьте учащегося к ресурсу, где он может найти ответ.
- Отложите вопрос до более подходящего времени, если вопрос не связан с материалом, который вы освещаете.
 Обязательно запишите вопрос и учащегося и вернитесь к вопросу в более подходящее время.
Обязательно запишите вопрос и учащегося и вернитесь к вопросу в более подходящее время.
Независимо от того, какую стратегию вы используете, вы должны вернуться к учащемуся после ответа на вопрос и определить, удовлетворил ли его ответ.
Если вы не знаете ответа на вопрос студента , никогда не подделывайте ответ . Признайтесь, что вы не можете ответить на вопрос, а затем выберите одну из этих стратегий или другие, которые вы считаете подходящими:
- Спросите, может ли кто-нибудь в классе ответить на вопрос. В большинстве случаев после занятий вы должны попытаться определить, была ли предоставленная информация точной или основана на разумных рассуждениях и достоверных источниках.
- Либо предложите план получения доказательств для ответа на вопрос, либо попросите учащихся предложить, как можно исследовать этот вопрос.
- Если возможно, предложите ресурс, где учащийся может найти информацию. Ресурс может быть письменным материалом, другим преподавателем или сотрудником, студентом или кем-то из сообщества.

- Вызовитесь найти ответ самостоятельно и доложите об этом классу. Убедитесь, что вы действительно вернетесь с ответом, если выберете этот вариант.
Стратегии, которые можно использовать, когда учащиеся не отвечают
- Перенаправление: Когда учащийся отвечает на вопрос, преподаватель может попросить другого учащегося прокомментировать его утверждение. Одной из целей использования этого метода является предоставление возможности участвовать большему количеству студентов. Эту стратегию также можно использовать, чтобы позволить учащемуся исправить неверное утверждение другого учащегося или ответить на вопрос другого учащегося. Инструктор: Али, ты согласен с комментарием Марка? Инструктор: По вашему опыту, Аиша, то, что сказал Вито, кажется правдой? Преподаватель: Ли, можете ли вы привести пример концепции, которую упомянула Пэт?
- Перефразируя: Этот метод используется, когда учащийся дает неправильный ответ или не отвечает.
 Вместо того, чтобы говорить учащемуся, что он не прав, или призывать другого учащегося, преподаватель может попробовать одну из трех стратегий:
Вместо того, чтобы говорить учащемуся, что он не прав, или призывать другого учащегося, преподаватель может попробовать одну из трех стратегий:- Преподаватель может попробовать переформулировать вопрос, чтобы сделать его более понятным. Возможно, вопрос был плохо сформулирован. I Инструктор : Что такое невроз? Студент: (Нет ответа) Инструктор : Каковы отличительные характеристики невротика?
- Преподаватель может предоставить некоторую информацию, чтобы помочь учащимся найти ответ. Преподаватель: Как далеко упал мяч через 3 секунды? Студент: Понятия не имею. Инструктор : Давайте разберем вопрос, Энн. Как мы измеряем расстояние?
- Преподаватель может разбить вопрос на более понятные части.
 Инструктор : Какова эпидемиология полиомиелита? Студент : Не уверен. Инструктор : Что означает «эпидемиология»?
Инструктор : Какова эпидемиология полиомиелита? Студент : Не уверен. Инструктор : Что означает «эпидемиология»?
- Преподаватель может попробовать переформулировать вопрос, чтобы сделать его более понятным. Возможно, вопрос был плохо сформулирован. I Инструктор : Что такое невроз? Студент: (Нет ответа) Инструктор : Каковы отличительные характеристики невротика?
- Использование «времени ожидания»: Одним из факторов, который может сильно повлиять на участие студентов, является количество времени, в течение которого преподаватель делает паузу между тем, чтобы задать вопрос и сделать что-то еще (позвонить студенту или переформулировать вопрос). Исследования вопросов в классе и обработки информации показывают, что учащимся требуется не менее трех секунд, чтобы понять вопрос, обдумать имеющуюся информацию, сформулировать ответ и начать отвечать.Напротив, то же исследование показало, что в среднем классный руководитель допускает менее одной секунды ожидания. После того, как учителей научили ждать от трех до пяти секунд, в их классах произошли следующие существенные изменения (из Rowe, 1974):
- Количество учащихся, которые не ответили на вызов, уменьшилось.

- Увеличилось количество нежелательных, но правильных ответов.
- Увеличена длина ответов учащихся.
- Увеличилось количество утверждений учащихся, в которых для выводов использовались доказательства.
- Увеличилось количество ответов от учеников, которые были определены учителем как менее способные.
- Увеличилось количество взаимодействий между учениками.
- Увеличилось количество вопросов учеников.
Разрешение на ожидание после ответа или вопроса учащегося также привело к значительным изменениям во взаимодействии в классе. Наиболее заметным изменением стало то, что преподаватель совершал меньше ошибок в обучении, характеризующихся нелогичными или неадекватными ответами на комментарии учащихся.
С другой стороны, слишком долгое ожидание также может отрицательно сказаться на взаимодействии учащихся. Когда кажется, что никто не может ответить на вопрос, дополнительное время ожидания не обязательно решит проблему.




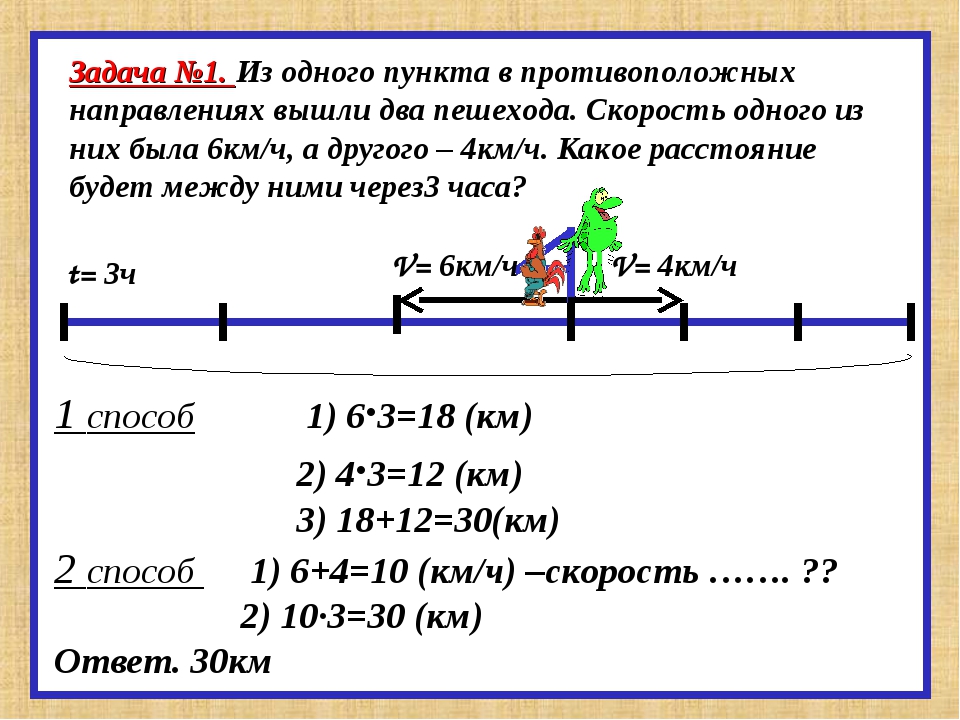


 Они раздают припасы, сортируют припасы, собирают припасы. Цель состоит в том, чтобы у них всегда была какая-то двигательная задача».
Они раздают припасы, сортируют припасы, собирают припасы. Цель состоит в том, чтобы у них всегда была какая-то двигательная задача». 
 Эту форму для печати можно настроить. Адаптируйте PDF-файл к вашим потребностям в обучении, набрав…
Эту форму для печати можно настроить. Адаптируйте PDF-файл к вашим потребностям в обучении, набрав… Все, что вам нужно сделать, это загрузить,…
Все, что вам нужно сделать, это загрузить,… Их также просят …
Их также просят … Ваша цель должна помочь вам определить, какие уровни вопросов вы будете задавать.
Ваша цель должна помочь вам определить, какие уровни вопросов вы будете задавать. Однако наличие подготовленного списка вопросов поможет убедиться, что вы задаете вопросы, соответствующие вашим целям и представляющие важный материал.
Однако наличие подготовленного списка вопросов поможет убедиться, что вы задаете вопросы, соответствующие вашим целям и представляющие важный материал. Вы можете рассмотреть следующее:
Вы можете рассмотреть следующее:
 Преподаватель: Какие предположения вы делаете о поведении потребителей, когда предлагаете это решение?
Преподаватель: Какие предположения вы делаете о поведении потребителей, когда предлагаете это решение?  Инструктор : Какое юридическое определение безумия? Студент : Это было нарушение процессуальных норм. Преподаватель: Можете объяснить почему?
Инструктор : Какое юридическое определение безумия? Студент : Это было нарушение процессуальных норм. Преподаватель: Можете объяснить почему?  Риск заключается в том, что процесс может быть смущающим или настолько угрожающим, что учащийся будет слишком напуган, чтобы задавать вопросы в будущем. Очевидно, что при использовании этой стратегии требуется некоторое человеческое сострадание.
Риск заключается в том, что процесс может быть смущающим или настолько угрожающим, что учащийся будет слишком напуган, чтобы задавать вопросы в будущем. Очевидно, что при использовании этой стратегии требуется некоторое человеческое сострадание. Обязательно запишите вопрос и учащегося и вернитесь к вопросу в более подходящее время.
Обязательно запишите вопрос и учащегося и вернитесь к вопросу в более подходящее время.
 Вместо того, чтобы говорить учащемуся, что он не прав, или призывать другого учащегося, преподаватель может попробовать одну из трех стратегий:
Вместо того, чтобы говорить учащемуся, что он не прав, или призывать другого учащегося, преподаватель может попробовать одну из трех стратегий: Инструктор : Какова эпидемиология полиомиелита? Студент : Не уверен. Инструктор : Что означает «эпидемиология»?
Инструктор : Какова эпидемиология полиомиелита? Студент : Не уверен. Инструктор : Что означает «эпидемиология»? 