Задача на круги эйлера с решением: ГБОУ Школа № 1492, Москва — Детская игровая комната «Волшебный лес»

Posted on 08.02.197010.06.2021 by alexxlab

Содержание

круги Эйлера — Основы логики и логические основы компьютера

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.

Опираясь на условия задачи, составим уравнения:

Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение

Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.

Обозначим каждый сектор отдельной буквой (А, Б, В).

Из условия задачи следует:

Торты │Пироги = А+Б+В = 12000

Торты & Пироги = Б = 6500

Пироги = Б+В = 7700

Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.

Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300

Сектор А равен 4300, следовательно

Торты = А+Б = 4300+6500 = 10800

Задача 3

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Пироженое & Выпечка	5100
Пироженое	9700
Пироженое \| Выпечка	14200

Какое количество страниц (в тысячах) будет найдено по запросуВыпечка?

Для решения задачи отобразим множестваПироженых и Выпечек в виде кругов Эйлера.

Обозначим каждый сектор отдельной буквой (А, Б, В).

Из условия задачи следует:

Пироженое & Выпечка = Б = 5100

Пироженое = А+Б = 9700

Пироженое │ Выпечка = А+Б+В = 14200

Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти секторВ, для этого из общего множества (Пироженое │ Выпечка ) отнимем множество Пироженое.

Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500

Сектор В равен 4500, следовательно Выпечка = Б + В = 4500+5100 =9600

Задача 4
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

1	спаниели \| (терьеры & овчарки)
2	спаниели \| овчарки
3	спаниели \| терьеры \| овчарки
4	терьеры & овчарки

Решение

Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).

Преобразим условие задачи в виде суммы секторов:

спаниели │(терьеры & овчарки) = Г + Б

спаниели│овчарки = Г + Б + В

спаниели│терьеры│овчарки = А + Б + В + Г

терьеры & овчарки = Б

Из сумм секторов мы видим какой запрос выдал больше количества страниц.

Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4

Задача 5

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

1	барокко \| классицизм \| ампир
2	барокко \| (классицизм & ампир)
3	классицизм & ампир
4	барокко \| классицизм

Решение

Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).

Преобразим условие задачи в виде суммы секторов:

барокко│ классицизм │ампир = А + Б + В + Г
барокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А

Из сумм секторов мы видим какой запрос выдал больше количества страниц.

Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1

Задача 6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

1	канарейки \| щеглы \| содержание
2	канарейки & содержание
3	канарейки & щеглы & содержание
4	разведение & содержание & канарейки & щеглы

Решение

Для решения задачи представим запросы в виде кругов Эйлера.

K — канарейки,

Щ – щеглы,

С – содержание,

Р – разведение.

Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.

канарейки \| терьеры \| содержание	канарейки & содержание	канарейки & щеглы & содержание	разведение & содержание & канарейки & щеглы

Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.

В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1

Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.

Только при таких условиях мы можем быть уверены, что правильно решили задачу.

Задача 7 (ЕГЭ 2013)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Фрегат \| Эсминец	3400
Фрегат & Эсминец	900
Фрегат	2100

Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Ответ: 2200

Решение: Запрос «Фрегат» обозначим символом «Ф», «Эсминец» — символом «Э».

Э=(Ф|Э)-Ф+(Ф&Э)=3400-2100+900=2200.

Разбор задачи B12 (демо ЕГЭ 2012)

Время выполнения-2 мин, уровень сложности-повышенный

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Шахматы \| Теннис	7770
Теннис	5500
Шахматы & Теннис	1000

Какое количество страниц (в тысячах) будет найдено по запросу Шахматы?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Ответ: 3270

Решение: Изобразим запросы в виде диаграмм Эйлера-Венна.

Запрос «Шахматы» обозначим символом «Ш», «Теннис» — символом «Т».

Ш=(Ш|Т)-Т+(Ш&Т)=7770-5500+1000=3270.

Задачи для самостоятельного решения

Задача 1

1	принтеры & сканеры & продажа
2	принтеры & продажа
3	принтеры \| продажа
4	принтеры \| сканеры \| продажа

Задача 2

1	физкультура
2	физкультура & подтягивания & отжимания
3	физкультура & подтягивания
4	физкультура \| фитнесс

Решение задач с помощью кругов Эйлера

Пояснительная записка

Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.

В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.

Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.

Основные понятия

Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.

Пересечение множеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

2. Решение задач с помощью кругов Эйлера

2.1. «Обитаемый остров» и «Стиляги»

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Решение:

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

1. 15 — 6 = 9 — человек, которые смотрели только «Обитаемый остров»,

2. 11- 6 = 5 — человек, которые смотрели только «Стиляги».

Получаем:

Ответ: 5 человек.

2.2. Задача про библиотеки

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 — в районной.

Сколько шестиклассников:

Являются читателями обеих библиотек;
Не являются читателями районной библиотеки;
Не являются читателями школьной библиотеки;
Являются читателями только районной библиотеки;
Являются читателями только школьной библиотеки?

Решение:

Чертим два множества таким образом:

1) 20+ 25 — 35 = 10 (человек) — являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2) 35 — 20 = 15 (человек) — не являются читателями районной библиотеки,

3) 35 — 25 = 10 (человек) — не являются читателями школьной библиотеки,

4) 35- 20 = 10 (человек) — являются читателями только районной библиотеки,

5) 35- 20 = 15 (человек) — являются читателями только школьной библиотеки.

Очевидно, что вопросы 2 и 5, а также 3 и 4 — равнозначны и ответы на них совпадают.

Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.

2.3. Гарри Поттер, Рон и Гермиона

На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер.

Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

Решение:

Учитывая условия задачи, сделаем чертеж:

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги — Гермиона, то 11 — 4 — 2 = 5 — книг прочитал только Гарри.

Следовательно, 26 — 7 — 2 — 5 — 4 = 8 — книг прочитал только Рон.

Ответ: 8 книг.

2.4. Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.

У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Чертим три круга, таким образом:

Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым — «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.

Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 — 3 = 2 — ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».

1) 21 — 3 — 1 — 6 = 11 — учеников выбрали только «Белоснежка и семь гномов»,

2) 13 — 3 — 1 — 2 = 7 — учеников выбрали — «Волк и теленок»,

3) 38 — (11 + 3 + 1 + 2 + 6 + 7) = 8 — ребят выбрали «Губка Боб Квадратные Штаны».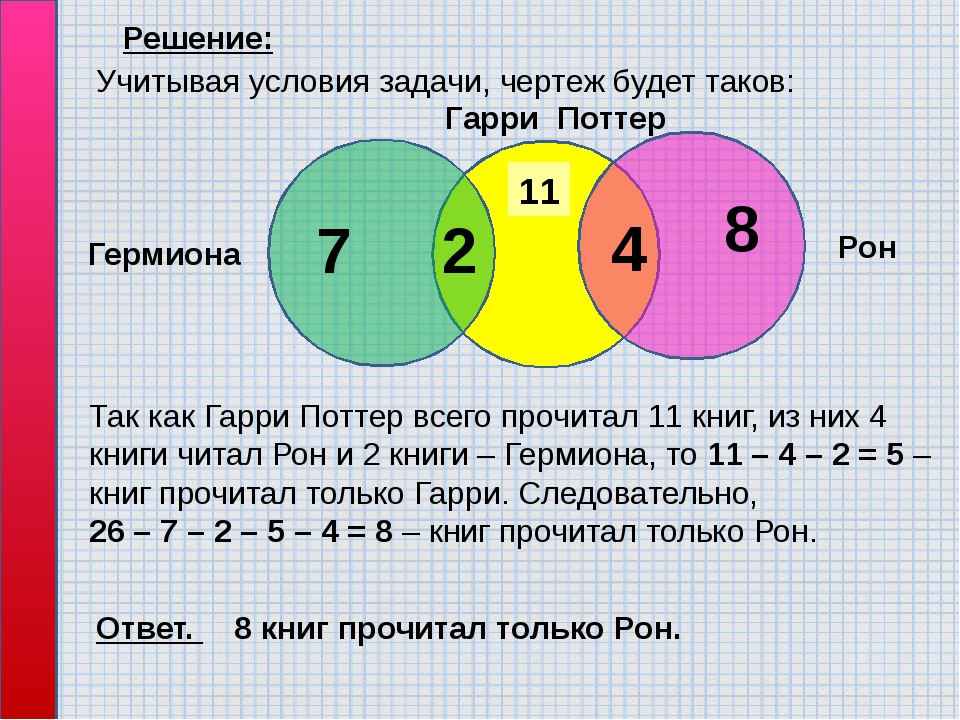

4) 8 + 2 + 1 + 6 = 17 — человек выбрали мультик «Губка Боб Квадратные Штаны».

Ответ: 17 учеников.

2.5. Задача про Крейсер и Линкор

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц, тыс.
Крейсер и Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов. )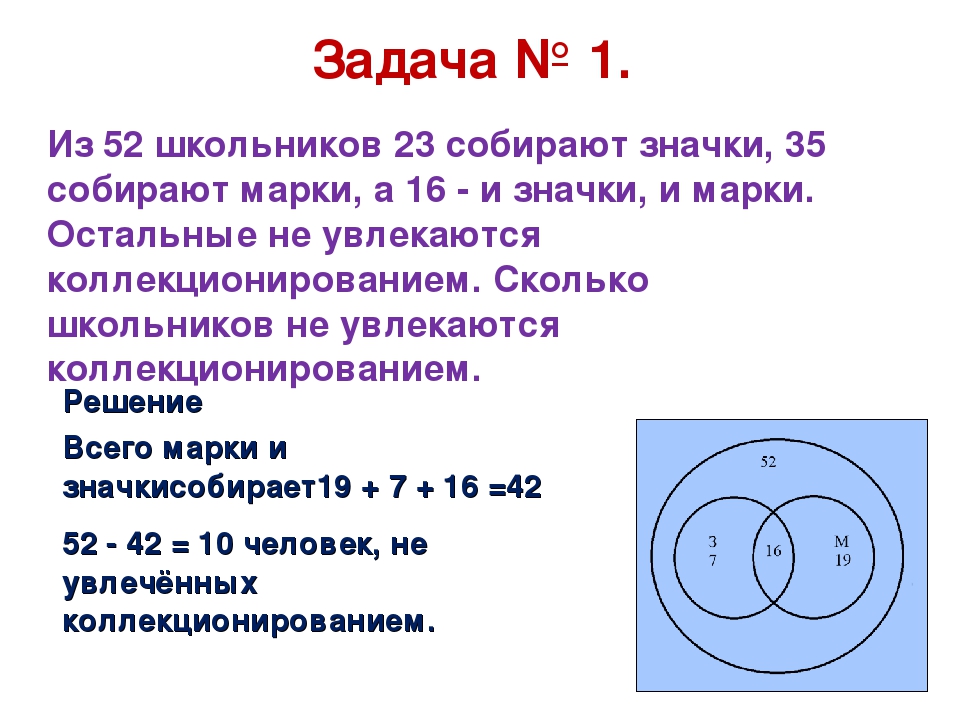

Решение:

При помощи кругов Эйлера изобразим условия задачи.

1) 4800 + 4500 — 7000 = 2300 (тыс. страниц) — найдено по запросу Крейсер и Линкор,

2) 4800 — 2300 = 2500 (тыс. страниц) — найдено по запросу Крейсер,

3) 4500 — 2300 = 2200 (тыс. страниц) — найдено по запросу Линкор.

Ответ: 2300 тыс. страниц.

2.6. Задача про блондинок

Каждый ученик класса — либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика — блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?

Решение:

Изобразим с помощью кругов Эйлера данные из задачи:

1) 12 — 1 = 11 (учеников) — девочек блондинок,

2) 12 — 1 = 11 (учеников) — блондины и любят математику,

3) 6 — 1 = 5 (учеников) — девочек, которые любят математику,

4) 20 — 11 — 1 — 5 = 3 (ученика) — девочки,

5) 24 — 11 — 1 — 11 = 1 (ученик) — блондин,

6) 17- 5 — 1 — 11 = 0 (учеников) — любят математику,

7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) — всего в классе.

Ответ: 32 ученика.

2.7. Задача про кружки

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение:

Учитывая условия задачи, сделаем чертеж:

1) 10 — 3 = 7 (ребят) — посещают драмкружок и хор,

2) 6 — 3 = 3 (ребят) — поют в хоре и занимаются спортом,

3) 8 — 3 = 5 (ребят) — занимаются спортом и посещают драмкружок,

4) 27 — 7 — 3 — 5 = 12 (ребят) — посещают драмкружок,

5) 32 — 7 3 — 3 = 19 (ребят) — поют в хоре,

6) 22 — 5 — 3 — 3 = 11 (ребят) — увлекаются спортом,

7) 70 — (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) — не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.

Ответ: 10 человек и 11 человек.

Задачи для самостоятельного решения

1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?

2. Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

3. 12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?

5. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?

6. В одном классе 25 учеников. Из них 7 любят груши, 11 — черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?

7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?

8. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?

9. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

10. Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Список использованных источников

1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.

2. Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.

3. https://ru.wikipedia.org/wiki/

4. http://logika.vobrazovanie.ru

5. http://www.otvet-prost.ru/load/diskretnaja_matematika/na_krugi_ehjlera/zadacha_na_krugi_ehjlera/18-1-0-22

6. http://urok.1sept.ru/articles/550092/

7. http://www.tutoronline.ru/blog/reshit-zadachu-pomogut-krugi-jejlera

Круги эйлера примеры решения. Отношения между понятиями. круги эйлера. Изучение нового материала

Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь. На самом деле вы наверняка не раз с ними сталкивались, просто не знали, как это называется. Где именно? Схемы в виде кругов Эйлера легли в основу многих популярных интернет-мемов (растиражированных в сети изображений на определенную тему).

Давайте вместе разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться для решения многих задач.

Происхождение термина

– это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

Пока не очень понятно, верно? Посмотрите на этот рисунок:

На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.

Ну что, так стало понятнее? Именно поэтому круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.

Автор метода — ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.

До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.

Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.

Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).

Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна.

Зачем нужны круги Эйлера?

Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.

Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение каких-то понятий (например, соотношение рода и вида) – мы их рассмотрели на примере в начале статьи.

А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера:

Забавно, правда? И главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать простую схему, которая сразу расставит все по местам.

Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:

Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.

Решение задач с помощью кругов Эйлера

Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.

Вот на этом сайте — http://logika.vobrazovanie.ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и несложные задачи, для решения которых потребуется метод Эйлера. Используя логику и математику, разберем одну из них.

Задача про любимые мультфильмы

Решение:

Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:

Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:

Выходит, что:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».

13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».

Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».

Теперь смело можем сложить все полученные цифры и выяснить, что:

мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.

А еще давайте рассмотрим задачу , которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник — http://eileracrugi.narod.ru/index/0-6).

Условия задачи:

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц (в тысячах)
Крейсер \| Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор ?

Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

Опираясь на условия задачи, составим уравнения:

Крейсер | Линкор: 1 + 2 + 3 = 7000
Крейсер: 1 + 2 = 4800
Линкор: 2 + 3 = 4500

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.

Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

Заключение

Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.

Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение не только в виде мемов, но и в популярных сериалах. Таких, как «Теория большого взрыва» и «4исла».

Используйте это полезный и наглядный метод для решения задач. И обязательно расскажите о нем друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Каждый предмет или явление обладает некими свойствами (признаками).

Получается, что составить понятие об объекте означает, прежде всего, умение отличить его от других сходных с ним объектов.

Можно сказать, что понятие — это мысленное содержание слова.

Понятие — это форма мысли, отображающая предметы в их наиболее общих и существенных признаках.

Понятие — это форма мысли, а не форма слова, так как слово лишь метка, которой мы помечаем ту или иную мысль.

Слова могут быть различны, но при этом обозначать одно и то же понятие. По-русски — «карандаш», по-английски — «pencil», по-немецки — bleistift. Одна и та же мысль в разных языках имеет разное словесное выражение.

ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ. КРУГИ ЭЙЛЕРА.

Понятия, имеющие в своих содержаниях общие признаки, называются СРАВНИМЫМИ («адвокат» и «депутат»; «студент» и «спортсмен»).

В противном случае, понятия считаются НЕСРАВНИМЫМИ («крокодил» и «блокнот»; «человек» и «пароход»).

Если кроме общих признаков понятия имеют и общие элементы объёма, то они называются СОВМЕСТИМЫМИ .

Существует шесть видов отношений между сравнимыми понятиями. Отношения между объёмами понятий удобно обозначать с помощью кругов Эйлера (круговые схемы, где каждый круг обозначает объём понятия).

ВИД ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ	ИЗОБРАЖЕНИЕ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА
РАВНОЗНАЧНОСТЬ (ТОЖДЕСТВЕННОСТЬ) Объёмы понятий полностью совпадают. Т.е. это понятия, которые различаются по содержанию, но в них мыслятся одни и те же элементы объёма.	1) А — Аристотель В — основатель логики 2) А — квадрат В — равносторонний прямоугольник
ПОДЧИНЕНИЕ (СУБОРДИНАЦИЯ) Объём одного понятия полностью входит в объём другого, но не исчерпывает его.	1) А — человек В — студент 2) А — животное В — слон
ПЕРЕСЕЧЕНИЕ (ПЕРЕКРЕЩИВАНИЕ) Объёмы двух понятий частично совпадают. То есть понятия содержат общие элементы, но и включают элементы, принадлежащие только одному из них.	1) А — юрист В — депутат 2) А — студент В — спортсмен
СОПОДЧИНЕНИЕ (КООРДИНАЦИЯ) Понятия, не имеющие общих элементов, полностью входят в объём третьего, более широкого понятия.	1) А — животное В — кот; С — собака; D — мышь 2) А — драгоценный металл В — золото; С — серебро; D — платина
ПРОТИВОПОЛОЖНОСТЬ (КОНТРАРНОСТЬ) Понятия А и В не просто включены в объём третьего понятия, а как бы находятся на его противоположных полюсах. То есть, понятие А имеет в своём содержании такой признак, которых в понятии В заменён на противополжный.	1) А — белый кот; В — рыжий кот (коты бывают и чёрными и серыми) 2) А — горячий чай; холодный чай (чай может быть и тёплым) Т.е. понятия А и В не исчерпывают всего объёма понятия, в которое они входят.
ПРОТИВОРЕЧИЕ (КОНТРАДИКТОРНОСТЬ) Отношение между понятиями, одно из которых выражает наличие каких-либо признаков, а другое — их отсутствие, то есть просто отрицает эти признаки, не заменяя их никакими другими.	1) А — высокий дом В — невысокий дом 2) А — выигрышный билет В — невыигрышный билет Т.е. понятия А и не-А исчерпывают весь объём понятия, в которое они входят, так как между ними нельзя поставить никакое дополнительное понятие.

Упражнение : Определите вид отношений по объёму приведённых ниже понятий. Изобразите их с помощью кругов Эйлера .

1) А — горячий чай; В — холодный чай; С — чай с лимоном

Горячий чай (В) и холодный чай (С) — находятся в отношении противоположности.

Чай с лимоном (С) может быть как горячим,

так и холодным, но может быть и, например, тёплым.

2) А — деревянный; В — каменный; С — строение; D — дом.

Всякое ли строение (С) — дом (D)? — Нет.

Всякий ли дом (D) — строение (С)? — Да.

Что-то деревянное (А) обязательно ли дом (D) или строение (С) — Нет.

Но можно найти деревянное строение (например, будка),

также можно найти деревянный дом.

Что-то каменное (В) не обязательно дом (D) или строение (С).

Но может быть и каменное строение, и каменный дом.

3) А — российский город; В — столица России;

С — Москва; D — город на Волге; Е — Углич.

Столица России (В) и Москва (С) — один и тот же город.

Углич (Е) является городом на Волге (D).

При этом, Москва, Углич, как и любой город на Волге,

являются российскими городами (А)

Задача 1 .

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.

Сколько шестиклассников:

1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?

Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.

Решение.

1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.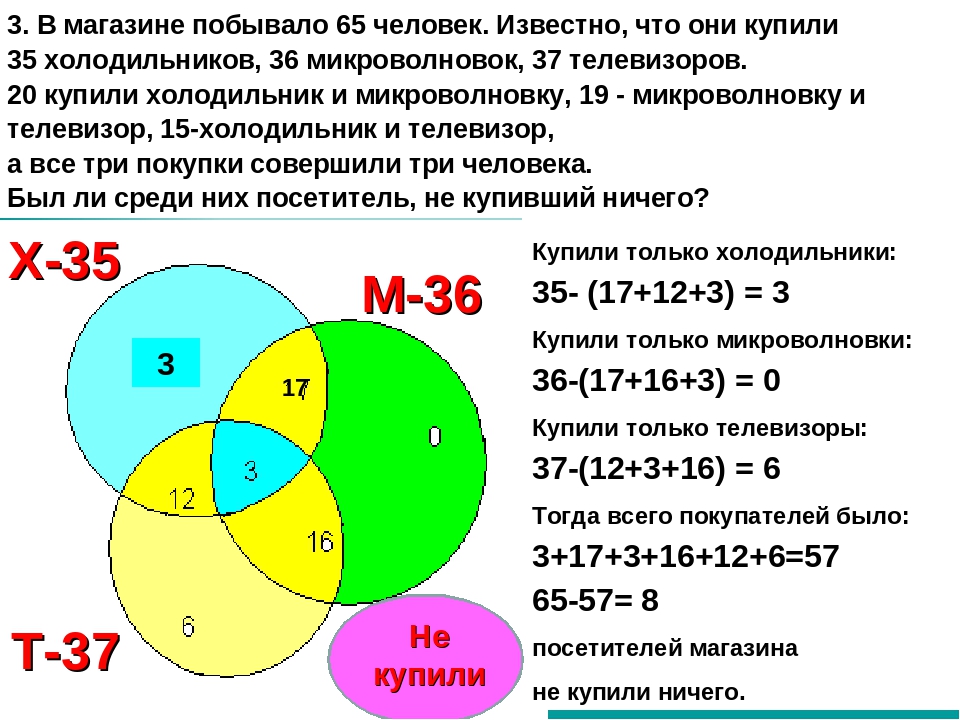

2. 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга)

3. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки. (На схеме правая часть правого круга)

4. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга)

5. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга).

Очевидно, что 2 и 5 , а также 3 и 4 – равнозначны и ответы на них совпадают .

При решении данной задачи мы использовали способ ее графического представления при помощи так называемых кругов Эйлера. Этот способ был предложен Леонардом Эйлером и широко используется при решении логических задач.

Леона́рд Э́йлер (4(15) апреля 1707, Базель, Швейцария – 7(18) сентября 1783, Санкт-Петербург, Российская империя) – швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. Некоторые из его потомков до сих пор живут в России.

Рассмотрим еще один пример.

Задача 2.

Часть жителей нашего дома выписывают только газету «Комсомольская правда», часть – только газету «Известия», а часть – и ту, и другую газету. Сколько процентов жителей дома выписывают обе газеты, если на газету «Комсомольская правда» из них подписаны 85%, а на «Известия» – 75%?

Решение.

Здесь нет принципиального отличия от решения предыдущей. На готовом рисунке заменим данные: 25 на 85% и 20 на 75%. Учитывая, что все жители дома составляют 100%, заменяем 35 на 100% и получаем готовое решение: 85% + 75% – 100% = 60%.

Ответ: обе газеты выписывают 60% жителей.

Чем более сложная и запутанная логическая задача, связанная с множествами, тем более очевиден эффект от применения кругов Эйлера. Только после составления рисунка их решение становится достаточно очевидным.

Задача 3.

Решение.

Пусть
Д – драмкружок,
Х – хор,
С – спорт.

Тогда
в круге Д – 27 ребят,
в круге Х – 32 человека,
в круге С – 22 ученика.

Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8 – 3 = 5 спортсменов, не поющих в хоре и 6 – 3 = 3, не посещающих драмкружок.

Легко видеть, что 5 + 3 + 3 = 11 спортсменов посещают хор или драмкружок,

22 – (5 + 3 + 3) = 11 занимаются только спортом;

70 – (11 + 12 + 19 + 7 + 3 + 3 + 5) = 10 – не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.

Ответ: 10 человек и 11 человек.

Задача 4.

В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?

Решение.

1 способ. Для решения опять воспользуемся кругами Эйлера. Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются
только метро и троллейбусом – (10 – х) человек,
только автобусом и троллейбусом – (9 – х) человек,
только метро и автобусом – (12 – х) человек.

Найдем, сколько человек пользуется одним только метро:
20 – (12 – х) – (10 – х) – х = х – 2.

Аналогично получаем: х – 6 – только автобусом и х + 4 – только троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30,
отсюда х = 3.

2 способ. А можно эту задачу решить задачу другим способом: 20 + 15 + 23 – 10 – 12 – 9 + х = 30, 27 + х = 30, х = 3 . Здесь сложили количество учеников, которые пользуются хотя бы одним видом транспорта и из полученной суммы вычли количество тех, кто пользуется двумя или тремя видами и, поэтому, вошли в сумму 2-3 раза. Таким образом, получили количество всех учеников в классе.

Ответ. 3 человека ежедневно пользуются всеми тремя видами транспорта.

Остались вопросы? Не знаете, как решить задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

кругами Эйлера называют фигуры, условно изображающие множества и наглядно иллюстрирующие некоторые свойства операций над множествами. В литературе круги Эйлера иногда называют диаграммами Вен на (или диаграммами Эйлера — Венна).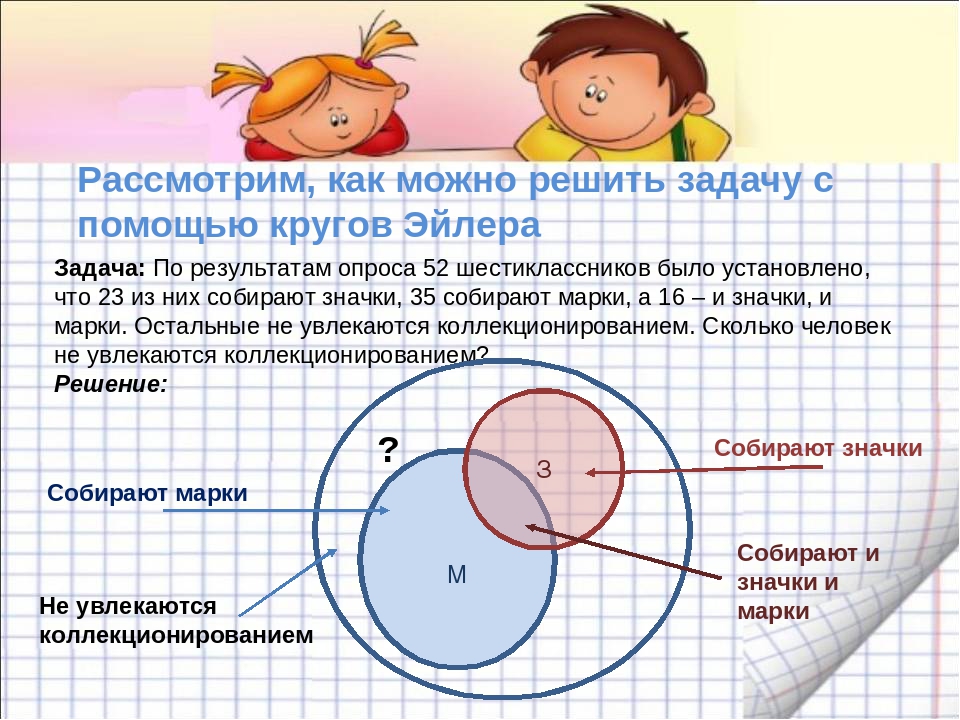 Круги Эйлера, иллюстрирующие основные операции над множествами, представлены на рис. 1.2 (множества, полученные в результате этих операций, отмечены штриховкой). АПВ 00 АЬВ Рис. 1.2 Пример 1.8. При помощи кругов Эйлера установим сначаг ла справедливость первого соотношения, выражающего свойство дистрибутивности операций объединения и пересечения множеств, На рис. 1.3,а вертикально заштрихован круг, изображающий множество А) а горизонтально — область, отвечающая пересечению множеств В и С. В итоге тем или иным способом заштрихована область, изображающая множество A U (БПС). На рис. 1.3,5 вертикально заштрихована область, соответствующая объединению множеств Л и Б, а горизонтально — объединению множеств Л и С, так что обоими способами заштрихована область, изображающая множество (A U В) П (A U С) и совпадающая с областью, заштрихованной каким-либо способом на рис. 1.3,а. Таким образом, круги Эйлера позволяют установить справедливость (1.10). Теперь рассмотрим второй закон де Моргана (1. 7) Заштрихованная на рис. 1.4,а область изображает множество ЛИВ, а незаштрихованная часть прямоугольника Q (внешняя по отношению к заштрихованной) соответствует множеству ЛПВ. На рис. 1.4,5 части прямоугольника 12, заштрихованные вертикально и горизонтально, отвечают соответственно А и В. Тогда множеству Ли В отвечает область, заштрихованная хотя бы одним из указанных способов. Она совпадает с областью, не заштрихованной на рис. 1.4,а и отвечающей множеству ЛПБ, что устанавливает справедливость (1.11). Вопросы и задачи 1.1. Запись m|n, где m,n € Z, означает, что число m нацело делит число п (то — делитель п). Описать заданные множества при условии, что х € N: 1.2. Доказать следующие соотношения и проиллюстрировать их кругами Эйлера: . 1.3. Установить, в каком отношении (X С Y, X Э У или X = Y) находятся множества X и У, если: а Использовать для иллюстрации круги Эйлера. 1.4. Пусть Aj — множество точек, образующих стороны некоторого треугольника, вписанного в заданную окружность. Описать объединение и пересечение всех таких множеств, если треугольники: а) произвольные; б) правильные; в) прямоугольные. Найти IK и flAi ieN i en для заданных семейств множеств: 1.6. Указать, какие из представленных ниже соотношений неверны, и объяснить, почему: 1.7. Указать, какие из множеств равны между собой: . 1.8. Найти множества Ли В, АГ\В, А\В, В\А и изобразить их на числовой прямой, если А = (1.0. Считая отрезок универсальным множеством, найти и изобразить на числовой прямой дополнения множеств: . 1.10. По приведенным ниже описаниям множеств людей подберите для каждой записи высказывания на языке множеств подходящую пословицу или поговорку. Надеемся, что это позволит лишний раз проанализировать смысл народных изречений. Например, если Z -множество людей, которые сами как следует не знают того, о чем говорят, то запись х £ Z можно отнести к пословице „Слышал звон, да не знает, где он, поскольку именно так говорят о человеке, наделенном указанным свойством (в данном случае — характеристическим свойством множества Z, см. 1.1). Множества людей ft — универсальное множество всех людей, Л — добрые, 5е В — незаурядные, с большими способностями, С — глупые, D — умные, Е — поступающие по своему, не слушающие советов, F — связанные корыстными отношениями, G — много обещающие, Я — не выполняющие своих обещаний, J — злоупотребляющие своим служебным положением, К — слишком важничающие, задающиеся, L — вмешивающиеся не в свое дело, М — предприимчивые, ловкие, умеющие устраиваться, Р — берущиеся за несколько дел сразу, Q — плодотворно работающие, S — ошибающиеся, Т — чувствующие вину и возможность расплаты, U — не добивающиеся результатов, V — выдающие себя своим поведением, W- недальновидные, X — действующие заодно, не предающие друг друга, У — бывалые, опытные люди. 1 + ns, Vs>-1 (неравенство Бернулли). 1.14. Доказать, что среднее арифметическое п положительных действительных чисел не меньше их среднего геометрического, т.е. п 1.15. Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что это был синий „Бьюик», Джонс — голубой „Крайслер», а Смит — „Форд Мустанг», но не синий. Какого цвета был автомобиль и какой марки, если известно, что, желая запутать следствие, каждый из них указал правильно либо только марку машины, либо только ее цвет? 1.1в. Для полярной экспедиции из восьми претендентов А, В, С, Д J5, F, G и Я надо отобрать шесть специалистов: биолога, гидролога, синоптика, радиста, механика и врача. Обязанности биолога могут выполнять Е и G, гидролога — В и F, синоптика — F и G, радиста — С и Д механика — С и Я, врача — А и Д но каждый из них, если будет в экспедиции, сможет выполнять лишь одну обязанность. Кого и кем следует взять в экспедицию, если F не может ехать без D — без Я и без С, С не может ехать с G, а Д — с В?

Леонард Эйлер – величайший из математиков,написал более 850 научных работ.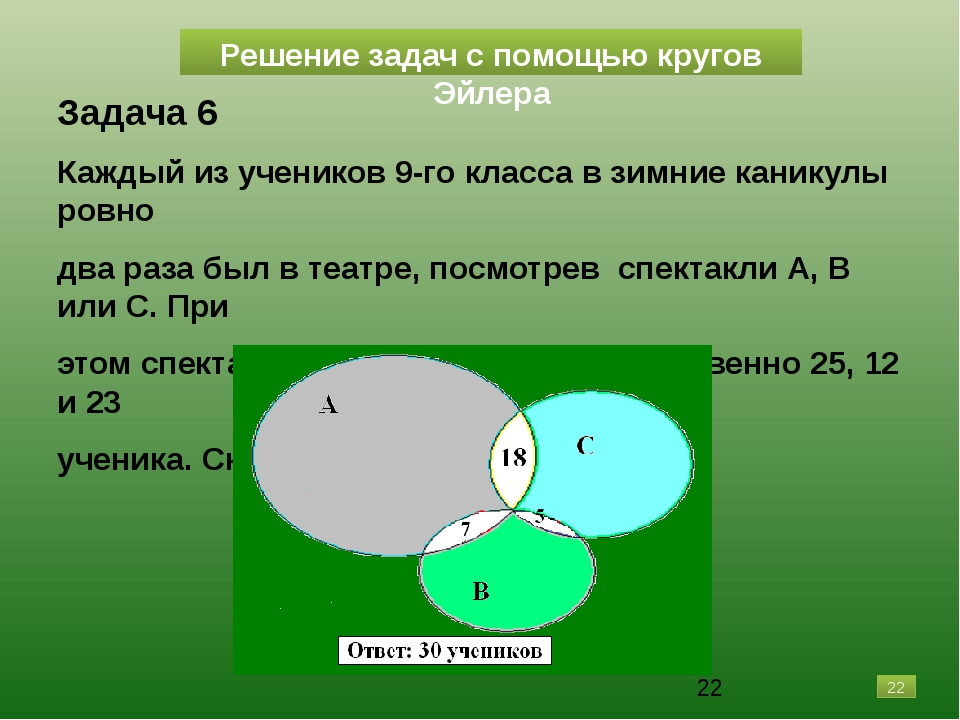 В одной из них и появились эти круги.

Учёный писал, что «они очень подходят для того, чтобы облегчить наши размышления».

Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

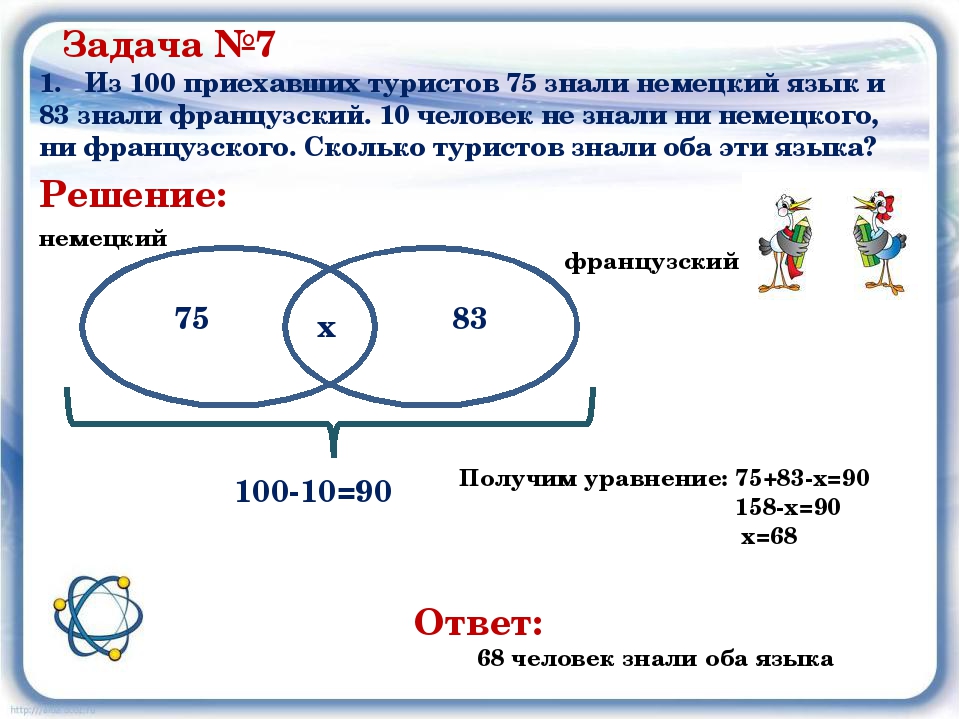
Задача 1

Из 90 туристов, отправляющихся в путешествие, немецким языком владеют 30 человек, английским – 28 чел, французским – 42 чел. Английским и немецким одновременно владеют 8 человек, английским и французским -10 чел, немецким и французским – 5 чел, всеми тремя языками – 3 чел. Сколько туристов не владеют ни одним языком?

Решение:

Покажем условие задачи графически – с помощью трёх кругов

Ответ: 10 человек.

Задача 2

Многие ребята нашего класса любят футбол, баскетбол и волейбол. А некоторые — даже два или три из этих видов спорта. Известно, что 6 человек из класса играют только в волейбол, 2 – только в футбол, 5 – только в баскетбол. Только в волейбол и футбол умеют играть 3 человека, в футбол и баскетбол – 4, в волейбол и баскетбол – 2. Один человек из класса умеет играть во все игры, 7 не умеют играть ни в одну игру. Требуется найти:

Сколько всего человек в классе?

Сколько человек умеют играть в футбол?

Сколько человек умеют играть в волейбол?

Задача 3

В детском лагере отдыхало 70 ребят. Из них 20 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов, а 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Задача 4

Из сотрудников фирмы 16 побывали во Франции, 10 – в Италии, 6 – в Англии. В Англии и Италии – пятеро, в Англии и Франции – 6, во всех трёх странах – 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работает 19 человек, и каждый их них побывал хотя бы в одной из названных стран?

Задача 5

Задачи для решения учащимися

1. В классе 35 учеников. Все они являются читателями школьной и районной библиотек. Из них 25 берут книги в школьной библиотеке, 20 — в районной. Сколько из них:

а) не являются читателями школьной библиотеки;

б) не являются читателями районной библиотеки;

в) являются читателями только школьной библиотеки;

г) являются читателями только районной библиотеки;

д) являются читателями обеих библиотек?

2. Каждый ученик в классе изучает английский или немецкий язык, или оба этих языка. Английский язык изучают 25 человек, немецкий — 27 человек, а тот и другой — 18 человек. Сколько всего учеников в классе?

3.На листе бумаги начертили круг площадью 78 см2 и квадрат площадью 55 см2. Площадь пересечения круга и квадрата равна 30 см2. Не занятая кругом и квадратом часть листа имеет площадь 150 см2. Найдите площадь листа.

4. В группе туристов 25 человек. Среди них 20 человек моложе 30 лет и 15 человек старше 20 лет. Может ли так быть? Если может, то в каком случае?

5. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое, или то и другое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?

6. В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек -.и математический, и физический, 5 — и математический, и химический, 3 — и физический, и химический кружки. Сколько учеников класса не посещают никакие кружки?

7. После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?

Решение задач ЕГЭ с помощью кругов Эйлера

Задача 1

Крейсер & Линкор ? Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Запрос	Найдено страниц (в тысячах)
Крейсер \| Линкор	7000
Крейсер	4800
Линкор	4500

Решение:

Опираясь на условия задачи, составим уравнения:

Крейсер | Линкор: 1 + 2 + 3 = 7000
Крейсер: 1 + 2 = 4800
Линкор: 2 + 3 = 4500

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.

Задача 2

В языке запросов поискового сервера для обозначения

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Торты \| Пироги	12000
Торты & Пироги	6500
Пироги	7700

Какое количество страниц (в тысячах) будет найдено по запросу Торты ?

Решение

Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.

А , Б , В ).

Из условия задачи следует:

Торты │Пироги = А + Б + В = 12000

Торты & Пироги = Б = 6500

Пироги = Б + В = 7700

Чтобы найти количество Тортов (Торты = А + Б ), надо найти сектор А Торты│Пироги ) отнимем множество Пироги.

Торты│Пироги – Пироги = А + Б + В -(Б + В ) = А = 1200 – 7700 = 4300

Сектор А равен 4300, следовательно

Торты = А + Б = 4300+6500 = 10800

Задача 3

|», а для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Пироженое & Выпечка	5100
Пироженое	9700
Пироженое \| Выпечка	14200

Какое количество страниц (в тысячах) будет найдено по запросуВыпечка ?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение

Для решения задачи отобразим множества Пироженых и Выпечек в виде кругов Эйлера.

Обозначим каждый сектор отдельной буквой (А , Б , В ).

Из условия задачи следует:

Пироженое & Выпечка = Б = 5100

Пироженое = А + Б = 9700

Пироженое │ Выпечка = А + Б + В = 14200

Чтобы найти количество Выпечки (Выпечка = Б + В ), надо найти сектор В , для этого из общего множества (Пироженое │ Выпечка) отнимем множество Пироженое .

Пироженое │ Выпечка – Пироженное = А + Б + В -(А + Б ) = В = 14200–9700 = 4500

Сектор В равен 4500, следовательноВыпечка = Б + В = 4500+5100 = 9600

Задача 4
убывания
Для обозначения логической операции «ИЛИ» используется символ » |», а для логической операции «И» — символ «&».
Решение

Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (

А , Б , В , Г ).

с паниели │(терьеры & овчарки) = Г + Б

с паниели│овчарки = Г + Б + В

спаниели│терьеры│овчарки = А + Б + В + Г

терьеры & овчарки = Б

Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4

Задача 5

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ » |», а для логической операции «И» — символ «&».

1	барокко \| классицизм \| ампир
2	барокко \| (классицизм & ампир)
3	классицизм & ампир
4	барокко \| классицизм

Решение

Преобразим условие задачи в виде суммы секторов:

Из сумм секторов мы видим какой запрос выдал больше количества страниц.

Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1

Задача 6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ » |», а для логической операции «И» — символ «&».

1	канарейки \| щеглы \| содержание
2	канарейки & содержание
3	канарейки & щеглы & содержание
4	разведение & содержание & канарейки & щеглы

Решение

Для решения задачи представим запросы в виде кругов Эйлера.

K — канарейки,

Щ – щеглы,

Р – разведение.

канарейки \| терьеры \| содержание	канарейки & содержание	канарейки & щеглы & содержание	разведение & содержание & канарейки & щеглы

В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1

Только при таких условиях мы можем быть уверены, что правильно решили задачу.

Задача 7 (ЕГЭ 2013)

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Фрегат \| Эсминец	3400
Фрегат & Эсминец	900
Фрегат	2100

Какое количество страниц (в тысячах) будет найдено по запросу Эсминец ?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение логических задач с помощью кругов эйлера

Муниципальное общеобразовательное учреждение

лицей № 8 «Олимпия»

Дзержинского района г. Волгограда

Телефоны (8442) 58-80-83, 51-81-31 адрес электронной почты lyceum8@mail.ru

Решение логических задач с помощью кругов Эйлера

Выполнил:

Назаретян Сюзана Горовна,

ученица 5 Б класса

Учитель:

Кокиева Лилия Диляверовна, учитель

математики высшей категории

Волгоград, 2011

Оглавление	С.
Введение……………………………………………………………………………………	3 — 4
Глава I. Логические задачи и круги Эйлера ……………..…….……	5 — 9
1.1. Трудно решать логические задачи? …..…………………….	5 — 6
1.2. Немного о множествах ………..……………………………	6 — 8
1.3. Из истории кругов Эйлера …….……..…………………….	8 — 9
Глава II. Решение логических задач с помощью кругов Эйлера…..	7 — 14
2.1. Задачи на пересечение и объединение двух множеств…….	9 —12
2.2. Задачи на пересечение и объединение трёх множеств ……	12 — 14
Заключение………………………………………………………………………………..	15
Список источников и литературы……………………………………………….	16
Приложения ………………………………………………………………………………	17—20

Введение.

Сколько гостей Вам встречать, если собираются друзья с 15 угощениями и 20 украшениями? Может ли хватить всем места за столом, вмещающем 22 человека? Первое, что приходит на ум, это 35 человек. А причём здесь 22 человека? Есть подвох? Конечно! Ведь надо рассмотреть несколько вариантов.

Как узнать количество учащихся класса, посещающих одновременно две или три секции, если известны количества участников каждой секции отдельно? Можно ли научиться решать такие задачи, планируя результат? Хочется ответить положительно.

А как решить такую задачу: «Министерство послало в один из лицеев инспектора для проверки, как в нём ведётся преподавание иностранных языков. Сотрудник министерства в отчёте записал, что в лицее учатся 100 детей. Каждый изучает по крайней мере один из трёх языков: французский, немецкий и испанский. Причём все три языка изучают 5 человек; немецкий и испанский 10;французский и испанский 8; немецкий и французский 20; испанский 30, немецкий 23, французский 50. Инспектор, представивший отчёт, был уволен. Почему?»? Такое длинное условие: пока дочитали до конца – забыли начало. Что делать?

Оказывается, такие задачи решаются с помощью кругов Эйлера. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению.

Актуальность нашей работы заключается в том, чтобы такие задачи не ставили нас «в тупик» и мы могли их решать.

С учетом этого и была выбрана тема исследования: «Решение логических задач с помощью кругов Эйлера».

Объект исследования — логические задачи.

Предмет исследования —использование кругов Эйлера для решения логических задач .

Гипотеза исследования. Можно решать логические задачи определённого вида специальными способами и в 5 – 6 классах.

Целью нашего исследования является исследование механизма решения определённых логических задач при помощи кругов Эйлера.

Для достижения цели исследования и обоснования гипотезы нам необходимо решить ряд задач:

Найти необходимые сведения о пересечении и объединении множеств, о кругах Эйлера.
Рассмотреть способы решения логических задач на пересечение и объединение двух и трёх множеств.
Вывести в общем виде способ решения логических задач определённого вида с помощью кругов Эйлера.
Научиться решать конкретные логические задачи с помощью кругов Эйлера.
Создать модели «Круги Эйлера» для решения задач с двумя и тремя множествами в помощь учащимся.

Методы исследования:

1. Поиск, анализ и синтез различных источников информации.

2. Интервьюирование, беседы.

Практическая значимость заключается в расширении аппарата для решения логических задач. Данный материал можно будет использовать на некоторых уроках, для проведения кружков, факультативных занятий по математике. Применение кругов Эйлера придает задачам наглядность и простоту.

Теоретическая значимость заключается в разработке способа действий при решении логических задач с помощью кругов Эйлера в общем виде.

Здесь будет выводиться история переписки.

Глава I. Логические задачи и круги Эйлера

1.1. Трудно решать логические задачи?

Логика – это искусство рассуждать, умение делать правильные выводы. Это не всегда легко, потому что очень часто необходимая информация «замаскирована», представлена неявно, и надо уметь её извлечь.

Решение логических задач – одно из важнейших средств развития мыслительных способностей.

Логические задачи обладают рядом достоинств, позволяющих использовать их для развития соображения и улучшения логического мышления детей, начиная с детского сада и заканчивая старшими классами средней школы. Логические задачи допускают изложение в занимательной, игровой форме. С другой стороны, такие задачи труднее, для их решения часто не требуется глубоких знаний, а следует применить смекалку.

Вдоль овражка
Шла фуражка,
Две косынки,
Три корзинки
И от них не отставала
Белоснежная панама.
Посчитай поскорей
Сколько было детей?

Задача предполагает несколько решений. Потому что мы точно не знаем, носил ли кто — нибудь и головной убор, и корзинку.
1 Решение. Предполагается, что каждый ребёнок носил 1 предмет. Значит, детей было 7.
2 Решение. Предполагается, что 1 из детей нёс корзинку и головной убор. Следовательно, детей было 6.
3 Решение. Предполагается, что 2 из детей носили и корзинку, и головной убор. Следовательно, детей было 5 .
4 Решение. Предполагается, что 3 из детей носили и корзинку, и головной убор. Следовательно, детей было 4.

1.2. Немного о множествах

Множество – одно из основных понятий математики. Его смысл выражается словами: совокупность, собрание, класс, набор, команда и т.д. Этот смысл поясняется многочисленными примерами. Так, можно говорить о множестве всех учащихся 5-го класса, о множестве всех жителей Волгограда, о множестве всех натуральных чисел, о множестве корней данного уравнения. Основатель теории множеств немецкий математик Георг Кантор (1845–1918) так определил множество – «многое, мыслимое как единое, целое».

Множества обозначаются прописными буквами латинского алфавита А, В, С, …

О предметах, составляющих множество, говорят, что они принадлежат этому множеству или являются его элементами. Множества, элементами которых являются числа, называются числовыми множествами.

Множество может быть задано перечислением всех его элементов в произвольном порядке. Такое множество называют конечным. Мы будем рассматривать только конечные множества.

Множество, в котором нуль элементов, называют пустым.

Над множествами, как и над числами, производят операции. Рассмотрим некоторые из них: пересечение, объединение и разность.

Пересечение множеств

Возьмем множество X, состоящее из букв а, б, в, г, д, и множество Y, состоящее из букв г, д, е, ж:

X = {а, б, в, г, д}, Y= {г, д, е, ж}.

Эти множества имеют общие элементы гид. Множества X и Y называются пересекающимися множествами. Множество общих элементов X и Y называют пересечением множеств X и Y и обозначают с помощью знака :Х Y={г, д} (рис. 1).

Пусть множество А = {1, 3, 5}. Множества А и X не имеют ни одного общего элемента. В таком случае множества А и X называются непересекающимися множествами. Пересечением множеств А и X является пустое множество: А  Х=  (рис. 2).

Пересечением множеств называется новое множество, состоящее
из элементов, принадлежащих одновременно нескольким множествам

Рис. 1

Рис. 2

Объединение множеств

Если из элементов множеств X и Y составить новое множество, состоящее из всех элементов этих множеств и не содержащее других элементов, то получится объединение множеств Х и Y, которое обозначают с помощью знака :

X и Y= {а, б, в, г, д, е, ж) (рис. 4).

Объединение множеств А и X не является пустым:

А X = {1, 3, 5, а, б, в, г, д) (рис. 5).

Объединением множеств называется новое множество, состоящее
из элементов, принадлежащих хотя бы одному из множеств.

Рис. 3

Рис. 4

Разность

Разность множеств X и Y — это множество всех элементов из X, не являющихся элементами из Y.Разность обозначают Х\Y = {а, б, в} (рис. 5).

Рис. 5

1.3. Из истории кругов Эйлера

Часто множество изображают кругами, эти круги обычно называют «кругами Эйлера» по имени величайшего математика Леонарда Эйлера.

Леонард Эйлер (Euler) (1707 – 1783 г.г.) – математик, механик, физик и астроном. По происхождению швейцарец, а работал в основном в Росси и в Германии. В 1726 году был приглашен в Петербургскую АН и в 1727 году переехал в Россию. В 1741 – 1766 годах работал в Берлине, член Берлинской АН. Эйлер – ученый необычайной широты интересов и творческой продуктивности. Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавших значительное влияние на развитие науки.

Одним из первых, кто разрабатывал метод решения задач с помощью кругов Эйлера, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил швейцарский математик Леонард Эйлер (1707 – 1783). Он долгие годы работал в Петербургской Академии наук. К этому времени относятся его знаменитые «Письма к немецкой принцессе», написанные в период с 1761 по 1768 год. В некоторых из этих «Писем…» Эйлер как раз и рассказывает о кругах, которые «очень подходят для того, чтобы облегчить наши размышления». После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848).

Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов пользовался и немецкий математик Эрнест Шредер (1841 – 1902). Этот метод широко используется в книге «Алгебра логики». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.

Глава II. Решение логических задач с помощью кругов Эйлера

2.1. Задачи на пересечение и объединение двух множеств

К Лене на День Рождения пришли гости с подарками. Получилось так, что подарили только букеты цветов и воздушные шарики. Шесть гостей подарили букеты цветов, четыре — воздушные шарики. Сколько было гостей?
Задача предполагает несколько решений. Потому что мы точно не знаем, брал ли кто — нибудь из гостей два подарка.

1 Решение. Предполагается, что каждый гость с одним подарком. Следовательно, гостей 10.

2 Решение. Предполагается, что 1 из гостей пришел и с шариком, и с букетом цветов. Следовательно, 6 + 3 = 9 гостей.

3 Решение. Предполагается, что 2 из гостей пришли с двумя подарками. Следовательно, гостей 8.

4 Решение. Предполагается, что 3 из гостей пришли и с шариком, и с букетом цветов. Следовательно, 6 + 1 = 7.

5 Решение. Предполагается, 4 из гостей пришли с 2 подарками. Следовательно, 4 + 2 = 6 гостей.

) 2)

) 4)

В одном множестве 40 элементов, а в другом 30. Сколько элементов может быть в их:

а) пересечении; б) объединении?

Ответ: а) от 0 до 30; б) от 40 до 70.

«Ёлки» и «Неудержимый»: Некоторые ребята из нашего класса любят ходить в кино. Известно, что 12 ребят смотрели фильм «Ёлки», 9 человек – фильм «Неудержимый», из них 6 смотрели и «Ёлки», и «Неудержимый». Сколько человек смотрели только фильм «Неудержимый»?
Сначала заполняем пересечение. Это будет число 6. Потом заполняем множество ребят, смотревших фильм «Ёлки». Это будет число 6. Так как 6 из двенадцати к тому же ещё смотрели фильм «Неудержимый». После заполняем множество ребят, смотревших фильм «Неудержимый». Это будет число 3. Так как 6 из 9 к тому же ещё смотрели фильм «Ёлки».
Ответ: 3 человека смотрели только фильм «Неудержимый».

20 человек знают английский и 10 — немецкий, из них 5 знают и английский, и немецкий. Сколько человек всего?

Способ 1. С помощью модели «Круги Эйлера» (Приложение 1).

10+20 – 5=25 человек.

Способ 2.

1) 20 – 5 = 15(чел.) – знают только английский язык;

2) 10 – 5 = 5 (чел.) – знают только немецкий язык;

3) 15+5+5 = 25 (чел.) – всего.

Можно решать и короче:

20 – 5 = 15(чел.) – знают только английский язык;
10+15 = 25 (чел.) — знают немецкий и только английский

2.2. Задачи на пересечение и объединение трёх множеств

В классе всего 36 человек. Учащиеся посещают математический, физический и химический кружки, причем, математический кружок посещают 18 человек, физический — 14 человек, химический — 10 человек. Кроме того, известно, что все три кружка посещают 2 человека, математический и физический -8,математический и химический — 5, физический и химический — 3.

Сколько учеников класса не посещают никаких кружков?

Способ 1. На рисунке большой круг изображает множество всех учеников класса. Внутри этого круга расположены три пересекающихся круга меньшего диаметра: эти круги изображают соответственно множества членов математического, физического и химического кружков. Эти круги обозначены буквами М, Ф, Х.

Общей части всех трех кругов соответствует множество ребят, посещающих все три кружка, поэтому она обозначена МФХ.

Через обозначено множество ребят, посещающих математический и физический кружки, но не посещающих химический кружок. Аналогичным образом обозначены и все остальные области. Здесь для удобства обозначений мы будем отсутствие отмечать чертой над символом.

Теперь обратимся к числовым данным (см. Приложение 2).

В область МФХ впишем число 2, т.к. все три кружка посещают 2 ученика. Далее известно, что ребят, посещающих математический и физический кружки, было 8. Значит, в область МФ надо вписать число 8. Но область МФ состоит из двух частей: и МФХ, причем в МФХ входят 2 человека. Значит, на долю остается 6 человек.

Теперь рассмотрим множество МХ, на которое приходится 5 человек. Эта область также состоит из двух частей. На МФХ приходится 2 человека, значит, на приходится 3.

Рассмотрим теперь множество М, в которое входят 18 учеников. Оно состоит из 4 частей. Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 3. Значит, в четвертое подмножество входит 18 – (2+3+6) = 7 человек.

Рассмотрим множество ФХ, на которое приходится 3 человека. Эта область также состоит из двух частей. На МФХ приходится 2 человека, значит, на приходится 1.

Рассмотрим множество Ф, в которое входят 14 учеников. Оно состоит из 4 частей. Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 1. Значит, в четвертое подмножество входит 14 – (2+1+6) = 5 человек.

36 – (10+7+6+5) = 8 человек. Таким образом, в классе 8 ребят, не посещающих никаких кружков.

? 8

Способ 2. С помощью модели «Круги Эйлера» (Приложение 1).

Представим множества учащихся, посещающих математический, физический и химический кружки, в виде кругов, вырезанных из плотной бумаги. Будем считать, что площадь каждого из этих кругов равна числу учащихся, посещающих соответствующий кружок. Наложим круги друг на друга так, чтобы было понятно, что есть учащиеся, посещающие один, два или три кружка. Вычислим площадь получившейся фигуры:

14 + 18 + 10 – ((8 + 5 + 3)  2) – 2 = 8 (чел.)— не посещают кружки.

Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским — 28, французским — 42. Английским и немецким одновременно владеют 8 человек, английским и французским — 10, немецким и французским — 5, всеми тремя языками — 3. Сколько туристов не владеют ни одним языком?

Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.

Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста.

Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек,а одним французским — 30.

Всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.

Заключение

Существует множество приемов, которые используются при решении текстовых логических задач (Приложение 3). Очень часто решение задачи помогает найти рисунок, он делает решение простым и наглядным. Задачи, решаемые с помощью кругов Эйлера, предлагаются на математических олимпиадах, но в школьной программе не отводятся часы на изучение данной темы. Ценность использования кругов Эйлера состоит в том, что решения задач с громоздкими условиями и со многими данными становятся проще.

Подобные задачи часто имеют практический характер, что немаловажно в современной жизни. Они заставляют задумываться, подходить к решению какой-либо проблемы с разных сторон, уметь выбирать из множества способов решения наиболее простой, легкий путь.

Нами созданы модели «Круги Эйлера» для решения логических задач на пересечение двух и трёх множеств, которыми можно пользоваться как на месте (за партой), так и у доски (Приложение 4).

Поиск готовых способов решения выделенных логических задач, самостоятельное описание способа действий при использовании кругов Эйлера для их решения, а также попытки рассмотрения другой формы представления данных условия позволили нам решить поставленные задачи.

Цель была достигнута. С результатами работы были ознакомлены наши одноклассники, что позволило решать логические задачи этого вида не только нам.

Теперь наши одноклассники решают такие задачи, используя не только модели, но и памятку со способом действий, написанных нами.

Теперь мы точно будем знать, сколько друзей нам надо встречать в гости. От 20 до 35! А значит, и за стол всех всё же можно будет посадить.

Данная тема, безусловно, расширяет математический кругозор учащихся, обогащает арсенал средств, используемых в решении разнообразных задач.

Литература

Задачи для внеклассной работы по математике в V – VI классах: Пособие для учителей Текст/ Сост. В.Ю. Сафонова. Под ред. Д.Б. Фукса, А. Л. Гавронского. М.: МИРОС, 1993. с. 42. – ISBN 5-7084-0023-4
Занимательная математика. 5 – 11 классы. Текст: (Как сделать уроки нескучными) / Авт. – сост. Т.Д. Гаврилова. Волгоград: Учитель, 2005. с.32-38. – 10000 экз. –5-7057-0482-8
Депман,И.Я., Виленкин, Н.Я. За страницами учебника математики Пособие для учащихся 5 – 6 кл. Текст/ И.Я Депман. М.: Просвещение, 1999. с. 189 – 191, 231. – 10000 экз. – ISBN 5-09-007107-1
Смыкалова, Е.В. Дополнительные главы по математике для учащихся 5 класса. Текст: СПб: СМИО Пресс, 2009. с.14-20. – 2000 экз. – ISBN 5-7704-0055-2
Фарков, А.В. Математические олимпиады в школе.5–11 классы.Текст / А.В. Фарков. М.: Айрис–пресс, 2007. с. 27, 34, 61. – 7000 экз. – ISBN 978-5-8112-2394-7
Энциклопедия для детей. Т. 11. Математика Текст/ Глав.ред. М.Д. Аксёнова. М.: Аванта +,2001. с. 537 — 542. – 20000экз. – ISBN 5-8483-0015-1
Иванищев, Д. М. Поляна загадок – математика царица.

Дистанционная обучающая олимпиада по математике (ДООМ)

Сопова, С. С. Диаграмма Эйлера-Вена и «дерево». Взаимодополнение.

Приложение 1

Модель «Круги Эйлера» на пересечение двух множеств

На листе бумаги нарисовать два круга.
Разрезать по пунктирным линиям и получить детали.
На бумаге цвета 1 обвести и вырезать детали № 1 () (), № 2 ().

На бумаге цвета 2 обвести и вырезать детали № 2, № 3 () ().

 — окошко для названия множества,  — окошко для числа

Модель «Круги Эйлера» на пересечение трёх множеств

На листе бумаги нарисовать три круга.
Разрезать по пунктирным линиям и получить детали.
На бумаге цвета 1 обвести и вырезать детали № 5 () (), № 2, № 1, № 4.

На бумаге цвета 2 обвести и вырезать детали № 6 (), (), № 2, № 1, № 3.

На бумаге цвета 3 обвести и вырезать детали № 7 (), (), № 4 (), № 1 (),

№ 3 ().

Приложение 2.

Способ действий при решении задач

на пересечение и объединение трёх множеств с помощью кругов Эйлера

Начертить три пересекающихся круга. Обозначить множества: A, B, C.
Начертить большой круг, в котором окажутся три маленьких. Это общее количество объектов – множество Е.
Начертить отдельное множество D – подмножество множества E Это те, кто не является элементом множеств А, В и С.
Найти часть круга, являющуюся общей для всех трёх множеств (№1) и записать данные.
Найти часть круга, являющуюся общей для двух множеств (№1 и №2) и записать данные в №2.

Найти часть круга, являющуюся общей для двух множеств (№1 и №3) и записать данные в №3.

Найти часть круга, являющуюся общей для двух множеств (№1 и №4) и записать данные в №4.

Найти часть круга, отвечающую за каждое множество в отдельности:

5 = А – (1 + 2 + 4), 6 = В – (1 + 2 + 3), 7 = С – (1 + 3 + 4).

Должно выполняться: 1 + 2 + 3 + 4 + 5 + 6 + 7 + D = E/
Записываем ответ на вопрос задачи.

Приложение 3.

Задача (/). а) На 3 курсе факультета обучается 81 студент. Многие из них выбрали одинаковые дисциплины, посещают одни и те же лекции и хорошо знают друг друга. б) 43 студента посещают лекции по философии, в)32 — по логике и г)41 — по естествознанию. д) Философию и логику выбрали 11 человек. е) Философию и естествознание посещает 21 студент, ж)а логику и естествознание — 16. з) 4 человека выбрали только философию и логику.

Сколько студентов посещают лекции:

1) по всем трём предметам,

2)только по философии и естествознанию,

3)только по логике и естествознанию,

4)только по философии,

5)только по естествознанию,

6)только по логике,

7)не выбрали ни одну из этих дисциплин.

Каждое высказывание из условия записать в виде логического выражения, строго подписывая друг под другом элементы. Решать систему будем с тех уравнений, где меньше всего неизвестных, попарно вычитая уравнения. При решении стремимся убрать как можно больше неизвестных.

1) Возможные варианты перебираем с учетом

а) + + + + + + + = 81

б) + 0 + 0 + + + 0 + + 0 = 43

в) 0 + + 0 + + 0 + + + 0 = 32

г) 0 + 0 + + 0 + + + + 0 = 41

д) 0 + 0 + 0 + + 0 + 0 + + 0 = 11

е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21

ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16

з) 0 + 0 + 0 + + 0 + 0 + 0 + 0 = 4

2) Четко видно, что = 4. Подписываем под чертой вычисленные значения и убираем использованные уравнения. Ниже приведен подробный ход решения.

а) + + + + + + + = 81

б) + 0 + 0 + + + 0 + + 0 = 43

в) 0 + + 0 + + 0 + + + 0 = 32

г) 0 + 0 + + 0 + + + + 0 = 41

д) 0 + 0 + 0 + + 0 + 0 + + 0 = 11

е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21

ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16

и) 4

а) + + + + + + + = 81

б) + 0 + 0 + + + 0 + + 0 = 43

в) 0 + + 0 + + 0 + + + 0 = 32

г) 0 + 0 + + 0 + + + + 0 = 41

е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21

ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16

и) 4 7

а) + + + + + + + = 81

б) + 0 + 0 + + + 0 + + 0 = 43

в) 0 + + 0 + + 0 + + + 0 = 32

г) 0 + 0 + + 0 + + + + 0 = 41

и) 4 14 9 7

а) + + + + + + + = 81

и) 18 12 11 4 14 9 7

0) + + ++ + + + = 81

и) 18 12 11 4 14 9 7 6

Ответ:1) по всем трём предметам, , 7

2)только по философии и естествознанию, , 14

3)только по логике и естествознанию, , 9

4)только по философии, , 18

5)только по естествознанию, , 11

6)только по логике, , 12

7)не выбрали ни одну из этих дисциплин, , 6

Приложение 4

Отчёт о проделанной работе перед коллегами

6 класс Математика. Решение задач с помощью кругов Эйлера | Презентация к уроку по математике (6 класс):

Конспект урока

6 класс

Предмет: Математика

Тема: Решение задач с помощью кругов Эйлера

Здравствуйте, ребята! Сегодня на занятии мы с вами познакомимся с новым для вас методом решения логических задач — кругами Эйлера. Мы научимся решать некоторые из тех задач, которые входят в группу конкурсных и олимпиадных. Целью нашего урока: является познакомиться с решением простейших логических задач методом кругов.

Разминка

Устно:

Кирпич весит 3кги ещё полкирпича. Сколько весит кирпич?
Два спортсмена на соревновании пробежали по стадиону 8 кругов. Сколько кругов пробежал каждый?
Назовите два числа, разность которых равна их сумме.
Сколько будет: два плюс пять умножить на три?

Изучение нового материала

В математике рисунки в виде кругов, изображающих множества, используются очень давно. Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646-1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил и Леонард Эйлер. Он долгие годы работал в Петербургской Академии наук.

Для наглядной геометрической иллюстрации понятий и соотношений между ними используется диаграммы Эйлера-Венна (круги Эйлера). Если имеются какие-либо понятия А, В, С и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объектами (множествами) — в виде пересекающихся кругов.

Перед решением задачи ответьте сначала на следующие вопросы:

О скольких множествах идет речь в данной задаче?
Какие из перечисленных в задаче данных относятся к разным множествам одновременно?

Задачи разобрать и записать в тетрадь с правильным оформлением: дано, рисунок (круги Эйлера), решение, ответ.

Задача 1. Домашние любимцы. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро — собак. И только у двоих есть и те и другие. Угадайте, сколько у меня подруг?

Решение: Изобразим два круга, так как у нас два вида питомцев. В одном будем фиксировать владелиц кошек, в другом — собак. Поскольку у некоторых подруг есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих. В оставшейся части «кошачьего» круга ставим цифру 4 (6 — 2 = 4). В свободной части «собачьего» круга ставим цифру 3 (5 — 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.

Ответ. 9 подруг.

Задача 2. Библиотеки. В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 — в районной. Сколько учеников не являются читателями школьной библиотеки?

Решение: Пусть круг Ш изображает читателей только школьной библиотеки, круг Р — только районной. Тогда ШР — изображение читателей и районной, и школьной библиотек одновременно. Из рисунка следует, что число учеников, не являющихся читателями школьной библиотеки, равно:

(не Шк.биб) = Р — ШР.

Всего 30 учеников,

Ш = 20 человек,

Р = 15 человек.

Тогда значение ШР может быть найдено так (см. рисунок): ШР = (Ш + Р) — 30 = (20 + 15) — 30 = 5, т.е. 5 учеников являются читателями школьной и районной библиотек одновременно.

Тогда (не Шк.биб) = Р — ШР= 15 — 5= 10.

Ответ: 10 учеников не являются читателями школьной библиотеки.

Задача 3. Любимые мультфильмы. Среди школьников пятого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Винни Пух», «Микки Маус». Всего в классе 28 человек. «Белоснежку и семь гномов» выбрали 16 учеников, среди которых трое назвали еще «Микки Маус», шестеро — «Винни Пух», а один написал все три мультфильма. Мультфильм «Микки Маус» назвали 9 ребят, среди которых пятеро выбрали по два мультфильма. Сколько человек выбрали мультфильм «Винни Пух»?

Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только «Белоснежку» выбрали 16-6-3-1=6 человек. Только «Микки-Маус» выбрали 9-3-2-1=3 человека.

Только «Винни-Пух» выбрали 28-(6+3+3+2+6+1)=7 человек. Тогда, учитывая, что некоторые выбрали по несколько мультфильмов, получаем, что «Винни-Пух» выбрали 7+6+1+2=16 человек.

Задачи на оценку:

Задача 1. Спортивный класс. В классе 35 учеников. 24 из них играют в футбол, 18 — в волейбол, 12 — в баскетбол. 10 учеников одновременно играют в футбол и волейбол, 8 — в футбол и баскетбол, а 5 — в волейбол и баскетбол. Сколько учеников играют и в футбол, и в волейбол, и в баскетбол одновременно?

Задача 2. Из 40 учащихся нашего класса 32 любят молоко, 21 – лимонад, а 15 – и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

Задача 3. 12 моих одноклассников любят читать детективы , 18 – фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

Домашнее задание:

Задача 1. Хобби. Из 24 учеников 5 класса музыкальную школу посещают 10 человек, художественную школу — 8 человек, спортивную школу — 12 человек, музыкальную и художественную школу- 3, художественную и спортивную школу — 2, музыкальную и спортивную школу — 2, все три школы посещает 1 человек. Сколько учеников посещают только одну школу? Сколько учащихся ни в чем себя не развивают?

КОМБИНАТОРИКА. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА.

Щербакова А.Ю. 1

Коренец Е.И. 1

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Именно математика дает

надежнейшие правила:

кто им следует – тому не опасен

обман чувств.

Л. Эйлер

Введение

Во все времена представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов.

Комбинаторика – раздел математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из данных объектов. Особая примета комбинаторных задач – это вопрос, который можно сформулировать таким образом, что он начинался бы словами:

Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».

Выбор объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например конструктору, разрабатывающему новую модель механизма, учёному-агроному, планирующему распределение сельскохозяйственных культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав.

Гипотеза работы: Решение комбинаторных задач с помощью кругов Эйлера развивает творческие способности, помогает при решении олимпиадных задач, имеет практическое применение.

Основополагающий вопрос: А все ли я знаю о комбинаторике?

Проблемный вопрос: Может ли помочь комбинаторика в реальной жизни?

Цель работы: изучить решение логических задач путем построения кругов (диаграмм)Эйлера.

Задачи:

Познакомиться с историей возникновения науки комбинаторики;
Находить возможные комбинации для решения комбинаторных задач
Уметь составлять и решать задачи с помощью кругов Эйлера;
Поработать с ресурсами Internet;
Применять полученные знания в дальнейшем обучении;
Расширить и углубить представление о практическом значении математики в жизни;
Уметь работать с научно-познавательной литературой, анализировать, делать выводы.

Объект исследования : логические задачи.

Методы:отбор источников информации, изучение материала и анализ его.

Актуальность выбранной темы заключается в необходимости решения комбинаторных задач на уроках математики, применении их в жизни, т.к. они имеют социальную значимость, помогают разобраться в новых веяниях жизни. Основа хорошего понимания комбинаторики – умение считать, думать, рассуждать, находить удачные решения задач.

История комбинаторики

Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Комбинаторные мотивы можно заметить в символике китайской «Книги Перемен»(Vвек до н.э.). По мнению её авторов, все в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо. Большой интерес математиков вызывали магические квадраты.(см.Приложение 1) Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Индийцы умели вычислять числа, которые сейчас называют «сочетания».Античные греки рассматривали комбинаторные задачи. Хрисипп (IIIв. до н. э.) и Гиппарх(II в.до н.э.) подсчитывали сколько следствий можно получить из 10 аксиом. У Хрисиппа получилось более миллиона. Во все века математики исследовали задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями. Позднее Д.Кардано провел исследование азартной игры в кости . (Азартными называют те игры, в которых выигрыш зависит не только от умения игрока, но и от случайности). Было замечено, что при многократном бросании однородного кубика (все шесть граней которого отмечены соответственно числами 1, 2, 3, 4, 5, 6) число очков от 1 до 6 выпадают в среднем одинаково часто, иными словами, выражаясь языком математики, выпадение определённого числа очков имеет вероятность, равную 1/6. Аналогично вероятность появления на верхней грани кости чётного числа очков равна 3/6, так как из шести равновозможных случаев чётное число появляется только в трёх. Математически заинтересовались азартной игрой П.Ферма и Б.Паскаль. Помимо азартных игр, комбинаторные методы использовались в криптографии — как для разработки шифров, так и их взломов. Комбинаторика и треугольник Паскаля. Паскаль много занимался биномиальными коэффициентами и открыл их способ вычисления. Число сочетаний можно вычислять не через факториал, а с помощью арифметического треугольника. Строится треугольник: его бедра и вершина состоят из единиц, а в основании каждый элемент строки получается суммированием двух стоящих непосредственно над ним элементов.(см.Приложение 2) Паскаль также как и Лейбниц считается основоположником современной комбинаторики .(см.Приложение 3) А вот сам термин комбинаторика придумал Лейбниц. В 1666г. он опубликовал книгу «Рассуждения о комбинаторном искусстве ». Его ученик — Якоб Бернулли (см.Приложение 4) — основатель теории вероятности, изложил много интересного о комбинаторике. Дал научное обоснование теории сочетаний и перестановок. Изучением размещений занимался Я. Бернулли во второй части своей книги «Искусство предугадывания» в 1713 г., в которой указал формулы для числа размещений из n элементов по k, выводились выражения для степенных сумм .

Позднее обнаружили тесную связь между комбинаторными и аналитическими задачами Абрахам де Муавр Джеймс Стирлинг. Они нашли формулы для нахождения факториала. Окончательно комбинаторику, как раздел математики, оформил в своих трудах Эйлер. Кроме перестановок и сочетаний Эйлер изучал разбиение, а также сочетания и размещения с условиями.

Современным отцом комбинаторики считается Пал Эрдёш. (см.Приложение 5) Он ввел вероятностный анализ. Внимание к комбинаторике повысился во второй половине XX века, с появлением компьютеров.

Многие специалисты в области математики и физики считают, что именно комбинаторная задача может стать толчком в развитии всех технических наук. Некоторые из них всерьез утверждают, что комбинаторика является подспорьем для всех современных наук, особенно космонавтики.

Области применения комбинаторики:

учебные заведения ( составление расписаний)
сфера общественного питания (составление меню)
лингвистика (рассмотрение вариантов комбинаций букв)
география (раскраска карт)
спортивные соревнования (расчёт количества игр между участниками)
производство (распределение нескольких видов работ между рабочими)
агротехника (размещение посевов на нескольких полях)
азартные игры (подсчёт частоты выигрышей)
химия (анализ возможных связей между химическими элементами)
экономика (анализ вариантов купли-продажи акций)
криптография (разработка методов шифрования)
доставка почты (рассмотрение вариантов пересылки)
биология (расшифровка кода ДНК)
военное дело (расположение подразделений)
астрология (анализ расположения планет и созвездий

Теория конфигураций и теория перечисления

Наиболее разработанным разделом комбинаторики является теория конфигураций. Она рассматривает задачи выбора и расположения элементов некоторого множества, в соответствии с заданными правилами. Элементарными комбинаторными конфигурациями являются сочетания, размещения, перестановки. Для подсчёта числа этих конфигураций используются правила суммы и произведения.

Правило суммы:

Если элемент A можно выбрать m способами, а элемент B можно выбрать k способами, то выбор элемента A или B можно осуществить m + k способами.

Правило суммы можно перефразировать на теоретико-множественном языке. Обозначим через | A | число элементов множества A, через A B — объединение множеств A и B, через AxB — декартово произведение множеств A и B. Тогда для непересекающихся множеств A и B выполняется равенство:

| A B | = | A | + | B |.

Обобщением правила суммы является правило произведения.

Правило произведения:

Если элемент A можно выбрать m способами, а после каждого выбора элемента A элемент B можно выбрать k способами, тогда, упорядоченную пару элементов (A, B) можно выбрать m*k способами.

Правило произведения можно распространить на выбор последовательности (x₁, x₂, …, xn) произвольной конечной длиныn. На теоретико-множественном языке правило произведения формулируется так:

| Aх B | = | A | | B |.

Правило размещения.

Назовём множество, содержащееn элементов, n-множеством.

Последовательность (x₁, x₂, …, x_k ) длины k без повторяющихся элементов из элементов данного n-множества назовём k-размещением.

Обозначим символом число размещений из n по k элементов (от фран. «arrangement» — размещение). Используя правило произведения, вычислим число . Пусть произвольное размещение длины k имеет вид: (x₁, x₂, …, x_k ).

Элемент x₁ можно выбрать n способами. После каждого выбора x₁ элемент x₂ можно выбрать (n — 1) способами. После каждого выбора элементов x₁ и x₂ элемент x₃ можно выбрать (n — 2) способами, и т.д. После каждого выбора элементов x₁, x₂, …, x_k-1 элемент x_k можно выбрать (n -(k — 1)) = (n — k + 1) способами. Тогда, по правилу произведения, последовательность (x₁; x₂; , …, x_k ) можно выбрать числом способов, равным

n(n — 1)(n — 2) … (n — k + 1) = (1.1)

Произведение в левой части равенства (1.1) умножим и разделим на (n — k)!, получим:

. (1.2)

Если в форуме (1.2) k = n, то есть число Pn перестановок из n элементов

Pn = n! (от «permutation»- перестановка).

Правило сочетания.

k-подмножество данного n-множества называется k-сочетанием.

Обозначим через число k-сочетаний из данныхn элементов. Формулу для числа получим, рассуждая следующим образом. Если каждое сочетание упорядочить всеми возможными способами, то получим все k-последовательностей изn элементов, без повторений, то есть все k-размещения. Иными словами, Откуда: (1.3) или Предполагая, что n и k — целые положительные числа и 0!=1, сформулируем основные свойства сочетаний.

Основные свойства сочетаний.

Условились, что

Как выбрать формулу? (см.Приложение 6) Сводка формул для всех видов соединений. (см.Приложение 7)

Сочетания и размещения широко используются при вычислении классической вероятности случайных событий.

Пример. В корзине находятся 20 орехов, из которых 7 грецких. Наудачу выбирают 5 орехов. Найти вероятность того, что среди выбранных орехов содержатся 2 грецких.

Решение. Число исходов опыта . Случайное событие A — среди пяти выбранных орехов содержатся 2 грецких ореха. Число исходов, благоприятствующих событию A, равно: . Искомая вероятность .

Задачи.

Найти вероятность того, что случайно выбранное 5-значное (десятичное) число не содержит цифры 5.
Предприятие располагает 5 вакансиями для мужчин, 5 вакансиями для женщин и 4 вакансиями для работников любого пола. В отдел кадров предприятия обратилось 20 человек, среди которых 12 мужчин и 8 женщин. Сколькими способами предприятие может заполнить имеющиеся вакансии?
В классе 25 учеников, из которых 13 юношей и 12 девушек. Сколькими способами 25 учеников могут встать в шеренгу так, чтобы юноши после удаления из строя девушек, оказались построенными по росту; аналогично девушки после удаления из строя юношей оказались построенными по росту?

Круги Эйлера

Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

Автор метода — ученый Леонард Эйлер (1707-1783) (см.Приложение 8) . Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки. Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами. Круги Эйлера имеют прикладное назначение. С их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике. Круги Эйлера можно разделить их на те, что описывают объединение каких-то понятий и описывают пересечение множеств по какому-то признаку. (см.Приложение9)

Пример пересечения — какую профессию выбрать? Нарисую схему в виде кругов Эйлера. Схема сразу расставит все по местам и поможет определиться с выбором. То, что окажется на пересечении всех трех кругов, и есть профессия, которая не только сможет прокормить, но и будет нравиться.

Чертеж, вроде этого, поможет определиться с выбором:

Рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц (в тысячах)
Крейсер \| Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?

Решение:

Опираясь на условия задачи, составим уравнения:

Крейсер | Линкор: 1 + 2 + 3 = 7000
Крейсер: 1 + 2 = 4800
Линкор: 2 + 3 = 4500

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.

Вывод

Круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи. Для этого необходимо запомнить порядок этапов :

Записать краткое условие.
Выполнить рисунок.
Записать данные в круги Эйлера.
Анализировать, рассуждать и записывать результаты в части круга.
Записать ответ.

Задачи:

1. Сколько существует натуральных чисел, меньших 1000, которые делятся на 3 , но не делятся на 2 и на 5?

2. Сколько существует различных десятизначных чисел, состоящих только из нулей и единиц, которые содержат не более трех единиц ?

3. Биатлонист проходит четыре огневые точки, на каждой он делает по 5 выстрелов. Сколько существует различных способов промахнуться не более 4?

4. По результатам одного социологического исследования, было установлено, что из 200 людей смотрящих телевизор, 110 человек смотрят спортивную передачу, 120 – комедии, 85 предпочитаю драмы, 50 смотрят драмы и спорт, 70 – комедии и спорт, 55 смотрят комедии и драмы и 30 человек смотрят все три вида передач. Сколько человек, смотрят спорт или комедии или драмы? сколько человек не смотрят ничего из вышеперечисленного?

5. Человек имеет 10 друзей и течение нескольких дней, приглашает некоторых из них в гости, так что компания, ни разу не повторяется. Сколько дней он может так делать?

6. Найти количество трехзначных чисел, которые делятся на 7, но не делятся на 2 и на 5.

7. На данный момент, в классе 20 учеников, получивших сначала учебного года, хотя одну двойку, 17 учеников, получивших не менее двух двоек, 8 учеников, получивших не менее трех двоек, три ученика получивших не менее 4 двоек, один ученик получивший 5 двоек, больше пяти двое нет ни у кого. Сколько всего двое в журнале?

Задача 1.

Решение:

Определение: множество А называется подмножество множества В, если каждый элемент множества А принадлежит множеству В.

Если в некоторой задаче считается что элементы принадлежат некоторым множествам, то это множество называется универсальным.

Например, в задаче № 1 универсальным множеством можно считать множество чисел, от 1 до 999.

A = количество элементов во множестве А

В = 333

Если число делится на 2 и 3, то число делится на 6

A В = 166

Если число делится на 3 и 5, то число делится на 15

В D = 66

При таком подсчете, мы дважды посчитали числа, которые входят во множество

АВD = 33

(В/А)/D = В — AВ — ВD + AВD = 333 – 166 – 66 + 33 = 134

Задача 2

Определение: Правило суммы.

Все множества способов подсчета можно разбить на пересекающиеся множества. Тогда общее количество способов вычисляется как сумма множеств.

С = = 1-0 единиц

С = = 10-1 единица

С = = 45

С = = 120

120+45+10+1=176

Задача 3.

С = = 1 способ – 0 промахов

C = = 20 способов – 1 промах

С = = 190 способов – 2 промаха

С = =1140 способов – 3 промаха

С = =4845 способов – 4 промаха

Всего 1 + 20 + 190 +1140 + 4845= 6196 способов

Задача 4.

Формула включений и исключений

А ВD = A + В +D — AВ — AD — ВD — AВD

а) А ВD = 110 + 120 + 85 – 70 -55 – 50 + 30 =170

б)200-170=30 человек ничего не смотрят

Задача 5.

Составим таблицу друзей

С = = 10 компаний из 1 человека

С = = 45 компаний из 2 человек

С = = 120 компаний из 3 человек

С = = 210 компаний из 4 человек

С = = 252 компании из 5 человек

С ==210 компаний из 6 человек

С = = 120 компаний из 7 человек

С = =45 компаний из 8 человек

С = =10 компаний из 9 человек

С = = 1 компания из 10 человек

Итого 10+45+120+210+252+210+120+45+10+1= 1023 способов

Задача 6.

Всего 900 трехзначных чисел.

A = 900:7=128 чисел

АВ =900:14=64 числа

АD = 900: 35=25 чисел

АВD =900:70=12 чисел

А = А — АВ — АD + АВD = 128 – 64 – 25 + 12 = 51 число

Задача 7.

Найдем количество учеников, получивших ровно четыре двойки.

3 – 1= 2 ученика получили 4 двойки

Теперь узнаем количество учеников , получивших ровно три двойки, ровно две двойки и ровно одну двойку.

8 – 2 — 1 = 5 учеников получили 3 двойки
17 – 5 – 2 – 1 = 9 учеников получили 2 двойки
20 – 9 – 5 – 2 – 1 = 3 ученика получили 1 двойку
1×3 + 2×9 + 3×5 + 4×2 + 5×1 = 49 двоек в журнале

Вывод

Для решения данных логических задач, использовала круги Эйлера, что позволило успешно решить поставленные задачи. Этот способ показался мне удобным и надежным, так как он упрощает путь к решению задачи, делая его наглядным.

Заключение

В процессе изучения данной темы, я научилась грамотно оперировать такими понятиями как «множество», «объединение множеств», «пересечение множеств», «разность множеств» и использовать их при решении задач. В процессе решения задач я расширила свои знания по математике, познакомилась с ещё одним способом решения задач, который был мне мало знаком. Для решения задач с помощью кругов Эйлера можно воспользоваться алгоритмом, состоящим из нескольких этапов.

Применение кругов Эйлера позволяет легко решить задачи, которые обычным путем разрешимы составлением сложных уравнений. Моя гипотеза подтвердилась. Решения задач с громоздкими условиями и со многими данными просты и не требуют особых умозаключений. Применение кругов Эйлера придает задачам наглядность и простоту.

Практическая значимость заключается в расширении возможностей при решении логических задач. Пригодится для решения задач занимательного характера, позволит применять методы и правила для решения нетрадиционных задач. Приобретенные сведения и знания способствуют повышению интеллектуального развития, помогают развить умение наблюдать и анализировать.

Круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьных уроках, но и вполне себе житейских проблем. Они заставляют задумываться, подходить к решению какой-либо проблемы с разных сторон, уметь выбирать из множества способов решения наиболее простой, легкий путь. Сам Леонард Эйлер говорил: «круги подходят для того, чтобы облегчить наши размышления».

Список использованной литературы

Галеева Р. А. Тренируем мышление. Задачи на сообразительность / Р. А. Галеева, Г. С. Курбанов, И. В. Мельченко – Изд. 2 – е – Ростов н/Д: Феникс, 2006.
Игнатьев. Е.И. В царстве смекалки, или Арифметика для всех: Книга для семьи и школы. Опыт математической хрестоматии в 3 книгах/Худож. Н.Я. Бойко. – Ростов н/Д: Кн. Изд-во, 1995.
Рыбников К.А.Комбинаторный анализ. Очерки истории.-М.: Изд.мехмата МГУ1996.-124с.
История математики под редакцией Юшкевича А.П. М.: Наука Том 1.С древнейших времен до начала Нового времени.1970.
Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4-8 кл. сред. Шк. – 5-е изд. – М.: Просвещение, 1988.
Увлекательные логические задачки, которые будут интересны детям и взрослым. http://logika.vobrazovanie.ru

Приложение

Приложение 1.

Приложение 2.

Приложение 3.

Приложение 4.

Якоб Бернулли.

Приложение 5.

Математика — это орудие, с помощью которого человек познает и покоряет себе окружающий мир.

Пал Эрдеш.

Приложение 6.

Приложение 7.

Приложение 8.

Приложение 9.

Просмотров работы: 5692

Круги Эйлера в информатике

Сегодня разберём задачи на круги Эйлера в информатике.

Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.

Задача (Простая)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Пушкин	3500
Лермонтов	2000
Пушкин \| Лермонтов	4500

Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

Видим, что по запросу «Пушкин» в поисковике нашлось 3500 страниц. По запросу «Лермонтов» — 2000 страниц.

Запрос «Пушкин | Лермонтов» обозначает, что поисковик выдаст страницы, где есть слова про «Пушкина», и страницы, где есть слова про «Лермонтова», а так же могут быть страницы, где написано и про «Пушкина», и про «Лермонтова» одновременно.

Если сложить страницы, в которых написано про «Пушкина» и про «Лермонтова» получается 3500 + 2000 = 5500 страниц. Но почему же при запросе «Пушкин | Лермонтов» получается меньше страниц, всего 4500 ?

Этот факт обозначает то, что когда мы подсчитывали страницы про «Пушкина» (3500 страниц), мы подсчитали и те страницы, где было написано и про «Пушкина», и про «Лермонтова» одновременно.

Тоже самое и для количества страниц, где написано про «Лермонтова» (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про «Пушкина», и про «Лермонтова».

В вопросе спрашивается, сколько страниц будет по запросу «Пушкин & Лермонтов«. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про «Пушкина», и про «Лермонтова».

Отсюда получается:

Пушкин & Лермонтов = (3500 + 2000) — 4500 = 5500 — 4500 = 1000 страниц.

Это и будет ответ!

Теперь решим эту задачу с помощью Кругов Эйлера!

У нас всего есть две сущности: «Пушкин» и «Лермонтов». Поэтому рисуем два пересекающихся круга, желательно разными цветами.

Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию «Пушкин | Лермонтов». Эта операция всегда стремится увеличить площадь, объединить площади других фигур!

Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» «Пушкин | Лермонтов» (4500).

Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.

Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).

Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:

Пушкин & Лермонтов (Количество страниц) = 2000 — 1000 = 1000

Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.

Ответ: 1000

Рассмотрим ещё одну не сложную разминочную задачу.

Задача (Разминочная)

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Кокос \| Ананас	3400
Кокос & Ананас	900
Кокос	2100

Какое количество страниц (в тысячах) будет найдено по запросу Ананас?

Решение:

У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.

Найдём заштрихованную часть красного круга.

Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 — 900 = 1200.

После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!

Ананас (Количество страниц) = 3400 — 1200 = 2200
Ответ: 2200

Разберём классическую задачу из информатики по кругам Эйлера.

Задача (Классическая)

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
(Космос & Звезда) \| (Космос & Планета)	1100
Космос & Планета	600
Космос & Планета & Звезда	50

Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?

Решение:

В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.

Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического «ИЛИ».

Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).

Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда

Теперь отметим вторую скобку Космос & Планета.

В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического «ИЛИ». Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!

Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.

Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!

Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.

Теперь у нас есть все компоненты, чтобы решить эту задачу.

Найдём заштрихованную область.

Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).

Количество страниц в заштрихованной части = 600 — 50 = 550

Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).

Количество страниц (при запросе Космос & Звезда) = 1100 — 550 = 550
Ответ: 550

Закрепляем материал по задачам на Круги Эйлера.

Задача (На закрепление)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Море & Солнце	290
Море & Пляж	355
Море & (Пляж \| Солнце)	465

Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.

Отметим все области для которых нам даны количество страниц.

В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)

Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.

Теперь отметим Море & Пляж.

Теперь отметим Море & Солнце.

Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!

Найдём заштрихованную область!

Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) — Море & Солнце =
= 465 — 290 = 175

Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).

Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) — Количество страниц (в заштрихованной области) 175 =
= 355 — 175 = 180
Ответ: 180

Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.

Задача (с 4 сущностями)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Англия & (Уэльс & Шотландия \| Ирландия)	450
Англия & Уэльс & Шотландия	213
Англия & Уэльс & Шотландия & Ирландия	87

Какое количество страниц (в тысячах) будет найдено по запросу

Англия & Ирландия?

Решение:

Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.

Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.

Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.

Область Уэльс & Шотландия выглядит так:

Добавим к этой области Ирландию через логическое «ИЛИ». Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!

Теперь нужно сделать операцию логического «И» получившийся области с «Англией». Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:

Т.е. это общее между предыдущем серым контуром и красным кругом!

Отметим Англия & Уэльс & Шотландия — это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.

Отметим Англия & Уэльс & Шотландия & Ирландия — это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.

Отметим то, что нужно найти Англия & Ирландия чёрным цветом.

Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!

Найдём, сколько страниц приходится на бирюзовый кусочек:

Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) — Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 — 87 = 126

Найдём искомую чёрную область.

Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) — Количество (для бирюзового кусочка) =
450 — 126 = 324

Это и будет ответ!

Ответ: 324.

Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)

Задача (ЕГЭ по информатике, 2019, Москва)

В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:

Запрос	Найдено страниц (в тысячах)
Суфле	450
Корзина	200
Эклер	490
Суфле & Корзина	70
Суфле & Эклер	160
Корзина & Эклер	0

Сколько страниц (в тысячах) будет найдено по запросу

Суфле | Корзина | Эклер
Решение:

Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!

Так же видим, что логическое «И» между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического «ИЛИ» совпадала бы с суммой этих кругов.

Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.

Отметим всё, что нам дано в условии.

Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.

Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.

Левая заштрихованная область находится просто:

Количество страниц (лев. заштрих. область) =
= Эклер (490) — Суфле & Эклер (160) = 330

Так же найдём площадь правой заштрихованной области:

Количество страниц (прав. заштрих. область) =
= Корзина (200) — Суфле & Корзина (70) = 130

Теперь можно найти искомую жёлтую область

Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910

Задача решена, можно писать ответ.

Ответ: 910

Разберём ещё одну задачу из реального ЕГЭ уже 2020 года

Задача (ЕГЭ по информатике, 2020, Москва)

Запрос	Найдено страниц (в тысячах)
Аврора	50
Крейсер	45
Заря	23
Аврора & Заря	9
Заря & Крейсер	0
Заря \| Крейсер \| Аврора	93

Сколько страниц (в тысячах) будет найдено по запросу

Аврора & Крейсер
Решение:

Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.

Нарисуем все данные на рисунке.

Нужно найти для начала заштрихованную правую часть.

Количество страниц (для двух заштрих. частей) =
З | К | А (93) — Красный круг (50) = 43

Левую заштрихованную область легко найти.

Количество страниц (для левой заштрих. части) =
Синий круг (23) — А & З (9) = 14

Тогда для правой заштрихованной области получается:

Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) — Колич. страниц (для лев. заштрих. части) (14) =
= 43 — 14 = 29

Тогда искомую область легко найти:

Колич. страниц (А & K) =
Зелёный круг (45) — Колич. страниц (для правой заштрих. части) (29) =
45 — 29 = 16
Ответ: 16

На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.

Комбинаторика — круг Эйлера

Комбинаторика (Летняя сессия 1, 2021 г.) — это математика конечных или дискретных объектов. Часто и наиболее классически нас интересует подсчет количества способов, которыми может быть решена определенная проблема. Например, количество способов разбить прямоугольник с использованием прямоугольников и прямоугольников без промежутков или перекрытий — это число Фибоначчи, очень знакомая последовательность чисел. Ответы на многие другие простые задачи подсчета включают биномиальные коэффициенты.

В этом классе мы будем предполагать, что учащиеся уже знакомы с этими основными комбинаторными проблемами и их решениями, чтобы мы могли изучать комбинаторику на более высоком уровне. После краткого обзора комбинаторики на уровне типичных задач конкуренции мы рассмотрим другие, менее известные типы специальных чисел, такие как числа Стирлинга, числа Белла и числа Эйлера. Эти числа удовлетворяют соотношениям, напоминающим отношения биномиальных коэффициентов, но также имеют свои отличительные особенности.Они проявляются в нескольких различных контекстах математики, от задач подсчета до полиномиальных тождеств, что предполагает, что они являются фундаментальными объектами математики.

Мы также изучим методы сита, которые позволяют нам подсчитывать объекты только с желаемыми свойствами. Очень известная проблема ситового метода — проблема расстройства, которая требует от людей количества способов переставить шляпы так, чтобы у каждого была неправильная шляпа. Менее известная, но все же важная проблема метода решета спрашивает для данного подмножества доски, сколько способов разместить ладьи, чтобы никакие двое не атаковали.Фактически, проблема расстановки — это частный случай этой проблемы с расстановкой ладьи!

Мы также рассмотрим частично заказанные наборы. Упорядочивание (или полный порядок) в наборе — это способ взять любые два элемента и сказать, что либо или. Частичное упорядочение — это обобщение, которое позволяет нам сравнивать некоторые пары элементов, говоря, что другие элементы несопоставимы. Например, положительные целые числа с делимостью представляют собой частично упорядоченный набор: заданы два положительных целых числа и, может быть, что или, но может случиться так, что ни одно из них не делит другое.С любым частично упорядоченным набором связан набор функций, называемых алгеброй инцидентности, каждую из которых можно представить в виде матрицы. Алгебра инцидентности фиксирует всю комбинаторную информацию о ЧУМе в простой для использования форме и содержит элементы, которые ведут себя так же, как дзета-функция и функция Мёбиуса для целых чисел.

Наконец, мы изучим производящие функции. Теория производящих функций — очень мощный способ решения комбинаторных задач и исследования их асимптотик.Генерирующие функции обычно хорошо сочетаются с повторениями: они делают решение линейных повторений столь же простым, как нахождение корней многочленов, и мы также можем использовать их для получения повторений, что приводит к некоторым впечатляющим последствиям. Например, существует красивая и полностью явная взаимно однозначная взаимосвязь между двоичными деревьями и семерками двоичных деревьев. Это неверно, если 7 заменяется меньшим числом, отличным от 1. Производящие функции также полезны при изучении асимптотической комбинаторики, где нас может не заботить точное количество решений проблемы, а только приближение, данное в терминах более знакомые функции, такие как многочлены и экспоненциальные функции.

Наборы задач в этом классе будут содержать множество возможных исследовательских задач, над которыми могут работать заинтересованные студенты.

Этот класс будет проходить утром в понедельник, вторник, четверг и пятницу с 9:30 до 11:30 по тихоокеанскому времени в течение 5 недель, начиная с 7 июня. Заявки принимаются 25 апреля . Нажмите здесь, чтобы подать заявку!

Нравится:

Нравится Загрузка …

человек — круг Эйлера

Инструкторы

Саймон Рубинштейн-Сальзедо — основатель и главный преподаватель Euler Circle.Саймон получил докторскую степень в Стэнфордском университете в 2012 году под руководством Акшая Венкатеша в области алгебраической теории чисел. Он провел исследования во многих областях математики, включая теорию чисел, алгебраическую геометрию, комбинаторику, теорию игр, вероятность и комплексный анализ. До основания Euler Circle Саймон преподавал математику в Стэнфордском университете и Дартмутском колледже.

Помимо преподавания в университетах, Саймон более десяти лет преподает математику старшим и старшим школьникам и пользуется огромной популярностью среди своих учеников.В настоящее время он читает лекции по Программе II в математическом лагере Стэнфордского университета (SUMaC), где преподает алгебраическую топологию. Он работал в The Art of Problem Solving, преподавал на многих математических мероприятиях и руководил многими математическими кружками в Bay Area. Он также является тренером команды ARML области залива Сан-Франциско, которая выиграла национальный чемпионат три года подряд. Его самое большое притязание на известность в жизни, вероятно, связано с тем, что в его честь назван трюк с факторингом.

Саймон также успешно руководил исследовательскими проектами по математике для старшеклассников, в результате чего на данный момент было написано пять оригинальных статей в соавторстве со студентами, и в настоящее время ведется работа над другими проектами.Его статьи можно найти на его сайте. Пожалуйста, свяжитесь с ним по адресу [email protected].

Помимо математики, Саймон также заядлый музыкант, шахматист и каллиграф.

Помощники учителя

Аарон Кауфер — младший студент Стэнфорда, изучает математику и информатику. Интересуется алгеброй и теорией чисел. Он любит репетиторство и работает преподавателем математического факультета Стэнфорда. Он провел исследования в области коммутативной алгебры, написал статью и выступил с докладом о своих результатах.Помимо математики, ему нравится стрельба из лука и кубики Рубика.

Аарон Лин — недавний выпускник Массачусетского технологического института по математике и информатике, его особенно интересуют темы, связанные с топологией, комбинаторикой и теорией сложности вычислений. Он всегда ищет новые книги для чтения, головоломки и кого-нибудь, с кем можно поиграть в го (Weiqi).

Алекс ДеВиз в настоящее время изучает информатику в Калифорнийском университете в Беркли. Его основные исследовательские интересы связаны с машинным обучением и его приложениями.Помимо учебы, он любит рисовать и изучать языки (корейский и японский).

Александр Ричардсон — старший преподаватель Калифорнийского университета в Беркли по специальности математика и второстепенная физика. В настоящее время занимается исследованиями в области дифференциальной геометрии, но интересуется анализом, комбинаторикой, дифференциальными уравнениями, алгеброй. По сути, любой урок математики, который он посещал, вызывает новый интерес.

Помимо академических кругов, он увлекается пешим туризмом, скалолазанием, пением, театром, музыкальным театром и поиском новых впечатлений.

Элис Ян — студентка старшего курса Стэнфордского университета, изучает математику. Ее интересы включают области вероятности и оптимизации / динамических систем. Ранее она учила студентов как соревновательной, так и неконкурентной математике. Помимо математики, она любит играть и слушать музыку.

Энни Чен — студентка Стэнфордского университета, изучает математику. Ее интересы включают анализ, вероятность и комбинаторику.Она провела исследования в области арифметической динамики и теории вероятностей, написала доклад и выступила с презентацией на конференции о своей работе. Кроме того, ранее она обучала математике многих учеников средних и старших классов средней школы. В свободное время Энни любит играть в теннис и карточные игры.

Анника Мауро — студентка факультета математики в Стэнфорде. Она широко интересуется математикой, особенно комплексным анализом, алгебраической топологией и комбинаторикой, а также проводила исследования в области дискретной математики.Она также увлечена информатикой и физикой. В свободное время она любит читать, проводить время на свежем воздухе и рисовать.

Бен Хеллер — студент Стэнфорда, изучает математику. Его интересы охватывают практически все области математики, но он питает слабость к математической логике, анализу и дифференциальной топологии. Он проводил исследования в области теории вероятностей и имеет опыт преподавания студентов в рамках программы взаимного обучения на математическом факультете Стэнфордского университета.Помимо математики, ему нравится возиться с Linux и слушать музыку.

Брайан Ху — аспирант UCSD, изучает математику. Его интересы включают теорию чисел, алгебраическую геометрию и комбинаторику. Ранее он был помощником инструктора в математическом кружке Лос-Анджелеса. Помимо математики, Брайан любит баскетбол и всевозможные игры.

Кейси Войчик — аспирант Стэнфорда, занимается топологической фотоникой.У него широкий интерес к математике и физике, и ему особенно нравится видеть, как разнообразные математические концепции могут помочь объяснить простые и универсальные физические явления. В свободное время он любит понаблюдать за птицами и заниматься другими видами активного отдыха.

Кэтрин Валенмайер — растущая аспирантка второго курса Калифорнийского университета в Сан-Диего. Ей интересно узнать больше о дискретной геометрии, комбинаторике и математическом образовании. Она работала онлайн-преподавателем в Larson Texts, Inc. и ТА в Университете Ганнона и UCSD, и она хотела бы продолжить карьеру преподавателя.Помимо математики, Екатерина любит готовить и печь и впервые с нетерпением ждет прыжков с парашютом.

Клайд Хьюбрегтсе окончил Массачусетский технологический институт в 2020 году со степенью в области физики и математики для компьютерных наук. В настоящее время он работает инженером-программистом в стартапе в области ядерной энергетики под названием Oklo в Саннивейле. Он работает на стыке научных вычислений и машинного обучения в разработке нелинейных моделей динамики ядра. В колледже он был игроком в водное поло NCAA и до сих пор проводит время, тренируясь и соревнуясь в Bay Area.

Доминик Джу — студентка Брауна, изучает математику. Его особенно интересуют геометрия и топология, а также среднее математическое образование. Его другие академические интересы включают лингвистику и музыку. В свободное время играет в шахматы, разгадывает кроссворды и читает.

Даун Ким — недавний выпускник Калифорнийского университета в Беркли в области статистики и анализа данных. Его интересы включают теорию вероятностей, машинное обучение и случайные процессы.Вне школы он увлекается гольфом, сноубордом и историей.

Эрик Франкель учится на втором курсе Стэнфорда, изучает математику. Он интересуется анализом, вероятностью, комбинаторикой и динамическими системами, а также проводил исследования в области теории вероятностей. Эрик является членом правления Стэнфордской математической организации и обучал студентов соревновательной и неконкурентной математике. Помимо математики, Эрик любит заниматься спортом, есть, программировать и плохо стричься.

Эрик Ким — недавний выпускник Стэнфордского университета по математике.Его интересы включают алгебру, теорию чисел, функциональный анализ, вероятность и дифференциальные уравнения. Он провел исследования в области комплексного анализа и получил диплом бакалавриата. Помимо математики, он любит петь и решать кубики Рубика.

Эйоб Цегайе — младший студент Стэнфорда, изучает математику. Его интересы включают алгебру и комбинаторику. Он имеет опыт исследований в области аддитивной комбинаторики, теории вероятностей и теории конечных групп. Кроме того, ранее он обучал несколько старшеклассников.Помимо математики, он любит читать, слушать музыку и играть в суперсемейку.

Гаутам Манохар — первокурсник Стэнфорда, изучает математику. Он увлекается анализом, дифференциальными уравнениями и теорией чисел. Он также интересуется математическим письмом и коммуникацией, а также информатикой, особенно алгоритмами и структурами данных. В свободное время он любит изучать языки, заниматься баскетболом и писать.

Хавьер Эчеваррия — старший преподаватель Стэнфордского университета, изучает математику и информатику.Его интересуют уравнения в частных производных, дифференциальная геометрия и математическая физика. Помимо оценки курсов бакалавриата, он также был наставником для сокурсников со времен старшей школы. В свободное время любит плавать и играть на пианино.

Джейдип Сингх — выпускник Стэнфордского университета, изучает математику. Он интересуется пересечениями математики и физики, поскольку они проявляются в вероятности, PDE и геометрическом анализе. Он имеет опыт исследований в области общей математической теории относительности и калибровочной теории, а также работал преподавателем математического анализа в Стэнфорде.Вне школы он любит печь, играть в теннис и слушать музыку.

Цзячжэнь Тан — аспирант Калифорнийского университета в Беркли, изучает математику. Ее интересы включают теорию чисел, алгебру, функциональный анализ и классическую геометрию. Будучи старшекурсником, она организовывала занятия по паззлу для математического клуба Корнелла и преподавала в Центре поддержки математики при кафедре. Летом она также работала консультантом в Росс и ПРОМИС. Ей нравится делать многогранные модели (модульное оригами, воздушные шары), учить кататься на коньках, чернику и число 1207.

Карен Ге — студентка Стэнфорда, которая надеется улучшить математическое образование. Она интересуется областями теории чисел, алгебраической топологии и криптографии. Карен имеет обширный опыт преподавания и обучения как в соревновательной, так и в неконкурентной математике. Помимо математики, она любит играть в настоящую фрисби, увлекаться чудесами оркестровой музыки и писать стихи.

Кэти Ву — старший изучает математику.Она интересуется теорией чисел и криптографией, и проводит их исследования. Она была президентом студенческой математической организации Стэнфорда, а в настоящее время является консультантом математического факультета. Она также была консультантом математического лагеря Стэнфордского университета и ассистентом курса криптографии на факультете компьютерных наук. Помимо математики, она увлекается танцами и оригами.

Матео Аттанасио учится в Стэнфорде, изучает математику. Его интересы включают алгебру, теорию чисел и топологию.У него есть опыт преподавания на математическом факультете Стэнфордского университета. Помимо математики, его интересы включают скалолазание и историю.

Матин «Мат» Гавамизаде недавно с отличием окончил Калифорнийский университет в Беркли со степенью в области электротехники и информатики (EECS) и прикладной математики с акцентом на теорию вероятностей. В настоящее время он является приглашенным исследователем в MIT Probabilistic Computing Project (ProbComp). Перед тем, как поступить в докторантуру Массачусетского технологического института, Матен в следующем году уходит, чтобы закончить Часть III математических испытаний по статистике в Кембриджском университете.Его математические интересы — анализ, теория вероятностей, статистика и вычисления, особенно вероятностные вычисления. Помимо математики и компьютеров, Матин любит читать, думать, готовить и комедии.

Максим Гилула переехал из Москвы, Россия, в Сан-Матео, Калифорния, со своей семьей, когда ему было шесть лет. Он получил степень бакалавра в Калифорнийском университете в Ирвине, а затем переехал в Филадельфию для учебы в аспирантуре по математике в Университете Пенсильвании. Его наставниками в UCI были Сара Эйххорн, Мартин Земан и Светлана Житомирская; в UPenn Ричард Кадисон и Фил Грессман.Проработав в течение трех лет приглашенным доцентом в Университете штата Мичиган, он вернулся домой в Район залива, чтобы присоединиться к Stanford OHS. Сейчас он живет в Фостер-Сити с сыном, женой и котом.

В свободное время он любит играть в видеоигры, гулять и находить новые вкусные места, где можно поесть. Он также всю жизнь любил теннис, играл в лигах и соревновался, когда мог.

Его исследования включали бесконечные серии, осциллирующие интегралы и развязку, хотя в последние несколько лет он не проводил никаких исследований.

Майя Санкар — студентка первого курса математического факультета Стэнфорда. Ее интересы лежат в области теории графов и комбинаторики. Вне школы Майя любит заниматься музыкой, читать и вязать, и рада вернуться домой в Калифорнию, где она может круглый год наслаждаться солнцем.

Можган Мирзаи — недавний выпускник Калифорнийского университета в Сан-Диего по специальности «математика». В частности, она интересуется комбинаторикой, вычислительной геометрией и теорией графов. Помимо математики, Можган любит заниматься спортом, играть в шахматы и рисовать.

Никлас Маджамаки — младший студент Калифорнийского университета в Беркли, изучает электротехнику и информатику. Он интересуется вероятностью, теорией чисел и глубоким обучением. Он преподавал как в средней школе, так и на курсах бакалавриата. Помимо учебы, он входит в команду Cal Triathlon и любит ходить в походы, ходить на пляж и есть хорошую еду.

Ник Кастро — выпускник Стэнфордского университета, изучает математику. Его интересы включают реальный анализ, вероятность, алгебраическую топологию и теорию алгебраических чисел.Он закончил курсы бакалавриата и магистратуры и работал консультантом в математическом лагере Стэнфордского университета. Помимо математики, ему нравится заниматься боевыми искусствами.

Никхил Саху — недавний выпускник Калифорнийского университета в Беркли, где он получил степень бакалавра математики. Его основные математические интересы связаны с дифференциальной топологией, но он выполнял исследовательские проекты в области симплектической топологии, исчисления Шуберта и геометрии Минковского. С 2018 года Нихил также читал лекции и выставлял оценки в кружке математики Беркли, где ему очень нравится делиться интересной математикой со студентами всех уровней.Помимо учебы и преподавания, Нихил любит пешие прогулки и скалолазание.

Нина Зубрилина — студентка Стэнфордского университета, изучает математику. Она увлекается комбинаторикой, аналитической теорией чисел, анализом, геометрией и всем, что связано с упаковкой сфер. Она провела исследования в области комбинаторики и теории чисел и написала четыре статьи о своей работе.

Помимо кружка Эйлера, ее педагогический опыт включает в себя работу TA для других математических кругов, TA в классе в Московской средней школе № 57, работу консультантом и TA в летнем математическом лагере, а также чтение серии лекций в Московском отделении Московской средней школы №57. Высшая школа экономики.

Нитья Мани — студент, изучающий математику в Стэнфордском университете. Она увлечена проблемами алгебраической теории чисел и экстремальной комбинаторики и провела исследования в обеих областях. Некоторые текущие области, в которых она изучает больше, включают геометрическую теорию меры и теорию поля локальных классов. В дополнение к тому, что последние 3 года Нитья работает ассистентом преподавателя в Euler Circle, она координирует программу обучения сверстников на факультете математики Стэнфорда и закончила многие математические классы Стэнфорда.

Нивен Ахенджанг — старший преподаватель Стэнфорда, изучает математику. Его математические интересы включают алгебраическую теорию чисел, алгебраическую топологию и комплексную геометрию, и он опубликовал исследования по теории чисел. В Стэнфорде он оценивал и обучал студентов в математических классах, а также был консультантом и техническим специалистом в математическом лагере Стэнфордского университета. Помимо математики, Нивен любит видеоигры, всевозможные виды спорта и выступает в Стэнфордской команде по прыжкам со скакалкой.

Онебучи Экента — аспирант математического факультета Калифорнийского университета в Беркли. Он изучает вычислительную линейную алгебру и научные вычисления. Он также интересуется теорией сложности вычислений. Из хобби ему нравится смотреть аниме и играть с компьютерными программами и схемами.

Пит Ригас — недавний выпускник Корнельского университета, получивший диплом бакалавра математики с отличием и степень магистра статистики.Он интересуется теорией вероятностей, статистической механикой, вариационными квантовыми вычислениями, синтетической биологией и прогнозированием автономных космических аппаратов. Он провел исследования во всех этих областях, уделяя особое внимание количественной оценке точности оценок вероятности пересечения для разбавленной модели Поттса, которая имеет общие связи с моделью Loop O (n), в дополнение к нескольким предстоящим работам по различным статистическим моделям. . В свободное время он любит бегать, ходить на пляж и исследовать разные части Южной Калифорнии.

Куинн Грейсиус — выпускник Стэнфордского университета, изучает математику. Он интересуется алгебраической геометрией, теорией чисел и алгебраической топологией, а также провел исследования представлений Галуа, возникающих из абелевых многообразий. Ранее он преподавал алгебру и теорию чисел для старшеклассников в районе залива. В свободное время Куинн любит играть на пианино, читать и играть в футбол.

Рачана Мадукара — студентка Массачусетского технологического института, изучает математику.Она в первую очередь интересуется элементарной и аналитической теорией чисел и имеет опыт исследований в этих областях. Помимо математики, Рачана любит квесты, скалолазание, готовку и путешествия.

Раджашри (Раджи) Агравал — первокурсник Университета Джорджа Мейсона. Ранее Раджи бросил школу в Индии, чтобы продолжить самостоятельное обучение. В настоящее время она использует свой образовательный опыт, чтобы проводить эксперименты в обучении, особенно в области муссонной математики.орг. Больше всего ей нравится логика, теория категорий и комбинаторика. Помимо математики, Раджи интересует надежность машинного обучения, экономики свободного рынка и финансового инжиниринга. В свободное время она поет классическую хиндустани, танцует свинг, готовит и занимается групповой медитацией с друзьями.

Ричард Йи только что окончил Массачусетский технологический институт по специальности математика и физика. Начиная с этой осени, он будет защищать докторскую степень по математике в Калифорнийском университете в Сан-Диего. Интересуется теорией чисел и алгебраической геометрией.Он тренировал несколько студентов по соревновательной математике. Помимо математики, этим летом он проводил время, играя в шахматы, размышляя о философии и читая разные книги.

Райан Смит — студент магистратуры по информатике в Стэнфорде. Его интересы лежат в области криптографии, теории сложности вычислений и теории алгебраических чисел. У него есть опыт TA в математическом лагере Стэнфордского университета, а также на факультете информатики в Стэнфорде.Помимо математики, он любит читать, играть в музыкальный театр и всевозможные игры.

Сойер Добсон — студентка бакалавриата Стэнфорда, изучает математику. Он в первую очередь интересуется теорией чисел и криптографией, и у него есть опыт написания задач для математических соревнований. Перед тем, как поступить в Стэнфорд, он преподавал в математическом клубе в старшей школе в Сан-Франциско. Помимо математики, Сойер увлекается программированием, волейболом и настольными играми.

Сойер Робертсон в настоящее время учится на первом курсе аспирантуры по математике Калифорнийского университета в Сан-Диего.Его исследовательские интересы обычно связаны с комбинаторикой и приложениями к науке о данных, с особым упором на теорию спектральных графов.

Шардул Чиплункар — студент 22 года в Массачусетском технологическом институте, изучает математику и информатику. Его математические интересы включают логику, формальные системы, теорию вычислений и теорию языков программирования; Его другие академические интересы включают лингвистику и вычислительную когнитивную науку. В настоящее время он занимается исследованиями в области формальной верификации и синтеза программ.Он также любит слушать и создавать музыку (особенно классическую хиндустани), преподавать и вращать огонь.

Шерри Саркар — старший специалист по информатике в Технологическом институте Джорджии. Ее научные интересы — комбинаторика, теоретическая информатика и дискретная геометрия. У нее есть несколько докладов и выступлений на конференциях в этих областях. Шерри также закончила несколько курсов по математике и информатике в Технологическом институте Джорджии. Помимо исследований, она катается на валунах и смотрит аниме.

Соня Чу — первокурсница Стэнфордского университета.Она интересуется широким спектром областей математики, а также междисциплинарными исследованиями между математикой и другими областями. Соня обучала учеников от начальной до средней школы как по соревновательной, так и по внеконкурсной математике. Кроме того, она является автором лабораторных руководств для курсов по криптографии в колледжах. Помимо математики, она любит читать, играть на кларнете и кататься на лыжах.

Тим Ву — студент Стэнфорда, изучает математику. Его интересы включают теорию чисел, комбинаторику и теорию графов, и он провел исследования в области теории графов.Перед тем, как присоединиться к Euler Circle, Тим работал и преподавал математический кружок дома в Мичигане. Помимо математики, он любит слушать музыку и торговать акциями.

Тайлер Шибата учится на втором курсе Стэнфорда, изучает математику. Хотя его математические интересы охватывают множество областей, ему особенно нравится изучение линейной алгебры, случайных процессов и реального анализа. Несмотря на то, что до колледжа у него не было формального интереса к математике, он влюбился в мотивацию, лежащую в основе определенных тем, после просмотра вдохновляющих видеороликов 3Blue1Brown.Помимо математики, он любит заниматься академической греблей в Стэнфордском университете, готовить и есть вкусные блюда, а также играть на саксофоне.

Уильям Си — студент Стэнфордского университета, изучает математику и информатику. Он интересуется всеми видами математики, особенно алгеброй, теорией чисел и комбинаторикой. На протяжении многих лет он обучал студентов как соревновательной, так и неконкурентной математике и получил оценки за несколько онлайн-классов по математике. Помимо математики, Уильям любит программировать, заниматься физикой, играть в баскетбол и есть.

Елена Мандельштам — старший преподаватель Стэнфорда, изучает математику. С 2016 года она работала ассистентом в Euler Circle, а зимой 2017-18 года — в лагере Эйлера в Ирвине. Помимо кружка Эйлера, у Елены есть опыт преподавания математического кружка в своей русской школе, когда она училась в старшей школе, в качестве консультанта в математическом лагере Стэнфордского университета и индивидуального обучения студентов. Ее основные научные интересы — комбинаторика и анализ. Она провела исследования в области математической биологии, комбинаторики и эргодической теории и написала пять статей о своей работе.Помимо математики, Елена любит скалолазание, играет в настольные игры, а также читает и пишет стихи.

Юзу Идо учится на втором курсе Стэнфордского университета, изучает математику и музыку. Она интересуется несколькими областями математики, в настоящее время уделяет особое внимание алгебре. Она провела исследования по целочисленным формам и эллиптическим кривым и работает преподавателем в Стэнфордской математической организации бакалавриата. Помимо математики, она любит заниматься музыкой, посещать интересные курсы по разным предметам и хорошо поесть.

Зизай Цуй учится в Duke. Он хочет изучить идеи и силы, которые сформировали современное общество. Его цель — быть человеком эпохи Возрождения.

Он намеревается посвятить свою жизнь поискам Истины и Красоты, и математика кажется комбинацией этих двух!

Более подробную информацию можно найти на его веб-сайте.

Зои Химвич изучает математику в старшем классе Стэнфорда. С зимы 2018 года она работает техническим специалистом в Euler Circle.Другой ее опыт преподавания включает обучение TA в Стэнфордском математическом кружке и аттестацию на курсах математики в бакалавриате. Она провела исследования в нескольких областях математики, включая теорию графов, топологические квантовые теории поля и математику филогенетики. В свободное от математики время Зоя изучает английскую литературу и любит изучать новые языки.

Нравится:

Нравится Загрузка …

Классы — круг Эйлера

Каждую четверть мы проводим два класса.

Наши продвинутые классы встречаются вечером по вторникам и средам с 18:30 до 20:30 в Пало-Альто.По вторникам новый материал представлен в формате интерактивной лекции. По средам проводятся тематические занятия, на которых учащиеся работают в небольших группах, чтобы укрепить понимание материала, представленного накануне, а также обсуждают проблемы с предыдущей недели. Студенты также пишут пояснительную работу по выбранной ими теме, относящейся к учебному материалу, но не освещенной в нем напрямую, а особенно целеустремленные студенты будут иметь возможность работать над открытыми исследовательскими проблемами.
Наш промежуточный класс по математике, основанный на доказательствах, проводится по понедельникам с 17:30 до 20:30 в Пало-Альто. В начале урока вводится новый материал, после чего студенты работают над задачами и корректурой, а также перебирают задачи предыдущей недели. Эта последовательность рассчитана на год, после чего успешные ученики будут подготовлены к занятиям на курсах продвинутого уровня в следующем году. Осенью класс будет посвящен доказательствам по теории чисел; зимой речь пойдет о доказательствах в комбинаторике; Весной речь пойдет о пруфах в разборе.Это занятие повторяется каждый год.

Летом 2021 года мы предлагаем продвинутые занятия по комбинаторике и комбинаторной теории игр.

В 2021–2022 году темами для продвинутых классов являются производящие функции осенью, доказательства из КНИГИ зимой и дифференциальная геометрия весной.

Вот расширенные классы, которые мы предлагали в прошлые годы: В 2015–2016 году мы предлагали занятия по абстрактной алгебре, криптографии и комплексному анализу.В 2016–2017 годах мы предлагали занятия по комбинаторной теории игр, доказательствам из КНИГИ и теории колец / алгебраической геометрии. В 2017–2018 годах мы предлагали занятия по комбинаторике, математике Эйлера и p-адическому анализу. В 2018–2019 году мы предлагали занятия по теории чисел, эргодической теории и аналитической теории чисел. В 2019–2020 годах мы предлагали занятия по криптографии, бесконечным рядам и абстрактной алгебре. Летом 2020 года мы предложили уроки теории колец и алгебраической геометрии и доказательства из КНИГИ.В 2020–2021 году мы предложили занятия по цепям Маркова и комплексному анализу.

В будущем мы предложим множество других классов, основанных на интересах студентов и преподавателей, включая различные классы по теории чисел, абстрактной алгебре, анализу, комбинаторике, топологии, вероятности, теории игр и многому другому.

Сейчас мы принимаем заявки на занятия летом и осенью 2021 года. Нажмите здесь, чтобы подать заявку! Заявки принимаются до 30 мая и 25 июля для летнего и осеннего классов соответственно.

Как это:

Нравится Загрузка …

Эйлеровы и гамильтоновы пути и схемы

Результаты обучения

Определить, есть ли у графа путь Эйлера и / или схема
Используйте алгоритм Флери, чтобы найти схему Эйлера
Добавьте ребра к графу, чтобы создать схему Эйлера, если таковой не существует
Определите, имеет ли граф гамильтонову схему или путь
Найдите оптимальную гамильтонову схему для графа, используя алгоритм грубой силы, алгоритм ближайшего соседа и алгоритм сортировки ребер
Определите связный граф, который является остовным деревом
Используйте алгоритм Крускала для формирования остовного дерева и остовного дерева с минимальной стоимостью

В следующем уроке мы исследуем определенные виды путей через граф, называемый эйлеровыми путями и схемами.Пути Эйлера — это оптимальный путь через граф. Они названы в его честь, потому что первым их определил Эйлер.

Подсчитав количество вершин графа и их степень, мы можем определить, есть ли у графа путь Эйлера или схема. Мы также изучим другой алгоритм, который позволит нам найти схему Эйлера, как только мы определим, что в графе она есть.

Схемы Эйлера

В первом разделе мы построили график мостов Кенигсберга и спросили, можно ли пройти через каждый мост один раз.Поскольку Эйлер впервые изучил этот вопрос, эти типы путей названы в его честь.

Путь Эйлера

Путь Эйлера — это путь, который использует каждое ребро в графе без повторов. Будучи путем, он не должен возвращаться в начальную вершину.

Пример

На графике, показанном ниже, есть несколько путей Эйлера. Один из таких путей — CABDCB. Путь показан стрелками вправо с порядком нумерации ребер.

Схема Эйлера

Схема Эйлера — это схема, которая использует каждое ребро графа без повторов.Поскольку цепь является схемой, она должна начинаться и заканчиваться в одной и той же вершине.

Пример

На приведенном ниже графике показано несколько возможных схем Эйлера. Вот пара, начинающаяся и заканчивающаяся в вершине A: ADEACEFCBA и AECABCFEDA. Второй показан стрелками.

Вернитесь к примеру с путями Эйлера — есть ли в этом графе контур Эйлера? Несколько попыток скажут вам нет; в этом графе нет схемы Эйлера. Когда мы работали с кратчайшими путями, нас интересовал оптимальный путь.В случае эйлеровских путей и схем нас в первую очередь интересует, существует ли эйлеров путь или схема .

Почему нас волнует, существует ли схема Эйлера? Вспомните нашего инспектора газонов жилищного строительства из начала главы. Инспектор газона заинтересован в том, чтобы как можно меньше гулять. Идеальной ситуацией была бы трасса, которая охватывает все улицы без повторов. Это схема Эйлера! К счастью, Эйлер решил вопрос о том, будет ли существовать путь или схема Эйлера.

Теоремы Эйлера о путях и цепях

Граф будет содержать путь Эйлера, если он содержит не более двух вершин нечетной степени.

Граф будет содержать схему Эйлера, если все вершины имеют четную степень

Пример

В приведенном ниже графе вершины A и C имеют степень 4, так как в каждую вершину ведет 4 ребра. B — степень 2, D — степень 3, а E — степень 1. Этот граф содержит две вершины с нечетной степенью (D и E) и три вершины с четной степенью (A, B и C), поэтому теоремы Эйлера говорят нам об этом. граф имеет путь Эйлера, но не контур Эйлера.

Пример

Есть ли схема Эйлера на графике инспектора газонов жилищного строительства, который мы создали ранее в этой главе? Все выделенные вершины имеют нечетную степень. Поскольку существует более двух вершин с нечетной степенью, на этом графе нет путей Эйлера или схем Эйлера. К сожалению, нашему инспектору газонов придется вернуться назад.

Пример

Когда идет снег в одной и той же жилой застройке, снегоочиститель должен обрабатывать обе стороны каждой улицы.Для простоты предположим, что плуг выключается достаточно рано, чтобы он мог игнорировать правила дорожного движения и ехать по любой стороне улицы в любом направлении. Это можно визуализировать на графике, нарисовав по два ребра для каждой улицы, представляющих две стороны улицы.

Обратите внимание, что каждая вершина в этом графе имеет четную степень, поэтому у этого графа есть схема Эйлера.

Следующее видео дает больше примеров того, как определить путь Эйлера и схему Эйлера для графа.

Алгоритм Флери

Теперь мы знаем, как определить, есть ли в графе цепь Эйлера, но если она есть, как ее найти? Хотя обычно можно найти схему Эйлера, просто вытащив карандаш и попытавшись найти ее, более формальным методом является алгоритм Флери.

Алгоритм Флери

1. Начните с любой вершины, если найдете схему Эйлера. Если вы найдете путь Эйлера, начните с одной из двух вершин с нечетной степенью.

2. Выберите любое ребро, выходящее из вашей текущей вершины, при условии, что удаление этого ребра не разделит граф на два несвязанных набора ребер.

3. Добавьте это ребро в схему и удалите его с графика.

4. Продолжайте, пока не закончите.

Пример

Найдите на этом графе схему Эйлера, используя алгоритм Флери, начиная с вершины A.

Попробуйте

Имеется ли на приведенном ниже графике схема Эйлера? Если да, то найдите его.

В следующем видео представлены другие примеры использования алгоритма Флери для поиска схемы Эйлера.

Эйлеризация и проблема китайского почтальона

Не на каждом графике есть эйлеров путь или цепь, но нашему инспектору газонов все равно нужно проводить проверки. Ее цель — свести к минимуму время ходьбы. Для этого ей придется дублировать некоторые ребра в графе, пока не появится схема Эйлера.

Эйлеризация

Эйлеризация — это процесс добавления ребер к графу для создания схемы Эйлера на графе.Чтобы эулеризовать граф, ребра дублируются, чтобы соединить пары вершин с нечетной степенью. Соединение двух вершин нечетной степени увеличивает степень каждой, давая им обе четные степени. Когда две вершины нечетной степени не связаны напрямую, мы можем продублировать все ребра пути, соединяющего их.

Обратите внимание, что мы можем только дублировать ребра, но не создавать ребра там, где их раньше не было. Дублирование краев означало бы идти или проезжать по дороге дважды, а создание края там, где раньше не было, сродни прокладке новой дороги!

Пример

Для показанного прямоугольного графика показаны три возможных эулеризации.Обратите внимание, что в каждом из этих случаев вершины, которые начинались с нечетных степеней, имеют четные степени после эулеризации, что позволяет использовать схему Эйлера.

В приведенном выше примере вы заметите, что последняя эулеризация потребовала дублирования семи ребер, в то время как первые два потребовали дублирования только пяти ребер. Если бы мы выполняли эулеризацию графа, чтобы найти пешеходный путь, нам бы потребовалась эулеризация с минимальным дублированием. Если бы у ребер были веса, представляющие расстояния или затраты, тогда мы хотели бы выбрать эулеризацию с минимальным общим добавленным весом.

Попробовать

Эйлеризовать показанный граф, затем найти схему Эйлера на эйлеризованном графе.

Пример

Еще раз посмотрев на график нашего инспектора лужайки из примеров 1 и 8, вершины с нечетной степенью будут выделены. С восемью вершинами нам всегда придется дублировать как минимум четыре ребра. В этом случае нам нужно продублировать пять ребер, поскольку две вершины нечетной степени не связаны напрямую. Без утяжелителей мы не можем быть уверены, что это эулеризация, которая сводит к минимуму пешую прогулку, но выглядит она неплохо.

Проблема поиска оптимальной эулеризации называется проблемой китайского почтальона. Это имя дал американец в честь китайского математика Мей-Ко Квана, который впервые изучил проблему в 1962 году, пытаясь найти оптимальные маршруты доставки для почтовых перевозчиков. Эта проблема важна при определении эффективных маршрутов для мусоровозов, школьных автобусов, счетчиков парковок, дворников и т. Д.

К сожалению, алгоритмы решения этой проблемы довольно сложны.Некоторые более простые случаи рассматриваются в упражнениях

На следующем видео показан другой вид поиска проблемы эйлеризации газонокосилки.

Гамильтоновы схемы

Задача коммивояжера

В последнем разделе мы рассмотрели оптимизацию пешеходного маршрута для почтового перевозчика. Чем это отличается от требований драйвера доставки пакетов? В то время как почтовый перевозчик должен был пройти по каждой улице (краю), чтобы доставить почту, водителю, занимающемуся доставкой посылок, вместо этого необходимо посетить все из набора пунктов доставки.Вместо того, чтобы искать схему, которая покрывает каждое ребро один раз, поставщик пакета интересуется схемой, которая посещает каждую вершину один раз.

Гамильтоновы схемы и пути

Гамильтонова схема — это схема, которая посещает каждую вершину один раз без повторов. Поскольку цепь является схемой, она должна начинаться и заканчиваться в одной и той же вершине. Гамильтонов путь также посещает каждую вершину один раз без повторов, но не обязательно должен начинаться и заканчиваться в одной и той же вершине.

гамильтоновых схем названы в честь Уильяма Роуэна Гамильтона, который изучал их в 1800-х годах.

Пример

Одна гамильтонова схема показана на графике ниже. На этом графе возможно несколько других гамильтоновых схем. Обратите внимание, что схема должна посетить каждую вершину только один раз; нет необходимости использовать каждую грань.

Эту схему можно обозначить последовательностью посещенных вершин, начинающихся и заканчивающихся в одной и той же вершине: ABFGCDHMLKJEA. Обратите внимание, что одна и та же схема может быть записана в обратном порядке или начинаться и заканчиваться в другой вершине.

В отличие от схем Эйлера, здесь нет хорошей теоремы, позволяющей мгновенно определить, существует ли гамильтонова схема для всех графов. [1]

Пример

Существует ли гамильтонов путь или цепь на графике ниже?

Мы видим, что как только мы переместимся в вершину E, нет возможности уйти, не вернувшись в C, поэтому нет возможности гамильтоновой схемы. Если мы начнем с вершины E, мы можем найти несколько гамильтоновых путей, таких как ECDAB и ECABD

В случае гамильтоновых схем наше внимание будет сосредоточено не на существовании, а на вопросе оптимизации; учитывая граф, в котором ребра имеют веса, можем ли мы найти оптимальную гамильтонову схему; тот, у которого наименьший общий вес.

Посмотрите это видео, чтобы увидеть проработанные выше примеры.

Эта задача называется задачей коммивояжера (TSP), потому что вопрос может быть сформулирован следующим образом: предположим, что продавцу нужно провести презентацию о продажах в четырех городах. Он просматривает цены на авиабилеты между каждым городом и отображает стоимость на графике. В каком порядке он должен поехать, чтобы посетить каждый город один раз, а затем вернуться домой с наименьшими затратами?

Чтобы ответить на этот вопрос о том, как найти гамильтонову схему с наименьшей стоимостью, мы рассмотрим несколько возможных подходов.Первый вариант, который может прийти в голову, — это просто попробовать все возможные схемы.

Вопрос

можно сформулировать так: Предположим, продавцу нужно провести презентацию в четырех городах. Он просматривает цены на авиабилеты между каждым городом и отображает стоимость на графике. В каком порядке он должен поехать, чтобы посетить каждый город один раз, а затем вернуться домой с наименьшими затратами?

Алгоритм грубой силы (он же исчерпывающий поиск)

1. Перечислите все возможные гамильтоновы схемы

2. Найдите длину каждой цепи, добавив веса ребер

3. Выберите контур с минимальным общим весом.

Пример

Примените алгоритм грубой силы, чтобы найти гамильтонову схему минимальной стоимости на графике ниже.

Чтобы применить алгоритм грубой силы, мы перечисляем все возможные гамильтоновы схемы и вычисляем их вес:

Контур	Масса
ABCDA	4 + 13 + 8 + 1 = 26
ABDCA	4 + 9 + 8 + 2 = 23
ACBDA	2 + 13 + 9 + 1 = 25

Примечание. Это уникальные схемы на этом графике. Все другие возможные схемы являются обратными перечисленным или начинаются с другой вершины, но имеют те же веса.

Из этого видно, что вторая цепь, ABDCA, является оптимальной.

Посмотрите, как эти примеры работали еще раз в следующем видео.

Оптимален алгоритм грубой силы; он всегда будет производить гамильтонову схему с минимальным весом. Это эффективно? Чтобы ответить на этот вопрос, нам нужно подумать, сколько гамильтоновых схем может иметь граф. Для простоты давайте рассмотрим наихудший вариант, когда каждая вершина соединена со всеми остальными вершинами.Это называется полным графиком .

Предположим, что у нас есть полный граф с пятью вершинами, подобный приведенному выше графу авиаперелетов. Из Сиэтла мы можем сначала посетить четыре города. Из каждого из них есть три варианта. Из каждого из этих городов есть два возможных города, которые можно посетить следующим. Тогда есть только один выбор для последнего города перед возвращением домой.

Это можно показать визуально:

Подсчитав количество маршрутов, мы видим [latex] 4 \ cdot {3} \ cdot {2} \ cdot {1} [/ latex] маршрута.Для шести городов будут маршруты [latex] 5 \ cdot {4} \ cdot {3} \ cdot {2} \ cdot {1} [/ latex].

Количество возможных цепей

Для N вершин в полном графе будет [latex] (n-1)! = (N-1) (n-2) (n-3) \ dots {3} \ cdot {2} \ cdot {1} [/ latex] маршруты. Половина из них дублируются в обратном порядке, поэтому есть [latex] \ frac {(n-1)!} {2} [/ latex] уникальные схемы.

Восклицательный знак! Читается как «факториал» и является сокращением для показанного продукта.

Пример

Сколько цепей будет в полном графе с 8 вершинами?

Полный граф с 8 вершинами имел бы = 5040 возможных гамильтоновых схем. Половина цепей дублирует другие цепи, но в обратном порядке, оставляя 2520 уникальных маршрутов.

Хотя это много, это не кажется необоснованно огромным. Но посмотрим, что происходит с увеличением количества городов:

Города	Уникальные гамильтоновы схемы
9	8! / 2 = 20160
10	9! / 2 = 181 440
11	10! / 2 = 1,814,400
15	14! / 2 = 43,589,145,600
20	19! / 2 = 60 822 550 204 416 000

Посмотрите, как эти примеры работали еще раз в следующем видео.

Как видите, количество контуров растет очень быстро. Если бы компьютер просматривал один миллиард цепей в секунду, ему все равно потребовалось бы почти два года, чтобы исследовать все возможные цепи только с 20 городами! Конечно, Brute Force — это , а не — эффективный алгоритм.

Алгоритм ближайшего соседа (NNA)

1. Выберите начальную точку.

2. Перейти к ближайшей непосещенной вершине (ребру с наименьшим весом).

3. Повторяйте, пока цепь не будет завершена.

К сожалению, еще никто не нашел эффективных оптимальных алгоритмов и для решения TSP, и очень маловероятно, что кто-нибудь когда-нибудь это сделает. Поскольку для решения проблемы использовать грубую силу непрактично, мы обращаемся к эвристическим алгоритмам ; эффективные алгоритмы, дающие приближенные решения. Другими словами, эвристические алгоритмы работают быстро, но могут создавать или не создавать оптимальную схему.

Пример

Рассмотрим наш предыдущий график, показанный справа.

Начиная с вершины A, ближайшим соседом является вершина D с весом 1.

От D ближайшим соседом является C с весом 8.

Из C наш единственный вариант — переместиться в вершину B, единственную непосещаемую вершину, со стоимостью 13.

Из B мы возвращаемся в A с весом 4.

Результирующая схема представляет собой ADCBA с общим весом [латекс] 1 + 8 + 13 + 4 = 26 [/ латекс].

Посмотрите проработанный пример в следующем видео.

В итоге мы нашли худшую схему на графике! Что случилось? К сожалению, несмотря на то, что его очень легко реализовать, NNA представляет собой жадный алгоритм , что означает, что он учитывает только немедленное решение без учета последствий в будущем.В данном случае, следование кромке AD вынудило нас позже использовать очень дорогую кромку BC.

Пример

Взгляните еще раз на нашего продавца. Начиная с Сиэтла, ближайший сосед (самый дешевый рейс) — в Лос-Анджелес, его стоимость составляет 70 долларов. Оттуда:

Лос-Анджелес — Чикаго: 100 долларов

Чикаго — Атланта: 75 долларов

Атланта — Даллас: 85 долларов США

Даллас — Сиэтл: 120 долларов

Общая стоимость: 450 $

В данном случае ближайший сосед действительно нашел оптимальную схему.

Посмотрите этот отработанный пример еще раз в этом видео.

Возвращаясь к нашему первому примеру, как мы могли бы улучшить результат? Один из вариантов — повторить алгоритм ближайшего соседа с другой начальной точкой, чтобы увидеть, изменился ли результат. Поскольку ближайший сосед такой быстрый, сделать это несколько раз — не проблема.

Пример

Мы вернемся к графику из Примера 17.

Запуск в вершине A привел к цепи с весом 26.

Начиная с вершины B, ближайшей соседней схемой является BADCB с весом 4 + 1 + 8 + 13 = 26. Это та же схема, которую мы нашли, начиная с вершины A. Не лучше.

Начиная с вершины C, ближайшей соседней схемой является CADBC с весом 2 + 1 + 9 + 13 = 25. Лучше!

Начиная с вершины D, ближайшей соседней схемой является DACBA. Обратите внимание, что это на самом деле та же схема, которую мы нашли, начиная с C, только написанную с другой начальной вершиной.

RNNA смогла создать немного лучшую схему с весом 25, но все же не оптимальную схему в этом случае.Обратите внимание, что даже несмотря на то, что мы нашли схему, начиная с вершины C, мы все равно могли написать схему, начинающуюся с A: ADBCA или ACBDA.

Попробуйте

В таблице ниже показано время в миллисекундах, которое требуется для отправки пакета данных между компьютерами в сети. Если данные нужно было отправлять последовательно на каждый компьютер, а затем уведомление нужно было возвращать на исходный компьютер, мы бы решали TSP. Для удобства компьютеры обозначены буквами A-F.

	А	B	С	D	E	F
А	–	44	34	12	40	41
B	44	–	31	43	24	50
С	34	31	–	20	39	27
D	12	43	20	–	11	17
E	40	24	39	11	–	42
Ф.	41	50	27	17	42	–

а.Найдите схему, генерируемую NNA, начиная с вершины B.

г. Найдите цепь, генерируемую РННА.

Хотя, конечно, лучше, чем базовая NNA, к сожалению, RNNA все еще жадная и дает очень плохие результаты для некоторых графиков. В качестве альтернативы, в нашем следующем подходе мы сделаем шаг назад и посмотрим на «общую картину» — сначала выберем самые короткие края, а затем заполним пробелы.

Пример

Используя четырехвершинный граф, описанный ранее, мы можем использовать алгоритм Sorted Edges.

Самое дешевое ребро — AD, его стоимость 1. Мы выделяем это ребро, чтобы отметить его выбранным.

Следующее кратчайшее ребро — это AC с весом 2, поэтому мы выделяем это ребро.

Для третьего ребра мы хотели бы добавить AB, но это дало бы вершине A степень 3, что недопустимо в гамильтоновой схеме. Следующее кратчайшее ребро — это CD, но это ребро создаст схему ACDA, не включающую вершину B, поэтому мы отклоняем это ребро. Следующее кратчайшее ребро — это BD, поэтому мы добавляем это ребро в граф.

ПЛОХО

ОК

Затем мы добавляем последнее ребро, чтобы замкнуть цепь: ACBDA с весом 25.

Обратите внимание, что в этом случае алгоритм не создал оптимальную схему; оптимальная схема — ACDBA с массой 23.

Хотя алгоритм Sorted Edge преодолевает некоторые недостатки NNA, он по-прежнему является только эвристическим алгоритмом и не гарантирует оптимальную схему.

Пример

Группа вашего учителя, Derivative Work , проводит тур по барам в Орегоне.Расстояние проезда показано ниже. Спланируйте эффективный маршрут, чтобы ваш учитель посетил все города и вернулся в исходную точку. Используйте NNA, начиная с Портленда, а затем используйте Sorted Edges.

	Ашленд	Astoria	Отвод	Корваллис	Кратерное озеро	Евгений	Ньюпорт	Портленд	Салем	Приморский
Ашленд	–	374	200	223	108	178	252	285	240	356
Astoria	374	–	255	166	433	199	135	95	136	17
Отвод	200	255	–	128	277	128	180	160	131	247
Корваллис	223	166	128	–	430	47	52	84	40	155
Кратерное озеро	108	433	277	430	–	453	478	344	389	423
Евгений	178	199	128	47	453	–	91	110	64	181
Ньюпорт	252	135	180	52	478	91	–	114	83	117
Портленд	285	95	160	84	344	110	114	–	47	78
Салем	240	136	131	40	389	64	83	47	–	118
Приморский	356	17	247	155	423	181	117	78	118	–

Чтобы увидеть всю таблицу, прокрутите вправо

Используя NNA с большим количеством городов, вы можете отметить города по мере их посещения, чтобы случайно не посетить их снова.Если посмотреть в строке на Портленд, то наименьшее расстояние 47 до Салема. Следуя этой идее, наша схема будет:

Портленд — Салем 47

Салем — Корваллис 40

Корваллис — Юджину 47

Юджин в Ньюпорт 91

Ньюпорт-Сисайд 117

Побережье до Астории 17

Astoria до изгиба 255

Изгиб к Ашленду 200

Эшленд — Кратерное озеро 108

От озера Кратер до Портленда 344

Общая протяженность поездки: 1266 миль

Используя Sorted Edges, вы можете счесть полезным нарисовать пустой граф, возможно, нарисовав вершины по кругу.Добавление ребер к графу по мере их выбора поможет вам визуализировать любые цепи или вершины со степенью 3.

Начинаем складывать самые короткие ребра:

От моря до Астории 17 миль

Корваллис — Салем 40 миль

Портленд — Салем 47 миль

Корваллис — Юджин 47 миль

График после добавления этих ребер показан справа. Следующее кратчайшее преимущество — от Корваллиса до Ньюпорта на 52 мили, но добавление этого края даст Корваллису степень 3.

Продолжая, мы можем пропустить любую пару ребер, которая содержит Салема или Корваллиса, поскольку они оба уже имеют степень 2.

Портленд до побережья 78 миль

Юджин — Ньюпорт 91 миля

Портленд — Астория (отклонить — замыкает цепь)

Эшленд до кратера Lk 108 миль

График после добавления этих ребер показан справа. На этом этапе мы можем пропустить любую пару ребер, которая содержит Салем, Сисайд, Юджин, Портленд или Корваллис, поскольку они уже имеют степень 2.

Ньюпорт — Астория (отклонить — замыкает цепь)

Ньюпорт до Бенд 180 миль

Изгиб к Ашленду 200 миль

На данный момент единственный способ завершить цепь — это добавить:

Crater Lk до Астории 433 мили. Последняя схема, написанная для начала в Портленде:

Портленд, Салем, Корваллис, Юджин, Ньюпорт, Бенд, Эшленд, Кратерное озеро, Астория, Сисайд, Портленд.Общая протяженность поездки: 1241 миля.

Хотя алгоритм лучше, чем маршрут NNA, ни один алгоритм не дал оптимального маршрута. В 1069 миль можно пройти по следующему маршруту:

Портленд, Астория, Сисайд, Ньюпорт, Корваллис, Юджин, Эшленд, Кратерное озеро, Бенд, Салем, Портленд

Посмотрите пример алгоритма ближайшего соседа для путешествия из города в город с использованием таблицы, представленной на видео ниже.

В следующем видео мы используем ту же таблицу, но для планирования поездки используем отсортированные края.

Попробуйте

Найдите схему, созданную алгоритмом Sorted Edges, используя график ниже.

Связывающие деревья

Компании требуется надежный Интернет и телефонная связь между их пятью офисами (для простоты названными A, B, C, D и E) в Нью-Йорке, поэтому они решают арендовать выделенные линии у телефонной компании. Телефонная компания будет взимать плату за каждую сделанную ссылку. Затраты в тысячах долларов в год показаны на графике.

В этом случае нам не нужно искать цепь или даже конкретный путь; все, что нам нужно сделать, это убедиться, что мы можем позвонить из любого офиса в любой другой. Другими словами, мы должны быть уверены, что есть путь из любой вершины в любую другую вершину.

Связующее дерево

Остовное дерево — это связный граф, использующий все вершины, в котором нет цепей.

Другими словами, есть путь из любой вершины в любую другую вершину, но нет контуров.

Некоторые примеры остовных деревьев показаны ниже. Обратите внимание, что в деревьях нет цепей, и вполне нормально иметь вершины со степенью выше двух.

Обычно у нас есть начальный график для работы, как в примере с телефоном выше. В этом случае мы формируем остовное дерево, находя подграф — новый граф, сформированный с использованием всех вершин, но только некоторых ребер исходного графа. Ребра не будут созданы там, где их еще не было.

Конечно, любое случайное остовное дерево — это не совсем то, что нам нужно. Нам нужно связующее дерево минимальной стоимости (MCST) .

Связующее дерево минимальной стоимости (MCST)

Остовное дерево с минимальной стоимостью — это остовное дерево с наименьшим общим весом ребер.

Подход в стиле ближайшего соседа здесь не имеет большого смысла, поскольку нам не нужна схема, поэтому вместо этого мы воспользуемся подходом, аналогичным сортировке ребер.

Алгоритм Краскала

Выберите самое дешевое неиспользуемое ребро на графике.
Повторите шаг 1, добавив самый дешевый неиспользуемый край, если:
добавление ребра приведет к созданию цепи

Повторяйте, пока не сформируется остовное дерево

Пример

Используя наш телефонный линейный график сверху, начните добавлять ребра:

AB $ 4 ОК

AE $ 5 ОК

BE $ 6 отклонить — замыкает цепь ABEA

DC $ 7 ОК

AC $ 8 ОК

На этом мы останавливаемся — теперь все вершины связаны, поэтому мы сформировали остовное дерево стоимостью 24 тысячи долларов в год.

Примечательно, что алгоритм Крускала одновременно оптимален и эффективен; мы гарантируем, что всегда произведем оптимальную MCST.

Пример

Энергетической компании необходимо проложить обновленные распределительные линии, соединяющие десять городов Орегона ниже с энергосистемой. Как они могут свести к минимуму количество новой укладки?

	Ашленд	Astoria	Отвод	Корваллис	Кратерное озеро	Евгений	Ньюпорт	Портленд	Салем	Приморский
Ашленд	–	374	200	223	108	178	252	285	240	356
Astoria	374	–	255	166	433	199	135	95	136	17
Отвод	200	255	–	128	277	128	180	160	131	247
Корваллис	223	166	128	–	430	47	52	84	40	155
Кратерное озеро	108	433	277	430	–	453	478	344	389	423
Евгений	178	199	128	47	453	–	91	110	64	181
Ньюпорт	252	135	180	52	478	91	–	114	83	117
Портленд	285	95	160	84	344	110	114	–	47	78
Салем	240	136	131	40	389	64	83	47	–	118
Приморский	356	17	247	155	423	181	117	78	118	–

Чтобы увидеть всю таблицу, прокрутите вправо

Используя алгоритм Крускала, мы добавляем ребра от самых дешевых к самым дорогим, отбрасывая те, которые замыкают цепь.Останавливаемся, когда граф подключен.

от моря до Астории 17 миль от Корваллиса до Салема 40 миль

Портленд — Салем 47 миль

Корваллис — Юджин 47 миль

Корваллис — Ньюпорт 52 мили

Салем к Юджину отклонить — замыкает цепь

Портленд до побережья 78 миль

График до этого момента показан ниже.

Продолжение,

Отклонение из Ньюпорта в Салем

Корваллис в Портленд отклонить

Юджин в Ньюпорт отклонить

из Портленда в Асторию отклонить

Эшленд до кратера Lk 108 миль

Юджин в Портленд отклонить

Ньюпорт — Портленд отклонить

Отклонение от Ньюпорта до Сисайд

От Салема до приморского отклонения

Поверните к Юджину 128 миль

Изгиб до Салема отклонить

Астория — Ньюпорт отклонить

Салем — Астория отклонить

Corvallis to Seaside отклонить

Portland to Bend отклонить

Астория — Корваллису отклонить

Юджин — Ашленд 178 миль

Это соединяет график.Общая длина прокладываемого кабеля составит 695 миль.

Посмотрите приведенный выше пример без таблицы в следующем видео.

Теперь мы представляем тот же пример с таблицей в следующем видео.

Попробуйте

Найдите остовное дерево минимальной стоимости на графике ниже, используя алгоритм Краскала.

[1] Есть некоторые теоремы, которые можно использовать в определенных обстоятельствах, например теорема Дирака, которая гласит, что гамильтонова схема должна существовать на графе с n вершинами, если каждая вершина имеет степень n /2 или больше.

(PDF) Решение задачи о треугольнике Эйлера с помощью карандаша Понселе

Решение задачи о треугольнике Эйлера с помощью карандаша Понселе 129

W (K), Jlie на той же прямой, поскольку F + и F − являются обратными в ортоцентроидной окружности

с центром J [7].

Гипербола Киперта — это изотомическое преобразование линии, проходящей через Hsand

G, где Hsis — изотомическое преобразование H [4]. Поскольку G является фиксированной точкой изотомического преобразования

, эта прямая касается гиперболы в точке G.Как показано в [3],

Hsis — симедиана антикомплементарного треугольника, так что фактически K также находится на

этой прямой и HsG: GL = 2: 1.

Пусть Y — двойник прямой GH в гиперболе Киперта; затем Ylies на касательной

линии HsGto G; следовательно, двойник J проходит через Y. Поскольку J является средней точкой

GH, то линия JY проходит через центр W (K). Но мы уже

показали, что K находится на линии JW (K) и HsG; таким образом, Y = K. Следовательно,

, двойственный любой точке на GH, проходит через K; в частности, двойственная точка в бесконечности

на GH проходит через K и центр W (K).Следовательно, два пересечения

этой прямой с коникой F + и F − имеют свои касательные, параллельные

прямой Эйлера GH.

Замечание. Редакция указала на самую последнюю ссылку [9].

Ссылки

[1] Р. К. Альперин, Карандаш Понселе прямоугольных гипербол, Forum Geom., 10 (2010) 15–20.

[2] К. Дж. Брэдли и Г. К. Смит, Расположение центров треугольников, Форум. Геом., 6 (2006) 57–70.

[3] Натан Альтшиллер-Корт, College Geometry, Barnes & Noble, 1952.

[4] Р. Х. Эдди, Р. Фрич, Коники Людвига Киперта, Math. Mag., 67 (1994) 188–205.

[5] А. Гинанд, Прямые Эйлера, трикасательные центры и их треугольники, Amer. Математика. Ежемесячно, 91 (1984)

290–300.

[6] Р. А. Джонсон, Современная геометрия, Houghton-Mifin, 1929.

[7] К. Кимберлинг, Центральные точки и центральные линии в плоскости треугольника, Math. Mag., 67 (1994)

163–187.

[8] К. Кимберлинг, Энциклопедия треугольных центров,

http: // faculty.evansville.edu/ck6/encyclopedia/ETC.html

[9] А. Рыба и Дж. Стерн, Эквимодулярные многочлены и теоремы о тритангентности Эйлера, Фейера-

, Баха и Гинанда, Amer. Математика. Ежемесячно, 117 (2011) 217–228.

[10] Б. Шимеми, Складывание бумаги и повторение теоремы Эйлера, Forum Geom., 2 (2002) 93–104.

[11] Г. К. Смит, Статика и пространство модулей треугольников, Forum Geom., 5 (2005) 181–190.

[12] П. Ю, Задача определения треугольника Эйлера, Журнал геометрии и графики, 12 (2008)

75–80.

Роджер С. Альперин: Департамент математики Государственного университета Сан-Хосе, Сан-Хосе, Калифорния

95192, США

Адрес электронной почты: [email protected]

Пути и схемы Эйлера

Расследуй! 35

Путь Эйлера в графе или мультиграфе — это обход графа, при котором каждое ребро используется ровно один раз. Схема Эйлера — это путь Эйлера, который начинается и заканчивается в одной и той же вершине. Наша цель — найти быстрый способ проверить, есть ли в графе (или мультиграфе) эйлеров путь или цепь.

В каком из графов ниже есть пути Эйлера? Какие есть схемы Эйлера?
Перечислите степени каждой вершины графов выше. Есть ли связь между степенями и существованием путей и цепей Эйлера?
Может ли граф с вершиной степени 1 иметь схему Эйлера? Если да, нарисуйте один. Если нет, объясните, почему нет. А как насчет пути Эйлера?
Что делать, если каждая вершина графа имеет степень 2.Есть ли путь Эйлера? Схема Эйлера? Нарисуйте графики.
Ниже часть графика. Несмотря на то, что вы можете видеть только некоторые из вершин, можете ли вы определить, будет ли граф иметь путь Эйлера или схему?

Если мы начнем с вершины и проследим вдоль ребер, чтобы добраться до других вершин, мы создадим обход по графу. Точнее, обход в графе — это последовательность вершин, такая что каждая вершина в последовательности смежна с вершинами до и после нее в последовательности.Если прогулка проходит по каждому ребру ровно один раз, то она называется Эйлеровской дорогой (или Эйлеровской ). Если, кроме того, начальная и конечная вершины совпадают (так что вы проводите вдоль каждого ребра ровно один раз и заканчиваете там, где вы начали), то переход называется контуром Эйлера (или обходом Эйлера ). Конечно, если граф не связан, нет никакой надежды найти такой путь или цепь. В оставшейся части этого раздела предполагаем, что все обсуждаемые графы связаны.

Мосты в Кенигсбергской проблеме — это действительно вопрос о существовании путей Эйлера. Будет маршрут, который пересекает каждый мост ровно один раз тогда и только тогда, когда в приведенном ниже графике есть путь Эйлера:

Этот граф достаточно мал, чтобы мы могли проверить все возможные обходы, не использующие повторно ребра, и тем самым убедить себя, что пути Эйлера (не говоря уже о схеме Эйлера) не существует. На небольших графах, у которых есть путь Эйлера, найти его обычно не сложно.Наша цель — найти быстрый способ проверить, есть ли в графе путь или цепь Эйлера, даже если граф довольно большой.

Один из способов гарантировать, что граф не имеет схему Эйлера, — это включить «пик», вершину степени 1.

Вершина \ (a \) имеет степень 1, и если вы попытаетесь составить схему Эйлера, вы увидите, что застрянете в вершине. Это тупик. То есть, если вы не начнете с этого. Но тогда нет возможности вернуться, поэтому нет никакой надежды найти схему Эйлера.Однако существует путь Эйлера. Он начинается с вершины \ (a \ text {,} \), затем обходит треугольник. Вы закончите в вершине степени 3.

Вы сталкиваетесь с подобной проблемой всякий раз, когда у вас есть вершина какой-либо нечетной степени. Если вы начнете с такой вершины, вы не сможете там закончить (после прохождения каждого ребра ровно один раз). После использования одного ребра для выхода из начальной вершины у вас останется четное количество ребер, исходящих из вершины. Половину из них можно было использовать для возврата в вершину, а другую половину — для ухода.Итак, вы вернетесь, а затем уйдете. Возвращайся, потом уходи. Единственный способ использовать все ребра — использовать последнее, оставив вершину. С другой стороны, если у вас есть вершина с нечетной степенью, с которой вы не начинаете путь, то в конечном итоге вы застрянете в этой вершине. Путь будет использовать пары ребер, инцидентных вершине, чтобы снова прийти и уйти. В конце концов все эти ребра, кроме одного, будут израсходованы, и останется только одно ребро, которое нужно будет пройти, и ни одно ребро, которое можно будет покинуть снова.

Все это говорит о том, что если у графа есть путь Эйлера и две вершины с нечетной степенью, то путь Эйлера должен начинаться в одной из вершин нечетной степени и заканчиваться на другой.В такой ситуации каждая вторая вершина должна иметь четную степень , поскольку нам нужно равное количество ребер, чтобы добраться до этих вершин, чтобы выйти из них. Как у нас могла быть схема Эйлера? Граф не может иметь вершину нечетной степени, поскольку путь Эйлера должен начинаться или заканчиваться там, но не то и другое вместе. Таким образом, чтобы граф имел схему Эйлера, все вершины должны иметь четную степень.

Верно и обратное: если все вершины графа имеют четную степень, то у графа есть схема Эйлера, а если есть ровно две вершины с нечетной степенью, у графа есть путь Эйлера.Доказать это немного сложно, но основная идея состоит в том, что вы никогда не застрянете, потому что для каждого «входящего» ребра в каждой вершине существует «исходящее» ребро. Если вы попытаетесь построить путь Эйлера и пропустите некоторые ребра, вы всегда сможете «соединить» схему, используя ребра, которые вы ранее пропустили.

Пути и цепи Эйлера

Поскольку в мостах графа Кенигсберга все четыре вершины имеют нечетную степень, нет пути Эйлера через граф. Таким образом, у горожан нет возможности пересечь каждый мост ровно один раз.

Подраздел Пути Гамильтона

Предположим, вы хотите совершить поездку по Кенигсбергу таким образом, чтобы посетить каждый массив суши (два острова и оба берега) ровно один раз. Это можно сделать. В терминах теории графов мы спрашиваем, существует ли путь, который посещает каждую вершину ровно один раз. Такой путь называется гамильтоновым путем (или гамильтоновым путем ). Мы также могли бы рассмотреть циклов Гамильтона , которые являются путями Гамлитона, которые начинаются и заканчиваются в одной и той же вершине.

Пример4.4.1

Определите, есть ли в приведенных ниже графиках путь Гамильтона.

Решение

На графике слева есть путь Гамильтона (на самом деле много разных), как показано здесь:

На графике справа нет пути Гамильтона. Вам нужно будет посетить каждую из «внешних» вершин, но как только вы посетите одну из них, вы застрянете. Обратите внимание, что у этого графа нет пути Эйлера, хотя есть графы с путями Эйлера, но нет путей Гамильтона.

Похоже, что найти пути Гамильтона было бы проще, потому что графы часто имеют больше ребер, чем вершин, поэтому требуется меньше требований. Однако никто не знает, правда ли это. Не существует известного простого теста на наличие в графе пути Гамильтона. Для небольших графов это не проблема, но по мере того, как размер графа увеличивается, становится все труднее и труднее проверить, существует ли путь Гамильтона. Фактически, это пример вопроса, который, насколько нам известно, слишком сложно решить для компьютеров; это пример NP-полной задачи.

Подраздел Упражнения

1

Вы и ваши друзья хотите совершить поездку по юго-западу на машине. Вы посетите следующие девять штатов со следующим довольно странным правилом: вы должны пересечь каждую границу между соседними штатами ровно один раз (так, например, вы должны пересечь границу Колорадо и Юты только один раз). Ты можешь сделать это? Если да, имеет ли значение, откуда вы начнете свое путешествие? Какой факт в теории графов решает эту проблему?

Решение

Это вопрос о поиске путей Эйлера.Нарисуйте граф с вершиной в каждом состоянии и соедините вершины, если их состояния имеют общую границу. Ровно две вершины будут иметь нечетную степень: вершины для Невады и Юты. Таким образом, вы должны начать свое путешествие в одном из этих состояний и закончить его в другом.

2

Какой из следующих графов содержит путь Эйлера? Какие содержат схему Эйлера?

\ (К_4 \)
\ (K_5 \ text {.} \)
\ (K_ {5,7} \)
\ (K_ {2,7} \)
\ (C_7 \)
\ (P_7 \)

Решение

\ (K_4 \) не имеет пути или цепи Эйлера.
\ (K_5 \) имеет схему Эйлера (а также путь Эйлера).
\ (K_ {5,7} \) не имеет пути или цепи Эйлера.
\ (K_ {2,7} \) имеет путь Эйлера, но не контур Эйлера.
\ (C_7 \) имеет схему Эйлера (это схемный граф!)
\ (P_7 \) имеет путь Эйлера, но не контур Эйлера.

3

Эдвард А. Маус только что закончил строительство своего нового дома. План этажа показан ниже:

Эдвард хочет показать свой новый коврик подруге-мышке.Могут ли они пройти через каждый дверной проем ровно один раз? Если да, то в каких комнатах они должны начать и закончить экскурсию? Объяснять.
Можно ли совершить поездку по дому, посещая каждую комнату ровно один раз (не обязательно через каждый дверной проем)? Объяснять.
Через несколько мышиных лет Эдвард решает переделать. Он хотел бы добавить новые двери между комнатами, которые у него есть. Конечно, он не может добавлять двери снаружи дома. Возможно ли, чтобы в каждой комнате было нечетное количество дверей? Объяснять.

4

Для какого \ (n \) граф \ (K_n \) содержит схему Эйлера? Объяснять.

Решение

Когда \ (n \) нечетно, \ (K_n \) содержит схему Эйлера. Это потому, что каждая вершина имеет степень \ (n-1 \ text {,} \), поэтому при нечетном \ (n \) все степени будут четными.

5

Для каких \ (m \) и \ (n \) граф \ (K_ {m, n} \) содержит путь Эйлера? Схема Эйлера? Объяснять.

Решение

Если и \ (m \), и \ (n \) четные, то \ (K_ {m, n} \) имеет схему Эйлера.Когда оба нечетные, эйлеров путь или цепь отсутствуют. Если один равен 2, а другой нечетный, то существует путь Эйлера, но не контур Эйлера.

6

Для какого \ (n \) \ (K_n \) содержит путь Гамильтона? Цикл Гамильтона? Объяснять.

Решение

Все значения \ (n \ text {.} \) В частности, \ (K_n \) содержит \ (C_n \) как подгруппу, которая представляет собой цикл, включающий каждую вершину.

7

Для каких \ (m \) и \ (n \) граф \ (K_ {m, n} \) содержит путь Гамильтона? Цикл Гамильтона? Объяснять.

Решение

Пока \ (| m-n | \ le 1 \ text {,} \) граф \ (K_ {m, n} \) будет иметь путь Гамильтона. Чтобы иметь цикл Гамильтона, мы должны иметь \ (m = n \ text {.} \)

8

В Кенигсберг приехал мостостроитель и хочет добавить мосты, чтобы можно было проехать по по каждому мосту ровно один раз. Сколько мостов нужно построить?

Решение

Если мы построим один мост, у нас будет путь Эйлера. Для схемы Эйлера необходимо построить два моста.

9

Ниже приведен график, представляющий дружбу между группой студентов (каждая вершина — ученик, а каждое ребро — дружба).Могут ли ученики сесть за круглый стол так, чтобы каждый ученик сидел между двумя друзьями? Какое отношение этот вопрос имеет к путям?

Решение

Мы ищем гамильтонов цикл, и на этом графике он есть:

10

Предположим, что у графа есть путь Гамильтона. Какое максимальное количество вершин первой степени может иметь граф? Объясните, почему ваш ответ правильный.
Найдите граф, в котором нет пути Гамильтона, хотя ни одна вершина не имеет степени один.Объясните, почему ваш пример работает.

11

Рассмотрим следующий график:

Найдите путь Гамильтона. Можно ли продлить ваш путь до цикла Гамильтона?
Является ли граф двудольным? Если да, сколько вершин в каждой «части»?
Используйте свой ответ на часть (b), чтобы доказать, что в графе нет цикла Гамильтона.
Предположим, у вас есть двудольный граф \ (G \), в котором одна часть имеет как минимум на две вершины больше, чем другая. Докажите, что \ (G \) не имеет гамильтонова пути.

дискретная математика — «Хитрые» вопросы по теории графов

Существует граф с 1871 вершиной, который является эйлеровым и двудольным. Верно это или нет?

Это пытается ввести вас в заблуждение нечетным числом вершин, что означает, что две части двойного разбиения не могут иметь одинаковый размер. Но это проблема только для гамильтоновых циклов, а не для циклов Эйлера.

На этом рисунке показано, что вы можете создать двудольный граф Эйлера для любого нечетного числа ($ \ ge 7 $) вершин:

Неважно, что обычный красный узор заканчивается на той же стороне, что и начался, вы можете просто добавить еще 2 (зеленых) края, чтобы получить цикл Эйлера.

Каково максимальное значение ребер для простого (без параллельных ребер) неориентированного графа с $ n \ ge 10 $, который является эйлеровым и имеет по крайней мере две разные окружности Гамильтона?

Для нечетных $ n $ это просто: это полный $ K_n $ с $ {n \ choose 2} = \ frac {n (n-1)} 2 $ ребрами.

Для четных $ n $ хотя бы одно возможное ребро на вершину не может быть в графе (чтобы степень каждой вершины была четной). Это означает, что вам нужно удалить не менее $ \ frac {n} 2 $ ребер из полного графа.Если вы сделаете это, объединив вершины, вы получите полный граф за вычетом идеального совпадения. Этот граф эйлеров и (поскольку $ n $ достаточно велик) по-прежнему имеет 2 разных гамильтоновых цикла). Итак, ответ здесь: $ {n \ choose 2} — \ frac {n} 2 = \ frac {n (n-2)} 2 $

ДОБАВЛЕНО: Почему графики для второго примера имеют как минимум два гамильтоновых цикла? Потому что они предназначены для нечетных $ n $ точно, а для четных $ n $ почти полного графа $ K_n $! С заданным набором вершин, чем больше у вас ребер, тем лучше (поскольку вам это не нужно, но вы можете использовать их для гамильтонова цикла).В этих графах много-много гамильтоновых циклов, 2 — это очень простая нижняя граница.

Давайте посмотрим на случай четных $ n $:

Приведенная выше конструкция означает, что все ребра между точками находятся в графе, за исключением красных «ступенек лестницы». Я просто выделил 2 цикла зеленого цвета с каждой стороны лестницы и еще несколько краев (синий и фиолетовый).

Вы получите один гамильтониан, если начнете где-нибудь с левой стороны лестницы, поднимитесь вверх, пока не дойдете до первого синего края, затем перейдете на правую сторону с этим синим краем, затем возьмете нисходящий «внешний» зеленый край и продолжите движение. снова вверх с правой стороны, пока не встретитесь с другим синим краем, пересеките его обратно в левую сторону, поверните левый «внешний» зеленый край вниз и поднимайтесь вверх, пока не дойдете до начальной точки.

Вы получите другой гамильтониан, если проделаете эту процедуру еще раз, но с использованием фиолетовых краев для пересечения слева направо и обратно.

Должно быть ясно, что существует так много способов, которыми вы можете выбрать левую и правую точки и выбрать порядок их расположения в зеленых циклах, что «всего 2» гамильтоновых цикла уже является большим преуменьшением для минимальных $ n $ 10.

1	спаниели \| (терьеры & овчарки)
2	спаниели \| овчарки
3	спаниели \| терьеры \| овчарки
4	терьеры & овчарки

1	барокко \| классицизм \| ампир
2	барокко \| (классицизм & ампир)
3	классицизм & ампир
4	барокко \| классицизм

1	барокко \| классицизм \| ампир
2	барокко \| (классицизм & ампир)
3	классицизм & ампир
4	барокко \| классицизм