Математика, 5 класс: уроки, тесты, задания
Натуральные числа
-
Десятичная система счисления. Римская нумерация
-
Числовые и буквенные выражения
-
Начальные геометрические понятия: прямая, отрезок, луч, ломаная, прямоугольник
-
Определение координатного луча
-
Округление чисел.
 Прикидка и оценка результатов вычислений
Прикидка и оценка результатов вычислений
-
Законы арифметических действий. Вычисления с многозначными числами
-
Решение текстовых задач арифметическим способом
-
Формулы. Уравнения. Упрощение выражений
-
Математический язык и математическая модель
Обыкновенные дроби
-
Деление с остатком.
 Понятие обыкновенной дроби
Понятие обыкновенной дроби
-
Основное свойство дроби. Сокращение и расширение дробей
-
Правильные и неправильные дроби. Смешанные числа. Понятие, запись и чтение
-
Сравнение обыкновенных дробей
-
Сложение и вычитание обыкновенных дробей и смешанных чисел
-
Умножение и деление обыкновенной дроби на натуральное число
-
Нахождение части от целого и числа по его части
-
Геометрические понятия: окружность и круг
Геометрические фигуры
-
Угол.
 Измерение углов
Измерение углов
-
Биссектриса угла. Свойство биссектрисы угла
-
Треугольник. Площадь треугольника
-
-
Расстояния между двумя точками.
 Масштаб. Виды масштаба
Масштаб. Виды масштаба
-
Перпендикулярность прямых. Расстояние от точки до прямой. Серединный перпендикуляр
Десятичные дроби
-
Понятие десятичной дроби. Представление десятичной дроби в виде обыкновенной дроби и наоборот
-
Десятичные дроби.
 Сравнение
Сравнение
-
-
Десятичные дроби. Умножение
-
Степень с натуральным показателем
-
Десятичные дроби.
 Среднее арифметическое, деление на натуральное число
Среднее арифметическое, деление на натуральное число
-
Десятичные дроби. Деление на десятичную дробь
-
Проценты. Задачи на проценты: нахождение процента от величины и величины по её проценту
Геометрические тела
-
Прямоугольный параллелепипед.
 Определение, свойства
Определение, свойства
-
Прямоугольный параллелепипед. Развёртка
-
Прямоугольный параллелепипед. Объём
Тест по математике на тему «Задачи на движение» (5 класс)
Тест по математике на тему «Задачи на движение».
Вариант №1.
1.Скорость катера в стоячей воде 19 , скорость реки 3 . Какова скорость катера по течению? Ответ дайте в
2 Найдите скорость течения реки, если скорость катера по течению 15 , против течения 9 . Ответ дайте в
3.Найдите скорость моторной лодки в стоячей воде, если её скорость по течению реки равна 49 , а против течения реки 41 . Ответ дайте в
4. Из одной станции одновременно в противоположных направлениях вышли два поезда. Их скорости равны 72 и 73 . Какое расстояние будет между ними через 2 часа?
5.Из турбазы одновременно в противоположных направлениях вышли две группы туристов. Скорость одной из групп 4 . Найдите скорость второй группы, если известно, что через 4 часа расстояние между группами было 36 км. Ответ дайте в
Вариант №2.
1.Скорость катера в стоячей воде 17 , скорость реки 2 . Какова скорость катера против течения? Ответ дайте в
2.Скорость катера по течению 15 , против течения 13 . Найдите скорость течения реки. Ответ дайте в
Ответ дайте в
3.Найдите собственную скорость теплохода, если его скорость по течению реки равна 36 , а против течения реки 30 . Ответ дайте в
4.Из одного населённого пункта в одном направлении выехали одновременно два велосипедиста. Скорость первого 13 , скорость второго 10 . Какое расстояние будет между велосипедистами через 3 часа?
5.Из двух городов, расстояние между которыми 462 км, одновременно навстречу друг другу выехали два мотоциклиста. Скорость первого 80 . Найдите скорость второго мотоциклиста , если известно, что встретились мотоциклисты через 3 часа. Ответ дайте в
Ответы.
1 | 2 | 3 | 4 | 5 | |
Вариант №1. | 22 | 3 | 45 | 290 | 5 |
Вариант №2. | 15 | 1 | 33 | 9 | 74 |
Самостоятельная работа по математике — 5 класс: Уравнения, задачи на уравнения, порядок действий. Вариант-1
Самостоятельная работа по математике — 5 класс: уравнения, задачи на уравнения, порядок действий.
Вариант-1
№1. У Пети было в 5 раз меньше карандашей, чем у Маши. При этом у Маши было на 12 карандашей больше. Сколько было карандашей у каждого ребенка?
№2. Решите уравнения: а) 3*(x+4)-12=24; б)45:(17-x)+9=24;
№3. Вычислите: 23*5-(12+4*2):5+13
Вариант-2
№1. Для приготовления мороженого взяли 3 части молока, 2 части сахара и 1 часть масла. Всего мороженое весило 120 грамм. Сколько грамм сахара взяли?
№2. Решите уравнения: а) 54:(x-7)+22=31; б)(29-x)*2-7=45;
Решите уравнения: а) 54:(x-7)+22=31; б)(29-x)*2-7=45;
№3. Вычислите: 27*2-54:(16+34:17)
Самостоятельная работа по математике — 5 класс: уравнения, задачи на уравнения, порядок действий.
Вариант-1
№1. У Пети было в 5 раз меньше карандашей, чем у Маши. При этом у Маши было на 12 карандашей больше. Сколько было карандашей у каждого ребенка?
№2. Решите уравнения: а) 3*(x+4)-12=24; б)45:(17-x)+9=24;
№3. Вычислите: 23*5-(12+4*2):5+13
Вариант-2
№1. Для приготовления мороженого взяли 3 части молока, 2 части сахара и 1 часть масла. Всего мороженое весило 120 грамм. Сколько грамм сахара взяли?
№2. Решите уравнения: а) 54:(x-7)+22=31; б)(29-x)*2-7=45;
№3. Вычислите: 27*2-54:(16+34:17)
Задачи по математике для учеников 5 класса на составление уравнений.
Задача №11. Для приготовления салата берут 4 части помидор, 3 части огурцов и 1 часть зелени. Всего получилось 480 грамм салата. Сколько грамм помидор было взято?
Всего получилось 480 грамм салата. Сколько грамм помидор было взято?
Задача №12. У Веры было в 5 раз больше слив, чем у Даши. При этом у Даши было на 16 слив меньше. Сколько слив было у Даши? У Веры?
Задача №13. У Дениса было в 3 раз больше монет, чем у Васи. А у Димы в 2 раза больше монет, чем у Дениса. Всего же монет было 50. Сколько монет было у Васи? У Дениса?
Задача №14. Для приготовления варенья взяли 4 части сахара и 7 частей фруктов. Всего получилось 660 грамм варенья. Сколько грамм сахара было взято?
Задачи по математике для учеников 5 класса на составление уравнений.
Задача №6. У Насти было в 3 раза больше груш, чем у Иры. При этом, у Иры было на 14 груш меньше, чем у Насти. Сколько груш было у Иры? У Насти?
Задача №7. Для приготовления теста взяли 5 частей муки, 2 части молока и 1 часть масла. Общий вес теста составил 960 грамм. Сколько грамм молока было взято?
Задача №8. У Ивана было в 6 раз меньше мандарин, чем у Пети. При этом у Пети было на 15 мандарин больше. Сколько мандарин было у Ивана? У Пети?
При этом у Пети было на 15 мандарин больше. Сколько мандарин было у Ивана? У Пети?
Задача №9. Мальчик проехал на автобусе 3 части пути от дома, а пешком прошел 2 части пути. Всего же он преодолел 15 км. Сколько км мальчик прошел?
Задача №10. У Вики было в 4 раза меньше апельсин, чем у Оли. При этом у Оли было на 12 апельсин больше, чем у Вики. Сколько апельсин было у Вики? У Оли?
Математика 5 класс: Уравнения и составление уравнений по условию задачи.
Решите уравнения:
Задание по математике №1.
а) 34-x+12=9; б)4x-(12-25+3x)=87.
Задание по математике №2.
а) 5x-(7+8+4x)=56; б)12-2x+3x-7=29;
Задание по математике №3.
а) 4x+(15-3x)-12=26; б)23-x+1=11
Задание по математике №4.
а)27-(x-3)+12=10; б)2x-4-13-x=47;
Задание по математике №5.
а) (21+x)-34=11; б)19+(13-7x+8x)=59;
Задачи на составление уравнений:
Карточка №6. Составьте уравнение по условию задачи и решите его:
В корзине было неизвестное количество яблок. Сначала из нее взяли 12 яблок, а потом положили туда 5 яблок. В результате в корзине стало 24 яблока. Сколько яблок было в корзине первоначально?
Карточка №7. Составьте уравнение по условию задачи и решите его:
В корзине было 15 груш. Сначала из нее взяли 7 груш, а потом положили в нее неизвестное количество груш. В результате в корзине стало 34 груши. Сколько груш положили в корзину?
Карточка №8. Составьте уравнение по условию задачи и решите его:
В коробке было 65 конфет. Вначале из нее взяли неизвестное количество конфет, а потом доложили 7 конфет. В результате в коробке стало 34 конфеты. Сколько конфет было взято?
Сколько конфет было взято?
Карточка №9. Составьте уравнение по условию задачи и решите его:
Турист прошел часть пути за 45 минут, затем отдыхал неизвестное количество времени, и оставшуюся часть пути прошел за 34 минуты. В результате весь путь турист преодолел за 2 часа 18 минут. Сколько минут отдыхал турист?
Карточка №10. Составьте уравнение по условию задачи и решите его:
Температура воздуха была 23 градуса. В первый день она опустилась на неизвестное количество градусов, а во второй день поднялась на 5 градусов. В результате температура воздуха стала 19 градусов.
На сколько градусов опустилась температура в первый день?
ГДЗ по Математике 5 класс: Никольский С.М. Решебник
Решебник по математике для 5 класса Никольский – это онлайн-решебник, содержащий комплекс решенных примеров и задач по учебнику группы российских авторов Никольского С. М., Потапова М.К., Решетникова Н.Н. и Шевкина А.В. Его используют во многих общеобразовательных школах России в качестве пособия для обучения пятиклассников основам арифметики.
М., Потапова М.К., Решетникова Н.Н. и Шевкина А.В. Его используют во многих общеобразовательных школах России в качестве пособия для обучения пятиклассников основам арифметики.
Готовые домашние задания по математике Никольского – стоит ли пятиклассникам ими пользоваться?
В 5 классе учебная программа не отличается повышенной сложностью, однако с ее усвоением нередко испытывают сложности даже ребята-отличники. Главная причина – переход из начальной школы в среднее звено. Родителям на этом этапе не следует сразу бросаться за помощью к репетиторам: надо позволять ребенку выбраться из сложной ситуации самостоятельно с опорой на готовые домашние задания.
ГДЗ по математике за 5 класс Никольский помогают разобрать примеры и задачи, которые ребенок не успел понять в классе, запомнить алгоритм их выполнения и особенности оформления. Родители на основе решебников могут проверять домашние работы и контролировать успеваемость своих детей.
Использование онлайн-ответов на упражнения учебника Никольского С. М. на сайте ГДЗ Путина обеспечивает к тому же и экономию времени:
М. на сайте ГДЗ Путина обеспечивает к тому же и экономию времени:
- найти нужный ответ можно по его номеру в таблице;
- на одно упражнение может приходиться несколько вариантов решения;
- использовать базу ответов можно с любого устройства – телефона, планшета, ноутбука.
В дополнение – база решебников на сайте регулярно обновляется, оттого номера решений в таблице соответствуют упражнениям последних изданий учебников.
Какие задачи помогает выполнить решебник по математике за 5 класс от Никольского?
Несмотря на то, что в 5 классе учебная программа не отличается высоким уровнем сложности, однако спектр рассматриваемых тем чрезвычайно широк:
- натуральные числа, их свойства, математические действия с натуральными числами;
- прямая, отрезов, луч, угол и особенности их измерения;
- прямоугольники и треугольники, определение их площади;
- делимость натуральных числе и ее особенности, НОК и НОД;
- обыкновенные дроби, равенство дробей, их приведение к общему знаменателю, математические действия с дробями.

Особенностью учебника по математике для 5 класса Никольского С.М. в его 13-м издании 2014 года выступает наличие в нем нескольких видов задач – заданий для устной работы, повышенной трудности, старинных задач, а также задачек на построение. Любая из них найдет свое решение в решебнике по математике за 5 класс Никольский.
На основе готовых домашних заданий пятиклассники могут не только разобраться в практическом применении формул и теорем, но также подготовиться к самостоятельным и контрольным работам, олимпиадам и экзаменам.
Качественное усвоение учебной программы по математике в 5 классе – гарантия успеха в изучении предмета в последующие годы.
Контрольные работы по математике за 5 класс, УМК Виленкин (с ответами по паролю)
Виленкин — один из старых, известных многим, авторов учебников математики. Учебники довольно логично построены, материал не поверхностный, но и не слишком углубленный, то что нужно в пятом классе и ничего более. А чтобы проверить усвоенные учениками знания, обязательно нужно проводить самостоятельные и контрольные работы по математике. Вот такие работы к учебнику Виленкина за пятый класс мы и предлагаем вашему вниманию.
Вот такие работы к учебнику Виленкина за пятый класс мы и предлагаем вашему вниманию.
Контрольная работа №1 за 5 класс (Виленкин)
Вариант 1
1. Найдите сумму:
а) 3000000+5000+7
б) 654+765
2. Выполните действия:
(60+40):2 – 30:5
3. Сравните числа и поставьте вместо звездочки знак < или >
а) 63001 * 63002
б) 41527 * 42326
4. Задача. От туристского лагеря до города 84 км. Турист ехал на велосипеде из лагеря в город со скоростью 12 км/ч., а возвращался по той же дороге со скоростью 14 км/ч. На какой путь турист затратил больше времени и на сколько часов.
Вариант 2
1. Найдите сумму:
а) 2000000+7000+300+2
б) 763+448
2. Выполните действия:
(70-50)∙5:20+55
3. Сравните числа и поставьте вместо звездочки знак < или >
а) 20850 * 20860
б) 31255 * 32254
4. Задача. Игорь живет на расстоянии 48 км от районного центра. Путь от дома до райцентра он проехал на велосипеде со скоростью 16 км/ч, а обратный путь по той же дороге он проехал со скоростью 12 км/ч. На какой путь Игорь затратил меньше времени и насколько часов.
На какой путь Игорь затратил меньше времени и насколько часов.
Контрольная работа №1 за 5 класс (Виленкин)
Вариант 1
1. Найдите сумму: а) 3000000+5000+7=3005004 б) 654+765=1419
2. Выполните действия: (60+40):2 – 30:5=100:2-6 = 50-6 = 44
3. Сравните числа и поставьте вместо звездочки знак < или > а) 63001 < 63002 б) 41527 < 42326
4. Задача. От туристского лагеря до города 84 км. Турист ехал на велосипеде из лагеря в город со скоростью 12 км/ч., а возвращался по той же дороге со скоростью 14 км/ч. На какой путь турист затратил больше времени и на сколько часов.
1) 84:12=7 (ч.) ехал из лагеря в город.
2) 84:14=6 (ч.) ехал из города в лагерь.
3) 7-6=1 (ч.) на 1 час дольше ехал из лагеря в город.
Ответ: на 1 час дольше ехал из лагеря в город.
Вариант 2
1. Найдите сумму:
а) 2000000+7000+300+2=2007300
б) 763+448=1211
Найдите сумму:
а) 2000000+7000+300+2=2007300
б) 763+448=1211
2. Выполните действия: (70-50)∙5:20+55=20*5:20+55=5+55=60
3. Сравните числа и поставьте вместо звездочки знак < или > а) 20850 < 20860 б) 31255 < 32254
4. Задача. Игорь живет на расстоянии 48 км от районного центра. Путь от дома до райцентра он проехал на велосипеде со скоростью 16 км/ч, а обратный путь по той же дороге он проехал со скоростью 12 км/ч. На какой путь Игорь затратил меньше времени и насколько часов.
1) 48:16=3
(ч.) ехал дома до райцентра.
2) 48:12=4
(ч.) ехал от райцентра до дома.
3) 4-3=1 (ч.) на 1 час дольше ехал от райцентра до дома.
Ответ: на 1 час дольше ехал от райцентра до дома.
Контрольная работа №2 за 5 класс (Виленкин)
Вариант 1
1. Выполнить действия:
а) (829-239)*75
б) 8991:111:3
2. Задача. Периметр треугольника 36 см, а периметр прямоугольника в 3 раза меньше. На сколько сантиметров периметр треугольника больше периметра прямоугольника?
На сколько сантиметров периметр треугольника больше периметра прямоугольника?
3. Вычислить:
4 кг – 80 гр
4.
а) На сколько число 59345 больше числа 53568?
б) На сколько число 59345 меньше числа 69965?
5. Задача. Вдоль аллеи (по прямой) высадили 15 кустов. Расстояние между любыми двумя соседними кустами одинаковое. Найдите это расстояние, если между крайними кустами 210 дм.
Вариант 2
1. Выполнить действия:
а) 2000 – (859+1085):243
б) 3969:(305 – 158)
2. Задача. Туристы в первый день ехали на велосипедах 6 часов со скоростью 12 км/ч, во — второй день они проехали с одинаковой скоростью такой же путь за 4 часа. С какой же скоростью ехали туристы во – второй день?
3. Вычислить:
2 кг – 60 гр
4.
а) на сколько число 38954 больше числа 22359
б) На сколько число 38954 меньше числа 48234.
5. Задача. Вдоль шоссе (по прямой) высадили 20 деревьев. Расстояние между любыми двумя соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 380 м.
Найдите это расстояние, если между крайними деревьями 380 м.
Контрольная работа №2 за 5 класс (Виленкин)
Вариант 1
1. Выполнить действия: а) (829-239)*75=590*75=44250
*590
75
+ 2950
4130
44250
б) 8991:111:3=81:3=27
2. Задача. Периметр треугольника 36 см, а периметр прямоугольника в 3 раза меньше. На сколько сантиметров периметр треугольника больше периметра прямоугольника?
1) 36:3=12 (см) периметр прямоугольника.
2) 36-12=24 (см) на столько периметр треугольника больше периметра
прямоугольника.
Ответ: на 24 см периметр треугольника больше периметра прямоугольника.
3. Вычислить: 4кг – 80г = 3 кг 920 г
4. а) На сколько число 59345 больше числа 53568?
-59345
53568
5777
б) На сколько число 59345 меньше числа 69965?
-69965
59345
10620
5. Задача. Вдоль аллеи (по прямой) высадили 15 кустов. Расстояние между любыми
двумя соседними кустами одинаковое. Найдите это расстояние, если между крайними
кустами 2100 дм.
Задача. Вдоль аллеи (по прямой) высадили 15 кустов. Расстояние между любыми
двумя соседними кустами одинаковое. Найдите это расстояние, если между крайними
кустами 2100 дм.
2100 дм = 21000 см = 21м
1) 21:14=1,5 (м) между соседними кустами
Ответ: 1,5 метра между соседними кустами.
Вариант 2
1. Выполнить действия: а) 2000 – (859+1085):243=2000-1944:243=2000-8=1992 б) 3969:(305 – 158)=3969:147=27
2. Задача. Туристы в первый день ехали на велосипедах 6 часов со скоростью 12 км/ч, во — второй день они проехали с одинаковой скоростью такой же путь за 4 часа. С какой же скоростью ехали туристы во – второй день?
1) 6*12=72 (км) проехали туристы в 1 день.
2) 72:4=18 (км/ч) скорость туристов во второй день.
Ответ: 18 км/ч скорость туристов во второй день.
3. Вычислить: 2кг – 60г = 1 кг 940г
4.
а) на сколько число 38954 больше числа 22359.
— 38954
22359
16595
б) На сколько число 38954 меньше числа 48234.
-48234
38954
9280
5. Задача. Вдоль шоссе (по прямой) высадили 20 деревьев. Расстояние между любыми двумя соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 380 м.
380:19=20 (м) между соседними деревьями.
Ответ: 20 метров.
Контрольная работа №3 за 5 класс (Виленкин)
Вариант 1
1. Решите уравнение:
а) 21+х=56
б) у-89=90
2. Найти значение выражения:
260+в – 160, если в=93
3. Вычислите, выбирая удобный порядок действий
а) 5+1977+1515
б) 863 – (163+387)
4. Решить задачу с помощью уравнения.
В автобусе было 78 пассажиров. После того, как на остановке из него несколько человек вышли, в автобусе осталось 59 пассажиров. Сколько человек вышли из автобуса на остановке.
5.
На отрезке MN =19, отметили точку К такую, что МК=15 и точку F такую, что FN=13. Найти длину отрезка KF.
Вариант 2
1. Решите уравнение:
а) х+32=68
б) 76 – у=24
2. Найти значение выражения:
340+к – 240, если к=87
3. Вычислите, выбирая удобный порядок действий
а) 7231+1437+563
б) (964+479) – 264
4. Решить задачу с помощью уравнения.
В санатории было 97 отдыхающих. После того, как несколько человек уехали на экскурсию, в санатории осталось 78 отдыхающих. Сколько отдыхающих уехали на экскурсию.
5.
На отрезке DE=25 отметили точку L такую, что DL=19, и точку Р такую, что РЕ=17. Найдите длину отрезка LP.
Контрольная работа №3 за 5 класс (Виленкин)
Вариант 1
1. Решите уравнение:
а) 21+х=56
х=56-21
х=35
б) у-89=90
у=90+89
у=179
2. Найти значение выражения:
260+ в – 160, если в = 93
260+93-160=193
3. Вычислите, выбирая удобный порядок действий
а) 5 + 1977 + 1515 = 1520 + 1977 = 34197
б) 863 – (163 + 387) = 700 + 387 = 1087
Вычислите, выбирая удобный порядок действий
а) 5 + 1977 + 1515 = 1520 + 1977 = 34197
б) 863 – (163 + 387) = 700 + 387 = 1087
4. Решить задачу с помощью уравнения. В автобусе было 78 пассажиров. После того, как на остановке из него несколько человек вышли, в автобусе осталось 59 пассажиров. Сколько человек вышли из автобуса на остановке.
78 — х = 59
78 — 59 = х
х = 19
Ответ: 19 человек
5. На отрезке MN = 19 мм, отметили точку К такую, что МК=15 мм и точку F такую, что FN=13 мм. Найти длину отрезка KF.
1) 19 — 15 = 4 (мм) длина отрезка KN.
2) 19 — 13 = 6 (мм) длина отрезка MF
3) 19 — (4 + 6) = 10 (мм) длина отрезка
KF.
Ответ: 10 мм.
Вариант 2
1. Решите уравнение:
а) х+32=68
х=68-32
х = 36
б) 76 – у = 24
76 — 24 = y
y = 52
2. Найти значение выражения:
Найти значение выражения:
340 + к – 240, если к = 87
340 + 87 — 240 = 187
3. Вычислите, выбирая удобный порядок действий
а) 7231 + 1437 + 563 = 7231 + 2000 = 9 231
б) (964 + 479) – 264 = 964 — 264 + 479 = 700 + 469 = 1 169
4. Решить задачу с помощью уравнения. В санатории было 97 отдыхающих. После того, как несколько человек уехали на экскурсию, в санатории осталось 78 отдыхающих. Сколько отдыхающих уехали на экскурсию.
97 — x = 78
x = 97 — 78
x = 19
Ответ: 19 человек.
5. На отрезке DE = 25 мм отметили точку L такую, что DL = 19 мм, и точку Р такую, что РЕ = 17 мм. Найдите длину отрезка LP.
1) 25 — 19 = 6 (мм) длина LE.
2) 25 — 17 = 8 (мм) длина DP.
3) 25 — (6+8) = 9 (мм) длина LP
Ответ: 9 мм
Контрольная работа №4 за 5 класс (Виленкин)
Вариант 1
1. Найдите значение выражения:
Найдите значение выражения:
а) 58∙196
б) 405∙208
в) 36490:178
2. Решите уравнение
а) х∙14=112
б) 133:у=19
в) m:15=90
3. Вычислите, выбирая удобный порядок действий.
а) 4∙289∙25
б) 50∙97∙20
4. Задача. Коля задумал число, умножил его на 3 и от произведения отнял 8. Он получил 50. Какое число задумал Коля?
5. Вычислите корень уравнения и сделайте проверку:
х+х – 20=х+5
Вариант 2
1. Найдите значение выражения:
а) 67∙189
б) 306∙805
в) 38130:186
2. Решите уравнение
а) х∙13=182
б) 187:у=17
в) n:14=98
3. Вычислите, выбирая удобный порядок действий.
а) 25∙197∙4
б) 50∙23∙40
4. Задача. Света задумала число, умножила его на 4 и к произведению прибавила 8. Получила 60. Какое число задумала Света?
5. Угадайте корень уравнения и сделайте проверку:
у+у – 25=у+10
Контрольная работа №4 за 5 класс (Виленкин)
Вариант 1
1. Найдите значение выражения:
а) 58∙196
Найдите значение выражения:
а) 58∙196
* 196
58
+ 1568
980
11368
б) 405∙208
*405
208
+3240
810
84240
в) 36490:178
-36490|178
356 |205
-890
890
0
2. Решите уравнение а) х∙14=112
х = 112 : 14
х= 8
б) 133:у=19
у = 133 * 19
у = 2527
в) m:15=90
m = 90 * 15
m = 1350
3. Вычислите, выбирая удобный порядок действий.
а) 4∙289∙25 = 289 * 100 = 28 900
б) 50∙97∙20 = 97 * 1000 = 97 000
4. Задача. Коля задумал число, умножил его на 3 и от произведения отнял 8. Он получил 50. Какое число задумал Коля?
х — задуманное число.
х * 3 — 8 = 50
х * 3 = 50 — 8
х = 42 : 3
х = 14
5. Вычислите корень уравнения и сделайте проверку:
х + х – 20 = х + 5
Вычислите корень уравнения и сделайте проверку:
х + х – 20 = х + 5
х + х — х = 20 + 5
х = 25
Вариант 2
1. Найдите значение выражения: а) 67∙189
*189
67
+1323
1134
12663
б) 306∙805
*306
805
+1530
2448
246330
в) 38130:186
-38130|186
372 |205
-930
930
0
2. Решите уравнение
а) х∙13=182
х = 182 : 13
х = 14
б) 187:у=17
у = 187 : 17
у = 11
в) n:14=98
n = 98 * 14
n = 1372
3. Вычислите, выбирая удобный порядок действий.
а) 25∙197∙4 = 197 *100 = 19 700
б) 50∙23∙40 = 2000 * 23 = 46 000
4. Задача. Света задумала число, умножила его на 4 и к произведению прибавила 8. Получила 60. Какое число задумала Света?
Получила 60. Какое число задумала Света?
х — задуманное число
х * 4 + 8 = 60
х * 4 = 60 — 8
х = 52 : 4
х = 13
5. Вычислите корень уравнения и сделайте проверку: у + у – 25 = у + 10
у + у — у = 25 + 10
у = 35
Контрольная работа №5 за 5 класс (Виленкин)
Вариант 1
1. Найдите значение выражения:
а) 684∙397 — 584∙397
б) 39∙58 – 9720:27+33
в) 23 + 32
2. Решите уравнение:
а) 7у – 39=717
б) х+3х=76
3. Упростите выражение:
а) 24а+16+13а
б) 25∙m∙16
4. Задача. В книге напечатаны 2 сказки. Первая занимает в 4 раза больше страниц, чем вторая, а обе они занимают 30 стр. Сколько страниц занимает каждая сказка?
5. Имеет ли корни уравнение:
х2=х:х
Вариант 2
1. Найдите значение выражения:
а) 798∙349-798∙249
б) 57∙38-8640:24+66
в) 52+33
2. Решите уравнение:
Решите уравнение:
а) 8х+14=870
б) 5у-у=68
3. Упростите выражение:
а) 37к+13+22к
б) 50∙n∙12
4. Задача. В двух корзинах 98 яблок. В первой яблок в шесть раз меньше, чем во второй. Сколько яблок в каждой корзине?
5. Имеет ли корни уравнение:
у3=у∙у
Вариант 1
1. Найдите значение выражения:
а) 684∙397 — 584∙397 = (684 — 584 ) * 397 = 39 700
б) 39 ∙ 58 – 9720 : 27 + 33 = 1935
1) 39 * 58 = 2262
2) 9720 : 27 = 360
3) 2262 — 360 = 1902
4) 1902 + 33 = 1935
в) 23 + 32 = 55
2. Решите уравнение:
а) 7у – 39 = 717
7у = 717 + 39
7у = 756
у = 108
б) х + 3х = 76
4 * х = 76
х = 76 : 4
х = 19
3. Упростите выражение:
а) 24а + 16 + 13а = 37а + 16
б) 25∙m∙16 = 400m
4. Задача. В книге напечатаны 2 сказки. Первая занимает в 4 раза больше страниц,
чем вторая, а обе они занимают 30 стр. Сколько страниц занимает каждая сказка?
Сколько страниц занимает каждая сказка?
Решение:
х — страниц перва сказка.
4х — вторая сказка
Составляем уравнение
х + 4 х = 30
х = 30 : 5
х = 6
5. Имеет ли корни уравнение:
х2=х:х
Имеет при х = 0 или 1.
Вариант 2
1. Найдите значение выражения:
а) 798∙349-798∙249 = 798 (349 — 249) = 79 800
б) 57∙38-8640:24+66 = 1872
1) 57 * 38 = 2166
2) 8640 : 24 = 360
3) 2166 — 360 = 1806
4) 1806 + 66 = 1872
в) 52 + 33 = 85
2. Решите уравнение:
а) 8х+14=870
8х = 870 — 14
х = 856 : 8
х = 107
б) 5у-у=68
4у = 68
у = 68 : 4
у = 22
3. Упростите выражение:
а) 37к+13+22к = 59к + 13
б) 50∙n∙12 = 62n
4. Задача. В двух корзинах 98 яблок. В первой яблок в шесть раз меньше, чем во второй. Сколько яблок в каждой корзине?
x — в первой корзине
6х — во второй корзине
х + 6х = 98
7х = 98
х = 14
5. Имеет ли корни уравнение:
Имеет ли корни уравнение:
у3=у∙у
Имеет при у = 0 или 1.
Контрольная работа №6 за 5 класс (Виленкин)
Вариант 1
1. Вычислите:
а) (53+132):21
б) 180∙94-47700:45+4946
2. Задача. Длина прямоугольного участка земли 125 м, а ширина 96 м. Найдите площадь поля и выразите её в арах.
3. Задача. Найдите объем прямоугольного параллелепипеда, измерения которого равны 4 м, 3 м и 5 дм.
4. Используя формулу пути s=v∙t, найдите:
а) путь, пройденный автомашиной за 3 ч, если её скорость 80 км/ч,
б) время движения катера, прошедшего 90 км со скоростью 15 км/ч
5. Задача. Найдите площадь поверхности и объем куба, ребро которого равно 6 дм. Во сколько раз уменьшится площадь поверхности и во сколько раз – объем куба, если ребро уменьшить вдвое?
Вариант 2
1. Вычислите:
а) (63+122):15
б) 86∙170-5793+72800:35
2. Задача. Ширина прямоугольного поля 375 м, а длина 1600 м. Найдите площадь поля и выразите её в гектарах.
Ширина прямоугольного поля 375 м, а длина 1600 м. Найдите площадь поля и выразите её в гектарах.
3. Задача. Найдите объем прямоугольного параллелепипеда, измерения которого равны 2 дм, 6 дм и 5 см.
4. Используя формулу пути s=v∙t, найдите:
а) путь, пройденный моторной лодкой за 2 часа, если её скорость 18 км/ч
б) скорость движения автомобиля, за 3 ч прошедшего 150 км.
5. Задача. Ребро куба равно 5 см. Найдите площадь поверхности и объем этого куба. Во сколько раз увеличится площадь поверхности и во сколько раз – объем куба, если его ребро увеличить вдвое?
В РАБОТЕ
Контрольная работа №7 за 5 класс (Виленкин)
Вариант 1
1. Примите за единичный отрезок длину 8 клеток тетради и отметьте на координатном луче точки А( 3/8 ), М( 1/2 ), К( 7/8 ), Т( 1/4 ), Р ( 11/8 )
2. Сравните числа:
а) 5/13 и 7/13, б) 11/15 и 8/15, в) 1 и 7/6, г) 8/9 и 5/4
3. Сложите 3/5 числа 30 и 2/7 числа 14.
4. Какую часть составляют:
а) 9 см2 от квадратного дециметра,
б) 17 дм3 от кубического метра,
в) 13 кг от 2 ц?
5. Задача. Ширина прямоугольника 48 см, что составляет 3/16 его периметра. Найдите длину этого прямоугольника.
Вариант 2
1. Примите за единичный отрезок длину 12 клеток тетради и отметьте на координатном луче точки В( 5/12 ), С( 1/2 ), Е( 1/3 ), О( 3/4 ), Н( 17/12 )
2. Сравните числа:
а) 6/11 и 3/11, б) 11/17 и 12/17, в) 1 и 3/8, г) 6/7 и 5/3
3. Сложите 2/9 числа 18 и 2/5 числа 40.
4. Какую часть составляют:
а) 7 дм2 от квадратного метра,
б) 19 см3 от кубического дециметра,
в) 9 ц от 4 т?
5. Задача. Длина прямоугольника составляет 5/16 его периметра. Найдите ширину этого прямоугольника, если его длина равна 80 см.
В РАБОТЕ
Контрольная работа №8 за 5 класс (Виленкин)
Вариант 1
1. Выполните действия:
Выполните действия:
а) 10/11 — 4/11 + 3/11 б) 4 5/9 + 3 8/9
в) 6 — 2 3/8 г) 5 6/13 — 1 11/13
2. Задача. Турист шел с постоянной скоростью и за 3 часа прошел 14 км. С какой скоростью он шел?
3. Задача. В гараже 45 автомобилей. Из них 5/9 — легковые. Сколько легковых автомобилей в гараже.
4. Решите уравнение:
а) 5 6/7 — х = 3 2/7 б) у + 4 8/11 = 10 7/11
5. Какое число надо разделить на 8, чтобы частное равнялось 5 7/8?
Вариант 2
1. Выполните действия:
а) 12/13 — 5/13 + 4/13 б) 5 — 2 3/8
в) 5 7/11 + 1 9/11 г) 6 5/11 — 4 9/11
2. Задача. Автомобиль, двигаясь с постоянной скоростью, прошел 14 км за 9 мин. Какова скорость автомобиля?
3. Задача. В классе 40 учеников. Из них 5/8 занимаются в спортивных секциях. Сколько учеников класса занимаются спортом?
4. Решите уравнение:
Решите уравнение:
а) х + 2 5/13 = 4 11/13 б) 6 3/7 — у = 3 5/7
5. Какое число надо разделить на 6, чтобы частное равнялось 8 5/6?
В РАБОТЕ
Контрольная работа №9 за 5 класс (Виленкин)
Вариант 1
1. Сравните числа: 7,195 и 12,1; 8,276 и 8,3; 0,76 и 0,7598
2. Выполните действия:
а) 12,3 + 5,26 в) 79,1-6,08
б) 0,48 + 0,057 г) 5-1,63
3. Округлите:
а) 3,18; 30,625; 257,51; 0,28 до единиц
б) 0,531; 12,467; 8,5452 и 0,009 до сотых
4. Задача. Собственная скорость лодки 3,4 км/ч. Скорость лодки против течения реки 0,8 км/ч. Найдите скорость лодки по течению.
5. Запишите четыре значения m, при которых верно неравенство 0,71<m<0,74.
Вариант 2
1. Сравните числа: 8,2 и 6,984; 7,6 и 7,596; 0,6387 и 0,64
2. Выполните действия:
а) 15,4+3,18 в) 86,3 – 5,07
в) 0,068+0,39 г) 7 – 2,78
3. Округлите:
Округлите:
а) 8,72; 40,198; 164,53 и 0,61 до единиц
б) 0,834; 19,471; 6,352 и 0,08 до десятых.
4. Задача. Собственная скорость катера 32,8 км/ч. Скорость катера по течению реки 34,2 км/ч. Найдите скорость катера против течения.
5. Запишите четыре значения n, при которых верно неравенство 0,65<n<0,68.
В РАБОТЕ
Контрольная работа №10 за 5 класс (Виленкин)
Вариант 1
1. Вычислите:
а) 4,35∙18 г) 53,3:26
б) 6,25∙108 д) 6:24
в) 126,385∙10 е) 126,385:100
2. Решить уравнение:
7у+2,6=27,8
3. Найдите значение выражения
90-16,2:9+0,08
4. Задача. На автомобиль погрузили 6 контейнеров и 8 одинаковых ящиков по 0,28т каждый. Какова масса одного ящика, если масса всего груза 2,4т?
5. Задача. Как изменится произведение двух десятичных дробей, если в одном множителе перенести запятую вправо через две цифры, а в другом – влево через четыре цифры?
Вариант 2
1. Вычислите:
Вычислите:
а) 3,85∙24; г) 35,7:34
б) 4,75∙116; д) 7:28
в) 234,166∙100 е) 234,166:10
2. Решить уравнение:
6х+3,8=20,6
3. Найдите значение выражения
40-23,2:8+0,07
4. Задача. Из 7,7 м ткани сшили 7 платьев для кукол и 9 одинаковых полотенец. Сколько ткани пошло на одно полотенце, если на каждое платье потребовалось 0,65 м ткани?
5. Задача. Как изменится произведение двух десятичных дробей, если в одном множителе перенести запятую влево через четыре цифры, а в другом — вправо через две цифры?
В РАБОТЕ
Контрольная работа №11 за 5 класс (Виленкин)
Вариант 1
1. Выполните действия:
а) 0,872∙6,3 г) 30,42:7,8
б) 1,6∙7,625 д) 0,702:0,065
в) 0,045∙0,1 е) 0,026:0,01
2. Найдите среднее арифметическое чисел 32,4; 41; 27,95; 46,9; 55,75.
3. Найдите значение выражения 296,2 – 2,7∙6,6 + 6:0,15.
4. Задача. Поезд 3 ч шел со скоростью 63,2 км/ч и 4 ч со скоростью 76,5 км/ч. Найдите среднюю скорость поезда на всем пути.
Найдите среднюю скорость поезда на всем пути.
5. Задача. Сумма трех чисел 10,23, а среднее арифметическое шести других чисел 2,9. Найти среднее арифметическое всех этих девяти чисел.
Вариант 2
1. Выполните действия:
а) 0,964∙7,4 г) 25,23:8,7
б) 2,4∙7,375 д) 0,0918:0,0085
в) 0,72∙0,01 е) 0,39:0,1
2. Найдите среднее арифметическое чисел 63; 40,63; 70,4; 67,97
3. Найдите значение выражения 398,6 – 3,8∙7,7 + 3:0,06
4. Задача. Легковой автомобиль шел 2 ч со скоростью 55,4 км/ч и ещё 4 ч со скоростью 63,5 км/ч. Найдите среднюю скорость автомобиля на всем пути.
5. Задача. Среднее арифметическое пяти чисел 4,7, а сумма других трех чисел 25,14. Найдите среднее арифметическое всех этих восьми чисел.
В РАБОТЕ
Контрольная работа №12 за 5 класс (Виленкин)
Вариант 1
1. Задача. Площадь поля 260 га. Горохом засеяно 35% поля. Какую площадь занимают посевы гороха?
2. Найдите значение выражения 201 – (176,4:16,8+9,68)∙2,5.
Найдите значение выражения 201 – (176,4:16,8+9,68)∙2,5.
3. Задача. В библиотеке 12% всех книг – словари. Сколько книг в библиотеке, если словарей в ней 900?
4. Решите уравнение 12+8,3х+1,5х = 95,3
5. Задача. От мотка провода отрезали сначала 30%, а затем ещё 60% остатка. После этого в мотке осталось 42 м провода. Сколько метров провода было в мотке первоначально?
Вариант 2
1. Задача. В железной руде содержится 45% железа. Сколько тонн железа содержится в 380 т руды?
2. Найдите значение выражения (299,3:14,6 – 9,62)∙3,5+72,2
3. Задача. За день вспахали 18% поля. Какова площадь всего поля, если вспахали 1170 га?
4. Решите уравнение 6,7у+13+3,1у=86,5
5. Задача. Израсходовали сначала 40% имевшихся денег, а затем ещё 30% оставшихся. После этого осталось 105р. Сколько было денег первоначально?
В РАБОТЕ
Контрольная работа №13 за 5 класс (Виленкин)
Вариант 1
1. Постройте углы, если:
Постройте углы, если:
а) <ВМЕ = 68° б) <СКР = 115°
2. Начертите треугольник AKN такой, чтобы <A = 120°. Измерьте и запишите градусные меры остальных углов треугольника.
3. Луч ОК делит прямой угол DOS на два угла так, что угол DOK составляет 0,7 угла DOS. Найдите градусную меру угла KOS.
4. Развернутый угол AMF разделен лучом МС на два угла АМС и CMF. Найдите градусные меры этих углов, если угол АМС вдвое больше угла CMF.
5. Из вершины развернутого угла DKP проведены его биссектриса КВ и луч КМ так, что <ВКМ =38°. Какой может быть градусная мера угла DKM?
Вариант 2
1. Постройте углы, если:
а) <ADF = 110° б) <HON = 73°
2. Начертите треугольник BCF такой, чтобы <В = 105°. Измерьте и запишите градусные меры остальных углов треугольника.
3. Луч АР делит прямой угол CAN на два угла так, что угол NAP составляет 0,3 угла CAN. Найдите градусную меру угла РАС.
4. Развернутый угол ВОЕ разделен лучом ОТ на два угла ВОТ и ТОЕ. Найдите градусные меры этих углов, если угол ВОТ втрое меньше угла ТОЕ.
Найдите градусные меры этих углов, если угол ВОТ втрое меньше угла ТОЕ.
5. Из вершины развернутого угла MNR проведены его биссектриса NB и луч NP так, что <BNP = 26°. Какой может быть градусная мера угла MNP?
В РАБОТЕ
Контрольная работа №14 за 5 класс (Виленкин)
Вариант 1
1. Вычислите: 2,66:3,8 – 0,81∙0,12 + 0,0372
2. В магазине 240 кг фруктов. За день продали 65% фруктов. Сколько килограммов фруктов осталось.
3. Найдите высоту прямоугольного параллелепипеда, объем которого равен 25,2 дм3, длина 3,5 дм и ширина 16 см.
4. Собственная скорость теплохода 24,5 км/ч, скорость течения реки 1,3 км/ч. Сначала теплоход 0,4 ч плыл по озеру, а затем 3,5 ч по реке против течения. Какой путь прошел теплоход за все это время?
5. Постройте углы МОК и КОС, если <МОК = 110°, <КОС = 46°. Какой может быть градусная мера угла СОМ?
Вариант 2
1. Вычислите: 7,8∙0,26 – 2,32:2,9 + 0,672.
2. В цистерне 850 л молока. 48% молока разлили в бидоны. Сколько литров молока осталось в цистерне?
3. Объем прямоугольного параллелепипеда равен 1,35 м3, высота 2,25 м и длина 8 дм. Найдите его ширину.
4. Катер плыл 3,5 ч по течению реки и 0,6 ч по озеру. Найдите путь, пройденный катером за все это время, если собственная скорость катера 16,5 км/ч, а скорость течения реки 2,1 км/ч.
5. Постройте углы AND и NDB, если <ADN = 34°, <NDB = 120°. Какой может быть градусная мера угла ADB?
Вариант 1
1. Вычислите: 2,66 : 3,8 – 0,81 ∙ 0,12 + 0,0372 = 0,6628
1) 2,66 : 3,8 = 0,7
2) 0,81 * 0,12 = 0,0972
3) 0,7 — 0,0972 = 0,6028
4) 0,6028 + 0,0372 = 0,6628
2. В магазине 240 кг фруктов. За день продали 65% фруктов. Сколько килограммов фруктов осталось.
1) 240 : 100 = 2,4 (кг) фруктов это 1 процент от всех фруктов.
2) 2,4 * 65 = 156 (кг) фруктов продали.
3) 240 — 156 = 84 (кг) осталось.
Ответ: 84 кг
3. Найдите высоту прямоугольного параллелепипеда, объем которого равен 25,2 дм3, длина 3,5 дм и ширина 16 см.
1) 3,5 * 1.6 = 5,6 (дм2) площадь одной стороны.
2) 25,2 : 5,6 = 4,5 (дм) высота прямоугольного параллелепипеда.
Ответ: 4,5 дм.
4. Собственная скорость теплохода 24,5 км/ч, скорость течения реки 1,3 км/ч. Сначала теплоход 0,4 ч плыл по озеру, а затем 3,5 ч по реке против течения. Какой путь прошел теплоход за все это время?
1) 24,5 * 0,4 = 9,8 (км) проплыл теплоход по озеру.
2) 24,5 — 1,3 = 23,2 (км/ч) скорость теплохода по реке, против течения реки.
3) 23,2 * 3,5 = 81,2 (км) проплыл теплоход по реке, против течения реки.
4) 81,2 + 9,8 = 91 (км) проплыл параход.
Ответ: 91 км.
5. Постройте углы МОК и КОС, если <МОК = 110°, <КОС = 46°. Какой может быть градусная мера угла СОМ?
Строим в тетради с помощью транспортира. COM может быть: 110° — 46° = 64° или 180° — 110° — 46° = 24°
Вариант 2
1. Вычислите: 7,8 ∙ 0,26 – 2,32 : 2,9 + 0,672 = 1,9
Вычислите: 7,8 ∙ 0,26 – 2,32 : 2,9 + 0,672 = 1,9
1) 7,8 ∙ 0,26 = 2.028
2) 2,32 : 2,9 = 0,8
3) 2,028 — 0,8 = 1.228
4) 1,228 + 0,672 = 1,9
2. В цистерне 850 л молока. 48% молока разлили в бидоны. Сколько литров молока осталось в цистерне?
1) 850 : 100 = 8,5 (л) 1 процент от 850 литров.
2) 8,5 * 48 = 408 (л) разлили в бидоны.
3) 850 — 408 = 442 (л)молока осталось в цистерне.
Ответ: 442 л
3. Объем прямоугольного параллелепипеда равен 1,35 м3, высота 2,25 м и длина 8 дм. Найдите его ширину.
1) 2.25 * 0.8 = 1,8 (м2) площадь одной из сторон прямоугольного параллелепипеда.
2) 1,35 : 1,8 = 0,75 (м) высота прямоугольного параллелепипеда.
Ответ: 0,75 м.
4. Катер плыл 3,5 ч по течению реки и 0,6 ч по озеру. Найдите путь, пройденный катером за все это время, если собственная скорость катера 16,5 км/ч, а скорость течения реки 2,1 км/ч.
1) 16.5 + 2,1 = 18. 6 (км/ч) скорость по течению реки.
6 (км/ч) скорость по течению реки.
2) 18,6 * 3,5 = 65.1 (км) проплыл по течению реки.
3) 16.5 * 0,6 = 9,9 (км) проплыл по озеру.
4) 9,9 + 65,1 = 75 (км) проплыл катер.
Ответ: 75 км.
5. Постройте углы AND и NDB, если <ADN = 34°, <NDB = 120°. Какой может быть градусная мера угла ADB?
Строим в тетради с помощью транспортира. ADB может быть: 120° — 34° = 86° или 180° — 120° — 34° = 26°
Итоговая контрольная работа за 5 класс (Виленкин)
Вариант 1
1. Вычислите: 8,45 + (346 – 83,6):12,8
2. Вычислите площадь прямоугольника, если его ширина 1,9 дм, а длина вдвое больше.
3. Катер шел 3ч против течения реки и 2ч по течению. Какой путь прошел катер за эти 5 ч, если собственная скорость катера 18,6 км/ч, а скорость течения реки 1,3 км/ч?
4. Начертите треугольник АОВ, в котором угол АОВ равен 75°.
5. В классе 30 учеников. Оценку «5» на экзамене получили 30% учеников. Сколько учеников получили на экзамене пятерки?
Сколько учеников получили на экзамене пятерки?
Вариант 2
1. Вычислите 6,35 + (359 – 63,8):14,4.
2. Длина прямоугольника 12,6 см, а ширина втрое меньше. Найдите площадь этого прямоугольника.
3. Собственная скорость моторной лодки 6,7 км/ч. Скорость течения реки 1,2 км/ч. Лодка шла 2ч против течения и 2ч по течению реки. Какой путь прошла моторная лодка за эти 4 ч?
4. Начертите треугольник ВСК, в котором угол ВСК равен 110°.
5. Площадь поля 120 га. Тракторист вспахал 70% поля. Сколько гектаров земли вспахал тракторист?
Вариант 1
1. Вычислите: 8,45 + (346 – 83,6):12,8 = 20.45
1) 346 — 83.6 = 262.4
2) 262.4 : 12.8 = 20,5
3) 8.45 + 20.5 = 28.45
2. Вычислите площадь прямоугольника, если его ширина 1,9 дм, а длина вдвое больше.
1) 1,9 * 2 = 3,8 (дм) длина прямоугольника.
2) 1,9 * 3,8 = 4,142 (дм2) площадь.
Ответ: 4.142 дм2
3. Катер шел 3ч против течения реки и 2 ч по течению. Какой путь прошел катер за
эти 5 ч, если собственная скорость катера 18,6 км/ч, а скорость течения реки 1,3
км/ч?
Какой путь прошел катер за
эти 5 ч, если собственная скорость катера 18,6 км/ч, а скорость течения реки 1,3
км/ч?
Решение:
каждый час туда и обратно можно представить как выражение:
а + b — (b — a) = 2a, где
а — скорость реки;
b — скорость катера.
В итоге у нас остается один час против течения реки, к которому надо прибавить два значения скорости реки.
1) 18.6 — 1.3 = 17.3 (км) прошел катер за 1 час против течения.
2) 17.3 + 1,3 * 2 = 19.9 (км) катер прошел за 5 часов.
Ответ: 19.9 км
4. Начертите треугольник АОВ, в котором угол АОВ равен 75°.
Самостоятельно. Первым чертим угол именно 75 градусов, а дальше продолжаем построение треугольника!
5. В классе 30 учеников. Оценку «5» на экзамене получили 30% учеников. Сколько учеников получили на экзамене пятерки?
1) 30 : 100 * 30 = 0,3 * 30 = 9 (уч.) получили 5.
Ответ: 9 учеников.
Вариант 2
1. Вычислите 6,35 + (359 – 63,8) : 14,4 = 26. 85
85
1) 359 – 63,8 = 295.2
2) 295.2 : 14.4 = 20.5
3) 6.35 + 20.5 = 26.85
2. Длина прямоугольника 12,6 см, а ширина втрое меньше. Найдите площадь этого прямоугольника.
1) 12.6 : 3 = 4.2 (см) ширина прямоугольника.
2) 12.6 * 4,2 = 52.92 (см2) площадь прямоугольника.
Ответ: 52.92 см2
3. Собственная скорость моторной лодки 6,7 км/ч. Скорость течения реки 1,2 км/ч. Лодка шла 2ч против течения и 2ч по течению реки. Какой путь прошла моторная лодка за эти 4 ч?
Решение:
каждый час туда и обратно можно представить как выражение:
а + b — (b — a) = 2a, где
а — скорость реки;
b — скорость лодки.
В итоге у нас остается два значения скорости реки умноженное на количество часов.
2 * 1,2 * 2 = 4.8 (км) прошла лодка.
Ответ: 4,8 км.
4. Начертите треугольник ВСК, в котором угол ВСК равен 110°.
Самостоятельно. Первым чертим угол именно 110 градусов, а дальше продолжаем построение треугольника!
5. Площадь поля 120 га. Тракторист вспахал 70% поля. Сколько гектаров земли
вспахал тракторист?
Площадь поля 120 га. Тракторист вспахал 70% поля. Сколько гектаров земли
вспахал тракторист?
120 : 100 * 70 = 1.2 * 70 = 84 (га) вспахал тракторист.
Ответ: 84 га.
Самостоятельная работа по теме: «Комбинаторные задачи» 5 класс
Самостоятельная работа по теме:
«Комбинаторные задачи»
Вариант 1
1. В 5 классе в четверг пять уроков: литература, математика, обществознание, физкультура, музыка. Сколько вариантов составления расписания на этот день существует?
2. Школьные туристы решили совершить путешествие к горному озеру. Первый этап пути можно преодолеть на поезде или автобусе. Второй этап — на байдарках, велосипедах или пешком. И третий этап пути — пешком или с помощью канатной дороги. Какие возможные варианты путешествия есть у школьных туристов?
3. Сколько
двузначных чисел существует, для записи которых используются только цифры 9, 3
и 1 (цифры не могут повторяться).
4. В алфавите племени уауа имеются только две буквы «а», «у». Сколько различных слов из трех букв можно составить используя алфавит этого племени?
5. В кружок бального танца записались Петя, Коля, Витя, Игорь, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?
Самостоятельная работа по теме:
«Комбинаторные задачи»
Вариант 2
1. Сколько различных видов бутербродов может приготовить Маша, если в доме есть белый хлеб, черный хлеб, сыр, колбаса и варенье?
2. Запишите все трёхзначные числа, для записи которых используются только цифры 1, 5 и 0 (цифры не могут повторяться).
3. В школьной столовой за столом четыре стула. Одноклассницы Таня, Маша, Лера и Оля решили каждый день за обедом рассаживаться на эти стулья по — разному. Сколько дней девочки будут это делать без повторений?
4. Прямоугольник
состоит из трех квадратов. Сколькими способами можно раскрасить эти квадраты
тремя красками: зеленой, желтой и синей?
Сколькими способами можно раскрасить эти квадраты
тремя красками: зеленой, желтой и синей?
5. Вася решил пойти на новогодний карнавал в костюме мушкетёра. В ателье проката ему предложили на выбор: три вида брюк, два камзола, три шляпы. Сколько различных карнавальных костюмов можно составить из этих предметов?
Критерии оценивания
«5» — 5 правильно выполненных заданий
«4» — 4 правильно выполненных задания
«3» — 3 правильно выполненных задания
«2» менее 3 правильно выполненных заданий
Ответы
№ задания | 1 вариант | 2 вариант |
1 | 120 | 6 |
2 | 12 | 4 |
3 | 9 | 24 |
4 | 8 | 6 |
5 | 16 | 18 |
Скачано с www. znanio.ru
znanio.ru
Занимательные задачи
1 260
Занимательные задачи!
Чем хороши занимательные задачи — ими можно интересно занять детей по в дороге, по пути в школу или устроить конкурс на школьном празднике. Обратите внимание, что мало кто сможет дать правильный ответ сразу, потому не забывайте о маленьких подсказках, разгадывание задачек от этого будет не менее интересным.
Занимательные задачи по математике1.В каждом из 4 углов комнаты сидит кошка. Напротив каждой из этих кошек сидят три кошки. Сколько всего в этой комнате кошек?
2. У отца шесть сыновей. Каждый сын имеет сестру. Сколько всего детей у этого отца?
3. В мастерской по пошиву одежды от куска сукна в 200 м ежедневно, начиная с 1 марта, отрезали по 20 м. Когда был отрезан последный кусок?
4. В клетке находятся 3 кролика. Три девочки попросили дать им по одному кролику. Каждой девочке дали кролика. И все же в клетке остался один кролик. Как так получилось?
В клетке находятся 3 кролика. Три девочки попросили дать им по одному кролику. Каждой девочке дали кролика. И все же в клетке остался один кролик. Как так получилось?
5. 6 рыбаков съели 6 судаков за 6 дней. За сколько дней 10 рыбаков съедят 10 судаков?
6. На одном дереве сидело 40 сорок. Проходил охотник, выстрелил и убил 6 сорок. Сколько сорок осталось на дереве?
7.Два землекопа за 2 часа работы выкопают 2 м канавы. Сколько нужно землекопов, чтобы они за 100 часов работы выкопали 100 м такой же канавы?
8. Два отца и два сына разделили между собой 3 апельсина так, что каждому досталось по одному апельсину. Как это могло получиться?
9. По стеблю растения, высота которого 1 м, от земли ползет гусеница. Днем она поднимается на 3 дм, а ночью опускается на 2 дм. Через сколько суток гусеница доползет до верхушки растения?
10. Есть два ведра емкостью 4 и 9 литров. Как с их помощью принести из речки ровно 6 литров воды?
Как с их помощью принести из речки ровно 6 литров воды?
Ответы:
1.4
2.Одной девочке дали клетку с кроликом.
3.9марта
4.7
5. 6 рыбаков за день едят 1 судака.
Один рыбак есть 1/6 судака в день.
10 рыбаков едят за день 10/6 судака.
10 судаков делим на 10/6 судака = 6 дней
6.Все улетели
7. 2
8. Дед, отец и внук = 2 отца и 2 сына
9.Через 7/12 суток.
10. Из полного девятилитрового ведра нужно вылить в реку 8литров воды, пользуясь ведром в 4 литра. Затем литр, оставшийся в большом ведре, нужно перелить в пустое четырехлитровое ведро. Если в него теперь добавить три литра из полного большого ведра, то в девятилитровом ведре как раз останется шесть литров воды.
Подумай и сосчитай
Чтоб одеть тепло сыночков,
Не хватает двух носочков.
Сколько же в семье сынков,
Если в доме шесть носков?
Ответ:четверо
Столько книжек у ребяток,
Сколько у Алеши пяток.
Принесла ребяткам Галя
Мячик, книжку, мишек.
Вы, ребята, посчитали,
Сколько стало книжек?
Ответ: три
******************
К трем лягушкам у болота
Прибежали два енота,
Прискакала тетя жаба
И пришла наседка Ряба.
Сколько в камышах болотных
Оказалось земноводных?
Ответ: четверо
Задачи на внимание
1. Подумай и скажи — кто быстрее переплывет речку — утята или цыплята?
2. Подумай и скажи — какого цвета волосы у колобка?
3. Отгадай загадку:
Лежали конфетки в кучке.
Две матери, две дочки
Да бабушка с внучкой
Взяли конфет по штучке,
И не стало этой кучки.
Сколько конфет было в кучке?
4. Росли 5 берез. На каждой березе по 5 больших веток. На каждой ветке по 5 маленьких веток. На каждой маленькой ветке — по 5 яблок. Сколько всего яблок?
На каждой маленькой ветке — по 5 яблок. Сколько всего яблок?
5. Подумай и скажи — что помогает выжить белым медведям в пустыне, где нет воды?
6. На каких деревьях вьют свои гнезда страусы?
7. На столе лежит 2 яблока и 4 груши. Сколько всего овощей лежит на столе?
8. Подумай и скажи — кто громче рычит: тигр или буйвол?
9. Посмотрел Ваня утром в окно и говорит:
— А на улице, оказывается, очень сильный ветер. Нужно теплее одеваться.
Как он догадался, что на улице ветер? Что он увидел?
10. Пошли 2 девочки в лес за грибами, а навстречу 2 мальчика. Сколько всего детей идет в лес? (подсказка: 2 — остальные идут обратно)
11. В комнате горело 5 свечей. Зашел человек, потушил 2 свечи. Сколько осталось? ( подсказка: 2- остальные сгорели)
12. Бревно распилили на 4 части. Сколько сделали распилов?
13. Прочитай слова и скажи — какое слово лишнее в каждом ряду?
— диван, стул, шкаф, конура, тумбочка,
— гвоздика, ромашка, камыш, лилия, астра,
— боровик, мухомор, сыроежка, подберезовик, лисичка.
14. Подумай и скажи — сколько земли будет в яме глубиной 1 метр, длиной 1 метр и шириной 1 метр?
15. У шестилетней девочки была кошка с коротким хвостом. Она съела мышку с длинным хвостом, а мышка проглотила 2 зернышка и съела тонкий кусочек сыра. Скажи, сколько лет было девочке, у которой была кошка?
16. На одном берегу реки стоит петух, а на другом индюк. Посреди реки — островок. Кто из этих птиц быстрее долетит до островка?
17. Скажи сколько грибов можно вырастить из 5 семечек?
18. Скажи, кто обитает в море на большей глубине: щука, рак или форель?
19. Гусь на двух ногах весит 2 кг. Сколько он будет весить, стоя на одной ноге?
20. На клене 5 веток. На каждой ветке по 2 яблока. Cколько яблок на клене?
Мой блог находят по следующим фразам
Задание первой недели 1: Математика 5 класс
5 класс
Задание первой недели 1
Перейти к содержанию Приборная доскаАвторизоваться
Приборная панель
Календарь
Входящие
История
Помощь
- Мой Dashboard
- 5 класс
- Страницы
- Задание первой недели 1
- Home
- Мартики
- BACKURE
- Resource Bank
- класс 4 курс
- класс 5 G / T
- класс 5 G / T
- класс 5 CURIELULUL CUSICT
- Семья класса и сообщества
- СОЕДИНЕНИЯ
- Google Диск
- HCPSS.
 я
я
EM4 в домашних условиях 5 класс
EM4 на домашнем уровне 5
Выберите единицу измерения
- Раздел 1 Площадь и объем
- Модуль 2 Значение целого числа и операции
- Блок 3 Понятия дробей, сложение и вычитание
- Раздел 4 Десятичные понятия; Координатные сетки
- Блок 5 Операции с дробями
- Блок 6 Исследования в области измерения; Десятичное умножение и деление
- Блок 7 Умножение смешанных чисел; Геометрия; Графики
- Блок 8 Приложения измерения, вычислений и построения графиков
Поиск номеров модулей и уроков
Повседневная математика разделен на разделы, которые разделены на уроки. В верхнем левом углу домашней ссылки вы должны увидеть такой значок:
В верхнем левом углу домашней ссылки вы должны увидеть такой значок:
.
Номер модуля — это первое число, которое вы видите на значке, а номер урока — второе число. В этом случае учащийся работает в Блоке 5, Урок 4. Чтобы получить доступ к справочным ресурсам, выберите «Блок 5» из списка выше, а затем найдите строку в таблице с надписью «Урок 5-4».
Математика на каждый день для родителей: Что нужно знать, чтобы помочь вашему ребенку добиться успеха
Школьный математический проект Чикагского университета
Чикагский университет Press
Подробнее >>
Ссылки по теме
Математика на каждый день ОнлайнС помощью логина, предоставленного учителем вашего ребенка, вы можете получить доступ к ресурсам, которые помогут вашему ребенку с домашним заданием или освежить свои математические навыки.
Понимание
Математика на каждый день Для родителей Узнайте больше об учебной программе EM и о том, как помочь своему ребенку.
Планы уроков математики в пятом классе
Посмотреть наши демонстрации уроковУчебная программа по математике Time4Learning доступна для учащихся от дошкольного до двенадцатого класса. Родители могут ожидать, что будут рассмотрены такие темы, как закономерности в алгебре, построение графиков, сравнение и упорядочивание десятичных знаков и многое другое.
Подробные планы уроков, представленные ниже, содержат подробный список учебных программ Time4Learning по математике для пятого класса.
Участники часто используют эту страницу в качестве ресурса для более подробного планирования, в качестве руководства по выбору конкретных занятий с помощью средства поиска занятий или для сравнения нашей учебной программы со стандартами штата и законами о домашнем обучении.
Что входит в планы уроков Time4Learning?
- Полная учебная программа по математике для пятого класса, состоящая из 12 глав, более 416 заданий, рабочих листов и тестов
- Уроки по главам с подробным описанием изучаемого содержания
- Несколько типов заданий для отработки навыков, включая действия без оценки, викторины и распечатываемые ответы на вопросы викторины
- Рабочие листы и ключи к ответам на представленные материалы
- Легкий доступ к дополнительным главам по каждому предмету
- Time4MathFacts, который использует забавные игры, чтобы вовлечь вашего ребенка в изучение основ математики
Учащиеся, зачисленные на математическую программу Time4Learning для пятого класса, получат доступ к урокам как в четвертом, так и в шестом классе в рамках своего членства, поэтому они могут двигаться вперед или повторять в своем собственном темпе.
План урока математики – учебная программа пятого класса
Учащиеся будут использовать римские и греческие цифры.
Учащиеся будут использовать числовые цифры и слова для чтения и записи чисел до сотен миллиардов.
Учащиеся будут показывать числа в стандартной и расширенной форме до разряда миллиардов.
Учащиеся будут сравнивать и упорядочивать числа, используя таблицу стоимостных значений и числовые ряды.
Учащиеся будут округлять числа до миллиарда и использовать концепцию округления для решения реальных задач.
Учащиеся будут использовать стратегии оценивания для решения реальных задач, в которых они будут находить сумму и разность.
Учащиеся будут оценивать и оценивать вопросы на предмет обоснованности и определять обоснованность данных ответов.
Учащиеся будут складывать и вычитать целые числа.
Учащиеся будут умножать целые числа.
Учащиеся будут решать задачи на умножение, включающие умножение двух цифр на две цифры, а также умножение трех цифр на две цифры.
Учащиеся решат реальную задачу, включающую оценку с умножением двух цифр на две, а также на умножение трех цифр на две цифры.
Учащиеся определят наибольший общий делитель заданных чисел.
Найдите наименьшее общее кратное заданных чисел.
Студенты будут использовать показатели для решения задачи.
Учащиеся определят степени от 10 до 6 степени.
Учащиеся будут использовать закономерности при умножении на степень десяти.
Учащиеся будут изучать показатели степени как многократное умножение.
Ученики разделятся, чтобы решить задачи.
Учащиеся будут использовать совместимые числа для оценки частных.
Учащиеся будут применять правила делимости на 2, 3, 5, 9 и 10 к различным числам.
Учащиеся будут интерпретировать остатки и применять понятия, чтобы определить, что означают остатки.
Учащиеся будут использовать порядок действий для решения задач.
Учащиеся определят и найдут простые и составные числа до 50. Учащиеся найдут разложение чисел до 50 на простые множители.
Учащиеся будут записывать множители чисел, используя только простые числа и факторизацию простых чисел.
Студенты будут решать реальные задачи.
Учащиеся поймут, что цифра в одном разряде представляет в 10 раз больше, чем она представляет в разряде справа от нее, и одну десятую того, что она представляет в разряде слева от нее.
Учащиеся будут читать и записывать числа с точностью до тысячных в письменной и стандартной форме и показывать эквивалентность между ними.
Учащиеся определят число и поместят его в числовую строку, чтобы обозначить данные десятичные дроби.
Учащиеся будут использовать <, > и = для сравнения десятичных долей до тысячных. Студенты закажут десятичные дроби через тысячи.
Учащиеся будут округлять десятичные дроби до определенного разряда и до ближайшей половины или целого числа.
Учащиеся будут складывать и вычитать десятичные дроби.
Учащиеся будут вычислять суммы и разности с помощью десятичных дробей.
Учащиеся будут умножать десятичные дроби на другие десятичные дроби.
Учащиеся будут делить десятичные дроби на десятичные дроби и целые числа как на делитель, так и на делимое.
Учащиеся будут вычислять произведения и частные, используя десятичные дроби.
Учащиеся определят проценты.
Учащиеся найдут проценты от числа и решат реальные задачи, используя проценты.
Учащиеся определят неправильные и смешанные числа и продемонстрируют свою способность находить эквиваленты между ними.
Учащиеся найдут наименьший общий знаменатель дробей с разными знаменателями.
Учащиеся упрощают дроби, находя наименьший общий знаменатель.
Учащиеся найдут эквивалентные формы дробей, не включающие смешанные числа.
Учащиеся будут сравнивать и упорядочивать дроби.
Учащиеся будут округлять дроби до половины или целого числа.
Учащиеся будут складывать дроби, не включая смешанные числа, с одинаковыми и разными знаменателями.
Учащиеся будут вычитать дроби, не включая смешанные числа, с одинаковыми и разными знаменателями.
Учащиеся будут решать реальные задачи на вычитание дробей с разными знаменателями.
Учащиеся будут складывать смешанные числа с перегруппировкой и без нее.
Учащиеся будут вычитать смешанные числа с перегруппировкой и без нее.
Учащиеся представят произведение двух дробей, используя модель площади.
Учащиеся определят результат умножения целого числа на дробь меньше 1 и на дробь больше 1.
Учащиеся будут умножать дроби, не включая смешанные числа, и упрощать ответы.
Учащиеся будут решать задачи на умножение дроби на смешанное число и на умножение смешанного числа на смешанное число.
Учащиеся смоделируют деление целых чисел на дроби и дроби на целые числа.
Учащиеся будут решать реальные задачи на деление на единичные дроби.
Учащиеся будут делить дроби, не включая смешанные числа, используя обратные числа и упрощая ответы.
Учащиеся будут вычислять произведения и частные, используя дроби.
Учащиеся будут интерпретировать дробь как деление.
Учащиеся будут записывать дроби в виде десятичных дробей.
Учащиеся продемонстрируют свое понимание взаимосвязи между десятичными числами и дробями и дробями с десятичными знаками, а также того, как они эквивалентны процентам.
Ученики выучат дроби как отношения.
Учащиеся найдут эквивалентные соотношения.
Учащиеся узнают знак процента и поймут значение процента как сто. Студенты будут выражать эквивалентности между дробями, десятичными знаками и процентами и знать общие эквивалентности.
Учащиеся будут описывать жизненные ситуации, используя целые числа, и определять целые числа на числовой прямой.
Учащиеся определят закономерности на картинках и в таблицах и опишу правило функции.
Учащиеся будут писать и оценивать алгебраические выражения.
Учащиеся найдут правило в реальных задачах и определят правила функций из таблиц.
Учащиеся будут решать одношаговые уравнения с целыми, десятичными и дробными числами на сложение.
Учащиеся будут решать одношаговые уравнения с целыми, десятичными и дробными числами, включая вычитание.
Учащиеся будут решать одношаговые уравнения с целыми и десятичными дробями, включая умножение.
Учащиеся будут решать одношаговые уравнения с целыми числами и десятичными дробями с делением.
Учащиеся будут применять формулы для решения обычных задач на длину. Учащиеся узнают, какие инструменты следует использовать для решения обычных проблем длины, и применят концепции оценки для получения ответов.
Учащиеся будут применять формулы для решения обычных задач с весом. Учащиеся узнают, какие инструменты следует использовать для решения обычных задач с весом, и применят концепции оценки для получения ответов.
Учащиеся узнают, какие инструменты следует использовать для решения обычных задач с весом, и применят концепции оценки для получения ответов.
Учащиеся будут применять формулы для решения обычных задач на емкость. Учащиеся узнают, какие инструменты следует использовать для решения обычных проблем с пропускной способностью, и применят концепции оценки для получения ответов.
Учащиеся будут применять формулы с температурой в градусах Фаренгейта для решения реальных задач.
Учащиеся узнают о метрической системе и узнают, как умножение и деление на десять влияет на положение в системе.
Учащиеся будут применять формулы для решения задач на длину в метрических единицах. Учащиеся узнают, какие инструменты следует использовать для решения задач метрической длины, и применят концепции оценки для получения ответов.
Учащиеся будут применять формулы для решения задач с метрическим весом. Учащиеся узнают, какие инструменты следует использовать для решения задач с метрическим весом, и применят концепции оценки для получения ответов.
Учащиеся будут применять формулы для решения задач на метрическую емкость. Учащиеся узнают, какие инструменты следует использовать для решения проблем с метрической емкостью, и применят концепции оценки для получения ответов.
Учащиеся будут применять формулы с температурой в градусах Цельсия для решения реальных задач.
Учащиеся решают задачи на прошедшее время.
Учащиеся будут решать задачи, показывающие прошедшее время, включая дни, недели, месяцы, годы и столетия.
Учащиеся найдут периметры многоугольников и правильных многоугольников с пропущенными значениями и без них.
Учащиеся найдут площади квадратов и прямоугольников.
Учащиеся найдут площади треугольников.
Учащиеся найдут объем кубов и прямоугольных призм.
Учащиеся найдут объем прямоугольной призмы, считая кубы.
Учащиеся найдут объем прямоугольной призмы, умножив длины ребер или умножив площадь основания на высоту.
Учащиеся найдут объем прямоугольной призмы по формуле V = B × h.
Учащиеся найдут объем объемной фигуры, составленной из двух прямоугольных призм.
Учащиеся будут использовать совпадающие, коллинеарные, параллельные и перпендикулярные для описания относительной ориентации на координатной сетке.
Учащиеся узнают параллельные, перпендикулярные, пересекающиеся и наклонные линии.
Учащиеся будут измерять градусы прямых, острых, тупых и прямых углов с помощью транспортира.
Учащиеся узнают о различных видах треугольников.
Учащиеся будут сортировать многоугольники по атрибутам. Учащиеся классифицируют четырехугольники как параллелограммы, трапеции, ромбы, прямоугольники и квадраты.
Учащиеся будут классифицировать четырехугольники как параллелограммы, трапеции, ромбы, прямоугольники и квадраты.
Учащиеся узнают о трехмерных фигурах.
Учащиеся будут сортировать многогранники по их атрибутам.
Учащиеся определят дугу, хорду, радиус и диаметр окружностей.Учащиеся вычисляют радиус или диаметр окружности.
Учащиеся будут строить трехмерные фигуры из набора видов.
Учащиеся определят и создадут двухмерное представление трехмерной фигуры (сети) на сетке или точечной бумаге.
Учащиеся найдут измерение углов.
Учащиеся узнают об упорядоченных парах.
Учащиеся будут классифицировать плоские фигуры как имеющие линейную симметрию, точечную симметрию, и то, и другое или отсутствие симметрии.
Учащиеся будут применять множественные преобразования к плоской фигуре, предсказывать результат и определять изображение плоской фигуры в результате многократного преобразования, включая повороты на 90 и 180 градусов.
Учащиеся будут использовать масштаб для отображения относительного размера на карте или чертеже.
Учащиеся исследуют сходство, используя конгруэнтные углы. Учащиеся изучают конгруэнтность, используя конгруэнтные сегменты и конгруэнтные углы.
Учащиеся определят и представят все возможные исходы для определенного вероятностного события, используя диаграммы, списки или древовидные диаграммы.
Учащиеся вычисляют вероятность события.
Учащиеся будут делать прогнозы будущих событий на основе предыдущих событий.
Учащиеся будут интерпретировать и анализировать гистограммы.
Учащиеся будут интерпретировать линейные графики (интерполяция и экстраполяция).
Учащиеся будут создавать и интерпретировать круговые диаграммы с использованием обыкновенных дробей.
Учащиеся будут интерпретировать, анализировать и создавать гистограммы.
Учащиеся будут интерпретировать и анализировать диаграммы Венна.
Учащиеся выбирают наиболее подходящий график для набора данных и делают выводы из графиков.
Учащиеся будут сравнивать и переводить данные из информации, подсчетов и данных в график.
Учащиеся будут собирать, систематизировать и описывать данные, используя медиану, моду и диапазон.
Учащиеся найдут среднее значение заданного набора чисел.
Учащиеся будут использовать знания о графиках ствола и листа, чтобы решить, чтобы определить среднее значение, медиану, моду и диапазон.
Инструмент поиска занятий
Поиск занятий — один из многих полезных инструментов, которые Time4Learning предлагает своим членам. Поиск занятий — это ярлык, который позволяет родителям легко просматривать уроки или находить дополнительную практику для своего ребенка.
Каждый урок в учебной программе имеет уникальный номер занятия, который в планах уроков называется «Номер LA». Эти номера можно найти либо на страницах объема и последовательности, либо в планах уроков на родительской панели.
Дополнительные ресурсы, связанные с математикой в пятом классе
Если вас интересуют планы уроков математики в пятом классе, вам также могут быть интересны:
Онлайн-учебная программа для домашнего обучения, послешкольного и летнего использования
Если вы только знакомитесь с Time4Learning, мы рекомендуем узнать больше об учебной программе Time4Learning на дому или о том, как использовать программу для повышения квалификации после школы.
Богатые задачи — Часть 1 — Математика для всех
- Ожидание, что учащийся сможет изложить свои идеи и защитить свой подход.
- Возможность для учащихся выбирать из ряда инструментов и стратегий для решения проблемы на основе их собственных сильных сторон в развитии нервной системы.
- Возможность изучить новую математику (математический остаток) в процессе работы над задачей.
- Возможность отработать рутинные навыки для решения сложной проблемы.
- Возможность для учителя углубить свое понимание своих учеников как учащихся и построить новые уроки на основе того, что знают учащиеся, их уровня развития, а также их сильных и слабых сторон в развитии нервной системы.
Все взрослые нуждаются в математических знаниях для решения задач в повседневной жизни. Большинство взрослых используют калькуляторы и компьютеры для выполнения рутинных вычислений, выходящих за рамки того, что они могут сделать в уме. Однако они должны достаточно понимать математику, чтобы знать, что вводить в машины и как оценивать то, что выходит. Наше личное финансовое положение сильно зависит от нашего понимания схем ценообразования на вещи, которые мы покупаем, ипотечных кредитов, которые мы держим, и сборов, которые мы платим.Как граждане, понимание математики может помочь нам оценивать политику правительства, понимать политические опросы и принимать решения. Строительство и проектирование наших домов, а также масштабирование рецептов для толпы также требуют математики. Особенно сейчас математическое понимание имеет решающее значение для понимания политики, связанной с пандемией. Решения о закрытии, лечении и вакцинах основаны на математике. По всем этим причинам важно, чтобы учащиеся развивали свои способности рассуждать о математике.Исследования показали, что опыт решения сложных задач улучшает математическое мышление детей (Hattie, Fisher, & Frey, 2017).
Однако они должны достаточно понимать математику, чтобы знать, что вводить в машины и как оценивать то, что выходит. Наше личное финансовое положение сильно зависит от нашего понимания схем ценообразования на вещи, которые мы покупаем, ипотечных кредитов, которые мы держим, и сборов, которые мы платим.Как граждане, понимание математики может помочь нам оценивать политику правительства, понимать политические опросы и принимать решения. Строительство и проектирование наших домов, а также масштабирование рецептов для толпы также требуют математики. Особенно сейчас математическое понимание имеет решающее значение для понимания политики, связанной с пандемией. Решения о закрытии, лечении и вакцинах основаны на математике. По всем этим причинам важно, чтобы учащиеся развивали свои способности рассуждать о математике.Исследования показали, что опыт решения сложных задач улучшает математическое мышление детей (Hattie, Fisher, & Frey, 2017).
Несколько типов сложных задач доступны онлайн, готовые к использованию или адаптации. Сайты ниже являются одними из многих мест, где можно найти богатые задачи:
Сайты ниже являются одними из многих мест, где можно найти богатые задачи:
- Какой из них не принадлежит? Эти задачи состоят из квадратов, разделенных на 4 квадранта с числами, формами или графиками. В каждой задаче есть по крайней мере один способ, которым каждый из квадрантов «не принадлежит».Таким образом, можно утверждать, что любой квадрант отличается от других.
- Задачи «Открытая середина» — это задачи с одним ответом, но с множеством способов получить ответ. Они организованы как по темам, так и по классам.
- NRICH Maths — это многогранный сайт Кембриджского университета в Великобритании. В нем есть как статьи, так и готовые задачи. На сайте представлены задачи для 1–5 классов (листайте до раздела «Сборники») и задачи для детей младшего возраста.Мы также рекомендуем вам более полно изучить NRICH. На сайте много познавательных статей и обсуждений.
- Богатые задачи из Вирджинии — это задачи, опубликованные Департаментом образования Вирджинии.
 Они поставляются с полными планами уроков, а также примерами ожидаемых ответов учащихся.
Они поставляются с полными планами уроков, а также примерами ожидаемых ответов учащихся. - Расширенные задания из Джорджии. Этот сайт содержит полную систему заданий, разработанных для соответствия всем стандартам для всех классов. Они включают в себя задачи 3-Act, задачи YouCubed и многие другие задачи с открытым концом или подходом с открытой серединой.
Задачи можно использовать «как есть» или адаптировать к конкретным сильным сторонам и проблемам развития нервной системы ваших учащихся. Тщательно адаптированные, они могут вовлечь ВСЕХ ваших учеников в размышления о математических идеях различными способами, тем самым не только улучшая их навыки, но и их способности мыслить гибко и глубоко.
Поиск высококачественных математических задач для начальных классов в Интернете
Интернет может быть отличным ресурсом для поиска математических задач на любом уровне когнитивных потребностей.В то время как учащимся начальных классов необходимо знакомиться с задачами на всех уровнях — как на более низком, так и на более высоком — акцент следует делать на более высоких уровнях. Это означает, что нам нужны навыки для оценки того, что является когнитивно сложным, а что нет.
Это означает, что нам нужны навыки для оценки того, что является когнитивно сложным, а что нет.
Чтобы определить качество онлайн-активности, мои партнеры по исследованию и я использовали «Руководство по анализу задач» (TAG) Маргарет Шван Смит и Мэри Кей Стейн 1998 года, которое состоит из четырех различных уровней когнитивных требований: запоминание, процедуры без связей, процедуры со связями, и заниматься математикой.
При запоминании критическое мышление не требуется, не делается никакой связи с пониманием того, почему ответ работает, и процедуры обходят. Задание такого типа может выглядеть как припоминание фактов. Процедуры без соединений алгоритмичны; учащиеся придумывают ответ, не связывая его с другими математическими понятиями, и им не требуется объяснять свою работу. В эту категорию попадают задачи, которые требуют простых процедур, таких как требование стандартного алгоритма США для сложения.Запоминание и действия без связей — это задачи с низкой когнитивной нагрузкой, потому что они не требуют много размышлений.
Учителя часто представляют визуальные диаграммы или манипуляции, такие как кубы Unifix или блоки с основанием 10, для решения математических задач, которые представляют собой процедуры со связями, которые позволяют учащимся подойти к проблеме с разных сторон. В этих задачах используются процедуры, такие как алгоритм частичного произведения для умножения, чтобы помочь учащимся понять, почему ответ работает, а не просто знать, как найти ответ.
Задачи самого высокого уровня, связанные с математикой, требуют неалгоритмического мышления, требуют самоконтроля и позволяют использовать несколько стратегий — учащиеся на этом этапе изучают математические концепции.
По словам Смита и Штейна, процедуры со связями и выполнение математических задач требуют высокой когнитивной нагрузки, потому что учащиеся должны устанавливать связи, анализировать информацию и делать выводы для их решения.
Математические задачи нужно выбирать критически
Для того, чтобы ставить перед учащимися начальной школы проблемы на каждом когнитивном уровне, учителя должны критически относиться к имеющимся ресурсам. В нашем исследовании следующие моменты помогли мне и моим коллегам оценить познавательную потребность и качество онлайн-задач.
В нашем исследовании следующие моменты помогли мне и моим коллегам оценить познавательную потребность и качество онлайн-задач.
Возраст имеет значение. Уровень познавательной потребности может меняться в зависимости от возраста детей, для которых создавалась задача. Например, заполнение рабочего листа основных задач на сложение одной цифры будет закодировано как запоминание для четвероклассника, который, как ожидается, запомнит их (даже в большей степени, если учащийся измеряет время), но это будет считаться выполнением процедур без связи для детсадовцев, которые только учатся тому, что значит сложить две части, чтобы получилось одно целое.
Если вы ищете задачи с высокими когнитивными требованиями, ресурс, отвечающий любому из следующих критериев, может считаться процедурой со связями; чтобы считаться занятием по математике, должно быть несколько способов решения задачи:
- Проблема обычно связана с манипуляциями (например, 10 кадров, блоки с основанием 10, числовые линии, числовые сетки).

- Существуют указания, призывающие учащихся объяснить, как они нашли ответ (с помощью моделей, слов или того и другого).
- Требуется высокий уровень критического мышления. Например, учащиеся решают, как решить проблему, которую можно решить более чем одним способом, устанавливают реальные связи с математикой или объясняют свое математическое мышление.
Оценивая математическое задание, учителя также должны оценивать все изображения, сопровождающие его. Включено ли изображение исключительно в декоративных целях или оно играет функциональную роль в решении проблемы? Изображения с функциональными ролями включают циферблаты, 10 кадров и графики.Если у деятельности есть декоративный образ, это, скорее всего, будет задачей с низким когнитивным спросом; если у него есть функциональный образ, он, скорее всего, будет закодирован на высоком уровне когнитивного запроса. В то время как деятельность может быть популярной из-за своих декоративных, симпатичных изображений, визуальная привлекательность не коррелирует с высоким уровнем когнитивного спроса. Важно сосредоточиться на содержании, а не на искусстве.
Важно сосредоточиться на содержании, а не на искусстве.
Где найти сложные математические задачи
У вас гораздо больше шансов найти математические задания с высоким уровнем когнитивного спроса на веб-сайтах, где ресурсы проверяются перед публикацией, в отличие от таких сайтов, как «Учителя платят учителям» или Pinterest, где любой может публиковать сообщения.Следующие веб-сайты публикуют проверенные ресурсы:
- Illustrative Mathematics позволяет учителям искать задачи на основе стандартов содержания по предметной области или классу для K–12 (бесплатно).
- EngageNY — это набор учебных программ по английскому языку, искусству и математике для учащихся от дошкольного до 8-го класса, разработанный Департаментом образования штата Нью-Йорк. В нем также есть учебные программы по математике для старших классов — алгебра I и II, геометрия, предварительное исчисление и выше (бесплатно).
- NRICH, находящийся в ведении Кембриджского университета в Англии, предоставляет библиотеку ресурсов и картографических документов для учащихся в возрасте от 3 до 18 лет (бесплатно).

- youcubed, основанный профессором математического образования Стэнфордского университета Джо Болером, предоставляет высококачественные математические задачи, которые можно искать по классам (K–12) или темам. Некоторые задачи были созданы исследователями, управляющими youcubed, в то время как другие взяты с различных сайтов, включая NRICH (бесплатно).
- Illuminations — это онлайн-ресурс, доступный через Национальный совет учителей математики (NCTM), который предоставляет материалы, основанные как на стандартах NCTM, так и на общих базовых государственных стандартах для классов от pre-K до 12.Для доступа требуется членство в NCTM (стоимость: от 49 до 139 долларов в год).
Контрольные задания для 3–5 классов
Урок для третьего, четвертого и пятого классов
Линда Дейси и Джейн Бэмфорд Линч
Открытые задачи могут стать отличной последующей оценкой. Хотите знать, как вы можете разработать эффективные задачи после оценивания для ваших студентов? Этот урок предлагает план из четырех шагов, включая 3–5 примеров заданий и соответствующие аутентичные ответы учащихся.Урок адаптирован из книги Линды Дейси и Джейн Бэмфорд Линч по математике для All: Differentiating Instruction, Classs 3–5, . Посетите www.mathsolutions.com , чтобы узнать больше.
Хотите знать, как вы можете разработать эффективные задачи после оценивания для ваших студентов? Этот урок предлагает план из четырех шагов, включая 3–5 примеров заданий и соответствующие аутентичные ответы учащихся.Урок адаптирован из книги Линды Дейси и Джейн Бэмфорд Линч по математике для All: Differentiating Instruction, Classs 3–5, . Посетите www.mathsolutions.com , чтобы узнать больше.
Шаг 1I. Разработайте задачу, которая будет охватывать широкий спектр ответов
Открытые задания позволяют учащимся самостоятельно контролировать некоторые уровни сложности. В приведенном ниже примерном задании учащиеся могут ограничить свое рассмотрение лишь несколькими фигурами или сосредоточиться исключительно на двумерных фигурах.Точно так же учащиеся могут использовать рисунки, схемы или диаграммы для передачи своих идей или они могут больше полагаться на прозу.
Образец 3–5 Задача
Что вы знаете о формах? Пишите и рисуйте, чтобы поделиться своими идеями.
Шаг II: Обсудите с учащимися ожидания от задания
Всем классом составьте список, которым учащиеся будут руководствоваться в работе над заданием.
Образец 3–5 Список
- Сосредоточьтесь на формах.
- Используйте слова и рисунки, чтобы объяснить, что вы знаете.
- Используйте словарь геометрии.
- Организуйте свои идеи.
- Дайте несколько образцов.
- Подумайте о реальных связях.
Шаг III: Предложите учащимся ответить на задание
После краткого обсуждения ожиданий от задания учащиеся обычно готовы приступить к выполнению задания. Некоторые учащиеся могут подумать минуту или около того, прежде чем начать записывать свои идеи, но большинство начинают сразу же. Ниже приведены примеры, в том числе подлинные студенческие работы, того, как учащиеся отреагировали на указанное выше задание.
Некоторые учащиеся использовали шаблоны фигур, в то время как другие предпочитали рисовать от руки. Большинство учеников начинали с того, что рисовали фигуру на бумаге, а затем писали над ней или под ней несколько слов. Несколько студентов начали с того, что написали идею или название фигуры, которую затем проиллюстрировали.
Большинство учеников начинали с того, что рисовали фигуру на бумаге, а затем писали над ней или под ней несколько слов. Несколько студентов начали с того, что написали идею или название фигуры, которую затем проиллюстрировали.
Образец ответа 1: двумерные фигуры
Ответ третьеклассницы Лизы был сосредоточен на двухмерных формах. Она классифицировала фигуры по количеству сторон и дала правильные названия трех-, четырех-, пяти-, шести- и восьмигранным фигурам.Хотя она не назвала фигуры, которые нарисовала в своей категории четырехугольников, она включила в нее трапецию, квадрат и параллелограмм. Она привела один пример треугольника, пятиугольника и шестиугольника.
Ответ третьеклассницы Лизы
Четвертоклассник Тай включил ссылки на вогнутые формы и многоугольники, а также провел связи между двухмерными и трехмерными фигурами. Он также ввел пирамиды, прямые углы и термин параллель. Он был взволнован, когда работал.Он записал одну идею, а затем его глаза загорелись, когда он подумал о другой. Поскольку эти идеи не обязательно были связаны между собой, он часто записывал мысль, а затем обводил ее кольцом, чтобы отделить ее от других своих записей.
Поскольку эти идеи не обязательно были связаны между собой, он часто записывал мысль, а затем обводил ее кольцом, чтобы отделить ее от других своих записей.
Ответ четвероклассника Тая
Ответ Рафаэля был особенно интересен. Рафаэль был сильным визуалом. Он часто делал диаграммы, чтобы обобщить события в рассказе, и его язык часто отражал его визуальные предпочтения. Как раз в то утро учительница слушал, как другой ученик объяснял Рафаэлю, почему они должны сегодня днем играть в футбол, а не кататься на велосипеде.Выслушав доводы другого ученика, Рафаэль ответил: «Хорошо, я понимаю, что вы имеете в виду». Наряду с иллюстрацией и обозначением многих геометрических форм и понятий, Рафаэль рисовал инструменты, которые он ассоциировал с геометрией. Обратите внимание на два его изображения, которые соединяют метрические и английские единицы измерения, а также геодоску, розу ветров и транспортир.
Ответ пятиклассника Рафаэля
Шаг IV: просмотр ответов учащихся и планирование следующих шагов
Узнайте, что каждый учащийся выбрал для включения; возможно, это то, что он знает лучше всего, или то, что она считает наиболее важным, или то, что он находит наиболее интересным. Также отметьте, для каких концепций учащиеся не предоставили доказательств или для которых доказательств
Также отметьте, для каких концепций учащиеся не предоставили доказательств или для которых доказательств
неполный или неточный. Поделитесь своими выводами с другими учителями. Посмотрите на сходства и различия между уровнями обучения. Ниже приведены наблюдения и планы, сделанные учителями после просмотра ответов на типовое задание.
Примеры отзывов и планов учителей
Учителя были поражены различиями между классами. Учительница третьего класса была удивлена тем, насколько более сложными были ответы учеников старших классов.Он отметил, что в ответе своей третьеклассницы Лизы (см. Ответ
Образец 1), стороны внутри ее треугольника, пятиугольника и шестиугольника имели примерно одинаковую длину, а фигуры были нарисованы с основанием, параллельным нижней части страницы. Такие ориентации распространены; на самом деле, многие учащиеся не идентифицируют некоторые из этих фигур, когда их стороны не конгруэнтны или когда они не расположены в традиционном положении.
Учителя решили включить эту работу в портфолио учеников.В следующем году они хотели, чтобы у учителей студентов были эти артефакты, чтобы помочь им определить готовность к будущей работе по геометрии. Им также было интересно наблюдать за эволюцией работы студентов с течением времени. Возможно, они могли бы повторить задание позже в этом году, а в следующем году они могли бы использовать его в качестве предварительной и последующей оценки.
Опубликовано в информационном бюллетене Math Solutions Online, выпуск 32
Связанная публикация:
Математика для всех: дифференцированное обучение, классы 3–5
Линда Дейси и Джейн Бэмфорд Линч
Математика — 5 класс — 5012070
Карнавальное безумие!: В этом интерактивном руководстве вы научитесь делить целые числа на дроби, помогая Элли и Кэмерон создавать равные доли конфет и призов для гостей карнавала.
Тип: Оригинальное учебное пособие для учащихся
Задача шоколадного магазина, часть 2: деление дробей и целых чисел с помощью числовых линий:В этом интерактивном учебном пособии, посвященном шоколадной тематике, решите реальные задачи со словами, включающие деление дробной части на целое число и деление целого числа на дробную часть с помощью числовых линий.
Это вторая часть серии из двух частей. Нажмите ЗДЕСЬ , чтобы открыть «Задание в магазине шоколада, часть 1: деление дробей единиц и целых чисел с использованием моделей дробных стержней»
Нажмите ЗДЕСЬ , чтобы открыть соответствующее руководство «Дэвид делит десерты: разделите дробную часть на целое число»
Тип: Оригинальное учебное пособие для учащихся
Делитесь и делитесь одинаково: Из этого интерактивного руководства вы узнаете, как разделить дробную часть на целое число, чтобы поровну разделить вкусняшки для пикника.
Тип: Оригинальное учебное пособие для учащихся
Создание искусства, часть 2: решение задач на сложение и вычитание дробей:Научитесь решать задачи на сложение и вычитание с участием дробей с разными знаменателями. По мере прохождения этого интерактивного учебного пособия, посвященного искусству, вы будете использовать визуальные модели, писать и решать уравнения, а также проверять обоснованность результатов на основе оценок.
Это вторая часть серии из двух частей. Нажмите ниже, чтобы открыть часть 1.
Тип: Оригинальное учебное пособие для учащихся
Четырехугольники — Часть 5: В этом интерактивном учебном пособии вы узнаете, как классифицировать четырехугольники, включая параллелограммы, прямоугольники, ромбы и квадраты, на основе определяющих их атрибутов с помощью диаграмм.
Это пятая часть из шести частей. Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Круговая гонка:Изучите округление десятичных долей до тысячных, помогая Черепахе Тайрезу тренироваться, чтобы участвовать в гонках на зайца, в этом интерактивном учебном пособии.
Тип: Оригинальное учебное пособие для учащихся
День в парке: Время: Узнайте, как преобразовать время из секунд в минуты, минут в часы и часов в дни. В этом интерактивном учебном пособии вы также попрактикуетесь в преобразовании времени в дробные значения.
Тип: Оригинальное учебное пособие для учащихся
Пекарня Баффи, часть 2: умножение дробей:Помогите пекарю Баффи умножить дроби меньше единицы, связав стандартный алгоритм с визуальными моделями, когда он управляет своей пекарней, в этом интерактивном руководстве.
Это вторая часть серии из 4 частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Хижина кузнечика для Гаса: линейные сюжеты: Помогите построить хижину кузнечика для Гаса, создав линейные графики и ответив на вопросы о линейных графиках в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Магазин видеоигр: Volume!:Помогите решить проблему доставки видеоигр и аксессуаров клиентам, рассчитав объем контейнеров, необходимых в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Строительные блоки объема:Используя этот интерактивный учебник, вы сможете расширить свои знания о площади и научиться вычислять объем в кубических единицах.
Тип: Оригинальное учебное пособие для учащихся
База десяти и экспоненты: Изучите основание 10 и показатели степени в этом интерактивном учебном пособии на тему бейсбола.
Тип: Оригинальное учебное пособие для учащихся
Проектирование игровых площадок для собак: умножение десятичных знаков:Помогите своему городу построить парк для собак, умножая целые числа на десятичные до десятых в этом интерактивном руководстве.
Примечание. Это вводное руководство по умножению целых чисел на десятичные, прежде чем учащиеся перейдут к умножению десятичных чисел на десятичные.
Тип: Оригинальное учебное пособие для учащихся
Topsy-Turvy Playground: вычитание десятичных знаков: В этом интерактивном учебном пособии научитесь вычитать десятичные дроби до сотых, используя модели разрядных значений и письменные выражения, исправляя перевернутую игровую площадку.
Тип: Оригинальное учебное пособие для учащихся
Масштабирование до побега:Попробуйте выбраться из этой комнаты, используя умножение в качестве масштабирования в этом интерактивном руководстве.
Примечание: это руководство является вводным уроком по умножению заданного числа без вычислений перед работой с дробями.
Тип: Оригинальное учебное пособие для учащихся
«Выяснение» 2D-фигур — Часть 1: Изучите 2D (двумерные) фигуры и узнайте, как каждая 2D фигура обладает уникальными атрибутами в этом интерактивном учебном пособии.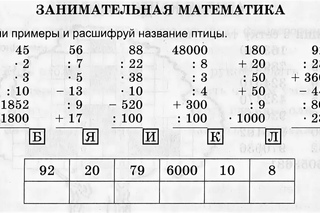
Это первая часть из четырех. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Просто переходите к делу!:Попрактикуйтесь в построении координат в квадранте I с использованием упорядоченных пар в этом интерактивном учебном пособии для учащихся.
Тип: Оригинальное учебное пособие для учащихся
Bee A Coder Часть 4: Повторяющиеся циклы: Узнайте, как использовать повторяющиеся циклы в этом интерактивном руководстве. Циклы повторения перебирают список инструкций заданное количество раз. В сочетании с переменными, условными операторами, операторами if и повторяющимися циклами мы практикуем использование порядка операций в коде.
Циклы повторения перебирают список инструкций заданное количество раз. В сочетании с переменными, условными операторами, операторами if и повторяющимися циклами мы практикуем использование порядка операций в коде.
Это первая часть из четырех частей. Нажмите ниже, чтобы ознакомиться с другими руководствами из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Bee A Coder Часть 3: Операторы If:В этом интерактивном учебном пособии вы узнаете, как выполнять инструкции с помощью оператора if и изучите операторы отношения (меньше, больше, равно и не равно) и как они используются для сравнения со значениями.
Тип: Оригинальное учебное пособие для учащихся
Bee A Coder, часть 2: Заявления об условиях: Создавайте эффективные строки кода, используя операторы условий и операторов if для решения уравнений по мере выполнения этого интерактивного руководства. Вы также просмотрите порядок операций в выражениях.
Вы также просмотрите порядок операций в выражениях.
Это вторая часть из четырех статей о кодировании. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Bee A Coder Часть 1: Объявление переменных:Из этого интерактивного руководства вы узнаете, как определять, объявлять и инициализировать переменные, когда начинаете свой путь к кодеру.Переменные — это структуры, используемые компьютерными программами для хранения информации. Вы будете использовать свои математические навыки для представления дроби в виде десятичной дроби, которая будет храниться в переменной.
Это первая часть из четырех статей о программировании. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Приключение Саманты по сбору ракушек: Научитесь интерпретировать данные, представленные на линейном графике, и используйте операции над дробями для решения задач, связанных с информацией, представленной на линейных графиках, по мере выполнения этого интерактивного учебного пособия на пляжную тематику.
Тип: Оригинальное учебное пособие для учащихся
Измерение для постройки пандуса:В этом интерактивном учебном пособии вы узнаете, как преобразовывать обычные единицы веса, длины, вместимости и времени в скейт-парке.
Тип: Оригинальное учебное пособие для учащихся
Дебаты о выражении: Научитесь оценивать выражения, в которых есть все четыре операции (умножение, деление, сложение и вычитание) и круглые скобки, при разрешении дебатов в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Взлом десятичного кода:К концу этого урока вы сможете читать и записывать десятичные дроби до тысячных, используя десятичные числа, названия чисел и расширенную форму.
Тип: Оригинальное учебное пособие для учащихся
#InterpretAFractionAsDivision:В этом интерактивном учебном пособии вы научитесь определять дробь как деление числителя на знаменатель, используя модели дробей.
Тип: Оригинальное учебное пособие для учащихся
Ты потопил мой линкор! : Узнайте, как точно нанести координаты на плоскость, из интерактивного руководства.
Тип: Оригинальное учебное пособие для учащихся
Работа на Вонка:В этом интерактивном учебном пособии продемонстрируйте, как можно аккуратно заполнить прямоугольную призму без пробелов или перекрытий, используя единичные кубы одинакового размера, а затем используйте эту модель для определения ее объема.
Тип: Оригинальное учебное пособие для учащихся
Ice Ice Maybe: игра по оценке операций:
Эта увлекательная интерактивная игра помогает тренировать навыки оценивания с использованием различных операций по выбору, включая сложение, вычитание, умножение, деление, использование десятичных дробей, дробей и процентов.
Различные уровни сложности делают эту игру подходящей для разных возрастов и уровней способностей.
Сложение/ Вычитание: Сложение и вычитание целых чисел, сложение и вычитание десятичных дробей.
Умножение/Деление: Умножение и сложение целых чисел.
Проценты: Определение процента от целого числа.
Дроби: Умножение и деление целого числа на дробь, а также применение свойств операций.
Тип: обучающая игра
Цветочная сила: игра в упорядочение рациональных чисел:
Это веселая интерактивная игра, которая помогает учащимся практиковаться в упорядочивании рациональных чисел, включая десятичные дроби, дроби и проценты. Вы сажаете и собираете цветы за деньги. Позвольте пчелам опылять, и вы сможете умножить свой урожай и денежные вознаграждения!
Вы сажаете и собираете цветы за деньги. Позвольте пчелам опылять, и вы сможете умножить свой урожай и денежные вознаграждения!
Тип: обучающая игра
Фракция Викторина:Проверьте свои навыки фракции, отвечая на вопросы на этом сайте.В этом тесте вам предлагается упростить дроби, преобразовать дроби в десятичные числа и проценты, а также ответить на вопросы по алгебре, связанные с дробями. Вы даже можете выбрать уровень сложности, типы вопросов и ограничение по времени.
Тип: обучающая игра
Оценщик четыре: В этом упражнении учащиеся играют в игру «Соедини четыре», но чтобы разместить фигуру на доске, они должны правильно решить задачу на сложение, умножение или процентное соотношение. Студенты могут регулировать сложность задач, а также то, насколько близко оценка должна быть к фактическому результату. Это задание позволяет учащимся попрактиковаться в оценке сложения, умножения и процентного соотношения больших чисел (сотни). Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Студенты могут регулировать сложность задач, а также то, насколько близко оценка должна быть к фактическому результату. Это задание позволяет учащимся попрактиковаться в оценке сложения, умножения и процентного соотношения больших чисел (сотни). Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: обучающая игра
Оценочная викторина: В этом упражнении учащихся проверяют на их способность вычислять суммы, произведения и проценты.Студент может регулировать сложность задач и то, насколько они должны быть близки к фактическому ответу. Это задание позволяет учащимся попрактиковаться в оценке сложения, умножения или процента от больших чисел. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: обучающая игра
Создатель изменений: Этот интерактивный апплет позволяет учащимся попрактиковаться в внесении изменений в U.долларов США и в четырех других валютах. Студентам предоставляется сумма покупки и уплаченная сумма, и они должны ввести количество каждого номинала, которое составляет правильное изменение. Студенты награждаются за правильные ответы и показывают правильное изменение, если они ошибаются. Существует четыре уровня сложности: от суммы менее доллара до суммы более 100 долларов.
Тип: обучающая игра
Лабиринт игры:В этом упражнении учащиеся вводят координаты, чтобы проложить путь к месту назначения, минуя мины.Это задание позволяет учащимся изучить декартовы координаты и плоскость декартовых координат. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: обучающая игра
Прогресс вычислительного тома 1: Учащихся просят определить количество единичных кубов, необходимых для построения кубов заданных размеров.
Тип: Задача решения проблем
Прогресс вычислительного тома 3:Учеников просят найти высоту прямоугольной призмы, зная длину, ширину и объем.
Тип: Задача решения проблем
Прогресс вычислительного тома 4:Учащихся просят применить знания об объеме прямоугольных призм, чтобы найти объем объекта неправильной формы, используя принцип смещения.
Тип: Задача решения проблем
Сравнение двух разных пицц: Основное внимание в этой задаче уделяется пониманию того, что дроби в явном контексте являются дробями определенного целого. В этой задаче есть три разных целого: средняя пицца, большая пицца и две пиццы вместе взятые.Это задание лучше всего подходит для обучения. Студенты могут практиковаться в объяснении своих рассуждений друг другу в парах или в рамках группового обсуждения.
В этой задаче есть три разных целого: средняя пицца, большая пицца и две пиццы вместе взятые.Это задание лучше всего подходит для обучения. Студенты могут практиковаться в объяснении своих рассуждений друг другу в парах или в рамках группового обсуждения.
Тип: Задача решения проблем
Сравнение сумм дробей единиц:Цель этого задания – помочь учащимся понять сложение дробей; он задуман как учебная задача.Обратите внимание, что учащимся не предлагается найти сумму, поэтому это может быть дано учащимся, которые ограничены вычислением суммы дробей с одним и тем же знаменателем. Скорее, им нужно четко понимать единичные дроби (дроби с единицей в числителе) и рассуждать об их относительном размере.
Тип: Задача решения проблем
Билеты на карнавал: Целью этого задания является решение учащимися многоступенчатых задач в контексте концепции, поддерживающей финансовую грамотность, а именно инфляции. Инфляция – это устойчивый рост среднего уровня цен. В этом задании учащиеся видят, что если уровень цен растет, а доходы людей не растут, они не могут покупать столько товаров и услуг; другими словами, их покупательная способность снижается.
Инфляция – это устойчивый рост среднего уровня цен. В этом задании учащиеся видят, что если уровень цен растет, а доходы людей не растут, они не могут покупать столько товаров и услуг; другими словами, их покупательная способность снижается.
Тип: Задача решения проблем
Результаты видеоигр: В этом задании учащимся предлагается использовать оба этих дополнительных навыка, написав выражение в части (а) и интерпретировав данное выражение в (б).Числа, приведенные в задаче, преднамеренно большие и «уродливые», чтобы отбить у учащихся желание подсчитывать баллы Эрика и Лейлы. Основное внимание в этой задаче уделяется не числовым ответам, а построению и интерпретации выражений, которые можно ввести в калькулятор или сообщить другому учащемуся, не знакомому с контекстом.
Тип: Задача решения проблем
Коробка с глиной:Цель этого задания — помочь учащимся понять, что происходит при масштабировании размеров прямоугольного твердого тела.Эта задача дает возможность сравнить относительные объемы ящиков, чтобы вычислить массу глины, необходимую для их заполнения. Эти относительные объемы можно рассчитать геометрически, заполняя большую коробку меньшими коробками, или арифметически, используя заданные размеры.
Тип: Задача решения проблем
Что такое 23 ÷ 5?: Когда задача на деление, включающая целые числа, не приводит к целочисленному частному, важно, чтобы учащиеся могли решить, требует ли контекст, чтобы результат сообщался как целое число с остатком (как в части (b)) или смешанное число/десятичное число (как в Части (c)). Часть (а) представляет два варианта контекста, которые требуют, чтобы эти два разных ответа подчеркивали различие между ними.
Часть (а) представляет два варианта контекста, которые требуют, чтобы эти два разных ответа подчеркивали различие между ними.
Тип: Задача решения проблем
Сколько пирога?:Цель этого задания – помочь учащимся увидеть связь между a÷b и a/b в конкретном конкретном примере.Это задание, вероятно, лучше всего подходит для обучения или формирующего оценивания.
Тип: Задача решения проблем
Сколько порций овсянки?: Эта задача предоставляет контекст для выполнения деления целого числа на дробную часть. Эта задача представляет собой пример деления «Сколько групп?»: «группами» в данном случае являются порции овсянки, и вопрос заключается в том, сколько порций (или групп) в упаковке.
Эта задача представляет собой пример деления «Сколько групп?»: «группами» в данном случае являются порции овсянки, и вопрос заключается в том, сколько порций (или групп) в упаковке.
Тип: Задача решения проблем
Покраска комнаты:Цель этого задания — представить учащимся ситуацию, в которой для них естественно делить единичную дробь на ненулевое целое число.Определение количества краски, которое нужно Кулани для каждой стены, иллюстрирует понимание значения деления единичной дроби на ненулевое целое число.
Тип: Задача решения проблем
Покраска стены: Цель этого задания – помочь учащимся найти ответ на вопрос в контексте, который может быть представлен умножением дробей. Это задание подходит как для обучения, так и для оценивания, в зависимости от того, как оно используется и на каком уровне учащиеся понимают умножение дробей.
Это задание подходит как для обучения, так и для оценивания, в зависимости от того, как оно используется и на каком уровне учащиеся понимают умножение дробей.
Тип: Задача решения проблем
Звезды оригами:Цель этого задания — представить учащимся ситуацию, в которой им необходимо разделить целое число на дробную часть, чтобы найти решение.Подсчет количества звезд оригами, которые Эйвери и Меган могут сделать, иллюстрирует понимание учащимися процесса деления целого числа на дробную часть.
Тип: Задача решения проблем
Смешанные числа с разными знаменателями: Цель этого задания — помочь учащимся осознать, что существуют разные способы сложения смешанных чисел, и они наиболее подходят для использования в учебной среде. Два основных способа, которыми учащиеся могут складывать, — это преобразование смешанных чисел в дроби, большие 1, или сложение целых чисел и дробных частей по отдельности. Для учащихся полезно развить чувство того, какой подход будет лучше в конкретном контексте.
Два основных способа, которыми учащиеся могут складывать, — это преобразование смешанных чисел в дроби, большие 1, или сложение целых чисел и дробных частей по отдельности. Для учащихся полезно развить чувство того, какой подход будет лучше в конкретном контексте.
Тип: Задача решения проблем
Приготовление смора:Цель этого учебного задания — мотивировать дискуссию о сложении дробей и значении общего знаменателя.В различных частях задания учащиеся перемещаются между абстрактным представлением дробей и значением дробей в контексте.
Тип: Задача решения проблем
Создание куки: Эта задача очень хорошо поддается множественному решению. Студенты могут многому научиться, сравнивая различные методы. Учащиеся, которые уже знакомы с умножением дробей, могут сразу перейти к числовым решениям, приведенным ниже. Учащиеся, которые еще не уверены в значении этих операций, могут нарисовать рисунки или диаграммы.
Студенты могут многому научиться, сравнивая различные методы. Учащиеся, которые уже знакомы с умножением дробей, могут сразу перейти к числовым решениям, приведенным ниже. Учащиеся, которые еще не уверены в значении этих операций, могут нарисовать рисунки или диаграммы.
Тип: Задача решения проблем
Бег-А-Тон:Цель этого задания — представить учащимся ситуацию, когда естественно складывать дроби с разными знаменателями; его можно использовать как для оценки, так и для учебных целей.Учителя должны предусмотреть два типа решений: в одном учащиеся вычисляют расстояние, которое пробежал Алекс, чтобы определить ответ, а в другом учащиеся сравнивают две части его бега с эталонными дробями.
Тип: Задача решения проблем
Умножать или не умножать?: Цель этого задания — познакомить учащихся с умножением дробей с помощью реальных вопросов.
Тип: Задача решения проблем
Пока не увижу, не поверю:Цель этого задания — помочь учащимся увидеть, что 4×(9+2) в четыре раза больше, чем (9+2). Хотя эта задача может показаться очень простой, она предоставляет учащимся и учителям очень полезную визуальную информацию для интерпретации выражения без его оценки, поскольку они могут сами убедиться, что 4×(9+2) в четыре раза больше, чем (9+2). .
Тип: Задача решения проблем
Заправка для салата: Цель этого задания – научить учащихся складывать дроби с разными знаменателями и делить единичную дробь на целое число. Этот доступный контекст реальной жизни дает учащимся возможность применить свое понимание сложения как объединения двух отдельных величин.
Этот доступный контекст реальной жизни дает учащимся возможность применить свое понимание сложения как объединения двух отдельных величин.
Тип: Задача решения проблем
Бегом в школу:Задание может быть одним из первых занятий по ознакомлению с умножением дробей. В задаче есть дроби, которые легко рисовать, и обеспечивает линейную ситуацию.Учащимся полезно рассуждать о решении таких текстовых задач до того, как им скажут, что их можно решить путем умножения дробей; это помогает им развить смысл умножения дробей.
Тип: Задача решения проблем
Пробежать милю: В решении используется идея о том, что умножение на дробь меньше 1 дает меньшее значение. Учащимся необходимо объяснить, почему это так.
Учащимся необходимо объяснить, почему это так.
Тип: Задача решения проблем
Рассуждения об умножении:Это хорошая задача для работы с детьми, чтобы попытаться ясно и точно объяснить их мышление, хотя учителя должны быть готовы работать с множеством различных способов объяснения взаимосвязи между величиной факторов и величиной продукта.
Тип: Задача решения проблем
Сравнение продуктов: Цель этого задания — организовать обсуждение в классе, которое поможет учащимся обобщить то, что они узнали об умножении в предыдущих классах. Он основан на применении свойств операций как стратегий умножения и деления и интерпретации уравнения умножения как сравнения.
Он основан на применении свойств операций как стратегий умножения и деления и интерпретации уравнения умножения как сравнения.
Тип: Задача решения проблем
Слова к выражениям 1:Эта задача позволяет учащимся увидеть слова, которые могут описывать выражение, хотя для решения требуются вложенные скобки.Кроме того, слова (сложение, сумма) и (произведение, умножение) используются стратегически, чтобы учащийся мог видеть, что эти слова имеют связанные значения.
Тип: Задача решения проблем
Обратите внимание на скобки 1: В этой задаче учащемуся предлагается оценить шесть числовых выражений, которые содержат одни и те же целые числа и операции, но имеют разные результаты из-за размещения скобок. Этот тип задач помогает учащимся увидеть структуру числовых выражений. В более поздних классах они будут работать с аналогичными идеями в контексте видения и использования структуры в алгебраических выражениях.
Этот тип задач помогает учащимся увидеть структуру числовых выражений. В более поздних классах они будут работать с аналогичными идеями в контексте видения и использования структуры в алгебраических выражениях.
Тип: Задача решения проблем
Минуты и дни:Эта задача требует деления многозначных чисел в контексте изменения единиц измерения.Кроме того, проблема преобразования требует двух шагов, так как 2011 минут необходимо преобразовать сначала в часы и минуты, а затем в дни, часы и минуты.
Тип: Задача решения проблем
Половина рецепта: Это третья задача в серии из трех задач на умножение дробей, которые можно решить с помощью рисунков или числовых линий. Первый, «Бег в школу», не требует, чтобы единичные дроби, составляющие 3/4, были разделены, чтобы найти 1/3 от 3/4. Второе задание, «Питьевой сок», требует, чтобы учащиеся разделили дроби, составляющие 1/2, чтобы найти 3/4 от 1/2. Эта задача также требует подразделения и включает в себя умножение дроби и смешанного числа.
Первый, «Бег в школу», не требует, чтобы единичные дроби, составляющие 3/4, были разделены, чтобы найти 1/3 от 3/4. Второе задание, «Питьевой сок», требует, чтобы учащиеся разделили дроби, составляющие 1/2, чтобы найти 3/4 от 1/2. Эта задача также требует подразделения и включает в себя умножение дроби и смешанного числа.
Тип: Задача решения проблем
Рассада травы:Цель этого задания — лучше понять, как умножать дроби.Учащиеся должны использовать представленную диаграмму для обоснования своих выводов.
Тип: Задача решения проблем
Сбор средств: Эта задача помогает учащимся лучше понять умножение на дроби.
Тип: Задача решения проблем
Складывание полосок бумаги:Цель этого задания — дать учащимся конкретный опыт, который они могут применить к умножению дробей.Возможно, более важно то, что задание также целенаправленно связывает длину и расположение точек на числовой прямой, что часто вызывает затруднения у учащихся. Это задание предназначено для обучения и может быть полезно как часть вводного раздела по умножению дробей.
Тип: Задача решения проблем
Нахождение общих знаменателей для вычитания: В части (a) этого задания учащимся предлагается использовать два разных знаменателя для вычитания дробей. Цель этого состоит в том, чтобы помочь учащимся понять, что любой общий знаменатель будет работать, а не только наименьший общий знаменатель. Часть (b) не требует от учащихся делать это более чем одним способом; цель состоит в том, чтобы дать им возможность выбрать знаменатель и, возможно, сравнить с другим студентом, который выбрал другой знаменатель. Цель части (с) — помочь учащимся отказаться от рисования картинок. Учащиеся могут нарисовать картинку, если хотят, но эту задачу на вычитание легче решить символически, что помогает учащимся оценить силу символической записи.
Цель этого состоит в том, чтобы помочь учащимся понять, что любой общий знаменатель будет работать, а не только наименьший общий знаменатель. Часть (b) не требует от учащихся делать это более чем одним способом; цель состоит в том, чтобы дать им возможность выбрать знаменатель и, возможно, сравнить с другим студентом, который выбрал другой знаменатель. Цель части (с) — помочь учащимся отказаться от рисования картинок. Учащиеся могут нарисовать картинку, если хотят, но эту задачу на вычитание легче решить символически, что помогает учащимся оценить силу символической записи.
Тип: Задача решения проблем
Нахождение общих знаменателей для добавления: В части (а) этого задания учащимся предлагается найти и использовать два различных общих знаменателя, чтобы сложить данные дроби. Цель этого вопроса — помочь учащимся понять, что они могут использовать любой общий знаменатель для поиска решения, а не только наименьший общий знаменатель.Часть (б) не просит студентов решить данную задачу на сложение более чем одним способом. Вместо этого цель этого вопроса состоит в том, чтобы дать учащимся возможность выбрать знаменатель и, возможно, сравнить свой метод решения с другим учащимся, выбравшим другой знаменатель. Цель части (с) — дать учащимся, готовым к символической работе, возможность работать более эффективно.
Цель этого вопроса — помочь учащимся понять, что они могут использовать любой общий знаменатель для поиска решения, а не только наименьший общий знаменатель.Часть (б) не просит студентов решить данную задачу на сложение более чем одним способом. Вместо этого цель этого вопроса состоит в том, чтобы дать учащимся возможность выбрать знаменатель и, возможно, сравнить свой метод решения с другим учащимся, выбравшим другой знаменатель. Цель части (с) — дать учащимся, готовым к символической работе, возможность работать более эффективно.
Тип: Задача решения проблем
Сколько шариков?: Это задание предназначено для дополнения задания «Сколько порций овсянки?» и «Бег Молли. » Все три задачи решают проблему деления 4÷1/3, но с разных точек зрения. В этом задании указано, сколько в каждой группе вариантов 4÷1/3. Это задание следует выполнять вместе с заданием «Сколько порций овсянки», уделяя особое внимание очень разным картинкам, изображающим две ситуации.
» Все три задачи решают проблему деления 4÷1/3, но с разных точек зрения. В этом задании указано, сколько в каждой группе вариантов 4÷1/3. Это задание следует выполнять вместе с заданием «Сколько порций овсянки», уделяя особое внимание очень разным картинкам, изображающим две ситуации.
Тип: Задача решения проблем
Египетские дроби:Одна из целей этого задания — помочь учащимся научиться легко и удобно складывать дроби с разными знаменателями.Другая цель состоит в том, чтобы помочь им развить чувство числа дробей, попросив учащихся разложить дроби.
Тип: Задача решения проблем
Питьевой сок: Это вторая задача в серии из трех задач на умножение дробей, которые можно решить с помощью картинок или числовых линий. Это задание требует, чтобы учащиеся разделили дроби, составляющие 1/2, чтобы найти 3/4 от 1/2.
Это задание требует, чтобы учащиеся разделили дроби, составляющие 1/2, чтобы найти 3/4 от 1/2.
Тип: Задача решения проблем
Это складывается?:Это задание устраняет распространенные ошибки, которые допускают учащиеся при интерпретации словесных задач на сложение дробей.Учащимся очень важно понимать, что они складывают дроби только тогда, когда дроби относятся к одному и тому же целому, а также когда дроби складываемого целого не перекрываются. Этот набор вопросов предназначен для улучшения понимания учащимися того, когда уместно и неуместно складывать дроби.
Тип: Задача решения проблем
Деление на половину: Это задание требует, чтобы учащиеся распознали проблемы деления как «количество групп неизвестно» (часть (a)) так и «неизвестный размер группы» (часть (d)) в контексте деления целого числа на дробную часть. В нем также рассматривается распространенное заблуждение учащихся, когда они путают деление на 2 или умножение на 1/2 с делением на 1/2.
В нем также рассматривается распространенное заблуждение учащихся, когда они путают деление на 2 или умножение на 1/2 с делением на 1/2.
Тип: Задача решения проблем
Коннор и Макайла обсуждают умножение:Цель этого задания — заставить учащихся задуматься о значении умножения числа на дробь и использовать это растущее понимание умножения дробей, чтобы понять коммутативное свойство умножения в случае дробей.
Тип: Задача решения проблем
Сравнение числа и произведения: Цель этого задания состоит в том, чтобы учащиеся сравнили число и его произведение с другими числами, которые больше и меньше единицы. Как написано, это задание можно использовать в контексте итогового оценивания, но оно может быть более полезным в учебной обстановке, когда учащихся просят объяснить свои ответы либо партнеру, либо в ходе обсуждения в классе.
Как написано, это задание можно использовать в контексте итогового оценивания, но оно может быть более полезным в учебной обстановке, когда учащихся просят объяснить свои ответы либо партнеру, либо в ходе обсуждения в классе.
Тип: Задача решения проблем
Проблема с калькулятором:Эта конкретная задача связана с умножением. Хотя учащиеся могут решить эту задачу путем умножения, маловероятно, что они это сделают. Здесь намного проще ответить на вопрос, если вы можете думать об умножении числа на коэффициент как о масштабировании числа.
Тип: Задача решения проблем
Банановый пудинг: Цель этого задания — предоставить учащимся конкретную ситуацию, которую они могут смоделировать, разделив целое число на дробную часть. Для учащихся, которые только начинают задумываться о значении деления на единичную дробь (или для учащихся, которые никогда не готовили), учитель может принести мерный стакан на 1/4 чашки, чтобы учащиеся могли разыграть его.Если учащиеся смогут успешно рассуждать в частях (а) и (б), у них будет хорошая возможность подумать о части (в), которая может привести к различным методам решения.
Для учащихся, которые только начинают задумываться о значении деления на единичную дробь (или для учащихся, которые никогда не готовили), учитель может принести мерный стакан на 1/4 чашки, чтобы учащиеся могли разыграть его.Если учащиеся смогут успешно рассуждать в частях (а) и (б), у них будет хорошая возможность подумать о части (в), которая может привести к различным методам решения.
Тип: Задача решения проблем
Умножение десятичной дроби на степень 10:В этом обучающем видео Академии Хана объясняются закономерности размещения десятичной точки, когда десятичная дробь умножается на степень 10.Показатели НЕ обсуждаются.
Тип: Учебник
Умножение и деление степеней 10: нулевые закономерности: В этом обучающем видеоролике Академии Хана представлена методология понимания и использования шаблонов числа нулей продуктов , имеющих коэффициент, равный 10. Хотя в стандарте не упоминаются показатели степени, понимание разрядности умножения или деления на степени десяти поможет учащимся понять умножение и деление на десятичные дроби.
Хотя в стандарте не упоминаются показатели степени, понимание разрядности умножения или деления на степени десяти поможет учащимся понять умножение и деление на десятичные дроби.
Тип: Учебник
Степени 10: Шаблоны:В этом обучающем видеоролике Академии Хана представлена схема умножения десятков, которая получается, когда мы сравниваем количество десятков в множителях с количеством нулей в произведении.Введен словарь, экспонента и основание .
Тип: Учебник
Вычислите выражение с круглыми скобками и без них: В этом обучающем видеоролике Академии Хана показано влияние нотации скобок в выражении. Поскольку учебник решает одну и ту же задачу со скобками и без них, отрицательные числа являются частью решения.
Поскольку учебник решает одну и ту же задачу со скобками и без них, отрицательные числа являются частью решения.
Тип: Учебник
Метрическая система: Единицы объема:Этот обучающий видеоролик Академии Хана иллюстрирует эквивалент преобразования литров, миллилитров и килолитров.
Тип: Учебник
Распространение Trail Mix: В этом обучающем видео Академии Хана представлена стратегия решения следующей задачи: по точечному графику с различными измерениями следовой смеси в мешках найти количество следовой смеси, которое содержалось бы в каждом мешке, если бы общее количество во всех мешках было равномерно перераспределено. .
.
Тип: Учебник
Объем через разложение:В этом обучающем видео Академии Хана показано, как найти объем неправильной объемной фигуры, разделив фигуру на две прямоугольные призмы и найдя объем каждой из них.Хотя учебник работает с чертежом, отдельные объемные кубы не рисуются, поэтому учащиеся должны работать с формулой.
Тип: Учебник
Том: Разложение сплошной фигуры Пример: В этом обучающем видео Академии Хана показано, как найти объем неправильной фигуры, состоящей из единичных кубов, путем разделения фигуры на две прямоугольные призмы и определения объема каждой части.
Тип: Учебник
Том: четыре примера подсчета единиц кубов:В этом обучающем видео Академии Хана показано измерение объема путем подсчета кубов. Модели в этом видео включают в себя составную фигуру из прямоугольных призм, хотя для нахождения объема используется только счет, а не уравнение.
Тип: Учебник
Объем: как его измерить: В этом учебном видео Академии Хана описываются измерения в одном, двух и трех измерениях.
Тип: Учебник
Обзор четырехугольника:В этом учебном видео Академии Хана представлены четырехугольники.их категории и подкатегории.
Тип: Учебник
Раздел: Важность позиционного значения:В этом видеоруководстве от Академии Хана вы узнаете о важности разряда при делении.В учебнике используется разрядное значение до тысяч, чтобы помочь учащимся подумать о делении.
Тип: Учебник
Умножение: как использовать модель области:В этом видеоруководстве от Khan Academy показано, как настроить площадную модель для умножения двузначного числа на двузначное число на миллиметровой или сетчатой бумаге, а затем связать ее со стандартным алгоритмом.
Тип: Учебник
Умножение: 4 цифры умножить на 1 цифру (с использованием расширенной формы):В этом видеоруководстве Академии Хана показан пример умножения 4-значного числа на однозначное путем расширения 4-значного числа и умножения на каждую цифру отдельно в модели площади.Это видео поможет сформировать понимание перед обучением стандартному алгоритму. Умножение на 4-значный коэффициент больше, чем в некоторых стандартах, которые ограничивают множители 3-значным числом.
Тип: Учебник
Арифметические операции с дробями:В этом руководстве четыре операции применяются к дробям с визуализацией числовой прямой.Это руководство начинается со сложения дробей с одинаковыми знаменателями и объясняет логику умножения дробей. В этом руководстве также освещается применение и расширение предыдущего понимания умножения для умножения дроби или целого числа на дробь.
а. Интерпретировать продукт ( A / B ) x Q q As A 60101 A Части разбиения Q на B Равные детали; эквивалентно, в результате последовательности операций a x qb .В общем, ( A / B ) x ( C / D ) = AC / BD .
Тип: Учебник
Создание общих знаменателей:В этом учебном пособии изучается сложение и вычитание дробей с разными знаменателями.Используя числовую прямую, этот математический процесс можно легко визуализировать и связать с конечной стратегией умножения знаменателей (a/b + c/d = ad +bc/bd). Строка номера видео показывает отрицательные числа, которые выходят за рамки элементарных стандартов, поэтому учителю начальных классов необходимо подумать о том, обогатит ли это видео знания учащихся или вызовет путаницу.
Тип: Учебник
Наименьшие общие знаменатели:В этом уроке учащиеся познакомятся со стратегией нахождения наименьшего общего знаменателя для определенных случаев.Учителя начальных классов должны помнить, что это не является обязательным требованием для начальных стандартов, и подумать, будет ли это видео способствовать углублению знаний учащихся или создаст путаницу. В этой главе объясняется, как найти наименьший возможный общий знаменатель. Например, 2/3 + 5/4 = 8/12 + 15/12 = 23/12.
Тип: Учебник
Декартова система координат:Декартова система координат, образованная декартовым произведением действительной числовой прямой на саму себя, позволяет визуализировать алгебраические уравнения в виде геометрических фигур в двух или трех измерениях.Хотя это руководство включает в себя основы системы координат, оно также включает в себя идеи, выходящие за рамки стандартов пятого класса. Скорее всего, это видео понравится только продвинутым пятиклассникам.
Тип: Учебник
Сложение и вычитание с десятичными дробями:Этот учебник для студенческой аудитории поможет учащимся лучше понять правила сложения и вычитания десятичных дробей.Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Тип: Учебник
Сложение и вычитание дробей:Этот учебник для студенческой аудитории поможет учащимся лучше понять правила сложения и вычитания дробей.Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Тип: Учебник
Преобразование единиц скорости:На этом уроке учащиеся будут просматривать видео Академии Хана, в котором показано, как преобразовывать отношения с использованием единиц измерения скорости.
Тип: Учебник
Умножение дробей:В видео рассказывается, как умножать дроби и формулировать ответ в минимальных выражениях.
Тип: Учебник
. Прикидка и оценка результатов вычислений
Прикидка и оценка результатов вычислений
 Понятие обыкновенной дроби
Понятие обыкновенной дроби
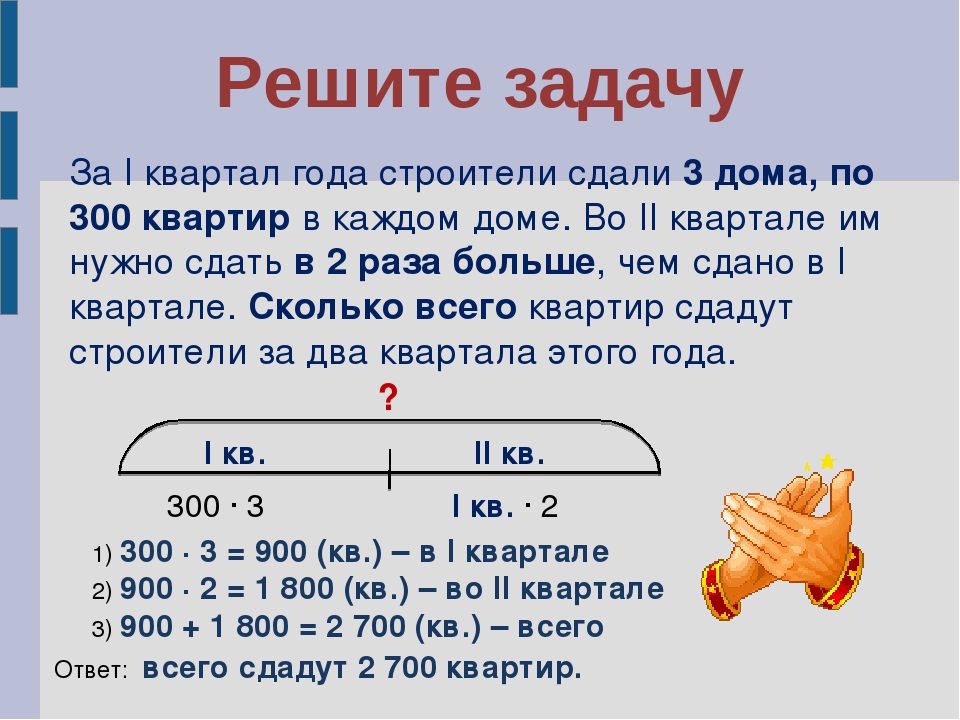 Измерение углов
Измерение углов
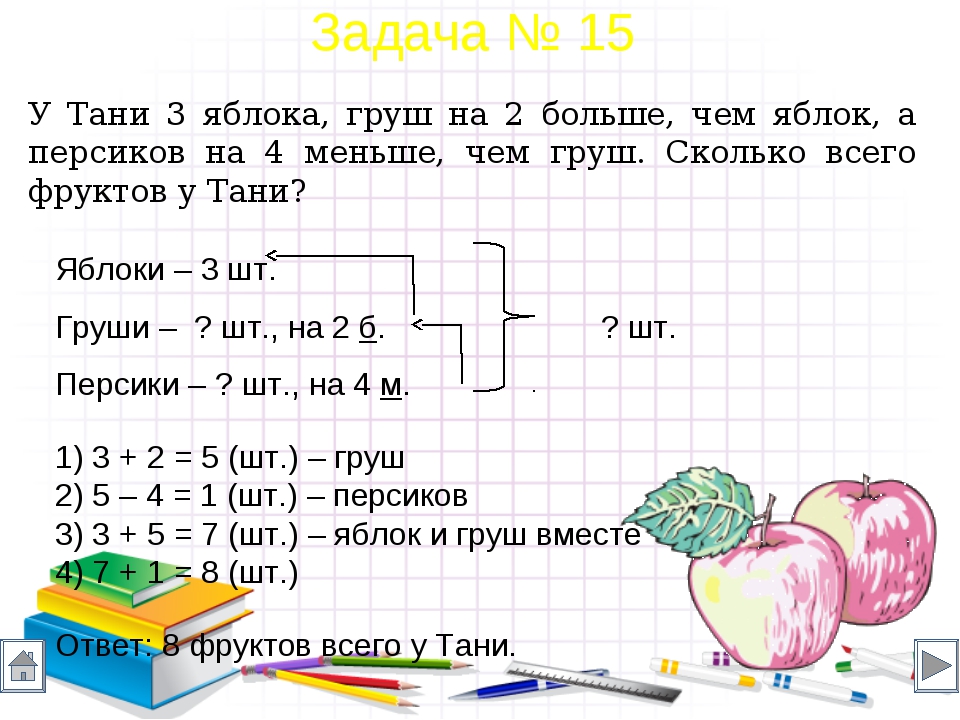 Масштаб. Виды масштаба
Масштаб. Виды масштаба
 Сравнение
Сравнение
 Среднее арифметическое, деление на натуральное число
Среднее арифметическое, деление на натуральное число
 Определение, свойства
Определение, свойства


 я
я Они поставляются с полными планами уроков, а также примерами ожидаемых ответов учащихся.
Они поставляются с полными планами уроков, а также примерами ожидаемых ответов учащихся.
