Задачи движение по окружности физика – Решение задач на движение по окружности (в том числе и на поворотах)

Posted on by alexxlab

Задачи на тему Равномерное движение тела по окружности

Частота обращения ветроколеса ветродвигателя 30 об/мин, якоря электродвигателя 1500 об/мин, барабана сепаратора 8400 об/мин, шпинделя шлифовального станка 96 000 об/мин. Вычислить их периоды
РЕШЕНИЕ

Найти частоту обращения Луны вокруг Земли (см. табл. 14).
РЕШЕНИЕ

Скорость точек рабочей поверхности наждачного круга диаметром 300 мм не должна превышать 35 м/с. Допустима ли посадка круга на вал электродвигателя, совершающего 1400 об/мин; 2800 об/мин
РЕШЕНИЕ

Частота обращения воздушного винта самолета 1500 об/мин. Сколько оборотов делает винт на пути 90 км при скорости полета 180 км/ч
РЕШЕНИЕ

Период обращения платформы карусельного станка 4 с. Найти скорость крайних точек платформы, удаленных от оси вращения на 2 м
РЕШЕНИЕ

Диаметр передних колес трактора в 2 раза меньше, чем задних. Сравнить частоты обращения колес при движении трактора
РЕШЕНИЕ

Радиус рукоятки колодезного ворота в 3 раза больше радиуса вала, на который наматывается трос. Какова линейная скорость конца рукоятки при поднятии ведра с глубины 10 м за 20 с
РЕШЕНИЕ

С какой скоростью и в каком направлении должен лететь самолет по шестидесятой параллели, чтобы прибыть в пункт назначения раньше (по местному времени), чем он вылетел из пункта отправления? Возможно ли это для современных пассажирских самолетов
РЕШЕНИЕ

Первая в мире орбитальная космическая станция, образованная в результате стыковки космических кораблей Союз-4 и Союз-5 16 января 1969 г., имела период обращения 88,85 мин и среднюю высоту над поверхностью Земли 230 км (считая орбиту круговой). Найти среднюю скорость движения станции
РЕШЕНИЕ

При увеличении в 4 раза радиуса круговой орбиты искусственного спутника Земли период его обращения увеличивается в 8 раз. Во сколько раз изменяется скорость движения спутника по орбите
РЕШЕНИЕ

Минутная стрелка часов в 3 раза длиннее секундной. Найти отношение скоростей концов стрелок
РЕШЕНИЕ

Движение от шкива I (рис. 21) к шкиву IV передается при помощи двух ременных передач. Найти частоту обращения (в об/мин) шкива IV, если шкив I делает 1200 об/мин, а радиусы шкивов r1 = 8 см, r2 = 32 см, r3 = 11 см,r4 = 55 см. Шкивы II и III жестко укреплены на одном валу
РЕШЕНИЕ

Циркулярная пила имеет диаметр 600 мм. На ось пилы насажен шкив диаметром 300 мм, который приводится во вращение посредством ременной передачи от шкива диаметром 120 мм, насаженного на вал электродвигателя. Какова скорость зубьев пилы, если вал двигателя совершает 1200 об/мин
РЕШЕНИЕ

Диаметр колеса велосипеда Пенза d 70 см, ведущая зубчатка имеет z1 = 48 зубцов, а ведомая z2 = 18 зубцов. С какой скоростью движется велосипедист на этом велосипеде при частоте вращения педалей n= 1 об/с? С какой скоростью движется велосипедист на складном велосипеде Кама при той же частоте вращения педалей, если у этого велосипеда соответственно d = 50 см,z1 = 48 зубцов, z2 = 15 зубцов
РЕШЕНИЕ

Каково центростремительное ускорение поезда, движущегося по закруглению радиусом 800 м со скоростью 20 м/с
РЕШЕНИЕ

Скорость точек экватора Солнца при его вращении вокруг своей оси равна 2 км/с. Найти период обращения Солнца вокруг своей оси и центростремительное ускорение точек экватора
РЕШЕНИЕ

Период обращения молотильного барабана комбайна Нива диаметром 600 мм равен 0,046 с. Найти скорость точек, лежащих на ободе барабана, и их центростремительное ускорение
РЕШЕНИЕ

С какой скоростью автомобиль должен проходить середину выпуклого моста радиусом 40 м, чтобы центростремительное ускорение было равно ускорению свободного падения
РЕШЕНИЕ

Рабочее колесо турбины Красноярской ГЭС имеет диаметр 7,5 м и вращается с частотой 93,8 об/мин. Каково центростремительное ускорение концов лопаток турбины
РЕШЕНИЕ

Найти центростремительное ускорение точек колеса автомобиля, соприкасающихся с дорогой, если автомобиль движется со скоростью 72 км/ч и при этом частота обращения колеса 8 с-1
РЕШЕНИЕ

Две материальные точки движутся по окружности радиусами R1 и R2, причем R1 = 2R2. Сравнить их центростремительные ускорения в случаях: равенства их скоростей; равенства их периодов обращения
РЕШЕНИЕ

Радиус рабочего колеса гидротурбины в 8 раз больше, а частота обращения в 40 раз меньше, чем у паровой турбины. Сравнить скорости и центростремительные ускорения точек обода колес турбин
РЕШЕНИЕ

Детский заводной автомобиль, двигаясь равномерно, прошел расстояние s за время *. Найти частоту обращения и центростремительное ускорение точек на ободе колеса, если диаметр колеса равен d. По возможности конкретные данные задачи получите опытным путем
РЕШЕНИЕ

famiredo.ru

Прямолинейное и криволинейное движение. Движение тела по окружности с постоянной по модулю скоростью

1624. Что означает выражение «машину занесло на повороте»? Почему это происходит?

1625. Почему при быстрой езде по кругу мотоциклист сильно наклоняется к центру круга?

1626. При повороте в воздухе самолет опускает вниз то крыло, в какую сторону поворачивает. Корабль при повороте в воде опускает вниз борт, противоположный стороне поворота. Почему?

1627. Почему наездники в цирке свободно держатся на том боку седла, который обращен к центру арены, а на противоположном боку седла им удержаться гораздо труднее?

1628. При вращении шарика на резинке, резинка растягивается, причем тем сильнее, чем быстрее вращается шарик. Почему резинка растягивается?


1629. Велосипедист, двигаясь на большой скорости, может преодолеть чертово колесо (рис. 220). Почему велосипедист не падает в верхней точке петли?

1630. Кубик массой 0,4 кг положили на грампластинку на расстоянии 0,2 м от ее центра (рис. 221). При вращении пластинки линейная скорость кубика равна 0,2 м/с. Каково ускорение кубика? Какая сила удерживает кубик на пластинке и чему она равна?

1631. Мотоцикл проходит поворот радиусом 20 м. Коэффициент трения между колесами и землей равен 0,7. С какой наибольшей скоростью может двигаться мотоцикл, чтобы не возникло заноса?

1632. Во время дождя коэффициент трения между колесами мотоцикла и землей уменьшается до 0,1. Решите предыдущую задачу для дождливой погоды. Во сколько раз найденная вами скорость мотоцикла из предыдущей задачи будет меньше во время дождя?

1633. Определите центростремительную силу, действующую на вагон метро массой 16 т, когда он движется со скоростью 8 м/с по закруглению радиусом 80 м.

1634. Постройте траекторию движения тела, брошенного горизонтально со скоростью 30 м/сек с высоты 80 м. Определите, на каком расстоянии от места бросания тело упадет на землю и скорость его в момент удара о землю. Сопротивление воздуха не учитывать. Принять g = 10 м/сек2.

1635. С мачты парохода с высоты 10 м над палубой уронили мяч. Скорость парохода 18 км/час. На сколько успеет переместиться пароход за время падения мяча? Где упадет мяч? Какова траектория движения мяча по отношению к поверхности моря? Какова скорость мяча в момент удара о палубу?

1636. На краю стола лежит кусочек мела. Мелу сообщили горизонтальный толчок по направлению, перпендикулярному к классной доске. След от удара мела о доску лежит на 20 см ниже поверхности стола. Расстояние доски от края стола 1 м. Определите начальную скорость мела.

1637. С какой скоростью надо бросить тело в горизонтальном направлении с высоты 20 м, чтобы скорость его в момент падения на землю была 25 м/сек?
(Указание. Решите эту задачу на основании закона сохранения энергии.)

1638. Грузовик массой 5000 кг движется со скоростью 28,8 км/ч по выпуклому мосту с радиусом кривизны 0,04 км. С какой силой давит грузовик на середину моста? С какой скоростью он должен ехать, чтобы не оказывать давления на верхнюю точку моста?

1639. Тепловоз массой 15 т движется по вогнутому мосту с радиусом кривизны 0,05 км. Сила давления тепловоза на середину моста равна 149,5 кН. Какова скорость тепловоза?

1640. Автофургон идет по закруглению радиусом 200 м со скоростью 72 км/ч. При этом внутри фургона производится взвешивание на пружинных весах груза массой 49 кг. Определите показания пружинных весов.

1641. Самолет делает «мертвую петлю» радиусом 0,245 км в вертикальной плоскости. При какой наименьшей скорости самолета в верхней части петли летчик не будет отрываться от кресла?

1642. Самолет, летящий со скоростью 360 км/ч, описывает в вертикальной плоскости «петлю Нестерова» радиусом 0,2 км. Во сколько раз сила, прижимающая летчика к сиденью в нижней точке петли, больше его веса?

1643. Самолет, летящий со скоростью 540 км/ч, описывает в вертикальной плоскости «мертвую петлю» радиусом 500 м. Во сколько раз сила, прижимающая летчика к сиденью, в нижней точке петли больше силы, прижимающей летчика к сиденью, в верхней точке петли?

1644. Коленчатый вал двигателя делает 3600 об/мин. Найдите угловую скорость и период вращения коленчатого вала.

1645. Винт вертолета вращается с частотой 1500 об/мин. Скорость полета вертолета 72 км/ч. Сколько оборотов сделает винт на пути 120 км?

1646. Определите угол поворота Земли вокруг собственной оси за 120 мин.

1647. Коленчатый вал радиусом 2 см делает два оборота за ОД с. Какова частота вращения вала? Найдите угловую и линейную скорости точек поверхности вала.

1648. Самолет летит на широте Санкт-Петербурга (60°). Его пассажиры и экипаж видят, что за окнами иллюминаторов все время светло, ночь не наступает. В каком направлении и с какой скоростью летит самолет? (Радиус Земли 6400 км.)

1649. Вал радиусом 10 см с прикрепленной к нему нитью начал равномерно вращаться. Через 5 с на него намоталось 15 м нити. Найти период, частоту и угловую скорость вращения вала.

1650. Диаметр точильного камня равен 0,3 м. Линейная скорость точек на его рабочей поверхности равна 10 м/с. Определите угловую скорость, частоту и период вращения точильного камня. Сколько оборотов он сделает за 1,5 мин? На какой угол он повернется за это же время?

1651. Шкив радиусом 50 см делает 110 об/мин. Определите период вращения и линейную скорость точек, лежащих на окружности шкива. Какой путь пройдет одна из этих точек за 2 мин?

1652. Капля краски на ободе колеса, имеющего диаметр 20 см движется с линейной скоростью 628 см/с. Сколько оборотов шкив делает за минуту?

1653. Для качественной шлифовки поверхность наждачного круга не должна иметь линейную скорость более 50 м/с. На шлифовальной машине такой круг диаметром в 200 мм делает 3000 оборотов в минуту. Допустима ли такая скорость?

1654. Шлифовальный круг радиусом 30 см равномерно вращается вокруг оси в его центре О (рис. 222). Линейная скорость точки А на круге равна 3,5 м/с. Определите линейную скорость точки Б, расположенной на расстоянии 5 см от оси вращения.

1655. Укажите направление ускорения движущегося тела в положениях А и В, показанных на рисунке 223.

1656. На рисунке 224 показана рука, вращающая камень, привязанный к веревке. Укажите, какие силы действуют на камень, на веревку, на руку, и изобразите их векторами. Если в положении, показанном на рисунке, веревка оборвется, то как будет двигаться камень?

1657. На прибор, состоящий из стержня, по которому могут скользить два шарика: масса одного в 2 раза больше массы другого. Оба шарика связаны нитью так, что центры тяжести их расположены друг от друга на расстоянии 12 см. Весь прибор приводится во вращение вокруг вертикальной оси. Рассчитайте, на каком расстоянии от оси вращения должны быть расположены шарики, чтобы при вращении прибора они оставались на месте, не скользили по стержню.

1658. Если на веревке привязать маленькое ведерко с водой, то можно это ведерко вращать по кругу и вода из него не выльется. Изготовьте ведерко из жестяной банки и проделайте такой опыт. Постарайтесь объяснить его.

 

1659. Радиус окружности, по которой движется конец секундной стрелки, 0,8 см, минутной — 2 см, часовой — 1,5 см. Найдите линейные и угловые скорости стрелок.

1660. Ведущее колесо паровоза диаметром 1,6 м делает 120 оборотов в минуту. С какой скоростью движется паровоз?

1661. Найдите линейную и угловую скорости точки земной поверхности на широте Москвы при суточном вращении Земли вокруг оси. Считать радиус Земли равным 6400 км.

1662. Во сколько раз линейная скорость конца минутной стрелки больше линейной скорости конца часовой стрелки, если минутная стрелка в 1,2 раза длиннее часовой?

1663. Колесо катится без проскальзывания со скоростью 5 м/с. Найдите скорости точек А, В, С, D, Е (рис. 226) относительно Земли. Расстояние от точки Е до центра колеса равно половине радиуса.

1664. Скорость движения электровоза 90 км/ч, диаметр его колес 1,2 м. Каков период вращения колес?

1665. Велосипед движется по закруглению радиусом 10 м со скоростью 21,6 км/ч. Каково центростремительное ускорение велосипеда?

1666. Мотокар движется по закруглению радиусом 20 м с центростремительным ускорением 5 м/с2. Какова скорость мотокара?

1667. Масса планеты Марс составляет 0,11 массы Земли. Во сколько раз первая космическая скорость для Марса меньше, чем для Земли, если его радиус равен 0,53 радиуса Земли?

1668. Космический корабль удалился от поверхности Земли на расстояние, равное радиусу Земли. Какую скорость он должен развить, чтобы вращаться по окружности вокруг Земли?

1669. Искусственный спутник Земли движется по круговой орбите вокруг Земли на высоте, равной 4000 км над поверхностью Земли. Найдите его скорость и период обращения.

1670. Искусственный спутник Земли находится на круговой орбите на расстоянии 6600 км от центра Земли. Какова скорость его движения? Сколько оборотов вокруг Земли за сутки совершит спутник?

1671. Астероид удален от центра Солнца в среднем на расстояние 1,7 • 108 км. Оцените скорость его движения по орбите и период обращения вокруг Солнца.

1672. Искусственный спутник движется в плоскости земного экватора и с Земли кажется неподвижным. Какова скорость спутника? Найдите расстояние от спутника до центра Земли.

kupuk.net

Решение задач ЕГЭ по теме «Движение тела по окружности»

ЕГЭ. Задание 28(С2). Механика (расчетная задача). Движение по окружности.

Полый конус с углом при вер­ши­не 2α вра­ща­ет­ся с уг­ло­вой ско­ро­стью ω во­круг вер­ти­каль­ной оси, сов­па­да­ю­щей с его осью сим­мет­рии. Вер­ши­на ко­ну­са об­ра­ще­на вверх. На внеш­ней по­верх­но­сти ко­ну­са на­хо­дит­ся не­боль­шая шайба, ко­эф­фи­ци­ент тре­ния ко­то­рой о по­верх­ность ко­ну­са равен μ. При каком мак­си­маль­ном рас­сто­я­нии L от вер­ши­ны шайба будет не­по­движ­на от­но­си­тель­но ко­ну­са? Сде­лай­те схе­ма­ти­че­ский ри­су­нок с ука­за­ни­ем сил, дей­ству­ю­щих на шайбу.

За­да­ние 28 № 6401

Ре­ше­ние.

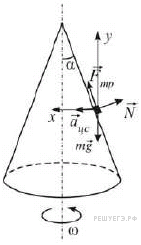hello_html_79befd56.pngЗа­пи­шем вто­рой закон Нью­то­на для шайбы:

 

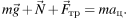
hello_html_m7b52cd64.png

 

Про­ек­ции урав­не­ния на оси OX и OY в инер­ци­аль­ной си­сте­ме отсчёта, свя­зан­ной с Зем­лей:

 

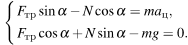
hello_html_m78167ef0.png

 

По­сколь­ку 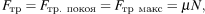hello_html_m36535d9d.pngси­сте­ма урав­не­ний при­ни­ма­ет вид:

 

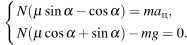
hello_html_m4638cfdb.png

 

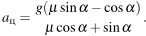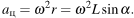От­ку­да hello_html_m3e3b4819.pngНо hello_html_m1bc8371a.pngСле­до­ва­тель­но,

 

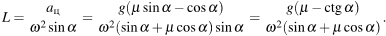
hello_html_m31b391.png

 

Ответ: 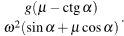hello_html_7d39d76e.png

В вер­ти­каль­ной плос­ко­сти рас­по­ло­же­на глад­кая труб­ка, изо­гну­тая пе­ри­о­ди­че­ски в виде дуг окруж­но­стей оди­на­ко­вым ра­ди­у­сом R (см. рис.). В верх­нее от­вер­стие труб­ки без на­чаль­ной ско­ро­сти за­пус­ка­ют шарик мас­сой m = 10 г. С какой по мо­ду­лю силой F шарик дей­ству­ет на труб­ку в точке А, в конце пер­вой по­ло­ви­ны пе­ри­о­да сво­е­го дви­же­ния по труб­ке?

За­да­ние 28 № 5778

Ре­ше­ние.

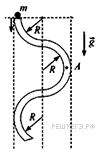
hello_html_m4a2bea75.png

Как видно из ри­сун­ка, к концу пер­во­го по­лу­пе­ри­о­да дви­же­ния по труб­ке шарик опу­стит­ся по вы­со­те на рас­сто­я­ние 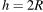hello_html_m41e54472.jpg. По­сколь­ку по­терь ме­ха­ни­че­ской энер­гии нет (по усло­вию труб­ка глад­кая), то ско­рость ша­ри­ка к этому мо­мен­ту будет равна hello_html_m1e0b6fe4.png.

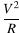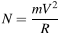В точке A шарик дви­жет­ся по окруж­но­сти с цен­тро­стре­ми­тель­ным уско­ре­ни­ем, рав­ным hello_html_7cfde839.jpg, ко­то­рое, со­глас­но вто­ро­му за­ко­ну Нью­то­на, создаётся нор­маль­ной силой дав­ле­ния со сто­ро­ны труб­ки: hello_html_337ba951.png.

По тре­тье­му за­ко­ну Нью­то­на эта сила по мо­ду­лю равна ис­ко­мой силе дав­ле­ния ша­ри­ка на труб­ку: 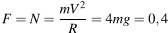hello_html_m228b721e.pngН.

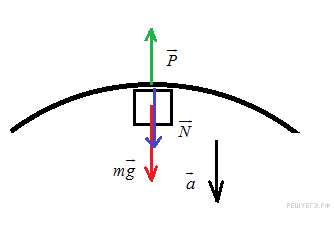
В ат­трак­ци­о­не че­ло­век мас­сой 60 кг дви­жет­ся на те­леж­ке по рель­сам и со­вер­ша­ет «мерт­вую петлю» в вер­ти­каль­ной плос­ко­сти. Каков ра­ди­ус кру­го­вой тра­ек­то­рии, если в ниж­ней точке при дви­же­нии те­леж­ки со ско­ро­стью 10 м/с сила дав­ле­ния че­ло­ве­ка на си­де­ние те­леж­ки была равна 1800 Н? Уско­ре­ние сво­бод­но­го па­де­ния при­нять рав­ным 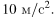hello_html_m642c87e5.png

За­да­ние 28 № 2963

Ре­ше­ние.

 

этапа

Со­дер­жа­ние этапа ре­ше­ния

Чертёж, гра­фик, фор­му­ла

Оцен­ка этапа в бал­лах

1

Вы­пол­ня­ет­ся вто­рой закон Нью­то­на. Сила P дав­ле­ния на си­де­ние по тре­тье­му за­ко­ну Нью­то­на равна по мо­ду­лю силе N упру­го­сти, дей­ству­ю­щей на че­ло­ве­ка.

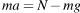
hello_html_0.gifhello_html_m5c050e3.png

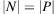
hello_html_0.gifhello_html_m23e8d3fc.png

1

2

Из ки­не­ма­ти­че­ских усло­вий цен­тро­стре­ми­тель­ное уско­ре­ние равно:

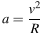
hello_html_0.gifhello_html_m265eb159.png

1

3

Из урав­не­ний пунк­тов 1 и 2 сле­ду­ет:

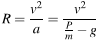
hello_html_m7fb7b053.png

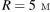
hello_html_751bbbad.jpg

1

Мак­си­маль­ный балл

3

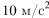
В ат­трак­ци­о­не че­ло­век мас­сой 70 кг дви­жет­ся на те­леж­ке по рель­сам и со­вер­ша­ет «мерт­вую петлю» в вер­ти­каль­ной плос­ко­сти. С какой ско­ро­стью дви­жет­ся те­леж­ка в верх­ней точке кру­го­вой тра­ек­то­рии ра­ди­у­сом 20 м, если в этой точке сила дав­ле­ния че­ло­ве­ка на си­де­ние те­леж­ки равна 700 Н? Уско­ре­ние сво­бод­но­го па­де­ния при­нять рав­ным hello_html_0.gifhello_html_m77e59ca1.png

Ре­ше­ние.

 

этапа

Со­дер­жа­ние этапа ре­ше­ния

Чертёж, гра­фик, фор­му­ла

Оцен­ка этапа в бал­лах

1

При дви­же­нии по окруж­но­сти со­глас­но вто­ро­му за­ко­ну Нью­то­на рав­но­дей­ству­ю­щая силы тя­же­сти и силы упру­го­сти со­зда­ет цен­тро­стре­ми­тель­ное уско­ре­ние. Сила P дав­ле­ния на си­де­ние по тре­тье­му за­ко­ну Нью­то­на равна по мо­ду­лю силе N упру­го­сти, дей­ству­ю­щей на че­ло­ве­ка.

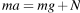
hello_html_0.gifhello_html_125dc3b2.png

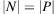
hello_html_m23e8d3fc.png

1

2

Из ки­не­ма­ти­че­ских усло­вий цен­тро­стре­ми­тель­ное уско­ре­ние равно:

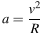
hello_html_m265eb159.png

1

3

Из урав­не­ний пунк­тов 1 и 2 сле­ду­ет:

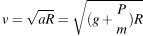hello_html_m5cb2683b.png,

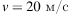
hello_html_0.gifhello_html_m1a150d7e.png

1

Мак­си­маль­ный балл

3

hello_html_m240f65f3.png

infourok.ru

Трение и движение по окружности

В этой статье собраны задачи, затрагивающие одновременно как тему “сила трения”, так и тему “движение по окружности”, придется вспомнить, что такое центробежная сила и как рассчитывается нормальное ускорение.

Задача 1. На горизонтальной дороге автомобиль делает поворот радиусом 16 м. Какова наибольшая скорость, которую может развить автомобиль, чтобы его не занесло, если коэффициент трения скольжения колес о дорогу равен 0,4? Во сколько раз изменится эта скорость зимой, когда коэффициент трения станет меньше в 4 раза?

трение

К задаче 1

Чтобы автомобиль не занесло, необходимо чтобы сила трения была не меньше, чем центробежная сила. Поэтому

    \[F_{n}=\frac{m \upsilon^2}{R}\]

    \[F_{tr}=\mu m g\]

Приравняем:

    \[\frac{m \upsilon^2}{R}=\mu m g\]

Откуда скорость:

    \[\upsilon^2=\mu g R\]

    \[\upsilon=\sqrt{\mu g R }=\sqrt{0,4 \cdot 9,8 \cdot 16}=7,9\]

Если коэффициент трения уменьшится вчетверо, скорость придется уменьшить вдвое: \upsilon_1=3,96 м/с.

Ответ: \upsilon=7,9 м/с, \upsilon_1=3,96 м/с.

 

Задача 2. Горизонтально расположенный диск проигрывателя вращается с частотой 78 об/мин. На него поместили небольшой предмет. Расстояние от оси вращения до предмета составляет 7 см. На этом расстоянии предмет удерживается на диске. Каков коэффициент трения между предметом и диском?

Необходимо, чтобы сила трения была не меньше, чем центробежная сила. Поэтому

    \[F_{n}=\frac{m \upsilon^2}{R}=m \omega^2 R\]

    \[F_{tr}=\mu m g\]

Приравняем:

    \[m \omega^2 R =\mu m g\]

    \[\omega^2 R =\mu g\]

    \[4 \pi^2 \nu^2 R=\mu g\]

Зная частоту вращения, определим коэффициент трения:

    \[\mu=\frac{4 \pi^2 \nu^2 R }{g}=\frac{4 \cdot 3,14^2 \cdot1,3^2 \cdot 0,07 }{9,8}=0,48\]

Ответ: \mu=0,48.

 

Задача 3. Определите, какого радиуса круг может описать велосипедист, если он едет со скоростью 25 км/ч, а предельный угол наклона велосипедиста к земле равен 60^{\circ}?

трение

К задаче 3

Чтобы велосипедиста не занесло, необходимо чтобы сила трения была не меньше, чем центробежная сила. Но колесо наклонено под углом 60^{\circ}, поэтому введем систему координат  (ось x – горизонтальна, ось y – направлена вертикально вверх):

    \[N=mg\]

    \[\operatorname{ctg}{\alpha}=\frac{ F_{tr}}{N}\]

Следовательно, так как по определению F_{tr}=\mu N, то

    \[\mu=\operatorname{ctg}{\alpha}\]

Теперь определим радиус из условия равенства силы трения и центробежной силы:

    \[F_{n}=F_{tr}\]

Приравняем:

    \[\frac{m \upsilon^2}{R}= mg \operatorname{ctg}{\alpha}\]

    \[R=\frac{ \upsilon^2}{ g \operatorname{ctg}{\alpha}}=\frac{ \upsilon^2\operatorname{tg}{\alpha}}{ g }=\frac{ 25000^2\cdot \sqrt{3}}{ 9,8\cdot 3600^2 }=8,51\]

Ответ: 8,5 м

 

Задача 4. Описывая окружность радиусом 30 м, конькобежец наклонился в сторону поворота на угол 72^{\circ} к горизонту. С какой скоростью двигался конькобежец? Каков коэффициент трения коньков о лед?

Введем систему координат и разложим силу реакции опоры на проекции на оси:

    \[N\sin{\alpha}=mg\]

    \[N\cos{\alpha}= F_{tr}\]

Найдем силу реакции опоры:

    \[N=\frac{ mg }{\sin{\alpha}}\]

Найдем F_{tr}:

    \[F_{tr}=\frac{ mg\cos{\alpha} }{\sin{\alpha}}=mg \operatorname{ctg}{\alpha}\]

Теперь определим скорость:

    \[F_{n}=\frac{m \upsilon^2}{R}=F_{tr}\]

    \[\frac{m \upsilon^2}{R}= mg \operatorname{ctg}{\alpha}\]

    \[\upsilon^2= g R\operatorname{ctg}{\alpha}\]

    \[\upsilon=\sqrt{ g R\operatorname{ctg}{\alpha}}=\sqrt{ 9,8 \cdot 30 \cdot0,325=9,77\]

Определим коэффициент трения:

    \[F_{tr}=\mu mg =\frac{m \upsilon^2}{R}\]

    \[\mu=\frac{\upsilon^2}{gR}=0,32\]

Ответ: \upsilon=9,77 м/с, \mu=0,32.

easy-physic.ru

на движение по окружности; на нахождение длины движущегося объекта; на нахождение средней скорости

В статье рассмотрены задачи в помощь учащимся: для отработки навыков решения текстовых задач при подготовке к ЕГЭ, при обучении решению задач на составление математической модели реальных ситуаций во всех параллелях основной и старшей школы. В ней представлены задачи: на движение по окружности; на нахождение длины движущегося объекта; на нахождение средней скорости.

I. Задачи на движение по окружности.

Задачи на движение по окружности оказались сложными для многих школьников. Решаются они почти так же, как и обычные задачи на движение. В них также применяется формула . Но есть момент, на который обратим внимание.

Задача 1. Из пункта А круговой трассы выехал велосипедист, а через 30 мин следом за ним отправился мотоциклист. Через 10 мин после отправления он догнал велосипедиста в первый раз, а еще через 30 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.

Решение. Скорости участников примем за х км/ч и у км/ч. В первый раз мотоциклист обогнал велосипедиста через 10 мин, то есть через ч после старта. До этого момента велосипедист был в пути 40 мин, то есть ч. Участники движения проехали одинаковые расстояния, то есть y =x. Внесем данные в таблицу.

Таблица 1

Участник движенияv (км/ч.)t(ч)s(км)
велосипедистх
мотоциклисту

Мотоциклист затем второй раз обогнал велосипедиста. Произошло это через 30 мин, то есть через ч после первого обгона. Какие расстояния они проехали? Мотоциклист обогнал велосипедиста. А это значит, он проехал на один круг больше. Вот тот момент,

на который надо обратить внимание. Один круг – это длина трассы, Она равна 30 км. Составим другую таблицу.

Таблица 2

Участник движенияv(км/ч.)t(ч)s(км)
велосипедистх
мотоциклисту

Получим второе уравнение: y — x = 30. Имеем систему уравнений: В ответе укажем скорость мотоциклиста.

Ответ: 80 км/ч.

Задачи (самостоятельно).

I.1.1. Из пункта “А” круговой трассы выехал велосипедист, а через 40 мин следом за ним отправился мотоциклист. Через 10 мин после отправления он догнал велосипедиста в первый раз, а еще через 36 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 36 км. Ответ дайте в км/ч.

I.1. 2. Из пункта “А” круговой трассы выехал велосипедист, а через 30 мин следом за ним отправился мотоциклист. Через 8 мин после отправления он догнал велосипедиста в первый раз, а еще через 12 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 15 км. Ответ дайте в км/ч.

I.1. 3. Из пункта “А” круговой трассы выехал велосипедист, а через 50 мин следом за ним отправился мотоциклист. Через 10 мин после отправления он догнал велосипедиста в первый раз, а еще через 18 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 15 км. Ответ дайте в км/ч.

Задача 2.

Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 20 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 15 км/ч больше скорости другого?

Решение.

Рисунок 1

При одновременном старте мотоциклист, стартовавший из “А”, проехал на полкруга больше, стартовавший из “В”. То есть на 10 км. При движении двух мотоциклистов в одном направлении скорость удаления v = -. По условию задачи v= 15 км/ч =км/мин = км/мин – скорость удаления. Находим время, через которое мотоциклисты поравняются в первый раз.

10:= 40(мин).

Ответ: 40 мин.

Задачи (самостоятельно).

I.2.1. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 27 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 27 км/ч больше скорости другого?

I.2.2. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 6 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 9 км/ч больше скорости другого?

Задача 3.

Из одной точки круговой трассы, длина которой равна 8 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 89 км/ч, и через 16 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Решение.

16 мин == .

х км/ч – скорость второго автомобиля.

(89 – х) км/ч – скорость удаления.

8 км – длина круговой трассы.

Уравнение.

(89 – х) = 8,

89 – х = 2· 15,

89 – х = 30,

х = 59.

Ответ: 59 км/ч.

Задачи (самостоятельно).

I.3.1. Из одной точки круговой трассы, длина которой равна 12 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 103 км/ч, и через 48 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

I.3.2 . Из одной точки круговой трассы, длина которой равна 6 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 114 км/ч, и через 9 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

I.3.3. Из одной точки круговой трассы, длина которой равна 20 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 105 км/ч, и через 48 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

I.3.4. Из одной точки круговой трассы, длина которой равна 9 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 93 км/ч, и через 15 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Задача 4.

Часы со стрелками показывают 8 ч 00 мин. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Решение. Предполагаем, что экспериментально не решаем задачу.

За один час минутная стрелка проходит один круг, а часовая часть круга. Пусть их скорости равны 1 (круг в час) и Старт — в 8.00. Найдем время, за которое минутная стрелка в первый раз догонит часовую.

Минутная стрелка пройдет на больше, поэтому получим уравнение

1 — .

Значит, в первый раз стрелки поравняются через

Пусть во второй раз стрелки поравняются через время z. Минутная стрелка пройдет расстояние 1·z, а часовая причем минутная стрелка пройдет на один круг больше. Запишем уравнение:

1· z — = 1.

Решив его, получим, что .

Итак, через стрелки поравняются во второй раз, еще через – в третий, и ещё через – в четвертый раз.

Следовательно, если старт был в 8.00., то в четвертый раз стрелки поравняются через

4ч = 60 * 4 мин = 240 мин.

Ответ: 240 минут.

Задачи (самостоятельно).

I.4.1.Часы со стрелками показывают 4 ч 45 мин. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

I.4.2.Часы со стрелками показывают 2 ч ровно. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

I.4.3. Часы со стрелками показывают 8 ч 20 мин. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой? четвертый

II. Задачи на нахождение длины движущегося объекта.

Задача 1.

Поезд, двигаясь равномерно со скоростью 80км/ч, проезжает мимо придорожного столба за 36 с. Найдите длину состава поезда в метрах.

Решение. Так как скорость поезда указана в часах, то переведем секунды в часы.

1) 36 сек =

2) найдем длину состава поезда в километрах.

80·

Ответ: 800м.

Задачи (самостоятельно).

II. 2.Поезд, двигаясь равномерно со скоростью 60км/ч, проезжает мимо придорожного столба за 69 с. Найдите длину поезда в метрах. Ответ: 1150м.

II. 3. Поезд, двигаясь равномерно со скоростью 60км/ч, проезжает мимо лесополосы, длина которой 200 м, за 1мин 21 с. Найдите длину поезда в метрах. Ответ: 1150м.

III. Задачи на среднюю скорость.

На экзамене по математике может встретиться задача о нахождении средней скорости. Надо запомнить, что средняя скорость не равна среднему арифметическому скоростей. Средняя скорость находится по специальной формуле:

= .

Если участков пути было два, то.

Задача 1.

Расстояние между двумя селами 18 км. Велосипедист ехал из одного села в другое 2ч, а возвращался по той же дороге 3ч. Какова средняя скорость движения велосипедиста на всем участке пути?

Решение:

2 ч+3 ч = 5 ч — затратил на всё движение,

.

Ответ: .

Задача 2.

Турист шел со скоростью 4км/ч, потом точно такое же время со скоростью 5 км/ч. Какова средняя скорость движения туриста на всем участке пути?

Решение:

Пусть турист шел t ч со скоростью 4 км/ч и t ч со скоростью 5 км/ч. Тогда за 2t ч он прошел 4t + 5t = 9t (км). Средняя скорость движения туриста равна = 4,5 (км/ч).

Ответ: 4,5 км/ч.

Замечаем, средняя скорость движения туриста оказалась равной среднему арифметическому двух данных скоростей. Можно убедиться в том, что если время движения на двух участках пути одинаково, то средняя скорость движения равна среднему арифметическому двух данных скоростей. Для этого решим эту же задачу в общем виде.

Задача 3.

Турист шел со скоростью км/ч, потом точно такое же время со скоростью км/ч. Какова средняя скорость движения туриста на всем участке пути?

Решение:

Пусть турист шел t ч со скоростью км/ч и t ч со скоростью км/ч. Тогда за 2t ч он прошел t + t = t (км). Средняя скорость движения туриста равна

= (км/ч).

Задача 4.

Некоторое расстояние автомобиль преодолел в гору со скоростью 42 км/ч, а с горы – со скоростью 56 км/ч.

Какова средняя скорость движения автомобиля на всем участке пути?

Решение:

Пусть длина участка пути равна s км. Тогда в оба конца автомобиль проехал 2 s км, затратив на весь путь .

Средняя скорость движения равна 2 s: (км/ч).

Ответ: 48 км/ч.

Задача 5.

Некоторое расстояние автомобиль преодолел в гору со скоростью км/ч, а с горы – со скоростью км/ч.

Какова средняя скорость движения автомобиля на всем участке пути?

Решение:

Пусть длина участка пути равна s км. Тогда в оба конца автомобиль проехал 2 s км, затратив на весь путь .

Средняя скорость движения равна 2 s: (км/ч).

Ответ:км/ч.

Рассмотрим задачу, в которой средняя скорость задана, а одну из скоростей нужно определить. Потребуется применение уравнения.

Задача 6.

В гору велосипедист ехал со скоростью 10 км/ч, а с горы – с некоторой другой постоянной скоростью. Как он подсчитал, средняя скорость движения оказалась равной 12 км/ч.

С какой скоростью велосипедист ехал с горы?

Решение:

Пусть в гору и с горы велосипедист проехал по s км, всего 2s км. Так как средняя скорость равна 12 км/ч, то на путь туда и обратно затрачено Пусть скорость движения с горы равна, тогда на путь туда и обратно затрачено Составим уравнение:

urok.1sept.ru

ЭОР по физике «Решение задач на движение тел по окружности». 9 класс

Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №18» г. Белгорода

Урок физики в 9 классе по теме «Решение задач на движение тел по окружности»

Учитель физики

Н. П. Серечева

2017 – 2018 год

Тема урока: «Решение задач на движение тел по окружности»

Цель урока: 1. Содействовать формированию знаний о равномерном движении тел по окружности.

2. Способствовать формированию навыков решения задач на движение тел по окружности, закон всемирного тяготения, закон динамики.

3. Воспитывать аккуратность, вычислительные навыки.

Тип урока: урок закрепления и обобщения знаний.

Ход урока:

I. Организационный момент

а) Приветствие учащихся

б) Пожелание плодотворной (хорошей) работы на уроке.

в) Постановка целей и задач урока

II. Актуализация знаний

  1. Какой раздел физики мы изучаем?

2. По каким причинам можно судить, как тело движется?

3. а). Дать определение равномерного движения

б). Дать определение равноускоренного движения

в). Дать определение криволинейного движения

4. Как направлена легковая скорость тела, движущегося по окружности

5. Куда направлено ускорение теля, движущегося по окружности?

6. Как рассчитать скорость движения тела по окружности скорость = S/T; ʊ = 2TR/T

7. Как рассчитать модуль вектора центростремительного ускорения

8. Примените второй закон Ньютона к движению тела по окружности? F = mʊ2/R

III. Проверка домашнего задания

Учащимся предложено выполнить тест , содержащий 6 вопросов.

I V . Закрепление изученного материала:

Задача№1

Определите период вращение токарного станка, если его чистота вращения 125 1/с?

Задача№2

Шкив диаметром 16 см делает 300 оборотов за 3 минуты. Какова, частота вращение шкива и какова, скорость равномерного движения точек оборота этого шкива?

Задача№3

Какую скорость имеют точки обода колеса мотоцикла, радиуса 32см, если они движутся с ускорением 2 м/с2 ? С какой частотой вращается колесо?

Задача№4

Определите силу тяжести, действующей на тело, массой 12 кг, поднятье над Землёй на расстоянии, равный 1/3 земного радиуса.

V. Итог урока:

  1. Что нового узнали на уроке?

  2. С каким новым типом задач познакомились?

3. Оценки за урок.

V I. Домашнее задание:

Повторить параграфы 10-19 упр. 1814 и 1815

VI I Рефлексия (смайлики)

Электронно – образовательный ресурс по теме «: Решение задач по теме «Механические движения», « Масса тела», « Плотность вещества»», содержит план урока физики в 7 классе. Здесь показано, как организовать урок, где учащиеся восстановят полученные ранее знания по указанным темам. Проверка готовности учащихся к контрольной работе проводится методом тестирования, что позволит учителю оценить глубину и объем знаний сформированных при изучении темы «Механические движения», « Масса тела», « Плотность вещества». С целью закрепления материала подобраны задачи через которые демонстрируется практическое применение знаний темы.

Электронно – образовательный ресурс по теме «Решение задач на движение тел по окружности», содержит план урока физики в 9 классе. Здесь показано, как организовать урок, где учащиеся восстановят полученные ранее знания по указанным темам. Проверка готовности учащихся к уроку проводится методом тестирования, что позволит учителю оценить глубину и объем знаний сформированных при изучении темы «Решение задач на движение тел по окружности». С целью закрепления материала подобраны задачи, через которые демонстрируется практическое применение знаний этой темы.

infourok.ru

Задачи «Движение по окружности»

Вариант № 3305874(Движение по окружности)

1. Задание 1 № 6144

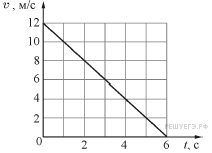hello_html_7834c9b4.pngМатериальная точка движется по окружности радиусом 4 м. На графике показана зависимость модуля её скорости v от времени t. Чему равен модуль центростремительного ускорения точки в момент t = 5 с? (Ответ дайте в метрах в секунду в квадрате.)

2. Задание 1 № 6260

Груз, подвешенный на нити длиной 2 м, отведён в сторону и отпущен. Нижнюю точку траектории он проходит со скоростью 1,4 м/с. Найдите центростремительное ускорение груза в нижней точке траектории. (Ответ дайте в метрах в секунду в квадрате и округлите до целых.)

3. Задание 1 № 3463

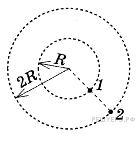
hello_html_m212ce02f.png

Два велосипедиста совершают кольцевую гонку с одинаковой угловой скоростью. Положения и траектории движения велосипедистов показаны на рисунке. Чему равно отношение центростремительных ускорений велосипедистов ?

4. Задание 1 № 6223

Спутник движется по круговой орбите радиусом 6,6·106 м, имея скорость 7,8 км/с. Чему равно центростремительное ускорение спутника? (Ответ дайте в метрах в секунду в квадрате и округлите до десятых.)

5. Задание 1 № 6296

Автомобиль движется по окружности радиусом 100 м со скоростью 10 м/с. Чему равно центростремительное ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)

infourok.ru

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *