Задачи первой части огэ по геометрии
1. | Найдите площадь прямоугольного треугольника, если его катет и |
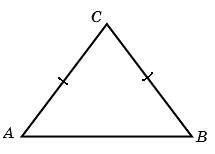
2.Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
3. В треугольнике со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведённая к первой из этих сторон, равна 4. Чему равна высота, проведённая ко второй стороне? 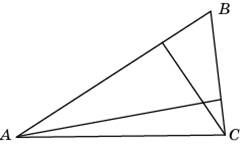
4. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
5.Периметр равнобедренного треугольника равен 16, а основание — 6.
Найдите площадь треугольника.
6.
В треугольнике АВС проведена биссектриса AL, угол ALC равен 1500, угол ABC равен 1270. Найдите угол ACB. Ответ дайте в градусах.
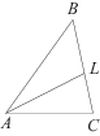
8. На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что угол DMC = 600. Найдите угол CMA. Ответ дайте в градусах.

10. Высота равностороннего треугольника равна
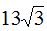 . Найдите его периметр.
. Найдите его периметр. 11. В треугольнике ABC AB = BC = 25, AC = 14. Найдите длину медианы BM.
12. В треугольнике ABC BM — медиана и BH — высота. Известно, что AC = 13 и BC = BM. Найдите AH.
14. Найдите площадь треугольника, изображённого на рисунке. 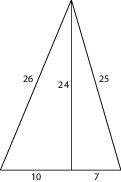
7. В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 5.
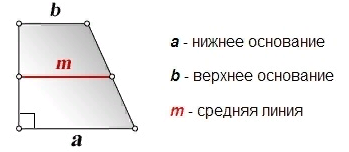
В трапецию, сумма длин боковых сторон которой равна 16, вписана окружность. Найдите длину средней линии трапеции.
9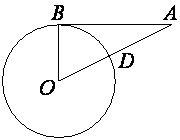
Окружность пересекает отрезок AO в точке D. Найдите AD.
15. Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=14.
16.На клетчатой бумаге с размером клетки 1×1 изображен параллелограмм. Найдите его площадь.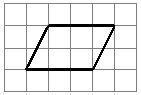
12.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите ее площадь.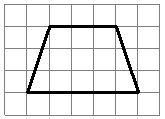
infourok.ru
Карточка 1 1) Найти АВ
2) Найти угол АСВ, если угол АОВ = 84°
3) 4) Найдите площадь равностороннего треугольника, отсекаемого от данного треугольника его средней линией, если площадь данного треугольника равна 48см2. 5) Периметр равностороннего треугольника АВС равен 24см. Найдите длину средней линии этого треугольника.
| Карточка 2 1) Найти угол АСВ, если угол АОВ равен 160°
2) 3) Найдите площадь данного равностороннего треугольника, если площадь треугольника, отсекаемого от него средней линией, равна 6 см2.
4) Средняя линия равностороннего треугольника АВС равна 8см. Найдите периметр этого треугольника
5) Из квадрата со стороной 10см вырезан прямоугольник со сторонами 3см и 4см. Найдите площадь оставшейся части. | Карточка 3 1) Найти угол ВАС, если угол ВОС = 160° 2) Найдите площадь прямоугольного треугольника, если его гипотенуза равна 16см, а один из углов треугольника равен 45°.
3) Найти угол ВАС
4) Найти длину меньшей средней линии треугольника 5) В прямоугольнике одна сторона равна 28см, а диагональ равна 35см. Найдите площадь прямоугольника. | |
Карточка 4 1) Найти угол ВАС
2) Найти угол АОВ, если угол АСВ = 25°
3) Найти площадь четырёхугольника
4) Найти длину большей высоты параллелограмма
5) Найти косинус угла | Карточка 5 1) В треугольнике АВС угол В равен 46°, угол С равен 71°, ВD – биссектриса. Найдите угол АDВ.
2) Найти радиус окружности, если АВ = 12см, ОА = 13см.
3) Найти длину отрезка НМ, Если АМ=3см, АН=НС=2
4) Найти угол ВОС, если угол ВАС = 70° 5) Найти площадь треугольника АВС, если высота, проведённая к одной из его сторон равна 11, а средняя линия, параллельная этой стороне, равна 10. | Карточка 6 1) Найти угол АОВ, если точки А и В делят окружность на две дуги в отношении 9 : 11. 2) Найти площадь параллелограмма
3) КВСD — параллелограмм. Найдите длину отрезка АВ. 4) Найдите косинус угла 5) Найдите площадь четырёхугольника | |
Карточка 7
1) Найти угол 3, если угол 1 равен 40°, а угол 2 равен 55°. 2) Основания трапеции равны 48 и 24, высота 4. Найдите площадь трапеции. 3) На рисунке изображён параллелограмм. Найти: х. 4) Из квадрата со стороной 8см вырезан прямоугольник со сторонами 3см и 2см. Найдите площадь оставшейся части.
5) Стороны прямоугольника равны 10 и 24. Найдите радиус окружности, описанной около этого прямоугольника. | Карточка 8 1) Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции.
2) Найдите угол α 3) Прямоугольный треугольник вписан в окружность. Найдите радиус этой окружности. 4) Найдите тангенс угла А.
5) Из прямоугольника со сторонами 8см и 10см вырезан квадрат со стороной 5см. Найдите площадь оставшейся части. | Карточка 9
1) Найдите тангенс угла А. 2) Найти длину медианы проведённой из вершины прямого угла. 3) Стороны параллелограмма равны 10 и 35. Высота, опущенная на первую сторону, равна 21. Найдите высоту, опущенную на вторую сторону.
4) Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
5) Найти площадь трапеции. | |
Карточка 10 1) Найти больший угол параллелограмма АВСD
2)
3) Найти угол ОСD 4) ВС = 8, соsВ = 0,8 Найти АВ 5) АВСD — равнобедренная трапеция Найти угол АВC
| Карточка 11 1) Найти меньший угол параллелограмма АВСD
2) Найти угол ОСD
3)
4) 5) Найти тангенс угла С | Карточка 12 1) АВСD — равнобедренная трапеция Найти угол АDC Найти угол ОDС 2)
3) АС = 6, соsA = 0,6 Найти АВ 4) 5) Найти площадь параллелограмма | |
Карточка 13 1) В трапеции АВСD АВ=СD ∟ВDА=18° и ∟ВDС=97°. Найдите угол АВD. 2) Найдите тангенс угла АОВ 3) Найдите расстояние от точки А до середины отрезка СВ 4) Найдите угол АВС 5) Колесо имеет 8 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы. | Карточка 14 1) В трапеции АВСD АВ=СD ∟ВDА=40° и ∟ВDС=24°. Найдите угол АВD. 2) Найдите расстояние от точки А до середины отрезка СВ Найдите котангенс угла АОВ 3) 4) Найдите угол АВС 5) Угол АОВ = 63°. Найдите угол АСВ. | Карточка 15 1) В трапеции АВСD АВ=СD ∟ВDА=24° и ∟ВDС=70°. Найдите угол АВD. 2) Найдите расстояние от точки А до середины отрезка СВ 3) Найдите котангенс угла АОВ 4) Из квадрата Вырезали прямоугольник. Найдите площадь получившейся фигуры. 5) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,6 м и 3,6 м? | |
Карточка 16 1) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 4,6 м? 2) Сколько спиц в колесе, если угол между соседними спицами равен 40°? 3) Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85. 4) Найдите тангенс угла АОВ 5) Найдите площадь фигуры | Карточка 17 1) Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек? 2) Сколько спиц в колесе, если угол между соседними спицами равен 9°? 3) Колесо имеет 40 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы. 4) Найдите тангенс угла АОВ 5) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота средней опоры 3,1 м, высота большей опоры 3,3 м. Найдите высоту малой опоры. | Карточка 18 1) Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек? 2) Сколько спиц в колесе, если угол между соседними спицами равен 15°? 3) Колесо имеет 6 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы. 4) Найдите котангенс угла АОВ 5) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,5 м, высота средней опоры 2,65 м. Найдите высоту большей опоры. | |
Карточка 19 1) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,95 м, высота большей опоры 3,65 м. Найдите высоту средней опоры. 2) Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,7 м и 3 м? 3) Человек ростом 1,8 м стоит на расстоянии 10 м от столба, на котором висит фонарь на высоте 7,8 м. Найдите длину тени человека в метрах. 4) Найдите площадь трапеции 5) Прямые m и n параллельны. Найдите ∟3, если ∟1 = 117°, ∟2 = 24°. | Карточка 20 1) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,25 м, высота большей опоры 2,85 м. Найдите высоту средней опоры. 2) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 4,2 м? 3) Человек ростом 1,6 м стоит на расстоянии 15 м от столба, на котором висит фонарь на высоте 9,6 м. Найдите длину тени человека в метрах. 4) Найдите площадь трапеции 5) Прямые m и n параллельны. Найдите ∟3, если ∟1 = 74°, ∟2 = 39°. | Карточка 21
80 см. Расстояние между точками А и В составляет 41 м. Найдите высоту, на которую поднимается лестница (в метрах). 2) Человек ростом 1,5 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 10,5 м. Найдите длину тени человека в метрах. 3) Найдите площадь трапеции 4) 5) Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности. | |
Карточка 22
сторону на два отрезка. Каковы длины этих отрезков? 2) 3) Найдите тангенс угла АВС 4) 5) На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A , проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности. | Карточка 23 1) 2) MN и АВ – диаметры окружности. ∟NВА=73°. Найти угол NMB 3) ∟DMC=24°. Найдите угол СМА. 4)Найти площадь трапеции. 5) Найти площадь параллелограмма | Карточка 24 1) Прямая касается окружности в точке K . Точка O – центр окружности. Хорда КМ образует с касательной угол, равный 7°. Найдите величину угла ОМК 2) Найти площадь трапеции 3) 4) Найти радиус окружности 5) В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB. |
intolimp.org
Конспект урока-тренинга по геометрии «Решение планиметрических задач из ОГЭ» (9 класс)
Урок-тренинг по геометрии в 9 классе
«Решение планиметрических задач из ОГЭ»
Цель и задачи урока:
• отработка умений решать задачи по планиметрии, предлагаемые в тестах ОГЭ;
• развитие внимания, памяти, логического мышления, интереса к предмету,
математически грамотной речи;
• воспитание трудолюбия, усидчивости, чувства ответственности,
познавательной активности.
Тип урока: урок-тренинг.
Оборудование: компьютер, мультимедийный проектор, сборник «Математика.
9 класс. Подготовка к ОГЭ – 2015» под редакцией Ф.Ф.Лысенко,
С.Ю.Кулабухова.
Ход урока
I. Организационный момент.
Геометрия – это не просто наука о свойствах геометрических
фигур. Геометрия – это целый мир, который окружает нас с
самого рождения. Ведь все, что мы видим вокруг, так или иначе
относится к геометрии, ничто не ускользает от ее внимательного
взгляда. Геометрия помогает человеку идти по миру с широко
открытыми глазами, учит внимательно смотреть вокруг и видеть
красоту обычных вещей, смотреть и думать, думать и делать
выводы.
В качестве эпиграфа нашего урока мы возьмем слова известного математика Пойа:
«Лучше решить одну задачу несколькими способами,
чем несколько задач – одним»
II. Актуализация знаний учащихся.
Задания на экзамене предлагаются каждый год разные. Мы с вами не можем знать заранее, какие задачи будут на экзамене. Поэтому, чтобы уверенно решать предложенные задачи, надо хорошо знать теорию, т.е. определения и формулировки теорем. Кроме того, в экзаменационной работе есть задание № 13, проверяющее, как ученик ориентируется в теоретическом материале. В каждом варианте в задании №13 предлагается по три вопроса, и надо из них выбрать либо верные утверждения, либо неверные. Иногда из-за одного пропущенного слова меняется смысл сказанного. Поэтому мы начнём наш тренинг с проверки знания теории.
На слайдах вы увидите задания, предлагавшиеся на экзамене в прошлом году, а также задания из сборника для подготовки к экзамену в 2015 году.
Какие из следующих утверждений верны?
1. Через любые три точки на плоскости можно провести окружность.
2. Площадь трапеции равна половине высоты, умноженной на разность
оснований.
Неверно.
3. Существует прямоугольник, диагонали которого взаимно перпендикулярны.
Верно.
4. В любой четырехугольник можно вписать окружность.
Неверно.
5. Отношение площадей подобных треугольников равно коэффициенту подобия.
Неверно.
6. Площадь параллелограмма равна половине произведения его диагоналей.
Неверно.
7. Отношение стороны треугольника к синусу противолежащего угла равно
диаметру описанной окружности.
Верно.
8. Одна из высот прямоугольного треугольника всегда делит его на два
подобных треугольника.
Верно.
9. Биссектрисы любого треугольника точкой пересечения делятся в отношении
2 : 1, считая от вершины.
Неверно.
10. Угол, вписанный в окружность, равен соответствующему центральному углу,
опирающемуся на ту же дугу.
Неверно.
11. Две прямые, перпендикулярные третьей прямой, параллельны друг другу.
Верно.
12. Биссектрисы треугольника пересекаются в центре вписанной в него
окружности.
Верно.
III. Тренинг по решению задач.
Начнем мы с вами с решения задач из первой части экзамена, т.е. с задач, оцениваемых в 1 балл. Вы знаете, что на экзамене при решении этих задач надо только дать правильный ответ, записав его в бланк ответов.
Задача на 1 балл
В треугольнике АВС точка К – середина стороны ВС, точка Р лежит на отрезке АК, АР = 10, РК = 5, ВР = 9. Найдите ВМ.
Решение.
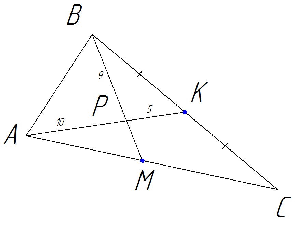
Т. к. точка К – середина стороны ВС, то АК – медиана. Точка Р делит АК в отношении 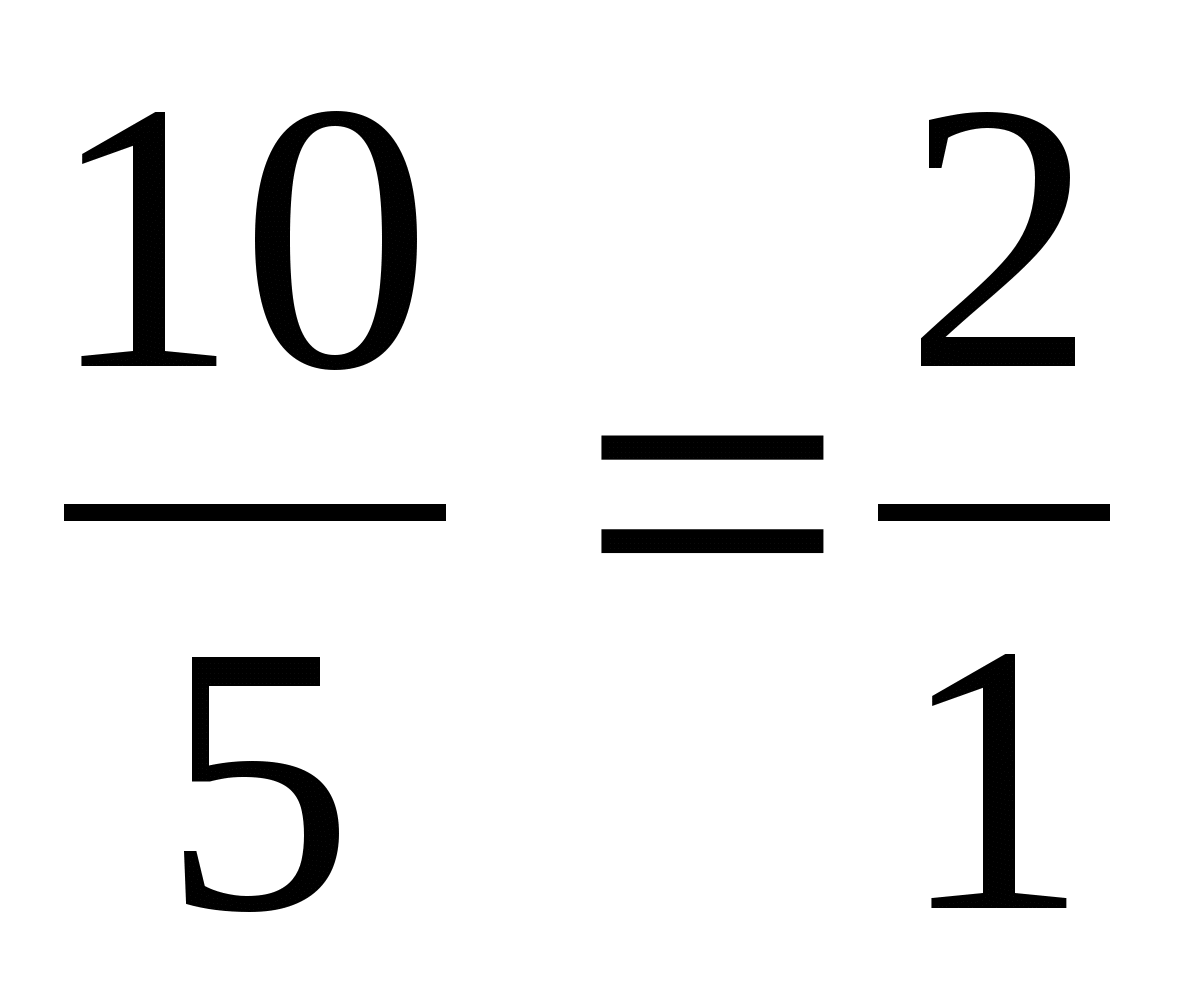 . Значит, точка Р – точка пересечения медиан треугольника.
. Значит, точка Р – точка пересечения медиан треугольника.
Следовательно, ВМ тоже медиана и 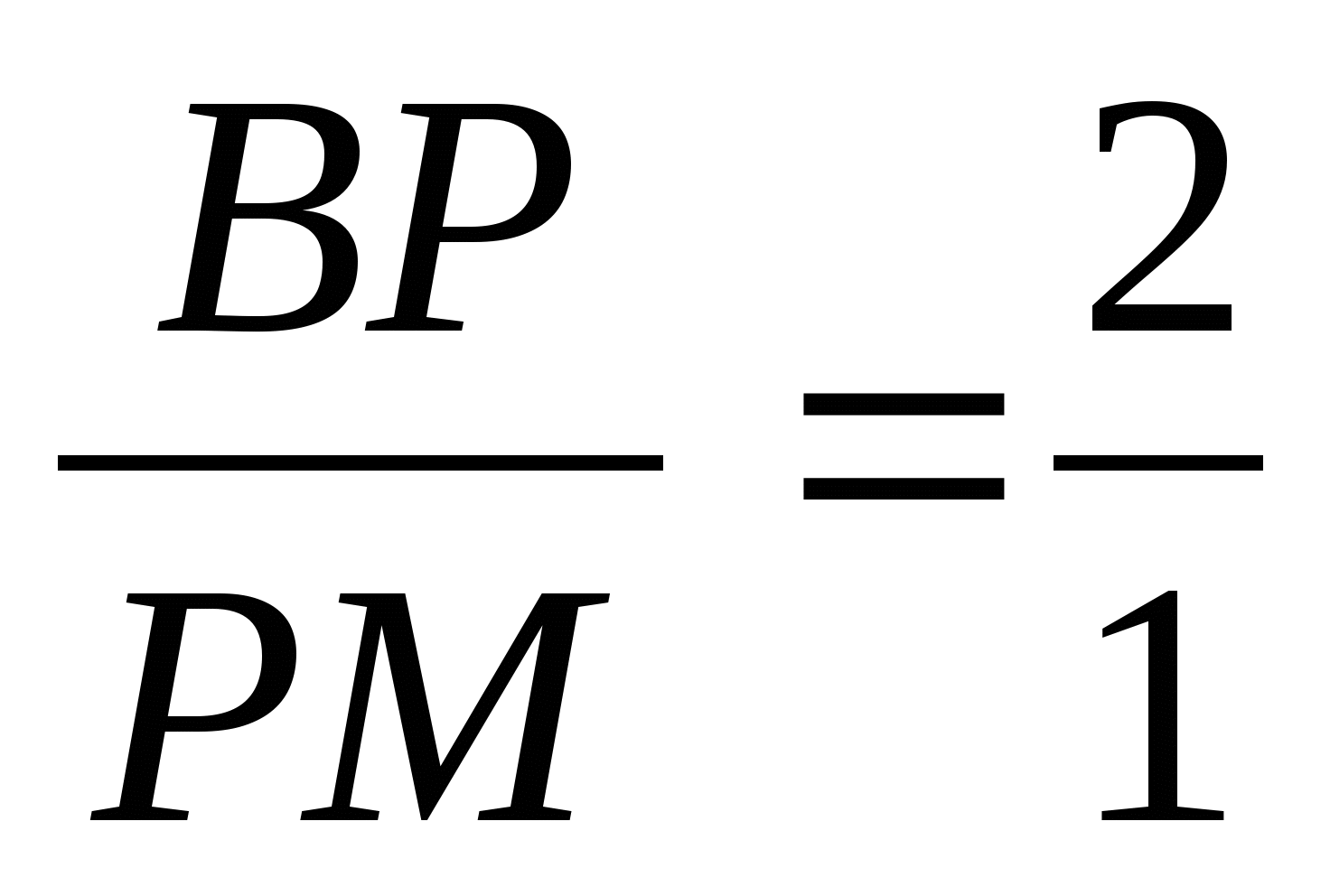

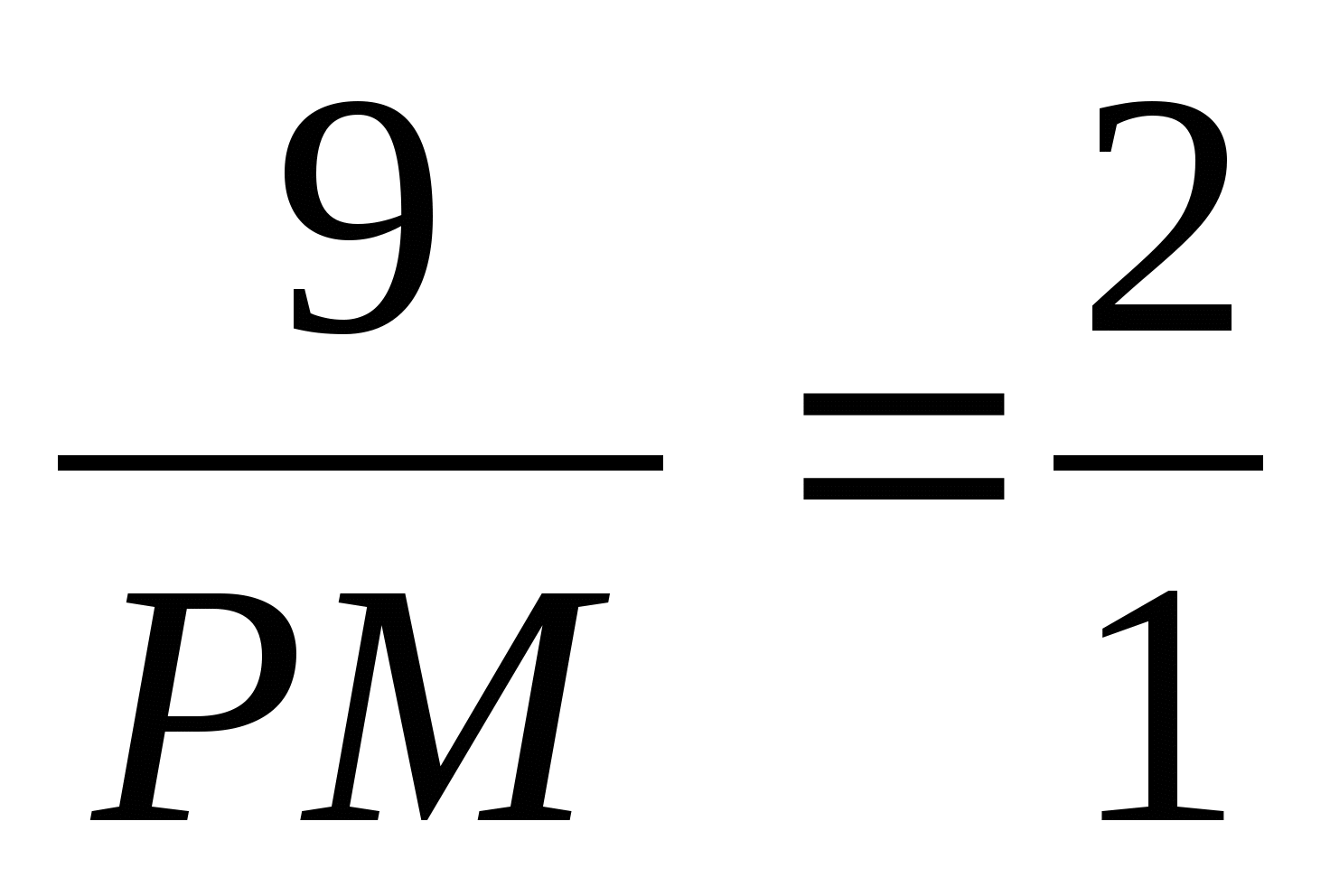
 РМ = 4,5.
РМ = 4,5.
ВМ = ВР + РМ = 9 + 4,5 = 13,5.
Ответ: 13,5.
Задача на 1 балл
Найдите длину отрезка АN, если радиус изображенной на рисунке окружности ОК =3, АК = 2.
Решение.
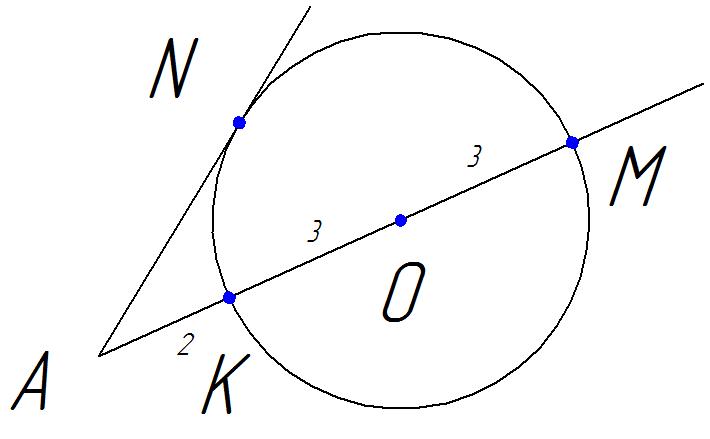
1 способ.
АN – касательная к окружности, АМ – секущая. Если из точки А к окружности проведены касательная и секущая, то квадрат отрезка касательной от точки А до точки касания равен произведению отрезков секущей от точки А до точек пересечения секущей с окружностью. АN2 = АК ∙ АМ = 2 ∙ 8 = 16  АN = 4.
АN = 4.
2 способ
Проведем радиус О
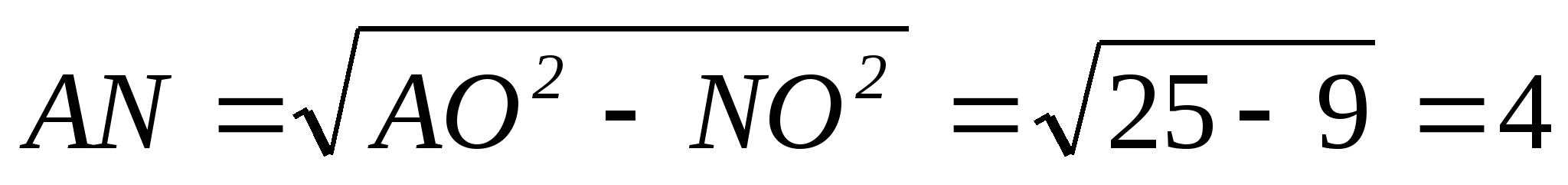 .
.3 способ
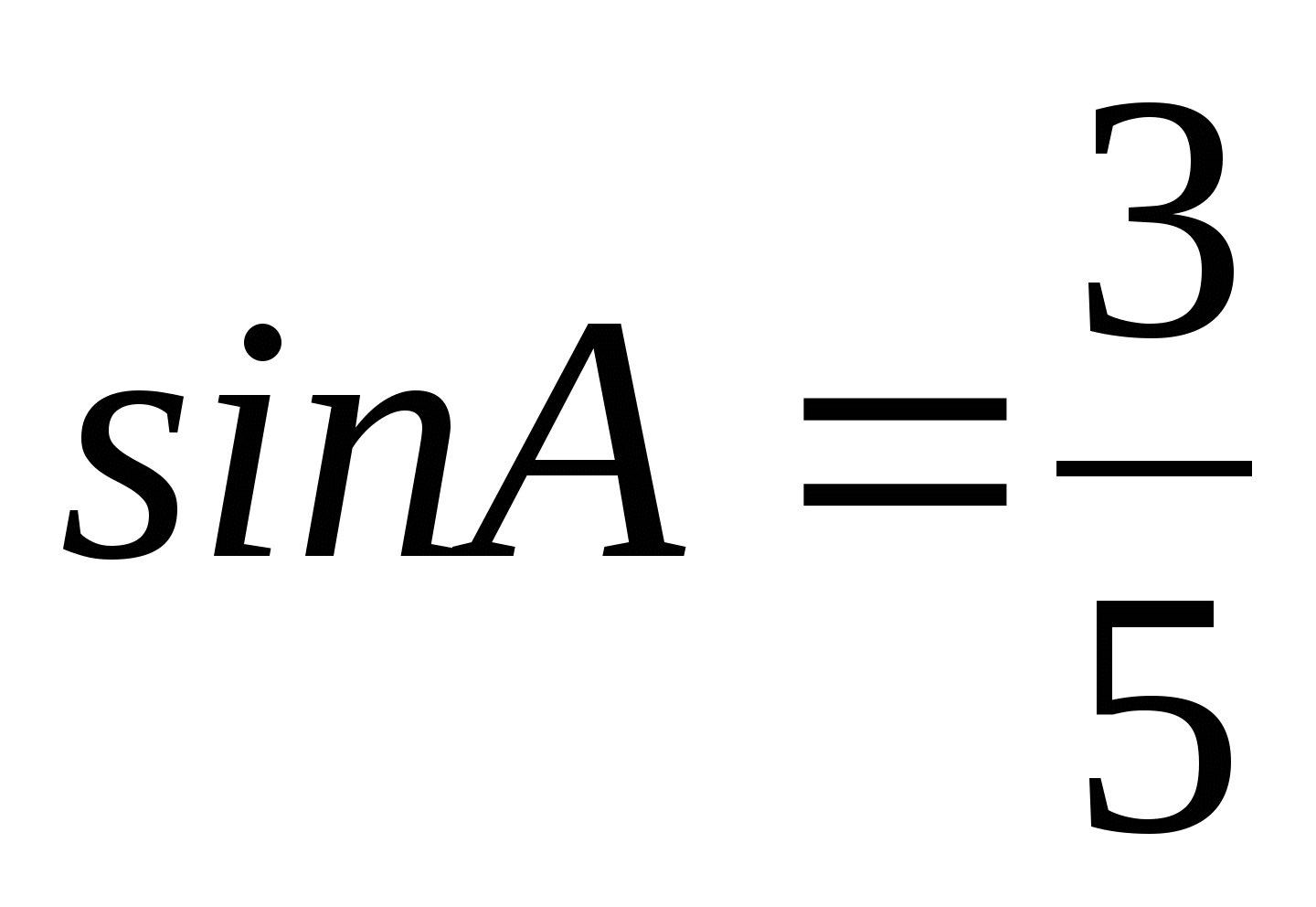 . По основному тригонометрическому тождеству
. По основному тригонометрическому тождеству 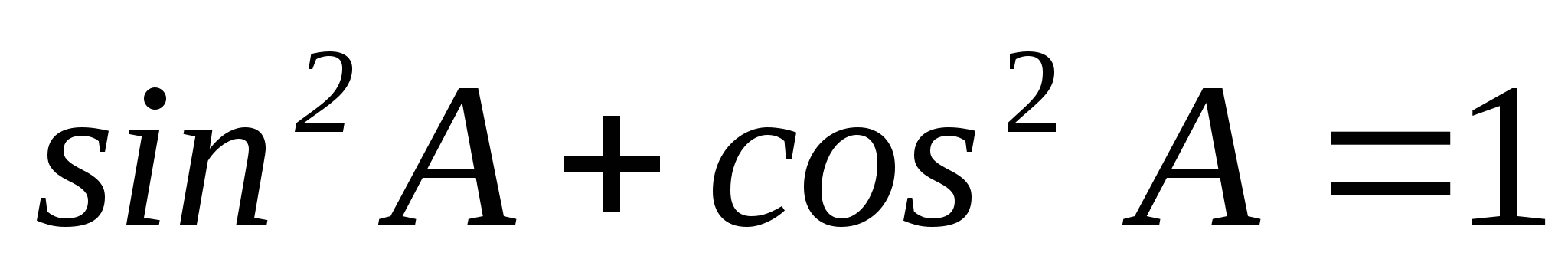 .
.
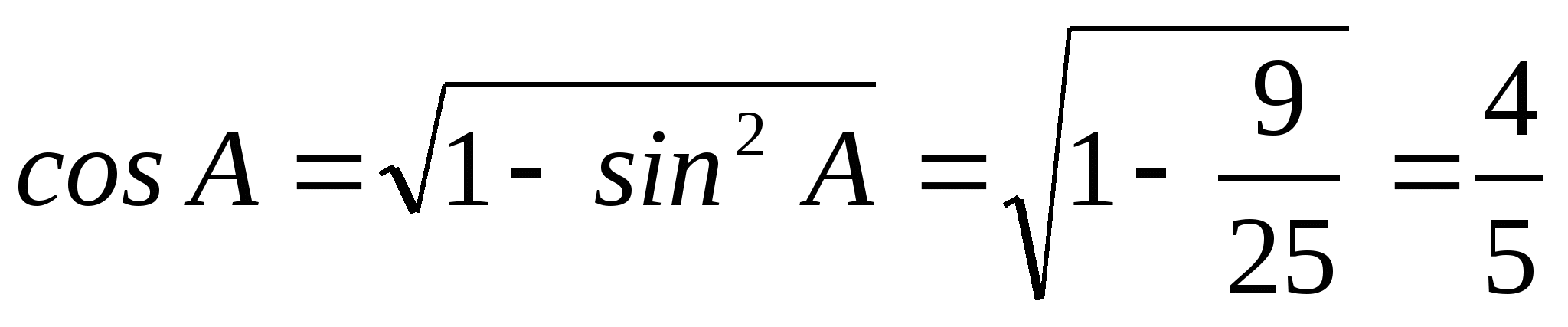 .
. 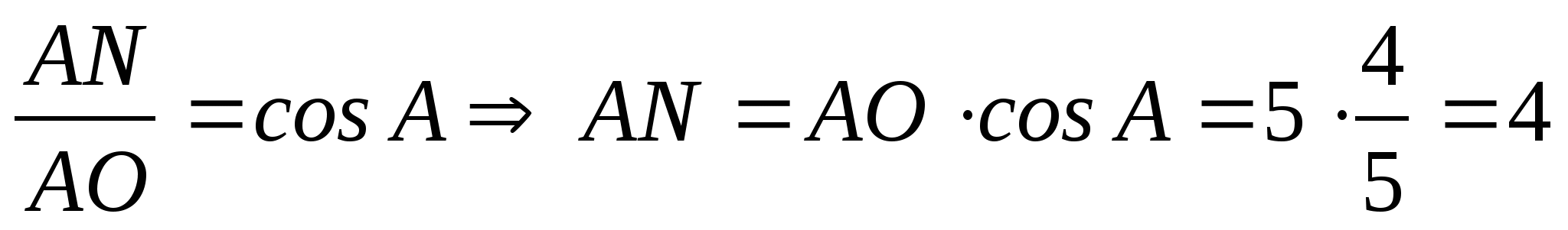 .
.
Ответ: 4.
Во второй части экзаменационной работы есть задачи на 2, 3 и 4 балла.
Задача на 2 балла
В параллелограмме АВСD биссектриса острого угла С пересекает сторону АВ в точке М. Найдите расстояние от В до прямой СМ, если СМ = 30, СВ = 17.
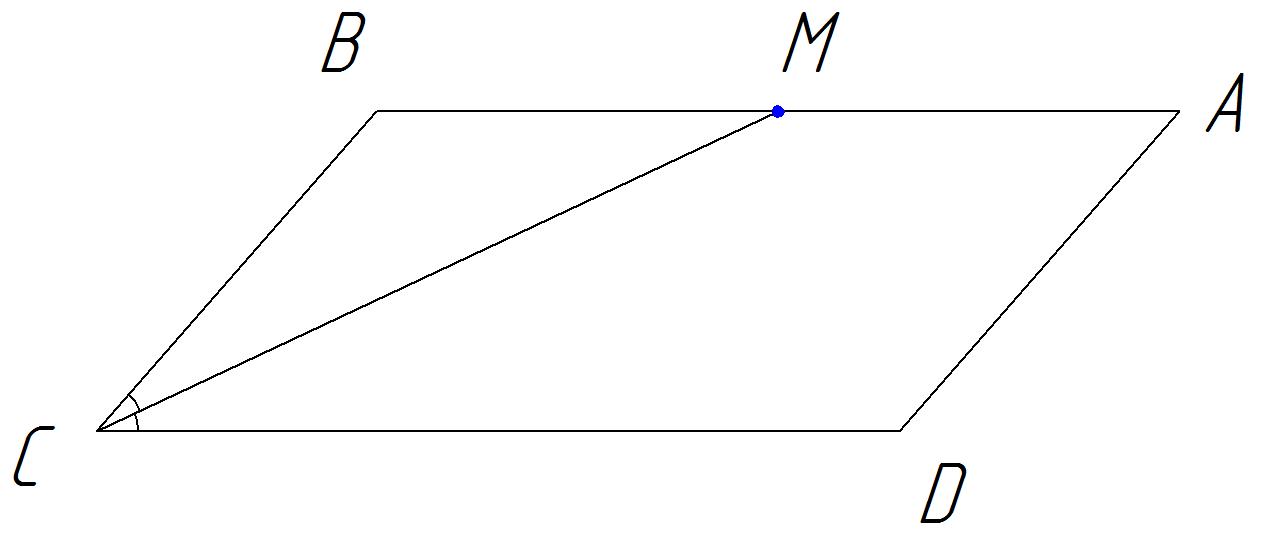
Решение.
Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из этой точки к прямой. Проведем из точки В к прямой СМ перпендикуляр ВН.
Значит, ρ(В; СМ) = ВН.
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Значит, ∆СВМ – равнобедренный. В равнобедренном треугольнике высота, проведенная к основанию, является медианой. Следовательно, ВН – медиана, т.е.
СН = НМ = 15. По теореме Пифагора ВН = 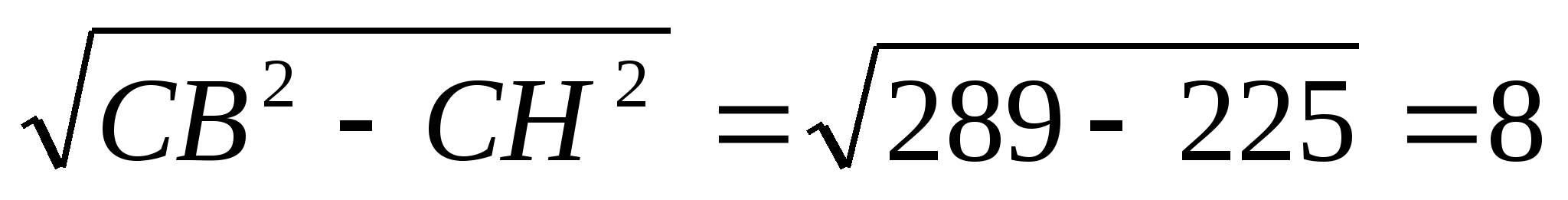 .
.
Ответ: 8.
Задача на 3 балла
В трапеции АВСD точка К – середина основания АВ. Известно, что СК = КD. Докажите, что трапеция равнобедренная.
Решение.
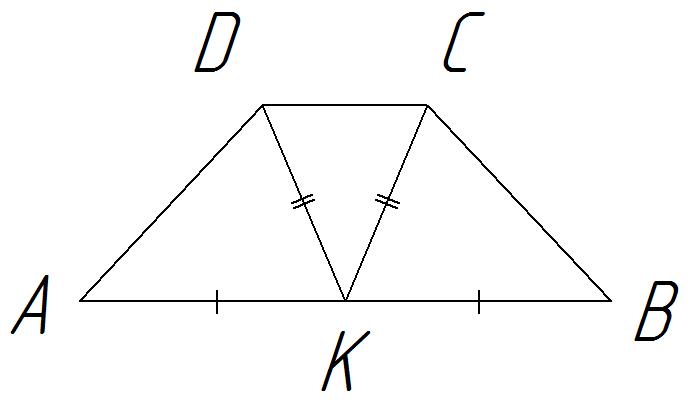
1 способ
Т. к. СК = КD, то ∆СКD – равнобедренный, а в равнобедренном треугольнике углы при основании равны 
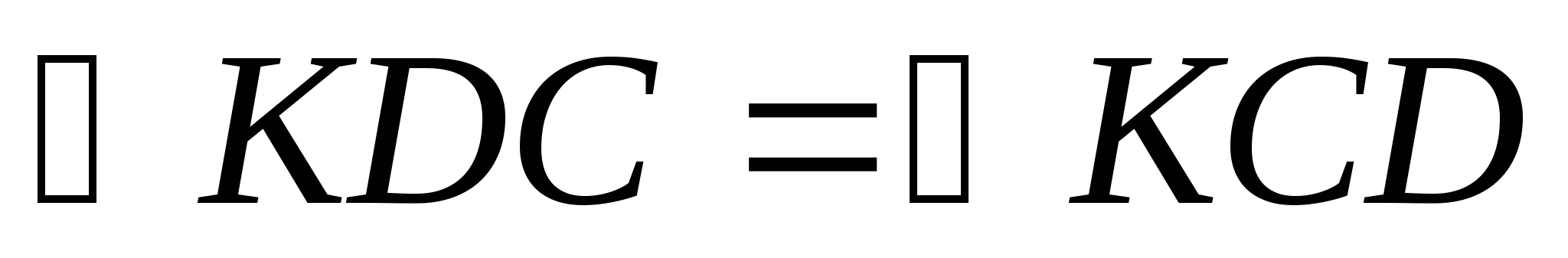 .
. 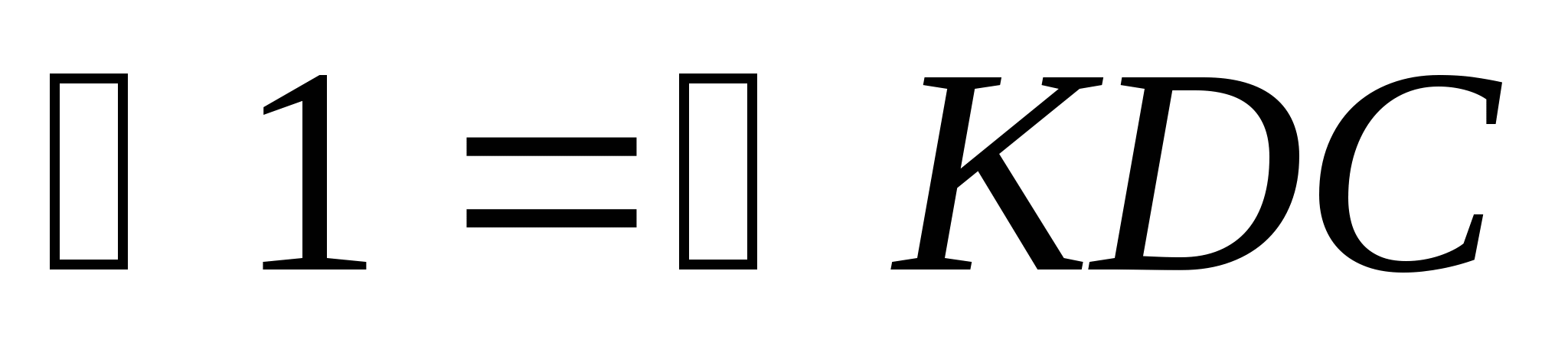 как накрест лежащие при пересечении параллельных прямых DС и АВ секущей DК,
как накрест лежащие при пересечении параллельных прямых DС и АВ секущей DК, 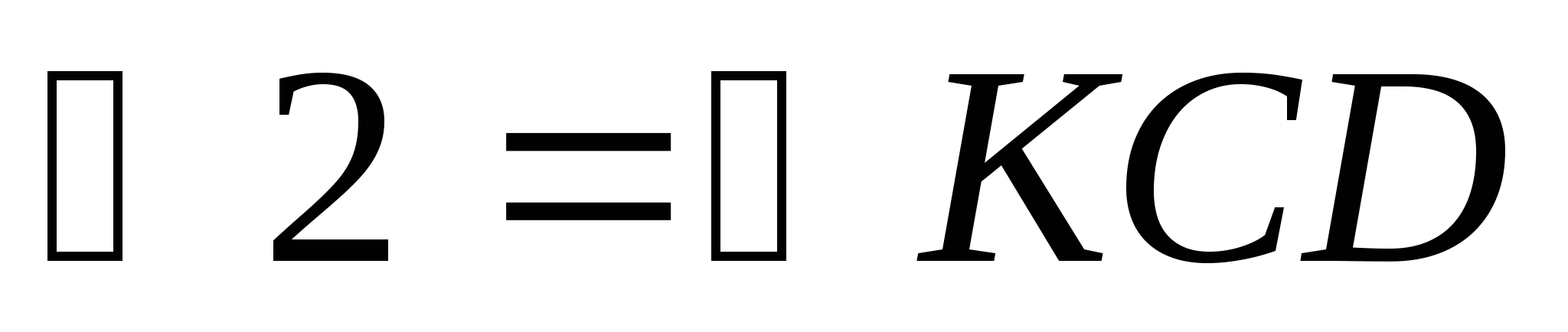 как накрест лежащие при пересечении параллельных прямых DС и АВ секущей СК.
как накрест лежащие при пересечении параллельных прямых DС и АВ секущей СК.
Т. к. 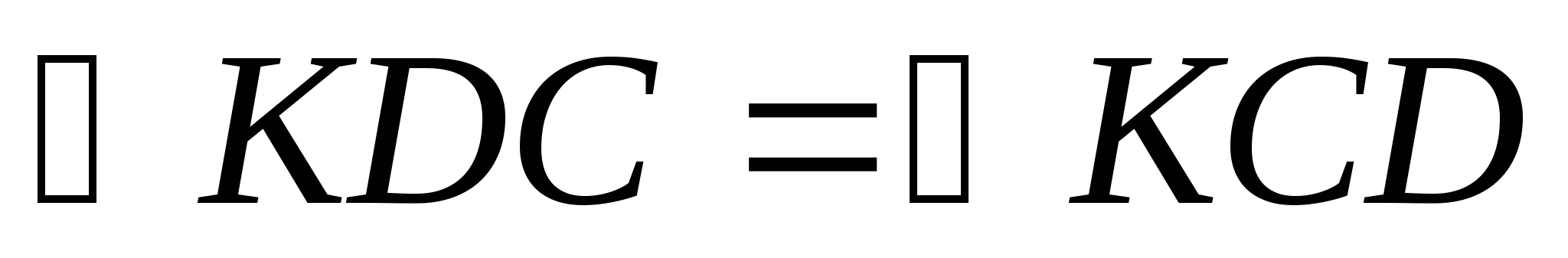 , то
, то 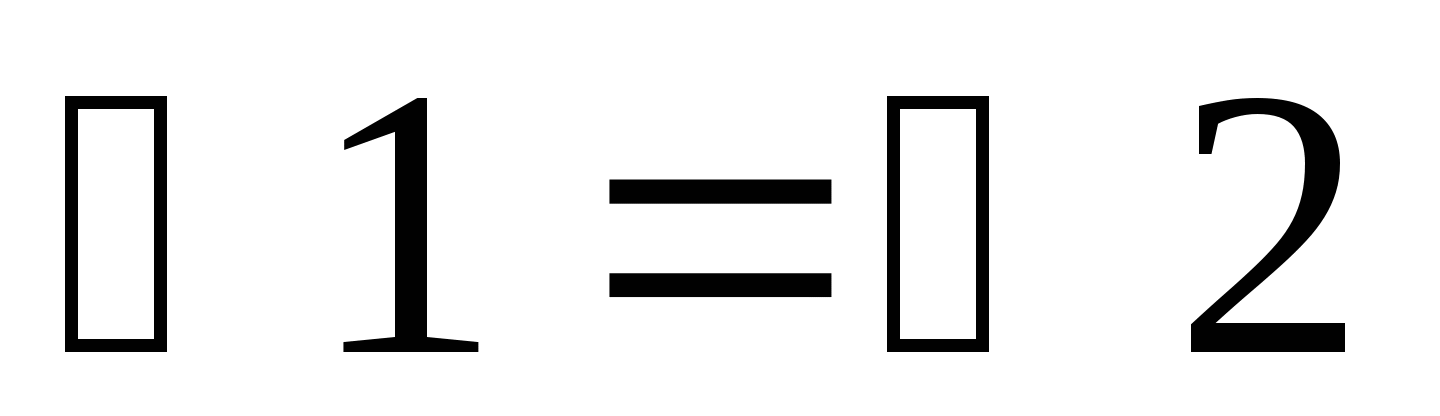 .
.
Рассмотрим ∆АКD и ∆ВКС. АК = КВ, DК = СК – по условию, 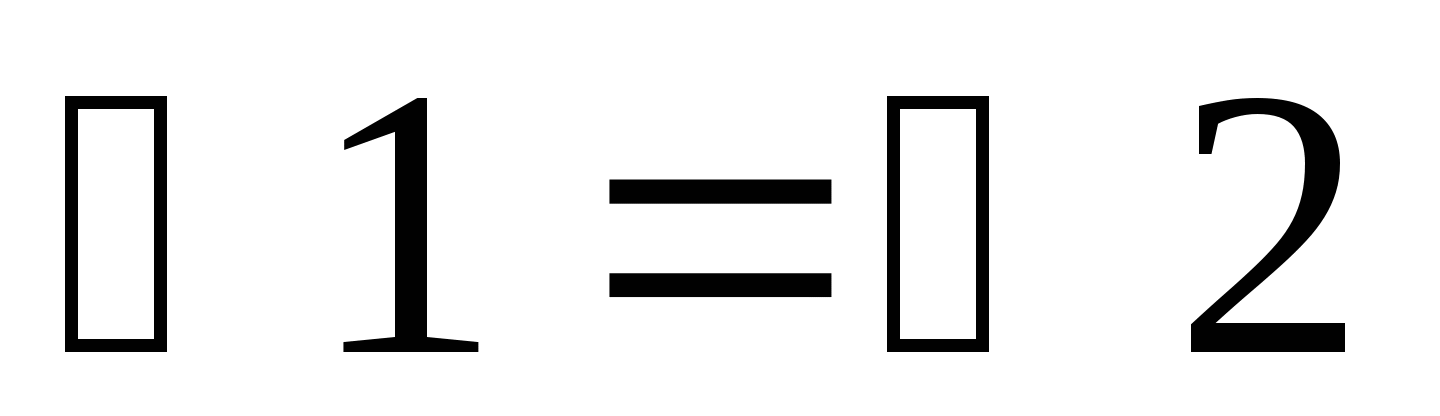 − по доказанному, то ∆АКD = ∆ВКС по первому признаку равенства треугольников.
− по доказанному, то ∆АКD = ∆ВКС по первому признаку равенства треугольников.
Из равенства треугольников следует, что АD= СВ  трапеция АВСD – равнобедренная.
трапеция АВСD – равнобедренная.
2 способ
Проведем высоты DН и СМ. ∆DКН = ∆СКМ по гипотенузе и катету (DН = СМ как расстояния между параллельными прямыми, DК = СК – по условию) 
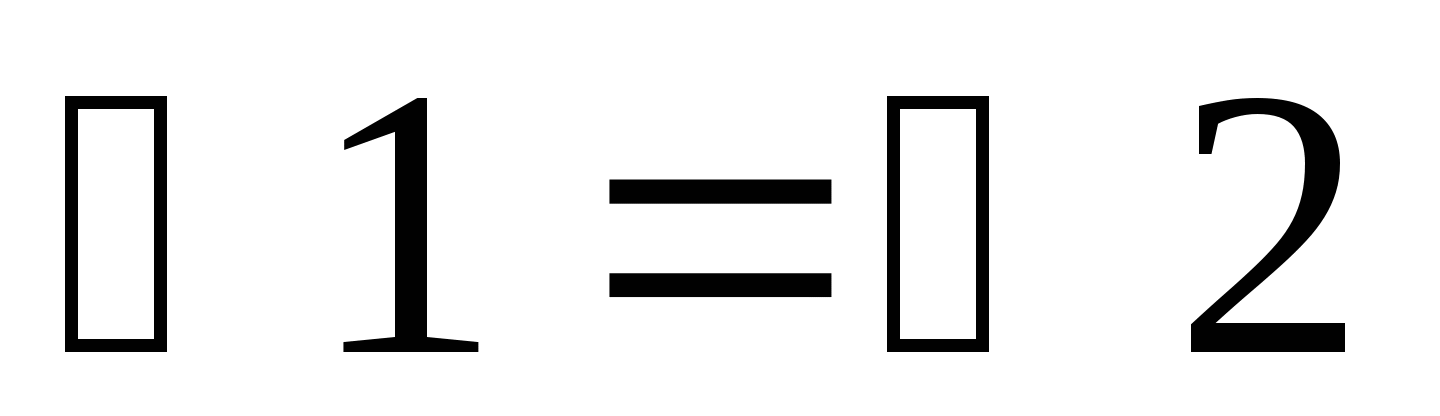 . (Дальше как в первом способе).
. (Дальше как в первом способе).
3 способ
Из равенства ∆DКН и ∆СКМ следует, что НК = КМ.
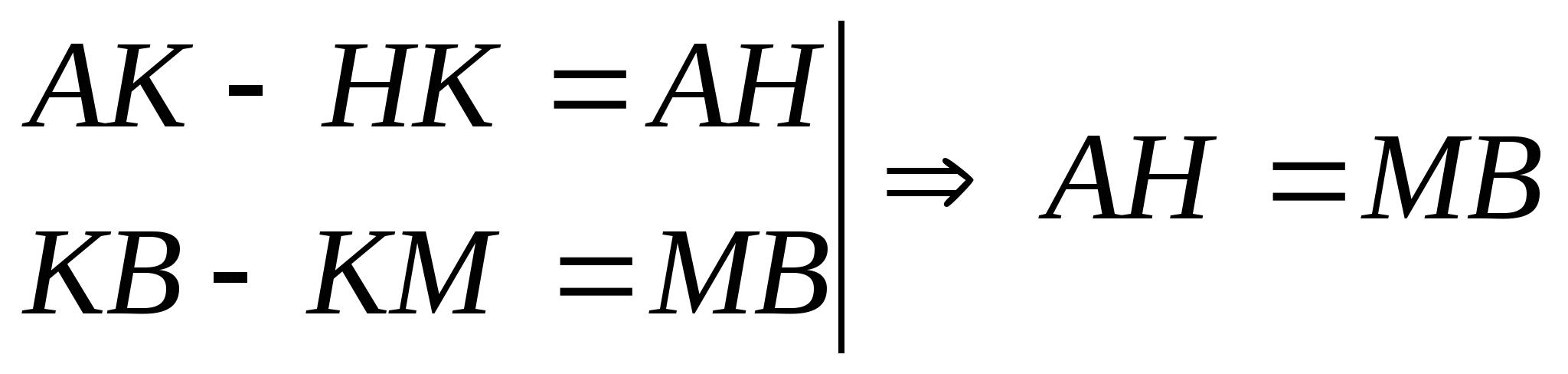 .
.
Значит, прямоугольные треугольники АDН и ВСМ равны по двум катетам
(DН = СМ как расстояния между параллельными прямыми, АН = МВ по доказанному). Из равенства треугольников следует, что АD= СВ  трапеция АВСD – равнобедренная.
трапеция АВСD – равнобедренная.
Задача на 4 балла
В равнобедренном треугольнике АВС стороны АВ = ВС = 10, соsАВС = 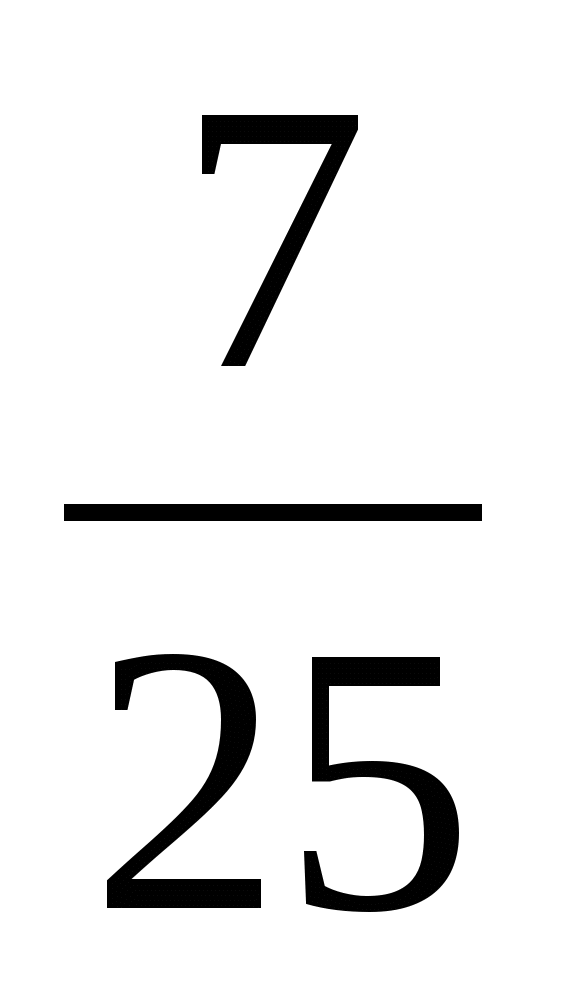 . Найдите радиус окружности, вписанной в треугольник.
. Найдите радиус окружности, вписанной в треугольник.
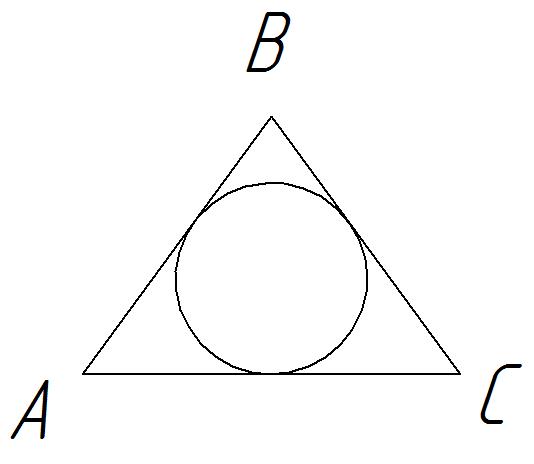
Решение.
По теореме косинусов 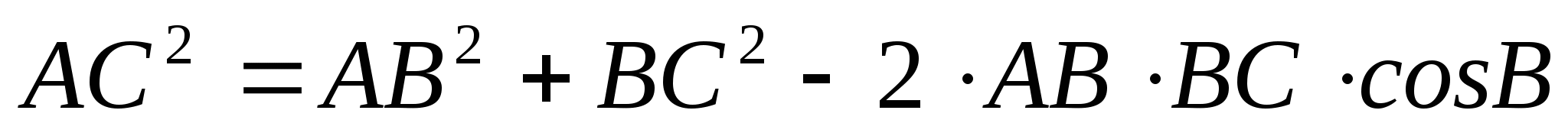
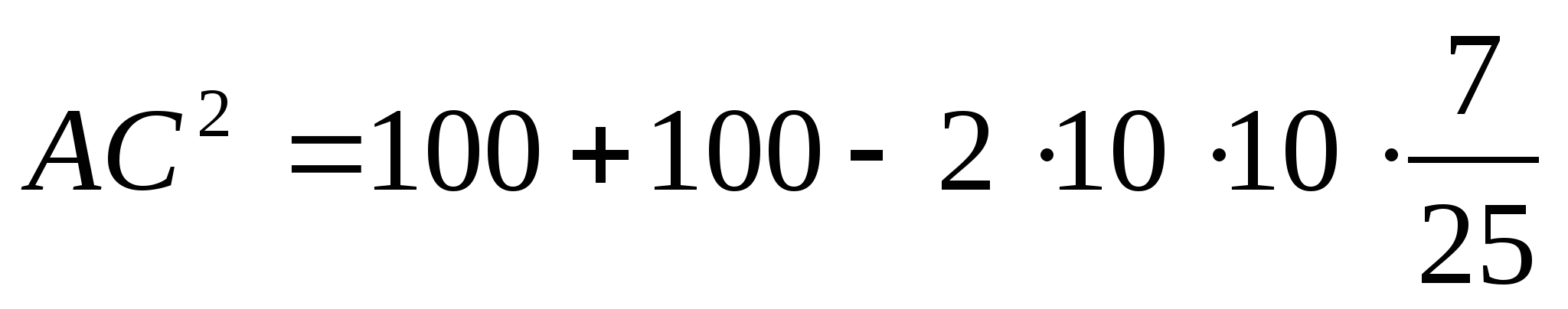
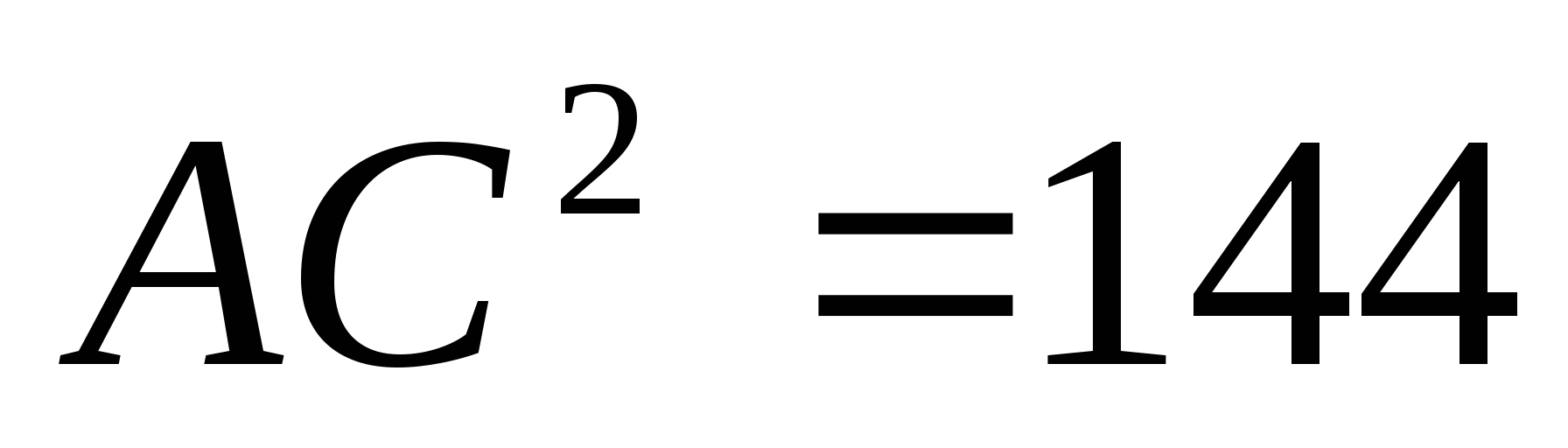
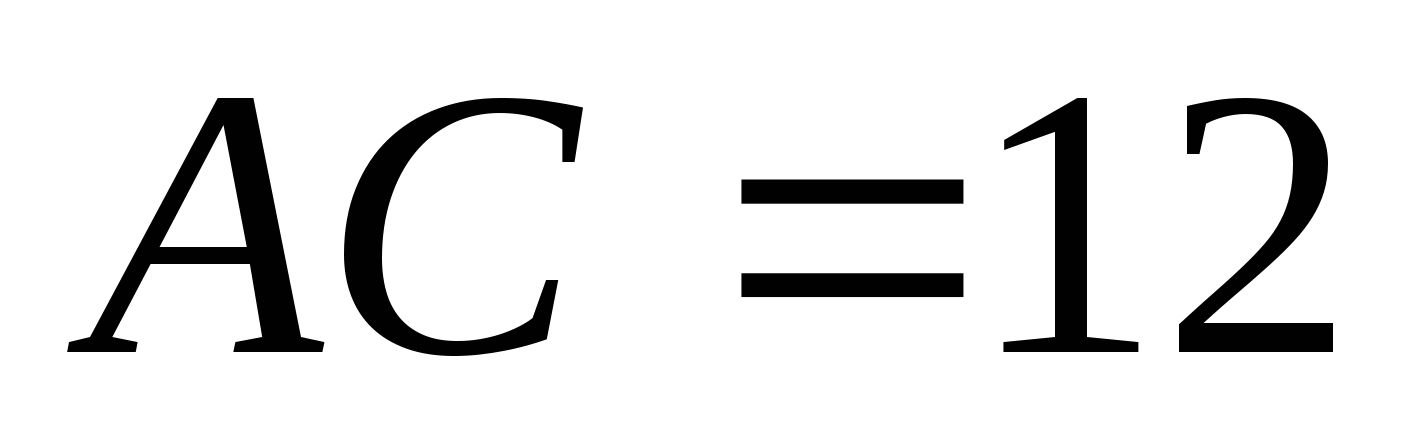
1 способ
Радиус окружности, вписанной в треугольник, можно найти с помощью формулы 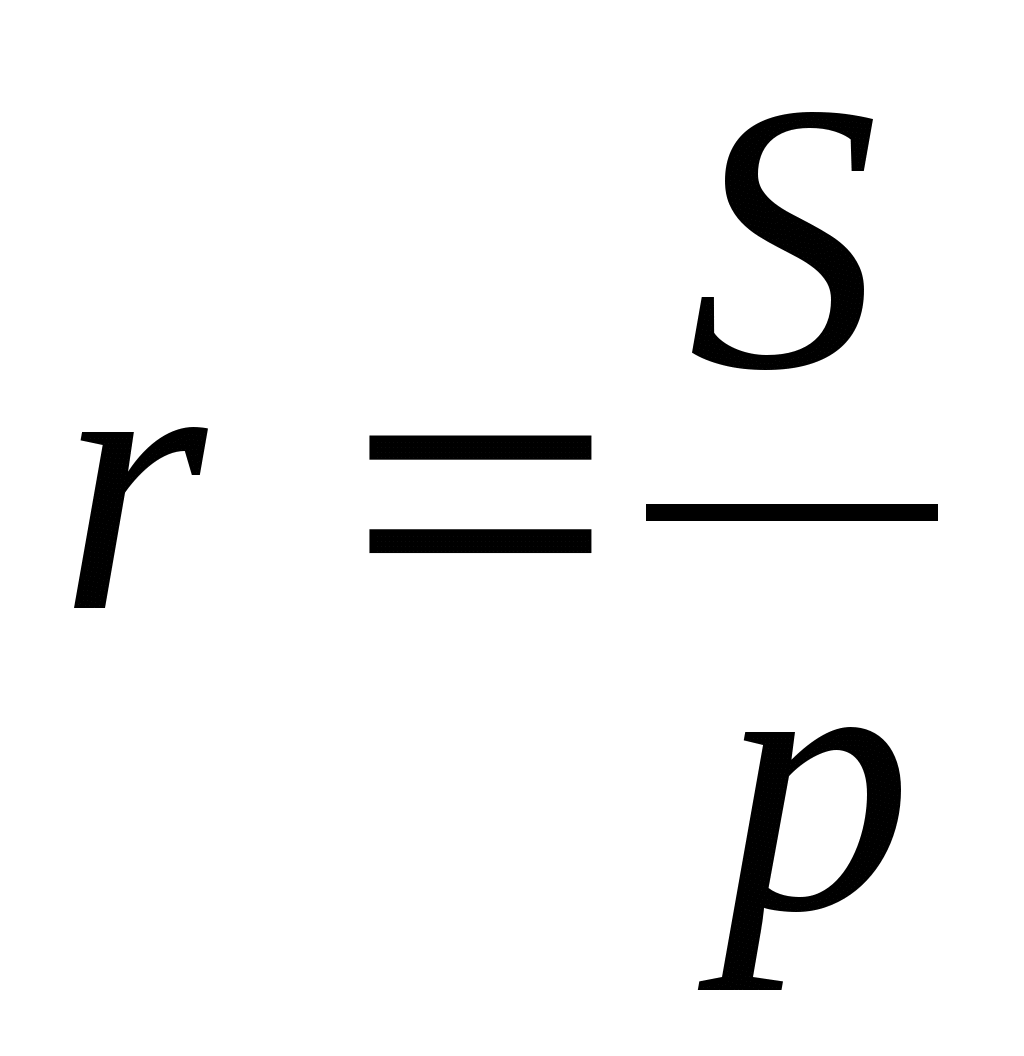 . Площадь данного треугольника можно найти следующими способами:
. Площадь данного треугольника можно найти следующими способами:
1. 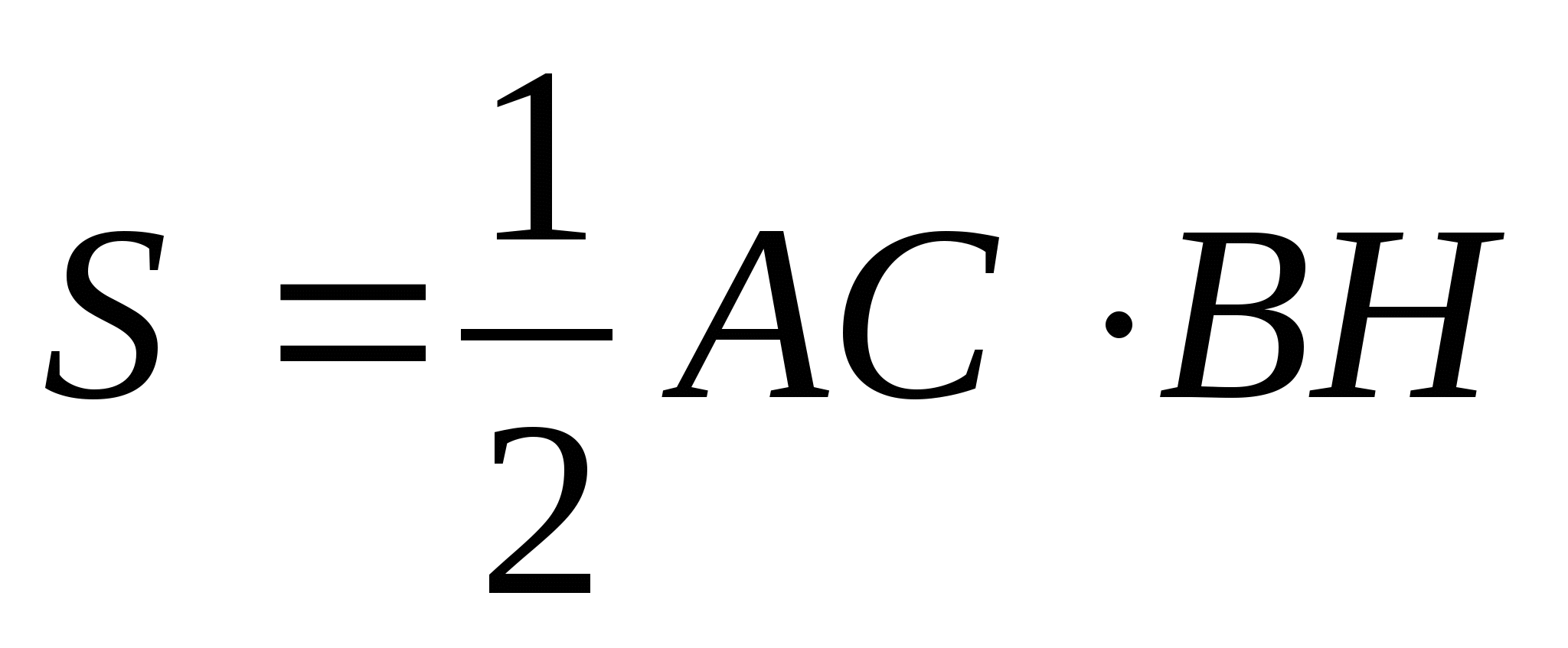 ; 2.
; 2. 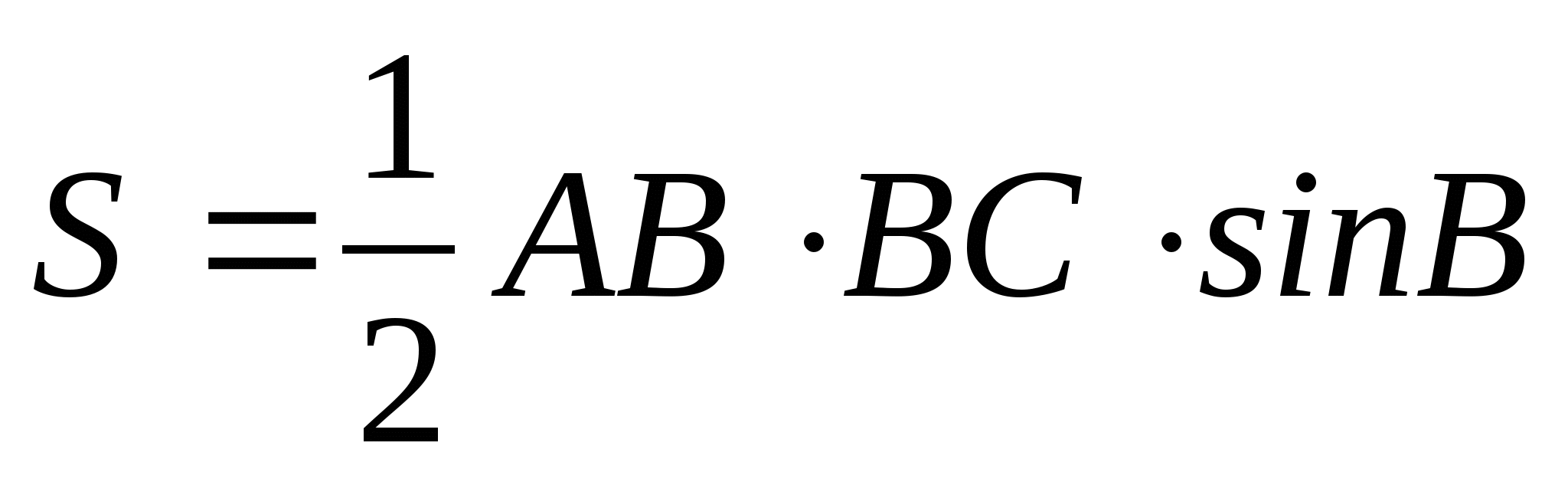 ; 3.
; 3. 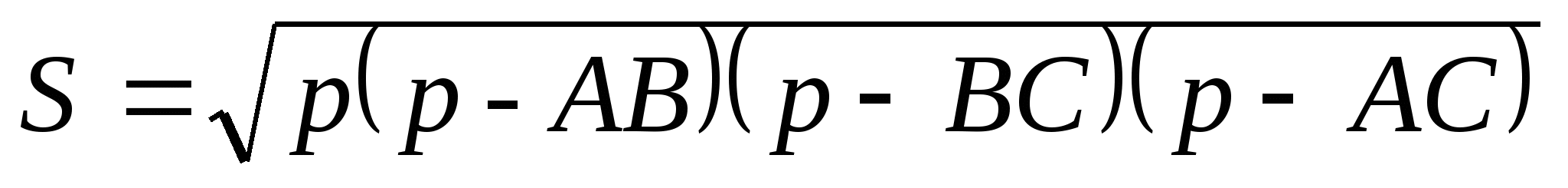 .
.
р = 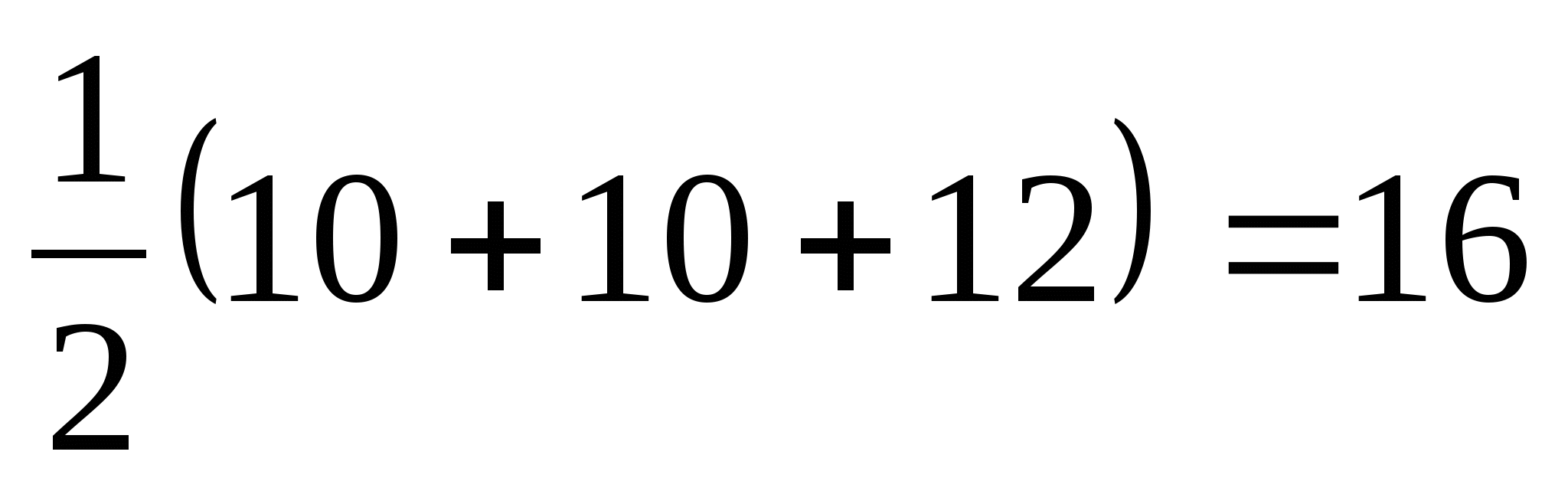 .
. 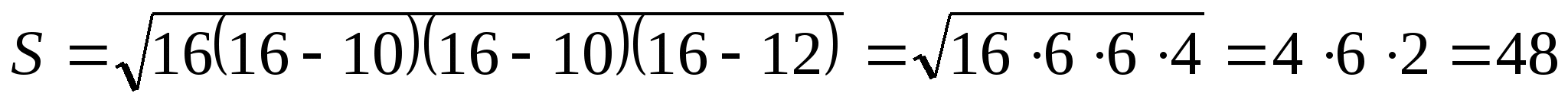 . Значит,
. Значит, 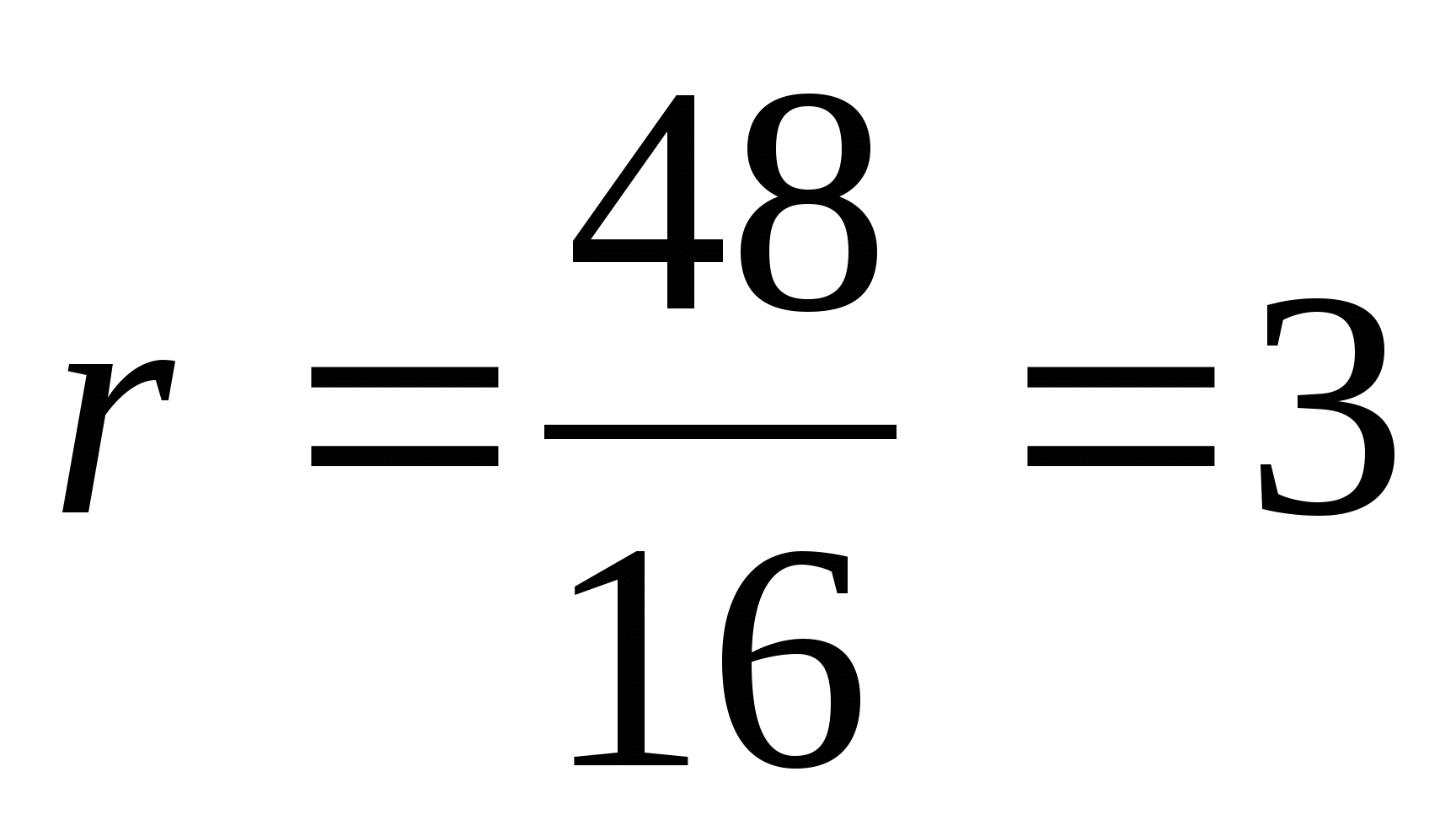 .
.
2 способ.
Мы знаем, что центром окружности, вписанной в треугольник, является точка пересечения его биссектрис. Проведем биссектрису ВН. Т. к. в равнобедренном треугольнике высота, медиана и биссектриса, проведенные к основанию, совпадают, то биссектриса ВН будет и медианой, и высотой.
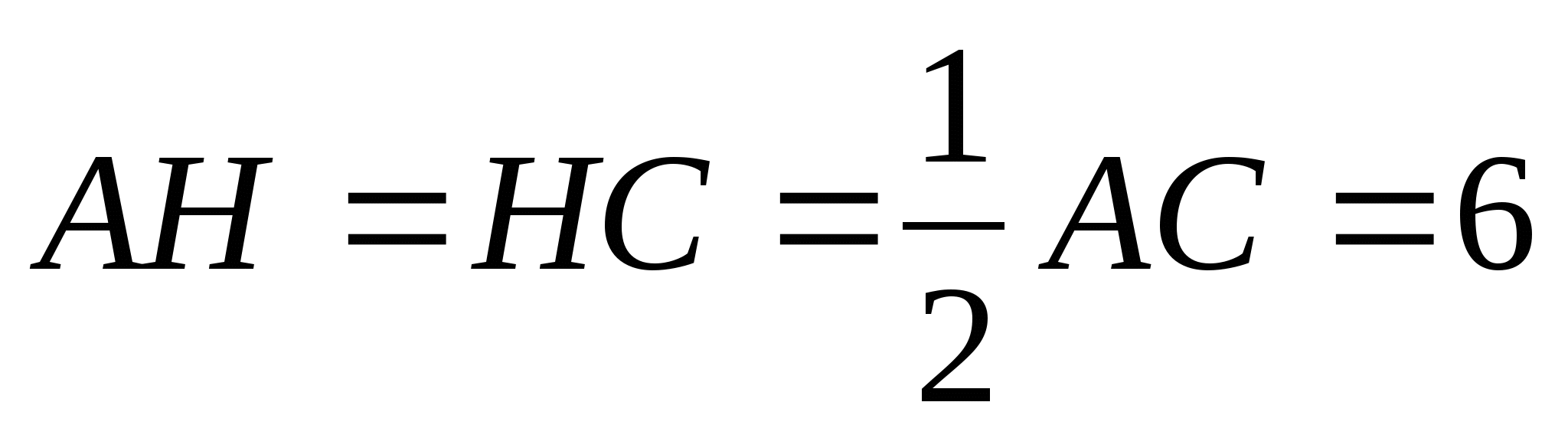 .
.
Из ∆АВН по теореме Пифагора 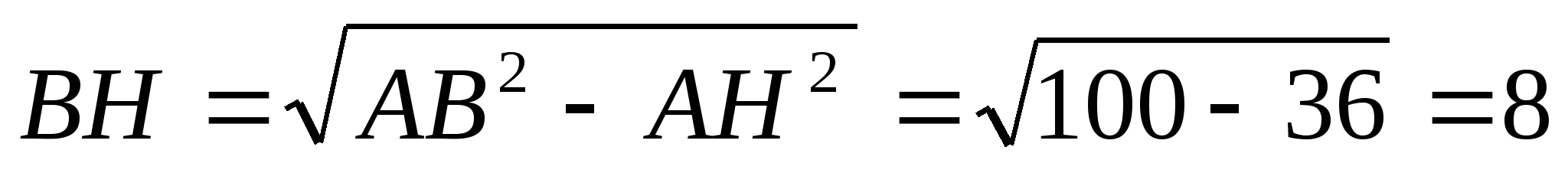 .
.
Проведем радиус ОD в точку касания. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Прямоугольные треугольники АВН и ОВD подобны по двум углам (угол АВН – общий, углы Н и D равны как прямые). В подобных треугольниках сходственные стороны пропорциональны.
Пусть ОН= х, тогда ВО = 8 – х.
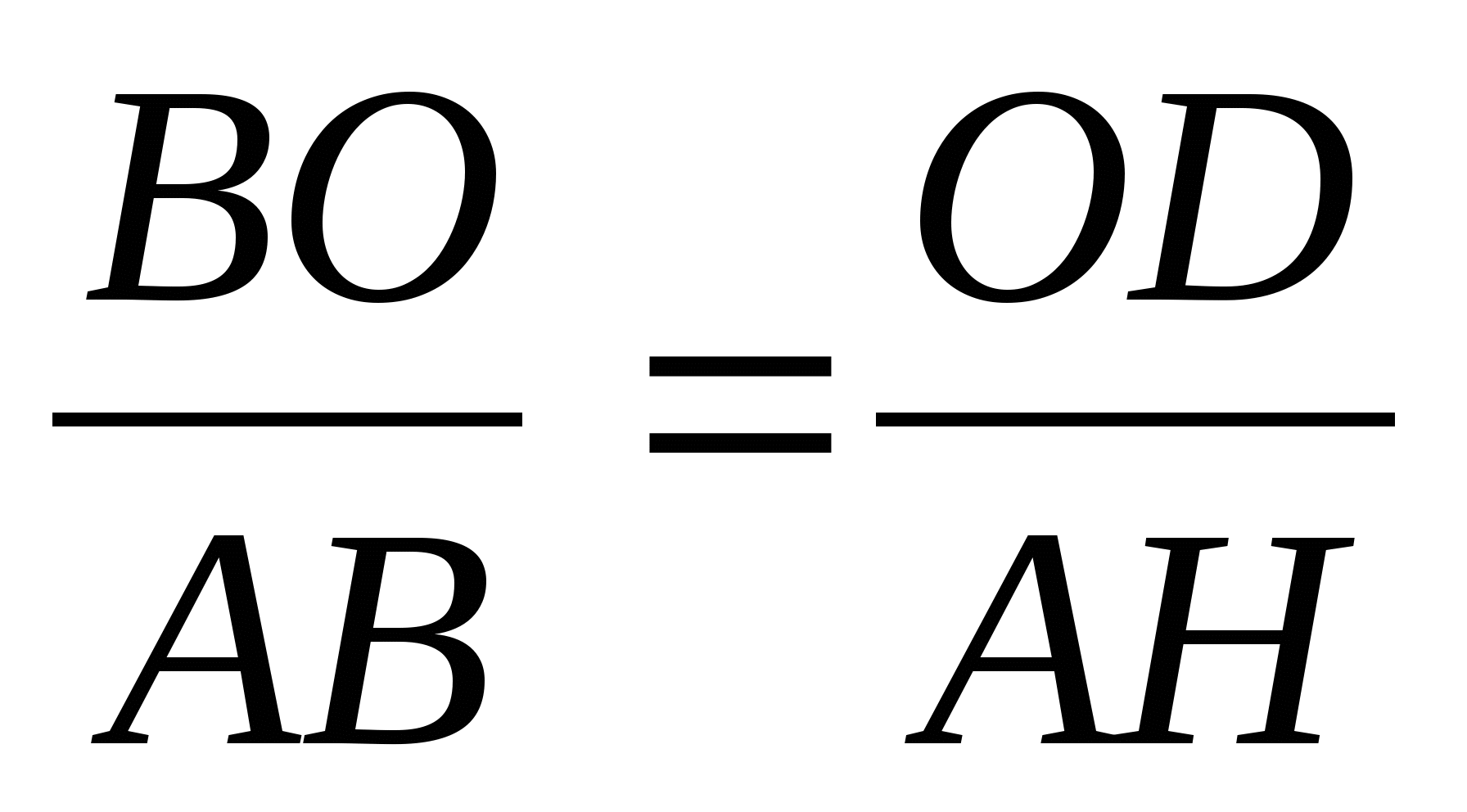

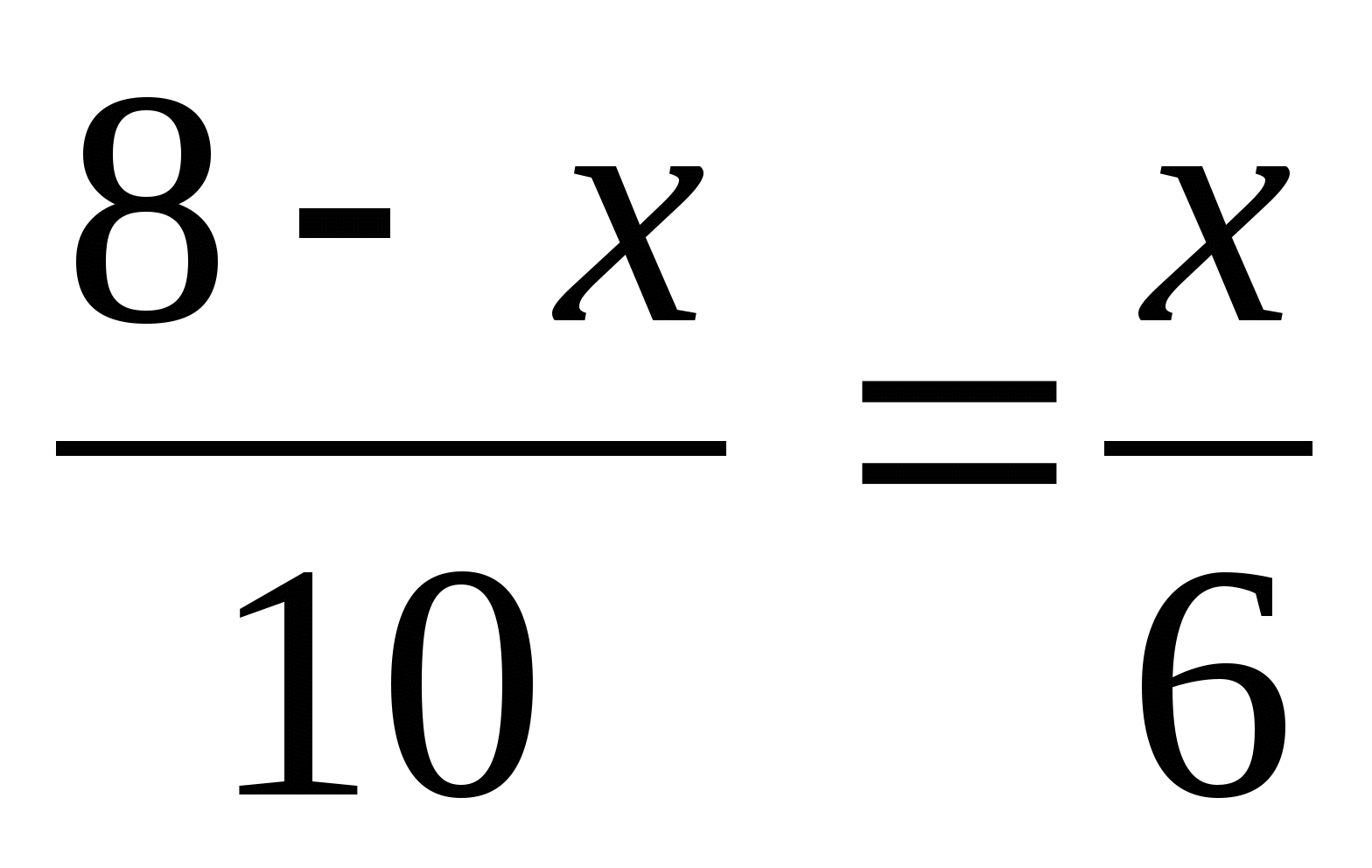

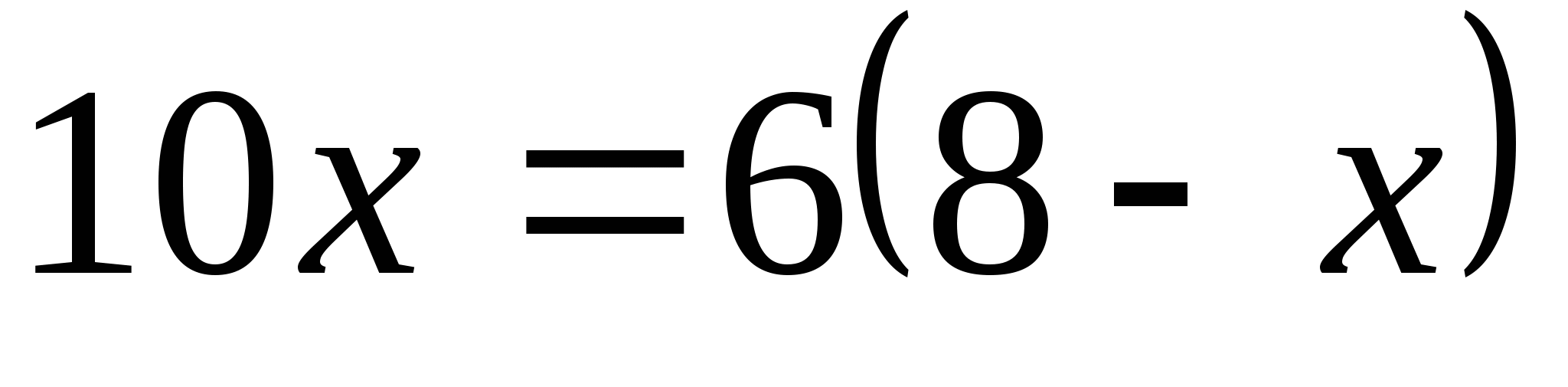
 х = 3. Значит, радиус ВО = 3.
х = 3. Значит, радиус ВО = 3.
3 способ
Начало такое же, как во 2-м способе. Только рассмотрим не подобные треугольники, а прямоугольный треугольник ОВD.
Отрезки касательных к окружности, проведенные из одной точки, равны. Значит, АD = АН = 6. ВD = 10 – 6 = 4.
Пусть ОН = ОD = х, тогда ВО = 8 – х. По теореме Пифагора имеем уравнение:
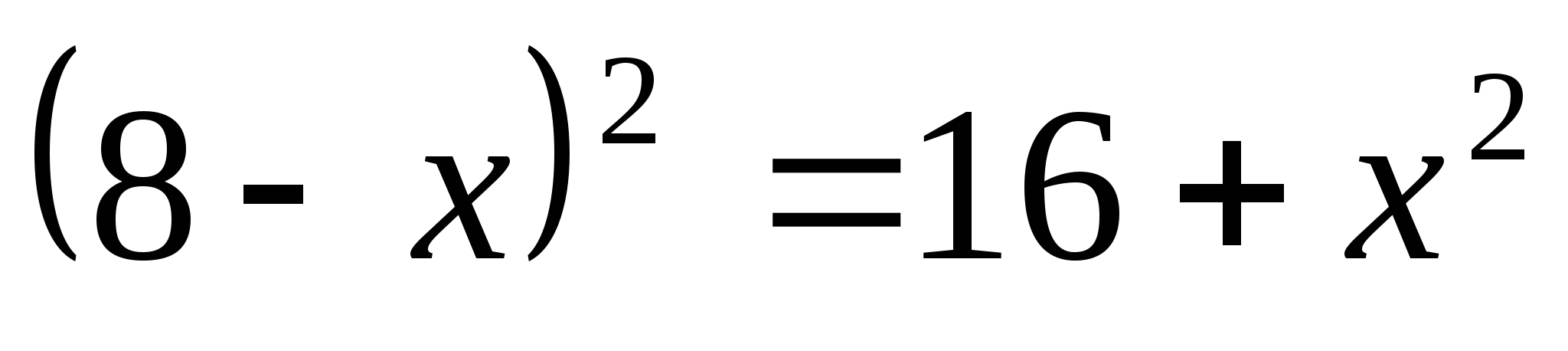
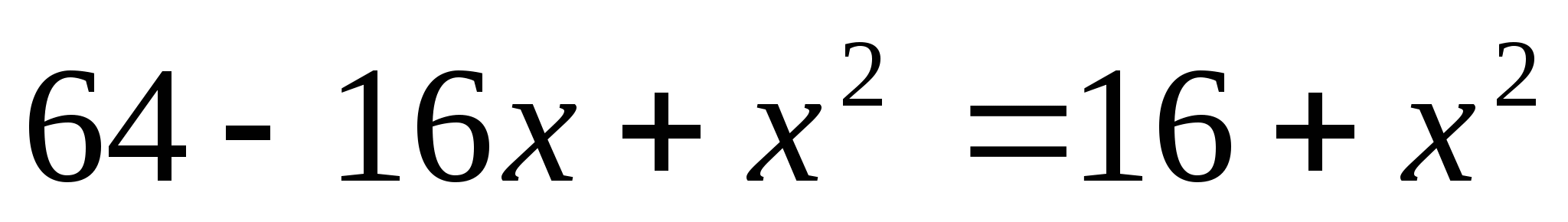
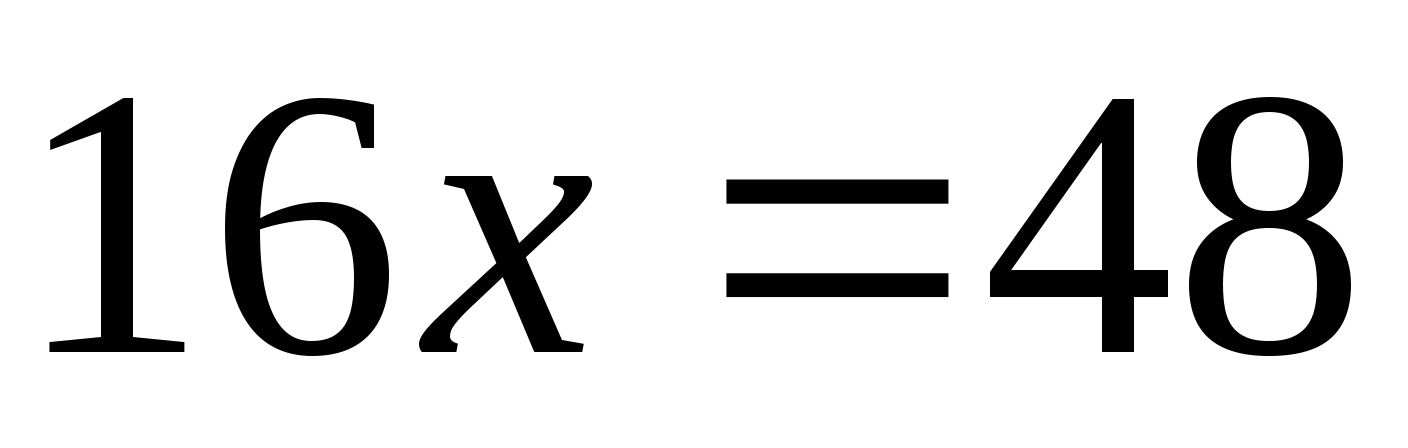
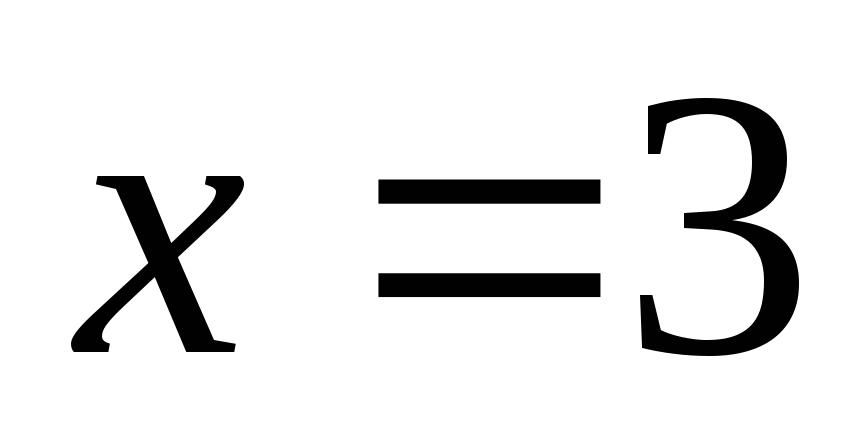
Значит, радиус ВО = 3.
4 способ
Проведем ВН (не будем проводить ОD, но точку касания D обозначим).
Из второго способа 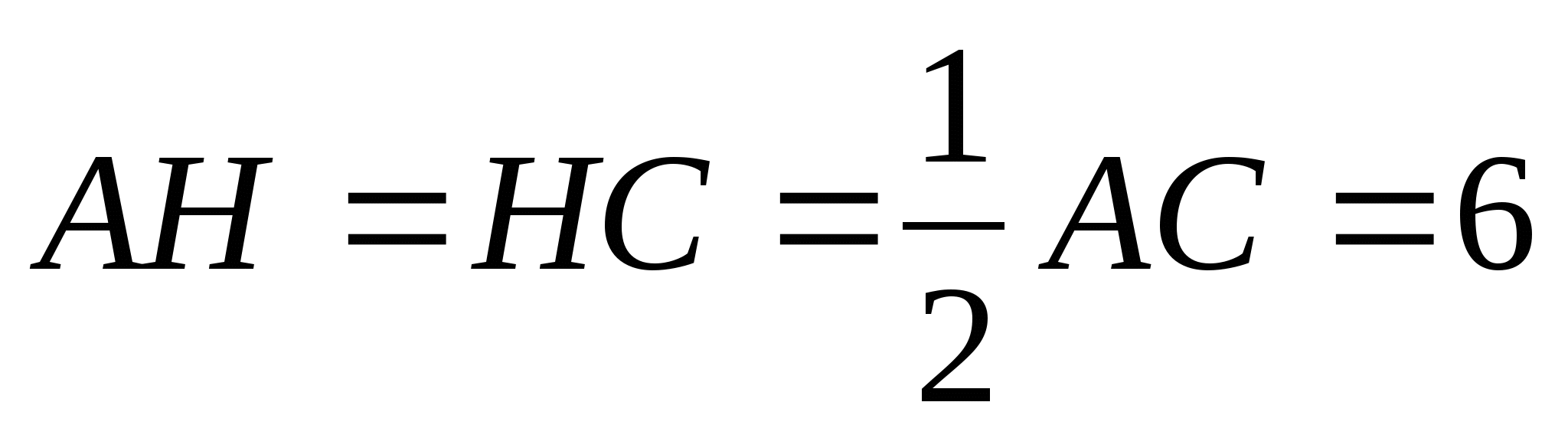 .
.
Из ∆АВН по теореме Пифагора 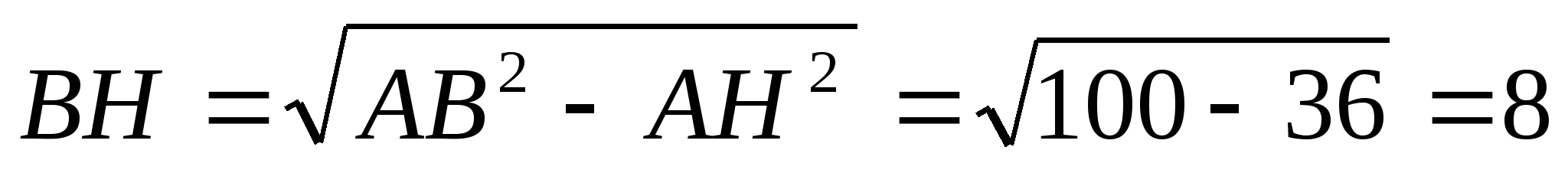 .
.
Отрезки касательных к окружности, проведенные из одной точки, равны. Значит, АD = АН = 6. ВD = 10 – 6 = 4.
По теореме о касательной и секущей ВD2 = ВМ ∙ ВН
16 = ВМ ∙ 8
ВМ = 2
МН = 2r = 8 – 2 = 6  r = 3.
r = 3.
Значит, радиус ВО = 3.
5 способ
Проведем ВН и АО. Т.к. центром окружности, вписанной в треугольник, является точка пересечения биссектрис, то АО – биссектриса угла А, а значит, и биссектриса треугольника АВН. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
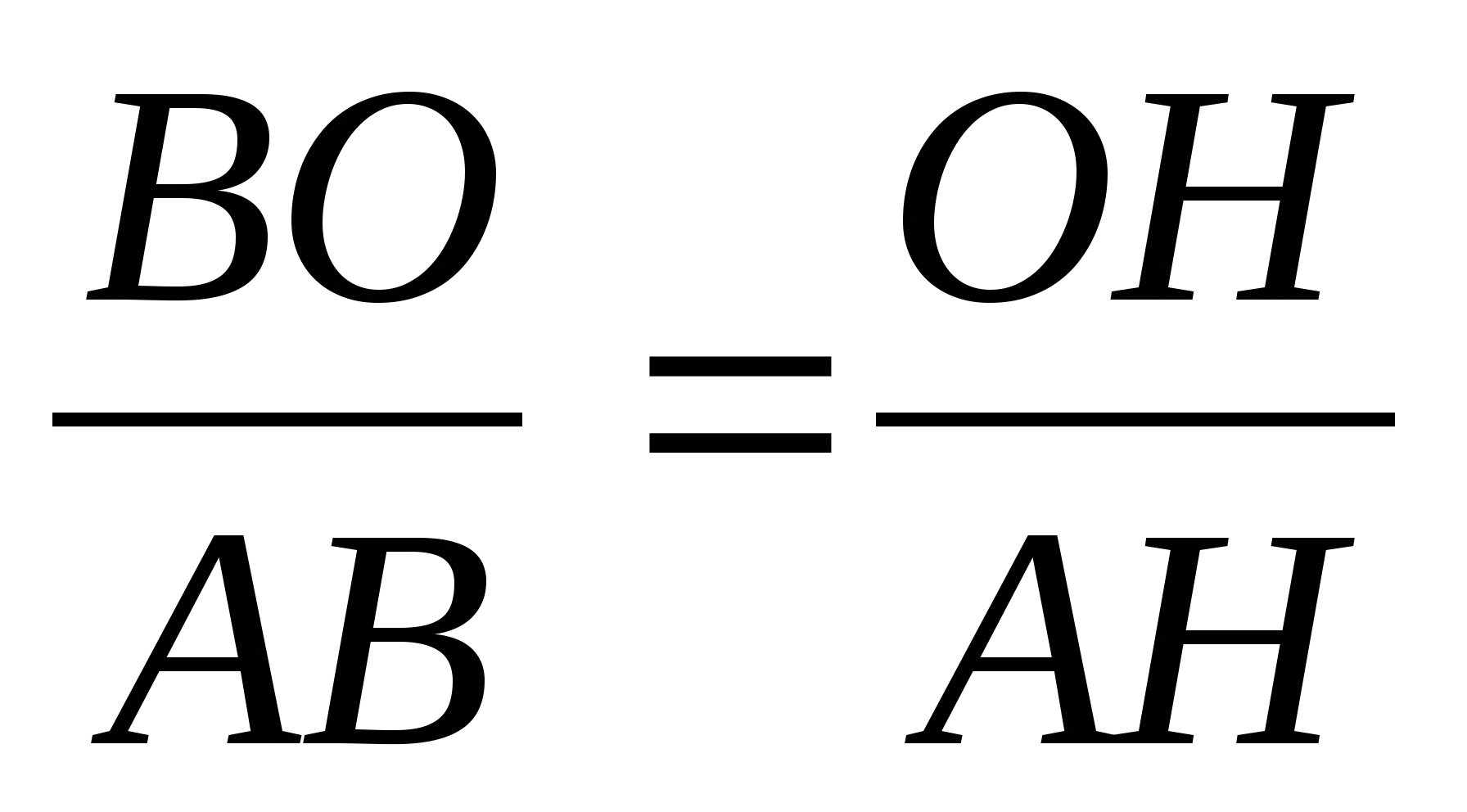 . Пусть ОН = х, тогда ВО = 8 – х.
. Пусть ОН = х, тогда ВО = 8 – х. 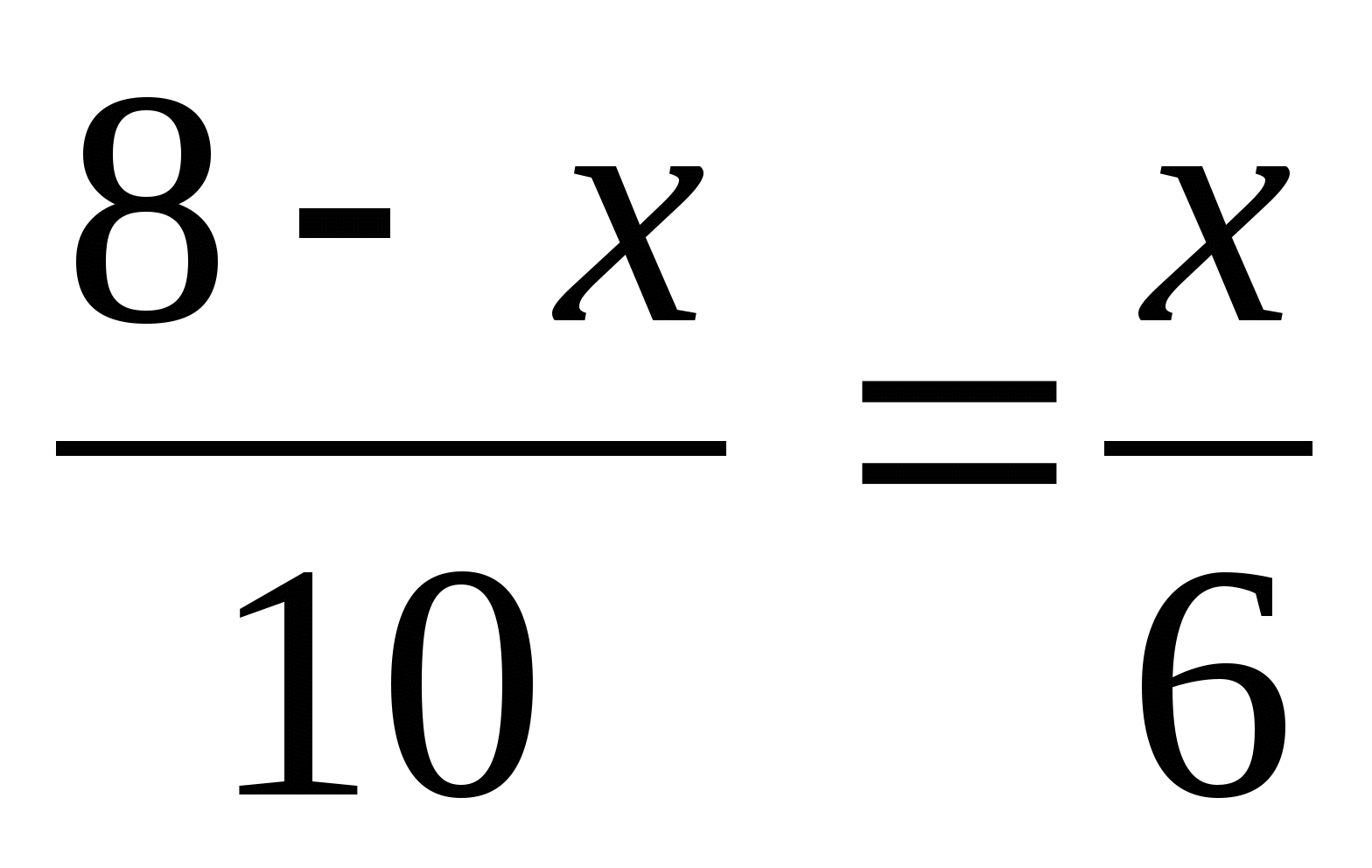
 16х = 48
16х = 48  х = 3.
х = 3.
Значит, радиус ВО = 3.
6 способ
Из ∆АВН: 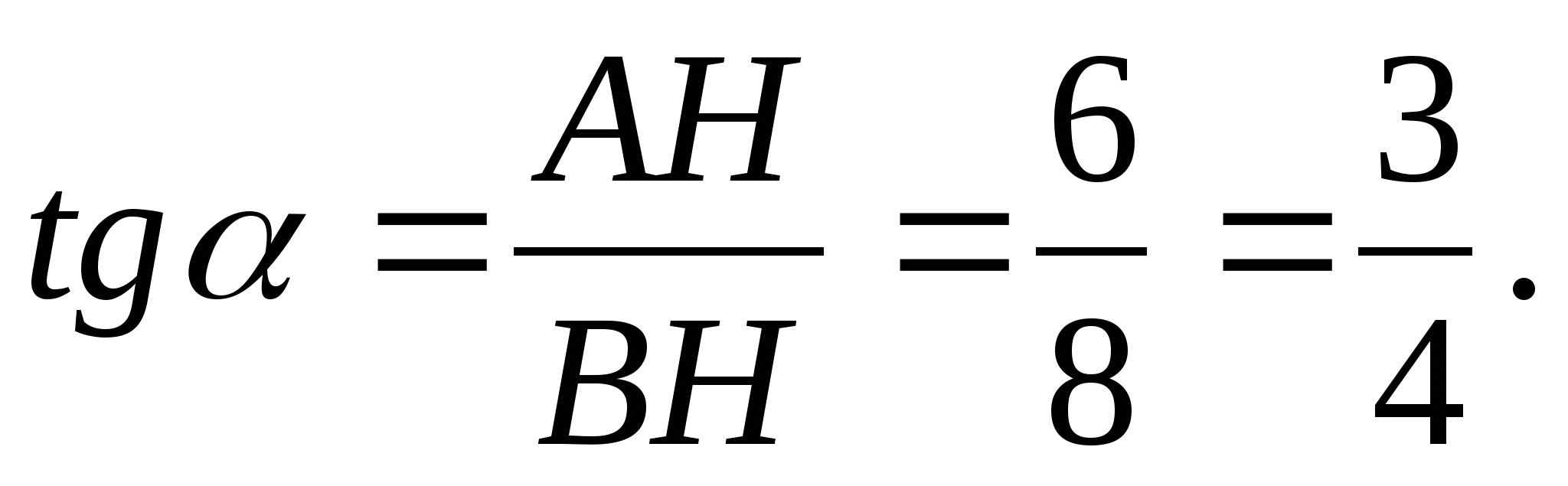 ВD = 4.
ВD = 4.
Из ∆ОВD: 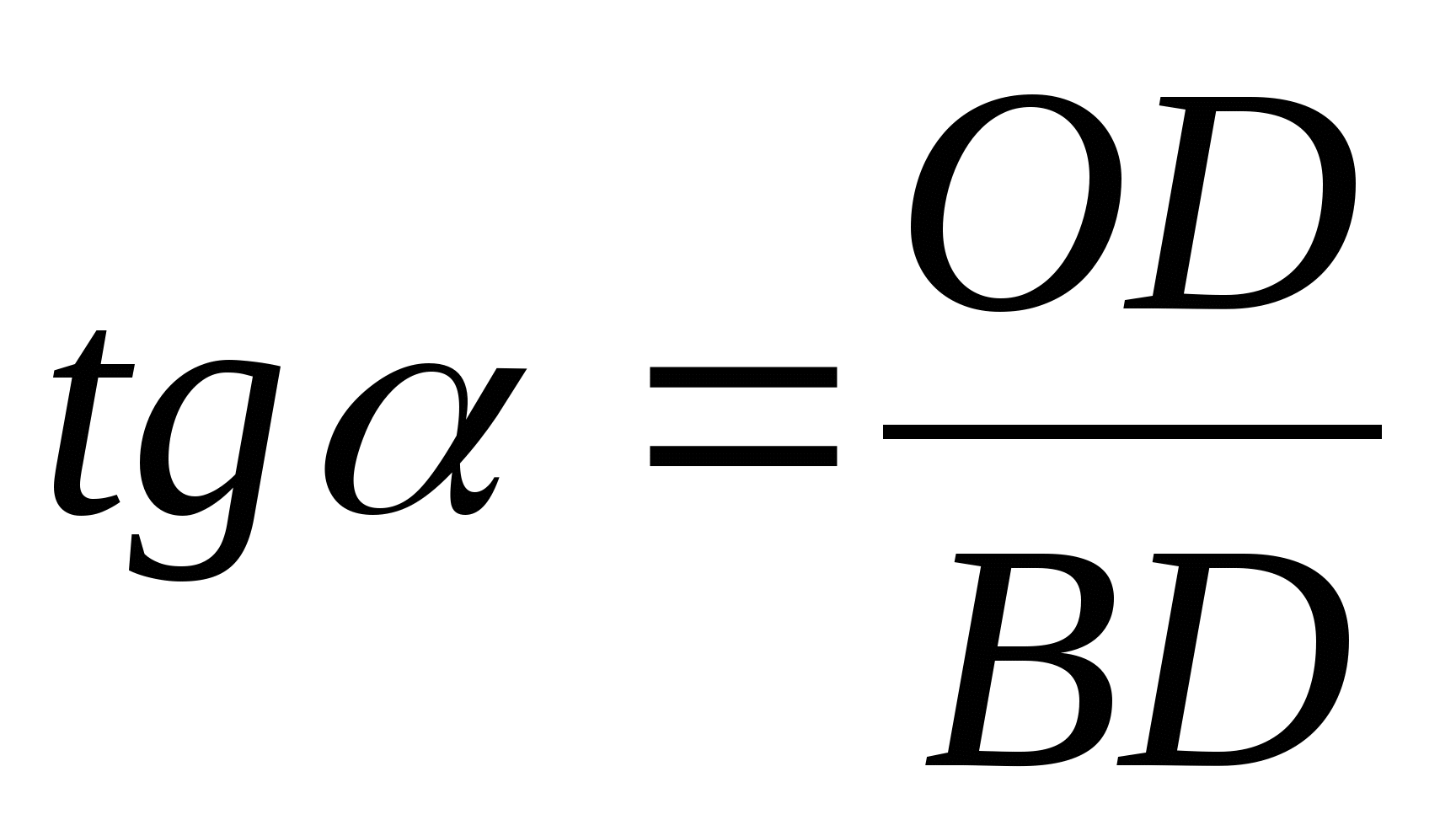

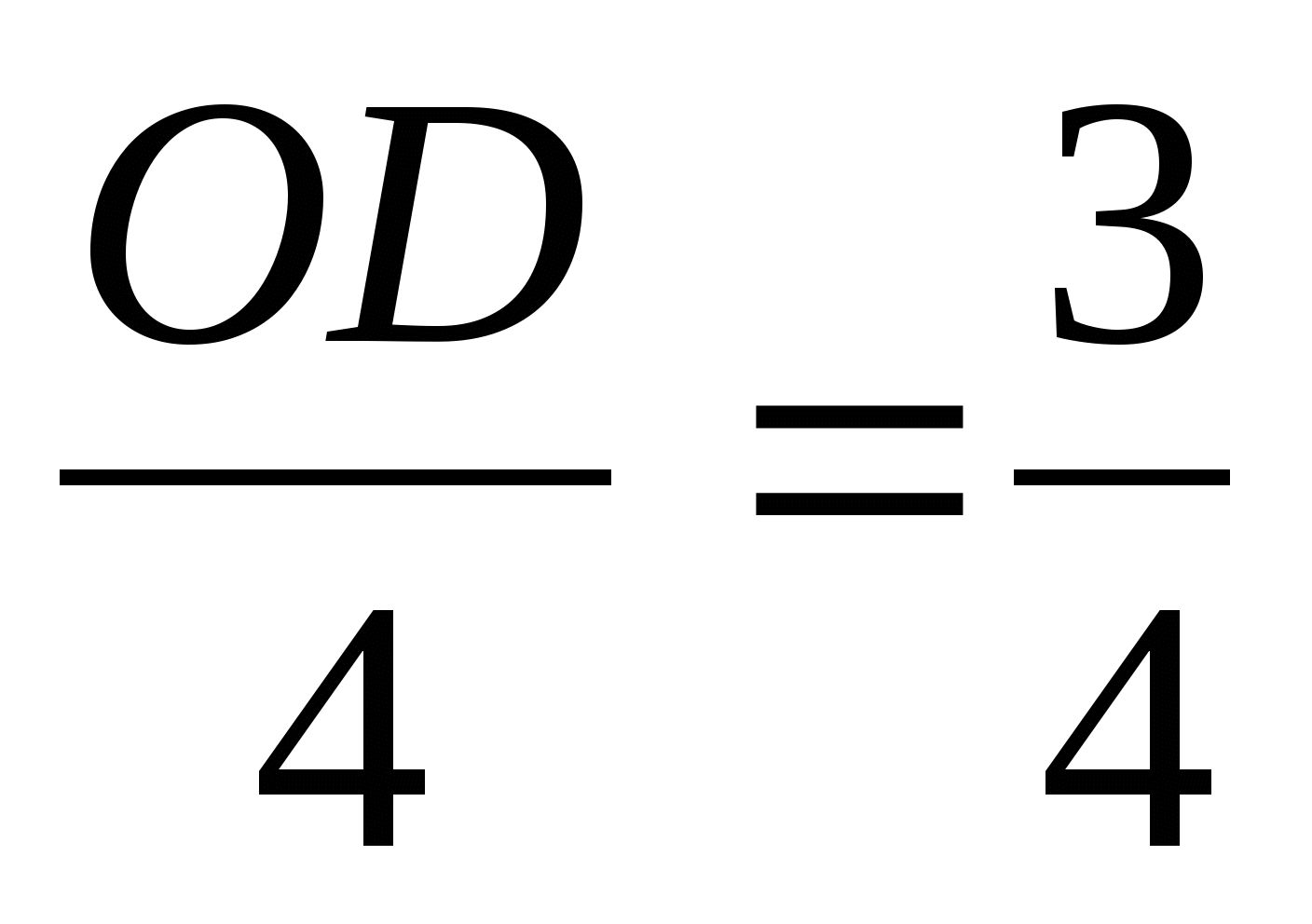
 ОD = 3.
ОD = 3.
Значит, радиус ВО = 3.
Ответ: 3.
Домашнее задание.
Задача на 2 балла
Найдите углы вписанного в окружность четырехугольника, если три угла (в последовательном порядке) относятся как 3 : 7 : 5. В ответе укажите больший из них в градусах.
Задача на 4 балла
В равнобедренную трапецию с верхним основанием, равным 2, вписана окружность радиуса 2. Найдите нижнее основание трапеции.
Пожелания и советы учащимся
• Помни и понимай, что подготовка к ОГЭ – это тяжелый труд, где
результат будет прямо пропорционален времени, потраченному на
активную подготовку к экзамену.
• Выполняй как можно больше различных тестов по предмету.
• Тренируйся с секундомером в руках, засекай время выполнения тестов.
• Готовясь к экзаменам, мысленно рисуй себе картину успеха.
Рефлексия
Подведение итогов
Выставление оценок
Литература
1. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений / Л.С.Атанасян, В.Ф.Бутузов и др. − М. : Просвещение, 2009.
2. Математика. 9 класс. Подготовка к ОГЭ – 2015. Учебно-тренировочные тесты по новой демоверсии / Под ред. Ф.Ф.Лысенко, С.Ю.Кулабухова – Ростов-на-Дону: Легион, 2015.
infourok.ru
Задания по геометрии для подготовки слабого учащегося к сдаче ОГЭ
Задачи по геометрии для 8 класса
Подготовка к ОГЭ
1 задача
 Какой угол (в градусах) образуют минутная и часовая стрелки часов в 18:00?
Какой угол (в градусах) образуют минутная и часовая стрелки часов в 18:00?
(в окружности 360°)
2 задача
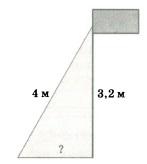
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,2 метра от земли. Длина троса равна 4 метра. Найдите расстояние от основания флагштока до места крепления троса на земле. Ответ дайте в метрах.
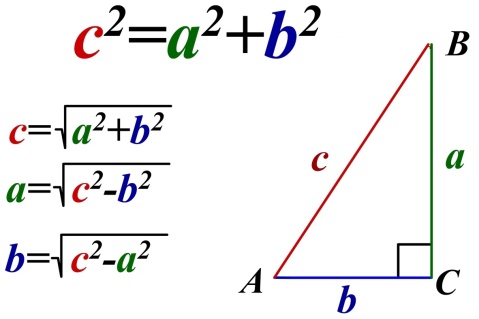
3 задача
Какой угол (в градусах) описывает минутная стрелка за 4 минуты?
 (Всего в окружности 360°, а минут в часах 60. 360°:60 – это в 1 минуте, а надо в 4)
(Всего в окружности 360°, а минут в часах 60. 360°:60 – это в 1 минуте, а надо в 4)
4 задача
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите меньший угол параллелограмма.
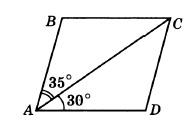
(угол А и есть меньший)
5 задача
Найдите площадь трапеции, изображённой на рисунке.
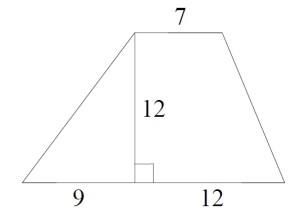
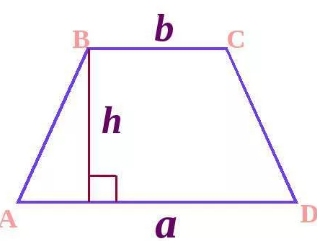
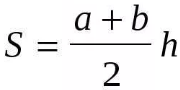
6 задача
На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.
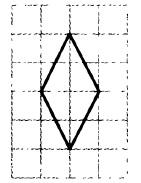
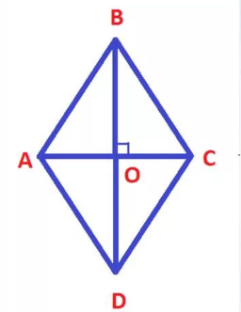 АС и ВD – ээто диагонали
АС и ВD – ээто диагонали
7 задача
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии
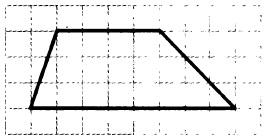
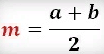
8 задача
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
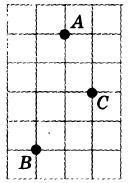 (Найди середину отрезка ВС, соедини его с А, посчитай клетки)
(Найди середину отрезка ВС, соедини его с А, посчитай клетки)
9 задача
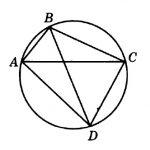
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
10 задача
Касательные в точках A и B к окружности с центром O пересекаются под углом 2º. Найдите угол ABO. Ответ дайте в градусах.
11 задача
Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в
12 задача
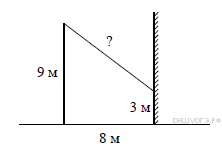
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
13 задача
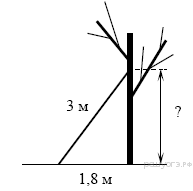
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
14 задача
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
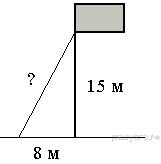
15 задача
Пожарную лестницу приставили к окну, расположенному на высоте 12 м
от земли. Нижний конец лестницы отстоит от стены на 5 м. Какова длина лестницы? Ответ дайте в метрах.
 16 задача
16 задача
Колесо имеет 18 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.
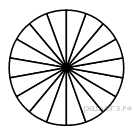 ( рис 17 задачи)
( рис 17 задачи)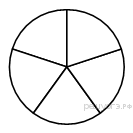
17 задача
На рисунке изображено колесо с пятью спицами.Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 18°?
18 задача
В треугольнике два угла равны 36° и 73°. Найдите его
третий угол. Ответ дайте в градусах
19 задача

infourok.ru
Подборка задач по геометрии для подготовки к ОГЭ 9 класс
Подборка задач по геометрии из ОГЭ.
1) Два угла треугольника равны 40∘ и 130∘. Найдите величину внешнего угла при третьей вершине. Ответ дайте в градусах.
2) В прямоугольном треугольнике внешний угол при вершине острого угла равен 110∘. Найдите другой острый угол треугольника. Ответ дайте в градусах.
3) Два угла треугольника равны 40∘ и 80∘. Найдите наибольший угол этого треугольника. Ответ дайте в градусах.
4) В равнобедренном треугольнике ABC с основанием AC угол B равен 42∘. Найдите величину угла CAK, если AK — биссектриса угла A. Ответ дайте в градусах.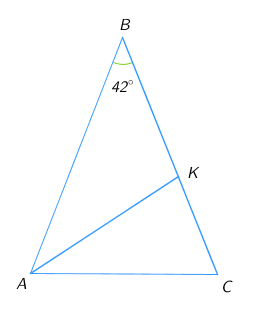 5) В треугольнике ABC, углы которого равны ∠B=40∘ и ∠C=80∘, проведена высота CH.
5) В треугольнике ABC, углы которого равны ∠B=40∘ и ∠C=80∘, проведена высота CH.
Найдите величину угла ACH (в градусах).
6) Параллельные прямые AB и CD пересечены секущей AC. CB — биссектриса угла C, ∠CAB=50∘. Найдите угол ACB.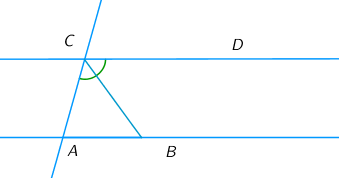 7) Один из внешних углов равнобедренного треугольника равен 40∘. Найдите угол при основании этого треугольника. Ответ дайте в градусах.
7) Один из внешних углов равнобедренного треугольника равен 40∘. Найдите угол при основании этого треугольника. Ответ дайте в градусах.
8) В равнобедренном треугольнике угол при основании в два раза больше угла при вершине. Найдите угол при вершине. Ответ дайте в градусах.
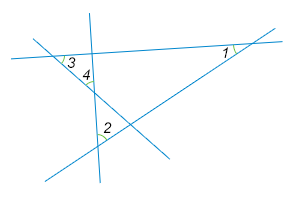
9) Про углы на рисунке известно, что ∠1=40∘, ∠2=20∘, ∠3=30∘. Найдите ∠4. Ответ дайте в градусах
10) Два угла вписанного в окружность четырехугольника равны 72∘ и 118∘. Найдите меньший из оставшихся углов. Ответ дайте в градусах.11) Дан прямоугольный треугольник, один из острых углов которого равен 24∘. Найдите угол между биссектрисой и высотой, проведенными из вершины прямого угла.
12) Острый угол A параллелограмма ABCD равен 40∘. BM — биссектриса угла B. Найдите угол BMC. Ответ дайте в градусах. 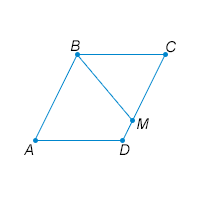 13) В треугольнике ABC проведена биссектриса BD. Известно,
13) В треугольнике ABC проведена биссектриса BD. Известно, 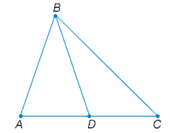 что ∠ACB=40∘, ∠BDC=110∘. Найдите ∠BAC. Ответ дайте в градусах.
что ∠ACB=40∘, ∠BDC=110∘. Найдите ∠BAC. Ответ дайте в градусах.
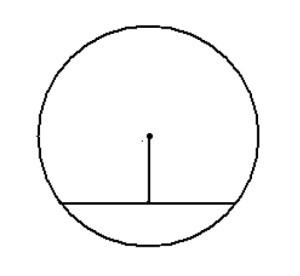
14) В трапеции ABCD AB=BC=CD. Точки K, L, M и N — середины сторон трапеции. Найдите наибольший угол четырёхугольника KLMN, если угол BAD равен 40∘. Ответ дайте в градусах.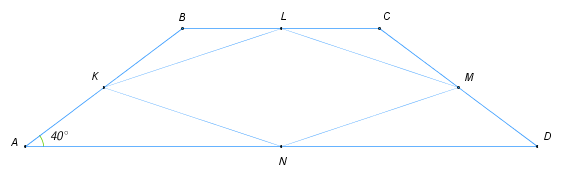 15) На рисунке изображена окружность с центром O. Угол BON равен 50∘, а угол MAB равен 20∘. Найдите величину дуги NBM. Ответ дайте в градусах.
15) На рисунке изображена окружность с центром O. Угол BON равен 50∘, а угол MAB равен 20∘. Найдите величину дуги NBM. Ответ дайте в градусах.
 16) Треугольник ABC вписан в окружность. Известны два его угла ∠A=80∘, ∠B=55∘. Найдите градусную меру меньшей дуги AB.
16) Треугольник ABC вписан в окружность. Известны два его угла ∠A=80∘, ∠B=55∘. Найдите градусную меру меньшей дуги AB. 17) На рисунке точка O — центр окружности, а треугольник OAB — равносторонний. Найдите величину угла ACB в градусах.
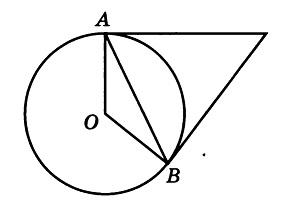
17) На рисунке точка O — центр окружности, а треугольник OAB — равносторонний. Найдите величину угла ACB в градусах. 18) Правильный шестиугольник вписан в окружность. С — произвольная точка окружности. Найдите угол ACB в градусах.
18) Правильный шестиугольник вписан в окружность. С — произвольная точка окружности. Найдите угол ACB в градусах.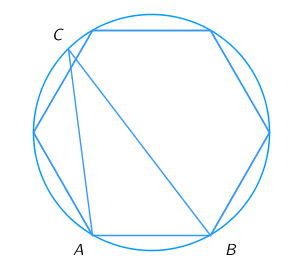 19) К окружности с центром O проведена касательная KA. Радиус окружности равен 2. Расстояние от точки K до центра окружности равно 11. Найдите AK.
19) К окружности с центром O проведена касательная KA. Радиус окружности равен 2. Расстояние от точки K до центра окружности равно 11. Найдите AK.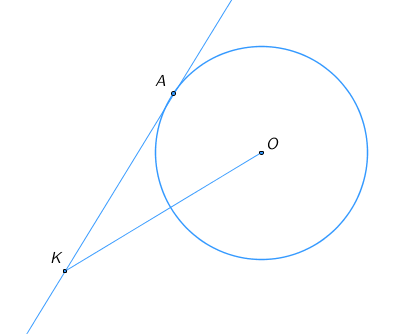 20) AB — касательная к окружности, AC и AD — хорды, причем AC и AB перпендикулярны. Найдите градусную меру угла CAD, если дуга AD равна 112∘.
20) AB — касательная к окружности, AC и AD — хорды, причем AC и AB перпендикулярны. Найдите градусную меру угла CAD, если дуга AD равна 112∘.
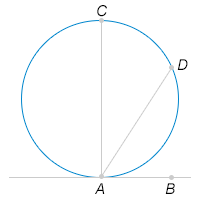 21) Точки A и B расположены на окружности с центром O, при этом градусная мера дуги AB равна 70∘. Найдите угол OAB. Ответ дайте в градусах.
21) Точки A и B расположены на окружности с центром O, при этом градусная мера дуги AB равна 70∘. Найдите угол OAB. Ответ дайте в градусах.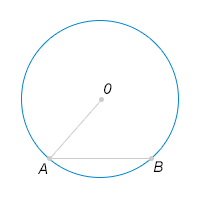 22) Из точки K к окружности проведены касательные KM и KN. Меньшая дуга MN равна 100∘. Найдите угол MKN. Ответ дайте в градусах.
22) Из точки K к окружности проведены касательные KM и KN. Меньшая дуга MN равна 100∘. Найдите угол MKN. Ответ дайте в градусах. 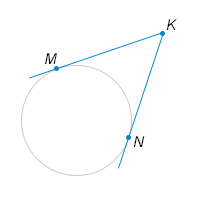
infourok.ru
Задачи для подготовки к ОГЭ по геометрии 7 класс
Задачи для подготовки к ОГЭ по геометрии 7 класс.
Тема «Углы»
1.
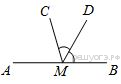
На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 60°. Найдите угол CMA. Ответ дайте в градусах.
2.
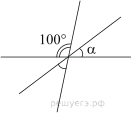
Углы, отмеченные на рисунке одной дугой, равны. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
3.
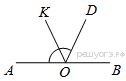
Найдите величину угла AOK, если OK — биссектриса угла AOD, ∠DOB = 64°. Ответ дайте в градусах.
4.
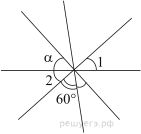
Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α. Ответ дайте в градусах.
5.
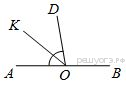
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах.
6.
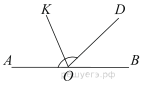
Найдите величину угла AOK, если OK — биссектриса угла AOD, ∠DOB = 52°. Ответ дайте в градусах.
7.
В треугольнике два угла равны 54° и 58°. Найдите его третий угол. Ответ дайте в градусах.
8.
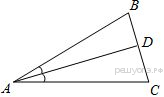
В треугольнике 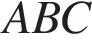 известно, что
известно, что  ,
,  — биссектриса. Найдите угол
— биссектриса. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
9
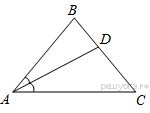
В треугольнике 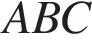 известно, что
известно, что  ,
,  — биссектриса. Найдите угол
— биссектриса. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
10.
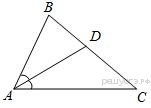
В треугольнике 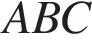 известно, что
известно, что  ,
,  — биссектриса. Найдите угол
— биссектриса. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
11.

В треугольнике 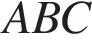 известно, что
известно, что  ,
,  — биссектриса. Найдите угол
— биссектриса. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
Тема «Равнобедренные треугольники»
1.
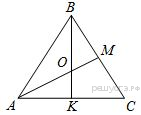 В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите
В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите 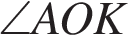 .
.
2.
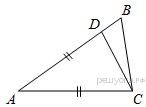 Точка D на стороне AB треугольника ABC выбрана так, что AD = AC. Известно, что ∠CAB = 80° и ∠ACB=59∘. Найдите угол DCB. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD = AC. Известно, что ∠CAB = 80° и ∠ACB=59∘. Найдите угол DCB. Ответ дайте в градусах.
3.
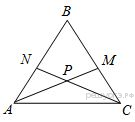
В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите 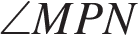 .
.
4.
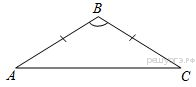
В треугольнике 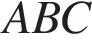 известно, что
известно, что 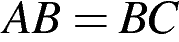 ,
,  . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
5.
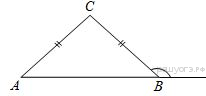 В треугольнике ABC AC = BC. Внешний угол при вершине B равен 140°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC = BC. Внешний угол при вершине B равен 140°. Найдите угол C. Ответ дайте в градусах.
6.
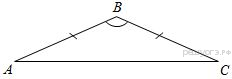 В треугольнике
В треугольнике 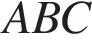 известно, что
известно, что 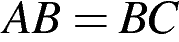 ,
,  . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
7.

В треугольнике 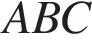 известно, что
известно, что 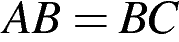 ,
,  . Найдите угол
. Найдите угол . Ответ дайте в градусах.
. Ответ дайте в градусах.
8.
Тема «Треугольники общего вида»
6.
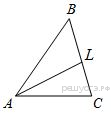
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
8.
В треугольнике два угла равны 38° и 89°. Найдите его третий угол. Ответ дайте в градусах.
9.
В треугольнике два угла равны 36° и 73°. Найдите его третий угол. Ответ дайте в градусах.
Тема «Прямоугольные треугольники»
1.
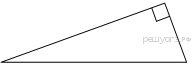 Один из острых углов прямоугольного треугольника равен 43°. Найдите его другой острый угол. Ответ дайте в градусах.
Один из острых углов прямоугольного треугольника равен 43°. Найдите его другой острый угол. Ответ дайте в градусах.
2. .
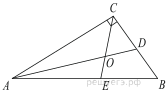 Острый угол прямоугольного треугольника равен 32°. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
Острый угол прямоугольного треугольника равен 32°. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
3.
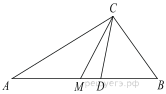 Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
4.
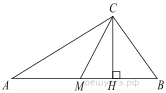 В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
5.
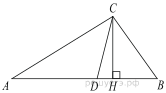 Один из углов прямоугольного треугольника равен
Один из углов прямоугольного треугольника равен  °. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
°. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
infourok.ru
Решение задач ОГЭ по геометрии
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РД
Открытый урок
ПО ГЕОМЕТРИИ
8 класс
Тема «Задачи ОГЭ»
Учитель математики МКОУ СОШ № 14
Саярсанова Марьян Абдулмаликовна
Решение задач ОГЭ
Цели урока:
1.Закрепить знания, полученные по темам: « Площади фигур», «Прямоугольные треугольники», «Подобие фигур». Вести подготовку учащихся к экзамену ОГЭ в ходе решения задач из брошюр.
2.Показать учащимся примеры использования изученного теоретического материала в ходе решения задач.
3. Совершенствовать знания решения задач.
Ход урока
1. Организационный момент
Сообщить тему урока, сформулировать цели урока
2. Актуализация знаний учащихся
Теоретические вопросы по пройденным темам
1 Свойства площадей
2 Формула вычисления площади квадрата
3 Формула вычисления площади прямоугольника
4 Формула вычисления площади треугольник
5 Формула вычисления площади трапеции
6 Формула вычисления площади ромба
7 Теорема Пифагора
8 Опреде ление подобия треугольников.
9 Средняя линия треугольника
10 пропорциональные отрезки.
Учитель решает задачи с ОГЭ с объяснением:
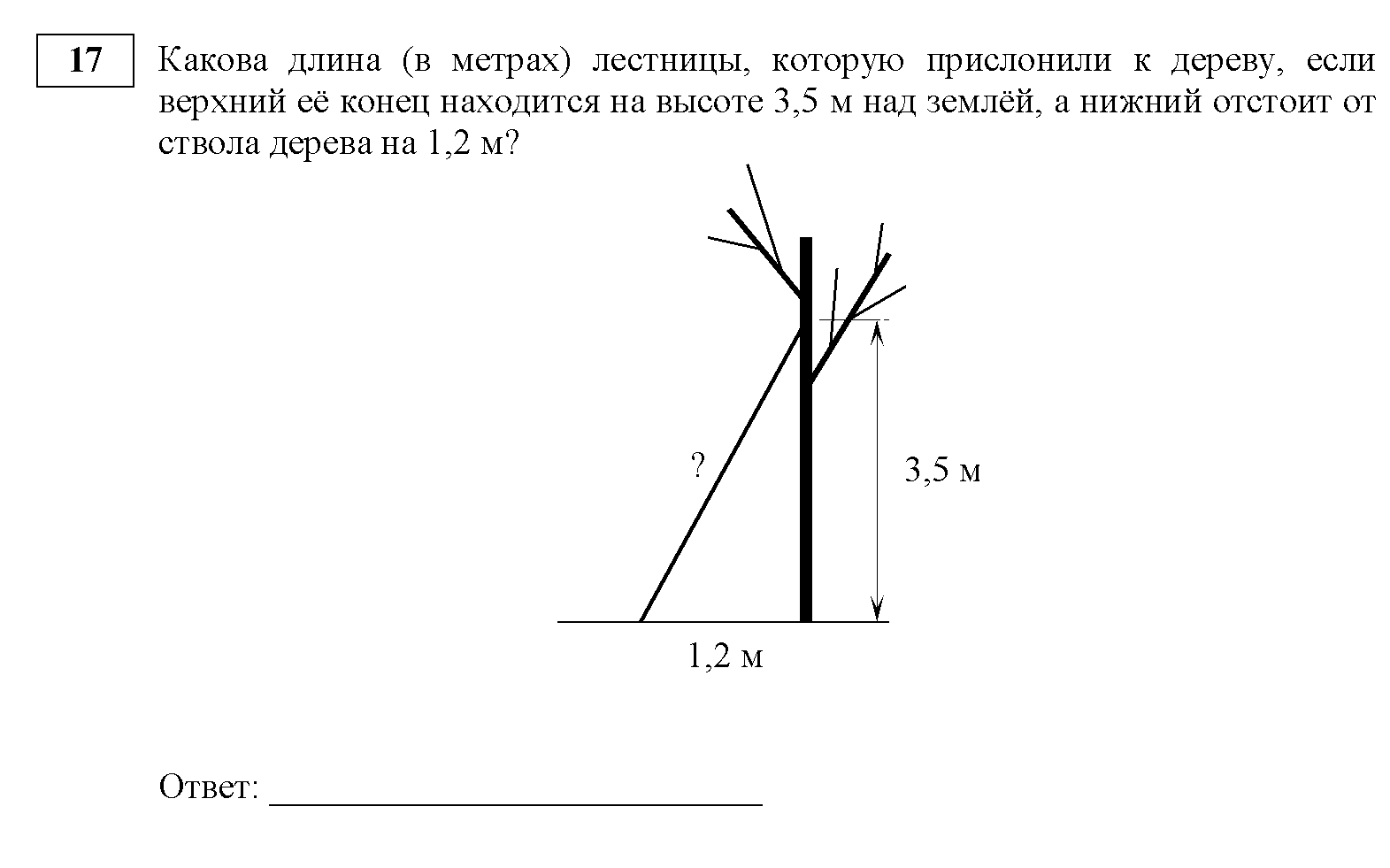
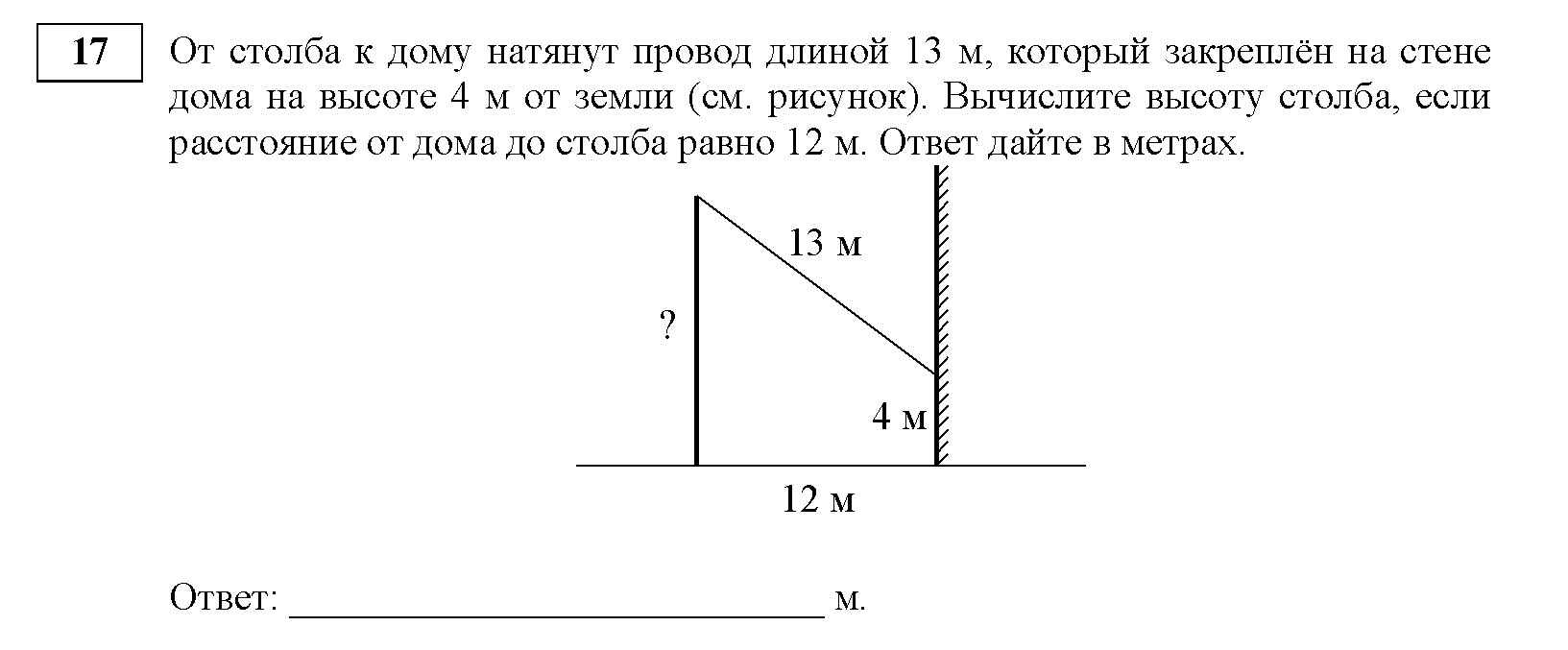
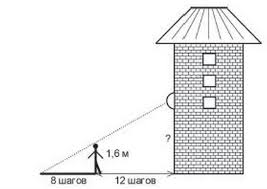
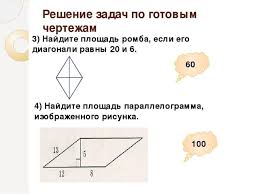
Самостоятельная работа по карточкам ( два варианта)
Карточки для второго варианта те же задачи с измененными данными
Проверка самостоятельной работы
Подведение итогов
Домашняя работа.



infourok.ru
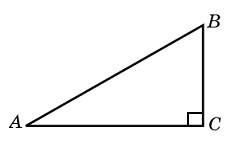 гипотенуза равны соответственно 6 и 10.
гипотенуза равны соответственно 6 и 10. 













































