Решение задач на проценты (урок изучения нового материала). 5-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели:
- научить решать основные задачи на проценты: нахождение процента от величины, нахождение величины по её проценту, нахождение процента одной величины от другой;
- способствовать развитию творческой активности учащихся;
- развивать познавательный интерес к предмету путем применения информационных технологий;
- способствовать развитию математической речи.
Метод обучения: лекция, объяснение, устные упражнения, письменные упражнения, самостоятельная работа.
Формы контроля: проверка самостоятельно решенных задач.
Учебник: Математика: Учеб. Для 5 кл. общеобразоват. Учреждений/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С. И. Шварцбурд.
Ход урока
I. Актуализация прежних знаний.
1. Устная работа (на закрепление понятия «процент») Предлагаются упражнения по переводу дроби в проценты, а процентов в десятичные дроби.
| 1. Представьте данные десятичные дроби в процентах: (слайд №2) | ||
| 0,5= : (50%) | 0,01=: (1%) | 0,42=: (42%) |
| 123=: (12300%) | 0,123=: (12,3%) | 7,2=: (720%) |
| 0,045=: (4,5%) | 70,5=: (7050%) | 1,5=: (150%) |
| 0,6=: (60%) | 0,0035=: (0,35%) | 10= : (1000%) |
| 2. Представьте проценты десятичными дробями: (слайд №3) | ||
| 100%=: | 1000%=: | 72,1%=: |
| 230%=: | 3,17%=: | 0,5%=: |
| 0,08%=: | 133%=: | 94,8%=: |
3. Заполнить таблицу: (слайд №4)
| Обыкновенная дробь | 1/2 | 1/5 | 4/5 | ||||||
| Десятичная дробь | 0,25 | 0,4 | 0,75 | ||||||
| Проценты | 10% | 60% | 100% |
II. Изучение нового материала
1). Простейшие задачи на проценты. Существует три типа задач на проценты. Сегодня на уроке вы научитесь их различать и решать, используя определение процента.
1 тип. Нахождение процентов данного числа (дано все и процент, найти часть). (Слайд №5)
В книге 600 страниц. Мальчик прочитал 23% книги. Сколько страниц прочитал мальчик?
2 тип. Нахождение числа по его процентам (дана часть и процент, найти всё). (Слайд №6)
Мальчик прочитал 138 страниц — это 23% всей книги. Сколько страниц в книге?
3 тип. Нахождение процентного отношения чисел (дано два числа, найти процент одного от другого) (слайд №7)
В книге 600 страниц. Мальчик прочитал 138 страниц. Сколько процентов всей книги он прочитал?
(Учащимся раздаются памятки, в которых написаны три типа задач на проценты и их признаки).
Задание 1. Устно определить тип задачи: №1536, №1543, №1544, №1555, №1540 (учебника)
При решении задач на проценты удобно пользоваться следующим алгоритмом (слайд 8):
- Попытаться определить тип задачи;
- Определить, что принимаем за 100%;
- Первым действием находим, сколько приходится на 1%.
Учащиеся вместе с учителем решают задачи 1-3.
Задача 1. (Слайд 9)
Решение. Задача на нахождение процента от числа.
600стр. — 100%
?стр. — 23%
600 : 100 = 6 (стр.) — 1% книги
6 x 23 = 138 (стр.) — прочитал мальчик
Ответ: 138 страниц.
Задача 2. (Слайд 10)
Решение. Задача на нахождение числа по проценту.
?стр. — 100%
138стр. — 23%
138 : 23 = 6 (стр.) — 1% книги.
6 x 100 = 600 (стр.) — в книге.
Ответ: 600 страниц.
Задача 3. (Слайд 11)
Решение. Задача на процентное отношение.
600стр. — 100%
138стр. — ?%
600 : 100 = 6 (стр.) — 1% книги
138 : 6 = 23 % книги прочитал мальчик
Ответ: 23%.
III. Тренировочные упражнения
№1538 (учебника) На поле, площадь которого 620 га, работали хлопкоуборочные машины. За сутки они убрали 15% всего поля. Сколько гектаров поля убрали за сутки?
Решение. Задача на нахождение процента от числа.
620 га — 100%
? га — 15%
620 : 100 = 6,2(га) — 1% поля
6,2x 15 = 93 (га) — убрали за сутки.
Ответ: 93га.
№1548 (учебника) Масса медвежонка составляет 15% массы белого медведя. Найдите массу белого медведя, если масса медвежонка 120 кг.
Решение. Задача на нахождение числа по проценту.
? кг — 100%
120 кг — 15%
120 :15 = 8 (кг)- 1% массы белого медведя.
8 x 100 = 800 (кг) — масса белого медведя.
Ответ: 800 кг.
№1551 (учебника) В школе 700 учащихся. Среди них 357 мальчиков. Сколько процентов учащихся этой школы составляют мальчики?
Решение. Задача на процентное отношение.
700 учащихся — 100%
357 учащихся — ?%
700 : 100 = 7(уч.) — 1 % учащихся школы.
357 : 7 = 51 (%) — составляют мальчики.
Ответ: 51%.
IV. Обучающая самостоятельная работа (7 минут) (Слайд №12)
Вариант №1.
1. Из сахарного тростника получается 18% сахара. Сколько тонн сахара получится из 42,5 т сахарного тростника?
2. Засеяли 65% поля, что составило 325 га. Найдите площадь всего поля.
Вариант №2.
1. Площадь поля 450 га. В первую смену засеяли 270 га. Сколько процентов всей площади засеяли в первую смену?
2. Из овса получается 40% муки. Сколько муки получится из 26,5 т овса?
Работу сдают на проверку.
V. Подведение итогов урока, выставление отметок.
VI. Домашнее задание. п.40; №1571, 1575. (Слайд 13)
urok.1sept.ru
Конспект урока «Решение задач на проценты» МАТЕМАТИКА 5 класс
Технологическая карта урока
«Решение задач на проценты»
В любом открытии есть 99 % труда и потения
И только 1% таланта и способностей.
Л. Магницкий
Проценты(«Решение задач на проценты»)
Тип урока
Урок обобщения и систематизации знаний.
Цель
совершенствование навыков решения задач на проценты и умение применять их в реальных жизненных ситуациях
Планируемые образовательные результаты
Предметные
Метапредметные
Личностные
уметь в процессе реальной ситуации использовать понятие процента и умения решать основные типы задач на проценты
регулятивные – уметь определять и формулировать цель урока; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать свое действие в соответствии с поставленной задачей; вносить необходимы коррективы в действия после его завершения на основе его оценки и учета характера сделанных ошибок;
коммуникативные – уметь оформлять свои мыслив устной форме; слушать и понимать речь других; уметь выражать свои мысли полно и точно; уметь договариваться в совместном общении;
познавательные – уметь использовать схемы и таблицы; выполнять действия по алгоритму; преобразовывать информацию из одной формы в другую.
уметь работать в парах, слушать собеседника и вести диалог, аргументировать свою точку зрения, осознавать ответственность за общее дело, уметь осуществлять самооценку.
Основные понятия, изучаемые на уроке
процент, перевод десятичной дроби в проценты и процентов в десятичную дробь, решение задач трех основных видов: нахождение процента от числа, числа по его проценту и процентного отношения чисел.
Методы
частично-поисковый
Формы работы
Фронтальная, индивидуальная, работа в парах.
Средства ИКТ и оборудование, используемые на занятии
Компьютер, проектор, экран, раздаточный материал (карточки с заданием)
Ресурсы, используемые на уроке
электронная презентация, выполненная в программе Power Point, карточки с заданием, таблицы для самооценки.
Ребята, давайте вместе с вами выясним, что объединяет понятия: производительность труда, успеваемость в классе, всхожесть семян, итоги голосования, ставка в банке по кредиту и т.д.Учащиеся рассуждают, включаются в деловой ритм урока и делают вывод, что это «проценты» или «все перечисленные величины выражаются в процентах».
2.Актуализация опорных знаний.
2мин
5мин
Прием «Корзина идей».
(На доске или слайде изображение корзины) (слайд3).
Давайте наполним «Корзину идей», вспомнив все, что мы знаем о процентах, правила, которые необходимы при выполнении действий с процентами и дробями, основные виды задач на проценты.
(Учитель фиксирует на доске варианты ответов, которые предлагают учащиеся.)
Организация устного счета и повторения основных типов задач на проценты. (слайд4-9)
1)Заполните пропуски в таблице:
1Сотая часть числа
1%
2
Десятая часть числа
… %
3
0,65
…%
4
…
30%
5
0,2
…%
6
1,45
…%
7
0,07
…%
8
1/2
…%
9
Половина
…%
10
Четверть числа
…%
11
Три четверти числа
…%
12
1/3
…%
12
Увеличить в 2 раза —
это значит увеличить на …%
13
Уменьшить в … раза-
это значит уменьшить на 50%.
2)Определите сколько процентов от заданной фигуры составляют заштрихованные в ней части 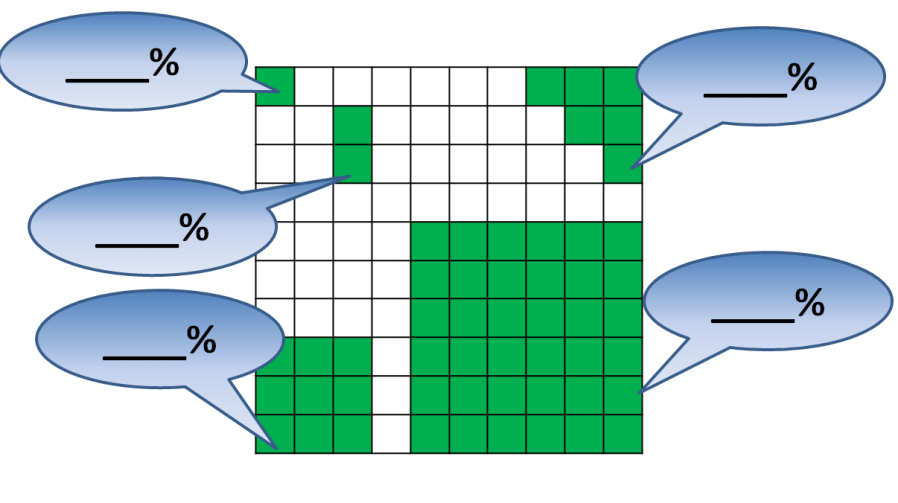 3)Определите сколько процентов от заданной фигуры составляют заштрихованные в ней части
3)Определите сколько процентов от заданной фигуры составляют заштрихованные в ней части
 4)Туристическая фирма предлагает отдых на море, отдых в горах, отдых с лечением , сафари. По диаграмме определите сколько процентов от общего числа приобретенных путевок составляют туры в горы? На сколько процентов отдых на море популярнее сафари?
4)Туристическая фирма предлагает отдых на море, отдых в горах, отдых с лечением , сафари. По диаграмме определите сколько процентов от общего числа приобретенных путевок составляют туры в горы? На сколько процентов отдых на море популярнее сафари?

5)
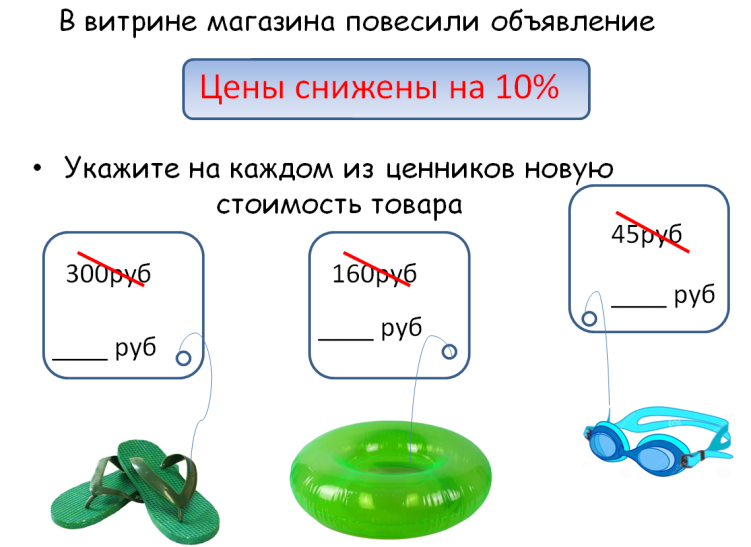
6) На сколько единиц 40 больше, чем 32? А на сколько процентов число 40 больше числа 32? На сколько единиц 32 меньше, чем 40? А на сколько процентов число 32 меньше числа 40?
Учащиеся предлагают свои варианты, «наполняя корзину идей»:
Процент – это сотая часть числа;
Чтобы перейти от десятичной дроби к процентам, надо умножить дробь на 100;
Чтобы перейти от процентов к десятичной дроби, надо разделить количество процентов на 100;
и т.д.
Учащиеся устно выполняют предложенные задания
3.Постановка цели и задач урока.
2мин
Итак, рассмотрев даже небольшое количество задач, мы выяснили, что в нашей жизни человек очень часто сталкивается с понятием процента. Давайте сформулируем тему и целили сегодняшнего урока.
Учащиеся формулируют тему и цель урока, записывают в тетради дату и тему урока:
«Решение задач на проценты», делают выводы о цели урока:
обобщить знания по теме «Проценты» и суметь применить их в реальных жизненных ситуациях.
4.Применение знаний и умений в новой ситуации
20мин
Работа в парах. Выполнение обучающимися компетентностно-ориентированного задания (Приём «гипер-текст»).
А в каких ещё сферах человеческой деятельности встречаются проценты и какие при этом возникают задачи выясним, работая в парах. (Вариан1, приложение1) (слайд10-11)
«Проценты вокруг нас»
Употребление термина «процент» в России начинается в конце XVIII в. Проценты применялись только в торговых и денежных сделках. Затем область их применения расширилась. Проценты — одно из математических понятий, которое часто встречается в повседневной жизни. Можно прочитать или услышать, например, что производительность труда в конце квартала составила 125%, 1% — это 1/100 числа, на данном участке в выборах приняли участие 57,6% избирателей, успеваемость в классе 99%, банк начисляет 8% годовых, молоко содержит 3,2% жира, 86% воды содержится в теле у новорожденного и до 50% у пожилых людей, концентрация активного вещества в растворе 0,4% и т.д. Встречается этот термин и в разговорной речи: «ручаюсь на все сто процентов», «пятьдесят на пятьдесят».
1.Прочитав текст, выполните задания :
Переведите все проценты, встречающиеся в тексте, в десятичные дроби.
На сколько процентов повысилась производительность труда в течении квартала?
Верно ли , что в организме новорожденного ребенка весом 4кг содержится не менее 3 кг 400г воды?
Сколько процентов избирателей не принимали участие в выборах?
Сколько могло бы всего избирателей проголосовать на данном участке , если в выборах на этом участке приняли участие 2880 человек?
2.Решите задачу: Из 120 обточенных деталей 6 деталей оказались бракованными. Сколько процентов составляет брак?
3.Решите задачу: Мальчик предложил младшему брату увеличить число 8 на 30%, а затем результат уменьшить на 30%. « Тут и решать нечего! Ясно, что снова получится число 8.» — воскликнул брат. Согласны ли Вы с таким ответом? Проверьте, прав ли младший брат.
(Учитель может предложить для работы в парах и задания 2-го, 3-го и 4-го вариантов, Приложение 2-4) (слайд 20-28)
Учащиеся в парах выполняют решение предложенных задач.
5. Физкультминутка
1мин
(Учитель проводит разминку) (слайд 29)
Дружно встали, потянулись,
Руки на пояс, повернулись.
Вправо, влево, раз, другой,
Повертели головой.
На носочках постояли,
Спинку стрункой подержали.
А теперь, тихонько сели.
Мы еще не все успели!
Учащиеся поднимаются с мест, повторяют действия за учителем.
6.Контроль усвоения, обсуждение допущенных ошибок и их коррекция.
4мин
Самопроверка выполненной работы (ответы на доске) и корректировка ошибок (если необходимо) (15-19слайды)
Учащиеся сверяются с ответами на доске, анализируют свою работу, выставляют себе отметки (критерий оценивания на доске).
Верных ответов 3 — «3»
Верных ответов 4-5 — «4»
Верных ответов 6-7 — «5»
7. Домашнее задание
1мин
Домашнее задание (учащиеся получают карточки с домашним заданием, приложение5)Учитель комментирует домашние задание и акцентирует внимание на том, что необходимо будет найти концентрацию вещества (процентную концентрацию).
Прочитав текст, выполните задания :
Концентрацией вещества (процентной концентрацией) называют число, показывающее, какую часть массы раствора составляет растворенное вещество. Концентрацию обычно записывают в процентах. Например, если в 100г раствора содержится 5г йода, то концентрация равна 5%.
1. Какую концентрацию будет иметь рассол, если в 1кг воды растворить 250г соли?
2. Для засолки огурцов используют раствор соли (рассол) следующих концентраций: 8% для крупных огурцов, 7% для средних и 6% для мелких. Сколько соли надо взять , чтобы приготовить 10 кг рассола для крупных плодов и 10кг рассола для мелких?
Дополнительное задание :
3.Оля в стакан чая кладет обычно 2 чайные ложки сахара и считает такой чай сладким. Масса чая в стакане 200г, масса сахара в одной ложке 10г. Какова концентрация сахара в Олином чае? (Ответ округлите до целых)
4.Исследуйте, при какой концентрации сахара Вы считаете чай сладким.
Учащиеся записывают домашнее задание, задают вопросы.
Принимают решение относительно дополнительной задачи.
8.Рефлексия (подведение итогов урока)
3мин
1мин
Приём «Синквейн»
Учитель предлагает составить синквейн по данной теме урока, используя следующий алгоритм:
1 строка – кто? что? – 1 существительное.
2 строка – какой? – 2 прилагательных,
описание темы.
действия относящиеся к теме.
фраза из 4-5 слов, пословица,
поговорка, крылатое выражение.
новое осмысление темы –
существительное.
Подведение итогов урока.
Учитель дает оценку работы класса и отдельных учащихся.
Учащиеся предлагают свои варианты, например:
Проценты
Интересные, полезные
Изучают, вычисляют, применяют
В жизни важную роль играют
Концентрация
Учащиеся сдают тетради на проверку.
infourok.ru
Разработка урока математики 5 класса «Решение задач на проценты»
Урок математики по теме: «Решение задач на проценты»
Класс: 5
Формы работы учащихся на уроке: фронтальная — повторение, объяснение нового материала, индивидуальная — проверка знаний, закрепление нового материала, групповая (в парах) – закрепление нового материала.
Конспект урока.
Постановка цели урока (1 минута).
Учитель: Ребята, на прошлом уроке мы познакомились с новым для вас понятием «процент». Вы научились обращать проценты в числа и наоборот. Но как вы считаете для чего необходимо все знать о процентах?
Учащиеся приводят ситуации из бытовой, финансовой и производственной сторон жизни.
Учитель объявляет тему урока «Решение задач на проценты»
Актуализация опорных знаний (5 минут).
Повторение ранее изученного материала, необходимого для изучения темы урока. Форма работы — фронтальная с использованием мультимедийного проектора, используется не только связь «учитель-ученик», но и «ученик-ученик».
На слайдах записаны задания. Первое задание на каждом слайде обсуждается фронтально. Затем учащиеся выполняют оставшиеся задания и обсуждают результаты в парах. Затем заслушивается по одному ответу от пары. Если первая пара ошиблась, то предоставляется возможность второй паре исправить и объяснить правильный ответ. Аналогично по всем слайдам.
Презентация по теме: «Повторение. Проценты» прилагается (Приложение 1).
Проверка знаний (10-11 минут)
Учащиеся разделены на две группы. Первая группа (каждый учащийся индивидуально) выполняет тест на компьютере по теме «Процент» (5 минут). Вторая группа учащихся (каждый учащийся индивидуально) выполняет задания самостоятельной работы по карточкам в тетрадях по теме повторения «Все действия с десятичными дробями»(5 минут). По истечении времени (5 минут) группы учащихся меняют рабочие места: первая группа приступает к выполнению самостоятельной работы в тетрадях, вторая приступает к выполнению теста на компьютерах.
Карточка для выполнения самостоятельной работы на повторение по теме «Все действия с десятичными дробями»:
Выполните действия:а) 3,785∙1000; б) 2,09:0,1; в) 34,71:10; г) 50,01∙0,01.
2. Найдите значение выражения:
а) 58,78 – 1,38 ∙ (275,4 : 6,8).
Тест по теме «Процент» прилагается (Приложение 2)
Физкультминутка. Гимнастика для глаз. (1 минута)
Рефлексия (2 минуты).
Учитель: Какое на ваш взгляд задание вызвало больше всего затруднений при выполнении теста или при работе по карточкам?
Учащиеся высказывают свои мнения по очереди (обязательно каждый учащийся), учитель фиксирует затруднения учащихся с целью дальнейшей индивидуальной коррекционной работы.
Объяснение нового материала (8 минут).
На доске три схемы (три вида) задач на проценты:
Нахождение А% от числа ВВ : 100 = С – число, приходящееся на 1%
С ∙ А = число, соответствующее А%
Нахождение числа М по заданным N%, соответствующих числу Р
Р : N = К – число, приходящееся на 1%
К ∙ 100 = М
Нахождение числа R от числа S в %
R : S = D
D ∙ 100
Учитель читает первую схему и приводит пример задачи. Далее предлагает учащимся привести пример данной задачи, слушает два-три примера, корректировать условия предложенных задач предлагает учащимся. Далее учитель выбирает один из примеров задач и показывает решение задачи согласно первой схемы. Аналогично учитель работает по двум другим видам задач.
Тексты задач:
№1. Завод выпустил 800 телевизоров. Из них 15% были проданы в магазинах города за первую неделю. Сколько телевизоров было продано за первую неделю?
№2. За контрольную работу по математике оценку «4» получили 6 учеников, что составляет 40% всех учеников. Сколько учеников в классе всего?
№3. Из 500га поля в первый день пшеницей засеяли 125га. Какой процент поля засеяли пшеницей в первый день?
VII. Закрепление изученного материала (14 минут)
Первичное закрепление нового материала проходит по методике «Каждый учит каждого». Каждый учащийся получает карточку А, В или С. Каждому номеру карточки соответствует один из трех видов задач на проценты. Карточка оформлена следующим образом: с одной стороны задача, с другой стороны указан номер схемы и решение задачи. Далее учащиеся работают по инструкции (инструкция висит на классной доске):
Прочитайте задачу, определите номер схемы (№1, №2 или №3), решите задачу в тетради.Проверьте решение задачи, используя готовое решение на обратной стороне карточки (в случае наличия ошибок, исправьте их).
Создай пару с учащимся другой карточки.
Задай свою задачу учащемуся, который должен определить номер схемы и решить ее в тетради.
Проконтролируй решение задачи, в случае ошибок исправь и объясни решение.
Выполни задание учащегося из пары.
После того, как в твоей тетради будет решено две задачи из трех, создай пару с учащимся такой карточки, которая у тебя отсутствует.
Выполни пункты 4,5,6.
Итог работы: в твоей тетради решены задачи на три различные схемы задач на проценты.
Учитель во время работы учащихся по инструкции наблюдает, направляет, корректирует действия учеников. А также фиксирует действия учеников в листе учета, отмечая в ячейках того учащегося, с кем работал ученик в паре (например):
VIII.Подведение итогов работы (1 минута).
Учитель анализирует работу учащихся на уроке, выставляет оценки.
IX. Комментирование домашнего задания (1 минута).
Учитель комментирует домашнее задание из учебника: №1600, №1605 – два вида задач на проценты, №1612(а) – задание на повторение (действия с десятичными дробями).
X. Рефлексия (1 минута).
Учитель: Ребята, чем больше всего вам запомнился урок?
Учащиеся высказывают коротко свое мнение.
Приложение 1.
Презентация по теме: «Повторение. Проценты»
1 слайд
ПОВТОРЕНИЕ.
ПРОЦЕНТЫ.
2 слайд
Умножение на 10, 100, 1000,…Вспомните правило умножения десятичной дроби на 10, 100, 1000, …— приведите пример умножения десятичной дроби на 100 устно;
— запишите в тетради пример умножения десятичной дроби на 10;
— проверьте друг у друга правильность умножения.
3 слайд
Деление на 10, 100, 1000,…Вспомните правило деления десятичной дроби на 10, 100, 1000, …
— приведите пример деления десятичной дроби на 100 устно;— запишите в тетради пример деления десятичной дроби на 10;
— проверьте друг у друга правильность деления.
4 слайд
Чтобы перевести обыкновенную дробь в десятичную, надо…
Переведите обыкновенную дробь в десятичную:
3 18 206
5 20 25
5 слайд
Чтобы перевести десятичную дробь в обыкновенную, надо…Переведите десятичную дробь в обыкновенную:
0,32 0,09 3,55
6 слайд
Процент – это … часть числа.1% метра — это ?
1% сотки — это?
1% центнера — это?
1% числа 300 — это?
7 слайд
50% — это . . . числа20% — это . . . часть числа
10% — это . . . часть числа
25% — это . . . часть числа
5% — это . . . часть числа
8 слайд
НАЙДИТЕ:50% от 40; 20% от 150;
10% от 80; 5% от 680;
25% от 48.
9 слайд
Чтобы перевести проценты в десятичную дробь, надо…Запишите в виде десятичной дроби:
48% = … ; 3% = … ;
6,3% = … ; 208% = … .
10 слайд
Чтобы перевести десятичную дробь в проценты, надо…Запишите в виде процентов:
0,31 = …% ; 0,08 = …%;
0,017 = …% ; 4,35 = …% .
Приложение 2.
Тест по теме «Процент»
1% от числа 2500 – это
А) 100; Б) 250; В) 25; Г)2.
2. Выполните умножение 3,2∙100
А) 32; Б) 320; В) 3200; Г) 0,032.
3. 2% — это
А) пятая часть числа; Б) двадцатая часть числа;
В) десятая часть числа; Г) пятидесятая часть числа.
4. Выполните деление 4,23:10
А) 42,3; Б) 0,423; В) 423; Г) 0,0423.
5. Найдите 25% от числа 800
А) 200; Б) 400; В) 160; Г) 100.
6. Переведите обыкновенную дробь 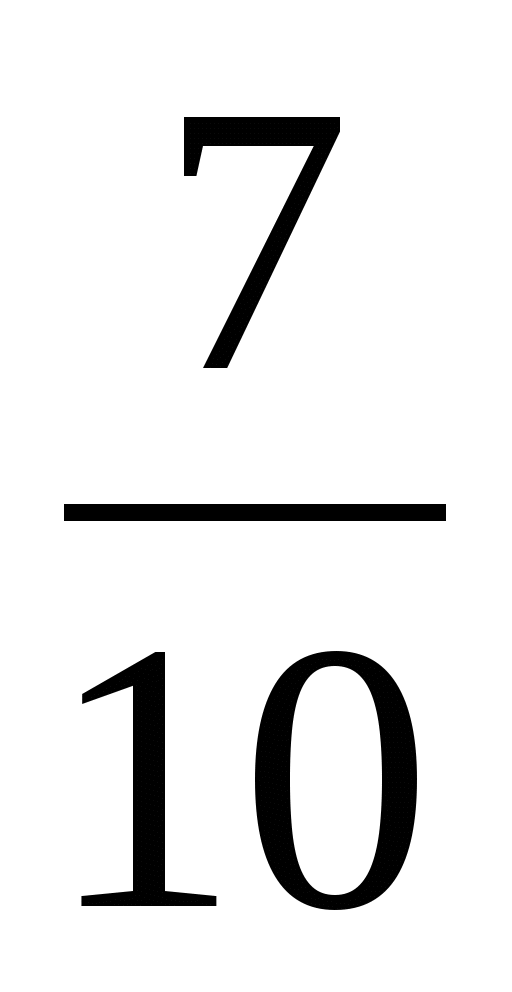 в десятичную
в десятичную
А) 0,07; Б) 0,77; В) 0,007; Г) 0,7.
7. Переведите 79% в десятичную дробь
А) 7,09; Б) 0,79; В) 7,9; Г) 0,079.
8. Переведите десятичную дробь 0,13 в обыкновенную дробь
А)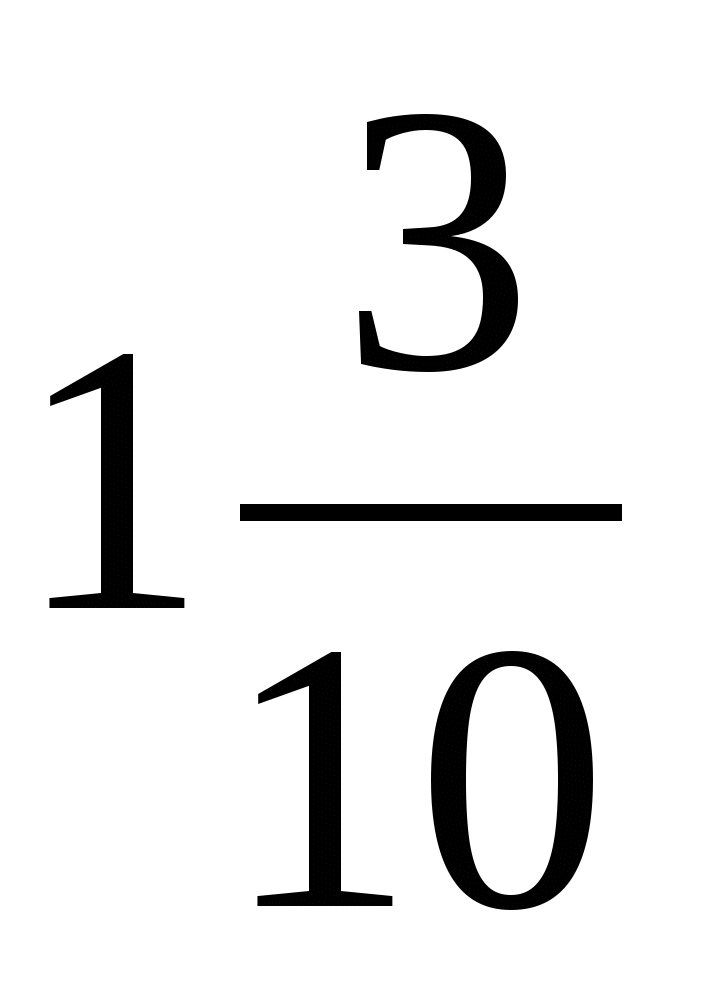 ; Б)
; Б) 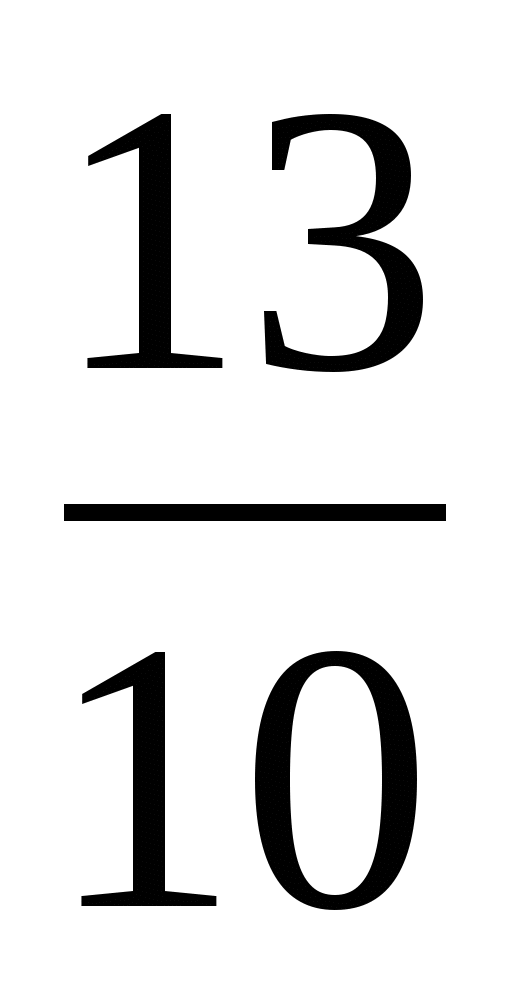 ; В)
; В) 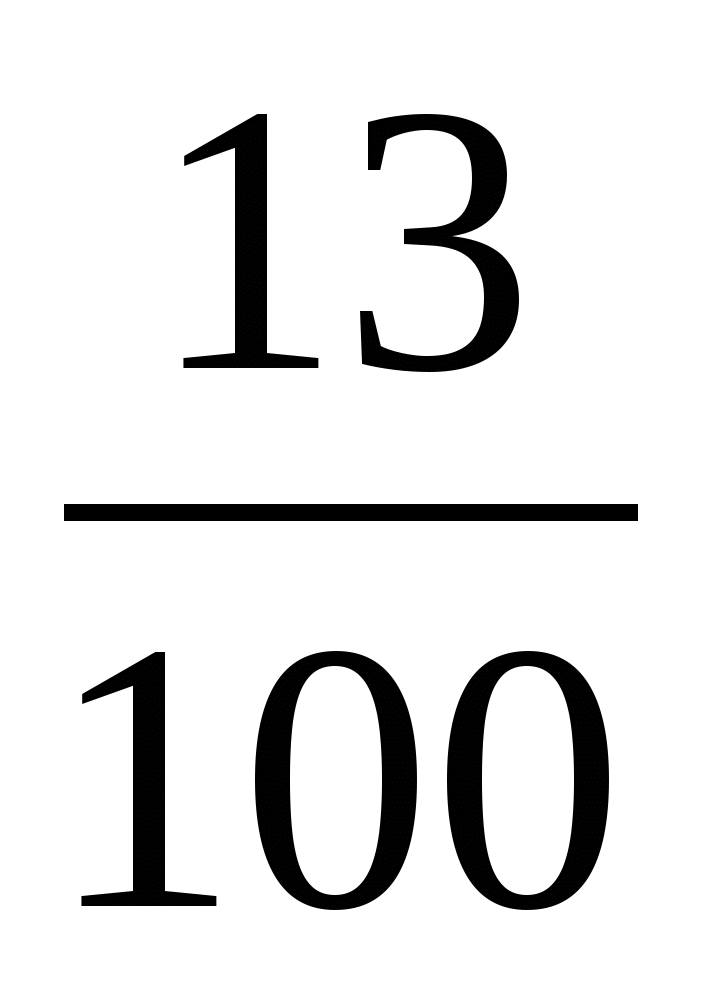 ; Г)
; Г)  .
.
9. Переведите десятичную дробь 0,07 в проценты
А) 7%; Б) 70%; В) 0,7%; Г) 70,7%.
10. Найдите 10% от 280
А) 2,8; Б) 0,28; В) 14; Г) 28.
infourok.ru
Математика. 5 класс. Решение задач на нахождение процента от числа. Для обновленного содержания
План урока
Раздел долгосрочного планирования: 5.4.А:Проценты
Школа: СОШ №34 инновационного типа г.Павлодара
Дата:
ФИО учителя: Антонович А.М.
Класс: 5
Участвовали:
Не участвовали:
Тема урока
Решение задач на нахождение процента от числа
Цели обучения, достигаемые на этом уроке (Ссылка на учебный план)
5.1.1.6
решать текстовые задачи на проценты
Цель урока
— применять понятие «процент» при решении задач;
— решать текстовые задачи на нахождение процента от числа.
Критерии оценивания
— применяет проценты при решении задач;
— решает текстовые задачи на нахождение процента от числа.
Языковые задачи
Лексика и терминология, специфичная для предмета:
— процент, доля;
— один процент, сто процентов;
— процент от числа;
Набор полезных фраз для диалога/письма:
— один процент – это одна сотая часть;
— чтобы выразить дробь, натуральное число в процентах…;
— умножить дробь на натуральное число, дробь…;
— записать краткое условие задачи.
Воспитание ценностей
Независимость Казахстана и Астана – воспитывать гражданский патриотизм. Формировать уважение друг к другу, уважение мнений других, учить работать с карточкой, правильно оформлять результаты самостоятельной работы, проводить работу по правильной формулировке определений математических терминов, вести диалог, дискуссию, доказывать, делать выводы и обобщения. Формативное оценивание позволяет выявить уровень достижения целей урока.
Межпредметная связь
Геометрия, естествознание, химия, физика, экономика.
Предыдущие знания
Дроби и действия над ними, метрическая система мер и весов, прямоугольник и его площадь, процент, нахождение процента от числа.
Ход урока
Запланированные этапы урока
Виды упражнений, запланированных на урок:
Ресурсы
Начало урока
6 мин
Приветствие. Психологическая подготовка.
Учащиеся в парах пожимают друг другу руки и желают удачи на уроке.
Актуализация опорных знаний.
Учащиеся получают карточки с заданиями по вариантам.
Найдите:1) 20% от 100
2) 12% от 50
Найдите:
1) 40% от 100
2) 16% от 50
Дескриптор:
— делит процент на 100;
— умножает полученную дробь на число.
Ответы:
Найдите:1) 20
2) 6
Найдите:
1) 40
2) 8
Проверка осуществляется путем взаимопроверки по готовым ответам, вынесенным учителем на доску.
Обратная связь: поднятие руки вверх
— один палец – одно задание с ошибкой;
— два пальца – оба задания выполнены неверно;
— жест «ok» – оба задания выполнены верно.
Выход на тему и цели урока:
Прием «Могу ли я?»
Учитель задает учащимся наводящие вопросы, которые помогут им самостоятельно сформулировать тему и цели урока.
— Где встречается понятие «Процент» в повседневной жизни? (Магазин, Интернет и т.д.)
— Можно ли посчитать, например, стоимость товара со скидкой? (Да)
— Можно ли из подобной жизненной ситуации сформулировать текстовую задачу? (Да)
— А сможем ли мы её решить? (Не все)
После того, как учащиеся сфомулируют тему и цели урока, учитель, при необходимости, корректирует.
Карточки
Середина урока
31 мин
«Индивидуализация-дифференциация»
Уровень А
1. Цена холодильника понизилась на 15%. Какова цена после снижения, если его первоначальная цена 62 000 тенге?
Дескриптор:
— записывает краткое условие задачи;
— находит новую стоимость в процентах;
— делит процент на 100;
— умножает первоначальную стоимость на полученную дробь;
— выполняет действия и записывает ответ.
2. В клубнике содержится 6% сахара. Сколько килограммов сахара содержится в 35 кг клубники?
Дескриптор:
— записывает краткое условие задачи;
— делит процент на 100;
— умножает первоначальную стоимость на полученную дробь;
— выполняет действия и записывает ответ.
3. Морская вода содержит 95% воды, остальное – соль. Солько тонн соли содержится в 6 т морской воды?
Дескриптор:
— записывает краткое условие задачи;
— находит количество соли в процентах;
— делит процент на 100;
— умножает количество морской воды на полученную дробь;
— выполняет действия и записывает ответ.
Уровень В
1. Банк города Астаны начисляет на вклад ежегодно 5% от внесенной суммы. Клиент сделал вклад в размере 3 750 000 тг. Какая сумма будет на его счету через год?
Дескриптор:
— записывает краткое условие задачи;
— делит процент на 100;
— умножает первоначальный вклад на полученную дробь;
— складывает первоначальный вклад с полученной суммой вознаграждения;
— выполняет действия и записывает ответ.
2. Ширина прямоугольника 6 см, а длина на 75% больше ширины. Найдите площадь прямоугольника.
Дескриптор:
— записывает краткое условие задачи;
— делит процент на 100;
— умножает ширину на полученную дробь;
— находит длину прямоугольника;
— записывает формулу нахождения площади прямоугольника;
— умножает длину прямоугольника на его ширину;
— выполняет действия и записывает ответ.
Уровень С
Туристы преодолели расстояние 180 км. Из них 40% пути они проехали на автомашине, 95% оставшегося пути – на мотоцикле, а остальную часть пути они прошли пешком. Сколько километров туристы прошли пешком?
Дескриптор:
— записывает краткое условие задачи;
— делит процент пройденного на машине пути на 100;
— находит расстояние, пройденное на машине;
— находит, какое расстояние осталось пройти;
— делит процент пройденного на мотоцикле пути на 100;
— находит расстояние, пройденное на мотоцикле;
— находит расстояние, пройденное пешком;
— выполняет действия и записывает ответ.
Проверка и обратная связь методом «Пирамида»
Тот, кто выполнил первым, приносит выполненное задание на проверку учителю. Если задание выполнено верно, то он получает право проверить работы двух одноклассников, после чего приступает к выполнению задания следующего уровня. Каждый из тех, кого проверил данный ученик, при условии правильности выполнения, проверяет в свою очередь ещё двух учащихся данного класса. Таким образом получается пирамида.
Решения и ответы:
Уровень А
1. Первоначальная цена – 62000 тг;
Цена снизилась на 15%
Новая цена – ?
Решение:
100% — 15% = 85%
(тг)
Ответ: новая цена холодильника – 52700 тенге.
2. Сахара – 6%;
Клубники – 35 кг;
Сколько кг сахара – ?
Решение:
(кг)
Ответ: 2,1 кг сахара.
3. Воды – 95%;
Морской воды – 6 т;
Сколько тонн соли – ?
Решение:
100% – 95% = 5%
(т)
Ответ: 0,3 тонны соли.
Уровень В
1. Размер вклада – 3 750 000 тг;
Ежегодный процент – 5%;
Сколько будет через год – ?
Решение:
(тг)
(тг)
Ответ: Через год на счете будет 3937500 тенге.
2. Ширина – 6 см;
Длина на 75% больше ширины;
Площадь прямоугольника – ?
Решение:
(см) – длина прямоугольника
(см2)
Ответ: площадь прямоугольника равна 63 см2.
Уровень С
Расстояние – 180 км;
На машине – 40% всего пути;
На мотоцикле – 95% оставшегося пути;
Остальной путь – пешком;
Сколько прошли пешком – ?
Решение:
(км) – проехали на машине.
(км) осталось.
(км) – проехали на мотоцикле.
(км) – прошли пешком.
Ответ: Туристы прошли пешком 5,4 км.
Физминутка.
Зарядка для глаз.
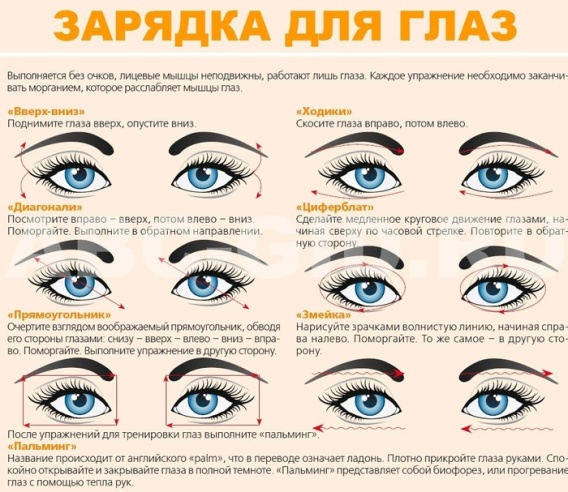
Индививидуальная работа
Учащиеся получают карточки с заданиями по вариантам.
Взаимопроверка по готовым ответам. Учитель выносит решение на флип-чарт, крепит на доску по истечению времени.
Обратная связь – жест «ok», если задача решена верно.
Дескриптор:
— записывает краткое условие;
— делит процент на 100;
— находит количество первого вещества;
— находит количество второго вечества;
— находит разность первого и второго веществ;
— выполняет действия и записывает ответ.
Ответы:
Меди – 85%;Бронзы – 5 кг;
На сколько меди больше, чем олова?
Решение:
(кг) – меди
(кг) – олова
(кг)
Ответ: Меди в бронзе на 3,5 кг больше, чем олова.
Железа – 95%;
Чугуна – 10 кг;
На сколько железа больше, чем примесей?
Решение:
(кг) – железо
(кг) – примеси
(кг)
Ответ: Железа в чугуне на 9 кг больше, чем примесей.
Учебник «Математика» 5 класс, часть 2;
Карточки
Учебник «Математика» 5 класс, часть 2;
Карточки
Конец урока
3 мин
Домашнее задание
Составить задачу, подобную пройденным на уроке. Уровень сложности по выбору.
Рефлексия
Стратегия «Телеграмма»
Кратко написать самое важное, что узнал на уроке и с пожеланиями отправить соседу по парте.
Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими?
Оценивание – как Вы планируете проверять уровень усвоения материала учащимися?
Охрана здоровья и соблюдение техники безопасности
Использование приема «Индивидуализация –дифференциация», сопровождаемое контролем учителя, взаимопроверкой и обратной связью мотодом «Пирамида» позволяет эффективно достигать целей урока, учитывая познавательные потребности каждого ученикака, при этом рационально используя время.
На уроке применялись методы взаимопроверки по готовым ответам, в том числе с помощью флип-чарта, «Пирамида».
В качестве обратной связи применялся метод «ok», формативное оценивание.
Соблюдение правил Техники Безопасности. Проведение физминутки (зарядка для глаз).
Рефлексия по уроку
Была ли реальной и доступной цель урока или учебные цели?
Все ли учащиесы достигли цели обучения? Если ученики еще не достигли цели, как вы думаете, почему? Правильно проводилась дифференциация на уроке?
Эффективно ли использовали вы время во время этапов урока? Были ли отклонения от плана урока, и почему?
Используйте данный раздел урока для рефлексии. Ответьте на вопросы, которые имеют важное значение в этом столбце.
Итоговая оценка
Какие две вещи прошли действительно хорошо (принимайте в расчет, как преподавание, так и учение)?
1:
2:
Какие две вещи могли бы улучшить Ваш урок (принимайте в расчет, как преподавание, так и учение)?
1:
2:
Что нового я узнал из этого урока о своем классе или об отдельных учениках, что я мог бы использовать при планировании следующего урока?
infourok.ru