Закон Ампера
ⓘ Закон Ампера
Закон Ампера — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила оказывается линейно зависимой как от тока, так и от магнитной индукции B {\displaystyle B}. Выражение для силы d F → {\displaystyle d{\vec {F}}}, с которой магнитное поле действует на элемент объема d V {\displaystyle dV} проводника с током плотности j → {\displaystyle {\vec {j}}}, находящегося в магнитном поле с индукцией B → {\displaystyle {\vec {B}}}, в Международной системе единиц имеет вид:
d F (Д) → = j → × B → d V. {\displaystyle d{\vec {F}}={\vec {j}}\times {\vec {B}}dV.} ({Б}}дв.})Направлении действия силы d F (Д) → {\свойства стиль отображения значение д{\ВМК {F}}} определяется по расчету правилу векторного произведения, который легко запомнить с помощью правила левой руки.
Модуль силы Ампера можно найти по формуле:
d F = I B d l sin (Д Ф = я б д л грех) α, {\displaystyle dF=IBdl\sin \alpha,}где α {\свойства стиль отображения значение \альфа } — угол между направлениями вектора магнитной индукции и направления, вдоль которых течет ток.
Сила F {\свойства стиль отображения значение F} максимальна, когда проводник перпендикулярен линиям магнитной индукции α = 90 ∘, sin (грех) α = 1 {\свойства стиль отображения значение \альфа =90^{\п },\грех \альфа =1}:
F = B L I (Ф = Б Л) {\displaystyle F=BLI} (Ф=БЛИ}), где L {\displaystyle L} — длина проводника.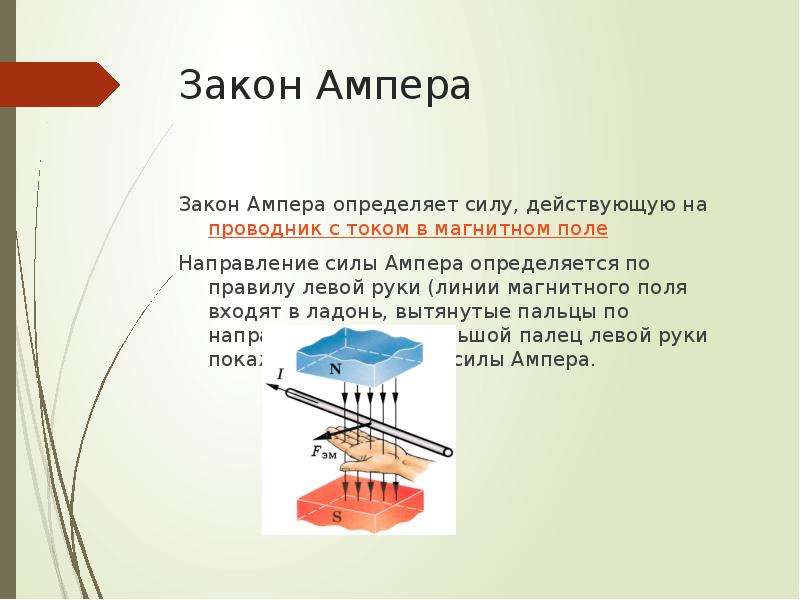
3.4 Закон Ампера. В 1820 году Ампер установил, что сила с которой магнитное поле действует на элемент проводника с током dl, равна (3.4.
Лекция 7 Магнитное поле
Восточно-Сибирский государственный университет технологий и управления Лекция 7 Магнитное поле ВСГУТУ, кафедра «Физика» План Магнитная индукция Магнитное поле движущегося заряда Действие магнитного поля
ПодробнееТема 2.2. МАГНИТНОЕ ПОЛЕ
Тема.. МАГНИТНОЕ ПОЛЕ. Магнитное поле и его характеристики. Закон Био Савара — Лапласа и его применение к расчету магнитного поля 3. Закон Ампера. Взаимодействие параллельных токов 4. Магнитная постоянная.
ПодробнееЛекция 5. Магнитное поле в вакууме.
Лекция 5 Магнитное поле в вакууме Вектор индукции магнитного поля Закон Био-Савара Принцип суперпозиции магнитных полей Поле прямого и кругового токов Теорема о циркуляции вектора индукции магнитного поля
ПодробнееРешение задач по теме «Магнетизм»
Решение задач по теме «Магнетизм» Магнитное поле- это особая форма материи, которая возникает вокруг любой заряженной движущейся частицы. Электрический ток- это упорядоченное движение заряженных частиц
ПодробнееОсновные теоретические сведения
Тема: Основы электростатики Д/З -4 Сав 3. 4. Д-Я План:. Основные понятия и определения. основные характеристики электростатического поля 3. графическое изображение электростатического поля 4. закон Кулона
графическое изображение электростатического поля 4. закон Кулона
Таким образом, мы пришли к закону (5).
Конспект лекций по курсу общей физики Часть II Электричество и магнетизм Лекция. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ (продолжение).4. Теорема Остроградского Гаусса. Применение теоремы Докажем теорему для частного
ПодробнееЛекция 2.5 Магнитное поле
План Лекция.5 Магнитное поле 1) Магнитная индукция ) Закон Био Савара Лапласа 3) Закон Ампера 4) Магнитная постоянная 5) Магнитное поле движущегося заряда 6) Действие магнитного поля на движущийся заряд
ПодробнееЭЛЕКТРОСТАТИКА И МАГНИТОСТАТИКА
Агентство образования администрации Красноярского края Красноярский государственный университет Заочная естественно-научная школа при КрасГУ Физика: Модуль 4 для 10 класса. Учебно-методическая часть. /
ПодробнееМагнитные взаимодействия
Магнитные взаимодействия В пространстве, окружающем намагниченные тела, возникает магнитное поле. Помещенная в это поле маленькая магнитная стрелка устанавливается в каждой его точке вполне определенным
ПодробнееГлава 11 Магнитное поле 88
Глава Магнитное поле 88 Магнитное поле и его характеристики Важнейшей особенностью магнитного поля является то, что оно действует только на движущиеся в этом поле электрические заряды Характер взаимодействия
ПодробнееМагнитное поле токов
И. В. Яковлев Материалы по физике MathUs.ru Магнитное поле токов В основе учения о магнитном поле лежат два экспериментальных наблюдения: 1) магнитное поле действует на движущиеся заряды; ) магнитное поле
ПодробнееЭкзамен.
 Закон Ампера и сила Ампера. I c
Закон Ампера и сила Ампера. I cПостоянное магнитное поле. Факультатив. Магнитные полюса и направление магнитного поля. Магнитные заряды. 1. Назовем северным полюсом магнитной стрелки конец, который показывает на север. 2. Северный полюс
Подробнее1.3. Теорема Гаусса.
1 1.3. Теорема Гаусса. 1.3.1. Поток вектора через поверхность. Поток вектора через поверхность одно из важнейших понятий любого векторного поля, в частности электрического d d. Рассмотрим маленькую площадку
Магнитное поле. Тест 1
Магнитное поле. Тест 1 1. Магнитное поле: чем создается, чем обнаруживается. 1.1 Магнитное поле создается (выберите правильные варианты ответа): 1) заряженными частицами 2)!!! постоянными магнитами 3)!!!
ПодробнееЭкзамен. Закон Био-Савара (-Лапласа).
Экзамен Закон Био-Савара (-Лапласа) I dl, db поле элемента тока Idl, где вектор, направленный из элемента тока в точку наблюдения Другие формы закона Био-Савара: 1 j, db dv 1 i, db ds q [ V,] B магнитное
ПодробнееОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА
КАЗАНСКАЯ ГОСУДАРСТВЕННАЯ АРХИТЕКТУРНО-СТРОИТЕЛЬНАЯ АКАДЕМИЯ Кафедра физики МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО ФИЗИКЕ для студентов специальностей 903, 906, 907, 908, 910 Лабораторная работа
Подробнее4. Электромагнитная индукция
1 4 Электромагнитная индукция 41 Закон электромагнитной индукции Правило Ленца В 1831 г Фарадей открыл одно из наиболее фундаментальных явлений в электродинамике явление электромагнитной индукции: в замкнутом
ПодробнееМАГНИТНОЕ ПОЛЕ.
 Лекция 2.5.
Лекция 2.5.МАГНИТНОЕ ПОЛЕ Лекция 2.5. План 1.Магнитные взаимодействия 2.Закон Био-Савара-Лапласа 3.Магнитное поле движущегося заряда 4.Напряженность магнитного поля 5.Магнитное поле прямого тока 6. Магнитное поле
Подробнее) (Плотность линий поля E ) ~ E, здесь ds
Экзамен. Линии электрического поля E. Линия векторного поля это линия, касательная в каждой точке к которой совпадает с направлением векторного поля. В физике к линиям поля есть дополнительное требование.
Магнитное поле. Лукьянов И.В.
Магнитное поле. Лукьянов И.В. Содержание: 1. Магнитное поле в вакууме. 2. Электромагнитная индукция. 3. Магнитное поле в веществе. Магнитное поле в вакууме. Содержание раздела: 1. Понятие магнитного поля
ПодробнееЧАСТЬ ТРЕТЬЯ КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
ЧАСТЬ ТРЕТЬЯ КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА ГЛАВА 7 Введение в электродинамику 7 Основные понятия и величины электродинамики Электрический заряд Плотность заряда и плотность тока Многие наблюдаемые макроскопические
ПодробнееФИЗИКА МАГНИТНЫХ ЯВЛЕНИЙ
9 ФИЗИКА МАГНИТНЫХ ЯВЛЕНИЙ КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ СИЛА ЛОРЕНЦА И СИЛА АМПЕРА Все проявления магнетизма в природе и технике могут быть сведены к фундаментальному взаимодействию
ПодробнееТеоретическая справка к лекции 5
Теоретическая справка к лекции 5 Электрический заряд. 19 Элементарный электрический заряд e 1, 6 1 Кл. Заряд электрона отрицательный ( e e), заряд протона положительный ( p N e электронов и N P протонов
ПодробнееТема 9.
 Электромагнетизм
Электромагнетизм1 Тема 9. Электромагнетизм 01. Магнитное поле создается постоянными магнитами и движущимися зарядами (токами) и изображается с помощью силовых линий линий вектора магнитной индукции. Рис. 9.1 Силовые линии
ПодробнееПерсональный сайт — 35. Силы, действующие на проводники с током в магнитном поле. Закон Ампера.
Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля:
F = BIlsina (a — угол между направлением тока и индукцией магнитного поля ). Эта формула закона Ампера оказывается справедливой для прямолинейного проводника и однородного поля.
Если проводник имеет произвольную формулу и поле неоднородно, тоЗакон Ампера принимает вид:
dF = I*B*dlsina
Закон Ампера в векторной форме:
dF = I [dl B]
Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B.
Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.
Сила, действующая на проводник с током в магнитном поле
Мы видели, что на заряженную частицу действует сила, равная . Ток в проводнике есть результат движения заряженных частиц тела, то есть равномерно размазанного заряда в пространстве нет, заряд локализован в каждой частице. Плотность тока . На i-ую частицу действует сила .
Выберем элемент объёма и просуммируем силы, действующие на все частицы этого элемента объёма . Сила, действующая на все частицы в данном элементе объёма, определяется как плотность тока на магнитное поле и на величину элемента объёма. А теперь перепишем её в дифференциальном виде: , отсюда – это плотность силы, сила, действующая на единицу объёма. Тогда мы получим общую формулу для силы:.
Тогда мы получим общую формулу для силы:.
Обычно ток течёт по линейным проводникам, редко мы сталкиваемся с случаями, когда ток размазан как-то по объёму. Хотя, между прочим, Земля имеет магнитное поле, а от чего это поле? Источник поля это магнитный момент, это означает, что Земля обладает магнитным моментом. А это означает, что тот рецепт для магнитного момента показывает, что должны быть какие-то токи внутри Земли, они по необходимости должны быть замкнутыми, потому что не может быть стационарного разомкнутого поля. Откуда эти токи, что их поддерживает? Я не специалист в земном магнетизме. Какое-то время назад определённой модели этих токов ещё не было. Они могли быть там когда-то индуцированы и ещё не успели там затухнуть. На самом деле, ток можно возбудить в проводнике, и потом он быстро сам кончается за счёт поглощения энергии, выделения тепла и прочего. Но, когда мы имеем дело с такими объёмами как Земля, то там время затухания этих токов, однажды каким-то механизмом возбуждённых, это время затухания может быть очень длительным и длиться геологические эпохи. Может быть, так оно и есть. Ну, скажем, мелкий объект типа Луны имеет очень слабое магнитное поле, это означает, что оно затухло там уже, скажем, магнитное поле Марса тоже значительно слабее поля Земли, потому что и марс меньше Земли. Это я к чему? Конечно, есть случаи, когда токи текут в объёмах, но то, что мы здесь на Земле имеем это обычно линейные проводники, поэтому эту формулу сейчас трансформируем применительно к линейному проводнику.
Пусть имеется линейный проводник, ток течёт с силой Á. Выберем элемент проводника , объём этого элемента dV, , . Сила, действующая на элемент проводника перпендикулярна плоскости треугольника, построенного на векторах и , то есть направлена перпендикулярно к проводнику, а полная сила находится суммированием. Вот, две формулы решают эту задачу.
Экзамен. Закон Ампера и сила Ампера. I c
Экзамен.
 Закон Био-Савара (-Лапласа).
Закон Био-Савара (-Лапласа).Экзамен Закон Био-Савара (-Лапласа) I dl, db поле элемента тока Idl, где вектор, направленный из элемента тока в точку наблюдения Другие формы закона Био-Савара: 1 j, db dv 1 i, db ds q [ V,] B магнитное
ПодробнееТема 2.2. МАГНИТНОЕ ПОЛЕ
Тема.. МАГНИТНОЕ ПОЛЕ. Магнитное поле и его характеристики. Закон Био Савара — Лапласа и его применение к расчету магнитного поля 3. Закон Ампера. Взаимодействие параллельных токов 4. Магнитная постоянная.
ПодробнееЛекция 7 Магнитное поле
Восточно-Сибирский государственный университет технологий и управления Лекция 7 Магнитное поле ВСГУТУ, кафедра «Физика» План Магнитная индукция Магнитное поле движущегося заряда Действие магнитного поля
ПодробнееМАГНИТНОЕ ПОЛЕ. Лекция 2.5.
МАГНИТНОЕ ПОЛЕ Лекция 2.5. План 1.Магнитные взаимодействия 2.Закон Био-Савара-Лапласа 3.Магнитное поле движущегося заряда 4.Напряженность магнитного поля 5.Магнитное поле прямого тока 6. Магнитное поле
ПодробнееМагнитные взаимодействия
Магнитные взаимодействия В пространстве, окружающем намагниченные тела, возникает магнитное поле. Помещенная в это поле маленькая магнитная стрелка устанавливается в каждой его точке вполне определенным
Магнитное поле токов
И. В. Яковлев Материалы по физике MathUs.ru Магнитное поле токов В основе учения о магнитном поле лежат два экспериментальных наблюдения: 1) магнитное поле действует на движущиеся заряды; ) магнитное поле
ПодробнееЧАСТЬ ТРЕТЬЯ КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
ЧАСТЬ ТРЕТЬЯ КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА ГЛАВА 7 Введение в электродинамику 7 Основные понятия и величины электродинамики Электрический заряд Плотность заряда и плотность тока Многие наблюдаемые макроскопические
ПодробнееРешение задач по теме «Магнетизм»
Решение задач по теме «Магнетизм» Магнитное поле- это особая форма материи, которая возникает вокруг любой заряженной движущейся частицы. Электрический ток- это упорядоченное движение заряженных частиц
Электрический ток- это упорядоченное движение заряженных частиц
Магнитное поле. Лукьянов И.В.
Магнитное поле. Лукьянов И.В. Содержание: 1. Магнитное поле в вакууме. 2. Электромагнитная индукция. 3. Магнитное поле в веществе. Магнитное поле в вакууме. Содержание раздела: 1. Понятие магнитного поля
Подробнееc током I, расположенным в начале
Компьютерная лабораторная работа 4.3 МАГНИТНОЕ ПОЛЕ 1. ЦЕЛЬ РАБОТЫ Ознакомиться с компьютерным моделированием магнитного поля от различных источников. Ознакомиться с видом линий магнитной индукции для
Подробнее9. МАГНИТНОЕ ПОЛЕ ТОКА
Тема 9. МАГНИТНОЕ ПОЛЕ ТОКА 9.1. Магнитные взаимодействия 9.. 3акон Био Савара Лапласа и его применение к расчету полей 9..1. Магнитное поле прямого тока 9… Магнитное поле кругового тока 9..3. Магнитное
ПодробнееЗадачи по магнитостатике
Версия (последняя версия доступна по ссылке) Задачи по магнитостатике Примечание Читая задачи имейте в виду что в печатном тексте вектор обозначается просто жирной буквой без черты или стрелки над буквой
ПодробнееРАБОТА 7 ИЗУЧЕНИЕ МАГНИТНЫХ ПОЛЕЙ
РАБОТА 7 ИЗУЧЕНИЕ МАГНИТНЫХ ПОЛЕЙ Цель работы: Исследование магнитного поля прямого тока, определение магнитной постоянной. Введение Магнитное поле возникает в пространстве, окружающем проводники с током,
Подробнее‘. И пусть для простоты dl dl F V, B
Экзамен Закон электромагнитной индукции Фарадея (продолжение) ЭДС возникает, если поток изменяется по любым причинам ЭДС возникает, если контур перемещается, поворачивается, деформируется, и если контур
ПодробнееЛекция 5.
 Магнитное поле в вакууме.
Магнитное поле в вакууме.Лекция 5 Магнитное поле в вакууме Вектор индукции магнитного поля Закон Био-Савара Принцип суперпозиции магнитных полей Поле прямого и кругового токов Теорема о циркуляции вектора индукции магнитного поля
ПодробнееЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики
Ю. В. Тихомиров ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики С ЭЛЕМЕНТАМИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. ОПТИКА для студентов всех специальностей всех форм обучения МОСКВА — 1 ЛАБОРАТОРНАЯ
ПодробнееМагнитное поле. Тест 1
Магнитное поле. Тест 1 1. Магнитное поле: чем создается, чем обнаруживается. 1.1 Магнитное поле создается (выберите правильные варианты ответа): 1) заряженными частицами 2)!!! постоянными магнитами 3)!!!
ПодробнееКомпас. Магнитное поле Земли.
Магнитное поле Магнитный момент контура с током. Вращающий момент, действующий на контур с током в однородном магнитном поле. Вектор магнитной индукции. Закон Био Савара Лапласа. Расчет полей, создаваемых
ПодробнееЗакон Био-Савара-Лапласа
Министерство образования Российской Федерации Томский политехнический университет Кафедра теоретической и экспериментальной физики «УТВЕРЖДАЮ» Декан ЕНМФ И.П. Чернов г. Закон Био-Савара-Лапласа Методические
ПодробнееКонтур с током в магнитном поле
Лабораторная работа 1 Контур с током в магнитном поле Цель работы: измерение момента M сил Ампера, действующих на рамку с током в магнитном поле, экспериментальная проверка формулы M = [ pmb], где p m
ПодробнееПрактическая работа по теме Решение задач на вычисление силы Ампера и силы Лоренца
Практическая работа № 18
Решение задач на применение закона Ампера Лоренца
Цель: научиться применять закон Ампера и формулу силы Лоренца при решении задач.
Краткая теория
Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля:
FA= IlBsinα
.
Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B. Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.
Fл= qvBsinα,
где q – модуль заряда, v – скорость движения заряженной частицы, α – угол между вектором скоростью и вектором магнитной индукции.
Практическая работа № 18
Решение задач на применение закона Ампера Лоренца
Вариант 1.
1. Какая сила действует на протон, движущийся со скоростью 106 м/с в магнитном поле с индукцией 0.2 Тл перпендикулярно линиям индукции?
2. Определите модуль силы, действующей на проводник длиной 20 см при силе тока 10 А в магнитном поле с индукцией 0.13 Тл, если угол α между вектором В и проводником равен а) 90°; б) 30°.
3. Определите, с какой силой магнитное поле, созданное током, действует на проводник, если магнитная индукция поля 1.5 Тл, рабочая длина проводника 0.4 м и по нему протекает ток 50 А.
4. Вычислите магнитную индукцию поля, если оно действует на проводник с силой 6 Н. Рабочая длина проводника, помещенного в магнитное поле, составляет 60 см, а ток, протекающий в нем, равен 15 А.
5. Параллельно пластинам плоского конденсатора создано однородное магнитное поле индукцией В = 4 мТл. Между пластинами перпендикулярно направлению магнитного поля и параллельно пластинам движется электрон со скоростью v = 5 000 км/с. Определите напряженность Е электрического поля между пластинами.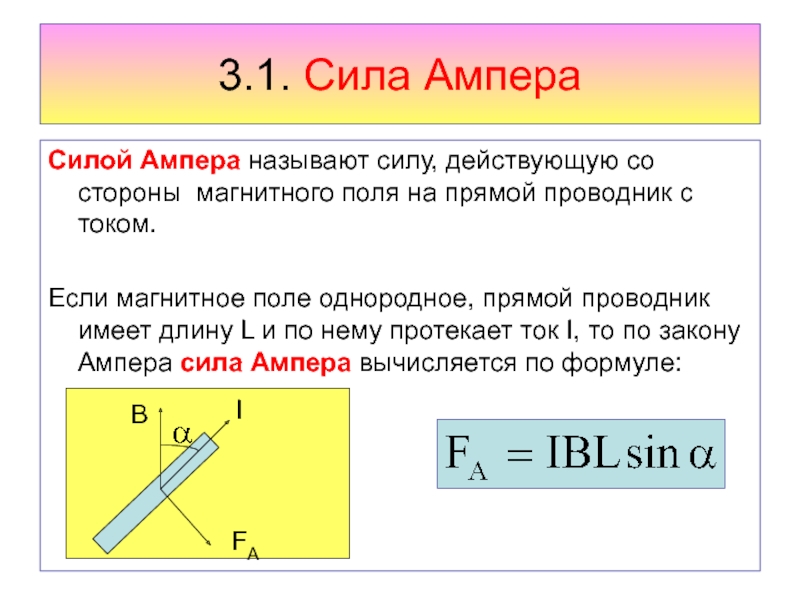
6. Заряженная частица электрон влетает в однородное магнитное поле с индукцией 2 Тл в вакууме со скоростью 10⁵ м/с перпендикулярно линиям магнитной индукции. Вычислим силу, действующую на электрон.
7. Проводник с током удерживается в магнитном поле, индукция которого равна 2 Тл, силой 4 Н. Определить длину проводника, если его сопротивление 3 Ом, разность потенциалов на концах составляет 20 В, а направление тока с линиями индукции образует угол, равный 90°.
8. В проводнике с длиной активной части 8 см сила тока равна 50 А. Он находится в однородном магнитном поле с индукцией 20 мТл. Какую работу совершил источник тока, если проводник переместился на 10 см перпендикулярно линиям индукции?
Практическая работа № 18
Решение задач на применение закона Ампера Лоренца
Вариант 2.
1. По проводнику длиной 45 см протекает ток силой 20 А. Чему равна индукция магнитного поля, в которое помещен проводник, если на проводник действует сила 9 мН?
2. Сила тока в проводнике 4 А, длина активной части проводника 0.2 м, магнитное поле действует на проводник с силой 0.1 Н. Определите индукцию магнитного поля, если линии индукции поля и ток взаимно перпендикулярны.
3. Индукция магнитного поля, созданная прямолинейным проводником в точке, находящейся на расстоянии 20 см от проводника, равна 2·10⁻⁵ Тл. Какой ток проходит по проводнику?
4. С какой силой взаимодействуют два параллельных проводника длиной 1 м каждый, по которым текут токи силой 10 и 40 А в одном направлении, если они находятся в воздухе на расстоянии 0.5 м друг от друга?
5. На проводник длиной 50 см, находящийся в однородном магнитном поле с магнитной индукцией 0.1 Тл, действует сила 0.05 Н. Вычислите угол между направлением силы тока и вектором магнитной индукции, если сила тока равна 2 А.
6. С какой скоростью должен двигаться проводник длиной 20 см в магнитном поле с индукцией 8·10⁻² Тл, чтобы в нем возникла ЭДС индукции 40 мВ.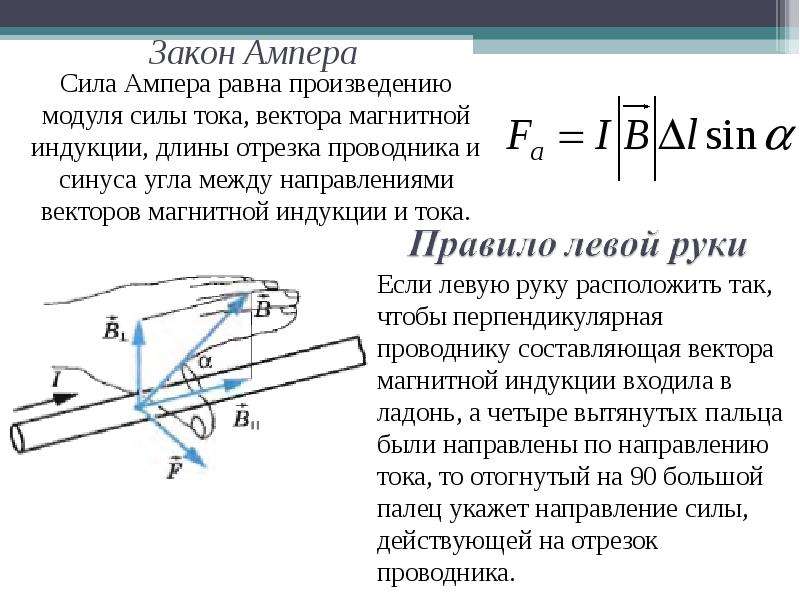 Проводник движется под углом 90° к вектору магнитной индукции.
Проводник движется под углом 90° к вектору магнитной индукции.
7. Электрон движется в вакууме в однородном магнитном поле с индукцией 5·10⁻³ Тл. Радиус окружности, по которой он движется, равен 1 см. Определите модуль скорости движения электрона, если она направлена перпендикулярно к линиям индукции.
8. В однородном магнитном поле, индукция которого равна 0.5 Тл, движется равномерно проводник длиной 10 см. По проводнику течет ток в 2 А. Скорость движения проводника 20 см/с и направлена перпендикулярно к направлению магнитного поля. Найти работу перемещения проводника за 10 с движения.
Закон Ампера и сила Лоренца
Цель:научиться применять закон Ампера и формулу силы Лоренца при решении задач.
Место проведения: учебная аудитория.
Средства обучения:
— методические рекомендации к практической работе № 12.
Виды самостоятельной работы:
Решение тренировочных заданий.
Краткая теория
Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля:
.
Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B. Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.
,
где Q – модуль заряда, v – скорость движения заряженной частицы, α – угол между вектором скоростью и вектором магнитной индукции.
Задания для аудиторной работы
1. Какова индукция магнитного поля, в котором на проводник с длиной активной части 5 см действует сила 50 мН? Сила тока в проводнике 25 А. Проводник расположен перпендикулярно индукции магнитного поля.
2. Под каким углом к линиям индукции однородного магнитного поля должен быть расположен проводник длиной 0,4 м, чтобы поле индукцией 0,8 Тл действовало на проводник силой 1,6 Н, если по нему проходит ток 5 А?
3. Какая сила действует на электрон, движущийся со скоростью 20 Мм/с в магнитном поле индукцией 0,4 Тл под углом 45°?
Самостоятельная работа
Вариант 1
1. Куда будет направлена сила, действующая на проводник с током, находящийся в магнитном поле?
2. Прямолинейный проводник длиной Δl = 0,1 м, по которому течет ток I = 3 А, находится в однородном магнитном поле с индукцией B = 4 Тл и расположен под углом 60° к вектору B. Чему равна сила, действующая на проводник со стороны магнитного поля?
3. В однородное магнитное поле индукцией 10 мТл перпендикулярно линиям индукции влетает электрон с кинетической энергией 48· Дж. Каков радиус кривизны траектории движения электрона в поле?
4. Какая сила действует на протон, движущийся со скоростью 10 Мм/с в магнитном поле индукцией 0,2 Тл под углом 30°?
Вариант 2
1. Куда будет направлена сила, действующая на проводник с током, находящийся в магнитном поле?
2. Какая сила действует на провод длиной 10 см в однородном магнитном поле с магнитной индукцией 2,6 Тл, если ток в проводе 12 А, а угол между направлением тока и линиями магнитной индукции 30º?
3. В направлении, перпендикулярном линиям индукции, влетает в магнитное поле электрон со скоростью 10 Мм/с. Найти индукцию поля, если электрон описал в поле окружность радиусом 1 см.
4. Какая сила действует на электрон, движущийся со скоростью 5 Мм/с в магнитном поле индукцией 4 Тл под углом 45°?
Контрольные вопросы
1. Сформулируйте закон Ампера.
2. Как определить направление силы Ампера? Силы Лоренца?
3. Запишите формулу силы Лоренца.
Практическая работа № 13
Решение задач по теме «Закон электромагнитной индукции.
Самоиндукция»
Цель:научиться применять закон электромагнитной индукции, формулу магнитного потока при решении задач.
Место проведения: учебная аудитория.
Средства обучения:
— методические рекомендации к практической работе № 13.
Виды самостоятельной работы:
Решение тренировочных заданий.
Краткая теория
Электромагнитная индукция – это явление образования электродвижущей силы в проводнике, который помещен в изменяющееся магнитное поле. Кроме того, электромагнитная индукция может возникать при движении проводника относительно постоянного магнитного поля.
Закон Фарадея электромагнитной индукции выражается следующей формулой:
,
где Е- это электродвижущая сила, действующая вдоль произвольно выбранного контура;
ΔФ — магнитный поток, проходящий через поверхность, ограниченную этим контуром.
Согласно правилу Ленца в формуле стоит знак «-» (минус). Правило Ленца гласит: индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Закон Фарадея для катушки, помещенной в переменное магнитное поле, выглядит немного иначе:
,
где Е — электродвижущая сила;
N — число витков;
ΔФ — магнитный поток через один виток.
Электричество и магнетизм
Применим закон Ампера для вычисления силы взаимодействия двух длинных прямолинейных проводников с токами I1 и I2, находящихся на расстоянии d друг от друга (рис. 6.26).
Рис. 6.26. Силовое взаимодействие прямолинейных токов:
1 — параллельные токи; 2 — антипараллельные токи
Видео 6. 2. Взаимодействие двух параллельных проводников с током.
2. Взаимодействие двух параллельных проводников с током.
Проводник с током I1 создает кольцевое магнитное поле, величина которого в месте нахождения второго проводника равна
|
(6.23) |
Это поле направлено «от нас» ортогонально плоскости рисунка. Элемент второго проводника испытывает со стороны этого поля действие силы Ампера
|
(6.24) |
Подставляя (6.23) в (6.24), получим
|
(6.25) |
При параллельных токах сила F21 направлена к первому проводнику (притяжение), при антипараллельных — в обратную сторону (отталкивание).
Аналогично на элемент проводника 1 действует магнитное поле, создаваемое проводником с током I2 в точке пространства с элементом с силой F12. Рассуждая таким же образом, находим, что F12 = –F21, то есть в этом случае выполняется третий закон Ньютона.
Итак, сила взаимодействия двух прямолинейных бесконечно длинных параллельных проводников, рассчитанная на элемент длины проводника, пропорциональна произведению сил токов I1 и I2 протекающих в этих проводниках, и обратно пропорциональна расстоянию между ними. В электростатике по аналогичному закону взаимодействуют две длинные заряженные нити.
На рис. 6.27 представлен опыт, демонстрирующий притяжение параллельных токов и отталкивание антипараллельных. Для этого используются две алюминиевые ленты, подвешенные вертикально рядом друг с другом в слабо натянутом состоянии. При пропускании через них параллельных постоянных токов силой около 10 А ленты притягиваются. а при изменении направления одного из токов на противоположное — отталкиваются.
Для этого используются две алюминиевые ленты, подвешенные вертикально рядом друг с другом в слабо натянутом состоянии. При пропускании через них параллельных постоянных токов силой около 10 А ленты притягиваются. а при изменении направления одного из токов на противоположное — отталкиваются.
Рис. 6.27. Силовое взаимодействие длинных прямолинейных проводников с током
На основании формулы (6.25) устанавливается единица силы тока — ампер, являющаяся одной из основных единиц в СИ.
|
Ампер — это сила неизменяюшегося тока, который, протекая по двум длинным параллельным проводникам, расположенным в вакууме на расстоянии 1 м, вызывает между ними силу взаимодействия 2×10–7 Н на каждый метр длины провода. |
Пример. По двум тонким проводам, изогнутым в виде одинаковых колец радиусом R = 10 см, текут одинаковые токи I = 10 А в каждом. Плоскости колец параллельны, а центры лежат на ортогональной к ним прямой. Расстояние между центрами равно d = 1 мм. Найти силы взаимодействия колец.
Решение. В этой задаче не должно смущать, что мы знаем лишь закон взаимодействия длинных прямолинейных проводников. Поскольку расстояние между кольцами много меньше их радиуса, взаимодействующие элементы колец «не замечают» их кривизны. Поэтому сила взаимодействия дается выражением (6.25), куда вместо надо подставить длину окружности колец Получаем тогда
Магнитные поля, создаваемые токами: закон Ампера
Цели обучения
К концу этого раздела вы сможете:
- Вычислить ток, создающий магнитное поле.
- Используйте правило правой руки 2, чтобы определить направление тока или направление контуров магнитного поля.

Какой ток нужен для создания значительного магнитного поля, возможно, такого же сильного, как поле Земли? Геодезисты скажут вам, что воздушные линии электропередач создают магнитные поля, которые мешают показаниям их компаса.Действительно, когда Эрстед в 1820 году обнаружил, что ток в проводе воздействует на стрелку компаса, он не имел дела с очень большими токами. Как форма проводов, по которым проходит ток, влияет на форму создаваемого магнитного поля? Ранее мы отметили, что токовая петля создает магнитное поле, подобное магнитному полю, но как насчет прямого провода или тороида (бублика)? Как направление создаваемого током поля связано с направлением тока? Ответы на эти вопросы исследуются в этом разделе вместе с кратким обсуждением закона, регулирующего поля, создаваемые токами.
Магнитное поле, создаваемое длинным прямым токопроводящим проводом: Правило правой руки 2
Магнитные поля имеют направление и величину. Как отмечалось ранее, один из способов исследовать направление магнитного поля — это использовать компасы, как показано для длинного прямого токоведущего провода на рисунке 1. Датчики Холла могут определять величину поля. Поле вокруг длинной прямой проволоки находится в виде кольцевых петель. Правило правой руки 2 (RHR-2) возникло в результате этого исследования и справедливо для любого текущего сегмента — направляет большой палец в направлении тока, и пальцы сгибаются в направлении петель магнитного поля , созданных Это.
Рис. 1. (a) Компасы, помещенные рядом с длинным прямым токопроводящим проводом, показывают, что силовые линии образуют круговые петли с центром на проводе. (b) Правило 2 правой руки гласит, что, если большой палец правой руки указывает в направлении тока, пальцы сгибаются в направлении поля. Это правило согласуется с полем, отображаемым для длинного прямого провода, и действительно для любого текущего сегмента.
Напряженность (величина) магнитного поля , создаваемая длинным прямым проводом с током , экспериментально определена равной
. {- 7} \ text {T } \ cdot \ text {m / A} \\ [/ latex] — проницаемость свободного пространства .( μ 0 — одна из основных констант в природе. Позже мы увидим, что μ 0 связано со скоростью света.) Поскольку провод очень длинный, величина поля зависит только от на расстоянии от провода r , а не на расстоянии вдоль провода.
{- 7} \ text {T } \ cdot \ text {m / A} \\ [/ latex] — проницаемость свободного пространства .( μ 0 — одна из основных констант в природе. Позже мы увидим, что μ 0 связано со скоростью света.) Поскольку провод очень длинный, величина поля зависит только от на расстоянии от провода r , а не на расстоянии вдоль провода.Пример 1. Расчет тока, создающего магнитное поле
Найдите ток в длинном прямом проводе, который создаст магнитное поле, вдвое превышающее земное, на расстоянии 5.0 см от проволоки.
СтратегияПоле Земли составляет около 5,0 × 10 −5 Тл, поэтому здесь B из-за проволоки принимается равным 1,0 × 10 −4 Тл. Уравнение [латекс] B = \ frac {\ mu_ {0} I} {2 \ pi r} \\ [/ latex] можно использовать для поиска I , так как все другие величины известны.
РешениеРешение для I и ввод известных значений дает
[латекс] \ begin {array} {lll} I & = & \ frac {2 \ pi rB} {\ mu _ {0}} = \ frac {2 \ pi \ left (5.{-7} \ text {T} \ cdot \ text {m / A}} \\ & = & 25 \ text {A} \ end {array} \\ [/ latex]
ОбсуждениеТаким образом, умеренно большой ток создает значительное магнитное поле на расстоянии 5,0 см от длинного прямого провода. Обратите внимание, что ответ состоит только из двух цифр, поскольку поле Земли в этом примере указано только из двух цифр.
Закон Ампера и другие
Магнитное поле длинного прямого провода имеет большее значение, чем вы можете сначала подумать. Каждый сегмент тока создает магнитное поле, подобное тому, которое имеет длинный прямой провод, а полное поле тока любой формы является векторной суммой полей, создаваемых каждым сегментом. Формальное определение направления и величины поля, создаваемого каждым сегментом, называется законом Био-Савара . Интегральное исчисление необходимо для суммирования поля для тока произвольной формы. Это приводит к более полному закону, называемому законом Ампера , который связывает магнитное поле и ток в общем виде.Закон Ампера, в свою очередь, является частью уравнений Максвелла , которые дают полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла выглядят для разных наблюдателей, привело к современной теории относительности и к осознанию того, что электрические и магнитные поля являются разными проявлениями одного и того же. Большая часть этого выходит за рамки этого текста как на математическом уровне, требующем вычислений, так и в объеме места, которое может быть отведено под него. Но для заинтересованного студента, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы, как элегантные, так и глубокие.В этом тексте мы будем иметь в виду общие особенности, такие как RHR-2 и правила для линий магнитного поля, перечисленные в разделе «Магнитные поля» и «Линии магнитного поля», концентрируясь при этом на полях, создаваемых в определенных важных ситуациях.
Установление связей: относительностьСлушая все, что мы делаем об Эйнштейне, у нас иногда складывается впечатление, что он из ничего изобрел теорию относительности. Напротив, одной из мотиваций Эйнштейна было решить трудности, связанные с пониманием того, как разные наблюдатели видят магнитные и электрические поля.
Магнитное поле, создаваемое токонесущей круговой петлей
Магнитное поле около токоведущей петли показано на рисунке 2. Как направление, так и величина магнитного поля, создаваемого токоведущей петлей, являются сложными. RHR-2 можно использовать для определения направления поля около петли, но для получения более подробной информации необходимы картографирование с помощью компасов и правила о силовых линиях, приведенные в разделах «Магнитные поля» и «Магнитные линии поля».Существует простая формула для напряженности магнитного поля в центре круговой петли . Это
[латекс] B = \ frac {\ mu_ {0} I} {2R} \ left (\ text {в центре петли} \ right) \\ [/ latex],
, где R — радиус петли. Это уравнение очень похоже на уравнение для прямого провода, но действительно только в центре кольцевой петли провода. Сходство уравнений указывает на то, что аналогичная напряженность поля может быть получена в центре петли.Один из способов получить большее поле — это N петель; тогда поле будет B = Nμ 0 I / (2 R ). Обратите внимание, что чем больше петля, тем меньше поле в ее центре, потому что ток дальше.
Рис. 2. (a) RHR-2 показывает направление магнитного поля внутри и снаружи токоведущей петли. (б) Более подробное картирование с помощью компасов или зонда Холла завершает картину. Поле похоже на поле стержневого магнита.
Магнитное поле, создаваемое токопроводящим соленоидом
Соленоид представляет собой длинную катушку провода (с большим количеством витков или петель, в отличие от плоской петли). Из-за своей формы поле внутри соленоида может быть как очень однородным, так и очень сильным. Поле сразу за катушками почти равно нулю. На рисунке 3 показано, как поле выглядит и как его направление задается RHR-2.
Рис. 3. (a) Из-за своей формы поле внутри соленоида длиной l заметно однородно по величине и направлению, на что указывают прямые и равномерно разнесенные силовые линии.Поле вне катушек почти равно нулю. (b) Этот разрез показывает магнитное поле, создаваемое током в соленоиде.
Магнитное поле внутри соленоида с током очень однородно по направлению и величине. Только ближе к концам он начинает ослабевать и менять направление. Поле снаружи имеет те же сложности, что и плоские петли и стержневые магниты, но напряженность магнитного поля внутри соленоида просто равна
.[латекс] B = {\ mu} _ {0} nI \ left (\ text {внутри соленоида} \ right) \\ [/ latex],
, где n — количество петель на единицу длины соленоида ( n = N / l , где N — количество петель, а l — длина).Обратите внимание, что B — это напряженность поля в любом месте однородной внутренней части, а не только в центре. Как следует из примера 2, с соленоидами возможны большие однородные поля, распределенные по большому объему.
Пример 2. Расчет напряженности поля внутри соленоида
Что такое поле внутри соленоида длиной 2,00 м, имеющего 2000 петель и пропускающего ток 1600 А?
СтратегияЧтобы найти напряженность поля внутри соленоида, мы используем [latex] B = {\ mu} _ {0} nI \\ [/ latex].{-1} \ right) \ left (1600 \ text {A} \ right) \\ & = & 2.01 \ text {T} \ end {array} \\ [/ latex]
ОбсуждениеЭто большая напряженность поля, которая может быть установлена над соленоидом большого диаметра, например, при использовании в медицине магнитно-резонансной томографии (МРТ). Однако очень большой ток указывает на то, что поля такой силы нелегко получить. Такой большой ток через 1000 петель, сжатых до метра, приведет к значительному нагреву.Более высокие токи могут быть достигнуты с помощью сверхпроводящих проводов, хотя это дорого. Существует верхний предел тока, поскольку сверхпроводящее состояние нарушается очень сильными магнитными полями.
Есть интересные варианты плоской катушки и соленоида. Например, тороидальная катушка, используемая для удержания реактивных частиц в токамаках, очень похожа на соленоид, изогнутый в круг. Поле внутри тороида очень сильное, но круглое. Заряженные частицы движутся по кругу, следуя силовым линиям поля, и сталкиваются друг с другом, возможно, вызывая синтез.Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. {- 7} \ text {T } \ cdot \ text {m / A} \\ [/ latex] — проницаемость свободного пространства.
[латекс] B = \ frac {\ mu_ {0} I} {2R} \ left (\ text {в центре петли} \ right) \\ [/ latex]
, где R — радиус петли. Это уравнение принимает вид B = μ 0 nI / (2 R ) для плоской катушки из N петель. RHR-2 дает направление поля вокруг петли. Длинная катушка называется соленоидом.
[латекс] B = {\ mu} _ {0} \ text {nI} \ left (\ text {внутри соленоида} \ right) \\ [/ latex]
, где n — количество витков на единицу длины соленоида.Поле внутри очень однородно по величине и направлению.
Концептуальные вопросы
1. Сделайте чертеж и используйте RHR-2, чтобы найти направление магнитного поля токовой петли в двигателе (например, на Рисунке 1 из «Крутящий момент на токовой петле»). Затем покажите, что направление крутящего момента на петле такое же, как и при отталкивании одинаковых полюсов и притяжении разных полюсов.
Глоссарий
- линейка правая 2 (RHR-2):
- правило для определения направления магнитного поля, создаваемого токоведущим проводом: направьте большой палец правой руки в направлении тока, а пальцы согнуты в направлении петель магнитного поля
- Напряженность (величина) магнитного поля, создаваемого длинным прямым проводом с током:
- определяется как [latex] B = \ frac {\ mu_ {0} I} {2 \ pi r} \\ [/ latex], где I — ток, r — кратчайшее расстояние до провода, и μ 0 — проницаемость свободного пространства
- проницаемость свободного пространства:
- — мера способности материала, в данном случае свободного пространства, поддерживать магнитное поле; константа [латекс] \ mu_ {0} = 4 \ pi \ times 10 ^ {- 7} T \ cdot \ text {m / A} \\ [/ latex]
- Напряженность магнитного поля в центре круговой петли:
- определяется как [латекс] B = \ frac {{\ mu} _ {0} I} {2R} \\ [/ latex], где R — радиус петли
- соленоид:
- Тонкая проволока, намотанная на катушку, которая создает магнитное поле при прохождении через нее электрического тока
- Напряженность магнитного поля внутри соленоида:
- определяется как [латекс] B = {\ mu} _ {0} \ text {nI} \\ [/ latex], где n — количество петель на единицу длины соленоида n = N / l , где N — количество петель и l — длина)
- Закон Био-Савара:
- физический закон, который описывает магнитное поле, создаваемое электрическим током, с помощью специального уравнения
- Закон Ампера:
- физический закон, который гласит, что магнитное поле вокруг электрического тока пропорционально току; каждый сегмент тока создает магнитное поле, подобное тому, которое имеет длинный прямой провод, а общее поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым сегментом
- Уравнения Максвелла:
- Набор из четырех уравнений, описывающих электромагнитные явления
Ампера: определение и примеры — видео и стенограмма урока
Уравнение
Поле, создаваемое длинным прямым проводом с током, имеет форму концентрических окружностей.И по мере того, как вы удаляетесь от проволоки, эти круги отдаляются друг от друга — или, другими словами, поле становится слабее. Мы могли бы создать уравнение для этого, используя закон Ампера и выполнив некоторые вычисления. Но на самом деле мы можем вывести это уравнение вообще без каких-либо исчислений.
Вместо интеграла воспользуемся суммой. Сумма всех элементов магнитного поля, составляющих концентрическую окружность: магнитное поле B, , умноженное на длину элемента delta-L, , равно mu-zero (проницаемость свободного пространства), умноженное на ток в провод I .Это закон Ампера.
Затем поймите, что, суммируя все эти элементы, ваша delta-L становится окружностью концентрической окружности, 2pi r . Переставьте это так, чтобы магнитное поле стало объектом, и вы получите ЭТО окончательное уравнение для поля, созданного токоведущим проводом.
Здесь B — магнитное поле в определенной точке пространства, измеренное в теслах.-6. I — ток, протекающий по проводу, измеряется в амперах. А r — это радиальное расстояние от провода, измеренное в метрах. Таким образом, вы можете использовать это уравнение, чтобы вычислить напряженность магнитного поля на расстоянии х от токоведущего провода.
Благодаря уравнению можно рассчитать напряженность поля. Но как насчет направления? Для этого мне нужно, чтобы ты показал мне большой палец правой руки. Нет, серьезно, сделай это прямо сейчас.
Используя эту схему токоведущего провода, укажите большим пальцем в направлении, в котором движется ток, в направлении стрелки, обозначенной I . А теперь представьте, что вы обвиваете пальцами проволоку, хватая ее. Направление, указываемое вашими пальцами, соответствует направлению, в котором указывают линии поля — куда идут стрелки на концентрических кругах. Это называется правилом правой руки, и жизненно важно, чтобы вы случайно не использовали левую руку, потому что вы получите совершенно неправильный ответ.
Примеры
Хорошо, давайте рассмотрим пример. Допустим, у вас есть токоведущий провод, направленный на север. Если по проводу течет ток 0,1 А, каковы величина и направление магнитного поля на расстоянии 0,01 метра над проводом?
Прежде всего, давайте запишем то, что мы знаем. Ток I равен 0,1, расстояние от провода r равно 0.-6 тесла. И это наша величина.
В качестве направления вы можете провести ток на листе бумаги, направив его вверх к верхней части страницы, которую вы можете отметить на севере. Теперь поднимите большой палец правой руки, направьте большой палец к верхней части страницы и представьте, как вы сгибаете пальцы вокруг проволоки. Если вы сделаете это правильно, вы увидите, что ваши пальцы будут указывать налево под проводом и направо над проводом. Если вверх по странице север, то вправо будет восток.-6 тесла к востоку.
Краткое содержание урока
Полная версия закона Ампера — это одно из уравнений Максвелла, описывающих электромагнитную силу. Закон Ампера , в частности, гласит, что магнитное поле, создаваемое электрическим током, пропорционально величине этого электрического тока с константой пропорциональности, равной проницаемости свободного пространства. Стационарные заряды создают электрические поля, пропорциональные величине заряда. Но движущиеся заряды создают магнитные поля, пропорциональные току (заряд и движение).
Единственная проблема с законом Ампера заключается в том, что это дифференциальное уравнение — другими словами, вам нужно провести некоторое исчисление, чтобы его использовать. Но мы можем избежать этого, посмотрев на результат всех этих вычислений для конкретной ситуации. Если мы изучим магнитное поле, создаваемое длинным прямым проводом с током, мы получим это окончательное уравнение для поля, создаваемого проводом с током.
Здесь B — магнитное поле в определенной точке пространства, измеренное в теслах.-6. I — ток, протекающий по проводу, измеряется в амперах. А r — это радиальное расстояние от провода, измеренное в метрах. Таким образом, вы можете использовать это уравнение, чтобы вычислить напряженность магнитного поля на расстоянии х от токоведущего провода. Чтобы получить направление этого поля, мы должны использовать правило правой руки и указывать большими пальцами в направлении тока.
Результаты обучения
После завершения этого урока вы должны уметь:
- Закон штата Ампера
- Рассчитайте магнитное поле токоведущего провода, используя закон Ампера
- Вспомните правило правой руки при вычислении текущего направления
Уравнения Максвелла: Закон Ампера
Четвертое уравнение Максвелла
На этой странице мы объясним значение последнего из уравнений Максвелла, Закон Ампера , который дан в уравнении [1]:
| [Уравнение 1] |
|---|
Ампер был ученым, экспериментировавшим с силами на проводах, по которым проводился электрический ток.Он проводил эти эксперименты еще в 1820-х годах, примерно в то же время, что и Фардей работал над законом Фарадея. Ампер и Фарде не знали, что там работа будет объединена самим Максвеллом, примерно 4 десятилетия спустя.
Силы на проводах мне не особо интересны, потому что у меня никогда не было иногда использовать очень сложные уравнения в ходе моей работы (который включает докторскую степень, некоторые работы в национальной лаборатории, а также занятость в обеих сторонах защиты и промышленность бытовой электроники).Итак, я начну с представляя закон Ампера, который связывает электрический ток, протекающий и магнитное поле вокруг него:
| [Уравнение 2] |
|---|
Уравнение [2] можно объяснить: Предположим, у вас есть проводник, несущий ток, I . Тогда этот ток производит Магнитное поле который обводит проволоку.
Левая часть уравнения [2] означает: если вы возьмете любое воображаемое путь, опоясывающий проволоку, и вы складываете магнитное поле в каждой точке на этом пути, а затем будет численно равняться количеству тока, окруженного этот путь (поэтому мы пишем для замкнутого или замкнутого тока).
Давайте сделаем пример для развлечения. Предположим, у нас есть длинный провод, по которому постоянный электрический ток, I [Ампер]. Что такое магнитное поле вокруг провод, на любое расстояние r [метров] от провода?
Давайте посмотрим на схему на рисунке 1. У нас есть длинный провод, по которому течет ток. I Ампер. Мы хотим знать, что такое магнитное поле на расстоянии р из проволоки. Итак, мы проводим воображаемый путь вокруг провода, который синяя пунктирная линия справа на рисунке 1:
Фигура 1.Расчет магнитного поля по закону Ампера.
Закон Ампера [Уравнение 2] гласит, что если мы сложим (интегрируем) Магнитные Поле вдоль этого синего пути, тогда численно это должно быть равно вложенный ток I .
Теперь в силу симметрии магнитное поле будет однородным (не меняющимся) при расстояние r от провода. Длина пути синего пути на рисунке 1 окружность равна окружности радиуса r : .
Если мы складываем постоянное значение магнитного поля (назовем его H ), то левая часть уравнения [2] становится простой:
| [Уравнение 3] |
|---|
Таким образом, мы выяснили, какова величина поля H . А поскольку r было произвольным, мы знаем, что такое H-поле везде. Уравнение [3] утверждает, что магнитное поле уменьшается по величине при движении. дальше от провода (из-за члена 1 / r).
Итак, мы использовали закон Ампера (Уравнение [2]), чтобы найти величину Магнитное поле вокруг провода. Однако поле H является Векторное поле, Это означает, что в каждом месте есть как величина, так и направление. Направление H-поля везде касательно мнимых петель, как показано на рисунке 2. Правило правой руки определяет направление магнитного поля:
Рис. 2. Величина и направление магнитного поля вокруг провода.
Манипулирование математикой закона Ампера
Мы собираемся проделать тот же трюк с теоремой Стокса, который мы сделали. когда смотришь на Закон Фарадея. Мы можем переписать закон Ампера в уравнении [2]:
| [Уравнение 4] |
|---|
В правой части равенства в уравнении [4] мы использовали теорему Стокса изменить линейный интеграл вокруг замкнутого контура на завиток того же поля через поверхность, заключенную в петлю ( S ).
Мы также можем переписать общий ток () как поверхностный интеграл Плотность тока ( Дж ):
| [Уравнение 5] |
|---|
Итак, теперь у нас есть исходный закон Ампера (уравнение [2]), переписанный в терминах поверхностные интегралы (уравнения [4] и [5]). Следовательно, мы можем заменить их вместе и получите новую форму закона Ампера:
| [Уравнение 6] |
|---|
Теперь у нас есть новая форма закона Ампера: ротор магнитного поля равен к Плотность электрического тока.Если вы проницательный ученик, вы можете заметить, что уравнение [6] не окончательная форма, которая записана в уравнении [1]. Существует проблема с уравнением [6], но только в 1860-х годах Джеймс Клерк Максвелл разобрались в проблеме и объединили электромагнетизм с уравнениями Максвелла.
Плотность тока смещения
Закон Ампера был записан как в Уравнении [6] до Максвелла. Итак, начнем посмотрите, что с этим не так. Сначала я должен выбросить еще один векторная идентичность — расхождение завиток любого векторного поля всегда равно нулю:
| [Уравнение 7] |
|---|
Итак, давайте рассмотрим расхождение закона Ампера, записанное в уравнении [6]:
| [Уравнение 8] |
|---|
Таким образом, уравнение [8] следует из уравнений [6] и [7].Но там сказано, что дивергенция плотности тока Дж, всегда равна нулю. Это правда?
Если расхождение J всегда равно нулю, это означает, что электрическая ток, текущий в любую область, всегда равен электрическому току, текущему вне региона (без расхождения). Это кажется несколько разумным, поскольку электрический ток в цепях течет по петле. Но давайте посмотрим, что будет, если мы поставить в цепь конденсатор:
Рисунок 3. Напряжение, приложенное к конденсатору.
Теперь мы знаем из теории электрических цепей, что если напряжение непостоянно (например, любая периодическая волна, такая как напряжение 60 Гц, выходящее из вашего розетки), то через конденсатор будет протекать ток. То есть у нас есть I не равно нулю на рисунке 3.
Однако конденсатор в основном представляет собой две параллельные проводящие пластины, разделенные воздуха. Следовательно, нет токопроводящего пути для протекания тока. Это означает, что электрический ток не может проходить через воздух конденсатора.Это проблема, если мы подумаем об уравнении [8]. Чтобы показать это более наглядно, давайте возьмем объем, который проходит через конденсатор, и посмотрим, дивергенция J равна нулю:
Рис. 4. Дивергенция J не равна нулю.
На рисунке 4 мы нарисовали воображаемый объем красным цветом и хотим проверить если расходимость плотности тока равна нулю. Выбранный нами объем, имеет один конец (обозначенный стороной 1), где ток поступает в объем через черный провод.Другой конец нашего объема (обозначенный стороной 2) делит конденсатор пополам.
Мы знаем, что ток течет в петле. Итак, ток поступает через сторону 1 нашего красного тома. Однако на стороне 2 отсутствует электрический ток. В воздухе конденсатора ток не течет. Это означает, что текущий входит в объем, но из него ничего не выходит — поэтому расхождение J составляет не ноль. Мы только что нарушили наше уравнение [8], что означает, что теория не верна.И так было до тех пор, пока пришел наш друг Максвелл.
Максвелл знал, что электрическое поле (и Плотность электрического потока ( D ) внутри конденсатора менялся. И он знал, что изменяющееся во времени магнитное поле возникло соленоидальное электрическое поле (т.е. это закон Фарде — curl E равен производной по времени B ). Итак, почему это не так изменяющееся во времени поле D вызовет соленоидальное поле H (я.е. рождает завиток H ). Вселенная любит симметрию, так почему бы не ввести этот термин? И другие Максвелл это сделал, и он назвал этот термин плотностью тока смещения :
| [Уравнение 9] |
|---|
Этот термин «исправит» проблему схемы, показанную на рисунке 4, и сделает Закон Фарде и Закон Ампера более симметричны. Это был большой вклад Максвелла. И можно подумать, что это слабый вклад.Но существование этого термина объединил уравнения и привел к пониманию распространения электромагнитных волны и доказательство того, что все волны движутся с одинаковой скоростью (скоростью света)! И именно это объединение уравнений, которое представил Максвелл, привело к коллективное множество, известное как уравнения Максвелла. Итак, если мы добавим ток смещения согласно закону Ампера, как записано в уравнении [6], тогда мы имеют окончательную форму закона Ампера:
| [Уравнение 10] |
|---|
Так появился Закон Ампера!
Толкование закона Ампера
Итак, что означает уравнение [10]? Следующие последствия этого закона:
Закон Ампера с участием Максвелла заложил основу для Электромагнетизм, как мы это понимаем сейчас.Итак, мы знаем, что изменяющийся во времени D дает начало H поле, но от Фардея Мы знаем, что изменяющееся поле H порождает поле E …. и так далее, и так далее, и распространяются электромагнитные волны — и это круто.
Уравнения Максвелла
Эта страница о Законе Ампера для цепей или о том, что защищено авторским правом, в частности поскольку это относится к уравнениям Максвелла. Авторские права www.maxwells-equations.com, 2012.
Закон Ампера, декабрь 1972 г. Популярная электроника
Декабрь 1972 г. Популярная электроника ОглавлениеВоск, ностальгирующий по истории ранней электроники. См. Статьи с Популярная электроника, опубликовано с октября 1954 года по апрель 1985 года. Настоящим подтверждаются все авторские права. |
Вот краткая, но информативная введение в историю открытия французским физиком Андре Мари Ампером одноименный закон, регулирующий отношения между током и магнитным поле.Как известно большинству посетителей RF Cafe, как постоянный, так и изменяющийся во времени ток будут генерировать магнитное поле, но только изменяющееся во времени магнитное поле может генерировать ток поток. Менее чем через неделю после свидетельства Ганс Кристиан Эрстед демонстрирует влияние токоведущего провода на компас иглой, Ампер обнаружил Правило правой руки текущего направления потока на основе направления магнитное поле.
Закон Ампера
Дэвид Л.Heiserman
Ампера Закон гласит, что пара проводников, несущих электрические токи, оказывает магнитное воздействие на друг друга. Кроме того, величина этой силы зависит от величины протекающего тока. в каждом проводнике, а также расстояние и угол между ними. Андре Мари Ампер, французский физик и математик, объявил об этом новом законе природы 18 сентября 1820 года. Как будто открывая такого закона было недостаточно, Ампер использовал его, чтобы заложить теоретические основы для совершенно нового Раздел электричества и физики называется электродинамикой — и он сделал это всего за семь лет.
Ранние годы. Оглядываясь на работы Ампера с нашей современной точки зрения, кажется, что что мужчина провел первые сорок пять лет своей жизни, готовясь к семи годам Открытие: Родившись в умеренно обеспеченной и образованной семье, юный Ампер имел большую часть преимущества, доступные французским детям, выросшим во время Великой революции. Более того, он был вундеркиндом, изучившим геометрию и математику в возрасте двенадцати лет, читая тексты которые были написаны на их оригинальной латыни.
Когда Ампера было восемнадцать, его отец был казнен во время кровавого «правления террора», прокатилась по Франции. Виды и звуки революции, завершенные жестоким отцом смерть, потрясла разум Ампера. Следующие шесть лет своей жизни он провел в бесцельных блужданиях. о деревне, строительстве замков из песка на берегу моря и сочинении бессмысленных стихов.
В конце этого потерянного периода времени Ампер женился и перешел на более традиционный стиль жизни.Его блестящий ум вернулся, но семейные деньги пропали. Итак, Ампер устроился на свою первую работу профессором в Университете Бурген-Бресс. Не прошло и трех лет прошел до того, как умерла его жена, что привело Ампера в ступор еще на год.
Наполеон слышал о талантах этого несчастного юного гения и предложил Амперу должность преподавателя в школе в Париже. Расстроен жизнью, но очень хочет вернуться в свою работу, Ампер принял эту должность и оставался там до конца своих профессиональных занятий. жизнь.
Ампер начал писать статьи по широкому кругу предметов, включая химию, математику, молекулярная физика и биология. В то время его особый интерес была к теории игр. Эти работы были важны для других ученых, но они не относились к категории тех, которые подпадают под категория особого величия.
Новое открытие. 11 сентября 1820 года Ампер посетил демонстрацию произведений Эрстеда. новое открытие.Демонстрация показала, что ток, протекающий по прямому отрезку провод заставляет стрелку компаса поворачиваться в положение под прямым углом к проводнику. Даже в то время как эта демонстрация все еще продолжалась, должно быть, подумал Ампер: «Поскольку один проводник нес электрический ток может воздействовать на стрелку компаса, почему два токонесущих проводники оказывают друг на друга силу? »
Возбужденный представлением о том, что токоведущие провода производят точно такие же магнитные сил в качестве грузовых камней и постоянных магнитов, Ампер немедленно отказался от всех своих других работ. и начал исследовать этот «искусственный» источник магнетизма.За семь дней Ампер развил фундаментальные теории электродинамики, спроектированные и построенные экспериментальные установки, выполненные необходимые эксперименты, и представил свои открытия научному миру. Никаких других крупных научное открытие когда-либо было задумано и проверено за такой короткий период времени. Ампер действительно был полностью готов к этой неделе великих открытий.
Две очень важные идеи возникли в результате экспериментов Ампера на той неделе.Для во-первых, он разработал то, что мы теперь обычно называем «правилом правой руки». Согласно этому правило, с большим пальцем правой руки, указывающим в направлении обычного электрического тока (положительный к отрицательному) через провод, скрученные пальцы этой руки указывают направление результирующего магнитного поля. Эрстед уже пришел к выводу, что магнитные силовые линии выходят под прямым углом из проводника. Ампер, однако, усовершенствовал это понятие, сделав можно предсказать смысл или полярность этого поля.
Другая важная идея в первой статье Ампера касалась притяжения и отталкивания. двух параллельных проводов, по которым проходит электрический ток. Ампер показал, что токи текут через провода в одном направлении заставлял их притягиваться друг к другу, в то время как токи текли в противоположных направлениях заставили провода отталкиваться.
Открытия Ампера о направлении магнитных полей вокруг проводника и силы, действующие на пару токоведущих проводов, сегодня так же важны, как и раньше. 150 лет назад.Что, пожалуй, еще более примечательно, так это почти невероятная простота лабораторного оборудования, которое он использовал. Ему удалось открыть совершенно новую технологию, не используя ничего лишнего. чем несколько отрезков медного провода, компас и пара батареек Вольта.
В течение семи лет после его предварительного объявления бумаги Ампера становились все более популярными. приправлен сложными уравнениями. Его ранние исследования геометрии и исчисления приносили прибыль. выключенный. Другие европейские исследователи тоже переняли несколько хороших идей из работ Эрстеда; но большинству из этих людей не хватало высокого уровня математических знаний и творческой проницательности Ампер одержим.
Снова в лабораторию. Его работа вскоре достигла точки, когда ему пришлось вернуться в лабораторию. чтобы подтвердить его уравнения. На этот раз ему нужно было получить точные цифры количества текущих поток и силы между проводниками. Используя то, что тогда было революционно новым измерением прибор, гальванометр, Ампер смог измерить количество тока, протекающего через провода. Его собственная оригинальная работа с катушками из проволоки и соленоидами, кстати, была непосредственно ответственным за изобретение того самого гальванометра, который он использовал.
Поскольку он также должен был знать точное количество силы, с которой два проводника действуют друг на друга, Ампер изобрел несколько специализированных инструментов. Одна из них была обычная лаборатория баланс, у которого был соленоид, прикрепленный к одной стороне балки. Этот соленоид помещается внутри большего один прикреплен к нижней части весов. Ток, протекающий через два соленоида, заставил меньшее движение внутри большего. Поместив калиброванные гири на чашку весов на противоположный конец балки, Ампер мог определить точное количество силы, которое два набора проводники давили друг на друга.
По словам известного ученого Джеймса Клерка Максвелла, фундаментальные уравнения Ампера «выпрыгнул из разума электричества Ньютона взрослым и во всеоружии». Ампера уравнения были практически завершены еще до того, как он намеревался продемонстрировать их справедливость в лаборатория. Составление уравнений перед проведением экспериментов противоречило общепринятым научная процедура того времени, но один простой факт заставил замолчать всех критиков — уравнения и лабораторные эксперименты всегда соглашались.И в честь этого «Ньютона электричества» Международный Конгресс электриков назвал в его честь основную единицу тока — ампер.
Ампер был трудолюбивым и научным гением. Даже когда он концентрировался работая над созданием основ электродинамики, он преподавал в университете. Возможно, это была ошибка. Ампер был известен тем, что останавливал свои лекции в середине предложение, в то время как его разум блуждает по какой-то новой идее или уравнению.У него также была привычка позволяя своей работе за доской извиваться в какую-то новую линию математических рассуждений, оставляя его ученики ломают голову над нагромождением непонятных фигур, связанных с какой-то новой идеей в электродинамике.
Ampere действительно был классическим примером рассеянного профессора. Не может быть никаких сомнений, тем не менее, что он был одним из самых успешных рассеянных профессоров всех времен. в отличие доски, унесшие его идеи в небытие, основные уравнения Ампера, по сути, стоят без изменений по сей день.
Опубликовано: 25 июля, 2017
B35: Новый взгляд на закон Гаусса для магнитного поля и закон Ампера
Закон Гаусса для магнитного поля
Помните закон Гаусса для электрического поля? Это тот, который в концептуальном плане утверждает, что количество силовых линий электрического поля, выходящих наружу через замкнутую поверхность, пропорционально количеству электрического заряда внутри замкнутой поверхности. В форме уравнения мы записали это как:
\ [\ oint \ vec {E} \ cdot \ vec {dA} = \ frac {Q _ {\ mbox {enclosed}}} {\ epsilon_o} \]
Мы назвали величину слева электрическим потоком \ (\ Phi_E = \ oint \ vec {E} \ cdot \ vec {dA} \).
Что ж, есть закон Гаусса и для магнитного поля. В каком-то смысле он очень похож, потому что он включает в себя величину, называемую магнитным потоком, которая математически выражается как \ (\ Phi_B = \ oint \ vec {B} \ cdot \ vec {dA} \) и представляет собой количество магнитного поля. линии, торчащие наружу через закрытую поверхность. Большая разница заключается в том, что не существует такого понятия, как «магнитный заряд». Другими словами, магнитного монополя не существует. В законе Гаусса для электрического поля электрический заряд (деленный на \ (\ epsilon_o \)) справа.В законе Гаусса для магнитного поля справа \ (0 \):
\ [\ oint \ vec {B} \ cdot \ vec {dA} = 0 \]
Что касается расчета магнитного поля, полезность этого уравнения ограничена. Но в сочетании с законом Ампера в интегральной форме (см. Ниже) он может пригодиться для расчета магнитного поля в случаях, связанных с большой симметрией. Кроме того, его можно использовать в качестве проверки для случаев, когда магнитное поле было определено другими способами.
Закон Ампера
Мы уже довольно много говорили о законе Ампера.Это тот, который говорит, что ток вызывает магнитное поле. Обратите внимание, что в этом ничего не говорится об изменении. Это просто причинно-следственная связь. Интегральная форма закона Ампера одновременно широка и конкретна. Читается:
\ [\ oint \ vec {B} \ cdot \ vec {d \ ell} = \ mu_o I _ {\ small THROUGH} \]
где:
\ (\ circ \) круг на знаке интеграла и \ (\ vec {d \ ell} \), дифференциальная длина, вместе говорят вам, что интеграл (бесконечная сумма) находится вокруг воображаемого замкнутого контура .
\ (\ vec {B} \) — магнитное поле,
\ (\ vec {d \ ell} \) — бесконечно малый элемент пути замкнутого цикла,
\ (\ mu_o \) — универсальная постоянная, называемая магнитной проницаемостью свободного пространства, а
\ (I _ {\ small THROUGH} \) — это ток, проходящий через область, заключенную в петлю.
Закон Ампера в интегральной форме говорит о том, что если вы суммируете магнитное поле вдоль сегмента пути, умноженное на длину сегмента пути для всех сегментов пути, составляющих воображаемый замкнутый контур, вы получите ток через область заключенный в цикл, умноженный на универсальную константу.Интеграл \ (\ oint \ vec {B} \ cdot \ vec {d \ ell} \) на любом замкнутом пути, по которому он выполняется, называется циркуляцией магнитного поля на этом замкнутом пути. Итак, другой способ сформулировать интегральную форму закона Ампера — сказать, что циркуляция магнитного поля на любом замкнутом пути прямо пропорциональна току через область, ограниченную этим путем. Вот изображение:
На картинке я показываю все, кроме магнитного поля.Идея состоит в том, что для каждого бесконечно малого сегмента \ (\ vec {d \ ell} \) воображаемой петли вы ставите точки магнитного поля \ (\ vec {B} \) в позиции сегмента на \ ( \ vec {d \ ell} \). Сложите все такие скалярные произведения. Общая сумма равна \ (\ mu _ {\ small 0} \), умноженному на \ (I \) через цикл.
Итак, для чего он нужен? Закон Ампера в интегральной форме имеет для нас ограниченную пользу. Его можно использовать в качестве отличной проверки для случая, когда кто-то вычислил магнитное поле, обусловленное некоторым набором проводников с током, другим способом (например,грамм. используя закон Био-Савара, который будет представлен в следующей главе). Кроме того, в случаях, связанных с высокой степенью симметрии, мы можем использовать его для расчета магнитного поля из-за некоторого тока.
Например, мы можем использовать закон Ампера, чтобы получить математическое выражение для величины магнитного поля, создаваемого бесконечно длинным прямым проводом. Я собираюсь включить наше понимание того, что для сегмента провода с током в нем ток создает магнитное поле, которое образует петли вокруг провода в соответствии с правилом правой руки для чего-то изогнутого и прямого.Другими словами, мы уже знаем, что для длинного прямого провода, по которому ток идет прямо от вас, магнитное поле распространяется петлями вокруг провода, которые, с вашей точки зрения, идут по часовой стрелке.
Исходя из симметрии, мы можем утверждать, что величина магнитного поля такая же для данной точки, как и в любой другой точке, которая находится на том же расстоянии от провода, что и данная точка. При реализации закона Ампера нам необходимо выбрать воображаемую петлю, называемую в данном контексте петлей Ампера, которая позволяет нам получить некоторую полезную информацию из закона Ампера.В этом случае разумным выбором будет круг, плоскость которого перпендикулярна прямому проводу, а центр лежит на прямом проводе.
Здесь \ (I \) хочу поделиться с вами некоторой информацией об интегральной форме закона Ампера. Что касается \ (\ vec {d \ ell} \): каждый вектор \ (\ vec {d \ ell} \) с данной точки зрения может быть охарактеризован как представляющий либо шаг по часовой стрелке по пути, либо против часовой стрелки. шагать по тропинке. И, если один по часовой стрелке, все они должны быть по часовой стрелке.Если один против часовой стрелки, все они должны быть против часовой стрелки. Таким образом, при выполнении интеграла по замкнутому контуру обход контура осуществляется либо по часовой стрелке, либо против часовой стрелки с заданной точки обзора. Теперь вот важная информация о направлении: ток, который проходит через петлю в том направлении, которое связано со смыслом (по часовой стрелке или против часовой стрелки) обхода петли в соответствии с правилом правой руки для чего-то вьющегося, чего-то прямого (с петлей, являющейся чем-то кудрявый, а текущее — прямое) считается положительным.Итак, для рассматриваемого случая, если я выберу обход цикла по часовой стрелке, если смотреть с точки зрения, которая заставляет вещи выглядеть так:
, то текущий \ (I \) считается положительным. Если вы согнете пальцы вокруг петли по часовой стрелке, большой палец будет направлен от вас. Это означает, что ток через петлю, направленный от вас, положительный. Именно такой ток мы имеем в данном случае. Итак, когда мы подставляем \ (I \) для рассматриваемого случая в общее уравнение (закон Ампера),
\ [\ oint \ vec {B} \ cdot \ vec {d \ ell} = \ mu_o I _ {\ small THROUGH} \]
для текущего \ (\ mu_o I _ {\ small THROUGH} \) идет со знаком «+».
\ [\ oint \ vec {B} \ cdot \ vec {d \ ell} = \ mu_o I \]
Теперь, с выбранной мной петлей, каждый \ (\ vec {d \ ell} \) точно параллелен магнитному полю \ (\ vec {B} \) в месте расположения \ (\ vec {d \ ell } \), поэтому \ (\ vec {B} \ cdot \ vec {d \ ell} \) — это просто \ (B \ space d \ ell \). То есть, с нашим выбором петли Ампера закон Ампера упрощается до:
\ [\ oint B d \ ell = \ mu_o I \]
Кроме того, исходя из симметрии, с нашим выбором петли Ампера, величина магнитного поля \ (B \) имеет одно и то же значение в каждой точке петли.Это означает, что мы можем вынести величину магнитного поля \ (B \) из интеграла. Это дает:
\ [B \ oint d \ ell = \ mu_o I \]
Хорошо, теперь мы находимся на легкой улице. \ (\ Oint d \ ell \) — это просто сумма всех \ (d \ ell \), составляющих нашу воображаемую петлю (круг) радиуса \ (r \). Эй, это просто длина окружности \ (2 \ pi r \). Итак, закон Ампера принимает вид:
.\ [B (2 \ pi r) = \ mu_o I \]
, что означает
\ [B = \ frac {\ mu_o I} {2 \ pi r} \]
Это наш конечный результат.Величина магнитного поля, создаваемого длинным прямым проводом, прямо пропорциональна току в проводе и обратно пропорциональна расстоянию от провода.
Длинный прямой соленоид
Соленоид представляет собой катушку из проволоки в виде цилиндрической оболочки. Рассматриваемый здесь идеализированный соленоид бесконечно длинный, но он имеет фиксированный конечный радиус \ (R \) и постоянный конечный ток \ (I \).
Он также характеризуется числом витков на длину, \ (n \), где каждый «виток» (a.к.а. обмотка) представляет собой одну круговую токовую петлю. Фактически, мы еще больше идеализируем наш соленоид, думая о нем как о бесконечном множестве круговых токовых петель. Настоящий соленоид приближается к этому идеализированному соленоиду, но за один оборот (на изображении выше) конец поворота смещается влево или вправо от начала поворота на величину, равную диаметру провода. В результате в реальном соленоиде у нас есть (на изображении выше) некоторый ток слева направо или справа налево (в зависимости от того, в какую сторону наматывается провод).Мы пренебрегаем этим током и считаем, что он просто циркулирует по кругу.
Наша цель здесь — найти магнитное поле, создаваемое идеальным бесконечно длинным соленоидом, который имеет число витков на длину \ (n \), имеет радиус \ (R \) и пропускает ток \ (Я\).
Начнем с рассмотрения соленоида в разрезе. Относительно изображения выше, мы представим, что смотрим на соленоид с левого конца. С этой точки зрения поперечное сечение представляет собой круг с током по часовой стрелке:
Давайте попробуем амперовскую петлю в форме круга, плоскость которого перпендикулярна оси симметрии соленоида, круг с центром на оси симметрии соленоида.
Исходя из симметрии, мы можем утверждать, что если магнитное поле имеет компоненту, параллельную изображенному \ (d \ ell \), то оно должно иметь точно такую же составляющую для каждого \ (d \ ell \) на замкнутом пути. Но это сделало бы циркуляцию \ (\ oint \ vec {B} \ cdot \ vec {d \ ell} \) ненулевой, что противоречит тому факту, что ток не проходит через область, заключенную в петлю. Это верно для любого значения \ (r \). Таким образом, магнитное поле не может иметь компоненты, касательной к окружности, плоскость которой перпендикулярна оси симметрии соленоида, окружности с центром на оси симметрии соленоида.
Теперь предположим, что магнитное поле имеет радиальную составляющую. По симметрии он должен быть везде направлен радиально наружу от оси симметрии соленоида или всюду радиально внутрь. В любом случае мы могли бы построить воображаемую цилиндрическую оболочку, ось симметрии которой совпадает с осью соленоида. Чистый магнитный поток через такую гауссову поверхность был бы ненулевым в нарушение закона Гаусса для магнитного поля. Следовательно, соленоид не может иметь радиальной компоненты магнитного поля.
Единственный вид поля, который мы не исключили, — это поле, которое всюду параллельно оси симметрии соленоида. Посмотрим, приведет ли такое поле к каким-либо противоречиям.
Здесь мы видим соленоид в разрезе сбоку. Вверху катушки мы видим ток, направленный к нам, а внизу — прочь. Возможное продольное (параллельно оси симметрии соленоида) магнитное поле включено в диаграмму.
Прямоугольники на диаграмме представляют собой амперовские петли.Чистый ток через любую из петель в любом направлении (от вас или к вам) равен нулю. Таким образом, тираж \ (\ oint \ vec {B} \ cdot \ vec {d \ ell} \) равен нулю. Поскольку магнитное поле справа и слева от любой из петель перпендикулярно правой и левой сторонам любой из петель, оно не влияет на циркуляцию там. По симметрии магнитное поле в одной позиции на вершине петли такое же, как и в любой другой точке на вершине той же петли. Следовательно, если мы пройдем любую из петель против часовой стрелки (с нашей точки зрения), вклад в циркуляцию будет \ (- B _ {\ small TOP} L \), где \ (L \) — длина верхнего и нижнего сегментов какой бы цикл вы ни выбрали, чтобы сосредоточить свое внимание.Знак «-» обусловлен тем фактом, что \ (I \) выбрано (произвольно) обходить цикл против часовой стрелки, и при этом каждый \ (\ vec {d \ ell} \) в верхнем сегменте находится в направление, противоположное направлению магнитного поля в верхней части петли. Вклад нижнего сегмента той же петли в циркуляцию равен \ (+ B _ {\ small BOTTOM} L \). На данный момент у нас есть:
\ [\ oint \ vec {B} \ cdot \ vec {d \ ell} = \ mu_o I _ {\ small THROUGH} \]
\ [\ oint \ vec {B} \ cdot \ vec {d \ ell} = 0 \]
(где чистый ток через любую из изображенных петель равен нулю при осмотре.)
\ [0 + -B _ {\ small TOP} L + 0 + B _ {\ small BOTTOM} L = 0 \]
(два нуля в левой части уравнения находятся в правой и левой частях петли, где магнитное поле перпендикулярно петле.)
Решая для \ (B _ {\ small BOTTOM} \), мы обнаруживаем, что для каждого цикла на диаграмме (и бесконечного числа циклов, содержащих нулевой чистый ток, как и у них):
\ [B _ {\ small BOTTOM} = B _ {\ small TOP} \]
Это означает, что магнитное поле во всех точках вне соленоида имеет одну и ту же величину.То же самое можно сказать обо всех точках внутри соленоида, но внутреннее значение соленоида может отличаться от внешнего значения. Фактически, давайте рассмотрим петлю, в которой чистый ток не равен нулю:
Опять же, я предпочитаю обходить петлю против часовой стрелки (с нашей точки зрения). Таким образом, по правилу правой руки для чего-то вьющегося, чего-то прямого, ток, направленный к нам через петлю, положительный. Вспоминая, что количество витков на длину соленоида равно \ (n \), мы имеем для петли, изображенной выше,
\ [\ oint \ vec {B} \ cdot \ vec {d \ ell} = \ mu_o I _ {\ small THROUGH} \]
\ [0 + -B _ {\ small TOP} L + 0 + B _ {\ small BOTTOM} L = \ mu_o n L I \]
\ [B _ {\ small BOTTOM} = B _ {\ small TOP} + \ mu_o n I \]
Нижняя часть петли находится внутри соленоида, и мы установили, что величина магнитного поля внутри соленоида имеет одну и ту же величину во всех точках внутри соленоида.Я назову это \ (B _ {\ small INSIDE} \), что означает \ (B _ {\ small BOTTOM} = B _ {\ small INSIDE} \). Точно так же мы обнаружили, что величина магнитного поля имеет одно и то же (другое) значение во всех точках вне соленоида. Назовем это \ (B _ {\ small OUTSIDE} \), что означает \ (B _ {\ small TOP} = B _ {\ small OUTSIDE} \). Таким образом:
\ [B _ {\ small INSIDE} = B _ {\ small OUTSIDE} + \ mu_o n I \]
Это все, что я могу сделать с помощью закона Гаусса для магнитного поля, симметрии и только закона Ампера.Отсюда я перехожу к экспериментальным результатам с длинными конечными соленоидами. Экспериментально мы обнаруживаем, что магнитное поле вне соленоида исчезающе мало, а внутри соленоида есть заметное магнитное поле. Настройка
\ [B _ {\ small OUTSIDE} = 0 \]
мы находим, что магнитное поле внутри длинного прямого соленоида равно:
\ [B _ {\ small INSIDE} = \ mu_o n I \]
Авторы и авторство
Окружной закон Ампера
Окружной закон АмпераДалее: Теорема Гельмгольца Up: Не зависящие от времени уравнения Максвелла Предыдущий: Магнитные монополи? Рассмотрим, опять же, бесконечный прямой провод, выровненный по оси и несущий ток.Поле, создаваемое таким проводом, записывается
| (257) |
в цилиндрических полярных координатах. Рассмотрим круговую петлю в плоскости — который центрируется на проволоке. Предположим, что радиус этой петли равен. Оценим линейный интеграл . Этот интеграл легко выполнить, поскольку магнитное поле всегда параллельно линейный элемент. У нас есть
| (258) |
Однако мы знаем из теоремы Стокса, что
| (259) |
где любая поверхность, прикрепленная к петле.
Оценим
напрямую. Согласно формуле. (254),
где использовались , и т. Д. Теперь у нас проблема. Из уравнений (258) и (259) следует, что
| (263) |
Но мы только что продемонстрировали, что . Эта проблема очень напоминает трудности, с которыми мы раньше сталкивались . Напомним, что для тома, содержащего дискретный заряд, но это в общем.Мы обошли эту проблему говоря, что это трехмерный дельта-функция, пик которой совпадает с положением заряда. Точно так же мы можем обойти нашу настоящую трудность, сказав, что — двумерная дельта-функция. Трехмерная дельта-функция является сингулярной (но интегрируемой) точкой в пространстве, тогда как двумерная дельта-функция — это особая строка в пространстве. Это ясно из рассмотрения уравнений. (260) — (262), что единственная составляющая которая может быть сингулярной, является -компонента, и что эта может быть единственным числом на оси -оси ( i.е. ,). Таким образом, особенность совпадает с положением тока, и мы можем написать
| (264) |
Вышеприведенное уравнение, безусловно, дает , а также везде отдельно от -оси, в соответствии с уравнениями. (260) — (262). Предположим, что мы интегрируем по плоская поверхность, соединенная с петлей. Элемент поверхности , так
| (265) |
где интегрирование ведется по области .Однако, поскольку единственная часть, которая на самом деле в поверхностный интеграл вносит бит, который лежит бесконечно близко к оси -оси, мы можем интегрировать по всем и без изменения результата. Таким образом, получаем
| (266) |
что согласуется с формулой. (263).
Но почему мы так старались доказать
что-то с помощью теории векторного поля, которое можно продемонстрировать
в одну линию через обычные
анализ [см.(258)]? Ответ, конечно же, таков: векторное поле
результат легко обобщается, тогда как
обычный результат — это просто частный случай.
Например, ясно, что уравнение. (266) верно для любой поверхности , прикрепленной к петле
C, а не просто плоская поверхность.
Более того, предположим, что мы искажаем нашу простую круговую петлю
так что он больше не круглый и даже не лежит в одной плоскости.
Что сейчас такое линейный интеграл
вокруг петли? Это уже не простая проблема для обычных
анализ, потому что магнитное поле не параллельно линейному элементу
петля.Однако согласно теореме Стокса
| (267) |
с участием дается формулой. (264). Обратите внимание, что единственная часть который дает вклад в поверхностный интеграл, представляет собой бесконечно малую область с центром на оси. Итак, пока фактически пересекает ось, не имеет значения, какой формы остальная поверхность, и мы всегда получаем один и тот же ответ для поверхностного интеграла:
| (268) |
Таким образом, при условии, что кривая перемещается по оси, и, следовательно, любая поверхность присоединенный к пересекает ось, линейный интеграл равно .Конечно, если не циркулирует ось, тогда прикрепленная поверхность не пересекает ось и равно нулю. Есть еще одна оговорка. Линия интеграл для цикла, который циркулирует ось по часовой стрелке (если смотреть вверх -ось). Однако, если петля движется против часовой стрелки направлении, то интеграл равен. Это следует потому, что в последнем случае -компонента поверхностного элемента противоположно направлена к текущий поток в точке, где поверхность пересекает провод.
Рассмотрим теперь провода, направленные вдоль оси -оси с координатами
(,) в плоскости -, каждая из которых несет ток в
положительное направление. Совершенно очевидно, что уравнение. (264) обобщает
к
| (269) |
Если мы проинтегрируем магнитное поле вокруг некоторой замкнутой кривой, которая может иметь любой формы и не обязательно лежат в одной плоскости, то теорема Стокса и из приведенного выше уравнения следует, что
| (270) |
где — полный ток, ограниченный кривой.Опять же, если кривая перемещает th провод по часовой стрелке (если смотреть вниз направление тока), то провод способствует к совокупному току. С другой стороны, если кривая движется против часовой стрелки, то провод способствует . Наконец, если кривая вообще не перемещает проволоку, тогда провод ничего не способствует.
Уравнение (269) — это уравнение поля, описывающее, как набор -направленных
токоведущие провода создают магнитное поле.Эти провода имеют
нулевой толщины, что означает, что мы пытаемся сжать конечное количество
ток в бесконечно малую область. Этот
учитывает дельта-функции в правой части
уравнение. Точно так же мы получили дельта-функции в разд. 3,4
потому что мы имели дело с точечными обвинениями. Давайте теперь обобщим на более
реалистичный случай диффузных токов. Предположим, что -ток, текущий через
маленький
прямоугольник в плоскости — с центром в координатах (,) и размеров
и является
.Здесь называется плотностью тока в
направление. Интегрируем
над этим прямоугольником.
Предполагается, что прямоугольник достаточно мал, чтобы существенно не меняется. Согласно формуле. (270) этот интеграл равен
равный умноженному на общий ток, протекающий через прямоугольник. Таким образом,
| (271) |
откуда следует, что
| (272) |
Конечно, в -оси нет ничего особенного.Предположим, у нас есть набор диффузные токи, текущие в -направлении. Ток, протекающий через небольшой прямоугольник в плоскости — с центром в координатах (,) и размеров и определяется выражением , где — плотность тока в -направлении. Совершенно очевидно, что мы можем написать
| (273) |
с аналогичным уравнением для диффузного токи, протекающие по оси. Мы можем совместить эти уравнения с формулой. (272) для формирования единого уравнения векторного поля который описывает, как электрические токи создают магнитные поля,
| (274) |
где — векторная плотность тока.Это третье уравнение Максвелла. Электрический ток, протекающий через небольшая площадь, расположенная на позиции, . Предположим, что пространство заполнено частицами заряда, плотность которых , а скорость . Плотность заряда дано . Плотность тока дана от , и, очевидно, является собственным векторным полем (скорости являются правильными векторами, поскольку они в конечном итоге являются производными от смещений).
Если мы составим линейный интеграл вокруг некоторой общей замкнутой кривой
, используя теорему Стокса и уравнение поля (274), то
получать
| (275) |
Другими словами, линейный интеграл магнитного поля вокруг любого замкнутого контура равна умноженному на поток плотности тока через.Этот Результат называется по закону Ампера . Если токи текут в проводов нулевой толщины, то закон Ампера сводится к формуле (270).
Поток плотности тока
сквозной оценивается путем интегрирования
по любой поверхности
прикреплен к. Предположим, что мы берем две разные поверхности и
. Ясно, что если схема Ампера
закон должен иметь какой-то смысл, тогда поверхностный интеграл
лучше сравнять интеграл
. То есть, когда мы вычисляем поток тока
хотя, используя две разные прикрепленные поверхности, нам лучше получить
тот же ответ, иначе уравнение.(275) неверно (поскольку левая часть явно независима
поверхности, охватывающей C).
Мы видели в разд. 2 что если интеграл от векторного поля
на некоторой поверхности, прикрепленной к петле, зависит только от петли и
независимо от покрывающей его поверхности, то это означает, что . Поток тока
плотность через любую петлю
вычисляется путем вычисления интеграла
для
любая поверхность, которая охватывает петлю. В соответствии с
По закону оборота Ампера этот интеграл зависит только от
и полностью не зависит от
( я.е. , он равен линейному интегралу от около, который зависит от
включен, но не включен). Это означает, что
. Фактически, мы
можно получить это соотношение непосредственно из уравнения поля (274). Мы знаем это
расхождение завитка автоматически равно нулю, поэтому расхождение
уравнения (274), получаем
| (276) |
Мы показали, что для того, чтобы закон Ампера имел какой-либо смысл, нам нужно .Физически это означает, что текущий текущий ток через любую замкнутую поверхность равен нулю. До сих пор мы рассматривали только стационарные заряды и установившиеся токи. Понятно, что если все обвинения стационарный, и все токи устойчивы, значит, чистый ток не может протекать через закрытую поверхность, так как это будет означать накопление заряда в том в комплекте. Другими словами, пока мы ограничиваем наше расследование к стационарным зарядам и постоянным токам, то мы ожидаем , и закон Ампера имеет смысл.Однако предположим, что теперь мы ослабим это ограничение. Предположим, что некоторые из зарядов в томе решают переместиться за пределами . Ясно, что чистый поток электрического тока через ограничивающая поверхность, пока это происходит. Это следует из Теорема Гаусса о том, что . В этих условиях Окружной закон Ампера рушится в кучу. Позже мы увидим, что можем спасти Обходной закон Ампера путем добавления дополнительного члена, включающего производную по времени, к правая часть уравнения поля (274).Для стационарных ситуаций ( т. Е. , ), это дополнительным сроком можно пренебречь. Таким образом, уравнение поля фактически составляет лишь две трети третьего уравнения Максвелла: отсутствует член с правой стороны.
Мы вывели два уравнения поля, включающие магнитные поля (фактически,
мы получили только один
и две трети):
Мы получили эти уравнения, рассматривая поля, порождаемые бесконечно длинные, прямые, устойчивые токи.Это, конечно, довольно особый класс токи. Теперь мы должны вернуться и повторить процесс для обычных токов. По факту, если бы мы сделали это, мы бы обнаружили, что приведенные выше уравнения поля все еще выполняются (при условии, что что токи устойчивы). К сожалению, это демонстрация довольно беспорядочная и чрезвычайно утомительная. Есть подход получше. Допустим, предположим, что приведенные выше уравнения поля верны для любого набор установившихся токов. Тогда мы можем с относительно небольшими усилиями используйте эти уравнения, чтобы получить правильную формулу для магнитного поля. индуцируется общим набором установившихся токов, тем самым доказывая, что наше предположение верно.Подробнее об этом позже.
Далее: Теорема Гельмгольца Up: Не зависящие от времени уравнения Максвелла Предыдущий: Магнитные монополи? Ричард Фицпатрик 2006-02-02
Закон Ампера — Урок — TeachEngineering
Быстрый просмотр
Уровень оценки: 12 (11-12)
Требуемое время: 45 минут
Зависимость урока:
Тематические области: Физика
Подпишитесь на нашу рассылку новостей
Резюме
Демонстрация в классе знакомит студентов с силой между двумя токонесущими петлями, сравнивая притяжение и отталкивание между петлями и между двумя магнитами.После лекции по закону Ампера (включая некоторые примеры случаев и задач) студенты начинают использовать эти концепции для расчета магнитного поля вокруг петли. Это применяется для определения магнитного поля тороида, представляя тороид как соленоид с петлей. Студенты используют закон Ампера для решения некоторых домашних заданий. Эта инженерная программа соответствует научным стандартам нового поколения (NGSS).Инженерное соединение
Понимание закона Ампера позволяет инженерам вычислять магнитное поле вокруг петли, что полезно при изучении магнитного поля, создаваемого магнитами МРТ.Помимо расчета магнитного поля, инженеры используют закон Ампера для определения величины тока и напряжения, необходимых для создания работающей печатной платы для выполнения желаемых задач.
Цели обучения
После этого урока учащиеся должны уметь
- Примените закон Ампера для расчета магнитных полей в симметричных ситуациях.
- Опишите магнитное поле тороида.
Образовательные стандарты
Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными дисциплинами K-12, образовательные стандарты в области технологий, инженерии или математики (STEM).
Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты иерархически структурированы: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика; внутри типа по подтипу, затем по классу, и т. д. .
NGSS: научные стандарты нового поколения — наука| Ожидаемые характеристики NGSS | ||
|---|---|---|
HS-PS3-2.Разработайте и используйте модели, чтобы проиллюстрировать, что энергия в макроскопическом масштабе может быть учтена либо как движение частиц, либо как энергия, запасенная в полях. (9–12 классы) Вы согласны с таким раскладом? Спасибо за ваш отзыв! | ||
| Нажмите, чтобы просмотреть другие учебные программы, соответствующие этим ожиданиям от результатов. | ||
| Этот урок посвящен следующим аспектам трехмерного обучения NGSS: | ||
| Наука и инженерная практика | Основные дисциплинарные идеи | Сквозные концепции |
| Разработайте и используйте модель, основанную на доказательствах, для иллюстрации взаимосвязей между системами или между компонентами системы. Соглашение о выравнивании: Спасибо за ваш отзыв! | Энергия — это количественное свойство системы, которое зависит от движения и взаимодействия материи и излучения внутри этой системы. То, что существует единственная величина, называемая энергией, объясняется тем фактом, что общая энергия системы сохраняется, даже если внутри системы энергия непрерывно передается от одного объекта к другому и между его различными возможными формами. Соглашение о выравнивании: Спасибо за ваш отзыв! В макроскопическом масштабе энергия проявляется множеством способов, таких как движение, звук, свет и тепловая энергия.Соглашение о выравнивании: Спасибо за ваш отзыв! Эти отношения лучше понять в микроскопическом масштабе, в котором все различные проявления энергии могут быть смоделированы как комбинация энергии, связанной с движением частиц, и энергии, связанной с конфигурацией (относительное положение частиц). В некоторых случаях энергия относительного положения может рассматриваться как хранимая в полях (которые опосредуют взаимодействия между частицами).Эта последняя концепция включает излучение, явление, при котором энергия, запасенная в полях, перемещается в пространстве.Соглашение о выравнивании: Спасибо за ваш отзыв! | Энергия не может быть создана или уничтожена — она только перемещается между одним местом и другим местом, между объектами и / или полями или между системами. Соглашение о выравнивании: Спасибо за ваш отзыв! |
- Энергию можно разделить на основные формы: тепловую, лучистую, электрическую, механическую, химическую, ядерную и другие.(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Технологические инновации часто возникают в результате обмена идеями, знаниями или навыками в рамках технологии, между технологиями или в других областях.(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
Какое альтернативное выравнивание вы предлагаете для этого контента?
Рабочие листы и приложения
Посетите [www.teachengineering.org/lessons/view/van_mri_lesson_7], чтобы распечатать или загрузить.Больше подобной программы
Изменение полейУчащиеся индуцируют ЭДС в катушке с проволокой с помощью магнитных полей. Студенты рассматривают кросс-произведение относительно магнитной силы и вводят магнитный поток, закон индукции Фарадея, закон Ленца, вихревые токи, ЭДС движения и индуцированную ЭДС.
Закон Био-СавараНачиная с демонстрации в классе, учащимся предлагается подумать о том, как ток создает магнитное поле, и о направлении создаваемого поля. Во время лекции студенты изучают закон Био-Савара (и решают некоторые типовые задачи), чтобы проще всего рассчитать магнитное поле, создаваемое в…
Да пребудет с вами магнитная силаПосле демонстрации отклонения электронного луча учащиеся повторяют свои знания о перекрестном произведении и правиле правой руки с примерами задач. Учащиеся применяют эти концепции, чтобы понять магнитную силу, действующую на провод с током.Посредством сопутствующей деятельности студенты продвигаются вперед …
СоленоидыВ этом уроке о соленоидах учащиеся узнают, как рассчитать магнитное поле вдоль оси соленоида, а затем выполняют задание по изучению магнитного поля металлической обтяжки.Соленоиды составляют основу магнитов МРТ. Изучение свойств этого соленоида помогает студентам и …
Введение / Мотивация
Чтобы решить проблему безопасности МРТ (данного устройства), нам необходимо понять и измерить магнитное поле, создаваемое токовыми петлями.Инженеры продолжают изучать магнитные поля и вместе с другими инженерами стремятся разработать более мощные аппараты МРТ мощностью около 7 Тесла по сравнению с обычными 1,5 Тесла, используемыми в большинстве средств визуализации.
Демонстрация класса: сила между двумя токовыми петлями
Цель: Цель демонстрации — показать силу между двумя токоведущими петлями. Притяжение и отталкивание между петлями очень похоже на силу между магнитами и может помочь студентам начать визуализировать силу между петлями тока, связанную с током внутри твердого тела или магнитным моментом.
Материалы:
- 2 катушки малого диаметра
- 2 Источник питания 5 В постоянного тока мощностью 30 Вт или выше
- 2 лабораторных стенда
- 1 тонкая фольга алюминиевая
- 4 провода с зажимом типа «крокодил»
- 1 рулон ленты
* Эта демонстрация была протестирована с катушкой диаметром 2 дюйма на 100 витков с использованием магнитного провода 20 калибра, скрепленного изолентой.
Рисунок A. Демонстрационная установка класса.
Перед тем, как представить демонстрацию, поставьте задачу о двух коротких сегментах провода, выровненных параллельно, и попросите учащихся определить направление магнитного поля в каждом сегменте, создаваемом другим сегментом.Затем попросите их определить направление магнитной силы на каждом сегменте. Затем рассмотрим, как многие из этих сегментов образуют петлю, в которой каждый сегмент петли притягивается к соответствующему сегменту другой петли. Попросите учащихся определить вектор магнитного момента каждой катушки, чтобы сделать вывод, что петли с параллельными магнитными моментами будут притягиваться.
Настройте демонстрацию, как показано на рисунке A. Подключите каждую петлю к собственному источнику питания, но не замыкайте схему, пока не будете готовы начать демонстрацию, поскольку провода могут перегреться.Не оставляйте цепи подключенными более чем на несколько секунд. На мгновение замкните цепь до обеих катушек и посмотрите, как они притягиваются. Измените направление тока в одной из петель, чтобы увидеть, как они отталкиваются.
Предпосылки и концепции урока для учителей
Устаревшая информация о цикле
Этот урок вписывается в фазу исследования и проверки наследия, во время которой учащимся предоставляется дополнительная информация, позволяющая им пересмотреть свои первоначальные идеи для решения задачи.Аспект исследования состоит из демонстрации в классе силы между двумя токовыми петлями и лекции о законе Ампера и его приложениях.
Закон Ампера
Хотя полный магнитный поток через замкнутую поверхность должен быть равен нулю, сумма магнитного поля вокруг замкнутого контура не должна быть нулем. Более конкретно, если вообразить замкнутый цикл в пространстве, мы можем создать вектор в каждом крошечном сегменте, называемый dl, указывающий в направлении цикла, с величиной, равной длине сегмента.Затем мы посмотрим на магнитное поле в этой точке, возьмем скалярное произведение и представим его как магнитное поле вдоль этого сегмента петли. Интеграл этих скалярных произведений вокруг контура является математически точным способом рассмотрения магнитного поля вокруг замкнутого контура (см. Рисунок B).
Рисунок B Авторские права
Авторские права © 2006 Эрик Аппельт, Университет Вандербильта
Как вы можете себе представить, магнитное поле вокруг петли было бы больше, если бы провод, по которому проводился ток, проходил через внутреннюю часть петли.Фактически, точное значение поля вокруг контура — это где I — полный ток, проходящий через контур.
Этот результат назван законом Ампера в честь его первооткрывателя.
Как и закон Гаусса, он полезен для определения величины магнитного поля в высокосимметричных ситуациях.
Пример: Определите магнитное поле вне бесконечно длинного прямого провода.
Решение: Рассмотрим замкнутую круговую петлю радиуса R вокруг провода с центром на оси провода, как показано на рисунке C.Обратите внимание, что диаграмма вращательно-симметрична, поэтому магнитное поле вокруг контура должно иметь постоянную величину.
Рисунок Ccopyright
Copyright © 2006 Эрик Аппельт, Университет Вандербильта
Таким образом,.
Теперь по закону Ампера,
Этот результат соответствует закону Био-Савара. Обратите внимание, что это, по-видимому, работает для конечного отрезка провода и дает тот же результат, что противоречит результату закона Био-Савара, согласно которому
Экспериментально доказано, что закон Био-Савара верен.Это несоответствие можно понять, осознав, что сегмент провода должен быть частью более крупной цепи, нарушая симметрию и делая недействительным использование закона Ампера, или что ток должен быть нестационарным течением от одного проводника к другому. Исходя из этого, мы можем предположить, что закон Ампера должен выполняться только для установившихся токов.
Тороид
Рисунок D
Тороид в основном представляет собой соленоид, изогнутый в круг, как показано на рисунке D. Эта фигура в форме пончика имеет внутренний радиус a , внешний радиус b , ток I и общее количество оборотов Н .Чтобы определить магнитное поле с помощью закона амперов, представьте себе круговую петлю радиусом r , разделяющую центр с тороидом в плоскости тороида.
Если r , то через контур не проходит ток, поэтому
Поскольку диаграмма обладает осевой симметрией, магнитное поле должно иметь одинаковую величину в любом месте контура, поэтому B = 0 везде внутри внутреннего радиуса.
Случай 2: a
В этом случае каждый виток проходит через петлю в одном направлении, как показано на виде в разрезе на Рисунке E.
Рисунок Ecopyright
Copyright © 2006 Эрик Аппельт, Университет Вандербильта
Случай 3: r> b
В этом случае для каждого внутреннего витка, пропускающего ток I через петлю в одном направлении, есть внешний виток, пропускающий ток I через петлю в другом направлении, так что общий ток через петлю Ампера равен нулю. , таким образом, B = 0 везде за пределами внешнего радиуса.
Словарь / Определения
тороид: поверхность, образованная вращением любой замкнутой плоской кривой или контура вокруг оси, лежащей в его плоскости.
Оценка
Домашнее задание: Поручите студентам заполнить вопросы домашнего задания Закона Ампера, чтобы оценить их прогресс в понимании понятий.
