Задачи по теме «Арифметическая прогрессия»
Арифметическая прогрессия
Задачи обязательного уровня
№1. Определите, является ли заданная последовательность арифметической прогрессией.
2; 4; 6; 8; 10; 12;…
б) 3; 1; 3; 1; 3; …
№2. Доказать, что последовательность, заданная формулой n-ого члена an=-1,5+4n, является арифметической прогрессией.
№3. Записать первые шесть членов арифметической прогрессии, если
а) a1=-3; d=2 b) an=3-2n
Ответ: -3; -1; 1; 3; 5; 7.
Ответ: 1; -1; -3; -5; -7; -9.
№4. Найдите сто тридцатый член арифметической прогрессии, если a1=-1,2; d=
№5. Число –29 является членом арифметической прогрессии 21; 16; 11; …
Найдите номер этого члена. a11=-29.
б) Является ли число –10 членом этой прогрессии? нет
в) Является ли число 30 членом этой прогрессии? нет
№6. Найдите разность арифметической прогрессии 100; 90; 80; 70; …
Ответ: d=10
№7. Решить следующие задачи, где по трем известным величинам требуется определить две неизвестные.
a1
d
N
an
Sn
1.
1,5
1,5
3,654
999
2.
-28
7
9
28
0
3.
10
10
14
140
1050
4.
0
0,5
11
5
27,5
5.
-38
2
15
-10
-360
6.
-9
0,5
25;12
3;-3,5
-75
7.
1
100
67
3400
8.
-45
3
31
45
0
9.
0,2
0,1
51
5,2
137,7
Полезно научить учащихся выражать неизвестную величину из формулы n-ого члена и суммы n-первых членов арифметической прогрессии.
an=a1+(n-1)d3. an=a1+nd-d
3.
1. a1=an-(n-1)d
2.
1.
2.
№8. Составьте формулу n-ого члена арифметической прогрессии 2; 5; 8; 11; …
Ответ: an=3n-1№9. Найдите двенадцатый член арифметической прогрессии, если известно, что a11+a13=122.
Ответ:а12=61
№10. Найдите a3+a15, если известно, что a1+a17=35. a3+a15= a1+a17=35
Задачи среднего уровня
№11. Выясните, является ли последовательность, заданная формулой n-ого члена, арифметической прогрессией? Если да, то укажите первый член и разность прогрессии.
а) an=3*2n нет
б) an= d=-1. Да, a1=.
№12. Запишите формулу n-ого члена арифметической прогрессии, если известно, что a7=-5; a12=55.
Ответ: an=12n-89 .
№13. Найдите седьмой член арифметической прогрессии, если известно, что a3+a11=20.
Ответ: а7=10
№14. Сколько нужно взять членов в арифметической прогрессии, первый член которой равен 16, а разность равна 8, чтобы сумма членов составила 1840?
Ответ: n=20.
№15. Найдите те значения x, при которых числа 5х+2; 7х+1; 3х-6 образуют арифметическую прогрессию.
Ответ: х=-1.
№16. Между числами –8 и –35 вставьте два числа так, чтобы получились четыре последовательных члена арифметической прогрессии.
Ответ: -17; -26.
№17. Найдите сумму всех натуральных чисел от 2 до 98 включительно.
Ответ: S97=4850.
№18. Начиная с какого номера n все члены арифметической прогрессии будут больше заданного числа А, если an=7n-121; A=?
Ответ: n=18.
№19. Являются ли числа 4,6 и –1,2 членами арифметической прогрессии, заданной формулой n-ого члена an=13-0,4n? Да, нет
№20. Второй член арифметической прогрессии составляет 96% от первого. Сколько % от первого члена составляет семнадцатый член этой прогрессии?
Ответ: 36%
№21. Найдите сумму всех трехзначных чисел, не делящихся на 19.
Ответ: 468653.
№22. Найдите пятнадцатый член арифметической прогрессии и сумму ее первых двадцати членов, если известно, что a7=-100; a9=-78.
Ответ: a15= -12; S20=1850.
№23. Улитка ползет по дереву. За первую минуту она проползла 30см, а за каждую следующую минуту – на 5см больше, чем за предыдущую. За какое время улитка достигнет вершины дерева длиной 5,25 м, если считать, что движение начато от его основания?
Ответ: 10 минут.
№24. Определить первый член и разность арифметической прогрессии, в которой:
а) a7-a3=8; a2*a7=75 б) a4:a6=-1; a2*a8=-1 в) a42+a122=1170; a7+a15=60
Ответ: а) a1=3; d=2 или a1=-17; d=2 б) a1=4/3; d=-1/3 или a1=-4/3; d=1/3 в) a1=-12; d=4,2 или a1=0; d=3.
№25. Найдите сумму членов арифметической прогрессии с шестого по двадцать пятый включительно, если первый ее член равен 21, а разность равна –0,5?
Решение задачи сводится к нахождению суммы S=S25-S5.
Задачи повышенной сложности
№26. При каких значениях a корни уравнения 3х3-(а+1)х2+(а-2)х=0, взятые в определенном порядке, составляют арифметическую прогрессию?
Ответ: a=-1; 3,5; 8
№27. Найти х из уравнения (х+1)+(х+4)+(х+7)+…+(х+28)=155
Ответ: x=1.
№28. В арифметической прогрессии Sn-a1-an=21; Sn-a2-an-a1-an-1=7. Найдите Sn и n.
Ответ: Sn=35; n=5.
№29. Вычислите первый член арифметической прогрессии с разностью 8, зная, что сумма первых десяти членов в 4 раза больше суммы первых пяти членов.
Ответ: a1=4.
№30. Найти сумму первых тридцати нечетных чисел, которые при делении на 5 дают в остатке 1.
Ответ: S30=4380.
№31. Найти арифметическую прогрессию с положительными членами, если дано: a1+a2+a3+a4+a5=25 (1) a1*a2*a3*a4*a5=945 (2)
Ответ: 1; 3; 5; 7; 9; …
№32. Найти m-ый член арифметической прогрессии, в которой Sn=pn+qn2.
Ответ: am=2qm+p-q.
№33. Первый член арифметической прогрессии равен числу, логарифм которого при основании равен 1,5. Если произведение первых трех членов арифметической прогрессии разделить в отдельности на каждый из них, то сумма полученных частных равна 167. Найти сумму десяти первых членов этой прогрессии.
Ответ: S10= -600 или S10=255.
№34. Сумма n членов арифметической прогрессии определяется из уравнения
, где an=7n-6. Определить число членов n прогрессии.
Ответ: n=8
№35. Найдите стороны прямоугольного треугольника, если известно, что они составляют арифметическую прогрессию, разность которой d=25.
Ответ: 75; 100; 125.
№36. Доказать, что для арифметической прогрессии с отличными от 0 членами имеет место равенство:
Задачи для самостоятельного решения
№37. В возрастающей арифметической прогрессии а4 и а7 являются корнями квадратного уравнения 0,1х2-5х+58,9=0. Сумма n членов на 30 больше наименьшего целого числа, которое при делении на 37 дает остаток 33, а при делении на 53 – остаток 12. определить число членов n.
Ответ: n=30
№38. Найти сумму четырех членов арифметической прогрессии, содержащей целые и положительные члены, если известно, что произведение этих чисел равно 1680, а разность прогрессии равна модулю при переходе от системы логарифмов с основанием 81 к системе логарифмов с основанием 3.
Ответ: 32
№39. Определить х из уравнения 1+7+13+ … +х=280
Ответ: х=55
№40. Найти все арифметические прогрессии с целыми и положительными членами, в которых S5=35
Ответ: 1) a1=5; d=1 2) a1=3; d=2 3) a1=1; d=3
№41. В арифметической прогрессии a1+a3+a5+ … +a2n+1=25; a1+a2n-1=10. Найдите n.
Ответ: n=4
№42. В арифметической прогрессии Sn=7; S2n=34; a1+a2n=17. Найти S30.
Ответ: S30=2205.
№43. Найти Sn арифметической прогрессии, любой член которой равенam=2m-1.
Ответ: Sn=n2
№44. Найти n= таких дробей, числители которых составляют возрастающую арифметическую прогрессию, а знаменатели – арифметическую убывающую. Разности обеих этих прогрессий по абсолютной величине равны между собой. Предпоследняя из искомых дробей равна обратному значению последней; знаменатель второй больше ее числителя на n единиц, а сумма всех числителей искомых дробей относится к сумме их знаменателей, как (n-1):(n+2).
Ответ:
№45. Разность арифметической прогрессии равна 27; седьмой и восьмой члены ее соответственно равны квадратам двух последовательных натуральных чисел. Найти эту прогрессию.
Ответ: 7; 34; 61; …
№46. Определить при каком значении m корни уравнения x4-(3m-5)x2+(m+1)2=0 составляют арифметическую прогрессию.
Ответ: m=-25; -.
Задачи по теме «Арифметическая прогрессия» 1. Найдите первые пять членов арифметической прогрессии, если (an): 4; 1;… 2. По формуле n-го члена найти: а41, если а1=0,6; d= –1,7. 3. Найти разность арифметической прогрессии, если у1 = 10; у5 = 22. 4. Найти первый член арифметической прогрессии, если а9 = – 37; d =5. 5. По формуле распознавания арифметической прогрессии найти: с1; с2; с31, если сn = 4n – 1. 6. Найти номер члена арифметической прогрессии (уn), равного 17,2, если у1 = 5,3; d = 0,7. 7. Встретится ли число 50 среди членов арифметической прогрессии (аn): 14; 17;.. 8. (хn) – арифметическая прогрессия, х6 = 24, х21 = 12. Найдите х42. 9. Найдите первый отрицательный член арифметической прогрессии (аn):135; 125; 115;… 10. В арифметической прогрессии аn = 0,7n – 35,1. Найти наименьший положительный член прогрессии. 11. Найти седьмой член арифметической прогрессии, если а3 + а11 = 20. | Задачи по теме «Арифметическая прогрессия» 1. Найдите первые пять членов арифметической прогрессии, если (an): 4; 1;… 2. По формуле n-го члена найти: а41, если а1=0,6; d= –1,7. 3. Найти разность арифметической прогрессии, если у1 = 10; у5 = 22. 4. Найти первый член арифметической прогрессии, если а9 = – 37; d =5. 5. По формуле распознавания арифметической прогрессии найти: с1; с2; с31, если сn = 4n – 1. 6. Найти номер члена арифметической прогрессии (уn), равного 17,2, если у1 = 5,3; d = 0,7. 7. Встретится ли число 50 среди членов арифметической прогрессии (аn): 14; 17;.. 8. (хn) – арифметическая прогрессия, х6 = 24, х21 = 12. Найдите х42. 9. Найдите первый отрицательный член арифметической прогрессии (аn):135; 125; 115;… 10. В арифметической прогрессии аn = 0,7n – 35,1. Найти наименьший положительный член прогрессии. 11. Найти седьмой член арифметической прогрессии, если а3 + а11 = 20. | Задачи по теме «Арифметическая прогрессия» 1. Найдите первые пять членов арифметической прогрессии, если (an): 4; 1;… 2. По формуле n-го члена найти: а41, если а1=0,6; d= –1,7. 3. Найти разность арифметической прогрессии, если у1 = 10; у5 = 22. 4. Найти первый член арифметической прогрессии, если а9 = – 37; d =5. 5. По формуле распознавания арифметической прогрессии найти: с1; с2; с31, если сn = 4n – 1. 6. Найти номер члена арифметической прогрессии (уn), равного 17,2, если у1 = 5,3; d = 0,7. 7. Встретится ли число 50 среди членов арифметической прогрессии (аn): 14; 17;.. 8. (хn) – арифметическая прогрессия, х6 = 24, х21 = 12. Найдите х42. 9. Найдите первый отрицательный член арифметической прогрессии (аn):135; 125; 115;… 10. В арифметической прогрессии аn = 0,7n – 35,1. Найти наименьший положительный член прогрессии. 11. Найти седьмой член арифметической прогрессии, если а3 + а11 = 20. | Задачи по теме «Арифметическая прогрессия» 1. Найдите первые пять членов арифметической прогрессии, если (an): 4; 1;… 2. По формуле n-го члена найти: а41, если а1=0,6; d= –1,7. 3. Найти разность арифметической прогрессии, если у1 = 10; у5 = 22. 4. Найти первый член арифметической прогрессии, если а9 = – 37; d =5. 5. По формуле распознавания арифметической прогрессии найти: с1; с2; с31, если сn = 4n – 1. 6. Найти номер члена арифметической прогрессии (уn), равного 17,2, если у1 = 5,3; d = 0,7. 7. Встретится ли число 50 среди членов арифметической прогрессии (аn): 14; 17;.. 8. (хn) – арифметическая прогрессия, х6 = 24, х21 = 12. Найдите х42. 9. Найдите первый отрицательный член арифметической прогрессии (аn):135; 125; 115;… 10. В арифметической прогрессии аn = 0,7n – 35,1. Найти наименьший положительный член прогрессии. 11. Найти седьмой член арифметической прогрессии, если а3 + а11 = 20. |
Решение типовых задач на арифметическую прогрессию. Часть 1
Пример 1. Выписать первые пять членов арифметической прогрессии 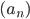 , если:
, если: 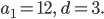
Решение.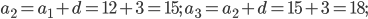
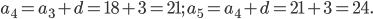
Ответ: 12; 15; 18; 21; 24.
Пример 2. Найти одиннадцатый член арифметической прогрессии
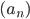 , если
, если 
Решение.

Ответ: {4}.
Пример 3. Найти семнадцатый член арифметической прогрессии
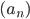 , если арифметическая прогрессия имеет вид 3; 7; 11; 15.
, если арифметическая прогрессия имеет вид 3; 7; 11; 15.Решение.
Находим разность прогрессии:

Ответ: {67}
Пример 4. Последовательность
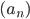 — арифметическая прогрессия.
— арифметическая прогрессия.Найти:
a)
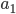 , если
, если 
б)
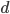 , если
, если 
Решение.
а)

б)

Ответ: a) {1,5}; 6) {0,8}.
Пример 5. Разность арифметической прогрессии равна 3, а сумма первых ее шести членов равна 57. Найти
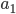 ,
,  .
.Решение.
 Имеем
Имеем


Ответ:

Пример 6. Найти первый член арифметической прогрессий и количество членов
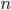 , если
, если 
Решение.
Подставив данные значения из условия примера в формулы

получаем систему уравнении

Решая второе уравнение системы, получаем
 (это значение
(это значение 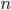 не подходит, т. к.
не подходит, т. к.  ).
).Итак,

Ответ:

Пример 7. Найти арифметическую прогрессию
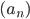 , если
, если
Решение.

Подставив в исходную систему, получаем:

Из первого уравнения системы

Подставив это значение во второе уравнение системы, получаем

Отсюда имеем равносильную исходной систему

Выпишем несколько первых членов: -2; 5; 12; 19.
Ответ:

Решение прикладных задач по теме «Арифметическая и геометрическая прогрессии».

Последовательности
МБОУ «Койинская СОШ»
9 класс

Арифметическая и геометрическая прогрессии. Решение прикладных задач.
«Все познается в сравнении»

Цели урока :
1) образовательные :
- продолжить работу над определениями арифметической, геометрической прогрессий;
- формулами n-го члена, суммы n первых членов; характеристическими свойствами,
которым обладают члены прогрессий;
— убедится, что раздел математики «Прогрессии» являются неотъемлемой частью общечеловеческой культуры;
— продолжать формировать навыки применения прогрессии к решению прикладных задач;
— обобщить и систематизировать знания учащихся по данной теме.
2) воспитательные:
- содействовать воспитанию интереса к математике и ее приложениям, активности,
умению общаться, аргументировано отстаивать свои взгляды.
3) развивающие:
- продолжить дальнейшую работу по выработке умения сравнивать математические понятия,
- находить сходства и различия, умения наблюдать, подмечать закономерности;
- учиться проводить рассуждения по аналогии; формировать умение строить и интерпретировать математическую модель некоторой реальной ситуации.

Определение
Арифметической Геометрической
прогрессией
а 1 ,а 2 ,а 3 ,…а n ,.. b 1 ,b 2 ,b 3 ,…b n ,…
называется п оследовательность ,
отличных от нуля чисел
каждый член которой, начиная со второго,
равен предыдущему члену,
сложенному с одним
и тем же числом.
умноженному на одно
и то же число.

Определите закономерность
в таблице

Определите вид прогрессии
- В третьем тысячелетии високосными годами будут 2008, 2012 ,2016, 2020. В какой последовательности записаны года?
- В искусственном водоеме 10 кг
водорослей. Через три дня их
стало 20 кг. Через шесть дней
– 40 кг, а через девять – 80 кг.
В какой последовательности
увеличивается масса
водорослей?


Задача (экономика)
Вкладчик положил в банк 5000р. на счёт, по которому
сумма вклада ежегодно возрастает на 8%. Какая сумма
будет у него на счету через 6 лет?
Решение:
Начальная сумма вклада составляла 5000р. Через год эта сумма возрастёт на 8%
и составит 108% от 5000р., т.е. будет равна 5000 ∙1,08р. Через 2 года накопленная
сумма составит (5000 ∙ 1,08) ∙ 1,08р., т.е. 5000 ∙ 1,08 ² р. Через 3 года на счету у
вкладчика будет (5000 ∙ 1,08 ² ) ∙ 1,08р., т.е. 5000 ∙ 1,08³ р. и т.д.
Мы имеем дело с геом. прогрессией:
5000; 5000 ∙ 1,08; 5000 ∙ 1,08 ² ; 5000 ∙ 1,08³ ; ….
Сумма, накопленная на счету у вкладчика, через 6 лет будет равна
седьмому члену этой прогрессии, т.е. составит 5000 ∙ 1,08
Выполнив вычисления, найдём, что

Задача (медицина).
Человек, заболевший гриппом, может заразить четырех
человек. Через сколько дней заболеет все население
поселка в количестве 341 человека?
Решение:
Дано:
Решение:
Найти:
n -?

Задача (физики).
Свободно падающее тело проходит в первую секунду 5 м, а в каждую следующую секунду на 10 м больше, чем в предыдущую. Найдите глубину шахты, если свободно падающее тело достигло дна шахты через 5 секунд после начала падения.
Дано:
( а n ) – А.П.
а 1 = 5
d = 10
S 5 = ?
S 5 =125 м

Задача (медицина).
Курс воздушных ванн начинают с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1 час 45 минут.


1. Составим последовательность чисел
2. Данная последовательность является геометрической
прогрессией со знаменателем q =2, n = 24.
3. Попытаемся подсчитать сумму
4 . Зная формулу
5.Имеем

Если бы удалось царю засеять пшеницей площадь
всей поверхности Земли, считая и моря, и океаны, и горы,
и пустыни, и Арктику с Антарктидой, и получить
удовлетворительный урожай, то пожалуй, лет за пять смог бы
рассчитаться. Чтобы поместить это зерно в амбаре,
то его размеры будут: высота – 4м, ширина – 10м,
длина – 30 000 000км – это вдвое больше, чем расстояние
от Земли до Солнца.
Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать!
18 446 744 073 709 551 615

Математику должны учить в школе
ещё с той целью, чтобы познания,
здесь приобретаемые были
достаточными для обыкновенных
потребностей жизни.
И.Л.Лобачевский

Составьте геометрическую прогрессию:
Дима на перемене съел булочку. Во время еды в
кишечник попало 30 дизентерийных палочек. Через
каждые 20 минут происходит деление бактерий
(они удваиваются).
30; 60; 120; 240;…
Каждый курильщик выкуривает в среднем
8 сигарет в сутки. После выкуривания одной
сигареты в легких оседает 0,0002 грамма
никотина и табачного дегтя. С каждой
последующей сигаретой это количество
увеличивается в два раза.
0,0002; 0,0004; 0,0008;…

МАНГУСТ
Мангуст – пушистый зверёк, родина которого – Индия.
Длина тела ~ 50-60см. Даёт потомство 3 раза в год, в помёте в среднем по 4 детёныша.

1 пара=2 мангуста
через год
4 детёныша
4 детёныша
4 детёныша

Сколько будет детёнышей, если образовалось 6 пар и каждая пара даёт 12 детёнышей?
- 1–й год – 2 мангуста
- 2-й год – 12 детёнышей
- 3-й год – 72 детёныша!!!

Сколько детёнышей мангустов появится на 10-й год?
в 10 = 20 155 392 детёныша

8. Рефлексия
1.На уроке я работал активно / пассивно
2.Своей работой на уроке я доволен / не доволен
3.Урок для меня показался коротким / длинным
4.За урок я не устал / устал
5.Мое настроение стало лучше / стало хуже
6.Материал урока мне был понятен / не понятен
полезен / бесполезен
легким / трудным
интересным / неинтересным
«Решение задач на арифметическую и геометрическую прогрессию»
Урок № __ класс 9 предмет алгебра дата 23.12.2014
Тема урока: «Решение задач на арифметическую и геометрическую прогрессию»
Цели:
Обучающая – формирование и развитие специальных и общеучебных умений; закрепление навыков решения задач по нахождению суммы n первых членов геометрической прогрессии;
Развивающая – развивать познавательные процессы, память, воображение, мышление, сообразительность, речь учащихся;
Воспитывающая – повысить интерес к решению нестандартных задач, сформировать положительный мотив учения.
Тип урока: урок обобщения и систематизации ЗУН
Вид урока: урок практических работ
Формы работы на уроке: индивидуальная, парная, групповая
Оборудование: интерактивная доска, карточки с заданиями, слайды с презентацией
Прогнозируемый результат:
знать: формулы арифметической и геометрической прогрессии
уметь: применять полученные знания при решении стандартных и нестандартных задач
Ход урока
1. Организационный момент (4 мин.)
Цель: проверить готовность учащихся к уроку (рабочее место, классная доска, необходимое оборудование).
Психологический настрой учащихся «Дерево».
Разделение учащихся по группам «Пазл»(3 группы)
2. Сообщение темы и целей урока (1 мин.)
Учитель: ребята, сегодня мы продолжаем изучать геометрическую прогрессию и тема сегодняшнего урока: «Решение задач».
3. Актуализация знаний учащихся ( 14 мин.)
Цель: повторение теоретического материала, подготовка учащихся к работе на уроке
1) Каждому из учеников дается следующее задание: Заполнить таблицу.
Данная стадия дает целостное осмысление, обобщение полученной информации. (Заполненная таблица показывается на слайде)
Форма работы: индивидуальная (3 мин)
Формула n-го члена
Изменение последующего
члена по отношению к
предыдущему происходит
на или в
Как это число найти
Как называется это число
Формула суммы
n- первых членов
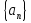
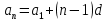
на
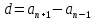
разность
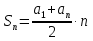
или
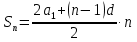
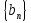
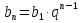
в
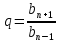
знаменатель
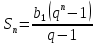
2) Распределите последовательности, определив какая из них является арифметической , а какая геометрической. Указав значение знаменателя и разности в прогрессиях
Форма работы: парная (3 мин)
1; 5; 25; 125;…;
1; 6; 11; 16;…;
4; 7; 10; 13;…;
3; 9; 27; 81;…
55; 45; 35; …
1000; 100; 10; ….
3) «Я сам» (Марафон) Выполнить задание(8 мин)
Каждый ученик решает самостоятельно, и каждый ученик решает одно задание у доски (заранее разрезать таблицу и каждому ученику раздать по одному заданию)
Таблица
№1. В арифметической прогрессии  : -10;-7;-4;-1;… .Найти
: -10;-7;-4;-1;… .Найти  .
.
№2. Найдите четвертый член геометрической прогрессии , если
, если  .
.
№3. Найдите сумму семи первых членов арифметической прогрессии 10;6;2;… .
№4. В геометрической прогрессии 
№5. В геометрической прогрессии 
4. Осознанное применение умений и навыков вычислительной деятельности учащихся при решении стандартных и нестандартных задач. (9 мин.)
Форма организации: групповая
1. (Физика) Имеется радиоактивное вещество массой 256г, масса которого за сутки уменьшается вдвое. Какова станет масса вещества на пятые сутки? (256; 128;64; 32; 16;…)
2. (Экономика) Срочный вклад, положенный в сберегательный банк, ежегодно увеличивается на 5%. Каким станет вклад через 5 лет, если вначале он был равен 1000 €? (1000; 1050; 1102,5; 1157,625;1215,5025;…)
3 (Биология) Бактерия за 1 секунду делится на три. Сколько бактерий будет в пробирке через 5 секунд? (1; 3; 9; 27; 81;…)
4. (Биология) Отдыхающий, следуя совету врача. В первый день загорал 5 минут. А в каждый последующий день увеличивал время пребывания на солнце на 5 минут. В какой день время пребывания на солнце будет равно 40 минут?
ТЕСТ (8 мин)
Вариант 1.
В геометрической прогрессии b1; b2; 4; 8;…. Найди b1.
1) – 4;
2) 1;
3) 1/4;
4) 1/8;
5) – 1.
(bn) – геометрическая прогрессия. Найди b6 , если b1 = 4; q = 1/2
1)– 1/8;
2) 1,25;
3) 1/8;
4)12,5;
5) – 1,25.
Найди S4 , (bn) – геометрическая прогрессия и b1 = 1, q = 3.
1) 81;
2) 40;
3) 80;
4) –80;
5) – 40.
Чему может быть равен знаменатель геометрической прогрессии (bn), если b10 = 10, а b12 = 40?
2;
2 и -2;
4;
15;
10.
В геометрической прогрессии (bn) найдите b5, если b3 = 8 + 2
 , а b4 = 1 +
, а b4 = 1 +  .
.
7 +
 ;
;1;
2;
3;
-1.
Код ответов 23222
Вариант 2.
В геометрической прогрессии b1; b2; 3; 9;…. Найди b1.
5;
1;
-1/4;
1/3;
– 1.
(bn) – геометрическая прогрессия. Найди b6 , если b1 = 5 q = 1/5
1)– 1/25;
2) 1,25;
3) 1/625;
4)12,5;
5) – 6,25.
Найди S4 , (bn) – геометрическая прогрессия и b1 = 1, q = 5.
81;
156;
80;
60;
– 40.
Чему может быть равен знаменатель геометрической прогрессии (bn), если b5 = 6, а b8 = 48?
1) 2 и -2;
2) 8;
3) 2;
4) 4;
5) 10.
5. В геометрической прогрессии (cn) найдите c6, если c4 = 3 + 2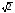 , а c5 = 1 +
, а c5 = 1 + 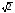 .
.
2 +
 ;
;1;
2;
3;
-1.
Код ответов 43232
5. Дополнительный исторический материал. (3 мин.)
Цель: расширить кругозор учащихся; показать исторические корни возникновения понятия геометрической прогрессии.
Сообщение учащегося:
Индийский принц Сирам предложил изобретателю шахматной игры просить у него награду, какую захочет. Тот попросил, чтобы ему дали за первый квадрат шахматной доски 1 рисовое зерно, за второй квадрат 2 зерна, за третий квадрат 4 зерна и т. д., увеличивая число зерен вдвое за каждый следующий квадрат. Принц согласился. Но когда подсчитали количество риса, которое следует выдать за все 64 квадрата шахматной доски, то оказалось, что награда в таком размере не может быть выдана по недостатку риса. Оказывается, когда точно подсчитали общее количество зерен риса, то их получилось 18 446 744 073 709 551 615. В этой задаче речь идет о геометрической прогрессии с первым членом 1 и знаменателем 2. Необходимо найти сумму 64 первых членов геометрической прогрессии.
Такое количество зерен можно собрать лишь с урожая планеты, поверхность которой примерно в 2000 раз больше поверхности Земли.
Задачи на геометрические и арифметические прогрессии встречаются у вавилонян, в египетских папирусах, в древнекитайском трактате «Математика в 9 книгах».Отметим также, что Архимед знал, что такое геометрическая прогрессия, и умел вычислять сумму любого числа ее членов. Правило нахождения суммы членов арифметической прогрессии впервые встречается в «Книге абака» (1202) Леонардо Пизанского.
Цель: проверить и оценить знания учащихся по данной теме.
6. Домашнее задание. (3 мин.)
Уровень 1.
Найдите сумму первых 5 членов геометрической прогрессии: 2; 4; …
b1 = -4, q = 2. Найдите сумму первых пяти членов геометрической прогрессии.
Уровень 2.
b1 = 8, q = 1/2. Найдите сумму пяти первых членов геометрической прогрессии.
Найдите сумму шести первых членов геометрической прогрессии: 3; — 6; ….
Уровень 3.
Найдите сумму пяти первых членов геометрической прогрессии, если b1 = 36, q = -2.
Докажите, что последовательность (bn) является геометрической прогрессией, и найдите сумму n первых ее членов, если bn = 3*2n-1.
Найдите сумму четырех первых членов геометрической прогрессии (bn), в которой: b2 = 6, b4 = 24, q > 0.
7. Подведение итогов (3 мин). Рефлексия «Сказочное дерево»
Плод — урок прошел очень интересно, я работал с удовольствием
Цветок — урок прошел хорошо, но были затруднения с решением задач
Зеленый листок- урок прошел хорошо, но у меня остались вопросы по применению формул
Желтый листок — мне было не интересно на уроке
Формула n-го члена
Изменение последующего
члена по отношению к
предыдущему происходит
на или в
Как это число найти
Как называется это число
Формула суммы
n- первых членов
Арифметическая
прогрессия
Геометрическая
прогрессия
Ф.И.О. учащегося:__________________________________________________
Формула n-го члена
Изменение последующего
члена по отношению к
предыдущему происходит
на или в
Как это число найти
Как называется это число
Формула суммы
n- первых членов
Арифметическая
прогрессия
Геометрическая
прогрессия
Ф.И.О. учащегося:__________________________________________________
№1 В арифметической прогрессии  : -10;-7;-4;-1;… .Найти
: -10;-7;-4;-1;… .Найти  .
.
№2 Найдите четвертый член геометрической прогрессии , если
, если  .
.
№3 Найдите сумму семи первых членов арифметической прогрессии 10;6;2;… .
№4 В геометрической прогрессии 
№ 5 В геометрической прогрессии 
№1 В арифметической прогрессии  : -10;-7;-4;-1;… .Найти
: -10;-7;-4;-1;… .Найти  .
.
№2 Найдите четвертый член геометрической прогрессии , если
, если  .
.
№3 Найдите сумму семи первых членов арифметической прогрессии 10;6;2;… .
№4 В геометрической прогрессии 
№ 5 В геометрической прогрессии 
№1 В арифметической прогрессии  : -10;-7;-4;-1;… .Найти
: -10;-7;-4;-1;… .Найти  .
.
№2 Найдите четвертый член геометрической прогрессии , если
, если  .
.
№3 Найдите сумму семи первых членов арифметической прогрессии 10;6;2;… .
№4 В геометрической прогрессии 
№ 5 В геометрической прогрессии 
1. (Физика) Имеется радиоактивное вещество массой 256г, масса которого за сутки уменьшается вдвое. Какова станет масса вещества на пятые сутки? (256; 128;64; 32; 16;…)
2 (Экономика) Срочный вклад, положенный в сберегательный банк, ежегодно увеличивается на 5%. Каким станет вклад через 5 лет, если вначале он был равен 1000 €.? (1000; 1050; 1102,5; 1157,625;1215,5025;…)
3 (Биология1) Бактерия за 1 секунду делится на три. Сколько бактерий будет в пробирке через 5 секунд? (1; 3; 9; 27; 81;…)
4. (Биология2) Отдыхающий, следуя совету врача. В первый день загорал 5 минут. А в каждый последующий день увеличивал время пребывания на солнце на 5 минут. В какой день время пребывания на солнце будет равно 40 минут?
Ф.И. учащегося________________________________________
Вариант 1.
В геометрической прогрессии b1; b2; 4; 8;…. Найди b1.
1) – 4;
2) 1;
3) 1/4;
4) 1/8;
5) – 1.
(bn) – геометрическая прогрессия. Найди b6 , если b1 = 4; q = 1/2
1)– 1/8;
2) 1,25;
3) 1/8;
4)12,5;
5) – 1,25.
Найди S4 , (bn) – геометрическая прогрессия и b1 = 1, q = 3.
1) 81;
2) 40;
3) 80;
4) –80;
5) – 40.
Чему может быть равен знаменатель геометрической прогрессии (bn), если b10 = 10, а b12 = 40?
2;
2 и -2;
4;
15;
10.
В геометрической прогрессии (bn) найдите b5, если b3 = 8 + 2
 , а b4 = 1 +
, а b4 = 1 +  .
.
7 +
 ;
;1;
2;
3;
-1.
Ответы:
№
1
2
3
4
5
Вариант ответа
Ф.И. учащегося________________________________________
Вариант 2.
В геометрической прогрессии b1; b2; 3; 9;…. Найди b1.
5;
1;
-1/4;
1/3;
– 1.
(bn) – геометрическая прогрессия. Найди b6 , если b1 = 5 q = 1/5
1)– 1/25;
2) 1,25;
3) 1/625;
4)12,5;
5) – 6,25.
Найди S4 , (bn) – геометрическая прогрессия и b1 = 1, q = 5.
81;
156;
80;
60;
– 40.
Чему может быть равен знаменатель геометрической прогрессии (bn), если b5 = 6, а b8 = 48?
1) 2 и -2;
2) 8;
3) 2;
4) 4;
5) 10.
5. В геометрической прогрессии (cn) найдите c6, если c4 = 3 + 2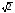 , а c5 = 1 +
, а c5 = 1 + 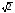 .
.
2 +
 ;
;1;
2;
3;
-1.
Ответы:
№
1
2
3
4
5
Вариант ответа
ДЕРЕВО
Выбор позиции № 1, 3, 6, 7 характеризует установку на преодоление препятствий.
№ 2, 11, 12, 18, 19 — общительность, дружескую поддержку.
№ 4 — устойчивость положения (желание добиваться успехов, не преодолевая трудности).
№ 5 — утомляемость, общая слабость, небольшой запас сил, застенчивость.
№ 9 — мотивация на развлечения.
№ 13, 21 — отстраненность, замкнутость, тревожность.
№ 8 — отстраненность от учебного процесса, уход в себя.
№ 10, 15 — комфортное состояние, нормальная адаптация.
№ 14 — кризисное состояние, «падение в пропасть».
Позицию № 20 часто выбирают как перспективу учащиеся с завышенной самооценкой и установкой на лидерство.
Следует заметить, что позицию № 16 дети не всегда понимают как позицию «человечка, который несет на себе человечка № 17», а склонны видеть в ней человека, поддерживаемого и обнимаемого другим.
ДЕРЕВО
Выбор позиции № 1, 3, 6, 7 характеризует установку на преодоление препятствий.
№ 2, 11, 12, 18, 19 — общительность, дружескую поддержку.
№ 4 — устойчивость положения (желание добиваться успехов, не преодолевая трудности).
№ 5 — утомляемость, общая слабость, небольшой запас сил, застенчивость.
№ 9 — мотивация на развлечения.
№ 13, 21 — отстраненность, замкнутость, тревожность.
№ 8 — отстраненность от учебного процесса, уход в себя.
№ 10, 15 — комфортное состояние, нормальная адаптация.
№ 14 — кризисное состояние, «падение в пропасть».
Позицию № 20 часто выбирают как перспективу учащиеся с завышенной самооценкой и установкой на лидерство.
Следует заметить, что позицию № 16 дети не всегда понимают как позицию «человечка, который несет на себе человечка № 17», а склонны видеть в ней человека, поддерживаемого и обнимаемого другим.
































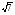 , а b4 = 1 +
, а b4 = 1 +