Решение задач по теме параллелограмм 8 класс

На прошлом уроке мы изучили параллелограмм. Вы узнали свойства и признаки параллелограмма. Сегодня мы обобщим наши знания по этой теме, отработаем навыки и умения решать задачи.

2

Вначале для успешной работы освежим в памяти наши знания. Какую фигуру называют параллелограммом?

Сколько параллелограммов изображено на рисунке? / 9 /

3

Вспомним свойства параллелограмма. Также вспомним графическую иллюстрацию данных свойств.

4

Устно решить по готовым чертежам. Первое задание найти периметр

а) 20

б) 14

5

Второе задание. Найти углы параллелограмма

а) 110 и 70

б) 110 и 70

6

Чему равен полупериметр?

/10/

Вспоминаем неравенство треугольника: /каждая сторона треугольника меньше суммы длин других сторон/

значит /9/

7

Следующую задачу оформим в тетрадях. Запишите №1, сделайте чертёж.

Что неопределенно в этой задаче?

Как поступить в этом случае?

8

Проверяем ответы / 70 и 50 /

9

Задача вторая… Чертёж выполняем самостоятельно.

Давайте подумаем, может и здесь тоже несколько случаев?

Какой ещё чертёж можно начертить, следуя условиям задачи?

Решаем оба случая

В каком случае задача не имеет решения?

Почему? / Значит задача имеет одно решение / 3, 2, 3 /

Итак, как мы видим, при решении задач по геометрии необходимо разбирать все случаи.

10

Теперь вспомним признаки параллелограмма. По каким критериям можно сказать, что четырёхугольник является параллелограммом?

11

Устно доказать, что фигура параллелограмм и почему?

12

Ученики проговаривают решение устно, затем самостоятельно оформляют решение в тетради.

/ Проверка см. слайд 17/

13

И, наконец, обобщим наши знания признаков параллелограмма. №4. Сначала сформулируйте, условие задачи

Докажем, что четырёхугольник – параллелограмм разными способами:

по определению,

используя тот факт, что две стороны равны и параллельны,

противоположные стороны попарно равны.

1 способ: проговаривают, оформляют в тетради, проверка на экране

2 и 3 способы:

АВС = СDА по стороне и двум прилежащим углам

далее самостоятельно 1 вариант – по 1 признаку, 2 вариант – по 2 признаку; самопроверка в парах 2 минуты

14

№5 Вам предлагается выбрать два способа из четырёх предложенных и полностью самостоятельно оформить доказательство данной задачи двумя способами.

15

Подведём итоги:

Что нового узнали на уроке?

16

Задание на дом: п. 43 – 44 повторить теорию; № 376(д), 425, 429.

infourok.ru

Конспект «ЗАДАЧИ по теме Параллелограмм»

ЗАДАЧИ по теме Параллелограмм

---

---

Признаки параллелограмма:
— две противолежащие стороны равны и параллельны,
— противолежащие стороны попарно равны,
— диагонали пересекаются и точкой пересечения делятся пополам,
— каждая диагональ делит четырехугольник на два равных треугольника.

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

Задача № 1. Дано: ABCD — параллелограмм; BC — AB = 5 см; P_ABCD = 40 см.  Найти: AB; BC.

Задача № 2. Дано: ABCD — параллелограмм; AB : BC= 4 : 5; P_ABCD = 10,8 см.  Найти: AB; BC; CD; AD.

Задача № 3. Дано: ABCD — параллелограмм; ∠В больше ∠А на 40°. Найти: ∠A; ∠B; ∠C; ∠D.

Задача № 4. Дано: ABCD — параллелограмм; AC — диагональ; ∠BAC = 35°; ∠CAD = 25°. Найти: ∠A; ∠B; ∠C; ∠D.

Задача № 5. Дано: ABCD — параллелограмм; P_ABCD = 10 см; P_ABD = 8 см. Найти: BD.

Задача № 6. Дано: ABCD — параллелограмм; AK — биссектриса ∠A; BK : KC = 2 : 1; P

ABCD = 50 см. Найти: AB; BC; CD; AD.

---

Это конспект по теме «ЗАДАЧИ по теме Параллелограмм». Выберите дальнейшие действия:

 

uchitel.pro

Признаки параллелограмма. 8-й класс

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока: рассмотреть признаки параллелограмма и закрепить полученные знания в процессе решения задач.

Задачи:

• образовательная: формирование умений применять признаки параллелограмма для решения задач;
• развивающая: развитие логического мышления, внимания, навыков самостоятельной работы, навыков самооценки;
• воспитательная: воспитание интереса к предмету, умение работать в коллективе, культуре общения.

Тип урока: изучение нового материала, первичное закрепление.

Оборудование: интерактивная доска, проектор, карточки с заданием, презентация.

Ход урока

1. Организационный момент.

У: Добрый день, ребята! Сегодня на уроке мы опять будем говорить о параллелограмме. Нам предстоит выполнить много заданий, доказать теоремы и научиться применять их при решении задач. Девизом нашего урока будут слова Ле Карбюзье: «Всё вокруг — геометрия».

2. Актуализация знаний учащихся.

Теоретический опрос

Некоторым учащимся дать индивидуальные задания по карточкам на тему свойства параллелограмма (задания выбирает каждый самостоятельно на слайде презентации по гиперссылке, наводя указатель мышки на фигуру, но не на цифру) , выслушать индивидуально каждого отвечающего.

С остальным — доказать дополнительные свойства параллелограмма. (Сначала обсудить устно доказательство, затем сверить с интерактивной доской).

1°. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

2°. Биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы противоположных углов параллельны или лежат на одной прямой.

После подготовки выслушать доказательства дополнительных свойств параллелограмма.

Дано:

ABCD -параллелограмм,

AE -биссектриса угла BAD.

Доказать: ABE — равнобедренный.

Доказательство:

Так как ABCD — параллелограмм, значит BC || AD, тогда угол EAD = углу BEA как накрест лежащие при параллельных прямых BC и AD и секущей AE. AE - биссектриса угла BAD, значит, угол BAE = углу EAD, поэтому угол BAE = углу BEA.

В ABE угол BAE =углу BEA, значит, ABE - равнобедренный с основанием AE.

Наводящие вопросы:

Сформулируйте признак равнобедренного треугольника.

Какие углы в BAE могут быть равными? Почему?

Дано:

ABCD -параллелограмм,

BE -биссектриса угла CBA,

AE — биссектриса угла BAD.

Наводящие вопросы:

Когда прямые AE и CK будут параллельными?

Равны ли углы BEA и <3? Почему?

В каком случае AE и CK совпадут?

Подготовка к изучению нового материала

Фронтальная работа с классом (устно).

• Что означают слова «свойства» и «признак»? Приведите примеры.
• Что такое обратная теорема?
• Всегда ли верно утверждение обратное данному? Приведите примеры.

3. Объяснение нового материала.

У.: У каждого объекта есть свои свойства и признаки. Скажите, пожалуйста, чем отличаются свойства от признаков.

Давайте попробуем разобраться в этом вопросе на простом примере. Дан объект — осень. Назовите его свойства: Его признаки:

• Какими утверждениями являются по отношению друг к другу свойство и признак объекта? (ответ: обратными)
• Какие свойства в курсе геометрии мы уже изучали? Сформулируйте их. (называют несколько)

Для любого ли свойства можно построить верное обратное утверждение? (разные ответы).

Проверим это на следующих свойствах:

Сделайте вывод: Для любого ли свойства можно построить верное обратное утверждение? (нет, не для любого)

Теперь, давайте вернёмся к нашему четырёхугольнику, вспомним его свойства и сформулируем обратные для них утверждения, т.е:.. (ответ — признаки параллелограмма). Итак, тема сегодняшнего урока: «Признаки параллелограмма».

Итак, назовите свойства параллелограмма.

Сформулируйте обратные свойствам утверждения. (ученики формулируют признаки, учитель их корректирует и формулирует повторно)

Докажем, эти признаки. Первый признак - подробно, второй — коротко, третий - самостоятельно дома.

 

4. Закрепление изученного материала.

Работа в рабочих тетрадях: решить задачу №11 на интерактивной доске к доске вызвать менее подготовленного учащегося.

Решение задачи № 379 (решение записать на интерактивной доске). Из вершин B и D параллелограмма ABCD, у которого AB BC и А острый, проведены перпендикуляры ВК и DМ к прямой АС. Докажите, что четырёхугольник BMDK - параллелограмм.

Даю время ученикам, чтобы подготовили чертёж.

Дано: ABCD — параллелограмм, BKAC, DM

Доказать, что: BMDK — параллелограмм.

Доказательство:

BKC= DMA по гипотенузе и острому углу ( как накрест лежащие углы при параллельных прямых AD и BC и секущей AC, BC=AD как противолежащие стороны параллелограмма, BKC и DMA прямоугольные), значит MD=BK.

BMK и DKM — прямоугольные, BMK = DKM по двум катетам (MD=BK, KM- общий катет), значит BM=DK.

В четырехугольнике BMDK противолежащие стороны равны (MD=BK и BM=DK), следовательно, BMDK - параллелограмм.

5. Самостоятельное решение задач (задачи выбирают учащиеся на интерактивной доске, решение сверяют с доской, перейдя по гиперссылке)

Обратно к выбору задач можно вернуться по гиперссылке.

6. Итог урока. Задание на дом.

Итак, подведём итог сегодняшнего урока. Ответьте, пожалуйста, на мои вопросы:

1. Какими утверждениями являются по отношению друг к другу свойство и признак объекта?
2. Сформулируйте признаки параллелограмма?
3. Для чего нужны нам признаки параллелограмма?

Домашнее задание: п. 43, доказательство второго и третьего признака закончить, № 380, № 383.

7. Рефлексия.

У.: Ребята, мы сегодня изучили признаки параллелограмма, доказали их и мне хочется узнать, как вы поняли материал урока? (оставить на рабочем столе нужную полоску)

Приложение 1

Приложение 2

Приложение 3

Приложение 4

Приложение 5

urok.1sept.ru

Задачи на параллелограмм — Математика

Просмотр содержимого документа
«Задачи на параллелограмм»

Самостоятельная работа «Задачи на параллелограмм» вар 1

1. Один из углов параллелограмма равен 40⁰. Найдите остальные углы.

1. Найдите периметр параллелограмма, если его стороны равны 3,6 см и 5,8 см.

2. Диагональ  BD  па­рал­ле­ло­грам­ма  ABCD  об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 50° и 85°. Най­ди­те мень­ший угол параллелограмма

1. Найдите углы параллелограмма, зная, что один из них больше другого на 50⁰.

1. В параллелограмме биссектриса угла В делит сторону АД на отрезки, равные 2 см и 6 см. Найдите его периметр.

6. Найдите все углы параллелограмма, если сумма двух из них равна 240⁰

Самостоятельная работа «Задачи на параллелограмм» вар 2

1. Один из углов параллелограмма равен 105⁰. Найдите остальные углы.

2. Найдите периметр параллелограмма, если его стороны равны 3,9 см и 7,6 см.

3.Диагональ BD па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 65° и 50°. Най­ди­те мень­ший угол параллелограмма

4. В параллелограмме биссектриса угла А делит сторону ВС на отрезки, равные 3 и 5 см. Найдите его периметр

5. Найдите углы параллелограмма, зная, что

6. . Найдите все углы параллелограмма, если сумма двух из них равна 100 .

multiurok.ru

Признаки параллелограмма

На прошлом уроке мы с вами говорили, что параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. Также мы рассмотрели некоторые свойства параллелограмма. Вспомним их.

Свойство 1. Сумма углов при соседних вершинах параллелограмма равна .

Свойство 2. Диагональ разбивает параллелограмм на два равных треугольника.

Свойство 3. У параллелограмма противоположные стороны равны.

Свойство 4. У параллелограмма противоположные углы равны.

Свойство 5. Диагонали параллелограмма точкой пересечения делятся пополам.

На этом уроке мы рассмотрим три признака параллелограмма. Отметим, что свойство – это то, чем обладает данная фигура. А признак – это то, чем фигура отличается от других, то есть черты, по которым мы можем отличить данную фигуру от других.

Теорема. 1-й признак параллелограмма. Если у четырёхугольника две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

Докажем это.

Рассмотрим  и .

,.

Сторона  – общая, по условию,как накр. лежащие при и секущей .

по первому признаку. Следовательно, . , – накр. лежащие при  и  и секущей .

Так как , то .

, ,следовательно,  – параллелограмм.

Теорема доказана.

Теорема. 2-й признак. Если в четырёхугольнике противоположные стороны равны, то этот четырёхугольник – параллелограмм.

Доказательство.

 Пусть в четырёхугольнике ABCD сторона,.

 Проведём диагональ AC, которая разделяет четырёхугольник на два треугольника ABC и CDA.

Рассмотрим  и .

Сторона  – общая, по условию, по условию.

по третьему признаку.

Следовательно, .

Так как , – накр. лежащие при  и  и секущей ,то .

,,тогда по 1-му признаку  – параллелограмм.

Теорема доказана.

Теорема. 3-й признак. Если у четырёхугольника диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

Доказательство.

Пусть в четырёхугольнике ABCD диагонали AC и BD пересекаются в точке О и делятся этой точкой пополам.

Рассмотрим  и .

 по условию, по условию, как вертикальные.

по первому признаку.

Следовательно, ,.Так как , – накр. лежащие при  и  и секущей ,то .

,,тогда по 1-му признаку  – параллелограмм.

Теорема доказана.

Теперь решим несколько задач.

Задача. Докажите, что четырёхугольник  является параллелограммом, если  – диагональ, а  и .

Доказательство.

, – накр. лежащие при  и и секущей .

Так как , то .

, – накр. лежащие при  и и секущей .

Так как , то ., ,следовательно,  – параллелограмм.

Решим эту задачу ещё одним способом.

Рассмотрим  и .Сторона  – общая, ,по условию.

по второму признаку, следовательно, ,.

Тогда – параллелограмм по 2-му признаку.

Что и требовалось доказать.

Задача. Отрезки  и  – диагонали четырёхугольника , которые пересекаются в точке . , а . Докажите, что четырёхугольник  – параллелограмм.

Доказательство.

Рассмотрим  и .

 по условию,

 по условию,

как вертикальные.

по второму признаку.

Следовательно, .

Тогда  – параллелограмм по 3-му признаку.

Что и требовалось доказать.

videouroki.net

8 класс. Геометрия. Признаки параллелограмма. Задачи на параллелограмм. — Признаки параллелограмма.

Комментарии преподавателя

При­зна­ки па­рал­ле­ло­грам­ма

Нач­нем с того, что вспом­ним опре­де­ле­ние па­рал­ле­ло­грам­ма.

Опре­де­ле­ние. Па­рал­ле­ло­грамм – че­ты­рех­уголь­ник, у ко­то­ро­го каж­дые две про­ти­во­по­лож­ные сто­ро­ны па­рал­лель­ны (см. Рис. 1).

 

Рис. 1. Па­рал­ле­ло­грамм

Вспом­ним ос­нов­ные свой­ства па­рал­ле­ло­грам­ма:

 

Для того, чтобы иметь воз­мож­ность поль­зо­вать­ся всеми этими свой­ства­ми, необ­хо­ди­мо быть уве­рен­ным, что фи­гу­ра, о ко­то­рой идет речь, – па­рал­ле­ло­грамм. Для этого необ­хо­ди­мо знать такие факты, как при­зна­ки па­рал­ле­ло­грам­ма. Пер­вые два из них мы се­год­ня и рас­смот­рим.

Тео­ре­ма. Пер­вый при­знак па­рал­ле­ло­грам­ма. Если в че­ты­рех­уголь­ни­ке две про­ти­во­по­лож­ные сто­ро­ны равны и па­рал­лель­ны, то этот че­ты­рех­уголь­ник – па­рал­ле­ло­грамм. .

Рис. 2. Пер­вый при­знак па­рал­ле­ло­грам­ма

До­ка­за­тель­ство. Про­ве­дем в че­ты­рех­уголь­ни­ке диа­го­наль  (см. Рис. 2), она раз­би­ла его на два тре­уголь­ни­ка. За­пи­шем, что мы знаем об этих тре­уголь­ни­ках:

 

по пер­во­му при­зна­ку ра­вен­ства тре­уголь­ни­ков.

Из ра­вен­ства ука­зан­ных тре­уголь­ни­ков сле­ду­ет, что  по при­зна­ку па­рал­лель­но­сти пря­мых при пе­ре­се­че­нии их се­ку­щей. Имеем, что:

 па­рал­ле­ло­грамм по опре­де­ле­нию. Что и тре­бо­ва­лось до­ка­зать.

До­ка­за­но.

Тео­ре­ма. Вто­рой при­знак па­рал­ле­ло­грам­ма. Если в че­ты­рех­уголь­ни­ке каж­дые две про­ти­во­по­лож­ные сто­ро­ны равны, то этот че­ты­рех­уголь­ник – па­рал­ле­ло­грамм. .

Рис. 3. Вто­рой при­знак па­рал­ле­ло­грам­ма

До­ка­за­тель­ство. Про­ве­дем в че­ты­рех­уголь­ни­ке диа­го­наль 

www.kursoteka.ru

Какие задачи использует репетитор по математике на параллелограмм в 8 классе

Предлагаю Вашему вниманию страницы своей коллекции задач по геометрии для 8 класса. Это авторские номера, составлены мной собственноручно к рядовому уроку со средним (но способным) учеником. Репетитору по математике для разработки индивидуального урока.

Задачи репетитора на параллелограмм и свойство угла в 30 градусов.

1) На стороне AB параллелограмма ABCD отмечена середина M. Найдите расстояние от M до AD, если 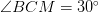и MC=10 см.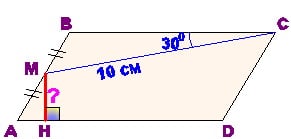

2) Точка P — середина стороны AD параллелограмма ABCD. Известно, что PC=8 см, 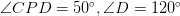. Найдите расстояние от P до стороны AB. Задача на дом.

Задачи на биссектрисы углов:
Точка М середина стороны BC параллелограмма ABCD, причем AM и DM — биссектрисы углов BAD и ADC. Найдите DM, если 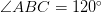и BC=6 см.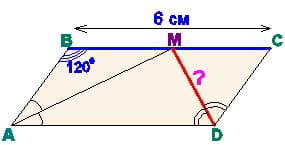

2) На стороне AD параллелограмма ABCD отмечена точка N так, что BN и CN — биссектрисы его углов B и C. Известно, что BN=4 и AD=8см. Найдите градусную меру угла А. (Обратная задача, составленная репетитором на биссектрисы ). Для домашней работы ученика.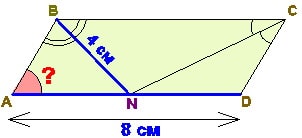

Репетитору по математике в копилку красивых задач на параллелограмм

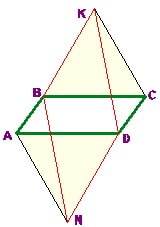На сторонах параллелограмма ABCD построены равносторонние треугольники BKC и AND. Докажите, что BKDN — параллелограмм.

Школьная математика (особенно геометрия) сильно ограничивает репетитора в варьировании простейшими объектами для составления с их участием комбинированных задач под конкретную учебную ситуацию. В начале 8 класса список пройденных теорем и понятий весьма невелик. Поэтому репетитор по математике всегда испытывает определенный недостаток в материале узкого назначения. Простые задачи — однотипные, а сложных не так много. Первые не дают развития, а последние доступны далеко не всем учащимся. Найди что-то интересное посередине — отличительная черта хорошего репетитора по математике. Недавно летом я попал ситуацию, когда со средним учеником 8 класса были перерешены все виды типовых номеров учебника и дидактических материалов (я не беру задачи — клоны). Пришлось составлять оригинальные упражнения. Причем к их подбору я всегда подхожу методически аккуратно и выдерживаю главное правило любого комплекта упражнений: если репетитор по математике разбирает на уроке какую-либо задачу, то аналогичная ей обязательно должна задаваться на дом.

Задача, которая была представлена выше явилась результатом таких поисков. Для того, чтобы получить правильную домашнюю задачу на параллелограмм и треугольники 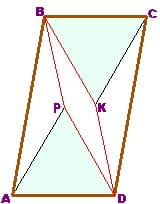репетитору по математике достаточно симметрично отобразить эти треугольники относительно сторон BC и AD. Вы видите их на рисунке справа. Нужно доказать, что BPDK — параллелограмм.

Как репетитор по математике растягивает задачи?

Как правило, любую задачу можно «дожать» или «растянуть», оптимизируя ее под конкретные цели повторения тех или иных теорем и формул. Я ругулярно комплектую задачи по геометрии несколькими пунктами в графе «докажите». В каждый номер с равносторонними треугольниками репетитору по математике можно посоветовать включить еще один пункт: докажите, что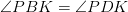

Вы можете изучить рабочий листочек (план на урок) с этими задачами, который я обычно готовлю каждому ученику. Кликните на него и он откроется в отдельном окне. В него включены еще две задачи на биссектрисы внутренних и внешних углов параллелограмма.

Надеюсь, что репетиторам по базовой математике 8 класса пригодятся предоставленные материалы для работы со средним и даже сильным учеником. Удачного плана на урок!

Репетитор по математике в Москве ( м. Строгино ). А.Н. Колпаков

ankolpakov.ru