Задачи на движение 8 класс

Posted on 20.07.202028.12.2019 by alexxlab

Содержание

Света (svt)

1.Из двух пунктов, расстояние между которыми равно 24 км, выехали навстречу друг другу два велосипедиста. Скорость первого, который выехал на 20 мин раньше второго, на 6 км/ч меньше скорости второго. Встретились велосипедисты на середине пути. Каковы скорости велосипедистов?

2.Из двух пунктов, расстояние между которыми 30 км, выехали навстречу друг другу велосипедист и мотоциклист. Мотоциклист выехал на 40 мин позже велосипедиста. Встретились они на середине пути. Скорость мотоциклиста на 30 км/ч больше скорости велосипедиста. Найдите скорости мотоциклиста и велосипедиста.

3.Из пункта А в пункт В, расстояние между которыми равно 60 км, выехал автобус, а через 20 мин вслед за ним выехал легковой автомобиль, скорость которого на 20 км/ч больше скорости автобуса. Автобус пришел в пункт В на 10 мин позже легкового автомобиля. Найдите скорости автобуса и легкового автомобиля.

4.Из пункта А в пункт В, расстояние между которыми равно 20 км, выехал мотоциклист, а через 6 мин вслед за ним выехал автобус, скорость которого на 10 км/ч больше скорости мотоциклиста. Автобус прибыл в пункт В на 4 мин раньше мотоциклиста. Найдите скорости автобуса и мотоциклиста.

5.Лодка прошла 3 км по течению реки и 2 км против течения за тоже время, за которое она могла бы пройти 6 км в стоячей воде. Скорость течения равна 2 км/ч. Найдите скорость лодки в стоячей воде.

6.Лодочник проплыл 3 км по течению реки и 2 км против течения за тоже время,

за которое мог бы проплыть плот 3 км по течению. Собственная скорость

лодки 2 км/ч. Найдите скорость течения реки.

7.Завод по плану должен был изготовить 180 станков к определенному сроку.

Перевыполняя дневную норму на 2 станка, завод выполнил задание на 1 день

раньше срока. За сколько дней завод выполнил план?

8.Завод должен был по плану изготовить 800 деталей к определенному сроку. Перевыполняя дневную норму на 20 деталей, завод выполнил задание на 2 дня раньше срока. За сколько дней завод выполнил план?

9.Первая мастерская получила заказ сшить 600 рубашек, а вторая –560 рубашек. Первая мастерская выполнила заказ за 4 дня до срока, а вторая за 1 день до срока, причем первая мастерская шила ежедневно на 4 рубашки больше, чем вторая. 10.Сколько рубашек шила каждая мастерская ежедневно.

Велосипедист и мотоциклист проехали 60 км, причем мотоциклист был в пути на 3 ч меньше. Вычислите скорость велосипедиста и мотоциклиста, если скорость велосипедиста была на 18 км/ч меньше скорости мотоциклиста.

11.Тракторист должен был вспахать поле площадью 200 га. Он пахал ежедневно на 5 га больше, чем планировал, а поэтому вспахал поле на 2 дня раньше срока. За сколько дней вспахал тракторист поле?

12.Комбайнер должен убрать поле площадью 60 га. Он убирал ежелневно на 2 га больше, чем планировал, а поэтому уборку закончил на 1 день рантше срока. За сколько дней планировал убрать поле комбайнер?

13.Моторная лодка прошла 28 км по течению реки и 25 км против течения, затратив на весь путь столько же времени, сколько ей потребовалось на прохожление 54 км по озеру. Найдите скорость моторной лодки по озеру, если скорость течения реки равна 2 км/ч.

Света (svt)

6.Лодочник проплыл 3 км по течению реки и 2 км против течения за тоже время,

за которое мог бы проплыть плот 3 км по течению. Собственная скорость

лодки 2 км/ч. Найдите скорость течения реки.

7.Завод по плану должен был изготовить 180 станков к определенному сроку.

Перевыполняя дневную норму на 2 станка, завод выполнил задание на 1 день

раньше срока. За сколько дней завод выполнил план?

infourok.ru

Задачи на движение — Математика

ЗАНЯТИЕ № 3

ЗАДАЧИ НА ДВИЖЕНИЕ

УЧИТЕЛЬ МАТЕМАТИКИ

НАЗАРОВА Л.М.

КОГОБУ ЦДОД город КИРОВ

ЦЕЛЬ: формирование умений

решения задач данного типа :

-сформировать представление о

составлении математической модели;

-рассмотреть особенности решения

задач на движение;

-умение проводить самооценку решения.

ВИДЕОУРОК НА ДВИЖЕНИЕ https://www.youtube.com/watch?v=KDveB1VyeOo

https://www.youtube.com/watch?time_continue=3&v=Muh-inqocNc

В задачах на движение рассматриваются три взаимосвязанные величины:

S — расстояние (пройденный путь),

t — время движения и

V — скорость – расстояние, пройденное

за единицу времени.

ЭТО СТОИТ ЗАПОМНИТЬ!

Расстояние – это произведение скорости на время движения;

S = V t

Скорость – это расстояние, которое тело проходит за единицу времени;
Скорость — это частное от деления расстояния на время движения;

V = S / t

Время – это частное от деления расстояния на скорость движения

t = S / V

1 . Задача

Расстояние в 480 км автомобиль прошел за 8 часов. С какой скоростью должен ехать этот автомобиль на обратном пути, чтобы пройти это же расстояние за 6 часов?

V = S : t

км/ч

6 ч

480 км

Встречное движение

V1+V2 =V СБЛИЖЕНИЯ

Движение в противоположных

направлениях

V1+V2 ==V УДАЛЕНИЯ

Движение в одном направлении

V1-V2 = V СБЛИЖЕНИЯ

2 . Задача

Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?

1) 80 – 60 = 20 (км/ч) – скорость удаления

2) 280 : 20 = 14 (ч) – время движения

1) 80 + 60 = 140 (км/ч) – скорость удаления

2) 280 : 140 = 2 (ч) – время движения

ОТВЕТ: 2 ЧАСА

3. Задача

Из двух городов выехали одновременно навстречу друг другу мотоциклист и велосипедист. Мотоциклист ехал со скоростью 48 км/ч, велосипедист – 12 км/ч. Они встретились. Найди расстояние между городами.

t 1 = t 2 = 4 ч

V1 = 48 км/ч

V2 = 12 км/ч

S = ?

4 . Задача

Самолет и вертолет вылетели одновременно

в одном направлении. Какое было расстояние между ними в момент вылета, если скорость самолета – 500 км/ч, скорость вертолета –

200 км/ч, и самолет догнал вертолет за 2 часа?

V 1 = 500 км/ч

V 2 = 200 км/ч

t = 2ч

1. 500-200=300(км/ч)-скорость сближения

2. 300*2=600 (км)- было такое расстояние

ОТВЕТ : 600м

ЗАДАЧА 5

В данный момент расстояние между двумя таксистами 345 км. На каком расстоянии будут находиться таксисты через два часа, если скорость одного 72 км /ч., а другого -68 км /ч., и они выезжают навстречу друг другу одновременно?

РЕШЕНИЕ: 1) 72 + 68 =140 (км /ч.) – скорость сближения таксистов. 2).140 * 2 = 280 (км) – на такое расстояние таксисты приблизятся друг к другу за 2 часа. 3). 345 – 280 = 65 (км) – на таком расстоянии будут таксисты через 2 часа. Ответ: 65 км.

ЗАДАЧА 6

Расстояние между городами А и В 720км. Из А в В вышел скорый поезд со скоростью 80 км /ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км /ч. Через сколько часов после выхода пассажирского поезда эти поезда встретятся?

РЕШЕНИЕ:

1)80*2=160(км)-прошёл скорый поезд за 2 часа.

2)720-160=560(км)-осталось пройти поездам.

3)80+60=140(км/ч)-скорость сближения 2 поездов.

4)560:140=4(ч)-был в пути пассажирский поезд.

Ответ:4часа.

ЗАДАЧА 7

Стоянка геологов находится на расстоянии 340 км от

города. Чтобы добраться до стоянки, геологи сначала ехали из города 4 часа на машине со скоростью 75 км/ч, затем 3 часа ехали на лошадях со скоростью 8 км/ч, а после этого 4 часа шли пешком. С какой скоростью они шли пешком?

РЕШЕНИЕ:

1) 75* 4= 300 (км) – проехали на машине.

2) 8 *3= 24 (км) – проехали на лошадях.

3) 300+ 24= 324 (км) – проехали на машине и на лошадях

вместе.

4) 340- 324= 16 (км) – прошли пешком.

5) 16 : 4= 4 (км/ч) – с такой скоростью они шли пешком.

ОТВЕТ: 4 км/ч

ЗАДАНИЕ НА ДОМ

задача 1 .Из двух пунктов навстречу друг другу одновременно выехали два автобуса. Скорость одного автобуса 45 км /ч, а скорость другого автобуса 72 км /ч. Первый автобус до встречи проехал 135км.

Найдите расстояние между пунктами.

задача 2. Максим и Саша вышли из школы со скоростью 50 м/мин. Рома вышел вслед за ними через 6 минут со скоростью 80 м/мин. Через сколько минут Рома догонит Максима и Сашу?

3. Расстояние между городами А и В равно 720 км. Из А в В вышел

скорый поезд со скоростью 80 км/ч. Через 2 ч навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км/ч. Через сколько часов после выхода скорого поезда они встретятся?

4. Два поезда движутся навстречу друг другу — один со скоростью

70 км/ч, другой со скоростью 80 км/ч. Пассажир, сидящий во втором поезде, заметил, что первый поезд прошел мимо него за 12 с. Какова длина первого поезда?

5. Из пункта А в пункт В вышел пешеход со скоростью 5 км/ч. Одновременно с ним из А в В вы¬ехал велосипедист со скоростью 10 км/ч. Велосипедист доехал до В, повернул назад и поехал с той же скоростью навстречу пешеходу. Через сколько часов после начала движения они встретятся, если расстояние между А и В равно 30 км?

http://www.yaklass.ru/p/algebra/8-klass/kvadratnye-uravneniia-11021/ratcionalnye-uravneniia-kak-matematicheskie-modeli-realnykh-situatcii-12479/re-0c0f870b-47fd-4d13-a964-991841af4dfe

https://www.youtube.com/watch?v=KDveB1VyeOo

multiurok.ru

Система тренировочных упражнений 8-9 класс по теме «Решение задач на движение по и против течения»

Система тренировочных задач (для 8-9 классов).

Тема: «Движения тел по течению и против течения».

Задача№1

Моторная лодка прошла 21км против течения реки и 8км по течению, затратив на весь путь 2ч. Найдите скорость лодки в стоячей воде, если скорость течения реки составляет 1км.ч.

Задача № 2

Катер проплыл 24км против течения реки и 27км по озеру, потратив на весь путь 3 часа. Найдите собственную скорость катера, если скорость течения реки равна 2км.ч.

Задача № 3

Лодка прошла 8км по течению реки и 6км против течения, затратив на весь путь 1ч. 12мин. Скорость течения реки составляет 3км.ч. Найдите скорость лодки по течению.

Задача № 4

Пароход прошел 17км по течению реки на 2 ч быстрее, чем 75км против течения. Найдите скорость течения, если собственная скорость парохода равна 32км.ч.

Задача №5

Моторная лодка проплыла 48км по течению реки и возвратилась назад, затратив на обратный путь на 1ч. больше. Найдите скорость течения, если собственная скорость лодки равна 14км.ч.

Задача №6

Моторная лодка проплыла 9км по течению реки и 14 км против течения за то же время, какое необходимо ей, чтобы проплыть 24км в стоячей воде. Найдите скорость лодки в стоячей воде, если скорость течения составляет 3км.ч.

Задача №7

Лодка проплывает 9км по течению реки и 1км против течения за то же время, которое необходимо плоту, чтобы проплыть 4км по этой реке. Найдите скорость течения, если собственная скорость лодки составляет 8км.ч.

Задача№8

Расстояние между двумя пристанями по реке равно 60км. Катер проходит этот путь туда и обратно за 3ч 40мин. Определите скорость течения, если собственная скорость катера равна 33км.ч.

Задача№9

По течению реки от пристани отошел плот. Через 9ч от этой пристани в том же направлении отошел катер, который догнал плот на расстоянии 20км от пристани. Найдите скорость течения, если собственная скорость катера составляет 18км.ч.

Задача№10

По течению реки от пристани отошел плот. Через 4ч от этой пристани в том же направлении отошла лодка, которая догнала плот на расстоянии 15км от пристани. Найдите скорость течения, если собственная скорость лодки составляет 12км.ч.

videouroki.net

Урок по алгебре 8 класс по теме «Решение задач на движение по реке»

Урок алгебры, 8 класс.

Тема:

«Решение задач, на движение по реке, составлением дробных рациональных уравнений».

Учитель Иванова Л. А.

МБОУ «СОШ № 14» г. Выборг

Тема урока: «Решение задач на движение по реке».

Цель: формирование программных знаний с учётом дифференцируемого подхода;

Задачи:

1. Образовательные:

2. Развивающие:

развитие памяти и речи на языке предмета;
развитие умения преодолевать трудности при решении рациональных уравнений и заданий, связанных с использованием дробно-рациональных уравнений;
развитие познавательного интереса, умения переносить знания в новые условия.

3. Воспитательные:

воспитание внимания, аккуратности, чёткости записи;
умения работать в паре и самостоятельно, оказывать помощь товарищу, умение провести самооценку и оценить деятельность товарищей.

Оборудование: компьютер, презентация, раздаточный материал: тест, карточка-помощник по решению дробных рациональных уравнений, карточка-помощник по составлению уравнения по условию задачи.

Ход урока.

1 этап. Проверка домашней задачи из учебника Магницкого (слайд №2).

2 этап. Повторение темы «Квадратные корни». Тест из шести заданий, повышающегося уровня сложности, таким образом, каждый может проявить себя. Самопроверка (слайд №4-5).

3 этап.

1) Подготовка к изучению нового материала. Устная фронтальная работа (слайд № 7, 8).

2) Изучение нового материала. Решение задач на движение по реке.

Задача № 1(слайд №9).

Турист проехал на моторной лодке вверх по реке 25 км, а обратно спустился на плоту. В лодке он плыл на 10 ч меньше, чем на плоту. Найдите скорость течения, если скорость лодки в стоячей воде 12 км/ч.

Учитель: Что нужно, чтобы решить задачу?

Ученик: Составить математическую модель задачи, используя таблицу.

Учитель: Какие величины должны быть в нашей таблице?

Заполнение таблицы на доске и в тетради. Выявление логических связей. Составление уравнения. Решение уравнения. Отбор корней на предмет условия задачи.

По течению реки (плот)

25 км

Против течения реки (лодка)

25 км

12-х

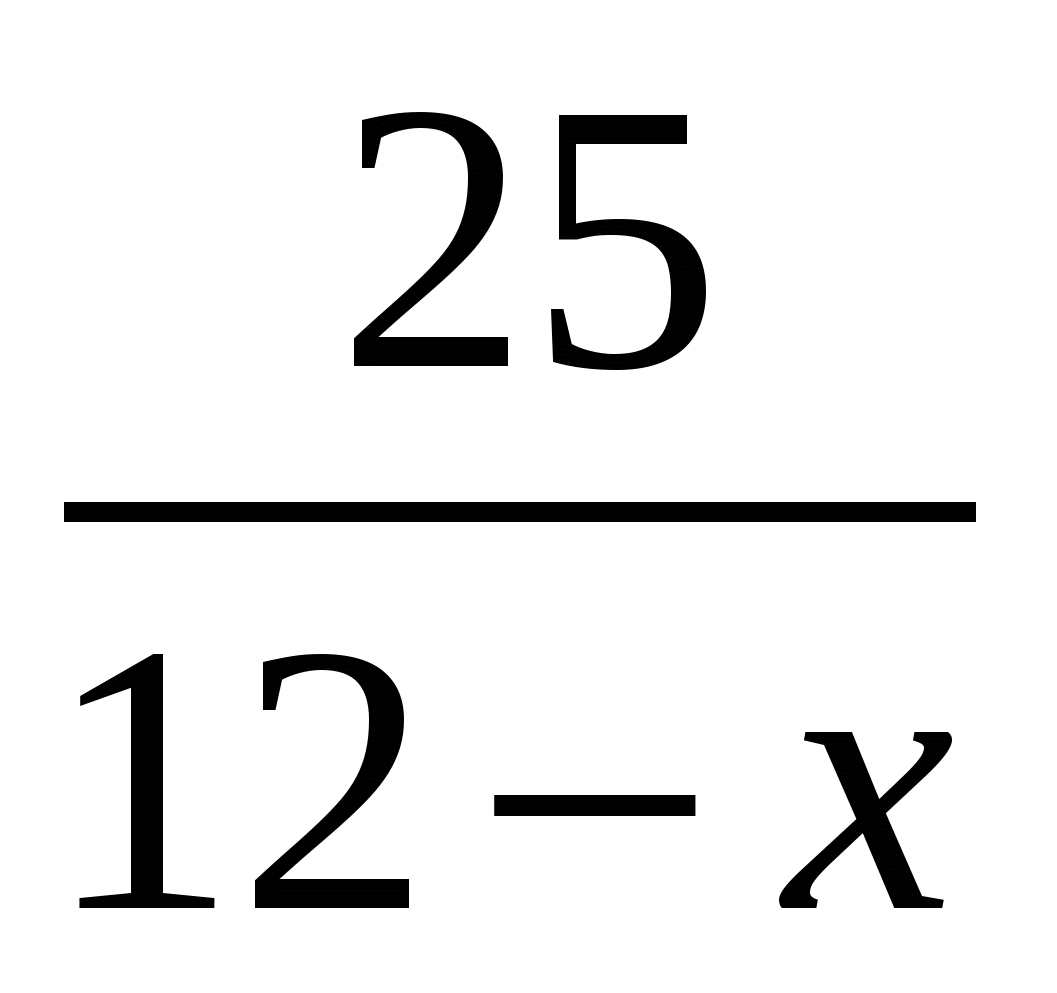
Скорость теч. реки

Х км/ч

Собственная скорость лодки

12 км/ч

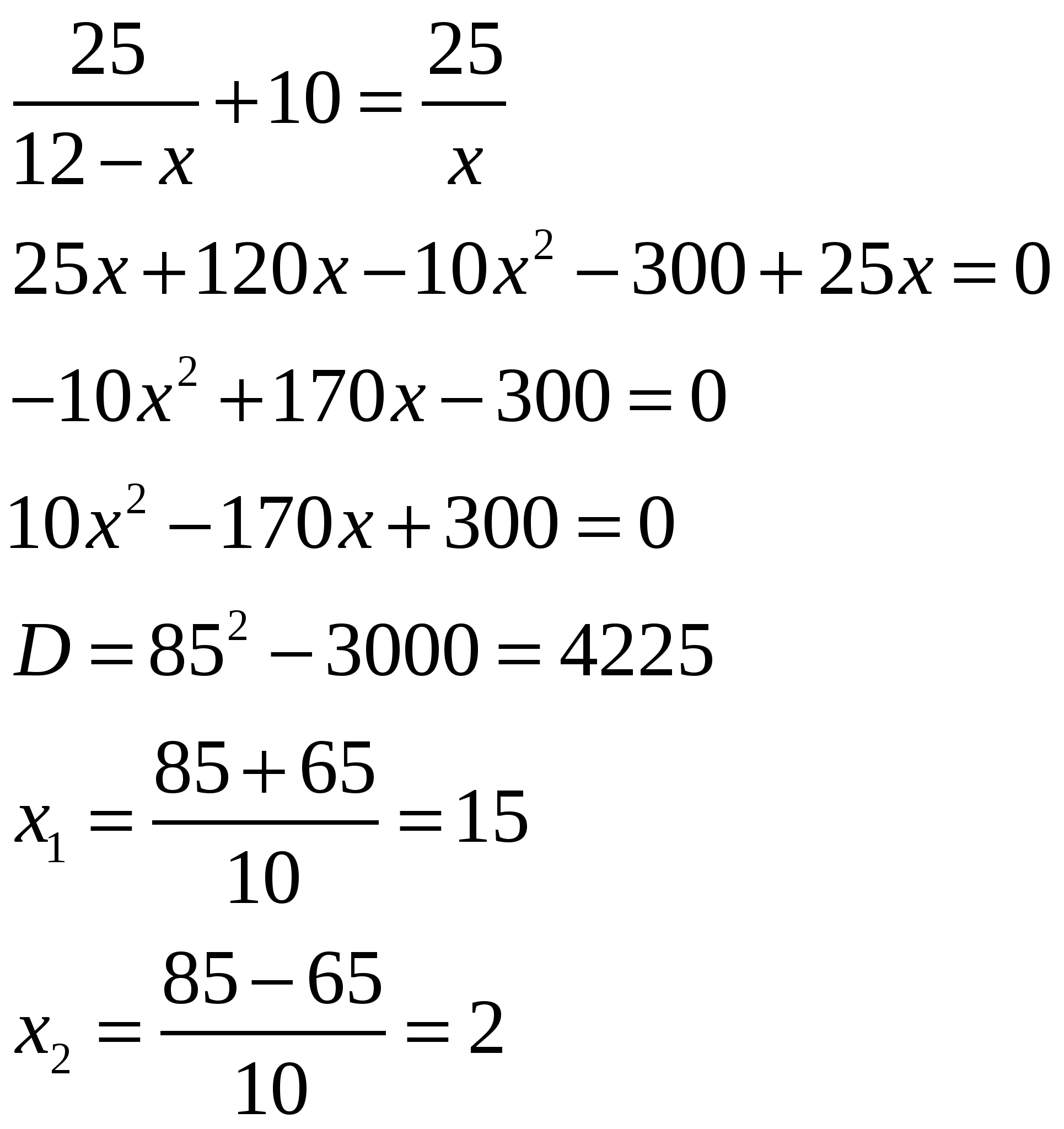
Ответ: скорость течения реки 2 км/ч.

3) Физкультминутка.

4) Учитель: А теперь поговорим о задачах древнего Китая (слайды № 10,11).

5) Составить уравнение по условию задачи № 629 (работа в парах, карточка-помощник). Самопроверка (слайд № 9). Дорешать задачу дома.

6) Самостоятельное решение задач по уровням. 1 уровень №628, 2 уровень № 627 (дополнительно № 703). Проверка учителем.

5 этап. Домашнее задание № 629, 636(а), Китайская задача.

Итог урока.

Задача №703

Моторная лодка прошла 35 км вверх по реке и на 18 км поднялась по ее притоку, затратив на весь путь 8ч. Скорость течения в реке на 1 км/ч меньше скорости течения в ее притоке. Найдите скорость течения в реке, если скорость лодки в стоячей воде 10 км/ч?

Против течения реки

(10-х)

8 ч

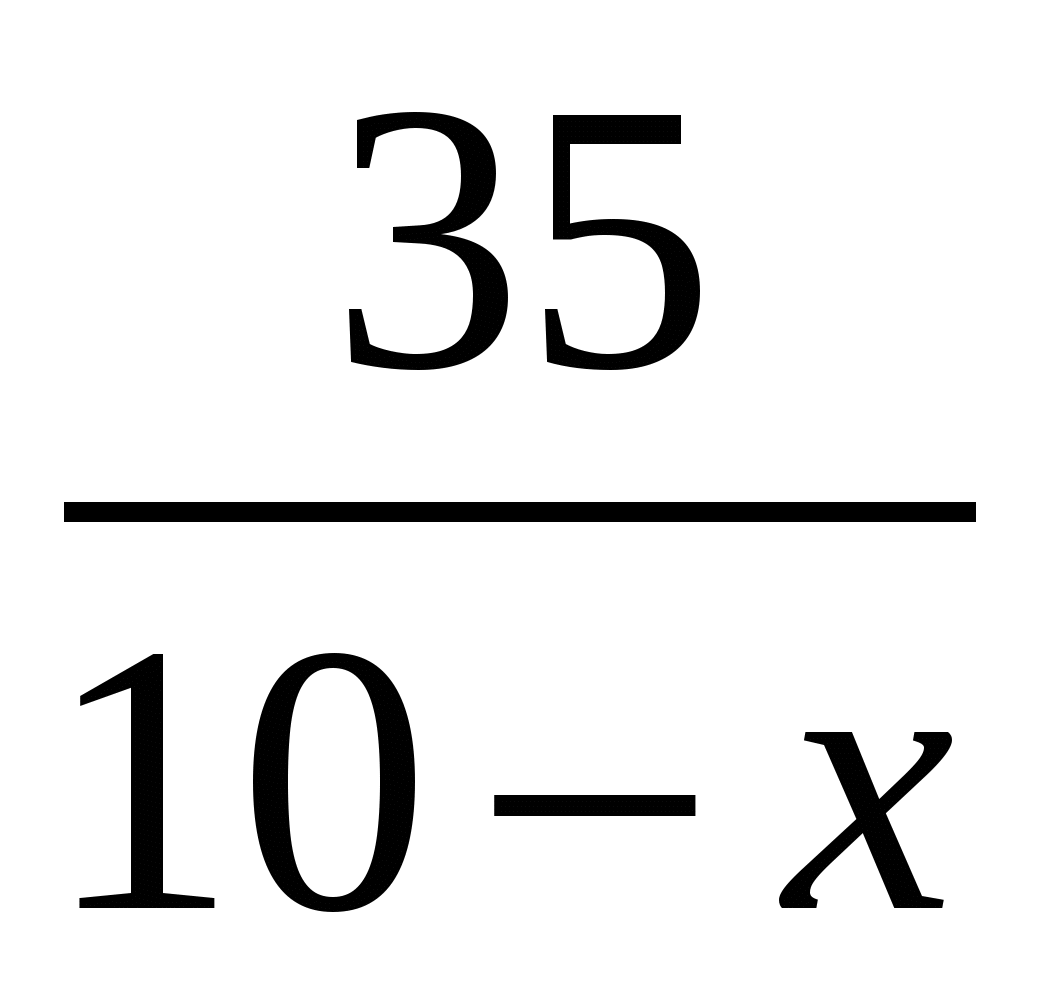
Против течения притока

(10-х-1)

Скорость теч. реки

Скорость теч.в притоке

X+1

Собственная скорость лодки

10 км/ч

Составим уравнение, решим его.

Ответ: скорость течения реки 3 км/ч.

Карточка-помощник по составлению уравнения.

По течению реки

Против течения

Собственная скорость лодки (скорость лодки в стоячей воде)

Скорость течения реки

Заполните таблицу. Для этого внимательно читая текст задачи, постепенно заполните столбец s.

В столбце v введите переменную х (для этого посмотрите на вопрос задачи, что необходимо найти), заполните остальные строчки, используя правило нахождения скорости лодки по течению реки и против течения. Заполните последний столбец, используя правило нахождения времени через расстояние и скорость. Что еще известно по условию задачи? Как это использовать, чтобы составить уравнение? Составьте уравнение.

infourok.ru

Подготовка к олимпиадам: относительность движения. 8 класс.

Продолжаем подготовку к олимпиадам. Сегодня закрепляем тему «относительность движения».

Задача 1. Человек, идущий вниз по опускающемуся эскалатору, затрачивает на спуск t_1=1 мин. Если человек будет идти вдвое быстрее, он затратит на $\Delta t=15$ с меньше. Сколько времени он будет спускаться, стоя на эскалаторе? Ответ выразить в секундах, округлив до целых.

Если длина эскалатора , а скорость человека $\upsilon$ , то

$l=(\upsilon+\upsilon_e)t_1$

$\upsilon_e$ – скорость эскалатора.

Для второй ситуации

$l=(2\upsilon+\upsilon_e)(t_1-15)$

Найти нам надо величину $\frac{l}{\upsilon_e }$ – это и будет временем пассивного спуска.

Приравняем правые части:

$(\upsilon+\upsilon_e)t_1=(2\upsilon+\upsilon_e)(t_1-15)$

Откуда

$2\upsilon=\upsilon_e$

Подставим в первое уравнение:

$l=(\frac{\upsilon_e}{2}+\upsilon_e)t_1$

Или

$\frac{l}{\upsilon_e }=90$

Ответ: 90 с.

Задача 2. Собака в лесу погналась за зайцем. За сколько скачков собака догонит зайца, если расстояние, которое собака пробегает за 5 скачков, равно расстоянию, которое заяц пробегает за 6 скачков? Начальное расстояние между собакой и зайцем равно 40 скачков собаки, а скачки собака и заяц делают одновременно.

Одно и то же расстояние собака преодолевает за 5 скачков, или за 5 единиц времени. Заяц – за шесть. Следовательно, скорость собаки

$\upsilon_s=\frac{l}{t_s}$

Скорость зайца –

$\upsilon_z=\frac{l}{t_z}$

Или

$\frac{\upsilon_s }{\upsilon_z}=\frac{ t_z }{ t_s}=\frac{6}{5}$

скорость зайца – $\upsilon_z=\frac{5}{6}\upsilon_s$ , а скорость сближения собаки и зайца равна

$\upsilon=\upsilon_s-\frac{5}{6}\upsilon_s=\frac{1}{6}\upsilon_s$

Время погони –

$t=\frac{S}{\upsilon}=\frac{40}{\frac{1}{6}\upsilon_s }=\frac{240}{\upsilon_s }$

Таким образом, придется 240 скачков собаке пробежать.

Ответ: 240.

Задача 3. В море при штиле навстречу друг другу плывут два мальчика. Скорость первого $\upsilon_1=1$ км/ч, скорость второго $\upsilon_2=2$ км/ч. Одновременно между ними плавает дельфин со скоростью U=10 км/ч. Подплыв к одному из мальчиков, он тотчас поворачивает обратно к другому. Так он и плавает между сближающимися мальчиками. Определите путь, который проделает дельфин за время, в течение которого расстояние между мальчиками сократилось от S_1=1 км до S_2=400 м. Ответ выразить в км, округлив до целых.

Мальчики сближаются со скоростью 3 км/ч. В общей сложности проплыли они вместе 600 м. Посчитаем, сколько времени это отняло:

$t=\frac{S}{\upsilon_1+\upsilon_2}=\frac{0,6}{3}=0,2$

Все это время дельфин шнырял туда-сюда, поэтому проплыл

$l=Ut=10\cdot0,2=2$

Ответ: 2 км.

Задача 4. По дороге, параллельной железнодорожным путям, едет велосипедист со скоростью u=14,4 км/ч. Его догоняет поезд длинной L=120 м и обгоняет за t_0=6 с. Определите скорость поезда $\upsilon$ . Ответ выразить в м/с, округлив до целых.

Поезд протаскивает свою длину мимо велосипедиста. Сближаются поезд и велосипедист со скоростью

$\upsilon-u=\upsilon-\frac{14400}{3600}=\upsilon-4$

Тогда

$\upsilon-4=\frac{L}{t_0}=20$

Тогда

$\upsilon=24$

Ответ: 24 м/с.

Задача 5. Вдоль железной дороги через каждые 100 м расставлены столбики с номерами 1, 2, …, 10, 1, 2, …, 10, …. Через 2 минуты после того, как кабина машиниста равномерно движущегося поезда проехала столбик с цифрой «1», машинист увидел в окне столбик с цифрой «2». Известно, что скорость поезда меньше 100 км/ч. С какой максимальной скоростью мог ехать поезд? Ответ дать в м/мин, округлив до целых.

Поезд мог проехать 100 м – тогда машинист увидел бы следующий по порядку столбик. Если поезд проехал 1100 м – то машинист увидел столбик следующего километра. Он также мог увидеть столбик с цифрой 2 и через 2100 м, или через 3100. Определим скорость в каждом случае (кроме первого случая – для поезда маловато):

$\upsilon_1=\frac{1100}{120}=9,1$

Это 33 км/ч.

$\upsilon_2=\frac{2100}{120}=17,5$

Это 63 км/ч.

$\upsilon_3=\frac{3100}{120}=25,8$

Это 93 км/ч.

Видимо, это и есть максимальная скорость, меньшая 100 км/ч.

Ответ: 93 км/ч.

Задача 6. Два автомобиля стартуют одновременно и движутся по прямолинейной дороге к финишу. Первый автомобиль первую половину времени своего движения до финиша движется со скоростью $\upsilon_1=100$ км/ч, а вторую половину времени – со скоростью $\upsilon_2=160$ км/ч. Второй автомобиль первую половину времени своего движения имеет скорость $\upsilon_3=120$ км/ч, а вторую половину времени – скорость $\upsilon_4=140$ км/ч. Какое максимальное расстояние будет между автомобилями в процессе движения, если длина трассы S=32,5 км? Ответ выразить в км, округлив до десятых.

Весь путь первого автомобиля

$S_1=\upsilon_1\cdot\frac{t}{2}+\upsilon_2\cdot\frac{t}{2}=50t+80t=130t$

Весь путь второго

$S_2=\upsilon_3\cdot\frac{t}{2}+\upsilon_4\cdot\frac{t}{2}=60t+70t=130t$

Таким образом, они финишируют одновременно.

$130t=32,5$

$t=0,25$

$\frac{t}{2}=0,125$

На первой половине времени расстояние между автомобилями увеличивается постоянно. А на второй – постоянно уменьшается. Поэтому максимальное расстояние между ними – как раз по истечении первой половины времени.

$l=(\upsilon_3-\upsilon_1) \frac{t}{2}=20\cdot0,125=2,5$

Ответ: 2,5 км.

Задача 7. Петя ездит в школу на автобусе, который всегда ходит точно по расписанию. Его дом стоит на обочине дороги между остановками A и B на расстоянии S=400 м от остановки A. Расстояние между остановками L=900 м. Автобус едет в направлении от A к B с постоянной скоростью u=10 м/с. Найдите, за какой минимальный промежуток времени Петя может добраться до пункта B, если он ходит со скоростью $\upsilon=2$ м/с, а время, в течение которого автобус стоит на остановке, пренебрежимо мало по сравнению с нахождением Пети в пути. Ответ выразить в с, округлив до целых.

Петя может идти от дома вдоль дороги до остановки , а потом ехать на автобусе до . Или он может идти сразу к остановке . Тогда в первом случае время равно

$t_1=\frac{S}{\upsilon}+\frac{L}{u}=200+90=290$

Во втором случае

$t_2=\frac{L-S}{\upsilon}=250$

Во втором случае мальчик быстрее попадет на остановку .

Ответ: 250 с.

easy-physic.ru

Урок в 8 классе «Задачи на движение

Алгебра 8 класс Алимов

Урок 63. Решение задач на движение с помощью квадратных уравнений.

Цели: Научить решать задачи на движение; составлять уравнение по условию задачи; составлять таблицу для краткой записи условия задачи.

Ход урока.

Организационный момент.
Устная работа.

Составить уравнение по условию задачи.

Произведение двух натуральных чисел равно 273. Найдите эти числа, если одно из них на 8 больше другого.
Одно из двух натуральных чисел на 7 меньше другого. Найдите эти числа, если их произведение равно 330.

Объяснение нового материала.

Задачи на движение – чаще всего встречающиеся задачи. При их решении нужно выделять три величины: скорость, время, расстояние и записать между ними зависимость. Чтобы это было нагляднее, лучше записывать все данные в таблицу.

Рассмотрим пример.

Чтобы ликвидировать опоздание на 1 час, поезд на перегоне в 720 км увеличил скорость, с которой должен был идти по расписанию, на 10 км/ч. Какова скорость поезда по расписанию?

Решение.

Обозначим скорость поезда по расписанию Х км/ч, тогда после увеличения скорости она будет равняться (Х+10) км/ч. Рассмотрим скорость, время и расстояние для двух видов движения:

720

Не по расписанию

(Х+10)км/ч

720 км

720_

Х+10

Используя такую таблицу, легко составить уравнение.

По расписанию поезд должен был проехать расстояние в 720 км за часов, а он после увеличения скорости был в пути часов. По условию задачи известно, что разность во времени составляет 1 час. Для данной задачи можно составить несколько уравнений, например,

Решая любое из них, находим Х₁=80; Х₂= — 90. По условию задачи скорость поезда может быть числом только положительным, значит, скорость поезда по расписанию составляет 80 км/ч.

Ответ: 80 км/ч.

Следует обратить внимание, что если в задаче несколько неизвестных величин, то за Х лучше обозначить меньшую величину. Иногда в задачах для обозначения одной величины используются разные единицы измерения, например, часы и минуты, их следует всегда переводить в одни единицы измерения.

Закрепление нового материала.

Разобрать задачу № 480

Решение:

400

Х+20

400 км

Товарный поезд

Х км/ч

400

400 км

По условию задачи время скорого меньше времени товарного поезда.

Составим и решим уравнение.

Самостоятельная работа.

Решение задачи № 485

30_

Х+3

30 км

2-й лыжник

Х км/ч

30 км

По условию задачи время 1-го лыжника меньше времени 2-го лыжника на

20 мин = 1/3 часа.

Составим и решим уравнение

Итоги урока.
Домашнее задание

§31. № 488.

infourok.ru

Текстовые задачи. Алгебра 8 класс ИДЗ 3 ЗАДАНИЕ 2

8 класс Алгебра ИДЗ 3

Задание 2. Решите задачи

Вариант 1.

1. Путь от города до поселка автомобиль проезжает за 2,5 ч. Если он увеличит скорость на 20 км/ч, то за 2 ч проедет путь на 15 км/ч больший, чем расстояние от города до поселка. Найдите это расстояние.

2. Один рабочий затрачивает на изготовление болта на 6 мин меньше, чем второй. Сколько болтов может изготовить каждый из них за 7 ч, если первый изготавливает за это время на 8 болтов больше?

Вариант 2.

1. Из Москвы в Санкт-Петербург выехал автобус. Спустя 1 ч за ним вышла легковая машина, скорость которой на 20 км/ч больше скорости автобуса. Машина обогнала автобус и через 5 ч после своего выхода находилась впереди него на 70 км. Найдите скорость автобуса.

2. Ученик тратит На обработку одной детали на 12 мин больше, чем мастер. Сколько деталей обработает каждый из них за 6 ч, если ученик обрабатывает на 5 деталей меньше, чем мастер?

Вариант 3

1. Товарный поезд был задержан в пути на18 мин, а затем на расстоянии в 60 км наверстал это время, увеличив скорость на 10 км/ч. Найти первоначальную скорость поезда.

2. Две бригады, работая совместно, закончили посадку деревьев за 4 дня. Сколько дней потребовалось бы на эту работе каждой бригаде, если одна из них может выполнить работу на 15 дней быстрее другой?

Вариант 4

1. Мотоциклист проехал 40 км от пункта А до пункта В. Возвращаясь обратно со скоростью на 10 км/ч меньше первоначальной, он затратил на 20 мин больше. Найти первоначальную скорость мотоциклиста.

2. Двое рабочих, работая вместе, могут выполнить оклейку комнаты обоями за 6 ч. За какое время каждый из них может оклеить эту комнату обоями, если один из них тратит на это на 5 ч меньше, чем другой?

Вариант 5

1. Теплоход прошел 4 км против течения реки и затем прошел еще 33 км по течению, затратив на весь путь 1 ч. Найдите скорость теплохода в стоячей воде, если скорость течения реки равна 6,5 км/ч.

2. Два экскаватора, работая совместно, могут вырыть котлован за 48 ч. За какое время каждый из них может вырыть котлован, работая в отдельности, если первому нужно на40 ч больше, чем второму?

Вариант 6

1. Моторная лодка прошла по течению 25 км и против течения 3 км, затратив на весь путь 2 ч. Какова скорость течения реки, если известно, что она не превосходит 5 км/ч, а скорость лодки в стоячей воде 12 км/ч.

2.Две трубы, работая вместе, наполнили бассейн за 12 ч. Первая труба, работая в отдельности, наполняет бассейн на 18 ч быстрее, чем вторая. За сколько ч наполняет бассейн вторая труба?

Вариант 7

1. Теплоход прошел по течению реки 48 км и столько же обратно, затратив на весь путь 5 ч. Определите собственную скорость теплохода, если скорость течения реки 4 км/ч.

2. Два сборщика винограда, работая вместе, собрали виноград с участка за 12ч. Первый сборщик мог бы собрать виноград с этого участка на 10 ч быстрее, чем второй. За какое время каждый сборщик может выполнить эту работу?

Вариант 8

1. Катер, собственная скорость которого 20 кем/ч, прошел расстояние по реке, равное 60 км, и вернулся обратно. Определите скорость течения реки, если на весь путь катер потратил 6,25 ч.

2. Два компьютера, работая совместно, могут выполнить определенный объем работы за 3,75 ч. Работая отдельно, один из них выполнил бы эту работу на 4 ч быстрее другого. Сколько времени потребовалось бы каждому компьютеру для выполнения этой работы?

Вариант 9

1. Пешеход должен был пройти 12 км за определенный срок, но он был задержан с выходом на 1ч, поэтому ему пришлось увеличить скорость на 1 км/ч. С какой скоростью шел пешеход?

2. Аквариум наполняется водой, поступающей в него через две трубки, за3 ч. За сколько ч может наполнить аквариум первая трубка, если ей потребуется для этого на 2,5 меньше, чем второй?

Вариант 10

1. Велосипедист проехал с определенной скоростью путь 10 км от города до турбазы. Возвращаясь обратно, он снизил скорость на 5 км/ч. НА весь путь туда и обратно потрачено 1 ч 10 мин. Найти его скорость от турбазы до города.

2. Двое рабочих вместе могут убрать помещение за 2 ч. Первому рабочему на эту работу потребовалось бы на 3 ч больше, чем второму. За какое время может убрать помещение первый рабочий?

Вариант 11

1. Расстояние между городами 200 км. Мотоциклист проходит это расстояние на 5 ч быстрее велосипедиста. Найти их скорости, если скорость велосипедиста на 20 км/ч меньше скорости мотоциклиста.

2. Два крана, работая вместе, разгрузили баржу за 6 ч. За какое время могут разгрузить баржу, работая отдельно, каждый кран, если одному из них нужно на 9 ч меньше, чем другому?

Вариант 12

1. Яхта прошла по течению реки 9 км и такой же путь против течения. Путь по течению занял на 2 ч меньше, чем путь против течения. Найти скорость яхты в стоячей воде, если скорость течения реки 3 км/ч.

2. Два грузовика, работая вместе, могут перевезти зерно за 4 ч. За какое время перевезет то же количество зерна каждый грузовик в отдельности, если первому нужно для этого на 6 ч больше, чем второму?

Вариант 13

Вариант 14

Вариант 15

Вариант 16

Вариант 17

Вариант 18

2. Две трубы, работая вместе, наполнили бассейн за 12 ч. Первая труба, работая в отдельности, наполняет бассейн на 18 ч быстрее, чем вторая. За сколько ч наполняет бассейн вторая труба?

Вариант 19

1. Теплоход прошел по течению реки48 км и столько же обратно, затратив на весь путь 5 ч. Определите собственную скорость теплохода, если скорость течения реки 4 км/ч.

Вариант 20

Вариант 21

Вариант 22

Вариант 23

Вариант 24

multiurok.ru