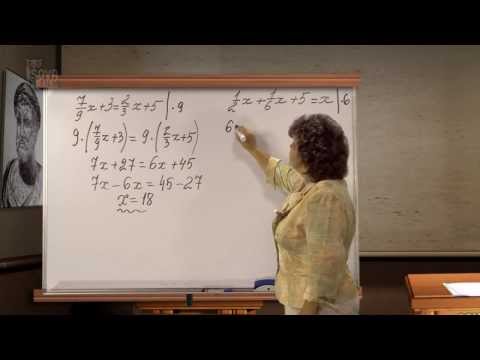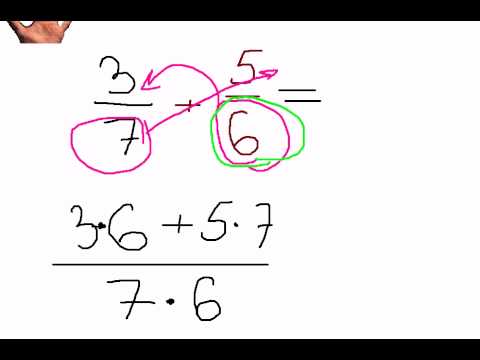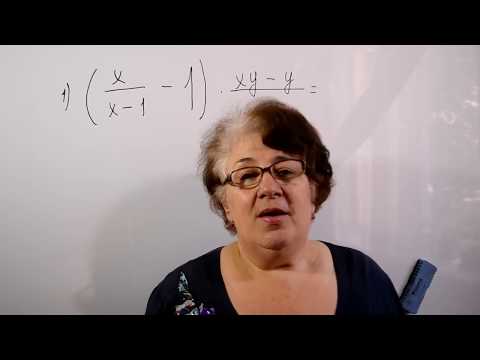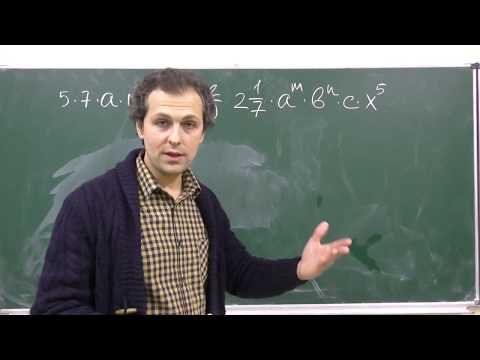Презентация к уроку по алгебре (7 класс) на тему: Урок математики в 7 классе по теме «Алгебраические выражения».
Слайд 1
Алгебраические выражения.Слайд 2
Проверка домашнего задания. Какие сведения из математики вам пришлось вспомнить в процессе выполнения домашнего задания ?
Слайд 3
Порядок арифметических действий. Переместительный закон сложения: a + b = b + a Переместительный закон умножения: a * b = b * a Сочетательный закон сложения: a + b + c = (a + b) + c = a + (b + c) Сочетательный закон умножения: abc = (ab)c = a(bc) Понятие обыкновенной дроби, десятичной дроби, отрицательного числа. Арифметические операции с десятичными дробями. Арифметические операции с обыкновенными дробями. Основное свойство обыкновенной дроби: Правила действий с десятичными дробями.
Слайд 4
Пример 1 Один холодильник стоит 350 $ . Тогда два холодильника стоят в два раза больше, т.е. 350·2=700 $ ; пять холодильников стоят в пять раз дороже, т.е. 350·5=1750 $ . Легко сообразить, что а холодильников стоят в а раз больше, т.е. 350· а $ С помощью выражения 350· а можно находить стоимость различного числа а холодильников, подставляя различные значения а и выполняя умножение. Так как буква а может принимать различные натуральные значения, то а – переменная 350· а – алгебраическое выражение (или выражение с переменной)
Слайд 5
Пример 2. Пусть длина одной стороны прямоугольника а см, другой – b см. Найдем периметр прямоугольника. b a P = 2 a + 2 b a , b – переменные 2 a + 2 b – алгебраическое выражение
Слайд 6
Пример 3. Запись 2a – 3b + 5 – алгебраическое выражение с переменными a и b . — алгебраическое выражение с переменными x и y .
Слайд 7
Пример 4. Найдем значение выражения при a = 3 , b = 4 и с =2 В данное алгебраическое выражение подставим значения переменных a = 3 , b = 4 , c = 2 . Получаем числовое выражение. Выполнив действия, найдем его значение: = = = 9 Число 9 является значением алгебраического выражения для данных значений переменных. Значение числового выражения , которое получается при подстановке выбранных значений переменных в алгебраическое выражение, называют значением алгебраического выражения.
Слайд 8
Задания. 1.18(а, в) 1.20(а) 1.22(а, г) 1.24(б) 1.29 (а) 1.39(а, б) 1.42(а, в)
Слайд 9
Контрольные вопросы. Чем отличаются числовые и алгебраические выражения? Что называется алгебраическим выражением и переменной? Как вычислить значение алгебраического выражения для данных значений переменных? Всегда ли это можно сделать?
Слайд 10
Задание на дом. 1.18(б, г) 1.20(в) 1.22(б, в) 1.24(г) 1.30(в) 1.40(б, г) 1.42(б, г)
Слайд 11
Спасибо з а урок
План-конспект урока по алгебре (7 класс) на тему: Алгебраические выражения
МБОУ «Прииртышская средняя общеобразовательная школа»
Алгебраические выражения
(урок алгебры в 7 классе)
Учитель: Голубева О.А.
п.Прииртышский, 2012 г
Развивающая: Развивать и совершенствовать умение применять имеющиеся знания в измененной ситуации; развивать научную речь и творческое мышление через создание условий для самореализации и творческого потенциала учащихся. |
Воспитательная: Содействовать воспитанию интереса к математике, активности, взаимопомощи, умения общаться через ситуацию успеха и доверия. |
Общедидактическая цель:
Познавательная: Отработать и закрепить навыки решения и преобразования алгебраических выражений; сформировать умение применять свойства тождественных преобразований. |
— обеспечить закрепление знаний и способов деятельности и организовать работу учащихся по первичному обобщению знаний и способов деятельности.
Уровневые цели:
- репродуктивный уровень: уметь применять навыки решения буквенных выражений;
- конструктивный уровень: использование высокого уровня суждений:
- творческий уровень: нахождение рационального способа решения.
Тип урока: закрепление новых знаний
Методы: рассуждающий, диалогический, эвристический, исследовательский
Форма: фронтальная, индивидуальная, дифференцированно-групповая, парная.
Оборудование: компьютер
учебник: Алгебра 7 класс
карточки
тест
Оборудование: компьютеры, презентация, набор карточек
О, сколько нам открытий чудных
Готовит просвещенья дух
И опыт, сын ошибок трудных,
И гений парадоксов друг!
А.С.Пушкин
Ход урока
I.Организационный момент.
Приветствие, мобилизация на учебную деятельность, запись числа в тетрадях.
II. Актуализация знаний.
- Какое выражение называется числовым?
- Какое выражение называется буквенным?
- Что значит найти значение выражения?
Сформулировать тему урока нам поможет следующее задание:
Задание: найти значение выражения (ответ укажет номер места на доске)
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
2х-3 | + 3х При х = | Х2 +2 | 6х + 3,8 | 4х-15 При х=2.5 | 28 – 4х | 3х – 2 | 26 – 2х2 |
АЛГ | ЕБР | АИЧ | ЕСК | ИЕ | ВЫР | АЖЕ | НИЯ |
Одновременно ведется индивидуальная работа со слабоуспевающими учащимися:
( выполнение тестового задания на компьютере) Учитель отслеживает ответы.
III. Отработка навыков преобразования алгебраических выражений.
1.Индивидуальная работа.
задание. Найти значение выражения 3х2 + 2, если
А | Х=- | 1 | 1 |
2 | — | ||
Б | Х=2 | 3 | -0,25 |
4 | 0 | ||
В | Х=0,5 | 5 | -12 |
6 | — 1075 | ||
Г | Х=0 | 7 | 2,5 |
8 | 16 |
Соедините стрелками значение Х с правильным ответом и запишите в таблицу
2. Работа в дифференцированных группах (по карточкам)
1.задание: Составить буквенное выражение для решения задачи и найти его значение. (Самопроверка)
Карточка №3
1 уровень: Две команды играли в баскетбол. Первая команда забросила а мячей, вторая – в мячей. Сколько мячей было забито за время матча? Найдите значение выражения при а=36, в=48 (ответ 84)
2 уровень: Две команды играли в баскетбол. В первой команде каждый из 3-х игроков забил а мячей, во второй команде каждый 2-ой игрок забросил в мячей. Сколько мячей было забито за время матча? Найдите значение выражения при а=15, в=20. (ответ 85)
2 задание. Работа по учебнику № 143(дополнительное задание)
3.Устная работа
Закончить свойства и сопоставить формулы с названием свойств
| A – распределительное свойство умножения относительно сложения |
| Б – переместительное свойство сложения |
| В – сочетательное свойство умножения |
| Г – переместительное свойство умножения |
| Д – сочетательное свойство сложения |
Ответ:
4. Работа в дифференцированных парах
1 уровень: Найти значение числового выражения
2 уровень: Найти значение числового выражения рациональным способом, ответ записать десятичной дробью
2 — 4 + 3 – 2 ;
Решение:
1. 2 + 3 = 6
2.- (4 + 2) = — 6
3. -6 + 6 = — = — 0,8
5. Индивидуальная работа у доски
1 ученик (слева): упростить выражение 0,5 (2а — 3) + 0,2(2а – 3) и найти его значение при а=2 (2 уровень) ответ: 0,7
2 ученик (справа): составить разность выражений 15а — 11в + 6 и 18а + 4в, упростить выражение (1 уровень) ответ: -3а – 15в + 6
IV. Подведение итогов урока. Рефлексия
1.Настроение: создадим букет: из ромашек (все понравилось), васильков (не всем доволен).
2. Уровень знаний: старт—————финиш расположить свой символ на дистанции.
V. Домашняя работа:
Разноуровневые задания (по выбору обучающегося):
1 уровень:
- Найдите значение выражения 8 — 5 + 2 ;
- Сравнить значения выражений 3х и при а) х = 9, б) х = — 15;
- Вычислить значение буквенного выражения 2 () при х=10, у=-5.
2 уровень:
- Преобразовать выражение 6,9 – 4,1m + (2,1 + 1,3n) – (0,3n + 0,9m) и найти его значение при n=2, m=3
- Составить выражение для решения задачи.
Площадь прямоугольника равна 42см2, одна из его сторон равна х см. Чему равен периметр данного прямоугольника? Найти его значение при х = 6 с
Материал по алгебре (7 класс) на тему: Алгебраические выражения,Алгебра,7 класс
правило «фонтанчика» | 1) вынесение общего множителя за скобки (количество слагаемых 2, 3, 4, 5…) | |
Общий множитель это | а) НОД коэффициентов б) степень с меньшим показателем | |
первый многочлен умножить на первое слагаемое второго многочлена, потом первый многочлен умножить на второе слагаемое второго многочлена, результаты сложить |
сгруппировали парами, между скобками + общий множитель вынесли за скобки | |
произведение разности двух выражений и их суммы равно разности квадратов этих выражений |
разность квадратов двух выражений равна произведению разности этих выражений и их суммы | |
квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого выражения на второе, плюс квадрат второго выражения |
| |
квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого выражения на второе, плюс квадрат второго выражения | 5) разложение на множители с помощью формулы квадрата разности двух выражений (количество слагаемых 3)
| |
произведение суммы двух выражений и неполного квадрата разности равно сумме кубов двух выражений | 6) разложение на множители суммы кубов двух выражений (количество слагаемых 2)
сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности | |
произведение разности двух выражений и неполного квадрата суммы равно разности кубов двух выражений |
(количество слагаемых 2)
разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы | |
💣алгебраические выражения 7 класс примеры ✔️
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
💣алгебраические выражения 7 класс примеры математика ✔️
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||