Задачи на движение. ЕГЭ по математике. Разбор задач.

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Если прочитаешь эту статью — гарантирую — ты научишься решать задачи на движение.

И вообще… умение решать задачи на движение может перевесить чашу весов в ту или иную сторону…сдашь ты экзамен или нет… поступишь на бюджет или нет…

В общем, думаю, никого убеждать не надо. Читай эту статью и РЕШАЙ ЗАДАЧИ!

Let’s dive right in… (Поехали!) 

Без чего нельзя решать задачи на движение (или без чего трудно хорошо сдать ЕГЭ по математике!) 

Для успешного решения задач на движение нужно все время держать в голове одну простую формулу:

Чтобы легче запомнить эту формулу, подумай, что ты ответишь на такой вопрос:

«Сколько километров я проеду на велосипеде за   часа, двигаясь со скоростью   км/ч?»

Ты, не задумываясь, ответишь –   км. Ну вот. Поздравляю! Эту формулу ты всегда хорошо знал, просто не мог сформулировать.

Из нашей формулы легко выразить все ее составляющие:

Очень многим запомнить формулу помогает вот такая пирамидка:

Усвоил? А теперь рассмотрим подробный алгоритм решения задачна движение. Он состоит из   больших этапов.

Разберем немного подробнее некоторые особенности и тонкости, возникающие при решении задач на движение.

Немного о внимательности в прочтении задач на движение

Прочитай задачу несколько раз. Осознай ее настолько, чтобы тебе было понятно абсолютно все.

Например, часто возникают трудности с понятием «собственная скорость лодки/катера» и т.д.

Подумай, что это может значить? Правильно, скорость лодки в стоячей воде, например, в пруду, когда на нее НЕ влияет скорость течения.

Кстати, в задачах иногда пишут «найти скорость лодки в стоячей воде».

Теперь ты знаешь, что собственная скорость лодки и скорость лодки в стоячей воде – одно и тоже, так что не теряйся, если встретишь оба этих определения.

Кто куда едет, кто к кому приехал, и где они все встретились

Сделай рисунок, попутно записывая на нем все известные величины (ну либо под ним, если не знаешь, как их отобразить схематически).

Рисунок должен четко отражать весь смысл задачи. Его следует сделать таким образом, чтобы на нем была видна динамика движения – направления движения, встречи, развороты, повороты.

Качественный рисунок позволяет понять задачу, не заглядывая в ее текст. Он – твоя основная подсказка для дальнейшего составления уравнения.

Рассмотрим возможные виды движения двух тел…

Не веришь? Давай посмотрим на практике.

Допустим, из точки   и из точки   навстречу друг другу выехали две машины. Скорость одной машины –   км/ч, а скорость   машины –   км/ч. Они встретились через   часа. Какое расстояние между пунктами   и  ?

Просто второе более рационально, так что запоминай формулу (она абсолютно логична, правда?), а для усвоения реши следующую задачу:

Оба решения являются верными.

Миша и Вася ехали на велосипеде навстречу друг к другу. Скорость Миши-  км/ч, скорость Васи –   км/ч. Ребята встретились через   часа. Какой совместный путь они проделали?

Решил? У меня получилось, что скорость сближения равна   км/ч, а путь равен   км.

Теперь разберемся, как вычисляется время при подобном случае

Исходя из предыдущей формулы, это вполне логично, однако, попробуем проверить на практике.

Итак, задача – Из пункта   и пункта   машины движутся навстречу друг другу со скоростями   км/ч и   км/ч. Расстояние между пунктами –   км. Через сколько времени машины встретятся?

Пусть   – время, которое едут машины, тогда путь первой машины –  , а путь второй машины –  .

Их сумма и будет равна расстоянию между пунктами   и   —  .

  (ч) – время, через которое встретились машины.

Попробуй самостоятельно решить задачу и доказать верность данной формулы как в предыдущем случае.

Из Москвы в противоположные стороны выехало   машины. Скорость одной машины –   км/ч, скорость другой –   км/ч. На каком расстоянии друг от друга будут находиться машины через   часа?

Решая первым способом, у меня получилось, что путь, проделанный первой машиной, равен   км, а второй –   км. Соответственно, расстояние между машинами –   км.

Решая вторым способом, выходит, что скорость удаления равна \displaystyle 145  км/ч, а путь равен \displaystyle 145  км/ч   = \displaystyle 290 км.

Теперь разберемся, как вычисляется время при подобном случае.

Как ты видишь, формула, аналогичная выведенной нами при

движении тел навстречу друг другу. Считаешь, что такого не может быть? Проверь ее на практике!

Допустим, что две машины двигаются в противоположных направлениях со скоростями   и   км/ч. При остановке, расстояние между ними составляло   км. Сколько времени ехали машины?

Попробуй решить эту задачу теми двумя способам, которые были описаны при движении на встречу.

Решил? Формула подтвердилась? Давай сравнивать ответы.

Уравнение, получаемое при решении 1 вариантом —  ; при решении 2 вариантом — скорость удаления –   км/ч, время в пути –   часа.

А что если, тела изначально находятся на неком расстоянии   друг от друга? Это выглядит примерно так:

Как решать подобные задачи тогда? Очень просто. При решении нам необходимо обязательно учитывать  .

Логично? Вырази из этой формулы время встречи двух тел, а потом сравним что у нас получилось.

Справился? Тогда решим задачу на данную формулу.

Из разных точек города N в стороны, противоположные друг другу, выехало два мотоциклиста. Изначальное расстояние между ними составляло   км. Скорость первого мотоциклиста составляла   км/ч; скорость второго –   км/ч.

Через какое время расстояние между ними будет равно   км?

Какой ответ ты получил? У меня получилось   часа.

Давай проверим все обстоятельно. Путь, который мотоциклисты действительно ехали равен  км км км. Скорость их удаления друг от друга равна   км/ч.

Делим   км на   км/ч и получаем   часа – время, которое мотоциклисты провели в дороге.

 

Итак, допустим, наши тела двигаются в одном направлении. Как ты думаешь, сколько случаев может быть для такого условия? Правильно, два.

Почему так получается? Уверена, что после всех примеров ты с легкостью сам разберешься, как вывести данные формулы.

Разобрался? Молодец! Пришло время решить задачу.

Четвертая задача

Коля едет на работу на машине со скоростью   км/ч. Коллега Коли Вова едет со скоростью   км/ч. Коля от Вовы живет на расстоянии   км.

Через сколько времени Вова догонит Колю, если из дома они выехали одновременно?

Посчитал? Сравним ответы – у меня получилось, что Вова догонит Колю через   часа или через   минут.

Сравним наши решения…

Рисунок выглядит вот таким образом:

Похож на твой? Молодец!

Так как в задаче спрашивается, через сколько ребята встретились, а выехали они одновременно, то время  , которое они ехали, будет одинаковым, так же как место встречи   (на рисунке оно обозначено точкой  ). Составляя уравнения, возьмем время за  .

Итак, Вова до места встречи проделал путь  . Коля до места встречи проделал путь  . Это понятно. Теперь разбираемся с осью передвижения.

Начнем с пути, который проделал Коля. Его путь ( ) на рисунке изображен как отрезок  . А из чего состоит путь Вовы ( )? Правильно, из суммы отрезков   и  , где   – изначальное расстояние между ребятами, а   равен пути, который проделал Коля.

Исходя из этих выводов, получаем уравнение:

 

Разобрался? Если нет, просто прочти это уравнение еще раз и посмотри на точки, отмеченные на оси. Рисунок помогает, не правда ли?

Решаем дальше и получаем:

 

 

  часа или   минут   минут.

Надеюсь, на этом примере ты понял, насколько важную роль играет грамотно составленный рисунок!

А мы плавно переходим, точнее, уже перешли к следующему пункту нашего алгоритма – приведение всех величин к одинаковой размерности.

 

Правило трех «Р» — размерность, разумность, расчет.

Размерность.

Далеко не всегда в задачах дается одинаковая размерность для каждого участника движения (как это было в наших легких задачках).

Например, можно встретить задачи, где сказано, что тела двигались определенное количество минут, а скорость их передвижения указана в км/ч.

Мы не можем просто взять и подставить значения в формулу – ответ получится неверный. Даже по единицам измерения наш ответ «не пройдет» проверку на разумность. Сравни:

Видишь? При грамотном перемножении у нас также сокращаются единицы измерения, и, соответственно, получается разумный и верный результат.

А что происходит, если мы не переводим в одну систему измерения? Странная размерность у ответа и  % неверный результат.

Итак, напомню тебе на всякий случай значения основных единиц измерения длины и времени.

  сантиметр =   миллиметров

  дециметр =   сантиметров =   миллиметров

  метр =   дециметров =   сантиметров =   миллиметров

  километр =   метров

  минута =   секунд

  час =   минут =   секунд

  сутки =   часа =   минут =   секунд

Совет: Переводя единицы измерения, связанные с временем (минуты в часы, часы в секунды и т.д.) представь в голове циферблат часов. Невооруженным глазом видно, что   минут это четверть циферблата, т.е.   часа,   минут это треть циферблата, т.е.   часа, а   минута это   часа.

А теперь совсем простенькая задача:

Маша ехала на велосипеде из дома в деревню со скоростью   км/ч на протяжении   минут. Какое расстояние между машиным домом и деревней?

Посчитал? Правильный ответ –   км.

  минут – это час, и еще   минут от часа (мысленно представил себе циферблат часов, и сказал, что   минут – четверть часа), соответственно –   мин =   ч.

  км

Разумность.

Ты же понимаешь, что скорость машины не может быть   км/ч, если речь, конечно, идет не о спортивном болиде? И уж тем более, она не может быть отрицательной, верно? Так вот, разумность, это об этом)

Расчет.

Посмотри, «проходит» ли твое решение на размерность и разумность, и только потом проверяй расчеты. Логично же – если с размерностью и разумностью получается несостыковочка, то проще все зачеркнуть и начать искать логические и математические ошибки.

 

«Любовь к таблицам» или «когда рисунка недостаточно»

Далеко не всегда задачи на движение такие простые, как мы решали раньше. Очень часто, для того, чтобы правильно решить задачу, нужно не просто нарисовать грамотный рисунок, но и составить таблицу со всеми данными нам условиями.

Первая задача

Из пункта   в пункт  , расстояние между которыми   км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на   км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт   на   минут позже, чем мотоциклист.

Вот такая вот задача. Соберись, и прочитай ее несколько раз. Прочитал? Начинай рисовать – прямая, пункт  , пункт  , две стрелочки…

В общем рисуй, и сейчас сравним, что у тебя получилось.

Пустовато как-то, правда? Рисуем таблицу.

Как ты помнишь, все задачи на движения состоят из   компонентов: скорость, время и путь. Именно из этих граф и будет состоять любая таблица в подобных задачах.

Правда, мы добавим еще один столбец – имя, про кого мы пишем информацию – мотоциклист и велосипедист.

Так же в шапке укажи размерность, в какой ты будешь вписывать туда величины. Ты же помнишь, как это важно, правда?

У тебя получилась вот такая таблица?

	Скорость км/ч	Время t, часов	Путь S, км
велосипедист
мотоциклист

 

Теперь давай анализировать все, что у нас есть, и параллельно заносить данные в таблицу и на рисунок.

Первое, что мы имеем – это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен   км. Вносим!

	Скорость км/ч	Время t, часов	Путь S, км
велосипедист			30
мотоциклист			30

 

Рассуждаем дальше. Мы знаем, что мотоциклист проезжает на   км/ч больше, чем велосипедист, да и в задаче нужно найти скорость велосипедиста…

Возьмем скорость велосипедиста за  , тогда скорость мотоциклиста будет  …

Если с такой переменной решение задачи не пойдет – ничего страшного, возьмем другую, пока не дойдем до победного. Такое бывает, главное не нервничать!

	Скорость км/ч	Время t, часов	Путь S, км
велосипедист			30
мотоциклист			30

 

Таблица преобразилась. У нас осталась не заполнена только одна графа – время. Как найти время, когда есть путь и скорость?

Правильно, разделить путь на скорость. Вноси это в таблицу.

	Скорость км/ч	Время t, часов	Путь S, км
велосипедист			30
мотоциклист			30

 

Вот и заполнилась наша таблица, теперь можно внести данные на рисунок.

Что мы можем на нем отразить?

Молодец. Скорость передвижения мотоциклиста и велосипедиста.

Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу.

Какие данные не отражены ни в таблице, ни на рисунке?

Верно. Время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени –   минут.

Что мы должны сделать следующим шагом? Правильно, перевести данное нам время из минут в часы, ведь скорость дана нам в км/ч.

  минут /   минут =   часа.

И что дальше, спросишь ты? А дальше числовая магия!

Магия формул: составление и решение уравнений – манипуляции, приводящие к единственно верному ответу.

Итак, как ты уже догадался, сейчас мы будем составлять уравнение.

Составление уравнения:

Взгляни на свою таблицу, на последнее условие, которое в нее не вошло и подумай, зависимость между чем и чем мы можем вынести в уравнение?

Правильно. Мы можем составить уравнение, основываясь на разнице во времени!

 

Логично? Велосипедист ехал больше, если мы из его времени вычтем время движения мотоциклиста, мы как раз получим данную нам разницу.

Это уравнение – рациональное. Если не знаешь, что это такое, прочти тему «Рациональные уравнения».

Приводим слагаемые к общему знаменателю:

 

Раскроем скобки и приведем подобные слагаемые:Уф! Усвоил? Попробуй свои силы на следующей задаче.

Решение уравнения:

 

Из этого уравнения мы получаем следующее:

 

 

 

Раскроем скобки и перенесем все в левую часть уравнения:

 

Вуаля! У нас простое квадратное уравнение. Решаем!

 

 

 

 

 

 

 

Мы получили два варианта ответа. Смотрим, что мы взяли за  ? Правильно, скорость велосипедиста.

Вспоминаем правило «3Р», конкретнее «разумность». Понимаешь о чем я? Именно! Скорость не может быть отрицательной, следовательно, наш ответ –   км/ч.

Вторая задача

Два велосипедиста одновременно отправились в  -километровый пробег. Первый ехал со скоростью, на   км/ч большей, чем скорость второго, и прибыл к финишу на   часов раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

Напоминаю алгоритм решения:

• Прочитай задачу пару раз – усвой все-все детали. Усвоил?
• Начинай рисовать рисунок – в каком направлении они двигаются? какое расстояние они прошли? Нарисовал?
• Проверь, все ли величины у тебя одинаковой размерности и начинай выписывать кратко условие задачи, составляя табличку (ты же помнишь какие там графы?).
• Пока все это пишешь, думай, что взять за  ? Выбрал? Записывай в таблицу! Ну а теперь просто: составляем уравнение и решаем. Да, и напоследок – помни о «3Р»!
• Все сделал? Молодец! У меня получилось, что скорость велосипедиста –   км/ч.

-«Какого цвета твоя машина?» — «Она красивая!» Правильные ответы на поставленные вопросы

Продолжим наш разговор. Так какая там скорость у первого велосипедиста?   км/ч? Очень надеюсь, что ты сейчас не киваешь утвердительно!

Внимательно прочти вопрос: «Какая скорость у первого велосипедиста?»

Понял, о чем я?

Именно! Полученный   – это не всегда ответ на поставленный вопрос!

Вдумчиво читай вопросы — возможно, после нахождения   тебе нужно будет произвести еще некоторые манипуляции, например, прибавить   км/ч, как в нашей задаче.

Еще один момент — часто в задачах все указывается в часах, а ответ просят выразить в минутах, или же все данные даны в км, а ответ просят записать в метрах.

Смотри за размерностью не только в ходе самого решения, но и когда записываешь ответы.

Задачи на движение по кругу

Тела в задачах могут двигаться не обязательно прямо, но и по кругу, например, велосипедисты могут ехать по круговой трассе. Разберем такую задачу.

Задача №1

Из пункта   круговой трассы выехал велосипедист. Через   минут он еще не вернулся в пункт   и из пункта   следом за ним отправился мотоциклист. Через   минут после отправления он догнал велосипедиста в первый раз, а еще через   минут после этого догнал его во второй раз.

Найдите скорость велосипедиста, если длина трассы равна   км. Ответ дайте в км/ч.

Решение задачи №1

Попробуй нарисовать рисунок к этой задаче и заполнить для нее таблицу. Вот что получилось у меня:

Пусть скорость велосипедиста будет  , а мотоциклиста –  . До момента первой встречи велосипедист был в пути   минут, а мотоциклист –  .

При этом они проехали равные расстояния:

 

Между встречами велосипедист проехал расстояние  , а мотоциклист –  .

Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:

Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили – спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.

Значит,

 

Полученные уравнения решаем в системе:

 

 

Ответ:  .

Разобрался? Попробуй решить самостоятельно следующие задачи:

Задачи для самостоятельной работы:

1. Два мо­то­цик­ли­ста стар­ту­ют од­но­вре­мен­но в одном на­прав­ле­нии из двух диа­мет­раль­но про­ти­во­по­лож­ных точек кру­го­вой трас­сы, длина ко­то­рой равна   км. Через сколь­ко минут мо­то­цик­ли­сты по­рав­ня­ют­ся в пер­вый раз, если ско­рость од­но­го из них на   км/ч боль­ше скорости дру­го­го?
2. Из одной точки кру­го­вой трас­сы, длина ко­то­рой равна   км, од­н­времен­но в одном на­прав­ле­нии стар­то­ва­ли два мотоциклиста. Ско­рость пер­во­го мотоцикла равна   км/ч, и через   минут после стар­та он опе­ре­дил вто­рой мотоцикл на один круг. Най­ди­те ско­рость вто­ро­го мотоцикла. Ответ дайте в км/ч.

Решения задач для самостоятельной работы:

1. Пусть   км/ч — ско­рость пер­во­го мо­то­цик­ли­ста, тогда ско­рость вто­ро­го мо­то­цик­ли­ста равна   км/ч. Пусть пер­вый раз мо­то­цик­ли­сты по­рав­ня­ют­ся через   часов. Для того, чтобы мо­то­цик­ли­сты по­рав­ня­лись, более быст­рый дол­жен пре­одо­леть из­на­чаль­но раз­де­ля­ю­щее их рас­сто­я­ние, рав­ное по­ло­ви­не длины трас­сы.
    
   Получаем, что время равно   часа =   минут.
2. Пусть ско­рость вто­ро­го мотоцикла равна   км/ч. За   часа пер­вый мотоцикл про­шел на   км боль­ше, чем вто­рой, соответственно, получаем уравнение:
    
   Скорость второго мотоциклиста равна   км/ч.

 

Задачи на течение

Теперь, когда ты отлично решаешь задачи «на суше», перейдем в воду, и рассмотрим страаашные задачи, связанные с течением.

Представь, что у тебя есть плот, и ты спустил его в озеро. Что с ним происходит? Правильно. Он стоит, потому что озеро, пруд, лужа, в конце концов, – это стоячая вода.

Скорость течения в озере равна  .

Плот поедет, только если ты сам начнешь грести. Та скорость, которую он приобретет, будет собственной скоростью плота. Неважно куда ты поплывешь – налево, направо, плот будет двигаться с той скоростью, с которой ты будешь грести. Это понятно? Логично же.

А сейчас представь, что ты спускаешь плот на реку, отворачиваешься, чтобы взять веревку…, поворачиваешься, а он … уплыл…

Это происходит потому что у реки есть скорость течения, которая относит твой плот по направлению течения.

Его скорость при этом равна нулю (ты же стоишь в шоке на берегу и не гребешь) – он движется со скоростью течения.

Разобрался?

Тогда ответь вот на какой вопрос – «С какой скоростью будет плыть плот по реке, если ты сидишь и гребешь?» Задумался?

Здесь возможно два варианта.

1-й вариант — ты плывешь по течению.

И тогда ты плывешь с собственной скоростью + скорость течения. Течение как бы помогает тебе двигаться вперед.

2-й вариант — ты плывешь против течения.

Тяжело? Правильно, потому что течение пытается «откинуть» тебя назад. Ты прилагаешь все больше усилий, чтобы проплыть хотя бы   метров, соответственно скорость, с которой ты передвигаешься, равна собственная скорость – скорость течения.

Допустим, тебе надо проплыть   км. Когда ты преодолеешь это расстояние быстрее? Когда ты будешь двигаться по течению или против?

Решим задачку и проверим.

Добавим к нашему пути данные о скорости течения –   км/ч и о собственной скорости плота –   км/ч. Какое время ты затратишь, двигаясь по течению и против него?

Конечно, ты без труда справился с этой задачей! По течению –   час, а против течения аж   часа!

В этом и есть вся суть задач на движение с течением.

Несколько усложним задачу.

Задача №1

Лодка с моторчиком плыла из пункта   в пункт     часа, а обратно –   часа.

Найдите скорость течения, если скорость лодки в стоячей воде –   км/ч

Решение задачи №1

Обозначим расстояние между пунктами, как  , а скорость течения – как  .

Все данные из условия занесем в таблицу:

	Путь S	Скорость v, км/ч	Время t, часов
A –> B (против течения)			3
B –> A (по течению)			2

 

Мы видим, что лодка проделывает один и тот же путь, соответственно:

 

 

 

 

Что мы брали за  ?

Скорость течения. Тогда это и будет являться ответом:)

Скорость течения равна   км/ч.

Задача №2

Байдарка в   вышла из пункта   в пункт  , расположенный в   км от  . Пробыв в пункте    час   минут, байдарка отправилась назад и вернулась в пункт   в  .

Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки   км/ч.

Решение задачи №2

Итак, приступим. Прочитай задачу несколько раз и сделай рисунок. Думаю, ты без труда сможешь решить это самостоятельно.

Все величины у нас выражены в одном виде? Нет. Время отдыха у нас указано и в часах, и в минутах.

Переведем это в часы:

  час   минут =   ч.

Теперь все величины у нас выражены в одном виде. Приступим к заполнению таблицы и поиску того, что мы возьмем за  .

Пусть   – собственная скорость байдарки. Тогда, скорость байдарки по течению равна  , а против течения равна  .

Запишем эти данные, а так же путь (он, как ты понимаешь, одинаков) и время, выраженное через путь и скорость, в таблицу:

	Путь S	Скорость v, км/ч	Время t, часов
Против течения	26
По течению	26

 

Посчитаем, сколько времени байдарка затратила на свое путешествие:

  часов.

Все ли   часов она плыла? Перечитываем задачу.

Нет, не все. У нее был отдых   час   минут, соответственно, из   часов мы вычитаем время отдыха, которое, мы уже перевели в часы:

   ч байдарка действительно плыла.

Догадываешься, что мы делаем дальше? Правильно! Приравниваем полученное время к тому времени, которое мы выразили в таблице через путь и скорость. Получаем:

 

Приведем все слагаемые к общему знаменателю   :

 

Раскроем скобки и приведем подобные слагаемые. Далее решаем получившееся квадратное уравнение. 

С этим, я думаю, ты тоже справишься самостоятельно. Какой ответ у тебя получился? У меня   км/ч.

 

 

Подведем итоги

1. Основная формула:  
   
2. Алгоритм решения задач на движение подразумевает выполнение двух больших этапов:
   
3. В задачах на движение обязательно необходимо рисовать чертеж. Тела могут двигаться навстречу друг другу, в противоположные стороны и догонять друг друга.
4. Все цифры нужно привести в единой размерности – только км или только м; только часы или минуты, и т.д.
5. Решая задачи, удобно записывать данные в виде таблицы с обязательными графами – путь, скорость и время.
6. За   можно брать как то, что нужно найти в задаче, так и другое неизвестное.
7. Внимательно читай, что спрашивается в задаче!   – не всегда ответ. Кроме этого, в ответе могут попросить указать величину в другой единице измерения (не в той, которая вышла у тебя, решая уравнение).
8. Задачи на движение по течению решаются в две формулы:
   

 

ПРОДВИНУТЫЙ УРОВЕНЬ

Задачи на движение. Примеры

Рассмотрим примеры с решениями для каждого типа задач.

Движение с течением

Одни из самых простых задач – задачи на движение по реке. Вся их суть в следующем:

• если движемся по течению, к нашей скорости прибавляется скорость течения;
• если движемся против течения, из нашей скорости вычитается скорость течения.

Пример №1:

Катер плыл из пункта A в пункт B   часов а обратно –   часа. Найдите скорость течения, если скорость катера в стоячей воде   км/ч.

Решение №1:

Обозначим расстояние между пунктами, как AB, а скорость течения – как  .

 

Все данные из условия занесем в таблицу:

	Путь S	Скорость v, км/ч	Время t, часов
A –> B (против течения)	AB	50–x	5
B –> A (по течению)	AB	50+x	3

Для каждой строки этой таблицы нужно записать формулу:

 

 

На самом деле, можно не писать уравнения для каждой из строк таблицы. Мы ведь видим, что расстояние, пройденное катером туда и обратно одинаково.

Значит, расстояние мы можем приравнять. Для этого используем сразу формулу для расстояния:

 .

Часто приходится использовать и формулу для времени:

 .

Пример №2:

Против течения лодка проплывает расстояние в   км на   час дольше, чем по течению. Найдите скорость лодки в стоячей воде, если скорость течения равна   км/ч.

Решение №2 :

Попробуем сразу составить уравнение. Время против течения на   час больше, чем время по течению.

Это записывается так:

 

Теперь вместо каждого времени подставим формулу:

 

Получили обычное рациональное уравнение, решим его:

 

Очевидно, что скорость не может быть отрицательным числом, значит, ответ:   км/ч.

Относительное движение

Если какие-то тела движутся друг относительно друга, часто бывает полезно посчитать их относительную скорость. Она равна:

• сумме скоростей, если тела движутся навстречу друг другу;
• разности скоростей, если тела движутся в одном направлении.

Пример №1

Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля со скоростями   км/ч и   км/ч. Через сколько минут они встретятся. Если расстояние между пунктами   км?

I способ решения:

 

Относительная скорость автомобилей   км/ч. Это значит, что если мы сидим в первом автомобиле, то он нам кажется неподвижным, но второй автомобиль приближается к нам со скоростью   км/ч. Так как между автомобилями изначально расстояние   км, время, через которое второй автомобиль проедет мимо первого:

 .

II способ решения:

Время от начала движения до встречи у автомобилей, очевидно, одинаковое. Обозначим его  . Тогда первый автомобиль проехал путь  , а второй –  .

В сумме они проехали все   км. Значит,

 .

 

Другие задачи на движение

Пример №1:

Из пункта А в пункт В выехал автомобиль. Одновременно с ним выехал другой автомобиль, который ровно половину пути ехал со скоростью на   км/ч меньшей, чем первый, а вторую половину пути он проехал со скоростью   км/ч.

В результате автомобили прибыли в пункт В одновременно.

Найдите скорость первого автомобиля, если известно, что она больше   км/ч.

Решение №1:

Слева от знака равно запишем время первого автомобиля, а справа – второго:

 .

Упростим выражение в правой части:

 .

Поделим каждое слагаемое на АВ:

 .

Получилось обычное рациональное уравнение. Решив его, получим два корня:

 

Из них только один больше  .

Ответ:   км/ч.

Если тебе непонятно, как получились эти корни, прочитай тему «Рациональные уравнения».

 

Пример №2

Из пункта A круговой трассы выехал велосипедист. Через   минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через   минут после отправления он догнал велосипедиста в первый раз, а еще через   минут после этого догнал его во второй раз. Найдите скорость велосипедиста, если длина трассы равна   км. Ответ дайте в км/ч.

Решение:

Здесь будем приравнивать расстояние.

Пусть скорость велосипедиста будет  , а мотоциклиста –  . До момента первой встречи велосипедист был в пути   минут, а мотоциклист –  .

При этом они проехали равные расстояния:

 

Между встречами велосипедист проехал расстояние  , а мотоциклист –  . Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:

Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили– спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.

Значит,

 

Полученные уравнения решаем в системе:

 

Ответ:  .

КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ

1. Основная формула

 , или  

2. Относительное движение

• Это сумма скоростей, если тела движутся навстречу друг другу;
• разность скоростей, если тела движутся в одном направлении.

3. Движение с течением:

• Если движемся по течению, к нашей скорости прибавляется скорость течения;
• если движемся против течения, из скорости вычитается скорость течения.

Мы помогли тебе разобраться с задачами на движение…

Теперь твой ход…

Если ты внимательно прочитал текст и прорешал самостоятельно все примеры, готовы спорить, что ты все понял. 

И это уже половина пути.

Напиши внизу в комментариях разобрался ли ты с задачами на движение?

Какие вызывают наибольшие трудности?

Понимаешь ли ты, что задачи на «работу» — это почти тоже самое? 

Напиши нам и удачи на экзаменах!

 

 

 

Получить доступ к учебнику YouClever без ограничений можно кликнув по этой ссылке:

youclever.org

Задачи на движение | Фізика — легко!

Для начала вспомним формулы, которые используют при решении подобных задач:  S = υ·t,   υ = S : t,   t = S : υ
где S – расстояние, υ – скорость движения, t – время движения.

Когда два объекта движутся равномерно с разными скоростями, то расстояние между ними за каждую единицу времени или увеличивается, или уменьшается.

Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.

Движение на сближение можно разделить на два вида: встречное движение и движение вдогонку. Движение на удаление можно разделить на два вида: движение в противоположных направлениях и движение с отставанием.

Трудность для некоторых учеников заключается в том, чтобы правильно поставить «+» или «–» между скоростями при нахождении скорости сближения объектов или скорости удаления.

Рассмотрим таблицу.

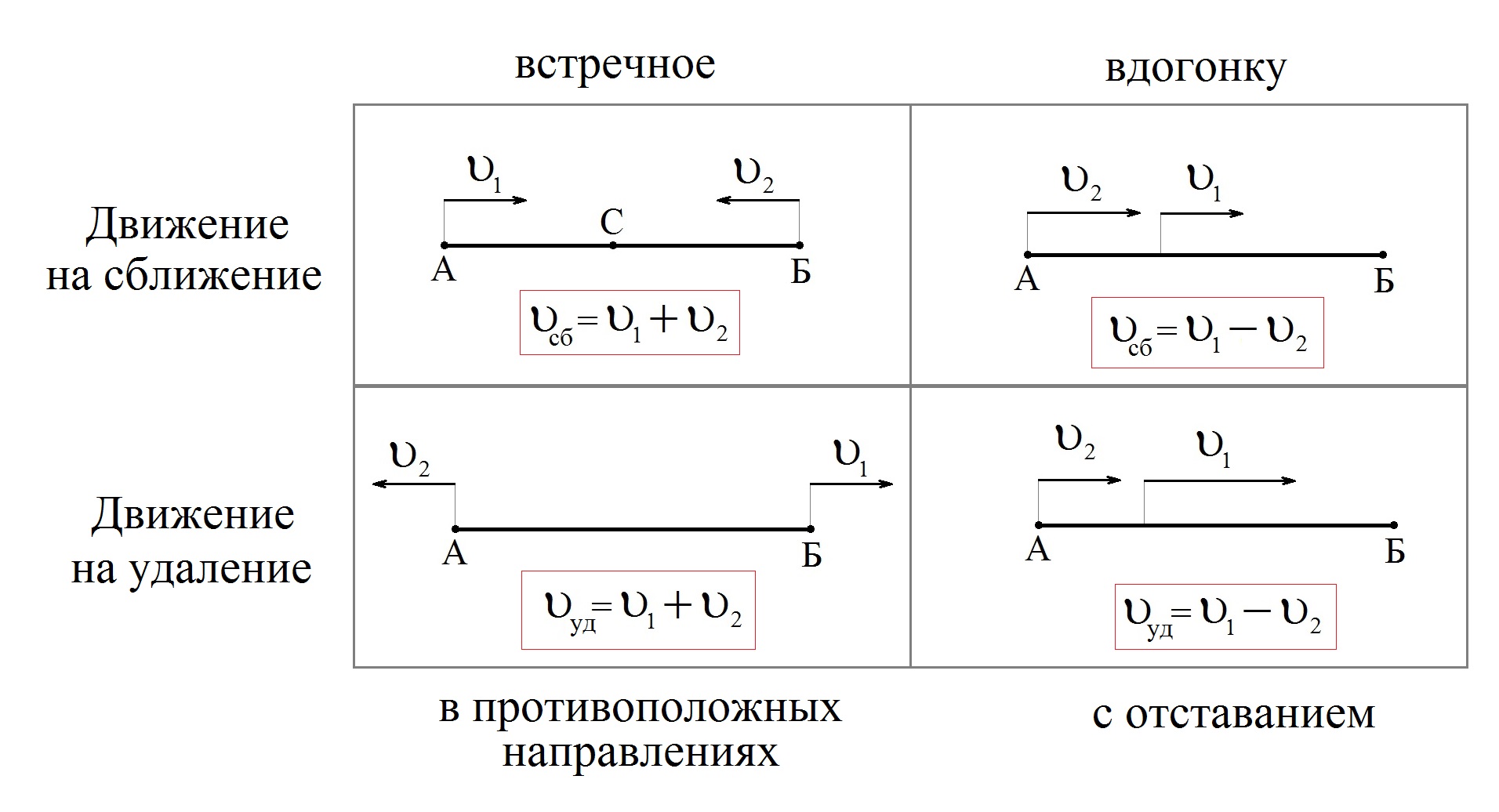
Из неё видно, что при движении объектов в противоположные стороны их скорости складываются. При движении в одну сторону – вычитаются.

Примеры решения задач.

Задача №1.  Две автомашины движутся навстречу друг другу со скоростями 60км/ч и 80 км/ч. Определите скорость сближения машин.
υ₁ = 60 км/ч
υ₂ = 80 км/ч
Найти υ_сб
Решение.
υ_сб = υ₁ + υ₂ – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υ_сб = 60 + 80 = 140 (км/ч)
Ответ:  скорость сближения 140 км/ч.

Задача №2. Из одного пункта в противоположных направлениях выехали две автомашины со скоростями 60 км/ч и 80 км/ч. Определите скорость удаления машин.
υ₁ = 60 км/ч
υ₂ = 80 км/ч
Найти υ_уд
Решение.
υ_уд = υ₁ + υ₂ – скорость удаления (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υ_уд = 80 + 60 = 140 (км/ч)
Ответ: скорость удаления 140 км/ч.

Задача №3. Из одного пункта в одном направлении выехали сначала автомобиль со скоростью 60 км/ч, а затем мотоцикл со скоростью 80 км/ч. Определите скорость сближения машин.
(Видим, что здесь случай движения вдогонку, поэтому находим скорость сближения)
υ_ав = 60 км/ч
υ_мот = 80 км/ч
Найти υ_сб
Решение.
υ_сб =  υ₁ – υ₂– скорость сближения (знак «–» так как из условия понятно, что машины движутся в одном направлении)
υ_сб = 80 – 60 = 20 (км/ч)
Ответ: скорость сближения 20 км/ч.

То есть название скорости – сближения или удаления – не влияют на знак между скоростями. Имеет значение только направление движения.

Рассмотрим другие задачи.

Задача № 4. Из одного пункта в противоположных направлениях вышли два пешехода. Скорость одного из них 5 км/ч, другого – 4 км/ч. Какое расстояние будет между ними через 3 ч?
υ₁ = 5 км/ч
υ₂ = 4 км/ч
t = 3 ч
Найти S
Решение.
υ_уд = υ₁ + υ₂ – скорость удаления (знак «+» так как из условия понятно, что пешеходы движутся в разных направлениях)
υ_уд = 5 + 4 = 9 (км/ч)
(Пройденное расстояние находим по формуле)
S = υ_уд·t
S =  9·3 = 27 (км)
Ответ: через 3 ч расстояние будет 27 км.

Задача № 5. Два велосипедиста одновременно выехали навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого 10 км/ч, второго 8 км/ч. Через сколько часов они встретятся?
S = 36 км
υ₁ = 10 км/ч
υ₂ = 8 км/ч
Найти t
Решение.
υ_сб = υ₁ + υ₂ – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υ_сб = 10 + 8 = 18 (км/ч)
(время встречи можно рассчитать по формуле)
t = S : υ_сб
t = 36 : 18 = 2 (ч)
Ответ:  встретятся через 2 ч.

Задача №6. Два поезда отошли от одной станции в противоположных направлениях. Их скорости 60 км/ч и 70км/ч. Через сколько часов расстояние между ними будет 260 км?
υ₁ = 60 км/ч
υ₂ = 70 км/ч
S = 260 км
Найти t
Решение.
1 способ
υ_уд = υ₁ + υ₂ – скорость удаления (знак «+» так как из условия понятно, что пешеходы движутся в разных направлениях)
υ_уд = 60 + 70 = 130 (км/ч)
(Пройденное расстояние находим по формуле)
S = υ_уд·t    ⇒   t = S : υ_уд
t =  260 : 130 = 2 (ч)
Ответ: через 2 ч расстояние между ними будет 260 км.
2 способ
Сделаем пояснительный рисунок:

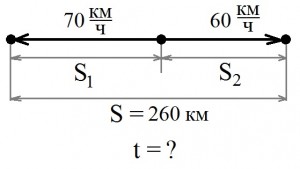
Из рисунка видно, что
1) через заданное время расстояние между поездами будет равно сумме расстояний, которые прошли каждый из поездов:
S = S₁ + S₂;
2) каждый из поездов ехал одинаковое время (из условия задачи), значит, 
S₁ =υ₁· t — расстояние которое проехал 1 поезд
S₂ =υ₂· t — расстояние которое проехал 2 поезд
Тогда,
S = S₁ + S₂ = υ₁· t  + υ₂· t  =  t · (υ₁ + υ₂) = t · υ_уд  
t = S : (υ₁ + υ₂)  — время за которое оба поезда проедут 260 км
t =  260 : (70 + 60) = 2 (ч)
Ответ:  расстояние между поездами будет 260 км через 2 ч . 

1. Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18 км. Скорость одного из них 5 км/ч, другого – 4 км/ч. Через сколько часов они встретятся? (2 ч)
2. Два поезда отошли от одной станции в противоположных направлениях. Их скорости 10 км/ч и 20 км/ч. Через сколько часов расстояние между ними будет 60 км? (2 ч)
3. Из двух сел, расстояние между которыми 28 км, одновременно навстречу друг другу вышли два пешехода. Скорость первого 4 км/ч, скорость второго 5 км/ч. На сколько километров за час пешеходы сближаются друг с другом? Какое расстояние будет между ними через 3 часа? (9 км, 27 км)
4. Расстояние между двумя городами 900 км. Два поезда вышли из этих городов навстречу друг другу со скоростями 60 км/ч и 80 км/ч. На каком расстоянии друг от друга были поезда за 1 час до встречи? Есть ли в задаче лишнее условие? (140 км, есть)
5. Велосипедист и мотоциклист выехали одновременно из одного пункта в одном направлении. Скорость мотоциклиста 40 км/ч, а велосипедиста 12 км/ч. Какова скорость их удаления друг от друга? Через сколько часов расстояние между ними будет 56 км? (28 км/ч, 2 ч)
6. Из двух пунктов, удаленных друг от друга на 30 км, выехали одновременно в одном направлении два мотоциклиста. Скорость первого 40 км/ч, второго 50 км/ч. Через сколько часов второй догонит первого?
7. Расстояние между городами А и В 720 км. Из А в В вышел скорый поезд со скоростью 80 км/ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км/ч. Через сколько часов они встретятся?
8. Из села вышел пешеход со скоростью 4 км/ч. Через 3 часа вслед за ним выехал велосипедист со скоростью 10 км/ч. За сколько часов велосипедист догонит пешехода?
9. Расстояние от города до села 45 км. Из села в город вышел пешеход со скоростью 5 км/ч. Через час навстречу ему из города в село выехал велосипедист со скоростью 15 км/ч. Кто из них в момент встречи будет ближе к селу?
10. Старинная задача.  Некий юноша пошел из Москвы к Вологде. Он проходил в день 40 верст. Через день вслед за ним был послан другой юноша, проходивший в день 45 верст. Через сколько дней второй догонит первого?
11. Старинная задача. Собака усмотрела в 150 саженях зайца, который пробегает в 2 минуты по 500 сажен, а собака за 5 минут – 1300 сажен. Спрашивается, в какое время собака догонит зайца?
12. Старинная задача. Из Москвы в Тверь вышли одновременно 2 поезда. Первый проходил в час 39 верст и прибыл в Тверь двумя часами раньше второго, который проходил в час 26 верст. Сколько верст от Москвы до Твери?

www.easyphysics.in.ua

Как научить ребенка решать задачи на движение

В четвертом классе многих детей и родителей пугают задачи на движение. Сегодня мы поделимся, как одно небольшое изменение подачи формулы, может научить ребенка щелкать подобные задачи, словно орешки.

Пример задач на движение:

Лыжник шел со скоростью 18 км/ч и был в пути 3 часа. Сколько времени потребуется пешеходу, чтобы пройти такое же расстояние, если его скорость 9 км час

Расстояние между селами 48 км. Через сколько часов встретятся два пешехода, которые вышли одновременны навстречу друг другу, если скорость одного 3 км/ч, а другого 5 км/ч?

В этой статье вы узнаете простую технику, которая позволяет детям легко применять практически первую в их жизни серьезную математическую формулу (до этого дети применяли формулу вычисления площади и периметра)

В школе, по традиционной программе, детей знакомят с формулой в линейной структуре, записывая ее на доске и поясняя S=v*t

Опытный учитель не только расскажет, что S — расстояние v — скорость t — время, а обязательно объяснит, почему обозначение происходит именно такими буквами.

Дальше ребенку последовательно предлагается блок задач, сначала на применение прямой формулы S=v*t

Потом обратной. V=S:t t=S:v

Конечно ребенку нужно будет выучить правило нахождения расстояния, времени или скорости.  Правила с одной стороны, очень понятны взрослым, с другой очень трудны для детей.

Потому что читая задачу, маленький ученик, который только учится решать задачи, в голове прокручивает алгоритм:

1. Известно, что …
2. Надо узнать…
3. Чтобы ответить на вопрос, надо … (тут происходит процесс определения нужной формулы, обычно это самая трудная часть)
4. Можем сразу ответить на вопрос? Нет. Сразу мы не можем ответить на вопрос задачи, так как не знаем…
5. Поэтому в первом действии мы узнаем …
6. Во втором действии мы ответим на вопрос задачи. Для этого …

Сложный алгоритм, но именно так решают задачи младшие школьники! Некоторые делают это очень быстро, а некоторые продумывают каждый шаг.

Упростите ребенку решение задач. Станьте для него магом и лучшим проводником по школе.

Нарисуйте вместе с ним треугольник. И впишите в него формулу следующим образом:

Закройте карточкой или рукой то, что нужно найти (например, время) Тогда сразу найдется «нужная формула»

Горизонтальная черта в треугольнике обозначает деление. Вертикальная — умножение. Ребенку можно поставить точку (знак умножения), что будет для него подсказкой.

Так подбор правильной формулы для решения задачи на движение становится не только простым, но и интересным ребенку.

У меня дети просили все больше и больше задач, закрывали разные части формулы, и тем самым, запоминали ее.

Если речь идет о двух, трех движущихся объектах, то треугольник с формулой применяется для каждого в отдельности. Хотя об этом обычно догадываются сами дети.

Взаимодействие и обмен полезными техниками между родителями и учениками может помочь ребенку как добиться хороших результатов в учебе, так и улучшить свою самооценку.

Используйте техники эффективного обучения, помогайте детям учиться.

Ведь очень часто одно простое действие может убрать непонимание, слезы, истерики, нежелание ребенка учиться, замотивировать его на учебу и показать ему простые и легкие способы решения сложных для него задач.

• Можно стирать белье руками, а можно в стиральной машинке
• Можно идти пешком, а можно доехать на автомобиле
• Можно делать дырку в стене ручной дрелью, а можно перфоратором
• Можно решеть задачи по-старинке, а можно дать ребенку техники эффективного решения задач.

Результат одинаков — усилие разное

Именно для этих целей, создана Школа умных детей.

В каждом классе по курсу «Математика», в уроках школы по блоку «решение задач» Вы узнаете:

• Как научить ребенка понимать текст задачи
• Как научить ребенка оформлять краткую запись
• Как научить ребенка определить, как решать задачу
• Сможете объяснить разницу между 2*9 и 9*2 в задаче
• Получите простой Алгоритм-инструкцию «Как решать задачи»
• Узнаете типы задач 1 класса и способы простого объяснения
• Узнаете типы задач 2 класса и способы простого объяснения
• Узнаете типы задач 3 класса и способы простого объяснения
• Узнаете типы задач 4 класса и способы простого объяснения
• Узнаете Формулу «треугольник» для решения задач на движение, цену, количество и стоимость и все тонкости ее применения

Присоединяйтесь прямо сейчас, пока действует специальная цена на участие

Хочу учить ребенка эффективно>>

Вам понравилась статья? Сохраните себе на стену, чтобы не потерять

Похожее

gladtolearn.ru

Физика. Формула времени. Решение задач

«Формула времени. Решение задач»

Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.

Время обозначается как t. Единица измерения времени – с (секунды).

Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.

При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v₀) / a  или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v₀).

Решение задач через формулу времени

Задача № 1.

Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

 Ответ: 200 с.

---

Задача № 2.

Двигаясь с ускорением 5 м/с² скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?

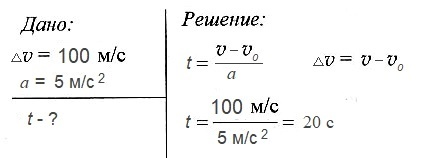 Ответ: 20 с.

---

Задача № 3.

Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t₁ = 3 ч, а плот то же расстояние – за время t₀ =12 ч. Какое время t₂ затратит моторная лодка на обратный путь?

Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через v_л , а скорость течения через v_т. Тогда t₀ = L / v_т ,  t₁ = L / (v_л +  v_т) ,  t₂ = L / (v_л —  v_т) . Исключая из записанной системы уравнений L, v_л и  v_т
находим 

Ответ: 6 ч.

---

Конспект урока «Формула времени. Решение задач».

Следующая тема: «».

 

uchitel.pro

Задачи на движение протяженных тел

Задачи на движение протяженных тел

Протяженными будем считать тела, длина которых соизмерима с расстоянием, которое они проезжают.

В задачах на движение протяженных тел обычно требуется определить длину одного из них. Наиболее типичные ситуации, предлагаемые в таких задачах, — определить длину поезда проезжающего мимо:

• придорожного столба;

• идущего параллельно путям пешехода;

• лесополосы определенной длины;

• другого двигающегося поезда.

Помним, что во всех задачах на движение используется только одна формула: это формула пути

Если поезд движется мимо столба, то он проходит расстояние равное его длине. Обозначим:

l – длина поезда,

v – скорость поезда,

Если поезд движется мимо протяженной лесополосы (платформы), то он проходит расстояние равное сумме длины самого поезда и лесополосы. Обозначим:

l₁ – длина поезда,

l₂ – длина лесополосы (платформы),

v – скорость поезда,

Если поезд движется мимо движущегося человека, то учитываем направление движения человека. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:

l – длина поезда,

v₁ – скорость поезда,

v₂ – скорость человека,

В одну сторону:

В разные стороны:

Если поезд движется мимо движущегося поезда, то учитываем направление движения второго поезда. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:

l₁ – длина первого поезда,

l₂ – длина второго поезда,

v₁ – скорость первого поезда,

v₂ – скорость второго поезда,

В одну сторону:

В разные стороны:

Рассмотрим несколько задач.

Задача 1. Поезд, двигаясь равномерно со скоростью 60км/ч, проезжает мимо придорожного столба за 30 секунд. Найти длину поезда в метрах.

Решение:

v = 60 км/ч = 1000 м/мин, t = 30 сек. = 1/2 мин. Длину поезда находим как пройденное расстояние:

Ответ: 500 метров.

Задача 2. Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо лесополосы, длина которой равна 800 метрам, за 1 минуту. Найти длину поезда в метрах.

Решение:

v = 90 км/ч = 1500 м/мин, t = 1 мин. Тогда пройденное поездом расстояние:

Это собственная длина поезда плюс длина лесополосы. Длина поезда равна: 1500 – 800 = 700 (м).

Ответ: 700 метров.

Задача 3. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.

Решение: Так как поезда двигаются в одном направлении, их относительная скорость равна:

v = 90 – 30 = 60 км/ч =

За 60 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:

Это длина пассажирского и товарного поездов. Тогда длина пассажирского поезда равна:

1000 – 600 = 400 (м).

Ответ: 400 метров.

Задача 4. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.

Решение: Так как поезда двигаются в противоположных направлениях, их относительная скорость равна:

v = 65 + 35 = 100 км/ч =

За 36 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:

Это расстояние, равное сумме длин обоих поездов. Значит, длина скорого поезда равна:

1000 – 700 = 300 (м).

Ответ: 300 метров.

Задача 5.  Поезд проходит мимо неподвижного наблюдателя за 7 секунд, а мимо платформы длиной 378 метров – за 25 секунд. Найдите длину поезда. 

Решение: Из первого условия следует, что за 7 секунд поезд проедет расстояние, равное собственной длине поезда. За 25 же секунд ему надо проехать собственно саму длину платформы, т.е. 378 метров и ещё надо «вытащить» головной вагон вперед на расстояние, равное длине поезда.

1) 25 – 7 = 18 (с) – время, за которое поезд проехал 378 м

2) 378 : 18 = 21 (м/с) – скорость поезда

3) 21

Ответ: 144 м.

Задача 6. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и скорый поезда. Скорый поезд, двигаясь со скоростью 120 км/ч, догнал пассажирский поезд и прошёл мимо него за 100 секунд. Найдите скорость пассажирского поезда, если его длина составляет 800 метров, а длина скорого поезда – 700 метров. Ответ дайте в км/ч.

Решение: Считаем, что пассажирский поезд неподвижен, а скорый приближается к нему со скоростью, равной разности скоростей поездов.

1) 700 + 800 = 1500 (м) – прошёл скорый поезд за 100 секунд

2) 1500 : 100 = 15 (м/с) – разность скоростей (скорость вдогонку)

15 м/с = км/ч = 54 км/ч

3) 120 – 54 = 66 (км/ч) – скорость пассажирского поезда.

Ответ: 66 км/ч.

Задача 7. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 110 метров, второй — длиной 90 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 1000 метров. Через 16 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 400 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

Решение: Пока сухогрузы перейдут из первого положения во второе, второй сухогруз переместился относительно первого на

1000 + 110 + 90 + 400 = 1600 (м).

Пусть v — разность скоростей сухогрузов, тогда

v = 1600 : 16 = 100 м/мин = 6 км/ч.

Ответ: на 6 км/ч.

multiurok.ru

Урок по теме «Решение текстовых задач на движение». 8-й класс

Цели:

сформировать представление о составлении математической модели;

рассмотреть особенности решения задач на движение.

отработать умение составлять дробное рациональное уравнение по условию текстовой задачи.

Универсальные учебные действия:

• регулятивные: составление плана и последовательности действий;
• коммуникативные
: построение речевых высказываний;
• познавательные
: формулировка проблемы и создание способов ее решения; структуирование знаний;
• личностные
: самооценка.

Вид урока: урок усвоения знаний, умений и навыков.

Ход урока

1. Организационный момент.
2. Актуализация опорных знаний учащихся.
3. Мотивация учебной деятельности учащихся.
4. Изучение нового материала.
5. Закрепление. Коррекция умений и навыков учащихся.
6. Проверка уровня усвоения новых знаний, умений и навыков.
7. Итог урока.

Решение задач на движение с помощью рациональных уравнений

1. Организационный момент.

2. Актуализация опорных знаний учащихся.

Наиболее удобные обозначения при решении задач на движение

S (км)– путь, расстояние;

V (км/ч) – скорость;

t (ч) – время.

Связь при равномерном движении по прямой между этими величинами такова:

S=V*t

При х>0 1х>1х+2; 15у-2>15у+2; 60х-7>60х; Из двух дробей с равными числителями больше та, у которой знаменатель меньше:

Условия задачи удобно анализировать, заполняя таблицу.

	Путь S (км)	Скорость V (км/ч)	Время t (ч)
По течению
Против течения

3. Мотивация учебной деятельности учащихся.

4. Изучение нового материала.

Основные этапы решения текстовой задачи алгебраическим методом

1. Анализ условия задачи и его схематическая запись.

2. Перевод естественной ситуации на математический язык (построение математической модели: введение переменной и составление дробного рационального уравнения).

3. Решение полученного уравнения.

4. Интерпретация полученного результата.

Решение задачи.

Турист проплыл на лодке против течения реки 6 км и по озеру 15 км, затратив на путь по озеру на 1 час больше чем на путь по реке. Зная, что скорость течения реки равна 2 км/ч, найдите скорость лодки при движении по озеру.

	Путь S (км.)	Скорость V (км/ч.)	Время t (ч)
Против течения	6 км	(х-2)км/ч
По озеру	15 км	х км/ч

На 1 час больше.

Пусть х км/ч скорость движения лодки по озеру. По условию х > 0.

то х=6 или х=5.

Ответ: собственная скорость лодки 6 км/ч или 5 км/ч.

5. Закрепление. Коррекция умений и навыков учащихся.

Учащимся предлагается выбрать правильный ответ. Приложение 1

Учащиеся выходят к доске по одному, заполняют таблицу и составляют уравнение. Для экономии времени всем учащимся раздаются листы с условиями задач и пустыми таблицами. Успешным учащимся предлагается для одной из задач провести полное решение.

1. Теплоход проходит по течению до пункта назначения 126 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения 2 км/ч, стоянка длится 8 ч, а в пункт отправления теплоход возвращается ровно через сутки после отплытия из него. Ответ дайте в км/ч.

	Путь S (км)	Скорость V (км/ч)	Время t (ч)
По течению	126 км	(х+2)км/ч
Против течения	126 км	(х-2)км/ч

Возвращается через 24 ч.

Стоянка 8 ч.

В пути 24-8=16 (ч.).

Пусть х км/ч собственная скорость теплохода. По условию х > 2.

Ответ: 16 км/ч

2. Пристани А и В, расстояние между которыми равно 120 км, расположены на реке, скорость течения которой на этом участке равна 5 км/ч. Катер проходит от А до В и обратно без остановок со средней скоростью 24 км/ч. Найдите собственную скорость катера.

	Путь S (км)	Скорость V (км/ч)	Время t (ч)
Из А в В.	120 км	(х+5)км/ч
Из В в А.	120 км	(х-5)км/ч
Туда и обратно.	240 км	24 км/ч

Пусть х км/ч собственная скорость катера. По условию х > 5.

Ответ: 25 км/ч

3. Из пункта А в пункт В, расположенного на расстоянии 100 км, отправился автобус со скоростью 36 км/ч. Как только автобус проехал пятую часть пути, вслед за ним выехала машина. В пункт В они прибыли одновременно. Найдите скорость машины в км/ч.

	Путь S (км.)	Скорость V (км/ч.)	Время t (ч)
Автобус	100 км	36 км/ч
Машина	100 км	Х км/ч

Больше на ч

Ответ: 45 км/ч

4. Из пункта А в пункт В, расстояние между которыми 80 км, выехал автобус. В середине пути он был задержан на 10 минут, но, увеличив скорость на 20 км/ч, прибыл в В вовремя. С какой скоростью автобус проехал первую половину пути?

	Путь S (км.)	Скорость V (км/ч.)	Время t (ч)
I половина	40 км	х км/ч
II половина	40 км	(х+20)км/ч

На 10 мин меньше

Ответ: 60 км/ч

5. Дополнительно: Велосипедист проехал из поселка до станции с некоторой постоянной скоростью, а возвращался со скоростью на 5 км/ч большей. Какова была первоначальная скорость велосипедиста, если известно, что средняя скорость на всем пути следования составляла 12 км/ч?

6. Проверка уровня усвоения новых знаний, умений и навыков.

7. Итог урока.

Приложение 2

urok.1sept.ru