6.1.2. Задачи на пропорцию математика-повторение
Задача 1. Толщина 300 листов бумаги для принтера составляет 3, 3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги?
Решение. Пусть х см — толщина пачки бумаги из 500 листов. Двумя способами найдем толщину одного листа бумаги:
3,3:300 или х:500.
Так как листы бумаги одинаковые, то эти два отношения равны между собой. Получаем пропорцию (напоминание: пропорция — это равенство двух отношений):
3,3:300=х:500. Неизвестный средний член пропорции равен произведению крайних членов пропорции, деленному на известный средний член. (Подробно о пропорции и нахождению ее крайнего, среднего членов читайте в статье: «6.1.1. Пропорция. Основное свойство пропорции.»)
х=(3,3·500):300;
х=5,5. Ответ: пачка 500 листов бумаги имеет толщину
Это классическое рассуждение и оформление решения задачи. Такие задачи часто включают в тестовые задания для выпускников, которые обычно записывают решение в таком виде:

или решают устно, рассуждая так: если 300 листов имеют толщину 3,3 см, то 100 листов имеют толщину в 3 раза меньшую. Делим 3,3 на 3, получаем 1,1 см. Это толщина 100 листовой пачки бумаги. Следовательно, 500 листов будут иметь толщину в 5 раз большую, поэтому, 1,1 см умножаем на 5 и получаем ответ: 5,5 см.
Разумеется, это оправдано, так как время тестирования выпускников и абитуриентов ограничено. Однако, на этом занятии мы будем рассуждать и записывать решение так, как положено это делать в 6 классе.
Задача 2. Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды?
Решение.
Вся масса арбуза (5 кг) составляет 100%. Вода составит х кг или 98%. Двумя способами можно найти, сколько кг приходится на 1% массы.
5:100 или х:98. Получаем пропорцию:
5:100 = х:98.
х=(5·98):100;
х=4,9 Ответ: в 5кг арбуза содержится 4,9 кг воды.
Задача 3. Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти?
Решение.
Пусть масса 35 литров нефти составляет х кг. Тогда двумя способами можно найти массу 1 литра нефти:
16,8:21 или х:35. Получаем пропорцию:
16,8:21=х:35.
 Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (
Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (
Умножаем числитель и знаменатель дроби на 10, чтобы в числителе и знаменателе были только натуральные числа. Сокращаем дробь на 5 (5 и 10) и на 3 (168 и 3).
Ответ: 35 литров нефти имеют массу 28 кг.
Задача 4. После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?
Решение.
Пусть площадь всего поля х га, что составляет 100%. Осталось вспахать 9 га, что составляет 100% — 82% = 18% всего поля. Двумя способами выразим 1% площади поля. Это:
х:100 или 9:18. Составляем пропорцию:
х:100 = 9:18.

Ответ: площадь всего поля 50 га.
www.mathematics-repetition.com
Конспект «Пропорции. Решение задач с помощью пропорций» урок математика 7 класс
ООО Учебный центр «ПРОФЕССИОНАЛ»
План-конспект урока
по математике
в 7 классе
Муниципальное общеобразовательное учреждение основная общеобразовательная школа Бельговского сельского поселения Комсомольского муниципального района Хабаровского края
По теме: «Пропорции. Решение задач с помощью пропорций»
Разработал: Приймаков Евгений Альфредович
слушатель курсов профессиональной переподготовки «Математика: теория и методика преподавания в образовательной организации» (300 часов).
Проверил: Дигор А.К.
с. Бельго 2017
7 класс
Технологическая карта
Урок 1 по теме: «Пропорции. Решение задач с помощью пропорций»
Тема урока: «Пропорции»
Цель урока: создание условий для изучения, осмысления и понимания нового учебного материала на основе применения ранее полученных знаний и умений учащихся путём вовлечения в исследование и открытие новых знаний.
Задачи урока:
1.Образовательные: изучить понятия: пропорция, члены пропорции, верная и неверная пропорция; сформулировать основное свойство пропорции и научиться применять его для определения верной и неверной пропорции, определять крайние и средние члены пропорции.
2. Развивающие: развивать умение ставить перед собой цель – целеполагание, как постановку учебной задачи на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно; добывать новые знания путём исследования; учиться оформлять свои мысли в устной и письменной речи, высказывать свою точку зрения, пытаясь ее обосновать, приводя аргументы; развивать умения анализировать, сравнивать, делать соответствующие выводы.
3. Воспитательные: развивать познавательные интересы и учебные мотивы обучающихся, формировать позитивную самооценку; формировать опыт равноправного взаимодействия (сотрудничества) учителя и учащихся на уроке.
Тип урока: Урок первичного предъявления новых знаний
Необходимое оборудование: учебник, доска, мел, задания на карточках
Технологическая карта урока
Содержание учебного материала.Деятельность учителя
Формирование УУД
1.Организационный момент
Приветствие учителя. Настрой на урок.
Приветствие. Создание благоприятной рабочей обстановки. Проверка готовности.
Здравствуйте, ребята. Я рад вас видеть. Мы начинаем наш урок. Сегодня на уроке вы узнаете, что знания математики нам нужны в реальной жизни. Я хочу, чтобы этот урок принес вам новые открытия, и надеюсь, что вы с успехом будете применять имеющиеся у вас знания в решении практических задач. И всерьез задумаетесь над темой нашего разговора.
Личностные: самоопределение, настрой на работу
Регулятивные: целеполагание.
2. Актуализация субъектного опыта учащихся.
1. Отвечают на вопрос учителя, выполняют задания
2. Выполняют вычисления, сопоставляют с кодом и получают тему урока
Что мы знаем и умеем по теме отношения?
1.Из выражений назвать отношения, прочитать и вычислить (записать на доске):
57-14;
8:1
2,5:5;
1,2+3,5
2.Выполнить преобразования обыкновенных дробей в десятичные и в проценты, расшифровать тему урока (карточка):
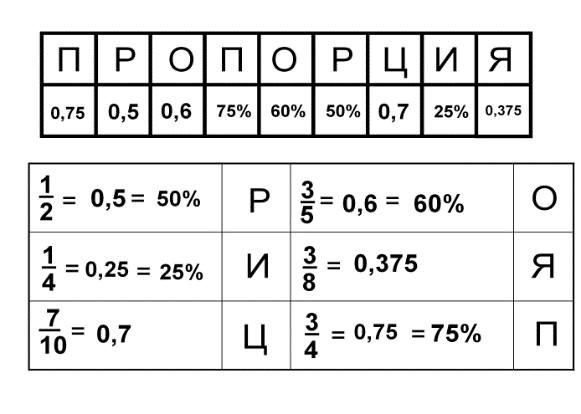
Познавательные: структурирование собственных знаний
(анализ, сравнение)
Коммуникативные: организация и планирование учебного сотрудничества с учителем и сверстниками
3. Постановка цели и задач урока
Формулируют задачи урока и план урока.
Записывают в тетради тему урока. Называют критерии оценивания.
Зная тему урока, попробуйте составить план урока.
Что вы должны узнать сегодня на уроке?
Что вы хотите узнать?
Чему хотите научиться на уроке?
По каким критериям мы можем оценить себя по окончании урока?
Регулятивные: целеполагание
Личностные:
Самоопределение
Коммуникативные:
Умение вступать в диалог, участвовать в коллективном обсуждении вопроса
4.Открытие новых знаний и первичное восприятие нового учебного материала
Слушают учителя и записывают определения и примеры
1. Найдем числовые значения двух отношений: 6 : 3 и 10 : 5. Мы видим, что они равны: 6 : 3 = 2 и 10 : 5 = 2, следовательно, можно записать равенство 6 : 3 = 10 : 5. Такое равенство отношений называют пропорцией.
2. Определение. Пропорцией называется равенство двух отношений. Числа, составляющие пропорцию (6; 3; 10; 5), называются членами пропорции.
3. Пропорцию можно записать с помощью букв: а : b = с : d
, или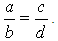 .
.4. Эти записи читают: «Отношение а к b равно отношению с к d» или «а так относится к в, как с относится к d».
5. Числа а и d называют крайними членами, а числа b и с – средними членами.
В дальнейшем считают, что все члены пропорции отличны от нуля:
а 0, b 0, с 0, d 0.
6. Чтобы проверить, верно ли составлена пропорция, вычисляют числовое значение каждого отношения, составляющего пропорцию. Если эти отношения равны, то пропорция составлена верно; если не равны, то пропорция составлена неверно.
Примеры: 1) Пропорция 40 : 8 = 65 : 13 составлена верно, так как 40 : 8 = 5 и 65 : 13 = 5.
2) Пропорция 2,7 : 9 = 2 : 5 составлена неверно, так как
2,7 : 9 = 0,3, а 2 : 5 = 0,4.
Регулятивные:
коррекция, планирование
Коммуникативные;
выражение и аргументация своих мыслей с достаточной полнотой и точностью
Личностные: формирование готовности к самообразованию
5.Физкультминутка
Учащиеся поднимаются с мест, повторяют действия за учителем.
Учащиеся сменили вид деятельности и готовы продолжить работу.
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.
Давайте немного отдохнем.
Мы топаем ногами,
Мы хлопаем руками,
Киваем головой.
Мы руки поднимаем,
Мы руки опускаем,
И вновь писать начнем.
6. Усвоение новых знаний и способов действий
Поочередно выходят к доске, объясняя решение заданий
С 54-55, № 177, 178, 180(а)
Коммуникативные:
учебное сотрудничество с учителем и сверстниками
Регулятивные:
коррекция, оценка
7. Информация о домашнем задании
Записывают в дневник домашнее задание. Слушают пояснение домашнего задания
П. 2.3 – читать, выучить определение. №179, 180(б), р/т №_37-39
8. Подведение итогов урока.
Отвечают на вопросы:
а) Пропорцией называется равенство двух отношений
б)Числа x и y называют крайними членами
в) Числа m и n называют – средними членами
1. Вопросы:
а) Что такое пропорция?
б) Как называются числа х и у в пропорции х : а = b : у?
в) Как называются числа m и n в пропорции а : m = n : b?
2. Привести свои примеры верных пропорций.
Регулятивные: коррекция, оценка, как осознание того, что уже усвоено, умение самостоятельно адекватно анализировать
Личностные: формирование позитивной самооценки
9. Рефлексия
Осуществляют самооценку собственной учебной деятельности, в листок самооценки
Поставьте «+» в пустые клетки, где по вашему верно указано утверждение
Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли;
Познавательные: рефлексия.
Выполнить преобразования обыкновенных дробей в десятичные и в проценты, расшифровать тему урока:
Выполнить преобразования обыкновенных дробей в десятичные и в проценты, расшифровать тему урока:
Оцени сегодняшний урок знаком «+»:
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!
Оцени сегодняшний урок знаком «+»:
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!
Оцени сегодняшний урок знаком «+»:
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!
Оцени сегодняшний урок знаком «+»:
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!
Оцени сегодняшний урок знаком «+»:
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!
Оцени сегодняшний урок знаком «+»:
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!
Оцени сегодняшний урок знаком «+»:
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!
Оцени сегодняшний урок знаком «+»:
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!
infourok.ru
«Решение задач с помощью пропорции»
Тип урока: закрепление изученного материала.
Цели урока:
Образовательные:
закрепление понятия пропорции и основного свойства пропорции; отработка умения решать задачи с помощью пропорции, решать уравнения , записанные в виде пропорции; продолжение формирования навыков самоконтроля.
Воспитательные:
содействие формированию интеллектуальных умений и мыслительных навыков учащихся: обдуманность действий, выбор рационального пути решения, умение работать в коллективе, самоконтроль;
Развивающие:
развитие умения выделять главное в изучаемом материале, обобщать и систематизировать изучаемые факты; развитие самостоятельности, умения преодолевать трудности; развитие творческой деятельности и познавательного интереса школьников.
Оборудование: компьютер, мультимедиа,
ХОД УРОКА
Проверка готовности к уроку. Сообщение темы и цели.
Сегодня у нас урок по теме “Решение задач с помощью пропорции”. Попробуйте сформулировать, каждый для себя цель урока.
Учащиеся формулируют цели. Далее обобщая всё ,что сказали учащиеся учитель делает вывод:
– Итак, на предыдущих уроках мы рассматривали
прямую пропорциональную зависимость величин,
обратную пропорциональную зависимость величин.
Сегодня на уроке мы будем решать разные задачи,
анализируя условия которых находить прямую или
обратную пропорциональные зависимости величин,
составлять пропорции.
Перед вами стоит цель – показать свои знания и
умения при решении задач с помощью пропорции. Эти
знания вам пригодятся при решении задач по химии,
физике, геометрии, географии, черчению и
технологии. А умения могут пригодиться и
водителю в дороге (чтобы рассчитать количество
бензина) , и хозяйке на кухне (чтобы рассчитать
необходимый расход продуктов).
Графический диктант.
“Да” и “нет” не говорите,
А значком изобразите.
“Да” значком “+”, нет значком “-”.
Ученики работают самостоятельно.
Затем обмениваются тетрадями в парах для проверки.
- Две величины называют прямо пропорциональными, если при увеличении одной из них в 3 раза, другая уменьшается в 3 раза.
- Зависимость между временем и расстоянием при постоянной скорости является прямой пропорциональностью.
- Возраст человека и размер его обуви обратно пропорциональны.
- Скорость и расстояние при постоянном времени движения обратно пропорциональны.
- Число дней работы трактора и площадь, которую он вспашет, прямо пропорциональны.
- Покупают одинаковые тетради. Количество тетрадей и стоимость покупки прямо пропорциональны.
Карта ответов: -, +, -, -, +, +.
Ребята проверяют работу соседа и выставляют оценку по следующим критериям.
- 5– 6 правильных ответов – “5”.
- 4– правильных ответов – “4”.
- 3– правильных ответов – “3”.
- 2– это “2”.
Решение задач. На предыдущем уроке были введены понятия прямой и обратной пропорциональности, отработаны данные понятия на задачах. На данном уроке решаем задачи с помощью пропорций. Мы вывели алгоритм решения задач: слайд 6.
1. За 6 ч поезд прошел 480 км. Какой путь прошел поезд за первые 2 ч, если его скорость была постоянна.
Составим краткую запись условия задачи:
Краткая запись заранее оформляется на плакате. В процессе устного обсуждения выясняем, что время и путь уменьшились в одно и то же число раз, так как при постоянной скорости эти величины прямо пропорциональны.
Затем, составляем пропорцию и решаем её: ; Х= 160 (км)
2. Расстояние между городами пассажирский поезд прошел со скоростью 80 км/ч за 3 ч. За сколько часов товарный поезд пройдет то же расстояние, со скоростью 40 км/ч?
Решение.
В процессе устного обсуждения выясняем, что скорость уменьшилась, а время увеличилось в одно и то же число раз, следовательно, эти величины при одном и том же расстоянии являются обратно пропорциональными.
(ч)
3. За 2 ч поймали 12 карасей. Сколько карасей поймали за 3 ч?
Физкультминутка. Слайд 9.
А теперь, ребята, встали.
Быстро руки вверх подняли,
В стороны, вперед, назад.
Повернулись вправо, влево,
Тихо сели, вновь за дело.
Самостоятельная работа. Цель: проверка сформированности умений и навыков, выявление недостатков и причин их появления, побуждение учащихся к самообразованию. Уч-ся получают листы с печатной основой.
Вариант №1
1) Из 5 кг свежих слив получается 1,5 кг чернослив. Сколько чернослива получится их 17,5 кг свежих слив?
Закончите решение задачи.
| Свежие сливы | Чернослив | |
| 5 кг | — | 1,5 кг |
| 17,5 кг | — | х кг |
Так как величины пропорциональны, то можно составить пропорцию:
Ответ:
2). На путь от одного поселка до другого со скоростью 12,5 км/ч велосипедист затратил 0,7 ч. С какой скоростью он должен был ехать, чтобы преодолеть этот путь за 0,5 ч?
Закончите решение задачи.
Ответ:
Вариант №2
1) 3а 4 ч поезд, не останавливаясь, прошел 280 км. Сколько километров он пройдет с той же скоростью за 6 ч?
Закончите решение задачи.
Так как величины пропорциональны, то можно составить пропорцию.
Ответ:
2) Чтобы вывезти товар, прибывший на железнодорожную станцию, потребуется 21 автомашина грузоподъемностью 2,5 т. Сколько потребовалось бы автомашин грузоподъемностью 3.5 т?
Закончите решение задачи.
Ответ:
Задание на дом №210, 212.
Цель
: дать домашнее задание, которое дало бы возможность ребятам реализовать себя творчески, применить полученные знания в новой ситуации.– Подобрать, а лучше придумать самим, задачи с использованием прямой и обратной пропорциональных зависимостей. Оформить красочно содержание и решение задач на альбомном листе.
– Спасибо за работу!
Итог урока. (Ставим оценки)
Цель
: проанализировать степень успешности овладения знаниями, выявить недостатки и наметить пути их устранения.– Итак, наш урок близится к концу. Давайте вспомним, какие цели мы ставили в начале урока. Удалось ли их достичь? Что запомнилось на уроке?
Рефлексия. Слайд 9.
Презентация
urok.1sept.ru
Самостоятельная работа «Задачи на пропорции и их решение»
Просмотр содержимого документа
«Самостоятельная работа «Задачи на пропорции и их решение»»
Самостоятельная работа
Задачи на пропорции и их решение
Вариант 1
Задание 1. Найдите неизвестный член пропорции: а) 4:5=х:100; б) 12:х=2:3
Задание 2. Разделите число 120 в отношении 4:4:3:1.
Задание 3. При выпечке хлеба из килограмма ржаной муки получается 1,4 кг хлеба. Сколько килограммов муки расходует завод на выпечку 21 центнера ржаного хлеба?
Задание 4. 16 каменщиков могут вымостить улицу за 21 день. Сколько каменщиков нужно, чтобы вымостить ту же улицу за 14 дней?
Задание 5. На собрании цеха присутствовало 69 человек, что составило 92% всех рабочих. Сколько человек отсутствовало на собрании?
Самостоятельная работа
Задачи на пропорции и их решение
Вариант 2
Задание 1. Найдите неизвестный член пропорции: а) 3 : х =18 : 24; б) 15 : 5 = х : 3.
Задание 2. Разделите число 126 в отношении 3 : 2 : 3 : 1
Задание 3. 190 т овса обменяли на кукурузу. Сколько надо получить кукурузы, если 100 кг овса обменивают на 78 кг кукурузы?
Задание 4. 18 лесорубов могут вырубить участок леса за 46 дней. За сколько дней смогут вырубить тот же участок леса 23 лесоруба при той же производительности труда?
Задание 5. В туристическом походе не участвовало 4 ученика, что составляет 5% от числа учащихся этих классов. Сколько учащихся участвовало в походе?
Самостоятельная работа
Задачи на пропорции и их решение
Вариант 1
Задание 1. Найдите неизвестный член пропорции: а) 4:5=х:100; б) 12:х=2:3
Задание 2. Разделите число 120 в отношении 4:4:3:1.
Задание 3. При выпечке хлеба из килограмма ржаной муки получается 1,4 кг хлеба. Сколько килограммов муки расходует завод на выпечку 21 центнера ржаного хлеба?
Задание 4. 16 каменщиков могут вымостить улицу за 21 день. Сколько каменщиков нужно, чтобы вымостить ту же улицу за 14 дней?
Задание 5. На собрании цеха присутствовало 69 человек, что составило 92% всех рабочих. Сколько человек отсутствовало на собрании?
Самостоятельная работа
Задачи на пропорции и их решение
Вариант 2
Задание 1. Найдите неизвестный член пропорции: а) 3 : х =18 : 24; б) 15 : 5 = х : 3.
Задание 2. Разделите число 126 в отношении 3 : 2 : 3 : 1
Задание 3. 190 т овса обменяли на кукурузу. Сколько надо получить кукурузы, если 100 кг овса обменивают на 78 кг кукурузы?
Задание 4. 18 лесорубов могут вырубить участок леса за 46 дней. За сколько дней смогут вырубить тот же участок леса 23 лесоруба при той же производительности труда?
Задание 5. В туристическом походе не участвовало 4 ученика, что составляет 5% от числа учащихся этих классов. Сколько учащихся участвовало в походе?
multiurok.ru
«Пропорции. Решение задач с помощью пропорций»
Тема урока: «Пропорции. Решение задач с помощью пропорций»
Дата проведения: 25.09.2017 г.
Тип урока: Урок первичного предъявлений новых знаний
Технология урока: Технология деятельностного обучения
Цель урока: создание условий для изучения, осмысления и понимания нового учебного материала на основе применения ранее полученных знаний и умений, учащихся путём вовлечения в исследование и открытие новых знаний
Знать/понимать понятия: что такое пропорция, определение пропорции, основное свойство пропорции, что такое масштаб;
Уметь: находить неизвестный член пропорции, применяя определение пропорции и основное свойство пропорции, анализировать условие задач, уметь применять полученные знания на других уроках;
анализировать текст задачи, моделировать условие с помощью схем, рисунков, реальных предметов; строить логическую цепочку рассуждений
Личностные: проявлять интерес к познавательной деятельности, активности при подготовке творческих отчетов.
Метапредметные (универсальные учебные действия):
Познавательные: анализировать (выделяют главное, разделяют на части) и обобщать.
Регулятивные: критически оценивать полученный ответ, осуществлять самоконтроль, проверяя ответ на соответствие условию.
Коммуникативные: осуществлять контроль, коррекцию, оценку собственных действий и действий другого ученика.
Основные термины понятия: пропорция, члены пропорции, верная и неверная пропорция; сформулировать основное свойство пропорции и научиться применять его для определения верной и неверной пропорции, определять крайние и средние члены пропорции.
Оборудования: Учебник, рабочая тетрадь, доска, мел, карточки с заданиями
Структура урока соответствует целям урока и его типу — это урок изучения нового материала:
Содержание учебного материала.Деятельность учителя
Деятельность обучающихся
Формирование УУД
1.Организационный момент
Приветствие. Создание благоприятной рабочей обстановки. Проверка готовности.
Здравствуйте, ребята. Я рад вас видеть. Мы начинаем наш урок. Сегодня на уроке вы узнаете, что знания математики нам нужны в реальной жизни. Я хочу, чтобы этот урок принес вам новые открытия, и надеюсь, что вы с успехом будете применять имеющиеся у вас знания в решении практических задач. И всерьез задумаетесь над темой нашего разговора.
Приветствие учителя. Настрой на урок.
Личностные: самоопределение, настрой на работу
Регулятивные: целеполагание.
2. Актуализация субъектного опыта учащихся
Что мы знаем и умеем по теме отношения?
1.Из выражений назвать отношения, прочитать и вычислить (записать на доске):
57-14;
8:1
2,5:5;
1,2+3,5
2.Выполнить преобразования обыкновенных дробей в десятичные и в проценты, расшифровать тему урока (карточка):
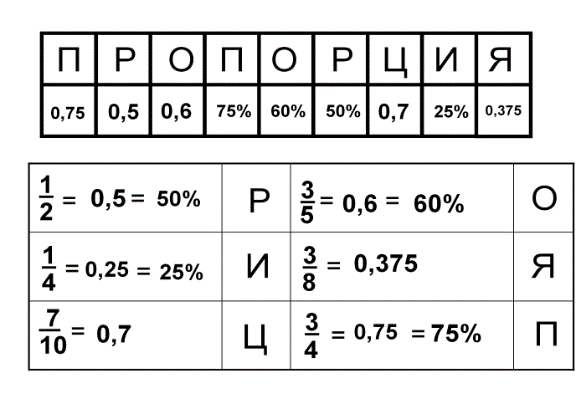
1. Отвечают на вопрос учителя, выполняют задания
2. Выполняют вычисления, сопоставляют с кодом и получают тему урока
Познавательные: структурирование собственных знаний
(анализ, сравнение)
Коммуникативные: организация и планирование учебного сотрудничества с учителем и сверстниками
3. Постановка цели и задач урока
Зная тему урока, попробуйте составить план урока.
Что вы должны узнать сегодня на уроке?
Что вы хотите узнать?
Чему хотите научиться на уроке?
По каким критериям мы можем оценить себя по окончании урока?
Формулируют задачи урока и план урока.
Записывают в тетради тему урока. Называют критерии оценивания.
Регулятивные: целеполагание
Личностные:
Самоопределение
Коммуникативные:
Умение вступать в диалог, участвовать в коллективном обсуждении вопроса
4.Открытие новых знаний и первичное восприятие нового учебного материала
1. Найдем числовые значения двух отношений: 6 : 3 и 10 : 5. Мы видим, что они равны: 6 : 3 = 2 и 10 : 5 = 2, следовательно, можно записать равенство 6 : 3 = 10 : 5. Такое равенство отношений называют пропорцией.
2. Определение. Пропорцией называется равенство двух отношений. Числа, составляющие пропорцию (6; 3; 10; 5), называются членами пропорции.
3. Пропорцию можно записать с помощью букв: а : b = с : d, или 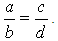 .
.
4. Эти записи читают: «Отношение а к b равно отношению с к d» или «а так относится к в, как с относится к d».
5. Числа а и d называют крайними членами, а числа b и с – средними членами.
В дальнейшем считают, что все члены пропорции отличны от нуля:
а 0, b 0, с 0, d 0.
6. Чтобы проверить, верно ли составлена пропорция, вычисляют числовое значение каждого отношения, составляющего пропорцию. Если эти отношения равны, то пропорция составлена верно; если не равны, то пропорция составлена неверно.
Примеры: 1) Пропорция 40 : 8 = 65 : 13 составлена верно, так как 40 : 8 = 5 и 65 : 13 = 5.
2) Пропорция 2,7 : 9 = 2 : 5 составлена неверно, так как
2,7 : 9 = 0,3, а 2 : 5 = 0,4.
Слушают учителя и записывают определения и примеры
Регулятивные:
коррекция, планирование
Коммуникативные;
выражение и аргументация своих мыслей с достаточной полнотой и точностью
Личностные: формирование готовности к самообразованию
5.Физкультминутка
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.
Давайте немного отдохнем.
Мы топаем ногами,
Мы хлопаем руками,
Киваем головой.
Мы руки поднимаем,
Мы руки опускаем,
И вновь писать начнем.
Учащиеся поднимаются с мест, повторяют действия за учителем.
Учащиеся сменили вид деятельности и готовы продолжить работу.
6. Усвоение новых знаний и способов действий
С 54-55, № 177, 178, 180(а)
Поочередно выходят к доске, объясняя решение заданий
Коммуникативные:
учебное сотрудничество с учителем и сверстниками
Регулятивные:
коррекция, оценка
7. Информация о домашнем задании
П. 2.3 – читать, выучить определение. №179, 180(б), р/т №_37-39
Записывают в дневник домашнее задание. Слушают пояснение домашнего задания
8. Подведение итогов урока.
1. Вопросы:
а) Что такое пропорция?
б) Как называются числа х и у в пропорции х : а = b : у?
в) Как называются числа m и n в пропорции а : m = n : b?
2. Привести свои примеры верных пропорций.
Отвечают на вопросы:
а) Пропорцией называется равенство двух отношений
б)Числа x и y называют крайними членами
в) Числа m и n называют – средними членами
Регулятивные: коррекция, оценка, как осознание того, что уже усвоено, умение самостоятельно адекватно анализировать
Личностные: формирование позитивной самооценки
9. Рефлексия
Поставьте «+» в пустые клетки, где по-вашему верно указано утверждение
Осуществляют самооценку собственной учебной деятельности, в листок самооценки
Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли;
Познавательные: рефлексия.
Формы контроля и оценки результатов их деятельности: На определенных этапах урока старался применять разнообразные формы контроля и оценки знаний учащихся, а именно: устный опрос, карточки, решение задач с объяснением.
Информация о домашнем задании: Задания было задано с закреплением пройденного на уроке, п. 2.3 – читать, выучить определение. №179, 180(б), р/т № 37-39
infourok.ru
Решение задач с помощью пропорции
Презентация позволяет провести урок в соревновательном духе, закрепить материал, поддержать интерес учащихся к предмету.
Просмотр содержимого документа
«Решение задач с помощью пропорции»

17.01.08 « Решение задач с помощью пропорции»

Эпиграф
Каждая решенная мною задача становилась образцом, который служил впоследствии для решения других задач
Декарт
Вопросы для повторения
Частное двух чисел
Если при увеличении (уменьшении) одной другая наоборот уменьшается пропорции):
двух крайних
и
двух средних
(увеличивается), то зависимость является обратной пропорциональной зависимостью
Если
поменять местами
средние или крайние члены то получится снова верная пропорция
Произведение крайних членов равно произведению средних
Если при увеличении (уменьшении) одной другая также увеличивается (уменьшается), то зависимость между ними является прямой пропорциональной зависимостью
Равенство двух отношений
- Что называется отношением двух чисел?
- Что показывает отношение?
- Что называется пропорцией?
- Из чего состоит пропорция?
- В чем заключается основное свойство пропорции?
- Каким еще свойством обладает пропорция?
- Чему равен неизвестный член пропорции ?
- Какая зависимость между двумя величинами называется прямой пропорциональной зависимостью?
- Какая зависимость между двумя величинами называется прямой пропорциональной зависимостью?
Отношение большего к меньшему показывает во сколько раз одно число больше другого
Отношение меньшего к большему показывает какую часть одно число составляет от другого
Пропорция состоит из четырех чисел (членов
х = 8

Задача № 1
- Малыш и Карлсон любили пить чай. Малыш наливал себе 100 г заваренного чая и добавлял в него 3 ложечки сахара. Карлсон наливал себе 200 г чая. Сколько ложечек сахара должен добавить в свой чай Карлсон, чтобы чай его был таким же сладким , как у Малыша?
- Ответ: 6 ложечек
↓
Вода
Малыш
Сахар
100г
Карлсон
3 лож.
200г
↓
Х лож

Задача № 2
- За 4 м ткани заплатили 180 р. Сколько стоят 14 м этой ткани?
Кол-во ткани
I покупка
Стоимость
II покупка

Алгоритм составления пропорции
- Внимательно прочитайте условие задачи.
- Найдите в условии 3 известных величины и 1 неизвестную.
- 4 найденные величины впишите в таблицу из 2 строк и 2 столбцов, так чтобы в строках стояли величины связанные между собой, а в столбцах величины одинаковой размерности (неизвестную величину при этом нужно обозначить буквой!).
- Определите характер зависимости между взаимосвязанными величинами и укажите его в краткой записи с помощью стрелок.
- Преобразуйте краткую запись условия в пропорцию учитывая характер зависимости (если зависимость обратная и стрелки направлены в разные стороны то при записи пропорции вторую дробь необходимо перевернуть!).
- Найдите неизвестный член пропорции.
- Запишите ответ.

Задача 3
- Чтобы покрасить стены дома за 2 дня требуется 20 маляров. За сколько дней эту работу выполнят 4 маляра?
↑
20 маляров
4 маляра
2 дня
↓
х дней

Задача №4 (на проценты)
- Из свежей малины получается 15% сухой. Сколько взяли свежей малины, если получили при ее сушке 6 кг сухой?
↓
кг
Свежая
%
Сухая
х
100
6
15
↓

Задачи для классной работы
Стр. 130
- № 783
- № 784
- № 785
- № 786
- № 787
- № 788
- № 789
- № 784
Решите, составив пропорцию.
- Ответ: 19,5 г.
- Ответ: 1,7 кг.
- Ответ: 150 мин.
- Ответ: 40 машин.
- Ответ: 85 %.
- Ответ: 60 лип.
- Ответ: 40% д., 60 % м
- Ответ:1125 т.

Пропорция находит себе множество применений. С ее помощью вы сможете сейчас или в будущем решать следующие задачи:
- Задачи на проценты
- Задачи на деньги
- Задачи на выполнение работы
- Задачи на движение
- Задачи на смеси и сплавы
- Нахождение расстояний с помощью карты
- Геометрические задачи
- Физические задачи
- Химические задачи
- Многие другие задачи в самых различных отраслях знаний и деятельности.

Интересные задачи
- Сколько воды надо добавить к 600г жидкости, содержащей 40% соли, чтобы получить раствор, содержащий 12% этой соли.
- Поезд проходит мимо светофора за 5 с, а мимо платформы длиной 150 м за 15 с. Найдите длину поезда и его скорость.

Домашнее задание
п. 22, № 811 – 813
Желаю успеха!
kopilkaurokov.ru
Конспект урока с презентацией на тему «Пропорция. Основное свойство пропорции», алгебра 7 класс
ПЛАН-КОНСПЕКТ ОТКРЫТОГО УРОКА
по теме:
«Пропорция. Основное свойство пропорций»
1. ФИО Носкова Елена Викторовна
2. Место работы МОУ СОШ №2 г. Пошехонье Ярославской области
3. Должность учитель математики
4. Предмет математика
5. Класс 7
6. Тема и номер урока в теме «Пропорция. Основное свойство пропорций», 7 -ой урок
7. Базовый учебник «Алгебра 7», под ред. Г.В. Дорофеева. – М.: Просвещение, 2013
8. Цель урока: ввести понятие пропорции, рассмотреть основное свойство пропорции.
9. Задачи:
— обучающие: ввести понятие пропорции, крайних и средних членов пропорции, основного свойства пропорции, способствовать формированию у учащихся навыков вычисления отношения величин, закрепить и усовершенствовать навыки применения основного свойства пропорции.
— развивающие: развивать логическое мышление, внимание, алгоритмическую культуру учащихся; способствовать формированию навыка построения высказываний с использованием математических терминов;
— воспитательные: способствовать формированию культуры общения, самостоятельности, интереса к изучению математики.
10. Тип урока урок введения нового материала
11. Формы работы учащихся фронтальная, групповая, самостоятельная, индивидуальная
12. Необходимое техническое оборудование
• ПК
• проектор
• экран
СТРУКТУРА И ХОД УРОКА
«3нание только тогда знание,
когда оно приобретено усилиями
своей мысли, а не памятью».
Л.Н. Толстой
1. Организационный момент (приветствие учащихся, гостей урока,
запись в тетради числа, вида работы)
2. Девиз урока:
Думать — коллективно!
Решать — оперативно!
Отвечать — доказательно!
Стараться — обязательно!
3. Давайте вспомним, какие новые понятия мы изучил на предыдущих уроках,
с чем мы работали?
(отношения, прямая пропорциональность, обратная пропорциональность)
4 Повторение изученного
Задание 1. Вычислить отношения
1,5 к 3; 24 к 8; 5 к 25; 8 к 40; 0, 48 к 0,16; 17 к 51
Что наблюдаем в результате вычислений? Какую группу отношений можно
выделить? (равные отношения)
Задание 2. Запишите равенство пар отношений
Отношения равны, значит можно записать равенства
24 : 8 =48 : 0,16;
5:25=8 : 40 Прочитайте полученные отношения
5 Изучение нового материала
5.1. Фронтальная работа
Итак, мы получили равенства двух отношений.
РАВЕНСТВО ДВУХ ОТНОШЕНИЙ
НАЗЫВАЮТ ПРОПОРЦИЕЙ.
-Это новое понятие. Значит, какая у нас сегодня новая тема?
-(Пропорции)
-Запишите в тетрадь тему урока.
-Значит, равенства (1) и (2) – пропорции.
В этих пропорциях участвуют числа.
Попробуйте записать пропорцию с помощью букв а, b, с, d.
а : b = с : d
-Прочитайте эти записи.
-( «Отношение а к b равно отношению с к d»
или « а так относится к b, как с относится к d» )
-Итак, в пропорции участвуют 4 числа.
Их принято называть членами пропорции.
А в зависимости от их расположения в пропорции они могут быть разбиты на две группы. Каким образом? Как бы вы назвали члены каждой пары?
Вызвать к доске 4 чел (2 дев., 2 мал.; девочки – посередине, мальчики – по краям).
-Как бы вы назвали расположение девочек и мальчиков в ряду?
(Девочки в середине, мальчики скраю)
Вернёмся к пропорции. Как бы вы назвали члены каждой пары?
( Средние и крайние члены пропорции )
-Назовите средние и крайние члены в полученных пропорциях
5.2 Работа в группах
Класс делится на группы.
Задание 3.
Каждая группа получает карточку с заданием: заполнить таблицу.
Группа 1. Дана пропорция 1,2:6=0,6:3
Группа 2. Дана пропорция 7:5=14:10
Группа 3. Дана пропорция 0,5:0,2=1:0,4
Группа 4. Дана пропорция 35:0,7=10:0,2
Группа 5. Дана пропорция 3,4:2=68:40
Группа 6. Дана пропорция 35:0,1=700:2
На основании полученных данных нужно заполнить таблицу
ПропорцияКрайние члены
Средние члены
Произведение крайних членов
Произведение средних членов
Какой вывод можно сделать на основании полученных результатов?
(произведение крайних членов равно произведению средних членов)
Сводная таблица всех групп
Пропорция1,2:6=0,6:3
7:5=14:10
0,5:0,2=1:0,4
35:0,7=10:0,2
3,4:2=68:40
35:0,1=700:2
Крайние члены
1,2 и 3
7 и 10
0,5 и 0,4
35 и 0,2
3,4 и 40
35 и 2
Средние члены
6 и 0,6
5 и 14
0,2 и 1
0,7 и 10
2 и 68
0,1 и 700
Произведение крайних членов
3,6
70
0,2
7
136
70
Произведение средних членов
3,6
70
0,2
7
136
70
Итак, мы сформулировали основное свойство пропорции: произведение крайних членов пропорции равно произведению средних членов
6. Закрепление изученного материала.
ЗАДАНИЕ № 3. (устно)
Среди равенств найдите верные пропорции и назовите их средние и крайние члены:
а) 25 + 13 = 8 + 30 г) 90 : 3 = 5 · 6
б) 33 : 11 = 6 : 2 д) 3 : 4 = 6 : 8
в) 5 + 15 = 50 – 30 е) 10 : 5 = 20 : 4
ЗАДАНИЕ № 4.
1) Составьте верную пропорцию из данных отношений:
8 : 24 ; 7 : 28 ; 2 : 6 .
2) Пользуясь основным свойством пропорции, проверьте, верна ли эта пропорция.
3) Верна ли пропорция 7 : 28 = 2 : 6 ? Почему?
7. Контроль полученных знаний.
САМОСТОЯТЕЛЬНАЯ РАБОТА по карточкам.
Заполните пропущенные места в карточке.
(Приложение 1 – карточки с самостоятельной работой)
По окончании самостоятельной работы учащиеся меняются своими работами, проверяют по образцу, ставят оценки:
«5» — за 3 задание
«4» — за 2 задания
«3» — за 1 задание
8. Рефлексия
Давайте подведём итоги:
Что нового вы узнали сегодня на уроке?
( Понятие «Пропорция»,
название членов пропорции,
основное свойство пропорции )
Оцените свое настроение в конце нашего урока (смайлики)
СПАСИБО ЗА УРОК!
САМОСТОЯТЕЛЬНАЯ РАБОТА.
1 вариант
«5» — за 3 задание
«4» — за 2 задания
«3» — за 1 задание
№ 1. Укажите средние и крайние члены пропорции,
вычислите их произведения: 21 : 42 = 2 : 4 .
Средние члены _______________________________ +
Их произведение ______________________________ + —
Крайние члены _______________________________ + —
Их произведение _______________________________ + —
№ 2. Из данных отношений выберите те, из которых можно
составить верную пропорцию:
6 : 4 ; 10 : 4 ; 9 : 6 .
Верная пропорция: _____________________________ + —
№ 3. Пользуясь основным свойством пропорции, проверьте,
верна ли пропорция:
а) 52 : 208 = 2 : 8
Решение: ______________________________________
______________________________________
Ответ: пропорция ( верна или не верна) ____________ + —
б) 8 : 3 = 13 : 5
Решение: ______________________________________
______________________________________
Ответ: пропорция ( верна или не верна) ____________ + —
САМОСТОЯТЕЛЬНАЯ РАБОТА.
2 вариант
«5» — за 3 задание
«4» — за 2 задания
«3» — за 1 задание
№ 1. Укажите средние и крайние члены пропорции,
вычислите их произведения: 12 : 6 = 4 : 2 .
Средние члены _________________________________ + —
Их произведение ______________________________ + —
Крайние члены _________________________________ + —
Их произведение _______________________________ + —
№ 2. Из данных отношений выберите те, из которых можно
составить верную пропорцию:
6 : 4 ; 5 : 4 ; 3: 2 .
Верная пропорция: _____________________________ + —
№ 3. Пользуясь основным свойством пропорции, проверьте,
верна ли пропорция:
а) 21 : 42 = 4 : 8
Решение: ______________________________________
______________________________________
Ответ: пропорция ( верна или не верна) ____________ + —
б) 6 : 3 = 12 : 5
Решение: ______________________________________
______________________________________
Ответ: пропорция ( верна или не верна) ____________ + —
Проверка самостоятельной работы.
1 вариант
№ 1. Средние члены 42 и 2
Их произведение 84
Крайние члены 21 и 4
Их произведение 84
№2. верная пропорция 6:4=9:6
№3. а) Решение: 52 · 8 = 416 , 208 · 2 = 416
Ответ: пропорция верна.
б) Решение: 8 · 5 = 40 , 3 · 13 = 39
Ответ: пропорция не верна.
2 вариант
№ 1. Средние члены 6 и 4
Их произведение 24
Крайние члены 12 и 2
Их произведение 24
№2. верная пропорция 6:4=3:2
№3. . а) Решение: 21 · 8 = 168, 42 · 4 = 168
Ответ: пропорция верна.
б) Решение: 5 · 5 = 30 , 3 · 12 = 36
Ответ: пропорция не верна.
infourok.ru