Исследование функций с помощью производной | LAMPA
Монотонная функция
Возрастающая функция на отрезке [a,b][a,b][a,b] (или интервале, или множестве) — это такая функция f(x)f(x)f(x), что для любых x1<x2x_1\lt x_2x1<x2 из отрезка (интервала, множества) выполняется неравенство f(x1)<f(x2)f(x_1)\lt f(x_2)f(x1)<f(x2). В случае выполнения нестрогого неравенства f(x1)≤f(x2)f(x_1)\le f(x_2)f(x1)≤f(x2) функция называется неубывающей на отрезке.
Убывающая функция на отрезке [a,b][a,b][a,b] (или интервале, или множестве) — это такая функция f(x)f(x)f(x), что для любых x1<x2x_1\lt x_2x1<x2 из отрезка (интервала, множества) выполняется неравенство f(x1)>f(x2)f(x_1)\gt f(x_2)f(x1)>f(x2). В случае выполнения нестрогого неравенства f(x1)≥f(x2)f(x_1)\ge f(x_2)f(x1)≥f(x2) функция называется невозрастающей на отрезке.
Если функция является убывающей или возрастающей, то она называется монотонной функцией.
Пример: функция является возрастающей.
Пример: функция y=−3x+2y=-3x+2y=−3x+2 является убывающей.
Точки экстремума
x0x_0x0 — точка максимума функции f(x)f(x)f(x), если для всех достаточно близких точек xxx верно неравенство f(x)≤f(x0)f(x)\le f(x_0)f(x)≤f(x0).
x0x_0x0 — точка минимума функции f(x)f(x)f(x), если для всех достаточно близких точек верно неравенство f(x)≥f(x0)f(x)\ge f(x_0)f(x)≥f(x0).
Точка экстремума — это либо функции.
Признак возрастания и убывания функции
Функция f(x)f(x)f(x) возрастает на промежутке (a;b)(a;b)(a;b), если f′(x)>0f'(x)\gt 0f′(x)>0 на этом промежутке.
Функция f(x)f(x)f(x) убывает на промежутке (a;b), если производная f′(x)<0f'(x)\lt 0f′(x)<0 на этом промежутке.
Признаки максимума и минимума функции
Если функция f(x)f(x)f(x) непрерывна на промежутке (a;b)(a; b)(a;b), возрастает на промежутке (a;x0)(a;x_0)(a;x0) и убывает на промежутке (x0;b)(x_0;b)(x0;b), то x0x_0x0 является .
Признак максимума функции выполняется, если:
- f′(x)>0f'(x)\gt 0f′(x)>0 на промежутке (a;x0)(a; x_0)(a;x0)
- f′(x)=0f'(x)=0f′(x)=0 в точке x0x_0x0
- f′(x)<0f'(x)\lt 0f′(x)<0 на промежутке (x0;b)(x_0; b)(x0;b)
Если функция f(x)f(x)f(x) непрерывна на промежутке (a;b)(a; b)(a;b), убывает на промежутке (a;x0)(a;x_0)(a;x0) и возрастает на промежутке (x0;b)(x_0;b)(x0;b), то x0x_0x0 является .
Признак минимума функции выполняется, если:
- f′(x)<0f'(x)\lt 0f′(x)<0 на промежутке (a;x0)(a; x_0)(a;x0)
- f′(x)=0f'(x)=0f′(x)=0 в точке x0x_0x0
- f′(x)>0f'(x)\gt 0f′(x)>0 на промежутке (x0;b)(x_0; b)(x0;b)
Критическая точка
Точка, в которой производная функции равна нулю.
В критических точках является горизонтальной линией, так как тангенс угла наклона касательной (значение производной в точке касания) равен нулю.
Три типа критических точек:
x1x_1x1 – точка локального , является ;
x2x_2x2 – точка перегиба, НЕ является точкой экстремума.
x3x_3x3 – точка локального , является точкой экстремума;
Как искать точки максимума и минимума функции
Задачи на нахождение функции решаются по стандартной схеме в 333 шага.
Шаг 1. Найдите производную функции
- Запомните функции и основные , чтобы найти производную.
y′(x)=(x3−243x+19)′=3×2−243.y'(x)=(x^3-243x+19)’=3x^2-243.y′(x)=(x3−243x+19)′=3×2−243.
Шаг 2. Найдите
- Решите полученное уравнение, чтобы найти .
3×2−243=0⇔x2=81⇔x1=−9,×2=9.3x^2-243=0 \,\,\,\,\Leftrightarrow \,\,\,\, x^2=81 \,\,\,\,\Leftrightarrow \,\,\,\, x_1=-9, \,\,\,\, x_2=9.3×2−243=0⇔x2=81⇔x1=−9,×2=9.
Шаг 3. Найдите точки экстремума
- Используйте , чтобы определить знаки производной;
- В равна нулю и меняет знак с минуса на плюс, а в – с плюса на минус.
Применим этот подход, чтобы решить следующую задачу:
Найдите точку максимума функции y=x3−243x+19y=x^3-243x+19y=x3−243x+19.
1) Найдем производную: y′(x)=(x3−243x+19)′=3×2−243;y'(x)=(x^3-243x+19)’=3x^2-243;y′(x)=(x3−243x+19)′=3×2−243;
2) Решим уравнение y′(x)=0y'(x)=0y′(x)=0: 3×2−243=0⇔x2=81⇔x1=−9,×2=93x^2-243=0 \,\,\,\,\Leftrightarrow \,\,\,\, x^2=81 \,\,\,\,\Leftrightarrow \,\,\,\, x_1=-9, \,\,\,\, x_2=93×2−243=0⇔x2=81⇔x1=−9,×2=9
3) Производная положительная при x>9x\gt 9x>9 и x<−9x\lt -9x<−9 и отрицательная при −9<x<9.-9\lt x\lt 9.−9<x<9. Поэтому x=−9x=-9x=−9 — точка максимума.
Как искать наибольшее и наименьшее значение функции
Для решения задачи на поиск наибольших и наименьших значений функции необходимо:
- Найти функции на отрезке (интервале).
- Найти значения в концах отрезка и выбрать наибольшее или наименьшее величину из значений в точках экстремума и в концах отрезка.
Во многих задачах помогает теорема:
Если на отрезке только одна , причем это точка минимума, то в ней достигается наименьшее значение функции. Если это точка максимума, то в ней достигается наибольшее значение.
lampa.io
Исследование функций с помощью второй производной. Точки перегиба

Из рисунка ясно, | что функция имеет максимум в точке x1 = −1 и минимум в точке | |
x2 = 3 . В точке разрыва характер монотонности не меняется. | ||
Определение 1 |
|
|
Функция f (x) | называется выпуклой вниз (выпуклой) на промежутке (a, b), если ее | |
график лежит выше касательной, проведенной в любой точке x0 (a, b) (рис.14 a). | ||
Определение 2 |
|
|
Функция f (x) | называется выпуклой вверх (вогнутой) на промежутке (a, b), если ее | |
график лежит ниже касательной, проведенной в любой точке x0 (a, b) (рис.14 b). | ||
| y | y |
a | x0 | b | x | a | x0 | b | x |
|
| Рис. 14 a. |
|
| Рис. 14 b. |
| |
Теорема 1 | f (x) |
|
|
|
| промежутке (a, b) и вторая | |
Если функция | дважды | дифференцируема | на | ||||
производная f »(x)> 0 для всех значений | x (a, b), то | f (x) | выпукла вниз на промежутке | ||||
(a, b). |
|
|
|
|
|
|
|
Доказательство
1) Возьмем произвольную точку x0 (a, b). Уравнение касательной к графику функции
в этой точке имеет вид:
y = f (x0 )+ f ′(x0 ) (x − x0 ).
Покажем, что в любой точке x (a, b) график функции расположен выше этой касательной.
Рассмотрим любую точку x (a, b), удовлетворяющую условию x > x0 , и вычислим разность ординат функции (f (x)) и касательной (y) в этой точке:
f (x)− y = f (x)−(f (x0 )+ f ′(x0 ) (x − x0 ))= (f (x)− f (x0 ))− f ′(x0 ) (x − x0 ).
Поскольку функция f (x) удовлетворяет условиям теоремы Лагранжа на промежутке (x0 , x), то найдется точка c1 (x0 , x), для которой справедливо равенство
f (x)− f (x0 )= f ′(c1 ) (x − x0 ).
Учитывая это, разность ординат функции и касательной в точке x можно представить в виде
f (x)− y = f ′(c1 ) (x − x0 )− f ′(x0 ) (x − x0 )= (f ′(c1 )− f ′(x0 )) (x − x0 ).
Производная f ′(x) удовлетворяет условиям теоремы Лагранжа на промежутке (x0 , с1). Значит, найдется точка c2 (x0 , с1), для которой справедливо равенство
f ′(c1 )− f ′(x0 )= f ′′(c1 ) (с1 − x0 ).
Учитывая это, разность ординат функции и касательной в точке x можно записать в виде f (x)− y = f ′′(c2 ) (c1 − x0 ) (x − x0 ).
25

Так как f ′′(x)> 0 при всех x (a,b), а x0 < c2 < c1 < x (рис.15), то f ′′(с2 )>0 , | c1 − x0 > 0 и | |||||
x − x0 > 0 . Следовательно, f (x)− y > 0 | и график функции в точке x > x0 | расположен | ||||
выше касательной. |
|
|
|
|
| |
|
|
|
|
|
| |
| x0 | c | c | x |
|
|
|
| 2 | 1 |
|
|
|
Рис. 15
2) Рассмотрим любую точку x (a, b), удовлетворяющую условию x < x0 , и вычислим
разность ординат функции (f (x)) и касательной (y) в этой точке:
f (x)− y = f (x)− (f (x0 )+ f ′(x0 ) (x − x0 ))= (f (x)− f (x0 ))− f ′(x0 ) (x − x0 )= = −(f (x0 )− f (x))+ f ′(x0 ) (x0 − x).
Поскольку функция f (x) удовлетворяет условиям теоремы Лагранжа на промежутке
(x, x0 ), то найдется точка c1 (x, x0 ), для которой справедливо равенство f (x0 )− f (x)= f ′(c1 ) (x0 − x).
Учитывая это, разность ординат функции и касательной в точке x можно записать в виде f (x)− y = − f ′(c1 ) (x0 − x)+ f ′(x0 ) (x0 − x)= (f ′(x0 )− f ′(c1 )) (x0 − x).
Производная f ′(x) удовлетворяет условиям теоремы Лагранжа на промежутке (с1, x0 ). Значит, найдется точка c2 (с1, x0 ), для которой справедливо равенство
f ′(x0 )− f ′(c1 )= f ′′(c2 ) (x0 −c1 ).
Учитывая это, разность ординат функции и касательной в точке x можно записать в виде
| f (x)− y = f ′′(c2 ) (x0 −c1 ) (x0 − x). |
|
| ||||
Так как f ′′(x)> 0 при всех x (a,b), а x < c1 < c2 < x0 (рис. 16), то | f ′′(с2 )>0 , x0 −c1 > 0 и | ||||||
x0 − x > 0 . Следовательно, f (x)− y > 0 . | Тогда график функции в точке x < x0 | также | |||||
расположен выше касательной. |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| x | c1 | c2 | x0 |
|
| |
|
|
| Рис. 16 |
|
|
|
|
Теорема 2 |
|
|
|
|
|
| |
Если функция f (x) дважды | дифференцируема | на промежутке (a,b) и | вторая | ||||
′′ |
|
|
|
| (a,b) выпукла вверх. | ||
производная f (x)< 0 для всех x (a,b), то f (x) на промежутке | |||||||
Доказательство
аналогично доказательству теоремы 1.
Определение 3
Точки, в которых меняется характер выпуклости функции, называются точками перегиба.
Теорема 3
Если f ′′(x0 )= 0 и f ′′(x) меняет знак при переходе через точку x0 , то функция f (x) имеет в точке x0 перегиб.
ЗАМЕЧАНИЕ
Вторая производная может менять знак и в точке разрыва. Поэтому точками перегиба являются точки, в которых вторая производная обращается в ноль или бесконечна (а функция определена) и меняет знак.
26

Чтобы найти точки перегиба графика функции нужно:
•вычислить вторую производную заданной функции;
•найти все точки, в которых вторая производная равна нулю или не существует;
•нанести эти точки, а также точки разрыва функции на числовую ось;
•определить знак второй производной на каждом из полученных интервалов;
•по знаку второй производной определить характер выпуклости функции;
•точками перегиба будут те точки, в которых меняется характер выпуклости функции, исключая точки разрыва.
Пример 1
Определите точки перегиба графика функции f (x)= ln(x2 +1).
Решение
Первая производная заданной функции равна |
| f | ′ |
|
|
|
| 1 |
|
|
|
|
|
|
| Исследуя первую | |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||
|
| (x)= x2 +1 2x . |
| ||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x = 0 |
| . |
|
|
|
|
| ||||
производную легко убедиться, что функция имеет минимум в точке |
| = 0 |
|
|
|
|
| ||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| y |
|
|
|
|
|
| |||||
Теперь вычислим вторую производную |
|
|
|
|
|
| 2 (1− x) (1+ x) |
|
|
|
|
|
|
|
| ||||||||||||||||||||
|
| y′′ | = 2 | x2 | +1− x 2x | = 2 | 1− x2 |
| = |
|
|
|
|
|
|
|
|
| |||||||||||||||||
|
|
| (x2 +1)2 | (x2 +1)2 |
|
|
|
| (x2 +1)2 |
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
и исследуем ее. Вторая производная меняет знак в точках |
| x = ±1. По знаку второй | |||||||||||||||||||||||||||||||||
производной y′′ можно выяснить характер выпуклости функции (рис. 17). |
|
|
|
|
|
|
| ||||||||||||||||||||||||||||
| − |
| + |
| y′ |
|
|
|
|
|
| y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
| min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| − | + |
| − |
| y′′ |
|
|
|
|
| ln 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
| −1 |
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
| перегиб | перегиб |
|
|
| Рис. 17 | −1 |
| 0 |
| 1 |
|
|
|
|
|
|
|
|
|
|
| x |
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Из рисунка видно, что функция имеет две точки перегиба |
| x = ±1 | . На рисунке 17 | ||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| y = ln 2 |
|
|
|
|
|
|
| |||||||
показан график заданной функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
Пример 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Исследуйте характер выпуклости графика функции |
| y = 3 x5 |
|
| и |
| найдите | точки | |||||||||||||||||||||||||||
перегиба. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| 3 |
|
| 5 | ′ |
|
| 5 |
| ′ |
| 5 |
|
| 2 |
|
|
| 5 3 |
| 2 |
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
| 3 |
|
|
|
|
| |||||||||||
Поскольку первая | производная функции | y = |
| x |
|
|
|
|
| = x |
|
|
| = |
|
| x |
|
| = |
| x |
| всюду | |||||||||||
|
|
|
|
|
|
| 3 |
|
|
| 3 |
| |||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
положительна, то функция возрастает при всех значениях x .
27
studfile.net
Исследование функции с помощью производной онлайн · Как пользоваться Контрольная Работа РУ
Вы можете выполнить исследование функции с помощью производной. Для этого воспользуйтесь онлайн калькулятором с подробным решением, как исследовать функцию.
Для это введите свою функцию в калькулятор:

Где при исследовании функции пригодится помощь производной?
Здесь перечислим, где используется производная, чтобы исследовать функцию:
- Чтобы найти точки экстремумов: найти наименьшее или наибольшее значение функции, а также промежутки возрастания и убывания функции
- Также чтобы найти точки перегибов функции — интервалы выпуклости и вогнутости (здесь используется производная второго порядка).
Рассмотрим пример
Найдём с помощью производной экстремумы и точки перегибов для функции (x^2 — 1)/(x^2 + 1):
Получим результат:
Для того, чтобы найти экстремумы, нужно решить уравнение
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
Первая производная
/ 2 \
2*x 2*x*\x - 1/
------ - ------------ = 0
2 2
x + 1 / 2 \
\x + 1/ Решаем это уравнение
Корни этого ур-ния
Зн. экстремумы в точках:
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
Максимумов у функции нет
Убывает на промежутках
Возрастает на промежутках
Найдем точки перегибов, для этого надо решить уравнение
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
Вторая производная
/ 2 2 2 / 2\\
| -1 + x 4*x 4*x *\-1 + x /|
2*|1 - ------- - ------ + --------------|
| 2 2 2 |
| 1 + x 1 + x / 2\ |
\ \1 + x / /
----------------------------------------- = 0
2
1 + x Решаем это уравнение
Корни этого ур-ния
Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
Выпуклая на промежутках
(-oo, -sqrt(3)/3] U [sqrt(3)/3, oo)
www.kontrolnaya-rabota.ru
Тема исследование функций с помощью производных
Лекция 12
§1. Условие постоянства функции
Теорема. Если функция 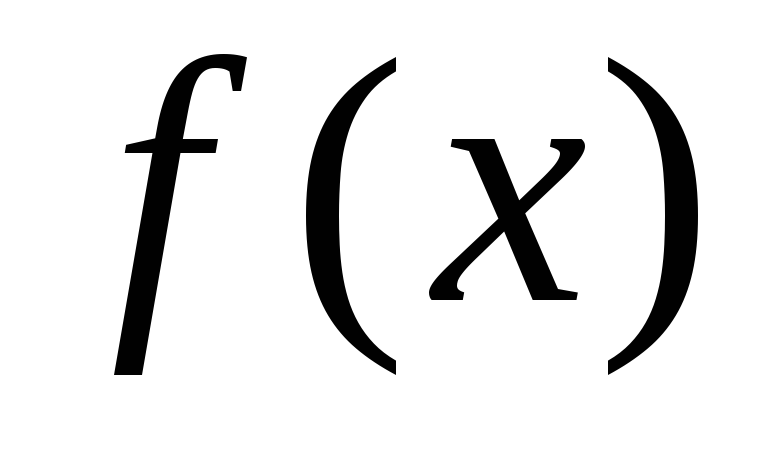 непрерывна
на промежутке
непрерывна
на промежутке и во всех внутренних
точках отрезка
и во всех внутренних
точках отрезка  ,
то
,
то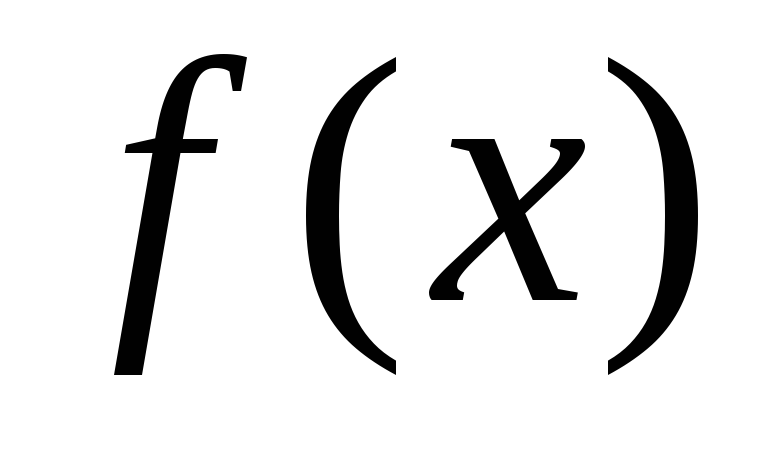 постоянна
на этом промежутке.
постоянна
на этом промежутке.
Доказательство. Пусть 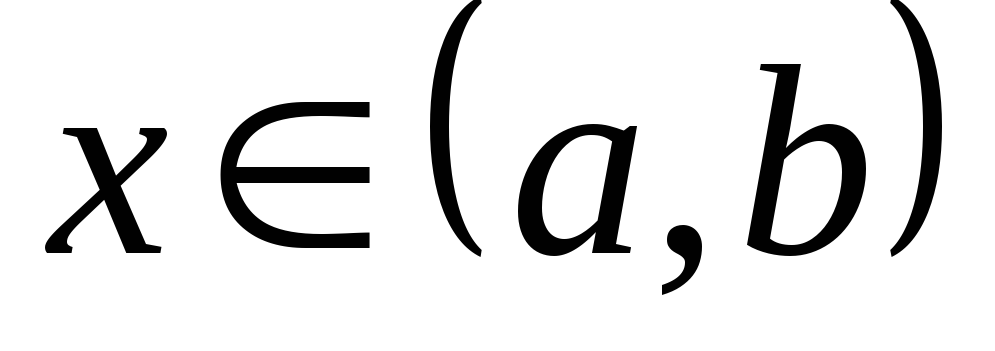 .
Применим теорему Лагранжа к функции
.
Применим теорему Лагранжа к функции  на
промежутке
на
промежутке 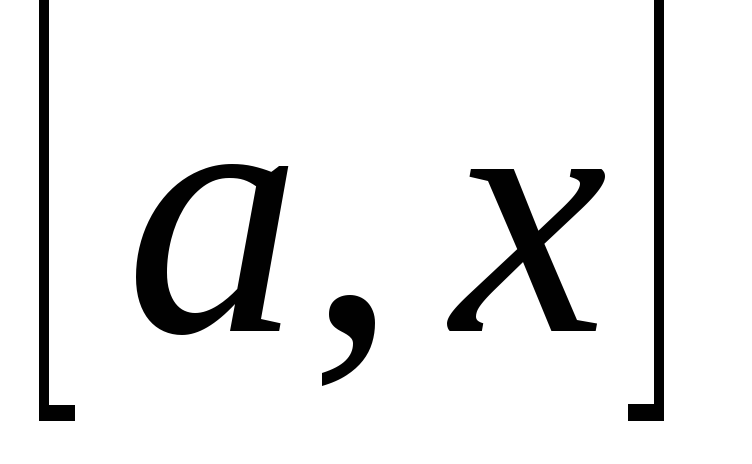 :
:
 .
Но по условию
.
Но по условию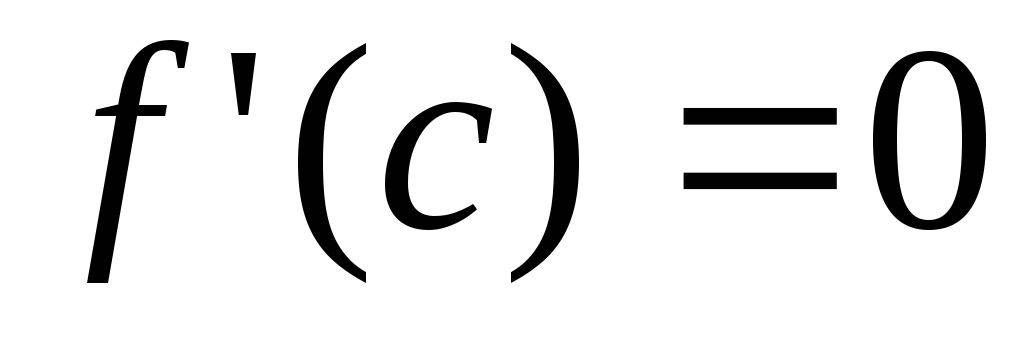 ,
следовательно,
,
следовательно,  и поэтому
и поэтому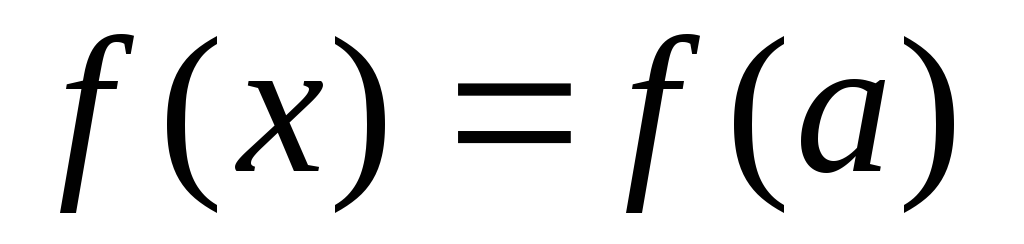
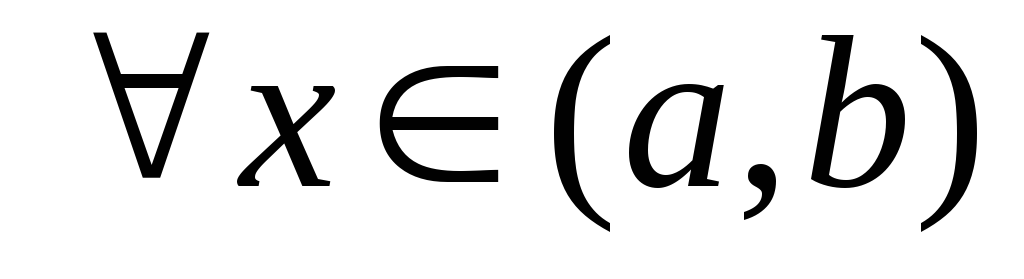 (на правом конце
(на правом конце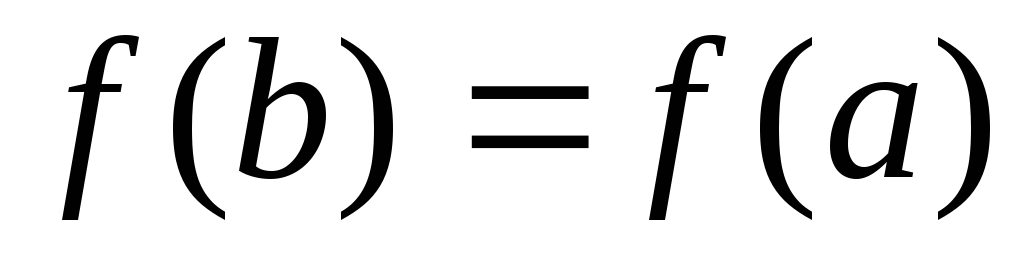 в силу непрерывности).
в силу непрерывности).
Пример. Рассмотрим функцию 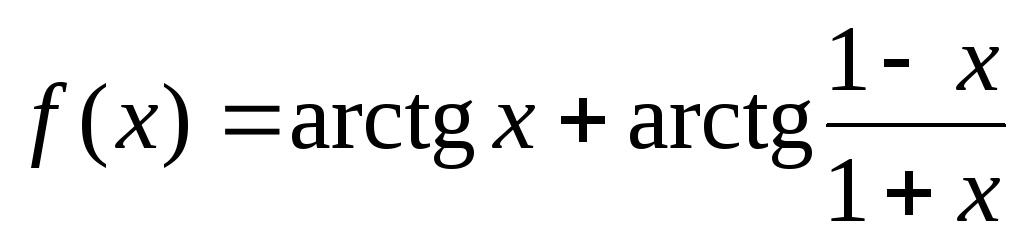 на промежутке
на промежутке 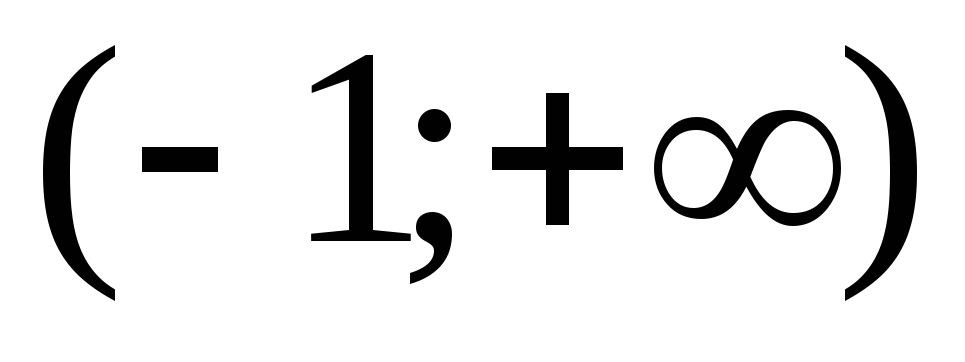 .
Её производная:
.
Её производная: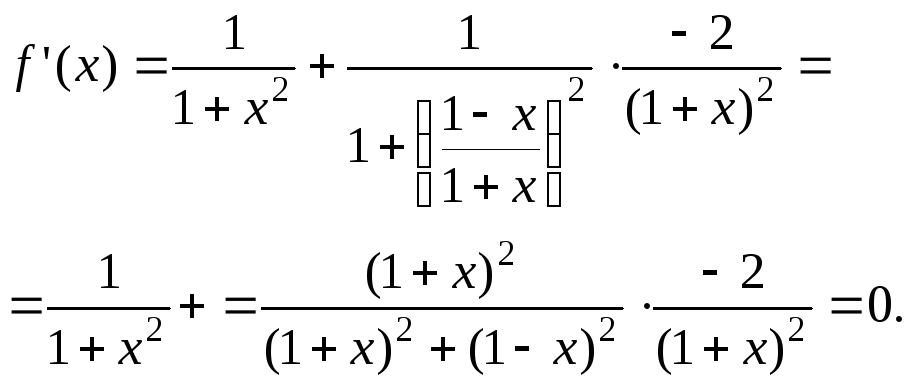
Следовательно, 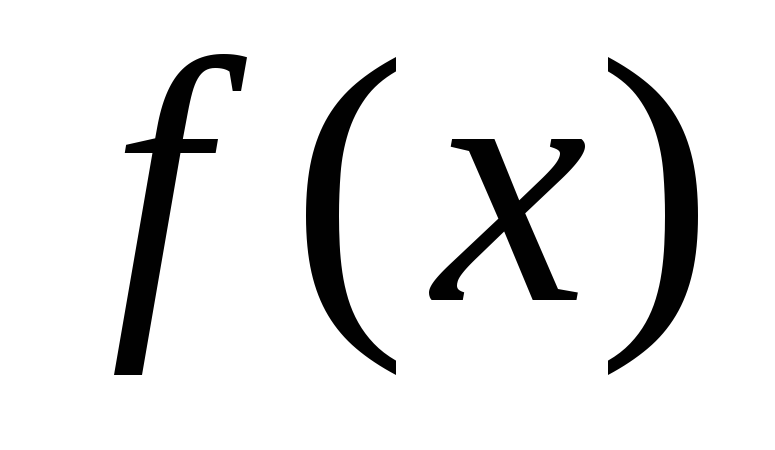
 const
на
const
на 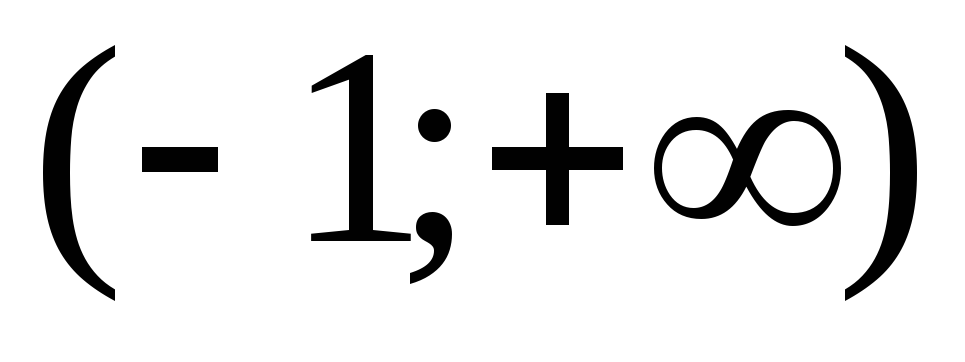 .
Чтобы найти эту константу, достаточ-но
вычислить
.
Чтобы найти эту константу, достаточ-но
вычислить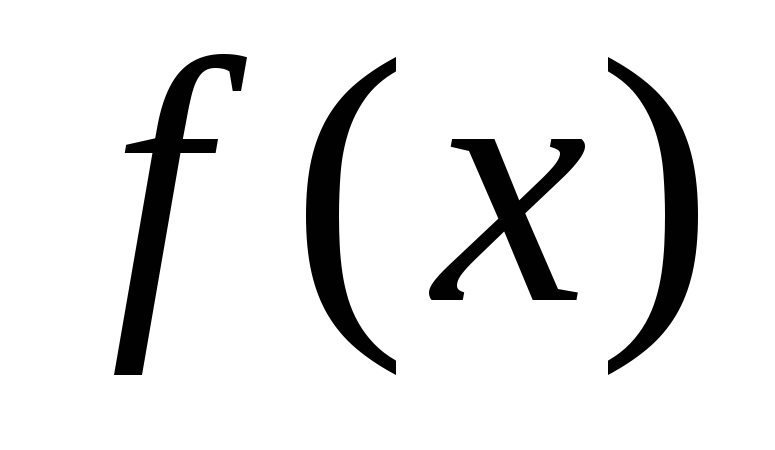 в любой точке, например,
в любой точке, например, . Итак, мы доказали тождество
. Итак, мы доказали тождество  .
.
В интегральном исчислении важное приложение найдет следствие, вытекающее из доказанной теоремы.
Следствие. Если функции и
и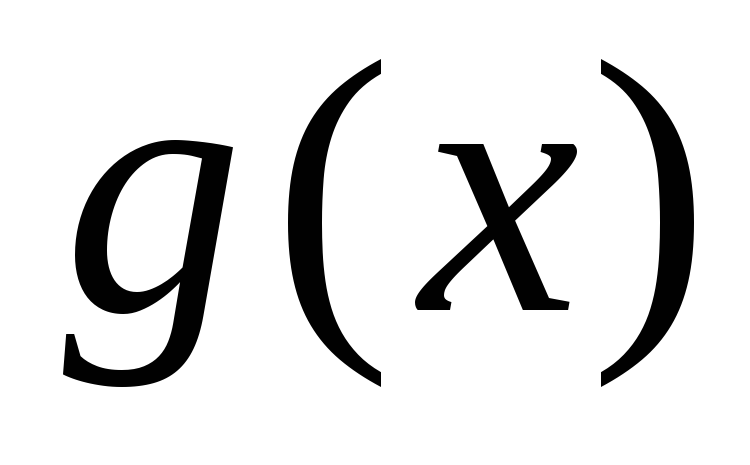 непрерывны
на промежутке
непрерывны
на промежутке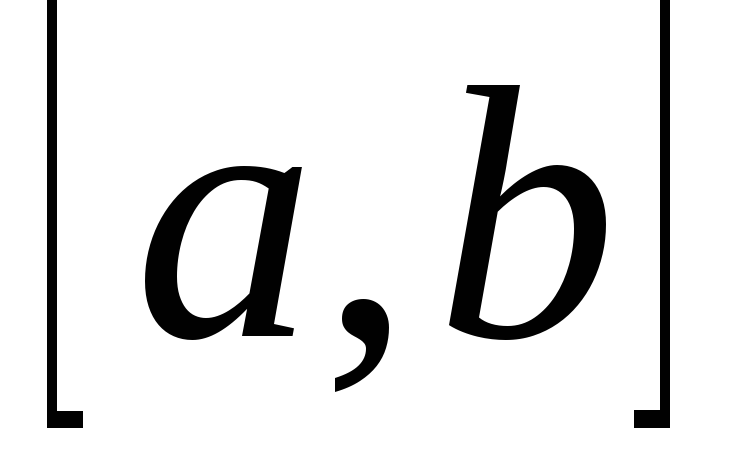 и имеют равные
производные во всех внутренних точках
промежутка, то эти функции всюду в
и имеют равные
производные во всех внутренних точках
промежутка, то эти функции всюду в 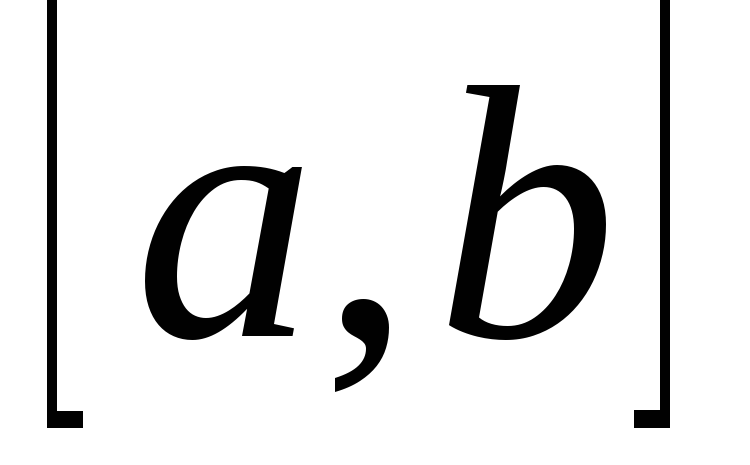 отличаются лишь на постоянную:
отличаются лишь на постоянную: .
.
Для
доказательства достаточно применить
теорему к вспомогательной функции 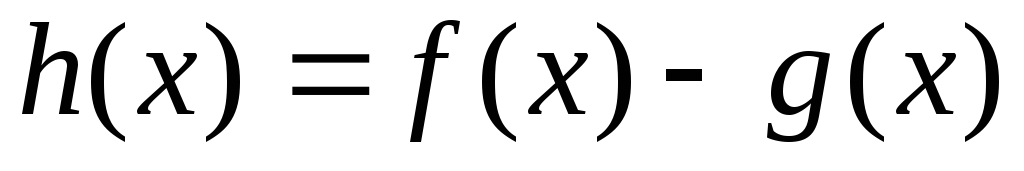 .
Тогда
.
Тогда и
и .
.
§2. Условие монотонности функции
Известно,
что функция 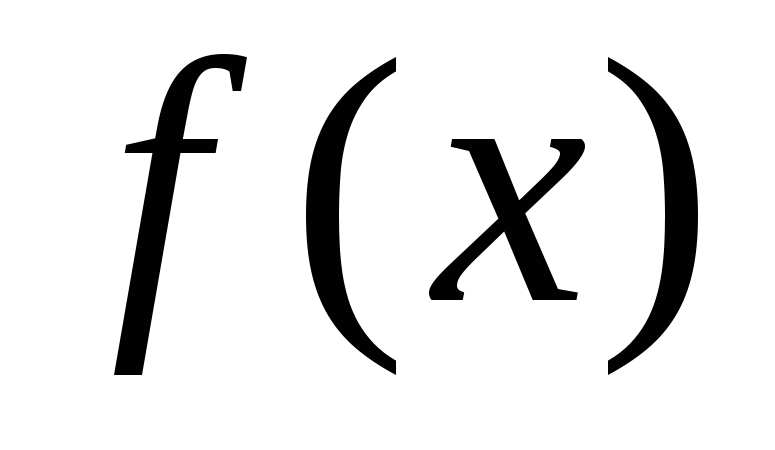 называется
строго возрастающей на
называется
строго возрастающей на  ,
если для любых точек
,
если для любых точек из
неравенства
из
неравенства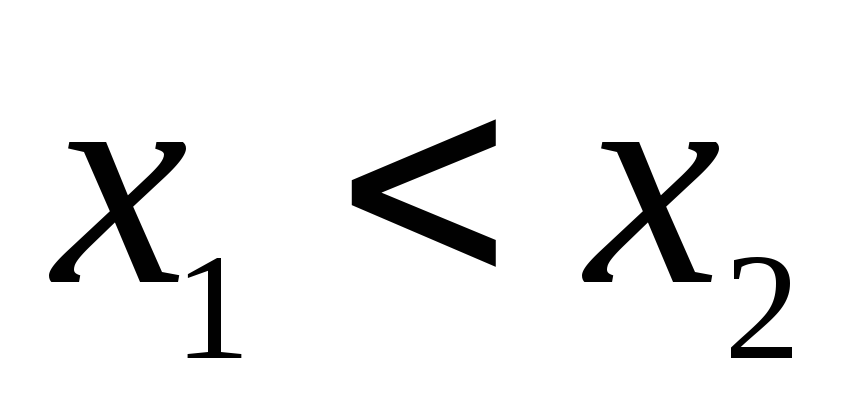 следует неравенство
следует неравенство .
Другими словами знак приращения функции
совпадает со знаком приращения аргумента:
.
Другими словами знак приращения функции
совпадает со знаком приращения аргумента: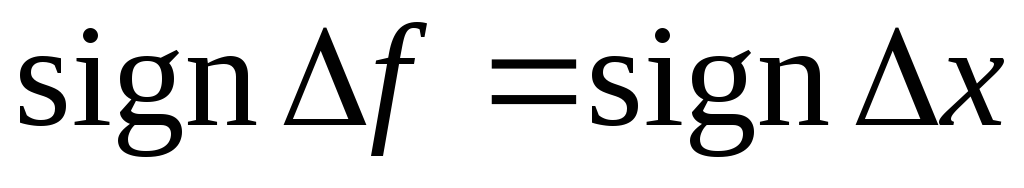 .
Для убывающей функции, естественно,
.
Для убывающей функции, естественно, .
.
Теорема. (Достаточное
условие монотонности). Пусть функция 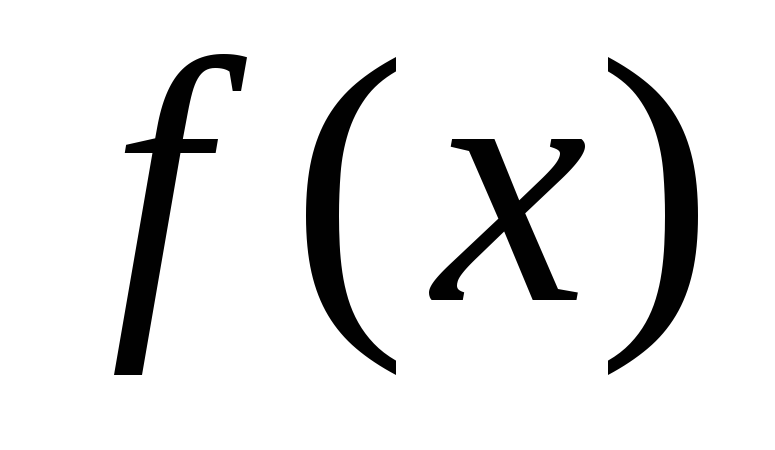 дифференцируема
на
дифференцируема
на  .
Тогда:
.
Тогда:
1) если  на
на 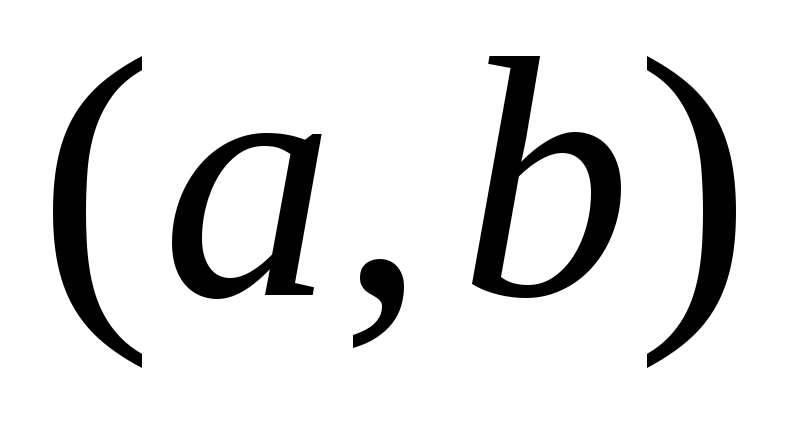 ,то
,то 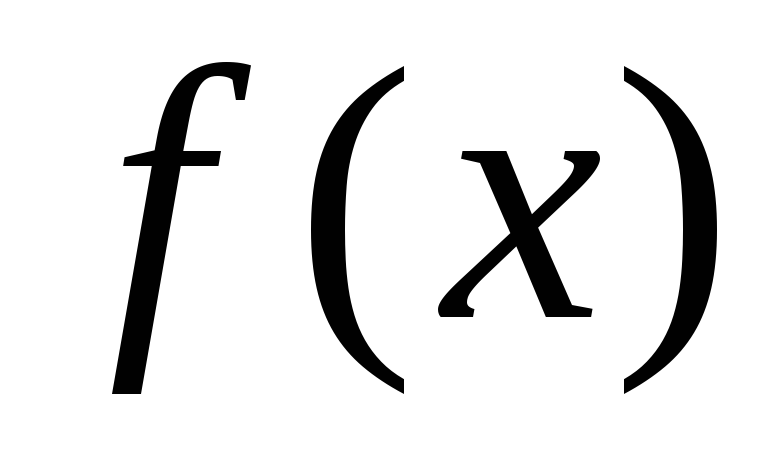 строго возрастает на
строго возрастает на 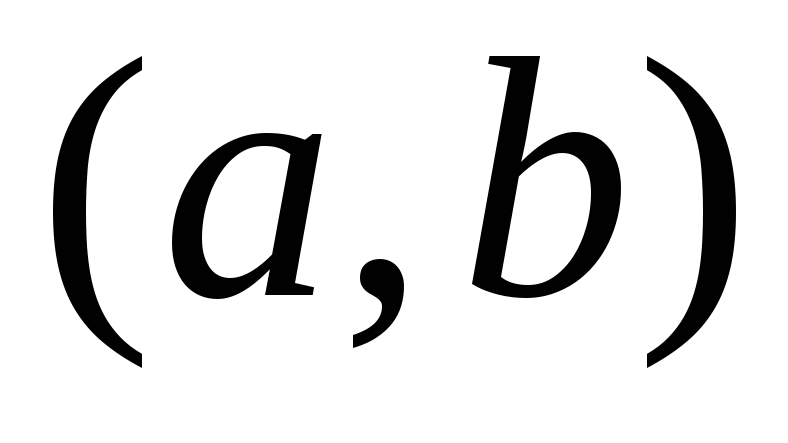 ;
;
2) если  на
на 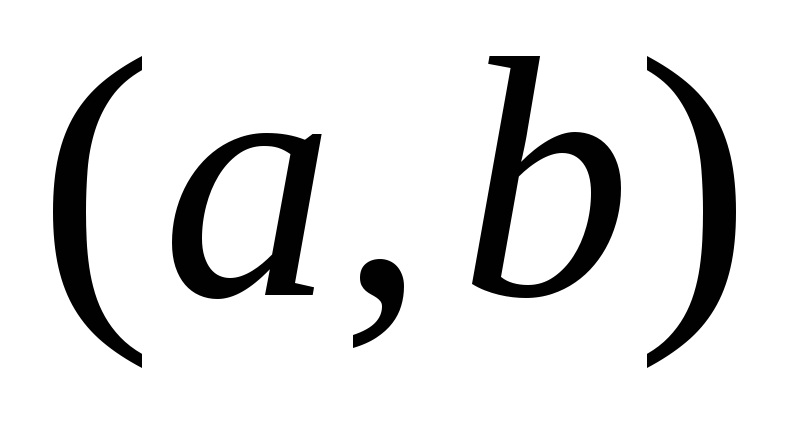 ,то
,то 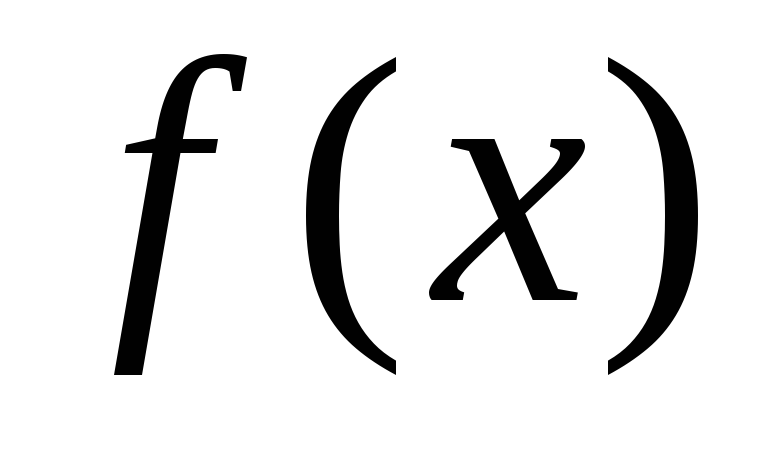 строго убывает на
строго убывает на 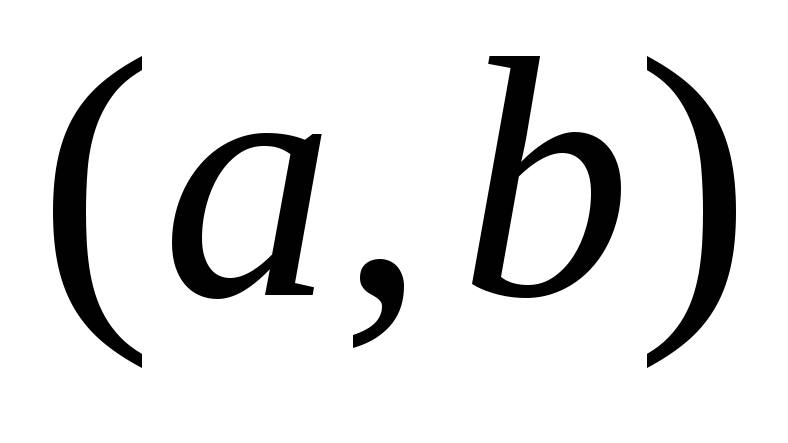 .
.
Доказательство. Возьмём две произвольные точки  ,
причём пусть
,
причём пусть 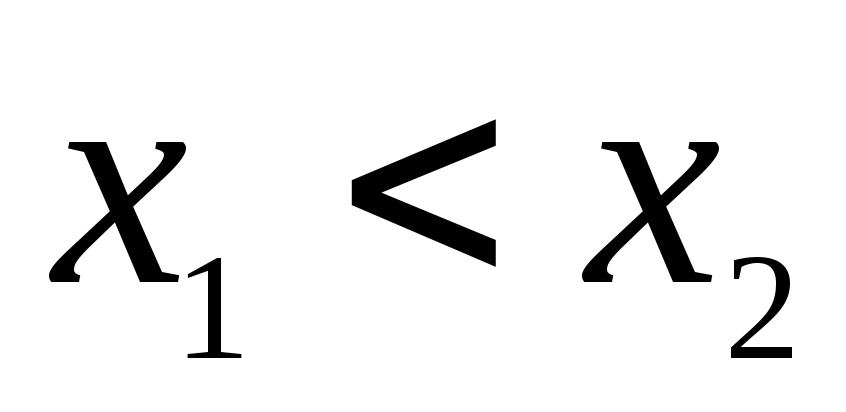 .
Применим теорему Лагранжа к функции
.
Применим теорему Лагранжа к функции 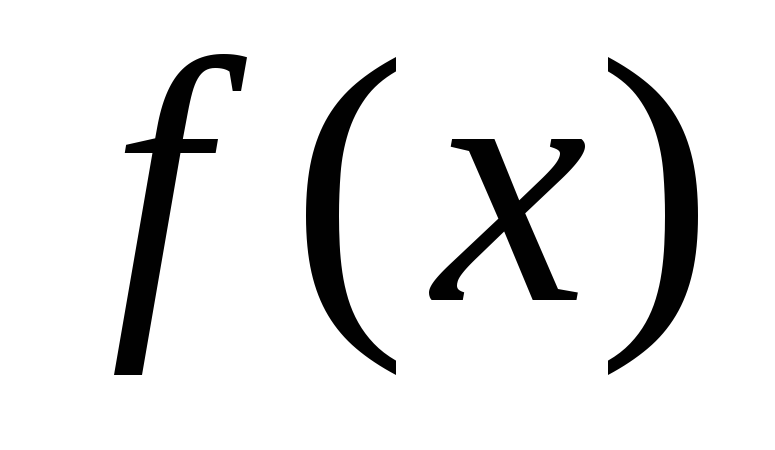 на
промежутке
на
промежутке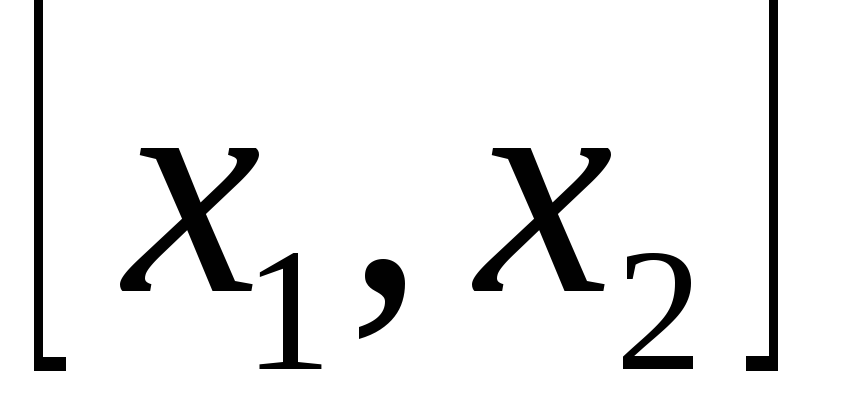 (условия теоремы выполнены, ибо
непрерывность
(условия теоремы выполнены, ибо
непрерывность вытекает из её дифференцируемости):
вытекает из её дифференцируемости): По предположению
По предположению 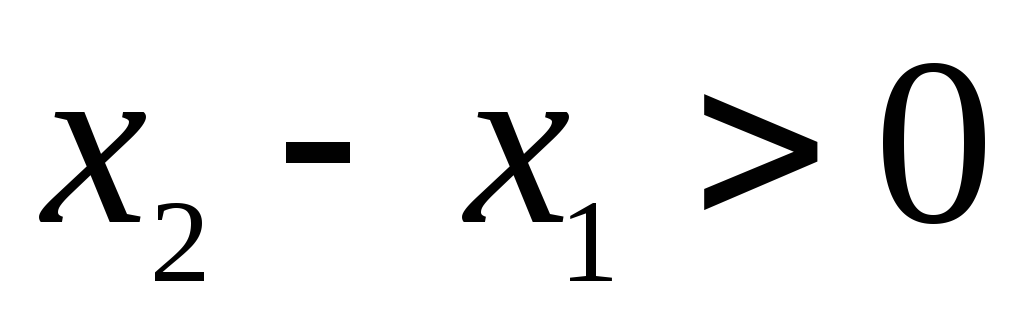 ,
следовательно,знак
,
следовательно,знак 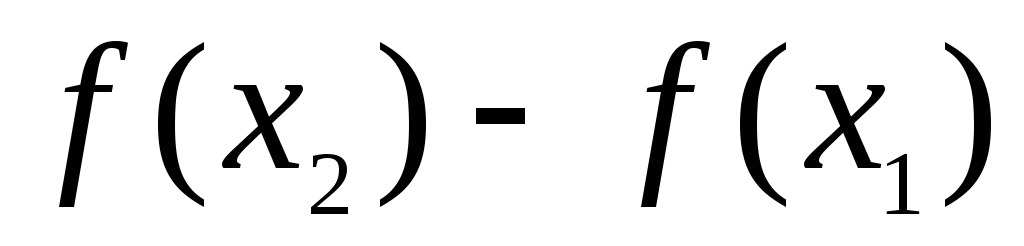 определяется
знаком производной. 1) Если
определяется
знаком производной. 1) Если ,
то и
,
то и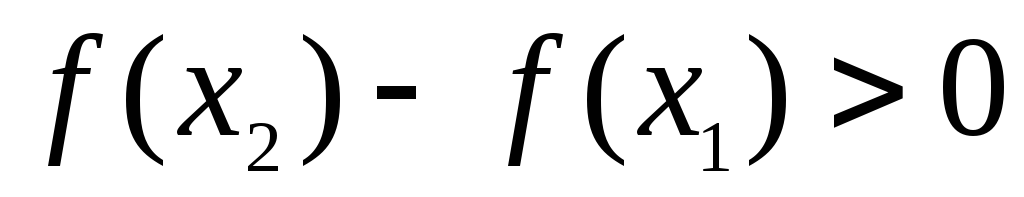 и
и ;
т.к. это верно для любых
;
т.к. это верно для любых ,
то
,
то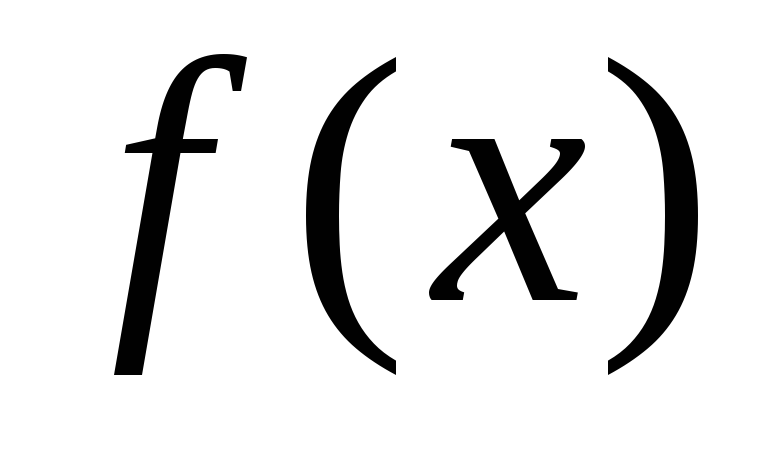 возрастает
на
возрастает
на 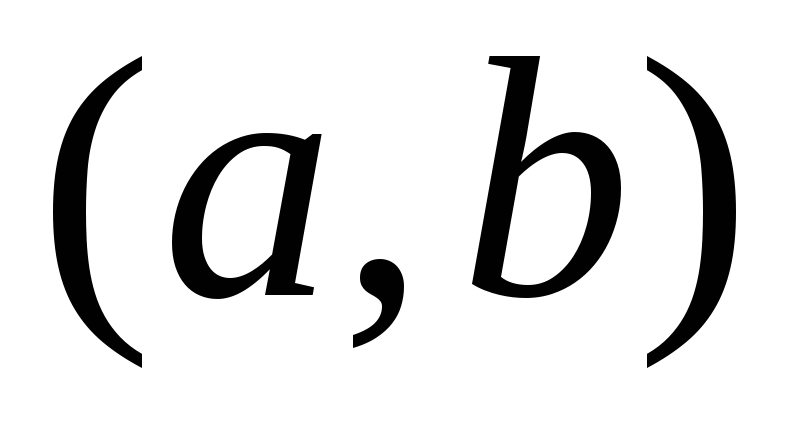 .
2) Если
.
2) Если 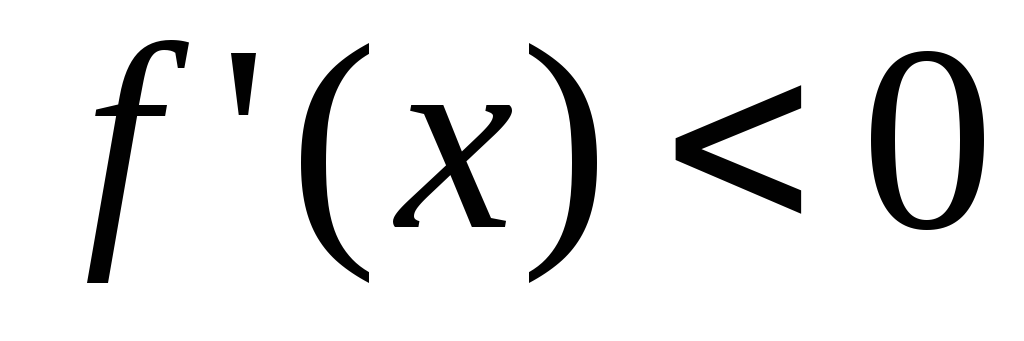 ,
то и
,
то и и
и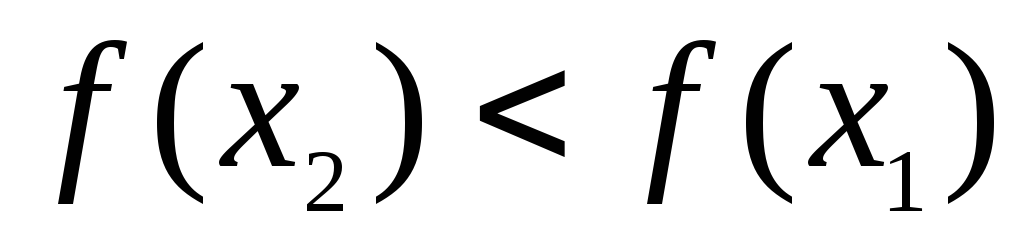 ,
что означает убывание
,
что означает убывание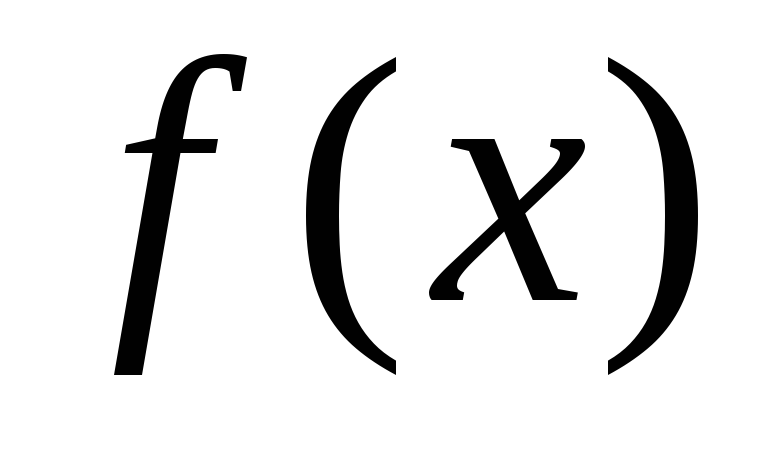 .
.
Замечание. Связь между знаком 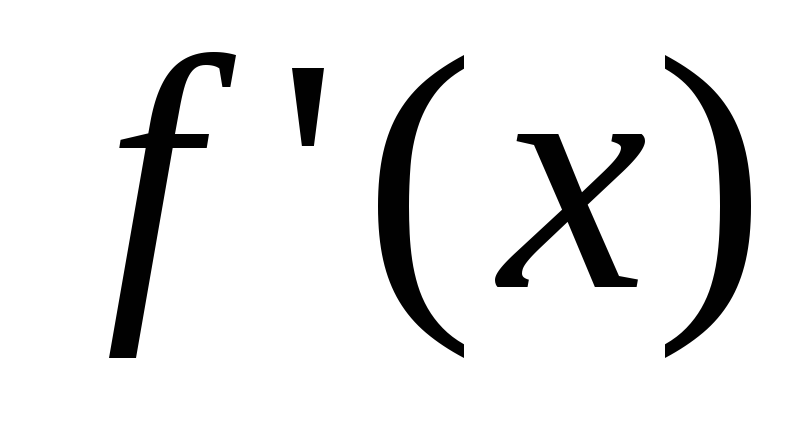 и направлением изменения
и направлением изменения геометрически
очевидна, если вспомнить, что производная
– это угловой коэффициент касательной
к графику
геометрически
очевидна, если вспомнить, что производная
– это угловой коэффициент касательной
к графику .
Однако, даже у строго монотонной функции
.
Однако, даже у строго монотонной функции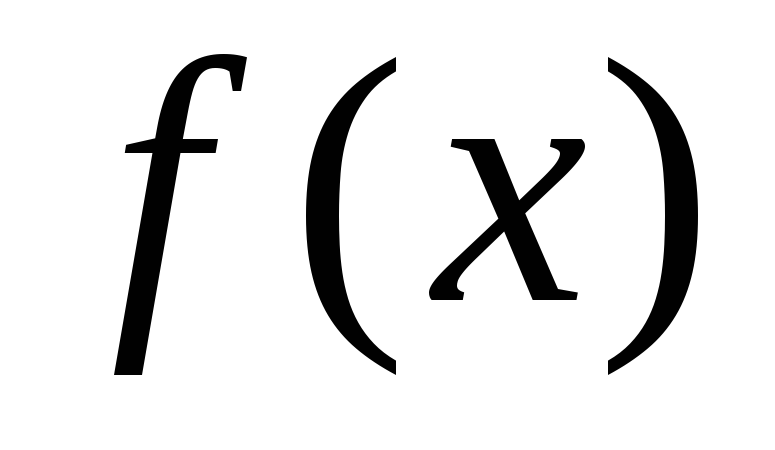 касательная может быть и горизонтальной,
т.е.
касательная может быть и горизонтальной,
т.е.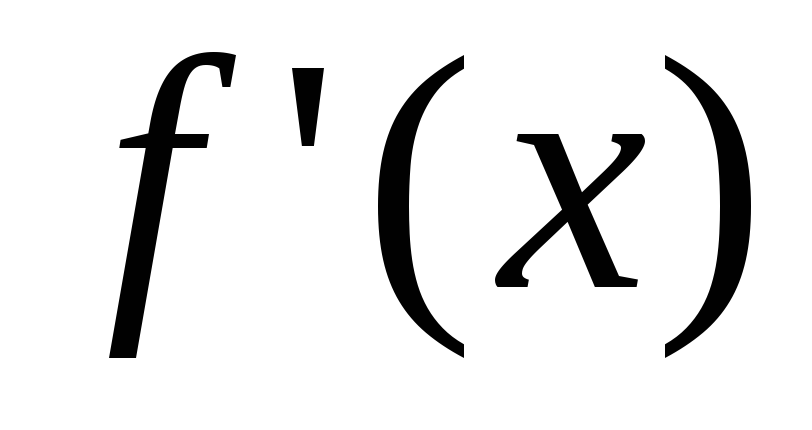 для
отдельных значений
для
отдельных значений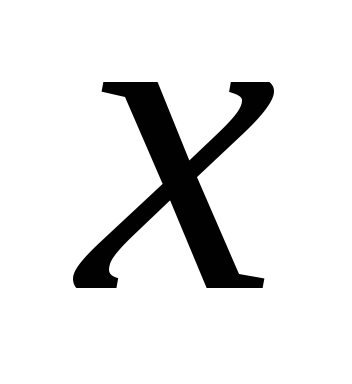 может обращаться в0.
Примером служит функция
может обращаться в0.
Примером служит функция 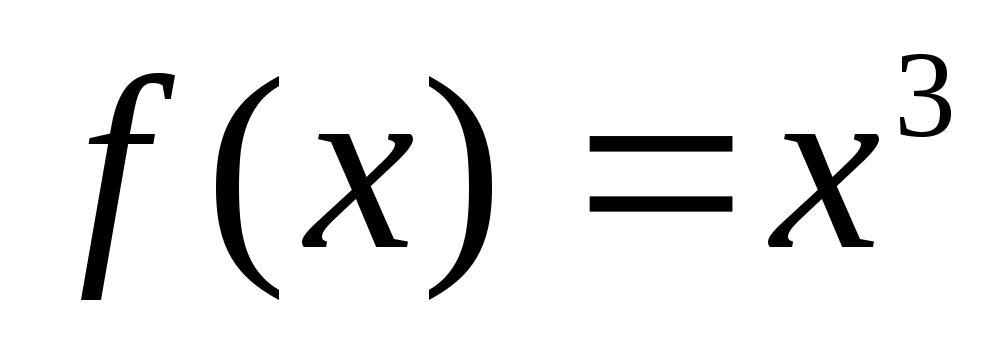 :
она строго возрастает, но производная
:
она строго возрастает, но производная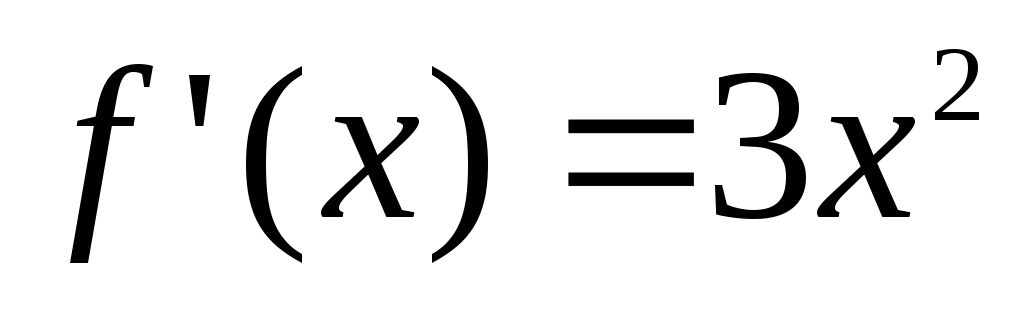 при
при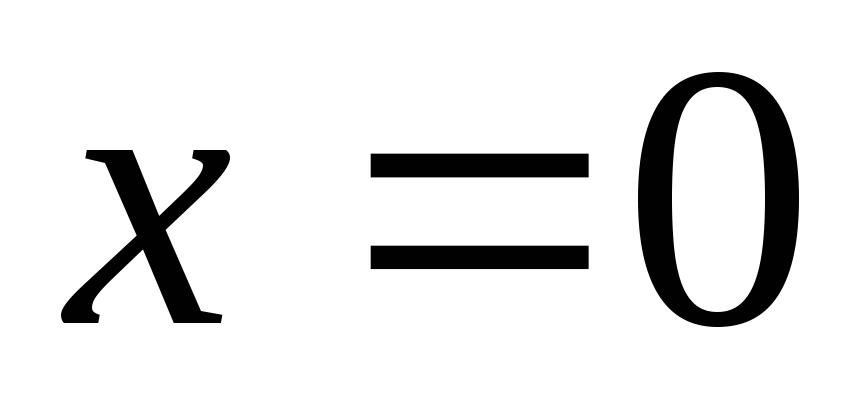 обращается в ноль.
обращается в ноль.
Итак, теорема
сводит вопрос о возрастании (убывании)
функции 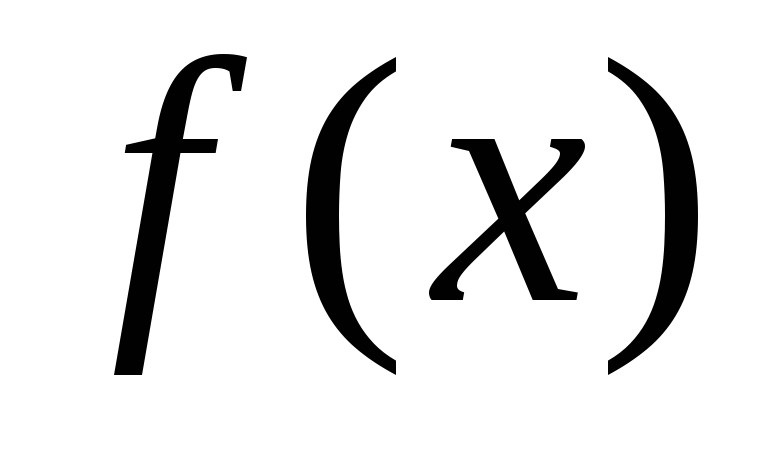 к
решению неравенства
к
решению неравенства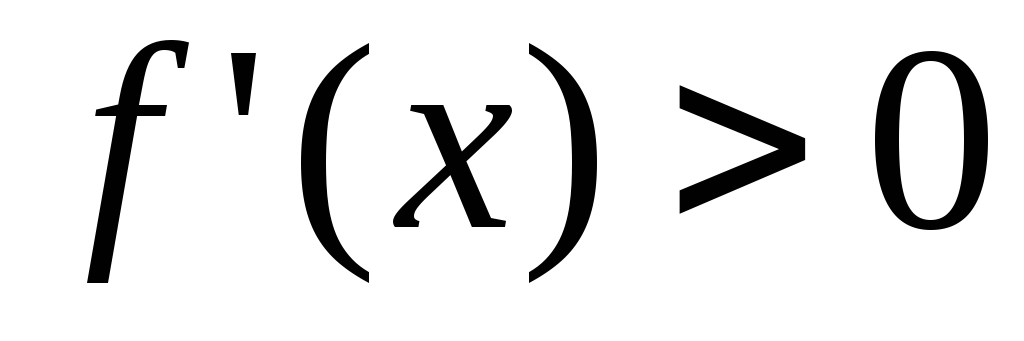 (
( ).
).
Пример. Исследовать на монотонность функцию  .
Находим производную и разлагаем её на
множители:
.
Находим производную и разлагаем её на
множители: .
Метод интервалов позволяет определить
знак
.
Метод интервалов позволяет определить
знак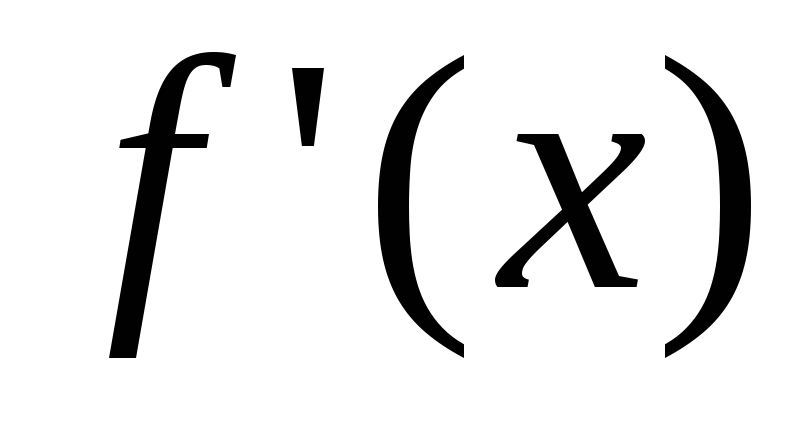 :
:
—

На интервалах 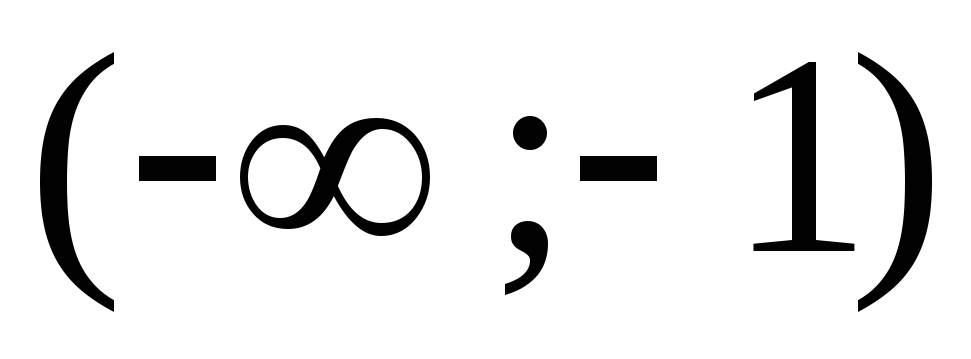 и
и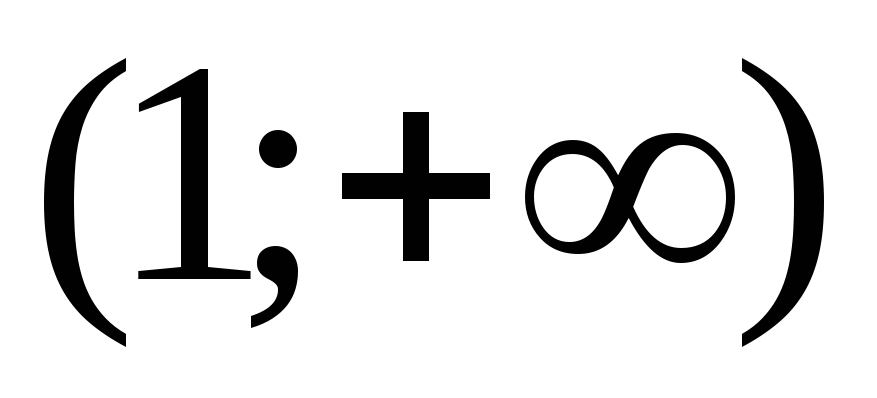 функция возрастает, а на
функция возрастает, а на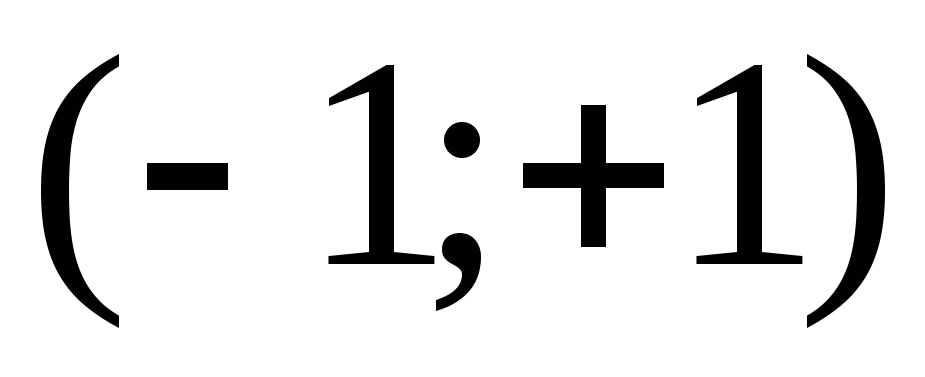 – убывает.
– убывает.
§3. Исследование функции на экстремум
Напомним уже известные факты. Во-первых, точка экстремума – это всегда внутренняя точка области определения функции; она характеризуется тем, что знак приращения функции не зависит от знака приращения аргумента, если последнее достаточно мало. Во-вторых, необходимое условие экстремума даётся теоремой Ферма: если в точке экстремума функция дифференцируема (т.е. обладает конечной производной), то производная в этой точке равна 0.
Точки, в которых производная функции обращается в ноль, принято называть стационарными точками.
Однако, если
рассматривать функции, не имеющие в
отдельных точках конечной двусторонней
производной, то не исключена возможность,
что экстремум придётся на какую на
какую-либо из таких точек. Например,
функции  и
и имеют в
имеют в минимумы, в тоже время
минимумы, в тоже время ,
,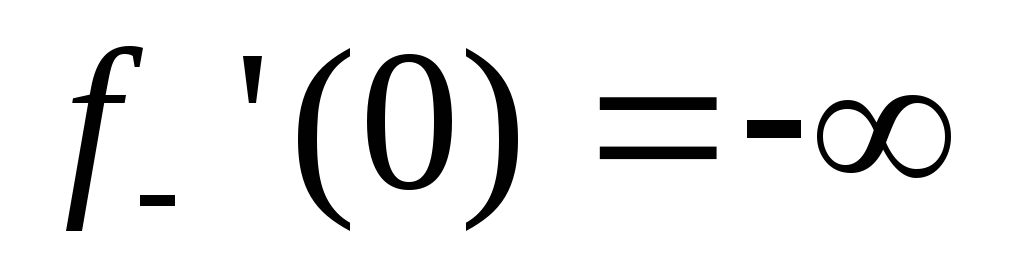 и
и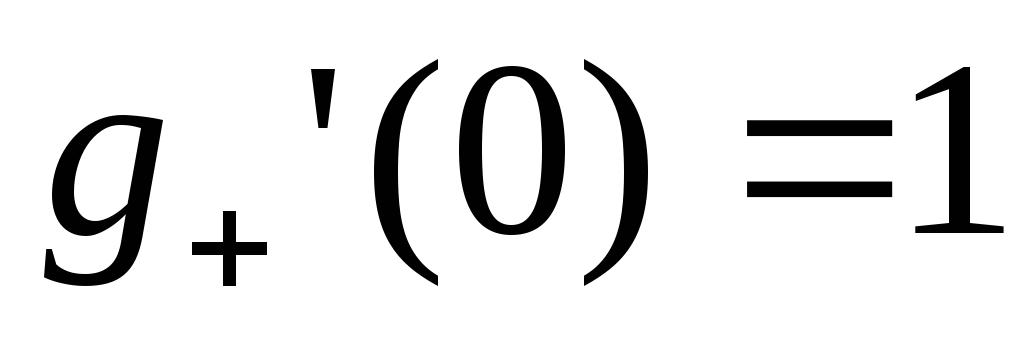 ,
,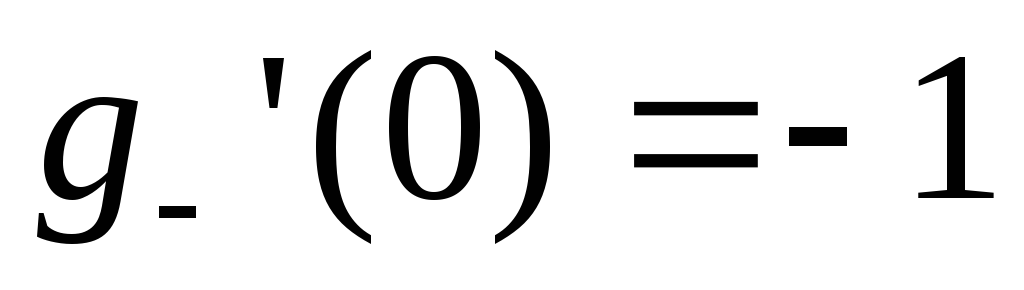 .
.
Определение. Точку  называют критической точкой первого
порядка функции
называют критической точкой первого
порядка функции ,
если
,
если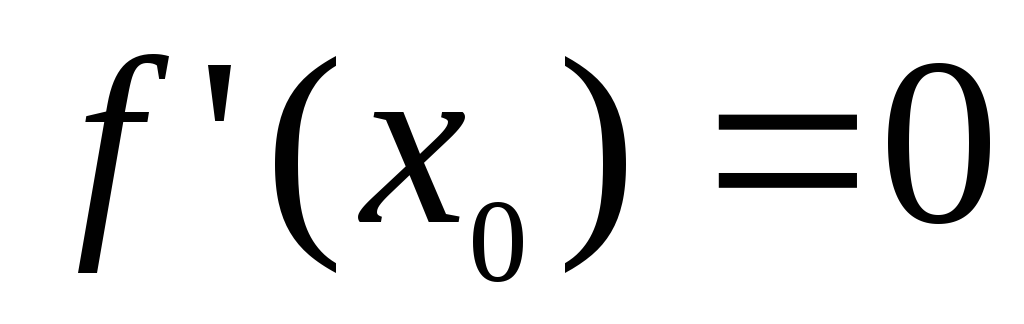 или
или 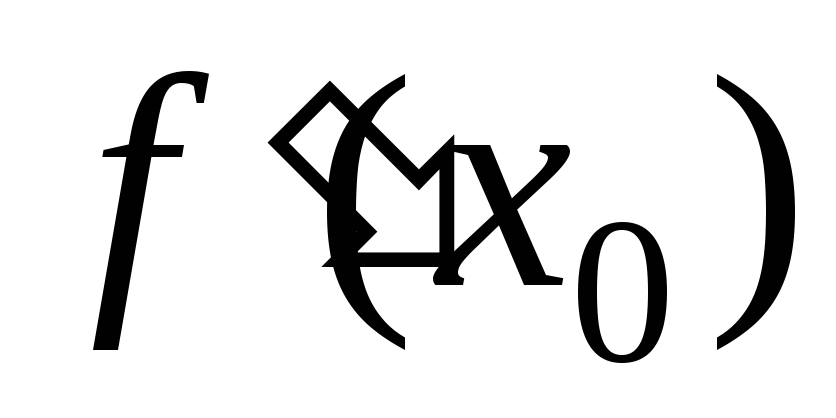 не существует.
не существует.
Из теоремы Ферма следует, что точки экстремума следует искать среди критических точек (их ещё называют точками возможного экстремума). Требуется дополнительное исследование таких точек, чтобы отобрать среди них точки экстремума. Это исследование выполняется с помощью достаточных условий экстремума.
Теорема
1 (первое
достаточное условие экстремума). Пусть 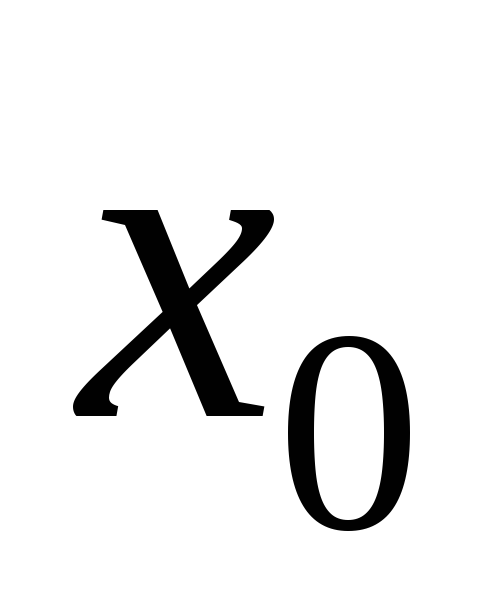 – крити-ческая точка первого порядка
непрерывной функции
– крити-ческая точка первого порядка
непрерывной функции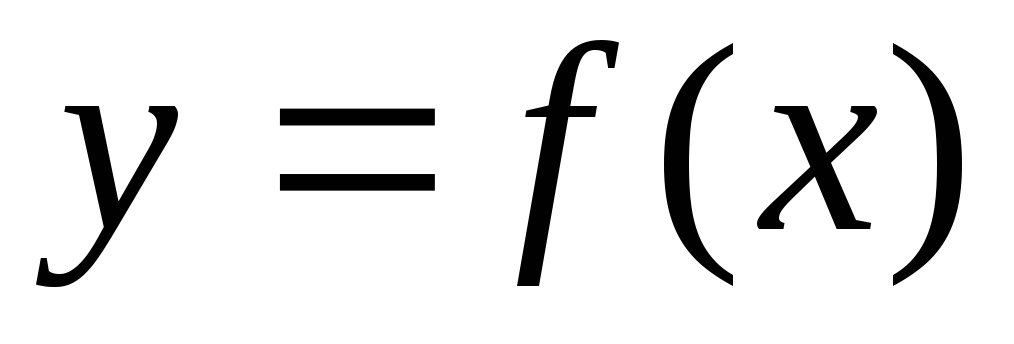 и пусть существует
и пусть существует такое, что в односторонних окрестностях
этой точки:
такое, что в односторонних окрестностях
этой точки: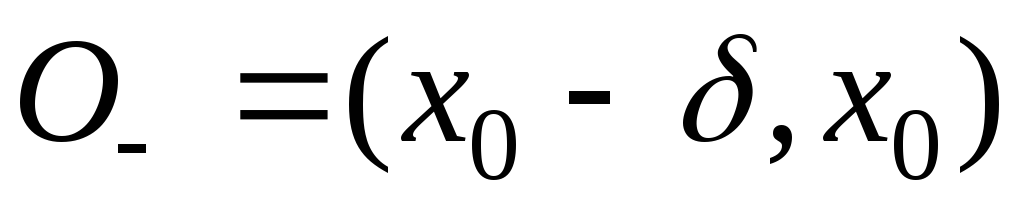 и
и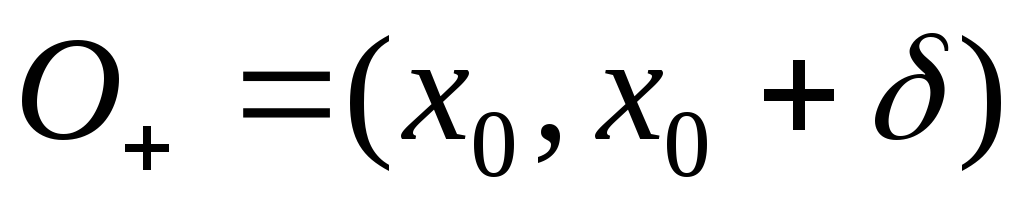 – функция
– функция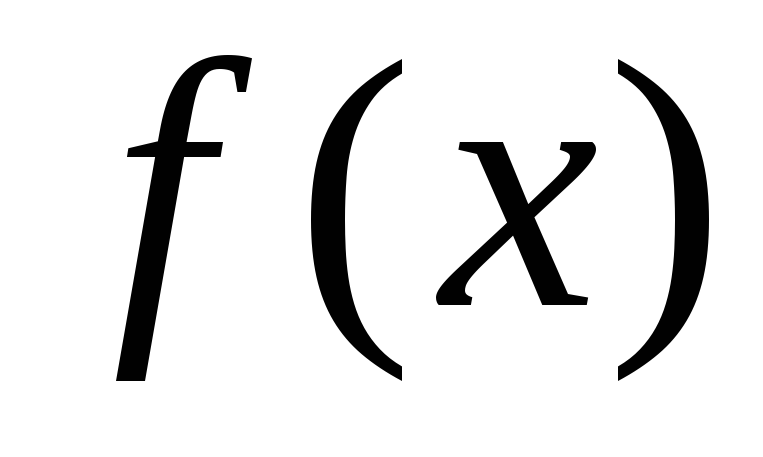 дифференцируема и её производная
сохраняет знак. Тогда:
дифференцируема и её производная
сохраняет знак. Тогда:
1) если 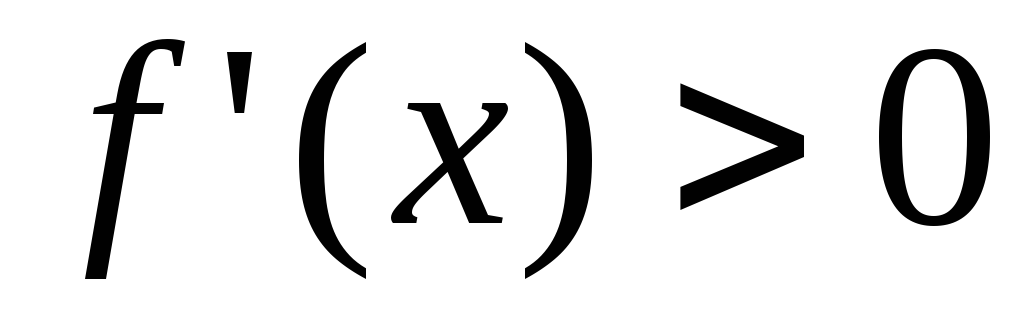 в
в и
и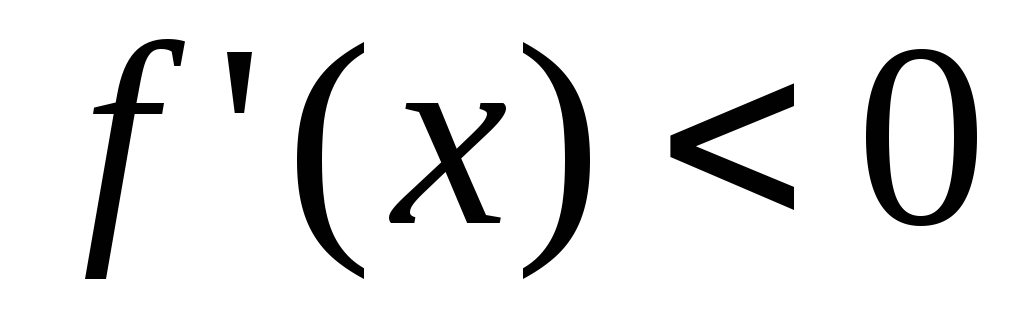 в
в ,
то
,
то – точка максимума;
– точка максимума;
2) если 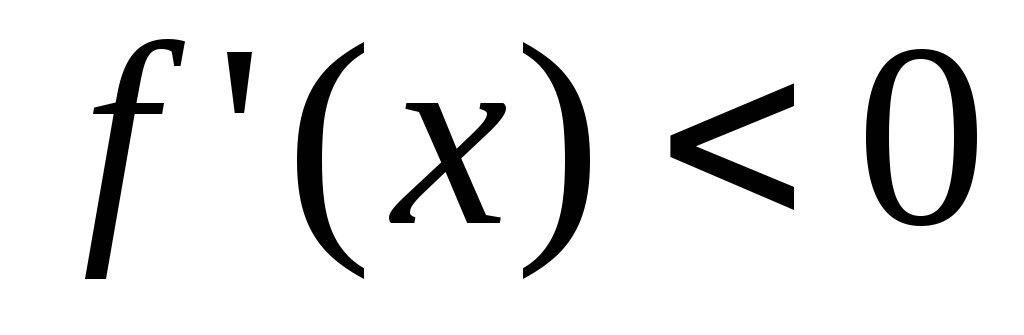 в
в и
и в
в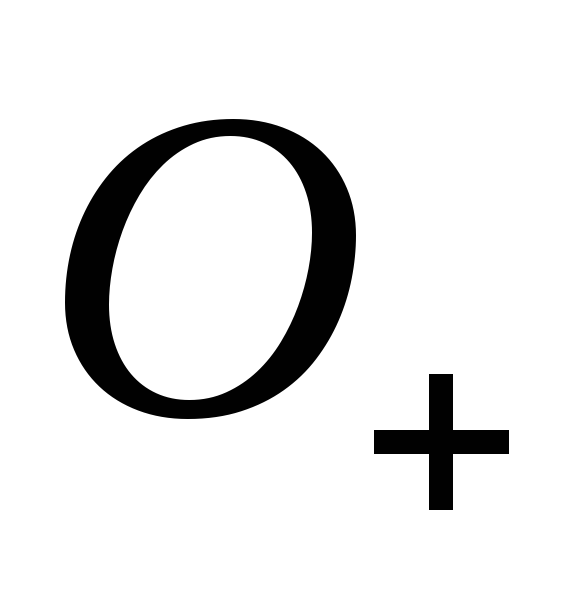 ,
то
,
то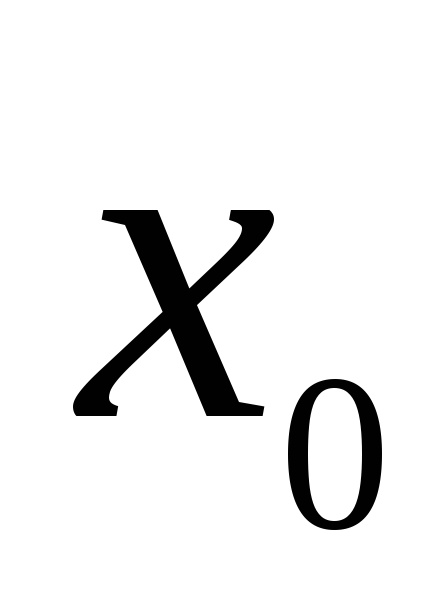 – точка минимума;
– точка минимума;
3) если 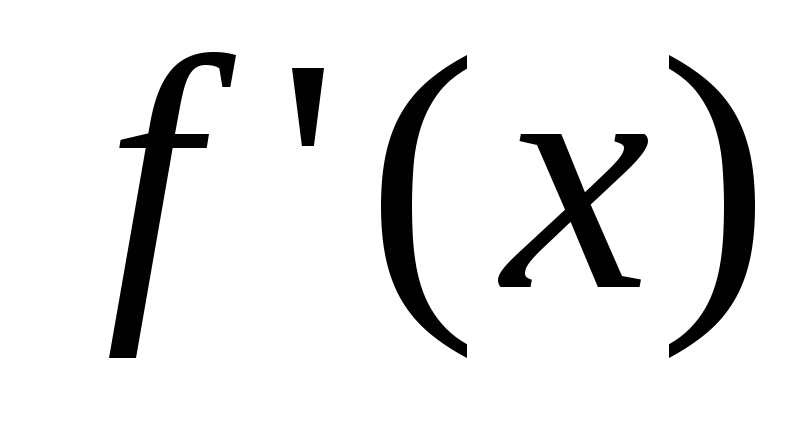 одного знака в
одного знака в и
и ,
то в точке
,
то в точке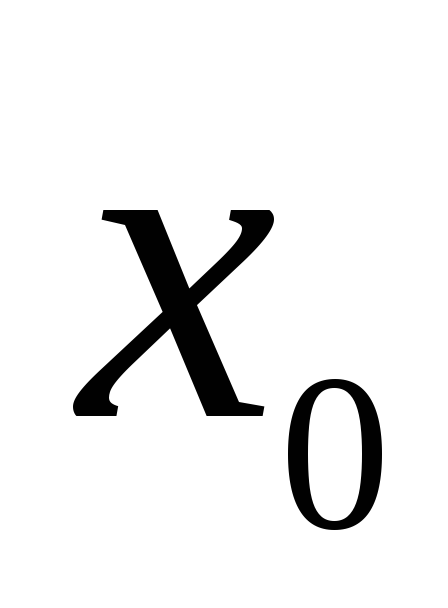 нет экстремума.
нет экстремума.
Доказательство. 1) Возьмём произвольные точки  и
и и рассмотрим функцию
и рассмотрим функцию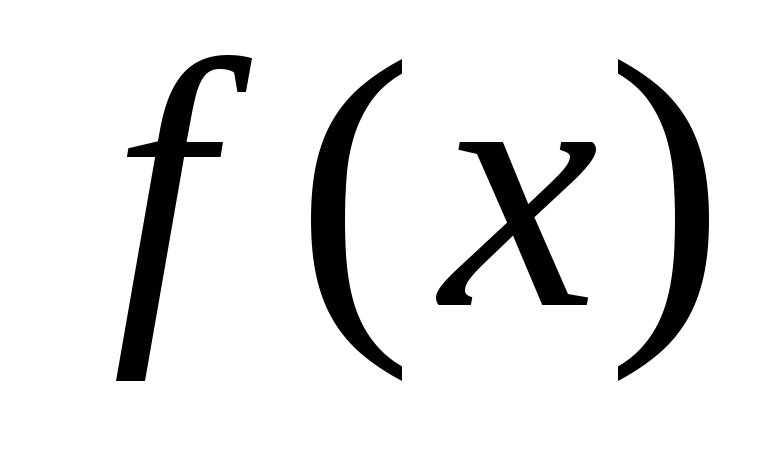 на двух промежутках:
на двух промежутках: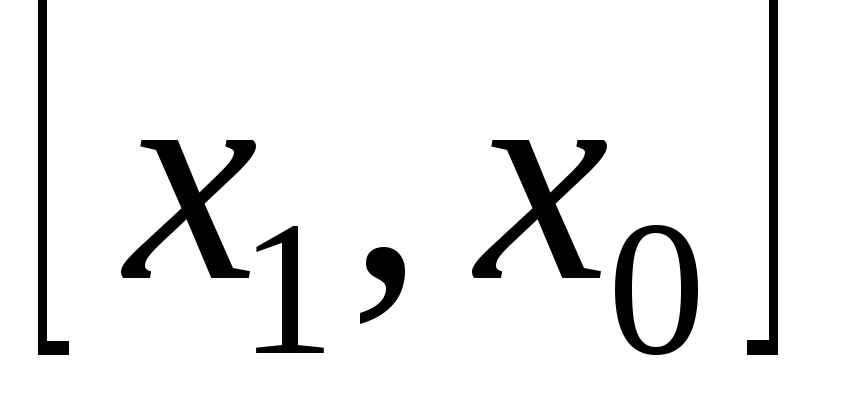 и
и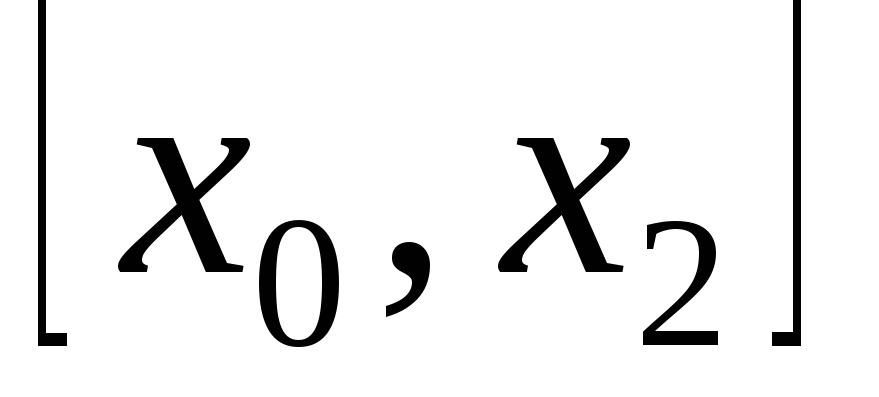 .
На каждом из этих промежутков функция
.
На каждом из этих промежутков функция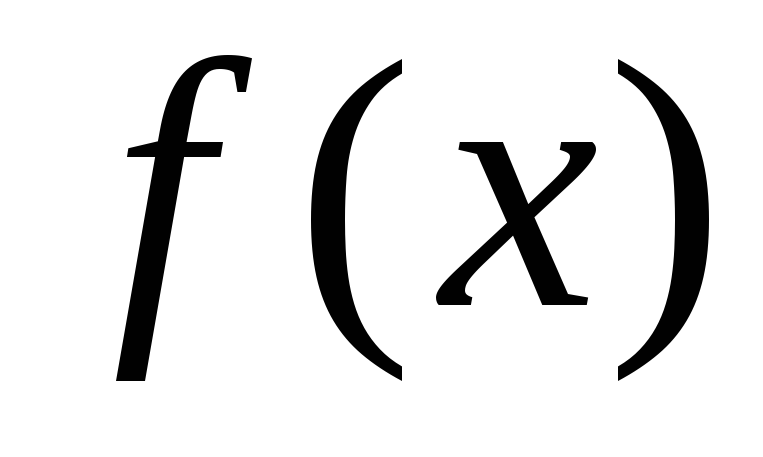 удовлетворяет условиям теоремы Лагранжа,
следовательно, существуют точки
удовлетворяет условиям теоремы Лагранжа,
следовательно, существуют точки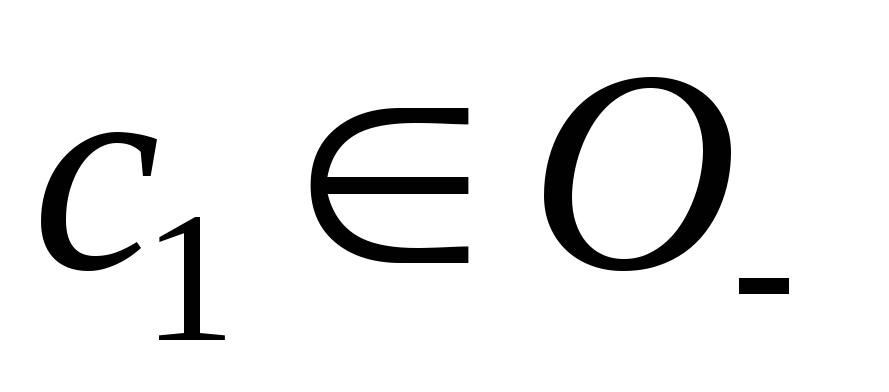 и
и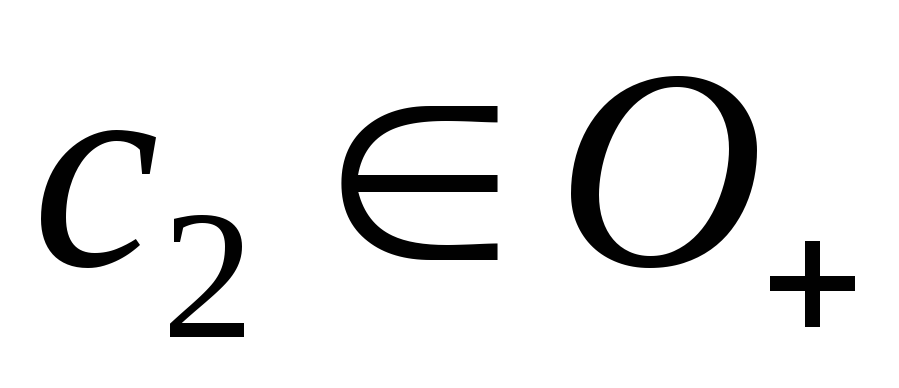 такие, что:
такие, что:
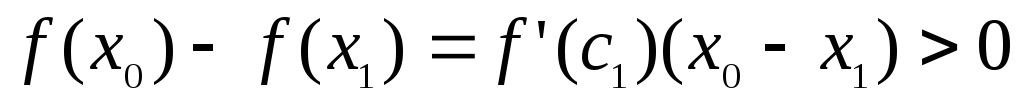 ,
,
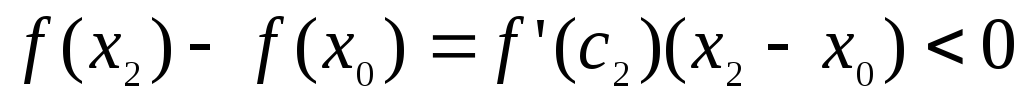 .
.
Из этих неравенств
вытекает, что 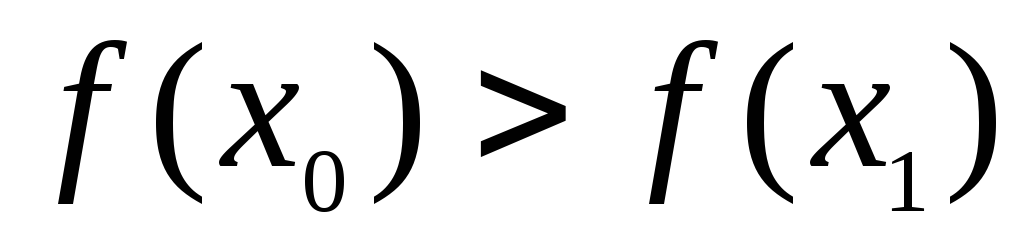 и
и
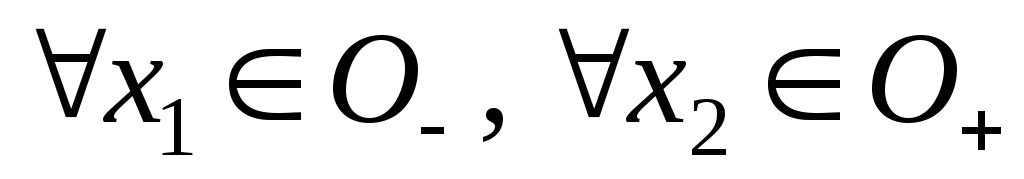 .
Таким образом значение
.
Таким образом значение 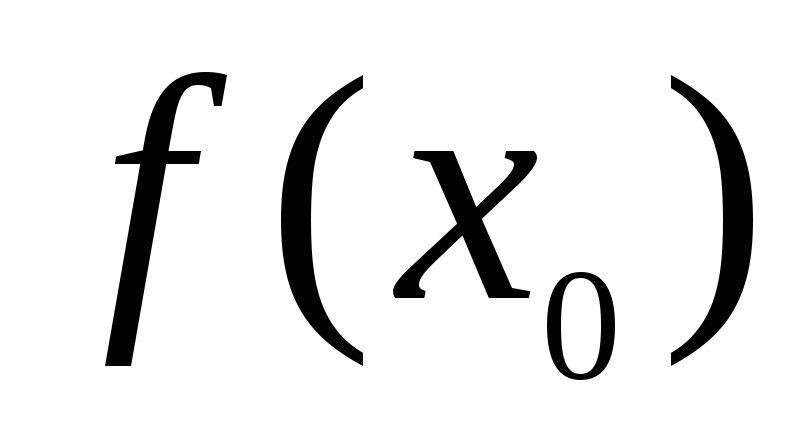 – самое большое среди значений
– самое большое среди значений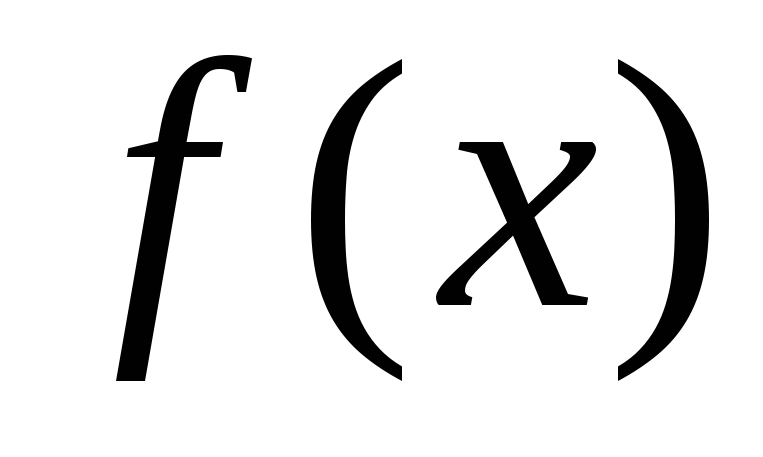 для
для .
Это и означает:
.
Это и означает: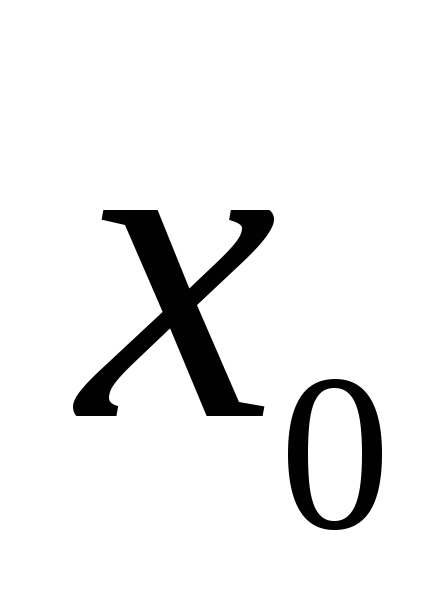 – точка максимума.
– точка максимума.
2) Доказывается аналогично.
3) Если  ,
то
,
то возрастает как в
возрастает как в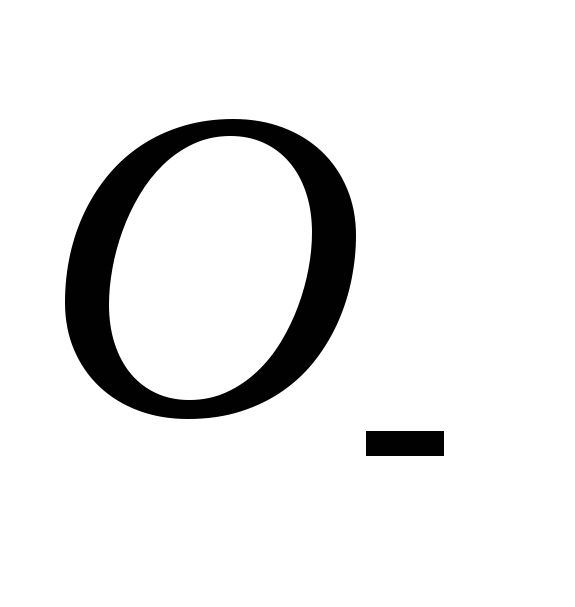 ,
так и в
,
так и в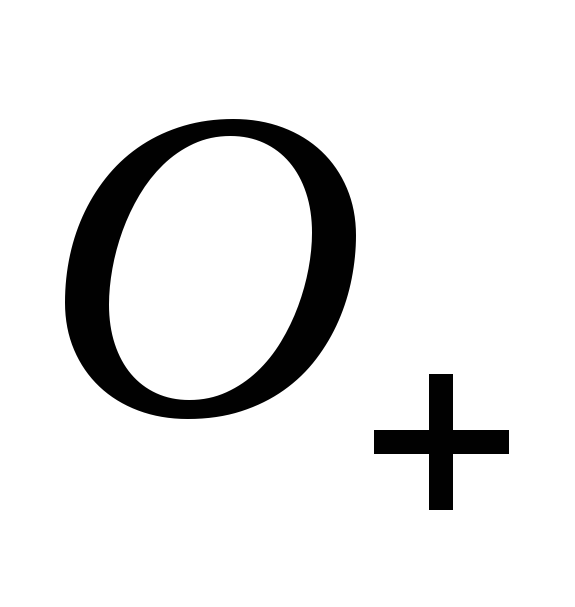 .
Если же
.
Если же ,
то
,
то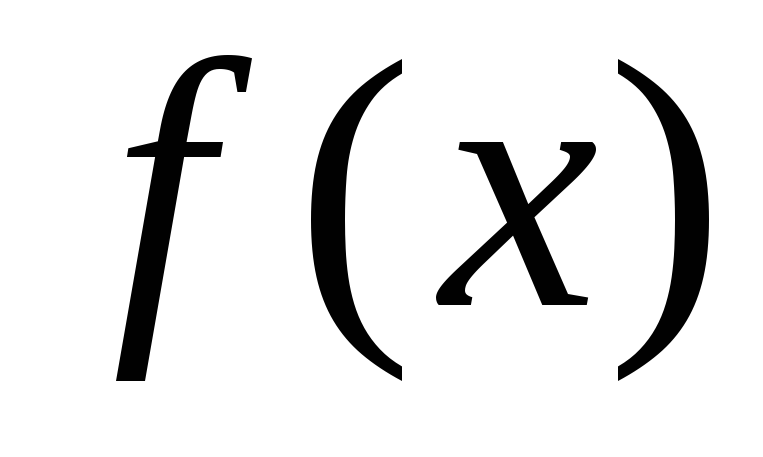 убывает в тех же окрестностях. В обоих
случаях такое поведение функции говорит
о том, что в точке
убывает в тех же окрестностях. В обоих
случаях такое поведение функции говорит
о том, что в точке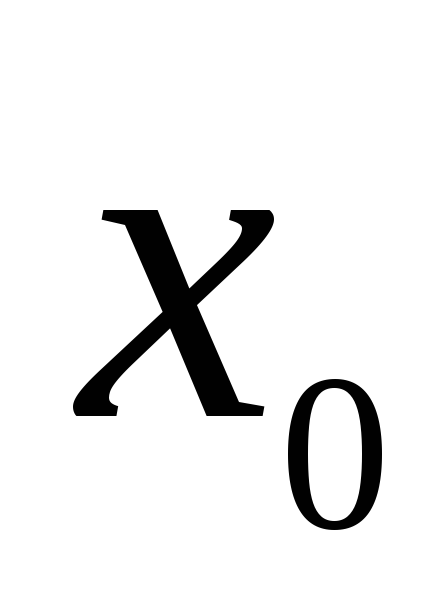 у неё нет
у неё нет
экстремума.
Замечание
1. Требование
непрерывности
функции
нельзя ослабить, о чем свидетельствует
рисунок:
в точке 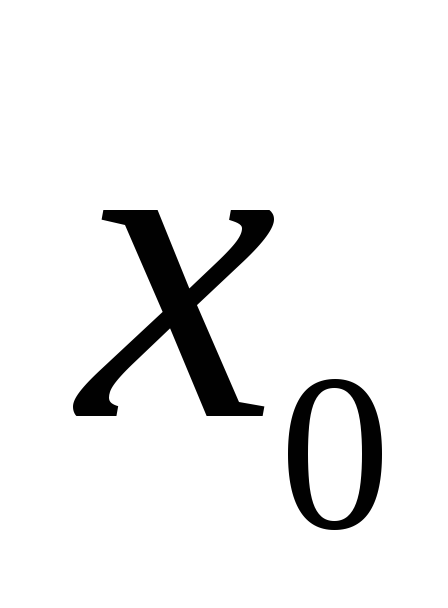 функция имеет максимум,
в то же
время при переходе через эту
точку
производная не меняет знак.
функция имеет максимум,
в то же
время при переходе через эту
точку
производная не меняет знак.
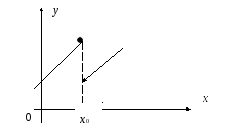
Замечание 2. Доказанную теорему не всегда можно применить, ибо для некоторых функций требование сохранения знака производной не выполняется. Например, для функции
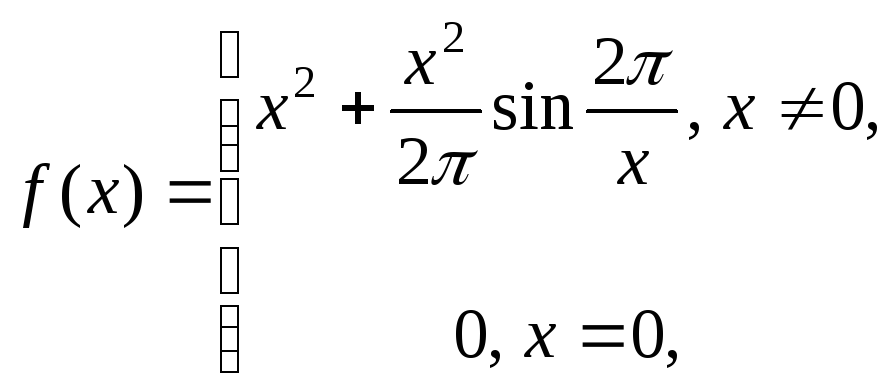
имеем:
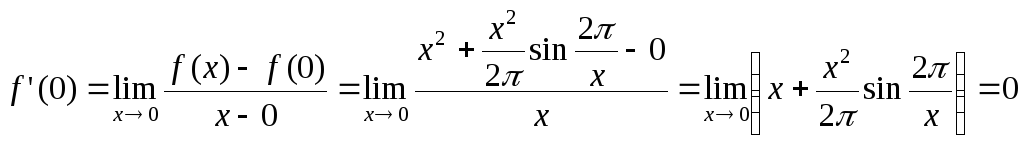 ,
значит, точка 0
– критическая точка. Далее, для
,
значит, точка 0
– критическая точка. Далее, для 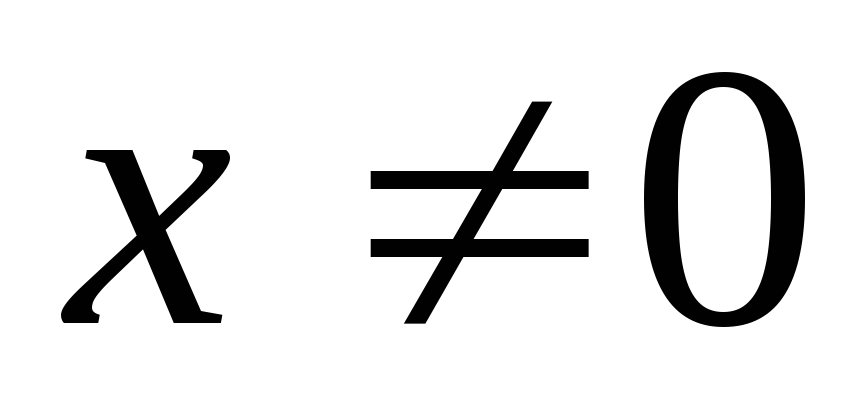

Выражение в скобках
ограничено, поэтому при  близких
к нулю первый член полученной разности
также близок к нулю, а второй член
принимает значения от –1 до +1. Значит,
знак
близких
к нулю первый член полученной разности
также близок к нулю, а второй член
принимает значения от –1 до +1. Значит,
знак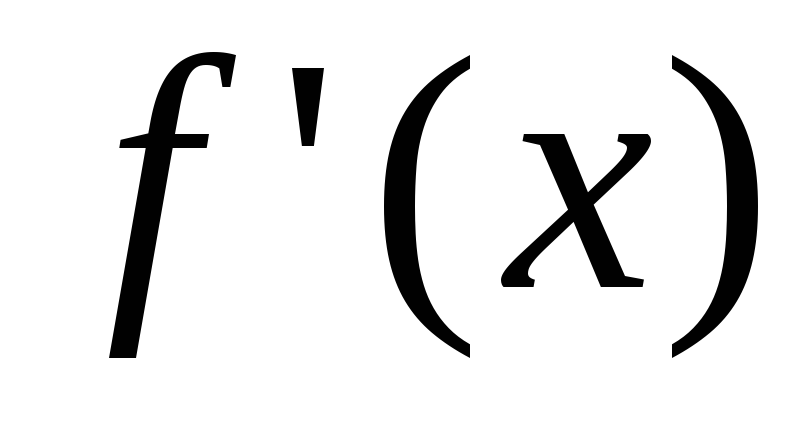 определяется членом
определяется членом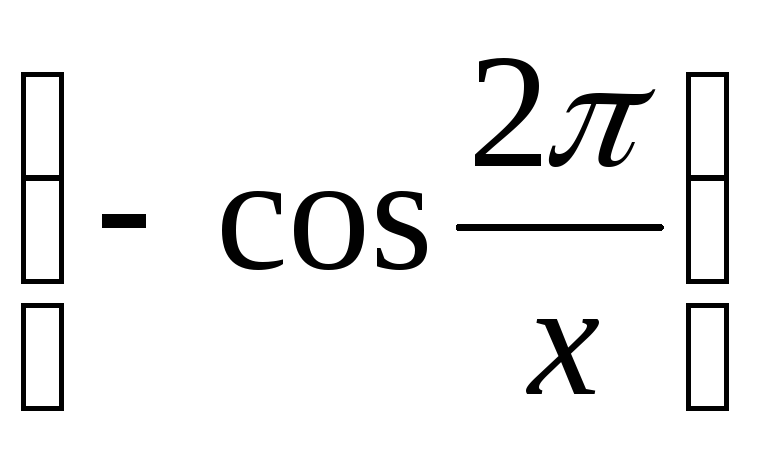 .
Но в точках вида
.
Но в точках вида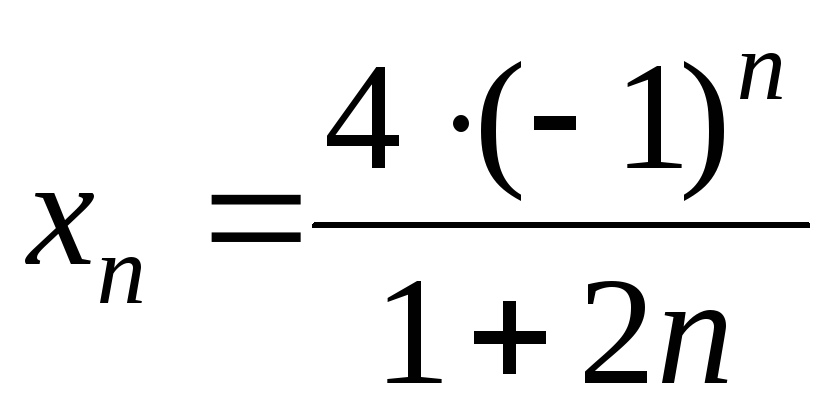 этот член обращается
в ноль и меняет знак. А так как
этот член обращается
в ноль и меняет знак. А так как 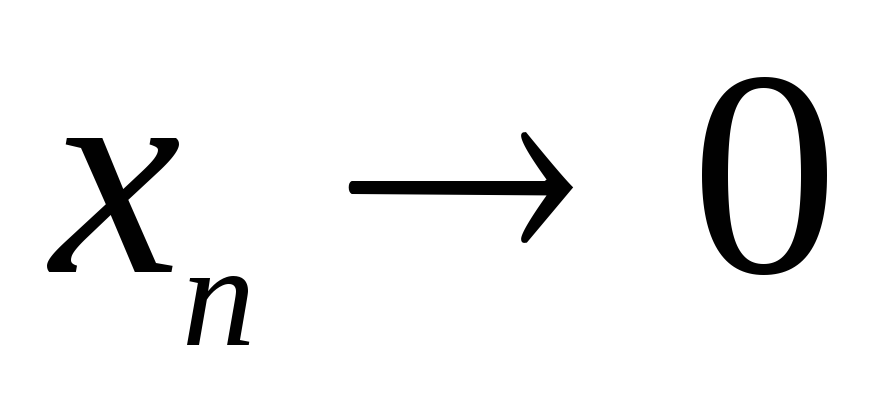 при
при  ,
то в любой сколь угодно малой окрестности
нуля
,
то в любой сколь угодно малой окрестности
нуля 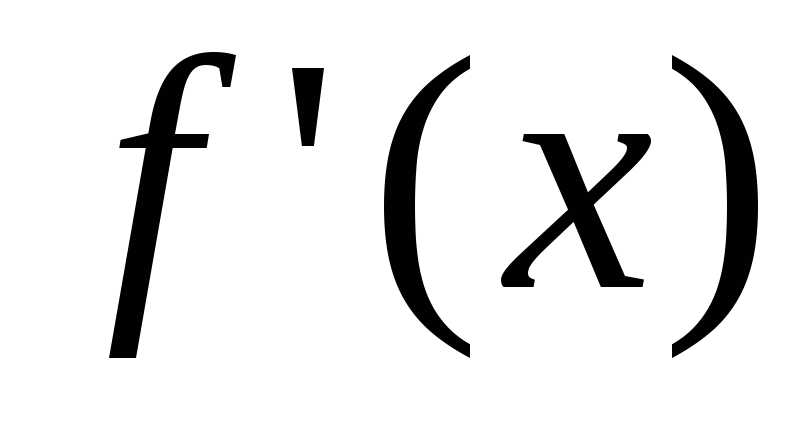 бесконечное число раз меняет знак.
бесконечное число раз меняет знак.
Теорема
2 (второе
достаточное условие экстремума). Пусть
функция  имеет в критической точке
имеет в критической точке конечную вторую производную. Тогда:
конечную вторую производную. Тогда:
1) если 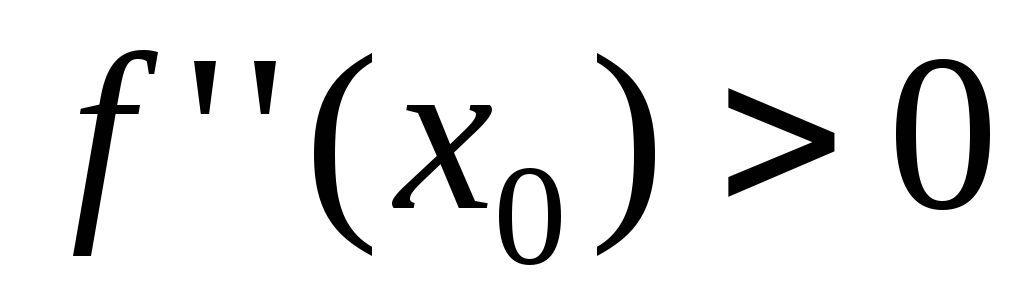 ,
то
,
то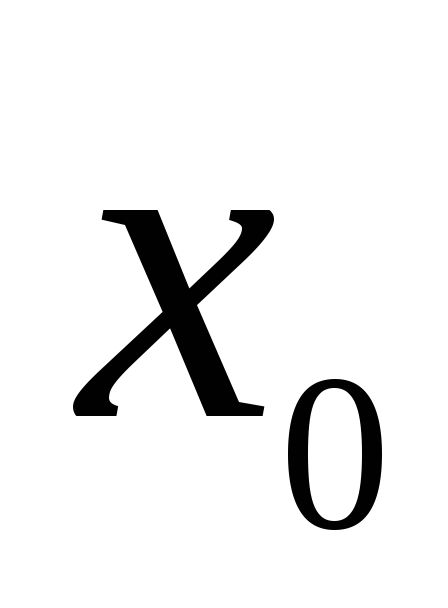 – точка минимума;
– точка минимума;
2) если 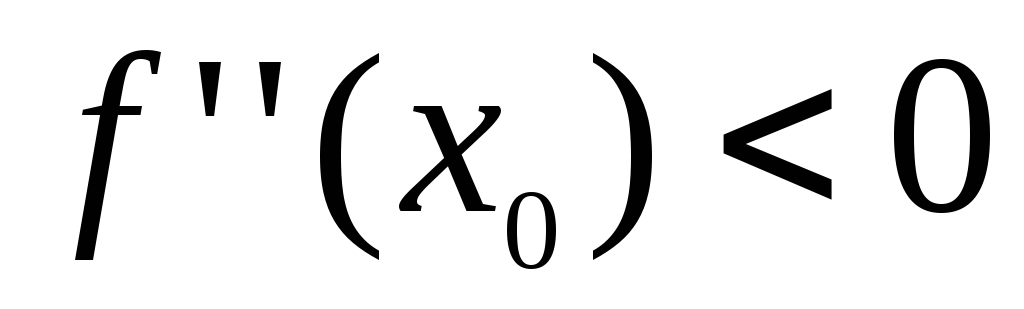 ,
то
,
то – точка максимума;
– точка максимума;
3) если  ,
то требуется дополнительное исследование.
,
то требуется дополнительное исследование.
Доказательство. Существование конечной производной 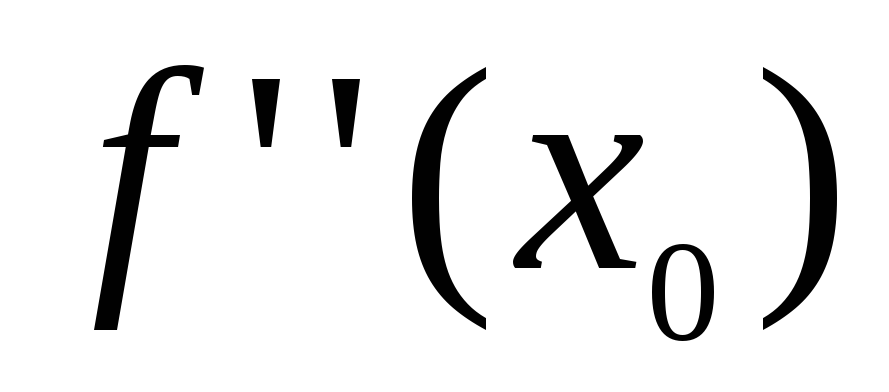 означает, что существует конечная
производная
означает, что существует конечная
производная в некоторой окрестности точки
в некоторой окрестности точки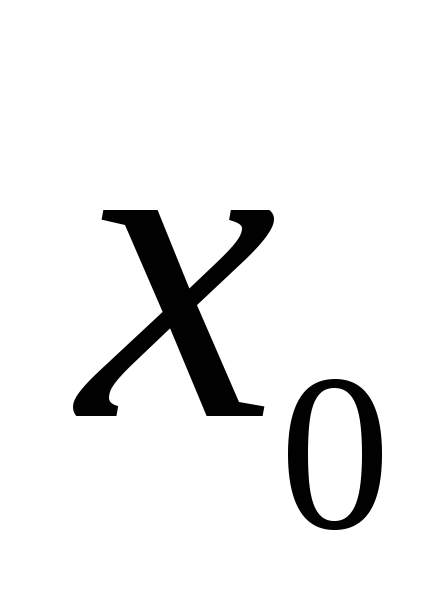 и
и ,
ибо
,
ибо –
критическая точка. Обозначим
–
критическая точка. Обозначим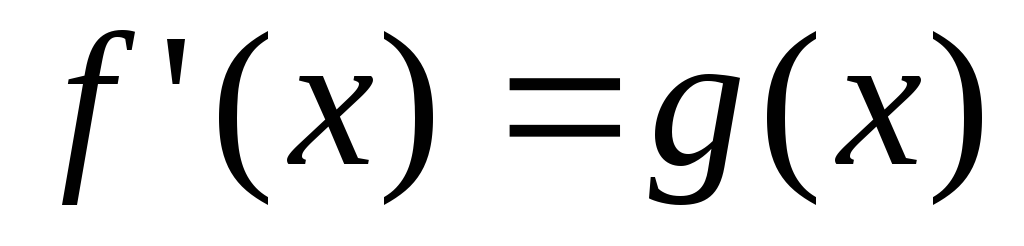 .
Тогда условия теоремы означают, что
существует конечный предел
.
Тогда условия теоремы означают, что
существует конечный предел
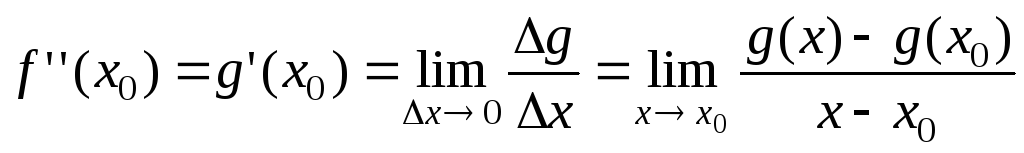 .
.
Пусть, например, 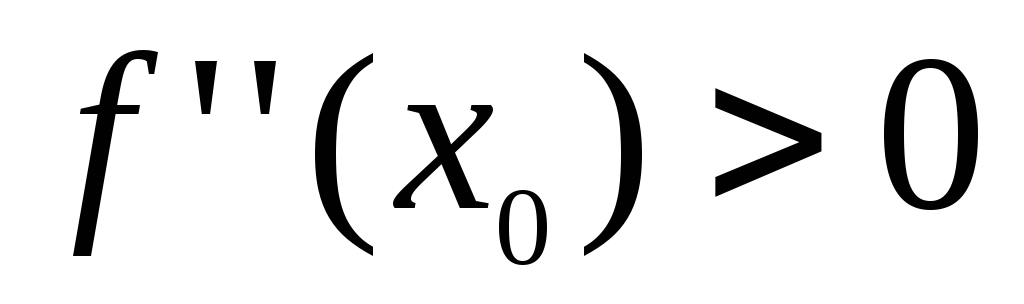 .
Тогда для
.
Тогда для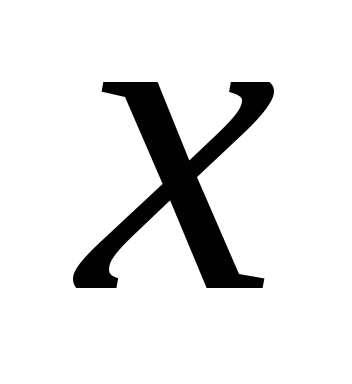 близких к
близких к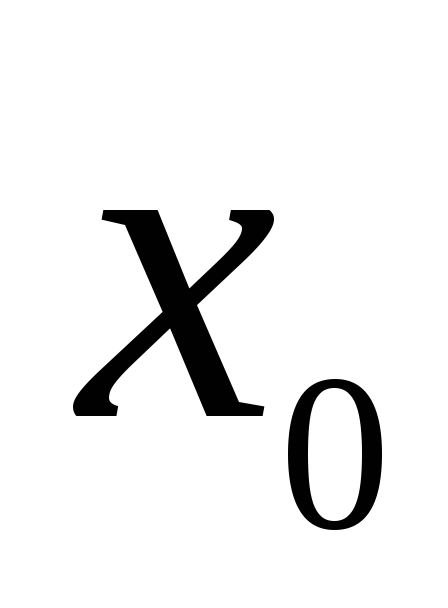 и
и ,
то есть
,
то есть 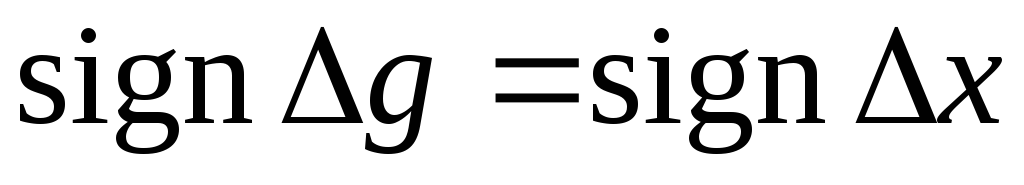 .
Это означает, что функция
.
Это означает, что функция  возрастает в некоторой окрестности
точки
возрастает в некоторой окрестности
точки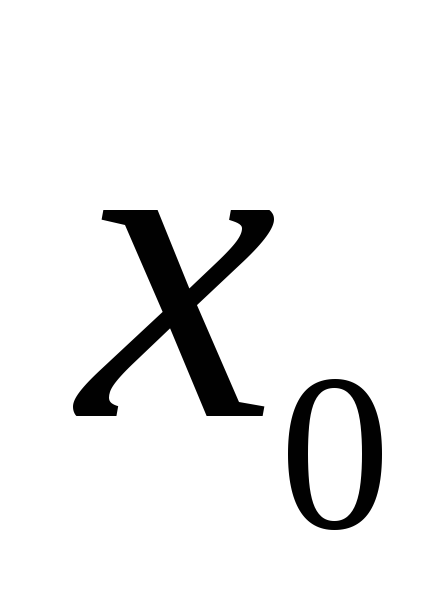 .
Но
.
Но .
Следовательно, левее точки
.
Следовательно, левее точки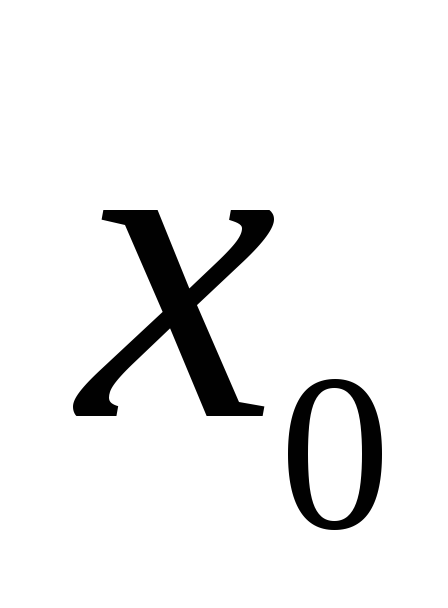 функция
функция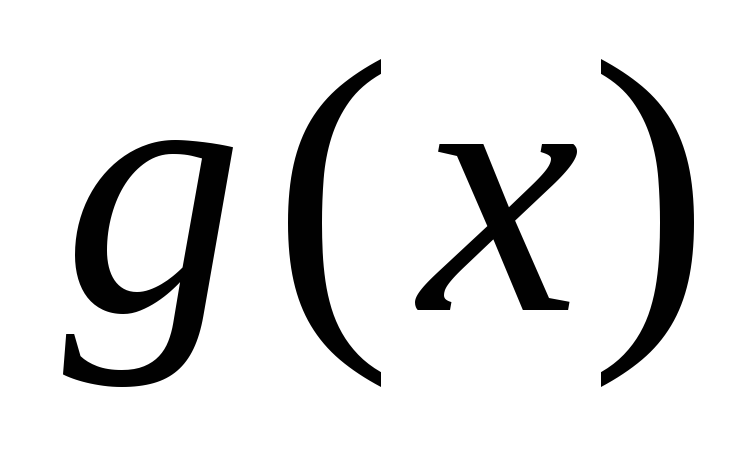 отрицательна, а правее – положительна.
Однако,
отрицательна, а правее – положительна.
Однако,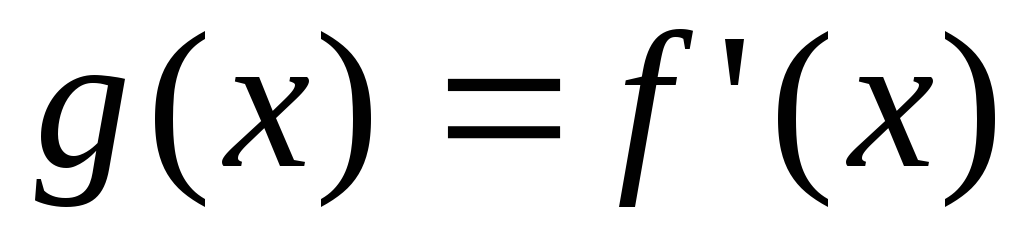 .
Значит, первая производная данной
функции при переходе через точку
.
Значит, первая производная данной
функции при переходе через точку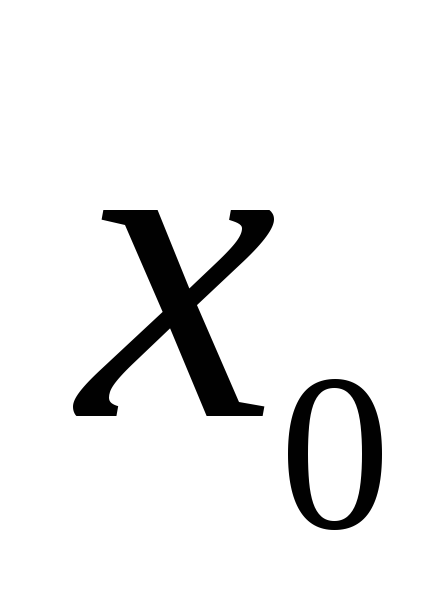 меняет знак с «–» на «+». Это означает,
что точка
меняет знак с «–» на «+». Это означает,
что точка – точка минимума. Аналогично рассматривается
и случай
– точка минимума. Аналогично рассматривается
и случай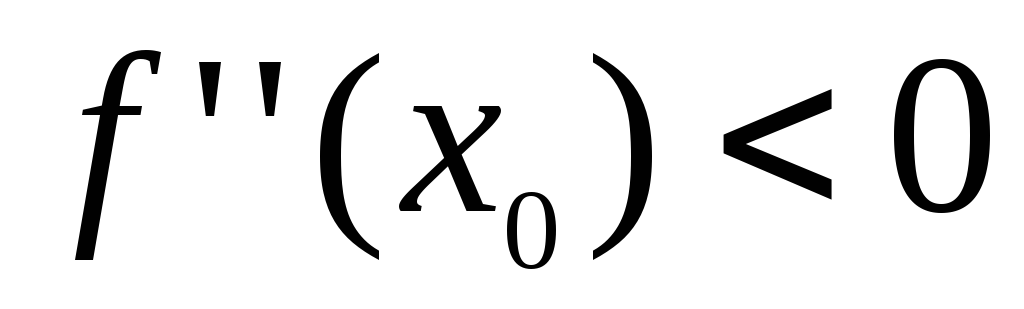 .
В необходимости дополнительного
исследования, когда
.
В необходимости дополнительного
исследования, когда ,
убеждают две функции:
,
убеждают две функции: и
и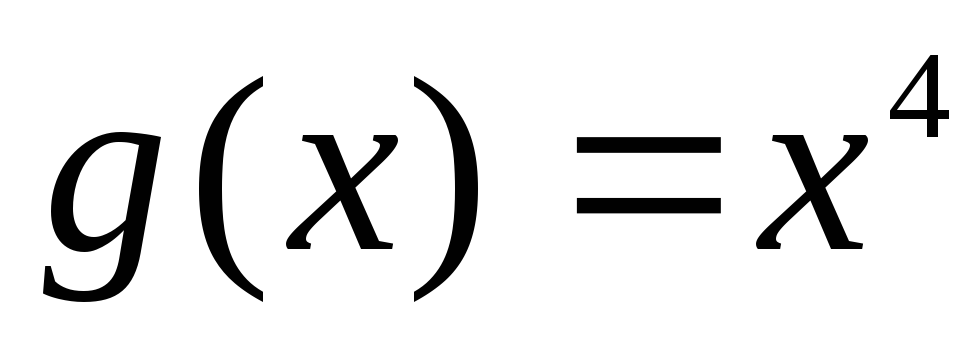 .
Очевидно, что
.
Очевидно, что – точка0
критическая для обеих функций, и
– точка0
критическая для обеих функций, и  .
Однако, для
.
Однако, для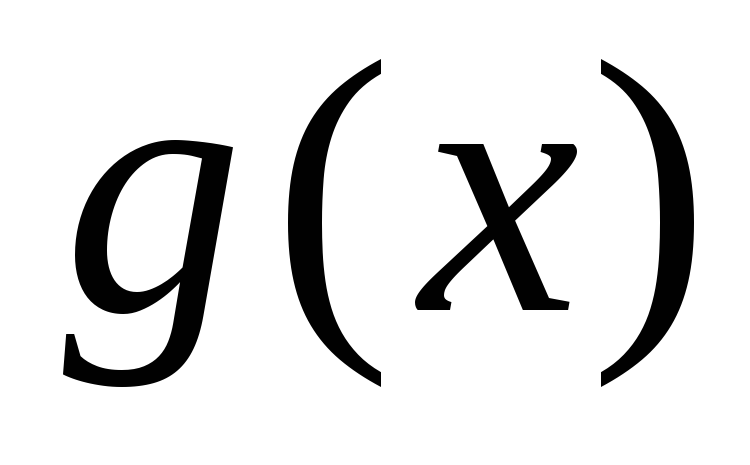 ноль – это точка минимума, а
ноль – это точка минимума, а в
нуле не имеет экстремума.
в
нуле не имеет экстремума.
Замечание 3. В теме «Формулы Тейлора и Маклорена» будет сформулировано и доказано третье достаточное условие экстремума, с помощью которого и производится это дополнительное исследование.
Пример 1. Найти точки экстремума функции 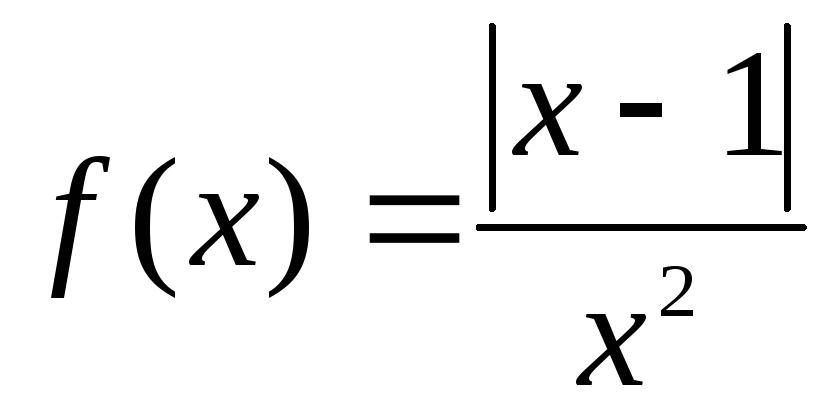 .
.
Решение. Раскроем знак модуля и вычислим производную:
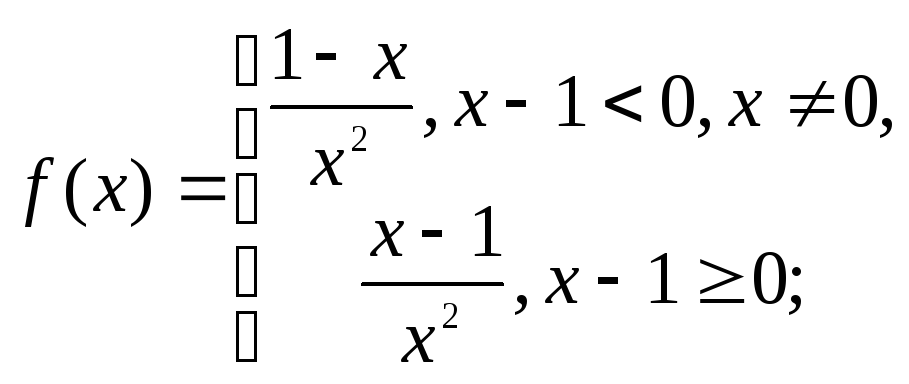

Наличие модуля в
выражении для 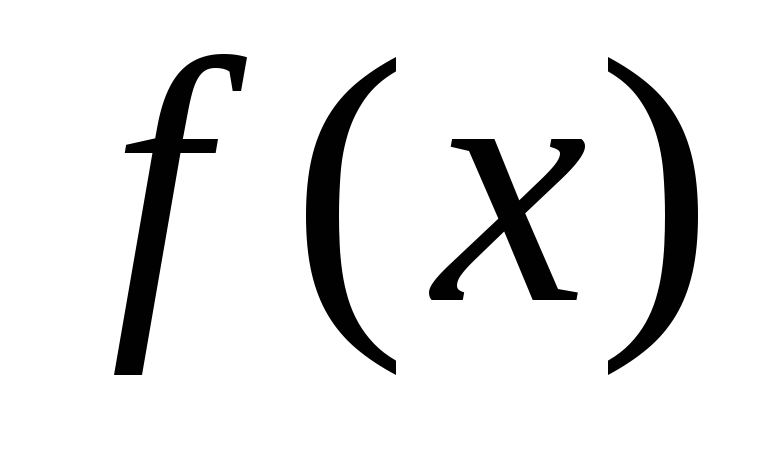 может
привести, и в нашем случае приводит, к
несуществованию
может
привести, и в нашем случае приводит, к
несуществованию в точке, где модуль обращается в ноль.
Действительно,
в точке, где модуль обращается в ноль.
Действительно,
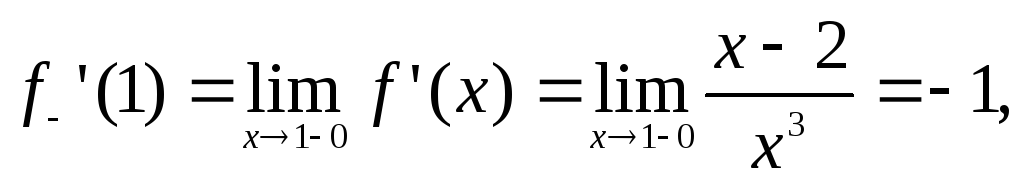
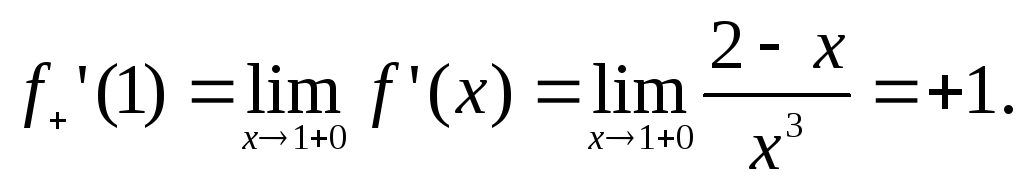
Отличие левой
производной от правой и означает
отсутствие производной в точке 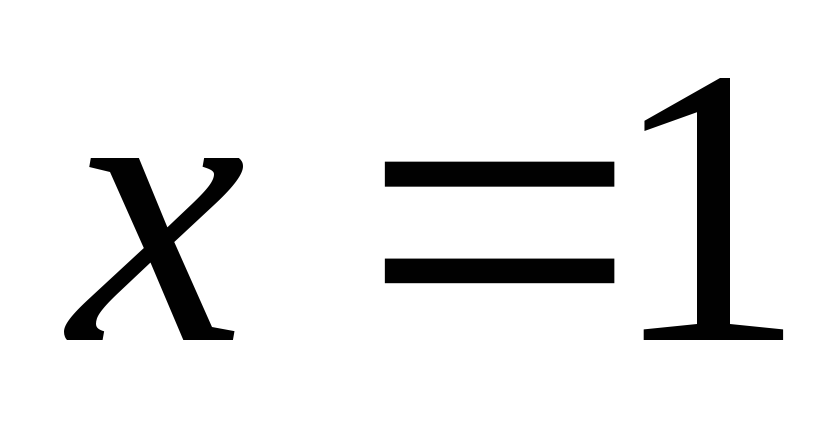 ,
т.е. эта точка – критическая. Другие
критические точки – это нули производной:
,
т.е. эта точка – критическая. Другие
критические точки – это нули производной: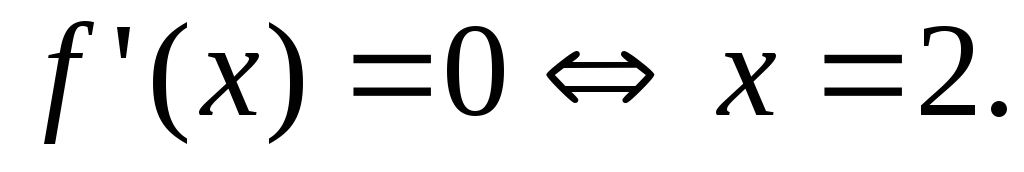
Итак, имеем две
критические точки 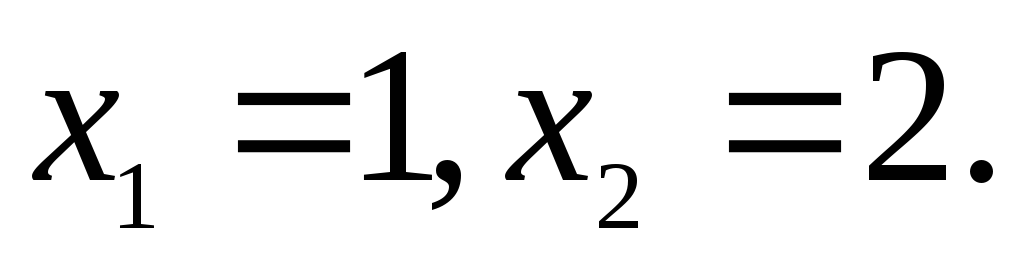 Они разбивают область определения
функции
Они разбивают область определения
функции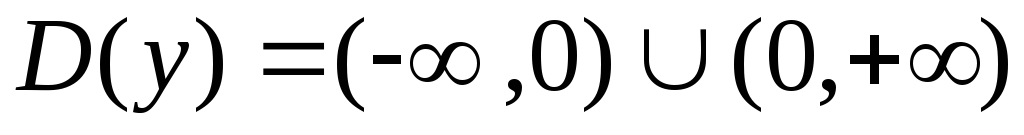 на интервалы знакопостоянства производной,
т.е. на интервалы монотонности функции.
Для определения знака
на интервалы знакопостоянства производной,
т.е. на интервалы монотонности функции.
Для определения знака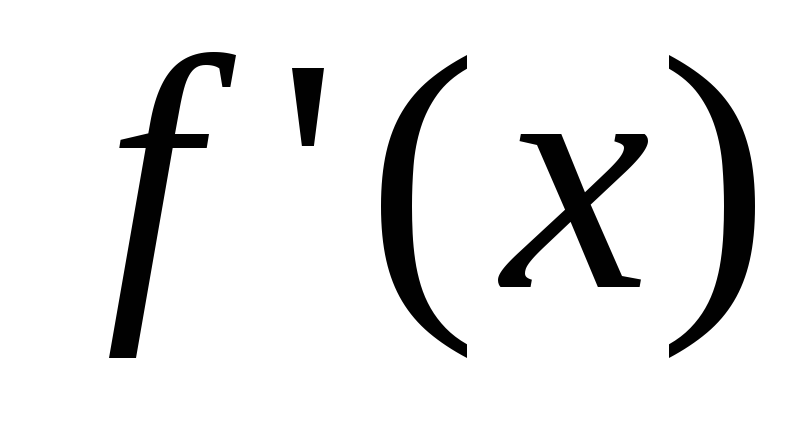 на интервале достаточно определить
этот знак в какой-либо точке интервала.
Дальнейшее исследование удобно вести,
нарисовав вспомогательный чертёж:
на интервале достаточно определить
этот знак в какой-либо точке интервала.
Дальнейшее исследование удобно вести,
нарисовав вспомогательный чертёж:

Еще раз напомним,
что критические точки наносятся на
область определения. Мы получаем 4
интервала. Определяем знаки  :
:
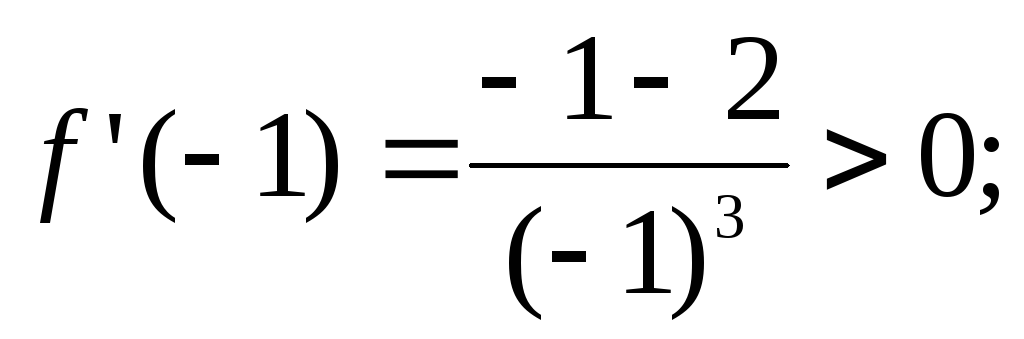

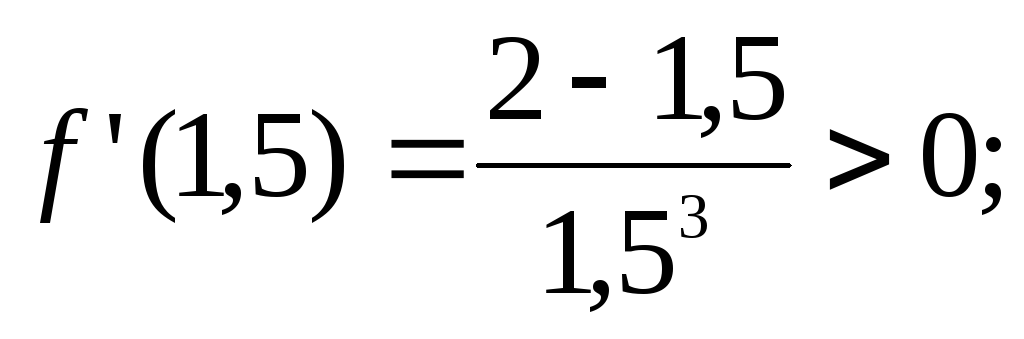
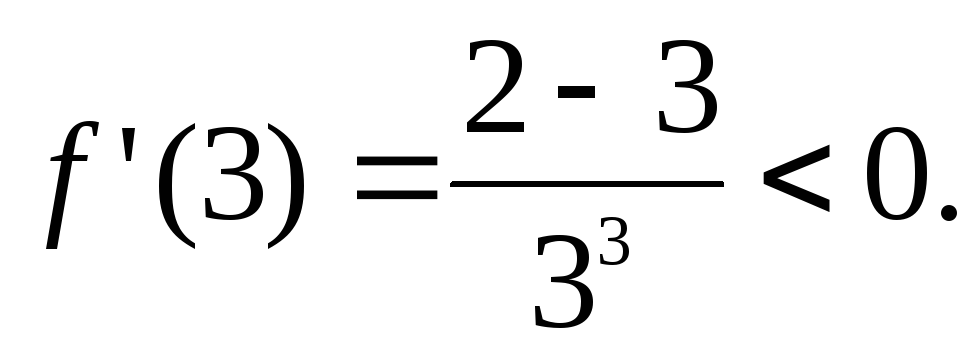
Анализ чертежа
показывает: в точке  функция имеет локальный минимум, причём
функция имеет локальный минимум, причём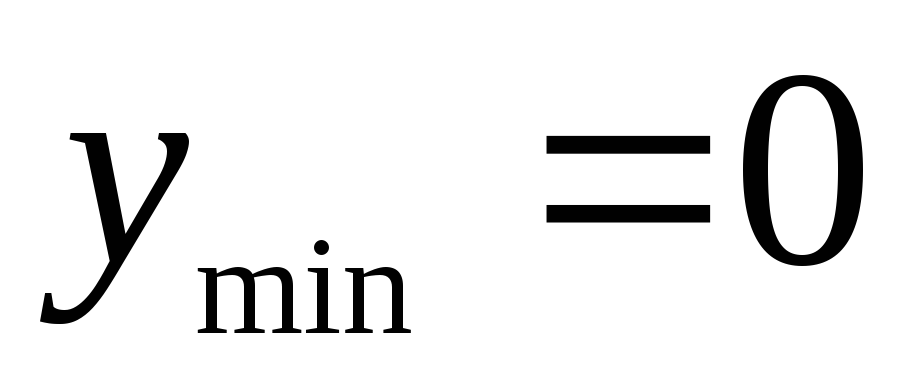 ,
а в точке
,
а в точке – локальный максимум:
– локальный максимум: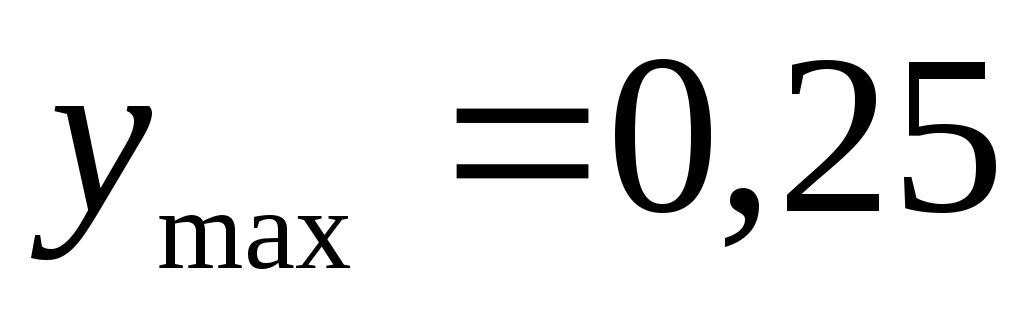 .
.
На чертеже
видны и интервалы монотонности 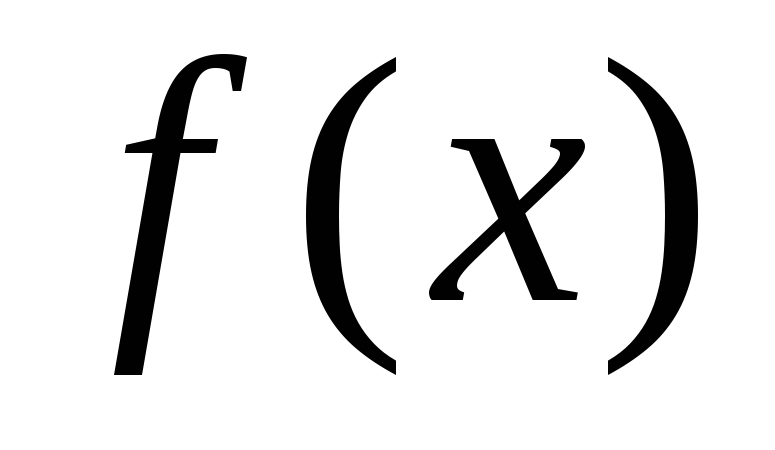 :
на
:
на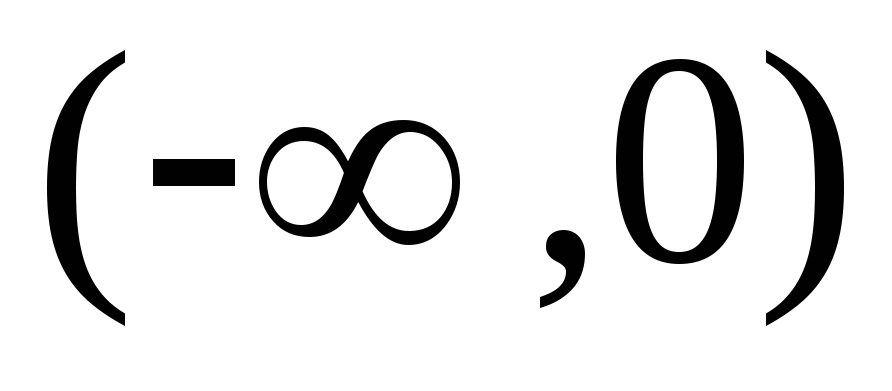 и
и функция возрастает, а на
функция возрастает, а на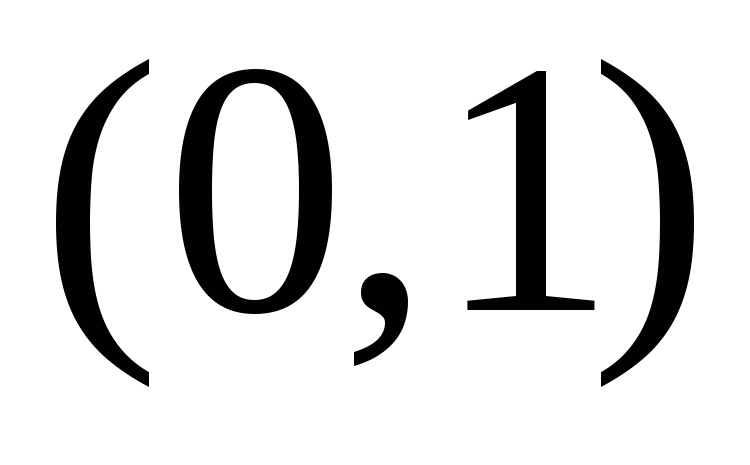 и
и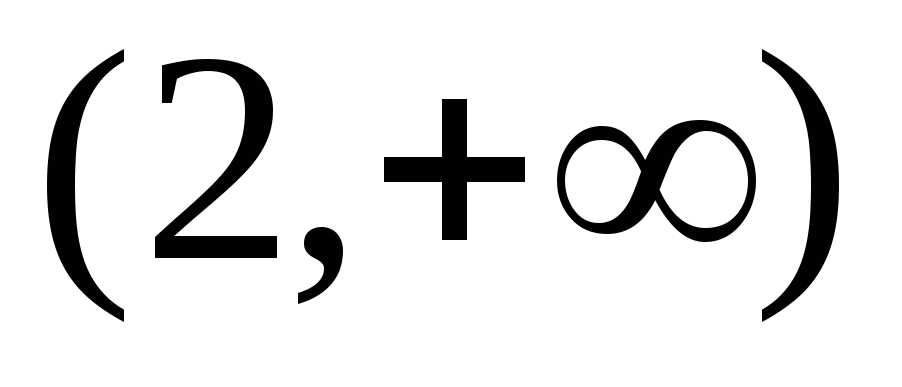 –
убывает.
–
убывает.
Замечание
4. В
точке максимума  рассмотренная функция имеет нулевую
производную и касательная к графику
функции – горизонтальна. О таком
максимуме говорят «гладкий максимум»
(аналогично «гладкий минимум»). В
противоположность этому, точка
рассмотренная функция имеет нулевую
производную и касательная к графику
функции – горизонтальна. О таком
максимуме говорят «гладкий максимум»
(аналогично «гладкий минимум»). В
противоположность этому, точка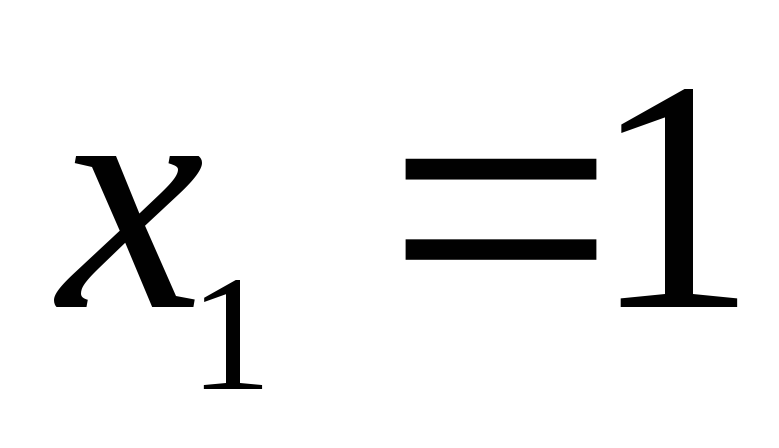 является точкой «негладкого минимума»
– в этой точке производная не существует,
хотя есть односторонние производные.
Соответствующая точка графика
является точкой «негладкого минимума»
– в этой точке производная не существует,
хотя есть односторонние производные.
Соответствующая точка графика называетсяугловой
точкой графика.
называетсяугловой
точкой графика.
Пример 2. Найти
экстремумы функции  .
.
Решение. 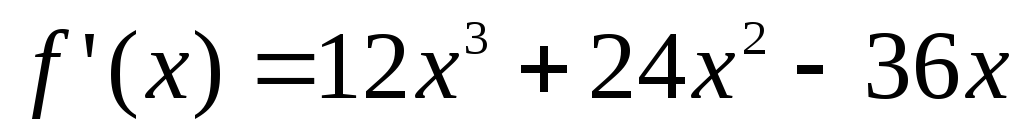 – существует везде.
– существует везде.
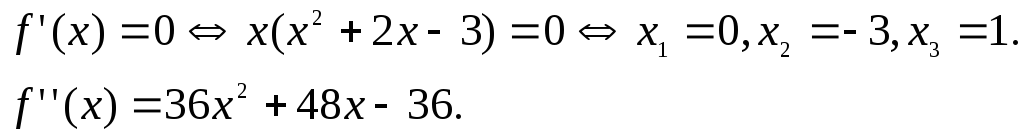
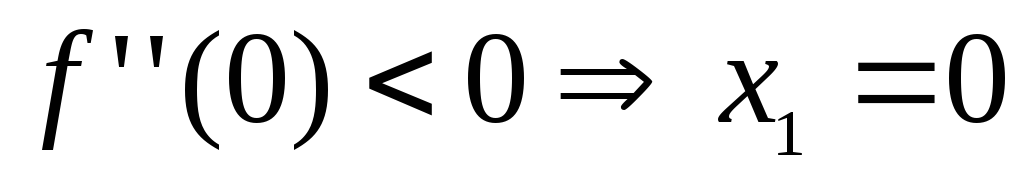 –точка максимума;
–точка максимума;
 –точка минимума;
–точка минимума;
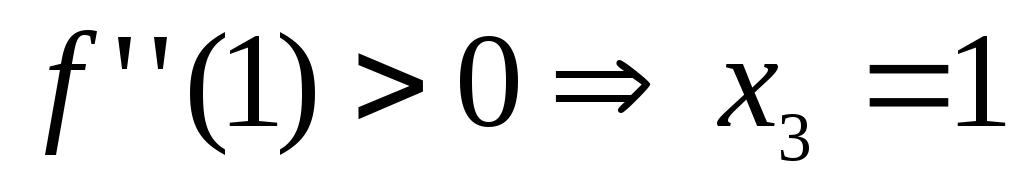 –точка минимума.
–точка минимума.
Лекция 13
studfile.net
Исследование функций с помощью производных
Лекция 26
Лекция 26. Исследование поведения функций с помощью первой и второй производной, асимптоты. Построение графиков функций.
Теорема 1.
Если функция 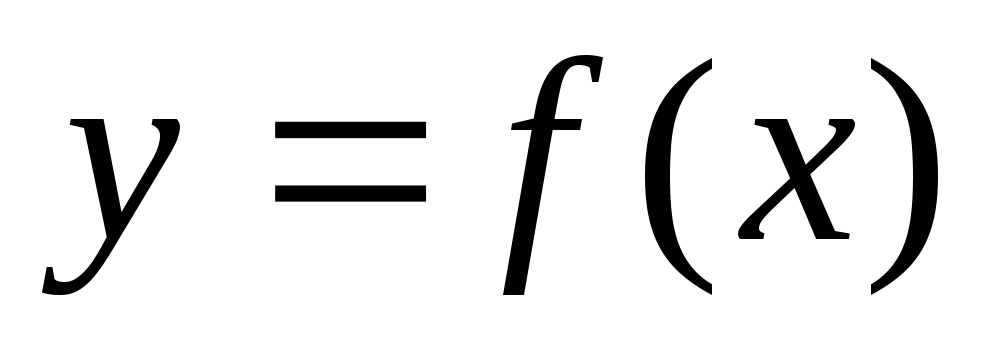 возрастает на некотором интервале
возрастает на некотором интервале 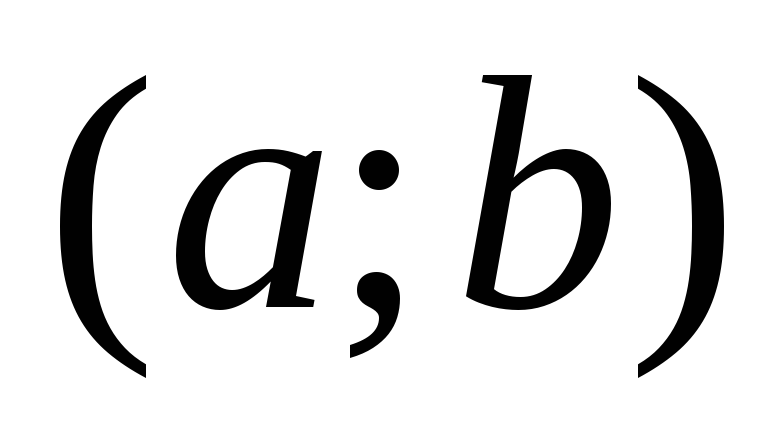 оси ох (с ростом x растет и y)
и дифференцируема на этом интервале,
то для любого x из этого интервала
оси ох (с ростом x растет и y)
и дифференцируема на этом интервале,
то для любого x из этого интервала  (производная имеет знак (+)). А если она
убывает на этом интервале (y убывает с ростом x)
и дифференцируема на нем, то для любого x из этого интервала
(производная имеет знак (+)). А если она
убывает на этом интервале (y убывает с ростом x)
и дифференцируема на нем, то для любого x из этого интервала 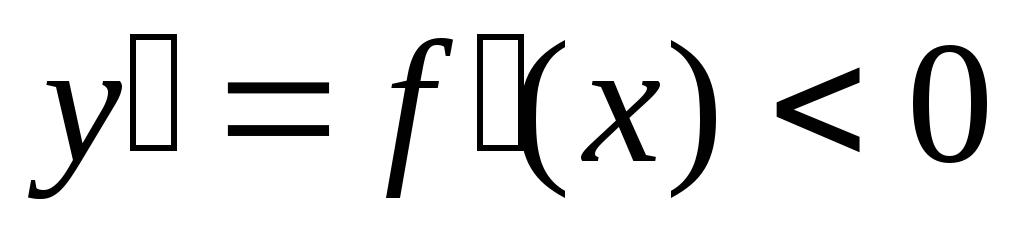 (производная
имеет знак (–)).
(производная
имеет знак (–)).
Доказательство.

Рассмотрим сначала
рис.1. На нем изображен график возрастающей
и дифференцируемой на интервале 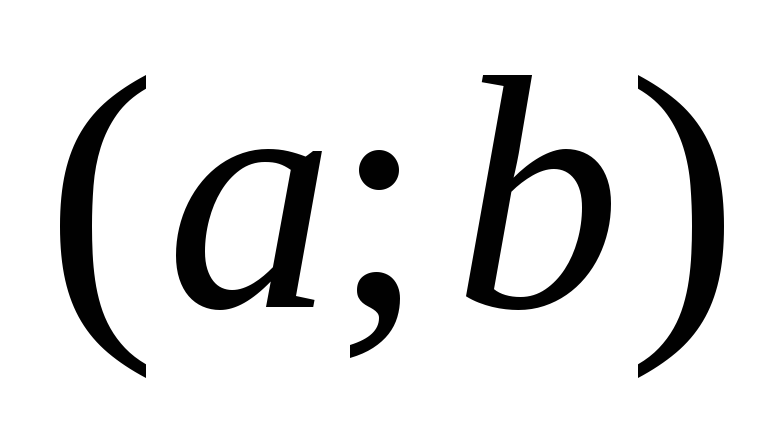 функции
функции 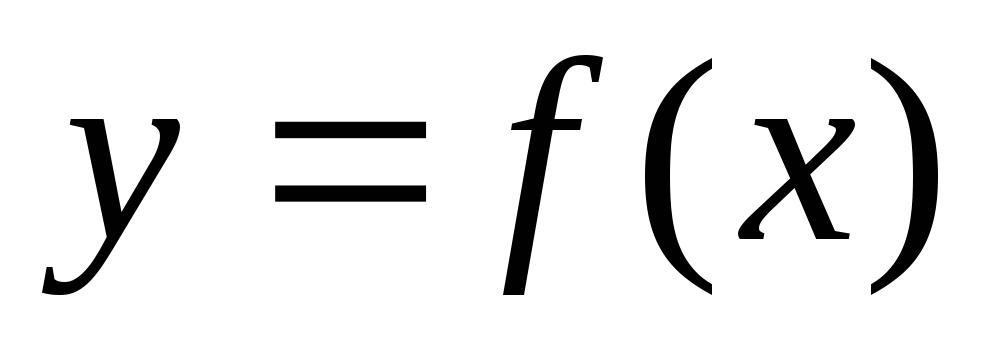 .
В каждой точке M этого графика касательная составляет
с осью ох острый угол
.
В каждой точке M этого графика касательная составляет
с осью ох острый угол  (
( ).
Но тангенсы острых углов, как известно,
положительны. Значит, согласно
геометрического смысла производной,
производная
).
Но тангенсы острых углов, как известно,
положительны. Значит, согласно
геометрического смысла производной,
производная 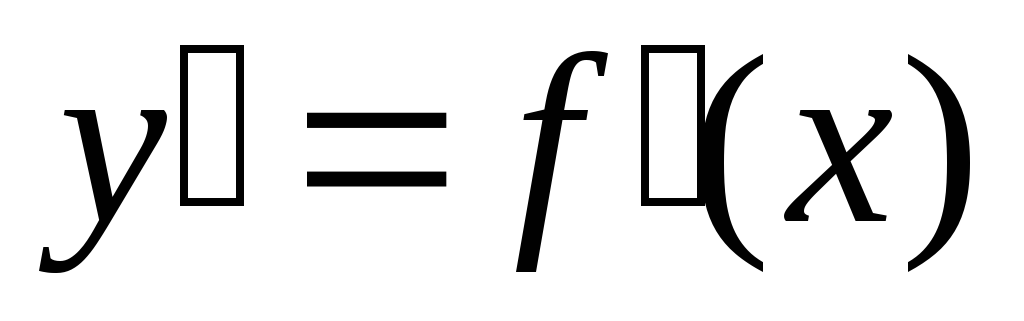 положительна для любых x из интервала
положительна для любых x из интервала 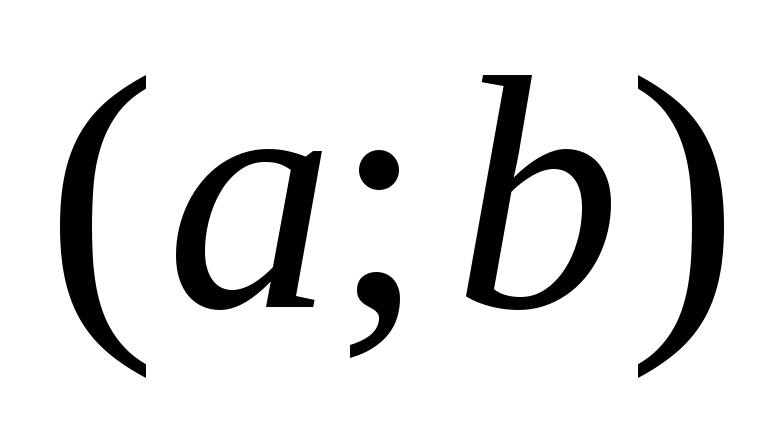 возрастания функции.
возрастания функции.
А теперь рассмотрим
рис. 2, на котором изображен график
убывающей на интервале 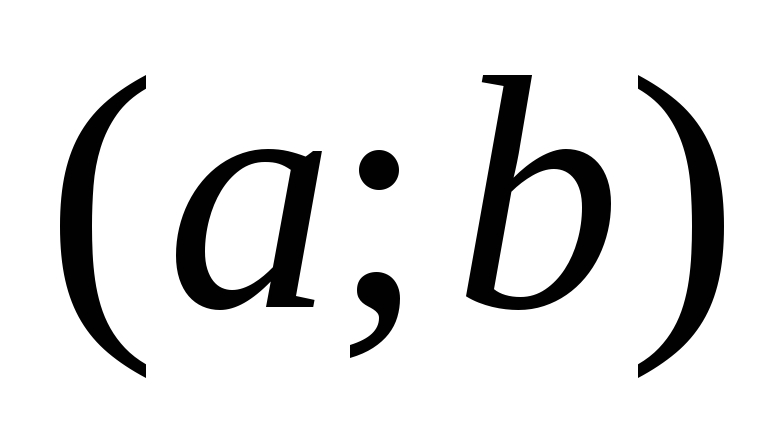 функции
функции  .
Здесь для любой точки М графика функции (а значит, для любого x из интервала
.
Здесь для любой точки М графика функции (а значит, для любого x из интервала 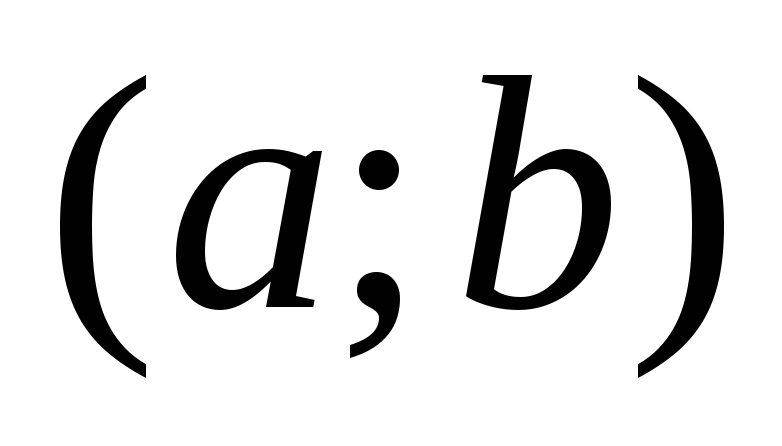 )
угол
)
угол  наклона касательной, проведенной к
графику функции, тупой (
наклона касательной, проведенной к
графику функции, тупой (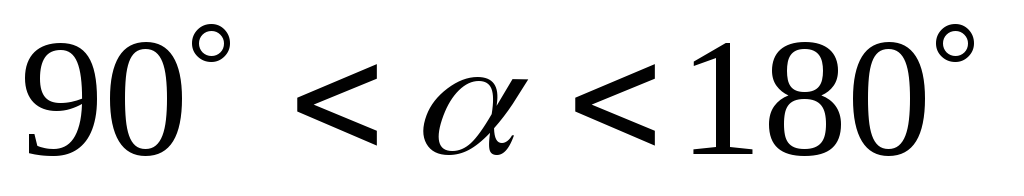 ).
Но тангенсы таких углов отрицательны.
А значит и производная
).
Но тангенсы таких углов отрицательны.
А значит и производная 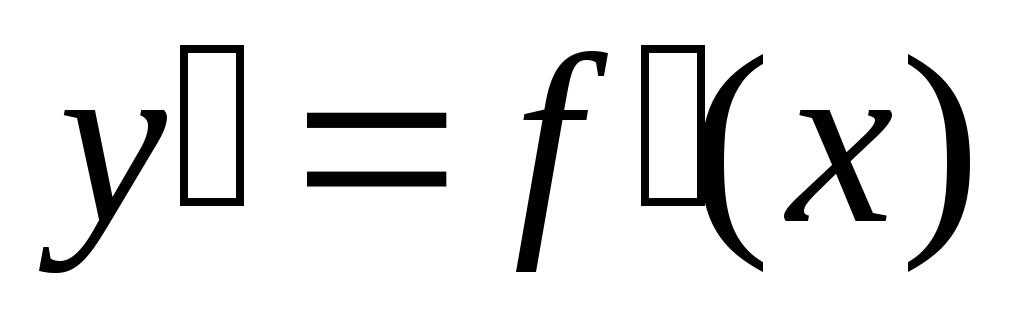 отрицательна.
отрицательна.
Следствие теоремы
1. Если на
некотором интервале 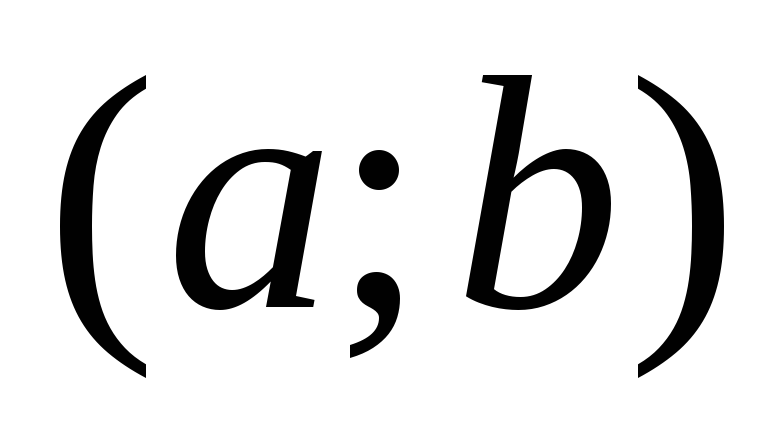 оси ох в любой его точке x производная функции
оси ох в любой его точке x производная функции 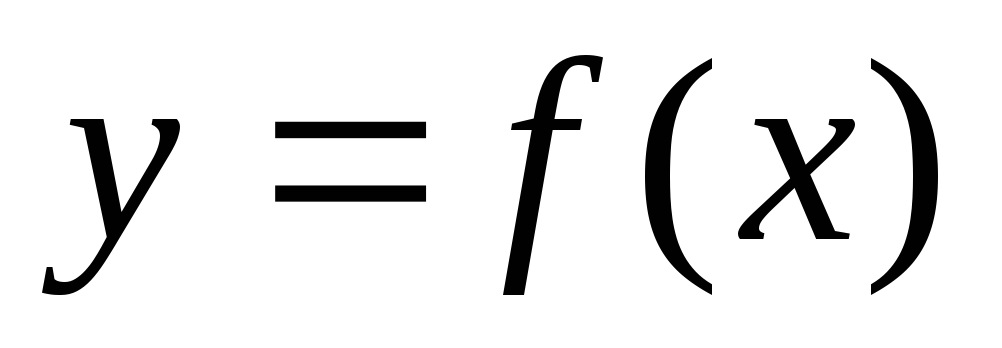 положительна, то функция возрастает на
этом интервале. А если отрицательна –
то убывает. Это следствие играет очень
важную роль в исследовании функций. Оно
позволяет по знаку производной функции
определять, растет или убывает функция,
и где именно (для каких x)
растет, и где (для каких x)
убывает.
положительна, то функция возрастает на
этом интервале. А если отрицательна –
то убывает. Это следствие играет очень
важную роль в исследовании функций. Оно
позволяет по знаку производной функции
определять, растет или убывает функция,
и где именно (для каких x)
растет, и где (для каких x)
убывает.
Докажем более строгий вариант теоремы 1.
Теорема 2.
1). Если функция 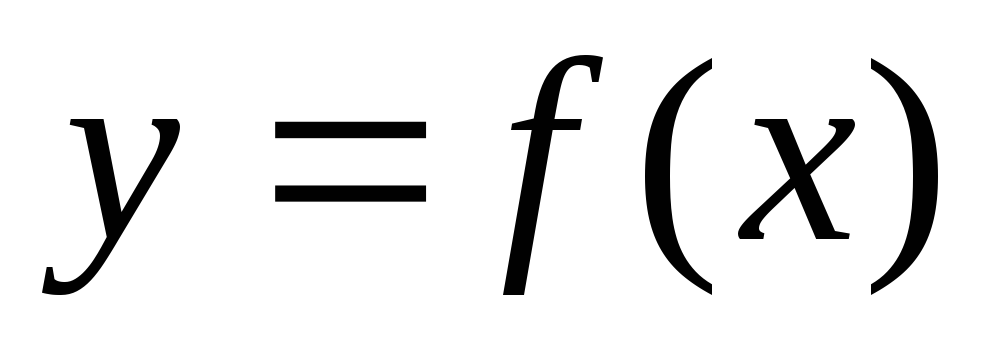 ,
имеющая производную на отрезке
,
имеющая производную на отрезке  ,
возрастает на этом отрезке, то ее
производная на отрезке
,
возрастает на этом отрезке, то ее
производная на отрезке 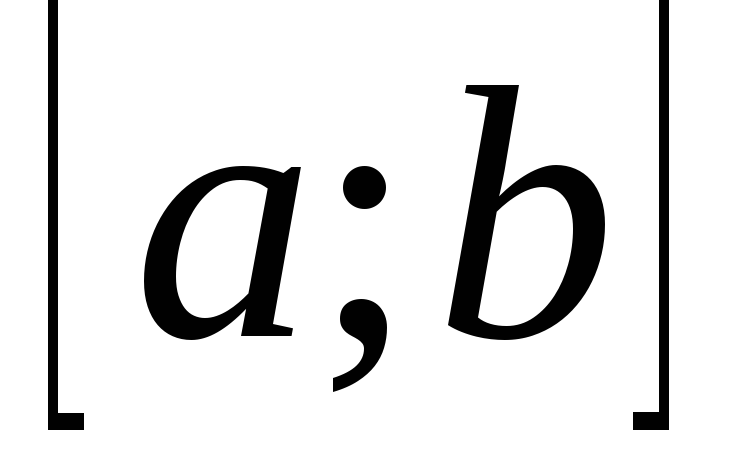 не отрицательна, т.е.
не отрицательна, т.е. 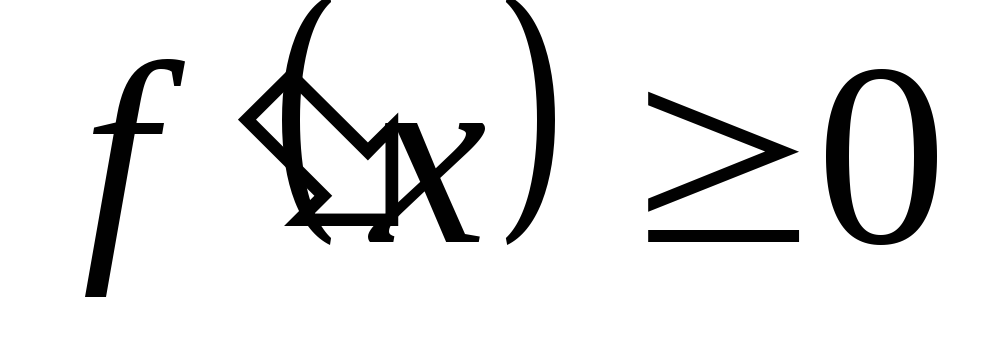 .
.
2) Если функция  непрерывна на отрезке
непрерывна на отрезке  и дифференцируема в промежутке
и дифференцируема в промежутке  ,
причем
,
причем  для
для  ,
то эта функция возрастает на отрезке
,
то эта функция возрастает на отрезке 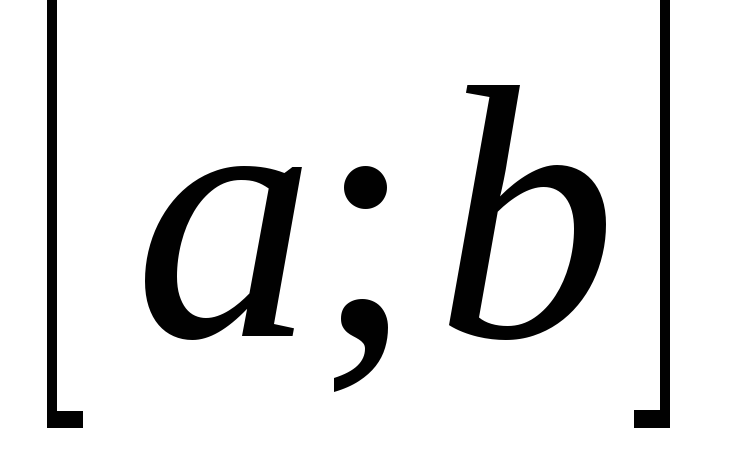 .
.
Доказательство. 1) Пусть y=f(x) возрастает на отрезке 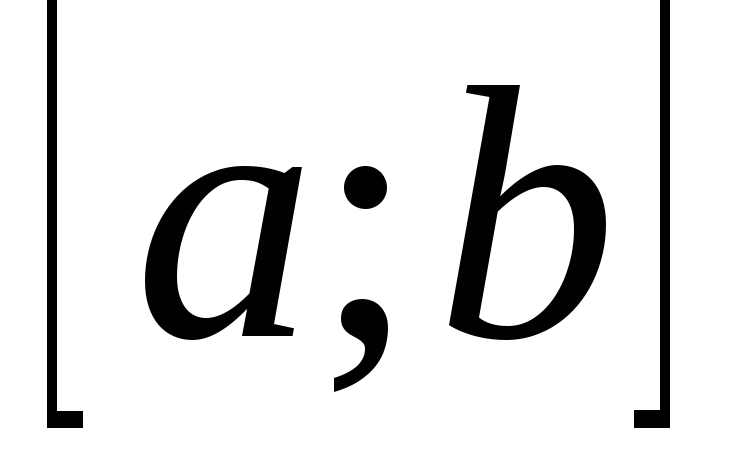 .
Придадим аргументу х приращение
.
Придадим аргументу х приращение 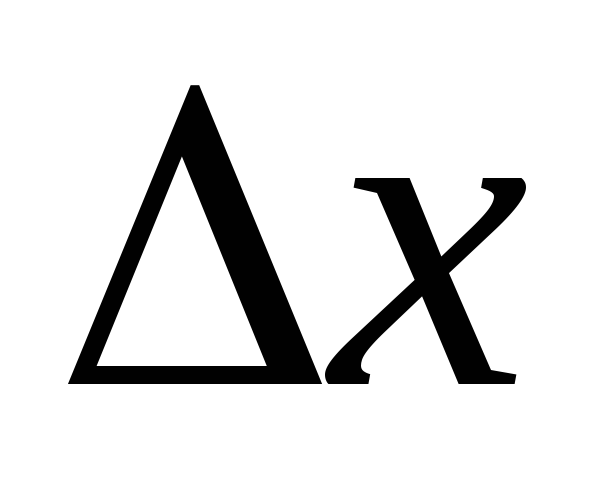 и рассмотрим отношение
и рассмотрим отношение
. (*)
Так как f(x) – функция возрастающая, то

В обоих случаях  по свойствам пределов функций. Т.е.
по свойствам пределов функций. Т.е.  ,
что и требовалось доказать.
,
что и требовалось доказать.
2) Пусть  при всех значениях х,
принадлежащих промежутку
при всех значениях х,
принадлежащих промежутку 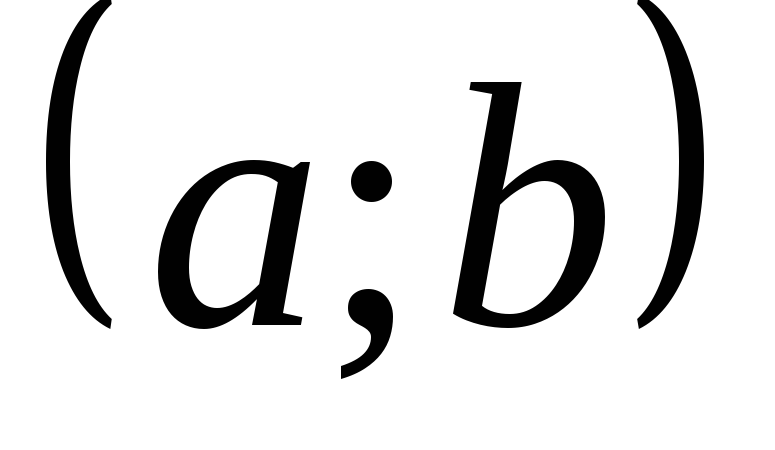 .
Рассмотрим два любых значения x1 и x2, x1 < x2,
принадлежащих отрезку
.
Рассмотрим два любых значения x1 и x2, x1 < x2,
принадлежащих отрезку  .
По теореме Лагранжа
о конечных приращениях имеем:
.
По теореме Лагранжа
о конечных приращениях имеем:

По условию 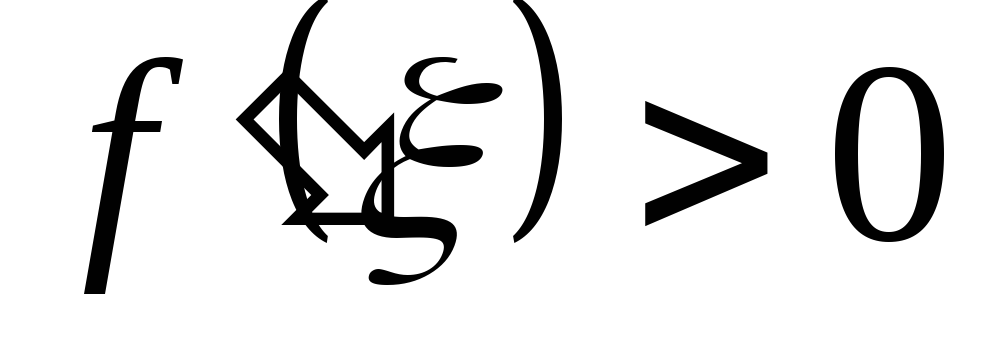 ,
следовательно
,
следовательно 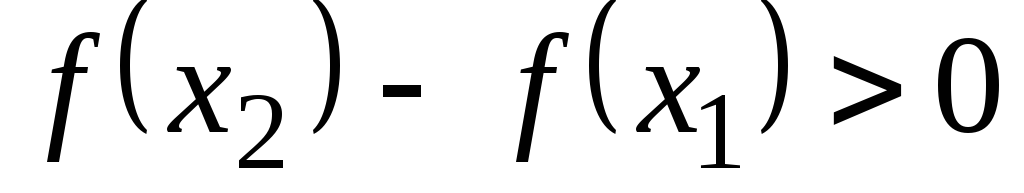 ,
а это означает, что f(x) – возрастающая функция.
,
а это означает, что f(x) – возрастающая функция.
Аналогичная теорема имеет место и для убывающей дифференцируемой функции.
Теорема 3. 1). Если функция 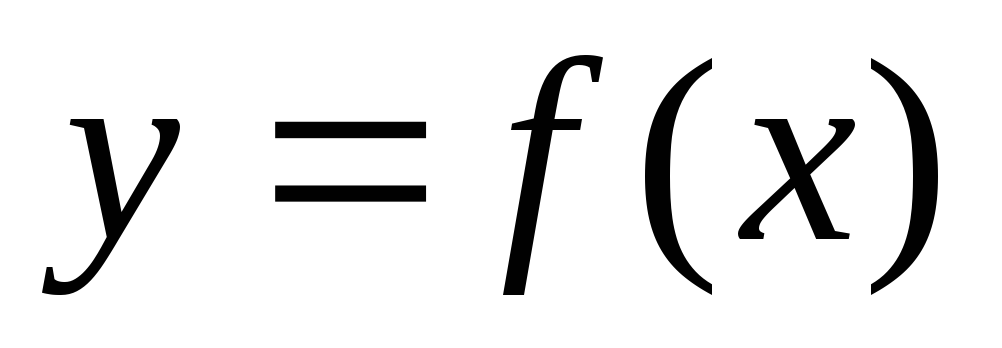 ,
имеющая производную на отрезке
,
имеющая производную на отрезке  ,
убывает на этом отрезке, то ее производная
на отрезке
,
убывает на этом отрезке, то ее производная
на отрезке 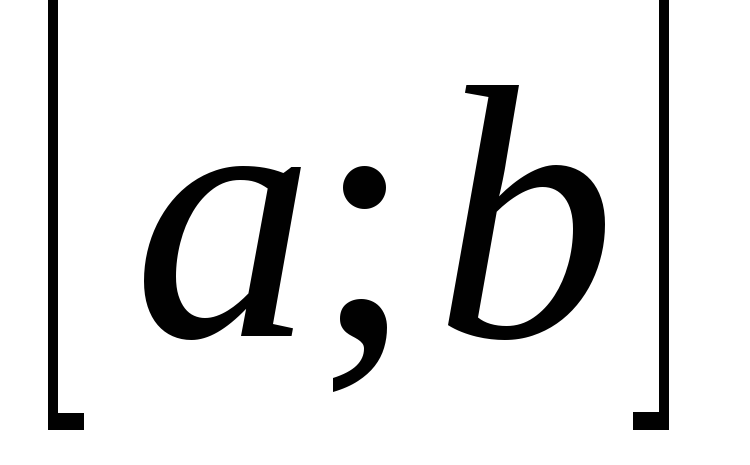 не положительна, т.е.
не положительна, т.е.  .
.
2) Если функция 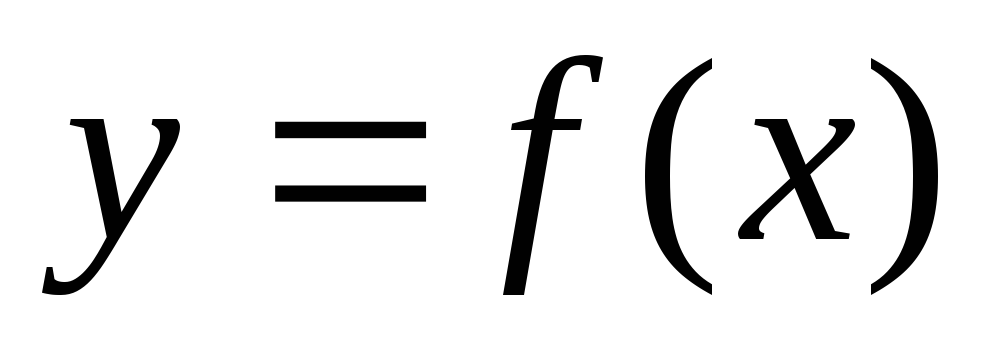 непрерывна на отрезке
непрерывна на отрезке 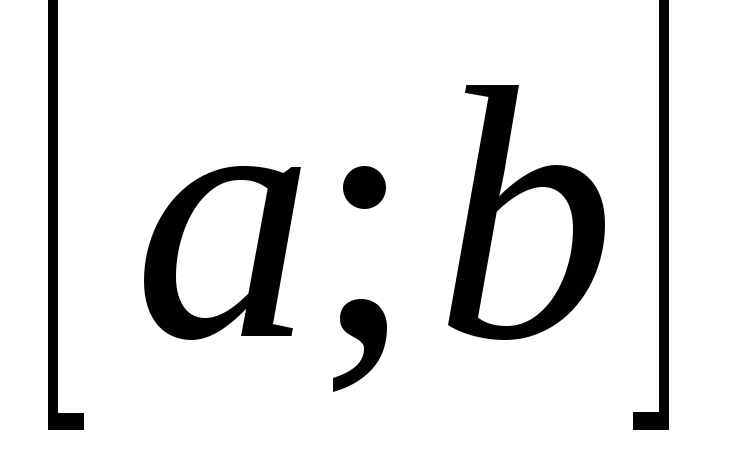 и дифференцируема в промежутке
и дифференцируема в промежутке  ,
причем
,
причем 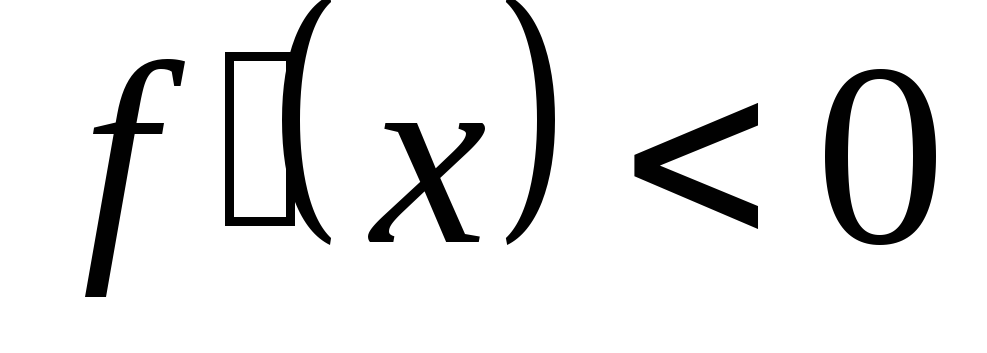 для
для 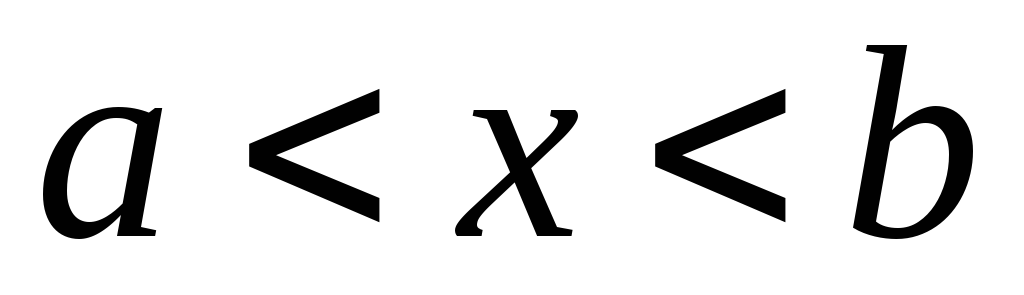 ,
то эта функция убывает на отрезке
,
то эта функция убывает на отрезке  .
.
Пример 1.
Рассмотрим функцию 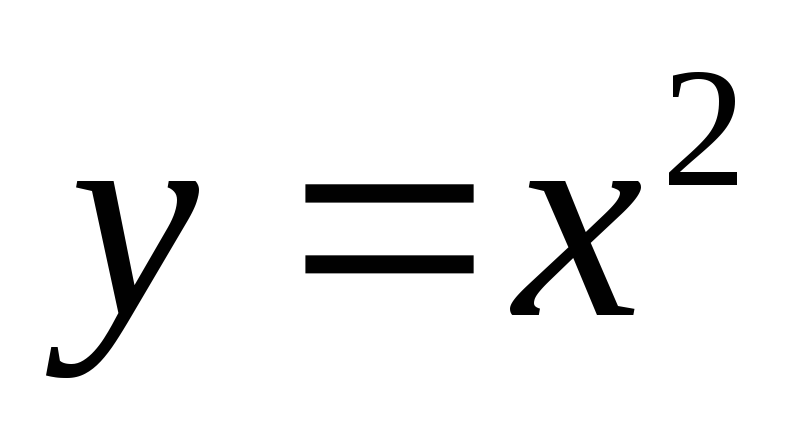 .
Ее производная
.
Ее производная 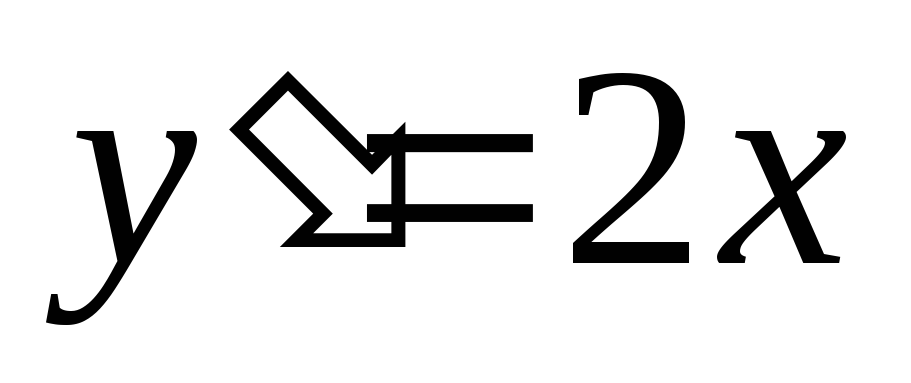 .
Она положительна при
.
Она положительна при 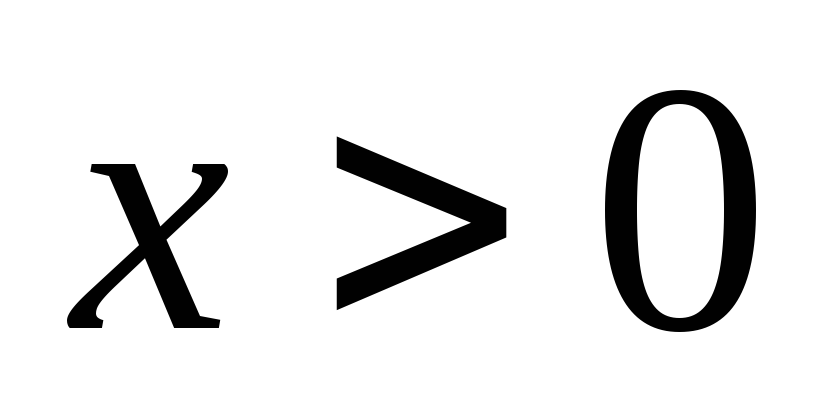 и отрицательна при
и отрицательна при 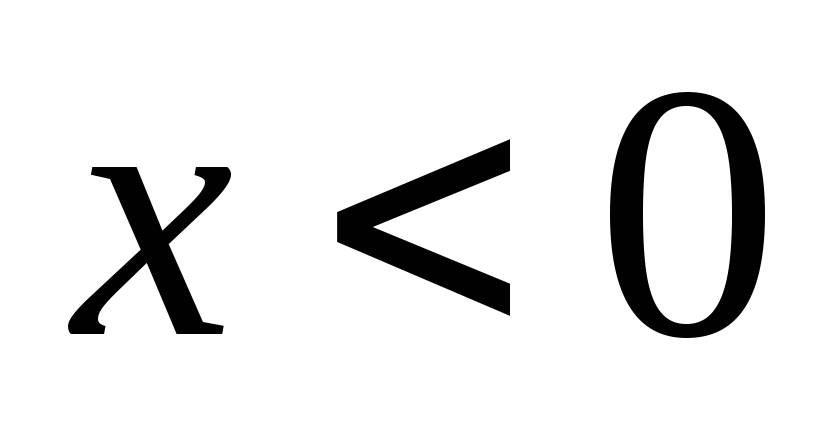 .
Значит, при
.
Значит, при  функция
функция 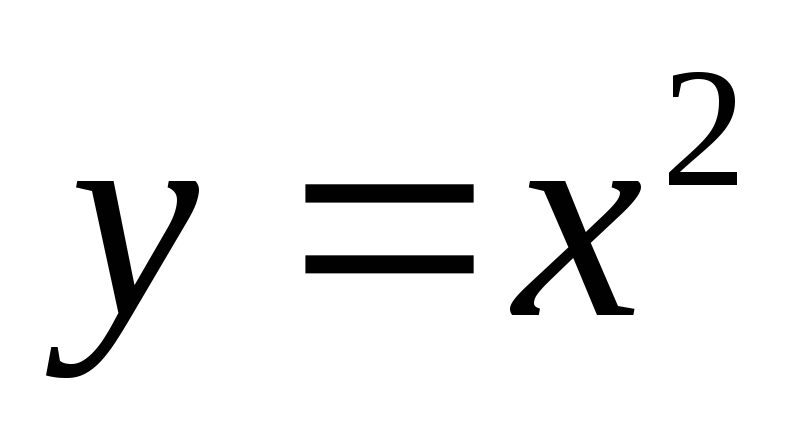 возрастает, а при
возрастает, а при 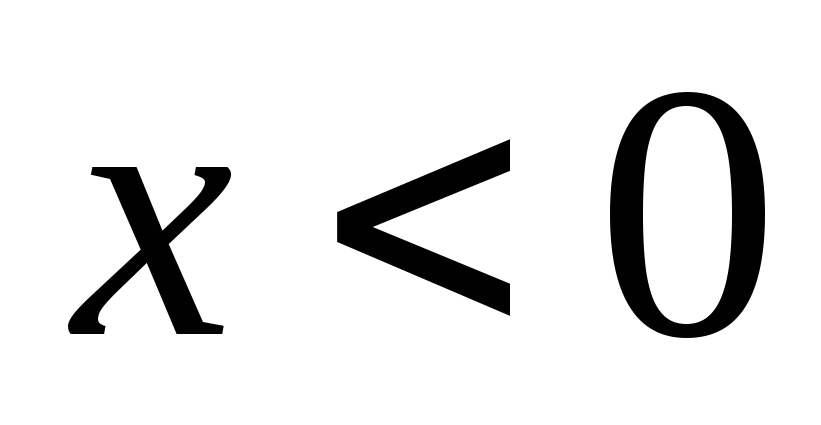 она убывает. График этой функции
(парабола) наглядно подтверждает
сказанное.
она убывает. График этой функции
(парабола) наглядно подтверждает
сказанное.
Применение производной функции к нахождению точек экстремума функции
Напомним, что
термин «точки экстремума» – это общее
название точек максимума и минимума
функции. А под ними, в свою очередь,
понимаются абсциссы вершин и впадин
графика функции (проекции вершин и
впадин на ось ох).
Или, если не прибегать к геометрической
трактовке, точки экстремума функции –
это те значения ее аргумента x,
при которых функция  принимает экстремальные (пиковые)
значения – максимальные или минимальные.
Точек экстремума у функции
принимает экстремальные (пиковые)
значения – максимальные или минимальные.
Точек экстремума у функции 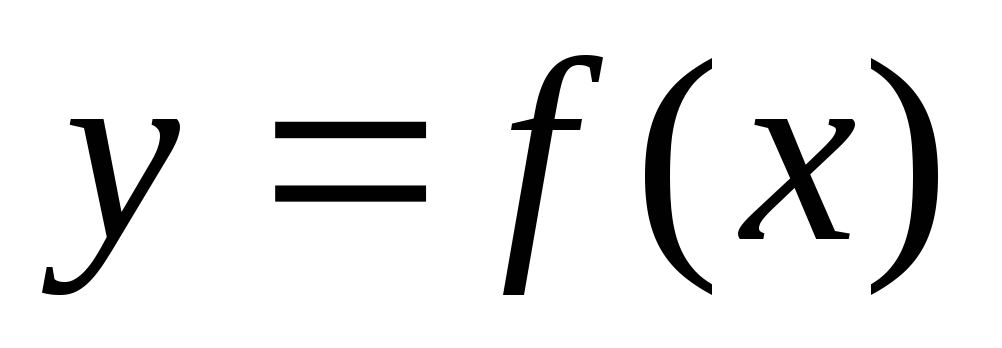 столько, сколько вершин и впадин у ее
графика.
столько, сколько вершин и впадин у ее
графика.
Определение 1: функция f(x) в точке х1 имеет максимум,
если значение функции f(x) в точке х1 больше, чем ее значения во всех точках
некоторого интервала, содержащего точку х1. Другими словами, функция f(x) в точке х=х1 имеет максимум,
если  при любых
при любых 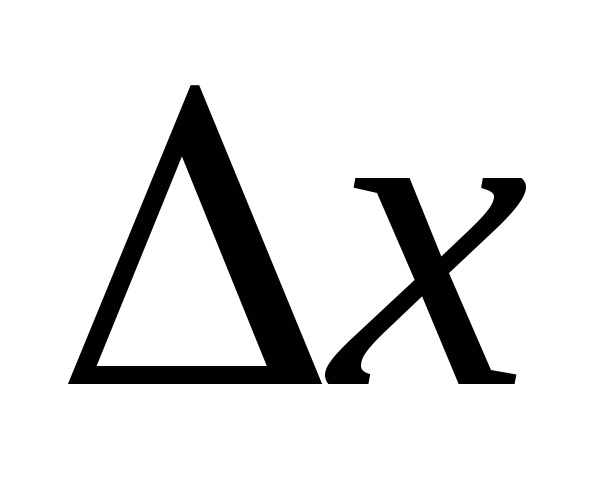 (
положительных и отрицательных ),
достаточно малых по абсолютной величине.
(
положительных и отрицательных ),
достаточно малых по абсолютной величине.
Определение 2: функция f(x) в точке х2 имеет минимум,
если значение функции f(x) в точке х1 меньше, чем ее значения во всех точках
некоторого интервала, содержащего точку х2. Другими словами, функция f(x) в точке х=х2 имеет минимум,
если  при любых
при любых 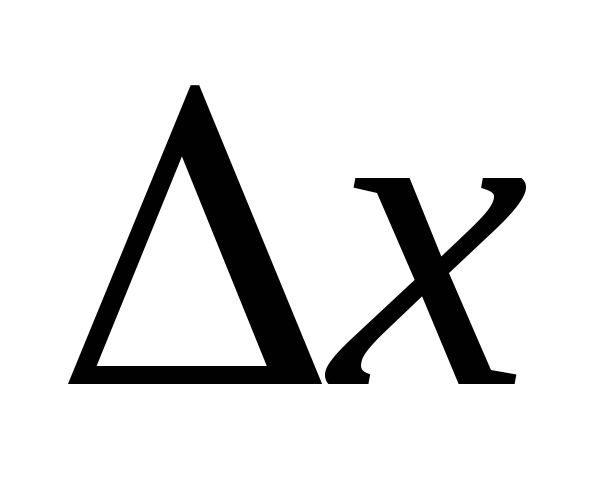 (
положительных и отрицательных ),
достаточно малых по абсолютной величине.
(
положительных и отрицательных ),
достаточно малых по абсолютной величине.
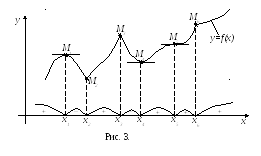
Рассмотрим рис.3. На нем изображен график непрерывной функции , имеющей и интервалы возрастания, и интервалы убывания, и точки экстремума:
Интервалы возрастания
функции помечены знаком (+), а интервалы
убывания – знаком (–). Согласно доказанной
выше теореме 1, это заодно и знаки
производной функции  .
.
Точками экстремума данной функции являются точки (x1, x2, x3, x4). Причем точки x1 и x3 – точки максимума, а x2 и x4 – точки минимума. Точки x5 и x6 точками экстремума функции не являются, так как соответствующие им точки графика М5 и М6 – не вершины и не впадины этого графика.
Точки экстремума разделяют интервалы возрастания и убывания функции. В точках максимума совершается переход от возрастания функции (слева от точки максимума) к ее убыванию (справа от точки максимума). То есть в точках максимума знак производной функции меняется с (+) слева на (–) справа. А в точках минимума, наоборот, совершается переход от убывания функции к ее возрастанию. То есть в точках минимума знак производной функции меняется с (–) слева на (+) справа.
Сами же точки экстремума не принадлежат ни к интервалам возрастания, ни к интервалам убывания функции. Потому в точках экстремума производная не может быть ни положительной, ни отрицательной. Значит, в этих точках она или равна нулю, или ее не существует вообще.
Этот вывод понятен
и с геометрической точки зрения.
Действительно, производная функции,
согласно ее геометрического смысла,
связана с касательной к графику функции.
А именно, представляет собой тангенс
угла наклона этой касательной к оси ох.
Но точкам экстремума функции соответствуют
на ее графике вершины и впадины, в которых
касательная к графику или параллельна
оси ох (если вершина или впадина графика
округлая), или эта касательная отсутствует
вообще (если вершина или впадина острая).
В первом случае угол наклона  касательной к оси ох равен нулю. Значит, и
касательной к оси ох равен нулю. Значит, и 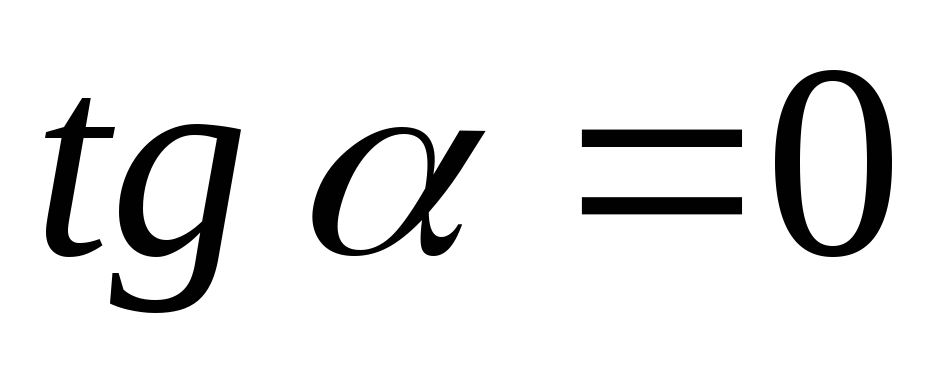 ,
а значит, и производная
,
а значит, и производная 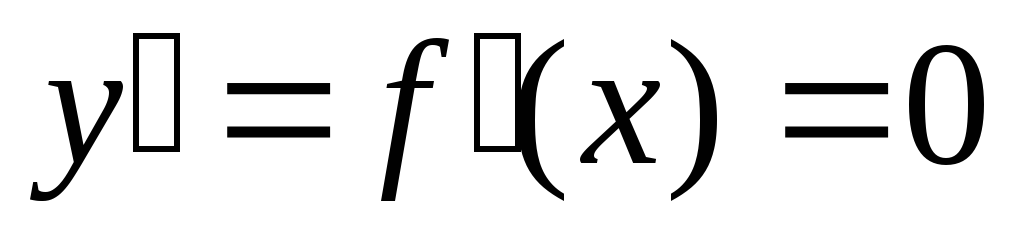 .
Во втором случае угол
.
Во втором случае угол  не существует вообще, а значит, не
существует для данной точки экстремума x и производная
не существует вообще, а значит, не
существует для данной точки экстремума x и производная 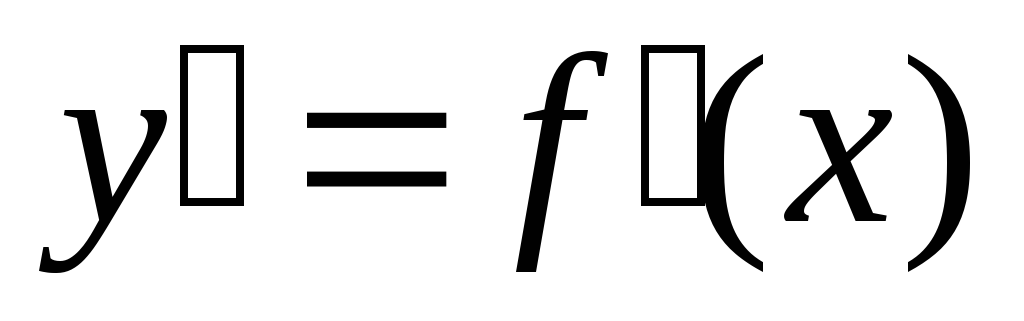 .
В частности, для рис. 3 имеем:
.
В частности, для рис. 3 имеем:
 ;
;  – не сущ.;
– не сущ.; 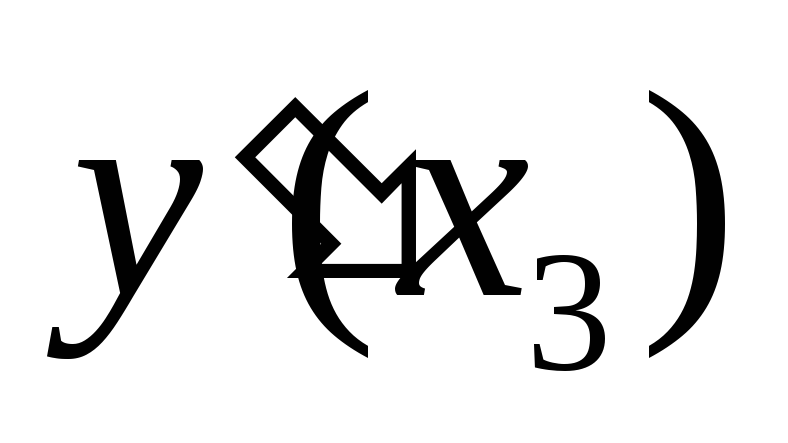 – не сущ.;
– не сущ.; 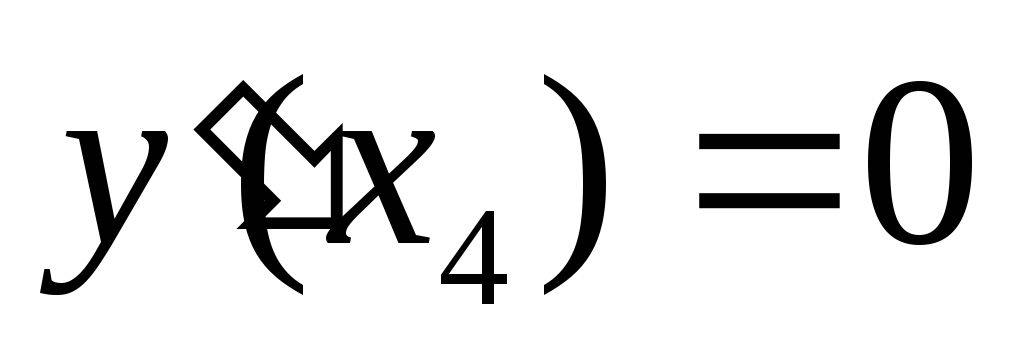 .
.
Однако заметим,
что не любая точка x,
в которой производная равна нулю или
не существует, непременно будет точкой
экстремума. В частности, на рис. 3 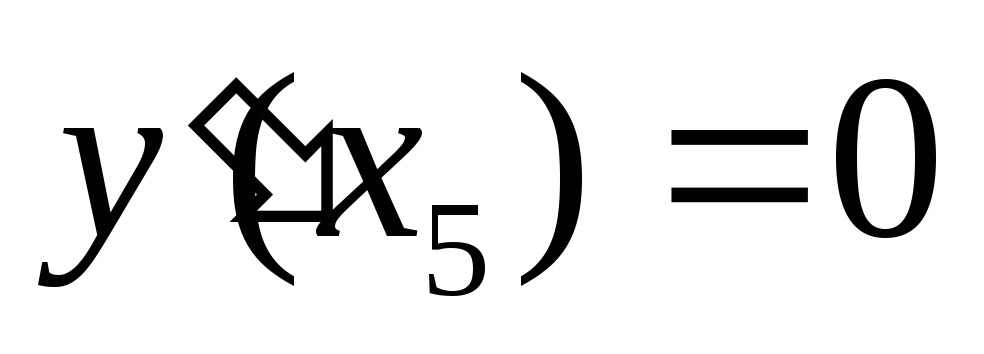 ;
; 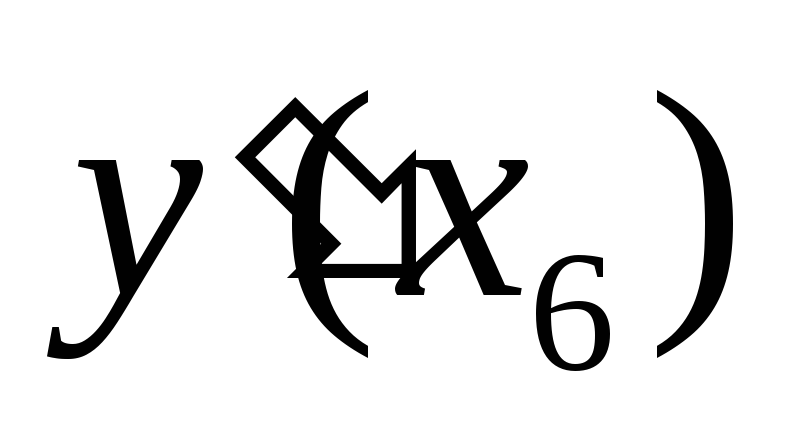 не существует, и тем не менее ни точка x5,
ни точка x6 не являются точками экстремума функции
не существует, и тем не менее ни точка x5,
ни точка x6 не являются точками экстремума функции  .
.
Все сказанное выше о точках экстремума функции можно оформить в виде теоремы.
Теорема 4. Необходимое условие экстремума.
Для того, чтобы
некоторая точка x являлась точкой экстремума функции  ,
необходимо, чтобы в этой точке производная
,
необходимо, чтобы в этой точке производная 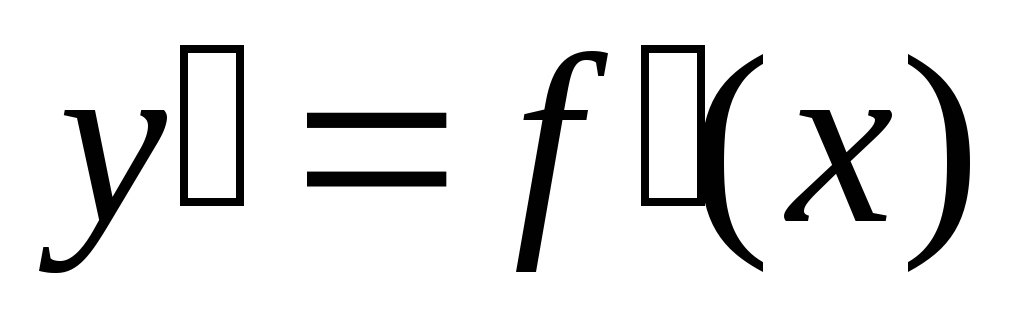 этой
функции или равнялась нулю, или не
существовала. Это условие не является
достаточным.
этой
функции или равнялась нулю, или не
существовала. Это условие не является
достаточным.
Таким образом,
лишь те точки (значения x),
в которых производная 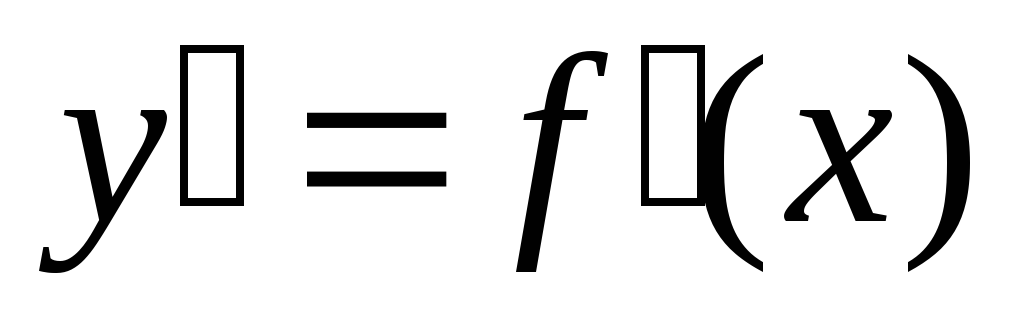 функции равна нулю или не существует,
могут быть точками экстремума этой
функции. Но еще не факт, что все такие
точки будут точками экстремума. Иначе
говоря, точки (значения x),
в которых
функции равна нулю или не существует,
могут быть точками экстремума этой
функции. Но еще не факт, что все такие
точки будут точками экстремума. Иначе
говоря, точки (значения x),
в которых 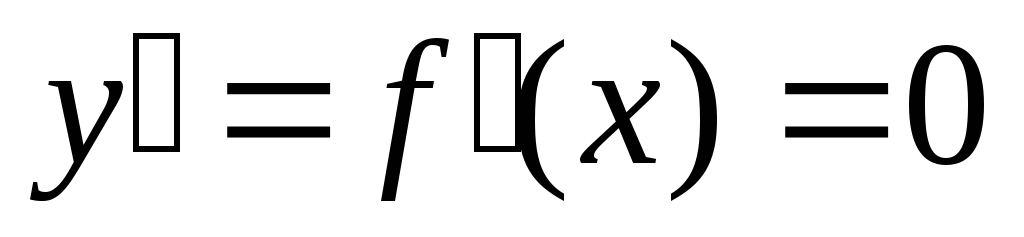 или
или 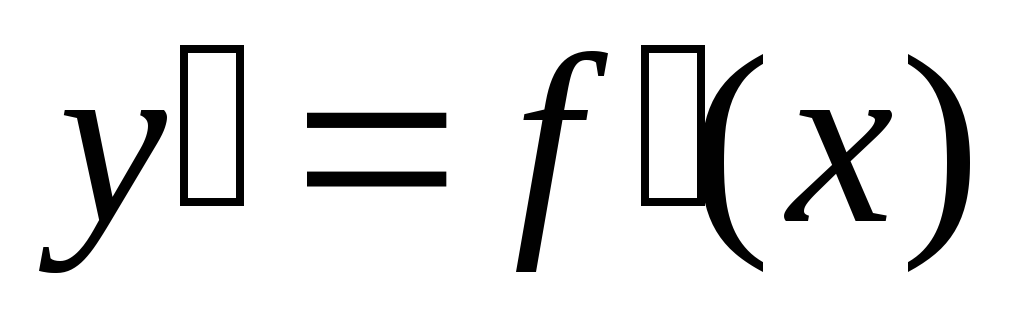 не существует, являются лишь
подозрительными на экстремум или
критическими точками.
Чтобы выяснить суть каждой подозрительной
точки, нужно посмотреть знак производной
слева и справа от неё. Здесь возможны
три варианта:
не существует, являются лишь
подозрительными на экстремум или
критическими точками.
Чтобы выяснить суть каждой подозрительной
точки, нужно посмотреть знак производной
слева и справа от неё. Здесь возможны
три варианта:
Если слева от подозрительной на экстремум точки знак производной (+), а справа (–), то эта подозрительная точка – точка максимума.
Если справа от подозрительной на экстремум точки знак производной (–), а справа (+), то эта подозрительная точка – точка минимума.
Если слева и справа от подозрительной на экстремум точки знак производной один и тот же, то эта подозрительная точка – не точка экстремума.
Сказанное наглядно иллюстрирует рис. 3. Таким образом, становится понятной и очевидной следующая
Схема исследования
функции 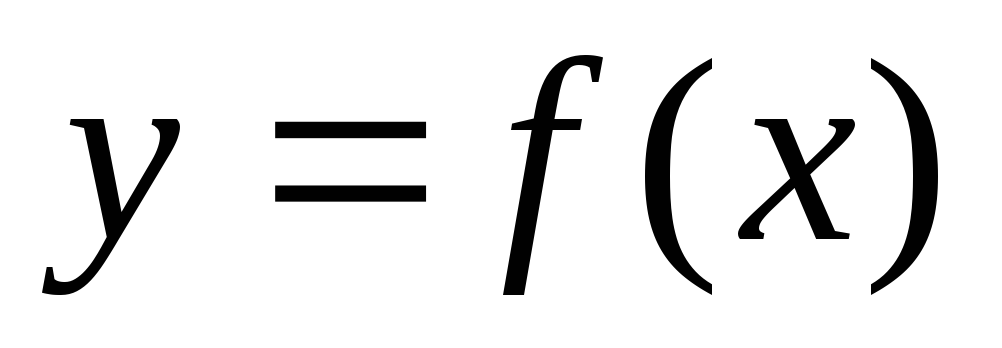 на возрастание-убывание
и точки
экстремума.
на возрастание-убывание
и точки
экстремума.
Находим область определения функции. То есть находим все те значения x, для которых существует (можно найти) значение функции
 .
Заодно устанавливаем интервалы
непрерывности и точки разрыва функции.
.
Заодно устанавливаем интервалы
непрерывности и точки разрыва функции.Находим производную
 .
.Находим точки (значения x), подозрительные на экстремум ( критические точки ). То есть находим те точки (значения x), в которых производная функции или равна нулю, или не существует:
а) 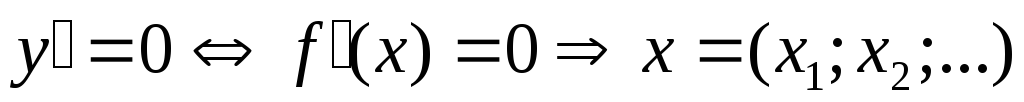
б)  не существует
не существует 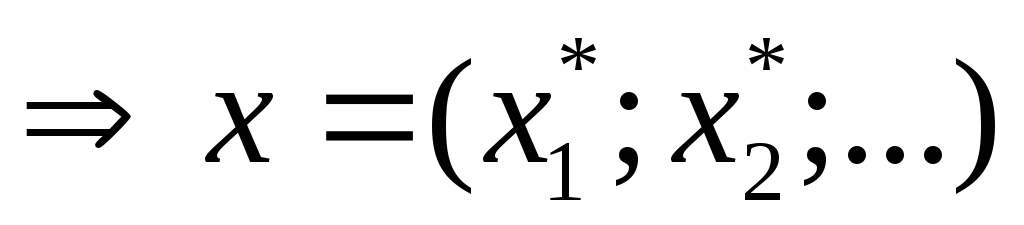
Наносим все найденные в пунктах (а) и (б) подозрительные на экстремум точки на область определения функции (на ось ох) и фиксируем (например, дугами) интервалы, на которые разобьется область определения этими точками. Так как внутри каждого такого интервала производная функции существует и не обращается в нуль, то в каждом интервале производная сохраняет свой знак, который может измениться лишь при переходе к другому интервалу. С помощью вычисления производной в пробных внутренних точках определяем знак производной в каждом интервале. По найденным знакам производной устанавливаем интервалы возрастания и убывания функции, а по смене знака производной определяем точки экстремума функции (точки максимума и минимума).
В найденных точках максимума и минимума вычисляем значения функции
 и тем самым определяем вершины и впадины
графика функции, отмечая заодно, округлые
они или острые.
и тем самым определяем вершины и впадины
графика функции, отмечая заодно, округлые
они или острые.
Пример 2.
Исследовать функцию 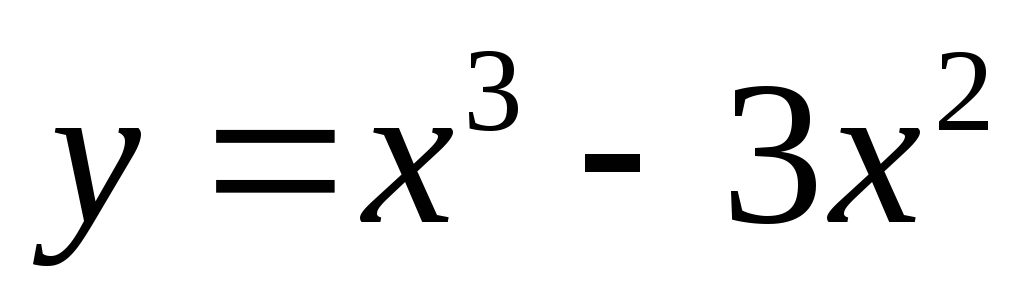 на
возрастание-убывание и точки экстремума.
на
возрастание-убывание и точки экстремума.
Решение. Действуем по изложенной выше схеме.
Функция
 определена (а следовательно, и непрерывна)
для любых x,
то есть на всей числовой оси ох (
определена (а следовательно, и непрерывна)
для любых x,
то есть на всей числовой оси ох ( ).
Значит, её график – сплошная (без
разрывов) линия.
).
Значит, её график – сплошная (без
разрывов) линия.Найдем производную
 :
:
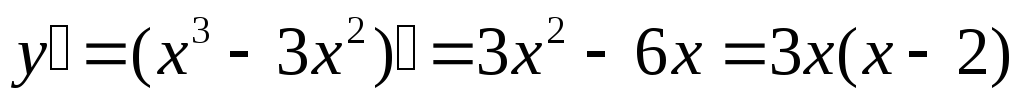 .
.
Найдем точки (значения x), подозрительные на экстремум:
а)  .
.
б)  не существует
таких x нет.
не существует
таких x нет.
Нанесем найденные подозрительные на экстремум точки
 и
и  на область определения функции (на ось ох).
Ось ох этими точками разобьется на три
интервала:
на область определения функции (на ось ох).
Ось ох этими точками разобьется на три
интервала:

Определяем знаки
производной  в этих интервалах (они отмечены на рис.
выше). Тем самым устанавливаем интервалы
возрастания функции
в этих интервалах (они отмечены на рис.
выше). Тем самым устанавливаем интервалы
возрастания функции 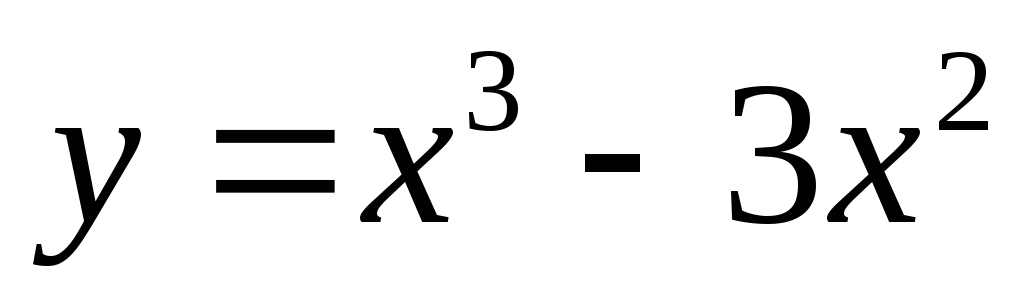 (они помечены стрелкой вверх) и интервал
ее убывания (стрелка вниз), а также
устанавливаем, что точка
(они помечены стрелкой вверх) и интервал
ее убывания (стрелка вниз), а также
устанавливаем, что точка  – точка максимума функции, а точка
– точка максимума функции, а точка 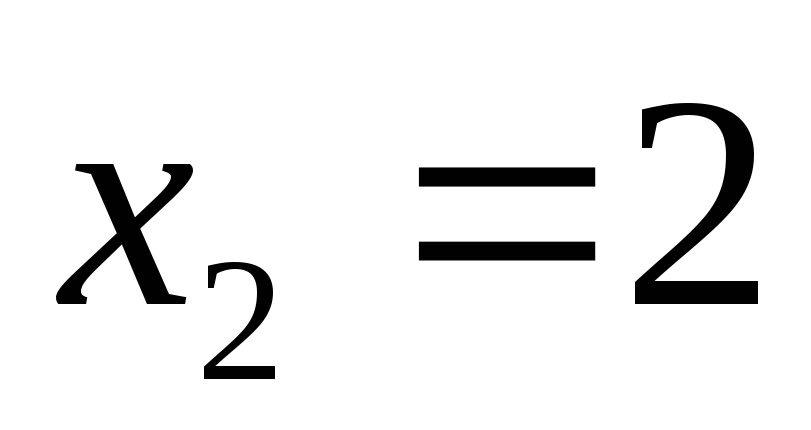 – точка ее минимума.
– точка ее минимума.
Находим (вычисляем) значения функции
 в точках ее максимума и минимума,
устанавливая тем самым вершины и впадины
графика функции:
в точках ее максимума и минимума,
устанавливая тем самым вершины и впадины
графика функции:
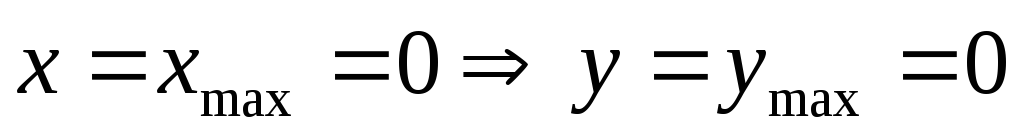 ;
точка
;
точка 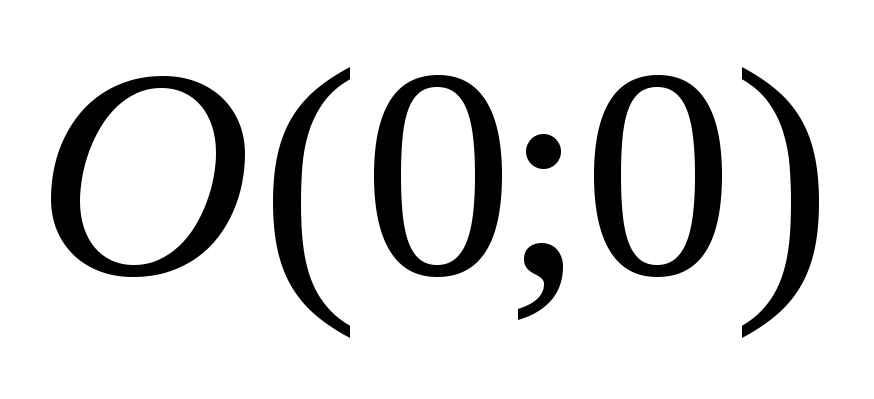 – вершина графика функции (округлая,
т.к.
– вершина графика функции (округлая,
т.к. 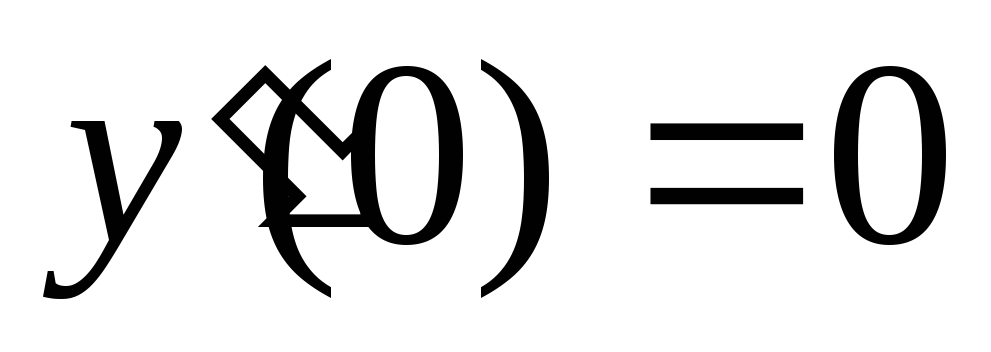 ).
).
 ;
точка
;
точка 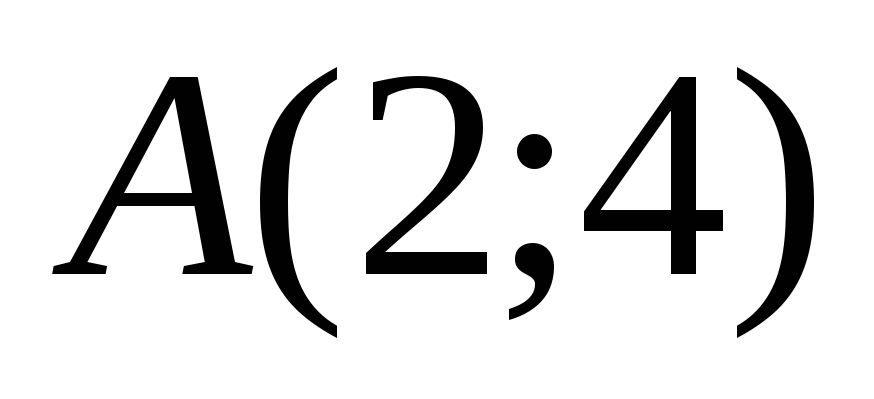 – впадина графика функции (округлая,
т.к.
– впадина графика функции (округлая,
т.к.  ).
).
В
 дополнение к проведенному исследованию
найдем еще точки пересечения графика
функции с осями координат:
дополнение к проведенному исследованию
найдем еще точки пересечения графика
функции с осями координат:
а) С осью ох:
б) С осью оу:
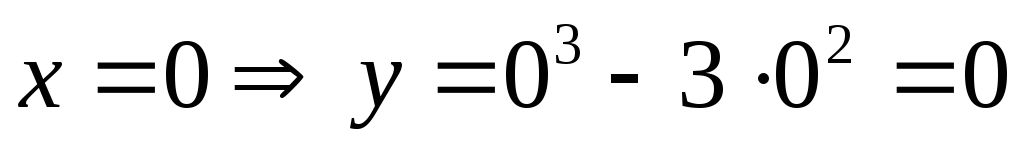
А теперь построим этот график (рис. 4):
studfile.net
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Интервалы возрастания и убывания функции
Для того, чтобы найти интервалы, на которых функция возрастает или убывает, часто используется метод, основанный на анализе знаков производной рассматриваемой функции. Суть этого метода состоит в следующем.
Если на интервале (a, b) функция y = f (x) строго возрастает и в каждой точке x0 интервала имеет производную, то, как показано на рисунке 1, а также на рисунке 2,

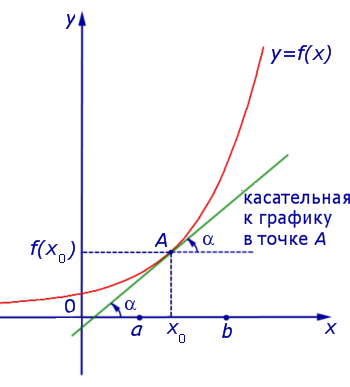
Рис.1
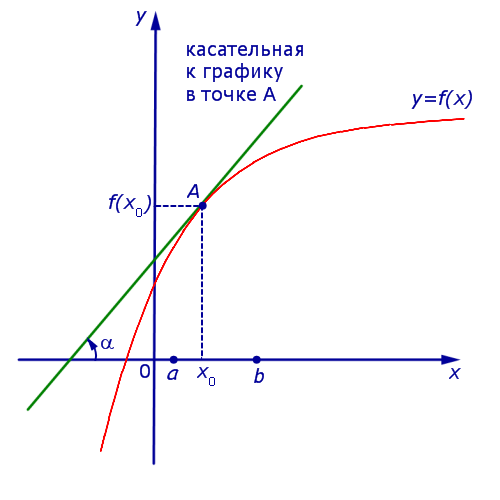
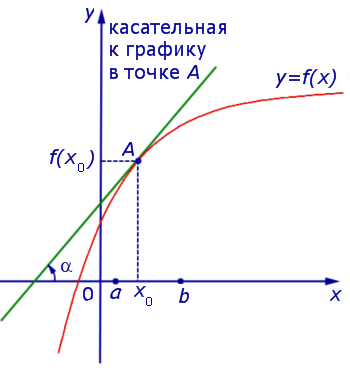
Рис.2
угол α наклона касательной к графику функции будет острым, откуда вытекает неравенство:
f ‘ (x0) = tg α > 0
Если же на интервале (a, b) функция y = f (x) строго убывает и в каждой точке x0 интервала имеет производную, то, как показано на рисунках 3 и 4,
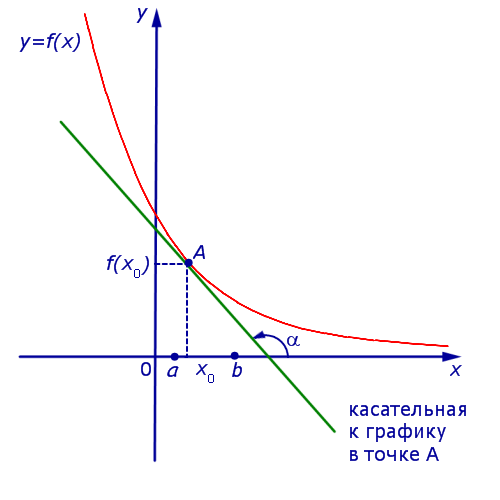
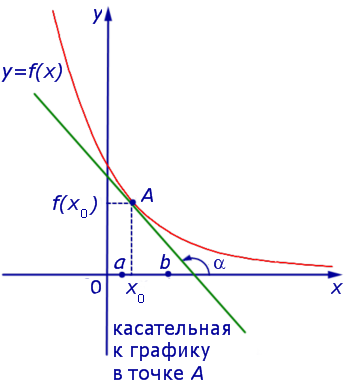
Рис.3
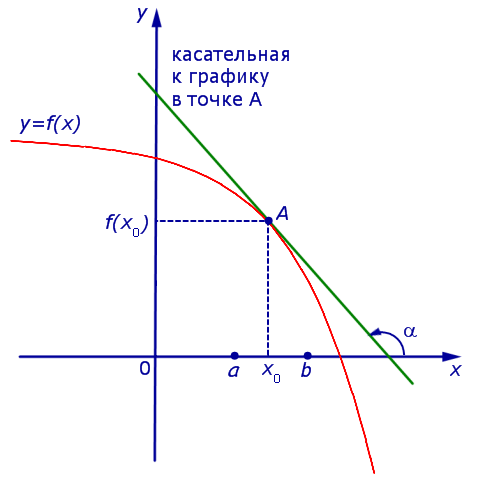
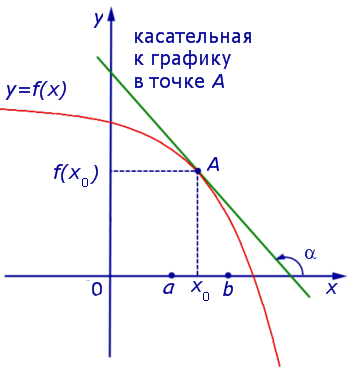
Рис.4
угол α наклона касательной к графику функции будет тупым, откуда вытекает неравенство:
f ‘ (x0) = tg α < 0
Достаточные условия для возрастания и убывания функции
В следующем утверждении, доказательство которого выходит за рамки школьного курса математики, сформулированы достаточные условия для возрастания и убывания функции.
Утверждение 1.
а). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
f ‘ (x) > 0 ,
то функция f (x) строго возрастает на интервале (a, b) .
б). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
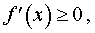
то функция f (x) возрастает (не убывает) на интервале (a, b) .
в). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
f ‘ (x) < 0 ,
то функция f (x) строго убывает на интервале (a, b) .
г). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
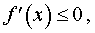
то функция f (x) убывает (не возрастает) на интервале (a, b) .
Экстремумы (максимумы и минимумы) функции
Определение 1. Точку x0 называют точкой максимума функции f (x) , если существует интервал (a, b) , такой, что a 0b , для точек x которого выполнено неравенство
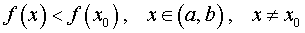 .
.
Таким образом, если x0 – точка максимума функции f (x) , то в интервале (a, b) значение функции f (x0) больше всех остальных значений функции.
Определение 2. Точку x0 называют точкой минимума функции f (x) , если существует интервал (a, b) , такой, что a < x0 < b , для точек x которого выполнено неравенство
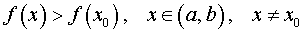 .
.
Другими словами, если x0 – точка минимума функции f (x) , то в интервале (a, b) значение функции f (x0) меньше всех остальных значений функции.
Определение 3. Точки максимума и минимума функции называют точками экстремума функции, а значения функции в точках экстремума называют экстремумами функции.
«Подозрительные» на наличие экстремума точки функции.
Теорема Ферма
Определение 4.Стационарной точкой функции называют такую точку, в которой производная функции равна нулю.
Определение 5.Критической точкой функции называют такую точку, в которой производная функции равна нулю или не существует.
Таким образом, если точка x0 является критической точкой функции, то точка x0 либо является стационарной точкой функции, либо производная функции в точке x0 не существует.
Теорема Ферма. Если точка x0 является точкой экстремума функции f (x) , то точка x0 является критической точкой функции f (x) .
Доказательство. Если в точке x0 у функции y = f (x) не существует производная, то точка x0 является критической точкой по определению. Докажем, что если в точке x0 у функции y = f (x) существует производная, то точка x0 является стационарной, то есть f ‘ (x0) = 0 .
Предположим сначала, что точка x0 является точкой максимума функции y = f (x) (рис. 5).
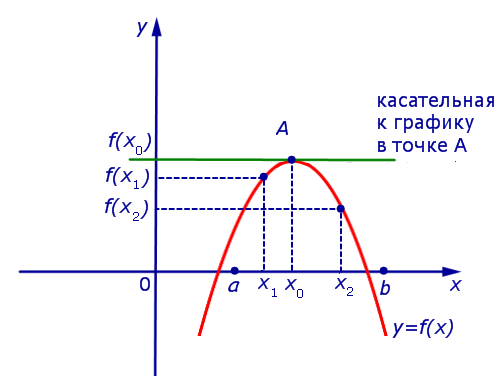
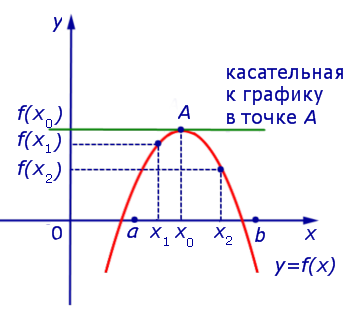
Рис.5
Поскольку x0 – точка максимума, то для любой точки x1 такой, что x1x0 , выполнено неравенство f (x1) < f (x0) , поэтому
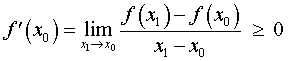 .
.
Точно так же, для любой точки x2 такой, что x2 > x0 , выполнено неравенство f (x2) < f (x0) , поэтому
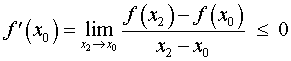 .
.
Таким образом, в случае, когда точка x0 является точкой максимума функции y = f (x), выполнено равенство f ‘ (x0) = 0 . Касательная к графику функции y = f (x) в точке A= (x0; f (x0)) параллельна оси Ox.
Совершенно аналогично доказывается, что и в случае, когда точка x0 является точкой минимума функции y = f (x), выполнено равенство f ‘ (x0) = 0 .
Замечание 1. Из утверждения 2 следует, что точки экстремумов функции (точки максимумов и точки минимумов) нужно искать лишь среди критических точек функции, так как в других (некритических) точках экстремумов быть не может. По этой причине критические точки функции часто называют точками, подозрительными на экстремум.
Достаточные условия для существования экстремума функции
В следующем утверждении, доказательство которого выходит за рамки школьного курса математики и в нашем справочнике не приводится, сформулированы достаточные условия для экстремума функции.
Утверждение 3. Рассмотрим функцию f (x) , непрерывную в интервале (a, b), содержащем точку x0 , производная которой существует в каждой точке этого интервала, кроме, быть может, самой точки x0 .
а). Если для точек 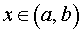 выполнено условие:
выполнено условие:
f ‘ (x) > 0 при x 0 и f ‘ (x) < 0 при x > x0 ,
то точка x0 является точкой максимума функции f (x) (рис. 6).
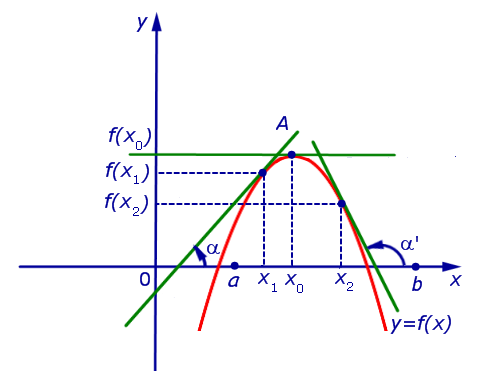
Рис.6
б). Если для точек  выполнено условие:
выполнено условие:
f ‘ (x) < 0 при x < x0 и f ‘ (x) > 0 при x > x0 ,
то точка x0 является точкой минимума функции f (x) (рис. 7).
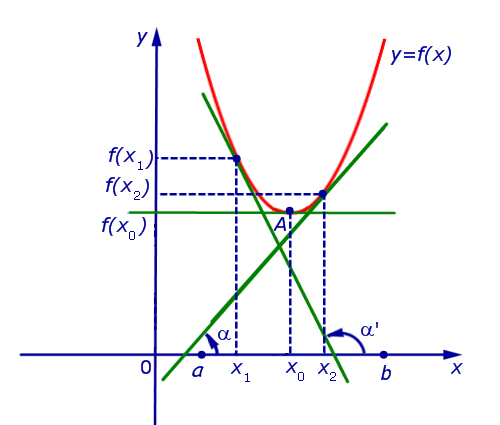
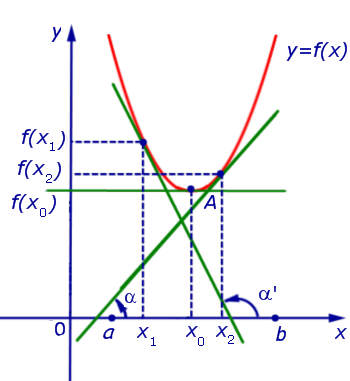
Рис.7
Замечание 2. Условия а) и б) утверждения 3 часто формулируют так: «Если при переходе через точку x0 производная функции меняет знак с «+» на «–» , то точка x0 является точкой максимума функции. Если при переходе через точку x0 производная функции меняет знак с «–» на «+» , то точка x0 является точкой минимума функции».
Пример исследования поведения функции
Пример. Найти интервалы возрастания, убывания и экстремумы функции
Решение. Исследуем сначала на возрастание, убывание и экстремумы функцию
и построим ее график. Для этого представим формулу (2) в виде
y1 = x2 (x + 3)
и заметим, что
а) y1 = 0 при x = 0 и x = – 3 ,
б) y1 > 0 при x > – 3 ; y1 < 0 при x < – 3 .
Теперь вычислим производную функции (2):
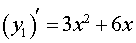 | (3) |
и разложим на множители правую часть формулы (3):
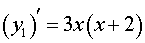 | (4) |
На рисунке 8 при помощи метода интервалов изобразим на числовой оси знаки производной (4)
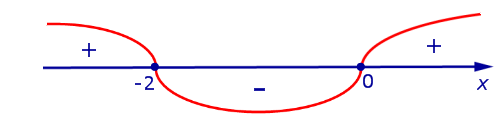
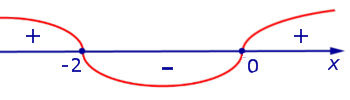
Рис.8
Поскольку решением неравенства
3x (x + 2) > 0
является множество
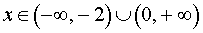 , , | (5) |
то в соответствии с утверждением 1 функция y1 возрастает на каждом из интервалов 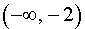 и
и  .
.
С другой стороны, поскольку решением неравенства
3x (x + 2)
является интервал
то в соответствии с утверждением 1 функция y1 убывает на интервале (– 2, 0) .
Так как решениями уравнения
3x (x + 2) = 0
являются точки
то эти точки являются стационарными точками функции y1 .
Поскольку при переходе через точку x = – 2 производная функции y1 меняет знак с «+» на «–» (рис. 8), то в соответствии с утверждением 3 точка x = – 2 является точкой максимума функции y1 , при этом
y1 (– 2) = 4 .
При переходе через точку x = 0 производная функции y1 меняет знак с «–» на «+» (рис. 8), поэтому в соответствии с утверждением 3 точка x = 0 является точкой минимума функции y1, при этом
y1 (0) = 0 .
Заметим, что при анализе поведения функции по знакам ее производной, удобно использовать следующую диаграмму, на которой стрелками указаны интервалы возрастания и убывания функции (рис. 9).
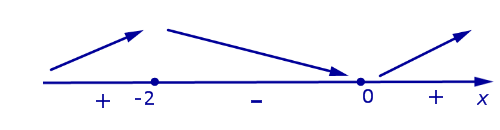
Рис.9
Теперь мы можем построить график функции y1 (рис. 10).
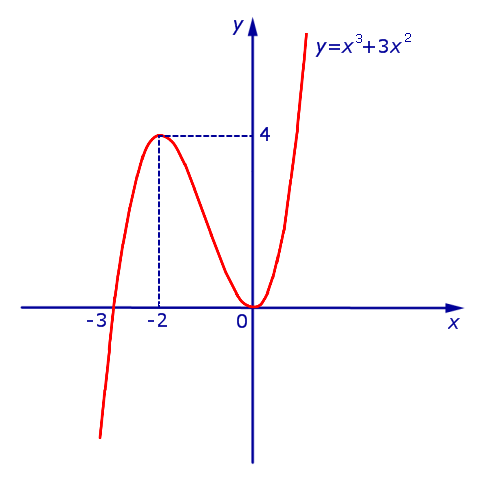
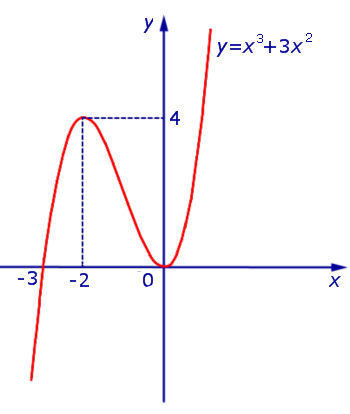
Рис.10
Перейдем к построению графика функции y = | x3 + 3x2 | .
В силу определения модуля, справедливо равенство
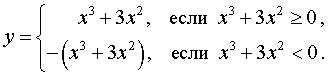
Из этого равенства вытекает, что, если мы симметрично отразим относительно оси Ox часть графика функции y1 = x3 + 3x2 (рис. 10), лежащую в нижней полуплоскости, оставив без изменения часть этого графика, лежащую в верхней полуплоскости, то мы получим график функции y = | x3 + 3x2 | (рис.11) .
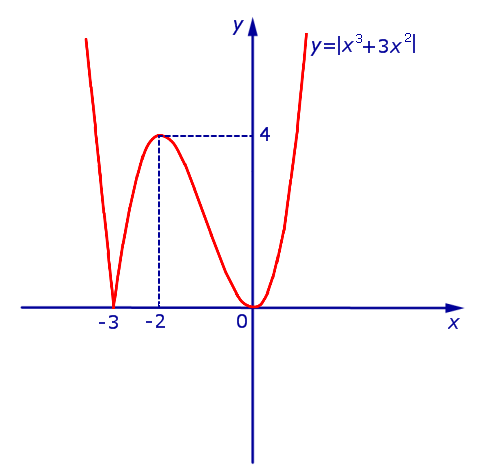
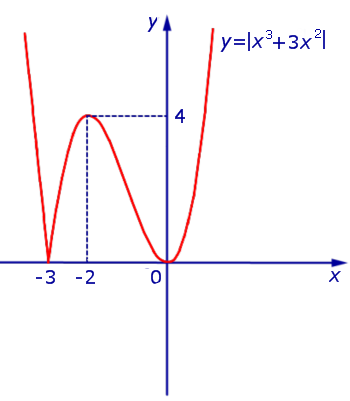
Рис.11
В точке x = – 3 производная функции y = | x3 + 3x2 | не существует. Во всех остальных точках числовой оси производная функции y = | x3 + 3x2 | существует.
Точки x = – 3 и x = 0 являются точками минимума, причем y ( – 3) = y (0) = 0 .
Точка x = – 2 является точкой максимума, причем y ( – 2) = 4 .
Функция y = | x3 + 3x2 | возрастает на каждом из интервалов (– 3, – 2) и 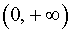 .
.
Функция y = | x3 + 3x2 | убывает на каждом из интервалов 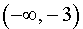 и (– 2, 0).
и (– 2, 0).

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
www.resolventa.ru
Применение производной к построению графиков функций
Понятие производной можно применять для построения графиков функций, так как с помощью производных мы можем выяснить промежутки возрастания и убывания, промежутки выпуклости и вогнутости функции, найти точки экстремума функции (точки минимума и максимума), а также наибольшее и наименьшее значения функции данной функции. Однако, помимо этих данных, для более точного построения графиков функции нам необходимы еще некоторые сведения. Поэтому вначале приведем схему исследования функций, которой и будем пользоваться в дальнейшем.
Схема для исследования функций
Найти область определения функции;
Найти область значения функции;
Выяснить является ли функция четной, нечетной и периодической.
Найти точки пересечения с осями координат;
Выяснить промежутки знакопостоянства функции;
Найти производную функции;
Найти точки минимума и максимума функции;
Найти промежутки монотонности функции;
Найти наибольшее и наименьшее значение функции;
Найти вторую производную функции;
Найти промежутки выпуклости и вогнутости функции;
Найти пределы функции на концах области определения;
Если необходимо, найти значение функции в дополнительных точках;
Построить график функции.
Задачи на исследование и построение графиков функций.
Пример 1
Исследовать и построить график функции:
\[y=2x+1\]Область определении — все действительные числа.
Область значения — все действительные числа.
функция ни четна, ни нечетна, непериодическая.
Точки пересечения с осями координат:
При $y=0$, $2x+1=0,\ x=-\frac{1}{2}$. Точка пересечения с осью $Ox:\left(-\frac{1}{2},0\right)$.
При $x=0$, $y=1$. Точка пересечения с осью $Ox:\left(0,1\right)$.
При $x\in \left(-\infty ,-\frac{1}{2}\right)$ функция отрицательна, при $x\in \left(-\frac{1}{2},\infty \right)$ функция положительна.
Производная:
\[y’=2>0\]Точек минимума и максимума нет.
Функция возрастает на всей области определения.
Функция не имеет наибольшего и наименьшего значений.
$y»=0$
Функция не имеет промежутков выпуклости и вогнутости.
${\mathop{lim}_{x\to -\infty } y\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } y\ }=+\infty $
График:
Рисунок 1.
Пример 2
Исследовать и построить график функции:
\[y=\frac{5x^2+x+1}{x}\]Область определения: $\left(-\infty ,0\right)(0,\infty )$.
Область значения:$\left(-\infty ,1-2\sqrt{5}\right][1+2\sqrt{5},\infty )$
Функция ни четна, ни нечетна, непериодическая.
Точек пересечения с осями координат нет.При $x\in \left(-\infty ,0\right)$ функция отрицательна, при $x\in \left(0,\infty \right)$ функция положительна.
При $x\in \left(-\infty ,0\right)$ функция отрицательна, при $x\in \left(0,\infty \right)$ функция положительна.
Производная:
\[y’=\frac{10x^2+x-5x^2-x-1}{x^2}=\frac{5x^2-1}{x^2}\]Найдем точки минимума:
\[\frac{5x^2-1}{x^2}=0\] \[x\ne 0,\ x=\pm \frac{\sqrt{5}}{5}\]
Рисунок 2.
Максимум функции: $\left(-\frac{\sqrt{5}}{5},1-2\sqrt{5}\right)$
Минимум функции: $\left(\frac{\sqrt{6}}{6},1+2\sqrt{5}\right)$
Из рисунка выше видим, что функция возрастает при $x\in \left(-\infty ,-\frac{\sqrt{5}}{5}\right)\left(\frac{\sqrt{5}}{5},\infty \right)$ и убывает при $x\in \left(-\frac{\sqrt{5}}{5},0\right)\left(0,\frac{\sqrt{5}}{5}\right)$
Наибольшее и наименьшее значение:
$f\left(-\frac{\sqrt{5}}{5}\right)=1-2\sqrt{5}$ — наименьшее значение,
$f\left(\frac{\sqrt{5}}{5}\right)=1-2\sqrt{5}$ — наибольшее значение.
$y»=\frac{{10x}^3-{10x}^3+2x}{x^4}=\frac{2}{x^3}$
Найдем промежутки выпуклости и вогнутости:
\[\frac{2}{x^3}=0\] \[x\ne 0\]Методом интервалов получаем, что
Функция вогнута при $x\in \left(0,\infty \right)$ и выпукла при $x\in \left(-\infty ,0\right)$.
${\mathop{lim}_{x\to 0-0} y\ }=-\infty $, ${\mathop{lim}_{x\to 0+0} y\ }=+\infty $, ${\mathop{lim}_{x\to -\infty } y\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } y\ }=+\infty $
График:

Рисунок 3.
spravochnick.ru
 .
Заодно устанавливаем интервалы
непрерывности и точки разрыва функции.
.
Заодно устанавливаем интервалы
непрерывности и точки разрыва функции. .
. и тем самым определяем вершины и впадины
графика функции, отмечая заодно, округлые
они или острые.
и тем самым определяем вершины и впадины
графика функции, отмечая заодно, округлые
они или острые.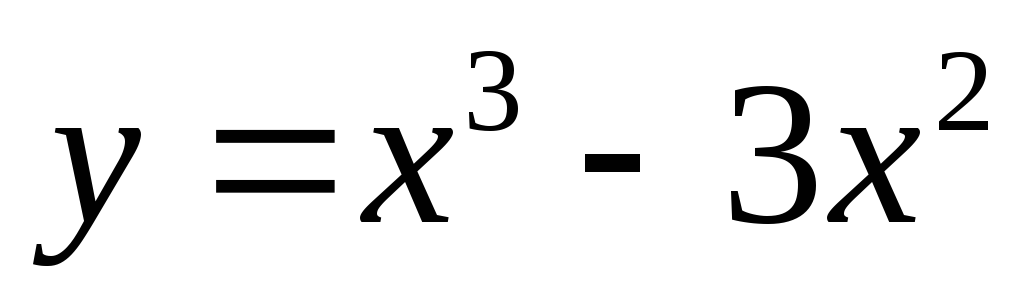 определена (а следовательно, и непрерывна)
для любых x,
то есть на всей числовой оси ох (
определена (а следовательно, и непрерывна)
для любых x,
то есть на всей числовой оси ох (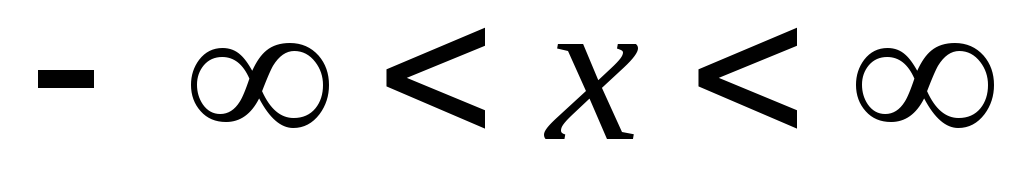 ).
Значит, её график – сплошная (без
разрывов) линия.
).
Значит, её график – сплошная (без
разрывов) линия. :
: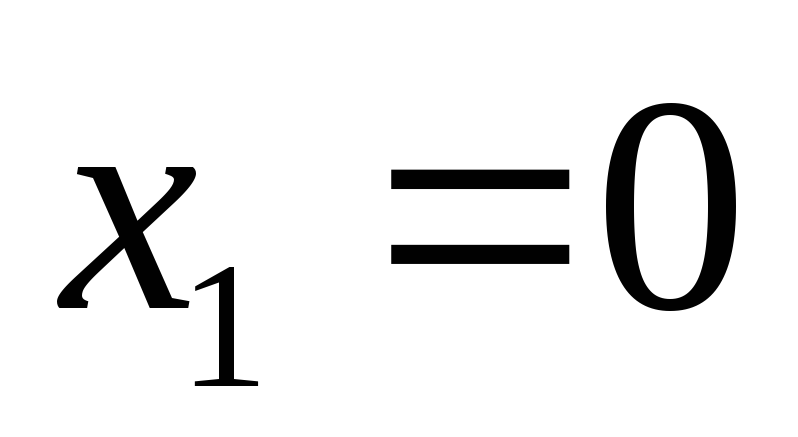 и
и 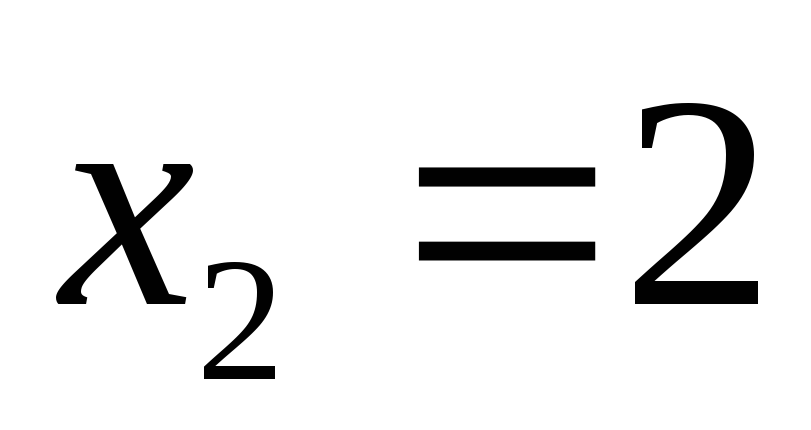 на область определения функции (на ось ох).
Ось ох этими точками разобьется на три
интервала:
на область определения функции (на ось ох).
Ось ох этими точками разобьется на три
интервала: в точках ее максимума и минимума,
устанавливая тем самым вершины и впадины
графика функции:
в точках ее максимума и минимума,
устанавливая тем самым вершины и впадины
графика функции: дополнение к проведенному исследованию
найдем еще точки пересечения графика
функции с осями координат:
дополнение к проведенному исследованию
найдем еще точки пересечения графика
функции с осями координат: